В электронной таблице excel приведен фрагмент банковских расчетов по вкладам населения таблица

В электронной таблице Excel приведен фрагмент банковских расчетов по вкладам населения. Таблица отражает фамилии вкладчиков, процентные ставки по вкладам за два фиксированных одногодичных промежутка времени и суммы вкладов с начисленными процентами за соответствующие истекшие периоды времени. Также приведены общие суммы всех вкладов в банке после начисления процентов и доход вкладчиков за истекший двухгодичный период.

	Вклад, р.	4 %	5 %	Сумма начислений за два периода
Осин	2100000	2184000	2293200	193200
Пнев	200000	208000	218400	18400
Чуйкин	50000	52000	54600	4600
Шаталов	2400000	2496000	2620800	220800
Общая сумма	4750000	4940000	5187000	437000

Определите, кто из вкладчиков за истекшее с момента открытия вклада время получил средний ежемесячный доход от вклада более 9000 рублей.

Егэ по информатике таблица эксель

В электронной таблице Excel приведен фрагмент банковских расчетов по вкладам населения. Таблица отражает фамилии вкладчиков, процентные ставки по вкладам за два фиксированных одногодичных промежутка времени и суммы вкладов с начисленными процентами за соответствующие истекшие периоды времени. Также приведены общие суммы всех вкладов в банке после начисления процентов и доход вкладчиков за истекший двухгодичный период.

Вклад, р.	4 %	5 %	Сумма начислений за два периода
Осин	2100000	2184000	2293200	193200
Пнев	200000	208000	218400	18400
Чуйкин	50000	52000	54600	4600
Шаталов	2400000	2496000	2620800	220800
Общая сумма	4750000	4940000	5187000	437000

Определите, кто из вкладчиков за истекшее с момента открытия вклада время получил средний ежемесячный доход от вклада более 9 000 рублей.

Для определения среднемесячного дохода необходимо разделить доход каждого на количество месяцев вклада, т. е. на 24 месяца.

Осин: 193200 / 24 = 8 050,

Пнев: 18400 / 24 = 766,7,

Чуйкин: сам доход меньше 9 000, поэтому он не подходит,

Источник

ЕГЭ по информатике 2021 — Задание 9 (Таблица Excel)

Девятое задание из ЕГЭ по информатике нового формата 2021 основывается на работе с таблицами Excel.

Это задание выполняется на компьютере в новом формате ЕГЭ 2021 года. Будет выдан файл Excel, по которому нужно получить правильный ответ и записать его в бланк заданий.

Если Вам урок удобнее смотреть в видеоформате, то можете перейти на ролик по 9 заданию из ЕГЭ по информатике 2021 на Youtube. Подписывайтесь на канал!

Вступление к 9 заданию ЕГЭ по информатике 2021

Рассмотрим таблицу Excel:

Вот как она выглядит:

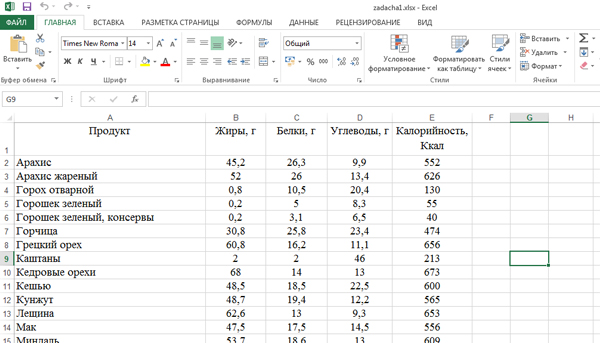
Здесь имеется столбец «Продукт». Другие столбцы: «Жиры», «Белки», «Углеводы», «Калорийность» – это характеристики этих продуктов.

В Excel можно каждой ячейке задавать какие-нибудь формулы. Например, пусть в ячейке F2 будет писаться СУММА из ячеек B2 (Жиры) и С2 (Белки).

Кликаем по ячейке F2, а затем на значок «вставить функцию».

Появится окно «Вставка функции«. Здесь все функции разбиты на категории: Финансовые, математические, логические и т.д. По умолчанию стоит категория «10 недавно используемых функций». В этой категории уже есть нужная нам функция СУММ. Выбираем её и кликаем «ОК». (Основная категория для функции СУММ является «математические»)

Появляется окно для функции СУММ.

Если мы напишем в поле Число1: «B2:E2» ,– то у нас суммируются три ячейки: B2, C2, E2. Таким образом, мы задали интервал.

Можно суммировать и вниз, т.е. ячейки одного столбца (B2:B1001).

Чтобы просуммировать отдельные ячейки, без интервала – необходимо уже использовать поле Число2.

Нам нужно просуммировать два числа: значение ячейки B2 и значение С2. Значит, пишем в поле Число1 — B2, а в поле Число2 — C2.

Нажимаем «Ок». Теперь у нас в ячейке F2 сумма значений ячеек B2 и С2.

Примечание 1: Мы могли сделать данную операцию с помощью интервала. Для этого нужно было написать в поле Число1: B2:C2.

Примечание 2: Так же мы могли суммировать и без вставки функции. Для этого нужно кликнуть по ячейке F2 и затем в поле, на которое показывает стрелка на рисунке, вписать формулу: «=B2+C2«. И нажать «Enter».

Как нам распространить данную формулу для всего столбца F ?

Необходимо подвести мышку к нижнему правому углу ячейки с формулой, чтобы появился чётный крестик:

И нажав левую кнопку мыши, тянем вниз. Таким образом, у нас формула распространится на весь столбец.

При изменении данных в ячейках столбцов В и С – значения в ячейках столбца F меняется автоматически.

Выводы:

• Excel – Программа для расположения и обработки данных в таблице.
• Ячейке можно присвоить формулу, которая будет брать данные из других ячеек и обрабатывать их. (Например: Суммирование, среднее значение и т.д. )
• Можно распространять формулу на весь столбец.

Примерные задачи 9 задания ЕГЭ по информатике 2021

Задача (Среднее значение с условием)

Откройте файл электронной таблицы, содержащей результаты тестирования обучающихся по математике и информатике. Каков средний балл по информатике среди участников тестирования, получивших зачётные баллы по этому предмету (т.е. не менее 44 баллов)? В ответе округлить число до двух знаков после запятой.

Для решения этой задачи будем использовать функцию =СРЗНАЧЕСЛИ().

Кликнем в свободную ближайшую ячейку E2. Здесь мы хотим получить ответ на задачу. Нажмём на кнопку «Вставить функцию«, выберем категорию «статистические«, а затем выберем функцию СРЗНАЧЕСЛИ.

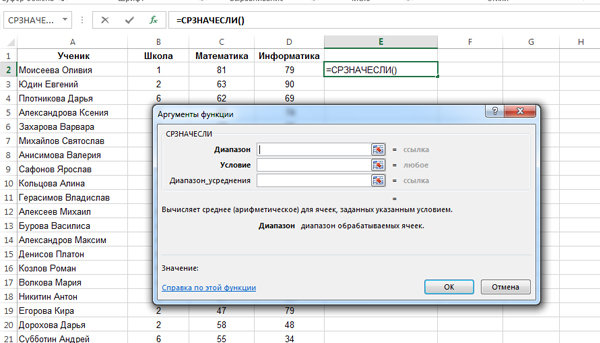
В диапазоне нужно указать все ячейки с числами столбца «Информатика» (Столбец D). Значит, напишем: D2:D273 (Чтобы понять сколько строчек в таблице, нужно прокрутить всю таблицу до самого конца вниз.). В условии напишем: >=44 (Т.к. мы должны считать среднее значение для тех ячеек, где число не меньше 44).

Нажимаем «ОК» и получаем в ячейке E2 число 68,60851064. Нам его нужно округлить до 2 знаков после запятой. Воспользуемся инструментом в программе Excel для округления.

Найдём кнопки «Уменьшить разрядность» и «Увеличить разрядность«. Их можно применять к выделенной ячейке.

Уменьшим разрядность до 2 знаков. Получается число 68,61. Это и будет ответ!

Примечание 1: Если мы хотим найти среднее значение без условия, есть функция СРЗНАЧ.

Примечание 2: СРЗНАЧЕСЛИ (СРЗНАЧ)- это и есть среднее арифметическое значение.

Посмотрим ещё один важный пример 9 задания ЕГЭ по информатике нового формата 2021.

Задача (Количество с условием)

Откройте файл электронной таблицы, содержащей данные о сотрудниках одного из предприятий города Москвы. Сколько человек в таблице имеют возраст меньше 30 лет, и их вес превышает 100 кг? В ответе напишите одно целое число.

Сначала поставим 1 в столбце F в тех строчках, которые удовлетворяют нашему условию: человек имеет возраст меньше 30 лет, и его вес превышает 100 кг. Если строчка не удовлетворяет условию, значит, в ячейке столбца F поставим 0.

Сначала настроим формулу для одной строчки, а затем формулу распространим на весь столбец.

Кликаем по ячейке F2. Нажимаем на кнопку «Вставить функцию«. Выбираем функцию ЕСЛИ из категории «Логические«.

В поле «Лог_выражение» задаём условие : И(C2>100; E2

В поле «Значение_если_истина» ставим 1. В поле «Значение_если_ложь» ставим 0. Нажимаем «ОК».

Получилось, что в ячейке F2 высветился ноль. Значит, первый сотрудник не удовлетворяет условию задачи.

Теперь распространим формулу на весь столбец F. Подводим мышку к ячейке F2 к правому нижнему углу. Когда появился чёрный крестик, нажимаем левую кнопку мыши и тянем вниз, распространяя формулу на весь столбец.

Где-то будут получатся нули, а где-то единицы. Всё зависит от характеристик сотрудника.

После того, как формула будет распространена на весь столбец F, нам нужно посчитать количество единиц в столбце F. Это количество и покажет число сотрудников, которые подходят под условие задачи.

Воспользуемся функцией СУММ. Кликнем по ячейке G2. Именно здесь получим ответ. Затем нажмём на кнопку «Вставить функцию» и выберем СУММ из категории «Математические«.

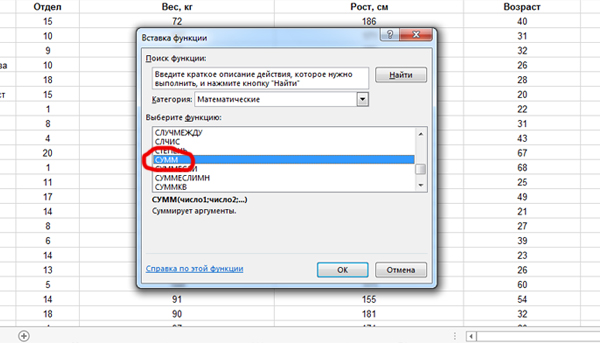
В поле Число1 зададим интервал F2:F301 (Ведь всего у нас 301 строчка в таблице).

Нажимаем «ОК» и получаем в ячейке G2 ответ на нашу задачу. В ответе напишем 14.

Примечание: Для подчёта количества с условием можно использовать функцию СЧЁТЕСЛИ. Попробуйте решить с помощью неё самостоятельно.

Продолжаем тренироваться решать 9 задания из ЕГЭ по информатике нового формата 2021.

Задача (Наименьшее значение + условие ИЛИ)

Откройте файл электронной таблицы, содержащей результаты тестирования обучающихся по математике, информатике и физике. Чему равна наименьшая сумма баллов по математике и информатике среди школьников, получивших более 50 баллов по математике или информатике?

В ответе запишете целое число.

В начале нужно выписать отдельно сумму баллов по математике и информатике для тех школьников, которые подходят под условие.

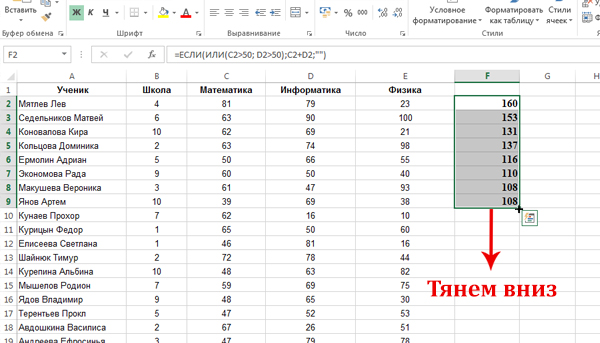
Выпишем сумму двух предметов, для удовлетворяющих условию строчек, в столбец F, с помощью функции ЕСЛИ.

В начале нужно задать формулу для одной ячейки F2. Кликаем по ячейке F2, нажимаем на кнопку «Вставить функцию«, выбираем функцию ЕСЛИ.

В поле «Лог_выражение» пишем: ИЛИ(C2>50; D2>50). В поле «Значение_если_истина«: C2+D2. В поле «Значение_если_ложь«: «» (Пустые двойные кавычки).

Важно: Здесь мы в поле «Значение_если_ложь» должны поставить пустые двойные кавычки, ведь, если поставить ноль, тогда, при поиске минимального значения будем находить всегда этот ноль. Мы ноль ставим в это поле только тогда, когда ищем количество строчек, ведь, тогда мы суммируем единицы, а ноль при суммировании не влияет на результат.

Нажимаем «ОК», и в ячейке F2 получается число 160. Это говорит о том, что первая строчка удовлетворяет условию задачи. И теперь в ячейке F2 лежит сумма баллов по математике и информатике для первого учащегося.

Распространим данную формулу на весь столбец F.

В основном получатся числа, но где-то ячейки останутся пустыми. Это значит, что эти строчки не подошли под условие задачи.

Теперь нужно с помощью функции МИН найти минимальное значение в столбце F.

Кликаем по ячейке G2, нажимаем «Вставить функцию«, выбираем функцию МИН из категории «Статистические«.

В поле Число1 пишем диапазон столбца F: F2:F273.

Получаем ответ 75.

Продолжаем оттачивать навыки работы с электронными таблицами в 9 задании из ЕГЭ по информатике нового формата 2021.

Задача (Среднее значение + сложное условие)

Откройте файл электронной таблицы, содержащей результаты тестирования обучающихся по математике, информатике и физике. Каков средний балл по математике обучающихся, набравших не менее 60 баллов по информатике?

В ответе запишите только целую часть получившегося числа.

Эту задачу решим двумя способами.

В этом способе решения будем снова использовать функцию СРЗНАЧЕСЛИ.

Кликаем по ячейке F2 и вставляем функцию СРЗНАЧЕСЛИ из категории «Статистические«.

Т.к. столбец, по которому мы будем проверять условие, отличается от того, по которому нужно искать среднее значение, то мы напишем следующие параметры:

В поле «Диапазон» пишем: D2:D273 (Это диапазон, который участвует в условии).

В поле «Условие«: >=60 (Это само условие, которое работает в диапазоне, написанный выше).

В поле «Диапазон_усреднения«: C2:C273 (Это диапазон, для которого будет найдено среднее арифметическое значение. Будут участвовать только те строчки, которые прошли условие).

Если последнее поле остаётся пустым, то среднее значение ищется по первому полю.

Нажимаем «ОК», и получаем число 60,0301205. Округлим это число до целых, получим число 60.

Этот способ подходит и для более запутанных ситуаций.

Для строчек, где выполняется условие задачи, перенесём значения столбца С в столбец F.

Кликаем в ячейку F2, нажимаем кнопку «Вставить функцию«, выбираем функцию Если.

Сначала нужно записать формулу для одной строки.

В поле «Лог_выражение» пишем: D2>=60 (Условие того, что человек набрал не менее 60 баллов по информатике)

В поле «Значение_если_истина» пишем: C2 (Переносим само значение столбца математики. Именно впоследствии мы должны найти среднее значение баллов по математике).

В поле «Значение_если_ложь» пишем: «» (Пустые кавычки. Нельзя писать ноль, иначе мы сильно занизим реальное среднее значение).

Нажимаем «ОК». Получается число 81 в ячейке F2.Оно перенеслось из ячейки C2, ведь значение по информатике больше 60 для этой строчки.

Распространяем формулу на весь столбец.

В строках, которые не удовлетворяют условию задачи, будут пустые ячейки.

Когда столбец готов, легко найти среднее значение для столбца F.

Кликаем в ячейку G2 и вставляем функцию СРЗНАЧ. В этой функции указываем диапазон F2:F273.

Получается число 60,0301205. Округляем его до целых, получается число 60.

Не редкий гость в примерных задачах 9 задания из ЕГЭ по информатике 2021.

Откройте файл электронной таблицы, содержащей данные о количестве белков, жиров и углеводов для различных продуктов. Сколько процентов от общего числа составили продукты, у которых более 10 г белка?

В ответе напишите одно целое число.

Задачи на проценты обычно сводятся к нахождению количества.

Найдём сколько продуктов, у которых белка более 10 г.

Кликаем по полю E2. Применим функцию СЧЕТЕСЛИ из категории «Статестические«.

Диапазон указываем: C2:C1001 (Столбец белка).

В поле критерий пишем: >10.

Нажимаем кнопку «ОК». В поле E2 получается число 373.

Чтобы найти проценты, нужно это количество, которое мы нашли, разделить на всё количество продуктов и умножить на сто.

Кликаем по верхнему полю («строка формул»):

Дописываем: =СЧЁТЕСЛИ(C2:C1001;»>10″) /1000 * 100

Всего у нас 1000 наименований продуктов. Строчек 1001, но начинаются продукты со второй строчки. Поэтому делим на 1000 (1001 — 1). Умножаем на 100, чтобы найти проценты.

Нажимаем Enter. Получается число 37,3. Округлим до целого числа, ответом будет 37.

В следующей примерной задаче 9 задания ЕГЭ по информатике 2021 будем комбинировать уже изученные приёмы.

Откройте файл электронной таблицы, содержащей вещественные числа – ведомость продуктового магазина. Наценкой товара считается разность между закупочной ценой и ценой реализации. Прибыль – количество проданных товаров, умноженное на значение наценки. Найдите товар с наценкой выше среднего значения, который принесет максимальную прибыль после его полной продажи. В качестве ответа укажите одно число – полученную после продажи найденного товара прибыль. Ответ округлите до целых чисел.

Сначала нужно найти среднее значение наценки. Запишем наценку в столбце E.

Запишем формулу сначала для одной ячейки E2. Кликаем по ячейки E2, затем кликаем по верхнему полю («строка формул») и пишем: =C2-B2.

Примечание: Формула начинается со знака «равно»!

Нажимаем Enter. Получается число 9,42.

Подводим курсор мышки к правому нижнему углу. После появления чёрного крестика, нажимаем левую кнопку мышку и тянем вниз. Тем самым распространим формулу на весь столбец.

Найдём среднее значение наценки, которая находится в столбце E.

Кликаем по ячейке F2, затем на кнопку «Вставить функцию«, выбираем СРЗНАЧ. Диапазон указываем: E2:E100. Нажимаем «ОК» и получаем число 58,25. Это и есть среднее значение для наценки.

Теперь напишем в столбец G прибыль, но только для тех товаров, у которых наценка выше среднего значения.

Сначала запишем формулу для одной строчки. Кликаем по ячейки G2, нажимаем «Вставить функцию«, выбираем ЕСЛИ.

В поле «Лог_выражение» пишем: E2>58,25. Если наценка выше среднего, то будем считать прибыль.

Т.к. в столбце E все числа имеют не более двух знаков после запятой и число 58,25 тоже имеет два знака после запятой, то мы не получим ошибок из-за округления среднего значения.

В поле «Значение_если_истина» : E2 * D2 (Умножаем наценку на количество проданных товаров. Получаем прибыль).

В поле «Значение_если_ложь«: «» (Пустые кавычки. Ведь мы потом будем искать максимальное значение для прибыли, для товаров, у которых наценка выше среднего значения).

Нажимаем «ОК». Получается в G2 пустое окошко. Значит, для этого товара наценка не выше среднего значения.

Распространим формулу на весь столбец G. Где-то окажутся числа, а где-то пустые ячейки.

Кликнем по ячейке H2 и найдём с помощью функции МАКС (категория «Статистические») максимальную прибыль, в диапазоне указав: G2:G100. Округлив до целых, в ячейке H2 получается ответ 10185.

Примечание: Мы могли при составлении условия E2>58,25 использовать название ячейки F2 вместо числа 58,25. Но тогда нужно её «зацементировать» т.е. E2>$F$2 (Использовать абсолютную адресацию). Если мы всё-таки решили написать число, то нужно следить, чтобы точность была одинаковая у среднего значения, и у тех ячеек, которые мы сравниваем с этим средним значением.

Последнее. Если в задаче говорится о значении по абсолютной величине, т.е. о значении по модулю, то нужно использовать конструкцию ABS(). Например, разница по абсолютной величине двух ячеек A2 и B2 равна ABS(A2-B2). Это можно использовать при составлении формул.

Так же при подготовке к 9 заданию может быть полезна статья, которая была написана под старый формат ЕГЭ по информатике.

На этом всё. Комбинируйте приёмы, которые мы рассмотрели в этом уроке при подготовке к 9 заданию из ЕГЭ по информатике нового формата 2021. Удачи!

Источник

№1. В ячей­ке D3 элек­трон­ной таб­ли­цы за­пи­са­на
фор­му­ла =B$2+$B3. Какой вид при­об­ре­тет фор­му­ла, после того как ячей­ку
D3 ско­пи­ру­ют в ячей­ку E4?

При­ме­ча­ние: знак $ ис­поль­зу­ет­ся для обо­зна­че­ния
аб­со­лют­ной ад­ре­са­ции.

1) =C$2+$B4

2) =A$2+$B1

3) =B$3+$C3

4) =B$1+$A3

По­яс­не­ние.

B$2: ме­ня­ет­ся стол­бец и не ме­ня­ет­ся номер стро­ки.

$B3: стол­бец не ме­ня­ет­ся, ме­ня­ет­ся номер стро­ки.

Номер столб­ца Е боль­ше но­ме­ра столб­ца D на 1. Зна­чит
стол­бец B ста­нет столб­цом С.

Номер стро­ки 4 на 1 боль­ше но­ме­ра стро­ки 3, зна­чит,
стро­ка 3 ста­нет стро­кой 4.

Окон­ча­тель­ный вид =С$2+$B4.

Пра­виль­ный ответ ука­зан под но­ме­ром 1.

№2 была ско­пи­ро­ва­на фор­му­ла. При ко­пи­ро­ва­нии
ад­ре­са ячеек в фор­му­ле ав­то­ма­ти­че­ски из­ме­ни­лись, и зна­че­ние фор­му­лы
стало рав­ным 8. В какую ячей­ку была ско­пи­ро­ва­на фор­му­ла? В от­ве­те ука­жи­те
толь­ко одно число – номер стро­ки, в ко­то­рой рас­по­ло­же­на ячей­ка.

	A	B	C	D	E
1	1	2	3	4
2	2	3	4	= B$3 + $C2
3	3	4	5	6
4	4	5	6	7

При­ме­ча­ние.

Знак $ обо­зна­ча­ет аб­со­лют­ную ад­ре­са­цию.

По­яс­не­ние.

При ко­пи­ро­ва­нии фор­му­лы из ячей­ки D2 у пер­во­го сла­га­е­мо­го
может из­ме­нять­ся толь­ко номер столб­ца, а у вто­ро­го — толь­ко номер стро­ки.
Таким об­ра­зом фор­му­лы в ячей­ках E1—E4:

E1 = C$3+$C1 = 8  E2 = C$3+$C2 = 9  E3 = C$3+$C3 =
10  E4 = C$3+$C4 = 11.

Таким об­ра­зом, фор­му­ла была ско­пи­ро­ва­на в ячей­ку
E1.

Ответ: 1.

№3. Саше нужно с по­мо­щью элек­трон­ных таб­лиц
по­стро­ить таб­ли­цу зна­че­ний вы­ра­же­ния a² + b²,
где a и b — целые числа, a ме­ня­ет­ся от 1 до 10, а b — от 6 до 15. Для этого
сна­ча­ла в диа­па­зо­не В1:К1 он за­пи­сал числа от 1 до 10, и в диа­па­зо­не
А2:А11 он за­пи­сал числа от 6 до 15. Затем в ячей­ку С3 за­пи­сал фор­му­лу
суммы квад­ра­тов чисел (А3 — зна­че­ние b; С1 — зна­че­ние a), после чего ско­пи­ро­вал
её во все ячей­ки диа­па­зо­на B2:К11. В итоге по­лу­чил таб­ли­цу сумм квад­ра­тов
дву­знач­ных чисел. На ри­сун­ке ниже пред­став­лен фраг­мент этой таб­ли­цы.

	A	B	C	D	E
1		1	2	3	4
2	6	37	40	45	52
3	7	50	53	58	65
4	8	65	68	73	80
5	9	82	85	90	97

В ячей­ке С3 была за­пи­са­на одна из сле­ду­ю­щих фор­мул:

1) =С1^2+A3^2

2) =$С$1^2+$A$3^2

3) =С$1^2+$A3^2

4) =$С1^2+A$3^2

Ука­жи­те в от­ве­те номер фор­му­лы, ко­то­рая была за­пи­са­на
в ячей­ке С3.

По­яс­не­ние.

Фор­му­ла, за­пи­сан­ная в ячей­ку С3, долж­на иметь знак аб­со­лют­ной
ад­ре­са­ции перед бук­вой А, по­сколь­ку в про­тив­ном слу­чае, при ко­пи­ро­ва­нии
фор­му­лы в ячей­ку B2, номер столб­ца будет ав­то­ма­ти­че­ски умень­шать­ся,
по­явит­ся не­вер­ная ссыл­ка, про­изойдёт ошиб­ка. Кроме того, фор­му­ла долж­на
иметь знак аб­со­лют­ной ад­ре­са­ции перед циф­рой 1, по­сколь­ку в про­тив­ном
слу­чае, при ко­пи­ро­ва­нии фор­му­лы, на­при­мер, в ячей­ку С2, номер стро­ки
будет ав­то­ма­ти­че­ски умень­шать­ся, по­явит­ся не­вер­ная ссыл­ка.

Пра­виль­ный ответ ука­зан под но­ме­ром 3.

№4. Дан фраг­мент элек­трон­ной таб­ли­цы:

	A	B	C
1		3	4
2	=(A1 + B1+2)/(C1 – B1)	=( 2*C1 – 2)/ A1	=B1*C1/(B1 – A1)

 

Какое целое число долж­но быть за­пи­са­но в ячей­ке A1,
чтобы по­стро­ен­ная после вы­пол­не­ния вы­чис­ле­ний диа­грам­ма по зна­че­ни­ям
диа­па­зо­на ячеек A2:С2 со­от­вет­ство­ва­ла ри­сун­ку?

По­яс­не­ние.

По ри­сун­ку видно, что зна­че­ния всех трёх ячеек диа­па­зо­на
A2:С2 равны. При­рав­ня­ем зна­че­ния в ячей­ках B2 и C2:

( 2*C1 – 2)/ A1 = B1*C1/(B1 – A1) ⇔ 6/ A1 =
12/(3 – A1) ⇔ A1 = 1 и A1
= 4.

При­рав­няв вы­ра­же­ние в ячей­ке A2 и ячей­ке B2, на­хо­дим
что A1 = 1.

Ответ: 1.

№5. Дан фраг­мент элек­трон­ной таб­ли­цы. Из
ячей­ки B2 в одну из ячеек диа­па­зо­на A1:A4 была ско­пи­ро­ва­на фор­му­ла.
При ко­пи­ро­ва­нии ад­ре­са ячеек в фор­му­ле ав­то­ма­ти­че­ски из­ме­ни­лись,
и чис­ло­вое зна­че­ние в этой ячей­ке стало рав­ным 8. В какую ячей­ку была
ско­пи­ро­ва­на фор­му­ла? В от­ве­те ука­жи­те толь­ко одно число — номер стро­ки,
в ко­то­рой рас­по­ло­же­на ячей­ка.

	A	B	C	D	E
1		4	3	2	1
2		= D$3 + $C2	4	3	2
3		6	5	4	3
4		7	6	5	4

При­ме­ча­ние. Знак $ обо­зна­ча­ет аб­со­лют­ную ад­ре­са­цию.

По­яс­не­ние.

При ко­пи­ро­ва­нии фор­му­лы в в одну из ячеек диа­па­зо­на
A1:A4 фор­му­ла при­мет вид = C$3 + $Cn, где n — номер стро­ки той ячей­ки в ко­то­рую
ско­пи­ро­ва­ли фор­му­лу. Чис­ло­вое зна­че­ние в этой ячей­ке стало равно 8,
сле­до­ва­тель­но, для того, чтобы вы­пол­ня­лось ра­вен­ство 5 + Cn = 8, n
долж­но быть рав­ным 1.

Ответ: 1.

№6. В ячей­ке F7 элек­трон­ной таб­ли­цы за­пи­са­на
фор­му­ла =D$12+$D13. Какой вид при­об­ре­тет фор­му­ла, после того как ячей­ку
F7 ско­пи­ру­ют в ячей­ку G8?

При­ме­ча­ние: знак $ ис­поль­зу­ет­ся для обо­зна­че­ния
аб­со­лют­ной ад­ре­са­ции.

1) =C$12+$D11

2) =D$11+$C13

3) =D$13+$E13

4) =E$12+$D14

По­яс­не­ние.

D$12: ме­ня­ет­ся стол­бец и не ме­ня­ет­ся номер стро­ки.

$D13: стол­бец не ме­ня­ет­ся, ме­ня­ет­ся номер стро­ки.

Номер столб­ца G боль­ше но­ме­ра столб­ца F на 1. Зна­чит
стол­бец D ста­нет столб­цом Е.

Номер стро­ки 8 на 1 боль­ше но­ме­ра стро­ки 7, зна­чит,
стро­ка 13 ста­нет стро­кой 14.

Окон­ча­тель­ный вид =Е$12+$D14.

Пра­виль­ный ответ ука­зан под но­ме­ром 4.

№7. В ячей­ке D3 элек­трон­ной таб­ли­цы за­пи­са­на
фор­му­ла =B$2-$B3. Какой вид при­об­ре­тет фор­му­ла, после того как ячей­ку
D3 ско­пи­ру­ют в ячей­ку С4?

При­ме­ча­ние: знак $ ис­поль­зу­ет­ся для обо­зна­че­ния
аб­со­лют­ной ад­ре­са­ции.

1) =C$2-$B4

2) =A$2-$B4

3) =B$1-$C4

4) =B$1-$B4

По­яс­не­ние.

B$2: ме­ня­ет­ся стол­бец и не ме­ня­ет­ся номер стро­ки.

$B3: стол­бец не ме­ня­ет­ся, ме­ня­ет­ся номер стро­ки.

Номер столб­ца C мень­ше но­ме­ра столб­ца D на 1. Зна­чит
стол­бец B ста­нет столб­цом A.

Номер стро­ки 4 на 1 боль­ше но­ме­ра стро­ки 3, зна­чит,
стро­ка 3 ста­нет стро­кой 4.

Окон­ча­тель­ный вид =A$2-$B4.

Пра­виль­ный ответ ука­зан под но­ме­ром 2.

№8. В ячей­ке F7 элек­трон­ной таб­ли­цы за­пи­са­на
фор­му­ла =D$12-$D13. Какой вид при­об­ре­тет фор­му­ла, после того как ячей­ку
F7 ско­пи­ру­ют в ячей­ку E8?

При­ме­ча­ние: знак $ ис­поль­зу­ет­ся для обо­зна­че­ния
аб­со­лют­ной ад­ре­са­ции.

1) =C$12-$C14

2) =D$12-$D13

3) =D$13-$D14

4) =C$12-$D14

По­яс­не­ние.

D$12: ме­ня­ет­ся стол­бец и не ме­ня­ет­ся номер стро­ки.

$D13: стол­бец не ме­ня­ет­ся, ме­ня­ет­ся номер стро­ки.

Номер столб­ца Е мень­ше но­ме­ра столб­ца F на 1. Зна­чит
стол­бец D ста­нет столб­цом С.

Номер стро­ки Е8 на 1 боль­ше но­ме­ра стро­ки F7, зна­чит,
стро­ка 13 ста­нет стро­кой 14.

Окон­ча­тель­ный вид =С$12-$D14.

Пра­виль­ный ответ ука­зан под но­ме­ром 4.

№9. В ячей­ке B1 за­пи­са­на фор­му­ла =2*$A1.
Какой вид при­об­ре­тет фор­му­ла, после того как ячей­ку B1 ско­пи­ру­ют в
ячей­ку C2?

1) =2*$B1

2) =2*$A2

3) =3*$A2

4) =3*$B2Н

По­яс­не­ние.

За­пись $A1 озна­ча­ет , что стол­бец не ме­ня­ет­ся, ме­ня­ет­ся
номер стро­ки.

Номер стро­ки 2 на 1 боль­ше но­ме­ра стро­ки 1, зна­чит,
при ко­пи­ро­ва­нии в ячей­ку C2 стро­ка 1 ста­нет стро­кой 2.

Окон­ча­тель­ный вид =2*$A2.

Пра­виль­ный ответ ука­зан под но­ме­ром 2.

№10. В ячей­ке C2 за­пи­са­на фор­му­ла
=$E$3+D2. Какой вид при­об­ре­тет фор­му­ла, после того как ячей­ку C2 ско­пи­ру­ют
в ячей­ку B1?

1) =$E$3+C1

2) =$D$3+D2

3) =$E$3+E

4) =$F$4+D2

По­яс­не­ние.

За­пись $E$3 озна­ча­ет, что стол­бец не ме­ня­ет­ся и номер
стро­ки не ме­ня­ет­ся.

Номер стро­ки 2 умень­шил­ся на 1, зна­чит, при ко­пи­ро­ва­нии
в ячей­ку B1 из C2 стро­ка 2 ста­нет стро­кой 1.

Номер столб­ца С умень­шил­ся на 1, зна­чит, при ко­пи­ро­ва­нии
в ячей­ку B1 из C2 стол­бец D ста­нет столб­цом С.

Окон­ча­тель­ный вид =$E$3+С1.

Пра­виль­ный ответ ука­зан под но­ме­ром 1.

       Определения значения формулы

№1. В элек­трон­ной таб­ли­це зна­че­ние фор­му­лы
=CP3HAЧ(A3:D3) равно 5. Чему равно зна­че­ние фор­му­лы =СУММ(АЗ:СЗ), если зна­че­ние
ячей­ки D3 равно 6?

1) 1

2) -1

3) 14

4) 4

По­яс­не­ние.

Функ­ция СРЗНАЧ(A3:D3) счи­та­ет сред­нее ариф­ме­ти­че­ское
диа­па­зо­на A3:D3, т. е. сумму зна­че­ний четырёх ячеек A3, B3, C3, D3,
делённую на 4. Умно­жим сред­нее зна­че­ние на число ячеек и по­лу­чим сумму
зна­че­ний ячеек A3 + B3 + C3 + D3 = 5 * 4 = 20.

Те­перь вы­чтем зна­че­ние ячей­ки D3 и найдём ис­ко­мую
сумму: A3 + B3 + C3 = 20 — 6 = 14.

Пра­виль­ный ответ ука­зан под но­ме­ром 3.

№2. В элек­трон­ной таб­ли­це зна­че­ние фор­му­лы
=СРЗНАЧ(С2:С5) равно 3. Чему равно зна­че­ние фор­му­лы =СУММ(С2:С4), если зна­че­ние
ячей­ки С5 равно 5?

1) 1

2) 7

3) -4

4) 4

По­яс­не­ние.

*Для луч­ше­го по­ни­ма­ния ре­ко­мен­ду­ет­ся на­ри­со­вать
таб­ли­цу.

Функ­ция СРЗНАЧ(С2:С5) счи­та­ет сред­нее ариф­ме­ти­че­ское
диа­па­зо­на С2:С5, т. е. сумму зна­че­ний четырёх ячеек С2, С3, C4, С5,
делённую на 4. Умно­жим сред­нее зна­че­ние на число ячеек и по­лу­чим сумму
зна­че­ний ячеек С2 + С3 + C4 + С5 = 3 * 4 = 12

Те­перь, вы­чтем зна­че­ние ячей­ки С5 и найдём ис­ко­мую
сумму: С2 + С3 + C4 = 12 — 5 = 7

Пра­виль­ный ответ ука­зан под но­ме­ром 2.

№3. В элек­трон­ной таб­ли­це зна­че­ние фор­му­лы
=СУММ(А5:D5) равно 6. Чему равно зна­че­ние фор­му­лы =СРЗНАЧ(А5:С5), если зна­че­ние
ячей­ки D5 равно 9?

1) 1

2) -3

3) 3

4) -1

По­яс­не­ние.

*Для луч­ше­го по­ни­ма­ния ре­ко­мен­ду­ет­ся на­ри­со­вать
таб­ли­цу.

Функ­ция СУММ(А5:D5) счи­та­ет сумму зна­че­ний ячеек диа­па­зо­на
A5:D5, т. е. A5 + B5 + C5 + D5 = 6

Функ­ция СРЗНАЧ(А5:С5) счи­та­ет сред­нее ариф­ме­ти­че­ское
диа­па­зо­на А5:С5, т. е. сумму зна­че­ний трёх ячеек A5, B5, C5, делённую на
3.

Вы­чтем зна­че­ние ячей­ки D5 из пер­вой суммы и найдём
сумму: A5 + B5 + C5 = 6 — 9 = -3.

Те­перь раз­де­лим ответ на 3 и найдём ис­ко­мое сред­нее
зна­че­ние: СРЗНАЧ(А5:С5) = -3 / 3 = -1.

Пра­виль­ный ответ ука­зан под но­ме­ром 4.

№4. В элек­трон­ной таб­ли­це зна­че­ние фор­му­лы
=CУMM(D2:D5) равно 10. Чему равно зна­че­ние фор­му­лы =CP3HAЧ(D2:D4), если зна­че­ние
ячей­ки D5 равно −2?

1) 6

2) 2

3) 8

4) 4

По­яс­не­ние.

*Для луч­ше­го по­ни­ма­ния ре­ко­мен­ду­ет­ся на­ри­со­вать
таб­ли­цу.

Функ­ция СУММ(D2:D5) счи­та­ет сумму зна­че­ний ячеек диа­па­зо­на
D2:D5, т. е. D2 + D3 + D4 + D5 = 10

Функ­ция СРЗНАЧ(D2:D4) счи­та­ет сред­нее ариф­ме­ти­че­ское
диа­па­зо­на D2:D4, т. е. сумму зна­че­ний трёх ячеек D2, D3, D4, делённую на
3.

Вы­чтем зна­че­ние ячей­ки D5 из пер­вой суммы и найдём
сумму: D2 + D3 + D4 = 10 — (-2) = 12.

Те­перь раз­де­лим ответ на 3 и найдём ис­ко­мое сред­нее
зна­че­ние: СРЗНАЧ(D2:D4) = 12 / 3 = 4.

Пра­виль­ный ответ ука­зан под но­ме­ром 4.

№5. В элек­трон­ной таб­ли­це зна­че­ние фор­му­лы
=СРЗНАЧ(А4:С4) равно 5. Чему равно зна­че­ние фор­му­лы СУММ(А4:D4), если зна­че­ние
ячей­ки D4 равно 6?

1) 1

2) 11

3) 16

4) 21

По­яс­не­ние.

*Для луч­ше­го по­ни­ма­ния ре­ко­мен­ду­ет­ся на­ри­со­вать
таб­ли­цу.

Функ­ция СРЗНАЧ(A4:C4) счи­та­ет сред­нее ариф­ме­ти­че­ское
диа­па­зо­на A4:C4, т. е. сумму зна­че­ний трёх ячеек A4, B4, C4, делённую на
3. Умно­жим сред­нее зна­че­ние на ко­ли­че­ство ячеек дан­но­го диа­па­зо­на и
найдём: A4 + B4 + C4 = 5 * 3 = 15

Те­перь при­ба­вим к по­лу­чен­но­му ре­зль­та­ту зна­че­ние
ячей­ки D4 и найдём ис­ко­мую сумму:

A4 + B4 + C4 +
D4 = 15 + 6 = 21

Пра­виль­ный ответ ука­зан под но­ме­ром 4.

№6. В элек­трон­ной таб­ли­це зна­че­ние фор­му­лы
=СРЗНАЧ(Е2:Е4) равно 3,

чему равно зна­че­ние фор­му­лы =СУММ(Е2:Е5), если зна­че­ние
ячей­ки Е5 равно 5?

1) 11

2) 2

3) 8

4) 14

По­яс­не­ние.

*Для луч­ше­го по­ни­ма­ния ре­ко­мен­ду­ет­ся на­ри­со­вать
таб­ли­цу.

Функ­ция СРЗНАЧ(Е2:Е4) счи­та­ет сред­нее ариф­ме­ти­че­ское
диа­па­зо­на Е2:Е4, т. е. сумму зна­че­ний трёх ячеек E2, E3, E4, делённую на
3. Умно­жим сред­нее зна­че­ние на ко­ли­че­ство ячеек дан­но­го диа­па­зо­на и
найдём: E2 + E3 + E4 = 3 * 3 = 9

Те­перь при­ба­вим к по­лу­чен­но­му ре­зль­та­ту зна­че­ние
ячей­ки E5 и найдём ис­ко­мую сумму:

E2 + E3 + E4 + E5 = 9 + 5 = 14

Пра­виль­ный ответ ука­зан под но­ме­ром 4.

№7. В элек­трон­ной таб­ли­це зна­че­ние фор­му­лы
=СУММ(А7:С7) равно 9. Чему равно зна­че­ние фор­му­лы =CPЗHAЧ(A7:D7). если зна­че­ние
ячей­ки D7 равно 3?

1) -6

2) 6

3) 3

4) 4

По­яс­не­ние.

*Для луч­ше­го по­ни­ма­ния ре­ко­мен­ду­ет­ся на­ри­со­вать
таб­ли­цу.

Функ­ция СУММ(А7:С7) счи­та­ет сумму зна­че­ний ячеек А7, B7
и С7, по­это­му А7 + B7 + С7 = 9.

Функ­ция СРЗНАЧ(A7:D7) счи­та­ет сред­нее ариф­ме­ти­че­ское
диа­па­зо­на A7:D7, т. е. сумму зна­че­ний четырёх ячеек А7, B7, С7, D7,
делённую на 4. По­это­му при­ба­вим к пер­вой сумме зна­че­ние ячей­ки D7 и
найдём:

А7 + B7 + С7 + D7 = 9 + 3 = 12.

Те­перь раз­де­лим по­лу­чен­ный ре­зль­тат на число ячеек и
найдём ис­ко­мую ве­ли­чи­ну:

СРЗНАЧ(A7:D7) = 12 / 4 = 3.

Пра­виль­ный ответ ука­зан под но­ме­ром 3.

№8. В элек­трон­ной таб­ли­це зна­че­ние фор­му­лы
=СУММ(В2:В4) равно 6. Чему равно зна­че­ние фор­му­лы =СРЗНАЧ(В2:В5), если зна­че­ние
ячей­ки В5 равно 14?

1) 5

2) 8

3) 10

4) 20

По­яс­не­ние.

*Для луч­ше­го по­ни­ма­ния ре­ко­мен­ду­ет­ся на­ри­со­вать
таб­ли­цу.

Функ­ция СУММ(В2:В4) счи­та­ет сумму зна­че­ний ячеек B2, B3
и B4, по­это­му B2 + B3 + B4 = 6.

Функ­ция СРЗНАЧ(В2:В5) счи­та­ет сред­нее ариф­ме­ти­че­ское
диа­па­зо­на В2:В5, т. е. сумму зна­че­ний четырёх ячеек B2, B3, B4, B5,
делённую на их ко­ли­че­ство. По­это­му при­ба­вим к пер­вой сумме зна­че­ние
ячей­ки В5 и найдём: B2 + B3 + B4 + В5 = 6 + 14 = 20.

Те­перь раз­де­лим по­лу­чен­ный ре­зль­тат на 4 и найдём ис­ко­мую
ве­ли­чи­ну: СРЗНАЧ(В2:В5) = 20 / 4 = 5.

Пра­виль­ный ответ ука­зан под но­ме­ром 1.

№9. В элек­трон­ной таб­ли­це зна­че­ние фор­му­лы
=CPЗHAЧ(A3:D4) равно 5. Чему равно зна­че­ние фор­му­лы =СРЗНАЧ(АЗ:С4), если
зна­че­ние фор­му­лы =CУMM(D3:D4) равно 4?

1) 1

2) 6

3) 3

4) 4

По­яс­не­ние.

*Для луч­ше­го по­ни­ма­ния ре­ко­мен­ду­ет­ся на­ри­со­вать
таб­ли­цу.

Функ­ция СУММ(D3:D4) счи­та­ет сумму зна­че­ний ячеек D3 и
D4: D3 + D4 = 4.

Функ­ция СРЗНАЧ(A3:D4) счи­та­ет сред­нее ариф­ме­ти­че­ское
диа­па­зо­на A3:D4, т. е. сумму зна­че­ний вось­ми ячеек A3, B3, C3, D3, A4,
B4, C4, D4, делённую на их ко­ли­че­ство. Умно­жим сред­нее зна­че­ние на 8 и
найдём сумм­му зна­че­ний этих ячеек: СУММ(A3:D4) = 5 * 8 = 40.

Вы­чтем из по­лу­чен­ной суммы СУММ(A3:D4) зна­че­ние суммы
D3 + D4 и найдём зна­че­ние суммы СУММ(A3:C4): оно равно 40 — 4 = 36.

Те­перь раз­де­лим по­лу­чен­ный ре­зль­тат на ко­ли­че­ство
ячеек дан­ной суммы (их здесь 6) и найдём ис­ко­мую ве­ли­чи­ну: СРЗНАЧ(АЗ:С4)
= 36 / 6 = 6.

Пра­виль­ный ответ ука­зан под но­ме­ром 2.

№10. В элек­трон­ной таб­ли­це зна­че­ние фор­му­лы
=CPЗHAЧ(C2:D5) равно 4. Чему равно зна­че­ние фор­му­лы =CУMM(C5:D5), если зна­че­ние
фор­му­лы =CPЗHAЧ(C2:D4) равно 5

1) -6

2) 2

3) -4

4) 4

По­яс­не­ние.

*Для луч­ше­го по­ни­ма­ния ре­ко­мен­ду­ет­ся на­ри­со­вать
таб­ли­цу.

Функ­ция СРЗНАЧ(C2:D5) счи­та­ет сред­нее ариф­ме­ти­че­ское
диа­па­зо­на C2:D5, т. е. сумму зна­че­ний вось­ми ячеек С2, D2, C3, D3, C4,
D4, C5, D5, делённую на их ко­ли­че­ство. Умно­жим сред­нее зна­че­ние на 8 и
найдём сумм­му зна­че­ний этих ячеек: СУММ(C2:D5) = 4 * 8 = 32.

Ана­ло­гич­но для CPЗHAЧ(C2:D4), ко­ли­че­ство ячеек 6:
СУММ(C2:D4) = 5 * 6 = 30.

Вы­чтем из СУММ(C2:D5) зна­че­ние СУММ(C2:D4) и найдём зна­че­ние
суммы С5 + D5: оно равно

32 — 30 = 2.

Пра­виль­ный ответ ука­зан под но­ме­ром 2.

      Работа с таблицами

№1. В элек­трон­ной таб­ли­це Excel от­ра­же­ны
дан­ные о де­я­тель­но­сти стра­хо­вой ком­па­нии за 4 ме­ся­ца. Стра­хо­вая
ком­па­ния осу­ществ­ля­ет стра­хо­ва­ние жизни, не­дви­жи­мо­сти, ав­то­мо­би­лей
и фи­нан­со­вых рис­ков своих кли­ен­тов. Суммы по­лу­чен­ных по каж­до­му виду
дея­тель­но­сти за эти ме­ся­цы стра­хо­вых взно­сов (в ты­ся­чах руб­лей)
также вы­чис­ле­ны в таб­ли­це.

	Стра­хо­ва­ние	Стра­хо­ва­ние	Стра­хо­ва­ние	Стра­хо­ва­ние
	жизни	ав­то­мо­би­лей	фин. рис­ков	не­дви­жи­мо­сти
	тыс. р.	тыс. р.	тыс. р.	тыс. р.
Май	10	3	20	11
Июнь	2	4	8	10
Июль	4	6	8	5
Ав­густ	6	12	7	4
Сумма	22	25	43	30

Из­вест­но, что за эти 4 ме­ся­ца ком­па­нии при­ш­лось вы­пла­тить
двум кли­ен­там по 20 000 руб­лей каж­до­му.

Каков общий доход стра­хо­вой ком­па­нии в руб­лях за про­шед­шие
4 ме­ся­ца?

1) 120 000

2) 100 000

3) 80 000

4) 60 000

По­яс­не­ние.

Найдём сумму зна­че­ний из стро­ки Сумма: 22 + 25 + 43 + 30
= 120(тыс. р.).

Двум кли­ен­там ком­па­ния вы­пла­ти­ла 2 * 20000 = 40000.
Со­от­вет­ствен­но общий доход со­ста­вит:

120000 — 40000 = 80000 руб.

Пра­виль­ный ответ ука­зан под но­ме­ром 3.

№2. В элек­трон­ной таб­ли­це Excel при­ве­ден
фраг­мент бан­ков­ских расче­тов по вкла­дам на­се­ле­ния. Таб­ли­ца от­ра­жа­ет
фа­ми­лии вклад­чи­ков, про­цент­ные став­ки по вкла­дам за два фик­си­ро­ван­ных
од­но­го­дич­ных про­ме­жут­ка вре­ме­ни и суммы вкла­дов с на­чис­лен­ны­ми
про­цен­та­ми за со­от­вет­ству­ю­щие ис­тек­шие пе­ри­о­ды вре­ме­ни. Также
при­ве­де­ны общие суммы всех вкла­дов в банке после на­чис­ле­ния про­цен­тов
и доход вклад­чи­ков за ис­тек­ший двух­го­дич­ный пе­ри­од.

Опре­де­ли­те, кто из вклад­чи­ков за ис­тек­шее с мо­мен­та
от­кры­тия вкла­да время по­лу­чил сред­ний еже­ме­сяч­ный доход от вкла­да
более 9 000 руб­лей.

1) Осин

2) Пнев

3) Чуй­кин

4) Ша­та­лов

По­яс­не­ние.

Для опре­де­ле­ния сред­не­ме­сяч­но­го до­хо­да не­об­хо­ди­мо
раз­де­лить доход каж­до­го на ко­ли­че­ство ме­ся­цев вкла­да, т. е. на
24 ме­ся­ца.

Осин: 193200 / 24 = 8 050,

Пнев: 18400 / 24 = 766,7,

Чуй­кин: сам доход мень­ше 9 000, по­это­му он не под­хо­дит,

Ша­та­лов: 220800 / 24 = 9 200.

Более 9 000 руб­лей имеет Ша­та­лов.

Пра­виль­ный ответ ука­зан под но­ме­ром 4.

№3. В элек­трон­ной таб­ли­це Excel при­ве­ден
фраг­мент бан­ков­ских расче­тов по вкла­дам на­се­ле­ния. Таб­ли­ца от­ра­жа­ет
фа­ми­лии вклад­чи­ков, про­цент­ные став­ки по вкла­дам за фик­си­ро­ван­ные
про­ме­жут­ки вре­ме­ни и суммы вкла­дов с на­чис­лен­ны­ми про­цен­та­ми за со­от­вет­ству­ю­щие
ис­тек­шие пе­ри­о­ды вре­ме­ни. Также при­ве­де­ны общие суммы всех вкла­дов в
банке после на­чис­ле­ния про­цен­тов.

Опре­де­ли­те общую сумму вкла­дов на­се­ле­ния в банке в
руб­лях по­сле оче­ред­но­го на­чис­ле­ния про­цен­тов, если про­цент­ная став­ка
бу­дет со­став­лять 10%.

1) 5 000 000

2) 5 134 567

3) 5 345 678

4) 5 479 188

По­яс­не­ние.

Общая сумма вкла­дов после на­чис­ле­ния про­цен­тов со­ста­ви­ла
4 981 080. Уве­ли­че­ние на 10% можно за­ме­нить опе­ра­ци­ей умно­же­ния
на 1,1. Тогда общая сумма со­ста­вит: 4 981 080 · 1,1 = 5 479 188.

Пра­виль­ный ответ ука­зан под но­ме­ром 4.

№4. В элек­трон­ной таб­ли­це Excel от­ра­же­ны
дан­ные по про­да­же не­ко­то­рого штуч­но­го то­ва­ра в тор­го­вых цен­трах го­ро­да
за че­ты­ре ме­ся­ца. За каж­дый месяц в таб­ли­це вы­чис­ле­ны сум­мар­ные про­да­жи
и сред­няя по го­ро­ду цена на товар, ко­то­рая на 2 рубля боль­ше цены по­став­щи­ка
дан­но­го то­ва­ра.

Из­вест­но, что весь по­сту­пив­ший от по­став­щи­ка в те­ку­щем
ме­ся­це товар ре­а­ли­зу­ет­ся в этом же ме­ся­це.

В каком ме­ся­це вы­руч­ка по­став­щи­ка дан­но­го то­ва­ра
была мак­си­маль­на?

1) Ян­варь

2) Фев­раль

3) Март

4) Ап­рель

По­яс­не­ние.

Найдём вы­руч­ку за про­да­жи в тор­го­вых цен­трах на каж­дый
месяц. В том ме­ся­це, где она мак­си­маль­на, по­став­щик также по­лу­чил наи­боль­шую
при­быль.

Ян­варь: 21 * 14 = 294,

Фев­раль: 15 * 15 = 225,

Март: 22 * 13 = 286,

Ап­рель: 16 * 15 = 240.

Наи­боль­шая при­быль в ян­ва­ре.

Пра­виль­ный ответ ука­зан под но­ме­ром 1.

№5. В элек­трон­ной таб­ли­це Excel от­ра­же­ны
дан­ные о де­я­тель­но­сти стра­хо­вой ком­па­нии за 4 ме­ся­ца. Стра­хо­вая
ком­па­ния осу­ществ­ля­ет стра­хо­ва­ние жизни, не­дви­жи­мо­сти,/ав­то­мо­би­лей
и фи­нан­со­вых рис­ков своих кли­ен­тов. Суммы по­лу­чен­ных по каж­до­му виду
дея­тель­но­сти за эти ме­ся­цы стра­хо­вых взно­сов (в ты­ся­чах руб­лей)
также вы­чис­ле­ны в таб­ли­це.

Из­вест­но, что за эти 4 ме­ся­ца ком­па­нии при­ш­лось вы­дать
трем кли­ен­там стра­хо­вые вы­пла­ты по 30 000 руб­лей каж­до­му. Каков общий
доход стра­хо­вой ком­па­нии в руб­лях за про­шед­шие 4 ме­ся­ца?

1) 310 000

2) 200 000

3) 210 000

4) 300 000

По­яс­не­ние.

Найдём общую сумму: 67 + 23 + 115 + 95 = 300 (тыс. р).

Вы­пла­ты кли­ен­там: 30 000 * 3 = 90 000 (р).

Общий доход: 300 000 — 90 000 = 210 000 руб­лей.

Пра­виль­ный ответ ука­зан под но­ме­ром 3.

№6. В элек­трон­ной таб­ли­це Excel при­ве­ден
фраг­мент бан­ков­ских рас­четов по вкла­дам на­се­ле­ния. Таб­ли­ца от­ра­жа­ет
фа­ми­лии вклад­чиков, про­цент­ные став­ки по вкла­дам за два фик­си­ро­ван­ных
од­но­го­дич­ных про­ме­жут­ка вре­ме­ни и суммы вкла­дов с на­чис­лен­ны­ми
про­цен­та­ми за со­от­вет­ству­ю­щие ис­тек­шие пе­ри­о­ды вре­ме­ни. Также
при­ве­де­ны общие суммы всех вкла­дов в банке по­сле на­чис­ле­ния про­цен­тов
и доход вклад­чи­ков за ис­тек­ший двух­го­дич­ный пе­ри­од.

Опре­де­ли­те, кто из вклад­чи­ков за ис­тек­шее с мо­мен­та
от­кры­тия вкла­да время по­лу­чил сред­ний еже­ме­сяч­ный доход от вкла­да
менее 2 000 руб­лей.

1) Стол­ков

2) Чин

3) Про­коп­чин

4) Щег­лов

По­яс­не­ние.

Сумма на­чис­ле­ний ука­за­на за 2 года, т. е. за 24 ме­ся­ца.
Чем мень­ше сумма, тем мень­ше сред­ний доход. Самая ма­лень­кая сумма у Про­коп­чи­на.
Про­ве­рим 36800 / 24 = 1533,33.

Пра­виль­ный ответ ука­зан под но­ме­ром 3.

№7. В 2000 году в РФ со­зда­но 7 фе­де­раль­ных
окру­гов. Ис­поль­зуя пред­став­лен­ную таб­ли­цу ука­жи­те номер ре­ги­о­на с
наи­мень­шей плот­но­стью на­се­ле­ния.

На­зва­ние	Со­став	Пло­щадь (тыс.км2)	На­се­ле­ние (2002 г.)
1. Се­ве­ро-За­пад­ный	11 ре­ги­о­нов −  субъ­ек­тов РФ, центр — г. Санкт-Пе­тер­бург	1677,9	14158
2. Цен­траль­ный	18 ре­ги­о­нов −  субъ­ек­тов РФ, центр — г. Москва	650,7	36482
3. При­волж­ский	15 ре­ги­о­нов −  субъ­ек­тов РФ, центр — г. Ниж­ний Нов­го­род	1038	31642
4. Южный	13 ре­ги­о­нов −  субъ­ек­тов РФ, центр — г. Ро­стов-на-Дону	589,2	21471
5. Ураль­ский	6 ре­ги­о­нов −  субъ­ек­тов РФ, центр — г. Ека­те­рин­бург	1788,9	12520
6. Си­бир­ский	16 ре­ги­о­нов −  субъ­ек­тов РФ, центр — г. Но­во­си­бирск	5114,8	20542
7. Даль­не­во­сточ­ный	10 ре­ги­о­нов −  субъ­ек­тов РФ, центр — г. Ха­ба­ровск	6515,9	7038

1) 4

2) 5

3) 6

4) 7

По­яс­не­ние.

Про­ве­рим все ва­ри­ан­ты. Для этого найдём плот­ность на­се­ле­ния
в окру­гах 4—7, по­де­лив на­се­ле­ние на пло­щадь.

Уви­дим, что седь­мой округ имеет наи­мень­шую плот­ность на­се­ле­ния.

Пра­виль­ный ответ ука­зан под но­ме­ром 4.

№8. В 2000 году в РФ со­зда­но 7 фе­де­раль­ных
окру­гов. Ис­поль­зуя пред­став­лен­ную таб­ли­цу ука­жи­те номер ре­ги­о­на с
наи­боль­шей плот­но­стью на­се­ле­ния.

На­зва­ние	Со­став	Пло­щадь (тыс.км2)	На­се­ле­ние (2002 г.)
1. Се­ве­ро-За­пад­ный	11 ре­ги­о­нов −  субъ­ек­тов РФ, центр — г. Санкт-Пе­тер­бург	1677,9	14158
2. Цен­траль­ный	18 ре­ги­о­нов −  субъ­ек­тов РФ, центр — г. Москва	650,7	36482
3. При­волж­ский	15 ре­ги­о­нов −  субъ­ек­тов РФ, центр — г. Ниж­ний Нов­го­род	1038	31642
4. Южный	13 ре­ги­о­нов −  субъ­ек­тов РФ, центр — г. Ро­стов-на-Дону	589,2	21471
5. Ураль­ский	6 ре­ги­о­нов −  субъ­ек­тов РФ, центр — г. Ека­те­рин­бург	1788,9	12520
6. Си­бир­ский	16 ре­ги­о­нов −  субъ­ек­тов РФ, центр — г. Но­во­си­бирск	5114,8	20542
7. Даль­не­во­сточ­ный	10 ре­ги­о­нов −  субъ­ек­тов РФ, центр — г. Ха­ба­ровск	6515,9	7038

1) 1

2) 2

3) 3

4) 4

По­яс­не­ние.

Про­ве­рим все ва­ри­ан­ты. Для этого найдём плот­ность на­се­ле­ния
в окру­гах 1—4, по­де­лив на­се­ле­ние на пло­щадь.

Уви­дим, что вто­рой окур­га имеет наи­боль­шую плот­ность
на­се­ле­ния.

Пра­виль­ный ответ ука­зан под но­ме­ром 2.

№9. Коле нужно с по­мо­щью элек­трон­ных таб­лиц
по­стро­ить таб­ли­цу умно­же­ния чисел от 3 до 6.

Для этого сна­ча­ла в диа­па­зо­нах В1:Е1 и А2:А5 он за­пи­сал
числа от 3 до 6. Затем в ячей­ку Е2 за­пи­сал фор­му­лу умно­же­ния, после чего
ско­пи­ро­вал её во все ячей­ки диа­па­зо­на В2:Е5. В итоге на экра­не по­лу­чил­ся
фраг­мент таб­ли­цы умно­же­ния (см. ри­су­нок).

	A	B	C	D	E
1		3	4	5	6
2	3	9	12	15	18
3	4	12	16	20	24
4	5	15	20	25	30
5	6	18	24	30	36

Какая фор­му­ла была за­пи­са­на в ячей­ке Е2?

1) =А$2*$Е1

2) =А2*Е1

3) =$А2*$Е1

4) =$А2*Е$1

По­яс­не­ние.

Фор­му­ла, за­пи­сан­ная в ячей­ку Е2, долж­на иметь знак аб­со­лют­ной
ад­ре­са­ции перед бук­вой А, по­сколь­ку в про­тив­ном слу­чае, при ко­пи­ро­ва­нии
фор­му­лы в диа­па­зон B2:D2, номер столб­ца будет ав­то­ма­ти­че­ски умень­шать­ся,
по­явит­ся не­вер­ная ссыл­ка. про­изойдёт ошиб­ка. Кроме того, фор­му­ла долж­на
иметь знак аб­со­лют­ной ад­ре­са­ции перед циф­рой 1, по­сколь­ку в про­тив­ном
слу­чае, при ко­пи­ро­ва­нии фор­му­лы в диа­па­зон E3:E5, номер стро­ки будет
ав­то­ма­ти­че­ски уве­ли­чи­вать­ся, по­явит­ся не­вер­ная ссыл­ка.

Сле­до­ва­тель­но, ответ 4.

№10. Коле нужно с по­мо­щью элек­трон­ных таб­лиц
по­стро­ить таб­ли­цу дву­знач­ных чисел от 50 до 89.

Для этого сна­ча­ла в диа­па­зо­не В1:К1 он за­пи­сал числа
от 0 до 9, и в диа­па­зо­не А2:А5 он за­пи­сал числа от 5 до 8. Затем в ячей­ку
В2 за­пи­сал фор­му­лу дву­знач­но­го числа (А2 — число де­сят­ков;
В1 — число еди­ниц), после чего ско­пи­ро­вал её во все ячей­ки диа­па­зо­на
В2:К5. В итоге по­лу­чил таб­ли­цу дву­знач­ных чисел. На ри­сун­ке ниже пред­став­лен
фраг­мент этой таб­ли­цы.

	A	B	C	D	E
1		0	1	2	3
2	5	50	51	52	53
3	6	60	61	62	63
4	7	70	71	72	73
5	8	80	81	82	83

Какая фор­му­ла была за­пи­са­на в ячей­ке В2?

1) =А$2*10+$В1

2) =$А2*10+$В1

3) =А2*10+В1

4) =$А2*10+В$1

По­яс­не­ние.

Фор­му­ла, за­пи­сан­ная в ячей­ку В2, долж­на иметь знак аб­со­лют­ной
ад­ре­са­ции перед бук­вой А, по­сколь­ку в про­тив­ном слу­чае,при ко­пи­ро­ва­нии
фор­му­лы в диа­па­зон B5:E5, номер столб­ца будет ав­то­ма­ти­че­ски уве­ли­чи­вать­ся,
по­явит­ся не­вер­ная ссыл­ка. Кроме того, фор­му­ла долж­на иметь знак аб­со­лют­ной
ад­ре­са­ции перед циф­рой 1, по­сколь­ку в про­тив­ном слу­чае, при ко­пи­ро­ва­нии
фор­му­лы в диа­па­зон B3:B5, номер стро­ки будет ав­то­ма­ти­че­ски уве­ли­чи­вать­ся,
по­явит­ся не­вер­ная ссыл­ка.

Сле­до­ва­тель­но, ответ 4.

       Составление диаграмм по данным

№1. Сплав­ля­ют­ся два ве­ще­ства, со­сто­я­щие
из серы, же­ле­за, во­до­ро­да и меди. Мас­со­вые доли серы (S), же­ле­за (Fe),
во­до­ро­да (Н) и меди (Си) в каж­дом ве­ще­стве при­ве­де­ны на диа­грам­мах.

Опре­де­ли­те, какая из диа­грамм пра­виль­но от­ра­жа­ет со­от­но­ше­ние
эле­мен­тов в спла­ве.

По­яс­не­ние.

От­тал­ки­ва­ем­ся от же­ле­за: в каж­дом ве­ще­стве же­ле­за
было боль­ше по­ло­ви­ны, сле­до­ва­тель­но, и в смеси его будет по­ло­ви­на
или более, такой ва­ри­ант изоб­ражён на диа­грам­ме 3.

Пра­виль­ный ответ: 3.

№2. На диа­грам­ме пред­став­лен уро­вень зар­плат
трех чле­нов семьи за два ме­ся­ца.

Какая из диа­грамм пра­виль­но от­ра­жа­ет сум­мар­ный за
два ме­ся­ца доход каж­до­го члена семьи?

По­яс­не­ние.

Ви­зу­аль­но видно, что за два ме­ся­ца папа на­би­ра­ет наи­боль­шую
из всех сумму,

дочка на вто­ром месте (ста­биль­но за оба ме­ся­ца), и на
тре­тьем месте — мама.

Сразу от­се­и­ва­ем диа­грам­му 2 и 3, а вот для 4ой ска­жем,
что за­ра­бо­ток отца во много боль­ше до­че­ри, сле­до­ва­тель­но оста­ет­ся
диа­грам­ма 1.

Пра­виль­ный ответ: 1.

№3. Диа­грам­ма от­ра­жа­ет ко­ли­че­ство (в ки­ло­грам­мах)
со­бран­но­го за че­тыре ме­ся­ца уро­жая двух сор­тов огур­цов в пар­ни­ко­вом
хо­зяй­стве.

Какая из диа­грамм пра­виль­но от­ра­жа­ет объ­е­мы сум­мар­но­го
за че­тыре ме­ся­ца со­бран­но­го уро­жая по каж­до­му из сор­тов?

По­яс­не­ние.

1 сорт: 10+20+30+30=90 кг.

2 сорт: 20+40+30+30=120 кг.

2го сорта боль­ше, чем 1го на 120 — 90 = 30 кг или на
30*100/120=25%, что со­от­вет­ству­ет гра­фи­ку 4.

Пра­виль­ный ответ: 4.

№4. На диа­грам­ме по­ка­за­но ко­ли­че­ство
участ­ни­ков те­сти­ро­ва­ния по пред­ме­там в раз­ных ре­ги­о­нах Рос­сии.

Какая из диа­грамм пра­виль­но от­ра­жа­ет со­от­но­ше­ние
об­ще­го коли­че­ства участ­ни­ков (из всех трех ре­ги­о­нов) по каж­до­му из
пред­ме­тов те­сти­ро­ва­ния?

По­яс­не­ние.

При по­мо­щи столб­ча­тых диа­грамм можно найти общее ко­ли­че­ство
уче­ни­ков:

400+100+200+400+200+200+400+300+200=2400

Кру­го­вые диа­грам­мы дают нам пред­став­ле­ние о долях от­дель­ных
со­став­ля­ю­щих в общей сумме. Со­от­вет­ствен­но под­счи­та­ем, какую долю те­сти­ру­е­мых
со­став­ля­ют уча­щи­е­ся, те­сти­ру­е­мые по раз­лич­ным пред­ме­там:

Био­ло­гия: 12002400=0,5=50%

Ис­то­рия: 6002400=0,25=25%

Химия: 6002400,25=25%

Этим дан­ным со­от­вет­ству­ет пер­вая диа­грам­ма

№5. На диа­грам­ме по­ка­за­но ко­ли­че­ство
участ­ни­ков те­сти­ро­ва­ния по пред­ме­там в раз­ных ре­ги­о­нах Рос­сии.

Какая из диа­грамм пра­виль­но от­ра­жа­ет со­от­но­ше­ние
об­ще­го коли­че­ства участ­ни­ков те­сти­ро­ва­ния по ре­ги­о­нам?

По­яс­не­ние.

При по­мо­щи столб­ча­тых диа­грамм можно найти общее ко­ли­че­ство
уче­ни­ков:

200+100+200+200+200+200+400+300+200=2000

Кру­го­вые диа­грам­мы дают нам пред­став­ле­ние о долях от­дель­ных
со­став­ля­ю­щих в общей сумме. Со­от­вет­ствен­но под­счи­та­ем, какую долю те­сти­ру­е­мых
со­став­ля­ют уча­щи­е­ся из раз­лич­ных ре­ги­о­нов:

Та­тар­стан: 5002000=0,25=25%

Чу­ва­шия: 6002000=0,30=30%

Яку­тия: 9002000=0,45=45%

Этим дан­ным со­от­вет­ству­ет тре­тья диа­грам­ма

№6. На диа­грам­ме по­ка­за­но ко­ли­че­ство
участ­ни­ков те­сти­ро­ва­ния по пред­ме­там в раз­ных ре­ги­о­нах Рос­сии.

Какая из диа­грамм пра­виль­но от­ра­жа­ет со­от­но­ше­ние
ко­ли­че­ства участ­ни­ков те­сти­ро­ва­ния по химии в ре­ги­о­нах?

По­яс­не­ние.

Из усло­вия видно, что со­от­но­ше­ние для всех ре­ги­о­нов
по участ­ни­кам те­сти­ро­ва­ния по химии оди­на­ко­во.

Пра­виль­ный ответ со­от­вет­ству­ет чет­вер­той диа­грам­ме

№7. На диа­грам­ме по­ка­за­но ко­ли­че­ство
участ­ни­ков те­сти­ро­ва­ния по пред­ме­там в раз­ных ре­ги­о­нах Рос­сии.

Какая из диа­грамм пра­виль­но от­ра­жа­ет со­от­но­ше­ние
ко­ли­че­ства участ­ни­ков те­сти­ро­ва­ния по ис­то­рии в ре­ги­о­нах?

По­яс­не­ние.

При по­мо­щи столб­ча­тых диа­грамм можно найти общее ко­ли­че­ство
уче­ни­ков, при­ни­мав­ших уча­стие в те­сти­ро­ва­нии по ис­то­рии:

100+200+300=600

Кру­го­вые диа­грам­мы дают нам пред­став­ле­ние о долях от­дель­ных
со­став­ля­ю­щих в общей сумме. Со­от­вет­ствен­но под­счи­та­ем, какую долю те­сти­ру­е­мых
со­став­ля­ют уча­щи­е­ся из раз­лич­ных ре­ги­о­нов:

Та­тар­стан: 100600=0,17=17%

Чу­ва­шия: 200600=0,33=33%

Яку­тия: 300600=0,5=50%

Этим дан­ным со­от­вет­ству­ет вто­рая диа­грам­ма

№8. На диа­грам­ме по­ка­за­но ко­ли­че­ство
участ­ни­ков те­сти­ро­ва­ния по пред­ме­там в раз­ных ре­ги­о­нах Рос­сии.

Какая из диа­грамм пра­виль­но от­ра­жа­ет со­от­но­ше­ние
ко­ли­че­ства участ­ни­ков те­сти­ро­ва­ния по рус­ско­му языку в ре­ги­о­нах?

По­яс­не­ние.

При по­мо­щи столб­ча­тых диа­грамм можно найти общее ко­ли­че­ство
уче­ни­ков, при­ни­мав­ших уча­стие в те­сти­ро­ва­нии по рус­ско­му языку:

200+200+200=600

Кру­го­вые диа­грам­мы дают нам пред­став­ле­ние о долях от­дель­ных
со­став­ля­ю­щих в общей сумме. Со­от­вет­ствен­но под­счи­та­ем, какую долю те­сти­ру­е­мых
со­став­ля­ют уча­щи­е­ся из раз­лич­ных ре­ги­о­нов:

Баш­ки­рия: 200600=0,33=33%

Кал­мы­кия: 200600=0,33=33%

Уд­мур­тия: 200600=0,33=33%

Этим дан­ным со­от­вет­ству­ет четвёртая диа­грам­ма.

Вто­рой ва­ри­ант рас­суж­де­ния

Про­ана­ли­зи­ро­вав диа­грам­му, уви­дим, что те­сти­ро­ва­ние
по рус­ско­му языку про­хо­ди­ло рав­ное ко­ли­че­ство уче­ни­ков во всех трех
ре­ги­о­нах. Таким об­ра­зом, диа­грам­ма под но­ме­ром 4 пра­виль­но от­ра­жа­ет
со­от­но­ше­ние ко­ли­че­ства участ­ни­ков те­сти­ро­ва­ния по рус­ско­му
языку.

Пра­виль­ный ответ ука­зан под но­ме­ром 4.

№9. В таб­ли­це пред­став­ле­ны сред­ние ры­ноч­ные
цены для 4–х типов то­варов на на­ча­ло и конец года. Какая из диа­грамм наи­бо­лее
верно от­ра­жа­ет рост цен этих то­ва­ров в про­цен­тах от­но­си­тель­но на­ча­ла
года?

По­яс­не­ние.

Най­дем на сколь­ко про­цен­тов из­ме­ни­лась цена, для
этого нужно найти из­ме­не­ние цены каж­до­го то­ва­ра, а затем от­не­сти его к
цене то­ва­ра в на­ча­ле года:

1-ый товар: 

2-ой товар: 

3-ий товар: 

4-ый товар: 

Ана­ли­зи­руя столб­ча­тые диа­грам­мы, при­хо­дим к вы­во­ду,
что таким дан­ным наи­бо­лее точно со­от­вет­ству­ет 2-ая диа­грам­ма.

№10. На про­тя­же­нии 3–х минут цен­траль­ный
про­цес­сор ком­пью­те­ра был за­гру­жен сле­ду­ю­щим об­ра­зом: 1–ю ми­ну­ту
был за­гру­жен на 30%, 2–ю – на 10% и 3–ю – на 60%. Какая из диа­грамм со­от­вет­ству­ет
за­гру­жен­но­сти про­цес­со­ра на про­тя­же­нии 3–х минут?

По­яс­не­ние.

Для ана­ли­за кру­го­вых диа­грамм не­об­хо­ди­мо вы­яс­нить,
какая доля па­мя­ти вы­де­ля­лась про­грам­ме в те­че­ние каж­до­го про­ме­жут­ка
вре­ме­ни. Ана­ли­зи­руя кру­го­вые диа­грам­мы, видим, что 1-я со­от­вет­ству­ет
усло­вию за­да­чи.

На вто­рой диа­грам­ме все части рав­ные, что не­вер­но.

На диа­грам­ме 3 тре­тья ми­ну­та не за­ни­ма­ет 60 %. На
четвёртой тре­тья ми­ну­та также мень­ше 60 %.

Ответ: 1.

       Столбчатая и круговая диаграммы

№1. Все уче­ни­ки стар­ших клас­сов (с 9-го по
11-й) участ­во­вали в школь­ной спар­та­киа­де. По ре­зуль­та­там со­рев­но­ва­ний
каж­дый из них по­лу­чил от 0 до 3-х бал­лов. На диа­грам­ме I от­ра­же­но рас­пре­де­ле­ние
уче­ни­ков по клас­сам, а на диа­грам­ме II — ко­ли­че­ство уче­ни­ков, на­брав­ших
бал­лы от 0 до 3-х. На обеих диа­грам­мах каж­дый уче­ник учтён толь­ко один
раз.

Име­ют­ся че­ты­ре утвер­жде­ния:

1 ) Среди уче­ни­ков 9-го клас­са есть хотя бы один, на­брав­ший
2 или 3 балла.

2 ) Все уче­ни­ки, на­брав­шие 0 бал­лов, могут быть 9-класс­ни­ка­ми.

3 ) Все 10-класс­ни­ки могли на­брать ровно по 2 балла.

4 ) Среди на­брав­ших 3 балла нет ни од­но­го 10-класс­ни­ка.

Какое из этих утвер­жде­ний сле­ду­ет из ана­ли­за обеих диа­грамм?

По­яс­не­ние.

Столб­ча­тая диа­грам­ма дает нам пред­став­ле­ние о чис­лен­ных
дан­ных. Из нее мы вы­яс­ня­ем, что всего уче­ни­ков 45 + 30 + 20 + 15 = 110.

Кру­го­вая диа­грам­ма дает нам пред­став­ле­ние о долях от­дель­ных
со­став­ля­ю­щих в общей сумме. Из нее мы вы­яс­ня­ем, что

«9 класс»,=50%=55

«11 класс»,

«10 класс» .

Те­перь рас­смот­рим утвер­жде­ния:

1. Од­но­знач­но не сле­ду­ет из ана­ли­за обеих диа­грамм,
по­сколь­ку сум­мар­ное ко­ли­че­ство уче­ни­ков, на­брав­ших 2 или 3 балла
равно 20 + 15 = 35, а уче­ни­ков де­вя­то­го клас­са 55.

2. Могут, так как 0 бал­лов на­бра­ло 45, а 9-класс­ни­ков
55.

3. Не могли, так как 10-класс­ни­ков 37, а ровно по 2 балла
на­бра­ло всего 20.

4. Од­но­знач­но не сле­ду­ет из ана­ли­за обеих диа­грамм.

№2. В ма­га­зи­не про­да­ют­ся мячи четырёх цве­тов
(синие, зе­лёные, крас­ные и жёлтые) и трёх раз­ме­ров (боль­шие, сред­ние и ма­лень­кие).
На диа­грам­ме I от­ра­же­но ко­ли­че­ство мячей раз­но­го раз­ме­ра, а на диа­грам­ме
II — рас­пре­де­ле­ние мячей по цве­там.

Име­ют­ся че­ты­ре утвер­жде­ния:

1 ) Среди боль­ших мячей дол­жен быть хотя бы один синий.

2 ) Ни один мяч сред­не­го раз­ме­ра не может быть крас­ным.

3 ) Все ма­лень­кие мячи могут быть зелёными.

4 ) Все зелёные мячи могут быть ма­лень­ки­ми.

Какое из этих утвер­жде­ний сле­ду­ет из ана­ли­за обеих диа­грамм?

По­яс­не­ние.

Столб­ча­тая диа­грам­ма дает нам пред­став­ле­ние о чис­лен­ных
дан­ных. Из нее мы вы­яс­ня­ем, что всего мячей 30+40+35+15=120.

Кру­го­вая диа­грам­ма дает нам пред­став­ле­ние о долях от­дель­ных
со­став­ля­ю­щих в общей сумме. Из нее мы вы­яс­ня­ем, что М=50%=60, Ср=25%=30,
Б=25%=30.

Те­перь рас­смот­рим утвер­жде­ния:

1. Может, но не обя­за­тель­но.

2. Может, так как Ср=30, а крас­ных 35.

3. Не могут, так как М=60, а зе­ле­ных всего 40.

4. Могут так как зе­ле­ных всего 40, а М=60.

№3. В ма­га­зи­не про­да­ют­ся мячи четырёх цве­тов
(синие, зе­лёные, крас­ные и жёлтые) и трёх раз­ме­ров (боль­шие, сред­ние и ма­лень­кие).
На диа­грам­ме I от­ра­же­но ко­ли­че­ство мячей раз­но­го раз­ме­ра, а на диа­грам­ме
II — рас­пре­де­ле­ние мячей по цве­там.

Име­ют­ся че­ты­ре утвер­жде­ния:

1 ) Все ма­лень­кие мячи могут быть си­ни­ми или жёлтыми.

2 ) Среди боль­ших мячей найдётся хотя бы один крас­ный.

3 ) Среди ма­лень­ких мячей найдётся хотя бы один зелёный
или крас­ный.

4 ) Все крас­ные мячи могут быть сред­не­го раз­ме­ра.

Какое из этих утвер­жде­ний сле­ду­ет из ана­ли­за обеих диа­грамм?

По­яс­не­ние.

Столб­ча­тая диа­грам­ма дает нам пред­став­ле­ние о чис­лен­ных
дан­ных. Из нее мы вы­яс­ня­ем, что всего мячей 30+40+35+15=120.

Кру­го­вая диа­грам­ма дает нам пред­став­ле­ние о долях от­дель­ных
со­став­ля­ю­щих в общей сумме. Из нее мы вы­яс­ня­ем, что М=50%=60, Ср=25%=30,
Б=25%=30.

Те­перь рас­смот­рим утвер­жде­ния:

1. Не могут, так как М=60, а синих 30, жёлтых 15.

2. Может, но не обя­за­тель­но.

3. Най­дет­ся, так как не­вер­но «1.»

4. Не могут так как крас­ных 35, а Ср=30.

№4. За­ве­ду­ю­щая дет­ским садом об­на­ру­жи­ла,
что в её саду все дети на­зы­ва­ют­ся толь­ко че­тырь­мя раз­ны­ми име­на­ми;
Саша, Валя, Миша и Ира. По цвету волос каж­до­го из них можно чёт­ко от­не­сти
к блон­ди­нам, ша­те­нам или брю­не­там. На диа­грам­ме I от­ра­же­но ко­ли­че­ство
детей каж­до­го имени, а на диа­грам­ме II — рас­пре­де­ле­ние детей по цвету
волос.

Име­ют­ся че­ты­ре утвер­жде­ния:

1 ) Всех брю­не­тов могут звать Саша.

2 ) Все Иры могут быть ша­тен­ка­ми.

3 ) Среди Миш найдётся хотя бы один блон­дин.

4 ) Среди Саш нет ни од­но­го ша­те­на.

Какое из этих утвер­жде­ний сле­ду­ет из ана­ли­за обеих диа­грамм?

По­яс­не­ние.

Столб­ча­тая диа­грам­ма дает нам пред­став­ле­ние о чис­лен­ных
дан­ных. Из нее мы вы­яс­ня­ем, что всего детей 

40+20+35+25=120

Кру­го­вая диа­грам­ма дает нам пред­став­ле­ние о долях от­дель­ных
со­став­ля­ю­щих в общей сумме. Из нее мы вы­яс­ня­ем, что

«Бр»,=50%=60

«Бл»,

«Ш» .

Те­перь рас­смот­рим утвер­жде­ния:

1. Не могут, так «Бр»=60, а Саш 40.

2. Могут, так как «Ш»=45, а Ир 25.

3. Од­но­знач­но не сле­ду­ет из ана­ли­за обеих диа­грамм.

4. Од­но­знач­но не сле­ду­ет из ана­ли­за обеих диа­грамм.

№5. За­ве­ду­ю­щая дет­ско­го сада об­на­ру­жи­ла,
что в сад ходят дети толь­ко четырёх имен: Саши, Вали, Миши и Иры. По цвету
волос каж­до­го из них можно чётко от­не­сти к блон­ди­нам, шате­нам и брю­не­там.
На диа­грам­ме I от­ра­же­но ко­ли­че­ство детей каж­до­го имени, а на диа­грам­ме
II — рас­пре­де­ле­ние детей по цвету волос.

Име­ют­ся че­ты­ре утвер­жде­ния:

1) Всех блон­ди­нов зовут Саша.

2) Все Миши могут быть блон­ди­на­ми.

3) Среди Саш может не быть ни од­но­го ша­те­на.

4) Среди брю­не­тов есть хотя бы один ребёнок по имени Валя
или Ира.

Какое из этих утвер­жде­ний сле­ду­ет из ана­ли­за обеих диа­грамм?

По­яс­не­ние.

Столб­ча­тая диа­грам­ма дает нам пред­став­ле­ние о чис­лен­ных
дан­ных. Из нее мы вы­яс­ня­ем, что всего детей 

40+20+35+25=120

Кру­го­вая диа­грам­ма дает нам пред­став­ле­ние о долях от­дель­ных
со­став­ля­ю­щих в общей сумме. Из нее мы вы­яс­ня­ем, что

«Бр»,=50%=60

«Бл»,

«Ш» .

Те­перь рас­смот­рим утвер­жде­ния:

1. Од­но­знач­но не сле­ду­ет из ана­ли­за обеих диа­грамм.

2. Не могут, так как «Бл»=20, а Миш 35.

3. Может не быть.

4. Од­но­знач­но не сле­ду­ет из ана­ли­за обеих диа­грамм.

№6. В ма­га­зи­не про­да­ют­ся го­лов­ные уборы
трёх видов (па­намки, шляпы и бейс­бол­ки) и четырёх ма­те­ри­а­лов (бре­зент,
хло­пок, шёлк и со­лом­ка).На диа­грам­ме 1 от­ра­же­но ко­ли­че­ство го­лов­ных
убо­ров каж­дого вида, а на диа­грам­ме II — рас­пре­де­ле­ние го­лов­ных убо­ров
по ма­те­ри­а­лам.

Име­ют­ся че­ты­ре утвер­жде­ния:

A) Все шляпы могут быть из шёлка.

Б) Все па­на­мы могут быть из со­лом­ки.

B) Среди го­лов­ных убо­ров из со­лом­ки найдётся хотя бы
одна па­на­ма.

Г) Все бейс­бол­ки долж­ны быть из хлоп­ка.

Какое из этих утвер­жде­ний сле­ду­ет из ана­ли­за обеих диа­грамм?

По­яс­не­ние.

Столб­ча­тая диа­грам­ма дает нам пред­став­ле­ние о чис­лен­ных
дан­ных. Из нее мы вы­яс­ня­ем, что всего го­лов­ных убо­ров

 45+35+20=100

Кру­го­вая диа­грам­ма дает нам пред­став­ле­ние о долях от­дель­ных
со­став­ля­ю­щих в общей сумме. Из нее мы вы­яс­ня­ем, что

«Х»

«Б»,

«С»,

«Ш» .

Те­перь рас­смот­рим утвер­жде­ния:

1. Могут, так как шляп 45, а «Ш»=50.

2. Не могут, так как «С»=25, а панам 35.

3. Од­но­знач­но не сле­ду­ет из ана­ли­за обеих диа­грамм.

4. Од­но­знач­но не сле­ду­ет из ана­ли­за обеих диа­грамм.

№7. В ма­га­зи­не про­да­ют­ся го­лов­ные уборы
трёх видов (па­намки, шляпы и бейс­бол­ки) и четырёх ма­те­ри­а­лов (бре­зент,
хло­пок, шёлк и со­лом­ка).На диа­грам­ме I от­ра­же­но ко­ли­че­ство го­лов­ных
убо­ров каж­дого вида, а на диа­грам­ме II — рас­пре­де­ле­ние го­лов­ных убо­ров
по ма­те­ри­а­лам.

Име­ют­ся че­ты­ре утвер­жде­ния:

A) Все со­ло­мен­ные из­де­лия могут быть бейс­бол­ка­ми.

Б) Все па­нам­ки могут быть из хлоп­ка или бре­зен­то­вы­ми.

B) Среди из­де­лий из шёлка может не быть ни одной шляпы.

Г) Среди из­де­лий, сде­лан­ных не из со­лом­ки, может не
быть ни одной па­на­мы.

Какое из этих утвер­жде­ний сле­ду­ет из ана­ли­за обеих диа­грамм?

По­яс­не­ние.

Столб­ча­тая диа­грам­ма дает нам пред­став­ле­ние о чис­лен­ных
дан­ных. Из нее мы вы­яс­ня­ем, что всего го­лов­ных убо­ров 

45+35+20=100

Кру­го­вая диа­грам­ма дает нам пред­став­ле­ние о долях от­дель­ных
со­став­ля­ю­щих в общей сумме. Из нее мы вы­яс­ня­ем, что

«Х»

«Б»,

«С»,

«Ш» .

Те­перь рас­смот­рим утвер­жде­ния:

1. Не могут, так как «С»=25 а бейс­бо­лок 20.

2. Не могут, так как панам 35, а «Б» и
«Х» мень­ше 20.

3. Может, так как «Ш»=50, а шляп всего 45.

4. Не может.

№8. Мо­ло­дой че­ло­век решил сде­лать по­да­рок
своей не­ве­сте и пришёл в юве­лир­ный ма­га­зин. Там он об­на­ру­жил коль­ца
из зо­ло­та, се­реб­ра и пла­ти­ны, каж­дое из ко­то­рых было укра­ше­но одним
дра­го­цен­ным кам­нем (то­па­зом, изу­мру­дом, ал­ма­зом или ру­би­ном). Он ис­сле­до­вал
со­от­но­ше­ние ко­ли­че­ства колец с раз­ными кам­ня­ми (ре­зуль­та­ты от­ра­же­ны
на диа­грам­ме I) и коли­че­ство колец раз­ных ма­те­ри­а­лов (ре­зуль­та­ты от­ра­же­ны
на диа­грам­ме II).

Мо­ло­дой че­ло­век сде­лал че­ты­ре пред­по­ло­же­ния:

A) Все коль­ца с изу­мру­да­ми могут быть из зо­ло­та.

Б) Среди се­реб­ря­ных колец найдётся хотя бы одно с изу­мру­дом.

B) Все коль­ца с ру­би­на­ми и ал­ма­за­ми могут быть пла­ти­но­вы­ми.

Г) Все зо­ло­тые коль­ца могут быть с ал­ма­за­ми.

Какое из этих пред­по­ло­же­ний сле­ду­ет из ана­ли­за обеих
диа­грамм?

По­яс­не­ние.

Столб­ча­тая диа­грам­ма дает нам пред­став­ле­ние о чис­лен­ных
дан­ных. Из нее мы вы­яс­ня­ем, что коли­че­ство колец раз­ных ма­те­ри­а­лов 

45+35+20=100

Кру­го­вая диа­грам­ма дает нам пред­став­ле­ние о долях от­дель­ных
со­став­ля­ю­щих в общей сумме. Из нее мы вы­яс­ня­ем, что

«P» ,=25%*100=25

«A» ,=25%*100=25

«И» .

«Т» .

Те­перь рас­смот­рим утвер­жде­ния:

1. Могут, так как «И»=33, а зо­ло­тых 45.

2. Од­но­знач­но не сле­ду­ет из ана­ли­за обеих диа­грамм.

3. Не могут, так как пла­ти­но­вых всего 20, а
«P»+»A»=50.

4. Не могут, так как зо­ло­тых 45, а «A»=25.

№9. Мо­ло­дой че­ло­век решил сде­лать по­да­рок
своей не­ве­сте и пришёл в юве­лир­ный ма­га­зин. Там он об­на­ру­жил коль­ца
из зо­ло­та, се­реб­ра и пла­ти­ны, каж­дое из ко­то­рых было укра­ше­но одним
дра­го­цен­ным кам­нем (то­па­зом, изу­мру­дом, ал­ма­зом или ру­би­ном). Он ис­сле­до­вал
со­от­но­ше­ние ко­ли­че­ства колец с раз­ными кам­ня­ми (ре­зуль­та­ты от­ра­же­ны
на диа­грам­ме I) и коли­че­ство колец раз­ных ма­те­ри­а­лов (ре­зуль­та­ты от­ра­же­ны
на диа­грам­ме И).

Мо­ло­дой че­ло­век сде­лал че­ты­ре пред­по­ло­же­ния:

A) Все коль­ца с изу­мру­да­ми не могут быть се­реб­ря­ны­ми.

Б) Среди зо­ло­тых и се­реб­ря­ных колец найдётся хотя бы
одно с ру­би­ном.

B) Все зо­ло­тые коль­ца могут быть с то­па­за­ми.

Г) Все ру­би­ны на­хо­дят­ся в се­реб­ря­ных коль­цах.

Какое из этих пред­по­ло­же­ний сле­ду­ет из ана­ли­за обеих
диа­грамм?

По­яс­не­ние.

Столб­ча­тая диа­грам­ма дает нам пред­став­ле­ние о чис­лен­ных
дан­ных. Из нее мы вы­яс­ня­ем, что коли­че­ство колец раз­ных ма­те­ри­а­лов 

45+35+20=100

Кру­го­вая диа­грам­ма дает нам пред­став­ле­ние о долях от­дель­ных
со­став­ля­ю­щих в общей сумме. Из нее мы вы­яс­ня­ем, что

«P» ,=25%*100=25

«A» ,=25%*100=25

«И» .

«Т» .

Те­перь рас­смот­рим утвер­жде­ния:

1. Могут, так как «И»=33, а се­реб­ря­ных 35.

2. Най­дет­ся, так как пла­ти­но­вых всего 20, а
«Р»=25, сле­до­ва­тель­но, 5 колец либо зо­ло­тые, либо се­реб­рян­ные.

3. Не могут, так как зо­ло­тых 45, а «Т»=17.

4. Од­но­знач­но не сле­ду­ет из ана­ли­за обеих диа­грамм.

№10. Все уче­ни­ки стар­ших клас­сов (с 9–го по
11–й) участ­во­вали в школь­ной спар­та­киа­де. По ре­зуль­та­там со­рев­но­ва­ний
каж­дый из них по­лу­чил от 0 до 3–х бал­лов. На диа­грам­ме I от­ра­же­но рас­пре­де­ле­ние
уче­ни­ков по клас­сам, а на диа­грам­ме II – ко­ли­че­ство уче­ни­ков, на­брав­ших
бал­лы от 0 до 3–х. На обеих диа­грам­мах каж­дый уче­ник учтён толь­ко один
раз.

Име­ют­ся че­ты­ре утвер­жде­ния:

А) Среди уче­ни­ков 9–го клас­са есть хотя бы один, кто на­брал
0 бал­лов.

Б) Все 11–класс­ни­ки на­бра­ли боль­ше 0 бал­лов.

В) Все уче­ни­ки 11–го клас­са могли на­брать ровно один
балл.

Г) Среди уче­ни­ков 10–го клас­са есть хотя бы один, кто на­брал
2 балла.

Какое из этих утвер­жде­ний сле­ду­ет из ана­ли­за обеих диа­грамм?

По­яс­не­ние.

Столб­ча­тая диа­грам­ма дает нам пред­став­ле­ние о чис­лен­ных
дан­ных. Из нее мы вы­яс­ня­ем, что всего уче­ни­ков 

45+30+20+110

Кру­го­вая диа­грам­ма дает нам пред­став­ле­ние о долях от­дель­ных
со­став­ля­ю­щих в общей сумме. Из нее мы вы­яс­ня­ем, что

«9 класс»,=50%=55

«11 класс»,

«10 класс» .

Те­перь рас­смот­рим утвер­жде­ния:

A)Нель­зя од­но­знач­но утвер­ждать из ана­ли­за обеих диа­грамм

Б)Нель­зя од­но­знач­но утвер­ждать из ана­ли­за обеих диа­грамм

В)Да, могли, т.к. 11-класс­ни­ков 18, а уче­ни­ков, на­брав­ших
один балл 30.

Г)Нель­зя од­но­знач­но утвер­ждать из ана­ли­за обеих диа­грамм

       Электронные таблицы и диаграммы 

№1. Дан фраг­мент элек­трон­ной таб­ли­цы:

	A	B	C
1	4	2
2	=2*(A1–C1)	=(2*B1+A1)/4	=C1-1

Какое целое число долж­но быть за­пи­са­но в ячей­ке C1,
чтобы по­стро­ен­ная после вы­пол­не­ния вы­чис­ле­ний диа­грам­ма по зна­че­ни­ям
диа­па­зо­на ячеек A2:С2 со­от­вет­ство­ва­ла ри­сун­ку?

По­яс­не­ние.

По ри­сун­ку видно, что зна­че­ния всех трёх ячеек диа­па­зо­на
A2:С2 равны. По дан­ным таб­ли­цы найдём зна­че­ние B2: B2 = (2 * 2 + 4) / 4 =
2.

Вы­ра­зим С1 из зна­че­ния С2: С1 = С2 + 1 = B2 + 1 = 2 + 1
= 3.

Ответ: 3.
Источник: Яндекс: Тре­ни­ро­воч­ная работа ЕГЭ по информатике. Ва­ри­ант 1.

№2. Дан фраг­мент элек­трон­ной таб­ли­цы:

	A	B	C
1	4	2
2	=A1+C1	=B1+A1	=3*C1

Какое целое число долж­но быть за­пи­са­но в ячей­ке C1,
чтобы по­стро­ен­ная после вы­пол­не­ния вы­чис­ле­ний диа­грам­ма по зна­че­ни­ям
диа­па­зо­на ячеек A2:С2 со­от­вет­ство­ва­ла ри­сун­ку?

По­яс­не­ние.

В ячей­ке В2 будет зна­че­ние 6. Из диа­грам­мы сле­ду­ет,
что зна­че­ния в ячей­ках равны между собой. Сле­до­ва­тель­но, из того, что
6=3*C1 => C1= 2.

№3.

Дан фраг­мент элек­трон­ной таб­ли­цы.

	A	B	C
1	2	4
2	= (B1 – A1)/2	= 2 – A1/2	= (C1 – A1)*2 – 4

Какое целое число долж­но быть за­пи­са­но в ячей­ке C1,
чтобы по­стро­ен­ная после вы­пол­не­ния вы­чис­ле­ний диа­грам­ма по зна­че­ни­ям
диа­па­зо­на ячеек A2 : С2 со­от­вет­ство­ва­ла ри­сун­ку? Из­вест­но, что все
зна­че­ния диа­па­зо­на, по ко­то­рым по­стро­е­на диа­грам­ма, имеют один и
тот же знак.

По­яс­не­ние.

В ячей­ке А₂ будет зна­че­ние 1. В ячей­ке В₂ будет
зна­че­ние 1. Из диа­грам­мы сле­ду­ет, что зна­че­ния в ячей­ке С₂ в
2 раза боль­ше. Сле­до­ва­тель­но, из того, что 2 = (C1 – A1)*2 – 4, сле­ду­ет,
что ответ 5.

№4. Дан фраг­мент элек­трон­ной таб­ли­цы:

	A	B	C
1	2		=A1+1
2	=C1-B1	=(3*B1+C1)/3	=B2+A1

Какое число долж­но быть за­пи­са­но в ячей­ке B1, чтобы по­стро­ен­ная
после вы­пол­не­ния вы­чис­ле­ний диа­грам­ма по зна­че­ни­ям диа­па­зо­на ячеек
A2:С2 со­от­вет­ство­ва­ла ри­сун­ку? Из­вест­но, что все зна­че­ния диа­па­зо­на,
по ко­то­рым по­стро­е­на диа­грам­ма, имеют один и тот же знак.

По­яс­не­ние.

В ячей­ке С₁ будет зна­че­ние 3. С₁ =
3, А₁ = 2, сле­до­ва­тель­но В₂ = В₁ +
1, С₂ = В₂ + 2 = В₁ + 3. Сле­до­ва­тель­но,
B₂не равно С₂, то есть, одно из них (судя по диа­грам­ме)
боль­ше дру­го­го в 2 раза. Решим эти урав­не­ния по­сле­до­ва­тель­но для В₂ =
2С₂ и С₂ = 2В₂. В пер­вом слу­чае В₁ =
-5, А₂ = 8, В₂ = −4, C₂ = −2.
Это не со­от­вет­ству­ет диа­грам­ме. Во вто­ром слу­чае В₁ =
1, А₂ = В₂ = 2, C₂ = 4. Этот ва­ри­ант
со­от­вет­ству­ет диа­грам­ме, сле­до­ва­тель­но, пра­виль­ный ответ — 1.

№5. Дан фраг­мент элек­трон­ной таб­ли­цы:

	A	B	C
1	2	1
2	=C1-B1*5	=(B1+C1)/A1	=C1-5

Какое число долж­но быть за­пи­са­но в ячей­ке С1, чтобы по­стро­ен­ная
после вы­пол­не­ния вы­чис­ле­ний диа­грам­ма по зна­че­ни­ям диа­па­зо­на
ячеек А2:С2 со­от­вет­ство­ва­ла ри­сун­ку?

Из­вест­но, что все зна­че­ния диа­па­зо­на, по ко­то­рым по­стро­е­на
диа­грам­ма, имеют один и тот же знак.

По­яс­не­ние.

По ри­сун­ку видно, что зна­че­ния всех трёх ячеек диа­па­зо­на
A2:С2 равны. При­рав­ня­ем зна­че­ния ячеек А2 и В2, решим урав­не­ние: C1 − B1
* 5 = (B1 + C1) / A1, из него C1 = 11 при А1 рав­ном 2, В1 рав­ном 1.

Ответ: 11.

№6. Дан фраг­мент элек­трон­ной таб­ли­цы:

	A	B	C
1	2	1
2	=C1-B1*3	=(B1+C1)/A1	=C1-3

Какое число долж­но быть за­пи­са­но в ячей­ке С1, чтобы по­стро­ен­ная
после вы­пол­не­ния вы­чис­ле­ний диа­грам­ма по зна­че­ни­ям диа­па­зо­на
ячеек А2:С2 со­от­вет­ство­ва­ла ри­сун­ку?

Из­вест­но, что все зна­че­ния диа­па­зо­на, по ко­то­рым по­стро­е­на
диа­грам­ма, имеют один и тот же знак.

По­яс­не­ние.

По ри­сун­ку видно, что зна­че­ния всех трёх ячеек диа­па­зо­на
A2:С2 равны. При­рав­ня­ем зна­че­ния ячеек А2 и В2, решим урав­не­ние: C1 − B1
* 3 = (B1 + C1) / A1, из него C1 = 7 при А1 рав­ном 2, В1 рав­ном 1.

Ответ: 7.

№7.

Дан фраг­мент элек­трон­ной таб­ли­цы.

	A	B	C
1	5		=A1*2
2	=(B1-A1)/2	=B1-C1	=B2+A1

Какое число долж­но быть за­пи­са­но в ячей­ке В1, чтобы по­стро­ен­ная
после вы­пол­не­ния вы­чис­ле­ний диа­грам­ма по зна­че­ни­ям диа­па­зо­на
ячеек А2:С2 со­от­вет­ство­ва­ла ри­сун­ку?

Из­вест­но, что все зна­че­ния диа­па­зо­на, по ко­то­рым по­стро­е­на
диа­грам­ма, имеют один и тот же знак.

По­яс­не­ние.

В ячей­ке С₁ будет зна­че­ние 10. С₁ =
10, А₁ = 5, сле­до­ва­тель­но, В₂ = В₁ −
10, С₂ = В₂ + 5 = В₁ − 5. По­это­му
B₂ не равно С₂, одно из них, судя по диа­грам­ме,
боль­ше дру­го­го в 2 раза.

Решим эти урав­не­ния по­сле­до­ва­тель­но для В₂ =
2С₂ и С₂ = 2В₂. В пер­вом слу­чае: В₁ =
−5, А₂ = 8, В₂ = −4, C₂ = 5.
Это не со­от­вет­ству­ет диа­грам­ме. Во вто­ром слу­чае: В₁ =
15, А₂ = В₂ = 5, C₂ = 10. Этот
ва­ри­ант со­от­вет­ству­ет диа­грам­ме, сле­до­ва­тель­но, пра­виль­ный ответ
— 15.

№8. Дан фраг­мент элек­трон­ной таб­ли­цы

Какое число долж­но быть за­пи­са­но в ячей­ке B1, чтобы по­стро­ен­ная
после вы­пол­не­ния вы­чис­ле­ний диа­грам­ма по зна­че­ни­ям диа­па­зо­на
ячеек A2:C2 со­от­вет­ство­ва­ла ри­сун­ку?

Из­вест­но, что все зна­че­ния диа­па­зо­на, по ко­то­рым по­стро­е­на
диа­грам­ма, имеют один и тот же знак.

По­яс­не­ние.

По­счи­та­ем зна­че­ния в тех клет­ках, в ко­то­рых это воз­мож­но.

Из диа­грам­мы видно, что две ячей­ки долж­ны быть равны
друг другу. B2 не равно C2 зна­чит, A2 = B2, а зна­че­ние в ячей­ке C2 в два
раза боль­ше.

Таким об­ра­зом: B1/2 = 8/B1, B1 = 4.

№9. Дан фраг­мент элек­трон­ной таб­ли­цы:

	A	B	C
1	5		=A1*2
2	=B1/5	=A1/B1	=B2+C1/10

Какое число долж­но быть за­пи­са­но в ячей­ке B1, чтобы по­стро­ен­ная
после вы­пол­не­ния вы­чис­ле­ний диа­грам­ма по зна­че­ни­ям диа­па­зо­на
ячеек A2:C2 со­от­вет­ство­ва­ла ри­сун­ку?

Из­вест­но, что все зна­че­ния диа­па­зо­на, по ко­то­рым по­стро­е­на
диа­грам­ма, имеют один и тот же знак.

По­яс­не­ние.

Вы­чис­лим зна­че­ния в тех клет­ках, в ко­то­рых это воз­мож­но.

Из диа­грам­мы видно, что две ячей­ки долж­ны быть равны
друг другу, а зна­че­ние в ячей­ке C2 в два раза боль­ше. По­сколь­ку B2 не
равно C2, имеем B1/5 = 5/B1, B1 = 5 и B1 = −5. По­сколь­ку по усло­вию все зна­че­ния
диа­па­зо­на, по ко­то­рым по­стро­е­на диа­грам­ма, имеют один и тот же знак,
ответ 5.

№10.

Дан фраг­мент элек­трон­ной таб­ли­цы:

	A	B	C
1	2		44
2	=С1 − В1*В1*5	=(В1*В1+С1)/А1	=C1−20

Какое целое число долж­но быть за­пи­са­но в ячей­ке B1,
чтобы по­стро­ен­ная после вы­пол­не­ния вы­чис­ле­ний диа­грам­ма по зна­че­ни­ям
диа­па­зо­на ячеек A2:С2 со­от­вет­ство­ва­ла ри­сун­ку? Из­вест­но, что все
зна­че­ния диа­па­зо­на А1 :С2 имеют один и тот же знак.

По­яс­не­ние.

Пре­об­ра­зу­ем таб­ли­цу:

	A	B	C
1	2		44
2	=44 − В1·В1·5	=В1·В1/2+22	44−20

Из диа­грам­мы сле­ду­ет, что зна­че­ния в ячей­ках равны
между собой. Сле­до­ва­тель­но, из того, что
В1·В1/2 + 22 = 24, В1 = 2, либо
В1 = −2. Все зна­че­ния диа­па­зо­на А1 :С2 имеют один и тот же знак,
сле­до­ва­тель­но, ответ 2.

---

A7 В ячейке D3 электронной таблицы записана формула =B$2+$B3. Какой вид приобретет
формула, после того как ячейку D3 скопируют в ячейку E4?
Примечание: знак $ используется для обозначения абсолютной адресации.
1) =C$2+$B4
2) =A$2+$B1
3) =B$3+$C3
4) =B$1+$A3
Пояснение.
B$2: меняется столбец и не меняется номер строки.
$B3: столбец не меняется, меняется номер строки.
Номер столбца Е больше номера столбца D на 1. Значит столбец B станет столбцом С.
Номер строки 4 на 1 больше номера строки 3, значит, строка 3 станет строкой 4.
Окончательный вид =С$2+$B4.
Правильный ответ указан под номером 1.
A7 В электронной таблице значение формулы =CP3HAЧ(D1:D4) равно 5. Чему равно значение
ячейки D1, если значение формулы =СУММ(D2:D4) равно 12?
1) 4
2) 6
3) 8
4) 17
Пояснение.
Функция СРЗНАЧ(D1:D4) считает среднее арифметическое диапазона D1:D4, т. е. сумму значений
четырёх ячеек D1, D2, D3, D4, делённую на 4. Сначала найдём сумму значений ячеек D1 + D2 +
D3 + D4 = 5 * 4 = 20.
Теперь, вычтем из полученной суммы значение =CУMM(D2:D4) и найдём D1: D1 = 20 — 12 = 8.
Правильный ответ указан под номером 3.
A7 В ячейке G4 электронной таблицы записана формула =D$22*$D23. Какой вид приобретет
формула, после того как ячейку G4 скопируют в ячейку F3?
Примечание: знак $ используется для обозначения абсолютной адресации.
1) =C$22*$C23
2) =D$21*$D22
3) =D$21*$C23
4) =C$22*$D22
Пояснение.
D$22: меняется столбец и не меняется номер строки.
$D23: столбец не меняется, меняется номер строки.
Номер столбца F меньше номера столбца G на 1, значит, при копировании из G4 в F3 столбец D в
формуле станет столбцом C.
Номер строки 3 на 1 меньше номера строки 4, значит, строка 23 в формуле станет строкой 22.
Окончательный вид =С$22*$D22.
Правильный ответ указан под номером 4.
A7 В ячейке D6 электронной таблицы записана формула =F$12-$F13.
Примечание: знак $ используется для обозначения абсолютной адресации.
Какой вид приобретет формула, после того как ячейку D6 скопируют в ячейку E7?
1) =G$12-$G13
2) =F$13-$F14
3) =F$13-$G13
4) =G$12-$F14
Пояснение.
F$12: меняется столбец и не меняется номер строки.
$F13: столбец не меняется, меняется номер строки.
Номер столбца E больше номера столбца D на 1, значит, при копировании из D6 в E7 столбец F в
формуле станет столбцом G.
Номер строки 7 на 1 больше номера строки 6, значит, строка 13 в формуле станет строкой 14.
Окончательный вид =G$12-$F14.
Правильный ответ указан под номером 4.
A7 В электронной таблице значение формулы =CP3HAЧ (D1:D4) равно 8. Чему равно значение
формулы = СРЗНАЧ (D2:D4), если значение ячейки D1 равно 11?
1) 19
2) 21
3) 7
4) 32
Пояснение.
Функция СРЗНАЧ(D1:D4) считает среднее арифметическое диапазона D1:D4, т. е. сумму значений
четырёх ячеек D1, D2, D3, D4, делённую на 4. Умножим среднее значние на число ячеек и
получим сумму значений ячеек D1 + D2 + D3 + D4 = 8 * 4 = 32.
Теперь, вычтем значение ячейки D1 и найдём сумму СУММ(D2:D4): D2 + D3 + D4 = 32 — 11 = 21.

Разделим полученный результат на 3 (число ячеек) и найдём СРЗНАЧ(D2:D4): 21 / 3 = 7.
Правильный ответ указан под номером 3.
A7 В электронной таблице значение формулы =CP3HAЧ(D1:D4) равно 8. Чему равно значение
формулы =СУММ(D2:D4), если значение ячейки D1 равно 11?
1) 7
2) 21
3) 32
4) 19
Пояснение.
Функция СРЗНАЧ(D1:D4) считает среднее арифметическое диапазона D1:D4, т. е. сумму значений
четырёх ячеек D1, D2, D3, D4, делённую на 4. Умножим среднее значние на число ячеек и
получим сумму значений ячеек D1 + D2 + D3 + D4 = 8 * 4 = 32.
Теперь, вычтем значение ячейки D1 и найдём сумму СУММ(D2:D4): D2 + D3 + D4 = 32 — 11 = 21.
Правильный ответ указан под номером 2.
A7 В электронной таблице Excel приведен фрагмент банковских расчетов по вкладам населения.
Таблица отражает фамилии вкладчиков, процентные ставки по вкладам за два фиксированных
одногодичных промеж утка времени и суммы вкладов с начисленными процентами за
соответствующие истекшие периоды времени. Такж е приведены общие суммы всех вкладов в
банке после начисления процентов и доход вкладчиков за истекший двухгодичный период.
 Вклад р. 4 % 5 % Сумма начислений за два периода
Столков 3200000 3328000 3494400 294400
Чин 3212000 3340480 3507504 295504
Прокопчин 400000 416000 436800 36800
Щ еглов 1000000 1040000 1092000 92000
 Общая сумма: 7812000 8124480 8530704 718704
Определите, кто из вкладчиков за истекшее с момента открытия вклада время получил средний
еж емесячный доход от вклада менее 2 000 рублей.
1) Столков
2) Чин
3) Прокопчин
4) Щ еглов
Пояснение.
Сумма начислений указана за 2 года, т. е. за 24 месяца. Чем меньше сумма, тем меньше средний
доход. Самая маленькая сумма у Прокопчина. Проверим 36800 / 24 = 1533,33.
Правильный ответ указан под номером 3.
A7 В электронной таблице значение формулы =СРЗНАЧ(С2:С5) равно 3. Чему равно значение
формулы =СУММ(С2:С4), если значение ячейки С5 равно 5?
1) 1
2) 7
3) -4
4) 4
Пояснение.
*Для лучшего понимания рекомендуется нарисовать таблицу.
Функция СРЗНАЧ(С2:С5) считает среднее арифметическое диапазона С2:С5, т. е. сумму значений
четырёх ячеек С2, С3, C4, С5, делённую на 4. Умножим среднее значение на число ячеек и
получим сумму значений ячеек С2 + С3 + C4 + С5 = 3 * 4 = 12
Теперь, вычтем значение ячейки С5 и найдём искомую сумму: С2 + С3 + C4 = 12 — 5 = 7
Правильный ответ указан под номером 2.
A7 Дан фрагмент электронной таблицы.
A B C D
1 1 2 3
2 5 4 = $A$2 + B$3
3 6 7 = A3 + B3
Чему станет равным значение ячейки D1, если в неё скопировать формулу из ячейки С2?
Примечание: знак $ обозначает абсолютную адресацию.
1) 18
2) 12
3) 14
4) 17
Пояснение.
$A$2: ничего не меняется.
B$3: столбец меняется, не меняется номер строки.
Номер столбца D больше номера столбца C на 1, значит, при копировании из С2 в D1 столбец B в
формуле станет столбцом C.
Окончательный вид =$A$2 + C$3, т. е. D1 = A2 + A3 + B3
Подставим имеющиеся значения: D1 = 5 + 6 + 7 = 18.
Правильный ответ указан под номером 1.

A7 В электронной таблице значение формулы =CУMM(B2:D2) равно 15. Чему равно значение
ячейки А2, если значение формулы =CP3HAЧ(A2:D2) равно 4?
1) 1
2) 5
3) 16
4) 20
Пояснение.
Функция СРЗНАЧ(A2:D2) считает среднее арифметическое диапазона A2:D2, т. е. сумму значений
четырёх ячеек A2, B2, C2, D2, делённую на 4. Умножим среднее значние на число ячеек и
получим сумму значений ячеек A2 + B2 + C2 + D2 = 4 * 4 = 16.
Теперь, вычтем из полученной сумы значение =CУMM(B2:D2) и найдём A2: A2 = 16 — 15 = 1.
Правильный ответ указан под номером 1.
A7 В электронной таблице значение формулы =СУММ(В2:D2) равно 16. Чему равно значение
формулы =CP3HAЧ(A2:D2), если значение ячейки А2 равно 4?
1) 20
2) 12
3) 5
4) 4
Пояснение.
Функция СРЗНАЧ(A2:D2) считает среднее арифметическое диапазона A2:D2, т. е. сумму значений
четырёх ячеек A2, B2, C2, D2, делённую на 4. Добавим к СУММ(В2:D2) значение элемента A2 и
разделим результат на 4 (число ячеек): A2 + B2 + C2 + D2 = 16 + 4 = 20,
СРЗНАЧ(A2:D2) = 20 / 4 = 5.
Правильный ответ указан под номером 3.
A7 В электронной таблице значение формулы =СУММ(В2:В4) равно 6. Чему равно значение
формулы =СРЗНАЧ(В2:В5), если значение ячейки В5 равно 14?
1) 5
2) 8
3) 10
4) 20
Пояснение.
*Для лучшего понимания рекомендуется нарисовать таблицу.
Функция СУММ(В2:В4) считает сумму значений ячеек B2, B3 и B4, поэтому B2 + B3 + B4 = 6.
Функция СРЗНАЧ(В2:В5) считает среднее арифметическое диапазона В2:В5, т. е. сумму значений
четырёх ячеек B2, B3, B4, B5, делённую на их количество. Поэтому прибавим к первой сумме
значение ячейки В5 и найдём: B2 + B3 + B4 + В5 = 6 + 14 = 20.
Теперь разделим полученный резльтат на 4 и найдём искомую величину: СРЗНАЧ(В2:В5) = 20 / 4 =
5.
Правильный ответ указан под номером 1.
A7 В ячейке F15 электронной таблицы записана формула. Эту формулу скопировали в ячейку
E14. В результате значение в ячейке E14 вычисляется по формуле x+2y, где x — значение в
ячейке C42, а y — значение в ячейке D42. Укажите, какая формула НЕ могла быть написана в
ячейке F15.
Примечание: знак $ используется для обозначения абсолютной адресации.
1) =$C$42+2*$D$42
2) =$C43+2*E$42
3) =C42+2*D42
4) =D$42+2*$D43
Пояснение.
По условию ясно, что в ячейке E14 записана формула 2D42 + C42.
Вариант 3 не мог быть записан в ячейку F15, так как при копировании формула изменилась бы,
поскольку отсутствуют знаки абсолютной адресации.
Следовательно, ответ 3.
A7 В ячейке М21 электронной таблицы записана формула. Эту формулу скопировали в ячейку
L22. В соответствии с формулой, полученной в ячейке L22, значение в этой ячейке равно
произведению значений в ячейках В36 и A37. Напишите, сколько из следующих четырёх
утверждений не противоречат этим данным.
A) Значение в ячейке М21 равно х·у, где х — значение в ячейке В36, а у — значение в ячейке A37.
Б) Значение в ячейке М21 равно х·у, где х — значение в ячейке С35, а у — значение в ячейке
A37.
В) Значение в ячейке М21 вычисляется по формуле х·у, где х — значение в ячейке С36, ау —
значение в ячейке А36.
Г) Значение в ячейке М21 равно 2·х , где х — значение в ячейке В36.
1) 1
2) 2
3) 3
4) 4
Пояснение.
По условию ясно, что в ячейке L22 записана формула В36 + A37, в которой каждая ссылка мож ет
быть как относительной, так и абсолютной.
Рассмотрим все варианты:
А) Не противоречит, так как в таком случае М21 = $B$36 + $A$37, а L22 = $B$36 + $A$37.
Б) Не противоречит, так как в таком случае М21 = C35 + $A$37, а L22 = B36 + $A$37.
В) Не противоречит, так как в таком случае М21 = C$36 + $A36, а L22 = B$36 + $A37.

Г) Не противоречит, так как в таком случае М21 = $B$36 + B36, а L22 = $B$36 + A37.
Следовательно, ответ 4.
A7 В электронной таблице значение формулы =СУММ(А7:С7) равно 9. Чему равно значение
формулы =CPЗHAЧ(A7:D7). если значение ячейки D7 равно 3?
1) -6
2) 6
3) 3
4) 4
Пояснение.
*Для лучшего понимания рекомендуется нарисовать таблицу.
Функция СУММ(А7:С7) считает сумму значений ячеек А7, B7 и С7, поэтому А7 + B7 + С7 = 9.
Функция СРЗНАЧ(A7:D7) считает среднее арифметическое диапазона A7:D7, т. е. сумму значений
четырёх ячеек А7, B7, С7, D7, делённую на 4. Поэтому прибавим к первой сумме значение ячейки
D7 и найдём:
А7 + B7 + С7 + D7 = 9 + 3 = 12.
Теперь разделим полученный резльтат на число ячеек и найдём искомую величину:
СРЗНАЧ(A7:D7) = 12 / 4 = 3.
Правильный ответ указан под номером 3.
A7 В 2000 году в РФ создано 7 федеральных округов. Используя представленную таблицу
укажите номер региона с наибольшей плотностью населения.
1) 1
2) 2
3) 3
4) 4
Пояснение.
Проверим все варианты. Для этого найдём плотность населения в округах 1—4, поделив
население на площадь.
Увидим, что второй окурга имеет наибольшую плотность населения.
Правильный ответ указан под номером 2.
A7 В электронной таблице значение формулы =CPЗHAЧ(C2:D5) равно 4. Чему равно значение
формулы =CУMM(C5:D5), если значение формулы =CPЗHAЧ(C2:D4) равно 5
1) -6
2) 2
3) -4
4) 4
Пояснение.
*Для лучшего понимания рекомендуется нарисовать таблицу.
Функция СРЗНАЧ(C2:D5) считает среднее арифметическое диапазона C2:D5, т. е. сумму значений
восьми ячеек С2, D2, C3, D3, C4, D4, C5, D5, делённую на их количество. Умножим среднее
значение на 8 и найдём суммму значений этих ячеек: СУММ(C2:D5) = 4 * 8 = 32.
Аналогично для CPЗHAЧ(C2:D4), количество ячеек 6: СУММ(C2:D4) = 5 * 6 = 30.

Вычтем из СУММ(C2:D5) значение СУММ(C2:D4) и найдём значение суммы С5 + D5: оно равно
32 — 30 = 2.
Правильный ответ указан под номером 2.
A7 В электронной таблице значение формулы =CУMM(D2:D5) равно 10. Чему равно значение
формулы =CP3HAЧ(D2:D4), если значение ячейки D5 равно −2?
1) 6
2) 2
3) 8
4) 4
Пояснение.
*Для лучшего понимания рекомендуется нарисовать таблицу.
Функция СУММ(D2:D5) считает сумму значений ячеек диапазона D2:D5, т. е. D2 + D3 + D4 + D5 =
10
Функция СРЗНАЧ(D2:D4) считает среднее арифметическое диапазона D2:D4, т. е. сумму значений
трёх ячеек D2, D3, D4, делённую на 3.
Вычтем значение ячейки D5 из первой суммы и найдём сумму: D2 + D3 + D4 = 10 — (-2) = 12.
Теперь разделим ответ на 3 и найдём искомое среднее значение: СРЗНАЧ(D2:D4) = 12 / 3 = 4.
Правильный ответ указан под номером 4.
A7 В ячейке F10 электронной таблицы записана формула. Эту формулу скопировали в ячейку
Е11. В соответствии с формулой, полученной в ячейке Е11, значение в этой ячейке равно сумме
значений в ячейках В16 и А17.
Напишите, сколько из следующих четырёх утверждений не противоречат этим данным.
A)Значение в ячейке F10 равно х+у, где х — значение в ячейке В16, а у — значение в ячейке А17.
Б)Значение в ячейке F10 равно х+у, где х — значение в ячейке С15, а у — значение в ячейке А17.
В)Значение в ячейке F10 вычисляется по формуле х+у, где х — значение в ячейке С16, а у —
значение в ячейке A16.
Г)Значение в ячейке F10 равно 2 · х, где х — значение в ячейке В16.
1) 1
2) 2
3) 3
4) 4
Пояснение.
По условию ясно, что в ячейке Е11 записана формула В16 + А17, в которой каждая ссылка мож ет
быть как относительной, так и абсолютной.
Рассмотрим все варианты:
А) Не противоречит, так как в таком случае F10 = $А$17 + $B$16, а Е11 = $А$17 + $B$16.
Б) Не противоречит, так как в таком случае F10 = $А$17 + С15, а Е11 = $А$17 + B16.
В) Не противоречит, так как в таком случае F10 = $А16 + С16, а Е11 = $А17 + B$16.
Г) Не противоречит, так как в таком случае F10 = B16 + $B$16, а Е11 = $А17 + $B$16.
Следовательно, ответ 4.
A7 В электронной таблице Excel отраж ены данные о деятельности страховой компании за 4
месяца. Страховая компания осуществляет страхование жизни, недвижимости,/автомобилей и
финансовых рисков своих клиентов. Суммы полученных по каждому виду деятельности за эти
месяцы страховых взносов (в тысячах рублей) такж е вычислены в таблице.
 Страхование жизни, тыс. р. Страхование автомобилей, тыс. р. Страхование фин. рисков, тыс. р. Страхование
недвижимости, тыс, р.
январь 10 4 20 11
 февраль 8 4 80 14
март 43 3 8 5
апрель 6 12 7 65
сумма 67 23 115 95
Известно, что за эти 4 месяца компании пришлось выдать трем клиентам страховые выплаты по
30 000 рублей каждому. Каков общий доход страховой компании в рублях за прошедшие 4
месяца?
1) 310 000
2) 200 000
3) 210 000
4) 300 000
Пояснение.
Найдём общую сумму: 67 + 23 + 115 + 95 = 300 (тыс. р).
Выплаты клиентам: 30 000 * 3 = 90 000 (р).
Общий доход: 300 000 — 90 000 = 210 000 рублей.
Правильный ответ указан под номером 3.

A7 В электронной таблице Excel отраж ены данные о деятельности страховой компании за 4
месяца. Страховая компания осуществляет страхование жизни, недвижимости, автомобилей и
финансовых рисков своих клиентов. Суммы полученных по каждому виду деятельности за эти
месяцы страховых взносов (в тысячах рублей) такж е вычислены в таблице.
 Страхование Страхование Страхование Страхование
жизни автомобилей фин. рисков недвижимости
тыс. р. тыс. р. тыс. р. тыс. р.
май 10 3 20 11
 июнь 2 4 8 10
 июль 4 6 8 5
 август 6 12 7 4
 Сумма 22 25 43 30
Известно, что за эти 4 месяца компании пришлось выплатить двум клиентам по 20 000 рублей
каждому.
Каков общий доход страховой компании в рублях за прошедшие 4 месяца?
1) 120 000
2) 100 000
3) 80 000
4) 60 000
Пояснение.
Найдём сумму значений из строки Сумма: 22 + 25 + 43 + 30 = 120(тыс. р.).
Двум клиентам компания выплатила 2 * 20000 = 40000. Соответственно общий доход составит:
120000 — 40000 = 80000 руб.
Правильный ответ указан под номером 3.
A7 В ячейке D5 электронной таблицы записана формула. Эту формулу скопировали в ячейку C4. В
результате значение в ячейке C4 вычисляется по формуле 3x+y, где x — значение в ячейке C22, а
y — значение в ячейке D22. Укажите, какая формула могла быть написана в ячейке D5.
1) =3*C22+D22
2) =3*$C22+$D22
3) =3*C$22+D$22
4) =3*D$22+$D23
Пояснение.
Вариант 1 не подходит, так как при переносе формулы =3*C22 + D22 из D5 в C4 она изменится на
=3*B21 + C21.
Вариант 2 не подходит, так как при переносе формулы =3*$C22 + $D22 из D5 в C4 она изменится
на =3*$C21 + $D21.
Вариант 3 не подходит, так как при переносе формулы =3*C$22 + D$22 из D5 в C4 она изменится
на =3*B$22 + C$22.
Вариант 4 подходит, так как при переносе формулы =3*D$22 + $D23 из D5 в C4 она изменится на
=3*C$22 + $D22.
Правильный ответ указан под номером 4.
A7 В электронной таблице значение формулы =CPЗHAЧ(A3:D4) равно 5. Чему равно значение
формулы =СРЗНАЧ(АЗ:С4), если значение формулы =CУMM(D3:D4) равно 4?
1) 1
2) 6
3) 3
4) 4
Пояснение.
*Для лучшего понимания рекомендуется нарисовать таблицу.
Функция СУММ(D3:D4) считает сумму значений ячеек D3 и D4: D3 + D4 = 4.
Функция СРЗНАЧ(A3:D4) считает среднее арифметическое диапазона A3:D4, т. е. сумму значений
восьми ячеек A3, B3, C3, D3, A4, B4, C4, D4, делённую на их количество. Умножим среднее
значение на 8 и найдём суммму значений этих ячеек: СУММ(A3:D4) = 5 * 8 = 40.
Вычтем из полученной суммы СУММ(A3:D4) значение суммы D3 + D4 и найдём значение суммы
СУММ(A3:C4): оно равно 40 — 4 = 36.
Теперь разделим полученный резльтат на количество ячеек данной суммы (их здесь 6) и найдём
искомую величину: СРЗНАЧ(АЗ:С4) = 36 / 6 = 6.
Правильный ответ указан под номером 2.
A7 В ячейке СЗ электронной таблицы записана формуле =$А$1+В1. Какой вид будет иметь
формула, если ячейку СЗ скопировать в ячейку ВЗ?
1) =$A$1+А1
2) =$В$1+ВЗ
3) =$А$1+ВЗ
4) =$B$1+C1
Пояснение.
Запись $А$1 означает, что столбец не меняется и номер строки не меняется.
При копировании в ячейку ВЗ из СЗ номер строки не изменился, а столбец уменьшился на 1,
значит, строка 1 в формуле останется строкой 1, а столбец B станет столбцом А.
Окончательный вид =$А$1+A1.
Правильный ответ указан под номером 1.

A7 В ячейке F7 электронной таблицы записана формула =D$12-$D13. Какой вид приобретет
формула, после того как ячейку F7 скопируют в ячейку E8?
Примечание: знак $ используется для обозначения абсолютной адресации.
1) =C$12-$C14
2) =D$12-$D13
3) =D$13-$D14
4) =C$12-$D14
Пояснение.
D$12: меняется столбец и не меняется номер строки.
$D13: столбец не меняется, меняется номер строки.
Номер столбца Е меньше номера столбца F на 1. Значит столбец D станет столбцом С.
Номер строки Е8 на 1 больше номера строки F7, значит, строка 13 станет строкой 14.
Окончательный вид =С$12-$D14.
Правильный ответ указан под номером 4.
A7 В электронной таблице Excel приведен фрагмент банковских расчетов по вкладам населения.
Таблица отражает фамилии вкладчиков, процентные ставки по вкладам за фиксированные
промеж утки времени и суммы вкладов с начисленными процентами за соответствующие истекшие
периоды времени. Такж е приведены общие суммы всех вкладов в банке после начисления
процентов.
 Вклад, р. 4 % 3 %
Агеев 2100000 2184000 2249520
Агнесян 200000 208000 214240
Сестров 50000 52000 53560
Кучкин 2300000 2392000 2463760
 Общая сумма 4650000 4836000 4981080
Определите общую сумму вкладов населения в банке в рублях после очередного начисления
процентов, если процентная ставка будет составлять 10%.
1) 5 000 000
2) 5 134 567
3) 5 345 678
4) 5 479 188
Пояснение.
Увеличение на 10% можно заменить операцией умнож ения на 1,1.
Тогда общая сумма составит: 4 981 080 * 1,1 = 5 479 188.
Правильный ответ указан под номером 4.
A7 В ячейке D5 электронной таблицы записана формула. Эту формулу скопировали в ячейку C4. В
результате значение в ячейке C4 вычисляется по формуле 3x+y, где x — значение в ячейке C22, а
y — значение в ячейке D22. Укажите, какая формула НЕ могла быть написана в ячейке D5.
Примечание: знак $ используется для обозначения абсолютной адресации.
1) =3*С22 + D22
2) =3*$C$22+$D$22
3) =3*D$22+$D23
4) =3*$C23+E$22
Пояснение.
По условию ясно, что в ячейке С4 записана формула 3С22 + D22.
Вариант 1 не мог быть записан в ячейку D5, так как при копировании формула изменилась бы,
поскольку отсутствуют знаки абсолютной адресации.
Следовательно, ответ 1.
A7 В ячейке B11 электронной таблицы записана формула. Эту формулу скопировали в ячейку
A10. В результате значение в ячейке A10 вычисляется по формуле x-3y, где x — значение в
ячейке C22, а y — значение в ячейке D22. Укажите, какая формула могла быть написана в ячейке
B11.
1) =C22-3*D22
2) =$C22-3*$D22
3) =C$22-3*D$22
4) =D$22-3*$D23
Пояснение.
Вариант 1 не подходит, так как при переносе формулы =C22-3*D22 из B11 в A10 она изменится
на =B21-3*C21.
Вариант 2 не подходит, так как при переносе формулы =$C22-3*$D22 из B11 в A10 она изменится
на =$C21-3*$D21.
Вариант 3 не подходит, так как при переносе формулы =C$22-3*D$22 из B11 в A10 она изменится
на =B$22-3*C$22.
Вариант 4 подходит, так как при переносе формулы =D$22-3*$D23 из B11 в A10 она изменится на
=3*C$22 + $D22.
Правильный ответ указан под номером 4.

A7 В ячейки диапазона C3:F6 электронной таблицы записаны числа, как показано на рисунке.
В ячейке А1 записали формулу =E$5-$D4. После этого ячейку А1 скопировали в ячейку В2. Какое
число будет показано в ячейке В2? Примечание: знак $ используется для обозначения
абсолютной адресации.
1) 6
2) 14
3) 16
4) 24
Пояснение.
Сначала запишем вид формулы после копирования в ячейку В2.
Запись $D4 означает, что столбец не меняется, а номер строки меняется. Запись E$5 означает,
что строка не меняется, а номер столбца меняется. Номер строки 1 увеличился на 1, значит, при
копировании в ячейку B2 из A1 строка 4 станет строкой 5, а строка 5 останется строкой 5. Номер
столбца A увеличился на 1, значит, при копировании в ячейку B2 из А1 столбец E станет столбцом
F.
Окончательный вид: F$5-$D5.
Вычислим значение в ячейке В2, оно равно 30 − 24 = 6.
Правильный ответ указан под номером 1.
A7 В электронной таблице Excel отраж ены данные по продаж е некоторого штучного товара в
торговых центрах города за четыре месяца. За каждый месяц в таблице вычислены суммарные
продажи и средняя по городу цена на товар, которая на 2 рубля больше цены поставщика
данного товара.
ТЦ Январь Февраль Март Апрель
 Продано, шт. Цена, р. Продано, шт. Цена, р. Продано, шт. Цена, р. Продано, шт. Цена, р.
Эдельвейс 5 14 1 17 5 15 4 15
Покупочка 6 13 2 16 6 11 4 14
Кошелек 2 17 5 14 4 15 1 18
Солнечный 8 12 7 13 7 11 7 13
 Продано
всего
21 15 22 16
 Средняя
цена
14 15 13 15
Известно, что весь поступивший от поставщика в текущем месяце товар реализуется в этом ж е
месяце.
В каком месяце выручка поставщика данного товара была максимальна?
1) Январь
2) Февраль
3) Март
4) Апрель
Пояснение.
Найдём выручку за продажи в торговых центрах на каждый месяц . В том месяце, где она
максимальна, поставщик такж е получил наибольшую прибыль.
Январь: 21 * 14 = 294,
Февраль: 15 * 15 = 225,
Март: 22 * 13 = 286,
Апрель: 16 * 15 = 240.
Наибольшая прибыль в январе.
Правильный ответ указан под номером 1.
A7 В ячейке G4 электронной таблицы записана формула =D$22∗$E11.
Примечание: знак $ используется для обозначения абсолютной адресации.
Какой вид приобретет формула, после того как ячейку G4 скопируют в ячейку F5?
1) =C$22∗$D11
2) =C$22∗$E12
3) =C$23∗$D12
4) =D$23∗$E12
Пояснение.
D$22: меняется столбец и не меняется номер строки.
$Е11: столбец не меняется, меняется номер строки.
Номер столбца F меньше номера столбца G на 1, значит, при копировании из G4 в F5 столбец D в
формуле станет столбцом C.
Номер строки 5 на 1 больше номера строки 4, значит, строка 11 в формуле станет строкой 12.
Окончательный вид =С$22*$E12.

Правильный ответ указан под номером 2.
A7 В электронной таблице значение формулы =СУММ(D2:D4) равно 15. Чему равно значение
формулы =CУMM(Dl:D4), если значение ячейки D1 равно 5?
1) 5
2) 10
3) 20
4) 4
Пояснение.
=CУMM(Dl:D4) = 5 + 15 = 20.
Правильный ответ указан под номером 3.
A7 В ячейке B1 записана формула =2*$A1. Какой вид приобретет формула, после того как ячейку
B1 скопируют в ячейку C2?
1) =2*$B1
2) =2*$A2
3) =3*$A2
4) =3*$B2Н
Пояснение.
Запись $A1 означает , что столбец не меняется, меняется номер строки.
Номер строки 2 на 1 больше номера строки 1, значит, при копировании в ячейку C2 строка 1
станет строкой 2.
Окончательный вид =2*$A2.
Правильный ответ указан под номером 2.
A7 В электронной таблице значение формулы =СРЗНАЧ(Е2:Е4) равно 3,
чему равно значение формулы =СУММ(Е2:Е5), если значение ячейки Е5 равно 5?
1) 11
2) 2
3) 8
4) 14
Пояснение.
*Для лучшего понимания рекомендуется нарисовать таблицу.
Функция СРЗНАЧ(Е2:Е4) считает среднее арифметическое диапазона Е2:Е4, т. е. сумму значений
трёх ячеек E2, E3, E4, делённую на 3. Умножим среднее значение на количество ячеек данного
диапазона и найдём: E2 + E3 + E4 = 3 * 3 = 9
Теперь прибавим к полученному резльтату значение ячейки E5 и найдём искомую сумму:
E2 + E3 + E4 + E5 = 9 + 5 = 14
Правильный ответ указан под номером 4.
A7 В ячейке А1 электронной таблицы записана формула =D1-$D2. Какой вид приобретет
формула после того, как ячейку А1 скопируют в ячейку В1?
1) =E1-$E2
2) =E1-$D2
3) =E2-$D2
4) =D1-$E2
Пояснение.
Запись $D2 означает, что столбец не меняется, а номер строки меняется.
Номер строки 1 не изменился, значит, при копировании в ячейку B1 из A1 строка 2 останется
строкой 2, а строка 1 останется строкой 1.
Номер столбца A увеличился на 1, значит, при копировании в ячейку B1 из А1 столбец D станет
столбцом E.
Окончательный вид =E1-$D2.
Правильный ответ указан под номером 2.
A7 В ячейке В2 записана формула =$D$2+Е2. Какой вид будет иметь формула, если ячейку В2
скопировать в ячейку А1?
1) =$D$2+E
2) =$D$2+C2
3) =$D$2+D2
4) =$D$2+D1
Пояснение.
Запись $D$2 означает, что столбец не меняется и номер строки не меняется.
При копировании в ячейку А1 из В2 номер строки 2 уменьшился на 1 и номер столбца B
уменьшился на 1 , значит, строка 2 в формуле станет строкой 1, а столбец E станет столбцом D.
Окончательный вид =$D$2+D1.
Правильный ответ указан под номером 4.
A7 В электронной таблице значение формулы =СРЗНАЧ(А4:С4) равно 5. Чему равно значение
формулы СУММ(А4:D4), если значение ячейки D4 равно 6?
1) 1
2) 11
3) 16

4) 21
Пояснение.
*Для лучшего понимания рекомендуется нарисовать таблицу.
Функция СРЗНАЧ(A4:C4) считает среднее арифметическое диапазона A4:C4, т. е. сумму значений
трёх ячеек A4, B4, C4, делённую на 3. Умножим среднее значение на количество ячеек данного
диапазона и найдём: A4 + B4 + C4 = 5 * 3 = 15
Теперь прибавим к полученному резльтату значение ячейки D4 и найдём искому сумму:
A4 + B4 + C4 + D4 = 15 + 6 = 21
Правильный ответ указан под номером 4.
A7 В электронной таблице значение формулы =CP3HA4(A2:D2) равно 5. Чему равно значение
формулы =СУММ(В2:D2), если значение ячейки А2 равно 4?
1) 20
2) 16
3) 5
4) 4
Пояснение.
Функция СРЗНАЧ(A2:D2) считает среднее арифметическое диапазона A2:D2, т. е. сумму значений
четырёх ячеек A2, B2, C2, D2, делённую на 4. Умножим среднее значние на число ячеек и
получим сумму значений ячеек A2 + B2 + C2 + D2 = 5 * 4 = 20.
Теперь, вычтем значение ячейки A2 и найдём искомую сумму: B2 + C2 + D2 = 20 — 4 = 16.
Правильный ответ указан под номером 2.
A7 В электронной таблице значение формулы =CУMM(C2:D2) равно 16. Чему равно значение
ячейки В2, если значение формулы =СРЗНАЧ(В2:D2) равно 7?
1) 5
2) 8
3) 21
4) 23
Пояснение.
Функция СРЗНАЧ(B2:D2) считает среднее арифметическое диапазона B2:D2, т. е. сумму значений
трёх ячеек B2, C2, D2, делённую на 3. Умножим среднее значние на число ячеек и получим сумму
значений ячеек B2 + C2 + D2 = 7 * 3 = 21.
Теперь, вычтем из полученной суммы значение =CУMM(С2:D2) и найдём В2: В2 = 21 — 16 = 5.
Правильный ответ указан под номером 1.
A7 В электронной таблице значение формулы =CУMM(D2:D4) равно 16. Чему равно значение
ячейки D1, если значение формулы =CP3HAЧ(D1:D4) равно 5?
1) 5
2) 11
3) 21
4) 4
Пояснение.
Функция СРЗНАЧ(D1:D4) считает среднее арифметическое диапазона D1:D4, т. е. сумму значений
четырёх ячеек D1, D2, D3, D4, делённую на 4. Сначала найдём сумму значений ячеек D1 + D2 +
D3 + D4 = 5 * 4 = 20.
Теперь, вычтем из полученной суммы значение =CУMM(D2:D4) и найдём D1: D1 = 20 — 16 = 4.
Правильный ответ указан под номером 4.
A7 В ячейки диапазона C3:F6 электронной таблицы записаны числа, как показано на рисунке.
В ячейке В2 записали формулу =E$5-$D4. После этого ячейку В2 скопировали в ячейку А1. Какое
число будет показано в ячейке А1?
Примечание: знак $ используется для обозначения абсолютной адресации.
1) 22
2) 14
3) 12
4) 4
Пояснение.
Сначала запишем вид формулы после копирования в ячейку А1.
Запись $D4 означает, что номер столбца при копировании не меняется, а номер строки меняется.
Запись E$5 означает, что номер строки не меняется, а номер столбца меняется. Номер строки 1
уменьшился на 1, значит, при копировании в ячейку А1 из В2 строка 4 станет строкой 3, а строка
5 останется строкой 5. Номер столбца В уменьшился на 1, значит, при копировании в ячейку А1 из
В2 столбец E станет столбцом D.
Окончательный вид: D$5-$D3.
Вычислим значение в ячейке В2: оно равно 24 − 2 = 22.

Правильный ответ указан под номером 1.
A7 В 2000 году в РФ создано 7 федеральных округов. Используя представленную таблицу
укажите номер региона с наименьшей плотностью населения.
1) 4
2) 5
3) 6
4) 7
Пояснение.
Проверим все варианты. Для этого найдём плотность населения в округах 4—7, поделив
население на площадь.
Увидим, что седьмой округ имеет наименьшую плотность населения.
Правильный ответ указан под номером 4.
A7 В электронной таблице значение формулы =CУMM(D2:D4) равно 15. Чему равно значение
формулы = СРЗНАЧ (D1:D4), если значение ячейки D1 равно 5?
1) 5
2) 10
3) 20
4) 4
Пояснение.
Функция СРЗНАЧ(D1:D4) считает среднее арифметическое диапазона D1:D4, т. е. сумму значений
четырёх ячеек D1, D2, D3, D4, делённую на 4. Сначала найдём сумму значений ячеек D1 + D2 +
D3 + D4 = 15 + 5 = 20.
Теперь, разделим её на 4 (число элементов) и получим СРЗНАЧ (D1:D4): 20 / 4 = 5.
Правильный ответ указан под номером 1.
A7 В ячейке D3 электронной таблицы записана формула =B$2-$B3. Какой вид приобретет
формула, после того как ячейку D3 скопируют в ячейку С4?
Примечание: знак $ используется для обозначения абсолютной адресации.
1) =C$2-$B4
2) =A$2-$B4
3) =B$1-$C4
4) =B$1-$B4
Пояснение.
B$2: меняется столбец и не меняется номер строки.
$B3: столбец не меняется, меняется номер строки.
Номер столбца C меньше номера столбца D на 1. Значит столбец B станет столбцом A.
Номер строки 4 на 1 больше номера строки 3, значит, строка 3 станет строкой 4.
Окончательный вид =A$2-$B4.
Правильный ответ указан под номером 2.

A7 В ячейки диапазона C3:F6 электронной таблицы записаны числа, как показано на рисунке.
В ячейке А1 записали формулу =$D4+E$5. После этого ячейку А1 скопировали в ячейку В2. Какое
число будет показано в ячейке В2? Примечание: знак $ используется для обозначения
абсолютной адресации.
1) 40
2) 54
3) 56
4) 70
Пояснение.
Сначала запишем вид формулы после копирования в ячейку В2.
Запись $D4 означает, что столбец не меняется, а номер строки меняется. Запись E$5 означает,
что строка не меняется, а номер столбца меняется. Номер строки 1 увеличился на 1, значит, при
копировании в ячейку B2 из A1 строка 4 станет строкой 5, а строка 5 останется строкой 5. Номер
столбца A увеличился на 1, значит, при копировании в ячейку B2 из А1 столбец E станет столбцом
F.
Окончательный вид: $D5+F$5.
Вычислим значение в ячейке В2, оно равно 24 + 32 = 56.
Правильный ответ указан под номером 3.
A7 В электронной таблице Excel приведен фрагмент банковских расчетов по вкладам населения.
Таблица отражает фамилии вкладчиков, процентные ставки по вкладам за два фиксированных
одногодичных промеж утка времени и суммы вкладов с начисленными процентами за
соответствующие истекшие периоды времени. Такж е приведены общие суммы всех вкладов в
банке после начисления процентов и доход вкладчиков за истекший двухгодичный период.
 Вклад, р. 4 % 5 % Сумма начислений за два периода
Осин 2100000 2184000 2293200 193200
Пнев 200000 208000 248400 18400
Чуйкин 50000 52000 54600 4600
Шаталов 2400000 2496000 2620800 220800
 Общая сумма 4750000 4940000 5187000 437000
Определите, кто из вкладчиков за истекшее с момента открытия вклада время получил средний
еж емесячный доход от вклада более 9 000 рублей.
1) Осин
2) Пнев
3) Чуйкин
4) Шаталов
Пояснение.
Для определения среднемесячного дохода необходимо разделить доход каждого на количество
месяцев вклада, т. е. на 24 месяца.
Осин: 193200 / 24 = 8 050,
Пнев: 18400 / 24 = 766,7,
Чуйкин: сам доход меньше 9 000, поэтому он не подходит,
Шаталов: 220800 / 24 = 9 200.
Более 9 000 рублей имеет Шаталов.
Правильный ответ указан под номером 4.
A7 В ячейке C2 записана формула =$E$3+D2. Какой вид приобретет формула, после того как
ячейку C2 скопируют в ячейку B1?
1) =$E$3+C1
2) =$D$3+D2
3) =$E$3+E
4) =$F$4+D2
Пояснение.
Запись $E$3 означает, что столбец не меняется и номер строки не меняется.
Номер строки 2 уменьшился на 1, значит, при копировании в ячейку B1 из C2 строка 2 станет
строкой 1.
Номер столбца С уменьшился на 1, значит, при копировании в ячейку B1 из C2 столбец D станет
столбцом С.
Окончательный вид =$E$3+С1.
Правильный ответ указан под номером 1.
A7 В электронной таблице значение формулы =CP3HAЧ(A3:D3) равно 5. Чему равно значение
формулы =СУММ(АЗ:СЗ), если значение ячейки D3 равно 6?

1) 1
2) -1
3) 14
4) 4
Пояснение.
Функция СРЗНАЧ(A3:D3) считает среднее арифметическое диапазона A3:D3, т. е. сумму значений
четырёх ячеек A3, B3, C3, D3, делённую на 4. Умножим среднее значние на число ячеек и
получим сумму значений ячеек A3 + B3 + C3 + D3 = 5 * 4 = 20.
Теперь, вычтем значение ячейки D3 и найдём искомую сумму: A3 + B3 + C3 = 20 — 6 = 14.
Правильный ответ указан под номером 3.
A7 В электронной таблице значение формулы =СУММ(А5:D5) равно 6. Чему равно значение
формулы =СРЗНАЧ(А5:С5), если значение ячейки D5 равно 9?
1) 1
2) -3
3) 3
4) -1
Пояснение.
*Для лучшего понимания рекомендуется нарисовать таблицу.
Функция СУММ(А5:D5) считает сумму значений ячеек диапазона A5:D5, т. е. A5 + B5 + C5 + D5 = 6
Функция СРЗНАЧ(А5:С5) считает среднее арифметическое диапазона А5:С5, т. е. сумму значений
трёх ячеек A5, B5, C5, делённую на 3.
Вычтем значение ячейки D5 из первой суммы и найдём сумму: A5 + B5 + C5 = 6 — 9 = -3.
Теперь разделим ответ на 3 и найдём искомое среднее значение: СРЗНАЧ(А5:С5) = -3 / 3 = -1.
Правильный ответ указан под номером 4.
A7 В ячейке F7 электронной таблицы записана формула =D$12+$D13. Какой вид приобретет
формула, после того как ячейку F7 скопируют в ячейку G8?
Примечание: знак $ используется для обозначения абсолютной адресации.
1) =C$12+$D11
2) =D$11+$C13
3) =D$13+$E13
4) =E$12+$D14
Пояснение.
D$12: меняется столбец и не меняется номер строки.
$D13: столбец не меняется, меняется номер строки.
Номер столбца G больше номера столбца F на 1. Значит столбец D станет столбцом Е.
Номер строки 8 на 1 больше номера строки 7, значит, строка 13 станет строкой 14.
Окончательный вид =Е$12+$D14.
Правильный ответ указан под номером 4.

• 1
• 2
• 3
• 4
• 5

Категория: по информатике | Добавил: Просмотров: 1 | Теги: ЕГЭ | Рейтинг: 0.0/0

top of page

bottom of page

Задача. Человек положил деньги в банк под n процентов годовых. Проценты начисляются ежеквартально и зачисляются на счет. С помощью электронной таблицы рассчитать, какое количество денег получит человек чрез два года.

Решение. Спланируем расчетную форму. Сумму денег, которая помещается первоначально на счет, и начисляемые проценты занесем в отдельные ячейки. При необходимости они могут быть изменены, и результат будет пересчитан.

На рисунке представлены результаты расчетов для некоторого набора данных.

Ниже – тот же фрагмент таблицы в режиме отображения формул.

Литература:

Газета «Первое сентября», «Информатика», №10, 2007.

1


Обработка информации посредством табличных процессоров Тяпкина Е.В. МОУ «СОШ 77» ГИА ЕГЭ 5А7 19В3

2


Распределение правильных ответов по заданиям ГИА Части 1

3


Распределение правильных ответов по заданиям ЕГЭ части В

4


Распределение правильных ответов по заданиям ЕГЭ части А Процент решений

5


Электронные таблицы Что нужно знать: адрес ячейки в электронных таблицах состоит из имени столбца и следующего за ним номера строки, например, C15 Типы данных: числа, текст, формулы формулы в электронных таблицах начинаются со знака «=» («равно») Знаки операций: +, –, *, / и ^ Приоритет: (), ^, */, +-

6


Диапазон ячеек запись (B2:C4) означает диапазон, то есть, все ячейки внутри прямоугольника, ограниченного ячейками B2 и C4: Минимальный диапазон – одна ячейка (В2;С4) – перечисление двух ячеек

7


Встроенные функции =СУММ(B2:C4) — сумма значений ячеек B2, B3, B4, C2, C3 и C4 =СЧЕТ (количество непустых ячеек), =СРЗНАЧ (среднее значение), =МИН (минимальное значение), =МАКС (максимальное значение) =СЧЕТЕСЛИ(количество ячеек, удовлетворяющих критерию)

8


=СРЗНАЧ(A1:B2) — при вычислении среднего арифметического не учитывает пустые ячейки и ячейки, заполненные текстом; например, после ввода формулы в C2 появится значение 2 (ячейка А2 – пустая) =СЧЕТ(A1:B2) в этом случае выдаст значение 3 (а не 4)

9


Д.П.Кириенко, П.О.Осипов ABCD ГИА: повышенный уровень, примерное время выполнения – 6 мин

10


С.С.Крылов, Т.Е.Чуркина ABCD ИНФ-9 Демо-2014

11


Л.Н.Евич, С.Ю.Кулабухов ИНФ ЕГЭ Демо-2014

12


Л.Н.Евич, С.Ю.Кулабухов

13

14


9 кл =57 10 кл =60 11 кл =59 Ответ: 1)

15


inf.reshuege.ru Мама заработала меньше дочки, дочка заработала меньше, чем папа

16


=100 Шелк – 50% = 50 Соломка – 25% = 25 Брезент + Хлопок = 25

17

18


A7 (базовый уровень, время – 3 мин)

19


Адресация ячеек адреса ячеек (или ссылки на ячейки) бывают относительные, А3 абсолютные, $A$3 смена клавишейF4 смешанные A$3 $A3 Выражается наличием или отсутствием знака $ и проявляется при копировании формулы в другую ячейку

20


– в абсолютных адресах $B$2+$C$3 имена ячеек не изменяются при копировании Знак $ как бы «фиксирует» значение: в абсолютных адресах и имя столбца, и номер строки зафиксированы

21


в относительных адресах знаков доллара нет, такие адреса при копировании изменяются: номер столбца (строки) изменяется на столько, на сколько отличается номер столбца (строки), где оказалась скопированная формула, от номера столбца (строки) исходной ячейки

22


в смешанных адресах часть адреса (строка или столбец) – абсолютная, она «зафиксирована» знаком $, а вторая часть – относительная; относительная часть изменится при копировании так же, как и для относительной ссылки:

23


A7 (базовый уровень, время – 3 мин) D2=Если($A$1>1;C2-B2;0) Ответ: 2

24


В ячейке B4 электронной таблицы записана формула = $C3*2. Какой вид приобретет формула, после того как ячейку B4 скопируют в ячейку B6? Примечание: знак $ используется для обозначения абсолютной адресации. 1)=$C5*4 2)=$C5*2 3)$C3*4 4)=$C3*2 Решение: ссылка $C3 – это смешанная ссылка, в которой «заблокирован» столбец C, а строка 3 – это относительный адрес; после того, как ячейку B4 скопировали в B6, номер строки увеличился на 2, поэтому и в ссылке $C3 номер строки (относительная часть) также увеличится на 2, ссылка превратится в $C5 константы при копировании формул не меняются, поэтому получится =$C5*2 таким образом, правильный ответ – 2.

25


reshuege.ru A В электронной таблице значение формулы =СРЗНАЧ(С2:С5) равно 3. Чему равно значение формулы =СУММ(С2:С4), если значение ячейки С5 равно 5? 1) 1 2) 7 3) -4 4) 4 Понимание сущности функции СРЗНАЧ C2:С4 содержит 4 ячейки 3*4= =7 Ответ 2)

26


Нужно с помощью электронных таблиц построить таблицу значений формулы 2х+3у для значений х и у от 4 до 7. Для этого сначала в диапазонах В1:Е1 и А2:А5 записали числа от 4 до 7. Затем в ячейку В5 записали формулу (А5 — значение х, В1 – значение y), после чего эта формула была скопирована во все ячейки диапазона В2:Е5. В итоге на экране получился фрагмент таблицы. Какая формула была записана в ячейку В5? 1) =$А5*2+В$1*32) =А5*2+В1*33) =$А5*2+$В1*3 4) =А$5*2+$В1*3 АВСDЕ ДЕМО ЕГЭ-2014 (аналог)

27


Нужно с помощью электронных таблиц построить таблицу значений формулы 2х+3у для значений х и у от 4 до 7 Какая формула была записана в ячейку В5? 1)=$А5*2+В$1*3 2)=А5*2+В1*3 3)=$А5*2+$В1*3 4)=А$5*2+$В1*3 Решение (частный случай, А.Н. Носкин с сайта К.Ю.Полякова): проанализируем предлагаемые формулы 1) =$А5*2+В$1*32) =А5*2+В1*33) =$А5*2+$В1*34) =А$5*2+$В1*3 формулы 2, 3 и 4 содержат ссылки на B1, в которых номер строки 1 не закреплён абсолютной ссылкой, то есть будет изменяться при копировании поэтому при копировании формул 2, 3 и 4 из В5 вверх (в строку с меньшим номером) номер строки должен получиться меньше 1, что приведет к ошибочной ссылке следовательно, варианты 2, 3 и 4 не подходят Ответ: 1. АВСDЕ

28


В ячейке E15 электронной таблицы записана формула. Эту формулу скопировали в ячейки D17 и C18. В соответствии с формулой, полученной в ячейке D17, значение в этой ячейке равно разности значений в ячейках D32 и C32; в соответствии с формулой, полученной в ячейке C18, значение в этой ячейке равно разности значений в ячейках D33 и B32. Укажите, какая формула могла быть написана в ячейке E15. 1) =E$32-D$30 2) =$D$32-$B$32 3) =$D$30-$C$32 4) =$D30-D$32

29


В ячейке E15 электронной таблицы записана формула. Эту формулу скопировали в ячейки D17 и C18. В соответствии с формулой, полученной в ячейке D17, значение в этой ячейке равно разности значений в ячейках D32 и C32; в соответствии с формулой, полученной в ячейке C18, значение в этой ячейке равно разности значений в ячейках D33 и B32. Укажите, какая формула могла быть написана в ячейке E15. 1)=E$32-D$30 2)=$D$32-$B$32 3)=$D$30-$C$32 4)=$D30-D$32 Решение: одну и ту же формулу скопировали в две ячейки и получили: в E15 ? ? в D17 D32 – C32 ? в C18 D33 – B32 Ответ: 4. BCDE

30


ДЕМО ЕГЭ-2013 Решение $A$2 – абсолютная ссылка и не изменяется B$3 – фиксируется только номер строки, при копировании на один столбец вправо, изменится на С$3 C3=6+7=13 D1=$A$2+C$3=5+13=18 Ответ 1)

31


Три страны: Королевство Бельгия, Королевство Нидерланды и Великое Герцогство Люксембург образуют экономико-политический союз, который носит название Бенилюкс. Ниже приведен фрагмент электронной таблицы, характеризующий каждую из стран союза и союз в целом: Какое значение должно стоять в ячейке D5? 1) 365 2) 9293) 3104) 2,74 АBCD 1 Страна Население (тыс. чел) Площадь (кв. км) Плотность населения (чел / кв.км) 2 Бельгия Нидерланды Люксембург Бенилюкс в целом

32


Три страны: Королевство Бельгия, Королевство Нидерланды и Великое Герцогство Люксембург образуют экономико-политический союз, который носит название Бенилюкс. Ниже приведен фрагмент электронной таблицы, характеризующий каждую из стран союза и союз в целом: Какое значение должно стоять в ячейке D5? 1)365 2)929 3)310 4)2,74 Решение: нужно не забыть, что плотность населения вычисляется как отношение населения к площади (не наоборот!); население не забываем перевести из тысяч человек в единицы: чел поэтому для всего Бенилюкса получаем / таким образом, правильный ответ – 1. АBCD 1 Страна Население (тыс. чел) Площадь (кв. км) Плотность населения (чел / кв.км) 2 Бельгия Нидерланды Люксембург Бенилюкс в целом

33


Дан фрагмент электронной таблицы: Как изменится значение ячейки С3, если после ввода формул переместить содержимое ячейки В2 в В3? («+1» означает увеличение на 1, а «–1» – уменьшение на 1) 1) –22) –1 3) 04) +1 АВС =СЧЁТ(A1:B2) 3=СРЗНАЧ(A1:C2)

34


Дан фрагмент электронной таблицы: Как изменится значение ячейки С3, если после ввода формул переместить содержимое ячейки В2 в В3? 1) –2 2) –1 3) 0 4) +1 («+1» означает увеличение на 1, а «–1» – уменьшение на 1) Решение: это задача на знание особенностей функций СЧЕТ и СРЗНАЧ, которые не учитывают пустые ячейки после ввода формул в С2 окажется количество непустых ячеек диапазона А1:В2, равное 4 в С3 будет выведено среднее значение диапазона А1:С2 равное ( )/5 = 3 после перемещения (не копирования!) содержимого ячейки В2 в В3 ячейка В2 окажется пустой, поэтому в С2 выводится число 3 – количество непустых ячеек диапазона А1:В2 в С3 будет выведено среднее значение диапазона А1:С2 равное ( )/4 = 2, то есть значение С3 уменьшится на 1 таким образом, правильный ответ – 2. Возможные ловушки и проблемы: нужно помнить, что при перемещении содержимого ячейки в другое место она становится пустой нужно помнить, что функции СЧЕТ и СРЗНАЧ не учитывают пустые ячейки АВС =СЧЁТ(A1:B2) 3=СРЗНАЧ(A1:C2)

35


A В электронной таблице Excel приведен фрагмент банковских расчетов по вкладам населения. Таблица отражает фамилии вкладчиков, процентные ставки по вкладам за фиксированные промежутки времени и суммы вкладов с начисленными процентами за соответствующие истекшие периоды времени. Также приведены общие суммы всех вкладов в банке после начисления процентов. Определите общую сумму вкладов населения в банке в рублях после очередного начисления процентов, если процентная ставка будет составлять 10%. 1) ) ) ) Вклад, р. 4 %3 % Агеев Агнесян Сестров Кучкин Общая сумма

36


A В электронной таблице Excel приведен фрагмент банковских расчетов по вкладам населения. Таблица отражает фамилии вкладчиков, процентные ставки по вкладам за фиксированные промежутки времени и суммы вкладов с начисленными процентами за соответствующие истекшие периоды времени. Также приведены общие суммы всех вкладов в банке после начисления процентов. Определите общую сумму вкладов населения в банке в рублях после очередного начисления процентов, если процентная ставка будет составлять 10%. 1) ) ) ) Решение Общая сумма вкладов после начисления процентов составила Увеличение на 10% можно заменить операцией умножения на 1,1. Тогда общая сумма составит: · 1,1 = Правильный ответ указан под номером 4. Вклад, р. 4 %3 % Агеев Агнесян Сестров Кучкин Общая сумма

37


В ячейке X15 электронной таблицы записана формула. Эту формулу скопировали в ячейку Z13. В соответствии с формулой, полученной в ячейке Z13, значение в этой ячейке равно произведению значений в ячейках D20 и E25. Напишите, сколько из следующих четырёх утверждений не противоречат этим данным. 1. Значение в ячейке X15 равно х*у, где х — значение в ячейке D20, а у — значение в ячейке C Значение в ячейке X15 равно х*у, где х — значение в ячейке B20, а у — значение в ячейке E Значение в ячейке X15 вычисляется по формуле х*у, где х — значение в ячейке D22, а у — значение в ячейке C Значение в ячейке X15 равно х 2, где х — значение в ячейке E27. 1) 12) 23) 34) 4

38


по условию мы знаем, что в ячейке Z13 записана формула =D20*E25, в которой каждая ссылка может быть абсолютной, относительной и смешанной, то есть возможны, например, такие варианты =$D$20*$E$25, =D$20*$E25 и т.д. для того, чтобы определить, какая формула была в X15, нужно скопировать формулу из Z13 в X15, поменяв соответствующим образом ссылки, тип которых мы не знаем начнём с варианта с относительными ссылками: при копировании формулы из Z13 в X15 номер столбца уменьшается на 2 (Z X), а номер строки – увеличивается на 2 (13 15), поэтому формула с относительными ссылками изменится так: Z13: =D20*E25 X15: =B22*C27 кроме того, каждая часть ссылки может быть защищена от изменений знаком $; например, для первой ссылки получаем такие варианты преобразования D20 B22, $D20 $D22, D$20 B$20, $D$20 $D$20, то есть первая ссылка может превратиться в B20, B22, D20 и D22 аналогично вторая ссылка (E25) при копировании может превратиться в C25, C27, E25 и E27 при проверке утверждений 1, 2 и 3 выясняется, что все адреса ячеек допустимые, то есть входят в перечисленные в пп. 4 и 5, поэтому эти утверждения не противоречат исходным данным. в утверждении 4 обе ссылки должны стать равны E27, это возможно для второй ссылки, но не для первой (см. п. 4), поэтому это утверждение не может быть верным. Ответ: 3.

39


Источники Информатика. 9 класс. Тематические тесты для подготовки к ГИА-9: базовый, повышенный, высокий уровни./ Под ред. Ф.Ф.Лысенко, Л.Н.Евич. – Изд. 2-е, доп. – Ростов-на-Дону: Легион Решу ЕГЭ. Образовательный портал для подготовки к экзаменам Результаты ЕГЭ по информатике (Лапшева Е.Е.), результаты ГИА-2013 по информатике (Синаторов С.В.)

40


Спасибо за внимание! Вопросы?