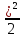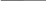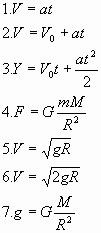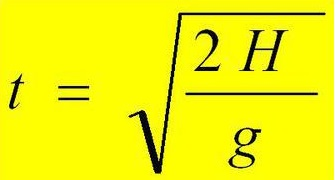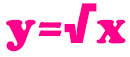Ускорение свободного падения excel

Решение задач физике средствами MS Excel

MS Excel является удобным средством решения разнооб­разных расчетных задач.

Рассмотрим решение задачи по физике средствами Excel, требующих выполне­ния значительного числа шагов, что делает эти задачи излишне трудоемкими для решения вручную.

Задача о горизонтально брошенном теле.

Тело брошено горизонтально над поверхностью земли с некоторой начальной скоростью. Ускорение свободного падения равно 9,8 м/с2. Сопротивлением воздуха можно пренебречь. Рассчитать траекторию движения тела.

Решение.

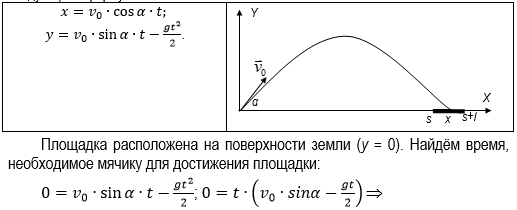
На тело действуют две силы: в горизонтальном направлении действует сила инер­ции, под действием которой тело движется равномерно, а в вертикальном – сила тяжести, под действием которой тело падает с ускорением. Горизонтальный путь под­считываем как скорость, умноженною на время, а вертикальную составляющую — по известной формуле

,умноженной на -1, чтобы указать направление оси на графике.

Решим задачу с помощью электронной таблицы. Выполним расчеты по шагам, разделив время падения на 15 интервалов по 0,1 с. При вычислении величины свободного падения все значений, как сказано выше, умножим на — 1, чтобы на диаграмме, свободное падение было направлено вниз.

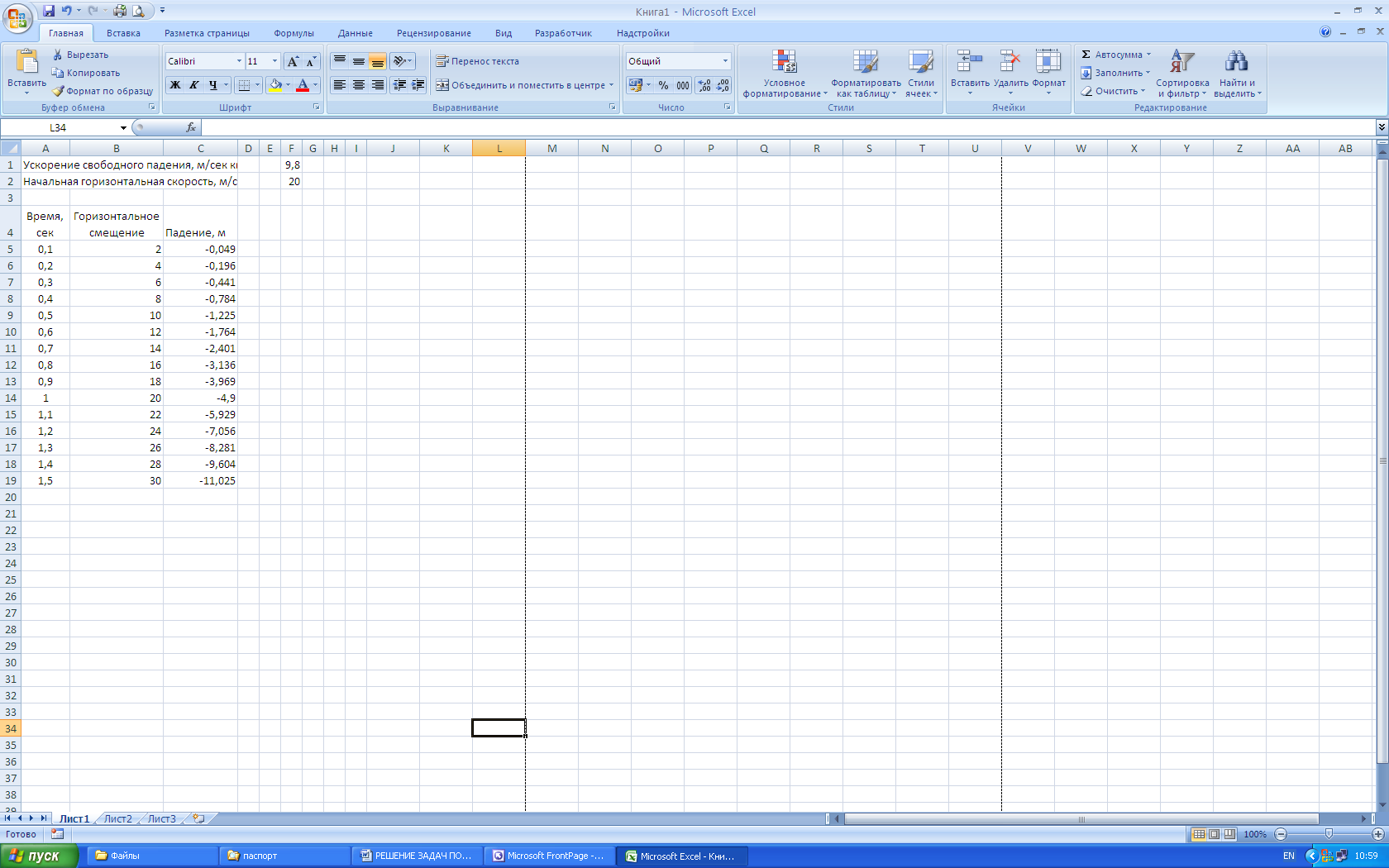
Формулы, по которым выполняются вычисления, представлены в таблице

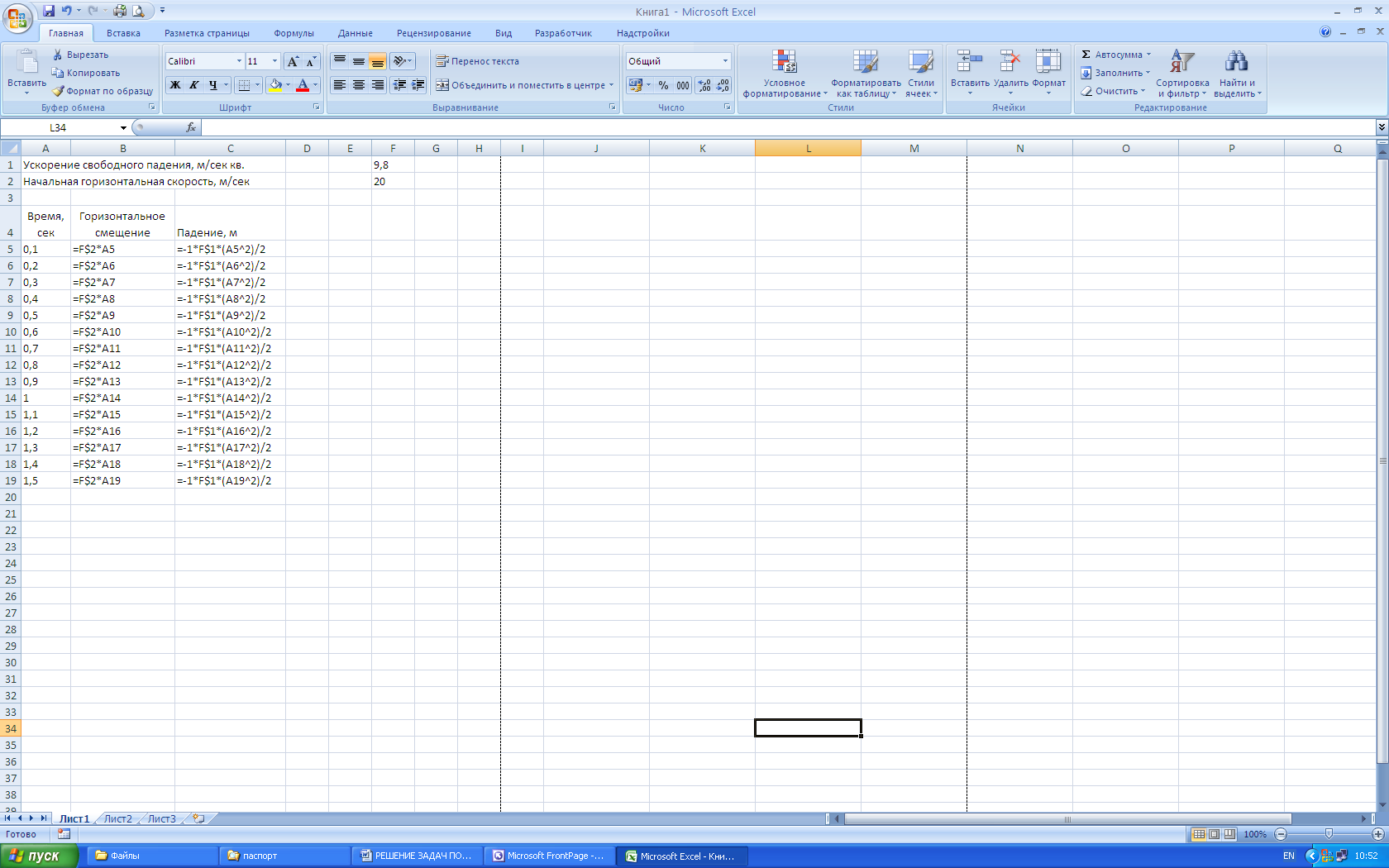
Рис. 1. Формулы для расчёта траекторий движения тела, брошенного горизонтально

Рис.2. Таблица с результатами вычислений.

Рис.3. Траектория движения тела

Литература:

  1. Понятный самоучитель работы в Excel. СПб,: Питер, 2002

  2. Информатика и образование. №4, 2003.

Источник

Как
и в случае математического маятника
любые из измеренных значений представленных
в таблицах
1-4
не являются точными величинами, так как
они измерены с погрешностями.

В
таких случаях в качестве точных значений
указанных величин, как и в случае
математического маятника, принимаются
их средние арифметические, вычисляемые
по формуле (11):


 (11)

где
n
число измерений.

Тогда
под погрешностью измерения будем
подразумевать модуль величины
максимального отклонения всех измеренных
величин от их среднего арифметического.
А именно, погрешность измерения времени
падения Δ2
будем определять как

Δ2
= max
|Ti
— Tср
|, (12)

В
формуле (12)
индекс i
= 1,2,3,4,5 пробегает все номера измерений
соответствующих величин.

Обработку
результатов измерений будем производить
на компьютере в программе Microsoft
Excel
и продемонстрируем технологию необходимых
при этом расчётов на конкретных
результатах измерений.

Задание
№1

Расчёт
ускорения свободного падения по
измерениям периода свободных колебаний
физического маятника.

Для
вычисления ускорения свободного падения
необходимо заполнить таблицы 1, 2, 3.

Таблица 1

φ=100

серия
1

серия
4

серия
6

серия
8

а,
м

0,1

0,2

0,3

0,4

Lср,
м

Т1

Т2

Т3

Т4

Т5

Тср

Δ2

Δ2

Δ2

Δ2

Δ2

max
Δ2

Δ1

Lср+Δ1

Lср-Δ1

Тср2

Начнём
вычисления с занесения в таблицу
приведенной длины физического маятника.
Вычислим приведенную длину Lср
физического маятника по формуле

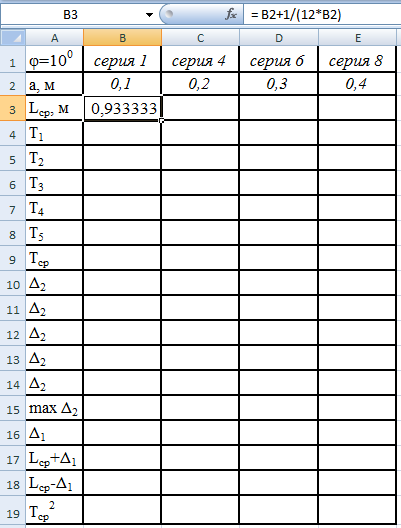
или используем следующую формулу для
вычисления в Excel
= B2+1/(12*B2)
в ячейке В3. Для этого активируем ячейку
В3 и введём в неё формулу.

Далее
распространим формулу на ячейки С3 –
Е3 для этого активируем ячейку, а затем
подведём отметку мыши к правому нижнему
углу ячейки, при этом отметка от мыши
превратиться в крест в этот момент надо
нажать левую кнопку и не отпуская
протянуть по ячейкам С3 – Е3 и отпустить.
Получим
таблицу изображённую на рис.5.

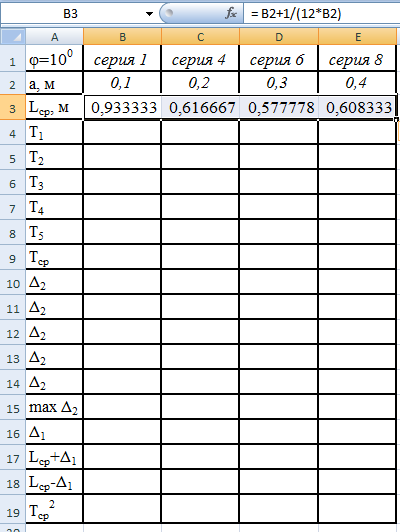
Рис.5.

Далее
в ячейки А4 – Е8 внесём результаты
измерений периода колебаний для различной
длины маятника и получим таблицу на
рис.6.

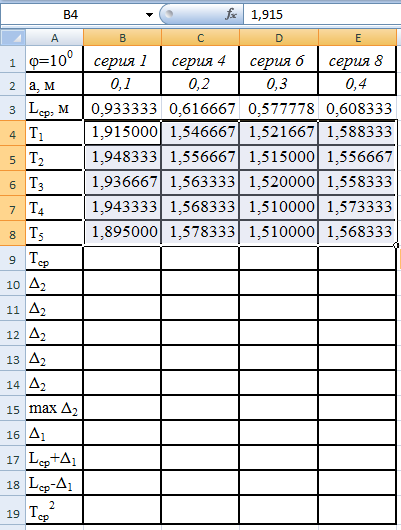
Рис.6.

В
ячейках В9 – Е9 проведём вычисление
средних периодов колебаний используя
стандартную статистическую функцию
СРЗНАЧ по периодам Т1
— Т5
для каждой длины а.
Для вставки функции активизируем ячейку
В9 и введём в неё функцию через мастер
функций рис.7 и выберем функцию СРЗНАЧ
рис.8 и нажмём OK,
откроется вкладка рис.9, на ней указываем
по каким ячейкам проводиться усреднение
см.рис.10 для этого активируем ячейки В4
– В8 и нажмём OK,
получим результат, изображённый на
рис.11. Распространим формулу на ячейки
С9 – Е9, как делали ранее см.рис.12.

Рис.7.

Рис.8.

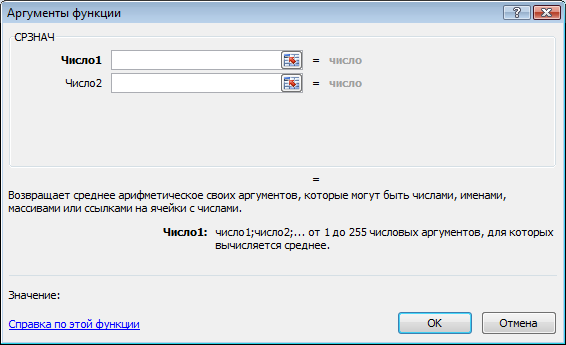
Рис.9.

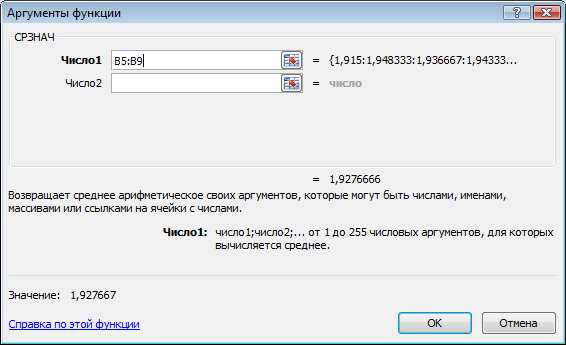
Рис.10.

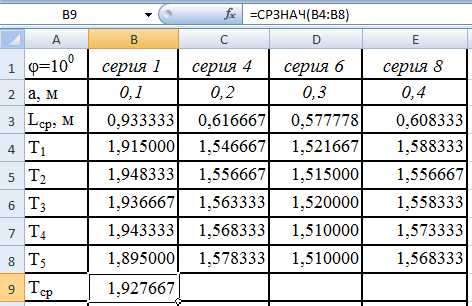
Рис.11.

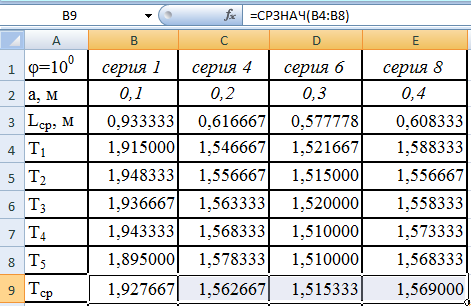
Рис.12.

Вычислим
Δ2
по формуле Δ2
= max
|Ti
— Tср
| или в обозначениях Excel
формула имеет вид =ABS($B$9-B4)
и внесём в ячейку B10
см. рис.13 и выберем на вкладке значения
по которым вычисляется Δ2,
что изображено на рис.14, а затем
распространим все формулы на ячейки
В10 – Е14 так же, как и ранее см.рис.15.

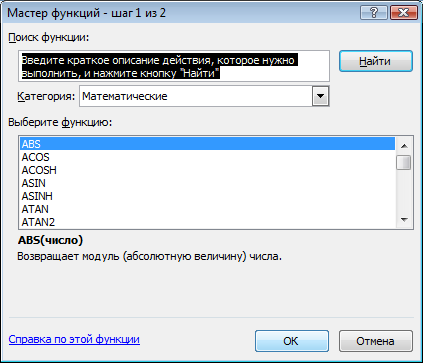
Рис.13.

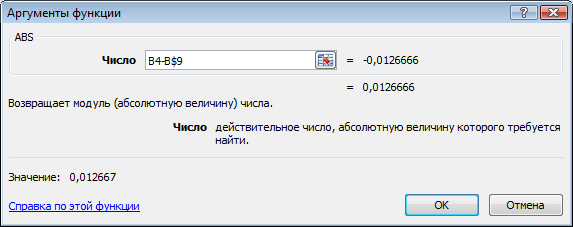
Рис.14.

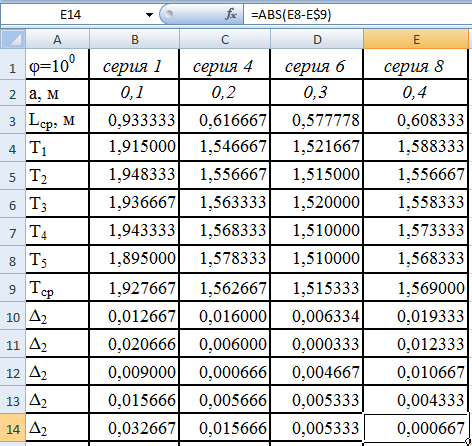
Рис.15.

В
ячейки В15 – Е15 введём наибольшее значение
Δ2
из каждого столбца по формуле
=МАКС(B10:B14),
а далее распространим формулу на ячейки
С15 – Е15 и в результате получим данные
приведенные на рис.16.

Для
вычисления наибольшего значения
активизируем ячейку В15 и введём в неё
статистическую формулу используя мастер
формул см. рис.17. Далее нажимаем OK
и выбираем диапазон значений ячеек по
которым выбирается наибольший элемент
см. рис.18. Затем проведём выбор наибольшего
элемента ошибки Δ2
по всем ячейкам 15 строки распространив
формулу из ячейки В15 в ячейки С15-Е15
см.рис.19.

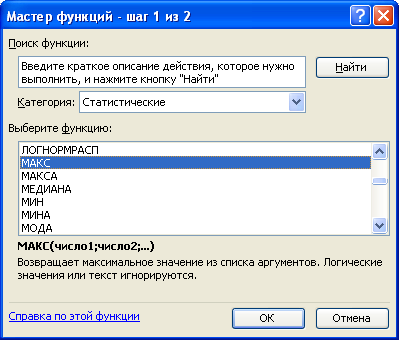
Рис.17.

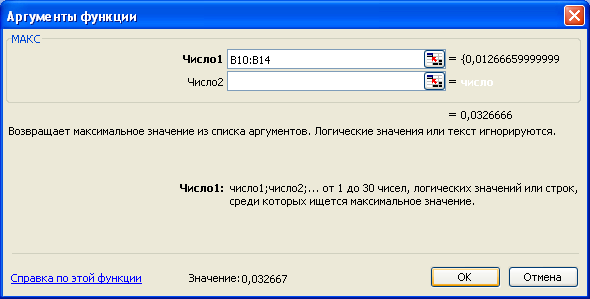
Рис.18.

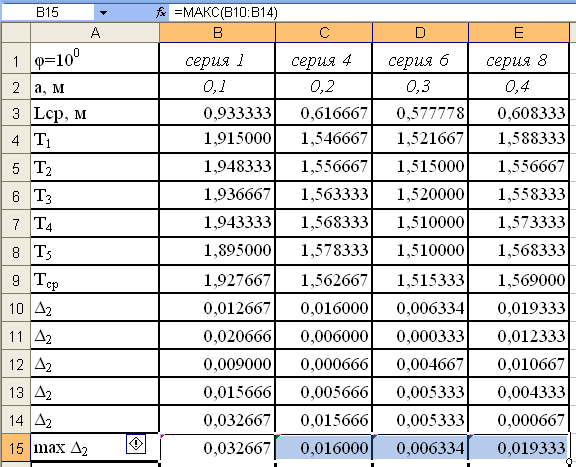
Рис.19.

Для
заполнения следующей строки необходимо
учесть, что величина ошибки измерения
длины маятника Δ1
определяется ценой деления линейки и
равна 0,0005 метра. Занесём в ручную
указанное значение во все ячейки 16-ой
строки см.результат на рис.20.

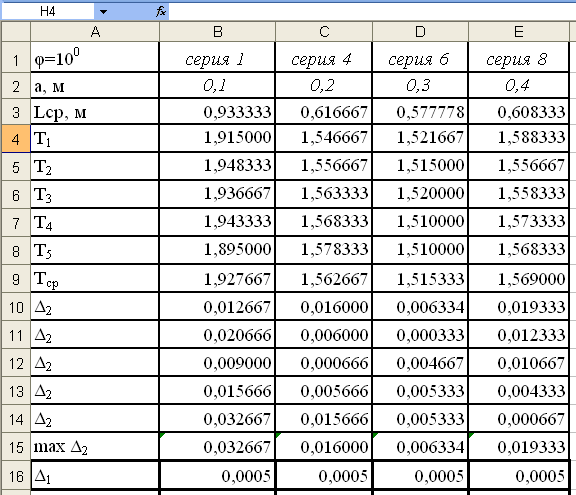
Рис.20.

Далее
проведём вычисления приведенной длины
маятника с учётом ошибок его измерения
т.е. Lср+Δ1
и Lср-Δ1.
Вычисленные значения
Lср+Δ1
и Lср-Δ1
занесём в строки 17 и 18. Для этого
активизируем ячейку В17 и введём в неё
формулу =B3+B16
затем нажмём кнопку ОК получим результат
(см.рис.21).

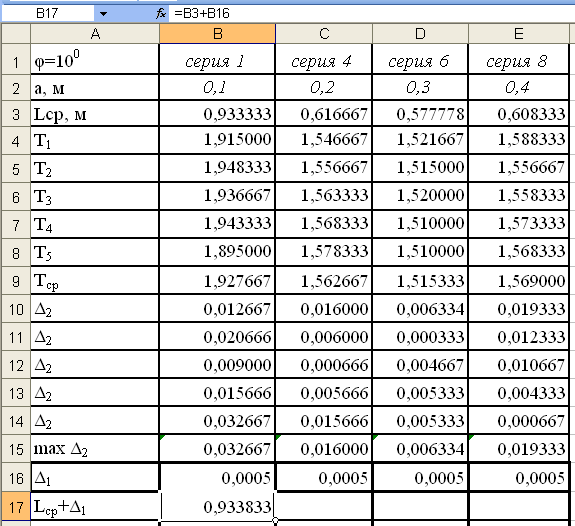
Рис.21.

Далее
распространим формулу на ячейки С17-Е18
см.рис.22.

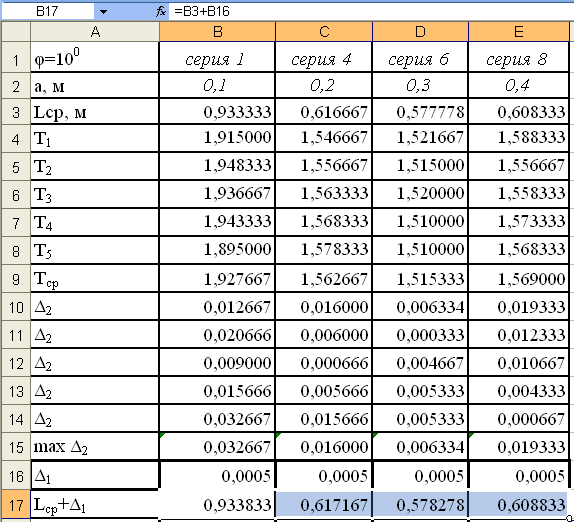
Рис.22.

Проделаем
аналогичные вычисления для расчёта
Lср-Δ1
и получим таблицу на рис.23.

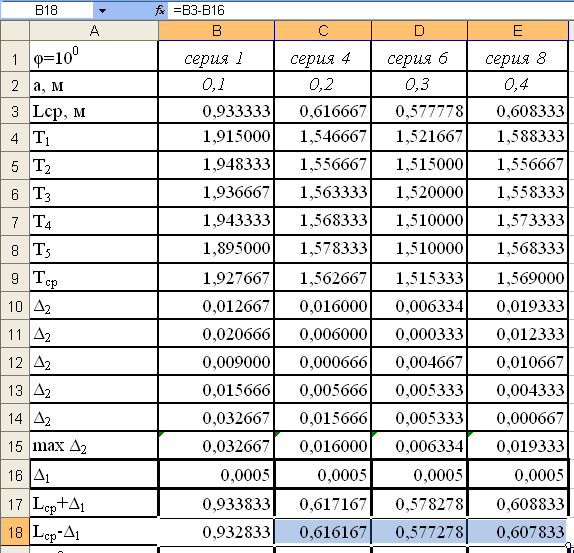
Рис.23.

Вычислим
квадрат значения Tср
в ячейках 19 строки, для этого введём в
ячейку В19 формулу =B9^2,
а затем продолжим формулу в ячейки
С19-Е19 см.рис.24.

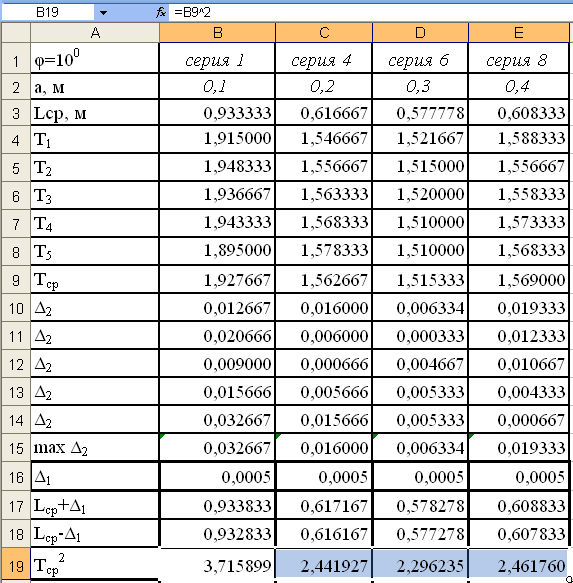
Рис.24.

Далее
введём 20 строку формулу (Тср+max
Δ2)2,
а в 21 строку формулу (Тср-max
Δ2)2.

Для
этого активизируем ячейку В20 и введём
неё формулу =(B9+B15)^2
см.рис.25 и распространим формулу в ячейки
С20-Е20 см.рис.26.

Рис.25.

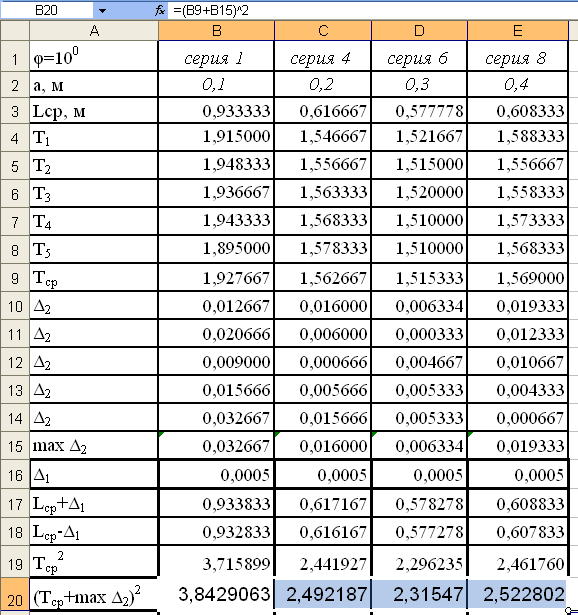
Рис.26.

Далее
проделаем аналогичную операцию в строке
21, для чего введём в ячейку В21 формулу
=(B9-B15)^2,
а затем распространим её на ячейки С21
— Е21. Получим
таблицу приведенную на рис. 27.

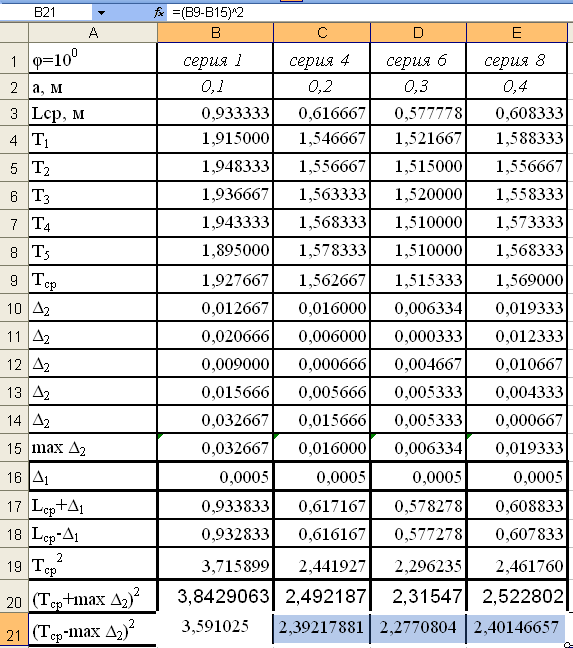
Рис.27.

Выберем
из таблицы необходимые для построения
графиков значения в отдельные таблицы
5 – 7.

Таблица
5.

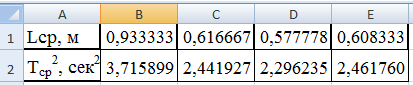
Таблица
6.

Таблица
7.

Построим
график по таблице 5. Для этого выделим
ячейки В1-Е2, а затем в меню вставка
выбрать «Вставить диаграмму» при
этом откроется окно см.рис.28.

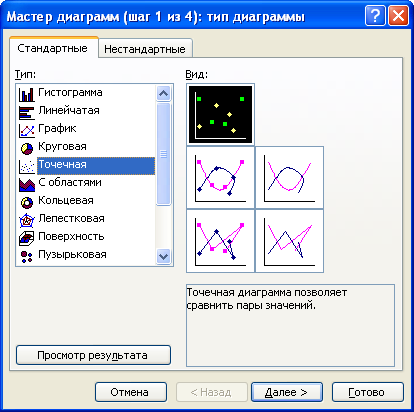
Рис.28.

Выберем
тип диаграмм «Точечная» и нажмём
клавишу «Далее» см.рис.29

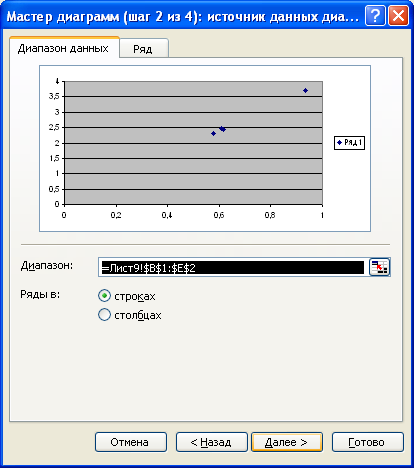
Рис.29.

Далее
выбираем закладку «Заголовки» и
вводим названия осей и всего графика
см. рис.30

Рис.30.

После
введения названий получим график в виде
рис.31.

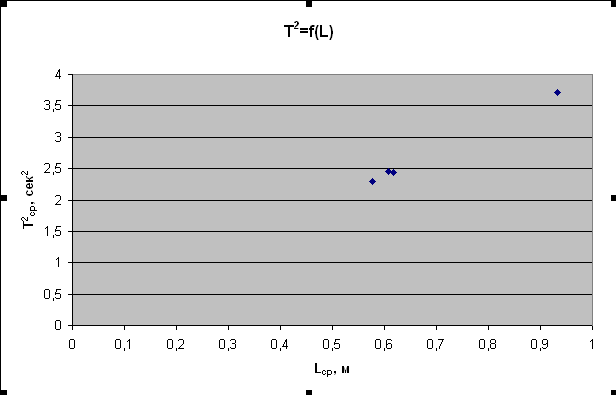
Рис.31.

После
этого в меню «Диаграмма» выбираем
«Добавить линию тренда», при этом
открывается окно в котором выбираем
линейный тренд см.рис.32.

Рис.32.

Затем
во вкладке «параметры» устанавливаем
«пересечение с кривой Y
в точке: 0» и помечаем «показывать
уравнение на диаграмме» см. рис.33, а
затем нажимаем ОК.

Рис.33.

В
результате получим график 34.

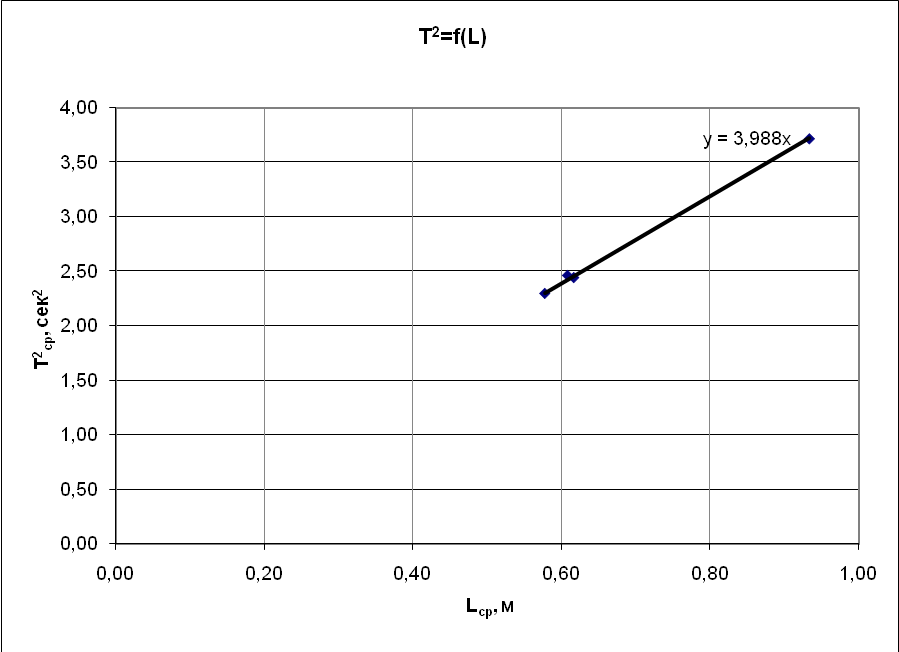
Рис.34.

Из
графика определяем К=3,988
сек2/м.

По
таблицам 6 и 7 аналогично построим
графики.

Таблица
6.

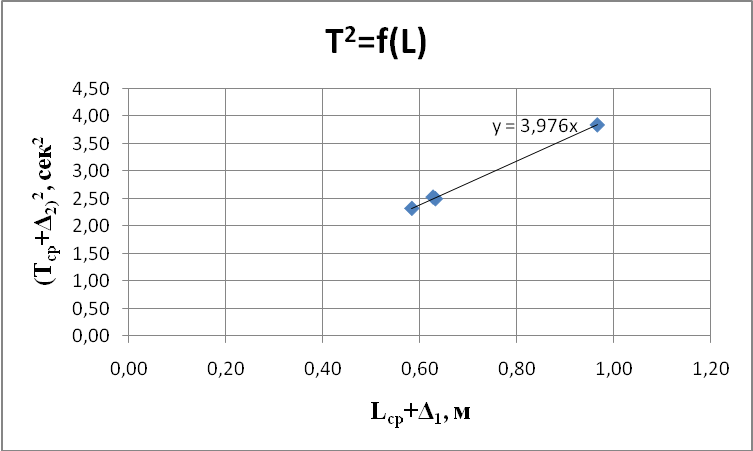
Из
графика определяем К=3,976
сек2/м.

Таблица
7.

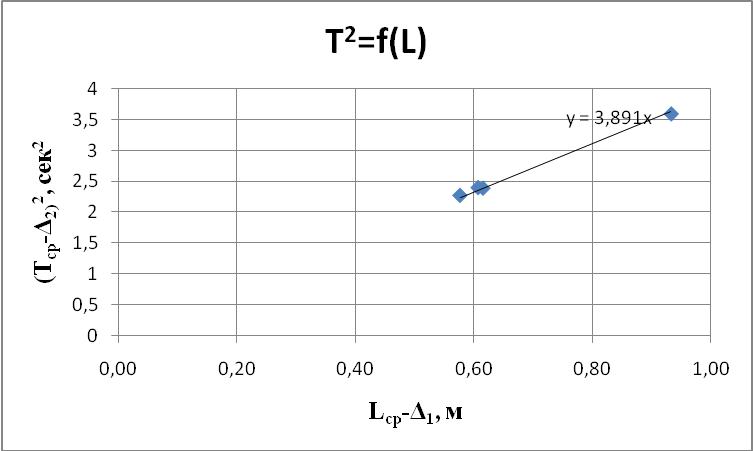
Из
графика определяем К=3,891
сек2/м.

Сведём
в одну таблицу 8 все коэффициенты наклона
прямых.

Таблица
8.

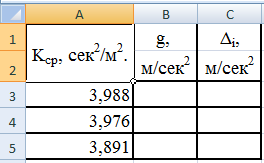
Пересчитаем
ускорение свободного падения по формуле
g=4π2/K
см.рис35.
Для этого введём формулу в ячейку В3 и
распространим её на ячейки В4-В5 см.рис.36.

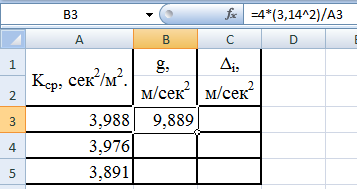
Рис.35.

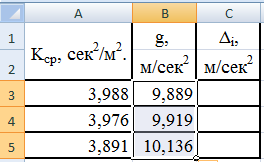
Рис.36.

Вычислим
gср
в
ячейке В4 см.рис37.

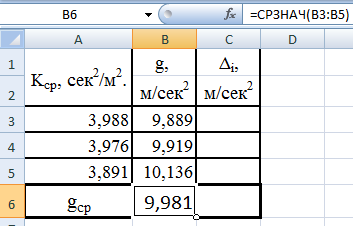
Рис.37.

Найдём
ошибки Δi=ABS(gi-gср)
по формуле см.рис.38.

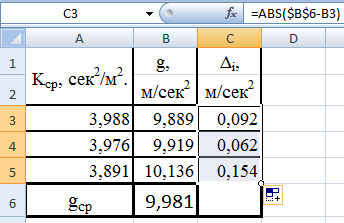
Рис.38.

Окончательно,
получим значение ускорение свободного
падения с вычисленными ошибками.

Таблица 9.

Средние
значения

Округленные
значения

gср=

9,981

10,0

Δ=

0,154

0,2

g
= gср
± Δ = 10,0 ± 0,2 м/с2

Задание
№2

Проверка
зависимости относительного периода
колебаний физического маятника Т/Т0
от положения опорной
призмы

З
аполнение
таблицы начнём с введения функции
y=√x+1/(12x)
в ячейку В3 таблицы см.рис.39.

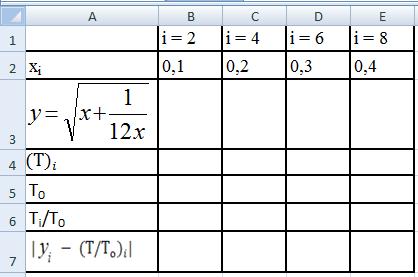
Рис.39.

Зависимость
представлена на рис.40.

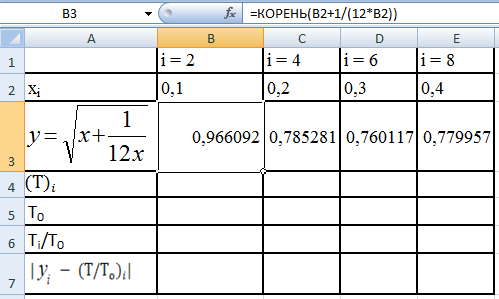
Рис.40.

В

качестве величины Ti
возьмём средние значения периода из
таблицы 1, а T0
рассчитаем по формуле T0=2π√l/g,
где

.

Таблица
10.

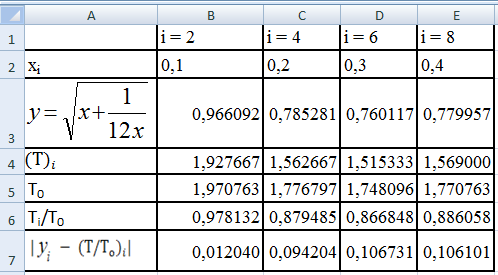
Далее
строим зависимость Yi
и Ti/T0
от х с помощью мастера функций см.рис.41
по значениям из таблицы 9, а затем
рассчитаем ошибку | Yi
— Ti/T0|
от х см.рис 42.

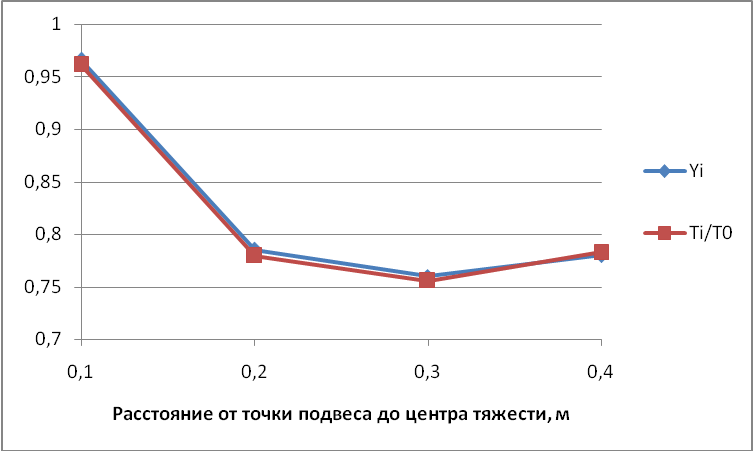
Рис.41.

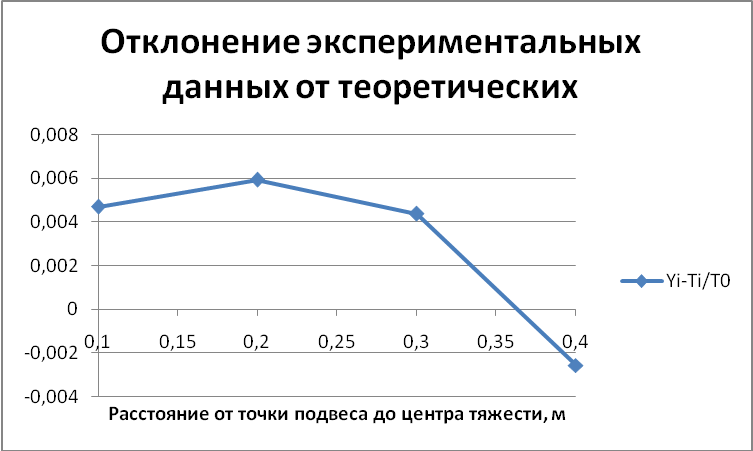
Рис.42.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник

Муниципальное общеобразовательное учреждение

«Лицей» г. Дедовска

«Решение задач по механики в Microsoft Excel и с помощью программы КАЛЬКУЛЯТОР»

Физика

Сердюченко Антон, 9 Б

Научный руководитель:

Семишина Нина Борисовна

Учитель физики МОУ «Лицей» г. Дедовска

Дедовск-2009

СОДЕРЖАНИЕ

ВВЕДЕНИЕ        .        .        .        .        .        .        .        .        .        .        3

ГЛАВА 1. ПРОГРАММА Microsoft Excel        .        .        .        .        .        .        4

        1.1 Работа в программе Microsoft Excel        .        .        .        .        .        4

        1.2 История        .        .        .        .        .        .        .        .        .        4

        1.3 Форматы файлов        .        .        .        .        .        .        .        .        6

        1.4 Новые форматы Excel 2007        .        .        .        .        .        .        6

        1.5 Экспорт и перемещение таблиц. Основы электронных таблиц        7

        1.6 Формулы и функции. Выбор встроенных функций        .        .        9

        1.7 Программирование        .        .        .        .        .        .        .        .        10

ГЛАВА 2. НЕМНОГО О МЕХАНИКЕ        .        .        .        .        .        .        11

        2.1 Механика        .        .        .        .        .        .        .        .        .        11

        2.2 Разделы механики. Классическая механика        .        .        .        .        11

        2.3 Кинематика и динамика        .        .        .        .        .        .        .        12

        2.4 Принцип относительности Галилея. Работа, мощность, энергия        14

ГЛАВА 3. РЕШЕНИЕ ЗАДАЧ В ПРОГРАММАХ MICROSOFT EXCEL И КАЛЬКУЛЯТОР        .        .        .        .        .        .        .        .        .        .        16

        3.1 Второй закон Ньютона        .        .        .        .        .        .        .        16

        3.2 Движение искусственных спутников и планет        .        .        .        17

        3.3 Движение по наклонной плоскости        .        .        .        .        .        19

        3.4 Движение под действием силы тяжести по вертикали        .        .        25

        3.5 Движение связанных тел        .        .        .        .        .        .        .        27

ЗАКЛЮЧЕНИЕ        .        .        .        .        .        .        .        .        .        .        29

СПИСОК ЛИТЕРАТУРЫ        .        .        .        .        .        .        .        .        30

ВВЕДЕНИЕ

Моя работа адресована всем, кто интересуется физикой. В наше время знание основ физики необходимо каждому, и особенно тем, кто решил избрать физику своей профессией.

        А что может быть важнее выбора профессии? Найти любимое дело – значит не только приносить пользу обществу, но и постоянно испытывать чувство внутреннего удовлетворения.

        Одна из главных задач моей работы – показать, как с помощью компьютерных программ Microsoft Excel и КАЛЬКУЛЯТОР решаются сложные задачи по физике.

ГЛАВА 1. ПРОГРАММА Microsoft Excel

1.1 Работа в программе Microsoft Excel

Microsoft Excel (также иногда называется Microsoft Office Excel) — программа для работы с электронными таблицами, созданная корпорацией Microsoft для Microsoft Windows, Windows NT и Mac OS. Она предоставляет возможности расчетов, графические инструменты, и, за исключением Excel 2008 под Mac OS X, язык макропрограммирования VBA (Visual Basic для приложений). Фактически это самый популярный табличный процессор, доступный на этих платформах, и является таковым с версии 5 от 1993 года, входя в состав Microsoft Office. На сегодняшний день Excel является одним из наиболее популярных приложений в мире [2, c.20].

1.2 История

В 1982 году Microsoft запустила на рынок первый электронный табличный процессор Multiplan, который был очень популярен на CP/M системах, но на MS-DOS системах он уступал Lotus 1-2-3. Первая версия Excel предназначалась для Mac и была выпущена в 1985 году, а первая версия для Windows была выпущена в ноябре 1987 года. Lotus не торопилась выпускать 1-2-3 под Windows, и Excel с 1988 года начала обходить по продажам 1-2-3, что в конечном итоге помогло Microsoft достичь позиций ведущего разработчика программного обеспечения. Microsoft укрепляла свое преимущество с выпуском каждой новой версии, что имело место примерно каждые два года. Текущая версия для платформы Windows — Excel 12, также известная как Microsoft Office Excel 2007 [4]. Текущая версия для платформы Mac OS X — Microsoft Excel 2008. В начале своего пути Excel стал причиной иска о товарном знаке от другой компании, уже продававшей пакет программ под названием «Excel». В результате спора Microsoft был обязана использовать название «Microsoft Excel» во всех своих официальных пресс-релизах и юридических документах. Однако со временем эта практика была позабыта, и Microsoft окончательно устранила проблему, приобретя товарный знак другой программы. Microsoft также решила использовать буквы XL как сокращенное название программы: иконка Windows-программы состоит из стилизованного изображения этих двух букв, а расширение файлов по умолчанию в Excel — .xls. В сравнении с первыми табличными процессорами Excel представляет множество новых функций пользовательского интерфейса, но суть остается прежней: как и в программе-родоначальнике VisiCalc ячейки расставляются в строки и столбцы и могут содержать данные или формулы с относительными или абсолютными ссылками на другие клетки.

Excel был первым табличным процессором, позволявшим пользователю менять внешний вид таблицы (шрифты, символы и внешний вид ячеек). Он также первым представил метод умного пересчета ячеек, когда обновляются только те ячейки, которые зависят от измененных ячеек (раньше табличные процессоры либо постоянно пересчитывали все ячейки или ждали команды пользователя). Будучи впервые объединенными в Microsoft Office в 1993 году, Microsoft Word и Microsoft PowerPoint получили новый графический интерфейс для соответствия Excel, главного стимула модернизации ПК в то время [5, c.12].

Начиная с 1993 года, в состав Excel входит Visual Basic для приложений (VBA), язык программирования, основанный на Visual Basic, позволяющий автоматизировать задачи Excel. VBA является мощным дополнением к приложению, которое в более поздних версиях стало включать полную интегрированную среду разработки. Можно создать VBA-код, повторяющий действия пользователя, позволяя таким образом автоматизировать простые задачи. VBA позволяет создавать формы для общения с пользователем. Язык поддерживает использование (но не создание) DLL от ActiveX; более поздние версии позволяют использовать основы объектно-ориентированного программирования. Функциональность VBA сделала Excel мишенью для макровирусов. Это было серьезной проблемой до тех пор, пока антивирусные продукты не стали их обнаруживать. Microsoft с опозданием приняла меры для уменьшения риска, добавив возможность полностью отключить макросы, включить макросы при открытии документа или доверять всем макросам, подписанных с использованием достоверных сертификатов. Версии Excel от 5.0 до 9.0 содержат различные «пасхальные яйца», хотя, начиная с версии 10 Microsoft начала принимать меры для ликвидации таких недокументированных возможностей своих продуктов.

1.3 Форматы файлов

Microsoft Excel вплоть до 2007 версии использовал свой собственный бинарный формат файлов (BIFF) в качестве основного. Excel 2007 использует Microsoft Office Open XML в качестве своего основного формата. Не смотря на то, что Excel 2007 поддерживает и направлен на использование новых XML-форматов в качестве основных, он по-прежнему совместим с традиционными бинарными форматами. Кроме того, большинство версий Microsoft Excel могут читать CSV, DBF, SYLK, DIF и другие форматы [3, c.30].

1.4 Новые форматы Excel 2007

Формат

Расширение

Примечания

Рабочая книга Excel

.xlsx

Стандартный формат рабочих книг Excel 2007. В действительности это сжатый ZIP-архив каталога XML документов. Является заменой бывшего бинарного формата .xls, хотя и не поддерживает макросы по соображениям безопасности.

Рабочая книга Excel с макросами

.xlsm

Та же рабочая книга Excel, но с поддержкой макросов.

Бинарная рабочая книга Excel

.xlsb

Та же рабочая книга Excel с макросами, но хранящая информацию в бинарном формате, открывая документы быстрее чем XML. В особенности часто используется для очень больших документов с десятками тысяч строк иили сотнями колонок.

Шаблон Excel с макросами

.xltm

Шаблон, созданный как основа для рабочих книг, включена поддержка макросов. Заменяет старый формат .xlt.

Надстройка Excel

.xlam

Надстройка Excel, направленная на добавление дополнительных функциональных возможностей и инструментов.

1.5 Экспорт и перемещение таблиц. Основы электронных таблиц

API позволяет открывать таблицы Excel в ряде других приложений. Это включает в себя открытие документов Excel на веб-страницах с помощью ActiveX или таких плагинов, как Adobe Flash Player. Проект Apache POI представляет Java-библиотеки для чтения и записи электронных таблиц Excel. Так же предпринимались попытки копировать таблицы Excel в веб-приложения с использованием разделенных запятыми значений.

Электронные таблицы (такие как Microsoft Excel) позволяют составить бюджет, проводить инвентаризацию или следить за расходами организации с помощью персонального компьютера.

Если необходимо оперировать формулами и работать с числами, можно воспользоваться карандашом или калькулятором. Однако вполне вероятно, что мы напишем неверное число, а еще придется самостоятельно пересчитывать все формулы при изменении любого из чисел. Поскольку в состав Microsoft Office входит программа Excel, можно сэкономить свои силы и время, используя для обработки чисел электронные таблицы. Просто вводить числа, создавать формулы и добавлять текстовые строки, чтобы понимать, какую величину представляет каждое число таблицы. Выполнив эту работу, мы сможем отформатировать числа и текстовые строки, чтобы придать таблицам более привлекательный вид.

Рабочий лист, разделенный на строки и столбцы. Рабочий лист выполняет роль обычного бумажного листа, на котором можно писать числа и буквы. Каждый рабочий лист состоит из 256 вертикальных столбцов и 16384 горизонтальных строк. Столбцы обозначают буквами (А, В, С и т.д.). Строки последовательно нумеруются (1,2,3 и т.д.) [5, c. 63].

Ячейки. Ячейка образуется в месте пересечения строки со столбцом. Если мы хотим ввести данные в рабочий лист, то должны ввести их в определенную ячейку. Каждая ячейка задается заголовком столбца и следующим за ним номером строки. Например, ячейка, образованная пересечением столбца G и строки 12, называется G12.

Числа. Числа могут представлять собой денежные суммы, размеры или количество, например 50000 руб., 309 или 0,094.

Текстовые строки. Текстовые строки указывают, что означает то или иное число на тот случай если мы это забудем. Примерами текстовых строк могут быть подписи типа Май, западные области или Сумма, потерянная нами по глупости тетушка [5, c. 64].

Формулы. Формула позволяет нам получать результат математических преобразований введенных чисел. Формула может быть очень простой, как, например, суммирование двух чисел, либо очень сложной, как, например, взятие тройного интеграла от уравнения, которое никому не нужно [5, c. 67].

1.6 Формулы и функции. Выбор встроенных функций

Можно потратить всю ночь, пересчитывая в столбик, суммируя на бумаге или с помощью калькулятора цифры в строках и столбцах огромной таблицы, но лучше сделать это с помощь программы Microsoft Excel. Просто необходимо сказать Excel, что мы хотим сосчитать и откуда взять исходные данные, а программа сама в считанные секунды выполнит всю работу за вас и покажет результат. Помимо простого суммирования, вычитания, деления и умножения, в Excel можно выполнять более сложные функции. У нас всегда будут под рукой встроенные статистические, математические и финансовые функции, которые скажут, сколько денег ежемесячно могли бы получить, если бы вложили все наличные в акции компании Рога и копыта [3, c. 57].

Необходимо написать формулу расчета амортизации имущества за указанный период с использованием метода постоянного учета амортизации. Вместо того чтобы составлять громоздкие и сложные формулы, можно воспользоваться списком формул, встроенных в Excel, которые называются функциями. Главное отличие функции от формулы состоит в том, что функция спрашивает, из каких ячеек использовать данные для выполнения операции, в то время как при составлении формул необходимо последовательно выбирать ссылки на ячейки и указывать Excel, надо ли значения из этих ячеек сложить, отнять, умножить или разделить. Для простых вычислений можно использовать свои собственные формулы, но для выполнения действительно сложных расчетов не обойтись без встроенных функций Excel.

1.7 Программирование

Ценной возможностью Excel является возможность писать код на основе Visual Basic для приложений (VBA). Этот код пишется с использованием отдельного от таблиц редактора. Записи таблицы управляются с помощью объектов. С помощью этого кода любые функции или подпрограммы, которые могут быть созданы в семействах языков Basic или Fortran, могут запущены на основе входных данных таблиц, а результаты будут мгновенно записываться кодом в электронные таблицы или будут отображены на диаграммах (графиках). Таблица становятся интерфейсом кода, позволяя легко работать с кодом и его расчетами.

Также можно воспользоваться программой КАЛЬКУЛЯТОР. Калькулятор можно использовать для выполнения операций сложения, вычитания, умножения и деления. Кроме того, калькулятор выполняет и более сложные инженерные и статистические вычисления. Можно производить вычисления, нажимая на кнопки калькулятора или вводя символы с клавиатуры. Кроме того, если включена клавиша NUM LOCK, доступен ввод цифр и действий с цифровой клавиатуры [4].

ГЛАВА 2. НЕМНОГО О МЕХАНИКЕ

2.1 Механика

Механика (греч. μηχανική — искусство построения машин) — наука о движении материальных объектов и взаимодействии между ними; в узком смысле — техническая наука, выделившаяся из прикладной физики. Предельными случаями механики являются небесная механика (механика движения небесных тел и гравитации) и квантовая механика (механика элементарных частиц и других малых тел).

2.2 Разделы механики. Классическая механика

Разделы механики: кинематика, статика, динамика. Основной математический аппарат классической механики: дифференциальное и интегральное исчисление, разработанное специально для этого Ньютоном и Лейбницем. В классической формулировке, механика строится на трёх законах Ньютона. Решение многих задач механики упрощается, если ограничиться только потенциальным взаимодействием тел, поскольку в этом случае интегрирование уравнений движения приводит к закону сохранения энергии.

Классическая механика основана на законах Ньютона, преобразовании скоростей Галилея и существовании инерциальных систем отсчёта. В настоящее время известно три типа ситуаций, в которых классическая механика перестаёт отражать реальность. Свойства микромира не могут быть поняты в рамках классической механики. В частности, в сочетании с термодинамикой она порождает ряд противоречий. Адекватным языком для описания свойств атомов и субатомных частиц является квантовая механика. Подчеркнём, что переход от классической к квантовой механике — это не просто замена уравнений движения, а полная перестройка всей совокупности понятий (что такое физическая величина, наблюдаемое, процесс измерения и т. д.) При скоростях, близких к скорости света, классическая механика также перестаёт работать, и необходимо переходить к специальной теории относительности. Опять же, этот переход подразумевает полный пересмотр парадигмы, а не простое видоизменение уравнений движения.

Если же, пренебрегая новым взглядом на реальность, попытаться всё же привести уравнение движения к виду F = ma, то придётся вводить тензор масс, компоненты которого растут с ростом скорости. Эта конструкция уже долгое время служит источником многочисленных заблуждений, поэтому пользоваться ей не рекомендуется.

Классическая механика становится неэффективной при рассмотрении систем с очень большим числом частиц. В этом случае практически целесообразно переходить к статистической физике [4].

2.3 Кинематика и динамика

Кинематика — изучает геометрические свойства движения тел без учета их масс и действующих на них сил. Рассматривает движение тел без выяснения причин этого движения.

Материальная точка — тело, размерами и формой которого в данных условиях можно пренебречь. Система отсчёта — совокупность тела отсчёта, связанной с ним системы координат и часов. Часы — устройство, в котором протекает периодический процесс, положенный в основу отсчета времени [4]. Траектория движения материальной точки — линия, описываемая этой точкой в пространстве. В зависимости от формы траектории движение может быть прямолинейным или криволинейным. Вектор перемещения — вектор, начальная точка которого совпадает с начальной точкой движения, конец вектора — с конечной. Путь — сумма длин всех участков траектории, пройденных точкой за определенное время. Средняя скорость — отношение модуля вектора перемещения к промежутку времени, в течение которого это перемещение произошло. Мгновенная скорость (скорость) — предел отношения вектора перемещения к промежутку времени, за который это перемещение произошло, при стремлении длительности промежутка времени к нулю. Ускорение  — характеристика степени неравномерности движения. Определяет быстроту изменения скорости по модулю и направлению.

Динамика (греч. δύναμις — сила) — раздел механики, в котором изучаются причины возникновения механического движения.

Динамика оперирует такими понятиями, как масса, сила, импульс, энергия. Динамика, базирующаяся на законах Ньютона, называется классической динамикой. Классическая динамика описывает движения объектов со скоростями от долей миллиметров в секунду до километров в секунду. Однако эти методы перестают быть справедливыми для движения объектов очень малых размеров и при движениях со скоростями, близкими к скорости света. Такие движения подчиняются другим законам.

Первый закон Ньютона: существуют такие системы отсчета, в которых изолированная материальная точка сохраняет состояние покоя или равномерно прямолинейно движется. Такие системы отсчета называются инерциальными.

Второй закон Ньютона: в инерциальных системах отсчета геометрическая сумма всех сил действующих на тело равно произведению массы тела на его ускорение. F=ma

Третий закон Ньютона: в инерциальных системах отсчета всякое действие одной (первой) материальной точки на другую (вторую), сопровождается воздействием второй материальной точки на первую, т.е. имеет характер взаимодействия; силы, с которыми взаимодействуют материальные точки, всегда равны по модулю, противоположно направлены, действуют вдоль прямой, соединяющей эти точки, являются силами одной природы и приложены к разным материальным точкам.

2.4 Принцип относительности Галилея. Работа, мощность, энергия

Принцип относительности Галилея: никакими механическими опытами, проводимыми внутри данной инерциальной системы, нельзя установить, покоится эта система или движется. Во всех инерциальных системах отсчета законы механики одинаковы.

Вес тела — сила, с которой тело давит на опору.  

Работа силы равна произведению модуля силы на перемещение и на косинус угла между ними. cosα

Мощность — отношение работы ко времени, за которое эта работа была совершена

Кинетическая энергия — величина, равная половине произведения массы тела на квадрат его скорости.

Величину, равную произведению массы тела на g и на высоту тела над поверхностью Земли, называют потенциальной энергией тела в поле силы тяжести.

Консервативные силы — силы, работа которых не зависит от пути, пройденного материальной точкой. Зависит только от перемещения.

Механическая энергия системы — величина, равная сумме кинетической и потенциальной энергий системы. .  

Закон сохранения механической энергии ─ в замкнутой системе, в которой действуют только консервативные силы, механическая энергия сохраняется.

Закон всемирного тяготения ─ два любых тела притягиваются друг к другу с силой, прямо пропорциональной массе каждого из них и обратно пропорциональной квадрату расстояния между ними.

Первая космическая скорость.

ГЛАВА 3. РЕШЕНИЕ ЗАДАЧ В ПРОГРАММАХ MICROSOFT EXCEL И КАЛЬКУЛЯТОР

3.1 Второй закон Ньютона

Задача № 1

        Найти силу F, под действием которой тело массой m приобрело ускорение a.

a

0.25м/с2

2 м/с2

0.4 м/с2

2 км/с2

0.1 м/с2

5 см/с2

m

8 кг

3 г

200 кг

10 г

200 кг

20 т

Решение:

  1. Переведем в систему СИ ускорение (м/с2) и массу (кг)
  2. Запишем второй закон Ньютона:

F = ma

3) Воспользуемся программой Microsoft Excel:

а) столбец А – ускорение

    столбец В – масса

    столбец С – сила

б) Заполним столбцы А и В данными.

в) В столбец С1 введем расчетную формулу:

= ПРОИЗВЕД (Число1 А1:В1)

Далее получаем ответы:

А

В

С

1

0,25

8

2

2

2

0,003

0,006

3

0,4

200

80

4

2000

0,01

20

5

0,1

200

20

6

0,05

20000

1000

3.2 Движение искусственных спутников и планет

Задача № 2

Найти ускорение свободного падения g и первую космическую скорость v для планет Солнечной системы, где М-масса планеты, R-средний радиус планеты.

G=6,67×10-11 

Планета

M, кг

R, м

Меркурий

3,26∙1023

2,42∙106

Венера

4,88∙1024

6,10∙106

Марс

6,43∙1023

3,38∙106

Юпитер

1,90∙1027

7,13∙107

Сатурн

5,69∙1026

6,04∙107

Уран

8,69∙1025

2,38∙107

Нептун

1,04∙1026

2,22∙107

Решение:

1. Запишем расчетные формулы для задачи:

1)  –  ускорение свободного падения

2)  – первая космическая скорость для планеты Солнечной системы

2. Для решения воспользуемся программой Microsoft Excel:

а) Столбец А ─ планета

    Столбец В ─ масса

    Столбец С ─ радиус

    Столбец D ─ ускорение свободного падения

    Столбец E ─ первая космическая скорость

б) Для g: [ = ЧАСТНОЕ(ПРОИЗВЕД(В1;ПРОИЗВЕД(6,67;СТЕПЕНЬ(10;-11)));СТЕПЕНЬ(С1;2))

Для V: [ = КОРЕНЬ(ПРОИЗВЕД(С1:D1))

3. Получаем результат

A

B

C

D

E

Планета

3,26E+23

2,42E+0,6

3,00E+00

2,69E+0,3

Меркурий

4,88E+24

6,10E+0,6

8,00E+00

6,99E+0,3

Венера

6,43E+23

3,38E+0,6

3,00E+00

3,18E+0,3

Марс

1,90E+27

7,13E+0,7

2,40E+01

4,14E+0,4

Юпитер

5,69E+26

6,04E+0,7

1,00E+01

2,46E+0,4

Сатурн

8,69E+25

2,28E+0,7

1,00E+01

1,54E+0,4

Уран

1,04E+26

2,22E+0,7

1,40E+01

1,76E+0,4

4. Благодаря данным мы можем в этой же программе построить диаграмму:

5. Так же можно решить с помощью КАЛЬКУЛЯТОРА (в инженерном режиме):

0

1

2

3

4

5

6

7

8

9

0

6

∙

6

7

ВП

1

1

/-/

П→x1

×

1

П→x2

F x2

÷

С/П

П→x2

×

F√

1

0

0

2

0

÷

С/П

F ABT; M – x → П1; R — x→ П2; В/О; С/П ─ ответ g; С/П ─ ответ v, км/с.

3.3Движение по наклонной плоскости

Задача № 3

        Поезд массой 3000т движется вниз под уклон, равный 0,003. Коэффициент сопротивления движению равен 0,008. С каким ускорением движется поезд, если сила тяги локомотива равна: а)300 кН; б)150 кН; в)90кН?

Из условия дано:

m =3000т = 3000000кг

 sin α = 0,003

µ = 0,008

F1 = 300кН = 300000Н

F2 = 150кН = 150000Н

F3 = 90кН = 90000Н

Найти: а — ?

Решение:

  1. Начертим рисунок:

  1. Запишем второй закон Ньютона

  1. Проекции на оси:

x: -ma = -F+Fтр – mgsinα

y: 0 = N – mgcosα ; Fтр = µN

a = g sinα – µg cosα +

  1. Подставим данные и получим расчетную формулу:

а = -0,05 +

  1. Продолжим решение в Microsoft Excel

Столбец А ─ силы

Столбец В ─ ускорение

а: =СУММ (-0,05;ЧАСТНОЕ (А1:3000000))

А

В

300000

0,05

150000

0

90000

-0,02

Задача № 4

        В момент начала наблюдения расстояние между автобусом 1 и мотоциклом 2 было равно S и автобус проходил начало координат (x01=0). Проекции скоростей тел соответственно равны v1x и v2x. Для каждой строки сформулировать условие задачи. Найти: 1) время t встречи автобуса и мотоциклиста; 2) координату x места их встречи; 3) координату x2 мотоцикла в момент времени прохождения автобусом точки, координата которой x1. (S=x02 – x01).

№

1

600

10

-20

250

2

1400

18,6

-18,6

1400

3

0

14

18

630

4

-283

-18

-12

-364

5

148

17

21

548

Решение:

1. Запишем расчетные формулы для задачи:

1) — время встречи автобуса и мотоциклиста

 2)  — координата между их встречами

3). – координата мотоцикла в момент времени прохождения автобуса точки, координаты которой .

2. Для решения задачи воспользуемся программой КАЛЬКУЛЯТОР.

0

1

2

3

4

5

6

7

8

9

0

П→x1

П→x2

П→x3

−

÷

C/П

П→x2

×

С/П

П→x4

1

П→x3

×

П→x2

÷

П→x1

+

С/П

F ABT; s ─ x → П1; V1x ─ x → П2; V1x ─ x → П3; x1 ─ x → П4; В/О; С/П ─ ответ t; С/П ─ ответ .

3. Подставив необходимые числа, получается следующий результат.

№

t, с

x, м

1

20

200

100

2

37,6

700

0

3

0

0

810

4

47,2

-849

-526

5

-37

-629

825

Задача № 5

Уравнения движения двух тел заданы выражениями: x1=x01+v1x t  и  x2=x02+ v2x t. Найти время и координату места встречи тел.

№

x01, м

x02, м/с

v1x, м/с

v2x, м/с

1

24

87

4,2

2,7

2

63

-12

-6,2

4,1

3

0

-17

1,1

2,6

4

263

0

0

4,9

5

12

-12

2,1

-2,1

Решение:

1. Запишем расчетные формулы для задачи:

1) – время встречи тел

 2) – координата места встречи

2. Для решения задачи воспользуемся программой КАЛЬКУЛЯТОР.

0

1

2

3

4

5

6

7

8

9

1

П→x2

П→x1

П→x3

П→x4

—

x→Па       (v1x—v2x)

÷

С/П

П→x3

2

П→x2

×

П→x1

П→x4

×

—

П→xa

÷

С/П

F ABT; x01 ─ x → П1; x02 – x → П2; v1x – x → П3; v2x — x→ П4; В/О; С/П ─ ответ t; С/П ─ ответ x.

3. Подставив необходимые числа, получается следующий результат.

№

t, c

x, м

1

42

200

2

7,3

17,8

3

11,3

12,5

4

53,7

263

5

-5,7

0

Задача № 6

        Судну (лодке, катеру и т.д.) необходимо проехать расстояние s туда и обратно один раз по реке, а другой раз по озеру. Скорость течения воды v1. Скорость судна относительно воды v2. На сколько больше времени займет движение по реке, чем по озеру?

№

v1, м/с

v2, м/с

s, м

1

1

5

240

2

2,13

18,6

1410

3

0,27

3,2

480

4

4,2

4,6

310

5

2,1

2,2

68

Решение:

1. Запишем расчетную формулу для задачи:

— время движения судна.

2. Для решения задачи воспользуемся программой Microsoft Excel, которая позволит быстро решить задачу.

0

1

2

3

4

5

6

7

8

9

0

П→x2

Fx2

П→x1

Fx2

─

П→x2

×

П→x3

÷

П→x1

1

Fx2

÷

2

÷

F 1/x

С/П

F ABT; v1 – x → П1; v2 — x→ П2; s ─ x → П3; В/О; С/П ─ ответ 𝜟t.

3. Подставив необходимые числа, получается следующий результат.

1) 4; 2) 2,01; 3) 2,15; 4) 675; 5) 634 с.

3.4 Движение под действием силы тяжести по вертикали

Задача № 7

Тело брошено вертикально вверх со скоростью 20м/с. Написать уравнение y=y(t). Найти, через какой промежуток времени тело будет на высоте: а)15 м; б) 20 м; в) 25 м.

        Указание. Ось Y направить вертикально вверх; принять, что при t=0 y=0

1) Запишем уравнение движения тела s в проекции на ось:

   =>  =>

 =>

 
2) Далее воспользуемся программой Microsoft Excel

а) Столбец А – необходимая h

    Столбец В – расчет t1

    Столбец С – расчет t2

б) Для t1: = ЧАСТНОЕ (20 — КОРЕНЬ(400-ПРОИЗВЕД (А1;20));10)

t2: = ЧАСТНОЕ (20 + КОРЕНЬ (400-ПРОИЗВЕД (А1;20));10)

И получаем ответ:

А

В

С

15

1

3

20

2

2

25

—

—

Задача № 8

Мальчик вращает в вертикальной плоскости камень, привязанный к веревке длиною r, с частотой . На какую максимальную высоту h может подняться камень после того, как мальчик отпустит веревку?

№

1

2

3

4

5

r, м

0,62

0,81

0,92

1,06

1,14

v, c-1

2,11

1,93

1,82

1,71

1,89

Решение:

1. Запишем расчетные формулы для задачи:

 — максимальная высота

2. Для решения задачи воспользуемся программой КАЛЬКУЛЯТОР.

0

1

2

3

4

5

6

7

8

9

0

×

F

×

Fx2

2

×

9

.

8

1

1

÷

С/П

F ABT; r; В↑; ; В/О; С/П ─ ответ h.

3. Подставив необходимые числа, получается следующий результат.

1)3,44; 2) 4,92; 3) 5,89; 4) 6,61; 5) 9,34 м.

3.5 Движение связанных тел

Задача № 9

С каким ускорением a движутся связанные тела и какова сила натяжения нити Fн? Трением пренебречь. Составить программу для условия: если тело массой m2 движется вправо (вниз), то a>0.                  

№

1

2

3

4

5

6

7

8

m2, кг

0,27

0,19

0,19

0,19

0,19

0,19

0,19

0,19

β,°

22

22

90

90

90

48

48

90

m1, кг

0,19

0,27

0,27

0,27

0,27

0,27

0,19

0,19

a,°

22

22

0

90

11

0

48

90

Решение:

1. Запишем расчетные формулы для задачи:

1) — ускорение связанных тел

 2) — сила натяжения нити

2. Для решения задачи воспользуемся программой КАЛЬКУЛЯТОР.

0

1

2

3

4

5

6

7

8

9

0

П→x1

П→x2

F sin

×

П→x3

П→x4

F sin

×

─

П→x5

1

×

П→x1

П→x3

+

÷

С/П

П→x4

F sin

П→x5

×

2

+

П→x3

×

С/П

F ABT; m2 – x → П1; β ─ x→ П2; m1 – x → П3; α ─ x → П4; g ─ x → П5; В/О; С/П ─ ответ a; С/П ─ ответ FH.

3. Подставив необходимые числа, получается следующий результат.

№

1

2

3

4

5

6

7

8

a, м/с2

0,64

-0,64

4,05

-1,71

2,95

3,01

0

0

FH, H

0,82

0,82

1,09

2,19

1,3

0,81

1,39

1,86

ЗАКЛЮЧЕНИЕ

        Многим из нас после окончания школы доведется работать квалифицированными рабочими, лаборантами, техниками, инженерами, врачами – знание физики и информатики поможет нам лучше овладеть своей профессией.

В своей работе я доказал, что даже очень сложные задачи по физике можно решить легкой подстановкой чисел в специальные компьютерные программы. И наверняка не запутаешься в подстановке больших чисел в сложные формулы!

СПИСОК ЛИТЕРАТУРЫ

1. Левин Александр. Самоучитель полезных программ. Питер, 2007. ─ 794с

2. Левина М. П. 100% Самоучитель работы на компьютере. Технолоджи – 3000, триумф, издательская группа, триумф, технолоджи – 3000, 2007. ─ 240с

3. Рымкевич А. П. Физика. Задачник. 10-11 классы. Дрофа, 2000. ─ 208с

4. Уоллес Вонг Office XP для «Чайников». Диалектика, 2005. ─ 288с

5. http://www.wikipedia.ru

Источник

Цель урока:

1.Образовательная: научить
учащихся применять знания по использованию
средств MS Excel для решения физических задач.

2.Развивающая: обеспечить развитие
у учащихся навыков, способствующих применению
имеющихся знаний и умений, логического мышления.

3.Воспитательная: формирование
информационной культуры, умения и навыков
самостоятельного овладения знаниями.

Тип урока: урок совершенствования
ЗУН.

Вид урока: тренировочный.

Оборудование: компьютеры с
установленной программой MS Excel, презентация,
листы с заданиями, проектор.

План урока:


  1. Организационный момент.
  2. Актуализация знаний.
  3. Изучение нового материала.
  4. Практическая работа учащихся.
  5. Заключение.
  6. Домашняя работа.

Ход урока

1. Организационный момент

Взаимное приветствие учителя и
учащихся. Фиксация отсутствующих, проверка
состояния классного помещения.

2. Актуализация знаний

Учитель: На прошлых уроках мы с вами
познакомились средствами MS Excel: правилами записи
соотношений, построение диаграмм и графиков.
Повторим пройденный материал:

Учитель

Ученики

Объяснить правило записи формул

Признаком формулы является
знак “=” стоящий перед совокупностью символов.

Перечислить правила записи
арифметических выражений

Запись выражения
осуществляется в одну сроку, без надстрочных и
подстрочных знаков;

Для обозначения операций используется
определенный набор символов;

Для определения приоритетов
выполнения действий используются скобки
При отсутствии скобок, объяснить
порядок вычисления выражений

1. Вычисляются значения
функций

2. Возводится в степень

3. Умножение и деление

4. Сложение и вычитание
Объяснить формулы

(Можно проецировать
на экран)

1. Формула вычисления
скорости при отсутствии начальной скорости

2. Формула вычисления скорости при
равноускоренном движении

3. Формула вычисления координаты при
равноускоренном движении

4. Формула вычисления силы всемирного
тяготения

5. Формула первой космической скорости

6. Формула второй космической скорости.

7. Формула вычисления ускорения
свободного падения.

3. Объяснение нового материала:

(Объяснение ведется в ходе показа слайдов.
Ученики следят за ходом объяснения). Приложение
1

Учитель Программная система MS Excel
является удобным средством решения
разнообразных расчетных задач. Электронные
таблицы, первоначально использовавшиеся для
финансовых расчетов, все шире применяются для
сложных многошаговых технических расчетов.

На уроках физики мы познакомились с
равномерным и равноускоренным движениями и
изучили закон всемирного тяготения. Программная
система MS Excel позволяет наглядно демонстрировать
траектории движения и позволяет быстрее решить
трудоемкие задачи

Рассмотрим этапы решения задачи при
помощи слайдов.

И так, тема нашего урока: Решение задач
по физике средствами MS Excel (1 слайд)

Рассмотрим использование электронных
таблиц в процессе решения задачи

Задача 1. Тело брошено горизонтально
над поверхностью земли с некоторой начальной
скоростью. Ускорение свободного падения равно 9,8
м/с2.. Сопротивлением воздуха пренебречь.
Рассчитать траекторию движения тела. (2 слайд)

Решим задачу графически: На тело
действуют две силы: в горизонтальном направлении
действует сила инерции, под действием которой
тело движется равномерно, а в вертикальном –
сила тяжести, под действием которой тело падает с
ускорением. Горизонтальный путь подсчитываем
как скорость, умноженное на время, а вертикальную
составляющую – по формуле, умноженной на -1, чтобы указать
направление оси на графике. (3 слайд)

Формулы, по которым выполняются
вычисления, представлены на фрагменте таблицы (4.
слайд)

По результатам вычислений заполним
таблицу и построим диаграмму, в нашем случае это
график, где видна траектория движения тела (5
слайд). По графику видим, что траектория
движения – это часть параболы.

При помощи средств MS Excel, можно решить
задачи на вычисления силы всемирного тяготения,
первой и второй космической скорости, периодов
вращения планет вокруг Солнца и др. А теперь
решим задачи при помощи подготовленных шаблонов.
Приложение 2

4. Практическая работа учащихся.

(На каждом листе представлены
задания, которые должны выполнить учащиеся. По
ходу работы учащиеся переходят из одного листа в
другой, объясняют процесс выполнения, отвечают
на вопросы).

Представленные задания:

  1. Изучение движения тел под действием силы
    тяжести. Заполнить цветные прямоугольники
    значениями ускорения свободного падения и
    начальной скорости: в первом случае V0=0 м/с, а во
    втором случае V0=10 м/с. Проследить за изменениями
    скорости и координаты, объяснить формулы.
  2. Изучение движения тел, брошенных горизонтально.
    Заполнить цветные прямоугольники
    соответствующими значениями и проследить за
    изменением значений.


  3. Использование закона всемирного тяготения.
    Задания: 1) Используя формулы, заполнить
    ячейки и вычислить скорость движения планет в
    км/с.
    2) Построить диаграмму, характеризующую сил
    притяжения планет к Солнцу.
    3) Дополнительное: Найти периоды вращения планет
    вокруг Солнца.
  4. Нахождение первой и второй космических
    скоростей и ускорения свободного падения.
    Используя формулы, заполнить пустующие ячейки.
    Объяснить эти формулы.

5. Заключение.

На нашем уроке мы использовали среду MS
Excel для решения физических задач. При помощи
программы мы облегчили свою работу, сделали
процесс решения более наглядно и интереснее.
Электронные таблицы позволяют автоматизировать
процесс решения не только физических, но и
математических, химических задач, а диаграммы
очень удобны при изучении тем по географии. Все
вы справились хорошо. Спасибо вам за работу. (Оценивание
работ учащихся)

6. Домашнее задание

При помощи калькулятора найти силы
притяжения Луны – Солнца и Луны – Земли,
сравнить результаты вычислений. (Справочный
материал находится в тетрадях учащихся.)

Источник

Содержание

  1. Excel ускорение свободного падения
  2. Движение тела, брошенного под углом к горизонту!
  3. Математика и физика полета баскетбольного мяча.
  4. Исходные данные:
  5. Результаты расчетов:
  6. Иные варианты расчетов:
  7. Ответ на вопрос:

Excel ускорение свободного падения

Что такое модель объекта или процесса и зачем её создавать? Какие бывают модели? Что такое информационная модель? Основные этапы моделирования Алгоритмическая модель Моделирование в языках программирования Моделирование в среде MS Excel

MS Excel – разновидность электронной таблицы. Это программа обработки числовых данных, хранящая и обрабатывающая данные в прямоугольных таблицах.

Таким образом, с помощью этой программы можно решать задачи исследовательского характера, требующие большого количества вычислений.

Рассмотрим задачу и сследовани я физических моделей . П остро им информационн ую модел ь движения тела, брошенного под углом к горизонту

1 этап. Содержательная постановка задачи «Бросание мячика в площадку». В процессе тренировок теннисистов используются автоматы по бросанию мячика в определенное место площадки. Необходимо задать автомату необходимую скорость и угол бросания мячика для попадания в площадку определенной длины, находящуюся на известном расстоянии.

Проведём формализацию задачи. Формулируем основные предположения:

· мячик мал по сравнению с Землей, поэтому его можно считать материальной точкой;

· изменение высоты мячика мало, поэтому ускорение свободного падения можно считать постоянной величиной g = 9,8 м/с 2 и движение по оси 0 Y можно считать равноускоренным;

· скорость бросания тела мала, поэтому сопротивлением воздуха можно пренебречь и движение по оси О X можно считать равномерным.

Вывод: можно использовать формулы для равноускоренного движения, известные из курса физики.

При заданных начальной скорости v 0 и угле бросания α значения координат дальности полета x и высоты y от времени можно описать следующими формулами:

Площадка расположена на расстоянии s и имеет длину l . Попадание произойдет, если значение координаты х мячика будет удовлетворять условию: s ≤ х ≤ s + l . Если х s , то это означает «недолет», а если х > s + l , то это означает «перелет».

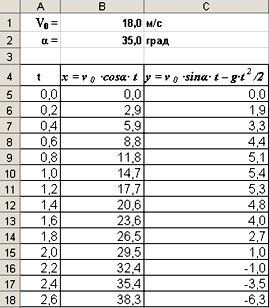
2 этап. Построение компьютерной модели движения тела в среде MS Excel .

В ячейки B 5 и C 5 введем формулы для вычисления х и у :

=$B$1*COS( РАДИАНЫ ($B$2))*A5

=$B$1*SIN( РАДИАНЫ ($B$2))*A5-4,9*A5*A5

1 Для ввода начальной скорости будем использовать ячейку B 1, а для ввода угла – ячейку B 2. Введём значения, как показано на рисунке.
2
3 Введем в ячейки A 5: A 18 значения времени с интервалом в 0,2 с.
4 Скопируем формулы в ячейки В6:В18 и С6:С18 соответственно. После этого должно получиться так, как показано на рисунке:
5 Построи м диаграмму типа График, в которой используется в качестве категории диапазон ячеек B 5: B 18, а в качестве значений — диапазон ячеек С5:С18.

3 этап. Исследование модели. Исследуем модель и определим с заданной точностью 0,1 градуса значения диапазона углов бросания, которые обеспечивают попадание мячика в мишень (например, при скорости бросания v 0 = 18 м/с в площадку длиной l = 1 м , находящуюся на расстоянии S = 30 м ).

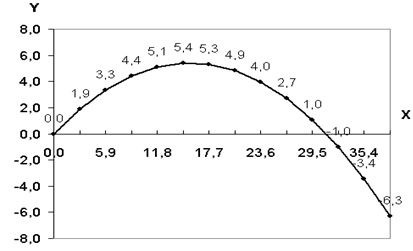Установить для ячеек точность один знак после запятой.

· в ячейку B 21 значение начальной скорости;

· в ячейку B 22 – значение угла бросания;

· в ячейку B 23 – значение расстояния до мишени;

· в ячейку B 25 формулу для вычисления координаты x мячика на поверхности для заданных начальных условий: =B21^2*SIN(РАДИАНЫ(2*B22))/9,81. Получится так, как показано на рисунке:

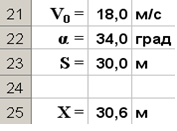
Для определения диапазона углов используем метод Подбор параметра. Этот метод позволяет задать значение функции и найти значение аргумента функции, который обеспечивает требуемое значение функции.

Функцией в нашем случае будет являться зависимость координаты тела x от параметра, т.е. угла бросания α. Для определения диапазона углов, необходимо определить два угла, которые обеспечивают попадания в ближний и дальний края площадки. Для заданных начальных условий (скорости бросания и расстояния до мишени) проведем поиск углов, которые дают попадание в площадку на расстояниях S = 30 м и S + l = 31 м.

Ищем значение угла бросания, которое обеспечит попадание мячика в ближний край площадки, т.е. какой угол α обеспечивает значение функции x = 30 метров .

Выделить ячейку В25, содержащую значение высоты мячика, и ввести команду [Сервис-Подбор параметра…].

В появившемся диалоговом окне ввести в поле Значение: расстояние до ближнего края площадки (т.е. 30).

В поле Изменяя значение ячейки: ввести адрес ячейки В$22, содержащей значение угла бросания.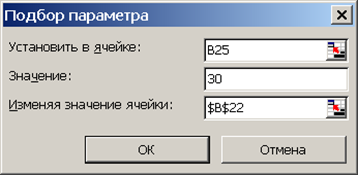

В ячейке В22 появится значение 32,6, т.е. значение минимального угла бросания мячика, которое обеспечивает попадание в площадку при заданных начальных условиях.

Далее, найдем угол бросания, который обеспечит попадание мячика в дальний край площадки, т.е. какой угол α обеспечивает значение функции x = 30 м + 1 м = 31 м .

Выделить ячейку В25, содержащую значение координаты х мячика, и ввести команду [Сервис-Подбор параметра…].

В появившемся диалоговом окне ввести в поле Значение: расстояние до дальнего края площадки (т.е. 30).

В поле Изменяя значение ячейки: ввести адрес ячейки В$22, содержащей значение угла бросания.

В ячейке В22 появится значение 34,9, т.е. значение максимального угла бросания мячика, которое обеспечивает попадание в площадку при заданных начальных условиях.

Итак, существует диапазон значений угла бросания мячика от 32,6 ° до 34,9 ° , в котором обеспечивается попадание в площадку длиной 1 м, находящуюся на расстоянии 30 м, мячиком, брошенным со скоростью 18 м/с.

Можно п овторит ь исследование модели при другом начальном значении угла (например, 55°).

Источник

Движение тела, брошенного под углом к горизонту!

Опубликовано 22 Апр 2014
Рубрика: О жизни | 9 комментариев

До конца финального матча баскетбольного турнира Олимпиады в Мюнхене 1972-ого года оставалось 3 секунды. Американцы – сборная США — уже во всю праздновали победу! Наша команда – сборная СССР – выигрывала около 10-и очков у великой dream Team.

. за несколько минут до окончания матча. Но, растеряв в концовке все преимущество, уже уступала одно очко 49:50. Дальше произошло невероятное! Иван Едешко бросает мяч из-за лицевой линии через всю площадку под кольцо американцев, где наш центровой Александр Белов принимает мяч в окружении двух соперников и вкладывает его в корзину. 51:50 – мы олимпийские чемпионы.

Я, будучи тогда ребенком, испытал сильнейшие эмоции – сначала разочарование и обиду, затем сумасшедший восторг! Эмоциональная память об этом эпизоде врезалась в мое сознание на всю жизнь! Посмотрите видео в Интернете по запросу «золотой бросок Александра Белова», не пожалеете.

Американцы тогда не признали поражения и отказались от получения серебряных медалей. Возможно ли за три секунды сделать то, что совершили наши игроки? Вспомним физику!

В этой статье мы рассмотрим движение тела, брошенного под углом к горизонту, составим в Excel программу решения этой задачи при различных сочетаниях исходных данных и попытаемся ответить на поставленный выше вопрос.

Это достаточно широко известная задача в физике. В нашем случае тело, брошенное под углом к горизонту – это баскетбольный мяч. Мы рассчитаем начальную скорость, время и траекторию полета мяча, брошенного через всю площадку Иваном Едешко и попавшего в руки Александра Белова.

Математика и физика полета баскетбольного мяча.

Представленные ниже формулы и расчет в excel являются универсальными для широкого круга задач о телах, брошенных под углом к горизонту и летящих по параболической траектории без учета влияния трения о воздух.

Расчетная схема представлена на рисунке, расположенном ниже. Запускаем программу MS Excel или OOo Calc.

Исходные данные:

1. Так как мы находимся на планете Земля и рассматриваем баллистическую задачу – движение тел в поле тяжести Земли, то первым делом запишем основную характеристику гравитационного поля – ускорение свободного падения g в м/с 2

в ячейку D3: 9,81

2. Размеры баскетбольной площадки – 28 метров длина и 15 метров ширина. Расстояние полета мяча почти через всю площадку до кольца от противоположной лицевой линии по горизонтали x в метрах впишем

в ячейку D4: 27,000

3. Если принять, что бросок Едешко совершил с высоты около двух метров, а Белов поймал мяч как раз где-то на уровне кольца, то при высоте баскетбольного кольца 3,05 метра расстояние между точками вылета и прилета мяча составит по вертикали 1 метр. Запишем вертикальное перемещение y в метрах

в ячейку D5: 1,000

4. По моим замерам на видеозаписи угол вылета мяча α0 из рук Едешко не превышал 20°. Введем это значение

в ячейку D6: 20,000

Результаты расчетов:

Основные уравнения, описывающие движение тела, брошенного под углом к горизонту без учета сопротивления воздуха:

5. Выразим время t из первого уравнения, подставим во второе и вычислим начальную скорость полета мяча v0 в м/с

в ячейке D8: =(D3*D4^2/2/COS (РАДИАНЫ(D6))^2/(D4*TAN (РАДИАНЫ (D6)) -D5))^0,5 =21,418

6. Время полета мяча от рук Едешко до рук Белова t в секундах рассчитаем, зная теперь v0 , из первого уравнения

в ячейке D9: =D4/D8/COS (РАДИАНЫ(D6)) =1,342

7. Найдем угол направления скорости полета мяча αi в интересующей нас точке траектории. Для этого исходную пару уравнений запишем в следующем виде:

Это уравнение параболы – траектории полета.

Нам необходимо найти угол наклона касательной к параболе в интересующей нас точке – это и будет угол αi . Для этого возьмем производную, которая представляет собой тангенс угла наклона касательной:

Рассчитаем угол прилета мяча в руки Белова αi в градусах

в ячейке D10: =ATAN (TAN (РАДИАНЫ(D6)) -D3*D4/D8^2/COS (РАДИАНЫ (D6))^2)/ПИ()*180 =-16,167

Расчет в excel, в принципе, закончен.

Иные варианты расчетов:

Используя написанную программу, можно быстро и просто при других сочетаниях исходных данных произвести вычисления.

Пусть, даны горизонтальная x =27 метров, вертикальная y =1 метр дальности полета и начальная скорость v0 =25 м/с.

Требуется найти время полета t и углы вылета α0 и прилета αi

Воспользуемся сервисом MS Excel «Подбор параметра». Я неоднократно в нескольких статьях блога подробно рассказывал, как им пользоваться. Детальнее об использовании этого сервиса можно почитать здесь.

Устанавливаем в ячейке D8 значение 25,000 за счет изменения подбором значения в ячейке D6. Результат на рисунке внизу.

Исходные данные в этом варианте расчета в excel (как, впрочем, и в предыдущем) выделены синими рамками, а результаты обведены красными прямоугольными рамками!

Устанавливая в таблице Excel некоторое интересующее значение в одной из ячеек со светло-желтой заливкой за счет подбора измененного значения в одной из ячеек со светло-бирюзовой заливкой, можно получить в общем случае десять различных вариантов решения задачи о движении тела, брошенного под углом к горизонту при десяти разных наборах исходных данных.

Ответ на вопрос:

Ответим на вопрос, поставленный в начале статьи. Мяч, посланный Иваном Едешко, долетел до Белова по нашим расчетам за 1,342с. Александр Белов поймал мяч, приземлился, подпрыгнул и бросил. На все это у него было «море» времени – 1,658с! Это действительно достаточное с запасом количество времени! Детальный просмотр по кадрам видеозаписи подтверждает вышесказанное. Нашим игрокам хватило трех секунд, чтобы доставить мяч от своей лицевой линии до щита соперников и забросить его в кольцо, вписав золотом свои имена в историю баскетбола!

Источник

Источник

Функция КОРЕНЬ принадлежит к категории Математических функций в Excel и возвращает положительное значение квадратного корня из числа.

Примеры использования функции КОРЕНЬ для математических расчетов в Excel

Пример 1. С помощью секундомера и небольшого предмета (например, камня), можно определить высоту здания (отпустить камень в свободное падение и засечь на секундомере моменты между началом движения и соприкосновения с поверхностью земли). Однако, зная высоту, можно рассчитать время, которое потребуется предмету на свободное падение. Для этого можно использовать следующую формулу: t=√(2H/g).

.

Где:

  • t – искомая величина времени падения;
  • H – высота, с которой предмет запущен в свободное падения;
  • g – ускорение свободного падения (пример равным 9,81).

Рассчитаем, сколько будет падать предмет с высоты 200 м (сопротивлением воздуха пренебрежем).

Внесем исходные данные в таблицу:

.

Для расчета используем следующую формулу:

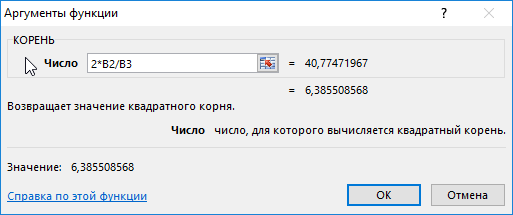
=КОРЕНЬ(2*B2/B3)

.

В качестве параметра функция принимает выражение 2*B2/B3, где:

  • B2 – ячейка с данными о высоте, с которой запущен предмет;
  • B3 – ячейка, содержащая данные об ускорении свободного падения.

В результате получим:

.

То есть, время падения составит примерно 6,4 с.



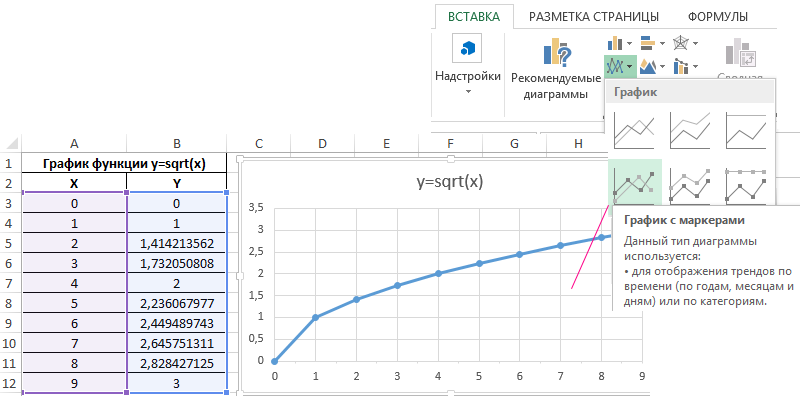
Как построить график функции в Excel?

Пример 2. Функцию КОРЕНЬ удобно использовать для построения графика следующего типа:

.

Рассмотрим на примере, как построить график данной функции в Excel.

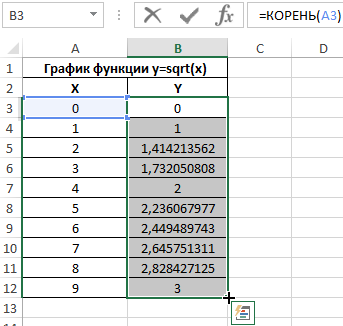
Заполним таблицу данных:

.

Для расчета значения функции y используем следующую формулу:

=КОРЕНЬ(A3)

A3 – соответствующее значение аргумента x. Аналогичным способом рассчитаем значение функции y в ячейке B4, а затем заполним таблицу следующим способом: выделим ячейки B3 и B4, поместим курсор мыши в правый нижний угол области выделения до появления знака «+».

Нажмем правую кнопку мыши и перетащим область выделения вниз до последней ячейки таблицы:

.

Так Excel по аналогии произведет расчет остальных значений функции с использованием функции КОРЕНЬ, принимающей аргументы из соответствующих ячеек.

В меню Вставка находим график с маркерами и вставляем его на лист Excel. В качестве данных для осей указываем значения аргументов x и функции y:

график с маркерами.

Как найти квадратный корень из дискриминанта в Excel?

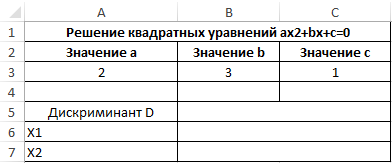
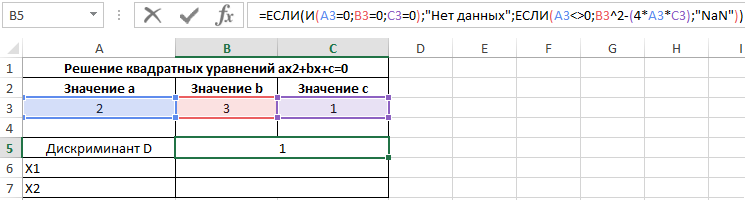
Пример 3. Для решения квадратных уравнений зачастую используют метод нахождения дискриминанта числа. Для нахождения квадратного корня из дискриминанта будет использована функция КОРЕНЬ. Создадим форму для расчета значений x1 и x2 (корней уравнения).

Для примера найдем корни уравнения 2×2+3x+c=0.

Таблица имеет следующий вид:

Таблица.

Рассмотрим формулу, введенную в ячейку B5:

Рассмотрим формулу.

С помощью формулы ЕСЛИ выполняется проверка наличия данных в ячейках A3, B3 и C3, которые содержат значения коэффициентов a, b и с. Если они пустые, в ячейке B5 отобразится текстовая строка «Значения не введены». Если A3 содержит значение, не равное нулю, производится расчет дискриминанта по известной формуле. Иначе будет выведена текстовая строка «NaN», то есть, уравнение не является квадратным, вычислить значение дискриминанта невозможно.

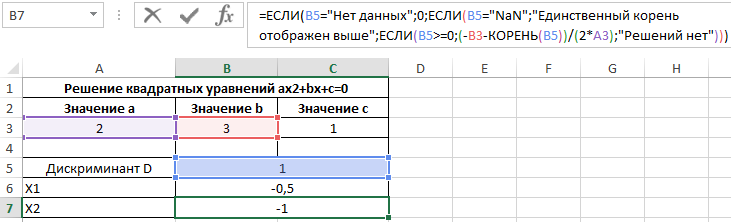
Ячейка B6 содержит следующую формулу:

содержит формулу.

Формула ЕСЛИ выполняет проверку условия ввода данных (если не введены, будет выведено значение 0). Следующая функция ЕСЛИ проверяет ячейку B5 на наличие значения «NaN». Если содержится «NaN», мы имеем дело с обычным линейным уравнением типа bx+c=0, единственный корень которого будет отображен в ячейке B6. Далее выполняется проверка дискриминанта на принадлежность к диапазону отрицательных чисел. Если дискриминант больше или равен нулю, производится расчет первого корня уравнения по известной формуле, иначе будет выведена текстовая строка «Решений нет».

Формула в ячейке B7 имеет лишь 2 отличия:

корни уравнения.

Во избежание дублирования результата в случае единственного решения уравнения, будет отображен текст «Единственный корень отображен выше». Также изменена формула расчета второго корня уравнения.

То есть, данное уравнение имеет два корня: -0,5 и -1.

Функция КОРЕНЬ в Excel и особенности ее синтаксической записи

Данная функция используется наряду с прочими математическими функциями Excel, такими как ЗНАК, КОРЕНЬПИ, ДВФАКТР и другими. Она имеет следующий синтаксис:

=КОРЕНЬ(число)

Функция принимает единственный параметр число, который принимает данные в виде числа, квадратный корень из которого требуется вычислить. Параметр обязателен для заполнения.

Примечания:

  1. В качестве параметра может быть передана ссылка на ячейку, содержащую числовые данные, либо указано определенное значение непосредственно в записи функции (например, КОРЕНЬ(A2) или КОРЕНЬ(144)).
  2. Если в качестве параметра функции КОРЕНЬ была передана ссылка на ячейку, не содержащую данных, результатом работы функции КОРЕНЬ будет 0 (нуль).
  3. Если в качестве параметра число были передано число из диапазона отрицательных чисел, функция КОРЕНЬ вернет код ошибки #ЧИСЛО!. При необходимости получения корня из отрицательного числа можно воспользоваться функцией ABS, которая возвращает модуль данного числа (абсолютное, то есть положительное значение). Например, результатом выполнения функции =КОРЕНЬ(ABS(-169)) будет число 13.
  4. Для расчета квадратного корня из числа можно использовать функцию =СТЕПЕНЬ(число;степень), где смысл параметра число эквивалентен смыслу одноименного параметра функции КОРЕНЬ, а в качестве параметра степень необходимо ввести число 0,5 (с точки зрения математики, корень квадратный из числа соответствует возведению данного числа в степень ½ или 0,5 в десятичной записи дроби).
  5. Также в Excel можно использовать математический символ «^» (Shift+6). Это означает, что еще одним эквивалентом записи «=КОРЕНЬ(A1)» является «=A1^0,5».
Источник

Использование
графических возможностей программы

 «Microsoft Office Excel»
для решения задач.

Задачей называется небольшая проблема,
которая решается с использованием логических умозаключений, эксперимента и
математических действий. Задачи являются неотъемлемым звеном учебного процесса,
обучение учащихся их решению относится к практическим методам обучения.

В процессе решения задач знания учащихся
конкретизируются, создаётся понимание сущности явлений, понятия и величины
приобретают реальный смысл, у ученика появляется способность рассуждать,
устанавливать причинно-следственные связи, выделять главное и отбрасывать
несущественное. Решение задач позволяет сделать знания учащихся осознанными,
избавить их от формализма.

Таким образом, решение задач имеет
образовательное значение, так как оно способствует усвоение учащимися курса
физики и математики.

Обучение решению
задач имеет и воспитательное значение, так как позволяет влиять на воспитание
личности ученика. Для развития личности ученика важна сама деятельность по
решению задач, когда ученик должен проявить волю, настойчивость, усидчивость,
самостоятельность.

Очень большое
значение имеет решение задач для развития учащихся, для развития их логического
мышления. В процессе решения задач могут быть созданы проблемные ситуации.

Задачи
классифицируются по содержанию, способам решения, способам задания условия
задачи, по степени сложности и т.п.

По основному
способу решения задач можно выделить качественные (задачи-вопросы),
вычислительные, графические и экспериментальные задачи. Качественные задачи
предполагают, что при их решении не выполняются вычисления, анализ задачной
ситуации осуществляется на качественном уровне. При решении вычислительных
задач выполняются вычисления; при решении экспериментальных задач применяют
физический эксперимент; при решении графических задач используют графики.

Нас интересует
графический способ решения задач. В этом случае объектом исследования является
график. В одних задачах он является условием и график надо проанализировать,
как говорят, «прочитать график». В других задачах график должен построить сам
учащийся по тем данным, которые приведены в условии задачи или которые он
получает в результате решения задачи.

Не секрет,
учащиеся «боятся» графиков, не понимают их, в то время как графики во многом
помогают решить задачу, а подчас и вовсе упрощают её. Необходимо «подружить»
детей с графиками, научить строить их, анализировать и использовать при решении
задач. Учащимся было предложено овладеть построением графиков различных
функций, используя компьютерную программу «Excel».
Таким образом, данную работу можно считать интегрированной: учащиеся овладевают
компьютерной грамотностью и закрепляют материал по физике и математике.

Приведу
несколько примеров решения задач по физике и математике:

Задача
№ 1

Тело
брошено вертикально вверх с начальной скоростью 40 м/с. Через сколько секунд
оно окажется на высоте 60 м?

Решение:

Если
не учитывать сопротивление воздуха, то высота h(м), на которой
брошенное вертикально вверх тело окажется через t(c), может
быть найдено по формуле:

h = vot – gt2/2,

где vo (м/с) –
начальная скорость

g – ускорение
свободного падения, приближённо равное 10 м/с2.

Создадим
таблицу для функции h(t), t – меняется
в интервале от 0 до 8 с шагом 1и построим график.

t

h

0

0

1

35

2

60

3

75

4

80

5

75

6

60

7

35

8

0

Анализируя график,
видим, что 4с тело поднималось вверх до высоты 80 м, а затем начинает падать.

Ответ:
на высоте 60 м тело побывает дважды через 2с и через 6с

Задача
№ 2

Тело брошено
вертикально вверх с начальной скоростью 20 м/с. Когда оно достигло высшей точки
пути, из того же начального пункта с той же скоростью 20 м/с брошено второе тело.
На какой высоте от начального пункта они встретятся?

Решение:

Если
не учитывать сопротивление воздуха, то высота h(м), на которой
брошенное вертикально вверх тело окажется через t(c), может
быть найдено по формуле:

h = vot – gt2/2,

где vo (м/с) –
начальная скорость

g – ускорение
свободного падения, приближённо равное 10 м/с2.

Время
подъёма первого тела на h max   определим
по формуле t = vo/g  (2c)

Создадим
таблицу для функции h(t), t – меняется
в интервале от 0 до 4 с шагом 0.5 и построим график.

t1

h1

t2

h2

0

0

0,5

8,75

1

15

1,5

18,75

2

20

0

0

2,5

18,75

0,5

8,75

3

15

1

15

3,5

8,75

1,5

18,75

4

0

2

20

Анализируя график,
видим, что через 3с  на высоте 15м тела встретятся.

Используя
компьютерную программу «Excel»,
продемонстрируем графический способ решения   систем уравнений.

№
1. Решить систему линейных уравнений графическим способом (на интервале

от
-5 до 5, шаг 0,5)

         

x

y1

y2

-5

-13,3333

-11,25

-4,5

12,6667

-10,875

-4

-12

-10,5

-3,5

-11,3333

-10,125

-3

-10,6667

-9,75

-2,5

-10

-9,375

-2

-9,33333

-9

-1,5

-8,66667

-8,625

-1

-8

-8,25

-0,5

-7,33333

-7,875

0

-6,66667

-7,5

0,5

-6

-7,125

1

-5,33333

-6,75

1,5

-4,66667

-6,375

2

-4

-6

2,5

-3,33333

-5,625

3

-2,66667

-5,25

3,5

-2

-4,875

4

-1,33333

-4,5

4,5

-0,66667

-4,125

5

0

-3,75

По графику видно, что система имеет
единственное решение.

№
2. Решить систему линейных уравнений графическим способом

 (на
интервале   от -3 до 3, шаг 0,5)

x

y1

y2

-3

10

10

-2,5

9

9

-2

8

8

-1,5

7

7

-1

6

6

-0,5

5

5

0

4

4

0,5

3

3

1

2

2

1,5

1

1

2

0

0

2,5

-1

-1

3

-2

-2

Ответ: бесконечное
множество

№
3. Решить систему линейных уравнений графическим способом

 (на
интервале   от -3 до 3, шаг 0,5)

x

y1

y2

-3

-9

-4,5

-2,5

-8,5

-4

-2

-8

-3,5

-1,5

-7,5

-3

-1

-7

-2,5

-0,5

-6,5

-2

0

-6

-1,5

0,5

-5,5

-1

1

-5

-0,5

1,5

-4,5

0

2

-4

0,5

2,5

-3,5

1

3

-3

1,5

Ответ: решений нет

№
4. Решить систему уравнений графическим способом

(на
интервале   от -3 до 3, шаг 0,5)

       

x

y1

y2

-3

9

-3

-2,5

6,25

-2

-2

4

-1

-1,5

2,25

0

-1

1

1

-0,5

0,25

2

0

0

3

0,5

0,25

4

1

1

5

1,5

2,25

6

2

4

7

2,5

6,25

8

3

9

9

Ответ:
(-1,1), (3,9)  — решения системы

№
5. Решить систему уравнений графическим способом

(на
интервале   от -5 до 5, шаг 0,5)

x

y1

y2

y3

-5

0

0

-7

-4,5

2,17945

-2,1794

-6

-4

3

-3

-5

-3,5

3,57071

-3,5707

-4

-3

4

-4

-3

-2,5

4,33013

-4,3301

-2

-2

4,58258

-4,5826

-1

-1,5

4,7697

-4,7697

0

-1

4,89898

-4,899

1

-0,5

4,97494

-4,9749

2

0

5

-5

3

0,5

4,97494

-4,9749

4

1

4,89898

-4,899

5

1,5

4,7697

-4,7697

6

2

4,58258

-4,5826

7

2,5

4,33013

-4,3301

8

3

4

-4

9

3,5

3,57071

-3,5707

10

4

3

-3

11

4,5

2,17945

-2,1794

12

5

0

0

13

Используя
компьютерную программу «Excel»,
можно создавать рисунки, например «зонтик».

Построить
графики функций, где х принимает значения от -12 до 12, шаг 0,1

Y1
= -x2 /18 + 12                 xÎ(-12;
12)

Y2
= -x2 /8 + 6                     xÎ
(-
4; 4)

Y3
= -(x + 8) 2 /8 + 6            xÎ
(-
12; -4)

Y4
= -(x — 8) 2 /8 + 6             xÎ
(4;
12)

Y5
= 2(x + 3)2
— 9               xÎ
(-4; -0,3)

Y6
= 1.5(x + 3)2
— 10           xÎ (-4;
0,2)

Microsoft
Excel — одна из самых загадочных и интересных программ в пакете MS Office.
Интересна она многочисленными средствами автоматизации работы, оформления
документов и богатыми вычислительными возможностями. Загадочность ее состоит в
том, что большинство пользователей применяют лишь малую толику того, что может
дать им Excel. Это тем более удивительно, что спектр возможностей программы
практически безграничен: от создания простых таблиц, построения диаграмм и
графиков до решения сложных вычислительных задач и моделирования различных
процессов.

Источник

Понравилась статья? Поделить с друзьями:
  • Уроки работы office word
  • Уроки по word формулы
  • Уроки работы excel 2010
  • Уроки по word списки
  • Уроки программирования на excel для начинающих