Excel for Microsoft 365 Excel for Microsoft 365 for Mac Excel for the web Excel 2021 Excel 2021 for Mac Excel 2019 Excel 2019 for Mac Excel 2016 Excel 2016 for Mac Excel 2013 Excel 2010 Excel for Mac 2011 Excel Starter 2010 More…Less
Returns the probability associated with a Student’s t-Test. Use T.TEST to determine whether two samples are likely to have come from the same two underlying populations that have the same mean.
Syntax
T.TEST(array1,array2,tails,type)
The T.TEST function syntax has the following arguments:
-
Array1 Required. The first data set.
-
Array2 Required. The second data set.
-
Tails Required. Specifies the number of distribution tails. If tails = 1, T.TEST uses the one-tailed distribution. If tails = 2, T.TEST uses the two-tailed distribution.
-
Type Required. The kind of t-Test to perform.
Parameters
|
If type equals |
This test is performed |
|
1 |
Paired |
|
2 |
Two-sample equal variance (homoscedastic) |
|
3 |
Two-sample unequal variance (heteroscedastic) |
Remarks
-
If array1 and array2 have a different number of data points, and type = 1 (paired), T.TEST returns the #N/A error value.
-
The tails and type arguments are truncated to integers.
-
If tails or type is nonnumeric, T.TEST returns the #VALUE! error value.
-
If tails is any value other than 1 or 2, T.TEST returns the #NUM! error value.
-
T.TEST uses the data in array1 and array2 to compute a non-negative t-statistic. If tails=1, T.TEST returns the probability of a higher value of the t-statistic under the assumption that array1 and array2 are samples from populations with the same mean. The value returned by T.TEST when tails=2 is double that returned when tails=1 and corresponds to the probability of a higher absolute value of the t-statistic under the “same population means” assumption.
Example
Copy the example data in the following table, and paste it in cell A1 of a new Excel worksheet. For formulas to show results, select them, press F2, and then press Enter. If you need to, you can adjust the column widths to see all the data.
|
Data 1 |
Data 2 |
|
|
3 |
6 |
|
|
4 |
19 |
|
|
5 |
3 |
|
|
8 |
2 |
|
|
9 |
14 |
|
|
1 |
4 |
|
|
2 |
5 |
|
|
4 |
17 |
|
|
5 |
1 |
|
|
Formula |
Description |
Result |
|
=T.TEST(A2:A10,B2:B10,2,1) |
Probability associated with a Student’s paired t-Test, with a two-tailed distribution. |
0.196016 |
Need more help?
A T-test in excel helps compare the means (average) of two samples and make inferences for the entire populations. By performing a t-test, one can say whether the difference between the two means is statistically significant or by chance alone. An outcome (result) is said to be statistically significant if the reason behind its occurrence can be attributed to a specific cause rather than to coincidence (or chance). Such results are reliable and provide confidence in decision-making.
For example, an organization launches a new policy for the employees (customer service associates or CSA) of its marketing department. According to this policy, if the number of customer complaints resolved in a day crosses 50, two additional leaves (in a month) will be granted to an employee.
Further, the organization performs the following tasks:
- Collects the data of complaints addressed and resolved (before and after the policy) by a sample of CSAs.
- Conducts a paired t-test in excel (refer to the heading “types of t-tests” of this article) to determine whether there is any difference in the productivity of the CSAs before and after the introduction of the policy.
- Interprets and analyzes the findings of the excel t-test to determine whether the results are statistically significantStatistical significance is the probability of an observation not being caused by a sampling error.read more or caused by chance.
The aim of conducting this paired t-test is to assess whether the productivity of employees is impacted positively or negatively by the introduction of the new policy. Moreover, if the productivity increases, similar policies can be launched for the employees of other departments as well.
T-tests are used for testing a hypothesisHypothesis Testing is the statistical tool that helps measure the probability of the correctness of the hypothesis result derived after performing the hypothesis on the sample data. It confirms whether the primary hypothesis results derived were correct.read more. A hypothesis is an assumption that is tested to check whether it holds true or false. The null and alternative hypotheses are two opposing statements.
A null hypothesis is created using the operators, “equal to,” “greater than or equal to” or “less than or equal to.” In contrast, an alternative hypothesis uses the operators, “not equal to,” “greater than,” or “less than.”
A t-test in excel can be conducted by using the Data Analysis ToolPakExcel’s data analysis toolpak can be used by users to perform data analysis and other important calculations. It can be manually enabled from the addins section of the files tab by clicking on manage addins, and then checking analysis toolpak.read more or the TTEST function of Excel. The TTEST function was replaced by the T.TEST function in Excel 2010. However, in this article, we use the TTEST function of Excel for performing the t-test.
The TTEST or the T.TEST functions are categorized under the Statistical functions of Excel.
Table of contents
- T-test in Excel
- Syntax of the TTEST Function of Excel
- Types of T-tests
- How to use the TTEST Function in Excel?
- Example #1–Paired Sample T-test Using One-tail Distribution
- Example #2–Two-sample Equal Variance T-test Using One-tail Distribution
- Example #3–Two-sample Unequal Variance T-test Using One-tail Distribution
- Example #4–Paired Excel T-test Using One-tail Distribution in VBA
- The Errors Returned by the TTEST Function of Excel
- T-TEST in Excel Video
- Frequently Asked Questions
- Recommended Articles
Syntax of the TTEST Function of Excel
The syntax of the TTEST function is shown in the following image:
The TTEST function accepts the following arguments:
- Array1: This is the first dataset on which the excel t-test is to be performed.
- Array2: This is the second dataset on which the excel t-test is to be performed.
- Tails: This specifies the kind of distribution to be used. This argument can take either of the following values:
- 1–This implies a one-tailed distribution. A one-tailed t-test is performed when one wants to study the specific direction (only positive direction or only negative direction) of difference between the two means.
- 2–This implies a two-tailed distribution. A two-tailed t-test is performed when one wants to find out whether the two population means are different from one another or not.
- Type: This is the kind of t-testA T-test is a method to identify whether the means of two groups differ from one another significantly. It is an inferential statistics approach that facilitates the hypothesis testing.read more to be performed. This argument can take any of the following values:
- 1–This implies that a paired samples t-test is to be performed.
- 2–This implies that a two-sample equal variance t-test is to be performed. One must perform this test when there are two independent samples having the same (equal) population variances. The feature of the same variance is known as homoscedasticity.
- 3–This implies that a two-sample unequal variance t-test (or the Welch t-test) is to be performed. One must perform this test when there are two independent samples having unequal or unknown variances. The feature of unequal variances is known as heteroscedasticity.
All the preceding arguments are mandatorily required when conducting a t-test in Excel.
Note: For information about the kind of t-tests, refer to the next heading, “types of t-tests.”
Types of T-tests
A t-test can be of the following types:
- Independent samples t-test–It compares the means of two independent or unrelated samples or groups. It is also called an unpaired t-test or a two-sample t-test. It is used when the population mean or standard deviation is unknown.
- Paired samples t-test–It compares the means of the same group at different time periods. In other words, the t-test is conducted on dependent or related samples. The paired samples t-test is also conducted when the samples are different but subjected to the same conditions. For instance, one may want to measure the effectiveness (using the same technique) of the same product manufactured by two different manufacturers. The paired samples t-test is also called the dependent samples t-test.
- One-sample t-test–It compares the mean of a single sample with the known mean (target value or hypothetical value) of a population (from which this sample is drawn).
Note 1: Select the type of t-test to be conducted by taking into account the kind of data and the kind of analysis required. For instance, if the two sample sets are related, use the paired t-test. Further, the paired samples t-test must be performed when both the sample sets are of the same size. This implies that the number of data points of both samples is the same.
If the samples are independent, use the two-sample equal variance or two-sample unequal variance t-tests depending on whether the variances are equal or unequal respectively.
Note 2: For more information on the type of t-test to be performed, refer to the heading “frequently asked questions” at the end of this article.
How to use the TTEST Function in Excel?
The TTEST function of Excel is simple and easy to use. Let us consider some examples to understand the working of the TTEST function in Excel.
You can download this TTEST Function Excel Template here – TTEST Function Excel Template
Example #1–Paired Sample T-test Using One-tail Distribution
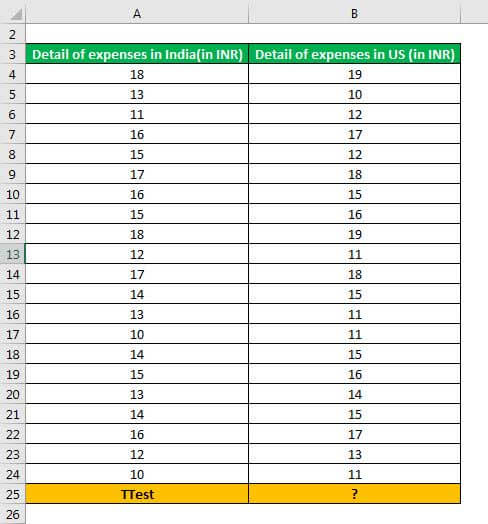
The following image shows the expenses incurred (in INR) by an organization in two countries, India and USA. Perform a paired sample t-test in excel using a one-tail distribution.
The steps to perform a paired t-test with one-tail distribution are listed as follows:
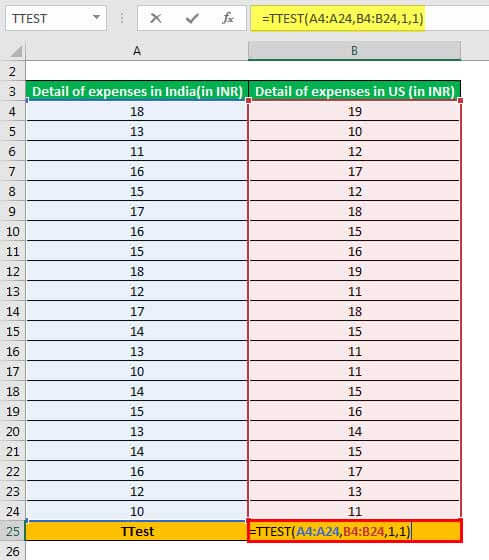
Step 1: Enter the following formula in cell B25.
“=TTEST(A4:A24,B4:B24,1,1)”
The same is shown in the following image.
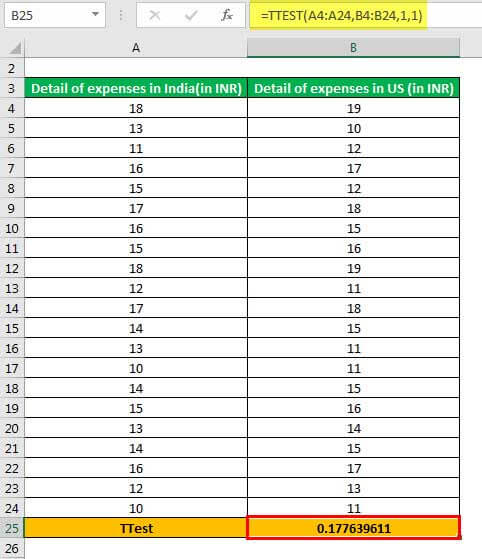
Step 2: Press the “Enter” key. The output in cell B25 is 0.177639611, as shown in the following image.
Explanation: The range A4:A24 (entered in step 1 of the formula) is the first array on which the excel t-test is to be performed. Likewise, the range B4:B24 is the second array on which the t-test is to be performed.
Further, we have entered the “tails” and “type” arguments as 1. This is because a one-tailed, paired t-test needs to be performed.
Interpretation: To accept or reject the null hypothesisNull hypothesis presumes that the sampled data and the population data have no difference or in simple words, it presumes that the claim made by the person on the data or population is the absolute truth and is always right. So, even if a sample is taken from the population, the result received from the study of the sample will come the same as the assumption.read more, perform the following tasks:
- Calculate the t-table value by referring to the one-tail t-distribution table, at a certain significance level (alpha) with the specific degrees of freedomDegrees of freedom (df) refers to the number of independent values (variable) in a data sample used to find the missing piece of information (fixed) without violating any constraints imposed in a dynamic system. These nominal values have the freedom to vary, making it easier for users to find the unknown or missing value in a dataset.read more (df). Compare the t-table value with the calculated t-value (0.177639611). If the calculated t-value is greater than the t-table value, reject the null hypothesis.
- Calculate the p-value based on the t-table value. Compare the p-valueP-Value, or Probability Value, is the deciding factor on the null hypothesis for the probability of an assumed result to be true, being accepted or rejected, & acceptance of an alternative result in case of the assumed results rejection. read more with the significance level. Since the significance level (alpha) is not specified in the question, consider it as 0.05 or 5%. If the p-value is less than the significance level, reject the null hypothesis.
The acceptance or rejection of the null hypothesis should be carried out by using a combination of the p and t values (obtained in the preceding pointers a and b). Further, rejecting a null hypothesis implies accepting the alternative hypothesis.
Note 1: The negative sign (if any) can be ignored when comparing the t-values.
Note 2: The null hypothesis of a paired sample excel t-test assumes that the mean difference of paired observations is zero. In other words, the mean of paired observations is equal.
The alternative hypothesis of a paired sample t-test assumes that the mean difference of paired observations is not equal to zero. For instance, the difference between the paired observations for row 4 is (18-19) or (cell A4-cell B4).
Rejecting the null hypothesis implies that the mean difference of paired observations does exist. In other words, this mean difference is not equal to zero.
Example #2–Two-sample Equal Variance T-test Using One-tail Distribution
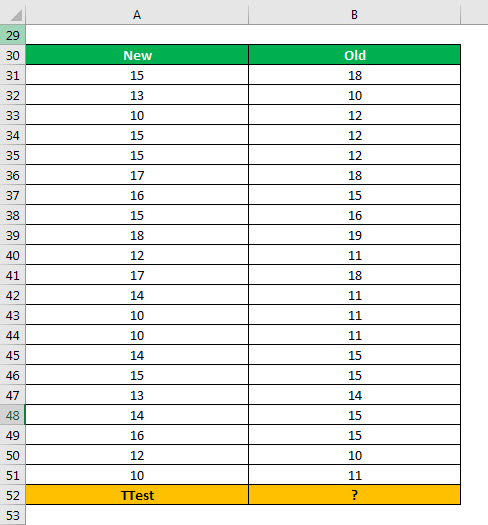
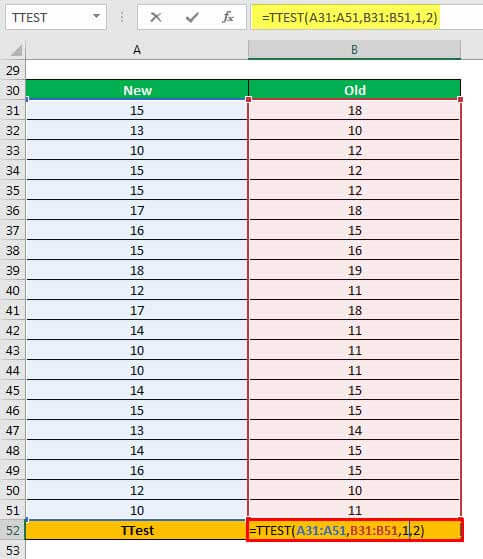
An organization has introduced a new flavor of a beverage in the market. To test the effectiveness of this flavor, two samples (consisting of 21 people in each sample) are created.
The different people who tasted the new flavor are listed in the column “new.” The different people who tasted the old flavor are listed in the column “old.” Consider the groups “new” and “old” as independent samples.
The population variancesPopulation variance can be calculated using this formula: σ2 = ∑ni=1 (xi – μ)2 / N, where, σ2 is population variance, x1, x2, x3,…..xn are the observations, N is the number of observations and µ is the mean of the data set.read more of both samples, “new” and “old,” are equal. Calculate the two-sample equal variance t-test in excel using a one-tail distribution.
The steps to perform the two-sample equal variance t-test using a one-tail distribution are listed as follows:
Step 1: Enter the following formula in cell B52.
“=TTEST(A31:A51,B31:B51,1,2)”
The same is shown in the following image.
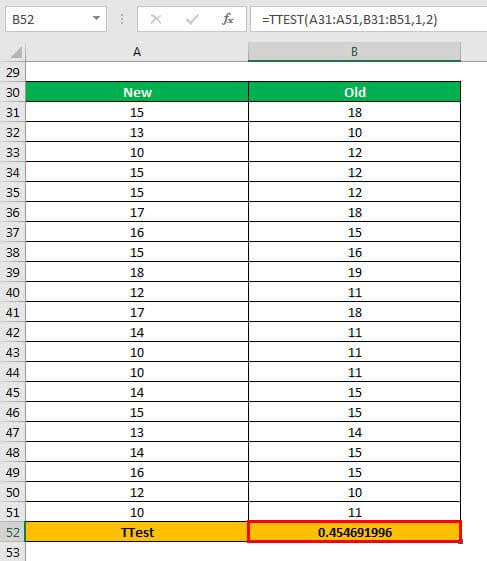
Step 2: Press the “Enter” key. The output in cell B52 is 0.454691996.
Explanation: The first array (in the formula entered in step 1) is A31:A51 and the second array is B31:B51. The argument 1 indicates that a one-tailed test is to be performed. The argument 2 implies that a two-sample equal variance t-test is to be conducted.
Interpretation: To accept or reject the null hypothesis, compare the calculated t-value with the t-table value. At the same time, compare the p-value with the standard significance level (0.05).
Note 1: The null hypothesis of the two-sample equal variance t-test in excel states that the difference between the two sample means is zero. In other words, the two sample means are equal. The alternative hypothesis states that the two sample means are not equal.
Note 2: If one is using the Data Analysis Toolpak, compare the t-statistic of the results obtained with the t-critical one-tail value. If the t-statistic is larger than the t-critical one-tail value, reject the null hypothesis.
Likewise, compare the p one-tail value with the significance level. If the former (p one-tail value) is less than the latter (significance level), reject the null hypothesis.
Rejecting a null hypothesis implies that there is a difference between the two sample means. Moreover, this difference is not explainable by chance alone.
Note 3: While using the Data Analysis Toolpak, if one does not know which t-values (of one-tail or two-tail test) are to be compared, always compare the t-statistic with the t-critical two-tail value.
Example #3–Two-sample Unequal Variance T-test Using One-tail Distribution
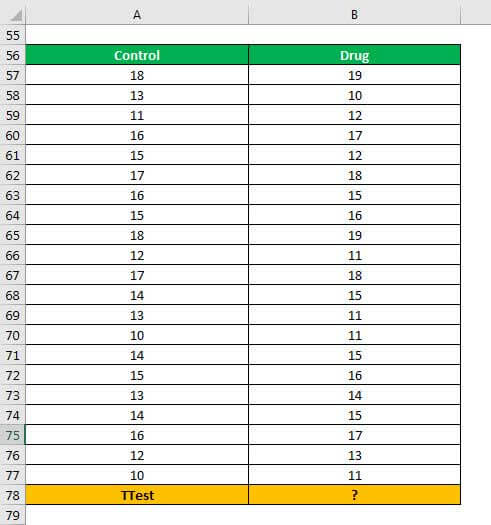
A researcher wants to study the impact of a new drug on the car driving skills of a person. A total of 21 individuals were administered the drug prior to being given a driving test.
The column A of the following image shows the score assigned to each driver. The column B shows the level of drug (in percentage) given to each driver.
The population variances of both the samples are unequal. Perform the two-sample unequal variance test using a one-tail distribution.
The steps to perform the two-sample unequal variance test using a one-tail distribution are listed as follows:
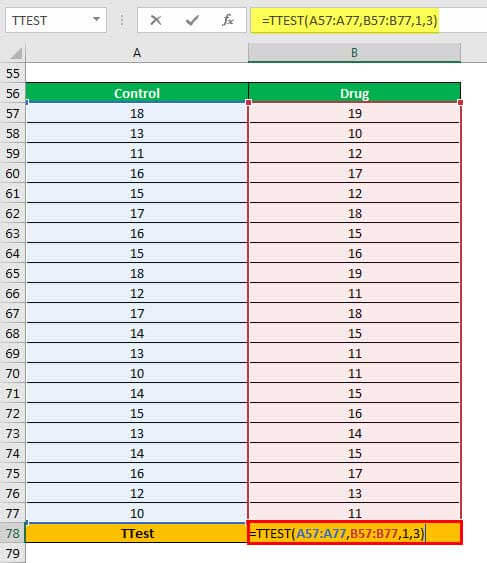
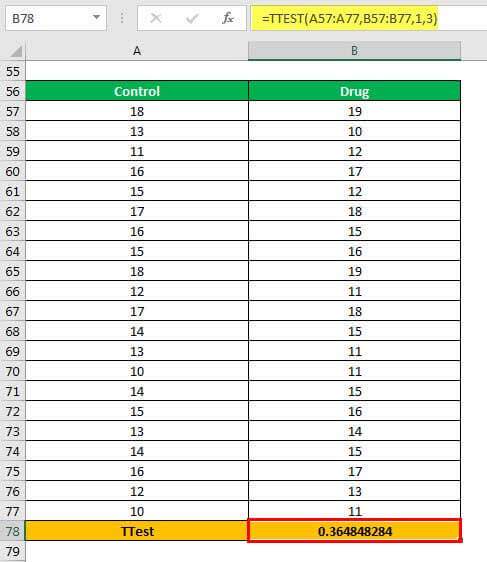
Step 1: Enter the following formula in cell B78.
“=TTEST(A57:A77,B57:B77,1,3)”
The same is shown in the following image.
Step 2: Press the “Enter” key. The output is 0.364848284, as shown in the following image.
Explanation: The range A57:A77 represents the first array (in the formula entered in step 1). The range B57:B77 represents the second array on which the excel t-test is to be performed.
Since a one-tailed test is to be performed, we enter 1 in the “tails” argument. The 3 in the “type” argument implies that the two-sample unequal variance t-test is to be performed.
Interpretation: Compare the t-calculated value with the t-table value. If the former is greater than the latter at the given significance level, reject the null hypothesis. Likewise, if the p-value is smaller than the significance level, reject the null hypothesis and accept the alternative hypothesis.
Note: The null hypothesis for the two-sample unequal variance t-test states that the mean of the two samples is the same (or equal). The alternative hypothesis states that the mean of the two samples is not the same (or unequal).
Example #4–Paired Excel T-test Using One-tail Distribution in VBA
There are two datasets in the ranges A4:A24 and B4:B24 of Excel. Write the VBA codeVBA code refers to a set of instructions written by the user in the Visual Basic Applications programming language on a Visual Basic Editor (VBE) to perform a specific task.read more to conduct a t-test on the given ranges.
The VBA code is written as follows:
Sub TTESTcal() // start the TTEST function scope
Dim TTEST as interger
TTEST = Application.WorksheetFunction.TTest(Range(“A4:A24”),Range(“B4:B24”),1,1)
MsgBox TTEST // print the TTEST value in the message box.
End sub // End the TTEST function
The Errors Returned by the TTEST Function of Excel
The TTEST function can return the following types of errors:
- “#N/A” error: This is displayed if the two arrays supplied are of different lengths and a paired t-test is to be performed.
- “#NAME?” error: This is displayed if either of the arguments “tails” or “type” is provided as a text value.
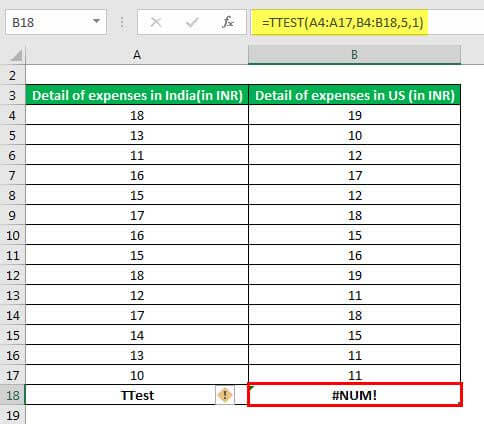
- “#NUM!” error: This is displayed on account of either of the following reasons:
- If the “tails” argument is other than the numbers 1 or 2
- If the “type” argument is other than the numbers 1, 2 or 3
The “#NUM!” error is shown in the following image. It must be observed that the “tails” argument in the TTEST formula has been entered as 5. Moreover, the two arrays supplied are of different sizes.
Had the arrays been equal in length and the “tails” and “type” arguments had remained 5 and 1 respectively, the “#NUM!” error would still have been displayed.
T-TEST in Excel Video
Frequently Asked Questions
1. Define t-test and state its syntax used in Excel.
A t-test is a hypothesis test that is conducted on random samples drawn from a population. By performing a t-test, the means of two samples are compared. The t-test is a parametric test which assumes that the population data is normally distributed.
A t-test can be performed either by using the Data Analysis ToolPak or the TTEST (or T.TEST) function of Excel. The syntax of the TTEST function of Excel is stated as follows:
“TTEST(array1,array2,tails,type)”
Note 1: A normal distribution is represented by a bell-shaped curve which shows the distribution of the data points.
Note 2: For an explanation related to the arguments of the TTEST function, refer to the heading “syntax of the TTEST function of Excel” of this article.
2. Which t-test should be used in Excel?
One can perform any of the following t-tests on the basis of the given considerations:
a. Independent samples t-test–Perform this test if the two datasets pertain to unrelated or independent samples. In other words, the two datasets come from two different populations. Each population consists of unique data points. Further, the population means and/or the standard deviations are unknown.
b. Paired sample t-test–Perform this test if the two samples are related or dependent on each other. In other words, the two datasets come from the same population and have the same number of data points.
c. One sample t-test–Perform this test if the single sample mean is to be compared with a hypothetical value.
d. Two-sample equal variance t-test–Perform this test if the variances of the two populations are known to be equal.
e. Two-sample unequal variance t-test–Perform this test if the variances of the two populations are unequal. One can also perform this test when he/she does not know whether the variances of the two populations are equal or not.
f. One-tail t-test–Perform this test if one wants to study the specific direction of difference between the two sample means. In other words, the user is interested in one direction of difference (sample A mean is greater than the sample B mean) and not interested in the opposite direction of difference (sample A mean is lesser than the sample B mean). A one-tail t-test can detect differences between the two means in a single direction only.
g. Two-tail t-test–Perform this test if one wants to know whether a difference between the two sample means exists or not. A two-tail t-test can detect both positive and negative differences between the two means. For instance, one may want to find out if sample A mean is greater than or lesser than the sample B mean.
Note: If more than two groups are to be compared, use ANOVA (Analysis of Variance) instead of the t-test.
3. How should the t-test of Excel be interpreted?
Interpreting the results of a t-test helps in accepting or rejecting the null hypothesis. For interpretation, one must perform the following tasks:
a. Compare the calculated t-value or the t-statistic with the t-table value. If the former is more than the latter, reject the null hypothesis.
b. Compare the p-value with the significance level (if not given in the question, assume the standard significance level of 0.05). If the former is less than the latter, reject the null hypothesis.
Prior to carrying out the calculations, it is essential to state the null and alternative hypotheses clearly and precisely. This provides a direction to the process of interpretation of results.
The null and alternative hypotheses are contradictory to each other. To accept or reject either of them, strong evidence is required. So, one must ensure that the sample data supports the acceptance or rejection decision.
Recommended Articles
This has been a guide to t-test in Excel. Here we discuss the t-test formula in Excel and how to use it along with examples and downloadable Excel templates. You may also look at these useful functions in Excel–
- Quartile FormulaQuartile Formula is a statistical tool to calculate the variance from the given data by dividing the same into four defined intervals. First Quartile could be calculated as follows: (Q1) = ((n + 1)/4)th Term.read more
- Mode Formula ExcelThe MODE Function in Excel is a statistical function that returns the most often occurring value in a dataset. In case there are multiple modes, it will return the lowest one. read more
- VBA “MsgBox”VBA MsgBox function is an output function which displays the generalized message provided by the developer. This statement has no arguments and the personalized messages in this function are written under the double quotes while for the values the variable reference is provided.read more
- Not Equal to in Excel“Not Equal to” argument in excel is inserted with the expression <>. The two brackets posing away from each other command excel of the “Not Equal to” argument, and the user then makes excel checks if two values are not equal to each other.read more
17 авг. 2022 г.
читать 3 мин
Двухвыборочный t-критерий используется для проверки того, равны ли средние значения двух совокупностей.
В этом руководстве представлено полное руководство по интерпретации результатов двухвыборочного t-теста в Excel.
Шаг 1: Создайте данные
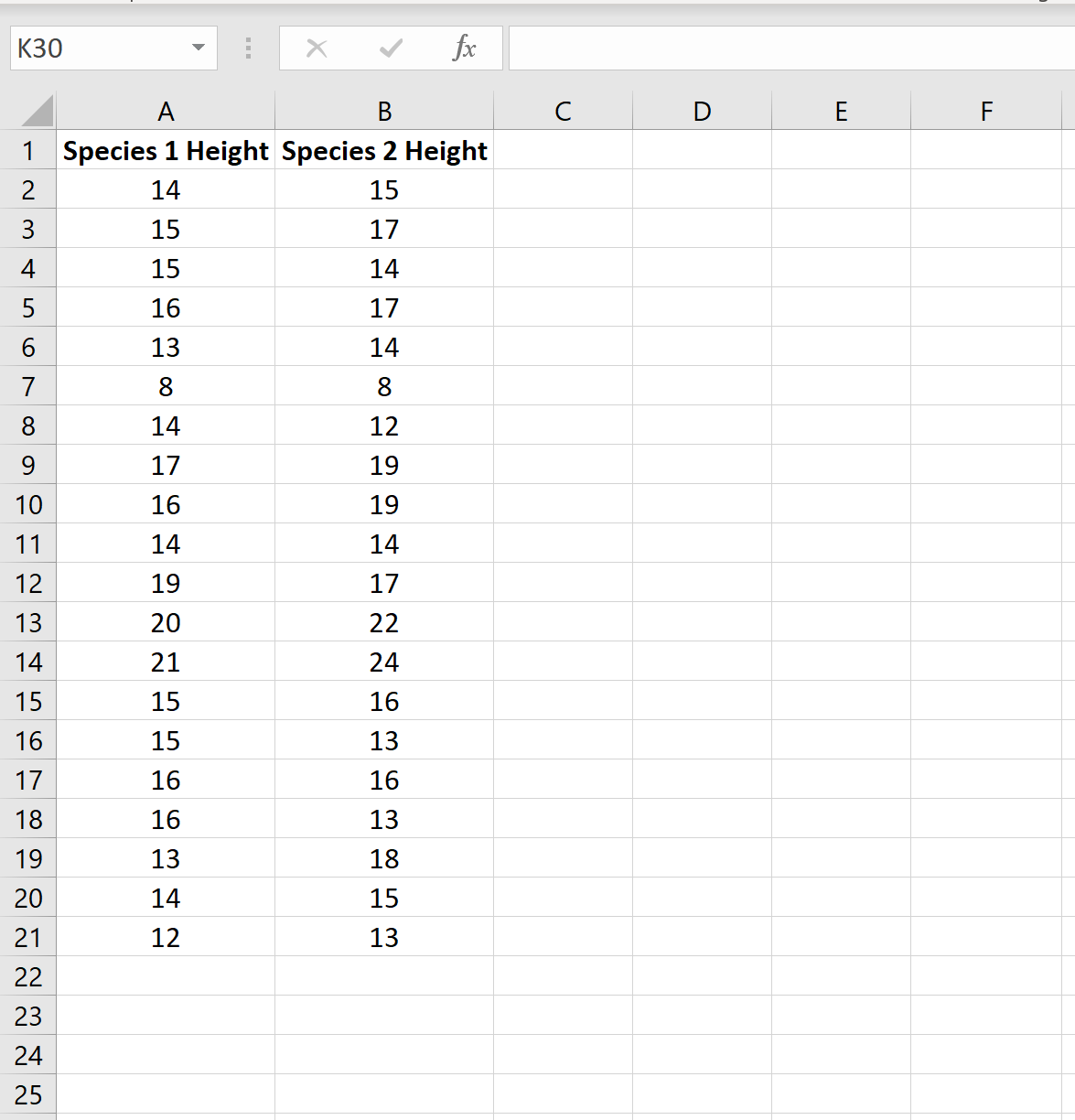
Предположим, биолог хочет знать, имеют ли два разных вида растений одинаковую среднюю высоту.
Чтобы проверить это, она собирает простую случайную выборку из 20 растений каждого вида:
Шаг 2. Выполните t-тест для двух выборок.
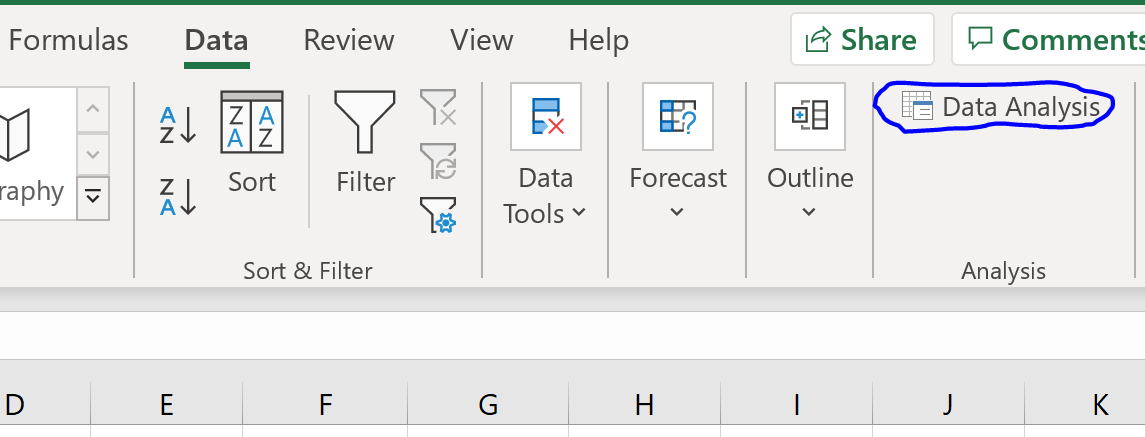
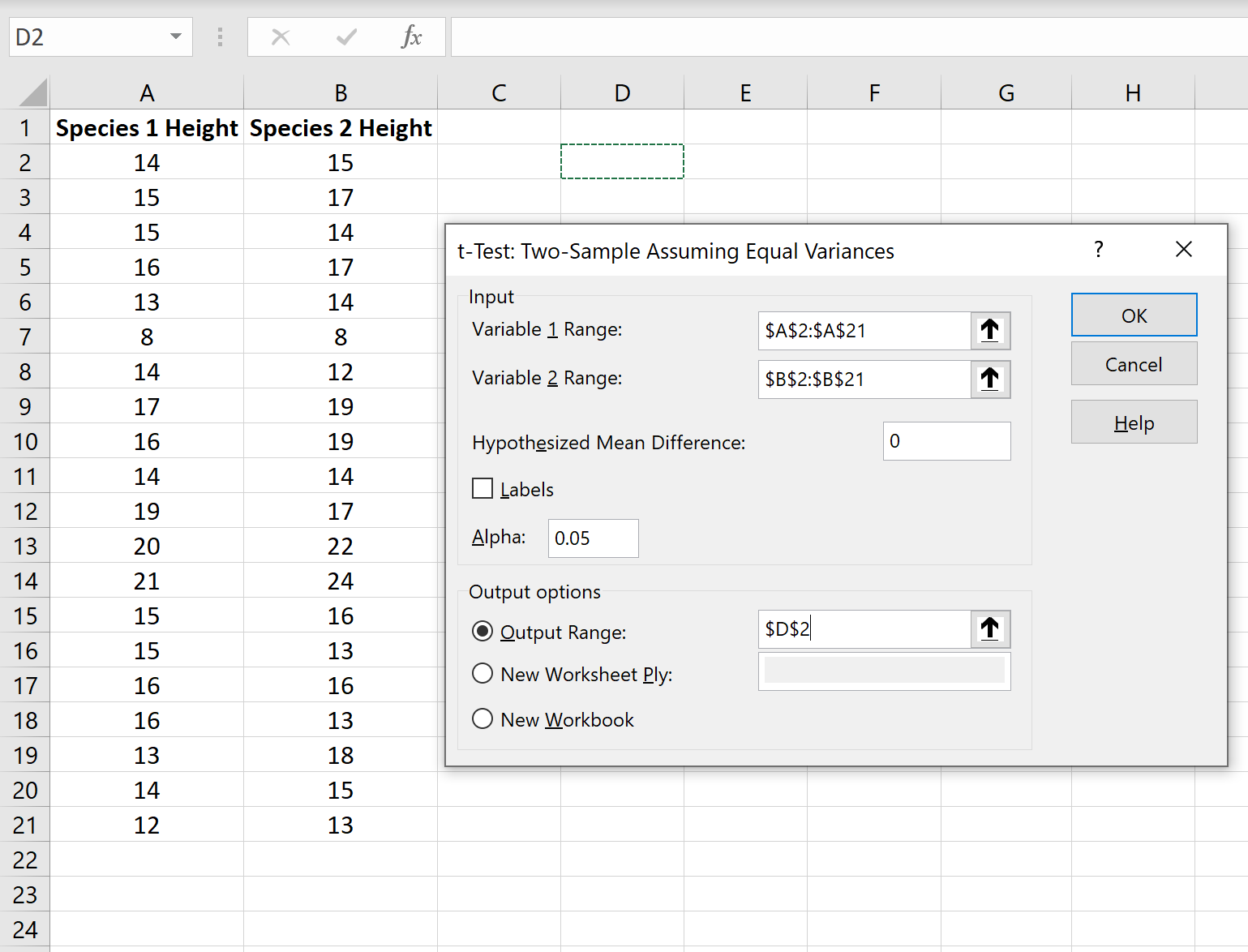
Чтобы выполнить двухвыборочный t-критерий в Excel, щелкните вкладку « Данные » на верхней ленте, а затем щелкните « Анализ данных» :
Если вы не видите эту опцию, вам необходимо сначала загрузить пакет инструментов анализа .
В появившемся окне выберите параметр под названием t-Test: Two-Sample, предполагающий равные отклонения , а затем нажмите OK.Затем введите следующую информацию:
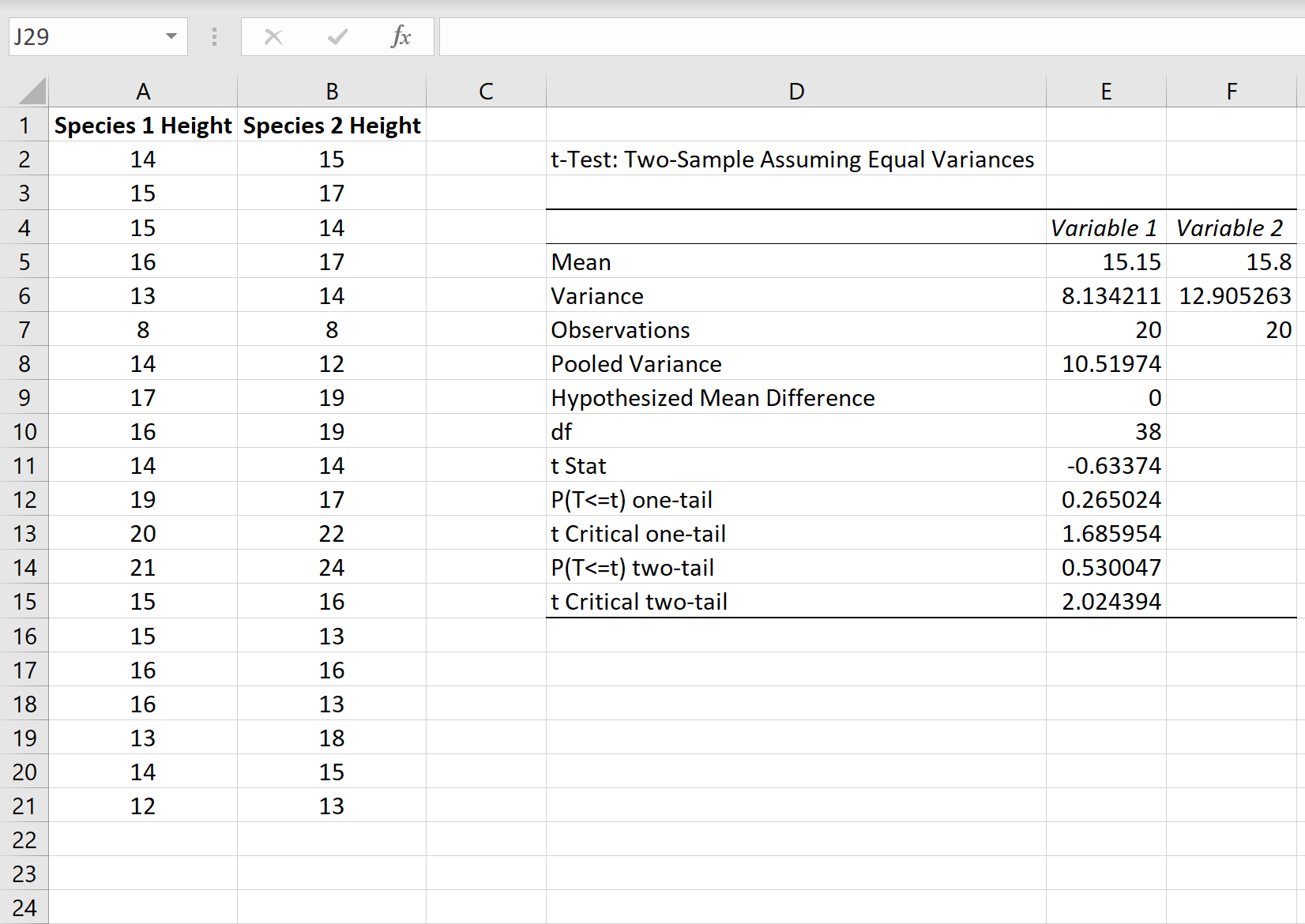
После того, как вы нажмете OK , отобразятся результаты t-теста:
Шаг 3: интерпретируйте результаты
Вот как интерпретировать каждую строку в результатах:
Среднее значение: среднее значение каждого образца.
- Образец 1 Среднее значение: 15,15
- Образец 2 Среднее значение: 15,8
Дисперсия: Дисперсия каждого образца.
- Образец 1 Дисперсия: 8,13
- Образец 2 Дисперсия: 12,9
Наблюдения: количество наблюдений в каждой выборке.
- Образец 1 Наблюдения: 20
- Образец 2 Наблюдения: 20
Объединенная дисперсия: средняя дисперсия выборок, рассчитанная путем «объединения» дисперсий каждой выборки вместе по следующей формуле:
- s 2 p = ((n 1 -1)s 2 1 + (n 2 -1)s 2 2 ) / (n 1 +n 2 -2)
- с 2 р = ((20-1)8,13 + (20-1)12,9) / (20+20-2)
- с 2 р = 10,51974
Гипотетическая средняя разница: число, которое мы «предполагаем», представляет собой разницу между двумя средними значениями совокупности. В этом случае мы выбрали 0 , потому что хотим проверить, равна ли разница между двумя популяциями в среднем 0.
df: Степени свободы для t-критерия, рассчитанные как:
- df = n 1 + n 2 – 2
- df = 20 + 20 – 2
- дф = 38
t Stat: тестовая статистика t , рассчитанная как:
- т знак равно ( Икс 1 — Икс 2 ) / √ с 2 п (1 / п 1 + 1 / п 2 )
- t = (15,15–15,8) / √ 10,51974 (1/20+1/20)
- т = -0,63374
P(T<=t) двухсторонний: значение p для двустороннего t-критерия. Это значение можно найти с помощью любого калькулятора T Score to P Value, используя t = -0,63374 с 38 степенями свободы.
В этом случае р = 0,530047.Это больше, чем 0,05, поэтому мы не можем отвергнуть нулевую гипотезу. Это означает, что у нас нет достаточных доказательств, чтобы сказать, что средние значения двух популяций различны.
t Критический двухсторонний: это критическое значение теста. Это значение можно найти с помощью Калькулятора критического значения t с 38 степенями свободы и уровнем достоверности 95%.
В этом случае критическое значение оказывается равным 2,024394.Поскольку наша тестовая статистика t меньше этого значения, мы не можем отвергнуть нулевую гипотезу. Еще раз, это означает, что у нас нет достаточных доказательств, чтобы сказать, что два средних значения населения различны.
Примечание № 1. Вы придете к одному и тому же выводу независимо от того, используете ли вы метод p-значения или метод критического значения.
Примечание № 2. Если вы выполняете односторонний тест гипотезы , вместо этого вы будете использовать значения для одностороннего P(T<=t) и критического одностороннего t.
Дополнительные ресурсы
В следующих руководствах представлены пошаговые примеры выполнения различных t-тестов в Excel.
Как провести одновыборочный t-тест в Excel
Как провести двухвыборочный t-тест в Excel
Как провести t-тест для парных выборок в Excel
Как выполнить t-критерий Уэлча в Excel
In this tutorial, I will show you how to perform a one-sample T-test by using Microsoft Excel.
What is a one-sample T-test?
A one-sample T-test is a statistical test to determine if a sample mean is significantly different from a hypothesized mean.
Example data
For this tutorial, I have a sample of 12 young female adults (18 years old). I measured their height in inches and entered the data into a single column in Excel.
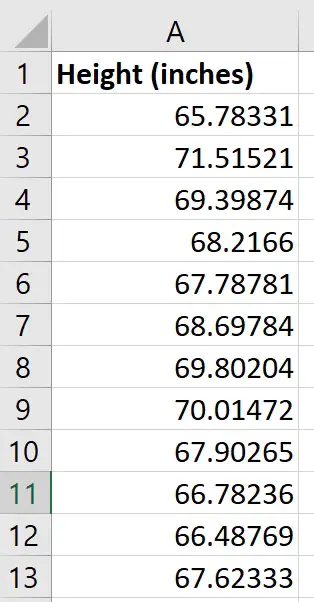
Hypotheses
For the purpose of this example, I will pretend the national average height of 18-year-old girls is 66.5 inches.
I want to perform a one-sample T-test in Excel to determine if there is any significant difference between the heights of my sample compared with the national average height (66.5 inches).
The null and alternative hypothesis are:
- Null hypothesis – There is no significant difference between the heights of the sample, compared with the national average
- Alternative hypothesis – There is a significant difference between the heights of the sample, compared with the national average
There is no function in Excel to perform a one-sample T-test. Instead, I will show you a step-by-step process on how to achieve this.
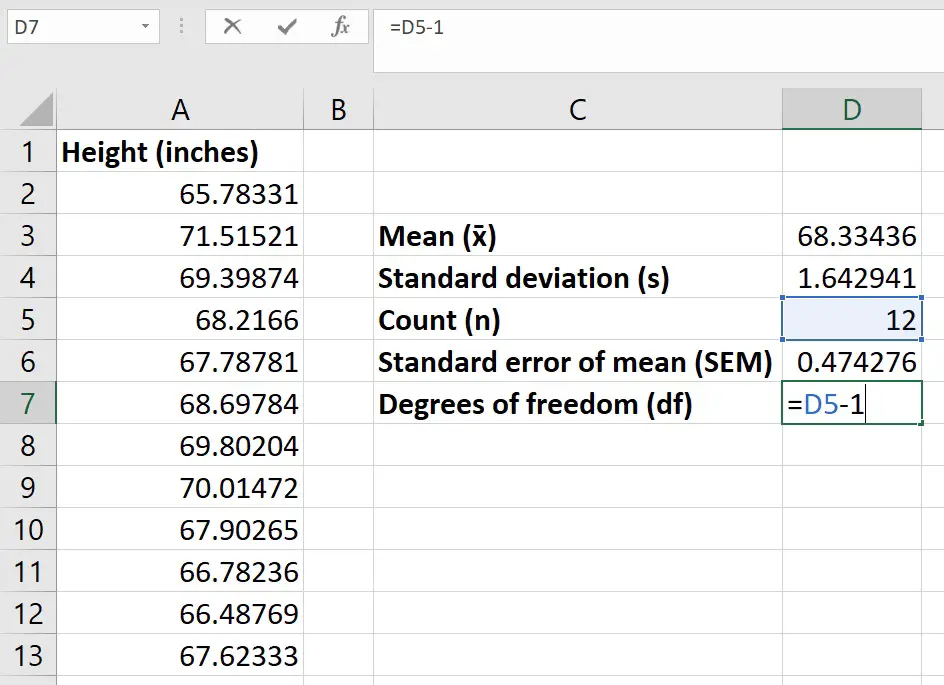
Firstly, calculate the mean, standard deviation (SD) and standard error of the mean (SEM) in Excel. Then, use this information to determine the t-statistic and ultimately the p-value.
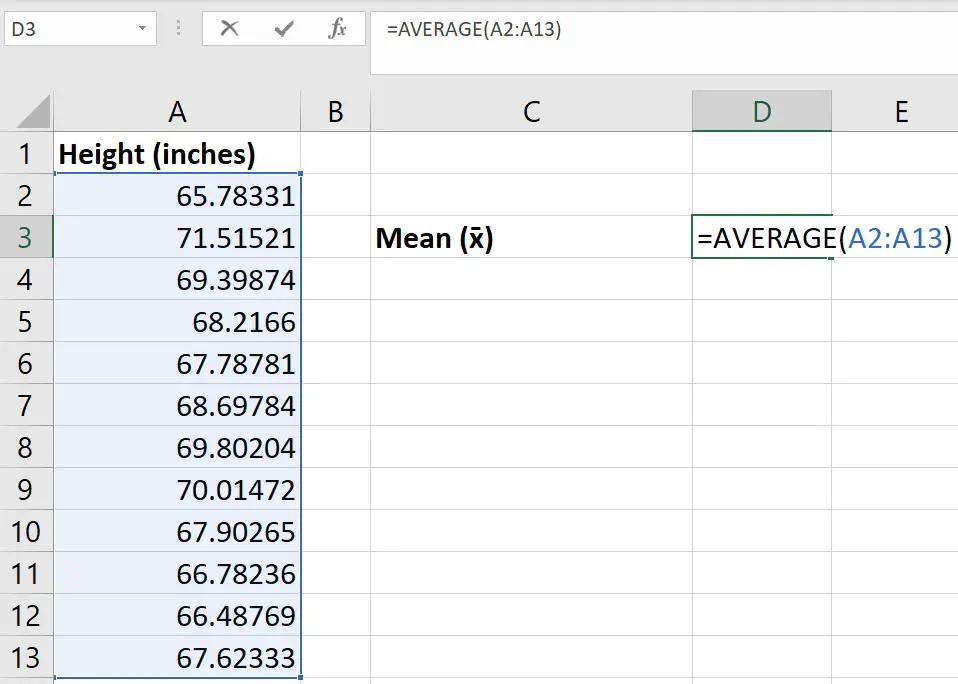
Step 1: Calculate the average
The first thing you should do is to calculate the average value of the sample data.
This can be easily calculated by using the AVERAGE function in Excel.
In Excel, click on an empty cell and enter the following…
=AVERAGE(cell1:cell2)
Replace cell1 in the equation with the cell containing the first data point and replace cell2 with the cell containing the last data point.
Below is a screenshot of what my example looks like.
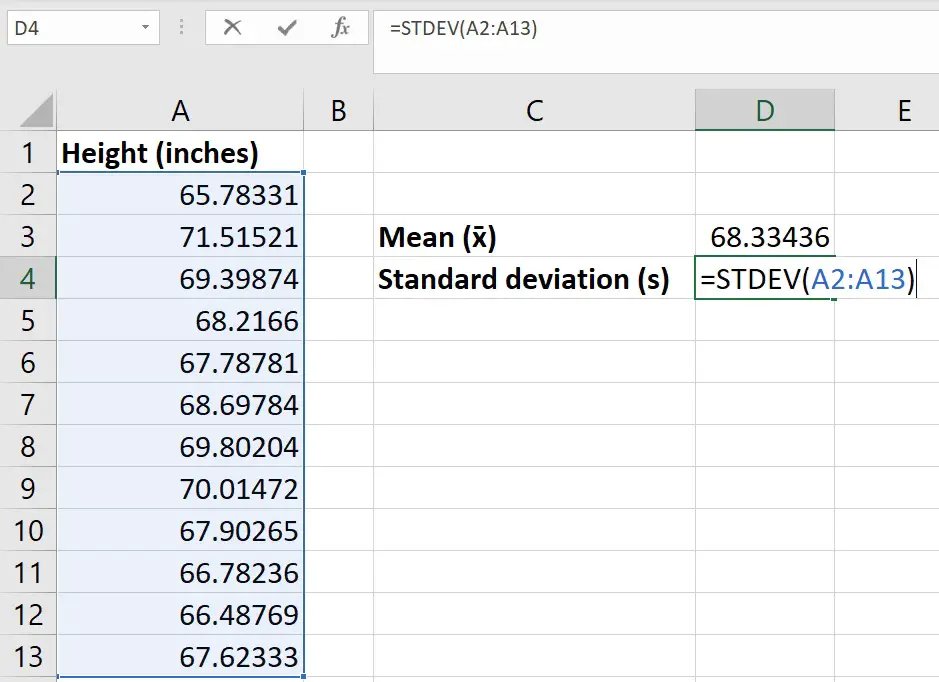
Step 2: Calculate the standard deviation
The next step is the calculate the SD of the sample data.
To do this, use the STDEV function.
In an empty cell, enter the following…
=STDEV(cell1:cell2)
Again, replace cell1 and cell 2 in the equation with the cell containing the first and last data points, respectively.
Note, you can also use the STDEV.S function to achieve the same result.
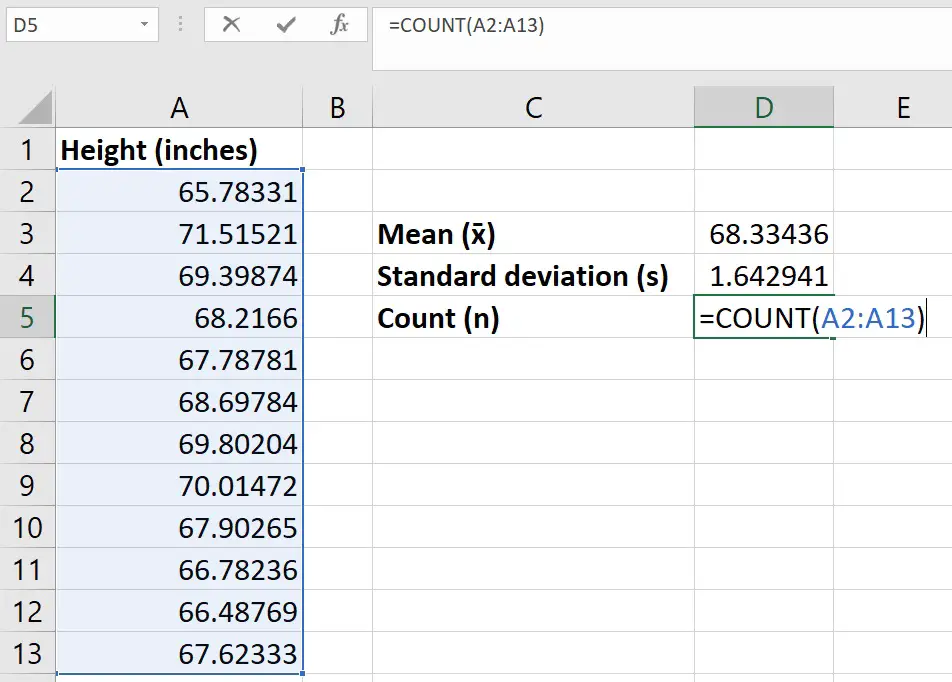
Step 3: Calculate the number of observations
For the next step, simply count the number of observations in the sample.
This can be easily done if you have relatively small numbers. Otherwise, use the COUNT function to get Excel to count them for you.
In an empty cell, enter the following…
=COUNT(cell1:cell2)
As before, replace the cell1 and cell2 with the respected first and last cells.
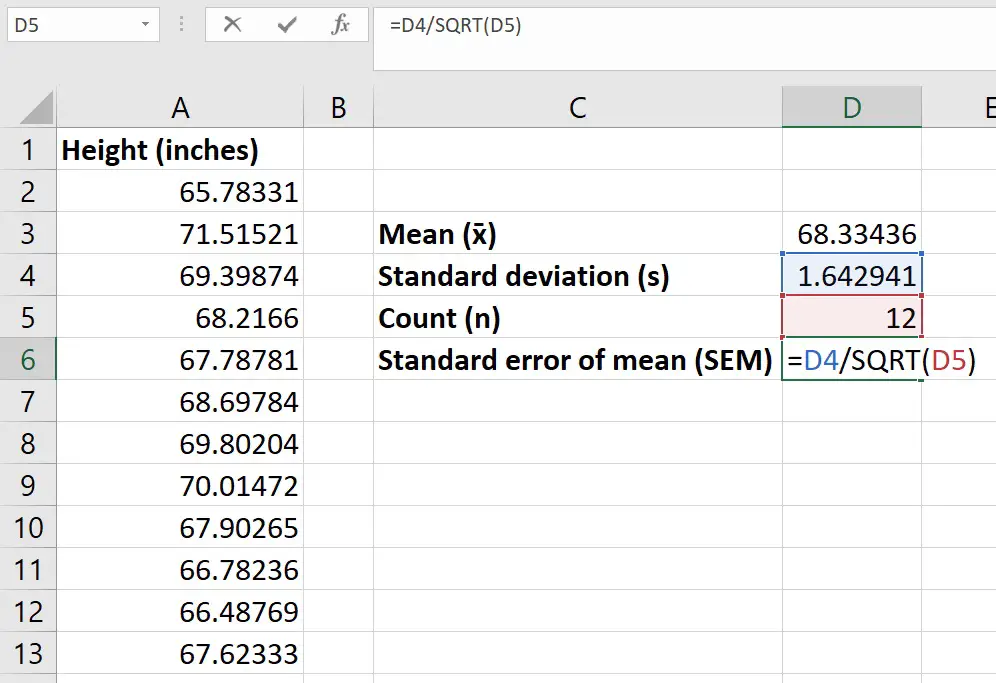
Step 4: Calculate the standard error of the mean
Now we have the mean and n, we can now work out the standard error of the mean (SEM).
To manually calculate the SEM, simply divide the SD by the square root of n.
In Excel, click on an empty cell and enter the following…
=SD/SQRT(n)
Replace the following:
- SD – With the cell containing the SD
- n – With the cell containing the n
Step 5: Calculate the degrees of freedom
To calculate the degrees of freedom (df) in this case, simply subtract 1 from the n.
In a new cell, enter the following…
=n-1
Replace n with the cell containing the n.
Step 6: Calculate the t-statistic
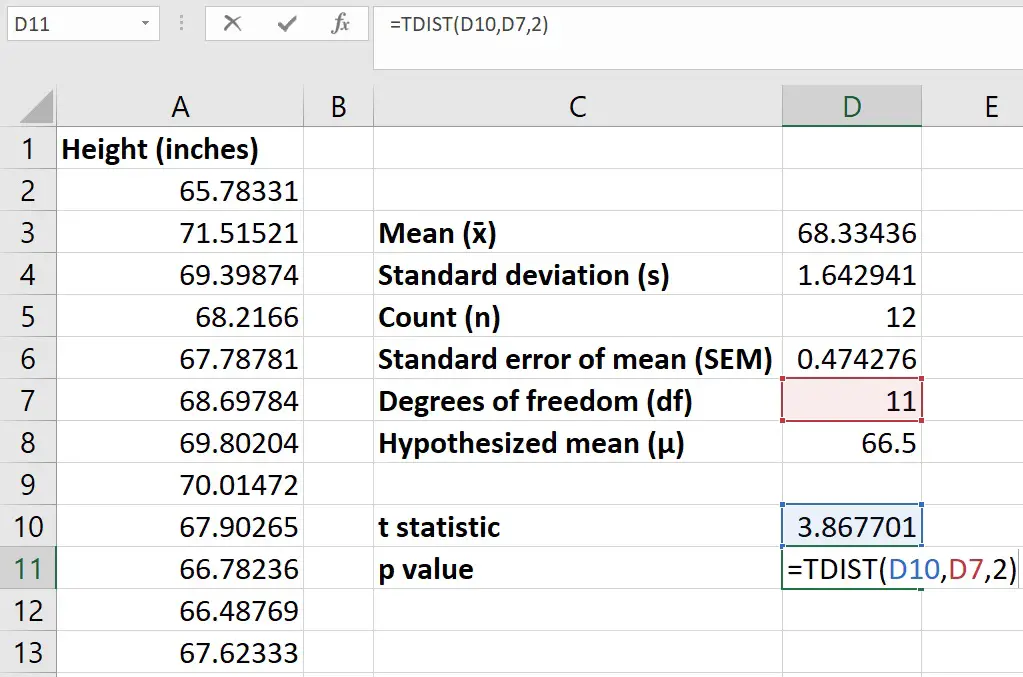
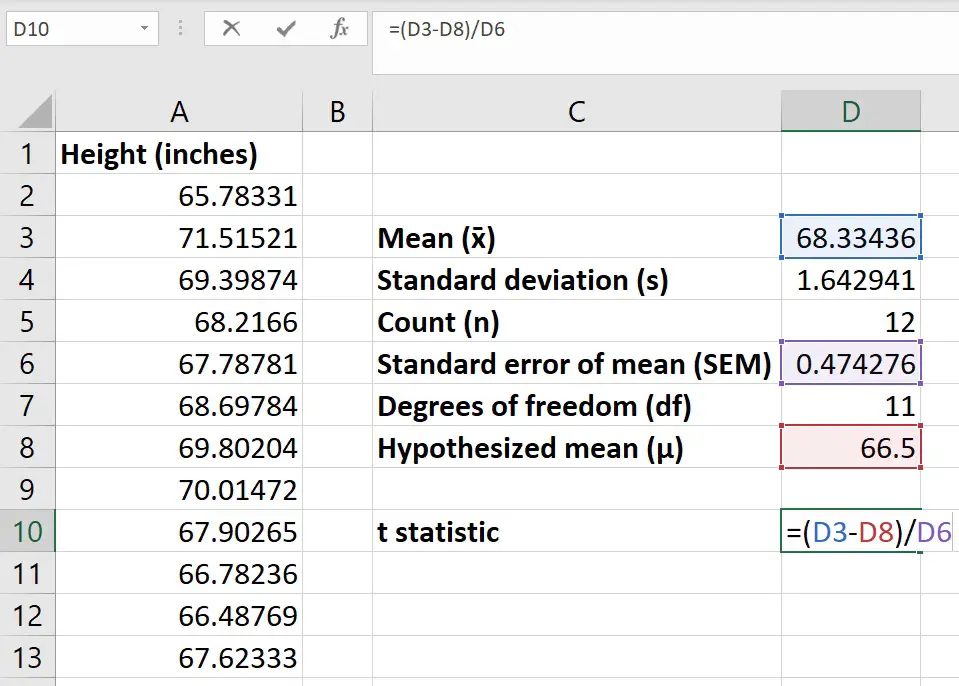
Before calculating the t-statistic, enter the hypothesized mean into a new cell in Excel.
The hypothesized mean is the value you want to compare your sample data to. So, in my example, this will be the national average height of 18-year-old girls – 66.5.
The formula to calculate the t-statistic for a one-sample T-test is shown below.
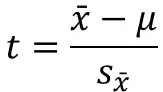
Where:
- x̄ – The sample mean
- μ – The hypothesized mean; in this case, the population mean
- sx̄ – The SEM
So, to work this out in Excel, click on an empty cell and enter the following…
=(x̄ - μ)/sx̄
Replace each component of the formula with the cell containing the corresponding value.
Step 7: Calculate the p-value
The last step is to calculate the p-value by using the t-statistic and the df. This is achieved by using the TDIST function.
In an empty cell, enter the following…
=TDIST(t, df, tails)
Replace the following components of the function with…
- t – The cell containing the t-statistic
- df – The cell containing the df
- tails – Enter 1 if you want to perform a one-tailed analysis, or a 2 if you want to do a two-tailed analysis
For my example, I did not hypothesize if my sample data was greater or lower than the national average. Therefore, I will perform a two-tailed analysis.
If I hypothesized the sample data will be greater than the national average, then I would select to do a one-tailed analysis instead.
So, the p-value for my example is 0.0026.
If my alpha level was set at 0.05, then since the p-value is below the alpha level, I will reject the null hypothesis and accept the alternative hypothesis.
In other words, there is a significant difference between the heights of the sample, compared with the national average.
Wrapping up
In this tutorial, I have shown you how to perform a one-sample T-test in Excel. There is no function to perform a one-sample T-test in Excel. However, you can still perform this by using a stepwise approach.
Microsoft Excel version used: 365 ProPlus
A one sample t-test is used to test whether or not the mean of a population is equal to some value.
This tutorial explains how to conduct a one sample t-test in Excel.
Suppose a botanist wants to know if the mean height of a certain species of plant is equal to 15 inches. She collects a random sample of 12 plants and records each of their heights in inches.
The following image shows the height (in inches) for each plant in the sample:
We can use the following steps to conduct a one sample t-test to determine if the mean height for this species of plant is actually equal to 15 inches.
Step 1: Find the sample size, sample mean, and sample standard deviation.
First, we need to find the sample size, sample mean, and sample standard deviation, which will all be used to conduct the one sample t-test.
The following image shows the formulas we can use to calculate these values:
Step 2: Calculate the test statistic t.
Next, we will calculate the test statistic t using the following formula:
t = x – µ / (s/√n)
where:
x = sample mean
µ = hypothesized population mean
s = sample standard deviation
n = sample size
The following image shows how to calculate t in Excel:
The test statistic t turns out to be -1.68485.
Step 3: Calculate the p-value of the test statistic.
Next, we need to calculate the p-value associated with the test statistic using the following function in Excel:
=T.DIST.2T(ABS(x), deg_freedom)
where:
x = test statistic t
deg_freedom = degrees of freedom for the test, which is calculated as n-1
Technical Notes:
The function T.DIST.2T() returns the p-value for a two-tailed t-test. If you’re instead conducting a left-tailed t-test or a right-tailed t-test, you would instead use the functions T.DIST() or T.DIST.RT(), respectively.
The following image shows how to calculate the p-value for our test statistic:
The p-value turns out to be 0.120145.
Step 4: Interpret the results.
The two hypotheses for this particular one sample t test are as follows:
H0: µ = 15 (the mean height for this species of plant is 15 inches)
HA: µ ≠15 (the mean height is not 15 inches)
Because the p-value of our test (0.120145) is greater than alpha = 0.05, we fail to reject the null hypothesis of the test.
We do not have sufficient evidence to say that the mean height for this particular species of plant is different from 15 inches.
Additional Resources
The following tutorials explain how to perform other common types of t-tests in Excel:
How to Conduct a Two Sample t-Test in Excel
How to Conduct a Paired Samples t-Test in Excel