Дадим определение терминам уровень надежности и уровень значимости. Покажем, как и где они используется в
MS
EXCEL
.
Уровень значимости
(Level of significance) используется в
процедуре проверки гипотез
и при
построении доверительных интервалов
.
СОВЕТ
: Для понимания терминов
Уровень значимости и
Уровень надежности
потребуется знание следующих понятий:
-
выборочное распределение среднего
;
-
стандартное отклонение
;
-
проверка гипотез
;
-
нормальное распределение
.
Уровень значимости
статистического теста – это вероятность отклонить
нулевую гипотезу
, когда на самом деле она верна. Другими словами, это допустимая для данной задачи вероятность
ошибки первого рода
(type I error).
Уровень значимости
обычно обозначают греческой буквой α (
альфа
). Чаще всего для
уровня значимости
используют значения 0,001; 0,01; 0,05; 0,10.
Например, при построении
доверительного интервала для оценки среднего значения распределения
, его ширину рассчитывают таким образом, чтобы вероятность события «
выборочное среднее (Х
ср
) находится за пределами доверительного интервала
» было равно
уровню значимости
. Реализация этого события считается маловероятным (практически невозможным) и служит основанием для отклонения нулевой гипотезы о
равенстве среднего заданному значению
.
Ошибка первого рода
часто называется риском производителя. Это осознанный риск, на который идет производитель продукции, т.к. он определяет вероятность того, что годная продукция может быть забракована, хотя на самом деле она таковой не является. Величина
ошибки первого рода
задается перед
проверкой гипотезы
, таким образом, она контролируется исследователем напрямую и может быть задана в соответствии с условиями решаемой задачи.
Чрезмерное уменьшение
уровня значимости α
(т.е. вероятности
ошибки первого рода
) может привести к увеличению вероятности
ошибки второго рода
, то есть вероятности принять
нулевую гипотезу
, когда на самом деле она не верна. Подробнее об
ошибке второго рода
см. статью
Ошибка второго рода и Кривая оперативной характеристики
.
Уровень значимости
обычно указывается в аргументах
обратных функций MS EXCEL
для вычисления
квантилей
соответствующего распределения:
НОРМ.СТ.ОБР()
,
ХИ2.ОБР()
,
СТЬЮДЕНТ.ОБР()
и др. Примеры использования этих функций приведены в статьях про
проверку гипотез
и про построение
доверительных интервалов
.
Уровень надежности
Уровень
доверия
(этот термин более распространен в отечественной литературе, чем
Уровень надежности
) — означает вероятность того, что
доверительный интервал
содержит истинное значение оцениваемого параметра распределения.
Уровень
доверия
равен
1-α,
где α –
уровень значимости
.
Термин
Уровень надежности
имеет синонимы:
уровень доверия, коэффициент доверия, доверительный уровень
и
доверительная вероятность (англ.
Confidence
Level
,
Confidence
Coefficient
).
В математической статистике обычно используют значения
уровня доверия
90%; 95%; 99%, реже 99,9% и т.д.
Например,
Уровень
доверия
95% означает, что событие, вероятность которого 1-0,95=5% исследователь считать маловероятным или невозможным. Разумеется, выбор
уровня доверия
полностью зависит от исследователя. Так, степень доверия авиапассажира к надежности самолета, несомненно, должна быть выше степени доверия покупателя к надежности электрической лампочки.
Примечание
: Стоит отметить, что математически не корректно говорить, что
Уровень
доверия
является вероятностью, того что оцениваемый параметр распределения принадлежит
доверительному интервалу
, вычисленному на основе
выборки
. Поскольку, считается, что в математической статистике отсутствуют априорные сведения о параметре распределения. Математически правильно говорить, что
доверительный интервал
, с вероятностью равной
Уровню
доверия,
накроет истинное значение оцениваемого параметра распределения.
Уровень надежности в MS EXCEL
В MS EXCEL
Уровень надежности
упоминается в
надстройке Пакет анализа
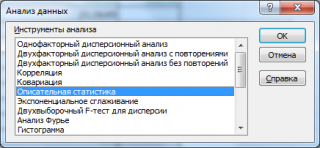
. После вызова надстройки, в диалоговом окне необходимо выбрать инструмент
Описательная статистика
.
После нажатия кнопки
ОК
будет выведено другое диалоговое окно.
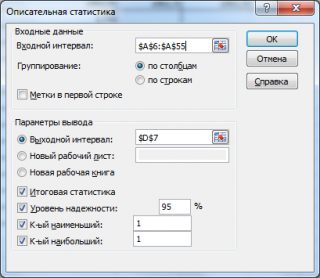
В этом окне задается
Уровень надежности,
т.е.значениевероятности в процентах. После нажатия кнопки
ОК
в
выходном интервале
выводится значение равное
половине ширины
доверительного интервала
. Этот
доверительный интервал
используется для оценки
среднего значения распределения, когда дисперсия не известна
(подробнее см.
статью про доверительный интервал
).
Необходимо учитывать, что данный
доверительный интервал
рассчитывается при условии, что
выборка
берется из
нормального распределения
. Но, на практике обычно принимается, что при достаточно большой
выборке
(n>30),
доверительный интервал
будет построен приблизительно правильно и для распределения, не являющегося
нормальным
(если при этом это распределение не будет иметь
сильной асимметрии
).
Примечание
: Понять, что в диалоговом окне речь идет именно об оценке
среднего значения распределения
, достаточно сложно. Хотя в английской версии диалогового окна это указано прямо:
Confidence
Level
for
Mean
.
Если
Уровень надежности
задан 95%, то
надстройка Пакет анализа
использует следующую формулу (выводится не сама формула, а лишь ее результат):
=СТАНДОТКЛОН.В(Выборка)/КОРЕНЬ(СЧЁТ(Выборка)) *СТЬЮДЕНТ.ОБР.2Х(1-0,95;СЧЁТ(Выборка)-1)
или эквивалентную ей
=СТАНДОТКЛОН.В(Выборка)/КОРЕНЬ(СЧЁТ(Выборка)) *СТЬЮДЕНТ.ОБР((1+0,95)/2;СЧЁТ(Выборка)-1)
где
=СТАНДОТКЛОН.В(Выборка)/КОРЕНЬ(СЧЁТ(Выборка))
– является
стандартной ошибкой среднего
(формулы приведены в
файле примера
).
или
=ДОВЕРИТ.СТЬЮДЕНТ(1-0,95; СТАНДОТКЛОН.В(Выборка); СЧЁТ(Выборка))
Подробнее см. в
статьях про доверительный интервал
.
Программа Эксель используется для выполнения различных статистических задач, одной из которых является вычисление доверительного интервала, который применяется как наиболее подходящая замена точечной оценки при малом объеме выборки.
Хотим сразу заметить, что сама процедура вычисления доверительного интервала довольно непростая, однако, в Excel существует ряд инструментов, призванных облегчить выполнение данной задачи. Давайте рассмотрим их.
Содержание
- Вычисление доверительного интервала
- Метод 1: оператор ДОВЕРИТ.НОРМ
- Метод 2: оператор ДОВЕРИТ.СТЬЮДЕНТ
- Заключение
Вычисление доверительного интервала
Доверительный интервал нужен для того, чтобы дать интервальную оценку каким-либо статическим данным. Основная цель этой операции – убрать неопределенности точечной оценки.
В Microsoft Excel существует два метода выполнения данной задачи:
- Оператор ДОВЕРИТ.НОРМ – применяется в случаях, когда дисперсия известна;
- Оператор ДОВЕРИТ.СТЬЮДЕНТ– когда дисперсия неизвестна.
Ниже мы пошагово разберем оба метода на практике.
Метод 1: оператора ДОВЕРИТ.НОРМ
Данная функция впервые была внедрена в арсенал программы в редакции Эксель 2010 года (до этой версии ее заменял оператор “ДОВЕРИТ”). Оператор входит в категорию “статистические”.
Формула функции ДОВЕРИТ.НОРМ выглядит так:
=ДОВЕРИТ.НОРМ(Альфа;Станд_откл;Размер)
Как мы видим, у функции есть три аргумента:
- “Альфа” – это показатель уровня значимости, который берется за основу при расчете. Доверительный уровень считается так:
1-"Альфа". Это выражение применимо в случае, если значение “Альфа” представлено в виде коэффициента. Например, 1-0,7=0,3, где 0,7=70%/100%.(100-"Альфа")/100. Применятся это выражение, если мы считаем доверительным уровень со значением “Альфа” в процентах. Например, (100-70)/100=0,3.
- “Стандартное отклонение” — соответственно, стандартное отклонение анализируемой выборки данных.
- “Размер” – объем выборки данных.
Примечание: У данной функции наличие всех трех аргументов является обязательным условием.
Оператор “ДОВЕРИТ”, который применялся в более ранних редакциях программы, содержит такие же аргументы и выполняет те же самые функции.
Формула функции ДОВЕРИТ выглядит следующим образом:
=ДОВЕРИТ(Альфа;Станд_откл;Размер)
Отличий в самой формуле нет никаких, лишь название оператора иное. В редакциях приложения Эксель 2010 года и последующих этот оператор находится в категории “Совместимость”. В более же старых версиях программы он находится в разделе статических функций.
Граница доверительного интервала определяется следующей формулой:
X+(-)ДОВЕРИТ.НОРМ
где Х – это среднее значение по заданному диапазону.
Теперь давайте разберемся, как применять эти формулы на практике. Итак, у нас есть таблица с различными данными 10-ти проведенных замеров. При этом, стандартное отклонение совокупности данных равняется 8.
Перед нами стоит задача – получить значение доверительного интервала с 95%-ым уровнем доверия.
- Первым делом выбираем ячейку для вывода результата. Затем кликаем по кнопке “Вставить функцию” (слева от строки формул).
- Откроется окно Мастера функций. Кликнув по текущей категории функций, раскрываем список и щелкаем в нем по строке “Статистические”.
- В предложенном перечне кликаем по оператору “ДОВЕРИТ.НОРМ”, затем жмем OK.
- Перед нами появится окно с настройками аргументов функции, заполнив которые нажимаем кнопку OK.
- в поле “Альфа” указываем уровень значимости. В нашей задаче предполагается 95%-ый уровень доверия. Подставив данное значение в формулу расчета, которую мы рассматривали выше, получаем выражение:
(100-95)/100. Пишем его в поле аргумента (или можно сразу написать результат вычисления, равный 0,05). - в поле “Станд_откл” согласно нашим условия, пишем цифру 8.
- в поле “Размер” указываем количество исследуемых элементов. В нашем случае было проведено 10 замеров, значит пишем цифру 10.
- в поле “Альфа” указываем уровень значимости. В нашей задаче предполагается 95%-ый уровень доверия. Подставив данное значение в формулу расчета, которую мы рассматривали выше, получаем выражение:
- Чтобы при изменении данных не пришлось заново настраивать функцию, можно автоматизировать ее. Для это применим функцию “СЧЁТ”. Ставим указатель в область ввода информации аргумента “Размер”, затем щелкаем по значку треугольника с левой стороны от строки формул и кликаем по пункту “Другие функции…”.
- В результате откроется еще одно окно Мастера функций. Выбрав категорию “Статистические”, кликаем по функции “СЧЕТ”, затем – OK.
- На экране отобразится еще одно окно с настройками аргументов функции, которая применяется для определения числа ячеек в заданном диапазоне, в которых находятся числовые данные.
Формула функции СЧЕТ пишется так:=СЧЁТ(Значение1;Значение2;...).
Количество доступных аргументов этой функции может достигать 255 штук. Здесь можно прописать, либо конкретные числа, либо адреса ячеек, либо диапазоны ячеек. Мы воспользуемся последним вариантом. Для этого кликаем по области ввода информации для первого аргумента, затем зажав левую кнопку мыши выделяем все ячейки одного из столбцов нашей таблицы (не считая шапки), после чего жмем кнопку OK. - В результате проделанных действий в выбранной ячейке будет выведено результат расчетов по оператору ДОВЕРИТ.НОРМ. В нашей задаче его значение оказалось равным 4,9583603.
- Но это еще не конечный результат в нашей задаче. Далее требуется рассчитать среднее значение по заданному интервалу. Для этого потребуется применить функцию “СРЗНАЧ”, которая выполняет задачу по вычислению среднего значения в пределах указанного диапазона данных.
Формула оператора пишется так:=СРЗНАЧ(число1;число2;...).
Выделяем ячейку, куда планируем вставить функцию и жмем кнопку “Вставить функцию”. - В категории “Статистические” выбираем нудный оператор “СРЗНАЧ” и кликаем OK.
- В аргументах функции в значении аргумента “Число” указываем диапазон, в который входят все ячейки со значениями всех замеров. Затем кликаем OK.
- В результате проделанных действий среднее значение будет автоматически подсчитано и выведено в ячейку с только что вставленной функцией.
- Теперь нам нужно рассчитать границы ДИ (доверительного интервала). Начнем с расчета значения правой границы. Выбираем ячейку, куда хотим вывести результат, и выполняем в ней сложение результатов, полученных с помощью операторов “СРЗНАЧ” и “ДОВЕРИТ.НОРМ”. В нашем случае формула выглядит так:
A14+A16. После ее набора жмем Enter. - В результате будет произведен расчет и результат немедленно отобразится в ячейке с формулой.
- Затем аналогичным способом выполняем расчет для получения значения левой границы ДИ. Только в этом случае значение результата “ДОВЕРИТ.НОРМ” нужно не прибавлять, а вычитать из результата, полученного при помощи оператора “СРЗНАЧ”. В нашем случае формула выглядит так:
=A16-A14. - После нажатия Enter мы получим результат в заданной ячейке с формулой.
Примечание: В пунктах выше мы постарались максимально подробно расписать все шаги и каждую применяемую функцию. Однако все прописанные формулы можно записать вместе, в составе одной большой:
- Для определения правой границы ДИ общая формула будет выглядеть так:
=СРЗНАЧ(B2:B11)+ДОВЕРИТ.НОРМ(0,05;8;СЧЁТ(B2:B11)). - Точно также и для левой границы, только вместо плюса нужно поставить минус:
=СРЗНАЧ(B2:B11)-ДОВЕРИТ.НОРМ(0,05;8;СЧЁТ(B2:B11)).
Метод 2: оператор ДОВЕРИТ.СТЬЮДЕНТ
Теперь давайте познакомимся со вторым оператором для определения доверительного интервала – ДОВЕРИТ.СТЬЮДЕНТ. Данная функция была внедрена в программу относительно недавно, начиная с версии Эксель 2010, и направлена на определение ДИ выбранной совокупности данных с применением распределения Стьюдента, при неизвестной дисперсии.
Формула функции ДОВЕРИТ.СТЬЮДЕНТ выглядит следующим образом:
=ДОВЕРИТ.СТЬЮДЕНТ(Альфа;Cтанд_откл;Размер)
Давайте разберем применение данного оператора на примере все той же таблицы. Только теперь стандартное отклонение по условиям задачи нам неизвестно.
- Сначала выбираем ячейку, куда планируем вывести результат. Затем кликаем по значку “Вставить функцию” (слева от строки формул).
- Откроется уже хорошо знакомое окно Мастера функций. Выбираем категорию “Статистические”, затем из предложенного списка функций щелкаем по оператору “ДОВЕРИТ.СТЬЮДЕНТ”, после чего – OK.
- В следующем окне нам нужно настроить аргументы функции:.
- В выбранной ячейке отобразится значение доверительного интервала согласно заданным нами параметрам.
- Далее нам нужно рассчитать значения границ ДИ. А для этого потребуется получить среднее значение по выбранному диапазону. Для этого снова применим функцию “СРЗНАЧ”. Алгоритм действий аналогичен тому, что был описан в первом методе.
- Получив значение “СРЗНАЧ”, можно приступать к расчетам границ ДИ. Сами формулы ничем не отличаются от тех, что использовались с оператором “ДОВЕРИТ.НОРМ”:
- Правая граница ДИ=СРЗНАЧ+ДОВЕРИТ.СТЬЮДЕНТ
- Левая граница ДИ=СРЗНАЧ-ДОВЕРИТ.СТЬЮДЕНТ
Заключение
Арсенал инструментов Excel невероятно большой, и наряду с распространенными функциями, программа предлагает большое разнообразие специальных функций, которые помогут существенно облегчить работу с данными. Возможно, описанные выше шаги некоторым пользователям, на первый взгляд, могут показаться сложными. Но после детального изучения вопроса и последовательности действий, все станет намного проще.
history 23 ноября 2016 г.
- Группы статей
- Статистический вывод
Дадим определение терминам уровень надежности и уровень значимости. Покажем, как и где они используется в MS EXCEL .
СОВЕТ : Для понимания терминов Уровень значимости и Уровень надежности потребуется знание следующих понятий:
Уровень значимости статистического теста – это вероятность отклонить нулевую гипотезу , когда на самом деле она верна. Другими словами, это допустимая для данной задачи вероятность ошибки первого рода (type I error).
Уровень значимости обычно обозначают греческой буквой α ( альфа ). Чаще всего для уровня значимости используют значения 0,001; 0,01; 0,05; 0,10.
Например, при построении доверительного интервала для оценки среднего значения распределения , его ширину рассчитывают таким образом, чтобы вероятность события « выборочное среднее (Х ср ) находится за пределами доверительного интервала » было равно уровню значимости . Реализация этого события считается маловероятным (практически невозможным) и служит основанием для отклонения нулевой гипотезы о равенстве среднего заданному значению .
Ошибка первого рода часто называется риском производителя. Это осознанный риск, на который идет производитель продукции, т.к. он определяет вероятность того, что годная продукция может быть забракована, хотя на самом деле она таковой не является. Величина ошибки первого рода задается перед проверкой гипотезы , таким образом, она контролируется исследователем напрямую и может быть задана в соответствии с условиями решаемой задачи.
Чрезмерное уменьшение уровня значимости α (т.е. вероятности ошибки первого рода ) может привести к увеличению вероятности ошибки второго рода , то есть вероятности принять нулевую гипотезу , когда на самом деле она не верна. Подробнее об ошибке второго рода см. статью Ошибка второго рода и Кривая оперативной характеристики .
Уровень значимости обычно указывается в аргументах обратных функций MS EXCEL для вычисления квантилей соответствующего распределения: НОРМ.СТ.ОБР() , ХИ2.ОБР() , СТЬЮДЕНТ.ОБР() и др. Примеры использования этих функций приведены в статьях про проверку гипотез и про построение доверительных интервалов .
Уровень надежности
Уровень доверия (этот термин более распространен в отечественной литературе, чем Уровень надежности ) — означает вероятность того, что доверительный интервал содержит истинное значение оцениваемого параметра распределения.
Уровень доверия равен 1-α, где α – уровень значимости .
Термин Уровень надежности имеет синонимы: уровень доверия, коэффициент доверия, доверительный уровень и доверительная вероятность (англ. Confidence Level , Confidence Coefficient ).
В математической статистике обычно используют значения уровня доверия 90%; 95%; 99%, реже 99,9% и т.д.
Например, Уровень доверия 95% означает, что событие, вероятность которого 1-0,95=5% исследователь считать маловероятным или невозможным. Разумеется, выбор уровня доверия полностью зависит от исследователя. Так, степень доверия авиапассажира к надежности самолета, несомненно, должна быть выше степени доверия покупателя к надежности электрической лампочки.
Примечание : Стоит отметить, что математически не корректно говорить, что Уровень доверия является вероятностью, того что оцениваемый параметр распределения принадлежит доверительному интервалу , вычисленному на основе выборки . Поскольку, считается, что в математической статистике отсутствуют априорные сведения о параметре распределения. Математически правильно говорить, что доверительный интервал , с вероятностью равной Уровню доверия, накроет истинное значение оцениваемого параметра распределения.
Уровень надежности в MS EXCEL
В MS EXCEL Уровень надежности упоминается в надстройке Пакет анализа . После вызова надстройки, в диалоговом окне необходимо выбрать инструмент Описательная статистика .
После нажатия кнопки ОК будет выведено другое диалоговое окно.
В этом окне задается Уровень надежности, т.е.значениевероятности в процентах. После нажатия кнопки ОК в выходном интервале выводится значение равное половине ширины доверительного интервала . Этот доверительный интервал используется для оценки среднего значения распределения, когда дисперсия не известна (подробнее см. статью про доверительный интервал ).
Необходимо учитывать, что данный доверительный интервал рассчитывается при условии, что выборка берется из нормального распределения . Но, на практике обычно принимается, что при достаточно большой выборке (n>30), доверительный интервал будет построен приблизительно правильно и для распределения, не являющегося нормальным (если при этом это распределение не будет иметь сильной асимметрии ).
Примечание : Понять, что в диалоговом окне речь идет именно об оценке среднего значения распределения , достаточно сложно. Хотя в английской версии диалогового окна это указано прямо: Confidence Level for Mean .
Если Уровень надежности задан 95%, то надстройка Пакет анализа использует следующую формулу (выводится не сама формула, а лишь ее результат):
или эквивалентную ей
где =СТАНДОТКЛОН.В(Выборка)/КОРЕНЬ(СЧЁТ(Выборка)) – является стандартной ошибкой среднего (формулы приведены в файле примера ).
=ДОВЕРИТ.СТЬЮДЕНТ(1-0,95; СТАНДОТКЛОН.В(Выборка); СЧЁТ(Выборка))
Решение задач описательной статистики средствами пакета анализа Microsoft Excel Текст научной статьи по специальности « Компьютерные и информационные науки»
CC BY
Аннотация научной статьи по компьютерным и информационным наукам, автор научной работы — Трущелёв Сергей Андреевич
Представлено определение описательной статистики , изложены методика вычисления основных ее показателей, а также пошаговая процедура статистического анализа. Сообщение содержит обучающий компонент.
Похожие темы научных работ по компьютерным и информационным наукам , автор научной работы — Трущелёв Сергей Андреевич
Descriptive statistics using the Data Analysis Toolpak in Microsoft Excel
The paper presents a definition of descriptive statistics , and its main indicators. The necessity of their calculation is set out step by step in the procedure of statistical analysis. The message is a training component with.
Текст научной работы на тему «Решение задач описательной статистики средствами пакета анализа Microsoft Excel»
МЕТОДОЛОГИЯ НАУЧНО-ИССЛЕДОВАТЕЛЬСКОЙ ДЕЯТЕЛЬНОСТИ
Уважаемые читатели, коллеги!
В связи с возрастающими требованиями к качеству публикаций результатов научно-исследовательских работ в «Российском психиатрическом журнале» открыта новая рубрика «Методология научно-исследовательской деятельности». Планируется публикация обучающих и информационно-разъяснительных материалов по разным разделам науковедения, организации научной работы, биоинформатике, биостатистике, биоэтике и т.д. Приглашаем ученых и исследователей поделиться опытом в этой области. Надеемся, что наша инициатива будет поддержана не только в научном сообществе, но и воспринята в среде практикующих специалистов.
© С.А. Трущелёв, 2013 Для корреспонденции
УДК 311:004 Трущелёв Сергей Андреевич — кандидат медицинских наук,
доцент, ведущий научный сотрудник ФГБУ «Московский научно-исследовательский институт психиатрии Минздрава России»
Адрес: 107076, г. Москва, ул. Потешная, д. 3 Телефон: (495) 963-25-31 E-mail: sat-geo@mail.ru
Решение задач описательной статистики средствами пакета анализа Microsoft Excel
Descriptive statistics using the Data Analysis Toolpak in Microsoft Excel
The paper presents a definition of descriptive statistics, and its main indicators. The necessity of their calculation is set out step by step in the procedure of statistical analysis. The message is a training component with. Key words: science of science, biostatistics, descriptive statistics, data analysis toolpak, Excel
ФГБУ «Московский научно-исследовательский институт психиатрии Минздрава России»
Moscow Research Institute of Psychiatry
Представлено определение описательной статистики, изложены методика вычисления основных ее показателей, а также пошаговая процедура статистического анализа. Сообщение содержит обучающий компонент.
Ключевые слова: науковедение, биостатистика, описательная статистика, пакет анализа, Excel
Каждое явление (предмет исследования) определяется многими факторами. В научном исследовании полностью учесть все факторы и обеспечить их стабильность удается редко. Следовательно, явление, определяемое этими факторами, не поддается точному предсказанию — оно приобретает вероятностные черты, т.е. ведет себя случайным образом. Этому подвержены многие явления, поэтому они определяются случайной величиной, которая принимает в результате опыта или наблюдения одно из множества значений. Случайные величины могут быть дискретными (прерывными) и непрерывными. Немаловажно их распределение — правило, которое устанавливает связь между значениями случайной величины и вероятностями (частотами) их появления.
Наглядное представление о распределении случайных величин дает разброс песчинок, образующих кучу при высыпании (рассеивании) из некоторого точечного источника. Его проекция является параметром положения и соответствует математическому ожиданию распределения, если куча симметрична. Разброс песчинок (параметр рассеяния) характеризуется радиусом кучи на высоте примерно 2/3. Такой параметр рассеяния соответствует так называемому стандартному (среднеквадратичному) отклонению случайных величин в распределении. Горизонтальные расстояния песчинок от проекции источника (математического ожидания) моделируют рассеяние случайной величины. Поверхность кучи (ее высоты) соответствует частоте случайных величин на разных расстояниях от центра. Вершина кучи, расположенная под источником, отвечает максимуму частоты. На периферии высота кучи уменьшается до нуля, что соответствует уменьшению частот больших отклонений от центра рассеяния. Статистическая обработка совокупности данных состоит в некоторых осредняющих вычислительных процедурах, погашающих сугубо индивидуальные особенности — отклонения от общей закономерности и подчеркивающих типичные (популяцион-ные) свойства явления в целом. Начальный раздел математической статистики — описательная статистика — занимается характеристикой (описанием) картины случайного рассеяния по совокупности данных. В соответствии с законом распределения данных решаются вопросы выбора и вычислений надлежащих показателей. Описательная статистика включает методы организации, суммирования и описания данных. Дескриптивные (от англ. descriptive — описательный) показатели позволяют быстро обобщать данные. К описательным методам относят частотные распределения, меры централь-
ной тенденции и меры относительного положения [4, с. 95].
К основным показателям описательной статистики относятся среднее значение (среднее арифметическое, медиана, мода), усредненное значение, разброс (диапазон разброса данных), дисперсия, стандартное среднеквадратное отклонение (СКО), квартили, доверительный интервал [2, с. 28].
Статистическая обработка результатов исследований и получение показателей описательной статистики в недалеком прошлом обычно занимали много времени, однако с внедрением средств компьютерной техники многое изменилось — вычислительные процессы стали происходить очень быстро. Для проведения статистических расчетов в электронной таблице Microsoft Excel имеется пакет анализа. Надстройка «Анализ данных» располагается во вкладке «Данные», в крайне правом блоке ленты (рис. 1).
Для демонстрации вычислений будем использовать гипотетический набор данных. Далее приведем пошаговую инструкцию по созданию описательной статистики признака (показателя систолического давления), измеренного до лечения и после него, в группе наблюдения (n=60).
Для проведения вычисления обратитесь к ленте: Данные ^ Анализ данных ^ Описательная статистика ^ ОК. Затем, перейдя в окно инструмента, выберите входной интервал, группирование (по столбцам), поставьте галочку, если в первой строке выделены метки; в параметрах вывода на поле электронной страницы выберите ячейку вывода результатов, установите галочку рядом с итоговой статистикой. Потом нажмите кнопку ОК. После этого вы получите результаты описательной статистики выбранных признаков (рис. 2 и 3).
[й1 A «ï- V m И^ЭгшИ Главная Ш I» 1 Описательная статистика — Microsoft Excel □ 0 й Вставка Разметка страницы Формулы Данные Рецензирование Вид Разработчик Надстройки MetaXL Л □ S3
П внец m 1олучение jних данныхт ч [^Подключения ^Свойства Обновить все т && Изменить связи Подключения A I AIЯ I Я + Я 1А1 Я| Сортировка Со pi ч Ш ^ Очистить ^ Повторить Фильтр ™ № Дополнительно ировка и фильтр S Ii ы» вш а в Текст по Удалить ,—, столбцам дубликаты » Работа сданными Ф Фор» орма Jbi ssprfa ф ^ ^Анализданных Поиск решения Стр^И^ра Анализ
А в с D Е F G У 1 J К 1 L _
1 Номер_исс Признак_1 Признак_2 у
3 2 178 143 Анализ данным lia
Инструменты анализа У _ 1 о, 1
4 3 320 188 Двухфакторный дисперсионный^нализ без повторений Корреляция Л* 3 J d Отмена |
6 5 159 161 Экспоненциальное сглаживание Двухвыборочный Р-тест для дисперсии Анализ Фурье Гистограмма Скользящее среднее 1 Генерация случайных чисел_| Справка
Рис. 1. Пошаговый выбор инструмента анализа данных
Рис. 2. Окно инструмента описательной статистики
Среднее (арифметическое; М; х ) — одна из наиболее распространенных мер центральной тенденции, представляющая собой сумму всех значений, деленную на их количество. Если значения интересующего нас признака у большинства объектов близки к их среднему и с равной вероятностью отклоняются от него в большую или меньшую сторону, лучшими характеристиками совокупности будут само среднее значение и стандартное отклонение. Напротив, когда значения признака распределены несимметрично относительно среднего, совокупность лучше описать с помощью медианы и процен-тилей [1, с. 27].
Стандартная ошибка (т) — показатель надежности расчетного параметра; стандартное отклонение оценок, которые будут получены при многократной случайной выборке данного размера из одной и той же совокупности. Стандартная ошибка — это убывающая функция объема выборки: чем меньше стандартная ошибка, тем более достоверной является оценка параметра. Весьма часто для описания непрерывных количественных данных используют стандартную ошибку, которая (в отличие от СКО) является не характеристикой, описывающей распределение наблюдений исследуемой выборки по области значений, а только мерой точности оценки популяционного среднего и, следовательно, не характеризует дисперсию (разброс) в анализируемой выборке. Однако часто именно стандартную ошибку среднего приводят в качестве параметра описательной статистики, пытаясь продемонстрировать тем самым малую вариабельность своих данных, так как всегда (по определению) т Не можете найти то, что вам нужно? Попробуйте сервис подбора литературы.
60 Среднее 161,77 Среднее 134,03
61 Стандартная ошибка 12,46 Стандартная ошибка 6.59
62 Медиана 167 Медиана 121,5
63 Мода 72 Мода 141
64 Стандартное отклонение 96.54 Стандартное отклонение 51,03
65 Дисперсия выборки 9320.59 Дисперсия выборки 2604.34
66 Эксцесс 0.89 Эксцесс 2.75
67 Асимметричность 0.96 Асимметричность 1,43
68 Интервал 420 Интервал 254
69 Минимум 50 Минимум 55
70 Максимум 470 Максимум 309
71 Сумма 9706 Сумма 8042
72 Счет 60 Счет 60
73 74 Уровень надежности(95.0%) 24.94 Уровень надежности(95.0%) 13,18
Коэффициент вариации 60% Коэффициент вариации 38%
Рис. 3. Результаты описательной статистики двух признаков
Медиану и интерквартильный размах рекомендуется применять для описания распределения, не являющегося нормальным (а это большинство распределений медико-биологических параметров) [1, с. 34]. Интерквартильный размах указывают в виде процентилей. Рекомендуется указывать уровни 25 и 75%, которые соответствуют верхней границе 1-го и нижней границе 4-го квартилей. Пример описания: Me (25%; 75%) = 60 (23; 78).
Мода (Мо) — значение, которое встречается наиболее часто во множестве. Иногда в совокупности встречается более одной моды. Тогда говорят, что совокупность мультимодальна — свидетельство того, что набор данных не подчиняется нормальному распределению. Мода как средняя величина употребляется чаще для данных, имеющих нечисловую природу. Например, в группе пациентов наибольшая частота тяжести болезни будет равна моде. При экспертной оценке с помощью этого показателя определяют предпочтения участников исследования. Недостаток — показатель не учитывает поведение распределения в других точках.
Стандартное отклонение (синонимы: среднеквадратичное отклонение, квадратичное отклонение; стандартный разброс; СКО; в; о) — в теории вероятностей и статистике наиболее распространенный показатель рассеивания значений случайной величины относительно ее математического ожидания. Измеряется в единицах случайной величины. Равно корню квадратному из дисперсии случайной величины. Стандартное отклонение используют при расчете стандартной ошибки среднего арифметического, построении доверительных интервалов, статистической проверке гипотез, измерении линейной взаимосвязи между случайными величинами. Большое значение СО показывает большой разброс значений в представленном множестве со средней величиной множества; маленькое значение, соответственно, показывает, что значения во множестве сгруппированы вокруг среднего. Если среднее значение измерений сильно отличается от предсказанных теорией значений (большое значение среднеквадратичного отклонения), то полученные значения или метод их получения следует перепроверить.
Дисперсия (D; о2) — мера разброса случайной величины, т.е. ее отклонения от математического ожидания. Квадратный корень из дисперсии называется стандартным отклонением. Дисперсия измеряется в квадратах единицы измерения. Однако в самостоятельном виде (как, например, средняя арифметическая) дисперсия используется редко. Это скорее вспомогательный и промежуточный показатель, который применяют в других методах статистического анализа.
Эксцесс — скалярная характеристика островершинности графика плотности вероятности унимо-
дального распределения, которую используют в качестве некоторой меры отклонения рассматриваемого распределения от нормального. Если коэффициент эксцесса равен нулю или близок к нему, то плотность вероятности распределения имеет нормальный эксцесс. Если коэффициент эксцесса сильно больше нуля, то плотность вероятности имеет положительный эксцесс. Это, как правило, соответствует тому, что график плотности рассматриваемого распределения в окрестности моды имеет более острую и более высокую вершину, чем нормальная кривая. Когда коэффициент эксцесса сильно больше нуля, говорят об отрицательном эксцессе плотности, при этом плотность вероятности имеет в окрестности моды более низкую и плоскую вершину, чем плотность нормального закона. Для генеральных совокупностей больших объемов его малыми значениями можно пренебречь.
Асимметричность (коэффициент асимметрии или скоса) — величина, характеризующая асимметрию распределения данной случайной величины. Коэффициент асимметрии положителен, если правый хвост распределения длиннее левого, и отрицателен в альтернативном случае. Если распределение симметрично относительно математического ожидания, то его коэффициент асимметрии равен нулю.
Интервал — размах показателей, т.е. разность между максимумом и минимумом значений вариант.
Максимум — наибольшее значение вариант.
Минимум — наименьшее значение вариант.
Сумма — сумма значений вариант.
Счет — количество вариант.
Уровень надежности — свойство объекта сохранять в установленных пределах значения всех параметров. Показывает величину доверительного интервала для математического ожидания согласно заданному уровню надежности или доверия. По умолчанию уровень надежности принят равным 95%.
Коэффициент вариации случайной величины -мера относительного разброса случайной величины. Показывает, какую долю среднего значения этой величины составляет ее средний разброс. Исчисляется в процентах. Вычисляется только для количественных данных. В отличие от стандартного отклонения, он измеряет не абсолютную, а относительную меру разброса значений признака в статистической совокупности. В Excel нет готовой функции для расчета коэффициента вариации. Расчет можно провести простым делением стандартного отклонения на среднее значение. Эти значения имеются в таблице описательной статистики. Для вычисления этого важного показателя в ячейке ниже надписи Уровень надежности пишем Коэффициент вариации, затем в ячейке справа делаем запись: =G64/G60. То же необходимо по-
вторить для вычисления коэффициента вариации для другого измерения.
Коэффициент вариации обычно выражается в процентах, поэтому ячейку с формулой можно обрамить процентным форматом. Нужная кнопка находится на панели инструментов в закладке «Главная». Коэффициент вариации, в отличие от других показателей разброса значений, используется как самостоятельный и весьма информативный индикатор вариации данных. В статистике принято считать, что совокупность данных является однородной, если коэффициент вариации менее 33%, неоднородной — если более 33%. Эта информация может быть полезна для предварительного описания данных и определения возможностей проведения дальнейшего анализа. Кроме того, коэффициент вариации, измеряемый в процентах, позволяет сравнивать степень разброса различных данных независимо от их масштаба и единиц измерений.
Анализ показателей описательной статистики
При сравнении значений среднего, медианы, моды в каждом измерении следует отметить, что эти показатели сильно отличаются друг от друга.
Коэффициенты эксцесса и асимметрии значимо отличаются от установленных границ, коэффициенты вариации больше критического (предельного) значения. Следовательно, распределение данных в обеих группах измерений отлично от нормального. В последующем необходимо применять непараметрические методы статистического анализа. Для быстрой сравнительной оценки можно использовать показатели доверительных интервалов.
Для представления результатов сравнения обычно используют формат в виде М (95% ДИ) — значение среднего и указание 95% доверительного интервала. В тексте публикации запись может выглядеть следующим образом: Средний уровень систолического давления в группе пациентов до лечения составил 161,77 мм рт. ст. (95% ДИ от 136,83 до 186,71 мм рт. ст.), после лечения -134,03 мм рт. ст. (95% ДИ от 120,85 до 147,21 мм рт. ст.). Указанные доверительные интервалы имеют зону совмещения, следовательно, существенного различия в изменении признака нет. Исходя из этого с большой долей вероятности можно утверждать, что для данной группы пациентов лекарственный препарат, примененный для снижения уровня систолического артериального давления, был не эффективен.
1. Гланц С. Медико-биологическая статистика / Пер. с англ. -М., Практика, 1998. — 459 с.
2. Ланг Т.А., Сесик М. Как описывать статистику в медицине. Аннотированное руководство для авторов, редакторов и рецензентов / Пер. с англ. под ред. В.П. Леонова. -М.: Практическая медицина, 2011. — 480 с.
3. Леонов В.П. Ошибки статистического анализа биомедицинских данных // Междунар. журн. мед. практики. — 2007. -№ 2. — С. 19-35.
4. Трущелев С.А. Медицинская диссертация: руководство: 3-е изд. / Под ред. проф. И.Н. Денисова. — М.: ГЭОТАР-Медиа, 2009. — 416 с.
Сводка
В этой статье описана функция ДОВЕРИТ в Microsoft Office Excel 2003 и Microsoft Office Excel 2007, а также сравнивает результаты функции для Excel 2003 и Excel 2007 с результатами функции ДОВЕРИТ в более ранних версиях Excel.
Значение доверительных интервалов часто неправильно интерпретировано, и мы стараемся предоставить объяснение допустимой и недопустимой выписки, которые могут быть сделаны после определения доверительного значения на основе данных.
Дополнительные сведения
Функция ДОВЕРИТ(альфа; сигма, n) возвращает значение, которое можно использовать для построения доверительный интервал для многая населения. Доверительный интервал — это диапазон значений, вы центр на основе известного значения выборки. Предполагается, что результаты наблюдений в выборке взяты из нормального распределения с известным стандартным отклонением, сигмой, а количество наблюдений в выборке — n.
Синтаксис
CONFIDENCE(alpha,sigma,n)
Параметры: альфа — вероятность и 0 < альфа < 1. Сигма — это положительное число, а n — положительное integer, соответствующее размеру выборки.
Обычно альфа — это небольшая вероятность, например 0,05.
Пример использования
Предположим, что оценки коэффициента аналитики следуют за обычным распределением со стандартным отклонением 15. Вы тестировали IQ-тест для 50 учащихся в вашем учебном замещаемом учебном замещаке и получили пример средней 105. Необходимо вычислить доверительный интервал в 95 % для математических вычислений. Доверительный интервал 95 % или 0,95 соответствует альфа = 1 – 0,95 = 0,05.
Чтобы проиллюстрировать функцию ДОВЕРИТ, создайте пустой Excel, скопируйте таблицу ниже и выберите ячейку A1 на Excel листе. В меню Правка выберите команду Вставить.
Примечание: В Excel 2007 нажмите кнопку Вировать в группе Буфер обмена на вкладке Главная.
Элементы в таблице ниже заполняют ячейки A1:B7 на вашем компьютере.
|
Альфа |
0,05 |
|
Stdev |
15 |
|
м |
50 |
|
выборка «вехи» |
105 |
|
=ДОВЕРИТ(B1;B2;B3) |
|
|
=НОРМСИНВ(1 — B1/2)*B2/SQRT(B3) |
После вжатия этой таблицы на новый Excel нажмите кнопку Параметры вжатия и выберите пункт Найти формат назначения.
Вы можете выбрать в меню Формат пункт Столбец, а затем выбрать пункт Авто подбор по столбцу.
Примечание: В Excel 2007 г. с выбранным диапазоном ячеек нажмите кнопку Формат в группе Ячейки на вкладке Главная, а затем выберите Авто ширина столбца.
Ячейка A6 отображает значение ДОВЕРИТ. Ячейка A7 имеет то же значение, так как звонок на значение ДОВЕРИТ(альфа; сигма, n) возвращает результат вычисления:
NORMSINV(1 – alpha/2) * sigma / SQRT(n)
Непосредственно в доверии не внося изменений, но в Microsoft Excel 2002 г. была улучшена норм.В.ВОСЬМ, а затем в Excel 2002 и Excel 2007 г. были внесены дополнительные улучшения. Поэтому в этих более поздних версиях стандарта ДОВЕРИТ могут возвращаться другие (и улучшенные Excel) результаты, так как доверит их на основе нормСИНВ.
Это не означает, что в более ранних версиях Excel доверие к доверию. Неточности в нормОЛИНВ обычно связаны со значениями аргумента, близкими к 0 или очень близко к 1. На практике альфа обычно имеет 0,05, 0,01 или, возможно, 0,001. Значения альфа-значения должны быть намного меньше, чем это, например 0,0000001, прежде чем ошибки округления в НОРМСИНВ, скорее всего, будут заметили.
Примечание: В этой статье на сайте НОРМ.В.ВН можно узнать о различиях в вычислениях в нормСИНХНОВ.
Для получения дополнительных сведений щелкните номер следующей статьи, чтобы просмотреть статью в базе знаний Майкрософт:
826772 Excel статистические функции: НОРМСИНВ
Интерпретация результатов проверки доверия
Файл Excel справки для confidence был перезаписан в Excel 2003 и Excel 2007, так как все более ранние версии файла справки вводили в заблуждение при интерпретации результатов. В примере говорится: «Предположим, что в нашем примере из 50 сотрудников в пути средняя продолжительность поездки на работу составляет 30 минут со стандартным отклонением в 2,5. Мы можем быть уверены в том, что значение «0,692951» находится в интервале 30 +/- 0,692951″, где значение 0,692951 — это значение, возвращаемого значением ДОВЕРИТ(0,05, 2,5, 50).
В этом же примере в заключение говорится, что средняя продолжительность поездки на работу равна 30 ± 0,692951 минуты или от 29,3 до 30,7 минуты. Это также утверждение о том, что численность населения находится в интервале [30 –0,692951, 30 + 0,692951] с вероятностью 0,95.
Перед проведением эксперимента, который дает данные в данном примере, статистический статистик (в отличие от байеса) не может делать никаких заявлений о распределении вероятности распределения по численности населения. Вместо этого статистический статистик в классической версии имеет дело с проверкой гипотез.
Например, классическому статистику может потребоваться провести двухбоговую проверку гипотезы на основе гипотезы на основе гипотезы о нормальном распределении с известным стандартным отклонением (например, 2,5), заранее выбранным значением μ0 и предопределенным уровнем значимости (например, 0,05). Результат проверки будет основан на значении наблюдаемого значения выборки (например, 30), а гипотеза null о том, что это μ0, будет отклонена на уровне значимости 0,05, если наблюдаемое значение имеет значение слишком далеко от μ0 в любом направлении. Если гипотеза NULL отклонена, то интерпретация состоит в том, что выборка означает, что выборка означает, что гораздо больше μ0 может возникнуть менее 5 % времени при позиции, что μ0 — это истинное подмногление численности населения. После проведения этого теста статистический статистик по-прежнему не может сделать никаких заявлений о распределении вероятностей для распределения по численности населения.
С другой стороны, байесский статистический статистик начинается с предполагается распределение вероятности для распределения по численности населения (априори), собирает экспериментальные признаки так же, как и статистический статистик, и использует его для изменения его распределения вероятности для многубного распределения по численности населения и тем самым получения задняя часть распределения. Excel не предусмотрены статистические функции, которые помогли бы байесам в этом случае. Excel статистические функции классической статистики.
Доверительный интервал связан с проверкой гипотез. Учитывая экспериментальные признаки, доверительный интервал делает краткое утверждение о значениях среднего среднего гипотезы μ0, которое позволит принять нулевую гипотезу о том, что это μ0, и значения μ0, которые подавят отклонение гипотезы null о том, что это значение имеет значение μ0. Статистический статистик не может сделать ни одного заявления о вероятности того, что оно попадает в определенный интервал, так как он никогда не делает предопределенные предположения относительно этого распределения вероятности, и такие предположения потребуются, если они будут использовать экспериментальные признаки для их изменения.
Изучение связи между проверками гипотез и доверитными интервалами с помощью примера в начале этого раздела. Связь между доверим и НОРМСИНХОV, которая была заверяема в последнем разделе, имеется:
CONFIDENCE(0.05, 2.5, 50) = NORMSINV(1 – 0.05/2) * 2.5 / SQRT(50) = 0.692951
Так как выборка имеет 30-е, доверительный интервал составляет 30 +/- 0,692951.
Теперь рассмотрим двухбудную проверку гипотезы с уровнем значимости 0,05, как описано выше, в котором предполагается нормальное распределение со стандартным отклонением 2,5, выборку размером 50 и определенным гипотезой о среднего распределения ( μ0). Если это истинное решение по численности населения, то выборка будет взята из нормального распределения со стандартным отклонением μ0 и стандартным отклонением 2,5/SQRT(50). Это распределение симметрично о μ0, и вы хотите отклонить гипотезу null, если abS(выборка μ0) > некого конечного значения. Конечное значение будет таким, что если μ0 — это истинное значение по численности населения, значение выборки — μ0 больше, чем это обрезка, или значение μ0 — выборочная величина выше, чем это обрезка будет возникать с вероятностью 0,05/2. Это вырезание
NORMSINV(1 – 0.05/2) * 2.5/SQRT(50) = CONFIDENCE(0.05, 2.5, 50) = 0. 692951
Отклонить нулевую гипотезу (о численности населения = μ0), если одно из следующих заявлений истинно:
выборка «mean» — μ0 > 0. 692951
0 — пример > 0. 692951
Так как в нашем примере примере выборка » = 30″, эти две выписки становятся следующими:
30 — μ0 > 0. 692951
μ0 –30 > 0. 692951
При переописи слева отображается только μ0, что приводит к следующим утверждениям:
μ0 < 30-0. 692951
μ0 > 30 + 0. 692951
Это точно те значения μ0, которые не находятся в доверительный интервал [30 – 0,692951, 30 + 0,692951]. Поэтому доверительный интервал [30 –0,692951, 30 + 0,692951] содержит значения μ0, где null-гипотеза о том, что это μ0, не будет отклонена с учетом примеров признаков. Для значений μ0 вне этого интервала гипотеза null о том, что это μ0, будет отклонена с учетом примеров признаков.
Выводы
Неточности в более ранних версиях Excel обычно возникают при очень небольших или очень больших значениях p в нормУРОВН(p). Доверит оценивается с помощью вызовов НОРМ.СТ.ВВ(p), поэтому точность НОРМСИНВ является потенциальной проблемой для пользователей ДОВЕРИТ. Однако значения p, которые используются на практике, вряд ли являются достаточно крайними, чтобы вызывать существенные ошибки округленного округления в нормУРОВН, и производительность доверит пользователям любой версии Excel.
В большинстве статей основное внимание уделялось анализу результатов проверки доверить. Другими словами, мы спросили: «В чем смысл доверительный интервал?» Доверительный интервал часто неправильно понимается. К сожалению, Excel этой теме были Excel справки во всех версиях Excel 2003. Улучшен Excel 2003.
- Авторы
- Файлы работы
- Сертификаты
Коваль О.В. 1, Аверьянова С.Ю. 2
1Филиал Южного федерального универстета в г.Новошахтинске
2Филиал Южного федерального университета в г.Новошахтинске Ростовской области
Комментарии
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF
овладеть навыками расчета числовых характеристик выборки с помощью Надстройки Пакет Анализа ЭТ MS Excel.
Краткая теория
В ЭТ MS Excel имеется набор мощных инструментов для работы с выборками и углубленного статистического анализа данных, называемый Пакет анализа, который может быть использован для решения задач статистической обработки выборочных данных.
Надстройка Пакет анализа вызывается командой главного меню Данные → Анализ данных. В появившемся окне Анализ данных выбираем пункт Описательная статистика.
Далее откроется окно Описательная статистика, в котором необходимо сделать нужные установки.
Входной диапазон. Ссылка на диапазон, содержащий анализируемые данные. Ссылка должна состоять не менее чем из двух смежных диапазонов данных, данные в которых расположены по строкам или столбцам.
Группирование. Установите переключатель в положение «По столбцам» или «По строкам» в зависимости от расположения данных во входном диапазоне.
Метки в первой строке/Метки в первом столбце. Если первая строка исходного диапазона содержит названия столбцов, установите переключатель в положение Метки в первой строке. Если названия строк находятся в первом столбце входного диапазона, установите переключатель в положение Метки в первом столбце. Если входной диапазон не содержит меток, то необходимые заголовки в выходном диапазоне будут созданы автоматически.
Уровень надежности. Установите флажок, если в выходную таблицу необходимо вывести границу доверительного интервала для среднего. В поле введите требуемое значение в процентах. Например, значение 95% вычисляет уровень надежности среднего с уровнем значимости 0,05.
К-ый наибольший. Установите флажок, если в выходную таблицу необходимо включить строку для k-го наибольшего значения для каждого диапазона данных. В соответствующем окне введите число k. Если k равно 1, эта строка будет содержать максимальное значение выборки.
К-ый наименьший. Установите флажок, если в выходную таблицу необходимо включить строку для k-го наименьшего значения для каждого диапазона данных. В соответствующем окне введите число k. Если k равно 1, эта строка будет содержать минимальное значение выборки.
Выходной диапазон. Введите ссылку на левую верхнюю ячейку выходного диапазона. Этот инструмент анализа выводит два столбца сведений для каждого набора данных. Левый столбец содержит метки статистических данных; правый столбец содержит статистические данные. Состоящий их двух столбцов диапазон статистических данных будет выведен для каждого столбца или для каждой строки входного диапазона в зависимости от положения переключателя Группирование.
Если хотим вывести результаты расчета на новый лист, то установите переключатель, чтобы открыть новый лист в книге и вставить результаты анализа, начиная с ячейки A1. Если в этом есть необходимость, введите имя нового листа в поле, расположенном напротив соответствующего положения переключателя.
Если хотим вывести результаты расчета в новой книге, то установите переключатель, чтобы открыть новую книгу и вставить результаты анализа в ячейку A1 на первом листе в этой книге.
Итоговая статистика. Установите флажок, если в выходном диапазоне необходимо получить по одному полю для каждого из следующих видов статистических данных, представленных в таблице 2.
Таблица 2.
|
Значение |
Примечания |
|
Среднее |
Выборочное среднее х=1n∙i=1nxi. Функция СРЗНАЧ. |
|
Стандартная ошибка |
Оценка среднеквадратичного отклонения выборочного среднего. Вычисляется по формуле 1n∙(n-1)∙i=1n(xi-x)2 |
|
Медиана |
Число, которое является серединой множества чисел, то есть половина чисел имеют значения большие, чем медиана, а половина чисел имеют значения меньшие, чем медиана. Функция МЕДИАНА. |
|
Мода |
Наиболее часто встречающееся значение в выборке. Если нет одинаковых значений, то возвращается значение ошибки #Н/Д. Функция МОДА.ОДН. |
|
Стандартное отклонение |
Оценка среднеквадратичного отклонения генеральной совокупности S=1n-1∙i=1n(xi-x)2. Функция СТАНДОТКЛОН.В. |
|
Дисперсия выборки |
Оценка дисперсии генеральной совокупности . Функция ДИСП.В. |
|
Эксцесс |
Выборочный эксцесс. Функция ЭКСЦЕСС. |
|
Асимметрич-ность |
Коэффициент асимметрии. Функция СКОС. |
|
Интервал |
Размах варьирования R = xmax ‒ xmin . |
|
Минимум |
Минимальное значение в выборке. Функция МИН. |
|
Максимум |
Максимальное значение в выборке. Функция МАКС. |
|
Сумма |
Сумма всех значений в выборке. Функция СУММ. |
|
Счет |
Объем выборки. Функция СЧЕТ. |
|
Наибольший |
k-тое наибольшее значение выборки. Если k=1, то выводится максимальное значение. Функция НАИБОЛЬШИЙ. |
|
Наименьший |
k-тое наименьшее значение выборки. Если k=1, то выводится минимальное значение. Функция НАИМЕНЬШИЙ |
|
Уровень надежности |
Параметр показывает возможность отклонения среднего по выборке, от среднего для генеральной совокупности, при заданном уровне надежности. |
Замечание. Следует обратить внимание на то, что расчет параметров в режиме Описательная статистика имеет ряд важных особенностей:
1. В качестве значений параметров: Стандартное отклонение, Дисперсия выборки, Эксцесс, Асимметричность – Excel генерирует оценки соответствующих параметров для генеральной совокупности, а не для выборки.
2. Для применения Описательной статистики предварительное ранжирование исходных данных не требуется: при вычислении показателей ранжирование выполняется автоматически.
3. Появление в ячейке Мода индикатора ошибки #Н/Д указывает на то, что в анализируемых данных нет одинаковых значений признака. В этом случае в качестве моды Мо выбирается то значение признака, которое соответствует максимальной ординате теоретической кривой распределения.
4. Индикатор ошибки #ДЕЛ/0! В ячейке Эксцесс и/или Асимметричность означает, что в результативной таблице стандартное отклонение является нулевым или же заданный входной диапазон данных содержит менее четырех элементов данных
5. Стандартная ошибка ‒ это разность между ожидаемыми и наблюдаемыми значениями исследуемого признака.
Стандартная ошибка или ошибка среднегонаходится из выражения
m=Sn .
Стандартная ошибка – это параметр, характеризующий степень возможного отклонения среднего значения, полученного на исследуемой ограниченной выборке, от истинного среднего значения, полученного на всей совокупности элементов. С помощью стандартной ошибки задается так называемый доверительный интервал. 95%-ый доверительный интервал, равный х ± 2т , обозначает диапазон, в который с вероятностью р = 0,95 (при достаточно большом числе наблюдений п>30) попадает среднее значение генеральной совокупности.
Пример выполнения
Постановка задачи. Приведены объемы дневной выручки (в тыс. руб.) 24 продавцов колбасных изделий, работающих в разных районах города (см. табл.1).
Таблица 1.
|
20,2 |
19,3 |
19,9 |
23,1 |
18,8 |
17,4 |
|
19,9 |
18,3 |
16,4 |
17,3 |
18,3 |
15,8 |
|
20,5 |
20,6 |
19,4 |
18,7 |
16,3 |
18,4 |
|
21,6 |
21,2 |
19,3 |
19,1 |
19,3 |
18,8 |
Требуется: выполнить описательную статистику выборки с помощью Надстройки Пакет Анализа ЭТ MS Excel.
Решение задачи в среде ЭТ MSExcel. Для решения задачи в среде ЭТ MS Excel необходимо выполнить следующие действия:
1. Идентифицируйте свою работу, переименовав Лист1 в Титульный лист и записав номер лабораторной работы, ее название, кто выполнил и проверил.
2. Переименуйте Лист 2 в Исходные данные и наберите столбец исходных данных.
3. Вычислите величины хmax, хmin, R, n, N, Nокругл., Δ и Δокругл. , используя встроенные функции Excel МАКС, МИН, СЧЕТ, КОРЕНЬ и ОКРУГЛ.
4. Сформируйте столбец интервалов группировки. Наберите команду Данные → Анализ данных → Гистограмма и в появившемся диалоговом окне выполните нужные установки. Отформатируйте полученную таблицу и построенную гистограмму выборки.
5. Наберите команду Данные → Анализ данных → Описательная статистика и в появившемся диалоговом окне выполните нужные установки.
6. Щелчок по кнопке «ОК» приводит к появлению результирующей таблицы статистических характеристик выборки.
7. Повторно вычислим найденные характеристики с помощью встроенных функций MS Excel или формул. Сравним полученные результаты.
8. Сделайте выводы и сохраните работу в вашем каталоге.
Исходные данные для самостоятельного решения
Задание. Имеется выборка объема n = 27 (табл. 2).
Требуется: выполнить описательную статистику выборки с помощью Надстройки Пакет Анализа ЭТ MS Excel.
Таблица 2.
|
№ варианта |
Выборка |
||||||||
|
1 |
22,5 |
20,2 |
19,3 |
19,9 |
23,1 |
18,8 |
17,4 |
21,6 |
19,1 |
|
21,6 |
19,9 |
18,3 |
16,4 |
17,3 |
18,3 |
15,8 |
21,2 |
19,3 |
|
|
17,8 |
20,5 |
20,6 |
19,4 |
18,7 |
16,3 |
18,4 |
19,3 |
18,8 |
|
|
2 |
18,8 |
20,2 |
19,3 |
19,9 |
23,2 |
22,5 |
17,4 |
21,8 |
19,2 |
|
19,4 |
18,7 |
16,3 |
18,4 |
19,3 |
18,8 |
19,4 |
18,7 |
16,3 |
|
|
20,5 |
20,6 |
19,4 |
18,7 |
16,3 |
18,4 |
19,3 |
18,8 |
17,8 |
|
|
2 |
20,2 |
19,3 |
19,9 |
23,1 |
18,8 |
17,4 |
21,6 |
19,1 |
22,4 |
|
18,7 |
20,2 |
19,3 |
19,9 |
23,2 |
22,5 |
17,4 |
21,8 |
19,2 |
|
|
18,1 |
19,8 |
18,2 |
16,4 |
17,2 |
21,8 |
15,8 |
21,2 |
19,2 |
|
|
3 |
19,4 |
18,7 |
16,3 |
18,4 |
19,3 |
18,8 |
19,4 |
18,7 |
16,3 |
|
18,5 |
20,6 |
19,4 |
20,7 |
16,3 |
18,4 |
19,3 |
18,8 |
17,8 |
|
|
20,1 |
19,3 |
19,9 |
23,1 |
18,8 |
17,4 |
21,6 |
19,1 |
22,4 |
|
|
4 |
19,7 |
20,2 |
19,3 |
18,9 |
23,2 |
22,5 |
17,4 |
21,8 |
19,2 |
|
18,3 |
19,8 |
18,2 |
16,4 |
17,2 |
21,8 |
15,8 |
21,2 |
19,2 |
|
|
19,7 |
18,7 |
16,3 |
18,4 |
19,3 |
18,8 |
19,4 |
18,7 |
16,3 |
|
|
5 |
19,4 |
20,7 |
16,3 |
18,4 |
19,3 |
18,8 |
17,8 |
18,7 |
20,2 |
|
19,9 |
23,1 |
18,8 |
17,4 |
21,6 |
19,1 |
22,4 |
18,1 |
19,8 |
|
|
19,3 |
18,9 |
23,2 |
22,5 |
17,4 |
21,8 |
19,2 |
19,4 |
18,7 |
|
|
6 |
18,7 |
16,3 |
18,4 |
19,3 |
18,8 |
19,4 |
18,7 |
18,5 |
20,6 |
|
20,6 |
19,4 |
20,7 |
16,3 |
18,4 |
19,3 |
18,8 |
18,4 |
19,3 |
|
|
19,3 |
19,9 |
23,1 |
18,8 |
17,4 |
21,6 |
19,1 |
18,4 |
19,3 |
|
|
7 |
16,3 |
18,4 |
19,3 |
18,8 |
19,4 |
18,7 |
18,5 |
20,6 |
18,7 |
|
19,4 |
20,7 |
16,3 |
18,4 |
19,3 |
18,8 |
18,4 |
19,3 |
20,6 |
|
|
19,9 |
23,1 |
18,8 |
17,4 |
21,6 |
19,1 |
18,4 |
19,3 |
19,3 |
|
|
8 |
19,3 |
19,9 |
23,1 |
18,8 |
17,4 |
21,6 |
19,1 |
22,5 |
20,2 |
|
18,3 |
16,4 |
17,3 |
18,3 |
15,8 |
21,2 |
19,3 |
21,6 |
19,9 |
|
|
20,6 |
19,4 |
18,7 |
16,3 |
18,4 |
19,3 |
18,8 |
17,8 |
20,5 |
|
|
9 |
19,4 |
20,7 |
16,3 |
18,4 |
19,3 |
18,8 |
17,8 |
18,7 |
20,2 |
|
19,9 |
23,1 |
18,8 |
17,4 |
21,6 |
19,1 |
22,4 |
18,1 |
19,8 |
|
|
19,3 |
18,9 |
23,2 |
22,5 |
17,4 |
21,8 |
19,2 |
19,4 |
18,7 |
|
|
10 |
18,7 |
16,3 |
18,4 |
19,3 |
18,8 |
19,4 |
18,7 |
18,5 |
20,6 |
|
20,6 |
19,4 |
20,7 |
16,3 |
18,4 |
19,3 |
18,8 |
18,4 |
19,3 |
|
|
16,4 |
20,4 |
20,8 |
19,4 |
18,7 |
17,8 |
18,4 |
19,4 |
18,8 |
Просмотров работы: 3443
Код для цитирования: