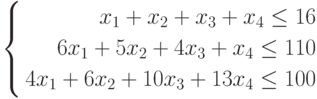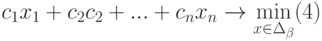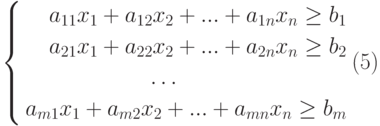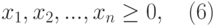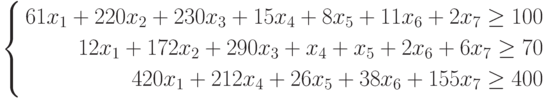Урок задачи оптимизации excel

Решение задач оптимизации с помощью электронных таблиц

Оглавление

Задачи оптимизации в ЕXCEL        1

Надстройки в электронных таблицах        1

Алгоритм решения задач        2

Задача 1. «Покраска пола»        3

        Решение на компьютере:        4

Задача 2        6

Задача 3        6

Задача 4        7

Задача 5        8

Задача 6        8

Задача 7        9

Надстройки в электронных таблицах

        Возможности электронных таблиц не ограничиваются вычислениями по формулам и построением диаграмм и графиков. С помощью надстроек электронных таблиц можно строить информационные модели, приближенно с заданной точностью решать уравнения методом подбора параметра, решать задачи оптимизационного моделирования методом поиска решений и т.д. Некоторые из надстроек не устанавливаются по умолчанию и требуют установки.

        Поиск решения. Поиск решения является надстройкой (рис. 1.1.5.), которая позволяет решать задачи оптимизационного моделирования. Процедура поиска решения позволяет найти оптимальное значение формулы, содержащейся в ячейке, которая называется целевой. Эта процедура работает с группой ячеек, прямо или косвенно связанных с формулой в целевой ячейке. Чтобы получить по формуле, содержащейся в целевой ячейке, искомый результат, процедура изменяет значения во влияющих ячейках. Чтобы сузить множество значений, используемых в модели, применяются ограничения. Эти ограничения могут содержать ссылки на другие влияющие ячейки.

Рисунок 1.1.5.

Задача оптимизации – поиск оптимального (наилучшего) решения данной задачи при соблюдении некоторых условий.

Алгоритм решения задач

1. Разобрать условие задачи.
2. Построить математическую модель.
3. Выбрать поисковые переменные.
4. Задать ограничения.
5. Выбрать критерий оптимизации.
6. Решить задачу на компьютере.
7. Проанализировать полученные результаты.

Выбрать Главное меню – Данные – группа Работа с данными – кнопка Анализ «Что-если».

Подбор параметра является одним из инструментов анализа «что-если». Этот метод используется при поиске значения аргумента функции, который обеспечивает требуемое значение функции. При подборе параметра изменяется значение в ячейке аргумента функции до тех пор, пока значение в ячейке самой функции не будет возвращать нужный результат. Это как бы подгонка исходных данных задачи к требуемому ответу, известному заранее.

Задача 1. «Покраска пола»

Вычислить количество краски для покрытия пола в спортивном зале.

Сначала измеряют длину a (18,1 ≤ а ≤ 18,3) и

ширину b (7,6 ≤ b ≤ 7,7) пола.

Реальный объект – пол зала – заменяют прямоугольником, для которого S = ab.

При покупке краски выясняют, какую площадь S1 можно покрыть содержимым  одной банки (предположим меньше 10 м2), вычисляют необходимое количество банок  n=ab/S1.

а, b, S1 – поисковые переменные, значения которых можно изменять.

Необходимо задать ограничения: а ≥ 18,1;  а ≤ 18,3;  b ≤ 7,6;  b ≥7,7;  S1 ≤ 10.

Критерий оптимизации: количество банок должно быть минимальным, т.е. n=ab/S1 = min.

Решение на компьютере:

1. Заполнить таблицу, указав произвольные значения для поисковых переменных.

	А	В
1	Поисковые переменные
2	имя	значение
3	а	18,1
4	b	7,6
5	S1	10
6	Критерий оптимизации
7	n	=B3*B4/B5
8

1. Найти оптимальное решение,  для этого:

• Выделить целевую ячейку В7;
• Нажать кнопку MS Office    – кнопка Параметры Excel – Надстройки – Поиск решения (находится во

вкладке Данные)

• Установить целевую ячейку, равную минимальному значению.
• Указать мышью диапазон изменяемых ячеек.

• Выбрать кнопку Добавить для записи ограничений.

• После записи ограничения нажать Добавить (для последнего ограничения – ОК).
• Нажать кнопку Выполнить.
• Выбрать Тип отчета, Результаты и нажать ОК.
• На новом листе Отчет по результатам1 можно увидеть:

В электронных таблицах найдено оптимальное решение: для покраски пола в актовом зале необходимо не более 14 банок краски.

Задача 2

На научный семинар собрались ученые и обменялись визитными карточками. Число визитных карточек составило 210 штук. Сколько ученых приехало на семинар, если их было не более 20?

Решение:

х – количество ученых

n – количество карточек

Подумайте, определите, составьте:

• Математическая модель
• Поисковые переменные
• Ограничения
• Критерий оптимизации

Найдите поиск решения в Еxcel,  создайте отчет и сохраните документ под именем семинар.xls.

Задача 3

Какие размеры должен иметь бак объемом V = abh = 2000 куб.см, чтобы на его изготовление пошло как можно меньше материала? Сторона а должна быть не менее 10 см.

Выполните поиск решения, заполнив таблицу:

Задача 4

На участке работает 20 человек; каждый из них в среднем работает 1800 часов в год. Выделенные ресурсы: 32 т металла, 54 тыс кВт.ч электроэнергии. План реализации: не менее 2 тыс. изделий А и не менее 3 тыс. изделий Б. На выпуск 1 тыс. изделий А затрачивается 3 т металла, 3 тыс. кВт.ч электроэнергии и 3 тыс. ч рабочего времени. На выпуск 1 тыс. изделий Б затрачивается 1 т металла, 6 тыс. кВт.ч электроэнергии и 3 тыс. ч рабочего времени.

От реализации 1 тыс. изделий А завод получает прибыль 500 тыс.р., от реализации 1 тыс. изделий Б – 700 тыс.р.

Выпуск какого количества изделий А и Б (в тыс. штук) надо запланировать, чтобы прибыль от их реализации была наибольшей? Составьте модель и решите задачу.

Выполните поиск решения, заполнив таблицу. Создайте отчет и сохраните документ под именем работа5.xls.

Задача 5

Кооператив из 20 человек выпускает изделия А и Б (смотри задание 5). Кооператив намерен получать прибыль не менее 6,5 млн. руб. в год. Ему выделили 54 тыс. кВт.ч электроэнергии. Какое минимальное количество металла потребуется кооперативу, чтобы обеспечить нужную прибыль?

Составьте модель и решите задачу. Создайте отчет и сохраните документ под именем работа6.xls.

Задача 6

Начальник участка изучает возможность расширить ассортимент товаров – добавить к выпускаемым изделиям А и Б еще два вида изделий В и Г. Предварительное изучение спроса показало, что можно реализовать не более 5 тыс. изделий В, получив при этом прибыль в размере 1200 руб. с каждого изделия. Можно также реализовать не более 4 тыс. изделий Г, получив прибыль 1000 руб. с изделия. На 1 тыс. изделий В расход металла составляет 0,5 тонн, электроэнергии 4 тыс. кВт.ч, рабочего времени 5 тыс.час.  Для выпуска 1 тыс. изделий Г требуется 1,5 т металла, 4 тыс. кВт.ч электроэнергии, 6 тыс. ч рабочего времени. Расширение ассортимента изделий потребует приобретение дополнительного оборудования на сумму 800 тыс. рублей, которая будет возмещена из прибыли. Целесообразно ли расширение ассортимента выпускаемых товаров (можно ли спланировать выпуск товаров А, Б, В, Г так, чтобы получить прибыль большую, чем при выпуске только товаров А и Б)?

Выполните поиск решения, создайте отчет и сохраните документ под именем работа7.xls.

Задача 7

Заведующий хозрасчетной больницей должен составить штатное расписание, т.е. определить, сколько сотрудников, на какие должности и с каким окладом он должен принять на работу. Общий месячный фонд зарплаты составляет 10 000 у.е. Известно, что для нормальной работы больницы нужно 5-7 санитарок, 8-10 медсестер, 10-12 врачей, 1 зав. аптекой, 1 зав. отделением, 1 главный врач, 1 завхоз, 1 зав. больницей.

За основу берется оклад санитарки, а все остальные вычисляются по формуле:

АВ + С, где С – оклад санитарки, А и В – коэффициенты, которые для каждой должности определяются решением совета трудового коллектива.

Допустим, совет решил, что:

— медсестра должна получать в 1,5 раза больше санитарки (А = 1,5; В = 0);

— врач – в 3 раза больше санитарки;

— зав.отделением – на 30 у.е. больше, чем врач;

— зав.аптекой – в 2 раза больше санитарки;

— завхоз – на 40 у.е. больше медсестры;

— главный врач – в 4 раза больше санитарки;

— зав.больницей – на 20 у.е. больше главного врача.

Составьте модель и решите задачу.

1. Заполните таблицу, установив зарплату санитарки 150 у.е. Расположите таблицу на листе Расписание.

1. Составьте штатное расписание с использованием функции автоматизации расчетов Подбор параметра  (Меню – Данные – (блок Работа с данными) – Анализ «Что-если»

1. Составьте несколько вариантов штатного расписания, изменяя количество сотрудников на должностях санитарки, медсестры, врача. Подберите зарплату санитарки в новых условиях. Расположите таблицу на листе Варианты.
2. Удалите остальные листы.
3. Сохраните документ под именем госпиталь.xls.

Задание №1.

Тема: Решение задач оптимизации в EXCEL

План занятия:

1. Оптимизационные модели при экономической и технической сфере.

Цель занятия: подобрать сбалансированное решение, оптимальное в конкретных условиях (количество продаж для получения определенной выручки, лучшее меню, число рейсов и т.п.).

В Excel для решения задач оптимизации используются следующие команды:

• Подбор параметров («Данные» — «Работа с данными» — «Анализ «что-если»» — «Подбор параметра») – находит значения, которые обеспечат нужный результат.

• Поиск решения (надстройка Microsoft Excel; «Данные» — «Анализ») – рассчитывает оптимальную величину, учитывая переменные и ограничения. Перейдите по ссылке и узнайте как подключить настройку «Поиск решения».

• Диспетчер сценариев («Данные» — «Работа с данными» — «Анализ «что-если»» — «Диспетчер сценариев») – анализирует несколько вариантов исходных значений, создает и оценивает наборы сценариев.

Для решения простейших задач применяется команда «Подбор параметра». Самых сложных – «Диспетчер сценариев». Рассмотрим пример решения оптимизационной задачи с помощью надстройки «Поиск решения».

Условие. Фирма производит несколько сортов йогурта. Условно – «1», «2» и «3». Реализовав 100 баночек йогурта «1», предприятие получает 200 сом. «2» — 250 сом. «3» — 300 сом. Сбыт, налажен, но количество имеющегося сырья ограничено. Нужно найти, какой йогурт и в каком объеме необходимо делать, чтобы получить максимальный доход от продаж.

Известные данные (в т.ч. нормы расхода сырья) занесем в таблицу:

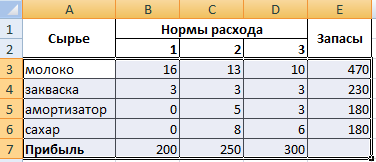
На основании этих данных составим рабочую таблицу:

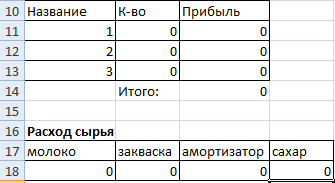
1. Количество изделий нам пока неизвестно. Это переменные.

2. В столбец «Прибыль» внесены формулы: =200*B11, =250*В12, =300*В13.

3. Расход сырья ограничен (это ограничения). В ячейки внесены формулы: =16*B11+13*B12+10*B13 («молоко»); =3*B11+3*B12+3*B13 («закваска»); =0*B11+5*B12+3*B13 («амортизатор») и =0*B11+8*B12+6*B13 («сахар»). То есть мы норму расхода умножили на количество.

4. Цель – найти максимально возможную прибыль. Это ячейка С14.

Активизируем команду «Поиск решения» и вносим параметры.

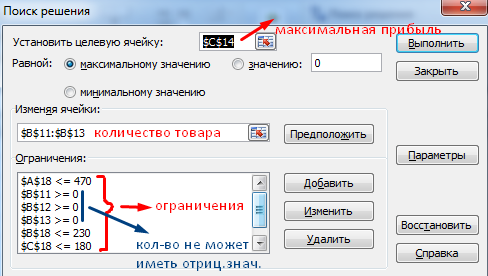
После нажатия кнопки «Выполнить» программа выдает свое решение.

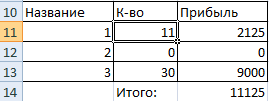
Оптимальный вариант – сконцентрироваться на выпуске йогурта «3» и «1». Йогурт «2» производить не стоит.

во втором поле выбрать оператор ограничения (>, Поиск решения).

Найденные решения (значения изменяемых ячеек) можно сохранить в качестве сценария. Для этого нужно:

1. В диалоговом окне Результаты поиска решения выбрать Сохранить сценарий.
2. В поле Название сценария ввести имя сценария. Просмотреть сценарии можно с помощью команды Данные > Работа с данными > Анализ что-если > Диспетчер сценариев > Сценарии.

С помощью программы Поиск решения можно создать три типа отчетов по результатам, полученным при успешном завершении процедуры решения.

Каждый отчет создается на отдельном листе текущей рабочей книги.

Для создания отчета надо в диалоговом окне Результаты поиска решения выбрать нужный тип отчета в поле Тип отчета. Можно выбрать сразу несколько типов (при выделении нескольких строк используется клавиша ).

• Результаты – отчет содержит целевую ячейку, список изменяемых ячеек, их исходные и конечные значения, ограничения и сведения о них.
• Устойчивость – отчет содержит сведения о степени зависимости модели от изменений величин, входящих в формулы, применяемые в задаче (формулы модели и формулы ограничений).
• Пределы – выводится целевая ячейка и ее значение, а также список изменяемых ячеек, их значений, нижних и верхних пределов и целевых результатов.

Рассмотрим применение процессора Excel для решения ЗЛП на примерах.

Задача 1. Планирование производства

Модель линейного программирования дает возможность определить наиболее выгодную производственную программу выпуска нескольких видов продукции при заданных ограничениях на ресурсы.

МП выпускает товары х₁,х₂,х₃,х₄, получая от реализации каждого прибыль в 60,70,120,130 руб. соответственно. Затраты на производство приведены в таблице.

Затраты	х1	х2	x3	х4	Всего
Трудовые	1	1	1	1	16
Сырьевые	6	5	4	1	110
Финансы	4	6	10	13	100

1. Максимум прибыли в зависимости от оптимального распределения затрат.
2. Минимум ресурсов, необходимых для получения максимальной прибыли.

Решение задачи средствами Excel состоит из 4 этапов:

1. Создание математической модели задачи ЛП.
2. Создание формы для ввода условий задачи, ввод в неё исходных данных и зависимостей из математической модели.
3. Ввод данных из формы в окно Excel Поиск решения из меню Данные.
4. Задание параметров поиска и решение задачи.

Создание математической модели задачи

Составим математическую модель процесса по описанию задачи:

— целевая функция прибыли.

— граничные условия модели, так как количество производимых товаров не может быть отрицательной величиной.

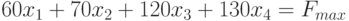
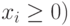
Для решения данной задачи c помощью программы MS Excel создадим новую книгу с именем Линейное программирование и изменим имя ее первого рабочего листа на Задача о производстве.

Создание формы

• Составление формы в виде:

A	B	C	D	E	F	G	H
1	Переменная	х7	х2	x3	х4	Формула	Знак	Св.член
2	Значение
3	Коэф. ЦФ	60	70	120	130	=СУММПРОИЗВ(В$2:Е$2;В3:Е3)	Max
4	Трудовые	1	1	1	1	=СУММПРОИЗВ(В$2:Е$2;В4:Е4)		16
5	Сырьевые	6	5	4	1	=СУММПРОИЗВ(В$2:Е$2;В5:Е5)		110
6	Финансы	4	6	10	13	=СУММПРОИЗВ(В$2:Е$2;В6:Е6)		100

• Запись в ячейки В3:Е3 коэффициентов целевой функции F (1), в В4:Е6 коэффициентов из системы ограничений (2) и в ячейки Н4:Н6 – свободных членов из системы (2).
• Ввод формул с помощью f_x – Мастера функций.

Для ввода формулы в целевую ячейку (целевой функции): щелкнуть левой клавишей мыши по ячейке F3 , затем по значку Мастера функций f_x на панели инструментов, в появившемся окне «Мастер функций, Шаг 1» выбрать категорию «Математические», далее выбрать функцию СУММПРОИЗВ, нажать клавишу ОК, в окне «Мастер функций Шаг 2» в поле Массив 1 ввести с клавиатуры В2:Е2 (ячейки, в которых будут варьироваться х₁..х₄), в поле Массив 2 ввести В3:Е3 (коэффициенты целевой функции ЦФ).

Примечание. Можно вводить В2:Е2 не с клавиатуры, а поставить курсор в окно Массив 1, а затем протащить курсор при нажатой левой клавише мыши по ячейкам В2:Е2, имена ячеек сами запишутся в окно. Аналогично поступить с полем Массив 2.

Нажать клавишу ОК, в ячейку F3 запишется формула 60х₁+70х₂+120х₃+ 130х₄ в виде СУММПРОИЗВ(В2:Е2;В3:Е3).

Чтобы не вводить формулы в другие ячейки, необходимо изменить тип адресации для ячеек В2:Е2 с относительной на абсолютную $B$2:$E$2 , установив курсор перед нужным адресом B2 и нажав функциональную клавишу F4 , затем повторить эти действия для адреса E2 . Формула примет следующий вид:

После внесенных изменений необходимо скопировать формулу в ячейки F4:F6 c помощью маркера заполнения. Для этого необходимо выделить ячейку F3 , содержащую нужную формулу, установить указатель мыши на черный квадратик в правом нижнем углу ячейки (он примет форму черного крестика) и протащить с помощью левой кнопки мыши на весь требуемый диапазон.

В результате копирования мы увидим следующие формулы:

• в ячейке F4 – СУММПРОИЗВ($В$2:$Е$2;В4:Е4),
• в ячейке F5 – СУММПРОИЗВ($В$2:$Е$2;В5:Е5),
• в ячейке F6 – СУММПРОИЗВ($В$2:$Е$2;В6:Е6).

Заполнение окна Поиск решения

Выбрать в пункте меню Данные команду Поиск решения, поставить курсор в поле целевой функции, выделить ячейку F3 в форме (или ввести F3 с клавиатуры), поставить переключатель в положение «Максимальному значению» (см. рис. 12.1 рис. 12.1). В поле «Изменяя ячейки» ввести $В$2:$Е$2(с клавиатуры или протащив мышью).

Нажать клавишу «Добавить», в окне «Добавление ограничения» в поле «Ссылка на ячейку» ввести F4 , выбрать через «стрелка вниз» знак ««, в поле справа ввести Н4 (рис. 12. рис. 12.2).

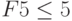
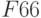
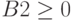
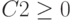
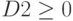
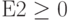
Аналогично через «Добавить» ввести , для системы ограничений (2), а также , , и .

Также необходимо добавить ограничения для получения целочисленных величин по количеству товаров: B2=цел, C2=цел, D2=цел и Е2=цел.

После ввода последнего граничного условия вместо «Добавить» нажать клавишу ОК, появится окно «Поиск решения».

Для изменения или удаления ограничений и граничных условий используются клавиши Изменить, Удалить.

Параметры поиска

В окне «Поиск решения» нажать клавишу «Параметры», выбрать по умолчанию Максимальное время – 100 с, число итераций – 100 (для большинства задач это количество просчётов подходит с большим запасом), установить флажок в строке «Линейная модель», нажать ОК, в появившемся окне Поиск Решения нажать Выполнить (рис. 12. рис. 12.3).

Результаты поиска решения с таблицей результатов:

A	B	C	D	E	F	G	H
1	Переменная	X1	X2	X3	X4	Формула	Знак	Св.член
2	Значение	10	0	6	0
3	Коэф. ЦФ	60	70	120	130	1320	Max
4	Трудовые	1	1	1	1	16		16
5	Сырьевые	6	5	4	1	84		110
6	Финансы	4	6	10	13	100		100

Таким образом оптимальный план Х(Х₁,Х₂,Х₃,Х₄)=(10,0,6,0) при минимальном использовании ресурсов

• Трудовые – 16 (У₁)
• Сырьевые – 84 (У₂)
• Финансы – 100 (У₃)

даёт максимум прибыли F в 1320 руб.

_Вывод: Максимальная прибыль F в 1320 руб. получается при выпуске только товаров Х₁ и Х₃ в количестве 10 и 6 штук соответственно, товары Х₃ и Х₄ выпускать не нужно (это приведёт к снижению прибыли). Трудовые (У₁) и финансовые (У₃) ресурсы используются полностью, по сырьевым ресурсам (У₂) есть запас в 110-84=26 ед.

Кроме того, это означает, что изменение трудовых ( y₁ ) и финансовых ( y₃ ) ресурсов приведёт к изменению прибыли F , а изменение сырьевых ресурсов ( y₂ ) – нет.

Разности между плановыми ресурсами и использованными являются двойственными переменными y₁, y₂ и y₃ сопряжённой задачи линейного программирования. В данном случае y₁=y₃=0 , а y₂=26 ед. Таким образом, ресурс y₂ можно уменьшить на 26 ед., тогда план по сырью тоже будет оптимальным.

Задача 2. Задача об оптимальной диете

Имеется n видов продуктов питания, в которых содержится m типов питательных веществ (белки, жиры, углеводы). В одной весовой единице продукта i-го типа содержится а_i единиц питательного вещества j-го вида . Известна минимальная суточная потребность b _j (j in <1,2. т>) человека в каждом из видов питательных веществ. Задана калорийность с_i одной весовой единицы i-го продукта ( i принадлежит <1, 2, . n>).

Требуется определить оптимальный состав рациона продуктов, такой, чтобы каждое питательное вещество содержалось в нем в необходимом количестве, обеспечивающем суточную потребность человека, и при этом суммарная калорийность рациона была минимальной.

Ведем в рассмотрение следующие переменные: х – весовое количество продукта питания i-го типа в суточном рационе.

Тогда в общем случае математическая постановка задачи об оптимальной диете может быть сформулирована следующим образом:

где множество допустимых альтернатив 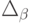формируется следующей системой ограничений типа неравенств:

Для решения задачи об оптимальной диете с помощью программы MS Excel необходимо задать конкретные значения параметрам исходной задачи.

Для определенности предположим, что в качестве исходных типов продуктов рассматриваются: хлеб, мясо, сыр, бананы, огурцы, помидоры, виноград ( n = 7), а в качестве питательных веществ рассматриваются белки, жиры, углеводы ( m = 3).

Калорийность одной весовой единицы каждого из продуктов следующая:с₁ = 2060,с₂= 2430,с₃= 3600,с₄= 890,с₅= 140,с₆= 230, с₇ = 650. Содержание питательных веществ в каждом из продуктов может быть задано в форме нижеприведенной таблицы.

Минимальная суточная потребность в питательных веществах следующая: в белках b ₁ = 100, в жирах b ₂= 70, в углеводах b3 = 400.

Для решения данной задачи c помощью программы MS Excel создадим новую книгу с именем Линейное программирование и изменим имя ее второго рабочего листа на Задача о диете.

Таблица 1. Содержание питательных веществ в продуктах питания

Продукты/питательные вещества	Хлеб ржаной	Мясо баранина	Сыр «Российский»	Банан	Огурцы	Помидоры	Виноград
Белки	61	220	230	15	8	11	6
Жиры	12	172	290	1	1	2	2
Углеводы	420	0	0	212	26	38	155

Создание математической модели задачи

Составим математическую модель процесса по описанию задачи:

– целевая функция (суммарная калорийность продуктов).

– граничные условия

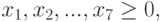
Создание формы

Для решения поставленной задачи выполним следующие подготовительные действия:

1. Внесем необходимые надписи в ячейки A1:I1, A2:A7, B4, I4, J4 .
2. В ячейки ВЗ:НЗ введем значения коэффициентов целевой функции: с₁ = 2060, с₂ = 2430, с₃ = 3600, с₄ = 890, с₅ = 140, с₆ = 230, с₇ = 650.
3. В ячейку I2 введем формулу: =СУММПРОИЗВ( b ₂:Н2;B3:H3), которая представляет целевую функцию (4).
4. В ячейки В5:Н7 введем значения коэффициентов ограничений, взятых из таблицы.

1. В ячейки J5 :J7 введем значения правых частей ограничений, соответствующих минимальной суточной потребности в питательных веществах: в белках b ₁=100 , жирах b ₂= 70 и углеводах b3 = 400.
2. В ячейку I5 введем формулу: =СУММПРОИЗВ($B$2:$H$2;В5:Н5), которая представляет левую часть первого ограничения (5).
3. Скопируем формулу, введенную в ячейку I5 , в ячейки I6 и I7 .
4. Внешний вид рабочего листа MS Office Excel с исходными данными для решения задачи об оптимальном рационе питания имеет следующий вид (pиc. 12.4).

Для отображения формул в ячейках рабочего листа необходимо выполнить команду меню: Формулы и на панели инструментов в группе Зависимости формул выбрать Показать формулы.

Заполнение окна Поиск решения

Для дальнейшего решения задачи следует вызвать мастер поиска решения, для чего необходимо выполнить операцию: Данные > Поиск решения.

После появления диалогового окна Поиск решения следует выполнить следующие действия:

1. В поле с именем Установить целевую ячейку: ввести абсолютный адрес ячейки $I$2 .
2. Для группы Равной: выбрать вариант поиска решения – минимальному значению.
3. В поле с именем Изменяя ячейки: ввести абсолютный адрес ячеек $B$2:$H$2 .
4. Добавить 3 ограничения, представляющие минимальные суточные потребности в питательных веществах. С этой целью выполнить следующие действия:
   • для задания первого ограничения в исходном диалоговом окне Поиск решения нажать кнопку с надписью Добавить (рис. 12.5 рис. 12.5, а);
   • в появившемся дополнительном окне выбрать ячейку $I$5 , которая должна отобразиться в поле с именем Ссылка на ячейку;
   • в качестве знака ограничения из выпадающего списка выбрать нестрогое неравенство » «;
   • в качестве значения правой части ограничения выбрать ячейку $J$5 ;
   • для добавления первого ограничения в дополнительном окне нажать кнопку с надписью Добавить;
   • аналогичным образом задать оставшиеся два ограничения (рис. 12.5 рис. 12.5, б).

Параметры

В окне «Поиск решения» нажать клавишу «Параметры», выбрать «Поиск решения Линейных задач симплекс-методом», нажать ОК, затем нажать Найти Решение (рис. 12.6 рис. 12.6, б).

После задания ограничений и целевой функции можно приступить к поиску численного решения, для чего следует нажать кнопку Выполнить. После выполнения расчетов программой MS Excel будет получено количественное решение, которое имеет вид, представленный на рис. 12. рис. 12.7.

Результатом решения задачи об оптимальной диете являются найденные оптимальные значения переменных: х₁ = 0, х₂ = 0,211, 3 = 0,109, х₄= 1,887, х₅ = 0, х₆ = 0, х₇ = 0, которым соответствует значение целевой функции: f_опт= 2587,140. При выполнении расчетов для ячеек В2:I2 был выбран числовой формат с 3 знаками после запятой.

Анализ найденного решения показывает, что для удовлетворения суточной потребности в питательных веществах (белки, жиры, углеводы) следует использовать 211 г мяса баранины, 109 г сыра и 1887 г бананов, совсем отказавшись от хлеба, огурцов, помидоров и винограда. При этом общая калорийность найденной оптимальной диеты будет приближенно равна 2590 ккал, что вполне соответствует малоактивному образу жизни без серьезных физических нагрузок. Напомним, что согласно медицинским данным, энергетические затраты работников интеллектуального труда (юристы, бухгалтера, врачи, педагоги) лежат в пределах 3000 ккал.

ЗАДАНИЕ

1. Составить математическую модель задачи линейного программирования.
2. Решить задачу линейного программирования в Excel с помощью Поиска решения.
3. Сохранить в виде модели установочные параметры.

Предприятие легкой промышленности выпускает две модели машин, причем каждая модель производится на отдельной технологической линии. Суточный объем производства первой линии – 80 изделий, второй линии – 85 изделий. На машину первой модели расходуются 12 однотипных элементов электронных схем, на машину второй модели – 6 таких же элементов. Максимальный суточный запас используемых элементов равен 800 единицам. Прибыль от реализации одной машины первой и второй моделей равна $30 и $40 соответственно. Определить оптимальный суточный объем производства первой и второй моделей.

Процесс изготовления двух видов промышленных изделий состоит в последовательной обработке каждого из них на трех приборах. Время использования этих приборов для производства данных изделий ограничено 10 ч. в сутки. Найти оптимальный объем производства изделий каждого вида.

Фирма имеет возможность рекламировать свою продукции, используя местные радио- и телевизионную сеть. Затраты на рекламу в бюджете фирмы ограничены $1000 в месяц. Каждая минута радиорекламы обходится в $5, а минута телерекламы – в $100. Фирма хотела бы использовать радиосеть, по крайней мере, в два раза чаще, чем сеть телевидения. Опыт прошлых лет показал, что объем сбыта, который обеспечивает каждая минута телерекламы, в 25 раз больше сбыта, обеспечиваемого одной минутой радиорекламы. Определить оптимальное распределение ежемесячно отпускаемых средств между радио- и телерекламой.

Фирма производит два вида продукции – А и B . Объем сбыта продукции вида A составляет не менее 70% общего объема реализации продукции обоих видов. Для изготовления продукции А и В используется одно и то же сырье, суточный запас которого ограничен величиной 120 кг. Расход сырья на единицу продукции A составляет 3 кг, а на единицу продукции В – 5 кг. Цены продукции А и В равны $20 и $60 соответственно. Определить оптимальное распределение сырья для изготовления продукции А и В.

Фирма выпускает женские шляпы двух фасонов. Трудоемкость изготовления шляпы фасона 1 вдвое выше трудоемкости изготовления шляпы фасона 2. Если бы фирма выпускала только шляпы фасона 1, суточный объем производства мог бы составить 60 шляп. Суточный объем сбыта шляп обоих фасонов ограничен диапазоном от 50 до 100 штук. Прибыль от продажи шляпы фасона 1 равна $6, а фасона 2 – $7. Определить какое количество шляп каждого фасона следует изготавливать, чтобы максимизировать прибыль.

Изделия четырех типов проходят последовательную обработку на двух станках. Время обработки одного изделия каждого типа на каждом из станков:

Затраты на производство одного изделия каждого типа определяются как величины, прямо пропорциональные времени использования станков (в машино-часах). Стоимость машино-часа составляет $10 и $15 для станка 1 и 2 соответственно. Допустимое время для использования станков для обработки изделий всех типов ограничено следующими значениями: 500 машино-часов – для станка 1 и 380 машино-часов для станка 2. Цены изделий типов 1,2,3 и 4 равны $65, $70, $55 и $45 соответственно. Составить план производства, максимизирующий чистую прибыль.

Завод выпускает изделия трех моделей ( I, II III ) Для их изготовления используется два вида ресурсов (А и В), запасы которых составляют – 5000 и 6000 единиц. Расходы ресурсов на одно изделие каждой модели:

Трудоемкость изготовления модели I вдвое больше, чем изделия модели II , и втрое больше, чем изделие модели III . Численность рабочих завода позволяет выпускать 1500 изделий I . Анализ условий сбыта показывает, что минимальный спрос на продукцию завода составляет 200, 200 и 150 изделий моделей I,II и III соответственно. Однако соотношение выпуска изделий моделей I,II и III должно быть равно 3:2:5. Удельная прибыль от реализации изделий моделей I,II и III составляет $30, $20 и $50 соответственно. Определить выпуск изделий, максимизирующий прибыль.

Требуется распределить имеющиеся денежные средства по четырем альтернативным вариантам. Игра имеет три исхода. Ниже приведены размеры выигрыша (или проигрыша) на каждый доллар, вложенный в соответствующий альтернативный вариант, для любого из трех исходов. У игрока имеется $500, причем, использовать в игре их можно только один раз. Точный исход игры заранее неизвестен, и, учитывая эту неопределенность, игрок решил распределить деньги так, чтобы максимизировать максимальную отдачу от этой суммы.

Бройлерное хозяйство птицеводческой фермы насчитывает 80000 цыплят, которые выращиваются до 8-недельного возраста и после соответствующей обработки поступают в продажу. Хотя недельный рацион цыплят зависит от их возраста, в дальнейшем будем считать, что в среднем (за 8 недель) он составляет 1 фунт.

Для того чтобы цыплята достигли к восьмой неделе необходимых весовых кондиций, кормовой рацион должен удовлетворять определенным требованиям по питательности. Этим требованиям могут соответствовать смеси различных видов кормов или ингредиентов. Ограничим наше рассмотрение только тремя ингредиентами: известняком, зерном и соевыми бобами. Ниже приведены данные, характеризующие содержание (по весу) питательных веществ в каждом из ингредиентов и удельную стоимость каждого ингредиента.

Смесь должна содержать:

• не менее 0.8%, но не более 1.2% кальция;
• не менее 22% белка;
• не более 5% клетчатки.

Необходимо определить количество каждого из трех ингредиентов, образующих смесь минимальной стоимости при соблюдении требований к общему расходу кормовой смеси и ее питательности.

Имеется n видов продуктов питания, в которых содержится m типов питательных веществ (белки, жиры, углеводы). В одной весовой единице продукта i-го типа содержится а_i единиц питательного вещества j-го вида . Известна минимальная суточная потребность b _j человека в каждом из видов питательных веществ. Задана калорийность сi одной весовой единицы i-го продукта ( i принадлежит <1, 2, . n >). Требуется определить оптимальный состав рациона продуктов, такой, чтобы каждое питательное вещество содержалось в нем в необходимом количестве, обеспечивающем суточную потребность человека, и при этом суммарная калорийность рациона была минимальной.

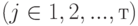
Для решения задачи об оптимальной диете с помощью программы MS Excel необходимо задать конкретные значения параметрам исходной задачи. Для определенности предположим, что в качестве исходных типов продуктов рассматриваются: хлеб, мясо, сыр, бананы, огурцы, помидоры, виноград ( n = 7), а в качестве питательных веществ рассматриваются белки, жиры, углеводы ( m = 3). Калорийность одной весовой единицы каждого из продуктов следующая:с₁ = 2060,с₂= 2430,с₃= 3600,с₄= 890,с₅= 140,с₆= 230, с₇ = 650. Содержание питательных веществ в каждом из продуктов может быть задано в форме следующей таблицы (см. табл.).

Таблица 1. Содержание питательных веществ в продуктах питания

Продукты/питательные вещества	Хлеб ржаной	Мясо баранина	Сыр «Российский»	Банан	Огурцы	Помидоры	Виноград
Белки	66	225	235	20	13	16	11
Жиры	17	177	295	1	1	7	7
Углеводы	425	0	0	217	31	43	200

Минимальная суточная потребность в питательных веществах следующая: в белках b ₁ = 105, в жирах b ₂ = 75, в углеводах b ₃ = 405.

Определить суточную потребности в питательных веществах (белки, жиры, углеводы) и общую калорийность оптимальной диеты.

Предприятие электронной промышленности выпускает две модели радиоприемников, причем каждая модель производится на отдельной технологической линии. Суточный объем производства первой линии – 60 изделий, второй линии – 75 изделий. На радиоприемник первой модели расходуются 10 однотипных элементов электронных схем, на радиоприемник второй модели – 8 таких же элементов. Максимальный суточный запас используемых элементов равен 800 единицам. Прибыль от реализации одного радиоприемника первой и второй моделей равна $30 и $20 соответственно. Определить оптимальный суточный объем производства первой и второй моделей.

Процесс изготовления двух видов промышленных изделий состоит в последовательной обработке каждого из них на трех станках. Время использования этих станков для производства данных изделий ограничено 10 ч. в сутки. Найти оптимальный объем производства изделий каждого вида.

Фирма имеет возможность рекламировать свою продукции, используя местные радио- и телевизионную сеть. Затраты на рекламу в бюджете фирмы ограничены $1000 в месяц. Каждая минута радиорекламы обходится в $5, а минута телерекламы – в $100. Фирма хотела бы использовать радиосеть, по крайней мере, в два раза чаще, чем сеть телевидения. Опыт прошлых лет показал, что объем сбыта, который обеспечивает каждая минута телерекламы, в 25 раз больше сбыта, обеспечиваемого одной минутой радиорекламы. Определить оптимальное распределение ежемесячно отпускаемых средств между радио- и телерекламой.

Фирма производит два вида продукции – A и B . Объем сбыта продукции вида A составляет не менее 60% общего объема реализации продукции обоих видов. Для изготовления продукции А и В используется одно и то же сырье, суточный запас которого ограничен величиной 100 кг. Расход сырья на единицу продукции A составляет 2 кг, а на единицу продукции В – 4 кг. Цены продукции А и В равны $20 и $40 соответственно. Определить оптимальное распределение сырья для изготовления продукции А и В.

Фирма выпускает ковбойские шляпы двух фасонов. Трудоемкость изготовления шляпы фасона 1 вдвое выше трудоемкости изготовления шляпы фасона 2. Если бы фирма выпускала только шляпы фасона 1, суточный объем производства мог бы составить 60 шляп. Суточный объем сбыта шляп обоих фасонов ограничен диапазоном от 50 до 100 штук. Прибыль от продажи шляпы фасона 1 равна $8, а фасона 2 – $5. Определить какое количество шляп каждого фасона следует изготавливать, чтобы максимизировать прибыль.

Изделия четырех типов проходят последовательную обработку на двух станках. Время обработки одного изделия каждого типа на каждом из станков:

Затраты на производство одного изделия каждого типа определяются как величины, прямо пропорциональные времени использования станков (в машино-часах). Стоимость машино-часа составляет $10 и $15 для станка 1 и 2 соответственно. Допустимое время для использования станков для обработки изделий всех типов ограничено следующими значениями: 500 машино-часов – для станка 1 и 380 машино-часов для станка 2. Цены изделий типов 1,2,3 и 4 равны $65, $70, $55 и $45 соответственно. Составить план производства максимизирующий чистую прибыль.

Завод выпускает изделия трех моделей ( I, II III ). Для их изготовления используется два вида ресурсов (А и В), запасы которых составляют – 4000 и 6000 единиц. Расходы ресурсов на одно изделие каждой модели:

Трудоемкость изготовления модели I вдвое больше, чем изделия модели II , и втрое больше, чем изделие модели III . Численность рабочих завода позволяет выпускать 1500 изделий I . Анализ условий сбыта показывает, что минимальный спрос на продукцию завода составляет 200, 200 и 150 изделий моделей I,II и III соответственно. Однако соотношение выпуска изделий моделей I,II и III должно быть равно 3:2:5. Удельная прибыль от реализации изделий моделей I,II и III составляет $30, $20 и $50 соответственно. Определить выпуск изделий, максимизирующий прибыль.

Некоторое производственное предприятие выпускает три вида клея. Для производства клея используется 4 типа химических веществ: крахмал, желатин, квасцы и мел. Расход этих веществ в кг для получения 1 кг каждого вида клея и их запас на складе предприятия представлены в таблице.

Таблица 1. Расход химических веществ на изготовления клея, их запас на складе

Вид клея /Химические вещества	Клей № 1	Клей № 2	Клей № 3	Запас на складе
Крахмал	0,4	0,3	0,2	20
Желатин	0,2	0,3	0,4	35
Квасцы	0,05	0,07	0,1	7
Мел	0,01	0,05	0,15	10

Стоимость каждого вида клея для оптовых покупателей следующая:с₁ = 380 руб/кг,с₂ =430 руб/кг,с₃ = 460 руб/кг. Требуется определить оптимальный объем выпуска клея каждого вида, обеспечивающий максимум общей стоимости готовой продукции.

Бройлерное хозяйство птицеводческой фермы насчитывает 20000 цыплят, которые выращиваются до 8-недельного возраста и после соответствующей обработки поступают в продажу. Хотя недельный рацион цыплят зависит от их возраста, в дальнейшем будем считать, что в среднем (за 8 недель) он составляет 1 фунт.

Для того чтобы цыплята достигли к восьмой неделе необходимых весовых кондиций, кормовой рацион должен удовлетворять определенным требованиям по питательности. Этим требованиям могут соответствовать смеси различных видов кормов или ингредиентов. Ограничим наше рассмотрение только тремя ингредиентами: известняком, зерном и соевыми бобами. Ниже приведены данные, характеризующие содержание (по весу) питательных веществ в каждом из ингредиентов и удельную стоимость каждого ингредиента.

Смесь должна содержать:

• не менее 0.8%, но не более 1.2% кальция;
• не менее 22% белка;
• не более 5% клетчатки.

Необходимо определить количество каждого из трех ингредиентов, образующих смесь минимальной стоимости при соблюдении требований к общему расходу кормовой смеси и ее питательности.

Имеется конечное число видов продуктов питания: ананас, арбуз, грейпфрут, язык говяжий, сардельки говяжьи, хлеб «Бородинский», картофель ( n = 7), а в качестве питательных веществ рассматриваются белки, жиры, углеводы ( m = 3). Калорийность 1 кг каждого из продуктов следующая:с₁ = 470,с₂= 380,с₃ = 350,с₄ = 1460,с₅ = 2150,с₆ = 2070, с₇ = 800. Минимальная суточная потребность в питательных веществах следующая: в белках b ₁ = 100, в жирах b ₂ = 70, в углеводах b3 = 400. Содержание питательных веществ в каждом из продуктов может быть задано в форме нижеприведенной таблицы (табл.).

Требуется определить такой рацион питания, чтобы каждое питательное вещество содержалось в нем в необходимом количестве, обеспечивающем суточную потребность человека, и при этом суммарная калорийность рациона была минимальной.

Поиск решения задач в Excel с примерами

Пользователи Excel давно и успешно применяют программу для решения различных типов задач в разных областях.

Excel – это самая популярная программа в каждом офисе во всем мире. Ее возможности позволяют быстро находить эффективные решения в самых разных сферах деятельности. Программа способна решать различного рода задачи: финансовые, экономические, математические, логические, оптимизационные и многие другие. Для наглядности мы каждое из выше описанных решение задач в Excel и примеры его выполнения.

Решение задач оптимизации в Excel

Оптимизационные модели применяются в экономической и технической сфере. Их цель – подобрать сбалансированное решение, оптимальное в конкретных условиях (количество продаж для получения определенной выручки, лучшее меню, число рейсов и т.п.).

В Excel для решения задач оптимизации используются следующие команды:

Для решения простейших задач применяется команда «Подбор параметра». Самых сложных – «Диспетчер сценариев». Рассмотрим пример решения оптимизационной задачи с помощью надстройки «Поиск решения».

Условие. Фирма производит несколько сортов йогурта. Условно – «1», «2» и «3». Реализовав 100 баночек йогурта «1», предприятие получает 200 рублей. «2» — 250 рублей. «3» — 300 рублей. Сбыт, налажен, но количество имеющегося сырья ограничено. Нужно найти, какой йогурт и в каком объеме необходимо делать, чтобы получить максимальный доход от продаж.

Известные данные (в т.ч. нормы расхода сырья) занесем в таблицу:

На основании этих данных составим рабочую таблицу:

1. Количество изделий нам пока неизвестно. Это переменные.
2. В столбец «Прибыль» внесены формулы: =200*B11, =250*В12, =300*В13.
3. Расход сырья ограничен (это ограничения). В ячейки внесены формулы: =16*B11+13*B12+10*B13 («молоко»); =3*B11+3*B12+3*B13 («закваска»); =0*B11+5*B12+3*B13 («амортизатор») и =0*B11+8*B12+6*B13 («сахар»). То есть мы норму расхода умножили на количество.
4. Цель – найти максимально возможную прибыль. Это ячейка С14.

Активизируем команду «Поиск решения» и вносим параметры.

После нажатия кнопки «Выполнить» программа выдает свое решение.

Оптимальный вариант – сконцентрироваться на выпуске йогурта «3» и «1». Йогурт «2» производить не стоит.

Решение финансовых задач в Excel

Чаще всего для этой цели применяются финансовые функции. Рассмотрим пример.

Условие. Рассчитать, какую сумму положить на вклад, чтобы через четыре года образовалось 400 000 рублей. Процентная ставка – 20% годовых. Проценты начисляются ежеквартально.

Оформим исходные данные в виде таблицы:

Так как процентная ставка не меняется в течение всего периода, используем функцию ПС (СТАВКА, КПЕР, ПЛТ, БС, ТИП).

1. Ставка – 20%/4, т.к. проценты начисляются ежеквартально.
2. Кпер – 4*4 (общий срок вклада * число периодов начисления в год).
3. Плт – 0. Ничего не пишем, т.к. депозит пополняться не будет.
4. Тип – 0.
5. БС – сумма, которую мы хотим получить в конце срока вклада.

Вкладчику необходимо вложить эти деньги, поэтому результат отрицательный.

Для проверки правильности решения воспользуемся формулой: ПС = БС / (1 + ставка) кпер . Подставим значения: ПС = 400 000 / (1 + 0,05) 16 = 183245.

Решение эконометрики в Excel

Для установления количественных и качественных взаимосвязей применяются математические и статистические методы и модели.

Дано 2 диапазона значений:

Значения Х будут играть роль факторного признака, Y – результативного. Задача – найти коэффициент корреляции.

Для решения этой задачи предусмотрена функция КОРРЕЛ (массив 1; массив 2).

Решение логических задач в Excel

В табличном процессоре есть встроенные логические функции. Любая из них должна содержать хотя бы один оператор сравнения, который определит отношение между элементами (=, >, =, Пример задачи. Ученики сдавали зачет. Каждый из них получил отметку. Если больше 4 баллов – зачет сдан. Менее – не сдан.

1. Ставим курсор в ячейку С1. Нажимаем значок функций. Выбираем «ЕСЛИ».
2. Заполняем аргументы. Логическое выражение – B1>=4. Это условие, при котором логическое значение – ИСТИНА.
3. Если ИСТИНА – «Зачет сдал». ЛОЖЬ – «Зачет не сдал».

Решение математических задач в Excel

Средствами программы можно решать как простейшие математические задачки, так и более сложные (операции с функциями, матрицами, линейными уравнениями и т.п.).

Условие учебной задачи. Найти обратную матрицу В для матрицы А.

1. Делаем таблицу со значениями матрицы А.
2. Выделяем на этом же листе область для обратной матрицы.
3. Нажимаем кнопку «Вставить функцию». Категория – «Математические». Тип – «МОБР».
4. В поле аргумента «Массив» вписываем диапазон матрицы А.
5. Нажимаем одновременно Shift+Ctrl+Enter — это обязательное условие для ввода массивов.

Возможности Excel не безграничны. Но множество задач программе «под силу». Тем более здесь не описаны возможности которые можно расширить с помощью макросов и пользовательских настроек.

Государственное автономное профессиональное образовательное учреждение

Тюменской области

 «Тюменский колледж транспортных технологий и сервиса»

Разработка учебного занятия

Тема: Решение стратегических задач, задач оптимизации (поиск решения) в MS Excel.

Цель учебного занятия:

образовательные:

сформировать умения использовать возможности ВТ для решения конкретных физических задач; совершенствовать навыки работы в среде электронных таблиц при моделировании процессов и явлений;

развивающие:

развитие коммуникативных способностей у студентов, исследовательской, творческой и познавательной деятельности;

расширение кругозора студентов в области информационных ресурсов и программного обеспечения;

развитие коммуникационной компетентности у студентов;

развитие интереса к физике, информатике и истории посредством применения информационных технологий.

воспитательные:

воспитание бережного отношения к компьютерной технике;

выработка навыков грамотной устной речи

воспитание патриотизма, любви к Родине.

Таблица 1

Результаты обучения на учебном занятии

Таблица 2

Формируемые общие и профессиональные компетенции на учебном занятии

Таблица 3

Межпредметные связи учебной дисциплины с другими дисциплинами, междисциплинарными курсам основной профессиональной образовательной программы по специальности

Тип занятия: комбинированное занятие.

Вид занятия: практическая работа.

Таблица 4

Методы обучения, используемые на учебном занятии

Приемы обучения:

— выполнение заданий на проверку;

— представление результатов выполнения практических заданий;

— ответы на поставленные вопросы;

— рефлексия (оформление технологической карты)

Общее время: 90 минут.

Оснащение занятия:

Компьютеры (программа MS Excel), дидактический раздаточный материал (технологические карты).

Используемая основная литература:

Макарова. Н.В., Николайчук Г.С., Титова Ю.Ф., Информатика и ИКТ. Учебник. 11 класс. Базовый уровень. – СПб.: Питер, 2009.-224с.

Цветкова М. С. Информатика и ИКТ: учебник для нач. и сред проф. образования / М. С. Цветкова, Л. С. Великович. – М.: Издательский центр «Академия», 2011. – 352 с.

Макарова Н.В., . Задачник по моделированию. 9 -11 класс. Базовый уровень, СПб.: Питер, 2011;

Макарова Н.В., Николайчук Г.С., Титова Ю.Ф. под ред. Макаровой Н.В. Информатика и ИКТ 10 класс (базовый уровень) 2-е изд., СПб.: Питер, 2010;

Макарова Н.В., Информатика и ИКТ: Методическое пособие для учителей. Часть 2. Программное обеспечение информационных технологий. /под ред. Макаровой Н. В., СПб.: Питер, 2010;

Касьянов В.А., Физика – 10 класс, М.: Дрофа, 2010.

Кузнецов А.А. и др. Информатика, тестовые задания. – М., 2010. -152с.

Михеева Е.В. Практикум по информации: учеб. пособие. – М., 2010. – 190с.

Михеева Е.В., Титова О.И. Информатика: учебник. – М., 2013. -350с.

Михеева Е.В., Титова О.И., Информатика: учебник для студентов сред. проф. образования. – М.: Издательский центр «Академия», 2013.-352с.

Таблица 5

Структура учебного занятия

Приложение 1

Технологическая карта

Тема занятия:

Группа № _1_

Название группы: «Центральный фронт»

Состав группы:

Теоретическая часть

В состав табличного процессора Microsoft Excel входит более 300 встроенных функций, дающих возможность выполнять самую разнообразную обработку данных.

Параметры (аргументы) функций записываются после имени функции в круглых скобках, отделяются они друг от друга точкой с запятой. В качестве параметров функций могут указываться числа, текст, адреса или имена ячеек и их диапазонов, выражения и другие встроенные функции.

Практическая часть

Задача:

Исследовать движение снаряда, выпущенного из танка с начальной скоростью υ0=700 м/с под углом α=25 к горизонту, сопротивлением воздуха можно пренебречь. Определить попадание снаряда в противника, если расстояние до противника, т.е. до танка «Тигр» 500 м, время падения снаряда от 0 до 2 с, шаг изменения времени 0,2с. (Длина танка «Тигр» = 8,5 м). Построить на отдельных листах два графика:

1) график скорости снаряда

2) график траектории движения снаряда.

Решение:

Для того чтобы решить эту задачу необходимо исследовать движение снаряда, выпущенного из танковой пушки с начальной скоростью под углом к горизонту, определить место падения снаряда.

Создание компьютерной модели.

Оформите таблицу в программе Excel по образцу (рис. 1).

Рисунок № 1

Формулы

vу = v0*sing*t, скорость по оси у

vх = v0 *cos, скорость по оси х

v =  v2х + v2у скорость тела в любой точке траектории

х = v0 *cos*t, координаты полета дальности

у = v0 *sin*t – g*t2 /2, высота полета

S + l, расстояние до противника

S  х  S + l. попадание в цель

Если координата дальности (х) больше расстояния (20 м), и меньше расстояния до противника (20+9=29 м), то снаряд попал в цель, то есть в танк, иначе выстрел произведен мимо. (=Если(И(координата дальности> расстояния; координата дальности<расстояния до противника; «ПОПАЛ»; «МИМО»)

Заполнение ячеек формулами

Для преобразования значений углов из градусов в радианы используем функцию РАДИАНЫ(адрес).

В формулах, данные ячеек В2 (начальная скорость), В3 (угол), В4(расстояние), В5(длина) не изменяются. Поэтому мы дадим ячейкам имена, чтобы было проще работать. Ячейке В2 (рис. 1) дадим имя скорость, ячейке В3 – имя угол, B4 – имя расстояние, В5- имя длина, В6 – имя время.

Рисунок 1

При записи формул достаточно будет, щелкнуть по этой ячейке мышью.

Тогда наши формулы будут выглядеть так:

=скорость*SIN(РАДИАНЫ(угол))-9,8*А7 в ячейке В6

=скорость*COS(РАДИАНЫ(угол)) в ячейке С6

=скорость*COS(РАДИАНЫ(угол))*А7

=скорость*SIN(РАДИАНЫ(угол))*A7-9,8*A7^2/2

ПРИМЕЧАНИЕ: функцию РАДИАНЫ( ) лучше набирать с клавиатуры.

COS или SIN – использовать мастер функции fx.

Ссылки на ячейки выбирать, щелкнув по ячейке мышью (при работе по второму способу).

График скорости построить на отдельном листе по скорости движения снаряда в любой точке траектории и времени.

График траектории движения снаряда построить на отдельном листе по координатам высоты и дальности полета снаряда.

Вывод:

При высоте полета______________ снаряд достигнет своей цели спустя ____________ секунды, при скорости в любой точке траектории ________, противник будет уничтожен. График траектории ___________________________ (увеличивается / уменьшается), а график скорости _____________(увеличивается/уменьшается).

Технологическая карта

Тема занятия:

Группа № _2_

Название группы: «Воронежский фронт»

Состав группы:

Теоретическая часть

В состав табличного процессора Microsoft Excel входит более 300 встроенных функций, дающих возможность выполнять самую разнообразную обработку данных.

Параметры (аргументы) функций записываются после имени функции в круглых скобках, отделяются они друг от друга точкой с запятой. В качестве параметров функций могут указываться числа, текст, адреса или имена ячеек и их диапазонов, выражения и другие встроенные функции.

Практическая часть

Задача:

Рассчитать траекторию полета снаряда по формулам и построить график, отражающий траекторию полета снаряда.

Решение:

Создание компьютерной модели.

Оформите таблицу в программе Excel по образцу (рис. 1).

Рисунок № 1

Формулы

vу = v0*sing*t, скорость по оси у

vх = v0 *cos, скорость по оси х

v =  v2х + v2у скорость тела в любой точке траектории

х = v0 *cos*t, координаты полета дальности

у = v0 *sin*t – g*t2 /2, высота 

S + l, расстояние до противника

S  х  S + l. попадание в цель

Если координата дальности (х) больше расстояния (20 м), и меньше расстояния до противника (20+9=29 м), то снаряд попал в цель, то есть в танк, иначе выстрел произведен мимо. (=Если(И(координата дальности> расстояния; координата дальности<расстояния до противника; «ПОПАЛ»; «МИМО»)

Заполнение ячеек формулами

Для преобразования значений углов из градусов в радианы используем функцию РАДИАНЫ(адрес).

В формулах данные ячеек В2 (начальная скорость), В3 (угол), В4(расстояние), В5(длина) не изменяются. Поэтому мы дадим ячейкам имена, чтобы было проще работать. Ячейке В2 (рис. 1) дадим имя скорость, ячейке В3 – имя угол, B4 – имя расстояние, В5- имя длина, В6 – имя время.

Рисунок 1

При записи формул достаточно будет, щелкнуть по этой ячейке мышью.

Тогда наши формулы будут выглядеть так:

=скорость*SIN(РАДИАНЫ(угол))-9,8*А7 в ячейке В6

=скорость*COS(РАДИАНЫ(угол)) в ячейке С6

=скорость*COS(РАДИАНЫ(угол))*А7

=скорость*SIN(РАДИАНЫ(угол))*A7-9,8*A7^2/2

ПРИМЕЧАНИЕ: функцию РАДИАНЫ( ) лучше набирать с клавиатуры.

COS или SIN – использовать мастер функции fx.

Ссылки на ячейки выбирать, щелкнув по ячейке мышью (при работе по второму способу).

График скорости построить на отдельном листе по скорости движения снаряда в любой точке траектории и времени.

График траектории движения снаряда построить на отдельном листе по координатам высоты и дальности полета снаряда.

Вывод:

При высоте полета______________ снаряд достигнет своей цели спустя ____________ секунды, при скорости в любой точке траектории ________, противник будет уничтожен. График траектории ___________________________ (увеличивается / уменьшается), а график скорости _____________(увеличивается/уменьшается).

Технологическая карта

Тема занятия:

Группа № _3_

Название группы: «Степной фронт»

Состав группы:

Теоретическая часть

В состав табличного процессора Microsoft Excel входит более 300 встроенных функций, дающих возможность выполнять самую разнообразную обработку данных.

Параметры (аргументы) функций записываются после имени функции в круглых скобках, отделяются они друг от друга точкой с запятой. В качестве параметров функций могут указываться числа, текст, адреса или имена ячеек и их диапазонов, выражения и другие встроенные функции.

Практическая часть

Задача:

Необходимо сбросить со штурмовика ИЛ-2 противотанковые авиабомбы (ПТАБ) для уничтожения вражеских танков.

Решение: для решения задачи необходимо исследовать движение снаряда, выпущенного из пушки под углом к горизонту, подобрать начальные значения скорости и угла выстрела так, чтобы снаряд попал в цель.

Исходные данные задачи – это начальная скорость,

угол выстрела снаряда,

координаты цели,

точность попадания;

Расчётные данные задачи – это координаты положения снаряда,

время движения снаряда,

Результат – расстояние между снарядом и самолетом.

Оформите таблицу в программе Excel по образцу (рис. 1).

Рисунок 1

Формулы

Начальная горизонтальная скорость: v0*cos(*3,14/180)

Начальная вертикальная скорость: v0*sin(*3,14/180)

Время [0….2,4], с шагом 0,2

Координата х v(нач.горизонт)*t

Координата у v(нач.вертик)*t-g*t2/2

Расстояние до цели горизонтальное Sгоризонт: v(нач.горизонт)-х(цели)

Расстояние до цели вертикальное Sвертик: v(нач.вертик)- у(цели)

Расстояние до цели полное:

Попадание в цель: если расстояние до цели стало меньше заданной точности, значит, снаряд попал в цель. (=ЕСЛИ(Sполное<точности попадания; «ПОПАЛ»; МИМО)

Введите в ячейки соответствующие формулы.

Постройте диаграмму движения снаряда.

В процессе выполнения работы вы должны проследить, как изменяется высота подъёма снаряда и дальность полёта при изменении начальной скорости, а затем, как они меняются при изменении угла выстрела снаряда. Результаты экспериментов вы должны записать в таблицы.

Вывод:

 

При координатах полета______________ бомба достигнет своей цели спустя ____________ секунды, при расстоянии до цели _________ м, противник будет уничтожен. График движения бомбы ___________________________ (увеличивается / уменьшается).