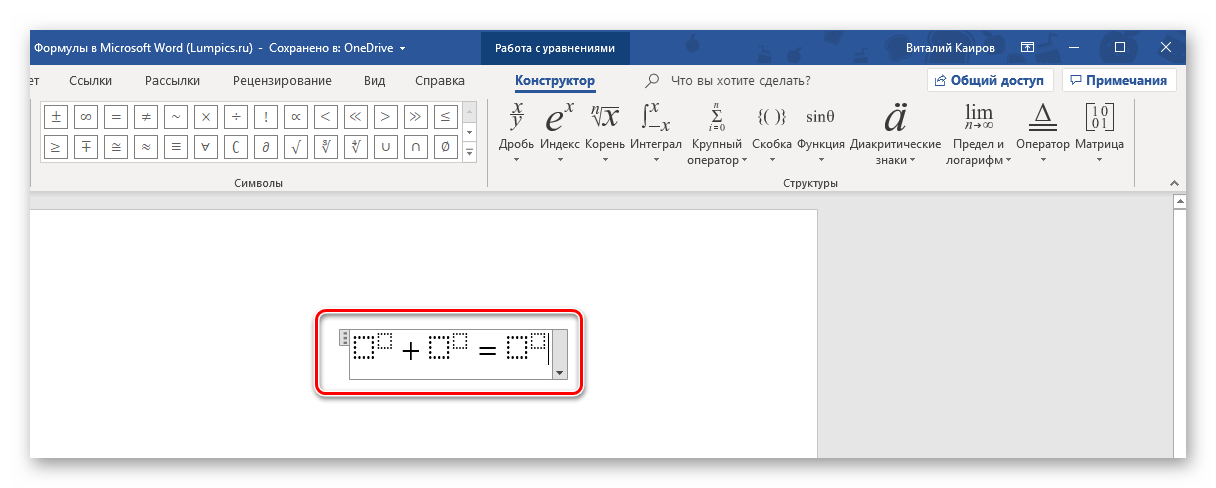
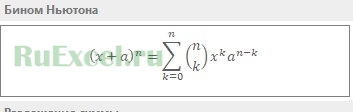Excel 2016 Word 2016 Outlook 2016 PowerPoint 2016 Excel 2013 Word 2013 Outlook 2013 PowerPoint 2013 Excel 2010 Word 2010 Outlook 2010 PowerPoint 2010 Excel 2007 Word 2007 Outlook 2007 PowerPoint 2007 Еще…Меньше
Редактор уравнений (Microsoft Equation 3,0) был добавлен в более ранние версии Word, но был удален из всех версий, указанных в общедоступном обновлении для 2018 января (ОБЩЕДОСТУПНОЕ обновление за), и заменен новым редактором уравнений.
Содержимое здесь описывает эту функцию для пользователей, которые установили это обновление.
Важно: Редактор уравнений 3,0 она была удалена из-за проблем с безопасностью в ее реализации. Пользователи, которые пытаются изменить формулу, созданную в редакторе уравнений 3,0, получат сообщение об ошибке «Microsoft Equation недоступен». Если вы установили шрифт «MT Extra» (если у вас нет шрифта, вы можете скачать его), вы увидите, что они будут отображаться в 3,0 редакторе уравнений в обычном режиме. Тем не менее, пользователи могут редактировать эти уравнения только путем загрузки программных средств Мастипе, предоставленных ВИРИС. Посмотрите, как мастипе классическое приложение для пользователей «редактор уравнений».
Вставка уравнения с помощью редактора формул
-
На вкладке Вставка в группе Текст нажмите кнопку Объект.
-
В диалоговом окне Объект откройте вкладку Создание.
-
В поле Тип объекта выберите значение Microsoft Equation 3.0 и нажмите кнопку ОК.
-
Измените уравнение с помощью символов, шаблонов и структур на панели инструментов Формула.
-
Чтобы вернуться к документу, в Word, Excel или Outlook щелкните в любом месте документа.
Чтобы вернуться к презентации в PowerPoint, в меню Файлредактора формул щелкните Выход и возврат к презентации.
Изменение уравнения с помощью редактора формул
Если вы использовали редактор формул для вставки уравнения, изменить его также можно с помощью этого редактора.
-
Дважды щелкните уравнение, которое вы хотите изменить.
-
Измените уравнение с помощью символов, шаблонов и структур на панели инструментов Формула.
-
Чтобы вернуться к документу, в Word, Excel или Outlook щелкните в любом месте документа.
Чтобы вернуться к презентации в PowerPoint, в меню Файлредактора формул щелкните Выход и возврат к презентации.
Вставка уравнения с помощью редактора формул
-
На вкладке Вставка в группе Текст нажмите кнопку Объект.
-
В диалоговом окне Объект откройте вкладку Создание.
-
В поле Тип объекта выберите значение Microsoft Equation 3.0.
Если редактор уравнений недоступен, возможно, потребуется установить его.
Установка редактора формул
-
Закройте все программы.
-
На панели управления щелкните Установка и удаление программ.
-
В поле Установленные программы выберите Microsoft Office <выпуск> 2007 и нажмите кнопку Изменить.
-
На странице Изменение установленного пакета Microsoft Office <suite> 2007. выберите команду Добавить или удалить компонентыи нажмите кнопку продолжить.
-
На вкладке Параметры установки щелкните индикатор развертывания (+) рядом с компонентом Средства Office.
-
Щелкните стрелку рядом с названием Редактор формул и выберите Запускать с моего компьютера.
-
Нажмите кнопку Продолжить.
-
После того как вы закончите установку редактора формул, перезапустите приложение Office, которое вы используете.
-
-
В диалоговом окне Объект нажмите кнопку ОК.
-
Измените уравнение с помощью символов, шаблонов и структур на панели инструментов Формула.
-
Чтобы вернуться к документу, в Word, Excel или Outlook щелкните в любом месте документа.
Чтобы вернуться к презентации в PowerPoint, в меню Файлредактора формул щелкните Выход и возврат к презентации.
Изменение уравнения с помощью редактора формул
Если вы использовали редактор формул для вставки уравнения, изменить его также можно с помощью этого редактора.
-
Дважды щелкните уравнение, которое вы хотите изменить.
-
Измените уравнение с помощью символов, шаблонов и структур на панели инструментов Формула.
-
Чтобы вернуться к документу, в Word, Excel или Outlook щелкните в любом месте документа.
Чтобы вернуться к презентации в PowerPoint, в меню Файлредактора формул щелкните Выход и возврат к презентации.
Сведения о том, как использовать встроенные уравнения с помощью кнопки » уравнение «, можно узнать в статье написание формулы или формулы.
См. также
Формулы в линейном формате и функция автозамены математическими символами в Word
Создание уравнений и формул
Нужна дополнительная помощь?
Редактор формул
Редактор уравнений (Microsoft Equation 3,0) был добавлен в более ранние версии Word, но был удален из всех версий, указанных в общедоступном обновлении для 2018 января (ОБЩЕДОСТУПНОЕ обновление за), и заменен новым редактором уравнений.
Содержимое здесь описывает эту функцию для пользователей, которые установили это обновление.
Важно: Редактор уравнений 3,0 она была удалена из-за проблем с безопасностью в ее реализации. Пользователи, которые пытаются изменить формулу, созданную в редакторе уравнений 3,0, получат сообщение об ошибке «Microsoft Equation недоступен». Если вы установили шрифт «MT Extra» (если у вас нет шрифта, вы можете скачать его), вы увидите, что они будут отображаться в 3,0 редакторе уравнений в обычном режиме. Тем не менее, пользователи могут редактировать эти уравнения только путем загрузки программных средств Мастипе, предоставленных ВИРИС. Посмотрите, как мастипе классическое приложение для пользователей «редактор уравнений».
Вставка уравнения с помощью редактора формул
На вкладке Вставка в группе Текст нажмите кнопку Объект.
В диалоговом окне Объект откройте вкладку Создание.
В поле Тип объекта выберите значение Microsoft Equation 3.0 и нажмите кнопку ОК.
Измените уравнение с помощью символов, шаблонов и структур на панели инструментов Формула.
Чтобы вернуться к документу, в Word, Excel или Outlook щелкните в любом месте документа.
Чтобы вернуться к презентации в PowerPoint, в меню Файл редактора формул щелкните Выход и возврат к презентации.
Изменение уравнения с помощью редактора формул
Если вы использовали редактор формул для вставки уравнения, изменить его также можно с помощью этого редактора.
Дважды щелкните уравнение, которое вы хотите изменить.
Измените уравнение с помощью символов, шаблонов и структур на панели инструментов Формула.
Чтобы вернуться к документу, в Word, Excel или Outlook щелкните в любом месте документа.
Чтобы вернуться к презентации в PowerPoint, в меню Файл редактора формул щелкните Выход и возврат к презентации.
Вставка уравнения с помощью редактора формул
На вкладке Вставка в группе Текст нажмите кнопку Объект.
В диалоговом окне Объект откройте вкладку Создание.
В поле Тип объекта выберите значение Microsoft Equation 3.0.
Если редактор уравнений недоступен, возможно, потребуется установить его.
Установка редактора формул
Закройте все программы.
На панели управления щелкните Установка и удаление программ.
В поле Установленные программы выберите Microsoft Office 2007 и нажмите кнопку Изменить.
На странице Изменение установленного пакета Microsoft Office 2007. выберите команду Добавить или удалить компонентыи нажмите кнопку продолжить.
На вкладке Параметры установки щелкните индикатор развертывания (+) рядом с компонентом Средства Office.
Щелкните стрелку рядом с названием Редактор формул и выберите Запускать с моего компьютера.
Нажмите кнопку Продолжить.
После того как вы закончите установку редактора формул, перезапустите приложение Office, которое вы используете.
В диалоговом окне Объект нажмите кнопку ОК.
Измените уравнение с помощью символов, шаблонов и структур на панели инструментов Формула.
Чтобы вернуться к документу, в Word, Excel или Outlook щелкните в любом месте документа.
Чтобы вернуться к презентации в PowerPoint, в меню Файл редактора формул щелкните Выход и возврат к презентации.
Изменение уравнения с помощью редактора формул
Если вы использовали редактор формул для вставки уравнения, изменить его также можно с помощью этого редактора.
Дважды щелкните уравнение, которое вы хотите изменить.
Измените уравнение с помощью символов, шаблонов и структур на панели инструментов Формула.
Чтобы вернуться к документу, в Word, Excel или Outlook щелкните в любом месте документа.
Чтобы вернуться к презентации в PowerPoint, в меню Файл редактора формул щелкните Выход и возврат к презентации.
Сведения о том, как использовать встроенные уравнения с помощью кнопки » уравнение «, можно узнать в статье написание формулы или формулы.
Графика точных наук: изображения формул в Excel
Здравствуйте, уважаемые читатели. В последнее время мне приходит много вопросов о том, как можно оформить в Экселе целую научную работу. Пишут студенты, аспиранты, иногда – преподаватели. Все знают, как записать текст в ячейку, эффективно отформатировать его, провести расчеты с помощью формул и функций. Для большей информативности вставить диаграммы, а получившийся документ вывести на печать.
Но возникает вопрос: как нам в Экселе написать уравнение или формулу, чтобы она была картинкой, и описывала то, что мы считаем? Если написать ее как текст в ячейке – способов форматирования недостаточно, чтобы записать правильную дробь, корень n-й степени или, например, интеграл. И как же быть?
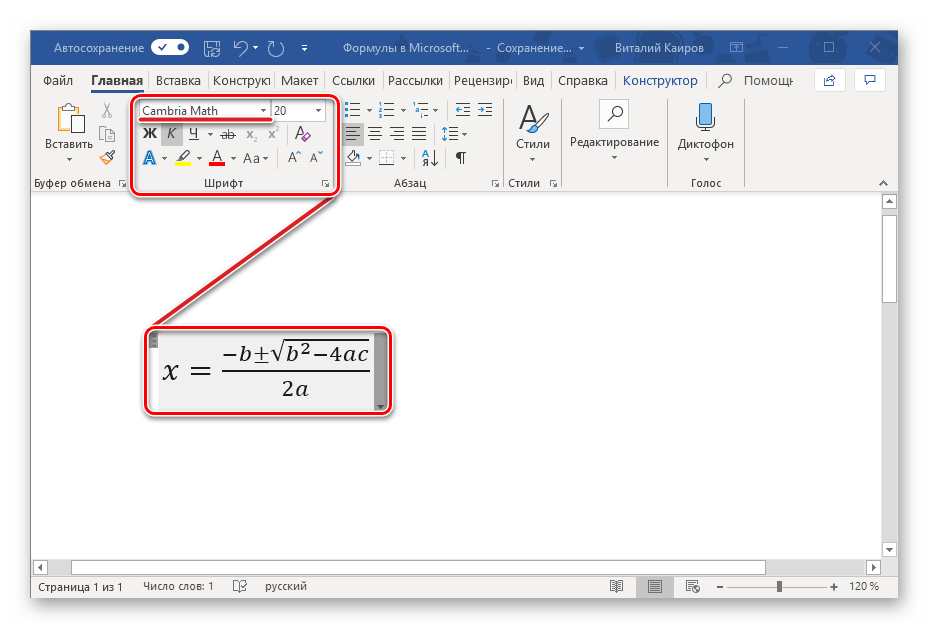
Выход есть. Начиная с Excel 2010, разработчики предлагают нам средство для рисования формул и уравнений. Оно называется редактором уравнений и позволяет записать формулы вот такого вида:
Как вставить уравнение в Excel
Чтобы вставить уравнение или формулу, найдите на ленте команду: Вставка – Символы – Уравнение . Если кликнуть на стрелке вниз – откроется перечень самых популярных уравнений, их можно вставить одним нажатием мыши.
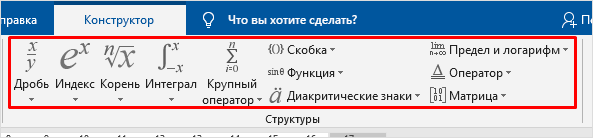
Если же нужной формулы в списке нет, нажимайте кнопку «Уравнение». На листе появится текстовый объект в рамке, а на ленте две новые вкладки:
- Средства рисования – Формат . Служит для оформления графического объекта с формулой
- Работа с уравнениями – Конструктор . Предназначена для создания макета формулы.
Перейдите на вкладку «Конструктор», чтобы начать верстку формулы. Сам процесс заключается в подборе структур для последующего заполнения ее данными. Структура представляет собой ячейки, оформленные под выбранный тип данных. Каждая ячейка структуры обведена пунктирной линией, и в нее можно вставить значение, или другую структуру. Принцип построения формул предлагаю разобрать на примере, построим вместе формулу с рисунка выше:
- В левой части уравнения – степень. В разделе «Индекс» выберем «Верхний индекс»;
- Далее у нас знак равно и сумма единицы бесконечным множеством дробей. Давайте вставим все знаки, кроме дробей. Вот, что получилось:
Знак бесконечности и символы сравнения берем из на ленте: Работа с уравнениями – Конструктор – Символы ;
- Везде, где должны быть правильные дроби – вставим их макеты ( Структуры – Дробь – Вертикальная простая дробь ). Заполним те данные, которые уже можем заполнить;
- В числителях двух последних дробей – степени. Вставим их так же, как и в п.1.:
- Осталось лишь заполнить недостающие данные и формула (в данном случае, ряд Тейлора) готова:
Как видите, все очень просто. Конечно, такие формулы не будут участвовать в расчетах, они лишь визуализируют какие-то вычисления, законы, и нужны для оформления рабочего пространства. Наверняка, Вы оцените мощь инструмента при работе с тригонометрическими расчетами, например.
Давайте подведем итог. В блоке статей о графических объектах Эксель мы с вами:
- Научились строить геометрические фигуры
- Нарисовали схемы SmartArt
- Сделали красивый текст с помощью WordArt
- Научились вставлять картинки на лист несколькими способами
- Написали уравнение с помощью редактора уравнений.
Этих знаний графических объектов достаточно, чтобы быть уверенными в своих силах при вставке и форматировании рисунков. Поэтому, в следующих постах я буду рассматривать уже другую тематику, и планирую в ближайшее время рассказать, как настраивать пользовательский интерфейс. Тогда и увидимся, до встречи!
Как добавить красивую математическую формулу со знаменателем, делителем и степенью на лист Excel.
Иногда при оформлении таблиц в программе «Excel» приходится добавлять в ячейки математические формулы. Эти формулы не используются в расчетах, а несут функцию декоративных элементов таблицы. Можно конечно прописать формулы в строчку обычным шрифтом, но это будет не очень красиво.
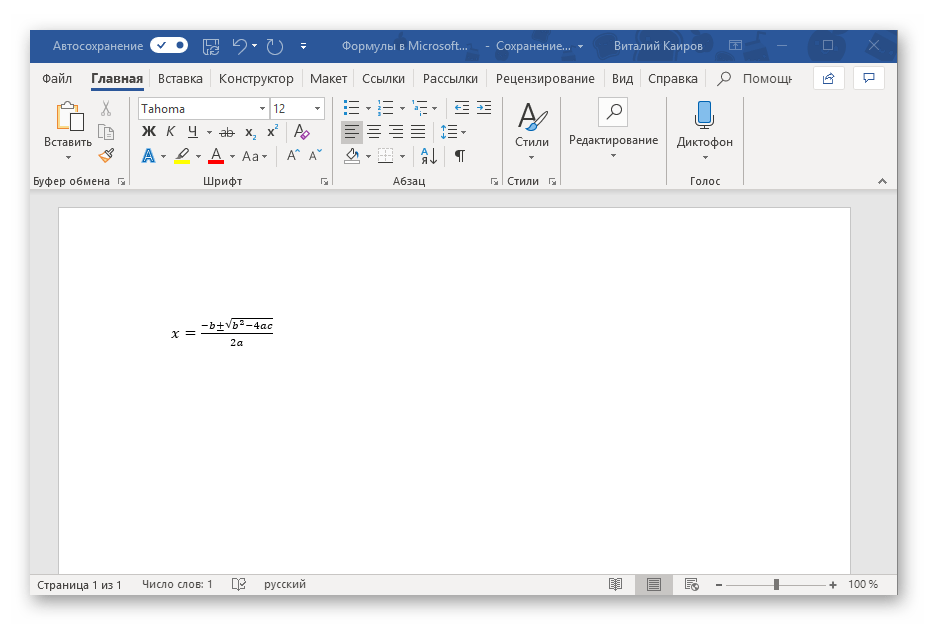
Рассмотрим добавление формулы на лист «Excel» на примере формулы площади круга: Пи*D^2/4.
Как видите, выглядит она не очень презентабельно.
Попробуем отобразить ее в виде математической функции.
Устанавливаем курсор в нужную ячейку.
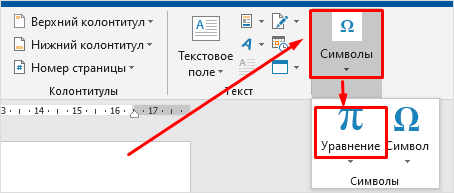
Во вкладке «Вставка» панели инструментов кликаем по значку «Уравнение».
При нажатии на значок «Уравнение» выпадает целый список готовых распространенных формул. Среди который есть и площадь круга, правда в ином формате.
Для того что бы записать формулу в том формате, который нам требуется, вставляем из списка уже готовое уравнение площади круга, а затем изменяем его при помощи пункта «Вставить новое уравнение»
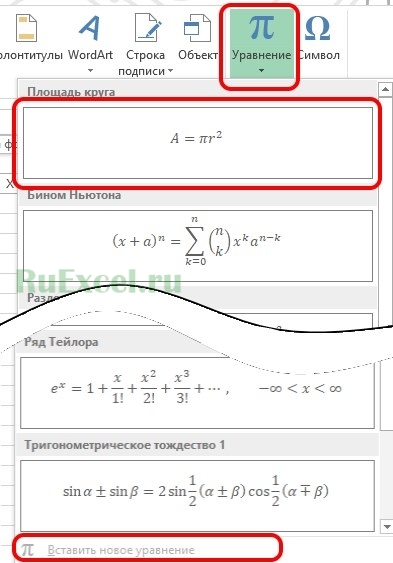
После выбора пункта «Вставить новое уравнение» открывается конструктор с помощью которого можно изменить вид полученной формулы.

источники:
http://officelegko.com/2017/01/27/grafika-tochnyih-nauk-izobrazheniya-formul-v-excel/
http://ruexcel.ru/uravnenie/
Использование формул в таблице Word или Outlook
Вычисления и логические сравнения можно выполнять с помощью формул. Команда Формула находится в разделе Работа с таблицами на вкладке Макет в группе Данные.
В приложении Word формулы обновляются автоматически при открытии документа, который их содержит. Результаты формул также можно обновлять вручную. Дополнительные сведения см. в разделе Обновление результатов формул.
Примечание: Формулы в таблицах Word и Outlook — это тип кода поля. Дополнительные сведения о кодах полей см. в разделе См. также.
В этой статье
Вставка формулы в ячейку таблицы
Выделите ячейку таблицы, в которой должен находиться результат. Если ячейка не пустая, удалите ее содержимое.
В разделе Работа с таблицами на вкладке Макет в группе Данные нажмите кнопку Формула.
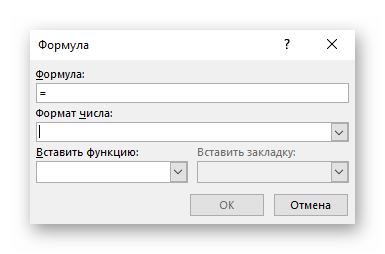
С помощью диалогового окна Формула создайте формулу. Можно ввести формулу в поле Формула, выбрать формат числа в поле Формат числа, а также вставить функции и закладки, используя списки Вставить функцию и Вставить закладку.
Обновление результатов вычислений
В Word результат формулы рассчитывается при ее вставке, а также при открытии содержащего ее документа. В Outlook результат формулы рассчитывается только при ее вставке, и получатель сообщения не сможет его изменить.
Кроме того, поддерживается ручное обновление следующих элементов:
результатов отдельных формул;
результатов всех формул в отдельной таблице;
всех кодов полей в документе, включая формулы.
Обновление результатов отдельных формул
Выделите формулы, которые необходимо обновить. Чтобы выделить несколько формул, удерживайте нажатой клавишу CTRL.
Выполните одно из указанных ниже действий.
Щелкните формулу правой кнопкой мыши и выберите команду Обновить поле.
Нажмите клавишу F9.
Обновление результатов всех формул в таблице
Выделите таблицу, содержащую результаты формул, которые необходимо обновить, и нажмите клавишу F9.
Обновление всех формул в документе
Важно: В результате выполнения этой процедуры будут обновлены не только формулы, а все коды полей в документе.
Нажмите клавиши CTRL+A.
Нажмите клавишу F9.
Примеры: сложение чисел в таблице с помощью позиционных аргументов
Позиционные аргументы (LEFT, RIGHT, ABOVE, BELOW) можно использовать для следующих функций:
В качестве примера рассмотрим процедуру сложения чисел с помощью функции SUM и позиционных аргументов.
Важно: Чтобы при нахождении суммы в таблице с помощью позиционных аргументов не возникло ошибки, введите в пустые ячейки, учитываемые при вычислении, нуль (0).
Выделите ячейку таблицы, в которой должен находиться результат. Если ячейка не пустая, удалите ее содержимое.
В разделе Работа с таблицами на вкладке Макет в группе Данные нажмите кнопку Формула.
В диалоговом окне Формула выполните одно из указанных ниже действий.
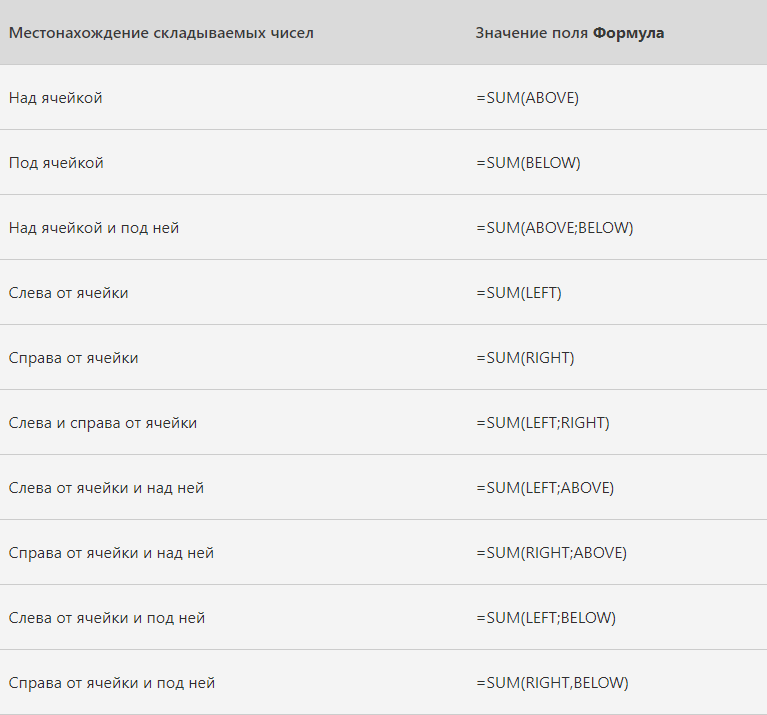
Местонахождение складываемых чисел
Значение поля Формула
Над ячейкой и под ней
Слева от ячейки
Справа от ячейки
Слева и справа от ячейки
Слева от ячейки и над ней
Справа от ячейки и над ней
Слева от ячейки и под ней
Справа от ячейки и под ней
Нажмите кнопку «ОК».
Доступные функции
Примечание: Формулы, в которых используются позиционные аргументы (например, LEFT), не учитывают значения в строке заголовков.
В формулах, располагаемых внутри таблиц Word и Outlook, можно использовать перечисленные ниже функции.
Определяет абсолютную величину числа в скобках
Определяет, все ли аргументы внутри скобок являются истинными.
1, если сумма значений, находящихся слева от формулы (в той же строке), меньше 10 исумма значений, находящихся над формулой (в том же столбце, исключая ячейки заголовка) больше или равна 5; в противном случае — 0.
Находит среднее арифметическое значение элементов, указанных в скобках.
Среднее арифметическое всех значений, находящихся справа от ячейки с формулой (в той же строке).
Определяет количество элементов, указанных в скобках.
Количество значений, находящихся слева от ячейки с формулой (в той же строке).
Устанавливает, определен ли аргумент внутри скобок. Возвращает значение 1, если аргумент определен и вычисляется без ошибок, или 0, если аргумент не определен или возвращает ошибку.
1, если элемент «валовой_доход» определен и вычисляется без ошибок; в противном случае — 0.
Не имеет аргументов. Всегда возвращает значение 0.
Вычисляет первый аргумент. Если первый аргумент является истинным, возвращает второй аргумент; если ложным — третий.
Примечание: Необходимо задать все три аргумента.
10, если сумма значений, находящихся слева от формулы, больше или равна 10; в противном случае — 0.
Округляет значение в скобках до ближайшего целого числа (меньшего).
Возвращает наибольшее значение среди элементов, указанных в скобках.
Наибольшее из значений, находящихся в ячейках над формулой (за исключением ячеек строк заголовков).
Возвращает наименьшее значение среди элементов, указанных в скобках.
Наименьшее из значений, находящихся в ячейках над формулой (за исключением ячеек строк заголовков).
Имеет два аргумента (числа или выражения, результатами которых являются числа). Возвращает остаток от деления первого аргумента на второй. Если остаток равен нулю (0), возвращает значение 0,0.
Имеет один аргумент. Определяет истинность аргумента. Если аргумент является истинным, возвращает значение 0; если ложным — 1. В основном используется в функции IF.
Имеет два аргумента. Если хотя бы один из них является истинным, возвращает значение 1. Если оба аргумента являются ложными, возвращает значение 0. В основном используется в функции IF.
Вычисляет произведение элементов, указанных в скобках.
Произведение всех значений, находящихся в ячейках слева от формулы.
Имеет два аргумента (первый аргумент должен быть числом или выражением, результатом которого является число, второй — целым числом или выражением, результатом которого является целое число). Округляет первый аргумент до заданного вторым аргументом количества десятичных разрядов. Если второй аргумент больше нуля (0), первый аргумент округляется до указанного количества десятичных разрядов (в меньшую сторону). Если второй аргумент равен нулю (0), первый аргумент округляется до ближайшего целого числа (в меньшую сторону). Если второй аргумент меньше нуля, первый аргумент округляется слева от десятичной запятой (в меньшую сторону).
Имеет один аргумент, который должен быть числом или выражением, результатом которого является число. Сравнивает указанный в скобках элемент с нулем (0). Если этот элемент больше нуля, возвращает значение 1; если равен нулю — 0; если меньше нуля — -1.
Вычисляет сумму элементов, указанных в скобках.
Сумма значений, находящихся в ячейках справа от формулы.
Имеет один аргумент. Определяет истинность аргумента. Если аргумент является истинным, возвращает значение 1, если ложным — 0. В основном используется в функции IF.
Использование в формуле закладок и ссылок на ячейки
В формулу можно вставить ссылку на ячейку, для которой создана закладка, используя имя этой закладки. Например, если для ячейки, содержащей число или выражение, результатом которого является число, создана закладка с именем валовой_доход, формула =ROUND( валовой_доход,0) округлит значение этой ячейки до ближайшего целого числа в меньшую сторону.
В формуле также можно использовать ссылки на столбцы и строки. Существует два формата записи ссылок: RnCn и A1.
Примечание: Ячейки с формулами не учитываются в вычислениях, в которых используются ссылки. Если ячейка является частью ссылки, она игнорируется.
Ссылки формата RnCn
Для записи ссылки на строку, столбец или ячейку таблицы в формуле можно использовать формат RnCn. Здесь Rn соответствует n-ой строке, а Cn — n-му столбцу. Например, ссылка R1C2 указывает на ячейку в первой строке и втором столбце. Приведенная ниже таблица содержит примеры записи ссылок в таком формате.
Как в Ворде посчитать сумму и другие показатели
Здравствуйте, уважаемые читатели. Не многие знают, что расчеты в Word существуют, доступны всем и отлично работают. А это так, поверьте. Каждый из Вас может этому научиться. Главное – внимательно дочитать эту статью до конца, а потом немного попрактиковаться.
Конечно, вычислительные возможности Ворда и близко не соизмеримы с формулами Excel, но и задачи перед этими двумя программами стоят разные. Тем не менее, когда нужно в таблице Word что-то посчитать – мы можем это сделать. А потом еще и диаграмму построить. Не ожидали такого от Word? Думаю, нет. Так давайте же скорее разбираться.
Как делать расчеты в Word
Давайте сразу смотреть на примере. Пусть у нас есть таблица с продажами некоторых работников помесячно. И мы хотим посчитать, к примеру, итоговые данные.
Да, удобнее было бы сделать это в Excel, но таблица эта является частью некоего пакета документов, портфеля, если хотите. Вот, что у нас есть:
Видим, что у нас предусмотрены столбцы для заполнения итогов. Как нам их считать? Не вручную же, верно? Давайте просуммируем продажи Ивана Алексеева по месяцам. Для этого выполняем такую последовательность:
- Выделяем пока еще пустую ячейку, где у нас будет сумма
- На ленте нажимаем Макет – Данные – Формула . Открывается окно вставки формулы
Записываем формулу: =SUM(LEFT) . Это будет значить, что нужно просуммировать все числовые значения слева от этой ячейки. То есть все продажи по месяцам.
Формат числа мы пока не трогаем, я расскажу о нем в одном из следующих постов
Так что же за формулу мы записали? Она одновременно и похожа и не похожа на формулы в Экселе. Давайте разберем ее на части:
- Знак «=», как и в Excel, сигнализирует о том, что сейчас будет формула
- SUM – это функция суммирования, которая вернет сумму значений, указанных в аргументе
- LEFT – аргумент функции, указывающий, что суммировать нужно все числовые данные расположенные слева от данной. Такая запись обусловлена тем, что в Ворде нет явной адресации ячеек таблицы. Адресация, как таковая, есть, я опишу это ниже, но она нигде на экране не обозначается.
Перед тем, как мы приступим к списку доступных функций, давайте уточним, как еще в аргументах можно указывать ссылки на ячейки. Хотя, конечно, вместо ссылок можно указать и просто значения. Получится такой себе калькулятор в Word.
Ссылки на ячейки в формулах Ворд
Ниже я привел Вам таблицу возможных обращений к ячейкам Ворда:
| Запись обращения | Расшифровка |
| LEFT | Все ячейки слева от формулы |
| RIGHT | Все ячейки справа от формулы |
| ABOVE | Все ячейки над формулой |
| BELOW | Все ячейки под формулой |
| LEFT;RIGHT | Все ячейки слева и справа |
| ABOVE;BELLOW | Все ячейки сверху и снизу |
| LEFT;ABOVE | Все ячейки слева и сверху |
| RIGHT;ABOVE | Все ячейки справа и сверху |
| LEFT;BELLOW | Все ячейки слева и снизу |
| RIGHT;BELLOW | Все ячейки справа и снизу |
| Cn | Весь столбец. Например, C1 обратится к первому столбцу |
| Rn | Вся строка. R1 ссылается на первую строку |
| RnCn | Ячейка на пересечении указанной строки и столбца. Например, R3C2 – ячейка во третьей строке и втором столбце |
| R | Строка с формулой |
| C | Столбец с формулой |
| RnCn:RnCn | Диапазон между ячейками, указанными через двоеточие |
| Bookmarkname RnCn | Ячейка в таблице с закладками |
| Bookmarkname RnCn:RnCn | Диапазон в таблице с закладками |
| Ссылки А1 | Тип ссылок аналогичный Excel, где строки нумеруются цифрами, а столбцы – буквами. То есть, B3 укажет на ячейку в третьей строке второго столбца |
В этих параметрах все просто, думаю, Вы не запутаетесь. А если запутаетесь – задавайте вопросы в комментариях – разберемся вместе.
Теперь переходим к функциям, доступным в этом инструменте. Они, так же, очень похожи на функции в Экселе, но их значительно меньше.
Функции расчетов в Ворде
Выше в тексте мы уже рассмотрели функцию SUM , а теперь я опишу Вам все функции, доступные в Ворде.
Как пересчитать результаты вычисления
В отличие от Excel, в Ворде формулы не пересчитываются после изменения исходных данных. Для пересчета можно воспользоваться одним из следующих приемов:
- Сохраните, закройте и снова откройте документ. Все формулы во всех таблицах будут пересчитаны
- Выделите таблицу, в которой нужно пересчитать результат и нажмите F9
- Выделите ячейки, в которых нужно пересчитать результат и нажмите F9 . Чтобы выделить несмежные ячейки – зажмите Ctrl в процессе выделения.
Примеры вычислений в Word
Вначале статьи я привел таблицу, с который мы будем работать. Давайте заполним недостающие поля.
Вычислим сумму продаж всех менеджеров за 3 месяца. Выделяем первую ячейку столбца «Сумма» и кликаем на ленте Макет – Данные – Формула. В окне записываем нашу формулу =SUM(LEFT) и жмем Ок .
Далее поочередно выделяем оставшиеся ячейки столбца и жмем F4 , программа автоматически запишет в них такую же формулу. Вот, что у нас получилось:
Теперь посчитаем средние продажи каждого менеджера за эти три месяца. Обратите внимание, использовать указатель LEFT уже не получится, потому что слева от столбца с формулами будут не только продажи по месяцам, а и сумма продаж за 3 месяца. Поэтому, формула для первой строки будет такой: =AVERAGE(B3:D3) . Для остальных строк нужно будет увеличивать на единицу номер строки. Т.е. у второго менеджера диапазон будет B4:D4 , у третьего B5:D5 и так далее.
Заполняем все строки и получаем результат:
Теперь просчитаем бонусы. Предположим, руководители решили мотивировать самых старательных продавцов. И для тех, у кого средние продажи выше 10% от общей выручки, выплатить 5% от их личных средних продаж. Надеюсь, логика расчета ясна, давайте писать сложную формулу для первой строки:
- Сначала вычислим суммарные средние продажи: =SUM(F3:F12)
- Теперь вычислим долю продаж для первого менеджера: =F3/SUM(F3:F12) . Кстати, результат будет 12%, т.е. этот продавец должен получить свой бонус. Проверим, получится ли это вычислить
- И наконец, проверим условие начисления бонусов: =IF(F3/SUM(F3:F12)>0,1; F3*0,05;0) . Формула проверит, если доля продаж менеджера больше 0,1 (10%) – вернет 5% от его средних продаж. Если нет- вернет 0. Для первой строки у нас получилось 313,33, это правильный результат, можете проверить вручную
- Вставляем такую формулу во все строки, не забываем менять номера строк. Так, для второго продавца формула будет такой: = IF(F4/SUM(F3:F12)>0,1; F4*0,05;0) . Для остальных аналогично.
Вот какая в итоге у нас вышла таблица:
Как видим, у нас есть три человека, которые работали не в полную силу и премию не заслужили.
Теперь можно изменять исходные данные и клавишей F9 выполнять пересчет формул.
Вот, пожалуй, и всё о расчетах в таблицах Word. Хотел написать статью покороче, но не хотелось что-то вычеркивать из материалов, поэтому, получилось, как есть. За то, у Вас в руках целый гид по расчетам в Ворде. Если пост Вам понравился – поделитесь с другом. Возможно, ему она тоже пригодится! Ну и подписывайтесь на обновления блога – здесь только полезные советы и нужные уроки, от простого к сложному.
У нас осталось всего два поста о таблицах Word – это форматирование и Экспресс-таблицы. Там будем учиться делать Ваши выкладки более читаемыми с профессиональным оформлением. До встречи там, друзья!
Добавить комментарий Отменить ответ
4 комментариев
Николай :
Функция автосуммы в Microsoft Word
Далеко не все пользователи Microsoft Word знают, что в этой программе можно производить вычисления по заданным формулам. Конечно, до возможностей собрата по офисному пакету, табличного процессора Excel, текстовый редактор не дотягивает, тем не менее такие простые расчеты, как суммирование данных, в нем выполнить можно. Сегодня расскажем о том, как это делается.
Подсчет суммы в Ворде
Хотя Microsoft Word и ориентирован в первую очередь на работу с текстом, помимо этого в нем можно работать с графическими элементами, всевозможными фигурами и объектами, таблицами и математическими выражениями. Последняя «пара» нередко подразумевает и необходимость подсчета суммы, то есть получить ее может потребоваться как в таблице, так и в примере, формуле или уравнении. В каждом из этих случаем необходимо действовать по-разному. Как именно, узнаете далее.
Способ 1: Формулы и уравнения
Если в Ворде вам необходимо посчитать сумму чисел или неизвестных переменных, записанных в математическом выражении, уравнении или формуле, потребуется обратиться к соответствующему инструментарию текстового редактора. Представлен он в разделе вставки, создания и изменения уравнений, о работе с которым мы подробно писали в отдельной статье на нашем сайте — ссылка на нее представлена ниже.
Способ 2: Сумма в таблице
Куда более часто перед пользователями Майкрософт Ворд возникает несколько более простая задача, чем создание математических выражений и уравнений. Необходимость в подсчете суммы появляется при работе с таблицами, когда требуется получить общее значение чисел, записанных в ее отдельном столбце или строке. Это тоже делается с помощью формулы, но совсем по иному, отличному от рассмотренного выше алгоритму.
Итак, у вас есть таблица, в одну из ячеек которой (наверняка крайнюю) требуется вывести сумму чисел, записанных в строке или столбце – с ней и будем работать. Если же место для суммирования отсутствует, ознакомьтесь с одной из представленных по ссылкам ниже статей, в зависимости от того, расчет какой части будет производиться.
Читайте также: Как в Ворде добавить строку или столбец в таблицу
- Кликните по той ячейке таблицы, в которую будет выводиться сумма.
Перейдите во вкладку «Макет», входящую в состав основного раздела «Работа с таблицами».
В группе «Данные», расположенной в этой вкладке, нажмите на кнопку «Формула».
В открывшемся диалоговом окне в разделе «Вставить функцию» выберите «SUM» — это и будет основой для нашей будущей формулы.
Выделить или указать ячейки так, как это можно сделать в Excel, в Word не получится. Поэтому местоположение ячеек, которые нужно суммировать, придется указывать по-другому.
После =SUM (без каких-либо отступов) в строке «Формула» введите одно из следующих значений:
- (ABOVE) — если требуется сложить данные из всех ячеек, расположенных выше формулы;
- (BELOW) — суммирование данных в ячейках, расположенных ниже той, в которую вписывается формула;
- (ABOVE;BELOW) — сумма чисел в ячейках выше и ниже;
- (LEFT) — суммирование данных слева от ячейки;
- (RIGHT) — сумма чисел справа от нее;
- (LEFT;RIGHT) — сложение чисел слева и справа от выделенной ячейки.
Указав необходимые сведения для расчета, нажмите «ОК», чтобы закрыть диалоговое окне «Формула».
В выбранной вами ячейке будет указана сумма данных, записанных в обозначенной вами строке или столбце либо их части.
Помимо данных, содержащихся только в строке или столбце таблицы либо же в части таковых, Ворд позволяет высчитывать сумму чисел в обоих этих диапазонах одновременно, например, слева и снизу или справа и сверху от ячейки, в которую выводится формула. Синтаксис таковых показан на изображении ниже, а под ним есть ссылка на официальный сайт Майкрософт, где можно узнать и о других математических выражениях для работы с таблицами.
Особенности работы формулы суммы
Производя расчеты в таблице, созданной в Word, следует знать о нескольких важных нюансах.
- Если вы изменяете содержимое ячеек, входящих в состав формулы, сумма чисел не будет обновляться автоматически. Чтобы получить корректный результат, необходимо кликнуть правой кнопкой мышки в ячейке с формулой и выбрать пункт «Обновить поле».
Заключение
Как видите, посчитать сумму чисел в Microsoft Word можно двумя разными методами. Первый подразумевает работу с математическими выражениями, а второй – с таблицами и содержащимися в их ячейках данными.
Мы рады, что смогли помочь Вам в решении проблемы.
Помимо этой статьи, на сайте еще 11905 инструкций.
Добавьте сайт Lumpics.ru в закладки (CTRL+D) и мы точно еще пригодимся вам.
Отблагодарите автора, поделитесь статьей в социальных сетях.
Опишите, что у вас не получилось. Наши специалисты постараются ответить максимально быстро.
Содержание
- 1 Варианты решений
- 1.1 Способ 1: матричный метод
- 1.2 Способ 2: подбор параметров
- 1.3 Способ 3: метод Крамера
- 1.4 Способ 4: метод Гаусса
- 1.5 Помогла ли вам эта статья?
- 2 Решение уравнений методом подбора параметров Excel
- 3 Как решить систему уравнений матричным методом в Excel
- 4 Решение системы уравнений методом Крамера в Excel
- 5 Решение систем уравнений методом Гаусса в Excel
- 6 Примеры решения уравнений методом итераций в Excel
Умение решать системы уравнений часто может принести пользу не только в учебе, но и на практике. В то же время, далеко не каждый пользователь ПК знает, что в Экселе существует собственные варианты решений линейных уравнений. Давайте узнаем, как с применением инструментария этого табличного процессора выполнить данную задачу различными способами.
Варианты решений
Любое уравнение может считаться решенным только тогда, когда будут отысканы его корни. В программе Excel существует несколько вариантов поиска корней. Давайте рассмотрим каждый из них.
Способ 1: матричный метод
Самый распространенный способ решения системы линейных уравнений инструментами Excel – это применение матричного метода. Он заключается в построении матрицы из коэффициентов выражений, а затем в создании обратной матрицы. Попробуем использовать данный метод для решения следующей системы уравнений:
14x1+2x2+8x4=218
7x1-3x2+5x3+12x4=213
5x1+x2-2x3+4x4=83
6x1+2x2+x3-3x4=21
- Заполняем матрицу числами, которые являются коэффициентами уравнения. Данные числа должны располагаться последовательно по порядку с учетом расположения каждого корня, которому они соответствуют. Если в каком-то выражении один из корней отсутствует, то в этом случае коэффициент считается равным нулю. Если коэффициент не обозначен в уравнении, но соответствующий корень имеется, то считается, что коэффициент равен 1. Обозначаем полученную таблицу, как вектор A.
- Отдельно записываем значения после знака «равно». Обозначаем их общим наименованием, как вектор B.
- Теперь для нахождения корней уравнения, прежде всего, нам нужно отыскать матрицу, обратную существующей. К счастью, в Эксель имеется специальный оператор, который предназначен для решения данной задачи. Называется он МОБР. Он имеет довольно простой синтаксис:
=МОБР(массив)Аргумент «Массив» — это, собственно, адрес исходной таблицы.
Итак, выделяем на листе область пустых ячеек, которая по размеру равна диапазону исходной матрицы. Щелкаем по кнопке «Вставить функцию», расположенную около строки формул.
- Выполняется запуск Мастера функций. Переходим в категорию «Математические». В представившемся списке ищем наименование «МОБР». После того, как оно отыскано, выделяем его и жмем на кнопку «OK».
- Запускается окно аргументов функции МОБР. Оно по числу аргументов имеет всего одно поле – «Массив». Тут нужно указать адрес нашей таблицы. Для этих целей устанавливаем курсор в это поле. Затем зажимаем левую кнопку мыши и выделяем область на листе, в которой находится матрица. Как видим, данные о координатах размещения автоматически заносятся в поле окна. После того, как эта задача выполнена, наиболее очевидным было бы нажать на кнопку «OK», но не стоит торопиться. Дело в том, что нажатие на эту кнопку является равнозначным применению команды Enter. Но при работе с массивами после завершения ввода формулы следует не кликать по кнопке Enter, а произвести набор сочетания клавиш Ctrl+Shift+Enter. Выполняем эту операцию.
- Итак, после этого программа производит вычисления и на выходе в предварительно выделенной области мы имеем матрицу, обратную данной.
- Теперь нам нужно будет умножить обратную матрицу на матрицу B, которая состоит из одного столбца значений, расположенных после знака «равно» в выражениях. Для умножения таблиц в Экселе также имеется отдельная функция, которая называется МУМНОЖ. Данный оператор имеет следующий синтаксис:
=МУМНОЖ(Массив1;Массив2)Выделяем диапазон, в нашем случае состоящий из четырех ячеек. Далее опять запускаем Мастер функций, нажав значок «Вставить функцию».
- В категории «Математические», запустившегося Мастера функций, выделяем наименование «МУМНОЖ» и жмем на кнопку «OK».
- Активируется окно аргументов функции МУМНОЖ. В поле «Массив1» заносим координаты нашей обратной матрицы. Для этого, как и в прошлый раз, устанавливаем курсор в поле и с зажатой левой кнопкой мыши выделяем курсором соответствующую таблицу. Аналогичное действие проводим для внесения координат в поле «Массив2», только на этот раз выделяем значения колонки B. После того, как вышеуказанные действия проведены, опять не спешим жать на кнопку «OK» или клавишу Enter, а набираем комбинацию клавиш Ctrl+Shift+Enter.
- После данного действия в предварительно выделенной ячейке отобразятся корни уравнения: X1, X2, X3 и X4. Они будут расположены последовательно. Таким образом, можно сказать, что мы решили данную систему. Для того, чтобы проверить правильность решения достаточно подставить в исходную систему выражений данные ответы вместо соответствующих корней. Если равенство будет соблюдено, то это означает, что представленная система уравнений решена верно.
Урок: Обратная матрица в Excel
Способ 2: подбор параметров
Второй известный способ решения системы уравнений в Экселе – это применение метода подбора параметров. Суть данного метода заключается в поиске от обратного. То есть, основываясь на известном результате, мы производим поиск неизвестного аргумента. Давайте для примера используем квадратное уравнение
3x^2+4x-132=0
- Принимаем значение x за равное 0. Высчитываем соответствующее для него значение f(x), применив следующую формулу:
=3*x^2+4*x-132Вместо значения «X» подставляем адрес той ячейки, где расположено число 0, принятое нами за x.
- Переходим во вкладку «Данные». Жмем на кнопку «Анализ «что если»». Эта кнопка размещена на ленте в блоке инструментов «Работа с данными». Открывается выпадающий список. Выбираем в нем позицию «Подбор параметра…».
- Запускается окно подбора параметров. Как видим, оно состоит из трех полей. В поле «Установить в ячейке» указываем адрес ячейки, в которой находится формула f(x), рассчитанная нами чуть ранее. В поле «Значение» вводим число «0». В поле «Изменяя значения» указываем адрес ячейки, в которой расположено значение x, ранее принятое нами за 0. После выполнения данных действий жмем на кнопку «OK».
- После этого Эксель произведет вычисление с помощью подбора параметра. Об этом сообщит появившееся информационное окно. В нем следует нажать на кнопку «OK».
- Результат вычисления корня уравнения будет находиться в той ячейке, которую мы назначили в поле «Изменяя значения». В нашем случае, как видим, x будет равен 6.
Этот результат также можно проверить, подставив данное значение в решаемое выражение вместо значения x.
Урок: Подбор параметра в Excel
Способ 3: метод Крамера
Теперь попробуем решить систему уравнений методом Крамера. Для примера возьмем все ту же систему, которую использовали в Способе 1:
14x1+2x2+8x4=218
7x1-3x2+5x3+12x4=213
5x1+x2-2x3+4x4=83
6x1+2x2+x3-3x4=21
- Как и в первом способе, составляем матрицу A из коэффициентов уравнений и таблицу B из значений, которые стоят после знака «равно».
- Далее делаем ещё четыре таблицы. Каждая из них является копией матрицы A, только у этих копий поочередно один столбец заменен на таблицу B. У первой таблицы – это первый столбец, у второй таблицы – второй и т.д.
- Теперь нам нужно высчитать определители для всех этих таблиц. Система уравнений будет иметь решения только в том случае, если все определители будут иметь значение, отличное от нуля. Для расчета этого значения в Экселе опять имеется отдельная функция – МОПРЕД. Синтаксис данного оператора следующий:
=МОПРЕД(массив)Таким образом, как и у функции МОБР, единственным аргументом выступает ссылка на обрабатываемую таблицу.
Итак, выделяем ячейку, в которой будет выводиться определитель первой матрицы. Затем жмем на знакомую по предыдущим способам кнопку «Вставить функцию».
- Активируется окно Мастера функций. Переходим в категорию «Математические» и среди списка операторов выделяем там наименование «МОПРЕД». После этого жмем на кнопку «OK».
- Запускается окно аргументов функции МОПРЕД. Как видим, оно имеет только одно поле – «Массив». В это поле вписываем адрес первой преобразованной матрицы. Для этого устанавливаем курсор в поле, а затем выделяем матричный диапазон. После этого жмем на кнопку «OK». Данная функция выводит результат в одну ячейку, а не массивом, поэтому для получения расчета не нужно прибегать к нажатию комбинации клавиш Ctrl+Shift+Enter.
- Функция производит подсчет результата и выводит его в заранее выделенную ячейку. Как видим, в нашем случае определитель равен -740, то есть, не является равным нулю, что нам подходит.
- Аналогичным образом производим подсчет определителей для остальных трех таблиц.
- На завершающем этапе производим подсчет определителя первичной матрицы. Процедура происходит все по тому же алгоритму. Как видим, определитель первичной таблицы тоже отличный от нуля, а значит, матрица считается невырожденной, то есть, система уравнений имеет решения.
- Теперь пора найти корни уравнения. Корень уравнения будет равен отношению определителя соответствующей преобразованной матрицы на определитель первичной таблицы. Таким образом, разделив поочередно все четыре определителя преобразованных матриц на число -148, которое является определителем первоначальной таблицы, мы получим четыре корня. Как видим, они равны значениям 5, 14, 8 и 15. Таким образом, они в точности совпадают с корнями, которые мы нашли, используя обратную матрицу в способе 1, что подтверждает правильность решения системы уравнений.
Способ 4: метод Гаусса
Решить систему уравнений можно также, применив метод Гаусса. Для примера возьмем более простую систему уравнений из трех неизвестных:
14x1+2x2+8x3=110
7x1-3x2+5x3=32
5x1+x2-2x3=17
- Опять последовательно записываем коэффициенты в таблицу A, а свободные члены, расположенные после знака «равно» — в таблицу B. Но на этот раз сблизим обе таблицы, так как это понадобится нам для работы в дальнейшем. Важным условием является то, чтобы в первой ячейке матрицы A значение было отличным от нуля. В обратном случае следует переставить строки местами.
- Копируем первую строку двух соединенных матриц в строчку ниже (для наглядности можно пропустить одну строку). В первую ячейку, которая расположена в строке ещё ниже предыдущей, вводим следующую формулу:
=B8:E8-$B$7:$E$7*(B8/$B$7)Если вы расположили матрицы по-другому, то и адреса ячеек формулы у вас будут иметь другое значение, но вы сможете высчитать их, сопоставив с теми формулами и изображениями, которые приводятся здесь.
После того, как формула введена, выделите весь ряд ячеек и нажмите комбинацию клавиш Ctrl+Shift+Enter. К ряду будет применена формула массива и он будет заполнен значениями. Таким образом мы произвели вычитание из второй строки первой, умноженной на отношение первых коэффициентов двух первых выражений системы.
- После этого копируем полученную строку и вставляем её в строчку ниже.
- Выделяем две первые строки после пропущенной строчки. Жмем на кнопку «Копировать», которая расположена на ленте во вкладке «Главная».
- Пропускаем строку после последней записи на листе. Выделяем первую ячейку в следующей строке. Кликаем правой кнопкой мыши. В открывшемся контекстном меню наводим курсор на пункт «Специальная вставка». В запустившемся дополнительном списке выбираем позицию «Значения».
- В следующую строку вводим формулу массива. В ней производится вычитание из третьей строки предыдущей группы данных второй строки, умноженной на отношение второго коэффициента третьей и второй строки. В нашем случае формула будет иметь следующий вид:
=B13:E13-$B$12:$E$12*(C13/$C$12)После ввода формулы выделяем весь ряд и применяем сочетание клавиш Ctrl+Shift+Enter.
- Теперь следует выполнить обратную прогонку по методу Гаусса. Пропускаем три строки от последней записи. В четвертой строке вводим формулу массива:
=B17:E17/D17Таким образом, мы делим последнюю рассчитанную нами строку на её же третий коэффициент. После того, как набрали формулу, выделяем всю строчку и жмем сочетание клавиш Ctrl+Shift+Enter.
- Поднимаемся на строку вверх и вводим в неё следующую формулу массива:
=(B16:E16-B21:E21*D16)/C16Жмем привычное уже нам сочетание клавиш для применения формулы массива.
- Поднимаемся ещё на одну строку выше. В неё вводим формулу массива следующего вида:
=(B15:E15-B20:E20*C15-B21:E21*D15)/B15Опять выделяем всю строку и применяем сочетание клавиш Ctrl+Shift+Enter.
- Теперь смотрим на числа, которые получились в последнем столбце последнего блока строк, рассчитанного нами ранее. Именно эти числа (4, 7 и 5) будут являться корнями данной системы уравнений. Проверить это можно, подставив их вместо значений X1, X2 и X3 в выражения.
Как видим, в Экселе систему уравнений можно решить целым рядом способов, каждый из которых имеет собственные преимущества и недостатки. Но все эти методы можно условно разделить на две большие группы: матричные и с применением инструмента подбора параметров. В некоторых случаях не всегда матричные методы подходят для решения задачи. В частности тогда, когда определитель матрицы равен нулю. В остальных же случаях пользователь сам волен решать, какой вариант он считает более удобным для себя.
Мы рады, что смогли помочь Вам в решении проблемы.
Задайте свой вопрос в комментариях, подробно расписав суть проблемы. Наши специалисты постараются ответить максимально быстро.
Помогла ли вам эта статья?
Да Нет
В программе Excel имеется обширный инструментарий для решения различных видов уравнений разными методами.
Рассмотрим на примерах некоторые варианты решений.
Инструмент «Подбор параметра» применяется в ситуации, когда известен результат, но неизвестны аргументы. Excel подбирает значения до тех пор, пока вычисление не даст нужный итог.
Путь к команде: «Данные» — «Работа с данными» — «Анализ «что-если»» — «Подбор параметра».
Рассмотрим на примере решение квадратного уравнения х2 + 3х + 2 = 0. Порядок нахождения корня средствами Excel:
- Введем в ячейку В2 формулу для нахождения значения функции. В качестве аргумента применим ссылку на ячейку В1.
- Открываем меню инструмента «Подбор параметра». В графе «Установить в ячейку» — ссылка на ячейку В2, где находится формула. В поле «Значение» вводим 0. Это то значение, которое нужно получить. В графе «Изменяя значение ячейки» — В1. Здесь должен отобразиться отобранный параметр.
- После нажатия ОК отобразится результат подбора. Если нужно его сохранить, вновь нажимаем ОК. В противном случае – «Отмена».
Для подбора параметра программа использует циклический процесс. Чтобы изменить число итераций и погрешность, нужно зайти в параметры Excel. На вкладке «Формулы» установить предельное количество итераций, относительную погрешность. Поставить галочку «включить итеративные вычисления».
Как решить систему уравнений матричным методом в Excel
Дана система уравнений:
- Значения элементов введем в ячейки Excel в виде таблицы.
- Найдем обратную матрицу. Выделим диапазон, куда впоследствии будут помещены элементы матрицы (ориентируемся на количество строк и столбцов в исходной матрице). Открываем список функций (fx). В категории «Математические» находим МОБР. Аргумент – массив ячеек с элементами исходной матрицы.
- Нажимаем ОК – в левом верхнем углу диапазона появляется значение. Последовательно жмем кнопку F2 и сочетание клавиш Ctrl + Shift + Enter.
- Умножим обратную матрицу Ах-1х на матрицу В (именно в таком порядке следования множителей!). Выделяем диапазон, где впоследствии появятся элементы результирующей матрицы (ориентируемся на число строк и столбцов матрицы В). Открываем диалоговое окно математической функции МУМНОЖ. Первый диапазон – обратная матрица. Второй – матрица В.
- Закрываем окно с аргументами функции нажатием кнопки ОК. Последовательно нажимаем кнопку F2 и комбинацию Ctrl + Shift + Enter.
Получены корни уравнений.
Решение системы уравнений методом Крамера в Excel
Возьмем систему уравнений из предыдущего примера:
Для их решения методом Крамера вычислим определители матриц, полученных заменой одного столбца в матрице А на столбец-матрицу В.
Для расчета определителей используем функцию МОПРЕД. Аргумент – диапазон с соответствующей матрицей.
Рассчитаем также определитель матрицы А (массив – диапазон матрицы А).
Определитель системы больше 0 – решение можно найти по формуле Крамера (Dx / |A|).
Для расчета Х1: =U2/$U$1, где U2 – D1. Для расчета Х2: =U3/$U$1. И т.д. Получим корни уравнений:
Решение систем уравнений методом Гаусса в Excel
Для примера возьмем простейшую систему уравнений:
3а + 2в – 5с = -1
2а – в – 3с = 13
а + 2в – с = 9
Коэффициенты запишем в матрицу А. Свободные члены – в матрицу В.
Для наглядности свободные члены выделим заливкой. Если в первой ячейке матрицы А оказался 0, нужно поменять местами строки, чтобы здесь оказалось отличное от 0 значение.
- Приведем все коэффициенты при а к 0. Кроме первого уравнения. Скопируем значения в первой строке двух матриц в ячейки В6:Е6. В ячейку В7 введем формулу: =B3:Е3-$B$2:$Е$2*(B3/$B$2). Выделим диапазон В7:Е7. Нажмем F2 и сочетание клавиш Ctrl + Shift + Enter. Мы отняли от второй строки первую, умноженную на отношение первых элементов второго и первого уравнения.
- Копируем введенную формулу на 8 и 9 строки. Так мы избавились от коэффициентов перед а. Сохранили только первое уравнение.
- Приведем к 0 коэффициенты перед в в третьем и четвертом уравнении. Копируем строки 6 и 7 (только значения). Переносим их ниже, в строки 10 и 11. Эти данные должны остаться неизменными. В ячейку В12 вводим формулу массива.
- Прямую прогонку по методу Гаусса сделали. В обратном порядке начнем прогонять с последней строки полученной матрицы. Все элементы данной строки нужно разделить на коэффициент при с. Введем в строку формулу массива: {=B12:E12/D12}.
- В строке 15: отнимем от второй строки третью, умноженную на коэффициент при с второй строки ({=(B11:E11-B16:E16*D11)/C11}). В строке 14: от первой строки отнимаем вторую и третью, умноженные на соответствующие коэффициенты ({=(B10:E10-B15:E15*C10-B16:E16*D10)/B10}). В последнем столбце новой матрицы получаем корни уравнения.
Примеры решения уравнений методом итераций в Excel
Вычисления в книге должны быть настроены следующим образом:
Делается это на вкладке «Формулы» в «Параметрах Excel». Найдем корень уравнения х – х3 + 1 = 0 (а = 1, b = 2) методом итерации с применением циклических ссылок. Формула:
Хn+1 = Xn– F (Xn) / M, n = 0, 1, 2, … .
M – максимальное значение производной по модулю. Чтобы найти М, произведем вычисления:
f’ (1) = -2 * f’ (2) = -11.
Полученное значение меньше 0. Поэтому функция будет с противоположным знаком: f (х) = -х + х3 – 1. М = 11.
В ячейку А3 введем значение: а = 1. Точность – три знака после запятой. Для расчета текущего значения х в соседнюю ячейку (В3) введем формулу: =ЕСЛИ(B3=0;A3;B3-(-B3+СТЕПЕНЬ(B3;3)-1/11)).
В ячейке С3 проконтролируем значение f (x): с помощью формулы =B3-СТЕПЕНЬ(B3;3)+1.
Корень уравнения – 1,179. Введем в ячейку А3 значение 2. Получим тот же результат:
Скачать решения уравнений в Excel
Корень на заданном промежутке один.
Задача решения уравнения встает не только перед студентами и школьниками. В Excel можно использовать различные способы выполнения этой задачи. О способе решения путем подбора параметра пойдет речь в этой статье.
Нахождение корней нелинейного уравнения с использованием средства
«Подбор параметра» сводится в двум этапам:
- определение приблизительных границ отрезков и количества корней графическим методом;
- подбор на каждом отрезке значения корня, удовлетворяющего заданной точности вычислений.
Примером может служить решение квадратного уравнения, которое в общем виде задается выражением
«Y(x) = ax2 + bx +
c» . Для того, чтобы построенная электронная таблица позволяла бы находить решения подобных уравнений с любыми коэффициентами, лучше вынести коэффициенты в отдельные ячейки, а в формулах для вычисления значений функции использовать ссылки на эти ячейки. Впрочем, это дело вкуса. Можно при составлении формулы использовать значения коэффициентов, а не ссылки на них.
Чтобы оценить примерные границы отрезков и количество корней, можно использовать табличное задание значений функции, т.е. задать несколько значений переменной и вычислить соответствующие значения функции. Опять же, для того, чтобы можно было моделировать расчеты для квадратных уравнений с различными коэффициентами, шаг табулирования лучше задать в отдельной ячейке. Начальное значение переменной можно будет изменять путем ввода в ячейку «
А6» . Для вычисления следующего значения в ячейку
«А7» введена формула «
=А6+$
B$4» , т.е. использована абсолютная ссылка на ячейку с шагом табулирования.
Далее с помощью
маркера заполнения формируется ряд формул для вычисления последующих значений переменной, в приведенном примере используется 20 значений.
Вводится формула для вычисления значения функции (для рассматриваемого примера в ячейку «
В6» ) и формируется ряд аналогичных формул для остальных ячеек. В формуле использованы абсолютные ссылки на ячейки с коэффициентами уравнения.
По построенной таблице строится
точечная диаграмма .
Если начальное значение Х и шаг выбраны неудачно, и на диаграмме нет пересечений с осью абсцисс, то можно ввести другие значения и добиться нужного результата.
Можно было бы найти решение уже на этом шаге, но для этого понадобилось бы гораздо больше ячеек и шаг, равный заданной точности вычислений (0,001). Чтобы не создавать громоздких таблиц, далее используется
«Подбор параметра» из группы
«Прогноз» на вкладке
«Данные» . Предварительно необходимо выделить место под начальные значения переменной (корней в примере два) и соответствующие значения функции. В качестве «
х1» выбирается первое из значений, дающих наиболее близкое к нулю значение функции (в примере 0,5). В
ячейку
L6 введена формула для вычисления функции. В окне подбора параметра необходимо указать для какой ячейки (
L6 ), какое значение (
) нужно получить, и в какой ячейке для этого изменять значения (
К6 ).
Для поиска второго корня необходимо ввести второе из значений, дающих наиболее близкое к нулю значение функции (в примере 9,5), и повторить подбор параметра для ячейки
L9 (в ячейку скопирована формула из ячейки
L6 ).
Предложенное оформление коэффициентов функции в отдельные ячейки позволяет без изменения формул решать другие подобные уравнения.
Подбор параметра имеется и в более ранних версиях программы.
Вставка формулы в Microsoft Word
Функциональные возможности текстового редактора Microsoft Word на деле не ограничиваются одной только работой с текстом. Так, это офисное приложение позволяет создавать таблицы, диаграммы и графики, добавлять и изменять изображения и много чего другого. Одной из наиболее интересных, хотя и не самых очевидных функций является вставка формул и уравнений, а также их создание с нуля. О том, как это делается, расскажем в данной статье.
Добавление формулы в Ворде
Как и в случае с большинством объектов, работа с которыми поддерживается Word, добавление и создание формул в текстовом документе осуществляется во вкладке «Вставка». На выбор пользователю предоставляется четыре различных варианта — от использования готовых шаблонов до самостоятельного создания записи и даже ее ручного ввода. Все это, а также некоторые дополнительные возможности и нюансы, подробнее рассмотрим далее, но прежде всего расскажем и покажем, как перейти к интересующему нас разделу программы.
-
Из главного окна Майкрософт Ворд перейдите во вкладку «Вставка».
Примечание: В Microsoft Word 2003 встроенные средства для создания уравнений и работы с ними отсутствуют. Если вы до сих пор пользуетесь этой версией программы, ознакомьтесь с последней частью данной статьи.
Способ 1: Выбор шаблонных и часто используемых примеров
В меню создания уравнений Microsoft Word есть несколько готовых шаблонов, для добавления любого из которых в документ достаточно просто нажать по нему ЛКМ. В числе таковых следующие:
- Бином Ньютона;
- Квадратное уравнение;
- Площадь круга;
- Разложение суммы;
Конечно же, большинству пользователей этого будет недостаточно, а потому неудивительно, что столь скромный список можно пополнить как собственными формулами, так и дополнительными уравнениями на сайте Office.com, которые на самом деле доступны прямо в программе. Для их выбора и последующей вставки просто наведите указатель курсора на соответствующий пункт меню добавления новой записи.
Далее кратко расскажем о том, каким образом осуществляется работа с изначально отформатированными, шаблонными математическими записями в Ворде.
Примечание: Для всех формул и уравнений, как шаблонных, так и записанных вручную, применяется шрифт Cambria Math, и изменить его невозможно. Все остальные параметры (изменение типа начертания, размера, цвета и т. д.) при этом остаются доступными.
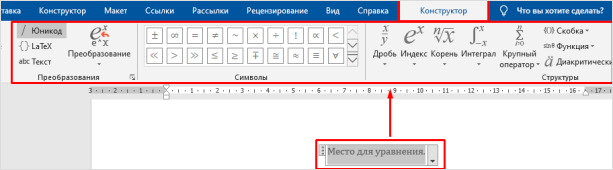
Сразу же после добавления шаблонного уравнения (как и любого другого) вы будете перенаправлены на вкладку «Конструктор» (не путайте с той, что изначально присутствует не панели инструментов Microsoft Word и расположена между вкладками «Вставка» и «Макет», ранее она называлась «Дизайн»).
Примечание: Вкладка «Конструктор», посредством которой осуществляется вся работа с формулами, активна и открыта исключительно в то время, когда выделено поле вставки нового уравнения и/или вы с ним взаимодействуете.
Здесь представлены три основных категории инструментов, а именно:
- Преобразования;
- Символы;
- Структуры.
Получить доступ к возможностям «Преобразования» можно и через меню с блоком добавленной формулы – просто нажмите ЛКМ на указывающий вниз треугольник. Помимо прочего, отсюда же можно сохранить уравнение в виде шаблона, о чем мы еще расскажем, и определить тип его выравнивания на странице документа. 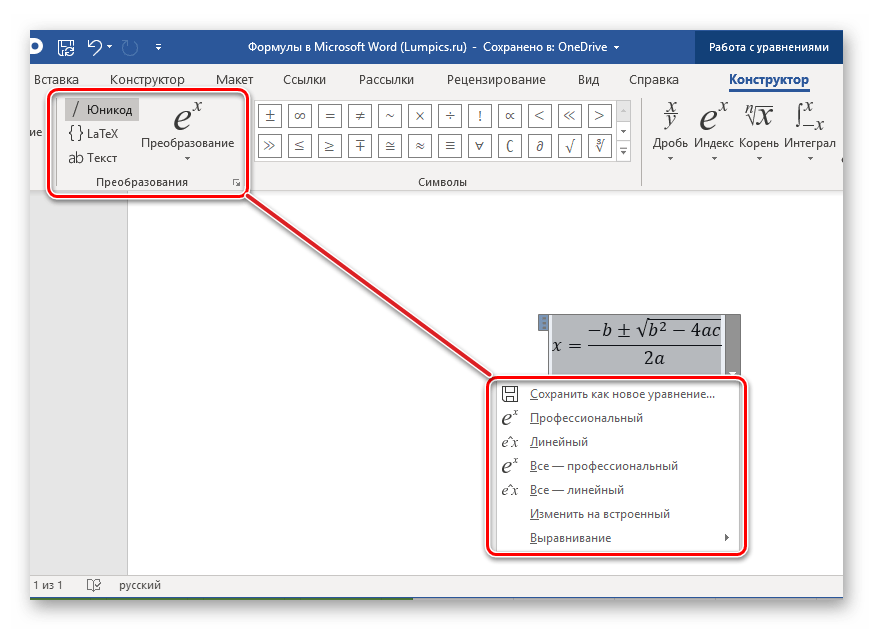
Если в добавленную запись потребуется внести изменения, используйте инструментарий разделов «Символы» и «Структуры». 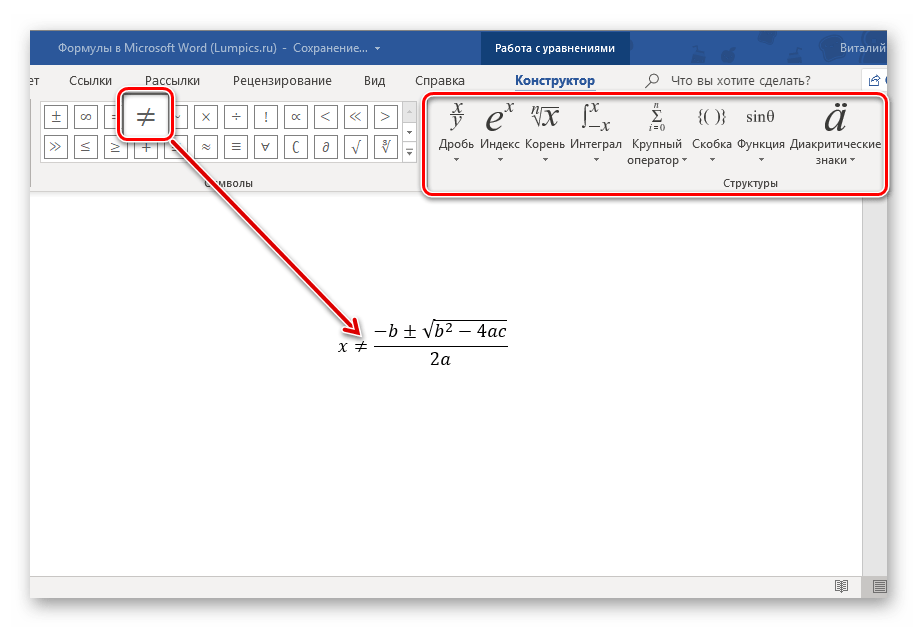
Закончив работу с уравнением, просто кликните по пустой области страницы. Если нажать после этого на пробел, запись, изначально вставленная посередине, будет выровнена по левому краю (или по тому, который задан в качестве параметров выравнивания по умолчанию для текущего документа).
Способ 2: Самостоятельное создание уравнений
Куда более часто требуется добавить в текстовый документ не шаблонную запись, а произвольное или просто отсутствующее в списке «Встроенные» уравнение. Делается это следующим образом:
-
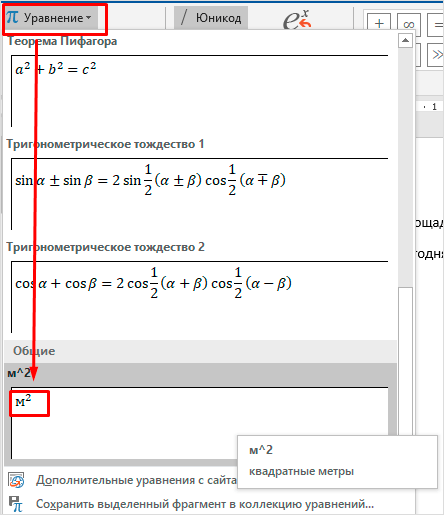
В выпадающем списке меню «Уравнение» выберите пункт «Вставить новое уравнение», после чего на страницу будет добавлено поле для записи.
Примечание: Для вставки поля для ввода формулы, которое называется «Место для уравнения», можно воспользоваться горячими клавишами, а именно, комбинацией «ALT+=».
- Дробь;
- Индекс;
- Корень;
- Интеграл;
- Крупный оператор;
- Скобка;
- Функция;
- Диакритические знаки;
- Предел и логарифм;
- Оператор;
- Матрица.
Вот пример того, как можно записать простое уравнение:
- Для начала выбираем подходящую структуру (в нашем примере это «Верхний индекс»).
- Затем ставим символ (такие как плюс, минус, равно, умножить можно ввести и с клавиатуры, остальные же выбираются на панели «Символы»).
- Аналогичным образом записываем остальные элементы примера.
Способ 3: Рукописный ввод уравнений
Если набор математических символов и структур, представленных во вкладке «Конструктор» и предназначенных для самостоятельного создания записей, вас по каким-то причинам вас не устраивает, формулу или уравнение можно добавить и старым-добрым способом – написав его от руки, а точнее, с помощью мышки (или стилуса на устройствах с сенсорным экраном). Делается это следующим образом:
-
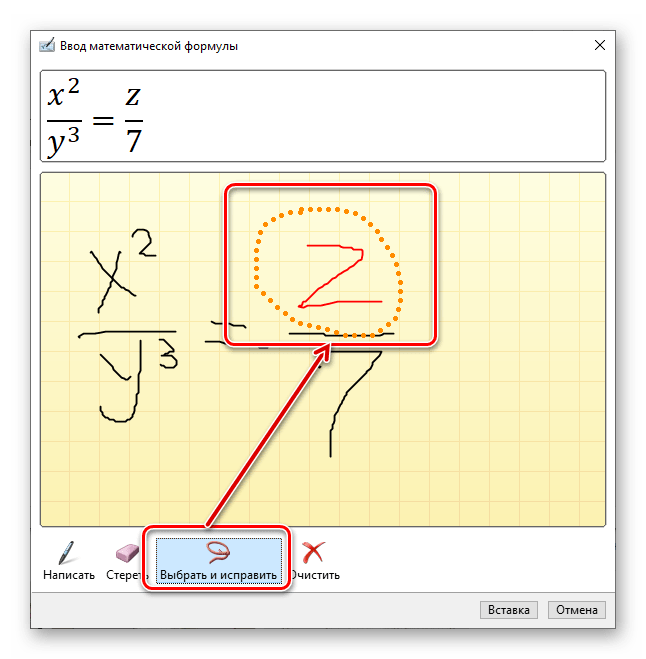
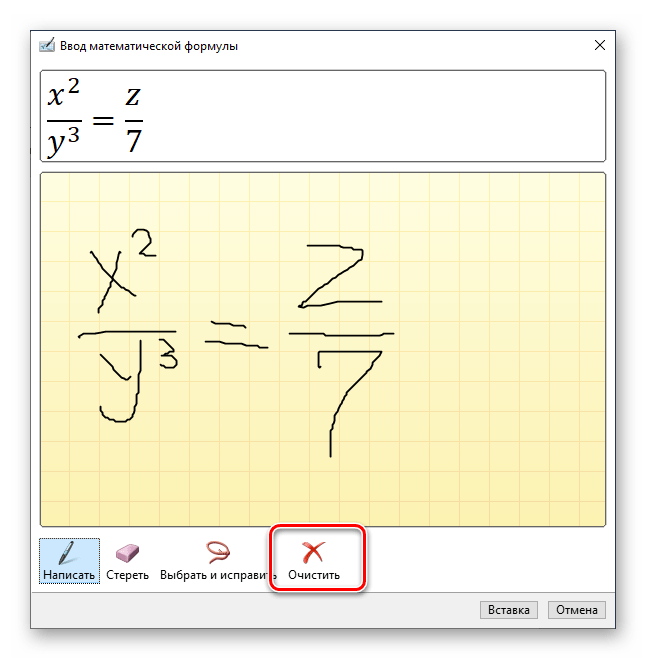
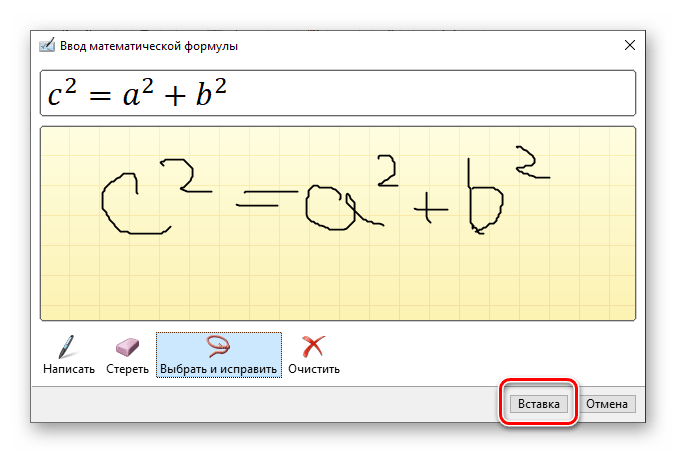
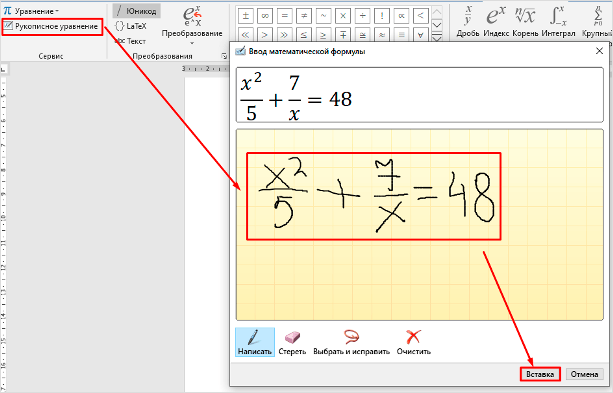
В меню вставки нового уравнения выберите предпоследний пункт «Рукописное уравнение».
Примечание: По ходу написания формулы поле для ее ввода будет автоматически расширяться.
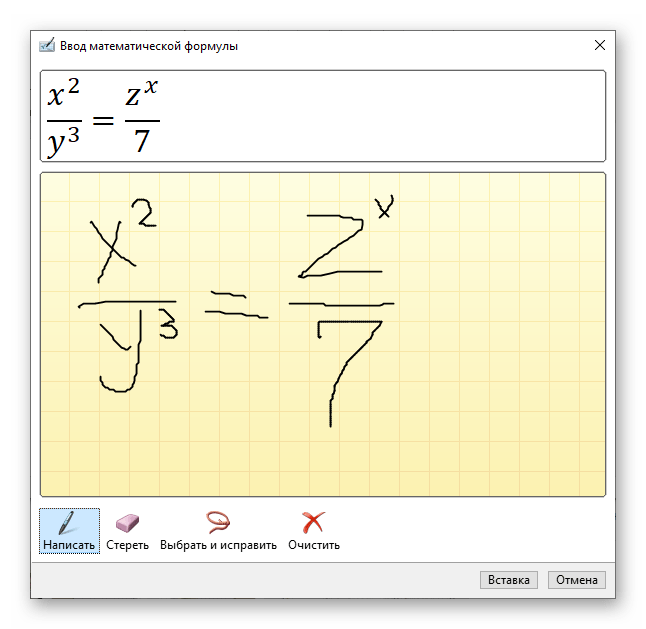
Если вы допустили ошибку, воспользуйтесь инструментом «Стереть», который удаляет сразу весь выбранный символ. 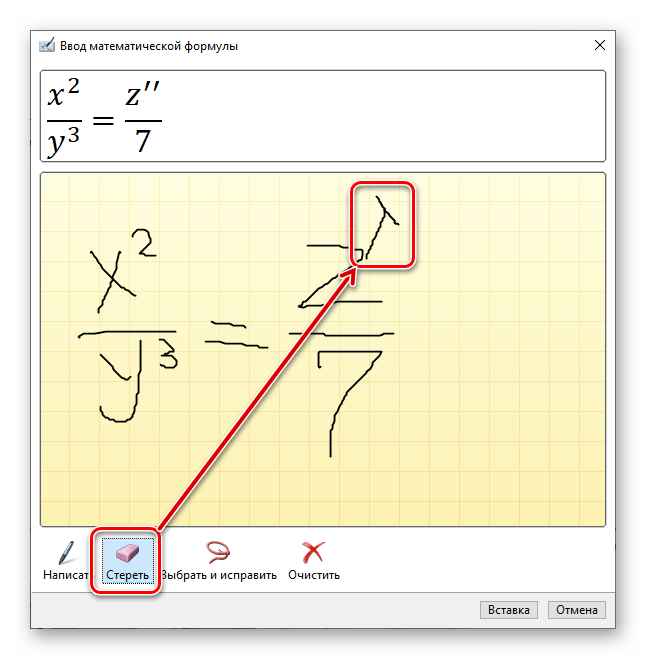
Помимо удаления, доступно и исправление ошибок, что делается инструментом «Выбрать и исправить». С его помощью выделяете символ, обводя его по кругу, а затем из выпадающего меню выбираете то, на что вы хотите его заменить.
Сохранение собственных формул в качестве шаблона
Если в процессе работы с документами вам часто требуется записывать одни и те же формулы, разумно будет добавить их в список часто используемых. Таким образом вы создадите готовый шаблон, который будет доступен из меню вставки буквально в пару кликов мышкой.
-
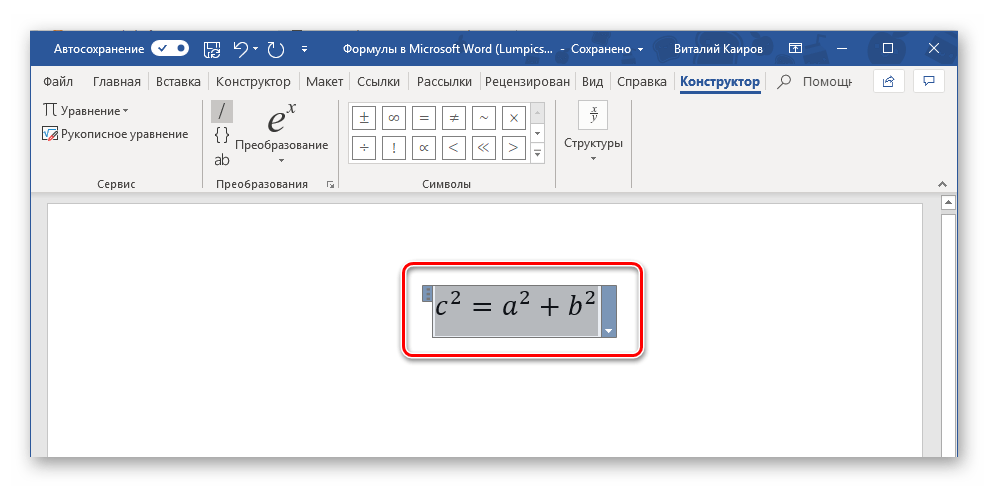
Создайте формулу, которую хотите добавить в список шаблонов, а затем выделите ее нажатием ЛКМ по «рамке».
Вставка формулы в ячейку таблицы
Несмотря на то что в пакете Microsoft Office за работу с таблицами отвечает Excel, Word тоже позволяет создавать и обрабатывать элементы данного типа. Да, возможности текстового редактора в этом плане куда более скромные, чем у его собрата, но для решения базовых задач встроенной функциональности будет достаточно.
Вставка непосредственно уравнений, шаблонных или самостоятельно созданных, в таблицу осуществляется ровно по тому же алгоритму, что и во всех рассмотренных нами случаях, что можно понять из представленного выше скриншота. Однако помимо этого в программе имеется возможность добавления именно формулы в любую ячейку таблицы Ворд, по типу того, как это делается в Экселе. Об этом далее и расскажем.
- Создайте таблицу, если не сделали это заранее, а затем выделите кликом ЛКМ ту ее ячейку, в которую будет добавлена формула.
- Перейдите во вкладку «Макет», но не ту, что в основной группе вкладок, а ту, которая располагается в категории «Работа с таблицами», и нажмите там по кнопке «Формула» (группа инструментов «Данные»).
Примечание: Если просто навести указатель курсора на кнопку «Формула», можно увидеть краткое описание того, что данная функция позволяет. С ее помощью можно добавить в ячейку таблицы формулу для выполнения простого расчета, например, среднего значения или суммы.
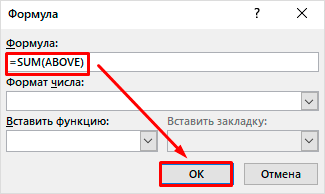
У вас может возникнуть вполне логический вопрос – как правильно записывать такие формулы, какой у них должен быть синтаксис? Общий алгоритм в данном случае мало чем отличается от такового в MS Excel, с той лишь разницей, что переменными в записи выступают не адреса ячеек, а их расположение – над ячейкой (ABOVE) или под ней (BELOW), справа (RIGHT) или слева от нее (LEFT). Например, вот так будет выглядеть формула суммы значений:
=SUM(ABOVE) 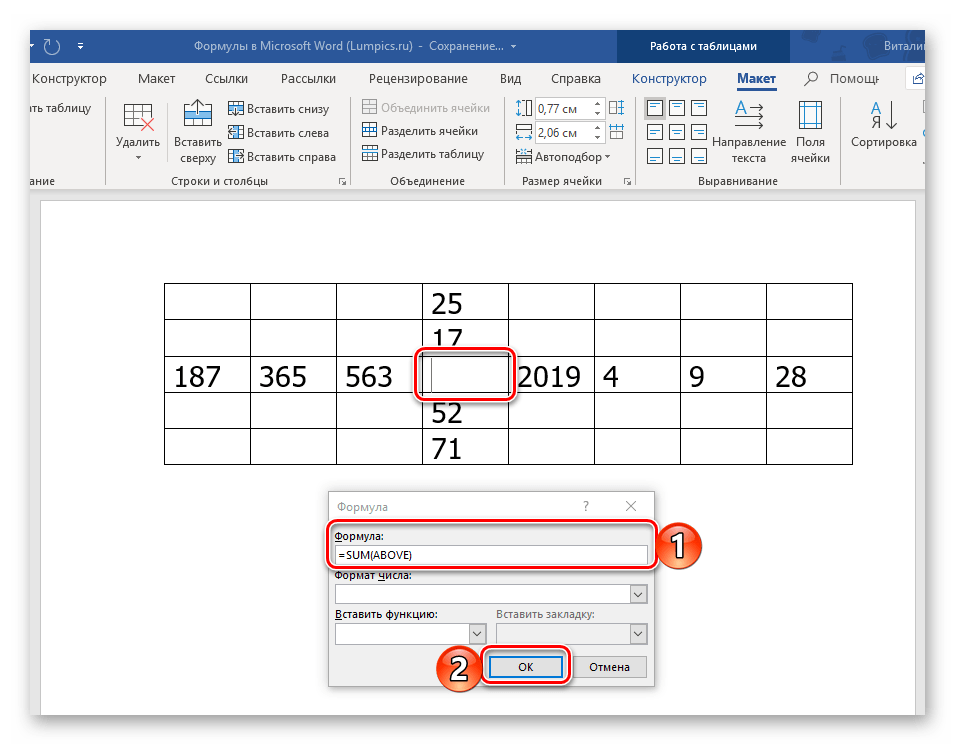
В нашем примере она записана в в четвертую ячейку третьей строки таблицы, а значит, будет суммировать указанные над ней значения: 25+17, что равно 42. 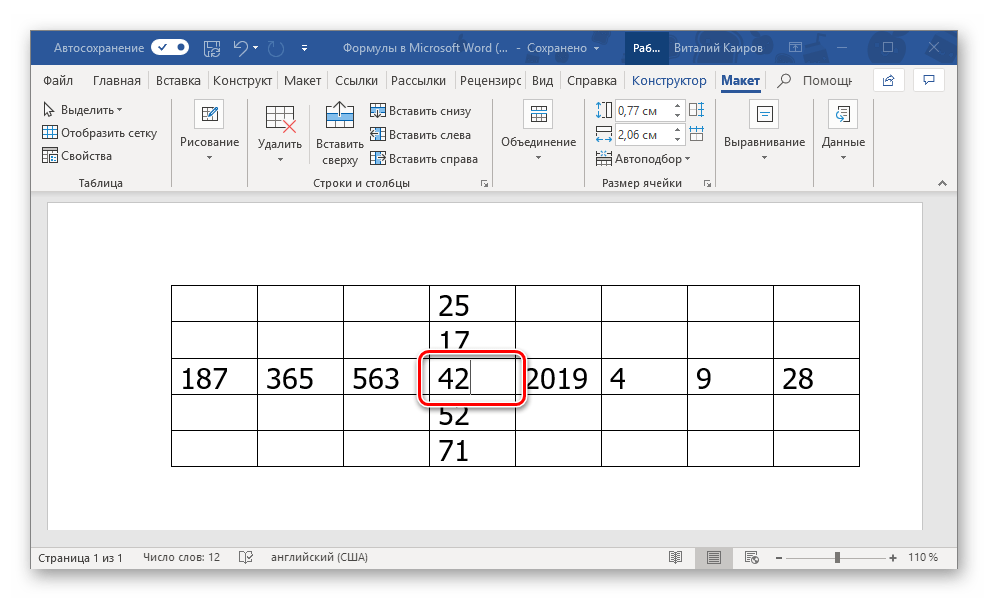
Остальные примеры различных вариантов записи формулы суммы для таблиц в Ворде показаны на следующем изображении, а под ним есть ссылка на официальную страницу поддержки на сайте Microsoft, посвященную данной теме — на ней можно найти синтаксис всех поддерживаемых программой формул и подробное описание их использования.
Работа с формулами в Microsoft Word 2003
Как было сказано во вступлении, в Ворд 2003 нет собственных средств для добавления, изменения и создания уравнений и формул. Но решение нашей сегодняшней задачи, хоть и весьма ограниченное, доступно и в этой версии программы. Используются для этих целей специальные надстройки — Microsoft Equation и Math Type, об использовании которых мы кратко расскажем далее.
- Откройте вкладку «Вставка» и выберите пункт «Объект».
- В открывшемся диалоговом окне выберите «Microsoft Equation 3.0» и нажмите на кнопку «ОК».
- Сразу же после этого будет открыто небольшое окно под названием «Формула», в котором можно выбирать математические символы и структуры, аналогичные таковым в более новых версиях Microsoft Word, и использовать их для создания формул и уравнений любой сложности.
Заключение
Несмотря на то что Microsoft Word предназначен в первую очередь для работы с текстом, в нем возможно в том числе и выполнение таких отнюдь не рутинных задач, как вставка шаблонных уравнений и формул, их изменение или создание с нуля, и даже рукописный ввод.

Как вставить формулу в Word: подробная инструкция с примерами для новичков
В студенческие годы мне тяжело давалась работа с текстом, лабораторные и особенно курсовые проекты. Курсовую по программированию мне возвращали 3 или 4 раза из-за недоработок именно в тексте, а не в программе. Я терпеть не могла этот Word и требования к оформлению документов: то поля не такие, то шрифт, то отступы.
Но времена меняются, и сейчас текстовый редактор от компании Microsoft стал моим лучшим помощником, и я с радостью поделюсь с вами навыками работы в нем. Мы уже говорили о том, как делать таблицы и гиперссылки в тексте, а сегодня разберемся, как вставить формулу в Word, отредактировать ее и перенести в другое место, создать свои шаблоны для упрощения работы.
Зачем и кому нужны формулы
Конечно, не все функции текстового редактора нужны каждому пользователю. Их очень много, и вряд ли кто-то из нас владеет всеми. Мне, например, редко приходится делать сноски внизу документа, но если вы пишете книгу, то без них не обойтись.
Работа с формулами нужна не только студентам и тем, кто пишет научные работы по математике, физике или химии. На самом деле иногда нужно поставить значок градуса, добавить верхний или нижний индекс в самом простом тексте для широкого круга читателей. Можно обойтись без стандартных функций программы, набрать текст вручную, но выглядеть это будет некрасиво и непрофессионально.
Многие простые и не очень задачи решаются при помощи вставки формул в документ, поэтому, я думаю, эта опция полезна для всех.
Как добавить формулу в Word
Расположение и название функций отличаются в разных версиях программы. У меня недавно появился Office 2019, и я буду показывать все действия на его примере. Если у вас более ранние выпуски текстового редактора, то повторяйте за мной, но будьте внимательны, названия и внешний вид пунктов меню могут немного отличаться. Я об этом еще скажу.
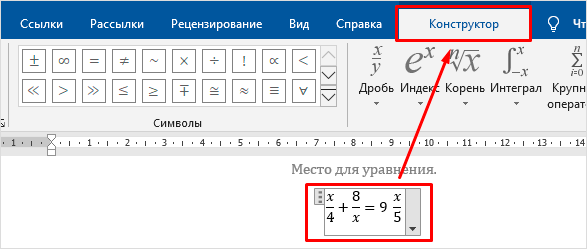
Чтобы добавить формулу, установите курсор в нужное место документа и отправляйтесь во вкладку “Вставка” или “Вставить” основного меню.
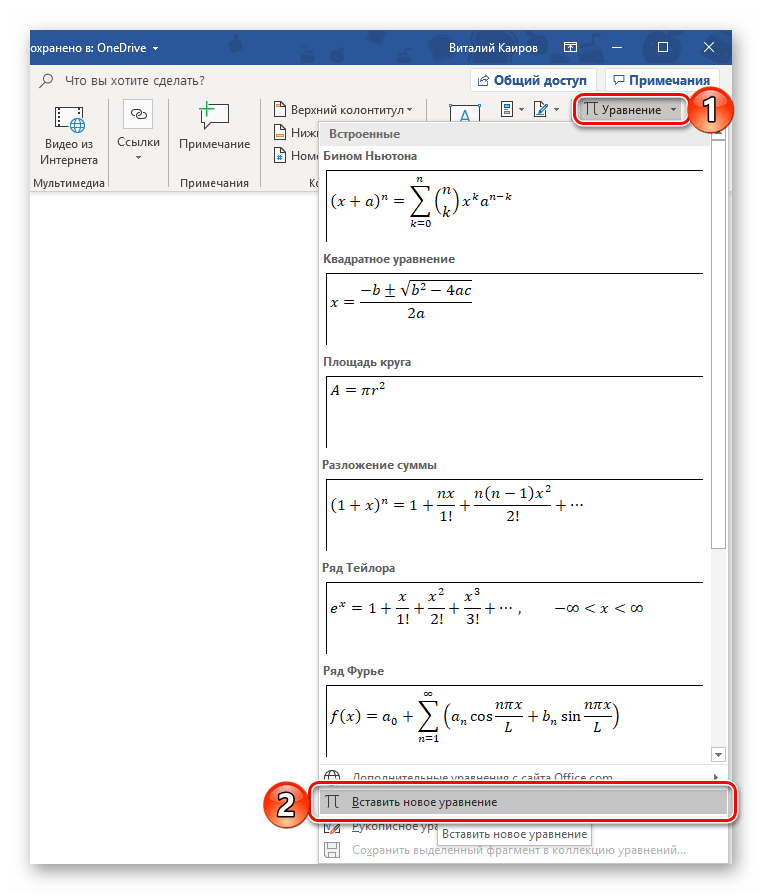
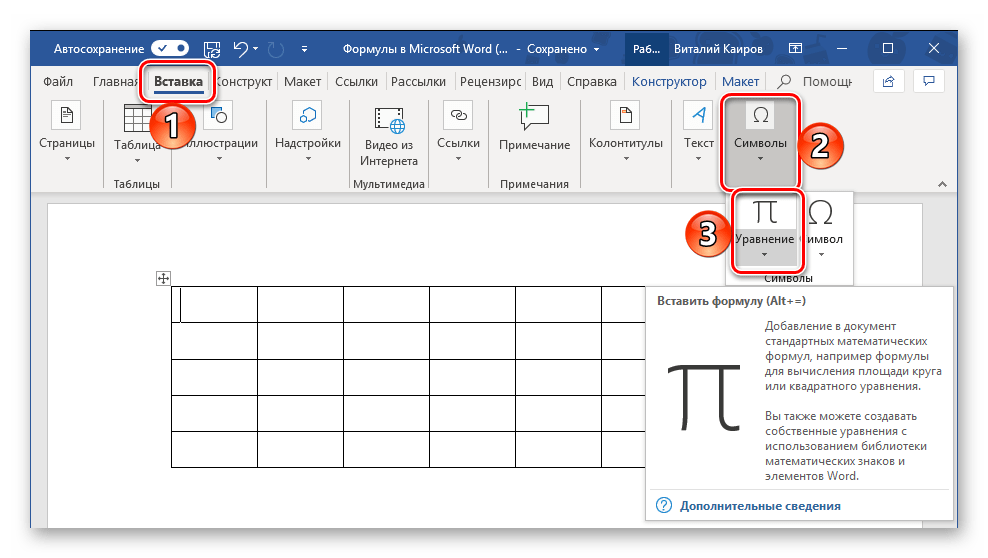
Теперь справа в панели инструментов находим опцию “Символы”, нажимаем на нее и выбираем раздел “Уравнение”.
Примечание: в Word 2007 и 2010 эта функция называется “Формула”, а в выпусках 2013, 2016 и 2019 годов – “Уравнение”.
После этого появится специальная рамка для ввода математического выражения, и мы окажемся в новой вкладке “Конструктор”, где отображаются все доступные шаблоны для работы с формулами в Word.
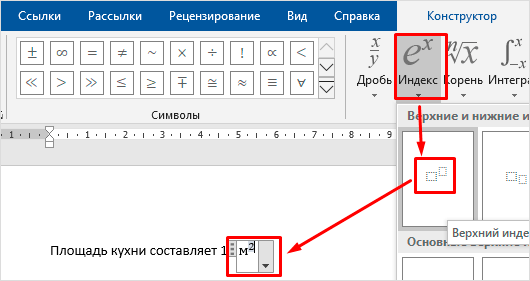
Давайте рассмотрим простой и довольно распространенный пример. Мне нужно написать площадь помещения в квадратных метрах. Чтобы сократить единицы измерения, нам понадобится верхний индекс.
Я пишу текст, затем иду во вкладку “Вставка”, “Символы”, “Уравнение”, выбираю опцию “Индекс” и кликаю по соответствующему моей задаче варианту. Затем ввожу букву “м” и верхний индекс “2” в появившееся на экране поле.
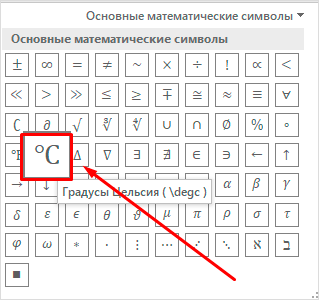
Еще одна популярная задача – это корректное отображение значка градусов, когда мы пишем температуру воздуха или чего-то еще. Снова идем в меню “Вставка”, “Символы”, “Уравнение”. Чтобы написать нужный текст, нам понадобится перечень встроенных математических символов.
Находим нужный нам значок и кликаем по нему.
Основные возможности редактора формул
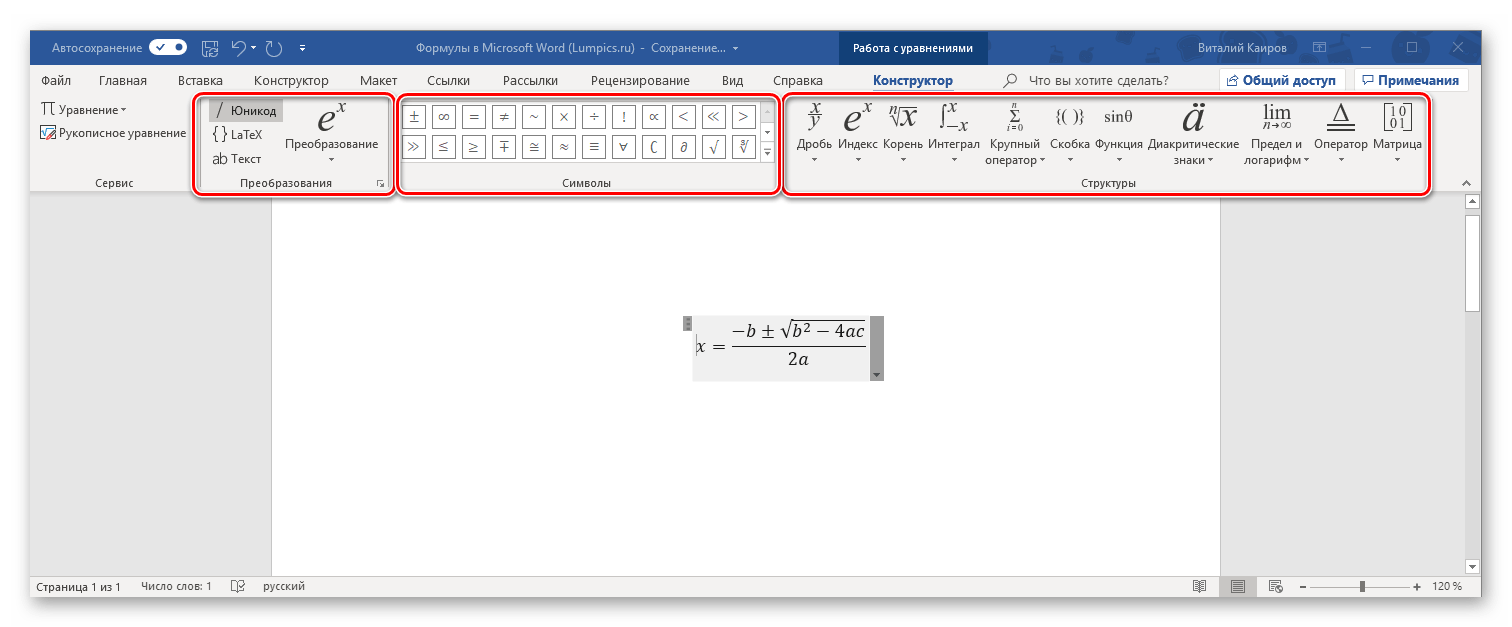
Мы рассмотрели с вами самые простые примеры использования редактора уравнений. Давайте теперь подробнее остановимся на доступных опциях. Добавляем новую формулу и смотрим на меню вкладки “Конструктор”.
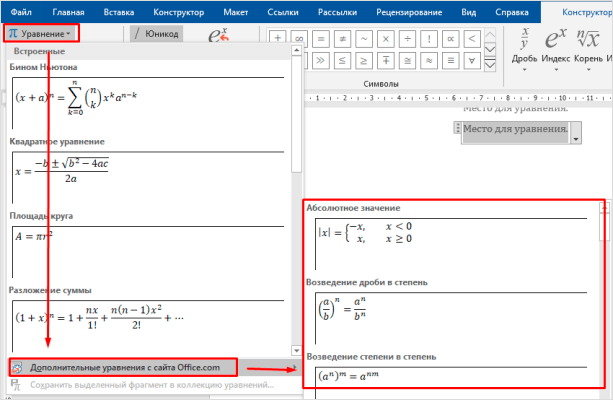
Слева есть вкладка “Уравнение”, в ней собраны стандартные математические выражения и дополнительные материалы с сайта office.com. Просмотрите их, возможно, какие-то шаблоны вам пригодятся, и не надо будет набирать их вручную.
В том же левом углу есть опция, которая позволяет написать выражение вручную, как в тетради, а редактор сделает из нашей “писанины” печатные символы. Классная функция, но пока не до конца доработана, так что будьте внимательны. Если требуется строгое оформление документа, лучше все-таки набрать уравнение с использованием встроенных операторов или подправить его при необходимости.
С доступными математическими символами мы уже знакомились, тут есть весь необходимый набор: от сложения и умножения до знака бесконечности и оператора “не равно”.
Чтобы раскрыть полный перечень и выбрать соответствующую категорию букв и знаков, нажмите сначала на стрелочку вниз, а затем на надпись “Основные математические символы”.
Идем дальше вправо по панели инструментов. Теперь посмотрим, какие типичные выражения встроены в программу:
- простые дроби;
- значения с одинарными и двойными индексами, что позволяет легко сделать не только математическую или физическую, но и химическую формулу;
- кубические, квадратные и любые другие корни;
- обычные, двойные, тройные и контурные интегралы (о последних я, к счастью, мало что знаю, а вы?);
- операторы суммы, произведения и пересечения (последний, насколько я понимаю, применяется для множеств);
- всевозможные скобки, которые позволяют, например, записывать системы уравнений;
- тригонометрические функции;
- диакритические знаки, которые могут быть вам знакомы, если вы изучали логику или дискретный анализ в институте;
- логарифмы и пределы;
- различные операторы, отличные от стандартных “умножить”, “сложить”, “равно”;
- матрицы – моя любимая тема из высшей математики.
Все эти шаблоны собраны в подразделе “Структуры”.
Создание своих шаблонов
Если вы часто набираете одни и те же математические выражения, то их можно внести в библиотеку вашего текстового редактора Word и в нужный момент вставить в документ за несколько секунд.
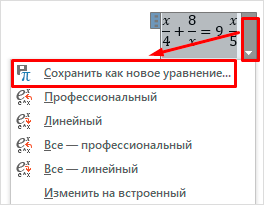
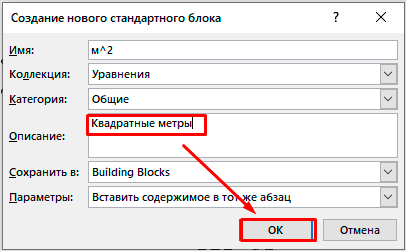
Для этого нажмите на треугольник рядом с готовой формулой и выберите пункт “Сохранить как новое уравнение”.
Дополните описание, если хотите, и подтвердите действие.
Теперь, чтобы ввести это выражение в другом месте текста, нажмите на слово “Уравнение” в левом углу панели инструментов, пролистайте вниз и найдите свой шаблон.
Как редактировать и перемещать готовые формулы
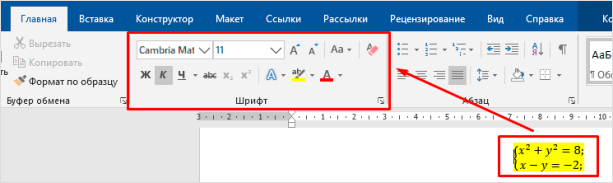
С созданием уравнений мы разобрались, переходим к редактированию. Чтобы изменить формулу, кликните по ней левой кнопкой мыши. Изменить параметры можно просто вручную, а если нужно воспользоваться встроенными функциями, то перейдите во вкладку “Конструктор”.
Чтобы изменить шрифт, выделить цветом формулу или внести другие изменения в ее внешний вид, используйте стандартный набор функций Word. Выделите объект и выберите подходящий инструмент во вкладке меню “Главная” на панели “Шрифт”.
Чтобы переместить готовое математическое выражение, есть 2 пути. Кликните по нему левой кнопкой мыши, затем, удерживая ее на 3 точках в левом углу, перетяните объект по документу. Следите за темной черной полосой, это курсор. Где он находится, там и появится формула, когда мы отпустим кнопку мыши.
Я чаще пользуюсь другим способом. Выделяю формулу и нажимаю “Ctrl + X”, чтобы вырезать ее. Затем перемещаю курсор в то место, куда нужно переместить уравнение, и использую комбинацию клавиш “Ctrl + V”.
Этот способ особенно хорош, если “тащить” выражение нужно далеко.
Как работать с формулами в таблицах
В текстовом редакторе можно делать и некоторые вычисления. Для этого мы создаем таблицу и заполняем ее данными. Затем идем во вкладку “Макет” и вставляем в нужную ячейку формулу.
Теперь выбираем функцию из предложенного стандартного набора. Я, например, хочу посчитать сумму элементов в столбце. Выглядеть формула будет так.
Какие действия доступны в таблицах Word:
- ABS – абсолютное значение числа;
- AND – проверка истинности выражения;
- AVERAGE – вычисление среднего арифметического значения;
- COUNT – подсчет количества элементов в диапазоне;
- DEFINED – показывает, правильно ли составлено выражение в скобках;
- FALSE – функция всегда возвращает 0;
- IF – проверка истинности условия;
- INT – округление до ближайшего целого числа;
- MAX – поиск наибольшего значения из заданных;
- MIN – определение минимального значения;
- MOD – нахождение остатка от деления;
- NOT – еще один оператор для проверки истинности выражения;
- OR – проверка на истинность хотя бы одного из двух условий;
- PRODUCT – произведение элементов;
- ROUND – округление с заданной точностью;
- SUM – сумма;
- SIGN – определяем, является ли число положительным или отрицательным;
- TRUE – проверка истинности выражения.
Заключение
Мы с вами разобрали основы работы с формулами, надеюсь, теперь создание подобных объектов в Word не вызовет у вас трудностей. Если все же попалась необычная задача, которую не получается решить стандартным набором инструментов, расскажите о ней в комментариях, я с удовольствием подумаю над ней и постараюсь помочь.
Сохраняйте статью в закладки и делитесь ей с друзьями в социальных сетях. Если эта тема актуальна для вас, то, думаю, придется не раз вернуться к этой инструкции, пока все основные шаги не останутся в памяти. Тогда вы сможете быстро и без ошибок записывать любые математические выражения в текстовом редакторе.
Подписывайтесь на новые материалы сайта iklife.ru, мы будем и дальше разбирать возможности программ из пакета Microsoft Office. Кроме того, у нас вы сможете найти статьи по другим интересным и актуальным темам.
А на сегодня у меня все. Если у вас все получилось, поздравляю! Если остались вопросы, пишите.
Расчет в Ворде или как использовать Word вместо Excel

Например, не так давно я получил сообщение с просьбой рассказать, как в Экселе создать электронный классный журнал, в который бы выставлялись оценки, а затем автоматически вычислялся средний балл.
Давайте решим эту задачу, но воспользуемся для этого Вордом!
Для журнала логичным образом подходит таблица и я уже прикинул необходимые размеры, поэтому создам таблицу в семь строк и семь столбцов.
Далее объединю некоторые ячейки, сформировав строку заголовка.
Заполним заголовки столбцов. 
Далее можно добавить заливку для ячеек-заголовков.
Введем в таблицу данные — ФИО учеников и их оценки.
Ну а теперь первая малоизвестная фишка Ворд.
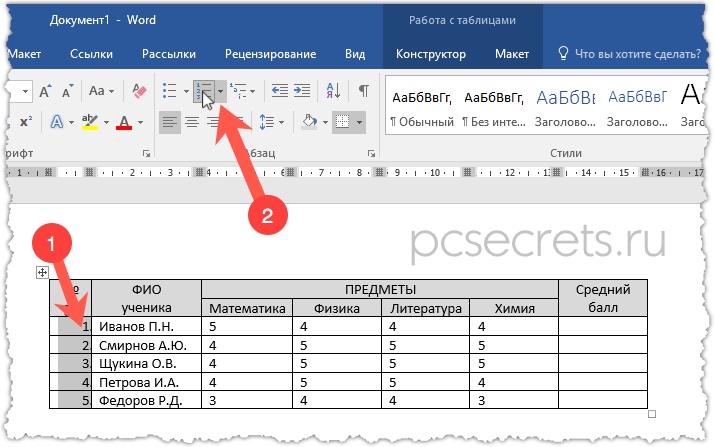
Уверен, вы обратили внимание, что я не заполнял первый столбец с порядковым номером ученика. Мы можем это сделать автоматически! Выделим ячейки первого столбца и затем щелкнем по нумерованному списку.
Вот и все! Теперь, если в таблице будут добавляться новые строки, то нумерация никак не нарушится и вам не нужно будет ее редактировать вручную.
Ну и давайте рассмотрим основную задачу — расчет среднего балла.
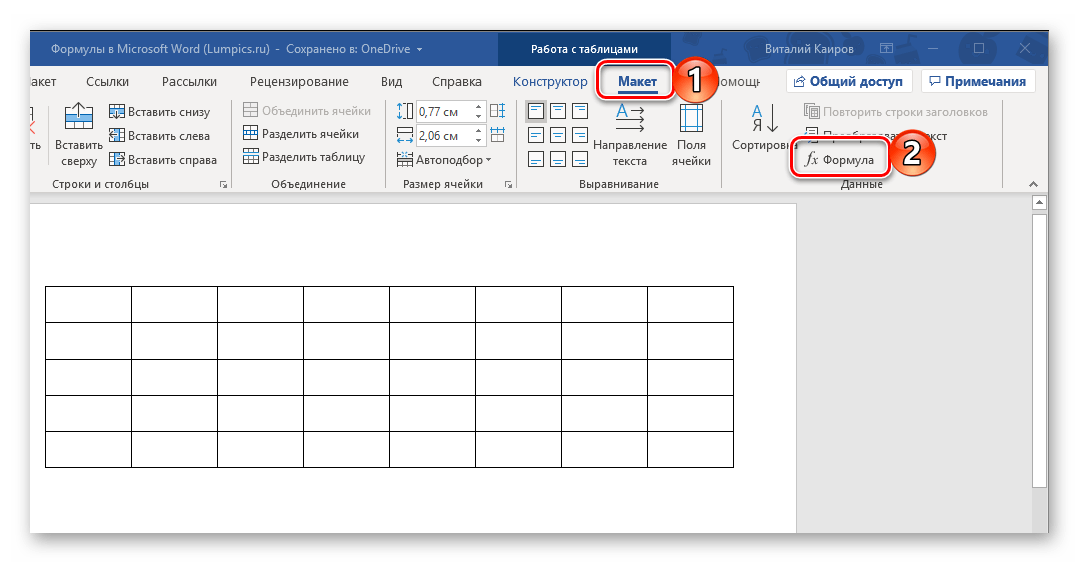
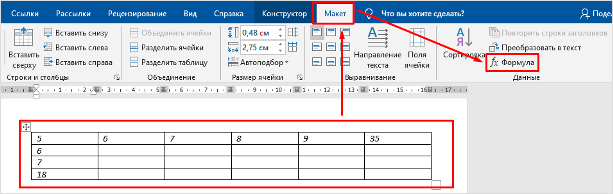
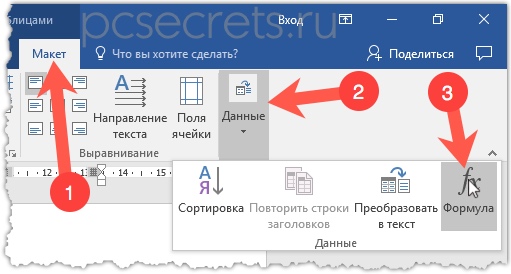
Установим текстовый курсор в первую ячейку соответствующего столбца, перейдем на вкладку Макет и найдем команду Формула.
Ворд, в отличие от Экселя, не очень богат на функции и они представлены в выпадающем списке.
Нам нужно вычислить среднее арифметическое значений в строках, поэтому нам подойдет функция AVERAGE (). В скобках мы должны указать ячейки, над значениями которых операция производится. И тут, в отличии от Экселя, мы можем воспользоваться в качестве аргумента направлением, а не указанием координат ячеек.
Нам нужно получить среднее арифметическое всех ячеек, находящихся левее нашей ячейки. Поэтому в качестве аргумента указываем английское слово LEFT (слева). В расчете будут принимать участие все ячейки с числовыми значениями, которые идут подряд и находятся левее ячейки с результатом.
Аналогично можно проделать и для остальных ячеек, но так как у нас формула будет одинакова для всех других ячеек столбца «Средний балл», то просто скопируем значение из первой ячейки и вставим его в остальные. Теперь выделим все ячейки с формулами и обновим их значения, нажав функциональную клавишу F9 на клавиатуре.
Вот так без лишних заморочек с Экселем можно сделать расчет в привычном Ворде.
Ну а если у вас есть желание узнать о Ворд больше и более эффективно применять программу для решения своих задач, то обратите внимание на мои видеокурсы «Microsoft Word Шаг за Шагом».
В первой части курса изложены основные принципы Word и дано объяснение, почему правильно применять программу и ее инструменты именно так, а не как-то иначе. Весь учебный процесс проходит на рассмотрении конкретных примеров и курс снабжен упражнениями, решение которых также представлено в видео-формате.
Данного уровня знаний будет вполне достаточно, для использования Word в повседневных целях. Однако, если вы захотите расширить свои знания и область применения программы Ворд, то обратите внимание и на второй уровень — ПОЛЬЗОВАТЕЛЬ.
Это на 100% практический курс, в котором рассматриваются конкретные примеры и их реализация средствами Word.