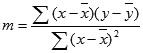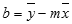Как построить прямую в экселе по двум точкам?
Построить прямую линию по двум точкам в программе эксель задача дольно легко решаема. Рассмотрим подробную инструкцию, как это сделать.
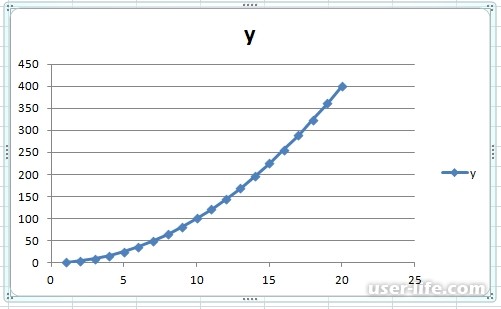
Первый этап. Построим прямую линию функции y=x+6. Чтобы её построить, нужно получить две координаты, для этого в экселе рисуем небольшую таблицу с двумя столбцами и задаем вручную координаты «Х».
Второй этап. Посчитает координаты точек «Y», для этого пропишем в ячейке «В2» формулу: =A2+6, а в ячейке «В3»: =A3+6.
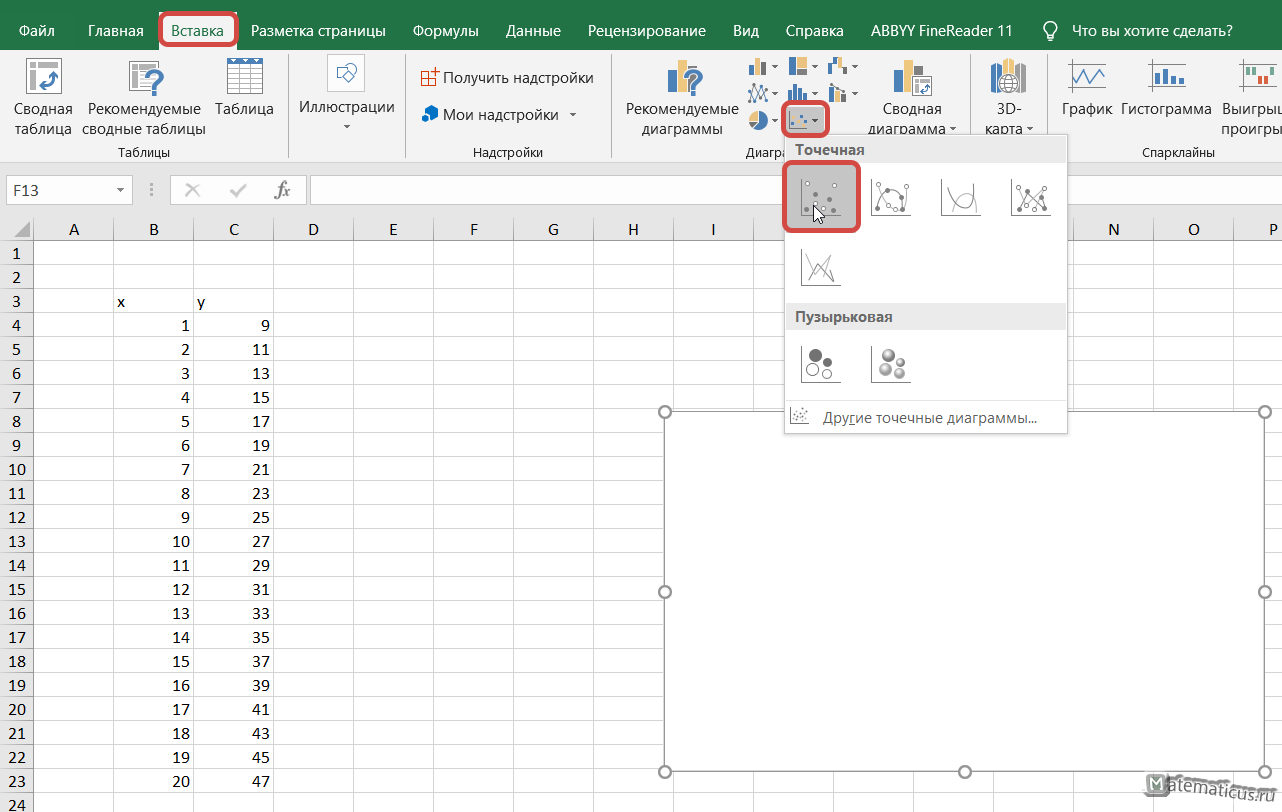
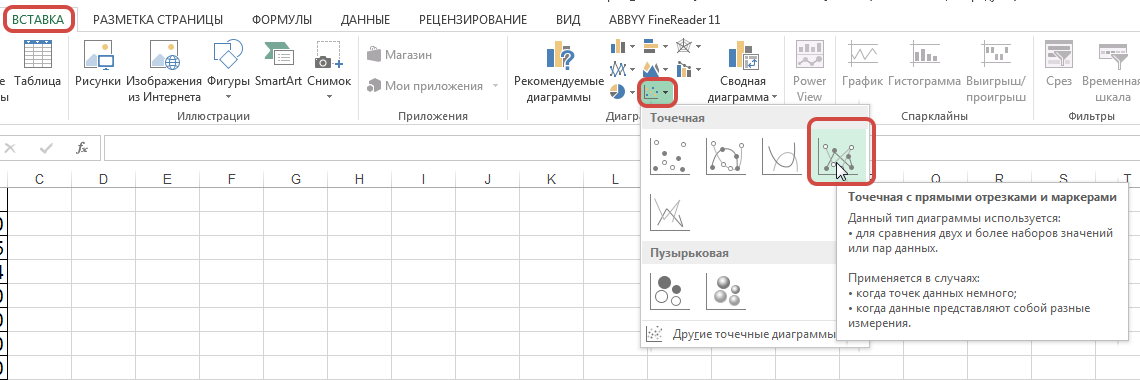
Третий этап. Выделим четыре данных точки, а на верхней панели настроек, провалимся в закладку «Вставка», чтобы в блоке «Диаграммы» отыскать иконку в виде осей и точек с подписью «Точечная».
Четвертый этап. Нажав на данную иконку, программа предложить выбрать тип диаграммы, выберем ту, что предлагает соединять прямыми линиями точки, она будет четвертой по счету.
В итоге мы построили в программе эксель прямую линию по двум точкам, что и требовалось сделать.
Видео
Вывести уравнение прямой по координатам двух точек
По введенным пользователем координатам двух точек вывести уравнение прямой, проходящей через эти точки.
Общее уравнение прямой имеет вид y = kx + b . Для какой-то конкретной прямой в уравнении коэффициенты k и b заменяются на числа, например, y = 4x — 2 . Задача сводится именно к нахождению этих коэффициентов.
Так как координаты точки это значения x и y , то мы имеем два уравнения. Пусть, например, координаты точки А(3;2), а координаты B(-1;-1). Получаем уравнения:
2 = k*3 + b,
-1 = k*(-1) + b.
Решая полученную систему уравнений находим значения k и b :
b = 2 — 3k
-1 = -k + 2 — 3k
4k = 3
k = 3/4 = 0.75
b = 2 — 3 * 0.75 = 2 — 2.25 = -0.25
Таким образом, получается уравнение конкретной прямой, проходящей через указанные точки: y = 0.75x — 0.25.
Алгоритм решения данной задаче на языке программирования будет таков:
- Получить значения координат первой точки и присвоить их переменным, например x1 и y1 .
- Получить значения координат ( x2, y2 ) второй точки.
- Вычислить значение k по формуле k = (y1 — y2) / (x1 — x2) .
- Вычислить значение b по формуле b = y2 — k * x2 .
- Вывести на экран полученное уравнение.
Функция ЛИНЕЙН
В этой статье описаны синтаксис формулы и использование функции LINEST в Microsoft Excel. Ссылки на дополнительные сведения о диаграммах и выполнении регрессионного анализа можно найти в разделе См. также.
Описание
Функция ЛИНЕЙН рассчитывает статистику для ряда с применением метода наименьших квадратов, чтобы вычислить прямую линию, которая наилучшим образом аппроксимирует имеющиеся данные и затем возвращает массив, который описывает полученную прямую. Функцию ЛИНЕЙН также можно объединять с другими функциями для вычисления других видов моделей, являющихся линейными по неизвестным параметрам, включая полиномиальные, логарифмические, экспоненциальные и степенные ряды. Поскольку возвращается массив значений, функция должна задаваться в виде формулы массива. Инструкции приведены в данной статье после примеров.
Уравнение для прямой линии имеет следующий вид:
y = m1x1 + m2x2 +. + b
если существует несколько диапазонов значений x, где зависимые значения y — функции независимых значений x. Значения m — коэффициенты, соответствующие каждому значению x, а b — постоянная. Обратите внимание, что y, x и m могут быть векторами. Функция ЛИНЕЙН возвращает массив . Функция ЛИНЕЙН может также возвращать дополнительную регрессионную статистику.
Синтаксис
ЛИНЕЙН(известные_значения_y; [известные_значения_x]; [конст]; [статистика])
Аргументы функции ЛИНЕЙН описаны ниже.
Синтаксис
Известные_значения_y. Обязательный аргумент. Множество значений y, которые уже известны для соотношения y = mx + b.
Если массив известные_значения_y имеет один столбец, то каждый столбец массива известные_значения_x интерпретируется как отдельная переменная.
Если массив известные_значения_y имеет одну строку, то каждая строка массива известные_значения_x интерпретируется как отдельная переменная.
Известные_значения_x. Необязательный аргумент. Множество значений x, которые уже известны для соотношения y = mx + b.
Массив известные_значения_x может содержать одно или несколько множеств переменных. Если используется только одна переменная, то массивы известные_значения_y и известные_значения_x могут иметь любую форму — при условии, что они имеют одинаковую размерность. Если используется более одной переменной, то известные_значения_y должны быть вектором (т. е. интервалом высотой в одну строку или шириной в один столбец).
Если массив известные_значения_x опущен, то предполагается, что это массив <1;2;3;. >, имеющий такой же размер, что и массив известные_значения_y.
Конст. Необязательный аргумент. Логическое значение, которое указывает, требуется ли, чтобы константа b была равна 0.
Если аргумент конст имеет значение ИСТИНА или опущен, то константа b вычисляется обычным образом.
Если аргумент конст имеет значение ЛОЖЬ, то значение b полагается равным 0 и значения m подбираются таким образом, чтобы выполнялось соотношение y = mx.
Статистика. Необязательный аргумент. Логическое значение, которое указывает, требуется ли вернуть дополнительную регрессионную статистику.
Если статистика имеет true, то LINEST возвращает дополнительную регрессию; в результате возвращается массив .
Если аргумент статистика имеет значение ЛОЖЬ или опущен, функция ЛИНЕЙН возвращает только коэффициенты m и постоянную b.
Дополнительная регрессионная статистика.
Стандартные значения ошибок для коэффициентов m1,m2. mn.
Стандартное значение ошибки для постоянной b (seb = #Н/Д, если аргумент конст имеет значение ЛОЖЬ).
Коэффициент определения. Сравнивает предполагаемые и фактические значения y и диапазоны значений от 0 до 1. Если значение 1, то в выборке будет отличная корреляция— разница между предполагаемым значением y и фактическим значением y не существует. С другой стороны, если коэффициент определения — 0, уравнение регрессии не помогает предсказать значение y. Сведения о том, как вычисляется 2, см. в разделе «Замечания» далее в этой теме.
Стандартная ошибка для оценки y.
F-статистика или F-наблюдаемое значение. F-статистика используется для определения того, является ли случайной наблюдаемая взаимосвязь между зависимой и независимой переменными.
Степени свободы. Степени свободы используются для нахождения F-критических значений в статистической таблице. Для определения уровня надежности модели необходимо сравнить значения в таблице с F-статистикой, возвращаемой функцией ЛИНЕЙН. Дополнительные сведения о вычислении величины df см. ниже в разделе «Замечания». Далее в примере 4 показано использование величин F и df.
Регрессионная сумма квадратов.
Остаточная сумма квадратов. Дополнительные сведения о расчете величин ssreg и ssresid см. в подразделе «Замечания» в конце данного раздела.
На приведенном ниже рисунке показано, в каком порядке возвращается дополнительная регрессионная статистика.
Замечания
Любую прямую можно описать ее наклоном и пересечением с осью y:
Наклон (m):
Чтобы найти наклон линии, обычно записанной как m, возьмите две точки на строке (x1;y1) и (x2;y2); наклон равен (y2 — y1)/(x2 — x1).
Y-перехват (b):
Y-пересечение строки, обычно записанное как b, — это значение y в точке, в которой линия пересекает ось y.
Уравнение прямой имеет вид y = mx + b. Если известны значения m и b, то можно вычислить любую точку на прямой, подставляя значения y или x в уравнение. Можно также воспользоваться функцией ТЕНДЕНЦИЯ.
Если имеется только одна независимая переменная x, можно получить наклон и y-пересечение непосредственно, воспользовавшись следующими формулами:
Наклон:
=ИНДЕКС( LINEST(known_y,known_x’s);1)
Y-перехват:
=ИНДЕКС( LINEST(known_y,known_x),2)
Точность аппроксимации с помощью прямой, вычисленной функцией ЛИНЕЙН, зависит от степени разброса данных. Чем ближе данные к прямой, тем более точной является модель ЛИНЕЙН. Функция ЛИНЕЙН использует для определения наилучшей аппроксимации данных метод наименьших квадратов. Когда имеется только одна независимая переменная x, значения m и b вычисляются по следующим формулам:
где x и y — выборочные средние значения, например x = СРЗНАЧ(известные_значения_x), а y = СРЗНАЧ( известные_значения_y ).
Функции ЛИННЕСТРОЙ и ЛОГЪЕСТ могут вычислять наилучшие прямые или экспоненциальное кривой, которые подходят для ваших данных. Однако необходимо решить, какой из двух результатов лучше всего подходит для ваших данных. Вы можетевычислить known_y( known_x) для прямой линии или РОСТ( known_y, known_x в ) для экспоненциальной кривой. Эти функции без аргумента new_x возвращают массив значений y, спрогнозируемых вдоль этой линии или кривой в фактических точках данных. Затем можно сравнить спрогнозируемые значения с фактическими значениями. Для наглядного сравнения можно отобразить оба этих диаграммы.
Проводя регрессионный анализ, Microsoft Excel вычисляет для каждой точки квадрат разности между прогнозируемым значением y и фактическим значением y. Сумма этих квадратов разностей называется остаточной суммой квадратов (ssresid). Затем Microsoft Excel подсчитывает общую сумму квадратов (sstotal). Если конст = ИСТИНА или значение этого аргумента не указано, общая сумма квадратов будет равна сумме квадратов разностей действительных значений y и средних значений y. При конст = ЛОЖЬ общая сумма квадратов будет равна сумме квадратов действительных значений y (без вычитания среднего значения y из частного значения y). После этого регрессионную сумму квадратов можно вычислить следующим образом: ssreg = sstotal — ssresid. Чем меньше остаточная сумма квадратов по сравнению с общей суммой квадратов, тем больше значение коэффициента определения r 2 — индикатор того, насколько хорошо уравнение, выданное в результате регрессионного анализа, объясняет связь между переменными. Значение r 2 равно ssreg/sstotal.
В некоторых случаях один или несколько столбцов X (предполагается, что значения Y и X — в столбцах) могут не иметь дополнительного прогнозируемого значения при наличии других столбцов X. Другими словами, удаление одного или более столбцов X может привести к одинаковой точности предсказания значений Y. В этом случае эти избыточные столбцы X следует не использовать в модели регрессии. Этот вариант называется «коллинеарность», так как любой избыточный X-столбец может быть выражен как сумма многих не избыточных X-столбцов. Функция ЛИНЕЙН проверяет коллинеарность и удаляет все избыточные X-столбцы из модели регрессии при их идентификации. Удалены столбцы X распознаются в результатах LINEST как имеющие коэффициенты 0 в дополнение к значениям 0 se. Если один или несколько столбцов будут удалены как избыточные, это влияет на df, поскольку df зависит от числа X столбцов, фактически используемых для прогнозирования. Подробные сведения о вычислении df см. в примере 4. Если значение df изменилось из-за удаления избыточных X-столбцов, это также влияет на значения Sey и F. Коллинеарность должна быть относительно редкой на практике. Однако чаще всего возникают ситуации, когда некоторые столбцы X содержат только значения 0 и 1 в качестве индикаторов того, является ли тема в эксперименте участником определенной группы или не является ее участником. Если конст = ИСТИНА или опущен, функция LYST фактически вставляет дополнительный столбец X из всех 1 значений для моделирования перехвата. Если у вас есть столбец с значением 1 для каждой темы, если мальчик, или 0, а также столбец с 1 для каждой темы, если она является женщиной, или 0, последний столбец является избыточным, так как записи в нем могут быть получены из вычитания записи в столбце «самец» из записи в дополнительном столбце всех 1 значений, добавленных функцией LINEST.
Вычисление значения df для случаев, когда столбцы X удаляются из модели вследствие коллинеарности происходит следующим образом: если существует k столбцов известных_значений_x и значение конст = ИСТИНА или не указано, то df = n – k – 1. Если конст = ЛОЖЬ, то df = n — k. В обоих случаях удаление столбцов X вследствие коллинеарности увеличивает значение df на 1.
При вводе константы массива (например, в качестве аргумента известные_значения_x) следует использовать точку с запятой для разделения значений в одной строке и двоеточие для разделения строк. Знаки-разделители могут быть другими в зависимости от региональных параметров.
Следует отметить, что значения y, предсказанные с помощью уравнения регрессии, возможно, не будут правильными, если они располагаются вне интервала значений y, которые использовались для определения уравнения.
Основной алгоритм, используемый в функции ЛИНЕЙН, отличается от основного алгоритма функций НАКЛОН и ОТРЕЗОК. Разница между алгоритмами может привести к различным результатам при неопределенных и коллинеарных данных. Например, если точки данных аргумента известные_значения_y равны 0, а точки данных аргумента известные_значения_x равны 1, то:
Функция ЛИНЕЙН возвращает значение, равное 0. Алгоритм функции ЛИНЕЙН используется для возвращения подходящих значений для коллинеарных данных, и в данном случае может быть найден по меньшей мере один ответ.
Наклон и ОТОКП возвращают #DIV/0! ошибка «#ЗНАЧ!». Алгоритм функций НАКЛОН и ОТОКП предназначен для поиска только одного ответа, и в этом случае может быть несколько ответов.
Помимо вычисления статистики для других типов регрессии с помощью функции ЛГРФПРИБЛ, для вычисления диапазонов некоторых других типов регрессий можно использовать функцию ЛИНЕЙН, вводя функции переменных x и y как ряды переменных х и у для ЛИНЕЙН. Например, следующая формула:
работает при наличии одного столбца значений Y и одного столбца значений Х для вычисления аппроксимации куба (многочлен 3-й степени) следующей формы:
y = m1*x + m2*x^2 + m3*x^3 + b
Формула может быть изменена для расчетов других типов регрессии, но в отдельных случаях требуется корректировка выходных значений и других статистических данных.
Значение F-теста, возвращаемое функцией ЛИНЕЙН, отличается от значения, возвращаемого функцией ФТЕСТ. Функция ЛИНЕЙН возвращает F-статистику, в то время как ФТЕСТ возвращает вероятность.
Примеры
Пример 1. Наклон и Y-пересечение
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
источники:
http://gospodaretsva.com/straight.html
http://support.microsoft.com/ru-ru/office/%D1%84%D1%83%D0%BD%D0%BA%D1%86%D0%B8%D1%8F-%D0%BB%D0%B8%D0%BD%D0%B5%D0%B9%D0%BD-84d7d0d9-6e50-4101-977a-fa7abf772b6d
Содержание
- Как в excel построить график с двумя осями x и y
- Как построить прямую в экселе по двум точкам?
- Видео
- Как построить график по точкам в Excel пошагово (Эксель)
Как в excel построить график с двумя осями x и y
Допустим, нам надо построить график линейной функции, заданной уравнением
y=2x+7
Для этой функции сделаем таблицу с двумя колонками. В первой колонки будут находится произвольные значения X от 1 до 20, в данном случае шаг у нас единица. Если функция сложная, то шаг лучше взять меньше. Чем меньше шаг, тем точность построения графика выше. Во второй колонки – расчёт значений Y в зависимости от значения x.
Формула для определения Y первой ячейки C4 в нашем случае будет иметь вид:
=2*B4+7
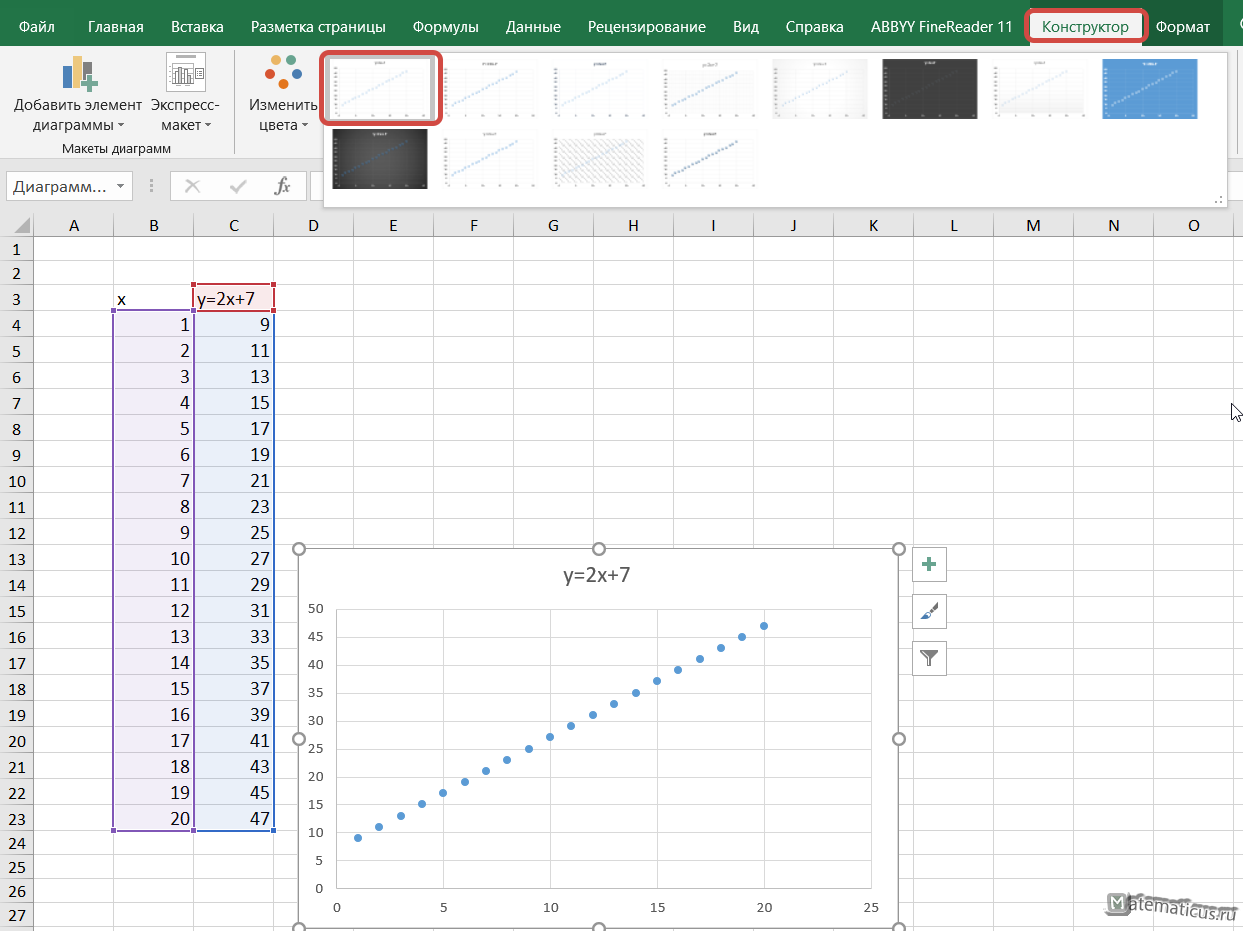
Для остальных ячеек формула аналогичная. Переходим на вкладку Вставка -> Точечная (можно выбрать точечная с гладкими кривыми и маркерами)
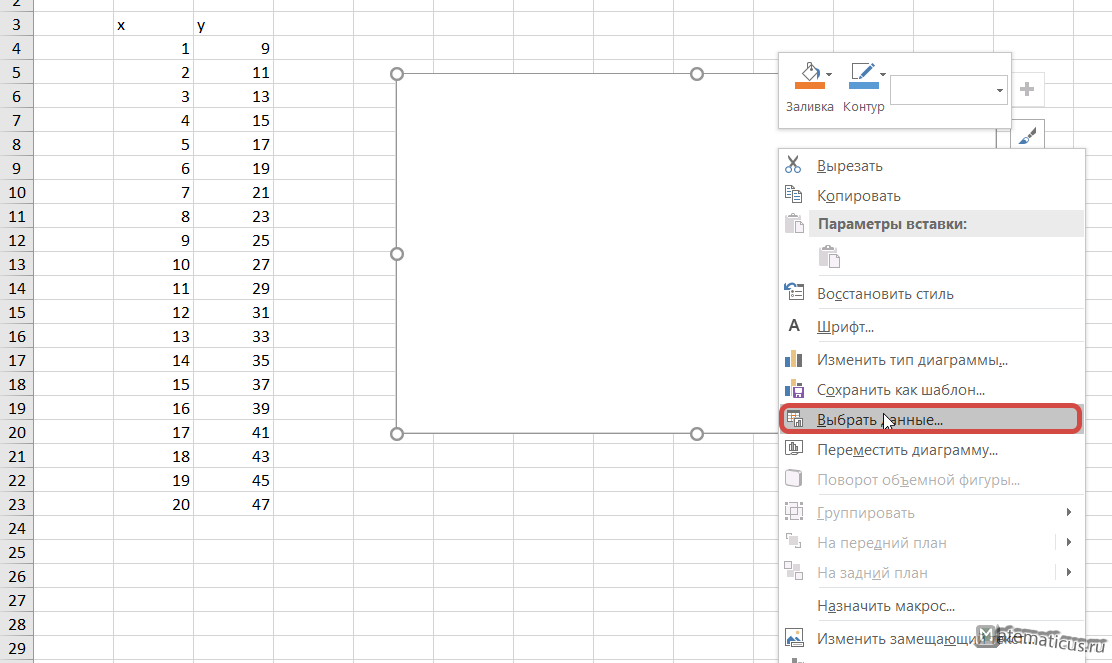
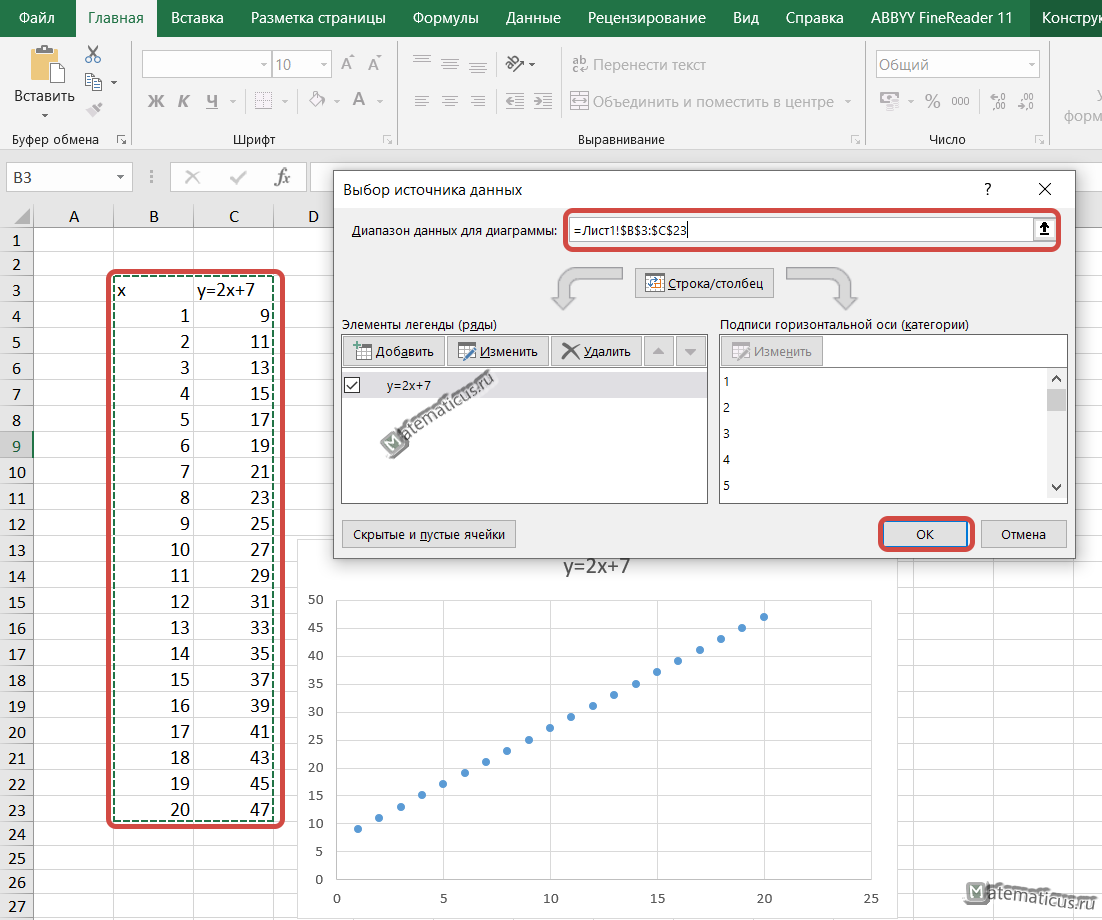
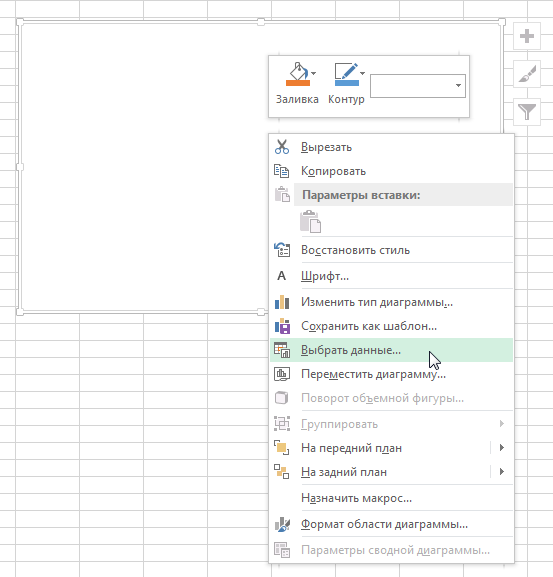
Появится белая прямоугольная область, кликаем на неё правым указателем мыши и из пункта меню выбираем Выбрать данные, появляется окошко Выбора источника данных и выбираем весь диапазон данных в ячейках.
В итоги получается вот такой точечный график.
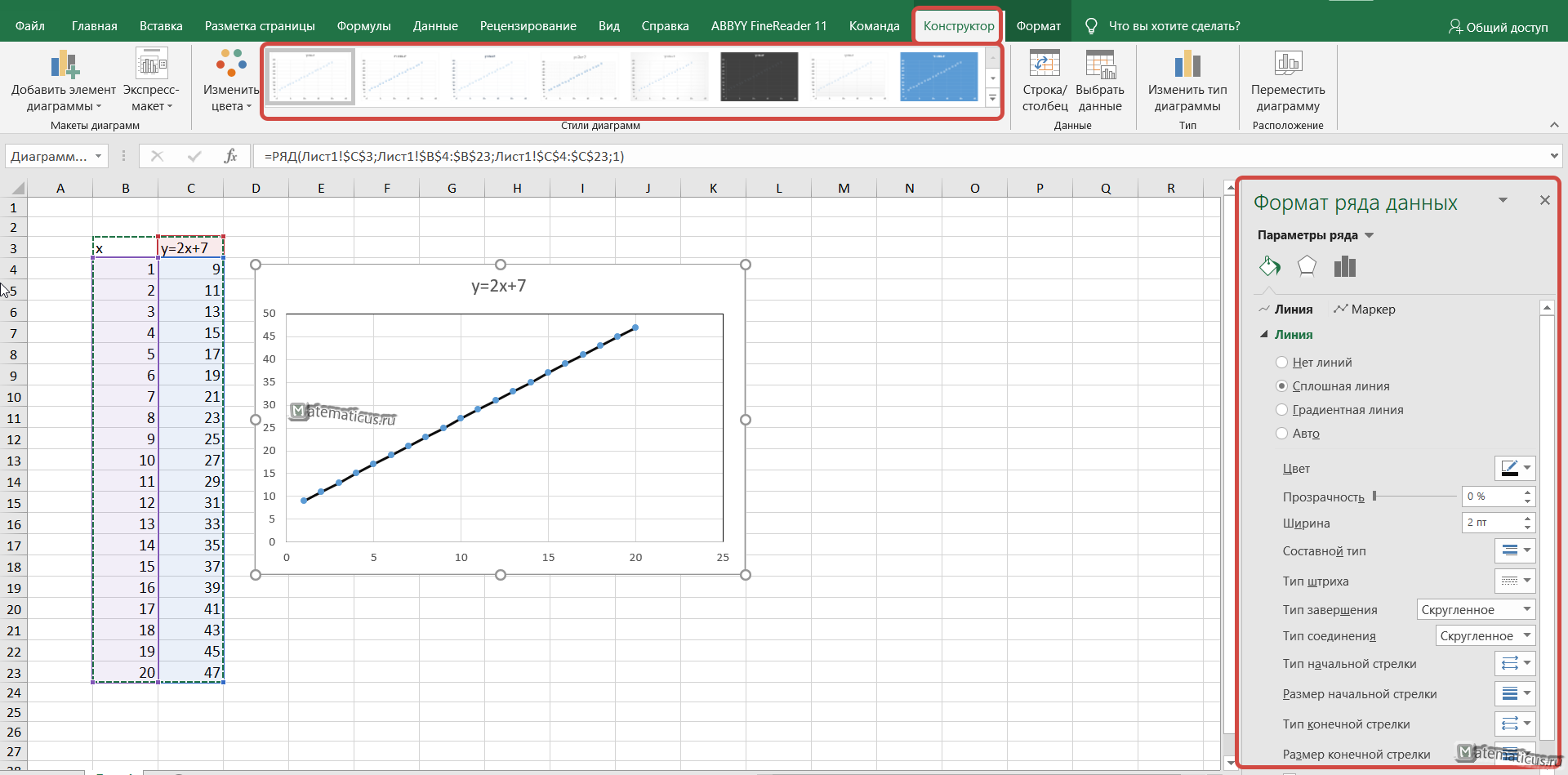
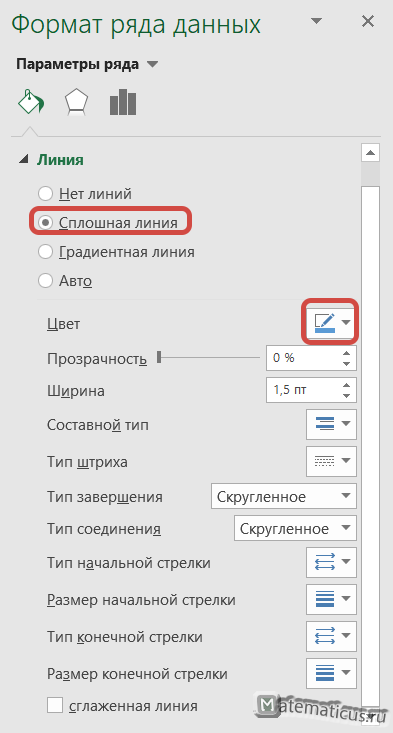
Чтобы добавить линию, необходимо два раза быстро кликнуть на точку графика. Справа появится окошко Формат ряда данных -> Заливка и границы. Здесь можно настроить наш график, укать тип линии (в нашем случае сплошная), цвет, штрихи и т.д.
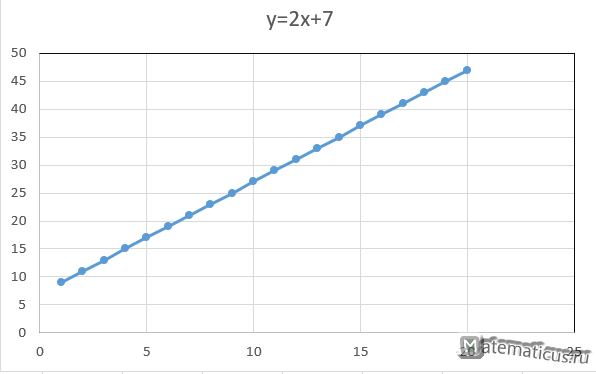
Таблица исходных данных для построения линейной функции в Excel.
| x | y=2x+7 |
| 1 | 9 |
| 2 | 11 |
| 3 | 13 |
| 4 | 15 |
| 5 | 17 |
| 6 | 19 |
| 7 | 21 |
| 8 | 23 |
| 9 | 25 |
| 10 | 27 |
| 11 | 29 |
| 12 | 31 |
| 13 | 33 |
| 14 | 35 |
| 15 | 37 |
| 16 | 39 |
| 17 | 41 |
| 18 | 43 |
| 19 | 45 |
| 20 | 47 |
Пример построение графика для разного шага по оси Х.
Возьмём данные для первого столбца c разным шагом (ось X — первый столбец)
Далее в Excell переходим на вкладку Вставка -> Точечная с прямыми отрезками и маркерами
Далее появляется график, правой клавишей мыши нажимаем на него и в меню выбираем Выбрать данные
Далее выбираем Диапазон данных для диаграммы и жмём Ок
Источник
Как построить прямую в экселе по двум точкам?
Построить прямую линию по двум точкам в программе эксель задача дольно легко решаема. Рассмотрим подробную инструкцию, как это сделать.
Первый этап. Построим прямую линию функции y=x+6. Чтобы её построить, нужно получить две координаты, для этого в экселе рисуем небольшую таблицу с двумя столбцами и задаем вручную координаты «Х».
Второй этап. Посчитает координаты точек «Y», для этого пропишем в ячейке «В2» формулу: =A2+6, а в ячейке «В3»: =A3+6.
Третий этап. Выделим четыре данных точки, а на верхней панели настроек, провалимся в закладку «Вставка», чтобы в блоке «Диаграммы» отыскать иконку в виде осей и точек с подписью «Точечная».
Четвертый этап. Нажав на данную иконку, программа предложить выбрать тип диаграммы, выберем ту, что предлагает соединять прямыми линиями точки, она будет четвертой по счету.
В итоге мы построили в программе эксель прямую линию по двум точкам, что и требовалось сделать.
Видео
Источник
Как построить график по точкам в Excel пошагово (Эксель)
Как построить график в Excel
Многие задаются вопросом «Как построить график в Excel?». Хотя на самом деле это довольно простая задача, но неопытные пользователи порой сбиваются с толку и теряются, в выборе типа диаграмм, и правильном построении таблиц с данными.
В Excel имеется два варианта диаграмм для создания графиков:
• точечная диаграмма;
• график.
Точечные диаграммы зачастую применяют при наличии двух рядов данных, и показатели одного из рядов, используют для определения второго. Наилучшим примером этого, является диаграмма функции y=x 2.
Что же касается графика, то его используют для обычного просмотра изменения данных.
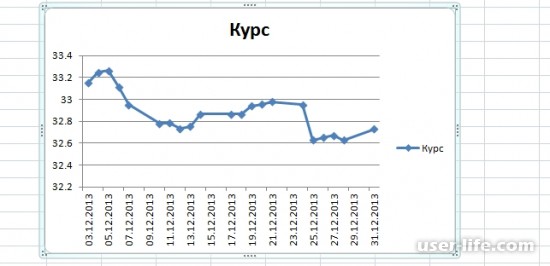
Чтобы построить график, вам достаточно совершить не больше одного-двух касаний. В качестве примера, возьмем показатели доллара в декабре.
Следует выделить таблицу, и на вкладке «Вставка», выберите кнопку «График». После нажатия вы получите несколько вариантов графика.
Среди предложенных вариантов, выберете наиболее подходящий. В качестве примера мы выбрали график с маркерами.
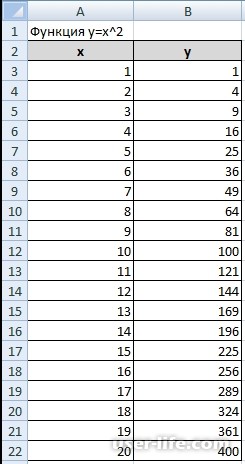
Теперь давайте рассмотрим способ создания графика, через точечную диаграмму. Зачастую ее применяют для создания графиков функций. В качестве примера, возьмем формулу y=x 2.
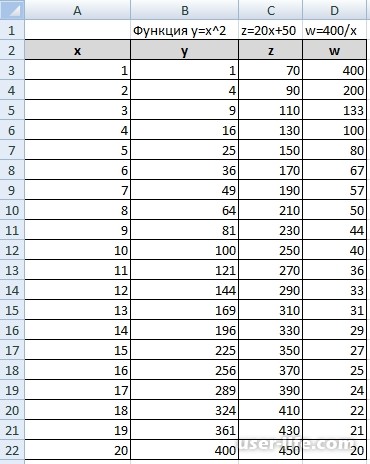
Теперь нам нужно составить таблицу с данными из двух столбиков.
Выделяем таблицу и заходим в панель управление, в «Вставку», выбирая там «точечную диаграмму».
Далее как и в прошлый раз мы получаем варианты диаграммы, мы выбрали диаграмму с маркерами.
Теперь давайте поработаем с вкладкой «Конструктор». Тут следует добавить несколько рядов данных:
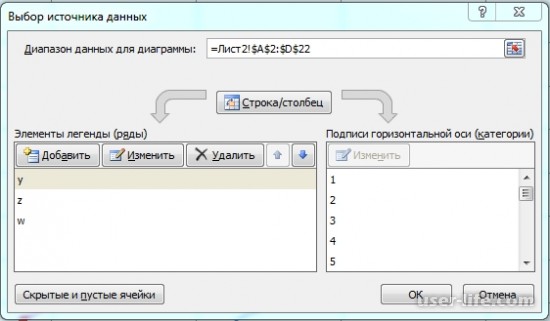
Возвращаемся к таблице и выбираем вкладку «конструктор». Там нажимаем клавишу «Выбрать данные». Вам будет представлено окно, в котором мы можем выбрать как диапазон нашу новую табличку.
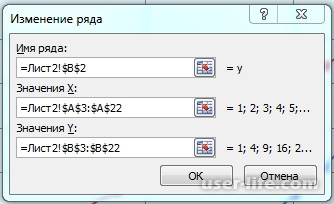
Тут же, мы можем поменять параметры любого из рядов таблицы.
Теперь на диаграмме появятся новые функции.
Таким образом, мы рассмотрели два варианта построения графиков, и на этом примере, отчетливо видно, что сделать это и вправду очень просто.
Источник
Содержание
- 0.1 Вам понадобится
- 0.2 Инструкция
- 1 Инструкция
- 2 Инструкция
- 3 Инструкция
- 4 Инструкция
- 5 Инструкция
- 6 Инструкция
- 7 Инструкция
- 8 Инструкция
- 9 Инструкция
- 9.1 Сглаживание графика в Excel. Как быстро сделать?
- 9.2 Экспоненциальное сглаживание в Excel
- 9.3 Как найти прямую приближенных значений
Приложение Microsoft Office Excel имеет встроенные инструменты, позволяющие на основе табличных данных создавать диаграммы разных типов. График, на котором можно отобразить прямую линию, здесь тоже отнесен к диаграммам. Есть в Excel и возможность заполнить таблицу данными, вычисляемыми по заданной пользователем формуле, поэтому задачу построения прямой с использованием этой программы можно отнести к разряду не очень сложных.
Вам понадобится
- Табличный редактор Microsoft Office Excel 2007 или 2010.
Инструкция
Запустите Excel и заполните две колонки на созданном им по умолчанию листе с пустой таблицей. Первая колонка должна содержать перечень точек вдоль оси абсцисс, которые должны присутствовать на графике с прямой линией. Поместите в верхнюю ячейку (A1) этой колонки минимальное значение вдоль оси X — например, -15.Во вторую строку колонки введите знак равенства, затем кликните указателем мыши на предыдущую ячейку, введите знак плюс и наберите число, соответствующее величине приращения для каждой последующей точки по оси абсцисс. Например, чтобы между точками по оси X было расстояние в 2,5 пункта, содержимое этой ячейки (A2) должно быть таким: =A1+2,5. Чтобы закончить ввод формулы используйте клавишу Enter.Наведите указатель мыши на правый нижний угол заполненной клетки таблицы, а когда указатель трансформируется в черный плюсик, растяните ячейку вниз до последней строки колонки данных. Например, если вы хотите, чтобы прямая была построена по 15 точкам, дотащите выделение до ячейки A15.В первую строку второй колонки (B1) введите алгоритм расчета точек прямой. Скажем, если их надо вычислять по формуле y=3x-4, содержимое этой ячейки должно выглядеть так: =3*A1-4. После нажатия клавиши Enter растяните эту ячейку на всю высоту таблицы способом, который описан в предыдущем шаге.Выделите обе заполненные колонки и перейдите на вкладку «Вставка» в меню Excel. В группе команд «Диаграммы» раскройте выпадающий список «Точечная» и выберите наиболее подходящий вид графика. Сразу после этого табличный редактор рассчитает точки и поместит график в этот же лист документа.С использованием блока из трех вкладок, объединенных заголовком «Работа с диаграммами», придайте нужный вид созданному графику. Эти вкладки приложение добавляет в меню сразу после создания новой диаграммы, а позже вы можете вызвать их, выделив график щелчком мышки. Оцените статью!
Построение графиков функций в Excel
Февраль 9th, 2014
Andrey K
Построение графиков функций — одна из возможностей Excel. В этой статье мы рассмотрим процесс построение графиков некоторых математических функций: линейной, квадратичной и обратной пропорциональности.
Функция, это множество точек (x, y), удовлетворяющее выражению y=f(x). Поэтому, нам необходимо заполнить массив таких точек, а Excel построит нам на их основе график функции.
1) Рассмотрим пример построения графика линейной функции: y=5x-2
Графиком линейной функции является прямая, которую можно построить по двум точкам. Создадим табличку
В нашем случае y=5x-2. В ячейку с первым значением y введем формулу: =5*D4-2. В другую ячейку формулу можно ввести аналогично (изменив D4 на D5) или использовать маркер автозаполнения.
В итоге мы получим табличку:
Теперь можно приступать к созданию графика.
Выбираем: ВСТАВКА — > ТОЧЕЧНАЯ -> ТОЧЕЧНАЯ С ГЛАДКИМИ КРИВЫМИ И МАРКЕРАМИ (рекомендую использовать именно этот тип диаграммы)
Появиться пустая область диаграмм. Нажимаем кнопку ВЫБРАТЬ ДАННЫЕ
Выберем данные: диапазон ячеек оси абсцисс (х) и оси ординат (у). В качестве имени ряда можем ввести саму функцию в кавычках «y=5x-2» или что-то другое. Вот что получилось:
Нажимаем ОК. Перед нами график линейной функции.
2) Рассмотрим процесс построения графика квадратичной функции — параболы y=2×2-2
Параболу по двум точкам уже не построить, в отличии от прямой.
Зададим интервал на оси x, на котором будет строиться наша парабола. Выберу .
Задам шаг. Чем меньше шаг, тем точнее будет построенный график. Выберу .
Заполняю столбец со значениями х, используя маркер автозаполнения до значения х=5.
Столбец значений у рассчитывается по формуле: =2*B4^2-2. Используя маркер автозаполнения, рассчитываем значения у для остальных х.
Выбираем: ВСТАВКА — > ТОЧЕЧНАЯ -> ТОЧЕЧНАЯ С ГЛАДКИМИ КРИВЫМИ И МАРКЕРАМИ и действуем аналогично построению графика линейной функции.
Получим:
Чтобы не было точек на графике, поменяйте тип диаграммы на ТОЧЕЧНАЯ С ГЛАДКИМИ КРИВЫМИ.
Любые другие графики непрерывных функций строятся аналогично.
3) Если функция кусочная, то необходимо каждый «кусочек» графика объединить в одной области диаграмм.
Рассмотрим это на примере функции у=1/х.
Функция определена на интервалах (- беск;0) и (0; +беск)
Создадим график функции на интервалах: .
Подготовим две таблички, где х изменяется с шагом :
Находим значения функции от каждого аргумента х аналогично примерам выше.
На диаграмму вы должны добавить два ряда — для первой и второй таблички соответственно
Далее нажимаем кнопочку ДОБАВИТЬ и заполняем табличку ИЗМЕНЕНИЕ РЯДА значениями из второй таблички

В дополнение привожу видео — где показан порядок действий, описанный выше.
В следующей статье расскажу как создать 3-мерные графики в Excel.
Спасибо за внимание!
Вы можете
оставить комментарий
, или
ссылку
на Ваш сайт.
Душевые термостаты, лучшие модели на
http://tools-ricambi.ru/
изготавливаются из материалов высшего качества
Приложение Microsoft Office Excel имеет встроенные инструменты, дозволяющие на основе табличных данных создавать диаграммы различных типов. График, на котором дозволено отобразить прямую линию, тут тоже отнесен к диаграммам. Есть в Excel и вероятность заполнить таблицу данными, вычисляемыми по заданной пользователем формуле, следственно задачу построения прямой с применением этой программы дозволено отнести к разряду не дюже трудных.
Вам понадобится
- Табличный редактор Microsoft Office Excel 2007 либо 2010.
Инструкция
1. Запустите Excel и заполните две колонки на сделанном им по умолчанию листе с пустой таблицей. Первая колонка должна содержать перечень точек по оси абсцисс, которые обязаны присутствовать на графике с прямой линией. Разместите в верхнюю ячейку (A1) этой колонки минимальное значение по оси X — скажем, -15.
2. Во вторую строку колонки введите знак равенства, после этого кликните указателем мыши на предыдущую ячейку, введите знак плюс и наберите число, соответствующее величине приращения для всякой дальнейшей точки по оси абсцисс. Скажем, дабы между точками по оси X было расстояние в 2,5 пункта, содержимое этой ячейки (A2) должно быть таким: =A1+2,5. Дабы завершить ввод формулы используйте клавишу Enter.
3. Наведите указатель мыши на правый нижний угол заполненной клетки таблицы, а когда указатель трансформируется в черный плюсик, растяните ячейку вниз до последней строки колонки данных. Скажем, если вы хотите, дабы прямая была построена по 15 точкам, дотащите выделение до ячейки A15.
4. В первую строку 2-й колонки (B1) введите алгорифм расчета точек прямой. Скажем, если их нужно вычислять по формуле y=3x-4, содержимое этой ячейки должно выглядеть так: =3*A1-4. Позже нажатия клавиши Enter растяните эту ячейку на всю высоту таблицы методом, тот, что описан в предыдущем шаге.
5. Выделите обе заполненные колонки и перейдите на вкладку «Вставка» в меню Excel. В группе команд «Диаграммы» раскройте выпадающий список «Точечная» и выберите особенно подходящий вид графика. Сразу позже этого табличный редактор рассчитает точки и разместит график в данный же лист документа.
6. С применением блока из 3 вкладок, объединенных заголовком «Работа с диаграммами», придайте надобный вид сделанному графику. Эти вкладки приложение добавляет в меню сразу позже создания новой диаграммы, а позднее вы можете вызвать их, выделив график щелчком мышки.
В приложении Microsoft Excel существует масса вероятностей для всесторонней обработки данных, проведения обзора и выдачи итоговых итогов в комфортном виде. Составление таблиц, диаграмм, создание функций и выдача готовых расчетов проводится дюже стремительно. Подсознательно доступный интерфейс легко понимается даже новичками-пользователями. Построение в Excel таблиц одна из самых примитивных и актуальных функций, где дозволено обширно применять все средства приложения.
Вам понадобится
- Приложение Microsoft Excel
Инструкция
1. Запустите приложение Microsoft Excel. Выделите первую строку нового листа. Увеличьте ширину строки и включите режим толстого шрифта и центрального выравнивания текста. Щелкните на первую ячейку строки. Напишите заголовок создаваемой таблицы.
2. На 2-й строке листа Excel напишите заголовки столбца. Один заголовок должен быть в одной ячейке. Раздвигайте столбцы на максимальную ширину для заполнения всей ячейки. Выделите всю строку и поставьте выравнивание во всех ее ячейках по центру.
3. Заполните все столбцы ниже наименований соответствующей информацией. Установите ячейкам формат в соответствии с внесенными в них данными. Для этого выделите мышкой группу ячеек одного формата. Щелкнув правой кнопкой мышки, откройте для выделенных ячеек контекстное меню. Выберите в нем пункт «Формат ячеек».
4. В открывшемся окне во вкладке «Число» укажите требуемое представление внесенных данных. В иных вкладках окна при желании задайте выравнивание в ячейке, цвет, шрифт и другие параметры вводимого текста.
5. При наличии в вашей таблице итоговых полей с суммирующей информацией, внесите в них формулу для подсчета данных. Для этого выделите ячейку для итоговых значений. В панели управления в поле функции поставьте знак «=». Дальше нужно указать формулу расчета. При суммировании данных из ячеек, запишите наименование ячеек в функции и поставьте знак сложения между ними. Завершив формулу, нажмите клавишу «Enter». В итоговой ячейке в таблице отобразится итог записанной формулы. Причем, итоговое значение будет механически пересчитываться при изменении значений суммируемых ячеек.
6. С поддержкой режима «Формат ячеек» установите, где это нужно, границы строк, столбцов и каждой таблицы.
7. Таблица в Excel готова, сбережете ее с поддержкой пункта меню «Файл» и дальше «Сберечь».
Прямую линию дозволено возвести по двум точкам. Координаты этих точек «спрятаны» в уравнении прямой. Уравнение расскажет о линии все секреты: как повернута, в какой стороне координатной плоскости располагается и т.д.
Инструкция
1. Почаще требуется строить прямую линию в плоскости. У всякой точки будет две координаты: х, y. Обратите внимание на уравнение прямой, оно подчиняется всеобщему виду: y=k*x ±b, где k, b — свободные числа, а y, х – те самые координаты всех точек прямой.Из уравнения всеобщего вида внятно, что для нахождения координаты y нужно знать координату х. Самое увлекательное, что значение координаты х дозволено предпочесть всякое: из каждой бесконечности вестимых чисел. Дальше подставьте х в уравнение и, решив его, обнаружьте у. Пример. Пускай дано уравнение: у=4х-3. Придумайте два всяких значения для координат 2-х точек. К примеру, х1 = 1, х2 = 5.Подставьте эти значения в уравнения для нахождения координат у. у1 = 4*1 – 3 = 1. у2 = 4*5 – 3 = 17. Получились две точки А и В, с координатами А (1; 1) и В (5; 17).
2. Следует возвести обнаруженные точки в координатной оси, объединить их и увидеть ту самую прямую, которая была описана уравнением. Для построения прямой нужно трудиться в декартовой системе координат. Начертите оси Х и У. В точке пересечения поставьте значение «нуль». Нанесите числа на оси.
3. В построенной системе подметьте две обнаруженные в 1-м шаге точки. Тезис выставления указанных точек: точка А имеет координаты х1 = 1, у1 = 1; на оси Х выберите число 1, на оси У – число 1. В этой точке и находится точка А.Точка В задана значениями х2 = 5, у2 = 17. По аналогии обнаружьте точку В на графике. Объедините А и В, дабы получилась прямая.
Видео по теме
Программа для работы с электронными таблицами Excel открывает громадные вероятности для обработки цифровой информации. Но ни одна таблица не сумеет представить процесс столь наглядно, как это сделает график функции , которой он описывается. В Excel есть и такая вероятность в пункте меню Вставка – Диаграмма (для Microsoft Office 2003).
Вам понадобится
- Программное обеспечение Microsoft Excel 2003
Инструкция
1. Откройте чистый лист книги Microsoft Excel 2003. Продумайте, с каким шагом надобно вычислять точки посторенние график а функции в таблице. Чем труднее график функции , тем меньший шаг надобно брать для больше точного построения. В первом столбце таблицы, отведенном для значений довода функции , внесите первые два наименьших значения из волнующего диапазона. Позже этого выделите их блоком при помощи «мыши».
2. Подведите курсор «мыши» к правому нижнему углу выделенного диапазона, он примет вид черного крестика. Прижмите левую кнопку и проведите вниз, остановив курсор в конце волнующего диапазона. Так получится столбец доводов функции . К примеру, если надобно получить график функции в диапазоне (-10;10) с шагом 0,5, первые два значения составят -10 и -9,5, а остановить курсор необходимо позже того, как в столбце появится число 10.
3. Для того дабы возвести столбец значений, в ячейке соседней с наименьшим значением довода установите курсор и нажмите «=». Позже этого, наберите формулу функции , взамен довода (значения «х»), непрерывно щелкая «мышью» по соседней ячейке. Позже того, как формула набрана, нажмите клавишу Enter. В ячейке появится значение функции для довода из первого столбца. Установите курсор на это значение функции . Подведя курсор «мыши» к нижнему правому углу ячейки и увидев черный крестик, протяните его до конца диапазона, прижав левую кнопку. В столбце появятся значения функции , соответствующие доводам в первом столбце.
4. Выберите в меню пункты «Вставка» – «Диаграмма». В открывшемся окне выберите «Точечная». В правой части окна выберите вид диаграммы «Точечная диаграмма со значениями, объединенными сглаживающими линиями без маркеров». Нажмите кнопку «Дальше». В открывшемся окне установите точку на пункте «Ряды в: столбцах». Щелкните по флажку, тот, что находится справа строки «Диапазон» и прижав левую кнопку «мыши» выделите каждый диапазон доводов и значений. Щелкните по вкладке того же окна «Ряд» и в строке «значения Х» «мышью» укажите диапазон доводов. Двукратно щелкните кнопу «Дальше», после этого «Готово». Полученный график будет меняться в зависимости от изменений в формуле. В иных версиях алгорифм равен и отличается только деталями.
Видео по теме
Особенно распространенная задача в геометрии – построение прямой линии. И это недаром, именно с прямой начинается построение больше трудных фигур. Координаты, которые требуются для построения, находятся в уравнении прямой.
Вам понадобится
- — карандаш либо ручка;
- — лист бумаги;
- — линейка.
Инструкция
1. Для того дабы начертить прямую , нужны две точки. Именно с них начинается построение линии. У всякой точки на плоскости есть две координаты: х и у. Они будут являться параметрами уравнения прямой: у = k*х ±b, где k и b – это свободные числа, х и у – координаты точек прямой.
2. Для того дабы обнаружить координату у, вам нужно задать некоторое значение для координаты х и подставить ее в уравнение. При этом значение координаты х может быть любым из каждой бесконечности чисел, как правильным, так и негативным. Вследствие уравнению прямой, дозволено не только возвести надобную вам прямую линию , но и узнать, под каким углом она расположена, в какой части координатной плоскости находится, является она убывающей либо вырастающей.
3. Разглядите такой пример. Пускай дано уравнение: у = 3х-2. Возьмите два всяких значения для координаты х, возможен х1 = 1, х2 = 3. Подставьте эти значения в уравнение прямой: у1 = 3*1-2 = 1, у2 = 3*3-2 = 7. В вас получатся две точки с разными координатами: А (1;1), В (3;7).
4. После этого отложите полученный точки на координатной оси, объедините их и вы увидите прямую , которую нужно было возвести по заданному уравнению. Заранее вам следует начертить в декартовой системе координат оси Х (ось абсцисс), расположенную горизонтально, и У (ось ординат), расположенную вертикально. На пересечении осей подметьте «нуль». После этого отложите числа по горизонтали и вертикали.
5. Позже этого переходите к построению. Тезис построения достаточно примитивен. Вначале подметьте первую точку А. Для этого отложите на оси Х число 1 и на оси У это же число, от того что точка А имеет координаты (1;1). Аналогичным образом постройте точку В, отложив по оси Х три единицы, а по оси У – семь. Вам останется только в поддержкой линейки объединить полученные точки и получить требуемую прямую .
Программа Microsoft Office Excel имеет уйма использований в разных областях деятельности, в том числе, такая дисциплина, как эконометрика, также задействует в работе данную программную утилиту. Фактически все действия лабораторных и фактических работы выполняются в Excel.
Инструкция
1. Для того дабы возвести регрессию , воспользуйтесь программным обеспечением Microsoft Office Excel либо его аналогами, скажем, схожей утилитой в Open Office. При этом для вычисления показателя используйте его функцию ЛИНЕЙН():(Значения_y; Значения_x; Конст; статистика).
2. Вычислите уйма точек на линии регрессии при помощи функции с наименованием «СКЛОННОСТЬ» (Значения_y; Значения_x; Новые_значения_x; Конст). Вычислите при помощи заданных чисел неведомое значение показателей m и b. Действия тут могут варьироваться в зависимости от данного вам данные задачи, следственно уточните порядок вычисления, просмотрев добавочный материал по данной теме.
3. В случае если у вас появились загвоздки с построением уравнения регрессии, используйте особую литературу по эконометрике, а также пользуйтесь дополнительны материалом тематических сайтов, скажем, лабораторные работы по данной дисциплине — Обратите внимание, что также уравнения регрессии могут быть различными, следственно обращайте внимание на дополнительную информацию в теме.
4. В случае появления у вас задач с применением программы Microsoft Office Excel скачайте особые видеоуроки по теме, которая вызывает у вас затруднения, либо запишитесь на особые обучающие курсы, которые доступны фактически для всех городов.
5. При этом удостоверитесь также, что навыки эти сгодятся вам и в будущем, от того что эконометрика нередко входит в состав программ на гуманитарных факультетах для растяжения всеобщих познаний и вряд ли сгодится в будущем, скажем, адвокатам.
Полезный совет
Постигайте вероятности Excel для вычислений.
Точка и запятая могут исполнять функции разделителя разрядов в числах, записанных в формате десятичной дроби. В большинстве англоязычных стран в качестве такого разделителя применяется точка, а в России — запятая. С этим зачастую бывает связана надобность замены точек на запятые в табличном редакторе Microsoft Office Excel.
Вам понадобится
- Табличный редактор Microsoft Office Excel.
Инструкция
1. Если в настройках вашего табличного редактора точка задана в качестве десятичного разделителя, то изменить это дозволено в одном из разделов панели установок Excel. Дабы до нее добраться, раскройте меню приложения. Это дозволено сделать, нажав клавишу Alt, а позже нее — кнопку «Ф». В меню Excel 2010 пункт «Параметры» размещен в предпоследнюю строку списка команд, а в Excel 2007 кнопка «Параметры Excel» находится в правом нижнем углу меню.
2. Выберите строку «Добавочно» в левой колонке панели настроек и в разделе «Параметры правки» обнаружьте строку «Применять системные разделители». Если в чекбоксе у этой надписи отметка стоит, то необходимое вам поле «Разграничитель целой и дробной части» редактировать немыслимо. Уберите ее, поставьте запятую в текстовое поле и нажмите кнопку OK для фиксации метаморфозы в настройках редактора.
3. Если требуется заменить точку запятой в какой-то определенной ячейке электронной таблицы, сделать это дозволено несколькими методами. Вначале выделите надобную ячейку, после этого включите режим ее редактирования — нажмите клавишу F2 либо двукратно кликните эту клетку. Переместите курсор ввода к точке и замените ее запятой. Это же дозволено сделать не в ячейке, а в строке формул — там для включения режима редактирования довольно одного щелчка.
4. Для тотального замещения запятыми всех точек во всех ячейках электронной таблицы используйте диалог поиска и замены. Для его вызова предуготовлены «жгучие клавиши» Ctrl + H и пункт «Заменить» в выпадающем списке кнопки «Обнаружить и выделить» — она размещена в группу команд «редактирование» на вкладке «Основная».
5. В поле «Обнаружить» диалога поиска и замены поставьте точку, а запятую — в поле «Заменить на». Если использования этой операции только на нынешнем листе документа будет довольно, нажмите кнопку «Заменить все» и Excel приступит к выполнению команды. Для замены на всех листах открытого документа нажмите кнопку «Параметры», установите значение «в книге» в выпадающем списке у надписи «Искать» и лишь позже этого кликните по кнопке «Заменить все».
В программе Microsoft Office Excel дозволено создавать диаграммы разных типов. Гистограмма – это диаграмма, в которой данные представлены в виде вертикальных столбиков разной высоты, значения для которых берутся из заданных ячеек.
Инструкция
1. Запустите приложение Excel и введите данные, на основании которых будет сделана столбиковая диаграмма. Выделите надобный диапазон ячеек, включая наименования строк и столбцов, которые позднее будут использованы в легенде диаграммы.
2. Перейдите на вкладку «Вставка». На стандартной панели инструментов в разделе «Диаграммы» нажмите на кнопку-миниатюру «Гистограмма». В выпадающем меню выберите из предложенных вариантов тот пример, тот, что класснее каждого подойдет для ваших целей. Гистограмма может быть конической, пирамидальной, цилиндрической либо выглядеть, как обыкновенный прямоугольный столбик.
3. Выделите сделанную гистограмму , кликнув по ней левой кнопкой мыши. Станет доступно контекстное меню «Работа с диаграммами» с тремя вкладками: «Конструктор», «Макет» и «Формат». Дабы настроить вид диаграммы по своему усмотрению – изменить тип, расположить данные в ином порядке, предпочесть подходящий жанр оформления – воспользуйтесь вкладкой «Конструктор».
4. На вкладке «Макет» отредактируйте содержимое гистограммы: присвойте наименование диаграмме и осям координат, задайте метод отображения сетки и так дальше. Часть операций дозволено исполнить в окне самой диаграммы. Кликните, к примеру, по полю «Наименование диаграммы» левой кнопкой мыши, указанная область будет выделена. Удалите имеющийся текст и введите свой личный. Дабы выйти из режима редактирования выбранного поля, кликните левой кнопкой мыши в любом месте вне границ выделения.
5. С поддержкой вкладки «Формат» настройте размеры гистограммы, подберите цвет, силуэт и результаты для фигур, применяя соответствующие разделы на панели инструментов. Часть операций с диаграммой также может быть исполнена с поддержкой мыши. Так, дабы изменить размер области гистограммы, вы можете либо воспользоваться разделом «Размер», либо подвести курсор к углу диаграммы и, удерживая нажатой левую кнопку мыши, потянуть силуэт в надобную сторону.
6. Также для настройки гистограммы дозволено воспользоваться контекстным меню, вызываемым через щелчок правой кнопкой мыши по области гистограммы. Если выделена диаграмма целиком, будут доступны всеобщие настройки. Дабы отредактировать определенную группу данных, вначале выделите ее, тогда в выпадающем меню появятся опции для выделенного фрагмента.
Программа MS Excel, даже не будучи полновесным статистическим пакетом, владеет достаточно огромным спектром вероятностей по прогнозированию событий на основе теснее имеющихся данных. Одним из особенно примитивных, на 1-й взор, методов такого предсказания является построение линии тренда.
Инструкция
1. Проще каждого возвести график функции тренда непринужденно сразу позже внесения имеющихся данных в массив. Для этого на листе с таблицей данных выделите не менее 2-х ячеек диапазона, для которого будет построен график, и сразу позже этого вставьте диаграмму. Вы можете воспользоваться такими видами диаграмм, как график, точечная, гистограмма, пузырьковая, биржевая. Остальные виды диаграмм не поддерживают функцию построения тренда.
2. В меню «Диаграмма» выберите пункт «Добавить линию тренда». В открывшемся окне на вкладке «Тип» выберите нужный тип линии тренда, что в математическом эквиваленте также обозначает и метод аппроксимации данных. При применении описываемого способа вам придется делать это «на глаз», т.к. никаких математических вычислений для построения графика вы не проводили.
3. Следственно примитивно прикиньте, какому типу функции больше каждого соответствует график имеющихся данных: линейной, логарифмической, экспоненциальной, степенной либо другой. Если же вы сомневаетесь в выборе типа аппроксимации, можете возвести несколько линий, а для большей точности прогноза на вкладке «Параметры» этого же окна подметить флажком пункт «разместить на диаграмму величину достоверности аппроксимации (R^2)».
4. Сопоставляя значения R^2 для различных линий, вы сумеете предпочесть тот тип графика, тот, что характеризует ваши данные особенно верно, а, следственно, строит особенно подлинный прогноз. Чем ближе значение R^2 к единице, тем вернее вы предпочли тип линии. Тут же, на вкладке «Параметры», вам нужно указать период, на тот, что делается прогноз.
5. Такой метод построения тренда является крайне примерным, следственно отличнее все-таки произвести правда бы самую простую статистическую обработку имеющихся данных. Это дозволит возвести прогноз больше верно.
6. Если вы полагаете, что имеющиеся данные описываются линейным уравнением, примитивно выделите их курсором и произведите автозаполнение на нужное число периодов, либо число ячеек. В данном случае нет необходимости находить значение R^2, т.к. вы предварительно подогнали прогноз к уравнению прямой.
7. Если же вы считаете, что вестимые значения переменной класснее каждого могут быть описаны с поддержкой экспоненциального уравнения, также выделите начальный диапазон и произведите автозаполнение нужного числа ячеек, удерживая правую клавишу мыши. При помощи автозаполнения вы не сумеете возвести других типов линий, помимо 2-х указанных.
8. Следственно для наибольшей точности построения прогноза вам придется воспользоваться одной из нескольких статистических функций: «ПРЕДСКАЗ», «СКЛОННОСТЬ», «РОСТ», «ЛИНЕЙН» либо «ЛГРФПРИБЛ». В этом случае вам придется высчитывать значение для всякого дальнейшего периода прогноза вручную. Если вам нужно произвести больше трудный регрессионный обзор данных, вам потребуется надстройка «Пакет обзора», которая не входит в стандартную установку MS Office.
Видео по теме
Чуть ранее мы уже писали, как красиво оформить нулевые/пустые значения на графике, чтобы диаграмма не получалась «зубчатой». Помимо этого, для лучшей визуализации информации иногда нужно сделать сглаживание графика в Excel. Как это сделать? Читайте ниже
Сразу хотел бы написать где можно почитать, как создавать графики — тут и тут. Далее разберем как сделать линию графика чуть более красивее.
Сглаживание графика в Excel. Как быстро сделать?
Часто соединения узлов графика выглядят некрасиво, если линии на графике расположены под острыми углами. Как сделать плавную линию? Правой кнопкой мыши нажимаем на сам график — выплывает окно —
Формат ряда данных (см. первую картинку) выбираем — пункт Тип линии -ставим галочку — Сглаженная линия
Теперь линия сгладилась.
Экспоненциальное сглаживание в Excel
В Excel можно подключить пакет анализа для сглаживания самих данных.
Такое сглаживание это метод применяемый для сглаживания временных рядом — статья википедии
Зайдите в меню — Параметры Excel — Надстройки — Пакет анализа (в правом окне) и в самом низу нажимайте Перейти
В открывшемся окне находим Экспоненциальное сглаживание.
Как найти прямую приближенных значений
Всегда можно построить линию приближенных значений — линию тренда — она покажет куда идет динамика графика, какое направление имеют события графика
Поделитесь нашей статьей в ваших соцсетях:
(Visited 15 074 times, 34 visits today)
1
Как в эксель составить формулу для получения уравнения прямой по точкам?
Даны координаты двух точек надо составить формулу для получения уравнения прямой проходящей через эти точки.
1 ответ:
1
0
Уравнение прямой в общем виде имеет вид:
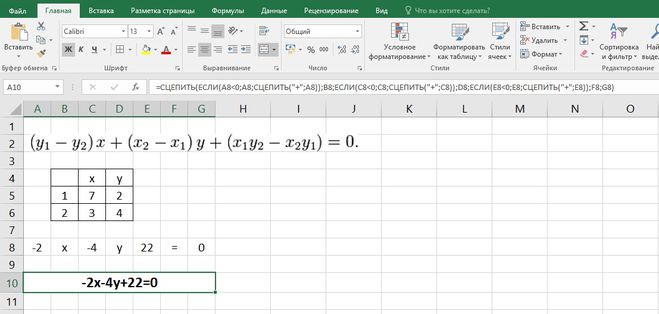
( у1-у2 ) x + ( x2-x1 ) y + ( x1y2 — x2y1 ) = 0
Создадим в Экселе табличку, в которую будем вбивать координаты точек 1 и 2.
Из формулы прямой видно, что нужно вычислить всего 3 числа, которые будут являться коэффициентами требуемого уравнения прямой.
Значит в столбце А будет вычисляться коэффициент первого слагаемого, в столбце B будет стоять «Х», в столбце С будет вычисляться коэффициент второго слагаемого, в столбце D будет стоять «y», в столбце E будет вычисляться третье слагаемое, в столбце F будет стоять «=», в столбце G будет стоять «0».
Теперь только остается сцепить все это в одно уравнение:
=СЦЕПИТЬ(ЕСЛИ(A8<0;A<wbr />8;СЦЕПИТЬ(«+»;A8));B8<wbr />;ЕСЛИ(C8<0;C8;СЦЕПИТЬSHY);D8;ЕСЛИ(E8<<wbr />0;E8;СЦЕПИТЬ(«+»;E8))<wbr />;F8;G8)
Вот, что получиться:
Теперь, меняя координаты точек 1 и 2 вы будете получать в Microsoft Excel новые уравнения прямой.
Читайте также
Для этого нужно в ветку «ложь» функции «ЕСЛИ» вложить следующую функцию «ЕСЛИ», в её ветку «ложь» — ещё одну функцию «ЕСЛИ» и так далее. Конечно не до бесконечности, но что-то около 40 вложений программа «Excel» (у меня версия от 2007 года) принимает. Выглядеть это будет так:
<hr />
=ЕСЛИ(C3=1;D3;ЕСЛИ(C3=2;E3;ЕСЛИ(C3=3;F3;»значение в ячейке С3 не равно ни 1, ни 2, ни 3″)))
<hr />
Во избежание путаницы саму (или самоё?) формулу выделил в отдельную строку.
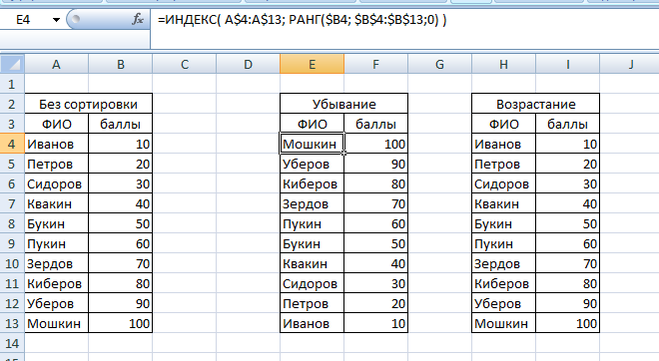
Сортировка формулами позволяет расположить на одном листе и таблицы, отсортированные по возрастанию и таблицы отсортированные, по убыванию рядом с исходной таблицей.
Алгоритм формулы:
- Составляем формулу для столбца по которому проходит сортировка (функции НАИБОЛЬШИЙ/НАИМЕНЬШИ<wbr />Й)
- Для каждой ячейки другого столбца находим соответствующие значение (функция ИНДЕКС)
Для сортировки столбца по которому проходит сортировка можно воспользоваться функцией РАНГ)
если данные находятся в диапазоне B4:B13
то номер ячейки в сортированной по убыванию таблице определим формулой:
=РАНГ( $B4 ; $B$4:$B$13 ; 0)
номер ячейки в сортированной по возрастанию таблице определим формулой:
=РАНГ( $B4 ; $B$4:$B$13 ; 1)
и затем растягиваем эту формулу на весь столбец
Формула сортировки по убыванию для ячейки B4 выглядит так:
=ИНДЕКС( A$4:A$13 ; РАНГ($B4; $B$4:$B$13 ;0) )
Формула сортировки по возрастанию для ячейки B4 выглядит так:
=ИНДЕКС( A$4:A$13 ; РАНГ($B4; $B$4:$B$13 ;1) )
Эта формула растягивается на весь диапазон таблицы.
Пример работы формулы:
- A$4:A$13 отображаемый столбец исходной таблицы
- $B4 текущая ячейка столбца, по которому проходит сортировка
- $B$4:$B$13 столбец, по которому проходит сортировка
Чтобы было понятно, проведём небольшую тренировку. Напишите в какой-либо ячейке формулу, например такую =(A1-C1)/B1. Теперь «встаньте в эту ячейку», нажмите клавишу F2 (включается режим редактирования формул непосредственно в ячейке). В ячейке появится формула и курсор (в виде палочки). Переместите курсор по ячейке так, чтобы он находился либо рядом с тем адресом, которым Вы хотите управлять (в данном случае B1), либо непосредственно внутри адреса, т.е. либо так =(A1-C1)/|B1, либо так (A1-C1)/B1|, либо так (A1-C1)/B|1.
Нажмите клавишу F4. Формула примет вид =(A1-C1)/$B$1.
Нажмите клавишу F4 ещё раз. Формула примет вид =(A1-C1)/B$1.
Нажмите клавишу F4 ещё раз. Формула примет вид =(A1-C1)/$B1.
Нажмите клавишу F4 ещё раз. Формула примет первоначальный вид =(A1-C1)/B1.
Нажмите клавишу F4 ещё раз. Формула примет вид =(A1-C1)/$B$1. И так далее по кругу.
Итак, имеется 4 представления адреса B1, $B$1, B$1, $B1. Значок доллара $ означает, что следующий за ним элемент адреса при копировании формулы не будет изменяться.
Если в формуле записано B1, то при копировании формулы могут изменяться и название столбца и номер строки.
Если записано $B$1, то при копировании формулы не будут изменяться ни название столбца ни номер строки.
Если записано B$1 то при копировании формулы название столбца будет изменяться, а номер строки изменяться не будет.
Если записано $B1 то при копировании формулы номер строки будет изменяться, а название столбца изменяться не будет.
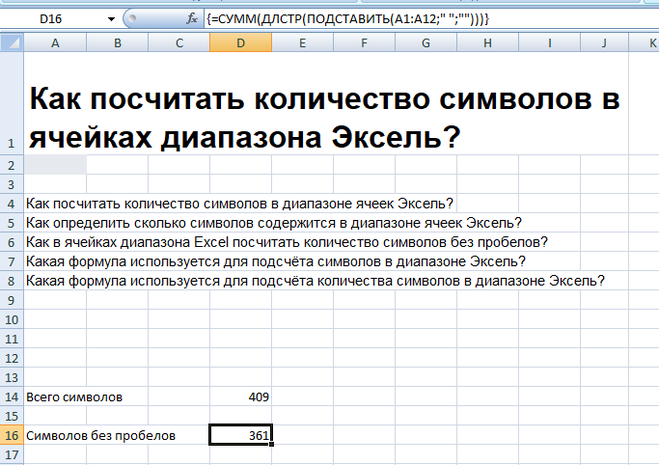
В Excel, чтобы определить количество символов в определённом диапазоне ячеек, придётся использовать формулу массива (вводится через CTRL+SHIFT+ENTER<wbr />).
Для диапазона ячеек A1:A12 формулы массива имеют вид:
найти количество символов: =СУММ(ДЛСТР( A1:A12 ))
найти количество символов без пробелов: =СУММ(ДЛСТР( ПОДСТАВИТЬ( A1:A12; » «; «»)))
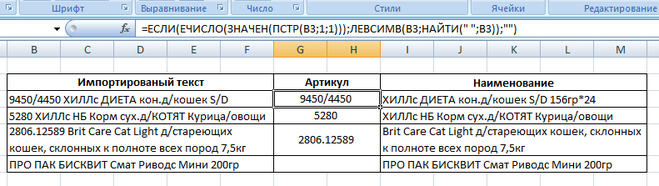
Допустим, что исходный текст записан в ячейке B3
Сначала надо проверить есть ли в начале текста артикул или условное цифровое обозначение, номер или код.
если текст начинается с цифры, то артикул есть
Формула для проверки (если есть артикул то результат ИСТИНА):
=ЕЧИСЛО( ЗНАЧЕН( ПСТР(B3;1;1) ))
Формула для столбца с цифрами:
=ЕСЛИ( ЕЧИСЛО( ЗНАЧЕН( ПСТР(B3;1;1) )) ; ЛЕВСИМВ( B3; НАЙТИ(» «; B3)) ; «»)
Формула для столбца с наименованием товара:
=ЕСЛИ( ЕЧИСЛО( ЗНАЧЕН( ПСТР( B3;1;1) )) ; ПРАВСИМВ( B3 ; ДЛСТР(B3)-НАЙТИ( » «;B3)) ; B3)
После копирования этих формул в свою таблицу надо заменить ячейку B3 на ту, в которой содержится текст, а потом растянуть на весь диапазон значений.
Аналитическая
геометрия в Excel
Декартова
система координат
В школьной
(элементарной) геометрии изучаются свойства прямолинейных фигур и окружности.
Основную роль играют построения, вычисления же, хотя их практическое значение
велико, в теории играют подчиненную роль.
Аналитическая
геометрия предлагает единообразные средства для решения для решения задач не
только элементарной геометрии, но и для изучения важных для практики кривых
линий различной формы. Эта цель достигается применением метода координат. Координаты
определяют положение точки в пространстве, на плоской или кривой поверхности,
на прямой или кривой линии. Значение координаты некоторой точки x зависит от выбора начальной точки 0,
от выбора положительного направления на прямой и от того, какой отрезок принят
за единицу масштаба.
Положение точки
на плоскости определяется двумя координатами. В прямоугольной системе координат
положение точки определяется значениями абсциссы) и ординаты y – рисунок 1. Положение точки в
декартовой прямоугольной системе координат определяется значениями абсциссы x, ординаты y и аппликаты z – рисунок 2.
 |
Линии на плоскости
Уравнение линии
на плоскости может быть записано по-разному.
1. Уравнение
прямой с угловым коэффициентом: где
— угловой коэффициент прямой, a – угол наклона прямой к оси X, a – абсцисса точки пересечения прямой с
осью X b – ордината точки пересечения прямой с осью Y – рисунок 3.
2. Уравнение
прямой, проходящая через данную точку (x1,y1) в данном направлении (с данным
углом наклона к оси X)
 |
3. Уравнение прямой,
проходящей через две данные точки (x1,y1) и (x2,y2): .
4. Уравнение
прямой «в отрезках» (рисунок 4)
5. Общее
уравнение прямой
В MS Excel для
построения прямых, а также кривых и поверхностей, может быть использован
специальный инструмент — Мастер диаграмм.
Пример. Построение прямой в Excel
на примере уравнения .
Пусть уравнение
имеет вид -2x+2y—1=0. Приведем это уравнение к виду
уравнения прямой с угловым коэффициентом: y = x – 0,5.
В Excel строится отрезок прямой. Выберем
область значений хÎ[-1;2]. Для построения отрезка
достаточно задать координаты начальной и конечной точек: A(0;2,5) и В(3;–1). Построение иллюстрируется
рисунком 5.
При построение
графика выбрано Мастер диаграмм – Стандартные –График – График с маркерами,
помечающими точки данных.
Функция ОТРЕЗОК(известные_значения_y;известные_значения_x) определяет точки пересечения прямой
с осями координат: (x0;0) и (y0;0).
Функция НАКЛОН(известные_значения_y;известные_значения_x) определяет угловой коэффициент
прямой.
 |
Рисунок 5 – Построение отрезка прямой -2x+2y—10=0
Полученные
значения наклона и отрезков позволяют, зная координаты двух точек, через
которые проходит прямая, записать уравнение прямой.
Пример. Прямая проходит через точки
(-1;3) и (2;-3) – рисунок 6.
По рассчитанным
значением отрезков, ограниченных началом системы координат и точками
пересечения осей прямой, можно записать уравнения прямой различным способом
(рисунок 6).
Рисунок 6 – Уравнения прямой
Условие
параллельности и перпендикулярности прямых
Если две прямые,
заданные уравнениями
характеризуются равенством угловых
коэффициентов, то они параллельны.
Угол между
двумя прямыми: .
Условие, при
котором три точки лежат на одной прямой
Три точки лежат
на одной прямой если

При вычислении
определителя квадратной матрицы используется функция =МОПРЕД(массив).
Расстояние от точки
до прямой
Расстояние от некоторой
точки с координатами (x1, y1) до прямой, заданной уравнением равно
Рисунок 7 – Комплекс примеров
Примеры, демонстрирующие вычисления
угла между двумя линиями, расстояния от точки до прямой, проверку условий
параллельности и перпендикулярности прямых, а также того, лежат ли три точки на
одной прямой, представлены на рисунке 7.
Полярные
параметры прямой

нельзя ими задать прямую, параллельную оси Y. В противоположность этому
полярными параметрами можно задать положение всякой прямой (рисунок 8).
Если прямая
представлена уравнением , то ее полярное расстояние
определяется по формуле 
,
, где верхние знаки берутся когда С >
0, а нижние – когда С < 0; при С = 0 произвольно берутся либо
верхние, либо только нижние знаки.

p и полярным углом a представляется уравнением . Оно называется нормальным уравнением
прямой. От нормального уравнения прямой можно перейти к полярному уравнению
(рисунок 9). Из рисунка видно, что прямая VU, не проходящая через полюс O, представляется в полярных координатах уравнением .
При построении прямой, заданной в полярных координатах, полярные
координаты переводят в декартовы. Если полюс имеет координаты (x0, y0),
то формулы преобразования таковы:
Уравнения для построения
прямой имеют вид:

 |
Пример
построения прямой приведен на рисунке 10.
Рисунок 10 – Построение прямой
Преобразование
координат
Одна и та же
линия представляется различными уравнениями в разных системах координат. Часто
требуется, зная уравнение некоторой линии в одной системе координат («старой»),
найти уравнение той же линии в другой системе («новой»). Это достигается
применением формул преобразования координат.
Любую новую
систему координат можно получить из старой путем смещения центра системы и
поворота ее осей (рисунок 11).

будут (x+Dx, y+Dу).
При повороте
системы координат на угол a с учетом предшествующего переноса новые координаты
точки определяются следующим образом:
Пример расчета
новых координат точки приведен на рисунке 12.
Рисунок 12 – Преобразование координат
Деление
отрезка в заданном отношении
Даны точки A1(x1;y1) и A2(x2;y2). Требуется найти координаты точки K(x;y), делящей отрезок A1A2 в данном отношении: (рисунок 13).
Координаты точки,
делящей отрезок в данном отношении находятся по формулам:
.
Пример решения
задачи приведен на рисунке 13.
 |
При построении отрезка
выбирается тип диаграммы: точечная, на которой значения соединены отрезками
Рисунок 13 – Деление отрезка
Задание
Задано уравнение
прямой (см. таблицу).
1.
Записать уравнение в виде
а) в)
,
с) , с)
, d)
.
2.
Построить прямую .
3.
Найти расстояние точки с
координатами (1; 2) до прямой.
4.
Построить прямую, заданную
в полярной системе координат .
Варианты:
|
№ п/п |
A |
B |
C |
|
1 |
3 |
-1 |
4 |
|
2 |
-1 |
3 |
2 |
|
3 |
-2 |
-1 |
5 |
|
4 |
2 |
4 |
-1 |
|
5 |
5 |
2 |
4 |
|
6 |
-4 |
5 |
3 |
|
7 |
-5 |
2 |
1 |
|
8 |
4 |
2 |
-4 |
|
9 |
5 |
1 |
2 |
|
10 |
-3 |
2 |
4 |
|
11 |
4 |
-3 |
-2 |
|
12 |
3 |
5 |
-4 |
|
13 |
6 |
2 |
-1 |
|
14 |
-1 |
5 |
-2 |