Опубликовано 15.05.2022 Обновлено 14.08.2022
Приветствую, друзья! В этой заметке вас ждут бесплатные Excel-программы для автоматического заполнения карты профессионального риска от наших коллег, которые любезно поделились своими наработками с подписчиками Блог—Инженера. Лучи добра и вопросы вы всегда можете послать в комментариях. Также приведём полезные ссылки касательно оценки профессиональных рисков.
Обновление от 15.05.2022 – Добавлены разработки (программы) для оценки и управления профессиональными рисками от Сергея Кубинова и Линара Муллахметова + Положение об управлении профессиональными рисками.
Содержание
- Программа по ОПР от Андрея Шакаева
- Программа по ОПР от Анатолия Юдина
- Программа по ОПР и Положение об управлении профессиональными рисками от Сергея Кубинова
- Программа по ОПР от Линара Муллахметова
- Программа по ОПР от Максима Жаренкова
- Дополнительная информация и материалы по оценке профессиональных рисков
Программа по ОПР от Андрея Шакаева
Программу я делал под себя.
Формулу в карте можно конечно усовершенствовать, но мне уже неохота, так как это вопрос мы для себя закрыли.
Краткая инструкция:
Открываете лист Карта – выделяете ячейку в столбце “Выявленные потенциальные…” – нажимаете кнопку на клавиатуре “=” – переходите в лист Реестр, выбираете (выделяете ячейку с опасностью) – нажимаете Еnter.
Всё просто, осталось скачать саму программку.
Скачать > Excel-программа для автоматического заполнения карты профессионального риска (1)
Программа по ОПР от Анатолия Юдина
Оценка профессиональных рисков и создание “Карт идентификации опасностей и оценки профессиональных рисков” производится в программе “MS Excel” на основе простого организационно-технологического решения.
Программа в “MS Excel” была применена при создание “Карт идентификации опасностей и оценки профессиональных рисков” в СПб ГУП “Петербургский спортивно-концертный комплекс” в 2019 г.
Для теоретической иллюстрации и понимания процессов при создании Карт и оценки профессиональных рисков приложена презентация к Системе управления профессиональными рисками (СУПР) из ИС Специалиста по охране труда v. 10.1, созданной в “MS Access”.
В ZIP-архиве:
Excel-программ для автоматического заполнения карты профессионального риска
Инструкция по работе с Excel-программой
Презентация “Система управления профессиональными рисками”
Положение о системе управления профессиональными рисками (пример)
Скачать > Excel-программа для автоматического заполнения карты профессионального риска (2)
Программа по ОПР и Положение об управлении профессиональными рисками от Сергея Кубинова
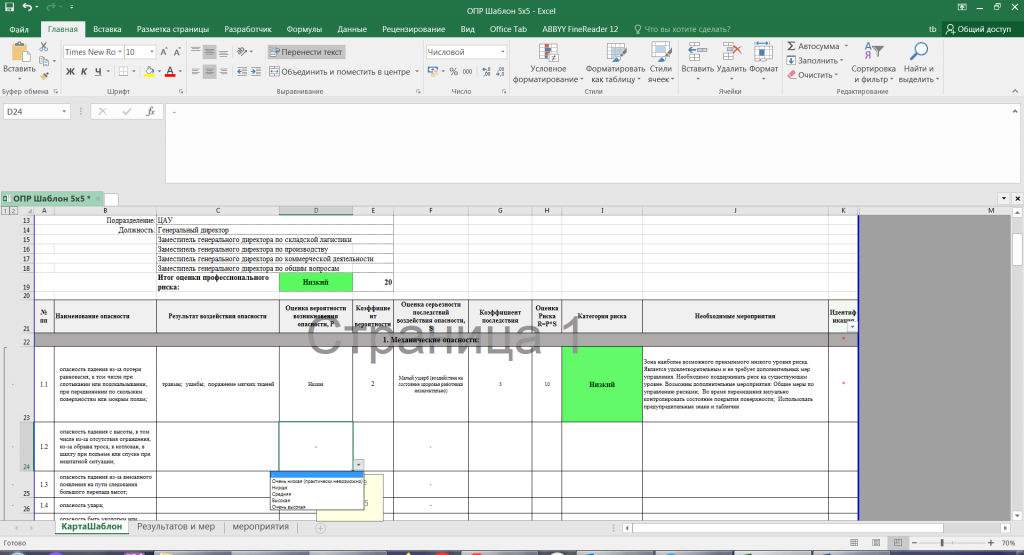
Предлагаю для помощи в создании карт риска программу по их созданию на основе методики 5х5.
Для работы в данной программе необходимо только выбрать два значения из выпадающего списка это в столбике Оценка вероятности возникновения опасности, Р и Оценка серьезности последствий воздействия опасности, S после чего можно получить быстрый результат
Все остальные действия подтянутся автоматически.
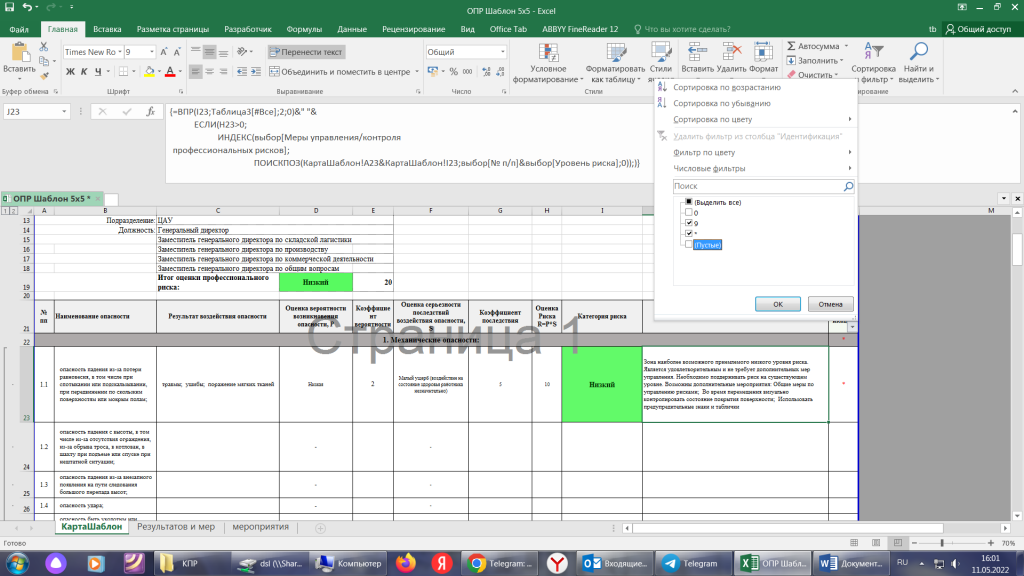
Чтобы убрать все ненужные пустые строчки, надо на столбике Идентификация убрать 2 галочки над значениями «0» и «Пустые» как показано на скриншоте 3
Остальные возможности программы как добавить мероприятия или изменить результат воздействия опасности опишу позднее.
Скачать > Excel-программа для автоматического заполнения карты профессионального риска (3)
Скачать > Положение об управлении профессиональными рисками (3)
Программа по ОПР от Линара Муллахметова
Решил поделится своей наработкой с целью упрощения составления карт идентификации, оценки и управления рисками. Форма конечно подойдёт не всем, т.к. сделана под мою организацию, но как пример или шаблон думаю можно использовать.
Как мы все знаем, руководители структурных подразделений обычно заняты и чтобы упростить задачу составления карт и хоть как-то вовлечь их в процесс оценки рисков, я разработал реестр основных операционных рисков, который и лёг в основу составления карт. Для работы с файлами у вас должны быть включены макросы, как это сделать, написано в интернете.
При запуске файла откроется вкладка “Реестр ОПР”, для очистки галочек ниже первого столбца нажмите на ячейку “Клац”, теперь выберите этап выполнения работ и щелкните один раз в первом столбце, при этом появится галочка и все значения, которые находятся правее галочки перенесутся во вкладку “Карта ОПР”. Далее можно просто скопировать значения в файл WORD или воспользоваться моим шаблоном – для этого во вкладке “Карта ОПР” нажмите на кнопку “Сформировать Карту” (при этом шаблон карты должен быть в одной папке с файлом), вуаля – карта готова, сохраните её.
Готов к любой критике или советам 🙂
Скачать > Excel-программа для автоматического заполнения карты профессионального риска (4)
Программа по ОПР от Максима Жаренкова
Так получилось, что программу опубликовали в отдельной заметке.
Скачать > Excel-программа для автоматического заполнения карты профессионального риска (5)
Дополнительная информация и материалы по оценке профессиональных рисков
- Кто не знает, вот здесь у нас народная копилка – Карты оценки рисков по профессиям и видам работ. Народные примеры и образцы
- Вот здесь можно заказать Оценку и управление профессиональными рисками:
01. Оценка профессиональных рисков “под заказ”
02. Практический курс “Оценка профессиональных рисков для работодателей”
03. Сервис РискПроф для экспертных компаний
04. Практический курс “Оценка профессиональных рисков для экспертных компаний” - Наш партнёр ФИНДИАС в рамках подписки PRO+ предлагает скидку 50% на сопровождение цифровой программы для ведения охраны труда в организациях (ФИ-ОТ), в которой есть модуль для расчёта профессиональных рисков.
На этом всё.
Продолжение следует …
В этом видео я знакомлю вас с методикой расчета риска в трейдинге в EXCEL, расчетом стоп-лосса и базовыми принципами управления капиталом. Привожу наглядные примеры для расчета риска по акциям, фьючерсам и CFD.
Также в вводной части высказываю свое мнение о проблемах неопытных трейдеров и об ошибках, которые приводят к потере депозита. У высказанной мысли имеется научное обоснование, поэтому пару слов сказал о Теории перспектив и ее влиянии на финрезультаты трейдеров.
Первая часть. Эту часть можно просто послушать.
00:00 — вступительное слово. Что вас ждет в этом видео, почему принципы управления капиталом так важны для трейдера, почему все новички сливаются и как этого избежать? Пара слов о теории перспектив и философия риск-менеджмента.
12:00 Вторая часть: работа в excel
12:01 — расчет риска для акций на примере акций Сбербанка;
19:42 — расчет риска для CFD на примерах валютных пар EUR/USD, USD/JPY, CFD на серебро;
33:02 — расчет риска для фьючерсов на примере фьючерсов на Московской бирже (РТС, нефть) и на Чикагской товарной бирже (Нефть, фьючерс на EUR/USD).
Все видео пропитано размышлениями и комментариями относительно риск-менеджмента и принципами управления капиталом.
====================================================================
За оперативной информацией по финансовым рынкам приглашаю всех желающих в свой канал Телеграмм: https://teleg.run/khtrader
Оценивание рисков представляет собой анализ каждого риска и определение его влияния на проект, в случае если данный риск воплотится в соответствующее нежелательное событие. Конечной целью процесса оценивания является определение рисков, для которых необходимо составить планы реагирования.
Например, мы определили, что одним из рисков, связанных с выполнением проекта Grant St.Move, является возможное увольнение главного исполнительного директора. Наша команда выяснила, что на данном этапе увольнение главного исполнительного директора не окажет существенного влияния на проект, поскольку договор об аренде нового здания на улице Grant St. уже подписан, а уведомление о прекращении действия договоров аренды старых зданий разослано в соответствующие инстанции. Иными словами, переезд в новое здание состоится независимо от появления в организации нового главного исполнительного директора, который если и посчитает переезд плохой идеей, повернуть данный процесс вспять (т.е. остановить выполнение проекта) все равно не сможет, поскольку это обошлось бы организации слишком дорого.
Таким образом, для указанного риска план реагирования не требуется. Это вовсе не означает, что событие, связанное с этим риском, не может наступить. Просто команда приняла осознанное решение такого плана не составлять, независимо от того, произойдет событие или нет. Проанализировав все риски в этом списке и взяв за основу степень серьезности каждого из них, мы должны решить, нуждаются ли они в составлении соответствующих планов реагирования. Прежде чем приступать к рассмотрению методов анализа, мы должны уяснить уровни допустимости рисков в нашей организации. Именно этот вопрос мы и рассмотрим.
Допустимость рисков
Риск, подобно другим процессам планирования проекта, связан с проблемой баланса. Определяя черту, до которой следует идти, чтобы извлечь из этого проекта выгоду, вы тем самым пытаетесь сбалансировать свою готовность рисковать со стремлением избежать последствий наступления соответствующего неблагоприятного события. У организаций, как и у людей, есть определенные уровни допустимости рисков. Вам нужно определить эти уровни для всех заинтересованных сторон, руководства организации, клиентов и других лиц, имеющих отношение к выполняемому проекту, т.е. необходимо заранее определить готовность тех или иных лиц брать на себя риск.
Возможно, разные категории риска будут характеризоваться разными уровнями допустимости рисков. Например, лица, заинтересованные в выполнении вашего проекта, могут быть в большей степени готовы к риску, связанному с календарным планом проекта, чем к финансовому риску. Воспользуйтесь методами интервьюирования: возможно, кому-то из исполнителей или руководителей других проектов уже приходилось работать с кем-то из лиц, заинтересованных в выполнении вашего проекта. Определяя уровни допустимости рисков для своего проекта, не забудьте ознакомиться с информацией о предыдущих проектах. Вы можете использовать специальные опросные листы, разместите их на press wall свадебный и периодически проверяйте заполнение их.
Определение уровней допустимости рисков
Рассмотрим понятие уровня допустимости риска на примере повседневной деятельности. Большинство из нас регулярно принимает ванну. И хотя всегда существует риск наступить на кусок мыла, случайно упавший на дно ванны, поскользнуться и ушибиться (или даже заработать серьезную травму), удерживает ли вас осознание этого риска от регулярного приема ванны или душа? Разумеется, нет (в противном случае вам следовало бы обратиться к психиатру, а не читать книги по управлению проектами). Таким образом, ваш уровень допустимости этого риска чрезвычайно высок. Иными словами, вы готовы мириться с возможностью весьма тяжелых последствий (в случае наступления события, связанного с этим риском) во имя того, чтобы воспользоваться таким благом современной цивилизации, как ванна.
Рассмотрим другой пример. Допустим, каждое утро по дороге на работу вам приходится пересекать оживленный перекресток. Этот перекресток печально известен тем, что здесь почти каждый день случаются дорожные происшествия, жертвами которых становятся как водители, так и пешеходы. Готовы ли вы перебегать этот перекресток на красный свет, лавируя между автомобилями с риском для жизни, только для того, чтобы вовремя прибыть на работу, или вы все же предпочитаете ждать минуту-другую, пока загорится зеленый сеет светофора, даже когда опаздываете на работу? Смеем предположить, что около 80% читателей будут ждать, пока загорится зеленый свет. Оставшиеся 20% еще приближаясь к перекрестку будут внимательно следить за сигналами светофора и постараются проскочить на зеленый свет, даже если останется всего пару секунд. Как нетрудно догадаться, у этих 20% пешеходов уровень допустимости риска, связанного с переходом оживленного перекрестка, выше, чем у тех, кто предпочитает дожидаться зеленого света.
Вероятность риска и его влияние
Есть несколько способов, с помощью которых можно определить вероятность риска и его влияние, из которых мы рассмотрим только два. Но сначала давайте разберемся, что же такое вероятность риска и в чем заключается его влияние.
Вероятность риска — это возможность наступления события, связанного с соответствующим риском. Например, когда вы подбрасываете монетку, вероятность выпадения «орла» и «решки» примерно одинакова и равняется 50%. Однако определить вероятность того или иного риска далеко не так просто. Как правило, для определения вероятности рисков, связанных с выполнением вашего проекта, приходится прибегать к помощи экспертов, которые высказывают собственные «предположения» относительно этих вероятностей. И зачастую такие предположения экспертов являются достаточно обоснованными, поскольку базируются на опыте выполнения аналогичных проектов в прошлом. В любом случае пользоваться оценками экспертов все же лучше, чем подбрасывать монетку.
Разумеется, точность оценки вероятности рисков зависит от того, насколько грамотно вы подберете экспертов и заинтересованных лиц, которые будут оценивать эти вероятности. Чтобы не попасть в ловушку так называемого группового мышления, вам потребуются эксперты с разным опытом работы. Если, например, все ваши эксперты являются специалистами по информационным технологиям и имеют соответствующий опыт работы, то вполне возможно, что им не удастся правильно оценить уровни вероятности рисков, связанных с бюджетами или маркетингом.
Влияние риска — это, так сказать, уровень неприятностей, которые может причинить событие, связанное с соответствующим отрицательным риском, или уровень «позитива», который может обусловить событие, связанное с соответствующим положительным риском. Влияние, как правило, зависит от конкретного риска и едва ли является более определенным, чем вероятность. Например, для определения влияния утраты какого-либо из ключевых ресурсов (специалиста редкой квалификации) по нашему проекту Grant St. Move нам нужно оценить приблизительно время, на которое задержится исполнение календарного плана этого проекта, пока мы будем подыскивать другого специалиста с аналогичной квалификацией (и пока этот специалист будет входить в курс дел и выходить на требуемый уровень производительности). Кроме того, нам потребуется оценить приблизительные затраты, связанные с задержкой выполнения заказов, продлением договоров с поставщиками (вызванным указанной задержкой) и т.п.
Схемы вероятности рисков и их влияния
Вероятность риска и его влияние можно выразить либо в виде числа, либо уровня. Числа всегда выражаются долями в диапазоне от 0,0 (означающем, что вероятность наступления события, связанного с соответствующим риском, равняется нулю) до 1,0 (а это означает, что вероятность наступления события, связанного с соответствующим риском, равняется единице, т.е. наступление этого события неизбежно). Уровни обычно измеряются по шкале «высокий-средненизкий» или с помощью того или иного отклонения. На рис. 1 представлен шаблон схемы вероятности рисков и их влияния. В этом шаблоне предусмотрен столбец «Величина риска» (Risk Score), который представляет собой интегральную оценку вероятности риска и его влияния. Ниже мы покажем (на примере проекта Grant St. Move), как заполнять такой шаблон.
Рис. 1. Схема вероятности рисков и их влияния (шаблон)
В нашей схеме вероятности рисков и их влияния мы использовали уровни (высокий, средний и низкий). Их можно применять для небольших и средних проектов, а иногда и для крупных проектов с минимальным количеством рисков. На рис. 2 показаны риски, обнаруженные нами для проекта Grant St.Move, причем для каждого из этих рисков указан соответствующий уровень. (Разумеется, этот перечень рисков ни в коем случае не является исчерпывающим.)
Рис. 2. Схема вероятности рисков и их влияния для проекта Grant St.Move
Рассмотрим подробно первый риск — «стабилизаторы электропитания выбраны неправильно». Вероятность этого риска («низкая») базируется на мнении наших экспертов. Однако влияние этого риска велико. Специалисты рассуждали так: если событие, связанное с этим риском, случится, то в лучшем случае серверы будут работать со сбоями, т.е. пользователи не смогут передавать электронную почту, запускать компьютерные программы, требующиеся для выполнения их работы, или обращаться в Интернет. А значит, наш проект не достигнет своей цели, поскольку его назначение в том, чтобы не допустить снижения производительности и простоев. Показатель «Величина риска» представляет собой интегральную оценку вероятности риска и его влияния (в данном случае эта интегральная оценка риска такова: «низкая-высокая»).
Чтобы определить уровни вероятности риска и его влияния, вы можете воспользоваться любым методом — мозгового штурма, номинально-групповым или интервью, задав такие вопросы: «Если событие, связанное с этим риском, действительно произойдет, то каким может быть самое негативное его влияние на выполняемый проект, клиентов, организацию и т.д.? И как в этом случае вы оцените уровень влияния этого риска (высокое, среднее, низкое)?»
Шкалы влияния риска
Теперь мы займемся созданием матрицы вероятности рисков и их влияния (Probability and Impact Matrix — PI matrix). Эта матрица похожа на только что рассмотренную схему в том отношении, что вы определяете вероятность и влияние событий, связанных с каждым из рисков, и присваиваете каждому такому риску соответствующую интегральную оценку вероятности/влияния. Как правило, в матрице PI вместо уровней используются числа. Поскольку до сих пор мы пользовались лишь такими оценками, как низкая, средняя и высокая, нам нужно в качестве первого шага построить шкалу влияния рисков.
Командам, по-видимому, гораздо легче при использовании шкалы влияния присваивать рискам привычные для себя уровни, нежели некий процент (долю). Разница в данном случае заключается лишь в том, что мы будем сопоставлять с уровнями определенные числа, что даст нам возможность затем использовать эти числа в матрице PI. Следующим этапом является шкала влияния рисков: она описывает диапазон возможных влиянии или последствий, что позволяет нам уточнить оценки влияния чех пли иных рисков. При оценке влияния рисков почти всегда учитываются факторы времени и затрат. В зависимости от природы выполняемого проекта вашей команде придется определять для своих шкал какие-то другие критерии. Для проекта Grant St. Move мы добавили в качестве еще одного критерия «Производительность» (невозможность использования компьютеров или телефонов). Соответствующая шкала влияния рисков показана на рис. 3.
Рис. 3. Шкала влияния рисков
С учетом такой шкалы команда сказала нам, что вследствие неправильного выбора стабилизаторов электропитания может пострадать производительность. Они определили, что влияние этого риска является высоким — 0,7. Теперь мы можем перейти к определению вероятности.
Если вы хотите также при оценке вероятности пользовать ся шкалой с уровнями от «очень низкой» до «очень высокой», то можно разработать такие шкалы, подобно разработанным нами шкалам влияния риска. Например, очень низкая вероятность для критерия «Производительность» может оцениваться величиной 0,05. У нас сложилось впечатление, что командам гораздо легче присвоить тот или иной процент вероятности события, связанного с риском, чем присвоить некий процент влияния этого риска на выполнение проекта.
Вероятность риска, связанного с неправильным выбором стабилизаторов электропитания, оценивается как низкая, поэтому вероятности такого события мы присвоили значение 0,2. Чтобы получить интегральную оценку этого риска, нужно вероятность умножить на влияние (0,2×0,7). Итак, в нашем случае интегральная оценка риска равняется 0.14. Чтобы определить, нужно ли для этого риска составлять план реагирования, следует рассмотреть матрицу PI.
Чтобы облегчить себе задачу определения интегральной оценки риска, можно воспользоваться электронной таблицей, которую мы сформировали в подразделе «Схемы вероятности рисков и их влияния» (см. рис. 1). Эту электронную таблицу необходимо модифицировать таким образом, чтобы в столбце «Величина риска» содержалась формула умножения вероятности на влияние.
ППП
EXCEL
предлагает широкий набор средств
автоматизации статистического
моделирования данных от вычисления
параметров описательной статистики до
построения сложных прогнозных моделей.
Для этих целей в нем реализована
специальная группа статистических и
математических функций, большинство
из которых содержится в дополнении
Пакет анализа.
Список и форматы некоторых функций,
использованных в процессе анализа
рисков, приведены в табл. 1.1.
-
Таблица 1.1.
Наименование функции
Формат функции
СРЗНАЧ
СРЗНАЧ(блок
ячеек)ДИСПР
ДИСПР(блок
ячеек)СКОС
СКОС(блок
ячеек)СТАНДОТКЛОНП
СТАНДОТКЛОНП(блок
ячеек)НОЕМОБР
НОРМОБР(вероятность;
средн_энач; станд отклон)НОРМРАСП
НОРМРАСП
(х; средн знач ; станд откл; интегральная)
4.3. Анализ рисков финансовых операций
Рассмотрим
типовые задачи, которые можно решать с
использованием стандартных функций
ППП EXCEL.
Определение
основных характеристик распределения
случайной величины (СВ). Возможны
два варианта расчетов: случай, когда
вероятность осуществления случайного
события не задана и , наоборот, вероятность
осуществления случайного события задана
явно.
Определение
характеристик СВ при незаданной
вероятности осуществления событий.
В этом случае полагаем вероятность
осуществления всех событий одинаковой,
т.е. p1
= p2
=…= pn=
1/n
и можем непосредственно применить
статистические функций ППП EXCEL,
вычисляющие основные характеристики
распределения СВ (среднее значение
М(Е), дисперсию VAR(E),
стандартное отклонение (Е)).
Продемонстрируем технику их расчетов
с применением встроенных функций ППП
EXCEL.
Подготовьте исходную таблицу (рис. 1.1. ) с данными следующего примера.
Пример
1.1. Рассмотрим
возможность покупки акции недавно
образованной фирмы «Н». Предполагается,
что прогнозируется доходность по акциям
этой фирмы через год будет зависеть от
состояния спроса на ее продукцию в
течение данного периода и соответственно
равна: 12% — в случае повышенного спроса;
9% — при обычном спросе; 6% — при пониженном
спросе.
|
А |
В |
С |
|
|
1 |
Анализ |
||
|
2 |
|||
|
3 |
Прогноз |
Доходность |
|
|
4 |
Пессимистический |
6% |
|
|
5 |
Вероятный |
9% |
|
|
6 |
Оптимистический |
12% |
|
|
7 |
|||
|
8 |
Ожидаемая |
||
|
9 |
Дисперсия |
||
|
10 |
Стандартное |
||
|
11 |
Коэффициент |
Рис.
1.1. Исходная таблица для решения примера
1.1.
Осуществим
анализ риска этой операции. Прежде всего
определим среднюю доходность по акциям
фирмы «Н». Поскольку наступление
любого события в данном примере считается
равновероятным, для расчета искомой
величины можно воспользоваться функцией
СРЗНАЧ (),
указав ей в качестве аргументов блок
ячеек В4,
В6,
содержащий предполагаемые значения
доходности. Введите в ячейку В8
формулу: =СРЗНАЧ
(В4: В6) (Результат
0,09, или 9%).
Для
вычисления дисперсии и стандартного
отклонения в ячейках В9
и В10
необходимо задать следующие формулы:
=ДИСПР(В4:В6) (Результат
0,0006)
=СТАНДОТКЛОНП
(В4: В6) (Результат
0,0245, или 2,45%)
Теперь
можно легко определить значение
коэффициента вариации из соотношения
(11). Для этого
в ячейке В11
вычислим результат отношения стандартного
отклонения (В10)
к величине среднего значения (В8):
=В10/В8 (Результат
0,27)
Полученные
значения параметров позволяют сделать
вывод о невысоком риске акций фирмы
«Н».
Определение
характеристик СВ при заданной вероятности
осуществления событий.
Рассчитаем
вероятность того, что доходность по
акциям «Н» будет меньше величины
а—
(9 — 2,45 = 6,55). При этом будем исходить из
предположения, что величина доходности
r
распределена по нормальному закону
Тогда из (10)
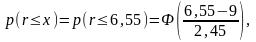
где
Ф — функция Лапласа.
Для
автоматизации расчетов, связанных с
нормальным распределением вероятностей,
в ППП EXCEL
реализован ряд специальных функций. Мы
будем использовать две функции —
НОРМРАСП()
и НОРМОБР().
Функция
НОРМРАСП (х; средн_знач; станд_откл;
интегральная)
Функция
НОРМРАСП ()
имеет следующие параметры:
х
— исследуемое значение случайной
величины,
средн_знач
— среднее значение;
станд_откл
— стандартное отклонение;
интегральная
— 0 или 1.
В
зависимости от заданного параметра
интегральная
— О (ложь) или 1 (истина) — она возвращает
плотность распределения (х)
или значение кумулятивной функции
распределения вероятностей F(x)
для нормальной случайной величины.
Определим
искомую вероятность р
(r
<. 6,55) Для
этого в ячейку В14
введем формулу:
=НОРМРАСП(6,55;
9; 2,45; 1)
(Результат 0,1586), или
=НОРМРАСП(В8-В10;
В8; В10; 1)
(Результат 0,1586)
Таким
образом, эта вероятность приблизительно
равна 16%. Соответственно вероятность
Р(r
> 6,55) будет
равна:
=1
— НОPМРАСП(В8-В10;
В8; В10; 1)
(Результат 0,8414)
На
рис. 1.2. приведен фрагмент ЭТ с расчетами
вероятностей для различных значений
ставки доходности r.
Выполнить эти расчеты самостоятельно.
Построить
графики плотности и кумулятивной функции
распределения вероятностей для примера
1.1. Для построения графиков необходимо
предварительно выполнить табуляцию
функций (х)
на интервале [а ± 3]
и F(x).
Для определения значений (х)
также используется функция НОРМРАСП
(), однако
значение параметра интегральная
при этом задается равным 0 (ложь).
|
А |
В |
С |
|
|
1 |
Анализ |
||
|
2 |
|||
|
3 |
Прогноз |
Доходность |
|
|
4 |
Пессимистический |
6% |
|
|
5 |
Вероятный |
9% |
|
|
6 |
Оптимистический |
12% |
|
|
7 |
|||
|
8 |
Ожидаемая |
9,00% |
|
|
9 |
Дисперсия |
0,0006 |
|
|
10 |
Стандартное |
2,45% |
|
|
11 |
Коэффициент |
0,27 |
|
|
12 |
|||
|
13 |
P |
0,1587 |
|
|
14 |
P |
0,8413 |
|
|
15 |
P |
0,0001 |
|
|
16 |
|||
|
17 |
рис.
1.2. Анализ риска (пример 1.1)
По
графикам убедиться, функция распределения
F(x)
возрастает на интервале от 0 до 1. Согласно
правилу сложения вероятностей при x1<x2
вероятность попадания значения случайной
величины Е
в интервал (x1;
x2)
равна
приращению функции распределения
вероятностей:
p(x1
E
< x2)=F(x2)
– F(x1)
Определим
вероятность попадания r
в интервал (а + ):
=НОРМРАСП(В8+В10;
В8; В10;1) — НОЕМРАСП(В8; В8; В10;1)
(Результат:
0,3414)
Соответственно
вероятность попадания r
в интервал (а ± )
будет равна:
=НОЕМРАСП(В8+В10;В8;В10;1)
— НОБМРАСП(В8-В10; В8; В10;1)
(Результат:
0,6828)
Вероятность
попадания г в интервал (а ± 2)
и (а ± З)
определите самостоятельно.
Полученные
результаты служат числовой иллюстрацией
правила трех сигм для нормального закона
распределения.
Функция
НОРМОБР (вероятность; средн_энач;
станд__откл)
Функция
имеет следующие параметры:
вероятность
—вероятность нормального распределения;
средн_знач
—среднее значение;
станд_откл
—стандартное отклонение.
Она
возвращает обратное нормальное
распределение для указанного среднего
и стандартного отклонения. Другими
словами, она позволяет по заданной
вероятности определить величину
исследуемой переменной (в нашем примере
доходности).
Определим
предельную величину доходности для
вероятности 84%:
=НОРМОБР
(0,84 ;В8 ;В10) (Результат:
11,45%).
Таким
образом, для заданной вероятности
величина доходности составит не более
11,45%: р(х 0,1145)
= 0,84.
Функции
ППП EXCEL,
определяющие значения параметров
распределения М(Е),
VAR(E)
и (Е),
следует применять только в тех случаях,
когда
вероятности событий равны.
Если же распределение вероятностей
задано (например, известно из предыдущего
опыта или получено методом экспертных
оценок), среднее значение, дисперсия и
стандартное отклонение рассчитываются
путем непосредственной реализации
средствами ППП EXCEL
соответствующих соотношений — (4),
(6), (7). Продемонстрируем
один из вариантов подобной реализации
на решении примера 1.2.
Пример
1.2.
Рассматривается возможность приобретения
акций двух фирм «А» и «В». Полученные
экспертные оценки предполагаемых
значений доходности по акциям и их
вероятности представлены в таблице
1.2.
Таблица
1.2.
|
Прогноз |
Вероятность |
Доходность, |
|
|
Фирма |
Фирма |
||
|
Пессимистический |
0,3 |
-70 |
10 |
|
Вероятный |
0,4 |
15 |
15 |
|
Оптимистический |
0,3 |
100 |
20 |
Подготовьте
исходную таблицу с данными примера, как
показано на рис. 1.3.
|
А |
В |
С |
D |
|
|
1 |
Анализ |
Взвешенные |
||
|
2 |
||||
|
3 |
Прогноз |
Вероятность |
Доходность |
|
|
5 |
Пессимистический |
0,30 |
-70,00% |
|
|
6 |
Вероятный |
0,40 |
15,00% |
|
|
7 |
Оптимистический |
0,30 |
100,00% |
|
|
8 |
||||
|
9 |
Ожидаемая |
|||
|
10 |
Стандартное |
|||
|
11 |
Коэффициент |
|||
|
12 |
||||
|
14 |
Интервал
(r1; |
Вероятность |
||
|
15 |
r1 |
r2 |
Рис.
1.3. Исходная таблица для решения примера
1.2.
Прежде
всего необходимо определить среднюю
величину доходности (соотношение (4)).
Наиболее простой способ — последовательно
перемножить каждую ячейку блока В5.
В7
на соответствующую ей ячейку блока С5.
С7 и суммировать
полученные значения. Нетрудно заметить,
что данная последовательность действий
представляет собой операцию нахождения
суммы произведений элементов двух
матриц. Поскольку матричные операции
достаточно часто встречаются в прикладном
анализе, для автоматизации их выполнения
в ППП EXCEL
реализована специальная группа
математических
функции..
В
частности, для выполнения необходимой
нам операции удобно использовать функцию
СУММПРОИЗВ (). Как следует из табл. 1.3.,
аргументами функции являются матрицы
одинакового размера. Введем в ячейку и
формулу:
=СУММПРОИЗВ
(В5: В7; С5: С7) (Результат:
0,15, или 15%)
Для
определения величины стандартного
отклонения необходимо сперва вычислить
дисперсию. Из (6) следует, что дисперсия
случайной величины представляет собой
сумму квадратов отклонений от среднего,
взвешенных на соответствующие вероятности.
Зададим в ячейке D5
формулу вычисления дисперсии для первого
события:
=В5*
(С5-$В$9) 2 (Результат:
0,2165).
Обратите
внимание на то, что для задания ячейки,
содержащей среднее значение (В9),
используется способ абсолютной адресации.
Это позволяет безболезненно скопировать
данную формулу в ячейки D6,D7
(в противном случае адрес ячейки,
содержащей среднее значение, был бы
настроен неправильно). Теперь можно
вычислить величину стандартного
отклонения, которая равна квадратному
корню из дисперсии (суммы ячеек D5:D7).
Для этого воспользуемся функцией КОРЕНЬ
() (см. табл. 1.3.). Введите в ячейку В10:
=КОРЕНЬ(СУММ(D5:D7)) (Результат:
0,6584, или 65,84%).
Вычисление
коэффициента вариации не представляет
особых трудностей. Для этого достаточно
просто разделить значение ячейки В10 на
значение В9. Введите в ячейку В11:
=В10/В9 (Результат:
4,39).
Вычислив
основные параметры распределения
случайной величины, можно определить
вероятность ее попадания в некоторый
интервал. В приведенной на рис. 1.4. таблице
границы первого интервала задаются в
ячейках В16
и С 16.
Определим вероятность того, что значение
доходности попадет в интервал (-70; 0).
Введите границы анализируемого интервала
в ячейки В16
и С16.
Формула вычисления вероятности в ячейке
D16
реализована с использованием уже
известной нам функцией НОРМРАСП
() и имеет
следующий вид:
=НОРМРАСП
(С16;$В$9;$В$10;1)-НОРМРАСП (В16;$В$9;$В$10;1)
(Результат:
0,31).
Снова
обращаем внимание на использование
абсолютной адресации при задании в
формулах ячеек, содержащих среднее
значение и стандартное отклонение.
|
А |
В |
С |
D |
|
|
1 |
Анализ |
|||
|
3 |
Прогноз |
Вероятность |
Доходность |
Взвешенные квадраты отклонений |
|
4 |
||||
|
5 |
Пессимистический |
0,30 |
-70,00% |
0,21675 |
|
6 |
Вероятный |
0,40 |
15,00% |
0 |
|
7 |
Оптимистический |
0,30 |
100,00% |
0,21675 |
|
9 |
Ожидаемая |
15,00% |
||
|
10 |
Стандартное |
65,84% |
||
|
11 |
Коэффициент |
4,39 |
||
|
14 |
Интервал
(r1; |
Вероятность (r1<=R<=r2) |
||
|
15 |
r1 |
r2 |
||
|
16 |
-70% |
0% |
0,31 |
|
|
17 |
15% |
65% |
0,28 |
|
|
18 |
15% |
100% |
0,4 |
|
|
19 |
-70% |
100% |
0,8 |
Рис.
1.4. Итоговая таблица анализа рисков
(фирма «А»).
Для
дальнейшего анализа достаточно указать
интересующие интервалы и скопировать
формулу в ячейке
D16
необходимое число раз. На рис 1.4. приведена
итоговая таблица, содержащая некоторые
результаты анализа риска по акциям
фирмы «А» (пример 2.) Аналогичная
таблица на рис 1.5. содержит результаты
анализа риска по акциям фирмы «В».
В
качестве упражнения попробуйте
разработать таблицу анализа рисков для
фирмы «В» самостоятельно, используя
рис 1.3. в качестве образца. Сравните
полученные результаты.
|
А |
В |
С |
D |
|
|
1 |
Анализ |
|||
|
2 |
||||
|
3 |
Прогноз |
Вероятность |
Доходность |
Взвешенные квадраты отклонений |
|
4 |
||||
|
5 |
Пессимистический |
0,3 |
10% |
0,00075 |
|
6 |
Вероятный |
0,4 |
15% |
0 |
|
7 |
Оптимистический |
0,3 |
20% |
0,00075 |
|
8 |
||||
|
9 |
Ожидаемая |
15,00% |
||
|
10 |
Стандартное |
3,87% |
||
|
11 |
Коэффициент |
0,26 |
||
|
12 |
||||
|
13 |
||||
|
14 |
Интервал (r1; r2) |
Вероятность (r1<=R<=r2) |
||
|
15 |
r1 |
r2 |
||
|
16 |
0% |
20% |
0,9 |
|
|
17 |
15% |
20% |
0,4 |
|
|
18 |
10% |
20% |
0,8 |
|
|
19 |
-10% |
0% |
0 |
Рис.
1.5. Итоговая таблица анализа рисков
(фирма «В»).
Пример
1.3.
Прогнозируемые
доходности по акциям фирм «К» и «Р»
имеют следующие распределения вероятностей
(табл.1.5)
Таблица
1.5.
|
Вероятность |
Доходность |
|
|
Акции |
Акции |
|
|
0,15 |
-15% |
—25% |
|
0,20 |
0% |
10% |
|
0,40 |
15% |
20% |
|
0,20 |
20% |
30% |
|
0,05 |
35% |
45% |
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Управление рисками проекта

Категория: РИСК МЕНЕДЖМЕНТ УПРАВЛЕНИЕ ПРОЕКТАМИ
Опубликовал:
10.01.2019
К списку статей
Каждый проект содержит риски. Риск — это сочетание вероятности и последствий наступления неблагоприятных событий. Если можно предположить, что в ходе проекта может (или не может) произойти что‑то негативное, то разумно управлять рисками. По мере развития проекта влияние рисков усиливается, поскольку ресурсы уже вложены, и, если прозевали какой-то риск, то его последствия могут вылиться в кругленькую сумму.
Перед началом проекта надлежит обязательно учесть все (максимально возможные) риски, чтобы потом не было мучительно больно за …
Направления, способы обнаружения рисков:
- Изучение документации по проекту (договор, техническое задание, функциональные требования и т.п.);
- Исследование бизнес- и технологических процессов;
- Анализ предположений, ограничений и допущений проекта;
- Интервьюирование / опросники ключевых участников проекта, их экспертные оценки;
- SWOT-анализ.
После того, как выявлены риски проекта, следует выделить наиболее важные, которые требуют первоочередного внимания и разрешения. Надобно подсчитать итоговые значения рисков, отсортировать их по данному параметру в порядке убывания. Образовавшийся порядковый номер — это ранг риска: 1 – самый тяжкий риск, 2 – серьезный и т. д. Риски с однаковым рангом не всегда равносильны: это могут быть риски с высокой вероятностью и низкой угрозой и наоборот.
Когда риски выявлены и оценены, необходимо решить, как реагировать на них, прежде всего на наиболее опасные.
Вашему вниманию предлагается Excel-шаблон (см. прикрепленный файл ниже) — инструмент классификации рисков посредством их идентификации, оценки влияния, вероятности, ранжирования последствий:
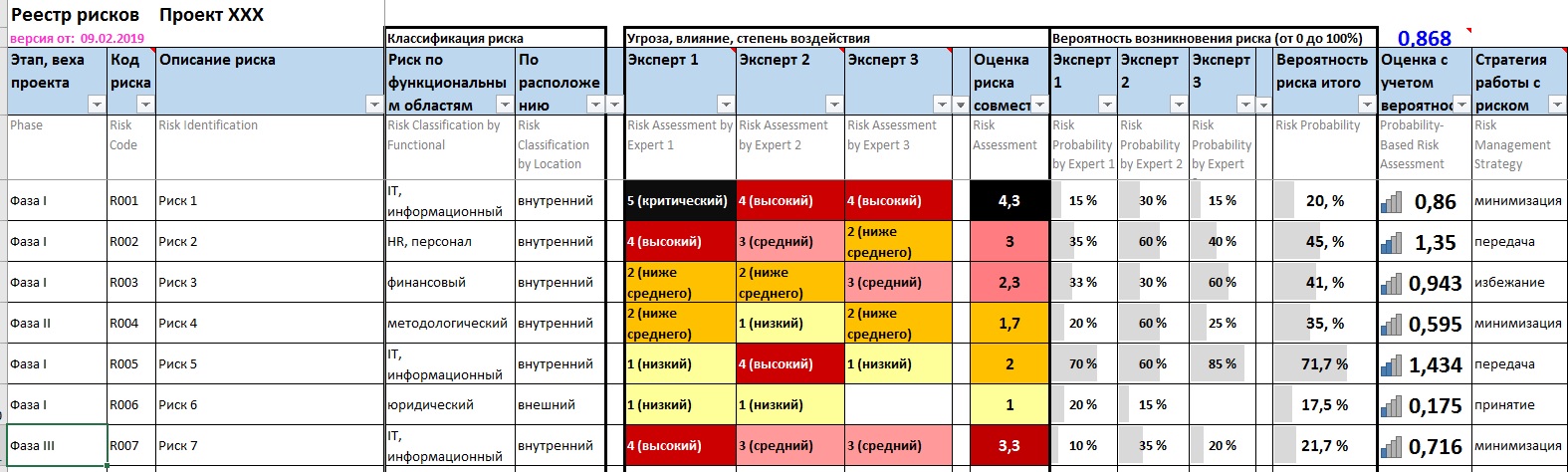
- В целях упрощения обсуждений каждому описываемому риску присваиваем уникальный код и соотносим к этапу проекта;
- Важно выявить и различать основные причины возникновения риска. У одного риска может быть несколько причин, а одна причина может являться источником нескольких рисков;
- Не менее важно заранее охарактеризовать признаки приближения риска, чтобы успеть заметить наступление риска и принять превентивные меры;
- Хорошо бы классифицировать риски как внутренние / внешние и по функциональным областям;
- Во избежание давления, взаимного влияния друг на друга ключевых участников проекта экспертные оценки по 5-ти бальной шкале степени воздействия (угрозы) рисков должны осуществляться тайным, обезличенным голосованием. Желательно учесть мнения не менее трёх специалистов, средняя совместная оценка угрозы каждого риска расчитается автоматически;
- Аналогичным способом каждый эксперт должен проставить вероятность возникновения риска (> 0 и < 100%), итоговая вероятность расчитается автоматически. Следует избегать значения 50%, которое означает, что над данным риском не думали либо старались соблюсти политес;
- Итоговая оценка по каждому риску автоматически рассчитывается как произведение совместной оценки угрозы риска и вероятности. Эти оценки ранжируем в порядке убывания и определяем самые важные риски;
- Изначально надо предотвратить такие риски, но если они все же случились, необходимо правильно реагировать на них. Нужно разработать стратегию работы с каждым риском проекта (Принятие, Избежание, Минимизация, Передача — частный случай минимизации) и выработать мероприятия по снижению риска;
- Следует зафиксировать срок реагирования по каждому риску. Некоторые риски могут требовать безотлагательной реакции, а иные терпят несколько дней;
- Необходимо определить владельца каждого риска — лицо или организационную единицу, которые имеют полномочия и несут ответственность за управление риском.
Оценивать риски нужно как перед стартом проекта, так и пересматривать их с некоторой разумной периодичностью в течение проекта, чтобы отслеживать динамику рисков и корректировать упредительные мероприятия.
dvbi.ru
2019-01-10 00:21:00Z
Последнее изменение: 2021-12-12 23:01:58Z
Возрастная аудитория: 14-70
Комментариев: 0
Теги: Примеры Управление
Связанные статьи:
Пожалуйста, проголосуйте и ниже поставьте лайк:
Следующая статья:
Обеспечение качества данных и информационных систем
Предыдущая статья:
SSAS — примеры документирования
К списку статей