|
0 / 0 / 0 Регистрация: 20.10.2014 Сообщений: 93 |
|
|
1 |
|
«Улитка» Паскаля12.11.2014, 15:52. Показов 13634. Ответов 9
Что то запутался в формулах, подскажите как правильно построить! Миниатюры
0 |
|
6599 / 4709 / 1961 Регистрация: 02.02.2014 Сообщений: 12,616 |
|
|
12.11.2014, 16:14 |
2 |
|
Решениеулитка… Кликните здесь для просмотра всего текста
4 |
|
0 / 0 / 0 Регистрация: 20.10.2014 Сообщений: 93 |
|
|
12.11.2014, 16:31 [ТС] |
3 |
|
Все разобрался, спасибо!) Добавлено через 13 минут
0 |
|
6599 / 4709 / 1961 Регистрация: 02.02.2014 Сообщений: 12,616 |
|
|
12.11.2014, 16:38 |
4 |
|
KNIGT, я желтым выделила правильную формулу для координаты y.
0 |
|
0 / 0 / 0 Регистрация: 20.10.2014 Сообщений: 93 |
|
|
12.11.2014, 16:48 [ТС] |
5 |
|
Это понятно, просто почему в задании одни формулы, у тебя свои, объясни этот момент пожалуйста!
0 |
|
6599 / 4709 / 1961 Регистрация: 02.02.2014 Сообщений: 12,616 |
|
|
12.11.2014, 17:01 |
6 |
|
в задании ошибка
0 |
|
0 / 0 / 0 Регистрация: 20.10.2014 Сообщений: 93 |
|
|
12.11.2014, 17:07 [ТС] |
7 |
|
Все, вопрос исчерпан, спасибо еще раз!
0 |
|
0 / 0 / 0 Регистрация: 27.11.2014 Сообщений: 4 |
|
|
22.06.2015, 15:08 |
8 |
|
Krasme, как правильно вписать cos^2? Добавлено через 34 минуты
0 |
|
0 / 0 / 0 Регистрация: 12.12.2018 Сообщений: 1 |
|
|
12.12.2018, 08:49 |
9 |
|
Можете прислать этот файл в электроне? Заранее спасибо) Добавлено через 1 минуту
в задании ошибка Krasme, Можете прислать этот файл в электроне? Заранее спасибо)
0 |
|
Krasme |
|
12.12.2018, 11:04
|
|
Не по теме: druha97, теме более 4-х лет, какие файлы?
0 |
|
Улитка Паскаля |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
Расчётно-графисечкие работы в MS Excel Стр. 1 из 13
|
MSExcel. Табулирование функции |
|||||||||
|
Задание: |
Протабулировать функцию y(x) на интервале |
||||||||
|
x [a |
x |
, b ], |
a |
x |
= −π |
2 |
, b = 2π c шагом h |
x |
= 0.1, варианты функций в |
|
x |
x |
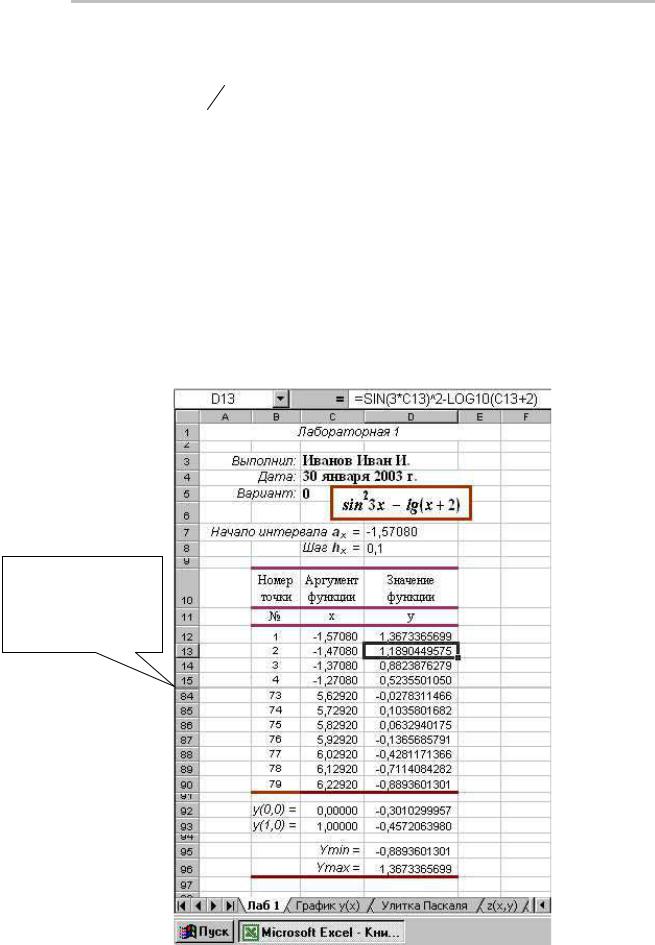
таблице 1 приложения. На защиту лабораторной подготовить лист электронной книги Excel по образцу на рисунке 1.
Ход работы:
1)Запустить программу Excel. Создать документ Книга1. Сохранить в свою папку на жестком диске под оригинальным именем, например, Книга Иванова, переименовать лист Лист1 на Лаб №.
2)Создать заголовок сверху по центру будущей таблицы, используя шрифты помельче, 12 пунктов, Аrial курсив и покрупнее, 14 пунктов, Times полужирный. Выделить название темы лабораторной цветом.
3)Сделать подпись Выполнил, Дата, Вариант. Дата должна пока-
Здесь скрыты строки с 16 по 83 для экономии места на рисунке.
Рисунок 1. Образец оформления лабораторной работы
на листе Excel (для 0-го варианта)
1
|
Расчётно-графисечкие работы в MS Excel |
Стр. 2 из 13 |
зывать текущую дату в заданном полном формате. Вставить свою функцию по варианту в математической нотации как объект MS Equation. Выделить формулу цветной рамкой.
4)Завести отдельные ячейки для начала интервала аx и шага табулирования hx, ячейки D7 и D8 на рисунке 1. Начало интервала определить через функцию ПИ(). Для заполнения диапазона ячеек со значениями аргумента функции использовать абсолютные адреса этих ячеек. В ячейки C7 и C8 вставьте пояснения Начало интервала аx =
иШаг hx =.
5)В строке 10 оформить шапку таблицы: Номер точки, Значение аргумента, Значение функции, и ниже, в строке 11 сокращенно: №, х, у.
6)Заполнение таблицы.
Создание столбца номеров точек. Набрать 1 в В12. Протащить маркер заполнения формул с нажатым Ctrl до 79 в всплывающем окне для получения арифметической прогрессии с приращением 1 в диапазоне ячеек B13:B90.
Создание столбца х. В первую сверху ячейку столбца, С12 набираем ссылку на начало интервала =$D$7 (абсолютный адрес). Под ней в ячейку C13 формулу для расчета следующего значения аргумента через предыдущее =C12+$D$8 (комбинация абсолютных и относительных адресов). Протаскиваем маркер заполнения через диапазон ячеек C14:C90 для получения в нем формул расчета значений аргумента.
Создание столбца y. В ячейку D12 набираем формулу расчета функции по варианту для первой строки таблицы. Для 0-го варианта =sin(3*C12)^2-log10(C12-2) (относительный адрес х). Далее используем технику протаскивания формулы для заполнения диапазона ячеек D13:D90 со значениями функции.
7)Форматирование таблицы. Вывести 5 значащих цифр для значений х и 10 для у. Выровнять по десятичной точке. Применяя условное форматирование, назначить холодный цвет (цвет шрифта, а не заливки), например, синий, отрицательным значениям и красный положительным. Навести рамки в таблице по образцу на рисунке 1.

9)Посчитать максимальное Ymax и минимальное Ymin значения функции в полученном диапазоне ячеек.
10)Сохранить книгу для использования в следующих лабораторных работах.
2
|
Расчётно-графисечкие работы в MS Excel |
Стр. 3 из 13 |
||
|
MS Excel. Построение графиков |
|||
|
Задание 1: Построить графики функции y(x) , |
x [ax , bx ] ломаной |
||
|
линией и сглаженной. |
Задание 2: Построить график кривой f (t) , заданной параметрически, и несколько вложенных в нее кривых.
Задание 3: Построить график трёхмерной поверхности z(x,y).
Вид функций и интервалы выбираются по варианту из таблиц 1, 3 Приложения.
Ход работы:
Построение на одних осях двух графиков функции y(x), x [ax,bx] ломаной линией и сглаженной.
1)График функции в Excel, как и все остальные диаграммы, строится по дискретным значениям. Исходные данные для графика получены в предыдущей лабораторной Лаб №[Книга Иванова].
2)Запускаем Мастера диаграмм. Выбираем тип диаграммы График. Во втором окне мастера указываем исходные данные для
первого ряда Значения: столбец y, Подписи оси Х: столбец x, Имя: набираем с клавиатуры Грубый график. Для второго ряда Значения и Подписи по оси Х те же, Имя: Сглаженный график. Лишние ряды удалить.
3) Отформатировать график по образцу рисунка 2.
На грубом графике соединить точки отрезками прямых сплошными, тонкими, синего цвета, в точках синие прозрачные квадратные маркеры 5 пунктов. На глаженном графике — соединяющие точки линии сплошные, толстые, красные, сглаженные, без маркеров. Настроить порядок рядов так, чтобы тонкие синие линии были видны на фоне красных. Оформить график заголовком, Equation скопировать с листа Лаб1 на график. Подписать оси как Ось Х и Ось Y. Ось Х провести че-
рез y=0. Проредить деления шкал, в подписях делений отобразить 2-3 цифры, чтобы не загромождали график. Настроить диапазон оси Y от ~Ymin до ~Ymax своей функции. Подпись Выполнил Дата Вариант подставить в шесть надписей из соответствующих ячеек листа. Выровнять и распределить надписи инструментами панели Рисование – Действия – Выровнять, Распределить, Группировка. Убрать серую заливку фона области построения. Линии сетки оставить только горизонтальные по основным делениям оси Y, уменьшить их яркость до штрих светло-серого цвета.
3
|
Расчётно-графисечкие работы в MS Excel |
Стр. 4 из 13 |
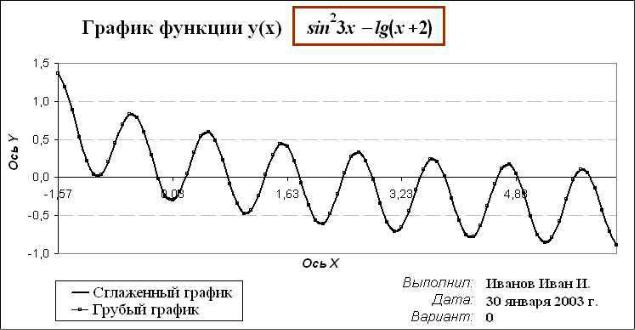
Рисунок 2. Образец оформления графика функции y(x)
4) Работа с книгой. Перенести диаграмму на отдельный лист под именем График y(x). Для обзора точности построения ломаной и сглаженной линий отобразить график в максимальном масштабе.
Построение графика кривой f(t), заданной параметрически, и
вложенных кривых при a=0.9, 0.8, 0.7,..
5)Задание выполняется на отдельном листе. Дать листу имя по названию кривой, Улитка Паскаля для 0-го варианта.
6)Предварительно перед построением графика рассчитать таб-
лицу значений x(t,a), y(t,a), комбинируя абсолютные и относительные
адреса ячеек со значениями t и а. Шаг по t подсчитать на этом же листе, чтобы можно было его изменить, если потребуется улучшить качество кривой. Достаточно взять 20 – 30 значений параметра t, диа-
грамма не будет их использовать, они нужны для расчета x,y— координат точек кривой. Примерный вид таблицы рассчитанных для графика данных смотри на рисунке 3. В строке формул показана фор-
мула в выделенной ячейке Е14 для x-координаты шестой точки при
t=1.31 кривой а=1.0.
7) Неоднозначные или с неравномерным шагом по аргументу кривые строятся по точкам на диаграммах типа Точечная. Запускаем Мастера диаграмм, выбираем тип диаграммы Точечная, подтип сглаженные линии без маркеров. Точечная диаграмма — это составная диаграмма, одна точка данных составляется из двух ячеек со значе-
4
|
Расчётно-графисечкие работы в MS Excel |
Стр. 5 из 13 |
ниями её x, y координат. То есть исходными данными для одного ряда будет диапазон из двух столбцов. Обратите внимание, что диапазон ячеек для первой кривой окружен пустыми клетками, чтобы Excel автоматически распознал непрерывный диапазон исходных данных =’Улитка Паскаля’!$E$9:$F$33, необходимо только перед вызовом Мастера диаграмм установить курсор внутри этого диапазона. Тогда окно предварительного просмотра мастера дает удовлетворительную картинку уже на первом шаге. В качестве имени ряда взять значение
а=1.0. На остальных шагах Мастер диаграмм может сделать название диаграммы, заголовки осей, размещение легенды и самой диаграммы.

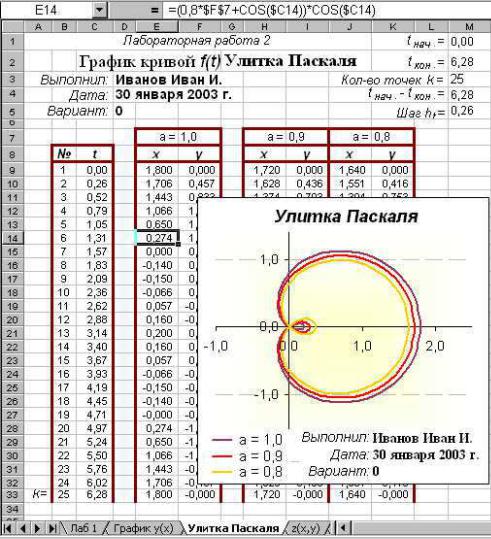
Рисунок 3. Вид таблицы значений x(t,a), y(t,a) и образец оформления графика f(t)
5
|
Расчётно-графисечкие работы в MS Excel |
Стр. 6 из 13 |
ний подобрать так, чтобы было 3 – 4 подписи на оси, в числовом формате подписей делений ограничиться одним знаком после запятой. Из формата выделенного ряда или ключа легенды настроить толщину и цвет линии – сглаженная, максимальной толщины, цвет красный, убрать маркеры точек.
9) Добавляем на диаграмму вложенные кривые. В окне Исходные данные на вкладке Ряд добавляем ряды, задавая диапазоны зна-
чений x и y. Например, для кривой а=0.9 Значения Х: =’Улитка Паска-
ля’!$H$9:$H$33, Значения Y: =’Улитка Паскаля’!$I$9:$I$33, Имя: =’Улитка Паскаля’!$H$7:$I$7. в окне предварительного просмотра сразу появляются кривые и их имена в легенде. Задать цвета кривым в
стиле Домна, плавно меняющиеся от красного для а=1.0 через оран-
жевые тона до желтого для последнего a.
Построение проекции графика функции двух переменных
z( x , y ) = y( x ) , x [—π/2; π], y [—π/2; π/2],
e x 2 +2 y2
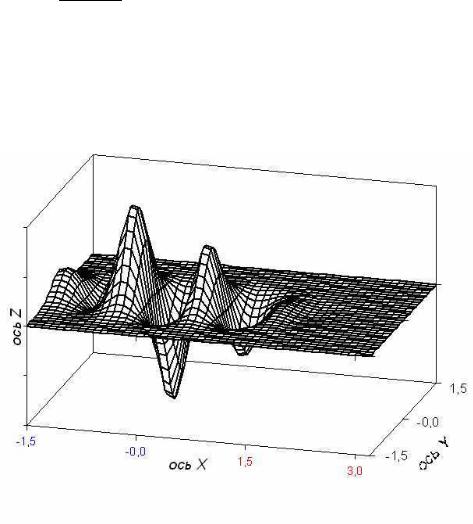
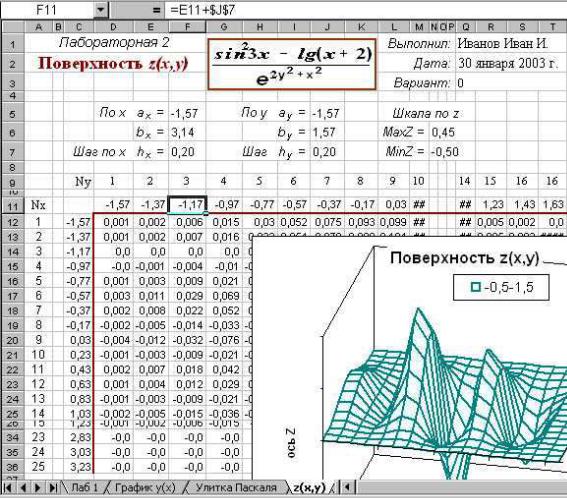
где y(x) выбирается по варианту из таблицы 1 приложения. Образец графика поверхности представлен на рисунке 4.
1)Заводим новый лист под именем z(x,y).
2)Строим таблицу значений x, y и z. Размещаем ее из сообра-
Рисунок 4. 3D-график функции z(x,y)
6
|
Расчётно-графисечкие работы в MS Excel |
Стр. 7 из 13 |
жений удобства работы на листе: чтоб она была компактная, то есть занимала меньше места на листе, чтобы направления роста х и у совпадали с направлением осей правосторонней системы координат. Образец на рисунке 5. Качество картинки зависит от шага, с которым посчитаны значения z(x,y). Поэтому рекомендуется разместить шаги изменения переменных на листе и использовать их адреса при расчете
xи y. Для начала возьмем hx=hy=0.2.
3)Устанавливаем курсор в диапазон значений z, запускаем Мастера диаграмм, заказываем тип Поверхность, единственный существенно трехмерный из стандартных автоформатов. Здесь каждая точка
данных составляется из трех ячеек с х, у и z значениями, где х и у задают равномерную сетку и расположены в первом столбце и первой строке прямоугольного диапазона.
4) Отказываемся от перспективного изображения Диаграмма – Объемный вид – Изометрия. Убираем серый фон стен и основания.
Рисунок 5. Образец расчёта данных для трёхмерного графика z(x,y)
7

|
Расчётно-графисечкие работы в MS Excel |
Стр. 8 из 13 |
Прореживаем деления и подписи осей. Формат оси категорий (оси X) – Шкала – Число категорий между делениями – увеличить — 8. И сразу убираем Пересечения с осью значений между категориями, это используется на гистограммах. Формат оси рядов (оси Y) – Число рядов между делениями – увеличить — 8. Формат оси значений (оси Z) – Вид
–Основные деления – Нет, Шкала – Цена основных делений >> ZmaxZmin, так как они задают не только деления оси значений, но и шкалу раскраски поверхности. И чтобы были деления на оси Z: Вид – Промежуточные деления – Наружу, Шкала — Цена промежуточных делений
–0.5.
5)Ключ легенды является ключом к раскраске поверхности. Выберите способ заливки поверхности посветлее или даже штриховым узором и в тон потемнее цвет линий сетки. Улучшает качество изображения подсветка: Формат ключа легенды — Параметры — Объемное заполнение.
Дополнительные задания
1)Улучшить внешний вид графика y(x) градиентной заливкой области построения.
2)Градиентная заливка центра фигуры, ограниченной замкнутой кривой f(t).
3)Построить поверхность z(x,y) с более мелким шагом по x и y. hx=hy=0.1. Образец на рисунке 4.
|
Приложение |
||||||||||||||||
|
Варианты функции y(x) |
||||||||||||||||
|
Таблица 1 |
||||||||||||||||
|
№ |
Функция |
y(x) |
Схематичный |
|||||||||||||
|
варианта |
график |
|||||||||||||||
|
0 |
sin2 3x |
− lg ( x + 2) |
||||||||||||||
|
2 |
x |
2 |
x |
|||||||||||||
|
1 |
sin |
+ 2 |
− |
|||||||||||||
|
5 |
||||||||||||||||
|
2 |
||||||||||||||||
|
2 |
sin (10 x −20 ) |
+ 0.25 x |
||||||||||||||
|
(x−2) 2 |
||||||||||||||||
|
e 5 |
||||||||||||||||
8

|
Расчётно-графисечкие работы в MS Excel |
Стр. 9 из 13 |
|||||||||||||||||||||||||||||||||||||
|
№ |
Функция y(x) |
Схематичный |
||||||||||||||||||||||||||||||||||||
|
варианта |
график |
|||||||||||||||||||||||||||||||||||||
|
3 |
1 cos |
x |
− sin2 3x |
|||||||||||||||||||||||||||||||||||
|
2 |
3 |
|||||||||||||||||||||||||||||||||||||
|
4 |
sin (10 x −20 ) |
− 0.25 x |
||||||||||||||||||||||||||||||||||||
|
( x−2) 2 |
||||||||||||||||||||||||||||||||||||||
|
e |
5 |
|||||||||||||||||||||||||||||||||||||
|
5 |
cos(x − 8)2 |
+ ln(x + 3)−1.5 |
||||||||||||||||||||||||||||||||||||
|
3 |
||||||||||||||||||||||||||||||||||||||
|
6 |
cos (x − 8)2 − sin (x + 1) |
− 0.2 |
||||||||||||||||||||||||||||||||||||
|
2 |
||||||||||||||||||||||||||||||||||||||
|
7 |
1 |
( x + 5) |
2 |
x − 2 |
2 |
|||||||||||||||||||||||||||||||||
|
sin |
+ |
|||||||||||||||||||||||||||||||||||||
|
2 |
2 |
4 |
||||||||||||||||||||||||||||||||||||
|
8 |
sin ( x |
2+ 3) + |
sin 2 x |
|||||||||||||||||||||||||||||||||||
|
2 |
||||||||||||||||||||||||||||||||||||||
|
9 |
2 sin 8 x |
+ |
3 cos x |
|||||||||||||||||||||||||||||||||||
|
3 |
4 |
|||||||||||||||||||||||||||||||||||||
|
10 |
cos 5x |
ln |
x + 3 |
|||||||||||||||||||||||||||||||||||
|
2 |
||||||||||||||||||||||||||||||||||||||
|
11 |
3 |
2 x + 6 |
2 |
|||||||||||||||||||||||||||||||||||
|
sin |
||||||||||||||||||||||||||||||||||||||
|
x + 3 |
3 |
|||||||||||||||||||||||||||||||||||||
|
( x +2)2 |
+ |
3 |
||||||||||||||||||||||||||||||||||||
|
12 |
cos |
ln |
x |
|||||||||||||||||||||||||||||||||||
|
2 |
2 |
|||||||||||||||||||||||||||||||||||||
|
13 |
cos ((x −5 )2 +1) |
ln(x +2.5 ) |
||||||||||||||||||||||||||||||||||||
|
2 |
||||||||||||||||||||||||||||||||||||||
|
14 |
sin(x −1)2 |
− 0.1 |
||||||||||||||||||||||||||||||||||||
|
x |
4 |
|||||||||||||||||||||||||||||||||||||
|
e |
||||||||||||||||||||||||||||||||||||||
|
( |
)2 |
|||||||||||||||||||||||||||||||||||||
|
15 |
1 sin |
x+3 |
ln (x +2 ) |
|||||||||||||||||||||||||||||||||||
|
2 |
||||||||||||||||||||||||||||||||||||||
|
2 |
||||||||||||||||||||||||||||||||||||||
9

|
Расчётно-графисечкие работы в MS Excel |
Стр. 10 из 13 |
|||||||||||||||||||||||||||||||||||
|
№ |
Функция y(x) |
Схематичный |
||||||||||||||||||||||||||||||||||
|
варианта |
график |
|||||||||||||||||||||||||||||||||||
|
1 |
( |
)2 |
ln |
(x +2 ) |
||||||||||||||||||||||||||||||||
|
16 |
x+3 |
+ |
−1 |
|||||||||||||||||||||||||||||||||
|
2 sin |
2 |
2 |
||||||||||||||||||||||||||||||||||
|
17 |
sin(2(x − 2)2 ) |
− 0.1x |
||||||||||||||||||||||||||||||||||
|
e |
x |
|||||||||||||||||||||||||||||||||||
|
4 |
||||||||||||||||||||||||||||||||||||
|
18 |
sin10 x + 0.5 |
|||||||||||||||||||||||||||||||||||
|
(x−2) 2 |
||||||||||||||||||||||||||||||||||||
|
e |
5 |
|||||||||||||||||||||||||||||||||||
|
19 |
sin |
x |
− cos2 3x |
|||||||||||||||||||||||||||||||||
|
3 |
||||||||||||||||||||||||||||||||||||
|
20 |
cos (5 x +10) |
|||||||||||||||||||||||||||||||||||
|
ln (4 x |
+ 8) |
|||||||||||||||||||||||||||||||||||
|
21 |
2 cos 5x − |
x |
+ 1 |
|||||||||||||||||||||||||||||||||
|
3 |
6 |
3 |
||||||||||||||||||||||||||||||||||
|
22 |
2 2cos2( |
x |
+2)2 +2 |
− |
x |
−3 |
||||||||||||||||||||||||||||||
|
2 |
5 |
|||||||||||||||||||||||||||||||||||
|
sin(x − 8)2 |
x − 2 |
|||||||||||||||||||||||||||||||||||
|
23 |
− |
|||||||||||||||||||||||||||||||||||
|
3 |
5 |
|||||||||||||||||||||||||||||||||||
|
24 |
log (x+4) − 1 |
(sin ( |
x+6 )3+5) |
|||||||||||||||||||||||||||||||||
|
2 |
2 |
3 |
||||||||||||||||||||||||||||||||||
|
25 |
0.2 x − cos 2 3 x |
|||||||||||||||||||||||||||||||||||
Контрольные ответы
|
Таблица 2 |
||||
|
№ |
y(x=0.0) |
y(x=1.0) |
Ymin |
Ymax |
|
вари- |
||||
|
анта |
||||
|
0 |
-0,3010299957 |
-0,4572063980 |
-0,8893601301 |
1,3673365699 |
|
1 |
0,5727500169 |
-0,1988991396 |
-1,2056587561 |
1,3050593587 |
10
Соседние файлы в папке Лева_2.0
- #
14.03.201658.79 Кб23Kniga3.xlsx
- #
14.03.201641.89 Кб25Kniga_Dukhovny.xlsx
- #
- #
- #
14.03.201615.48 Кб18Суперплоховсе.xlsm
Содержание
- Как построить улитку паскаля в excel
- «Улитка» Паскаля
- Решение
- Разработка урока «Красивые графики. Построение графиков функций в полярной системе координат в электронных таблицах Excel»
- Практическая работа в MS Excel «Графики»
- Просмотр содержимого документа «Практическая работа в MS Excel «Графики»»
- Практическая работа в MS EXCEL «Красивые графики»
- Лемниската бернулли уравнение и график в excel
- Формула Бернулли в Excel
- Схема независимых испытаний
- Формула Бернулли в Эксель
- Примеры решений задач
- Плоские алгебраические кривые в EXCEL
- Разработка урока «Красивые графики. Построение графиков функций в полярной системе координат в электронных таблицах Excel»
Как построить улитку паскаля в excel
«Улитка» Паскаля
Помощь в написании контрольных, курсовых и дипломных работ здесь.
Улитка паскаля
Люди добрые помогите построить улитку паскаля. Улитка Паскаля, 0 «»;O4:R4=0;O4:R4<>«»)> — которая в ячейках H4:K4, O4:R4 — выбирает.
Как сделать: если во всех ячейках диапазона знач.=»выполнено», то в данной ячейке тоже «выполнено» иначе «в работе»
Прилагаю файл. В ячейке G17 формула, в которой надо упростить условие: Если в диапазоне ячеек.
Сообщение было отмечено chumich как решение
Решение
Все разобрался, спасибо!)
Добавлено через 13 минут
У тебя какая то другая формула!
Разработка урока «Красивые графики. Построение графиков функций в полярной системе координат в электронных таблицах Excel»
Практическая работа «Красивые графики функций»
Построить спираль Архимеда по следующим данным:
— в столбце А – значения угла t в радианах от 0 до 10 с шагом 0,2
— в столбце В – значения r = 0,5* t
— в столбце С – значения х = r * cos ( t )
— в столбце D – значения y = r * sin ( t )
— выделить значения в столбцах С и D и построить диаграмму
(тип: точечная с гладкими кривыми )
Построить астроиду по следующим данным:
— в столбце А – значения угла t в радианах от 0 до 7 с шагом 0,2
— в столбце В – значения х = 2*( cos ( t )) 3
— в столбце С – значения y = 2*( sin ( t )) 3
— выделить значения в столбцах B и С и построить диаграмму
(тип: точечная с гладкими кривыми )
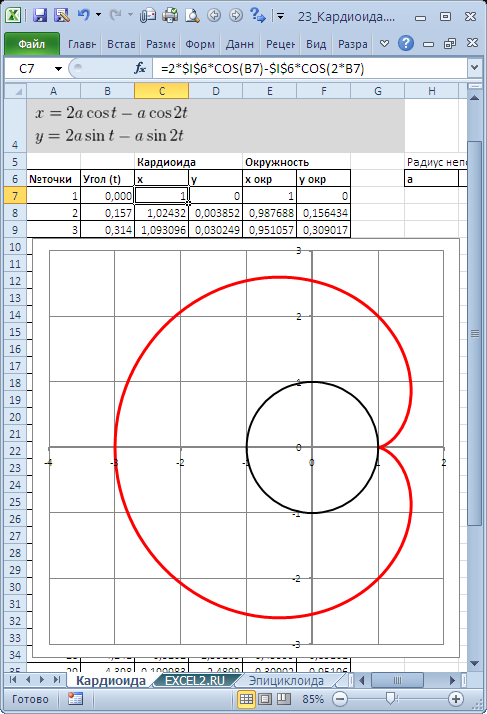
П остроить улитку Паскаля по следующим данным:
— в столбце А – значения a от 0 до 360 с шагом 10 (угол в градусах)
— в столбце В – значения t = a * π/180 (угол в радианах)
— в столбце С – значения p = cos ( t )–0,5
— в столбце D – значения x = p * cos ( t )
— в столбце Е – значения у = p * sin ( t )
— выделить значения в столбцах D и E и построить диаграмму
(тип: точечная с гладкими кривыми )
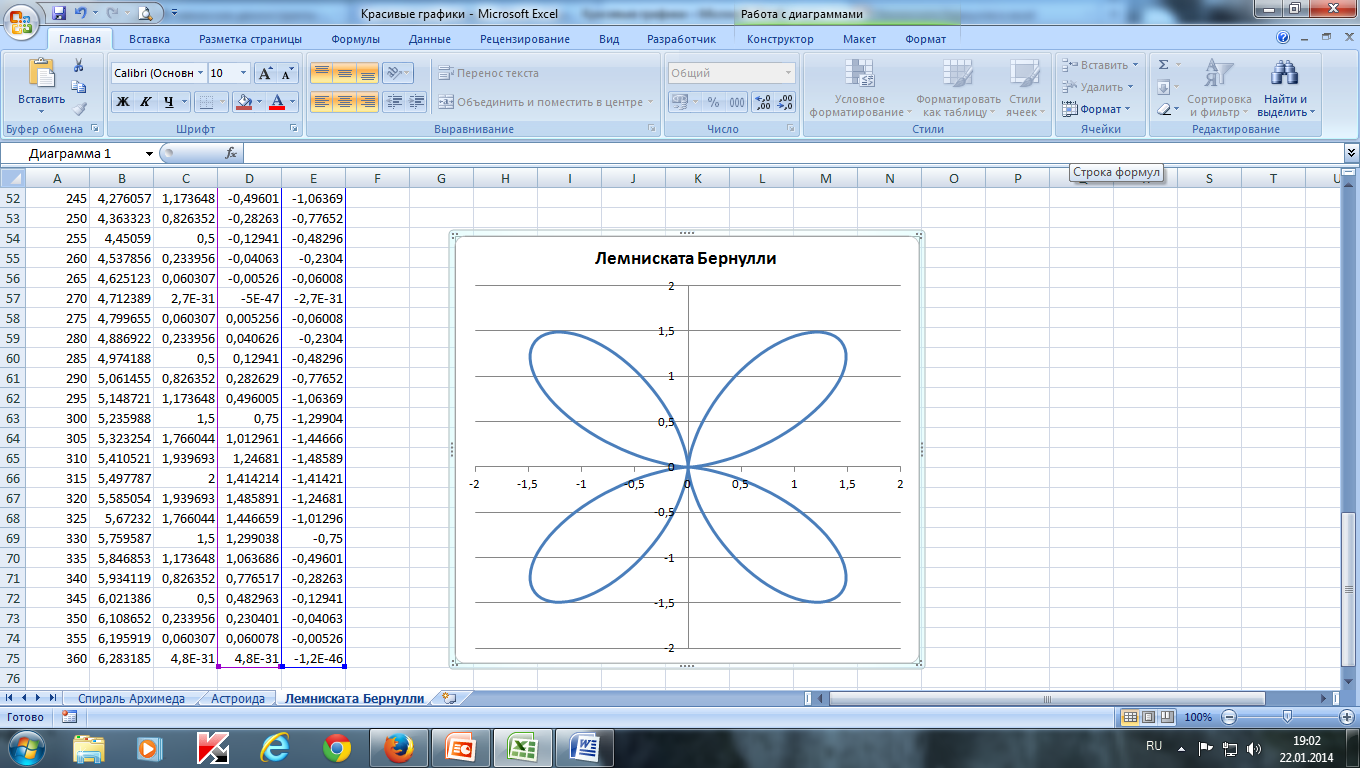
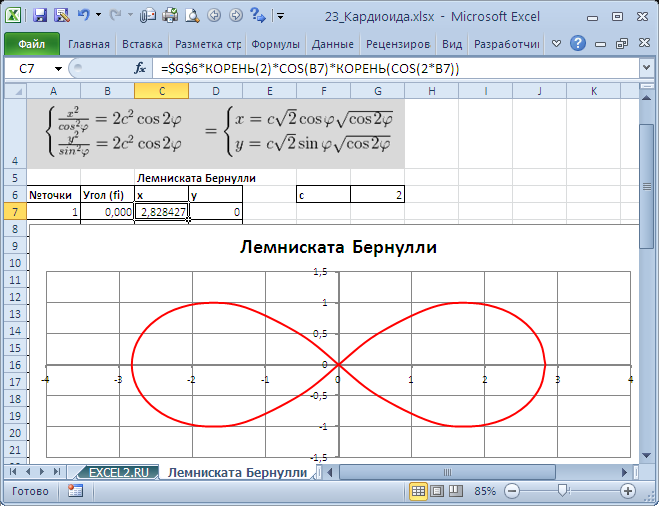
Построить лемнискату Бернулли по следующим данным:
— в столбце А – значения a от 0 до 360 с шагом 10 (угол в градусах)
— в столбце В – значения t = a * π/180 (угол в радианах)
— в столбце С – значения r = 2* sin (2* t ) 2
— в столбце D – значения x = r * cos ( t )
— в столбце E – значения y = r * sin ( t )
— выделить значения в столбцах D и E и построить диаграмму
(тип: точечная с гладкими кривыми )
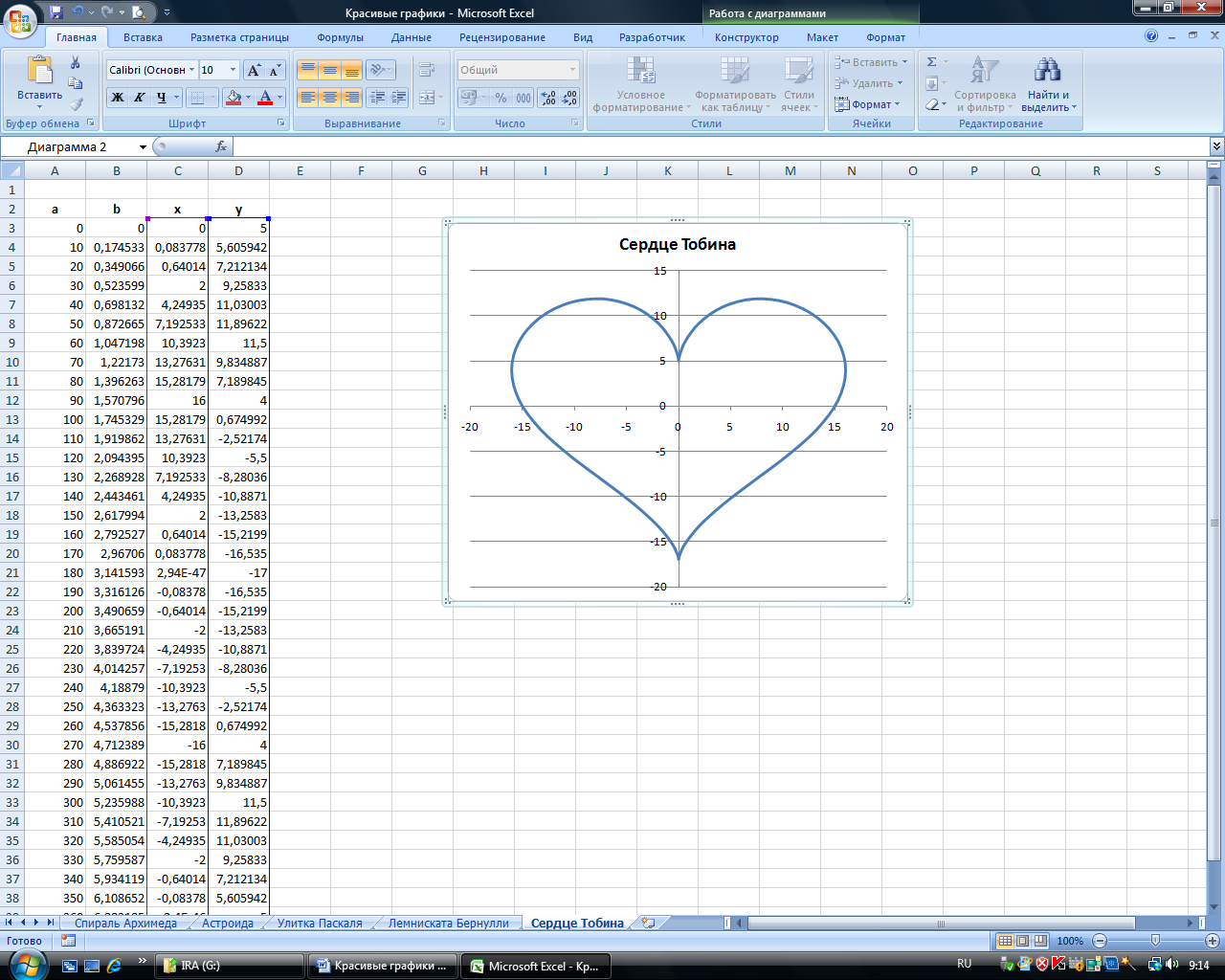
П остроить график в форме сердца по следующим данным:
— в столбце А – значения a от 0 до 360 с шагом 10 (угол в градусах)
— в столбце В – значения t = a * π/180 (угол в радианах)
— в столбце С – значения x = 16*( sin ( t )) 3
— в столбце D – значения у =13* cos ( t )–5* cos (2* t )–2* cos (3* t )– cos (4* t )
— выделить значения в столбцах C и D и построить диаграмму
(тип: точечная с гладкими кривыми )
Источник
Практическая работа в MS Excel «Графики»

Работа в формате .docx
Просмотр содержимого документа
«Практическая работа в MS Excel «Графики»»
Практическая работа «Красивые графики функций»
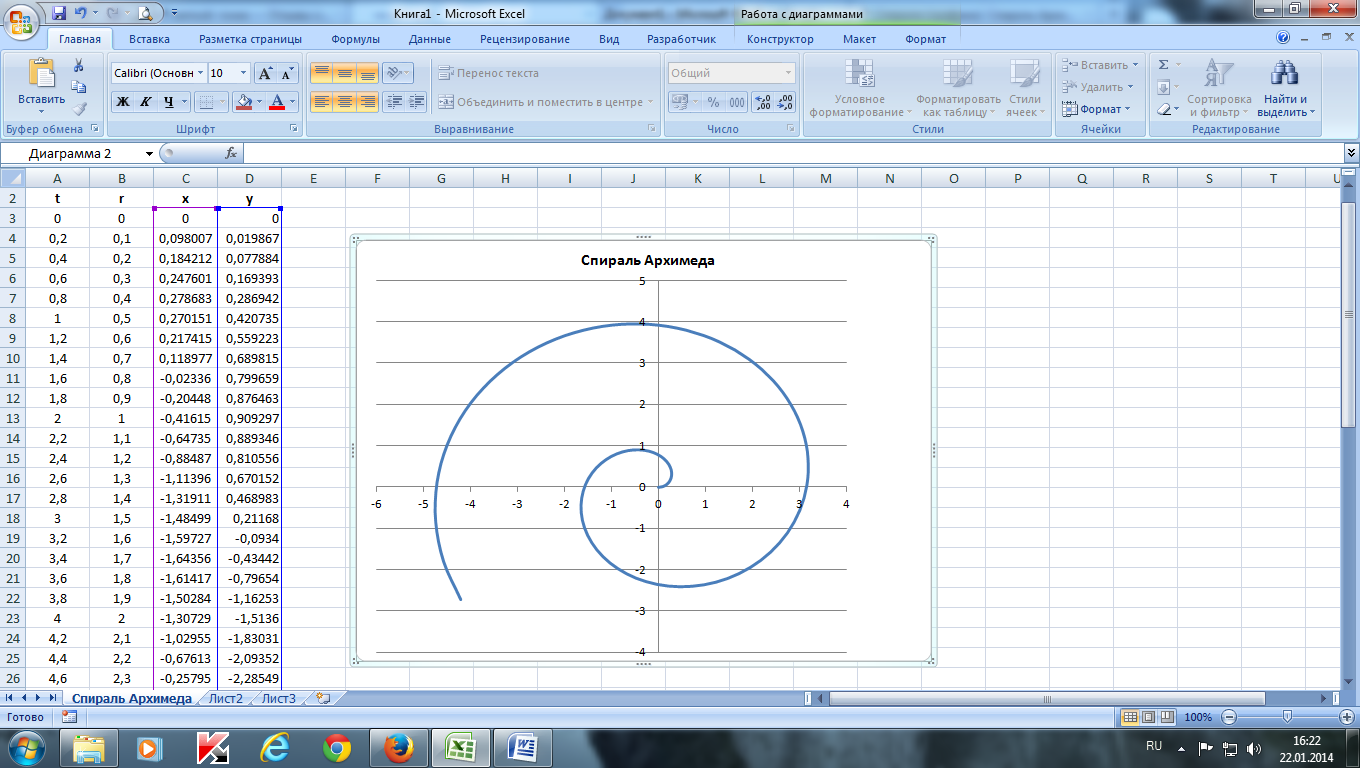
Построить спираль Архимеда по следующим данным:
— в столбце А – значения угла t в радианах от 0 до 10 с шагом 0,2
— в столбце В – значения r = 0,5*t
— в столбце С – значения х = r*cos(t)
— в столбце D – значения y = r*sin(t)
— выделить значения в столбцах С и D и построить диаграмму
(тип: точечная с гладкими кривыми)
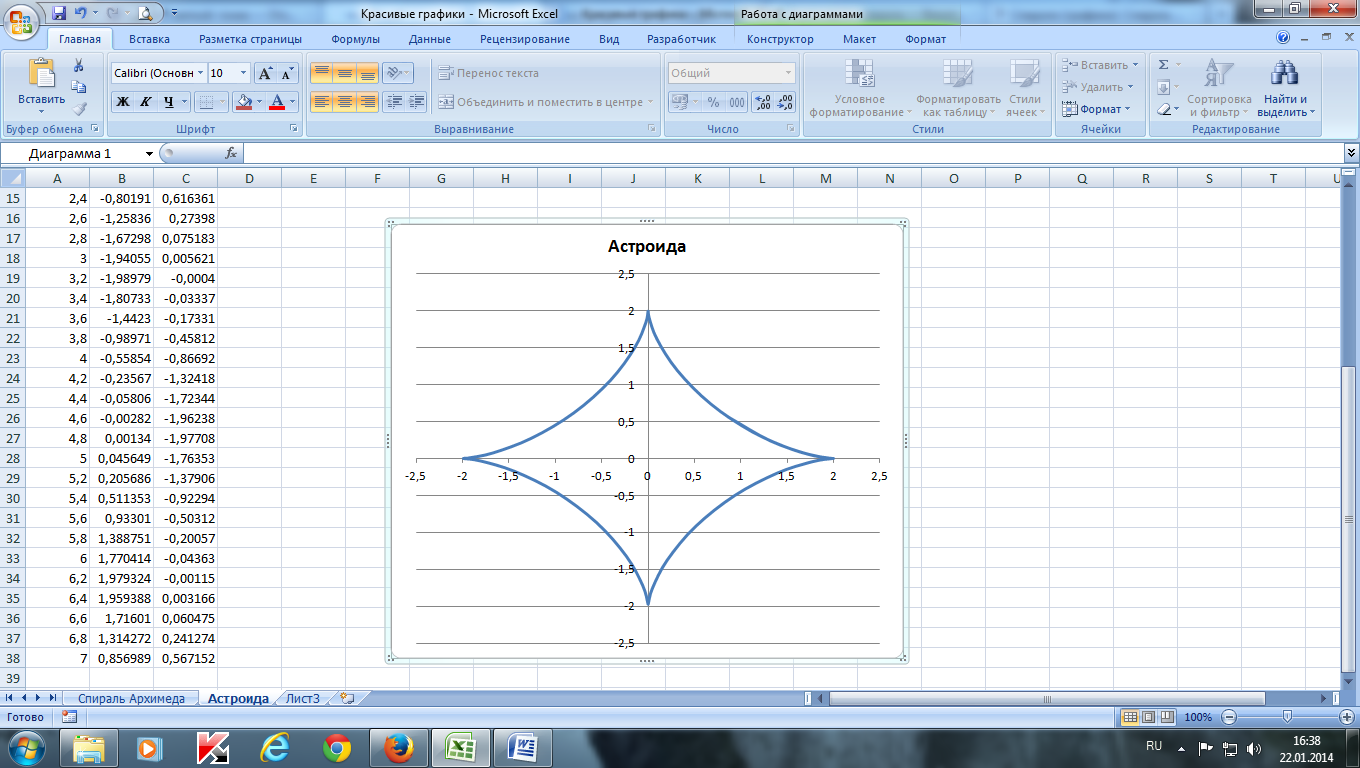
Построить астроиду по следующим данным:
— в столбце А – значения угла t в радианах от 0 до 7 с шагом 0,2
— в столбце В – значения х = 2*(cos (t)) 3
— в столбце С – значения y = 2*(sin (t)) 3
— выделить значения в столбцах B и С и построить диаграмму
(тип: точечная с гладкими кривыми)
Построить улитку Паскаля по следующим данным:
— в столбце А – значения a от 0 до 360 с шагом 10 (угол в градусах)
— в столбце В – значения t = a*π/180 (угол в радианах)
— в столбце С – значения p = cos(t)–0,5
— в столбце D – значения x = p*cos(t)
— в столбце Е – значения у = p*sin(t)
— выделить значения в столбцах D и E и построить диаграмму
(тип: точечная с гладкими кривыми)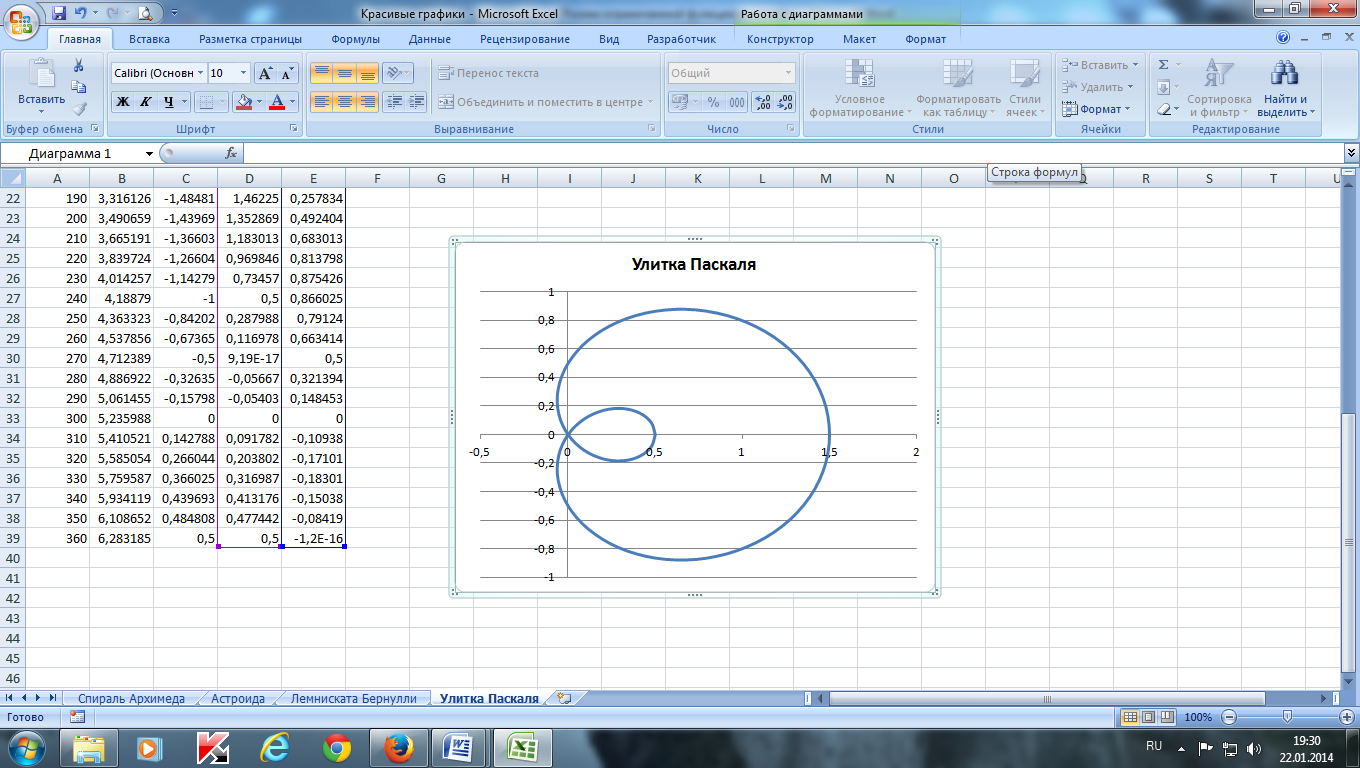
Построить лемнискату Бернулли по следующим данным:
— в столбце А – значения a от 0 до 360 с шагом 10 (угол в градусах)
— в столбце В – значения t = a*π/180 (угол в радианах)
— в столбце С – значения r = 2*sin(2*t) 2
— в столбце D – значения x = r*cos(t)
— в столбце E – значения y = r*sin(t)
— выделить значения в столбцах D и E и построить диаграмму
(тип: точечная с гладкими кривыми)
Построить график в форме сердца по следующим данным:
— в столбце А – значения a от 0 до 360 с шагом 10 (угол в градусах)
— в столбце В – значения t = a*π/180 (угол в радианах)
— в столбце С – значения x = 16*(sin(t)) 3
— в столбце D – значения у =13*cos(t)–5*cos(2*t)–2*cos(3*t)–cos(4*t)
— выделить значения в столбцах C и D и построить диаграмму
(тип: точечная с гладкими кривыми)
Источник
Практическая работа в MS EXCEL «Красивые графики»
Практическая работа «Красивые графики функций»
1) Построить спираль Архимеда по следующим данным:
— в столбце А – значения угла t в радианах от 0 до 10 с шагом 0,2
— в столбце В – значения r = 0,5* t
— в столбце С – значения х = r * cos ( t )
— в столбце D – значения y = r * sin ( t )
— выделить значения в столбцах С и D и построить диаграмму
(тип: точечная с гладкими кривыми)
2) Построить астроиду по следующим данным:
— в столбце А – значения угла t в радианах от 0 до 7 с шагом 0,2
— в столбце В – значения х = 2*( cos ( t )) 3
— в столбце С – значения y = 2*( sin ( t )) 3
— выделить значения в столбцах B и С и построить диаграмму
(тип: точечная с гладкими кривыми)
3) 

— в столбце А – значения a от 0 до 360 с шагом 10 (угол в градусах)
— в столбце В – значения t = a * π/180 (угол в радианах)
— в столбце С – значения p = cos ( t )–0,5
— в столбце D – значения x = p * cos ( t )
— в столбце Е – значения у = p * sin ( t )
— выделить значения в столбцах D и E и построить диаграмму
(тип: точечная с гладкими кривыми)
4) Построить лемнискату Бернулли по следующим данным:
— в столбце А – значения a от 0 до 360 с шагом 10 (угол в градусах)
— в столбце В – значения t = a * π/180 (угол в радианах)
— в столбце С – значения r = 2* sin (2* t ) 2
— в столбце D – значения x = r * cos ( t )
— в столбце E – значения y = r * sin ( t )
— выделить значения в столбцах D и E и построить диаграмму
(тип: точечная с гладкими кривыми)
5) 
— в столбце А – значения a от 0 до 360 с шагом 10 (угол в градусах)
— в столбце В – значения t = a * π/180 (угол в радианах)
— в столбце С – значения x = 16*( sin ( t )) 3
— в столбце D – значения у =13* cos ( t )–5* cos (2* t )–2* cos (3* t )– cos (4* t )
— выделить значения в столбцах C и D и построить диаграмму
(тип: точечная с гладкими кривыми)
Источник
Лемниската бернулли уравнение и график в excel
Формула Бернулли в Excel
В этой статье я расскажу о том, как решать задачи на применение формулы Бернулли в Эксель. Разберем формулу, типовые задачи — решим их вручную и в Excel. Вы разберетесь со схемой независимых ипытаний и сможете использовать расчетный файл эксель) для решения своих задач. Удачи!
Схема независимых испытаний
В общем виде схема повторных независимых испытаний записывается в виде задачи:
Пусть производится $n$ опытов, вероятность наступления события $A$ в каждом из которых (вероятность успеха) равна $p$, вероятность ненаступления (неуспеха) — соответственно $q=1-p$. Найти вероятность, что событие $A$ наступит в точности $k$ раз в $n$ опытах.
Эта вероятность вычисляется по формуле Бернулли:
$$ P_n(k)=C_n^k cdot p^k cdot (1-p)^ =C_n^k cdot p^k cdot q^ . qquad(1) $$
Данная схема описывает большой пласт задач по теории вероятностей (от игры в лотерею до испытания приборов на надежность), главное, выделить несколько характерных моментов:
- Опыт повторяется в одинаковых условиях несколько раз. Например, кубик кидается 5 раз, монета подбрасывается 10 раз, проверяется 20 деталей из одной партии, покупается 8 однотипных лотерейных билетов.
- Вероятность наступления события в каждом опыте одинакова. Этот пункт связан с предыдущим, рассматриваются детали, которые могут оказаться с одинаковой вероятностью бракованными или билеты, которые выигрывают с одной и той же вероятностью.
- События в каждом опыте наступают или нет независимо от результатов предыдущих опытов. Кубик падает случайно вне зависимости от того, как упал предыдущий и т.п.
Если эти условия выполнены — мы в условиях схемы Бернулли и можем применять одноименную формулу. Если нет — ищем дальше, ведь классов задач в теории вероятностей существенно больше (и о решении некоторых написано тут): классическая и геометрическая вероятность, формула полной вероятности, сложение и умножение вероятностей, условная вероятность и т.д.
Подробнее про формулу Бернулли и примеры ее применения можно почитать в онлайн-учебнике. Мы же перейдем к вычислению с помощью программы MS Excel.
Формула Бернулли в Эксель
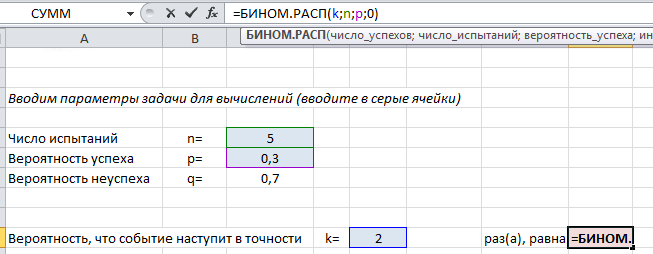
Для вычислений с помощью формулы Бернулли в Excel есть специальная функция =БИНОМ.РАСП() , выдающая определенную вероятность биномиального распределения.
Чтобы найти вероятность $P_n(k)$ в формуле (1) используйте следующий текст =БИНОМ.РАСП($k$;$n$;$p$;0) .
Покажем на примере. На листе подкрашены ячейки (серые), куда можно ввести параметры задачи $n, k, p$ и получить искомую вероятность (текст полностью виден в строке формул вверху).
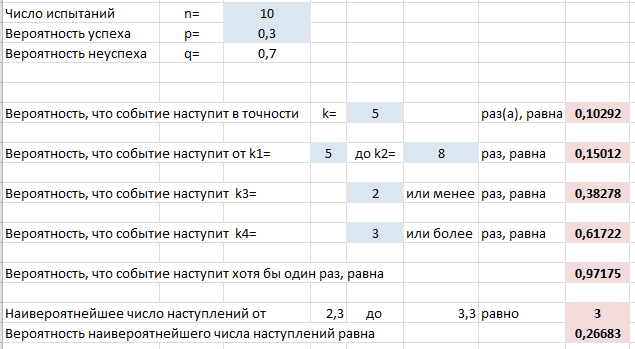
Пример применения формулы на конкретных задачах мы рассмотрим ниже, а пока введем в лист Excel другие нужные формулы, которые пригодятся в решении:
Выше на скриншоте введены формулы для вычисления следующих вероятностей (помимо самих формул для Excel ниже записаны и исходные формулы теории вероятностей):
- Событие произойдет в точности $k$ раз из $n$:
=БИНОМ.РАСП(k;n;p;0)
$$P_n(k)=C_n^k cdot p^k cdot q^ $$ - Событие произойдет от $k_1$ до $k_2$ раз:
=БИНОМ.РАСП(k_2;n;p;1) — БИНОМ.РАСП(k_1;n;p;1) + БИНОМ.РАСП(k_1;n;p;0)
$$P_n(k_1le X le k_2)=sum_ ^ C_n^i cdot p^i cdot q^ $$ - Событие произойдет не более $k_3$ раз:
=БИНОМ.РАСП(k_3;n;p;1)
$$P_n(0le X le k_3)=sum_ ^ C_n^i cdot p^i cdot q^ $$ - Событие произойдет не менее $k_4$ раз:
=1 — БИНОМ.РАСП(k_4;n;p;1) + БИНОМ.РАСП(k_4;n;p;0)
$$P_n(k_4le X le n)=sum_ ^ C_n^i cdot p^i cdot q^ $$ - Событие произойдет хотя бы один раз:
=1-БИНОМ.РАСП(0;n;p;0)
$$P_n( X ge 1)=1-P_n(0)=1-q^ $$ - Наивероятнейшее число наступлений события $m$:
=ОКРУГЛВВЕРХ(n*p-q;0)
$$np-q le m le np+p$$
Вы видите, что в задачах, где нужно складывать несколько вероятностей, мы уже используем функцию вида =БИНОМ.РАСП(k;n;p;1) — так называемая интегральная функция вероятности, которая дает сумму всех вероятностей от 0 до $k$ включительно.
Примеры решений задач
Рассмотрим решение типовых задач.
Пример 1. Произвели 7 выстрелов. Вероятность попадания при одном выстреле равна 0,75. Найти вероятность того, что при этом будет ровно 5 попаданий; от 6 до 7 попаданий в цель.
Решение. Получаем, что в задаче идет речь о повторных независимых испытаниях (выстрелах), всего их $n=7$, вероятность попадания при каждом одинакова и равна $p=0,75$, вероятность промаха $q=1-p=1-0,75=0,25$. Нужно найти, что будет ровно $k=5$ попаданий. Подставляем все в формулу (1) и получаем:
$$ P_7(5)=C_ ^5 cdot 0,75^5 cdot 0,25^2 = 21cdot 0,75^5 cdot 0,25^2= 0,31146. $$
Для вероятности 6 или 7 попаданий суммируем:
$$ P_7(6)+P_7(7)=C_ ^6 cdot 0,75^6 cdot 0,25^1+C_ ^7 cdot 0,75^7 cdot 0,25^0= \ = 7cdot 0,75^6 cdot 0,25+0,75^7=0,44495. $$
А вот это решение в файле эксель:
Пример 2. В семье десять детей. Считая вероятности рождения мальчика и девочки равными между собой, определить вероятность того, что в данной семье:
1. Ровно 2 мальчика
2. От 4 до 5 мальчиков
3. Не более 2 мальчиков
4. Не менее 7 мальчиков
5. Хотя бы один мальчик
Каково наиболее вероятное число мальчиков и девочек в семье?
Решение. Сначала запишем данные задачи: $n=10$ (число детей), $p=0,5$ (вероятность рождения мальчика). Формула Бернулли принимает вид: $$P_ (k)=C_ ^k cdot 0,5^kcdot 0,5^ =C_ ^k cdot 0,5^ $$ Приступим к вычислениям:
$$1. P_ (2)=C_ ^2 cdot 0,5^ = frac cdot 0,5^ approx 0,044.$$ $$2. P_ (4)+P_ (5)=C_ ^4 cdot 0,5^ + C_ ^5 cdot 0,5^ =left( frac + frac right)cdot 0,5^ approx 0,451.$$ $$3. P_ (0)+P_ (1)+P_ (2)=C_ ^0 cdot 0,5^ + C_ ^1 cdot 0,5^ + C_ ^2 cdot 0,5^ =left( 1+10+ frac right)cdot 0,5^ approx 0,055.$$ $$4. P_ (7)+P_ (8)+P_ (9)+P_ (10)=\ = C_ ^7 cdot 0,5^ + C_ ^8 cdot 0,5^ + C_ ^9 cdot 0,5^ + C_ ^10 cdot 0,5^ =\=left(frac + frac + 10 +1right)cdot 0,5^ approx 0,172.$$ $$5. P_ (ge 1)=1-P_ (0)=1-C_ ^0 cdot 0,5^ = 1- 0,5^ approx 0,999.$$
Наивероятнейшее число мальчиков найдем из неравенства:
$$ 10 cdot 0,5 — 0,5 le m le 10 cdot 0,5 + 0,5, \ 4,5 le m le 5,5,\ m=5. $$
Наивероятнейшее число — это 5 мальчиков и соответственно 5 девочек (что очевидно и по здравому смыслу, раз их рождения вероятность одинакова).
Проведем эти же расчеты в нашем шаблоне эксель, вводя данные задачи в серые ячейки:
Видно, что ответы совпадают.
Пример 3. Вероятность выигрыша по одному лотерейному билету равна 0,3. Куплено 8 билетов. Найти вероятность того, что а) хотя бы один билет выигрышный; б) менее трех билетов выигрышные. Какое наиболее вероятное число выигрышных билетов?
Решение. Полное решение этой задачи можно найти тут, а мы сразу введем данные в Эксель и получим ответы: а) 0,94235; б) 0,55177; в) 2 билета. И они совпадут (с точностью до округления) с ответами ручного решения.
Решайте свои задачи и советуйте наш сайт друзьям. Удачи!
Плоские алгебраические кривые в EXCEL
history 16 апреля 2015 г.
- Группы статей
- Диаграммы и графики
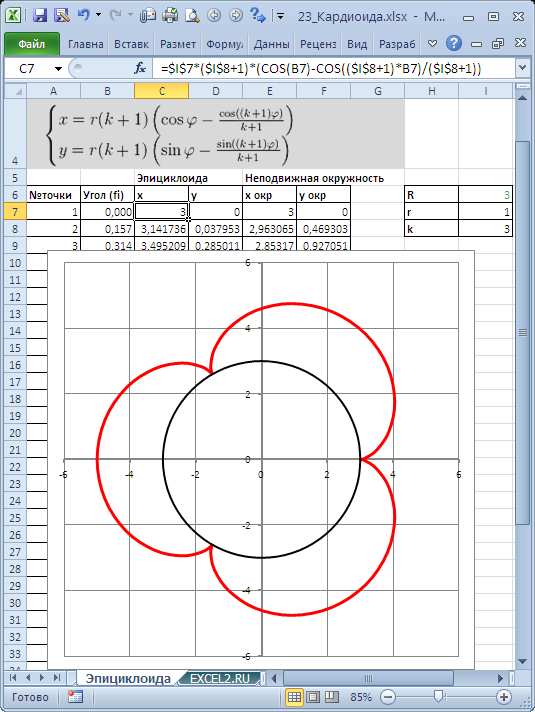
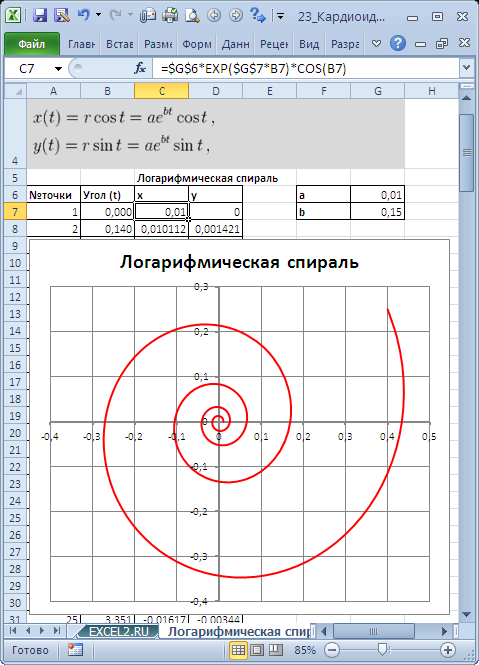
Построим в MS EXCEL несколько плоских алгебраических кривых: кардиоиду, эпициклоиду, логарифмическую спираль и лемнискату Бернулли.
Кривые будем строить с помощью уравнений в параметрической форме, где х и y зависят от одного парамеметра t. Например, для кардиоиды запишем уравнения в виде (см. файл примера ):
Для построения использован тип диаграммы Точечная с гладкими кривыми.
В статье Эллипс и окружность в MS EXCEL построены окружность и эллипс.
СОВЕТ : Для начинающих пользователей EXCEL советуем прочитать статью Основы построения диаграмм в MS EXCEL , в которой рассказывается о базовых настройках диаграмм, а также статью об основных типах диаграмм .
Разработка урока «Красивые графики. Построение графиков функций в полярной системе координат в электронных таблицах Excel»
Практическая работа «Красивые графики функций»
Построить спираль Архимеда по следующим данным:
— в столбце А – значения угла t в радианах от 0 до 10 с шагом 0,2
— в столбце В – значения r = 0,5* t
— в столбце С – значения х = r * cos ( t )
— в столбце D – значения y = r * sin ( t )
— выделить значения в столбцах С и D и построить диаграмму
(тип: точечная с гладкими кривыми )
Построить астроиду по следующим данным:
— в столбце А – значения угла t в радианах от 0 до 7 с шагом 0,2
— в столбце В – значения х = 2*( cos ( t )) 3
— в столбце С – значения y = 2*( sin ( t )) 3
— выделить значения в столбцах B и С и построить диаграмму
(тип: точечная с гладкими кривыми )
П остроить улитку Паскаля по следующим данным:
— в столбце А – значения a от 0 до 360 с шагом 10 (угол в градусах)
— в столбце В – значения t = a * π/180 (угол в радианах)
— в столбце С – значения p = cos ( t )–0,5
— в столбце D – значения x = p * cos ( t )
— в столбце Е – значения у = p * sin ( t )
— выделить значения в столбцах D и E и построить диаграмму
(тип: точечная с гладкими кривыми )
Построить лемнискату Бернулли по следующим данным:
— в столбце А – значения a от 0 до 360 с шагом 10 (угол в градусах)
— в столбце В – значения t = a * π/180 (угол в радианах)
— в столбце С – значения r = 2* sin (2* t ) 2
— в столбце D – значения x = r * cos ( t )
— в столбце E – значения y = r * sin ( t )
— выделить значения в столбцах D и E и построить диаграмму
(тип: точечная с гладкими кривыми )
П остроить график в форме сердца по следующим данным:
— в столбце А – значения a от 0 до 360 с шагом 10 (угол в градусах)
— в столбце В – значения t = a * π/180 (угол в радианах)
— в столбце С – значения x = 16*( sin ( t )) 3
— в столбце D – значения у =13* cos ( t )–5* cos (2* t )–2* cos (3* t )– cos (4* t )
— выделить значения в столбцах C и D и построить диаграмму
(тип: точечная с гладкими кривыми )
Источник
При работе с вычислениям в программе Excel иногда требуется узнать результат функции, значения которой находятся за рамками известной области (например для прогнозирования). Рассмотрим как это сделать с помощью нескольких способов.
Метод экстраполяции позволяет найти результат функции, значения которой могут находится за пределами конкретных рамок. Зачастую это используется в прогнозировании различных экономических процессов. В этом методе можно работать как с значениями в таблицах так и в работе с данными в графиках.
Имеется таблица с конкретным диапазоном аргументов от 5 до 50, которые относятся к функции (f(x)). В данном примере надо вычислить результат для числа, которое находится за рамкой изветсных аргументов. В данном случае это число 55. Чтобы это сделать надо работать с функцией ПРЕДСКАЗ.
Выбираем ту ячейку, которая в конечном итоге будет показывать результат. После этого нужно нажать на кнопку в строке формул, которая отвечает за вставку функций.
Появится новое окно, в нём нужно выбрать среди категорий именно категорию «Статистические» и после этого ниже в списке надо выбрать «ПРЕДСКАЗ» и в конце подтвердить действие.
В конечном итоге в нужной ячейке появится результат, который относится к числу 55.
Пример работы с данными в графиках линией тренда
Для начала важно построить правильный график, предварительно выделив таблицу, с которой будут проводится вычисления. Далее переходим в раздел «Вставка» в верхней панели программы Excel и выбираем в этом разделе пункт «Диаграммы» и кликаем на кнопку обозначающую построение графика, после этого нажимаем на самый оптимальный для вас график.
Далее будет отображен график по выбранными ранее данным. Важное примечание : нужно удалить в нём линию обозначающую аргумент (указана стрелкой на изображении).
После этих действий, есть также горизонтальная шкала, но в нам надо чтобы было отображены данные об аргументах. Чтобы именно эти данные были показано, нажимаем по графику ПКМ и в контекстном меню кликаем на «Выбрать данные».
Появится новое окно, в нём кликаем соответствующую кнопку для изменения данных.
Далее кликаем на «Диапазон подписей оси» и после этого нужно выделить столбец значений, которые надо ЛКМ выделить числа, которые нам нужны, в данном примере это столбец с значениями x, после этого подтверждаем действие. Также не забудьте подтвердить действие в окне выбора источника данных, которое было открыто ранее.
Чтобы сделать корректное отображение линии тренда, вновь нужно перейти с соответствующий пункт как на изображении выше, но в списке нажать на последний вариант, который позволит задать дополнительные параметры в линии тренда.
Далее будет открыто новое окно, в котором можно задать параметры линии тренда. Ищем в окне настройки прогноза, и задаем число 1 (период), так как пять единиц значений = одному периоду, это было сделано так как значение за пределами 50 возьмем вновь 55.
Результатом будет удлинение длины графика соответственно к параметрам линии тренда.
Как построить модель в Excel — Задача №3. Расчёт параметров регрессии и корреляции с помощью Excel — Как в офисе.
При этом количество столбцов аргумента массив1 должно быть таким же, как количество строк аргумента массив2, и оба массива должны содержать только числа. Результатом является массив с таким же числом строк, как массив1 и с таким же числом столбцов, как массив2.
Мнение эксперта
Витальева Анжела, консультант по работе с офисными программами
Со всеми вопросами обращайтесь ко мне!
Задать вопрос эксперту
Для массива А1 С3, состоящего из трёх строк и трёх столбцов матрица размером 3 3 , определитель вычисляется следующим образом. Если же вам нужны дополнительные объяснения, обращайтесь ко мне!
Обзор встроенных функции табличного процессора Microsoft Excel, особенности их практического использования. Создание таблиц и их заполнение данными, построение графиков. Применение математических формул для выполнения запросов пакетов прикладных программ.
Как построить кардиоиду в excel
- Выделяем ячейку, в которой будет отображаться результат проведенных вычислений. Кликаем по значку «Вставить функцию», который размещен у строки формул.
- Запускается окно Мастера функций. Выполняем переход в категорию «Статистические» или «Полный алфавитный перечень». В открывшемся списке производим поиск наименования «ПРЕДСКАЗ». Найдя его, выделяем, а затем щелкаем по кнопке «OK» в нижней части окна.
- Мы перемещаемся к окну аргументов вышеуказанной функции. Она имеет всего три аргумента и соответствующее количество полей для их внесения.
Для расчета в таблицах часто требуется значения одного столбца разделить на данные второй колонки. Конечно, можно делить значение каждой ячейки тем способом, который указан выше, но можно эту процедуру сделать гораздо быстрее.
Параметрические представления
Если объяснять просто, то параметрическое уравнение (представление) — это ещё один способ выражения функции. Обычно они используются в задачах или уравнениях кинематики (задачах основ физики) для описания таких свойств, как траектория ракеты или орбита планеты, вращающейся вокруг массивного объекта.
Давайте рассмотрим следующую функцию, которая создаёт параболу.
Чтобы получить эту функцию, мы можем разложить (при помощи вузовской алгебры) вышеприведённое уравнение, изолировав X и Y и сгенерировав отдельный параметр, входящими данными которого является t, как показано в функции ниже.
По сути, если мы создадим таблицу этих двух интерпретаций функции, то они будут давать одинаковые ответы.
Обычная функция (сверху) и параметрическая функция (снизу)
По сути, когда мы используем две функции для генерирования координат X и Y, то можем, как вы увидите ниже, создать огромное количество графики, примеры которой представлены в этом посте. (Помните, что это всего один набор уравнений).
А теперь самое интересное — ниже я опишу процесс, благодаря которому сгенерировал все представленные в посте изображения.
Экстраполяция в Excel (Эксель); Компьютерная помощь
Активируется окошко Мастера функций. В категории «Математические» или «Полный алфавитный перечень» ищем наименование «ПРЕДСКАЗ». После того, как соответствующее значение найдено, выделяем его и щелкаем по кнопке «OK».
Мнение эксперта
Витальева Анжела, консультант по работе с офисными программами
Со всеми вопросами обращайтесь ко мне!
Задать вопрос эксперту
Можно сделать даже проще, не запуская Мастер функций , а просто с клавиатуры вбить в пустую ячейку значение Н Д без кавычек. Если же вам нужны дополнительные объяснения, обращайтесь ко мне!
Методом (половинного деления или итерации)(нужно выбрать правильный) найти корень уравнения (x — 3) / (x ^ 2 + 2) = 0 расположенный на отрезке [ — 1 ; 4] с абсолютной погрешностью 10 ^ — 4 программа паскальи еще нужна блок схема.
Помогите пожалуйста сделать домашнее задание в паскале, экселе и блок — схему? Информатика
Но, что делать, если нужно разделить столбец на содержимое одной ячейки. Ведь по принципу относительности ссылок координаты делимого и делителя будут смещаться. Нам же нужно сделать адрес ячейки с делителем фиксированным.


 Сообщение было отмечено chumich как решение
Сообщение было отмечено chumich как решение



 _xlfn ……
_xlfn ……