Содержание
- Статистические функции
- МАКС
- МИН
- СРЗНАЧ
- СРЗНАЧЕСЛИ
- МОДА.ОДН
- МЕДИАНА
- СТАНДОТКЛОН
- НАИБОЛЬШИЙ
- НАИМЕНЬШИЙ
- РАНГ.СР
- Вопросы и ответы
Статистическая обработка данных – это сбор, упорядочивание, обобщение и анализ информации с возможностью определения тенденции и прогноза по изучаемому явлению. В Excel есть огромное количество инструментов, которые помогают проводить исследования в данной области. Последние версии этой программы в плане возможностей практически ничем не уступают специализированным приложениям в области статистики. Главными инструментами для выполнения расчетов и анализа являются функции. Давайте изучим общие особенности работы с ними, а также подробнее остановимся на отдельных наиболее полезных инструментах.
Статистические функции
Как и любые другие функции в Экселе, статистические функции оперируют аргументами, которые могут иметь вид постоянных чисел, ссылок на ячейки или массивы.
Выражения можно вводить вручную в определенную ячейку или в строку формул, если хорошо знать синтаксис конкретного из них. Но намного удобнее воспользоваться специальным окном аргументов, которое содержит подсказки и уже готовые поля для ввода данных. Перейти в окно аргумента статистических выражений можно через «Мастер функций» или с помощью кнопок «Библиотеки функций» на ленте.
Запустить Мастер функций можно тремя способами:
- Кликнуть по пиктограмме «Вставить функцию» слева от строки формул.
- Находясь во вкладке «Формулы», кликнуть на ленте по кнопке «Вставить функцию» в блоке инструментов «Библиотека функций».
- Набрать на клавиатуре сочетание клавиш Shift+F3.
При выполнении любого из вышеперечисленных вариантов откроется окно «Мастера функций».
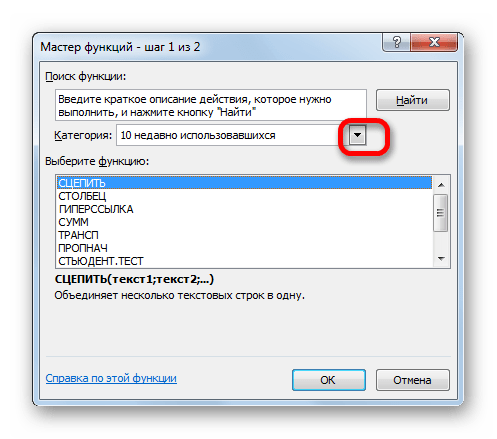
Затем нужно кликнуть по полю «Категория» и выбрать значение «Статистические».
После этого откроется список статистических выражений. Всего их насчитывается более сотни. Чтобы перейти в окно аргументов любого из них, нужно просто выделить его и нажать на кнопку «OK».
Для того, чтобы перейти к нужным нам элементам через ленту, перемещаемся во вкладку «Формулы». В группе инструментов на ленте «Библиотека функций» кликаем по кнопке «Другие функции». В открывшемся списке выбираем категорию «Статистические». Откроется перечень доступных элементов нужной нам направленности. Для перехода в окно аргументов достаточно кликнуть по одному из них.
Урок: Мастер функций в Excel
МАКС
Оператор МАКС предназначен для определения максимального числа из выборки. Он имеет следующий синтаксис:
=МАКС(число1;число2;…)
В поля аргументов нужно ввести диапазоны ячеек, в которых находится числовой ряд. Наибольшее число из него эта формула выводит в ту ячейку, в которой находится сама.
МИН
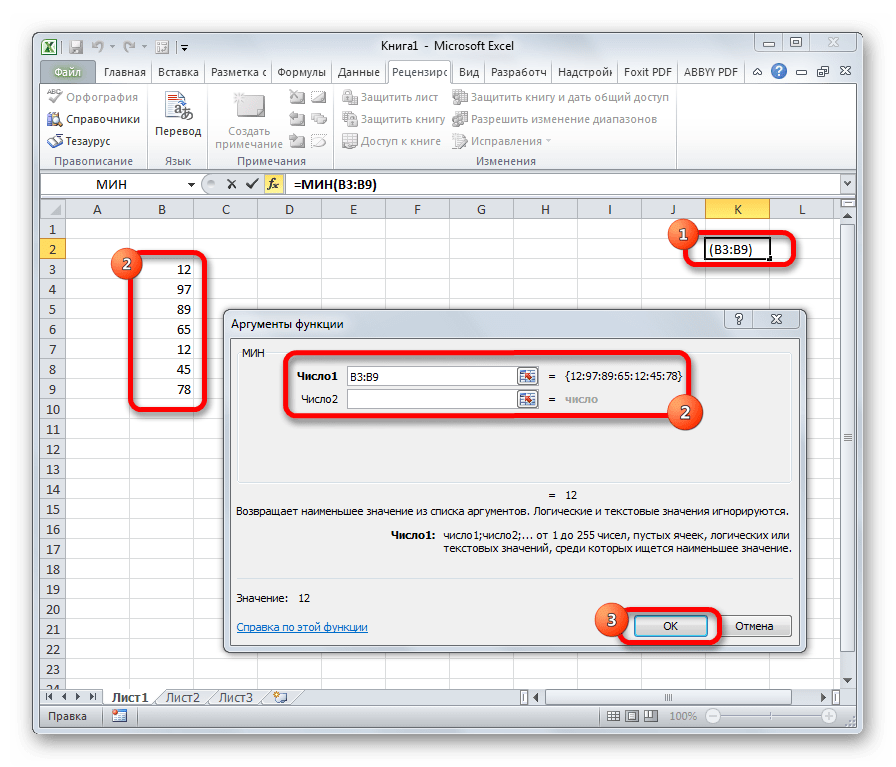
По названию функции МИН понятно, что её задачи прямо противоположны предыдущей формуле – она ищет из множества чисел наименьшее и выводит его в заданную ячейку. Имеет такой синтаксис:
=МИН(число1;число2;…)
СРЗНАЧ
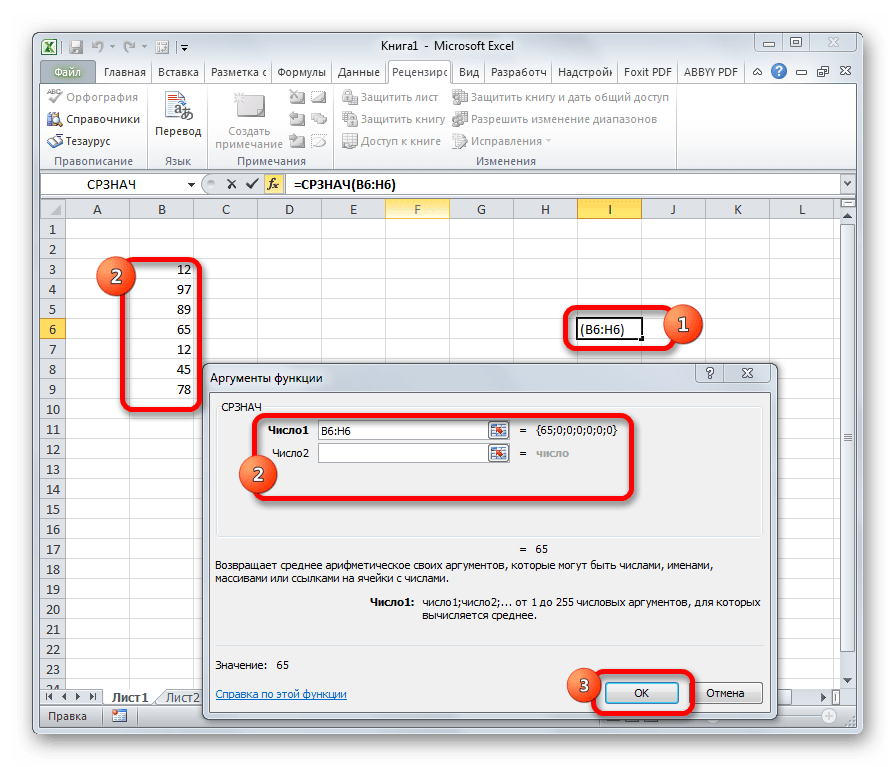
Функция СРЗНАЧ ищет число в указанном диапазоне, которое ближе всего находится к среднему арифметическому значению. Результат этого расчета выводится в отдельную ячейку, в которой и содержится формула. Шаблон у неё следующий:
=СРЗНАЧ(число1;число2;…)
СРЗНАЧЕСЛИ
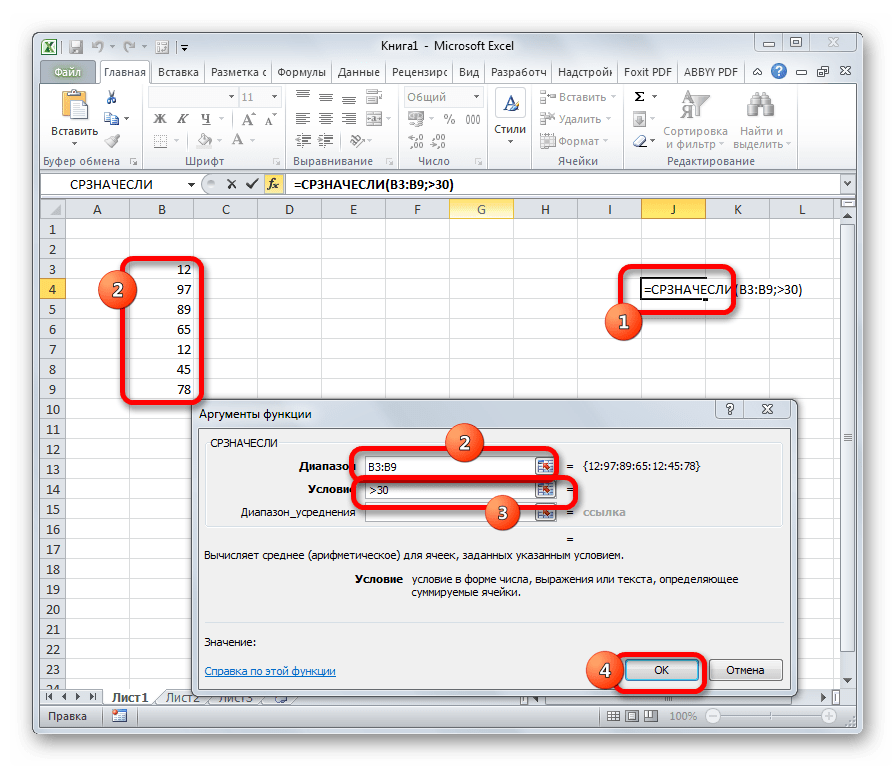
Функция СРЗНАЧЕСЛИ имеет те же задачи, что и предыдущая, но в ней существует возможность задать дополнительное условие. Например, больше, меньше, не равно определенному числу. Оно задается в отдельном поле для аргумента. Кроме того, в качестве необязательного аргумента может быть добавлен диапазон усреднения. Синтаксис следующий:
=СРЗНАЧЕСЛИ(число1;число2;…;условие;[диапазон_усреднения])
МОДА.ОДН
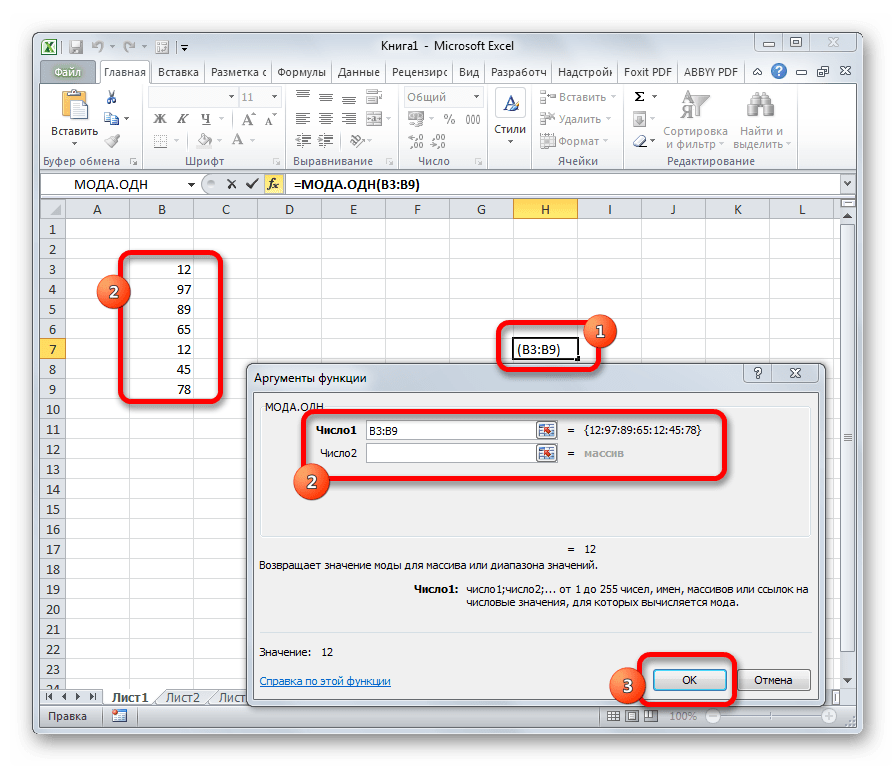
Формула МОДА.ОДН выводит в ячейку то число из набора, которое встречается чаще всего. В старых версиях Эксель существовала функция МОДА, но в более поздних она была разбита на две: МОДА.ОДН (для отдельных чисел) и МОДА.НСК(для массивов). Впрочем, старый вариант тоже остался в отдельной группе, в которой собраны элементы из прошлых версий программы для обеспечения совместимости документов.
=МОДА.ОДН(число1;число2;…)
=МОДА.НСК(число1;число2;…)
МЕДИАНА
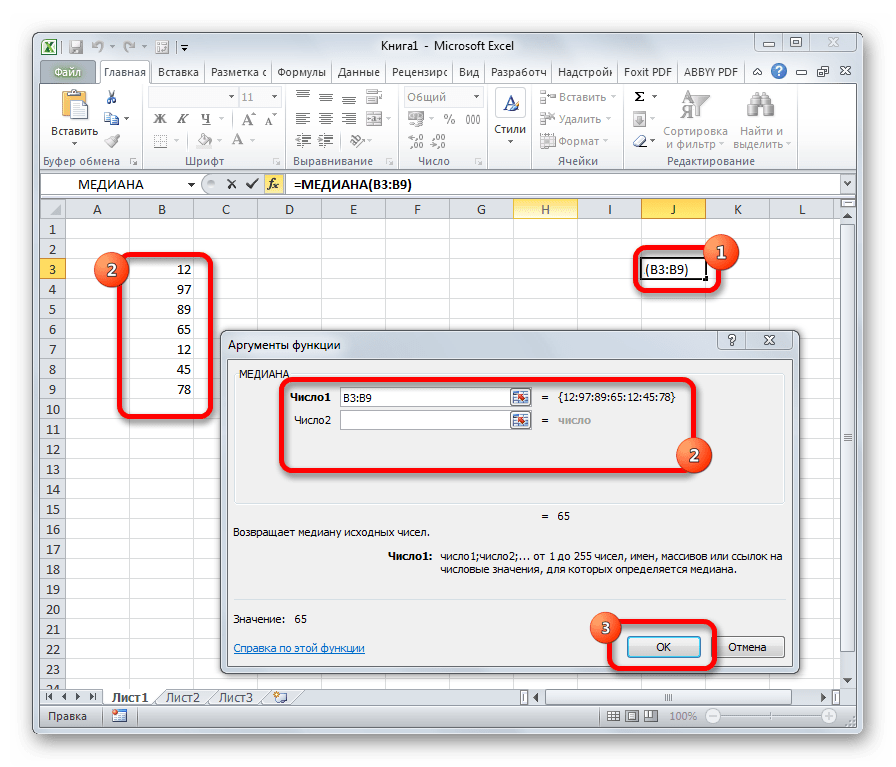
Оператор МЕДИАНА определяет среднее значение в диапазоне чисел. То есть, устанавливает не среднее арифметическое, а просто среднюю величину между наибольшим и наименьшим числом области значений. Синтаксис выглядит так:
=МЕДИАНА(число1;число2;…)
СТАНДОТКЛОН
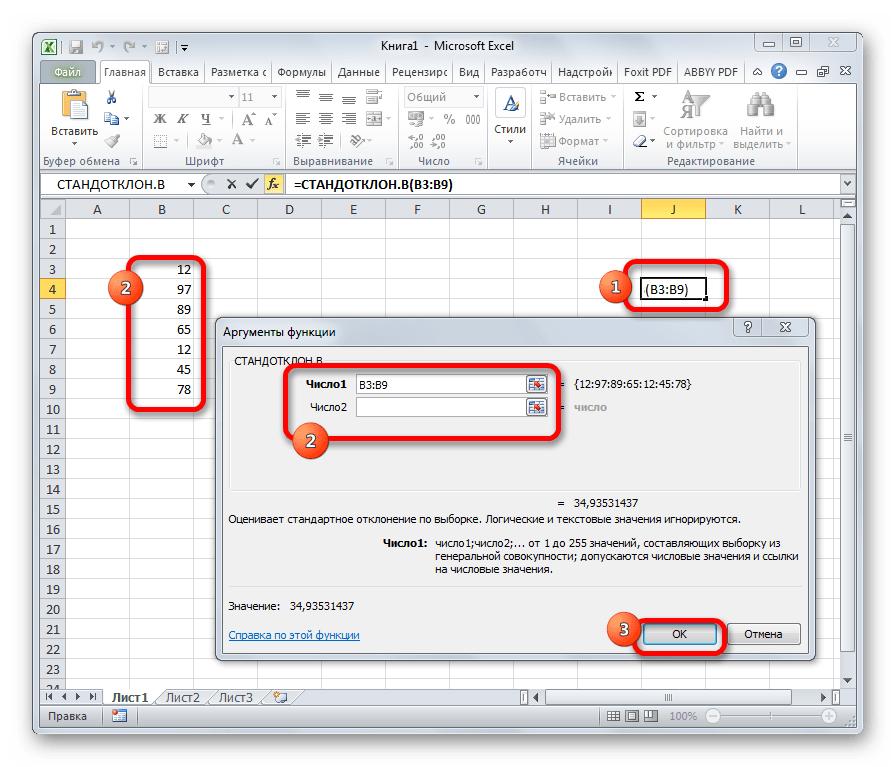
Формула СТАНДОТКЛОН так же, как и МОДА является пережитком старых версий программы. Сейчас используются современные её подвиды – СТАНДОТКЛОН.В и СТАНДОТКЛОН.Г. Первая из них предназначена для вычисления стандартного отклонения выборки, а вторая – генеральной совокупности. Данные функции используются также для расчета среднего квадратичного отклонения. Синтаксис их следующий:
=СТАНДОТКЛОН.В(число1;число2;…)
=СТАНДОТКЛОН.Г(число1;число2;…)
Урок: Формула среднего квадратичного отклонения в Excel
НАИБОЛЬШИЙ
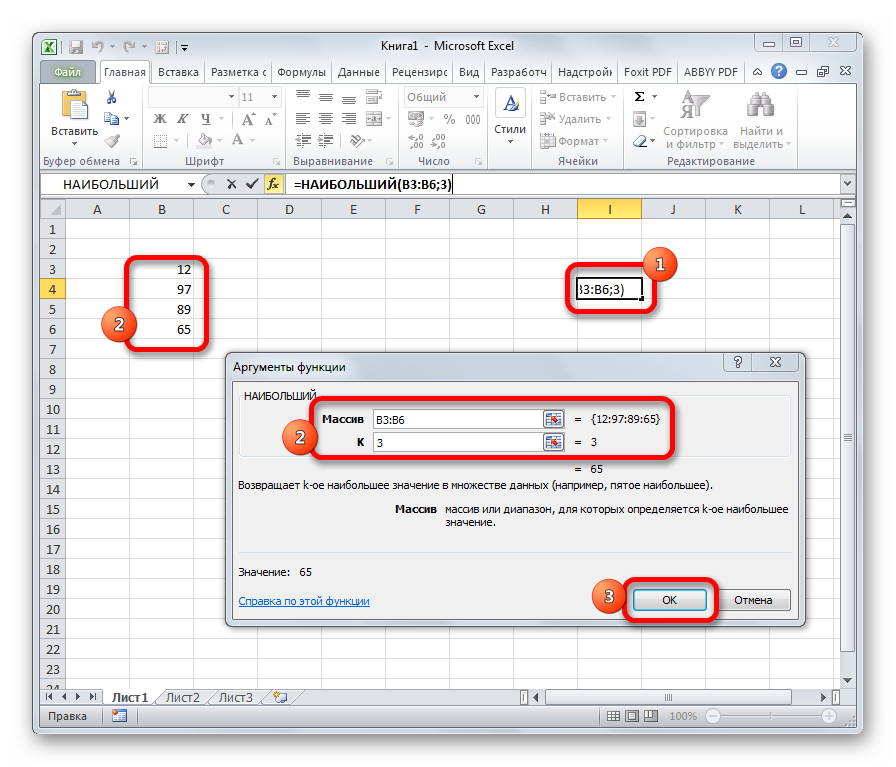
Данный оператор показывает в выбранной ячейке указанное в порядке убывания число из совокупности. То есть, если мы имеем совокупность 12,97,89,65, а аргументом позиции укажем 3, то функция в ячейку вернет третье по величине число. В данном случае, это 65. Синтаксис оператора такой:
=НАИБОЛЬШИЙ(массив;k)
В данном случае, k — это порядковый номер величины.
НАИМЕНЬШИЙ
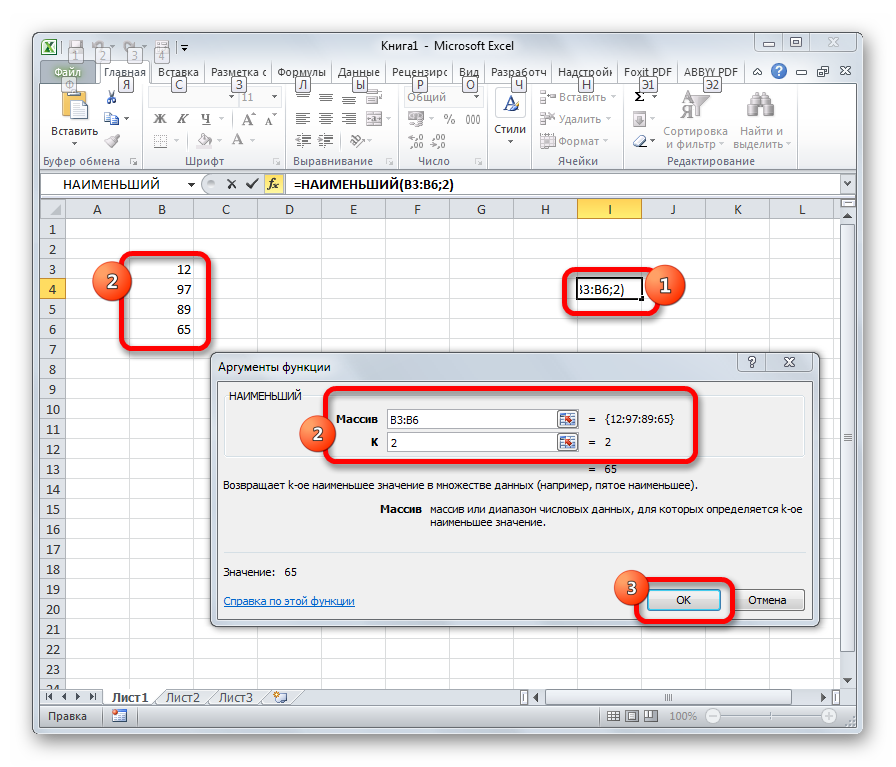
Данная функция является зеркальным отражением предыдущего оператора. В ней также вторым аргументом является порядковый номер числа. Вот только в данном случае порядок считается от меньшего. Синтаксис такой:
=НАИМЕНЬШИЙ(массив;k)
РАНГ.СР
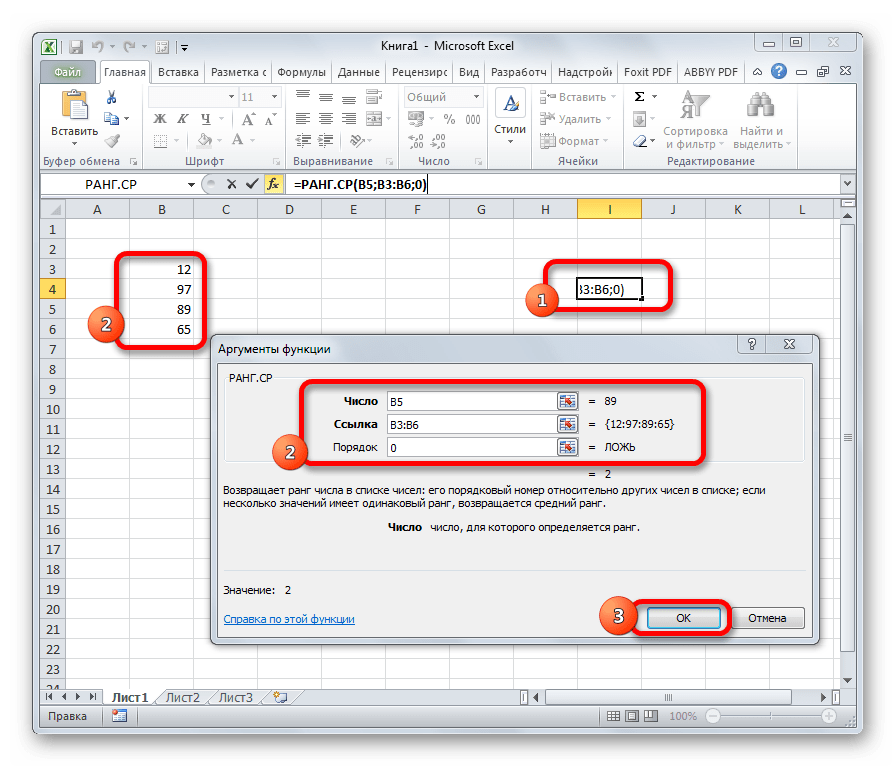
Эта функция имеет действие, обратное предыдущим. В указанную ячейку она выдает порядковый номер конкретного числа в выборке по условию, которое указано в отдельном аргументе. Это может быть порядок по возрастанию или по убыванию. Последний установлен по умолчанию, если поле «Порядок» оставить пустым или поставить туда цифру 0. Синтаксис этого выражения выглядит следующим образом:
=РАНГ.СР(число;массив;порядок)
Выше были описаны только самые популярные и востребованные статистические функции в Экселе. На самом деле их в разы больше. Тем не менее, основной принцип действий у них похожий: обработка массива данных и возврат в указанную ячейку результата вычислительных действий.
Чтобы просмотреть более подробные сведения о функции, щелкните ее название в первом столбце.
Примечание: Маркер версии обозначает версию Excel, в которой она впервые появилась. В более ранних версиях эта функция отсутствует. Например, маркер версии 2013 означает, что данная функция доступна в выпуске Excel 2013 и всех последующих версиях.
|
Функция |
Описание |
|
СРОТКЛ |
Возвращает среднее арифметическое абсолютных значений отклонений точек данных от среднего. |
|
СРЗНАЧ |
Возвращает среднее арифметическое аргументов. |
|
СРЗНАЧА |
Возвращает среднее арифметическое аргументов, включая числа, текст и логические значения. |
|
СРЗНАЧЕСЛИ |
Возвращает среднее значение (среднее арифметическое) всех ячеек в диапазоне, которые удовлетворяют заданному условию. |
|
СРЗНАЧЕСЛИМН |
Возвращает среднее значение (среднее арифметическое) всех ячеек, которые удовлетворяют нескольким условиям. |
|
БЕТА.РАСП |
Возвращает интегральную функцию бета-распределения. |
|
БЕТА.ОБР |
Возвращает обратную интегральную функцию указанного бета-распределения. |
|
БИНОМ.РАСП |
Возвращает отдельное значение вероятности биномиального распределения. |
|
БИНОМ.РАСП.ДИАП |
Возвращает вероятность пробного результата с помощью биномиального распределения. |
|
БИНОМ.ОБР |
Возвращает наименьшее значение, для которого интегральное биномиальное распределение меньше заданного значения или равно ему. |
|
ХИ2.РАСП |
Возвращает интегральную функцию плотности бета-вероятности. |
|
ХИ2.РАСП.ПХ |
Возвращает одностороннюю вероятность распределения хи-квадрат. |
|
ХИ2.ОБР |
Возвращает интегральную функцию плотности бета-вероятности. |
|
ХИ2.ОБР.ПХ |
Возвращает обратное значение односторонней вероятности распределения хи-квадрат. |
|
ХИ2.ТЕСТ |
Возвращает тест на независимость. |
|
ДОВЕРИТ.НОРМ |
Возвращает доверительный интервал для среднего значения по генеральной совокупности. |
|
ДОВЕРИТ.СТЬЮДЕНТ |
Возвращает доверительный интервал для среднего генеральной совокупности, используя t-распределение Стьюдента. |
|
КОРРЕЛ |
Возвращает коэффициент корреляции между двумя множествами данных. |
|
СЧЁТ |
Подсчитывает количество чисел в списке аргументов. |
|
СЧЁТЗ |
Подсчитывает количество значений в списке аргументов. |
|
СЧИТАТЬПУСТОТЫ |
Подсчитывает количество пустых ячеек в диапазоне. |
|
СЧЁТЕСЛИ |
Подсчитывает количество ячеек в диапазоне, удовлетворяющих заданному условию. |
|
СЧЁТЕСЛИМН |
Подсчитывает количество ячеек внутри диапазона, удовлетворяющих нескольким условиям. |
|
КОВАРИАЦИЯ.Г |
Возвращает ковариацию, среднее произведений парных отклонений. |
|
КОВАРИАЦИЯ.В |
Возвращает ковариацию выборки — среднее попарных произведений отклонений для всех точек данных в двух наборах данных. |
|
КВАДРОТКЛ |
Возвращает сумму квадратов отклонений. |
|
ЭКСП.РАСП |
Возвращает экспоненциальное распределение. |
|
F.РАСП |
Возвращает F-распределение вероятности. |
|
F.РАСП.ПХ |
Возвращает F-распределение вероятности. |
|
F.ОБР |
Возвращает обратное значение для F-распределения вероятности. |
|
F.ОБР.ПХ |
Возвращает обратное значение для F-распределения вероятности. |
|
F.ТЕСТ |
Возвращает результат F-теста. |
|
ФИШЕР |
Возвращает преобразование Фишера. |
|
ФИШЕРОБР |
Возвращает обратное преобразование Фишера. |
|
ПРЕДСКАЗ |
Возвращает значение линейного тренда. Примечание: В Excel 2016 эта функция заменена на ПРЕДСКАЗ.ЛИНЕЙН из нового набора функций прогнозирования. Однако она по-прежнему доступна для совместимости с предыдущими версиями. |
|
ПРЕДСКАЗ.ETS |
Возвращает будущее значение на основе существующих (ретроспективных) данных с использованием версии AAA алгоритма экспоненциального сглаживания (ETS). |
|
ПРЕДСКАЗ.ЕTS.ДОВИНТЕРВАЛ |
Возвращает доверительный интервал для прогнозной величины на указанную дату. |
|
ПРЕДСКАЗ.ETS.СЕЗОННОСТЬ |
Возвращает длину повторяющегося фрагмента, обнаруженного программой Excel в заданном временном ряду. |
|
ПРЕДСКАЗ.ETS.СТАТ |
Возвращает статистическое значение, являющееся результатом прогнозирования временного ряда. |
|
ПРЕДСКАЗ.ЛИНЕЙН |
Возвращает будущее значение на основе существующих значений. |
|
ЧАСТОТА |
Возвращает распределение частот в виде вертикального массива. |
|
ГАММА |
Возвращает значение функции гамма |
|
ГАММА.РАСП |
Возвращает гамма-распределение. |
|
ГАММА.ОБР |
Возвращает обратное значение интегрального гамма-распределения. |
|
ГАММАНЛОГ |
Возвращает натуральный логарифм гамма-функции, Γ(x). |
|
ГАММАНЛОГ.ТОЧН |
Возвращает натуральный логарифм гамма-функции, Γ(x). |
|
ГАУСС |
Возвращает значение на 0,5 меньше стандартного нормального распределения. |
|
СРГЕОМ |
Возвращает среднее геометрическое. |
|
РОСТ |
Возвращает значения в соответствии с экспоненциальным трендом. |
|
СРГАРМ |
Возвращает среднее гармоническое. |
|
ГИПЕРГЕОМ.РАСП |
Возвращает гипергеометрическое распределение. |
|
ОТРЕЗОК |
Возвращает отрезок, отсекаемый на оси линией линейной регрессии. |
|
ЭКСЦЕСС |
Возвращает эксцесс множества данных. |
|
НАИБОЛЬШИЙ |
Возвращает k-ое наибольшее значение в множестве данных. |
|
ЛИНЕЙН |
Возвращает параметры линейного тренда. |
|
ЛГРФПРИБЛ |
Возвращает параметры экспоненциального тренда. |
|
ЛОГНОРМ.РАСП |
Возвращает интегральное логарифмическое нормальное распределение. |
|
ЛОГНОРМ.ОБР |
Возвращает обратное значение интегрального логарифмического нормального распределения. |
|
МАКС |
Возвращает наибольшее значение в списке аргументов. |
|
МАКСА |
Возвращает наибольшее значение в списке аргументов, включая числа, текст и логические значения. |
|
МАКСЕСЛИ |
Возвращает максимальное значение из заданных определенными условиями или критериями ячеек. |
|
МЕДИАНА |
Возвращает медиану заданных чисел. |
|
МИН |
Возвращает наименьшее значение в списке аргументов. |
|
МИНЕСЛИ |
Возвращает минимальное значение из заданных определенными условиями или критериями ячеек. |
|
МИНА |
Возвращает наименьшее значение в списке аргументов, включая числа, текст и логические значения. |
|
МОДА.НСК |
Возвращает вертикальный массив наиболее часто встречающихся или повторяющихся значений в массиве или диапазоне данных. |
|
МОДА.ОДН |
Возвращает значение моды набора данных. |
|
ОТРБИНОМ.РАСП |
Возвращает отрицательное биномиальное распределение. |
|
НОРМ.РАСП |
Возвращает нормальное интегральное распределение. |
|
НОРМ.ОБР |
Возвращает обратное значение нормального интегрального распределения. |
|
НОРМ.СТ.РАСП |
Возвращает стандартное нормальное интегральное распределение. |
|
НОРМ.СТ.ОБР |
Возвращает обратное значение стандартного нормального интегрального распределения. |
|
ПИРСОН |
Возвращает коэффициент корреляции Пирсона. |
|
ПРОЦЕНТИЛЬ.ИСКЛ |
Возвращает k-ю процентиль для значений диапазона, где k — число от 0 и 1 (не включая эти числа). |
|
ПРОЦЕНТИЛЬ.ВКЛ |
Возвращает k-ю процентиль для значений диапазона. |
|
ПРОЦЕНТРАНГ.ИСКЛ |
Возвращает ранг значения в наборе данных как процентную долю набора (от 0 до 1, исключая границы). |
|
ПРОЦЕНТРАНГ.ВКЛ |
Возвращает процентную норму значения в наборе данных. |
|
ПЕРЕСТ |
Возвращает количество перестановок для заданного числа объектов. |
|
ПЕРЕСТА |
Возвращает количество перестановок для заданного числа объектов (с повторами), которые можно выбрать из общего числа объектов. |
|
ФИ |
Возвращает значение функции плотности для стандартного нормального распределения. |
|
ПУАССОН.РАСП |
Возвращает распределение Пуассона. |
|
ВЕРОЯТНОСТЬ |
Возвращает вероятность того, что значение из диапазона находится внутри заданных пределов. |
|
КВАРТИЛЬ.ИСКЛ |
Возвращает квартиль набора данных на основе значений процентили из диапазона от 0 до 1, исключая границы. |
|
КВАРТИЛЬ.ВКЛ |
Возвращает квартиль набора данных. |
|
РАНГ.СР |
Возвращает ранг числа в списке чисел. |
|
РАНГ.РВ |
Возвращает ранг числа в списке чисел. |
|
КВПИРСОН |
Возвращает квадрат коэффициента корреляции Пирсона. |
|
СКОС |
Возвращает асимметрию распределения. |
|
СКОС.Г |
Возвращает асимметрию распределения на основе заполнения: характеристика степени асимметрии распределения относительно его среднего. |
|
НАКЛОН |
Возвращает наклон линии линейной регрессии. |
|
НАИМЕНЬШИЙ |
Возвращает k-ое наименьшее значение в множестве данных. |
|
НОРМАЛИЗАЦИЯ |
Возвращает нормализованное значение. |
|
СТАНДОТКЛОН.Г |
Вычисляет стандартное отклонение по генеральной совокупности. |
|
СТАНДОТКЛОН.В |
Оценивает стандартное отклонение по выборке. |
|
СТАНДОТКЛОНА |
Оценивает стандартное отклонение по выборке, включая числа, текст и логические значения. |
|
СТАНДОТКЛОНПА |
Вычисляет стандартное отклонение по генеральной совокупности, включая числа, текст и логические значения. |
|
СТОШYX |
Возвращает стандартную ошибку предсказанных значений y для каждого значения x в регрессии. |
|
СТЬЮДРАСП |
Возвращает процентные точки (вероятность) для t-распределения Стьюдента. |
|
СТЬЮДЕНТ.РАСП.2Х |
Возвращает процентные точки (вероятность) для t-распределения Стьюдента. |
|
СТЬЮДЕНТ.РАСП.ПХ |
Возвращает t-распределение Стьюдента. |
|
СТЬЮДЕНТ.ОБР |
Возвращает значение t для t-распределения Стьюдента как функцию вероятности и степеней свободы. |
|
СТЬЮДЕНТ.ОБР.2Х |
Возвращает обратное t-распределение Стьюдента. |
|
СТЬЮДЕНТ.ТЕСТ |
Возвращает вероятность, соответствующую проверке по критерию Стьюдента. |
|
ТЕНДЕНЦИЯ |
Возвращает значения в соответствии с линейным трендом. |
|
УРЕЗСРЕДНЕЕ |
Возвращает среднее внутренности множества данных. |
|
ДИСП.Г |
Вычисляет дисперсию по генеральной совокупности. |
|
ДИСП.В |
Оценивает дисперсию по выборке. |
|
ДИСПА |
Оценивает дисперсию по выборке, включая числа, текст и логические значения. |
|
ДИСПРА |
Вычисляет дисперсию для генеральной совокупности, включая числа, текст и логические значения. |
|
ВЕЙБУЛЛ.РАСП |
Возвращает распределение Вейбулла. |
|
Z.ТЕСТ |
Возвращает одностороннее значение вероятности z-теста. |
Важно: Вычисляемые результаты формул и некоторые функции листа Excel могут несколько отличаться на компьютерах под управлением Windows с архитектурой x86 или x86-64 и компьютерах под управлением Windows RT с архитектурой ARM. Подробнее об этих различиях.
Статьи по теме
Excel (по категориям)
Excel (по алфавиту)
Зная статистические формулы и приемы можно обработать, проанализировать и упорядочить большое количество информации. В Эксель инструменты статистики выведены в отдельную категорию функций. Давайте посмотрим, как их найти, а также, какие из них являются наиболее популярными среди пользователей.
-
Использование статистических функций
- СРЗНАЧ
- МАКС
- МИН
- СРЗНАЧЕСЛИ
- МЕДИАНА
- НАИБОЛЬШИЙ
- НАИМЕНЬШИЙ
- МОДА.ОДН
- СТАНДОТКЛОН
- СРГЕОМ
- Заключение
Использование статистических функций
Формулы функций в Excel можно вводить вручную непосредственно в той ячейке, где планируется выполнить соответствующие расчеты. Это легко применимо к таким простым действиям, как сложение, вычитание, умножение и деление. Но запомнить формулы сложных функций уже непросто, поэтому проще воспользоваться специальным помощником, который встроен в программу.
Итак, чтобы вставить функцию в ячейку, выполняем одно из следующих действий:
- Находясь в любой вкладке программы щелкаем по значку “Вставить функцию” (fx), которая находится с левой стороны от строки формул.
- Переходим во вкладку “Формулы”, где видим в левом углу ленты инструментов кнопку “Вставить функцию”.
- Используем сочетание клавиш Shift+F3.
Независимо от выбранного способа выше перед нами появится окно вставки функций. Щелкаем по текущей категории и из раскрывшегося списка выбираем пункт “Статистические”.
Далее будет предложен на выбор один из статистических операторов. Отмечаем нужный и жмем OK.
На экране отобразится окно с аргументами выбранной функции, которые нужно заполнить.
Примечание: существует еще один способ выбора требуемой функции. Находясь во вкладке “Формулы” в блоке инструментов “Библиотека функций” щелкаем по значку “Другие функции”, затем выбираем пункт “Статистические” и, наконец, в открывшемся перечне (который можно листать вниз) – нужный оператор.
Давайте теперь рассмотрим наиболее популярные функции.
СРЗНАЧ
Оператор вычисляет среднее арифметическое значение из указанных значений (диапазона). Формула функции выглядит таким образом:
=СРЗНАЧ(число1;число2;…)
В качестве аргументов функции можно указать:
- конкретные числа;
- ссылки на ячейки, которые можно указать как вручную (напечатать с помощью клавиатуры), так и находясь в соответствующем поле щелкнуть по нужному элементу в самой таблице;
- диапазон ячеек – указывается вручную или путем выделения в таблице.
- переход к следующему аргументу происходит путем щелчка по соответствующему полю напротив него или просто нажатием клавиши Tab.
МАКС
Функция помогает определить максимальное значение из заданных чисел (диапазона). Формула оператора следующая:
=МАКС(число1;число2;…)
В аргументах функции, также, как и в случае с оператором СРЗНАЧ можно указать конкретные числа, ссылки на ячейки или диапазоны ячеек.
МИН
Функция находит минимальное число из указанных значений (диапазона ячеек). В общем виде синтаксис выглядит так:
=МИН(число1;число2;…)
Аргументы функции заполняются так же, как и для оператора МАКС.
СРЗНАЧЕСЛИ
Функция позволяет найти среднее арифметическое значение, но при выполнении заданного условия. Формула оператора:
=СРЗНАЧЕСЛИ(диапазон;условие;диапазон_усреднения)
В аргументах указываются:
- Диапазон ячеек – вручную или с помощью выделения в таблице;
- Условие отбора значений из заданного диапазона (больше, меньше, не равно) – в кавычках;
- Диапазон_усреднения – не является обязательным аргументом для заполнения.
МЕДИАНА
Оператор находит медиану заданного диапазона значений. Синтаксис функции:
=МЕДИАНА(число1;число2;…)
В аргументах указываются: конкретные числа, ссылки на ячейки или диапазоны элементов.
НАИБОЛЬШИЙ
Функция позволяет найти из указанного диапазона значений с заданной позицией (по убыванию). Формула оператора:
=НАИБОЛЬШИЙ(массив;k)
Аргумента функции два: массив и номер позиции – K.
Допустим, имеется ряд чисел 4, 6, 12, 24, 15, 9. Если мы укажем в качестве аргумента “K” число 2, результатом будет значение, равное 15, т.к. оно второе по величине в выбранном диапазоне.
НАИМЕНЬШИЙ
Функция также, как и оператор НАИБОЛЬШИЙ, выполняет поиск из указанного диапазона значений. Правда, в данном случае счет идет по возрастанию. Синтаксис оператора следующий:
=НАИМЕНЬШИЙ(массив;k)
МОДА.ОДН
Функция пришла на замену более старому оператору “МОДА” (теперь находится в категории “Полный алфавитный перечень”). Позволяет определять число, которое повторяется чаще остальных в выбранном диапазоне. Работает функция по формуле:
=МОДА.ОДН(число1;число2;…)
В значениях аргументов указываются конкретные числовые значения, отдельные ячейки или их диапазоны.
Для вертикальных массивов, также, используется функция МОДА.НСК.
СТАНДОТКЛОН
Функция СТАНДОТКЛОН также устарела (но ее все еще можно найти, выбрав алфавитный перечень) и теперь представлена двумя новыми:
- СТАДНОТКЛОН.В – находит стандартное отклонение выборки
- СТАДНОТКЛОН.Г – определяет стандартное отклонение по генеральной совопкупности
Формулы функций выглядят следующим образом:
- =СТАДНОТКЛОН.В(число1;число2;…)
- =СТАДНОТКЛОН.Г(число1;число2;…)
СРГЕОМ
Оператор находит среднее геометрическое значение для заданного массива или диапазона. Формула функции:
=СРГЕОМ(число1;число2;…)

Заключение
В программе Excel более 100 статистических функций. Мы лишь рассмотрели те, которые используются пользователями чаще других, а также, где их можно найти и как заполнить аргументы для получения корректного результата.
Содержание
- Использование описательной статистики
- Подключение «Пакета анализа»
- Размах вариации
- Вычисление коэффициента вариации
- Шаг 1: расчет стандартного отклонения
- Шаг 2: расчет среднего арифметического
- Шаг 3: нахождение коэффициента вариации
- Простая формула для расчета объема выборки
- Пример расчета объема выборки
- Задачи о генеральной доле
- По части судить о целом
- Как рассчитать объем выборки
- Как определить статистические выбросы и сделать выборку для их удаления в Excel
- Способ 1: применение расширенного автофильтра
- Способ 2: применение формулы массива
- СРЗНАЧ()
- СРЗНАЧЕСЛИ()
- МАКС()
- МИН()
Использование описательной статистики
Под описательной статистикой понимают систематизацию эмпирических данных по целому ряду основных статистических критериев. Причем на основе полученного результата из этих итоговых показателей можно сформировать общие выводы об изучаемом массиве данных.
В Экселе существует отдельный инструмент, входящий в «Пакет анализа», с помощью которого можно провести данный вид обработки данных. Он так и называется «Описательная статистика». Среди критериев, которые высчитывает данный инструмент следующие показатели:
- Медиана;
- Мода;
- Дисперсия;
- Среднее;
- Стандартное отклонение;
- Стандартная ошибка;
- Асимметричность и др.
Рассмотрим, как работает данный инструмент на примере Excel 2010, хотя данный алгоритм применим также в Excel 2007 и в более поздних версиях данной программы.
Подключение «Пакета анализа»
Как уже было сказано выше, инструмент «Описательная статистика» входит в более широкий набор функций, который принято называть Пакет анализа. Но дело в том, что по умолчанию данная надстройка в Экселе отключена. Поэтому, если вы до сих пор её не включили, то для использования возможностей описательной статистики, придется это сделать.
- Переходим во вкладку «Файл». Далее производим перемещение в пункт «Параметры».
- В активировавшемся окне параметров перемещаемся в подраздел «Надстройки». В самой нижней части окна находится поле «Управление». Нужно в нем переставить переключатель в позицию «Надстройки Excel», если он находится в другом положении. Вслед за этим жмем на кнопку «Перейти…».
- Запускается окно стандартных надстроек Excel. Около наименования «Пакет анализа» ставим флажок. Затем жмем на кнопку «OK».
После вышеуказанных действий надстройка Пакет анализа будет активирована и станет доступной во вкладке «Данные» Эксель. Теперь мы сможем использовать на практике инструменты описательной статистики.
Размах вариации
Размах вариации – разница между максимальным и минимальным значением:
Ниже приведена графическая интерпретация размаха вариации.

Видно максимальное и минимальное значение, а также расстояние между ними, которое и соответствует размаху вариации.
С одной стороны, показатель размаха может быть вполне информативным и полезным. К примеру, максимальная и минимальная стоимость квартиры в городе N, максимальная и минимальная зарплата по профессии в регионе и проч. С другой стороны, размах может быть очень широким и не иметь практического смысла, т.к. зависит лишь от двух наблюдений. Таким образом, размах вариации очень неустойчивая величина.
Вычисление коэффициента вариации
Этот показатель представляет собой отношение стандартного отклонения к среднему арифметическому. Полученный результат выражается в процентах.
В Экселе не существует отдельно функции для вычисления этого показателя, но имеются формулы для расчета стандартного отклонения и среднего арифметического ряда чисел, а именно они используются для нахождения коэффициента вариации.
Шаг 1: расчет стандартного отклонения
Стандартное отклонение, или, как его называют по-другому, среднеквадратичное отклонение, представляет собой квадратный корень из дисперсии. Для расчета стандартного отклонения используется функция СТАНДОТКЛОН. Начиная с версии Excel 2010 она разделена, в зависимости от того, по генеральной совокупности происходит вычисление или по выборке, на два отдельных варианта: СТАНДОТКЛОН.Г и СТАНДОТКЛОН.В.
Синтаксис данных функций выглядит соответствующим образом:
= СТАНДОТКЛОН(Число1;Число2;…)
= СТАНДОТКЛОН.Г(Число1;Число2;…)
= СТАНДОТКЛОН.В(Число1;Число2;…)
- Для того, чтобы рассчитать стандартное отклонение, выделяем любую свободную ячейку на листе, которая удобна вам для того, чтобы выводить в неё результаты расчетов. Щелкаем по кнопке «Вставить функцию». Она имеет внешний вид пиктограммы и расположена слева от строки формул.
Выполняется активация Мастера функций, который запускается в виде отдельного окна с перечнем аргументов. Переходим в категорию «Статистические» или «Полный алфавитный перечень». Выбираем наименование «СТАНДОТКЛОН.Г» или «СТАНДОТКЛОН.В», в зависимости от того, по генеральной совокупности или по выборке следует произвести расчет. Жмем на кнопку «OK».
Открывается окно аргументов данной функции. Оно может иметь от 1 до 255 полей, в которых могут содержаться, как конкретные числа, так и ссылки на ячейки или диапазоны. Ставим курсор в поле «Число1». Мышью выделяем на листе тот диапазон значений, который нужно обработать. Если таких областей несколько и они не смежные между собой, то координаты следующей указываем в поле «Число2» и т.д. Когда все нужные данные введены, жмем на кнопку «OK»
Шаг 2: расчет среднего арифметического
Среднее арифметическое является отношением общей суммы всех значений числового ряда к их количеству. Для расчета этого показателя тоже существует отдельная функция – СРЗНАЧ. Вычислим её значение на конкретном примере.
- Выделяем на листе ячейку для вывода результата. Жмем на уже знакомую нам кнопку «Вставить функцию».
В статистической категории Мастера функций ищем наименование «СРЗНАЧ». После его выделения жмем на кнопку «OK».
Запускается окно аргументов СРЗНАЧ. Аргументы полностью идентичны тем, что и у операторов группы СТАНДОТКЛОН. То есть, в их качестве могут выступать как отдельные числовые величины, так и ссылки. Устанавливаем курсор в поле «Число1». Так же, как и в предыдущем случае, выделяем на листе нужную нам совокупность ячеек. После того, как их координаты были занесены в поле окна аргументов, жмем на кнопку «OK».
Шаг 3: нахождение коэффициента вариации
Теперь у нас имеются все необходимые данные для того, чтобы непосредственно рассчитать сам коэффициент вариации.
- Выделяем ячейку, в которую будет выводиться результат. Прежде всего, нужно учесть, что коэффициент вариации является процентным значением. В связи с этим следует поменять формат ячейки на соответствующий. Это можно сделать после её выделения, находясь во вкладке «Главная». Кликаем по полю формата на ленте в блоке инструментов «Число». Из раскрывшегося списка вариантов выбираем «Процентный». После этих действий формат у элемента будет соответствующий.
Снова возвращаемся к ячейке для вывода результата. Активируем её двойным щелчком левой кнопки мыши. Ставим в ней знак «=». Выделяем элемент, в котором расположен итог вычисления стандартного отклонения. Кликаем по кнопке «разделить» (/) на клавиатуре. Далее выделяем ячейку, в которой располагается среднее арифметическое заданного числового ряда. Для того, чтобы произвести расчет и вывести значение, щёлкаем по кнопке Enter на клавиатуре.
Таким образом мы произвели вычисление коэффициента вариации, ссылаясь на ячейки, в которых уже были рассчитаны стандартное отклонение и среднее арифметическое. Но можно поступить и несколько по-иному, не рассчитывая отдельно данные значения.
- Выделяем предварительно отформатированную под процентный формат ячейку, в которой будет выведен результат. Прописываем в ней формулу по типу:
Вместо наименования «Диапазон значений» вставляем реальные координаты области, в которой размещен исследуемый числовой ряд. Это можно сделать простым выделением данного диапазона. Вместо оператора СТАНДОТКЛОН.В, если пользователь считает нужным, можно применять функцию СТАНДОТКЛОН.Г.
Существует условное разграничение. Считается, что если показатель коэффициента вариации менее 33%, то совокупность чисел однородная. В обратном случае её принято характеризовать, как неоднородную.
Как видим, программа Эксель позволяет значительно упростить расчет такого сложного статистического вычисления, как поиск коэффициента вариации. К сожалению, в приложении пока не существует функции, которая высчитывала бы этот показатель в одно действие, но при помощи операторов СТАНДОТКЛОН и СРЗНАЧ эта задача очень упрощается. Таким образом, в Excel её может выполнить даже человек, который не имеет высокого уровня знаний связанных со статистическими закономерностями.
Разделы: Математика
- Совершенствование умений и навыков нахождения статистических характеристик случайной величины, работа с расчетами в Excel;
- применение информационно коммутативных технологий для анализа данных; работа с различными информационными носителями.
- Сегодня мы научимся рассчитывать статистические характеристики для больших по объему выборок, используя возможности современных компьютерных технологий.
- Для начала вспомним:
– что называется случайной величиной? (Случайной величиной называют переменную величину, которая в зависимости от исхода испытания принимает одно значение из множества возможных значений.)
– Какие виды случайных величин мы знаем? (Дискретные, непрерывные.)
– Приведите примеры непрерывных случайных величин (рост дерева), дискретных случайных величин (количество учеников в классе).
– Какие статистические характеристики случайных величин мы знаем (мода, медиана, среднее выборочное значение, размах ряда).
– Какие приемы используются для наглядного представления статистических характеристик случайной величины (полигон частот, круговые и столбчатые диаграммы, гистограммы).
- Рассмотрим, применение инструментов Excel для решения статистических задач на конкретном примере.
Пример. Проведена проверка в 100 компаниях. Даны значения количества работающих в компании (чел.):
| 23 25 24 25 30 24 30 26 28 26 32 33 31 31 25 33 25 29 30 28 23 30 29 24 33 30 30 28 26 25 26 29 27 29 26 28 27 26 29 28 29 30 27 30 28 32 28 26 30 26 31 27 30 27 33 28 26 30 31 29 27 30 30 29 27 26 28 31 29 28 33 27 30 33 26 31 34 28 32 22 29 30 27 29 34 29 32 29 29 30 29 29 36 29 29 34 23 28 24 28 |
рассчитать числовые характеристики:
|
1. Занести данные в EXCEL, каждое число в отдельную ячейку.
| 23 | 25 | 24 | 25 | 30 | 24 | 30 | 26 | 28 | 26 |
| 32 | 33 | 31 | 31 | 25 | 33 | 25 | 29 | 30 | 28 |
| 23 | 30 | 29 | 24 | 33 | 30 | 30 | 28 | 26 | 25 |
| 26 | 29 | 27 | 29 | 26 | 28 | 27 | 26 | 29 | 28 |
| 29 | 30 | 27 | 30 | 28 | 32 | 28 | 26 | 30 | 26 |
| 31 | 27 | 30 | 27 | 33 | 28 | 26 | 30 | 31 | 29 |
| 27 | 30 | 30 | 29 | 27 | 26 | 28 | 31 | 29 | 28 |
| 33 | 27 | 30 | 33 | 26 | 31 | 34 | 28 | 32 | 22 |
| 29 | 30 | 27 | 29 | 34 | 29 | 32 | 29 | 29 | 30 |
| 29 | 29 | 36 | 29 | 29 | 34 | 23 | 28 | 24 | 28 |
2. Для расчета числовых характеристик используем опцию Вставка – Функция. И в появившемся окне в строке категория выберем – статистические, в списке: МОДА
В поле Число 1 ставим курсор и мышкой выделяем нашу таблицу:
Нажимаем клавишу ОК. Получили Мо = 29 (чел) – Фирм у которых в штате 29 человек больше всего.
Используя тот же путь вычисляем медиану.
Вставка – Функция – Статистические – Медиана.
В поле Число 1 ставим курсор и мышкой выделяем нашу таблицу:
Нажимаем клавишу ОК. Получили Ме = 29 (чел) – среднее значение сотрудников в фирме.
Размах ряда чисел – разница между наименьшим и наибольшим возможным значением случайной величины. Для вычисления размаха ряда нужно найти наибольшее и наименьшее значения нашей выборки и вычислить их разность.
Вставка – Функция – Статистические – МАКС.
В поле Число 1 ставим курсор и мышкой выделяем нашу таблицу:
Нажимаем клавишу ОК. Получили наибольшее значение = 36.
Вставка – Функция – Статистические – МИН.
В поле Число 1 ставим курсор и мышкой выделяем нашу таблицу:
Нажимаем клавишу ОК. Получили наименьшее значение = 22.
36 – 22 = 14 (чел) – разница между фирмой с наибольшим штатом сотрудников и фирмой с наименьшим штатом сотрудников.
Для построения диаграммы и полигона частот необходимо задать закон распределения, т.е. составить таблицу значений случайной величины и соответствующих им частот. Мы ухе знаем, что наименьшее число сотрудников в фирме = 22, а наибольшее = 36. Составим таблицу, в которой значения xi случайной величины меняются от 22 до 36 включительно шагом 1.
| xi | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 |
| ni |
Чтобы сосчитать частоту каждого значения воспользуемся
Вставка – Функция – Статистические – СЧЕТЕСЛИ.
В окне Диапазон ставим курсор и выделяем нашу выборку, а в окне Критерий ставим число 22
Нажимаем клавишу ОК, получаем значение 1, т.е. число 22 в нашей выборке встречается 1 раз и его частота =1. Аналогичным образом заполняем всю таблицу.
| xi | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 |
| ni | 1 | 3 | 4 | 5 | 11 | 9 | 13 | 18 | 16 | 6 | 4 | 6 | 3 | 0 | 1 |
Для проверки вычисляем объем выборки, сумму частот (Вставка – Функция – Математические – СУММА). Должно получиться 100 (количество всех фирм).
Чтобы построить полигон частот выделяем таблицу – Вставка – Диаграмма – Стандартные – Точечная (точечная диаграмма на которой значения соединены отрезками)
Нажимаем клавишу Далее, в Мастере диаграмм указываем название диаграммы (Полигон частот), удаляем легенду, редактируем шкалу и характеристики диаграммы для наибольшей наглядности.
Для построения столбчатой и круговой диаграмм используем тот же путь (выбирая нужный нам тип диаграммы).
Диаграмма – Стандартные – Круговая.
Диаграмма – Стандартные – Гистограмма.
4. Сегодня на уроке мы научились применять компьютерные технологии для анализа и обработки статистической информации.
Простая формула для расчета объема выборки
где: n – объем выборки;
z – нормированное отклонение, определяемое исходя из выбранного уровня доверительности. Этот показатель характеризует возможность, вероятность попадания ответов в специальный – доверительный интервал. На практике уровень доверительности часто принимают за 95% или 99%. Тогда значения z будут соответственно 1,96 и 2,58;
p – вариация для выборки, в долях. По сути, p – это вероятность того, что респонденты выберут той или иной вариант ответа. Допустим, если мы считаем, что четверть опрашиваемых выберут ответ «Да», то p будет равно 25%, то есть p = 0,25;
q = (1 – p);
e – допустимая ошибка, в долях.
Пример расчета объема выборки
Компания планирует провести социологическое исследование с целью выявить долю курящих лиц в населении города. Для этого сотрудники компании будут задавать прохожим один вопрос: «Вы курите?». Возможных вариантов ответа, таким образом, только два: «Да» и «Нет».
Объем выборки в этом случае рассчитывается следующим образом. Уровень доверительности принимается за 95%, тогда нормированное отклонение z = 1,96. Вариацию принимаем за 50%, то есть условно считаем, что половина респондентов может ответить на вопрос о том, курят ли они – «Да». Тогда p = 0,5. Отсюда находим q = 1 – p = 1 – 0,5 = 0,5. Допустимую ошибку выборки принимаем за 10%, то есть e = 0,1.
Подставляем эти данные в формулу и считаем:
Получаем объем выборки n = 96 человек.
Задачи о генеральной доле
На вопрос «Накрывает ли доверительный интервал заданное значение p0?» — можно ответить, проверив статистическую гипотезу H0:p=p0. При этом предполагается, что опыты проводятся по схеме испытаний Бернулли (независимы, вероятность p появления события А постоянна). По выборке объема n определяют относительную частоту p* появления события A: где m — количество появлений события А в серии из n испытаний. Для проверки гипотезы H0 используется статистика, имеющая при достаточно большом объеме выборки стандартное нормальное распределение (табл. 1).
Таблица 1 – Гипотезы о генеральной доле
|
Гипотеза |
H0:p=p0 | H0:p1=p2 |
| Предположения | Схема испытаний Бернулли | Схема испытаний Бернулли |
| Оценки по выборке |  |
|
| Статистика K |  |
 |
| Распределение статистики K | Стандартное нормальное N(0,1) | Стандартное нормальное N(0,1) |
Пример №1. С помощью случайного повторного отбора руководство фирмы провело выборочный опрос 900 своих служащих. Среди опрошенных оказалось 270 женщин. Постройте доверительный интервал, с вероятностью 0.95 накрывающий истинную долю женщин во всем коллективе фирмы.
Решение. По условию выборочная доля женщин составляет (относительная частота женщин среди всех опрошенных). Так как отбор является повторным, и объем выборки велик (n=900) предельная ошибка выборки определяется по формуле
(относительная частота женщин среди всех опрошенных). Так как отбор является повторным, и объем выборки велик (n=900) предельная ошибка выборки определяется по формуле
Значение uкр находим по таблице функции Лапласа из соотношения 2Ф(uкр)=γ, т.е. Функция Лапласа (приложение 1) принимает значение 0.475 при uкр=1.96. Следовательно, предельная ошибка
Функция Лапласа (приложение 1) принимает значение 0.475 при uкр=1.96. Следовательно, предельная ошибка и искомый доверительный интервал
(p – ε, p + ε) = (0.3 – 0.18; 0.3 + 0.18) = (0.12; 0.48)
Итак, с вероятностью 0.95 можно гарантировать, что доля женщин во всем коллективе фирмы находится в интервале от 0.12 до 0.48.
Пример №2. Владелец автостоянки считает день «удачным», если автостоянка заполнена более, чем на 80 %. В течение года было проведено 40 проверок автостоянки, из которых 24 оказались «удачными». С вероятностью 0.98 найдите доверительный интервал для оценки истинной доли «удачных» дней в течение года.
Решение. Выборочная доля «удачных» дней составляет
По таблице функции Лапласа найдем значение uкр при заданной
доверительной вероятности
По таблице функции Лапласа найдем значение uкр при заданной
доверительной вероятности
Ф(2.23) = 0.49, uкр = 2.33.
Считая отбор бесповторным (т.е. две проверки в один день не проводилось), найдем предельную ошибку:
где n=40, N = 365 (дней). Отсюда
где n=40, N = 365 (дней). Отсюда
и доверительный интервал для генеральной доли: (p – ε, p + ε) = (0.6 – 0.17; 0.6 + 0.17) = (0.43; 0.77)
С вероятностью 0.98 можно ожидать, что доля «удачных» дней в течение года находится в интервале от 0.43 до 0.77.
Пример №3. Проверив 2500 изделий в партии, обнаружили, что 400 изделий высшего сорта, а n–m – нет. Сколько надо проверить изделий, чтобы с уверенностью 95% определить долю высшего сорта с точностью до 0.01?
Решение ищем по формуле определения численности выборки для повторного отбора.
Ф(t) = γ/2 = 0.95/2 = 0.475 и этому значению по таблице Лапласа соответствует t=1.96
Выборочная доля w = 0.16; ошибка выборки ε = 0.01
Пример №4. Партия изделий принимается, если вероятность того, что изделие окажется соответствующим стандарту, составляет не менее 0.97. Среди случайно отобранных 200 изделий проверяемой партии оказалось 193 соответствующих стандарту. Можно ли на уровне значимости α=0,02 принять партию?
Решение. Сформулируем основную и альтернативную гипотезы.
H0:p=p0=0,97 — неизвестная генеральная доля p равна заданному значению p0=0,97. Применительно к условию — вероятность того, что деталь из проверяемой партии окажется соответствующей стандарту, равна 0.97; т.е. партию изделий можно принять.
H1:p<0,97 – вероятность того, что деталь из проверяемой партии окажется соответствующей стандарту, меньше 0.97; т.е. партию изделий нельзя принять. При такой альтернативной гипотезе критическая область будет левосторонней.
Наблюдаемое значение статистики K (таблица) вычислим при заданных значениях p0=0,97, n=200, m=193

Критическое значение находим по таблице функции Лапласа из равенства
По условию α=0,02 отсюда Ф(Ккр)=0,48 и Ккр=2,05. Критическая область левосторонняя, т.е. является интервалом (-∞;-Kkp)= (-∞;-2,05). Наблюдаемое значение Кнабл=-0,415 не принадлежит критической области, следовательно, на данном уровне значимости нет оснований отклонять основную гипотезу. Партию изделий принять можно.
Пример №5. Два завода изготавливают однотипные детали. Для оценки их качества сделаны выборки из продукции этих заводов и получены следующие результаты. Среди 200 отобранных изделий первого завода оказалось 20 бракованных, среди 300 изделий второго завода — 15 бракованных.
На уровне значимости 0.025 выяснить, имеется ли существенное различие в качестве изготавливаемых этими заводами деталей.
Решение. Это задача о сравнении генеральных долей двух совокупностей. Сформулируем основную и альтернативную гипотезы.
H0:p1=p2 — генеральные доли равны. Применительно к условию — вероятность появления бракованного изделия в продукции первого завода равна вероятности появления бракованного изделия в продукции второго завода (качество продукции одинаково).
H0:p1≠p2 — заводы изготавливают детали разного качества.
Для вычисления наблюдаемого значения статистики K (таблица) рассчитаем оценки по выборке.
Наблюдаемое значение равно

Так как альтернативная гипотеза двусторонняя, то критическое значение статистики K≈ N(0,1) находим по таблице функции Лапласа из равенства
Так как альтернативная гипотеза двусторонняя, то критическое значение статистики K≈ N(0,1) находим по таблице функции Лапласа из равенства
По условию α=0,025 отсюда Ф(Ккр)=0,4875 и Ккр=2,24. При двусторонней альтернативе область допустимых значений имеет вид (-2,24;2,24). Наблюдаемое значение Kнабл=2,15 попадает в этот интервал, т.е. на данном уровне значимости нет оснований отвергать основную гипотезу. Заводы изготавливают изделия одинакового качества.
По части судить о целом
О возможности судить о целом по части миру рассказал российский математик П.Л. Чебышев. «Закон больших чисел» простым языком можно сформулировать так: количественные закономерности массовых явлений проявляются только при
достаточном числе наблюдений
. Чем больше выборка, тем лучше случайные отклонения компенсируют друг друга и проявляется общая тенденция.
А.М. Ляпунов чуть позже сформулировал центральную предельную теорему. Она стала фундаментом для создания формул, которые позволяют рассчитать вероятность ошибки (при оценке среднего по выборке) и размер выборки, необходимый для достижения заданной точности.
Строгие формулировки:
С увеличением числа случайных величин их среднее арифметическое стремится к среднему арифметическому математических ожиданий и перестает быть случайным. Общий смысл закона больших чисел — совместное действие большого числа случайных факторов приводит к результату, почти не зависящему от случая.
Таким образом з.б.ч. гарантирует устойчивость для средних значений некоторых случайных событий при достаточно длинной серии экспериментов.
Распределение случайной величины, которая получена в результате сложения большого числа независимых случайных величин (ни одно из которых не доминирует, не вносит в сумму определяющего вклада и имеет дисперсию значительно меньшею по сравнению с дисперсией суммы) имеет распределение, близкое к нормальному.
Из ц.п.т. следует, что ошибки выборки также подчиняется нормальному распределению.
Еще раз: чтобы корректно оценивать популяцию по выборке, нам нужна не обычная выборка, а репрезентативная выборка достаточного размера. Начнем с определения этого самого размера.
Как рассчитать объем выборки
Достаточный размер выборки зависит от следующих составляющих:
- изменчивость признака (чем разнообразней показания, тем больше наблюдений нужно, чтобы это уловить);
- размер эффекта (чем меньшие эффекты мы стремимся зафиксировать, тем больше наблюдений необходимо);
- уровень доверия (уровень вероятности при который мы готовы отвергнуть нулевую гипотезу)
ЗАПОМНИТЕ
Объем выборки зависит от изменчивости признака и планируемой строгости эксперимента
Формулы для расчета объема выборки:
Формулы расчета объема выборки
Ошибка выборки значительно возрастает, когда наблюдений меньше ста. Для исследований в которых используется 30-100 объектов применяется особая статистическая методология: критерии, основанные на распределении Стьюдента или бутстрэп-анализ. И наконец, статистика совсем слаба, когда наблюдений меньше 30.
График зависимости ошибки выборки от ее объема при оценке доли признака в г.с.
Чем больше неопределенность, тем больше ошибка. Максимальная неопределенность при оценке доли — 50% (например, 50% респондентов считают концепцию хорошей, а другие 50% плохой). Если 90% опрошенных концепция понравится — это, наоборот, пример согласованности. В таких случаях оценить долю признака по выборке проще.
Для экспонирования и выделения цветом значений статистических выбросов от медианы можно использовать несколько простых формул и условное форматирование.
Первым шагом в поиске значений выбросов статистики является определение статистического центра диапазона данных. С этой целью необходимо сначала определить границы первого и третьего квартала. Определение границ квартала – значит разделение данных на 4 равные группы, которые содержат по 25% данных каждая. Группа, содержащая 25% наибольших значений, называется первым квартилем.
Границы квартилей в Excel можно легко определить с помощью простой функции КВАРТИЛЬ. Данная функция имеет 2 аргумента: диапазон данных и номер для получения желаемого квартиля.
В примере показанному на рисунке ниже значения в ячейках E1 и E2 содержат показатели первого и третьего квартиля данных в диапазоне ячеек B2:B19:

Вычитая от значения первого квартиля третьего, можно определить набор 50% статистических данных, который называется межквартильным диапазоном. В ячейке E3 определен размер межквартильного диапазона.
В этом месте возникает вопрос, как сильно данное значение может отличаться от среднего значения 50% данных и оставаться все еще в пределах нормы? Статистические аналитики соглашаются с тем, что для определения нижней и верхней границы диапазона данных можно смело использовать коэффициент расширения 1,5 умножив на значение межквартильного диапазона. То есть:
- Нижняя граница диапазона данных равна: значение первого квартиля – межкваритльный диапазон * 1,5.
- Верхняя граница диапазона данных равна: значение третьего квартиля + расширенных диапазон * 1,5.
Как показано на рисунке ячейки E5 и E6 содержат вычисленные значения верхней и нижней границы диапазона данных. Каждое значение, которое больше верхней границы нормы или меньше нижней границы нормы считается значением статистического выброса.
Чтобы выделить цветом для улучшения визуального анализа данных можно создать простое правило для условного форматирования.
Способ 1: применение расширенного автофильтра
Наиболее простым способом произвести отбор является применение расширенного автофильтра. Рассмотрим, как это сделать на конкретном примере.
- Выделяем область на листе, среди данных которой нужно произвести выборку. Во вкладке «Главная» щелкаем по кнопке «Сортировка и фильтр». Она размещается в блоке настроек «Редактирование». В открывшемся после этого списка выполняем щелчок по кнопке «Фильтр».
Есть возможность поступить и по-другому. Для этого после выделения области на листе перемещаемся во вкладку «Данные». Щелкаем по кнопке «Фильтр», которая размещена на ленте в группе «Сортировка и фильтр».
- После этого действия в шапке таблицы появляются пиктограммы для запуска фильтрования в виде перевернутых острием вниз небольших треугольников на правом краю ячеек. Кликаем по данному значку в заглавии того столбца, по которому желаем произвести выборку. В запустившемся меню переходим по пункту «Текстовые фильтры». Далее выбираем позицию «Настраиваемый фильтр…».
- Активируется окно пользовательской фильтрации. В нем можно задать ограничение, по которому будет производиться отбор. В выпадающем списке для столбца содержащего ячейки числового формата, который мы используем для примера, можно выбрать одно из пяти видов условий:
- равно;
- не равно;
- больше;
- больше или равно;
- меньше.
Давайте в качестве примера зададим условие так, чтобы отобрать только значения, по которым сумма выручки превышает 10000 рублей. Устанавливаем переключатель в позицию «Больше». В правое поле вписываем значение «10000». Чтобы произвести выполнение действия, щелкаем по кнопке «OK».
- Как видим, после фильтрации остались только строчки, в которых сумма выручки превышает 10000 рублей.
- Но в этом же столбце мы можем добавить и второе условие. Для этого опять возвращаемся в окно пользовательской фильтрации. Как видим, в его нижней части есть ещё один переключатель условия и соответствующее ему поле для ввода. Давайте установим теперь верхнюю границу отбора в 15000 рублей. Для этого выставляем переключатель в позицию «Меньше», а в поле справа вписываем значение «15000».
Кроме того, существует ещё переключатель условий. У него два положения «И» и «ИЛИ». По умолчанию он установлен в первом положении. Это означает, что в выборке останутся только строчки, которые удовлетворяют обоим ограничениям. Если он будет выставлен в положение «ИЛИ», то тогда останутся значения, которые подходят под любое из двух условий. В нашем случае нужно выставить переключатель в положение «И», то есть, оставить данную настройку по умолчанию. После того, как все значения введены, щелкаем по кнопке «OK».
- Теперь в таблице остались только строчки, в которых сумма выручки не меньше 10000 рублей, но не превышает 15000 рублей.
- Аналогично можно настраивать фильтры и в других столбцах. При этом имеется возможность сохранять также фильтрацию и по предыдущим условиям, которые были заданы в колонках. Итак, посмотрим, как производится отбор с помощью фильтра для ячеек в формате даты. Кликаем по значку фильтрации в соответствующем столбце. Последовательно кликаем по пунктам списка «Фильтр по дате» и «Настраиваемый фильтр».
- Снова запускается окно пользовательского автофильтра. Выполним отбор результатов в таблице с 4 по 6 мая 2016 года включительно. В переключателе выбора условий, как видим, ещё больше вариантов, чем для числового формата. Выбираем позицию «После или равно». В поле справа устанавливаем значение «04.05.2016». В нижнем блоке устанавливаем переключатель в позицию «До или равно». В правом поле вписываем значение «06.05.2016». Переключатель совместимости условий оставляем в положении по умолчанию – «И». Для того, чтобы применить фильтрацию в действии, жмем на кнопку «OK».
- Как видим, наш список ещё больше сократился. Теперь в нем оставлены только строчки, в которых сумма выручки варьируется от 10000 до 15000 рублей за период с 04.05 по 06.05.2016 включительно.
- Мы можем сбросить фильтрацию в одном из столбцов. Сделаем это для значений выручки. Кликаем по значку автофильтра в соответствующем столбце. В выпадающем списке щелкаем по пункту «Удалить фильтр».
- Как видим, после этих действий, выборка по сумме выручки будет отключена, а останется только отбор по датам (с 04.05.2016 по 06.05.2016).
- В данной таблице имеется ещё одна колонка – «Наименование». В ней содержатся данные в текстовом формате. Посмотрим, как сформировать выборку с помощью фильтрации по этим значениям.
Кликаем по значку фильтра в наименовании столбца. Последовательно переходим по наименованиям списка «Текстовые фильтры» и «Настраиваемый фильтр…».
- Опять открывается окно пользовательского автофильтра. Давайте сделаем выборку по наименованиям «Картофель» и «Мясо». В первом блоке переключатель условий устанавливаем в позицию «Равно». В поле справа от него вписываем слово «Картофель». Переключатель нижнего блока так же ставим в позицию «Равно». В поле напротив него делаем запись – «Мясо». И вот далее мы выполняем то, чего ранее не делали: устанавливаем переключатель совместимости условий в позицию «ИЛИ». Теперь строчка, содержащая любое из указанных условий, будет выводиться на экран. Щелкаем по кнопке «OK».
- Как видим, в новой выборке существуют ограничения по дате (с 04.05.2016 по 06.05.2016) и по наименованию (картофель и мясо). По сумме выручки ограничений нет.
- Полностью удалить фильтр можно теми же способами, которые использовались для его установки. Причем неважно, какой именно способ применялся. Для сброса фильтрации, находясь во вкладке «Данные» щелкаем по кнопке «Фильтр», которая размещена в группе «Сортировка и фильтр».
Второй вариант предполагает переход во вкладку «Главная». Там выполняем щелчок на ленте по кнопке «Сортировка и фильтр» в блоке «Редактирование». В активировавшемся списке нажимаем на кнопку «Фильтр».
При использовании любого из двух вышеуказанных методов фильтрация будет удалена, а результаты выборки – очищены. То есть, в таблице будет показан весь массив данных, которыми она располагает.
Способ 2: применение формулы массива
Сделать отбор можно также применив сложную формулу массива. В отличие от предыдущего варианта, данный метод предусматривает вывод результата в отдельную таблицу.
- На том же листе создаем пустую таблицу с такими же наименованиями столбцов в шапке, что и у исходника.
- Выделяем все пустые ячейки первой колонки новой таблицы. Устанавливаем курсор в строку формул. Как раз сюда будет заноситься формула, производящая выборку по указанным критериям. Отберем строчки, сумма выручки в которых превышает 15000 рублей. В нашем конкретном примере, вводимая формула будет выглядеть следующим образом:
=ИНДЕКС(A2:A29;НАИМЕНЬШИЙ(ЕСЛИ(15000<=C2:C29;СТРОКА(C2:C29);"");СТРОКА()-СТРОКА($C$1))-СТРОКА($C$1))Естественно, в каждом конкретном случае адрес ячеек и диапазонов будет свой. На данном примере можно сопоставить формулу с координатами на иллюстрации и приспособить её для своих нужд.
- Так как это формула массива, то для того, чтобы применить её в действии, нужно нажимать не кнопку Enter, а сочетание клавиш Ctrl+Shift+Enter. Делаем это.
- Выделив второй столбец с датами и установив курсор в строку формул, вводим следующее выражение:
=ИНДЕКС(B2:B29;НАИМЕНЬШИЙ(ЕСЛИ(15000<=C2:C29;СТРОКА(C2:C29);"");СТРОКА()-СТРОКА($C$1))-СТРОКА($C$1))Жмем сочетание клавиш Ctrl+Shift+Enter.
- Аналогичным образом в столбец с выручкой вписываем формулу следующего содержания:
=ИНДЕКС(C2:C29;НАИМЕНЬШИЙ(ЕСЛИ(15000<=C2:C29;СТРОКА(C2:C29);"");СТРОКА()-СТРОКА($C$1))-СТРОКА($C$1))Опять набираем сочетание клавиш Ctrl+Shift+Enter.
Во всех трех случаях меняется только первое значение координат, а в остальном формулы полностью идентичны.
- Как видим, таблица заполнена данными, но внешний вид её не совсем привлекателен, к тому же, значения даты заполнены в ней некорректно. Нужно исправить эти недостатки. Некорректность даты связана с тем, что формат ячеек соответствующего столбца общий, а нам нужно установить формат даты. Выделяем весь столбец, включая ячейки с ошибками, и кликаем по выделению правой кнопкой мыши. В появившемся списке переходим по пункту «Формат ячейки…».
- В открывшемся окне форматирования открываем вкладку «Число». В блоке «Числовые форматы» выделяем значение «Дата». В правой части окна можно выбрать желаемый тип отображения даты. После того, как настройки выставлены, жмем на кнопку «OK».
- Теперь дата отображается корректно. Но, как видим, вся нижняя часть таблицы заполнена ячейками, которые содержат ошибочное значение «#ЧИСЛО!». По сути, это те ячейки, данных из выборки для которых не хватило. Более привлекательно было бы, если бы они отображались вообще пустыми. Для этих целей воспользуемся условным форматированием. Выделяем все ячейки таблицы, кроме шапки. Находясь во вкладке «Главная» кликаем по кнопке «Условное форматирование», которая находится в блоке инструментов «Стили». В появившемся списке выбираем пункт «Создать правило…».
- В открывшемся окне выбираем тип правила «Форматировать только ячейки, которые содержат». В первом поле под надписью «Форматировать только ячейки, для которых выполняется следующее условие» выбираем позицию «Ошибки». Далее жмем по кнопке «Формат…».
- В запустившемся окне форматирования переходим во вкладку «Шрифт» и в соответствующем поле выбираем белый цвет. После этих действий щелкаем по кнопке «OK».
- На кнопку с точно таким же названием жмем после возвращения в окно создания условий.
Теперь у нас имеется готовая выборка по указанному ограничению в отдельной надлежащим образом оформленной таблице.
СРЗНАЧ()
Статистическая функция СРЗНАЧ возвращает среднее арифметическое своих аргументов.
Данная функция может принимать до 255 аргументов и находить среднее сразу в нескольких несмежных диапазонах и ячейках:
Если в рассчитываемом диапазоне встречаются пустые или содержащие текст ячейки, то они игнорируются. В примере ниже среднее ищется по четырем ячейкам, т.е. (4+15+11+22)/4 = 13
Если необходимо вычислить среднее, учитывая все ячейки диапазона, то можно воспользоваться статистической функцией СРЗНАЧА. В следующем примере среднее ищется уже по 6 ячейкам, т.е. (4+15+11+22)/6 = 8,6(6).
Статистическая функция СРЗНАЧ может использовать в качестве своих аргументов математические операторы и различные функции Excel:
СРЗНАЧЕСЛИ()
Если необходимо вернуть среднее арифметическое значений, которые удовлетворяют определенному условию, то можно воспользоваться статистической функцией СРЗНАЧЕСЛИ. Следующая формула вычисляет среднее чисел, которые больше нуля:
В данном примере для подсчета среднего и проверки условия используется один и тот же диапазон, что не всегда удобно. На этот случай у функции СРЗНАЧЕСЛИ существует третий необязательный аргумент, по которому можно вычислять среднее. Т.е. по первому аргументу проверяем условие, по третьему – находим среднее.
Допустим, в таблице ниже собрана статистика по стоимости лекарств в городе. В одной аптеке лекарство стоит дороже, в другой дешевле. Чтобы посчитать стоимость анальгина в среднем по городу, воспользуемся следующей формулой:
Если требуется соблюсти несколько условий, то всегда можно применить статистическую функцию СРЗНАЧЕСЛИМН, которая позволяет считать среднее арифметическое ячеек, удовлетворяющих двум и более критериям.
МАКС()
Статистическая функция МАКС возвращает наибольшее значение в диапазоне ячеек:
МИН()
Статистическая функция МИН возвращает наименьшее значение в диапазоне ячеек:
Источники
- https://lumpics.ru/descriptive-statistics-in-excel/
- https://statanaliz.info/statistica/opisanie-dannyx/variatsiya-razmakh-srednee-linejnoe-otklonenie/
- https://www.hd01.ru/info/kak-poschitat-razmah-v-excel/
- http://galyautdinov.ru/post/formula-vyborki-prostaya
- https://math.semestr.ru/group/interval-estimation-share.php
- https://tidydata.ru/sample-size
- https://exceltable.com/formuly/raschet-statisticheskih-vybrosov
- https://lumpics.ru/how-to-make-a-sample-in-excel/
- https://office-guru.ru/excel/statisticheskie-funkcii-excel-kotorye-neobhodimo-znat-96.html
Содержание
- 10 популярных статистических функций в Microsoft Excel
- Статистические функции
- СРЗНАЧ
- СРЗНАЧЕСЛИ
- МОДА.ОДН
- МЕДИАНА
- СТАНДОТКЛОН
- НАИБОЛЬШИЙ
- НАИМЕНЬШИЙ
- РАНГ.СР
- Статистические функции в Microsoft Excel
- Использование статистических функций
- СРЗНАЧ
- СРЗНАЧЕСЛИ
- МЕДИАНА
- НАИБОЛЬШИЙ
- НАИМЕНЬШИЙ
- МОДА.ОДН
- СТАНДОТКЛОН
- СРГЕОМ
- Заключение
10 популярных статистических функций в Microsoft Excel
Статистическая обработка данных – это сбор, упорядочивание, обобщение и анализ информации с возможностью определения тенденции и прогноза по изучаемому явлению. В Excel есть огромное количество инструментов, которые помогают проводить исследования в данной области. Последние версии этой программы в плане возможностей практически ничем не уступают специализированным приложениям в области статистики. Главными инструментами для выполнения расчетов и анализа являются функции. Давайте изучим общие особенности работы с ними, а также подробнее остановимся на отдельных наиболее полезных инструментах.
Статистические функции
Как и любые другие функции в Экселе, статистические функции оперируют аргументами, которые могут иметь вид постоянных чисел, ссылок на ячейки или массивы.
Выражения можно вводить вручную в определенную ячейку или в строку формул, если хорошо знать синтаксис конкретного из них. Но намного удобнее воспользоваться специальным окном аргументов, которое содержит подсказки и уже готовые поля для ввода данных. Перейти в окно аргумента статистических выражений можно через «Мастер функций» или с помощью кнопок «Библиотеки функций» на ленте.
Запустить Мастер функций можно тремя способами:
- Кликнуть по пиктограмме «Вставить функцию» слева от строки формул.
- Находясь во вкладке «Формулы», кликнуть на ленте по кнопке «Вставить функцию» в блоке инструментов «Библиотека функций».
При выполнении любого из вышеперечисленных вариантов откроется окно «Мастера функций».
Затем нужно кликнуть по полю «Категория» и выбрать значение «Статистические».
После этого откроется список статистических выражений. Всего их насчитывается более сотни. Чтобы перейти в окно аргументов любого из них, нужно просто выделить его и нажать на кнопку «OK».
Для того, чтобы перейти к нужным нам элементам через ленту, перемещаемся во вкладку «Формулы». В группе инструментов на ленте «Библиотека функций» кликаем по кнопке «Другие функции». В открывшемся списке выбираем категорию «Статистические». Откроется перечень доступных элементов нужной нам направленности. Для перехода в окно аргументов достаточно кликнуть по одному из них.
Оператор МАКС предназначен для определения максимального числа из выборки. Он имеет следующий синтаксис:
В поля аргументов нужно ввести диапазоны ячеек, в которых находится числовой ряд. Наибольшее число из него эта формула выводит в ту ячейку, в которой находится сама.
По названию функции МИН понятно, что её задачи прямо противоположны предыдущей формуле – она ищет из множества чисел наименьшее и выводит его в заданную ячейку. Имеет такой синтаксис:
СРЗНАЧ
Функция СРЗНАЧ ищет число в указанном диапазоне, которое ближе всего находится к среднему арифметическому значению. Результат этого расчета выводится в отдельную ячейку, в которой и содержится формула. Шаблон у неё следующий:
СРЗНАЧЕСЛИ
Функция СРЗНАЧЕСЛИ имеет те же задачи, что и предыдущая, но в ней существует возможность задать дополнительное условие. Например, больше, меньше, не равно определенному числу. Оно задается в отдельном поле для аргумента. Кроме того, в качестве необязательного аргумента может быть добавлен диапазон усреднения. Синтаксис следующий:
МОДА.ОДН
Формула МОДА.ОДН выводит в ячейку то число из набора, которое встречается чаще всего. В старых версиях Эксель существовала функция МОДА, но в более поздних она была разбита на две: МОДА.ОДН (для отдельных чисел) и МОДА.НСК(для массивов). Впрочем, старый вариант тоже остался в отдельной группе, в которой собраны элементы из прошлых версий программы для обеспечения совместимости документов.
МЕДИАНА
Оператор МЕДИАНА определяет среднее значение в диапазоне чисел. То есть, устанавливает не среднее арифметическое, а просто среднюю величину между наибольшим и наименьшим числом области значений. Синтаксис выглядит так:
СТАНДОТКЛОН
Формула СТАНДОТКЛОН так же, как и МОДА является пережитком старых версий программы. Сейчас используются современные её подвиды – СТАНДОТКЛОН.В и СТАНДОТКЛОН.Г. Первая из них предназначена для вычисления стандартного отклонения выборки, а вторая – генеральной совокупности. Данные функции используются также для расчета среднего квадратичного отклонения. Синтаксис их следующий:
НАИБОЛЬШИЙ
Данный оператор показывает в выбранной ячейке указанное в порядке убывания число из совокупности. То есть, если мы имеем совокупность 12,97,89,65, а аргументом позиции укажем 3, то функция в ячейку вернет третье по величине число. В данном случае, это 65. Синтаксис оператора такой:
В данном случае, k — это порядковый номер величины.
НАИМЕНЬШИЙ
Данная функция является зеркальным отражением предыдущего оператора. В ней также вторым аргументом является порядковый номер числа. Вот только в данном случае порядок считается от меньшего. Синтаксис такой:
РАНГ.СР
Эта функция имеет действие, обратное предыдущим. В указанную ячейку она выдает порядковый номер конкретного числа в выборке по условию, которое указано в отдельном аргументе. Это может быть порядок по возрастанию или по убыванию. Последний установлен по умолчанию, если поле «Порядок» оставить пустым или поставить туда цифру 0. Синтаксис этого выражения выглядит следующим образом:
Выше были описаны только самые популярные и востребованные статистические функции в Экселе. На самом деле их в разы больше. Тем не менее, основной принцип действий у них похожий: обработка массива данных и возврат в указанную ячейку результата вычислительных действий.
Источник
Статистические функции в Microsoft Excel
Зная статистические формулы и приемы можно обработать, проанализировать и упорядочить большое количество информации. В Эксель инструменты статистики выведены в отдельную категорию функций. Давайте посмотрим, как их найти, а также, какие из них являются наиболее популярными среди пользователей.
Использование статистических функций
Формулы функций в Excel можно вводить вручную непосредственно в той ячейке, где планируется выполнить соответствующие расчеты. Это легко применимо к таким простым действиям, как сложение, вычитание, умножение и деление. Но запомнить формулы сложных функций уже непросто, поэтому проще воспользоваться специальным помощником, который встроен в программу.
Итак, чтобы вставить функцию в ячейку, выполняем одно из следующих действий:
- Находясь в любой вкладке программы щелкаем по значку “Вставить функцию” (fx), которая находится с левой стороны от строки формул.
- Переходим во вкладку “Формулы”, где видим в левом углу ленты инструментов кнопку “Вставить функцию”.
- Используем сочетание клавиш Shift+F3.
Независимо от выбранного способа выше перед нами появится окно вставки функций. Щелкаем по текущей категории и из раскрывшегося списка выбираем пункт “Статистические”.
Далее будет предложен на выбор один из статистических операторов. Отмечаем нужный и жмем OK.
На экране отобразится окно с аргументами выбранной функции, которые нужно заполнить.
Примечание: существует еще один способ выбора требуемой функции. Находясь во вкладке “Формулы” в блоке инструментов “Библиотека функций” щелкаем по значку “Другие функции”, затем выбираем пункт “Статистические” и, наконец, в открывшемся перечне (который можно листать вниз) – нужный оператор.
Давайте теперь рассмотрим наиболее популярные функции.
СРЗНАЧ
Оператор вычисляет среднее арифметическое значение из указанных значений (диапазона). Формула функции выглядит таким образом:
=СРЗНАЧ(число1;число2;…)
В качестве аргументов функции можно указать:
- конкретные числа;
- ссылки на ячейки, которые можно указать как вручную (напечатать с помощью клавиатуры), так и находясь в соответствующем поле щелкнуть по нужному элементу в самой таблице;
- диапазон ячеек – указывается вручную или путем выделения в таблице.
- переход к следующему аргументу происходит путем щелчка по соответствующему полю напротив него или просто нажатием клавиши Tab.
Функция помогает определить максимальное значение из заданных чисел (диапазона). Формула оператора следующая:
=МАКС(число1;число2;…)
В аргументах функции, также, как и в случае с оператором СРЗНАЧ можно указать конкретные числа, ссылки на ячейки или диапазоны ячеек.
Функция находит минимальное число из указанных значений (диапазона ячеек). В общем виде синтаксис выглядит так:
=МИН(число1;число2;…)
Аргументы функции заполняются так же, как и для оператора МАКС.
СРЗНАЧЕСЛИ
Функция позволяет найти среднее арифметическое значение, но при выполнении заданного условия. Формула оператора:
=СРЗНАЧЕСЛИ(диапазон;условие;диапазон_усреднения)
В аргументах указываются:
- Диапазон ячеек – вручную или с помощью выделения в таблице;
- Условие отбора значений из заданного диапазона (больше, меньше, не равно) – в кавычках;
- Диапазон_усреднения – не является обязательным аргументом для заполнения.
МЕДИАНА
Оператор находит медиану заданного диапазона значений. Синтаксис функции:
=МЕДИАНА(число1;число2;…)
В аргументах указываются: конкретные числа, ссылки на ячейки или диапазоны элементов.
НАИБОЛЬШИЙ
Функция позволяет найти из указанного диапазона значений с заданной позицией (по убыванию). Формула оператора:
=НАИБОЛЬШИЙ(массив;k)
Аргумента функции два: массив и номер позиции – K.
Допустим, имеется ряд чисел 4, 6, 12, 24, 15, 9. Если мы укажем в качестве аргумента “K” число 2, результатом будет значение, равное 15, т.к. оно второе по величине в выбранном диапазоне.
НАИМЕНЬШИЙ
Функция также, как и оператор НАИБОЛЬШИЙ, выполняет поиск из указанного диапазона значений. Правда, в данном случае счет идет по возрастанию. Синтаксис оператора следующий:
=НАИМЕНЬШИЙ(массив;k)
МОДА.ОДН
Функция пришла на замену более старому оператору “МОДА” (теперь находится в категории “Полный алфавитный перечень”). Позволяет определять число, которое повторяется чаще остальных в выбранном диапазоне. Работает функция по формуле:
=МОДА.ОДН(число1;число2;…)
В значениях аргументов указываются конкретные числовые значения, отдельные ячейки или их диапазоны.
Для вертикальных массивов, также, используется функция МОДА.НСК.
СТАНДОТКЛОН
Функция СТАНДОТКЛОН также устарела (но ее все еще можно найти, выбрав алфавитный перечень) и теперь представлена двумя новыми:
- СТАДНОТКЛОН.В – находит стандартное отклонение выборки
- СТАДНОТКЛОН.Г – определяет стандартное отклонение по генеральной совопкупности
Формулы функций выглядят следующим образом:
- =СТАДНОТКЛОН.В(число1;число2;…)
- =СТАДНОТКЛОН.Г(число1;число2;…)
СРГЕОМ
Оператор находит среднее геометрическое значение для заданного массива или диапазона. Формула функции:
=СРГЕОМ(число1;число2;…)
Заключение
В программе Excel более 100 статистических функций. Мы лишь рассмотрели те, которые используются пользователями чаще других, а также, где их можно найти и как заполнить аргументы для получения корректного результата.
Источник