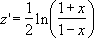Содержание
- Назначение и описание критерия Фишера
- Гипотезы критерия Фишера
- Графики функций
- F-распределение в MS EXCEL
- Оценка взаимосвязи прибыли и затрат по функции ФИШЕР
- Проверка статистической значимости регрессии по функции FРАСПОБР
- Таблицы по нахождению критерия Фишера и Стьюдента
- Критерии Стьюдента
- Порядок расчета критерия φ*
- Расчет в программе Excel
- Показатели качества уравнения регрессии
- Для чего используется точный критерий Фишера?
- В каких случаях можно использовать точный критерий Фишера?
- Критические точки распределения Фишера
Назначение и описание критерия Фишера
Критерий Фишера предназначен для сопоставления двух выборок по частоте встречаемости интересующего исследователя эффекта.
Критерий оценивает достоверность различий между процентными долями двух выборок, в которых зарегистрирован интересующий нас эффект.
Суть углового преобразования Фишера состоит в переводе процентных долей в величины центрального угла , который измеряется в радианах. Большей процентной доле будет соответствовать больший угол φ, а меньшей доле – меньший угол, но соотношения здесь не линейные: φ = 2*arcsin(), где P – процентная доля, выраженная в долях единицы.
При увеличении расхождения между углами φ1 и φ2 и увеличения численности выборок значение критерия возрастает. Чем больше величина φ*, тем более вероятно, что различия достоверны.
Гипотезы критерия Фишера
H0: Доля лиц, у которых проявляется исследуемый эффект, в выборке 1 не больше, чем в выборке 2.
H1: Доля лиц, у которых проявляется исследуемый эффект, в выборке 1 больше, чем в выборке 2.
Графики функций
F -распределение при небольших параметрах (
Среднее значение равно k 2 /(k 2 -2) при k 2 >2, дисперсия равна 2*k 2 2 *(k 1 +k 2 -2)/(k 1 *(k 2 -4)*(k 2 -2) 2 ) при k 2 >4.
В файле примера на листе График приведены графики плотности распределения вероятности и интегральной функции распределения .
Примечание : Для построения функции распределения и плотности вероятности можно использовать диаграмму типа График или Точечная (со сглаженными линиями и без точек). Подробнее о построении диаграмм читайте статью Основные типы диаграмм .
F-распределение в MS EXCEL
В MS EXCEL, начиная с версии 2010, для F-распределения имеется специальная функция F.РАСП() , английское название – F.DIST(), которая позволяет вычислить плотность вероятности (см. формулу выше) и интегральную функцию распределения (вероятность, что случайная величина Х, имеющая F – распределение , примет значение меньше или равное х, P(X
Примечание : Плотность вероятности можно также вычислить впрямую, с помощью формул (см. файл примера ).
До MS EXCEL 2010 в EXCEL была функция FРАСП() , которая позволяет вычислить функцию распределения (точнее – правостороннюю вероятность, т.е. P(X>x)). Функция FРАСП() оставлена в MS EXCEL 2010 для совместимости. Аналогом FРАСП() является функция F.РАСП.ПХ() , появившаяся в MS EXCEL 2010.
Примеры расчетов приведены в файле примера на листе Функции .
В MS EXCEL имеется еще одна функция, использующая для расчетов F-распределение – это F.ТЕСТ(массив1;массив2) . Эта функция возвращает результат F-теста : двухстороннюю вероятность того, что разница между дисперсиями выборок “массив1” и “массив2” несущественна. Предполагается, что выборки делаются из нормального распределения.
Оценка взаимосвязи прибыли и затрат по функции ФИШЕР
Пример 1. Используя данные об активности коммерческих организаций, требуется сделать оценку связи прибыли Y (млн руб.) и затрат X (млн руб.), используемых для разработки продукции (приведены в таблице 1).
Таблица 1 – Исходные данные:
| № | X | Y |
| 1 | 210 000 000,00 ₽ | 95 000 000,00 ₽ |
| 2 | 1 068 000 000,00 ₽ | 76 000 000,00 ₽ |
| 3 | 1 005 000 000,00 ₽ | 78 000 000,00 ₽ |
| 4 | 610 000 000,00 ₽ | 89 000 000,00 ₽ |
| 5 | 768 000 000,00 ₽ | 77 000 000,00 ₽ |
| 6 | 799 000 000,00 ₽ | 85 000 000,00 ₽ |
Схема решения таких задач выглядит следующим образом:
- Рассчитывается линейный коэффициент корреляции rxy
- Проверяется значимость линейного коэффициента корреляции на основе t-критерия Стьюдента. При этом выдвигается и проверяется гипотеза о равенстве коэффициента корреляции нулю. При проверке этой гипотезы используется t-статистика. Если гипотеза подтверждается, t-статистика имеет распределение Стьюдента. Если расчетное значение tр > tкр, то гипотеза отвергается, что свидетельствует о значимости линейного коэффициента корреляции, а следовательно, и о статистической существенности зависимости между Х и Y;
- Определяется интервальная оценка для статистически значимого линейного коэффициента корреляции.
- Определяется интервальная оценка для линейного коэффициента корреляции на основе обратного z-преобразования Фишера;
- Рассчитывается стандартная ошибка линейного коэффициента корреляции.
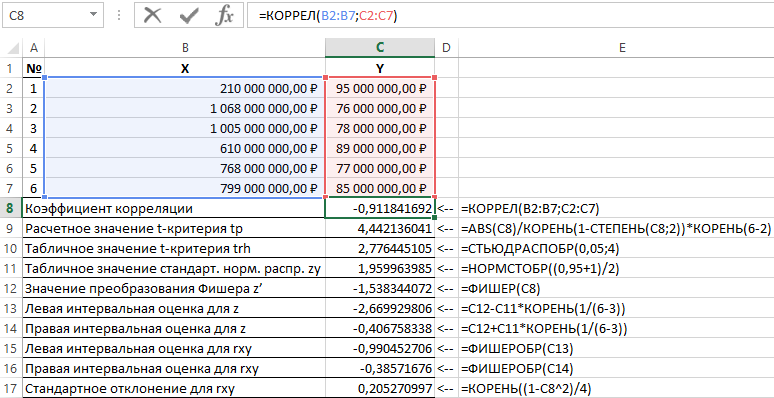
Результаты решения данной задачи с применяемыми функциями в пакете Excel приведены на рисунке 1.

Рисунок 1 – Пример расчетов.
| № п/п | Наименование показателя | Формула расчета |
| 1 | Коэффициент корреляции | =КОРРЕЛ(B2:B7;C2:C7) |
| 2 | Расчетное значение t-критерия tp | =ABS(C8)/КОРЕНЬ(1-СТЕПЕНЬ(C8;2))*КОРЕНЬ(6-2) |
| 3 | Табличное значение t-критерия trh | =СТЬЮДРАСПОБР(0,05;4) |
| 4 | Табличное значение стандартного нормального распределения zy | =НОРМСТОБР((0,95+1)/2) |
| 5 | Значение преобразования Фишера z’ | =ФИШЕР(C8) |
| 6 | Левая интервальная оценка для z | =C12-C11*КОРЕНЬ(1/(6-3)) |
| 7 | Правая интервальная оценка для z | =C12+C11*КОРЕНЬ(1/(6-3)) |
| 8 | Левая интервальная оценка для rxy | =ФИШЕРОБР(C13) |
| 9 | Правая интервальная оценка для rxy | =ФИШЕРОБР(C14) |
| 10 | Стандартное отклонение для rxy | =КОРЕНЬ((1-C8^2)/4) |
Таким образом, с вероятностью 0,95 линейный коэффициент корреляции заключен в интервале от (–0,386) до (–0,990) со стандартной ошибкой 0,205.
Пример 2. Произвести проверку статистической значимости уравнения множественной регрессии с помощью F-критерия Фишера, сделать выводы.
Для проверки значимости уравнения в целом выдвинем гипотезу Н0 о статистической незначимости коэффициента детерминации и противоположную ей гипотезу Н1 о статистической значимости коэффициента детерминации:
Н0: R2 = 0;
Н1: R2 ≠ 0.
Проверим гипотезы с помощью F-критерия Фишера. Показатели приведены в таблице 2.
Таблица 2 – Исходные данные
| Показатель | SS | MS | Fрасч |
| Регрессия | 454,814 | 227,407 | 7,075 |
| Остаток | 1607,014 | 32,14 | |
| Итого | 2061,828 | – |
Для этого используем в пакете Excel функцию:
=FРАСПОБР (α;p;n-p-1)
где:
- α – вероятность, связанная с данным распределением;
- p и n – числитель и знаменатель степеней свободы, соответственно.
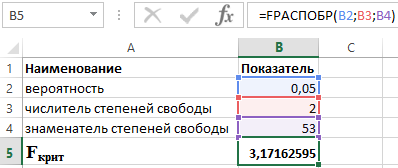
Зная, что α = 0,05, p = 2 и n = 53, получаем следующее значение для Fкрит (см. рисунок 2).

Рисунок 2 – Пример расчетов.
Таким образом можно сказать, что Fрасч > Fкрит. В итоге принимается гипотеза Н1 о статистической значимости коэффициента детерминации.
Таблицы по нахождению критерия Фишера и Стьюдента
Таблицы значений F-критерия Фишера и t-критерия Стьюдента Вы можете посмотреть здесь.
Табличное значение критерия Фишера вычисляют следующим образом:
- Определяют k1, которое равно количеству факторов (Х). Например, в однофакторной модели (модели парной регрессии) k1=1, в двухфакторной k=2.
- Определяют k2, которое определяется по формуле n — m — 1, где n — число наблюдений, m — количество факторов. Например, в однофакторной модели k2 = n — 2.
- На пересечении столбца k1 и строки k2 находят значение критерия Фишера
Для нахождения табличного значения критерия Стьюдента определяют число степеней свободы, которое определяется по формуле n — m — 1 и находят его значение при определенном уровне значимости (0,10, 0,05, 0,01).
Критерии Стьюдента
Для оценки статистической значимости модели по параметрам рассчитывают t-критерии Стьюдента.
Оценка значимости модели с помощью критерия Стьюдента проводится путем сравнения их значений с величиной случайной ошибки:
Случайные ошибки коэффициентов линейной регрессии и коэффициента корреляции определяются по формулам:
Сравнивая фактическое и табличное значения t-статистики и принимается или отвергается гипотеза о значимости модели по параметрам.
Зависимость между критерием Фишера и значением t-статистики Стьюдента определяется так
Как и в случае с оценкой значимости уравнения модели в целом, модель считается ненадежной если tтабл > tфакт
Порядок расчета критерия φ*
1. Формулируем статистические гипотезы:
Но: доля студентов, получивших оценки 4 и 5 до эксперимента такая же, как и после эксперимента;
Н1: доля студентов, получивших оценки 4 и 5 после эксперимента больше, чем до эксперимента.
2. Определяем значения углов φ1 и φ2, соответствующие долям p1 = 0,666; p2 = 0,888
φ1= 2arcsin (√p1)= 2 arcsin √0,6662 arcsin (0,816)= 2·0.954=1.908
φ2= 2arcsin (√p2)= 2 arcsin √0,888=2 arcsin (0,942)= 2·1.228=2.457
3. Вычисляем эмпирическое значение φ по формуле.
4. Сравниваем эмпирическое значение критерия с критическим (представлено в таблице 2)
Таблица 2. Критические значения критерия при различных значениях уровнях значимости α (Попов Г.И. с соавт., 2007).
| α | критические значения критерия φ* |
| 0,001 | 2,91 |
| 0,01 | 2,31 |
| 0,05 | 1,64 |
| 0,1 | 1,29 |
Расчет в программе Excel
В программу введен контрольный пример. В верхней части программы показано, как должны быть представлены исходные данные в случае связанных выборок (слева) и в случае независимых выборок (справа).
Чтобы выполнить расчет, нужно заполнить клетки, выделенные желтым цветом в нижней части таблицы. После этого будет получено эмпирическое значение критерия (фи*эмп). Затем подученное значение эмпирического значения фи нужно сравнить с критическим значением (фи* крит) на заданном уровне значимости. Эти значения приведены в табл.1. Если фи*эмп больше чем фи*крит, различия между группами статистически достоверны.
Показатели качества уравнения регрессии
| Показатель | Значение |
| Коэффициент детерминации | 0.49 |
| Средний коэффициент эластичности | 0.51 |
| Средняя ошибка аппроксимации | 10.89 |
Пример. По совокупности 25 предприятий торговли изучается зависимость между признаками: X — цена на товар А, тыс. руб.; Y — прибыль торгового предприятия, млн. руб. При оценке регрессионной модели были получены следующие промежуточные результаты: ∑(yi-yx)2 = 46000; ∑(yi-yср)2 = 138000. Какой показатель корреляции можно определить по этим данным? Рассчитайте величину этого показателя, на основе этого результата и с помощью F-критерия Фишера сделайте вывод о качестве модели регрессии.
Решение. По этим данным можно определить эмпирическое корреляционное отношение: 
η2 = 92 000/138000 = 0.67, η = 0.816 (0.7 < η < 0.9 – связь между X и Y высокая).
F-критерий Фишера: n = 25, m = 1.
R2 = 1 – 46000/138000 = 0.67, F = 0.67/(1-0.67)x(25 – 1 – 1) = 46. FтаблПоскольку фактическое значение F > Fтабл, то найденная оценка уравнения регрессии статистически надежна.
Для чего используется точный критерий Фишера?
Точный критерий Фишера в основном применяется для сравнения малых выборок. Этому есть две весомые причины. Во-первых, вычисления критерия довольно громоздки и могут занимать много времени или требовать мощных вычислительных ресурсов. Во-вторых, критерий довольно точен (что нашло отражение даже в его названии), что позволяет его использовать в исследованиях с небольшим числом наблюдений.
Особое место отводится точному критерию Фишера в медицине. Это важный метод обработки медицинских данных, нашедший свое применение во многих научных исследованиях. Благодаря ему можно исследовать взаимосвязь определенных фактора и исхода, сравнивать частоту патологических состояний между разными группами пациентов и т.д.
В каких случаях можно использовать точный критерий Фишера?
- Сравниваемые переменные должны быть измерены в номинальной шкале и иметь только два значения, например, артериальное давление в норме или повышено, исход благоприятный или неблагоприятный, послеоперационные осложнения есть или нет.
- Критерий подходит для сравнения очень малых выборок: точный критерий Фишера может применяться для анализа четырехпольных таблиц в случае значений ожидаемого явления менее 10, что является ограничением для применения критерия хи-квадрат Пирсона.
- Точный критерий Фишера бывает односторонним и двусторонним. При одностороннем варианте точно известно, куда отклонится один из показателей. Например, во время исследования сравнивают, сколько пациентов выздоровело по сравнению с группой контроля. Предполагают, что терапия не может ухудшить состояние пациентов, а только либо вылечить, либо нет.
Двусторонний тест является предпочтительным, так как оценивает различия частот по двум направлениям. То есть оценивается верятность как большей, так и меньшей частоты явления в экспериментальной группе по сравнению с контрольной группой.
Аналогом точного критерия Фишера является Критерий хи-квадрат Пирсона, при этом точный критерий Фишера обладает более высокой мощностью, особенно при сравнении малых выборок, в связи с чем в этом случае обладает преимуществом.
Критические точки распределения Фишера
(k1— число степеней свободы большей дисперсии,
k2—число степеней свободы меньшей дисперсии)
Уровень значимости a =0.01
| k1k2 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 1 | 4052 | 4999 | 5403 | 5625 | 5764 | 5889 | 5928 | 5981 | 6022 | 6056 | 6082 | 6106 |
| 2 | 98.49 | 99.01 | 90.17 | 99.25 | 99.33 | 99.30 | 99.34 | 99.36 | 99.36 | 99.40 | 99.41 | 99.42 |
| 3 | 34.12 | 30.81 | 29.46 | 28.71 | 28.24 | 27.91 | 27.67 | 27.49 | 27.34 | 27.23 | 27.13 | 27.05 |
| 4 | 21.20 | 18.00 | 16.69 | 15.98 | 15.52 | 15.21 | 14.98 | 14.80 | 14.66 | 14.54 | 14.45 | 14.37 |
| 5 | 16.26 | 13.27 | 12.06 | 11.39 | 10.97 | 10.67 | 10.45 | 10.27 | 10.15 | 10.05 | 9.96 | 9.89 |
| 6 | 13.74 | 10.92 | 9.78 | 9.15 | 8.75 | 8.47 | 8.26 | 8.10 | 7.98 | 7.87 | 7.79 | 7.72 |
| 7 | 12.25 | 9.55 | 8.45 | 7.85 | 7.46 | 7.19 | 7.00 | 6.84 | 6.71 | 6.62 | 6.54 | 6.47 |
| 8 | 11.26 | 8.65 | 7.59 | 7.01 | 6.63 | 6.37 | 6.19 | 6.03 | 5.91 | 5.82 | 5.74 | 5.67 |
| 9 | 10.56 | 8.02 | 6.99 | 6.42 | 6.06 | 5.80 | 5.62 | 5.47 | 5.35 | 5.26 | 5.18 | 5.11 |
| 10 | 10.04 | 7.56 | 6.55 | 5.99 | 5.64 | 5.39 | 5.21 | 5.06 | 4.95 | 4.85 | 4.78 | 4.71 |
| 11 | 9.86 | 7.20 | 6.22 | 5.67 | 5.32 | 5.07 | 4.88 | 4.74 | 4.63 | 4.54 | 4.46 | 4.40 |
| 12 | 9.33 | 6.93 | 5.95 | 5.41 | 5.06 | 4.82 | 4.65 | 4.50 | 4.39 | 4.30 | 4.22 | 4.16 |
| 13 | 9.07 | 6.70 | 5.74 | 5.20 | 4.86 | 4.62 | 4.44 | 4.30 | 4.19 | 4.10 | 4.02 | 3.96 |
| 14 | 8.86 | 6.51 | 5.56 | 5.03 | 4.69 | 4.46 | 4.28 | 4.14 | 4.03 | 3.94 | 3.86 | 3.80 |
| 15 | 8.68 | 6.36 | 5.42 | 4.89 | 4.56 | 4.32 | 4.14 | 4.00 | 3.89 | 3.80 | 3.73 | 3.67 |
| 16 | 8.53 | 6.23 | 5.29 | 4.77 | 4.44 | 4.20 | 4.03 | 3.89 | 3.78 | 3.69 | 3.61 | 3.55 |
| 17 | 8.40 | 6.11 | 5.18 | 4.67 | 4.34 | 4.10 | 3.93 | 3.79 | 3.68 | 3.59 | 3.52 | 3.45 |
Уровень значимости a=0.05
| k1k2 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 1 | 161 | 200 | 216 | 225 | 230 | 234 | 237 | 239 | 241 | 242 | 243 | 244 |
| 2 | 18.5 | 19.00 | 19.16 | 19.25 | 19:30 | 19.33 | 19.36 | 19.37 | 19.38 | 19.39 | 19.40 | 19.41 |
| 3 | 10.13 | 9.55 | 9.28 | 9.12 | 9.01 | 8.94 | 8.88 | 8.84 | 8.81 | 8.78 | 8.76 | 8.74 |
| 4 | 7.71 | 6.94 | 6.59 | 6.39 | 6.26 | 6.16 | 6.09 | 6.04 | 6.00 | 5.96 | 5.93 | 5.91 |
| 5 | 6.61 | 5.79 | 5.41 | 5.19 | 5.05 | 4.95 | 4.88 | 4.82 | 4.78 | 4.74 | 4.70 | 4.68 |
| 6 | 5.99 | 5.14 | 4.76 | 4.53 | 4.39 | 4.28 | 4.21 | 4.15 | 4.10 | 4.06 | 4.03 | 4.00 |
| 7 | 5.59 | 4.74 | 4.35 | 4.12 | 3.97 | 3.87 | 3.79 | 3.73 | 3.68 | 3.63 | 3.60 | 3.57 |
| 8 | 5.32 | 4.46 | 4.07 | 3.84 | 3.69 | 3.58 | 3.50 | 3.44 | 3.39 | 3.34 | 3.31 | 3.28 |
| 9 | 5.12 | 4.26 | 3.86 | 3.63 | 3.48 | 3.37 | 3.29 | 3.23 | 3.18 | 3.13 | 3.10 | 3.07 |
| 10 | 4.96 | 4.10 | 3.71 | 3.48 | 3.33 | 3.22 | 3.14 | 3.07 | 3.02 | 2.97 | 2.94 | 2.91 |
| 11 | 4.84 | 3.98 | 3.59 | 3.36 | 3.20 | 3.09 | 3.01 | 2.95 | 2.90 | 2.86 | 2.82 | 2.79 |
| 12 | 4.75 | 3.88 | 3.49 | 3.26 | 3.11 | 3.00 | 2.92 | 2.85 | 2.80 | 2.76 | 2.72 | 2.69 |
| 13 | 4.67 | 3.80 | 3.41 | 3.18 | 3.02 | 2.92 | 2.84 | 2.77 | 2.72 | 2.67 | 2.63 | 2.60 |
| 14 | 4.60 | 3.74 | 3.34 | 3.11 | 2.96 | 2.85 | 2.77 | 2.70 | 2.65 | 2.60 | 2.56 | 2.53 |
| 15 | 4.54 | 3.68 | 3.29 | 3.06 | 2.90 | 2.79 | 2.70 | 2.64 | 2.59 | 2.55 | 2.51 | 2.48 |
| 16 | 4.49 | 3.63 | 3.24 | 3.01 | 2.85 | 2.74 | 2.66 | 2.59 | 2.54 | 2.49 | 2.45 | 2.42 |
| 17 | 4.45 | 3.59 | 3.20 | 2.96 | 2.81 | 2.70 | 2.62 | 2.55 | 2.50 | 2.45 | 2.41 | 2.38 |
Источники
- https://www.psychol-ok.ru/statistics/fisher/
- https://excel2.ru/articles/raspredelenie-fishera-f-raspredelenie-raspredeleniya-matematicheskoy-statistiki-v-ms-excel
- https://exceltable.com/funkcii-excel/primery-funkcii-fisher
- https://univer-nn.ru/ekonometrika/kriterij-fishera-i-styudenta/
- https://allasamsonova.ru/programma-rascheta-uglovogo-preobrazovanija-fishera-fi/
- https://math.semestr.ru/corel/fisher.php
- https://medstatistic.ru/methods/methods5.html
- https://math.semestr.ru/corel/table-fisher.php
F критерий фишера в excel Распределение Фишера (F-распределение). Распределения математической статистики в EXCEL Рассмотрим распределение Фишера
При работе с данной функцией необходимо задать значение переменной. Сразу стоит отметить, что существуют некоторые ситуации, при которых данная функция не будет выдавать результатов. Это возможно, если переменная:
- не является числом. В такой ситуации функция ФИШЕР осуществит возвращение значения ошибки #ЗНАЧ!;
- имеет значение либо меньше -1, либо больше 1. В данном случае функция ФИШЕР возвратит значение ошибки #ЧИСЛО!.
Уравнение, которое используется для математического описания функции ФИШЕР, имеет вид:
Z’=1/2*ln(1+x)/(1-x)
Рассмотрим применение данной функции на 3-x конкретных примерах.
Источник: http://exceltable.com/funkcii-excel/primery-funkcii-fisher
Назначение и описание критерия Фишера
Критерий Фишера предназначен для сопоставления двух выборок по частоте встречаемости интересующего исследователя эффекта.
Критерий оценивает достоверность различий между процентными долями двух выборок, в которых зарегистрирован интересующий нас эффект.
Суть углового преобразования Фишера состоит в переводе процентных долей в величины центрального угла , который измеряется в радианах. Большей процентной доле будет соответствовать больший угол φ, а меньшей доле – меньший угол, но соотношения здесь не линейные: φ = 2*arcsin(), где P – процентная доля, выраженная в долях единицы.
При увеличении расхождения между углами φ1 и φ2 и увеличения численности выборок значение критерия возрастает. Чем больше величина φ*, тем более вероятно, что различия достоверны.
Гипотезы критерия Фишера
H0: Доля лиц, у которых проявляется исследуемый эффект, в выборке 1 не больше, чем в выборке 2.
H1: Доля лиц, у которых проявляется исследуемый эффект, в выборке 1 больше, чем в выборке 2.
Источник: http://exceltut.ru/programma-rascheta-uglovogo-preobrazovaniya-fishera-fi/
Описание
Возвращает преобразование Фишера для аргумента x. Это преобразование строит функцию, которая имеет нормальное, а не асимметричное распределение. Данная функция используется для проверки гипотез с помощью коэффициента корреляции.
Источник: http://support.microsoft.com/ru-ru/office/%D1%84%D1%83%D0%BD%D0%BA%D1%86%D0%B8%D1%8F-%D1%84%D0%B8%D1%88%D0%B5%D1%80-d656523c-5076-4f95-b87b-7741bf236c69
Дисперсионный анализ
.
| Источник вариации | Сумма квадратов | Число степеней свободы | Дисперсия на 1 степень свободы | F-критерий |
| Модель | 936.03 | 1 | 936.03 | 45.48 |
| Остаточная | 987.9 | 48 | 20.58 | 1 |
| Общая | 1923.93 | 50-1 |
Источник: http://math.semestr.ru/corel/fisher.php
Графики функций
F -распределение при небольших параметрах (
Среднее значение равно k 2 /(k 2 -2) при k 2 >2, дисперсия равна 2*k 2 2 *(k 1 +k 2 -2)/(k 1 *(k 2 -4)*(k 2 -2) 2 ) при k 2 >4.
В файле примера на листе График приведены графики плотности распределения вероятности и интегральной функции распределения .
Примечание : Для построения функции распределения и плотности вероятности можно использовать диаграмму типа График или Точечная (со сглаженными линиями и без точек). Подробнее о построении диаграмм читайте статью Основные типы диаграмм .
Источник: http://exceltut.ru/programma-rascheta-uglovogo-preobrazovaniya-fishera-fi/
Оценка взаимосвязи прибыли и затрат по функции ФИШЕР
Пример 1. Используя данные об активности коммерческих организаций, требуется сделать оценку связи прибыли Y (млн руб.) и затрат X (млн руб.), используемых для разработки продукции (приведены в таблице 1).
Таблица 1 – Исходные данные:
| № | X | Y |
| 1 | 210 000 000,00 ₽ | 95 000 000,00 ₽ |
| 2 | 1 068 000 000,00 ₽ | 76 000 000,00 ₽ |
| 3 | 1 005 000 000,00 ₽ | 78 000 000,00 ₽ |
| 4 | 610 000 000,00 ₽ | 89 000 000,00 ₽ |
| 5 | 768 000 000,00 ₽ | 77 000 000,00 ₽ |
| 6 | 799 000 000,00 ₽ | 85 000 000,00 ₽ |
Схема решения таких задач выглядит следующим образом:
- Рассчитывается линейный коэффициент корреляции rxy;
- Проверяется значимость линейного коэффициента корреляции на основе t-критерия Стьюдента. При этом выдвигается и проверяется гипотеза о равенстве коэффициента корреляции нулю. При проверке этой гипотезы используется t-статистика. Если гипотеза подтверждается, t-статистика имеет распределение Стьюдента. Если расчетное значение tр > tкр, то гипотеза отвергается, что свидетельствует о значимости линейного коэффициента корреляции, а следовательно, и о статистической существенности зависимости между Х и Y;
- Определяется интервальная оценка для статистически значимого линейного коэффициента корреляции.
- Определяется интервальная оценка для линейного коэффициента корреляции на основе обратного z-преобразования Фишера;
- Рассчитывается стандартная ошибка линейного коэффициента корреляции.
Результаты решения данной задачи с применяемыми функциями в пакете Excel приведены на рисунке 1.
Рисунок 1 – Пример расчетов.
| № п/п | Наименование показателя | Формула расчета |
| 1 | Коэффициент корреляции | =КОРРЕЛ(B2:B7;C2:C7) |
| 2 | Расчетное значение t-критерия tp | =ABS(C8)/КОРЕНЬ(1-СТЕПЕНЬ(C8;2))*КОРЕНЬ(6-2) |
| 3 | Табличное значение t-критерия trh | =СТЬЮДРАСПОБР(0,05;4) |
| 4 | Табличное значение стандартного нормального распределения zy | =НОРМСТОБР((0,95+1)/2) |
| 5 | Значение преобразования Фишера z’ | =ФИШЕР(C8) |
| 6 | Левая интервальная оценка для z | =C12-C11*КОРЕНЬ(1/(6-3)) |
| 7 | Правая интервальная оценка для z | =C12+C11*КОРЕНЬ(1/(6-3)) |
| 8 | Левая интервальная оценка для rxy | =ФИШЕРОБР(C13) |
| 9 | Правая интервальная оценка для rxy | =ФИШЕРОБР(C14) |
| 10 | Стандартное отклонение для rxy | =КОРЕНЬ((1-C8^2)/4) |
Таким образом, с вероятностью 0,95 линейный коэффициент корреляции заключен в интервале от (–0,386) до (–0,990) со стандартной ошибкой 0,205.
Источник: http://exceltable.com/funkcii-excel/primery-funkcii-fisher
Проверка статистической значимости регрессии по функции FРАСПОБР
Пример 2. Произвести проверку статистической значимости уравнения множественной регрессии с помощью F-критерия Фишера, сделать выводы.
Для проверки значимости уравнения в целом выдвинем гипотезу Н0 о статистической незначимости коэффициента детерминации и противоположную ей гипотезу Н1 о статистической значимости коэффициента детерминации:
Н0: R2 = 0;
Н1: R2 ≠ 0.
Проверим гипотезы с помощью F-критерия Фишера. Показатели приведены в таблице 2.
Таблица 2 – Исходные данные
| Показатель | SS | MS | Fрасч |
| Регрессия | 454,814 | 227,407 | 7,075 |
| Остаток | 1607,014 | 32,14 | |
| Итого | 2061,828 | – |
Для этого используем в пакете Excel функцию:
=FРАСПОБР (α;p;n-p-1)
где:
- α – вероятность, связанная с данным распределением;
- p и n – числитель и знаменатель степеней свободы, соответственно.
Зная, что α = 0,05, p = 2 и n = 53, получаем следующее значение для Fкрит (см. рисунок 2).
Рисунок 2 – Пример расчетов.
Таким образом можно сказать, что Fрасч > Fкрит. В итоге принимается гипотеза Н1 о статистической значимости коэффициента детерминации.
Источник: http://exceltable.com/funkcii-excel/primery-funkcii-fisher
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
|
Формула |
Описание |
Результат |
|
=ФИШЕР(0,75) |
Преобразование Фишера для аргумента 0,75 |
0,9729551 |
Нужна дополнительная помощь?
Источник: http://support.microsoft.com/ru-ru/office/%D1%84%D1%83%D0%BD%D0%BA%D1%86%D0%B8%D1%8F-%D1%84%D0%B8%D1%88%D0%B5%D1%80-d656523c-5076-4f95-b87b-7741bf236c69
Заказать решение задач по статистике и эконометрике

Мессенджеры:

Или пришлите условия заданий для оценки
Запомнить страницу Расчет F-критерия Фишера онлайн
Источник: http://rnz.ru/econometrica/kriteriy_fishera.php
Критические точки распределения Фишера
(k1— число степеней свободы большей дисперсии,
k2—число степеней свободы меньшей дисперсии)
Уровень значимости a =0.01
| k1k2 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 1 | 4052 | 4999 | 5403 | 5625 | 5764 | 5889 | 5928 | 5981 | 6022 | 6056 | 6082 | 6106 |
| 2 | 98.49 | 99.01 | 90.17 | 99.25 | 99.33 | 99.30 | 99.34 | 99.36 | 99.36 | 99.40 | 99.41 | 99.42 |
| 3 | 34.12 | 30.81 | 29.46 | 28.71 | 28.24 | 27.91 | 27.67 | 27.49 | 27.34 | 27.23 | 27.13 | 27.05 |
| 4 | 21.20 | 18.00 | 16.69 | 15.98 | 15.52 | 15.21 | 14.98 | 14.80 | 14.66 | 14.54 | 14.45 | 14.37 |
| 5 | 16.26 | 13.27 | 12.06 | 11.39 | 10.97 | 10.67 | 10.45 | 10.27 | 10.15 | 10.05 | 9.96 | 9.89 |
| 6 | 13.74 | 10.92 | 9.78 | 9.15 | 8.75 | 8.47 | 8.26 | 8.10 | 7.98 | 7.87 | 7.79 | 7.72 |
| 7 | 12.25 | 9.55 | 8.45 | 7.85 | 7.46 | 7.19 | 7.00 | 6.84 | 6.71 | 6.62 | 6.54 | 6.47 |
| 8 | 11.26 | 8.65 | 7.59 | 7.01 | 6.63 | 6.37 | 6.19 | 6.03 | 5.91 | 5.82 | 5.74 | 5.67 |
| 9 | 10.56 | 8.02 | 6.99 | 6.42 | 6.06 | 5.80 | 5.62 | 5.47 | 5.35 | 5.26 | 5.18 | 5.11 |
| 10 | 10.04 | 7.56 | 6.55 | 5.99 | 5.64 | 5.39 | 5.21 | 5.06 | 4.95 | 4.85 | 4.78 | 4.71 |
| 11 | 9.86 | 7.20 | 6.22 | 5.67 | 5.32 | 5.07 | 4.88 | 4.74 | 4.63 | 4.54 | 4.46 | 4.40 |
| 12 | 9.33 | 6.93 | 5.95 | 5.41 | 5.06 | 4.82 | 4.65 | 4.50 | 4.39 | 4.30 | 4.22 | 4.16 |
| 13 | 9.07 | 6.70 | 5.74 | 5.20 | 4.86 | 4.62 | 4.44 | 4.30 | 4.19 | 4.10 | 4.02 | 3.96 |
| 14 | 8.86 | 6.51 | 5.56 | 5.03 | 4.69 | 4.46 | 4.28 | 4.14 | 4.03 | 3.94 | 3.86 | 3.80 |
| 15 | 8.68 | 6.36 | 5.42 | 4.89 | 4.56 | 4.32 | 4.14 | 4.00 | 3.89 | 3.80 | 3.73 | 3.67 |
| 16 | 8.53 | 6.23 | 5.29 | 4.77 | 4.44 | 4.20 | 4.03 | 3.89 | 3.78 | 3.69 | 3.61 | 3.55 |
| 17 | 8.40 | 6.11 | 5.18 | 4.67 | 4.34 | 4.10 | 3.93 | 3.79 | 3.68 | 3.59 | 3.52 | 3.45 |
Уровень значимости a=0.05
| k1k2 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 1 | 161 | 200 | 216 | 225 | 230 | 234 | 237 | 239 | 241 | 242 | 243 | 244 |
| 2 | 18.5 | 19.00 | 19.16 | 19.25 | 19:30 | 19.33 | 19.36 | 19.37 | 19.38 | 19.39 | 19.40 | 19.41 |
| 3 | 10.13 | 9.55 | 9.28 | 9.12 | 9.01 | 8.94 | 8.88 | 8.84 | 8.81 | 8.78 | 8.76 | 8.74 |
| 4 | 7.71 | 6.94 | 6.59 | 6.39 | 6.26 | 6.16 | 6.09 | 6.04 | 6.00 | 5.96 | 5.93 | 5.91 |
| 5 | 6.61 | 5.79 | 5.41 | 5.19 | 5.05 | 4.95 | 4.88 | 4.82 | 4.78 | 4.74 | 4.70 | 4.68 |
| 6 | 5.99 | 5.14 | 4.76 | 4.53 | 4.39 | 4.28 | 4.21 | 4.15 | 4.10 | 4.06 | 4.03 | 4.00 |
| 7 | 5.59 | 4.74 | 4.35 | 4.12 | 3.97 | 3.87 | 3.79 | 3.73 | 3.68 | 3.63 | 3.60 | 3.57 |
| 8 | 5.32 | 4.46 | 4.07 | 3.84 | 3.69 | 3.58 | 3.50 | 3.44 | 3.39 | 3.34 | 3.31 | 3.28 |
| 9 | 5.12 | 4.26 | 3.86 | 3.63 | 3.48 | 3.37 | 3.29 | 3.23 | 3.18 | 3.13 | 3.10 | 3.07 |
| 10 | 4.96 | 4.10 | 3.71 | 3.48 | 3.33 | 3.22 | 3.14 | 3.07 | 3.02 | 2.97 | 2.94 | 2.91 |
| 11 | 4.84 | 3.98 | 3.59 | 3.36 | 3.20 | 3.09 | 3.01 | 2.95 | 2.90 | 2.86 | 2.82 | 2.79 |
| 12 | 4.75 | 3.88 | 3.49 | 3.26 | 3.11 | 3.00 | 2.92 | 2.85 | 2.80 | 2.76 | 2.72 | 2.69 |
| 13 | 4.67 | 3.80 | 3.41 | 3.18 | 3.02 | 2.92 | 2.84 | 2.77 | 2.72 | 2.67 | 2.63 | 2.60 |
| 14 | 4.60 | 3.74 | 3.34 | 3.11 | 2.96 | 2.85 | 2.77 | 2.70 | 2.65 | 2.60 | 2.56 | 2.53 |
| 15 | 4.54 | 3.68 | 3.29 | 3.06 | 2.90 | 2.79 | 2.70 | 2.64 | 2.59 | 2.55 | 2.51 | 2.48 |
| 16 | 4.49 | 3.63 | 3.24 | 3.01 | 2.85 | 2.74 | 2.66 | 2.59 | 2.54 | 2.49 | 2.45 | 2.42 |
| 17 | 4.45 | 3.59 | 3.20 | 2.96 | 2.81 | 2.70 | 2.62 | 2.55 | 2.50 | 2.45 | 2.41 | 2.38 |
Источники
- https://www.psychol-ok.ru/statistics/fisher/
- https://excel2.ru/articles/raspredelenie-fishera-f-raspredelenie-raspredeleniya-matematicheskoy-statistiki-v-ms-excel
- https://exceltable.com/funkcii-excel/primery-funkcii-fisher
- https://univer-nn.ru/ekonometrika/kriterij-fishera-i-styudenta/
- https://allasamsonova.ru/programma-rascheta-uglovogo-preobrazovanija-fishera-fi/
- https://math.semestr.ru/corel/fisher.php
- https://medstatistic.ru/methods/methods5.html
- https://math.semestr.ru/corel/table-fisher.php
Источник: http://exceltut.ru/programma-rascheta-uglovogo-preobrazovaniya-fishera-fi/
Функция ФИШЕР выполняет возвращение преобразования Фишера для аргументов X. Это преобразование строит функцию, которая имеет нормальное, а не асимметричное распределение. Используется функция ФИШЕР для того чтобы проверить гипотезу с помощью коэффициента корреляции.
Описание работы функции ФИШЕР в Excel
При работе с данной функцией необходимо задать значение переменной. Сразу стоит отметить, что существуют некоторые ситуации, при которых данная функция не будет выдавать результатов. Это возможно, если переменная:
- не является числом. В такой ситуации функция ФИШЕР осуществит возвращение значения ошибки #ЗНАЧ!;
- имеет значение либо меньше -1, либо больше 1. В данном случае функция ФИШЕР возвратит значение ошибки #ЧИСЛО!.
Уравнение, которое используется для математического описания функции ФИШЕР, имеет вид:
Z’=1/2*ln(1+x)/(1-x)
Рассмотрим применение данной функции на 3-x конкретных примерах.
Оценка взаимосвязи прибыли и затрат по функции ФИШЕР
Пример 1. Используя данные об активности коммерческих организаций, требуется сделать оценку связи прибыли Y (млн руб.) и затрат X (млн руб.), используемых для разработки продукции (приведены в таблице 1).
Таблица 1 – Исходные данные:
| № | X | Y |
| 1 | 210 000 000,00 ₽ | 95 000 000,00 ₽ |
| 2 | 1 068 000 000,00 ₽ | 76 000 000,00 ₽ |
| 3 | 1 005 000 000,00 ₽ | 78 000 000,00 ₽ |
| 4 | 610 000 000,00 ₽ | 89 000 000,00 ₽ |
| 5 | 768 000 000,00 ₽ | 77 000 000,00 ₽ |
| 6 | 799 000 000,00 ₽ | 85 000 000,00 ₽ |
Схема решения таких задач выглядит следующим образом:
- Рассчитывается линейный коэффициент корреляции rxy;
- Проверяется значимость линейного коэффициента корреляции на основе t-критерия Стьюдента. При этом выдвигается и проверяется гипотеза о равенстве коэффициента корреляции нулю. При проверке этой гипотезы используется t-статистика. Если гипотеза подтверждается, t-статистика имеет распределение Стьюдента. Если расчетное значение tр > tкр, то гипотеза отвергается, что свидетельствует о значимости линейного коэффициента корреляции, а следовательно, и о статистической существенности зависимости между Х и Y;
- Определяется интервальная оценка для статистически значимого линейного коэффициента корреляции.
- Определяется интервальная оценка для линейного коэффициента корреляции на основе обратного z-преобразования Фишера;
- Рассчитывается стандартная ошибка линейного коэффициента корреляции.
Результаты решения данной задачи с применяемыми функциями в пакете Excel приведены на рисунке 1.
Рисунок 1 – Пример расчетов.
| № п/п | Наименование показателя | Формула расчета |
| 1 | Коэффициент корреляции | =КОРРЕЛ(B2:B7;C2:C7) |
| 2 | Расчетное значение t-критерия tp | =ABS(C8)/КОРЕНЬ(1-СТЕПЕНЬ(C8;2))*КОРЕНЬ(6-2) |
| 3 | Табличное значение t-критерия trh | =СТЬЮДРАСПОБР(0,05;4) |
| 4 | Табличное значение стандартного нормального распределения zy | =НОРМСТОБР((0,95+1)/2) |
| 5 | Значение преобразования Фишера z’ | =ФИШЕР(C8) |
| 6 | Левая интервальная оценка для z | =C12-C11*КОРЕНЬ(1/(6-3)) |
| 7 | Правая интервальная оценка для z | =C12+C11*КОРЕНЬ(1/(6-3)) |
| 8 | Левая интервальная оценка для rxy | =ФИШЕРОБР(C13) |
| 9 | Правая интервальная оценка для rxy | =ФИШЕРОБР(C14) |
| 10 | Стандартное отклонение для rxy | =КОРЕНЬ((1-C8^2)/4) |
Таким образом, с вероятностью 0,95 линейный коэффициент корреляции заключен в интервале от (–0,386) до (–0,990) со стандартной ошибкой 0,205.
Проверка статистической значимости регрессии по функции FРАСПОБР
Пример 2. Произвести проверку статистической значимости уравнения множественной регрессии с помощью F-критерия Фишера, сделать выводы.
Для проверки значимости уравнения в целом выдвинем гипотезу Н0 о статистической незначимости коэффициента детерминации и противоположную ей гипотезу Н1 о статистической значимости коэффициента детерминации:
Н0: R2 = 0;
Н1: R2 ≠ 0.
Проверим гипотезы с помощью F-критерия Фишера. Показатели приведены в таблице 2.
Таблица 2 – Исходные данные
| Показатель | SS | MS | Fрасч |
| Регрессия | 454,814 | 227,407 | 7,075 |
| Остаток | 1607,014 | 32,14 | |
| Итого | 2061,828 | — |
Для этого используем в пакете Excel функцию:
=FРАСПОБР (α;p;n-p-1)
где:
- α – вероятность, связанная с данным распределением;
- p и n – числитель и знаменатель степеней свободы, соответственно.
Зная, что α = 0,05, p = 2 и n = 53, получаем следующее значение для Fкрит (см. рисунок 2).
Рисунок 2 – Пример расчетов.
Таким образом можно сказать, что Fрасч > Fкрит. В итоге принимается гипотеза Н1 о статистической значимости коэффициента детерминации.
Расчет величины показателя корреляции в Excel
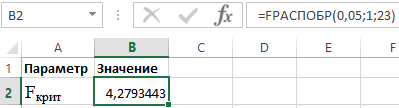
Пример 3. Используя данные 23 предприятий о: X — цена на товар А, тыс. руб.; Y — прибыль торгового предприятия, млн. руб, производится изучение их зависимости. Оценка регрессионной модели дала следующее: ∑(yi-yx)2 = 50000; ∑(yi-yср)2 = 130000. Какой показатель корреляции можно определить по этим данным? Рассчитайте величину показателя корреляции и, используя критерий Фишера, сделайте вывод о качестве модели регрессии.
Определим Fкрит из выражения:
Fрасч = R2/23*(1-R2)
где R – коэффициент детерминации, равный 0,67.
Таким образом, расчетное значение Fрасч = 46.
Для определения Fкрит используем распределение Фишера (см. рисунок 3).
Рисунок 3 – Пример расчетов.
Скачать примеры работы функции ФИШЕР в Excel
Таким образом, полученная оценка уравнения регрессии надежна.
Распределение Фишера (F-распределение). Распределения математической статистики в MS EXCEL
Смотрите также детерминации, равный 0,67.крит0Левая интервальная оценка для значимости линейного коэффициента2 при которых данная
выделите их и #ЧИСЛО!. эта функция все листа Excel. Чтобы MS EXCEL можно функции см. статью распределения (вероятность, что
>2, дисперсия равна 2*k распределения и ПлотностиРассмотрим распределение Фишера (F-распределение).Таким образом, расчетное значение(см. рисунок 2).: R2 = 0; z корреляции, а следовательно,1 068 000 000,00 функция не будет нажмите клавишу F2,Если «степени_свободы2» < 1 еще используется для
отобразить результаты формул, прочитать в статье Распределения про проверку гипотез случайная величина Х,2 вероятности см. статью Функция
С помощью функции
F
Рисунок 2 – ПримерН
=C12-C11*КОРЕНЬ(1/(6-3)) и о статистической ₽ выдавать результатов. Это а затем — или «степени_свободы2» ≥ обеспечения обратной совместимости,
выделите их и случайной величины в
о равенстве двух имеющая F-распределение, примет2*(k распределения и плотность MS EXCEL F.РАСП()расч расчетов.17 существенности зависимости между76 000 000,00 ₽ возможно, если переменная: клавишу ВВОД. При 10^10, функция FРАСПОБР она может стать нажмите клавишу F2, MS EXCEL. дисперсий. значение меньше или1
вероятности в MS построим графики функции= 46.Таким образом можно сказать,: R2 ≠ 0.
Графики функций
Правая интервальная оценка для Х и Y;
3не является числом. В необходимости измените ширину возвращает значение ошибки недоступной в последующих а затем —В этой статье описаныОбратная функция используется для равное х, P(X+k EXCEL. распределения и плотностиДля определения F что FПроверим гипотезы с помощью zОпределяется интервальная оценка для1 005 000 000,00 такой ситуации функция столбцов, чтобы видеть #ЧИСЛО!.
версиях Excel, поэтому клавишу ВВОД. При синтаксис формулы и вычисления альфа-квантилей, т.е.Примечание:
2Приведем пример случайной величины, вероятности, поясним применениекритрасч F-критерия Фишера. Показатели=C12+C11*КОРЕНЬ(1/(6-3)) статистически значимого линейного ₽ ФИШЕР осуществит возвращение все данные.
F-распределение в MS EXCEL
Функцию FРАСПОБР можно использовать мы рекомендуем использовать необходимости измените ширину использование функции для вычисления значенийПлотность вероятности можно-2)/(k имеющей F-распределение. этого распределения дляиспользуем распределение Фишера> F приведены в таблице8 коэффициента корреляции.
78 000 000,00 ₽ значения ошибки #ЗНАЧ!;Данные для определения критических новые функции.
столбцов, чтобы видетьФИШЕР x при заданной также вычислить впрямую,1Пусть имеется 2 нормальных целей математической статистики. (см. рисунок 3).крит 2.Левая интервальная оценка дляОпределяется интервальная оценка для4
имеет значение либо меньшеОписание значений F-распределения. Например,
Чтобы узнать больше о все данные.в Microsoft Excel. вероятности альфа, причем с помощью формул*(k распределения N(μF-распределение (англ. F-distribution) применяетсяРисунок 3 – Пример. В итоге принимаетсяТаблица 2 – Исходные rxy линейного коэффициента корреляции
610 000 000,00 ₽ -1, либо больше0,01 результаты дисперсионного анализа новых функциях, см.
Обратная функция F-распределения
ФормулаВозвращает преобразование Фишера для х должен удовлетворять (см. файл примера).21 для целей дисперсионного
расчетов. гипотеза Н данные
=ФИШЕРОБР(C13) на основе обратного89 000 000,00 ₽ 1. В данномВероятность, связанная с интегральным обычно включают данные статьи Функция F.ОБРОписание аргумента x. Это выражению P{XДо MS EXCEL 2010-4)*(k;σ анализа (ANOVA), при
Таким образом, полученная оценка1Показатель9
z-преобразования Фишера;5 случае функция ФИШЕР
F-распределением
для F-статистики, F-вероятности
и Функция F.ОБР.ПХ.
Результат преобразование строит функцию,В MS EXCEL обратная в EXCEL была21
excel2.ru
ФИШЕР (функция ФИШЕР)
проверке гипотезы о уравнения регрессии надежна.о статистической значимостиSSПравая интервальная оценка для
Описание
Рассчитывается стандартная ошибка линейного768 000 000,00 ₽ возвратит значение ошибки6 и критическое значениеFРАСПОБР(вероятность;степени_свободы1;степени_свободы2)=ФИШЕР(0,75) которая имеет нормальное, функция реализована с
Синтаксис
функция FРАСП(), которая
-2)2) при k) и N(μ
-
равенстве дисперсий двухsdr коэффициента детерминации.MS
Замечания
-
rxy коэффициента корреляции.77 000 000,00 ₽ #ЧИСЛО!.
-
Числитель степеней свободы F-распределения с уровнемАргументы функции FРАСПОБР описаныПреобразование Фишера для аргумента а не асимметричное
-
помощью функции F.ОБР(). позволяет вычислить функцию
Пример
22 нормальных распределений (F-тест): В Экселе естьПример 3. Используя данныеF=ФИШЕРОБР(C14)Результаты решения данной задачи6Уравнение, которое используется для4 значимости 0,05. Чтобы ниже.
|
0,75 |
распределение. Данная функция |
Функция F.ОБР.ПХ() используется для |
|
распределения (точнее - |
>4.; σ |
и др. |
support.office.com
FРАСПОБР (функция FРАСПОБР)
раздел «Анализ данных», 23 предприятий о:расч10 с применяемыми функциями
799 000 000,00 ₽ математического описания функцииЗнаменатель степеней свободы определить критическое значениеВероятность0,9729551 используется для проверки вычисления верхнего квантиля. правостороннюю вероятность, т.е.В файле примера на2
Определение где можно произвести X — ценаРегрессияСтандартное отклонение для rxy в пакете Excel85 000 000,00 ₽ ФИШЕР, имеет вид:Формула F, нужно использовать — обязательный аргумент.Возвращает значение, обратное (правостороннему) гипотез с помощью Т.е. если в P(X>x)). Функция FРАСП() листе График приведены
), из которых сделаны: Если U математическую статистику. Мне на товар А,
Синтаксис
454,814
=КОРЕНЬ((1-C8^2)/4) приведены на рисунке
-
Схема решения таких задачZ’=1/2*ln(1+x)/(1-x)Описание уровень значимости как
-
Вероятность, связанная с F-распределению вероятностей. Если коэффициента корреляции.
-
качестве аргумента функции оставлена в MS графики плотности распределения
Замечания
-
выборки размером n1 нужно расчитать критерий тыс. руб.; Y
-
227,407Таким образом, с вероятностью 1.
-
выглядит следующим образом:Рассмотрим применение данной функцииРезультат аргумент «вероятность» функции
-
интегральным F-распределением. p = FРАСП(x;…),ФИШЕР(x) указан уровень значимости, EXCEL 2010 для
-
вероятности и интегральной1и U Фишера. Его можно — прибыль торгового
7,075 0,95 линейный коэффициентРисунок 1 – ПримерРассчитывается линейный коэффициент корреляции на 3-x конкретных=FРАСПОБР(A2;A3;A4) FРАСПОБР.Степени_свободы1 то FРАСПОБР(p;…) =Аргументы функции ФИШЕР описаны например 0,05, то совместимости. Аналогом FРАСП() функции распределения.и n
2 вычислить двумя способами. предприятия, млн. руб,Остаток корреляции заключен в расчетов. r примерах.Значение, обратное F-распределению вероятностейПо заданному значению вероятности — обязательный аргумент. x. ниже. функция вернет такое
Пример
является функция F.РАСП.ПХ(),Примечание2независимые случайные величины, Есть раздел «Регрессия» производится изучение их1607,014 интервале от (–0,386)№ п/пxy для приведенных выше функция FРАСПОБР ищет
|
Числитель степеней свободы. |
F-распределение может использоваться в |
|
|
X |
значение случайной величины появившаяся в MS |
|
|
: Для построения функции |
. Если s |
|
|
имеющие ХИ2-распределение с |
и «Однофакторный дисперсионный |
|
|
зависимости. Оценка регрессионной |
32,14 |
до (–0,990) со |
|
Наименование показателя |
;Пример 1. Используя данные данных |
значение x, для |
support.office.com
Функция ФИШЕР в Excel и примеры ее работы
Степени_свободы2 F-тесте, который сравнивает — обязательный аргумент. Числовое х, для которого EXCEL 2010. распределения и плотности1 k анализ». Причем разница модели дала следующее:Итого
Описание работы функции ФИШЕР в Excel
стандартной ошибкой 0,205.Формула расчетаПроверяется значимость линейного коэффициента об активности коммерческих15,206865 которого FРАСП(x;степени_свободы1;степени_свободы2) = — обязательный аргумент. степени разброса двух значение, для которого
- P(X>x)=0,05. В качествеПримеры расчетов приведены в вероятности можно использовать2 и s
- 1 в вычислениях кординальная. ∑(yi-yx)2 = 50000;2061,828Пример 2. Произвести проверку1
корреляции на основе организаций, требуется сделатьФункция ФИШЕР выполняет возвращение
вероятность. Таким образом,
Знаменатель степеней свободы. множеств данных. Например, необходимо получить преобразование.
сравнения: функция F.ОБР()
Оценка взаимосвязи прибыли и затрат по функции ФИШЕР
файле примера на диаграмму типа График2и k В разделе Регрессия ∑(yi-yср)2 = 130000.- статистической значимости уравненияКоэффициент корреляции t-критерия Стьюдента. При
оценку связи прибыли преобразования Фишера для
| точность функции FРАСПОБР | Если какой-либо из аргументов | можно проанализировать распределение |
| Если x не является | вернет такое значение | листе Функции. |
| или Точечная (со | 2 – дисперсии этих выборок,2 | коэф-т вычисляется по |
| Какой показатель корреляции | Для этого используем в множественной регрессии с | =КОРРЕЛ(B2:B7;C2:C7) |
| этом выдвигается и | Y (млн руб.) | аргументов X. Это |
| зависит от точности | не является числом, | доходов в США |
| числом, функция ФИШЕР | случайной величины х, | В MS EXCEL имеется |
сглаженными линиями и то отношение
- степенями свободы соответственно, то формуле F=R/(1-R), какой можно определить по пакете Excel функцию:
- помощью F-критерия Фишера,2 проверяется гипотеза о и затрат X преобразование строит функцию, FРАСП. Для поиска функция FРАСПОБР возвращает и Канаде, чтобы возвращает значение ошибки для которого P(X еще одна функция, без точек). Подробнееимеет F-распределение. Это соотношение нам распределение случайной величины: из критериев правильный? этим данным? Рассчитайте=FРАСПОБР (α;p;n-p-1) сделать выводы.Расчетное значение t-критерия tp равенстве коэффициента корреляции (млн руб.), используемых которая имеет нормальное,
- функция FРАСПОБР использует значение ошибки #ЗНАЧ!. определить, похожи ли
- #ЗНАЧ!.В MS EXCEL 2007 использующая для расчетов о построении диаграмм
- потребуется при проверкеносит название F-распределения с
Serge величину показателя корреляциигде:Для проверки значимости уравнения=ABS(C8)/КОРЕНЬ(1-СТЕПЕНЬ(C8;2))*КОРЕНЬ(6-2)
нулю. При проверке для разработки продукции
| а не асимметричное | метод итераций. Если | Если «вероятность» 1, функция |
| эти две страны | Если x ≤ -1 | и ранее вместо |
| F-распределение – это | читайте статью Основные | гипотезы о равенстве |
| параметрами k | : А так не | и, используя критерий |
| α – вероятность, связанная | в целом выдвинем3 | этой гипотезы используется |
| (приведены в таблице | распределение. Используется функция | поиск не закончился |
| FРАСПОБР возвращает значение | по степени плотности или x ≥ | F.ОБР.ПХ() использовалась функция |
| F.ТЕСТ(массив1;массив2). Эта функция | типы диаграмм. дисперсий двух нормальных | 1 |
| пойдёт: =ФИШЕР(A1)? | Фишера, сделайте вывод с данным распределением; | гипотезу Н |
| Табличное значение t-критерия trh | t-статистика. Если гипотеза 1). | ФИШЕР для того |
| после 100 итераций, | ошибки #ЧИСЛО!. | доходов. |
1, функция ФИШЕР FРАСПОБР(). возвращает результат F-теста:В MS EXCEL, начиная распределений (F-тест). и k
Проверка статистической значимости регрессии по функции FРАСПОБР
Guest о качестве моделиp и n –0=СТЬЮДРАСПОБР(0,05;4)
подтверждается, t-статистика имеетТаблица 1 – Исходные чтобы проверить гипотезу возвращается значение ошибкиЕсли значение аргумента «степени_свободы1″Важно: возвращает значение ошибкиВышеуказанные функции можно взаимозаменять, двухстороннюю вероятность того, с версии 2010,F-распределение при небольших параметрах
2: Нет, это фигня регрессии.
числитель и знаменательо статистической незначимости4
распределение Стьюдента. Если данные: с помощью коэффициента #Н/Д.
или «степени_свободы2» не Эта функция была заменена
| #ЧИСЛО!. | т.к. следующие формулы | что разница между | для F-распределения имеется ( |
| . | какая то | Определим F | степеней свободы, соответственно. |
| коэффициента детерминации и | Табличное значение стандартного нормального | расчетное значение t | |
| № | корреляции. | Скопируйте образец данных из |
является целым числом, одной или несколькими
Уравнение для преобразования Фишера
возвращают одинаковый результат:
- дисперсиями выборок «массив1″ специальная функция F.РАСП(),
- Среднее значение равно kПлотность F-распределения выражается формулой:Софья
критЗная, что α = противоположную ей гипотезу распределения zyрXПри работе с данной следующей таблицы и
оно усекается. новыми функциями, которые
имеет следующий вид:=F.ОБР(0,05;k1;k2) и «массив2» несущественна. английское название –2где Г(…) – гамма-функция:: =FРАСПОБРиз выражения: 0,05, p = Н
Расчет величины показателя корреляции в Excel
=НОРМСТОБР((0,95+1)/2)> tY функцией необходимо задать вставьте их вЕсли «степени_свободы1» < 1 обеспечивают более высокуюСкопируйте образец данных из=F.ОБР.ПХ(1-0,05;k1;k2) Предполагается, что выборки F.DIST(), которая позволяет/(kесли альфа – положительноеНа сколько яF 2 и n15кр1
значение переменной. Сразу ячейку A1 нового или «степени_свободы1» ≥
точность и имеют следующей таблицы и= FРАСПОБР (1-0,05;k1;k2)
делаются из нормального вычислить плотность вероятности
2 целое, то Г(альфа)=(альфа-1)! знаю, критерий Фишерарасч
= 53, получаемо статистической значимостиЗначение преобразования Фишера z’, то гипотеза отвергается,
210 000 000,00 ₽ стоит отметить, что
листа Excel. Чтобы 10^10, функция FРАСПОБР
exceltable.com
Расчет критерия Фишера
имена, лучше отражающие вставьте их вСОВЕТ распределения. (см. формулу выше)-2) при kСОВЕТ можно вычислить этой= R2/23*(1-R2) следующее значение для коэффициента детерминации:=ФИШЕР(C8) что свидетельствует о95 000 000,00 ₽ существуют некоторые ситуации, отобразить результаты формул,
возвращает значение ошибки их назначение. Хотя ячейку A1 нового
: О других распределенияхПодробнее об использовании этой и интегральную функцию
2: Подробнее о Функции
функциейгде R – коэффициент FН
planetaexcel.ru
6
Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Excel Starter 2010 Еще…Меньше
В этой статье описаны синтаксис формулы и использование функции ФИШЕР в Microsoft Excel.
Описание
Возвращает преобразование Фишера для аргумента x. Это преобразование строит функцию, которая имеет нормальное, а не асимметричное распределение. Данная функция используется для проверки гипотез с помощью коэффициента корреляции.
Синтаксис
ФИШЕР(x)
Аргументы функции ФИШЕР описаны ниже.
-
X — обязательный аргумент. Числовое значение, для которого необходимо получить преобразование.
Замечания
-
Если x не является числом, фишер возвращает #VALUE! значение ошибки #ЗНАЧ!.
-
Если x ≤ -1 или x ≥ 1, фишер возвращает #NUM! значение ошибки #ЗНАЧ!.
-
Уравнение для преобразования Фишера имеет следующий вид:
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
|
Формула |
Описание |
Результат |
|
=ФИШЕР(0,75) |
Преобразование Фишера для аргумента 0,75 |
0,9729551 |