Time word problems with solutions

In today’s post, we are going to work with time word problems. We’ll take a look at some examples and solve them together.

Let’s begin!

Time Word Problem 1: The Sailboat Race

In a sailboat race, the winning boat completed two distances in the following times: 2 min 22 seconds and 3 min 45 seconds.  How much time did it take the sailboat to finish from the beginning to the end?

We want to know the total time that it took for the sailboat to finish.  So, we’ll need to add the times of the two distances. Here, we see that the seconds add up to 67 seconds, which is more than 60 seconds. We can’t leave the final answer in seconds. Instead, we’ll need to express the 67 seconds in minutes and seconds: As a result, it took the boat 6 minutes and 7 seconds to cross the finish line.

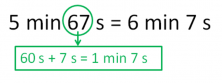
Time Word Problem 2: Flight to NYC

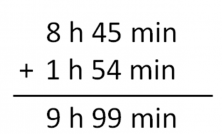
When Alex arrived at the airport, he looked at his watch and it was 5:45 a.m., exactly 3 hours before his next flight to NYC. If his next flight left on time and took exactly 114 minutes, what was the time on his watch when he arrived in NYC?

We need to calculate the amount of time that passed since the moment Alex looked at his watch until when he landed in NYC. The first thing we need to do is figure out when the plane took off. The text told us that exactly 3 hours passed, so he left at 8:45 a.m.

Now, we need to calculate when he landed. The flight took 114 minutes, which is more than 60 minutes. That means we need to change it so the answer is expressed in hours and minutes: Then, we can add on the time that passed to the initial time when the plane took off:99 minutes are more than 60, which means we need to change it to hours and minutes:

As we can see above, Alex’s plane landed in NYC at 10:39 a.m.

What did you think about this post? Did it help you understand how to solve time word problems?

If you want to practice more time word problems, and others, create an account on Smartick and try it for free!

Learn More:

Today we are going to learn the Word Problems on Measurement of Time, which helps students in every phase of their life. In order to solve problems on measuring time, first, we need to get knowledge on units of time and how to calculate and measure the time correctly. As you know, how time varies in different types of units, let’s have a glance at this Measurement of Time Word Problems.

While solving the time problems, time can be in the format of a.m. and p.m where the clock is 12-hour clock format. Here, we have compiled some examples for students to explain and understand the Time Problem Solving with Solution. So, practice with these Measuring Time Word Problems with Solutions PDF and improve your knowledge on 4th grade math time concepts.

Also Read:

• Time Duration
• Adding and Subtracting Time
• Worksheet on Conversion of Time

Example 1: 
Navya went to college at 7:00 a.m. It takes her 1 hr 30 min to reach the college. At what time will she reach the college?

Solution:

Navya went to college at                                 7 hr 00 min
Time taken to reach the college for her is       1 hr 30 min   +
Now, the time she reached college is              8 hr 30 min

Therefore, Navya reaches the college at 8:30 a.m.

---

Example 2: 
Chaitanya is feeding a dog. He starts at 10:45 a.m. and continues feeding for 15 minutes. When did he complete his feeding?

Solution:

Chaitanya started feeding a dog at 10:45 a.m.
He continued feeding for 15 minutes.
Now, have to find the time when he completed feeding.
We add both the timings and we will get the answer.
i.e., 10 hr 45 min + 15 min = 10 hr + 60 min = 10 hr + 1 hr = 11 hrs.
Hence, at 11:00 a.m. Chaitanya completed the feeding for his dog.

---

Example 3: 
Sam is getting her exam. She starts at 9:05 a.m. and continues her exam for 58 minutes. When did she finish her exam?

Solution:

Sam starts her exam at 9:05 a.m.
It continues for 58 minutes.
Now, add both the exam times to get the finish time of the exam.
9 hr 05 min + 58 min = 9 hr 63 min = 9 hr + 60 min + 3 min = 9 hr + 1 hr + 3 min = 10 hr 3 min.
So, Sam finishes her exam at 10:03 a.m.

---

Example 4: 
The train was scheduled to arrive at 6:40 p.m. However, it was delayed for 35 minutes. What is the time when the train arrives?

Solution:

The train schedules at 6:40 p.m. i.e., 6 hr 40 min.
The train delays for 35 minutes.
Arrived time of the train = 6 hr 40 min + 35 min = 6 hr 75 min = 6 hr + 60 min + 15 min = 6 hr + 1 hr + 15 min = 7 hr 15 min.
The train arrives at 7:15 p.m.

---

Example 5: 
Chetan’s birthday party started at 5:30 p.m. The last guest left at 7:05 p.m. How long did Chetan’s party last?

Solution:

Chetan’s birthday party starts at 5:30 p.m. i.e., 5 hr 30 min.
The last guest left the party at the time of 7:05 p.m i.e., 7 hr 5 min.
To know the time how long did Chetan’s party be. We subtract the left guest time with the time when the party started.
i.e., 7 hr 05 min – 5 hr 30 min = 2 hr 25 min.
Thus, Chetan’s party lasts for 2 hrs 25 min.

---

Example 6: 
Karan is practicing his violin. He finishes at 2:40 p.m. after 30 minutes. When did he start his violin?

Solution:

Karan completes his practice at 2:40 p.m. i.e., 2 hrs 40 min.
Next, we have to know when he starts his violin practice time.
From the given question, we have a clue that after 30 minutes. So, we subtract this 30 min time from the completed practice time i.e., 2 hr 40 min.
Now, 2 hr 40 min – 30 min = 2 hr 10 min.
Hence, Karan starts his violin practice session at 2:10 p.m.

---

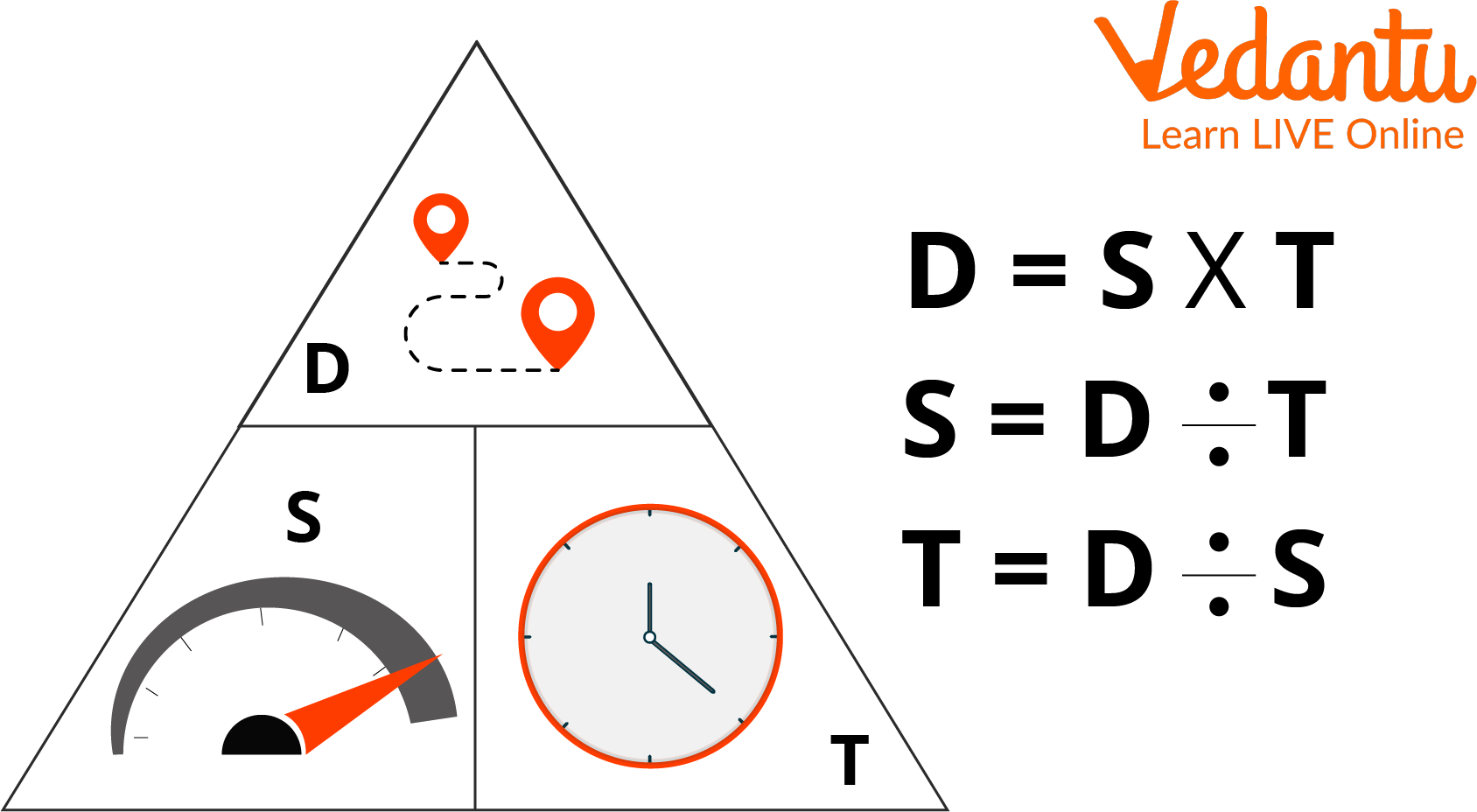
Speed, distance, and time are the three main pillars behind mathematics and physics. Whenever you are presented with a question related to any kind of transportation, you should immediately relate to these concepts. The train speed, the relation between the time taken by two cars at different speeds or even a simple question about a person walking from one place to another can be answered using simple formulas.

What is Speed?

When you think of speed, you must think of how fast? Speed is all about calculating the rate at which something can be accomplished.

A Device Used to Measure Speed Known as a ‘Speedometer’

What is Distance?

Distance in this concept refers to the distance travelled. It means how far? It can be measured in meters, for small distances and kilometres, for larger distances.

Distance is the Measurement From One Place to Another

What is Time?

Time is the answer to the question, how long? The best way to measure time is using the ‘world clock.’ In ancient times, time was measured with the help of the sun and the moon, and other celestial objects.

Time as Shown by a Clock

Relation Between Speed Distance and Time

There is a very simple mathematical relation between speed, distance and time.

$text{speed=}frac{text{distance}}{text{time}}$

$text{time=}frac{text{distance}}{text{speed}}$

$text{distance=speed }!!times!!text{ time}$

These relations can be memorised using the triangle method. See the following image to understand the use of this method.

Explaining the Triangle Method

Q1. A train is travelling at a speed of 160 km/hour. It takes 15 hours to cover the distance from city A to city B. Find the distance between the two cities.

Solution:

Speed= 160 km/hr

Time= 15 hours

Using the formula, $text{distance=speed }!!times!!text{ time}$

Distance= $160times 15=2400km$

Answer: The distance between city A and city B is 2400km

Q2. A car travelling from city A to city C completes the journey in 3 hours, whereas a person travelling on a bike completes the journey in 5 hours. What is the speed of the man on the bike if the car is travelling at 45 kmph?

Solution:

Find the distance using the information on the car

Using the formula, $text{distance=speed }!!times!!text{ time}$

Speed= 45km/hour

Time= 3 hours

$therefore text{distance}=45times 3=135km$

Using the distance, we can find the speed of the bike

Formula used, $text{speed=}frac{text{distance}}{text{time}}$

Time taken by bike is 5 hours

$therefore text{speed}=frac{135}{5}=27$

Answer: The bike is moving at a speed of 27 kmph.

Q3. A person travels at a speed of 15 kmph from point A to point B, which are 25 km from each other. Another person is travelling from point C to point B, 44 km from each other. Both people start their journey at the same time; the second person arrives at the point 2 hours after the first. What is the speed at which the second person was travelling?

Solution:

Speed of person 1 = 15km/hour

Distance travelled by person 1= 25 km/hour

Time taken by first-person = $frac{text{distance}}{text{speed}}=frac{25}{15}=frac{5}{3}$hours

Note: While solving the questions, keep the answers in fractions until you reach the final answer to make calculations easier.

Time taken by second person =$frac{5}{3}+2=frac{11}{3}$hours

Distance travelled by second person= 44 km

$therefore text{speed}=frac{text{distance}}{text{time}}=frac{44}{frac{11}{3}}=frac{44times 3}{11}=4times 3=12$kmph

Answer: The second person was travelling at a speed of 12kmph.

Q4. Raju is travelling from one station to another 560km away in a train which is moving at a speed of 125kmph. Monu is travelling to the same destination at a speed of 80kmph. Monu starts his journey 3 hours after Raju, from 120 km closer to the destination. How long will Raju have to wait at the train station for Monu to arrive?

Solution:

Distance travelled by Raju = 560km

Speed of Raju= 125km/hour

∴ Time taken by Raju to reach the station = $frac{text{distance}}{text{speed}}=frac{560}{125}=frac{112}{25}$hours

Distance travelled by Monu = $560-120=440$km

The speed at which Monu travelled = 80kmph

Time taken by Monu to complete journey = $frac{440}{80}=frac{22}{4}=frac{11}{2}$hours

Total time taken by Monu = $frac{11}{2}+3=frac{17}{2}$hours

Therefore, the time Raju had to wait = difference between the two times taken

$therefore frac{17}{2}-frac{112}{25}=frac{17times 25}{50}-frac{112times 2}{50}=frac{201}{50}=4.02$hours

Answer: Raju had to wait for 4.02 hours at the train station

Convert 4.02 hours to hours and minutes

$therefore 0.02=frac{2}{100}times 60=1.2$minutes

$therefore 0.2=frac{2}{10}times 60=12$seconds

Therefore, to be precise, Raju had to wait at the train station for 4 hours, 1 minute and 12 seconds.

Before you get into distance, time and speed word problems, take a few minutes to read this first and understand: How to build your credit score in USA as an international student.

Problems involving Time, Distance and Speed are solved based on one simple formula.

Distance = Speed * Time

Which implies →

Speed = Distance / Time   and

Time = Distance / Speed

Solution

Solution

Solution

Distance covered = 4*40 = 160 miles

Example 4. If a person walks at 4 mph, he covers a certain distance. If he walks at 9 mph, he covers 7.5 miles more. How much distance did he actually cover?

Now we can see that the direct application of our usual formula Distance = Speed * Time or its variations cannot be done in this case and we need to put in extra effort to calculate the given parameters.

Let us see how this question can be solved.

Solution

For these kinds of questions, a table like this might make it easier to solve.

Distance	Speed	Time
d	4	t
d+7.5	9	t

 
Let the distance covered by that person be ‘d’.

Walking at 4 mph and covering a distance ‘d’ is done in a time of ‘d/4’

IF he walks at 9 mph, he covers 7.5 miles more than the actual distance d, which is ‘d+7.5’.

He does this in a time of (d+7.5)/9.

Since the time is same in both the cases →

d/4 = (d+7.5)/9            →        9d = 4(d+7.5)   →        9d=4d+30        →        d = 6.

Solution

Here, we see that the distance is same.

Let us assume that its usual speed is ‘s’ and time is ‘t’, then

Distance	Speed	Time
d	s	t min
d	S+1/3	t+30 min

 
s*t = (1/3)s*(t+30)      →        t = t/3 + 10      →        t = 15.

So the actual time taken to cover the distance is 15 minutes.

Note: Note the time is expressed in terms of ‘minutes’. When we express distance in terms of miles or kilometers, time is expressed in terms of hours and has to be converted into appropriate units of measurement.

Solved Questions on Trains

Example 1. X and Y are two stations which are 320 miles apart. A train starts at a certain time from X and travels towards Y at 70 mph. After 2 hours, another train starts from Y and travels towards X at 20 mph. At what time do they meet?

Solution

Let the time after which they meet be ‘t’ hours.

Then the time travelled by second train becomes ‘t-2’.

Now,

Distance covered by first train+Distance covered by second train = 320 miles

70t+20(t-2) = 320

Solving this gives t = 4.

Solution

Let the speed of the first train be ‘s’.

Distance covered by the first train in (2+4) hours = Distance covered by second train in 4 hours

Therefore, 6s = 60*4

Solving which gives s=40.

So the slower train is moving at the rate of 40 mph.
 

Questions on Boats/Airplanes

For problems with boats and streams,

Speed of the boat upstream (against the current) = Speed of the boat in still water – speed of the stream

[As the stream obstructs the speed of the boat in still water, its speed has to be subtracted from the usual speed of the boat]

Speed of the boat downstream (along with the current) = Speed of the boat in still water + speed of the stream

[As the stream pushes the boat and makes it easier for the boat to reach the destination faster, speed of the stream has to be added]

Similarly, for airplanes travelling with/against the wind,

Speed of the plane with the wind = speed of the plane + speed of the wind

Speed of the plane against the wind = speed of the plane – speed of the wind

Let us look at some examples.

Example 1. A man travels at 3 mph in still water. If the current’s velocity is 1 mph, it takes 3 hours to row to a place and come back. How far is the place?

Solution

Let the distance be ‘d’ miles.

Time taken to cover the distance upstream + Time taken to cover the distance downstream = 3

Speed upstream = 3-1 = 2 mph

Speed downstream = 3+1 = 4 mph

Solution

Let the speed of the plane be ‘a’ and that of the wind be ‘w’.

Our table looks like this:
 

	Distance	Speed	Time
With the wind	2400	a+w	4
Against the wind	2400	a-w	6

 
4(a+w) = 2400 and 6(a-w) = 2400

Expressing one unknown variable in terms of the other makes it easier to solve, which means

a+w = 600 → w=600-a

Substituting the value of w in the second equation,

a-w = 400

a-(600-a) = 400 → a = 500

The speed of the plane is 500 kmph and that of the wind is 100 kmph.
 

More solved examples on Speed, Distance and Time

Example 1. A boy travelled by train which moved at the speed of 30 mph. He then boarded a bus which moved at the speed of 40 mph and reached his destination. The entire distance covered was 100 miles and the entire duration of the journey was 3 hours. Find the distance he travelled by bus.

Solution

	Distance	Speed	Time
Train	d	30	t
Bus	100-d	40	3-t

Let the time taken by the train be ‘t’. Then that of bus is ‘3-t’.

The entire distance covered was 100 miles

So, 30t + 40(3-t) = 100

Solving which gives t=2.

Substituting the value of t in 40(3-t), we get the distance travelled by bus is 40 miles.

Alternatively, we can add the time and equate it to 3 hours, which directly gives the distance.

d/30 + (100-d)/40 = 3

Solution

Our table looks like this.

	Distance	Speed	Time
1st part of journey	d	100	t
2nd part of journey	630-d	110	6-t

Assuming the distance covered in the 1^st part of journey to be ‘d’, the distance covered in the second half becomes ‘630-d’.

Assuming the time taken for the first part of the journey to be ‘t’, the time taken for the second half becomes ‘6-t’.

From the first equation, d=100t

The second equation is 630-d = 110(6-t).

Substituting the value of d from the first equation, we get

630-100t = 110(6-t)

Solving this gives t=3.

Solution

	Distance	Speed	Time
First person	d	3	t
Second person	20-d	4	t

 
Assuming the distance travelled by the first person to be ‘d’, the distance travelled by the second person is ’20-d’.

The time is ‘t’ for both of them because when they meet, they would have walked for the same time.

Since time is same, we can equate as

d/3 = (20-d)/4

Solving this gives d=60/7 miles (8.5 miles approximately)

Then t = 20/7 hours

So the two persons meet after 2 6/7 hours.
 

Practice Questions for you to solve

---

Problem 1: Click here

Answer 1: Click here

---

Problem 2: Click here

Answer 2: Click here

---

Related Topics:
Lesson
Plans and Worksheets for Grade 3
Lesson
Plans and Worksheets for all Grades
More
Lessons for Grade 3
Common Core For Grade 3

Videos, examples, solutions, and lessons to help Grade 3 students learn how to solve word problems involving time intervals within 1 hour by counting backward and forward using the number line and clock.

Common Core Standards: 3.NBT.2,
3.MD.1

New York State Common Core Math Grade 3, Module 2, Lesson 4

How many more minutes than Patrick did it take Lilly to finish her chores?
12 minutes more.

What strategy did you use to solve this problem?

• Show Step-by-step Solutions

Problem Set

1. Cole starts reading at 6:23 p.m. He stops at 6:49 p.m. How many minutes does Cole read?
Cole reads for __________ minutes.
2. Natalie finishes piano practice at 2:45 p.m. after practicing for 37 minutes. What time does Natalie’s
practice start?
Natalie’s practice starts at __________ p.m.

3. Genevieve works on her scrapbook from 11:27 a.m. to 11:58 a.m. How many minutes does she work on
her scrapbook?
Genevieve works on her scrapbook for __________minutes.

4. Nate finishes his homework at 4:47 p.m. after working on it for 38 minutes. What time does Nate start
his homework?
Nate starts his homework at __________ p.m.
5. Andrea goes fishing at 9:03 a.m. She fishes for 49 minutes. What time is Andrea done fishing?
6. Dion walks to school. The clocks below show when he leaves his house and when he arrives at school.
How many minutes does it take Dion to walk to school?

• Show Step-by-step Solutions

Homework Questions 1 to 6

Record your homework start time on the clock in Problem 6.
Directions: Use a number line to answer Problems 1 through 4.
1. Joy’s mom begins walking at 4:12 p.m. She stops at 4:43 p.m. How many minutes does she walk?
Joy’s mom walks for __________ minutes.
2. Cassie finishes softball practice at 3:52 p.m. after practicing for 30 minutes. What time does Cassie’s
practice start?
Cassie’s practice starts at ____________.
3. Jordie builds a model from 9:14 a.m. to 9:47 a.m. How many minutes does Jordie spend building his
model?
Jordie builds for _____________ minutes.
4. Cara finishes reading at 2:57 p.m. She reads for a total of 46 minutes. What time did Cara start reading?
Cara starts reading at ____________ p.m.
5. Jenna and her mom take the bus to the mall. The clocks below show when they leave their house and
when they arrive at the mall. How many minutes does it take them to get to the mall?
Time when they leave home:
Time when they arrive at the mall:
6. Record your homework start time:
Record the time you finish Problems 1–5:
How many minutes did you work on Problems 1–5?

• Show Step-by-step Solutions

Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.