Statistics (from German: Statistik, orig. «description of a state, a country»)[1][2] is the discipline that concerns the collection, organization, analysis, interpretation, and presentation of data.[3][4][5] In applying statistics to a scientific, industrial, or social problem, it is conventional to begin with a statistical population or a statistical model to be studied. Populations can be diverse groups of people or objects such as «all people living in a country» or «every atom composing a crystal». Statistics deals with every aspect of data, including the planning of data collection in terms of the design of surveys and experiments.[6]
When census data cannot be collected, statisticians collect data by developing specific experiment designs and survey samples. Representative sampling assures that inferences and conclusions can reasonably extend from the sample to the population as a whole. An experimental study involves taking measurements of the system under study, manipulating the system, and then taking additional measurements using the same procedure to determine if the manipulation has modified the values of the measurements. In contrast, an observational study does not involve experimental manipulation.
Two main statistical methods are used in data analysis: descriptive statistics, which summarize data from a sample using indexes such as the mean or standard deviation, and inferential statistics, which draw conclusions from data that are subject to random variation (e.g., observational errors, sampling variation).[7] Descriptive statistics are most often concerned with two sets of properties of a distribution (sample or population): central tendency (or location) seeks to characterize the distribution’s central or typical value, while dispersion (or variability) characterizes the extent to which members of the distribution depart from its center and each other. Inferences on mathematical statistics are made under the framework of probability theory, which deals with the analysis of random phenomena.
A standard statistical procedure involves the collection of data leading to a test of the relationship between two statistical data sets, or a data set and synthetic data drawn from an idealized model. A hypothesis is proposed for the statistical relationship between the two data sets, and this is compared as an alternative to an idealized null hypothesis of no relationship between two data sets. Rejecting or disproving the null hypothesis is done using statistical tests that quantify the sense in which the null can be proven false, given the data that are used in the test. Working from a null hypothesis, two basic forms of error are recognized: Type I errors (null hypothesis is falsely rejected giving a «false positive») and Type II errors (null hypothesis fails to be rejected and an actual relationship between populations is missed giving a «false negative»).[8] Multiple problems have come to be associated with this framework, ranging from obtaining a sufficient sample size to specifying an adequate null hypothesis.[7]
Statistical measurement processes are also prone to error in regards to the data that they generate. Many of these errors are classified as random (noise) or systematic (bias), but other types of errors (e.g., blunder, such as when an analyst reports incorrect units) can also occur. The presence of missing data or censoring may result in biased estimates and specific techniques have been developed to address these problems.
Introduction[edit]
Statistics is a mathematical body of science that pertains to the collection, analysis, interpretation or explanation, and presentation of data,[9] or as a branch of mathematics.[10] Some consider statistics to be a distinct mathematical science rather than a branch of mathematics. While many scientific investigations make use of data, statistics is concerned with the use of data in the context of uncertainty and decision making in the face of uncertainty.[11][12]
In applying statistics to a problem, it is common practice to start with a population or process to be studied. Populations can be diverse topics such as «all people living in a country» or «every atom composing a crystal». Ideally, statisticians compile data about the entire population (an operation called census). This may be organized by governmental statistical institutes. Descriptive statistics can be used to summarize the population data. Numerical descriptors include mean and standard deviation for continuous data (like income), while frequency and percentage are more useful in terms of describing categorical data (like education).
When a census is not feasible, a chosen subset of the population called a sample is studied. Once a sample that is representative of the population is determined, data is collected for the sample members in an observational or experimental setting. Again, descriptive statistics can be used to summarize the sample data. However, drawing the sample contains an element of randomness; hence, the numerical descriptors from the sample are also prone to uncertainty. To draw meaningful conclusions about the entire population, inferential statistics is needed. It uses patterns in the sample data to draw inferences about the population represented while accounting for randomness. These inferences may take the form of answering yes/no questions about the data (hypothesis testing), estimating numerical characteristics of the data (estimation), describing associations within the data (correlation), and modeling relationships within the data (for example, using regression analysis). Inference can extend to forecasting, prediction, and estimation of unobserved values either in or associated with the population being studied. It can include extrapolation and interpolation of time series or spatial data, and data mining.
Mathematical statistics[edit]
Mathematical statistics is the application of mathematics to statistics. Mathematical techniques used for this include mathematical analysis, linear algebra, stochastic analysis, differential equations, and measure-theoretic probability theory.[13][14]
History[edit]
Formal discussions on inference date back to Arab mathematicians and cryptographers, during the Islamic Golden Age between the 8th and 13th centuries. Al-Khalil (717–786) wrote the Book of Cryptographic Messages, which contains one of the first uses of permutations and combinations, to list all possible Arabic words with and without vowels.[15] Al-Kindi’s Manuscript on Deciphering Cryptographic Messages gave a detailed description of how to use frequency analysis to decipher encrypted messages, providing an early example of statistical inference for decoding. Ibn Adlan (1187–1268) later made an important contribution on the use of sample size in frequency analysis.[15]
The earliest writing containing statistics in Europe dates back to 1663, with the publication of Natural and Political Observations upon the Bills of Mortality by John Graunt.[16] Early applications of statistical thinking revolved around the needs of states to base policy on demographic and economic data, hence its stat- etymology. The scope of the discipline of statistics broadened in the early 19th century to include the collection and analysis of data in general. Today, statistics is widely employed in government, business, and natural and social sciences.
The mathematical foundations of statistics developed from discussions concerning games of chance among mathematicians such as Gerolamo Cardano, Blaise Pascal, Pierre de Fermat, and Christiaan Huygens. Although the idea of probability was already examined in ancient and medieval law and philosophy (such as the work of Juan Caramuel), probability theory as a mathematical discipline only took shape at the very end of the 17th century, particularly in Jacob Bernoulli’s posthumous work Ars Conjectandi.[17] This was the first book where the realm of games of chance and the realm of the probable (which concerned opinion, evidence, and argument) were combined and submitted to mathematical analysis.[18][19] The method of least squares was first described by Adrien-Marie Legendre in 1805, though Carl Friedrich Gauss presumably made use of it a decade earlier in 1795.[20]
The modern field of statistics emerged in the late 19th and early 20th century in three stages.[21] The first wave, at the turn of the century, was led by the work of Francis Galton and Karl Pearson, who transformed statistics into a rigorous mathematical discipline used for analysis, not just in science, but in industry and politics as well. Galton’s contributions included introducing the concepts of standard deviation, correlation, regression analysis and the application of these methods to the study of the variety of human characteristics—height, weight and eyelash length among others.[22] Pearson developed the Pearson product-moment correlation coefficient, defined as a product-moment,[23] the method of moments for the fitting of distributions to samples and the Pearson distribution, among many other things.[24] Galton and Pearson founded Biometrika as the first journal of mathematical statistics and biostatistics (then called biometry), and the latter founded the world’s first university statistics department at University College London.[25]
The second wave of the 1910s and 20s was initiated by William Sealy Gosset, and reached its culmination in the insights of Ronald Fisher, who wrote the textbooks that were to define the academic discipline in universities around the world. Fisher’s most important publications were his 1918 seminal paper The Correlation between Relatives on the Supposition of Mendelian Inheritance (which was the first to use the statistical term, variance), his classic 1925 work Statistical Methods for Research Workers and his 1935 The Design of Experiments,[26][27][28] where he developed rigorous design of experiments models. He originated the concepts of sufficiency, ancillary statistics, Fisher’s linear discriminator and Fisher information.[29] He also coined the term null hypothesis during the Lady tasting tea experiment, which «is never proved or established, but is possibly disproved, in the course of experimentation».[30][31] In his 1930 book The Genetical Theory of Natural Selection, he applied statistics to various biological concepts such as Fisher’s principle[32] (which A. W. F. Edwards called «probably the most celebrated argument in evolutionary biology») and Fisherian runaway,[33][34][35][36][37][38] a concept in sexual selection about a positive feedback runaway effect found in evolution.
The final wave, which mainly saw the refinement and expansion of earlier developments, emerged from the collaborative work between Egon Pearson and Jerzy Neyman in the 1930s. They introduced the concepts of «Type II» error, power of a test and confidence intervals. Jerzy Neyman in 1934 showed that stratified random sampling was in general a better method of estimation than purposive (quota) sampling.[39]
Today, statistical methods are applied in all fields that involve decision making, for making accurate inferences from a collated body of data and for making decisions in the face of uncertainty based on statistical methodology. The use of modern computers has expedited large-scale statistical computations and has also made possible new methods that are impractical to perform manually. Statistics continues to be an area of active research, for example on the problem of how to analyze big data.[40]
Statistical data[edit]
Data collection[edit]
Sampling[edit]
When full census data cannot be collected, statisticians collect sample data by developing specific experiment designs and survey samples. Statistics itself also provides tools for prediction and forecasting through statistical models.
To use a sample as a guide to an entire population, it is important that it truly represents the overall population. Representative sampling assures that inferences and conclusions can safely extend from the sample to the population as a whole. A major problem lies in determining the extent that the sample chosen is actually representative. Statistics offers methods to estimate and correct for any bias within the sample and data collection procedures. There are also methods of experimental design that can lessen these issues at the outset of a study, strengthening its capability to discern truths about the population.
Sampling theory is part of the mathematical discipline of probability theory. Probability is used in mathematical statistics to study the sampling distributions of sample statistics and, more generally, the properties of statistical procedures. The use of any statistical method is valid when the system or population under consideration satisfies the assumptions of the method. The difference in point of view between classic probability theory and sampling theory is, roughly, that probability theory starts from the given parameters of a total population to deduce probabilities that pertain to samples. Statistical inference, however, moves in the opposite direction—inductively inferring from samples to the parameters of a larger or total population.
Experimental and observational studies[edit]
A common goal for a statistical research project is to investigate causality, and in particular to draw a conclusion on the effect of changes in the values of predictors or independent variables on dependent variables. There are two major types of causal statistical studies: experimental studies and observational studies. In both types of studies, the effect of differences of an independent variable (or variables) on the behavior of the dependent variable are observed. The difference between the two types lies in how the study is actually conducted. Each can be very effective.
An experimental study involves taking measurements of the system under study, manipulating the system, and then taking additional measurements using the same procedure to determine if the manipulation has modified the values of the measurements. In contrast, an observational study does not involve experimental manipulation. Instead, data are gathered and correlations between predictors and response are investigated. While the tools of data analysis work best on data from randomized studies, they are also applied to other kinds of data—like natural experiments and observational studies[41]—for which a statistician would use a modified, more structured estimation method (e.g., Difference in differences estimation and instrumental variables, among many others) that produce consistent estimators.
Experiments[edit]
The basic steps of a statistical experiment are:
- Planning the research, including finding the number of replicates of the study, using the following information: preliminary estimates regarding the size of treatment effects, alternative hypotheses, and the estimated experimental variability. Consideration of the selection of experimental subjects and the ethics of research is necessary. Statisticians recommend that experiments compare (at least) one new treatment with a standard treatment or control, to allow an unbiased estimate of the difference in treatment effects.
- Design of experiments, using blocking to reduce the influence of confounding variables, and randomized assignment of treatments to subjects to allow unbiased estimates of treatment effects and experimental error. At this stage, the experimenters and statisticians write the experimental protocol that will guide the performance of the experiment and which specifies the primary analysis of the experimental data.
- Performing the experiment following the experimental protocol and analyzing the data following the experimental protocol.
- Further examining the data set in secondary analyses, to suggest new hypotheses for future study.
- Documenting and presenting the results of the study.
Experiments on human behavior have special concerns. The famous Hawthorne study examined changes to the working environment at the Hawthorne plant of the Western Electric Company. The researchers were interested in determining whether increased illumination would increase the productivity of the assembly line workers. The researchers first measured the productivity in the plant, then modified the illumination in an area of the plant and checked if the changes in illumination affected productivity. It turned out that productivity indeed improved (under the experimental conditions). However, the study is heavily criticized today for errors in experimental procedures, specifically for the lack of a control group and blindness. The Hawthorne effect refers to finding that an outcome (in this case, worker productivity) changed due to observation itself. Those in the Hawthorne study became more productive not because the lighting was changed but because they were being observed.[42]
Observational study[edit]
An example of an observational study is one that explores the association between smoking and lung cancer. This type of study typically uses a survey to collect observations about the area of interest and then performs statistical analysis. In this case, the researchers would collect observations of both smokers and non-smokers, perhaps through a cohort study, and then look for the number of cases of lung cancer in each group.[43] A case-control study is another type of observational study in which people with and without the outcome of interest (e.g. lung cancer) are invited to participate and their exposure histories are collected.
Types of data[edit]
Various attempts have been made to produce a taxonomy of levels of measurement. The psychophysicist Stanley Smith Stevens defined nominal, ordinal, interval, and ratio scales. Nominal measurements do not have meaningful rank order among values, and permit any one-to-one (injective) transformation. Ordinal measurements have imprecise differences between consecutive values, but have a meaningful order to those values, and permit any order-preserving transformation. Interval measurements have meaningful distances between measurements defined, but the zero value is arbitrary (as in the case with longitude and temperature measurements in Celsius or Fahrenheit), and permit any linear transformation. Ratio measurements have both a meaningful zero value and the distances between different measurements defined, and permit any rescaling transformation.
Because variables conforming only to nominal or ordinal measurements cannot be reasonably measured numerically, sometimes they are grouped together as categorical variables, whereas ratio and interval measurements are grouped together as quantitative variables, which can be either discrete or continuous, due to their numerical nature. Such distinctions can often be loosely correlated with data type in computer science, in that dichotomous categorical variables may be represented with the Boolean data type, polytomous categorical variables with arbitrarily assigned integers in the integral data type, and continuous variables with the real data type involving floating-point arithmetic. But the mapping of computer science data types to statistical data types depends on which categorization of the latter is being implemented.
Other categorizations have been proposed. For example, Mosteller and Tukey (1977)[44] distinguished grades, ranks, counted fractions, counts, amounts, and balances. Nelder (1990)[45] described continuous counts, continuous ratios, count ratios, and categorical modes of data. (See also: Chrisman (1998),[46] van den Berg (1991).[47])
The issue of whether or not it is appropriate to apply different kinds of statistical methods to data obtained from different kinds of measurement procedures is complicated by issues concerning the transformation of variables and the precise interpretation of research questions. «The relationship between the data and what they describe merely reflects the fact that certain kinds of statistical statements may have truth values which are not invariant under some transformations. Whether or not a transformation is sensible to contemplate depends on the question one is trying to answer.»[48]: 82
Methods[edit]
Descriptive statistics[edit]
A descriptive statistic (in the count noun sense) is a summary statistic that quantitatively describes or summarizes features of a collection of information,[49] while descriptive statistics in the mass noun sense is the process of using and analyzing those statistics. Descriptive statistics is distinguished from inferential statistics (or inductive statistics), in that descriptive statistics aims to summarize a sample, rather than use the data to learn about the population that the sample of data is thought to represent.[50]
Inferential statistics[edit]
Statistical inference is the process of using data analysis to deduce properties of an underlying probability distribution.[51] Inferential statistical analysis infers properties of a population, for example by testing hypotheses and deriving estimates. It is assumed that the observed data set is sampled from a larger population. Inferential statistics can be contrasted with descriptive statistics. Descriptive statistics is solely concerned with properties of the observed data, and it does not rest on the assumption that the data come from a larger population.[52]
Terminology and theory of inferential statistics[edit]
Statistics, estimators and pivotal quantities[edit]
Consider independent identically distributed (IID) random variables with a given probability distribution: standard statistical inference and estimation theory defines a random sample as the random vector given by the column vector of these IID variables.[53] The population being examined is described by a probability distribution that may have unknown parameters.
A statistic is a random variable that is a function of the random sample, but not a function of unknown parameters. The probability distribution of the statistic, though, may have unknown parameters. Consider now a function of the unknown parameter: an estimator is a statistic used to estimate such function. Commonly used estimators include sample mean, unbiased sample variance and sample covariance.
A random variable that is a function of the random sample and of the unknown parameter, but whose probability distribution does not depend on the unknown parameter is called a pivotal quantity or pivot. Widely used pivots include the z-score, the chi square statistic and Student’s t-value.
Between two estimators of a given parameter, the one with lower mean squared error is said to be more efficient. Furthermore, an estimator is said to be unbiased if its expected value is equal to the true value of the unknown parameter being estimated, and asymptotically unbiased if its expected value converges at the limit to the true value of such parameter.
Other desirable properties for estimators include: UMVUE estimators that have the lowest variance for all possible values of the parameter to be estimated (this is usually an easier property to verify than efficiency) and consistent estimators which converges in probability to the true value of such parameter.
This still leaves the question of how to obtain estimators in a given situation and carry the computation, several methods have been proposed: the method of moments, the maximum likelihood method, the least squares method and the more recent method of estimating equations.
Null hypothesis and alternative hypothesis[edit]
Interpretation of statistical information can often involve the development of a null hypothesis which is usually (but not necessarily) that no relationship exists among variables or that no change occurred over time.[54][55]
The best illustration for a novice is the predicament encountered by a criminal trial. The null hypothesis, H0, asserts that the defendant is innocent, whereas the alternative hypothesis, H1, asserts that the defendant is guilty. The indictment comes because of suspicion of the guilt. The H0 (status quo) stands in opposition to H1 and is maintained unless H1 is supported by evidence «beyond a reasonable doubt». However, «failure to reject H0» in this case does not imply innocence, but merely that the evidence was insufficient to convict. So the jury does not necessarily accept H0 but fails to reject H0. While one can not «prove» a null hypothesis, one can test how close it is to being true with a power test, which tests for type II errors.
What statisticians call an alternative hypothesis is simply a hypothesis that contradicts the null hypothesis.
Error[edit]
Working from a null hypothesis, two broad categories of error are recognized:
- Type I errors where the null hypothesis is falsely rejected, giving a «false positive».
- Type II errors where the null hypothesis fails to be rejected and an actual difference between populations is missed, giving a «false negative».
Standard deviation refers to the extent to which individual observations in a sample differ from a central value, such as the sample or population mean, while Standard error refers to an estimate of difference between sample mean and population mean.
A statistical error is the amount by which an observation differs from its expected value. A residual is the amount an observation differs from the value the estimator of the expected value assumes on a given sample (also called prediction).
Mean squared error is used for obtaining efficient estimators, a widely used class of estimators. Root mean square error is simply the square root of mean squared error.
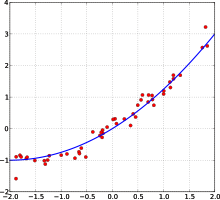
A least squares fit: in red the points to be fitted, in blue the fitted line.
Many statistical methods seek to minimize the residual sum of squares, and these are called «methods of least squares» in contrast to Least absolute deviations. The latter gives equal weight to small and big errors, while the former gives more weight to large errors. Residual sum of squares is also differentiable, which provides a handy property for doing regression. Least squares applied to linear regression is called ordinary least squares method and least squares applied to nonlinear regression is called non-linear least squares. Also in a linear regression model the non deterministic part of the model is called error term, disturbance or more simply noise. Both linear regression and non-linear regression are addressed in polynomial least squares, which also describes the variance in a prediction of the dependent variable (y axis) as a function of the independent variable (x axis) and the deviations (errors, noise, disturbances) from the estimated (fitted) curve.
Measurement processes that generate statistical data are also subject to error. Many of these errors are classified as random (noise) or systematic (bias), but other types of errors (e.g., blunder, such as when an analyst reports incorrect units) can also be important. The presence of missing data or censoring may result in biased estimates and specific techniques have been developed to address these problems.[56]
Interval estimation[edit]
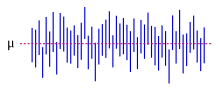
Confidence intervals: the red line is true value for the mean in this example, the blue lines are random confidence intervals for 100 realizations.
Most studies only sample part of a population, so results don’t fully represent the whole population. Any estimates obtained from the sample only approximate the population value. Confidence intervals allow statisticians to express how closely the sample estimate matches the true value in the whole population. Often they are expressed as 95% confidence intervals. Formally, a 95% confidence interval for a value is a range where, if the sampling and analysis were repeated under the same conditions (yielding a different dataset), the interval would include the true (population) value in 95% of all possible cases. This does not imply that the probability that the true value is in the confidence interval is 95%. From the frequentist perspective, such a claim does not even make sense, as the true value is not a random variable. Either the true value is or is not within the given interval. However, it is true that, before any data are sampled and given a plan for how to construct the confidence interval, the probability is 95% that the yet-to-be-calculated interval will cover the true value: at this point, the limits of the interval are yet-to-be-observed random variables. One approach that does yield an interval that can be interpreted as having a given probability of containing the true value is to use a credible interval from Bayesian statistics: this approach depends on a different way of interpreting what is meant by «probability», that is as a Bayesian probability.
In principle confidence intervals can be symmetrical or asymmetrical. An interval can be asymmetrical because it works as lower or upper bound for a parameter (left-sided interval or right sided interval), but it can also be asymmetrical because the two sided interval is built violating symmetry around the estimate. Sometimes the bounds for a confidence interval are reached asymptotically and these are used to approximate the true bounds.
Significance[edit]
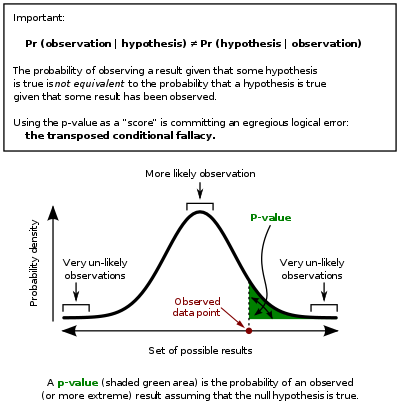
Statistics rarely give a simple Yes/No type answer to the question under analysis. Interpretation often comes down to the level of statistical significance applied to the numbers and often refers to the probability of a value accurately rejecting the null hypothesis (sometimes referred to as the p-value).
In this graph the black line is probability distribution for the test statistic, the critical region is the set of values to the right of the observed data point (observed value of the test statistic) and the p-value is represented by the green area.
The standard approach[53] is to test a null hypothesis against an alternative hypothesis. A critical region is the set of values of the estimator that leads to refuting the null hypothesis. The probability of type I error is therefore the probability that the estimator belongs to the critical region given that null hypothesis is true (statistical significance) and the probability of type II error is the probability that the estimator doesn’t belong to the critical region given that the alternative hypothesis is true. The statistical power of a test is the probability that it correctly rejects the null hypothesis when the null hypothesis is false.
Referring to statistical significance does not necessarily mean that the overall result is significant in real world terms. For example, in a large study of a drug it may be shown that the drug has a statistically significant but very small beneficial effect, such that the drug is unlikely to help the patient noticeably.
Although in principle the acceptable level of statistical significance may be subject to debate, the significance level is the largest p-value that allows the test to reject the null hypothesis. This test is logically equivalent to saying that the p-value is the probability, assuming the null hypothesis is true, of observing a result at least as extreme as the test statistic. Therefore, the smaller the significance level, the lower the probability of committing type I error.
Some problems are usually associated with this framework (See criticism of hypothesis testing):
- A difference that is highly statistically significant can still be of no practical significance, but it is possible to properly formulate tests to account for this. One response involves going beyond reporting only the significance level to include the p-value when reporting whether a hypothesis is rejected or accepted. The p-value, however, does not indicate the size or importance of the observed effect and can also seem to exaggerate the importance of minor differences in large studies. A better and increasingly common approach is to report confidence intervals. Although these are produced from the same calculations as those of hypothesis tests or p-values, they describe both the size of the effect and the uncertainty surrounding it.
- Fallacy of the transposed conditional, aka prosecutor’s fallacy: criticisms arise because the hypothesis testing approach forces one hypothesis (the null hypothesis) to be favored, since what is being evaluated is the probability of the observed result given the null hypothesis and not probability of the null hypothesis given the observed result. An alternative to this approach is offered by Bayesian inference, although it requires establishing a prior probability.[57]
- Rejecting the null hypothesis does not automatically prove the alternative hypothesis.
- As everything in inferential statistics it relies on sample size, and therefore under fat tails p-values may be seriously mis-computed.[clarification needed]
Examples[edit]
Some well-known statistical tests and procedures are:
- Analysis of variance (ANOVA)
- Chi-squared test
- Correlation
- Factor analysis
- Mann–Whitney U
- Mean square weighted deviation (MSWD)
- Pearson product-moment correlation coefficient
- Regression analysis
- Spearman’s rank correlation coefficient
- Student’s t-test
- Time series analysis
- Conjoint Analysis
Exploratory data analysis[edit]
Exploratory data analysis (EDA) is an approach to analyzing data sets to summarize their main characteristics, often with visual methods. A statistical model can be used or not, but primarily EDA is for seeing what the data can tell us beyond the formal modeling or hypothesis testing task.
Misuse[edit]
Misuse of statistics can produce subtle but serious errors in description and interpretation—subtle in the sense that even experienced professionals make such errors, and serious in the sense that they can lead to devastating decision errors. For instance, social policy, medical practice, and the reliability of structures like bridges all rely on the proper use of statistics.
Even when statistical techniques are correctly applied, the results can be difficult to interpret for those lacking expertise. The statistical significance of a trend in the data—which measures the extent to which a trend could be caused by random variation in the sample—may or may not agree with an intuitive sense of its significance. The set of basic statistical skills (and skepticism) that people need to deal with information in their everyday lives properly is referred to as statistical literacy.
There is a general perception that statistical knowledge is all-too-frequently intentionally misused by finding ways to interpret only the data that are favorable to the presenter.[58] A mistrust and misunderstanding of statistics is associated with the quotation, «There are three kinds of lies: lies, damned lies, and statistics». Misuse of statistics can be both inadvertent and intentional, and the book How to Lie with Statistics,[58] by Darrell Huff, outlines a range of considerations. In an attempt to shed light on the use and misuse of statistics, reviews of statistical techniques used in particular fields are conducted (e.g. Warne, Lazo, Ramos, and Ritter (2012)).[59]
Ways to avoid misuse of statistics include using proper diagrams and avoiding bias.[60] Misuse can occur when conclusions are overgeneralized and claimed to be representative of more than they really are, often by either deliberately or unconsciously overlooking sampling bias.[61] Bar graphs are arguably the easiest diagrams to use and understand, and they can be made either by hand or with simple computer programs.[60] Unfortunately, most people do not look for bias or errors, so they are not noticed. Thus, people may often believe that something is true even if it is not well represented.[61] To make data gathered from statistics believable and accurate, the sample taken must be representative of the whole.[62] According to Huff, «The dependability of a sample can be destroyed by [bias]… allow yourself some degree of skepticism.»[63]
To assist in the understanding of statistics Huff proposed a series of questions to be asked in each case:[58]
- Who says so? (Does he/she have an axe to grind?)
- How does he/she know? (Does he/she have the resources to know the facts?)
- What’s missing? (Does he/she give us a complete picture?)
- Did someone change the subject? (Does he/she offer us the right answer to the wrong problem?)
- Does it make sense? (Is his/her conclusion logical and consistent with what we already know?)
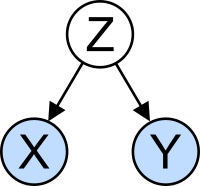
The confounding variable problem: X and Y may be correlated, not because there is causal relationship between them, but because both depend on a third variable Z. Z is called a confounding factor.
Misinterpretation: correlation[edit]
The concept of correlation is particularly noteworthy for the potential confusion it can cause. Statistical analysis of a data set often reveals that two variables (properties) of the population under consideration tend to vary together, as if they were connected. For example, a study of annual income that also looks at age of death, might find that poor people tend to have shorter lives than affluent people. The two variables are said to be correlated; however, they may or may not be the cause of one another. The correlation phenomena could be caused by a third, previously unconsidered phenomenon, called a lurking variable or confounding variable. For this reason, there is no way to immediately infer the existence of a causal relationship between the two variables.
Applications[edit]
Applied statistics, theoretical statistics and mathematical statistics[edit]
Applied statistics, sometimes referred to as Statistical science,[64] comprises descriptive statistics and the application of inferential statistics.[65][66] Theoretical statistics concerns the logical arguments underlying justification of approaches to statistical inference, as well as encompassing mathematical statistics. Mathematical statistics includes not only the manipulation of probability distributions necessary for deriving results related to methods of estimation and inference, but also various aspects of computational statistics and the design of experiments.
Statistical consultants can help organizations and companies that don’t have in-house expertise relevant to their particular questions.
Machine learning and data mining[edit]
Machine learning models are statistical and probabilistic models that capture patterns in the data through use of computational algorithms.
Statistics in academia[edit]
Statistics is applicable to a wide variety of academic disciplines, including natural and social sciences, government, and business. Business statistics applies statistical methods in econometrics, auditing and production and operations, including services improvement and marketing research.[67] A study of two journals in tropical biology found that the 12 most frequent statistical tests are: analysis of variance (ANOVA), chi-squared test, Student’s t-test, linear regression, Pearson’s correlation coefficient, Mann-Whitney U test, Kruskal-Wallis test, Shannon’s diversity index, Tukey’s range test, cluster analysis, Spearman’s rank correlation coefficient and principal component analysis.[68]
A typical statistics course covers descriptive statistics, probability, binomial and normal distributions, test of hypotheses and confidence intervals, linear regression, and correlation.[69] Modern fundamental statistical courses for undergraduate students focus on correct test selection, results interpretation, and use of free statistics software.[68]
Statistical computing[edit]
The rapid and sustained increases in computing power starting from the second half of the 20th century have had a substantial impact on the practice of statistical science. Early statistical models were almost always from the class of linear models, but powerful computers, coupled with suitable numerical algorithms, caused an increased interest in nonlinear models (such as neural networks) as well as the creation of new types, such as generalized linear models and multilevel models.
Increased computing power has also led to the growing popularity of computationally intensive methods based on resampling, such as permutation tests and the bootstrap, while techniques such as Gibbs sampling have made use of Bayesian models more feasible. The computer revolution has implications for the future of statistics with a new emphasis on «experimental» and «empirical» statistics. A large number of both general and special purpose statistical software are now available. Examples of available software capable of complex statistical computation include programs such as Mathematica, SAS, SPSS, and R.
Business statistics[edit]
In business, «statistics» is a widely used management- and decision support tool. It is particularly applied in financial management, marketing management, and production, services and operations management .[70][71] Statistics is also heavily used in management accounting and auditing. The discipline of Management Science formalizes the use of statistics, and other mathematics, in business. (Econometrics is the application of statistical methods to economic data in order to give empirical content to economic relationships.)
A typical «Business Statistics» course is intended for business majors, and covers [72] descriptive statistics (collection, description, analysis, and summary of data), probability (typically the binomial and normal distributions), test of hypotheses and confidence intervals, linear regression, and correlation; (follow-on) courses may include forecasting, time series, decision trees, multiple linear regression, and other topics from business analytics more generally. See also Business mathematics § University level. Professional certification programs, such as the CFA, often include topics in statistics.
Statistics applied to mathematics or the arts[edit]
Traditionally, statistics was concerned with drawing inferences using a semi-standardized methodology that was «required learning» in most sciences. This tradition has changed with the use of statistics in non-inferential contexts. What was once considered a dry subject, taken in many fields as a degree-requirement, is now viewed enthusiastically.[according to whom?] Initially derided by some mathematical purists, it is now considered essential methodology in certain areas.
- In number theory, scatter plots of data generated by a distribution function may be transformed with familiar tools used in statistics to reveal underlying patterns, which may then lead to hypotheses.
- Predictive methods of statistics in forecasting combining chaos theory and fractal geometry can be used to create video works.[73]
- The process art of Jackson Pollock relied on artistic experiments whereby underlying distributions in nature were artistically revealed.[74] With the advent of computers, statistical methods were applied to formalize such distribution-driven natural processes to make and analyze moving video art.[citation needed]
- Methods of statistics may be used predicatively in performance art, as in a card trick based on a Markov process that only works some of the time, the occasion of which can be predicted using statistical methodology.
- Statistics can be used to predicatively create art, as in the statistical or stochastic music invented by Iannis Xenakis, where the music is performance-specific. Though this type of artistry does not always come out as expected, it does behave in ways that are predictable and tunable using statistics.
Specialized disciplines[edit]
Statistical techniques are used in a wide range of types of scientific and social research, including: biostatistics, computational biology, computational sociology, network biology, social science, sociology and social research. Some fields of inquiry use applied statistics so extensively that they have specialized terminology. These disciplines include:
- Actuarial science (assesses risk in the insurance and finance industries)
- Applied information economics
- Astrostatistics (statistical evaluation of astronomical data)
- Biostatistics
- Chemometrics (for analysis of data from chemistry)
- Data mining (applying statistics and pattern recognition to discover knowledge from data)
- Data science
- Demography (statistical study of populations)
- Econometrics (statistical analysis of economic data)
- Energy statistics
- Engineering statistics
- Epidemiology (statistical analysis of disease)
- Geography and geographic information systems, specifically in spatial analysis
- Image processing
- Jurimetrics (law)
- Medical statistics
- Political science
- Psychological statistics
- Reliability engineering
- Social statistics
- Statistical mechanics
In addition, there are particular types of statistical analysis that have also developed their own specialised terminology and methodology:
- Bootstrap / jackknife resampling
- Multivariate statistics
- Statistical classification
- Structured data analysis
- Structural equation modelling
- Survey methodology
- Survival analysis
- Statistics in various sports, particularly baseball – known as sabermetrics – and cricket
Statistics form a key basis tool in business and manufacturing as well. It is used to understand measurement systems variability, control processes (as in statistical process control or SPC), for summarizing data, and to make data-driven decisions. In these roles, it is a key tool, and perhaps the only reliable tool.[citation needed]
See also[edit]
- Abundance estimation
- Glossary of probability and statistics
- List of academic statistical associations
- List of important publications in statistics
- List of national and international statistical services
- List of statistical packages (software)
- List of statistics articles
- List of university statistical consulting centers
- Notation in probability and statistics
- Statistics education
- World Statistics Day
- Foundations and major areas of statistics
- Foundations of statistics
- List of statisticians
- Official statistics
- Multivariate analysis of variance
References[edit]
- ^ «statistics». Oxford English Dictionary (Online ed.). Oxford University Press. (Subscription or participating institution membership required.)
- ^ “Statistik” in Digitales Wörterbuch der deutschen Sprache
- ^ «Statistics». Oxford Reference. Oxford University Press. January 2008. ISBN 978-0-19-954145-4. Archived from the original on 2020-09-03. Retrieved 2019-08-14.
- ^ Romijn, Jan-Willem (2014). «Philosophy of statistics». Stanford Encyclopedia of Philosophy. Archived from the original on 2021-10-19. Retrieved 2016-11-03.
- ^ «Cambridge Dictionary». Archived from the original on 2020-11-22. Retrieved 2019-08-14.
- ^ Dodge, Y. (2006) The Oxford Dictionary of Statistical Terms, Oxford University Press. ISBN 0-19-920613-9
- ^ a b Lund Research Ltd. «Descriptive and Inferential Statistics». statistics.laerd.com. Archived from the original on 2020-10-26. Retrieved 2014-03-23.
- ^ «What Is the Difference Between Type I and Type II Hypothesis Testing Errors?». About.com Education. Archived from the original on 2017-02-27. Retrieved 2015-11-27.
- ^ Moses, Lincoln E. (1986) Think and Explain with Statistics, Addison-Wesley, ISBN 978-0-201-15619-5. pp. 1–3
- ^ Hays, William Lee, (1973) Statistics for the Social Sciences, Holt, Rinehart and Winston, p.xii, ISBN 978-0-03-077945-9
- ^ Moore, David (1992). «Teaching Statistics as a Respectable Subject». In F. Gordon; S. Gordon (eds.). Statistics for the Twenty-First Century. Washington, DC: The Mathematical Association of America. pp. 14–25. ISBN 978-0-88385-078-7.
- ^ Chance, Beth L.; Rossman, Allan J. (2005). «Preface» (PDF). Investigating Statistical Concepts, Applications, and Methods. Duxbury Press. ISBN 978-0-495-05064-3. Archived (PDF) from the original on 2020-11-22. Retrieved 2009-12-06.
- ^ Lakshmikantham, D.; Kannan, V. (2002). Handbook of stochastic analysis and applications. New York: M. Dekker. ISBN 0824706609.
- ^ Schervish, Mark J. (1995). Theory of statistics (Corr. 2nd print. ed.). New York: Springer. ISBN 0387945466.
- ^ a b Broemeling, Lyle D. (1 November 2011). «An Account of Early Statistical Inference in Arab Cryptology». The American Statistician. 65 (4): 255–257. doi:10.1198/tas.2011.10191. S2CID 123537702.
- ^ Willcox, Walter (1938) «The Founder of Statistics». Review of the International Statistical Institute 5(4): 321–328. JSTOR 1400906
- ^ J. Franklin, The Science of Conjecture: Evidence and Probability before Pascal, Johns Hopkins Univ Pr 2002
- ^ Schneider, I. (2005). Jakob Bernoulli, Ars Conjectandi (1713). In I. Grattan-Guinness (Ed.), Landmark writings in Western Mathematics, 1640-1940 (pp. 88-103).
- ^ Sylla, E. D.; Bernoulli, Jacob (2006). The Art of Conjecturing, Together with Letter to a Friend on Sets in Court Tennis (trans.). JHU Press. ISBN 978-0-8018-8235-7.
- ^ Lim, M. (2021). «Gauss, Least Squares, and the Missing Planet». Actuaries Digital. Retrieved 2022-11-01.
- ^ Helen Mary Walker (1975). Studies in the history of statistical method. Arno Press. ISBN 9780405066283. Archived from the original on 2020-07-27. Retrieved 2015-06-27.
- ^ Galton, F (1877). «Typical laws of heredity». Nature. 15 (388): 492–553. Bibcode:1877Natur..15..492.. doi:10.1038/015492a0.
- ^ Stigler, S.M. (1989). «Francis Galton’s Account of the Invention of Correlation». Statistical Science. 4 (2): 73–79. doi:10.1214/ss/1177012580.
- ^ Pearson, K. (1900). «On the Criterion that a given System of Deviations from the Probable in the Case of a Correlated System of Variables is such that it can be reasonably supposed to have arisen from Random Sampling». Philosophical Magazine. Series 5. 50 (302): 157–175. doi:10.1080/14786440009463897. Archived from the original on 2020-08-18. Retrieved 2019-06-27.
- ^ «Karl Pearson (1857–1936)». Department of Statistical Science – University College London. Archived from the original on 2008-09-25.
- ^ Box, JF (February 1980). «R.A. Fisher and the Design of Experiments, 1922–1926». The American Statistician. 34 (1): 1–7. doi:10.2307/2682986. JSTOR 2682986.
- ^ Yates, F (June 1964). «Sir Ronald Fisher and the Design of Experiments». Biometrics. 20 (2): 307–321. doi:10.2307/2528399. JSTOR 2528399.
- ^ Stanley, Julian C. (1966). «The Influence of Fisher’s «The Design of Experiments» on Educational Research Thirty Years Later». American Educational Research Journal. 3 (3): 223–229. doi:10.3102/00028312003003223. JSTOR 1161806. S2CID 145725524.
- ^ Agresti, Alan; David B. Hichcock (2005). «Bayesian Inference for Categorical Data Analysis» (PDF). Statistical Methods & Applications. 14 (3): 298. doi:10.1007/s10260-005-0121-y. S2CID 18896230. Archived (PDF) from the original on 2013-12-19. Retrieved 2013-12-19.
- ^ OED quote: 1935 R.A. Fisher, The Design of Experiments ii. 19, «We may speak of this hypothesis as the ‘null hypothesis’, and the null hypothesis is never proved or established, but is possibly disproved, in the course of experimentation.»
- ^ Fisher|1971|loc=Chapter II. The Principles of Experimentation, Illustrated by a Psycho-physical Experiment, Section 8. The Null Hypothesis
- ^ Edwards, A.W.F. (1998). «Natural Selection and the Sex Ratio: Fisher’s Sources». American Naturalist. 151 (6): 564–569. doi:10.1086/286141. PMID 18811377. S2CID 40540426.
- ^ Fisher, R.A. (1915) The evolution of sexual preference. Eugenics Review (7) 184:192
- ^ Fisher, R.A. (1930) The Genetical Theory of Natural Selection. ISBN 0-19-850440-3
- ^ Edwards, A.W.F. (2000) Perspectives: Anecdotal, Historical and Critical Commentaries on Genetics. The Genetics Society of America (154) 1419:1426
- ^ Andersson, Malte (1994). Sexual Selection. Princeton University Press. ISBN 0-691-00057-3. Archived from the original on 2019-12-25. Retrieved 2019-09-19.
- ^ Andersson, M. and Simmons, L.W. (2006) Sexual selection and mate choice. Trends, Ecology and Evolution (21) 296:302
- ^ Gayon, J. (2010) Sexual selection: Another Darwinian process. Comptes Rendus Biologies (333) 134:144
- ^ Neyman, J (1934). «On the two different aspects of the representative method: The method of stratified sampling and the method of purposive selection». Journal of the Royal Statistical Society. 97 (4): 557–625. doi:10.2307/2342192. JSTOR 2342192.
- ^ «Science in a Complex World – Big Data: Opportunity or Threat?». Santa Fe Institute. Archived from the original on 2016-05-30. Retrieved 2014-10-13.
- ^ Freedman, D.A. (2005) Statistical Models: Theory and Practice, Cambridge University Press. ISBN 978-0-521-67105-7
- ^ McCarney R, Warner J, Iliffe S, van Haselen R, Griffin M, Fisher P (2007). «The Hawthorne Effect: a randomised, controlled trial». BMC Med Res Methodol. 7 (1): 30. doi:10.1186/1471-2288-7-30. PMC 1936999. PMID 17608932.
- ^ Rothman, Kenneth J; Greenland, Sander; Lash, Timothy, eds. (2008). «7». Modern Epidemiology (3rd ed.). Lippincott Williams & Wilkins. p. 100. ISBN 9780781755641.
- ^ Mosteller, F.; Tukey, J.W (1977). Data analysis and regression. Boston: Addison-Wesley.
- ^ Nelder, J.A. (1990). The knowledge needed to computerise the analysis and interpretation of statistical information. In Expert systems and artificial intelligence: the need for information about data. Library Association Report, London, March, 23–27.
- ^ Chrisman, Nicholas R (1998). «Rethinking Levels of Measurement for Cartography». Cartography and Geographic Information Science. 25 (4): 231–242. doi:10.1559/152304098782383043.
- ^ van den Berg, G. (1991). Choosing an analysis method. Leiden: DSWO Press
- ^ Hand, D.J. (2004). Measurement theory and practice: The world through quantification. London: Arnold.
- ^ Mann, Prem S. (1995). Introductory Statistics (2nd ed.). Wiley. ISBN 0-471-31009-3.
- ^ «Descriptive Statistics | Research Connections». www.researchconnections.org. Retrieved 2023-01-10.
- ^ Upton, G., Cook, I. (2008) Oxford Dictionary of Statistics, OUP. ISBN 978-0-19-954145-4.
- ^ «Basic Inferential Statistics — Purdue OWL® — Purdue University». owl.purdue.edu. Retrieved 2023-01-10.
- ^ a b Piazza Elio, Probabilità e Statistica, Esculapio 2007
- ^ Everitt, Brian (1998). The Cambridge Dictionary of Statistics. Cambridge, UK New York: Cambridge University Press. ISBN 0521593468.
- ^ «Cohen (1994) The Earth Is Round (p < .05)». YourStatsGuru.com. Archived from the original on 2015-09-05. Retrieved 2015-07-20.
- ^ Rubin, Donald B.; Little, Roderick J.A., Statistical analysis with missing data, New York: Wiley 2002
- ^ Ioannidis, J.P.A. (2005). «Why Most Published Research Findings Are False». PLOS Medicine. 2 (8): e124. doi:10.1371/journal.pmed.0020124. PMC 1182327. PMID 16060722.
- ^ a b c Huff, Darrell (1954) How to Lie with Statistics, WW Norton & Company, Inc. New York. ISBN 0-393-31072-8
- ^ Warne, R. Lazo; Ramos, T.; Ritter, N. (2012). «Statistical Methods Used in Gifted Education Journals, 2006–2010». Gifted Child Quarterly. 56 (3): 134–149. doi:10.1177/0016986212444122. S2CID 144168910.
- ^ a b Drennan, Robert D. (2008). «Statistics in archaeology». In Pearsall, Deborah M. (ed.). Encyclopedia of Archaeology. Elsevier Inc. pp. 2093–2100. ISBN 978-0-12-373962-9.
- ^ a b Cohen, Jerome B. (December 1938). «Misuse of Statistics». Journal of the American Statistical Association. JSTOR. 33 (204): 657–674. doi:10.1080/01621459.1938.10502344.
- ^ Freund, J.E. (1988). «Modern Elementary Statistics». Credo Reference.
- ^ Huff, Darrell; Irving Geis (1954). How to Lie with Statistics. New York: Norton.
The dependability of a sample can be destroyed by [bias]… allow yourself some degree of skepticism.
- ^ Nelder, John A. (1999). «From Statistics to Statistical Science». Journal of the Royal Statistical Society. Series D (The Statistician). 48 (2): 257–269. doi:10.1111/1467-9884.00187. ISSN 0039-0526. JSTOR 2681191. Archived from the original on 2022-01-15. Retrieved 2022-01-15.
- ^ Nikoletseas, M.M. (2014) «Statistics: Concepts and Examples.» ISBN 978-1500815684
- ^ Anderson, D.R.; Sweeney, D.J.; Williams, T.A. (1994) Introduction to Statistics: Concepts and Applications, pp. 5–9. West Group. ISBN 978-0-314-03309-3
- ^ «Journal of Business & Economic Statistics». Journal of Business & Economic Statistics. Taylor & Francis. Archived from the original on 27 July 2020. Retrieved 16 March 2020.
- ^ a b Natalia Loaiza Velásquez, María Isabel González Lutz & Julián Monge-Nájera (2011). «Which statistics should tropical biologists learn?» (PDF). Revista Biología Tropical. 59: 983–992. Archived (PDF) from the original on 2020-10-19. Retrieved 2020-04-26.
- ^ Pekoz, Erol (2009). The Manager’s Guide to Statistics. Erol Pekoz. ISBN 9780979570438.
- ^ «Aims and scope». Journal of Business & Economic Statistics. Taylor & Francis. Archived from the original on 23 June 2021. Retrieved 16 March 2020.
- ^ «Journal of Business & Economic Statistics». Journal of Business & Economic Statistics. Taylor & Francis. Archived from the original on 27 July 2020. Retrieved 16 March 2020.
- ^ Numerous texts are available, reflecting the scope and reach of the discipline in the business world:
- Sharpe, N. (2014). Business Statistics, Pearson. ISBN 978-0134705217
- Wegner, T. (2010). Applied Business Statistics: Methods and Excel-Based Applications, Juta Academic. ISBN 0702172863
Two open textbooks are:
- Holmes, L., Illowsky, B., Dean, S. (2017). Introductory Business Statistics Archived 2021-06-16 at the Wayback Machine
- Nica, M. (2013). Principles of Business Statistics Archived 2021-05-18 at the Wayback Machine
- ^ Cline, Graysen (2019). Nonparametric Statistical Methods Using R. EDTECH. ISBN 978-1-83947-325-8. OCLC 1132348139. Archived from the original on 2022-05-15. Retrieved 2021-09-16.
- ^ Palacios, Bernardo; Rosario, Alfonso; Wilhelmus, Monica M.; Zetina, Sandra; Zenit, Roberto (2019-10-30). «Pollock avoided hydrodynamic instabilities to paint with his dripping technique». PLOS ONE. 14 (10): e0223706. Bibcode:2019PLoSO..1423706P. doi:10.1371/journal.pone.0223706. ISSN 1932-6203. PMC 6821064. PMID 31665191.
Further reading[edit]
- Lydia Denworth, «A Significant Problem: Standard scientific methods are under fire. Will anything change?», Scientific American, vol. 321, no. 4 (October 2019), pp. 62–67. «The use of p values for nearly a century [since 1925] to determine statistical significance of experimental results has contributed to an illusion of certainty and [to] reproducibility crises in many scientific fields. There is growing determination to reform statistical analysis… Some [researchers] suggest changing statistical methods, whereas others would do away with a threshold for defining «significant» results.» (p. 63.)
- Barbara Illowsky; Susan Dean (2014). Introductory Statistics. OpenStax CNX. ISBN 9781938168208.
- Stockburger, David W. «Introductory Statistics: Concepts, Models, and Applications». Missouri State University (3rd Web ed.). Archived from the original on 28 May 2020.
- OpenIntro Statistics Archived 2019-06-16 at the Wayback Machine, 3rd edition by Diez, Barr, and Cetinkaya-Rundel
- Stephen Jones, 2010. Statistics in Psychology: Explanations without Equations[permanent dead link]. Palgrave Macmillan. ISBN 9781137282392.
- Cohen, J (1990). «Things I have learned (so far)» (PDF). American Psychologist. 45 (12): 1304–1312. doi:10.1037/0003-066x.45.12.1304. Archived from the original (PDF) on 2017-10-18.
- Gigerenzer, G (2004). «Mindless statistics». Journal of Socio-Economics. 33 (5): 587–606. doi:10.1016/j.socec.2004.09.033.
- Ioannidis, J.P.A. (2005). «Why most published research findings are false». PLOS Medicine. 2 (4): 696–701. doi:10.1371/journal.pmed.0040168. PMC 1855693. PMID 17456002.
External links[edit]
- (Electronic Version): TIBCO Software Inc. (2020). Data Science Textbook.
- Online Statistics Education: An Interactive Multimedia Course of Study. Developed by Rice University (Lead Developer), University of Houston Clear Lake, Tufts University, and National Science Foundation.
- UCLA Statistical Computing Resources (archived 17 July 2006)
- Philosophy of Statistics from the Stanford Encyclopedia of Philosophy
Statistics is a branch of applied mathematics that deals with collecting, organising, analysing, reading and presenting data.[1][2][3] Descriptive statistics make summaries of data.[4][5] Inferential statistics makes predictions.[6] Statistics helps in the study of many other fields, such as science, medicine,[7] economics,[8][9] psychology,[10] politics[11] and marketing.[12] Someone who works in statistics is called a statistician. In addition to being the name of a field of study, the word «statistics» can also mean numbers that are used to describe data or relationships.
History[change | change source]
The first known statistics are census data. The Babylonians did a census around 3500 BC, the Egyptians around 2500 BC, and the Ancient Chinese around 1000 BC.
Starting in the 16th century mathematicians such as Gerolamo Cardano developed probability theory,[13][14][15][16][17] which made statistics a science. Since then, people have collected and studied statistics on many things. Trees, starfish, stars, rocks, words, almost anything that can be counted has been a subject of statistics.
Collecting data[change | change source]
Before we can describe the world with statistics, we must collect data. The data that we collect in statistics are called measurements. After we collect data, we use one or more numbers to describe each observation or measurement. For example, suppose that we want to find out how popular a certain TV show is. We can pick a group of people (called a sample) out of the total population of viewers. Then we ask each viewer in the sample how often they watch the show. The sample is data that one can see, and the population is data that one cannot see (assuming that not every viewer in the population are asked). For another example, if we want to know whether a certain drug can help lower blood pressure, we could give the drug to people for some time and measure their blood pressure before and after.
Descriptive and inferential statistics[change | change source]
Numbers that describe the data one can see are called descriptive statistics. Numbers that make predictions about the data one cannot see are called inferential statistics.
Descriptive statistics involves using numbers to describe features of data. For example, the average height of women in the United States is a descriptive statistic: it describes a feature (average height) of a population (women in the United States).
Once the results have been summarized and described, they can be used for prediction. This is called inferential statistics. As an example, the size of an animal is dependent on many factors. Some of these factors are controlled by the environment, but others are by inheritance. A biologist might therefore make a model that says that there is a high probability that the offspring will be small in size—if the parents were small in size. This model probably allows to predict the size in better ways than by just guessing at random. Testing whether a certain drug can be used to cure a certain condition or disease is usually done by comparing the results of people who are given the drug against those who are given a placebo.
Methods[change | change source]
Most often, we collect statistical data by doing surveys or experiments. For example, an opinion poll is one kind of survey. We pick a small number of people and ask them questions. Then, we use their answers as the data.
The choice of which individuals to take for a survey or data collection is important, as it directly influences the statistics. When the statistics are done, it can no longer be determined which individuals are taken. Suppose we want to measure the water quality of a big lake. If we take samples next to the waste drain, we will get different results than if the samples are taken in a far-away and hard-to-reach spot of the lake.
There are two kinds of problems which are commonly found when taking samples:
- If there are many samples, the samples will likely be very close to what they are in the real population. If there are very few samples, however, they might be very different from what they are in the real population. This error is called a chance error (see also Errors and residuals in statistics).
- The individuals for the samples need to be chosen carefully. Usually, they will be chosen randomly. If this is not the case, the samples might be very different from what they really are in the total population. This is true even if a great number of samples is taken. This kind of error is called bias.
Errors[change | change source]
We can reduce chance errors by taking a larger sample, and we can avoid some bias by choosing randomly. However, sometimes large random samples are hard to take. And bias can happen if different people are not asked, or refuse to answer our questions, or if they know they are getting a fake treatment. These problems can be hard to fix. See standard error for more.
Descriptive statistics[change | change source]
Finding the middle of the data[change | change source]
The middle of the data is called an average. The average tells us about a typical individual in the population. There are three kinds of average that are often used: the mean, the median and the mode.
The examples below use this sample data:
| Name | A | B | C | D | E | F | G | H | I | J |
| Score | 23 | 26 | 49 | 49 | 57 | 64 | 66 | 78 | 82 | 92 |
Mean[change | change source]
The formula for the mean is[18]

Where 

This means that one calculates the mean by adding up all the values, and then divide by the number of values. For the example above, the mean is:

The problem with the mean is that it does not tell anything about how the values are distributed. Values that are very large or very small change the mean a lot. In statistics, these extreme values might be errors of measurement, but sometimes the population really does contain these values. For example, if there are 10 people in a room who make $10 per day and 1 who makes $1,000,000 per day. The mean of the data is $90,918 per day. Even though it is the average amount, the mean in this case is not the amount any single person makes, and thus is not very useful for some purposes.
The mean described above is the «arithmetic mean». Other kinds are useful for some purposes.
Median[change | change source]
The median is the middle item of the data. For a given data 

As another example, like the income example presented for the mean, consider a room with 10 people who have incomes of $10, $20, $20, $40, $50, $60, $90, $90, $100, and $1,000,000. Here, the median is $55, because $55 is the average of the two middle numbers, $50 and $60. If the extreme value of $1,000,000 is ignored, the mean is $53. In this case, the median is close to the value obtained when the extreme value is thrown out. The median solves the problem of extreme values as described in the definition of mean above.
Mode[change | change source]
The mode is the most frequent item of data. For example, the most common letter in English is the letter «e». We would say that «e» is the mode of the distribution of the letters.
As another example, if there are 10 people in a room with incomes of $10, $20, $20, $40, $50, $60, $90, $90, $90, $100, and $1,000,000, then the mode is $90, because $90 occurs three times and all other values occur fewer than three times.
There can be more than one mode. For example, if there are 10 people in a room with incomes of $10, $20, $20, $20, $50, $60, $90, $90, $90, $100, and $1,000,000, the modes are $20 and $90. This is bi-modal, or has two modes. Bi-modality is very common, and it often indicates that the data is the combination of two different groups. For instance, the average height of all adults in the U.S. has a bi-modal distribution. This is because males and females have separate average heights of 1.763 m (5 ft 9 + 1⁄2 in) for men and 1.622 m (5 ft 4 in) for women. These peaks are apparent when both groups are combined.
The mode is the only form of average that can be used for data that can not be put in order.
Finding the spread of the data[change | change source]
Another thing we can say about a set of data is how spread out it is. A common way to describe the spread of a set of data is the standard deviation. If the standard deviation of a set of data is small, then most of the data is very close to the average. If the standard deviation is large, though, then a lot of the data is very different from the average.
The standard deviation of a sample is generally different from the standard deviation of its originating population . Because of that, we write 

If the data follows the common pattern called the normal distribution, then it is very useful to know the standard deviation. If the data follows this pattern (we would say the data is normally distributed), about 68 of every 100 pieces of data will be off the average by less than the standard deviation. Not only that, but about 95 of every 100 measurements will be off the average by less than two times the standard deviation, and about 997 in 1000 will be closer to the average by less than three standard deviations.
Other descriptive statistics[change | change source]
We also can use statistics to find out that some percent, percentile, number, or fraction of people or things in a group do something or fit in a certain category.
For example, social scientists used statistics to find out that 49% of people in the world are males.
[change | change source]
In order to support statisticians, many statistical software have been developed:
- MATLAB[19][20]
- R[21][22][23][24][25][26]
- SAS Institute[27]
- SPSS[28][29][30][31][32][33] (made by IBM)
References[change | change source]
- ↑ DeGroot, M. H., & Schervish, M. J. (2012). Probability and statistics. Pearson Education.
- ↑ Johnson, R. A., Miller, I., & Freund, J. E. (2000). Probability and statistics for engineers (Vol. 2000, p. 642p). London: Pearson Education.
- ↑ Walpole, R. E., Myers, R. H., Myers, S. L., & Ye, K. (1993). Probability and statistics for engineers and scientists (Vol. 5). New York: Macmillan.
- ↑ Dean, Susan; Illowsky, Barbara. «Descriptive Statistics: Histogram». cnx.org. Retrieved 2020-10-13.
{{cite web}}: CS1 maint: url-status (link) - ↑ Larson, M. G. (2006). Descriptive statistics and graphical displays. Circulation, 114(1), 76-81.
- ↑ Asadoorian, M. O., & Kantarelis, D. (2005). Essentials of inferential statistics. University Press of America.
- ↑ Lang, T. A., Lang, T., & Secic, M. (2006). How to report statistics in medicine: annotated guidelines for authors, editors, and reviewers. ACP Press.
- ↑ Wonnacott, T. H., & Wonnacott, R. J. (1990). Introductory statistics for business and economics (Vol. 4). New York: Wiley.
- ↑ Newbold, P., Carlson, W. L., & Thorne, B. (2013). Statistics for business and economics. Boston, MA: Pearson.
- ↑ Aron, A., & Aron, E. N. (1999). Statistics for psychology. Prentice-Hall, Inc.
- ↑ Fioramonti, D. L. (2014). How numbers rule the world: The use and abuse of statistics in global politics. Zed Books Ltd..
- ↑ Rossi, P. E., Allenby, G. M., & McCulloch, R. (2012). Bayesian statistics and marketing. John Wiley & Sons.
- ↑ Chow, Y. S., & Teicher, H. (2003). Probability theory: independence, interchangeability, martingales. Springer Science & Business Media.
- ↑ Feller, W. (2008). An introduction to probability theory and its applications (Vol. 2). John Wiley & Sons.
- ↑ Durrett, R. (2019). Probability: theory and examples (Vol. 49). Cambridge University Press.
- ↑ Jaynes, E. T. (2003). Probability theory: The logic of science. Cambridge University Press.
- ↑ Chung, K. L., & Zhong, K. (2001). A course in probability theory. Academic Press.
- ↑ 18.0 18.1 18.2 «List of Probability and Statistics Symbols». Math Vault. 2020-04-26. Retrieved 2020-10-13.
- ↑ Cho, M., & Martinez, W. L. (2014). Statistics in Matlab: A primer (Vol. 22). CRC Press.
- ↑ Martinez, W. L. (2011). Computational statistics in MATLAB®. Wiley Interdisciplinary Reviews: Computational Statistics, 3(1), 69-74.
- ↑ Crawley, M. J. (2012). The R book. John Wiley & Sons.
- ↑ Dalgaard, P. (2008). Introductory statistics with R. Springer.
- ↑ Maronna, R. A., Martin, R. D., & Yohai, V. J. (2019). Robust statistics: theory and methods (with R). John Wiley & Sons.
- ↑ Ugarte, M. D., Militino, A. F., & Arnholt, A. T. (2008). Probability and Statistics with R. CRC Press.
- ↑ Bruce, P., Bruce, A., & Gedeck, P. (2020). Practical Statistics for Data Scientists: 50+ Essential Concepts Using R and Python. O’Reilly Media.
- ↑ Kruschke, J. (2014). Doing Bayesian data analysis: A tutorial with R, JAGS, and Stan. Academic Press.
- ↑ Khattree, R., & Naik, D. N. (2018). Applied multivariate statistics with SAS software. SAS Institute Inc..
- ↑ Wagner III, W. E. (2019). Using IBM® SPSS® statistics for research methods and social science statistics. Sage Publications.
- ↑ Pollock III, P. H., & Edwards, B. C. (2019). An IBM® SPSS® Companion to Political Analysis. Cq Press.
- ↑ Babbie, E., Wagner III, W. E., & Zaino, J. (2018). Adventures in social research: Data analysis using IBM SPSS statistics. Sage Publications.
- ↑ Aldrich, J. O. (2018). Using IBM® SPSS® Statistics: An interactive hands-on approach. Sage Publications.
- ↑ Stehlik-Barry, K., & Babinec, A. J. (2017). Data Analysis with IBM SPSS Statistics. Packt Publishing Ltd.
- ↑ Parametric & Nonparametric Data Analysis for Social Research: IBM SPSS, Hary Gunarto. LAP Academic Publishing. 2019. ISBN 978-6200118721.
Other websites[change | change source]
Media related to Statistics at Wikimedia Commons
Statistics may be defined as the collection, presentation, analysis and interpretation of numerical data.
Statistics is a set of decision-making techniques which helps businessmen in making suitable policies from the available data. In fact, every businessman needs a sound background of statistics as well as of mathematics.
The purpose of statistics and mathematics is to manipulate, summarize and investigate data so that the useful decision-making results can be executed.
Table of Content
- 1 What is Statistics?
- 2 Statistics Meaning
- 3 Statistics Definition
- 4 Uses of Statistics in Business Decision Making
- 4.1 Uses of Statistics in Business
- 4.2 Uses of Mathematics for Decision Making
- 4.3 Uses of Statistics in Economics
- 5 Functions of Statistics
- 5.1 Condensation
- 5.2 Comparison
- 5.3 Forecast
- 5.4 Testing of hypotheses
- 5.5 Preciseness
- 5.6 Expectation
- 6 Importance of Statistics
- 6.1 Importance of Statistics in Business and Industry
- 6.2 Importance in the Field of Science and Research
- 6.3 Importance in the Field of Banking
- 6.4 Importance to the State
- 6.5 Importance in planning
- 7 Scope of Statistics
- 7.1 Presents facts in numerical figures
- 7.2 Presents complex facts in a simplified form
- 7.3 Studies relationship between two or more phenomena
- 7.4 Helps in the formulation of policies
- 7.5 Helps in forecasting
- 7.6 Provides techniques for testing of hypothesis
- 7.7 Provides techniques for making decisions under uncertainty
- 8 Limitations of Statistics
- 8.1 Statistics Suits to the Study of Quantitative Data Only
- 8.2 Statistical Results are not Exact
- 8.3 Statistics Deals with Aggregates Only
- 8.4 Statistics is Useful for Experts Only
- 8.5 Statistics does not Provide Solutions to the Problems
- 9 Summary
Statistics Meaning
The term ‘statistics’ has been derived from the Latin word ‘status’ Italian word ‘statista’ or German word ‘statistik’.
All these words mean ‘Political state’. In ancient days, the states were required to collect statistical data mainly for the number of youngmen so that they can be recruited in the Army.
Also to calculate the total amount of land revenue that can be collected. Due to this reason, statistics is also called ‘Political Arithmetic’.
Statistics Definition
Statistics has been defined in different ways by different authors.
Statistics are numerical statements of facts in any department of enquiry placed in relation to each other.Bowley
By statistics, we mean quantitative data affected to a marked extend by multiplicity of causesYule and Kendall
By statistics, we mean aggregate of facts affected to a marked extent by multiplicity of causes, numerically expressed, enumerated or estimated according to reasonable standards of accuracy, collected in a systematic manner for a predetermined purpose and placed in relation to each other.Horace Secrist
Statistics may be defined as the collection, presentation, analysis and interpretation of numerical data.Croxton and Cowden
Uses of Statistics in Business Decision Making
Uses of Statistics in Business
The following are the main uses of statistics in various business activities:
- With the help of statistical methods, quantitative information about production, sale, purchase, finance, etc. can be obtained. This type of information helps businessmen in formulating suitable policies.
- By using the techniques of time series analysis which are based on statistical methods, the businessman can predict the effect of a large number of variables with a fair degree of accuracy.
- In business decision theory, most of the statistics techniques are used in taking a business decision which helps us in doing the business without uncertainty.
- Nowadays, a large part of modern business is being organised around systems of statistical analysis and control.
- By using ‘Bayesian Decision Theory’, the businessmen can select the optimal decisions for the direct evaluation of the payoff for each alternative course of action.
Uses of Mathematics for Decision Making
- The number of defects in a roll of paper, bale of cloth, sheet of a photographic film can be judged by means of Control Chart based on Normal distribution.
- In statistical quality control, we analyse the data which are based on the principles involved in Normal curve.
Uses of Statistics in Economics
Statistics is the basis of economics. The consumer’s maximum satisfaction can be determined on the basis of data pertaining to income and expenditure. The various laws of demand depend on the data concerning price and quantity. The price of a commodity is well determined on the basis of data relating to its buyers, sellers, etc.
Functions of Statistics
Statistics can be well-defined as a branch of research which is concerned with the development and application of techniques for collecting, organising, presenting, analysing and interpreting data in such a manner that the reliability of conclusions may be evaluated in terms of probability statements.
Statistical methods and processes are useful for business development and, hence, applied to enormous numerical facts with an objective that “behind every figure, there’s a story”.
Some key functions of statistics are as follows:
- Condensation
- Comparison
- Forecast
- Testing of hypotheses
- Preciseness
- Expectation
Condensation
Statistics can be used to compress a large amount of data into small meaningful information; for example, aggregated sales forecast, BSE indices, GDP growth rate, etc. It is almost impossible to get a complete idea of the profitability of a company by looking at the records of its income and expenditure. Financial ratios such as return on investment, earnings per share, profit margins, etc., however, can be easily remembered and thus can be used in quick decision making.
Comparison
Statistics facilitate comparing different quantities. For example, the price-to-earnings ratio of ITC as of January 22, 2021 is 19.54 as compared to HUL. HUL is overvalued, quoting a price-to-earnings ratio of 71 times.
Forecast
Statistics helps forecast by looking at trends of a variable. It is essential for planning and decision-making. Predictions or forecasts based on intuition can be disastrous for any business.
For example, to decide the production capacity for a vehicle-manufacturing plant, we need to predict the demand for the product mix, supply of components, cost of manpower, competitor strategy, etc., over the next 5 to 10 years, before committing an investment.
Testing of hypotheses
Hypotheses are statements about population parameters based on knowledge from literature that a researcher would like to test for validity in the light of new information. Drawing inferences about the population using sample estimates involves an element of risk.
Preciseness
Statistics visualises and presents facts precisely in a quantitative form. Facts and information conveyed in quantitative terms are more convincing than qualitative data. For example, ‘increase in profit margin is less in the year 2020 than in the year 2019’ does not convey a precise and complete piece of information.
On the other hand, statistics summarise the information more precisely. For example, ‘profit margin is 5% of the turnover in the year 2020 against 7% in the year 2019’.
Expectation
Statistics can act as the basic building block for framing clear plans and policies. For example, how much raw material to be imported in a year, how much capacity to be expanded, or manpower to be recruited, etc., depends on the expected value of outcome of our decisions taken under different situations.
Importance of Statistics
Statistics in today’s life has become an essential part of various business activities which is clear from the following points.
The importance of statistics in the following major areas:
- Importance of Statistics in Business and Industry
- Importance in the Field of Science and Research
- Importance in the Field of Banking
- Importance to the State
- Importance in planning
Importance of Statistics in Business and Industry
In past days, decisions regarding business were made only on personal judgement. However, in these days, they are based on several mathematical and statistical techniques and the best decision is arrived by using all these techniques.
For example, by using the testing hypothesis, we can reject or accept the null hypothesis which are based upon the assumption made from the population or universe
By using ‘Bayesian Decision Theory’ or ‘Decision Theory’, we can select the optimal decisions for the direct evaluation of the payoff for each alternative course of action.
Mathematics and statistics have become ingredients of various decisions problems which is clear from the following:
- In Selecting Alternative Course of Action: The process of business decisions involve the selection of a single action among some set of alternative actions. When there are two or more alternative courses of action, and we need only one course of action, statistical decisions theory helps us in selecting the required course of action by applying Bayesian decision theory and thus saves lot of time.
- In Removing Uncertainty: In decision-making problems, uncertainty is very common in a situation, when the course of action is not known to us. When there are many possible outcomes of an event, we cannot predict with certainty that what will happen. By applying the concept of joint and conditional probability, the uncertainty about the event can be removed very easily.
- In Calculating E.O.L., C.O.L., etc.: In business, the opportunity loss is very often, which can be defined as the difference between the highest possible profit for an event and the actual profit obtained for the actual action taken. The expected opportunity loss (E.O.L.) and conditional opportunity loss (C.O.L.) can be easily calculated by using the concept of maximum and minimum criteria of pay-off.
Importance in the Field of Science and Research
Statistics has great significance in the field of physical and natural sciences. It is widely used in verifying scientific laws and phenomenon.
For example, to formulate standards of body temperature, pulse rate, blood pressure, etc. The success of modern computers depends on the conclusions drawn on the basis of statistics.
Importance in the Field of Banking
In banking industry, the bankers have to relate demand deposits, time deposits, credit etc. It is on the basis of data relating to demand and time deposits that the bankers determine the credit policies. The credit policies are based on the theory of probability.
Importance to the State
We know that the subject of statistics originated for helping the ancient rulers in the assessment of their military and economic strength. Gradually its scope was enlarged to tackle other problems relating to political activities of the State.
In the modern era, the role of State has increased and various governments of the world also take care of the welfare of its people. Therefore, these governments require much greater information in the form of numerical figures for the fulfilment of welfare objectives in addition to the efficient running of their administration.
Importance in planning
Planning is indispensable for achieving faster rate of growth through the best use of a nation’s resources. It also requires a good deal of statistical data on various aspects of the economy.
One of the aims of planning could be to achieve a specified rate of growth of the economy. Using statistical techniques, it is possible to assess the amounts of various resources available in the economy and accordingly determine whether the specified rate of growth is sustainable or not.
Scope of Statistics
The following are the main scope of statistics:
- Presents facts in numerical figures
- Presents complex facts in a simplified form
- Studies relationship between two or more phenomena
- Helps in the formulation of policies
- Helps in forecasting
- Provides techniques for testing of hypothesis
- Provides techniques for making decisions under uncertainty
Presents facts in numerical figures
The first function of statistics is to present a given problem in terms of numerical figures. We know that the numerical presentation helps in having a better understanding of nature an of problem.
Presents complex facts in a simplified form
Generally, a problem to be investigated is represented by a large mass of numerical figures which are very difficult to understand and remember. Using various statistical methods, this large mass of data can be presented in a simplified form.
Studies relationship between two or more phenomena
Statistics can be used to investigate whether two or more phenomena are related. For example, the relationship between income and consumption, demand and supply, etc.
Helps in the formulation of policies
Statistical analysis of data is the starting point in the formulation of policies in various economic, business and government activities.
For example, using statistical techniques a firm can know the tastes and preferences of the consumers and decide to make its product accordingly.
Helps in forecasting
The success of planning by the Government or of a business depends to a large extent upon the accuracy of their forecasts. Statistics provides a scientific basis for making such forecasts.
Provides techniques for testing of hypothesis
A hypothesis is a statement about some characteristics of a population (or universe).
Provides techniques for making decisions under uncertainty
Many times we face an uncertain situation where any one of the many alternatives may be adopted. A businessman might face a situation of uncertain investment opportunities in which he can lose or gain.
He may be interested in knowing whether to undertake a particular investment or not. The answer to such problems are provided by the statistical techniques of decision-making under uncertainty.
Limitations of Statistics
Statistics is considered to be a science as well as an art, which is used as an instrument of research in almost every sphere of our activities.
Some of the limitations of statistics are as follows:
- Statistics Suits to the Study of Quantitative Data Only
- Statistical Results are not Exact
- Statistics Deals with Aggregates Only
- Statistics is Useful for Experts Only
- Statistics does not Provide Solutions to the Problems
Statistics Suits to the Study of Quantitative Data Only
Statistics deals with the study of quantitative data only. By using the methods of statistics, the problems regarding production, income, price, wage, height, weight etc. can be studied. Such characteristics are quantitative in nature.
The characteristics like honesty, goodwill, duty, character, beauty, intelligence, efficiency, integrity etc. are not capable of quantitative measurement and hence cannot be directly dealt with statistical methods. These characteristics are qualitative in nature.
In such type of characteristics, only comparison is possible The use of statistical methods is limited to quantitative characteristics and those qualitative characteristics which are capable of being expressed numerically.
Statistical Results are not Exact
The task of statistical analysis is performed under certain conditions. It is not always possible, rather not advisable, to consider the entire population during statistical investigations.
The use of samples is called for in statistical investigations. And the results obtained by using samples may not be universally true for the entire population. Data collected for a statistical enquiry may not be hundred percent true. Statistical results are true on an average.
Statistics Deals with Aggregates Only
Statistics does not recognise individual items. Consider the statement, “The weight of Mr X in the college is 70 kg”. This statement does not constitute statistical data. Statistical methods are not going to investigate anything about this statement. Whereas, if the weights of all the students of the college are given, the statistical methods may be applied to analyse that data.
According to Tippett, “Statistics is essentially totalitarian because it is not concerned with individual values, but only with classes”. Statistics is used to study group characteristics of aggregates.
Statistics is Useful for Experts Only
Statistics is both a science and an art. It is systematic and finds applications in studying problems in Economics, Business, Astronomy, Physics, Medicines etc. Statistical methods are sophisticated in nature. Everyone is not expected to possess the intelligence required to understand and to apply these methods to practical problems. This is the job of an expert, who is well-versed with statistical methods
Statistics does not Provide Solutions to the Problems
The statistical methods are used to explore the essentials of problems. It does not find use in inventing solutions to problems. For example, the methods of statistics may reveal the fact that the average result of a particular class in a college is deteriorating for the last ten years, i.e., the trend of the result is downward, but statistics cannot provide solution to this problem.
It cannot help in taking remedial steps to improve the result of that class. Statistics should be taken as a means and not as an end. The methods of statistics are used to study the various aspects of the data.
Summary
- Statistics is a set of decision-making techniques which helps businessmen in making suitable policies from the available data.
- “Statistics may be defined as the collection, presentation, analysis and interpretation of numerical data.”
- With the help of statistical methods, quantitative information about production, sale, purchase, finance etc. can be obtained.
- Statistics is the basis of economics. The consumer’s maximum satisfaction can be determined on the basis of data pertaining to income and expenditure.
- By using ‘Bayesian Decision Theory’ or ‘Decision Theory’, we can select the optimal decisions for the direct evaluation of the payoff for each alternative course of action.
- Statistics is considered to be a science as well as an art, which is used as an instrument of research in almost every sphere of our activities.
- W.I. King says, “Statistics is a most useful servant but only of great value to those who understand its proper use.”
- Yule and Kendall has rightly said that “statistical methods are most dangerous tools in the hands of inexperts.”
- The statistical methods are used to explore the essentials of problems.
The post is about “The Word Statistics Meaning and Use”.
The word statistics was first used by German scholar Gottfried Achenwall in the middle of the 18th century as the science of statecraft concerning the collection and use of data by the state.
The word statistics comes from the Latin word “Status” or Italian word “Statistia” or German word “Statistik” or the French word “Statistique”; meaning a political state, and originally meant information useful to the state, such as information about sizes of the population (human, animal, products, etc.) and armed forces.
According to pioneer statistician Yule, the word statistics occurred at the earliest in the book “the element of universal erudition” by Baron (1770). In 1787 a wider definition was used by E.A.W. Zimmermann in “A Political survey of the present state of Europe”. It appeared in the encyclopedia of Britannica in 1797 and was used by Sir John Sinclair in Britain in a series of volumes published between 1791 and 1799 giving a statistical account of Scotland. In the 19th century, the word statistics acquired a wider meaning covering numerical data of almost any subject whatever and also interpretation of data through appropriate analysis.
Now statistics are being used in different meanings.
- Statistics refers to “numerical facts that are arranged systematically in the form of tables or charts etc. In this sense, it is always used a plural i.e. a set of numerical information. For instance statistics of prices, road accidents, crimes, births, educational institutions etc.
- The word statistics is defined as a discipline that includes procedures and techniques used to collect, process and analyze the numerical data to make inferences and to reach an appropriate decision in a situation of uncertainty (uncertainty refers to incompleteness, it does not imply ignorance). In this sense word statistic is used in the singular sense. It denotes the science of basing the decision on numerical data.
- The word statistics are numerical quantities calculated from sample observations; a single quantity calculated from sample observations is called statistics such as the mean. Here word statistics is plural.
“We compute statistics from statistics by statistics”
The first place of statistics is plural of statistics, in second place is plural sense data, and in third place is singular sense methods.
For learning about Basics of Statistics Follow the link Basic Statistics
Muhammad Imdad Ullah
Currently working as Assistant Professor of Statistics in Ghazi University, Dera Ghazi Khan.
Completed my Ph.D. in Statistics from the Department of Statistics, Bahauddin Zakariya University, Multan, Pakistan.
l like Applied Statistics, Mathematics, and Statistical Computing.
Statistical and Mathematical software used is SAS, STATA, GRETL, EVIEWS, R, SPSS, VBA in MS-Excel.
Like to use type-setting LaTeX for composing Articles, thesis, etc.
Statistics is a broad mathematical discipline which studies ways to collect, summarize, and draw conclusions from data.
It is applicable to a wide variety of academic fields from the physical and social sciences to the humanities, as well as to business, government and industry.
Once data is collected, either through a formal sampling procedure or some other, less formal method of observation, graphical and numerical summaries may be obtained using the techniques of descriptive statistics. The specific summary methods chosen depend on the method of data collection. The techniques of descriptive statistics can also be applied to census data, which is collected on entire populations.
If the data can be viewed as a sample (a subset of some population of interest), inferential statistics can be used to draw conclusions about the larger, mostly unobserved population.
These inferences, which are usually based on ideas of randomness and uncertainty quantified through the use of probabilities, may take any of several forms:
- Answers to essentially yes/no questions (hypothesis testing)
- Estimates of numerical characteristics (estimation)
- Predictions of future observations (prediction)
- Descriptions of association (correlation)
- Modeling of relationships (regression)
The procedures by which such inferences are made are sometimes collectively known as applied statistics. In contrast, statistical theory (or, as an academic subject sometimes called mathematical statistics) is the subdiscipline of applied mathematics which uses probability theory and mathematical analysis to place statistical practice on a firm theoretical basis. (If applied statistics is what you do in statistics, statistical theory tells you why it works.)
In academic statistics courses, the word statistic (no final s) is usually defined as a numerical quantity calculated from a set of data. In this usage, statistics would be the plural form meaning a collection of such numerical quantities. See Statistic for further discussion.
Less formally, the word statistics (singluar statistic) is often used in a way roughly synonymous with data or simply numbers, a common example being sports «statistics» published in newspapers. In the United States, the Bureau of Labor Statistics collects data on employment and general economic conditions; also, the Census Bureau publishes a large annual volume called the Statistical Abstract of the United States based on census data.
Etymology
The word statistics comes from the modern Latin phrase statisticum collegium (lecture about state affairs), which gave rise to the Italian word statista (statesman or politician — compare to status) and the German Statistik (originally the analysis of data about the state). It acquired the meaning of the collection and classification of data generally in the early 19th century. The collection of data about states and localities continues, largely through national and international statistical services.
History of statistics
In the 9th century, the Islamic mathematician, Al-Kindi, was the first to use statistics to decipher encrypted messages and developed the first code-breaking algorithm in the House of Wisdom in Baghdad, based on frequency analysis. He wrote a book entitled Manuscript on Deciphering Cryptographic Messages, containing detailed discussions on statistics.[1] It covers methods of cryptanalysis, encipherments, cryptanalysis of certain encipherments, and statistical analysis of letters and letter combinations in Arabic.[2]
In the early 11th century, Al-Biruni’s scientific method emphasized repeated experimentation. Biruni was concerned with how to conceptualize and prevent both systematic errors and observational biases, such as «errors caused by the use of small instruments and errors made by human observers.» He argued that if instruments produce errors because of their imperfections or idiosyncratic qualities, then multiple observations must be taken, analyzed qualitatively, and on this basis, arrive at a «common-sense single value for the constant sought», whether an arithmetic mean or a «reliable estimate.»[3]
Modern history
- History of Statistics by Prof. Noelson Manilay
The Word statistics have been derived from Latin word “Status” or the Italian word “Statista”, meaning of these words is “Political State” or a Government. Shakespeare used a word Statist is his drama Hamlet (1602). In the past, the statistics was used by rulers. The application of statistics was very limited but rulers and kings needed information about lands, agriculture, commerce, population of their states to assess their military potential, their wealth, taxation and other aspects of government.
Gottfried Achenwall used the word statistik at a German University in 1749 which means that political science of different countries. In 1771 W. Hooper (Englishman) used the word statistics in his translation of Elements of Universal Erudition written by Baron B.F Bieford, in his book statistics has been defined as the science that teaches us what is the political arrangement of all the modern states of the known world. There is a big gap between the old statistics and the modern statistics, but old statistics also used as a part of the present statistics.
During the 18th century the English writer have used the word statistics in their works, so statistics has developed gradually during last few centuries. A lot of work has been done in the end of the nineteenth century.
At the beginning of the 20th century, William S Gosset was developed the methods for decision making based on small set of data. During the 20th century several statistician are active in developing new methods, theories and application of statistics. Now these days the availability of electronics computers is certainly a major factor in the modern development of statistics.
Basic concepts
There are several approaches to statistics, most of which rely on a few basic concepts.
Population vs. sample
In statistics, a population is the set of all objects (people, etc.) that one wishes to make conclusions about. In order to do this, one usually selects a sample of objects: a subset of the population. By carefully examining the sample, one may make inferences about the larger population.
For example, if one wishes to determine the average height of adult women aged 20–29 in the U.S., it would be impractical to try to find all such women and ask or measure their heights. However, by taking small but representative sample of such women, one may determine the average height of all young women quite closely. The matter of taking representative samples is the focus of sampling.
Randomness, probability and uncertainty
The concept of randomness is difficult to define precisely. In general, any outcome of an action, or series of actions, which cannot be predicted beforehand may be described as being random. When statisticians use the word, they generally mean that while the exact outcome cannot be known beforehand, the set of all possible outcomes is known — or, at least in theory, knowable. A simple example is the outcome of a coin toss: whether the coin will land heads up or tails up is (ideally) unknowable before the toss, but what is known is that the outcome will be one of these two possibilities and not, say, on edge (assuming that the coin cannot stand upright on its edge). The set of all possible outcomes is usually called the sample space.
The probability of an event is also difficult to define precisely but is basically equivalent to the everyday idea of the likelihood or chance of the event happening. An event that can never happen has probability zero; an event that must happen has probability one. (Note that the reverse statements are not necessarily true; see the article on probability for details.) All other events have a probability strictly between zero and one. The greater the probability the more likely the event, and thus the less our uncertainty about whether it will happen; the smaller the probability the greater our uncertainty.
There are several basic interpretations of probability used to assign or compute probabilities in statistics:
- Relative frequency interpretation: The probability of an event is the long-run relative frequency of occurrence of the event. That is, after a long series of trials, the probability of event A is taken to be:
- To make this definition rigorous, the right-hand side of the equation should be preceded by the limit as the number of trials grows to infinity.
- Subjective interpretation: The probability of an event reflects our subjective assessment of the likelihood of the event happening. This idea can be made rigorous by considering, for example, how much one should be willing to pay for the chance to win a given amount of money if the event happens. For more information, see Bayesian probability.
- Classical approach to assigning probability: This approach requires that each outcome is equally likely. In this case, the probability that event A occurs is equal to the number of ways that A can occur divided by the number of possible outcomes of the experiment.
Note that the relative frequency interpretation does not require that a long series of trials actually be conducted. Typically probability calculations are ultimately based upon perceived equally-likely outcomes — as obtained, for example, when one tosses a so-called «fair» coin or rolls or «fair» die. Many frequentist statistical procedures are based on simple random samples, in which every possible sample of a given size is as likely as any other.
Prior information and loss
Once a procedure has been chosen for assigning probabilities to events, the probabilistic nature of the phenomenon under consideration can be summarized in one or more probability distributions. The data collected is then viewed as having been generated, in a sense, according to the chosen probability distribution.
Section requires expansion…
Data collection
Sampling
Main article: Sampling (statistics)
If your business has a million customers, it isn’t really feasible to ask them all what their experience of your business was like. In order to take a survey of a population, statisticians use a sample of the population. For example, you might survey five thousand people instead of a million and still come up with some answers that are close to what you would have obtained if you had surveyed everyone.
Experimental design
Main article: Experimental design (statistics)
Data summary: descriptive statistics
Main article: Descriptive statistics
Levels of measurement
Main article: Level of measurement
- Qualitative (categorical)
- Nominal
- Ordinal
- Quantitative (numerical)
- Interval
- Ratio
Graphical summaries
Main article: Statistical graphs
Numerical summaries
Main article: Summary statistics
Data interpretation: inferential statistics
Main article: Statistical inference
Estimation
Main article: Statistical estimation
Prediction
Main article: Statistical prediction
Hypothesis testing
Main article: Statistical hypothesis testing
Relationships and modeling
Correlation
Main article: Correlation
Two quantities are said to be correlated if greater values of one tend to be associated with greater values of the other (positively correlated) or with lesser values of the other (negatively correlated). In the case of interval or ratio variables, this is often apparent in a scatterplot of the data: positive correlation is reflected in an overall increasing trend in the data points when viewed left to right on the graph; negative correlation appears as an overall decreasing trend.
The correlation between two variables is a number measuring the strength and usually the direction of this relationship. Most measures of correlation take on values from -1 to 1 or from 0 to 1. Zero correlation means that greater values of one variable are associated with neither higher nor lower values of the other, or possibly with both. A correlation of 1 implies a perfect positive correlation, meaning that an increase in one variable is always associated with an increase in the other (and possibly always of the same size, depending on the correlation measure used). Finally, a correlation of -1 means that an increase in one variable is always associated with a decrease in the other.
See the article on correlation for more information.
Regression
Main article: Regression
Time series
Main article: Time series
Data mining
Main article: Data mining
Statistics in other fields
- Biostatistics
- Business statistics
- Chemometrics
- Demography
- Economic statistics
- Engineering statistics
- Epidemiology
- Geostatistics
- Psychometrics
- Statistical physics
Subfields or specialties in statistics
- Mathematical statistics
- Reliability
- Survival analysis
- Quality control
- Time series
- Categorical data analysis
- Multivariate statistics
- Large-sample theory
- Bayesian inference
- Regression
- Sampling theory
- Design of experiments
- Statistical computing
- Non-parametric statistics
- Density estimation
- Simultaneous inference
- Linear inference
- Optimal inference
- Decision theory
- Linear models
- Data modeling
- Sequential analysis
- Spatial statistics
Probability:
- Stochastic processes
- Queueing theory
- Probability
- Set theory
- Finite mathematics
- Discrete mathematics
- Combinatorics
- Analysis
- Calculus
- Real analysis
- Measure theory
- Probability theory
- Distribution theory
- Asymptotic analysis
- Linear algebra
- Matrix theory
- Numerical analysis
- Scientific computing
Statistical software
- Main article: List of statistical software
Commercial
- CART
- ECHIPS (EChips)
- Excel
- add-ins: Analyse-It, SigmaXL, statistiXL, WinSTAT, XLSTAT (XLSTAT)
- JMP
- Minitab
- NCSS
- nQuery
- PASS
- SAS System (SAS)
- S
- descendents: S-PLUS (S-Plus), S2, S3, S4, S5, S6
- SPSS
- Stata
- STATISTICA (Statistica)
- StatXact, LogXact
- SUDAAN (Sudaan)
- SYSTAT (Systat)
Free versions of commercial software
- Gnumeric — not a clone of Excel, but implements many of the same functions
- R — free version of S
- FIASCO or PSPP — free version of SPSS
Other free software
- BUGS — Bayesian inference Using Gibbs Sampling
- ESS — a GNU Emacs add-on
- …
- see also [1]
Licensing unknown
- Genstat
- XLispStat
- …
World Wide Web
- StatLib — large repository of statistical software and data sets
Online data sources
- StatLib
- …
References
- ↑ Singh, Simon (2000). The Code Book: The Science of Secrecy from Ancient Egypt to Quantum Cryptography (1st Anchor Books ed. ed.). New York: Anchor Books. ISBN 0-385-49532-3.
- ↑ «Al-Kindi, Cryptgraphy, Codebreaking and Ciphers». http://www.muslimheritage.com/topics/default.cfm?ArticleID=372. Retrieved 2007-01-12.
- ↑ Glick, Thomas F.; Livesey, Steven John; Wallis, Faith (2005), Medieval Science, Technology, and Medicine: An Encyclopedia, Routledge, pp. 89–90, ISBN 0-415-96930-1
External links
- Wikipedia:List of statistical topics
- StatLib
Statistics |
|||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|||||||||||||||||||||||||
|
|||||||||||||||||||||||||
|
|||||||||||||||||||||||||
|
|||||||||||||||||||||||||
|
|||||||||||||||||||||||||
|
|||||||||||||||||||||||||
|
|
What do we mean by statistics?
The mathematics of the collection, organization, and interpretation of numerical data, especially the analysis of population characteristics by inference from sampling. noun
Numerical data. noun
A systematic collection of numbers relating to the enumeration of great classes, or to ratios of quantities connected with such classes, and ascertained by direct enumeration. noun
The study of any subject, especially sociology, by means of extensive enumerations; the science of human society, so far as deduced from enumerations. noun
The science which has to do with the collection, classification, and analysis of facts of a numerical nature regarding any topic. noun
Classified facts of a numerical nature regarding any topic. noun
Numerical facts respecting the condition of the people in a state, their health, their longevity, domestic economy, arts, property, and political strength, their resources, the state of the country, etc., or respecting any particular class or interest; especially, those facts which can be stated in numbers, or in tables of numbers, or in any tabular and classified arrangement. noun
Numerical facts regarding the performance of athletes or athletic teams, such as winning percentages, numbers of games won or lost in a season, batting averages (for baseball players), total yards gained (for football players). The creation and classification of such numbers is limited only by the imagination of those wishing to describe athletic performance numerically. noun
The branch of mathematics which studies methods for the calculation of probabilities. noun
A mathematical science concerned with data collection, presentation, analysis, and interpretation. noun
A systematic collection of data on measurements or observations, often related to demographic information such as population counts, incomes, population counts at different ages, etc. noun
Plural form of statistic. noun
A branch of applied mathematics concerned with the collection and interpretation of quantitative data and the use of probability theory to estimate population parameters noun
A mathematical science concerned with data collection, presentation, analysis, and interpretation.
The bastard child of math and psychology. Urban Dictionary
Statistics is a branch of science which deals with data collection,presentstion,analysis, and drawing conclusion for any problem under study. Urban Dictionary
The mathamatical study of the distribution of data on any subject to prove any point you’re trying to make, when whining about it doesn’t work. Urban Dictionary
Bullshit alot of the time. Urban Dictionary
The study of percentages, bars, graphs, and charts, all in an attempt to make some sort of logical conclusion out of a bunch of numbers so that even more percentages, bars, graphs, and charts can be made. Urban Dictionary
Also known as a useless subject one is forced to do to complete one’s degree in Capitalism 1001 so one can get a piece of paper at the end of four years to be part of a globalised world so one can feed one’s children (if one chooses to have any) and live happily ever after.
so if one does not do statistics one will lead a sad and lonely life. Urban Dictionary
A fire song made by lil timmy tim aka 2 inches proud aka timothee chalamet Urban Dictionary
Someone who believes in the practice or doctrine of giving a centralized government control over economic planning and policy. Urban Dictionary
The scientific way to say I am not sure Urban Dictionary
Modern day supporter of political slavery; A secular State-Worshiper; Member of the cult of the State; An irrational, immoral, collectivist parasite which leeches off the productive private sector at the point of a gun, while attempting to justify such behavior through invalid, unethical, altruistic arguments. Uses statist law (oppressive edicts backed by criminal violence) to intimidate and run the neo-slave racket. Typically found in government, politics, bureaucracy, police, military and law; aka Supporter of such; Governmentalist; Nationalist; A degenerate sub-human who makes your life a living hell; An accident just waiting to happen… Urban Dictionary
Statistics Meaning
Statistics transforms raw data into meaningful results. It is the science behind the identification, collection, organization, interpretation, and presentation of data. Data could be qualitative or quantitative. Statistics makes information-based decision-making easier.
Statistics comprises useful data interpretation tools like mean, median, mode, standard deviation, coefficient of variance, and sample tests. Raw financial data in a numerical format is interpreted using mathematical formulas. Many sectors like science, government, manufacturing, population, psychology, banking, and financial markets rely on statistical data.
Table of contents
- Statistics Meaning
- Statistics Explained
- Application of Statistics
- Role of Statistics in Finance
- Statistics Example
- Properties
- Types of Statistics
- #1 – Descriptive
- #2 – Inferential
- Limitations of Statistics
- Frequently Asked Questions (FAQs)
- Recommended Articles
- Statistics is a discipline that applies various tools and techniques to process raw data and ultimately outputs conclusive results.
- The statistical process includes collection, organization, summarization, interpretation, and reporting of information.
- This mathematical discipline is broadly classified into descriptive and inferential sub-divisions. The descriptive branch deals with the quantitative representation of data. In contrast the inferential statistics focuses on interpreting results.
- For decision making crucial statistical properties like uniformity, efficiency, sufficiency, and quantitative analysis are focused upon.
You are free to use this image on your website, templates, etc, Please provide us with an attribution linkArticle Link to be Hyperlinked
For eg:
Source: Statistics (wallstreetmojo.com)
Statistics Explained
Statistics is the systematic processing and interpretation of raw data to compile a conclusive result. These reports are drafted in a numerical format. They are presented in a succinct manner so that one can read and understand easily. One should be able to comprehend them at a mere glance.
Financial data is in a numerical format and includes details about portfolios, investments, and assets. Historical data and present data are interpreted using mathematical formulas. Forecasts are based on available information and requirements.
Application of Statistics
Statistics is indispensable for decision-making in various sectors and verticals. It is applied in marketing, e-commerce, banking, finance, human resource, production, and information technology. In addition, this mathematical discipline has been a prominent part of research and is widely used in data mining, medicine, aerospace, robotics, psychology, and machine learning.
Not to forget the economicsEconomics is an area of social science that studies the production, distribution, and consumption of limited resources within a society.read more, government, and public sectors where statistical data is a significant part of decision-making. For example, it is used for public surveys, weather forecasts, sports scoring, and budgetingBudgeting is a method used by businesses to make precise projections of revenues and expenditure for a future specific period of time while taking into account various internal and external factors prevailing at that time.read more.
Role of Statistics in Finance
In the finance sector, statistical data facilitate decision-making. For instance, a watch manufacturing company can use statistical tools to determine the percentage of defective watches in every lot.
At a macro level, it helps in understanding a country’s financial state and measuring economic growthEconomic growth refers to an increase in the aggregated production and market value of economic commodities and services in an economy over a specific period.read more. At a micro-level, statistics helps analysts determine a company’s business income, earningsEarnings are usually defined as the net income of the company obtained after reducing the cost of sales, operating expenses, interest, and taxes from all the sales revenue for a specific time period. In the case of an individual, it comprises wages or salaries or other payments.read more, and revenue-generating capacity.
Be it preparing budgets, financial forecastsFinancial Forecasting is the process of predicting or estimating future stats of an organization i.e. how business will perform in the future based on historical data like by analyzing the income statement, position statement, current conditions, past trends of the financial, future internal and external environment which is usually undertaken with the objective of preparing and developing budget and allocating available resources to ensure best possible utilization.read more, monitoring a company, or a country’s performance, statistics is everywhere.
Statistics Example
Lets’ take an example to understand the application of statistics. PNU Productions manufactures fashion clothes for kids. Now, the company is planning to expand into a new line of business, i.e., fashion garments for women. However, before expanding, the management prepares a forecast of customer preferences and expectations.
There are around 5 million women who can potentially be target customers. So, the management decided to survey 1000 women from different areas and of varying age groups. The survey aimed to find out needs and choices in fashion outfits. This way, the statistical analysis helped the company make an effective decision.
In the practical world, this mathematical discipline is applied widely to catch the nerves of a particular stock movement. Also, statistical computer models consider the historical prices of a specific stock to interpret its future performance and returns. These tools analyze economic trends and determine the business cycleThe business cycle refers to the alternating phases of economic growth and decline.read more.
Properties
Various statistical properties make this discipline useful for crucial decision-making and research in different fields. Let us discuss some of these:
- Uniformity: Most data sets used in evaluations are similar. To ensure consistency; data is collected using a set base of parameters.
- Efficiency: If the available information deviates from sample data, it can still be interpreted using specific formulas.
- Sufficiency: The sample data analysis represents complete information about the whole population, which makes this method apt for extensive data sets.
- Quantitative Analysis: The numerical form of statistical data makes it easier to understand and interpret results.
- Unbiased: It is purely based on parameters and mechanisms, and therefore, reliable, offering no adjustments.
Types of Statistics
Given below are the two different forms of statistical approaches:
#1 – Descriptive
Descriptive StatisticsDescriptive statistics is used to summarize information available in statistics, and there is a descriptive statistics function in Excel as well. This built-in tool is found in the data tab, in the data analysis section.read more refers to data that shows the fundamental aspects of a selected population. Also, it establishes how it was organized and presented. The data can be analyzed by simply looking at the provided information and referring to how it is arranged. It is further classified as follows.
- Tendency Descriptive: It uses simple mathematical calculations and can be analyzed by computing the mean, median, and mode for the data under consideration.
- Spread Descriptive: This form focuses on whether different sets of data are relative to each other or not. Generally, it includes a description using variances, deviation methods, range of data, and distribution.
#2 – Inferential
The inferential discipline focuses on arriving at a conclusion based on the sample evaluation. It is further classified into:
- Confidence Interval Inferential: It refers to statistical data drawn from real numbers. However, the parameter concerning its actual data size may not be known.
- Hypothesis Inferential: This type analyzes extensive data based on a small sample sizeThe sample size formula depicts the relevant population range on which an experiment or survey is conducted. It is measured using the population size, the critical value of normal distribution at the required confidence level, sample proportion and margin of error.read more.
Limitations of Statistics
There is a downside to relying on statistical data. Following are its limitations:
- It emphasizes average values, but the individual data can vary to a great extent.
- Most of the time, the qualitative aspect of data analysis is overlooked.
- In the absence of relevant data, a statistical conclusion has no significance.
- Statistical analysis is always prone to human errors, and this may result in false conclusions.
- There are numerous statistical formulas to choose form making it difficult for the researcher.
- Using this mathematical discipline to solve problems requires a lot of expertise.
- Statistical processes end with a result but often fail to find the reasons behind the result.
Frequently Asked Questions (FAQs)
What does statistics mean?
It is the science behind identifying, collecting, organizing, summarizing, analyzing, interpreting, and presenting data. The data could be either qualitative or quantitative. This mathematical decision is employed in decision-making.
Why is statistics important?
Statistical data analysis plays a crucial role in scientific discoveries, research, economic decisions, government budgeting, public welfare activities, weather forecast, and stock analysis. In addition, this mathematical discipline makes decision-making more objective.
It is an essential part of day-to-day life even. For instance, it is used in schools and colleges to find the average percentage of the students. Similarly, In households, it is used to determine the per-day expense.
What is the difference between descriptive and inferential statistics?
Descriptive discipline is the quantitative part of the statistical analysis. The raw data is first collected and organized. Then it is presented in a succinct manner. The inferential subtype, on the other hand, focuses on interpreting sample data to form conclusions.
Recommended Articles
This has been a guide to What is Statistics and its Meaning. Here we explain how statistics work, its application, types, roles, properties, and limitations. You may also have a look at related articles on finance –
- Statistics in Excel
- Descriptive Statistics in Excel
- Confidence Interval Formula
- Standard Error
Essay on Statistics: Meaning and Definition of Statistics
Meaning:
“Statistics”, that a word is often used, has been derived from the Latin word ‘Status’ that means a group of numbers or figures; those represent some information of our human interest.
We find statistics in everyday life, such as in books or other information papers or TV or newspapers.
Although, in the beginning it was used by Kings only for collecting information about states and other information which was needed about their people, their number, revenue of the state etc.
This was known as the science of the state because it was used only by the Kings. So it got its development as ‘Kings’ subject or ‘Science of Kings’ or we may call it as “Political Arithmetic’s”. It was for the first time, perhaps in Egypt to conduct census of population in 3050 B.C. because the king needed money to erect pyramids. But in India, it is thought, that, it started dating back to Chandra Gupta Maurya’s kingdom under Chankya to collect the data of births and deaths. TM has also been stated in Chankya’s Arthshastra.
But now-a-days due to its pervading nature, its scope has increased and widened. It is now used in almost in all the fields of human knowledge and skills like Business, Commerce, Economics, Social Sciences, Politics, Planning, Medicine and other sciences, Physical as well as Natural.
Definition:
The term ‘Statistics’ has been defined in two senses, i.e. in Singular and in Plural sense.
“Statistics has two meanings, as in plural sense and in singular sense”.
—Oxford Dictionary
In plural sense, it means a systematic collection of numerical facts and in singular sense; it is the science of collecting, classifying and using statistics.
A. In the Plural Sense:
“Statistics are numerical statements of facts in any department of enquiry placed in relation to each other.” —A.L. Bowley
“The classified facts respecting the condition of the people in a state—especially those facts which can be stated in numbers or in tables of numbers or in any tabular or classified arrangement.” —Webster
These definitions given above give a narrow meaning to the statistics as they do not indicate its various aspects as are witnessed in its practical applications. From the this point of view the definition given by Prof. Horace Sacrist appears to be the most comprehensive and meaningful:
“By statistics we mean aggregates of facts affected to a marked extent by multiplicity of causes, numerically expressed, enumerated or estimated according to reasonable standard of accuracy, collected in a systematic manner for a predetermined purpose, and placed in relation to each other.”—Horace Sacrist
B. In the Singular Sense:
“Statistics refers to the body of technique or methodology, which has been developed for the collection, presentation and analysis of quantitative data and for the use of such data in decision making.” —Ncttor and Washerman
“Statistics may rightly be called the science of averages.” —Bowleg
“Statistics may be defined as the collection, presentation, analysis, and interpretation of numerical data.” —Croxton and Cowden
Stages of Investigations:
1. Collection of Data:
It is the first stage of investigation and is regarding collection of data. It is determined that which method of collection is needed in this problem and then data are collected.
2. Organisation of Data:
It is second stage. The data are simplified and made comparative and are classified according to time and place.
3. Presentation of Data:
In this third stage, organised data are made simple and attractive. These are presented in the form of tables diagrams and graphs.
4. Analysis of Data:
Forth stage of investigation is analysis. To get correct results, analysis is necessary. It is often undertaken using Measures of central tendencies, Measures of dispersion, correlation, regression and interpolation etc.
5. Interpretation of Data:
In this last stage, conclusions are enacted. Use of comparisons is made. On this basis, forecasting is made.
Some Modern Definitions:
From the above two senses of statistics, modem definitions have emerged as given below:
“Statistics is a body of methods for making wise decisions on the face of uncertainty.” —Wallis and Roberts
“Statistics is a body of methods for obtaining and analyzing numerical data in order to make better decisions in an uncertain world.” —Edward N. Dubois
So, from above definitions we find that science of statistics also includes the methods of collecting, organising, presenting, analysing and interpreting numerical facts and decisions are taken on their basis.
The most proper definition of statistics can be given as following after analysing the various definitions of statistics.
“Statistics in the plural sense are numerical statements of facts capable of some meaningful analysis and interpretation, and in singular sense, it relates to the collection, classification, presentation and interpretation of numerical data.”
Page load link
Go to Top