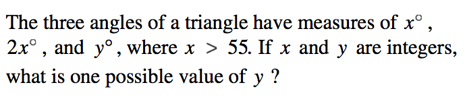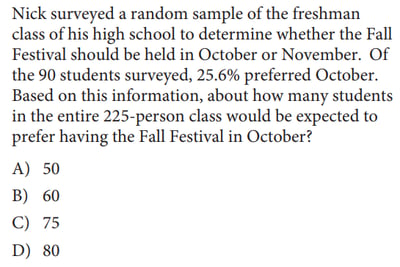From Wikipedia, the free encyclopedia
This article is about algorithmic word problems in mathematics and computer science. For other uses, see Word problem.
In computational mathematics, a word problem is the problem of deciding whether two given expressions are equivalent with respect to a set of rewriting identities. A prototypical example is the word problem for groups, but there are many other instances as well. A deep result of computational theory is that answering this question is in many important cases undecidable.[1]
Background and motivation[edit]
In computer algebra one often wishes to encode mathematical expressions using an expression tree. But there are often multiple equivalent expression trees. The question naturally arises of whether there is an algorithm which, given as input two expressions, decides whether they represent the same element. Such an algorithm is called a solution to the word problem. For example, imagine that 

EQUAL, and similarly produce NOT_EQUAL from 
The most direct solution to a word problem takes the form of a normal form theorem and algorithm which maps every element in an equivalence class of expressions to a single encoding known as the normal form — the word problem is then solved by comparing these normal forms via syntactic equality.[1] For example one might decide that 



While the word problem asks whether two terms containing constants are equal, a proper extension of the word problem known as the unification problem asks whether two terms 


while 

History[edit]
One of the most deeply studied cases of the word problem is in the theory of semigroups and groups. A timeline of papers relevant to the Novikov-Boone theorem is as follows:[3][4]
- 1910: Axel Thue poses a general problem of term rewriting on tree-like structures. He states «A solution of this problem in the most general case may perhaps be connected with unsurmountable difficulties».[5][6]
- 1911: Max Dehn poses the word problem for finitely presented groups.[7]
- 1912: Dehn presents Dehn’s algorithm, and proves it solves the word problem for the fundamental groups of closed orientable two-dimensional manifolds of genus greater than or equal to 2.[8] Subsequent authors have greatly extended it to a wide range of group-theoretic decision problems.[9][10][11]
- 1914: Axel Thue poses the word problem for finitely presented semigroups.[12]
- 1930 – 1938: The Church-Turing thesis emerges, defining formal notions of computability and undecidability.[13]
- 1947: Emil Post and Andrey Markov Jr. independently construct finitely presented semigroups with unsolvable word problem.[14][15] Post’s construction is built on Turing machines while Markov’s uses Post’s normal systems.[3]
- 1950: Alan Turing shows the word problem for cancellation semigroups is unsolvable,[16] by furthering Post’s construction. The proof is difficult to follow but marks a turning point in the word problem for groups.[3]: 342
- 1955: Pyotr Novikov gives the first published proof that the word problem for groups is unsolvable, using Turing’s cancellation semigroup result.[17][3]: 354 The proof contains a «Principal Lemma» equivalent to Britton’s Lemma.[3]: 355
- 1954 – 1957: William Boone independently shows the word problem for groups is unsolvable, using Post’s semigroup construction.[18][19]
- 1957 – 1958: John Britton gives another proof that the word problem for groups is unsolvable, based on Turing’s cancellation semigroups result and some of Britton’s earlier work.[20] An early version of Britton’s Lemma appears.[3]: 355
- 1958 – 1959: Boone publishes a simplified version of his construction.[21][22]
- 1961: Graham Higman characterises the subgroups of finitely presented groups with Higman’s embedding theorem,[23] connecting recursion theory with group theory in an unexpected way and giving a very different proof of the unsolvability of the word problem.[3]
- 1961 – 1963: Britton presents a greatly simplified version of Boone’s 1959 proof that the word problem for groups is unsolvable.[24] It uses a group-theoretic approach, in particular Britton’s Lemma. This proof has been used in a graduate course, although more modern and condensed proofs exist.[25]
- 1977: Gennady Makanin proves that the existential theory of equations over free monoids is solvable.[26]
The word problem for semi-Thue systems[edit]
The accessibility problem for string rewriting systems (semi-Thue systems or semigroups) can be stated as follows: Given a semi-Thue system 




The accessibility and word problems are undecidable, i.e. there is no general algorithm for solving this problem.[28] This even holds if we limit the systems to have finite presentations, i.e. a finite set of symbols and a finite set of relations on those symbols.[27] Even the word problem restricted to ground terms is not decidable for certain finitely presented semigroups.[29][30]
The word problem for groups[edit]
Given a presentation 
The word problem in combinatorial calculus and lambda calculus[edit]
One of the earliest proofs that a word problem is undecidable was for combinatory logic: when are two strings of combinators equivalent? Because combinators encode all possible Turing machines, and the equivalence of two Turing machines is undecidable, it follows that the equivalence of two strings of combinators is undecidable. Alonzo Church observed this in 1936.[32]
Likewise, one has essentially the same problem in (untyped) lambda calculus: given two distinct lambda expressions, there is no algorithm which can discern whether they are equivalent or not; equivalence is undecidable. For several typed variants of the lambda calculus, equivalence is decidable by comparison of normal forms.
The word problem for abstract rewriting systems[edit]
Solving the word problem: deciding if 

The word problem for an abstract rewriting system (ARS) is quite succinct: given objects x and y are they equivalent under 

The Knuth-Bendix completion algorithm can be used to transform a set of equations into a convergent term rewriting system.
The word problem in universal algebra[edit]
In universal algebra one studies algebraic structures consisting of a generating set A, a collection of operations on A of finite arity, and a finite set of identities that these operations must satisfy. The word problem for an algebra is then to determine, given two expressions (words) involving the generators and operations, whether they represent the same element of the algebra modulo the identities. The word problems for groups and semigroups can be phrased as word problems for algebras.[1]
The word problem on free Heyting algebras is difficult.[34]
The only known results are that the free Heyting algebra on one generator is infinite, and that the free complete Heyting algebra on one generator exists (and has one more element than the free Heyting algebra).
The word problem for free lattices[edit]
|
|
The word problem on free lattices and more generally free bounded lattices has a decidable solution. Bounded lattices are algebraic structures with the two binary operations ∨ and ∧ and the two constants (nullary operations) 0 and 1. The set of all well-formed expressions that can be formulated using these operations on elements from a given set of generators X will be called W(X). This set of words contains many expressions that turn out to denote equal values in every lattice. For example, if a is some element of X, then a ∨ 1 = 1 and a ∧ 1 = a. The word problem for free bounded lattices is the problem of determining which of these elements of W(X) denote the same element in the free bounded lattice FX, and hence in every bounded lattice.
The word problem may be resolved as follows. A relation ≤~ on W(X) may be defined inductively by setting w ≤~ v if and only if one of the following holds:
- w = v (this can be restricted to the case where w and v are elements of X),
- w = 0,
- v = 1,
- w = w1 ∨ w2 and both w1 ≤~ v and w2 ≤~ v hold,
- w = w1 ∧ w2 and either w1 ≤~ v or w2 ≤~ v holds,
- v = v1 ∨ v2 and either w ≤~ v1 or w ≤~ v2 holds,
- v = v1 ∧ v2 and both w ≤~ v1 and w ≤~ v2 hold.
This defines a preorder ≤~ on W(X), so an equivalence relation can be defined by w ~ v when w ≤~ v and v ≤~ w. One may then show that the partially ordered quotient set W(X)/~ is the free bounded lattice FX.[35][36] The equivalence classes of W(X)/~ are the sets of all words w and v with w ≤~ v and v ≤~ w. Two well-formed words v and w in W(X) denote the same value in every bounded lattice if and only if w ≤~ v and v ≤~ w; the latter conditions can be effectively decided using the above inductive definition. The table shows an example computation to show that the words x∧z and x∧z∧(x∨y) denote the same value in every bounded lattice. The case of lattices that are not bounded is treated similarly, omitting rules 2 and 3 in the above construction of ≤~.
Example: A term rewriting system to decide the word problem in the free group[edit]
Bläsius and Bürckert
[37]
demonstrate the Knuth–Bendix algorithm on an axiom set for groups.
The algorithm yields a confluent and noetherian term rewrite system that transforms every term into a unique normal form.[38]
The rewrite rules are numbered incontiguous since some rules became redundant and were deleted during the algorithm run.
The equality of two terms follows from the axioms if and only if both terms are transformed into literally the same normal form term. For example, the terms
, and
share the same normal form, viz. 
As another example, the term 



| A1 |  |

|
| A2 |  |

|
| A3 |  |

|
| R1 |  |

|
| R2 |  |

|
| R3 |  |

|
| R4 |  |

|
| R8 |  |

|
| R11 |  |

|
| R12 |  |

|
| R13 |  |

|
| R14 |  |

|
| R17 |  |

|
See also[edit]
- Conjugacy problem
- Group isomorphism problem
References[edit]
- ^ a b c d Evans, Trevor (1978). «Word problems». Bulletin of the American Mathematical Society. 84 (5): 790. doi:10.1090/S0002-9904-1978-14516-9.
- ^ Cohen, Joel S. (2002). Computer algebra and symbolic computation: elementary algorithms. Natick, Mass.: A K Peters. pp. 90–92. ISBN 1568811586.
- ^ a b c d e f g Miller, Charles F. (2014). Downey, Rod (ed.). «Turing machines to word problems» (PDF). Turing’s Legacy: 330. doi:10.1017/CBO9781107338579.010. hdl:11343/51723. ISBN 9781107338579. Retrieved 6 December 2021.
- ^ Stillwell, John (1982). «The word problem and the isomorphism problem for groups». Bulletin of the American Mathematical Society. 6 (1): 33–56. doi:10.1090/S0273-0979-1982-14963-1.
- ^ Müller-Stach, Stefan (12 September 2021). «Max Dehn, Axel Thue, and the Undecidable». p. 13. arXiv:1703.09750 [math.HO].
- ^ Steinby, Magnus; Thomas, Wolfgang (2000). «Trees and term rewriting in 1910: on a paper by Axel Thue». Bulletin of the European Association for Theoretical Computer Science. 72: 256–269. CiteSeerX 10.1.1.32.8993. MR 1798015.
- ^ Dehn, Max (1911). «Über unendliche diskontinuierliche Gruppen». Mathematische Annalen. 71 (1): 116–144. doi:10.1007/BF01456932. ISSN 0025-5831. MR 1511645. S2CID 123478582.
- ^ Dehn, Max (1912). «Transformation der Kurven auf zweiseitigen Flächen». Mathematische Annalen. 72 (3): 413–421. doi:10.1007/BF01456725. ISSN 0025-5831. MR 1511705. S2CID 122988176.
- ^ Greendlinger, Martin (June 1959). «Dehn’s algorithm for the word problem». Communications on Pure and Applied Mathematics. 13 (1): 67–83. doi:10.1002/cpa.3160130108.
- ^ Lyndon, Roger C. (September 1966). «On Dehn’s algorithm». Mathematische Annalen. 166 (3): 208–228. doi:10.1007/BF01361168. hdl:2027.42/46211. S2CID 36469569.
- ^ Schupp, Paul E. (June 1968). «On Dehn’s algorithm and the conjugacy problem». Mathematische Annalen. 178 (2): 119–130. doi:10.1007/BF01350654. S2CID 120429853.
- ^ Power, James F. (27 August 2013). «Thue’s 1914 paper: a translation». arXiv:1308.5858 [cs.FL].
- ^ See History of the Church–Turing thesis. The dates are based on On Formally Undecidable Propositions of Principia Mathematica and Related Systems and Systems of Logic Based on Ordinals.
- ^ Post, Emil L. (March 1947). «Recursive Unsolvability of a problem of Thue» (PDF). Journal of Symbolic Logic. 12 (1): 1–11. doi:10.2307/2267170. JSTOR 2267170. S2CID 30320278. Retrieved 6 December 2021.
- ^ Mostowski, Andrzej (September 1951). «A. Markov. Névožmoinost’ nékotoryh algoritmov v téorii associativnyh sistém (Impossibility of certain algorithms in the theory of associative systems). Doklady Akadémii Nauk SSSR, vol. 77 (1951), pp. 19–20». Journal of Symbolic Logic. 16 (3): 215. doi:10.2307/2266407. JSTOR 2266407.
- ^ Turing, A. M. (September 1950). «The Word Problem in Semi-Groups With Cancellation». The Annals of Mathematics. 52 (2): 491–505. doi:10.2307/1969481. JSTOR 1969481.
- ^ Novikov, P. S. (1955). «On the algorithmic unsolvability of the word problem in group theory». Proceedings of the Steklov Institute of Mathematics (in Russian). 44: 1–143. Zbl 0068.01301.
- ^ Boone, William W. (1954). «Certain Simple, Unsolvable Problems of Group Theory. I». Indagationes Mathematicae (Proceedings). 57: 231–237. doi:10.1016/S1385-7258(54)50033-8.
- ^ Boone, William W. (1957). «Certain Simple, Unsolvable Problems of Group Theory. VI». Indagationes Mathematicae (Proceedings). 60: 227–232. doi:10.1016/S1385-7258(57)50030-9.
- ^ Britton, J. L. (October 1958). «The Word Problem for Groups». Proceedings of the London Mathematical Society. s3-8 (4): 493–506. doi:10.1112/plms/s3-8.4.493.
- ^ Boone, William W. (1958). «The word problem» (PDF). Proceedings of the National Academy of Sciences. 44 (10): 1061–1065. Bibcode:1958PNAS…44.1061B. doi:10.1073/pnas.44.10.1061. PMC 528693. PMID 16590307. Zbl 0086.24701.
- ^ Boone, William W. (September 1959). «The Word Problem». The Annals of Mathematics. 70 (2): 207–265. doi:10.2307/1970103. JSTOR 1970103.
- ^ Higman, G. (8 August 1961). «Subgroups of finitely presented groups». Proceedings of the Royal Society of London. Series A. Mathematical and Physical Sciences. 262 (1311): 455–475. Bibcode:1961RSPSA.262..455H. doi:10.1098/rspa.1961.0132. S2CID 120100270.
- ^ Britton, John L. (January 1963). «The Word Problem». The Annals of Mathematics. 77 (1): 16–32. doi:10.2307/1970200. JSTOR 1970200.
- ^ Simpson, Stephen G. (18 May 2005). «A Slick Proof of the Unsolvability of the Word Problem for Finitely Presented Groups» (PDF). Retrieved 6 December 2021.
- ^ «Subgroups of finitely presented groups». Mathematics of the USSR-Sbornik. 103 (145): 147–236. 13 February 1977. doi:10.1070/SM1977v032n02ABEH002376.
- ^ a b Matiyasevich, Yuri; Sénizergues, Géraud (January 2005). «Decision problems for semi-Thue systems with a few rules». Theoretical Computer Science. 330 (1): 145–169. doi:10.1016/j.tcs.2004.09.016.
- ^ Davis, Martin (1978). «What is a Computation?» (PDF). Mathematics Today Twelve Informal Essays: 257–259. doi:10.1007/978-1-4613-9435-8_10. ISBN 978-1-4613-9437-2. Retrieved 5 December 2021.
- ^ a b Baader, Franz; Nipkow, Tobias (5 August 1999). Term Rewriting and All That. Cambridge University Press. pp. 59–60. ISBN 978-0-521-77920-3.
- ^
- Matiyasevich, Yu. V. (1967). «Простые примеры неразрешимых ассоциативных исчислений» [Simple examples of undecidable associative calculi]. Doklady Akademii Nauk SSSR (in Russian). 173 (6): 1264–1266. ISSN 0869-5652.
- Matiyasevich, Yu. V. (1967). «Simple examples of undecidable associative calculi». Soviet Mathematics. 8 (2): 555–557. ISSN 0197-6788.
- ^ Novikov, P. S. (1955). «On the algorithmic unsolvability of the word problem in group theory». Trudy Mat. Inst. Steklov (in Russian). 44: 1–143.
- ^ Statman, Rick (2000). «On the Word Problem for Combinators». Rewriting Techniques and Applications. Lecture Notes in Computer Science. 1833: 203–213. doi:10.1007/10721975_14. ISBN 978-3-540-67778-9.
- ^ Beke, Tibor (May 2011). «Categorification, term rewriting and the Knuth–Bendix procedure». Journal of Pure and Applied Algebra. 215 (5): 730. doi:10.1016/j.jpaa.2010.06.019.
- ^ Peter T. Johnstone, Stone Spaces, (1982) Cambridge University Press, Cambridge, ISBN 0-521-23893-5. (See chapter 1, paragraph 4.11)
- ^ Whitman, Philip M. (January 1941). «Free Lattices». The Annals of Mathematics. 42 (1): 325–329. doi:10.2307/1969001. JSTOR 1969001.
- ^ Whitman, Philip M. (1942). «Free Lattices II». Annals of Mathematics. 43 (1): 104–115. doi:10.2307/1968883. JSTOR 1968883.
- ^ K. H. Bläsius and H.-J. Bürckert, ed. (1992). Deduktionsssysteme. Oldenbourg. p. 291.; here: p.126, 134
- ^ Apply rules in any order to a term, as long as possible; the result doesn’t depend on the order; it is the term’s normal form.
Download Article
Download Article
You can solve many real world problems with the help of math. In order to familiarize students with these kinds of problems, teachers include word problems in their math curriculum. However, word problems can present a real challenge if you don’t know how to break them down and find the numbers underneath the story. Solving word problems is an art of transforming the words and sentences into mathematical expressions and then applying conventional algebraic techniques to solve the problem.
-
1
Read the problem carefully.[1]
A common setback when trying to solve algebra word problems is assuming what the question is asking before you read the entire problem. In order to be successful in solving a word problem, you need to read the whole problem in order to assess what information is provided, and what information is missing.[2]
-
2
Determine what you are asked to find. In many problems, what you are asked to find is presented in the last sentence. This is not always true, however, so you need to read the entire problem carefully.[3]
Write down what you need to find, or else underline it in the problem, so that you do not forget what your final answer means.[4]
In an algebra word problem, you will likely be asked to find a certain value, or you may be asked to find an equation that represents a value.- For example, you might have the following problem: Jane went to a book shop and bought a book. While at the store Jane found a second interesting book and bought it for $80. The price of the second book was $10 less than three times the price of he first book. What was the price of the first book?
- In this problem, you are asked to find the price of the first book Jane purchased.
Advertisement
-
3
Summarize what you know, and what you need to know. Likely, the information you need to know is the same as what information you are asked to find. You also need to assess what information you already know. Again, underline or write out this information, so you can keep track of all the parts of the problem. For problems involving geometry, it is often helpful to draw a sketch at this point.[5]
- For example, you know that Jane bought two books. You know that the second book was $80. You also know that the second book cost $10 less than 3 times the price of the first book. You don’t know the price of the first book.
-
4
Assign variables to the unknown quantities. If you are being asked to find a certain value, you will likely only have one variable. If, however, you are asked to find an equation, you will likely have multiple variables. No matter how many variables you have, you should list each one, and indicate what they are equal to.[6]
-
5
Look for keywords.[7]
Word problems are full of keywords that give you clues about what operations to use. Locating and interpreting these keywords can help you translate the words into algebra.[8]
- Multiplication keywords include times, of, and factor.[9]
- Division keywords include per, out of, and percent.[10]
- Addition keywords include some, more, and together.[11]
- Subtraction keywords include difference, fewer, and decreased.[12]
- Multiplication keywords include times, of, and factor.[9]
Advertisement
-
1
Write an equation. Use the information you learn from the problem, including keywords, to write an algebraic description of the story.[13]
-
2
Solve an equation for one variable. If you have only one unknown in your word problem, isolate the variable in your equation and find which number it is equal to. Use the normal rules of algebra to isolate the variable. Remember that you need to keep the equation balanced. This means that whatever you do to one side of the equation, you must also do to the other side.[14]
-
3
Solve an equation with multiple variables. If you have more than one unknown in your word problem, you need to make sure you combine like terms to simplify your equation.
-
4
Interpret your answer. Look back to your list of variables and unknown information. This will remind you what you were trying to solve. Write a statement indicating what your answer means.[15]
Advertisement
-
1
Solve the following problem. This problem has more than one unknown value, so its equation will have multiple variables. This means you cannot solve for a specific numerical value of a variable. Instead, you will solve to find an equation that describes a variable.
- Robyn and Billy run a lemonade stand. They are giving all the money that they make to a cat shelter. They will combine their profits from selling lemonade with their tips. They sell cups of lemonade for 75 cents. Their mom and dad have agreed to double whatever amount they receive in tips. Write an equation that describes the amount of money Robyn and Billy will give to the shelter.
-
2
Read the problem carefully and determine what you are asked to find.[16]
You are asked to find how much money Robyn and Billy will give to the cat shelter. -
3
Summarize what you know, and what you need to know. You know that Robyn and Billy will make money from selling cups of lemonade and from getting tips. You know that they will sell each cup for 75 cents. You also know that their mom and dad will double the amount they make in tips. You don’t know how many cups of lemonade they sell, or how much tip money they get.
-
4
Assign variables to the unknown quantities. Since you have three unknowns, you will have three variables. Let
equal the amount of money they will give to the shelter. Let
equal the number of cups they sell. Let
equal the number of dollars they make in tips.
-
5
Look for keywords. Since they will “combine” their profits and tips, you know addition will be involved. Since their mom and dad will “double” their tips, you know you need to multiply their tips by a factor of 2.
-
6
Write an equation. Since you are writing an equation that describes the amount of money they will give to the shelter, the variable
will be alone on one side of the equation.
-
7
Interpret your answer. The variable
equals the amount of money Robyn and Billy will donate to the cat shelter. So, the amount they donate can be found by multiplying the number of cups of lemonade they sell by .75, and adding this product to the product of their tip money and 2.
Advertisement
Add New Question
-
Question
How do you solve an algebra word problem?
Daron Cam is an Academic Tutor and the Founder of Bay Area Tutors, Inc., a San Francisco Bay Area-based tutoring service that provides tutoring in mathematics, science, and overall academic confidence building. Daron has over eight years of teaching math in classrooms and over nine years of one-on-one tutoring experience. He teaches all levels of math including calculus, pre-algebra, algebra I, geometry, and SAT/ACT math prep. Daron holds a BA from the University of California, Berkeley and a math teaching credential from St. Mary’s College.
Academic Tutor
Expert Answer
Carefully read the problem and figure out what information you’re given and what that information should be used for. Once you know what you need to do with the values they’ve given you, the problem should be a lot easier to solve.
-
Question
If Deborah and Colin have $150 between them, and Deborah has $27 more than Colin, how much money does Deborah have?
Let x = Deborah’s money. Then (x — 27) = Colin’s money. That means that (x) + (x — 27) = 150. Combining terms: 2x — 27 = 150. Adding 27 to both sides: 2x = 177. So x = 88.50, and (x — 27) = 61.50. Deborah has $88.50, and Colin has $61.50, which together add up to $150.
-
Question
Karl is twice as old Bob. Nine years ago, Karl was three times as old as Bob. How old is each now?
Let x be Bob’s current age. Then Karl’s current age is 2x. Nine years ago Bob’s age was x-9, and Karl’s age was 2x-9. We’re told that nine years ago Karl’s age (2x-9) was three times Bob’s age (x-9). Therefore, 2x-9 = 3(x-9) = 3x-27. Subtract 2x from both sides, and add 27 to both sides: 18 = x. So Bob’s current age is 18, and Karl’s current age is 36, twice Bob’s current age. (Nine years ago Bob would have been 9, and Karl would have been 27, or three times Bob’s age then.)
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Video
-
Word problems can have more than one unknown and more the one variable.
-
The number of variables is always equal to the number of unknowns.
-
While solving word problems you should always read every sentence carefully and try to extract all the numerical information.
Show More Tips
Advertisement
References
About This Article
Article SummaryX
To solve word problems in algebra, start by reading the problem carefully and determining what you’re being asked to find. Next, summarize what information you know and what you need to know. Then, assign variables to the unknown quantities. For example, if you know that Jane bought 2 books, and the second book cost $80, which was $10 less than 3 times the price of the first book, assign x to the price of the 1st book. Use this information to write your equation, which is 80 = 3x — 10. To learn how to solve an equation with multiple variables, keep reading!
Did this summary help you?
Thanks to all authors for creating a page that has been read 56,462 times.
Reader Success Stories
-
James Carson
Sep 13, 2019
«I think this is amazing because it explains how and what you need to do.This helped me in algebra, and I recommend…» more
Did this article help you?
Solving Word Problems in Mathematics
What Is a Word Problem? (And How to Solve It!)
Learn what word problems are and how to solve them in 7 easy steps.
Real life math problems don’t usually look as simple as 3 + 5 = ?. Instead, things are a bit more complex. To show this, sometimes, math curriculum creators use word problems to help students see what happens in the real world. Word problems often show math happening in a more natural way in real life circumstances.
As a teacher, you can share some tips with your students to show that in everyday life they actually solve such problems all the time, and it’s not as scary as it may seem.
As you know, word problems can involve just about any operation: from addition to subtraction and division, or even multiple operations simultaneously.
If you’re a teacher, you may sometimes wonder how to teach students to solve word problems. It may be helpful to introduce some basic steps of working through a word problem in order to guide students’ experience. So, what steps do students need for solving a word problem in math?
Steps of Solving a Word Problem
To work through any word problem, students should do the following:
1. Read the problem: first, students should read through the problem once.
2. Highlight facts: then, students should read through the problem again and highlight or underline important facts such as numbers or words that indicate an operation.
3. Visualize the problem: drawing a picture or creating a diagram can be helpful.
Students can start visualizing simple or more complex problems by creating relevant images, from concrete (like drawings of putting away cookies from a jar) to more abstract (like tape diagrams). It can also help students clarify the operations they need to carry out. (next step!)
4. Determine the operation(s): next, students should determine the operation or operations they need to perform. Is it addition, subtraction, multiplication, division? What needs to be done?
Drawing the picture can be a big help in figuring this out. However, they can also look for the clues in the words such as:
– Addition: add, more, total, altogether, and, plus, combine, in all;
– Subtraction: fewer, than, take away, subtract, left, difference;
– Multiplication: times, twice, triple, in all, total, groups;
– Division: each, equal pieces, split, share, per, out of, average.
These key words may be very helpful when learning how to determine the operation students need to perform, but we should still pay attention to the fact that in the end it all depends on the context of the wording. The same word can have different meanings in different word problems.
Another way to determine the operation is to search for certain situations, Jennifer Findley suggests. She has a great resource that lists various situations you might find in the most common word problems and the explanation of which operation applies to each situation.
5. Make a math sentence: next, students should try to translate the word problem and drawings into a math or number sentence. This means students might write a sentence such as 3 + 8 =.
Here they should learn to identify the steps they need to perform first to solve the problem, whether it’s a simple or a complex sentence.
6. Solve the problem: then, students can solve the number sentence and determine the solution. For example, 3 + 8 = 11.
7. Check the answer: finally, students should check their work to make sure that the answer is correct.
These 7 steps will help students get closer to mastering the skill of solving word problems. Of course, they still need plenty of practice. So, make sure to create enough opportunities for that!
At Happy Numbers, we gradually include word problems throughout the curriculum to ensure math flexibility and application of skills. Check out how easy it is to learn how to solve word problems with our visual exercises!
Word problems can be introduced in Kindergarten and be used through all grades as an important part of an educational process connecting mathematics to real life experience.
Happy Numbers introduces young students to the first math symbols by first building conceptual understanding of the operation through simple yet engaging visuals and key words. Once they understand the connection between these keywords and the actions they represent, they begin to substitute them with math symbols and translate word problems into number sentences. In this way, students gradually advance to the more abstract representations of these concepts.
For example, during the first steps, simple wording and animation help students realize what action the problem represents and find the connection between these actions and key words like “take away” and “left” that may signal them.
From the beginning, visualization helps the youngest students to understand the concepts of addition, subtraction, and even more complex operations. Even if they don’t draw the representations by themselves yet, students learn the connection between operations they need to perform in the problem and the real-world process this problem describes.
Next, students organize data from the word problem and pictures into a number sentence. To diversify the activity, you can ask students to match a word problem with the number sentence it represents.
Solving measurement problems is also a good way of mastering practical math skills. This is an example where students can see that math problems are closely related to real-world situations. Happy Numbers applies this by introducing more complicated forms of word problems as we help students advance to the next skill. By solving measurement word problems, students upgrade their vocabulary, learning such new terms as “difference” and “sum,” and continue mastering the connection between math operations and their word problem representations.
Later, students move to the next step, in which they learn how to create drawings and diagrams by themselves. They start by distributing light bulbs equally into boxes, which helps them to understand basic properties of division and multiplication. Eventually, with the help of Dino, they master tape diagrams!
To see the full exercise, follow this link.
The importance of working with diagrams and models becomes even more apparent when students move to more complex word problems. Pictorial representations help students master conceptual understanding by representing a challenging multi-step word problem in a visually simple and logical form. The ability to interact with a model helps students better understand logical patterns and motivates them to complete the task.
Having mentioned complex word problems, we have to show some of the examples that Happy Numbers uses in its curriculum. As the last step of mastering word problems, it is not the least important part of the journey. It’s crucial for students to learn how to solve the most challenging math problems without being intimidated by them. This only happens when their logical and algorithmic thinking skills are mastered perfectly, so they easily start talking in “math” language.
These are the common steps that may help students overcome initial feelings of anxiety and fear of difficulty of the task they are given. Together with a teacher, they can master these foundational skills and build their confidence toward solving word problems. And Happy Numbers can facilitate this growth, providing varieties of engaging exercises and challenging word problems!
: Decision problem pertaining to equivalence of expressions
In computational mathematics, a word problem is the problem of deciding whether two given expressions are equivalent with respect to a set of rewriting identities. A prototypical example is the word problem for groups, but there are many other instances as well. A deep result of computational theory is that answering this question is in many important cases undecidable.[1]
Background and motivation
In computer algebra one often wishes to encode mathematical expressions using an expression tree. But there are often multiple equivalent expression trees. The question naturally arises of whether there is an algorithm which, given as input two expressions, decides whether they represent the same element. Such an algorithm is called a solution to the word problem. For example, imagine that [math]displaystyle{ x,y,z }[/math] are symbols representing real numbers — then a relevant solution to the word problem would, given the input [math]displaystyle{ (x cdot y)/z mathrel{overset{?}{=}} (x/z)cdot y }[/math], produce the output EQUAL, and similarly produce NOT_EQUAL from [math]displaystyle{ (x cdot y)/z mathrel{overset{?}{=}} (x/x)cdot y }[/math].
The most direct solution to a word problem takes the form of a normal form theorem and algorithm which maps every element in a equivalence class of expressions to a single encoding known as the normal form — the word problem is then solved by comparing these normal forms via syntactic equality.[1] For example one might decide that [math]displaystyle{ x cdot y cdot z^{-1} }[/math] is the normal form of [math]displaystyle{ (x cdot y)/z }[/math], [math]displaystyle{ (x/z)cdot y }[/math], and [math]displaystyle{ (y/z)cdot x }[/math], and devise a transformation system to rewrite those expressions to that form, in the process proving that all equivalent expressions will be rewritten to the same normal form.[2] But not all solutions to the word problem use a normal form theorem — there are algebraic properties which indirectly imply the existence of an algorithm.[1]
While the word problem asks whether two terms containing constants are equal, a proper extension of the word problem known as the unification problem asks whether two terms [math]displaystyle{ t_1,t_2 }[/math] containing variables have instances that are equal, or in other words whether the equation [math]displaystyle{ t_1 = t_2 }[/math] has any solutions. As a common example, [math]displaystyle{ 2 + 3 stackrel{?}{=} 8 + (-3) }[/math] is a word problem in the integer group ℤ,
while [math]displaystyle{ 2 + x stackrel{?}{=} 8 + (-x) }[/math] is a unification problem in the same group; since the former terms happen to be equal in ℤ, the latter problem has the substitution [math]displaystyle{ {x mapsto 3} }[/math] as a solution.
History
One of the most deeply studied cases of the word problem is in the theory of semigroups and groups. A timeline of papers relevant to the Novikov-Boone theorem is as follows:[3][4]
- 1910: Axel Thue poses a general problem of term rewriting on tree-like structures. He states «A solution of this problem in the most general case may perhaps be connected with unsurmountable difficulties».[5][6]
- 1911: Max Dehn poses the word problem for finitely presented groups.[7]
- 1912: Dehn presents Dehn’s algorithm, and proves it solves the word problem for the fundamental groups of closed orientable two-dimensional manifolds of genus greater than or equal to 2.[8] Subsequent authors have greatly extended it to a wide range of group theoretic decision problems.[9][10][11]
- 1914: Axel Thue poses the word problem for finitely presented semigroups.[12]
- 1930 – 1938: The Church-Turing thesis emerges, defining formal notions of computability and undecidability.[13]
- 1947: Emil Post and Andrey Markov Jr. independently construct finitely presented semigroups with unsolvable word problem.[14][15] Post’s construction is built on Turing machines while Markov’s uses Post’s normal systems.[3]
- 1950: Alan Turing shows the word problem for cancellation semigroups is unsolvable,[16] by furthering Post’s construction. The proof is difficult to follow but marks a turning point in the word problem for groups.[3]:342
- 1955: Pyotr Novikov gives the first published proof that the word problem for groups is unsolvable, using Turing’s cancellation semigroup result.[17][3]:354 The proof contains a «Principal Lemma» equivalent to Britton’s Lemma.[3]:355
- 1954 – 1957: William Boone independently shows the word problem for groups is unsolvable, using Post’s semigroup construction.[18][19]
- 1957 – 1958: John Britton gives another proof that the word problem for groups is unsolvable, based on Turing’s cancellation semigroups result and some of Britton’s earlier work.[20] An early version of Britton’s Lemma appears.[3]:355
- 1958 – 1959: Boone publishes a simplified version of his construction.[21][22]
- 1961: Graham Higman characterises the subgroups of finitely presented groups with Higman’s embedding theorem,[23] connecting recursion theory with group theory in an unexpected way and giving a very different proof of the unsolvability of the word problem.[3]
- 1961 – 1963: Britton presents a greatly simplified version of Boone’s 1959 proof that the word problem for groups is unsolvable.[24] It uses a group-theoretic approach, in particular Britton’s Lemma. This proof has been used in a graduate course, although more modern and condensed proofs exist.[25]
- 1977: Gennady Makanin proves that the existential theory of equations over free monoids is solvable.[26]
The word problem for semi-Thue systems
The accessibility problem for string rewriting systems (semi-Thue systems or semigroups) can be stated as follows: Given a semi-Thue system [math]displaystyle{ T:=(Sigma, R) }[/math] and two words (strings) [math]displaystyle{ u, v in Sigma^* }[/math], can [math]displaystyle{ u }[/math] be transformed into [math]displaystyle{ v }[/math] by applying rules from [math]displaystyle{ R }[/math]? Note that the rewriting here is one-way. The word problem is the accessibility problem for symmetric rewrite relations, i.e. Thue systems.[27]
The accessibility and word problems are undecidable, i.e. there is no general algorithm for solving this problem.[28] This even holds if we limit the systems to have finite presentations, i.e. a finite set of symbols and a finite set of relations on those symbols.[27] Even the word problem restricted to ground terms is not decidable for certain finally presented semigroups.[29][30]
The word problem for groups
- Main page: Word problem for groups
Given a presentation [math]displaystyle{ langle Smid mathcal{R} rangle }[/math] for a group G, the word problem is the algorithmic problem of deciding, given as input two words in S, whether they represent the same element of G. The word problem is one of three algorithmic problems for groups proposed by Max Dehn in 1911. It was shown by Pyotr Novikov in 1955 that there exists a finitely presented group G such that the word problem for G is undecidable.[31]
The word problem in combinatorial calculus and lambda calculus
One of the earliest proofs that a word problem is undecidable was for combinatory logic: when are two strings of combinators equivalent? Because combinators encode all possible Turing machines, and the equivalence of two Turing machines is undecidable, it follows that the equivalence of two strings of combinators is undecidable. Alonzo Church observed this in 1936.[32]
Likewise, one has essentially the same problem in (untyped) lambda calculus: given two distinct lambda expressions, there is no algorithm which can discern whether they are equivalent or not; equivalence is undecidable. For several typed variants of the lambda calculus, equivalence is decidable by comparison of normal forms.
The word problem for abstract rewriting systems
Solving the word problem: deciding if [math]displaystyle{ x stackrel{*}{leftrightarrow} y }[/math] usually requires heuristic search (red, green), while deciding [math]displaystyle{ xdownarrow = ydownarrow }[/math] is straightforward (grey).
The word problem for an abstract rewriting system (ARS) is quite succinct: given objects x and y are they equivalent under [math]displaystyle{ stackrel{*}{leftrightarrow} }[/math]?[29] The word problem for an ARS is undecidable in general. However, there is a computable solution for the word problem in the specific case where every object reduces to a unique normal form in a finite number of steps (i.e. the system is convergent): two objects are equivalent under [math]displaystyle{ stackrel{*}{leftrightarrow} }[/math] if and only if they reduce to the same normal form.[33]
The Knuth-Bendix completion algorithm can be used to transform a set of equations into a convergent term rewriting system.
The word problem in universal algebra
In universal algebra one studies algebraic structures consisting of a generating set A, a collection of operations on A of finite arity (typically binary operations), and a finite set of identities that these operations must satisfy. The word problem for an algebra is then to determine, given two expressions (words) involving the generators and operations, whether they represent the same element of the algebra modulo the identities. The word problems for groups and semigroups can be phrased as word problems for algebras.[1]
The word problem on free Heyting algebras is difficult.[34]
The only known results are that the free Heyting algebra on one generator is infinite, and that the free complete Heyting algebra on one generator exists (and has one more element than the free Heyting algebra).
The word problem for free lattices
|
|
The word problem on free lattices and more generally free bounded lattices has a decidable solution. Bounded lattices are algebraic structures with the two binary operations ∨ and ∧ and the two constants (nullary operations) 0 and 1. The set of all well-formed expressions that can be formulated using these operations on elements from a given set of generators X will be called W(X). This set of words contains many expressions that turn out to denote equal values in every lattice. For example, if a is some element of X, then a ∨ 1 = 1 and a ∧ 1 =a. The word problem for free bounded lattices is the problem of determining which of these elements of W(X) denote the same element in the free bounded lattice FX, and hence in every bounded lattice.
The word problem may be resolved as follows. A relation ≤~ on W(X) may be defined inductively by setting w ≤~ v if and only if one of the following holds:
- w = v (this can be restricted to the case where w and v are elements of X),
- w = 0,
- v = 1,
- w = w1 ∨ w2 and both w1 ≤~ v and w2 ≤~ v hold,
- w = w1 ∧ w2 and either w1 ≤~ v or w2 ≤~ v holds,
- v = v1 ∨ v2 and either w ≤~ v1 or w ≤~ v2 holds,
- v = v1 ∧ v2 and both w ≤~ v1 and w ≤~ v2 hold.
This defines a preorder ≤~ on W(X), so an equivalence relation can be defined by w ~ v when w ≤~ v and v ≤~ w. One may then show that the partially ordered quotient space W(X)/~ is the free bounded lattice FX.[35][36] The equivalence classes of W(X)/~ are the sets of all words w and v with w ≤~ v and v ≤~ w. Two well-formed words v and w in W(X) denote the same value in every bounded lattice if and only if w ≤~ v and v ≤~ w; the latter conditions can be effectively decided using the above inductive definition. The table shows an example computation to show that the words x∧z and x∧z∧(x∨y) denote the same value in every bounded lattice. The case of lattices that are not bounded is treated similarly, omitting rules 2 and 3 in the above construction of ≤~.
Example: A term rewriting system to decide the word problem in the free group
Bläsius and Bürckert
[37]
demonstrate the Knuth–Bendix algorithm on an axiom set for groups.
The algorithm yields a confluent and noetherian term rewrite system that transforms every term into a unique normal form.[38]
The rewrite rules are numbered incontiguous since some rules became redundant and were deleted during the algorithm run.
The equality of two terms follows from the axioms if and only if both terms are transformed into literally the same normal form term. For example, the terms
- [math]displaystyle{ ((a^{-1} cdot a) cdot (b cdot b^{-1}))^{-1} stackrel{R2}{rightsquigarrow} (1 cdot (b cdot b^{-1}))^{-1} stackrel{R13}{rightsquigarrow} (1 cdot 1)^{-1} stackrel{R1}{rightsquigarrow} 1 ^{-1} stackrel{R8}{rightsquigarrow} 1 }[/math], and
- [math]displaystyle{ b cdot ((a cdot b)^{-1} cdot a) stackrel{R17}{rightsquigarrow} b cdot ((b^{-1} cdot a^{-1}) cdot a) stackrel{R3}{rightsquigarrow} b cdot (b^{-1} cdot (a^{-1} cdot a)) stackrel{R2}{rightsquigarrow} b cdot (b^{-1} cdot 1) stackrel{R11}{rightsquigarrow} b cdot b^{-1} stackrel{R13}{rightsquigarrow} 1 }[/math]
share the same normal form, viz. [math]displaystyle{ 1 }[/math]; therefore both terms are equal in every group.
As another example, the term [math]displaystyle{ 1 cdot (a cdot b) }[/math] and [math]displaystyle{ b cdot (1 cdot a) }[/math] has the normal form [math]displaystyle{ a cdot b }[/math] and [math]displaystyle{ b cdot a }[/math], respectively. Since the normal forms are literally different, the original terms cannot be equal in every group. In fact, they are usually different in non-abelian groups.
| A1 | [math]displaystyle{ 1 cdot x }[/math] | [math]displaystyle{ = x }[/math] |
| A2 | [math]displaystyle{ x^{-1} cdot x }[/math] | [math]displaystyle{ = 1 }[/math] |
| A3 | [math]displaystyle{ (x cdot y) cdot z }[/math] | [math]displaystyle{ = x cdot (y cdot z) }[/math] |
| R1 | [math]displaystyle{ 1 cdot x }[/math] | [math]displaystyle{ rightsquigarrow x }[/math] |
| R2 | [math]displaystyle{ x^{-1} cdot x }[/math] | [math]displaystyle{ rightsquigarrow 1 }[/math] |
| R3 | [math]displaystyle{ (x cdot y) cdot z }[/math] | [math]displaystyle{ rightsquigarrow x cdot (y cdot z) }[/math] |
| R4 | [math]displaystyle{ x^{-1} cdot (x cdot y) }[/math] | [math]displaystyle{ rightsquigarrow y }[/math] |
| R8 | [math]displaystyle{ 1^{-1} }[/math] | [math]displaystyle{ rightsquigarrow 1 }[/math] |
| R11 | [math]displaystyle{ x cdot 1 }[/math] | [math]displaystyle{ rightsquigarrow x }[/math] |
| R12 | [math]displaystyle{ (x^{-1})^{-1} }[/math] | [math]displaystyle{ rightsquigarrow x }[/math] |
| R13 | [math]displaystyle{ x cdot x^{-1} }[/math] | [math]displaystyle{ rightsquigarrow 1 }[/math] |
| R14 | [math]displaystyle{ x cdot (x^{-1} cdot y) }[/math] | [math]displaystyle{ rightsquigarrow y }[/math] |
| R17 | [math]displaystyle{ (x cdot y)^{-1} }[/math] | [math]displaystyle{ rightsquigarrow y^{-1} cdot x^{-1} }[/math] |
See also
- Conjugacy problem
- Group isomorphism problem
References
- ↑ 1.0 1.1 1.2 1.3 Evans, Trevor (1978). «Word problems». Bulletin of the American Mathematical Society 84 (5): 790. doi:10.1090/S0002-9904-1978-14516-9.
- ↑ Cohen, Joel S. (2002). Computer algebra and symbolic computation: elementary algorithms. Natick, Mass.: A K Peters. pp. 90–92. ISBN 1568811586.
- ↑ 3.0 3.1 3.2 3.3 3.4 3.5 3.6 Miller, Charles F. (2014). Downey, Rod. ed. «Turing machines to word problems». Turing’s Legacy: 330. doi:10.1017/CBO9781107338579.010. ISBN 9781107338579. http://minerva-access.unimelb.edu.au/bitstream/11343/51723/1/cfm-lnl42-turings-legacy-pp329-385-2014.pdf. Retrieved 6 December 2021.
- ↑ Stillwell, John (1982). «The word problem and the isomorphism problem for groups». Bulletin of the American Mathematical Society 6 (1): 33–56. doi:10.1090/S0273-0979-1982-14963-1.
- ↑ Müller-Stach, Stefan (12 September 2021). «Max Dehn, Axel Thue, and the Undecidable». p. 13. arXiv:1703.09750 [math.HO].
- ↑ Steinby, Magnus; Thomas, Wolfgang (2000). «Trees and term rewriting in 1910: on a paper by Axel Thue» (in English). Bulletin of the European Association for Theoretical Computer Science 72: 256–269.
- ↑ Dehn, Max (1911). «Über unendliche diskontinuierliche Gruppen». Mathematische Annalen 71 (1): 116–144. doi:10.1007/BF01456932. ISSN 0025-5831. http://gdz.sub.uni-goettingen.de/index.php?id=11&PPN=PPN235181684_0071&DMDID=DMDLOG_0013&L=1.
- ↑ Dehn, Max (1912). «Transformation der Kurven auf zweiseitigen Flächen». Mathematische Annalen 72 (3): 413–421. doi:10.1007/BF01456725. ISSN 0025-5831. http://gdz.sub.uni-goettingen.de/index.php?id=11&PPN=PPN235181684_0072&DMDID=DMDLOG_0039&L=1.
- ↑ Greendlinger, Martin (June 1959). «Dehn’s algorithm for the word problem». Communications on Pure and Applied Mathematics 13 (1): 67–83. doi:10.1002/cpa.3160130108.
- ↑ Lyndon, Roger C. (September 1966). «On Dehn’s algorithm». Mathematische Annalen 166 (3): 208–228. doi:10.1007/BF01361168. http://gdz.sub.uni-goettingen.de/index.php?id=11&PPN=GDZPPN002296799&L=1.
- ↑ Schupp, Paul E. (June 1968). «On Dehn’s algorithm and the conjugacy problem». Mathematische Annalen 178 (2): 119–130. doi:10.1007/BF01350654. http://gdz.sub.uni-goettingen.de/index.php?id=11&PPN=GDZPPN002300036&L=1.
- ↑ Power, James F. (27 August 2013). «Thue’s 1914 paper: a translation». arXiv:1308.5858 [cs.FL].
- ↑ See History of the Church–Turing thesis. The dates are based on On Formally Undecidable Propositions of Principia Mathematica and Related Systems and Systems of Logic Based on Ordinals.
- ↑ Post, Emil L. (March 1947). «Recursive Unsolvability of a problem of Thue». Journal of Symbolic Logic 12 (1): 1–11. doi:10.2307/2267170. https://www.wolframscience.com/prizes/tm23/images/Post2.pdf. Retrieved 6 December 2021.
- ↑ Mostowski, Andrzej (September 1951). «A. Markov. Névožmoinost’ nékotoryh algoritmov v téorii associativnyh sistém (Impossibility of certain algorithms in the theory of associative systems). Doklady Akadémii Nauk SSSR, vol. 77 (1951), pp. 19–20.». Journal of Symbolic Logic 16 (3): 215. doi:10.2307/2266407.
- ↑ Turing, A. M. (September 1950). «The Word Problem in Semi-Groups With Cancellation». The Annals of Mathematics 52 (2): 491–505. doi:10.2307/1969481.
- ↑ Novikov, P. S. (1955). «On the algorithmic unsolvability of the word problem in group theory» (in ru). Proceedings of the Steklov Institute of Mathematics 44: 1–143.
- ↑ Boone, William W. (1954). «Certain Simple, Unsolvable Problems of Group Theory. I». Indagationes Mathematicae (Proceedings) 57: 231–237. doi:10.1016/S1385-7258(54)50033-8.
- ↑ Boone, William W. (1957). «Certain Simple, Unsolvable Problems of Group Theory. VI». Indagationes Mathematicae (Proceedings) 60: 227–232. doi:10.1016/S1385-7258(57)50030-9.
- ↑ Britton, J. L. (October 1958). «The Word Problem for Groups». Proceedings of the London Mathematical Society s3-8 (4): 493–506. doi:10.1112/plms/s3-8.4.493.
- ↑ Boone, William W. (1958). «The word problem». Proceedings of the National Academy of Sciences 44 (10): 1061–1065. doi:10.1073/pnas.44.10.1061. PMID 16590307. PMC 528693. Bibcode: 1958PNAS…44.1061B. http://www.pnas.org/cgi/reprint/44/10/1061.pdf.
- ↑ Boone, William W. (September 1959). «The Word Problem». The Annals of Mathematics 70 (2): 207–265. doi:10.2307/1970103.
- ↑ Higman, G. (8 August 1961). «Subgroups of finitely presented groups». Proceedings of the Royal Society of London. Series A. Mathematical and Physical Sciences 262 (1311): 455–475. doi:10.1098/rspa.1961.0132. Bibcode: 1961RSPSA.262..455H.
- ↑ Britton, John L. (January 1963). «The Word Problem». The Annals of Mathematics 77 (1): 16–32. doi:10.2307/1970200.
- ↑ Simpson, Stephen G. (18 May 2005). «A Slick Proof of the Unsolvability of the Word Problem for Finitely Presented Groups». http://www.personal.psu.edu/t20/logic/seminar/050517.pdf.
- ↑ «Subgroups of finitely presented groups». Mathematics of the USSR-Sbornik 103 (145): 147–236. 13 February 1977. doi:10.1070/SM1977v032n02ABEH002376.
- ↑ 27.0 27.1 Matiyasevich, Yuri; Sénizergues, Géraud (January 2005). «Decision problems for semi-Thue systems with a few rules». Theoretical Computer Science 330 (1): 145–169. doi:10.1016/j.tcs.2004.09.016.
- ↑ Davis, Martin (1978). «What is a Computation?». Mathematics Today Twelve Informal Essays: 257–259. doi:10.1007/978-1-4613-9435-8_10. ISBN 978-1-4613-9437-2. https://www.cs.princeton.edu/courses/archive/spring11/cos116/handouts/daviscomputation.pdf. Retrieved 5 December 2021.
- ↑ 29.0 29.1 Baader, Franz; Nipkow, Tobias (5 August 1999) (in en). Term Rewriting and All That. Cambridge University Press. pp. 59–60. ISBN 978-0-521-77920-3. https://www.google.com/books/edition/Term_Rewriting_and_All_That/N7BvXVUCQk8C?hl=en&gbpv=1&pg=PA59.
- ↑
- Matiyasevich, Yu. V. (1967). «Простые примеры неразрешимых ассоциативных исчислений» (in Russian). Doklady Akademii Nauk SSSR 173 (6): 1264–1266. ISSN 0869-5652. http://mi.mathnet.ru/eng/dan/v173/i6/p1264.
- Matiyasevich, Yu. V. (1967). «Simple examples of undecidable associative calculi». Soviet Mathematics 8 (2): 555–557. ISSN 0197-6788.
- ↑ Novikov, P. S. (1955). «On the algorithmic unsolvability of the word problem in group theory» (in ru). Trudy Mat. Inst. Steklov 44: 1–143.
- ↑ Statman, Rick (2000). «On the Word Problem for Combinators». Rewriting Techniques and Applications. Lecture Notes in Computer Science 1833: 203–213. doi:10.1007/10721975_14. ISBN 978-3-540-67778-9.
- ↑ Beke, Tibor (May 2011). «Categorification, term rewriting and the Knuth–Bendix procedure». Journal of Pure and Applied Algebra 215 (5): 730. doi:10.1016/j.jpaa.2010.06.019.
- ↑ Peter T. Johnstone, Stone Spaces, (1982) Cambridge University Press, Cambridge, ISBN 0-521-23893-5. (See chapter 1, paragraph 4.11)
- ↑ Whitman, Philip M. (January 1941). «Free Lattices». The Annals of Mathematics 42 (1): 325–329. doi:10.2307/1969001.
- ↑ Whitman, Philip M. (1942). «Free Lattices II». Annals of Mathematics 43 (1): 104–115. doi:10.2307/1968883.
- ↑ K. H. Bläsius and H.-J. Bürckert, ed (1992). Deduktionsssysteme. Oldenbourg. pp. 291.; here: p.126, 134
- ↑ Apply rules in any order to a term, as long as possible; the result doesn’t depend on the order; it is the term’s normal form.
About 25% of your total SAT Math section will be word problems, meaning you will have to create your own visuals and equations to solve for your answers. Though the actual math topics can vary, SAT word problems share a few commonalities, and we’re here to walk you through how to best solve them.
This post will be your complete guide to SAT Math word problems. We’ll cover how to translate word problems into equations and diagrams, the different types of math word problems you’ll see on the test, and how to go about solving your word problems on test day.
Feature Image: Antonio Litterio/Wikimedia
What Are SAT Math Word Problems?
A word problem is any math problem based mostly or entirely on a written description. You will not be provided with an equation, diagram, or graph on a word problem and must instead use your reading skills to translate the words of the question into a workable math problem. Once you do this, you can then solve it.
You will be given word problems on the SAT Math section for a variety of reasons. For one, word problems test your reading comprehension and your ability to visualize information.
Secondly, these types of questions allow test makers to ask questions that’d be impossible to ask with just a diagram or an equation. For instance, if a math question asks you to fit as many small objects into a larger one as is possible, it’d be difficult to demonstrate and ask this with only a diagram.
Translating Math Word Problems Into Equations or Drawings
In order to translate your SAT word problems into actionable math equations you can solve, you’ll need to understand and know how to utilize some key math terms. Whenever you see these words, you can translate them into the proper mathematical action.
For instance, the word «sum» means the value when two or more items are added together. So if you need to find the sum of a and b, you’ll need to set up your equation like this: a+b.
Also, note that many mathematical actions have more than one term attached, which can be used interchangeably.
Here is a chart with all the key terms and symbols you should know for SAT Math word problems:
| Key Terms | Mathematical Action |
| Sum, increased by, added to, more than, total of | + |
| Difference, decreased by, less than, subtracted from | − |
| Product, times, __ times as much, __ times as many (a number, e.g., “three times as many”) | * or x |
| Divided by, per, __ as many, __ as much (a fraction, e.g., “one-third as much”) | / or ÷ |
| Equals, is, are, equivalent | = |
| Is less than | < |
| Is greater than | > |
| Is less than or equal to | ≤ |
| Is greater than or equal to | ≥ |
Now, let’s look at these math terms in action using a few official examples:
We can solve this problem by translating the information we’re given into algebra. We know the individual price of each salad and drink, and the total revenue made from selling 209 salads and drinks combined. So let’s write this out in algebraic form.
We’ll say that the number of salads sold = S, and the number of drinks sold = D. The problem tells us that 209 salads and drinks have been sold, which we can think of as this:
S + D = 209
Finally, we’ve been told that a certain number of S and D have been sold and have brought in a total revenue of 836 dollars and 50 cents. We don’t know the exact numbers of S and D, but we do know how much each unit costs. Therefore, we can write this equation:
6.50S + 2D = 836.5
We now have two equations with the same variables (S and D). Since we want to know how many salads were sold, we’ll need to solve for D so that we can use this information to solve for S. The first equation tells us what S and D equal when added together, but we can rearrange this to tell us what just D equals in terms of S:
S + D = 209
Now, just subtract S from both sides to get what D equals:
D = 209 − S
Finally, plug this expression in for D into our other equation, and then solve for S:
6.50S + 2(209 − S) = 836.5
6.50S + 418 − 2S = 836.5
6.50S − 2S = 418.5
4.5S = 418.5
S = 93
The correct answer choice is (B) 93.
This word problem asks us to solve for one possible solution (it asks for «a possible amount»), so we know right away that there will be multiple correct answers.
Wyatt can husk at least 12 dozen ears of corn and at most 18 dozen ears of corn per hour. If he husks 72 dozen at a rate of 12 dozen an hour, this is equal to 72 / 12 = 6 hours. You could therefore write 6 as your final answer.
If Wyatt husks 72 dozen at a rate of 18 dozen an hour (the highest rate possible he can do), this comes out to 72 / 18 = 4 hours. You could write 4 as your final answer.
Since the minimum time it takes Wyatt is 4 hours and the maximum time is 6 hours, any number from 4 to 6 would be correct.
Though the hardest SAT word problems might look like Latin to you right now, practice and study will soon have you translating them into workable questions.
Typical SAT Word Problems
Word problems on the SAT can be grouped into three major categories:
- Word problems for which you must simply set up an equation
- Word problems for which you must solve for a specific value
- Word problems for which you must define the meaning of a value or variable
Below, we look at each world problem type and give you examples.
Word Problem Type 1: Setting Up an Equation
This is a fairly uncommon type of SAT word problem, but you’ll generally see it at least once on the Math section. You’ll also most likely see it first on the section.
For these problems, you must use the information you’re given and then set up the equation. No need to solve for the missing variable—this is as far as you need to go.
Almost always, you’ll see this type of question in the first four questions on the SAT Math section, meaning that the College Board consider these questions easy. This is due to the fact that you only have to provide the setup and not the execution.
To solve this problem, we’ll need to know both Armand’s and Tyrone’s situations, so let’s look at them separately:
Armand: Armand sent m text messages each hour for 5 hours, so we can write this as 5m—the number of texts he sent per hour multiplied by the total number of hours he texted.
Tyrone: Tyrone sent p text messages each hour for 4 hours, so we can write this as 4p—the number of texts he sent per hour multiplied by the total number of hours he texted.
We now know that Armand’s situation can be written algebraically as 5m, and Tyrone’s can be written as 4p. Since we’re being asked for the expression that represents the total number of texts sent by Armand and Tyrone, we must add together the two expressions:
5m + 4p
The correct answer is choice (C) 5m + 4p
Word Problem Type 2: Solving for a Missing Value
The vast majority of SAT Math word problem questions will fall into this category. For these questions, you must both set up your equation and solve for a specific piece of information.
Most (though not all) word problem questions of this type will be scenarios or stories covering all sorts of SAT Math topics, such as averages, single-variable equations, and ratios. You almost always must have a solid understanding of the math topic in question in order to solve the word problem on the topic.
Let’s try to think about this problem in terms of x. If Type A trees produced 20% more pears than Type B did, we can write this as an expression:
x + 0.2x = 1.2x = # of pears produced by Type A
In this equation, x is the number of pears produced by Type B trees. If we add 20% of x (0.2x) to x, we get the number of pears produced by Type A trees.
The problem tells us that Type A trees produced a total of 144 pears. Since we know that 1.2x is equal to the number of pears produced by Type A, we can write the following equation:
1.2x = 144
Now, all we have to do is divide both sides by 1.2 to find the number of pears produced by Type B trees:
x = 144 / 1.2
x = 120
The correct answer choice is (B) 120.
You might also get a geometry problem as a word problem, which might or might not be set up with a scenario, too. Geometry questions will be presented as word problems typically because the test makers felt the problem would be too easy to solve had you been given a diagram, or because the problem would be impossible to show with a diagram. (Note that geometry makes up a very small percentage of SAT Math.)
This is a case of a problem that is difficult to show visually, since x is not a set degree value but rather a value greater than 55; thus, it must be presented as a word problem.
Since we know that x must be an integer degree value greater than 55, let us assign it a value. In this case, let us call x 56°. (Why 56? There are other values x could be, but 56 is guaranteed to work since it’s the smallest integer larger than 55. Basically, it’s a safe bet!)
Now, because x = 56, the next angle in the triangle—2x—must measure the following:
56*2 = 112
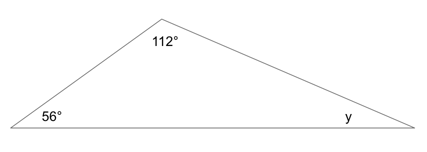
Let’s make a rough (not to scale) sketch of what we know so far:
Now, we know that there are 180° in a triangle, so we can find the value of y by saying this:
y = 180 − 112 − 56
y = 12
One possible value for y is 12. (Other possible values are 3, 6, and 9.)
Word Problem Type 3: Explaining the Meaning of a Variable or Value
This type of problem will show up at least once. It asks you to define part of an equation provided by the word problem—generally the meaning of a specific variable or number.
This question might sound tricky at first, but it’s actually quite simple.
We know that P is the number of phones Kathy has left to fix, and d is the number of days she has worked in a week. If she’s worked 0 days (i.e., if we plug 0 into the equation), here’s what we get:
P = 108 − 23(0)
P = 108
This means that, without working any days of the week, Kathy has 108 phones to repair. The correct answer choice, therefore, is (B) Kathy starts each week with 108 phones to fix.
To help juggle all the various SAT word problems, let’s look at the math strategies and tips at our disposal.
Ready to go beyond just reading about the SAT? Then you’ll love the free five-day trial for our SAT Complete Prep program. Designed and written by PrepScholar SAT experts, our SAT program customizes to your skill level in over 40 subskills so that you can focus your studying on what will get you the biggest score gains.
Click on the button below to try it out!
SAT Math Strategies for Word Problems
Though you’ll see word problems on the SAT Math section on a variety of math topics, there are still a few techniques you can apply to solve word problems as a whole.
#1: Draw It Out
Whether your problem is a geometry problem or an algebra problem, sometimes making a quick sketch of the scene can help you understand what exactly you’re working with. For instance, let’s look at how a picture can help you solve a word problem about a circle (specifically, a pizza):
If you often have trouble visualizing problems such as these, draw it out. We know that we’re dealing with a circle since our focus is a pizza. We also know that the pizza weighs 3 pounds.
Because we’ll need to solve the weight of each slice in ounces, let’s first convert the total weight of our pizza from pounds into ounces. We’re given the conversion (1 pound = 16 ounces), so all we have to do is multiply our 3-pound pizza by 16 to get our answer:
3 * 16 = 48 ounces (for whole pizza)
Now, let’s draw a picture. First, the pizza is divided in half (not drawn to scale):
We now have two equal-sized pieces. Let’s continue drawing. The problem then says that we divide each half into three equal pieces (again, not drawn to scale):
This gives us a total of six equal-sized pieces. Since we know the total weight of the pizza is 48 ounces, all we have to do is divide by 6 (the number of pieces) to get the weight (in ounces) per piece of pizza:
48 / 6 = 8 ounces per piece
The correct answer choice is (C) 8.
As for geometry problems, remember that you might get a geometry word problem written as a word problem. In this case, make your own drawing of the scene. Even a rough sketch can help you visualize the math problem and keep all your information in order.
#2: Memorize Key Terms
If you’re not used to translating English words and descriptions into mathematical equations, then SAT word problems might be difficult to wrap your head around at first. Look at the chart we gave you above so you can learn how to translate keywords into their math equivalents. This way, you can understand exactly what a problem is asking you to find and how you’re supposed to find it.
There are free SAT Math questions available online, so memorize your terms and then practice on realistic SAT word problems to make sure you’ve got your definitions down and can apply them to the actual test.
#3: Underline and/or Write Out Important Information
The key to solving a word problem is to bring together all the key pieces of given information and put them in the right places. Make sure you write out all these givens on the diagram you’ve drawn (if the problem calls for a diagram) so that all your moving pieces are in order.
One of the best ways to keep all your pieces straight is to underline your key information in the problem, and then write them out yourself before you set up your equation. So take a moment to perform this step before you zero in on solving the question.
#4: Pay Close Attention to What’s Being Asked
It can be infuriating to find yourself solving for the wrong variable or writing in your given values in the wrong places. And yet this is entirely too easy to do when working with math word problems.
Make sure you pay strict attention to exactly what you’re meant to be solving for and exactly what pieces of information go where. Are you looking for the area or the perimeter? The value of x, 2x, or y?
It’s always better to double-check what you’re supposed to find before you start than to realize two minutes down the line that you have to begin solving the problem all over again.
#5: Brush Up on Any Specific Math Topic You Feel Weak In
You’re likely to see both a diagram/equation problem and a word problem for almost every SAT Math topic on the test. This is why there are so many different types of word problems and why you’ll need to know the ins and outs of every SAT Math topic in order to be able to solve a word problem about it.
For example, if you don’t know how to find an average given a set of numbers, you certainly won’t know how to solve a word problem that deals with averages!
Understand that solving an SAT Math word problem is a two-step process: it requires you to both understand how word problems work and to understand the math topic in question. If you have any areas of mathematical weakness, now’s a good time to brush up on them—or else SAT word problems might be trickier than you were expecting!
All set? Let’s go!
Test Your SAT Math Word Problem Knowledge
Finally, it’s time to test your word problem know-how against real SAT Math problems:
Word Problems
1. No Calculator
2. Calculator OK
3. Calculator OK
4. Calculator OK
Answers: C, B, A, 1160
Answer Explanations
1. For this problem, we have to use the information we’re given to set up an equation.
We know that Ken spent x dollars, and Paul spent 1 dollar more than Ken did. Therefore, we can write the following equation for Paul:
x + 1
Ken and Paul split the bill evenly. This means that we’ll have to solve for the total amount of both their sandwiches and then divide it by 2. Since Ken’s sandwich cost x dollars and Paul’s cost x + 1, here’s what our equation looks like when we combine the two expressions:
x + x + 1
2x + 1
Now, we can divide this expression by 2 to get the price each person paid:
(2x + 1) / 2
x + 0.5
But we’re not finished yet. We know that both Ken and Paul also paid a 20% tip on their bills. As a result, we have to multiply the total cost of one bill by 0.2, and then add this tip to the bill. Algebraically, this looks like this:
(x + 0.5) + 0.2(x + 0.5)
x + 0.5 + 0.2x + 0.1
1.2x + 0.6
The correct answer choice is (C) 1.2x + 0.6
2. You’ll have to be familiar with statistics in order to understand what this question is asking.
Since Nick surveyed a random sample of his freshman class, we can say that this sample will accurately reflect the opinion (and thus the same percentages) as the entire freshman class.
Of the 90 freshmen sampled, 25.6% said that they wanted the Fall Festival held in October. All we have to do now is find this percentage of the entire freshmen class (which consists of 225 students) to determine how many total freshmen would prefer an October festival:
225 * 0.256 = 57.6
Since the question is asking «about how many students»—and since we obviously can’t have a fraction of a person!—we’ll have to round this number to the nearest answer choice available, which is 60, or answer choice (B).
3. This is one of those problems that is asking you to define a value in the equation given. It might look confusing, but don’t be scared—it’s actually not as difficult as it appears!
First off, we know that t represents the number of seconds passed after an object is launched upward. But what if no time has passed yet? This would mean that t = 0. Here’s what happens to the equation when we plug in 0 for t:
h(0) = -16(0)2 + 110(0) + 72
h(0) = 0 + 0 + 72
h(0) = 72
As we can see, before the object is even launched, it has a height of 72 feet. This means that 72 must represent the initial height, in feet, of the object, or answer choice (A).
4. You might be tempted to draw a diagram for this problem since it’s talking about a pool (rectangle), but it’s actually quicker to just look at the numbers given and work from there.
We know that the pool currently holds 600 gallons of water and that water has been hosed into it at a rate of 8 gallons a minute for a total of 70 minutes.
To find the amount of water in the pool now, we’ll have to first solve for the amount of water added to the pool by hose. We know that 8 gallons were added each minute for 70 minutes, so all we have to do is multiply 8 by 70:
8 * 70 = 560 gallons
This tells us that 560 gallons of water were added to our already-filled, 600-gallon pool. To find the total amount of water, then, we simply add these two numbers together:
560 + 600 = 1160
The correct answer is 1160.
Aaaaaaaaaaand time for a nap.
Key Takeaways: Making Sense of SAT Math Word Problems
Word problems make up a significant portion of the SAT Math section, so it’s a good idea to understand how they work and how to translate the words on the page into a proper expression or equation. But this is still only half the battle.
Though you won’t know how to solve a word problem if you don’t know what a product is or how to draw a right triangle, you also won’t know how to solve a word problem about ratios if you don’t know how ratios work.
Therefore, be sure to learn not only how to approach math word problems as a whole, but also how to narrow your focus on any SAT Math topics you need help with. You can find links to all of our SAT Math topic guides here to help you in your studies.
What’s Next?
Want to brush up on SAT Math topics? Check out our individual math guides to get an overview of each and every topic on SAT Math. From polygons and slopes to probabilities and sequences, we’ve got you covered!
Running out of time on the SAT Math section? We have the know-how to help you beat the clock and maximize your score.
Been procrastinating on your SAT studying? Learn how you can overcome your desire to procrastinate and make a well-balanced prep plan.
Trying to get a perfect SAT score? Take a look at our guide to getting a perfect 800 on SAT Math, written by a perfect scorer.
Want to improve your SAT score by 160 points?
Check out our best-in-class online SAT prep program. We guarantee your money back if you don’t improve your SAT score by 160 points or more.
Our program is entirely online, and it customizes what you study to your strengths and weaknesses. If you liked this Math strategy guide, you’ll love our program. Along with more detailed lessons, you’ll get thousands of practice problems organized by individual skills so you learn most effectively. We’ll also give you a step-by-step program to follow so you’ll never be confused about what to study next.
Check out our 5-day free trial:
Have friends who also need help with test prep? Share this article!
About the Author
Courtney scored in the 99th percentile on the SAT in high school and went on to graduate from Stanford University with a degree in Cultural and Social Anthropology. She is passionate about bringing education and the tools to succeed to students from all backgrounds and walks of life, as she believes open education is one of the great societal equalizers. She has years of tutoring experience and writes creative works in her free time.