The word mean for math - Word и Excel - помощь в работе с программами

From Wikipedia, the free encyclopedia

This article is about the mathematical concept. For other uses, see Mean (disambiguation). For the state of being mean or cruel, see Meanness. For broader coverage of this topic, see Average.

There are several kinds of mean in mathematics, especially in statistics. Each mean serves to summarize a given group of data, often to better understand the overall value (magnitude and sign) of a given data set.

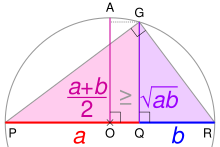
Pythagorean means consist of arithmetic mean (AM), geometric mean (GM), and harmonic mean (HM). The AM is the sum of numbers divided by the number of numbers, GM is an average for sets of positive numbers based on their product, and HM is an average for sets of numbers defined in relation to a unit of measurement. The relationship between AM, GM, and HM is represented by the inequality AM ≥ GM ≥ HM.

Statistical location covers mean, median, and mode, where mean may not always be the same as the median or mode for skewed distributions. The mean of a probability distribution is the long-run average value of a random variable with that distribution.

Generalized means include power mean and f-mean. The power mean is an abstraction of quadratic, arithmetic, geometric, and harmonic means, while the f-mean generalizes the concept further.

Other specialized means discussed are weighted arithmetic mean, truncated mean, interquartile mean, mean of a function, mean of angles and cyclical quantities, Fréchet mean, triangular sets, and Swanson’s rule.

For a data set, the arithmetic mean, also known as «arithmetic average», is a measure of central tendency of a finite set of numbers: specifically, the sum of the values divided by the number of values. The arithmetic mean of a set of numbers x₁, x₂, …, x_n is typically denoted using an overhead bar, .^{[note 1]} If the data set were based on a series of observations obtained by sampling from a statistical population, the arithmetic mean is the sample mean () to distinguish it from the mean, or expected value, of the underlying distribution, the population mean (denoted or $mu _{x}$ ^{[note 2]}).^[1]

Outside probability and statistics, a wide range of other notions of mean are often used in geometry and mathematical analysis; examples are given below.

Types of means[edit]

Pythagorean means[edit]

Arithmetic mean (AM)[edit]

The arithmetic mean (or simply mean) of a list of numbers, is the sum of all of the numbers divided by the number of numbers. Similarly, the mean of a sample $x_{1},x_{2},ldots ,x_{n}$ , usually denoted by , is the sum of the sampled values divided by the number of items in the sample.

${displaystyle {bar {x}}={frac {1}{n}}left(sum _{i=1}^{n}{x_{i}}right)={frac {x_{1}+x_{2}+cdots +x_{n}}{n}}}$

For example, the arithmetic mean of five values: 4, 36, 45, 50, 75 is:

${displaystyle {frac {4+36+45+50+75}{5}}={frac {210}{5}}=42.}$

Geometric mean (GM)[edit]

The geometric mean is an average that is useful for sets of positive numbers, that are interpreted according to their product (as is the case with rates of growth) and not their sum (as is the case with the arithmetic mean):

${displaystyle {bar {x}}=left(prod _{i=1}^{n}{x_{i}}right)^{frac {1}{n}}=left(x_{1}x_{2}cdots x_{n}right)^{frac {1}{n}}}$

^[2]

For example, the geometric mean of five values: 4, 36, 45, 50, 75 is:

${displaystyle (4times 36times 45times 50times 75)^{frac {1}{5}}={sqrt[{5}]{24;300;000}}=30.}$

Harmonic mean (HM)[edit]

The harmonic mean is an average which is useful for sets of numbers which are defined in relation to some unit, as in the case of speed (i.e., distance per unit of time):

${displaystyle {bar {x}}=nleft(sum _{i=1}^{n}{frac {1}{x_{i}}}right)^{-1}}$

For example, the harmonic mean of the five values: 4, 36, 45, 50, 75 is

${frac {5}{{tfrac {1}{4}}+{tfrac {1}{36}}+{tfrac {1}{45}}+{tfrac {1}{50}}+{tfrac {1}{75}}}}={frac {5}{;{tfrac {1}{3}};}}=15.$

Relationship between AM, GM, and HM[edit]

AM, GM, and HM satisfy these inequalities:

{displaystyle mathrm {AM} geq mathrm {GM} geq mathrm {HM} ,}

Equality holds if all the elements of the given sample are equal.

Statistical location[edit]

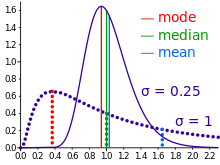
Geometric visualization of the mode, median and mean of an arbitrary probability density function.^[3]

In descriptive statistics, the mean may be confused with the median, mode or mid-range, as any of these may incorrectly be called an «average» (more formally, a measure of central tendency). The mean of a set of observations is the arithmetic average of the values; however, for skewed distributions, the mean is not necessarily the same as the middle value (median), or the most likely value (mode). For example, mean income is typically skewed upwards by a small number of people with very large incomes, so that the majority have an income lower than the mean. By contrast, the median income is the level at which half the population is below and half is above. The mode income is the most likely income and favors the larger number of people with lower incomes. While the median and mode are often more intuitive measures for such skewed data, many skewed distributions are in fact best described by their mean, including the exponential and Poisson distributions.

Mean of a probability distribution[edit]

The mean of a probability distribution is the long-run arithmetic average value of a random variable having that distribution. If the random variable is denoted by , then it is also known as the expected value of (denoted E(X) ). For a discrete probability distribution, the mean is given by , where the sum is taken over all possible values of the random variable and P(x) is the probability mass function. For a continuous distribution, the mean is $textstyle int _{-infty }^{infty }xf(x),dx$ , where f(x) is the probability density function.^[4] In all cases, including those in which the distribution is neither discrete nor continuous, the mean is the Lebesgue integral of the random variable with respect to its probability measure. The mean need not exist or be finite; for some probability distributions the mean is infinite (+∞ or −∞), while for others the mean is undefined.

Generalized means[edit]

Power mean[edit]

The generalized mean, also known as the power mean or Hölder mean, is an abstraction of the quadratic, arithmetic, geometric, and harmonic means. It is defined for a set of n positive numbers x_i by

${displaystyle {bar {x}}(m)=left({frac {1}{n}}sum _{i=1}^{n}x_{i}^{m}right)^{frac {1}{m}}}$ ^[2]

By choosing different values for the parameter m, the following types of means are obtained:

${displaystyle lim _{mto infty }}$: maximum of $x_{i}$
${displaystyle lim _{mto 2}}$: quadratic mean
${displaystyle lim _{mto 1}}$: arithmetic mean
${displaystyle lim _{mto 0}}$: geometric mean
${displaystyle lim _{mto -1}}$: harmonic mean
${displaystyle lim _{mto -infty }}$: minimum of $x_{i}$

f-mean[edit]

This can be generalized further as the generalized f-mean

${displaystyle {bar {x}}=f^{-1}left({{frac {1}{n}}sum _{i=1}^{n}{fleft(x_{i}right)}}right)}$

and again a suitable choice of an invertible f will give

Weighted arithmetic mean[edit]

The weighted arithmetic mean (or weighted average) is used if one wants to combine average values from different sized samples of the same population:

${displaystyle {bar {x}}={frac {sum _{i=1}^{n}{w_{i}{bar {x_{i}}}}}{sum _{i=1}^{n}w_{i}}}.}$

^[2]

Where ${displaystyle {bar {x_{i}}}}$ and $w_{i}$ are the mean and size of sample respectively. In other applications, they represent a measure for the reliability of the influence upon the mean by the respective values.

Truncated mean[edit]

Sometimes, a set of numbers might contain outliers (i.e., data values which are much lower or much higher than the others). Often, outliers are erroneous data caused by artifacts. In this case, one can use a truncated mean. It involves discarding given parts of the data at the top or the bottom end, typically an equal amount at each end and then taking the arithmetic mean of the remaining data. The number of values removed is indicated as a percentage of the total number of values.

Interquartile mean[edit]

The interquartile mean is a specific example of a truncated mean. It is simply the arithmetic mean after removing the lowest and the highest quarter of values.

${displaystyle {bar {x}}={frac {2}{n}};sum _{i={frac {n}{4}}+1}^{{frac {3}{4}}n}!!x_{i}}$

assuming the values have been ordered, so is simply a specific example of a weighted mean for a specific set of weights.

Mean of a function[edit]

In some circumstances, mathematicians may calculate a mean of an infinite (or even an uncountable) set of values. This can happen when calculating the mean value ${displaystyle y_{text{avg}}}$ of a function f(x) . Intuitively, a mean of a function can be thought of as calculating the area under a section of a curve, and then dividing by the length of that section. This can be done crudely by counting squares on graph paper, or more precisely by integration. The integration formula is written as:

${displaystyle y_{text{avg}}(a,b)={frac {1}{b-a}}int limits _{a}^{b}!f(x),dx}$

In this case, care must be taken to make sure that the integral converges. But the mean may be finite even if the function itself tends to infinity at some points.

Mean of angles and cyclical quantities[edit]

Angles, times of day, and other cyclical quantities require modular arithmetic to add and otherwise combine numbers. In all these situations, there will not be a unique mean. For example, the times an hour before and after midnight are equidistant to both midnight and noon. It is also possible that no mean exists. Consider a color wheel—there is no mean to the set of all colors. In these situations, you must decide which mean is most useful. You can do this by adjusting the values before averaging, or by using a specialized approach for the mean of circular quantities.

Fréchet mean[edit]

The Fréchet mean gives a manner for determining the «center» of a mass distribution on a surface or, more generally, Riemannian manifold. Unlike many other means, the Fréchet mean is defined on a space whose elements cannot necessarily be added together or multiplied by scalars.
It is sometimes also known as the Karcher mean (named after Hermann Karcher).

Trianglar sets[edit]

In geometry, there are thousands of different
definitions for the center of a triangle that can all be interpretted as the mean of a triangular set of points in the plane.^{[citation needed]}

Swanson’s rule[edit]

This is an approximation to the mean for a moderately skewed distribution.^[5] It is used in hydrocarbon exploration and is defined as:

${displaystyle m=0.3P_{10}+0.4P_{50}+0.3P_{90}}$

where P₁₀, P₅₀ and P₉₀ 10th, 50th and 90th percentiles of the distribution.

Other means[edit]

Arithmetic-geometric mean
Arithmetic-harmonic mean
Cesàro mean
Chisini mean
Contraharmonic mean
Elementary symmetric mean
Geometric-harmonic mean
Grand mean
Heinz mean
Heronian mean
Identric mean
Lehmer mean
Logarithmic mean
Moving average
Neuman–Sándor mean
Quasi-arithmetic mean
Root mean square (quadratic mean)
Rényi’s entropy (a generalized f-mean)
Spherical mean
Stolarsky mean
Weighted geometric mean
Weighted harmonic mean

Notes[edit]

^ Pronounced «x bar».
^ Greek letter μ, for «mean», pronounced /’mjuː/.

References[edit]

^ Underhill, L.G.; Bradfield d. (1998) Introstat, Juta and Company Ltd. ISBN 0-7021-3838-X p. 181
^ ^a ^b ^c «Mean | mathematics». Encyclopedia Britannica. Retrieved 2020-08-21.
^ «AP Statistics Review — Density Curves and the Normal Distributions». Archived from the original on 2 April 2015. Retrieved 16 March 2015.
^ Weisstein, Eric W. «Population Mean». mathworld.wolfram.com. Retrieved 2020-08-21.
^ Hurst A, Brown GC, Swanson RI (2000) Swanson’s 30-40-30 Rule. American Association of Petroleum Geologists Bulletin 84(12) 1883-1891

Источник

The term ‘Mean’ is used constantly in the field of Statistics and is one of the basic methods used to obtain a result. It is also known as arithmetic mean or the average of a given set of data. It also measures the central tendency of data. The definition of a mean for a given set of data is the average calculated for a given set of numbers or data. This is referred to as the total of all the values of data provided divided by the number of data values in total for any given set of data.

The mathematical symbol or notation for the mean is ‘x-bar’. This symbol appears on scientific calculators and in mathematical and statistical notations.

The ‘mean’ or ‘arithmetic mean is the most commonly used form of average. To calculate the mean, you need a set of related numbers (or data set). At least two numbers are needed in order to calculate the mean.

The formula denoting the mean of a given set of data is as follows:

Mean = Sum of Observations/Total number of observations

The other two statistical methods used are median and mode to obtain a result for a given set of data. The median is defined as the value present in the middle of a given set of data and the mode is the frequency with which a particular number occurs in a given set of data.

(Image will be uploaded soon)

In order to find the mean of 4, 5, 6, 3, and 7, first, we have to add the numbers and then divide the sum by the number of items.

4 + 5 + 6 + 3 + 7 = 25 i.e. the sum of the numbers is 25.

Mean = = = = 5

So, the mean of the data set 4, 5, 6, 3, and 7 is 5.

How to Find Mean?

The mean value for a given set of data is calculated in a two-step process:

The values given in the data set are added up together.
The total of the values obtained is then divided by the number of values given.

Mean Formula

The measure of central tendencies is used to describe data clusters around a central value. The mean definition indicates a varied formula used to calculate the mean depending on the data provided. The general formula to calculate the mean is as follows:

[Mean = frac{text{Sum of Given Data}}{text{Total Number of Data}}]

When using the Sigma (∑) notation, the mean formula is:

[frac{sum_{i=1}^{n} X_{i}}{N}]

Here,

N = it is the Total number provided in a given data set.

∑ Xi = Total sum of all the data values.

Mean of Negative Numbers

We have seen examples of finding the mean of positive numbers till now. But what if the numbers in the observation list include negative numbers. Let us understand with an instance,

Example: Find the mean of 9, 6, -3, 2, -7, 1.

Add all the numbers first:

Total: 9+6+(-3)+2+(-7)+1 = 9+6-3+2-7+1 = 8

Now divide the total from 6, to get the mean.

Mean = 8/6 = 1.33

Mean Formula with Example

Find the mean for the given set of random data,

3, 5, 9, 17, 19

The given set of data contains the numbers 3, 5, 9, 17, 19
The total number of numerals given is 5
Sum of the given numbers in the data set = 3 + 5 + 9 + 17 + 19 = 53

Therefore, Mean = Sum of given data/Total number of data

=[ frac{53}{5}] =10.6

Hence, the mean for the given data is 10.6.

Different Types of Mean

A. Arithmetic Mean

The arithmetic mean is one of the foremost methods used to obtain the central tendency of a set of data. It encompasses all the values provided by the data set. It is referred to as the ratio of the total sum of given observations to the total number of observations. The arithmetic mean can be positive, negative, or zero. There are two types of Arithmetic Mean,

Simple Arithmetic Mean.
Weighted Arithmetic Mean.

The formula to calculate Arithmetic mean is as follows:

[X = frac{sum_{i=1}^{n} x_{i}p_{i}}{N}]

The arithmetic mean is easy to calculate and is rigidly defined.

B. Geometric Mean

The second type of Mean is the Geometric Mean (GM). It is defined as the average value signifying the set of numbers of central tendencies by calculating the product of their values. Multiplication of the numbers provided and take out the nth root of the multiplied numbers.

Here, n is the total number of values.

Taking an example of two numbers in a given set of data as 4 and 2, the geometric mean is equal to. [sqrt{(4+2)} = sqrt{6} = 2.5]

The difference between the arithmetic mean and the geometric mean is the method. In the arithmetic mean, we add the numbers whereas in the geometric mean we calculate the product of the numbers.

[text{Geometric Mean = } sqrt[n]{prod_{i=1}^{n} x_{i}}]

C. Harmonic Mean

This is one of the methods of central tendency used in Statistics. It is the reciprocal of the arithmetic mean for a given set of data. The Harmonic Mean is based on all values from the data set and it is defined rigidly. It also provides the weightage of the mean in terms of large or small values depending on the data set. This is applied in time and average analysis.

To calculate the harmonic mean for a given set of data, where x1, x2, x3,…, xn are the individual items up to n terms, then,

[text{Harmonic Mean = } frac{n}{[(frac{1}{x_{1}}) + (frac{1}{x_{2}}) + (frac{1}{x_{3}}) + . . . + (frac{1}{x_{n}})]}]

(Image will be uploaded soon)

Properties of Mean

The sum of the deviations taken from the arithmetic mean is zero.
If the mean of n observations x1, x2, x3….,xn is x then (x1-x)+(x2-x)+(x3-x)…+(xn-x)=0. In short, ∑ (x-x)=0
If each observation is increased by p, the mean of new observations is also increased by p.
If the mean of n observations x1, x2, x3….,xn is x then the mean of (x1+p), (x2+p), (x3+p),….,(xn+p) is (x+p).
If each observation is decreased by p, the mean of new observations is also decreased by p.
If the mean of n observations x1, x2, x3….,xnis x then the mean of (x1-p), (x2-p), (x3-p),….,(xn-p) is (x-p).
If each observation is multiplied by p (where p≠0), the mean of new observations is also multiplied by p.
If the mean of n observations x1, x2, x3….,xn is x then the mean of px1, px2,px3,pxn is px.
If each observation is divided by p (where p≠0), the mean of new observations is also divided by p.
If the mean of n observations x1, x2, x3….,xn is x then the mean of

[ frac{X_{1}}{p} ,frac{X_{2}}{p} ,frac{X_{3}}{p} ,…frac{X_{n}}{p} is frac{bar{X}}{p}]

Why is the Average Called the Mean?

To find the mean, add all the data points and divide it by the total number of data points. In the case of Mathematics, we have been always taught that the average is the middle point of all the given numbers. The central value which is called the average in mathematics is called the mean in statistics.

Important points:

The mean is the mathematical average of a set of two or more numbers.
The arithmetic mean and the geometric mean are two types of mean that can be calculated.
Summing the numbers in a set and dividing by the total number gives you the arithmetic mean.
The geometric mean is more complicated and involves the multiplication of the numbers taking the nth root.
The mean helps to assess the performance of an investment or company over a period of time, and many other uses.

Источник

What is Mean in Statistics?

Mean in statistics refers to the average of a collection of values. The collection of values can be two or more. It is a measure of central tendency and output typical value in a collection or set of data.

In its simplest form, it is the mathematical average derived by adding the values given in a set and dividing it by the number of values in the set. In finance and probability, a similar concept is known as expected value, a synonym of mean or average value.

What is Mean in Statistics?
- Mean Explained
- How to Find Mean?
- Types
  - #1 – Arithmetic Mean
  - #2 – Geometric Mean
  - #3 – Harmonic Mean
  - #4 – Root Mean Square
  - #5 – Contraharmonic Mean
- Applications of Mean
- Frequently Asked Questions (FAQs)
- Recommended Articles

Mean refers to the average of values or items in a given set. In its simplest form, it is derived by adding the values given in a set and dividing it by the number of values in the set.
Mean is a central tendency measure. It is also known as the mathematical average or expected value.
The main types are arithmetic, geometric, harmonic, root mean square, and contra harmonic. Each type primarily differs by the formula used.
Its application is substantial in statistics and data analysis.
Example: The average of numbers 1, 3, 5, and 3 will be (1+3+5+3)/4, which is equal to 3.

Mean Explained

The mean is one of the simple methods employed in descriptive statistics used to interpret or summarize the given data set and derive relevant information or conclusion about the population or sample of a population represented by the data set. Most of the time, it is imperative to derive an average to understand the overall performance and simplify the statistical calculations.

It is also combined with the other central tendency measures like mode and median. These three central tendency measures are equal for a frequency distribution with a symmetrical frequency curve. In the case of a positively skewed distribution curve, the mean is greater than the median, and the median is greater than the mode. When the frequency distribution is negatively skewed, the mode is greater than the median, and the median is greater than the mean.

How to Find Mean?

Fundamentally, it is the value obtained by dividing the sum of all observations by the number of observations. The Greek letter μ denotes the population means, and X̄ is the symbol for the sample mean.

∑x: Sum of all observations or data values
X̄: Number of observations in the population (population size)
N: Number of observations in the sample (sample size)

Suppose, if a batch of nine people participated in a maths test; each student scored different marks out of 100 as given below:

Students	Marks
A1	18
B2	36
C3	27
D4	54
E5	72
F6	81
G7	99
H8	90
I9	45

The average mark is:

Sum of all the observations/total number of observations

= 522/9

= 58

So, 58 is the average mark.

Types of Mean

Let’s look into the brief description of a few significant types:

Arithmetic Mean (AM)

Arithmetic Mean is also referred to as the arithmetic average. It is calculated by summing all the observations and then dividing it by the total number of observations.

Geometric Mean (GM)

Geometric Mean involves finding the product of all observations or values and calculating the n^th root of the product of the observations. The value of n indicates the total number of observations. GM’s calculation method is complex compared to AM, and GM is generally less than the AM. GM is commonly used in investment scenarios and is favorable when the observations in the sample exhibit dependence and significant fluctuations.

Harmonic Mean (HM)

Harmonic Mean formula and approach are quite different from other averages as the total number of observations or values are divided by the sum of the reciprocal of each observation or value in the set. It is one of the three classical Pythagorean means; the other two are AM and GM.

Root Mean Square (RMS)

The Root Mean Square calculation starts with finding the AM of squares of the values in the set. Then the square root of the mean square obtained gives the RMS value.

Contraharmonic Mean

It is complementary to the HM. It is calculated by dividing AM of squares of the values by the AM of the values.

Applications of Mean

Its use is integral in experiments, statistics, and data analysis. For example, it is used in statistical testing, academic studies, geographical studies, and agricultural experiments.
Traders and investors derive meaningful information by calculating average returns based on proper context, forming an important input to investment decisions.
It is used in the calculation of dispersion and skewness.
It can be applied to complete a simple time-series data if any one of the data points is missing.
Examples of its application include a quasi-arithmetic mean-based filter for topology optimization and AM filter used for noise reduction.

Frequently Asked Questions (FAQs)

What is mean in math?

In math, it is the average value of a given data set or items in quantitative terms. It is determined to arrive at the most common value among all the data or frequencies collected to give out an average value of the scenario. For example, suppose in a classroom of twenty students all scored different marks on a given test; the mean computes the average marks scored by all the students, therefore the class’s average.

What is the mean, median, and mode formula?

The basic formulas are the following:
Mean = Sum of all the values/ Total number of values
Mode = The number that occurs the most
Median = Middle value in the data set
If the number of observations n is odd:
Median = [(n + 1)/2]^th term
If the number of observations n is an even number:
Median = [(n/2)^th term + ((n/2) + 1)^th term]/2

What is mean corpuscular volume?

It is also known as MCV, and the MCV blood test calculates the average size of red blood cells.

PRONUNCIATION OF MATH

GRAMMATICAL CATEGORY OF MATH

Math is a noun.

A noun is a type of word the meaning of which determines reality. Nouns provide the names for all things: people, objects, sensations, feelings, etc.

WHAT DOES MATH MEAN IN ENGLISH?

math

Mathematics

Mathematics is the study of topics such as quantity, structure, space, and change. There is a range of views among mathematicians and philosophers as to the exact scope and definition of mathematics. Mathematicians seek out patterns and use them to formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proof. When mathematical structures are good models of real phenomena, then mathematical reasoning can provide insight or predictions about nature. Through the use of abstraction and logic, mathematics developed from counting, calculation, measurement, and the systematic study of the shapes and motions of physical objects. Practical mathematics has been a human activity for as far back as written records exist. The research required to solve mathematical problems can take years or even centuries of sustained inquiry. Rigorous arguments first appeared in Greek mathematics, most notably in Euclid’s Elements.

Synonyms and antonyms of math in the English dictionary of synonyms

Translation of «math» into 25 languages

TRANSLATION OF MATH

Find out the translation of math to 25 languages with our English multilingual translator.

The translations of math from English to other languages presented in this section have been obtained through automatic statistical translation; where the essential translation unit is the word «math» in English.

Translator English — Chinese

数学

1,325 millions of speakers

Translator English — Spanish

matemáticas

570 millions of speakers

English

math

510 millions of speakers

Translator English — Hindi

गणित

380 millions of speakers

Translator English — Arabic

الرياضيات

280 millions of speakers

Translator English — Russian

математика

278 millions of speakers

Translator English — Portuguese

matemática

270 millions of speakers

Translator English — Bengali

গণিত

260 millions of speakers

Translator English — French

math

220 millions of speakers

Translator English — Malay

Matematik

190 millions of speakers

Translator English — German

mathe

180 millions of speakers

Translator English — Japanese

数学

130 millions of speakers

Translator English — Korean

수학

85 millions of speakers

Translator English — Javanese

Math

85 millions of speakers

Translator English — Vietnamese

toán học

80 millions of speakers

Translator English — Tamil

கணித

75 millions of speakers

Translator English — Marathi

गणित

75 millions of speakers

Translator English — Turkish

matematik

70 millions of speakers

Translator English — Italian

matematica

65 millions of speakers

Translator English — Polish

matematyka

50 millions of speakers

Translator English — Ukrainian

математика

40 millions of speakers

Translator English — Romanian

matematica

30 millions of speakers

Translator English — Greek

μαθηματικά

15 millions of speakers

Translator English — Afrikaans

wiskunde

14 millions of speakers

Translator English — Swedish

math

10 millions of speakers

Translator English — Norwegian

math

5 millions of speakers

Trends of use of math

TENDENCIES OF USE OF THE TERM «MATH»

The term «math» is very widely used and occupies the 4.721 position in our list of most widely used terms in the English dictionary.

Trends

FREQUENCY

Very widely used

The map shown above gives the frequency of use of the term «math» in the different countries.

Principal search tendencies and common uses of math

List of principal searches undertaken by users to access our English online dictionary and most widely used expressions with the word «math».

FREQUENCY OF USE OF THE TERM «MATH» OVER TIME

The graph expresses the annual evolution of the frequency of use of the word «math» during the past 500 years. Its implementation is based on analysing how often the term «math» appears in digitalised printed sources in English between the year 1500 and the present day.

Examples of use in the English literature, quotes and news about math

10 QUOTES WITH «MATH»

Famous quotes and sentences with the word math.

Music rhythms are mathematical patterns. When you hear a song and your body starts moving with it, your body is doing math. The kids in their parents’ garage practicing to be a band may not realize it, but they’re also practicing math.

Yes, I was a big math and computer geek, that’s true. I was driven by the scholastic side of things. For me, it was all about what I could do with math and computers.

I’ve always liked all the sciences, like math, physics and biology.

I liked English and art and did a lot of painting. And for some reason I was good at math, but I wasn’t an A student. I really had to work hard to get good grades.

I was dyslexic, so math and formulas were not necessarily my strong suit.

It was just like a digital fixation with cards and math and science and then I started to look at images of great magicians from Houdini down the line.

When I was growing up, I always knew I’d be in the top of my class in math, and that gave me a lot of self-confidence.

The average actor might only be able to book six to eight guest star jobs a year — that would be high. So when you start doing the math, you can’t live on that in Los Angeles.

It’s estimated that across Africa 100 elephants are killed for their tusks every day. It takes nothing more than simple math to get to what that adds up to in a year, and it’s a distressing figure.

I had decent but not great grades in high school because I was highly motivated in some subjects, like the arts, drama, English, and history, but in math and science I was a screw-up. Wooster saw something in me, and I really flourished there. I got into theatre, took photography and painting classes.

10 ENGLISH BOOKS RELATING TO «MATH»

Discover the use of math in the following bibliographical selection. Books relating to math and brief extracts from same to provide context of its use in English literature.

The Math Book: From Pythagoras to the 57th Dimension, 250 …

This book covers 250 milestones in mathematical history, beginning millions of years ago with ancient «ant odometers» and moving through time to our modern-day quest for new dimensions.

Clifford A. Pickover, 2009

«Combining mathematical rigor with light romance, Math Girls is a unique introduction to advanced mathematics, delivered through the eyes of three students as they learn to deal with problems seldom found in textbooks.» — Front flap.

Conquering Math Anxiety

This third edition of Arem’s CONQUERING MATH ANXIETY workbook presents a comprehensive, multifaceted treatment approach to reduce math anxiety and math avoidance.

Kaplan SAT Math Workbook

Includes everything students need to conquer the Math section of the exam with: In-depth coverage and targeted practice for the SAT Math section 2 realistic math tests with detailed answer explanations covering all parts of the SAT math …

Staff of Kaplan Test Prep and Admissions, 2008

Barron’s SAT Math Workbook

Presents a study guide which covers basic arithmetic skills, algebra, word problems, and geometry. (back cover) Exercises and practice tests to hone your math skills and prepare you to excel on the SAT Detailed solutions for all problems A …

Important Notice: Media content referenced within the product description or the product text may not be available in the ebook version.

The Math Behind the Music

Looks at the mathematical aspects of music, covering such topics as compositional techniques, scales, tuning systems, and music criticism.

Kaplan GMAT Math Workbook

Features: Targeted review of the math concepts students need to know Hundreds of exercises to help readers assess their current skill level and focus study efforts, as well as… explanations and practice for all the question types in the …

Mensa Challenge Your Brain Math and Logic Puzzles

Give your brain a workout on the type of brainteasers that challenge the best solvers at the World Puzzle Championships.

Dave Tuller, Michael Rios, 2005

Graduate Record Exam test takers who feel the need for extra help with math will value this brand-new workbook.

10 NEWS ITEMS WHICH INCLUDE THE TERM «MATH»

Find out what the national and international press are talking about and how the term math is used in the context of the following news items.

How Outwhiz Is Motivating The Unmotivated When It Comes To …

To survive in today’s digital world basic math proficiency is a prerequisite. It’s foundational for learning how to code, look at financial statements … «Forbes, Jul 15»

Signature graduate named Mr. Math by Gov. Pence

EVANSVILLE — Adam Lonnberg, a 2015 Signature School graduate, can now officially refer to himself as “Mr. Math.” Lonnberg, 18, who prefers … «Evansville Courier & Press, Jul 15»

The U.S.’s Math Olympiad Win Breaks China’s Dominance

The International Mathematical Olympiad (IMO) is a competition for high schoolers around the world. The U.S. ranks 36 of 65 countries and economies on math … «FiveThirtyEight, Jul 15»

Colonial Elementary student records perfect score in Math …

Last spring, for example, his perfect score in Math Olympiads competitions — as a fifth-grader at Colonial Elementary School — catapulted both … «Montgomery Newspapers, Jul 15»

Crazy 8s program at Conshohocken Free Library keeps children …

CONSHOHOCKEN >> A math-oriented kids’ group called the Crazy 8s Club has become “a major hit” at the Conshohocken Free Library, … «Montgomery Newspapers, Jul 15»

Why chirpy cicadas are a bunch of math geniuses

If you’re in the Midwest, your summer might have a very crunchy soundtrack: The sounds of hordes of cicadas emerging from the Earth, chirping … «Washington Post, Jul 15»

Raymond S. Gomez, longtime Falls math teacher

Sept. 18, 1939 – July 19, 2015. LEWISTON – Raymond Salvatore Gomez of Lewiston, a longtime mathematics teacher at Niagara Falls High … «Buffalo News, Jul 15»

Police Help Form Math And Science Club For West Side Kids

Officer Erin Carlquist (L) and Officer Lissette Rosado (R) working with youngsters in a math and science club designed to help children learn … «CBS Local, Jul 15»

Math Says This Is the Perfect Age to Get Married

A new study suggests that people should get married between the ages of 28 and 32 if they don’t want to get divorced, at least in the first five … «TIME, Jul 15»

Peg + Cat: Making Math Cool

When Jennifer Oxley and Billy Aronson pitched the idea for the math-focused preschool TV series Peg + Cat to PBS Kids – which was looking … «Publishers Weekly, Jul 15»

REFERENCE

« EDUCALINGO. Math [online]. Available <https://educalingo.com/en/dic-en/math>. Apr 2023 ».

Download the educalingo app

Discover all that is hidden in the words on

Источник

This is a glossary of common mathematical terms used in arithmetic, geometry, algebra, and statistics.

Abacus: An early counting tool used for basic arithmetic.

Absolute Value: Always a positive number, absolute value refers to the distance of a number from 0.

Acute Angle: An angle whose measure is between 0° and 90° or with less than 90° (or pi/2) radians.

Addend: A number involved in an addition problem; numbers being added are called addends.

Algebra: The branch of mathematics that substitutes letters for numbers to solve for unknown values.

Algorithm: A procedure or set of steps used to solve a mathematical computation.

Angle: Two rays sharing the same endpoint (called the angle vertex).

Angle Bisector: The line dividing an angle into two equal angles.

Area: The two-dimensional space taken up by an object or shape, given in square units.

Array: A set of numbers or objects that follow a specific pattern.

Attribute: A characteristic or feature of an object—such as size, shape, color, etc.—that allows it to be grouped.

Average: The average is the same as the mean. Add up a series of numbers and divide the sum by the total number of values to find the average.

Base: The bottom of a shape or three-dimensional object, what an object rests on.

Base 10: Number system that assigns place value to numbers.

Bar Graph: A graph that represents data visually using bars of different heights or lengths.

BEDMAS or PEMDAS Definition: An acronym used to help people remember the correct order of operations for solving algebraic equations. BEDMAS stands for «Brackets, Exponents, Division, Multiplication, Addition, and Subtraction» and PEMDAS stands for «Parentheses, Exponents, Multiplication, Division, Addition, and Subtraction».

Bell Curve: The bell shape created when a line is plotted using data points for an item that meets the criteria of normal distribution. The center of a bell curve contains the highest value points.

Binomial: A polynomial equation with two terms usually joined by a plus or minus sign.

Box and Whisker Plot/Chart: A graphical representation of data that shows differences in distributions and plots data set ranges.

Calculus: The branch of mathematics involving derivatives and integrals, Calculus is the study of motion in which changing values are studied.

Capacity: The volume of substance that a container will hold.

Centimeter: A metric unit of measurement for length, abbreviated as cm. 2.5 cm is approximately equal to an inch.

Circumference: The complete distance around a circle or a square.

Chord: A segment joining two points on a circle.

Coefficient: A letter or number representing a numerical quantity attached to a term (usually at the beginning). For example, x is the coefficient in the expression x(a + b) and 3 is the coefficient in the term 3y.

Common Factors: A factor shared by two or more numbers, common factors are numbers that divide exactly into two different numbers.

Complementary Angles: Two angles that together equal 90°.

Composite Number: A positive integer with at least one factor aside from its own. Composite numbers cannot be prime because they can be divided exactly.

Cone: A three-dimensional shape with only one vertex and a circular base.

Conic Section: The section formed by the intersection of a plane and cone.

Constant: A value that does not change.

Coordinate: The ordered pair that gives a precise location or position on a coordinate plane.

Congruent: Objects and figures that have the same size and shape. Congruent shapes can be turned into one another with a flip, rotation, or turn.

Cosine: In a right triangle, cosine is a ratio that represents the length of a side adjacent to an acute angle to the length of the hypotenuse.

Cylinder: A three-dimensional shape featuring two circle bases connected by a curved tube.

Decagon: A polygon/shape with ten angles and ten straight lines.

Decimal: A real number on the base ten standard numbering system.

Denominator: The bottom number of a fraction. The denominator is the total number of equal parts into which the numerator is being divided.

Degree: The unit of an angle’s measure represented with the symbol °.

Diagonal: A line segment that connects two vertices in a polygon.

Diameter: A line that passes through the center of a circle and divides it in half.

Difference: The difference is the answer to a subtraction problem, in which one number is taken away from another.

Digit: Digits are the numerals 0-9 found in all numbers. 176 is a 3-digit number featuring the digits 1, 7, and 6.

Dividend: A number being divided into equal parts (inside the bracket in long division).

Divisor: A number that divides another number into equal parts (outside of the bracket in long division).

Edge: A line is where two faces meet in a three-dimensional structure.

Ellipse: An ellipse looks like a slightly flattened circle and is also known as a plane curve. Planetary orbits take the form of ellipses.

End Point: The «point» at which a line or curve ends.

Equilateral: A term used to describe a shape whose sides are all of equal length.

Equation: A statement that shows the equality of two expressions by joining them with an equals sign.

Even Number: A number that can be divided or is divisible by 2.

Event: This term often refers to an outcome of probability; it may answers question about the probability of one scenario happening over another.

Evaluate: This word means «to calculate the numerical value».

Exponent: The number that denotes repeated multiplication of a term, shown as a superscript above that term. The exponent of 3⁴ is 4.

Expressions: Symbols that represent numbers or operations between numbers.

Face: The flat surfaces on a three-dimensional object.

Factor: A number that divides into another number exactly. The factors of 10 are 1, 2, 5, and 10 (1 x 10, 2 x 5, 5 x 2, 10 x 1).

Factoring: The process of breaking numbers down into all of their factors.

Factorial Notation: Often used in combinatorics, factorial notations requires that you multiply a number by every number smaller than it. The symbol used in factorial notation is ! When you see x!, the factorial of x is needed.

Factor Tree: A graphical representation showing the factors of a specific number.

Fibonacci Sequence: A sequence beginning with a 0 and 1 whereby each number is the sum of the two numbers preceding it. «0, 1, 1, 2, 3, 5, 8, 13, 21, 34…» is a Fibonacci sequence.

Figure: Two-dimensional shapes.

Finite: Not infinite; has an end.

Flip: A reflection or mirror image of a two-dimensional shape.

Formula: A rule that numerically describes the relationship between two or more variables.

Fraction: A quantity that is not whole that contains a numerator and denominator. The fraction representing half of 1 is written as 1/2.

Frequency: The number of times an event can happen in a given period of time; often used in probability calculations.

Furlong: A unit of measurement representing the side length of one square acre. One furlong is approximately 1/8 of a mile, 201.17 meters, or 220 yards.

Geometry: The study of lines, angles, shapes, and their properties. Geometry studies physical shapes and the object dimensions.

Graphing Calculator: A calculator with an advanced screen capable of showing and drawing graphs and other functions.

Graph Theory: A branch of mathematics focused on the properties of graphs.

Greatest Common Factor: The largest number common to each set of factors that divides both numbers exactly. The greatest common factor of 10 and 20 is 10.

Hexagon: A six-sided and six-angled polygon.

Histogram: A graph that uses bars that equal ranges of values.

Hyperbola: A type of conic section or symmetrical open curve. The hyperbola is the set of all points in a plane, the difference of whose distance from two fixed points in the plane is a positive constant.

Hypotenuse: The longest side of a right-angled triangle, always opposite to the right angle itself.

Identity: An equation that is true for variables of any value.

Improper Fraction: A fraction whose numerator is equal to or greater than the denominator, such as 6/4.

Inequality: A mathematical equation expressing inequality and containing a greater than (>), less than (<), or not equal to (≠) symbol.

Integers: All whole numbers, positive or negative, including zero.

Irrational: A number that cannot be represented as a decimal or fraction. A number like pi is irrational because it contains an infinite number of digits that keep repeating. Many square roots are also irrational numbers.

Isosceles: A polygon with two sides of equal length.

Kilometer: A unit of measure equal to 1000 meters.

Knot: A closed three-dimensional circle that is embedded and cannot be untangled.

Like Terms: Terms with the same variable and same exponents/powers.

Like Fractions: Fractions with the same denominator.

Line: A straight infinite path joining an infinite number of points in both directions.

Line Segment: A straight path that has two endpoints, a beginning and an end.

Linear Equation: An equation that contains two variables and can be plotted on a graph as a straight line.

Line of Symmetry: A line that divides a figure into two equal shapes.

Logic: Sound reasoning and the formal laws of reasoning.

Logarithm: The power to which a base must be raised to produce a given number. If nx = a, the logarithm of a, with n as the base, is x. Logarithm is the opposite of exponentiation.

Mean: The mean is the same as the average. Add up a series of numbers and divide the sum by the total number of values to find the mean.

Median: The median is the «middle value» in a series of numbers ordered from least to greatest. When the total number of values in a list is odd, the median is the middle entry. When the total number of values in a list is even, the median is equal to the sum of the two middle numbers divided by two.

Midpoint: A point that is exactly halfway between two locations.

Mixed Numbers: Mixed numbers refer to whole numbers combined with fractions or decimals. Example 3 ¹/₂ or 3.5.

Mode: The mode in a list of numbers are the values that occur most frequently.

Modular Arithmetic: A system of arithmetic for integers where numbers «wrap around» upon reaching a certain value of the modulus.

Monomial: An algebraic expression made up of one term.

Multiple: The multiple of a number is the product of that number and any other whole number. 2, 4, 6, and 8 are multiples of 2.

Multiplication: Multiplication is the repeated addition of the same number denoted with the symbol x. 4 x 3 is equal to 3 + 3 + 3 + 3.

Multiplicand: A quantity multiplied by another. A product is obtained by multiplying two or more multiplicands.

Natural Numbers: Regular counting numbers.

Negative Number: A number less than zero denoted with the symbol -. Negative 3 = -3.

Net: A two-dimensional shape that can be turned into a two-dimensional object by gluing/taping and folding.

Nth Root: The nth root of a number is how many times a number needs to be multiplied by itself to achieve the value specified. Example: the 4th root of 3 is 81 because 3 x 3 x 3 x 3 = 81.

Norm: The mean or average; an established pattern or form.

Normal Distribution: Also known as Gaussian distribution, normal distribution refers to a probability distribution that is reflected across the mean or center of a bell curve.

Numerator: The top number in a fraction. The numerator is divided into equal parts by the denominator.

Number Line: A line whose points correspond to numbers.

Numeral: A written symbol denoting a number value.

Obtuse Angle: An angle measuring between 90° and 180°.

Obtuse Triangle: A triangle with at least one obtuse angle.

Octagon: A polygon with eight sides.

Odds: The ratio/likelihood of a probability event happening. The odds of flipping a coin and having it land on heads are one in two.

Odd Number: A whole number that is not divisible by 2.

Operation: Refers to addition, subtraction, multiplication, or division.

Ordinal: Ordinal numbers give relative position in a set: first, second, third, etc.

Order of Operations: A set of rules used to solve mathematical problems in the correct order. This is often remembered with acronyms BEDMAS and PEMDAS.

Outcome: Used in probability to refer to the result of an event.

Parallelogram: A quadrilateral with two sets of opposite sides that are parallel.

Parabola: An open curve whose points are equidistant from a fixed point called the focus and a fixed straight line called the directrix.

Pentagon: A five-sided polygon. Regular pentagons have five equal sides and five equal angles.

Percent: A ratio or fraction with the denominator 100.

Perimeter: The total distance around the outside of a polygon. This distance is obtained by adding together the units of measure from each side.

Perpendicular: Two lines or line segments intersecting to form a right angle.

Pi: Pi is used to represent the ratio of a circumference of a circle to its diameter, denoted with the Greek symbol π.

Plane: When a set of points join together to form a flat surface that extends in all directions, this is called a plane.

Polynomial: The sum of two or more monomials.

Polygon: Line segments joined together to form a closed figure. Rectangles, squares, and pentagons are just a few examples of polygons.

Prime Numbers: Prime numbers are integers greater than 1 that are only divisible by themselves and 1.

Probability: The likelihood of an event happening.

Product: The sum obtained through multiplication of two or more numbers.

Proper Fraction: A fraction whose denominator is greater than its numerator.

Protractor: A semi-circle device used for measuring angles. The edge of a protractor is subdivided into degrees.

Quadrant: One quarter (qua) of the plane on the Cartesian coordinate system. The plane is divided into 4 sections, each called a quadrant.

Quadratic Equation: An equation that can be written with one side equal to 0. Quadratic equations ask you to find the quadratic polynomial that is equal to zero.

Quadrilateral: A four-sided polygon.

Quadruple: To multiply or to be multiplied by 4.

Qualitative: Properties that must be described using qualities rather than numbers.

Quartic: A polynomial having a degree of 4.

Quintic: A polynomial having a degree of 5.

Quotient: The solution to a division problem.

Radius: A distance found by measuring a line segment extending from the center of a circle to any point on the circle; the line extending from the center of a sphere to any point on the outside edge of the sphere.

Ratio: The relationship between two quantities. Ratios can be expressed in words, fractions, decimals, or percentages. Example: the ratio given when a team wins 4 out of 6 games is 4/6, 4:6, four out of six, or ~67%.

Ray: A straight line with only one endpoint that extends infinitely.

Range: The difference between the maximum and minimum in a set of data.

Rectangle: A parallelogram with four right angles.

Repeating Decimal: A decimal with endlessly repeating digits. Example: 88 divided by 33 equals 2.6666666666666…(«2.6 repeating»).

Reflection: The mirror image of a shape or object, obtained from flipping the shape on an axis.

Remainder: The number left over when a quantity cannot be divided evenly. A remainder can be expressed as an integer, fraction, or decimal.

Right Angle: An angle equal to 90°.

Right Triangle: A triangle with one right angle.

Rhombus: A parallelogram with four sides of equal length and no right angles.

Scalene Triangle: A triangle with three unequal sides.

Sector: The area between an arc and two radii of a circle, sometimes referred to as a wedge.

Slope: Slope shows the steepness or incline of a line and is determined by comparing the positions of two points on the line (usually on a graph).

Square Root: A number squared is multiplied by itself; the square root of a number is whatever integer gives the original number when multiplied by itself. For instance, 12 x 12 or 12 squared is 144, so the square root of 144 is 12.

Stem and Leaf: A graphic organizer used to organize and compare data. Similar to a histogram, stem and leaf graphs organize intervals or groups of data.

Subtraction: The operation of finding the difference between two numbers or quantities by «taking away» one from the other.

Supplementary Angles: Two angles are supplementary if their sum is equal to 180°.

Symmetry: Two halves that match perfectly and are identical across an axis.

Tangent: A straight line touching a curve from only one point.

Term: Piece of an algebraic equation; a number in a sequence or series; a product of real numbers and/or variables.

Tessellation: Congruent plane figures/shapes that cover a plane completely without overlapping.

Translation: A translation, also called a slide, is a geometrical movement in which a figure or shape is moved from each of its points the same distance and in the same direction.

Transversal: A line that crosses/intersects two or more lines.

Trapezoid: A quadrilateral with exactly two parallel sides.

Tree Diagram: Used in probability to show all possible outcomes or combinations of an event.

Triangle: A three-sided polygon.

Trinomial: A polynomial with three terms.

Unit: A standard quantity used in measurement. Inches and centimeters are units of length, pounds and kilograms are units of weight, and square meters and acres are units of area.

Uniform: Term meaning «all the same». Uniform can be used to describe size, texture, color, design, and more.

Variable: A letter used to represent a numerical value in equations and expressions. Example: in the expression 3x + y, both y and x are the variables.

Venn Diagram: A Venn diagram is usually shown as two overlapping circles and is used to compare two sets. The overlapping section contains information that is true of both sides or sets and the non-overlapping portions each represent a set and contain information that is only true of their set.

Volume: A unit of measure describing how much space a substance occupies or the capacity of a container, provided in cubic units.

Vertex: The point of intersection between two or more rays, often called a corner. A vertex is where two-dimensional sides or three-dimensional edges meet.

Weight: The measure of how heavy something is.

Whole Number: A whole number is a positive integer.

X-Axis: The horizontal axis in a coordinate plane.

X-Intercept: The value of x where a line or curve intersects the x-axis.

X: The Roman numeral for 10.

x: A symbol used to represent an unknown quantity in an equation or expression.

Y-Axis: The vertical axis in a coordinate plane.

Y-Intercept: The value of y where a line or curve intersects the y-axis.

Yard: A unit of measure that is equal to approximately 91.5 centimeters or 3 feet.

Источник

Types of means[edit]

Pythagorean means[edit]

Arithmetic mean (AM)[edit]

Geometric mean (GM)[edit]

Harmonic mean (HM)[edit]

Relationship between AM, GM, and HM[edit]

Statistical location[edit]

Mean of a probability distribution[edit]

Generalized means[edit]

Power mean[edit]

f-mean[edit]

Weighted arithmetic mean[edit]

Truncated mean[edit]

Interquartile mean[edit]

Mean of a function[edit]

Mean of angles and cyclical quantities[edit]

Fréchet mean[edit]

Trianglar sets[edit]

Swanson’s rule[edit]

Other means[edit]

See also[edit]

Notes[edit]

References[edit]

How to Find Mean?

Mean Formula

Mean of Negative Numbers

Mean Formula with Example

Different Types of Mean

Properties of Mean

Why is the Average Called the Mean?

What is Mean in Statistics?

Table of contents

Mean Explained

How to Find Mean?

Types of Mean

Arithmetic Mean (AM)

Geometric Mean (GM)

Harmonic Mean (HM)

Root Mean Square (RMS)

Contraharmonic Mean

Applications of Mean

Frequently Asked Questions (FAQs)

Recommended Articles

PRONUNCIATION OF MATH

GRAMMATICAL CATEGORY OF MATH

WHAT DOES MATH MEAN IN ENGLISH?

Mathematics

Synonyms and antonyms of math in the English dictionary of synonyms

Translation of «math» into 25 languages

TRANSLATION OF MATH

Translator English — Chinese

Translator English — Spanish

English

Translator English — Hindi

Translator English — Arabic

Translator English — Russian

Translator English — Portuguese

Translator English — Bengali

Translator English — French

Translator English — Malay

Translator English — German

Translator English — Japanese

Translator English — Korean

Translator English — Javanese

Translator English — Vietnamese

Translator English — Tamil

Translator English — Marathi

Translator English — Turkish

Translator English — Italian

Translator English — Polish

Translator English — Ukrainian

Translator English — Romanian

Translator English — Greek

Translator English — Afrikaans

Translator English — Swedish

Translator English — Norwegian

Trends of use of math

TENDENCIES OF USE OF THE TERM «MATH»

FREQUENCY OF USE OF THE TERM «MATH» OVER TIME

Examples of use in the English literature, quotes and news about math