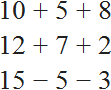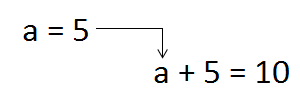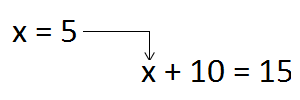From Wikipedia, the free encyclopedia
In mathematics, an expression or mathematical expression is a finite combination of symbols that is well-formed according to rules that depend on the context. Mathematical symbols can designate numbers (constants), variables, operations, functions, brackets, punctuation, and grouping to help determine order of operations and other aspects of logical syntax.
Many authors distinguish an expression from a formula, the former denoting a mathematical object, and the latter denoting a statement about mathematical objects.[citation needed] For example, 


Examples[edit]
The use of expressions ranges from the simple:
-
(linear polynomial)
-
(quadratic polynomial)
-
(rational fraction)
to the complex:
Syntax versus semantics[edit]
Syntax[edit]
An expression is a syntactic construct. It must be well-formed: the allowed operators must have the correct number of inputs in the correct places, the characters that make up these inputs must be valid, have a clear order of operations, etc. Strings of symbols that violate the rules of syntax are not well-formed and are not valid mathematical expressions.
For example, in the usual notation of arithmetic, the expression 1 + 2 × 3 is well-formed, but the following expression is not:
.
Semantics[edit]
Semantics is the study of meaning. Formal semantics is about attaching meaning to expressions.
In algebra, an expression may be used to designate a value, which might depend on values assigned to variables occurring in the expression. The determination of this value depends on the semantics attached to the symbols of the expression. The choice of semantics depends on the context of the expression. The same syntactic expression 1 + 2 × 3 can have different values (mathematically 7, but also 9), depending on the order of operations implied by the context (See also Operations § Calculators).
The semantic rules may declare that certain expressions do not designate any value (for instance when they involve division by 0); such expressions are said to have an undefined value, but they are well-formed expressions nonetheless. In general the meaning of expressions is not limited to designating values; for instance, an expression might designate a condition, or an equation that is to be solved, or it can be viewed as an object in its own right that can be manipulated according to certain rules. Certain expressions that designate a value simultaneously express a condition that is assumed to hold, for instance those involving the operator 
Formal languages and lambda calculus[edit]
Formal languages allow formalizing the concept of well-formed expressions.
In the 1930s, a new type of expressions, called lambda expressions, were introduced by Alonzo Church and Stephen Kleene for formalizing functions and their evaluation. They form the basis for lambda calculus, a formal system used in mathematical logic and the theory of programming languages.
The equivalence of two lambda expressions is undecidable. This is also the case for the expressions representing real numbers, which are built from the integers by using the arithmetical operations, the logarithm and the exponential (Richardson’s theorem).
Variables[edit]
Many mathematical expressions include variables. Any variable can be classified as being either a free variable or a bound variable.
For a given combination of values for the free variables, an expression may be evaluated, although for some combinations of values of the free variables, the value of the expression may be undefined. Thus an expression represents a function whose inputs are the values assigned to the free variables and whose output is the resulting value of the expression.[citation needed]
For example, the expression
evaluated for x = 10, y = 5, will give 2; but it is undefined for y = 0.
The evaluation of an expression is dependent on the definition of the mathematical operators and on the system of values that is its context.
Two expressions are said to be equivalent if, for each combination of values for the free variables, they have the same output, i.e., they represent the same function. Example:
The expression
has free variable x, bound variable n, constants 1, 2, and 3, two occurrences of an implicit multiplication operator, and a summation operator. The expression is equivalent to the simpler expression 12x. The value for x = 3 is 36.
See also[edit]
- Algebraic closure
- Algebraic expression
- Analytic expression
- Closed-form expression
- Combinator
- Computer algebra expression
- Defined and undefined
- Equation
- Expression (programming)
- Formal grammar
- Formula
- Functional programming
- Logical expression
- Term (logic)
- Well-defined expression
Notes[edit]
References[edit]
- Redden, John (2011). «Elementary Algebra». Flat World Knowledge. Archived from the original on 2014-11-15. Retrieved 2012-03-18.
Any real-life scenario containing unknown quantities can be modelled into mathematical statements. For instance, say you wanted to model the population of eagles and frogs in a particular habitat. Each year, the population of frogs double while the population of eagles halves. By creating a suitable expression that describes the decrease of eagles and the increase of frogs in this ecosystem, we can make predictions and identify trends in their population.
In this article, we will discuss expressions, what they look like, and how to factorise and simplify them.
Defining an Expression
An expression can be used to describe a scenario when an unknown number is present or when a variable value exists. It helps solve real-world problems in a more simplified and explicit manner.
A variable value is a value that changes over time.
To construct an expression of this kind, you would need to determine which quantity is unknown in the circumstance, and then define a variable to represent it. Before we dive into this topic further, let us first define expressions.
Expressions are mathematical statements that have two terms at least that contain variables, numbers, or both. Expressions are such that they contain also at least, one mathematical operation; addition, subtraction, multiplication, and division.
Let’s see an example of an expression.
The following is a mathematical expression,
[2x+1]
because it contains one variable, (x), two numbers, (2) and (1), and one mathematical operation, (+).
Expressions are very organised, in a way that a statement that has an operator come right after another one is not a valid expression. For example,
[2x+times 1.]
They are also organised in the sense that when a parenthesis opens, there needs to be a close. For example,
[3(4x+2)-6]
is a valid expression. However,
[6-4(18x]
is not a valid expression.
Components of an Expression
Expressions in algebra contain at least a variable, numbers, and an arithmetic operation. However, there are quite a number of terms related to the parts of an expression. These elements are described below.
-
Variables: Variables are the letters that represent an unknown value in a mathematical statement.
-
Terms: Terms are either numbers or variables (or numbers and variables) multiplying and dividing each other and are separated by either the addition (+) or subtraction sign (-).
-
Coefficient: Coefficients are the numbers that multiply variables.
-
Constant: Constants are the numbers in expressions that do not change.
Components of an expression
Examples of Expressions
Here are some examples of mathematical expressions.
1) ((x+1)(x+3))
2) (6a+3)
3) (6x-15y+12)
4) (y^2+4xy)
5) (frac{x}{4}+frac{x}{5})
Notice that all of them contain the necessary components to be considered expressions. They all have variables, numbers, and at least one mathematical operation composing them.
In particular, in the first example, you will find a multiplication implicit in the parenthesis that connects the two terms (x+1) and (x+3); so it is a valid expression. In the fourth example, in the second term, variables (x) and (y) are multiplying and it’s written as (xy). So, that one is also a valid expression.
Writing Expressions
In this segment of our discussion, we will be introduced to writing expressions, particularly translating word problems into mathematical ones. Such skill is important when solving a given question. By doing so, we can visualise anything in terms of numbers and arithmetic operations!
Translating Word Problems into Expressions
Given a sentence that illustrates a mathematical statement, we can translate them into expressions that involve the appropriate components of expressions we had mentioned before and mathematical symbols. The table below demonstrates several examples of word problems that have been translated into expressions.
|
Phrase |
Expression |
|
Five more than a number |
[x+5] |
|
Three-fourths of a number |
[frac{3y}{4}] |
|
Eight larger than a number |
[a+8] |
|
The product of a number with twelve |
[12z] |
|
The quotient of a number and nine |
[frac{x}{9}] |
Types of Maths Expressions
Numerical Expressions
In comparison to what expressions are, there are expressions that do not contain variables. These are called numerical expressions.
Numerical expressions are a combination of numbers with mathematical operators separating them.
They could be as long as possible, containing as many mathematical operators as possible also.
Here are a few examples of numerical expressions.
1) (13-3)
2) (3-7+14-9)
3) (12+frac{4}{17}-2times 11+1)
4) (4-2-1)
Algebraic Expressions
Algebraic expressions are expressions that contain unknowns. Unknowns are variables that are often represented by letters. In most cases throughout our syllabus, these letters are (x), (y) and (z).
However, we may sometimes get expressions that comprise Greek letters as well. For instance, (alpha), (beta) and (gamma). Below are several examples of algebraic expressions.
1) (frac{2x}{7}+3y^2)
2) (4alpha-3beta + 15)
3) (x^2+3y-4z)
Evaluating Maths Expressions
In this section, we will be introduced to evaluating math expression. Here, we would essentially solve a given expression based on the arithmetic operations between the numbers or variables. These basic arithmetic operations (or mathematical symbols) include addition, subtraction, multiplication and division. We will also see how these operations can help us factorise and simplify such expressions.
Addition and Subtraction of Expressions
Addition and subtraction are the primary actions done when adding and subtracting fractions. These are performed on like terms. There are two steps to consider here, namely
-
Step 1: Identify and rearrange like terms to be grouped.
-
Step 2: Add and subtract like terms.
Below is a worked example.
Add the expressions (5a-7b+3c) and (-4a-2b+3c).
Solution
Step 1: We will first put the two expressions together so we can rearrange them.
[5a-7b+3c+(-4a-2b+3c)]
Then,
[5a-7b+3c-4a-2b+3c]
Next,
[5a-4a-7b-2b+3c+3c]
Step 2: We can now successfully add all the like terms.
[a-9b+6c]
Here is another worked example for you.
Add the expressions
(7x^2+8y-9y), (3y+2-3x^2) and (3-y+3x^2).
Solution
Step 1: We will note them down so that they can be rearranged
[7x^2+8y-9+3y+2-3x^2+3-y+3x^2]
Then,
[7x^2+3x^2-3x^2+8y-y+3y-9+2+3]
Step 2: Add the like terms
[7x^2+10y-4]
Factorising Expressions
This is an important element when it comes to dealing with expressions. It helps us group like terms in order for us to perform arithmetic operations more structured manner.
Factorising is the process of reversing the expansion of brackets.
The factorised form of expressions is always in brackets. The process involves taking out the highest common factors (HCF) from all the terms such that when the factors are taken out and multiplied by the values in the brackets, we will arrive at the same expression we had in the first place.
For example, say you had the expression below.
[4x^2+6x]
Notice here that the coefficients of (x^2) and (x) both have a factor of 2 since 4 and 6 are divisible by 2. Furthermore, (x^2) and (x) have a common factor of (x). Thus, you can take these two factors out of this expression, making the factories form equivalent to
[2x(2x+3)]
Let’s explain this again with another example.
Factorise the expression
[6x+9]
Solution
To factorise this we need to find the HCF of (6x) and 9. That value happens to be 3. Therefore, we will note down the value and account for the bracket.
[3(?+?)]
The sign in the bracket above is gotten from the sign in the initial expression. To find out what values must be in the brackets, we will divide the terms in the expressions that we factorised the 3 from by the 3.
[frac{6x}{3}=2x]
and
[frac{9}{3}=3]
Then, we will arrive at
[3(2x+3)]
We can evaluate to see if the answer we have is right by expanding the brackets.
[(3times 2x)+(3times 3)=6x+9]
as we had before!
Let’s go through one more example.
Simplify the expression
[3y^2+12y]
Solution
We will need to find the HCF. Usually, these can be broken down just if they are a bit too complex at first. Looking at the coefficients, we realise that 3 is the HCF. That will be taken outside the bracket.
[3(?+?)]
We can now divide the expression from which the 3 was factored by the 3.
[frac{3y^2}{3}=y^2]
and
[frac{12y}{3}=4y]
This leaves us with the expression;
[3(y^2+4y)]
However, carefully looking at the expression, we will notice that this can be factored further. (y) can be factored out of the expression in the bracket.
[3y(?+?)]
We will go over the process again by dividing the values that y has been factored from by (y).
[frac{y^2}{y}=y]
and
[frac{4y}{y}=4]
This leaves us with the final expression in its factored form;
[3y(y+4)]
We can evaluate this by expanding the brackets.
[(3ytimes y)+(3ytimes 4)=3y^2+12y]
which again, is what we had at the beginning.
Simplifying Expressions
The term simplifying stems from the root word «simple». As the word suggests, simplifying a given expression allows us to solve them more efficiently. When we simplify an expression, we are reducing it into a simpler form by cancelling common factors and regrouping terms that share the same variable.
Simplifying expressions is the process of writing expressions in their most compact and simplest forms such that the value of the original expression is maintained.
This avoids all the lengthy working you might have to perform that may result in unwanted careless mistakes. Surely, you wouldn’t want to have any arithmetic errors now, would you?
There are three steps to follow when simplifying expressions.
-
Eliminate the brackets by multiplying out the factors (if any are present);
-
Remove exponents by using the exponent rules;
-
Add and subtract like terms.
Let’s go through some worked examples.
Simplify the expression
[3x+2(x-4).]
Solution
Here, we will first operate on the brackets by multiplying the factor (outside the bracket) by what is in the brackets.
[3x+2x-8]
We will add like terms, which will give us our simplified form as
[5x-8]
which indeed holds the same value as the expression we had in the beginning.
Here is another example.
Simplify the expression
[x(4-x)-x(3-x).]
Solution
With this problem, we will deal with the brackets first. We will multiply the factors by elements of the brackets.
[x(4-x)-x(3-x)]
This yields,
[4x-x^2-3x+x^2]
We can go ahead here to rearrange them such that like terms are grouped close together.
[4x-3x-x^2+x^2]
Let us now do the additions and subtractions, which will in turn leave us with:
[4x-3x-x^2+x^2=x]
Expressions — Key takeaways
- Expressions are mathematical statements that have two terms at least that contain variables, numbers, or both.
- Terms are either numbers or variables or numbers and variables multiplying each other.
- Numerical expressions are a combination of numbers with mathematical operators separating them.
- Factorising is the process of reversing the expansion of brackets.
- The factorising process involves taking out the highest common factors (HCF) from all the terms such that when the factors are taken out and multiplied by the values in the brackets, we will arrive at the same expression we had in the first place.
- Simplifying expressions is the process of writing expressions in their most compact and simplest forms such that the value of the original expression is maintained.
Expressions in math are mathematical statements that have a minimum of two terms containing numbers or variables, or both, connected by an operator in between. The mathematical operators can be of addition, subtraction, multiplication, or division. For example, x + y is an expression, where x and y are terms having an addition operator in between. In math, there are two types of expressions, numerical expressions — that contain only numbers; and algebraic expressions- that contain both numbers and variables.
In this article, we will discuss the concept of expressions in math and their different types. We will also understand the difference between an expression and an equation in a tabular way and different types of expressions with the help of examples for a better understanding.
| 1. | |
| 2. | Types of Expressions in Math |
| 3. | Expression vs Equation |
| 4. | Simplifying Expression in Math |
| 5. | FAQs on Expressions in Math |
What is an Expression in Math?
An expression in math is a sentence with a minimum of two numbers/variables and at least one math operation in it. Let us understand how to write expressions. A number is 6 more than half the other number, and the other number is x. This statement is written as x/2 + 6 in a mathematical expression. Mathematical expressions are used to solve complicated puzzles.
Expression Definition in Math
An expression is a combination of terms that are combined by using mathematical operations such as subtraction, addition, multiplication, and division. The terms involved in an expression in math are:
- Constant: A constant is a fixed numerical value.
- Variable: A variable is a symbol that doesn’t have a fixed value.
- Term: A term can be a single constant, a single variable, or a combination of a variable and a constant combined with multiplication or division.
- Coefficient: A coefficient is a number that is multiplied by a variable in an expression.
Expression in Math Example
There are infinite examples of an expression. For example, 2y-9, 3a×2, -7+6÷3, etc. Let us also look at a real-life example. Sarah told her younger brother Daniel that her age is 3 more than twice his age. She asked him to calculate her age if his age is x years. Let’s help him write an expression. Twice the age of Daniel can be written as 2x. Now Sarah’s age is 3 more than 2x. Therefore, Sarah’s age will be written as 2x+3.
Types of Expressions in Math
There are three basic types of mathematical expressions. Based on the terms that they have, they can be classified as arithmetic/numerical expressions, fractional expressions, and algebraic expressions. Let us learn more about each of them with the help of the table given below:
| Types of Mathematical Expressions | Definition of Expression | List of Mathematical Expressions |
|---|---|---|
| Numerical Expression | Contains only numbers and mathematical operators | 40-5+2 |
| Fractional Expression | Contains fractional numbers and mathematical operators | 5/3 — 7/6 |
| Algebraic Expression | Contains variables, numbers, and mathematical operators | 3x+2y |
Now, algebraic expressions are further classified into monomials, binomials, trinomials, etc. They are also termed as polynomials. Let us look at the types of algebraic expressions in the table given below:
| Category | Definition of Expression | Examples |
|---|---|---|
| Monomial | An expression having a single term with non-negative exponential integers. | 2x2 |
| Binomial | An expression formed by the addition or subtraction of two monomials. | 2x2+5xy |
| Trinomial | An expression formed by the addition or subtraction of three monomials. | 2x2+5xy+4yz |
| Polynomial | An expression formed by one or more monomials. | 2x2+5xy+4yz+2y+3 |
Expression vs Equation
In math, expressions and equations are two different concepts. Let us try to understand the difference between the two. An expression can be a number, a variable, or a combination of numbers and variables connected by mathematical operators, i.e., addition, subtraction, multiplication, and division. On the other hand, an equation is the equality relation between two expressions. Look at the table given below to understand it better:
| Expression | Equation |
|---|---|
| Expressions are only one-sided. | Equations are two-sided (left side and right side) |
| Expressions can be simplified to have a numerical answer. | Equations can be solved to verify the equality or to find the missing values. |
| Expression is the combination of terms having operators in between. |
Equation is the combination of two expressions having an ‘equal to’ (=) in between. |
| Example: 3x-8 | Example: 3x-8=16 |
Look at a few more examples of expressions and equations through the figure given below:
Simplifying Expression in Math
Expressions can be simplified to form an answer. For example, 3+6-2 is an expression that can be simplified to 7. There are two different ways to simplify arithmetic expressions and algebraic expressions. We use the BODMAS rule (PEMDAS rule) to simplify them. In case of algebraic expressions, like terms can be added or subtracted for simplification. Like terms are those that have the same variable raised to the same power. So, we can easily add or subtract two or more like terms by adding their coefficients. For example, 2x+5x results in 7x, whereas 7ab-b is an expression that has two unlike terms, which cannot be added.
In the case of expressions having multiple terms and operators, we apply the PEMDAS rule (BODMAS rule). For example, let us simplify 23 — 6 + 7 × 3. Here, as there are no brackets and exponents, we will first evaluate 7 × 3 which is 21. Now, the expression is 23-6+21. Now, there are two operators, addition and subtraction. Since both are same level operations and subtraction is first from the left side, we will subtract 6 from 23, i.e., 17. Now our expression has become 17+21, which results in 38 and 38 is the simplified value of the expression 23 — 6 + 7 × 3.
Important Notes on Expressions in Math:
- An expression has 3 parts: constant, variable, and term.
- There are 3 types of expressions: arithmetic/numerical, fractional, and algebraic.
- Polynomial is a type of variable expression.
Related Articles
- Division of Algebraic Expressions
- Subtraction of Algebraic Expressions
- Addition of Algebraic Expressions
- Simplifying Rational Expressions
FAQs on Expressions in Math
What is Expression in Math?
Expressions in math are mathematical statements that have a minimum of two terms containing numbers or variables, or both, connected by an operator in between. We have different types of expressions in math such as numerical expressions, algebraic expressions, fractional expressions, etc.
How do you Identify Like Terms in Mathematical Expressions?
Like terms, in an expression have the same variables raised to the same power. For example, 5x, −x, and −3x are all like terms.
How do you Write an Expression in Math?
We write an expression in math by using numbers or variables and mathematical operators which are addition, subtraction, multiplication, and division. For example, the expression of the mathematical statement «4 added to 2», will be 2+4.
What is a Numerical Expression?
A numerical expression consists of numbers and operators. Numerical expressions are also called number expressions. Examples of number expressions are 8 — 7, 3 + 6 × 7 — 3, etc.
How Many Terms are there in an Expression?
There can be any number of terms in an expression. Expression is a mathematical phrase that consists of terms separated by operators in between. So, we can have an expression with 1 term, 2 terms, 3 terms, or n number of terms.
What is the Difference Between Mathematical Expression and Algebraic Expression?
Generally, mathematical expressions or numerical expressions have only numbers and operators, while algebraic expressions have both numbers and variables in terms, separated by operators in between.
Can you Solve an Expression in Math?
Since expressions do not have an ‘equal to’ sign (=) we cannot solve them. We can only simplify expressions and find their reduced form using the given mathematical operators.
How to Simplify Expressions in Math?
We can simplify expressions in math by reducing the given expression in the simplest form. If it is a numerical expression, then it can be simplified by finding the value of the expression. If it is an algebraic expression, then it can be simplified by reducing it to the simplest form such that it cannot further be reduced.
An expression in math is a sentence with a minimum of two numbers or variables and at least one math operation. This math operation can be addition, subtraction, multiplication, or division. The structure of an expression is:
Expression is (Number/variable, Math Operator, Number/variable)
Expression Examples:
| Example 1: | $7 + 9$ |
| Example 2: | $23.5 times 4$ |
| Example 3: | $37text{s}$ $–$ $6text{t}$ |
| Example 4: | $25text{a}^4 + 9$ $–$ $4 ÷ 15$ |
In all the given expressions, a math operator is used between the two numbers.
Non Examples of Expressions:
Example 1: a
Example 2: $4$
Example 3: $7.89$
Related Games
Parts of an Expression in Math
An expression in Math is made up of the following:
a) Constant: it is a fixed numerical value.
Example: $7, 45, 4frac{1}{3}, −18, sqrt{5}, 7 + sqrt{11}$
b) Variables: they do not take any fixed values. Values are assigned according to the requirement.
Example: a, p, z
c) Terms: can be constants, variables or constants multiplied by variable/(s). Each term in an expression is separated by ‘+’ sign or ‘−’ sign
Example: In $5text{a} + 2text{b}$ $-$ $7$ the terms are: $5text{a}, 2text{b}$, and $7$.
d) Operators: The four operations of addition (+) , subtraction (−),multiplication (×), division (÷) are used to combine the terms of an expression and are called operators.
Related Worksheets
Types of Expression in Math
Numerical Expression
Numerical expression in Math consists of numbers and arithmetic operators. It does not contain any unknown variables, equality or inequality symbols.
Examples:
$65 + 9$ $–$ $4$
$frac{25}{4}+frac{36}{5}$
$42 div 7 times 4$ $–$ $9 + 7$
$14.5 + 9$
Algebraic Expression
An algebraic expression consists of unknown variables, numbers and arithmetic operators. It does not contain any equality or inequality symbols.
Examples:
$5z$
$3text{x}^2 + 5$
$frac{2}{5}text{a}$ $-$ $frac{7}{11}text{b} + 4.5text{c}$
$0.2text{p}^3$ $text{q}^2 + frac{2}{5}$ $text{p}^2$ $text{q}$
Types of Algebraic Expressions
Algebraic expressions are classified on the basis of the number of terms in the expression. The various types of algebraic expressions are:
- Monomial expressions contain only one term. E.g. $4text{x}$
- Binomial expressions contain two unlike terms. E.g. $2text{xy} +x$
- Trinomial expressions contain only three unlike terms. E.g. $3text{t}2$ $-$ $4text{t} + 9$
- Polynomial expressions have two or more terms. This includes binomials and trinomials too and all other expressions with four or more terms. E.g. $2text{x} + 3text{y} + 5text{z}; 4text{t} + 5$ $−$ $4text{u} + text{z}$
Expression vs Equation
A math expression is different from a math equation.
The difference between expressions and equations is that an expression signifies a combination of numbers, variables, and operation symbols whereas an equation will always use an equal (=) operator between two math expressions. Also both sides of the “equal to” sign have the same value.
For example,
| Expression | Equation |
| $22 + 5$ | $22 + 5 = 29$ $–$ $2$ |
| $9 times 5$ | $9 times 5 = 45$ |
| $50 div 10$ | $45 div 9 = 50 div 10$ |
| $15 + 7$ $–$ $6$ | $15 + 7$ $–$ $6 = 16$ |
| $25 + 7$ | $25 + 7 = 64 div 2$ |
| $20 times 5$ | $20 times 5 = 100$ |
Where are expressions used?
Expressions help us in solving word problems. Math expressions are formed using the words of a problem.
Let’s consider the following problem as an example:
Let’s consider a word problem and learn how to write expressions in math
1. Tom has to fill a box with oranges and apples. The number of apples should be 5 more than oranges. Tom picks 3 oranges each time and repeats it 5 times. Count the total number of oranges and apples.
To solve this, formulate the math expressions as follows:
Number of oranges = $3 times 5$
Number of oranges = $15$
Number of apples = Number of oranges $ + 5$
Number of apples = $15 + 5$
Number of apples = $20$
Total number of fruits = Number of oranges + Number of apples
Third math expression will be:
Total number of fruits = $15 + 20$ (Substituting the value of number of oranges and apples)
$= 35$
2. A class of students are going on a trip. Each student has to pay an individual fee of $$$8 and a group fee of $$$30. Write an algebraic expression for the total cost of the trip. Find the total cost of the trip if there are 56 students going on the trip.
Let n represent the number of students.
Algebraic expression will be:
$$$8n + $$$30
To find the total cost of the trip, when n = 56.
$$$8n + $$$30
$$$8(56) + $$$30 (Substituting n with 56)
$$$448 + $$$30
$$$478
PEDMAS
PEDMAS is an acronym where P stands for parenthesis, E for exponents, D for division, M for multiplication, A for addition, and S stands for subtraction.
The order of the letters indicate the order in which the operation must be performed.
The operations of multiplication and division have the same level of priority. Always perform the operation which appears first from left to right.
Similarly addition and subtraction have the same level of priority. Here also perform the one that appears first from left to right.
Example:
$(15 div 3 times 4$ $−$ $7) + (19$ $−$ $4^2)$
$= (5 × 4 − 7) + × (19 − 16)$
$= (20 − 7) + 3$
$= 13 + 3$
$= 16$
Application:
The knowledge of applying math operations on numbers is the first step towards building basic arithmetic reasoning and logic in children. Formulation of math expressions using the respective skill lays a strong foundation to learn algebra and translate real-life problems in suitable mathematical models.
Solved Examples on Expression:
Example 1: Write whether each is an expression or an equation.
| (a) $4 + 8$ | (b) $4 + 12 = 16$ | (c) $5 times 35$ |
| (d) $16 div 4 + 9$ $–$ $2$ | (e) $8 times 4 div 2 = 16$ | (f) $72+94$ |
Solution:
| Expression | Equation |
| $4 + 8$ | $4 + 12 = 16$ |
| $5 times 35$ | $8 times 4 div 2 = 16$ |
| $16 div 4 + 9$ $–$ $2$ | |
| $72+94$ |
Example 2: Write each word phrase as an expression.
- The sum of $10$ and $14$
- 3 more than a number $7$
- Two times $11$, increased by $1$
- 19 less than the product of $15$ and $4$
- The quotient of $33$ and $3$
Solution:
- $10 + 14$
- $7 + 3$
- $2 times 11 + 1$
- $15 times 4$ $–$ $19$
- $33 div 3$
Example 3: Classify the following expression as arithmetic or algebraic.
- $4text{a}$ $–$ $7text{b}$
- $23 + 42$ $–$ $6$
- $715$ $-$ $911$
- $2$ $-$ $5text{x}9text{y}$
- $22$ $–$ $5 + 8$
- $7text{y} + 19text{x}$ $–$ $4text{z}$
Solution:
| Arithmetic | Algebraic |
| $23 + 42$ $–$ $6$ | $4text{a}$ $–$ $7text{b}$ |
| $22$ $–$ $5 + 8$ | $7text{y} + 19text{x}$ $–$ $4text{z}$ |
| $715$ $-$ $911$ | $2$ $-$ $5x9y$ |
Example 4: Write the terms of the given expression $4uv + 7u − 9z + 6z$.
Solution:
$4text{uv}, 7text{u}$, $−$ $9text{z}$ and $6text{z}$ are terms of the given expression.
Example 5: A book has $250$ pages. Ron has $62$ pages left to read. Write an expression to find the number of pages he has read.
Solution:
$250$ $–$ $62$
Example 6: $X$, $Y$, and $Z$ have a few hairbands. $Y$ has $20$ more hairbands than $X$. $Z$ says that she has five more hairbands than the number of headbands that $X$ and $Y$ together have. Express this in the form of an expression?
Solution: Let the number of hair bands with $X$ be$ = text{x}$.
Then, $Y$ has $(text{x}+20)$ hairbands.
$Z$ has $text{x} + (text{x}+20) + 5=2text{x}+25$ hairbands.
Therefore, $Z$ has $(2text{x}+25)$ hairbands.
Practice Problem
$6 + 8 = 14$
$0$ $–$ $16 =$ $–$ $16$
$frac{4}{7}+ frac{4}{7}$ $-$ $frac{1}{7}$
$5text{x}$ $-$ $7text{y}=15$
Correct answer is: $frac{4}{7}+ frac{4}{7}$ $-$ $frac{1}{7}$
As it has numbers (fraction) and mathematical operators, other options are equations as it has equal $(=)$ operator between two math expressions.
$3text{a}+7text{b}$ $-$ $6text{c}=5text{x}$
$9$ $-$ $5text{w}$
$frac{1}{2}+frac{3}{4}$
$44 + 55$
Correct answer is: $9$ $-$ $5text{w}$
It contains variables, numbers, and mathematical operator.Option (a) is an equation, option (c) and option (d) are arithmetic expressions not algebraic as no variables are involved.
Monomial
Binomial
Trinomial
None of these
Correct answer is: Trinomial
If there are three terms in an expression, we call it trinomial expression.
Variable
Constant
Term
Coefficient
Correct answer is: Constant
The term that does not change its value is called a constant.
$3times14$
$10$ $−$ $3 times 14$
$3 times 10$ $−$ $14$
$3 times 14$ $−$ $10$
Correct answer is: $3 times 14$ $−$ $10$
Three times a number 14 is $3 times 14$.
This decreased by 10 equals $3 times 14$ $−$ $10$
$$$$(9.75 + 40)$
$$$$(40 $–$ 9.75)$
$$$$(9.75 times 40)$
$$$$(9.75 $–$ 40)$
Correct answer is: $$$$(9.75 times 40)$
Amount earned in an hour $=$ $$$9.75
Amount earned in 40 hours $=$ $$$$(9.75 times 40)$
Frequently Asked Questions
What is an expression in maths?
An expression is a set of numbers or variables combined using the operations $+$, $–$, $times$ or $div$.
What are types of expression?
Arithmetic expression that contains only numbers and mathematical operators and algebraic expression that contains variables, numbers and mathematical operators.
Can we solve a math expression?
No, we cannot solve a math expression as it does not have an ‘equal to’ sign $( = )$ but we can simplify expressions.
What is the difference between arithmetic expression and algebraic expression?
Mathematical expressions have only numbers and operators, while algebraic expressions have both numbers and variables in terms, separated by operators in between.
Difference Between Algebraic Expression And Equation
What are terms, factors, and coefficients in algebraic expressions? | 6th grade | Khan Academy
| Expression | Equation |
| An expression is a number, a variable, or a combination of numbers and variables and operation symbols. | An equation is made up of two expressions connected by an equal sign. |
| Word example: The sum of 8 and 3 | Word example: The sum of 8 and 3 is equal to 11. |
| Expression: 8 + 3 | |
| Expression with exponent: x2 4 | Equation with exponent: x2 4 = 0 |
What Is Numerical Expression
The term numerical expression is made up of two words, numerical meaning numbers, and expression meaning phrase. Thus, it is a phrase involving numbers.
A numerical expression in mathematics can be a combination of numbers, and integers combined using mathematical operators such as addition, subtraction, multiplication, or division.
Testing Knowledge Of Mathematical Phrasing For Addition
Use the following questions and answers to help your student learn the correct way to formulate Algebraic expressions based on mathematical phrasing:
- Question: Write seven plus n as an Algebraic expression.
- Question: What expression is used to mean “a number increased by eight.”
- Answer: n + 8 or 8 + n
- Question: Write an expression for “the sum of a number and 22.”
- Answer: n + 22 or 22 + n
As you can tell, all of the questions above deal with Algebraic expressions that deal with the addition of numbers remember to think “addition” when you hear or read the words add, plus, increase or sum, as the resulting Algebraic expression will require the addition sign .
Also Check: Differential Equations And Linear Algebra 4th Edition
Different Terms In Algebra
There are two kinds of terms in algebra: Like Terms and Unlike Terms.
Like Terms: Like terms are terms whose variables and exponent power are the same. They can be simplified by combining them. The operations of addition and subtraction can be performed on them together.
For example, 5x + 8x is an algebraic expression with like terms.
Unlike Terms: Unlike terms are those terms whose variables and their exponents are different from each other. They cannot be simplified by combining them. The operations of addition and subtraction cannot be performed on them together.
For example, 5x + 8y is an algebraic expression with unlike terms.
Let Us Learn about Polynomials
Polynomial comprises two Greek words: the word poly means many and nominal means terms. So, we get the phrase many terms. Polynomials are classified into three different types based on the number of terms it consists of.
The three types of polynomials are:
Algebra: Expressions And Equations
Mathematics is known as the Queen of Science. Algebra is a special branch of mathematics that deals with numbers, shapes and letters. We use concepts of mathematics everywhere, every day, almost in every situation. So far, we have used lots of numbers, lots of shapes and figures. Here, we are going to use some letters in math. Yes, it is algebra lets learn more about it.
- Algebraic Operations on Complex Numbers
Don’t Miss: What Is Density In Physics
Algebraic Expression And Equation Problem
Question: Find the value of x in the given equation: 4x + 10 = 30
Solution:
Given Equation: 4x + 10 = 30
Keep the variable term on the left-hand side, and move the constant term on the right-hand side.
So, the given equation is written as:
4x = 30-10
4x = 20
x = 20/4
x = 5.
Therefore, the value of x is 5.
Alternative Method:
How To Simplify Expressions In Math
We can simplify expressions in math by reducing the given expression in the simplest form. If it is a numerical expression, then it can be simplified by finding the value of the expression. If it is an algebraic expression, then it can be simplified by reducing it to the simplest form such that it cannot further be reduced.
You May Like: How To Know If You Have Chemistry With Someone
What Is An Expression In Math
An expression in math is a sentence with a minimum of two numbers/variables and at least one math operation in it. Let us understand how to write expressions. A number is 6 more than half the other number, and the other number is x. This statement is written as x/2 + 6 in a mathematical expression. Mathematical expressions are used to solve complicated puzzles.
Simplifying Expression In Math
What does factoring an expression mean
Expressions can be simplified to form an answer. For example, 3+6-2 is an expression that can be simplified to 7. There are two different ways to simplify arithmetic expressions and algebraic expressions. We use the BODMAS rule to simplify them. In case of algebraic expressions, like terms can be added or subtracted for simplification. Like terms are those that have the same variable raised to the same power. So, we can easily add or subtract two or more like terms by adding their coefficients. For example, 2x+5x results in 7x, whereas 7ab-b is an expression that has two unlike terms, which cannot be added.
In the case of expressions having multiple terms and operators, we apply the PEMDAS rule . For example, let us simplify 23 – 6 + 7 × 3. Here, as there are no brackets and exponents, we will first evaluate 7 × 3 which is 21. Now, the expression is 23-6+21. Now, there are two operators, addition and subtraction. Since both are same level operations and subtraction is first from the left side, we will subtract 6 from 23, i.e., 17. Now our expression has become 17+21, which results in 38 and 38 is the simplified value of the expression 23 – 6 + 7 × 3.
Important Notes on Expressions in Math:
- An expression has 3 parts: constant, variable, and term.
- There are 3 types of expressions: arithmetic/numerical, fractional, and algebraic.
- Polynomial is a type of variable expression.
Related Articles
You May Like: What Is The Definition Of Mantle In Geography
Formal Languages And Lambda Calculus
Formal languages allow formalizing the concept of well-formed expressions.
In the 1930s, a new type of expressions, called lambda expressions, were introduced by Alonzo Church and Stephen Kleene for formalizing functions and their evaluation. They form the basis for lambda calculus, a formal system used in mathematical logic and the theory of programming languages.
The equivalence of two lambda expressions is undecidable. This is also the case for the expressions representing real numbers, which are built from the integers by using the arithmetical operations, the logarithm and the exponential .
S Of An Expression In Math
An expression in Math is made up of the following:
a) Constant: itis a fixed numerical value.
Example: $7, 45, 4frac, 18, sqrt, 7 + sqrt$
b) Variables: they do not take any fixed values. Values are assigned according to the requirement.
Example: a, p, z
c) Terms: can be constants, variables or constants multiplied by variable/. Each term in an expression is separated by + sign or sign
Example: In $5a + 2b -7$ the terms are: $5a, 2b, and 7$.
d) Operators: The four operations of addition , subtraction ,multiplication , division are used to combine the terms of an expression and are called operators.
Read Also: What Is Grid In Geography
How To Simplify Math Expressions
wikiHow is a wiki, similar to Wikipedia, which means that many of our articles are co-written by multiple authors. To create this article, 19 people, some anonymous, worked to edit and improve it over time. This article has been viewed 304,150 times.Learn more…
Math students are often asked to give their answers in “the simplest terms”in other words, to write answers as small as possible. Though a long, ungainly expression and a short, elegant one may technically equal the same thing, often, a math problem isn’t considered “done” until the answer has been reduced to the simplest terms. In addition, answers in the simplest terms are almost always the easiest expressions to work with. For these reasons, learning how to simplify expressions is a crucial skill for aspiring mathematicians.
Basic Mathematical Symbols With Name Meaning And Examples
The basic mathematical symbols used in Maths help us to work with mathematical concepts in a theoretical manner. In simple words, without symbols, we cannot do maths. The mathematical signs and symbols are considered as representative of the value. The basic symbols in maths are used to express mathematical thoughts. The relationship between the sign and the value refers to the fundamental need of mathematics. With the help of symbols, certain concepts and ideas are clearly explained. Here is a list of commonly used mathematical symbols with names and meanings. Also, an example is provided to understand the usage of mathematical symbols.
| Symbol |
|---|
Recommended Reading: Is Psychology Part Of Stem
Translating Words Into Mathematical Expressions
In this section we turn our attention to translating word phrases into mathematical expressions. We begin with phrases that translate into sums. There is a wide variety of word phrases that translate into sums. Some common examples are given in Table , though the list is far from complete. In like manner, a number of phrases that translate into differences are shown in Table .
Table : Translating words into symbols.
| Phrase | |||
|---|---|---|---|
| sum of x and 12 | x + 12 | difference of x and 12 | x 12 |
| a) Phrases that are sums | b) Phrases that are differences |
Lets look at some examples, some of which translate into expressions involving sums, and some of which translate into expressions involving differences.
Example 1
Translate the following phrases into mathematical expressions:
Exercise
Translate the following phrases into mathematical expressions:
-
y 12
Example 2
Let W represent the width of the rectangle. The length of a rectangle is 4 feet longer than its width. Express the length of the rectangle in terms of its width W.
Solution
We know that the width of the rectangle is W. Because the length of the rectangle is 4 feet longer that the width, we must add 4 to the width to find the length.
Thus, the length of the rectangle, in terms of its width W, is 4 + W.
Exercise
- Answer
-
L 5
Example 3
What Does # Mean In A Mathematical Expression
What does # mean in this formula? )/)]1
I’ve tried to google it in various terms but haven’t found any examples of other formulas with it, and it’s also not explained in the appendices of the book I read.
- Dietrich BurdeSep 2 at 10:32
- $begingroup$But some people use this also in a different context, i.e., for matrices, $A^$, or $A^$.$endgroup$ Dietrich BurdeSep 2 at 10:39
- $begingroup$Thank you both for your comments. @lulu, so in my first equation, hn = #/), the # refers to the number of x such that its index is between 1 and n and the x itself is between aj-1 and aj, right?$endgroup$ Nin KhodorivskoSep 2 at 13:13
- $begingroup$Well, that’s hard to parse. I have no idea what $x_i$ means nor what the $a_j$ are .$endgroup$
Recommended Reading: What Is The Most Dangerous Biological Weapon
Example: Factor 4×2 9
Hmmm… there don’t seem to be any common factors.
But knowing the Special Binomial Products gives us a clue called the “difference of squares”:
Because 4×2 is 2, and 9 is 2,
So we have:
And that can be produced by the difference of squares formula:
= a2 b2
Where a is 2x, and b is 3.
So let us try doing that:
= 2 2 = 4×2 9
Yes!
So the factors of 4×2 9 are and :
Answer: 4×2 9 =
How can you learn to do that? By getting lots of practice, and knowing “Identities”!
Here is a list of common “Identities” .
It is worth remembering these, as they can make factoring easier.
There are many more like those, but those are the most useful ones.
What Does If And Only If Mean In Mathematics
Algebra Basics: What Are Polynomials? – Math Antics
To understand if and only if, we must first know what is meant by a conditional statement. A conditional statement is one that is formed from two other statements, which we will denote by P and Q. To form a conditional statement, we could say if P then Q.
The following are examples of this kind of statement:
- If it is raining outside, then I take my umbrella with me on my walk.
- If you study hard, then you will earn an A.
- If n is divisible by 4, then n is divisible by 2.
You May Like: How Is Sociology Different From Psychology
Other Forms Of Algebraic Expressions
Multiplication, division, exponentials, and parentheticals are all part of the ways in which Algebraic expressions function, all of which follow an order of operations when presented together. This order then defines the manner in which students solve the equation to get variables to one side of the equals sign and only real numbers on the other side.
Like with addition and subtraction, each of these other forms of value manipulation come with their own terms that help identify which type of operation their Algebraic expression is performing words like times and multiplied by trigger multiplication while words like over, divided by, and split into equal groups denote division expressions.
Once students learn these four basic forms of Algebraic expressions, they can then begin to form expressions that contain exponentials and parentheticals . An example of an exponential expression with parentheticals would be 2×2 + 2.
Are Algebraic Expressions Polynomials
No, not all algebraic expressions are polynomials. But all polynomials are algebraic expressions. The difference is polynomials include only variables and coefficients with mathematical operations but algebraic expressions include irrational numbers in the powers as well.
Also, polynomials are continuous function but algebraic expression may not be continuous sometimes .
Recommended Reading: Which Theorist Published Research Related To The Psychology Of Personality
Types Of Expressions In Math
There are three basic types of mathematical expressions. Based on the terms that they have, they can be classified as arithmetic/numerical expressions, fractional expressions, and algebraic expressions. Let us learn more about each of them with the help of the table given below:
| Types of Mathematical Expressions |
|---|
Look at a few more examples of expressions and equations through the figure given below:
Expression Definition In Math
An expression is a combination of terms that are combined by using mathematical operations such as subtraction, addition, multiplication, and division. The terms involved in an expression in math are:
- Constant: A constant is a fixed numerical value.
- Variable: A variable is a symbol that doesn’t have a fixed value.
- Term: A term can be a single constant, a single variable, or a combination of a variable and a constant combined with multiplication or division.
- Coefficient: A coefficient is a number that is multiplied by a variable in an expression.
Also Check: What Is An Experimental Group In Psychology
Examples Of Numerical Expressions
We can form a numerical expression by combining numbers with various mathematical operators. There is no limit to the number of operators a numerical expression may contain. Some numerical expressions use only one operator between two numbers, and some may contain more.
Some examples of numerical expression are given below:
10 + 5
72 ÷ 8 × 5 4 + 1
82 + 4 10
How To Derive Algebraic Expressions
An algebraic expression is a combination of constants, variables and algebraic operations . We can derive the algebraic expression for a given situation or condition by using these combinations.
For example, Sima age is thrice more than Tina. And the total age of Sima and Tina is 40. Expressing the algebraic form of this condition
3x + x = 40 4x = 40 where x is the age of Tina.
Don’t Miss: Holt Algebra 2 Powerpoint Presentations
How To Solve Algebraic Equations
An algebraic equation contains two algebraic expressions separated by an equal sign in between. The primary purpose of solving algebraic equations is to find the unknown variable in the given expression. While solving the equation, separate the variable terms on one side and constant terms on another side. The variable term can be isolated using the various arithmetic operations such as addition, subtraction, multiplication, division, and other operations like finding square roots, etc.
Types Of Algebraic Expressions
Algebra Basics: Exponents In Algebra – Math Antics
Algebraic expressions are classified on the basis of the number of terms in the expression. The various types of algebraic expressions are:
Also Check: What Does Standard Deviation Mean In Math
Using The Order Of Operations
In mathematics, an expression is a finite combination of symbols that is well-formed according to rules that depend on the context. Symbols can designate numbers (constants), variables, operations, functions, and other mathematical symbols, as well as punctuation, symbols of grouping, and other syntactic symbols. The use of expressions can range from the simple:
- 3 + 5
to the complex:
.
Strings of symbols that violate the rules of syntax are not well-formed and are not valid mathematical expressions. For example:
would not be considered a mathematical expression but only a meaningless jumble.[1]
In algebra an expression may be used to designate a value, which might depend on values assigned to variables occurring in the expression; the determination of this value depends on the semantics attached to the symbols of the expression. These semantic rules may declare that certain expressions do not designate any value; such expressions are said to have an undefined value, but they are well-formed expressions nonetheless. In general the meaning of expressions is not limited to designating values; for instance, an expression might designate a condition, or an equation that is to be solved, or it can be viewed as an object in its own right that can be manipulated according to certain rules. Certain expressions that designate a value simultaneously express a condition that is assumed to hold, for instance those involving the operator 
Being an expression is a syntactic concept; although different mathematical fields have different notions of valid expressions, the values associated to variables does not play a role. See formal language for general considerations on how expressions are constructed, and formal semantics for questions concerning attaching meaning (values) to expressions.
Variables
Many mathematical expressions include letters called variables. Any variable can be classified as being either a free variable or a bound variable.
For a given combination of values for the free variables, an expression may be evaluated, although for some combinations of values of the free variables, the value of the expression may be undefined. Thus an expression represents a function whose inputs are the value assigned the free variables and whose output is the resulting value of the expression.[2]
For example, the expression
- x / y
evaluated for x = 10, y = 5, will give 2; but is undefined for y = 0.
The evaluation of an expression is dependent on the definition of the mathematical operators and on the system of values that is its context.
Two expressions are said to be equivalent if, for each combination of values for the free variables, they have the same output, i.e., they represent the same function. Example:
The expression
has free variable x, bound variable n, constants 1, 2, and 3, two occurrences of an implicit multiplication operator, and a summation operator. The expression is equivalent with the simpler expression 12x. The value for x = 3 is 36.
The ‘+’ and ‘−’ (addition and subtraction) symbols have their usual meanings. Division can be expressed either with the ‘/’ or with a horizontal dash. Thus
are perfectly valid. Also, for multiplication one can use the symbols ‘×’ or a ‘·’ (mid dot), or else simply omit it (multiplication is implicit); so:
are all acceptable. However, notice in the first example above how the «times» symbol resembles the letter ‘x’ and also how the ‘·’ symbol resembles a decimal point, so to avoid confusion it’s best to use one of the later two forms.
An expression must be well-formed. That is, the operators must have the correct number of inputs, in the correct places. The expression 2 + 3 is well formed; the expression * 2 + is not, at least, not in the usual notation of arithmetic.
Expressions and their evaluation were formalised by Alonzo Church and Stephen Kleene[3] in the 1930s in their lambda calculus. The lambda calculus has been a major influence in the development of modern mathematics and computer programming languages.[4]
One of the more interesting results of the lambda calculus is that the equivalence of two expressions in the lambda calculus is in some cases undecidable. This is also true of any expression in any system that has power equivalent to the lambda calculus.
See also
- Algebraic closure
- Algebraic expression
- Combinator
- Defined and undefined
- Expression (programming)
- Formula
- Formal grammar
- Functional programming
References
- ^ Introduction to Algebra
- ^ TalkTalk Reference Encyclopedia
- ^ Biographical Memoir of Stephen Kleene
- ^ Programming Languages and Lambda Calculi
Definition. A mathematical expression is any combination of numbers, letters, and relational operators. We can say that all mathematics consists of expressions.
There are two kinds of expressions: numerical and alphabetical.
Numerical expressions consist of numbers and relational operators.
For example, the following expressions are numerical expressions:
An expression with unknown contain letters in addition to numbers and relational operators. For example, the following expressions are the expressions with unknown:
Letters that are contained in letter expressions are called variables. Remember this once and for all! Ask any schoolboy what a variable is — this question will put him in a stupor, despite the fact that he will solve complex math tasks without knowing what it is. In the meantime, variable is a fundamental concept without an understanding of which mathematics cannot be studied.
By the word «study» we mean independent reading of the relevant literature and the ability to understand what is written there. Otherwise, it seems that you know mathematics with a B grade, you can solve some problems, but you cannot understand what is written in lectures and books. Everyone knows this feeling, especially students.
Since the understanding of a variable is very important, let’s dwell on it in more detail. Look closely at the word «variable. Does it ring any bells? The word «variable» comes from the words «to change», «to change», «to change its value». A variable in mathematics is always expressed by some letter. For example, let’s write the following expression:
a + 5
This is an expression with unknown. There is one variable — a. Because it is a variable, it can change its value at any time. Anyone can change the value: you, your teacher, your friend, anyone. For example, let’s change the value of this variable. Let’s give it the value 5. So let’s write the variable itself, then let’s make an equal sign and write 5
a = 5
What happens as a result of this? The value of the variable a (which is 5) will go into the main expression a + 5, and will be substituted for a.
The value of the variable a is substituted into the original expression
The result is: 5 + 5 = 10
Of course, we have considered the simplest expressions. In practice, there are more complex expressions that contain fractions, powers, roots, and parentheses. This looks scary. But in fact, there’s nothing to be afraid of. The main thing is to understand the principle.
In textbooks, you will often find the following problem: Find the value of the expression x + 10 if x = 5. Such an expression requires that you substitute the value of the variable for it. Let’s do it. The value of the variable x is 5. Substitute that five into the original expression x + 10 and we get 5 + 10 = 15.
The value of the variable x is substituted into the expression x + 10
A variable is a kind of container where the value is stored. Variables are convenient because they allow you, without giving examples, to prove theorems, to write various formulas and laws.
Recall Lesson 2, Basic Operations. To understand what addition is, we gave the example 5 + 2 = 7, and said that the numbers 5 and 2 are the summands of, and the number 7 is the sum result. But we could have understood the topic without the example if we had used a letter expression. Denote the summands by any letters, for example a and b, and denote the sum result by c. Then we would have an expression with three variables a + b = c, and we would say that a and b are the summand and c is the sum.
So, having expression a + b = c, we can use it by substituting any numbers instead of variables a and b. And the variable c will get its value automatically, depending on what numbers we substitute instead of a and b
As practice you can do the following task. The expression a + b = c is given. Find its value if a = 10, b = 6. Variable c will get its value automatically. Write the answer as follows: If a = 10 and b = 6, the variable c is equal to …
Solution:
a + b = c
10 + 6 = 16
Answer: when a = 10 and b = 6, the variable c is 16.
Result of the expression
In elementary school textbooks, you will often find the task to solve something, followed by a list of exercises. When you have an assignment like this in front of you, you should immediately understand what you need to calculate. This is often sounds like «solve an example», but if we are more literate, we should say «evaluate an algebraic expression». Solving an example and finding the value of an expression are actually the same thing.
For example, an expression 10 + 6 is given, and we are asked to find the value of that expression. This means that we need to solve this example. Put an equal sign = and write down the answer:
10 + 6 = 16
The resulting sum (16) is called the value of the expression 10 + 6.
Definition. The value of an expression is the result of the computation described by this expression when the variables and constants in it are assigned values
Let’s look at some more examples:
- 16 is the value of the expression 4 × 4, because 4 × 4 = 16
- 20 is the value of the expression 10 + 10, because 10 + 10 = 20
- 5 is the value of the expression 10 ÷ 2, because 10 ÷ 2 = 5
Exercises
Task 1. Evaluate an algebraic expression 5 + x when x = 4
Task 2. Find the value of the expression a + 3 when a = 7
Task 3. Evaluate an algebraic expression a + a + a when a = 10
Task 4. Find the value of the expression a + b when a = 10 and b = 20
Task 5. Evaluate an algebraic expression b + b + b when b = 5
Video lesson
Continue Learning about Other Math
What does evalute mean in math?
It means to find the value of an expression or algebraic
expression
What is an impresion in math?
If you mean expression, then an expression is a math problem
like 2 multiplyed by 2 or 9-2+3
What is a variable expression in math?
a variable expression in math is a symbol that is in a
sentence
What does it mean to Evaluate a math expression?
evaluate means to figure out the value of something
In math how do you simplify an expression?
Math can be difficult at times. To simplify a math expression,
it is important to follow the order of operations, or PEMDAS.














 .
.