The word energy can be written in a

This article is about the scalar physical quantity. For an overview of and topical guide to energy, see Outline of energy. For other uses, see Energy (disambiguation).

Energy
A plasma lamp, using electrical energy to create plasma, light, heat, movement and a faint sound
Common symbols	E
SI unit	joule
Other units	kW⋅h, BTU, calorie, eV, erg, foot-pound
In SI base units	J = kg⋅m2⋅s−2
Extensive?	yes
Conserved?	yes
Dimension	M L2 T−2

In physics, energy (from Ancient Greek ἐνέργεια (enérgeia) ‘activity’) is the quantitative property that is transferred to a body or to a physical system, recognizable in the performance of work and in the form of heat and light. Energy is a conserved quantity—the law of conservation of energy states that energy can be converted in form, but not created or destroyed. The unit of measurement for energy in the International System of Units (SI) is the joule (J).

Common forms of energy include the kinetic energy of a moving object, the potential energy stored by an object (for instance due to its position in a field), the elastic energy stored in a solid object, chemical energy associated with chemical reactions, the radiant energy carried by electromagnetic radiation, and the internal energy contained within a thermodynamic system. All living organisms constantly take in and release energy.

Due to mass–energy equivalence, any object that has mass when stationary (called rest mass) also has an equivalent amount of energy whose form is called rest energy, and any additional energy (of any form) acquired by the object above that rest energy will increase the object’s total mass just as it increases its total energy.

Human civilization requires energy to function, which it gets from energy resources such as fossil fuels, nuclear fuel, or renewable energy. The Earth’s climate and ecosystems processes are driven by the energy the planet receives from the Sun (although a small amount is also contributed by geothermal energy).

Forms

The total energy of a system can be subdivided and classified into potential energy, kinetic energy, or combinations of the two in various ways. Kinetic energy is determined by the movement of an object – or the composite motion of the components of an object – and potential energy reflects the potential of an object to have motion, and generally is a function of the position of an object within a field or may be stored in the field itself.

While these two categories are sufficient to describe all forms of energy, it is often convenient to refer to particular combinations of potential and kinetic energy as its own form. For example, the sum of translational and rotational kinetic and potential energy within a system is referred to as mechanical energy, whereas nuclear energy refers to the combined potentials within an atomic nucleus from either the nuclear force or the weak force, among other examples.^[1]

Some forms of energy (that an object or system can have as a measurable property)

Type of energy	Description
Mechanical	the sum of macroscopic translational and rotational kinetic and potential energies
Electric	potential energy due to or stored in electric fields
Magnetic	potential energy due to or stored in magnetic fields
Gravitational	potential energy due to or stored in gravitational fields
Chemical	potential energy due to chemical bonds
Ionization	potential energy that binds an electron to its atom or molecule
Nuclear	potential energy that binds nucleons to form the atomic nucleus (and nuclear reactions)
Chromodynamic	potential energy that binds quarks to form hadrons
Elastic	potential energy due to the deformation of a material (or its container) exhibiting a restorative force as it returns to its original shape
Mechanical wave	kinetic and potential energy in an elastic material due to a propagating oscillation of matter
Sound wave	kinetic and potential energy in a material due to a sound propagated wave (a particular type of mechanical wave)
Radiant	potential energy stored in the fields of waves propagated by electromagnetic radiation, including light
Rest	potential energy due to an object’s rest mass
Thermal	kinetic energy of the microscopic motion of particles, a kind of disordered equivalent of mechanical energy

History

The word energy derives from the Ancient Greek: ἐνέργεια, romanized: energeia, lit. ‘activity, operation’,^[2] which possibly appears for the first time in the work of Aristotle in the 4th century BC. In contrast to the modern definition, energeia was a qualitative philosophical concept, broad enough to include ideas such as happiness and pleasure.

In the late 17th century, Gottfried Leibniz proposed the idea of the Latin: vis viva, or living force, which defined as the product of the mass of an object and its velocity squared; he believed that total vis viva was conserved. To account for slowing due to friction, Leibniz theorized that thermal energy consisted of the motions of the constituent parts of matter, although it would be more than a century until this was generally accepted. The modern analog of this property, kinetic energy, differs from vis viva only by a factor of two. Writing in the early 18th century, Émilie du Châtelet proposed the concept of conservation of energy in the marginalia of her French language translation of Newton’s Principia Mathematica, which represented the first formulation of a conserved measurable quantity that was distinct from momentum, and which would later be called «energy».

In 1807, Thomas Young was possibly the first to use the term «energy» instead of vis viva, in its modern sense.^[3] Gustave-Gaspard Coriolis described «kinetic energy» in 1829 in its modern sense, and in 1853, William Rankine coined the term «potential energy». The law of conservation of energy was also first postulated in the early 19th century, and applies to any isolated system. It was argued for some years whether heat was a physical substance, dubbed the caloric, or merely a physical quantity, such as momentum. In 1845 James Prescott Joule discovered the link between mechanical work and the generation of heat.

These developments led to the theory of conservation of energy, formalized largely by William Thomson (Lord Kelvin) as the field of thermodynamics. Thermodynamics aided the rapid development of explanations of chemical processes by Rudolf Clausius, Josiah Willard Gibbs, and Walther Nernst. It also led to a mathematical formulation of the concept of entropy by Clausius and to the introduction of laws of radiant energy by Jožef Stefan. According to Noether’s theorem, the conservation of energy is a consequence of the fact that the laws of physics do not change over time.^[4] Thus, since 1918, theorists have understood that the law of conservation of energy is the direct mathematical consequence of the translational symmetry of the quantity conjugate to energy, namely time.

Units of measure

In 1843, James Prescott Joule independently discovered the mechanical equivalent in a series of experiments. The most famous of them used the «Joule apparatus»: a descending weight, attached to a string, caused rotation of a paddle immersed in water, practically insulated from heat transfer. It showed that the gravitational potential energy lost by the weight in descending was equal to the internal energy gained by the water through friction with the paddle.

In the International System of Units (SI), the unit of energy is the joule, named after Joule. It is a derived unit. It is equal to the energy expended (or work done) in applying a force of one newton through a distance of one metre. However energy is also expressed in many other units not part of the SI, such as ergs, calories, British thermal units, kilowatt-hours and kilocalories, which require a conversion factor when expressed in SI units.

The SI unit of energy rate (energy per unit time) is the watt, which is a joule per second. Thus, one joule is one watt-second, and 3600 joules equal one watt-hour. The CGS energy unit is the erg and the imperial and US customary unit is the foot pound. Other energy units such as the electronvolt, food calorie or thermodynamic kcal (based on the temperature change of water in a heating process), and BTU are used in specific areas of science and commerce.

Scientific use

Classical mechanics

In classical mechanics, energy is a conceptually and mathematically useful property, as it is a conserved quantity. Several formulations of mechanics have been developed using energy as a core concept.

Work, a function of energy, is force times distance.

This says that the work () is equal to the line integral of the force F along a path C; for details see the mechanical work article. Work and thus energy is frame dependent. For example, consider a ball being hit by a bat. In the center-of-mass reference frame, the bat does no work on the ball. But, in the reference frame of the person swinging the bat, considerable work is done on the ball.

The total energy of a system is sometimes called the Hamiltonian, after William Rowan Hamilton. The classical equations of motion can be written in terms of the Hamiltonian, even for highly complex or abstract systems. These classical equations have remarkably direct analogs in nonrelativistic quantum mechanics.^[5]

Another energy-related concept is called the Lagrangian, after Joseph-Louis Lagrange. This formalism is as fundamental as the Hamiltonian, and both can be used to derive the equations of motion or be derived from them. It was invented in the context of classical mechanics, but is generally useful in modern physics. The Lagrangian is defined as the kinetic energy minus the potential energy. Usually, the Lagrange formalism is mathematically more convenient than the Hamiltonian for non-conservative systems (such as systems with friction).

Noether’s theorem (1918) states that any differentiable symmetry of the action of a physical system has a corresponding conservation law. Noether’s theorem has become a fundamental tool of modern theoretical physics and the calculus of variations. A generalisation of the seminal formulations on constants of motion in Lagrangian and Hamiltonian mechanics (1788 and 1833, respectively), it does not apply to systems that cannot be modeled with a Lagrangian; for example, dissipative systems with continuous symmetries need not have a corresponding conservation law.

Chemistry

In the context of chemistry, energy is an attribute of a substance as a consequence of its atomic, molecular, or aggregate structure. Since a chemical transformation is accompanied by a change in one or more of these kinds of structure, it is usually accompanied by a decrease, and sometimes an increase, of the total energy of the substances involved. Some energy may be transferred between the surroundings and the reactants in the form of heat or light; thus the products of a reaction have sometimes more but usually less energy than the reactants. A reaction is said to be exothermic or exergonic if the final state is lower on the energy scale than the initial state; in the less common case of endothermic reactions the situation is the reverse. Chemical reactions are usually not possible unless the reactants surmount an energy barrier known as the activation energy. The speed of a chemical reaction (at a given temperature T) is related to the activation energy E by the Boltzmann’s population factor e^−E/kT; that is, the probability of a molecule to have energy greater than or equal to E at a given temperature T. This exponential dependence of a reaction rate on temperature is known as the Arrhenius equation. The activation energy necessary for a chemical reaction can be provided in the form of thermal energy.

Biology

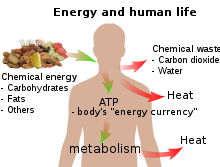
In biology, energy is an attribute of all biological systems, from the biosphere to the smallest living organism. Within an organism it is responsible for growth and development of a biological cell or organelle of a biological organism. Energy used in respiration is stored in substances such as carbohydrates (including sugars), lipids, and proteins stored by cells. In human terms, the human equivalent (H-e) (Human energy conversion) indicates, for a given amount of energy expenditure, the relative quantity of energy needed for human metabolism, using as a standard an average human energy expenditure of 12,500 kJ per day and a basal metabolic rate of 80 watts. For example, if our bodies run (on average) at 80 watts, then a light bulb running at 100 watts is running at 1.25 human equivalents (100 ÷ 80) i.e. 1.25 H-e. For a difficult task of only a few seconds’ duration, a person can put out thousands of watts, many times the 746 watts in one official horsepower. For tasks lasting a few minutes, a fit human can generate perhaps 1,000 watts. For an activity that must be sustained for an hour, output drops to around 300; for an activity kept up all day, 150 watts is about the maximum.^[6] The human equivalent assists understanding of energy flows in physical and biological systems by expressing energy units in human terms: it provides a «feel» for the use of a given amount of energy.^[7]

Sunlight’s radiant energy is also captured by plants as chemical potential energy in photosynthesis, when carbon dioxide and water (two low-energy compounds) are converted into carbohydrates, lipids, proteins and oxygen. Release of the energy stored during photosynthesis as heat or light may be triggered suddenly by a spark in a forest fire, or it may be made available more slowly for animal or human metabolism when organic molecules are ingested and catabolism is triggered by enzyme action.

All living creatures rely on an external source of energy to be able to grow and reproduce – radiant energy from the Sun in the case of green plants and chemical energy (in some form) in the case of animals. The daily 1500–2000 Calories (6–8 MJ) recommended for a human adult are taken as food molecules, mostly carbohydrates and fats, of which glucose (C₆H₁₂O₆) and stearin (C₅₇H₁₁₀O₆) are convenient examples. The food molecules are oxidized to carbon dioxide and water in the mitochondria

and some of the energy is used to convert ADP into ATP:

ADP + HPO₄²⁻ → ATP + H₂O

The rest of the chemical energy of the carbohydrate or fat are converted into heat: the ATP is used as a sort of «energy currency», and some of the chemical energy it contains is used for other metabolism when ATP reacts with OH groups and eventually splits into ADP and phosphate (at each stage of a metabolic pathway, some chemical energy is converted into heat). Only a tiny fraction of the original chemical energy is used for work:^{[note 1]}

gain in kinetic energy of a sprinter during a 100 m race: 4 kJ

gain in gravitational potential energy of a 150 kg weight lifted through 2 metres: 3 kJ

Daily food intake of a normal adult: 6–8 MJ

It would appear that living organisms are remarkably inefficient (in the physical sense) in their use of the energy they receive (chemical or radiant energy); most machines manage higher efficiencies. In growing organisms the energy that is converted to heat serves a vital purpose, as it allows the organism tissue to be highly ordered with regard to the molecules it is built from. The second law of thermodynamics states that energy (and matter) tends to become more evenly spread out across the universe: to concentrate energy (or matter) in one specific place, it is necessary to spread out a greater amount of energy (as heat) across the remainder of the universe («the surroundings»).^{[note 2]} Simpler organisms can achieve higher energy efficiencies than more complex ones, but the complex organisms can occupy ecological niches that are not available to their simpler brethren. The conversion of a portion of the chemical energy to heat at each step in a metabolic pathway is the physical reason behind the pyramid of biomass observed in ecology. As an example, to take just the first step in the food chain: of the estimated 124.7 Pg/a of carbon that is fixed by photosynthesis, 64.3 Pg/a (52%) are used for the metabolism of green plants,^[8] i.e. reconverted into carbon dioxide and heat.

Earth sciences

In geology, continental drift, mountain ranges, volcanoes, and earthquakes are phenomena that can be explained in terms of energy transformations in the Earth’s interior,^[9] while meteorological phenomena like wind, rain, hail, snow, lightning, tornadoes and hurricanes are all a result of energy transformations in our atmosphere brought about by solar energy.

Sunlight is the main input to Earth’s energy budget which accounts for its temperature and climate stability. Sunlight may be stored as gravitational potential energy after it strikes the Earth, as (for example when) water evaporates from oceans and is deposited upon mountains (where, after being released at a hydroelectric dam, it can be used to drive turbines or generators to produce electricity). Sunlight also drives most weather phenomena, save a few exceptions, like those generated by volcanic events for example. An example of a solar-mediated weather event is a hurricane, which occurs when large unstable areas of warm ocean, heated over months, suddenly give up some of their thermal energy to power a few days of violent air movement.

In a slower process, radioactive decay of atoms in the core of the Earth releases heat. This thermal energy drives plate tectonics and may lift mountains, via orogenesis. This slow lifting represents a kind of gravitational potential energy storage of the thermal energy, which may later be transformed into active kinetic energy during landslides, after a triggering event. Earthquakes also release stored elastic potential energy in rocks, a store that has been produced ultimately from the same radioactive heat sources. Thus, according to present understanding, familiar events such as landslides and earthquakes release energy that has been stored as potential energy in the Earth’s gravitational field or elastic strain (mechanical potential energy) in rocks. Prior to this, they represent release of energy that has been stored in heavy atoms since the collapse of long-destroyed supernova stars (which created these atoms).

Cosmology

In cosmology and astronomy the phenomena of stars, nova, supernova, quasars and gamma-ray bursts are the universe’s highest-output energy transformations of matter. All stellar phenomena (including solar activity) are driven by various kinds of energy transformations. Energy in such transformations is either from gravitational collapse of matter (usually molecular hydrogen) into various classes of astronomical objects (stars, black holes, etc.), or from nuclear fusion (of lighter elements, primarily hydrogen). The nuclear fusion of hydrogen in the Sun also releases another store of potential energy which was created at the time of the Big Bang. At that time, according to theory, space expanded and the universe cooled too rapidly for hydrogen to completely fuse into heavier elements. This meant that hydrogen represents a store of potential energy that can be released by fusion. Such a fusion process is triggered by heat and pressure generated from gravitational collapse of hydrogen clouds when they produce stars, and some of the fusion energy is then transformed into sunlight.

Quantum mechanics

In quantum mechanics, energy is defined in terms of the energy operator
(Hamiltonian) as a time derivative of the wave function. The Schrödinger equation equates the energy operator to the full energy of a particle or a system. Its results can be considered as a definition of measurement of energy in quantum mechanics. The Schrödinger equation describes the space- and time-dependence of a slowly changing (non-relativistic) wave function of quantum systems. The solution of this equation for a bound system is discrete (a set of permitted states, each characterized by an energy level) which results in the concept of quanta. In the solution of the Schrödinger equation for any oscillator (vibrator) and for electromagnetic waves in a vacuum, the resulting energy states are related to the frequency by Planck’s relation: (where is the Planck constant and the frequency). In the case of an electromagnetic wave these energy states are called quanta of light or photons.

Relativity

When calculating kinetic energy (work to accelerate a massive body from zero speed to some finite speed) relativistically – using Lorentz transformations instead of Newtonian mechanics – Einstein discovered an unexpected by-product of these calculations to be an energy term which does not vanish at zero speed. He called it rest energy: energy which every massive body must possess even when being at rest. The amount of energy is directly proportional to the mass of the body:

where

• m₀ is the rest mass of the body,
• c is the speed of light in vacuum,
• is the rest energy.

For example, consider electron–positron annihilation, in which the rest energy of these two individual particles (equivalent to their rest mass) is converted to the radiant energy of the photons produced in the process. In this system the matter and antimatter (electrons and positrons) are destroyed and changed to non-matter (the photons). However, the total mass and total energy do not change during this interaction. The photons each have no rest mass but nonetheless have radiant energy which exhibits the same inertia as did the two original particles. This is a reversible process – the inverse process is called pair creation – in which the rest mass of particles is created from the radiant energy of two (or more) annihilating photons.

In general relativity, the stress–energy tensor serves as the source term for the gravitational field, in rough analogy to the way mass serves as the source term in the non-relativistic Newtonian approximation.^[10]

Energy and mass are manifestations of one and the same underlying physical property of a system. This property is responsible for the inertia and strength of gravitational interaction of the system («mass manifestations»), and is also responsible for the potential ability of the system to perform work or heating («energy manifestations»), subject to the limitations of other physical laws.

In classical physics, energy is a scalar quantity, the canonical conjugate to time. In special relativity energy is also a scalar (although not a Lorentz scalar but a time component of the energy–momentum 4-vector).^[10] In other words, energy is invariant with respect to rotations of space, but not invariant with respect to rotations of spacetime (= boosts).

Transformation

Some forms of transfer of energy («energy in transit») from one object or system to another

Type of transfer process	Description
Heat	equal amount of thermal energy in transit spontaneously towards a lower-temperature object
Work	equal amount of energy in transit due to a displacement in the direction of an applied force
Transfer of material	equal amount of energy carried by matter that is moving from one system to another

Energy may be transformed between different forms at various efficiencies. Items that transform between these forms are called transducers. Examples of transducers include a battery (from chemical energy to electric energy), a dam (from gravitational potential energy to kinetic energy of moving water (and the blades of a turbine) and ultimately to electric energy through an electric generator), and a heat engine (from heat to work).

Examples of energy transformation include generating electric energy from heat energy via a steam turbine, or lifting an object against gravity using electrical energy driving a crane motor. Lifting against gravity performs mechanical work on the object and stores gravitational potential energy in the object. If the object falls to the ground, gravity does mechanical work on the object which transforms the potential energy in the gravitational field to the kinetic energy released as heat on impact with the ground. The Sun transforms nuclear potential energy to other forms of energy; its total mass does not decrease due to that itself (since it still contains the same total energy even in different forms) but its mass does decrease when the energy escapes out to its surroundings, largely as radiant energy.

There are strict limits to how efficiently heat can be converted into work in a cyclic process, e.g. in a heat engine, as described by Carnot’s theorem and the second law of thermodynamics. However, some energy transformations can be quite efficient. The direction of transformations in energy (what kind of energy is transformed to what other kind) is often determined by entropy (equal energy spread among all available degrees of freedom) considerations. In practice all energy transformations are permitted on a small scale, but certain larger transformations are not permitted because it is statistically unlikely that energy or matter will randomly move into more concentrated forms or smaller spaces.

Energy transformations in the universe over time are characterized by various kinds of potential energy, that has been available since the Big Bang, being «released» (transformed to more active types of energy such as kinetic or radiant energy) when a triggering mechanism is available. Familiar examples of such processes include nucleosynthesis, a process ultimately using the gravitational potential energy released from the gravitational collapse of supernovae to «store» energy in the creation of heavy isotopes (such as uranium and thorium), and nuclear decay, a process in which energy is released that was originally stored in these heavy elements, before they were incorporated into the Solar System and the Earth. This energy is triggered and released in nuclear fission bombs or in civil nuclear power generation. Similarly, in the case of a chemical explosion, chemical potential energy is transformed to kinetic and thermal energy in a very short time.

Yet another example is that of a pendulum. At its highest points the kinetic energy is zero and the gravitational potential energy is at its maximum. At its lowest point the kinetic energy is at its maximum and is equal to the decrease in potential energy. If one (unrealistically) assumes that there is no friction or other losses, the conversion of energy between these processes would be perfect, and the pendulum would continue swinging forever.

Energy is also transferred from potential energy () to kinetic energy () and then back to potential energy constantly. This is referred to as conservation of energy. In this isolated system, energy cannot be created or destroyed; therefore, the initial energy and the final energy will be equal to each other. This can be demonstrated by the following:

(4)

The equation can then be simplified further since (mass times acceleration due to gravity times the height) and (half mass times velocity squared). Then the total amount of energy can be found by adding .

Conservation of energy and mass in transformation

Energy gives rise to weight when it is trapped in a system with zero momentum, where it can be weighed. It is also equivalent to mass, and this mass is always associated with it. Mass is also equivalent to a certain amount of energy, and likewise always appears associated with it, as described in mass-energy equivalence. The formula E = mc², derived by Albert Einstein (1905) quantifies the relationship between relativistic mass and energy within the concept of special relativity. In different theoretical frameworks, similar formulas were derived by J.J. Thomson (1881), Henri Poincaré (1900), Friedrich Hasenöhrl (1904) and others (see Mass-energy equivalence#History for further information).

Part of the rest energy (equivalent to rest mass) of matter may be converted to other forms of energy (still exhibiting mass), but neither energy nor mass can be destroyed; rather, both remain constant during any process. However, since is extremely large relative to ordinary human scales, the conversion of an everyday amount of rest mass (for example, 1 kg) from rest energy to other forms of energy (such as kinetic energy, thermal energy, or the radiant energy carried by light and other radiation) can liberate tremendous amounts of energy (~ joules = 21 megatons of TNT), as can be seen in nuclear reactors and nuclear weapons. Conversely, the mass equivalent of an everyday amount energy is minuscule, which is why a loss of energy (loss of mass) from most systems is difficult to measure on a weighing scale, unless the energy loss is very large. Examples of large transformations between rest energy (of matter) and other forms of energy (e.g., kinetic energy into particles with rest mass) are found in nuclear physics and particle physics. Often, however, the complete conversion of matter (such as atoms) to non-matter (such as photons) is forbidden by conservation laws.

Reversible and non-reversible transformations

Thermodynamics divides energy transformation into two kinds: reversible processes and irreversible processes. An irreversible process is one in which energy is dissipated (spread) into empty energy states available in a volume, from which it cannot be recovered into more concentrated forms (fewer quantum states), without degradation of even more energy. A reversible process is one in which this sort of dissipation does not happen. For example, conversion of energy from one type of potential field to another is reversible, as in the pendulum system described above. In processes where heat is generated, quantum states of lower energy, present as possible excitations in fields between atoms, act as a reservoir for part of the energy, from which it cannot be recovered, in order to be converted with 100% efficiency into other forms of energy. In this case, the energy must partly stay as thermal energy and cannot be completely recovered as usable energy, except at the price of an increase in some other kind of heat-like increase in disorder in quantum states, in the universe (such as an expansion of matter, or a randomization in a crystal).

As the universe evolves with time, more and more of its energy becomes trapped in irreversible states (i.e., as heat or as other kinds of increases in disorder). This has led to the hypothesis of the inevitable thermodynamic heat death of the universe. In this heat death the energy of the universe does not change, but the fraction of energy which is available to do work through a heat engine, or be transformed to other usable forms of energy (through the use of generators attached to heat engines), continues to decrease.

Conservation of energy

The fact that energy can be neither created nor destroyed is called the law of conservation of energy. In the form of the first law of thermodynamics, this states that a closed system’s energy is constant unless energy is transferred in or out as work or heat, and that no energy is lost in transfer. The total inflow of energy into a system must equal the total outflow of energy from the system, plus the change in the energy contained within the system. Whenever one measures (or calculates) the total energy of a system of particles whose interactions do not depend explicitly on time, it is found that the total energy of the system always remains constant.^[11]

While heat can always be fully converted into work in a reversible isothermal expansion of an ideal gas, for cyclic processes of practical interest in heat engines the second law of thermodynamics states that the system doing work always loses some energy as waste heat. This creates a limit to the amount of heat energy that can do work in a cyclic process, a limit called the available energy. Mechanical and other forms of energy can be transformed in the other direction into thermal energy without such limitations.^[12] The total energy of a system can be calculated by adding up all forms of energy in the system.

Richard Feynman said during a 1961 lecture:^[13]

There is a fact, or if you wish, a law, governing all natural phenomena that are known to date. There is no known exception to this law – it is exact so far as we know. The law is called the conservation of energy. It states that there is a certain quantity, which we call energy, that does not change in manifold changes which nature undergoes. That is a most abstract idea, because it is a mathematical principle; it says that there is a numerical quantity which does not change when something happens. It is not a description of a mechanism, or anything concrete; it is just a strange fact that we can calculate some number and when we finish watching nature go through her tricks and calculate the number again, it is the same.

Most kinds of energy (with gravitational energy being a notable exception)^[14] are subject to strict local conservation laws as well. In this case, energy can only be exchanged between adjacent regions of space, and all observers agree as to the volumetric density of energy in any given space. There is also a global law of conservation of energy, stating that the total energy of the universe cannot change; this is a corollary of the local law, but not vice versa.^[12][13]

This law is a fundamental principle of physics. As shown rigorously by Noether’s theorem, the conservation of energy is a mathematical consequence of translational symmetry of time,^[15] a property of most phenomena below the cosmic scale that makes them independent of their locations on the time coordinate. Put differently, yesterday, today, and tomorrow are physically indistinguishable. This is because energy is the quantity which is canonical conjugate to time. This mathematical entanglement of energy and time also results in the uncertainty principle – it is impossible to define the exact amount of energy during any definite time interval (though this is practically significant only for very short time intervals). The uncertainty principle should not be confused with energy conservation – rather it provides mathematical limits to which energy can in principle be defined and measured.

Each of the basic forces of nature is associated with a different type of potential energy, and all types of potential energy (like all other types of energy) appear as system mass, whenever present. For example, a compressed spring will be slightly more massive than before it was compressed. Likewise, whenever energy is transferred between systems by any mechanism, an associated mass is transferred with it.

In quantum mechanics energy is expressed using the Hamiltonian operator. On any time scales, the uncertainty in the energy is by

which is similar in form to the Heisenberg Uncertainty Principle (but not really mathematically equivalent thereto, since H and t are not dynamically conjugate variables, neither in classical nor in quantum mechanics).

In particle physics, this inequality permits a qualitative understanding of virtual particles, which carry momentum. The exchange of virtual particles with real particles is responsible for the creation of all known fundamental forces (more accurately known as fundamental interactions). Virtual photons are also responsible for the electrostatic interaction between electric charges (which results in Coulomb’s law), for spontaneous radiative decay of excited atomic and nuclear states, for the Casimir force, for the Van der Waals force and some other observable phenomena.

Energy transfer

Closed systems

Energy transfer can be considered for the special case of systems which are closed to transfers of matter. The portion of the energy which is transferred by conservative forces over a distance is measured as the work the source system does on the receiving system. The portion of the energy which does not do work during the transfer is called heat.^{[note 3]} Energy can be transferred between systems in a variety of ways. Examples include the transmission of electromagnetic energy via photons, physical collisions which transfer kinetic energy,^{[note 4]} tidal interactions,^[16] and the conductive transfer of thermal energy.

Energy is strictly conserved and is also locally conserved wherever it can be defined. In thermodynamics, for closed systems, the process of energy transfer is described by the first law:^{[note 5]}

(1)

where is the amount of energy transferred,   represents the work done on or by the system, and represents the heat flow into or out of the system. As a simplification, the heat term, , can sometimes be ignored, especially for fast processes involving gases, which are poor conductors of heat, or when the thermal efficiency of the transfer is high. For such adiabatic processes,

(2)

This simplified equation is the one used to define the joule, for example.

Open systems

Beyond the constraints of closed systems, open systems can gain or lose energy in association with matter transfer (this process is illustrated by injection of an air-fuel mixture into a car engine, a system which gains in energy thereby, without addition of either work or heat). Denoting this energy by , one may write

(3)

Thermodynamics

Internal energy

Internal energy is the sum of all microscopic forms of energy of a system. It is the energy needed to create the system. It is related to the potential energy, e.g., molecular structure, crystal structure, and other geometric aspects, as well as the motion of the particles, in form of kinetic energy. Thermodynamics is chiefly concerned with changes in internal energy and not its absolute value, which is impossible to determine with thermodynamics alone.^[17]

First law of thermodynamics

The first law of thermodynamics asserts that the total energy of a system and its surroundings (but not necessarily thermodynamic free energy) is always conserved^[18] and that heat flow is a form of energy transfer. For homogeneous systems, with a well-defined temperature and pressure, a commonly used corollary of the first law is that, for a system subject only to pressure forces and heat transfer (e.g., a cylinder-full of gas) without chemical changes, the differential change in the internal energy of the system (with a gain in energy signified by a positive quantity) is given as

,

where the first term on the right is the heat transferred into the system, expressed in terms of temperature T and entropy S (in which entropy increases and its change dS is positive when heat is added to the system), and the last term on the right hand side is identified as work done on the system, where pressure is P and volume V (the negative sign results since compression of the system requires work to be done on it and so the volume change, dV, is negative when work is done on the system).

This equation is highly specific, ignoring all chemical, electrical, nuclear, and gravitational forces, effects such as advection of any form of energy other than heat and PV-work. The general formulation of the first law (i.e., conservation of energy) is valid even in situations in which the system is not homogeneous. For these cases the change in internal energy of a closed system is expressed in a general form by

where is the heat supplied to the system and is the work applied to the system.

Equipartition of energy

The energy of a mechanical harmonic oscillator (a mass on a spring) is alternately kinetic and potential energy. At two points in the oscillation cycle it is entirely kinetic, and at two points it is entirely potential. Over a whole cycle, or over many cycles, average energy is equally split between kinetic and potential. This is an example of the equipartition principle: the total energy of a system with many degrees of freedom is equally split among all available degrees of freedom, on average.

This principle is vitally important to understanding the behavior of a quantity closely related to energy, called entropy. Entropy is a measure of evenness of a distribution of energy between parts of a system. When an isolated system is given more degrees of freedom (i.e., given new available energy states that are the same as existing states), then total energy spreads over all available degrees equally without distinction between «new» and «old» degrees. This mathematical result is part of the second law of thermodynamics. The second law of thermodynamics is simple only for systems which are near or in a physical equilibrium state. For non-equilibrium systems, the laws governing the systems’ behavior are still debatable. One of the guiding principles for these systems is the principle of maximum entropy production.^[19][20] It states that nonequilibrium systems behave in such a way as to maximize their entropy production.^[21]

See also

Notes

References

Further reading

Journals

• The Journal of Energy History / Revue d’histoire de l’énergie (JEHRHE), 2018–

External links

• Energy at Curlie
• Differences between Heat and Thermal energy Archived 2016-08-27 at the Wayback Machine – BioCab

Energy
Forms of energy
The effects of energy can be seen, felt or heard in different ways, depending on the form of
energy in question. The main forms are listed below:
•
kinetic energy: energy in the form of movement - a type of mechanical energy
•
thermal energy: energy in the form of heat
•
electrical energy: the energy of an electric current
•
sound energy: energy in the form of noise
•
light energy: for example, light emitted from the sun or from a light bulb
•
chemical energy: energy within substances that can produce a chemical reaction
•
nuclear energy: energy from an atomic reaction.
Energy cannot be created or destroyed, only converted from one form to another. For
example, in a torch powered by batteries, chemical energy stored in the batteries is converted
to electrical energy, and the electrical energy is converted to light energy.
Mechanical energy can be stored as potential energy. An example is a load, lifted by a crane
and suspended at a high level. The weight has the potential (in the future) to be released and
allowed to fall, becoming kinetic energy. Energy can also be stored when a component is
elastically deformed. This is called strain energy. An example is the spring in a watch, which
is wound up, then progressively unwinds.
Note: For more on deformation, see Unit 18. For more on strain , see Unit 30.
Energy efficiency
Machines often convert an energy source,
such as electricity, to another form of useful
energy - in other words, energy used for
a purpose. For example, a motor converts
electrical energy (the energy source) into
kinetic energy (useful energy). But it also
converts some energy into heat and noise.
As this will be dissipated into the air, and not
used, it is waste energy.
A motor: electrical energy --> useful kinetic energy
--> wasted thermal and sound energy
If a machine converts a high percentage of energy into useful energy, it is efficient. For
example, if a motor converts 75% of the electrical energy it consumes into kinetic energy,
and wastes 25% as thermal and sound energy, it is seventy-five percent efficient. Improving
efficiency - making efficiency gains - is a key focus in engineering.
Work and power
The amount of energy needed to do a task - for example, lifting a load to a certain height
by crane - is called work. The amount of energy converted in order to perform tasks - in
other words, the amount of work done- is measured in joules (J). If a force of one newton is
required to keep an object moving, the work required to move that object over a distance of
one metre is equal to one joule.
The speed, or rate, at which work is done is called power, and is measured in watts (W).
One watt is one joule per second. Power, in watts, is often referred to as wattage. A powerful
motor will have a higher wattage than a less powerful one.
35.1
Make word combinations with energy using words from A and B opposite. Then match the
combinations with the descriptions (1-8).
1 ................................ energy
2 ................................ energy
3 ................................ energy
4 ................................ energy
5 ................... ............. energy
6 ................................ energy
7 ............... ................. energy
8 ................................ energy
35.2
=
=
=
=
=
=
=
=
energy stored within the liquids or solids in a battery
mechanical energy in the form of movement
potential energy stored in a deformed material
energy converted to the form required for a purpose
energy converted to a form that cannot be used
the form of energy that shines, and can be seen
the form of energy that can be heard
energy that results in an increase in temperature
Complete the article about electric and diesel-electric locomotives using the words in the box.
Look at A, B and C opposite to help you.
chemical
convert
dissipated
efficiency
efficient
electrical
form
gam
joules
kinetic
power
powered
An electric locomotive is one that is
(1) ................................ by an external energy
(2) ................................ , most often via overhead
electric lines. This differs from a diesel-electric
locomotive, which has an onboard fue l tank and
a diesel-powered generator to provide electricity
for its motors. Purely electric power has
numerous advantages over diesel-electric power,
explaining the choice of electric locomotives for
use in high-speed trains.
powerful
source
stored
thermal
useful
waste
wattage
work
.... An electric locomotive
Firstly, an electric locomotive needs to carry neither a generator nor fuel. Its mass is
therefore lower than a diesel-electric equivalent. This results in a significant efficiency
(3) ................................ ,as the electric locomotive's smal ler mass means less (4) ................................
is done - measured as a total number of (5) ................................ - on a given journey. For a
comparable rate of acceleration, its motors are also required to provide less
(6) ................................ . As they use a lower (7) ................................ ,this means less (8) ................................
motors can be used, making them smaller, thus further reducing weight and improving
(9) ................................. In addition, electric locomotives use only (10) ................................ energy.
This means there is no need to (11) ................................ energy from one (12) ................................ to
another on board the train (electricity can be generated more efficiently in power stations).
In a diesel-electric unit, the energy conversion process starts with (13) ................................
energy, which is (14) ................................ within the hydro-carbon compounds of diesel. This fuel is
burned to produce (15) ................................ energy, and the heat is then converted by the engine
into (16) ................................ energy, which provides the movement to drive the train. This process
is a very long way from being 100% (17) ................................ - only a small percentage of the
initial chemical energy is converted to the (18) ................................ energy that is actually used to
drive the train, with a significant percentage being (19) ................................ into the air in the form
of heat, constituting (20) ................................ energy.

Article Summary & FAQs

What is energy?

Energy is a scalar physical quantity. Energy is generally defined as the potential to do work or produce heat. Sometimes it is like the “currency” for performing work. You must have the energy to accomplish work. To do 1 kilojoule of work, you must expend 1 kilojoule of energy. The total energy cannot be created or destroyed.

Key Facts

• One of the most wonderful properties of the Universe is that energy can be transformed from one type to another and transferred from one object to another.
• The SI unit for energy is the same as the unit of work – the joule (J).
• 1 British Thermal Unit (BTU) = 1055 J
• One joule in everyday life and science corresponds to approximately the energy required to lift a medium-size apple (100 g) 1 meter vertically from the surface of the Earth.
• Energy exists in many forms. Common energy forms include mechanical energy, kinetic energy, or thermal energy.
• A fundamental aspect of the energy concept is that energy is conserved. This principle is known as the first law of thermodynamics.
• One of the striking results of Einstein’s theory of relativity is that mass and energy are equivalent and convertible, one into the other.
• The IEA estimates that, in 2013, the total primary energy supply (TPES) was 157.5 petawatt hours or 1.575×10¹⁷ Wh (157.5 thousand TWh; 5.67×10²⁰ J; 13.54 billion toes).

What are primary energy sources?

What are primary energy sources?

Primary energy (PE) is an energy resource found in nature that has not been subjected to any conversion or transformation process. It is the energy contained in raw fuels and other forms of energy received as input to a system. Primary energy sources take many forms, including nuclear energy, fossil energy — like oil, coal, and natural gas — and renewable sources like wind, solar, geothermal, and hydropower.

What is thermodynamics used for?

What is thermodynamics used for?

Despite the fact it is a very broad subject that affects most fields of science, including biology and microelectronics, we will concern mostly with large-scale observations. Knowledge of thermodynamics is essential to engineers who deal with power plants. Our goal here will be to introduce thermodynamics as the energy conversion science and introduce some of the fundamental concepts and definitions used in the study of engineering thermodynamics. These fundamental concepts and definitions will be further applied to energy systems and finally to thermal or nuclear power plants.

What is nuclear energy?

What is nuclear energy?

Nuclear energy comes either from spontaneous nuclei conversions or induced nuclei conversions. It is associated with nuclear binding energy. If nuclear energy is generated (splitting atoms, nuclear fission), a small amount of mass (saved in the nuclear binding energy) transforms into pure energy (such as kinetic energy, thermal energy, or radiant energy).

The term energy is very broad, and it has many definitions. Technically, energy is a scalar physical quantity that is associated with the state of one or more objects. Energy is generally defined as the potential to do work or produce heat. Sometimes it is like the “currency” for performing work. You must have the energy to accomplish work. To do 1 kilojoule of work, you must expend 1 kilojoule of energy. It must be added. This interpretation can be misleading because energy is not necessarily available to do work.

One of the most wonderful properties of the Universe is that energy can be transformed from one type to another and transferred from one object to another. Moreover, when transformed from one type to another and transferred from one object to another, the total amount of energy is always the same. It is one of the elementary properties of the Universe.

For example, burning gasoline to power cars is an energy conversion process we rely on. The chemical energy in gasoline is converted to thermal energy, then converted to mechanical energy that makes the car move. The mechanical energy has been converted to kinetic energy. When we use the brakes to stop a car, that kinetic energy is converted by friction back to heat or thermal energy.

Energy is generally defined as the potential to do work or produce heat. This definition causes the SI unit for energy to be the same as the unit of work – the joule (J). Joule is a derived unit of energy, and it is named in honor of James Prescott Joule and his experiments on the mechanical equivalent of heat. In more fundamental terms, 1 joule is equal to:

1 J = 1 kg.m²/s²

Since energy is a fundamental physical quantity used in various branches of physics and engineering, there are many units in physics and engineering. These units are summarized in the following points:

Joule (unit: J)

Joule (unit: J). Joule is a derived unit of energy. It is equal to the energy transferred to an object when a force of one newton acts on that object in the direction of its motion through a distance of one meter.

• • 1 joule = 0.239 Calories
  • 1 joule = 9.48 x 10^-4 BTU
  • 1 joule = 2.778 x 10^-7 kWh

Examples of Energy of 1 Joule:

One joule in everyday life and science corresponds to approximately:

• The kinetic energy of an object with mass 1 kg moving at √2 ≈ 1.4 m/s.
• The kinetic energy of a 50 kg object (e.g.,, human) moving very slowly – approximately 0.72 km/h.
• The energy required to lift a medium-size apple (100 g) 1 meter vertically from the surface of the Earth.
• The heat required to raise the temperature of 1 g of water by 0.24 °C.
• The heat required to evaporate of 0.00044 g of liquid water at 100°C.
• The amount of electricity required to light a 1 watt LED for 1 s.
• Is released by approximately 3.1⋅10¹⁰ fissions in a nuclear reactor.

Calorie (unit: cal)

Calorie (unit: cal). A calorie is a traditional unit of heat. It is part of the  International System of Units (SI). It is defined as the amount of heat that must be absorbed by 1 gram of water to raise its temperature by 1 °C. Its counterpart in the British Imperial system of units is the BTU, which is defined as the amount of heat required to raise the temperature of one pound of water by one degree Fahrenheit. But we have to distinguish between small calorie and large calorie. The large calorie (unit: Cal) is defined in terms of the kilogram rather than the gram. It is equal to 1000 small calories, and it is, i.e., 1 kilocalorie (unit: kcal).  Nutritionists use it to characterize the energy-producing potential in food.

• • 1 calorie = 4.184 J
  • 1 calorie = 0.00397 BTU
  • 1 calorie = 1.16 x 10^-6 kWh

British Thermal Unit (unit: BTU)

British Thermal Unit (unit: BTU).  British Thermal Unit is a traditional unit of heat. It is part of the British Imperial system of units. It is defined as the amount of heat that must be absorbed by 1 pound of water to raise its temperature by 1 °F at the temperature that water has its greatest density (approximately 39 degrees Fahrenheit). Its counterpart in the International System of Units (SI) is the calorie, defined as the amount of heat required to raise the temperature of one gram of water by one degree Celsius.

• • 1 British Thermal Unit (BTU) = 1055 J
  • 1 British Thermal Unit (BTU) = 252 calories
  • 1 British Thermal Unit (BTU) = 0.000293 kWh

Foot-pound force (unit: ft.lbf)

Foot-pound force (unit: ft.lbf). Foot-pound force is a derived unit of work and energy. It is equal to the energy transferred to an object when a force of one pound-force (lbf) acts on that object in the direction of its motion through a distance of one foot. The corresponding SI unit is the joule. The foot-pound is often used in ballistics, especially in the United States. Typically muzzle energies of bullets are given in foot-pound force.

• • 1 foot-pound force = 1.356 J
  • 1 foot-pound force = 0.324 cal
  • 1 foot-pound force = 0.00129 BTU

Kilowatt-hour (unit: kWh)

Kilowatt-hour (unit: kWh). Kilowatt-hour is a derived unit of energy. It is used to measure energy, especially electrical energy in commercial applications. One kilowatt-hour is equal to one kilowatt of power produced or consumed over a period of one hour (kilowatts multiplied by the time in hours). Electric utilities commonly use the kilowatt-hour as a billing unit for energy delivered to consumers. 1kW . h = 1kW . 3600s = 3600kWs = 3600kJ = 3600000J. One kilowatt-hour corresponds to the heat required to evaporate 1.58 kg of liquid water at 100°C. A radio rated at 100 watts continuously operating for 10 hours uses one kilowatt-hour.

• • 1 kWh = 3.6 x 10⁶ J
  • 1 kWh = 8.6 x 10⁵ cal
  • 1 kWh = 3412 BTU

Megawatt-day (unit: MWd)

Megawatt-day (unit: MWd).  Megawatt-day is a derived unit of energy. It is used to measure the energy produced, especially in power engineering. One megawatt-day is equal to one megawatt of power produced by a power plant over a period of one day (megawatts multiplied by the time in days). 1 MWd = 24,000 kWh. At nuclear power plants, there are also gigawatt-days because it approximately corresponds to energy produced by power plant over a period of one day. This unit (MWd) was also used to derive the unit of fuel burnup. The most commonly used measure of fuel burnup is the fission energy release per unit mass of fuel. Therefore fuel burnup of nuclear fuel normally has units of megawatt-days per metric tonne (MWd/MTU), where tonne refers to a metric ton of uranium metal (sometimes MWd/tU HM as Heavy Metal). In this field, the megawatt-day refers to the reactor’s thermal power, not the fraction converted to electricity. For example, for a typical nuclear reactor with thermal power of 3000 MWth, about ~1000MWe of electrical power is generated in the generator. For example, a reactor with 100 000 kg of fuel operating at 3000MWth power level for 1000 days would have a burnup increase of 30,000 MWd/MTU. In words of fissions, the fissioning of about 1 g of U-235 produces about 1 MWd of thermal energy (see: Energy Release per Fission).

• • 1 MWd = 8.64 x 10¹⁰ J
  • 1 MWd = 2.06 x 10¹⁰ cal
  • 1 MWd = 8.19 x 10⁷ BTU

Electronvolt (unit: eV)

Electronvolt (unit: eV). Electronvolts are a traditional unit of energy, particularly in atomic and nuclear physics. An electronvolt is equal to the energy gained by a single electron when accelerated through 1 volt of electric potential difference. The work done on the charge is given by the charge times the voltage difference, therefore the work W on electron is: W = qV = (1.6 x 10^-19 C) x (1 J/C) = 1.6 x 10^-19 J. Since this is a very small unit, it is more convenient to use multiples of electronvolts: kilo-electronvolts (keV), mega-electronvolts (MeV), giga-electronvolts (GeV), and so on. Since Albert Einstein showed that mass and energy are equivalent and convertible one into the other, the electronvolt is also a unit of mass. It is common in particle physics, where units of mass and energy are often interchanged, to express mass in units of eV/c², where c is the speed of light in a vacuum (from E = mc²). For example, it can be said the proton has a mass of 938.3 MeV, although strictly speaking, it should be 938.3 MeV/c². For another example, an electron-positron annihilation occurs when a negatively charged electron and a positively charged positron (each with a mass of 0.511 MeV/c²) collide. When an electron and a positron collide, they annihilate, resulting in the complete conversion of their rest mass to pure energy (according to the E=mc² formula) in the form of two oppositely directed 0.511 MeV gamma rays (photons).

e⁻ + e⁺ → γ + γ (2x 0.511 MeV)

• • 1 eV = 1.603 x 10^-19 J
  • 1 eV = 3.83 x 10^-20 cal
  • 1 eV = 1.52 x 10^-22 BTU

Example of Energies in Electronvolts

• Thermal neutrons are neutrons in thermal equilibrium with a surrounding medium of the temperature of 290K (17 °C or 62 °F). Most probable energy at 17°C (62°F) for Maxwellian distribution is 0.025 eV (~2 km/s).
• The thermal energy of a molecule is at room temperature, about 0.04 eV.
• Approximately 1 eV corresponds to an infrared photon of wavelength 1240 nm.
• Visible light photons have energies in range 1.65 eV (red) – 3.26 eV (violet).
• The first resonance in n + ²³⁸U reaction is at 6.67 eV (energy of incident neutron), which corresponds to the first virtual level in ²³⁹U, which has a total width of only 0.027 eV mean life of this state is 2.4×10^-14s.
• The ionization energy of atomic hydrogen is 13.6 eV.
• Carbon-14 decays into nitrogen-14 through beta decay (pure beta decay). The emitted beta particles have a maximum energy of 156 keV, while their weighted mean energy is 49 keV.
• High energy diagnostic medical x-ray photons have kinetic energies of about 200 keV.
• Thallium 208, one of the nuclides in the ²³²U decay chain, emits gamma rays of 2.6 MeV, which are very energetic and highly penetrating.
• The typical kinetic energy of alpha particle from radioactive decay is about 5 MeV. It is caused by the mechanism of their production.
• The total energy released in a reactor is about 210 MeV per ²³⁵U fission, distributed as shown in the table. In a reactor, the average recoverable energy per fission is about 200 MeV, being the total energy minus the energy of antineutrinos that are radiated away.
• Cosmic rays can have energies of 1 MeV – 1000 TeV.

Examples of Energy of 1 Joule

One joule in everyday life and science corresponds to approximately:

• The kinetic energy of an object with mass 1 kg moving at √2 ≈ 1.4 m/s.
• The kinetic energy of a 50 kg object (e.g.,, human) moving very slowly – approximately 0.72 km/h.
• The energy required to lift a medium-size apple (100 g) 1 meter vertically from the surface of the Earth.
• The heat required to raise the temperature of 1 g of water by 0.24 °C.
• The heat required to evaporate of 0.00044 g of liquid water at 100°C.
• The amount of electricity required to light a 1 watt LED for 1 s.
• Is released by approximately 3.1⋅10¹⁰ fissions in a nuclear reactor.

Forms of Energy

Energy exists in many forms. Common energy forms include mechanical energy that is classically divided into kinetic and potential energy. The kinetic energy is related to the velocity of a moving object. The potential energy is related to an object’s position in a force field (gravitational, electric, or magnetic). Tension in a spring or surface film tension is another form of potential mechanical energy (elastic energy). There are many other forms of energy, including electrical, magnetical, chemical, and nuclear energy.

In thermodynamics, the concept of energy is broadened to account for other observed changes. Thermodynamics deals with another type of energy called “thermal energy” or “internal energy”. The only ways the energy of a closed system can be changed are through the transfer of energy by work or by heat. Further, based on the experiments of Joule and others, a fundamental aspect of the energy concept is that energy is conserved. This principle is known as the first law of thermodynamics. In general, energy is a fundamental concept of thermodynamics and one of the most significant aspects of engineering analysis.

Mechanical energy

In physics, mechanical energy (E_mech) is the energy associated with the motion and position of an object, usually in some force field (e.g.,, gravitational field). Mechanical energy (and thermal energy) can be separated into two categories, transient and stored. Transient energy is energy in motion, that is, energy being transferred from one place to another. Stored energy is the energy contained within a substance or object. Transient mechanical energy is commonly referred to as work. Stored mechanical energy exists in one of two forms: kinetic or potential.

Kinetic energy

The kinetic energy, K, is defined as the energy stored in an object because of its motion. An object in motion can do work and thus can be said to have energy. It is called kinetic energy, from the Greek word kinetics, meaning “motion.”

The kinetic energy depends on the speed of an object and is the ability of a moving object to do work on other objects when it collides with them. On the other hand, the kinetic energy of an object represents the amount of energy required to increase the velocity of the object from rest (v = 0) to its final velocity. The kinetic energy also depends linearly on the mass, which is a numerical measure of an object’s inertia and the measure of an object’s resistance to acceleration when a force is applied.

We define the quantity:

K = ½ mv²

to be the translational kinetic energy of the object. It must be added, and it is called the “translational” kinetic energy to distinguish it from rotational kinetic energy

Potential energy

Potential energy, U, is defined as the energy stored in an object subjected to a conservative force. Common types include the gravitational potential energy, the elastic potential energy of an extended spring, and the electric potential energy of an electric charge in an electric field, and so on.

Gravitational energy

In classical mechanics, the gravitational potential energy (U) is the energy an object possesses because of its position in a gravitational field. Gravitational potential (V; the gravitational energy per unit mass) at a location is equal to the work (energy transferred) per unit mass that would be needed to move the object from a fixed reference location to the location of the object. The most common use of gravitational potential energy is for an object near the surface of the Earth, where the gravitational acceleration can be assumed to be constant at about 9.8 m/s².

U = mgh

Internal energy

In thermodynamics, internal energy (also called thermal energy) is defined as the energy associated with microscopic forms of energy. It is an extensive quantity, and it depends on the size of the system or on the amount of substance it contains. The SI unit of internal energy is the joule (J). It is the energy contained within the system, excluding the kinetic energy of motion of the system as a whole and the system’s potential energy. Microscopic forms of energy include those due to the rotation, vibration, translation, and interactions among the molecules of a substance. None of these forms of energy can be measured or evaluated directly. Still, techniques have been developed to evaluate the change in the total sum of all these microscopic forms of energy.

In addition, energy can be stored in the chemical bonds between the atoms that make up the molecules. This energy storage on the atomic level includes energy associated with electron orbital states, nuclear spin, and binding forces in the nucleus.

Enthalpy

In thermodynamics, the enthalpy is a measurement of energy in a thermodynamic system. It is the thermodynamic quantity equivalent to the total heat content of a system. The enthalpy is defined to be the sum of the internal energy E plus the product of the pressure p and volume V. In many thermodynamic analyses, the sum of the internal energy U and the product of pressure p and volume V appears. Therefore it is convenient to give the combination a name, enthalpy, and a distinct symbol, H.

The enthalpy is the preferred expression of system energy changes in many chemical, biological, and physical measurements at constant pressure. It is so useful that it is tabulated in the steam tables along with specific volume and specific internal energy. It is due to the fact. It simplifies the description of energy transfer. At constant pressure, the enthalpy change equals the energy transferred from the environment through heating (Q = H₂ – H₁) or work other than expansion work. For a variable-pressure process, the difference in enthalpy is not quite as obvious.

Entropy

In thermodynamics and statistical physics, entropy is a quantitative measure of disorder or the energy in a system to do work.

In statistical physics, entropy is a measure of the disorder of a system. What disorder refers to is the number of microscopic configurations, W, that a thermodynamic system can have when in a state as specified by certain macroscopic variables (volume, energy, pressure, and temperature). By “microscopic states”, we mean the exact states of all the molecules making up the system.

Mathematically, the exact definition is:

Entropy = (Boltzmann’s constant k) x logarithm of the number of possible states

S = k_B logW

This equation, which relates the microscopic details, or microstates, of the system (via W) to its macroscopic state (via the entropy S), is the key idea of statistical mechanics. In a closed system, entropy never decreases, so in the Universe, entropy is irreversibly increasing. In an open system (for example, a growing tree), entropy can decrease, and the order can increase, but only at the expense of increasing entropy somewhere else (e.g.,, in the Sun).

Gibbs Free Energy

In thermodynamics, the Gibbs free energy is a thermodynamic potential that is defined as the enthalpy of the system minus the product of the temperature times the entropy of the system. Since the enthalpy is defined to be the sum of the internal energy E plus the product of the pressure p and volume V.

Electrical Energy

Electrical energy is the energy derived from electric potential energy or kinetic energy. A typical nuclear power plant has an electric-generating capacity of 1000 MWe. It produces 1 000 000 000 joules of electrical energy per second. The heat source in the nuclear power plant is a nuclear reactor. As is typical in all conventional thermal power stations, the heat is used to generate steam which drives a steam turbine connected to a generator that produces electricity. The turbines are heat engines subject to the efficiency limitations imposed by the second law of thermodynamics. In modern nuclear power plants, the overall thermodynamic efficiency is about one-third (33%), so 3000 MWth of thermal power from the fission reaction is needed to generate 1000 MWe of electrical power.

Since voltage is electric potential energy per unit charge, Kirchhoff’s voltage law can be seen to be a consequence of the conservation of electrical energy. Kirchhoff’s voltage law states:

The algebraic sum of the voltages (drops or rises) encountered in traversing any loop of a circuit in a specified direction must be zero.

The algebraic sum of the voltages (drops or rises) encountered in traversing any loop of a circuit in a specified direction must be zero.

Simply, the voltage changes around any closed loop must sum to zero. The sum of the voltage rises is equal to the sum of the voltage drops in a loop. No matter what path you take through an electric circuit, if you return to your starting point, you must measure the same voltage, constraining the net change around the loop to be zero. This rule is equivalent to saying that each point on a mountain has only one elevation above sea level. If you start from any point and return to it after walking around the mountain, the algebraic sum of the elevation changes that you encounter must be zero.

Radiant Energy

In physics, radiant energy is the energy of electromagnetic and gravitational radiation. The term “radiant energy” is most commonly used in the fields of radiometry, solar energy, heating, and lighting. As energy, its SI unit is the joule (J). The quantity of radiant energy may be calculated by integrating radiant flux concerning time. Radiant heat transfer is very important in the power industry because it is one of the most important ways to transfer thermal energy. It does not need a medium, such as air or metal, to take place. Any material that has a temperature above absolute zero gives off some radiant energy. Most energy of this type is in the infra-red region of the electromagnetic spectrum, although some of it is in the visible region.

The radiant heat transfer rate from a body (e.g.,, a black body) to its surroundings is proportional to the fourth power of the absolute temperature. It can be expressed by the following equation:

q =  εσT⁴

where σ is a fundamental physical constant called the Stefan–Boltzmann constant, which is equal to 5.6697×10^-8 W/m²K⁴, this relationship is called the Stefan–Boltzmann law. The emissivity, ε, of the surface of a material is its effectiveness in emitting energy as thermal radiation and varies between 0.0 and 1.0. By definition, a black body in thermal equilibrium has an emissivity of ε = 1.0. It can be seen and radiation heat transfer is important at very high temperatures and in a vacuum.

Two bodies that radiate toward each other have a net heat flux between them. The net flow rate of heat between them is given by:

Q = εσA_1-2(T⁴₁ −T⁴₂)  [J/s]

q =  εσ(T⁴₁ −T⁴₂) [J/m²s]

The area factor A_1-2 is the area viewed by body 2 of body 1 and can become fairly difficult to calculate.

Ionization Energy

Ionization energy, also called ionization potential, is the energy necessary to remove an electron from the neutral atom.

X + energy → X⁺ + e⁻

where X is any atom or molecule capable of ionizing, X⁺ is that atom or molecule with an electron removed (positive ion), and e⁻ is the removed electron.

There is ionization energy for each successive electron removed. The electrons that circle the nucleus move in fairly well-defined orbits. Some of these electrons are more tightly bound in the atom than others. For example, only 7.38 eV is required to remove the outermost electron from a lead atom, while 88,000 eV is required to remove the innermost electron.

• Ionization energy is lowest for the alkali metals, which have a single electron outside a closed shell.
• Ionization energy increases across a row on the periodic maximum for the noble gases which have closed shells.

For example, sodium requires only 496 kJ/mol or 5.14 eV/atom to ionize it. On the other hand, neon, the noble gas, immediately preceding it in the periodic table, requires 2081 kJ/mol or 21.56 eV/atom.

The ionization energy associated with the removal of the first electron is most commonly used. The nth ionization energy refers to the energy required to remove an electron from the species with a charge of (n-1).

1st ionization energy

X → X⁺ + e⁻

2nd ionization energy

X⁺ → X²⁺ + e⁻

3rd ionization energy

X²⁺ → X³⁺ + e⁻

For example, only 7.38 eV is required to remove the outermost electron from a lead atom, while 88,000 eV is required to remove the innermost electron.

Nuclear Energy

Nuclear energy comes either from spontaneous nuclei conversions or induced nuclei conversions. Among these conversions (nuclear reactions) are nuclear fission, nuclear decay, and nuclear fusion. Conversions are associated with mass and energy changes. One of the striking results of Einstein’s theory of relativity is that mass and energy are equivalent and convertible, one into the other. Equivalence of the mass and energy is described by Einstein’s famous formula:

Mass-energy Equivalence

One of the striking results of Einstein’s theory of relativity is that mass and energy are equivalent and convertible, one into the other. Equivalence of the mass and energy is described by Einstein’s famous formula:

where M is the small amount of mass and C is the speed of light.

What does that mean? If nuclear energy is generated (splitting atoms, nuclear fusion), a small amount of mass (saved in the nuclear binding energy) transforms into pure energy (such as kinetic energy, thermal energy, or radiant energy).

The energy equivalent of one gram (1/1000 of a kilogram) of mass is equivalent to:

• 89.9 terajoules
• 25.0 million kilowatt-hours (≈ 25 GW·h)
• 21.5 billion kilocalories (≈ 21 Tcal)
• 85.2 billion BTUs

or to the energy released by combustion of the following:

• 21.5 kilotons of TNT-equivalent energy (≈ 21 kt)
• 568,000 US gallons of automotive gasoline

Any time energy is generated, the process can be evaluated from an E = mc² perspective.

Principle of Conservation of Energy

One of the most wonderful properties of the Universe is that energy can be transformed from one type to another and transferred from one object to another. Moreover, when transformed from one type to another and transferred from one object to another, the total amount of energy is always the same. It is one of the elementary properties of the Universe.

In thermodynamics, the concept of energy is broadened to account for other observed changes. The principle of conservation of energy is extended to include a wide variety of ways systems interact with their surroundings. The only ways the energy of a closed system can be changed are through the transfer of energy by work or by heat. Further, based on the experiments of Joule and others, a fundamental aspect of the energy concept is that energy is conserved. This principle is known as the first law of thermodynamics. The first law of thermodynamics can be written in various forms:

In words:

Equation form:

∆E_int = Q – W

where E_int represents the internal energy of the material, which depends only on the material’s state (temperature, pressure, and volume), Q is the net heat added to the system, and W is the net work done by the system. We must be careful and consistent in following the sign conventions for Q and W. Because W in the equation is the work done by the system, then if work is done on the system, W will be negative, and E_int will increase.

Similarly, Q is positive for heat added to the system, so if heat leaves the system, Q is negative. This tells us the following: The internal energy of a system tends to increase if the system absorbs heat or if positive work is done on the system. Conversely, the internal energy tends to decrease if heat is lost by the system or if negative work is done on the system. It must be added Q and W are path-dependent, while E_int is path-independent.

Differential form:

dE_int = dQ  – dW

The internal energy E_int of a system tends to increase if energy is added as heat Q and tends to decrease if energy is lost as work W is done by the system.

Energy Sources

Energy sources have always played a very important role in the development of human society. Since the industrial revolution, energy has been a driving force for modern civilization development. Technological development and consumption of primary energy and the increase of the world population are interdependent. In the past 20 years, the world around us has changed significantly. Technology has become one of the main drivers of economic and social development. The rapid advancement of Information Technology (IT) worldwide has transformed not only the way we think but also the way we act. It must be noted that practically all technologies run on electrical energy. Therefore, the share of electricity is increasing rapidly, faster than Total Primary Energy Supply (TPES –  the sum of production and imports subtracting exports and storage changes.).

At present, fossil fuel is still the world’s predominant energy source. Its extraction, production, and use are not considered efficient regardless of the new technologies available to improve its use and extraction. When studying energy resources, we have to distinguish the primary energy sources and secondary energy sources.

Primary Energy Sources

Primary energy (PE) is an energy resource found in nature that has not been subjected to any conversion or transformation process. It is the energy contained in raw fuels and other forms of energy received as input to a system. Primary energy sources take many forms, including nuclear energy, fossil energy — like oil, coal, and natural gas — and renewable sources like wind, solar, geothermal, and hydropower. These primary sources can be converted to secondary energy source, so-called energy carriers. Primary energy sources can be divided into:

• Non-renewable sources
  • Fossil fuels
    • Oil
    • Coal
    • Natural gas
  • Mineral fuels
    • Natural Uranium
    • Natural Thorium
• Renewable sources
  • Solar energy
  • Wind energy
  • Hydro and tidal energy
  • Geothermal energy
  • Biomass energy (if sustainably exploited)

Secondary Energy Sources – Energy Carriers

Secondary energy sources, also called energy carriers, are derived from the transformation of primary energy sources. They are called energy carriers because they move energy in a useable form from one place to another. The well-known energy carriers are:

• Electricity
• Petrol
• Hydrogen

Electricity and hydrogen are made from primary energy sources such as coal, natural gas, nuclear energy, petroleum, and renewable energy sources. Electricity is particularly useful since it has low entropy (is highly ordered) and can be converted into other forms of energy very efficiently. Simply, we cannot say that hydrogen has the potential to offset fossil fuels.

Secondary energy sources are used because their use is easier than using a primary energy source. For example, using electricity for lighting is safer than using petroleum in candles or kerosene lamps.

On the other hand, any conversion of primary energy to energy carrier is associated with some inefficiency. Therefore when dealing with the secondary energy source, we always have to consider the way, how the carrier was made.

References:

Reactor Physics and Thermal Hydraulics:

1. J. R. Lamarsh, Introduction to Nuclear Reactor Theory, 2nd ed., Addison-Wesley, Reading, MA (1983).
2. J. R. Lamarsh, A. J. Baratta, Introduction to Nuclear Engineering, 3d ed., Prentice-Hall, 2001, ISBN: 0-201-82498-1.
3. W. M. Stacey, Nuclear Reactor Physics, John Wiley & Sons, 2001, ISBN: 0- 471-39127-1.
4. Glasstone, Sesonske. Nuclear Reactor Engineering: Reactor Systems Engineering, Springer; 4th edition, 1994, ISBN: 978-0412985317
5. Todreas Neil E., Kazimi Mujid S. Nuclear Systems Volume I: Thermal Hydraulic Fundamentals, Second Edition. CRC Press; 2 edition, 2012, ISBN: 978-0415802871
6. Zohuri B., McDaniel P. Thermodynamics in Nuclear Power Plant Systems. Springer; 2015, ISBN: 978-3-319-13419-2
7. Moran Michal J., Shapiro Howard N. Fundamentals of Engineering Thermodynamics, Fifth Edition, John Wiley & Sons, 2006, ISBN: 978-0-470-03037-0
8. Kleinstreuer C. Modern Fluid Dynamics. Springer, 2010, ISBN 978-1-4020-8670-0.
9. U.S. Department of Energy, THERMODYNAMICS, HEAT TRANSFER, AND FLUID FLOW. DOE Fundamentals Handbook, Volume 1, 2, and 3. June 1992.

Presentation on theme: «What is Energy? Energy Is the Ability to Do Work. Energy can be found in a number of different forms. It can be chemical energy, electrical energy, heat.»— Presentation transcript:

1

What is Energy? Energy Is the Ability to Do Work. Energy can be found in a number of different forms. It can be chemical energy, electrical energy, heat (thermal energy), light (radiant energy), mechanical energy, and nuclear energy.

2

Stored and Moving Energy Energy makes everything happen and can be divided into two types: Stored energy is called potential energy. Moving energy is called kinetic energy. With a pencil, try this example to know the two types of energy. Put the pencil at the edge of the desk and push it off to the floor. The moving pencil uses kinetic energy. Belarus’ Yuliya Nesterenko runs on her way to winning gold in the women’s 100 metres final at the Athens 2004 Olympic Games on August 21. Nesterenko won the race with a time of 10.93 seconds. Reuters

3

How Do We Measure Energy? Energy is measured in many ways. One of the basic measuring blocks is called a Btu. This stands for British thermal unit and was invented by, of course, the English. Btu is the amount of heat energy it takes to raise the temperature of one pound of water by one degree Fahrenheit, at sea level. One Btu equals about one blue-tip kitchen match. One thousand Btus roughly equals: One average candy bar or 4/5 of a peanut butter and jelly sandwich. It takes about 2,000 Btus to make a pot of coffee. Energy also can be measured in joules. Joules sounds exactly like the word jewels, as in diamonds and emeralds. A thousand joules is equal to a British thermal unit. 1,000 joules = 1 Btu So, it would take 2 million joules to make a pot of coffee.

4

The term «joule» is named after an English scientist James Prescott Joule who lived from 1818 to 1889. He discovered that heat is a type of energy.James Prescott Joule One joule is the amount of energy needed to lift something weighing one pound to a height of nine inches. So, if you lifted a five-pound sack of sugar from the floor to the top of a counter (27 inches), you would use about 15 joules of energy. Around the world, scientists measure energy in joules rather than Btus. It’s much like people around the world using the metric system of meters and kilograms, instead of the English system of feet and pounds. Like in the metric system, you can have kilojoules — «kilo» means 1,000. 1,000 joules = 1 kilojoule = 1 Btu A piece of buttered toast contains about 315 kilojoules (315,000 joules) of energy. With that energy you could: Jog for 6 minutes Bicycle for 10 minutes Walk briskly for 15 minutes Sleep for 1-1/2 hours Run a car for 7 seconds at 80 kilometers per hour (about 50 miles per hour) Light a 60-watt light bulb for 1-1/2 hours Or lift that sack of sugar from the floor to the counter 21,000 times!

5

Heat Energy Heat is a form of energy. We use it for a lot of things, like warming our homes and cooking our food. Heat energy moves in three ways: 1.Conduction 2.Convection 3.Radiation Conduction occurs when energy is passed directly from one item to another. If you stirred a pan of soup on the stove with a metal spoon, the spoon will heat up. The heat is being conducted from the hot area of the soup to the colder area of spoon. Metals are excellent conductors of heat energy. Wood or plastics are not. These «bad» conductors are called insulators. That’s why a pan is usually made of metal while the handle is made of a strong plastic. Convection is the movement of gases or liquids from a cooler spot to a warmer spot. If a soup pan is made of glass, we could see the movement of convection currents in the pan. The warmer soup moves up from the heated area at the bottom of the pan to the top where it is cooler. The cooler soup then moves to take the warmer soup’s place. The movement is in a circular pattern within the pan (see picture above).

6

Electrical Energy is the movement of electrical charges. Everything is made of tiny particles called atoms. Atoms are made of even smaller particles called electrons, protons, and neutrons. Applying a force can make some of the electrons move. Electrical charges moving through a wire is called electricity. Lightning is another example of electrical energy.

7

Thermal Energy, or heat, is the internal energy in substances the vibration and movement of the atoms and molecules within substances. Geothermal energy is an example of thermal energy.

8

Chemical Energy is energy stored in the bonds of atoms and molecules. It is the energy that holds these particles together. Biomass, petroleum, natural gas, and propane are examples of stored chemical energy.

9

Nuclear Energy is energy stored in the nucleus of an atom the energy that holds the nucleus together. The energy can be released when the nuclei are combined or split apart. Nuclear power plants split the nuclei of uranium atoms in a process called fission. The sun combines the nuclei of hydrogen atoms in a process called fusion. Scientists are working on creating fusion energy on earth, so that someday there might be fusion power plants.