The problem of a word group

HistoryEdit

A more concrete descriptionEdit

ExamplesEdit

Partial solution of the word problemEdit

For every mapping of X into S
    If every relator in R is satisfied in S
        If w ≠ 1 in S
            return 0
        End if
    End if
End for

Unsolvability of the uniform word problemEdit

Let n = 0
    Let repeatable = TRUE
        while (repeatable)
            increase n by 1
            if (solution to word problem in G reveals hn(w) ≠ 1 in G)
                Let repeatable = FALSE
output 0.

Algebraic structure and the word problemEdit

See alsoEdit

NotesEdit

ReferencesEdit

В математике, особенно в области абстрактной алгебры, известной как комбинаторная теория групп, проблема слов для конечно порожденной группы G — это алгоритмическая проблема определения того, представляют ли два слова в генераторах один и тот же элемент. Точнее, если A — конечный набор образующих для G, то проблема слов — это проблема принадлежности для формального языка всех слов в A и формального набора обратных, которые отображают в тождество при естественном отображении свободного моноида с инволюцией на A в группу G. Если B — другое конечное порождающее множество для G, то проблема слов над порождающим множеством B эквивалентна слову проблема над порождающим множеством A. Таким образом, можно однозначно говорить о разрешимости проблемы слов для конечно порожденной группы G.

Родственная, но отличная равномерная проблема слов для класса K группы рекурсивно представленные группы — это алгоритмическая проблема решения, заданного в качестве входных данных презентации P для группы G в классе K и двух слов в образующих G, представляют ли слова один и тот же элемент группы G. авторы требуют, чтобы класс K определялся с помощью рекурсивно перечислимого набора представлений.

Содержание

• 1 История
• 2 Более конкретное описание
• 3 Примеры
• 4 Частичное решение проблемы слов
  • 4.1 Пример
• 5 Неразрешимость проблемы единообразных слов
  • 5.1 Доказательство того, что не существует универсальной решаемой группы проблем со словами
• 6 Алгебраическая структура и проблема со словами
• 7 См. Также
• 8 Примечания
• 9 Ссылки

История

На протяжении всей истории испытуемого, вычисления в группах проводились с использованием различных нормальных форм. Обычно они неявно решают проблему слов для рассматриваемых групп. В 1911 году Макс Ден предположил, что проблема слов была важной областью исследования сама по себе, вместе с проблемой сопряженности и проблемой группового изоморфизма. В 1912 году он дал алгоритм, который решает как проблему слова, так и проблему сопряженности для фундаментальных групп замкнутых ориентируемых двумерных многообразий рода больше или равного 2. Последующие авторы значительно расширили алгоритм Дена. и применил его к широкому кругу теоретико-групповых задач принятия решений.

В 1955 году Петр Новиков показал, что существует конечно представленная группа G такая, что проблема слов для G неразрешимый. Отсюда сразу следует, что проблема единообразного слова также неразрешима. Другое доказательство было получено Уильямом Бун в 1958 году.

Проблема слов была одним из первых примеров неразрешимой проблемы, которую нельзя было найти в математической логике или теория алгоритмов, но в одном из центральных разделов классической математики, алгебре. В результате его неразрешимости было показано, что некоторые другие проблемы комбинаторной теории групп также неразрешимы.

Важно понимать, что проблема слов на самом деле разрешима для многих групп G. Например, полициклические группы имеют разрешимые проблемы со словами, поскольку нормальная форма произвольного слова в полициклическом представление легко вычислимо; другие алгоритмы для групп могут, при подходящих обстоятельствах, также решить проблему слов, см. алгоритм Тодда – Кокстера и алгоритм завершения Кнута – Бендикса. С другой стороны, тот факт, что конкретный алгоритм не решает проблему слов для определенной группы, не показывает, что у группы есть неразрешимая проблема слов. Например, алгоритм Дена не решает проблему слов для фундаментальной группы тора . Однако эта группа является прямым произведением двух бесконечных циклических групп и поэтому имеет разрешимую проблему слов.

Более конкретное описание

В более конкретных терминах проблема единообразия слов может быть выражена как переписывание вопроса для буквальных строк. Для представления P группы G, P задает определенное количество образующих

x, y, z,…

для G. Нам нужно ввести одну букву для x и другую (для удобства) для элемент группы, представленный x. Назовите эти буквы (вдвое больше, чем образующих) алфавитом Σ { displaystyle Sigma}для нашей задачи. Тогда каждый элемент в G каким-либо образом представлен произведением

abc… pqr

символов из Σ { displaystyle Sigma}некоторой длины, умноженных на G. Строка длины 0 (нулевая строка ) обозначает элемент идентичности e группы G. Суть всей проблемы состоит в том, чтобы распознать все способы, которыми может быть e. представлены, учитывая некоторые отношения.

Эффект отношений в G состоит в том, что различные такие строки представляют один и тот же элемент G. Фактически отношения предоставляют список строк, которые могут быть либо введены, где мы хотим, либо отменены, когда мы видим их, без изменения «значения», то есть элемента группы, который является результатом умножения.

В качестве простого примера рассмотрим презентацию {a | а}. Написав A вместо символа a, мы получим возможные строки, объединяющие любое количество символов a и A. Когда мы видим aaa, aA или Aa, мы можем вычеркнуть их. Мы также должны не забыть вычеркнуть AAA; это говорит о том, что, поскольку куб для a является единичным элементом G, то же самое и с кубом, обратным к a. В этих условиях проблема слова становится легкой. Сначала сократите строки до пустой строки, a, aa, A или AA. Затем обратите внимание, что мы также можем умножить на aaa, чтобы мы могли преобразовать A в aa и преобразовать AA в a. В результате проблема слов для циклической группы третьего порядка разрешима.

Однако это не типичный случай. Например, у нас есть каноническая форма , которая сокращает любую строку до одной длины не более трех, монотонно уменьшая длину. В общем, неверно, что можно получить каноническую форму для элементов путем пошагового исключения. Возможно, придется использовать отношения для многократного расширения строки, чтобы в конечном итоге найти сокращение, которое сокращает длину строки.

В худшем случае получается, что отношение между строками, которое говорит, что они равны в G, является неразрешимой проблемой.

Примеры

Следующие группы имеют разрешимую проблема со словами:

• Автоматические группы, в том числе:
  • Конечные группы
  • Отрицательно изогнутые (или гиперболические) группы
  • Евклидовы группы
  • Группы Кокстера
  • Группы кос
  • Геометрически конечные группы
• Конечно порожденные свободные группы
• Конечно порожденные свободные абелевы группы
• Полициклические группы
• Конечно порожденные рекурсивно абсолютно представленные группы, в том числе:
  • Конечно определенные простые группы.
• Конечно определенные аппроксимируемые конечные группы
• Группы с одним соотношением (это теорема Магнуса), включая:
  • Фундаментальные группы замкнутых ориентируемые двумерные многообразия.
• Комбинируемые группы
• Автономные группы

Также известны примеры неразрешимых словесных проблем:

• Дано рекурсивно перечислимое множество A натуральные числа с неразрешимой проблемой принадлежности, a, b, c, d | aba = cdc: n ∈ A⟩ — конечно порожденная группа с рекурсивно перечислимым представлением, чья словесная проблема неразрешима
• Каждая конечно порожденная группа с рекурсивно перечислимым представлением и неразрешимой словесной проблемой является подгруппой конечно представленной группы с неразрешимой проблемой слов
• Число соотносителей в конечно представленной группе с неразрешимой проблемой слов может быть от 14 до 12 или даже 12 на.
• Явный пример разумного короткого представления с неразрешимая проблема слов дана в Collins 1986:

⟨a, b, c, d, e, p, q, r, t, k | p 10 a = ap, pacqr = rpcaq, ra = ar, p 10 b = bp, p 2 adq 2 r = rp 2 daq 2, rb = br, p 10 c = cp, p 3 bcq 3 r = rp 3 cbq 3, rc = cr, p 10 d = dp, p 4 bdq 4 r = rp 4 dbq 4, rd = dr, p 10 e = ep, p 5 ceq 5 r = rp 5 ecaq 5, re = er, aq 10 = qa, p 6 deq 6 r = rp 6 edbq 6, pt = tp, bq 10 = qb, p 7 cdcq 7 r = rp 7 cdceq 7, qt = tq, cq 10 = qc, p 8 ca 3 q 8 r знак равно rp 8 a 3 q 8, dq 10 = qd, p 9 da 3 q 9 r = rp 9 a 3 q 9, eq 10 = qe, a — 3 ta 3 k = ka — 3 ta 3⟩ { displaystyle { begin {array} {lllll} langle a, b, c, d, e, p, q, r, t, k | \ p ^ {10} a = ap, pacqr = rpcaq, ra = ar, \ p ^ {10} b = bp, p ^ {2} adq ^ {2} r = rp ^ {2} daq ^ {2}, rb = br, \ p ^ {10} c = cp, p ^ {3} bcq ^ {3} r = rp ^ {3} cbq ^ {3}, rc = cr, \ p ^ {10} d = dp, p ^ {4} bdq ^ {4} r = rp ^ {4} dbq ^ {4}, rd = dr, \ p ^ {10} e = ep, p ^ {5} ceq ^ {5} r = rp ^ {5} ecaq ^ {5 }, re = er, \ aq ^ {10} = qa, p ^ {6} deq ^ {6} r = rp ^ {6} edbq ^ {6}, pt = tp, \ bq ^ { 10} = qb, p ^ {7} cdcq ^ {7} r = rp ^ {7} cdceq ^ {7}, qt = tq, \ cq ^ {10} = qc, p ^ {8} ca ^ {3} q ^ {8} r = rp ^ {8} a ^ {3} q ^ {8}, \ dq ^ {10} = qd, p ^ {9} da ^ {3} q ^ {9} r = rp ^ {9} a ^ {3} q ^ {9}, \ eq ^ {10} = qe, a ^ {- 3} ta ^ {3} k = ka ^ {- 3} ta ^ { 3} rangle end {array}}}

Частичное решение проблемы слов

Проблема слов для рекурсивно представленной группы может быть частично решена в следующем смысле:

Учитывая рекурсивную представление P = ⟨X | R⟩ для группы G, определим:

S = {⟨u, v⟩: u и v — слова в X и u = v в G} { displaystyle S = { langle u, v rangle: u { text {и}} v { text {- слова в}} X { text {и}} u = v { text {in}} G }}

тогда существует частично рекурсивная функция f P такая, что:

f P (⟨u, v⟩) = {0, если ⟨u, v⟩ ∈ S undefined / не останавливается, если ⟨u, v⟩ ∉ S { displaystyle f_ {P} ( langle u, v rangle) = { begin {cases} 0 { text {if}} langle u, v rangle in S \ { text {undefined / не останавливается}} { text {if}} langle u, v rangle notin S end {cases}}}

Более неформально, существует алгоритм, который останавливается, если u = v, но не делает иначе.

Отсюда следует, что для решения проблемы слов для P достаточно построить рекурсивную функцию g такую, что:

g (⟨u, v⟩) = {0, если ⟨u, v⟩ ∉ S undefined / не останавливается, если ⟨u, v⟩ ∈ S { displaystyle g ( langle u, v rangle) = { begin {cases} 0 { text {if}} langle u, v rangle notin S \ { text {undefined / не останавливается}} { text {if}} langle u, v rangle in S end {case}}

Однако u = v в G тогда и только тогда, когда uv = 1 в G. Отсюда следует, что для решения проблемы слов для P достаточно построить рекурсивную функцию h такую, что:

h (x) = {0, если x ≠ 1 в G undefined / не останавливается, если x = 1 в G { displaystyle h (x) = { begin {cases} 0 { text {if}} x neq 1 { text {in}} G \ { text {undefined / не останавливается}} { text {if}} x = 1 { text {in}} G end {cases}}}

Пример

В качестве примера использования этой техники будет доказано следующее:

Теорема: Конечно представимая финитно аппроксимируемая группа имеет разрешимую проблему слов.

Доказательство: предположим, что G = ⟨X | R⟩ конечная представленная финитно аппроксимируемая группа.

Пусть S будет группой всех перестановок N, натуральных чисел, которая фиксирует все числа, кроме конечного, тогда:

1. S является локально конечным и содержит копию каждой конечной группы.
2. Проблема слов в S разрешима путем вычисления произведений перестановок.
3. Существует рекурсивное перечисление всех отображений конечного множества X в S.
4. Поскольку G финитно аппроксимируема, если w — слово в образующих X группы G, то w ≠ 1 в G тогда и только тогда, когда некоторое отображение X в S индуцирует гомоморфизм такой, что w ≠ 1 в S.

Учитывая эти факты, алгоритм определяется следующим псевдокодом:

Для каждое отображение X в S Если, каждый относитель в R удовлетворяется в S Если w ≠ 1 в S return 0 End if End if End for

определяет рекурсивную функцию h такую, что:

h (x) = {0, если x ≠ 1 в G undefined / не останавливается, если x = 1 в G { displaystyle h (x) = { begin {cases} 0 { text {if}} x neq 1 { текст {in}} G \ { tex t {undefined / не останавливается}} { text {if}} x = 1 { text {in}} G end {cases}}}

Это показывает, что G имеет решаемую проблему со словами.

Неразрешимость проблемы единого слова

Приведенный выше критерий разрешимости проблемы слова в одной группе может быть расширен простым аргументом. Это дает следующий критерий равномерной разрешимости проблемы слов для класса конечно представленных групп:

Для решения равномерной проблемы слов для класса групп K достаточно найти рекурсивную функцию f ( P, w) { displaystyle f (P, w)}, который принимает конечное представление P для группы G и слово w { displaystyle w}в генераторы G, такие, что всякий раз, когда G ∈ K:

f (P, w) = {0, если w ≠ 1 в G undefined / не останавливается, если w = 1 в G { displaystyle f (P, w) = { begin {case} 0 { text {if}} w neq 1 { text {in}} G \ { text {undefined / не останавливается}} { text {if} } w = 1 { text {in}} G end {cases}}}

Теорема Буна-Роджерса: Не существует единого частичного алгоритма, решающего проблему слов во всех конечно определенных группах с разрешимой проблемой слов.

Другими словами, равномерная проблема слов для класса всех конечно определенных групп с разрешимой проблемой слов неразрешима. Это имеет некоторые интересные последствия. Например, теорема вложения Хигмана может быть использована для построения группы, содержащей изоморфную копию каждой конечно представленной группы с разрешимой проблемой слов. Кажется естественным спросить, может ли эта группа иметь решаемую проблему слов. Но следствием результата Буна-Роджерса является следующее:

Следствие: Не существует универсальной решаемой группы словесных задач. То есть, если G — конечно определенная группа, которая содержит изоморфную копию каждой конечно определенной группы с разрешимой проблемой слов, то сама G должна иметь неразрешимую проблему слов.

Замечание: Предположим, что G = ⟨X | R⟩ — конечно определенная группа с разрешимой проблемой слов, а H — конечное подмножество в G. Пусть H = ⟨H⟩, — группа, порожденная H. Тогда проблема слов в H разрешима: даны два слова h, k в образующих H группы H, запишите их как слова в X и сравните их, используя решение проблемы слов в G. Легко подумать, что это демонстрирует равномерное решение проблемы слов для класса K (скажем) конечно порожденных групп, которые может быть вложено в G. Если бы это было так, то несуществование универсальной разрешимой группы проблем со словами легко вытекало бы из Бун-Роджерса. Однако только что представленное решение проблемы слов для групп из K не является однородным. Чтобы убедиться в этом, рассмотрим группу J = ⟨Y | T⟩ ∈ K; Чтобы использовать приведенный выше аргумент для решения проблемы слов в J, сначала необходимо показать отображение e: Y → G, которое продолжается до вложения e: J → G.Если бы существовала рекурсивная функция, отображающая (конечно порожденная) представления групп из K вложения в G, то действительно может быть построено равномерное решение проблемы слов в K. Но в общем случае нет оснований предполагать, что такая рекурсивная функция существует. Однако оказывается, что, используя более изощренный аргумент, проблема слов в J может быть решена без использования вложения e: J → G. Вместо этого используется перечисление гомоморфизмов, и, поскольку такое перечисление может быть построено единообразно, оно приводит к единообразному решению проблемы слов в K.

Доказательство того, что не существует универсальной разрешимой группы проблем со словами

Предположим, G была универсальной разрешимой группой проблем со словами. Учитывая конечное представление P = ⟨X | R⟩ группы H, можно рекурсивно перечислить все гомоморфизмы h: H → G, сначала перечислив все отображения h: X → G. Не все эти отображения продолжаются до гомоморфизмов, но, поскольку h (R) конечно, можно различать гомоморфизмы и негомоморфизмы, используя решение проблемы слов в G. «Отсечение» негомоморфизмов дает требуемое рекурсивное перечисление: h 1, h 2,…, h n,….

Если H имеет разрешимую проблему слов, то хотя бы один из этих гомоморфизмов должен быть вложением. Итак, дано слово w в образующих H:

Если w ≠ 1 в H, hn (w) ≠ 1 в G для некоторого hn { displaystyle { text {If}} w neq 1 { text {in}} H, h_ {n} (w) neq 1 { text {in}} G { text {для некоторых}} h_ {n}}

Если w = 1 в H, hn (w) = 1 в G для всех hn { displaystyle { text {If}} w = 1 { text {in}} H, h_ {n} (w) = 1 { text {in}} G { text {для всех}} h_ {n}}

Рассмотрим алгоритм, описанный псевдокодом:

Пусть n = 0 Пусть repeatable = TRUE в то время как (повторяемый) увеличивает n на 1, если (решение проблемы слов в G показывает h n (w) ≠ 1 в G) Пусть repeatable = FALSE вывод 0.

Это описывает рекурсивную функцию:

f (w) = {0, если w ≠ 1 в H undefined / не останавливается, если w = 1 в H. { displaystyle f (w) = { begin {cases} 0 { text {if}} w neq 1 { text {in}} H \ { text {undefined / не останавливается}} { text {if}} w = 1 { text {in}} H. end {cases}}}

Функция f явно зависит от представления P. Рассматривая ее как функцию из двух переменных была построена рекурсивная функция f (P, w) { displaystyle f (P, w)}, которая принимает конечное представление P для группы H и слово w в генераторах группы G, такой, что всякий раз, когда G имеет разрешимую проблему слов:

f (P, w) = {0, если w 1 в H, undefined / не останавливается, если w = 1 в H. { displaystyle f (P, w) = { begin {cases} 0 { text {if}} w neq 1 { text {in}} H \ { text {undefined / не останавливается }} { text {if}} w = 1 { text {in}} H. end {ases}}}

Но это единообразно решает проблему слов для класса всех конечно представленных группы с разрешимой проблемой слов, противоречащие Буну-Роджерсу. Это противоречие доказывает, что G не может существовать.

Алгебраическая структура и проблема слов

Существует ряд результатов, которые связывают разрешимость проблемы слов и алгебраическую структуру. Наиболее важным из них является следующее:

Конечно представленная группа имеет разрешимую проблему слов тогда и только тогда, когда она может быть вложена в простую группу, которая может быть вложена в конечно определенную группу.

Широко распространено мнение, что можно построить такую ​​конструкцию, чтобы сама простая группа была конечно представимой. Если это так, можно было бы ожидать, что это будет трудно доказать, поскольку отображение представлений в простые группы должно быть нерекурсивным.

Следующее было доказано Бернхардом Нойманом и Ангусом Макинтайром :

Конечно представленная группа имеет разрешимую проблему слов тогда и только тогда, когда она может быть вложена в каждое алгебраически замкнутая группа

Что примечательно в этом, так это то, что алгебраически замкнутые группы настолько дикие, что ни одна из них не имеет рекурсивного представления.

Самым старым результатом, связывающим алгебраическую структуру с разрешимостью проблемы слов, является теорема Кузнецова:

Рекурсивно представленная простая группа S имеет разрешимую проблему слов.

Чтобы доказать это, пусть ⟨X | R⟩ будет рекурсивное представление для S. Выберем a ∈ S так, чтобы a ≠ 1 в S.

Если w — слово на образующих X слова S, то пусть:

S w = ⟨X | R ∪ {w}⟩. { displaystyle S_ {w} = langle X | R cup {w } rangle.}

Существует рекурсивная функция f ⟨X | R ∪ {w}⟩ { displaystyle f _ { langle X | R cup {w } rangle}}такой, что:

f ⟨X | R ∪ {w}⟩ (x) = {0, если x = 1 в S w undefined / не останавливается, если x ≠ 1 в S w. { displaystyle f _ { langle X | R cup {w } rangle} (x) = { begin {cases} 0 { text {if}} x = 1 { text {in}} S_ {w} \ { text {undefined / не останавливается}} { text {if}} x neq 1 { text {in}} S_ {w}. End {case }}}

Запишите:

g (w, x) = f ⟨X | R ∪ {w}⟩ (х). { displaystyle g (w, x) = f _ { langle X | R cup {w } rangle} (x).}

Тогда, поскольку конструкция f была равномерной, это рекурсивная функция две переменные.

Отсюда следует, что: h (w) = g (w, a) { displaystyle h (w) = g (w, a)}является рекурсивным. По построению:

h (w) = {0, если a = 1 в S w undefined / не останавливается, если a 1 в S w. { displaystyle h (w) = { begin {cases} 0 { text {if}} a = 1 { text {in}} S_ {w} \ { text {undefined / не останавливается }} { text {if}} a neq 1 { text {in}} S_ {w}. end {cases}}}

Поскольку S — простая группа, ее единственное частное группы — это сама и тривиальная группа. Поскольку a 1 в S, мы видим a = 1 в S w тогда и только тогда, когда S w тривиально тогда и только тогда, когда w ≠ 1 в S. Следовательно:

h (w) = {0, если w ≠ 1 в S undefined / не останавливается, если w = 1 в S. { displaystyle h (w) = { begin {cases} 0 { text {if}} w neq 1 { text {in}} S \ { text {undefined / не останавливается}} { text {if}} w = 1 { text {in}} S. end {ases}}}

Существования такой функции достаточно, чтобы доказать, что проблема слов разрешима для S.

Это доказательство не доказывает существования единого алгоритма решения проблемы слов для этого класса групп. Неоднородность заключается в выборе нетривиального элемента простой группы. Нет оснований предполагать, что существует рекурсивная функция, которая отображает представление простой группы на нетривиальный элемент группы. Однако в случае конечно представленной группы мы знаем, что не все генераторы могут быть тривиальными (конечно, может быть любой отдельный генератор). Используя этот факт, можно изменить доказательство, чтобы показать:

Проблема слов равномерно разрешима для класса конечно определенных простых групп.

См. Также

• Комбинаторика слов
• SQ-универсальная группа
• Проблема со словами (математика)
• Проблема достижимости
• Вложенные стековые автоматы (использовались для решения задачи со словами для групп)

Примечания

1. ^Ден 1911.
2. ^Ден 1912.
3. ^Гриндлингер, Мартин (июнь 1959 г.), «Алгоритм Дена для словесной проблемы», Коммуникации по чистой и прикладной математике, 13 (1): 67–83, doi : 10.1002 / cpa.3160130108.
4. ^Линдон, Роджер К. (сентябрь 1966 г.), «По алгоритму Дена» , Mathematische Annalen, 166 (3): 208–228, doi : 10.1007 / BF01361168, hdl : 2027.42 / 46211.
5. ^Шупп, Пол Э. (июнь 1968 г.), «Об алгоритме Дена и проблеме сопряжения» , Mathematische Annalen, 178 (2): 119–130, doi : 10.1007 / BF01350654.
6. ^Новиков, ПС (195 5), «Об алгоритмической неразрешимости проблемы слова в теории групп», Труды Математического института им. В.А. Стеклова, 44 : 1–143, Zbl 0068.01301
7. ^Бун, Уильям У. (1958), «Проблема слова» (PDF), Proceedings of the National Academy of Sciences, 44 (10): 1061–1065, doi : 10.1073 / pnas.44.10.1061, PMC 528693, PMID 16590307, Zbl 0086.24701
8. ^JA Тодд и Х.С.М. Кокстер. «Практический метод перечисления смежных классов конечной абстрактной группы», Proc, Edinburgh Math Soc. (2), 5, 25 — 34. 1936
9. ^Д. Кнут и П. Бендикс. «Простые словесные задачи в универсальных алгебрах». Вычислительные проблемы в абстрактной алгебре (ред. Дж. Лич), стр. 263-297, 1970.
10. ^Ротман 1994.
11. ^Х. Симмонс, «Проблема слов для абсолютных представлений». J. London Math. Soc. (2) 6, 275-280 1973
12. ^Роджер К. Линдон, Пол Э. Шупп, Комбинаторная теория групп, Springer, 2001
13. ^Collins Zieschang 1990, p. 149.
14. ^Collins Zieschang 1993, Cor. 7.2.6. sfn error: no target: CITEREFCollinsZieschang1993 (help )
15. ^Collins 1969.
16. ^Borisov 1969.
17. ^Collins 1972.
18. ^Collins 1986.
19. ^Мы используем исправленную версию из Каталога алгебраических языков Джона Педерсена Системы

Ссылки

• «Проблема со словами». PlanetMath.
• У.В. Бун, Ф. Б. Каннонито и Р. К. Линдон. Проблемы со словами: проблема принятия решения в теории групп. Нидерланды: Северная Голландия. 1973.
• Бун, У.В.; Хигман, Г. (1974). «Алгебраическая характеристика разрешимости проблемы слов». J. Austral. Math. Soc. 18 : 41–53. doi : 10.1017 / s1446788700019108.
• Бун, WW; Роджерс-младший, Х. (1966). «О проблеме Дж. Х. К. Уайтхеда. и проблема Алонсо Черча ». Math. Scand. 19 : 185–192. doi : 10.7146 / math.scand.a-10808.
• Борисов, В.В. (1969), «Простые примеры групп с неразрешимой проблемой слов», Академия Наук СССР, Математические заметки, 6 : 521–532, ISSN 00 25-567X, MR 0260851
• Коллинз, Дональд Дж. (1969), «Проблемы слова и сопряжения в группах только с несколькими определяющими отношениями», Zeitschrift für Mathematische Logik und Grundlagen der Mathematik, 15 (20–22): 305–324, doi : 10.1002 / malq.19690152001, MR 0263903
• Коллинз, Дональд Дж. (1972), «О теореме группового вложения В.В. Борисов », Вестник Лондонского математического общества, 4(2): 145–147, doi : 10.1112 / blms / 4.2.145, ISSN 0024-6093, MR 0314998
• Коллинз, Дональд Дж. (1986), «Простое представление группы с неразрешимой проблемой слов», Illinois Journal of Mathematics, 30 ( 2): 230–234, doi : 10.1215 / ijm / 1256044631, ISSN 0019-2082, MR 0840121
• Коллинз, Дональд J.; Цишанг Х. (1990), Комбинаторная теория групп и фундаментальные группы, Берлин, Нью-Йорк: Springer-Verlag, p. 166, MR 1099152
• Ден, Макс (1911), «Über unndliche diskontinuierliche Gruppen» , Mathematische Annalen, 71(1): 116–144, doi : 10.1007 / BF01456932, ISSN 0025-5831, MR 1511645
• Ден, Макс (1912), » Transformation der Kurven auf zweiseitigen Flächen «, Mathematische Annalen, 72(3): 413–421, doi : 10.1007 / BF01456725, ISSN 0025-5831, MR 1511705
• А. В. Кузнецов, «Алгоритмы как операции в алгебраических системах», Известия Акад. АН СССР Сер мат (1958)
• С. Ф. Миллер. «Решение проблемы для группы — обзор и размышления». В «Алгоритмах и классификации в комбинаторной теории групп», страницы 1–60. Springer, 1991.
• Ротман, Джозеф (1994), Введение в теорию групп, Берлин, Нью-Йорк: Springer-Verlag, ISBN 978-0 -387-94285-8
• Стиллвелл, Дж. (1982). «Проблема слова и проблема изоморфизма для групп». Бюллетень АПП. 6 : 33–56. doi :10.1090/s0273-0979-1982-14963-1.

The word-group theory in Modern English

word-group
theory in Modern English

Content

Introduction

.
Definition and general characteristics of the
word-group

.
Classification of word-groups

.
Semantic features of word-groups

.
Motivated and non-motivated word-groups

.
Phraseological word-groups

Introduction

is a branch of linguistics — the
science of language. Lexicology as a branch of linguistics has its own aims and
methods of scientific research. Its basic task — being a study and systematic
description of vocabulary in respect to its origin, development and its current
use. Lexicology is concerned with words, variable word-groups, phraseological
units and morphemes which make up words.the object of the linguistic research
within the frameworks of the lexicological analysis, word-groups draw much
attention of different scientists at different stages of the research
history.linguists as Shveitser, Arnold, Nikitin, Akhmanova, Marchenko, and many
others devoted their research papers to the matter of the word-groups, their
classification, semantic features, and other specific characteristics. They
have contributed linguistic research with a number of works, connected with
this lexical units. The matter of the word-group thorough study is topical with
a glance at their specific features, some phraseological peculiarities and
semantic-grammatical structure.above-mentioned aspects have predetermined our
choice of the topic of the present report «The word-group theory in Modern
English».object of the investigation are word-groups of Modern
English.subject of the present report includes specific features and
characteristics of word-groups.purpose of the report writing is to investigate
word-groups functioning in the Modern English language.purporse of the report
has predetermined the following tasks of the investigation:

to define the notion of the
word-group and outline its general characteristics;

to suggest the classification of the
word-group;

to consider semantic features of
word-groups;

to characterize motivated and
non-motivated word-groups;

to specify peculiar features of
phraseological word-groups.practical value of the present report is performed
by the possibility of using its materials for the further thorough study of
this matter.

1. Definition and general
characteristics of the word-group

word group is the simplest
nonpredicative (as contrasted to the sentence) unit of speech. The word group
is formed on a syntactic pattern and based on a subordinating grammatical
relationship between two or more content words. This relationship may be one of
agreement, government, or subordination. The grammatically predominant word is
the main element of the word group, and the grammatically subordinated word the
dependent element.word group denotes a fragment of extralinguistic reality. The
word group combines formally syntactic and semantically syntactic features.
Such features reveal the compatibility of grammatical and lexical meanings with
the structure of the object-logical relations that these meanings
reflect.groups may be free or phraseological. Free word groups are formed in
accordance with regular and productive combinative principles; their meanings
may be deduced from those of the component words.are a lot of definitions
concerning the word-group. The most adequate one seems to be the following: the
word-group is a combination of at least two notional words which do not
constitute the sentence but are syntactically connected. According to some
other scholars (the majority of Western scholars and professors B.Ilyish and
V.Burlakova — in Russia), a combination of a notional word with a function word
(on the table) may be treated as a word-group as well. The problem is
disputable as the role of function words is to show some abstract relations and
they are devoid of nominative power. On the other hand, such combinations are
syntactically bound and they should belong somewhere.characteristics of the
word-group are:

) As a naming unit it differs from a
compound word because the number of constituents in a word-group corresponds to
the number of different denotates: a black bird — чорний птах (2), a blackbird
— дрізд (1);loud speaker (2), a loudspeaker (1).

) Each component of the word-group
can undergo grammatical changes without destroying the identity of the whole
unit: to see a house — to see houses.

) A word-group is a dependent
syntactic unit, it is not a communicative unit and has no intonation of its own
[4; p. 28].

groups can be classified on the
basis of several principles:

a)
According to the type of syntagmatic
relations: coordinate (you and me), subordinate (to see a house, a nice dress),
predicative (him coming, for him to come),

b)  
According to the structure: simple
(all elements are obligatory), expanded (to read and translate the text —
expanded elements are equal in rank), extended (a word takes a dependent
element and this dependent element becomes the head for another word: a beautiful
flower — a very beautiful flower).

1) Subordinate
word-groups.word-groups are based on the relations of dependence between the
constituents. This presupposes the existence of a governingwhich is called the
head and the dependent element which is called the adjunct (in noun-phrases) or
the complement (in verb-phrases).to the nature of their heads, subordinate
word-groups fall into noun-phrases (NP) — a cup of tea, verb-phrases (VP) — to
run fast, to see a house, adjective phrases (AP) — good for you, adverbial
phrases (DP) — so quickly, pronoun phrases (IP) — something strange, nothing to
do.formation of the subordinate word-group depends on the valency of its
constituents. Valency is a potential ability of words to combine. Actual
realization of valency in speech is called combinability [6; p. 162-163].

) The noun-phrase (NP).word-groups
are widely spread in English. This may be explained by a potential ability of
the noun to go into combinations with practically all parts of speech. The NP
consists of a noun-head and an adjunct or adjuncts with relations of
modification between them. Three types of modification are distinguished here:

a)
Premodification that comprises all
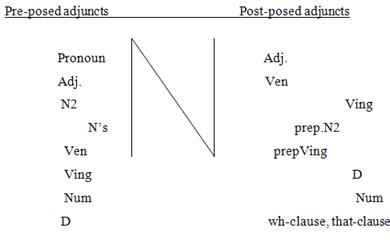
the units placed before the head: two smart hard-working students. Adjuncts used
in pre-head position are called pre-posed adjuncts.

b)  
Postmodification that comprises all
the units all the units placed after the head: students from Boston. Adjuncts
used in post-head position are called post-posed adjuncts.

c)
Mixed modification that comprises
all the units in both pre-head and post-head position: two smart hard-working
students from Boston.

) Noun-phrases with pre-posed
adjuncts.noun-phrases with pre-posed modifiers we generally find adjectives, pronouns,
numerals, participles, gerunds, nouns, nouns in the genitive case (see the
table) [8; p. 43]. According to their position all pre-posed adjuncts may be
divided into pre-adjectivals and adjectiavals. The position of adjectivals is
usually right before the noun-head. Pre-adjectivals occupy the position before
adjectivals. They fall into two groups: a) limiters (to this group belong
mostly particles): just, only, even, etc. and b) determiners (articles,
possessive pronouns, quantifiers — the first, the last).of nouns by nouns (N+N)
is one of the most striking features about the grammatical organization of
English. It is one of devices to make our speech both laconic and expressive at
the same time. Noun-adjunct groups result from different kinds of transformational
shifts. NPs with pre-posed adjuncts can signal a striking variety of
meanings:peace — peace all over the worldbox — a box made of silverlamp — lamp
for tableslegs — the legs of the tablesand — sand from the riverchild — a child
who goes to schoolgrammatical relations observed in NPs with pre-posed adjuncts
may convey the following meanings:

1)  
subject-predicate relations: weather
change;

2)  
object relations: health service,
women hater;

3)  
adverbial relations: a) of time:
morning star,

b) place: world peace, country
house,) comparison: button eyes,) purpose: tooth brush.is important to remember
that the noun-adjunct is usually marked by a stronger stress than the
head.special interest is a kind of ‘grammatical idiom’ where the modifier is
reinterpreted into the head: a devil of a man, an angel of a girl.

) Noun-phrases with post-posed
adjuncts.with post-posed may be classified according to the way of connection
into prepositionless and prepositional. The basic prepositionless NPs with post-posed
adjuncts are: Nadj. — tea strong, NVen — the shape unknown, NVing — the girl
smiling, ND — the man downstairs, NVinf — a book to read, NNum — room
ten.pattern of basic prepositional NPs is N1 prep. N2. The most common
preposition here is ‘of’ — a cup of tea, a man of courage. It may have quite
different meanings: qualitative — a woman of sense, predicative — the pleasure
of the company, objective — the reading of the newspaper, partitive — the roof
of the house.

) The verb-phrase.VP is a definite
kind of the subordinate phrase with the verb as the head. The verb is
considered to be the semantic and structural centre not only of the VP but of
the whole sentence as the verb plays an important role in making up primary
predication that serves the basis for the sentence. VPs are more complex than
NPs as there are a lot of ways in which verbs may be combined in actual usage.
Valent properties of different verbs and their semantics make it possible to
divide all the verbs into several groups depending on the nature of their
complements [7; p. 91].of verb-phrases.can be classified according to the
nature of their complements — verb complements may be nominal (to see a house)
and adverbial (to behave well). Consequently, we distinguish nominal, adverbial
and mixed complementation.complementation takes place when one or more nominal
complements (nouns or pronouns) are obligatory for the realization of potential
valency of the verb: to give smth. to smb., to phone smb., to hear smth.(smb.),
etc.complementation occurs when the verb takes one or more adverbial elements
obligatory for the realization of its potential valency: He behaved well, I
live …in Kyiv (here).complementation — both nominal and adverbial elements are
obligatory: He put his hat on he table (nominal-adverbial).to the structure VPs
may be basic or simple (to take a book) — all elements are obligatory; expanded
(to read and translate the text, to read books and newspapers) and extended (to
read an English book).

) Predicative word-groups.word
combinations are distinguished on the basis of secondary predication. Like
sentences, predicative word-groups are binary in their structure but actually
differ essentially in their organization. The sentence is an independent
communicative unit based on primary predication while the predicative
word-group is a dependent syntactic unit that makes up a part of the sentence.
The predicative word-group consists of a nominal element (noun, pronoun) and a
non-finite form of the verb: N + Vnon-fin. There are Gerundial, Infinitive and
Participial word-groups (complexes) in the English language: his reading, for
me to know, the boy running, etc.)

. Semantic features of word-groups

word-group is the largest two-facet
lexical unit comprising more than one word but expressing one global
concept.lexical meaning of the word groups is the combined lexical meaning of
the component words. The meaning of the word groups is motivated by the
meanings of the component members and is supported by the structural pattern.
But it’s not a mere sum total of all these meanings! Polysemantic words are
used in word groups only in 1 of their meanings. These meanings of the
component words in such word groups are mutually interdependent and inseparable
(blind man — «a human being unable to see», blind type — «the
copy isn’t readable).groups possess not only the lexical meaning, but also the
meaning conveyed mainly by the pattern of arrangement of their constituents.
The structural pattern of word groups is the carrier of a certain semantic component
not necessarily dependent on the actual lexical meaning of its members (school
grammar — «grammar which is taught in school», grammar school —
«a type of school»). We have to distinguish between the structural
meaning of a given type of word groups as such and the lexical meaning of its
constituents [11; p. 62-64].is often argued that the meaning of word groups is
also dependent on some extra-linguistic factors — on the situation in which
word groups are habitually used by native speakers.put together to form lexical
units make phrases or word-groups. One must recall that lexicology deals with
words, word-forming morphemes and word-groups.degree of structural and semantic
cohesion of word-groups may vary. Some word-groups, e.g. at least, point of
view, by means, to take place, etc. seem to be functionally and semantically
inseparable. They are usually described as set phrases, word-equivalents or
phraseological units and are studied by the branch of lexicology which is known
as phraseology. In other word-groups such as to take lessons, kind to people, a
week ago, the component-members seem to possess greater semantic and structural
independence. Word-groups of this type are defined as free word-groups or
phrases and are studied in syntax.discussing phraseology it is necessary to
outline the features common to various word-groups irrespective of the degree
of structural and semantic cohesion of the component-words [18; p. 231].are two
factors which are important in uniting words into word-groups:

the lexical valency of words;

. Motivated and non-motivated
word-groups

word group semantic
motivated

The term motivation is used to
denote the relationship existing between the phonemic or morphemic composition
and structural pattern of the word on the one hand and its meaning on the
other.are three main types of motivation:

) phonetical

) morphological

) semantic

. Phonetical motivation is used when
there is a certain similarity between the sounds that make up the word. For
example: buzz, cuckoo, gigle. The sounds of a word are imitative of sounds in
nature, or smth that produces a characteristic sound. This type of motivation
is determined by the phonological system of each language.

. Morphological motivation — the
relationship between morphemic structure and meaning. The main criterion in
morphological motivation is the relationship between morphemes. One-morphemed
words are non-motivated. Ex — means «former» when we talk about humans
ex-wife, ex-president. Re — means «again»: rebuild, rewrite. In
borrowed words motivation is faded: «expect, export, recover (get
better)». Morphological motivation is especially obvious in newly coined
words, or in the words created in this century. In older words motivation is
established etymologically.structure-pattern of the word is very important too:
«finger-ring» and «ring-finger». Though combined lexical
meaning is the same. The difference of meaning can be explained by the arrangement
of the components.motivation has some irregularities: «smoker» — si
not «the one who smokes», it is «a railway car in which
passenger may smoke».degree of motivation can be different:

«endless» is completely
motivated

«cranberry» is partially
motivated: morpheme «cran-» has no lexical meaning.

. Semantic motivation is based on
the co-existence of direct and figurative meanings of the same word within the
same synchronous system. «Mouth» denotes a part of the human face and
at the same time it can be applied to any opening: «the mouth of a
river». «Ermine» is not only the anme of a small animal, but
also a fur. In their direct meaning «mouth» and «ermine»
are not motivated [13; p. 86].compound words it is morphological motivation
when the meaning of the whole word is based on direct meanings of its
components and semantic motivation is when combination of components is used
figuratively. For example «headache» is «pain in the head»
(morphological) and «smth. annoying» (sematic).the connection between
the meaning of the word and its form is conventional (there is no perceptible
reason for the word having this phonemic and morphemic composition) the word is
non-motivated (for the present state of language development). Words that seem
non-motivated now may have lost their motivation: «earn» is derived
from «earnian — to harvest», but now this word is non-motivated.to
compounds, their motivation is morphological if the meaning of the whole is
based on the direct meaning of the components, and semantic if the combination
is used figuratively: watchdog — a dog kept for watching property
(morphologically motivated); — a watchful human guardian (semantically
motivated) [5; p. 94-95].vocabulary is in a state of constant development.
Words that seem non-motivated at present may have lost their motivation [16; p.
34]. When some people recognize the motivation, whereas others do not,
motivation is said to be faded.all word-groups may be classified into motivated
and non-motivated. Non-motivated word-groups are usually described as phraseological
units or idioms.groups may be described as lexically motivated if the combined
lexical meaning of the groups is based on the meaning of their components. Thus
take lessons is motivated; take place — ‘occur’ is lexically
non-motivated.groups are said to be structurally motivated if the meaning of
the pattern is deduced from the order and arrangement of the member-words of
the group. Red flower is motivated as the meaning of the pattern quality —
substance can be deduced from the order and arrangement of the words red and
flower, whereas the seemingly identical pattern red tape (‘official
bureaucratic methods’) cannot be interpreted as quality — substance.identical
word-groups are sometimes found to be motivated or non-motivated depending on
their semantic interpretation. Thus apple sauce, e.g., is lexically and
structurally motivated when it means ‘a sauce made of apples’ but when used to
denote ‘nonsense’ it is clearly non-motivated [15; p. 90].groups like words may
be also analyzed from the point of view of their motivation. Word-groups may be
called as lexically motivated if the combined lexical meaning of the group is
deducible from the meaning of the components. All free phrases are completely
motivated.follows from the above discussion that word-groups may be also
classified into motivated and non-motivated units. Non-motivated word-groups
are habitually described as phraseological units or idioms.

. Phraseological word-groups

of English phraseology began not
long ago. English and American linguists as a rule are busy collecting
different words, word-groups and sentences which are interesting from the point
of view of their origin, style, usage or some other features. All these units
are habitually described as «idioms», but no attempt has been made to
describe these idioms as a separate class of linguistic units or a specific
class of word-groups.in terminology («set-phrases»,
«idioms» and «word-equivalents») reflects certain
differences in the main criteria used to distinguish types of phraseological
units and free word-groups. The term «set phrase» implies that the
basic criterion of differentiation is stability of the lexical components and
grammatical structure of word-groups.is a certain divergence of opinion as to
the essential features of phraseological units as distinguished from other
word-groups and the nature of phrases that can be properly termed
«phraseological units». The habitual terms «set-phrases»,
«idioms», «word-equivalents» are sometimes treated
differently by different linguists. However these terms reflect to certain
extend the main debatable points of phraseology which centre in the divergent
views concerning the nature and essential features of phraseological units as
distinguished from the so-called free word-groups.term «set
expression» implies that the basic criterion of differentiation is
stability of the lexical components and grammatical structure of
word-groups.term «word-equivalent» stresses not only semantic but
also functional inseparability of certain word-groups, their aptness to
function in speech as single words [10; p. 31].term «idioms»
generally implies that the essential feature of the linguistic units under
consideration is idiomaticity or lack of motivation. Uriel Weinreich expresses
his view that an idiom is a complex phrase, the meaning of which cannot be
derived from the meanings of its elements. He developed a more truthful
supposition, claiming that an idiom is a subset of a phraseological unit. Ray
Jackendoff and Charles Fillmore offered a fairly broad definition of the idiom,
which, in Fillmore’s words, reads as follows: «…an idiomatic expression or
construction is something a language user could fail to know while knowing
everything else in the language». Chafe also lists four features of idioms
that make them anomalies in the traditional language unit paradigm:
non-compositionality, transformational defectiveness, ungrammaticality and
frequency asymmetry.work in this field has been done by the outstanding Russian
linguist A. Shakhmatov in his work «Syntax». This work was continued
by Acad. V.V. Vinogradov. Great investigations of English phraseology were done
by Prof. A. Cunin, I. Arnold and others [1; p. 121].units are habitually
defined as non-motivated word-groups that cannot be freely made up in speech
but are reproduced as ready-made units; the other essential feature of
phraseological units is stability of the lexical components and grammatical
structure.components of free word-groups which may vary according to the needs
of communication, member-words of phraseological units are always reproduced as
single unchangeable collocations. E.g., in a red flower (a free phrase) the
adjective red may be substituted by another adjective denoting colour, and the
word-group will retain the meaning: «the flower of a certain colour»
[2; p. 54].the phraseological unit red tape (bürokratik
metodlar) no such substitution is possible, as a change of the adjective would
cause a complete change in the meaning of the group: it would then mean «tape
of a certain colour». It follows that the phraseological unit red tape is
semantically non-motivated, i.e. its meaning cannot be deduced from the meaning
of its compo­nents, and that it exists as a ready-made linguistic unit which
does not allow any change of its lexical components and its grammatical
structure [9; p. 45-46].structure of phraseological units is to a certain
degree also stable:tape — a phraseological unit;tapes — a free word-group;go to
bed — a phraseological unit;go to the bed — a free word-group.ways of forming
phraseological units are those when a unit is formed on the basis of a free
word-group The most productive in Modern English is the formation of
phraseological units by means of transferring the meaning of terminological
word-groups, e.g. in cosmic technique we can point out the following phrases:
«launching pad» in its terminological meaning is «стартова
площадка», in its transferred meaning — «відправний пункт»,
«to link up» — «cтикуватися, стикувати космічні човни» in
its tranformed meaning it means -«знайомитися»;) a large group of
phraseological units was formed from free word groups by transforming their
meaning, e.g. «granny farm» — «пансионат для старих людей»,
«Troyan horse» — «компьютерна програма, яка навмиснестворена для
пвиведення з ладу компьютера»;) phraseological units can be formed by
means of alliteration, e.g. «a sad sack» — «нещасний
випадок», «culture vulture» — «людина, яка цікавиться
мистецтвом», «fudge and nudge» — «ухильність».) they
can be formed by means of expressiveness, especially it is characteristic for
forming interjections, e.g. «My aunt!», «Hear, hear !» etc)
they can be formed by means of distorting a word group, e.g. «odds and
ends» was formed from «odd ends»,) they can be formed by using
archaisms, e.g. «in brown study» means «in gloomy
meditation» where both components preserve their archaic meanings,) they
can be formed by using a sentence in a different sphere of life, e.g.
«that cock won’t fight» can be used as a free word-group when it is
used in sports (cock fighting ), it becomes a phraseological unit when it is
used in everyday life, because it is used metaphorically,) they can be formed
when we use some unreal image, e.g. «to have butterflies in the
stomach» — «відчувати хвилювання», «to have green
fingers» — «досягати успіхів як садовод-любитель» etc.) they can
be formed by using expressions of writers or polititions in everyday life, e.g.
«corridors of power» (Snow), «American dream» (Alby)
«locust years» (Churchil) , «the winds of change» (Mc
Millan).into consideration mainly the degree of idiomaticity phraseological
units may be classified into three big groups. This classification was first
suggested by Acad. V.V. Vinogradov. These groups are:

phraseological fusions,

phraseological unities,

phraseological collocations, or
habitual collocations.fusions are completely non-motivated word-groups.
Themeaning of the components has no connection at least synchronically with the
meaning of the whole group. Idiomaticity is combined with complete stability of
the lexical components and the grammatical structure of the fusion [19; p.
37].unities are partially non-motivated word-groups as their meaning can
usually be understood through (deduced from) the metaphoric meaning of the
whole phraseological unit [3; p. 84].unities are usually marked by a
comparatively high degree of stability of the lexical components and
grammatical structure. Phraseological unities can have homonymous free phrases,
used in direct meanings.

§  to skate on thin
ice — to skate on thin ice (to risk);

§  to wash one’s hands
off dirt — to wash one’s hands off (to withdraw from participance);

§  to play the first
role in the theatre — to play the first role (to dominate).must be not less
than two notional wordsin metaphorical meanings.collocations are partially
motivated but they are made up of words having special lexical valency which is
marked by a certain degree of stability in such word-groups. In phraseological
collocations variability of components is strictly limited. They differ from
phraseological unities by the fact that one of the components in them is used
in its direct meaning, the other — in indirect meaning, and the meaning of the
whole group dominates over the meaning of its components. As figurativeness is
expressed only in one component of the phrase it is hardly felt [14; p. 69].

§  to pay a visit,
tribute, attention, respect;

Conclusions

the course of the present report
writing we have specified the definition of the word-group and determined its
general characteristics. Specific attention has been drawn to the
classification of word-groups. We have thoroughly analyzed semantic features of
word-groups, their motivated and non-motivated types and their specific
subtype, i.e. phraseological word-groups.completed the report writing, we have
come to the following conclusions.word-group is a combination of at least two
notional words which do not constitute the sentence but are syntactically
connected.have concluded that according to the type of syntagmatic relations,
word-groups can be coordinate, subordinate and predicative, according to the
structure they are divided into simple, expanded and extended.lexical meaning
of the word groups is the combined lexical meaning of the component words. The
meaning of the word groups is motivated by the meanings of the component
members and is supported by the structural pattern.term motivation is used to
denote the relationship existing between the phonemic or morphemic composition
and structural pattern of the word on the one hand and its meaning on the
other.have come to the conclusion, that here are three main types of
motivation: 1) phonetical; 2) morphological; 3) semantic.have concluded,
phraseological units are created from free word-groups. But in the course of
time some words — constituents of phraseological units may drop out of the
language; the situation in which the phraseological unit was formed can be
forgotten, motivation can be lost and these phrases become phraseological
fusions.

Bibliography

1.      Арнольд
И.В. Аспекты семантических исследований. — М., 1980.

2.      Арнольд
И.В. Стилистика современного английского языка. — М., 1973.

.        Кунин
А.В. Фразеология современного английского языка. — М., 1970

.        Маковский
М.М. Английская этимология. — М., 1986

.        Мешков
О.Д. Словообразование современного английского языка. -М., 1976

.        Мостовий
М.I. Лексикологiя
англiйськоi
мови. — Харькiв, 1993

.        Никитин
М.В. Лексическое значение слова (структура и комбинаторика). — М., 1983
Смирницкий А.И. Лексикология английского языка. — М., 1956

.        Никитин
М.В. О предмете и понятиях комбинаторной семантики / Проблемы лексической и
грамматической семасиологии. Владимир, 1974 год выпуска

9.      Смит
Л.П. Фразеология английского языка. — М., 1959

.        Старикова
Е.Н.. Раевская Н.Н., Медведева Л.М. Лингвистические чтения. Проблемы
словообразования. Лингвистика текста. — К., 1985

11.    Телия
В.Н. Типы языковых значений. Связанное значение слова в языке — М., 1981
Теоретические проблемы социальной лингвистики. — М., 1981

.        Харитончик
З.А. Лексикология английского языка. — Минск, 1992

.        Швейцер
А.Д. Очерк современного английского языка США. — М.. 1963

.        Akhmanova
O. Lexicology. Theory and Method. — M., 1972 Ginsburg R.S. A Course in Modern
English Lexicology. M., 1979.

.        Arnold
I.V. The English Word. — M., 1986

.        Kuznetsova
V.S. Notes on English Lexicology.- K., 1968.

.        L.P.
Smith, Semantics. An introduction to the science of meaning. Oxford University
Press, 1962.

.        Vinogradov
V.V. Pixon P.G. Handbook of American Idioms and Idiomatic Usage, 1973.

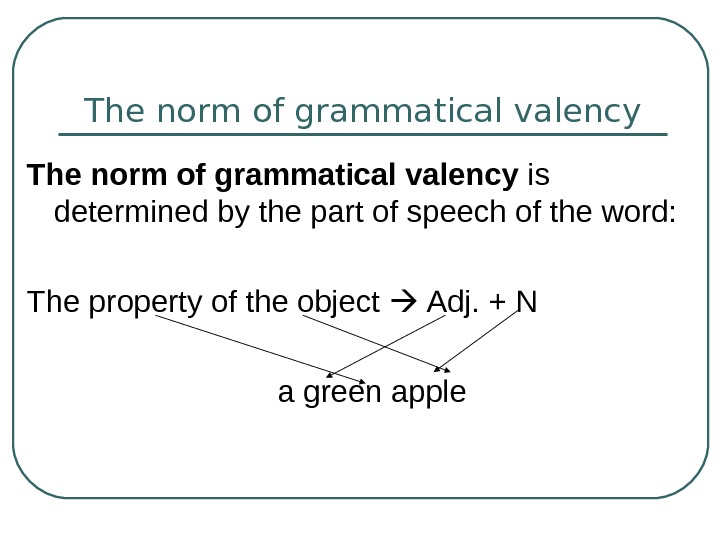
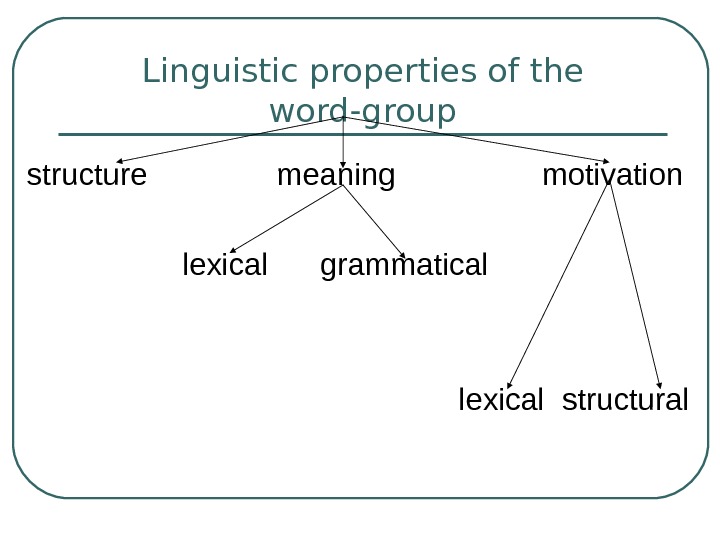
In mathematics, especially in the area of abstract algebra known as combinatorial group theory, the word problem for a finitely generated group G is the algorithmic problem of deciding whether two words in the generators represent the same element. More precisely, if A is a finite set of generators for G then the word problem is the membership problem for the formal language of all words in A and a formal set of inverses that map to the identity under the natural map from the free monoid with involution on A to the group G. If B is another finite generating set for G, then the word problem over the generating set B is equivalent to the word problem over the generating set A. Thus one can speak unambiguously of the decidability of the word problem for the finitely generated group G.

The related but different uniform word problem for a class K of recursively presented groups is the algorithmic problem of deciding, given as input a presentation P for a group G in the class K and two words in the generators of G, whether the words represent the same element of G. Some authors require the class K to be definable by a recursively enumerable set of presentations.

History

Throughout the history of the subject, computations in groups have been carried out using various normal forms. These usually implicitly solve the word problem for the groups in question. In 1911 Max Dehn proposed that the word problem was an important area of study in its own right, together with the conjugacy problem and the group isomorphism problem. In 1912 he gave an algorithm that solves both the word and conjugacy problem for the fundamental groups of closed orientable two-dimensional manifolds of genus greater than or equal to 2. Subsequent authors have greatly extended Dehn’s algorithm and applied it to a wide range of group theoretic decision problems.

It was shown by Pyotr Novikov in 1955 that there exists a finitely presented group G such that the word problem for G is undecidable. It follows immediately that the uniform word problem is also undecidable. A different proof was obtained by William Boone in 1958.

The word problem was one of the first examples of an unsolvable problem to be found not in mathematical logic or the theory of algorithms, but in one of the central branches of classical mathematics, algebra. As a result of its unsolvability, several other problems in combinatorial group theory have been shown to be unsolvable as well.

It is important to realize that the word problem is in fact solvable for many groups G. For example, polycyclic groups have solvable word problems since the normal form of an arbitrary word in a polycyclic presentation is readily computable; other algorithms for groups may, in suitable circumstances, also solve the word problem, see the Todd–Coxeter algorithm^[1] and the Knuth–Bendix completion algorithm.^[2] On the other hand, the fact that a particular algorithm does not solve the word problem for a particular group does not show that the group has an unsolvable word problem. For instance Dehn’s algorithm does not solve the word problem for the fundamental group of the torus. However this group is the direct product of two infinite cyclic groups and so has a solvable word problem.

A more concrete description

In more concrete terms, the uniform word problem can be expressed as a rewriting question, for literal strings. For a presentation P of a group G, P will specify a certain number of generators

x, y, z, …

for G. We need to introduce one letter for x and another (for convenience) for the group element represented by x^-1. Call these letters (twice as many as the generators) the alphabet

Sigma

for our problem. Then each element in G is represented in some way by a product

abc … pqr

of symbols from

Sigma

, of some length, multiplied in G. The string of length 0 (null string) stands for the identity element e of G. The crux of the whole problem is to be able to recognise all the ways e can be represented, given some relations.

The effect of the relations in G is to make various such strings represent the same element of G. In fact the relations provide a list of strings that can be either introduced where we want, or cancelled out whenever we see them, without changing the ‘value’, i.e. the group element that is the result of the multiplication.

For a simple example, take the presentation . Writing A for the inverse of a, we have possible strings combining any number of the symbols a and A. Whenever we see aaa, or aA or Aa we may strike these out. We should also remember to strike out AAA; this says that since the cube of a is the identity element of G, so is the cube of the inverse of a. Under these conditions the word problem becomes easy. First reduce strings to the empty string, a, aa, A or AA. Then note that we may also multiply by aaa, so we can convert A to aa and convert AA to a. The result is that the word problem, here for the cyclic group of order three, is solvable.

This is not, however, the typical case. For the example, we have a canonical form available that reduces any string to one of length at most three, by decreasing the length monotonically. In general, it is not true that one can get a canonical form for the elements, by stepwise cancellation. One may have to use relations to expand a string many-fold, in order eventually to find a cancellation that brings the length right down.

The upshot is, in the worst case, that the relation between strings that says they are equal in G is an Undecidable problem.

Examples

The following groups have a solvable word problem:

• Automatic groups, including:
  • Finite groups
  • Negatively curved (aka. hyperbolic) groups
  • Euclidean groups
  • Coxeter groups
  • Braid groups
  • Geometrically finite groups
• Finitely generated free groups
• Finitely generated free abelian groups
• Polycyclic groups
• Finitely generated recursively absolutely presented groups,^[3] including:
  • Finitely presented simple groups.
• Finitely presented residually finite groups
• One relator groups^[4] (this is a theorem of Magnus), including:
  • Fundamental groups of closed orientable two-dimensional manifolds.
• Combable groups
• Autostackable groups

Examples with unsolvable word problems are also known:

• Given a recursively enumerable set A of positive integers that has insoluble membership problem, ⟨a,b,c,d | aⁿbaⁿ = cⁿdcⁿ : n ∈ A⟩ is a finitely generated group with a recursively enumerable presentation whose word problem is insoluble
• Every finitely generated group with a recursively enumerable presentation and insoluble word problem is a subgroup of a finitely presented group with insoluble word problem
• The number of relators in a finitely presented group with insoluble word problem may be as low as 14 or even 12.
• An explicit example of a reasonable short presentation with insoluble word problem is given in Collins 1986:^[5]

begin{array}{lllll}langle&a,b,c,d,e,p,q,r,t,k&|&& 
&p¹⁰a=ap,&pacqr=rpcaq,&ra=ar,&\
&p¹⁰b=bp,&p^2adq2r=rp^2daq2,&rb=br,&\
&p¹⁰c=cp,&p^3bcq3r=rp^3cbq3,&rc=cr,&\
&p¹⁰d=dp,&p^4bdq4r=rp^4dbq4,&rd=dr,&\
&p¹⁰e=ep,&p^5ceq5r=rp^5ecaq5,&re=er,&\
&aq¹⁰=qa,&p^6deq6r=rp^6edbq6,&pt=tp,&\
&bq¹⁰=qb,&p^7cdcq7r=rp^7cdceq7,&qt=tq,&\
&cq¹⁰=qc,&p^8ca3q8r=rp^8a3q8,&&\
&dq¹⁰=qd,&p^9da3q9r=rp^9a3q9,&&\
&eq¹⁰=qe,&a^-3ta^3k=ka^-3ta³&&rangleend{array}

Partial solution of the word problem

The word problem for a recursively presented group can be partially solved in the following sense:

Given a recursive presentation P = ⟨X|R⟩ for a group G, define:

S={langleu,vrangle:uandvarewordsinXandu=vinG }

then there is a partial recursive function f_P such that:

f_P(langleu,vrangle)=begin{cases}0&if langleu,vrangleinS\
undefined/doesnothalt &if langleu,vranglenotinS
end{cases}

More informally, there is an algorithm that halts if u=v, but does not do so otherwise.

It follows that to solve the word problem for P it is sufficient to construct a recursive function g such that:

g(langleu,vrangle)=begin{cases}0&if langleu,vranglenotinS\
undefined/doesnothalt &if langleu,vrangleinS
end{cases}

However u=v in G if and only if in G. It follows that to solve the word problem for P it is sufficient to construct a recursive function h such that:

h(x)=begin{cases}0&if x ≠ 1 in G\
undefined/doesnothalt &if x=1 in G
end{cases}

Example

The following will be proved as an example of the use of this technique:

Theorem: A finitely presented residually finite group has solvable word problem.

Proof: Suppose G = ⟨X|R⟩ is a finitely presented, residually finite group.

Let S be the group of all permutations of N, the natural numbers, that fixes all but finitely many numbers then:

1. S is locally finite and contains a copy of every finite group.
2. The word problem in S is solvable by calculating products of permutations.
3. There is a recursive enumeration of all mappings of the finite set X into S.
4. Since G is residually finite, if w is a word in the generators X of G then in G if and only of some mapping of X into S induces a homomorphism such that in S.

Given these facts, algorithm defined by the following pseudocode:

For every mapping of X into S If every relator in R is satisfied in S If w ≠ 1 in S return 0 End if End if End for

defines a recursive function h such that:

h(x)=begin{cases}0&if x ≠ 1 in G\
undefined/doesnothalt &if x=1 in G
end{cases}

This shows that G has solvable word problem.

Unsolvability of the uniform word problem

The criterion given above, for the solvability of the word problem in a single group, can be extended by a straightforward argument. This gives the following criterion for the uniform solvability of the word problem for a class of finitely presented groups:

To solve the uniform word problem for a class K of groups, it is sufficient to find a recursive function that takes a finite presentation P for a group G and a word in the generators of G, such that whenever G ∈ K:

f(P,w)=begin{cases}0&if w ≠ 1 in G\
undefined/doesnothalt &if w=1 in G
end{cases}

Boone-Rogers Theorem: There is no uniform partial algorithm that solves the word problem in all finitely presented groups with solvable word problem.

In other words, the uniform word problem for the class of all finitely presented groups with solvable word problem is unsolvable. This has some interesting consequences. For instance, the Higman embedding theorem can be used to construct a group containing an isomorphic copy of every finitely presented group with solvable word problem. It seems natural to ask whether this group can have solvable word problem. But it is a consequence of the Boone-Rogers result that:

Corollary: There is no universal solvable word problem group. That is, if G is a finitely presented group that contains an isomorphic copy of every finitely presented group with solvable word problem, then G itself must have unsolvable word problem.

Remark: Suppose G = ⟨X|R⟩ is a finitely presented group with solvable word problem and H is a finite subset of G. Let H^* = ⟨H⟩, be the group generated by H. Then the word problem in H^* is solvable: given two words h, k in the generators H of H^*, write them as words in X and compare them using the solution to the word problem in G. It is easy to think that this demonstrates a uniform solution of the word problem for the class K (say) of finitely generated groups that can be embedded in G. If this were the case, the non-existence of a universal solvable word problem group would follow easily from Boone-Rogers. However, the solution just exhibited for the word problem for groups in K is not uniform. To see this, consider a group J = ⟨Y|T⟩ ∈ K; in order to use the above argument to solve the word problem in J, it is first necessary to exhibit a mapping e: Y → G that extends to an embedding e^*: J → G. If there were a recursive function that mapped (finitely generated) presentations of groups in K to embeddings into G, then a uniform solution of the word problem in K could indeed be constructed. But there is no reason, in general, to suppose that such a recursive function exists. However, it turns out that, using a more sophisticated argument, the word problem in J can be solved without using an embedding e: J → G. Instead an enumeration of homomorphisms is used, and since such an enumeration can be constructed uniformly, it results in a uniform solution to the word problem in K.

Proof that there is no universal solvable word problem group

Suppose G were a universal solvable word problem group. Given a finite presentation P = ⟨X|R⟩ of a group H, one can recursively enumerate all homomorphisms h: H → G by first enumerating all mappings h^†: X → G. Not all of these mappings extend to homomorphisms, but, since h^†(R) is finite, it is possible to distinguish between homomorphisms and non-homomorphisms, by using the solution to the word problem in G. «Weeding out» non-homomorphisms gives the required recursive enumeration: h₁, h₂, …, h_n, … .

If H has solvable word problem, then at least one of these homomorphisms must be an embedding. So given a word w in the generators of H:

If wne1 in H, h_n(w)ne1 in G forsome h_n

If w=1 in H, h_n(w)=1 in G forall h_n

Consider the algorithm described by the pseudocode:

Let n = 0 Let repeatable = TRUE while (repeatable) increase n by 1 if (solution to word problem in G reveals h_n(w) ≠ 1 in G) Let repeatable = FALSE output 0.

This describes a recursive function:

f(w)=begin{cases}0&if w ≠ 1 in H\
undefined/doesnothalt &if w=1 in H.
end{cases}

The function f clearly depends on the presentation P. Considering it to be a function of the two variables, a recursive function has been constructed that takes a finite presentation P for a group H and a word w in the generators of a group G, such that whenever G has soluble word problem:

f(P,w)=begin{cases}0&if w ≠ 1 in H\
undefined/doesnothalt &if w=1 in H.
end{cases}

But this uniformly solves the word problem for the class of all finitely presented groups with solvable word problem, contradicting Boone-Rogers. This contradiction proves G cannot exist.

Algebraic structure and the word problem

There are a number of results that relate solvability of the word problem and algebraic structure. The most significant of these is the Boone-Higman theorem:

A finitely presented group has solvable word problem if and only if it can be embedded in a simple group that can be embedded in a finitely presented group.

It is widely believed that it should be possible to do the construction so that the simple group itself is finitely presented. If so one would expect it to be difficult to prove as the mapping from presentations to simple groups would have to be non-recursive.

The following has been proved by Bernhard Neumann and Angus Macintyre:

A finitely presented group has solvable word problem if and only if it can be embedded in every algebraically closed group

What is remarkable about this is that the algebraically closed groups are so wild that none of them has a recursive presentation.

The oldest result relating algebraic structure to solvability of the word problem is Kuznetsov’s theorem:

A recursively presented simple group S has solvable word problem.

To prove this let ⟨X|R⟩ be a recursive presentation for S. Choose a ∈ S such that a ≠ 1 in S.

If w is a word on the generators X of S, then let:

S_w=langleX|Rcup{w}rangle.

There is a recursive function

f_langlerangle}

such that:

f_langlerangle}(x)=begin{cases}0&if x=1 in S_{w\
undefined/doesnothalt &if x ≠} 1 in S_{w.
end{cases}}

Write:

g(w,x)=f_langlerangle}(x).

Then because the construction of f was uniform, this is a recursive function of two variables.

It follows that: is recursive. By construction:

h(w)=begin{cases}
0&if a=1 in S_{w\
undefined/doesnothalt &if a ≠} 1 in S_{w.
end{cases}}

Since S is a simple group, its only quotient groups are itself and the trivial group. Since a ≠ 1 in S, we see a = 1 in S_w if and only if S_w is trivial if and only if w ≠ 1 in S. Therefore:

h(w)=begin{cases}
0&if wne1 in S\
undefined/doesnothalt &if w=1 in S.
end{cases}

The existence of such a function is sufficient to prove the word problem is solvable for S.

This proof does not prove the existence of a uniform algorithm for solving the word problem for this class of groups. The non-uniformity resides in choosing a non-trivial element of the simple group. There is no reason to suppose that there is a recursive function that maps a presentation of a simple groups to a non-trivial element of the group. However, in the case of a finitely presented group we know that not all the generators can be trivial (Any individual generator could be, of course). Using this fact it is possible to modify the proof to show:

The word problem is uniformly solvable for the class of finitely presented simple groups.

See also

• Combinatorics on words
• SQ-universal group
• Word problem (mathematics)
• Reachability problem
• Nested stack automata (have been used to solve the word problem for groups)

Notes

1. Todd . J. . Coxeter . H.S.M. . A practical method for enumerating cosets of a finite abstract group . Proceedings of the Edinburgh Mathematical Society . 5 . 1 . 26–34 . 1936 . 10.1017/S0013091500008221 .
2. Book: Knuth, D. . P. . Bendix . Simple word problems in universal algebras . https://www.google.com/books/edition/Computational_Problems_in_Abstract_Algeb/KIDiBQAAQBAJ?hl=en&pg=PA263 . J. . Leech . Computational Problems in Abstract Algebra: Proceedings of a Conference Held at Oxford Under the Auspices of the Science Research Council Atlas Computer Laboratory, 29th August to 2nd September 1967 . Springer . 2014 . 1970 . 9781483159423 . 263–297 .
3. H. . Simmons . The word problem for absolute presentations . J. London Math. Soc. . s2-6 . 2 . 275–280 . 1973 . 10.1112/jlms/s2-6.2.275 .
4. Book: Lyndon, Roger C. . Paul E . Schupp . Combinatorial Group Theory . Springer . 2001 . 9783540411581 . 1–60 .
5. We use the corrected version from John Pedersen’s A Catalogue of Algebraic Systems

References

• Book: Boone, W.W. . F.B. . Cannonito . Roger C. . Lyndon . Word problems : decision problems and the Burnside problem in group theory . North-Holland . 1973 . 9780720422719 . Studies in logic and the foundations of mathematics . 71.
• Boone . W. W. . Higman . G. . 1974 . An algebraic characterization of the solvability of the word problem . J. Austral. Math. Soc. . 18 . 41–53 . 10.1017/s1446788700019108. free .
• Boone . W. W. . Rogers Jr . H. . 1966 . On a problem of J. H. C. Whitehead and a problem of Alonzo Church . Math. Scand. . 19 . 185–192 . 10.7146/math.scand.a-10808. free .
  • • • • • • • A.V. . Kuznetsov . Algorithms as operations in algebraic systems . Izvestia Akad. Nauk SSSR Ser Mat . 13 . 3 . 81 . 1958 .
• Book: Miller, C.F. . Decision problems for groups — survey and reflections . https://link.springer.com/chapter/10.1007/978-1-4613-9730-4_1 . Algorithms and Classification in Combinatorial Group Theory . Springer . 1991 . 978-1-4613-9730-4 . 1–60 . 10.1007/978-1-4613-9730-4_1.
  • • Stillwell . J. . 1982 . The word problem and the isomorphism problem for groups . Bulletin of the AMS . 6 . 33–56 . 10.1090/s0273-0979-1982-14963-1. free .