Noun
The front of the car took the full force of the collision.
instruments used to measure the force of the wind
The police were accused of using excessive force when they made the arrest.
We discourage the use of force.
He used brute force to open the door.
I was impressed by the force of her personality.
Verb
They forced us to work long hours without pay.
The flooding forced hundreds of residents to flee their homes.
After seeing the evidence, I was forced to admit my error.
I am forced to conclude that more funding will be necessary.
The pilot was forced to land when one of the plane’s engines caught fire.
The scandal forced his resignation.
Lack of time may eventually force a compromise.
They are trying to force a vote on this issue.
The runner was forced out of bounds.
Their car was forced off the road.
See More
Recent Examples on the Web
The sides split in 1949 after a civil war, and the Communist Party says the island is obliged to rejoin the mainland, by force if necessary.
—
China, which has never renounced the use of force to bring the island under its control, says Taiwan is the most important and sensitive issue in its relations with the United States, and the topic is a frequent source of tensions.
—
In December 1958, a brutal Cuban dictator friendly with the United States, Fulgencio Batista, was deposed by forces led by Fidel Castro, who became a brutal Cuban dictator not friendly with the United States.
—
Police removed them by force, detaining hundreds and leaving dozens injured.
—
Almost a quarter of those allegations were for improper use of force.
—
An intense Chinese show of force could hamper Nationalist efforts to make its case to voters, said Lev Nachman, a political scientist at National Chengchi University in Taipei who studies electoral attitudes in Taiwan.
—
Geller said the Virginia State Police Bureau of Criminal Investigation is probing whether the troopers’ use of deadly force was justified.
—
On Thursday, text messages between Majors and the alleged victim were released by Chaudry, with Chaudry claiming that the exchange contained an admission of physical force by the alleged victim.
—
But one player who could force his way into the lineup is Pritchett, a Jackson native who transferred to South Alabama last season from Tuskegee.
—
According to New York State Police, Tatiana David was taken against her will from her Ithaca, N.Y., home Wednesday morning and forced into a white SUV.
—
Giant galaxies can merge with one another, too, forcing the black holes at their respective centers into close proximity.
—
Defense was a bit of a problem, but the Pacers forced him into difficult situations down the stretch of the season to try to move that along.
—
In the first two years of the tournament going into this week’s game, the seventh-place team is 4-0, yet to be forced into a second game.
—
Others who missed the cut included Bryson DeChambeau, who shot back-to-back 74s to miss by one, and 2003 champ Mike Weir, who also finished at 4 over after he was forced to play his second round Friday with a marker.
—
Others who missed the cut included Bryson DeChambeau, who shot back-to-back 74s to miss by one, and 2003 champ Mike Weir, who also finished at 4 over after he was forced to play his second round Friday with a marker.
—
Being forced to cede control is a big part of Lizzy’s life too.
—
See More
These examples are programmatically compiled from various online sources to illustrate current usage of the word ‘force.’ Any opinions expressed in the examples do not represent those of Merriam-Webster or its editors. Send us feedback about these examples.
| Force | |
|---|---|

Forces can be described as a push or pull on an object. They can be due to phenomena such as gravity, magnetism, or anything that might cause a mass to accelerate. |
|
|
Common symbols |
 , F, F , F, F |
| SI unit | newton (N) |
|
Other units |
dyne, pound-force, poundal, kip, kilopond |
| In SI base units | kg·m·s–2 |
|
Derivations from |
F = ma (formerly P = mf) |
| Dimension |  |
In physics, a force is an influence that causes the motion of an object with mass to change its velocity (e.g. moving from a state of rest), i.e., to accelerate. It can be a push or a pull, always with magnitude and direction, making it a vector quantity. It is measured in the SI unit of newton (N) and represented by the symbol F (formerly P).
The original form of Newton’s second law states that the net force acting upon an object is equal to the rate at which its momentum changes with time. If the mass of the object is constant, this law implies that the acceleration of an object is directly proportional to the net force acting on the object, is in the direction of the net force, and is inversely proportional to the mass of the object.
Concepts related to force include: thrust, which increases the velocity of an object; drag, which decreases the velocity of an object; and torque, which produces changes in rotational speed of an object. In an extended body, each part usually applies forces on the adjacent parts; the distribution of such forces through the body is the internal mechanical stress. Such internal mechanical stresses cause no acceleration of that body as the forces balance one another. Pressure, the distribution of many small forces applied over an area of a body, is a simple type of stress that if unbalanced can cause the body to accelerate. Stress usually causes deformation of solid materials, or flow in fluids.
Development of the concept[edit]
Philosophers in antiquity used the concept of force in the study of stationary and moving objects and simple machines, but thinkers such as Aristotle and Archimedes retained fundamental errors in understanding force. In part this was due to an incomplete understanding of the sometimes non-obvious force of friction, and a consequently inadequate view of the nature of natural motion.[1] A fundamental error was the belief that a force is required to maintain motion, even at a constant velocity. Most of the previous misunderstandings about motion and force were eventually corrected by Galileo Galilei and Sir Isaac Newton. With his mathematical insight, Sir Isaac Newton formulated laws of motion that were not improved for nearly three hundred years.[2] By the early 20th century, Einstein developed a theory of relativity that correctly predicted the action of forces on objects with increasing momenta near the speed of light, and also provided insight into the forces produced by gravitation and inertia.
With modern insights into quantum mechanics and technology that can accelerate particles close to the speed of light, particle physics has devised a Standard Model to describe forces between particles smaller than atoms. The Standard Model predicts that exchanged particles called gauge bosons are the fundamental means by which forces are emitted and absorbed. Only four main interactions are known: in order of decreasing strength, they are: strong, electromagnetic, weak, and gravitational.[3]: 2–10 [4]: 79 High-energy particle physics observations made during the 1970s and 1980s confirmed that the weak and electromagnetic forces are expressions of a more fundamental electroweak interaction.[5]
Pre-Newtonian concepts[edit]
Aristotle famously described a force as anything that causes an object to undergo «unnatural motion»
Since antiquity the concept of force has been recognized as integral to the functioning of each of the simple machines. The mechanical advantage given by a simple machine allowed for less force to be used in exchange for that force acting over a greater distance for the same amount of work. Analysis of the characteristics of forces ultimately culminated in the work of Archimedes who was especially famous for formulating a treatment of buoyant forces inherent in fluids.[1]
Aristotle provided a philosophical discussion of the concept of a force as an integral part of Aristotelian cosmology. In Aristotle’s view, the terrestrial sphere contained four elements that come to rest at different «natural places» therein. Aristotle believed that motionless objects on Earth, those composed mostly of the elements earth and water, to be in their natural place on the ground and that they will stay that way if left alone. He distinguished between the innate tendency of objects to find their «natural place» (e.g., for heavy bodies to fall), which led to «natural motion», and unnatural or forced motion, which required continued application of a force.[6] This theory, based on the everyday experience of how objects move, such as the constant application of a force needed to keep a cart moving, had conceptual trouble accounting for the behavior of projectiles, such as the flight of arrows. The place where the archer moves the projectile was at the start of the flight, and while the projectile sailed through the air, no discernible efficient cause acts on it. Aristotle was aware of this problem and proposed that the air displaced through the projectile’s path carries the projectile to its target. This explanation demands a continuum like air for change of place in general.[7]
Aristotelian physics began facing criticism in medieval science, first by John Philoponus in the 6th century.
The shortcomings of Aristotelian physics would not be fully corrected until the 17th century work of Galileo Galilei, who was influenced by the late medieval idea that objects in forced motion carried an innate force of impetus. Galileo constructed an experiment in which stones and cannonballs were both rolled down an incline to disprove the Aristotelian theory of motion. He showed that the bodies were accelerated by gravity to an extent that was independent of their mass and argued that objects retain their velocity unless acted on by a force, for example friction.[8]
In the early 17th century, before Newton’s Principia, the term «force» (Latin: vis) was applied to many physical and non-physical phenomena, e.g., for an acceleration of a point. The product of a point mass and the square of its velocity was named vis viva (live force) by Leibniz. The modern concept of force corresponds to Newton’s vis motrix (accelerating force).[9]
Newtonian mechanics[edit]
Sir Isaac Newton described the motion of all objects using the concepts of inertia and force, and in doing so he found they obey certain conservation laws. In 1687, Newton published his thesis Philosophiæ Naturalis Principia Mathematica.[2][10] In this work Newton set out three laws of motion that to this day are the way forces are described in physics.[10]
First law[edit]
Newton’s first law of motion states that objects continue to move in a state of constant velocity unless acted upon by an external net force (resultant force).[10] This law is an extension of Galileo’s insight that constant velocity was associated with a lack of net force (see a more detailed description of this below). Newton proposed that every object with mass has an innate inertia that functions as the fundamental equilibrium «natural state» in place of the Aristotelian idea of the «natural state of rest». That is, Newton’s empirical first law contradicts the intuitive Aristotelian belief that a net force is required to keep an object moving with constant velocity. By making rest physically indistinguishable from non-zero constant velocity, Newton’s first law directly connects inertia with the concept of relative velocities. Specifically, in systems where objects are moving with different velocities, it is impossible to determine which object is «in motion» and which object is «at rest». The laws of physics are the same in every inertial frame of reference, that is, in all frames related by a Galilean transformation.
For instance, while traveling in a moving vehicle at a constant velocity, the laws of physics do not change as a result of its motion. If a person riding within the vehicle throws a ball straight up, that person will observe it rise vertically and fall vertically and not have to apply a force in the direction the vehicle is moving. Another person, observing the moving vehicle pass by, would observe the ball follow a curving parabolic path in the same direction as the motion of the vehicle. It is the inertia of the ball associated with its constant velocity in the direction of the vehicle’s motion that ensures the ball continues to move forward even as it is thrown up and falls back down. From the perspective of the person in the car, the vehicle and everything inside of it is at rest: It is the outside world that is moving with a constant speed in the opposite direction of the vehicle. Since there is no experiment that can distinguish whether it is the vehicle that is at rest or the outside world that is at rest, the two situations are considered to be physically indistinguishable. Inertia therefore applies equally well to constant velocity motion as it does to rest.
Second law[edit]
A modern statement of Newton’s second law is a vector equation:[Note 1]

where 

By the definition of momentum,
where m is the mass and 
If Newton’s second law is applied to a system of constant mass,[Note 2] m may be moved outside the derivative operator. The equation then becomes
By substituting the definition of acceleration, the algebraic version of Newton’s second law is derived:

Newton never explicitly stated the formula in the reduced form above.[11]
Newton’s second law asserts the direct proportionality of acceleration to force and the inverse proportionality of acceleration to mass. Accelerations can be defined through kinematic measurements, which are well-described through reference frame analysis in advanced physics. General relativity offers an equivalence between space-time and mass, but lacking a coherent theory of quantum gravity, it is unclear as to how or whether this connection is relevant on microscales. With some justification, Newton’s second law can be taken as a quantitative definition of mass by writing the law as an equality; the relative units of force and mass then are fixed.
Some textbooks use Newton’s second law as a definition of force,[12][13][14] but this has been disparaged in other textbooks.[3]: 12–1 [4]: 59 Notable physicists, philosophers and mathematicians who have sought a more explicit definition of the concept of force include Ernst Mach and Walter Noll.[15][16]
Newton’s second law can be used to measure the strength of forces. For instance, knowledge of the masses of planets along with the accelerations of their orbits allows scientists to calculate the gravitational forces on planets.
Third law[edit]
Whenever one body exerts a force on another, the latter simultaneously exerts an equal and opposite force on the first. In vector form, if 

This law is sometimes referred to as the action-reaction law, with 

Newton’s Third Law is a result of applying symmetry to situations where forces can be attributed to the presence of different objects. The third law means that all forces are interactions between different bodies,[17][Note 3] and thus that there is no such thing as a unidirectional force or a force that acts on only one body.
In a system composed of object 1 and object 2, the net force on the system due to their mutual interactions is zero:
More generally, in a closed system of particles, all internal forces are balanced. The particles may accelerate with respect to each other but the center of mass of the system will not accelerate. If an external force acts on the system, it will make the center of mass accelerate in proportion to the magnitude of the external force divided by the mass of the system.[3]: 19–1 [4]
Combining Newton’s Second and Third Laws, it is possible to show that the linear momentum of a system is conserved.[18] In a system of two particles, if 

Using similar arguments, this can be generalized to a system with an arbitrary number of particles. In general, as long as all forces are due to the interaction of objects with mass, it is possible to define a system such that net momentum is never lost nor gained.[3][4]
Special theory of relativity[edit]
In the special theory of relativity, mass and energy are equivalent (as can be seen by calculating the work required to accelerate an object). When an object’s velocity increases, so does its energy and hence its mass equivalent (inertia). It thus requires more force to accelerate it the same amount than it did at a lower velocity. Newton’s Second Law,
remains valid because it is a mathematical definition.[19]: 855–876 But for relativistic momentum to be conserved, it must be redefined as:
where 

The relativistic expression relating force and acceleration for a particle with constant non-zero rest mass 

where

is called the Lorentz factor.
In the early history of relativity, the expressions 


If 


is a close approximation. Even for use in relativity, one can restore the form of
through the use of four-vectors. This relation is correct in relativity when 


Descriptions[edit]
Since forces are perceived as pushes or pulls, this can provide an intuitive understanding for describing forces.[2] As with other physical concepts (e.g. temperature), the intuitive understanding of forces is quantified using precise operational definitions that are consistent with direct observations and compared to a standard measurement scale. Through experimentation, it is determined that laboratory measurements of forces are fully consistent with the conceptual definition of force offered by Newtonian mechanics.
Forces act in a particular direction and have sizes dependent upon how strong the push or pull is. Because of these characteristics, forces are classified as «vector quantities». This means that forces follow a different set of mathematical rules than physical quantities that do not have direction (denoted scalar quantities). For example, when determining what happens when two forces act on the same object, it is necessary to know both the magnitude and the direction of both forces to calculate the result. If both of these pieces of information are not known for each force, the situation is ambiguous. For example, if you know that two people are pulling on the same rope with known magnitudes of force but you do not know which direction either person is pulling, it is impossible to determine what the acceleration of the rope will be. The two people could be pulling against each other as in tug of war or the two people could be pulling in the same direction. In this simple one-dimensional example, without knowing the direction of the forces it is impossible to decide whether the net force is the result of adding the two force magnitudes or subtracting one from the other. Associating forces with vectors avoids such problems.
Historically, forces were first quantitatively investigated in conditions of static equilibrium where several forces canceled each other out. Such experiments demonstrate the crucial properties that forces are additive vector quantities: they have magnitude and direction.[2] When two forces act on a point particle, the resulting force, the resultant (also called the net force), can be determined by following the parallelogram rule of vector addition: the addition of two vectors represented by sides of a parallelogram, gives an equivalent resultant vector that is equal in magnitude and direction to the transversal of the parallelogram.[3][4] The magnitude of the resultant varies from the difference of the magnitudes of the two forces to their sum, depending on the angle between their lines of action. If acting on an extended body, their respective lines of application must also be specified in order to account for their effects on the body’s motion.
Free-body diagrams can be used as a convenient way to keep track of forces acting on a system. Ideally, these diagrams are drawn with the angles and relative magnitudes of the force vectors preserved so that graphical vector addition can be done to determine the net force.[21]
As well as being added, forces can also be resolved into independent components at right angles to each other. A horizontal force pointing northeast can therefore be split into two forces, one pointing north, and one pointing east. Summing these component forces using vector addition yields the original force. Resolving force vectors into components of a set of basis vectors is often a more mathematically clean way to describe forces than using magnitudes and directions.[22] This is because, for orthogonal components, the components of the vector sum are uniquely determined by the scalar addition of the components of the individual vectors. Orthogonal components are independent of each other because forces acting at ninety degrees to each other have no effect on the magnitude or direction of the other. Choosing a set of orthogonal basis vectors is often done by considering what set of basis vectors will make the mathematics most convenient. Choosing a basis vector that is in the same direction as one of the forces is desirable, since that force would then have only one non-zero component. Orthogonal force vectors can be three-dimensional with the third component being at right-angles to the other two.[3][4]
Equilibrium[edit]
When all the forces that act upon an object are balanced, then the object is said to be in a state of equilibrium. Hence, equilibrium occurs when the resultant force acting on a point particle is zero (that is, the vector sum of all forces is zero). When dealing with an extended body, it is also necessary that the net torque be zero.
There are two kinds of equilibrium: static equilibrium and dynamic equilibrium.
Static[edit]
Static equilibrium was understood well before the invention of classical mechanics. Objects that are at rest have zero net force acting on them.[23]
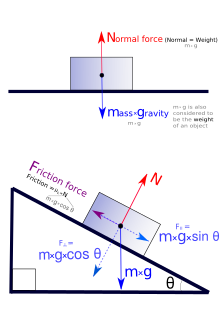
The simplest case of static equilibrium occurs when two forces are equal in magnitude but opposite in direction. For example, an object on a level surface is pulled (attracted) downward toward the center of the Earth by the force of gravity. At the same time, a force is applied by the surface that resists the downward force with equal upward force (called a normal force). The situation produces zero net force and hence no acceleration.[2]
Pushing against an object that rests on a frictional surface can result in a situation where the object does not move because the applied force is opposed by static friction, generated between the object and the table surface. For a situation with no movement, the static friction force exactly balances the applied force resulting in no acceleration. The static friction increases or decreases in response to the applied force up to an upper limit determined by the characteristics of the contact between the surface and the object.[2]
A static equilibrium between two forces is the most usual way of measuring forces, using simple devices such as weighing scales and spring balances. For example, an object suspended on a vertical spring scale experiences the force of gravity acting on the object balanced by a force applied by the «spring reaction force», which equals the object’s weight. Using such tools, some quantitative force laws were discovered: that the force of gravity is proportional to volume for objects of constant density (widely exploited for millennia to define standard weights); Archimedes’ principle for buoyancy; Archimedes’ analysis of the lever; Boyle’s law for gas pressure; and Hooke’s law for springs. These were all formulated and experimentally verified before Isaac Newton expounded his Three Laws of Motion.[2][3][4]
Dynamic[edit]
Galileo Galilei was the first to point out the inherent contradictions contained in Aristotle’s description of forces.
Dynamic equilibrium was first described by Galileo who noticed that certain assumptions of Aristotelian physics were contradicted by observations and logic. Galileo realized that simple velocity addition demands that the concept of an «absolute rest frame» did not exist. Galileo concluded that motion in a constant velocity was completely equivalent to rest. This was contrary to Aristotle’s notion of a «natural state» of rest that objects with mass naturally approached. Simple experiments showed that Galileo’s understanding of the equivalence of constant velocity and rest were correct. For example, if a mariner dropped a cannonball from the crow’s nest of a ship moving at a constant velocity, Aristotelian physics would have the cannonball fall straight down while the ship moved beneath it. Thus, in an Aristotelian universe, the falling cannonball would land behind the foot of the mast of a moving ship. When this experiment is actually conducted, the cannonball always falls at the foot of the mast, as if the cannonball knows to travel with the ship despite being separated from it. Since there is no forward horizontal force being applied on the cannonball as it falls, the only conclusion left is that the cannonball continues to move with the same velocity as the boat as it falls. Thus, no force is required to keep the cannonball moving at the constant forward velocity.[8]
Moreover, any object traveling at a constant velocity must be subject to zero net force (resultant force). This is the definition of dynamic equilibrium: when all the forces on an object balance but it still moves at a constant velocity.
A simple case of dynamic equilibrium occurs in constant velocity motion across a surface with kinetic friction. In such a situation, a force is applied in the direction of motion while the kinetic friction force exactly opposes the applied force. This results in zero net force, but since the object started with a non-zero velocity, it continues to move with a non-zero velocity. Aristotle misinterpreted this motion as being caused by the applied force. When kinetic friction is taken into consideration it is clear that there is no net force causing constant velocity motion.[3][4]
Quantum mechanics[edit]
The notion «force» keeps its meaning in quantum mechanics, though one is now dealing with operators instead of classical variables and though the physics is now described by the Schrödinger equation instead of Newtonian equations. This has the consequence that the results of a measurement are now sometimes «quantized», i.e. they appear in discrete portions. This is, of course, difficult to imagine in the context of «forces». The potentials V(x, y, z) or fields, from which the forces generally can be derived, are treated similarly to classical position variables, i.e., 
This becomes different only in the framework of quantum field theory, where these fields are also quantized.
Quantum mechanics has a caveat; the particles acting onto each other do not only possess the spatial variable, but also a discrete intrinsic angular momentum-like variable called the «spin», and there is the Pauli exclusion principle relating the space and the spin variables. Depending on the value of the spin, identical particles split into two different classes, fermions and bosons. If two identical fermions (e.g. electrons) have a symmetric spin function (e.g. parallel spins) the spatial variables must be antisymmetric (i.e. they exclude each other from their places much as if there was a repulsive force), and vice versa, i.e. for antiparallel spins the position variables must be symmetric (i.e. the apparent force must be attractive). Thus in the case of two fermions there is a strictly negative correlation between spatial and spin variables, whereas for two bosons (e.g. quanta of electromagnetic waves, photons) the correlation is strictly positive.
Thus the notion «force» loses already part of its meaning.
Feynman diagrams[edit]
Feynman diagram for the decay of a neutron into a proton. The W boson is between two vertices indicating a repulsion.
In modern particle physics, forces and the acceleration of particles are explained as a mathematical by-product of exchange of momentum-carrying gauge bosons. With the development of quantum field theory and general relativity, it was realized that force is a redundant concept arising from conservation of momentum (4-momentum in relativity and momentum of virtual particles in quantum electrodynamics). The conservation of momentum can be directly derived from the homogeneity or symmetry of space and so is usually considered more fundamental than the concept of a force. Thus the currently known fundamental forces are considered more accurately to be «fundamental interactions».[5]: 199–128 When particle A emits (creates) or absorbs (annihilates) virtual particle B, a momentum conservation results in recoil of particle A making impression of repulsion or attraction between particles A A’ exchanging by B. This description applies to all forces arising from fundamental interactions. While sophisticated mathematical descriptions are needed to predict, in full detail, the accurate result of such interactions, there is a conceptually simple way to describe such interactions through the use of Feynman diagrams. In a Feynman diagram, each matter particle is represented as a straight line (see world line) traveling through time, which normally increases up or to the right in the diagram. Matter and anti-matter particles are identical except for their direction of propagation through the Feynman diagram. World lines of particles intersect at interaction vertices, and the Feynman diagram represents any force arising from an interaction as occurring at the vertex with an associated instantaneous change in the direction of the particle world lines. Gauge bosons are emitted away from the vertex as wavy lines and, in the case of virtual particle exchange, are absorbed at an adjacent vertex.[24]
The utility of Feynman diagrams is that other types of physical phenomena that are part of the general picture of fundamental interactions but are conceptually separate from forces can also be described using the same rules. For example, a Feynman diagram can describe in succinct detail how a neutron decays into an electron, proton, and neutrino, an interaction mediated by the same gauge boson that is responsible for the weak nuclear force.[24]
Fundamental interactions[edit]
All of the known forces of the universe are classified into four fundamental interactions. The strong and the weak forces act only at very short distances, and are responsible for the interactions between subatomic particles, including nucleons and compound nuclei. The electromagnetic force acts between electric charges, and the gravitational force acts between masses. All other forces in nature derive from these four fundamental interactions. For example, friction is a manifestation of the electromagnetic force acting between atoms of two surfaces, and the Pauli exclusion principle,[25] which does not permit atoms to pass through each other. Similarly, the forces in springs, modeled by Hooke’s law, are the result of electromagnetic forces and the Pauli exclusion principle acting together to return an object to its equilibrium position. Centrifugal forces are acceleration forces that arise simply from the acceleration of rotating frames of reference.[3]: 12–11 [4]: 359
The fundamental theories for forces developed from the unification of different ideas. For example, Sir Isaac Newton unified, with his universal theory of gravitation, the force responsible for objects falling near the surface of the Earth with the force responsible for the falling of celestial bodies about the Earth (the Moon) and around the Sun (the planets). Michael Faraday and James Clerk Maxwell demonstrated that electric and magnetic forces were unified through a theory of electromagnetism. In the 20th century, the development of quantum mechanics led to a modern understanding that the first three fundamental forces (all except gravity) are manifestations of matter (fermions) interacting by exchanging virtual particles called gauge bosons.[26] This Standard Model of particle physics assumes a similarity between the forces and led scientists to predict the unification of the weak and electromagnetic forces in electroweak theory, which was subsequently confirmed by observation. The complete formulation of the Standard Model predicts an as yet unobserved Higgs mechanism, but observations such as neutrino oscillations suggest that the Standard Model is incomplete. A Grand Unified Theory that allows for the combination of the electroweak interaction with the strong force is held out as a possibility with candidate theories such as supersymmetry proposed to accommodate some of the outstanding unsolved problems in physics. Physicists are still attempting to develop self-consistent unification models that would combine all four fundamental interactions into a theory of everything. Einstein tried and failed at this endeavor, but currently the most popular approach to answering this question is string theory.[5]: 212–219
| Property/Interaction | Gravitation | Weak | Electromagnetic | Strong | |
|---|---|---|---|---|---|
| (Electroweak) | Fundamental | Residual | |||
| Acts on: | Mass — Energy | Flavor | Electric charge | Color charge | Atomic nuclei |
| Particles experiencing: | All | Quarks, leptons | Electrically charged | Quarks, Gluons | Hadrons |
| Particles mediating: | Graviton (not yet observed) |
W+ W− Z0 | γ | Gluons | Mesons |
| Strength in the scale of quarks: | 10−41 | 10−4 | 1 | 60 | Not applicable to quarks |
| Strength in the scale of protons/neutrons: |
10−36 | 10−7 | 1 | Not applicable to hadrons |
20 |
Gravitational[edit]
Images of a freely falling basketball taken with a stroboscope at 20 flashes per second. The distance units on the right are multiples of about 12 millimeters. The basketball starts at rest. At the time of the first flash (distance zero) it is released, after which the number of units fallen is equal to the square of the number of flashes.
What we now call gravity was not identified as a universal force until the work of Isaac Newton. Before Newton, the tendency for objects to fall towards the Earth was not understood to be related to the motions of celestial objects. Galileo was instrumental in describing the characteristics of falling objects by determining that the acceleration of every object in free-fall was constant and independent of the mass of the object. Today, this acceleration due to gravity towards the surface of the Earth is usually designated as 


For an object in free-fall, this force is unopposed and the net force on the object is its weight. For objects not in free-fall, the force of gravity is opposed by the reaction forces applied by their supports. For example, a person standing on the ground experiences zero net force, since a normal force (a reaction force) is exerted by the ground upward on the person that counterbalances his weight that is directed downward.[3][4]
Newton’s contribution to gravitational theory was to unify the motions of heavenly bodies, which Aristotle had assumed were in a natural state of constant motion, with falling motion observed on the Earth. He proposed a law of gravity that could account for the celestial motions that had been described earlier using Kepler’s laws of planetary motion.[29]
Newton came to realize that the effects of gravity might be observed in different ways at larger distances. In particular, Newton determined that the acceleration of the Moon around the Earth could be ascribed to the same force of gravity if the acceleration due to gravity decreased as an inverse square law. Further, Newton realized that the acceleration of a body due to gravity is proportional to the mass of the other attracting body.[29] Combining these ideas gives a formula that relates the mass (


where the vector direction is given by 
In this equation, a dimensional constant 





where 

This formula was powerful enough to stand as the basis for all subsequent descriptions of motion within the solar system until the 20th century. During that time, sophisticated methods of perturbation analysis[30] were invented to calculate the deviations of orbits due to the influence of multiple bodies on a planet, moon, comet, or asteroid. The formalism was exact enough to allow mathematicians to predict the existence of the planet Neptune before it was observed.[31]
Instruments like GRAVITY provide a powerful probe for gravity force detection.[32]
Mercury’s orbit did not match that predicted by Newton’s Law of Gravitation. Some astrophysicists predicted the existence of an undiscovered planet (Vulcan) that could explain the discrepancies. When Albert Einstein formulated his theory of general relativity (GR) he focused on Mercury’s problematic orbit and found that his theory added a correction, which could account for the discrepancy. This was the first time that Newton’s Theory of Gravity had been shown to be inexact.[33]
Since then, general relativity has been acknowledged as the theory that best explains gravity. In GR, gravitation is not viewed as a force, but rather, objects moving freely in gravitational fields travel under their own inertia in straight lines through curved space-time – defined as the shortest space-time path between two space-time events. From the perspective of the object, all motion occurs as if there were no gravitation whatsoever. It is only when observing the motion in a global sense that the curvature of space-time can be observed and the force is inferred from the object’s curved path. Thus, the straight line path in space-time is seen as a curved line in space, and it is called the ballistic trajectory of the object. For example, a basketball thrown from the ground moves in a parabola, as it is in a uniform gravitational field. Its space-time trajectory is almost a straight line, slightly curved (with the radius of curvature of the order of few light-years). The time derivative of the changing momentum of the object is what we label as «gravitational force».[4]
Electromagnetic[edit]
The electrostatic force was first described in 1784 by Coulomb as a force that existed intrinsically between two charges.[19]: 519 The properties of the electrostatic force were that it varied as an inverse square law directed in the radial direction, was both attractive and repulsive (there was intrinsic polarity), was independent of the mass of the charged objects, and followed the superposition principle. Coulomb’s law unifies all these observations into one succinct statement.[34]
Subsequent mathematicians and physicists found the construct of the electric field to be useful for determining the electrostatic force on an electric charge at any point in space. The electric field was based on using a hypothetical «test charge» anywhere in space and then using Coulomb’s Law to determine the electrostatic force.[35]: 4-6 to 4-8 Thus the electric field anywhere in space is defined as
where 
Meanwhile, the Lorentz force of magnetism was discovered to exist between two electric currents. It has the same mathematical character as Coulomb’s Law with the proviso that like currents attract and unlike currents repel. Similar to the electric field, the magnetic field can be used to determine the magnetic force on an electric current at any point in space. In this case, the magnitude of the magnetic field was determined to be

where 

Through combining the definition of electric current as the time rate of change of electric charge, a rule of vector multiplication called Lorentz’s Law describes the force on a charge moving in a magnetic field.[35] The connection between electricity and magnetism allows for the description of a unified electromagnetic force that acts on a charge. This force can be written as a sum of the electrostatic force (due to the electric field) and the magnetic force (due to the magnetic field). Fully stated, this is the law:

where 




The origin of electric and magnetic fields would not be fully explained until 1864 when James Clerk Maxwell unified a number of earlier theories into a set of 20 scalar equations, which were later reformulated into 4 vector equations by Oliver Heaviside and Josiah Willard Gibbs.[36] These «Maxwell Equations» fully described the sources of the fields as being stationary and moving charges, and the interactions of the fields themselves. This led Maxwell to discover that electric and magnetic fields could be «self-generating» through a wave that traveled at a speed that he calculated to be the speed of light. This insight united the nascent fields of electromagnetic theory with optics and led directly to a complete description of the electromagnetic spectrum.[37]
Attempts to reconcile electromagnetic theory with two observations, the photoelectric effect, and the nonexistence of the ultraviolet catastrophe, proved troublesome. Through the work of leading theoretical physicists, a new theory of electromagnetism was developed using quantum mechanics. This final modification to electromagnetic theory ultimately led to quantum electrodynamics (or QED), which fully describes all electromagnetic phenomena as being mediated by wave–particles known as photons. In QED, photons are the fundamental exchange particle, which described all interactions relating to electromagnetism including the electromagnetic force.[Note 4]
Strong nuclear[edit]
There are two «nuclear forces», which today are usually described as interactions that take place in quantum theories of particle physics. The strong nuclear force[19]: 940 is the force responsible for the structural integrity of atomic nuclei while the weak nuclear force[19]: 951 is responsible for the decay of certain nucleons into leptons and other types of hadrons.[3][4]
The strong force is today understood to represent the interactions between quarks and gluons as detailed by the theory of quantum chromodynamics (QCD).[38] The strong force is the fundamental force mediated by gluons, acting upon quarks, antiquarks, and the gluons themselves. The (aptly named) strong interaction is the «strongest» of the four fundamental forces.
The strong force only acts directly upon elementary particles. A residual is observed between hadrons (notably, the nucleons in atomic nuclei), known as the nuclear force. Here the strong force acts indirectly, transmitted as gluons that form part of the virtual pi and rho mesons, the classical transmitters of the nuclear force. The failure of many searches for free quarks has shown that the elementary particles affected are not directly observable. This phenomenon is called color confinement.
Weak nuclear[edit]
The weak force is due to the exchange of the heavy W and Z bosons. Since the weak force is mediated by two types of bosons, it can be divided into two types of interaction or «vertices» — charged current, involving the electrically charged W+ and W− bosons, and neutral current, involving electrically neutral Z0 bosons. The most familiar effect of weak interaction is beta decay (of neutrons in atomic nuclei) and the associated radioactivity. This is a type of charged-current interaction. The word «weak» derives from the fact that the field strength is some 1013 times less than that of the strong force. Still, it is stronger than gravity over short distances. A consistent electroweak theory has also been developed, which shows that electromagnetic forces and the weak force are indistinguishable at a temperatures in excess of approximately 1015 kelvins. Such temperatures have been probed in modern particle accelerators and show the conditions of the universe in the early moments of the Big Bang.
Non-fundamental types[edit]
Some forces are consequences of the fundamental ones. In such situations, idealized models can be used to gain physical insight.
Normal[edit]
The normal force is due to repulsive forces of interaction between atoms at close contact. When their electron clouds overlap, Pauli repulsion (due to fermionic nature of electrons) follows resulting in the force that acts in a direction normal to the surface interface between two objects.[19]: 93 The normal force, for example, is responsible for the structural integrity of tables and floors as well as being the force that responds whenever an external force pushes on a solid object. An example of the normal force in action is the impact force on an object crashing into an immobile surface.[3][4]
Friction[edit]
Friction is a surface force that opposes relative motion. The frictional force is directly related to the normal force that acts to keep two solid objects separated at the point of contact. There are two broad classifications of frictional forces: static friction and kinetic friction.
The static friction force (


The kinetic friction force (
where 
Tension[edit]
Tension forces can be modeled using ideal strings that are massless, frictionless, unbreakable, and unstretchable. They can be combined with ideal pulleys, which allow ideal strings to switch physical direction. Ideal strings transmit tension forces instantaneously in action-reaction pairs so that if two objects are connected by an ideal string, any force directed along the string by the first object is accompanied by a force directed along the string in the opposite direction by the second object.[39] By connecting the same string multiple times to the same object through the use of a set-up that uses movable pulleys, the tension force on a load can be multiplied. For every string that acts on a load, another factor of the tension force in the string acts on the load. Such machines allow a mechanical advantage for a corresponding increase in the length of displaced string needed to move the load. These tandem effects result ultimately in the conservation of mechanical energy since the work done on the load is the same no matter how complicated the machine.[3][4][40]
Elasticity[edit]
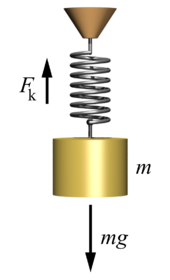
Fk is the force that responds to the load on the spring
An elastic force acts to return a spring to its natural length. An ideal spring is taken to be massless, frictionless, unbreakable, and infinitely stretchable. Such springs exert forces that push when contracted, or pull when extended, in proportion to the displacement of the spring from its equilibrium position.[41] This linear relationship was described by Robert Hooke in 1676, for whom Hooke’s law is named. If 

where 
Continuum mechanics[edit]
When the drag force (

Newton’s laws and Newtonian mechanics in general were first developed to describe how forces affect idealized point particles rather than three-dimensional objects. In real life, matter has extended structure and forces that act on one part of an object might affect other parts of an object. For situations where lattice holding together the atoms in an object is able to flow, contract, expand, or otherwise change shape, the theories of continuum mechanics describe the way forces affect the material. For example, in extended fluids, differences in pressure result in forces being directed along the pressure gradients as follows:
where 

A specific instance of such a force that is associated with dynamic pressure is fluid resistance: a body force that resists the motion of an object through a fluid due to viscosity. For so-called «Stokes’ drag» the force is approximately proportional to the velocity, but opposite in direction:

where:
More formally, forces in continuum mechanics are fully described by a stress–tensor with terms that are roughly defined as

where 
Fictitious[edit]
There are forces that are frame dependent, meaning that they appear due to the adoption of non-Newtonian (that is, non-inertial) reference frames. Such forces include the centrifugal force and the Coriolis force.[42] These forces are considered fictitious because they do not exist in frames of reference that are not accelerating.[3][4] Because these forces are not genuine they are also referred to as «pseudo forces».[3]: 12–11
In general relativity, gravity becomes a fictitious force that arises in situations where spacetime deviates from a flat geometry. As an extension, Kaluza–Klein theory and string theory ascribe electromagnetism and the other fundamental forces respectively to the curvature of differently scaled dimensions, which would ultimately imply that all forces are fictitious.
Rotation and torque[edit]
Relationship between force (F), torque (τ), and momentum vectors (p and L) in a rotating system.
Forces that cause extended objects to rotate are associated with torques. Mathematically, the torque of a force 

where 
Torque is the rotation equivalent of force in the same way that angle is the rotational equivalent for position, angular velocity for velocity, and angular momentum for momentum. As a consequence of Newton’s First Law of Motion, there exists rotational inertia that ensures that all bodies maintain their angular momentum unless acted upon by an unbalanced torque. Likewise, Newton’s Second Law of Motion can be used to derive an analogous equation for the instantaneous angular acceleration of the rigid body:
where
This provides a definition for the moment of inertia, which is the rotational equivalent for mass. In more advanced treatments of mechanics, where the rotation over a time interval is described, the moment of inertia must be substituted by the tensor that, when properly analyzed, fully determines the characteristics of rotations including precession and nutation.
Equivalently, the differential form of Newton’s Second Law provides an alternative definition of torque:[43]
where 
Newton’s Third Law of Motion requires that all objects exerting torques themselves experience equal and opposite torques,[44] and therefore also directly implies the conservation of angular momentum for closed systems that experience rotations and revolutions through the action of internal torques.
Centripetality[edit]
For an object accelerating in circular motion, the unbalanced force acting on the object equals:[45]

where 



Kinematic integrals[edit]
Forces can be used to define a number of physical concepts by integrating with respect to kinematic variables. For example, integrating with respect to time gives the definition of impulse:[46]
which by Newton’s Second Law must be equivalent to the change in momentum (yielding the Impulse momentum theorem).
Similarly, integrating with respect to position gives a definition for the work done by a force:[3]: 13–3

which is equivalent to changes in kinetic energy (yielding the work energy theorem).[3]: 13–3
Power P is the rate of change dW/dt of the work W, as the trajectory is extended by a position change 
so
with 
Potential energy[edit]
Instead of a force, often the mathematically related concept of a potential energy field can be used for convenience. For instance, the gravitational force acting upon an object can be seen as the action of the gravitational field that is present at the object’s location. Restating mathematically the definition of energy (via the definition of work), a potential scalar field 
Forces can be classified as conservative or nonconservative. Conservative forces are equivalent to the gradient of a potential while nonconservative forces are not.[3][4]
Conservation[edit]
A conservative force that acts on a closed system has an associated mechanical work that allows energy to convert only between kinetic or potential forms. This means that for a closed system, the net mechanical energy is conserved whenever a conservative force acts on the system. The force, therefore, is related directly to the difference in potential energy between two different locations in space,[47] and can be considered to be an artifact of the potential field in the same way that the direction and amount of a flow of water can be considered to be an artifact of the contour map of the elevation of an area.[3][4]
Conservative forces include gravity, the electromagnetic force, and the spring force. Each of these forces has models that are dependent on a position often given as a radial vector 
For gravity:
where 

For electrostatic forces:

where 

For spring forces:
where 
For certain physical scenarios, it is impossible to model forces as being due to gradient of potentials. This is often due to macrophysical considerations that yield forces as arising from a macroscopic statistical average of microstates. For example, friction is caused by the gradients of numerous electrostatic potentials between the atoms, but manifests as a force model that is independent of any macroscale position vector. Nonconservative forces other than friction include other contact forces, tension, compression, and drag. For any sufficiently detailed description, all these forces are the results of conservative ones since each of these macroscopic forces are the net results of the gradients of microscopic potentials.[3][4]
The connection between macroscopic nonconservative forces and microscopic conservative forces is described by detailed treatment with statistical mechanics. In macroscopic closed systems, nonconservative forces act to change the internal energies of the system, and are often associated with the transfer of heat. According to the Second law of thermodynamics, nonconservative forces necessarily result in energy transformations within closed systems from ordered to more random conditions as entropy increases.[3][4]
Units of measurement[edit]
The SI unit of force is the newton (symbol N), which is the force required to accelerate a one kilogram mass at a rate of one meter per second squared, or kg·m·s−2.[49] The corresponding CGS unit is the dyne, the force required to accelerate a one gram mass by one centimeter per second squared, or g·cm·s−2. A newton is thus equal to 100,000 dynes.
The gravitational foot-pound-second English unit of force is the pound-force (lbf), defined as the force exerted by gravity on a pound-mass in the standard gravitational field of 9.80665 m·s−2.[49] The pound-force provides an alternative unit of mass: one slug is the mass that will accelerate by one foot per second squared when acted on by one pound-force.[49]
An alternative unit of force in a different foot-pound-second system, the absolute fps system, is the poundal, defined as the force required to accelerate a one-pound mass at a rate of one foot per second squared.[49] The units of slug and poundal are designed to avoid a constant of proportionality in Newton’s Second Law.
The pound-force has a metric counterpart, less commonly used than the newton: the kilogram-force (kgf) (sometimes kilopond), is the force exerted by standard gravity on one kilogram of mass.[49] The kilogram-force leads to an alternate, but rarely used unit of mass: the metric slug (sometimes mug or hyl) is that mass that accelerates at 1 m·s−2 when subjected to a force of 1 kgf. The kilogram-force is not a part of the modern SI system, and is generally deprecated, sometimes used for expressing aircraft weight, jet thrust, bicycle spoke tension, torque wrench settings and engine output torque. Other arcane units include the sthène, which is equivalent to 1000 N, and the kip, which is equivalent to 1000 lbf.
|
newton | dyne | kilogram-force, kilopond |
pound-force | poundal |
|---|---|---|---|---|---|
| 1 N | ≡ 1 kg⋅m/s2 | = 105 dyn | ≈ 0.10197 kp | ≈ 0.22481 lbf | ≈ 7.2330 pdl |
| 1 dyn | = 10–5 N | ≡ 1 g⋅cm/s2 | ≈ 1.0197×10−6 kp | ≈ 2.2481×10−6 lbf | ≈ 7.2330×10−5 pdl |
| 1 kp | = 9.80665 N | = 980665 dyn | ≡ gn × 1 kg | ≈ 2.2046 lbf | ≈ 70.932 pdl |
| 1 lbf | ≈ 4.448222 N | ≈ 444822 dyn | ≈ 0.45359 kp | ≡ gn × 1 lb | ≈ 32.174 pdl |
| 1 pdl | ≈ 0.138255 N | ≈ 13825 dyn | ≈ 0.014098 kp | ≈ 0.031081 lbf | ≡ 1 lb⋅ft/s2 |
| The value of gn as used in the official definition of the kilogram-force (9.80665 m/s2) is used here for all gravitational units. |
See also Ton-force.
Force measurement[edit]
See force gauge, spring scale, load cell
See also[edit]
- Orders of magnitude (force)
- Parallel force system – Engineering
Notes[edit]
- ^ Newton’s Principia Mathematica actually used a finite difference version of this equation based upon impulse. See Impulse.
- ^ «It is important to note that we cannot derive a general expression for Newton’s second law for variable mass systems by treating the mass in F = dP/dt = d(Mv) as a variable. […] We can use F = dP/dt to analyze variable mass systems only if we apply it to an entire system of constant mass having parts among which there is an interchange of mass.» [Emphasis as in the original] (Halliday, Resnick & Krane 2001, p. 199)
- ^ «Any single force is only one aspect of a mutual interaction between two bodies.» (Halliday, Resnick & Krane 2001, pp. 78–79)
- ^ For a complete library on quantum mechanics see Quantum mechanics – References
References[edit]
- ^ a b Heath, T. L. (1897). The Works of Archimedes (1897). The unabridged work in PDF form (19 MB). Internet Archive. Retrieved 2007-10-14.
- ^ a b c d e f g h University Physics, Sears, Young & Zemansky, pp. 18–38.
- ^ a b c d e f g h i j k l m n o p q r s t u v w x y z aa ab Feynman volume 1
- ^ a b c d e f g h i j k l m n o p q r s t u v w x y Kleppner & Kolenkow 2010
- ^ a b c Weinberg, S. (1994). Dreams of a Final Theory. Vintage Books. ISBN 978-0-679-74408-5.
- ^ Lang, Helen S. (1998). The order of nature in Aristotle’s physics : place and the elements (1. publ. ed.). Cambridge: Cambridge Univ. Press. ISBN 9780521624534.
- ^ Hetherington, Norriss S. (1993). Cosmology: Historical, Literary, Philosophical, Religious, and Scientific Perspectives. Garland Reference Library of the Humanities. p. 100. ISBN 978-0-8153-1085-3.
- ^ a b Drake, Stillman (1978). Galileo At Work. Chicago: University of Chicago Press. ISBN 0-226-16226-5
- ^ Arnold, V. I.; Kozlov, V. V.; Neĩshtadt, A. I. (1988). «Mathematical aspects of classical and celestial mechanics». Encyclopaedia of Mathematical Sciences, Dynamical Systems III. Vol. 3. Anosov, D. V. Berlin: Springer-Verlag. ISBN 0-387-17002-2. OCLC 16404140.
- ^ a b c d e f Newton, Isaac (1999). The Principia Mathematical Principles of Natural Philosophy. Berkeley: University of California Press. ISBN 978-0-520-08817-7. This is a recent translation into English by I. Bernard Cohen and Anne Whitman, with help from Julia Budenz.
- ^ Howland, R. A. (2006). Intermediate dynamics a linear algebraic approach (Online-Ausg. ed.). New York: Springer. pp. 255–256. ISBN 9780387280592.
- ^ Landau, L. D.; Akhiezer, A. I.; Lifshitz, A. M. (1967). General Physics; mechanics and molecular physics (First English ed.). Oxford: Pergamon Press. ISBN 978-0-08-003304-4.
Translated by: J. B. Sykes, A. D. Petford, and C. L. Petford. LCCN 67—30260. In section 7, pp. 12–14, this book defines force as dp/dt. - ^ Kibble, Tom W. B.; Berkshire, Frank H. (2004). Classical Mechanics (Fifth ed.). London: Imperial College Press. ISBN 1860944248.
According to page 12, «[Force] can of course be introduced, by defining it through Newton’s second law». - ^ de Lange, O. L.; Pierrus, J. (2010). Solved Problems in Classical Mechanics (First ed.). Oxford: Oxford University Press. ISBN 978-0-19-958252-5.
According to page 3, «[Newton’s second law of motion] can be regarded as defining force». - ^ Jammer, Max (1999). Concepts of force : a study in the foundations of dynamics (Facsim. ed.). Mineola, N.Y.: Dover Publications. pp. 220–222. ISBN 9780486406893.
- ^ Noll, Walter (April 2007). «On the Concept of Force» (PDF). Carnegie Mellon University. Retrieved 28 October 2013.
- ^ Hellingman, C. (1992). «Newton’s third law revisited». Phys. Educ. 27 (2): 112–115. Bibcode:1992PhyEd..27..112H. doi:10.1088/0031-9120/27/2/011. S2CID 250891975.
Quoting Newton in the Principia: It is not one action by which the Sun attracts Jupiter, and another by which Jupiter attracts the Sun; but it is one action by which the Sun and Jupiter mutually endeavour to come nearer together.
- ^ Dr. Nikitin (2007). «Dynamics of translational motion». Retrieved 2008-01-04.
- ^ a b c d e Cutnell & Johnson 2003
- ^ Wilson, John B. «Four-Vectors (4-Vectors) of Special Relativity: A Study of Elegant Physics». The Science Realm: John’s Virtual Sci-Tech Universe. Archived from the original on 26 June 2009. Retrieved 2008-01-04.
- ^ «Introduction to Free Body Diagrams». Physics Tutorial Menu. University of Guelph. Archived from the original on 2008-01-16. Retrieved 2008-01-02.
- ^ Henderson, Tom (2004). «The Physics Classroom». The Physics Classroom and Mathsoft Engineering & Education, Inc. Archived from the original on 2008-01-01. Retrieved 2008-01-02.
- ^ «Static Equilibrium». Physics Static Equilibrium (forces and torques). University of the Virgin Islands. Archived from the original on October 19, 2007. Retrieved 2008-01-02.
- ^ a b Shifman, Mikhail (1999). ITEP lectures on particle physics and field theory. World Scientific. ISBN 978-981-02-2639-8.
- ^ Nave, Carl Rod. «Pauli Exclusion Principle». HyperPhysics. University of Guelph. Retrieved 2013-10-28.
- ^ «Fermions & Bosons». The Particle Adventure. Archived from the original on 2007-12-18. Retrieved 2008-01-04.
- ^ «Standard model of particles and interactions». Contemporary Physics Education Project. 2000. Retrieved 2 January 2017.
- ^ Cook, A. H. (1965). «A New Absolute Determination of the Acceleration due to Gravity at the National Physical Laboratory». Nature. 208 (5007): 279. Bibcode:1965Natur.208..279C. doi:10.1038/208279a0. S2CID 4242827.
- ^ a b Young, Hugh; Freedman, Roger; Sears, Francis; and Zemansky, Mark (1949) University Physics. Pearson Education. pp. 59–82.
- ^ Watkins, Thayer. «Perturbation Analysis, Regular and Singular». Department of Economics. San José State University. Archived from the original on 2011-02-10. Retrieved 2008-01-05.
- ^ Kollerstrom, Nick (2001). «Neptune’s Discovery. The British Case for Co-Prediction». University College London. Archived from the original on 2005-11-11. Retrieved 2007-03-19.
- ^ «Powerful New Black Hole Probe Arrives at Paranal». Retrieved 13 August 2015.
- ^ Siegel, Ethan (20 May 2016). «When Did Isaac Newton Finally Fail?». Forbes. Retrieved 3 January 2017.
- ^ Coulomb, Charles (1784). «Recherches théoriques et expérimentales sur la force de torsion et sur l’élasticité des fils de metal». Histoire de l’Académie Royale des Sciences: 229–269.
- ^ a b c Feynman volume 2
- ^ Scharf, Toralf (2007). Polarized light in liquid crystals and polymers. John Wiley and Sons. p. 19. ISBN 978-0-471-74064-3., Chapter 2, p. 19
- ^ Duffin, William (1980). Electricity and Magnetism, 3rd Ed. McGraw-Hill. pp. 364–383. ISBN 978-0-07-084111-6.
- ^ Stevens, Tab (10 July 2003). «Quantum-Chromodynamics: A Definition – Science Articles». Archived from the original on 2011-10-16. Retrieved 2008-01-04.
- ^ «Tension Force». Non-Calculus Based Physics I. Retrieved 2008-01-04.
- ^ Fitzpatrick, Richard (2006-02-02). «Strings, pulleys, and inclines». Retrieved 2008-01-04.
- ^ Nave, Carl Rod. «Elasticity». HyperPhysics. University of Guelph. Retrieved 2013-10-28.
- ^ Mallette, Vincent (1982–2008). «The Coriolis Force». Publications in Science and Mathematics, Computing and the Humanities. Inwit Publishing, Inc. Retrieved 2008-01-04.
- ^ Nave, Carl Rod. «Newton’s 2nd Law: Rotation». HyperPhysics. University of Guelph. Retrieved 2013-10-28.
- ^ Fitzpatrick, Richard (2007-01-07). «Newton’s third law of motion». Retrieved 2008-01-04.
- ^ Nave, Carl Rod. «Centripetal Force». HyperPhysics. University of Guelph. Retrieved 2013-10-28.
- ^ Hibbeler, Russell C. (2010). Engineering Mechanics, 12th edition. Pearson Prentice Hall. p. 222. ISBN 978-0-13-607791-6.
- ^ Singh, Sunil Kumar (2007-08-25). «Conservative force». Connexions. Retrieved 2008-01-04.
- ^ Davis, Doug. «Conservation of Energy». General physics. Retrieved 2008-01-04.
- ^ a b c d e Wandmacher, Cornelius; Johnson, Arnold (1995). Metric Units in Engineering. ASCE Publications. p. 15. ISBN 978-0-7844-0070-8.
Further reading[edit]
- Corben, H. C.; Stehle, Philip (1994). Classical Mechanics. New York: Dover publications. pp. 28–31. ISBN 978-0-486-68063-7.
- Cutnell, John D.; Johnson, Kenneth W. (2003). Physics, Sixth Edition. Hoboken, New Jersey: John Wiley & Sons Inc. ISBN 978-0471151838.
- Feynman, Richard P.; Leighton, Robert B.; Sands, Matthew (2010). The Feynman lectures on physics. Vol. I: Mainly mechanics, radiation and heat (New millennium ed.). New York: BasicBooks. ISBN 978-0465024933.
- Feynman, Richard P.; Leighton, Robert B.; Sands, Matthew (2010). The Feynman lectures on physics. Vol. II: Mainly electromagnetism and matter (New millennium ed.). New York: BasicBooks. ISBN 978-0465024940.
- Halliday, David; Resnick, Robert; Krane, Kenneth S. (2001). Physics v. 1. New York: John Wiley & Sons. ISBN 978-0-471-32057-9.
- Kleppner, Daniel; Kolenkow, Robert J. (2010). An introduction to mechanics (3. print ed.). Cambridge: Cambridge University Press. ISBN 978-0521198219.
- Parker, Sybil (1993). «force». Encyclopedia of Physics. Ohio: McGraw-Hill. p. 107. ISBN 978-0-07-051400-3.
- Sears, F.; Zemansky, M.; Young, H. (1982). University Physics. Reading, Massachusetts: Addison-Wesley. ISBN 978-0-201-07199-3.
- Serway, Raymond A. (2003). Physics for Scientists and Engineers. Philadelphia: Saunders College Publishing. ISBN 978-0-534-40842-8.
- Tipler, Paul (2004). Physics for Scientists and Engineers: Mechanics, Oscillations and Waves, Thermodynamics (5th ed.). W.H. Freeman. ISBN 978-0-7167-0809-4.
- Verma, H. C. (2004). Concepts of Physics Vol 1 (2004 Reprint ed.). Bharti Bhavan. ISBN 978-8177091878.
External links[edit]
Look up force in Wiktionary, the free dictionary.
- Video lecture on Newton’s three laws by Walter Lewin from MIT OpenCourseWare
- A Java simulation on vector addition of forces
- Force demonstrated as any influence on an object that changes the object’s shape or motion (video)
English[edit]
Pronunciation[edit]
- (General American) enPR: fôrs, IPA(key): /foɹs/, [fo̞ɹs]
- (Received Pronunciation) IPA(key): /fɔːs/
- (rhotic, without the horse–hoarse merger) enPR: fōrs, IPA(key): /fo(ː)ɹs/
- (non-rhotic, without the horse–hoarse merger) IPA(key): /foəs/
- Rhymes: -ɔː(ɹ)s
Etymology 1[edit]
From Middle English force, fors, forse, from Old French force, from Late Latin fortia, a noun derived from the neuter plural of Latin fortis (“strong”), ultimately from Proto-Indo-European *bʰerǵʰ- (“to rise, high, hill”).
Noun[edit]
force (countable and uncountable, plural forces)
- Strength or energy of body or mind; active power; vigour; might; capacity of exercising an influence or producing an effect.
-
the force of an appeal, an argument, or a contract
-
1849–1861, Thomas Babington Macaulay, chapter 14, in The History of England from the Accession of James the Second, volume (please specify |volume=I to V), London: Longman, Brown, Green, and Longmans, →OCLC:
-
He was, in the full force of the words, a good man.
-
-
- Power exerted against will or consent; compulsory power; violence; coercion.
-
1591 (date written), William Shakespeare, “The Second Part of Henry the Sixt, […]”, in Mr. William Shakespeares Comedies, Histories, & Tragedies. […] (First Folio), London: […] Isaac Iaggard, and Ed[ward] Blount, published 1623, →OCLC, (please specify the act number in uppercase Roman numerals, and the scene number in lowercase Roman numerals):
-
which now they hold by force, and not by right
-
-
- (countable) Anything that is able to make a substantial change in a person or thing.
- (countable, physics) A physical quantity that denotes ability to push, pull, twist or accelerate a body and which has a direction and is measured in a unit dimensioned in mass × distance/time² (ML/T²): SI: newton (N); CGS: dyne (dyn)
- Something or anything that has the power to produce a physical effect upon something else, such as causing it to move or change shape.
-
2012 March 1, Henry Petroski, “Opening Doors”, in American Scientist, volume 100, number 2, page 112-3:
-
A doorknob of whatever roundish shape is effectively a continuum of levers, with the axis of the latching mechanism—known as the spindle—being the fulcrum about which the turning takes place. Applying a force tangential to the knob is essentially equivalent to applying one perpendicular to a radial line defining the lever.
-
-
- (countable) A group that aims to attack, control, or constrain.
-
reinforcemented increased the American force in the area to 9,000
-
1611 April (first recorded performance), William Shakespeare, “The Tragedie of Cymbeline”, in Mr. William Shakespeares Comedies, Histories, & Tragedies […] (First Folio), London: […] Isaac Iaggard, and Ed[ward] Blount, published 1623, →OCLC, (please specify the act number in uppercase Roman numerals, and the scene number in lowercase Roman numerals):
-
Is Lucius general of the forces?
-
-
1910, Emerson Hough, chapter I, in The Purchase Price: Or The Cause of Compromise, Indianapolis, Ind.: The Bobbs-Merrill Company, →OCLC:
-
«A fine man, that Dunwody, yonder,» commented the young captain, as they parted, and as he turned to his prisoner. «We’ll see him on in Washington some day. He is strengthening his forces now against Mr. Benton out there. […].»
-
-
2004 April 15, “Morning swoop in hunt for Jodi’s killer”, in The Scotsman:
-
For Lothian and Borders Police, the early-morning raid had come at the end one of biggest investigations carried out by the force, which had originally presented a dossier of evidence on the murder of Jodi Jones to the Edinburgh procurator-fiscal, William Gallagher, on 25 November last year.
-
-
- (uncountable) The ability to attack, control, or constrain.
- (countable) A magic trick in which the outcome is known to the magician beforehand, especially one involving the apparent free choice of a card by another person.
- (law) Legal validity.
-
The law will come into force in January.
-
- (law) Either unlawful violence, as in a «forced entry«, or lawful compulsion.
- (linguistics, semantics, pragmatics) Ability of an utterance or its element (word, form, prosody, …) to effect a given meaning.
-
1962, J Gonda, The aspectual function of the R̥gvedic present and aorist, S̓-Gravenhage, Mouton, pages 43:
-
- (humorous or science fiction, with the, often capitalized) A metaphysical and ubiquitous power from the fictional Star Wars universe created by George Lucas. See usage note. [1977]
-
1999 September 28, Mike Selvey, “Crenshaw vindicated by a chain reaction”, in The Guardian[1]:
-
The Europeans tried, my goodness how they tried. But on the day the US proved too strong and too inspired. They were, dammit, just better. And when Leonard’s putt dropped they clearly had the force with them as well.
-
-
- (usually with «the», in the singular or plural) Synonym of police force
-
1880, [U.S.] House documents, page 64:
-
Q. All the time that he was on the force?
A. I cannot say that; but there were men on with me when I was on the force who were very good Republicans.
Q. During all this time you have been on the police force?
-
- 1992, Rage Against the Machine (band), Killing in the Name:
- Some of those that work forces / Are the same that burn crosses
-
2012 February 1, Janice Kay Johnson, Between Love and Duty, Harlequin, →ISBN, page 77:
-
Niall was on the force, too, a detective in major crimes.
-
-
Usage notes[edit]
- Adjectives often applied to «force»: military, cultural, economic, gravitational, electric, magnetic, strong, weak, positive, negative, attractive, repulsive, good, evil, dark, physical, muscular, spiritual, intellectual, mental, emotional, rotational, tremendous, huge.
- (science fiction): Outside of fiction, the force may be used as an alternative to invoking luck, destiny, or God. For example, the force was with him instead of luck was on his side, or may the force be with you instead of may God be with you.
Hyponyms[edit]
- air force
- armed forces
- breakout force
- brute force
- centrifugal force
- centripetal force
- conservative force
- Coriolis force
- Coulomb force
- fictitious force
- fundamental force
- g-force
- gale force
- police force
- restoring force
- spent force
- task force
- wind force
- workforce
Derived terms[edit]
- accelerating force
- antiforce
- atomic force microscope
- atomic force microscopy
- behavioral force
- brute-force
- by force of
- Casimir force
- color force
- colour force
- come into force
- coming into force
- constructive force
- counterforce
- driving force
- electromagnetic force
- electromotive force
- electrostatic force
- field of force
- force feed
- force field
- force in
- force justified
- force majeure
- force multiplier
- force of habit
- force of nature
- force of will
- force one’s way
- force out
- force play
- force quit
- force someone’s back to the wall
- force someone’s hand
- force something down someone’s throat
- force the pace
- force the voucher
- force to be reckoned with
- force-feed
- force-field
- force-out
- force-ripe
- four-force
- g force
- general of the air force
- gravitational force
- ground mobile force
- in force
- in full force
- intermolecular force
- job force
- kilogram-force
- labor force
- labour force
- life force
- life-force
- line of force
- Lorentz force
- magnetomotive force
- masticatory force
- may the Force be with you
- may the force be with you
- moment of force
- net force
- normal force
- nuclear force
- pinch force
- Planck force
- pound-force
- pressure gradient force
- pseudo force
- pseudo-force
- reconnaissance in force
- reduction in force
- sales force
- space force
- strike force
- strong force
- strong nuclear force
- support force
- task-force
- tidal force
- van der Waals force
- vital force
- weak force
- weak nuclear force
- will-force
- work force
- workforce
Translations[edit]
strength or energy of body or mind
- Arabic: قُوَّة (ar) f (quwwa)
- Finnish: voima (fi), tarmo (fi), (archaic) väki (fi)
- German: Kraft (de) f
- Hungarian: erő (hu)
- Irish: fórsa m
- Kazakh: пәрмен (kk) (pärmen)
- Latin: vīs f
- Marathi: शरीरउर्जा (śarīraurjā), मनःशक्ती (manaḥśaktī)
- Mòcheno: kròft f
- Old English: cræft m
- Papiamentu: forsa
- Plautdietsch: Krauft f
- Sanskrit: सहस् (sa) n (sahas)
- Slovak: sila
- Spanish: fuerza (es) f
power exerted against will or consent
- Finnish: voima (fi), voimakeinot pl, pakko (fi), pakottaminen (fi), pakkokeinot pl
- Greek:
- Ancient: βία f (bía)
- Hungarian: erőszak (hu), kényszer (hu), kényszerítés (hu)
- Irish: fórsa m
- Kurdish:
- Central Kurdish: زەبر (ckb) (zebir)
- Marathi: जबरदस्ती (jabardastī)
- Old English: nīed f
- Sanskrit: रभस् (sa) n (rabhas)
- Slovak: sila
- Spanish: fuerza (es) f
anything that is able to make a big change in person or thing
- Amharic: ኀይል (ḫäyl)
- Arabic: قُوَّة (ar) f (quwwa)
- Argobba: ሀይል (hayl)
- Armenian: ուժ (hy) (už), զորություն (hy) (zorutʿyun)
- Asturian: fuercia (ast) f, fuerza (ast) f
- Avar: гуч (guč), къуват (qxʼuwat)
- Azerbaijani: güc (az), qüvvə (az)
- Bashkir: көс (kös)
- Belarusian: сі́ла f (síla), моц f (moc)
- Bengali: জোর (bn) (zor)
- Bulgarian: си́ла (bg) f (síla), мощ (bg) f (mošt)
- Catalan: força (ca) f
- Chinese:
- Mandarin: 武力 (zh) (wǔlì)
- Corsican: forza (co) f
- Czech: síla (cs), moc (cs) f
- Danish: kraft (da) c
- Dutch: kracht (nl) f
- Finnish: voima (fi)
- French: force (fr) f
- Friulian: fuarce f
- Galician: forza (gl) f
- Ge’ez: ኀይል (ḫäyl)
- Georgian: ძალა (ʒala)
- German: Gewalt (de) f
- Greek: δύναμη (el) f (dýnami), ισχύς (el) f (ischýs), σθένος (el) n (sthénos)
- Hebrew: כוח כֹּחַ (he) m (kóakh)
- Hindi: ज़ोर m (zor), बल (hi) m (bal)
- Hungarian: erő (hu)
- Ido: violento (io), koakto (io)
- Indonesian: kekuatan (id)
- Ingush: низ (niz)
- Irish: fórsa m
- Istriot: forsa f
- Italian: forza (it) f
- Japanese: 力 (ja) (ちから, chikara)
- Korean: 힘 (ko) (him)
- Ladin: forza f
- Latin: vis (la) f, potentia f, fortitudo (la) f
- Latvian: spēks (lv) m, vara (lv) f
- Lezgi: гуж (guž), къуват (q̄uvat)
- Lithuanian: jėga f, galia (lt) f
- Macedonian: сила f (sila), моќ f (moḱ)
- Malay: daya (ms), kuasa (ms)
- Malayalam: ബലം (ml) (balaṃ), ശക്തി (ml) (śakti)
- Maori: tūkeri (of the wind, natural phenomena etc)
- Marathi: जोर (jor)
- Neapolitan: fuorza f
- Norwegian: kraft (no) m or f
- Occitan: fòrça (oc) f
- Old Church Slavonic:
- Cyrillic: сила f (sila), мощь f (moštĭ)
- Old East Slavic: сила f (sila), мочь f (močĭ)
- Oromo: humna
- Plautdietsch: Krauft f
- Polish: siła (pl) m, moc (pl) f
- Portuguese: força (pt) f
- Romanian: forță (ro) f
- Romansch: forza f
- Russian: си́ла (ru) f (síla), мощь (ru) f (moščʹ), (slang) дурь (ru) f (durʹ)
- Serbo-Croatian:
- Cyrillic: си̏ла f, мо̑ћ f
- Roman: sȉla (sh) f, mȏć f
- Sicilian: forza (scn) f
- Slovak: sila f, moc f
- Slovene: sila (sl) f, moč (sl) f
- Somali: quwad
- Spanish: fuerza (es) f
- Swahili: mabavu (sw)
- Swedish: kraft (sv) c
- Turkish: kuvvet (tr)
- Ukrainian: си́ла (uk) f (sýla), міць (uk) f (micʹ)
- Urdu: زور (ur) m (zor)
- Venetian: forsa f, força f
- Walloon: foice (wa) f
physical quantity
- Afrikaans: krag (af)
- Armenian: ուժ (hy) (už)
- Assamese: বল (bol)
- Azerbaijani: qüvvə (az)
- Bashkir: көс (kös)
- Basque: indar
- Bengali: বল (bn) (bol)
- Bulgarian: сила (bg) (sila)
- Catalan: força (ca) f
- Chinese:
- Hakka: 力 (li̍t)
- Min Nan: 力 (zh-min-nan) (la̍t)
- Corsican: forza (co) f
- Czech: síla (cs)
- Danish: kraft (da) c
- Dutch: kracht (nl) f
- Fiji Hindi: taagat (hif)
- Finnish: voima (fi)
- French: force (fr) f
- Friulian: fuarce f
- Galician: forza (gl) f
- Georgian: ძალა (ʒala)
- German: Kraft (de) f
- Greek: δύναμη (el) f (dýnami)
- Gujarati: બળ (gu) (baḷ)
- Hebrew: כח (he) m
- Higaonon: kusug
- Hindi: बल (hi) (bal)
- Hungarian: erő (hu), erősség (hu)
- Ido: forco (io), vigoro (io)
- Indonesian: gaya (id), kakas (id), forsa
- Interlingua: fortia
- Irish: fórsa m
- Istriot: forsa f
- Italian: forza (it) f
- Japanese: 力 (ja) (chikara)
- Javanese: ꦝꦪ (daya)
- Karakalpak: ku’sh
- Kazakh: күш (kk) (küş)
- Korean: 힘 (ko) (him)
- Kyrgyz: күч (ky) (küç)
- Ladin: forza f
- Latin: vis (la) f, potentia f
- Latvian: spēks (lv) m
- Lithuanian: galia (lt) f, jėga f
- Macedonian: сила f (sila)
- Malay: daya (ms)
- Malayalam: ബലം (ml) (balaṃ)
- Maori: tōpana
- Marathi: बळ (baḷ)
- Mongolian: хүч (mn) (xüč)
- Neapolitan: fuorza f
- Newar: तिबः (tiba:)
- Norwegian: kraft (no) m or f
- Occitan: fòrça (oc) f
- Persian: نیرو (fa) (niru)
- Plautdietsch: Krauft f
- Polish: siła (pl)
- Portuguese: força (pt) f
- Quechua: kallpa
- Romanian: forță (ro) f
- Romansch: forza f
- Russian: си́ла (ru) f (síla)
- Sanskrit: परस्परक्रिया (parasparakriyā)
- Shona: manikidzo
- Sicilian: forza (scn) f
- Sinhalese: බලය (balaya)
- Slovak: sila f
- Slovene: sila (sl) f
- Spanish: fuerza (es) f
- Sundanese: ᮌᮚ (gaya)
- Swedish: kraft (sv)
- Tagalog: isig, puwersa
- Thai: แรง (th) (rɛɛng)
- Turkish: kuvvet (tr)
- Ukrainian: си́ла (uk) (sýla)
- Uzbek: kuch (uz)
- Venetian: forsa f, força f
- Vietnamese: lực (vi)
- Walloon: foice (wa) f
- Waray-Waray: kusog
- Welsh: grym (cy)
- Yoruba: ipá
anything that has the power to produce an effect upon something else
- Finnish: voima (fi)
- Maori: tūkeri (of wind or water pushing), ākinga
- Marathi: प्रबळ (prabaḷ)
- Slovak: sila
group that aims to attack, control, or constrain
- Armenian: ուժեր (hy) (užer), զինված ուժեր (hy) (zinvac užer)
- Bashkir: көс (kös)
- Bulgarian: войска (bg) f (vojska)
- Danish: styrke c
- Dutch: macht (nl) f, troep (nl) f
- Finnish: voimat (fi) pl, joukot (fi) pl
- French: forces (fr) pl
- Georgian: ძალა (ʒala)
- German: Kräfte (de) f pl
- Greek: δύναμη (el) f (dýnami), σώμα (el) n (sóma)
- Hebrew: כח (he) m
- Hungarian: erő (hu), osztag (hu), sereg (hu), különítmény (hu), haderő (hu), hadsereg (hu), csapat (hu), egység (hu)
- Ido: trupi (io)
- Irish: fórsa m
- Italian: forza (it) f
- Kurdish:
- Central Kurdish: ھێز (ckb) (hêz)
- Latin: vis (la) f, potentia f
- Macedonian: сила f (sila)
- Marathi: प्रबळ गट (prabaḷ gaṭ)
- Norwegian: styrke (no) m
- Polish: siły (pl) pl
- Portuguese: força (pt) f
- Russian: отря́д (ru) f (otrjád)
- Slovak: sila f
- Swedish: styrka (sv)
- Turkish: zorlamak (tr)
- Ukrainian: загі́н m (zahín)
- Walloon: foice (wa) f
ability to attack, control, or constrain
- Bashkir: ҡеүәт (qewät), көс (kös)
- Bulgarian: сила (bg) f (sila)
- Danish: magt c
- Dutch: macht (nl) f
- Esperanto: forto (eo)
- Finnish: valta (fi), voima (fi)
- French: pouvoir (fr) m
- Georgian: ძალა (ʒala), ღონე (ka) (ɣone)
- German: Kraft (de) f
- Hungarian: erő (hu), hatalom (hu), képesség (hu)
- Ido: mov-energio (io)
- Macedonian: сила f (sila)
- Marathi: बळ (baḷ)
- Norwegian: styrke (no) m
- Polish: siła (pl) f
- Portuguese: força (pt) f
- Russian: си́ла (ru) f (síla)
- Scottish Gaelic: cumhachd m or f
- Slovak: sila f
- Ukrainian: си́ла (uk) (sýla)
law: legal validity
- Bashkir: ғәмәл (ğämäl)
- Bulgarian: действие (bg) n (dejstvie)
- Dutch: kracht (nl) f
- Finnish: voima (fi), voimassaolo
- Greek: ισχύς (el) f (ischýs), κύρος (el) n (kýros)
- Hungarian: hatály (hu), érvény (hu), érvényesség (hu)
- Macedonian: сила f (sila), полнова́жност f (polnovážnost)
- Polish: moc (pl) f
- Portuguese: validade (pt) f
- Russian: власть (ru) f (vlastʹ)
- Slovak: platnosť
- Ukrainian: чинність f (čynnistʹ), сила (uk) f (syla)
law: unlawful violence or lawful compulsion
- Bulgarian: насилие (bg) n (nasilie)
- Dutch: geweld (nl) n, macht (nl) f
- Esperanto: perforto
- Finnish: pakko (fi), pakottaminen (fi), voimakeinot pl, voimankäyttö, pakkokeinot pl
- Greek: βία (el) f (vía)
- Hungarian: kényszer (hu), kényszerítés (hu)
- Macedonian: сила f (sila), насилство n (nasilstvo)
- Norwegian: tvang (no)
- Old English: nīed
- Russian: си́ла (ru) f (síla), наси́лие (ru) n (nasílije)
- Slovak: sila
linguistics: ability of an utterance to effect a given meaning
- Finnish: voima (fi)
See also[edit]
- Imperial unit: pound, poundal
- metric unit: newton
References[edit]
force on Wikipedia.Wikipedia
Etymology 2[edit]
From Middle English forcen, from Old French forcier, from Late Latin *fortiāre, from Latin fortia.
Verb[edit]
force (third-person singular simple present forces, present participle forcing, simple past and past participle forced)
- (transitive) To violate (a woman); to rape. [from 14thc.]
-
1485, Sir Thomas Malory, chapter V, in Le Morte Darthur, book V:
-
For yf ye were suche fyfty as ye be / ye were not able to make resystence ageynst this deuyl / here lyeth a duchesse deede the whiche was the fayrest of alle the world wyf to syre Howel / duc of Bretayne / he hath murthred her in forcynge her / and has slytte her vnto the nauyl
- (please add an English translation of this quote)
-
-
1603, Michel de Montaigne, chapter 1, in John Florio, transl., The Essayes […], book II, London: […] Val[entine] Simmes for Edward Blount […], →OCLC:
-
a young woman not farre from mee had headlong cast her selfe out of a high window, with intent to kill herselfe, only to avoid the ravishment of a rascally-base souldier that lay in her house, who offered to force her […].
-
-
- (obsolete, reflexive, intransitive) To exert oneself, to do one’s utmost. [from 14thc.]
-
1470–1485 (date produced), Thomas Malory, “Capitulum xxi”, in [Le Morte Darthur], book XVIII, [London: […] by William Caxton], published 31 July 1485, →OCLC; republished as H[einrich] Oskar Sommer, editor, Le Morte Darthur […], London: David Nutt, […], 1889, →OCLC:
-
And I pray you for my sake to force yourselff there, that men may speke you worshyp.
- (please add an English translation of this quote)
-
-
- (transitive) To compel (someone or something) to do something. [from 15thc.]
-
1910, Emerson Hough, chapter I, in The Purchase Price: Or The Cause of Compromise, Indianapolis, Ind.: The Bobbs-Merrill Company, →OCLC:
-
Captain Edward Carlisle […] felt a curious sensation of helplessness seize upon him as he met her steady gaze, […]; he could not tell what this prisoner might do. He cursed the fate which had assigned such a duty, cursed especially that fate which forced a gallant soldier to meet so superb a woman as this under handicap so hard.
-
- 2011, Tim Webb & Fiona Harvey, The Guardian, 23 March:
- Housebuilders had warned that the higher costs involved would have forced them to build fewer homes and priced many homebuyers out of the market.
-
- (transitive) To constrain by force; to overcome the limitations or resistance of. [from 16thc.]
- (transitive) To drive (something) by force, to propel (generally + prepositional phrase or adverb). [from 16thc.]
-
1697, Virgil, “(please specify the book number)”, in John Dryden, transl., The Works of Virgil: Containing His Pastorals, Georgics, and Æneis. […], London: […] Jacob Tonson, […], →OCLC:
- It stuck so fast, so deeply buried lay / That scarce the victor forced the steel away.
-
c. 1591–1592 (date written), William Shakespeare, “The Third Part of Henry the Sixt, […]”, in Mr. William Shakespeares Comedies, Histories, & Tragedies […] (First Folio), London: […] Isaac Iaggard, and Ed[ward] Blount, published 1623, →OCLC, [Act III, scene iii]:
-
to force the tyrant from his seat by war
-
-
1655, Thomas Fuller, James Nichols, editor, The Church History of Britain, […], volume (please specify |volume=I to III), new edition, London: […] [James Nichols] for Thomas Tegg and Son, […], published 1837, →OCLC:
- Ethelbert […] ordered that none should be forced into religion.
- 2007, The Guardian, 4 November:
- In a groundbreaking move, the Pentagon is compensating servicemen seriously hurt when an American tank convoy forced them off the road.
-
- (transitive) To cause to occur (despite inertia, resistance etc.); to produce through force. [from 16thc.]
-
The comedian’s jokes weren’t funny, but I forced a laugh now and then.
- 2009, «All things to Althingi», The Economist, 23 July:
- The second problem is the economy, the shocking state of which has forced the decision to apply to the EU.
-
- (transitive) To forcibly open (a door, lock etc.). [from 17thc.]
-
To force a lock.
-
- To obtain or win by strength; to take by violence or struggle; specifically, to capture by assault; to storm, as a fortress.
- (transitive, baseball) To create an out by touching a base in advance of a runner who has no base to return to while in possession of a ball which has already touched the ground.
-
Jones forced the runner at second by stepping on the bag.
-
- (whist) To compel (an adversary or partner) to trump a trick by leading a suit that he/she does not hold.
- (archaic) To put in force; to cause to be executed; to make binding; to enforce.
- (archaic) To provide with forces; to reinforce; to strengthen by soldiers; to man; to garrison.
-
c. 1606 (date written), William Shakespeare, “The Tragedie of Macbeth”, in Mr. William Shakespeares Comedies, Histories, & Tragedies […] (First Folio), London: […] Isaac Iaggard, and Ed[ward] Blount, published 1623, →OCLC, [Act V, scene v], lines 5–7, page 150, column 1:
-
Were they not forc’d with thoſe that ſhould be ours, / We might haue met them darefull, beard to beard, / And beate them backward home.
-
-
- (obsolete) To allow the force of; to value; to care for.
Conjugation[edit]
Derived terms[edit]
- enforce
- forceful
- forcible
Translations[edit]
to violate a woman — see rape
to compel someone to do something
- Arabic: أَجْبَرَ (ar) (ʔajbara), اِضْطَرَّ (iḍṭarra)
- Egyptian Arabic: اجبر (ʾagbar)
- Armenian: ստիպել (hy) (stipel), հարկադրել (hy) (harkadrel), բռնանալ (hy) (bṙnanal)
- Asturian: forciar
- Belarusian: прымуша́ць impf (prymušácʹ), прыму́сіць pf (prymúsicʹ), змуша́ць impf (zmušácʹ), зму́сіць pf (zmúsicʹ)
- Bulgarian: принужда́вам (bg) impf (prinuždávam), прину́дя pf (prinúdja), заста́вям (bg) impf (zastávjam), заста́вя (bg) pf (zastávja)
- Catalan: forçar (ca)
- Cebuano: lugos
- Chinese:
- Cantonese: 逼 (bik1)
- Mandarin: 強迫/强迫 (zh) (qiǎngpò), 迫使 (zh) (pòshǐ), 迫 (zh) (pò), 逼迫 (zh) (bīpò), 逼 (zh) (bī), 脅迫/胁迫 (zh) (xiépò)
- Czech: nutit (cs) impf, donutit (cs) pf, přinutit (cs) pf
- Danish: tvinge (da)
- Dutch: dwingen tot (nl), overweldigen (nl)
- Esperanto: devigi
- Estonian: sundima
- Finnish: pakottaa (fi)
- French: forcer (fr), contraindre (fr)
- Galician: obrigar
- Georgian: იძულებულს ხდის (iʒulebuls xdis)
- German: zwingen (de)
- Gothic: 𐌰𐌽𐌰𐌵𐌹𐌿𐌾𐌰𐌽 (anaqiujan), 𐌱𐌰𐌹𐌳𐌾𐌰𐌽 (baidjan)
- Greek: αναγκάζω (el) (anagkázo)
- Ancient: ἀναγκάζω (anankázō), βιάζω (biázō)
- Hungarian: kényszerít (hu), erőltet (hu), rákényszerít (hu), ráerőszakol (hu)
- Italian: forzare (it), costringere (it)
- Japanese: 強いる (ja) (しいる, shiiru)
- Korean: 강요하다 (ko) (gang’yohada)
- Latin: obligo
- Latvian: piespiest
- Lithuanian: versti (lt), priversti
- Macedonian: тера impf (tera), присилува impf (prisiluva), принудува impf (prinuduva)
- Malagasy: manery (mg)
- Norman: forchi
- Norwegian: tvinge
- Old English: nīedan
- Polish: zmuszać (pl) impf, zmusić (pl) pf
- Portuguese: forçar (pt), obrigar (pt), compelir (pt)
- Romanian: forța (ro), supune (ro), violenta (ro)
- Russian: заставля́ть (ru) impf (zastavljátʹ), заста́вить (ru) pf (zastávitʹ), принужда́ть (ru) impf (prinuždátʹ), прину́дить (ru) pf (prinúditʹ)
- Serbo-Croatian:
- Cyrillic: си̏лити impf, прѝсилити pf, присиља́вати impf
- Roman: sȉliti (sh) impf, prìsiliti (sh) pf, prisiljávati (sh) impf
- Slovak: nútiť impf, donútiť pf, prinútiť pf
- Spanish: obligar (es)
- Swedish: tvinga (sv)
- Telugu: బలాత్కరించు (te) (balātkariñcu)
- Thai: บังคับ (th) (bang-káp)
- Ukrainian: приму́шувати (uk) impf (prymúšuvaty), приму́сити pf (prymúsyty), зму́шувати impf (zmúšuvaty), зму́сити pf (zmúsyty)
to constrain by force; to overcome the limitations or resistance of
to cause to occur, produce through force
baseball: to create an out by touching a base
whist: to compel to trump
See also[edit]
- coerce: To control by force.
Etymology 3[edit]
From Middle English force, forz, fors, from Old Norse fors (“waterfall”), from Proto-Germanic *fursaz (“waterfall”). Cognate with Icelandic foss (“waterfall”), Norwegian foss (“waterfall”), Swedish fors (“waterfall”). Doublet of foss.
Noun[edit]
force (plural forces)
- (countable, Northern England) A waterfall or cascade.
- 1778, Thomas West, A Guide to the Lakes in Cumberland, Westmorland, and Lancashire
- to see the falls or force of the river Kent
- 1778, Thomas West, A Guide to the Lakes in Cumberland, Westmorland, and Lancashire
Derived terms[edit]
- forcefall
Translations[edit]
Etymology 4[edit]
From Middle English forcen, forsen, a use of force, with confusion of farce (“to stuff”).
Verb[edit]
force (third-person singular simple present forces, present participle forcing, simple past and past participle forced)
- To stuff; to lard; to farce.
-
c. 1602, William Shakespeare, “The Tragedie of Troylus and Cressida”, in Mr. William Shakespeares Comedies, Histories, & Tragedies […] (First Folio), London: […] Isaac Iaggard, and Ed[ward] Blount, published 1623, →OCLC, [Act V, scene i]:
-
Wit larded with malice, and malice forced with wit.
-
-
Derived terms[edit]
- forcemeat
Further reading[edit]
- force at OneLook Dictionary Search
- force in Webster’s Revised Unabridged Dictionary, G. & C. Merriam, 1913
- “force”, in The Century Dictionary […], New York, N.Y.: The Century Co., 1911, →OCLC.
Anagrams[edit]
- Cofer, Corfe, corfe
French[edit]
Etymology[edit]
From Old French force, from Late Latin fortia, a noun derived from the neuter plural of Latin fortis (“strong”).
Pronunciation[edit]
- IPA(key): /fɔʁs/
-
Audio (France, Paris) (file) - Rhymes: -ɔʁs
- Homophones: forcent, forces
Noun[edit]
force f (plural forces)
- force
-
c. 1656–1662, Blaise Pascal, “Fragment Raisons des effets n° 20 / 21”, in Pensées [Thoughts][2]:
-
La justice sans la force est impuissante. La force sans la justice est tyrannique.
- Justice without force is powerless. Force without justice is tyrannical.
-
-
1897, Henri Poincaré, “Les idées de Hertz sur la mécanique [The ideas of Hertz on mechanics]”, in Revue générale des sciences pures et appliquées [General Review of Pure and Applied Sciences][3], volume 8, page 734:
-
— Qu’est-ce que la force ? C’est, répond Lagrange, une cause qui produit le mouvement d’un corps ou qui tend à le produire. — C’est, dira Kirchhoff, le produit de la masse par l’accélération. Mais alors, pourquoi ne pas dire que la masse est le quotient de la force par l’accélération ?
- «What is force? It is,» answers Lagrange, «a cause which produces the movement of a body or which tends to produce it.» «It is,» Kirchhoff will say, «the product of mass by acceleration.» But then why not say that mass is the quotient of force by acceleration?
-
-
- strength
Synonyms[edit]
- pouvoir
- puissance
- violence
Derived terms[edit]
- à bout de forces
- à force de
- à la force du poignet
- avoir force de loi
- camisole de force
- champ de force
- côté obscur de la force
- coup de force
- de force
- de gré ou de force
- de toutes ses forces
- de vive force
- démonstration de force
- en force
- forcé
- force de frappe
- force de la nature
- force de l’âge
- force majeure
- forcément
- forcer
- forces aériennes
- forces armées
- Forces canadiennes
- forces de l’ordre
- forces vives
- forces vives
- ligne de force
- l’union fait la force
- par la force des choses
- passage en force
- passer en force
- rapport de force
- tour de force
Descendants[edit]
- → Polish: forsa
Adjective[edit]
force (invariable)
- (archaic) Many; a lot of; a great quantity of
Verb[edit]
force
- inflection of forcer:
- first/third-person singular present indicative/subjunctive
- second-person singular imperative
Further reading[edit]
- “force”, in Trésor de la langue française informatisé [Digitized Treasury of the French Language], 2012.
Middle French[edit]
Etymology[edit]
From Old French force.
Noun[edit]
force f (plural forces)
- force (physical effort; physical might)
Descendants[edit]
- French: force
- → Polish: forsa
Old French[edit]
Alternative forms[edit]
- forche (northern)
- fors
Etymology[edit]
From Late Latin fortia, a noun derived from the neuter plural of Latin fortis (“strong”).
Pronunciation[edit]
- (classical) IPA(key): /ˈfɔɾt͡sə/, (northern) /-t͡ʃə/
- (late) IPA(key): /ˈfɔɾsə/, (northern) /-ʃə/
Noun[edit]
force f (oblique plural forces, nominative singular force, nominative plural forces)
- strength; might
[edit]
- esforcer
- esfort
- fort
- forteresce
Descendants[edit]
- Middle French: force
- French: force
- → Polish: forsa
- French: force
- Walloon: foice
- → Middle English: force, fors, forse
- English: force
- → Irish: fórsa
Portuguese[edit]
Verb[edit]
force
- inflection of forçar:
- first/third-person singular present subjunctive
- third-person singular imperative
Britannica Dictionary definition of FORCE
1
[noncount]
:
physical strength, power, or effect
-
The front of the car took the full force of the collision.
-
instruments used to measure the force of the wind
2
[noncount]
:
power or violence used on a person or thing
-
The police were accused of using excessive force when they made the arrest.
-
We discourage the use of force.
-
a show of force
-
He used brute force to open the door.
-
He took the purse from her by force. [=he used physical power to take her purse]
-
He feels that this conflict can only be resolved by force of arms. [=by using weapons; by military action]
3
[noncount]
:
strength or power that is not physical
-
I was impressed by the force of her personality.
-
lending force to his arguments [=making his arguments more effective/persuasive]
-
These regulations do not have the force of law. [=they do not have the power that laws have]
-
She succeeded by/through sheer force of will. [=because she was so determined to succeed]
-
Through/By force of circumstance(s) [=because of conditions that cannot be controlled], the company has had to lay off several hundred workers.
-
Even after he retired, he still woke up early every day by/from force of habit. [=he woke up early every day because he was in the habit of doing so]
4
technical
:
a natural power or effect that is able to change the speed or direction of something
[noncount]
-
the force of gravity
[count]
-
gravitational/electromagnetic forces
—
see also centrifugal force
5
[count]
:
something (such as rain or wind) that occurs in nature and that can be very powerful
— usually plural
-
The cliff was gradually eroded by the forces of nature.
-
natural forces
— sometimes used figuratively
-
She gets people to do whatever she wants: she’s a force of nature. [=she’s a very powerful person who cannot be easily controlled]
6
[count]
a
:
a group of soldiers trained to fight in a war
-
a force of 20,000 soldiers
-
He belonged to an elite fighting force.
-
The enemy forces had us surrounded.
-
ground forces
-
allied/rebel forces
—
see also air force
b
[count]
:
a group of people who do a particular job or are available for a particular purpose
-
our country’s labor/work force
-
The company has a very large sales force.
-
security forces
—
see also task force
c
the Force
informal
:
police force
-
After graduating from high school, he joined the Force.
d
the forces
British
:
armed forces
-
Will the new defense policy weaken the forces?
7
[count]
:
a person or group that has the power to do something or make something happen
-
The organization has been a strong force for good. [=has done a lot of good things]
-
He has been the driving/motivating force behind these changes. [=he has been the person who has caused these changes to occur]
-
He has become a force to be reckoned with [=a person who has power and influence] in politics.
8
— used to describe the strength of a wind
-
damage caused by a force 9 gale
-
The house was flattened by hurricane-force winds.
-
Storm-force winds [=very strong winds] are expected tonight.
9
[count]
baseball
:
force-out
-
a force at second base
in force
1
:
in large numbers
-
Picnickers were out in force today. [=there were many picnickers out today]
2
of a law, rule, etc.
:
actually working or operating
-
The ban remains in force. [=in effect]
-
The resolution remains in full force.
into force
:
into the condition of actually working or operating
-
The law came/went into force [=into effect] last year.
-
The regulations have not yet been put/brought into force.
join forces
also
combine forces
:
to begin working together in order to achieve something
-
We must all join forces to prevent violence.
— often + with
-
The company has joined forces with local environmental groups.
Britannica Dictionary definition of FORCE
[+ object]
1
:
to make (someone) do something that he or she does not want to do
-
They forced us to work long hours without pay.
-
He was forced to resign from office. = He was forced out of office.
-
I really have to force myself [=to make a great effort] to get up and go to work these days.
2
a
:
to make it necessary for (someone) to do something
-
The flooding forced hundreds of residents to flee their homes.
-
After seeing the evidence, I was forced to admit my error.
-
I am forced to conclude that more funding will be necessary.
-
The pilot was forced to land when one of the plane’s engines caught fire.
b
:
to make (something) necessary
-
The scandal forced his resignation.
-
Lack of time may eventually force a compromise.
c
:
to cause the occurrence of (something that other people do not want to happen)
-
They are trying to force a vote on this issue.
3
a
:
to move (someone or something) by physical effort
-
The runner was forced out of bounds.
-
Their car was forced off the road.
-
After hours of fighting, they were able to force back the enemy.
-
The pressure forces the water to the surface.
-
A pump forces air into the chamber.
-
The medicine tasted awful, but I managed to force it down. [=to swallow it by making an effort]
-
If the key doesn’t fit the lock, don’t force it. [=don’t use too much physical strength to make the key go into the lock]
b
:
to cause (something) to open by using physical effort or violence
-
They forced (open) the door.
-
It was clear that the door/lock had been forced.
4
:
to produce (something, such as a smile) by making an effort
-
She forced a smile.
5
baseball
:
to cause (a runner) to be put out by means of a force-out
-
He was forced (out) at second base.
force on/upon
[phrasal verb]
force (someone or something) on/upon (someone)
:
to cause (someone or something that is not wanted) to be accepted by (someone)
-
They resent having these decisions forced on them.
-
I don’t like the way he keeps forcing himself on us. [=the way he keeps coming to be with us when we do not want to be with him]
force someone’s hand
:
to make it necessary for someone to do something
-
She’d intended to postpone her decision, but events forced her hand.
force (something) down someone’s throat
—
see throat
force your way
:
to move ahead by pushing and making people move out of your way
-
They forced their way into the room.
-
He forced his way through the crowd.
Educalingo cookies are used to personalize ads and get web traffic statistics. We also share information about the use of the site with our social media, advertising and analytics partners.
Download the app
educalingo

The whole world is determined by trade — which is really the blood of the world. The driving force is everyone’s desire to have a better life. How? By consuming. For countries, the ‘Holy Grail’ is economic growth.
Yann Arthus-Bertrand
ETYMOLOGY OF THE WORD FORCE
From Old French, from Vulgar Latin fortia (unattested), from Latin fortis strong.
Etymology is the study of the origin of words and their changes in structure and significance.
PRONUNCIATION OF FORCE
GRAMMATICAL CATEGORY OF FORCE
Force is a verb and can also act as a noun.
A noun is a type of word the meaning of which determines reality. Nouns provide the names for all things: people, objects, sensations, feelings, etc.
The verb is the part of the sentence that is conjugated and expresses action and state of being.
See the conjugation of the verb force in English.
WHAT DOES FORCE MEAN IN ENGLISH?
Force
In physics, a force is any external effort that causes an object to undergo a certain change, either concerning its movement, direction, or geometrical construction. In other words, a force can cause an object with mass to change its velocity, i.e., to accelerate, or a flexible object to deform, or both. Force can also be described by intuitive concepts such as a push or a pull. A force has both magnitude and direction, making it a vector quantity. It is measured in the SI unit of newtons and represented by the symbol F. The original form of Newton’s second law states that the net force acting upon an object is equal to the rate at which its momentum changes with time. If the mass of the object is constant, this law implies that the acceleration of an object is directly proportional to the net force acting on the object, is in the direction of the net force, and is inversely proportional to the mass of the object. As a formula, this is expressed as: where the arrows imply a vector quantity possessing both magnitude and direction.
Definition of force in the English dictionary
The first definition of force in the dictionary is strength or energy; might; power. Other definition of force is exertion or the use of exertion against a person or thing that resists; coercion. Force is also a dynamic influence that changes a body from a state of rest to one of motion or changes its rate of motion. The magnitude of the force is equal to the product of the mass of the body and its acceleration.
CONJUGATION OF THE VERB TO FORCE
PRESENT
Present
I force
you force
he/she/it forces
we force
you force
they force
Present continuous
I am forcing
you are forcing
he/she/it is forcing
we are forcing
you are forcing
they are forcing
Present perfect
I have forced
you have forced
he/she/it has forced
we have forced
you have forced
they have forced
Present perfect continuous
I have been forcing
you have been forcing
he/she/it has been forcing
we have been forcing
you have been forcing
they have been forcing
Present tense is used to refer to circumstances that exist at the present time or over a period that includes the present time. The present perfect refers to past events, although it can be considered to denote primarily the resulting present situation rather than the events themselves.
PAST
Past
I forced
you forced
he/she/it forced
we forced
you forced
they forced
Past continuous
I was forcing
you were forcing
he/she/it was forcing
we were forcing
you were forcing
they were forcing
Past perfect
I had forced
you had forced
he/she/it had forced
we had forced
you had forced
they had forced
Past perfect continuous
I had been forcing
you had been forcing
he/she/it had been forcing
we had been forcing
you had been forcing
they had been forcing
Past tense forms express circumstances existing at some time in the past,
FUTURE
Future
I will force
you will force
he/she/it will force
we will force
you will force
they will force
Future continuous
I will be forcing
you will be forcing
he/she/it will be forcing
we will be forcing
you will be forcing
they will be forcing
Future perfect
I will have forced
you will have forced
he/she/it will have forced
we will have forced
you will have forced
they will have forced
Future perfect continuous
I will have been forcing
you will have been forcing
he/she/it will have been forcing
we will have been forcing
you will have been forcing
they will have been forcing
The future is used to express circumstances that will occur at a later time.
CONDITIONAL
Conditional
I would force
you would force
he/she/it would force
we would force
you would force
they would force
Conditional continuous
I would be forcing
you would be forcing
he/she/it would be forcing
we would be forcing
you would be forcing
they would be forcing
Conditional perfect
I would have force
you would have force
he/she/it would have force
we would have force
you would have force
they would have force
Conditional perfect continuous
I would have been forcing
you would have been forcing
he/she/it would have been forcing
we would have been forcing
you would have been forcing
they would have been forcing
Conditional or «future-in-the-past» tense refers to hypothetical or possible actions.
IMPERATIVE
Imperative
you force
we let´s force
you force
The imperative is used to form commands or requests.
NONFINITE VERB FORMS
Present Participle
forcing
Infinitive shows the action beyond temporal perspective. The present participle or gerund shows the action during the session. The past participle shows the action after completion.
WORDS THAT RHYME WITH FORCE
Synonyms and antonyms of force in the English dictionary of synonyms
SYNONYMS OF «FORCE»
The following words have a similar or identical meaning as «force» and belong to the same grammatical category.
Translation of «force» into 25 languages

TRANSLATION OF FORCE
Find out the translation of force to 25 languages with our English multilingual translator.
The translations of force from English to other languages presented in this section have been obtained through automatic statistical translation; where the essential translation unit is the word «force» in English.
Translator English — Chinese
力量
1,325 millions of speakers
Translator English — Spanish
fuerza
570 millions of speakers
English
force
510 millions of speakers
Translator English — Hindi
बल
380 millions of speakers
Translator English — Arabic
قُوَّة
280 millions of speakers
Translator English — Russian
сила
278 millions of speakers
Translator English — Portuguese
força
270 millions of speakers
Translator English — Bengali
বল
260 millions of speakers
Translator English — French
force
220 millions of speakers
Translator English — Malay
Memaksa
190 millions of speakers
Translator English — German
Kraft
180 millions of speakers
Translator English — Japanese
力
130 millions of speakers
Translator English — Korean
힘
85 millions of speakers
Translator English — Javanese
Pasukan
85 millions of speakers
Translator English — Vietnamese
lực
80 millions of speakers
Translator English — Tamil
படை
75 millions of speakers
Translator English — Marathi
शक्ती
75 millions of speakers
Translator English — Turkish
kuvvet
70 millions of speakers
Translator English — Italian
forza
65 millions of speakers
Translator English — Polish
siła
50 millions of speakers
Translator English — Ukrainian
сила
40 millions of speakers
Translator English — Romanian
forță
30 millions of speakers
Translator English — Greek
ισχύς
15 millions of speakers
Translator English — Afrikaans
krag
14 millions of speakers
Translator English — Swedish
styrka
10 millions of speakers
Translator English — Norwegian
styrke
5 millions of speakers
Trends of use of force
TENDENCIES OF USE OF THE TERM «FORCE»
The term «force» is very widely used and occupies the 2.009 position in our list of most widely used terms in the English dictionary.

FREQUENCY
Very widely used
The map shown above gives the frequency of use of the term «force» in the different countries.
Principal search tendencies and common uses of force
List of principal searches undertaken by users to access our English online dictionary and most widely used expressions with the word «force».
FREQUENCY OF USE OF THE TERM «FORCE» OVER TIME
The graph expresses the annual evolution of the frequency of use of the word «force» during the past 500 years. Its implementation is based on analysing how often the term «force» appears in digitalised printed sources in English between the year 1500 and the present day.
Examples of use in the English literature, quotes and news about force
10 QUOTES WITH «FORCE»
Famous quotes and sentences with the word force.
Our task force put to sea in early January 1942, to attack the Japanese in the Marshall and Gilbert islands, but the mission was called off on the eve of the attack.
I try to force myself to travel light; otherwise, I tend to bring a million things that I end up never using!
For the last 15 years that I have been performing, all I ever wanted to do was transcend poetry to the world. See, it wasn’t enough for me to write a book. It wasn’t enough for me to join a slam competition, and while those things hold weight, it wasn’t the driving force that pushes the pen to the pad.
The mercy caravans are through there the medicine refugees flowing out. It makes the United States look very bad here. And much more like an occupation force than it did before.
The whole world is determined by trade — which is really the blood of the world. The driving force is everyone’s desire to have a better life. How? By consuming. For countries, the ‘Holy Grail’ is economic growth.
My mind started wandering. I started playing carefully, instead of playing the way that had gotten me to that point. I had to force myself to keep driving the ball.
Population is a strong driver of the economy as well as the quality of the labor force.
The fatigue produced on the muscles of the human frame does not altogether depend on the actual force employed in each effort, but partly on the frequency with which it is exerted.
We must draw on our early roots and remind people why the Labour party was created and who it sought to represent. We have never been a sectional party promoting self-interest, but instead a force for engaging self-reliance and self-determination.
Sex, a great and mysterious motive force in human life, has indisputably been a subject of absorbing interest to mankind through the ages.
10 ENGLISH BOOKS RELATING TO «FORCE»
Discover the use of force in the following bibliographical selection. Books relating to force and brief extracts from same to provide context of its use in English literature.
1
Force: The Key To Capturing Life Through Drawing
Learn to approach drawing through Michael’s groundbreaking theory about force and its relationship to: · Rhythm · Form · Shape · Clothing · Reportage · Animals Animate objects are always full of «Force.
Michael D. Mattesi, Mike Mattesi, 2004
2
Ultimate Air Force Basic Training Guidebook: Tips, Tricks …
Beginning with the recruiting process and taking you all the way through basic training graduation day, this book answers all your questions and will help alleviate your fears and concerns as you enter this new and exciting period of your …
Nicholas Van Wormer, SrA Nicholas Van Wormer Wormer, 2010
3
Empty Force: The Power of Chi for Self-Defense and Energy …
This book reveals the secret of the empty force to the general reader for the very first time, and explains how martial arts masters use its power to defend themselves against opponents without making physical contact.
Paul Dong, Thomas Raffill, 2005
4
Atomic Force Microscopy: Biomedical Methods and Applications
Highly experienced physicians and biologists clearly explain the basic technical knowledge needed to use AFM and demonstrate its multifarious uses in biomedicine and the life sciences.
Pier Carlo Braga, Davide Ricci, 2004
5
Cultured Force: Makers and Defenders of the French Colonial …
Bridging gaps between intellectual history, biography, and military/colonial history, Barnett Singer and John Langdon provide a challenging, readable interpretation of French imperialism and some of its leading figures from the early modern …
Barnett Singer, John W. Langdon, 2004
6
Concepts of Force: A Study in the Foundations of Dynamics
This work by a noted physicist traces conceptual development from ancient to modern times.
The book also contains the Ambush Alley rules that allow players to recreate the intense counterinsurgency actions in an urban environment that have become the hallmark of 21st century warfare.
Shawn Carpenter, Robby Carpenter, 2011
8
Force.com Developer Certification Handbook (Dev401)
Developers who need to prepare for the Salesforce.com Certified Force.com Developer exam will benefit from this book. This book is ideal for developers who are new to Salesforce CRM and the Force.com platform.
INSIDE DELTA FORCE In this dramatic behind-the-scenes chronicle, Eric Haney, one of the founding members of Delta Force, takes us inside this legendary unit from the beginning.
10
International Law and the Use of Force
This fully revised and updated second edition of International Law and the Use of Force explores the whole of the large and controversial subject of the use of force in international law- not only the use of force by states but also the …
10 NEWS ITEMS WHICH INCLUDE THE TERM «FORCE»
Find out what the national and international press are talking about and how the term force is used in the context of the following news items.
Star Wars force awakens with standing ovation for Harrison Ford at …
Fans screamed for Harrison Ford at the Star Wars: The Force Awakens Comic-Con panel in San Diego on Friday evening, but the scene in the … «The Guardian, Jul 15»
Quiet Force speaks up in Arlington Handicap — ESPN.com
Kevin Warner’s Warner Thoroughbreds’ Quiet Force took command at the head of the lane in the Arlington Handicap July 11 and powered his … «ESPN, Jul 15»
Air Force launches inquiry into sex complaints | Stuff.co.nz
The Air Force has ordered an independent inquiry into the way it handles sexual assault complaints after lobbying by victims of a former … «Stuff.co.nz, Jul 15»
US Navy Triples Maternity Leave, Air Force Looks to Follow Suit …
The Air Force, apparently liking what they saw, is considering expanding their own maternity leave programs. A more lenient maternity policy … «Town Hall, Jul 15»
Metro Transit police force’s numbers are surging … quietly …
The Metro Transit police force’s full-time force has grown 67 percent in the past three years, Thursday, July 9, 2015. (Pioneer Press: Jean Pieri). «TwinCities.com-Pioneer Press, Jul 15»
Shane Watson’s lbw weakness could force Australia to dismiss …
Shane Watson was out lbw to England’s Mark Wood in Australia’s second innings to follow the all-rounder’s dismissal by Stuart Broad via the … «The Guardian, Jul 15»
Apple Prepares For Force Touch Based iPhone 7 — ValueWalk
This makes sense in many ways, with Apple Inc. (NASDAQ:AAPL) expected to incorporate the Force Touch technology that was introduced in … «ValueWalk, Jul 15»
Ben McCalman takes Force honour — The West Australian — News
McCalman, the incumbent Australian No.8 who re-signed with the Force for another three seasons last month, polled the most number of votes … «The West Australian, Jul 15»
Body of Air Force tech sergeant who drowned returned to Pittsburgh …
An American flag draped the casket of Air Force Tech Sgt. Lewis Barkley III as police, firefighters, members of the Air Force and his family met … «Tribune-Review, Jul 15»
Air Force veterans return to K.I. Sawyer after 20 years : News …
K.I. SAWYER — For the first time in almost 20 years, Air Force veterans are back at Sawyer Air Force Base. The reunion brought back a lot of … «UpperMichigansSource.com, Jul 15»
REFERENCE
« EDUCALINGO. Force [online]. Available <https://educalingo.com/en/dic-en/force>. Apr 2023 ».
Download the educalingo app


Discover all that is hidden in the words on