The definition of the word surface area - Word и Excel - помощь в работе с программами

From Wikipedia, the free encyclopedia

A sphere of radius r has surface area 4πr².

The surface area of a solid object is a measure of the total area that the surface of the object occupies.^[1] The mathematical definition of surface area in the presence of curved surfaces is considerably more involved than the definition of arc length of one-dimensional curves, or of the surface area for polyhedra (i.e., objects with flat polygonal faces), for which the surface area is the sum of the areas of its faces. Smooth surfaces, such as a sphere, are assigned surface area using their representation as parametric surfaces. This definition of surface area is based on methods of infinitesimal calculus and involves partial derivatives and double integration.

A general definition of surface area was sought by Henri Lebesgue and Hermann Minkowski at the turn of the twentieth century. Their work led to the development of geometric measure theory, which studies various notions of surface area for irregular objects of any dimension. An important example is the Minkowski content of a surface.

Definition[edit]

While the areas of many simple surfaces have been known since antiquity, a rigorous mathematical definition of area requires a great deal of care.
This should provide a function

which assigns a positive real number to a certain class of surfaces that satisfies several natural requirements. The most fundamental property of the surface area is its additivity: the area of the whole is the sum of the areas of the parts. More rigorously, if a surface S is a union of finitely many pieces S₁, …, S_r which do not overlap except at their boundaries, then

Surface areas of flat polygonal shapes must agree with their geometrically defined area. Since surface area is a geometric notion, areas of congruent surfaces must be the same and the area must depend only on the shape of the surface, but not on its position and orientation in space. This means that surface area is invariant under the group of Euclidean motions. These properties uniquely characterize surface area for a wide class of geometric surfaces called piecewise smooth. Such surfaces consist of finitely many pieces that can be represented in the parametric form

$S_D: vec{r}=vec{r}(u,v), quad (u,v)in D$

with a continuously differentiable function vec{r}. The area of an individual piece is defined by the formula

$A(S_D) = iint_Dleft |vec{r}_utimesvec{r}_vright | , du , dv.$

Thus the area of S_D is obtained by integrating the length of the normal vector $vec{r}_utimesvec{r}_v$ to the surface over the appropriate region D in the parametric uv plane. The area of the whole surface is then obtained by adding together the areas of the pieces, using additivity of surface area. The main formula can be specialized to different classes of surfaces, giving, in particular, formulas for areas of graphs z = f(x,y) and surfaces of revolution.

Schwarz lantern with axial slices and radial vertices. The limit of the area as and tend to infinity doesn’t converge. In particular it doesn’t converge to the area of the cylinder.

One of the subtleties of surface area, as compared to arc length of curves, is that surface area cannot be defined simply as the limit of areas of polyhedral shapes approximating a given smooth surface. It was demonstrated by Hermann Schwarz that already for the cylinder, different choices of approximating flat surfaces can lead to different limiting values of the area; this example is known as the Schwarz lantern.^[2]^[3]

Various approaches to a general definition of surface area were developed in the late nineteenth and the early twentieth century by Henri Lebesgue and Hermann Minkowski. While for piecewise smooth surfaces there is a unique natural notion of surface area, if a surface is very irregular, or rough, then it may not be possible to assign an area to it at all. A typical example is given by a surface with spikes spread throughout in a dense fashion. Many surfaces of this type occur in the study of fractals. Extensions of the notion of area which partially fulfill its function and may be defined even for very badly irregular surfaces are studied in geometric measure theory. A specific example of such an extension is the Minkowski content of the surface.

Common formulas[edit]

Surface areas of common solids

Shape	Equation	Variables
Cube	${displaystyle 6a^{2}}$	a = side length
Cuboid		l = length, b = breadth, h = height
Triangular prism		b = base length of triangle, h = height of triangle, l = distance between triangular bases, p, q, r = sides of triangle
All prisms		B = the area of one base, P = the perimeter of one base, h = height
Sphere	${displaystyle 4pi r^{2}=pi d^{2}}$	r = radius of sphere, d = diameter
Hemisphere	${displaystyle 3pi r^{2}}$	r = radius of the hemisphere
Hemispherical shell	${displaystyle pi left(3R^{2}+r^{2}right)}$	R = external radius of hemisphere, r = internal radius of hemisphere
Spherical lune	${displaystyle 2r^{2}theta }$	r = radius of sphere, θ = dihedral angle
Torus	${displaystyle left(2pi rright)left(2pi Rright)=4pi ^{2}Rr}$	r = minor radius (radius of the tube), R = major radius (distance from center of tube to center of torus)
Closed cylinder	${displaystyle 2pi r^{2}+2pi rh=2pi rleft(r+hright)}$	r = radius of the circular base, h = height of the cylinder
Cylindrical annulus	${displaystyle 2pi Rh+2pi rh+2(pi R^{2}-pi r^{2})=2pi (R+r)(R-r+h)}$	R = External radius r = Internal radius, h = height
Capsule		r = radius of the hemispheres and cylinder, h = height of the cylinder
Curved surface area of a cone	${displaystyle pi r{sqrt {r^{2}+h^{2}}}=pi rs}$	${displaystyle s={sqrt {r^{2}+h^{2}}}}$ s = slant height of the cone, r = radius of the circular base, h = height of the cone
Full surface area of a cone	${displaystyle pi rleft(r+{sqrt {r^{2}+h^{2}}}right)=pi rleft(r+sright)}$	s = slant height of the cone, r = radius of the circular base, h = height of the cone
Regular Pyramid	${displaystyle B+{frac {Ps}{2}}}$	B = area of base, P = perimeter of base, s = slant height
Square pyramid	${displaystyle b^{2}+2bs=b^{2}+2b{sqrt {left({frac {b}{2}}right)^{2}+h^{2}}}}$	b = base length, s = slant height, h = vertical height
Rectangular pyramid	${displaystyle lb+l{sqrt {left({frac {b}{2}}right)^{2}+h^{2}}}+b{sqrt {left({frac {l}{2}}right)^{2}+h^{2}}}}$	l = length, b = breadth, h = height
Tetrahedron	${sqrt {3}}a^{2}$	a = side length
Surface of revolution	${displaystyle 2pi int _{a}^{b}{f(x){sqrt {1+(f'(x))^{2}}}dx}}$
Parametric surface	${displaystyle iint _{D}leftvert {vec {r}}_{u}times {vec {r}}_{v}rightvert dA}$	= parametric vector equation of surface, ${vec {r}}_{u}$ = partial derivative of with respect to , ${displaystyle {vec {r}}_{v}}$ = partial derivative of with respect to , = shadow region

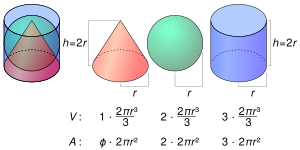
Ratio of surface areas of a sphere and cylinder of the same radius and height[edit]

A cone, sphere and cylinder of radius r and height h.

The below given formulas can be used to show that the surface area of a sphere and cylinder of the same radius and height are in the ratio 2 : 3, as follows.

Let the radius be r and the height be h (which is 2r for the sphere).

${displaystyle {begin{array}{rlll}{text{Sphere surface area}}&=4pi r^{2}&&=(2pi r^{2})times 2\{text{Cylinder surface area}}&=2pi r(h+r)&=2pi r(2r+r)&=(2pi r^{2})times 3end{array}}}$

The discovery of this ratio is credited to Archimedes.^[4]

In chemistry[edit]

Surface area of particles of different sizes.

Surface area is important in chemical kinetics. Increasing the surface area of a substance generally increases the rate of a chemical reaction. For example, iron in a fine powder will combust, while in solid blocks it is stable enough to use in structures. For different applications a minimal or maximal surface area may be desired.

In biology[edit]

The surface area of an organism is important in several considerations, such as regulation of body temperature and digestion. Animals use their teeth to grind food down into smaller particles, increasing the surface area available for digestion. The epithelial tissue lining the digestive tract contains microvilli, greatly increasing the area available for absorption. Elephants have large ears, allowing them to regulate their own body temperature. In other instances, animals will need to minimize surface area; for example, people will fold their arms over their chest when cold to minimize heat loss.

The surface area to volume ratio (SA:V) of a cell imposes upper limits on size, as the volume increases much faster than does the surface area, thus limiting the rate at which substances diffuse from the interior across the cell membrane to interstitial spaces or to other cells. Indeed, representing a cell as an idealized sphere of radius r, the volume and surface area are, respectively, V = (4/3)πr³ and SA = 4πr². The resulting surface area to volume ratio is therefore 3/r. Thus, if a cell has a radius of 1 μm, the SA:V ratio is 3; whereas if the radius of the cell is instead 10 μm, then the SA:V ratio becomes 0.3. With a cell radius of 100, SA:V ratio is 0.03. Thus, the surface area falls off steeply with increasing volume.

References[edit]

^ Weisstein, Eric W. «Surface Area». MathWorld.
^ «Schwarz’s Paradox» (PDF). Archived (PDF) from the original on 4 March 2016. Retrieved 21 March 2017.
^ «Archived copy» (PDF). Archived from the original (PDF) on 15 December 2011. Retrieved 24 July 2012.{{cite web}}: CS1 maint: archived copy as title (link)
^ Rorres, Chris. «Tomb of Archimedes: Sources». Courant Institute of Mathematical Sciences. Archived from the original on 9 December 2006. Retrieved 2 January 2007.

Yu.D. Burago; V.A. Zalgaller; L.D. Kudryavtsev (2001) [1994], «Area», Encyclopedia of Mathematics, EMS Press

External links[edit]

Surface Area Video at Thinkwell

Источник

The surface area of a three-dimensional object is the total area of all its faces. In real-life we use the concept of surface areas of different objects when we want to wrap something, paint something, and eventually while building things to get the best possible design. Let us learn all about the surface area of 3D shapes in this article.

1.	What is Surface Area?
2.	Surface Area Formulas
3.	Types of Surface Areas
4.	Surface Area of Prism
5.	FAQs on Surface Area

What is Surface Area?

The total area occupied by the surfaces of an object is called its surface area. In geometry, different 3D shapes have different surface areas which can be easily calculated using the formulas that we will be learning in this article. The surface area is classified into two categories:

Lateral surface area or Curved surface area
Total surface area

Let us learn about the general surface area formulas of various shapes.

Surface Area Formulas

There is a different surface area formula for every geometrical shape, but the idea behind all is to get the total area occupied by all the faces of the objects. In this section, we will learn about the various formulas used to calculate the surface area of different objects. The total surface area considers all the faces of the 3D shape including the flat surfaces and the curved surfaces, while the lateral surface area is calculated to find the area occupied by the curved surface of the shape. It does not include the area of the bases. A sphere is one 3D figure which has only one round surface with no flat base.

Observe the table given below to learn the surface area formulas of different 3D shapes.

3D Shape	Total Surface Area (TSA)	Lateral Surface Area (LSA)/Curved Surface Area
Cube	6a²	4a², where a is the length of each side
Cuboid	2 (lw + wh + lh)	2h (l + w), where l, w, and h are the length, width, and height of the cuboid
Cone	πr(r + l)	πrl, where r is the radius and l is the slant height of the cone
Cylinder	2πr(r + h)	2πrh, where r is the radius and h is the height of the cylinder
Sphere	4πr², where r is the radius of the sphere	Not applicable

Types of Surface Areas

As we have already discussed that there are two types of surface areas for three-dimensional shapes: total surface area and curved/lateral surface area. The total surface area includes the area of all the faces of the shape while the curved or lateral area includes only the area of the side faces of the shapes. Observe the cylinder given below to understand the difference between total surface area and curved surface area.

Surface Area of Prism

A prism is a 3D solid object made up of two congruent bases which are polygons and congruent lateral faces which are rectangular in shape. There are two types of areas that a prism has — the lateral surface area and the total surface area. The lateral area of a prism is the sum of the areas of all its lateral faces whereas the total surface area of a prism is the sum of its lateral area and area of its bases.

The lateral surface area of prism = base perimeter × height

The total surface area of a prism = Lateral surface area of prism + area of the two bases = (2 × Base Area) + Lateral surface area = (2 × Base Area) + (Base perimeter × height).

There are seven types of prisms based on the shape of the bases of prisms. The bases of different types of prisms are different so are the formulas to determine the surface area of the prism. Observe the table given below to understand this concept behind the surface area of various prisms:

Shape	Base	Surface Area of Prism = (2 × Base Area) + (Base perimeter × height)
Triangular Prism	Triangle	Surface area of triangular prism = bh + (s₁ + s₂ + b)H
Square Prism	Square	Surface area of square prism = 2a² + 4ah
Rectangular Prism	Rectangle	Surface area of rectangular prism = 2(lw + wh + lh)
Trapezoidal Prism	Trapezoid	Surface area of trapezoidal prism = h (b + d) + l (a + b + c + d)
Pentagonal Prism	Pentagon	Surface area of pentagonal prism = 5ab + 5bh
Hexagonal Prism	Hexagon	Surface area of hexagonal prism = 6ah + 3√3a²
Octagonal Prism	Octagon	Surface area of octagonal prism = 4a² (1 + √2) + 8aH

☛ Related Articles

Surface Area of Cube
Surface Area of Cuboid
Surface Area of Cone
Surface Area of Sphere
Surface Area of a Hemisphere
Surface Area of Cylinder
Surface Area of Pyramid
Difference Between Area and Surface Area

FAQs on Surface Area

What is the Definition of Surface Area?

The surface area is the total area covered by all the faces of a 3D object. For example, if we need to find the quantity of paint required to paint a cube, then the surface on which the paint will be applied is its surface area. It is always measured in square units.

What is the Formula for Surface Area?

The formula to find the surface areas of different geometrical shapes is to add the areas of each of their faces. It can be very tedious to find the area of each face individually, so we have surface area formulas for each of the geometrical figures. Some of the formulas are listed below:

Total surface area of a cube = 6 × (side)²
Surface area of sphere = 4πr²
Total surface area of cone = πr(r + l)

Is Surface Area the Same as Area?

The main difference between surface area and area is that surface area is the area of 3D shapes such as a sphere, cylinder, and so on, whereas, area is the measurement of the space occupied by 2D shapes such as triangles, squares, and so on.

How to Find the Surface Area of a Rectangular Prism?

The surface area of a rectangular prism can be calculated by using the following formula: Surface area of rectangular prism = 2(lw + wh + lh), where l, w, and h are the length, width, and height of the rectangular prism respectively.

What is the Surface Area of a Cube?

A cube is made up of 6 square faces. So, the surface area of a cube is the sum of the areas of all those 6 faces. We know that area of a square = a², where a is the side length of the square. So, the surface area of a cube with side length a is 6a².

What is the Surface Area of a Circle?

The surface area of a circle is the total area covered by the boundary of a circle. The area of a circle with radius ‘r’ is, Area of a circle = πr².

What is the Surface Area of a Cone?

The area occupied by a cone is referred to as the surface area of a cone. The total surface area of a cone is, T = πr(r + l), and the curved surface area of a cone, S = πrl. Here ‘r’ is the radius of the base and ‘l’ is the slant height of the cone.

What is the Surface Area of a Cylinder?

The surface area of a cylinder is the total region covered by the surface of the cylindrical shape. The total surface area of a cylinder is given as the sum of lateral surface area and the area of two bases. It is mathematically expressed as 2πr(r + h) and is expressed in square units, like m², in², cm², yd², etc. The curved or the lateral surface area of a cylinder is calculated with the formula, Curved surface area = 2πrh.

Источник

1
surface area

surface area

n

Англо-русский строительный словарь. — М.: Русский Язык.
.
1995.

* * *

surface area

n

Англо-русский строительный словарь.
Академик.ру.
2011.

Англо-русский словарь строительных терминов > surface area
2
surface area
1. удельная поверхность
2. площадь поверхности
Англо-русский словарь нормативно-технической терминологии > surface area
3
surface area

SA, surface area

морской район; площадь поверхности

————————

SURFA, surface area

морской район; площадь поверхности

English-Russian dictionary of planing, cross-planing and slotting machines > surface area
4
surface area

English-Russian big medical dictionary > surface area
5
surface area

English-Russian dictionary on nuclear energy > surface area
6
surface area

The English-Russian dictionary general scientific > surface area
7
surface area

Большой англо-русский и русско-английский словарь > surface area
8
surface area

Англо-русский словарь технических терминов > surface area
9
surface area

1) площадь поверхности

2) поверхность

Англо-русский технический словарь > surface area
10
surface area

Англо-русский словарь нефтегазовой промышленности > surface area
11
surface area

9) Авиационная медицина: площадь поверхности , участок поверхности

10) Макаров: площадь полной поверхности

Универсальный англо-русский словарь > surface area
12
surface area

Англо-русский универсальный дополнительный практический переводческий словарь И. Мостицкого > surface area
13
surface area

English-russian automobile dictionary > surface area
14
surface area

площадь поверхности, удельная поверхность.

English-Russian dictionary of terms for geological exploration drilling > surface area
15
surface area

English-Russian dictionary of terminology cable technology > surface area
16
surface area

English-Russian dictionary of computer science and programming > surface area
17
surface area

Англо-русский словарь по ядерным испытаниям и горному делу > surface area
18
surface area

Англо-русский словарь по авиационной медицине > surface area
19
surface area

English-Russian industrial glossariy > surface area
20
surface area

English-Russian military dictionary > surface area

Страницы

См. также в других словарях:

Surface area — is the measure of how much exposed area an object has. It is expressed in square units. If an object has flat faces, its surface area can be calculated by adding together the areas of its faces. Even objects with smooth surfaces, such as spheres … Wikipedia
surface area — surface ,area noun count the total area of a surface or surfaces, especially the outside surfaces of an object: enough paint to cover a surface area of 900 square feet … Usage of the words and phrases in modern English
surface area — surface .area n the area of the outside of an object that can be measured … Dictionary of contemporary English
surface area — noun the extent of a 2 dimensional surface enclosed within a boundary (Freq. 2) the area of a rectangle it was about 500 square feet in area • Syn: ↑area, ↑expanse • Derivationally related forms: ↑areal ( … Useful english dictionary
surface area — UK / US noun [countable] Word forms surface area : singular surface area plural surface areas maths the total area of a surface or surfaces, especially the outside surfaces of an object enough paint to cover a surface area of 900 square feet … English dictionary
surface area — paviršiaus plotas statusas T sritis Standartizacija ir metrologija apibrėžtis Nagrinėjamojo paviršiaus plotas. atitikmenys: angl. surface area vok. Oberflächeninhalt, m rus. площадь поверхности, f pranc. aire de surface, f … Penkiakalbis aiškinamasis metrologijos terminų žodynas
surface area — paviršiaus plotas statusas T sritis fizika atitikmenys: angl. surface area vok. Oberflächeninhalt, m rus. площадь поверхности, f pranc. aire de surface, f … Fizikos terminų žodynas
surface pressure-surface area isotherm — Surface Pressure Surface Area Isotherm Изотерма поверхностное давление площадь Зависимость поверхностного давления монослоя Ленгмюра на поверхности водной субфазы от площади, занимаемой молекулами поверхностно активного вещества в этом… … Толковый англо-русский словарь по нанотехнологии. — М.
Surface area to volume ratio — In chemical reactions involving a solid material, the surface area to volume ratio is an important factor for the reactivity, that is, the rate at which the chemical reaction will proceed. In some industries it is abbreviated sa/vol.Physical… … Wikipedia
Surface area, volume, and average depth of oceans and seas — ▪ Table Surface area, volume, and average depth of oceans and seas area volume average depth 000,000 sq km 000,000 sq mi 000,000 cu km 000,000 cu mi m ft Atlantic Ocean without marginal seas 82.440 31.830 324.600 77.900 3,930 12,890 with… … Universalium
surface area — noun The total area on the surface of a three dimensional figure … Wiktionary

Источник

Educalingo cookies are used to personalize ads and get web traffic statistics. We also share information about the use of the site with our social media, advertising and analytics partners.

Download the app
educalingo

With wok cooking, you chop things up into little pieces for maximum surface area, so they can cook in minutes, if not seconds. Sauteing is energy efficient; baking is not.

Jennifer Lee

PRONUNCIATION OF SURFACE AREA

GRAMMATICAL CATEGORY OF SURFACE AREA

Surface area is a noun.

A noun is a type of word the meaning of which determines reality. Nouns provide the names for all things: people, objects, sensations, feelings, etc.

WHAT DOES SURFACE AREA MEAN IN ENGLISH?

Surface area

The surface area of a solid object is the total area of the object’s faces and curved surfaces. The mathematical definition of surface area in the presence of curved surfaces is considerably more involved than the definition of arc length of one-dimensional curves, or of the surface area for polyhedra, for which the surface area is the sum of the areas of its faces. Smooth surfaces, such as a sphere, are assigned surface area using their representation as parametric surfaces. This definition of surface area is based on methods of infinitesimal calculus and involves partial derivatives and double integration. A general definition of surface area was sought by Henri Lebesgue and Hermann Minkowski at the turn of the twentieth century. Their work led to the development of geometric measure theory, which studies various notions of surface area for irregular objects of any dimension. An important example is the Minkowski content of a surface.

Definition of surface area in the English dictionary

The definition of surface area in the dictionary is the total area on the surface of a three-dimensional figure.

WORDS THAT RHYME WITH SURFACE AREA

Synonyms and antonyms of surface area in the English dictionary of synonyms

Translation of «surface area» into 25 languages

TRANSLATION OF SURFACE AREA

Find out the translation of surface area to 25 languages with our English multilingual translator.

The translations of surface area from English to other languages presented in this section have been obtained through automatic statistical translation; where the essential translation unit is the word «surface area» in English.

Translator English — Chinese

面积

1,325 millions of speakers

Translator English — Spanish

área de superficie

570 millions of speakers

Translator English — Hindi

सतह क्षेत्र

380 millions of speakers

Translator English — Arabic

مساحة السطح

280 millions of speakers

Translator English — Russian

площадь поверхности

278 millions of speakers

Translator English — Portuguese

área de superfície

270 millions of speakers

Translator English — Bengali

ভূপৃষ্ঠের

260 millions of speakers

Translator English — French

surface

220 millions of speakers

Translator English — Malay

kawasan permukaan

190 millions of speakers

Translator English — German

Oberfläche

180 millions of speakers

Translator English — Japanese

表面積

130 millions of speakers

Translator English — Korean

표면적

85 millions of speakers

Translator English — Javanese

Wilayah lumahing

85 millions of speakers

Translator English — Vietnamese

diện tích bề mặt

80 millions of speakers

Translator English — Tamil

மேற்பரப்பு

75 millions of speakers

Translator English — Marathi

पृष्ठभागाचे क्षेत्रफळ

75 millions of speakers

Translator English — Turkish

yüzey alanı

70 millions of speakers

Translator English — Italian

superficie

65 millions of speakers

Translator English — Polish

Powierzchnia

50 millions of speakers

Translator English — Ukrainian

Площа поверхні

40 millions of speakers

Translator English — Romanian

suprafață

30 millions of speakers

Translator English — Greek

επιφάνεια

15 millions of speakers

Translator English — Afrikaans

oppervlakte

14 millions of speakers

Translator English — Swedish

ytarea

10 millions of speakers

Translator English — Norwegian

flateareal

5 millions of speakers

Trends of use of surface area

TENDENCIES OF USE OF THE TERM «SURFACE AREA»

The term «surface area» is very widely used and occupies the 21.175 position in our list of most widely used terms in the English dictionary.

Trends

FREQUENCY

Very widely used

The map shown above gives the frequency of use of the term «surface area» in the different countries.

Principal search tendencies and common uses of surface area

List of principal searches undertaken by users to access our English online dictionary and most widely used expressions with the word «surface area».

FREQUENCY OF USE OF THE TERM «SURFACE AREA» OVER TIME

The graph expresses the annual evolution of the frequency of use of the word «surface area» during the past 500 years. Its implementation is based on analysing how often the term «surface area» appears in digitalised printed sources in English between the year 1500 and the present day.

Examples of use in the English literature, quotes and news about surface area

QUOTES WITH «SURFACE AREA»

Famous quotes and sentences with the word surface area.

With wok cooking, you chop things up into little pieces for maximum surface area, so they can cook in minutes, if not seconds. Sauteing is energy efficient; baking is not.

10 ENGLISH BOOKS RELATING TO «SURFACE AREA»

Discover the use of surface area in the following bibliographical selection. Books relating to surface area and brief extracts from same to provide context of its use in English literature.

Powder Surface Area and Porosity

An introduction to experimental methods used to study the surface area, porosity, density, and particle size of powders encountered in industry, for readers with little previous knowledge of solid surfaces but who, for example, just …

Seymour Lowell, Joan E. Shields, 1991

Adsorption, surface area, and porosity

The principal aim of the second edition of this book remains the same as that of the first edition: to give a critical exposition of the use of the adsorption methods for the assessment of the surface and pore size distribution of finely …

Sidney John Gregg, K. S. W. Sing, 1991

Characterization of Porous Solids and Powders: Surface Area, …

The growth of interest in newly developed porous materials has prompted the writing of this book for those who have the need to make meaningful measurements without the benefit of years of experience.

Surface Area and Porosity Determinations by Physisorption: …

Surface Area and Porosity Determinations by Physisorption is a practical guide for industry or academics to the measurement of surface area and pore size using the tool of physical adsorption.

The Growth of the Surface Area of the Human Body

This work provides an extensive analysis of one of the major body measures, surface area. It is strictly experimental and descriptive; numerical and graphic methods are used to present major findings.

Id). From the large body of information provided by electron micrographs, it has
been established that the majority of the clay minerals found in soils are platelike
or disk shaped. 1.1.6 Surface Area of Soil Particles Relationship to Particle Size …

William A. Jury, Robert Horton, 2004

TABLE 5.2 Comparison of Agar Cubes Cube Dimension Surface Area (cm2)
Volume (cm>) Surface Area: Volume (Simplest Form) 3 cm 2 cm 1 cm 3. Prepare
a data table like Table 5.2 and do the calculations necessary to complete it.

Wrappers Wanted: A Mathematical Adventure in Surface Area

Look no further! This unique tale takes the reader up to the North Pole and describes how Santa challenges his top elf, Snips Cleaver, to conserve paper because the North Pole is «going green.

Candice Yarbray Brucke, 2009

1.9 Surface area of particles Within the clay fraction there are particles small
enough to undergo erratic Brownian movement arising from bombardment by
water molecules in thermal motion. For this order of size, settling procedures are
…

T. J. Marshall, J. W. Holmes, C. W. Rose, 1996

He estimated the total ‘capillary’ surface area in an average man to be 6300
square metres. Intaglietta and Zweifach (1971) used an in-vivo technique to map
the vascular components of the rabbit’s mesentery and arrived at results that
appear …

10 NEWS ITEMS WHICH INCLUDE THE TERM «SURFACE AREA»

Find out what the national and international press are talking about and how the term surface area is used in the context of the following news items.

Surface of Pluto surprisingly young, say scientists

It is a well known fact that smaller objects cool faster than larger ones of the same shape because of their larger surface area. This principle also holds true for … «Youth Independent News, Jul 15»

Thick Cortex Could Be Key in Down Syndrome

Reductions in cortical surface area and increases in cortical thickness in brains of youth with Down Syndrome relative to typical controls. Panel (a) displays … «DrexelNow, Jun 15»

New ‘designer carbon’ from Stanford boosts battery performance

The activation process creates nanosized holes, or pores, that increase the surface area of the carbon, allowing it to catalyze more chemical reactions and store … «Stanford University News, May 15»

New Images Show Ceres is a Colorful Alien World

(Photo : NASA/JPL-Caltech/UCLA) Ceres has an estimated surface area of 2,850,000 km2. That’s just under seven times the total surface area of California state … «Nature World News, Apr 15»

Can money buy your kids a bigger brain?

«Money can buy better education, homes in areas further away from … Both income and education correlated with brain surface area, particularly in areas … «Sydney Morning Herald, Apr 15»

Nearly 81% of Great Lakes’ surface area covered with ice, for the …

The federal Great Lakes research laboratory in Ann Arbor reports Friday that nearly 81 percent of the five lakes’ surface area is ice-covered. On Thursday, the ice … «fox6now.com, Feb 15»

81% of Great Lakes’ surface area now covered in ice

Nearly 81 per cent of the lakes’ surface area was covered with ice, the NOAA Great Lakes Environmental Research Laboratory reported Friday. That was down … «CTV News, Feb 15»

Using Specific Surface Area Measurement for Pharmaceutical …

Hence, surface area measurement (Figure 2) can be incorporated as a quality control tool to the series of incoming raw materials analyses to determine the … «Azom.com, Sep 14»

Calculate plant surface area with smartphone app

«It has always been a challenge to measure leaf surface area without damaging the plants or spending long hours in the lab. I decided to attempt to write … «Business Standard, Aug 14»

Microsoft Offers Surface Pro 3 Buyers $650 on a MacBook Air Trade-In

The 12-inch 2160×1440 pixel display features a 3:2 aspect that supposedly delivers more surface area or visual real-estate to work with. The company boasts of … «NDTV, Jun 14»

REFERENCE

« EDUCALINGO. Surface area [online]. Available <https://educalingo.com/en/dic-en/surface-area>. Apr 2023 ».

Download the educalingo app

Discover all that is hidden in the words on

Источник

Fact-checked by

Paul Mazzola

Dimensionality

Surface area of three-dimensional solids refers to the measured area, in square units, of all the surfaces of objects like cubes, spheres, prisms and pyramids.

One-dimensional figures have only one dimension, one direction that can be measured. A line is one dimensional, since it has only length but no width or height.

One dimensional figures examples

Two-dimensional figures have two dimensions: width and length. All plane figures are two dimensional or 2D. Think of a square, circle, triangle or rectangle.

Two dimensional figures examples

Three-dimensional figures have three dimensions: width, length, and height or depth. When dealing with 3D, we can use height or depth interchangeably, based on what is being measured.

We would use height to describe a skyscraper, but we probably would use depth to describe a hole in the ground. Three-dimensional solids include everyday objects like people, pets, houses, vehicles, cubes, cereal boxes, donuts, planets, shoe boxes, and mathematics textbooks. We live in a 3D world.

Three dimensional figures examples

Defining our terms

A 3D solid is a closed, three-dimensional shape. Examples of 3D solids are cubes, spheres, and pyramids.

A face of a 3D solid is a polygon bound by edges, which are the line segments formed where faces meet. Spheres have no faces.

A cube is a rectangular prism with six congruent, square faces.

A sphere is the set of all points in three dimensions that are equidistant from a given point. A hemisphere is one-half a sphere, its surface area including the circular cross section.

Examples of 3D solid shapes

A prism is a 3D solid with two congruent, opposite faces (bases) with all other faces parallelograms of some sort. Examples of prisms are cubes and triangular, rectangular, hexagonal and octagonal prisms.

A right cylinder is a 3D solid with two circular, opposite faces (bases) and parallel sides connecting the circles. Any cross-section taken of a cylinder produces another circle congruent to the base.

A pyramid is a 3D solid with one polygon for a base (triangular, square, hexagonal — mathematically you have no limits) with all other faces being triangles. The Great Pyramid of Giza is a square pyramid.

A cone is a pyramid with a circular base. A cone has only one face, its base, and one vertex. It has height, h, the perpendicular measure from base to vertex, and slant height, l, which is the distance from base to vertex along its lateral surface.

Cone shape defined with example

Surface area formulas for prisms

For every 3D solid, we can examine each face or surface and calculate its surface area. Then, adding all the individual surface areas, we can find the surface area of the entire solid.

Think of it as unfolding the 3D shape like a cardboard box. Lay out every face, measure each, and add them. This is what occurs with geometry nets.

Formulas work for all the prisms. The faces of prisms will be recognizable polygons, so let’s review the area formulas for the basic polygons:

Try it!

Here is a triangular prism:

Total surface area of a triangular prism example

The area of each triangle is 12bhfrac{1}{2}bh:

Remember, though, we have two of these bases. Next, calculate the area of each of the three rectangular faces:

9cm×25cm=225cm29cmtimes 25cm=225c{m}^{2}

Then, add all the individual areas to find the total surface area:

Square centimeters derive from the linear unit, centimeters. All surface areas of 3D solids are measured in square units, even when the objects are spheres, cylinders or cones.

Here is a rectangular prism:

Total surface area of a rectangular prism example

What is it’s surface area?

Think: you need to measure three of the six faces, add them, and then multiply times 2, since the prism has three pairs of congruent faces. You must of course choose three dissimilar faces to capture length (l), width (w), and height (h):

Here is a cube representing all the gold that has ever been mined on earth:

Total surface area of a cube example

What is its surface area? Think: a cube is six squares, each with a length equal to width equal to height. For a cube with any side b, the formula is:

Surface area formulas for non-prisms

For pyramids, the surface area formula for a pyramid with a base area, A, perimeter of base, p, and slant height, l, is:

If you are fortunate enough to have a square pyramid with a base length, b, and slant height, l, its formula is:

For spheres, calculate the surface area if you know the radius, r:

For hemispheres, you calculate the surface area as the sum of the base surface area, πr2pi {r}^{2}, plus the half sphere, 2πr22pi {r}^{2}, which gives:

For cones with slant height, l, and radius, r, surface area is calculated using this formula:

If you do not know the slant height but know height, h, and radius, r, you can calculate slant height, l, using the Pythagorean Theorem:

For cylinders with height, h, and radius, r, the formula for surface area is:

Источник

Definition[edit]

Common formulas[edit]

Ratio of surface areas of a sphere and cylinder of the same radius and height[edit]

In chemistry[edit]

In biology[edit]

See also[edit]

References[edit]

External links[edit]

What is Surface Area?

Surface Area Formulas

Types of Surface Areas

Surface Area of Prism

FAQs on Surface Area

What is the Definition of Surface Area?

What is the Formula for Surface Area?

Is Surface Area the Same as Area?

How to Find the Surface Area of a Rectangular Prism?

What is the Surface Area of a Cube?

What is the Surface Area of a Circle?

What is the Surface Area of a Cone?

What is the Surface Area of a Cylinder?

См. также в других словарях:

PRONUNCIATION OF SURFACE AREA

GRAMMATICAL CATEGORY OF SURFACE AREA

WHAT DOES SURFACE AREA MEAN IN ENGLISH?

Surface area

Definition of surface area in the English dictionary

WORDS THAT RHYME WITH SURFACE AREA

Synonyms and antonyms of surface area in the English dictionary of synonyms

Translation of «surface area» into 25 languages

TRANSLATION OF SURFACE AREA

Translator English — Chinese

Translator English — Spanish

Translator English — Hindi

Translator English — Arabic

Translator English — Russian

Translator English — Portuguese

Translator English — Bengali

Translator English — French

Translator English — Malay

Translator English — German

Translator English — Japanese

Translator English — Korean

Translator English — Javanese

Translator English — Vietnamese

Translator English — Tamil

Translator English — Marathi

Translator English — Turkish

Translator English — Italian

Translator English — Polish

Translator English — Ukrainian

Translator English — Romanian

Translator English — Greek

Translator English — Afrikaans

Translator English — Swedish

Translator English — Norwegian

Trends of use of surface area

TENDENCIES OF USE OF THE TERM «SURFACE AREA»

FREQUENCY OF USE OF THE TERM «SURFACE AREA» OVER TIME

Examples of use in the English literature, quotes and news about surface area

QUOTES WITH «SURFACE AREA»

10 ENGLISH BOOKS RELATING TO «SURFACE AREA»

10 NEWS ITEMS WHICH INCLUDE THE TERM «SURFACE AREA»

Dimensionality

Defining our terms

Surface area formulas for prisms

Try it!

Surface area formulas for non-prisms