The definition of the word sequence - Word и Excel - помощь в работе с программами

In mathematics, a sequence is an enumerated collection of objects in which repetitions are allowed and order matters. Like a set, it contains members (also called elements, or terms). The number of elements (possibly infinite) is called the length of the sequence. Unlike a set, the same elements can appear multiple times at different positions in a sequence, and unlike a set, the order does matter. Formally, a sequence can be defined as a function from natural numbers (the positions of elements in the sequence) to the elements at each position. The notion of a sequence can be generalized to an indexed family, defined as a function from an arbitrary index set.

For example, (M, A, R, Y) is a sequence of letters with the letter ‘M’ first and ‘Y’ last. This sequence differs from (A, R, M, Y). Also, the sequence (1, 1, 2, 3, 5, 8), which contains the number 1 at two different positions, is a valid sequence. Sequences can be finite, as in these examples, or infinite, such as the sequence of all even positive integers (2, 4, 6, …).

The position of an element in a sequence is its rank or index; it is the natural number for which the element is the image. The first element has index 0 or 1, depending on the context or a specific convention. In mathematical analysis, a sequence is often denoted by letters in the form of $a_{n}$ , $b_{n}$ and $c_{n}$ , where the subscript n refers to the nth element of the sequence; for example, the nth element of the Fibonacci sequence is generally denoted as $F_{n}$ .

In computing and computer science, finite sequences are sometimes called strings, words or lists, the different names commonly corresponding to different ways to represent them in computer memory; infinite sequences are called streams. The empty sequence ( ) is included in most notions of sequence, but may be excluded depending on the context.

An infinite sequence of real numbers (in blue). This sequence is neither increasing, decreasing, convergent, nor Cauchy. It is, however, bounded.

Examples and notation[edit]

A sequence can be thought of as a list of elements with a particular order.^[1]^[2] Sequences are useful in a number of mathematical disciplines for studying functions, spaces, and other mathematical structures using the convergence properties of sequences. In particular, sequences are the basis for series, which are important in differential equations and analysis. Sequences are also of interest in their own right, and can be studied as patterns or puzzles, such as in the study of prime numbers.

There are a number of ways to denote a sequence, some of which are more useful for specific types of sequences. One way to specify a sequence is to list all its elements. For example, the first four odd numbers form the sequence (1, 3, 5, 7). This notation is used for infinite sequences as well. For instance, the infinite sequence of positive odd integers is written as (1, 3, 5, 7, …). Because notating sequences with ellipsis leads to ambiguity, listing is most useful for customary infinite sequences which can be easily recognized from their first few elements. Other ways of denoting a sequence are discussed after the examples.

Examples[edit]

A tiling with squares whose sides are successive Fibonacci numbers in length.

The prime numbers are the natural numbers greater than 1 that have no divisors but 1 and themselves. Taking these in their natural order gives the sequence (2, 3, 5, 7, 11, 13, 17, …). The prime numbers are widely used in mathematics, particularly in number theory where many results related to them exist.

The Fibonacci numbers comprise the integer sequence whose elements are the sum of the previous two elements. The first two elements are either 0 and 1 or 1 and 1 so that the sequence is (0, 1, 1, 2, 3, 5, 8, 13, 21, 34, …).^[1]

Other examples of sequences include those made up of rational numbers, real numbers and complex numbers. The sequence (.9, .99, .999, .9999, …), for instance, approaches the number 1. In fact, every real number can be written as the limit of a sequence of rational numbers (e.g. via its decimal expansion). As another example, π is the limit of the sequence (3, 3.1, 3.14, 3.141, 3.1415, …), which is increasing. A related sequence is the sequence of decimal digits of π, that is, (3, 1, 4, 1, 5, 9, …). Unlike the preceding sequence, this sequence does not have any pattern that is easily discernible by inspection.

Another example of sequences is a sequence of functions, where each member of the sequence is a function whose shape is determined by a natural number indexing that function.

The On-Line Encyclopedia of Integer Sequences comprises a large list of examples of integer sequences.^[3]

Indexing[edit]

Other notations can be useful for sequences whose pattern cannot be easily guessed or for sequences that do not have a pattern such as the digits of π. One such notation is to write down a general formula for computing the nth term as a function of n, enclose it in parentheses, and include a subscript indicating the set of values that n can take. For example, in this notation the sequence of even numbers could be written as ${displaystyle (2n)_{nin mathbb {N} }}$ . The sequence of squares could be written as ${displaystyle (n^{2})_{nin mathbb {N} }}$ . The variable n is called an index, and the set of values that it can take is called the index set.

It is often useful to combine this notation with the technique of treating the elements of a sequence as individual variables. This yields expressions like ${displaystyle (a_{n})_{nin mathbb {N} }}$ , which denotes a sequence whose nth element is given by the variable $a_{n}$ . For example:

${displaystyle {begin{aligned}a_{1}&=1{text{st element of }}(a_{n})_{nin mathbb {N} }\a_{2}&=2{text{nd element }}\a_{3}&=3{text{rd element }}\&;;vdots \a_{n-1}&=(n-1){text{th element}}\a_{n}&=n{text{th element}}\a_{n+1}&=(n+1){text{th element}}\&;;vdots end{aligned}}}$

One can consider multiple sequences at the same time by using different variables; e.g. ${displaystyle (b_{n})_{nin mathbb {N} }}$ could be a different sequence than ${displaystyle (a_{n})_{nin mathbb {N} }}$ . One can even consider a sequence of sequences: ${displaystyle ((a_{m,n})_{nin mathbb {N} })_{min mathbb {N} }}$ denotes a sequence whose mth term is the sequence ${displaystyle (a_{m,n})_{nin mathbb {N} }}$ .

An alternative to writing the domain of a sequence in the subscript is to indicate the range of values that the index can take by listing its highest and lowest legal values. For example, the notation ${displaystyle (k^{2})_{k=1}^{10}}$ denotes the ten-term sequence of squares . The limits infty and -infty are allowed, but they do not represent valid values for the index, only the supremum or infimum of such values, respectively. For example, the sequence ${displaystyle (a_{n})_{n=1}^{infty }}$ is the same as the sequence ${displaystyle (a_{n})_{nin mathbb {N} }}$ , and does not contain an additional term «at infinity». The sequence ${displaystyle (a_{n})_{n=-infty }^{infty }}$ is a bi-infinite sequence, and can also be written as ${displaystyle (ldots ,a_{-1},a_{0},a_{1},a_{2},ldots )}$ .

In cases where the set of indexing numbers is understood, the subscripts and superscripts are often left off. That is, one simply writes $(a_{k})$ for an arbitrary sequence. Often, the index k is understood to run from 1 to ∞. However, sequences are frequently indexed starting from zero, as in

${displaystyle (a_{k})_{k=0}^{infty }=(a_{0},a_{1},a_{2},ldots ).}$

In some cases, the elements of the sequence are related naturally to a sequence of integers whose pattern can be easily inferred. In these cases, the index set may be implied by a listing of the first few abstract elements. For instance, the sequence of squares of odd numbers could be denoted in any of the following ways.

Moreover, the subscripts and superscripts could have been left off in the third, fourth, and fifth notations, if the indexing set was understood to be the natural numbers. In the second and third bullets, there is a well-defined sequence ${displaystyle (a_{k})_{k=1}^{infty }}$ , but it is not the same as the sequence denoted by the expression.

Defining a sequence by recursion[edit]

Sequences whose elements are related to the previous elements in a straightforward way are often defined using recursion. This is in contrast to the definition of sequences of elements as functions of their positions.

To define a sequence by recursion, one needs a rule, called recurrence relation to construct each element in terms of the ones before it. In addition, enough initial elements must be provided so that all subsequent elements of the sequence can be computed by successive applications of the recurrence relation.

The Fibonacci sequence is a simple classical example, defined by the recurrence relation

${displaystyle a_{n}=a_{n-1}+a_{n-2},}$

with initial terms $a_{0}=0$ and $a_{1}=1$ . From this, a simple computation shows that the first ten terms of this sequence are 0, 1, 1, 2, 3, 5, 8, 13, 21, and 34.

A complicated example of a sequence defined by a recurrence relation is Recamán’s sequence,^[4] defined by the recurrence relation

${displaystyle {begin{cases}a_{n}=a_{n-1}-n,quad {text{if the result is positive and not already in the previous terms,}}\a_{n}=a_{n-1}+n,quad {text{otherwise}},end{cases}}}$

with initial term ${displaystyle a_{0}=0.}$

A linear recurrence with constant coefficients is a recurrence relation of the form

${displaystyle a_{n}=c_{0}+c_{1}a_{n-1}+dots +c_{k}a_{n-k},}$

where ${displaystyle c_{0},dots ,c_{k}}$ are constants. There is a general method for expressing the general term $a_{n}$ of such a sequence as a function of n; see Linear recurrence. In the case of the Fibonacci sequence, one has ${displaystyle c_{0}=0,c_{1}=c_{2}=1,}$ and the resulting function of n is given by Binet’s formula.

A holonomic sequence is a sequence defined by a recurrence relation of the form

${displaystyle a_{n}=c_{1}a_{n-1}+dots +c_{k}a_{n-k},}$

where ${displaystyle c_{1},dots ,c_{k}}$ are polynomials in n. For most holonomic sequences, there is no explicit formula for expressing $a_{n}$ as a function of n. Nevertheless, holonomic sequences play an important role in various areas of mathematics. For example, many special functions have a Taylor series whose sequence of coefficients is holonomic. The use of the recurrence relation allows a fast computation of values of such special functions.

Not all sequences can be specified by a recurrence relation. An example is the sequence of prime numbers in their natural order (2, 3, 5, 7, 11, 13, 17, …).

Formal definition and basic properties[edit]

There are many different notions of sequences in mathematics, some of which (e.g., exact sequence) are not covered by the definitions and notations introduced below.

Definition[edit]

In this article, a sequence is formally defined as a function whose domain is an interval of integers. This definition covers several different uses of the word «sequence», including one-sided infinite sequences, bi-infinite sequences, and finite sequences (see below for definitions of these kinds of sequences). However, many authors use a narrower definition by requiring the domain of a sequence to be the set of natural numbers. This narrower definition has the disadvantage that it rules out finite sequences and bi-infinite sequences, both of which are usually called sequences in standard mathematical practice. Another disadvantage is that, if one removes the first terms of a sequence, one needs reindexing the remainder terms for fitting this definition. In some contexts, to shorten exposition, the codomain of the sequence is fixed by context, for example by requiring it to be the set R of real numbers,^[5] the set C of complex numbers,^[6] or a topological space.^[7]

Although sequences are a type of function, they are usually distinguished notationally from functions in that the input is written as a subscript rather than in parentheses, that is, a_n rather than a(n). There are terminological differences as well: the value of a sequence at the lowest input (often 1) is called the «first element» of the sequence, the value at the second smallest input (often 2) is called the «second element», etc. Also, while a function abstracted from its input is usually denoted by a single letter, e.g. f, a sequence abstracted from its input is usually written by a notation such as ${displaystyle (a_{n})_{nin A}}$ , or just as ${displaystyle (a_{n}).}$ Here A is the domain, or index set, of the sequence.

Sequences and their limits (see below) are important concepts for studying topological spaces. An important generalization of sequences is the concept of nets. A net is a function from a (possibly uncountable) directed set to a topological space. The notational conventions for sequences normally apply to nets as well.

Finite and infinite[edit]

The length of a sequence is defined as the number of terms in the sequence.

A sequence of a finite length n is also called an n-tuple. Finite sequences include the empty sequence ( ) that has no elements.

Normally, the term infinite sequence refers to a sequence that is infinite in one direction, and finite in the other—the sequence has a first element, but no final element. Such a sequence is called a singly infinite sequence or a one-sided infinite sequence when disambiguation is necessary. In contrast, a sequence that is infinite in both directions—i.e. that has neither a first nor a final element—is called a bi-infinite sequence, two-way infinite sequence, or doubly infinite sequence. A function from the set Z of all integers into a set, such as for instance the sequence of all even integers ( …, −4, −2, 0, 2, 4, 6, 8, … ), is bi-infinite. This sequence could be denoted $(2n)_{n=-infty}^{infty}$ .

Increasing and decreasing[edit]

A sequence is said to be monotonically increasing if each term is greater than or equal to the one before it. For example, the sequence $(a_n)_{n=1}^{infty}$ is monotonically increasing if and only if a_n+1 geq a_n for all n ∈ N. If each consecutive term is strictly greater than (>) the previous term then the sequence is called strictly monotonically increasing. A sequence is monotonically decreasing if each consecutive term is less than or equal to the previous one, and is strictly monotonically decreasing if each is strictly less than the previous. If a sequence is either increasing or decreasing it is called a monotone sequence. This is a special case of the more general notion of a monotonic function.

The terms nondecreasing and nonincreasing are often used in place of increasing and decreasing in order to avoid any possible confusion with strictly increasing and strictly decreasing, respectively.

Bounded[edit]

If the sequence of real numbers (a_n) is such that all the terms are less than some real number M, then the sequence is said to be bounded from above. In other words, this means that there exists M such that for all n, a_n ≤ M. Any such M is called an upper bound. Likewise, if, for some real m, a_n ≥ m for all n greater than some N, then the sequence is bounded from below and any such m is called a lower bound. If a sequence is both bounded from above and bounded from below, then the sequence is said to be bounded.

Subsequences[edit]

A subsequence of a given sequence is a sequence formed from the given sequence by deleting some of the elements without disturbing the relative positions of the remaining elements. For instance, the sequence of positive even integers (2, 4, 6, …) is a subsequence of the positive integers (1, 2, 3, …). The positions of some elements change when other elements are deleted. However, the relative positions are preserved.

Formally, a subsequence of the sequence ${displaystyle (a_{n})_{nin mathbb {N} }}$ is any sequence of the form ${displaystyle (a_{n_{k}})_{kin mathbb {N} }}$ , where ${displaystyle (n_{k})_{kin mathbb {N} }}$ is a strictly increasing sequence of positive integers.

Other types of sequences[edit]

Some other types of sequences that are easy to define include:

An integer sequence is a sequence whose terms are integers.
A polynomial sequence is a sequence whose terms are polynomials.
A positive integer sequence is sometimes called multiplicative, if a_nm = a_n a_m for all pairs n, m such that n and m are coprime.^[8] In other instances, sequences are often called multiplicative, if a_n = na₁ for all n. Moreover, a multiplicative Fibonacci sequence^[9] satisfies the recursion relation a_n = a_n−1 a_n−2.
A binary sequence is a sequence whose terms have one of two discrete values, e.g. base 2 values (0,1,1,0, …), a series of coin tosses (Heads/Tails) H,T,H,H,T, …, the answers to a set of True or False questions (T, F, T, T, …), and so on.

Limits and convergence[edit]

The plot of a convergent sequence (a_n) is shown in blue. From the graph we can see that the sequence is converging to the limit zero as n increases.

An important property of a sequence is convergence. If a sequence converges, it converges to a particular value known as the limit. If a sequence converges to some limit, then it is convergent. A sequence that does not converge is divergent.

Informally, a sequence has a limit if the elements of the sequence become closer and closer to some value (called the limit of the sequence), and they become and remain arbitrarily close to , meaning that given a real number greater than zero, all but a finite number of the elements of the sequence have a distance from less than .

For example, the sequence ${textstyle a_{n}={frac {n+1}{2n^{2}}}}$ shown to the right converges to the value 0. On the other hand, the sequences ${textstyle b_{n}=n^{3}}$ (which begins 1, 8, 27, …) and ${displaystyle c_{n}=(-1)^{n}}$ (which begins −1, 1, −1, 1, …) are both divergent.

If a sequence converges, then the value it converges to is unique. This value is called the limit of the sequence. The limit of a convergent sequence $(a_{n})$ is normally denoted ${textstyle lim _{nto infty }a_{n}}$ . If $(a_{n})$ is a divergent sequence, then the expression ${textstyle lim _{nto infty }a_{n}}$ is meaningless.

Formal definition of convergence[edit]

A sequence of real numbers $(a_{n})$ converges to a real number if, for all , there exists a natural number such that for all ngeq N we have^[5]

${displaystyle |a_{n}-L|<varepsilon .}$

If $(a_{n})$ is a sequence of complex numbers rather than a sequence of real numbers, this last formula can still be used to define convergence, with the provision that |cdot | denotes the complex modulus, i.e. ${displaystyle |z|={sqrt {z^{*}z}}}$ . If $(a_{n})$ is a sequence of points in a metric space, then the formula can be used to define convergence, if the expression ${displaystyle |a_{n}-L|}$ is replaced by the expression ${displaystyle operatorname {dist} (a_{n},L)}$ , which denotes the distance between $a_{n}$ and .

Applications and important results[edit]

If $(a_{n})$ and $(b_{n})$ are convergent sequences, then the following limits exist, and can be computed as follows:^[5]^[10]

Moreover:

Cauchy sequences[edit]

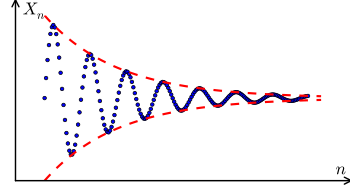
The plot of a Cauchy sequence (X_n), shown in blue, as X_n versus n. In the graph the sequence appears to be converging to a limit as the distance between consecutive terms in the sequence gets smaller as n increases. In the real numbers every Cauchy sequence converges to some limit.

A Cauchy sequence is a sequence whose terms become arbitrarily close together as n gets very large. The notion of a Cauchy sequence is important in the study of sequences in metric spaces, and, in particular, in real analysis. One particularly important result in real analysis is Cauchy characterization of convergence for sequences:

A sequence of real numbers is convergent (in the reals) if and only if it is Cauchy.

In contrast, there are Cauchy sequences of rational numbers that are not convergent in the rationals, e.g. the sequence defined by
x₁ = 1 and x_n+1 = x_n + 2/x_n/2
is Cauchy, but has no rational limit, cf. here. More generally, any sequence of rational numbers that converges to an irrational number is Cauchy, but not convergent when interpreted as a sequence in the set of rational numbers.

Metric spaces that satisfy the Cauchy characterization of convergence for sequences are called complete metric spaces and are particularly nice for analysis.

Infinite limits[edit]

In calculus, it is common to define notation for sequences which do not converge in the sense discussed above, but which instead become and remain arbitrarily large, or become and remain arbitrarily negative. If $a_{n}$ becomes arbitrarily large as , we write

$lim_{ntoinfty}a_n = infty.$

In this case we say that the sequence diverges, or that it converges to infinity. An example of such a sequence is a_n = n.

If $a_{n}$ becomes arbitrarily negative (i.e. negative and large in magnitude) as , we write

$lim_{ntoinfty}a_n = -infty$

and say that the sequence diverges or converges to negative infinity.

Series[edit]

A series is, informally speaking, the sum of the terms of a sequence. That is, it is an expression of the form ${textstyle sum _{n=1}^{infty }a_{n}}$ or ${displaystyle a_{1}+a_{2}+cdots }$ , where $(a_{n})$ is a sequence of real or complex numbers. The partial sums of a series are the expressions resulting from replacing the infinity symbol with a finite number, i.e. the Nth partial sum of the series ${textstyle sum _{n=1}^{infty }a_{n}}$ is the number

${displaystyle S_{N}=sum _{n=1}^{N}a_{n}=a_{1}+a_{2}+cdots +a_{N}.}$

The partial sums themselves form a sequence ${displaystyle (S_{N})_{Nin mathbb {N} }}$ , which is called the sequence of partial sums of the series ${textstyle sum _{n=1}^{infty }a_{n}}$ . If the sequence of partial sums converges, then we say that the series ${textstyle sum _{n=1}^{infty }a_{n}}$ is convergent, and the limit ${textstyle lim _{Nto infty }S_{N}}$ is called the value of the series. The same notation is used to denote a series and its value, i.e. we write ${textstyle sum _{n=1}^{infty }a_{n}=lim _{Nto infty }S_{N}}$ .

Use in other fields of mathematics[edit]

Topology[edit]

Sequences play an important role in topology, especially in the study of metric spaces. For instance:

A metric space is compact exactly when it is sequentially compact.
A function from a metric space to another metric space is continuous exactly when it takes convergent sequences to convergent sequences.
A metric space is a connected space if and only if, whenever the space is partitioned into two sets, one of the two sets contains a sequence converging to a point in the other set.
A topological space is separable exactly when there is a dense sequence of points.

Sequences can be generalized to nets or filters. These generalizations allow one to extend some of the above theorems to spaces without metrics.

Product topology[edit]

The topological product of a sequence of topological spaces is the cartesian product of those spaces, equipped with a natural topology called the product topology.

More formally, given a sequence of spaces ${displaystyle (X_{i})_{iin mathbb {N} }}$ , the product space

${displaystyle X:=prod _{iin mathbb {N} }X_{i},}$

is defined as the set of all sequences ${displaystyle (x_{i})_{iin mathbb {N} }}$ such that for each i, $x_{i}$ is an element of $X_{i}$ . The canonical projections are the maps p_i : X → X_i defined by the equation ${displaystyle p_{i}((x_{j})_{jin mathbb {N} })=x_{i}}$ . Then the product topology on X is defined to be the coarsest topology (i.e. the topology with the fewest open sets) for which all the projections p_i are continuous. The product topology is sometimes called the Tychonoff topology.

Analysis[edit]

In analysis, when talking about sequences, one will generally consider sequences of the form

${displaystyle (x_{1},x_{2},x_{3},dots ){text{ or }}(x_{0},x_{1},x_{2},dots )}$

which is to say, infinite sequences of elements indexed by natural numbers.

A sequence may start with an index different from 1 or 0. For example, the sequence defined by x_n = 1/log(n) would be defined only for n ≥ 2. When talking about such infinite sequences, it is usually sufficient (and does not change much for most considerations) to assume that the members of the sequence are defined at least for all indices large enough, that is, greater than some given N.

The most elementary type of sequences are numerical ones, that is, sequences of real or complex numbers. This type can be generalized to sequences of elements of some vector space. In analysis, the vector spaces considered are often function spaces. Even more generally, one can study sequences with elements in some topological space.

Sequence spaces[edit]

A sequence space is a vector space whose elements are infinite sequences of real or complex numbers. Equivalently, it is a function space whose elements are functions from the natural numbers to the field K, where K is either the field of real numbers or the field of complex numbers. The set of all such functions is naturally identified with the set of all possible infinite sequences with elements in K, and can be turned into a vector space under the operations of pointwise addition of functions and pointwise scalar multiplication. All sequence spaces are linear subspaces of this space. Sequence spaces are typically equipped with a norm, or at least the structure of a topological vector space.

The most important sequences spaces in analysis are the ℓ^p spaces, consisting of the p-power summable sequences, with the p-norm. These are special cases of L^p spaces for the counting measure on the set of natural numbers. Other important classes of sequences like convergent sequences or null sequences form sequence spaces, respectively denoted c and c₀, with the sup norm. Any sequence space can also be equipped with the topology of pointwise convergence, under which it becomes a special kind of Fréchet space called an FK-space.

Linear algebra[edit]

Sequences over a field may also be viewed as vectors in a vector space. Specifically, the set of F-valued sequences (where F is a field) is a function space (in fact, a product space) of F-valued functions over the set of natural numbers.

Abstract algebra[edit]

Abstract algebra employs several types of sequences, including sequences of mathematical objects such as groups or rings.

Free monoid[edit]

If A is a set, the free monoid over A (denoted A^*, also called Kleene star of A) is a monoid containing all the finite sequences (or strings) of zero or more elements of A, with the binary operation of concatenation. The free semigroup A⁺ is the subsemigroup of A^* containing all elements except the empty sequence.

Exact sequences[edit]

In the context of group theory, a sequence

$G_{0};{xrightarrow {f_{1}}};G_{1};{xrightarrow {f_{2}}};G_{2};{xrightarrow {f_{3}}};cdots ;{xrightarrow {f_{n}}};G_{n}$

of groups and group homomorphisms is called exact, if the image (or range) of each homomorphism is equal to the kernel of the next:

$mathrm {im} (f_{k})=mathrm {ker} (f_{k+1})$

The sequence of groups and homomorphisms may be either finite or infinite.

A similar definition can be made for certain other algebraic structures. For example, one could have an exact sequence of vector spaces and linear maps, or of modules and module homomorphisms.

Spectral sequences[edit]

In homological algebra and algebraic topology, a spectral sequence is a means of computing homology groups by taking successive approximations. Spectral sequences are a generalization of exact sequences, and since their introduction by Jean Leray (1946), they have become an important research tool, particularly in homotopy theory.

Set theory[edit]

An ordinal-indexed sequence is a generalization of a sequence. If α is a limit ordinal and X is a set, an α-indexed sequence of elements of X is a function from α to X. In this terminology an ω-indexed sequence is an ordinary sequence.

Computing[edit]

In computer science, finite sequences are called lists. Potentially infinite sequences are called streams. Finite sequences of characters or digits are called strings.

Streams[edit]

Infinite sequences of digits (or characters) drawn from a finite alphabet are of particular interest in theoretical computer science. They are often referred to simply as sequences or streams, as opposed to finite strings. Infinite binary sequences, for instance, are infinite sequences of bits (characters drawn from the alphabet {0, 1}). The set C = {0, 1}^∞ of all infinite binary sequences is sometimes called the Cantor space.

An infinite binary sequence can represent a formal language (a set of strings) by setting the n th bit of the sequence to 1 if and only if the n th string (in shortlex order) is in the language. This representation is useful in the diagonalization method for proofs.^[11]

Notes[edit]

References[edit]

^ ^a ^b «Sequences». www.mathsisfun.com. Archived from the original on 2020-08-12. Retrieved 2020-08-17.
^ Weisstein, Eric W. «Sequence». mathworld.wolfram.com. Archived from the original on 2020-07-25. Retrieved 2020-08-17.
^ Index to OEIS Archived 2022-10-18 at the Wayback Machine, On-Line Encyclopedia of Integer Sequences, 2020-12-03
^ Sloane, N. J. A. (ed.). «Sequence A005132 (Recamán’s sequence)». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 26 January 2018.
^ ^a ^b ^c Gaughan, Edward (2009). «1.1 Sequences and Convergence». Introduction to Analysis. AMS (2009). ISBN 978-0-8218-4787-9.
^ Edward B. Saff & Arthur David Snider (2003). «Chapter 2.1». Fundamentals of Complex Analysis. ISBN 978-01-390-7874-3. Archived from the original on 2023-03-23. Retrieved 2015-11-15.
^ James R. Munkres (2000). «Chapters 1&2». Topology. ISBN 978-01-318-1629-9. Archived from the original on 2023-03-23. Retrieved 2015-11-15.
^ Lando, Sergei K. (2003-10-21). «7.4 Multiplicative sequences». Lectures on generating functions. AMS. ISBN 978-0-8218-3481-7.
^ Falcon, Sergio (2003). «Fibonacci’s multiplicative sequence». International Journal of Mathematical Education in Science and Technology. 34 (2): 310–315. doi:10.1080/0020739031000158362. S2CID 121280842.
^ Dawikins, Paul. «Series and Sequences». Paul’s Online Math Notes/Calc II (notes). Archived from the original on 30 November 2012. Retrieved 18 December 2012.
^ Oflazer, Kemal. «FORMAL LANGUAGES, AUTOMATA AND COMPUTATION: DECIDABILITY» (PDF). cmu.edu. Carnegie-Mellon University. Archived (PDF) from the original on 29 May 2015. Retrieved 24 April 2015.

External links[edit]

Look up sequence in Wiktionary, the free dictionary.

«Sequence», Encyclopedia of Mathematics, EMS Press, 2001 [1994]
The On-Line Encyclopedia of Integer Sequences
Journal of Integer Sequences (free)

Источник

Noun

He listened to the telephone messages in sequence.

a chase sequence in a spy movie

I enjoyed the movie’s opening sequence.

Recent Examples on the Web

But a sequence almost immediately after gave perhaps the first public glimpse into what Burnes might become.

—Journal Sentinel, 24 Mar. 2023

The other two runs came on a sequence that went single-single-sacrifice bunt-single in the fifth.

—Theo Mackie, The Arizona Republic, 23 Mar. 2023

And to the disbelief of the Mavericks and the ire of team governor Mark Cuban, a bizarre third-quarter sequence gifted the Warriors a basket in what became a pivotal 127-125 Golden State victory.

—Brad Townsend, Dallas News, 22 Mar. 2023

While interrupting a chronological sequence to go back in time is an ancient narrative technique, flashback first appeared in 1916.

—Melissa Mohr, The Christian Science Monitor, 20 Mar. 2023

The blast, the third grand slam for the U.S. in WBC history, was another mesmerizing sequence in this tournament, much like how the bottom of the fifth inning ended after Altuve’s injury.

—Jorge Castillo, Los Angeles Times, 18 Mar. 2023

A few months later, the television network released a new opening titles sequence for season 7.

—Samantha Stutsman, Peoplemag, 17 Mar. 2023

The song’s video opens with a dream sequence as Quiles and Courtz rap from atop snowy mountains before falling from the peaks through a giant pair of legs before ending up lying down on the floor of a club, staring above at the dancing women.

—Tomás Mier, Rolling Stone, 16 Mar. 2023

Kraven the Hunter will follow Venom, Venom: Let There Be Carnage and Morbius in Columbia Pictures and Sony Entertainment’s sequence of movies based on Spider-Man villains.

—Philip Ellis, Men’s Health, 15 Mar. 2023

Love Dalén, a professor of evolutionary genomics at Stockholm University’s Centre for Paleogenetics who sequenced the world’s oldest mammoth DNA, knows what mammoth meat actually tastes like.

—Katie Hunt, CNN, 28 Mar. 2023

Other research projects had unsuccessfully tried to extract genetic material from Beethoven’s remains, but recent advances in sequencing DNA from very old samples made this new attempt possible, writes Nature News’Dyani Lewis.

—Will Sullivan, Smithsonian Magazine, 23 Mar. 2023

Two centuries later, a team of international researchers has answered that plea by sequencing Beethoven’s DNA, preserved in locks of his hair that collaborators and fans collected as treasured keepsakes.

—Carolyn Y. Johnson, Washington Post, 22 Mar. 2023

Two of the infants subsequently died, although Abbott maintains there has not been conclusive evidence that its formula caused the infant illnesses, since none of the Cronobacter strains found at their plant matched the two samples genetically sequenced from the sickened infants.

—Sasha Pezenik, ABC News, 18 Feb. 2023

Colossal is using the backing of a surprising government partner to sequence the dodo bird’s genome using stem cell technology, the company says.

—Tim Newcomb, Popular Mechanics, 31 Jan. 2023

The Wellcome Sanger Institute this week announced a project to collect and sequence millions of genomes of common respiratory pathogens, such as adenovirus, rhinovirus, and respiratory syncytial virus.

—Byscience News Staff, science.org, 12 Jan. 2023

Golden Gate plans to adapt and sequence the lectures for the degrees.

—Lindsay Ellis, WSJ, 7 Sep. 2022

There are already dozens of stool banks and numerous ongoing efforts by researchers to sequence human microbiomes, all of whom may want to keep their samples in the vault as a backup.

—Sabrina Weiss, WIRED, 4 Jan. 2023

See More

These examples are programmatically compiled from various online sources to illustrate current usage of the word ‘sequence.’ Any opinions expressed in the examples do not represent those of Merriam-Webster or its editors. Send us feedback about these examples.

Источник

se·quence

(sē′kwəns, -kwĕns′)

1. A following of one thing after another; succession.

2. An order of succession; an arrangement.

3. A related or continuous series. See Synonyms at series.

4. Games Three or more playing cards in consecutive order and usually the same suit; a run.

5. A series of related shots that constitute a complete unit of action in a movie.

6. Music A melodic or harmonic pattern successively repeated at different pitches with or without a key change.

7. Roman Catholic Church A hymn sung between the gradual and the Gospel.

8. Mathematics An ordered set of quantities, as x, 2x², 3x³, 4x⁴.

9. Biochemistry The order of constituents in a polymer, especially the order of nucleotides in a nucleic acid or of the amino acids in a protein.

tr.v. se·quenced, se·quenc·ing, se·quenc·es

1. To organize or arrange in a sequence.

2. To determine the order of constituents in (a polymer, such as a nucleic acid or protein molecule).

[Middle English, a type of hymn, from Old French, from Medieval Latin sequentia, hymn, that which follows (from its following the alleluia), from Late Latin, from Latin sequēns, sequent-, present participle of sequī, to follow; see sek^w— in Indo-European roots.]

American Heritage® Dictionary of the English Language, Fifth Edition. Copyright © 2016 by Houghton Mifflin Harcourt Publishing Company. Published by Houghton Mifflin Harcourt Publishing Company. All rights reserved.

sequence

(ˈsiːkwəns)

1. an arrangement of two or more things in a successive order

2. the successive order of two or more things: chronological sequence.

3. a sequentially ordered set of related things or ideas

4. an action or event that follows another or others

5. (Card Games) cards a set of three or more consecutive cards, usually of the same suit

6. (Bridge) bridge a set of two or more consecutive cards

7. (Music, other) music an arrangement of notes or chords repeated several times at different pitches

8. (Mathematics) maths

a. an ordered set of numbers or other mathematical entities in one-to-one correspondence with the integers 1 to n

b. an ordered infinite set of mathematical entities in one-to-one correspondence with the natural numbers

9. (Film) a section of a film constituting a single continuous uninterrupted episode

10. (Biochemistry) biochem the unique order of amino acids in the polypeptide chain of a protein or of nucleotides in the polynucleotide chain of DNA or RNA

11. (Roman Catholic Church) RC Church another word for prose⁴

vb (tr)

12. to arrange in a sequence

13. (Biochemistry) biochem to determine the order of the units comprising (a protein, nucleic acid, genome, etc)

[C14: from Medieval Latin sequentia that which follows, from Latin sequī to follow]

Collins English Dictionary – Complete and Unabridged, 12th Edition 2014 © HarperCollins Publishers 1991, 1994, 1998, 2000, 2003, 2006, 2007, 2009, 2011, 2014

se•quence

(ˈsi kwəns)

n., v. -quenced, -quenc•ing. n.

1. the following of one thing after another; succession.

2. order of succession.

3. a continuous connected series: a sonnet sequence.

4. result; consequence.

5. a melodic or harmonic pattern repeated three or more times at different pitches with or without modulation.

6. (often cap.) a hymn sometimes sung after the Gradual and before the Gospel in Masses for special occasions.

7. a series of related scenes or shots that make up one episode of a film narrative.

8. a series of three or more cards following one another in order of value, esp. of the same suit.

9. Genetics, Biochem. the linear order of monomers in a polymer, as nucleotides in DNA or amino acids in a protein.

v.t.

10. to place in a sequence.

11. Genetics, Biochem. to determine the order of (chemical units in a polymer chain), esp. nucleotides in DNA or RNA or amino acids in a protein.

[1350–1400; Middle English < Late Latin sequentia= Latin sequ- (s. of sequī to follow) + -entia -ence]

se·quence

(sē′kwəns)

1. Mathematics A set of quantities ordered in the same manner as the positive integers. A sequence can be finite, such as {1, 3, 5, 7, 9}, or it can be infinite, such as {1, ¹/₂ , ¹/₃ , ¹/₄ , … ¹/_n }.

2. Chemistry The order of molecules that make up the subunits of a chemical compound, especially the order of nucleotides in a nucleic acid or of the amino acids in a protein.

The American Heritage® Student Science Dictionary, Second Edition. Copyright © 2014 by Houghton Mifflin Harcourt Publishing Company. Published by Houghton Mifflin Harcourt Publishing Company. All rights reserved.

sequence

arithmetic progression — A sequence in which each term is obtained by the addition of a constant number to the preceding term, as 1, 4, 7, 10, 13.
initialism, alphabetism, acronym — Initialisms (sometimes called alphabetisms) are formed from the initial letters of a string of words and are pronounced as a sequence of letters, e.g. BYOB, USA, DVD. Acronyms are formed from the initial letters or parts of words in a sequence, but have the distinction of being pronounceable words, e.g. RADAR, SCUBA.
solfeggio, gamut — Solfeggio and gamut are words formed on the sequence of musical notes.
tier — From French tire, «order, sequence.»

Sequence

a continuous or connected series, 1575.

Examples: sequence of causes, 1829; of chambers, 1668; of reflections, 1823; of saints, 1589.

sequence

Past participle: sequenced
Gerund: sequencing

Imperative
sequence
sequence

Present
I sequence
you sequence
he/she/it sequences
we sequence
you sequence
they sequence

Preterite
I sequenced
you sequenced
he/she/it sequenced
we sequenced
you sequenced
they sequenced

Present Continuous
I am sequencing
you are sequencing
he/she/it is sequencing
we are sequencing
you are sequencing
they are sequencing

Present Perfect
I have sequenced
you have sequenced
he/she/it has sequenced
we have sequenced
you have sequenced
they have sequenced

Past Continuous
I was sequencing
you were sequencing
he/she/it was sequencing
we were sequencing
you were sequencing
they were sequencing

Past Perfect
I had sequenced
you had sequenced
he/she/it had sequenced
we had sequenced
you had sequenced
they had sequenced

Future
I will sequence
you will sequence
he/she/it will sequence
we will sequence
you will sequence
they will sequence

Future Perfect
I will have sequenced
you will have sequenced
he/she/it will have sequenced
we will have sequenced
you will have sequenced
they will have sequenced

Future Continuous
I will be sequencing
you will be sequencing
he/she/it will be sequencing
we will be sequencing
you will be sequencing
they will be sequencing

Present Perfect Continuous
I have been sequencing
you have been sequencing
he/she/it has been sequencing
we have been sequencing
you have been sequencing
they have been sequencing

Future Perfect Continuous
I will have been sequencing
you will have been sequencing
he/she/it will have been sequencing
we will have been sequencing
you will have been sequencing
they will have been sequencing

Past Perfect Continuous
I had been sequencing
you had been sequencing
he/she/it had been sequencing
we had been sequencing
you had been sequencing
they had been sequencing

Conditional
I would sequence
you would sequence
he/she/it would sequence
we would sequence
you would sequence
they would sequence

Past Conditional
I would have sequenced
you would have sequenced
he/she/it would have sequenced
we would have sequenced
you would have sequenced
they would have sequenced

sequence

A single episode in a film which is uninterrupted.

ThesaurusAntonymsRelated WordsSynonymsLegend:

Noun	1.	sequence — serial arrangement in which things follow in logical order or a recurrent pattern; «the sequence of names was alphabetical»; «he invented a technique to determine the sequence of base pairs in DNA» cistron, gene, factor — (genetics) a segment of DNA that is involved in producing a polypeptide chain; it can include regions preceding and following the coding DNA as well as introns between the exons; it is considered a unit of heredity; «genes were formerly called factors» string — a linear sequence of symbols (characters or words or phrases) combination — a sequence of numbers or letters that opens a combination lock; «he forgot the combination to the safe» combination — a coordinated sequence of chess moves Fibonacci sequence — a sequence of numbers in which each number equals the sum of the two preceding numbers series — similar things placed in order or happening one after another; «they were investigating a series of bank robberies» codon — a specific sequence of three adjacent nucleotides on a strand of DNA or RNA that specifies the genetic code information for synthesizing a particular amino acid
	2.	sequence — a following of one thing after another in time; «the doctor saw a sequence of patients» chronological sequence, chronological succession, succession, successiveness temporal arrangement, temporal order — arrangement of events in time pelting, rain — anything happening rapidly or in quick successive; «a rain of bullets»; «a pelting of insults» rotation — a planned recurrent sequence (of crops or personnel etc.); «crop rotation makes a balanced demand on the fertility of the soil»; «the manager had only four starting pitchers in his rotation» row — a continuous chronological succession without an interruption; «they won the championship three years in a row» run — an unbroken chronological sequence; «the play had a long run on Broadway»; «the team enjoyed a brief run of victories»
	3.	sequence — film consisting of a succession of related shots that develop a given subject in a movie episode photographic film, film — photographic material consisting of a base of celluloid covered with a photographic emulsion; used to make negatives or transparencies motion picture, motion-picture show, movie, moving picture, moving-picture show, pic, film, picture show, flick, picture — a form of entertainment that enacts a story by sound and a sequence of images giving the illusion of continuous movement; «they went to a movie every Saturday night»; «the film was shot on location»
	4.	sequence — the action of following in order; «he played the trumps in sequence» succession chess opening, opening — a recognized sequence of moves at the beginning of a game of chess; «he memorized all the important chess openings» ordering, order — the act of putting things in a sequential arrangement; «there were mistakes in the ordering of items on the list» alternation — successive change from one thing or state to another and back again; «a trill is a rapid alternation between the two notes»
	5.	sequence — several repetitions of a melodic phrase in different keys repeat, repetition — an event that repeats; «the events today were a repeat of yesterday’s»
Verb	1.	sequence — arrange in a sequence grade, rate, rank, place, range, order — assign a rank or rating to; «how would you rank these students?»; «The restaurant is rated highly in the food guide»
	2.	sequence — determine the order of constituents in; «They sequenced the human genome» ascertain, determine, find out, find — establish after a calculation, investigation, experiment, survey, or study; «find the product of two numbers»; «The physicist who found the elusive particle won the Nobel Prize»

sequence

Collins Thesaurus of the English Language – Complete and Unabridged 2nd Edition. 2002 © HarperCollins Publishers 1995, 2002

sequence

noun

1. Something brought about by a cause:

aftermath, consequence, corollary, effect, end product, event, fruit, harvest, issue, outcome, precipitate, ramification, result, resultant, sequel, sequent, upshot.

2. A way in which things follow each other in space or time:

3. A way or condition of being arranged:

arrangement, categorization, classification, deployment, disposal, disposition, distribution, formation, grouping, layout, lineup, order, organization, placement.

4. A number of things placed or occurring one after the other:

chain, consecution, course, order, procession, progression, round, run, series, string, succession, suite, train.

Источник

последовательность, ряд, эпизод, секвенция, череда, порядок следования, следствие

существительное ↓

- последовательность; ряд; порядок следования

- последствие, результат

a sequence to smth. — результат /последствие/ чего-л.
a natural sequence to folly — естественный результат безрассудства
a sequence of a crime is punishment — преступление неизбежно влечёт за собой наказание

- муз. секвенция
- кино, амер. тж. театр. несколько сцен, составляющих эпизод
- последовательный ряд кинокадров
- карт. три или более карты одной масти по старшинству
- серия; цикл

sequence of sonnets — цикл сонетов

прилагательное ↓

- последовательный

sequence automating call — последовательный автоматический вызов

глагол

- тех. задавать / устанавливать последовательность
- биохим. определение порядка химических единиц в полимерной цепи

Мои примеры

Словосочетания

a chase sequence in a spy movie — сцена погони в шпионском фильме
the regular sequence of the seasons — привычная череда времён года
confident sequence — доверительная последовательность
sequence of moves — последовательность движений
in chronological sequence — в хронологическом порядке
natural sequence — естественный результат
the straight sequence of events — правильный ход событий
sequence scheduling — планирование последовательности работ
sequence switch — программный переключатель
sequence number stamp — отметка порядкового номера
sequence cipher — поточный шифр
key bits sequence — ключевая последовательность

Примеры с переводом

Number them in sequence, 1,2,3 etc.

Пронумеруйте их по порядку: 1, 2, 3 и так далее.

The doctor saw a sequence of patients.

Доктор осмотрел ряд пациентов.

This sequence of events strains the reader’s credibility.

Такое развитие событий кажется читателю неправдоподобным.

Police are trying to reconstruct the sequence of events on the night of the murder.

Полиция пытается восстановить последовательность событий, произошедших в ночь убийства.

The number ‘one’ begins the sequence.

Число «один» является началом данной последовательности.

He invented a technique to determine the sequence of base pairs in DNA.

Он изобрёл способ определения последовательности пар оснований в ДНК.

He’s had a sequence of business failures.

Он потерпел ряд банкротств.

ещё 8 примеров свернуть

Примеры, ожидающие перевода

The chapters may be studied out of sequence.

The questions should be asked in a logical sequence.

Для того чтобы добавить вариант перевода, кликните по иконке ☰, напротив примера.

Возможные однокоренные слова

sequencing — упорядочение, секвенирование, установление последовательности, программирование

Формы слова

verb
I/you/we/they: sequence
he/she/it: sequencing
ing ф. (present participle): sequencing
2-я ф. (past tense): sequenced
3-я ф. (past participle): sequenced

noun
ед. ч.(singular): sequence
мн. ч.(plural): sequences

Источник

Other forms: sequences; sequencing; sequenced

When things come in sequence, they come in a specific order. It could be a chronological sequence, a sequence following a pattern (red-blue-brown, red-blue-brown), or a cause-and-effect sequence.

Sequence can also be a verb. When you sequence something, you put it in order. The prom committee had the task of sequencing dance music––even if playing «Celebrate» as the final dance and not the first felt out of sequence to the DJ, it was their call.

Definitions of sequence

noun

a following of one thing after another in time
noun

the action of following in order

“he played the trumps in
sequence”

synonyms:

succession
noun

serial arrangement in which things follow in logical order or a recurrent pattern

“the
sequence of names was alphabetical”

“he invented a technique to determine the
sequence of base pairs in DNA”

see moresee less

types:

show 30 types…

hide 30 types…

cistron, factor, gene

(genetics) a segment of DNA that is involved in producing a polypeptide chain; it can include regions preceding and following the coding DNA as well as introns between the exons; it is considered a unit of heredity

string

a linear sequence of symbols (characters or words or phrases)

combination

a sequence of numbers or letters that opens a combination lock

combination

a coordinated sequence of chess moves

Fibonacci sequence

a sequence of numbers in which each number equals the sum of the two preceding numbers

codon

a specific sequence of three adjacent nucleotides on a strand of DNA or RNA that specifies the genetic code information for synthesizing a particular amino acid

dominant gene

gene that produces the same phenotype in the organism whether or not its allele identical

allele, allelomorph

(genetics) either of a pair (or series) of alternative forms of a gene that can occupy the same locus on a particular chromosome and that control the same character

genetic marker

a specific gene that produces a recognizable trait and can be used in family or population studies

homeotic gene

one the genes that are involved in embryologic development

lethal gene

any gene that has an effect that causes the death of the organism at any stage of life

linkage group, linked genes

any pair of genes that tend to be transmitted together

modifier, modifier gene

a gene that modifies the effect produced by another gene

mutant gene

a gene that has changed so that the normal transmission and expression of a trait is affected

nonallele

genes that are not competitors at the same locus

operator gene

a gene that activates the production of messenger RNA by adjacent structural genes

oncogene, transforming gene

a gene that disposes normal cells to change into cancerous tumor cells

polygene

a gene that by itself has little effect on the phenotype but which can act together with others to produce observable variations

proto-oncogene

a normal gene that has the potential to become an oncogene

recessive gene

gene that produces its characteristic phenotype only when its allele is identical

regulator gene, regulatory gene

a gene that produces a repressor substance that inhibits an operator gene

repressor gene

gene that prevents a nonallele from being transcribed

structural gene

a gene that controls the production of a specific protein or peptide

suppresser, suppresser gene, suppressor, suppressor gene

a gene that suppresses the phenotypic expression of another gene (especially of a mutant gene)

transgene

an exogenous gene introduced into the genome of another organism

X-linked gene

a gene located on an X chromosome

Y-linked gene, holandric gene

a gene located on a Y chromosome

extension, file name extension, filename extension

a string of characters beginning with a period and followed by one or more letters; the optional second part of a PC computer filename

linguistic string, string of words, word string

a linear sequence of words as spoken or written

substring

a string that is part of a longer string

type of:

series

similar things placed in order or happening one after another
noun

several repetitions of a melodic phrase in different keys
noun

film consisting of a succession of related shots that develop a given subject in a movie

synonyms:

episode

see moresee less

types:

montage

a film sequence made by editing together a series of separate scenes or shots

type of:

film, photographic film

photographic material consisting of a base of celluloid covered with a photographic emulsion; used to make negatives or transparencies
verb

arrange in a sequence
verb

determine the order of constituents in

“They
sequenced the human genome”

DISCLAIMER: These example sentences appear in various news sources and books to reflect the usage of the word ‘sequence’.
Views expressed in the examples do not represent the opinion of Vocabulary.com or its editors.
Send us feedback

EDITOR’S CHOICE

Look up sequence for the last time

Close your vocabulary gaps with personalized learning that focuses on teaching the
words you need to know.

Sign up now (it’s free!)

Whether you’re a teacher or a learner, Vocabulary.com can put you or your class on the path to systematic vocabulary improvement.

Get started

Источник

Examples and notation[edit]

Examples[edit]

Indexing[edit]

Defining a sequence by recursion[edit]

Formal definition and basic properties[edit]

Definition[edit]

Finite and infinite[edit]

Increasing and decreasing[edit]

Bounded[edit]

Subsequences[edit]

Other types of sequences[edit]

Limits and convergence[edit]

Formal definition of convergence[edit]

Applications and important results[edit]

Cauchy sequences[edit]

Infinite limits[edit]

Series[edit]

Use in other fields of mathematics[edit]

Topology[edit]

Product topology[edit]

Analysis[edit]

Sequence spaces[edit]

Linear algebra[edit]

Abstract algebra[edit]

Free monoid[edit]

Exact sequences[edit]

Spectral sequences[edit]

Set theory[edit]

Computing[edit]

Streams[edit]

See also[edit]

Notes[edit]

References[edit]

External links[edit]

se·quence

sequence

se•quence

se·quence

sequence

Sequence

sequence

sequence

sequence

sequence

существительное ↓

прилагательное ↓

глагол

Мои примеры

Словосочетания

Примеры с переводом

Примеры, ожидающие перевода

Возможные однокоренные слова

Формы слова

Look up sequence for the last time

Sign up now (it’s free!)

Whether you’re a teacher or a learner, Vocabulary.com can put you or your class on the path to systematic vocabulary improvement.