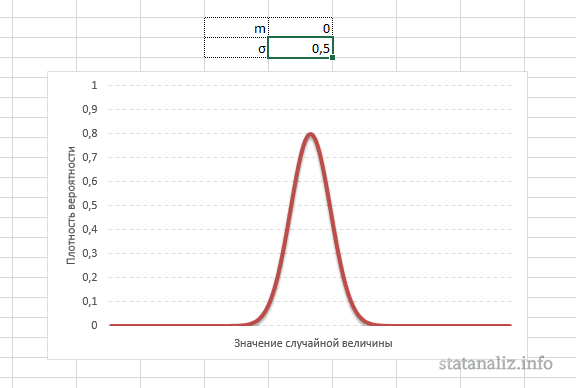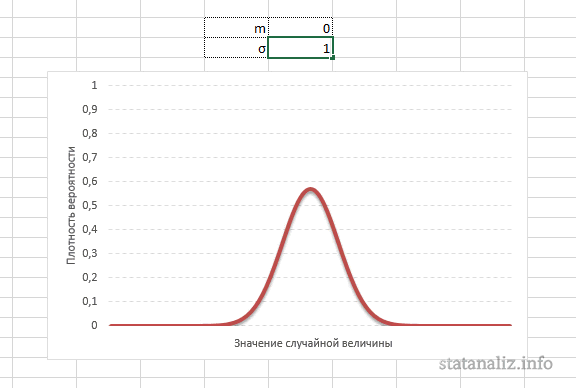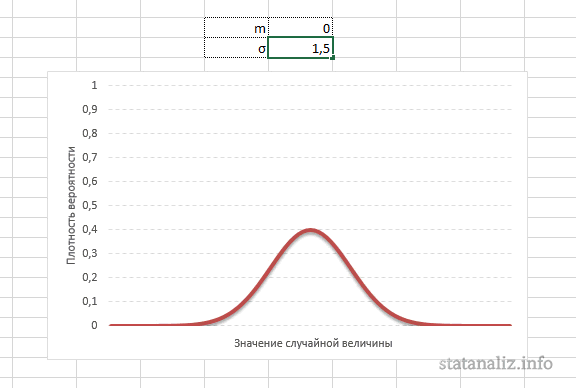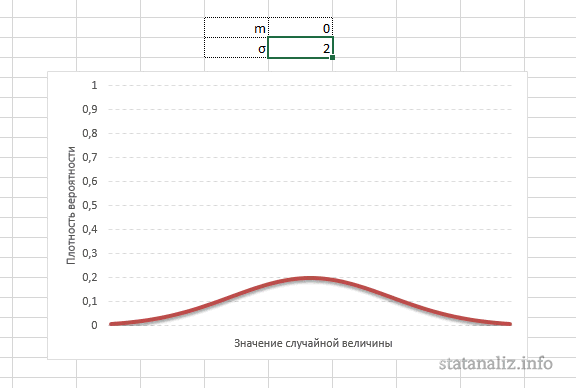
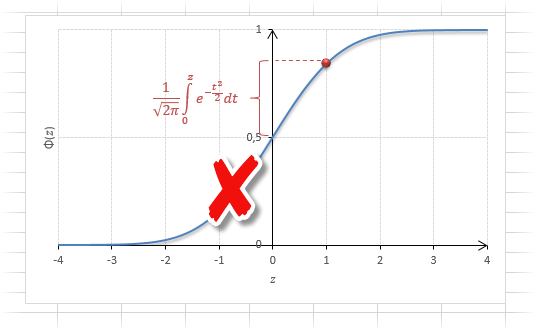
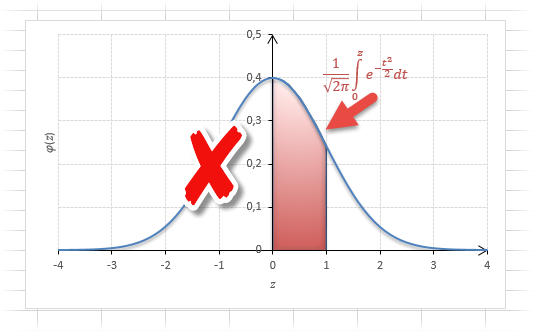
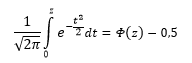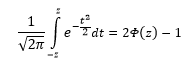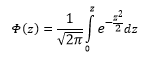Построение графика проверки распределения на нормальность (
Normal
Probability
Plot
) является графическим методом определения соответствия значений выборки нормальному распределению.
Предположим, что имеется некий набор данных. Требуется оценить, соответствует ли данная
выборка
нормальному распределению
.
Рассмотренный ниже графический метод основан на субъективной визуальной оценке данных. Объективным же подходом является, например,
анализ степени согласия гипотетического распределения с наблюдаемыми данными
(goodness-of-fit test), который рассмотрен в статье
Проверка простых гипотез критерием Пирсона ХИ-квадрат
.
Из-за наличия неустранимой статистической ошибки выборки, присущей случайной величине, невозможно однозначно ответить на вопрос «Взята ли данная выборка из
нормального распределения
или нет». Поэтому, рассмотренный графический метод, скорее, дает ответ на вопрос «Разумно ли предположение, что оцениваемая выборка взята из
нормального распределения
»?
Рассмотрим алгоритм построения графика проверки распределения на нормальность (
Normal
Probability
Plot
)
:
-
Отсортируйте значения выборки по возрастанию
(значения выборки x
j
будут отложены по горизонтальной оси Х); -
Каждому значению x
j
выборки
поставьте в соответствие значения (j-0,5)/n, где n – количество значений в
выборке
, j –порядковый номер
значения от 1 до n. Этот массив будет содержать значения от 0,5/n до (n-0,5)/n. Таким образом, диапазон от 0 до 1 будет разбит на равномерные отрезки. Этот диапазон соответствует
вероятности наблюдения значений случайной величины
Z<=z
j
; -
Преобразуем значения массива, полученные на предыдущем шаге, с помощью
обратной функции
стандартного нормального распределения
НОРМ.СТ.ОБР()
и отложим их по вертикальной оси Y.
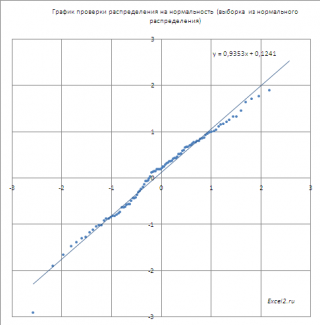
Если значения
выборки
, откладываемые по оси Х, взяты из
стандартного нормального распределения
, то на графике мы получим приблизительно прямую линию, проходящую примерно через 0 и под углом 45 градусов к оси х (если масштабы осей совпадают).
Расчеты и графики приведены в
файле примера на листе Нормальное
. О построении диаграмм см. статью
Основные типы диаграмм в MS EXCEL
.
Примечание
: Значения
выборки
в
файле примера
сгенерированы с помощью формулы
=НОРМ.СТ.ОБР(СЛЧИС())
. При перерасчете листа или нажатии клавиши
F9
происходит обновление данных в
выборке
. О генерации чисел, распределенных по
нормальному закону
см. статью
Нормальное распределение. Непрерывные распределения в MS EXCEL
. Таже значения выборки могут быть сгенерированы с помощью надстройки
Пакет анализа
.
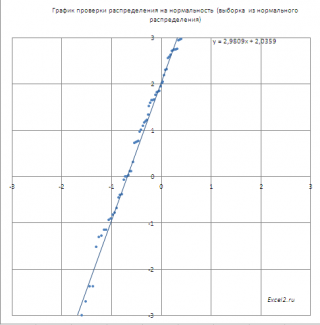
Если значения
выборки
взяты из
нормального распределения
(μ не обязательно равно 0, σ не обязательно равно 1), то угол наклона кривой даст оценку
стандартного отклонения
σ, а ордината точки пересечения оси Y – оценку
среднего значения
μ.
Данные оценки несколько отличаются от оценок параметров, полученных с помощью функций
СРЗНАЧ()
и
СТАНДОТКЛОН.В()
, т.к. они получены
методом наименьших квадратов
, рассмотренного в статье про регрессионный анализ.
Примечание
: Рассмотренный выше метод в отечественной литературе имеет название
Метод номограмм
. Номограмма – это листы бумаги, разлинованные определенным образом. Номограмма используется в различных областях знаний. В
математической статистике
номограмма называется вероятностной бумагой. Такую «вероятностную бумагу» мы практически построили самостоятельно, когда нелинейно изменили масштаб шкалы ординат:
=НОРМ.СТ.ОБР((j-0,5)/n)
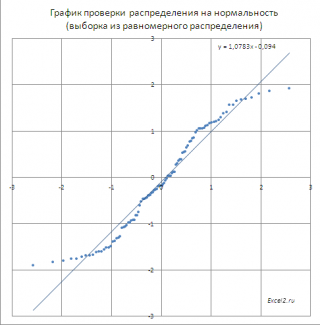
Интересно посмотреть, как будут выглядеть на диаграмме данные, полученные из
выборок
из других распределений (не из
нормального
). В
файле примера на листе Равномерное
приведен график, построенный на основе
выборки
из непрерывного равномерного распределения.
Очевидно, что значения
выборки
совсем не ложатся на прямую линию и предположение о
нормальности выборки
должно быть отвергнуто.
Подобная визуальная проверка
выборки
на соответствие другим распределениям может быть сделана при наличии соответствующих
обратных функций
. В статье
Статистики, их выборочные распределения и точечные оценки параметров распределений в MS EXCEL
приведены
графики
для следующих распределений:
Стьюдента
,
ХИ-квадрат распределения
,
F-распределения
. Подобный график также приведен в статье про
распределение Вейбулла
.
17 авг. 2022 г.
читать 2 мин
Многие статистические тесты предполагают, что значения в наборе данных имеют нормальное распределение .
Один из самых простых способов проверить это предположение — выполнить тест Харке-Бера , который представляет собой тест согласия, который определяет, имеют ли выборочные данные асимметрию и эксцесс, соответствующие нормальному распределению.
В этом тесте используются следующие гипотезы:
H 0 : Данные нормально распределены.
H A : Данные не распределены нормально.
Тестовая статистика JB определяется как:
JB = (n/6) * (S 2 + (C 2 /4))
куда:
- n: количество наблюдений в выборке
- S: асимметрия выборки
- C: образец эксцесса
При нулевой гипотезе нормальности JB ~ X 2 (2).
Если значение p , соответствующее тестовой статистике, меньше некоторого уровня значимости (например, α = 0,05), то мы можем отклонить нулевую гипотезу и сделать вывод, что данные не распределены нормально.
В этом руководстве представлен пошаговый пример того, как выполнить тест Харке-Бера для заданного набора данных в Excel.
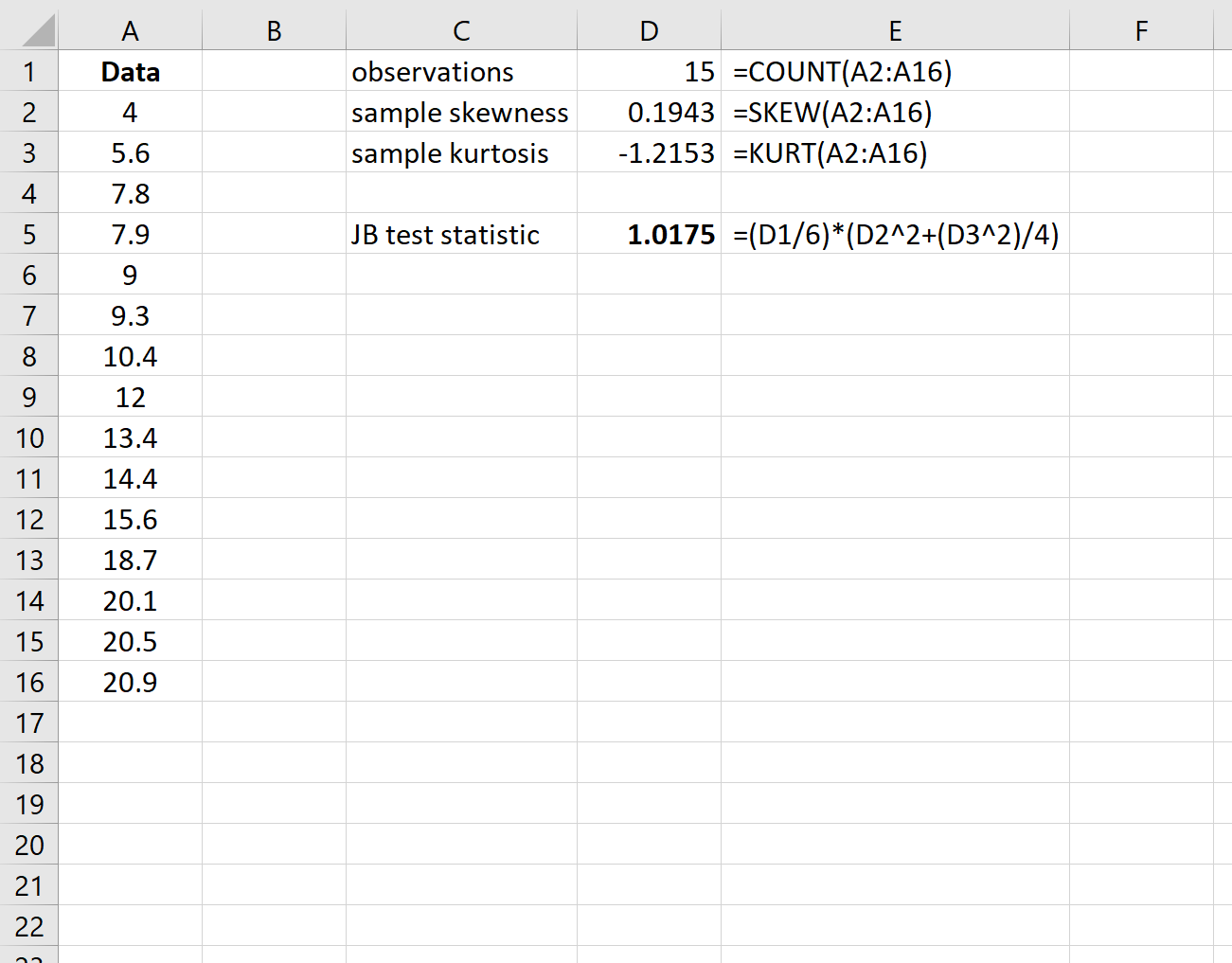
Шаг 1: Создайте данные
Во-первых, давайте создадим поддельный набор данных с 15 значениями:
Шаг 2: Рассчитайте тестовую статистику
Затем рассчитайте статистику теста JB. В столбце E показаны используемые формулы:
Тестовая статистика оказывается 1,0175 .
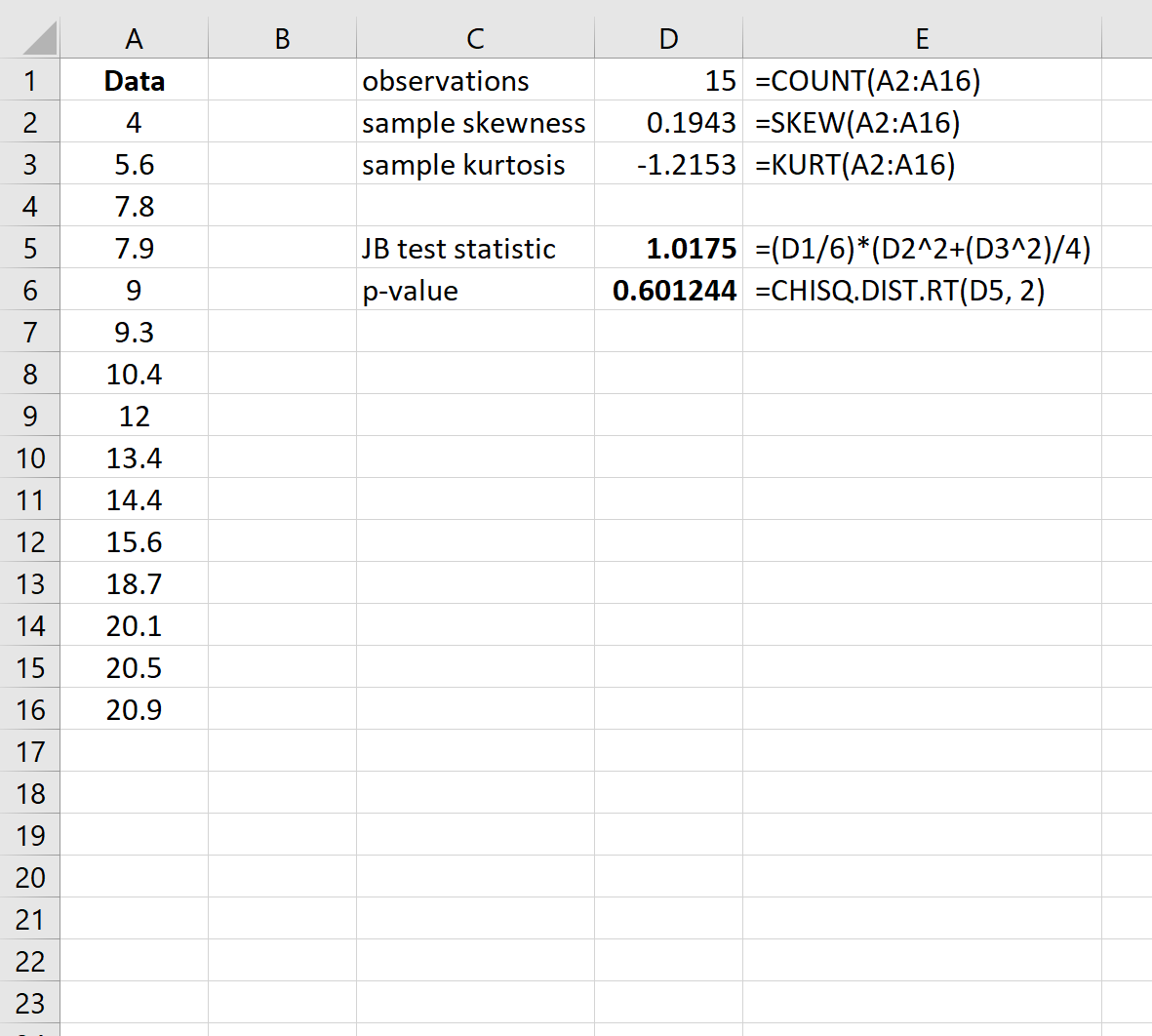
Шаг 3: Рассчитайте P-значение
При нулевой гипотезе нормальности тестовая статистика JB следует распределению хи-квадрат с 2 степенями свободы.
Итак, чтобы найти p-значение для теста, мы будем использовать следующую функцию в Excel: =CHISQ.DIST.RT(статистика теста JB, 2)
Значение p теста составляет 0,601244.Поскольку это p-значение не меньше 0,05, мы не можем отвергнуть нулевую гипотезу. У нас нет достаточных доказательств того, что набор данных не имеет нормального распределения.
Другими словами, мы можем предположить, что данные распределены нормально.
Дополнительные ресурсы
Как создать график QQ в Excel
Как выполнить критерий согласия хи-квадрат в Excel
This question borders on statistics theory too — testing for normality with limited data may be questionable (although we all have done this from time to time).
As an alternative, you can look at kurtosis and skewness coefficients. From Hahn and Shapiro: Statistical Models in Engineering some background is provided on the properties Beta1 and Beta2 (pages 42 to 49) and the Fig 6-1 of Page 197. Additional theory behind this can be found on Wikipedia (see Pearson Distribution).
Basically you need to calculate the so-called properties Beta1 and Beta2. A Beta1 = 0 and Beta2 = 3 suggests that the data set approaches normality. This is a rough test but with limited data it could be argued that any test could be considered a rough one.
Beta1 is related to the moments 2 and 3, or variance and skewness, respectively. In Excel, these are VAR and SKEW. Where … is your data array, the formula is:
Beta1 = SKEW(...)^2/VAR(...)^3
Beta2 is related to the moments 2 and 4, or the variance and kurtosis, respectively. In Excel, these are VAR and KURT. Where … is your data array, the formula is:
Beta2 = KURT(...)/VAR(...)^2
Then you can check these against the values of 0 and 3, respectively. This has the advantage of potentially identifying other distributions (including Pearson Distributions I, I(U), I(J), II, II(U), III, IV, V, VI, VII). For example, many of the commonly used distributions such as Uniform, Normal, Student’s t, Beta, Gamma, Exponential, and Log-Normal can be indicated from these properties:
Where: 0 <= Beta1 <= 4
1 <= Beta2 <= 10
Uniform: [0,1.8] [point]
Exponential: [4,9] [point]
Normal: [0,3] [point]
Students-t: (0,3) to [0,10] [line]
Lognormal: (0,3) to [3.6,10] [line]
Gamma: (0,3) to (4,9) [line]
Beta: (0,3) to (4,9), (0,1.8) to (4,9) [area]
Beta J: (0,1.8) to (4,9), (0,1.8) to [4,6*] [area]
Beta U: (0,1.8) to (4,6), [0,1] to [4.5) [area]
Impossible: (0,1) to (4.5), (0,1) to (4,1] [area]
Undefined: (0,3) to (3.6,10), (0,10) to (3.6,10) [area]
Values of Beta1, Beta2 where brackets mean:
[ ] : includes (closed)
( ) : approaches but does not include (open)
* : approximate
These are illustrated in Hahn and Shapiro Fig 6-1.
Granted this is a very rough test (with some issues) but you may want to consider it as a preliminary check before going to a more rigorous method.
There are also adjustment mechanisms to the calculation of Beta1 and Beta2 where data is limited — but that is beyond this post.
В статье рассматривается процедура создания шаблона Excel и опыт его применения для автоматического построения гистограмм и кривых Гаусса по результатам данных экспериментальных наблюдений с одновременной оценкой согласия по критерию Пирсона в учебном процессе. Показываются преимущества данного метода перед ручным счетом по проверке рассмотренного критерия.
Ключевые слова: шаблон Excel, гистограмма, кривая распределения, критерий согласия Пирсона
В современном мире к статистике проявляется большой интерес, поскольку это отличный инструмент для анализа и принятия решений, а также это отличное средство для поиска причин нарушений процесса и их устранения. Статистический анализ применим во многих сферах, где существуют большие массивы данных: металлургии, а также в экономике, биологии, политике, социологии и т. д. Рассмотрим использование некоторых средств статистического анализа, а именно — гистограмм для обработки больших массивов данных.
Целью первичной обработки экспериментальных наблюдений обычно является выбор закона распределения, наиболее хорошо описывающего случайную величину, выборку которой мы наблюдали. Проверка того, насколько хорошо наблюдаемая выборка описывается теоретическим законом, осуществляется с использованием различных критериев согласия. Целью проверки гипотезы о согласии опытного распределения с теоретическим является стремление удостовериться в том, что данная модель теоретического закона не противоречит наблюдаемым данным, и использование ее не приведет к существенным ошибкам при вероятностных расчетах. Некорректное использование критериев согласия может приводить к необоснованному принятию или необоснованному отклонению проверяемой гипотезы [1].
Сходимость результатов наблюдений можно оценить наиболее полно, если их распределение является нормальным. Поэтому исключительно важную роль при обработке результатов наблюдений играет проверка нормальности распределения.
Эта задача представляет собой частный случай более общей проблемы, заключающейся в подборе теоретической функции распределения, в некотором смысле наилучшим образом согласующейся с опытными данными. Сама процедура проверки нормальности распределения относится к распространенной стандартной и довольно тривиальной задаче обработки данных и достаточно подробно и широко описана в различной литературе по метрологии и статистической обработке данных измерений [2- 4].
Данные, получаемые в результате измерений при контроле технологических процессов, оценке характеристик различных объектов и др. для дальнейшей обработки желательно представлять в виде теоретического распределения, максимально соответствующего экспериментальному распределению. Проверку гипотезы о виде функции распределения в настоящее время проводят по различным критериям согласия — Пирсона, Колмогорова, Смирнова и другим в соответствии с новыми разработанными нормативными документами — рекомендациями по стандартизации [5, 6].
Наиболее часто используется критерий Пирсона 2. Однако применение критериев согласия требует обычно довольно значительного объёма данных. Так, критерий Пирсона обычно рекомендуется использовать при объёме выборки не менее 50…100. Поэтому при небольшом объёме выборки проверку гипотезы о виде функции распределения проводят приближёнными методами — графическим методом или по асимметрии и эксцессу. Применение критерия Пирсона для ручной обработки данных очень подробно было изложено в известной работе [2]. Как свидетельствует опыт проверок согласия экспериментальных данных с теоретическими по различным критериям, эта процедура является очень трудоемкой, требует некоторой усидчивости и особого внимания при обработке от исследователя, как правило, не исключает ошибок в работе и не вызывает особого энтузиазма у выполняющего эту работу.
Решение задач статистического анализа связано со значительными объемами вычислений. Проведение реальных многовариантных статистических расчетов в ручном режиме является очень громоздкой и трудоемкой задачей и без использования компьютера в настоящее время практически невозможно. В настоящее время разработано достаточное количество универсальных и специализированных программных средств для статистического анализа и обработки экспериментальных данных. Автор предлагает к рассмотрению достаточно простой и эффективный шаблон для быстрого построения гистограммы и кривой нормального распределения.
По виду гистограммы можно предположить (принять гипотезу) о том, что выборка случайных чисел подчиняется нормальному закону распределения. Далее, для того чтобы убедиться в правильности выбранной гипотезы надо, первое — построить график гипотетического нормального закона распределения, выбрав в качестве параметров (математического ожидания и среднего квадратического отклонения) их оценки (среднее и стандартное отклонение), и совместить график гипотетического распределения с графиком гистограммы. И, второе — используя в данном случае, как пример, критерий согласия Пирсона, установить справедливость выбранной гипотезы.
Рассмотрим порядок действий при работе с критерием Пирсона в среде Excel.
1. Полученные в результате измерений значения 100 случайных результатов измерений внести в ячейки A1:A100 шаблона Excel и приступить к построению гистограммы на основе данных, назначая длину интервала (карман) и выбирая необходимое число интервалов.
2. Затем на этом же листе создается таблица, в которую посредством формул Excel вносятся основные расчетные величины, используемые для построения гистограммы и кривой Гаусса: среднее арифметическое, стандартное отклонение, минимальное и максимальное значения выборки, размах, величина кармана (рис. 1).
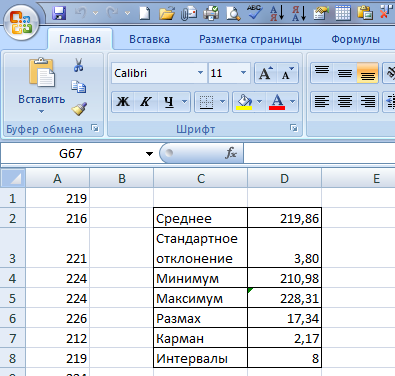
Рис. 1. Фрагмент таблицы с исходными данными
В ячейку D2 вносится формула =СРЗНАЧ(A1:A100), D3: =СТАНДОТКЛОН(A1:A100), D4: =МИН(A1:A100), D5: =МАКС(A1:A100), D6: =D5-D4, D7: =D6/D8. В ячейку D8 вводится число интервалов, которое для числа измерений, равным 100, может быть принято от 7 до 12.
Для оценки оптимального для нашего массива данных количества интервалов можно воспользоваться формулой Стерджесса: k~1+3,322lgN, где N— количество всех значений величины. Например, для N = 100, n = 7,6, которое должно быль округлено до целого числа, округляем до n = 8.
3. Интервал карманов вычисляют так: разность максимального и минимального значений массива, деленная на количество интервалов: .
4. Теперь в каждой ячейке шаг за шагом прибавляем полученное значение ширины кармана: сначала к минимальному значению нашего массива (ячейка D4), затем в следующей ячейке ниже — к полученной сумме и т. д. Так постепенно доходим до максимального значения. Таким образом, мы и построили интервалы карманов в виде столбца значений.
Интервалом считается следующий диапазон: (i-1; i] или i<значения<=i (нестрогая верхняя граница интервала — это значение в ячейке, нижняя строгая граница — значение в предыдущей ячейке).
5. Выделяем столбец рядом с нашими карманами, нажимаем «F2» и вводим функцию: =ЧАСТОТА (массив данных; диапазон карманов) и нажимаем Ctr+Shift+Enter.
6. В выделенном нами столбце напротив границ интервалов (а мы знаем, что это нестрогие верхние границы) появилось количество значений исходного массива, которые попадают в интервал (рис. 2).
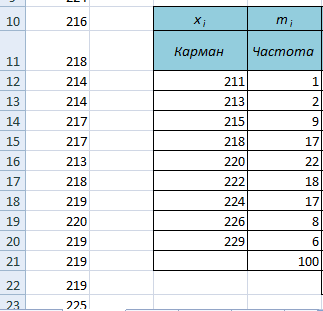
Рис. 2. Количество значений исходного массива, попавших в интервалы (частоты)
Построение теоретического закона распределения
Для построения теоретического закона распределения совместно с гистограммой и проверкой согласия по критерию хи-квадрат Пирсона автоматически заполняется таблица 1 после ввода экспериментальных данных в ячейки A1:A100.
Таблица 1
|
xi |
mi |
n∙pi |
|
|
карманы |
частота |
теоретическая частота |
статистика U |
Для построения этой таблицы надо воспользоваться таблицей карман — частота процедуры Гистограмма. В этой таблице обозначены:
xi — границы интервалов группировки (карманы — получены как результат выполнения процедуры Гистограмма);
mi — количество элементов выборки, попавших в i–ый интервал (частота — получена в результате процедуры Гистограмма).
Для построения этой таблицы в Excel к столбцам карман — частота процедуры Гистограмма надо добавить столбцы n∙pi (теоретическая частота) и (статистика U).
Проверка согласия эмпирического и теоретического законов распределения по критерию хи-квадрат Пирсона.
В ячейку столбца, помеченного именем U, вводим формулу,
, (1)
Критическое значение статистики U, которая имеет распределениес r степенями свободы (число степеней свободы определяется как число частичных интервалов минус 1), определяется при помощи функции ХИ2ОБР.
Функция ХИ2ОБР вызывается следующим образом. В главном меню Excel выбирается закладка Формулы → Вставить функцию →в диалоговом окне Мастер функций— шаг 1 из 2 вкатегории Статистические →ХИ2ОБР (рис. 3).
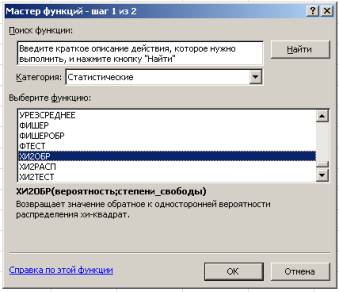
Рис. 3. Диалоговое окно выбора функции ХИ2ОБР
В диалоговом окне Аргументы функции ХИ2ОБР заполняются поля как показано на рис. 4, задаваясь уровнем значимости (например, 0,05, что соответствует доверительной вероятности Р = 0,95) и предварительно выбрав ячейку для результата вычисления функции.
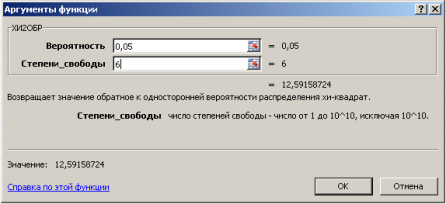
Рис. 4. Диалоговое окно функции ХИ2ОБР с заполненными полями ввода
Размножим формулу (1) в диапазонах ячеек [F12; F20] и [F51; F61]. В ячейке F21 получим сумму содержимого ячеек F12; F20 (рис. 5). В ячейке F62 получим сумму содержимого ячеек F51; F61 (рис. 6).
В ячейке F21 получено значение статистики: U = 2,09, а в ячейке F62 — U = 3,43 при доверительной вероятности Р = 0,95.
Теперь с помощью стандартного инструмента для построения гистограмм («вставка/гистограмма» и т. д.) на этом же листе Excel можно построить гистограммы распределения с кривой Гаусса для разных чисел интервалов (в данном случае n = 8 и n = 10) (рис. 5 и 6).
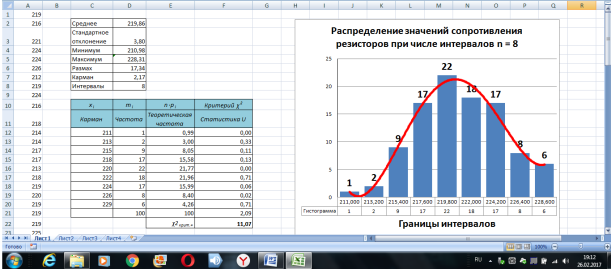
Рис. 5. Вид гистограммы и кривой распределения при числе интервалов n = 8 (пример)
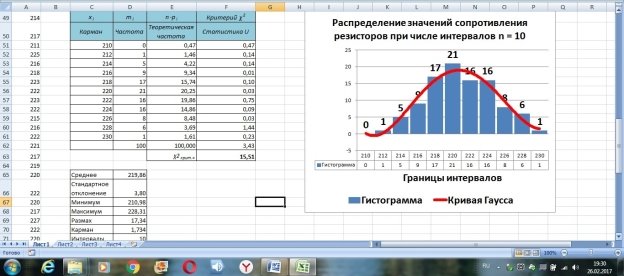
Рис. 6. Вид гистограммы и кривой распределения при числе интервалов n = 10 (пример)
Шаблон позволяет варьировать числом интервалов и величиной кармана, при этом автоматически изменяется внешний вид гистограммы и кривой нормального распределения. Исследователь может подобрать наиболее «красивый» вид гистограммы и аппроксимирующей кривой Гаусса, одновременно изменив значение доверительной вероятности и числа степеней свободы и добившись при этом выполнения критерия Пирсона.
Если значение статистики U оказалось меньше критического значения при заданной доверительной вероятности, то гипотеза, состоящая в том, что исследуемая выборка подчиняется нормальному закону распределения, принимается. Вданном примере значение обеих статистик U оказалось меньше критического значения
и
Следовательно, мы можем распространить данный закон распределения на всю генеральную совокупность исследуемых объектов (партию изделий, сменную выработку, месячный план и т. д.).
Более подробно указанная тема была рассмотрена в статье автора в сборнике «Законодательная и прикладная метрология» [7].
Выводы
- Существовавшая ранее традиционная «ручная» обработка данных при проверке нормального (и других) законов распределения и построении гистограмм являлась достаточно трудоемкой задачей, не исключавшей появление ошибок, обнаружение которых зачастую требовало значительных затрат времени и моральных сил исследователя.
- Появление пакетов офисных программ, в частности Excel 2010 и ее последующих версий, позволяет значительно сократить трудоемкость обработки данных и практически исключает появление ошибок в расчетах.
Литература:
1. Лемешко Б. Ю., Постовалов С. Н. О правилах проверки согласия опытного распределения с теоретическим. — Методы менеджмента качества. Надежность и контроль качества. — 1999, № 11. — С. 34–43.
2. Бурдун Г. Д., Марков Б. Н. Основы метрологии. Учебное пособие для вузов. — М.: Изд. стандартов, 1975. — 336 с.
3. Сулицкий В. Н. Методы статистического анализа в управлении: Учеб. пособие. — М.: Дело, 2002. — 520 с.
4. Иванов О. В. Статистика / Учебный курс для социологов и менеджеров. Часть 2. Доверительные интервалы. Проверка гипотез. Методы и их применение. — М.: Изд. МГУ им. М. В. Ломоносова, 2005. — 220 с.
5. Рекомендации по стандартизации Р 50.1.033–2001. Прикладная статистика. Правила проверки согласия опытного распределения с теоретическим. Часть 1. Критерии типа хи-квадрат. — М.: ФГУП «Стандартинформ», 2006. — 87 с.
6. Рекомендации по стандартизации Р 50.1.037–2002. Прикладная статистика. Правила проверки согласия опытного распределения с теоретическим. Часть II. Непараметрические критерии. — М.: ИПК Изд. стандартов, 2002. — 62 с.
7. Фаюстов А. А. Проверка гипотезы о нормальном распределении выборки по критерию согласия Пирсона средствами приложения Excel. — Законодательная и прикладная метрология, 2016, № 6. — С. 3–9.
Основные термины (генерируются автоматически): статистический анализ, критерий согласия, массив данных, вид функции распределения, интервал карманов, максимальное значение, минимальное значение, построение гистограммы, различный критерий согласия, стандартное отклонение.
Как определить, является ли распределение нормальным?
Если
установлено, что исследуемые значения
имеют количественный характер, следует
проверить выборку на нормальность
распределения. Это можно сделать
несколькими способами.
Первый
способ проверки выборки на нормальность
распределения
Прежде
всего, нужно вычислить показатели
асимметрии и эксцесса, используя
программу Excel,
имеющуюся практически на всех компьютерах.
Для этого в таблицу программы следует
поместить результаты измерений. Пусть
это будет ряд значений, полученных на
выборке из 25 объектов: 9 10 10 10 11
11 11 11 12 12 12 12 12 12 12 13 13 13 13
14 14 15 15 16 17
Данные
могут располагаться как в виде строки,
так и в виде колонки. Далее, нажатием
кнопки с символами fx,
расположенной
ниже панели инструментов, вызываем
мастер функций. В верхнем окне выбираем
категорию «Статистические», а в нижнем
— пункт «Скос». Возвращаемся к таблице
с результатами измерений, и, выделяя
набранные ранее цифры, помещаем их
значения в открывшееся окно «Аргументы
функций». На правой стороне окна
появляется результат вычислений –
0,579. Это и есть значение показателя
асимметрии, характеризующего степени
отклонения вершины кривой распределения
от его центра. Можно сказать, что
показатель асимметрии отражает отклонение
вершины реальной кривой распределения
от идеальной по оси абсцисс.
По
схожему алгоритму вычисляем величину
показателя эксцесса характеризующего
подъем или снижение вершины распределения,
то есть – отклонения по оси ординат.
Для того, чтобы произвести расчет данного
показателя, следует выбрать пункт
«эксцесс». В окне «Аргументы функций»
получим его значение – 0,116.
При
наличии статистических таблиц критических
значений асимметрии и эксцесса (в данном
учебном пособии это таблицы 9 и 10)
вычисленные значения сравниваются с
табличными. Если оба
(!) показателя окажутся меньше табличных
величин, то распределение может считаться
нормальным.
Для
нашего примера табличное значение
показателя асимметрии находим на
пересечении строки n
= 25 и колонки
р ≤ 0,01
(предположим,
что мы
анализируем
результаты
достаточно важных экспериментов и
считаем, что вероятность ошибки
статистического заключения не должна
превышать 1%). Это число составляет 1,061.
Так как вычисленное значение показателя
асимметрии 0,579 оказывается гораздо
меньше табличной величины 1,061, можно
сделать заключение, что отклонение
вершины распределения по оси абсцисс
не столь значительно, чтобы отказаться
от применения параметрических методов.
В
таблице 10 находим критическое значение
показателя эксцесса.
Для
n
= 26 (так как
в таблице
отсутствует строка для n
= 25, переходим
к ближайшей строке)
и
р
≤ 0,01 оно
составляет 0,869.
И снова
фактическое значение показателя 0,116
оказывается меньше табличного 0, 869.
Отсюда следует, что отклонение вершины
распределения по оси ординат также
несущественно и его можно считать
нормальным. То, что оба показателя
оказались меньше критических табличных
величин, дает основание для последующего
применения параметрических критериев.
Второй
способ проверки выборки на нормальность
распределения
При
отсутствии таблиц критических значений
асимметрии и эксцесса следует произвести
расчеты не только этих показателей, но
и их выборочных ошибок.
Ошибка
показателя асимметрии производится по
формуле:
Для
нашего примера
она составит:
Выборочная
ошибка эксцесса рассчитывается по
другой формуле:
в
результате получим:
Далее
следует разделить показатели асимметрии
и эксцесса на их ошибки.
Частное
от деления показателей асимметрии и
эксцесса на их ошибки определяется как
tф (фактическое
значение) и сравнивается с tт,табличное
значение),
взятым из
таблицы Стьюдента (таблица 6), при
соответствующем уровне значимости и
числе степеней свободы. Если фактическое
значение критерия Стьюдента окажется
меньше табличного, распределение
признается нормальным, и, наоборот, если
фактическое значение окажется больше
табличного, следует сделать вывод о
несоответствии распределения нормальному
закону.
Для
показателя асимметрии получаем следующее
значение t-критерия:
Число
степеней свободы (df),
определяющее строку в таблице Стьюдента,
находим как n-1.
Следовательно, df
= 25-1=24. Уровень значимости (вероятность
ошибки статистического заключения),
определяющий колонку в таблице Стьюдента,
оставляем 1%. На пересечении строки df
=24 и колонки р
≤ 0,01 находим
табличное значение критерия tт
= 2,80.
Так как tф (1,25)
оказывается
гораздо
меньше чем tт
(2,80), можно
заключить, что и второй способ проверки
указывает на незначительность асимметрии
кривой распределения.
Фактическое
значения t-критерия
для показателя эксцесса рассчитываем
по формуле
Таким образом, не только для асимметрии,
но и для эксцесса tф
(0,129)
оказывается
существенно
меньше чем tт
(2,80), что опять
же указывает на нормальность распределения.
Третий
способ проверки выборки на нормальность
распределения
Проще всего задача
решается, если имеется компьютер с
установленной на ней программой
Statistica. После ввода данных в таблицу
вызывается стартовая панель модуля
Основные
статистики и таблицы
(Basic
Statistics/Tables).
В средней части окна Descriptive
Statistics
(Описательные статистики) слева находится
блок проверки распределений (Distribution).
Чтобы проверить, относятся ли показатели
выбранной переменной к распределяемым
по нормальному закону, нужно поставить
галочку в окне возле пункта K-S
and Lilliefors test for normality (Критерий
Колмогорова-Смирнова и Лилиефорса для
нормальности)
и нажать на кнопку Histograms
(гистограммы). В появившемся окне
приводятся гистограмма распределения
значений переменной и наложенная на
нее кривая нормального распределения,
сопоставление которых позволяет
визуально оценить характер распределения.
В
верхней части окна указывается
достоверность отличия проверяемого
распределения от нормального,
характеризуемая уровнем значимости р
(вероятность неправильного отвержения
гипотезы, если она верна). Если уровень
значимости р<0,05, то распределение
отлично от нормального на основании
соответствующего критерия. И наоборот,
если р>0,05, как на рисунке, то наблюдаемая
величина распределена нормально. Зная
вид распределения, в дальнейшей обработке
можно применить оптимальные статистические
методы.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Нормальность распределения
В примерах в данной статье данные генерятся при каждой загрузке страницы. Если Вы хотите посмотреть пример с другими значениями —
обновите страницу .
Некоторые статистические инструменты исходят из предположения, что распределение
является нормальным. Ниже будет приведён алгоритм проверки нормальности распределения,
а также пример в excel.
Закон распределения
Проверка на соответствие нормальному распределению — это частный случай решения задачи
о нахождении среди известных функций распределения такой, максимально точно описывающей
данное распределение.
В первую очередь, необходимо структурировать имеющиеся значения, в статье
свойства
распределения
описано, как строится ряд распределения, поэтому здесь я опущу детали и приведу
исходные данные и обработанные значения:
| 154 | 142 | 135 | 149 | 149 | 159 | 150 | 148 | 163 | 156 |
| 151 | 130 | 136 | 155 | 141 | 164 | 159 | 163 | 157 | 141 |
| 150 | 156 | 154 | 134 | 142 | 161 | 144 | 141 | 159 | 130 |
| 153 | 159 | 156 | 142 | 152 | 159 | 163 | 144 | 159 | 151 |
| 150 | 156 | 164 | 161 | 163 | 152 | 129 | 155 | 135 | 164 |
| 156 | 162 | 164 | 142 | 142 | 158 | 155 | 166 | 158 | 155 |
| 154 | 153 | 135 | 145 | 135 | 151 | 157 | 153 | 158 | 147 |
| 158 | 166 | 151 | 158 | 163 | 146 | 138 | 150 | 155 | 171 |
| 149 | 154 | 150 | 153 | 151 | 149 | 153 | 168 | 139 | 155 |
| 152 | 136 | 163 | 140 | 137 | 151 | 150 | 149 | 163 | 163 |
| Таблица 1. Исходные данные для проверки нормальности распределения |
| # | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| x | 3 | 8 | 6 | 8 | 8 | 24 | 18 | 9 | 14 | 1 |
| pi | 0.03 | 0.08 | 0.06 | 0.08 | 0.08 | 0.24 | 0.18 | 0.09 | 0.14 | 0.01 |
| Таблица 2. Количество элементов в каждом интервале |
График 1. Ряд распределения
Независимо от того, что мы видим на графике, нам необходимо проверить, является
ли распределение нормальным.
Характеристики нормального распределения — это среднее значение и стандартное отклонение.
Вычислим эти значения для нашего распределения:
μ = 151.67
σ = 9.43
Расчёт среднего значения и стандартного отклонения описан в статье параметры распределения
Нормальное распределение
Кривая нормального распределения для μ=151.67 и σ=9.43:
P(x) = e^[-0.5((x-151.67)/9.43)2] / [9.43√2π]
Формула нормального распределения
График 2. Ряд распределения и нормальное распределение, μ = 151.67, σ = 9.43
Первое приближение
Попробуем изобрести критерий нормальности, самое простое,
что приходит в голову — это определить процент соответствия
нормальной кривой и существующего распределения.
Для этого сложим абсолютные значения разниц по всем точкам графика,
найдём площадь под графиком нормального распределения и вычислим
интересующее отклонение, я назову такой критерий
«критерий нормальности» и постановлю, что если отклонение
больше, допустим 30%, то распределение не является нормальным.
diff = Σ|D(X) — P(X)|
S = ΣP(X)
Δ = diff / S
diff = 49.77
S = 133.37
Δ = 37%
Отклонение составляет 37%, поэтому я делаю следующий вывод:
распределение не является нормальным по критерию нормальности.
Скачать статью в формате PDF.
Автор статьи:
Дата редакции статьи: 19.12.2019
Вам понравилась статья?
/
Просмотров: 3 741
В статье подробно показано, что такое нормальный закон распределения случайной величины и как им пользоваться при решении практически задач.
Нормальное распределение в статистике
История закона насчитывает 300 лет. Первым открывателем стал Абрахам де Муавр, который придумал аппроксимацию биномиального распределения еще 1733 году. Через много лет Карл Фридрих Гаусс (1809 г.) и Пьер-Симон Лаплас (1812 г.) вывели математические функции.
Лаплас также обнаружил замечательную закономерность и сформулировал центральную предельную теорему (ЦПТ), согласно которой сумма большого количества малых и независимых величин имеет нормальное распределение.
Нормальный закон не является фиксированным уравнением зависимости одной переменной от другой. Фиксируется только характер этой зависимости. Конкретная форма распределения задается специальными параметрами. Например, у = аx + b – это уравнение прямой. Однако где конкретно она проходит и под каким наклоном, определяется параметрами а и b. Также и с нормальным распределением. Ясно, что это функция, которая описывает тенденцию высокой концентрации значений около центра, но ее точная форма задается специальными параметрами.
Кривая нормального распределения Гаусса имеет следующий вид.
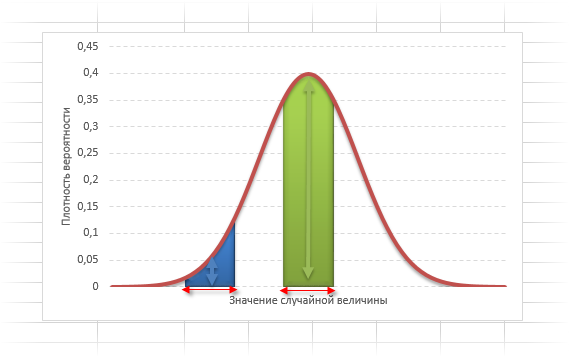
График нормального распределения напоминает колокол, поэтому можно встретить название колоколообразная кривая. У графика имеется «горб» в середине и резкое снижение плотности по краям. В этом заключается суть нормального распределения. Вероятность того, что случайная величина окажется около центра гораздо выше, чем то, что она сильно отклонится от середины.
На рисунке выше изображены два участка под кривой Гаусса: синий и зеленый. Основания, т.е. интервалы, у обоих участков равны. Но заметно отличаются высоты. Синий участок удален от центра, и имеет существенно меньшую высоту, чем зеленый, который находится в самом центре распределения. Следовательно, отличаются и площади, то бишь вероятности попадания в обозначенные интервалы.
Формула нормального распределения (плотности) следующая.
Формула состоит из двух математических констант:
π – число пи 3,142;
е – основание натурального логарифма 2,718;
двух изменяемых параметров, которые задают форму конкретной кривой:
m – математическое ожидание (в различных источниках могут использоваться другие обозначения, например, µ или a);
σ2 – дисперсия;
ну и сама переменная x, для которой высчитывается плотность вероятности.
Конкретная форма нормального распределения зависит от 2-х параметров: математического ожидания (m) и дисперсии (σ2). Кратко обозначается N(m, σ2) или N(m, σ). Параметр m (матожидание) определяет центр распределения, которому соответствует максимальная высота графика. Дисперсия σ2 характеризует размах вариации, то есть «размазанность» данных.
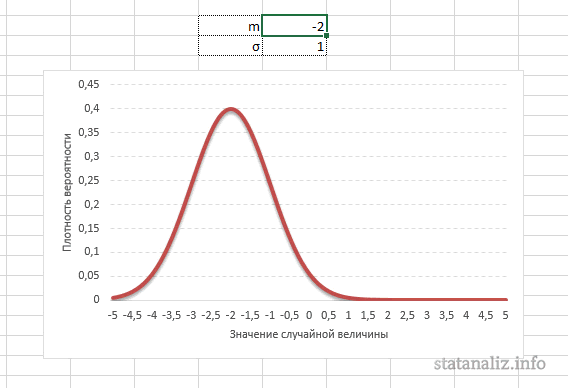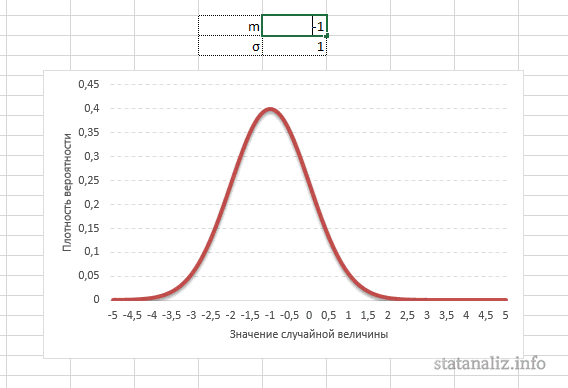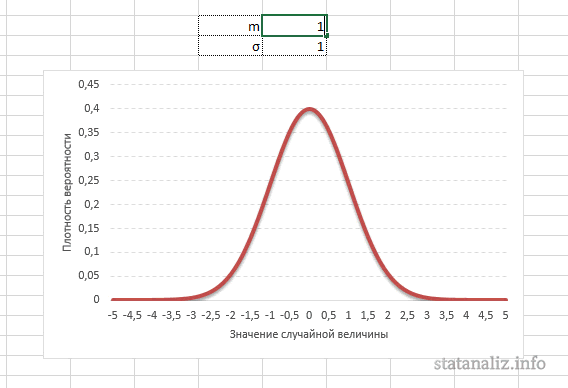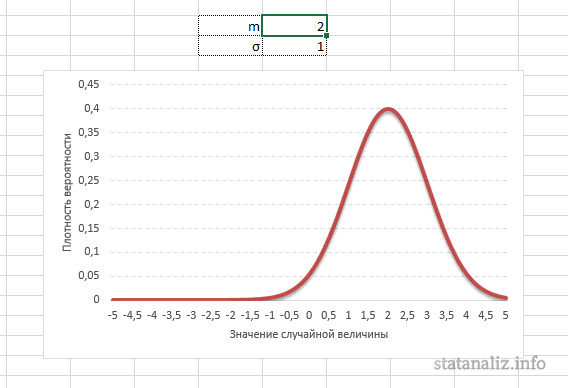
Параметр математического ожидания смещает центр распределения вправо или влево, не влияя на саму форму кривой плотности.
А вот дисперсия определяет остроконечность кривой. Когда данные имеют малый разброс, то вся их масса концентрируется у центра. Если же у данных большой разброс, то они «размазываются» по широкому диапазону.
Плотность распределения не имеет прямого практического применения. Для расчета вероятностей нужно проинтегрировать функцию плотности.
Вероятность того, что случайная величина окажется меньше некоторого значения x, определяется функцией нормального распределения:
Используя математические свойства любого непрерывного распределения, несложно рассчитать и любые другие вероятности, так как
P(a ≤ X < b) = Ф(b) – Ф(a)
Стандартное нормальное распределение
Нормальное распределение зависит от параметров средней и дисперсии, из-за чего плохо видны его свойства. Хорошо бы иметь некоторый эталон распределения, не зависящий от масштаба данных. И он существует. Называется стандартным нормальным распределением. На самом деле это обычное нормальное нормальное распределение, только с параметрами математического ожидания 0, а дисперсией – 1, кратко записывается N(0, 1).
Любое нормальное распределение легко превращается в стандартное путем нормирования:
где z – новая переменная, которая используется вместо x;
m – математическое ожидание;
σ – стандартное отклонение.
Для выборочных данных берутся оценки:
Среднее арифметическое и дисперсия новой переменной z теперь также равны 0 и 1 соответственно. В этом легко убедиться с помощью элементарных алгебраических преобразований.
В литературе встречается название z-оценка. Это оно самое – нормированные данные. Z-оценку можно напрямую сравнивать с теоретическими вероятностями, т.к. ее масштаб совпадает с эталоном.
Посмотрим теперь, как выглядит плотность стандартного нормального распределения (для z-оценок). Напомню, что функция Гаусса имеет вид:
Подставим вместо (x-m)/σ букву z, а вместо σ – единицу, получим функцию плотности стандартного нормального распределения:
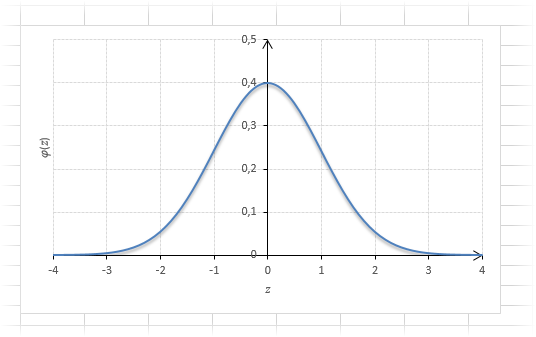
График плотности:
Центр, как и ожидалось, находится в точке 0. В этой же точке функция Гаусса достигает своего максимума, что соответствует принятию случайной величиной своего среднего значения (т.е. x-m=0). Плотность в этой точке равна 0,3989, что можно посчитать даже в уме, т.к. e0=1 и остается рассчитать только соотношение 1 на корень из 2 пи.
Таким образом, по графику хорошо видно, что значения, имеющие маленькие отклонения от средней, выпадают чаще других, а те, которые сильно отдалены от центра, встречаются значительно реже. Шкала оси абсцисс измеряется в стандартных отклонениях, что позволяет отвязаться от единиц измерения и получить универсальную структуру нормального распределения. Кривая Гаусса для нормированных данных отлично демонстрирует и другие свойства нормального распределения. Например, что оно является симметричным относительно оси ординат. В пределах ±1σ от средней арифметической сконцентрирована большая часть всех значений (прикидываем пока на глазок). В пределах ±2σ находятся большинство данных. В пределах ±3σ находятся почти все данные. Последнее свойство широко известно под названием правило трех сигм для нормального распределения.
Функция стандартного нормального распределения позволяет рассчитывать вероятности.
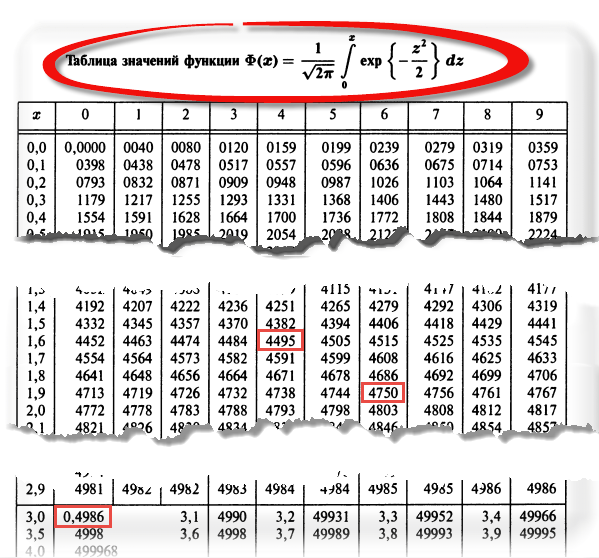
Понятное дело, вручную никто не считает. Все подсчитано и размещено в специальных таблицах, которые есть в конце любого учебника по статистике.
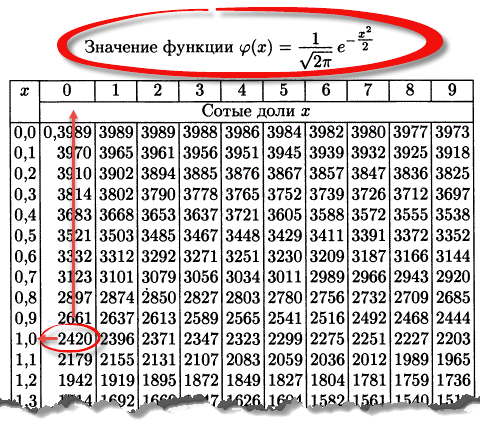
Таблица нормального распределения
Таблицы нормального распределения встречаются двух типов:
— таблица плотности;
— таблица функции (интеграла от плотности).
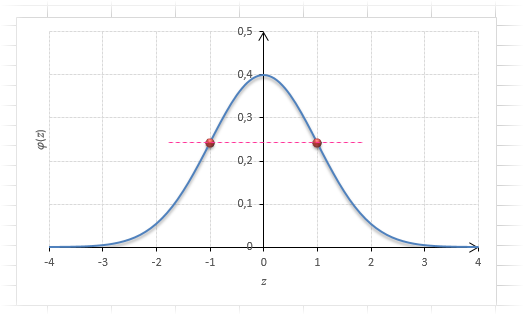
Таблица плотности используется редко. Тем не менее, посмотрим, как она выглядит. Допустим, нужно получить плотность для z = 1, т.е. плотность значения, отстоящего от матожидания на 1 сигму. Ниже показан кусок таблицы.
В зависимости от организации данных ищем нужное значение по названию столбца и строки. В нашем примере берем строку 1,0 и столбец 0, т.к. сотых долей нет. Искомое значение равно 0,2420 (0 перед 2420 опущен).
Функция Гаусса симметрична относительно оси ординат. Поэтому φ(z)= φ(-z), т.е. плотность для 1 тождественна плотности для -1, что отчетливо видно на рисунке.
Чтобы не тратить зря бумагу, таблицы печатают только для положительных значений.
На практике чаще используют значения функции стандартного нормального распределения, то есть вероятности для различных z.
В таких таблицах также содержатся только положительные значения. Поэтому для понимания и нахождения любых нужных вероятностей следует знать свойства стандартного нормального распределения.
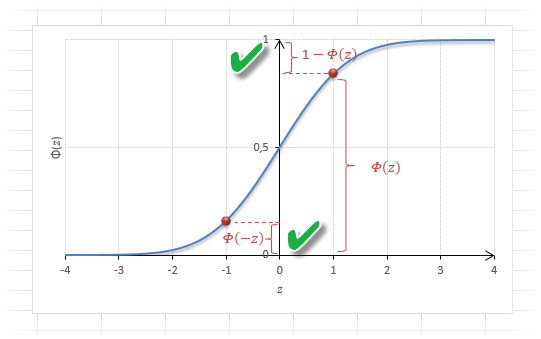
Функция Ф(z) симметрична относительно своего значения 0,5 (а не оси ординат, как плотность). Отсюда справедливо равенство:
Это факт показан на картинке:
Значения функции Ф(-z) и Ф(z) делят график на 3 части. Причем верхняя и нижняя части равны (обозначены галочками). Для того, чтобы дополнить вероятность Ф(z) до 1, достаточно добавить недостающую величину Ф(-z). Получится равенство, указанное чуть выше.
Если нужно отыскать вероятность попадания в интервал (0; z), то есть вероятность отклонения от нуля в положительную сторону до некоторого количества стандартных отклонений, достаточно от значения функции стандартного нормального распределения отнять 0,5:
Для наглядности можно взглянуть на рисунок.
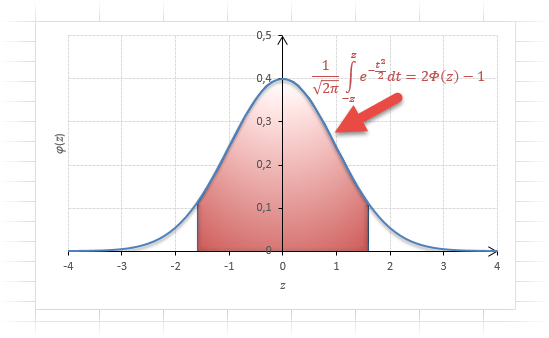
На кривой Гаусса, эта же ситуация выглядит как площадь от центра вправо до z.
Довольно часто аналитика интересует вероятность отклонения в обе стороны от нуля. А так как функция симметрична относительно центра, предыдущую формулу нужно умножить на 2:
Рисунок ниже.
Под кривой Гаусса это центральная часть, ограниченная выбранным значением –z слева и z справа.
Указанные свойства следует принять во внимание, т.к. табличные значения редко соответствуют интересующему интервалу.
Для облегчения задачи в учебниках обычно публикуют таблицы для функции вида:
Если нужна вероятность отклонения в обе стороны от нуля, то, как мы только что убедились, табличное значение для данной функции просто умножается на 2.
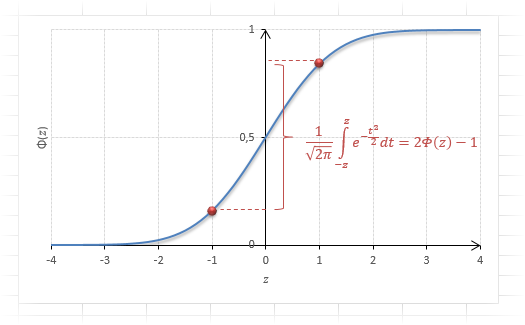
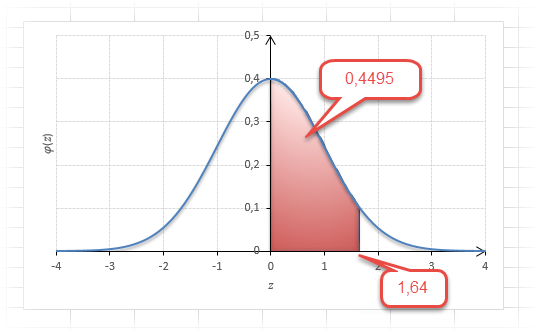
Теперь посмотрим на конкретные примеры. Ниже показана таблица стандартного нормального распределения. Найдем табличные значения для трех z: 1,64, 1,96 и 3.
Как понять смысл этих чисел? Начнем с z=1,64, для которого табличное значение составляет 0,4495. Проще всего пояснить смысл на рисунке.
То есть вероятность того, что стандартизованная нормально распределенная случайная величина попадет в интервал от 0 до 1,64, равна 0,4495. При решении задач обычно нужно рассчитать вероятность отклонения в обе стороны, поэтому умножим величину 0,4495 на 2 и получим примерно 0,9. Занимаемая площадь под кривой Гаусса показана ниже.
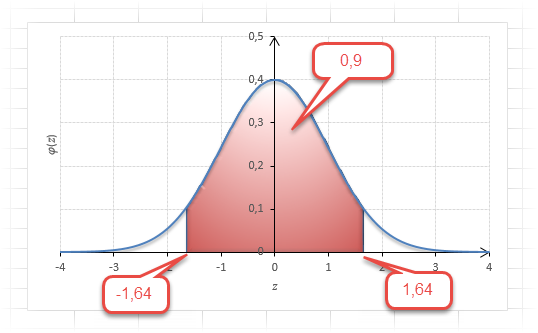
Таким образом, 90% всех нормально распределенных значений попадает в интервал ±1,64σ от средней арифметической. Я не случайно выбрал значение z=1,64, т.к. окрестность вокруг средней арифметической, занимающая 90% всей площади, иногда используется для проверки статистических гипотез и расчета доверительных интервалов. Если проверяемое значение не попадает в обозначенную область, то его наступление маловероятно (всего 10%).
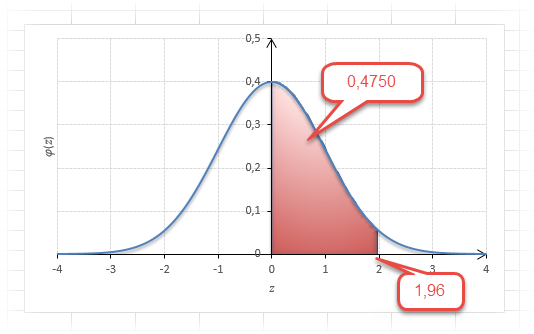
Для проверки гипотез, однако, чаще используется интервал, накрывающий 95% всех значений. Половина вероятности от 0,95 – это 0,4750 (см. второе выделенное в таблице значение).
Для этой вероятности z=1,96. Т.е. в пределах почти ±2σ от средней находится 95% значений. Только 5% выпадают за эти пределы.
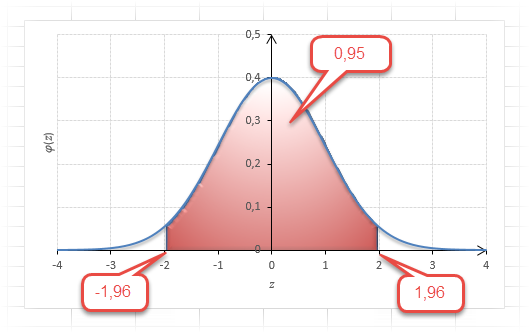
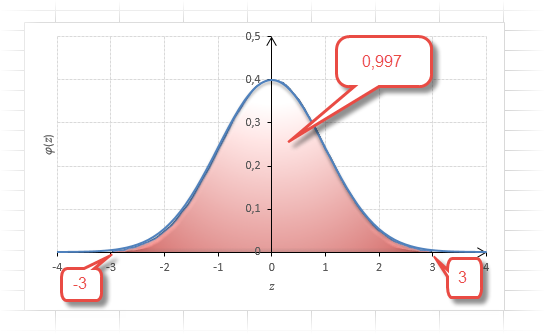
Еще одно интересное и часто используемое табличное значение соответствует z=3, оно равно по нашей таблице 0,4986. Умножим на 2 и получим 0,997. Значит, в рамках ±3σ от средней арифметической заключены почти все значения.
Так выглядит правило 3 сигм для нормального распределения на диаграмме.
С помощью статистических таблиц можно получить любую вероятность. Однако этот метод очень медленный, неудобный и сильно устарел. Сегодня все делается на компьютере. Далее переходим к практике расчетов в Excel.
В Excel есть несколько функций для подсчета вероятностей или обратных значений нормального распределения.
Функция НОРМ.СТ.РАСП
Функция НОРМ.СТ.РАСП предназначена для расчета плотности ϕ(z) или вероятности Φ(z) по нормированным данным (z).
=НОРМ.СТ.РАСП(z;интегральная)
z – значение стандартизованной переменной
интегральная – если 0, то рассчитывается плотность ϕ(z), если 1 – значение функции Ф(z), т.е. вероятность P(Z<z).
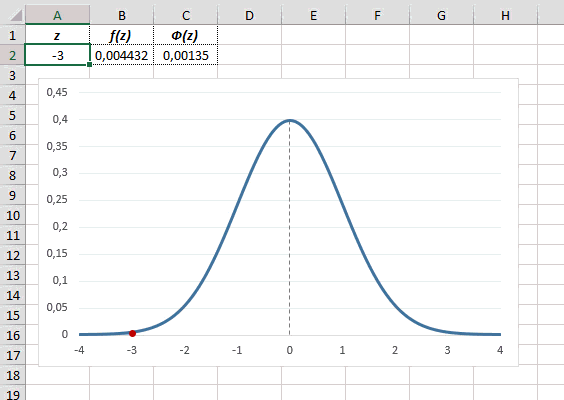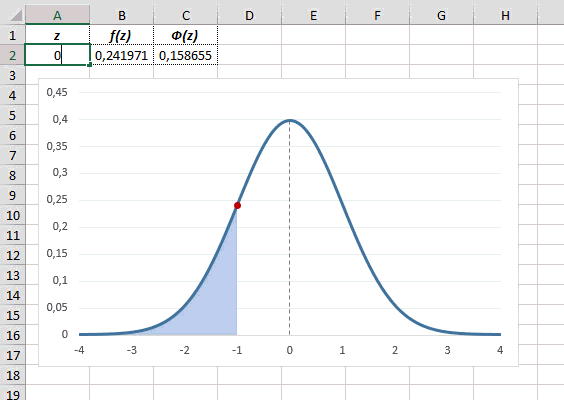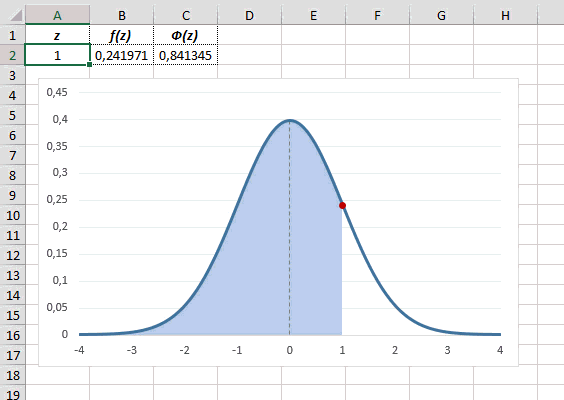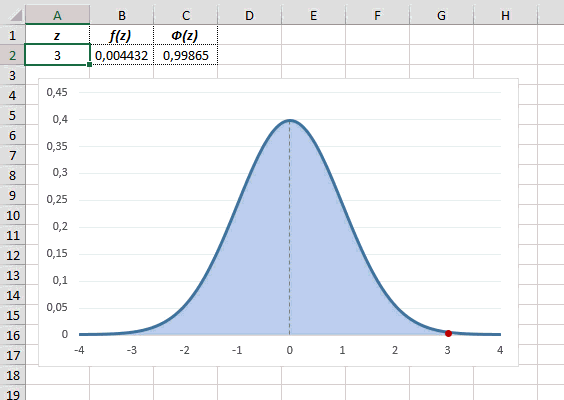
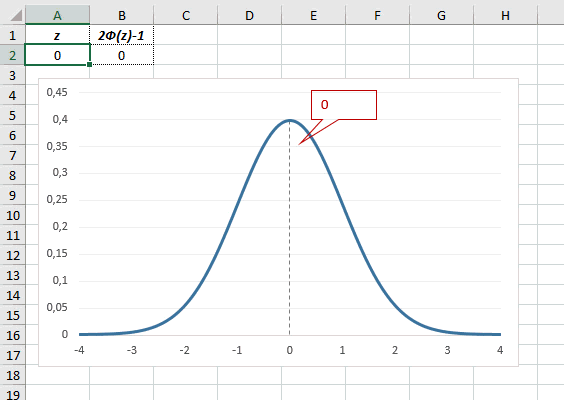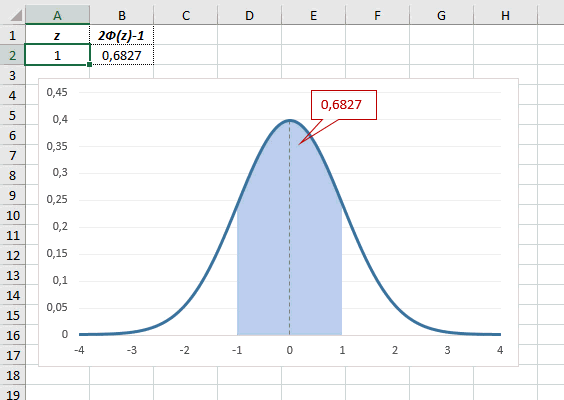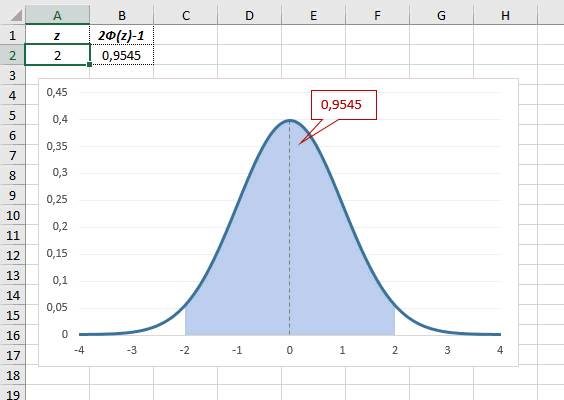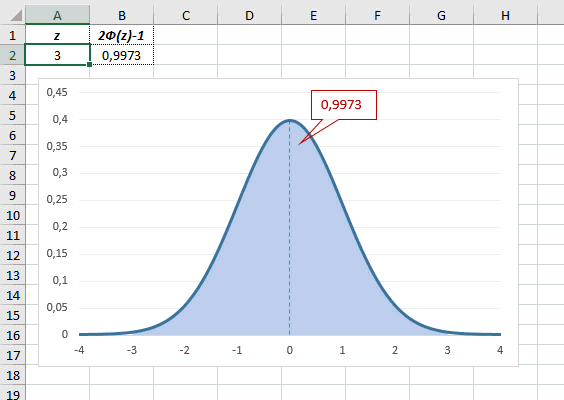
Рассчитаем плотность и значение функции для различных z: -3, -2, -1, 0, 1, 2, 3 (их укажем в ячейке А2).
Для расчета плотности потребуется формула =НОРМ.СТ.РАСП(A2;0). На диаграмме ниже – это красная точка.
Для расчета значения функции =НОРМ.СТ.РАСП(A2;1). На диаграмме – закрашенная площадь под нормальной кривой.
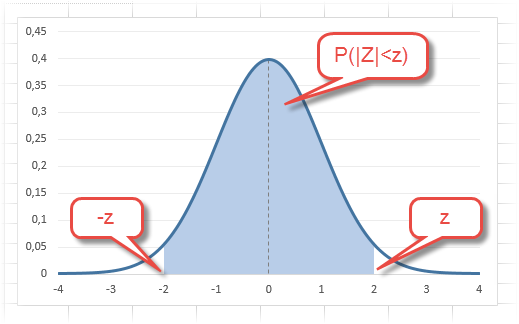
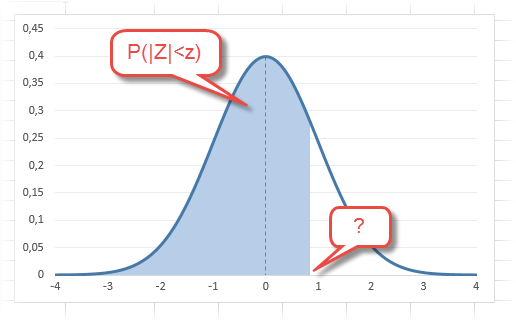
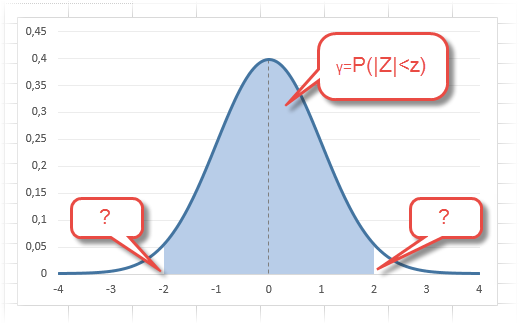
В реальности чаще приходится рассчитывать вероятность того, что случайная величина не выйдет за некоторые пределы от средней (в среднеквадратичных отклонениях, соответствующих переменной z), т.е. P(|Z|<z).
Определим, чему равна вероятность попадания случайной величины в пределы ±1z, ±2z и ±3z от нуля. Потребуется формула 2Ф(z)-1, в Excel =2*НОРМ.СТ.РАСП(A2;1)-1.
На диаграмме отлично видны основные основные свойства нормального распределения, включая правило трех сигм. Функция НОРМ.СТ.РАСП – это автоматическая таблица значений функции нормального распределения в Excel.
Может стоять и обратная задача: по имеющейся вероятности P(Z<z) найти стандартизованную величину z ,то есть квантиль стандартного нормального распределения.
Функция НОРМ.СТ.ОБР
НОРМ.СТ.ОБР рассчитывает обратное значение функции стандартного нормального распределения. Синтаксис состоит из одного параметра:
=НОРМ.СТ.ОБР(вероятность)
вероятность – это вероятность.
Данная формула используется так же часто, как и предыдущая, ведь по тем же таблицам искать приходится не только вероятности, но и квантили.
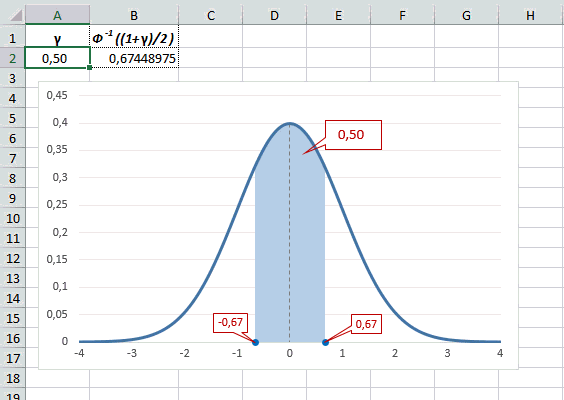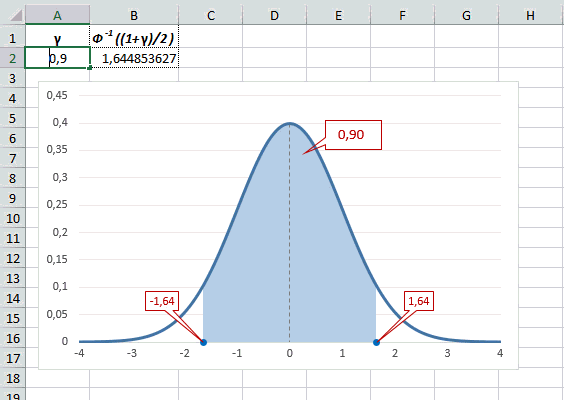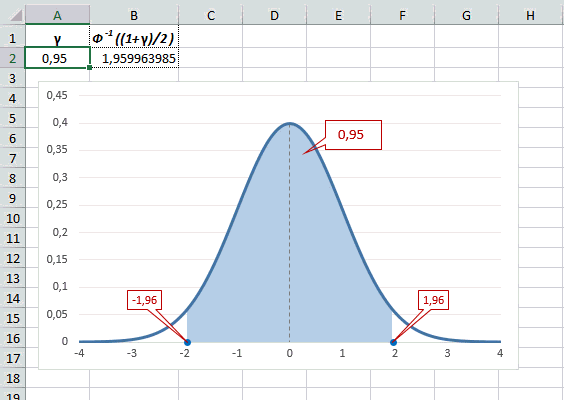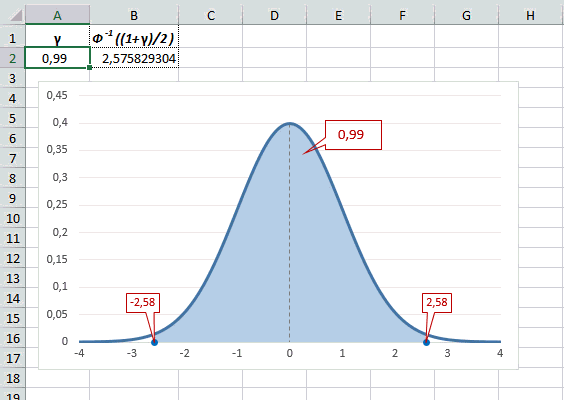
Например, при расчете доверительных интервалов задается доверительная вероятность, по которой нужно рассчитать величину z.
Учитывая то, что доверительный интервал состоит из верхней и нижней границы и то, что нормальное распределение симметрично относительно нуля, достаточно получить верхнюю границу (положительное отклонение). Нижняя граница берется с отрицательным знаком. Обозначим доверительную вероятность как γ (гамма), тогда верхняя граница доверительного интервала рассчитывается по следующей формуле.
Рассчитаем в Excel значения z (что соответствует отклонению от средней в сигмах) для нескольких вероятностей, включая те, которые наизусть знает любой статистик: 90%, 95% и 99%. В ячейке B2 укажем формулу: =НОРМ.СТ.ОБР((1+A2)/2). Меняя значение переменной (вероятности в ячейке А2) получим различные границы интервалов.
Доверительный интервал для 95% равен 1,96, то есть почти 2 среднеквадратичных отклонения. Отсюда легко даже в уме оценить возможный разброс нормальной случайной величины. В общем, доверительным вероятностям 90%, 95% и 99% соответствуют доверительные интервалы ±1,64, ±1,96 и ±2,58 σ.
В целом функции НОРМ.СТ.РАСП и НОРМ.СТ.ОБР позволяют произвести любой расчет, связанный с нормальным распределением. Но, чтобы облегчить и уменьшить количество действий, в Excel есть несколько других функций. Например, для расчета доверительных интервалов средней можно использовать ДОВЕРИТ.НОРМ. Для проверки статистической гипотезы о средней арифметической есть формула Z.ТЕСТ.
Рассмотрим еще пару полезных формул с примерами.
Функция НОРМ.РАСП
Функция НОРМ.РАСП отличается от НОРМ.СТ.РАСП лишь тем, что ее используют для обработки данных любого масштаба, а не только нормированных. Параметры нормального распределения указываются в синтаксисе.
=НОРМ.РАСП(x;среднее;стандартное_откл;интегральная)
x – значение (или ссылка на ячейку), для которого рассчитывается плотность или значение функции нормального распределения
среднее – математическое ожидание, используемое в качестве первого параметра модели нормального распределения
стандартное_откл – среднеквадратичное отклонение – второй параметр модели
интегральная – если 0, то рассчитывается плотность, если 1 – то значение функции, т.е. P(X<x).
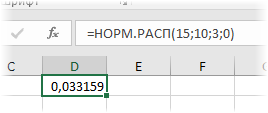
Например, плотность для значения 15, которое извлекли из нормальной выборки с матожиданием 10, стандартным отклонением 3, рассчитывается так:
Если последний параметр поставить 1, то получим вероятность того, что нормальная случайная величина окажется меньше 15 при заданных параметрах распределения. Таким образом, вероятности можно рассчитывать напрямую по исходным данным.
Функция НОРМ.ОБР
Это квантиль нормального распределения, т.е. значение обратной функции. Синтаксис следующий.
=НОРМ.ОБР(вероятность;среднее;стандартное_откл)
вероятность – вероятность
среднее – матожидание
стандартное_откл – среднеквадратичное отклонение
Назначение то же, что и у НОРМ.СТ.ОБР, только функция работает с данными любого масштаба.
Пример показан в ролике в конце статьи.
Моделирование нормального распределения
Для некоторых задач требуется генерация нормальных случайных чисел. Готовой функции для этого нет. Однако В Excel есть две функции, которые возвращают случайные числа: СЛУЧМЕЖДУ и СЛЧИС. Первая выдает случайные равномерно распределенные целые числа в указанных пределах. Вторая функция генерирует равномерно распределенные случайные числа между 0 и 1. Чтобы сделать искусственную выборку с любым заданным распределением, нужна функция СЛЧИС.
Допустим, для проведения эксперимента необходимо получить выборку из нормально распределенной генеральной совокупности с матожиданием 10 и стандартным отклонением 3. Для одного случайного значения напишем формулу в Excel.
=НОРМ.ОБР(СЛЧИС();10;3)
Протянем ее на необходимое количество ячеек и нормальная выборка готова.
Для моделирования стандартизованных данных следует воспользоваться НОРМ.СТ.ОБР.
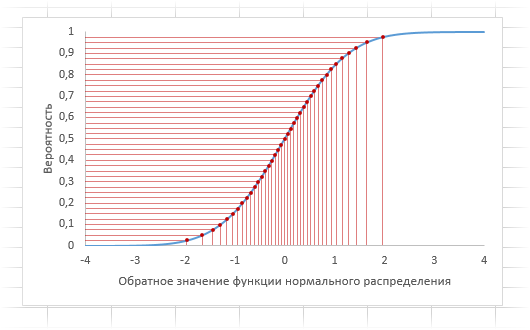
Процесс преобразования равномерных чисел в нормальные можно показать на следующей диаграмме. От равномерных вероятностей, которые генерируются формулой СЛЧИС, проведены горизонтальные линии до графика функции нормального распределения. Затем от точек пересечения вероятностей с графиком опущены проекции на горизонтальную ось.
На выходе получаются значения с характерной концентрацией около центра. Вот так обратный прогон через функцию нормального распределения превращает равномерные числа в нормальные. Excel позволяет за несколько секунд воспроизвести любое количество выборок любого размера.
Как обычно, прилагаю ролик, где все вышеописанное показывается в действии.
Скачать файл с примером.
Поделиться в социальных сетях: