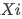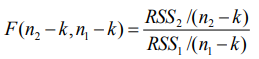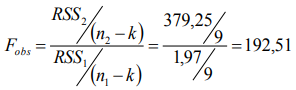|
адрес ячейки |
формула |
реализация в MS Excel |
|
сортировка по возрастанию |
||
|
=ДИСПР(G2:G9) |
||
|
=G10*$F$9 |
||
|
=G39/N39 |
||
|
|
=FРАСПОБР(0,05;(H27-H28-2*H29)/2;(H27-H28-2*H29)/2) |
4.3.3. Выводы по результатам проверки
предпосылки гомоскедастичности
возмущений. Оценка параметров
обобщенной линейной эконометрической
модели. На основании проведенных
расчетов делаем вывод (с надежностью
95%), что переменная
не является причиной гетероскедастичности
остатков модели, так как
.
Аналогично проводятся тесты
Гольфельда-Квандта по переменным
и
.
В результате получим, что
и
.
Следовательно, переменные
и
не являются причиной гетероскедастичности
остатков модели.
Можно заметить, что если из выборки
удалить два первых наблюдения
,
то по критерию
гипотеза о гетероскедастичности будет
отвергнута так как в этом случае
.
Модель, построенная по 22 наблюдениям,
будет иметь вид:
с коэффициентом детерминации
и средней относительной ошибкой
аппроксимации
и будет удовлетворять условию
гомоскедастичности.
Так как по критерию
массив данных
(24 наблюдения) признан гетероскедастичным
(при уровне значимости
),
а ни одна из переменных
,
,
не является источником гетероскедастичности,
то можно предположить, что причиной
гетероскедастичности являются факторы,
не учтенные в модели (3-ий случай — формула
(4.30)). Также следует отметить, что если
в тесте Гольфельда-Квандта по переменной
,
задать уровень значимости
то переменная
будет признана причиной гетероскедастичности
остатков модели, так как в этом случае
табличное значение
статистики
при уровне значимости
и степенях свободы
равно
и
.
Следовательно, для оценки параметров
необходимо использовать обобщённый
метод наименьших квадратов. Предположим,
что дисперсия остатков пропорциональна
квадрату значений переменной
(условие (4.29)). Тогда в матрице преобразований
(формула 4.27, ячейки
на рис. 4.14)
.
Используем оператор оценивания (4.29) для
оценки параметров ОМНК (рис. 4.14, 4.15).

Рис. 4.14. Расчет
параметров модели ОМНК.

Рис. 4.15. Расчет
матрицы
в ОМНК.
Таблица 4.5.
Реализация в MS Excel формул
при расчете параметров модели ОМНК
(рис. 4.14, 4.15)
|
адрес ячейки |
формула |
реализация в MS Excel |
|
G2=D2^2 |
||
|
|
=МОБР(G2:AD25) |
|
|
|
|
=ТРАНСП(B2:E25) |
|
|
|
=МУМНОЖ(B28:Y31;AG2:BD25) |
|
|
|
=МУМНОЖ(B34:Y37;B2:E25) |
|
|
|
=МОБР(B40:E43) |
|
|
|
=МУМНОЖ(B34:Y37;A2:A25) |
|
|
|
=МУМНОЖ(I40:L43;O40:O43) |
Модель, построенная ОМНК, будет иметь
вид:
с коэффициентом детерминации
и средней относительной ошибкой
аппроксимации
.
Так как в массиве данных наблюдалась
незначительная гетероскедастичность,
то качество моделей различаются
незначительно (1-2%). Для прогноза и
экономического анализа можно использовать
вторую или третью модель. Выберем,
например вторую модель. Рассчитаем ее
параметры матричным способом и используем
для прогноза и анализа.
Таблица 4.6.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Татьяна Олеговна Павловская
Эксперт по предмету «Экономика»
Задать вопрос автору статьи
Определение 1
Тест Голдфельда-Квандта (Goldfeld-Quandt test) – это процедура тестирования гетероскедастичности случайных ошибок в регрессионной модели, которая применяется при существовании основания полагать, что может быть пропорционально стандартное отклонение ошибок некоторой переменной.
Порядок проведения теста Голдфельда-Квандта
Самым распространенным видом гетероскедастичности является пропорциональность обычного отклонения возмущений от какой-либо объясняющей переменной.
Наиболее популярный формальный критерий – это критерий, предложенный Р. Квандтом и С. Голдфелдом. В процессе проведения проверки по данному критерию предполагается, что обычное отклонение распределения вероятностей случайной переменной в наблюдении $i$ будет прямо пропорционально $Xi$.
Сделаем домашку
с вашим ребенком за 380 ₽
Уделите время себе, а мы сделаем всю домашку с вашим ребенком в режиме online
Бесплатное пробное занятие
*количество мест ограничено
Основную и альтернативную гипотезы в тесте Голдфельда-Квандта можно сформулировать следующим образом:
$H_0$: гомоскедастичность, $H_1$ – гетероскедастичность.
Проведение теста включает следующие этапы:
-
Оценивается регрессия по всем существующим наблюдениям;
-
Выстраивается и анализируется график остатков. В отдельных случаях может появиться предположение о том, что дисперсия возмущений растет вместе с увеличением некоторой переменной, т.е. «подозрительная переменная»;
-
Упорядочиваются все наблюдения в соответствии с модулем «подозрительной переменной»;
-
Разделяются все наблюдения на 3 группы. В первой и третьей группах число наблюдений должно быть одинаковым;
-
Пренебрегают наблюдениями из средней группы, а по двум остальным n1 и n2 оцениваются отдельные регрессии и определяются для них суммы квадратов остатка RSS;
-
С использованием сумм квадратов остатков в оцененных регрессиях, рассчитывается тестовая статистика по следующей формуле:
Рисунок 1. Формула. Автор24 — интернет-биржа студенческих работ
«Тест Голдфельда-Квандта с примером» 👇
-
Сравнивается значение F-статистики и критическое;
-
В случае, если значение F-статистики выше критического, то отвергается нулевая гипотеза о гомоскедастичности.
Пример использования теста Голдфельда-Квандта
В качестве примера использования теста Голдфельда-Квандта рассмотрим зависимость расходов на образование($Y$) от объема ВВП ($X$) в отдельных странах мира в 1984 году.
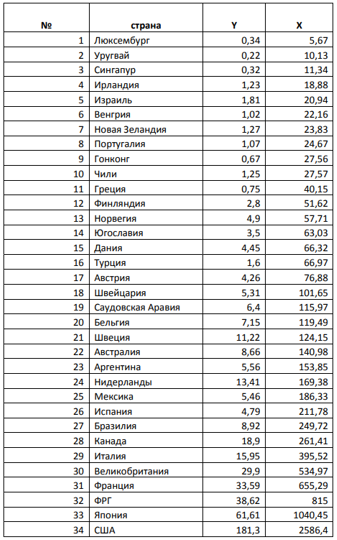
Необходимые исходные данные представлены на рисунке 2.
Рисунок 2. Исходные данные для теста. Автор24 — интернет-биржа студенческих работ
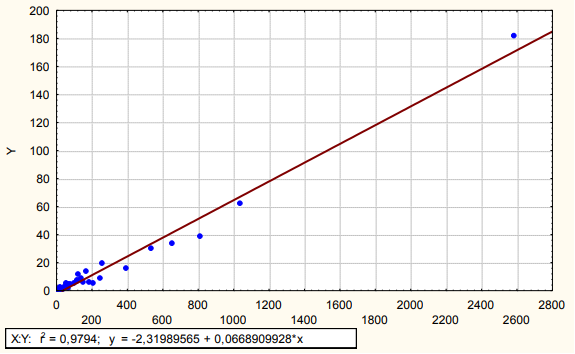
Для этого необходимо построить график зависимости (рис.3):
Рисунок 3. График зависимости. Автор24 — интернет-биржа студенческих работ
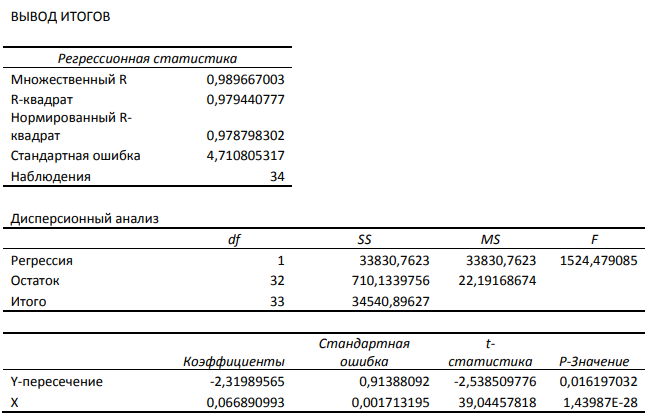
На рисунке 4 можно увидеть рецессию по всем имеющимся данным.
Рисунок 4. Рецессия. Автор24 — интернет-биржа студенческих работ
На рисунке 5 изображено поведение остатков в зависимости от $X$, что говорит о наличии гетероскедастичности.
Рисунок 5. Поведение остатков. Автор24 — интернет-биржа студенческих работ
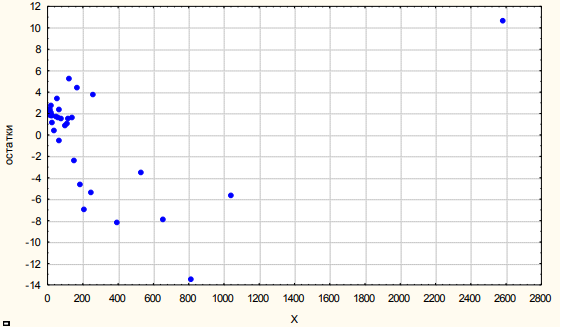
Необходимо взять первые и последние 11 наблюдений и построить вспомогательные регрессии (рис. 6 и 7)
Рисунок 6. До Греции включительно. Автор24 — интернет-биржа студенческих работ
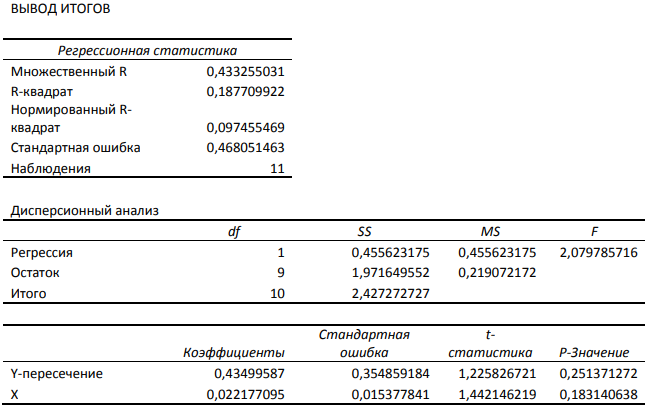
Рисунок 7. От Нидерландов. Автор24 — интернет-биржа студенческих работ
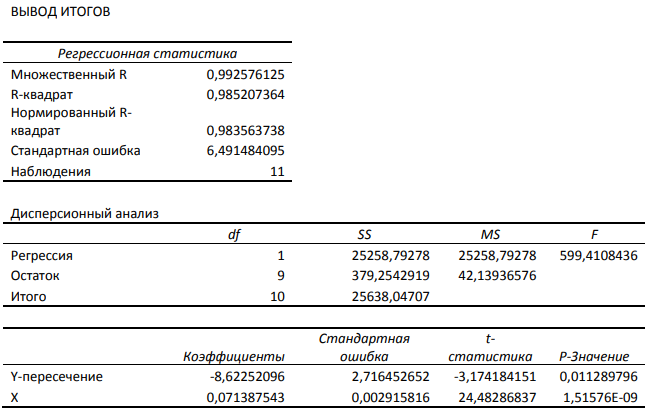
Производится расчет тестовой статистики (рисунок 8).
Рисунок 8. Значение тестовой статистики. Автор24 — интернет-биржа студенческих работ
Критическая точка будет равняться $F (0,05; 9; 9) = 3,18$
Таким образом, нулевая гипотеза по отношению к гомоскедастичности остатков будет отвергаться на 5%-ном уровне значимости.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Содержание:
Поскольку экономика стала серьезной самостоятельной наукой, исследователи пытаются дать представление о возможных путях экономического развития, предсказать ту или иную ситуацию, предсказать будущие значения экономических показателей, указать средства изменения ситуации в желаемом направлении. Однако в подавляющем большинстве случаев между экономическими переменными нет строгих корреляций.
Целью настоящей работы является установление взаимосвязи между такими факторами как: Потребление мяса, молока и молочных продуктов и среднедушевые доходы населения в Российской Федерации (79 регионов) для выявления.
Для проверки гипотезы о причинно-следственной связи между исследуемыми характеристиками были использованы следующие методы: График, корреляционная таблица и регрессионная модель. Построена эконометрическая модель, оценено ее качество и изучена проблема гетероскедастичности остатков. На основе этих методов формулируются утверждения о взаимосвязях между исследуемыми атрибутами.
Эконометрическая модель
Анализ множественной регрессии — это метод установления зависимости переменной от двух и более независимых переменных. Обычной формой представления данных является прямоугольная таблица, т.е. матрица, где каждая строка является результатом n наблюдений k характеристик на 1 объекте. Естественным требованием является то, что значения элементов этой матрицы должны быть одного типа.
Последствия неоднородности погрешностей:
Оценки дисперсии случайных величин (оценки коэффициентов линейной модели) оказываются смещенными.
Построенные доверительные интервалы не соответствуют заявленным уровням значимости.
Вычисленные значения коэффициентов — и — больше не могут рассматриваться как наблюдаемые значения случайных величин с распределениями — и -, соответствующими стандартным допущениям. Поэтому сравнение вычисленных значений коэффициентов — и — с квантилями этих — и — распределений может привести к статистически неверным выводам относительно гипотез о значениях коэффициентов линейной модели.
Тесты на гетероскедастичность проверяют основную гипотезу (т.е. модель гомоскедастична) против альтернативной гипотезы H1: а не H0 (т.е. модель гетероскедастична).
Помимо графических процедур, существует целый ряд процедур, предназначенных для проверки соответствия стандартных предположений о линейной модели наблюдений с использованием статистических критериев проверки гипотез. Мы сосредоточимся только на нескольких таких процедурах. Каждая из этих процедур принимает за нулевую гипотезу.
Однако соответствующие критерии адаптированы для выявления конкретных нарушений стандартных допущений, что делает каждый из критериев особенно чувствительным к нарушениям, на которые он «настраивается».
Тест Гольдфельда-Куандта (Goldfeld-Quandt) — это процедура тестирования гетероскедастичности случайных ошибок в регрессионной модели, применяемая в тех случаях, когда есть основания полагать, что может иметь место пропорциональное стандартное отклонение ошибок заданной переменной.
Последовательность теста Гольдфельда-Куандта
Наиболее распространенным типом гетероскедастичности является пропорциональность стандартного отклонения возмущений объясняющей переменной.
Самым известным формальным критерием является критерий Р. Квандта и С. Голдфельда. При проведении теста по данному критерию предполагается, что стандартное отклонение распределения вероятностей случайной величины при наблюдении i будет прямо пропорционально
Основные и альтернативные гипотезы в тесте Гольдфельда-Куандта могут быть сформулированы следующим образом:
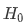
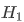
Тест включает в себя следующие этапы:
- Оценивается регрессия по всем имеющимся наблюдениям;
- Схематизация и анализ остатков. В некоторых случаях может существовать предположение, что дисперсия возмущений увеличивается с увеличением определенной переменной, т.е. «подозрительной переменной»;
- Все наблюдения упорядочены по модулю «подозрительная переменная»;
- Разделите все наблюдения на 3 группы. В первой и третьей группах количество наблюдений должно быть одинаковым;
- Наблюдениями из средней группы пренебрегают, для оставшихся двух n1 и n2 оценивают отдельные регрессии, а для них определяют суммы квадратов остатков RSS;
- Используя суммы квадратов остатков в расчетных регрессиях, тестовая статистика вычисляется по следующей формуле:
Рисунок 1: Формула.
- Сравниваются значения F-статистики и критического значения;
- Если значение F-статистики выше критического, то нулевая гипотеза о гомоскедастичности отвергается.
Пример использования теста Гольдфельда-Куандта
В качестве примера использования теста Гольдфельда-Куандта мы рассматриваем зависимость расходов на образование (Y) от ВВП (X) в отдельных странах мира в 1984 году.
Необходимые входные данные показаны на рисунке 2.
Рисунок 2: Входные данные для теста.
Для этого необходимо нарисовать диаграмму зависимости (рис. 3):
Рисунок 3: График зависимости.
На рисунке 4 мы видим рецессию для всех доступных данных.
Рисунок 4: Рецессия.
На рисунке 5 показано поведение остатков как функция Х, указывающая на наличие гетероскедастичности.
Рисунок 5. Поведение остатков.
Нужно взять первое и последние 11 наблюдений и построить вспомогательные регрессии (рис. 6 и 7).
Рисунок 6. до Греции включительно.
Рисунок 7: Из Нидерландов. Автор24 — Онлайн-рынок для студенческих исследовательских проектов
Вычисляется тестовая статистика (рис. 8).
Рисунок 8. значение статистики тестов.
Критическая точка тогда F(0.05;9;9)=3.18.
Таким образом, нулевая гипотеза отвергается с точки зрения гомоскедастичности остатков на 5%-м уровне значимости.
- Факторы и принципы оценки бизнеса — концепции, причины и суть
- Социально-экономическое равновесие — роль, особенности и определения
- Уровень технического развития средств производства в энергохозяйстве России — организация работы, особенности и энергетический сектор
- Особенности развития экономики России в период глобального экономического кризиса и после него — особенности кризиса, формы и периоды
- Значение антикризисного управления — концепция, необходимость, стратегия и важность
- Социальный бюджет — характеристика, концепция и виды
- Альтернативная стоимость — полезность, характеристики, закон и характер
- Рынок потребительского спроса — концепция, характер, определение и характеристики
17 авг. 2022 г.
читать 2 мин
Тест Гольдфельда-Квандта используется для определения наличия гетероскедастичности в регрессионной модели.
Гетероскедастичность относится к неравному разбросу остатков на разных уровнях переменной отклика в регрессионной модели.
Если присутствует гетероскедастичность, это нарушает одно из ключевых предположений линейной регрессии о том, что остатки одинаково разбросаны на каждом уровне переменной отклика.
В этом руководстве представлен пошаговый пример того, как выполнить тест Гольдфельда-Квандта в R, чтобы определить, присутствует ли гетероскедастичность в данной регрессионной модели.
Шаг 1: Постройте модель регрессии
Во-первых, мы построим модель множественной линейной регрессии, используя встроенный набор данных mtcars в R:
#fit a regression model
model <- lm(mpg~disp+hp, data=mtcars)
#view model summary
summary(model)
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 30.735904 1.331566 23.083 < 2e-16 ***
disp -0.030346 0.007405 -4.098 0.000306 ***
hp -0.024840 0.013385 -1.856 0.073679.
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 3.127 on 29 degrees of freedom
Multiple R-squared: 0.7482, Adjusted R-squared: 0.7309
F-statistic: 43.09 on 2 and 29 DF, p-value: 2.062e-09
Шаг 2. Выполните тест Гольдфельда-Квандта.
Далее мы будем использовать функцию gqtest() из пакета lmtest для выполнения теста Гольдфельда-Квандта, чтобы определить, присутствует ли гетероскедастичность.
Эта функция использует следующий синтаксис:
gqtest(модель, order.by, данные, дробь)
куда:
- модель: Модель линейной регрессии, созданная командой lm().
- order.by: предикторная переменная в модели.
- данные: имя набора данных.
- дробь*: количество центральных наблюдений, которые необходимо удалить из набора данных.
*Тест Голдфельда-Квандта работает, удаляя некоторое количество наблюдений, расположенных в центре набора данных, а затем проверяя, отличается ли разброс остатков от результирующих двух наборов данных, которые находятся по обе стороны от центральных наблюдений.
Обычно мы удаляем около 20% всех наблюдений. В этом случае у mtcars всего 32 наблюдения, поэтому мы можем удалить 7 центральных наблюдений:
#load lmtest library
library(lmtest)
#perform the Goldfeld Quandt test
gqtest(model, order.by = ~disp+hp, data = mtcars, fraction = 7)
Goldfeld-Quandt test
data: model
GQ = 1.0316, df1 = 10, df2 = 9, p-value = 0.486
alternative hypothesis: variance increases from segment 1 to 2
Вот как интерпретировать вывод:
- Статистика теста — 1,0316 .
- Соответствующее значение p равно 0,486 .
Тест Гольдфельда-Квандта использует следующие нулевые и альтернативные гипотезы:
- Null (H 0 ) : присутствует гомоскедастичность.
- Альтернатива ( HA ): присутствует гетероскедастичность.
Поскольку p-значение не меньше 0,05, мы не можем отвергнуть нулевую гипотезу. У нас нет достаточных доказательств того, что в регрессионной модели присутствует гетероскедастичность.
Что делать дальше
Если вы не можете отвергнуть нулевую гипотезу теста Гольдфельда-Квандта, тогда гетероскедастичность отсутствует, и вы можете приступить к интерпретации результатов исходной регрессии.
Однако если вы отвергаете нулевую гипотезу, это означает, что в данных присутствует гетероскедастичность. В этом случае стандартные ошибки, показанные в выходной таблице регрессии, могут быть ненадежными.
Есть несколько распространенных способов решить эту проблему, в том числе:
1. Преобразуйте переменную ответа.
Вы можете попробовать выполнить преобразование переменной ответа, например, взять логарифм, квадратный корень или кубический корень из переменной ответа. Как правило, это может привести к исчезновению гетероскедастичности.
2. Используйте взвешенную регрессию.
Взвешенная регрессия присваивает вес каждой точке данных на основе дисперсии ее подобранного значения. По сути, это дает небольшие веса точкам данных с более высокой дисперсией, что уменьшает их квадраты невязок.
При использовании правильных весов взвешенная регрессия может устранить проблему гетероскедастичности.
Дополнительные ресурсы
Как выполнить множественную линейную регрессию в R
Как выполнить тест Уайта в R
Как выполнить тест Бреуша-Пагана в R