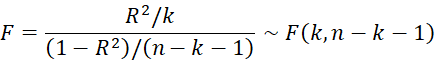A Breusch-Pagan Test is used to determine if heteroscedasticity is present in a regression analysis.
This tutorial explains how to perform a Breusch-Pagan Test in Excel.
Example: Breusch-Pagan Test in Excel
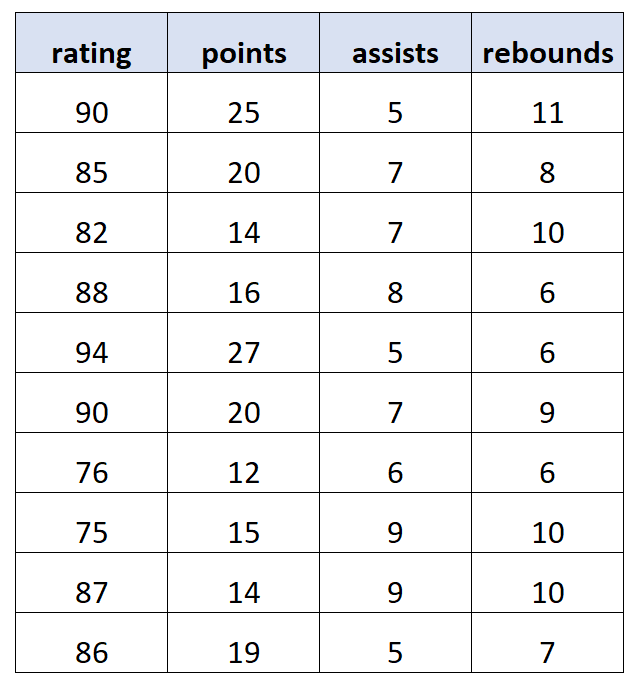
For this example we will use the following dataset that describes the attributes of 10 basketball players.
We will fit a multiple linear regression model using rating as the response variable and points, assists, and rebounds as the explanatory variables. Then we will perform a Breusch-Pagan Test to determine if heteroscedasticity is present in the regression.
Step 1: Perform multiple linear regression.
Along the top ribbon in Excel, go to the Data tab and click on Data Analysis. If you don’t see this option, then you need to first install the free Analysis ToolPak.
Once you click on Data Analysis, a new window will pop up. Select Regression and click OK. Fill in the necessary arrays for the response variables and the explanatory variables, then click OK.
This produces the following output:
Step 2: Calculate the squared residuals.
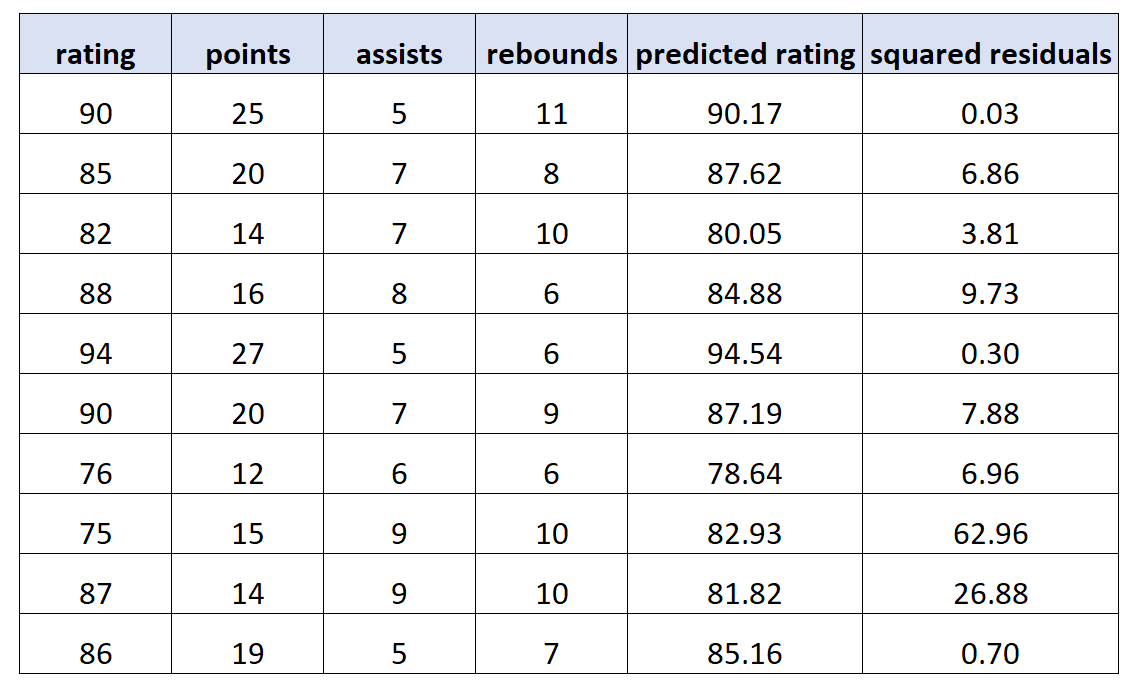
Next, we will calculate the predicted values and the squared residuals for each response value. To calculate the predicted values, we will use the coefficients from the regression output:
We will use the same formula to obtain each predicted value:
Next, we will calculate the squared residuals for each prediction:
We will use the same formula to obtain each squared residual:
Step 3: Perform a new multiple linear regression using the squared residuals as the response values.
Next, we will perform the same steps as before to conduct multiple linear regression using points, assists, and rebounds as the explanatory variables, except we will use the squared residuals as the response values this time. Here is the output of that regression:
Step 4: Perform the Breusch-Pagan Test.
Lastly, we will perform the Breusch-Pagan Test to see if heteroscedasticity was present in the original regression.
First we will calculate the Chi-Square test statistic using the formula:
X2 = n*R2new
where:
n = number of observations
R2new = R Square of the “new” regression in which the squared residuals were used as the response variable.
In our example, X2 = 10 * 0.600395 = 6.00395.
Next, we will find the p-value associated with this test statistic. We can use the following formula in Excel to do so:
=CHISQ.DIST.RT(test statistic, degrees of freedom)
In our case, the degrees of freedom is the number shown for df of regression in the output. In this case, it’s 3. Thus, our formula becomes:
=CHISQ.DIST.RT(6.00395, 3) = 0.111418.
Because this p-value is not less than 0.05, we fail to reject the null hypothesis. We do not have sufficient evidence to say that heteroscedasticity is present in the original regression model.
Тест Бреуша-Пагана: определение и пример
17 авг. 2022 г.
читать 3 мин
Одно из ключевых предположений линейной регрессии состоит в том, что остатки распределяются с одинаковой дисперсией на каждом уровне предиктора. Это предположение известно как гомоскедастичность .
Когда это предположение нарушается, говорят, что в остатках присутствует гетероскедастичность.Когда это происходит, результаты регрессии становятся ненадежными.
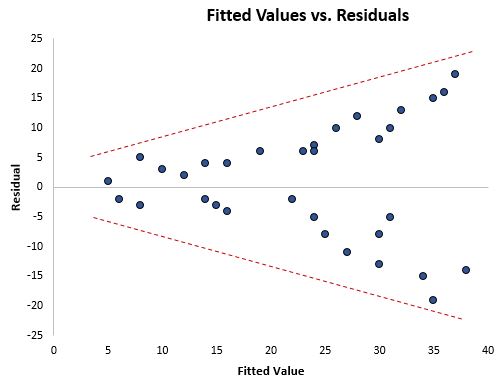
Один из способов визуально определить, присутствует ли гетероскедастичность, состоит в том, чтобы построить график остатков в зависимости от подогнанных значений регрессионной модели.
Если остатки становятся более разбросанными при более высоких значениях на графике, это явный признак наличия гетероскедастичности.
Формальный статистический тест, который мы можем использовать для определения наличия гетероскедастичности, — это тест Бреуша-Пагана .
Этот учебник содержит краткое объяснение теста Бреуша-Пагана вместе с примером.
Что такое тест Бреуша-Пагана?
Тест Бреуша-Пагана используется для определения наличия или отсутствия гетероскедастичности в регрессионной модели.
В тесте используются следующие нулевая и альтернативная гипотезы :
- Нулевая гипотеза (H 0 ): присутствует гомоскедастичность (остатки распределены с равной дисперсией)
- Альтернативная гипотеза ( HA ): присутствует гетероскедастичность (остатки не распределены с одинаковой дисперсией)
Если p-значение теста меньше некоторого уровня значимости (т. е. α = 0,05), то мы отклоняем нулевую гипотезу и делаем вывод, что в регрессионной модели присутствует гетероскедастичность.
Мы используем следующие шаги для выполнения теста Бреуша-Пагана:
1. Подберите регрессионную модель.
2. Рассчитайте квадраты невязок модели.
3. Подберите новую модель регрессии, используя квадраты невязок в качестве значений отклика.
4. Рассчитайте статистику критерия хи-квадрат X 2 как n*R 2 new , где:
- n: общее количество наблюдений
- R 2 new : R-квадрат новой регрессионной модели, в которой в качестве значений отклика использовались квадраты остатков.
Если значение p, соответствующее этой статистике критерия хи-квадрат с p (число предикторов) степеней свободы, меньше некоторого уровня значимости (т. е. α = 0,05), то нулевая гипотеза отвергается и делается вывод о наличии гетероскедастичности.
В противном случае не удастся отвергнуть нулевую гипотезу. В этом случае предполагается наличие гомоскедастичности.
Обратите внимание, что большинство статистических программ могут легко выполнить тест Бреуша-Пагана, поэтому вам, вероятно, никогда не придется выполнять эти шаги вручную, но полезно знать, что происходит за кулисами.
Пример теста Бреуша-Пагана
Предположим, у нас есть следующий набор данных, содержащий информацию о 10 разных баскетболистах:
Используя статистическое программное обеспечение, мы подогнали следующую модель множественной линейной регрессии :
рейтинг = 62,47 + 1,12*(очки) + 0,88*(передачи) – 0,43*(подборы)
Затем мы используем эту модель для прогнозирования рейтинга каждого игрока и рассчитываем квадраты остатков (т. е. квадрат разницы между прогнозируемым рейтингом и фактическим рейтингом):
Затем мы подгоняем новую модель регрессии, используя квадраты остатков в качестве значений отклика и исходные переменные-предикторы в качестве переменных-предикторов еще раз. Мы находим следующее:
- п: 10
- Р 2 новый : 0,600395
Таким образом, наша статистика критерия хи-квадрат для теста Бреуша-Пагана равна n*R 2 new = 10*0,600395 = 6,00395.Степени свободы — это p = 3 переменных-предиктора.
Согласно Калькулятору хи-квадрат для P-значения , p-значение, соответствующее X 2 = 6,00395 с 3 степенями свободы, составляет 0,111418 .
Поскольку это p-значение не меньше 0,05, мы не можем отвергнуть нулевую гипотезу. Таким образом, мы предполагаем, что гомоскедастичность присутствует.
Тест Бреуша-Пагана на практике
В следующих руководствах представлены пошаговые примеры выполнения теста Бреуша-Пагана в различных статистических программах:
Как выполнить тест Бреуша-Пагана в Excel
Как выполнить тест Бреуша-Пагана в R
Как выполнить тест Бреуша-Пагана в Python
Как выполнить тест Бреуша-Пагана в Stata
Suppose we have a sample {(Xi, yi): i = 1, …, n} of size n with k independent variables. We perform OLS regression based on this data and find the residuals ri based on the regression model. Next, perform OLS regression using the data {(Xi, ri2): i = 1, …, n} to find the coefficient of determination R2.
We test the null hypothesis that the original data is homoskedastic using the following test
Here, LM stands for the Lagrange Multiplier.
This test can only be used when your data is normally distributed; i.e. the residuals are normally distributed.
Essentially this test is testing whether the regression coefficients for all the independent variables are equal to zero. Thus, we can also use an F test comparing this second regression with the regression of the squared residuals only on the constant term. This is equivalent to the test
Example 1: Conduct the Breusch-Pagan test for the data in Example 2 of Multiple Regression Analysis using Excel.
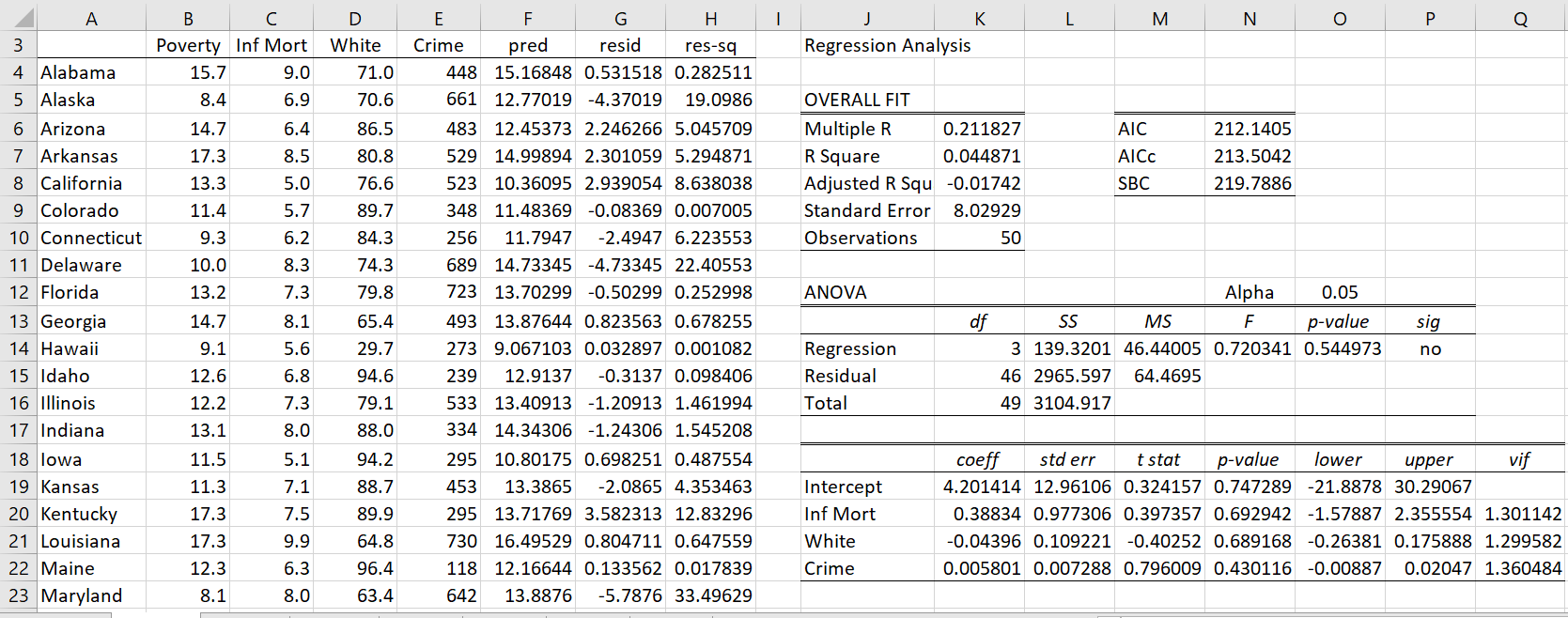
The data for the first 20 (of 50) states are shown in columns A through E of Figure 1.
Figure 1 – Breusch-Pagan Test (part 1)
Column F contains the predicted Poverty values for each state based on the linear regression of the Infant Mortality, White and Crime variables on Poverty. Here, range F4:F53 contains the array formula =TREND(B4:B53,C4:E53). Column G contains the residuals (i.e. the ri values); e.g. cell G4 contains the formula =B4-F4. Column H contains the squared residual values: e.g. cell H4 contains the formula =G4^2.
We now create the linear regression model with Infant Mortality, White and Crime as the independent variables and the squared residuals from column H as the dependent variable. The results are shown on the right side of Figure 1. We now use the results from this regression to conduct the Breusch-Pagan Test as shown in Figure 2.
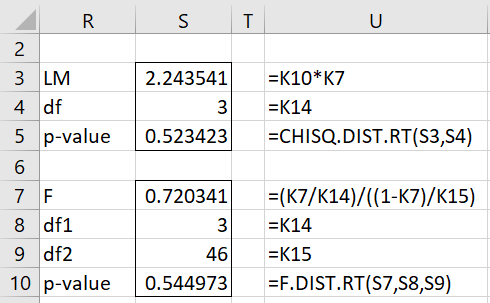
Figure 2 – Breusch-Pagan Test (part 2)
We see that the p-values of the two versions of the test are .52 and .54, which means there is no heteroskedasticity.
Real Statistics Functions: The following Real Statistics functions automate the Breusch-Pagan test in Excel.
BPagStat(R1, R2, chi) = Breusch-Pagan statistic for the X values in R1 and Y values in R2; if chi = TRUE (default) then the LM statistic is returned; otherwise the F statistic is returned.
BPagTest(R1, R2, chi) = p-value of the Breusch-Pagan test for the X values in R1 and Y values in R2; if chi = TRUE (default) then the chi-square test is used; otherwise the F test is used.
The values in Figure 1 can be achieved by placing the formulas
=BPagStat(C4:E53,B4:B53) in cell S3
=BPagTest(C4:E53,B4:B53) in cell S5
=BPagStat(C4:E53,B4:B53,FALSE) in S7
=BPagTest(C4:E53,B4:B53,FALSE) in S10
Скрипт в R для этого примера
Данные для этого примера.
Гетероскедастичность — это типичная «болезнь» пространственных данных, поэтому лучше по умолчанию исходить из того, что она в вашей модели есть. Тем не менее, иногда бывает полезно уметь аккуратно проверить её наличие. Для этого можно использовать два традиционных подхода: графический анализ данных и формальные статистические тесты.
Один из способов выявления гетероскедастичности при помощи графического анализа состоит в том, чтобы построить диаграммы рассеяния, в каждой из которых по оси ординат стоит зависимая переменная, а по оси абсцисс — один из регрессоров. Если, разглядывая подобную диаграмму, вы видите нечто похожее на рисунок 2.3б, то у вас есть гетероскедастичность, связанная с соответствующим регрессором. Другой вариант состоит в анализе графика остатков регрессии. Отсортируйте остатки по возрастанию какой-либо объясняющей переменной и постройте их график. Если разброс остатков вокруг нуля равномерен (как, например, на рис. 5.1), то можно заключить, что гетероскедастичность, связанная с этим регрессором, в данных отсутствует. Если же на графике остатков явно видно, что их разброс вокруг нуля зависит от значения регрессора (как, например, на рис. 5.2), значит, гетероскедастичность есть.
Рисунок 5.1. Поведение остатков регрессии говорит в пользу гомоскедастичности
Рисунок 5.2. Поведение остатков регрессии говорит в пользу гетероскедастичности
Анализ графиков не всегда позволяет сделать однозначный вывод по поводу наличия или отсутствия гетероскедастичности, поэтому помимо него могут быть полезны соответствующие формальные статистические тесты. Ниже приводятся два наиболее часто используемых в настоящее время теста.
Тест Бреуша — Пагана
Тестируемая гипотеза в данном тесте состоит в том, что гетероскедастичности в модели нет:
(H_{0}:{sigma_{1}^{2} = ldots = sigma_{n}^{2}})
Альтернативная гипотеза — дисперсия случайной ошибки (varepsilon_{i}) некоторым образом зависит от группы переменных:
(H_{1}:{sigma_{i}^{2} = {gamma_{0} + gamma_{1}}}{z_{i}^{(1)} + ldots + gamma_{p}}z_{i}^{(p)})
Здесь (z_{i}^{(1)},z_{i}^{(2)},ldots,z_{i}^{(p)}) — набор переменных, которые предположительно влияют на дисперсию случайной ошибки. Обычно в качестве таких переменных берутся регрессоры из исходной модели, а также их квадраты.
Процедура осуществления теста устроена так: сначала при помощи обычного МНК оценивается исходная модель (для которой мы хотим проверить отсутствие гетероскедастичности) и вычисляются соответствующие остатки (e_{i}). Далее вычисляется вспомогательное значение ({{overset{sim}{sigma}}^{2} = frac{1}{n}}{sum e_{i}^{2}}). После этого необходимо оценить вспомогательное уравнение, в котором справа стоят переменные, потенциально влияющие на дисперсию случайной ошибки:
({frac{e_{i}^{2}}{{overset{sim}{sigma}}^{2}} = {gamma_{0} + gamma_{1}}}{z_{i}^{(1)} + ldots + gamma_{p}}{z_{i}^{(p)} + u_{i}})
Далее вычисляется расчетное значение тестовой статистики по простой формуле: половина от объясненной суммы квадратов во вспомогательном уравнении.
Если верна нулевая гипотеза, то указанная статистика асимптотически имеет распределение Хи-квадрат с (p) степенями свободы. Поэтому, если расчетное значение больше критического значения, взятого из таблиц распределения (chi^{2}) с (p) степенями свободы для выбранного исследователем уровня значимости, то следует отвергнуть нулевую гипотезу и заключить, что в данных есть гетероскедастичность (необходимые таблицы доступны, например, в приложении к главе 6). В противном случае можно сделать вывод в пользу гомоскедастичности.
Тест Уайта
Тестируемая гипотеза в данном тесте снова состоит в том, что гетероскедастичности в модели нет:
(H_{0}:{sigma_{1}^{2} = ldots = sigma_{n}^{2}})
Альтернативная гипотеза — дисперсия случайной ошибки (varepsilon_{i}) произвольным (возможно, нелинейным) образом зависит от переменных модели.
Процедура теста устроена так: сначала при помощи обычного МНК оценивается исходная модель (для которой мы хотим проверить отсутствие гетероскедастичности) и вычисляются соответствующие остатки (e_{i}). После этого необходимо оценить вспомогательное уравнение, в котором слева стоит (e_{i}^{2}), а справа — константа, регрессоры исходного уравнения, их квадраты и попарные произведения1.
Далее вычисляется расчетное значение тестовой статистики по следующей формуле
({left( {R^{2}mathit{во}mathit{вспомогательном}mathit{уравнении}} right) ast n}.)
Если верна нулевая гипотеза, то указанная статистика асимптотически имеет распределение Хи-квадрат с (p) степенями свободы ((p) — число регрессоров во вспомогательном уравнении). Поэтому, если расчетное значение больше критического значения, взятого из таблиц распределения (chi^{2}) с (p) степенями свободы для выбранного исследователем уровня значимости, то следует отвергнуть нулевую гипотезу и заключить, что в данных есть гетероскедастичность. В противном случае можно сделать вывод в пользу гомоскедастичности2.
Закончить обсуждение вопроса выявления гетероскедастичности следует предостережением по поводу ложной гетероскедастичности. Ложной гетероскедастичностью называется ситуация, при которой формальные тесты указывают на наличие гетероскедастичности, однако в действительности дело вовсе не в ней, а в неверной спецификации уравнения. Хорошим примером может служить рисунок 4.5б, на котором представлена нелинейная зависимость между парой переменных. Если при этом ошибочно оценить линейную регрессию (соответствующая прямая линия изображена на рисунке), то статистические тесты будут говорить в пользу гетероскедастичности, так как поведение остатков технически будет зависеть от значения регрессора (см. нижний график на этом же рисунке). Однако в действительности гетероскедастичности в модели нет, а есть только нелинейная связь между переменными.
Важно различать истинную и ложную гетероскедастичность, так как они приводят к совершенно разным последствиям. Истинная гетероскедастичность не вызывает смещения оценок коэффициентов модели, в то время как ошибочная спецификация уравнения регрессии вызывает его, то есть является гораздо более серьезной проблемой.
Пример 5.3. Оценка эффективности использования удобрений (окончание)
Для модели, оцененной в примере 5.1, осуществите тест Уайта, используя пятипроцентный уровень значимости. Интерпретируйте полученные результаты.
Решение:
Результаты оценки вспомогательного уравнения для осуществления теста Уайта представлены ниже.
Тест Уайта на гетероскедастичностьМНК, использованы наблюдения 1-200
Зависимая переменная: квадраты остатков регрессии, оцененной в примере 5.1
Коэффициент Ст. ошибка t-статистика P-значение
--------------------------------------------------------------------
const -2270,16 5654,83 -0,4015 0,6886
FUNG1 0,482935 108,468 0,004452 0,9965
FUNG2 -150,789 95,3876 -1,581 0,1158
GIRB 1,82902 98,0229 0,01866 0,9851
INSEC 129,035 72,6436 1,776 0,0775 *
LABOUR 2,05511 4,84800 0,4239 0,6722
YDOB1 30,5354 43,6171 0,7001 0,4849
YDOB2 3,43369 50,1279 0,06850 0,9455
квадрат_FUNG1 0,0956897 0,0549105 1,743 0,0833 *
FUNG1*FUNG2 0,0294522 0,0492979 0,5974 0,5510
FUNG1*GIRB -0,0332633 0,0480171 -0,6927 0,4895
FUNG1*INSEC 0,0229300 0,0554156 0,4138 0,6796
FUNG1*LABOUR -0,00259087 0,00348456 -0,7435 0,4582
FUNG1*YDOB1 0,0104778 0,0246791 0,4246 0,6717
FUNG1*YDOB2 -0,0536699 0,0501448 -1,070 0,2861
квадрат_FUNG2 0,0919819 0,0646201 1,423 0,1565
FUNG2*GIRB -0,0931636 0,0529473 -1,760 0,0803 *
FUNG2*INSEC -0,0878293 0,0548646 -1,601 0,1113
FUNG2*LABOUR -0,00520969 0,00419928 -1,241 0,2165
FUNG2*YDOB1 0,0829467 0,0471221 1,760 0,0802 *
FUNG2*YDOB2 -0,0118900 0,0437395 -0,2718 0,7861
квадрат_GIRB -0,0598434 0,0581283 -1,030 0,3048
GIRB*INSEC -0,0361947 0,0561232 -0,6449 0,5199
GIRB*LABOUR 0,00279620 0,00413522 0,6762 0,4999
GIRB*YDOB1 0,0287539 0,0384965 0,7469 0,4562
GIRB*YDOB2 0,0537695 0,0489420 1,099 0,2735
квадрат_INSEC -0,0406052 0,0570708 -0,7115 0,4778
INSEC*LABOUR -0,00562133 0,00477862 -1,176 0,2412
INSEC*YDOB1 0,0367439 0,0296061 1,241 0,2163
INSEC*YDOB2 -0,0599689 0,0474392 -1,264 0,2080
квадрат_LABOUR -0,000342326 0,000950427 -0,3602 0,7192
LABOUR*YDOB1 -0,00130669 0,00215676 -0,6059 0,5454
LABOUR*YDOB2 0,00492378 0,00240166 2,050 0,0419 **
квадрат_YDOB1 -0,0176598 0,00913794 -1,933 0,0550 *
YDOB1*YDOB2 -0,0352604 0,0255207 -1,382 0,1690
квадрат_YDOB2 0,0194422 0,0232499 0,8362 0,4042
Неисправленный R-квадрат = 0,280856
Тестовая статистика: n*R-квадрат = 56,171138,
р-значение = P(Хи-квадрат(35) > 56,171138) = 0,013059
В учебных целях мы привели оцененное уравнение полностью, хотя обычно в этом нет нужды, так как для осуществления теста достаточно знать только количество переменных в этом уравнении, его R-квадрат и число наблюдений. Обратите внимание, что число регрессоров тут действительно велико из-за добавления квадратов и попарных произведений переменных из исходного уравнения.
В нашем случае P-значение для осуществляемого теста (представленное в самом низу таблицы с результатами) составляет 0,013. Это меньше, чем 0,05. Поэтому при уровне значимости 5% следует отвергнуть нулевую гипотезу данного теста. Напомним, что нулевая гипотеза теста Уайта состоит в том, что в модели нет гетероскедастичности. Следовательно, отвергая её, мы должны заключить: в нашем случае в данных наблюдается гетероскедастичность.
-
Обратите внимание, что добавлять нужно только такие квадраты и попарные произведения, включение которых в модель не приводит к чистой мультиколлинеарности. Например, квадраты фиктивных переменных добавлять не стоит, так как они будут принимать в точности такие же значения, что и исходные переменные ((0^{2} = 0) и (1^{2} = 1)).↩︎
-
В XX веке для выявления гетероскедастчиности использовался широкий спектр альтернативных тестов: Голдфелда — Квандта, Спирмена, Глейзера и Парка. Они остались за рамками этой книги, поскольку в современных исследованиях применяются редко.↩︎
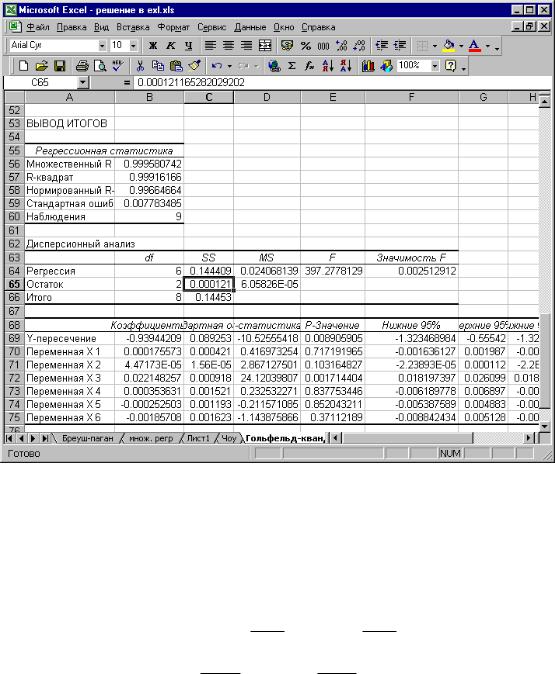
Рис. 3.16. Регрессия по последним 9 наблюдениям
Найдем статистику (3.5):
|
Fнабл = |
QII |
= |
0.000121 |
= 0.3 . |
|
ост |
||||
|
QI |
0.0004 |
|||
|
ост |
Так как
Fнабл = 0,3 < Fкрит (α;ν1 = n −2 d −k −1;ν2 = n −2 d −k −1) =
= Fкрит (0.05;ν1 = 252−7 −6 −1;ν2 = 252−7 −6 −1) =19,
то гипотеза о гомоскедастичности не отвергается.
Следует заметить, что переменная Х1 гомоскедастична, но это не значит, что по всем остальным переменным модель может быть гетероскедастичной. Поэтому необходима дальнейшая проверка по остальным переменным.
Предполагается, что дисперсия случайной ошибки зависит от
нескольких независимых переменных.
si2=γ0+γ1zi1+γ2zi2+…+γmzim.
Этапы тестирования:
1.Рассчитывают МНК-оценки коэффициентов регрессии.
2.Находят остатки ei.
3.Находят квадраты остатков ei2.
4.Рассчитывают коэффициент детерминации R2 для регрессии
|
ei2 = γ0+γ1zi1+γ2zi2+…+γmzim. |
|
|
5. Вычисляют X2набл = n R2. |
(3.6) |
6.Если X2набл превосходит критическое значение статистики Хи-квадрат для m степеней свободы, гетероскедастичность присутствует.
Задача 7
По данным таблицы 3.2 проверить гипотезу о гетероскедастичности, используя тест Бреуша-Пагана.
Решение
Рассчитаем регрессию по всем шести переменным, в результате получим регрессию (рис. 3.10). При построении регрессии необходимо вывести остатки ei, для этого следует поставить флажок «Остатки» в параметрах Регрессии (рис. 2.15).
В результате получим таблицу остатков. Найдем квадраты остатков
(рис. 3.17).

Рис. 3.17. Вывод остатка регрессии
Затем строим регрессию, в которой за зависимую переменную берется столбец квадратов остатков еi2, а за зависимые переменные –переменные Х1,
Х2, Х3, Х4, Х5, Х6.
Результат представлен на рис. 3.18.

Рис. 3.18. Вывод остатка регрессии
Найдена статистика (3.6): Χ2набл = nR2 = 25 0,68 =17,15 .
Так как Х2набл=17,15> Х2крит =12,59, то гипотеза о гомоскедастичности отвергается и модель считается гетероскедастичной.
Критическое значение распределения Хи-квадрат найдено с помощью действий: fx→Статистические→ХИ2ОБР(m), где m – число переменных, входящих в уравнение регрессии (в данном случае 6).
Тест Вайта (White)
Этот тест аналогичен тесту Бреуша-Пагана. В качестве независимых переменных используются все регрессоры, их квадраты и попарные
произведения.
si2=γ0+γ1xi1+γ2xi2+…+γkxik+ γk+1xi1 xi2+ γk+2xi1 xi3 +…+ γmxik2.
Этапы тестирования:
1.Рассчитывают МНК-оценки коэффициентов регрессии.
2.Находят остатки ei.
3.Находят квадраты остатков ei2.
4.Находят оценку остаточной дисперсии Sˆ 2 .
5.Рассчитывают R2 для регрессии

|
e |
2=γ |
+γ x +γ x +…+γ x + γ |
x |
x + γ |
x |
x +…+ γ x |
2. |
||
|
i |
0 |
1 i1 2 i2 |
k ik |
k+1 i1 |
i2 |
k+2 i1 |
i3 |
m |
ik |
|
6. Вычисляют X2набл = nR2. |
(3.7) |
7.Если X2набл превосходит критическое значение статистики Хи-квадрат для m степеней свободы, то гетероскедастичность присутствует.
Задача 8
По данным таблицы 3.2 проверить гипотезу о гетероскедастичности, используя тест Вайта.
Решение
Так как число переменных, входящих в уравнение не может быть больше 16, оставим только первые четыре переменных. В таблице построим данные, соответствующие квадратам переменных и их перекрестным произведениям (рис. 3.19).
Рис. 3.19. Данные для построения регрессии
Построим уравнение регрессии для этих переменных. Получим коэффициент детерминации, равный 0,98 (рис. 3.20).

Рис. 3.20. Расчет теста Вайта
Рассчитаем статистику по формуле (3.7).
Так как X2набл = nR2=24,64 > Х2крит =22,36 для числа степеней свободы, равного 13, то гипотеза о гомоскедастичности отвергается и модель можно считать гетероскедастичной.
3.5.2. Коррекция на гетероскедастичность
Рассмотрим модель:
yi = β0 + β1 xi +ui .
Пусть ошибки ui не коррелированны, но характеризуются разной дисперсией:
|
то есть модель гетероскедастична. |
D( ui ) =σi2 , |
||||
|
ошибок u имеет вид: |
|||||
|
Матрица ковариаций |
W |
вектора |
|||
|
2 |
0 … |
0 |
|||
|
σ1 |
|||||
|
0 |
σ22 … |
0 |
|||
|
Ω = |
… |
. |
|||
|
… … … |
|||||
|
0 |
0 … |
2 |
|||
|
σn |
Формула обобщенного метода наименьших квадратов
b = (X T Ω−1 X )−1 X T Ω−1Y
сводится к взвешенному методу наименьших квадратов, так как матрица
|
2 |
0 … |
0 |
||||||
|
1/σ1 |
||||||||
|
Ω |
-1 |
имеет простой вид:Ω |
−1 |
0 |
1/σ22 … |
0 |
||
|
= |
… … … |
. |
||||||
|
… |
||||||||
|
0 |
0 … |
2 |
||||||
|
1/σn |
Если s2i – известны, то получить модель с гомоскедастичными остатками можно, использовав в качестве весов наблюдений величины 1/σi .
Разделим каждую строку матрицы данных на σi:
|
yi |
= β0 |
1 |
+ β1 |
xi |
+ |
ui |
. |
(3.8) |
||||
|
σ |
||||||||||||
|
σ |
i |
i |
σ |
i |
σ |
i |
||||||
В результате получим преобразованную модель:
|
yi′ = β0 |
1 |
+ β1 xi′ |
+εi . |
(3.9) |
||||||||||||||
|
σ |
||||||||||||||||||
|
i |
||||||||||||||||||
|
Найдем дисперсию D(εi): |
σi2 |
|||||||||||||||||
|
D(εi ) = D ( |
ui |
) = |
D(ui ) |
= |
=1. |
|||||||||||||
|
σi2 |
σi2 |
|||||||||||||||||
|
σi |
||||||||||||||||||
|
В итоге получим пересмотренную модель: |
||||||||||||||||||
|
yi′ = β0 hi + β1 xi′ +εi , |
(3.10) |
|||||||||||||||||
|
yi |
1 |
xi |
ui |
|||||||||||||||
|
где |
yi′ = |
, |
hi = |
, |
xi′ = |
, εi = |
. |
|||||||||||
|
σi |
σi |
σi |
σi |
Заметим, что модель (3.10) не включает свободный член, bi –
коэффициент регрессии при новой переменной h.
На практике дисперсии ошибок почти никогда не известны.
Однако, иногда можно предположить, что σ2i пропорциональны некоторой переменной Zi.
yi = β0 + β1 xi +ui
D ui = σi2
σi = λZi .
Тогда в качестве весов наблюдений следует использовать величину 1/zi:
|
yi |
= β0 |
1 |
+ β1 |
zi |
+ |
ui |
. |
||||||||||||
|
zi |
zi |
zi |
zi |
||||||||||||||||
|
В итоге получим пересмотренную модель: |
|||||||||||||||||||
|
где |
yi′ = β0 hi + β1 xi′ +εi , |
(3.11) |
|||||||||||||||||
|
yi |
1 |
xi |
ui |
||||||||||||||||
|
yi′ = |
, |
hi = |
, |
xi′ = |
, εi |
= |
. |
(3.12)Подобрать простое |
|||||||||||
|
zi |
zi |
zi |
zi |
преобразование для того, чтобы добиться гомоскедастичности удается не всегда.Часто гетероскедастичность является сигналом о неправильной функциональной форме модели.
В общем случае для коррекции гетероскедастичности используют следующую процедуру:

|
1. |
Рассчитывают МНК-оценки коэффициентов регрессии. |
|||||||
|
2. |
Находят остатки ei. |
|||||||
|
3. |
Находят квадраты остатков e 2. |
|||||||
|
i |
||||||||
|
4. |
Находят логарифмы квадратов остатков ln(e |
2). |
||||||
|
i |
||||||||
|
5. |
Рассчитывают регрессиюln(ei2) = γ0+γ0zi1+γ0zi2+…+γ0zik+ui. |
|||||||
|
7. |
Получают |
прогноз |
ln(ei2)пр.Находят |
веса |
наблюдений |
|||
|
w = |
exp(ln(e2 |
прогноз |
)) . |
|||||
|
i |
i |
9.Полученные веса wi используют во взвешенном методе наименьших квадратов.
Задача 9
Для регрессии, рассчитанной по таблице 3.2 сделать коррекцию на гетероскедастичность.
Решение
Регрессия, рассчитанная в задаче 5 имеет вид:
уˆ = −0,6423−0,0005x1 +0,000043x2 +0,01858х3 + +0,00133х4 −0,0014х5 +0,00022х6.
Модель гетероскедастична согласно тесту Бреуша-Пагана (задача 7). Возможно, что модель имеет неправильную форму.
Построим модель
logY = β0 +log β1 X1 + β2 log X 2 +… + βk log X k +ε
и модель
logY = β0 + β1 X1 + β2 X 2 +… + βk X k +ε .
Проверим для каждой гипотезу о гетероскедастичности тестом БреушаПагана. Проделайте это самостоятельно, для нахождения логарифмов воспользуйтесь функцией: fx→Математические→LOG.
Сделаем коррекцию на гетероскедастичность, используя взвешенный метод наименьших квадратов.
Рассчитываем МНК-оценки коэффициентов регрессии, найдем остатки ei (не забудьте при нахождении регрессии поставить флажок «Остатки» в параметрах Регрессии).
Найдем квадраты остатков ei2, логарифмы квадратов остатков ln(ei2)
(рис.3.21).

Рис. 3.21. Нахождение логарифмов квадратов остатков
Построим регрессию от логарифмов остатков, независимые
переменные – значения Х1, Х2, Х3, Х4, Х5, Х6.
ln(ei2) = γ0+γ0zi1+γ0zi2+…+γ0zik+ui.

Найдем прогноз ln(ei2)пр и веса наблюдений wi = exp(ln(ei2 прогноз )) (рис.
3.22).
Рис. 3.22. Нахождение весов wi
Рассчитанные веса wi используют во взвешенном методе наименьших квадратов.
Преобразуем имеющиеся по условию данные. Поделим каждое значение таблицы на соответствующие веса, при этом по строке деление на вес не меняется, а по столбцу – меняется. Не забудьте клавишу F4 — при необходимости нажмите на нее два или три раза.
Получим преобразованные данные рис. 3.23 (обратите внимание на строку формул). Дополнительно необходимо построить столбец 1/Вес.

Рис. 3.23. Преобразование данных
Построим регрессию без свободного члена. Для этого в окне «Константа-ноль» поставьте флажок.
Получим результаты регрессии (рис. 3.24). Это модель гомоскедастична, ее коэффициенты имеют ту же самую интерпретацию, а стандартные ошибки более точные:
уˆ′= −0,618 1 −0,00036x1′ +0,0x2′ +0,018х3′ + wi
+0,0014х4′ −0,0014х5′ −0,00026х6′.
Как видно из модели значения коэффициентов поменялось незначительно, однако переменная х5 стала значимой, а х6 – поменяла знак.

Рис. 3.24. Регрессия, построенная взвешенным МНК
На значение коэффициента детерминации при взвешенном МНК обращать внимание не следует.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #