|
Автор: |
Проверьте Ваши знания и навыки работы в электронных таблицах Microsoft Excel. Задания теста основаны на реальных задачах по анализу и визуализации данных. Тест состоит из 10 вопросов, позволяющих осуществлять контроль знаний и проверку навыков работы в программе по следующим темам: • Применение категории встроенных функций «Ссылки и Массивы» и формул массивов • Прогнозирование данных • Диаграммы • Вариативный анализ «Что Если» и Оптимизация • Кубы данных OLAP для оперативного анализа данных в MS Excel Для успешной сдачи теста необходимо правильно ответить на 7 вопросов.
» Рекомендуемые курсы:
После прохождения теста сертификат тестирования не выдается Тест доступен после регистрации |
Статистика
|
Двухвыборочный t-критерий используется для проверки того, равны ли средние значения двух совокупностей.
В этом руководстве объясняется, как провести t-критерий с двумя образцами в Excel.
Как провести двухвыборочный t-тест в Excel
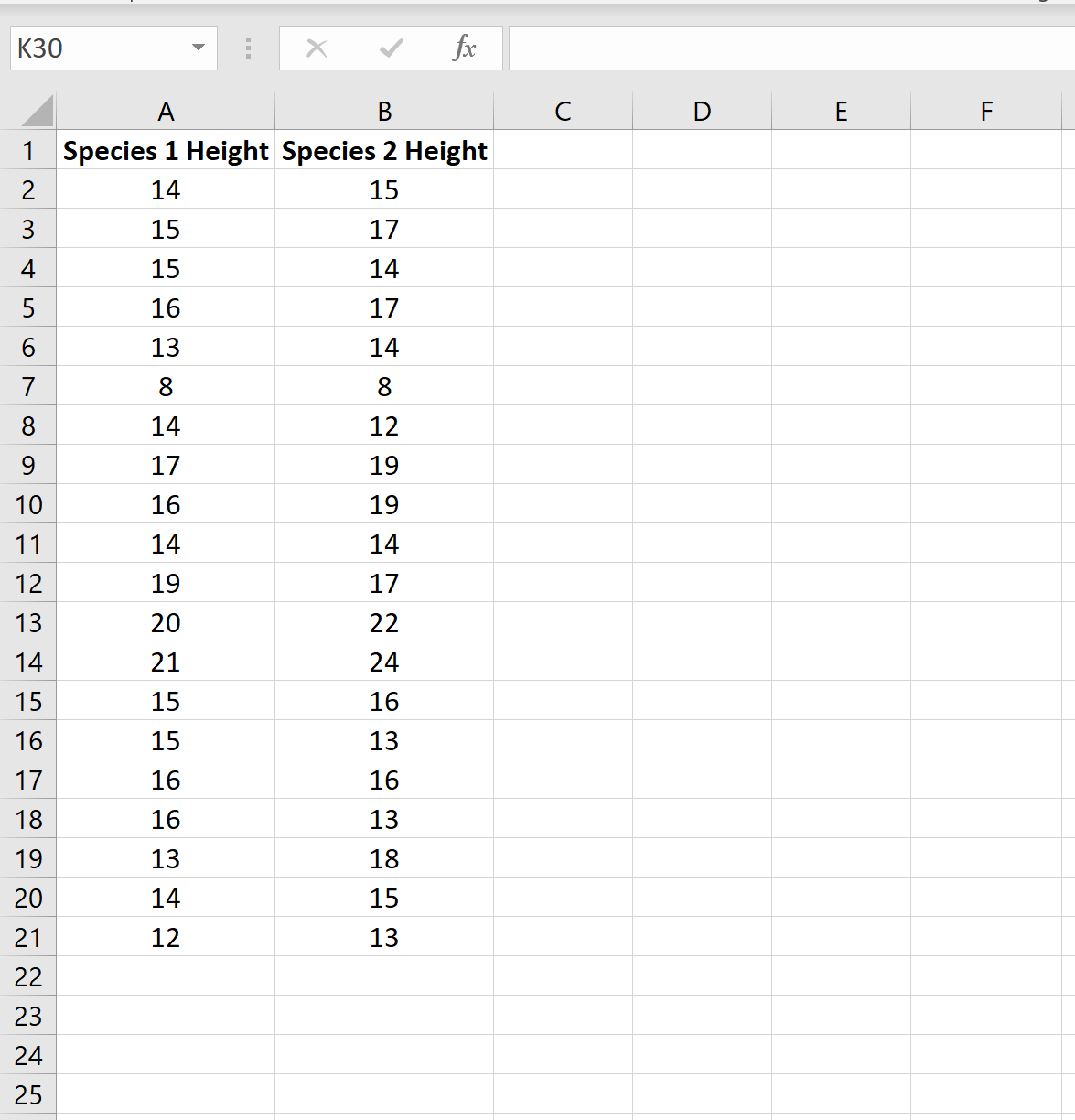
Предположим, исследователи хотят знать, имеют ли два разных вида растений в определенной стране одинаковую среднюю высоту. Поскольку обход и измерение каждого растения заняло бы слишком много времени, они решили собрать образец из 20 растений каждого вида.
На следующем изображении показана высота (в дюймах) каждого растения в каждом образце:
Мы можем провести двухвыборочный t-тест, чтобы определить, имеют ли два вида одинаковую среднюю высоту, используя следующие шаги:
Шаг 1: Определите, равны ли дисперсии генеральной совокупности .
Когда мы проводим двухвыборочный t-критерий, мы должны сначала решить, будем ли мы предполагать, что две совокупности имеют равные или неравные дисперсии. Как правило, мы можем предположить, что совокупности имеют равные дисперсии, если отношение большей выборочной дисперсии к меньшей выборочной дисперсии составляет менее 4:1.
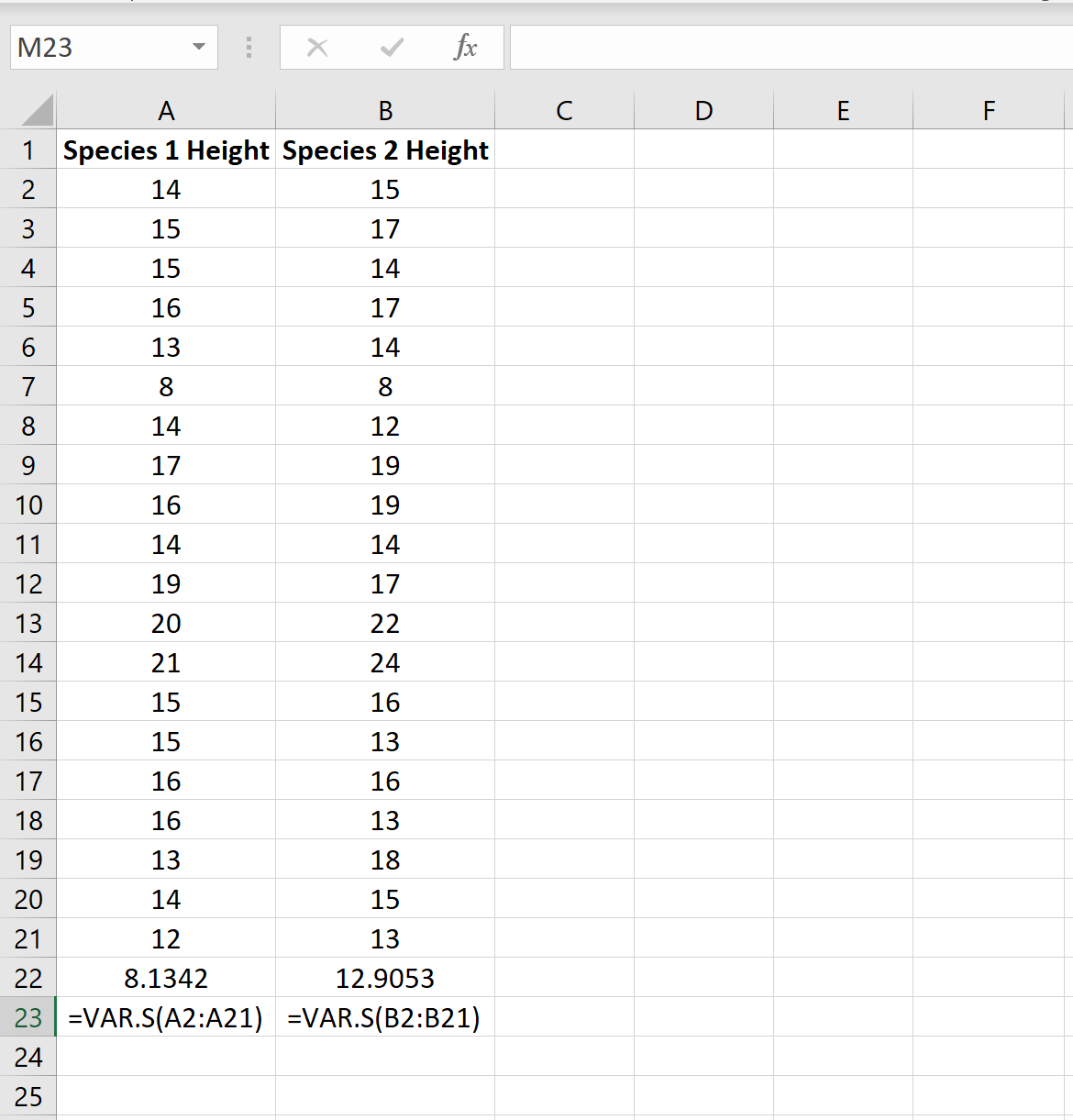
Мы можем найти дисперсию для каждого образца, используя функцию Excel =VAR.S(диапазон ячеек) , как показано на следующем рисунке:
Отношение большей дисперсии выборки к меньшей дисперсии выборки составляет 12,9053 / 8,1342 = 1,586 , что меньше 4. Это означает, что мы можем предположить, что дисперсии генеральной совокупности равны.
Шаг 2: Откройте пакет инструментов анализа .
На вкладке «Данные» на верхней ленте нажмите «Анализ данных».
Если вы не видите этот вариант для выбора, вам необходимо сначала загрузить пакет инструментов анализа , который является совершенно бесплатным.
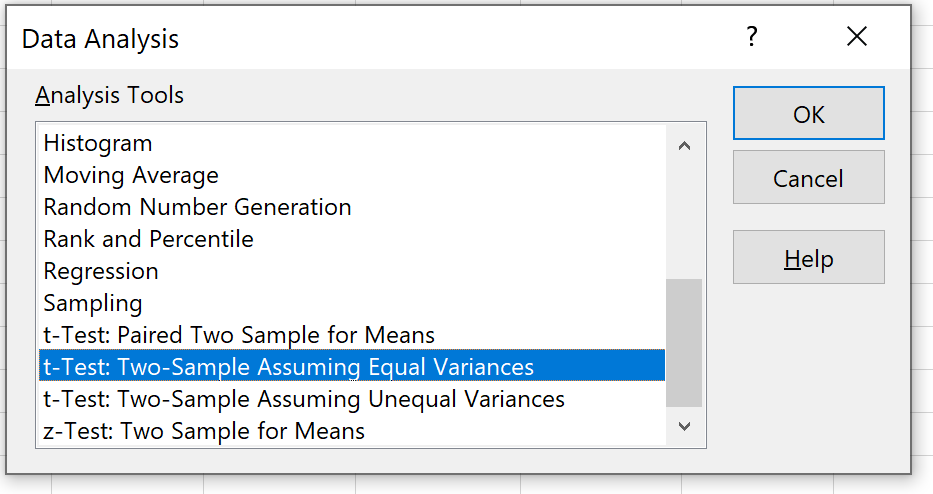
Шаг 3: Выберите подходящий тест для использования.
Выберите вариант с надписью t-Test: Two-Sample Assassining Equal Variances и нажмите OK.
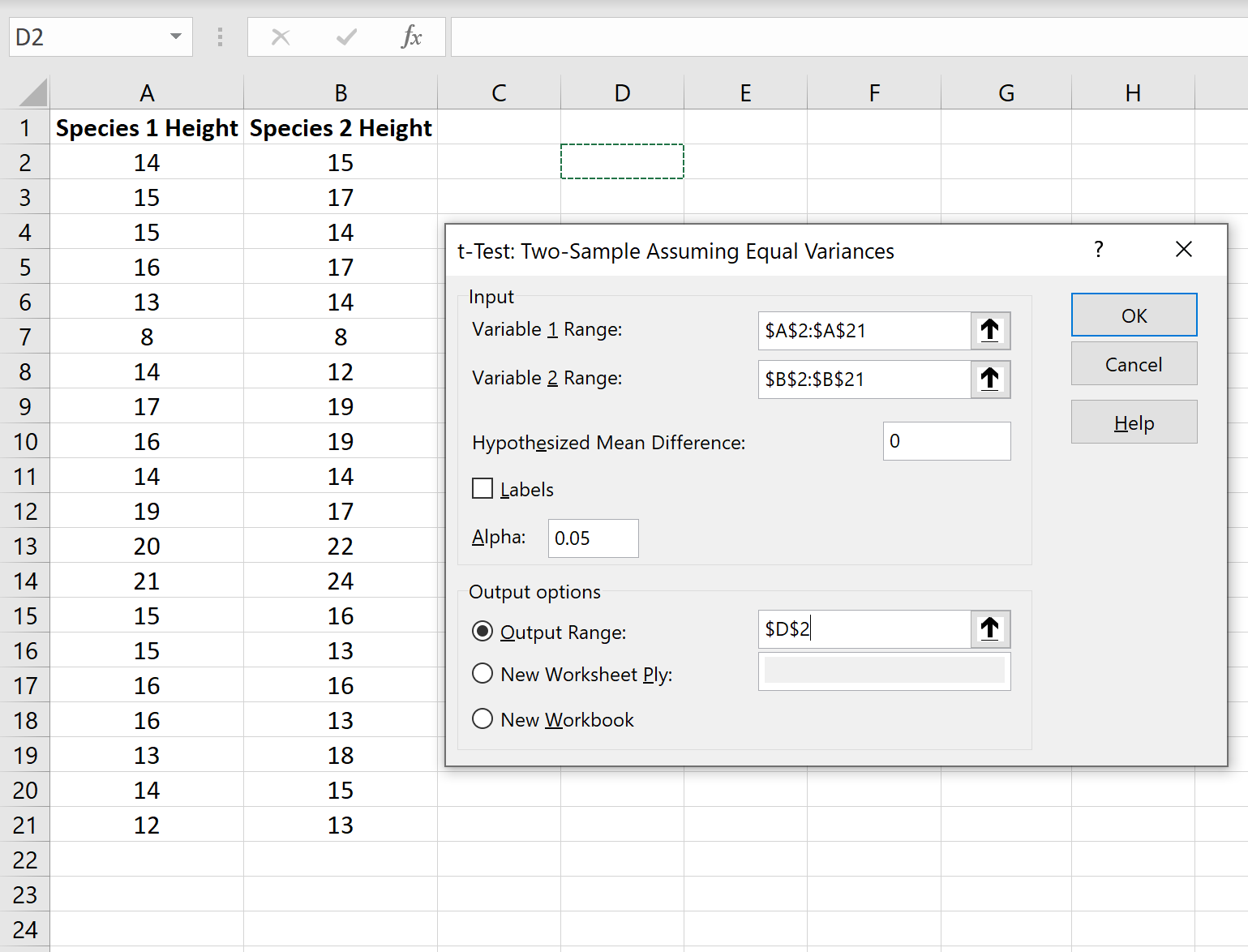
Шаг 4: Введите необходимую информацию .
Введите диапазон значений для переменной 1 (наша первая выборка), переменной 2 (наша вторая выборка), гипотетической средней разницы (в этом случае мы поместили «0», потому что мы хотим знать, равна ли истинная средняя разница генеральной совокупности 0), и выходной диапазон, в котором мы хотели бы видеть результаты t-теста. Затем нажмите ОК.
Шаг 5: интерпретируйте результаты .
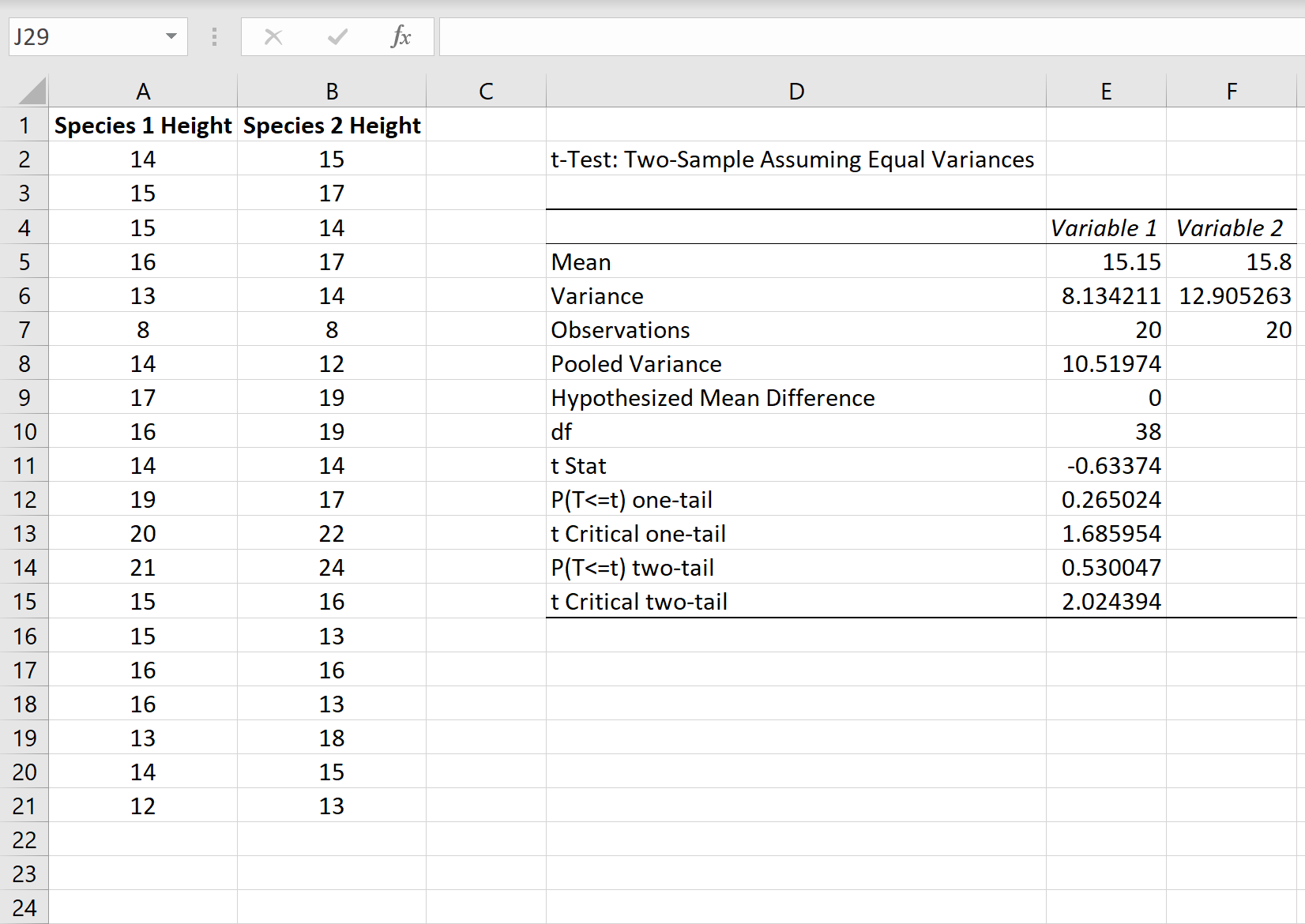
После того, как вы нажмете OK на предыдущем шаге, отобразятся результаты t-теста.
Вот как интерпретировать результаты:
Среднее значение: это среднее значение для каждого образца. Образец 1 имеет среднюю высоту 15,15 , а образец 2 имеет среднюю высоту 15,8 .
Дисперсия: это дисперсия для каждого образца. Выборка 1 имеет дисперсию 8,13 , а выборка 2 — 12,90 .
Наблюдения: это количество наблюдений в каждой выборке. Обе выборки содержат по 20 наблюдений (например, по 20 отдельных растений в каждой выборке).
Объединенная дисперсия: Число , которое рассчитывается путем «объединения» дисперсий каждой выборки вместе по формуле +n 2 -2), что оказывается равным 10,51974.Это число позже используется при вычислении тестовой статистики t .
Гипотетическая средняя разница: число, которое мы «предполагаем», представляет собой разницу между двумя средними значениями совокупности. В данном случае мы выбрали 0 , потому что хотим проверить, равна ли разница между двумя популяциями в среднем 0, например, разницы нет.
df: Степени свободы для t-критерия, рассчитанные как n 1 + n 2 -2 = 20 + 20 – 2 = 38 .
t Stat: тестовая статистика t , рассчитанная как t = [ x 1 – x 2 ] / √ [ s 2 p (1/n 1 + 1/n 2 )]
В этом случае t = [15,15-15,8] / √ [10,51974(1/20+1/20)] = -0,63374 .
P(T<=t) двухсторонний: значение p для двустороннего t-критерия. В этом случае р = 0,530047.Это намного больше, чем альфа = 0,05, поэтому мы не можем отвергнуть нулевую гипотезу. У нас нет достаточных доказательств, чтобы сказать, что два средних значения населения различны.
t Критический двухсторонний: это критическое значение теста, найденное путем определения значения в таблице распределения t , которое соответствует двустороннему тесту с альфа = 0,05 и df = 38. Получается 2,024394.Поскольку наша тестовая статистика t меньше этого значения, мы не можем отвергнуть нулевую гипотезу. У нас нет достаточных доказательств, чтобы сказать, что два средних значения населения различны.
Обратите внимание, что подход с использованием p-значения и критического значения приведет к одному и тому же выводу.
Дополнительные ресурсы
В следующих руководствах объясняется, как выполнять другие типы t-тестов в Excel:
Как провести одновыборочный t-тест в Excel
Как провести t-тест для парных выборок в Excel
Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Еще…Меньше
Если вам нужно разработать сложный статистический или инженерный анализ, вы можете сэкономить время и этапы с помощью этого средства. Вы предоставляете данные и параметры для каждого анализа, а средство использует соответствующие статистические или инженерные функции для вычисления и отображения результатов в выходной таблице. Некоторые средства создают диаграммы в дополнение к выходным таблицам.
Функции анализа данных можно применять только на одном листе. Если анализ данных проводится в группе, состоящей из нескольких листов, то результаты будут выведены на первом листе, на остальных листах будут выведены пустые диапазоны, содержащие только форматы. Чтобы провести анализ данных на всех листах, повторите процедуру для каждого листа в отдельности.
Ниже описаны инструменты, включенные в пакет анализа. Для доступа к ним нажмите кнопкуАнализ данных в группе Анализ на вкладке Данные. Если команда Анализ данных недоступна, необходимо загрузить надстройку «Пакет анализа».
-
Откройте вкладку Файл, нажмите кнопку Параметры и выберите категорию Надстройки.
-
В раскрывающемся списке Управление выберите пункт Надстройки Excel и нажмите кнопку Перейти.
Если вы используете Excel для Mac, в строке меню откройте вкладку Средства и в раскрывающемся списке выберите пункт Надстройки для Excel.
-
В диалоговом окне Надстройки установите флажок Пакет анализа, а затем нажмите кнопку ОК.
-
Если Пакет анализа отсутствует в списке поля Доступные надстройки, нажмите кнопку Обзор, чтобы выполнить поиск.
-
Если выводится сообщение о том, что пакет анализа не установлен на компьютере, нажмите кнопку Да, чтобы установить его.
-
Примечание: Чтобы включить Visual Basic для приложений (VBA) для надстройки «Надстройка анализа», вы можете загрузить надстройку VBA так же, как и надстройку «Надстройка анализа». В поле Доступные надстройки выберите «Надстройка анализа — VBA».
Существует несколько видов дисперсионного анализа. Нужный вариант выбирается с учетом числа факторов и имеющихся выборок из генеральной совокупности.
Однофакторный дисперсионный анализ
Этот инструмент выполняет простой анализ дисперсии данных для двух или более выборок. Анализ дает проверку гипотезы о том, что каждая выборка взята из одного и того же распределения вероятности на основе альтернативной гипотезы о том, что для всех выборок распределение вероятности не одно и то же. Если есть только два примера, можно использовать функцию T.ТЕСТ. В более чем двух примерах нет удобного обобщения T.ВМЕСТОэтого можно использовать модель Anova для одного фактора.
Двухфакторный дисперсионный анализ с повторениями
Этот инструмент анализа применяется, если данные можно систематизировать по двум параметрам. Например, в эксперименте по измерению высоты растений последние обрабатывали удобрениями от различных изготовителей (например, A, B, C) и содержали при различной температуре (например, низкой и высокой). Таким образом, для каждой из 6 возможных пар условий {удобрение, температура}, имеется одинаковый набор наблюдений за ростом растений. С помощью этого дисперсионного анализа можно проверить следующие гипотезы:
-
Извлечены ли данные о росте растений для различных марок удобрений из одной генеральной совокупности. Температура в этом анализе не учитывается.
-
Извлечены ли данные о росте растений для различных уровней температуры из одной генеральной совокупности. Марка удобрения в этом анализе не учитывается.
Извлечены ли шесть выборок, представляющих все пары значений {удобрение, температура}, используемые для оценки влияния различных марок удобрений (для первого пункта в списке) и уровней температуры (для второго пункта в списке), из одной генеральной совокупности. Альтернативная гипотеза предполагает, что влияние конкретных пар {удобрение, температура} превышает влияние отдельно удобрения и отдельно температуры.
Двухфакторный дисперсионный анализ без повторений
Этот инструмент анализа применяется, если данные можно систематизировать по двум параметрам, как в случае двухфакторного дисперсионного анализа с повторениями. Однако в таком анализе предполагается, что для каждой пары параметров есть только одно измерение (например, для каждой пары параметров {удобрение, температура} из предыдущего примера).
Функции CORREL и PEARSON вычисляют коэффициент корреляции между двумя переменными измерения, если для каждой переменной наблюдаемы измерения по каждому из N-объектов. (Любые отсутствующие наблюдения по любой теме вызывают игнорирование в анализе.) Средство анализа корреляции особенно удобно использовать, если для каждого субъекта N имеется более двух переменных измерения. Она содержит выходную таблицу — матрицу корреляции, которая показывает значение CORREL (или PEARSON),примененного к каждой из возможных пар переменных измерения.
Коэффициент корреляции, как и ковариана, — это мера степени, в которой две единицы измерения «различаются». В отличие от ковариации коэффициент корреляции масштабирован таким образом, что его значение не зависит от единиц измерения, выраженных в двух переменных измерения. (Например, если двумя переменными измерения являются вес и высота, то значение коэффициента корреляции не изменяется, если вес преобразуется из фунта в фунты.) Значение любого коэффициента корреляции должно быть включительно от -1 до +1 включительно.
Корреляционный анализ дает возможность установить, ассоциированы ли наборы данных по величине, т. е. большие значения из одного набора данных связаны с большими значениями другого набора (положительная корреляция) или наоборот, малые значения одного набора связаны с большими значениями другого (отрицательная корреляция), или данные двух диапазонов никак не связаны (нулевая корреляция).
Средства корреляции и коварианс могут использоваться в одном и том же параметре, если у вас есть N различных переменных измерения, наблюдаемые для набора людей. Каждый из инструментов корреляции и ковариции дает выходную таблицу — матрицу, которая показывает коэффициент корреляции или коварианс между каждой парой переменных измерения соответственно. Разница заключается в том, что коэффициенты корреляции масштабироваться в зависимости от -1 и +1 включительно. Соответствующие ковариансы не масштабироваться. Коэффициент корреляции и коварианс — это показатели степени, в которой две переменные «различаются».
Инструмент Ковариана вычисляет значение функции КОВАРИАНА. P для каждой пары переменных измерения. (Прямое использование КОВАРИАНА. P вместо ковариана является разумной альтернативой, если есть только две переменные измерения, то есть N=2.) Запись в диагонали выходной таблицы средства Коварица в строке i, столбце i — коварианс i-й переменной измерения. Это только дисперсия по численности населения для этой переменной, вычисляемая функцией ДИСПЕРС.P.
Ковариационный анализ дает возможность установить, ассоциированы ли наборы данных по величине, то есть большие значения из одного набора данных связаны с большими значениями другого набора (положительная ковариация) или наоборот, малые значения одного набора связаны с большими значениями другого (отрицательная ковариация), или данные двух диапазонов никак не связаны (ковариация близка к нулю).
Инструмент анализа «Описательная статистика» применяется для создания одномерного статистического отчета, содержащего информацию о центральной тенденции и изменчивости входных данных.
Инструмент анализа «Экспоненциальное сглаживание» применяется для предсказания значения на основе прогноза для предыдущего периода, скорректированного с учетом погрешностей в этом прогнозе. При анализе используется константа сглаживания a, величина которой определяет степень влияния на прогнозы погрешностей в предыдущем прогнозе.
Примечание: Для константы сглаживания наиболее подходящими являются значения от 0,2 до 0,3. Эти значения показывают, что ошибка текущего прогноза установлена на уровне от 20 до 30 процентов ошибки предыдущего прогноза. Более высокие значения константы ускоряют отклик, но могут привести к непредсказуемым выбросам. Низкие значения константы могут привести к большим промежуткам между предсказанными значениями.
Двухвыборочный F-тест применяется для сравнения дисперсий двух генеральных совокупностей.
Например, можно использовать F-тест по выборкам результатов заплыва для каждой из двух команд. Это средство предоставляет результаты сравнения нулевой гипотезы о том, что эти две выборки взяты из распределения с равными дисперсиями, с гипотезой, предполагающей, что дисперсии различны в базовом распределении.
С помощью этого инструмента вычисляется значение f F-статистики (или F-коэффициент). Значение f, близкое к 1, показывает, что дисперсии генеральной совокупности равны. В таблице результатов, если f < 1, «P(F <= f) одностороннее» дает возможность наблюдения значения F-статистики меньшего f при равных дисперсиях генеральной совокупности и F критическом одностороннем выдает критическое значение меньше 1 для выбранного уровня значимости «Альфа». Если f > 1, «P(F <= f) одностороннее» дает возможность наблюдения значения F-статистики большего f при равных дисперсиях генеральной совокупности и F критическом одностороннем дает критическое значение больше 1 для «Альфа».
Инструмент «Анализ Фурье» применяется для решения задач в линейных системах и анализа периодических данных на основе метода быстрого преобразования Фурье (БПФ). Этот инструмент поддерживает также обратные преобразования, при этом инвертирование преобразованных данных возвращает исходные данные.

Инструмент «Гистограмма» применяется для вычисления выборочных и интегральных частот попадания данных в указанные интервалы значений. При этом рассчитываются числа попаданий для заданного диапазона ячеек.
Например, можно получить распределение успеваемости по шкале оценок в группе из 20 студентов. Таблица гистограммы состоит из границ шкалы оценок и групп студентов, уровень успеваемости которых находится между самой нижней границей и текущей границей. Наиболее часто встречающийся уровень является модой диапазона данных.
Совет: В Excel 2016 теперь можно создавать гистограммы и диаграммы Парето.
Инструмент анализа «Скользящее среднее» применяется для расчета значений в прогнозируемом периоде на основе среднего значения переменной для указанного числа предшествующих периодов. Скользящее среднее, в отличие от простого среднего для всей выборки, содержит сведения о тенденциях изменения данных. Этот метод может использоваться для прогноза сбыта, запасов и других тенденций. Расчет прогнозируемых значений выполняется по следующей формуле:
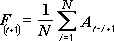
где
-
N — число предшествующих периодов, входящих в скользящее среднее;
-
A
j — фактическое значение в момент времени j; -
F
j — прогнозируемое значение в момент времени j.
Инструмент «Генерация случайных чисел» применяется для заполнения диапазона случайными числами, извлеченными из одного или нескольких распределений. С помощью этой процедуры можно моделировать объекты, имеющие случайную природу, по известному распределению вероятностей. Например, можно использовать нормальное распределение для моделирования совокупности данных по росту людей или использовать распределение Бернулли для двух вероятных исходов, чтобы описать совокупность результатов бросания монеты.
Средство анализа Ранг и процентиль создает таблицу, которая содержит порядковую и процентную ранг каждого значения в наборе данных. Можно проанализировать относительное положение значений в наборе данных. В этом средстве используются функции РАНГ. EQ и PERCENTRANK. INC. Если вы хотите учитывать связанные значения, используйте РАНГ. Функция EQ, которая обрабатывает связанные значения как имеющие одинаковый ранг или использует РАНГ.Функция AVG, которая возвращает средний ранг связанных значений.
Инструмент анализа «Регрессия» применяется для подбора графика для набора наблюдений с помощью метода наименьших квадратов. Регрессия используется для анализа воздействия на отдельную зависимую переменную значений одной или нескольких независимых переменных. Например, на спортивные качества атлета влияют несколько факторов, включая возраст, рост и вес. Можно вычислить степень влияния каждого из этих трех факторов по результатам выступления спортсмена, а затем использовать полученные данные для предсказания выступления другого спортсмена.
В средстве регрессии используется функция LINEST.
Инструмент анализа «Выборка» создает выборку из генеральной совокупности, рассматривая входной диапазон как генеральную совокупность. Если совокупность слишком велика для обработки или построения диаграммы, можно использовать представительную выборку. Кроме того, если предполагается периодичность входных данных, то можно создать выборку, содержащую значения только из отдельной части цикла. Например, если входной диапазон содержит данные для квартальных продаж, создание выборки с периодом 4 разместит в выходном диапазоне значения продаж из одного и того же квартала.
Двухвыборочный t-тест проверяет равенство средних значений генеральной совокупности по каждой выборке. Три вида этого теста допускают следующие условия: равные дисперсии генерального распределения, дисперсии генеральной совокупности не равны, а также представление двух выборок до и после наблюдения по одному и тому же субъекту.
Для всех трех средств, перечисленных ниже, значение t вычисляется и отображается как «t-статистика» в выводимой таблице. В зависимости от данных это значение t может быть отрицательным или неотрицательным. Если предположить, что средние генеральной совокупности равны, при t < 0 «P(T <= t) одностороннее» дает вероятность того, что наблюдаемое значение t-статистики будет более отрицательным, чем t. При t >=0 «P(T <= t) одностороннее» делает возможным наблюдение значения t-статистики, которое будет более положительным, чем t. «t критическое одностороннее» дает пороговое значение, так что вероятность наблюдения значения t-статистики большего или равного «t критическое одностороннее» равно «Альфа».
«P(T <= t) двустороннее» дает вероятность наблюдения значения t-статистики, по абсолютному значению большего, чем t. «P критическое двустороннее» выдает пороговое значение, так что значение вероятности наблюдения значения t- статистики, по абсолютному значению большего, чем «P критическое двустороннее», равно «Альфа».
Парный двухвыборочный t-тест для средних
Парный тест используется, когда имеется естественная парность наблюдений в выборках, например, когда генеральная совокупность тестируется дважды — до и после эксперимента. Этот инструмент анализа применяется для проверки гипотезы о различии средних для двух выборок данных. В нем не предполагается равенство дисперсий генеральных совокупностей, из которых выбраны данные.
Примечание: Одним из результатов теста является совокупная дисперсия (совокупная мера распределения данных вокруг среднего значения), вычисляемая по следующей формуле:
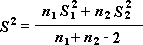
Двухвыборочный t-тест с одинаковыми дисперсиями
Этот инструмент анализа выполняет t-тест для двух образцов учащихся. В этой форме t-test предполагается, что два набора данных поступили из распределения с одинаковыми дисперсиями. Его называют гомике t-тестом. Этот t-тест можно использовать для определения вероятности того, что эти две выборки взяты из распределения с равными средствами распределения.
Двухвыборочный t-тест с различными дисперсиями
Этот инструмент анализа выполняет t-тест для двух образцов учащихся. В этой форме t-test предполагается, что два набора данных были полученными из распределения с неравными дисперсиями. Его называют гетероскестическими t-тестами. Как и в предыдущем примере с равными дисперсиями, этот t-тест можно использовать для определения вероятности того, что эти две выборки взяты из распределения с равными средствами распределения. Этот тест можно использовать, если в двух примерах есть отдельные объекты. Используйте тест Парный, описанный в примере, если существует один набор тем и две выборки представляют измерения по каждой теме до и после обработки.
Для определения тестовой величины t используется следующая формула.
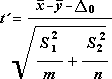
Следующая формула используется для вычисления степеней свободы (df). Так как результат вычисления обычно не является integer, значение df округлится до ближайшего другого, чтобы получить критическое значение из таблицы t. Функция Excel T .Test использует вычисляемую величину df без округлений, так как можно вычислить значение для T.ТЕСТ с неинтегрированной df. Из-за этих разных подходов к определению степеней свободы результаты T.Тест и этот t-тест будут отличаться в случае неравных дисперсий.
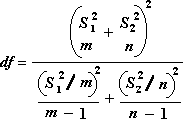
Z-тест. Средство анализа «Две выборки для середины» выполняет два примера z-теста для средств со известными дисперсиями. Этот инструмент используется для проверки гипотезы NULL о том, что между двумя значениями численности населения нет различий между односторонними или двухбокльными альтернативными гипотезами. Если дисперсии не известны, функция Z .Вместо этого следует использовать тест.
При использовании этого инструмента следует внимательно просматривать результат. «P(Z <= z) одностороннее» на самом деле есть P(Z >= ABS(z)), вероятность z-значения, удаленного от 0 в том же направлении, что и наблюдаемое z-значение при одинаковых средних значениях генеральной совокупности. «P(Z <= z) двустороннее» на самом деле есть P(Z >= ABS(z) или Z <= -ABS(z)), вероятность z-значения, удаленного от 0 в том же направлении, что и наблюдаемое z-значение при одинаковых средних значениях генеральной совокупности. Двусторонний результат является односторонним результатом, умноженным на 2. Инструмент «z-тест» можно также применять для гипотезы об определенном ненулевом значении разницы между двумя средними генеральных совокупностей. Например, этот тест можно использовать для определения разницы выступлений на соревнованиях двух автомобилей разных марок.
Дополнительные сведения
Вы всегда можете задать вопрос специалисту Excel Tech Community или попросить помощи в сообществе Answers community.
См. также
Создание гистограммы в Excel 2016
Создание диаграммы Парето в Excel 2016
Загрузка средства анализа в Excel
Инженерные функции (справка)
Общие сведения о формулах в Excel
Рекомендации, позволяющие избежать появления неработающих формул
Поиск ошибок в формулах
Сочетания клавиш и горячие клавиши в Excel
Функции Excel (по алфавиту)
Функции Excel (по категориям)
Нужна дополнительная помощь?
A T-test is a way of deciding if there are statistically significant differences between datasets, using a Student’s t-distribution. The T-Test in Excel is a two-sample T-test comparing the means of two samples. This article explains what statistical significance means and shows how to do a T-Test in Excel.
Instructions in this article apply to Excel 2019, 2016, 2013, 2010, 2007; Excel for Microsoft 365 and Excel Online.
What is Statistical Significance?
Imagine you want to know which of two dice will give a better score. You roll the first die and get a 2; you roll the second die and get a 6. Does this tell you the second die usually gives higher scores? If you answered, “Of course not,” then you already have some understanding of statistical significance. You understand the difference was due to the random change in the score, each time a die is rolled. Because the sample was very small (only one roll) it didn’t show anything significant.
Now imagine you roll each die 6 times:
- The first die rolls 3, 6, 6, 4, 3, 3; Mean = 4.17
- The second die rolls 5, 6, 2, 5, 2, 4; Mean = 4.00
Does this now prove the first die gives higher scores than the second? Probably not. A small sample with a relatively small difference between the means makes it likely the difference is still due to random variations. As we increase the number of dice rolls it becomes difficult to give a common sense answer to the question — is the difference between the scores the result of random variation or is one actually more likely to give higher scores than the other?
Significance is the probability that an observed difference between samples is due to random variations. Significance is often called the alpha level or simply ‘α.’ The confidence level, or simply ‘c,’ is the probability that the difference between the samples is not due to random variation; in other words, that there’s a difference between the underlying populations. Therefore: c = 1 – α
We can set ‘α’ at whatever level we want, to feel confident we’ve proven significance. Very often α=5% is used (95% confidence), but if we want to be really sure that any differences are not caused by random variation, we might apply a higher confidence level, using α=1% or even α=0.1%.
Various statistical tests are used to calculate significance in different situations. T-tests are used to determine whether the means of two populations are different and F-tests are used to determine whether the variances are different.
Why Test for Statistical Significance?
When comparing different things, we need to use significance testing to determine if one is better than the other. This applies to many fields, for example:
- In business, people need to compare different products and marketing methods.
- In sports, people need to compare different equipment, techniques, and competitors.
- In engineering, people need to compare different designs and parameter settings.
If you want to test whether something performs better than something else, in any field, you need to test for statistical significance.
What is a Student’s T-Distribution?
A Student’s t-distribution is similar to a normal (or Gaussian) distribution. These are both bell-shaped distributions with most results close to the mean, but some rare events are quite far from the mean in both directions, referred to as the tails of the distribution.
The exact shape of the Student’s t-distribution depends on the sample size. For samples of more than 30 it’s very similar to the normal distribution. As the sample size is reduced, the tails get larger, representing the increased uncertainty that comes from making inferences based on a small sample.
How to Do a T-Test in Excel
Before you can apply a T-Test to determine whether there’s a statistically significant difference between the means of two samples, you must first perform an F-Test. This is because different calculations are performed for the T-Test depending on whether there’s a significant difference between the variances.
You will need the Analysis Toolpak add-in enabled to perform this analysis.
Checking and Loading the Analysis Toolpak Add-In
To check and activate the Analysis Toolpak follow these steps:
-
Select the FILE tab >select Options.
-
In the Options dialogue box, select Add-Ins from the tabs on the left-hand side.
-
At the bottom of the window, select the Manage drop-down menu, then select Excel Add-ins. Select Go.
-
Ensure the check-box next to Analysis Toolpak is checked, then select OK.
-
The Analysis Toolpak is now active and you are ready to apply F-Tests and T-Tests.
Performing an F-Test and a T-Test in Excel
-
Enter two datasets into a spreadsheet. In this case, we’re considering the sales of two products during a week. The mean daily sales value for each product is also calculated, together with its standard deviation.
-
Select the Data tab > Data Analysis
-
Select F-Test Two-Sample for Variances from the list, then select OK.
The F-Test is highly sensitive to non-normality. It may therefore be safer to use a Welch test, but this is more difficult in Excel.
-
Select the Variable 1 Range and Variable 2 Range; set the Alpha (0.05 gives 95% confidence); select a cell for the top left corner of the output, considering that this will fill 3 columns and 10 rows. Select OK.
For the for Variable 1 Range, the sample with the largest standard deviation (or variance) must be selected.
-
View the F-Test results to determine whether there is a significant difference between the variances. The results give three important values:
- F: The ratio between the variances.
- P(F<=f) one-tail: The probability that variable 1 doesn’t actually have a larger variance than variable 2. If this is larger than alpha, which is generally 0.05, then there’s no significant difference between the variances.
- F Critical one-tail: The value of F that would be required to give P(F<=f)=α. If this value is greater than F, this also indicates there’s no significant difference between the variances.
P(F<=f) can also be calculated using the FDIST function with F and the degrees of freedom for each sample as its inputs. Degrees of freedom is simply the number of observations in a sample minus one.
-
Now that you know whether there is a difference between the variances you can select the appropriate T-Test. Select the Data tab > Data Analysis, then select either t-Test: Two-Sample Assuming Equal Variances or t-Test: Two-Sample Assuming Unequal Variances.
-
Regardless of which option you chose in the previous step, you will be presented with the same dialogue box to enter the details of the analysis. To start, select the ranges containing the samples for Variable 1 Range and Variable 2 Range.
-
Assuming you want to test for no difference between the means, set the Hypothesized Mean Difference to zero.
-
Set the significance level Alpha (0.05 gives 95% confidence), and select a cell for the top left corner of the output, considering that this will fill 3 columns and 14 rows. Select OK.
-
Review the results to decide if there’s a significant difference between the means.
Just as with the F-Test, if the p-value, in this case P(T<=t), is greater than alpha, then there’s no significant difference. However, in this case there are two p-values given, one for a one-tail test and the other for a two-tail test. In this case, use the two-tail value since either variable having a greater mean would be a significant difference.
Thanks for letting us know!
Get the Latest Tech News Delivered Every Day
Subscribe

С помощью t-критерия Стьюдента можно определить, имеются ли статистически значимые различия между наборами данных. T-тест в Excel — это T-тест с двумя образцами, сравнивающий средние значения двух образцов. В этой статье объясняется, что означает статистическая значимость, и показано, как выполнить T-тест в Excel.
Инструкции в этой статье относятся к Excel 2019, 2016, 2013, 2010, 2007; Excel для Office 365 и Excel Online.
Что такое статистическая значимость?
Представьте, что вы хотите знать, какая из двух костей даст лучший результат. Вы бросаете первый кубик и получаете 2; вы бросаете второй кубик и получаете 6. Это говорит вам, что второй кубик обычно дает более высокие оценки? Если вы ответили «Конечно, нет», то у вас уже есть некоторое понимание статистической значимости. Вы понимаете, что разница была связана со случайным изменением счета, каждый раз, когда бросали кубик. Поскольку образец был очень маленьким (только один рулон), он не показал ничего существенного.
Теперь представьте, что вы бросаете каждый кубик 6 раз:
- Первые кубики бросают 3, 6, 6, 4, 3, 3; Среднее = 4,17
- Второй бросает кубики 5, 6, 2, 5, 2, 4; Среднее = 4,00
Означает ли это, что первый кубик дает больше очков, чем второй? Возможно нет. Небольшая выборка с относительно небольшой разницей между средними значениями делает вероятным, что разница все же обусловлена случайными отклонениями. По мере того как мы увеличиваем количество бросков костей, становится трудно дать здравый смысл ответить на вопрос — является ли разница между оценками результатом случайного отклонения или один из них на самом деле с большей вероятностью дает более высокие оценки, чем другой?
Значимость — это вероятность того, что наблюдаемая разница между образцами обусловлена случайными колебаниями. Значение часто называют альфа-уровнем или просто «α». Уровень достоверности, или просто «с», — это вероятность того, что разница между выборками не обусловлена случайным изменением; другими словами, есть разница между основными группами населения. Следовательно: c = 1 — α
Мы можем установить «α» на любом желаемом уровне, чтобы чувствовать себя уверенно, что доказали свою значимость. Очень часто используется α = 5% (95% достоверности), но если мы хотим быть действительно уверенными в том, что какие-либо различия не вызваны случайными колебаниями, мы можем применить более высокий уровень достоверности, используя α = 1% или даже α = 0,1 %.
Зачем проверять статистическую значимость?
Сравнивая разные вещи, мы должны использовать тестирование значимости, чтобы определить, лучше ли одно, чем другое. Это относится ко многим полям, например:
- В бизнесе люди должны сравнивать разные продукты и методы маркетинга.
- В спорте люди должны сравнивать различное оборудование, техники и конкурентов.
- В разработке люди должны сравнивать различные проекты и настройки параметров.
Если вы хотите проверить, работает ли что-то лучше, чем что-либо, в любой области вам необходимо проверить статистическую значимость.
Что такое T-распределение студента?
T-распределение Стьюдента аналогично нормальному (или гауссовскому) распределению. Это оба распределения в форме колокола, большинство результатов которых близко к среднему, но некоторые редкие события довольно далеки от среднего значения в обоих направлениях, которые называются хвостами распределения.
Точная форма распределения Стьюдента зависит от размера выборки. Для образцов более 30 это очень похоже на нормальное распределение. По мере того как размер выборки уменьшается, хвосты становятся больше, что отражает возросшую неопределенность, возникающую в результате заключения на основе небольшой выборки.
Как сделать T-тест в Excel
Прежде чем вы сможете применить T-тест, чтобы определить, есть ли статистически значимая разница между средними значениями двух образцов, вы должны сначала выполнить F-тест. Это связано с тем, что для T-теста выполняются разные вычисления в зависимости от того, есть ли существенная разница между отклонениями.
Для выполнения этого анализа вам понадобится надстройка Пакет инструментов анализа.
Проверка и загрузка надстройки Toolpak для анализа
Чтобы проверить и активировать пакет инструментов анализа, выполните следующие действия.
-
Выберите вкладку ФАЙЛ > выберите Параметры .
-
В диалоговом окне «Параметры» выберите « Надстройки» на вкладках с левой стороны.
-
В нижней части окна выберите раскрывающееся меню «Управление» , затем выберите « Надстройки Excel» . Выберите Go .
-
Убедитесь, что установлен флажок рядом с Пакетом инструментов анализа , затем выберите ОК .
-
Пакет инструментов анализа теперь активен, и вы готовы применить F-тесты и T-тесты.
Выполнение F-теста и T-теста в Excel
-
Выберите вкладку « Данные »> « Анализ данных».
-
Выберите F-Test Two-Sample для отклонений из списка, затем нажмите OK .
F-тест очень чувствителен к ненормальности. Поэтому может быть безопаснее использовать тест Уэлча, но это сложнее в Excel.
-
Выберите диапазон переменной 1 и диапазон переменной 2; установить альфа (0,05 дает 95% уверенности); выберите ячейку для верхнего левого угла вывода, учитывая, что это заполнит 3 столбца и 10 строк. Выберите ОК .
Для диапазона переменной 1 необходимо выбрать выборку с наибольшим стандартным отклонением (или дисперсией).
-
Просмотрите результаты F-теста, чтобы определить, есть ли существенная разница между отклонениями. Результаты дают три важных значения:
- F : соотношение между дисперсиями.
- P (F <= f) one-tail : вероятность того, что переменная 1 на самом деле не имеет большей дисперсии, чем переменная 2. Если она больше, чем альфа, которая обычно равна 0,05, то нет существенной разницы между дисперсиями.
- F Критический односторонний : значение F, которое требуется, чтобы P (F <= f) = α. Если это значение больше, чем F, это также означает, что между отклонениями нет существенной разницы
P (F <= f) также можно рассчитать, используя функцию FDIST с F и степенями свободы для каждого сэмпла в качестве входных данных. Степени свободы — это просто число наблюдений в выборке минус один.
-
Теперь, когда вы знаете, есть ли разница между отклонениями, вы можете выбрать соответствующий T-критерий. Перейдите на вкладку « Данные »> « Анализ данных» , затем выберите « t-критерий: две выборки в предположении равных отклонений» или « t-критерий: две выборки в предположении неравных отклонений» .
-
Независимо от того, какой вариант вы выбрали на предыдущем шаге, вам будет предложено одно и то же диалоговое окно для ввода подробностей анализа. Чтобы начать, выберите диапазоны , содержащие образцы для переменных 1 Диапазона и переменных 2 Диапазона .
-
Предполагая, что вы хотите проверить отсутствие разницы между средними, установите гипотетическую среднюю разницу на ноль.
-
Установите уровень значимости Альфа (0,05 дает 95% достоверности) и выберите ячейку для верхнего левого угла выходных данных, учитывая, что это заполнит 3 столбца и 14 строк. Выберите ОК .
-
Просмотрите результаты, чтобы решить, есть ли существенная разница между средствами.
Как и в F-тесте, если значение p, в данном случае P (T <= t), больше, чем альфа, то существенной разницы нет. Однако в этом случае даются два значения p: одно для теста с одним хвостом, а другое для теста с двумя хвостами. В этом случае используйте значение с двумя хвостами, поскольку любая переменная, имеющая большее среднее значение, будет существенной разницей.