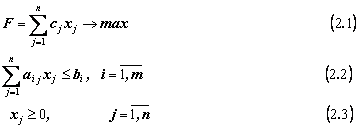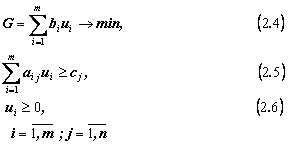Теневая цена в отчетах excel представляет собой двойственные переменные - Word и Excel

Рис.1.9. Симплекс таблица после второй итерации.

В строке, соответствующей целевой функции, нет
отрицательных элементов, следовательно, получено оптимальное решение (28/5,0,0,
1/5, 12/5) и F_max=11/5.
Заметим, что решения совпали.

2. ЗАДАЧА ОБ ОПТИМАЛЬНОМ РАСПРЕДЕЛЕНИЯ РЕСУРСОВ

Если финансы, оборудование, сырье и даже людей
полагать ресурсами, то значительное число задач в экономике можно рассматривать
как задачи распределения ресурсов. Достаточно часто математической моделью
таких задач является задача линейного программирования, которая записывается
следующим образом:

Здесь (2.1) — целевая
функция; (2.2) — система ограничений; (2.3) — естественные граничные условия;

x_j– количество выпускаемой продукции j-го типа, j=1,2,
…n;

b_i — количество располагаемого ресурса i-го вида, i=12,….,m;

a_ij— норма
расхода i-го ресурса для выпуска единицы продукции j-го
типа;

c_j—
прибыль, получаемая от реализации единицы продукции j-го типа.

В этом случае значение целевой функции — это суммарная
величина прибыли от реализации продукции, выпущенной в объемах x₁,x₂,…x_n. Левая
часть неравенства (2.2) представляет собой общее количество ресурса i,
используемое в соответствии с планом, правая часть — это имеющийся запас.

Эта
задача является частным случаем общей задачи линейного программирования, теория
применения которого была изучена в курсе Высшей математики [5]. Основными
положениями этой теории являются следующие положения:

Каждой задаче линейного программирования соответствует
двойственная задача, которая записывается по следующим правилам:

1.
Каждому i-му ограничению исходной задачи соответствует переменная двойственной
задачи z_i(двойственная переменная)

2.
Каждой j-ой переменной исходной задачи соответствует ограничение двойственной.
Матрица коэффициентов ограничений двойственной задачи является
транспонированной матрицей ограничений исходной. Если в исходной задаче
ограничения имеют знак £, то в двойственной — ³

3.
Коэффициенты при двойственных
переменных в целевой функции двойственной задачи равны правым частям
ограничений исходной задачи

4.
Если исходная задача была на
нахождение максимума, то двойственная будет на нахождение минимума:

§
Для оптимального решения значения
целевых функций прямой и двойственной задач совпадают (maxF=minG).

§
Если это записать в форме , то видно, что двойственная
переменная u_iявляется коэффициентом при b_i и, следовательно, показывает, как изменится целевая функция при
изменении ресурса b_i на единицу.
В литературе по оптимизации двойственные переменные принято называть
двойственными оценками. В отчетах Excel двойственная оценка
называется теневой ценой.

§
Теневая цена ресурса отлична от
нуля (точнее больше нуля) только для тех видов ресурсов, которые используются полностью,
т.е. ограничения (2.2) превращаются в равенства.

Принцип дополняющей полужесткости !!!!!!

§
Симметричность прямой и
двойственной задач заключается в том, что значения теневой цены в прямой задаче
совпадают с решением двойственной и наоборот

§ В теории ЛП также рассматриваются дополнительные
двойственные переменные, которые в Excel называются нормированной
стоимостью. Каждой основной переменной x_jсоответствует своя
нормированная стоимость v_j. Известно, что если x_j=0 (т.е.
продукцию j-го типа выпускать не целесообразно), то v_j отлична от нуля (точнее v_j<0) и
наоборот, если x_j>0
(продукцию выпускать целесообразно), то соответствующее v_j=0. Экономический
смысл нормированной стоимости — это величина, которая показывает, на сколько
уменьшится значение суммарной прибыли (ЦФ), при принудительном выпуске этой
продукции.

Уважаемый посетитель!

Чтобы распечатать файл, скачайте его (в формате Word).

Ссылка на скачивание — внизу страницы.

Источник

2.4. анализ решения злп на основе отчётов ms excel

Рассмотрим следующую ЗЛП:

f (x) =7,5х1+3х2+6х3+12х4—»max 2хі+х2+0,5х3+4х4 < 2400 х1+5х2+3х3 < 1200

3хі+6х3+х4 < 2000

Хі,2,3,4 ^0.

Начнём с отчёта результатов. Приведём его вид:

|ДІ В | С | D I Е | F | G | Н L

1	Целевая ячейка (Максим
7	Ячейка	Имя	Исходно	Результат
в	JGJ4	ЦФ	0,000	7884,296
9 10 11	Изменяемые ячейки
12	Ячейка	Имя	Исходно	Результат
13	JBJ4	продуктА	0,000	8,800
14	JCI4	продуктВ	0,000	148,760
15	JDJ4	продукте	0,000	152,066
16	JEI4	продукти	0,000	543,802
17 16 19	Ограничения
20	Ячейка	Имя	Значение	формула	Статус	Разница
21	JFJ12	ограничение!	2400,000 $F$12<=$H$12	связанное	0
22	JFJ13	ограничение!	1200,000 JF$13<=$H$13	связанное	0
23	JFJ14	ограничение!	I 2000,000 $F$14<=$H$14	связанное	0
24	ЇВЇ4	продуктА	0,000 JBt4>=0	связанное	0,000
25	JCJ4	продуктВ	146,760 JC(4>=0	не связан.	148,760
27	JDI4	продукте	152,066 IDt4>=0	не связан.	152,066
JEJ4	продукти	543,802 JEt4>=0	не связан.	543,802

Единственное, что здесь следует прокомментировать, это статус ресурсов. Т.к. все ограничения на ресурсы являются связанными, то это говорит о том, что все ресурсы были использованы. Другими словами, все ресурсы являются дефицитными.

I |Д| В | С | D | Е | F | G | Н I I |

7 Результ. Нормир. Целевой Допустимое Допустимое

8 Ячейка Имя значение стоимость Коэффициент Увеличение Уменьшение

1Г $Bt4 продуктА 8,800 -0,062 7,5 0,061983471 1Е+30

Ю_ КІА продуктВ 148,760 0,000 3 7,5 0,391304348

jj_ $Dt4 продукте 152,866 0,000 6 31,8 0,178571429

Г2_ ЦЕН продуктР 543,802 0,000 12 1,5 0,135135135

14 Ограничения

15 Результ. Теневая Ограничение Допустимое Допустимое

16 Ячейка Имя значение Цена Правая часть Увеличение Уменьшение

ТГ $F$12 ограничение! 2400,000 2,628 2400 1840 2193,333333

ГВ_ HFS13 ограничение!! 1200,000 0,074 1200 10966,66667 782,6086957

^9_ $Ft14 ограничение!!! 2000,000 0,744 2000 1500 920

Рассмотрим отчёт по устойчивости:

Нормированная стоимость (часто, редуцированная стоимость, от английского: cost reduction уменьшение затрат) представляет собой дополнительные двойственные переменные. Они показывают, насколько по модулю уменьшится целевая функция при принудительном выпуске единицы данной продукции. В нашем примере нормированная стоимость по продукту А не равна нулю. Следовательно, если мы будем принудительно выпускать единицу продукта А, то целевая функция уменьшится на 0,062. Другими словами, выпуск продукта А является нерентабельным (неприбыльным).

Допустимое увеличение показывает, насколько максимально можно увеличить коэффициент целевой функции (цену продукта), чтобы структура оптимального плана осталась прежней. Допустимое уменьшение, наоборот, показывает, насколько можно максимально уменьшить коэффициент ЦФ, чтобы осталась прежней структура оптимального плана. Например, в нашей задаче, чтобы выпуск продукта А оставался нерентабельным, максимально допустимое увеличение его цены составляет приблизительно 0.06. Допустимое же уменьшение представляет собой огромное число. Это понятно, т.к., ещё больше уменьшив цену нерентабельного продукта, сделать его рентабельным невозможно.

Теневая цена в отчётах Excel представляет собой двойственные переменные. Они показывают, как изменится целевая функция при изменения запаса ресурса на единицу. Понятно, что если ресурс использован полностью, то теневая цена этого ресурса положительна. Например, если мы увеличим запас ресурса I на единицу, то ЦФ возрастёт на 2,628 (ресурс I является самым приоритетным). Допустимое увеличение и уменьшение показывают границы, в которых могут изменяться ресурсы, чтобы структура оптимального решения, т.е. номенклатура выпускаемой продукции, остались без изменений.

Рассмотрим последний отчёт отчёт по пределам:

	А\| В	С I	D ІЕ	F	G \|Н	I	J I	к I
4 5
7	Ячейка	Имя	значение
І	SGJ4	ЦФ	7884,298
11		Изменяемое		Нижний	Целевое	Верхний	Целевое
12	Ячейка	Имя	значение	предел	результат	предел	результат
13	ЇВЇ4	продукгА	0,000	0,000	7884,233	0,000	7884,298
14	ICJ4	продукгВ	148,700	0,000	7438,017	148,760	7884,298
15	ШИ	продукте	152,066	0,000	6971,901	152,066	7884,298
16	ЇЕЇ4	продуктО	543,802	0,000	1358,673	543,802	7884,298

В отчёте указаны значения ЦФ при выпуске данного типа продукции на нижнем и верхнем пределах. Так, значение ЦФ 6971,901 соответствует тому, что продукт С не выпускается.

Отчёты Excel обеспечивают всей необходимой информацией для проведения полного анализа линейной модели.

Домашнее задание 2. 1.

Решить с помощью MS Excel следующие задачи (варианты 1-5, 610).

1-5.Для приготовления четырех видов продукции (A, B, C, D) используют три вида сырья. Ресурсы сырья, норма его расхода на единицу продукции и цена продукции заданы в соответствующей таблице.

Определите план выпуска продукции из условия максимизации его стоимости.

Определите статус, ценность каждого ресурса и его приоритет при решении задачи увеличения запаса ресурсов.

Определите максимальный интервал изменения запасов каждого из ресурсов, в пределах которого структура оптимального плана, то есть номенклатура выпускаемой продукции, остается без изменения.

Определите суммарную стоимостную оценку ресурсов, используемых при производстве единицы каждого изделия. Производство какой продукции нерентабельно?

На сколько уменьшится стоимость выпускаемой продукции при принудительном выпуске единицы нерентабельной продукции?

На сколько можно снизить запас каждого из ресурсов, чтобы это не привело к уменьшению прибыли?

Определите изменение стоимости продукции и количество выпускаемых изделий при увеличении второго вида сырья на Z единиц.

Определите оптимальное решение задачи для случая, когда вектор ресурсов задан в виде в -строки.

Определите интервалы изменения цен на каждую продукцию, при которых сохраняется оптимальный план.

продукции, чтобы сделать На сколько нужно снизить затраты каждого вида сырья на единицу производство нерентабельного изделия рентабельным?

На сколько нужно изменить запас каждого из дефицитных ресурсов, чтобы прибыль возросла на 20%?

6-і0.Из 4 видов кормов необходимо составить рацион, в состав которого должно входить не менее ві ед. вещества А, в2 ед. вещества В и в3 ед. вещества С. Количество единиц вещества, содержащегося в і кг корма каждого вида, указано в соответствующей таблице. В ней же приведена цена і кг корма каждого вида.

Составьте рацион, содержащий не менее нужного количества указанных питательных веществ и имеющий минимальную стоимость.

Определите, все ли виды кормов входят в рацион, ценность дополнительной единицы каждого питательного вещества и его приоритет при решении задач уменьшения стоимости рациона.

Определите суммарную стоимостную оценку питательных веществ в единице каждого корма, использование какого вида корма нерентабельно.

Содержание какого из питательных веществ превышает заданный минимальный уровень и на сколько?

Определите максимально возможное уменьшение содержания каждого из питательных веществ в рационе, при котором структура рациона остается без изменений.

На сколько уменьшится стоимость рациона и используемое количество кормов при снижении минимального уровня потребления питательного вещества В до Z ед.

Определите интервал изменения цен на каждый вид корма, при котором сохраняется структура рациона.

Возможно ли сделать выгодным использование корма, не вошедшего в рацион.

На сколько увеличится стоимость рациона при принудительном включении в рацион 1 кг нерентабельного вида корма.

На сколько нужно снизить минимальный уровень потребления каждого из питательных веществ, чтобы уменьшить стоимость рациона на 10%?.

і0.

2.5. Двойственный симплекс-метод (Р-метод)

Пример 2.9. Рассмотрим следующую ЗЛП:

min(2Xi + 4Х2 )

Х1 + Х2 > 3

Х1 + 3 Х2 > 6 Х1 + 2 Х2 < 3

Хі,2 > 0

Приведем рассматриваемую ЗЛП к каноническому виду

max (-2 Х1 -4 Х2 )

Х1 + Х2 S1 = 3

Х1 + 3 Х2 S2 = 6 Х1 + 2 Х2 S3 = 3

X, > 0, j = ГД, S, > 0, j =1,3.

(2.28)

или

max (-2 Х1 -4 Х2 )

3 Х1 — Х2 + S1 = 3

4 Х1 3 Х2 + S2 = -6

Х1 + 2 Х2+ S3 = 3

(2.29)

> 0, j = 1,2, S, > 0, i = 1,3. Рассмотрим расширенную матрицу системы линейных уравнений

(2.29):

	(-3	-1	1	0	0	31
P (°) =	4	-3	0	1	0	6
	v 1	2	0	0	1	3,

Матрица P(0) содержит единичную подматрицу порядка 3 и , следовательно, определяет базисное решение

An«0) = (-3; -6; 3); N (0)= (3; 4; 5)

системы уравнений , причем Cn(0) =( 0,0,0). Так как элементы ( n + 1 = 6 )-го столбца матрицы системы P(0) не являются неотрицательными, то она не является К-матрицей ЗЛП. Вычислим симплекс-разности матрицы P(0):

A(f = (Cn(0),а?) С, =-Cj > 0, j = 1,5

Так как все симплекс-разности матрицы то базисное решение XN(0) =

(0)

являются

При решении задачи симплекс-методом текущее базисное решение является опорным планом, но неоптимальным. Эти соображения позволяют построить метод решения определенного класса ЗЛП. В этом методе, называемом двойственным симплекс-методом, на каждой итерации обеспечивается выполнение условия оптимальности текущего базисного решения, не являющегося планом. Критерием окончания процесса итераций является получение опорного плана (неотрицательных свободных членов системы уравнений), который будет являться и оптимальным.

Определение P-матрицы ЗЛП.

Определение. Р-матрицей КЗЛП будем называть расширенную матрицу системы линейных уравнений, равносильной исходной системе, содержащую единичную подматрицу порядка m на месте n первых столбцов, все симплекс разности которой неотрицательны.

Очевидно, что всякая Р-матрица ЗЛП определяет некоторое базисное решение системы уравнений (2.29) (см.пример 2.9)

Определение. Базисное решение системы линейных уравнений (2.29), определяемое Р-матрицей, называется псевдопланом ЗЛП.

Условия перехода от одной P-матрицы ЗЛП к другой.

Пусть известна Р-матрица P(S) ЗЛП (2.28), определяющая псевдоплан

— —(S) (S)

Xn<s)= b ; N

Условия перехода от матрицы P(S) к матрице P(S+1) составляют

содержание теоремы і.

Теорема 1. Пусть bS )< 0 и в l -й строке матрицы P( S) есть хотя бы

один отрицательный элемент. Тогда одного шага метода Жордана-Гаусса можно построить новую Р-матрицу P(м), выбрав направляющий элемент из условия

д( s ) А(5)

°{S) =—7^ = min—(2 30) a7) *& of) (2.30)

Су<0

Замечание 1. Если в матрице P нет b( S )< 0, то определяемый ею псевдоплан является решением ЗЛП.

Теорема 2. Пусть ЦS )< 0 и в 1-й строке матрицы P( S) нет ни одного

отрицательного элемента. Тогда множество планов Р ЗЛП (2.28) пусто.

Замечание 2. При переходе от матрицы P( S) к матрице P(S+і) целевая функция изменяется в соответствии с формулой

(S)

f( XN(S+1)) = f ( XN(S)) + d(S)bS = f ( XN(S)) + bf (2.3і)

UIK откуда следует, что

f ( Xn(s+1)) < f ( Xn(s)), (2.32) так как ЪS)< 0 и aK) < 0. Из неравенства (2.32) следует, что при

переходе от одного псевдоплана к другому значение целевой функции f (x) не возрастает.

Алгоритм Р-метода.

Будем считать, что известна исходная Р-матрица P(0) задачи линейного программирования, определяющая исходный псевдоплан

X^0) = (Ъ(0),Ъ20),…,ъ<°>) ,

N(0) = (N(0), N 20),…, Ni0)).

В методе последовательного уточнения оценок последовательно

строят Р-матрицы P(1), P(2).., P(S), … задачи линейного

программирования, пока не получат Р-матрицу задачи линейного программирования, определяющую ее оптимальный план.

Рассмотрим алгоритм S-й итерации метода последовательного уточнения оценок. В начале S-й итерации имеем Р-матрицу P( S-1) задачи линейного программирования, определяющую псевдоплан

— (S-1) (S-1)

XN(S-1)= Ъ , N . Шаг 1. Найдем номер l из условия

Ъ( S-1) = min Ъ( S

1<i < m

Шаг 2. Если ЪS-1) > 0, то псевдоплан

—(S-1) (S-1)

Xn{ s-1)= Ъ1 , N является оптимальным опорным планом, а

f ( Xn(s-1) ) = (CNS-1), Xn(s-1)) _ есть оптимальное значение линейной формы f (x), иначе переходим к шагу 3. Шаг 3. Если

a(S-1) > 0, j = ,

то задача линейного программирования не имеет решения ( множество планов Р пусто), иначе переходим к шагу 4.

Шаг 4. Вычисляем для столбцов aj матрицы P(S-1) (j * N(si = 1,

2, .. .,m) симплекс-разности A(S-1) и находим номер К из условия

А(S-1) Г А(5-1)

Направляющий элемент на S-й итерации метода есть элемент Шаг 5. Вычисляем компоненты вектора N :

(S-1)

NS) = N(S-1), i = 1, m , i * і , NS) = K

Шаг 6. Производим один шаг метода Жордана-Гаусса с направляющим элементом a’K-1). Вычисляем элементы Р-матрицы

P(S) методом Жордана-Гаусса. Присваиваем переменной алгоритма S значение S+1 и переходим к шагу 1.

Решение задач Р-методом.

Так как компоненты псевдоплана Xn(x> =( 3/2, 3/2, 3/2) являются неотрицательными, то Xn(1> является оптимальным опорным планом ЗЛП (2.28). Итак,

Х*=( 3/2, 0, 3/2, 0, 3/2) и min f (Х)=3. Пример 2.10. Решим ЗЛП:

max f (x) = Х1 + 2Х2 -2 Х1 + Х2 > 2

Х1 + 2 Х2 < 4 (2.33) Х1 + 4 Х2 > 4

Х1,2 >0

Приведем рассматриваемую ЗЛП к каноническому виду max f (Х)= (Х1 + 2 Х2 )

2 Х1 + Х2 S1 = 2

Х1 + 2 Х2 + S2 = 4

Х1 + 4 Х2 S3 = 4

Xj > 0, j = 1,2, s, > 0, i = 1,3.

или

max f (X)= (Х1 + 2 Х2 )

(2.34)

2 Х1 Х2 + S1 = 2

Х1 + 2 Х2 + S2 = 4

i = 1,3.

Х1 4 Х2 + S3 = 4

Xj > 0, j = 1,2, s, > 0,

Расширенная матрица

ґ 2 і і 0 0 2^

Л(0) = і 2 0 і 0 4

vі 4 0 0 і 4у

системы линейных уравнений (3.42) не являются Р-матрицей рассматриваемой ЗЛП, так как

( 2) (Г)

А(0)=(0, 0, 0)

+ і = і > 0 , А(20)=(0, 0, 0)

2 = -2 < 0.

v 4У

Следовательно, к решению ЗЛП (3.4і) не применим Р-метод.

Пример 2.іі.

min f (x) = ( 6 Хі + 3Х2 ) -3 Хі + Х2 > і 2 Хі 3 Х2 > 2

Хі,2 > 0

j =і,2.

Решение. Приведем задачу к каноническому виду f(Х)= (6 Хі 3 Х2 ) -max 3 Хі — Х2 + Sl = і 2 Хі + 3 Х2 + S2 = 2

Xj > 0, j = ід, Sj > 0,

(0)

Так как расширенная матрица

( 3 і і 0 і)

2 3 0 і 2

(2.35)

системы линейных уравнений рассматриваемой задачи является Р-матрицей ( А(і0) = 6 >0; А(20) = 3 >0 ), то задачу можно решить Р-методом. Решение задачи ведем в симплексной таблице.

-6

-3

N(s)

C «

C N

X N

al(s)

a2(s)

a3(s)

a4(s)

Исследование операций в экономике

Предмет: Экономика
Автор: И.Н. Мастяева
Год издания: 2003
Язык учебника: русский
Рейтинг:
Просмотров: 534

Обсуждение Исследование операций в экономике

Комментарии, рецензии и отзывы

2.4. анализ решения злп на основе отчётов ms excel: Исследование операций в экономике, И.Н. Мастяева, 2003 читать онлайн, скачать pdf, djvu, fb2 скачать на телефон Рекомендовано Учебно-методическим объединением по образованию в области статистики в качестве учебного пособия для студентов высших учебных заведений, обучающихся по специальности 061700 «Статистика» и другим экономическим специальностям.

Источник

Проведем анализ устойчивости в Excel на примере задачи о прядильной фабрике.

Пример 2. Прядильная фабрика для производства четырех видов пряжи использует три типа сырья – чистую шерсть, капрон, акрил. В табл.1 указаны нормы расхода сырья, его общее количество, которое может быть использовано фабрикой в течение года; загрузка оборудования при производстве тонны пряжи и прибыль от реализации тонны пряжи каждого вида. Годовой ресурс оборудования составляет 140 тыс. маш.ч.

Требуется составить годовой план производства пряжи с целью максимизации суммарной прибыли.

Таблица 1. Исходные данные

Тип сырья	Нормы расхода сырья на 1 т. пряжи	Количество сырья (т.)
Вид 1	Вид 2	Вид 3	Вид 4
Шерсть Капрон Акрил	0,5 0,1 0,4	0,2 0,6 0,2	0,3 0,4 0,3	0,2 0,5 0,3
Загрузка оборудования в тыс. маш.ч	0,06	0,04	0,03	0,09
Прибыль от реализации 1 т пряжи (в $)

Обозначим: – объем производства пряжи i-го типа в тоннах.

На рис. 14 представлена заполненная форма для ввода условия задачи в Excel.

Диалоговое окно «Поиск решения» для рассматриваемой задачи с введенными данными приведено на рис. 15.

Рис. 15. Диалоговое окно «Поиск решения»

Рис. 16. Диалоговое окно «Результаты поиска решения»

Результаты решения задачи выводятся в форму ввода условий задачи: =235,29; =0; =0; =1352,9; ЦФz=18823529,41 (рис. 17), отчеты по результатам, по устойчивости и по пределам выводятся на отдельных листах в текущей рабочей книге Excel.

Microsoft Excel 11.0 Отчет по результатам
Целевая ячейка (Максимум)
Ячейка	Имя	Исходное значение	Результат
$F$6	коэффициенты ЦФ	0,00	18823529,41
Изменяемые ячейки
Ячейка	Имя	Исходное значение	Результат
$B$3	значение x1	235,29
$C$3	значение x2
$D$3	значение x3
$E$3	значение x4	1352,94
Ограничения
Ячейка	Имя	Значение	Формула	Статус	Разница
$F$12	Акрил левая часть	500,00	$F$12 =0	не связан.	235,3
$C$3	значение x2	$C$3>=0	связанное
$D$3	значение x3	$D$3>=0	связанное
$E$3	значение x4	1352,94	$E$3>=0	не связан.

Рис. 18- Отчет по результатам

По ресурсам приводится следующая информация: формула, соответствующая левой части ограничения; имя ограничения; значение (величина) использованного ресурса при оптимальном решении задачи; формула, задающая ограничение; статус ограничения и разница. Если ресурс используется полностью (то есть ресурс дефицитный), то в графе «Статус» («Состояние») соответствующее ограничение указывается как «связанное»; при неполном использовании ресурса (то есть ресурс недефицитный) в этой графе указывается «не связан». В графе «Разница» показана разность между значением использованного ресурса и исходно заданной величиной ресурса. Аналогичная информация приводится по переменным задачи: оптимальное значение, статус (связанная, если оптимальное значение переменной не нулевое; несвязанная в противном случае), разность между оптимальным значением переменной и заданным для нее граничным условием.

В задаче о прядильной фабрике полученное оптимальное решение означает выпуск первого и четвертого типов пряжи (базисные переменные: =235,29; =1352,9), выпускать пряжу второго и третьего типов не выгодно ( =0; =0). При таком плане выпуска полностью будут использованы ресурсы (запасы) акрила и капрона, а запасы шерсти и ресурс оборудования избыточны.

Отчет по результатам дает информацию для анализа возможного изменения запасов недефицитных ресурсов при сохранении полученного оптимального значения ЦФ. Если на ресурс наложено ограничение типа ≤, то в графе «Разница» дается количество ресурса, которое не используется при реализации оптимального решения. Например, используется 388.24 тонны шерсти. Неизрасходованным остается 211.76 тонн из общих запасов шерсти, на это количество можно уменьшить ресурс «шерсть» без изменения оптимального решения. Аналогично можно уменьшить ресурсы оборудования на 4.12 тыс. часов и это не повлияет на оптимальное решение.

Если на ресурс наложено ограничение типа ≥, то в графе «Разница» дается количество ресурса, на которое была превышена минимально необходимая норма. Если на эту величину увеличить ресурс, оптимальное решение задачи не изменится.

Отчет по устойчивости. На рис. 19 представлен отчет по устойчивости для задачи примера 1, который состоит из двух частей: информация по переменным и информация по ограничениям.

Microsoft Excel 11.00 Отчет по устойчивости
Изменяемые ячейки
Рез.	Нормир.	Целевой	Допусти -мое	Допусти -мое
Ячейка	Имя	знач.	стоимость	Коэфф.	увели -чение	умень- шение
$B$3	x1	235,3
$C$3	x2	-1352,9	1352,94	1E+30
$D$3	x3	-1617,7	1617,65	1E+30
$E$3	x4	1045,45
Ограничения
Рез.	Теневая	Ограни- чение	Допусти -мое	Допусти -мое
Ячейка	Имя	знач.	Цена	Правая часть	увели -чение	умень- шение
$F$12	акрил	25294,1	33,33
$F$11	капрон	8823,5	38,89	514,29
$F$10	шерсть	0,00	1E+30	211,76
$F$13	обору дование	0,00	1E+30	4,12

Рис. 19- Отчет по устойчивости

Нормированная стоимость показывает, на сколько изменится значение ЦФ в случае принудительного включения единицы этой продукции в оптимальное решение. Например, в отчете по устойчивости для рассматриваемой задачи нормированная стоимость для второго вида пряжи равна: -1352.94. Это означает, что если включить в план выпуска 1 тонну пряжи второго вида, то новый план выпуска принесет прибыль на 1352.94$ меньше, чем прежний оптимальный план. Нормированная стоимость для базисных переменных всегда равна нулю.

Предельные значения приращения целевых коэффициентов. Для каждой переменной указаны заданные коэффициенты ЦФ, допустимые увеличение и уменьшение коэффициентов при которых сохраняется оптимальное решение задачи. Например, допустимое увеличение цены на пряжу первого вида равно 2875$ за тонну, а допустимое уменьшение – 8600$. Это означает, что если цена на тонну пряжи первого вида возрастет не более чем на 2875$, например станет равной 13875$, то оптимальное решение сохранится, изменится только значение ЦФ в оптимальной точке.

При выходе за указанные в отчете по устойчивости пределы изменения цен оптимальное решение может измениться как по номенклатуре выпускаемой продукции, так и по объемам выпуска (без изменения номенклатуры).

Далее в отчете по устойчивости приводится информация, относящаяся к ограничениям. В колонке «Результирующее значение» приводится величина использованных ресурсов.

Предельные значения приращения ресурсов. В графах «Допустимое уменьшение» и «Допустимое увеличение» показано на сколько можно уменьшить (устранить излишек) или увеличить (повысить минимально необходимое требование) ресурс, сохранив при этом базис оптимального решения (изменить объем выпуска продукции без изменения номенклатуры). Рассмотрим анализ дефицитных ресурсов, так как анализ недефицитных ресурсов был дан при описании отчета по результатам. В рассматриваемой задаче такими ограничениями являются дефицитные ресурсы «акрил» и «капрон». Например, если ресурсы акрила уменьшатся не более чем на 80 тонн или возрастут не более чем на 33.33 тонны, базис задачи не изменится (по-прежнему будет оптимально выпускать пряжу первого и четвертого типов, хотя объемы выпуска изменятся).

Теневая цена (ценность дополнительной единицы i-го ресурса). Теневая цена показывает насколько возрастет значение ЦФ в случае выделения дополнительной единицы i-го ресурса. Очевидно, что теневая цена не нулевая только для дефицитных ресурсов. Например, если запасы акрила возрастут на 1 тонну, прибыль увеличится на 25294,12$, если запасы капрона возрастут на 1 тонну, то прибыль будет на 8823.53$ больше, чем исходная. Поэтому в первую очередь для фабрики выгодно увеличивать запасы акрила.

В терминах теории двойственности теневая цена соответствует значению двойственной оценки соответствующего ресурса, а нормированная стоимость – значению дополнительной двойственной оценки, которая равна разности между левой и правой частями в ограничениях двойственной задачи.

Отчет по пределам. Для рассматриваемой задачи отчет по пределам приведен на рис. 20.

Microsoft Excel 11.0 Отчет по пределам
Целевое
Ячейка	Имя	Знач.
$F$6	ЦФ
Изменяемое	Ниж.	Целевой	Верх.	Целевой
Ячейка	Имя	Знач.	пред.	результат	пред.	рез.
$B$3	x1	235,29	16235294,1	235,3
$C$3	x2	18823529,4
$D$3	x3	18823529,4
$E$3	x4	1352,94	2588235,3	1352,9

Рис. 20. Отчет по пределам

В отчете по пределам показано в каком диапазоне могут изменяться значения переменных, без изменения базиса (номенклатуры выпуска продукции). Например, если будет выпускаться 235 тонн пряжи первого вида, то в оптимальном решении ненулевые переменные будут соответствовать объемам выпуска первого и четвертого видов пряжи. В случае выпуска более чем 235.29 тонн пряжи первого типа номенклатура выпуска продукции изменится. Также в отчете по пределам приводится информация о величине ЦФ при нижнем и верхнем предельных значениях переменных задачи.

Содержание

1. Настройка MS Excel 4

2. Подготовка листа с исходными данными. 5

Порядок заполнения листа. 6

3. Установка данных для пакета «Поиск решения». 6

4. Получение результатов решения. 8

5. Типы отчетов: 9

6. Решение в Excel задач ЦЛП.. 10

7. Пример решения транспортной задачи. 11

8 Исследование устойчивости решения задачи ЛП.. 12

Анализ сокращения или увеличения ресурсов: 13

Microsoft Excel 8.0 Отчет по устойчивости

Отчет по устойчивости

Отчет по устойчивости имеет две различные формы: отчет по устойчивости решений, полученных с помощью линейных моделей оптимизации и нелинейных.

Результатам решения линейных задач можно дать наглядную экономическую интерпретацию. К сожалению, результаты, получаемые с помощью нелинейных моделей, в большинстве случаев не имеют такой интерпретации.

Часть 1. Поиск решений на электронных таблицах

Основной вопрос, освещаемый в этом отчете: насколько устойчиво найденное оптимальное решение по отношению к возможным изменениям параметров задачи. Любая строка любой таблицы этого отчета говорит о том, какие изменения можно произвести по отношению к ячейке (столбец «Ячейка») при условии, что содержимое остальных ячеек определяется оптимальным решением.

Отчет по устойчивости длялинейной модели

Отчет состоит из двух разделов: изменяемые ячейки и ограничения.

Рабочий лист: [Задача о красках.хфРешение задачи Отчет создан: 19.02.01 13:31:42

Ячейка	Имя	Результ. значение	Нормир. стоимость	Целевой Допустимое Коэффици- Увеличениеент	Допустимое Уменьшение
$В$23	Краска_Н	3,33	0,00	3 1
$В$24	Краска_В	1,33	0,00	2 4	0,5
Ограничения
Ячейка	Имя	Результ.значение	Теневая Цена	Ограничение Допустимое Правая часть Увеличение	Допустимое Уменьшение
$Е$16	П1 Суточ-ный_расход исх. продукте	6,00	0,33	6 1	1Е+30
$Е$17	П2 Суточ-	8,00	1,33	8 1Е+30	2′

ный_расход исх.продукто в(т)

Раздел «Ограничения» связан с анализом связанных ограничений на возможность изменения их правых частей (запасов дефицитных ресурсов) в пределах постоянства теневой цены.

Для дефицитных ресурсов (в нашей задаче это запасы исходных продуктов, сохраняемые в ячейках Е16, Е17) важен вопрос: какое дополнительное увеличение целевой функции может обеспечить увеличение запасов ресурса. Ответ на этот вопрос связан с использованием понятия теневой цены (скрытой цены, двойственной цены, ценности ресурса):

Теневая цена ресурса определяет прирост целевой функции, обеспечиваемый увеличением запаса дефицитного ресурса на единицу егоизмерения.

Анализ отчетов

Так, теневая цена продукта П1 (ячейка Е16) определена как 0,333333 (тыс. долл./т). Это означает, что увеличение запаса П1 на тонну увеличит целевую функцию примерно на 333 долл. Аналогичное влияние на изменение значения целевой функции оказывает теневая цена продукта Ш (ячейка Е17), которая определяется значением 1,333333 (тыс. долл./т).

Теневая цена определяет скрытые возможности реорганизации системы путем изменения запасов дефицитных ресурсов, изменения организации использования этих ресурсов (расширение складов и т. п.). Кроме того, теневая цена позволяет ранжировать такие ресурсы с точки зрения их полезности для расширения производства.

Например, в нашем примере сравнение теневых цен Ш и П2 показывает, что при стремлении увеличить общую прибыль от продажи краски предпочтение нужно отдать увеличению запасов продукта П2, поскольку он имеет большую теневую цену.

Однако анализ найденного оптимального решения с помощью теневых цен имеет смысл только в определенных пределах. Эти пределы указывают, в каких границах изменение запасов того или иного дефицитного ресурса влияет на найденное оптимальное решение задачи и значение целевой функции. В этом разделе отчета утверждается, что запасы ресурса П1 могут изменяться в пределах (6 — 1, 96; 6+1) тонн, дальнейшее увеличение или уменьшение запаса не будет оказывать влияния на оптимальное решение задачи (т. е. соответствующее ограничение по запасу ресурсов станет избыточным, а сам ресурс .перейдет в категорию недефицитных). Аналогично значения (8 — 1, 95) и (8 + 4) определяют пределы возможных изменений запасов другого дефицитного ресурса П2. Увеличение П2 в этом интервале от 8 т до 12 т приведет к изменению оптимального решения задачи и увеличению значения целевой функции, уменьшение запаса П2 с 8 т до примерно 6 т — к уменьшению найденного значения целевой функции.

Другими словами, четыре правых столбца таблицы ограничений определяют теневую цену ресурса и диапазон возможных изменений запасов этого ресурса, в котором теневая цена остается для данной задачи постоянной. Любое изменение дефицитного ресурса в пределах постоянства теневой цены приводит к изменению оптимального решения задачи и значения целевой функции.

Для любого недефицитного ресурса теневая цена равна нулю, поэтому для этого типа ресурсов интересен один вопрос: насколько можно снизить запасы ресурса при сохранении найденного оптимального решения. Ответ на этот вопрос можно получить при анализе отчета по результатам.

Часть 1. Поиск решений на электронных таблицах

Анализ Отчетов

Третья строка таблицы «Ограничения» отчета по устойчивости характеризует несвязанное ограничение по сбыту. Фактически эта строка не добавляет никакой информации к содержанию аналогичной строки в отчете по результатам: недефицитный ресурс сбыта может быть сокращен на 3 т и неограниченно увеличен (величина 1E + 30 в этом смысле просто большое число, представленное в научном формате).

В разделе «Изменяемые ячейки» определяется нормированная стоимость (редуцированная стоимость) единицы изменяемой ячейки (в нашем примере тонны краски) и анализируются возможные изменения коэффициентов целевой функции (в нашем примере это стоимости тонны краски Н и В).

Редуцируемая стоимость (Рс) единицы продукции определяет разницу между ее стоимостью (Ст) и производственными затратами на ее изготовление (Пз): Рс= Ст— Пз.

Первая строка таблицы «Изменяемые ячейки» посвящена анализу ячейки В23, в которой содержится оптимальное значение производимого объема краски Н — 3,33 т.

Целевой коэффициент, определяющий стоимость первой тонны краски Н, имеет значение 3 (тыс.$/т). Производственные затраты на изготовление тонны краски Н связаны с расходами исходных продуктов Ш и П2, которые относятся к дефицитным ресурсам.

В соответствии с условиями задачи на изготовление тонны краски Н требуется 1 т продукта Ш и 2 т продукта П2, следовательно, затраты на производство тонны краски Н определяются выражением:

Пз =1 (т П1/т Краски_Н) * Теневая_Цена_Ш (тыс.$/т П1) + + 2 (т П2/т Краски_Н) * Теневая_Цена_П2 (тыс. $/т П2).

Подставляя сюда значения теневых цен П1 и П2 из таблицы «Ограничения», получим:

Пз =1 * 0,333333 + 2 * 1,333333 = 3 (тыс.$/т краски_Н).

Поскольку стоимость тонны краски Н составляет 3 (тысдолл./т), редуцируемая стоимость тонны Краски_Н будет определяться значением:

Рс = Ст — Пз = 3 — 3 = 0 (тыс.$/т краски_Н).

Аналогично определяется редуцируемая стоимость единицы варь-ируемой переменной ячейки В24 — тонны краски В.

Нулевые значения редуцируемой стоимости свидетельствуют полной реализации всех потенциальных возможностей, связанных с по-!

лучением прибыли от данного вида производственной деятельности

(производства краски). В этом и заключается оптимальное решение задачи.

В общем случае редуцируемая стоимость может отличаться от нуля в сторону как увеличения, так и уменьшения, что свидетельствует о дисбалансе между стоимостью единицы продукции и производственными затратами на ее изготовление.

При упрощенном анализе этого раздела отчета редуцируемая стоимость показывает, насколько увеличится/уменьшится значение целевой ячейки при увеличении на единицу значения соответствующей изменяемой ячейки.

Два последних столбца таблицы «Изменяемые ячейки» определяют возможные вариации целевых коэффициентов, при которых сохраняется оптимальное решение задачи, но изменяется оптимальное значение целевой функции.

При изменении целевого коэффициента 3 (это стоимость 1 т краски Н, в тыс. долл.) в пределах (3 — 2 = 1;3 + 1 = 4)и изменении целевого коэффициента 2 (стоимость 1 т краски В) в пределах (1,5; 6) оптимальное решение в ячейках В23,В24 сохранится, но значение целевой функции изменится. Например, для прежних объемов производства краски (3,33 т краски Ни 1,33 т краски В) и допустимых новых целевых коэффициентах 4 и 6 значение общей прибыли будет:

4 (тыс.$/т) * 3,33т + 6 (тыс. $/т) * 1,33т = 21,33 (тыс.$).

С другой стороны использование минимально возможных значений целевых коэффициентов приведет к получению прибыли в размере:

1 (тысдолл./т) * 3,33т +1,5 (тысдолл./т) * 1,33т = 5,33 (тысдолл.).

Еще раз подчеркнем, что эти изменения общей прибыли могут быть получены только за счет изменения цен на краску без изменения оптимального соотношения объемов производства, т. е. фактически без какой-либо реорганизации исследуемой системы.

Отчет по устойчивости для нелинейной модели

При использовании нелинейной модели для решения той же задачи отчет по устойчивости оформляется программой поиска решения в виде таблицы, приведенной ниже.

Нормированный градиент является «нелинейным аналогом» редуцируемой стоимости для линейной модели, а множитель Лагранжа — аналогом теневой цены в малой окрестности точки оптимума. Это утверждение позволяет построить лишь некоторые весьма приблизительные аналогии с линейной моделью. Оба этих понятия являются

Часть 1. Поиск решений на электронных таблицах

Анализ отчетов

математическими, а не экономическими и должны интерпретироваться математиком, а не экономистом или менеджером.

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник