Теневая цена excel что это - Word и Excel - помощь в работе с программами

Самое понятное объяснение, как это работает + коллекция новых задач

25.07.2017, Елена Позднякова

Оглавление
Как это работает
Какой ассортимент выпускать
Трансфертные цены
Задача инвестора
Настройка надстройки

Приходилось ли Вам когда-нибудь составлять план продаж, маркетинговый бюджет или схему доставки грузов? Если да, то наверняка какое-то решение зависело только от вашего профессионального суждения… Вы когда-нибудь сомневались в том, что Ваше решение наилучшее? Сожалели ли Вы о том, что не имеете возможности просчитать все варианты, ведь факторов так много, а время ограничено?
Умение легко и быстро найти правильный ответ, а еще и своевременно сформулировать вопрос, отличает профессионала высокого класса от начинающего специалиста.

Программа Excel умеет находить наилучшее решение там, где, казалось бы, лучше уже нельзя.

Чтобы это сработало, нужно уметь правильно сформулировать условия, это мы и будем учиться делать в настоящей статье.

Поиск решения — это надстройка программы Excel, по умолчанию она не установлена, поэтому, если Вы никогда ранее ее не использовали, ее нужно настроить.

На одном листе Excel будут расположены все исходные данные, формулы, взаимосвязи и ограничения: это называется математическая модель. В составе модели пять типов данных:

Константы — это исходная информация, которая имеется в модели: маржинальная прибыль по каждому продукту, стоимости перевозки от каждого поставщика к каждому покупателю, нормы расхода материалов и т.д. Эти данные могут быть как внесены и виде констант, так и рассчитываться с помощью формул.

Изменяемые ячейки — это переменные, которые мы в итоге ищем: количество продукта, которое нужно производить, чтобы прибыль была максимальной или объемы перевозок от каждого поставщика к конкретному покупателю, чтобы затраты были минимальными и т.д.
Изменяемая ячейка может быть одна или диапазон из нескольких ячеек.
Эти ячейки мы будем указывать, но оставлять пустыми, надстройка «Поиск решения» сама заполнит их наилучшими данными.

Целевая функция— для того, чтобы программа понимала, какие данные считать наилучшими, мы зададим целевую функцию. Это всегда только одна ячейка, в которую внесена формула. Формула связана с теми данными, которые мы ищем. Например, если мы ищем ассортимент, максимизирующий прибыль, формула целевой функции будет задана как сумма произведений количества каждого продукта (изменяемые данные) и маржинальной прибыли по каждому продукту (константы, внесенные в модель).
При запуске надстройки мы будем указывать, какие данные будут наилучшими для целевой ячейки: максимальное значение, минимальное значение или конкретное число.
Подбор данных в изменяемых ячейках будет осуществляться таким образом, чтобы в ячейке с целевой функцией появилось наилучшее значение.

Ограничения — являются главным элементом в Поиске решения. Все ресурсы, которые участвуют в модели и имеют максимально допустимые значения — это ограничения: объем инвестирования, объем покупательского спроса, срок реализации проекта.
Например, на складе всего 5 000 кг материала, который входит в состав всех продуктов, а мы ищем ассортимент, который даст максимальную прибыль. Чтобы правильно учесть ограничение, потребуется внести формулу, которая рассчитает объем материала, который потребуется для производства ассортимента Х — наших переменных. Далее уже непосредственно в самой надстройке будет задано ограничение:

Важно учитывать, что если переменные должны быть выражены неотрицательным или целым числом — это тоже ограничения, которые необходимо задать.

Дополнительные формулы — в модель может быть внесено любое количество дополнительных формул, которые не влияют на целевую функцию и ограничения, а несут справочную информацию по проекту.

Как это работает: пошаговая инструкция

на примере задачи по распределению заказов

Попробуйте простыми расчетами решить такую задачу:

Компания занимается производством шкатулок ручной работы. В штате есть 4 мастера-надомника. Производительность мастеров в день представлена в таблице:

Мастер 1 — 3 шкатулки в день
Мастер 2 — 1,5 шкатулки в день
Мастер 3 — 2 шкатулки в день
Мастер 4 — 2,5 шкатулки в день

Поступил срочный заказ на 100 шкатулок и нужно раздать 100 заготовок, чтобы мастера успели справиться в самый короткий срок.
Сколько и кому раздать заготовок?

Эту задачу можно решить простыми расчетами, без использования поиска решений. Для начала так и поступим:

Рассчитаем, сколько шкатулок в день могут произвести все мастера:

3+1,5+2+2,5 = 9 шкатулок.

Теперь 100 шкатулок разделим на 9 шкатулок в день и получим 11,11 дней. Соответственно, сообщаем заказчику, что заказ будет готов за 12 дней

Распределим заготовки между мастерами с использованием округления:

Мастер 1: 3 х 11,11 = 33,33 Выдаем 34 заготовки
Мастер 2: 1,5 х 11,11 = 16,66 Выдаем 17 заготовок
Мастер 3: 2 х 11,11 = 22,22 Выдаем 21 заготовку
Мастер 4: 2,5 х 11,11 = 27,77 Выдаем 28 заготовок

А теперь дополним условие и введем индивидуальные тарифные ставки для мастеров за изготовление каждой шкатулки:

Мастер 1 — 1 500 руб
Мастер 2 — 950 руб
Мастер 3 — 1 100 руб
Мастер 4 — 1 150 руб

Рассчитаем для клиента, сколько стоит изготовить 100 шкатулок

34 х 1 500 = 51 000
17 х 950 = 16 150
21 х 1 100 = 23 100
28 х 1 150 = 32 200
Итого: 122 450

А теперь клиент задает нам вопрос, а если бы заказ был не срочный, во сколько минимально он мог бы обойтись? Как Вы думаете?

Посмотрим еще раз на таблицу с исходными данными:

Мы видим, что мастер 2, который работает медленнее всех — получает меньше всех. Значит, если мы не ограничены во времени и отдадим весь заказ ему, то вся работа будет стоить всего 95 000 (950 руб х 100 шкатулок). Но сколько это займет времени? 100/1,5 = 66,66 дней.

Таким образом, путем простых расчетов и логических рассуждений мы вывели основные отправные точки для диалога с клиентом:

Минимальный срок изготовления: 11,11 дней,
стоимость 122 450

Максимальный срок изготовления: 66,66 дней,
стоимость 95 000

Разница в сроке составляет 55,55 дней, а в сумме 27 450.

Вполне логично предположить, что клиент может задать вопрос:
А если я дам Вам срок 20 дней или месяц, как изменится стоимость?

Теоретически это задание можно решить простыми расчетами, но, надеюсь, Вы не затратили много времени на это, потому что нам пора применить опцию Поиск решения, чтобы мгновенно получать результат распределения заказов с учетом любых заданных ограничений!!!

Давайте вместе решим эту задачу с использованием надстройки «Поиск решения»

Создайте новый файл в программе Excel.
Проверьте, есть ли кнопка «Поиск решения» в закладке «Данные», если нет, то здесь инструкция, как ее установить.

Наша цель: как распределить заготовки, чтобы заказ был выполнен за 20 дней и стоимость была минимальной? Сколько будет стоить в этом случае выполнение заказа?Попытайтесь сами ответить на вопросы и записать ответы:
1. Какие у нас есть константы?
2. Что будет переменными?
3. Целевая функция
4. Ограничения

Константы: время выполнения заказа и ставка за одну шкатулку по каждому мастеру
Переменные: число заготовок, передаваемое каждому мастеру
Целевая функция: общая стоимость заказа (здесь формула: сумма произведений переменных на ставку за заказ), цель — минимум
Ограничения:
1. Число шкатулок в заказе = фиксированное значение 100 шт
2. Максимальное время для выполнения заказа <= фиксированное значение 20 дней
3. Переменные должны быть выражены неотрицательным и целым числом

А теперь найдите где какие данные расположены в этой таблице:

Заполните самостоятельно свою исходную таблицу в Excel в любой удобной для Вас форме.

Так выглядит окно Поиск решения
до того, как мы начали его заполнять,

После того, как Вы внесли все исходные данные, запускаем «Поиск решения» (вкладка «Данные»). Я покажу на примере Excel 2007 (Excel 2010 немножко отличается, но сам подход аналогичен).

1. Устанавливаем целевую ячейку E13. Это целевая функция, которая равна общей стоимости заказа. Переключаем цель, чтобы она была равной минимальному значению.

2. Вносим диапазон переменных D9:D12 в поле «Изменяя ячейки».

3. Вносим ограничения:
D13 (общее число заготовок) = 100 (внесем не значение 100, а ячейку D3, чтобы в дальнейшем можно было изменить количество шкатулок в задаче)
Диапазон переменных D9:D12 = целые
Диапазон переменных D9:D12 >= 0 (неотрицательные)
F13 (срок выполнения заказа: в эту ячейку внесена формула, которая выбирает максимальное значение из сроков по каждому мастеру, она выглядит так =МАКС(F9:F12)) <= 20 дней (внесем не значение 20, а ячейку D6, чтобы можно было изменять)

Осталось нажать кнопку «Выполнить»: переменные будут заполнены и появится окно с результатами. Обратите внимание на комментарий, что все ограничения и условия выполнены и решение найдено, если нет, возможно, исходные данные сформулированы неверно. Если все хорошо, нажимайте ОК, и ячейки с переменными останутся заполненными, если нажмете ОТМЕНА, заполненные данные не сохранятся.

Будьте внимательны! Всегда проверяйте, что написано в окне результаты, потому что результат бывает отрицательным: «Поиск не может найти подходящего решения».

В этом случае данные могут быть заполнены наилучшими по мнению надстройки, но эти данные могут быть неверными и не удовлетворять условию задачи!

Итоговый результат будет выглядеть так:

У Вас получилось? Если что-то непонятно или есть вопросы, скачайте мой файл с решением и проверьте в нем:

Теперь попробуйте самостоятельно рассчитать, сколько будет стоить заказ, если на него можно затратить 30 дней.

Молодцы, кто решил! С принципом работы надстройки Поиск решения мы разобрались, а теперь идем дальше — там еще интереснее!

Какой ассортимент выпускать, чтобы получить максимальную прибыль

классика жанра

Я решила не брать в качестве классического примера транспортную задачу, потому что она уже всем надоела, ее традиционно проходят в высших учебных заведениях и по ней написано множество инструкций в интернете.
В качестве классики приведу задачу из курса по управлению эффективностью бизнеса CIMA. Что интересно, сам поиск решения в рамках курса не проходят, а только учат формулировать целевую функцию и ограничения, а затем интерпретировать результаты. Что нужно сделать, чтобы этот результат получить, не знают даже выпускники CIMA!!!, но мы восполним этот пробел и раскроем тайну, как это делается.

Приведенную здесь задачу я взяла из курса подготовки к CIMA Кузьмина Михаила Юрьевича, который проходила в 2016 году. Было очень интересно, рекомендую и вам!

THS производит два продукта из различных комбинаций одних и тех же ресурсов. Ниже приведена информация о продуктах:

THS готовит план производства на следующий месяц. Максимально доступные (за месяц) объемы ресурсов приведены в таблице:
Материал А — 5 000 кг
Материал В — 5 400 кг
Работа оборудования — 3 000 часов
Квалифицированный труд — 4 500 часов

Задание:

Определить оптимальный план производства, максимизирующий прибыль.

Подготовим расчеты для компьютерной обработки данных

Для решения задачи требуется рассчитать маржинальную прибыль по каждому продукту:

Переменные:
х — количество продукта Е
у — количество продукта R

Маржинальная прибыль от всего объема выпуска будет рассчитана по формуле:
35x + 66y
Наша цель: найти такой объем выпуска, который даст максимальное значение

Ограничения:
Материал А: 3х+2у<=5000
Материал В: 4x+3у<=5400
Работа оборудования: 2х+3у<=3000
Квалифицированный труд: 2х+5у<=4500
Объем спроса: y<=1500
Неотрицательность: х>=0, y>=0

Подготовим в Excel таблицу для ввода данных

Колонка «Значение»
По строкам 1 и 2 в будет внесено оптимальное количество продуктов. Сейчас их оставляем пустыми, функция сама их заполнит. На эти ячейки ссылаются все последующие формулы.
По строке 3 «Целевая функция» — вносим формулу со ссылкой на ячейки Х и У выше. Пока она равна нулю, ПОИСК РЕШЕНИЯ будет ее максимизировать и заполнит значение.
Далее по строкам 4-10 вносим ограничения в виде формул. Например, 3х+2у, также со ссылками на ячейки Х и У.

Колонка «Ограничение»
Ограничения можно внести как в ячейки на листе, так и непосредственно в окне «Поиск решения». В данном случае они внесены в таблицу, чтобы можно было заполнить формулу в следующей колонке (которая называется «Излишек»), т.к. она участвует в финальной матрице.

Колонка «Излишек»
Здесь вносим формулу: Ограничение — Значение. После того, как функция рассчитает все значения, мы сразу сможем видеть ограниченные ресурсы и излишки.

Итак, таблица готова и выглядит, как приведено выше.

Переходим к функции «Поиск решения»

Нажимаем кнопку «Поиск решения» в закладке «Данные» (если нет кнопки, настройка здесь)

Ограничения вносятся так:

Ограничения НЕ ОТРИЦАТЕЛЬНОСТИ можно вносить, выделяя целый диапазон ячеек:

В окне «Результаты поиска решения» проверьте, что решение найдено. И еще выберите тип дополнительного отчета: «Устойчивость», он появится на дополнительном листе, там будет полезная информация о теневой цене (что это, поясню далее).

Интерпретация полученных результатов

В итоге таблица выглядит так:

Максимальное значение прибыли 62 625 долл, достигается при выпуске оптимального ассортимента: Продукт Е — 375 ед, Продукт R — 750 ед. Смотрим колонку «Избыток»
Имеется избыток Материала А и материала В в размере 2 375 ед и 1 650 ед, соответственно.
На продукт У имеется нереализованный спрос 750 ед.

Оборудование и труд являются ограничивающими ресурсами. Это значит, что если бы у нас имелись дополнительные единицы этих ресурсов, мы могли бы произвести еще продукт и получить дополнительную прибыль.

Поиск решения позволяет проводить углубленный анализ модели и рассчитывает «теневую цену» — сложнейшее для понимания экономистов понятие.
Надбавка к номинальной цене за единицу ограниченного ресурса, которую имело бы смысл заплатить, чтобы получить еще одну дополнительную единицу ограниченного ресурса, называется теневая цена.

Теневая цена ограниченного ресурса -это дополнительная маржинальная прибыль, которая возникла бы, если бы имелась одна дополнительная единица ограниченного ресурса, либо потерянная маржинальная прибыль, которая возникла бы, если бы объем ограниченного ресурса был на единицу меньше.

Теневую цену смотрим из отчета по устойчивости:

Теперь объясню, что это значит на цифрах.

Еще одна дополнительная единица продукта, которую мы могли бы произвести, при наличии еще одной единицы ограниченного ресурса, представляет собой условную единицу. Это не одна единица E или R, а условная единица, в состав которой входят и Е, и R в той пропорции, в которой определен оптимальный план

Продукты E и R входят в оптимальный план в пропорции 375:750 или 1:2. Давайте рассмотрим минимальный набор оптимального плана, который включает 3 единицы: 1 единицу продукта Е и 2 единицы продукта R.

Вернемся к таблице с расчетом маржинальной прибыли:

Если мы приобретем все ресурсы, которые входят в состав по тем же ценам, что и прежде, то получим маржинальную прибыль 1 х 35 + 2 х 66 = 167$

Однако ресурс работы оборудования и рабочее время рабочих исчерпаны, а все остальные ресурсы есть. Значит, если мы можем арендовать дополнительную единицу оборудования и нанять еще рабочих, можно было бы доплатить. Сейчас оборудование стоит 7$ в час, труд – 10$ в час и мы и имеем маржинальную прибыль. Теневая цена показывает, что можно доплатить за 1 час работы оборудования — 10,75 (тогда он будет стоить 17,75), а за 1 час труда — 6,75 (будет стоить 16,75) — это максимальные суммы, при которых маржинальная прибыль будет равна нулю:

Итак, мы можем вести переговоры о приобретении дополнительных ресурсов с надбавкой к текущей стоимости в пределах теневой цены и нам это будет выгодно.

Если остались вопросы, скачайте мой файл с решением:

Трансфертные цены

Как установить цену продажи внутри группы, чтобы минимизировать налоги

Когда я писала эту статью, мне очень хотелось придумать задачу на Поиск решения, которая была бы полезна в реальной практике. Я опросила множество экономистов, никто из моих знакомых Поиск решения в своей работе не применял.

А у Вас есть идея,
как применить Поиск решения на практике?
Пишите мне на почту или в комментариях.
Если идея будет рабочая, я составлю задачу и опубликую ее здесь!

За идею задачи про трансфертные цены, которую я привожу в этом разделе, благодарю очень талантливого экономиста Алексея Д.!

Есть группа из 3 компаний. ООО «Крона» закупает телефоны в Китае, ООО «Стрим» продает телефоны мелкооптовыми партиями по России, ООО «Маркет» торгует телефонами через розничные точки.

Стрим и Маркет закупают телефоны у Кроны. Учитывая, что все 3 юридических лица входят в группу и имеют одного собственника, их можно рассматривать как подразделения одной компании. Перед финансовым директором стоит задача запланировать оптимальные трансфертные цены.

Трансфертная цена – это цена, по которой товары или услуги передаются между подразделениями одной и той же компании.

Имеется следующая информация о показателях деятельности на квартал:

Маркет несет дополнительные расходы в виде 30% процентов от маржинальной прибыли по сделкам, это премия управляющему директору. Сумма премии при выполнении плана реализации в 1000 штук в квартал, не может быть меньше 150 000 руб.

Ограничения:
В целях минимизации налоговых рисков в задаче установлены следующие ограничения:

Цена
Минимальная трансфертная цена не может быть ниже себестоимости, увеличенной на 5%.
Максимальная трансфертная цена для компании не может быть больше чем средняя продажная цена покупателям уменьшенная на 5%.
Цены не должны отличаться между собой не более, чем на 20%.

Прибыль
Прибыль после уплаты налогов по каждой компании должна составить не менее 1% от выручки.

Задание. Найти оптимальные трансфертные цены для реализации с Крона на Стрим и Маркет, при которых прибыль после уплаты налогов будет максимальной.

Оптимальные трансфертные цены должны удовлетворять следующим условиям:

1) распределять налоговую нагрузку внутри компании с целью минимизации налога на прибыль

2) находиться в рамках допустимого диапазона, чтобы дать возможность обосновать для контролирующих органов, что аналогичные цены использовали бы компании, действующие независимо друг от друга

3) обеспечить справедливую оценку деятельности подразделений

Для решения перенесем данные в Excel.

Сначала заполним исходные данные, которые будут участвовать в расчетах:

Теперь подготовим поля для переменных. Это 2 ячейки: цена с Кроны на Стрим и цена с Кроны на Маркет. Пока они остаются пустыми, Поиск решений сам их заполнит.

Заполним таблицу с финансовыми результатами

Это нужно, чтобы рассчитать результат целевой функции. В формулах уже участвуют ячейки с трансфертными ценами, но пока они не заполнены, итоговые значения в формулах будут нулевыми.

Выручка по Кроне рассчитывается по формуле:
количество единиц, проданных со Стрима, умноженное на трансфертную цену + количество единиц проданных с Маркета, умноженное на трансфертную цену
Выручка по Стриму и Маркету нам известна: умножаем продажи на цену

Себестоимость по Кроне нам известна: умножаем общую сумму продаж со Стрима и Маркета на покупную цену.
По Стриму и Маркету в расчете себестоимости участвуют трансфертные цены, поэтому заполним формулы, но значения пока равны нулю.

Маржинальная прибыль рассчитывается по формуле: выручка минус себестоимость

Налог. Для Кроны и Стрима используется формула маржинальная прибыль на ставку налога, у Маркета другая формула: выручка на 6%.

Премия управляющему: вносим только для Маркета: маржинальная прибыль, умноженная на 30%

Прибыль после уплаты налога по формуле: маржинальная прибыль минус премия минус налог

Целевая функция. Сумма прибыли после уплаты налога по всем компаниям

Рядом с премией управляющему сразу установим ограничение >= 150 000

Минимальное ограничение цены: 4 400 х 1,05 = 4 620
Максимальная возможная цена на Стрим: 15 200 х 0,95 = 14 440
Максимальная возможная цена на Маркет: 17 860 х 0,95 = 17 860

Для того, чтобы задать ограничение по диапазону удобно использовать формулу отношение одной цены к другой. Предварительно требуется прикинуть, какая из цен будет стремиться в большую сторону. В данном случае я сделала оценку, что цена на Маркет чем больше, тем лучше, потому что ставка премии управляющему директору выше, чем ставка налога в Кроне, а цена на Стрим, наоборот, чем меньше, чем лучше, потому что ставка налога в Стриме ниже. Можно не делать предварительную оценку, а запустить поиск решения без учета этого ограничения: выяснить максимальную цену, а затем задать ограничение. Ограничение диапазона в пределах 20% будет выглядеть так:
Значение цена на Маркет/цена на Стрим <= 1,2

И последнее ограничение: минимальная сумма прибыли после уплаты налогов. Здесь значение будем задавать через формулу: выручка, умноженная на 1%, потому что на Кроне в зависимости от изменения трансфертных цен выручка будет изменяться.

Прибыль будет максимальной — 23 246 500 руб, если мы установим цену с Кроны на Стрим — 14 100 руб и цену на Маркет — 16 920.

Задача инвестора.
Что построить на участке?

Сможете сами решить?

Инвестор приобрел 400 соток земли под застройку. На участке можно построить 3 типа объектов: коттеджи, дуплексы и пятиэтажные дома на 30 квартир.

Имеется следующая информация об объектах:

По условиям договора с покупателями управляющая компания не может быть заменена в течение 5 лет с момента начала реализации проекта, а значит, управляющая компания инвестора будет получать в дальнейшем прибыль от эксплуатации объекта

Размер инвестиций ограничен суммой 330 млн.

Вопрос: что построить на участке, чтобы в течение 5 лет с начала проекта получить максимальную прибыль и сколько это будет?

Когда я составляла эту задачу, я подгоняла условия, чтобы получить наилучший ответ, который уже был мне известен. Каково же было мое удивление, когда я запустила Поиск решения – и получила совершенно другой результат! Специально пока его не публикую, чтобы было интереснее решать.

А Вы сможете решить эту задачу? Напишите свой ответ в комментариях, и нравятся ли Вам такие задачи? И идеи, идеи!

Как настроить функцию «Поиск решения»

если у вас нет кнопки «Поиск решения» во вкладке «Данные»

Поиск решения в Excel расположен на вкладке «Данные»

Если вы у себя в Excel не видите такой кнопки, значит нужно ее настроить. Делается это так. Шаг 1: Открыть «Параметры Excel»

Шаг 2: В открывшемся окне переключиться в закладку «Надстройки», выделить приложение «Поиск решения» и нажать на кнопку «Перейти».

Шаг 3: Появится окно «Надстройки», здесь отметить галочкой надстройку «Поиск решения», нажать «ОК» и все готово.

Понравилась статья?
Поделитесь в соцсетях:

Подпишитесь на обновления, чтобы первыми узнавать о публикации новых статей

Источник

Проведем анализ устойчивости в Excel на примере задачи о прядильной фабрике.

Пример 2. Прядильная фабрика для производства четырех видов пряжи использует три типа сырья – чистую шерсть, капрон, акрил. В табл.1 указаны нормы расхода сырья, его общее количество, которое может быть использовано фабрикой в течение года; загрузка оборудования при производстве тонны пряжи и прибыль от реализации тонны пряжи каждого вида. Годовой ресурс оборудования составляет 140 тыс. маш.ч.

Требуется составить годовой план производства пряжи с целью максимизации суммарной прибыли.

Таблица 1. Исходные данные

Тип сырья	Нормы расхода сырья на 1 т. пряжи	Количество сырья (т.)
Вид 1	Вид 2	Вид 3	Вид 4
Шерсть Капрон Акрил	0,5 0,1 0,4	0,2 0,6 0,2	0,3 0,4 0,3	0,2 0,5 0,3
Загрузка оборудования в тыс. маш.ч	0,06	0,04	0,03	0,09
Прибыль от реализации 1 т пряжи (в $)

Обозначим: – объем производства пряжи i-го типа в тоннах.

На рис. 14 представлена заполненная форма для ввода условия задачи в Excel.

Диалоговое окно «Поиск решения» для рассматриваемой задачи с введенными данными приведено на рис. 15.

Рис. 15. Диалоговое окно «Поиск решения»

Рис. 16. Диалоговое окно «Результаты поиска решения»

Результаты решения задачи выводятся в форму ввода условий задачи: =235,29; =0; =0; =1352,9; ЦФz=18823529,41 (рис. 17), отчеты по результатам, по устойчивости и по пределам выводятся на отдельных листах в текущей рабочей книге Excel.

Microsoft Excel 11.0 Отчет по результатам
Целевая ячейка (Максимум)
Ячейка	Имя	Исходное значение	Результат
$F$6	коэффициенты ЦФ	0,00	18823529,41
Изменяемые ячейки
Ячейка	Имя	Исходное значение	Результат
$B$3	значение x1	235,29
$C$3	значение x2
$D$3	значение x3
$E$3	значение x4	1352,94
Ограничения
Ячейка	Имя	Значение	Формула	Статус	Разница
$F$12	Акрил левая часть	500,00	$F$12 =0	не связан.	235,3
$C$3	значение x2	$C$3>=0	связанное
$D$3	значение x3	$D$3>=0	связанное
$E$3	значение x4	1352,94	$E$3>=0	не связан.

Рис. 18- Отчет по результатам

По ресурсам приводится следующая информация: формула, соответствующая левой части ограничения; имя ограничения; значение (величина) использованного ресурса при оптимальном решении задачи; формула, задающая ограничение; статус ограничения и разница. Если ресурс используется полностью (то есть ресурс дефицитный), то в графе «Статус» («Состояние») соответствующее ограничение указывается как «связанное»; при неполном использовании ресурса (то есть ресурс недефицитный) в этой графе указывается «не связан». В графе «Разница» показана разность между значением использованного ресурса и исходно заданной величиной ресурса. Аналогичная информация приводится по переменным задачи: оптимальное значение, статус (связанная, если оптимальное значение переменной не нулевое; несвязанная в противном случае), разность между оптимальным значением переменной и заданным для нее граничным условием.

В задаче о прядильной фабрике полученное оптимальное решение означает выпуск первого и четвертого типов пряжи (базисные переменные: =235,29; =1352,9), выпускать пряжу второго и третьего типов не выгодно ( =0; =0). При таком плане выпуска полностью будут использованы ресурсы (запасы) акрила и капрона, а запасы шерсти и ресурс оборудования избыточны.

Отчет по результатам дает информацию для анализа возможного изменения запасов недефицитных ресурсов при сохранении полученного оптимального значения ЦФ. Если на ресурс наложено ограничение типа ≤, то в графе «Разница» дается количество ресурса, которое не используется при реализации оптимального решения. Например, используется 388.24 тонны шерсти. Неизрасходованным остается 211.76 тонн из общих запасов шерсти, на это количество можно уменьшить ресурс «шерсть» без изменения оптимального решения. Аналогично можно уменьшить ресурсы оборудования на 4.12 тыс. часов и это не повлияет на оптимальное решение.

Если на ресурс наложено ограничение типа ≥, то в графе «Разница» дается количество ресурса, на которое была превышена минимально необходимая норма. Если на эту величину увеличить ресурс, оптимальное решение задачи не изменится.

Отчет по устойчивости. На рис. 19 представлен отчет по устойчивости для задачи примера 1, который состоит из двух частей: информация по переменным и информация по ограничениям.

Microsoft Excel 11.00 Отчет по устойчивости
Изменяемые ячейки
Рез.	Нормир.	Целевой	Допусти -мое	Допусти -мое
Ячейка	Имя	знач.	стоимость	Коэфф.	увели -чение	умень- шение
$B$3	x1	235,3
$C$3	x2	-1352,9	1352,94	1E+30
$D$3	x3	-1617,7	1617,65	1E+30
$E$3	x4	1045,45
Ограничения
Рез.	Теневая	Ограни- чение	Допусти -мое	Допусти -мое
Ячейка	Имя	знач.	Цена	Правая часть	увели -чение	умень- шение
$F$12	акрил	25294,1	33,33
$F$11	капрон	8823,5	38,89	514,29
$F$10	шерсть	0,00	1E+30	211,76
$F$13	обору дование	0,00	1E+30	4,12

Рис. 19- Отчет по устойчивости

Нормированная стоимость показывает, на сколько изменится значение ЦФ в случае принудительного включения единицы этой продукции в оптимальное решение. Например, в отчете по устойчивости для рассматриваемой задачи нормированная стоимость для второго вида пряжи равна: -1352.94. Это означает, что если включить в план выпуска 1 тонну пряжи второго вида, то новый план выпуска принесет прибыль на 1352.94$ меньше, чем прежний оптимальный план. Нормированная стоимость для базисных переменных всегда равна нулю.

Предельные значения приращения целевых коэффициентов. Для каждой переменной указаны заданные коэффициенты ЦФ, допустимые увеличение и уменьшение коэффициентов при которых сохраняется оптимальное решение задачи. Например, допустимое увеличение цены на пряжу первого вида равно 2875$ за тонну, а допустимое уменьшение – 8600$. Это означает, что если цена на тонну пряжи первого вида возрастет не более чем на 2875$, например станет равной 13875$, то оптимальное решение сохранится, изменится только значение ЦФ в оптимальной точке.

При выходе за указанные в отчете по устойчивости пределы изменения цен оптимальное решение может измениться как по номенклатуре выпускаемой продукции, так и по объемам выпуска (без изменения номенклатуры).

Далее в отчете по устойчивости приводится информация, относящаяся к ограничениям. В колонке «Результирующее значение» приводится величина использованных ресурсов.

Предельные значения приращения ресурсов. В графах «Допустимое уменьшение» и «Допустимое увеличение» показано на сколько можно уменьшить (устранить излишек) или увеличить (повысить минимально необходимое требование) ресурс, сохранив при этом базис оптимального решения (изменить объем выпуска продукции без изменения номенклатуры). Рассмотрим анализ дефицитных ресурсов, так как анализ недефицитных ресурсов был дан при описании отчета по результатам. В рассматриваемой задаче такими ограничениями являются дефицитные ресурсы «акрил» и «капрон». Например, если ресурсы акрила уменьшатся не более чем на 80 тонн или возрастут не более чем на 33.33 тонны, базис задачи не изменится (по-прежнему будет оптимально выпускать пряжу первого и четвертого типов, хотя объемы выпуска изменятся).

Теневая цена (ценность дополнительной единицы i-го ресурса). Теневая цена показывает насколько возрастет значение ЦФ в случае выделения дополнительной единицы i-го ресурса. Очевидно, что теневая цена не нулевая только для дефицитных ресурсов. Например, если запасы акрила возрастут на 1 тонну, прибыль увеличится на 25294,12$, если запасы капрона возрастут на 1 тонну, то прибыль будет на 8823.53$ больше, чем исходная. Поэтому в первую очередь для фабрики выгодно увеличивать запасы акрила.

В терминах теории двойственности теневая цена соответствует значению двойственной оценки соответствующего ресурса, а нормированная стоимость – значению дополнительной двойственной оценки, которая равна разности между левой и правой частями в ограничениях двойственной задачи.

Отчет по пределам. Для рассматриваемой задачи отчет по пределам приведен на рис. 20.

Microsoft Excel 11.0 Отчет по пределам
Целевое
Ячейка	Имя	Знач.
$F$6	ЦФ
Изменяемое	Ниж.	Целевой	Верх.	Целевой
Ячейка	Имя	Знач.	пред.	результат	пред.	рез.
$B$3	x1	235,29	16235294,1	235,3
$C$3	x2	18823529,4
$D$3	x3	18823529,4
$E$3	x4	1352,94	2588235,3	1352,9

Рис. 20. Отчет по пределам

В отчете по пределам показано в каком диапазоне могут изменяться значения переменных, без изменения базиса (номенклатуры выпуска продукции). Например, если будет выпускаться 235 тонн пряжи первого вида, то в оптимальном решении ненулевые переменные будут соответствовать объемам выпуска первого и четвертого видов пряжи. В случае выпуска более чем 235.29 тонн пряжи первого типа номенклатура выпуска продукции изменится. Также в отчете по пределам приводится информация о величине ЦФ при нижнем и верхнем предельных значениях переменных задачи.

Содержание

1. Настройка MS Excel 4

2. Подготовка листа с исходными данными. 5

Порядок заполнения листа. 6

3. Установка данных для пакета «Поиск решения». 6

4. Получение результатов решения. 8

5. Типы отчетов: 9

6. Решение в Excel задач ЦЛП.. 10

7. Пример решения транспортной задачи. 11

8 Исследование устойчивости решения задачи ЛП.. 12

Анализ сокращения или увеличения ресурсов: 13

Microsoft Excel 8.0 Отчет по устойчивости

Отчет по устойчивости

Отчет по устойчивости имеет две различные формы: отчет по устойчивости решений, полученных с помощью линейных моделей оптимизации и нелинейных.

Результатам решения линейных задач можно дать наглядную экономическую интерпретацию. К сожалению, результаты, получаемые с помощью нелинейных моделей, в большинстве случаев не имеют такой интерпретации.

Часть 1. Поиск решений на электронных таблицах

Основной вопрос, освещаемый в этом отчете: насколько устойчиво найденное оптимальное решение по отношению к возможным изменениям параметров задачи. Любая строка любой таблицы этого отчета говорит о том, какие изменения можно произвести по отношению к ячейке (столбец «Ячейка») при условии, что содержимое остальных ячеек определяется оптимальным решением.

Отчет по устойчивости длялинейной модели

Отчет состоит из двух разделов: изменяемые ячейки и ограничения.

Рабочий лист: [Задача о красках.хфРешение задачи Отчет создан: 19.02.01 13:31:42

Ячейка	Имя	Результ. значение	Нормир. стоимость	Целевой Допустимое Коэффици- Увеличениеент	Допустимое Уменьшение
$В$23	Краска_Н	3,33	0,00	3 1
$В$24	Краска_В	1,33	0,00	2 4	0,5
Ограничения
Ячейка	Имя	Результ.значение	Теневая Цена	Ограничение Допустимое Правая часть Увеличение	Допустимое Уменьшение
$Е$16	П1 Суточ-ный_расход исх. продукте	6,00	0,33	6 1	1Е+30
$Е$17	П2 Суточ-	8,00	1,33	8 1Е+30	2′

ный_расход исх.продукто в(т)

Раздел «Ограничения» связан с анализом связанных ограничений на возможность изменения их правых частей (запасов дефицитных ресурсов) в пределах постоянства теневой цены.

Для дефицитных ресурсов (в нашей задаче это запасы исходных продуктов, сохраняемые в ячейках Е16, Е17) важен вопрос: какое дополнительное увеличение целевой функции может обеспечить увеличение запасов ресурса. Ответ на этот вопрос связан с использованием понятия теневой цены (скрытой цены, двойственной цены, ценности ресурса):

Теневая цена ресурса определяет прирост целевой функции, обеспечиваемый увеличением запаса дефицитного ресурса на единицу егоизмерения.

Анализ отчетов

Так, теневая цена продукта П1 (ячейка Е16) определена как 0,333333 (тыс. долл./т). Это означает, что увеличение запаса П1 на тонну увеличит целевую функцию примерно на 333 долл. Аналогичное влияние на изменение значения целевой функции оказывает теневая цена продукта Ш (ячейка Е17), которая определяется значением 1,333333 (тыс. долл./т).

Теневая цена определяет скрытые возможности реорганизации системы путем изменения запасов дефицитных ресурсов, изменения организации использования этих ресурсов (расширение складов и т. п.). Кроме того, теневая цена позволяет ранжировать такие ресурсы с точки зрения их полезности для расширения производства.

Например, в нашем примере сравнение теневых цен Ш и П2 показывает, что при стремлении увеличить общую прибыль от продажи краски предпочтение нужно отдать увеличению запасов продукта П2, поскольку он имеет большую теневую цену.

Однако анализ найденного оптимального решения с помощью теневых цен имеет смысл только в определенных пределах. Эти пределы указывают, в каких границах изменение запасов того или иного дефицитного ресурса влияет на найденное оптимальное решение задачи и значение целевой функции. В этом разделе отчета утверждается, что запасы ресурса П1 могут изменяться в пределах (6 — 1, 96; 6+1) тонн, дальнейшее увеличение или уменьшение запаса не будет оказывать влияния на оптимальное решение задачи (т. е. соответствующее ограничение по запасу ресурсов станет избыточным, а сам ресурс .перейдет в категорию недефицитных). Аналогично значения (8 — 1, 95) и (8 + 4) определяют пределы возможных изменений запасов другого дефицитного ресурса П2. Увеличение П2 в этом интервале от 8 т до 12 т приведет к изменению оптимального решения задачи и увеличению значения целевой функции, уменьшение запаса П2 с 8 т до примерно 6 т — к уменьшению найденного значения целевой функции.

Другими словами, четыре правых столбца таблицы ограничений определяют теневую цену ресурса и диапазон возможных изменений запасов этого ресурса, в котором теневая цена остается для данной задачи постоянной. Любое изменение дефицитного ресурса в пределах постоянства теневой цены приводит к изменению оптимального решения задачи и значения целевой функции.

Для любого недефицитного ресурса теневая цена равна нулю, поэтому для этого типа ресурсов интересен один вопрос: насколько можно снизить запасы ресурса при сохранении найденного оптимального решения. Ответ на этот вопрос можно получить при анализе отчета по результатам.

Часть 1. Поиск решений на электронных таблицах

Анализ Отчетов

Третья строка таблицы «Ограничения» отчета по устойчивости характеризует несвязанное ограничение по сбыту. Фактически эта строка не добавляет никакой информации к содержанию аналогичной строки в отчете по результатам: недефицитный ресурс сбыта может быть сокращен на 3 т и неограниченно увеличен (величина 1E + 30 в этом смысле просто большое число, представленное в научном формате).

В разделе «Изменяемые ячейки» определяется нормированная стоимость (редуцированная стоимость) единицы изменяемой ячейки (в нашем примере тонны краски) и анализируются возможные изменения коэффициентов целевой функции (в нашем примере это стоимости тонны краски Н и В).

Редуцируемая стоимость (Рс) единицы продукции определяет разницу между ее стоимостью (Ст) и производственными затратами на ее изготовление (Пз): Рс= Ст— Пз.

Первая строка таблицы «Изменяемые ячейки» посвящена анализу ячейки В23, в которой содержится оптимальное значение производимого объема краски Н — 3,33 т.

Целевой коэффициент, определяющий стоимость первой тонны краски Н, имеет значение 3 (тыс.$/т). Производственные затраты на изготовление тонны краски Н связаны с расходами исходных продуктов Ш и П2, которые относятся к дефицитным ресурсам.

В соответствии с условиями задачи на изготовление тонны краски Н требуется 1 т продукта Ш и 2 т продукта П2, следовательно, затраты на производство тонны краски Н определяются выражением:

Пз =1 (т П1/т Краски_Н) * Теневая_Цена_Ш (тыс.$/т П1) + + 2 (т П2/т Краски_Н) * Теневая_Цена_П2 (тыс. $/т П2).

Подставляя сюда значения теневых цен П1 и П2 из таблицы «Ограничения», получим:

Пз =1 * 0,333333 + 2 * 1,333333 = 3 (тыс.$/т краски_Н).

Поскольку стоимость тонны краски Н составляет 3 (тысдолл./т), редуцируемая стоимость тонны Краски_Н будет определяться значением:

Рс = Ст — Пз = 3 — 3 = 0 (тыс.$/т краски_Н).

Аналогично определяется редуцируемая стоимость единицы варь-ируемой переменной ячейки В24 — тонны краски В.

Нулевые значения редуцируемой стоимости свидетельствуют полной реализации всех потенциальных возможностей, связанных с по-!

лучением прибыли от данного вида производственной деятельности

(производства краски). В этом и заключается оптимальное решение задачи.

В общем случае редуцируемая стоимость может отличаться от нуля в сторону как увеличения, так и уменьшения, что свидетельствует о дисбалансе между стоимостью единицы продукции и производственными затратами на ее изготовление.

При упрощенном анализе этого раздела отчета редуцируемая стоимость показывает, насколько увеличится/уменьшится значение целевой ячейки при увеличении на единицу значения соответствующей изменяемой ячейки.

Два последних столбца таблицы «Изменяемые ячейки» определяют возможные вариации целевых коэффициентов, при которых сохраняется оптимальное решение задачи, но изменяется оптимальное значение целевой функции.

При изменении целевого коэффициента 3 (это стоимость 1 т краски Н, в тыс. долл.) в пределах (3 — 2 = 1;3 + 1 = 4)и изменении целевого коэффициента 2 (стоимость 1 т краски В) в пределах (1,5; 6) оптимальное решение в ячейках В23,В24 сохранится, но значение целевой функции изменится. Например, для прежних объемов производства краски (3,33 т краски Ни 1,33 т краски В) и допустимых новых целевых коэффициентах 4 и 6 значение общей прибыли будет:

4 (тыс.$/т) * 3,33т + 6 (тыс. $/т) * 1,33т = 21,33 (тыс.$).

С другой стороны использование минимально возможных значений целевых коэффициентов приведет к получению прибыли в размере:

1 (тысдолл./т) * 3,33т +1,5 (тысдолл./т) * 1,33т = 5,33 (тысдолл.).

Еще раз подчеркнем, что эти изменения общей прибыли могут быть получены только за счет изменения цен на краску без изменения оптимального соотношения объемов производства, т. е. фактически без какой-либо реорганизации исследуемой системы.

Отчет по устойчивости для нелинейной модели

При использовании нелинейной модели для решения той же задачи отчет по устойчивости оформляется программой поиска решения в виде таблицы, приведенной ниже.

Нормированный градиент является «нелинейным аналогом» редуцируемой стоимости для линейной модели, а множитель Лагранжа — аналогом теневой цены в малой окрестности точки оптимума. Это утверждение позволяет построить лишь некоторые весьма приблизительные аналогии с линейной моделью. Оба этих понятия являются

Часть 1. Поиск решений на электронных таблицах

Анализ отчетов

математическими, а не экономическими и должны интерпретироваться математиком, а не экономистом или менеджером.

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник

Тема: Толкование отчетов: по устойчивости, по результатам, по пределам

Раздел: Бесплатные рефераты по ЭММ и ПМ

Вуз: ВЗФЭИ

Отчеты бывают трех типов: по результатам, по устойчивости, по пределам.
По найденным результатам можно создавать отчеты. Такие отчеты полезны для сравнения влияния на решение различных ограничений или исходных данных. Потому они являются очень важными инструментом для анализа полученных результатов и последующего их улучшения в зависимости от возможностей и ресурсов предприятия.

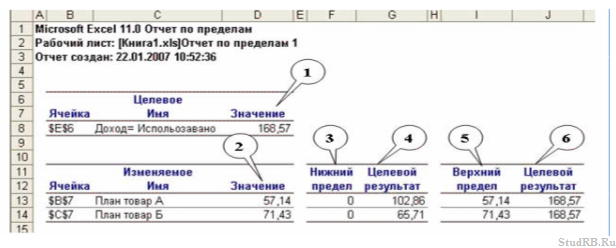
Отчет по пределам

Отчет по пределам состоит из двух частей, что касаются значений ЦФ (Целевое) и плана (Изменяемое).
1 – значение ЦФ (Доход);
2 – оптимальный план задачи;
3 – наименьшее значения, которое может принять неизвестное (в нашем случае количество товара А и Б имеет Нижний предел 0, поскольку мы в Параметрах Поиска решений отметили Неотрицательные значения);
4 – это значение, которое будет в целевой ячейке (Доход), если неизвестное будит равно Нижнему пределу;
5 – это наибольшее значение, которое может содержать неизвестные, чтобы получить максимальную ЦФ;
6 – это значение, которое будет в целевой ячейке (Доход), если неизвестные будут равны Верхнему пределу.
Вывод: как видим, отчет по пределам содержит результаты, которые мы уже имеем в таблице, потому его можно в дальнейшем не выводить.

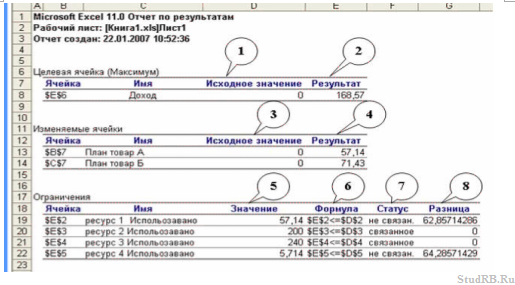
Отчет по результатам

Отчет по результатам содержит информацию о трех компонентах задачи оптимизации: целевой функции (Целевая ячейка), плана (Изменяемые ячейки), и ограничений (Ограничения).
1 – начальное значение целевой функции при начальном опорном плане (3);
2 – максимальное или минимальное значение (в зависимости от задачи) целевой функции. В нашем случае — 168,57 д. ед.;
3 – начальный опорный план;
4 – оптимальный план задачи. В нашем случае, чтобы получить максимальную выручку в размере 168,37 д. ед., нужно производить 57,14 единиц товара А и 71,43 единиц товара Б (понятно, что товар должен быть в целых единицах, но если бы мы задали такой параметр, то не получили отчеты, которые нужны для анализа и улучшение полученных результатов);
5 – показывает количество использованных ресурсов на производство при оптимальном плане;
6 – формулы ограничений;
7 – показывает влияние ограничений на конечный результат. Если статус «связанное», тогда данное ограничение влияет на полученный план, если «не связан» — значит не влияет. В нашем случае ресурс 1 и 4 имеют статус «не связан» — это значит, что эти ресурсы не ограничивают возможности в производстве, что не скажешь про ресурс 2 и 3, которые использованы полностью;
8 – разница между имеющемся в наличие количеством ресурсов и использованных при полученном плане.
Вывод: большинство данных отчета занесены в таблицу, другие – просто не нужны для анализа. Значит этот вид отчета можно не выводить!

Отчет по устойчивости

Отчет по устойчивости (более точным за содержанием был бы перевод с оригинала sensitivity — чувствительность) есть наиболее интересным и полезным – он определяет чувствительность структуры полученного плану до изменений начальных данных и, согласно, дальнейшие действия менеджера с целью улучшения результатов. Такой отчет не создается для моделей, значения в которых ограничены множеством целых чисел. В случае нелинейных моделей отчет содержит данные для градиентов и множителей Лагранжа.
1 – оптимальный план задачи. В нашем случае, чтобы получить максимальную выручку в размере 168,37 д. ед., нужно производить 57,14 единиц товара А и 71,43 единиц товара Б;
2 – нормированная стоимость касается неизвестных плана. Это неудачный перевод с оригинала reduced cost, которую можно было перевести, как «цена, которая уменьшает (целевую функцию)». Этот показатель, как изменится оптимальное значение ЦФ при выпуске продукции, которой нету в оптимальном плане. Например, если нормированная стоимость товара А была бы -3 (хотя в нашем случае это 0), то принудительный выпуск 2 единиц товара А, которых нету в оптимальном плане привел к уменьшению Дохода на 2•3=6 и составлял бы 168,57-6= 162, 57 д. ед.
3 – коэффициенты ЦФ;
4, 5 – границы изменений значений коэффициентов ЦФ при условии, что количество оптимальной продукции (план) не изменится. Например, если целевой коэффициент товара А (КА) равен 1,15 (цена за 1 единицу товара), то изменяя его в рамках 1,15-0,43< КА<1,15+0,074 > 0,72< КА<1,224 план не изменится, но значения дохода может уменьшится или увеличится. Это можно проверит если запустить программу «Поиск решений», после внесений в таблицу изменений данного коэффициента.
6 – количество использованных ресурсов;
7 – теневая цена(в нелинейной модели это множитель Лагранжа) касается ограничений, то есть, определенное значение указывает на «ценность» ограниченного ресурса в сравнении с другими ресурсами. Этот показатель указывает как изменится оптимальное значение ЦФ (Доход) при изменении запасов ресурсов на 1 единицу. Например, если увеличить запас ресурса 3 на 10 единиц, то доход увеличится на 10•0,61=6,1 и будет составлять 168,57+6,1=174,67 д. ед.
8 – запасы ресурсов;
9, 10 – задают диапазон для 8, в котором действует теневая цена 7 (аналогично 4, 5). Например, диапазон ресурса 3: 200<ресурс 3<340. Если ресурс 3 увеличить на 10 единиц, то доход увеличится на 6,1 и будет составлять 174,67. Если этот ресурс увеличить на 110 единиц, то про доход ничего сказать нельзя, поскольку мы вышли за указанные пределы.
Вывод: для конечного результата оптимизации нужен только отчет по устойчивости плана, поскольку там содержится наиболее существенная информация.

Чтобы полностью ознакомиться с толкованием, скачайте файл!

Внимание!

Если вам нужна помощь в написании работы, то рекомендуем обратиться к профессионалам. Более 70 000 авторов готовы помочь вам прямо сейчас. Бесплатные корректировки и доработки. Узнайте стоимость своей работы

Бесплатная оценка

Понравилось? Нажмите на кнопочку ниже. Вам не сложно, а нам приятно).

Чтобы скачать бесплатно Шпаргалки на максимальной скорости, зарегистрируйтесь или авторизуйтесь на сайте.

Важно! Все представленные Шпаргалки для бесплатного скачивания предназначены для составления плана или основы собственных научных трудов.

Друзья! У вас есть уникальная возможность помочь таким же студентам как и вы! Если наш сайт помог вам найти нужную работу, то вы, безусловно, понимаете как добавленная вами работа может облегчить труд другим.

Добавить работу

Если Шпаргалка, по Вашему мнению, плохого качества, или эту работу Вы уже встречали, сообщите об этом нам.

Добавление отзыва к работе

Добавить отзыв могут только зарегистрированные пользователи.

Похожие работы

Шпаргалки по ЭММ и ПМ на зачет
Ответы к экзамену по экономико-математическим методам
Экзаменационные задачи с решением в Excel по ЭММ и ПМ
Шпора по ЭММ и ПМ для экзамена
Ответы на вопросы к защите контрольной по ЭММ и ПМ
Шпаргалка по ЭММ и ПМ на экзамен

Источник

2.4. анализ решения злп на основе отчётов ms excel

Рассмотрим следующую ЗЛП:

f (x) =7,5х1+3х2+6х3+12х4—»max 2хі+х2+0,5х3+4х4 < 2400 х1+5х2+3х3 < 1200

3хі+6х3+х4 < 2000

Хі,2,3,4 ^0.

Начнём с отчёта результатов. Приведём его вид:

|ДІ В | С | D I Е | F | G | Н L

1	Целевая ячейка (Максим
7	Ячейка	Имя	Исходно	Результат
в	JGJ4	ЦФ	0,000	7884,296
9 10 11	Изменяемые ячейки
12	Ячейка	Имя	Исходно	Результат
13	JBJ4	продуктА	0,000	8,800
14	JCI4	продуктВ	0,000	148,760
15	JDJ4	продукте	0,000	152,066
16	JEI4	продукти	0,000	543,802
17 16 19	Ограничения
20	Ячейка	Имя	Значение	формула	Статус	Разница
21	JFJ12	ограничение!	2400,000 $F$12<=$H$12	связанное	0
22	JFJ13	ограничение!	1200,000 JF$13<=$H$13	связанное	0
23	JFJ14	ограничение!	I 2000,000 $F$14<=$H$14	связанное	0
24	ЇВЇ4	продуктА	0,000 JBt4>=0	связанное	0,000
25	JCJ4	продуктВ	146,760 JC(4>=0	не связан.	148,760
27	JDI4	продукте	152,066 IDt4>=0	не связан.	152,066
JEJ4	продукти	543,802 JEt4>=0	не связан.	543,802

Единственное, что здесь следует прокомментировать, это статус ресурсов. Т.к. все ограничения на ресурсы являются связанными, то это говорит о том, что все ресурсы были использованы. Другими словами, все ресурсы являются дефицитными.

I |Д| В | С | D | Е | F | G | Н I I |

7 Результ. Нормир. Целевой Допустимое Допустимое

8 Ячейка Имя значение стоимость Коэффициент Увеличение Уменьшение

1Г $Bt4 продуктА 8,800 -0,062 7,5 0,061983471 1Е+30

Ю_ КІА продуктВ 148,760 0,000 3 7,5 0,391304348

jj_ $Dt4 продукте 152,866 0,000 6 31,8 0,178571429

Г2_ ЦЕН продуктР 543,802 0,000 12 1,5 0,135135135

14 Ограничения

15 Результ. Теневая Ограничение Допустимое Допустимое

16 Ячейка Имя значение Цена Правая часть Увеличение Уменьшение

ТГ $F$12 ограничение! 2400,000 2,628 2400 1840 2193,333333

ГВ_ HFS13 ограничение!! 1200,000 0,074 1200 10966,66667 782,6086957

^9_ $Ft14 ограничение!!! 2000,000 0,744 2000 1500 920

Рассмотрим отчёт по устойчивости:

Нормированная стоимость (часто, редуцированная стоимость, от английского: cost reduction уменьшение затрат) представляет собой дополнительные двойственные переменные. Они показывают, насколько по модулю уменьшится целевая функция при принудительном выпуске единицы данной продукции. В нашем примере нормированная стоимость по продукту А не равна нулю. Следовательно, если мы будем принудительно выпускать единицу продукта А, то целевая функция уменьшится на 0,062. Другими словами, выпуск продукта А является нерентабельным (неприбыльным).

Допустимое увеличение показывает, насколько максимально можно увеличить коэффициент целевой функции (цену продукта), чтобы структура оптимального плана осталась прежней. Допустимое уменьшение, наоборот, показывает, насколько можно максимально уменьшить коэффициент ЦФ, чтобы осталась прежней структура оптимального плана. Например, в нашей задаче, чтобы выпуск продукта А оставался нерентабельным, максимально допустимое увеличение его цены составляет приблизительно 0.06. Допустимое же уменьшение представляет собой огромное число. Это понятно, т.к., ещё больше уменьшив цену нерентабельного продукта, сделать его рентабельным невозможно.

Теневая цена в отчётах Excel представляет собой двойственные переменные. Они показывают, как изменится целевая функция при изменения запаса ресурса на единицу. Понятно, что если ресурс использован полностью, то теневая цена этого ресурса положительна. Например, если мы увеличим запас ресурса I на единицу, то ЦФ возрастёт на 2,628 (ресурс I является самым приоритетным). Допустимое увеличение и уменьшение показывают границы, в которых могут изменяться ресурсы, чтобы структура оптимального решения, т.е. номенклатура выпускаемой продукции, остались без изменений.

Рассмотрим последний отчёт отчёт по пределам:

	А\| В	С I	D ІЕ	F	G \|Н	I	J I	к I
4 5
7	Ячейка	Имя	значение
І	SGJ4	ЦФ	7884,298
11		Изменяемое		Нижний	Целевое	Верхний	Целевое
12	Ячейка	Имя	значение	предел	результат	предел	результат
13	ЇВЇ4	продукгА	0,000	0,000	7884,233	0,000	7884,298
14	ICJ4	продукгВ	148,700	0,000	7438,017	148,760	7884,298
15	ШИ	продукте	152,066	0,000	6971,901	152,066	7884,298
16	ЇЕЇ4	продуктО	543,802	0,000	1358,673	543,802	7884,298

В отчёте указаны значения ЦФ при выпуске данного типа продукции на нижнем и верхнем пределах. Так, значение ЦФ 6971,901 соответствует тому, что продукт С не выпускается.

Отчёты Excel обеспечивают всей необходимой информацией для проведения полного анализа линейной модели.

Домашнее задание 2. 1.

Решить с помощью MS Excel следующие задачи (варианты 1-5, 610).

1-5.Для приготовления четырех видов продукции (A, B, C, D) используют три вида сырья. Ресурсы сырья, норма его расхода на единицу продукции и цена продукции заданы в соответствующей таблице.

Определите план выпуска продукции из условия максимизации его стоимости.

Определите статус, ценность каждого ресурса и его приоритет при решении задачи увеличения запаса ресурсов.

Определите максимальный интервал изменения запасов каждого из ресурсов, в пределах которого структура оптимального плана, то есть номенклатура выпускаемой продукции, остается без изменения.

Определите суммарную стоимостную оценку ресурсов, используемых при производстве единицы каждого изделия. Производство какой продукции нерентабельно?

На сколько уменьшится стоимость выпускаемой продукции при принудительном выпуске единицы нерентабельной продукции?

На сколько можно снизить запас каждого из ресурсов, чтобы это не привело к уменьшению прибыли?

Определите изменение стоимости продукции и количество выпускаемых изделий при увеличении второго вида сырья на Z единиц.

Определите оптимальное решение задачи для случая, когда вектор ресурсов задан в виде в -строки.

Определите интервалы изменения цен на каждую продукцию, при которых сохраняется оптимальный план.

продукции, чтобы сделать На сколько нужно снизить затраты каждого вида сырья на единицу производство нерентабельного изделия рентабельным?

На сколько нужно изменить запас каждого из дефицитных ресурсов, чтобы прибыль возросла на 20%?

6-і0.Из 4 видов кормов необходимо составить рацион, в состав которого должно входить не менее ві ед. вещества А, в2 ед. вещества В и в3 ед. вещества С. Количество единиц вещества, содержащегося в і кг корма каждого вида, указано в соответствующей таблице. В ней же приведена цена і кг корма каждого вида.

Составьте рацион, содержащий не менее нужного количества указанных питательных веществ и имеющий минимальную стоимость.

Определите, все ли виды кормов входят в рацион, ценность дополнительной единицы каждого питательного вещества и его приоритет при решении задач уменьшения стоимости рациона.

Определите суммарную стоимостную оценку питательных веществ в единице каждого корма, использование какого вида корма нерентабельно.

Содержание какого из питательных веществ превышает заданный минимальный уровень и на сколько?

Определите максимально возможное уменьшение содержания каждого из питательных веществ в рационе, при котором структура рациона остается без изменений.

На сколько уменьшится стоимость рациона и используемое количество кормов при снижении минимального уровня потребления питательного вещества В до Z ед.

Определите интервал изменения цен на каждый вид корма, при котором сохраняется структура рациона.

Возможно ли сделать выгодным использование корма, не вошедшего в рацион.

На сколько увеличится стоимость рациона при принудительном включении в рацион 1 кг нерентабельного вида корма.

На сколько нужно снизить минимальный уровень потребления каждого из питательных веществ, чтобы уменьшить стоимость рациона на 10%?.

і0.

2.5. Двойственный симплекс-метод (Р-метод)

Пример 2.9. Рассмотрим следующую ЗЛП:

min(2Xi + 4Х2 )

Х1 + Х2 > 3

Х1 + 3 Х2 > 6 Х1 + 2 Х2 < 3

Хі,2 > 0

Приведем рассматриваемую ЗЛП к каноническому виду

max (-2 Х1 -4 Х2 )

Х1 + Х2 S1 = 3

Х1 + 3 Х2 S2 = 6 Х1 + 2 Х2 S3 = 3

X, > 0, j = ГД, S, > 0, j =1,3.

(2.28)

или

max (-2 Х1 -4 Х2 )

3 Х1 — Х2 + S1 = 3

4 Х1 3 Х2 + S2 = -6

Х1 + 2 Х2+ S3 = 3

(2.29)

> 0, j = 1,2, S, > 0, i = 1,3. Рассмотрим расширенную матрицу системы линейных уравнений

(2.29):

	(-3	-1	1	0	0	31
P (°) =	4	-3	0	1	0	6
	v 1	2	0	0	1	3,

Матрица P(0) содержит единичную подматрицу порядка 3 и , следовательно, определяет базисное решение

An«0) = (-3; -6; 3); N (0)= (3; 4; 5)

системы уравнений , причем Cn(0) =( 0,0,0). Так как элементы ( n + 1 = 6 )-го столбца матрицы системы P(0) не являются неотрицательными, то она не является К-матрицей ЗЛП. Вычислим симплекс-разности матрицы P(0):

A(f = (Cn(0),а?) С, =-Cj > 0, j = 1,5

Так как все симплекс-разности матрицы то базисное решение XN(0) =

(0)

являются

При решении задачи симплекс-методом текущее базисное решение является опорным планом, но неоптимальным. Эти соображения позволяют построить метод решения определенного класса ЗЛП. В этом методе, называемом двойственным симплекс-методом, на каждой итерации обеспечивается выполнение условия оптимальности текущего базисного решения, не являющегося планом. Критерием окончания процесса итераций является получение опорного плана (неотрицательных свободных членов системы уравнений), который будет являться и оптимальным.

Определение P-матрицы ЗЛП.

Определение. Р-матрицей КЗЛП будем называть расширенную матрицу системы линейных уравнений, равносильной исходной системе, содержащую единичную подматрицу порядка m на месте n первых столбцов, все симплекс разности которой неотрицательны.

Очевидно, что всякая Р-матрица ЗЛП определяет некоторое базисное решение системы уравнений (2.29) (см.пример 2.9)

Определение. Базисное решение системы линейных уравнений (2.29), определяемое Р-матрицей, называется псевдопланом ЗЛП.

Условия перехода от одной P-матрицы ЗЛП к другой.

Пусть известна Р-матрица P(S) ЗЛП (2.28), определяющая псевдоплан

— —(S) (S)

Xn<s)= b ; N

Условия перехода от матрицы P(S) к матрице P(S+1) составляют

содержание теоремы і.

Теорема 1. Пусть bS )< 0 и в l -й строке матрицы P( S) есть хотя бы

один отрицательный элемент. Тогда одного шага метода Жордана-Гаусса можно построить новую Р-матрицу P(м), выбрав направляющий элемент из условия

д( s ) А(5)

°{S) =—7^ = min—(2 30) a7) *& of) (2.30)

Су<0

Замечание 1. Если в матрице P нет b( S )< 0, то определяемый ею псевдоплан является решением ЗЛП.

Теорема 2. Пусть ЦS )< 0 и в 1-й строке матрицы P( S) нет ни одного

отрицательного элемента. Тогда множество планов Р ЗЛП (2.28) пусто.

Замечание 2. При переходе от матрицы P( S) к матрице P(S+і) целевая функция изменяется в соответствии с формулой

(S)

f( XN(S+1)) = f ( XN(S)) + d(S)bS = f ( XN(S)) + bf (2.3і)

UIK откуда следует, что

f ( Xn(s+1)) < f ( Xn(s)), (2.32) так как ЪS)< 0 и aK) < 0. Из неравенства (2.32) следует, что при

переходе от одного псевдоплана к другому значение целевой функции f (x) не возрастает.

Алгоритм Р-метода.

Будем считать, что известна исходная Р-матрица P(0) задачи линейного программирования, определяющая исходный псевдоплан

X^0) = (Ъ(0),Ъ20),…,ъ<°>) ,

N(0) = (N(0), N 20),…, Ni0)).

В методе последовательного уточнения оценок последовательно

строят Р-матрицы P(1), P(2).., P(S), … задачи линейного

программирования, пока не получат Р-матрицу задачи линейного программирования, определяющую ее оптимальный план.

Рассмотрим алгоритм S-й итерации метода последовательного уточнения оценок. В начале S-й итерации имеем Р-матрицу P( S-1) задачи линейного программирования, определяющую псевдоплан

— (S-1) (S-1)

XN(S-1)= Ъ , N . Шаг 1. Найдем номер l из условия

Ъ( S-1) = min Ъ( S

1<i < m

Шаг 2. Если ЪS-1) > 0, то псевдоплан

—(S-1) (S-1)

Xn{ s-1)= Ъ1 , N является оптимальным опорным планом, а

f ( Xn(s-1) ) = (CNS-1), Xn(s-1)) _ есть оптимальное значение линейной формы f (x), иначе переходим к шагу 3. Шаг 3. Если

a(S-1) > 0, j = ,

то задача линейного программирования не имеет решения ( множество планов Р пусто), иначе переходим к шагу 4.

Шаг 4. Вычисляем для столбцов aj матрицы P(S-1) (j * N(si = 1,

2, .. .,m) симплекс-разности A(S-1) и находим номер К из условия

А(S-1) Г А(5-1)

Направляющий элемент на S-й итерации метода есть элемент Шаг 5. Вычисляем компоненты вектора N :

(S-1)

NS) = N(S-1), i = 1, m , i * і , NS) = K

Шаг 6. Производим один шаг метода Жордана-Гаусса с направляющим элементом a’K-1). Вычисляем элементы Р-матрицы

P(S) методом Жордана-Гаусса. Присваиваем переменной алгоритма S значение S+1 и переходим к шагу 1.

Решение задач Р-методом.

Так как компоненты псевдоплана Xn(x> =( 3/2, 3/2, 3/2) являются неотрицательными, то Xn(1> является оптимальным опорным планом ЗЛП (2.28). Итак,

Х*=( 3/2, 0, 3/2, 0, 3/2) и min f (Х)=3. Пример 2.10. Решим ЗЛП:

max f (x) = Х1 + 2Х2 -2 Х1 + Х2 > 2

Х1 + 2 Х2 < 4 (2.33) Х1 + 4 Х2 > 4

Х1,2 >0

Приведем рассматриваемую ЗЛП к каноническому виду max f (Х)= (Х1 + 2 Х2 )

2 Х1 + Х2 S1 = 2

Х1 + 2 Х2 + S2 = 4

Х1 + 4 Х2 S3 = 4

Xj > 0, j = 1,2, s, > 0, i = 1,3.

или

max f (X)= (Х1 + 2 Х2 )

(2.34)

2 Х1 Х2 + S1 = 2

Х1 + 2 Х2 + S2 = 4

i = 1,3.

Х1 4 Х2 + S3 = 4

Xj > 0, j = 1,2, s, > 0,

Расширенная матрица

ґ 2 і і 0 0 2^

Л(0) = і 2 0 і 0 4

vі 4 0 0 і 4у

системы линейных уравнений (3.42) не являются Р-матрицей рассматриваемой ЗЛП, так как

( 2) (Г)

А(0)=(0, 0, 0)

+ і = і > 0 , А(20)=(0, 0, 0)

2 = -2 < 0.

v 4У

Следовательно, к решению ЗЛП (3.4і) не применим Р-метод.

Пример 2.іі.

min f (x) = ( 6 Хі + 3Х2 ) -3 Хі + Х2 > і 2 Хі 3 Х2 > 2

Хі,2 > 0

j =і,2.

Решение. Приведем задачу к каноническому виду f(Х)= (6 Хі 3 Х2 ) -max 3 Хі — Х2 + Sl = і 2 Хі + 3 Х2 + S2 = 2

Xj > 0, j = ід, Sj > 0,

(0)

Так как расширенная матрица

( 3 і і 0 і)

2 3 0 і 2

(2.35)

системы линейных уравнений рассматриваемой задачи является Р-матрицей ( А(і0) = 6 >0; А(20) = 3 >0 ), то задачу можно решить Р-методом. Решение задачи ведем в симплексной таблице.

-6

-3

N(s)

C «

C N

X N

al(s)

a2(s)

a3(s)

a4(s)

Исследование операций в экономике

Предмет: Экономика
Автор: И.Н. Мастяева
Год издания: 2003
Язык учебника: русский
Рейтинг:
Просмотров: 534

Обсуждение Исследование операций в экономике

Комментарии, рецензии и отзывы

2.4. анализ решения злп на основе отчётов ms excel: Исследование операций в экономике, И.Н. Мастяева, 2003 читать онлайн, скачать pdf, djvu, fb2 скачать на телефон Рекомендовано Учебно-методическим объединением по образованию в области статистики в качестве учебного пособия для студентов высших учебных заведений, обучающихся по специальности 061700 «Статистика» и другим экономическим специальностям.

Источник