Темы исследований в excel

Управление
образования Администрации Ивдельского городского округа

МАОУ
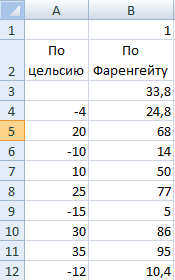
СОШ №7 г.Ивделя

Образовательная
область: математика и информатика

Предмет:
информатика

ИССЛЕДОВАНИЕ
ВОЗМОЖНОСТЕЙ

ТАБЛИЧНОГО
ПРОЦЕССОРА MS EXCEL

(за
страницами учебника)

Исполнители:
обучающиеся 11 класса

Васькин
Алексей,

Гутник
Андрей

Руководитель: Есаулкова М.А.,

учитель математики и информатики

Ивдель

2015

ОГЛАВЛЕНИЕ

ВВЕДЕНИЕ

ГЛАВА I.
Программа Microsoft Office Excel

1.1.         
Область применения табличного процессора MS Excel

1.2.         
Структура документа MS
Excel

1.3.         
Возможности программы MS
Excel

ГЛАВА
II.
Исследование возможностей MS Excel

2.1.
Создание расчетных таблиц с использованием элементов управления

2.2.
Решение системы уравнений графическим способом

ЗАКЛЮЧЕНИЕ

СПИСОК
ЛИТЕРАТУРЫ

ПРИЛОЖЕНИЕ
1. Таблицы данных для задания №1

ПРИЛОЖЕНИЕ
2. Примеры электронных таблиц, содержащие элементы управления

ВВЕДЕНИЕ

Программа
от Microsoft Excel или электронные таблицы была создана для более удобной
работы пользователя с таблицами данных, причём преимущественно данная работа
производится с числовыми значениями.

Основной
особенностью MS Excel выступает его возможность использовать формулы для того,
чтобы описывать между значениями разных ячеек различные связи. Следует
отметить, что по заданным формулам расчёт будет выполняться автоматически. Если
человек изменяет значение какой-либо ячейки, то сразу же автоматически
произойдёт перерасчёт значений всех остальных ячеек, которые связаны с ней
формульными отношениями, благодаря чему обновится вся таблица и данные, которые
находятся в ней.

В
основные возможности электронных таблиц входит:

·      
автоматизация всех итоговых вычислений;

·      
над большими наборами данных можно
производить однотипные расчёты;

·      
можно разрешать задачи с помощью подбора
значений с различными параметрами;

·      
можно обрабатывать результаты
экспериментов;

·      
производить табулирование функций и
формул;

·      
подготавливать табличные документы;

·      
проводить поиск наиболее оптимальных
значений для выбранных параметров;

·      
строить графики и диаграммы по уже
введённым данным.

Табличный
процессор Excel позволяет осуществлять вычисления. Там не одна сотня различных
функций (математических, логических, текстовых, статистических и т.д.). В Excel
можно осуществлять бухгалтерские расчеты, строить графики и диаграммы.

Можно
использовать Excel:

§  в
качестве простейшей базы данных, для этого имеются удобные средства:
фильтрация, сортировка, формы;

§  для
составления отчётов;

§  для
планирования и расчётов;

§  в
качестве тестовой оболочки для проверки знаний.

При
работе в MS Excel
на уроках информатики, заметили, что далеко не все функции редактора мы
изучили. Особенно стало интересно знать: где и как в расчетных таблицах применяются
элементы управления? Можно ли решить систему уравнений средствами табличного
процессора?

Представленная
работа состоит из двух частей. В первой рассматриваются структура, возможности
и области применения программы Excel.
Во второй части проведены исследования по изучению возможностей табличного
процессора: использование элементов управления и решение систем уравнений графическим
способом.

Цель
работы: рассмотреть возможности табличного
процессора, не изучаемые в школьной программе, на примерах решения задач с использованием
элементов управления и решения систем уравнений.

Задачи:

1.                
Рассмотреть программу Excel.

2.                
Выявить дополнительные возможности
табличного процессора Excel, которые мы еще не изучали.

3.                
Решить задачу с использованием элементов
управления.

4.                
Решить систему уравнений графическим
способом.

5.                
Провести анализ проделанной работы,
сделать выводы.

Методы
исследования:

§     Анализ
литературы по проблеме исследования.

§     Практическая
работа.

§     Анализ
результатов.

ГЛАВА
I.
ПРОГРАММА
MICROSOFT OFFICE EXCEL

1.1. Область применения табличного
процессора Excel

Программа
MS Excel, являясь лидером на рынке программ обработки электронных таблиц,
определяет тенденции развития в этой области. К значительным достижениям
программы Excel можно отнести появление трехмерных документов (блокнотов).
Дополнительные возможности программы облегчают решение сложных прикладных
задач. В программу Excel встроена удобная подсистема помощи, которая в любой
момент готова выдать необходимую справку. Описанные до сих пор новшества
касаются в основном комфорта в работе и быстрого освоения  программы.
Одним из важнейших функциональных расширений программы, предназначенным для
профессионалов, является встроенная в Excel среда программирования  Visual
Basic (VBA) для решения прикладных задач. Благодаря VBA фирме Microsoft удалось
не только расширить возможности языка макрокоманд Excel, но и ввести новый
уровень прикладного программирования, поскольку VBA позволяет создавать
полноценные прикладные пакеты, которые по своим функциям выходят далеко за
рамки обработки электронных таблиц.
Программа MS Excel позволяет решать сложные задачи, связанные с финансовой и
бухгалтерской работой предприятий: проводить широкий круг сложных вычислений в
электронных таблицах, легко и быстро анализировать большой объем данных; а
также приобретать навыки записи и редактирования макросов, с целью применения
их для часто повторяющихся операций и автоматизации работы. Программа Microsoft
Excel используется при составлении бизнес-анализа.

1.2. Структура документа Excel

Документом
MS Excel является рабочая книга. Рабочих книг создать можно столько, сколько
позволит наличие свободной памяти на соответствующем устройстве памяти. Однако
активной рабочей книгой может быть только текущая (открытая) книга.

 Рабочая
книга представляет собой набор рабочих листов, каждый из которых имеет
табличную структуру. В окне документа отображается только текущий (активный)
рабочий лист, с которым и ведётся работа. Каждый рабочий лист имеет название,
которое отображается на ярлычке листа в нижней части окна. С помощью ярлычков
можно переключаться к другим рабочим листам, входящим в ту же рабочую книгу.
Чтобы переименовать рабочий лист, надо дважды щёлкнуть мышкой на его ярлычке.
Рабочий лист состоит из строк и столбцов. Столбцы озаглавлены прописными
латинскими буквами и, далее, двухбуквенными комбинациями. Всего рабочий лист
содержит 256 столбцов, пронумерованных буквами латинского алфавита. Строки
последовательно нумеруются цифрами, от 1 до 65536.
На пересечении столбцов и строк образуются ячейки таблицы. Они являются
минимальными элементами для хранения данных. Каждая ячейка имеет свой адрес.
Адрес ячейки состоит из имени столбца и номера строки, на пересечении которых
расположена ячейка, например, A1, B5. Адреса ячеек используются при записи
формул, определяющих взаимосвязь между значениями, расположенными в разных
ячейках. В текущий момент времени активной может быть только одна ячейка,
которая активизируется щелчком мышки по ней и выделяется рамкой. Эта рамка в
программе Excel играет роль курсора. Операции ввода и редактирования данных
всегда производятся только в активной ячейке.

На
данные, расположенные в соседних ячейках, можно ссылаться в формулах, как на
единое целое. Такую группу ячеек называют диапазоном. Наиболее часто
используются прямоугольные диапазоны, образующиеся на пересечении группы
последовательно идущих строк и группы последовательно идущих столбцов. Диапазон
ячеек обозначают, указывая через двоеточие, номера ячеек, расположенных в
противоположных углах прямоугольника, например, B5:F15. Выделение диапазона
ячеек можно сделать протягиванием указателя мышки от одной угловой ячейки до
противоположной по диагонали. Рамка текущей (активной) ячейки при этом
расширяется, охватывая весь выбранный диапазон.

Отдельная
ячейка может содержать данные, относящиеся к одному из следующих типов: число,
дата, текст или формула, а также оставаться пустой.

Ввод
данных осуществляется непосредственно в текущую ячейку или в строку формул,
располагающуюся в верхней части окна программы непосредственно под панелями
инструментов.

1.3.  Возможности программы Excel

«Простые
задачи должны решаться просто». Этому постулату как нельзя лучше отвечают
вычислительные возможности программы MS Excel, которые без оговорки можно
назвать безграничными. Программа MS Excel (электронные таблицы) предназначена
для работы с таблицами данных, преимущественно числовых. Особенность
электронных таблиц заключается в возможности применения формул для описания
связи между значениями различных ячеек. Расчёт по заданным формулам выполняется
автоматически. Изменение содержимого какой-либо ячейки приводит к пересчёту
значений всех ячеек, которые с ней связаны формульными отношениями и, тем
самым, к обновлению всей таблицы в соответствии с изменившимися данными.

Применение
электронных таблиц упрощает работу с данными и позволяет получать результаты
без проведения расчётов вручную или специального программирования. Электронные
таблицы можно использовать эффективно для:

·  проведения
однотипных расчётов над большими наборами данных;

·  итоговых
вычислений;

·  решения
задач путём подбора значений параметров;

·  табулирования
формул (функций);

·  обработки
результатов экспериментов;

·  проведение
поиска оптимальных значений параметров;

·  подготовки
табличных документов;

·  построения
диаграмм и графиков по имеющимся данным.

Возможности
табличного процессора  MS Excel позволяют создавать электронные пособия
(учебники), состоящие из многих станиц (листов), переходы в которых можно
создавать с помощью гиперссылок и кнопок.

Рассмотрев
возможности и структуру табличного процессора MS Excel, нами было решено рассмотреть
задачи на создание таблиц с использованием элементов управления, а также решить
систему уравнения средствами Excel.

ГЛАВА
II.
ИССЛЕДОВАНИЕ ВОЗМОЖНОСТЕЙ MS EXCEL

2.1.
Создание таблиц с использованием элементов управления

Элементы
управления в Excel включают в себя флажки
опций, раскрывающиеся списки, счетчики и многое другое, что можно добавлять к
спискам данных, диаграмм и другим объектам рабочего листа для облегчения работы
с данными.

Элемент
управления привязывается к ячейке, и затем создается формула, использующая
адрес связи для поиска информации или проведения вычислений.

Для
вставки элементов управления на лист необходимо отобразить вкладку Разработчик.

·     В
MS Excel
2007 это можно сделать через меню Кнопка офис/ Параметры Excel/
Основные/ Показывать вкладку Разработчик на ленте.

·     В
MS Excel
2010 это можно сделать так: Откройте вкладку Файл; Нажмите кнопку Параметры;
Нажмите кнопку Настроить ленту; Выберите команду Настройка ленты и
в разделе Основные вкладки установить флажок Разработчик.

Для
добавления какого либо элемента управления на вкладке Разработчик в
группе Элементы управления используется кнопка Вставить.

Выделяют
следующие элементы управления:

ЗАДАНИЕ 1. Используя
данные Приложения 1, создать таблицу транспортных перевозок из Екатеринбурга в
города Свердловской области с учетом тарифа перевозок и оформить ее с помощью
элементов управления; выполнить соответствующие вычисления, используя формулы и
вычисления. Предполагаемый результат: При выборе города
назначения автоматически определяется расстояние, а при выборе веса груза
должна рассчитываться стоимость перевозки с учетом указанного тарифа.

Для начала, оформим таблицы с данными
по перевозкам в табличном процессоре MS Excel.
Примерно это будет выглядеть, как показано на рисунке 1.

Далее мы будем работать с ячейками,
выделенные жёлтым и красным цветом.

1.    
В жёлтую ячейку Город назначения мы
поместим список городов, из приведенной ниже таблицы, используя элемент
управления Поле со списком (Разработчик – Вставить – Поле со списком).

Рис.1.

2.    
Перенесём элемент управления на лист
электронной таблицы и придадим ему нужный размер (рис.2).

Рис.2.

3.    
Затем из вызванного контекстного меню
элемента управления выбираем команду Формат объекта. Появится окно Формат
элемента управления (рис.3).

Рис.3.

4.    
Выбираем вкладку Элемент управления.
В поле Формировать список по диапазону задаем диапазон данных, которые
должны входить в список (Город назначения).

5.    
В поле Связь с ячейкой вводим
ячейку, на которую будет ссылаться формула (А1). Указываем Количество строк
списка, выводящихся на экран. Установим флажок Объемное затенение (по
желанию). Нажимаем ОК.

6.    
Теперь, чтобы автоматически отобразить
расстояние, воспользуемся функцией ИНДЕКС. В ячейку В7 (Расстояние, км)
введем формулу: =ИНДЕКС(В10:В50;А1), в которой указывается столбец ссылка на
ячейку, содержащая номер строки.

7.    
Аналогично, добавляем элементы управления
в ячейку С7 (Вес груза), привязывая ее к ячейке связи В1, а в ячейку D7
введём формулу =ИНДЕКС(F10:F16;В1).

8.    
В ячейку F7
введём формулу для вычисления стоимости перевозки: =В7*D7.

Конечный
вариант таблицы изображён на рисунке 4.

Рис.4

Вывод:
Элементы управления формы (Поле со списком, Флажок, Счетчик и др.) помогают
менять данные на листе в определенном диапазоне, включать и выключать опции,
делать выбор и пр. В принципе, без них можно обойтись, но они делают управление
данными на листе более наглядным и уменьшают вероятность ввода некорректных
данных.

Мы
разобрали простой пример с использованием элементов управления, не усложнённый
логическими функциями. Используя совместно логические функции и элементы
управления, можно создавать тесты с выбором ответа, кроссворды, электронный
журнал, создавать сложные расчётные таблицы по экономике, логистике и пр.
Примеры таких таблиц приведены в Приложении 2.

2.2.
Решение систем уравнений средствами электронных таблиц

При
помощи табличного процессора можно решать уравнения и системы уравнений.
Корнями уравнения являются значения точек пересечения графика функции с осью
абсцисс. Решением системы уравнений являются точки пересечения графиков
функций. Такой метод нахождения корней называется графическим.

Для
графического решения подойдут средства построения диаграмм.

Рассмотрим
конкретный пример.

ЗАДАНИЕ 2.
Решить систему уравнений 

1. 
Преобразуем данную систему:    

2.  
Для оценки решений воспользуемся
диаграммой, на которой отобразим графики обеих функций. Для этого, на рабочем
листе (Лист1) MS Excel
создадим таблицу со следующими значениями (рис.5):

·    
1 строка – строка заголовков;

·    
столбец А: заполняем ячейки А2:А22 числами
от -10 до 10 с шагом 1;

·    
при заполнении столбца В в ячейку В2
заносим формулу =А2-1, которую затем копируем до ячейки В22;

·    
при заполнении столбца С в ячейку С2
заносим формулу =А2*А2-3, копируем ее до ячейки С22.

Рис.5.
Таблица с данными для приблизительного поиска решений

С
помощью мастера диаграмм выберем тип диаграммы График и построим
диаграмму первоначальной оценки решений (рис. 6).

На
рисунке 6 мы видим координаты точек пересечения графиков – решения системы.
Однако, пока мы получили только приближенные значения решений и точно не можем
определить координаты этих точек.

Рис.6.
 Диаграмма первоначальной оценки решения

Поэтому,
для уточнения значения решений (Лист 2) построим графики в интервалах от -3 до
-1, где находится первое решение, и от 0 до 2, где находится второе решение с
шагом  0,1 (рис. 7).

    

Рис.7.
Таблицы с данными для уточнения решений

3.    
Составляем новую таблицу для — 2 ≤ x
≤ 0(рис.7). Строим
точечную диаграмму для получения первого решения (рис.8).

Рис.8.
Поиск первого решения

4.    
Составляем новую таблицу для  1 ≤  x
≤ 3 (рис.7). Строим
точечную диаграмму для получения второго решения (рис.9).

Рис.9.
Поиск второго решения

Решением нашей системы будут координаты
точек пересечения графиков:(–1;–2) и (2;1).

 Вывод:
Нам удалось решить систему уравнений графическим
способом средствами MS Excel.
Учителя математики могут использовать табличный процессор на уроках при объяснении
тем, связанных с построением графиков функций.

ЗАКЛЮЧЕНИЕ

В
повседневной жизни человек постоянно использует таблицы: дневник в школе,
расписание электричек, расписание занятий и т.д. Персональный компьютер
расширяет возможности использования таблиц за счёт того, что позволяет не
только представлять данные в электронном виде, но и обрабатывать их.

Электронные
таблицы используются во всех сферах человеческой деятельности, но особо широко
используются для проведения экономических и бухгалтерских расчётов.

Главное
достоинство электронной таблицы – это возможность мгновенного пересчета всех
данных, связанных формульными зависимостями при изменении значения любого
операнда.

Основное
назначение табличного процессора – автоматизация расчётов в табличной форме.

Например,
в табличном процессоре можно вести журнал успеваемости, в случае отсутствия
Интернета. Учителя смогут заносить в него оценки учащихся, а встроенные формулы
позволят высчитывать средний балл для каждого ученика, общую успеваемость
класса по предмету и др. Каждый раз, когда учитель вносит новую оценку,
табличный процессор будет автоматически пересчитывать все результаты.

Когда
в повседневной жизни встречаются ситуации, связанные с обработкой информации в
объёмах, неподъёмных ручками, но не требующих применения дорогих и тяжелых
программных продуктов, типа  1С,  САПР  и тому подобное, в этом поможет Excel.

СПИСОК
ЛИТЕРАТУРЫ

1.                
Ефимова О.В., Морозов
В.В., Угринович Н.Д. Курс компьютерной технологии с основами информатики. –М.:
АБФ, ACT, 1999. –482 с.

2.                
Каратыгин С. и др. Базы
данных: Простейшие средства обработки информации. Электронные таблицы. Системы
управления базами данных. Т.1 /Каратыгин С., Тихонов А., Долголаптев В. –М.:
ABF, 1995. –533 с.

3.                
Программное обеспечение
персонального компьютера. http://www.tspu.tula.ru/ivt/umr/po/lection.htm/.

4.                
Прохоров А. Н. Учебный
курс Работа в современном офисе. http://www.intuit.ru/department/office/od/.

5.                
Работа с MS Excel.
http://avanta.vvsu.ru/met_supply/381/Index.htm/.

6.                
Практикум по экономической
информатике: Учебное пособие. Часть 1. /Под ред. Шуремова Е.Л., Тимаковой Н.А.,
Мамонтовой Е.А. – М.: Изд-во «Перспектива», 2000. – 300 c.

7.                
Попов А.А. Excel:
практическое руководство. — М.: ДЕСС КОМ, 2001. – 301 с.

8.                
Microsoft Excel. Версия
2002. Шаг за шагом: Практ. пособие/ Пер. с англ. – М.: Издательство ЭКОМ, 2003.
– 368 с.

9.                
Стоцкий Ю., Васильев А.,
Телина И. Office 2007. Самоучитель. – Спб.: Питер, 2007. – 524 с.

10.           
Киселев В.Г. ПРАКТИЧЕСКАЯ
РАБОТА В EXCEL 2007: Практикум. — Нижний Новгород: Нижегородский
госуниверситет, 2009. – 80 с.

11.           
Microsoft Office Excel
2007 Долженков В.А., Стученков А.Б.

12.           
Интернет-ресурсы:

·       
http://www.informika.ru

·       
http://www.rusedu.info/Downloads-index-req-viewdownload-cid-5.html
вся Информатика

Муниципальное бюджетное общеобразовательное учреждение средняя              общеобразовательная школа № 15 имени Пяти Героев Советского Союза

Иследовательская работа

Тема:

«Создание и исследование моделей

в электронной таблице Excel»

Секция информатики

Выполнила: Сотникова Полина Андреевна,

ученица 10 «А» класса

Руководитель: Титаренко Алексей Анатольевич,

учитель информатики

г. Хабаровск

2016

Содержание

Актуальность темы…………………………………………………………………………………………………………………3

Введение………………………………………………………………………………………………………………………………..4

Создание информационных моделей…………………………………………………………………………………..5

Формулы в Excel…………………………………………………………………………………………………………………….7

Этапы разработки и исследования моделей………………………………………………………………………..10

Исследование физических моделей в электронных таблицах…………………………………………..11

Исследование биологической модели развития популяций………………………………………………14

Оптимизационное моделирование в экономике…………………………………………………………………17

Заключение…………………………………………………………………………………………………………………………….20

Список использованной литературы…………………………………………………………………………………….21

2

Актуальность темы

Часто для исследования предметов, процессов и явлений человек создает модели окружающего мира.

Наглядные модели часто используются в процессе обучения. На уроке географии мы изучаем нашу планету используя её модели – карты и глобусы, при изучении химии мы используем модели молекул и кристаллических решеток, изучаем строение человека по анатомическим муляжам скелета и органов на биологии.

 Модели играют чрезвычайно важную роль в проектировании и создании различных технических устройств, машин и механизмов, зданий, электрических цепей и т.д. Без предварительного создания чертежей невозможно изготовить даже простую деталь, не говоря уже о сложном механизме. Кроме чертежей,в проектировании часто изготавливают макеты. Разработка электрической схемы обязательно предшествует созданию электрических цепей.

Развитие науки невозможно без создания теоретических моделей (теорий, законов, гипотез), отражающих строение, свойства и поведение реальных объектов. Соответствие теоретических моделей действительности проверяется с помощью опытов и экспериментов.

 Все художественное творчество фактически является процессом создания моделей. Например, такой литературный жанр, как басня, переносит реальные отношения между людьми на отношения между животными и фактически создает модели человеческих отношений.

3

Введение

Моделирование – это метод познания, состоящий в создании и исследовании моделей – неких новых объектов, которые отражают существенные особенности изучаемого объекта, явления или процесса.Модель – это некий новый объект, который отражает существенные особенности изучаемого объекта,явления или процесса. Модели позволяют представить в наглядной форме объекты и процессы, недоступные для непосредственного восприятия (очень большие или очень маленькие объекты, очень быстрые или очень медленные процессы).

Компьютерные модели стали обычным инструментом математического моделирования и применяются в физике, астрофизике, механике, химии, биологии, экономике, социологии, метеорологии, других науках и прикладных задачах в различных областях радиоэлектроники, машиностроения, автомобилестроения и прочих. Компьютерные модели используются для получения новых знаний о моделируемом объекте или для приближенной оценки поведения систем, слишком сложных для аналитического исследования. Компьютерное моделирование является одним из эффективных методов изучения сложных систем. Компьютерные модели проще и удобнее исследовать в силу их возможности проводить вычислительные эксперименты, в тех случаях когда реальные эксперименты затруднены из-за финансовых или физических препятствий или могут дать непредсказуемый результат. Логичность и формализованность компьютерных моделей позволяет определить основные факторы, определяющие свойства изучаемого объекта-оригинала (или целого класса объектов). В частности, моделирование в электронных таблицах может быть использовано для описания ряда объектов, обладающих одинаковыми наборами свойств. С помощью таблиц могут быть построены как статические, так и динамические информационные модели в различных предметных областях, а простота использования программ создания таблиц помогает составлять модели людям без знания сложных языков программирования.

4

Создание информационных моделей:

Информационные модели отражают различные типы систем объектов, в которых реализуются различные структуры взаимодействия и взаимосвязи между элементами системы. Для отражения систем с различными структурами используются различные типы информационных моделей: табличные, иерархические и сетевые. В программе Excelдоступно создание табличного типа моделей.

Табличные информационные модели:

Одним из наиболее часто используемых типов информационных моделей является прямоугольная таблица, состоящая из столбцов и строк. Такой тип моделей применяется для описания ряда объектов, обладающих одинаковыми наборами свойств.

В табличной информационной модели обычно перечень объектов размещен в ячейках первого столбца таблицы, а значения их свойств – в других столбцах.

С помощью электронной таблицы Excelпостроим таблицу стоимости продуктов. В первом столбце таблицы будет содержаться перечень продуктов, а во втором – интересующее нас свойство (цена).

С помощью специальных инструментов, встроенных в программу Excelможно визуализировать таблицу, представив ее в виде графика или круговой диаграммы. Для этого нужно выделить таблицу, зайти во вкладку «Вставка» и выбрать нужный формат визуализации.

5

Визуализация круговой диаграммой

Визуализация столбчатой диаграммой

6

Формулы в Excel

В таблицах Excelможно не только вводить и визуализировать данные, но и производить простые и сложные расчеты над данными.Все это реализуется при помощи формул в ячейках. Формула выполняет вычисления или другие действия с данными в листе.

Порядок ввода формулы

Для начала определим, в какой ячейке должен стоять результат расчета. Затем выделим эту ячейку (нажмем на нее левой кнопкой мышки и ячейка станет активной).

Вводить формулу надо со знака равенства. Это надо для того, чтобы Excel понял, что в ячейку вводится именно формула, а не данные.

Выделим произвольную ячейку, например D1. В строке формул введем =2+3 и нажмем Enter. В ячейке появится результат (5). А в строке формул сверху останется сама формула.

При обработке формулы с большим количеством вычислений, наблюдается определенный приоритет.

1. В первую очередь выполняются выражения внутри скобок.
2. Умножение и деление имеют более высокий приоритет чем сложение и вычитание.
3. Операторы с одинаковым приоритетом выполняются слева направо.

                         7

Так, в примере выше, сначала выполняется действие в скобках (5-4=1), потом первое умножение (100*1=100), затем второе умножение (38*2=76), сложение (100+26=126), и в конце вычитание (126-76=50).

Также, можно выполнять действия над числами, содержащимися в ячейках. Для этого, вместо цифр, в формулах нужно использовать ссылки на ячейки – букву латинского алфавита, обозначающую столбец и цифру, обозначающую строку.

Так, в ячейку D3 была введена формула D1+D2. В результате сложились числа,стоящие в ячейках D1(4) и D2(6) и полученный результат – 10 был записан в ячейку D3.

Для складывания нескольких ячеек используется функция СУММ. Для суммирования трех чисел формула запишется следующим образом

Но можно облегчить себе работу и вместо перечисления каждой ячейки записать диапазон, с помощью двоеточия

Истинное значение функции СУММ раскрывается, когда необходимо сложить большое количество ячеек в Excel. В примере ниже требуется просуммировать 12 значений. Функция СУММ позволяет сделать это несколькими щелчками мышью, если же использовать оператор сложения, то провозиться придется долго.

8

В таблицах Excelможно не только проводить простейшие вычисления над числами, но и возводить в степень, извлекать корень, производить сравнение чисел и многое другое.

9

Этапы разработки и исследования моделей

Использование компьютера для исследования информационных моделей различных объектов и систем позволяет изучить их изменения в зависимости от значения тех или иных параметров. Процесс разработки моделей и их исследования на компьютере можно разделить на несколько основных этапов.

 На первом этапе исследования объекта или процесса обычно строится описательная информационная модель. Такая модель выделяет существенные с точки зрения целей проводимого исследования параметры объекта, а несущественными параметрами пренебрегает.

На втором этапе создается формализованная модель, то есть описательная информационная модель записывается с помощью какого-либо формального языка. В такой модели с помощью формул, уравнений, неравенств и пр. фиксируются формальные соотношения между начальными и конечными значениями свойств объектов, а также накладываются ограничения на допустимые значения этих свойств.

 Однако далеко не всегда удается найти формулы, явно выражающие искомые величины через исходные данные. В таких случаях используются приближенные математические методы, позволяющие получать результаты с заданной точностью.

На третьем этапе необходимо формализованную информационную модель преобразовать в компьютерную модель, то есть выразить ее на понятном для компьютера языке. Существуют два принципиально различных пути построения компьютерной модели:

1) построение алгоритма решения задачи и его кодирование на одном из языков программирования;

2) построение компьютерной модели с использованием одного из приложений (электронных таблиц, СУБД и пр.).

 В процессе создания компьютерной модели полезно разработать удобный графический интерфейс, который позволит визуализировать формальную модель, а также реализовать интерактивный диалог человека с компьютером на этапе исследования модели.

Четвертый этап исследования информационной модели состоит в проведении компьютерного эксперимента. Если компьютерная модель существует в виде программы на одном из языков программирования, ее нужно запустить на выполнение и получить результаты.

Если компьютерная модель исследуется в приложении, например в электронных таблицах, можно провести сортировку или поиск данных, построить диаграмму или график и так далее.

Пятый этап состоит в анализе полученных результатов и корректировке исследуемой модели. В случае различия результатов, полученных при исследовании информационной модели, с измеряемыми параметрами реальных объектов можно сделать вывод, что на предыдущих этапах построения модели были допущены ошибки или неточности. Например, при построении описательной качественной модели могут быть неправильно отобраны существенные свойства объектов, в процессе формализации могут быть допущены ошибки в формулах и так далее. В этих случаях необходимо провести корректировку модели, причем уточнение модели может проводиться многократно, пока анализ результатов не покажет их соответствие изучаемому объекту.

10

Исследование физических моделей в электронных таблицах:

Рассмотрим процесс построения и исследования модели на конкретном примере движения тела, брошенного под углом к горизонту.

Задача: В процессе тренировке теннисистов используются автоматы по бросания мячика в определенное место площадки. Необходимо задать автомату необходимую скорость и угол бросания мячика для попадания в мишень определенного размера, находящуюся на известном расстоянии.

Качественная описательная модель: Сначала построим качественную описательную модель процесса движения тела с использованием физических объектов, понятия и законов, то есть в данном случае идеализированную модель движения объекта. Из условия задачи можно сформулировать следующие основные предположения:

• Мячик мал по сравнению с Землей, поэтому его можно считать материальной точкой;
• Изменение высоты мячика мало, поэтому ускорение свободного падения можно считать постоянной величиной g= 9,8 мс и движение по оси ОУ можно считать равноускоренным;
• Скорость бросания тела мала, поэтому сопротивлением воздуха можно пренебречь и движение по оси ОХ можно считать равномерным

Формальная модель: Для формализации модели используем известные из курса физики формулы равномерного и равноускоренного движения. При заданных начальной скорости v0 и угле бросания aзначения координат дальности полета х и высоты у от времени можно записать следующими формулами:

X=v0*cos*t;

Y=v0*sinα*t – g*t²/2

Пусть мишень высотой h будет размещаться на расстоянии sот автомата. Из первой формулы выражаем время, которое понадобится мячику, чтобы преодолеть расстояние s:

t = s/(v0*cos2α)

Представляем это значение для tв формулу для у. Получаем l – высоту мячика над землей на расстоянии s:

l = s*tgα – g*s²/(2*v0²*cosα²)

Формализуем теперь условие попадания мячика в мишень. Попадание произойдет, если значение высоты lмячика в мишень. Попадание произойдет, если значение высоты lмячика будет удовлетворять условию в форме неравенства:

0≤l ≤ h

Если l<0, то это означает «недолет», а если l>h, то это означает «перелет».

Создание модели:

1. Для ввода начальной скорости будем использовать ячейку В1, а для ввода угла – ячейку В2
2. Введем в ячейки А5:А18 значения времени с интервалом в 0,2 с.
3. В ячейки В5 и С5 введем формулы:

11

=$B$1*cos(Радианы($B$2))*А5

=$B$1*sin(РАДИАНЫ($B$2))*A5-4,9*A5*A5

1. Скопируем формулы в ячейки В6:В18 и С6:С18 соответственно.

Визуализируем модель, построив график зависимости координаты у от координаты х (траекторию движения тела).

1. Построить диаграмму типа График, в которой используется в качестве категории диапазон ячеек В5:В18, а в качестве значений – диапазон ячеек С5:С18.

Исследование модели: Исследуем модель и определим с заданной точностью 0,1 диапазон изменений угла, который обеспечивает попадание в мишень, находящуюся на расстоянии 30 м и имеющую высоту 1 м, при заданной начальной скорости 18 м/с. Воспользуемся для этого методом Подбор параметра.

1. Установить для ячеек точность один знак после запятой

12

1. Ввести в ячейки B21, B22 и В23 значения расстояния до мишени S = 30 м, начальной скорости Vо = 18 м/с и угла α= 35⁰, а в ячейку В25 – формулу для вычисления высоты мячика над поверхностью для заданных условий:

=B21*TAN(РАДИАНЫ(B23))-(9,81*B21^2)/(2*B22^2*COS(РАДИАНЫ(B23))^2)

Для заданных начальных условий определим углы, которые обеспечивают попадание в мишень на высотах 0 и 1 м.

1. Выделить ячейку В25 и ввести команду [Сервис-Подбор параметра…]. На появившейся диалоговой панели ввести в поле Значение: наименьшую высоту попадания в мишень ( то есть 0). В поле Изменяя значение ячейки: ввести адрес ячейки, содержащей значение угла (в данном случае $B$23).

1. В ячейке В23 появится значение 32,6. Повторить процедуру подбора параметра для максимальной высоты попадания в мишень – в ячейке В23 получим значение 36,1.

Таким образом, исследование компьютерной модели в электронных таблицах показало, что существует диапазон значений для угла бросания от 32,6 до 36,1⁰, который обеспечивает попадание в мишень высотой 1 м, находящуюся на расстоянии 30 м, мячиком брошенным со скоростью 18 м/с.

13

Исследование биологической модели развития популяций

В биологии при исследовании развития биосистем строятся динамические модели изменения численности популяций различных живых существ (бактерий, рыб, животных и пр.) с учетом различных факторов. Взаимовлияние популяций рассматривается в моделях типа «хищник-жертва».

Формальная модель. Изучение динамики численности популяций естественно начать с простейшей модели неограниченного роста, в которой численность популяции ежегодно увеличивается на определенный процент. Математическую модель можно записать с помощью рекуррентной формулы, связывающей численность популяции следующего года с численностью популяции текущего года, с использованием коэффициента роста а:

X(n+1) = a * x(n)

Например, если ежегодный прирост численности популяции составляет 5%, то а = 1,05. В модели ограниченного роста учитывается эффект перенаселенности, связанный с нехваткой питания, болезнями и так далее, который замедляет рост популяции с увеличением ее численности. Введем коэффициент перенаселенности b, значение которого обычно существенно меньше а (b<<а). Тогда коэффициент ежегодного увеличения численности равен (а — b*х(n)) и формула принимает вид:

X(n+1) = (a – b * x(n)) * x(n)

В модели ограниченного роста с отловом учитывается, что на численность популяций промысловых животных и рыб оказывает влияние величина ежегодного отлова. Если величина ежегодного отлова равна с, то формула принимает вид:

X(n+1) = (a – b * x(n)) * x(n) — c

Популяции обычно существуют не изолированно, а во взаимодействии с другими популяциями. Наиболее важным типом такого взаимодействия является взаимодействие между жертвами и хищниками (например, караси-щуки, зайцы-волки и так далее). В модели «хищник-жертва» количество жертв х(n) и количество хищников у(n) связаны между собой. Количество встреч жертв с хищниками можно считать пропорциональным произведению количеств жертв и хищников, а коэффициент f характеризует возможность гибели жертвы при встрече с хищниками. В этом случае численность популяции жертв ежегодно уменьшается на величину f * х(n)* у(n) и формула для расчета численности жертв принимает вид:

X(n+1) = (a – b * x(n)) * x(n) – c – f* x(n) * y(n)

Численность популяции хищников в отсутствие жертв (в связи с отсутствием пищи) уменьшается, что можно описать рекуррентной формулой

Y(n+1) = d* y(n)

где значение коэффициента d < 1 характеризует скорость уменьшения численности популяции хищников. Увеличение популяции хищников можно считать пропорциональной произведению собственно количеств жертв и хищников, а коэффициент е характеризует величину роста численности хищников за счет жертв. Тогда для численности хищников можно использовать

14

формулу:

y(n+1) = d*y(n) + e*x(n)*y(n)

Компьютерная модель. Построим в электронных таблицах компьютерную модель, позволяющую исследовать численность популяций с использованием различных моделей: неограниченного роста, ограниченного роста, ограниченного роста с отловом и «хищник—жертва».

1. В ячейки В1 и В6 внести начальные значения численности популяций жертв и хищников.

В ячейки В2:В5 внести значения коэффициентов a, b, cи f, влияющих на изменение численности жертв.

В ячейки В7 и В8 внести значения коэффициентов dи е, влияющих на изменение численности хищников

В столбце Dбудем вычислять численность популяции в соответствии с моделью неограниченного роста, в столбце Е – ограниченного роста, в столбце F–ограниченного роста с отловом, в столбцах Gи H–«хищник-жертва».

1. В ячейки D1, E1, F1 и G1 внести значения начальной численности популяций жертв, в ячейку Н1 – хищников.

В ячейку D2 внести рекуррентную формулу неограниченного роста =$B$2*D1

В ячейку Е2 внести рекуррентную формулу неограниченного роста =($B$2-$B$3*E1)*E1

В ячейку F2 внести рекуррентную формулу ограниченного роста с отловом =($B$2-$B$3*F1)*F1-$B$4

В ячейку G2 внести рекуррентную формулу изменения количества жертв =($B$2-$B$3*G1)*G1-$B$4-$B$5*G1*H1

В ячейку Н2 внести рекуррентную формулу изменения количества хищников =$B$7*H1+$B$8*G1*H1

1. Скопировать внесенные формулы в ячейки столбцов командой [Правка-Заполнить-Вниз].

В ячейках столбцов ознакомиться с динамикой изменения численности популяций.

15

1. Выделить столбцы данных и построить диаграмму типа График. Появятся графики изменения численности популяций в соответствии с моделями неограниченного роста, ограниченного роста, ограниченного роста с отловом, моделью хищник-жертва.

Исследование модели: Изменяя значения начальных численностей популяций, а также коэффициенты, можно получать различные варианты изменения численности популяций в зависимости от времени.

16

Оптимизационное моделирование в экономике

В сфере управления сложными системами (например, в экономике) применяется оптимизационное моделирование, в процессе которого осуществляется поиск наиболее оптимального пути развития системы.

Критерием оптимальности могут быть различные параметры; например, в экономике можно стремиться к максимальному количеству выпускаемой продукции, а можно к ее низкой себестоимости. Оптимальное развитие соответствует экстремальному (максимальному или минимальному) значению выбранного целевого параметра.

 Развитие сложных систем зависит от множества факторов (параметров), следовательно, значение целевого параметра зависит от множества параметров. Выражением такой зависимости является целевая функция

К = F(X1,X2,…,Xn),

где К — значение целевого параметра; X1,X2,…,Xn — параметры, влияющие на развитие системы.

Цель исследования состоит в нахождении экстремума этой функции и определении значений параметров, при которых этот экстремум достигается. Если целевая функция нелинейна, то она имеет экстремумы, которые находятся определенными методами.

 Однако часто целевая функция линейна и, соответственно, экстремумов не имеет. Задача поиска оптимального режима при линейной зависимости приобретает смысл только при наличии определенных ограничений на параметры. Если ограничения на параметры (система неравенств) также имеют линейный характер, то такие задачи являются задачами линейного программирования. (Термин «линейное программирование» в имитационном моделировании понимается как поиск экстремумов линейной функции, на которую наложены ограничения.) Рассмотрим в качестве примера экономического моделирования поиск вариантов оптимального раскроя листов материала на заготовки определенного размера.

Содержательная постановка проблемы. В ходе производственного процесса из листов материала получают заготовки деталей двух типов А и Б тремя различными способами, при этом количество получаемых заготовок при каждом методе различается.

Тип Заготовки	1 способ раскроя	2 способ раскроя	3 способ раскроя
А	10	3	8
Б	3	6	4

Необходимо выбрать оптимальное сочетание способов раскроя, для того чтобы получить 500 заготовок первого типа и 300 заготовок второго типа при расходовании наименьшего количества листов материала.

Формальная модель. Параметрами, значения которых требуется определить, являются количества листов материала, которые будут раскроены различными способами:

Х1 — количество листов, раскроенное способом 1;

Х2 — количество листов, раскроенное способом 2;

Х3 — количество листов, раскроенное способом 3.

Тогда целевая функция, значением которой является количество листов материала, примет вид:

17

F = Х1+ Х2 + Х3.

Ограничения определяются значениями требуемых количеств заготовок типа А и Б, тогда с учетом количеств заготовок, получаемых различными способами, должны выполняться два равенства: 10Х1+ ЗХ2 + 8Х3 = 500;

ЗХ1 + 6Х2 + 4Х3 = 300.

 Кроме того, количества листов не могут быть отрицательными, поэтому должны выполняться неравенства:

X1>= 0; Х2>= 0; Х3 >= 0.

Таким образом, необходимо найти удовлетворяющие ограничениям значения параметров, при которых целевая функция принимает минимальное значение. Компьютерная модель. Будем искать решение задачи путем создания и исследования компьютерной модели в электронных таблицах Excel.

Оптимизационное моделирование

1. Ячейки В2, С2 и D2 выделить для значений параметров Х1, Х2 и Х3.

В ячейку В4 ввести формулу для вычисления целевой функции:

=В2+С2+D2

В ячейку В7 ввести формулу вычисления количества заготовок типа А:

=10*B2+3*C2+8*D2.

В ячейку В8 ввести формулу вычислений количества заготовок типа Б:

=3*B2+6*C2+4*D2

Исследование модели: Для поиска оптимального набора значений параметров, который соотвествует минимальному значению целевой функции, воспользоваться надстройкой электронных таблиц Поиск решения.

1. На вкладке Данные нажмите кнопку Поиск решения.
2. На появившейся диалоговой панели Поиск решения установить:

• Адрес целевой ячейки
• Вариант оптимизации значения целевой ячейки (максимизация, минимизация или подбор значения)
• Адреса ячеек, значения которых изменяются в процессе поиска решения ( в которых хранятся значения параметров)

18

• Ограничения (типа «=» для ячеек, хранящих количество деталей, и типа «≥» для параметров).

• Щелкнуть по кнопке Выполнить. В ячейке целевой функции появится значение 69,4, а в ячейках параметров значения 0,11,58.

Таким образом, для изготовления 500 деталей А и 300 деталей Б требуется 71 лист материала, при этом 12 листов нужно раскроить по второму, а 59 по третьему способу.

19

Заключение

Моделирование глубоко проникает в теоретическое мышление. Более того, развитие любой науки в целом можно трактовать — в весьма общем, но вполне разумном смысле, — как «теоретическое моделирование». Важная познавательная функция моделирования состоит в том, чтобы служить импульсом, источником новых теорий. Нередко бывает так, что теория первоначально возникает в виде модели, дающей приближённое, упрощённое объяснение явления, и выступает как первичная рабочая гипотеза, которая может перерасти в «предтеорию» — предшественницу развитой теории. При этом в процессе моделирования возникают новые идеи и формы эксперимента, происходит открытие ранее неизвестных фактов. Такое «переплетение» теоретического и экспериментального моделирования особенно характерно для развития физических теорий.

 Моделирование — не только одно из средств отображения явлений и процессов реального мира, но и — несмотря на описанную выше его относительность — объективный практический критерий проверки истинности наших знаний, осуществляемой непосредственно или с помощьюустановления их отношения с другой теорией, выступающей в качестве модели, адекватность которой считается практически обоснованной. Применяясь в органическом единстве с другими методами познания, моделирование выступает как процесс углубления познания, его движения от относительно бедных информацией моделей к моделям более содержательным, полнее раскрывающим сущность исследуемых явлений действительности.

В своем проекте я показала, как использовать электронные таблицы Excelдля моделирования и анализа созданных моделей.

20

Список использованной литературы

1. Н. Угринович «Информатика и информационные технологии»
2. Н. Угринович «Информатика и ИКТ»
3. http://on-line-teaching.com/excel/lsn003.html
4. http://www.excel-office.ru/formulivexcel/formulivexcel

21

Муниципальное бюджетное общеобразовательное учреждение

средняя общеобразовательная школа села Синодское

Научно — исследовательская работа по математике

«Исследование графиков функций с помощью Excel»

Автор: учащийся 7 класса

МБОУ СОШ с.Синодское

Ворфоломеев Евгений Юрьевич

Научный руководитель:

учитель математики

МБОУ СОШ с.Синодское

Ромахина Каринэ Петросовна

2016 г.

Оглавление

1. Введение. Цели и задачи..………………………………………. 3

2. Теоретическая часть…………………………………………….. 4-5

3. Практическая часть……………………………………………… 6-8

а) Исследование графика линейной функции

б) Исследование системы линейных уравнений с двумя

переменными

1. Заключение ………………………………………………………….. 8

2. Список литературы ………………………………………………9

3. Приложение ……………………………………………………..10-17

Введение

На уроках алгебры мы изучаем функции и их свойства, строим графики функций, учимся решать уравнения и системы уравнений. В своей работе я показал способы построения графиков функций, исследовал свойства функций и графиков в зависимости от параметров, входящих в ее уравнение, графический способ решения уравнений и системы уравнений с двумя переменными – с помощью программы Microsoft Excel.

Программа MS Excel позволяет очень быстро создать любое количество графиков различных функций, а также рассмотреть большое количество примеров изменения графиков в зависимости от параметров.

Цели и задачи исследования:

исследовать изменение расположения графика линейной функции, в зависимости от параметров входящих в её уравнение; показать принцип построения графиков уравнений с помощью формул в электронных таблицах; ознакомиться с методами решения линейных уравнений с двумя переменными и систем уравнений с помощью электронной таблицы Microsoft Excel.

Выявить преимущества решения систем уравнений графическим способом.

Гипотеза:

Использование программы Microsoft Excel наглядно иллюстрирует построение графиков элементарных и более сложных функций, позволяет исследовать преобразование  графиков, изменение графика функции в зависимости от исходных данных.

1. Теоретическая часть

Линейной функцией называется функция, которую можно задать формулой вида y = kx + b, где x — независимая переменная, k и b — некоторые числа. Графиком линейной функции является прямая. Прямая определяется двумя точками. Значит, для построения графика линейной функции достаточно найти координаты двух точек графика, нанести полученные точки на координатную плоскость и через них провести прямую. Пусть в формуле у = kх + b число k равно нулю. Тогда формульное представление линейной функции получает вид у = 0 ∙ х + b, т. е. у = b. Функция, задаваемая формулой у = b, при любом значении аргумента принимает одно и то же значение b. Пусть в формуле у = kх + b число b это нуль. Тогда формульное представление линейной функции становится таким: у = kх. Прямой пропорциональностью называется функция, которую можно задать формулой вида y = kx, где x — независимая переменная, k — не равное нулю число. Графиком прямой пропорциональности является прямая, проходящая через начало координат. 
Для построения графика прямой пропорциональности достаточно отметить какую-либо точку графика, отличную от начала координат и провести через эту точку и начало координат прямую. Графики двух разных линейных функций вида у = kх + b: пересекаются, если коэффициенты k разные; параллельны, если коэффициенты k одинаковые.

Через свойства линейной функции можно решать системы линейных уравнений. Причем это решение изящно, а его графическая интерпретация помогает глубже вникнуть в смысл математических понятий.

Уравнение вида ах + ву = с — линейное уравнение с двумя переменным, где х и у переменные, а, в и с – некоторые числа. Если а = 0, то уравнение принимает вид 0· х + bу = с. Если b = 0, то уравнение принимает вид ах + 0· у = с.

Если a=0, b = 0, с = 0, то уравнение принимает вид 0· х+ 0·у= 0.

 Если а = 0, в = 0, с≠0, то уравнение принимает вид 0· х+ 0·у= с.

Графиком линейного уравнения с двумя переменными называется множество всевозможных точек координатной плоскости, координаты которых будут являться решениями этого линейного уравнения.  График представляет собой прямую линию. Поэтому такие уравнения и называются линейными.

Уравнение вида ах + ву = с — линейное уравнение с двумя переменным, где х и у переменные, а, в и с – некоторые числа. Если а = 0, то уравнение принимает вид 0· х + bу = с. Если b = 0, то уравнение принимает вид ах + 0· у = с.

Если a=0, b = 0, с = 0, то уравнение принимает вид 0· х+ 0·у= 0.

 Если а = 0, в = 0, с≠0, то уравнение принимает вид 0· х+ 0·у= с.

Графиком линейного уравнения с двумя переменными называется множество всевозможных точек координатной плоскости, координаты которых будут являться решениями этого линейного уравнения.  График представляет собой прямую линию. Поэтому такие уравнения и называются линейными.

Системой уравнений называется некоторое количество уравнений, объединенных фигурной скобкой. Решением системы уравнений с двумя переменными называется пара значений переменных, обращающих каждое уравнение системы в верное равенство. Решить систему уравнений – это означает найти их общие решения. Поиск общего решения нескольких уравнений называют решением системы уравнений.

II. Практическая часть

Исследование графика линейной функции.

1.Рассмотрим функцию y=kx+b такую, что k ≠ 0, b = 0.

Фyнкция вида y=kx (прямая пропорциональность).

В одной системе координат построим графики функций:

y=3x, y=x, y=-3x.
Вывод:
График линейной функции вида у=kх проходит через начало координат. (приложение 1)

2.Рассмотрим функцию y=kx+b такую, что k ≠ 0, b ≠ 0.

В одной системе координат построим графики функций:

y=2x+5, y=-2x+5
Вывод:
График линейной функции вида y = kx + b пересекает ось Оy в точке (0;b). (приложение 2)
3.Рассмотрим функцию y=kx+b, где k=0, b ≠ 0

y= b.

В одной системе координат построим графики функций: y=5, y=-5.
Вывод:
График линейной функции вида y = b проходит параллельно оси Оx и пересекает ось Оy в точке (0;b). (приложение 3)
4.В одной системе координат построим графики функций, где k – одно и то же число.

y=2x, y=2x+5, y=2x-5.
Вывод:
Графики линейных функций вида y=kx+b параллельны, если коэффициенты при х одинаковы.

(приложение 4)

5.В одной системе координат построим графики функций:

y=4x-5, y= -2x+7.
Вывод:
Графики двух линейных функций вида y=kx+b пересекаются, если коэффициенты при х различны. (приложение 5)
Коэффициент k называют угловым коэффициентом прямой – графика функции y=kx+ b.
Вывод:

Если kx тупой. Функция убывает.
Если k0 , то угол наклона графика к оси Оx острый. Функция возрастает. (приложение 6).

Итак, исследуя расположение прямой, в зависимости от изменения значения k можно сделать вывод, что внося изменения в одну ячейку электронной таблицы, не меняя более ничего, мы можем получать различные расположения прямой.

Исследование системы уравнений с двумя переменными.

1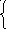.Решить систему уравнений y-2x=1

6x-y=7

В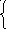ыразим y через x y=2x+1

y= 6x-7 и построим графики уравнений. (приложение 7)

Подводя курсор к точке пересечения линий легко можно увидеть решение уравнения (2;5).

2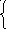.Решить систему уравнений

x-2y=6

3x+2y=-6

Выразим y через x y=x/2-3

y=-1,5x-3

Подводя курсор к точке пересечения линий легко можно увидеть решение уравнения (3;-1,5).

Применяя известный алгоритм построения графиков, получаем график. (приложение

Вывод:

Имея один шаблон для решения систем уравнений, не применяя особых усилий можно за короткое время решить много систем уравнений, а также использовать этот метод решения использовал для проверки домашних заданий.

Заключение:

Проделав данную исследовательскую работу, я пришел к следующим выводам: используя программу MS Excel на уроках математики можно получить наглядное представление о свойствах функции, графиках функций, взаимном расположении графиков, а также закрепить навыки и умения построения графиков функций, проводить исследования.

Использование компьютерных программ для построения графиков функций, изучение их свойств и закономерностей, дает возможность рассмотреть большое количество примеров с минимальными усилиями.

Список литературы

1.Алгебра. Учебник для 7 класса средней школы, под редакцией Теляковского С.А.

2.Д.В. Беклемишев. Курс аналитической геометрии и линейной алгебры. Москва, Наука, 1980 г.

3.М.Я. Выгодский. Справочник по высшей математике. Москва, 1977 г.

4. Математика. Учебное пособие под редакцией Муравья Л.Я., г. Москва Бридж 1994г.

5.В.С. Шипачёв. Основы высшей математики. Москва, Высшая школа, 1989 г.

9

Многие из вас уже знакомы с программой Excel от Microsoft, но используете ли вы ее по полной? Применяете ли вы в своей работе популярные функции или сводные таблицы? Создаете ли вы макросы для автоматизации своих действий? Действительно ли вы считаете себя опытным пользователем Excel, как это сейчас принято писать в резюме?

Если это не так, тогда добро пожаловать на наш полный курс по Excel. В этом объемном курсе вы узнаете не только о базовых манипуляциях в Excel, как добавление строк и столбцов, рабочих листов, создание таблиц и диаграмм, применение простых формул для подсчета ваших данных.

Здесь вы узнаете об условном форматировании. Как работать с фильтрами и применять срезы в ваших отчетах или презентациях. Вы узнаете, как быстро найти и заменить старые данные на новые. Научитесь работать в режиме нескольких окон и подсчитывать данные из нескольких листов или файлов excel.

Я расскажу вам, как делить данные в ячейках по разным столбцам и как создать выпадающий список. Вам будет нелишним узнать о полезной функции анализа «Что Если». Вы наконец-то научитесь применять популярные функции ЕСЛИ и ВПР в своей работе. Научитесь создавать сводные таблицы и создавать макросы для автоматизации ваших повторяющихся действий. Кстати, более углубленные знания в этом направлении, вы можете получить в платном курсе «Excel и Google-таблицы: от новичка до эксперта».

В конце вы узнаете, как защитить формулы в ваших таблицах от третьих лиц, как защитить рабочие листы и целые файлы. Также, я вам расскажу, как правильно оформить страницы перед печатью ваших таблиц Excel. Я уверен, что в каждом уроке вы узнаете что-то новое и откроете для себя новые возможности по работе с программой Excel.

Урок 1. Меню и вкладки в Excel

Первый урок я начну со знакомства с меню программы. Я уверен, что многие из вас уже знакомы с Excel, но данный курс будет неполным без ознакомительного урока с основными вкладками и командами.

Урок 2. Понимание книг и рабочих листов, строка состояния. Добавление и удаление строк и столбцов

Есть определенные термины Excel, которые мы должны постоянно использовать. В Excel файл – это книга. Книга — это файл. Каждая рабочая книга состоит как минимум из одного рабочего листа и в них производится основная работа в данной программе.

Урок 3. Изучение методов ввода и редактирования данных. Шаблоны Excel и заметки

Ввод данных — одно из самых основных действий, которые мы делаем в Excel, но есть некоторые правила, некоторые концепции, с которыми вам следует ознакомиться. Этим мы и займемся в нашем третьем уроке.

Урок 4. Создание и копирование простых формул в Excel

Для многих пользователей Excel написание формул, т.е. создание формул — одно из самых распространенных занятий. Формулы во многих случаях просты и удобны в использовании, но они работают по немного другой концепции. Давайте в этом разберемся.

Урок 5. Комбинированный подсчет, вычисление процентов, закрепить ячейку в формуле excel ($)

В предыдущем уроке мы с вами рассмотрели работу с простыми формулами и использование суммирования значений. В этот раз я покажу вам, как делать комбинированные расчеты, расчет процентов и фиксировать ячейку в формулах.

Урок 6. Функции СУММ, СРЕДНЕЕ, РАНГ, НАИБОЛЬШИЙ

В предыдущих уроках мы рассмотрели 3 метода суммирования данных и поиск среднего числа. В этом уроке я покажу вам быстрый метод подсчета суммы и средней, как узнать рейтинг из полученных результатов и другие чуть менее известные функции в Excel.

Урок 7. Регулирование размера строк и столбцов, объединение ячеек, перенос записи, выравнивание и работа с границами

Сегодня мы разберем способы форматирования рабочей области Excel. Я предполагаю, что вы уже знакомы с некоторыми продуктами Microsoft Office, как, например, Word, поэтому я не буду рассматривать те функции, с которыми вы, скорее всего, уже знаете.

Урок 8. Числовой и финансовый формат. Даты и условное форматирование

В данном уроке мы рассмотрим некоторые виды числового форматирования, чтобы вы знали, как обойти условные настройки программы и могли отредактировать данные ваших таблиц в более удобном для вас формате.

Урок 9. Создание и форматирование таблицы. Фильтрация и срезы в Excel

Если вы работаете со списками данных, возможно, с персоналом, или списком товара, или списком транзакций, например, то по мере увеличения или уменьшения списков вы можете упростить управление ими с помощью функции, называемой таблицей.

Урок 10. Работа с фигурами, добавление рисунков и схемы SmartArt в Excel

Для этого урока я создал простую таблицу, чтобы показать вам, каким образом мы можем добавлять в наши таблицы разного рода фигуры, картинки с компьютера или онлайн, элементы SmartArt и другое.

Урок 11. Копирование и перенос строк таблицы, скрытие строк и столбцов. Найти и заменить в Excel

Сегодня я вам покажу методы вставки и скрытия строк и столбцов, как быстро копировать и передвигать части таблицы без потерь. Мы также рассмотрим полезную функцию поиска и замены данных в ваших таблицах.

Урок 12. Как сделать диаграмму в excel

Люди не всегда быстро воспринимают информацию в цифрах, и иногда необходимо показать данные с помощью диаграмм. В Excel есть большое разнообразие диаграмм, которые вы можете использовать в ваших отчетах, презентациях и других методах демонстрации данных. Давайте рассмотрим, как с ними работать.

Урок 13. Форматирование диаграмм, Спарклайны, Гистограмма и диаграмма Парето в Excel

В прошлом уроке мы с вами рассмотрели несколько способов создания диаграмм и их форматирование, меняли стиль и добавляли записи. В этом видео я продолжу рассказывать вам о дополнительных функциях Excel для работы с диаграммами.

Урок 14. Как закрепить строку, разделить таблицу, и функция «группировать»  

Мы поговорим о некоторых настройках рабочего листа Excel для удобства работы с вашими таблицами и данными. Это одно из тех направлений, где встречаются множество вопросов пользователей по работе с программой. А значит, данный урок будет очень для вас полезен.

Урок 15. Как перемещаться между книгами Excel и упорядочить несколько окон

Если у вас открыто несколько книг Excel, то бывает необходимость переходить из одного файла в другой. Или, может быть, еще такая ситуация, что вы находитесь только в одной книге, но вам нужно перемещаться между рабочими листами внутри нее. Это довольно сложно сделать, если вы пытаетесь достичь и того и другого. Давайте рассмотрим несколько вариантов, как Excel может решить эту задачу.

Урок 16. Создание, копирование и группировка рабочих листов Excel

Здесь мы рассмотрим работу с рабочими листами. Вы научитесь создавать их, переименовывать, группировать и многое другое. Давайте начнем.

Урок 17. Как посчитать данные из разных листов и файлов в Excel

В предыдущих уроках мы с вами применяли формулы для подсчета данных в таблицах внутри рабочих листов. Но часто возникает потребность делать отчеты используя данные из нескольких листов или даже книг. В этом уроке я покажу, как все это работает.

Урок 18. Сортировка и фильтрация данных в Excel

Когда мы работаем с большими таблицами, в Excel имеется очень полезные функции сортировки и фильтрации данных. В этом уроке мы рассмотрим несколько примеров их использования.

Урок 19. Как разделить текст в ячейке excel по столбцам. Удаление дубликатов

Иногда возникают ситуации, когда вы получаете какой-нибудь отчет или проект, где данные находятся в одной ячейке, но вы хотите видеть их в разных столбцах. В этом уроке мы продолжим говорить о сортировке данных и разделении столбцов на отдельные части.

Урок 20. Проверка значений и как сделать выпадающий список в excel

В Excel имеется очень мощный инструмент по проверке вводимых значений. Он проверяет их не после ввода, а до него, чтобы данные в таблице были корректны. Сегодня мы рассмотрим данный инструмент и научимся создавать не только правила для вводимых данных, но и создавать выпадающие списки в ячейках.

Урок 21. Применение функции анализа «Что Если»

Сегодня мы рассмотрим полезную функцию Excel под названием «Анализ Что Если». Она будет вам полезна не только для подсчета финансовой деятельности предприятия, но и для собственных финансовых планов.

Урок 22. Функция ЕСЛИ в Excel. Подробное объяснение с примерами

Одна из самых мощных функций Excel называется функцией ЕСЛИ. По своей природе она почти похожа на программирование и открывает двери для другого образа мышления. Функция ЕСЛИ – это условная функция. Она позволяет нам давать несколько ответов в зависимости от условия. 

Урок 23. Функция ВПР в Excel. Подробное объяснение с примерами

Здесь мы рассмотрим очередную мощную функцию Excel, которая называется ВПР. В прошлом уроке мы рассматривали функцию ЕСЛИ, где мы задавали условие и, в зависимости от значения, программа предоставляла результат. Функция ВПР ищет значение в заданной области и предоставляет результат, который наиболее совместим с каким-нибудь заданным параметром.

Урок 24. Функции СЧЁТЕСЛИ и СУММЕСЛИ в Excel

Сегодня будет короткий урок, где мы закончим разбирать популярные функции Excel и рассмотрим две сразу: СЧЁТЕСЛИ и СУММЕСЛИ.

Урок 25. Как сделать сводную таблицу в Excel и манипулировать ее данными

Один из самых креативных и мощных инструментов Excel называется сводной таблицей. Это отдельная область, которую вы можете создать на основе данных.

Урок 26. Группировка и фильтры в сводной таблице excel. Сводные диаграммы.

Мы продолжаем работать со сводной таблицей, которую мы создали в прошлом уроке.

Урок 27. Создание простых макросов в Excel

Макрос – это способ автоматизировать вашу работу. Они применяются там, где пользователь изо дня в день выполняет определенные манипуляции в Excel и хочет вместо 5 или 10 шагов, выполнить действие одним сочетанием клавиш. Иногда применение некоторых макросов может занять две или три минуты, особенно если они связаны с большим количеством манипуляций с данными, но основная идея состоит в том, что вы определили конкретные действия, которые часто выполняете, и хотели бы их автоматизировать.

Урок 28. Как защитить рабочий лист или книгу и поделиться файлом Excel

В Excel имеется несколько вариантов защиты ваших таблиц, рабочих листов и целых книг. Бывают ситуации, что вы выполняете какой-нибудь проект в команде, и вам необходимо делится вашими файлами Excel. Чтобы защитить в них данные от разного рода манипуляций посторонних лиц, что нарушит целостность и правильность данных, вы можете применять разные методы защиты.

Урок 29. Как печатать страницы и заголовки на каждой странице. Как вставить колонтитул в excel

К последнему уроку данного курса мы с вами создали несколько Excel файлов и рабочих листов. Мы также создали множество таблиц и отчетов. Какие-то из них довольно длинные, а какие-то довольно широкие. Но мы бы хотели их распечатать таким образом, чтобы они выглядели целостными и привлекательными. Давайте рассмотрим, как мы это можем сделать.

Анализ данных в Excel предполагает сама конструкция табличного процессора. Очень многие средства программы подходят для реализации этой задачи.

Excel позиционирует себя как лучший универсальный программный продукт в мире по обработке аналитической информации. От маленького предприятия до крупных корпораций, руководители тратят значительную часть своего рабочего времени для анализа жизнедеятельности их бизнеса. Рассмотрим основные аналитические инструменты в Excel и примеры применения их в практике.

Инструменты анализа Excel

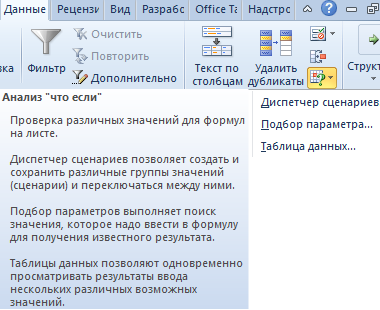
Одним из самых привлекательных анализов данных является «Что-если». Он находится: «Данные»-«Работа с данными»-«Что-если».

Средства анализа «Что-если»:

1. «Подбор параметра». Применяется, когда пользователю известен результат формулы, но неизвестны входные данные для этого результата.
2. «Таблица данных». Используется в ситуациях, когда нужно показать в виде таблицы влияние переменных значений на формулы.
3. «Диспетчер сценариев». Применяется для формирования, изменения и сохранения разных наборов входных данных и итогов вычислений по группе формул.
4. «Поиск решения». Это надстройка программы Excel. Помогает найти наилучшее решение определенной задачи.

Практический пример использования «Что-если» для поиска оптимальных скидок по таблице данных.

Другие инструменты для анализа данных:

Анализировать данные в Excel можно с помощью встроенных функций (математических, финансовых, логических, статистических и т.д.).



Сводные таблицы в анализе данных

Чтобы упростить просмотр, обработку и обобщение данных, в Excel применяются сводные таблицы.

Программа будет воспринимать введенную/вводимую информацию как таблицу, а не простой набор данных, если списки со значениями отформатировать соответствующим образом:

1. Перейти на вкладку «Вставка» и щелкнуть по кнопке «Таблица».
2. Откроется диалоговое окно «Создание таблицы».



3. Указать диапазон данных (если они уже внесены) или предполагаемый диапазон (в какие ячейки будет помещена таблица). Установить флажок напротив «Таблица с заголовками». Нажать Enter.

К указанному диапазону применится заданный по умолчанию стиль форматирования. Станет активным инструмент «Работа с таблицами» (вкладка «Конструктор»).

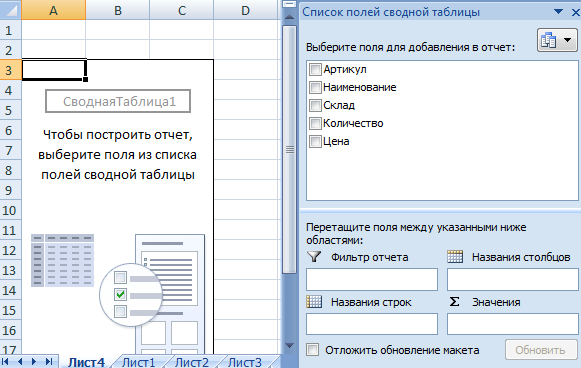
Составить отчет можно с помощью «Сводной таблицы».

1. Активизируем любую из ячеек диапазона данных. Щелкаем кнопку «Сводная таблица» («Вставка» — «Таблицы» — «Сводная таблица»).
2. В диалоговом окне прописываем диапазон и место, куда поместить сводный отчет (новый лист).
3. Открывается «Мастер сводных таблиц». Левая часть листа – изображение отчета, правая часть – инструменты создания сводного отчета.



4. Выбираем необходимые поля из списка. Определяемся со значениями для названий строк и столбцов. В левой части листа будет «строиться» отчет.

Создание сводной таблицы – это уже способ анализа данных. Более того, пользователь выбирает нужную ему в конкретный момент информацию для отображения. Он может в дальнейшем применять другие инструменты.

Анализ «Что-если» в Excel: «Таблица данных»

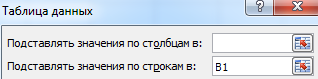
Мощное средство анализа данных. Рассмотрим организацию информации с помощью инструмента «Что-если» — «Таблица данных».

Важные условия:

• данные должны находиться в одном столбце или одной строке;
• формула ссылается на одну входную ячейку.

Процедура создания «Таблицы данных»:

1. Заносим входные значения в столбец, а формулу – в соседний столбец на одну строку выше.



2. Выделяем диапазон значений, включающий столбец с входными данными и формулой. Переходим на вкладку «Данные». Открываем инструмент «Что-если». Щелкаем кнопку «Таблица данных».



3. В открывшемся диалоговом окне есть два поля. Так как мы создаем таблицу с одним входом, то вводим адрес только в поле «Подставлять значения по строкам в». Если входные значения располагаются в строках (а не в столбцах), то адрес будем вписывать в поле «Подставлять значения по столбцам в» и нажимаем ОК.

Анализ предприятия в Excel: примеры

Для анализа деятельности предприятия берутся данные из бухгалтерского баланса, отчета о прибылях и убытках. Каждый пользователь создает свою форму, в которой отражаются особенности фирмы, важная для принятия решений информация.

• скачать систему анализа предприятий;
• скачать аналитическую таблицу финансов;
• таблица рентабельности бизнеса;
• отчет по движению денежных средств;
• пример балльного метода в финансово-экономической аналитике.

Для примера предлагаем скачать финансовый анализ предприятий в таблицах и графиках составленные профессиональными специалистами в области финансово-экономической аналитике. Здесь используются формы бухгалтерской отчетности, формулы и таблицы для расчета и анализа платежеспособности, финансового состояния, рентабельности, деловой активности и т.д.