Технология использования средств excel для финансовых расчетов

26

Использована
книга:ОВЧАРЕНКО Е.К., ИЛЬИНА О.П…..

ФИНАНСОВО-ЭКОНОМИЧЕСКИЕ
РАСЧЕТЫ В EXCEL.
1998г.

Модели и методы финансово-экономических
расчетов.

Условно
методы финансовой математики делятся
на две категории: базовые
и прикладные.
К базовым методам и моделям относятся:

1. простые
   и сложные
   проценты
   как основа операций, связанных с
   наращением или дисконтированием
   платежей;

2. расчет
   последовательностей
   (потоков) платежей применительно
   к различным видам финансовых рент.

К прикладным
методам финансовых расчетов относятся:

1. планирование и
   оценка эффективности финансово-кредитных
   операций;

2. расчет страховых
   аннуитетов;

3. планирование
   погашения долгосрочной задолженности;

4. планирование
   погашения ипотечных ссуд и потребительских
   кредитов;

5. финансовые расчеты
   по ценным бумагам;

6. лизинговые,
   факторинговые и форфейтинговые
   банковские операции;

7. планирование и
   анализ инвестиционных проектов и др.

Основными понятиями
финансовых методов расчета являются:

• процент
  —
  абсолютная величина дохода от
  предоставления денег в долг в любой
  его форме;

• процентная
  ставка
  — относительная величина дохода в
  зафиксированный интервал времени,
  измеряемая в процентах или в виде дроби;

• период
  начисления
  — интервал времени, к которому приурочена
  процентная ставка;

• капитализация
  процентов
  — присоединение начисленных процентов
  к основной сумме;

• наращение
  — увеличение первоначальной суммы в
  связи с капитализацией;

• дисконтирование
  — приведение стоимостной величины,
  относящейся к будущему, на некоторый,
  обычно более ранний момент времени
  (операция, обратная наращению).

В финансовых
расчетах используются следующие виды
процентных ставок:

• в
  зависимости от базы для начисления
  процентов различают простые
  проценты
  (постоянная база) и сложные
  проценты
  (переменная база);

• по
  принципу расчета различают ставку
  наращения — декурсивная ставка и
  учетную
  ставку — антисипативная ставка;

• по
  постоянству значения процентной ставки
  в течение действия контракта —
  фиксированные
  и
  плавающие (фиксируется
  ли изменяющаяся во времени база и размер
  надбавки к ней — маржи).
  
  

К средствам EXCELфинансового анализа относятся:

• финансовые функции
  EXCEL;

• подбор параметров;

• диспетчер сценариев:
  для создания, редактирования, объединения,
  удаления и просмотра созданных сценариев
  расчетов для ячеек текущего рабочего
  листа;

• таблица подстановки:
  для выбора наиболее оптимального
  варианта.

Финансовый
анализ инвестиций.

Описание аргументов
финансовых функций EXCEL,
использующих базовые модели.

АРГУМЕНТ в Excel2003-2007 (вExcel97-2000)	ОПИСАНИЕ АРГУМЕНТА
бс (бз)	Будущая стоимость фиксированных периодических выплат или единой суммы; баланс наличности, который нужно достичь после последней выплаты, по умолчанию равный 0 (например, будущая стоимость займа равна 0).
плт (выплата, пплат)	Фиксированная периодическая выплата.
дата0;дата1;…;датаN	Дата операций с наличными.
кпер (число_периодов)	Общее число периодов выплат.
пс (нз, пз, тс)	Текущая стоимость (начальное значение) вклада или займа.
ставка (норма)	Процентная ставка за период, норма дисконтирования.

сумма0;сумма1;…;суммаN	Значения выплат и поступлений.
значения
тип	Число 0 или 1, обозначающее, когда производится выплата (1- в начале периода, 0- в конце периода); по умолчанию равно 0.
предположение; предп; прогноз	Предполагаемое значение процентной ставки;по умолчанию равно 0,1.
период	Период, для которого требуется найти выплату по процентам; должен быть в интервале от 1 до кпер.
нач_период	Номер первого периода, участвующего в вычислениях.
кон_период	Номер последнего периода.
номинальная_ ставка	Номинальная годовая процентная ставка.
реинвест_ норма	Норма прибыли, получаемой за деньги,находящиеся в наличном обороте при реинвестировании.
финансовая_ норма	Норма прибыли, выплачиваемой за деньги, находящиеся в обороте.
эффект_ ставка	Эффективная годовая процентная ставка.

Функции excel для расчёта операций по кредитам и займам. Определение будущей стоимости.

Понятие будущей
стоимости основано на принципе
неравноценности денег, относящихся к
разным моментам времени. Вложения,
сделанные сегодня, в будущем составят
большую величину. Эта группа функций
позволяет рассчитать:

1. будущую или
   наращенную стоимость серии фиксированных
   периодических платежей, а также будущую
   стоимость текущего значения вклада
   или займа при постоянной процентной
   ставке (функция БС (БЗ));

2. будущее значение
   инвестиции после начисления сложных
   процентов при переменной процентной
   ставке (функция БЗРАСПИС).

Расчёты на основе постоянной процентной ставки. Функция бс (бз).

Синтаксис БС
(ставка; кпер; плт; пс; тип).

Рассмотрим различные
варианты использования этих функции
при решении конкретных задач.

1. Допустим, необходимо
   рассчитать будущую стоимость единой
   суммы вклада, по которой начисляются
   сложные проценты определённое число
   периодов.

В этом случае на
рабочем листе EXCELформула
примет вид:

=БС (ставка; кпер;
; пс).

При решении
конкретной задачи вместо названий
аргументов следует записать соответствующие
числа.

1. Рассмотрим
   ситуации, когда платежи производятся
   систематически, а не один раз, как в
   предыдущем примере. Эти платежи могут
   осуществляться в началекаждого
   расчетного периода (так называемые
   платежипренумерандоилиобязательные
   платежи) илив конце(постнумерандоилиобычные платежи) в течениеnпериодов. Допустим, что в каждом периоде
   вносится одинаковая сумма. Требуется
   найти совокупную величину таких вложений
   (их будущую стоимость) в концеn-ого
   периода для обоих случаев. Отличие в
   расчёте при этом заключается в том, что
   во втором случае не происходит начисления
   процентов на последний вклад, т.е. все
   вклады пренумерандо увеличиваются на
   сложные проценты на один расчётный
   период больше, чем вклады постнумерандо.

2.1. Для расчёта
будущей стоимости серии фиксированных
периодических платежей, если они вносятся
в начале каждого периода, формула имеет
вид:

=БС (ставка; кпер;
плт; ; 1).

2.2.Для расчёта
будущей стоимости серии фиксированных
периодических платежей, если выплаты
происходят в конце периода, формула
имеет вид:

=БС (ставка; кпер;
плт; ; 0).

Аргумент тип=0
можно опустить и записать:

=БС (ставка; кпер;
плт),

подставив вместо
аргумента соответствующие числа.

Соседние файлы в папке ФинФункции

• #
• #

Использование средств Excel для финансовых расчетов

1. Финансовые функции Excel 2. Подбор параметра 3. Диспетчер сценариев 4. Таблица подстановки

Финансовые функции EXCEL Предназначены для вычисления базовых величин, необходимых для проведения сложных финансовых расчетов

Группы финансовых функций 1. Для анализа инвестиционных проектов 2. Анализа ценных бумаг 3. Для расчета амортизации 4. Вспомогательные функции

Алгоритм расчета результата финансовой функции: 1. В ячейки рабочего листа ввести значения аргументов функции 2. Установить курсор в ячейку для ввода финансовой функции 3. Выполнить: Вставка Функция 4. Выбрать категорию Финансовые

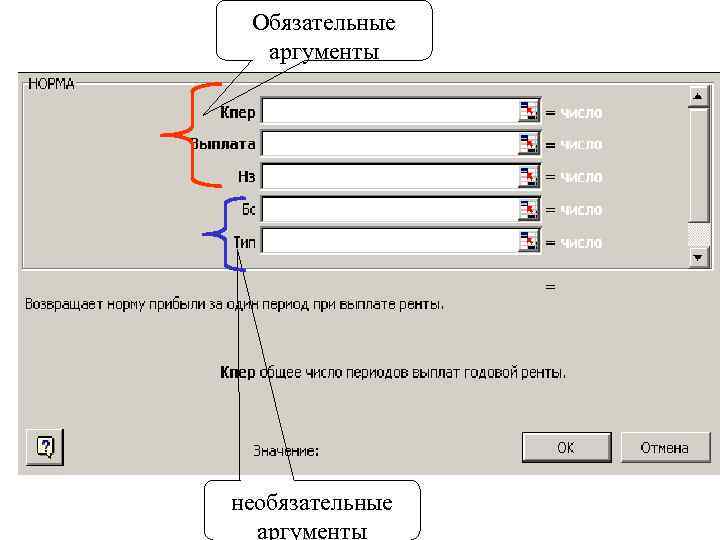
Обязательные аргументы необязательные аргументы

В Excel реализовано 15 встроенных и 37 дополнительных финансовых функций Дополнительные функции устанавливаются командой Сервис, Надстройки, Пакет анализа

Функции Excel для расчета финансовых операций по кредитам, займам, ссудам.

Расчеты основаны на концепции временной стоимости денег и предполагают неравноценность денег, относящихся к разным моментам времени

Данные функции позволяют определять: 1. Сумму наращенной стоимости (будущая стоимость) 2. Начальное значение (текущая стоимость) 3. Срок платежа и процентной ставки 4. Расчет периодических платежей, связанных с погашением займов.

Общая формула расчета, которую Excel использует при вычислении финансовых аргументов, связанных с денежными потоками: Формула 1

pmt – фиксированная (неизменная) сумма платежа; n – общее число периодов выплат r – процентная ставка за один период (норма) type – число 0 или 1, обозначающее когда производится выплата: 1 – в начале периода, 0 – в конце периода

pv – текущая стоимость вклада (займа), по которому начисляются проценты по ставке r % n-ое число периодов или текущая стоимость серии фиксированных периодических платежей fv – будущая стоимость вклада (займа) или будущая стоимость серии фиксированных периодических платежей.

Если процентная ставка за период начисления r = 0, то используется формула: Формула 2

Определение будущей стоимости Вложения сделанные сегодня, в будущем составят большую величину (принцип неравноценности денег)

Функция БЗ() рассчитывает будущую стоимость периодических постоянных платежей и будущее значение единой суммы вклада или займа на основе постоянной процентной ставки.

Синтаксис функции: БЗ(норма; число периодов; выплата; нз; тип) Возвращаемое значение функции БЗ() – аргумент fv формулы (1) Формула 3

Задача 1 Рассчитать будущую стоимость единой суммы вклада, по которой начисляются сложное проценты определенное число периодов

Эту величину можно рассчитать по формуле: fv — будущая стоимость вклада (займа) pv -текущая стоимость вклада (займа) n — общее число периодов начисления по % r -процентная ставка по вкладу (займу)

Эта формула соответствует классической формуле расчета наращенной суммы вклада (S) по методу сложных процентов: S = P*(1+i)n P- первоначальный размер долга i – ставка наращения по сложным процентам n – число лет наращения

Сложные проценты применяются в средних и долгосрочных финансово-кредитных операциях, если проценты не выплачиваются сразу после их начисления, а присоединяются к сумме долга

n P*(1+i) S= Проценты за n лет равны: i=S–P P*(1+i)n- P = P*((1+i)n-1) q q- множитель наращения по сложным процентам

Присоединение начисленных процентов к основной сумме называют капитализацией процентов

Задача 2 Рассчитать, какая сумма окажется на счете, если 27 тыс. руб. положены на 33 года под 13, 5% годовых. Проценты начисляются каждые полгода.

Решение Проценты начисляются несколько раз в год, значит необходимо рассчитать общее количество периодов начисления процентов и ставку % за период начисления.

% начисляется ежегодно: число периодов = n ставка % за период начисления k % начисляется 1 раз в полгода: число периодов = n*2 % за период начисления k/2

% начисляется каждый квартал n*4 k/4 % начисляется каждый месяц n*12 k/12 % начисляется каждый день n*365 k/365

В задаче общее число периодов = 33*2 Процент начисления = 13, 5%/2 По условию НЗ = -27 Отрицательное число — вложение денег =БЗ(13, 5%/2; 33*2; ; -27) = 2012, 07 тыс. руб

Задача 3 Два варианта инвестирования средств в течение 4 лет при ежегодном взносе 300 тыс. руб. : 1 -й – в начале каждого года под 26% годовых 2 -й – в конце каждого года под 38% годовых Определить сколько денег окажется на счете в конце каждого периода

Решение для 1 -го варианта: норма = 26% число_периодов=4 выплата = — 300 тип = 1 для 2 -го варианта: норма = 38% число_периодов=4 выплата = — 300 тип = 0

Расчеты показали – предпочтительнее первый вариант (инвестировать средства в начале года под 26%)

Функция НПЗ Вычисляет текущую стоимость (NPV) периодических платежей переменной величины как сумму ожидаемых расходов и доходов, дисконтированных нормой процента r

NPV – текущая стоимость периодических и поступлений r – норма дисконтирования (средняя цена капитала 0 n – количество выплат и поступлений valuei – значения выплат и поступлений

Дисконтирование – приведение стоимостной величины, относящейся к будущему, на некоторый, обычно более ранний момент времени (операция обратная наращиванию)

Метод определения чистой текущей стоимости применяется при оценке эффективности инвестиций. Позволяет определить нижнюю границу прибыльности и использовать ее как критерий выбора эффективного проекта

Синтаксис функции НПЗ(норма; значение 1; значение 2; … значение 29) (в XP НПЗ() соответствует ЧПС()

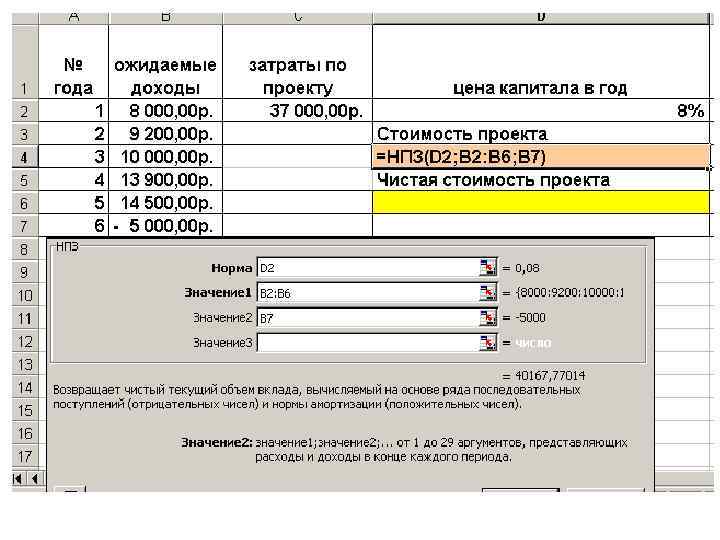
Задача 4 Затраты по проекту на начало его реализации составляют 37 000 р. , ожидаемые доходы в первые 5 лет: 8000 р. , 92000 р. , 10000 р. , 13900 р. , 14500 р. На 6 -й год ожидается убыток – 5000 р. Рассчитать чистую стоимость проекта

Текущая стоимость проекта : Значение функции НПЗ() -Затраты 3167, 77 р.

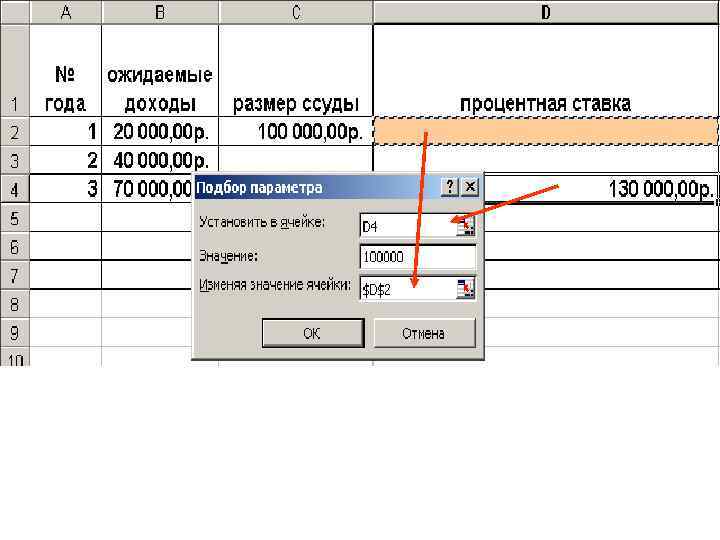
Задача 5 Вас просят дать в долг 100 000 руб. и обещают вернуть через год 20 000 руб. , через 2 года – 40 000 руб. , через 3 года 70 000 руб. При какой % ставке эта сделка выгодна (в банке ставка составляет 10% годовых)?

Решение Задачу следует решить с использованием средства Подбор параметра и функции НПЗ()

=НПЗ(D 2; B 2: B 4)

Задача 6 Оценка эффективности инвестиций В конце года кап. вложения по проекту составят 1280 млн. руб. Ожидается, что в последующие 3 года проект принесет доходы: 420, 490, 550, 590 млн. руб. Рассчитать чистую стоимость проекта для разных норм дисконтирования и объемов кап. вложений

Максимальная величина текущей прибыли достигается при минимальных кап. вложениях и минимальной ставке дисконтирования, например почти одинаковое значение NPV если Кап. вложения = 1310 млн. руб. и норма = 13, 8% Кап. вложения = 1270 млн. руб. и норма = 15%

Функция ПЗ() Возвращает текущий объем вклада на основе постоянных периодических платежей В отличии от НПЗ() допускает внесение денежного взноса в конце или в начале периода, которые должны быть постоянными на весь период инвестиции

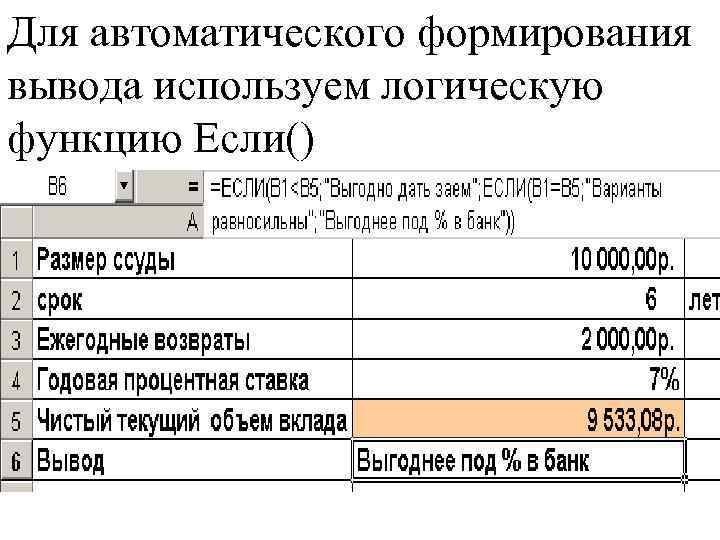
Задача 6 Заем в 10 000 руб. обещают возвращать по 2000 руб. в течение 6 лет. Будет ли выгодна сделка при годовой ставке 7%?

Для автоматического формирования вывода используем логическую функцию Если()

Для анализа вариантов используем Сервис, Сценарии, Добавить

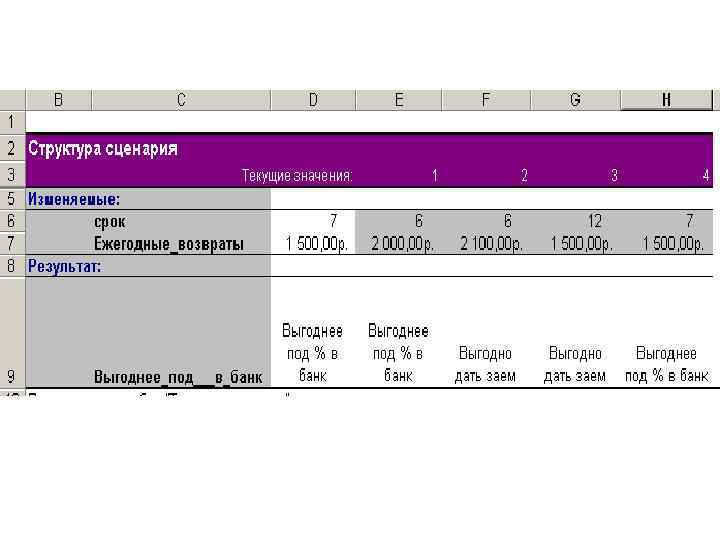
Создаем несколько сценариев и выводим отчет

На сегодняшний день разработано большое количество специализированных программных продуктов для проведения экономических расчетов, однако сотрудники финансово-экономических служб чаще всего пользуются табличным редактором Excel. Причина популярности данного инструмента — обширный функционал Excel и постоянное его развитие практически в каждой новой версии табличного редактора.

В рамках одной статьи невозможно рассмотреть все достоинства Excel, которые экономисты могут применить в своей работе, поэтому остановимся на анализе лучших функций редактора, используемых для решения экономических задач.

Для удобства восприятия материала сгруппируем эти функции в три блока:

1. Функционал расчетных формул в Excel.

2. Функционал Excel для обработки табличных данных.

3. Инструменты Excel для моделирования и анализа экономических данных.

ФУНКЦИОНАЛ РАСЧЕТНЫХ ФОРМУЛ В EXCEL

Расчетные формулы являются изначальным и основополагающим функционалом табличного редактора Excel, поэтому рассмотрим их в первую очередь.

Пакет встроенных расчетных формул включает в себя десятки наименований, но самыми востребованными в работе экономистов являются следующие формулы: ЕСЛИ, СУММЕСЛИ и СУММЕСЛИМН, ВПР и ГПР, СУММПРОИЗВ, СЧЕТЕСЛИ.

Решение экономической задачи с помощью формулы ЕСЛИ

Формула ЕСЛИ — расчетная функция Excel, которую наиболее часто используют для решения несложных экономических расчетов. Она относится к группе логических формул и позволяет рассчитать необходимые данные по условиям, заданным пользователями.

С помощью формулы ЕСЛИ можно сравнить числовые или текстовые значения по прописанным в формуле условиям.

Запись расчетной формулы в заданной ячейке в общем виде выглядит так:

=ЕСЛИ(логическое_выражение;[значение_если_истина];[значение_если_ложь]),

где логическое выражение — данные, которые нужно проверить/сравнить (числовые или текстовые значения в ячейках);

значение_если_истина — результат, который появится в расчетной ячейке, если значение будет верным;

значение_если_ложь — результат, который появится в расчетной ячейке при неверном значении.

Задача № 1. Предприятие реализует три номенклатурные группы продукции: лимонад, минеральная вода и пиво. С 01.09.2020 запланировано установить скидку в размере 15 % на пиво.

Чтобы сформировать новый прайс на продукцию, сохраняем ее перечень в виде таблицы Excel. В первом столбце таблицы отражена номенклатура всей продукции в алфавитном порядке, во втором — признак группы продукции.

Для решения задачи создаем в таблице третий столбец и прописываем в первой ячейке номенклатуры формулу: =ЕСЛИ(C4=»пиво»;15%;0).

Эту формулу продлеваем до конца перечня номенклатуры продукции. В итоге получаем сведения о продукции, на которую с сентября снизится цена (табл. 1).

В данном примере показано использование формулы ЕСЛИ для обработки текстовых значений в исходных данных.

Решение экономической задачи с помощью формулы СУММЕСЛИ

Формулы СУММЕСЛИ и СУММЕСЛИМН также используют для экономических расчетов, но они обладают более широкими возможностями для выборки и обработки данных. Можно задать не одно, а несколько условий отборов и диапазонов.

Задача № 2. На основе ведомости начисления заработной платы сотрудникам магазина нужно определить общую сумму зарплаты продавцов.

Чтобы решить эту задачу, сохраняем ведомость из учетной базы данных в виде таблицы Excel. В данном случае нам нужно не просто произвести выборку значений, но и суммировать их результат. Поэтому будем использовать более сложную разновидность формулы ЕСЛИ — СУММЕСЛИ.

Для решения задачи добавим внизу таблицы еще одну строку «Всего продавцы». В ее ячейке под суммой зарплаты, начисленной сотрудникам магазина, пропишем следующую формулу:=СУММЕСЛИ(C4:C13;»продавец»;D4:D13).

Таким образом мы задали условие, при котором табличный редактор обращается к столбцу с наименованием должностей (столбец С), выбирает в нем значение «Продавец» и суммирует данные ячеек с начисленной заработной платой из столбца D в привязке к этой должности.

Результат решения задачи — в табл. 2.

Решение экономической задачи с помощью формул ВПР и ГПР

Формулы ВПР и ГПР используют для решения более сложных экономических задач. Они популярны среди экономистов, так как существенно облегчают поиск необходимых значений в больших массивах данных. Разница между формулами:

• ВПР предназначена для поиска значений в вертикальных списках (по строкам) исходных данных;
• ГПР используют для поиска значений в горизонтальных списках (по столбцам) исходных данных.

Формулы прописывают в общем виде следующим образом:

=ВПР(искомое значение, которое требуется найти; таблица и диапазон ячеек для выборки данных; номер столбца, из которого будут подставлены данные; [интервал просмотра данных]);

=ГПР(искомое значение, которое требуется найти; таблица и диапазон ячеек для выборки данных; номер строки, из которой будут подставлены данные; [интервал просмотра данных]).

Указанные формулы имеют ценность при решении задач, связанных с консолидацией данных, которые разбросаны на разных листах одной книги Excel, находятся в различных рабочих книгах Excel, и размещении их в одном месте для создания экономических отчетов и подсчета итогов.

Задача № 3. У экономиста есть данные в виде таблицы Excel о реализации продукции за сентябрь в натуральном измерении (декалитрах) и данные о реализации продукции в сумме (рублях) в другой таблице Excel. Экономисту нужно предоставить руководству отчет о реализации продукции с тремя параметрами:

• продажи в натуральном измерении;
• продажи в суммовом измерении;
• средняя цена реализации единицы продукции в рублях.

Для решения этой задачи с помощью формулы ВПР нужно последовательно выполнить следующие действия.

Шаг 1. Добавляем к таблице с данными о продажах в натуральном измерении два новых столбца. Первый — для показателя продаж в рублях, второй — для показателя цены реализации единицы продукции.

Шаг 2. В первой ячейке столбца с данными о продажах в рублях прописываем расчетную формулу: =ВПР(B4:B13;Табл.4!B4:D13;3;ЛОЖЬ).

Пояснения к формуле:

В4:В13 — диапазон поиска значений по номенклатуре продукции в создаваемом отчете;

Табл.4!B4:D13 — диапазон ячеек, где будет производиться поиск, с наименованием таблицы, в которой будет организован поиск;

3 — номер столбца, по которому нужно выбрать данные;

ЛОЖЬ — значение критерия поиска, которое означает необходимость строгого соответствия отбора наименований номенклатуры таблицы с суммовыми данными наименованиям номенклатуры в таблице с натуральными показателями.

Шаг 3. Продлеваем формулу первой ячейки до конца списка номенклатуры в создаваемом нами отчете.

Шаг 4. В первой ячейке столбца с данными о цене реализации единицы продукции прописываем простую формулу деления значения ячейки столбца с суммой продаж на значение ячейки столбца с объемом продаж (=E4/D4).

Шаг 5. Продлим формулу с расчетом цены реализации до конца списка номенклатуры в создаваемом нами отчете.

В результате выполненных действий появился искомый отчет о продажах (табл. 3).

На небольшом количестве условных данных эффективность формулы ВПР выглядит не столь внушительно. Однако представьте, что такой отчет нужно сделать не из заранее сгруппированных данных по номенклатуре продукции, а на основе реестра ежедневных продаж с общим количеством записей в несколько тысяч.

Тогда эта формула обеспечит такую скорость и точность выборки нужных данных, которой трудно добиться другими функциями Excel.

Решение экономической задачи с помощью формулы СУММПРОИЗВ

Формула СУММПРОИЗВ позволяет экономистам справиться практически с любой экономической задачей, для решения которой нужно работать с несколькими массивами данных. Она обладает всеми возможностями рассмотренных выше формул, умеет суммировать произведения данных из списка до 255 источников (массивов).

Задача № 4. Есть реестр продаж различной номенклатуры продукции за сентябрь 2020 г. Нужно рассчитать из общего реестра данные о суммах реализации по основным номенклатурным группам продукции.

Чтобы выполнить задачу, добавим внизу реестра три новые строки с указанием групп продукции и пропишем в ячейке с будущими данными о продажах первой группы (пиво) следующую формулу: =СУММПРОИЗВ(((C4:C13=C16)*D4:D13)). Здесь указано, что в ячейке должно быть выполнено суммирование произведений значений диапазона ячеек столбца с наименованием групп продукции (C4:C13) с условием отбора наименования группы «Пиво» (С16) на значения ячеек столбца с суммами продаж (D4:D13).

Далее копируем эту формулу на оставшиеся две ячейки, заменив в них условия отбора на группу «Лимонад» (С17) и группу «Минеральная вода» (С18).

Выполнив указанные действия, получим искомое решение задачи в табл. 4.

Решение экономической задачи с помощью формулы СЧЕТЕСЛИ

Формула СЧЕТЕСЛИ используется не так широко, как предыдущие, но она выручает экономистов, если нужно минимизировать ошибки при работе с таблицами Excel. Эта формула удобна для проверки корректности вводимых данных и установке различного рода запретов, что особенно важно, если с данными работает несколько пользователей.

Задача № 5. Экономисту поручили провести корректировку справочника номенклатуры ТМЦ в учетной базе данных компании. Справочник долгое время не проверяли, данные в него вносили порядка 10 человек, поэтому появилось много некорректных и дублирующих наименований.

Чтобы повысить качество работы, приняли решение создать обновленный справочник в книге Excel, а затем сопоставить его с данными в учетной базе и исправить их. Проблема заключалась в том, что перечень номенклатуры составляет порядка 3000 наименований. Вносить его в книгу будут шесть человек, а это создает риск дублирования позиций.

Экономист может решить эту проблему с помощью формулы СЧЕТЕСЛИ. Нужно выполнить следующие действия:

• выбираем диапазон ячеек, куда будут вноситься наименования номенклатуры (В5:В3005);
• в меню редактора выбираем путь: Данные → Проверка данных;
• в появившемся диалоговом окне выбираем вкладку Параметры и указываем в выпадающем списке Тип данных вариант Другой;
• в строке Формула указываем: =СЧЕТЕСЛИ($В$5:$В$3005;В5)<=1;
• в диалоговом окне на вкладке Сообщение об ошибке вводим текст сообщения и нажимаем кнопку «ОК».

Если кто-либо из сотрудников будет пытаться ввести в указанный диапазон ячеек наименование ТМЦ, которое уже есть в диапазоне, у него это не получится. Excel выдаст сообщение в таком виде (рис. 1).

ФУНКЦИОНАЛ EXCEL ДЛЯ ОБРАБОТКИ ТАБЛИЧНЫХ ДАННЫХ

Помимо расчетных формул в табличном редакторе Excel присутствует набор инструментов, значительно облегчающих жизнь экономистам, которые работают с большими объемами данных. К наиболее популярным из них можно отнести функцию сортировки данных, функцию фильтрации данных, функцию консолидации данных и функцию создания сводных таблиц.

Решение экономической задачи с применением функции сортировки данных

Функционал сортировки данных позволяет изменить расположение данных в таблице и выстроить их в новой последовательности. Это удобно, когда экономист консолидирует данные нескольких таблиц и ему нужно, чтобы во всех исходных таблицах данные располагались в одинаковой последовательности.

Другой пример целесообразности сортировки данных — подготовка отчетности руководству компании. С помощью функционала сортировки из одной таблицы с данными можно быстро сделать несколько аналитических отчетов.

Сортировку данных выполнить просто:

• выделяем курсором столбцы таблицы;
• заходим в меню редактора: Данные → Сортировка;
• выбираем нужные параметры сортировки и получаем новый вид табличных данных.

Задача № 6. Экономист должен подготовить отчет о заработной плате, начисленной сотрудникам магазина, с последовательностью от самой высокой до самой низкой зарплаты.

Для решения этой задачи берем табл. 2 в качестве исходных данных. Выделяем в ней диапазон ячеек с показателями начисления зарплат (B4:D13).

Далее в меню редактора вызываем сортировку данных и в появившемся окне указываем, что сортировка нужна по значениям столбца D (суммы начисленной зарплаты) в порядке убывания значений.

Нажимаем кнопку «ОК», и табл. 2 преобразуется в новую табл. 5, где в первой строке идут данные о зарплате директора в 50 000 руб., в последней — данные о зарплате грузчика в 18 000 руб.

Решение экономической задачи с использованием функционала Автофильтр

Функционал фильтрации данных выручает при решении задач по анализу данных, особенно если возникает необходимость проанализировать часть исходной таблицы, данные которой отвечают определенным условиям.

В табличном редакторе Excel есть два вида фильтров:

• автофильтр — используют для фильтрации данных по простым критериям;
• расширенный фильтр — применяют при фильтрации данных по нескольким заданным параметрам.

Автофильтр работает следующим образом:

• выделяем курсором диапазон таблицы, данные которого собираемся отфильтровать;
• заходим в меню редактора: Данные → Фильтр → Автофильтр;
• выбираем в таблице появившиеся значения автофильтра и получаем отфильтрованные данные.

Задача № 7. Из общих данных о реализации продукции за сентябрь 2020 г. (см. табл. 4) нужно выделить суммы продаж только по группе лимонадов.

Для решения этой задачи выделяем в таблице ячейки с данными по реализации продукции. Устанавливаем автофильтр из меню: Данные → Фильтр → Автофильтр. В появившемся меню столбца с группой продукции выбираем значение «Лимонад». В итоге в табл. 6 автоматически остаются значения продаж лимонадов, а данные по группам «Пиво» и «Минеральная вода» скрываются.

Для применения расширенного фильтра нужно предварительно подготовить «Диапазон условий» и «Диапазон, в который будут помещены результаты».

Чтобы организовать «Диапазон условий», следует выполнить следующие действия:

• в свободную строку вне таблицы копируем заголовки столбцов, на данные которых будут наложены ограничения (заголовки несмежных столбцов могут оказаться рядом);
• под каждым из заголовков задаем условие отбора данных.

Строка копий заголовков вместе с условиями отбора образуют «Диапазон условий».

Порядок работы с функционалом консолидации данных

Функционал консолидации данных помогает экономистам в решении задач по объединению данных из нескольких источников в одну общую таблицу. Например, экономисты холдинговых компаний часто создают однотипные таблицы с данными по разным компаниям холдинга и им требуется предоставить руководству сводные данные о работе всей группы компаний. Для упрощения формирования сводных показателей как раз и подходит функционал консолидации данных.

Консолидация работает только с идентичными таблицами Excel, поэтому для успеха все объединяемые таблицы должны отвечать следующим требованиям:

• макеты всех консолидируемых таблиц одинаковые;
• названия столбцов во всех консолидируемых таблицах идентичные;
• в консолидируемых таблицах нет пустых столбцов и строк.

Работа с функционалом консолидации включает ряд последовательных действий:

1) открываем файлы со всеми таблицами, из которых собираемся консолидировать данные;

2) в отдельном файле, где будет находиться консолидированный отчет, ставим курсор на первую ячейку диапазона консолидированной таблицы;

3) в меню Excel открываем вкладки: Данные → Работа с данными → Консолидация;

4) в открывшемся диалоговом окне выбираем функцию консолидации (как правило, это «сумма», потому что нам требуется суммировать значения нескольких таблиц);

5) в диалоговом окне консолидации указываем ссылки на диапазоны объединяемых таблиц (диапазоны должны быть одинаковые);

6) если требуется автоматическое обновление данных консолидированной таблицы при изменении данных исходных таблиц, ставим галочку напротив «Создавать связи с исходными данными»;

7) завершаем консолидацию нажатием кнопки «ОК». В итоге получаем сводную структурированную таблицу, объединяющую данные всех исходных таблиц.

Решение экономической задачи с использованием функционала сводной таблицы для создания нового отчета

Функционал сводных таблиц позволяет сформировать различного рода отчеты из одного или нескольких массивов данных с возможностью обновления отчетных данных в случае изменения информации в исходных массивах. Используя сводные таблицы, можно быстро перенастроить параметры отчета.

Для создания сводной таблицы нужно зайти в меню Excel и вызвать Мастера сводных таблиц. В моей версии редактора это выполняется через Вставка → Сводная таблица, в некоторых версиях нужно выбрать Данные → Сводная таблица.

В появившемся диалоговом окне формируем параметры будущей таблицы:

• указываем исходную таблицу или диапазон ячеек Excel, откуда будут взяты данные для сводной таблицы. В последних версиях Excel также можно выбрать вариант обработки данных из внешних источников;
• указываем место, куда размещать создаваемый отчет сводной таблицы (новый лист, ячейки открытого листа);
• в открывшемся конструкторе отчета указываем, какие исходные данные будут выведены в строки и столбцы отчета, при необходимости настраиваем фильтры для показателей сводной таблицы и создаем новый отчет.

Задача № 8. Экономисту нужно создать отчет на основе реестра данных о реализации продукции за сентябрь 2020 г. В отчете должно быть два уровня группировки данных. На первом уровне нужно вывести итоги по группам продукции, на втором уровне — по ее номенклатурным позициям. Чтобы решить эту задачу, вызываем Мастера сводных таблиц. Указываем, что данные берем из ячеек табл. 4, а отчет будем размещать на новом листе книги Excel. В конструкторе отчета указываем, что в первой колонке отчета будут показатели групп и номенклатурных единиц продукции, во второй — данные о суммах реализации. После этого даем команду создать сводную таблицу. Результат — в табл. 7.

ИНСТРУМЕНТЫ EXCEL ДЛЯ МОДЕЛИРОВАНИЯ И АНАЛИЗА ЭКОНОМИЧЕСКИХ ДАННЫХ

Постоянное развитие функционала табличного редактора Excel привело к тому, что появилось много новых инструментов, которые могут помочь экономистам в решении выполняемых ими задач. К числу наиболее значимых можно отнести функцию «Поиск решения», пакет расширенного анализа данных и специализированные надстройки.

Решение экономической задачи с помощью надстройки «Поиск решения»

Функция «Поиск решения» позволяет найти наиболее рациональный способ решения экономической задачи математическими методами. Она может автоматически выполнить расчеты для задач с несколькими вводными данными при условии накладывания определенных ограничений на искомое решение.

Такими экономическими задачами могут быть:

• расчет оптимального объема выпуска продукции при ограниченности сырья;
• минимизация транспортных расходов на доставку продукции покупателям;
• решение по оптимизации фонда оплаты труда.

Функция поиска решения является дополнительной надстройкой, поэтому в стандартном меню Excel мы ее не найдем. Чтобы использовать в своей работе функцию «Поиск решения», экономисту нужно сделать следующее:

• в меню Excel выбрать путь: Файл → Параметры → Надстройки;
• в появившемся списке надстроек выбрать «Поиск решения» и активировать эту надстройку;
• вернуться в меню Excel и выбрать: Данные → Поиск решения.

Задача № 9. Туристической компании необходимо организовать доставку 45 туристов в четыре гостиницы города с трех пунктов прибытия при минимально возможной сумме затрат. Для решения задачи составляем таблицу с исходными данными:

1. Количество прибывающих с каждого пункта — железнодорожный вокзал, аэропорт и автовокзал (ячейки Н6:Н8).

2. Количество забронированных для туристов мест в каждой из четырех гостиниц (ячейки D9:G9).

3. Стоимость доставки одного туриста с каждого пункта прибытия до каждой гостиницы размещения (диапазон ячеек D6:G8).

Исходные данные, размещенные таким образом, показаны в табл. 8.1.

Далее приступаем к подготовке поиска решения.

1. Создаем внизу исходной таблицы такую же таблицу для расчета оптимального количества доставки туристов при условии минимизации затрат на доставку с диапазоном ячеек D15:G17.

2. Выбираем на листе ячейку для расчета искомой функции минимизации затрат (J4) и прописываем в ячейке расчетную формулу: =СУММПРОИЗВ(D6:G8;D15:G17).

3. Заходим в меню Excel, вызываем диалоговое окно надстройки «Поиск решения» и указываем там требуемые параметры и ограничения (рис. 2):

• оптимизировать целевую функцию — ячейка J4;
• цель оптимизации — до минимума;
• изменения ячейки переменных — диапазон ячеек второй таблицы D15:G17;
• ограничения поиска решения:

– в диапазоне ячеек второй таблицы D15:G17 должны быть только целые значения (D15:G17=целое);

– значения диапазона ячеек второй таблицы D15:G17 должны быть только положительными (D15:G17>=0);

– количество мест для туристов в каждой гостинице таблицы для поиска решения должно быть равно количеству мест в исходной таблице (D18:G18 = D9:G9);

– количество туристов, прибывающих с каждого пункта, в таблице для поиска решения должно быть равно количеству туристов в исходной таблице (Н15:Н17 = Н6:Н8).

Далее даем команду найти решение, и надстройка рассчитывает нам результат оптимальной доставки туристов (табл. 8.2).

При такой схеме доставки целевое значение общей суммы расходов действительно минимальное и составляет 1750 руб.

Пакет расширенного анализа данных

Пакет расширенного анализа данных применяют, если нужно исследовать различного рода статистические анализы, ряды данных, спрогнозировать тренды и т. д.

Пакет является надстройкой к Excel, устанавливается в основное меню аналогично функции поиска решений (Файл → Параметры → Надстройки → Пакет анализа). Вызвать его можно командой Данные → Анализ данных через диалоговое окно, в котором отражены все заложенные в надстройке виды анализа (рис. 3).

Специализированные надстройки для финансово-экономической работы

В последние годы значительно расширился перечень специализированных надстроек к табличному редактору Excel, которые могут использовать в своей работе экономисты. Практически все они бесплатные, легко устанавливаются самим пользователем.

Не будем останавливаться на таких надстройках, как Power Query, Power Pivot, Power Quick, так как они в большей степени используются в целях бизнес-аналитики, чем для решения экономических задач.

Есть и другие надстройки к Excel, которые могут облегчить работу специалистов финансово-экономических служб. Интерес представляют две бесплатные надстройки — «Финансист» и PowerFin.

Надстройку «Финансист» можно установить на свою версию Excel как в автоматическом, так и ручном режиме. В надстройке собрано много полезных для экономистов функций. Достаточно перечислить основные блоки данной надстройки:

• финансовые функции (ликвидность, платежеспособность, финансовая устойчивость, рентабельность, оборачиваемость, безубыточность продаж, отсрочка платежа, налоги и т. д.);
• работа с формулами;
• работа с текстом;
• работа с книгами и листами Excel;
• работа с ячейками Excel;
• поиск дубликатов и сравнение диапазонов данных;
• вставка дат и примечаний к диапазонам данных;
• загрузка курсов валют;
• создание выпадающих списков.

Надстройка PowerFin будет полезна прежде всего экономистам, которые работают с кредитами и инвестициями. Она без проблем устанавливается в меню надстроек Excel и имеет следующие функции:

• кредитный калькулятор (с функцией выведения калькулятора на лист, в том числе с возможностью автоматического формирования графика платежей);
• депозитный калькулятор для вычисления основных параметров инвестиций (с функцией выведения калькулятора на лист);
• вычисление требуемой процентной ставки исходя из первоначальной и будущей стоимости инвестиций;
• набор основных формул для расчета эффективности проекта: дисконтированного денежного потока, чистого денежного дохода, внутренней нормы доходности, срока окупаемости.

Excel имеет значительную популярность среди бухгалтеров, экономистов и финансистов не в последнюю очередь благодаря обширному инструментарию по выполнению различных финансовых расчетов. Главным образом выполнение задач данной направленности возложено на группу финансовых функций. Многие из них могут пригодиться не только специалистам, но и работникам смежных отраслей, а также обычным пользователям в их бытовых нуждах. Рассмотрим подробнее данные возможности приложения, а также обратим особое внимание на самые популярные операторы данной группы.

Выполнение расчетов с помощью финансовых функций

В группу данных операторов входит более 50 формул. Мы отдельно остановимся на десяти самых востребованных из них. Но прежде давайте рассмотрим, как открыть перечень финансового инструментария для перехода к выполнению решения конкретной задачи.

Переход к данному набору инструментов легче всего совершить через Мастер функций.

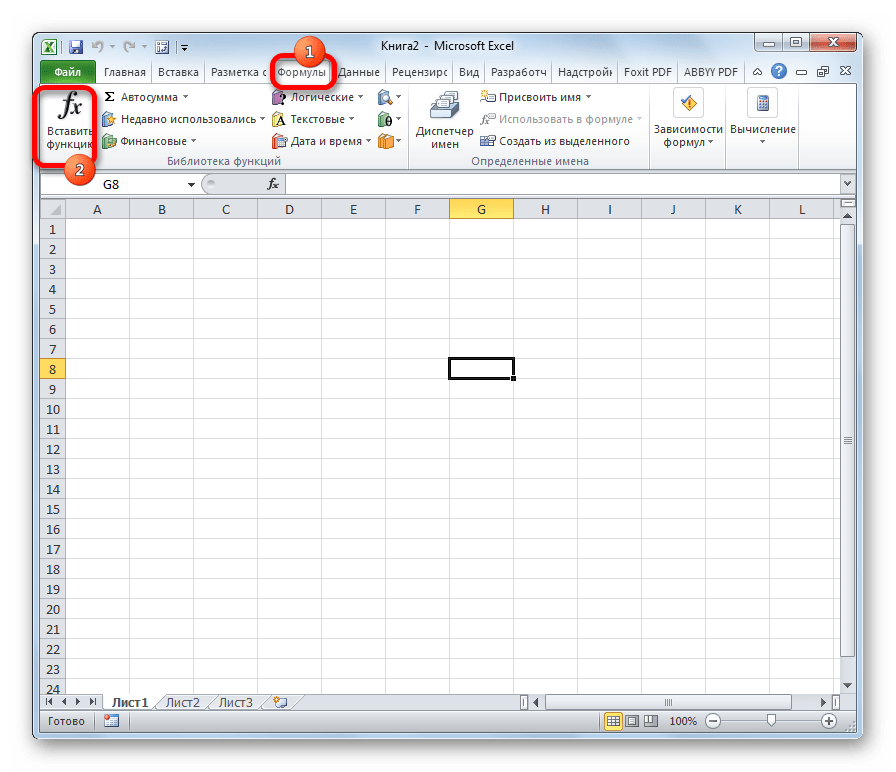
1. Выделяем ячейку, куда будут выводиться результаты расчета, и кликаем по кнопке «Вставить функцию», находящуюся около строки формул.



2. Запускается Мастер функций. Выполняем клик по полю «Категории».



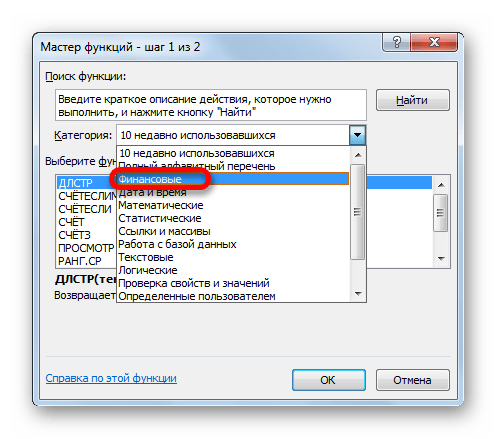
3. Открывается список доступных групп операторов. Выбираем из него наименование «Финансовые».



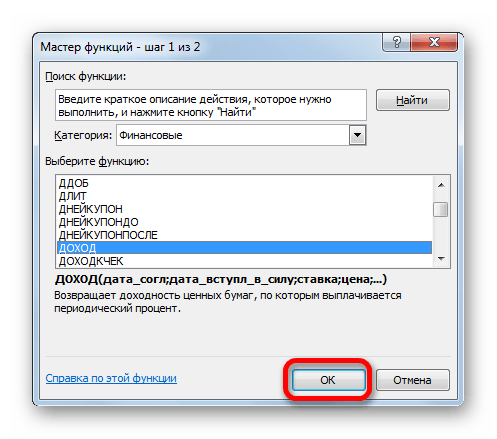
4. Запускается перечень нужных нам инструментов. Выбираем конкретную функцию для выполнения поставленной задачи и жмем на кнопку «OK». После чего открывается окно аргументов выбранного оператора.

В Мастер функций также можно перейти через вкладку «Формулы». Сделав переход в неё, нужно нажать на кнопку на ленте «Вставить функцию», размещенную в блоке инструментов «Библиотека функций». Сразу вслед за этим запустится Мастер функций.

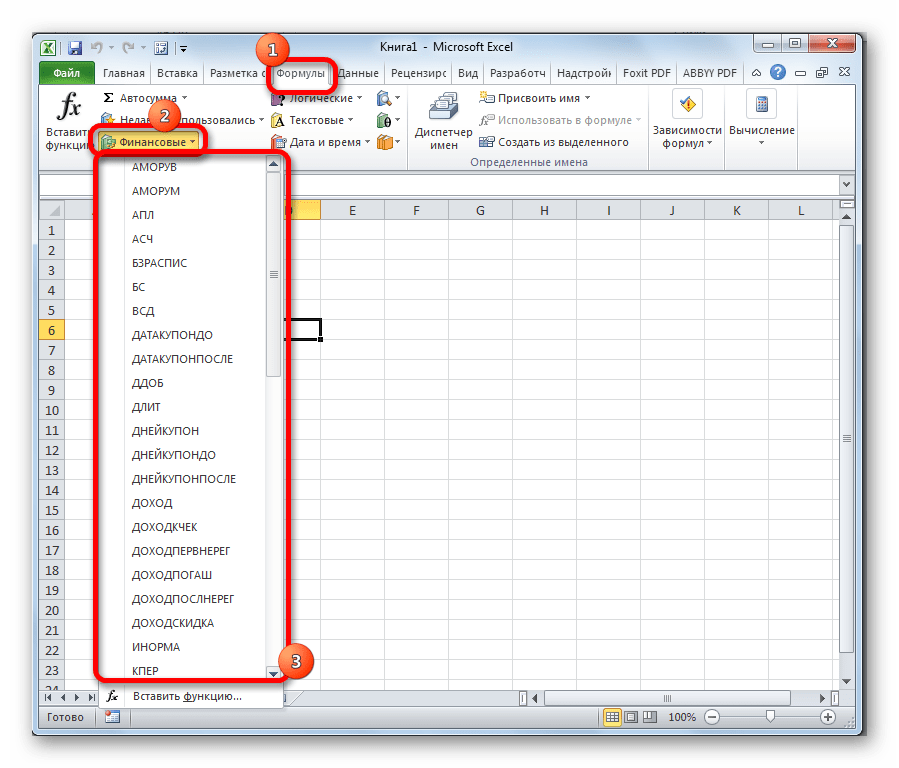
Имеется в наличии также способ перехода к нужному финансовому оператору без запуска начального окна Мастера. Для этих целей в той же вкладке «Формулы» в группе настроек «Библиотека функций» на ленте кликаем по кнопке «Финансовые». После этого откроется выпадающий список всех доступных инструментов данного блока. Выбираем нужный элемент и кликаем по нему. Сразу после этого откроется окно его аргументов.

Урок: Мастер функций в Excel

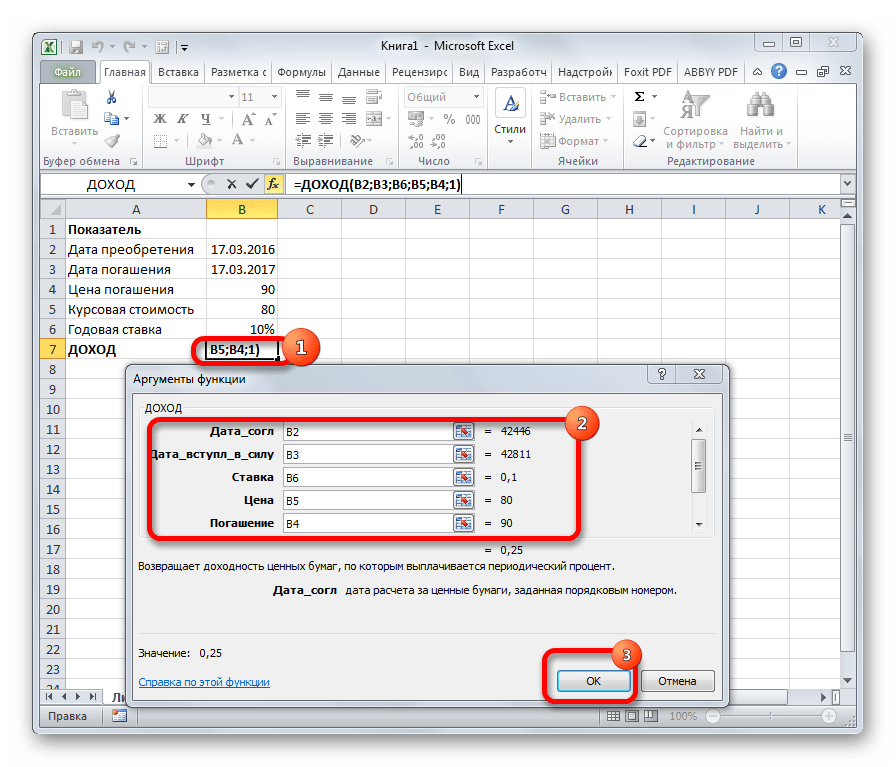
ДОХОД

Одним из наиболее востребованных операторов у финансистов является функция ДОХОД. Она позволяет рассчитать доходность ценных бумаг по дате соглашения, дате вступления в силу (погашения), цене за 100 рублей выкупной стоимости, годовой процентной ставке, сумме погашения за 100 рублей выкупной стоимости и количеству выплат (частота). Именно эти параметры являются аргументами данной формулы. Кроме того, имеется необязательный аргумент «Базис». Все эти данные могут быть введены с клавиатуры прямо в соответствующие поля окна или храниться в ячейках листах Excel. В последнем случае вместо чисел и дат нужно вводить ссылки на эти ячейки. Также функцию можно ввести в строку формул или область на листе вручную без вызова окна аргументов. При этом нужно придерживаться следующего синтаксиса:

=ДОХОД(Дата_сог;Дата_вступ_в_силу;Ставка;Цена;Погашение»Частота;[Базис])

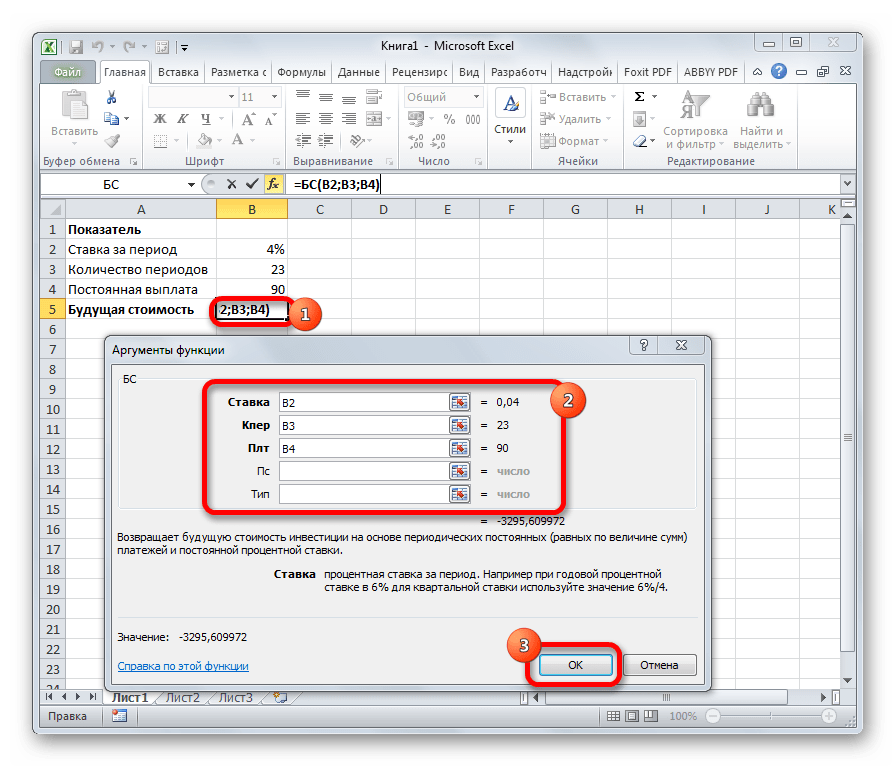
БС

Главной задачей функции БС является определение будущей стоимости инвестиций. Её аргументами является процентная ставка за период («Ставка»), общее количество периодов («Кол_пер») и постоянная выплата за каждый период («Плт»). К необязательным аргументам относится приведенная стоимость («Пс») и установка срока выплаты в начале или в конце периода («Тип»). Оператор имеет следующий синтаксис:

=БС(Ставка;Кол_пер;Плт;[Пс];[Тип])

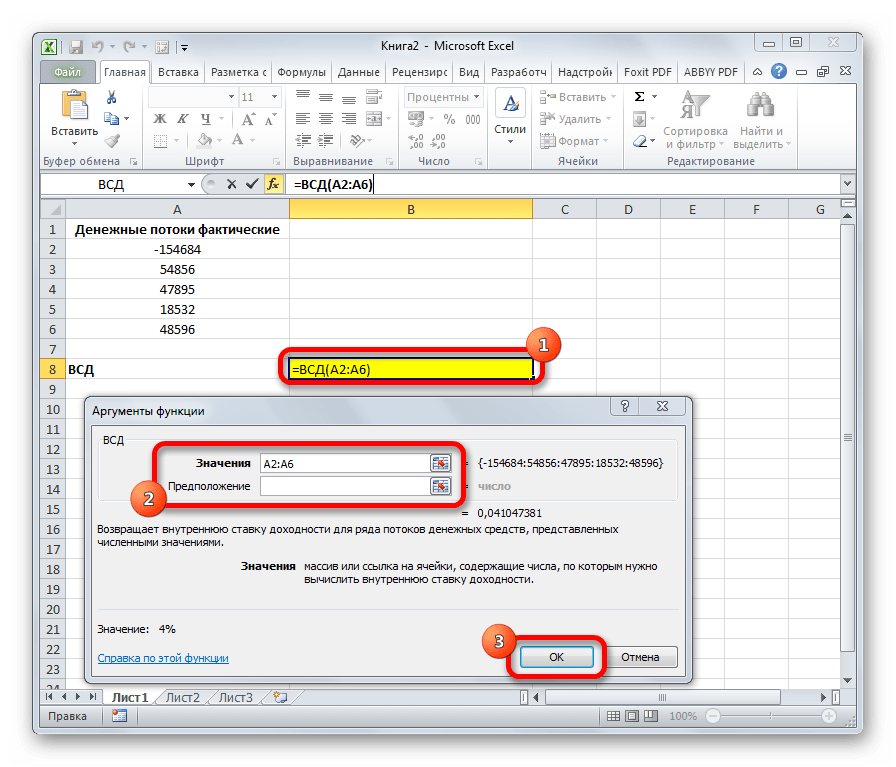
ВСД

Оператор ВСД вычисляет внутреннюю ставку доходности для потоков денежных средств. Единственный обязательный аргумент этой функции – это величины денежных потоков, которые на листе Excel можно представить диапазоном данных в ячейках («Значения»). Причем в первой ячейке диапазона должна быть указана сумма вложения со знаком «-», а в остальных суммы поступлений. Кроме того, есть необязательный аргумент «Предположение». В нем указывается предполагаемая сумма доходности. Если его не указывать, то по умолчанию данная величина принимается за 10%. Синтаксис формулы следующий:

=ВСД(Значения;[Предположения])

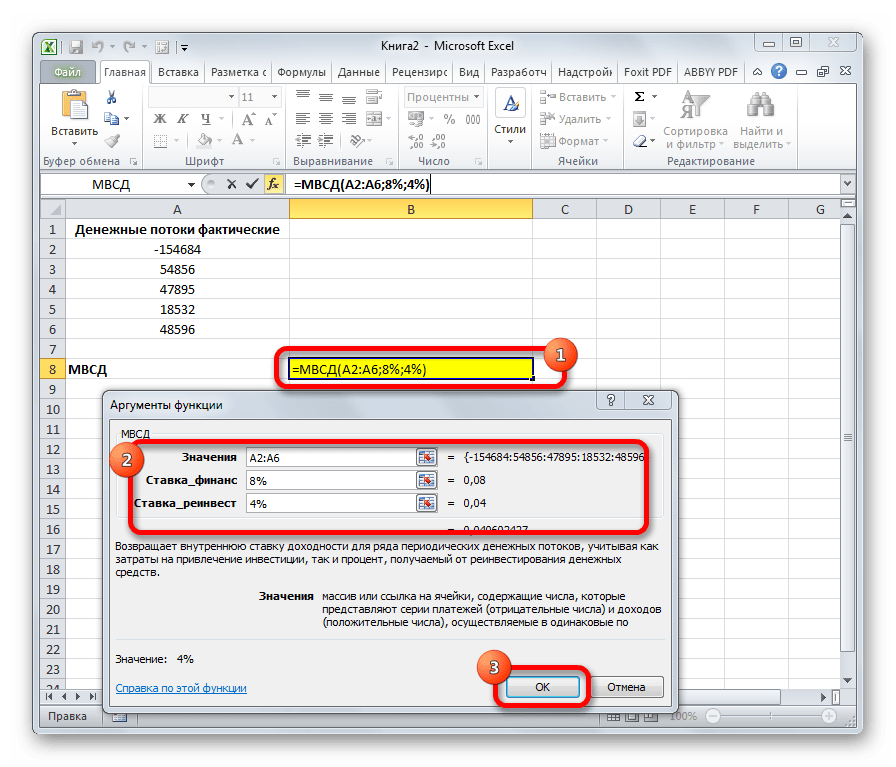
МВСД

Оператор МВСД выполняет расчет модифицированной внутренней ставки доходности, учитывая процент от реинвестирования средств. В данной функции кроме диапазона денежных потоков («Значения») аргументами выступают ставка финансирования и ставка реинвестирования. Соответственно, синтаксис имеет такой вид:

=МВСД(Значения;Ставка_финансир;Ставка_реинвестир)

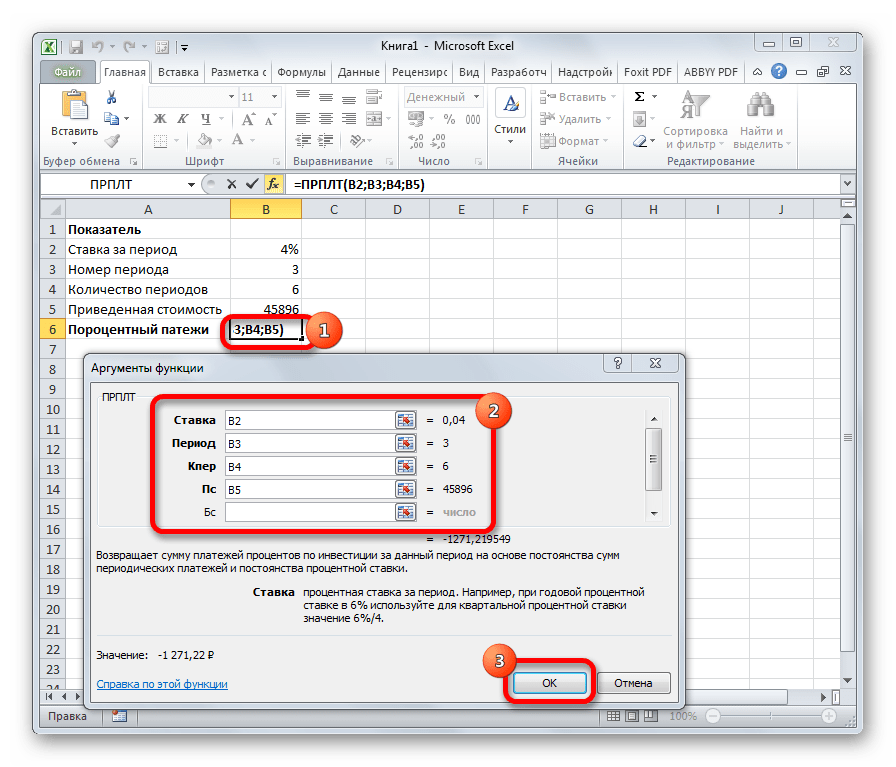
ПРПЛТ

Оператор ПРПЛТ рассчитывает сумму процентных платежей за указанный период. Аргументами функции выступает процентная ставка за период («Ставка»); номер периода («Период»), величина которого не может превышать общее число периодов; количество периодов («Кол_пер»); приведенная стоимость («Пс»). Кроме того, есть необязательный аргумент – будущая стоимость («Бс»). Данную формулу можно применять только в том случае, если платежи в каждом периоде осуществляются равными частями. Синтаксис её имеет следующую форму:

=ПРПЛТ(Ставка;Период;Кол_пер;Пс;[Бс])

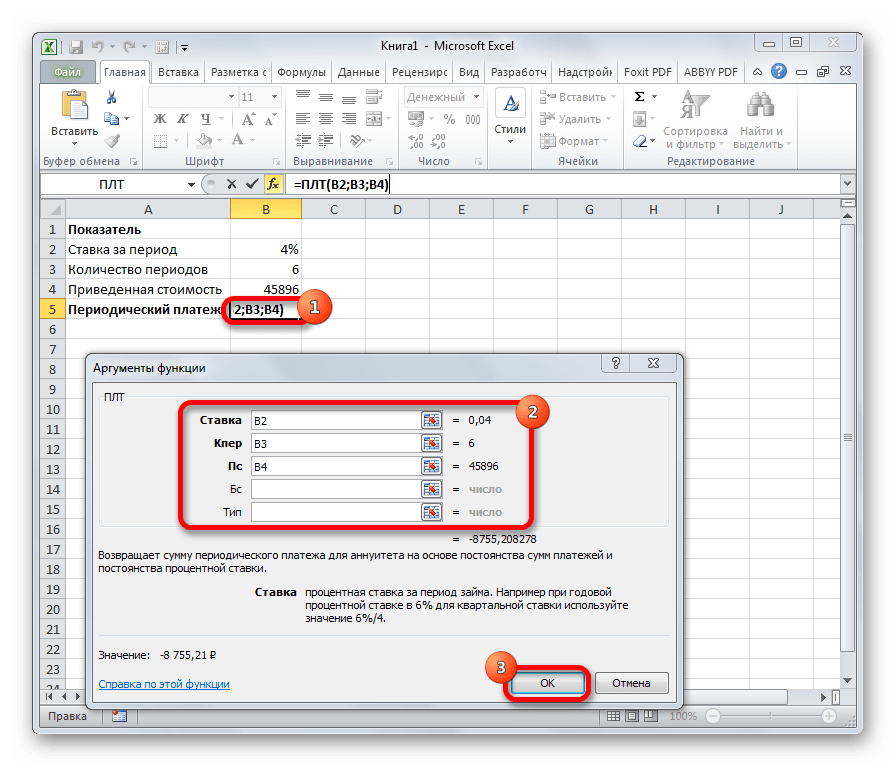
ПЛТ

Оператор ПЛТ рассчитывает сумму периодического платежа с постоянным процентом. В отличие от предыдущей функции, у этой нет аргумента «Период». Зато добавлен необязательный аргумент «Тип», в котором указывается в начале или в конце периода должна производиться выплата. Остальные параметры полностью совпадают с предыдущей формулой. Синтаксис выглядит следующим образом:

=ПЛТ(Ставка;Кол_пер;Пс;[Бс];[Тип])

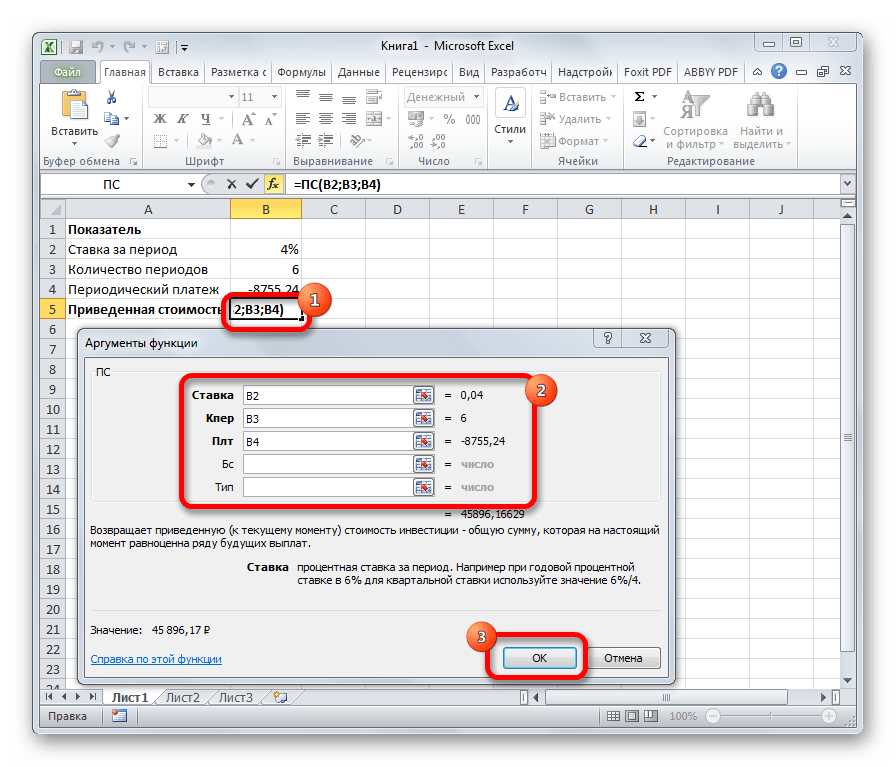
ПС

Формула ПС применяется для расчета приведенной стоимости инвестиции. Данная функция обратная оператору ПЛТ. У неё точно такие же аргументы, но только вместо аргумента приведенной стоимости («ПС»), которая собственно и рассчитывается, указывается сумма периодического платежа («Плт»). Синтаксис соответственно такой:

=ПС(Ставка;Кол_пер;Плт;[Бс];[Тип])

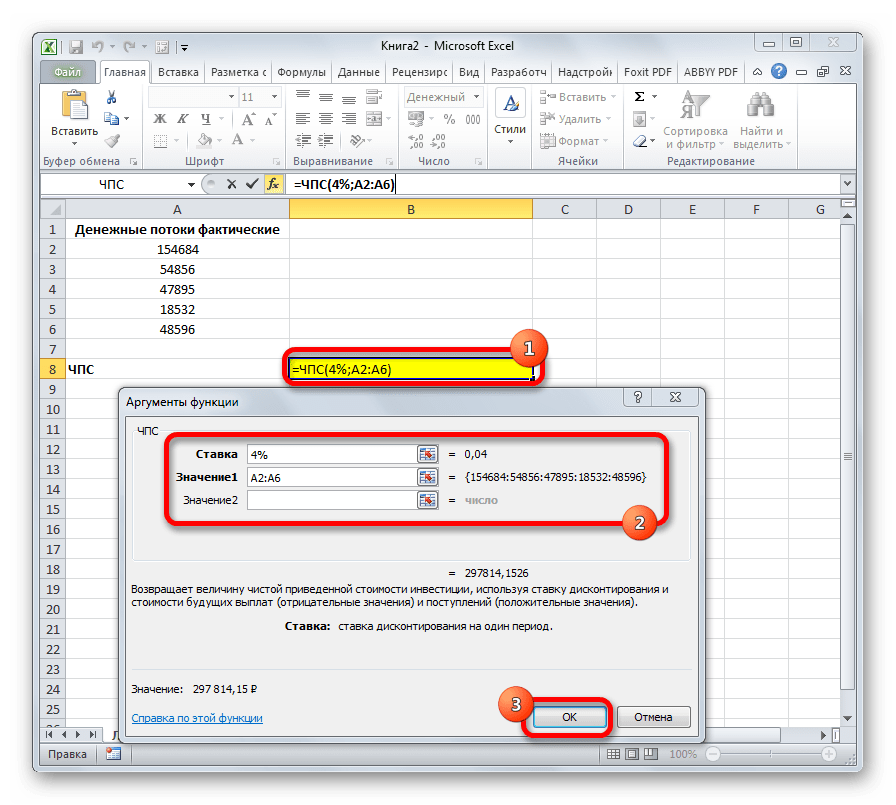
ЧПС

Следующий оператор применяется для вычисления чистой приведенной или дисконтированной стоимости. У данной функции два аргумента: ставка дисконтирования и значение выплат или поступлений. Правда, второй из них может иметь до 254 вариантов, представляющих денежные потоки. Синтаксис этой формулы такой:

=ЧПС(Ставка;Значение1;Значение2;…)

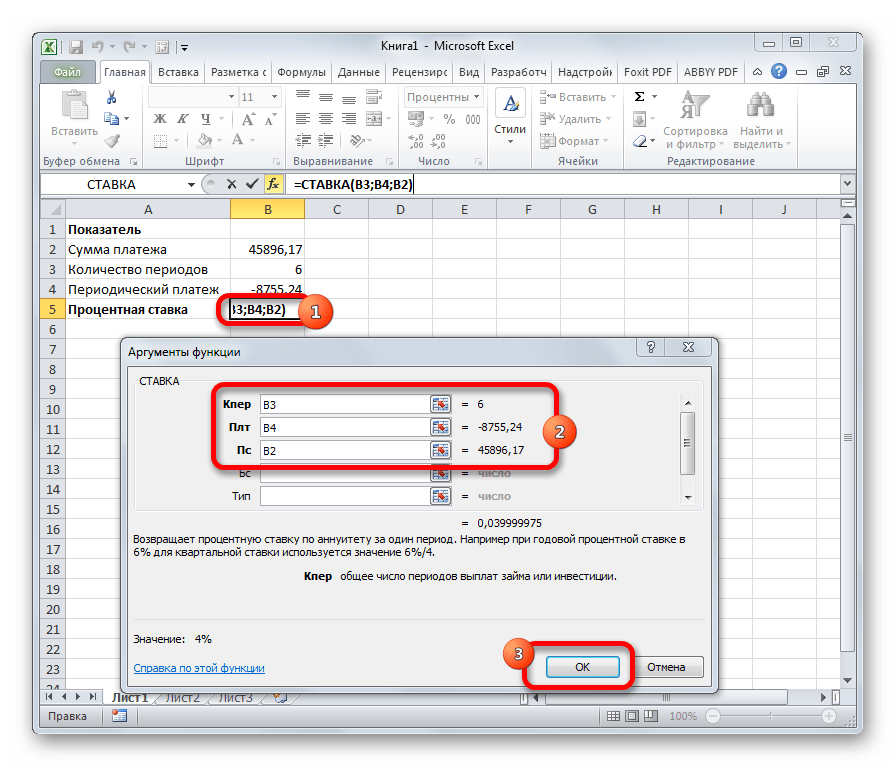
СТАВКА

Функция СТАВКА рассчитывает ставку процентов по аннуитету. Аргументами этого оператора является количество периодов («Кол_пер»), величина регулярной выплаты («Плт») и сумма платежа («Пс»). Кроме того, есть дополнительные необязательные аргументы: будущая стоимость («Бс») и указание в начале или в конце периода будет производиться платеж («Тип»). Синтаксис принимает такой вид:

=СТАВКА(Кол_пер;Плт;Пс[Бс];[Тип])

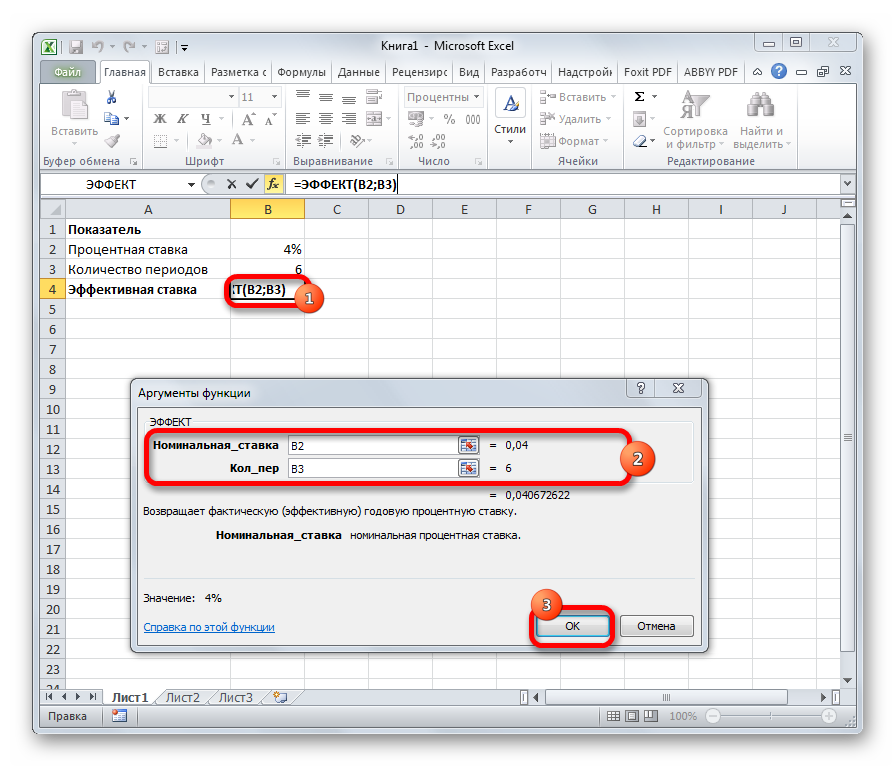
ЭФФЕКТ

Оператор ЭФФЕКТ ведет расчет фактической (или эффективной) процентной ставки. У этой функции всего два аргумента: количество периодов в году, для которых применяется начисление процентов, а также номинальная ставка. Синтаксис её выглядит так:

=ЭФФЕКТ(Ном_ставка;Кол_пер)

Нами были рассмотрены только самые востребованные финансовые функции. В общем, количество операторов из данной группы в несколько раз больше. Но и на данных примерах хорошо видна эффективность и простота применения этих инструментов, значительно облегчающих расчеты для пользователей.

Оглавление

Введение. 3

1. Теоретическая часть. 4

1.1 Особенности использования финансовых функций в MSExcel4

1.2 Технология работы и виды финансовых функций в области кредитования в MSExcel5

2. Практическая часть. 8

2.1 Постановка задачи:8

2.2 Решение поставленных задач.10

Выводы:18

Список литературы:19

Введение

В настоящее время трудно переоценить роль специалиста по финансовому анализу деятельности предприятия. Финансы являются «кровью» предприятия. Именно в деньгах оцениваются проданные товары и оказанные клиентам услуги. Именно деньги являются универсальным измерителем необходимых предприятию ресурсов – сырья и материалов, станков, человеческих ресурсов, информации и т.д. поэтому планирование и прогнозирование, контроль и оптимизация финансовых потоков являются жизненно важными задачами финансовой службы. (Л.А., 2006)

Финансовые функции применяются при планировании и анализе финансово-хозяйственной деятельности предприятия, а также при решении задач, связанных с инвестированием средств.

Данная работа посвящена рассмотрению различных задач связанных с расчетами по кредитам и вкладам в банки. В теоретической части рассмотрены особенности использования финансовых функций в MSExcel, а также описаны виды финансовых функций для расчетов в области кредитования в MSExcel.

В практической части рассмотрены различные задачи по кредитным вычислениям, с применением различных функций.

1. Теоретическая часть

1.1 Особенности использования финансовых функций в MSExcel

Сегодня нельзя всерьез претендовать на работу экономиста, менеджера, бухгалтера, финансиста, специалиста по ценным бумагам и т.п., если не уметь обращаться с компьютером. Умение работы с компьютером предполагает прежде всего знание текстовых процессоров, электронных таблиц, системы управления базами данных и систем для работы с графикой.

EXCEL является одной из самых популярных программ работающих в операционной среде Windows, поскольку объединяет возможности графического и текстового редактора с мощной математической поддержкой.

Функции EXCEL используют базовые модели финансовых операций, базирующиеся на математическом аппарате методов финансово-экономических расчетов. Использование возможностей компьютера и табличного процессора EXCEL позволяет облегчить выполнение расчетов и представить их в удобной для пользователя форме.

Финансовые функции EXCEL предназначены для проведения финансово-коммерческих расчетов по кредитам и займам, финансово-инвестиционного анализа, ценным бумагам.

Однако для ряда пользователей существуют трудности при использовании финансовых функций в среде EXCEL, поскольку синтаксис пакета использует иные обозначения основных понятий финансовых операций, нежели в классических расчетах. (Пикуза В., 2004)

На основной панели инструментов имеется кнопка «Мастер функций», с помощью которой открывается диалоговое окно Диспетчера функций. Оно организовано по тематическому принципу. Выбрав в списке тематическую группу Финансовые, получите полный перечень списка имен функций, содержащихся в данной группе. Когда курсор стоит на имени функции, в нижней части окна приводится краткая характеристика функции и синтаксис. Вызов функции осуществляется двойным щелчком на ее имени или нажатием кнопки «Далее» в диалоговом окне Диспетчера функций. Диалоговое окно Ввода аргументов функции для каждой финансовой функции регламентировано по составу и формату значений перечня аргументов.

При работе с финансовыми функциями необходимо учитывать специфику задания значения аргументов:

· можно вводить как сами значения аргументов, так и ссылки на адреса ячеек;

· все расходы денежных средств (платежи) представляются отрицательными числами, а все поступления денежных средств – положительными числами;

· процентная ставка вводится с использованием знака %;

· все даты как аргументы функций имеют числовой формат.

Функции, обслуживающие расчеты по операциям наращения позволяют рассчитать будущую стоимость разовой суммы по простым и сложным процентам, а также будущее значение потока платежей, как на основе постоянной процентной ставки, так и на основе переменной процентной ставки. (К., 2001)

Методика использования финансовых функций требует соблюдения определенной технологии.

1.2 Технология работы и виды финансовых функций в области кредитования в MS Excel

Технология работы с финансовыми функциями на рабочих листах Excel в целом не отличается от работы с другими функциями:

1) подготовка исходных значений основных аргументов функции;

2) для расчета финансовой функции курсор устанавливается в нужную ячейку и вызывается с панели задач Диспетчер функций;

3) из появившегося списка выбираем в разделе финансовых функций необходимую;

4) вводим аргументы функций;

5) получаем результат.

К основным финансовым функциям в Excel в области расчетов кредитования удобно использовать: ПС(), ПЛТ(), ОСПЛТ(), ПРПЛТ(), КПЕР(), БС(), СТАВКА().

Назначение финансовых функций представлено в таблице 1.1. (Куприянова А.В., 2007)

Таблица 1.1 Назначение финансовых функций

Название функции	Аргументы	Назначение
БС (ранее БЗ)	БС(ставка; кпер; плт; пс;[тип])	Рассчитывает будущую стоимость периодических постоянных платежей и будущее значение вклада (или займа) на основе постоянной процентной ставки
ПС (ранее ПЗ)	ПС(ставка; кпер; плт; бс;[тип])	Предназначена для расчета текущей стоимости, как единой суммы вклада (займа), так и будущих фиксированных периодических платежей
КПЕР	КПЕР(ставка; плт; пс; бс;[тип])	Вычисляет количество периодов начисления процентов исходя из известных величин ставки, платежа, и суммы займа (вклада)
ПЛТ	ПЛТ(ставка; кпер; пс; бс;[тип])	Позволяет рассчитать сумму постоянных периодических платежей, необходимых для равномерного погашения займа, при известных сумме займа, ставке процентов и сроках, на который он выдан
ПРПЛТ	ПРПЛТ(ставка; период; кпер; пс; бс)	Возвращает сумму платежей процентов по инвестиции за данный период, на основе постоянства сумм периодических платежей и постоянства процентной ставки
ОСПЛТ	ОСПЛТ(ставка; период; кпер; пс; бс)	Возвращает величину платежа в погашение основной суммы по инвестиции за данный период и на основании постоянства периодических платежей и процентной ставки.
СТАВКА	СТАВКА(кпер; плт; пс; бс;[тип])	Вычисляет процентную ставку, которая в зависимости от условий операции может выступать либо в качестве цены, либо в качестве нормы ее рентабельности

Как видно из таблицы, практически все функции содержат одинаковый набор аргументов:

Ставка – процентная ставка за период (норма доходности или цена заемных средств – r)

Кпер – срок (число периодов n) процедения операции.

Плт – выплата производимая каждый период и не меняющаяся за все время выплаты ренты.

Пс – это приведенная к текущему моменту стоимость, или общая сумма, которая на текущий момент равноценна ряду будущих платежей. Если аргумент ПС опущен, то он полагается равным 0. В этом случае должно быть указано значение аргумента Плт.

Бс – требуемое значение будущей стоимости или остатка средств после последней выплаты. Если аргумент опущен, он полагается равным 0 (например будущая стоимость займа равна 0)

[тип] – число 0 или 1, обозначающее когда должна производится выплата (1 – начало периода (обычная рента или пренумерандо), 0 – конец периода (постнумерандо)).

Как видно во многом функции перекрещиваются между собой, таким образом в решение одной финансовой задачи по расчету к примеру платежей по кредиту может использоваться несколько функций. (Мак-Федрис, 2006)

2. Практическая часть

2.1 Постановка задачи:

Необходимо на практике изучить финансовые функция для расчетов по кредитам: ПС(), БС(), ПЛТ(), ПРПЛТ(), ОСПЛТ(), КПЕР.

Для этого необходимо решить следующие задачи:

1) Рассчитать аннуитетные платежи по кредиту суммой 250 000 рублей, сроком на 1 год и под 17% годовых. Составить график платежей, с подробным описанием платежей непосредственно по кредиту, по процентам и оставшейся суммой платежа. (Использование функций ПС(), ПЛТ(), ПРПЛТ(), ОСПЛТ()).

2) Рассчитать сумму ежемесячного вложения под 10% годовых, которое через 15 лет составит сумму вклада в 50000 рублей. Выплата производится в начале периода. (Использование функции ПЛТ()).

3) Рассчитать сумму ежемесячного вложения под 10% годовых, которое через 15 лет составит сумму вклада 50000 рублей, при первоначальном взносе 1000 рублей. (Использование функции ПЛТ()).

4) Рассчитать величину вложений под 18 % годовых, которые будут приносить ежегодно в течение 5 лет 20 000 рублей. (Использование функции ПС()).

5) Рассчитать величину первоначальных вложений, под 15% годовых, которое через 10 лет принесет доход 100000 рублей, при условии внесении раз в год на счет 2000 рублей. (Использование функции ПС()).

6) Вычислить выплаты по процентам за первый месяц для трехгодичного займа в 100 000 рублей из расчета 10% годовых. (Использование функции ПРПЛТ()).

7) Вычислить доход за последний год от трехгодичного займа в 100000 рублей из расчета 10% годовых при ежегодных выплатах. (Использование функции ПРПЛТ()).

Вклад размером в 5000 рублей положен с 10.01.2010 по 03.04.2010 под 20% годовых. Найти величину капитала на 03.04.2010 при начислении простых процентов. (Использование функции БС()).

9) Определить сумму капитала, если изначально вложена сумма в размере 10 000 рублей, в банк на 3 года под 15% годовых, далее в течение всего периода раз в месяц вносится сумма 1000 рублей. Проценты начисляются раз в месяц, в начале. (Использование функции БС()).

10) Определить будущую стоимость капитала 15000 рублей, помещенных в банк под 18% годовых, сроком на 5 лет. Проценты начисляются раз в квартал. (Использование функции БС()).

11) Взята сумма в размере 90000 рублей сроком на 2 года под 15% годовых. Рассчитать сумму остаточных платежей для каждого года займа. (Использование функции ОСПЛТ()).

12) С кредитно-дебетовой карты взята сумма в размере 70000 рублей сроком на 3 года под 17% годовых. Рассчитать сумму остаточных платежей для каждого квартала займа, при условии, что конец периода на счету должна быть накоплена сумма 8000 рублей. (Использование функции ОСПЛТ()).

13) Рассчитать через сколько лет сумма вклада в размере 15 000 рублей достигнет 50000 рублей, при процентной ставке 15% годовых. (Использование функции КПЕР()).

14) Начиная с 30 лет каждый год на счет в банк вносится 1000 рублей. К какому возрасту человек станет миллионером, при условии, что процентная ставка равна 18% годовых. (Использование функции КПЕР()).

15) Рассчитать через сколько лет произойдет полное погашение займа размером 2500000 рублей, если выплаты 50000 рублей производятся в конце каждого квартала, а процентная ставка равна 17% годовых. (Использование функции КПЕР()).

2.2 Решение поставленных задач.

Для решение поставленных задач используются функции ПС(), БС(), ПЛТ(), ПРПЛТ(), ОСПЛТ(), КПЕР.

Алгоритм решения задач:

1) Внесение исходных данных;

2) Ввод функции с аргументными значениями;

3) Получение результата.

Задача 1.

Исходные данные:

Сумма кредита	250000
Срок кредита, лет	1
Процент	17%

Для решения поставленной задачи использовались функции ЕСЛИ(), ПС(), ПЛТ(), ПРПЛТ(), ОСПЛТ(), СУММ().

Ежемесячный платеж рассчитывается с помощью функции =ПЛТ(Процент/12; Срок кредита*12; Сумма кредита;;)

Аннуитет, платежи по кредиту, по процентам и остаток суммы задолженности рассчитывается по одинаковой формуле, с изменением № месяца, для которого производится расчет.

Формула расчета Аннуитета =ЕСЛИ(№ месяца>Срок кредита*12;0; Ежемесячный платеж)

Платежи по кредиту рассчитываются по формуле =ЕСЛИ(№ месяца>Срок кредита *12;0; ОСПЛТ(Процент/12;№месяца; Срок кредита*12; Сумма кредита)).

Процентные платежи рассчитываются по формуле ЕСЛИ(№месяца>Срок кредита*12;0; ПРПЛТ(Процент/12;№месяца; срок кредита*12; сумма кредита)).

Остаток суммы задолженности рассчитывается по формуле =ЕСЛИ(№месяца>Срок кредита*12;0; ПС(Процент/12;(Срок кредита *12)-№месяца; Ежемесячный платеж)).

Общая сумма процентов рассчитывается путем суммирований данных из столбца Проценты.

Мес. – рассчитывается путем умножения срока кредита (лет) на 12 месяцев.

Сумма аннуитета рассчитывается путем умножения суммы ежемесячного платежа на количество месяцев.

Результатом проведения вышеуказанных расчетом получаем график платежей.

Таблица 2.1 Решение задачи 1

Сумма кредита	250000
Срок кредита, лет	1	мес	Сумм. Аннуитет	Кредит	Проценты
Процент	17%	12	-273 614,26р.	-250 000,00р.	-23 614,26р.
Ежемесячный платеж	-22 801,19р.
№ месяца	Аннуитет	Кредит	Проценты	Остаток СЗ
1	-22 801,19р.	-19 259,52р.	-3 541,67р.	230 740,48р.
2	-22 801,19р.	-19 532,36р.	-3 268,82р.	211 208,11р.
3	-22 801,19р.	-19 809,07р.	-2 992,11р.	191 399,04р.
4	-22 801,19р.	-20 089,70р.	-2 711,49р.	171 309,34р.
5	-22 801,19р.	-20 374,31р.	-2 426,88р.	150 935,03р.
6	-22 801,19р.	-20 662,94р.	-2 138,25р.	130 272,09р.
7	-22 801,19р.	-20 955,67р.	-1 845,52р.	109 316,43р.
8	-22 801,19р.	-21 252,54р.	-1 548,65р.	88 063,89р.
9	-22 801,19р.	-21 553,62р.	-1 247,57р.	66 510,27р.
10	-22 801,19р.	-21 858,96р.	-942,23р.	44 651,31р.
11	-22 801,19р.	-22 168,63р.	-632,56р.	22 482,68р.
12	-22 801,19р.	-22 482,68р.	-318,50р.	0,00р.

Задача 2.

Исходные данные:

Годовая процентная ставка – 10%

Число лет хранения – 15

Необходимая величина сбережений – 50 000 руб.

Сумма ежемесячного платежа рассчитывается по формуле =ПЛТ(Процентная ставка/12; Число лет*12;; Необходимая сумма сбережений; момент выплаты) = ПЛТ(10%/12;15*12;;50000;1) = -119,64 руб.

Отрицательная сумма получилась, потому, что данную сумму необходимо платить.

При изменении момента выплаты на конец периода сумма несколько измениться = ПЛТ(10%/12;15*12;;50000;0) = -120,64 руб.

Задача 3.

Исходные данные:

Годовая процентная ставка – 10%

Число лет хранения – 15 лет

Необходимая величина сбережений – 50 000 руб.

Начальный взнос – 10 000 руб.

Сумма ежемесячного платежа рассчитывается по формуле =ПЛТ(Процент/12; Число лет*12; начальный взнос; необходимая величина сбережений)= ПЛТ(10%/12;15*12;10000;50000)=-228,10 руб.

Отрицательная сумма получилась, потому, что данную сумму необходимо платить.

Задача 4.

Исходные данные:

Ежегодный доход – 20 000 руб.

Процентная ставка – 18%

Число лет – 5

Величина вложений рассчитывается с помощью формулы =ПС(Ставка; Число лет; Ежегодный доход)=ПС(18%;5;20000)=-62 543,42 руб.

Отрицательная сумма получилась, потому, что данную сумму необходимо платить.

Задача 5.

Исходные данные:

Процентная ставка – 15%

Число лет – 10

Итоговый доход — 100 000 руб.

Ежегодный взнос – 2000 руб

Величина первоначальных вложений рассчитывается по формуле =ПС(Процент; Число лет; Ежегодный взнос; Итоговый доход)=ПС(15%;10;-2000;100000)=-14 680,933 руб.

Отрицательная сумма получилась, потому, что данную сумму необходимо платить.

Задача 6.

Исходные данные:

Процентная ставка – 10%

Месяц – 1

Срок кредита – 3 года

Сумма кредита – 100 000 руб.

Выплаты по процентам рассчитываются по формуле =ПРПЛТ(процентная ставка/12; Период (Месяц); Срок кредита*12; сумма кредита)= ПРПЛТ(10%/12;1;3*12;100000)= -833,33 руб.

Отрицательная сумма получилась, потому, что данную сумму необходимо платить.

Задача 7.

Исходные данные:

Процентная ставка – 10%

Срок кредита – 3 года

Момент дохода – 3-й год

Сумма кредита – 100000 руб.

Выплаты по процентам рассчитываются по формуле =ПРПЛТ(Ставка; Момент дохода; Срок кредита; Сумма кредита)=ПРПЛТ(10%;3;3;100000) = -3 655,59 руб.

Отрицательная сумма получилась, потому, что данную сумму необходимо платить.

В случае если не указан, хотя бы один из обязательных аргументов расчет будет невозможен.

Задача 8.

Исходные данные:

Процентная ставка – 30%

Вклад – 5000 рублей

Дата открытия вклада – 10.01.2010

Дата закрытия – 04.03.2010

Количество расчетных периодов – 1

Расчет суммы капитала производится через формулу =БС((Дата закрытия-Дата открытия)/360*Процент; Количество периодов;; вклад) = =БС((53)/360*30%;1;;-5000)= 5220,833.

В данном случае заполнение аргумента Плт не обязательно, т.к. заполняется необязательный аргумент Пс.

Задача 9.

Исходные данные:

Процентная ставка – 15%

Вклад – 10 000 руб.

Количество периодов – 3 года

Ежемесячные вклады – 1000 рублей.

Расчет накопленного капитала производится через формулу =БС(Процентная ставка/12; Количество периодов*12; Ежемесячный вклад; Первоначальный вклад; момент выплаты)= БС(15%/12;3*12;-1000;-10000;1)= 61318,89

Задача 10.

Исходные данные:

Процентная ставка – 18%

Вклад – 15 000 руб.

Количество периодов – 5 лет.

Расчет накопленного капитала производится через формулу =БС(Процентная ставка/4; Количество периодов*4;; вклад)= БС(18%/4;5*4;;-15000)=36 175,71 руб.

Задача 11.

Исходные данные:

Ссуда – 90 000 руб.

Процентная ставка – 15% годовых

Срок 2 года.

Расчет суммы остаточных платежей для каждого года производится по формуле =ОСПЛТ(Процентная ставка; Период; Ссуда; Срок кредита).

Для каждого периода в расчетной формуле меняется номер периода.

Таким образом для 1-го года остаточная сумма платежа равна =ОСПЛТ(15%;1;90000;2)=-41 860,47 руб.

Для 2-го года:

=ОСПЛТ(15;2;90000;2)=-48 139,53 руб.

Суммы отрицательны, т.к. их необходимо платить.

Задача 12.

Исходные данные:

Ссуда – 70 000 рублей

Процентная ставка – 17%

Срок кредита – 3 года

Накопления на счету – 8000 рублей.

Расчет платежей производится по формуле = ОСПЛТпроцентная ставка/4; период; срок кредита *4; ссуда; накопления).

Для каждого квартала изменяется только № периода. Результатом вычислений является таблица 2.2

Таблица 2.2 – Результаты расчетов по задаче 12

Ссуда	70 000,00р.
Процентная ставка	17%
Срок кредита	3
Период	Платеж
1	-5 117,07р.
2	-5 334,55р.
3	-5 561,27р.
4	-5 797,62р.
5	-6 044,02р.
6	-6 300,89р.
7	-6 568,68р.
8	-6 847,85р.
9	-7 138,88р.
10	-7 442,28р.
11	-7 758,58р.
12	-8 088,32р.
Итого	-78 000,00р.
Накопления	8 000,00р.

Задача 13.

Исходные данные:

Начальный платеж – 15 000 руб.

Необходимая сумма накоплений – 50 000 руб.

Процентная ставка – 15:

Срок накопления необходимых денежных средств рассчитывается по формуле=КПЕР(Процентная ставка;; Первоначальный платеж; Необходимая сумма)= КПЕР(15;;-15000;50000)=8,61 лет.

Не обязательно заполнение аргумента Плт при заполненном аргументе Бс.

Задача 14.

Исходные данные:

Ежемесячный платеж – 1000 рублей

Процентная ставка – 18% годовых

Необходимая сумма на счету – 1 000 000 руб.

Срок накопления необходимых денежных средств рассчитывается через формулу =КПЕР(процентная ставка/12;-ежемесячный платеж;; необходимая сумма на счету; момент выплаты)/12= КПЕР(18%/12;-1000;;1000000;0)/12=15,52 лет.

Таким образом возраст человека будет составлять = 30+15,52 = 45,52 лет.

Не обязательно заполнение аргумента Пс при заполненном аргументе Бс.

Задача 15.

Исходные данные:

Займ – 250 000 руб.

Ежеквартальные выплаты – 50 000 руб.

Процентная ставка – 17% годовых.

Срок погашение займа рассчитывается через формулу =КПЕР(процентная ставка/4; ежеквартальные выплаты; займ)/4 = КПЕР(17%/4;-50000;250000)/4=1,43 года.

Выводы:

Курсовой проект основывается на условных примерах, которые не отражает всех особенностей начисления кредитных платежей, вычисления сроков и т.п. Однако выполнение данного курсового проекта позволило ознакомиться и научиться применять все необходимые для современного финансиста-экономиста инструменты обработки финансовой информации.

В работе рассмотрены теоретические и практические основы использования финансовых функций, их возможности и способы использования

В практической части работы представлены 15 задач по использованию финансовых функций Excel при расчетах по кредитам. Рассмотрены различные варианты задач, а также способы заполнения аргументов функций (обязательные и необязательные аргументы).

Список литературы:

1) К., Карлберг (2001). Бизнес-анализ с помощью MS EXcel 2000. стр. 250.

2) Куприянова А.В., М. М. (2007). Вычисления и расчеты в Excel 2003 изд.2 Компьютерная шпаргалка. стр. 80.

3) Л.А., Левин (2006). «Финансовая математика в MS EXCEL» — Учебное-методическое пособие. стр. 111-5.

4) Мак-Федрис, П. (2006). Формулы и функции в Microsoft Excel 2003. стр. 576.

5) Пикуза В., Г. А. (2004). Экономические и финансовые расчеты в Excel. Самоучитель. стр. 397.

1. PMT (ПЛТ) — рассчитывает сумму ежемесячных платежей по долгам

Это сэкономит время, когда есть несколько кредитных предложений от разных банков и не хочется обращаться в каждый за подробностями.

Допустим, человек переехал в новую квартиру и решает отремонтировать её прямо сейчас. Свободных денег не осталось, поэтому он собирается занять их у банка.

Какие данные нужны

Для начала надо правильно написать формулу — в любой свободной ячейке.

=ПЛТ(ставка;кпер;пс)

В скобках стоят три обязательных аргумента, без которых не получится ничего посчитать:

1. Ставка — процент по кредиту, который предлагает банк. Пусть будет 9,5%.
2. Кпер — количество выплат по займу. Ремонт дорогой, но не смертельно, так что возьмём на полтора года: это 18 ежемесячных платежей.
3. Пс — сумма, которая нужна на обновление жилья. Оценим это дело в 300 000 рублей.

Как всё посчитать

Надо занести известные данные в таблицу, а потом напечатать формулу через знак «=». Вместо каждого из аргументов подставляем свои данные.

Ничего не мешает одновременно внести в таблицу несколько предложений с разными процентными ставками и сроками кредита и сравнить условия. Каждый раз переписывать формулу необязательно, её можно просто растянуть за уголок.

2. EFFECT (ЭФФЕКТ) — позволяет рассчитать сложный процент

Функция подойдёт инвестору, который выбирает облигации для своего портфеля и хочет понять, какую годовую доходность получит на самом деле.

Россия занимает деньги через множество облигаций федерального займа (ОФЗ). У каждого выпуска таких бумаг есть номинальная доходность, определяющая, какой процент годовых от вложенной суммы получит инвестор. Например, по ОФЗ 26209 обещают 7,6%, а по ОФЗ 26207 ещё больше — 8,15%.

Но если человеку не нужны деньги в ближайшее время, то он не станет забирать прибыль по облигациям. А, скорее всего, вложит её в те же бумаги, то есть реинвестирует. И тогда вырастет эффективная доходность облигаций. Это произойдёт из‑за механизма сложного процента: прибыль начисляется не только на первоначальные инвестиции, но и на последующие.

Какие данные нужны

Формула расчёта довольно простая:

=ЭФФЕКТ(номинальная_ставка;кол_пер)

В ней всего две переменные:

1. Номинальная_ставка — та доходность, которая обещана облигацией при выпуске. Это 7,6% и 8,15% в нашем примере.
2. Кол_пер — количество периодов в году, когда инвестору начисляется прибыль (в облигациях её называют купоном).

Как всё посчитать

Принцип сохраняется: вносим исходные данные в таблицу. Номинальную доходность и периодичность выплат по купонам обязательно публикуют для каждой облигации на Мосбирже в разделе «Параметры инструмента». Теперь легко всё посчитать:

Только заметим, что облигации устроены очень хитро, инвестору нужно учитывать и другие факторы, которые влияют на прибыльность. Например, номинал бумаги равен 1 000 рублей, а её продают за 996 — реальная доходность будет выше. С другой стороны, инвестору придётся заплатить ещё и накопленный купонный доход — автоматически рассчитываемая компенсация предыдущему владельцу облигации. Эта сумма может быть равна 20–30 рублям, из‑за чего доходность опять упадёт. Одной формулой здесь не обойтись.

3. XNPV (ЧИСТНЗ) — вычисляет общую прибыль инвестора

Порой люди накапливают много активов, каждый из которых нерегулярно приносит деньги: проценты по вкладам, выплаты купонов по облигациям, дивиденды от акций. У всех инструментов разная прибыль, поэтому полезно понимать, сколько выходит в сумме.

Функция позволяет рассчитать, какое количество денег вернётся через определённое время, например спустя четыре года. Так владелец активов поймёт, сможет ли реинвестировать доходы или купить что‑нибудь дорогое.

Какие данные нужны

Формула состоит из трёх компонентов:

=ЧИСТНЗ(ставка;значения;даты)

Второй и третий достаточно ясны:

2. Значения — сколько денег потрачено на инвестиции и сколько возвращается.
3. Даты — когда именно средства приходят или уходят.

Первый компонент формулы — ставка дисконтирования. Обычно деньги со временем обесцениваются, и на одну и ту же сумму в будущем можно купить меньше, чем сейчас. Это значит, что нынешние 100 рублей равны, допустим, 120 рублям в 2025 году.

Если инвестор хочет не просто сохранить деньги, но и заработать, ему нужно учесть постепенное обесценивание валюты. Есть много способов это сделать, но самый простой — посмотреть доходность по надёжным облигациям: к примеру, ОФЗ 26234 — 4,5%. Смысл в том, что инвестор почти гарантированно получит такую прибыль в будущем, это «безрисковая ставка». Оценивать потенциал инвестиций имеет смысл с поправкой на этот процент.

Как всё посчитать

Со знаком минус нужно внести затраты — в нашем случае деньги, израсходованные на ценные бумаги. Следом укажем поступления, которые для отдельных инвестиций доступны заранее.

Итоговое значение — фактическая прибыль инвестора через четыре года с учётом ставки дисконтирования. Она совсем маленькая, несмотря на 92 тысячи инвестиций: для больших поступлений нужно подбирать более рискованные, но доходные инструменты.

4. XIRR (ЧИСТВНДОХ) — оценивает доходность инвестиций по притокам денег

Обычно у любого инвестора есть выбор между разными финансовыми инструментами. Каждый обещает какую‑то прибыль, но не всегда понятно, что выгоднее.

Функция помогает сравнить доходность, если мы заранее не знаем процент годовых. К примеру, ставка по банковскому вкладу равна 6%. Можно вложить деньги туда, а можно в бизнес знакомого, который обещает раз в квартал платить плавающую сумму в зависимости от успехов.

Какие данные нужны

Чтобы определить более выгодное предложение, применим формулу:

=ЧИСТВНДОХ(значения;даты)

Достаточно знать всего две переменные:

1. Значения — сколько денег инвестор вложит и сколько ему обещают вернуть.
2. Даты — график платежей, по которым будут выплачивать прибыль.

Как всё посчитать

Допустим, человек вложил 100 000 рублей и получил четыре платежа, по одному в квартал. В конце года инвестор знает их размер и может вычислить доходность — больше 40%. Это на 37% выгоднее банковского вклада, хотя и рискованнее.

5. RATE (СТАВКА) — вычисляет месячную или годовую процентную ставку по займам

Бывают и такие ситуации, что заём уже есть, а процент не оговорён. Допустим, если человек взял в долг 100 000 рублей у знакомого и пообещал в течение полугода возвращать по 20 тысяч ежемесячно. Кредитор может захотеть узнать, какова выходит ставка.

Какие данные нужны

Полезной будет эта формула:

=СТАВКА(кпер;плт;пс)

Три переменных в ней означают следующее:

1. Кпер — количество выплат. В нашем примере заём полугодовой, то есть их будет шесть.
2. Плт — размер платежей. Считаются и основной долг, и проценты.
3. Пс — общая сумма займа. В нашем примере это 100 000 рублей.

Как всё посчитать

Нужно внести значения каждой переменной в свою ячейку и применить формулу. Главное — не забыть поставить перед суммой займа знак минуса, потому что это деньги, которые ушли.

6. PV (ПС) — подсказывает, сколько денег можно взять в долг

Люди иногда делают большие покупки. Например, приобретают автомобили. Они стоят дорого, и для машин берут автокредит, обслуживать который тоже недёшево. Если человек не готов отдавать всю зарплату на ежемесячные платежи, то может заранее прикинуть, какой заём будет комфортным.

Какие данные нужны

Пригодится формула расчёта текущей стоимости:

=ПС(ставка; кпер; плт)

Для этого потребуется информация, которая есть на сайте любого банка:

1. Ставка — под какой процент придётся брать деньги на покупку. Допустим, 9% годовых, или 0,75% в месяц.
2. Кпер — сколько времени предстоит выплачивать кредит. Например, четырёхлетний заём равен 48 ежемесячным переводам средств.
3. Плт — размер комфортного платежа.

Как всё посчитать

Предположим, что человеку будет по силам отдавать от 40 до 50 тысяч рублей в месяц. В этом случае нужны два столбца: ставка и срок постоянны, меняется только значение платежа. В результате увидим, что машина должна стоить не больше 1,6 или 2 миллионов рублей.

Автомобили с такой ценой не утянут в долговую яму. Значит, можно сокращать себе пространство для выбора и искать подходящие модели.

7. NPER (КПЕР) — помогает рассчитать время накоплений

Обычно банки объясняют, какой процент человек получит по их депозиту и сколько денег заработает. Но иногда у вкладчика другая цель — накопить конкретную сумму к определённой дате. Функция поможет высчитать этот срок.

Какие данные нужны

Чтобы узнать, за какое время соберутся деньги, используем формулу количества периодов:

=КПЕР(ставка/периоды_капитализации;плт;пс;бс)

Она состоит из четырёх основных значений и одного дополнительного:

1. Ставка — годовая процентная ставка, которую предлагают вкладчику. Предположим, что 7%.
2. Периоды_капитализации — количество раз в году, когда банк начисляет проценты. Это часто делают ежемесячно, поэтому пишем «12».
3. Плт — ежемесячный платёж. Скажем, вклад непополняемый, так что показатель будет равен нулю.
4. Пс — начальная сумма на депозите. Допустим, 100 000 рублей.
5. Бс — сумма, которую вкладчик намерен получить в конце срока. Например, 200 000 рублей.

Как всё посчитать

Человек собирается положить на депозит 100 000 рублей под 7% и хочет однажды забрать вдвое больше.

Для этого придётся подождать два с лишним года. Либо искать более доходную инвестицию, которая сократит срок.

Читайте также 🧐

• Как вести бюджет, если у вас непостоянный доход
• 20 полезных шаблонов «Google Таблиц» на все случаи жизни
• 10 крутых приложений, чтобы взять финансы под контроль

Дисциплина:

Раздел 5. Информационные технологии в профессиональной деятельности

ПМ.03. Организация деятельности структурных подразделений аптеки и руководство аптечной организацией при отсутствии специалиста с высшим образованием

МДК 03.01. Организация деятельности аптеки и её структурных подразделений

Специальность: 33.02.01 (060301.51) Фармация

Методическая разработка для проведения практического занятия по теме «Использование средств MS Excel для финансово – экономических расчетов»

Автор работы: Ельдецова Ирина Викторовна, преподаватель

колледж ГБОУ ВПО ОмГМУ Минздрава России

Тема занятия: Использование средств MS Excel для финансово – экономических расчетов.

Цели занятия:

1. Учебные.

Расширить знания по ведению первичной учетной документации, проведению экономического анализа отдельных производственных показателей деятельности аптечных организаций средствами Microsoft Office и специализированного программного обеспечения.

Умения: пользоваться компьютерным методом сбора, хранения и обработки профессиональной информации, прикладными программами обеспечения фармацевтической деятельности.

Знания: Основных задач и направлений информатизации аптечных организаций. Виды и тенденции развития программного обеспечения профессиональной направленности. Интерфейс ПО.

1. Развивающие.

Развить у студентов способность использовать полученные знания в профессиональной деятельности, умение оперировать формулировками, понятиями, определениями способствовать развитию творческого и логического мышлений, внимания при выполнении заданий, привить навыки самоорганизации и самостоятельной работы, развить умение частично — поисковой познавательной деятельности.

1. Воспитательные.

Выработать умение мыслить. Побудить к познавательной, научной, творческой, трудовой деятельности. Способствовать развитию умений преодолевать трудности, закалки воли, развитию познавательных интересов, убеждений, привитию взглядов, привычек.

Тип занятия: практическое

Междисциплинарные связи: все дисциплины и профессиональные модули основной профессиональной образовательной программы.

Формы и методы: метод анализа конкретных ситуаций (АКС), групповая работа, групповая дискуссия, самостоятельная работа по алгоритмам действий, машинно – программированный контроль.

Оснащение занятий.

Методические материалы: дидактический материал обучающего характера, задания с алгоритмами действий, вопросы для дискуссии, тестовые задания для машинно – программируемого контроля по разделу.

Материально – техническое оснащение: компьютеры с лицензионным программным обеспечением, мультимедийный проектор, экран, интерактивная приставка.

Перечень литературы:

Основная литература:

п/№

Наименование

Автор (ы)

Год, место издания

Кол-во экземпляров

Информационные технологии : учебник

Г. С. Гохберг, А. В. Зафиевский, А. А. Короткин

Москва : Академия, 2012

350

Дополнительная литература:

п/№

Наименование

Автор (ы)

Год, место издания

Кол-во экземпляров

2.

Информационные технологии [Электронный ресурс] : учеб. пособие. – Режим доступа: http://knigafund.ru/books/106847

Г. Н. Исаев

Москва : Омега-Л, 2012

доступ по индивидуальным картам для каждого обучающегося

Электронные образовательные ресурсы

Базы данных, информационно-справочные и поисковые системы:

1. Электронная библиотека ОмГМА: http://weblib.omsk-osma.ru/;

2. Электронно-библиотечная система «КнигаФонд»: http://www.knigafund.ru;

3. «Электронно-библиотечная система «Консультант студента. Электронная библиотека медицинского колледжа»: http://www.medcollegelib.ru;

СТРУКТУРА И СОДЕРЖАНИЕ ПРАКТИЧЕСКОГО ЗАНЯТИЯ

Этапы занятия

Код формируемых компетенций

Вре-мя

(мин)

1.

Организационный момент.

Проверка подготовленности кабинета к занятию, создание рабочей обстановки, формулировка целей занятия

ОК 1,2,4,5,9

ПК 1.8,3.1,

3.2, 3.3, 3.6

5

2.

Целевая установка.

Мотивация учебной деятельности:

Программа Excel имеет две отличительные особенности — эффективные вычислительные возможности и мощные визуальные средства для передачи цифровой информации. Именно такая комбинация открывает Excel особенно широкие перспективы для использования в деловой сфере.

С помощью электронных таблиц Microsoft Excel автоматизируется решение ряда типовых задач экономического анализа. Это, в частности, анализ безубыточности, эффективности сегментов бизнеса, планирование продаж коммерческой организации и анализ краткосрочных управленческих решений, возникающих в практике работы многих предприятий.

5

3.

Тестовый контроль для определения исходного уровня знаний по теме «Обработка информации средствами Microsoft Excel». В форме машинно – программированного контроля MTesting.

15

4.

Организация работы студентов с использованием метода анализа конкретных ситуаций (АКС).

Метод анализа конкретных ситуаций заключается в том, что в процессе обучения преподавателем создаются проблемные ситуации, взятые из профессиональной практики. От обучаемых требуется глубокий анализ ситуации и принятие соответствующего оптимального решения в данных условиях. АКС выполняет множество различных функций, служит инструментом исследования, изучения, оценки и выбора, обучения, воспитания, развития. Достоинство метода состоит в том, что в процессе решения конкретной ситуации участники обычно действуют по аналогии с реальной практикой, то есть используют свой опыт, применяют в учебной ситуации те способы, средства и критерии анализа, которые были ими приобретены в процессе обучения. Студенты не только получают нужные знания, но и учатся применять их на практике.

Этапы работы:

1-й этап. Введение в изучаемую проблему.

Перед руководством аптечной организации часто встают задачи анализа последствий принятия различных маркетинговых и управленческих решений, так или иначе влияющих на изменение затрат, выручки и прибыли аптеки. Поскольку принятие большинства экономических решений происходит в ситуации неопределённости, не существует точных оценок влияния последствий принимаемых решений на основные показатели функционирования организации. Поэтому приходится проводить многовариантные расчёты при различных оценках параметров, характеризующих экономические последствия мероприятий, связанных с развитием бизнеса. В принципе, чем больше таких расчётов проведено, тем более обоснованными могут быть решения, тем подробнее представление о возможных вариантах развития аптечной организации при осуществлении планируемых мероприятий. При выполнении такого рода расчётов эффективно используются компьютерные математические модели реализуемые возможностями электронных таблиц.

2-й этап. Постановка задачи.

Учебная группа делится на несколько подгрупп (по 2 человека в подгруппе — руководитель аптечной организации и его заместитель)

Преподаватель определяет круг задач для подгрупп:

1. Проанализировать примеры финансово – экономических ситуации.

2. Реализовать математические компьютерные модели их решений с помощью средств электронных таблиц.

3. Высказать свое мнение и рекомендации относительно предлагаемых компьютерных моделей и подготовиться к его публичной защите.

Преподаватель устанавливает время и режим самостоятельной работы:

Самостоятельная работа – 100 минут с перерывами через 30 мин на выполнение комплекса упражнений физкультурной паузы общего воздействия по 5 мин.

3-й этап. Групповая работа над финансово – экономическими ситуациями.

Преподаватель наблюдает за работой подгрупп, отвечает на возникшие вопросы, дает рекомендации.

4-й этап. Групповая дискуссия.

Представители подгрупп поочередно выступают с сообщением о результатах работы: излагают свое мнение о компьютерных моделях ситуаций, отвечают на поставленные вопросы, обосновывают предлагаемые рекомендации.

После выступлений представителей подгрупп начинается общая дискуссия: обсуждение точек зрения, оценка результатов анализа, формирование единого подхода к подобного рода проблемам и путям их решения, выбор наилучшего решения для данной ситуации.

Примерные вопросы для дискуссии:

1. Возможно, ли математическую модель ситуации №1 использовать для планирования и контроля правильности начисления налогов?

2. Как вы думаете, в математической модели ситуации №1 при изменении суммы реализации и издержек будет ли сразу виден фактический результат проведения будущей и прошедших операций?

3. На сколько универсальны предложенные Вам математические модели?

4. Возможно, ли с помощью математической модели ситуации №2 проанализировать влияние изменения выручки от реализации на сумму прибыли?

5. Если Вы как руководитель аптечной организации планируете арендовать дополнительную торговую точку, то какими моделями вы воспользуетесь и для чего?

6. Насколько на Ваш взгляд математическая модель «О назначении (assignment problem)» непосредственно исходить от практической кадровой ситуации?

7. При поиске наиболее удобного расположения центра обслуживания клиентов воспользовались бы вы математической моделью ситуации № 5?

5-й этап. Итоговая беседа.

Преподаватель выделяет общий положительный результат коллективной работы участников над ситуацией, обращает внимание на позиции подгрупп при анализе, сопоставляет их с тенденциями в реальной практике, выделяет правильные или ошибочные мнения, обосновывает оптимальный подход к подобным ситуациям, обращает внимание на круг знаний и навыков, необходимых для их решения. Выставляет оценки.

5

10

100

25

10

5.

Домашнее задание.

5

Время -180 мин

МЕТОДИЧЕСКИЕ УКАЗАНИЯ ДЛЯ СТУДЕНТОВ ПО ВЫПОЛНЕНИЮ 3-ГО ЭТАПА «ГРУППОВАЯ РАБОТА НАД ФИНАНСОВО – ЭКОНОМИЧЕСКИМИ СИТУАЦИЯМИ»

№ п/п

Этап

Ориентир. время

Методические указания

Форма отчетности

1

Групповая работа над финансово – экономическими ситуациями.

100

Вашей группе необходимо:

1. Проанализировать примеры финансово – экономических ситуации.

2. Реализовать математические компьютерные модели их решений с помощью средств электронных таблиц.

3. Подготовить сообщение о результатах работы, в котором вы изложите и обоснуете свое мнение о предложенных вам компьютерных моделях и эффективности их использования в деятельности руководителя аптечной организации, подготовиться к его публичной защите.

Демонстрация результатов решения своих финансово – экономических ситуаций средствами электронных таблиц.

Выступление с сообщением о результатах работы

ФИНАНСОВО – ЭКОНОМИЧЕСКИЕ СИТУАЦИИ ДЛЯ ГРУППОВОЙ РАБОТЫ СТУДЕНТОВ (3-Й ЭТАП)

Подбор ситуаций осуществляется по принципу от простого к сложному.

Пример финансово — экономической ситуации №1

Очень часто руководителю аптеки приходится производить расчет эффективности будущих операций. Для автоматизации подобных расчетов используют электронную таблицу. Пример упрощенной таблицы представлен на рис. 1.

Рис 1. Таблица расчета налогов и прибыли (с числовыми данными)

В данной таблице имеются четыре области:

-Ставки налогов (область А1:ВЗ). 
— Суммы реализованных товаров, издержек и дебетового НДС (область А5:В7). 
— Расчет НДС, подлежащего уплате в бюджет (область А9:В10). 
— Расчет прибыли и налогов на прибыль и с оборота (область А12:В17).

Заметим, что первые две области предназначены для ввода информации, а последние — для ее дальнейшей обработки. Рассмотрим формулы, введенные в область расчета (рис. 2.)

Формула для расчета налогового обязательства по НДС показана также на рис. 2.

Табличный вид этой формулы следующий:

=ОКРУГЛ(В5*(B1/(1+B1));2)

Формула расчета НДС, подлежащего уплате в бюджет, определяется вычитанием суммы налогового кредита из суммы налоговых обязательств (находится в ячейке В10):

=В9-В7

Валовая прибыль без НДС (формула в ячейке В12) равна разности суммы реализации и суммы налоговых обязательств:

=В5-В9

Рис. 2. Таблица расчета налогов и прибыли (с формулами)

Полученную в результате реализации прибыль можно определить путем вычитания издержек из суммы валовой прибыли:

=В12-В6

Налог с оборота рассчитывается умножением полученной валовой прибыли на ставку налога с оборота:

=ОКРУГЛ(В12*ВЗ;2)

Налогооблагаемая прибыль вычисляется как разность полученной прибыли и суммы налога с оборота:

=В13-В14

Налог на прибыль равен округленному до второго разряда (до копеек) произведению налогооблагаемой прибыли на действующую ставку налога на прибыль:

=ОКРУГЛ(В15*В2;2)

Чистая прибыль в результате реализации равняется разности налогооблагаемой прибыли и суммы налога на прибыль:

=В15-В16

Пример финансово — экономической ситуации №2

Необходимо провести расчёты по исследованию влияния различных вариантов (сценариев) изменения выручки от реализации, постоянных и переменных затрат на изменение прибыли и финансовой прочности аптечной организации.

Базовая компьютерная модель анализа «Затраты — Объём — Прибыль». Модель основана на предположении, что для каждого сценария, представленного отдельным столбцом электронной таблицы, может быть задана произвольная комбинация изменений параметров R, C и v. Изменения задаются как положительный или отрицательный прирост указанных параметров и рассчитываются по формулам:

1. R_j = R₀(1 + r_j⁽¹⁾) + R_j⁽²⁾;

2. C_j = C₀(1 + c_j⁽¹⁾) + C_j⁽²⁾;

3. v_j = v₀(1 + v_j⁽¹⁾) + v_j⁽²⁾, 

где R_j — сумма выручки от реализации в j-м сценарии; C_j — сумма постоянных затрат в j-м сценарии; v_j — переменные затраты на рубль реализации в j-м сценарии; R₀ — выручка от реализации базового периода; C₀ — постоянные затраты базового периода; v₀ — переменные затраты базового периода; r_j⁽¹⁾ — коэффициент относительного прироста выручки от реализации в j-м сценарии; c_j⁽¹⁾ — коэффициент относительного прироста постоянных затрат в j-м сценарии; v_j⁽¹⁾ — коэффициент относительного прироста переменных затрат на рубль реализации в j-м сценарии; R_j⁽²⁾ — абсолютная величина прироста выручки от реализации в j-м сценарии; C_j⁽²⁾ — абсолютная величина прироста постоянных затрат в j-м сценарии; v_j⁽²⁾ — абсолютная величина прироста переменных затрат на рубль реализации в j-м сценарии.

В соответствии с формулами 1–3 для удобства пользователя изменения базовых параметров могут задаваться в виде как относительных, так и абсолютных величин.

По заданным параметрам изменений, характеризующим отдельные сценарии, в модели рассчитываются все остальные зависимые показатели модели.

Общий вид компьютерной модели в формате электронной таблицы Excel представлен на рис. 3.

Рис. 3. Общий вид базовой модели 
анализа «Затраты — Объём — Прибыль»

В столбце A перечислены названия исследуемых показателей. В столбце B представлены базисные значения. Сценарии изменения суммы выручки, постоянных затрат и переменных затрат на рубль выручки могут задаваться в процентах от базисных значений или в виде абсолютного значения изменения по отношению к ним. Жирным шрифтом выделены ячейки, содержащие расчётные формулы, а обычным — ячейки, значения в которых задаются вручную. В соответствующих строках столбцов C–I содержатся значения показателей различных сценариев изменения затрат и выручки. В таблице на рис. 4 заданы семь сценариев. Однако формулы расчёта показателей для всех сценариев полностью идентичны. Их можно копировать для создания произвольного числа сценариев.

Основные формулы компьютерной модели приведены в таблице, изображенной на рис. 4.

Рис. 4. Основные формулы компьютерной модели

Поскольку в столбцах расчёта показателей сценариев формулы однотипны, они приводятся только для столбца C. В остальные столбцы их можно скопировать стандартными средствами электронных таблиц.

Порядок работы с таблицей таков. Вручную задаются базовые (текущие) показатели выручки от реализации (B3), переменных (B6) и постоянных (B11) затрат. На их основе вычисляются маржинальная прибыль (B10), прибыль (B14), порог рентабельности (B16) и запас финансовой прочности в процентах

Сценарии задаются с помощью отклонений показателей выручки от реализации, совокупных постоянных затрат и переменных затрат на рубль реализации от аналогичных показателей базового варианта. Для каждого сценария нужно вручную задать соответствующие ему величины отклонения от тех, которые зафиксированы в базовом варианте. Все остальные показатели и коэффициенты здесь являются расчётными.

Выручка в ячейке C3 рассчитывается по формуле $B$3*(1+C4)+С5. Расчёт производится путём умножения выручки в базовом периоде ($B$3) на коэффициент изменения, получаемый путём сложения 100 % базового уровня с отклонением (положительным или отрицательным), заданным в ячейке C4, и к этой величине прибавляется абсолютное значение заданного пользователем в ячейке C5 изменения суммы выручки.

Таким образом, изменение выручки можно задать как в процентах (ячейка C4), так и в виде конкретного значения. Можно одновременно задать и то и другое.

Поскольку все вычисления привязываются к базовому уровню выручки, используется абсолютная адресация. Процентный формат в электронной таблице подразумевает хранение в ячейке долей единицы. Например, вводится величина 30 %, а хранится и используется в расчётах коэффициент 0,3. Иными словами, в ячейке процентного отклонения хранится видимая на экране величина, делённая на 100 %. Это отличается от традиционной «бумажной» записи, где вместо выражения в скобках надо было бы записать (100 % – С4) / 100 %.

Переменные затраты в ячейке C6 рассчитываются как произведение суммы выручки по данному сценарию (ячейка C3) на изменённый в нём по отношению к базе коэффициент соотношения переменных затрат и выручки. В представленных на рис. 3 данных этот коэффициент неизменен для всех сценариев, потому что ни в одном из них не задано изменяющих его данных. Однако в дальнейшем мы рассмотрим ситуации, когда коэффициент переменных затрат может измениться.

Расчёт коэффициента переменных затрат осуществляется путём умножения его базового значения на величину коэффициента изменения, к которой добавляется предусмотренное сценарием изменение на абсолютную величину (ячейка C9).

Маржинальная прибыль рассчитывается как разность выручки от реализации (ячейка C3) и переменных затрат (ячейка C6).

Постоянные затраты в ячейке C7 рассчитываются по тем же принципам, что и сценарная сумма выручки от реализации.

Прибыль рассчитывается как разница между маржинальной прибылью (ячейка C10) и постоянными затратами (ячейка C11). В ячейке C15 вычисляется процент изменения прибыли в данном сценарии по отношению к её базовой величине. Порог рентабельности для данного сценария определяется как отношение постоянных затрат к разнице между единицей и коэффициентом переменных затрат.

Для большей наглядности представления данных в модель встроена диаграмма, характеризующая изменение прибыли в исследуемых сценариях. Кроме того, для диапазона С14–I14 задано условное форматирование, позволяющее выделять иным цветом ячейки расчёта прибыли в том случае, если достигнутая в данном сценарии прибыль превосходит базовую величину.

Базовая модель анализа «Затраты — Объём — Прибыль» позволяет решать широкий круг задач.

Прежде всего благодаря ей можно проанализировать влияние изменения выручки от реализации на сумму прибыли. В данных рис. 3 сценарии 1, 2, 4 и 5 определяют изменение выручки от реализации на –10 %, –20 %, 10 % и 20 % соответственно при сохранении прочих параметров модели неизменными. Из приведённых данных видно, что снижение выручки от реализации на 20 % (сценарий 1) приведёт к уменьшению прибыли на 50 % по сравнению с базовым уровнем, а увеличение выручки на 20 % (сценарий 5) увеличит прибыль на те же 50 %. Поскольку в сценариях 1–5 никакие другие параметры не изменяются, порог рентабельности остаётся неизменным — 6000.

Сценарии 6 и 7 характеризуются одновременным изменением выручки от реализации и постоянных затрат. Такой анализ может быть нужен, например, в том случае, когда предприятие планирует арендовать дополнительную торговую точку. Тогда постоянные затраты возрастают, но можно ожидать возрастания выручки от реализации. В соответствии с приведёнными на рис. 3 сведениями постоянные затраты возрастают на сумму 1500. Если при этом выручка от реализации увеличится на 30 %, то прибыль в целом останется неизменной. Если же при том же увеличении постоянных затрат удастся добиться увеличения выручки на 40 %, то по сравнению с базовым уровнем прибыль вырастет на 25 %. Однако в любом случае порог рентабельности вырастет, а финансовая прочность предприятия снизится по сравнению с базовым уровнем.

Построенная модель позволяет сравнивать одновременно несколько альтернативных управленческих решений, так или иначе комплексно влияющих на изменения в структуре и объёме затрат, а также выручки от реализации.

Пример финансово — экономической ситуации № 3

Инвестор, рискуя, планирует наилучшим образом определить части сумм денег общим объемом S д. ед., которые будут вложены у n предприятий путем покупки акций с целью получения прибыли у определенном последующем периоде.
Условие оптимально означает, что существует два альтернативные критерии оптимизации:

• минимизация риска при фиксированном доходе (аккуратный подход) или

• максимизация дохода при фиксированном риске.

В инвестиционном менеджменте набор частей сумм инвестирования называется портфель, оптимальным портфелем есть такой набор, который инвестор признает для себя наилучшим относительно дохода и риска. Чем больший доход, тем больший риск.
Наш инвестор хочет вложить деньги в суме 30000 д. ед. в акции 6 предприятий, для каждого с которых известны доходность акций (%), срок действия, оценка риска, максимальная величина инвестиций на одно предприятие не больше 7500 в предприятия с уровнем риска больше 3 вложить не больше 1/3 сумы всех денег, а в предприятия со сроком больше чем 5 лет не меньше ? сумы денег.
Инвестор должен выбрать на основе фиксированных предприятиями рисков оптимальный вариант – куда и сколько вложить денег, что бы получить максимальный доход.
Экономико-математическая модель.

• Найти план инвестирования при котором,

• Об_Доход=План*Доходность(%) — mах

• При ограничениях: План=30000; План_предприятие<=7500; План>=Мин_взнос Предприятия(риск>=3) <=10000; Предприятия(срок>5)>=15000.

Пример финансово — экономической ситуации № 4

Название задачи и соответственной модели – о назначении (assignment problem) – непосредственно исходить от практической кадровой ситуации, когда претендентов нужно назначить на вакантные должности  наилучшим образом.
Критерий максимизации общего аффекта используется тогда, когда известны о каждом претенденте заданные оценки способности исполнения определенной функции (чем выше, тем лучше), минимизации – когда, скажем, для каждого претендента заданная величина затрат на его подготовку для определенной деятельности (чем выше, тем хуже).  
Аптечная организация объявила набор работников для нового отдела – указало названия семи должностей и количество вакансий по каждой из них. Кадровая служба собрала от 18 претендентов на эти должности, провела тестирование по каждой из них и за результатами определила 5 групп с одинаковыми оценками и возможностями, получивши соответственную таблицу средних оценок их умений и знаний.
Нужно назначить на вакантные должности претендентов таким образом, что бы общая эффективность исполнения ними соответствующих обязанностей была максимальной.
Особенность – наличие высокой оценки еще не гарантирует успех, поскольку целью оптимизации о назначении есть максимальный общий эффект.
Экономико-математическая модель.

1. Найти такую матрицу назначений, чтобы

2. Общий эффект=Матрица_оценок*Матрица_назначений — mах

3. При ограничениях: Назначено<=Всего_претендентов; Занято=Всего_вакансий.
   

Пример финансово — экономической ситуации №5

Современный маркетинг все чаще использует количественные методы планирования соответствующих исследований. Эта особенность проявилась в появлении и активном развитии научного направления под названием Marketing Engineering, где для качественной деятельности маркетологов используются методы прогнозирования и оптимизации, развитые в сфере математического программирования и исследования операций.
В области маркетинговых исследований довольно типичной есть задачи размещения (location problem), скажем, сервисных центров (клиник, полицейских служб, учебных заведений), складов или производительных мощностей. Целью таких задач есть определения такого размещения, для которого минимизируется, например, расстояние между центром предоставления услуг та их потребителем. Задачи такого типа появляются в практике коммуникационного обеспечения (пути, железная дорога, кабельная связь), где нужно исполнить определенные работы с минимальной стоимостью.
Начальными данными для этой задачи есть координаты та весомые коэффициенты (количество населения, число школьников, пенсионеров или больных) клиентов, дополнительно учитываются определенные ограничения. «Клиентами» в данном примере есть 25 городов Европы. Нужно найти координаты оптимального центра, чтобы минимизировать суму расстояний от центра к всем другим городам.
Экономико-математическая модель.

• Найти координаты центра, чтобы

• Сума расстояний была минимальной

• При ограничениях: