Финансовые
функции ПП Excel, являющегося
составной частью MS Office,
предназначены для вычисления базовых
величин, необходимых при проведении
практически всех финансовых расчетов,
встречающихся в практике работы
финансиста – экономиста.
Функции
EXCEL используют базовые модели финансовых
операций, базирующиеся на математическом
аппарате методов финансово-экономических
расчетов. Использование возможностей
компьютера и табличного процессора
EXCEL позволяет облегчить выполнение
расчетов и представить их в удобной для
пользователя форме.
К
сожалению, существуют некоторые трудности
при использовании финансовых функций
в среде EXCEL, и, прежде всего потому, что
синтаксис функций использует иные
обозначения основных понятий финансовых
операций, нежели в рассмотренных выше
классических расчетах.
Методика
изучения и использования финансовых
функций требует соблюдения определенной
технологии.
2.1.Технология работы с финансовыми функциями Excel
FНа
рабочем листе в отдельных ячейках
осуществляется подготовка значений
основных аргументов функции.
F
Для расчета результата финансовой
функции Excel курсор
устанавливается в новую ячейку для
ввода формулы, использующей встроенную
финансовую функцию17.
F
Осуществляется вызов «Мастера
функций18»
На
основной панели инструментов имеются
кнопки «Мастер функций«, с
помощью которой открывается диалоговое
окно Диспетчера функций19.
Диалоговое
окно «Диспетчер функций»
организован по тематическому принципу.
После выбора в левом списке «Категории»
тематической группы «Финансовые»,
на экран будет выведено диалоговое окно
с полным перечнем списка имен функций,
содержащихся в данной группе20.
Поиск необходимой финансовой функции
осуществляется путем последовательного
просмотра списка.
ðДля
выбора функции курсор устанавливается
на имя функции.
Обратите
внимание,
что когда курсор устанавливается на
имени функции, то в нижней части окна
выбранной функции приводится краткий
синтаксис и назначение выбираемой
функции.
Рис. 2‑11 Последовательность
действий при выборе необходимой
финансовой функции
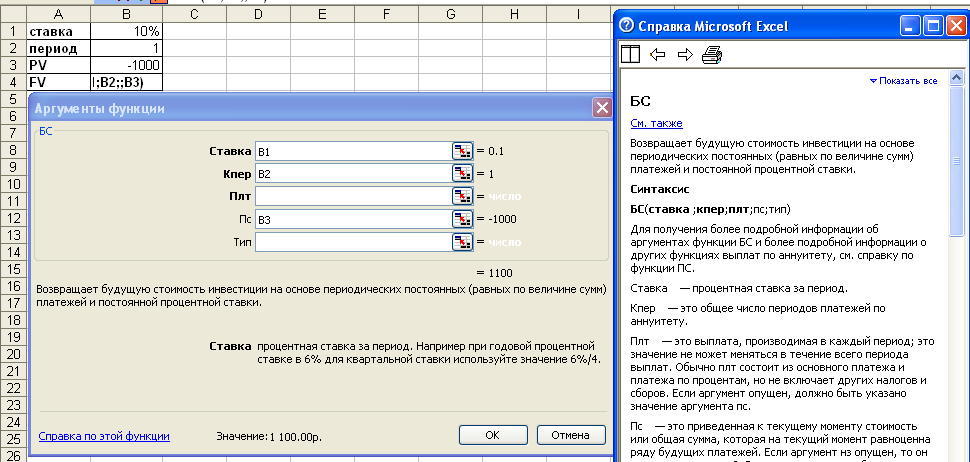
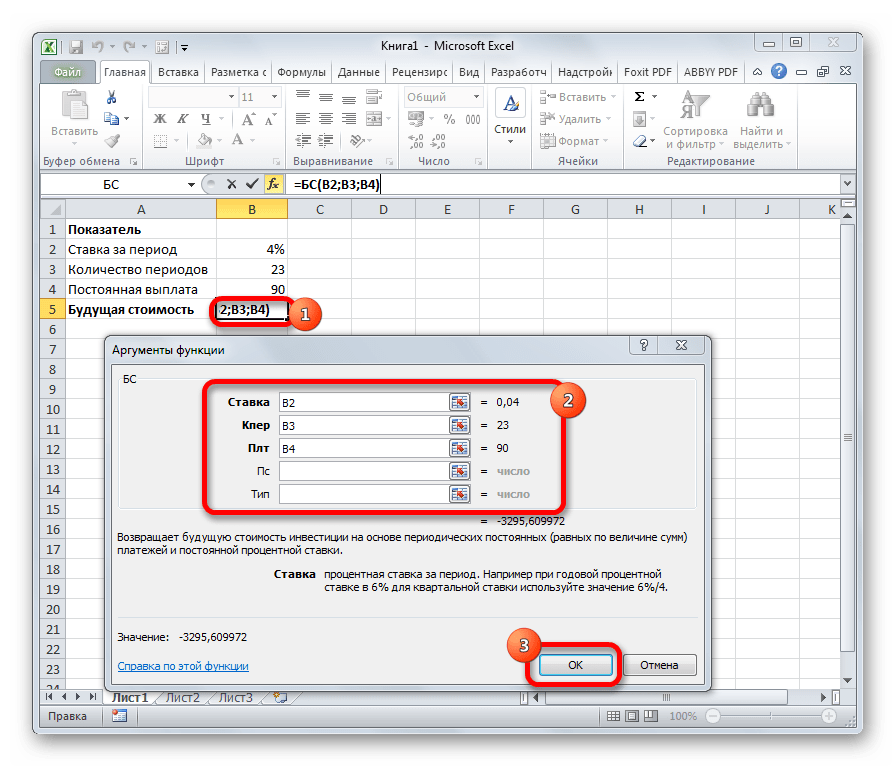
Рис. 2‑12 Фрагмент
листа Excel с диалоговым
окном финансовой функции БС (расчет
будущей стоимости инвестиции) и справочной
информацией
ðПеренос
формулы необходимой функции в ячейку
осуществляется двойным щелчком на ее
имени,21
либо щелчком на кнопке «ОК»
В
результате выполненных действий на
экране откроется диалоговое окно
выбранной функции.
FВ
поля диалогового окна функции:
-
можно
вводить как сами значения аргументов,
так и ссылки на адреса ячеек, содержащие
необходимые значения; -
все
расходы денежных средств (платежи)
представляются отрицательными
числами, а все поступления денежных
средств – положительными
числами; -
процентная
ставка вводится в виде десятичной
дроби, либо с использованием знака %; -
все
даты как аргументы функций имеют
числовой формат представления, например
дата 1 сентября 2006 года представляется
числом 3896122
Примечание
Если значение
аргумента типа «Дата» берется
из ячейки, то дата может быть записана
в обычном виде, например 1.09.2006.
При вводе аргумента типа «Дата»
непосредственно в поле ввода диалогового
окна финансовой функции, можно
воспользоваться встроенной функцией
«Дата», которая осуществляет
преобразование строки символов в дату23.
Для
исчисления характеристик финансовых
операций с наращением и дисконтированием
вложенных сумм удобно использовать
функции БС(), ПС(),
КПЕР(), НОРМА(), БЗРАСПИС(
, )НОМИНАЛ(), ЭФФЕКТ(). ПЛПРОЦ(), ОББШПЛАТ(),
ОСНПЛАТ(), ОБЩДОХОД().
Таблица 2‑1
Функции рабочего
листа Excel для оценки
разовых и периодических (потоков)
платежей
|
Наименование функции |
Формат функции |
Назначение функции |
|
БС
В младших версиях Excel эта функция |
БС (ставка; кпер; платеж; нc; [тип]) |
рассчитывает будущую стоимость |
|
ПС
В младших версиях Excel эта функция |
ПС(ставка; кпер; платеж; бс; [тип]) |
предназначена для расчета текущей
Текущий объем — это общая сумма,
Этот расчет является обратным к |
|
КПЕР |
КПЕР(ставка; платеж; нз; бс; [тип]) |
вычисляет количество периодов |
|
СТАВКА
В младших версиях Excel эта функция |
СТАВКА (кпер; платеж; нз; бс; [тип]) |
вычисляет процентную ставку, которая |
|
ПЛТ |
ПЛТ(ставка; кпер; нз; [бс]; [тип]) |
позволяет рассчитать сумму постоянных |
|
БЗРАСПИС |
БЗРАСПИС (сумма; массив ставок) |
удобно использовать для расчета |
|
НОМИНАЛ |
НОМИНАЛ (эф_ставка;кол_пер) |
Возвращает номинальную годовую |
|
ЭФФЕКТ |
ЭФФЕКТ(ном_ставка; кол_пер) |
Возвращает фактическую годовую |
|
ПЛПРОЦ |
ПЛПРОЦ(ставка; период;кпер;пс)) |
Вычисляет проценты, выплачиваемые |
|
ПРПЛТ(ставка ; период;кпер;пс;бс; тип) |
Возвращает сумму платежей процентов |
|
|
ОСПЛТ(ставка ; период; кпер;пс;бс; |
Возвращает величину платежа в |
|
|
ОБДОХОД( ставка; кпер; нз; нач_период; |
Вычисляет сумму основных платежей |
FКак
видно из приведенной таблицы, большинство
финансовых функций имеет одинаковый
набор базовых аргументов:
ставка
— процентная ставка за период (норма
доходности или цена заемных средств –
r).
Например, если получена ссуда на
автомобиль под 10 процентов годовых и
делаются ежемесячные выплаты, то
процентная ставка за месяц составит
10%/12 или 0,83%. В качестве значения аргумента
ставка нужно ввести в формулу 10%/12 или
0,83% или 0,0083
кпер
— срок (число
периодов n)
проведения операции. Например, если
получена ссуда на 4 года под приобретение
автомобиля и делаются ежемесячные
платежи, то ссуда имеет 4*12 (или 48) периодов.
В качестве значения аргумента кпер
в формулу нужно ввести число 48.
Плт
— выплата, производимая в каждый
период и не меняющаяся за все время
выплаты ренты. Обычно выплаты включают
основные платежи и платежи по процентам,
но не включают других сборов или налогов.
Например, ежемесячная выплата по
четырехгодичному займу в 10 000 руб. под
12 процентов годовых составит 263,33 руб.
В качестве значения аргумента выплата
нужно ввести в формулу число -263,33.
Пс
— это приведенная к текущему моменту
стоимость (величина PV)
или общая сумма, которая на текущий
момент равноценна ряду будущих платежей.
Если аргумент ПС опущен, то он
полагается равным 0. В этом случае должно
быть указано значение аргумента Плт.;
Бс
— требуемое значение будущей стоимости
(FV) или остатка
средств после последней выплаты. Если
аргумент опущен, он полагается равным
0 (будущая стоимость займа, например,
равна 0). Например, если предполагается
накопить 50000 руб. для оплаты специального
проекта в течение 18 лет, то 50 000 руб. это
и есть будущая стоимость
[тип]
— число 0 или 1, обозначающее, когда
должна производиться выплата
[1 — начало периода (обычная
рента или пренумерандо), 0 — конец
периода (постнумерандо)],
необязательный аргумент.
F
Завершение ввода аргументов и запуск
расчета значения функции выполняется
нажатием кнопки «ОК».
F
При необходимости корректировки значений
аргументов функции (изменении адресов
ссылок, постоянных значений и др.)
необходимо установить курсор в ячейку,
содержащую формулу:
ðВыполнить
редактирование аргументов функции в
строке формул
либо
ðповторно
вызвать, используя «Мастер функций»,
диалоговое окно функции и в нем выполнить
необходимую коррекцию24.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание
- Выполнение расчетов с помощью финансовых функций
- ДОХОД
- БС
- ВСД
- МВСД
- ПРПЛТ
- ПЛТ
- ПС
- ЧПС
- СТАВКА
- ЭФФЕКТ
- Вопросы и ответы
Excel имеет значительную популярность среди бухгалтеров, экономистов и финансистов не в последнюю очередь благодаря обширному инструментарию по выполнению различных финансовых расчетов. Главным образом выполнение задач данной направленности возложено на группу финансовых функций. Многие из них могут пригодиться не только специалистам, но и работникам смежных отраслей, а также обычным пользователям в их бытовых нуждах. Рассмотрим подробнее данные возможности приложения, а также обратим особое внимание на самые популярные операторы данной группы.
Выполнение расчетов с помощью финансовых функций
В группу данных операторов входит более 50 формул. Мы отдельно остановимся на десяти самых востребованных из них. Но прежде давайте рассмотрим, как открыть перечень финансового инструментария для перехода к выполнению решения конкретной задачи.
Переход к данному набору инструментов легче всего совершить через Мастер функций.
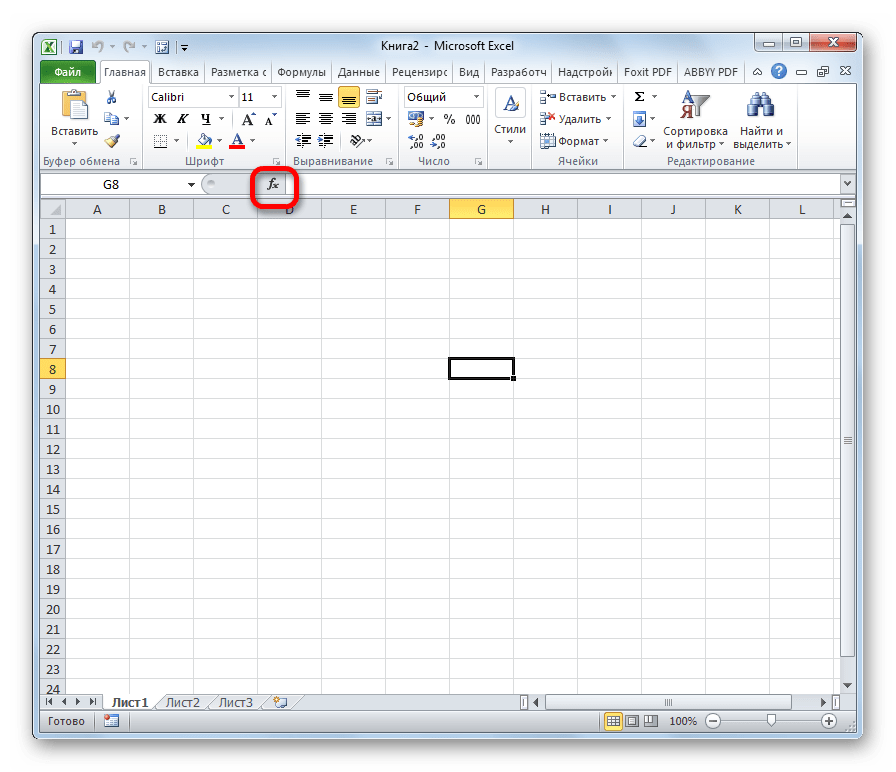
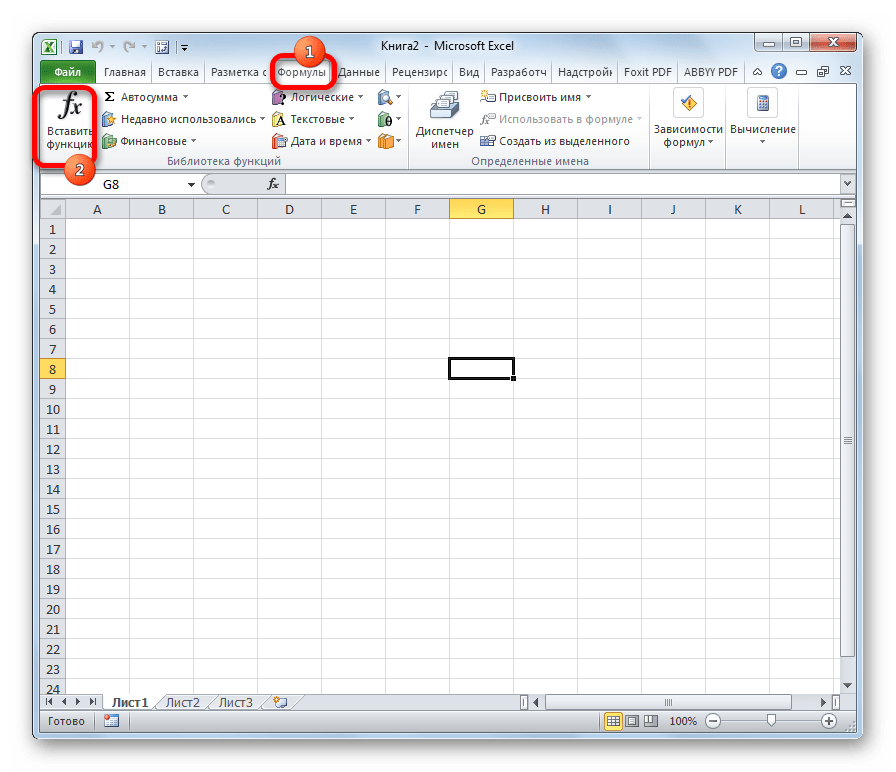
- Выделяем ячейку, куда будут выводиться результаты расчета, и кликаем по кнопке «Вставить функцию», находящуюся около строки формул.
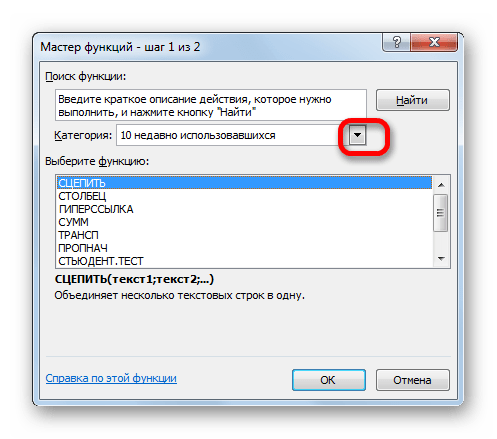
- Запускается Мастер функций. Выполняем клик по полю «Категории».
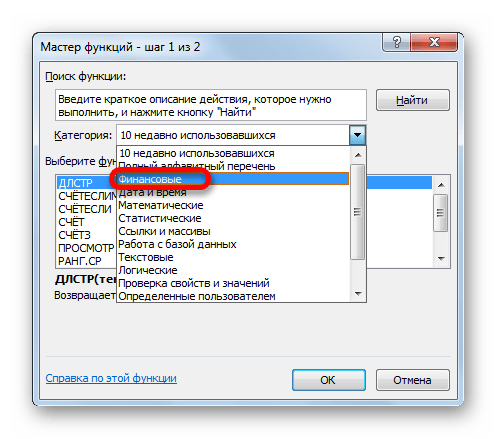
- Открывается список доступных групп операторов. Выбираем из него наименование «Финансовые».
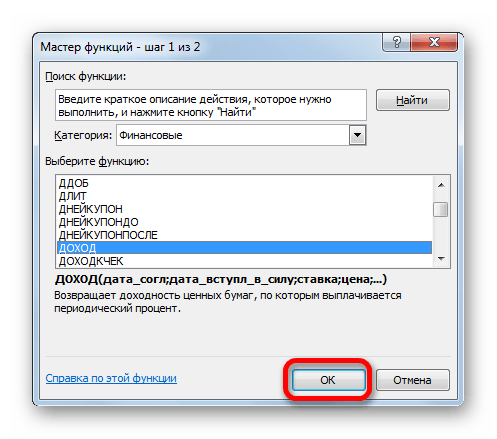
- Запускается перечень нужных нам инструментов. Выбираем конкретную функцию для выполнения поставленной задачи и жмем на кнопку «OK». После чего открывается окно аргументов выбранного оператора.
В Мастер функций также можно перейти через вкладку «Формулы». Сделав переход в неё, нужно нажать на кнопку на ленте «Вставить функцию», размещенную в блоке инструментов «Библиотека функций». Сразу вслед за этим запустится Мастер функций.
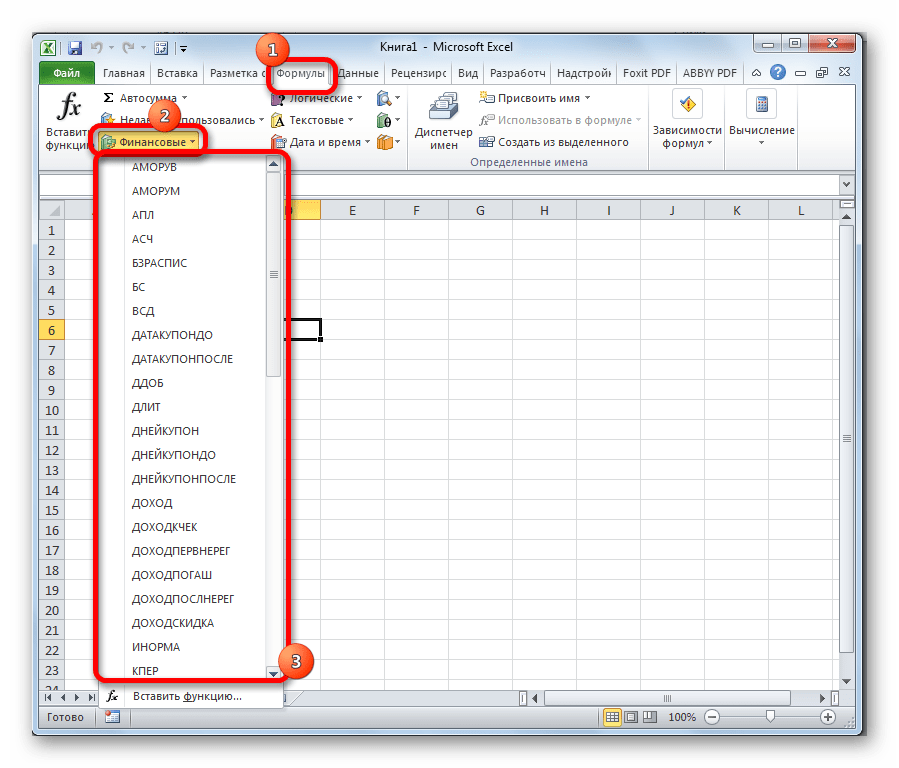
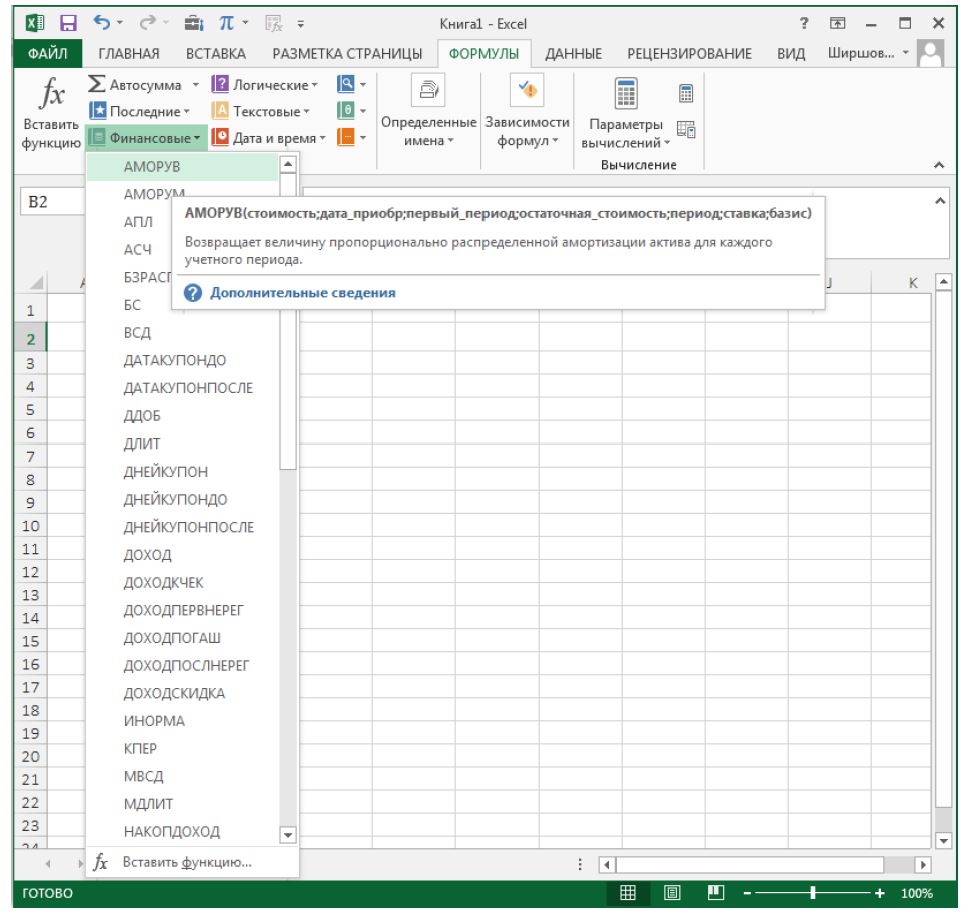
Имеется в наличии также способ перехода к нужному финансовому оператору без запуска начального окна Мастера. Для этих целей в той же вкладке «Формулы» в группе настроек «Библиотека функций» на ленте кликаем по кнопке «Финансовые». После этого откроется выпадающий список всех доступных инструментов данного блока. Выбираем нужный элемент и кликаем по нему. Сразу после этого откроется окно его аргументов.
Урок: Мастер функций в Excel
ДОХОД
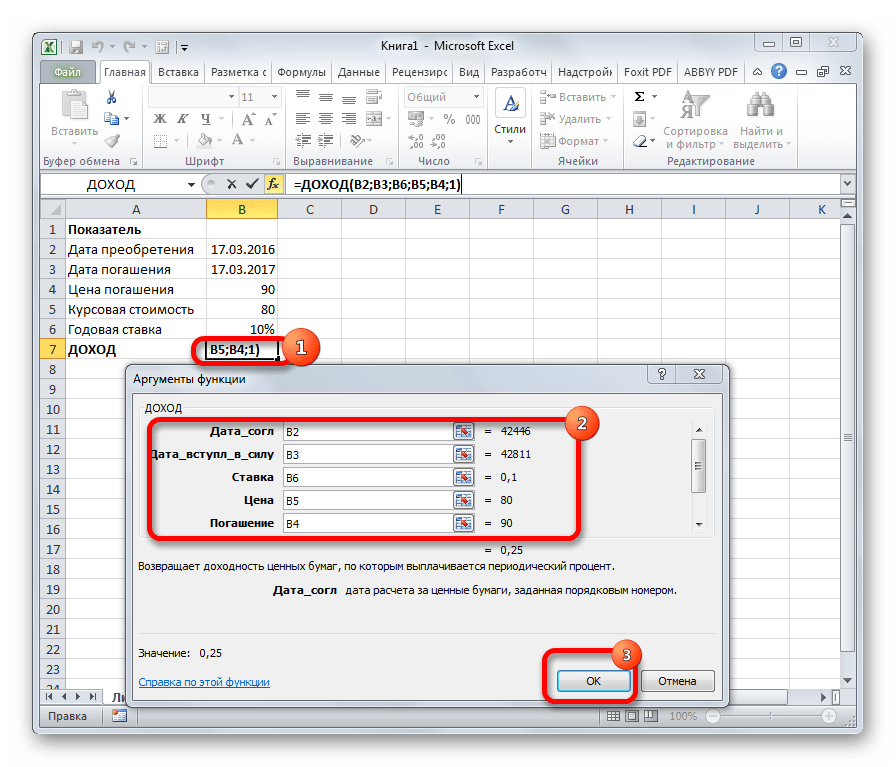
Одним из наиболее востребованных операторов у финансистов является функция ДОХОД. Она позволяет рассчитать доходность ценных бумаг по дате соглашения, дате вступления в силу (погашения), цене за 100 рублей выкупной стоимости, годовой процентной ставке, сумме погашения за 100 рублей выкупной стоимости и количеству выплат (частота). Именно эти параметры являются аргументами данной формулы. Кроме того, имеется необязательный аргумент «Базис». Все эти данные могут быть введены с клавиатуры прямо в соответствующие поля окна или храниться в ячейках листах Excel. В последнем случае вместо чисел и дат нужно вводить ссылки на эти ячейки. Также функцию можно ввести в строку формул или область на листе вручную без вызова окна аргументов. При этом нужно придерживаться следующего синтаксиса:
=ДОХОД(Дата_сог;Дата_вступ_в_силу;Ставка;Цена;Погашение»Частота;[Базис])
БС
Главной задачей функции БС является определение будущей стоимости инвестиций. Её аргументами является процентная ставка за период («Ставка»), общее количество периодов («Кол_пер») и постоянная выплата за каждый период («Плт»). К необязательным аргументам относится приведенная стоимость («Пс») и установка срока выплаты в начале или в конце периода («Тип»). Оператор имеет следующий синтаксис:
=БС(Ставка;Кол_пер;Плт;[Пс];[Тип])
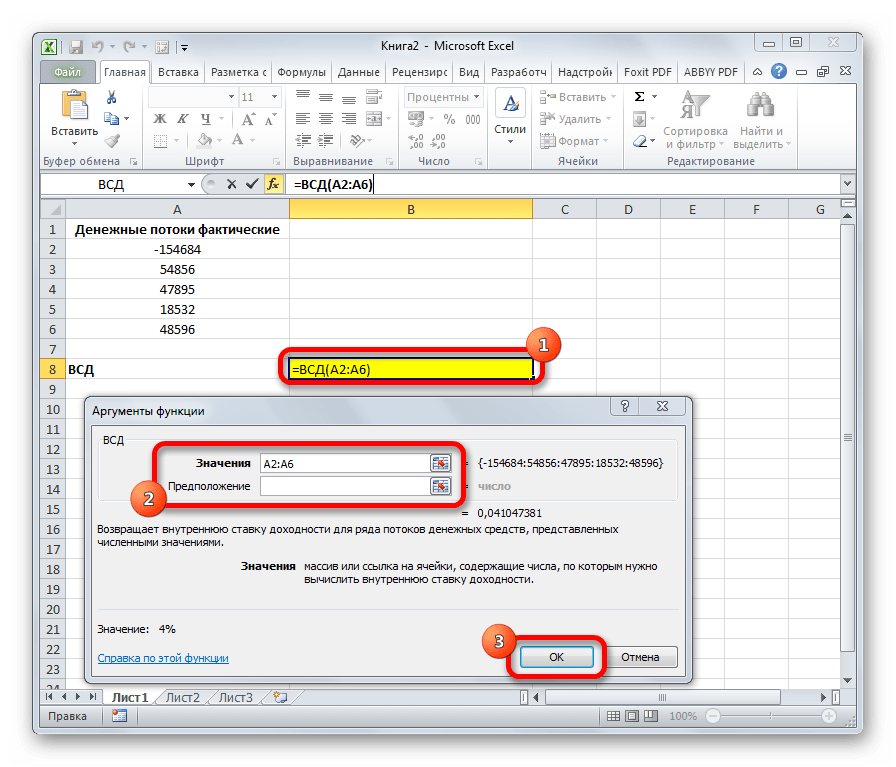
ВСД
Оператор ВСД вычисляет внутреннюю ставку доходности для потоков денежных средств. Единственный обязательный аргумент этой функции – это величины денежных потоков, которые на листе Excel можно представить диапазоном данных в ячейках («Значения»). Причем в первой ячейке диапазона должна быть указана сумма вложения со знаком «-», а в остальных суммы поступлений. Кроме того, есть необязательный аргумент «Предположение». В нем указывается предполагаемая сумма доходности. Если его не указывать, то по умолчанию данная величина принимается за 10%. Синтаксис формулы следующий:
=ВСД(Значения;[Предположения])
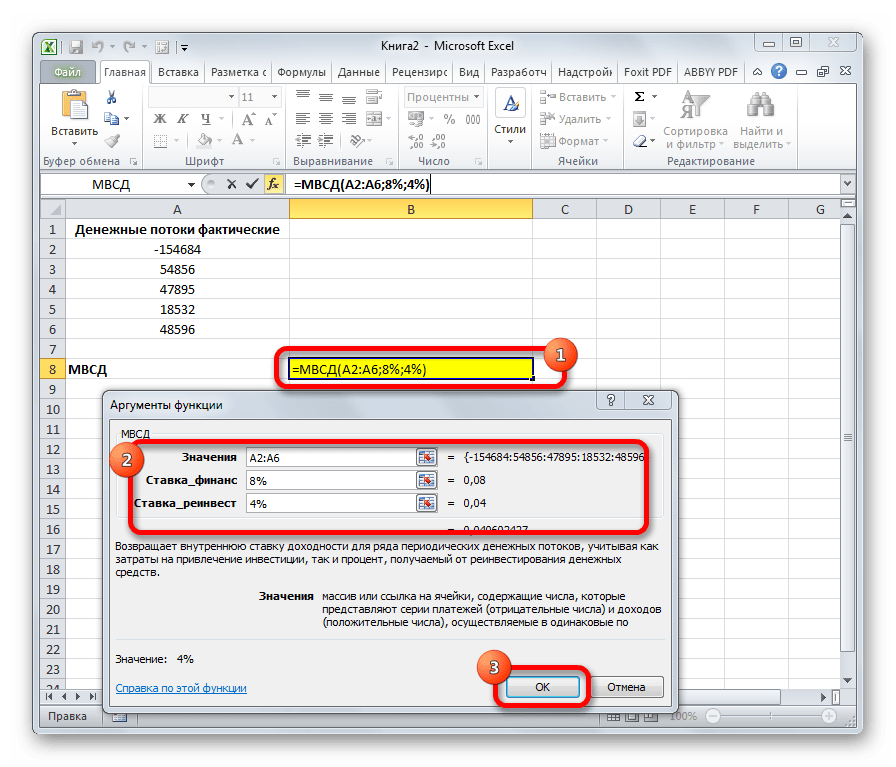
МВСД
Оператор МВСД выполняет расчет модифицированной внутренней ставки доходности, учитывая процент от реинвестирования средств. В данной функции кроме диапазона денежных потоков («Значения») аргументами выступают ставка финансирования и ставка реинвестирования. Соответственно, синтаксис имеет такой вид:
=МВСД(Значения;Ставка_финансир;Ставка_реинвестир)
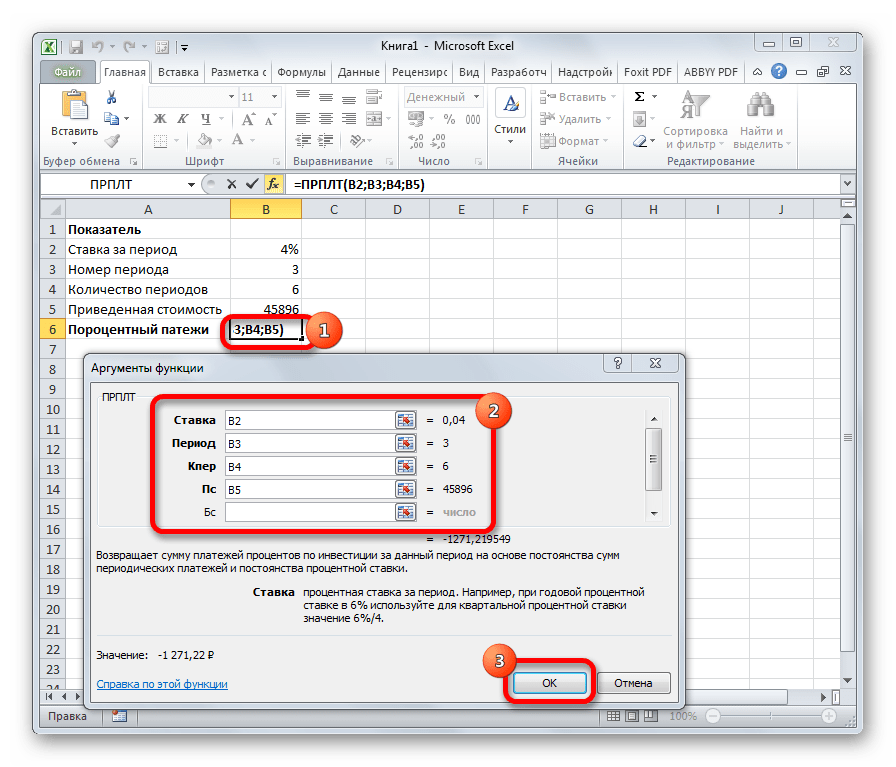
ПРПЛТ
Оператор ПРПЛТ рассчитывает сумму процентных платежей за указанный период. Аргументами функции выступает процентная ставка за период («Ставка»); номер периода («Период»), величина которого не может превышать общее число периодов; количество периодов («Кол_пер»); приведенная стоимость («Пс»). Кроме того, есть необязательный аргумент – будущая стоимость («Бс»). Данную формулу можно применять только в том случае, если платежи в каждом периоде осуществляются равными частями. Синтаксис её имеет следующую форму:
=ПРПЛТ(Ставка;Период;Кол_пер;Пс;[Бс])
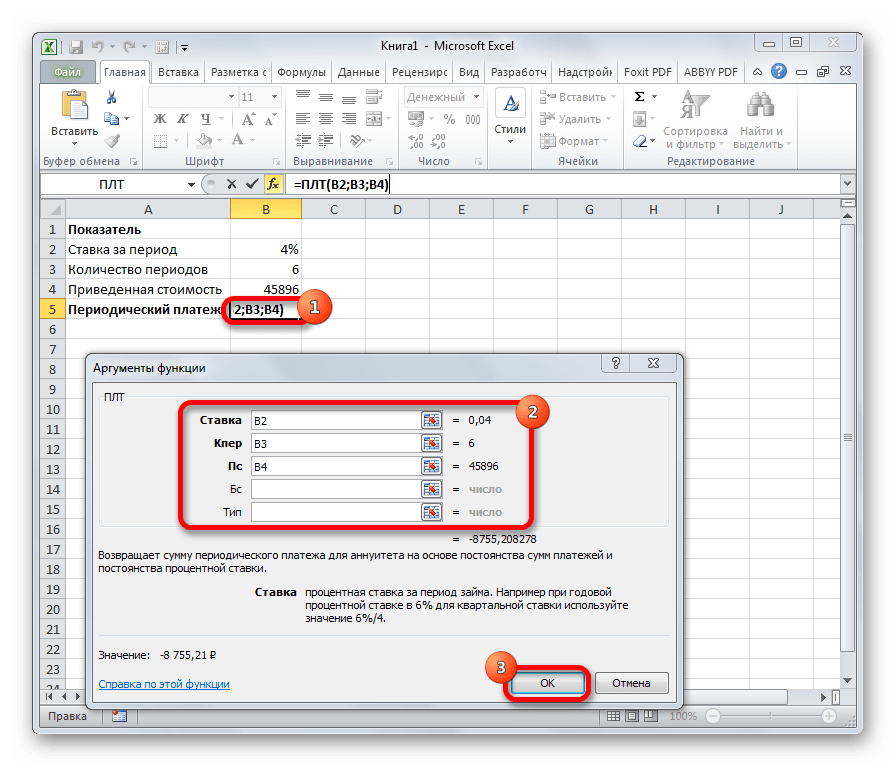
ПЛТ
Оператор ПЛТ рассчитывает сумму периодического платежа с постоянным процентом. В отличие от предыдущей функции, у этой нет аргумента «Период». Зато добавлен необязательный аргумент «Тип», в котором указывается в начале или в конце периода должна производиться выплата. Остальные параметры полностью совпадают с предыдущей формулой. Синтаксис выглядит следующим образом:
=ПЛТ(Ставка;Кол_пер;Пс;[Бс];[Тип])
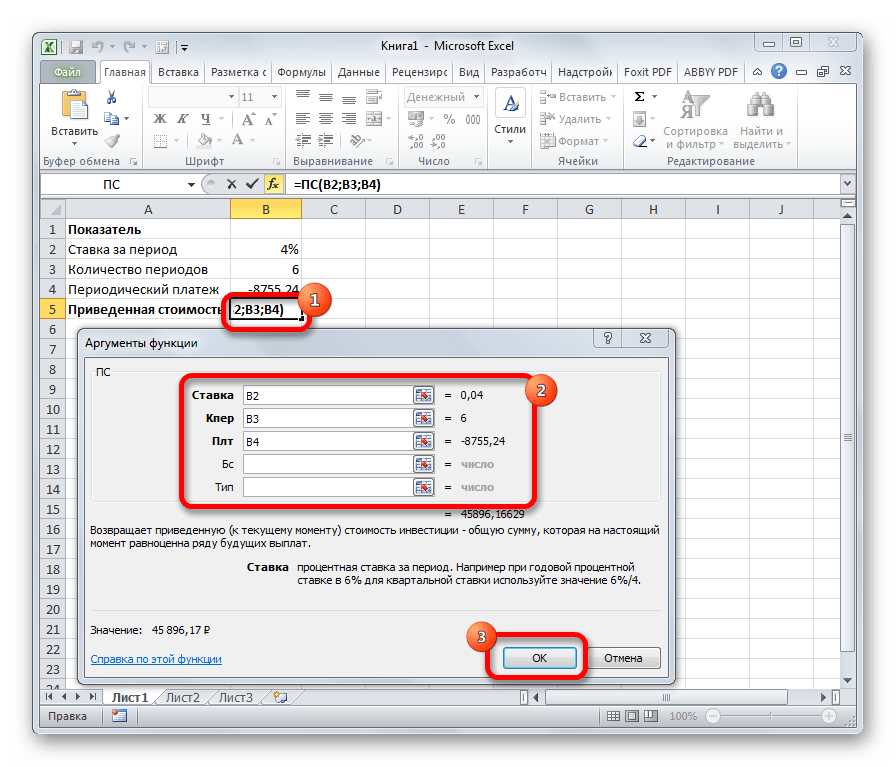
ПС
Формула ПС применяется для расчета приведенной стоимости инвестиции. Данная функция обратная оператору ПЛТ. У неё точно такие же аргументы, но только вместо аргумента приведенной стоимости («ПС»), которая собственно и рассчитывается, указывается сумма периодического платежа («Плт»). Синтаксис соответственно такой:
=ПС(Ставка;Кол_пер;Плт;[Бс];[Тип])
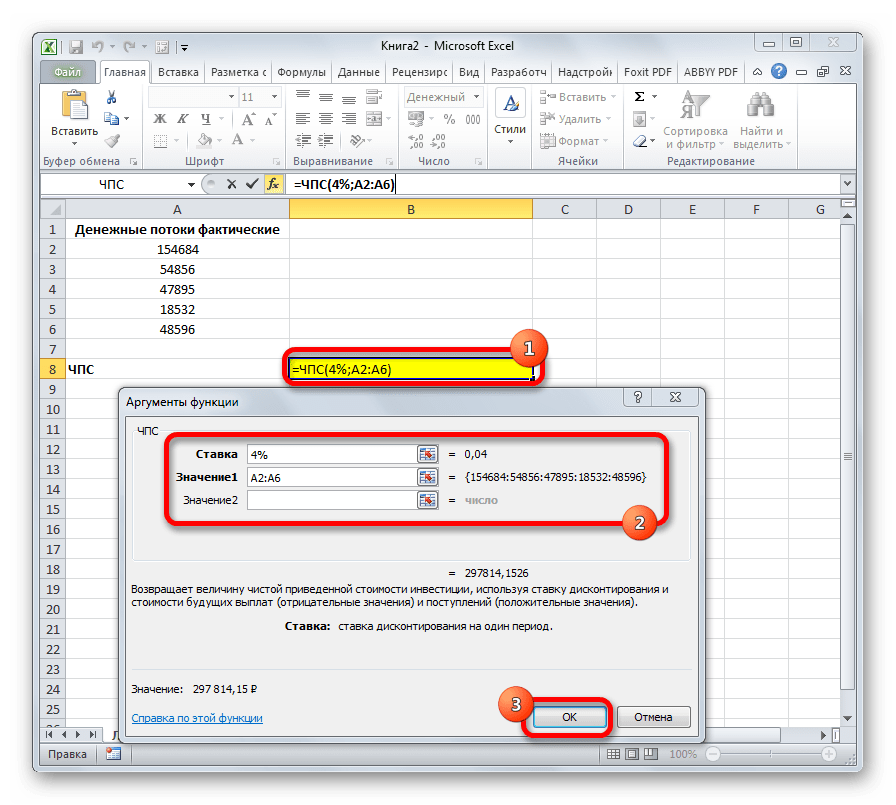
ЧПС
Следующий оператор применяется для вычисления чистой приведенной или дисконтированной стоимости. У данной функции два аргумента: ставка дисконтирования и значение выплат или поступлений. Правда, второй из них может иметь до 254 вариантов, представляющих денежные потоки. Синтаксис этой формулы такой:
=ЧПС(Ставка;Значение1;Значение2;…)
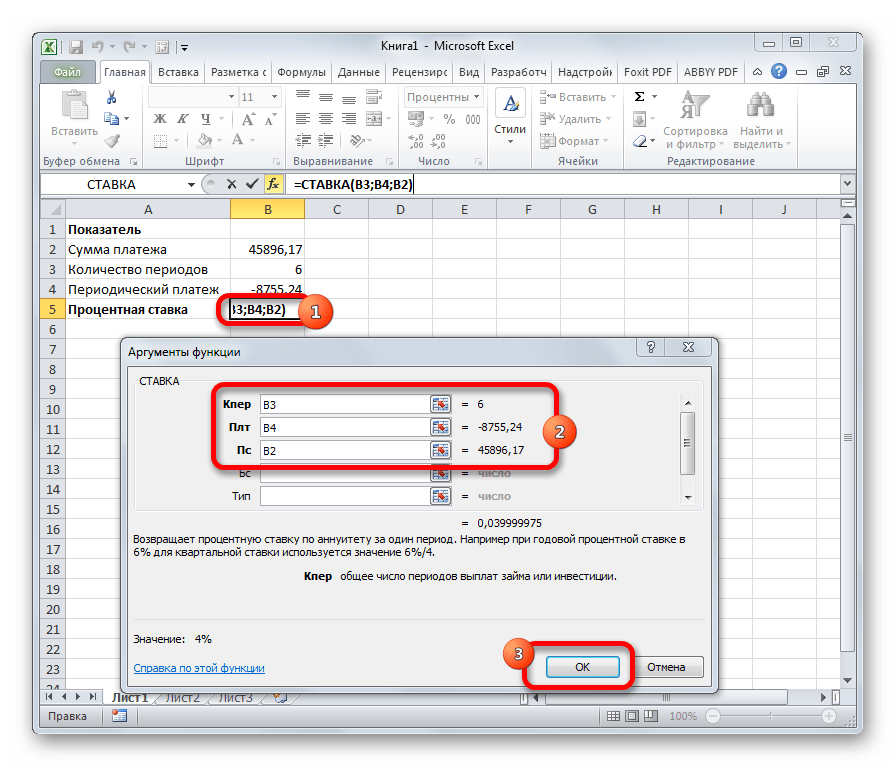
СТАВКА
Функция СТАВКА рассчитывает ставку процентов по аннуитету. Аргументами этого оператора является количество периодов («Кол_пер»), величина регулярной выплаты («Плт») и сумма платежа («Пс»). Кроме того, есть дополнительные необязательные аргументы: будущая стоимость («Бс») и указание в начале или в конце периода будет производиться платеж («Тип»). Синтаксис принимает такой вид:
=СТАВКА(Кол_пер;Плт;Пс[Бс];[Тип])
ЭФФЕКТ
Оператор ЭФФЕКТ ведет расчет фактической (или эффективной) процентной ставки. У этой функции всего два аргумента: количество периодов в году, для которых применяется начисление процентов, а также номинальная ставка. Синтаксис её выглядит так:
=ЭФФЕКТ(Ном_ставка;Кол_пер)
Нами были рассмотрены только самые востребованные финансовые функции. В общем, количество операторов из данной группы в несколько раз больше. Но и на данных примерах хорошо видна эффективность и простота применения этих инструментов, значительно облегчающих расчеты для пользователей.

В учебном пособии приведены материалы к заданиям для самостоятельного выполнения контрольных, лабораторных, практических работ, примеры и методика их решения. Предназначены для студентов, обучающихся по направлениям: 38.03.02 (080200.62) «Менеджмент» (профили: «Производственный менеджмент», «Финансовый менеджмент»), 38.03.01 (080100.62) «Экономика» (профили: «Финансы и кредит», «Экономика предприятия и организации») всех форм обучения, слушателей системы послевузовского образования, преподавателей. Рекомендовано УМО РАЕ по классическому университетскому и техническому образованию в качестве учебного пособия для студентов высших учебных заведений, обучающихся по направлениям подготовки: 38.03.02 (080200.62) – «Менеджмент», 38.03.01 (080100.62) – «Экономика».
Оглавление
1. Модели и методы финансово — экономических расчетов
1.1. Общие положения
Финансовые функции Excel предназначены для вычисления базовых величин, необходимых при проведении сложных финансовых расчетов. Их используют вместо финансовых уравнений. Они работают быстрее, чем введенные формулы, и с меньшей вероятностью ошибок.
Количественный финансовый анализ предполагает применение унифицированных моделей и методов расчета финансовых показателей.
В этом контексте, Microsoft Excel предоставляет широкий спектр функций для финансово-экономических расчетов: от нахождения выплат по процентам, реализации задач дисконтирования, посторения моделей расчета амортизации оборудования, анализа показателей ценных бумаг, регулярных выплат по займу до оценки эффективности капитальных вложений и инвестиций, моделирования финансово-экономических аспектов деятельности предприятия, фирмы и т.п.
Рис. 1. Обобщенная классификация финансовых функций
Условно методы финансовой математики делятся на две категории: базовые и прикладные. К базовым методам и моделям относятся:
— простые и сложные проценты. Простые проценты используются, как правило, в краткосрочных финансово-экономических операциях (продолжительностью до года). Базой для исчисления процентов за каждый период в этом случае служит исходная сумма сделки. Сложные проценты применяются в среднесрочных и долгосрочных финансовых операциях (более одного года), но могут применяться и в краткосрочных, если это вызвано объективной необходимостью (риски, высокий уровень инфляции и т.п.). При этом база для исчисления процентов за период включает в себя как исходную сумму сделки, так и сумму уже накопленных к этому времени процентов;
— расчет последовательностей (потоков) платежей. При проведении большинства финансовых операций возникают чередующиеся в течение ограниченного или неограниченного промежутка времени поступления и выплаты денежных средств. Поток состоит из отдельных элементов потока — платежей. Поступление денежных средств считают положительными платежами, а выплаты — отрицательными. Денежные потоки делятся:
— по распределению во времени: регулярные (периодические) и нерегулярные;
— по величине элементов: на постоянные и переменные.
Наращенная сумма может представлять собой общую сумму накопленной задолженности к концу срока, итоговый объем инвестиций, накопленный денежный резерв и т.д.
Современная стоимость характеризует приведенные к началу осуществления проекта затраты, капитализированный доход или чистую приведенную прибыль от реализации проекта и т.д.
К прикладным методам финансовых расчетов относятся:
— планирование и оценка эффективности финансово-кредитных операций;
— расчет страховых аннуитетов;
— планирование погашения долгосрочной задолженности;
— планирование погашения ипотечных ссуд и потребительских кредитов;
— финансовые расчеты по ценным бумагам;
— лизинговые, факторинговые и форфейтинговые банковские операции;
— планирование и анализ инвестиционных проектов и др.
Особенностью всех финансовых расчетов является временная ценность денег, то есть принцип неравноценности денег, относящихся к разным моментам времени. Деньги — это мера стоимости товаров и услуг. Предполагается, что полученная сегодня сумма обладает большей ценностью, чем ее эквивалент, полученный в будущем, то есть будущие поступления менее ценны, чем современные. Неравноценность одинаковых по абсолютной величине сумм связана, прежде всего, с тем, что имеющиеся сегодня деньги могут быть инвестированы и принести доход в будущем.
Основными понятиями финансовых методов расчета являются:
— процент — абсолютная величина дохода от предоставления денег в долг в любой его форме;
— процентная ставка — относительная величина дохода за фиксированный интервал времени, измеряемая в процентах или в виде дроби, которая используется в качестве измерителя уровня (нормы) доходности задачу — нахождение величины на заданный момент времени по ее известному или предполагаемому значению в будущем.
Ввиду ограниченного объема данного учебного пособия, теоретические вопросы описания методов, расчетов, способов, определений, а также и другие характеристики рекомендуется изучать в специальной литературе [7].
1.2. Специфика использования финансовых функций Excel
Финансовые функции Excel предназначены для вычисления базовых величин, необходимых при проведении сложных финансовых расчетов. Методика изучения и использования финансовых функций Excel требует соблюдения определенной технологии.
1. На рабочем листе в отдельных ячейках осуществляется подготовказначений основных аргументов функции.
2. Для расчета результата финансовой функции Excel курсор устанавливается в новую ячейку для ввода формулы, использующей встроенную финансовую функцию; если финансовая функция вызывается в продолжение ввода другой формулы, данный пункт опускается.
3. Осуществляется добавление финансовой функции на рабочий листс помощью команды Формулы, из библиотеки функций активизацией опции Финансовые функции или одновременным нажатием клавиш Shift-F3, а также нажатием одноименной кнопки fx — Вставить функцию на панели инструментов Стандартная.
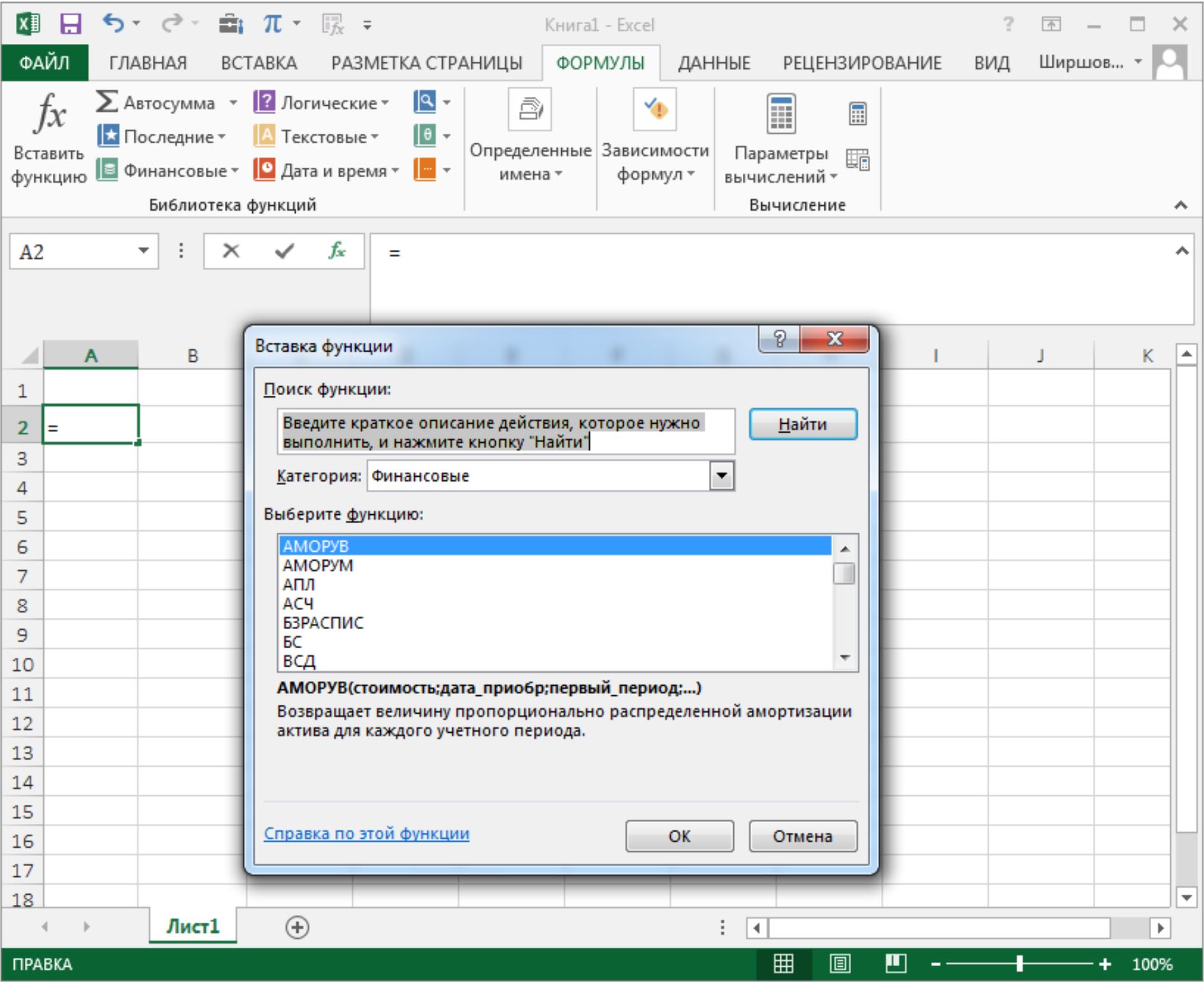
4. Выполняется выбор категории Финансовые (рис. 2). В списке Категория содержится полный перечень доступных функций выбранной категории. Поиск функции осуществляется путем последовательного просмотра списка. Для выбора функции курсор устанавливается на имя функции. В нижней части окна приведен краткий синтаксис и справка о назначении выбираемой функции. Кнопка Справка по этой функции вызывает экран справки для встроенной функции, на которой установлен курсор. Кнопка Отмена прекращает работу опции Вставка функции. При нажатии на кнопку ОК осуществляется переход к работе с диалоговым окном выбранной функции.
Рис. 2. Экран вызова опции Вставка функции
В списке Категория содержится полный перечень доступных функций выбранной категории. Поиск функции осуществляется путем последовательного просмотра списка. Для выбора функции курсор устанавливается на имя функции. В нижней части окна приведен краткий синтаксис и справка о назначении выбираемой функции. Кнопка Справка по этой функции вызывает экран справки для встроенной функции, на которой установлен курсор. Кнопка Отмена прекращает работу опции Вставка функции. При нажатии на кнопку ОК осуществляется переход к работе с диалоговым окном выбранной функции.
5. Выполняется выбор в списке требуемой финансовой функции, в результате выбора появляется диалоговое окно для ввода аргументов (рис. 2). Для каждой финансовой функции существует регламентированный по составу и формату значений перечень аргументов.
6. В поля ввода диалогового окна можно вводить как ссылки на адреса ячеек, содержащих собственно значения аргументов, так и сами значения аргументов.
7. Если аргумент является результатом расчета другой встроеннойфункции Excel, возможно организовать вычисление вложенной встроенной функции путем вызова опции Вставка функции одноименной кнопкой, расположенной перед полем ввода аргумента.
8. Возможна работа с экраном справки, поясняющей назначение иправила задания аргументов функции; вызов справки осуществляется путем нажатия кнопки Справка по этой функции.
9. Для отказа от работы со встроенной функцией нажимается кнопка Отмена.
10. Завершение ввода аргументов и запуск расчета значения встроенной функции выполняется нажатием кнопки ОК.
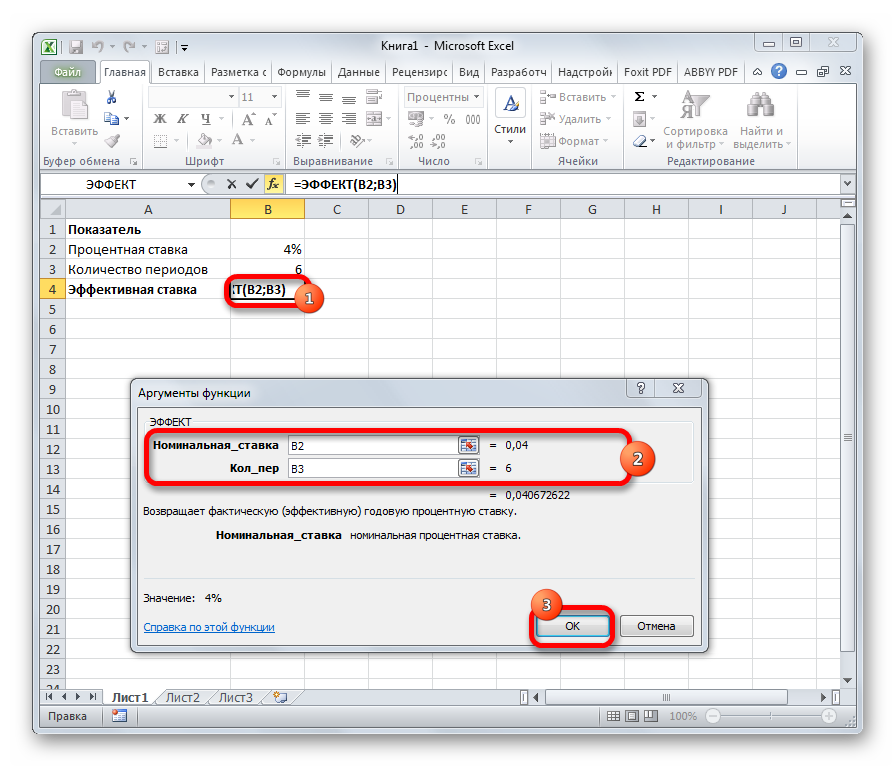
При необходимости корректировки значений аргументов функции (изменения ссылок, постоянных значений и т.п.) необходимо установить курсор в ячейку, содержащую формулу, и вызвать кнопку fx — Вставить функцию. При этом появляется окно для редактирования (рис. 3).
Рис.3. Диалоговое окно ввода аргументов функции
Возможен вариант непосредственного ввода формулы, содержащей имена и параметры встроенных финансовых функций.
Формула начинается со знака =. Далее следует имя функции, а в круглых скобках указываются её аргументы в последовательности, соответствующей синтаксису функции. В качестве разделителя аргументов используется выбранный при настройке Windows разделитель, обычно это точка с запятой или запятая.
Безусловно, функцию можно ввести, набрав ее прямо в ячейке. Однако Microsoft Excel предоставляет на стандартной панели инструментов кнопку fx — Вставить функцию (см. рис. 4).
Рис. 4. Стандартная панель инструментов (кнопка Вставитьфункцию)
Специфика задания значений аргументов финансовых функций заключается в следующем:
— все аргументы, означающие расходы денежных средств, представляются отрицательными числами (например, ежегодные платежи), а аргументы, означающие поступления, представляются положительными числами (например, дивиденды);
— все даты как аргументы функции имеют числовой формат представления, например, дата 1 января 1995 года представлена числом 34700. Если значение аргумента типа дата берется из ячейки, то дата в ячейке может быть записана в обычном виде;
— для аргументов типа логический возможен непосредственный ввод констант типа ИСТИНА или ЛОЖЬ, либо использование встроенных функций аналогичного названия категории Логические
Конец ознакомительного фрагмента.
Смотрите также
Финансовые функции Excel предназначены для вычисления базовых величин, необходимых при проведении сложных финансовых расчетов. Методика изучения и использования финансовых функций Excel требует соблюдения определенной технологии.
1. На рабочем листе в отдельных ячейках осуществляется подготовказначений основных аргументов функции.
2. Для расчета результата финансовой функции Excel курсор устанавливается в новую ячейку для ввода формулы, использующей встроенную финансовую функцию; если финансовая функция вызывается в продолжение ввода другой формулы, данный пункт опускается.
3. Осуществляется добавление финансовой функции на рабочий листс помощью команды Формулы, из библиотеки функций активизацией опции Финансовые функции или одновременным нажатием клавиш Shift-F3, а также нажатием одноименной кнопки fx – Вставить функцию на панели инструментов Стандартная.
4. Выполняется выбор категории Финансовые (рис. 2). В списке Категория содержится полный перечень доступных функций выбранной категории. Поиск функции осуществляется путем последовательного просмотра списка. Для выбора функции курсор устанавливается на имя функции. В нижней части окна приведен краткий синтаксис и справка о назначении выбираемой функции. Кнопка Справка по этой функции вызывает экран справки для встроенной функции, на которой установлен курсор. Кнопка Отмена прекращает работу опции Вставка функции. При нажатии на кнопку ОК осуществляется переход к работе с диалоговым окном выбранной функции.
Рис. 2. Экран вызова опции Вставка функции
В списке Категория содержится полный перечень доступных функций выбранной категории. Поиск функции осуществляется путем последовательного просмотра списка. Для выбора функции курсор устанавливается на имя функции. В нижней части окна приведен краткий синтаксис и справка о назначении выбираемой функции. Кнопка Справка по этой функции вызывает экран справки для встроенной функции, на которой установлен курсор. Кнопка Отмена прекращает работу опции Вставка функции. При нажатии на кнопку ОК осуществляется переход к работе с диалоговым окном выбранной функции.
5. Выполняется выбор в списке требуемой финансовой функции, в результате выбора появляется диалоговое окно для ввода аргументов (рис. 2). Для каждой финансовой функции существует регламентированный по составу и формату значений перечень аргументов.
6. В поля ввода диалогового окна можно вводить как ссылки на адреса ячеек, содержащих собственно значения аргументов, так и сами значения аргументов.
7. Если аргумент является результатом расчета другой встроеннойфункции Excel, возможно организовать вычисление вложенной встроенной функции путем вызова опции Вставка функции одноименной кнопкой, расположенной перед полем ввода аргумента.
8. Возможна работа с экраном справки, поясняющей назначение иправила задания аргументов функции; вызов справки осуществляется путем нажатия кнопки Справка по этой функции.
9. Для отказа от работы со встроенной функцией нажимается кнопка Отмена.
10. Завершение ввода аргументов и запуск расчета значения встроенной функции выполняется нажатием кнопки ОК.
При необходимости корректировки значений аргументов функции (изменения ссылок, постоянных значений и т.п.) необходимо установить курсор в ячейку, содержащую формулу, и вызвать кнопку fx – Вставить функцию. При этом появляется окно для редактирования (рис. 3).
Рис.3. Диалоговое окно ввода аргументов функции
Возможен вариант непосредственного ввода формулы, содержащей имена и параметры встроенных финансовых функций.
Формула начинается со знака =. Далее следует имя функции, а в круглых скобках указываются её аргументы в последовательности, соответствующей синтаксису функции. В качестве разделителя аргументов используется выбранный при настройке Windows разделитель, обычно это точка с запятой или запятая.
Безусловно, функцию можно ввести, набрав ее прямо в ячейке. Однако Microsoft Excel предоставляет на стандартной панели инструментов кнопку fx – Вставить функцию (см. рис. 4).
Рис. 4. Стандартная панель инструментов (кнопка Вставитьфункцию)
Специфика задания значений аргументов финансовых функций заключается в следующем:
– все аргументы, означающие расходы денежных средств, представляются отрицательными числами (например, ежегодные платежи), а аргументы, означающие поступления, представляются положительными числами (например, дивиденды);
– все даты как аргументы функции имеют числовой формат представления, например, дата 1 января 1995 года представлена числом 34700. Если значение аргумента типа дата берется из ячейки, то дата в ячейке может быть записана в обычном виде;
– для аргументов типа логический возможен непосредственный ввод констант типа ИСТИНА или ЛОЖЬ, либо использование встроенных функций аналогичного названия категории Логические;
– при непосредственном вводе формулы в ячейку необходимо следить за тем, чтобы каждый аргумент находился строго на своем месте. Если какие-то аргументы не используются, то необходимо поставить соответствующее число разделительных знаков. Если не используется последний аргумент или несколько идущих подряд последних аргументов, то соответствующие разделительные знаки можно опустить (в большинстве случаев это замечание относится к аргументам тип и базис).
Для облегчения восприятия материала учебно-методического пособия все финансовые функции и описание их аргументов представлены в прил. 1, табл. 1-6.
2. Функции для анализа инвестиций
2.1. Функции для расчета операций по кредитам и займам
В данном разделе показано применение функций Excel, использующих базовые модели финансовых операций. Изложение материала ведется в терминах пакета Excel.
В Excel существует группа функций, предназначенная для расчета финансовых операций по кредитам, ссудам, займам. Эти расчеты основаны на концепции временной стоимости денег, относящихся к разным моментам времени. Эта группа функций охватывает следующие расчеты:
– определение наращенной суммы (будущей стоимости);
– определение начального значения (текущей стоимости);
– определение срока платежа и процентной ставки;
– расчет периодических платежей, связанных с погашением займов.
Понятие будущей стоимости основано на принципе неравноценности денег, относящихся к разным моментам времени. Вложения, сделанные сегодня, в будущем составят большую величину. Эта группа функций позволяет рассчитать:
– будущую или наращенную стоимость серии фиксированных периодических платежей, а также будущую стоимость текущего значения вклада или займа при постоянной процентной ставке;
– будущее значение инвестиции после начисления сложных процентов при переменной процентной ставке.
Во многих задачах используется и понятие текущей (современной) стоимости будущих доходов и расходов. Это понятие базируется на положении о том, что на начальный момент времени полученная в будущем сумма денег имеет меньшую стоимость, чем ее эквивалент, полученный в начальный момент времени.
Согласно концепции временной стоимости денег, расходы и до ходы, не относящиеся к одному моменту времени, можно сопоставить путем приведения к одному сроку (т.е. путем дисконтирования). Текущая стоимость получается как результат приведения будущих доходов и расходов к начальному периоду времени. Excel содержит ряд функций, которые позволяют рассчитать:
– текущую стоимость единой суммы вклада (займа) и фиксированных периодических платежей;
– чистую текущую стоимость будущих периодических расходов и поступлений переменной величины;
– чистую текущую стоимость нерегулярных расходов и поступлений переменной величины.
Функции для определения срока платежа и процентной ставки позволяют находить величины, расчет которых весьма затруднен, если ведется вручную. К ним относятся:
– общее число периодов постоянных выплат, необходимых для достижения заданного будущего значения; число периодов, через которое начальная сумма займа (вклада) достигнет заданного значения;
– значение постоянной процентной ставки за один период серии фиксированных периодических платежей; значение ставки процента по вкладу или займу.
При выпуске ценных бумаг, заключении финансовых контрактов, займах на долговом соглашении указывается годовая номинальная процентная ставка и период начисления (год, полугодие, квартал).
Начисление процентов по номинальной ставке производится по формуле сложных процентов. Годовая ставка, обеспечивающая тот же доход, что и номинальная ставка после начисления сложных процентов, – это эффективная процентная ставка. Номинальная и эффективная процентная ставки эквивалентны по финансовому результату.
Функции Excel также позволяют вычислять следующие величины, связанные с периодическими выплатами:
– периодические платежи, осуществляемые на основе постоянной процентной ставки и не меняющиеся за все время расчета;
– платежи по процентам за конкретный период;
– сумму платежей по процентам за несколько периодов, идущих основные платежи по займу (за вычетом процентов) за конкретный период;
– сумму основных платежей за несколько периодов, идущих подряд.
Все эти величины вычисляются, например, при расчете схемы равномерного погашения займа. Допустим, что заем погашается одинаковыми платежами в конце каждого расчетного периода. Будущая стоимость этих платежей будет равна сумме займа с начисленными процентами к концу последнего расчетного периода, если в нем предполагается полное погашение займа.
С другой стороны, текущая стоимость выплат по займу должна равняться настоящей сумме займа. Если известна сумма займа, ставка процента, срок, на который выдан заем, то можно рассчитать сумму постоянных периодических платежей, необходимых для равномерного погашения займа.
Задача : Предположим, что открыт льготный (не облагаемый налогами) пенсионный счет. При этом планируется вносить на счет 2000$ в начале каждого года в расчете на среднюю скорость оборота 11 % в год на протяжении всего срока. Если считать, что клиенту сейчас 30 лет, то какая сумма будет аккумулирована на его счету, когда ему исполниться 65 лет, и если клиент открыл счет три года назад и на настоящий момент уже накопил 7500$?
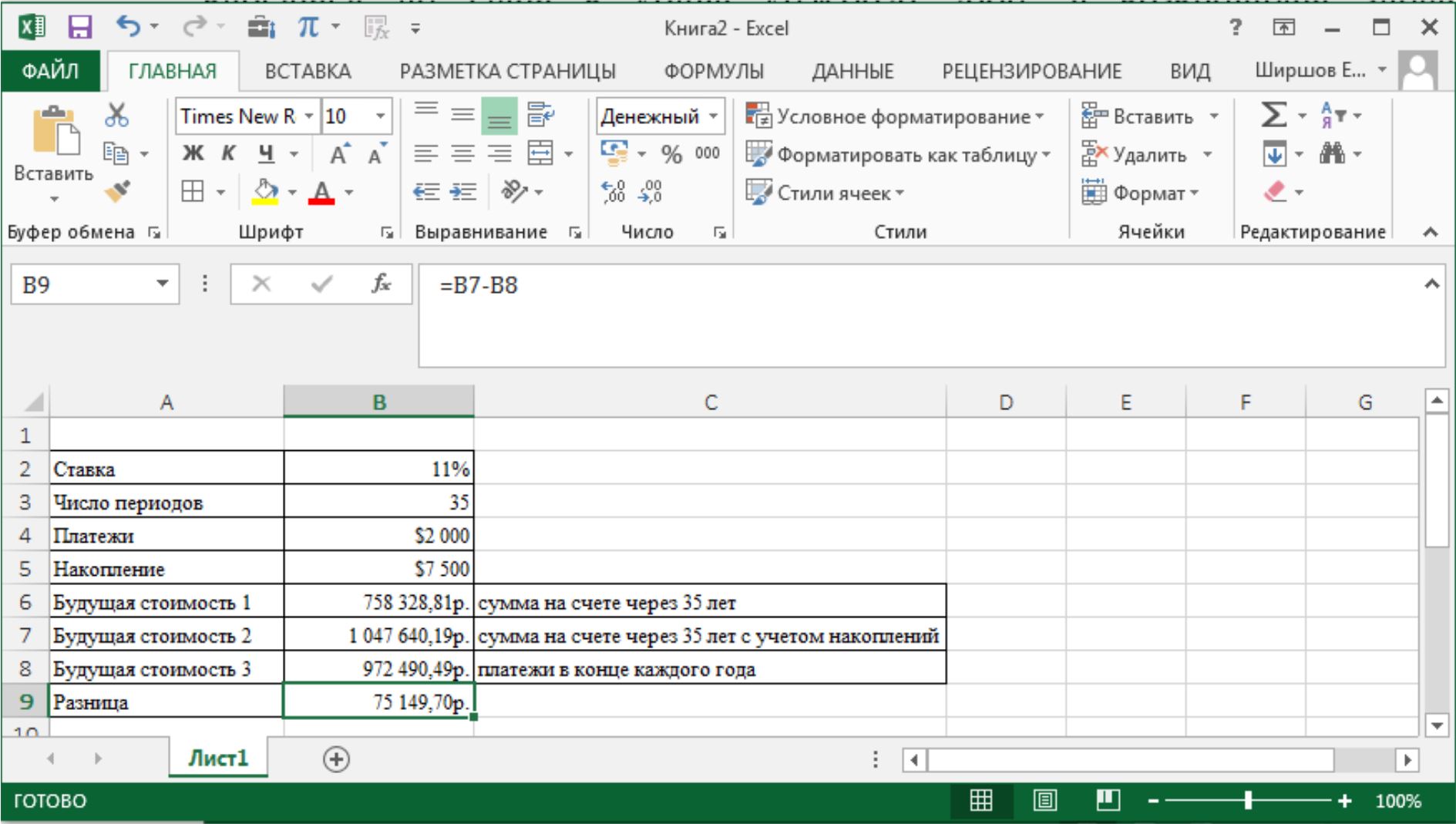
Ответ : = БС (11 %;35; -2000;; 1) через 35 лет на счете клиента будет 758328,81$; = БС (11 %; 35; -2000; -7500; 2) с накоплением через 35 лет на счете клиента будет 1047640,19$. В этих двух примерах аргумент тип равен 1, поскольку выплаты производятся в начале периодов. Если опуститьаргументтипвпоследнейформуле, т.е. предполагается, что деньгивносятсянасчетвконцекаждогогода, Excel возвращаетзначение 972490,49$. Разницасоставляетбольше 75000$!
Рис. 5. Пример решения задачи по теме: «Функции для расчета операций по кредитам и займам»
Задания для самостоятельной работы
1. Рассчитать, какая сумма окажется на счете, если 27 тыс. руб. положенына 33 года под 13,5 % годовых. Проценты начисляются каждые полгода.
2. Предположим, есть два варианта инвестирования средств в течение 4лет: в начале каждого года под 26 % годовых или в конце каждого года под 38 % годовых. Пусть ежегодно вносится 300 тыс. руб. Определить, сколько денег окажется на счете в конце 4-го года для каждого варианта.
3. Предположим, Вы хотите зарезервировать деньги для специального проекта, который будет осуществлен через год. Предположим, Вы собираетесь вложить 1000 рублей под 6 % годовых (что составит в месяц 6 %/12 или 0,5 %). Вы собираетесь вкладывать по 100 рублей в начале каждого следующего месяца в течение следующих 12 месяцев. Сколько денег будет на счету в конце 12 месяцев?
4. Рассчитать, какая сумма будет на счете, если сумма размером5000 тыс. руб. размещена под 12 % годовых на 3 года, а проценты начисляются каждые полгода.
5. По вкладу размером 2000 тыс. руб. начисляется 10 % годовых.Рассчитать, какая сумма будет на сберегательном счете через 5 лет, если проценты начисляются ежемесячно.
6. На сберегательный счет вносятся платежи по 200 тыс. руб. в начале каждого месяца. Рассчитать, какая сумма окажется на счете через 4 года при ставке процента 13,5 % годовых.
7. На сберегательный счет вносятся платежи по 200 тыс. руб. в конце каждого месяца. Рассчитать, какая сумма окажется на счете через 4 года при ставке процента 13,5 % годовых.
8. По облигации номиналом 100 тыс. руб., выпущенной на 6 лет, предусмотрен следующий порядок начисления процентов: в первый год – 10 %, в два последующих года – 20 %, в оставшиеся три года – 25 %. Рассчитать будущую (наращенную) стоимость облигации по сложной процентной ставке.
9. Исходя из плана начисления процентов, приведенного в предыдущей задаче, рассчитать номинал облигации, если известно, что ее будущая стоимость составила 1546,88 тыс. руб. При решении использовать аппарат подбора параметра программы Excel.
10. Рассчитать будущую стоимость облигации номиналом 300 тыс. руб., выпущенной на 5 лет, если предусмотрен следующий порядок начисления процентов: в первые два года – 13,5 % годовых, в следующие два года – 15 % и в последний год – 20 % годовых.
11. Ожидается, что будущая стоимость инвестиции размером 1500 тыс. руб. к концу 4-го года составит 3000 тыс. руб. При этом за первый год доходность составит 15 %, за второй – 17 %, за четвертый – 23 %. Рассчитать доходность инвестиции за третий год. При решении использовать аппарат Подбора параметра Excel.
12. Предположим, что представилась возможность вложения, которое ежегодно возвращает 1000$ в течение следующих пяти лет. Но для этого нужно вложить 4000$. Имеет ли смысл выкладывать 4000$ сегодня, чтобы заработать 5000$ в течение следующих пяти лет? Для решения задачи определить текущую стоимость ряда поступления, полагая, что деньги можно положить на краткосрочный счет под 4,5 % (барьерная ставка).
13. Используя данные из предыдущего примера, предположим, что клиент получит 5000$ в конце пятого года, а не по 1000$ в каждый из последующих пяти годов. Будет ли это вложение выгодным?
14. Имеется возможность вложения капитала, которое обещает принести убыток в размере 55000$ в конце первого года, но затем дать прибыль 95000$, 140000$ и 185000$ в конце второго, третьего и четвертого года. При этом необходимо вложить авансом 250000$, а барьерная ставка должна быть равна 12 %. Можно ли рассчитывать на получение чистой прибыли от этого вложения?
15. Предположим, что Вы намерены выкупить страховку, по которой выплачивается по 500 руб. в конце каждого месяца в течение 20 последующих лет. Стоимость ренты составляет 60 000 руб. и выплачиваемые деньги принесут 8 % годовых. Вы хотите определить, будет ли это хорошим способом инвестировать капитал. Какую финансовую функцию необходимо использовать, чтобы рассчитать настоящий объем вклада?
16. Фирме потребуется 5000 тыс. руб. через 12 лет. В настоящее время фирма располагает деньгами и готова положить их на депозит единым вкладом, чтобы через 12 лет он достиг 5000 тыс. руб. Определить необходимую сумму текущего вклада, если ставка процента по нему составляет 12 % в год.
17. Предположим, рассматриваются два варианта покупки дома: заплатить сразу 99000 тыс. руб. или в рассрочку – по 940 тыс. руб. ежемесячно в течение 15 лет. Определить, какой вариант предпочтительнее, если ставка процента – 8 % годовых.
18. Рассчитать текущую стоимость вклада, который через три года составить 15000 тыс. руб. при начислении 20 % в год.
19. Определить текущую стоимость обязательных ежемесячных платежей размером 100 тыс. руб. в течение 5 лет, если процентная ставка составляет 12 % годовых.
20. Определить текущую стоимость обычных ежемесячных платежейразмером 50 тыс. руб. в течение двух лет при начислении 18 % годовых.
21. Рассчитайте, какую сумму необходимо положить на депозит, чтобы через 4 года она достигла значение 20 млн. руб. при начислении 9 % годовых.
22. Определить текущую стоимость обычных ежеквартальных платежей размером 350 тыс. руб. в течение 7 лет, если ставка процента 11 % годовых.
23. Рассмотрим инвестицию, при которой Вы выплачиваете 10000 руб. через год после сегодняшнего дня и получаете годовые доходы 3000 руб., 4200 руб. 6800 руб. в последующие три года. Предположим, что учетная ставка составляет 10 %, в таком случае рассчитайте чистый текущий объем инвестиции.
24. Рассмотрим инвестиции, которые начинаются в начале первого периода. Допустим, Вы интересуетесь покупкой обувного магазина. Стоимость предприятия – 40 000 руб. и Вы ожидаете получить следующие доходы за первые пять лет: 8 000 руб., 9 200 руб., 10 000 руб., 12 000 руб. и 14 500 руб. Годовая учетная ставка равна 8 %. Она может представлять степень инфляции или учетную ставку конкурирующих инвестиций. Если стоимость и доходы от обувного магазина введены в ячейки от B1 до B6 соответственно, то чему будет равен чистый текущий объем инвестиции в обувной магазин?
25. На основании данных из предыдущей задачи (24) предположим, что на шестой год Ваш магазин потерпел крах, и Вы предполагаете убыток в 9000 руб. для шестого года. Чему будет равен чистый текущий объем инвестиции в обувной магазин после шести лет?
26. Инвестиции в проект к концу первого года его реализации составят 10000 руб. В последующие три года ожидаются годовые доходы по проекту 3000 руб., 4200 руб.. 6800 руб. Издержки привлечения капитала 10 %. Рассчитать чистую текущую стоимость проекта.
27. Можно приобрести оборудование за 40000 руб. наличными. Можно вложить наличность под 8 %. В течение пяти последующих лет в конце каждого года оборудование экономит: 9000, 6000, 6000, 5000 и 5000 руб. соответственно. В конце шестого года оборудование экономит 5000 руб., и его можно продать за 25000 руб. Стоит ли делать такую покупку?
28. Допустим затраты по проекту в начальный момент его реализации составляют 37000 руб., а ожидаемые доходы за первые пять лет: 8000 руб., 9200 руб., 10000 руб., 13900 руб. и 14500 руб. На шестой год ожидается убыток в 5000 руб. Цена капитала 8 % годовых. Рассчитать чистую текущую стоимость проекта.
29. Определить эффективность инвестиций размером 200 млн. руб.по NPV, если ожидаемые ежемесячные доходы за первые пять месяцев составят соответственно: 20, 40, 50, 80 и 100 млн. руб. Издержки привлечения капитала составляют 13,5 % годовых.
30. Рассчитать чистую текущую стоимость проекта, затраты по которому составят 400 млн. руб., а предполагаемые доходы за первые два года реали зации проекта – 40 и 80 млн. руб. Начало реализации проекта – через два года. Норма дисконтирования – 15 % годовых.
31. Инвестиция размером 10 млн. руб. от 01.07.1998 года, которая принесет доходы: 2750 тыс. руб. на 15.09.1998 года, 4250 тыс. руб. на 01.11.1998 года, 5250 тыс. руб. на 01.01.1999 года. Норма дисконтирования 9 %. Определить чистую текущую стоимость инвестиции на 01.07.1998 года и на 01.07.1997 года.
32. Определить чистую текущую стоимость проекта на 1.01.1998, затраты по которому на 20.12.1998 составят 100 млн. руб. Ожидается, что за первые полгода 1999 года проект принесет следующие доходы: на 01.03.1999 –18 млн. руб.; на 15.04.1999 – 40 млн. руб.; на 30.06.1999 – 51 млн. руб. Норма дисконтирования – 12 % годовых.
33. Рассмотрим инвестицию, при которой предполагается выплата наличными 10000 руб. 01.01.1992 года и поступления: 2750 руб. 01.03.1992 года, 4250 руб. 30.10.1992 года, 3250 руб. 15.02.1993 года и 2750 руб. 01.04.1993 года. Определить чистую текущую стоимость инвестиций.
34. Рассчитать, через сколько лет вклад размером 1 млн. руб. достигнет величины 1 млрд. руб., если годовая ставка процента по вкладу 16,79 % и начисление процентов производится ежеквартально.
35. Для обеспечения будущих расходов создается фонд. Средства в фонд поступают в виде постоянной годовой ренты постнумерандо. Размер разового платежа 16 млн. руб. На поступившие взносы начисляется 11,18 % годовых. Необходимо определить, когда величина фонда будет равна 100 млн. руб.
36. Ожидается, что ежегодные доходы от реализации проекта составят 33 млн. руб. Необходимо рассчитать срок окупаемости проекта, если инвестиции к началу поступления доходов составят 100 млн. руб., а норма дисконтирования 12,11 %.
37. Ссуда размером 66000 тыс. руб., выданная под 36 % годовых, погашается обычными ежемесячными платежами по 6630 тыс. руб. Определить срок погашения ссуды.
38. Клиент может выплачивать по закладной 1000$ в месяц. Каков срок, в течение которого он выплатит 100000$, взятых под 8 % годовых.
39. Определить общее количество периодов выплаты для вклада 10000 руб. на основе периодических постоянных выплат, составляющих 100 руб., при общей сумме всех будущих платежей в 1000 руб. и постоянной процентной ставке 12 % годовых.
40. Через сколько лет обязательные ежемесячные платежи размером 150 тыс. руб. принесут доход в 10 млн. руб. при ставке процента 13,5 % годовых?
41. Рассчитать, через сколько лет произойдет полное погашение займа размером 500 тыс. руб., если выплаты по 100 тыс. руб. производятся в конце каждого квартала, а ставка процента – 15 % годовых.
Данный текст является ознакомительным фрагментом.
В Microsoft Excel предусмотрено огромное количество разнообразных функций, позволяющих справляться с математическими, экономическими, финансовыми и другими задачами. Программа является одним из основных инструментов, использующихся в малых, средних и больших организациях для ведения различных видов учета, выполнения расчетов и т.д. Ниже мы рассмотрим финансовые функции, которые наиболее востребованы в Экселе.
- Вставка функции
-
Популярные финансовые функции
- БС
- ВСД
- ДОХОД
- МВСД
- ИНОРМА
- ПЛТ
- ПОЛУЧЕНО
- ПС
- СТАВКА
- ЦЕНА
- ЧПС
- Заключение
Вставка функции
Для начала вспомним, как вставить функцию в ячейку таблицы. Сделать это можно по-разному:
- Выбрав нужную ячейку щелкаем по значку “fx (Вставить функцию)” слева от строки формул.
- Или переключаемся во вкладку “Формулы” и жмем аналогичную кнопку, расположенную в левом углу ленты программы.
Независимо от выбранного варианта, откроется окно вставки функции, в котором требуется выбрать категорию “Финансовые”, определиться с нужным оператором (например, ДОХОД), после чего нажать кнопку OK.
На экране отобразится окно с аргументами функции, которые требуется заполнить, после чего нажать кнопку OK, чтобы добавить ее в выбранную ячейку и получить результат.
Указывать данные можно вручную, используя клавиши клавиатуры (конкретные значения или ссылки на ячейки), либо встав в поле напротив нужного аргумента, выбирать соответствующие элементы в самой таблице (ячейки, диапазон ячеек) с помощью левой кнопки мыши (если это допустимо).
Обратите внимание, что некоторые аргументы могут не показываться и необходимо пролистать область вниз для получения доступа к ним (с помощью вертикального ползункам справа).
Альтернативный способ
Находясь во вкладке “Формулы” можно нажать кнопку “Финансовые” в группе “Библиотека функций”. Раскроется список доступных вариантов, среди которых просто кликаем по нужному.
После этого сразу же откроется окно с аргументами функции для заполнения.
Популярные финансовые функции
Теперь, когда мы разобрались с тем, каким образом функция вставляется в ячейку таблицы Excel, давайте перейдем к перечню финансовых операторов (представлены в алфавитном порядке).
БС
Данный оператор применяется для вычисления будущей стоимости инвестиции исходя из периодических равных платежей (постоянных) и размера процентной ставки (постоянной).
Обязательными аргументами (параметрами) для заполнения являются:
- Ставка – процентная ставка за период;
- Кпер – общее количество периодов выплат;
- Плт – неизменная выплата за каждый период.
Необязательные аргументы:
- Пс – приведенная (нынешняя) стоимость. Если не заполнять, будет принято значение, равное “0”;
- Тип – здесь указывается:
- 0 – выплата в конце периода;
- 1 – выплата в начале периода
- если поле оставить пустым, по умолчанию будет принято нулевое значение.
Также есть возможность вручную ввести формулу функции сразу в выбранной ячейке, минуя окна вставки функции и аргументов.
Синтаксис функции:
=БС(ставка;кпер;плт;[пс];[тип])
Результат в ячейке и выражение в строке формул:
ВСД
Функция позволяет вычислить внутреннюю ставку доходности для ряда денежных потоков, выраженных числами.
Обязательный аргумент всего один – “Значения”, в котором нужно указать массив или координаты диапазона ячеек с числовыми значениями (по крайней мере, одно отрицательное и одно положительное число), по которым будет выполняться расчет.
Необязательный аргумент – “Предположение”. Здесь указывается предполагаемая величина, которая близка к результату ВСД. Если не заполнять данное поле, по умолчанию будет принято значение, равное 10% (или 0,1).
Синтаксис функции:
=ВСД(значения;[предположение])
Результат в ячейке и выражение в строке формул:
ДОХОД
С помощью данного оператора можно посчитать доходность ценных бумаг, по которым производится выплата периодического процента.
Обязательные аргументы:
- Дата_согл – дата соглашения/расчета по ценным бумагам (далее – ц.б.);
- Дата_вступл_в_силу – дата вступления в силу/погашения ц.б.;
- Ставка – годовая купонная ставка ц.б.;
- Цена – цена ц.б. за 100 рублей номинальной стоимости;
- Погашение – суммы погашения или выкупная стоимость ц.б. за 100 руб. номинальной стоимости;
- Частота – количество выплат за год.
Аргумент “Базис” является необязательным, в нем задается способ вычисления дня:
- 0 или не заполнен – армериканский (NASD) 30/360;
- 1 – фактический/фактический;
- 2 – фактический/360;
- 3 – фактический/365;
- 4 – европейский 30/360.
Синтаксис функции:
=ДОХОД(дата_согл;дата_вступл_в_силу;ставка;цена;погашение;частота;[базис])
Результат в ячейке и выражение в строке формул:
МВСД
Оператор используется для расчета внутренней ставки доходности для ряда периодических потоков денежных средств исходя из затрат на привлечение инвестиций, а также процента от реинвестирования денег.
У функции только обязательные аргументы, к которым относятся:
- Значения – указываются отрицательные (платежи) и положительные числа (поступления), представленные в виде массива или ссылок на ячейки. Соответственно, здесь должно быть указано, как минимум, одно положительное и одно отрицательное числовое значение;
- Ставка_финанс – выплачиваемая процентная ставка за оборачиваемые средства;
- Ставка _реинвест – процентная ставка при реинвестировании за оборачиваемые средства.
Синтаксис функции:
=МВСД(значения;ставка_финанс;ставка_реинвест)
Результат в ячейке и выражение в строке формул:
ИНОРМА
Оператор позволяет вычислить процентную ставку для полностью инвестированных ц.б.
Аргументы функции:
- Дата_согл – дата расчета по ц.б.;
- Дата_вступл_в_силу – дата погашения ц.б.;
- Инвестиция – сумма, вложенная в ц.б.;
- Погашение – сумма к получению при погашении ц.б.;
- аргумент “Базис” как и для функции ДОХОД является необязательным.
Синтаксис функции:
=ИНОРМА(дата_согл;дата_вступл_в_силу;инвестиция;погашение;[базис])
Результат в ячейке и выражение в строке формул:
ПЛТ
С помощью этой функции рассчитывается сумма периодического платежа по займу исходя из постоянства платежей и процентной ставки.
Обязательные аргументы:
- Ставка – процентная ставка за период займа;
- Кпер – общее количество периодов выплат;
- Пс – приведенная (нынешняя) стоимость.
Необязательные аргументы:
- Бс – будущая стоимость (баланс после последней выплаты). Если поле оставить незаполненным, по умолчанию будет принято значение, равное “0”.
- Тип – здесь указывается, как будет производиться выплата:
- “0” или не указано – в конце периода;
- “1” – в начале периода.
Синтаксис функции:
=ПЛТ(ставка;кпер;пс;[бс];[тип])
Результат в ячейке и выражение в строке формул:
ПОЛУЧЕНО
Применяется для нахождения суммы, которая будет получена к сроку погашения инвестированных ц.б.
Аргументы функции:
- Дата_согл – дата расчета по ц.б.;
- Дата_вступл_в_силу – дата погашения ц.б.;
- Инвестиция – сумма, инвестированная в ц.б.;
- Дисконт – ставка дисконтирования ц.б.;
- “Базис” – необязательный аргумент (см. функцию ДОХОД).
Синтаксис функции:
=ПОЛУЧЕНО(дата_согл;дата_вступл_в_силу;инвестиция;дисконт;[базис])
Результат в ячейке и выражение в строке формул:
ПС
Оператор используется для нахождения приведенной (т.е. к настоящему моменту) стоимости инвестиции, которая соответствует ряду будущих выплат.
Обязательные аргументы:
- Ставка – процентная ставка за период;
- Кпер – общее количество периодов выплат;
- Плт – неизменная выплата за каждый период.
Необязательные аргументы – такие же как и для функции “ПЛТ”:
- Бс – будущая стоимость;
- Тип.
Синтаксис функции:
=ПС(ставка;кпер;плт;[бс];[тип])
Результат в ячейке и выражение в строке формул:
СТАВКА
Оператор поможет найти процентную ставку по аннуитету (финансовой ренте) за 1 период.
Обязательные аргументы:
- Кпер – общее количество периодов выплат;
- Плт – неизменная выплата за каждый период;
- Пс – приведенная стоимость.
Необязательные аргументы:
- Бс – будущая стоимость (см. функцию ПЛТ);
- Тип (см. функцию ПЛТ);
- Предположение – предполагаемая величина ставки. Если не указывать, будет принято значение по умолчанию – 10% (или 0,1).
Синтаксис функции:
=СТАВКА(кпер;;плт;пс;[бс];[тип];[предположение])
Результат в ячейке и выражение в строке формул:
ЦЕНА
Оператор позволяет найти цену за 100 рублей номинальной стоимости ц.б., по которым производится выплата периодического процента.
Обязательные аргументы:
- Дата_согл – дата расчета по ц.б.;
- Дата_вступл_в_силу – дата погашения ц.б.;
- Ставка – годовая купонная ставка ц.б.;
- Доход – годовой доход по ц.б.;
- Погашение – выкупная стоимость ц.б. за 100 руб. номинальной стоимости;
- Частота – количество выплат за год.
Аргумент “Базис” как и для оператора ДОХОД является необязательным.
Синтаксис функции:
=ЦЕНА(дата_согл;дата_вступл_в_силу;ставка;доход;погашение;частота;[базис])
Результат в ячейке и выражение в строке формул:
ЧПС
С помощью данной функции можно определить чистую приведенную стоимость инвестиции исходя из ставки дисконтирования, а также размера будущих поступлений и платежей.
Аргументы функции:
- Ставка – ставка дисконтирования за 1 период;
- Значение1 – здесь указываются выплаты (отрицательные значения) и поступления (положительные значения) в конце каждого периода. Поле может содержать до 254 значений.
- Если лимит аргумента “Значение 1” исчерпан, можно перейти к заполнению следующих – “Значение2”, “Значение3” и т.д.
Синтаксис функции:
=ЧПС(ставка;значение1;[значение2];...)
Результат в ячейке и выражение в строке формул:
Заключение
Категория “Финансовые” в программе Excel насчитывает свыше 50 различных функций, но многие из них специфичны и узконаправлены, из-за чего используются редко. Мы же рассмотрели 11 самых востребованных, по нашему мнению.