На этой странице разберем подробные решения транспортной задачи (алгоритм и примеры разных типов) с использованием пакета электронных таблиц MS Excel (надстройка Поиск решения).
Как решить транспортную задачу в Excel
Ручное решение транспортной задачи занимает очень много времени и сил (скажем, даже для учебной задачи типа 3*5 решение может составлять от 4 до 10 страниц расчетов!). Тогда как решение в Эксель для задачи размерности как 3*3, так и 5*7 потребует буквально 10-15 минут и немного опыта (правда, если уже составлена математическая модель).
Использовать можно любую версию программы — 2003, 2007, 2010 и так далее, главное, включить использование надстройки Поиск решения (интерфейс может немного отличаться в разных версиях).
Алгоритм решения ТЗ в Эксель
- Составить математическую модель транспортной задачи — то есть получить таблицу со стоимостью перевозок, запасами груза у поставщиков и потребностями потребителей (и, возможно, дополнительными ограничениями).
- Если задача открытая (несбалансированная), то добавить потребителя или поставщика с нулевыми тарифами перевозки.
- Внести на лист таблицы Excel данную модель в виде матрицы тарифов (затрат).
- Создать рядом на листе еще одну таблицу, где будут выводиться искомые перевозки (такой же размерности, что и таблица тарифов). Просуммировать перевозки по строкам и столбцам (чтобы сравнивать с аналогичными ячейками — предельными ограничениями задачи — запасами поставщиков и потребностями потребителей).
- Ввести в ячейку формулу, подсчитывающую суммарную стоимость перевозок (это число мы должны минимизировать по смыслу транспортной задачи)
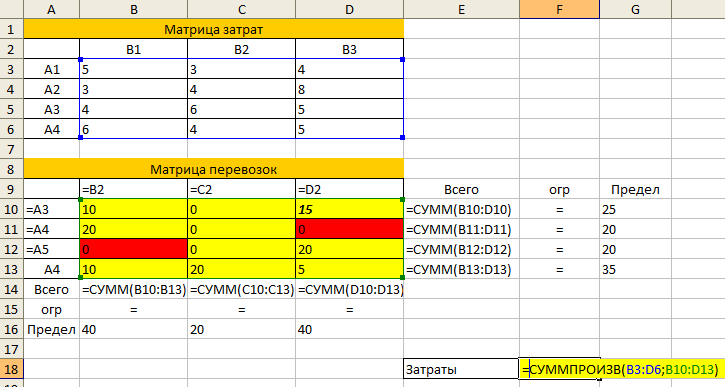
В режиме формул таблица будет выглядеть так:
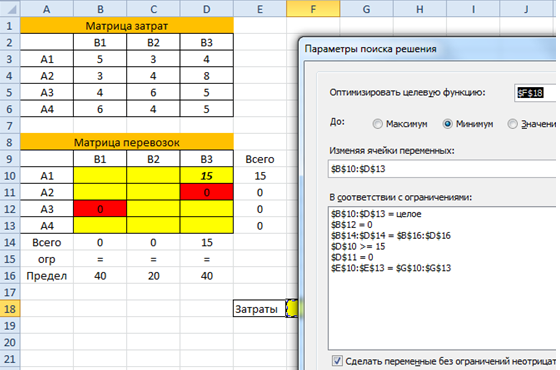
- Запустить надстройку Поиск решения и указать а) ячейку, которую мы минимизируем, б) все ограничения на запасы поставщиков и потребности потребителей, в) дополнительные ограничения (иногда бывают запреты перевозок или требования по минимальному объему груза между определенными пунктами, как в данном случае).
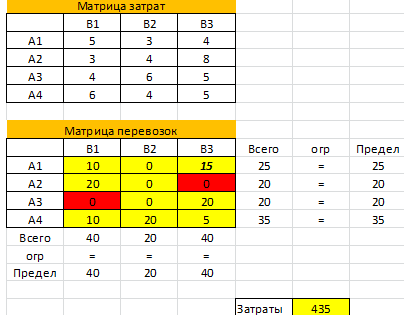
- Получить решение транспортной задачи: в целевой ячейке вы увидите минимальную стоимость перевозок (в примере 435), а в таблице перевозок — искомые значения объема перевозимого груза (см. желтые ячейки).
- Проанализировать решение, если требуется и записать более подробно, например
Минимальные затраты на перевозку составят 435. План перевозок:
Из 1 карьера 10 тонн везем на 1-й участок, 15 тонн на 3-й.
Из 2 карьера 20 тонн везем на 1-й участок.
Из 3 карьера 20 тонн везем на 3-й.
Из 4 карьера 10 тонн везем на 1-й участок, 20 тонн на 2-й, 5 тонн на 3-й.
Понравилось? Добавьте в закладки
Транспортные задачи: примеры в Excel
Задача 1. Решить транспортную задачу вручную (методом потенциалов) и в программе Эксель.
Задача 2. Исходные данные задачи приведены схематически: внутри прямоугольника заданы удельные транспортные затраты на перевозку единицы груза, слева указаны мощности поставщиков, а сверху — мощности потребителей.
Сформулировать экономико-математическую модель исходной транспортной задачи, найти оптимальный план закрепления поставщиков за потребителями, установить единственность или не единственность оптимального плана, используя Поиск решений.
Задача 3. Имеется 3 нефтеперерабатывающих завода, 4 спиртовых завода, 3 завода по производству синтетического каучука.
Схема кооперационных связей (см. файл).
Далее приведены производственные показатели предприятий.
Также заданы расстояния между предприятиями.
Необходимо найти решение транспортной задачи с ориентацией на спрос СК и минимизацией транспортных суммарных затрат.
Задача 4. Используя метод потенциалов, решить транспортную задачу. Выполнить проверку, используя табличный редактор Microsoft Excel Компания владеет тремя заводами А1, А2, А3. Соответствующие объемы производства равны 600, 300 и 330 единиц продукции. Компания обязалась поставить в города В1, В2, В3 и В4 соответственно 350, 350, 230 и 300 единиц. При заданных в таблице стоимостях перевозок единицы продукции составьте план ее распределения, чтобы общая стоимость перевозок была наименьшей.
Задача 5. Свести задачу к виду ТЗ и решить с помощью надстройки «Поиск решения»
Четыре ремонтные мастерские могут за год отремонтировать соответственно 400, 500, 450 и 550 машин при себестоимости ремонта одной машины в 500, 700, 650 и 600 рублей. Планируется годовая потребность в ремонте пяти автобаз: 550, 350, 300, 375 и 400 машин.
Ремонт машин с 1 автобазы должен осуществляться в 100% случаев силами ремонтных мастерских.
На 4 АБ возможно самостоятельное проведение ремонтных работ (бесплатное) в объеме, не превышающем 8% от планируемой годовой потребности этой мастерской. Платное (на стороне) — совсем не возможно.
Вторая, третья и пятая АБ могут «ремонтироваться» на стороне, стоимость ремонта +трансп.расходы каждой машины в таком случае составит 695 руб.
Дана матрица, характеризующая транспортные расходы на доставку машины с j-й автобазы в i-ю ремонтную мастерскую. Определить минимальную годовую потребность в кредитах на выполнение указанного объема работ по всем автобазам
Решаем транспортные задачи любой сложности
Полезные ссылки
|
|
Муниципальное общеобразовательное учреждение
«Лицей» г. Дедовска
«Решение задач по механики в Microsoft Excel и с помощью программы КАЛЬКУЛЯТОР»
Физика
Сердюченко Антон, 9 Б
Научный руководитель:
Семишина Нина Борисовна
Учитель физики МОУ «Лицей» г. Дедовска
Дедовск-2009
СОДЕРЖАНИЕ
ВВЕДЕНИЕ . . . . . . . . . . 3
ГЛАВА 1. ПРОГРАММА Microsoft Excel . . . . . . 4
1.1 Работа в программе Microsoft Excel . . . . . 4
1.2 История . . . . . . . . . 4
1.3 Форматы файлов . . . . . . . . 6
1.4 Новые форматы Excel 2007 . . . . . . 6
1.5 Экспорт и перемещение таблиц. Основы электронных таблиц 7
1.6 Формулы и функции. Выбор встроенных функций . . 9
1.7 Программирование . . . . . . . . 10
ГЛАВА 2. НЕМНОГО О МЕХАНИКЕ . . . . . . 11
2.1 Механика . . . . . . . . . 11
2.2 Разделы механики. Классическая механика . . . . 11
2.3 Кинематика и динамика . . . . . . . 12
2.4 Принцип относительности Галилея. Работа, мощность, энергия 14
ГЛАВА 3. РЕШЕНИЕ ЗАДАЧ В ПРОГРАММАХ MICROSOFT EXCEL И КАЛЬКУЛЯТОР . . . . . . . . . . 16
3.1 Второй закон Ньютона . . . . . . . 16
3.2 Движение искусственных спутников и планет . . . 17
3.3 Движение по наклонной плоскости . . . . . 19
3.4 Движение под действием силы тяжести по вертикали . . 25
3.5 Движение связанных тел . . . . . . . 27
ЗАКЛЮЧЕНИЕ . . . . . . . . . . 29
СПИСОК ЛИТЕРАТУРЫ . . . . . . . . 30
ВВЕДЕНИЕ
Моя работа адресована всем, кто интересуется физикой. В наше время знание основ физики необходимо каждому, и особенно тем, кто решил избрать физику своей профессией.
А что может быть важнее выбора профессии? Найти любимое дело – значит не только приносить пользу обществу, но и постоянно испытывать чувство внутреннего удовлетворения.
Одна из главных задач моей работы – показать, как с помощью компьютерных программ Microsoft Excel и КАЛЬКУЛЯТОР решаются сложные задачи по физике.
ГЛАВА 1. ПРОГРАММА Microsoft Excel
1.1 Работа в программе Microsoft Excel
Microsoft Excel (также иногда называется Microsoft Office Excel) — программа для работы с электронными таблицами, созданная корпорацией Microsoft для Microsoft Windows, Windows NT и Mac OS. Она предоставляет возможности расчетов, графические инструменты, и, за исключением Excel 2008 под Mac OS X, язык макропрограммирования VBA (Visual Basic для приложений). Фактически это самый популярный табличный процессор, доступный на этих платформах, и является таковым с версии 5 от 1993 года, входя в состав Microsoft Office. На сегодняшний день Excel является одним из наиболее популярных приложений в мире [2, c.20].
1.2 История
В 1982 году Microsoft запустила на рынок первый электронный табличный процессор Multiplan, который был очень популярен на CP/M системах, но на MS-DOS системах он уступал Lotus 1-2-3. Первая версия Excel предназначалась для Mac и была выпущена в 1985 году, а первая версия для Windows была выпущена в ноябре 1987 года. Lotus не торопилась выпускать 1-2-3 под Windows, и Excel с 1988 года начала обходить по продажам 1-2-3, что в конечном итоге помогло Microsoft достичь позиций ведущего разработчика программного обеспечения. Microsoft укрепляла свое преимущество с выпуском каждой новой версии, что имело место примерно каждые два года. Текущая версия для платформы Windows — Excel 12, также известная как Microsoft Office Excel 2007 [4]. Текущая версия для платформы Mac OS X — Microsoft Excel 2008. В начале своего пути Excel стал причиной иска о товарном знаке от другой компании, уже продававшей пакет программ под названием «Excel». В результате спора Microsoft был обязана использовать название «Microsoft Excel» во всех своих официальных пресс-релизах и юридических документах. Однако со временем эта практика была позабыта, и Microsoft окончательно устранила проблему, приобретя товарный знак другой программы. Microsoft также решила использовать буквы XL как сокращенное название программы: иконка Windows-программы состоит из стилизованного изображения этих двух букв, а расширение файлов по умолчанию в Excel — .xls. В сравнении с первыми табличными процессорами Excel представляет множество новых функций пользовательского интерфейса, но суть остается прежней: как и в программе-родоначальнике VisiCalc ячейки расставляются в строки и столбцы и могут содержать данные или формулы с относительными или абсолютными ссылками на другие клетки.
Excel был первым табличным процессором, позволявшим пользователю менять внешний вид таблицы (шрифты, символы и внешний вид ячеек). Он также первым представил метод умного пересчета ячеек, когда обновляются только те ячейки, которые зависят от измененных ячеек (раньше табличные процессоры либо постоянно пересчитывали все ячейки или ждали команды пользователя). Будучи впервые объединенными в Microsoft Office в 1993 году, Microsoft Word и Microsoft PowerPoint получили новый графический интерфейс для соответствия Excel, главного стимула модернизации ПК в то время [5, c.12].
Начиная с 1993 года, в состав Excel входит Visual Basic для приложений (VBA), язык программирования, основанный на Visual Basic, позволяющий автоматизировать задачи Excel. VBA является мощным дополнением к приложению, которое в более поздних версиях стало включать полную интегрированную среду разработки. Можно создать VBA-код, повторяющий действия пользователя, позволяя таким образом автоматизировать простые задачи. VBA позволяет создавать формы для общения с пользователем. Язык поддерживает использование (но не создание) DLL от ActiveX; более поздние версии позволяют использовать основы объектно-ориентированного программирования. Функциональность VBA сделала Excel мишенью для макровирусов. Это было серьезной проблемой до тех пор, пока антивирусные продукты не стали их обнаруживать. Microsoft с опозданием приняла меры для уменьшения риска, добавив возможность полностью отключить макросы, включить макросы при открытии документа или доверять всем макросам, подписанных с использованием достоверных сертификатов. Версии Excel от 5.0 до 9.0 содержат различные «пасхальные яйца», хотя, начиная с версии 10 Microsoft начала принимать меры для ликвидации таких недокументированных возможностей своих продуктов.
1.3 Форматы файлов
Microsoft Excel вплоть до 2007 версии использовал свой собственный бинарный формат файлов (BIFF) в качестве основного. Excel 2007 использует Microsoft Office Open XML в качестве своего основного формата. Не смотря на то, что Excel 2007 поддерживает и направлен на использование новых XML-форматов в качестве основных, он по-прежнему совместим с традиционными бинарными форматами. Кроме того, большинство версий Microsoft Excel могут читать CSV, DBF, SYLK, DIF и другие форматы [3, c.30].
|
1.4 Новые форматы Excel 2007 |
||
|
Формат |
Расширение |
Примечания |
|
Рабочая книга Excel |
.xlsx |
Стандартный формат рабочих книг Excel 2007. В действительности это сжатый ZIP-архив каталога XML документов. Является заменой бывшего бинарного формата .xls, хотя и не поддерживает макросы по соображениям безопасности. |
|
Рабочая книга Excel с макросами |
.xlsm |
Та же рабочая книга Excel, но с поддержкой макросов. |
|
Бинарная рабочая книга Excel |
.xlsb |
Та же рабочая книга Excel с макросами, но хранящая информацию в бинарном формате, открывая документы быстрее чем XML. В особенности часто используется для очень больших документов с десятками тысяч строк иили сотнями колонок. |
|
Шаблон Excel с макросами |
.xltm |
Шаблон, созданный как основа для рабочих книг, включена поддержка макросов. Заменяет старый формат .xlt. |
|
Надстройка Excel |
.xlam |
Надстройка Excel, направленная на добавление дополнительных функциональных возможностей и инструментов. |
1.5 Экспорт и перемещение таблиц. Основы электронных таблиц
API позволяет открывать таблицы Excel в ряде других приложений. Это включает в себя открытие документов Excel на веб-страницах с помощью ActiveX или таких плагинов, как Adobe Flash Player. Проект Apache POI представляет Java-библиотеки для чтения и записи электронных таблиц Excel. Так же предпринимались попытки копировать таблицы Excel в веб-приложения с использованием разделенных запятыми значений.
Электронные таблицы (такие как Microsoft Excel) позволяют составить бюджет, проводить инвентаризацию или следить за расходами организации с помощью персонального компьютера.
Если необходимо оперировать формулами и работать с числами, можно воспользоваться карандашом или калькулятором. Однако вполне вероятно, что мы напишем неверное число, а еще придется самостоятельно пересчитывать все формулы при изменении любого из чисел. Поскольку в состав Microsoft Office входит программа Excel, можно сэкономить свои силы и время, используя для обработки чисел электронные таблицы. Просто вводить числа, создавать формулы и добавлять текстовые строки, чтобы понимать, какую величину представляет каждое число таблицы. Выполнив эту работу, мы сможем отформатировать числа и текстовые строки, чтобы придать таблицам более привлекательный вид.
Рабочий лист, разделенный на строки и столбцы. Рабочий лист выполняет роль обычного бумажного листа, на котором можно писать числа и буквы. Каждый рабочий лист состоит из 256 вертикальных столбцов и 16384 горизонтальных строк. Столбцы обозначают буквами (А, В, С и т.д.). Строки последовательно нумеруются (1,2,3 и т.д.) [5, c. 63].
Ячейки. Ячейка образуется в месте пересечения строки со столбцом. Если мы хотим ввести данные в рабочий лист, то должны ввести их в определенную ячейку. Каждая ячейка задается заголовком столбца и следующим за ним номером строки. Например, ячейка, образованная пересечением столбца G и строки 12, называется G12.
Числа. Числа могут представлять собой денежные суммы, размеры или количество, например 50000 руб., 309 или 0,094.
Текстовые строки. Текстовые строки указывают, что означает то или иное число на тот случай если мы это забудем. Примерами текстовых строк могут быть подписи типа Май, западные области или Сумма, потерянная нами по глупости тетушка [5, c. 64].
Формулы. Формула позволяет нам получать результат математических преобразований введенных чисел. Формула может быть очень простой, как, например, суммирование двух чисел, либо очень сложной, как, например, взятие тройного интеграла от уравнения, которое никому не нужно [5, c. 67].
1.6 Формулы и функции. Выбор встроенных функций
Можно потратить всю ночь, пересчитывая в столбик, суммируя на бумаге или с помощью калькулятора цифры в строках и столбцах огромной таблицы, но лучше сделать это с помощь программы Microsoft Excel. Просто необходимо сказать Excel, что мы хотим сосчитать и откуда взять исходные данные, а программа сама в считанные секунды выполнит всю работу за вас и покажет результат. Помимо простого суммирования, вычитания, деления и умножения, в Excel можно выполнять более сложные функции. У нас всегда будут под рукой встроенные статистические, математические и финансовые функции, которые скажут, сколько денег ежемесячно могли бы получить, если бы вложили все наличные в акции компании Рога и копыта [3, c. 57].
Необходимо написать формулу расчета амортизации имущества за указанный период с использованием метода постоянного учета амортизации. Вместо того чтобы составлять громоздкие и сложные формулы, можно воспользоваться списком формул, встроенных в Excel, которые называются функциями. Главное отличие функции от формулы состоит в том, что функция спрашивает, из каких ячеек использовать данные для выполнения операции, в то время как при составлении формул необходимо последовательно выбирать ссылки на ячейки и указывать Excel, надо ли значения из этих ячеек сложить, отнять, умножить или разделить. Для простых вычислений можно использовать свои собственные формулы, но для выполнения действительно сложных расчетов не обойтись без встроенных функций Excel.
1.7 Программирование
Ценной возможностью Excel является возможность писать код на основе Visual Basic для приложений (VBA). Этот код пишется с использованием отдельного от таблиц редактора. Записи таблицы управляются с помощью объектов. С помощью этого кода любые функции или подпрограммы, которые могут быть созданы в семействах языков Basic или Fortran, могут запущены на основе входных данных таблиц, а результаты будут мгновенно записываться кодом в электронные таблицы или будут отображены на диаграммах (графиках). Таблица становятся интерфейсом кода, позволяя легко работать с кодом и его расчетами.
Также можно воспользоваться программой КАЛЬКУЛЯТОР. Калькулятор можно использовать для выполнения операций сложения, вычитания, умножения и деления. Кроме того, калькулятор выполняет и более сложные инженерные и статистические вычисления. Можно производить вычисления, нажимая на кнопки калькулятора или вводя символы с клавиатуры. Кроме того, если включена клавиша NUM LOCK, доступен ввод цифр и действий с цифровой клавиатуры [4].
ГЛАВА 2. НЕМНОГО О МЕХАНИКЕ
2.1 Механика
Механика (греч. μηχανική — искусство построения машин) — наука о движении материальных объектов и взаимодействии между ними; в узком смысле — техническая наука, выделившаяся из прикладной физики. Предельными случаями механики являются небесная механика (механика движения небесных тел и гравитации) и квантовая механика (механика элементарных частиц и других малых тел).
2.2 Разделы механики. Классическая механика
Разделы механики: кинематика, статика, динамика. Основной математический аппарат классической механики: дифференциальное и интегральное исчисление, разработанное специально для этого Ньютоном и Лейбницем. В классической формулировке, механика строится на трёх законах Ньютона. Решение многих задач механики упрощается, если ограничиться только потенциальным взаимодействием тел, поскольку в этом случае интегрирование уравнений движения приводит к закону сохранения энергии.
Классическая механика основана на законах Ньютона, преобразовании скоростей Галилея и существовании инерциальных систем отсчёта. В настоящее время известно три типа ситуаций, в которых классическая механика перестаёт отражать реальность. Свойства микромира не могут быть поняты в рамках классической механики. В частности, в сочетании с термодинамикой она порождает ряд противоречий. Адекватным языком для описания свойств атомов и субатомных частиц является квантовая механика. Подчеркнём, что переход от классической к квантовой механике — это не просто замена уравнений движения, а полная перестройка всей совокупности понятий (что такое физическая величина, наблюдаемое, процесс измерения и т. д.) При скоростях, близких к скорости света, классическая механика также перестаёт работать, и необходимо переходить к специальной теории относительности. Опять же, этот переход подразумевает полный пересмотр парадигмы, а не простое видоизменение уравнений движения.
Если же, пренебрегая новым взглядом на реальность, попытаться всё же привести уравнение движения к виду F = ma, то придётся вводить тензор масс, компоненты которого растут с ростом скорости. Эта конструкция уже долгое время служит источником многочисленных заблуждений, поэтому пользоваться ей не рекомендуется.
Классическая механика становится неэффективной при рассмотрении систем с очень большим числом частиц. В этом случае практически целесообразно переходить к статистической физике [4].
2.3 Кинематика и динамика
Кинематика — изучает геометрические свойства движения тел без учета их масс и действующих на них сил. Рассматривает движение тел без выяснения причин этого движения.
Материальная точка — тело, размерами и формой которого в данных условиях можно пренебречь. Система отсчёта — совокупность тела отсчёта, связанной с ним системы координат и часов. Часы — устройство, в котором протекает периодический процесс, положенный в основу отсчета времени [4]. Траектория движения материальной точки — линия, описываемая этой точкой в пространстве. В зависимости от формы траектории движение может быть прямолинейным или криволинейным. Вектор перемещения — вектор, начальная точка которого совпадает с начальной точкой движения, конец вектора — с конечной. Путь — сумма длин всех участков траектории, пройденных точкой за определенное время. Средняя скорость — отношение модуля вектора перемещения к промежутку времени, в течение которого это перемещение произошло. Мгновенная скорость (скорость) — предел отношения вектора перемещения к промежутку времени, за который это перемещение произошло, при стремлении длительности промежутка времени к нулю. Ускорение — характеристика степени неравномерности движения. Определяет быстроту изменения скорости по модулю и направлению.
Динамика (греч. δύναμις — сила) — раздел механики, в котором изучаются причины возникновения механического движения.
Динамика оперирует такими понятиями, как масса, сила, импульс, энергия. Динамика, базирующаяся на законах Ньютона, называется классической динамикой. Классическая динамика описывает движения объектов со скоростями от долей миллиметров в секунду до километров в секунду. Однако эти методы перестают быть справедливыми для движения объектов очень малых размеров и при движениях со скоростями, близкими к скорости света. Такие движения подчиняются другим законам.
Первый закон Ньютона: существуют такие системы отсчета, в которых изолированная материальная точка сохраняет состояние покоя или равномерно прямолинейно движется. Такие системы отсчета называются инерциальными.
Второй закон Ньютона: в инерциальных системах отсчета геометрическая сумма всех сил действующих на тело равно произведению массы тела на его ускорение. F=ma
Третий закон Ньютона: в инерциальных системах отсчета всякое действие одной (первой) материальной точки на другую (вторую), сопровождается воздействием второй материальной точки на первую, т.е. имеет характер взаимодействия; силы, с которыми взаимодействуют материальные точки, всегда равны по модулю, противоположно направлены, действуют вдоль прямой, соединяющей эти точки, являются силами одной природы и приложены к разным материальным точкам.
2.4 Принцип относительности Галилея. Работа, мощность, энергия
Принцип относительности Галилея: никакими механическими опытами, проводимыми внутри данной инерциальной системы, нельзя установить, покоится эта система или движется. Во всех инерциальных системах отсчета законы механики одинаковы.
Вес тела — сила, с которой тело давит на опору.
Работа силы равна произведению модуля силы на перемещение и на косинус угла между ними. cosα
Мощность — отношение работы ко времени, за которое эта работа была совершена
Кинетическая энергия — величина, равная половине произведения массы тела на квадрат его скорости.
Величину, равную произведению массы тела на g и на высоту тела над поверхностью Земли, называют потенциальной энергией тела в поле силы тяжести.
Консервативные силы — силы, работа которых не зависит от пути, пройденного материальной точкой. Зависит только от перемещения.
Механическая энергия системы — величина, равная сумме кинетической и потенциальной энергий системы. .
Закон сохранения механической энергии ─ в замкнутой системе, в которой действуют только консервативные силы, механическая энергия сохраняется.
Закон всемирного тяготения ─ два любых тела притягиваются друг к другу с силой, прямо пропорциональной массе каждого из них и обратно пропорциональной квадрату расстояния между ними.
Первая космическая скорость.
ГЛАВА 3. РЕШЕНИЕ ЗАДАЧ В ПРОГРАММАХ MICROSOFT EXCEL И КАЛЬКУЛЯТОР
3.1 Второй закон Ньютона
Задача № 1
Найти силу F, под действием которой тело массой m приобрело ускорение a.
|
a |
0.25м/с2 |
2 м/с2 |
0.4 м/с2 |
2 км/с2 |
0.1 м/с2 |
5 см/с2 |
|
m |
8 кг |
3 г |
200 кг |
10 г |
200 кг |
20 т |
Решение:
- Переведем в систему СИ ускорение (м/с2) и массу (кг)
- Запишем второй закон Ньютона:
F = ma
3) Воспользуемся программой Microsoft Excel:
а) столбец А – ускорение
столбец В – масса
столбец С – сила
б) Заполним столбцы А и В данными.
в) В столбец С1 введем расчетную формулу:
= ПРОИЗВЕД (Число1 А1:В1)
Далее получаем ответы:
|
А |
В |
С |
|
|
1 |
0,25 |
8 |
2 |
|
2 |
2 |
0,003 |
0,006 |
|
3 |
0,4 |
200 |
80 |
|
4 |
2000 |
0,01 |
20 |
|
5 |
0,1 |
200 |
20 |
|
6 |
0,05 |
20000 |
1000 |
3.2 Движение искусственных спутников и планет
Задача № 2
Найти ускорение свободного падения g и первую космическую скорость v для планет Солнечной системы, где М-масса планеты, R-средний радиус планеты.
G=6,67×10-11
|
Планета |
M, кг |
R, м |
|
Меркурий |
3,26∙1023 |
2,42∙106 |
|
Венера |
4,88∙1024 |
6,10∙106 |
|
Марс |
6,43∙1023 |
3,38∙106 |
|
Юпитер |
1,90∙1027 |
7,13∙107 |
|
Сатурн |
5,69∙1026 |
6,04∙107 |
|
Уран |
8,69∙1025 |
2,38∙107 |
|
Нептун |
1,04∙1026 |
2,22∙107 |
Решение:
1. Запишем расчетные формулы для задачи:
1) – ускорение свободного падения
2) – первая космическая скорость для планеты Солнечной системы
2. Для решения воспользуемся программой Microsoft Excel:
а) Столбец А ─ планета
Столбец В ─ масса
Столбец С ─ радиус
Столбец D ─ ускорение свободного падения
Столбец E ─ первая космическая скорость
б) Для g: [ = ЧАСТНОЕ(ПРОИЗВЕД(В1;ПРОИЗВЕД(6,67;СТЕПЕНЬ(10;-11)));СТЕПЕНЬ(С1;2))
Для V: [ = КОРЕНЬ(ПРОИЗВЕД(С1:D1))
3. Получаем результат
|
A |
B |
C |
D |
E |
|
Планета |
3,26E+23 |
2,42E+0,6 |
3,00E+00 |
2,69E+0,3 |
|
Меркурий |
4,88E+24 |
6,10E+0,6 |
8,00E+00 |
6,99E+0,3 |
|
Венера |
6,43E+23 |
3,38E+0,6 |
3,00E+00 |
3,18E+0,3 |
|
Марс |
1,90E+27 |
7,13E+0,7 |
2,40E+01 |
4,14E+0,4 |
|
Юпитер |
5,69E+26 |
6,04E+0,7 |
1,00E+01 |
2,46E+0,4 |
|
Сатурн |
8,69E+25 |
2,28E+0,7 |
1,00E+01 |
1,54E+0,4 |
|
Уран |
1,04E+26 |
2,22E+0,7 |
1,40E+01 |
1,76E+0,4 |
4. Благодаря данным мы можем в этой же программе построить диаграмму:
5. Так же можно решить с помощью КАЛЬКУЛЯТОРА (в инженерном режиме):
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
|
0 |
6 |
∙ |
6 |
7 |
ВП |
1 |
1 |
/-/ |
П→x1 |
× |
|
1 |
П→x2 |
F x2 |
÷ |
С/П |
П→x2 |
× |
F√ |
1 |
0 |
0 |
|
2 |
0 |
÷ |
С/П |
F ABT; M – x → П1; R — x→ П2; В/О; С/П ─ ответ g; С/П ─ ответ v, км/с.
3.3Движение по наклонной плоскости
Задача № 3
Поезд массой 3000т движется вниз под уклон, равный 0,003. Коэффициент сопротивления движению равен 0,008. С каким ускорением движется поезд, если сила тяги локомотива равна: а)300 кН; б)150 кН; в)90кН?
Из условия дано:
m =3000т = 3000000кг
sin α = 0,003
µ = 0,008
F1 = 300кН = 300000Н
F2 = 150кН = 150000Н
F3 = 90кН = 90000Н
Найти: а — ?
Решение:
- Начертим рисунок:
- Запишем второй закон Ньютона
- Проекции на оси:
x: -ma = -F+Fтр – mgsinα
y: 0 = N – mgcosα ; Fтр = µN
a = g sinα – µg cosα +
- Подставим данные и получим расчетную формулу:
а = -0,05 +
- Продолжим решение в Microsoft Excel
Столбец А ─ силы
Столбец В ─ ускорение
а: =СУММ (-0,05;ЧАСТНОЕ (А1:3000000))
|
А |
В |
|
300000 |
0,05 |
|
150000 |
0 |
|
90000 |
-0,02 |
Задача № 4
В момент начала наблюдения расстояние между автобусом 1 и мотоциклом 2 было равно S и автобус проходил начало координат (x01=0). Проекции скоростей тел соответственно равны v1x и v2x. Для каждой строки сформулировать условие задачи. Найти: 1) время t встречи автобуса и мотоциклиста; 2) координату x места их встречи; 3) координату x2 мотоцикла в момент времени прохождения автобусом точки, координата которой x1. (S=x02 – x01).
|
№ |
|
|
|
|
|
1 |
600 |
10 |
-20 |
250 |
|
2 |
1400 |
18,6 |
-18,6 |
1400 |
|
3 |
0 |
14 |
18 |
630 |
|
4 |
-283 |
-18 |
-12 |
-364 |
|
5 |
148 |
17 |
21 |
548 |
Решение:
1. Запишем расчетные формулы для задачи:
1) — время встречи автобуса и мотоциклиста
2) — координата между их встречами
3). – координата мотоцикла в момент времени прохождения автобуса точки, координаты которой
.
2. Для решения задачи воспользуемся программой КАЛЬКУЛЯТОР.
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
|
0 |
П→x1 |
П→x2 |
П→x3 |
− |
÷ |
C/П |
П→x2 |
× |
С/П |
П→x4 |
|
1 |
П→x3 |
× |
П→x2 |
÷ |
П→x1 |
+ |
С/П |
F ABT; s ─ x → П1; V1x ─ x → П2; V1x ─ x → П3; x1 ─ x → П4; В/О; С/П ─ ответ t; С/П ─ ответ .
3. Подставив необходимые числа, получается следующий результат.
|
№ |
t, с |
x, м |
|
|
1 |
20 |
200 |
100 |
|
2 |
37,6 |
700 |
0 |
|
3 |
0 |
0 |
810 |
|
4 |
47,2 |
-849 |
-526 |
|
5 |
-37 |
-629 |
825 |
Задача № 5
Уравнения движения двух тел заданы выражениями: x1=x01+v1x t и x2=x02+ v2x t. Найти время и координату места встречи тел.
|
№ |
x01, м |
x02, м/с |
v1x, м/с |
v2x, м/с |
|
1 |
24 |
87 |
4,2 |
2,7 |
|
2 |
63 |
-12 |
-6,2 |
4,1 |
|
3 |
0 |
-17 |
1,1 |
2,6 |
|
4 |
263 |
0 |
0 |
4,9 |
|
5 |
12 |
-12 |
2,1 |
-2,1 |
Решение:
1. Запишем расчетные формулы для задачи:
1) – время встречи тел
2) – координата места встречи
2. Для решения задачи воспользуемся программой КАЛЬКУЛЯТОР.
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
|
1 |
П→x2 |
П→x1 |
П→x3 |
П→x4 |
— |
x→Па (v1x—v2x) |
÷ |
С/П |
П→x3 |
|
|
2 |
П→x2 |
× |
П→x1 |
П→x4 |
× |
— |
П→xa |
÷ |
С/П |
F ABT; x01 ─ x → П1; x02 – x → П2; v1x – x → П3; v2x — x→ П4; В/О; С/П ─ ответ t; С/П ─ ответ x.
3. Подставив необходимые числа, получается следующий результат.
|
№ |
t, c |
x, м |
|
1 |
42 |
200 |
|
2 |
7,3 |
17,8 |
|
3 |
11,3 |
12,5 |
|
4 |
53,7 |
263 |
|
5 |
-5,7 |
0 |
Задача № 6
Судну (лодке, катеру и т.д.) необходимо проехать расстояние s туда и обратно один раз по реке, а другой раз по озеру. Скорость течения воды v1. Скорость судна относительно воды v2. На сколько больше времени займет движение по реке, чем по озеру?
|
№ |
v1, м/с |
v2, м/с |
s, м |
|
1 |
1 |
5 |
240 |
|
2 |
2,13 |
18,6 |
1410 |
|
3 |
0,27 |
3,2 |
480 |
|
4 |
4,2 |
4,6 |
310 |
|
5 |
2,1 |
2,2 |
68 |
Решение:
1. Запишем расчетную формулу для задачи:
— время движения судна.
2. Для решения задачи воспользуемся программой Microsoft Excel, которая позволит быстро решить задачу.
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
|
0 |
П→x2 |
Fx2 |
П→x1 |
Fx2 |
─ |
П→x2 |
× |
П→x3 |
÷ |
П→x1 |
|
1 |
Fx2 |
÷ |
2 |
÷ |
F 1/x |
С/П |
F ABT; v1 – x → П1; v2 — x→ П2; s ─ x → П3; В/О; С/П ─ ответ 𝜟t.
3. Подставив необходимые числа, получается следующий результат.
1) 4; 2) 2,01; 3) 2,15; 4) 675; 5) 634 с.
3.4 Движение под действием силы тяжести по вертикали
Задача № 7
Тело брошено вертикально вверх со скоростью 20м/с. Написать уравнение y=y(t). Найти, через какой промежуток времени тело будет на высоте: а)15 м; б) 20 м; в) 25 м.
Указание. Ось Y направить вертикально вверх; принять, что при t=0 y=0
1) Запишем уравнение движения тела s в проекции на ось:
=>
=>
=>
2) Далее воспользуемся программой Microsoft Excel
а) Столбец А – необходимая h
Столбец В – расчет t1
Столбец С – расчет t2
б) Для t1: = ЧАСТНОЕ (20 — КОРЕНЬ(400-ПРОИЗВЕД (А1;20));10)
t2: = ЧАСТНОЕ (20 + КОРЕНЬ (400-ПРОИЗВЕД (А1;20));10)
И получаем ответ:
|
А |
В |
С |
|
15 |
1 |
3 |
|
20 |
2 |
2 |
|
25 |
— |
— |
Задача № 8
Мальчик вращает в вертикальной плоскости камень, привязанный к веревке длиною r, с частотой . На какую максимальную высоту h может подняться камень после того, как мальчик отпустит веревку?
|
№ |
1 |
2 |
3 |
4 |
5 |
|
r, м |
0,62 |
0,81 |
0,92 |
1,06 |
1,14 |
|
v, c-1 |
2,11 |
1,93 |
1,82 |
1,71 |
1,89 |
Решение:
1. Запишем расчетные формулы для задачи:
— максимальная высота
2. Для решения задачи воспользуемся программой КАЛЬКУЛЯТОР.
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
|
0 |
× |
F |
× |
Fx2 |
2 |
× |
9 |
. |
8 |
1 |
|
1 |
÷ |
С/П |
F ABT; r; В↑; ; В/О; С/П ─ ответ h.
3. Подставив необходимые числа, получается следующий результат.
1)3,44; 2) 4,92; 3) 5,89; 4) 6,61; 5) 9,34 м.
3.5 Движение связанных тел
Задача № 9
С каким ускорением a движутся связанные тела и какова сила натяжения нити Fн? Трением пренебречь. Составить программу для условия: если тело массой m2 движется вправо (вниз), то a>0.
|
№ |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
m2, кг |
0,27 |
0,19 |
0,19 |
0,19 |
0,19 |
0,19 |
0,19 |
0,19 |
|
β,° |
22 |
22 |
90 |
90 |
90 |
48 |
48 |
90 |
|
m1, кг |
0,19 |
0,27 |
0,27 |
0,27 |
0,27 |
0,27 |
0,19 |
0,19 |
|
a,° |
22 |
22 |
0 |
90 |
11 |
0 |
48 |
90 |
Решение:
1. Запишем расчетные формулы для задачи:
1) — ускорение связанных тел
2) — сила натяжения нити
2. Для решения задачи воспользуемся программой КАЛЬКУЛЯТОР.
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
|
0 |
П→x1 |
П→x2 |
F sin |
× |
П→x3 |
П→x4 |
F sin |
× |
─ |
П→x5 |
|
1 |
× |
П→x1 |
П→x3 |
+ |
÷ |
С/П |
П→x4 |
F sin |
П→x5 |
× |
|
2 |
+ |
П→x3 |
× |
С/П |
F ABT; m2 – x → П1; β ─ x→ П2; m1 – x → П3; α ─ x → П4; g ─ x → П5; В/О; С/П ─ ответ a; С/П ─ ответ FH.
3. Подставив необходимые числа, получается следующий результат.
|
№ |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
a, м/с2 |
0,64 |
-0,64 |
4,05 |
-1,71 |
2,95 |
3,01 |
0 |
0 |
|
FH, H |
0,82 |
0,82 |
1,09 |
2,19 |
1,3 |
0,81 |
1,39 |
1,86 |
ЗАКЛЮЧЕНИЕ
Многим из нас после окончания школы доведется работать квалифицированными рабочими, лаборантами, техниками, инженерами, врачами – знание физики и информатики поможет нам лучше овладеть своей профессией.
В своей работе я доказал, что даже очень сложные задачи по физике можно решить легкой подстановкой чисел в специальные компьютерные программы. И наверняка не запутаешься в подстановке больших чисел в сложные формулы!
СПИСОК ЛИТЕРАТУРЫ
1. Левин Александр. Самоучитель полезных программ. Питер, 2007. ─ 794с
2. Левина М. П. 100% Самоучитель работы на компьютере. Технолоджи – 3000, триумф, издательская группа, триумф, технолоджи – 3000, 2007. ─ 240с
3. Рымкевич А. П. Физика. Задачник. 10-11 классы. Дрофа, 2000. ─ 208с
4. Уоллес Вонг Office XP для «Чайников». Диалектика, 2005. ─ 288с
5. http://www.wikipedia.ru
Пользователи Excel давно и успешно применяют программу для решения различных типов задач в разных областях.
Excel – это самая популярная программа в каждом офисе во всем мире. Ее возможности позволяют быстро находить эффективные решения в самых разных сферах деятельности. Программа способна решать различного рода задачи: финансовые, экономические, математические, логические, оптимизационные и многие другие. Для наглядности мы каждое из выше описанных решение задач в Excel и примеры его выполнения.
Решение задач оптимизации в Excel
Оптимизационные модели применяются в экономической и технической сфере. Их цель – подобрать сбалансированное решение, оптимальное в конкретных условиях (количество продаж для получения определенной выручки, лучшее меню, число рейсов и т.п.).
В Excel для решения задач оптимизации используются следующие команды:
Для решения простейших задач применяется команда «Подбор параметра». Самых сложных – «Диспетчер сценариев». Рассмотрим пример решения оптимизационной задачи с помощью надстройки «Поиск решения».
Условие. Фирма производит несколько сортов йогурта. Условно – «1», «2» и «3». Реализовав 100 баночек йогурта «1», предприятие получает 200 рублей. «2» — 250 рублей. «3» — 300 рублей. Сбыт, налажен, но количество имеющегося сырья ограничено. Нужно найти, какой йогурт и в каком объеме необходимо делать, чтобы получить максимальный доход от продаж.
Известные данные (в т.ч. нормы расхода сырья) занесем в таблицу:
На основании этих данных составим рабочую таблицу:
- Количество изделий нам пока неизвестно. Это переменные.
- В столбец «Прибыль» внесены формулы: =200*B11, =250*В12, =300*В13.
- Расход сырья ограничен (это ограничения). В ячейки внесены формулы: =16*B11+13*B12+10*B13 («молоко»); =3*B11+3*B12+3*B13 («закваска»); =0*B11+5*B12+3*B13 («амортизатор») и =0*B11+8*B12+6*B13 («сахар»). То есть мы норму расхода умножили на количество.
- Цель – найти максимально возможную прибыль. Это ячейка С14.
Активизируем команду «Поиск решения» и вносим параметры.
После нажатия кнопки «Выполнить» программа выдает свое решение.
Оптимальный вариант – сконцентрироваться на выпуске йогурта «3» и «1». Йогурт «2» производить не стоит.
Решение финансовых задач в Excel
Чаще всего для этой цели применяются финансовые функции. Рассмотрим пример.
Условие. Рассчитать, какую сумму положить на вклад, чтобы через четыре года образовалось 400 000 рублей. Процентная ставка – 20% годовых. Проценты начисляются ежеквартально.
Оформим исходные данные в виде таблицы:
Так как процентная ставка не меняется в течение всего периода, используем функцию ПС (СТАВКА, КПЕР, ПЛТ, БС, ТИП).
Заполнение аргументов:
- Ставка – 20%/4, т.к. проценты начисляются ежеквартально.
- Кпер – 4*4 (общий срок вклада * число периодов начисления в год).
- Плт – 0. Ничего не пишем, т.к. депозит пополняться не будет.
- Тип – 0.
- БС – сумма, которую мы хотим получить в конце срока вклада.
Вкладчику необходимо вложить эти деньги, поэтому результат отрицательный.
Для проверки правильности решения воспользуемся формулой: ПС = БС / (1 + ставка)кпер. Подставим значения: ПС = 400 000 / (1 + 0,05)16 = 183245.
Решение эконометрики в Excel
Для установления количественных и качественных взаимосвязей применяются математические и статистические методы и модели.
Дано 2 диапазона значений:
Значения Х будут играть роль факторного признака, Y – результативного. Задача – найти коэффициент корреляции.
Для решения этой задачи предусмотрена функция КОРРЕЛ (массив 1; массив 2).
Решение логических задач в Excel
В табличном процессоре есть встроенные логические функции. Любая из них должна содержать хотя бы один оператор сравнения, который определит отношение между элементами (=, >, <, >=, <=). Результат логического выражения – логическое значение ИСТИНА или логическое значение ЛОЖЬ.
Пример задачи. Ученики сдавали зачет. Каждый из них получил отметку. Если больше 4 баллов – зачет сдан. Менее – не сдан.
- Ставим курсор в ячейку С1. Нажимаем значок функций. Выбираем «ЕСЛИ».
- Заполняем аргументы. Логическое выражение – B1>=4. Это условие, при котором логическое значение – ИСТИНА.
- Если ИСТИНА – «Зачет сдал». ЛОЖЬ – «Зачет не сдал».
Решение математических задач в Excel
Средствами программы можно решать как простейшие математические задачки, так и более сложные (операции с функциями, матрицами, линейными уравнениями и т.п.).
Условие учебной задачи. Найти обратную матрицу В для матрицы А.
- Делаем таблицу со значениями матрицы А.
- Выделяем на этом же листе область для обратной матрицы.
- Нажимаем кнопку «Вставить функцию». Категория – «Математические». Тип – «МОБР».
- В поле аргумента «Массив» вписываем диапазон матрицы А.
- Нажимаем одновременно Shift+Ctrl+Enter — это обязательное условие для ввода массивов.
Скачать примеры
Возможности Excel не безграничны. Но множество задач программе «под силу». Тем более здесь не описаны возможности которые можно расширить с помощью макросов и пользовательских настроек.
Эксель можно использовать для решения широкого спектра задач, в том числе, для нахождения наилучшего способа осуществления перевозок от производителя (продавца) к потребителю (покупателю). Давайте посмотрим, каким образом это можно реализовать в программе.
Содержание
- Транспортная задача: описание
- Подготовительный этап: включение функции “Поиск решения”
- Пример задачи и ее решение
- Условия
- Алгоритм решения
- Заключение
Транспортная задача: описание
С помощью транспортной задачи можно найти наилучший вариант перевозки с минимальными издержками между двумя взаимодействующими контрагентами (в рамках данной статьи будем рассматривать покупателей и продавцов). Чтобы приступить к решению, нужно представить исходные данные в схематичном или матричном виде. Последний вариант применяется в Эксель.
Транспортные задачи бывают двух типов:
- Закрытая – совокупное предложение продавца равняется общему спросу.
- Открытая – спрос и предложение не равны. Чтобы решить такую задачу, нужно сначала привести ее к закрытому типу. В этом случае добавляется условный покупатель или продавец с недостающим количеством спроса или предложения. Также в таблицу издержек следует внести соответствующую запись (с нулевыми значениями).
Подготовительный этап: включение функции “Поиск решения”
Чтобы решить транспортную задачу в Эксель, нужно воспользоваться функцией “Поиск решения”, которую нужно предварительно активировать, т.к. изначально она не включена. Алгоритм действий следующий:
- Открываем меню “Файл”.
- В перечне слева выбираем пункт “Параметры”.
- В параметрах кликаем по подразделу “Надстройки”. Затем в правой части окна в самом низу, выбрав значение “Надстройки Excel” для параметра “Управление”, щелкаем по кнопке “Перейти”.
- В открывшемся окне ставим галочку напротив надстройки “Поиск решения” и жмем OK.
- В результате, если мы перейдем во вкладу “Данные”, то увидим здесь кнопку “Поиск решения” в группе инструментов “Анализ”.
Пример задачи и ее решение
Чтобы лучше понять, как решать транспортные задачи в Excel, давайте рассмотрим конкретный практический пример.
Условия задачи
Допустим, у нас есть 6 продавцов и 7 покупателей. Предложение продавцов составляет 36, 51, 32, 44, 35 и 38 единиц. Спрос покупателей следующий: 33, 48, 30, 36, 33, 24 и 32 единицы. Суммарные количества по спросу и предложению равны, следовательно, это транспортная задача закрытого типа.
Также, мы имеем данные по издержкам перевозок из одного пункта в другой (ячейки с желтым фоном).
Алгоритм решения
Итак, приступи к решению нашей задачи:
- Для начала строим таблицу, количество строк и столбцов в которой соответствует числу продавцов и покупателей, соответственно.
- Перейдя в любую свободную ячейку щелкаем по кнопке “Вставить функцию” (fx).
- В открывшемся окне выбираем категорию “Математические”, в списке операторов отмечаем “СУММПРОИЗВ”, после чего щелкаем OK.
- На экране отобразится окно, в котором нужно заполнить аргументы:
- в поле для ввода значения напротив первого аргумента “Массив1” указываем координаты диапазона ячеек матрицы затрат (с желтым фоном). Сделать это можно, используя клавиши на клавиатуре, или просто выделив нужную область в самой таблице с помощью зажатой левой кнопки мыши.
- в качестве значения второго аргумента “Массив2” указываем диапазон ячеек новой таблицы (либо вручную, либо выделив нужные элементы на листе).
- по готовности жмем OK.
- Щелкаем по ячейке, расположенной слева от самого верхнего левого элемента новой таблицы, после чего снова жмем кнопку “Вставить функцию”.
- На этот раз нам нужна функция “СУММ”, которая также, находится в категории “Математические”.
- Теперь нужно заполнить аргументы. В качестве значения аргумента “Число1” указываем верхнюю строку созданной для расчетов таблицы (целиком) – вручную или методом выделения на листе. Жмем кнопку OK, когда все готово.
- В ячейке с функцией появится результат, равный нулю. Наводим указатель мыши на ее правый нижний угол, и когда появится Маркер заполнения в виде черного плюсика, зажав левую кнопку мыши тянем его до конца таблицы.
- Это позволит скопировать формулу и получить аналогичные результаты для остальных строк.
- Выбираем ячейку, которая находится сверху от самого верхнего левого элемента созданной таблицы. Аналогично описанным выше действиям вставляем в нее функцию “СУММ”.
- В значении аргумента “Число1” теперь указываем (вручную или с помощью выделения на листе) все ячейки первого столбца, после чего кликаем OK.
- С помощью Маркера заполнения выполняем копирование формулы на оставшиеся ячейки строки.
- Переключаемся во вкладку “Данные”, где жмем по кнопке функции “Поиск решения” (группа инструментов “Анализ”).
- Перед нами появится окно с параметрами функции:
- в качестве значения параметра “Оптимизировать целевую функцию” указываем координаты ячейки, в которую ранее была вставлена функция “СУММПРОИЗВ”.
- для параметра “До” выбираем вариант – “Минимум”.
- в области для ввода значений напротив параметра “Изменяя ячейки переменных” указываем диапазон ячеек новой таблицы (без суммирующей строки и столбца).
- нажимаем кнопку “Добавить” в блоке “В соответствии с ограничениями”.
- Откроется небольшое окошко, в котором мы можем добавить ограничение – сумма значений первых столбцов исходной и созданной таблицы должны быть равны.
- становимся в поле “Ссылка на ячейки”, после чего указываем нужный диапазон данных в таблице для расчетов.
- затем выбираем знак “равно”.
- в качестве значения для параметра “Ограничение” указываем координаты аналогичного столбца в исходной таблице.
- щелкаем OK по готовности.
- Таким же способом добавляем условие по равенству сумм верхних строк таблиц.
- Также добавляем следующие условия касательно суммы ячеек в таблице для расчетов (диапазон совпадает с тем, который мы указали для параметра “Изменяя ячейки переменных”):
- больше или равно нулю;
- целое число.
- В итоге получаем следующий список условий в поле “В соответствии с ограничениями”. Проверяем, чтобы обязательно была поставлена галочка напротив опции “Сделать переменные без ограничений неотрицательными”, а также, чтобы в качестве метода решения стояло значение “Поиск решения нелинейных задач методов ОПГ”. Когда все готово, нажимаем “Найти решение”.
- В результате будет выполнен расчет и отобразится окно с результатами поиска решения. Оцениваем их, и в случае, когда они нас устраивают, нажимаем OK.
- Все готово, мы получили таблицу с заполненными данными и транспортную задачу можно считать успешно решенной.
Заключение
Таким образом, с помощью программы Эксель достаточно просто решить транспортную задачу. Самое главное – правильно заполнить начальные данные и четко следовать плану действий, и тогда проблем быть не должно, т.к. программа все расчеты выполнит сама.