Цель данной работы: показать, как
электронные таблицы MicrosoftExcel могут помочь
учителю математики в совершенствовании
преподавания и обучения.
В настоящее время уже нет ни одного учителя,
утверждающего, что применение компьютерных
технологий на уроке математики неэффективно.
Вопрос уже другой: как сделать чтобы применение
компьютера стало естественной потребностью, не
вызывало различных дополнительных проблем,
чтобы компьютер экономил время учителя,
разгружал его.
В большинстве же случаев учитель, применяя
информационные технологии, сталкивается с рядом
проблем:
- сложность приобретения электронных учебников;
- много времени тратится на ознакомление с их
структурой, особенностями поиска, использования,
редактирования материалов; - невозможность быстро адаптировать
мультимедийные материалы к своим конкретным
условиям; - задания трудно «вписать» в структуру урока;
- многие замечательные программы требуют
специального обучения.
Электронные таблицы MicrosoftExcelвходят в
полный пакет офисных программ Microsoft, что
позволяет учителю на любом компьютере применять
их на уроках математики, а также ученикам при
выполнении домашних заданий. В данной работе
представлены «наработки» использования
электронных таблиц MicrosoftExcel на уроках
математики.
1. Использование встроенных функций для
выполнения стандартных вычислений
Excelсодержит более 900 встроенных функций. Функции
– это уже готовые, встроенные в Excel
формулы, которым присвоены уникальные имена.
Среди этого разнообразия есть функции, созданные
специально для финансовых, инженерных,
статистических и других специфических расчётов.
Каждая функция состоит из трёх обязательных
элементов.
Знак равенства (=). Признак того, что в
данную ячейку введена функция или формула, а не
данные какого-либо другого типа.
Имя функции. Характеризует тип
выполняемых операций.
Аргументы. Значения, на основе которых
выполняются вычисления. Аргументы вводят в
круглых скобках сразу после имени функции.
Аргументами могут быть числа, адреса ячеек,
текст, выражения, содержащие другие функции.
Функции, используемые на уроках математики.
СУММ(В2:В5) – вычисление суммы числовых значений
диапазона ячеек начиная с В2 до В5.
СУММ(В2:В5;100;К4) – вычисление суммы числовых
значений диапазона ячеек В2:В5, числа 100 и значения
ячейки К4.
СУММЕСЛИ(В2:В5;”>10”) – вычисление суммы чисел,
больших 10, из диапазона ячеек В2:В5.
СРЗНАЧ(В2:В5) – вычисление среднего значения для
диапазона ячеек В2:В5.
МАКС(В2:В5) – вычисление максимального значения
из диапазона ячеек В2:В5.
МИН(В2:В5) – вычисление минимального значения из
диапазона ячеек В2:В5.
СЧЕТ(В2:В5) – подсчёт общего количества чисел из
диапазона ячеек В2:В5.
СЧЕТЕСЛИ(В2:В5;”<5”) – вычисление количества
чисел меньших 5, из диапазона ячеек В2:В5.
СТЕПЕНЬ(В1;А4) – вычисление значения степени с
основанием В1 и показателем степени А4.
КОРЕНЬ(В1) – вычисление значения квадратного
корня.
Задание 1.1:
Дана последовательность чисел: 25; –61; 0; –82;
18; –11; 0; 30; 15; –31; 0; –58; 22. С помощью встроенных
функций найдите: общее количество чисел,
количество положительных чисел, количество
отрицательных чисел, количество нулей,
максимальное значение, минимальное значение,
среднее значение, сумму всех чисел, сумму
положительных чисел, сумму отрицательных чисел,
сумму максимального и минимального значений.
Приложение 1_1.xls.
Задание 1.2:
Найти значение выражения: 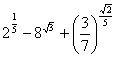
Приложение 1_2.xls.
2. Построение графиков функций
Рассмотрим примеры построения графиков
следующих функций с помощью ЭТ.
Пример 2.1:
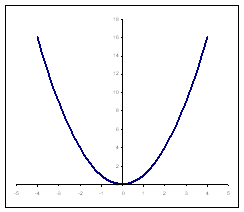
Построить график функции y= х2,
где –4 < х < 4, с шагом 0,5.
| А | В | |
| 1 | х | У |
| 2 | –4 | =А2^2 |
| 3 | –3,5 | 12,25 |
| 4 | –3 | 9 |
| 5 | –2,5 | 6,25 |
| 6 | –2 | 4 |
| 7 | –1,5 | 2,25 |
| 8 | –1 | 1 |
| 9 | –0,5 | 0,25 |
| 10 | 0 | 0 |
| 11 | 0,5 | 0,25 |
| … | … | … |
| 18 | 4 | 16 |
1. В диапазон ячеек А2:А18 введите
значение переменной х от –4 до 4 с шагом 0,5.
2. В ячейку В2 введите формулы:
=А2*А2 или А2^2 или СТЕПЕНЬ(А2;2).
3. Выделите ячейку В2, установите
указатель мыши на маркере заполнения этого
диапазона и протащите его вниз так, чтобы
заполнить диапазон В2:В18.
4. Выделить диапазон ячеек А2:В18.
5. Панель инструментов – Мастер
диаграмм – Тип (точечная) – Вид (плавная линия).
Готово.
Приложение 2_1.xls.
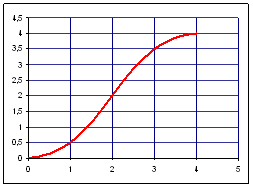
Пример 2.2:
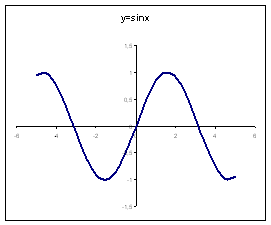
Построить график функции у = sinx, при
х є [–5;5], с шагом 0,5.
| А | В | |
| 1 | x |
y |
| 2 | –5 | =sin(A2) |
| 3 | –4,5 | 0,97753 |
| 4 | –4 | 0,756802 |
| 5 | –3,5 | 0,350783 |
| 6 | –3 | –0,14112 |
| 7 | –2,5 | –0,59847 |
| … |
… |
… |
| 18 | 3 | 0,14112 |
1. В диапазон ячеек А2:А20 введите
значение переменной х от –5 до 5 с шагом 0,5.
2. В ячейку В2 введите формулу: =sin(A2)
3. Выделите ячейку В2, установите
указатель мыши на маркере заполнения этого
диапазона и протащите его вниз так, чтобы
заполнить диапазон В2 : В22.
4. Выделить диапазон ячеек А2 : В18.
5. Панель инструментов – Мастер
диаграмм – Тип (точечная) – Вид (плавная линия).
Готово.
Приложение 2_2.xls.
Пример 2.3.
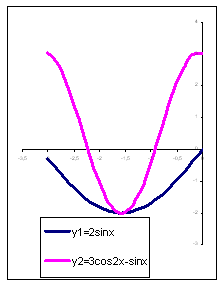
Построить в одной системе координат графики
следующих двух функций y1 = 2sinx и у2
= 3cos2x– sinx при x є [–3;0] с шагом 0,2.
|
А |
В |
С |
|
| 1 | х |
у1 |
у2 |
| 2 | –3 | =2*sin(A2) | =3*cos(2*A2)–sin(A2) |
| 3 | –2,8 | –0,66998 | 2,661686 |
| 4 | –2,6 | –1,031 | 1,921051 |
| 5 | –2,4 | –1,35093 | 0,93796 |
| 6 | –2,2 | –1,61699 | –0,1135 |
| 7 | –2 | –1,81859 | –1,05163 |
| 8 | –1,8 | –1,9477 | –1,71643 |
| 9 | –1,6 | –1,99915 | –1,99531 |
| 10 | –1,4 | –1,9709 | –1,84122 |
| … | … | … | |
| 17 | 0 | 0 | 2 |
1. В ячейки А1, В1 и С1 введите x, y1, у2
соответственно.
2. В диапазон ячеек А2:А17 введите
значения переменной от –3 до 0 с шагом 0,2.
3. В ячейку В2 и С2 ввести формулы: =2*sin(A2) и
=3*cos(2*A2)–sin(A2).
4. Заполнить оставшиеся ячейки с помощью
Автозаполнения. Для этого выделите диапазон
В2:С2, установив указатель мыши на маркере
заполнения этого диапазона и протащите его вниз
так, чтобы заполнить диапазон В2:С17.
5. Выделите диапазон ячеек А1: С17.
6. Панель инструментов – Мастер
диаграмм – Тип (точечная) – Вид (плавная линия).
Готово.
Приложение 2_3.xls.
3. Преобразование графика:
Пример 3.4.
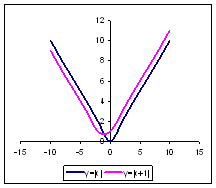
Постройте график функции у=|x| на отрезке
[–10;10] с шагом 2. Преобразовать его: построить
график y = |x +1|
| А | В | С | |
| 1 | х | у1 | у2 |
| 2 | –10 | =ABS(А2) | =ABS(A2+1) |
| 3 | –8 | 8 | 7 |
| 4 | –6 | 6 | 5 |
| 5 | –4 | 4 | 3 |
| 6 | –2 | 2 | 1 |
| 7 | 0 | 0 | 1 |
| 8 | 2 | 2 | 3 |
| 9 | 4 | 4 | 5 |
| 10 | 6 | 6 | 7 |
| 11 | 8 | 8 | 9 |
| 12 | 10 | 10 | 11 |
1. В столбце А постройте
таблицу значений при различных значениях
аргумента;
2. В ячейку В2 введите формулу =ABS(А2);
3. Постройте график функции на данном
листе с помощью Мастера Диаграмм.
4. Добавьте столбец y = |x + 1| и найдите
значения функции при данных значениях аргумента
– в ячейку С2 введите формулу =АBS(А2+1);
5. Выделите график и выполните команду
ДИАГРАММА – ДОБАВИТЬ ДАННЫЕ.
6. Выделите диапазон значений
функции y = | x + 1 | и постройте новый график.
7. Поменяйте y = | x + 1 | на y = | x –1 |, при
этом поменяйте формулу. Что произойдёт с
графиком?
Приложение3_4. xls.
4.1. Использование логических функций
при построении графиков функций
Логические функции предназначены для проверки
выполнения условия или для проверки нескольких
условий. Эта проверка осуществляется на основе
значений ИСТИНА или ЛОЖЬ.
=ЕСЛИ(условие; выражение1; выражение2)
Функция ЕСЛИ позволяет определить,
выполняется ли указанное условие. Если условие
истинно, то значением ячейки будет выражение 1,
в противном случае – выражение2.
Например: =ЕСЛИ(В5>20;”тепло”;”холодно”)
Если значение в ячейке В5>20, то выводится
сообщение «тепло», в противном случае – «холодно».
Совместно с функцией ЕСЛИ используются
логические операции И, ИЛИ, НЕ.
Например: =ЕСЛИ(И(Е4<3;Н92>=13);”выиграет”;”проиграет”)
Если значение в ячейке Е4<3 и Н92>=13, то выводится
сообщение «выиграет», в противном случае –
«проиграет».
Пример 4.5. (построение графика
функции с одним условием)
Постройте график функции у=х+0,5|x| на
отрезке [–5;5] с шагом 0,5.
Данную функцию можно задать двумя формулами. Используя эти
формулы, переведем на язык Электронных Таблиц.
| А | В | |
| 1 | х | у |
| 2 | –5 | =ЕСЛИ(А2<0;0,5*A2;1,5*A2) |
Приложение4_5. xls.
Пример 4.6
(построение графика функции с двумя
условиями)
Постройте график функции
| А | В | |
| 1 | х | у |
| 2 | 0 | 0 |
| 3 | 1 | =ЕСЛИ(И(A3>=0;A2<=2);1/2*A3^2;(4–0,5*(4–A3)^2)) |
Приложение4_6. xls.
4.2.Использование логических функций при
решение геометрических задач.
С помощью логических функций в Электронных
Таблицах можно выполнять решение геометрических
задач.
Пример 4.7
Построить таблицу для определения возможности
нахождения периметра треугольника по заданным
значениям его сторон. По теореме «Неравенство
треугольника» (Каждая сторона треугольника
меньше суммы двух других сторон), Электронная
Таблица проверяет, существует треугольник с
данными сторонами или не существует. Если
треугольник существует, то вычисляется периметр
треугольника.
| 1 сторона | 2 сторона | 3 сторона | существование треугольника | периметр треугольника |
| 3 | 5 | 7 | =ЕСЛИ(И(A2<E2;B2<F2;C2<D2);»существует»;»не существует») |
15 |
| 4 | 4 | 8 | не существует | нет |
| 1 | 2 | 3 | не существует | нет |
| 5 | 2 | 4 | существует | 11 |
| 0,7 | 1,2 | 3,5 | не существует | нет |
| 1,8 | 2 | 3 | существует | 6,8 |
| 5 | 5 | 10 | не существует | нет |
| 5,7 | 2,9 | 8 | существует | 16,6 |
Приложение4_7. xls.
5. Графическое решение уравнений
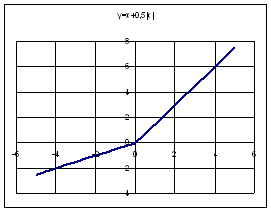
Пример 5.8: Решить графически
уравнение: 2х = – х + 1
Рассмотрим две функции: у1
= 2х и у2 = – х+ 1.
Построим в одной системе координат графики этих
функций на отрезке [– 4;4] с шагом 0,5. По графику
функции определяем решение уравнения: х = 0
| А | В | С | |
| 1 | х | у1 | у2 |
| 2 | –4 | =СТЕПЕНЬ(2;А2) | =–1*А2+1 |
| 3 | –3,5 | 0,088388 | 4,5 |
| … | … | … | … |
| 9 | 0 | 1 | 1 |
| .. | … | … | … |
| 18 | 4 | 16 | –3 |
Приложение5_8. xls.
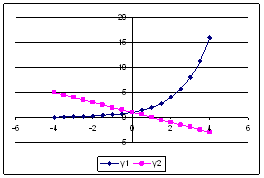
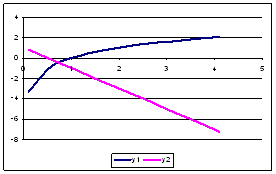
Пример 5.9: Показать графически,
что уравнение имеет решение:
Рассмотрим две функции: у1=
log2x и у2 = –2х+1.
Построим в одной системе координат графики этих
функций на отрезке [0,1;4,1] с шагом 0,5. При
построении видим, что графики пересекаются,
следовательно, уравнение имеет решение.
| А | В | С | |
| 1 | х | у1 | у2 |
| 2 | 0,1 | =LOG(A2;2) | =–2*A2+1 |
| 3 | 0,6 | –0,73697 | –0,2 |
Приложение5_9. xls.
6. Создание тренажёров и тестов в Excel
Создание теста и тренажёров по математике с
помощью электронных таблиц Excel,
предназначенного для заполнения на компьютере, с
автоматической проверкой правильных ответов.
Будем использовать функцию ЕСЛИ для
проверки правильности ответов.
Приведём пример создания теста: (Пример
6.10)
| А | В | С | D | E | |
| 1 | 1. Выполните действия: | 1) 1,52 | |||
| 2 | 0,256:0,8+1,2•0,01 | 2) 0,44 | =ЕСЛИ(С2=3;1;0) | ||
| 3 | 3) 0,332 | ||||
| 4 | 4) 4,52 | ||||
| … | |||||
| … | |||||
| 11 | 2. Укажите числа, кратные 9, | 1) 149; 154 | |||
| 12 | удовлетворяющие неравенству: | 2) 144; 152 | =ЕСЛИ(С12=4;1;0) | ||
| 13 | 142 < y <153 | 3) 145; 150 | |||
| 14 | 4) 144; 153 | ||||
| … | |||||
| … | |||||
| 30 | Всего баллов | =СУММ(D2;D7D12…) | |||
| 31 | оценка: | =ЕСЛИ(D30>=17;5;ЕСЛИ(D30>=11;4; ЕСЛИ(D30>=6;3;2))) |
Приложение6_10. xls.
Проверка правильностиответов:
Функция ЕСЛИ устанавливает одно
значение, если заданное условие истинно, и другое
– если оно ложно. В ячейки С2, С12…
вводятся варианты ответов 1, 2, 3 или 4. В ячейках D2,
D12… идёт проверка результатов. Таким
образом, наша функция ЕСЛИ будет
выдавать в ячейках D1, D12…будет выдавать единицу,
если ответ ученика совпал с правильным ответом, и
ноль в случае несовпадения.
Вычисление суммы:
В ячейке D30 находим сумму баллов, используя
функцию СУММ. При этом адреса ячеек отделяем “;”.
Отображение результатов теста:
С помощью функции ЕСЛИ в ячейке D31 идёт проверка
результатов.
Скрытые столбцы:
Наш тест вполне работоспособен, однако столбец
D было бы хорошо “спрятать”, чтобы учащийся не
мог сразу определить, что дал верный или неверный
ответ. Для этого выделите столбец D, щёлкнув в их
заголовки. В меню Формат выберите СтолбецСкрыть.
Столбец станет невидимым.
Если необходимо вновь сделать столбец доступным
для просмотра и редактирования, выделите два
соседних столбца, между которыми находится
скрытый столбец. В меню Формат выбрать СтолбецОтобразить.
Столбец станет видимым.
Приведём пример создания тренажёра: (Пример
6.11)
В столбце G с помощью функции ЕСЛИ
идёт проверка правильности ответов. Если в
ячейке F1 будет занесено число –3, то
таблица выдаст “Правильно”, в противном
случае “Неправильно”.
| А | И | С | D | E | F | G | |
| 1 | 1 | –9 | + | 6 | = | =ЕСЛИ(F5=0;»»;ЕСЛИ(F5=B5+D5; «Правильно»;»Неправильно»)) |
|
| 2 | 2 | –18 | + | 12 | = | ||
| 3 | 3 | –5 | + | –7 | = | ||
| 4 | 4 | 12 | + | –19 | = | ||
| 5 | 5 | 6 | + | 21 | = | ||
| 6 | 6 | 7 | + | 19 | = | ||
| 7 | 7 | 5 | + | –15 | = | ||
| 8 | 8 | 3,7 | + | 0,3 | = | ||
| 9 | 9 | –8 | + | –7,5 | = | ||
| 10 | 10 | –9 | + | 0,8 | = |
Приложение 6_11.xls.
Excel для Microsoft 365 Excel 2021 Excel 2019 Excel 2016 Excel 2013 Excel 2010 Excel 2007 Еще…Меньше
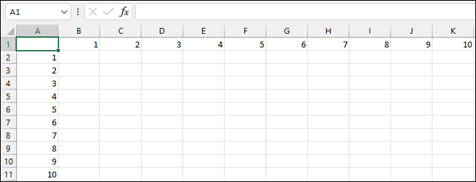
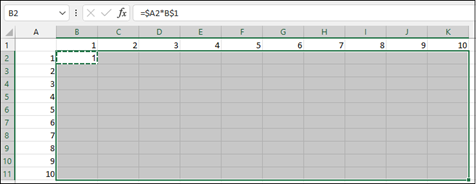
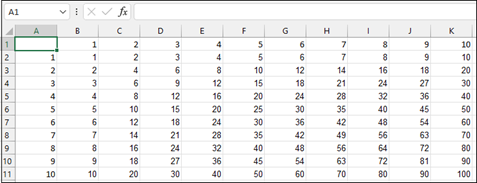
Предположим, вы хотите помочь ребенку лучше понять математические концепции, создав таблицу умножения.
-
Введите числа от 1 до 10 в ячейках A2–A11 и еще раз в ячейках B1–K1.
-
Введите эту формулу в ячейку B2. $блокирует значение строки заголовка, а формула умножает его на значение в строке.
=$A2*B$1
-
Скопируйте ячейку B2.
-
Выберите диапазон B2:K11.
-
Вставьте формулу в эти ячейки (Crtl + V).
Нужна дополнительная помощь?
Муниципальное бюджетное образовательное
учреждение
Досчатинская средняя школа
г.о.г. Выкса
Исследовательская работа на тему:
«Microsoft Excel –
на уроках математики»
Физико-математическое отделение
Секция математика
Работу выполнил: ученица 8Б класса
Обыденнова Дарья Сергеевна
Руководитель:
учитель математики и физики
Рощина Людмила Валерьевна,
2019
год
Оглавление
|
Введение |
3-4 |
|
Обзор |
5 |
|
Глава |
6-11 |
|
1.1 |
6-7 |
|
1.2 Таблицы в Microsoft |
7 |
|
1.3 Возможности табличного 1.4 |
8-9 9-11 |
|
Глава 2. Практическая часть…………………………………………. |
11-13 |
|
2.1 Решение уравнения графическим способом……………………. |
8-19 |
|
Заключение…………………………………………………………… |
20 |
|
Литература……………………………………………………………. |
21 |
|
Приложение…………………………………………………………… |
22-23 |
Введение
В школьной
программе по математике, в 7 классе изучаются линейные функции, их свойства и
графики, а в 8 – обратные пропорциональные, квадратичные и графики функций y=√х,
системы уравнений решающиеся графическим способом. При изучении, этой
темы возникает необходимость построения графиков элементарных функций и
уравнений выше второй степени. Для изучения свойств этих функций MicrosoftExcel
предлагает широкие возможности, которые в школьных учебниках по информатике не
оговариваются.
Программа от MicrosoftExcel или электронные таблицы была создана
для более удобной работы пользователя с таблицами данных, причём
преимущественно данная работа производится с числовыми значениями.
Основной особенностью MS Excel выступает его возможность
использовать формулы для того, чтобы описывать между значениями разных ячеек
различные связи. Следует отметить, что по заданным формулам расчёт будет
выполняться автоматически. Если человек изменяет значение какой-либо ячейки, то
сразу же автоматически произойдёт перерасчёт значений всех остальных ячеек,
которые связаны с ней формульными отношениями, благодаря чему обновится вся
таблица и данные, которые находятся в ней.
Табличный процессор Excel позволяет осуществлять вычисления. Там
не одна сотня различных функций (математических, логических, текстовых,
статистических и т.д.). В Excel можно осуществлять бухгалтерские расчеты,
строить графики и диаграммы.
При работе в MS Excelна уроках информатики, заметили, что далеко
не все функции редактора мы изучили. Особенно стало интересно знать: где и как
в расчетных таблицах применяются элементы управления? Можно
ли решить системы уравнений средствами табличного процессора?
Представленная работа состоит из двух частей. В первой
рассматриваются структура, возможности и области применения программыExcel. Во
второй части проведены исследования по изучению возможностей табличного
процессора: использование элементов управления и решение систем уравнений
графическим способом.
Гипотеза: С помощью MS
Excel можно решать математические уравнения и системы.
Цель работы: выявление возможности таблицы MS Excel на примерах построения
функции уравнения и решения графическим способом системы уравнений.
Задачи:
1.Рассмотреть программу Excel.
2. Выявить возможности
табличного процессора Excel.
3.Научится решать
уравнения графическим способом.
4.Решить систему
уравнений графическим способом.
5.Провести анализ
проделанной работы, сделать выводы.
Методы исследования:
·
Анализ литературы по проблеме исследования.
·
Практическая работа.
·
Анализ результатов.
Объектисследования – процесс
построения графиков элементарных функций при помощи ПК.
Предмет исследования — методика
использования ПК при построении графиков функций.
Обзор
литературы
1.
В своей работе я использовала несколько
книг. В книге Уокенбах Дж. «Диаграммы в Excel», перевод с английского
А.Г.Сысонюка. В книге рассматривается вопрос по построению диаграмм, подробно
рассказывается обо всех типах диаграмм их свойствах и возможностях.
2.
Из учебника алгебры 8 класса А.Г.Мерзляк,
я использовала линейные уравнения и системы уравнений, состоящие из нескольких
уравнений.
Глава 1. Теоретическая часть
1.1 Рассмотреть
программу Excel.
14
января 1985 года появилась самая популярная, на сегодняшний день, программа в
мире – Microsoft Excel. Excel был первым табличным процессором, позволявшим
пользователю менять внешний вид таблицы на экране: шрифты,
символыи
внешний вид ячеек. Он также первым представил метод умного пересчёта ячеек —
обновления только ячеек, зависящих от изменённых ячеек: раньше табличные
процессоры пересчитывали все ячейки; это делалось либо после каждого изменения
(что на больших таблицах долго), либо по команде пользователя (что могло
вводить пользователя в заблуждение не пересчитанными значениями). Excel – это
широко распространеннаякомпьютерная программа. Нужна она для
проведения расчетов, составления таблиц и диаграмм, вычисления простых и
сложных функций. Она входит в состав пакета Microsoft Office. Это такой набор
программ для работы в офисе. Самые популярные приложения в нем — Word и Excel.
Microsoft Excel представляет собой большую таблицу, в которую можно вносить
данные, то есть печатать слова и цифры. Также, используя функции этой
программы, можно производить с цифрами разные манипуляции: складывать,
вычитать, умножать, делить и многое другое.
Многие
люди думают, что Excel – это только таблицы. Они убеждены, что все таблицы на
компьютере составляются именно в этой программе. Но это не так. Эта программа
нужна, в первую очередь, для вычислений.
Если
требуется не только расчертить таблицу со словами и цифрами, но еще и
произвести с цифрами какие-либо действия (сложить, умножить, вычислить процент
и т.д), тогда Вам нужно работать в Microsoft Excel. А если же нужно составить
таблицу без вычислений, то есть ввести уже готовые данные, то быстрее и удобнее
это сделать в программе Microsoft Word.
Эксэль,
по сравнению с Вордом, конечно, сложнее. И лучше начинать работать в этой
программе уже после того, как освоите Word. Чтобы изучить Excel досконально, потребуется
немало времени. Но, как показывает практика, большинству для работы достаточно
лишь базовых навыков.
С помощьюмExcel можно анализировать большие
массивы данных. В Excel можно использовать больше 400 математических,
статистических, финансовых и других специализированных функций, связывать
разные таблицы между собой, выбирать произвольные форматы представления данных,
создавать иерархические структуры. Воистину безграничные методы графического
представления данных: кроме нескольких десятков встроенных типов диаграмм,
можно создавать свои, что настраиваются типы, помогают наглядно отобразить
тематику диаграммы.
1.2 Таблицы в Microsoft
Excel.
Построение
всякого графика начинается с таблицы. Самый быстрый способ построения диаграммы
– выделить таблицу и нажать F11,
но без таблицы даже самый простой метод не проходит. Размещать её можно на
любом для вас листе рабочей книге, а так же в любом месте страницы. Зачастую
таблица имеет самый простой и обычный вид, но иногда для получения нужного вида
графика приходится потрудиться. При наборе таблицы совершенно неважно, что у
вас будет строками, а что – столбцами. Можно набирать как вам удобно, и легко
потом менять строки и столбцы местами. Данные из одной и той же таблицы могут
использоваться в нескольких графиках и диаграммах. Дизайн таблицы ни в коем
случае не влияет на дизайн графика. После того как вы набрали таблицу, вам
нужно её выделить. Если это специально набранный квадрат данных, то здесь
проблем не возникнет. Если данные разбросаны по большей таблице, то выделяйте
куски, держа при этом нажатым CTRL.
Это позволяем выделять несмежные области.
1.3 Возможности
табличного процессора Microsoft Excel.
Табличные
процессоры имеют очень широкие функциональные и дополнительные возможности,
обеспечивающие удобную и продуктивную работу пользователя (Приложение 1).
Контекстная
подсказка. Вызывается из контекстного меню или нажатием соответствующей кнопки
в пиктографическом меню.
Контекстное
меню. Разворачивается по щелчку кнопки (правой) мыши на выбранном объекте. Речь
идет, например, о месте таблицы, где в данный момент хочет работать
пользователь. Наиболее часто используемые функции обработки, доступные в данной
ситуации, собраны в контекстном меню (Приложение 2).
Справочная
система. Организована в виде гипертекста и позволяет легко и быстро
осуществлять поиск нужной темы.
Рабочие
группы или рабочие папки. Документы можно соединять в рабочие папки, так что
они могут рассматриваться как одно единое целое, если речь идет о копировании,
загрузке, изменении или других процедурах. В нижней части электронной таблицы
расположен алфавитный указатель (регистр), который обеспечивает доступ к
рабочим листам. Пользователь может задавать название листам в папке (вместо
алфавитного указателя), что делает наглядным содержимое регистра, а значит
облегчает поиск и переход от документа к документу.
Средства
оформления и вывода на печать таблиц. Для удобства пользователя предусмотрены
все функции, обеспечивающие печать таблиц, такие как выбор размера страницы,
разбивка на страницы, установка размера полей страниц, оформление колонтитулов,
а также предварительный просмотр получившейся страницы
Для удобства вычисления в табличных процессорах имеются встроенные
функции, а именно: математические, статистические, финансовые, функции даты и
времени, логические и другие. Менеджер функций позволяет выбрать нужную функцию
и, проставив значения, получить результат (Приложение 3).
Диаграммы.Современный табличный процессор состоит из построения
различного типа двумерных, трехмерных и смешанных диаграмм. Насчитывается более
20 различных типов и подтипов диаграмм, которые можно построить в современной
системе данного класса. А возможности оформления диаграмм также многообразны и
доступны, например, вставка и оформление легенд, меток данных; оформление осей
— возможность вставки линий сеток и другие. Помимо этого, современные системы
работы с электронными таблицами снабжены такими мощными средствами построения и
анализа деловой графики, как вставка планок погрешностей, возможность
построения тренда и выбор функции линии тренда (Приложение 4).
1.4
Типы диаграмм в Microsoft Excel.
1.4.1
Гистограммы
Данные
в столбцах или строках листа можно представить в виде гистограммы. В гистограмме категории обычно отображаются по
горизонтальной оси, а значения — по вертикальной оси, как показано на этой
диаграмме (приложение 5).
1.4.2
Графики (приложение 6).
Данные,
расположенные в столбцах или строках листа, можно представить в виде графика.
Графики позволяют изображать непрерывное изменение данных с течением времени в
едином масштабе и идеально подходят для представления тенденций изменения
данных с равными интервалами. На графиках данные категорий равномерно
распределяются вдоль горизонтальной оси, а все значения равномерно
распределяются вдоль вертикальной оси. Графики можно использовать, если метки
категорий являются текстовыми и представляют значения, разделённые равными
интервалами, например, месяцы, кварталы или финансовые годы. Это особенно важно
при наличии нескольких рядов: для отображения одного ряда можно использовать
точечную диаграмму. Также графики можно использовать при наличии нескольких
разделённых равными интервалами числовых меток, в частности, лет. Если числовых
меток больше десяти, вместо графика лучше использовать точечную диаграмму.
1.4.3
Круговые диаграммы (приложение 7)
Данные
в одном столбце или строке листа можно представить в виде круговой диаграммы.
Круговая диаграмма демонстрирует размер элементов одного ряда данных
относительно суммы элементов. Точки данных на круговой диаграмме выводятся как
проценты от всего круга.
Круговую
диаграмму рекомендуется использовать, если:
-нужно
отобразить только один ряд данных;
-все
значения ваших данных неотрицательны;
-почти
все значения данных больше нуля;
—имеется
не более семи категорий, каждой из которых соответствуют части общего круга.
1.4.4 Линейчатые
диаграммы (приложение 
Данные
в столбцах или строках листа можно представить в виде линейчатой диаграммы.
Линейчатые диаграммы используют для сравнения отдельных элементов. В диаграммах
этого типа категории обычно располагаются по вертикальной оси, а
величины — по горизонтальной.
1.4.5 Точечные
диаграммы (приложение 9)
Данные
в столбцах и строках листа можно представить в виде точечной диаграммы.
Точечная диаграмма показывает отношения между численными значениями в
нескольких рядах данных или отображает две группы чисел как один ряд координат
x и y. Точечная диаграмма имеет две оси значений, при этом одни числовые
значения выводятся вдоль горизонтальной оси (оси X), а другие — вдоль
вертикальной оси (оси Y). На точечной диаграмме эти значения объединяются в
одну точку и выводятся через неравные интервалы или кластеры. Точечные
диаграммы обычно используются для иллюстрации и сравнения числовых значений,
например научных, статистических или технических данных.
1.4.6
Поверхностные
диаграммы (приложение 10)
Данные
в столбцах или строках листа можно представить в виде поверхностной диаграммы. Поверхностная
диаграмма полезна, если требуется найти оптимальные комбинации данных из двух
наборов. Как на топографической карте, области, относящиеся к одинаковым
диапазонам, при этом выделяются цветами и штриховкой. Поверхностные
диаграммы можно использовать для иллюстрации категорий и наборов данных,
представляющих собой числовые значения.
Глава
2. Практическая часть.
2.1
Решение уравнения графическим способом.
Работать
я буду в Microsoft Excel 2010.
Пример
1. Вначале я покажу, как строить простейшее
линейное уравнение у=2·х+5. Для этого зададим переменную х и
запишем уравнение в таблицу.
Зададим
переменную и составим формулу.
Создаем
значения для постоянной у.
Строим
график. Обводим ячейки А2:В9. Выбираем позицию «вставка», далее «точечная
диаграмма»
Получаем
график линейного уравнения.
Пример
2. Следующимя построю систему уравнений,
возьму её из учебника алгебры 8 класса.
Система:
Задаем
для первого уравнения переменную и находим постоянную.
Теперь
задаём для второго уравнения переменную и находим постоянную
Строим
график этих уравнений.
Получаем
точку пересечений (5,3), это и будет ответ нашей системы уравнения.
Пример
3. Возьмём более сложную функцию
Задаем
переменную и находим «у» для наших уравнений.
Выбираем
точечную диаграмму
Так как в нашей системе есть линейные уравнения и парабола, то для
каждого уравнения добавляем по отдельности линию тренда
Получаем графическое решение нашей системы, также можем поменять
название. Находим точку пересечения у=9, х=3.
Пример 4. Построим
более сложную систему, которую мы еще не проходили, и решить самостоятельно я
её не смогу. Моя система состоит из квадратного трёхчлена и кубического
уравнения.
Сначала введем переменную х и запишем формулы. Проведем
расчёты, вот что получили.
Выбираем
точечную диаграмму.
Нажимаем по очереди на точечную диаграмму, выбираем линию тренда.
Так как у нас уравнения со степенями, то нажимаем на полиномиальную линию
тренда, со степенью 2, и то же самое делаем с кубическим уравнением, только
ставим степень 3.
Построив
графики, выбираем источник данных и изменяем имя ряда.
Вывод.
Программа
MicrosoftExcel
– одна из наиболее практически значимых, востребованных. Электронные таблицы не
только позволяют автоматизировать расчеты, но и являются эффективным средством
моделирования различных вариантов и ситуаций. Меняя значения исходных данных,
можно проследить за изменением получаемых результатов и из множества вариантов
решения задачи выбрать наиболее подходящий.
Цель
моей работы достигнута, задачи выполнены. Я считаю, что моя гипотеза
подтвердилась, математические уравнения и системы можно решать графическим способом
с помощью программы MicrosoftExcel.
Использование
компьютерной программы при изучении позволяет повысить эффективность работы учеников
на уроке, избежать монотонных, однообразных действий при построении графиков
функций, поддержать интерес детей к математике. Использование ПК дает
возможность работать в одинаковом, достаточно быстром темпе. Конечно, на уроке
времени не хватает, но можно организовать
дополнительные занятия или задавать домашние задание предназначенные для
построения графиков функций при помощи компьютера, с целью повышения
эффективности работы учащихся на уроках, побуждение и поддержание интереса к
математике, показ необходимости знаний по математике и информатики в реальной
жизни
Литература
3.
Бурьков Д.В.: Практикум по информатике. — М.:
Дашков и К, 2010
4.
Гобарева Я.Л.: Технология экономических
расчетов средствами MS Exsel. — М.: КноРус, 2009
5.
Мерзляк А.Г.: Алгебра, 8 класс. – М.:
Вентана-Граф, 2018. – 256 с.
6.
Уокенбах Дж. Диаграммы в Excel
Интренет – ресурсы:
1. studbooks.net
2. lumpics.ru
3. exceltable.com
4. poisk-ru.ru
Приложение
|
Приложение 1. |
Приложение 2. Контекстное меню |
||
|
Приложение 3. Вычисления |
Приложение |
||
|
Приложение 5. Гистограмма |
Приложение |
||
|
Приложение |
Приложение |
||
|
Приложение 9. Точечные диаграммы. |
Приложение 10. Поверхностные диаграммы. |
||
Рецензия
на
исследовательскую работу: MicrosoftExcel – на
уроках математике.
Автор
работы: учащийся 8 класса, 14 лет
Работа
представлена на 17 страницах (основной текст – 15 страниц, приложение – 2
страницы). Структура работы соответствует требованиям конкурса.
Работа
носит исследовательский характер и посвящена изучению построения функций и
системы уравнений в программе Excel. Цели и
задачи соответствуют заданным исследованиям. В главе 1 рассмотрена сама
программа Excel и подробно
рассказывается об основных возможностях Всемирной паутины. В практической части
подробно рассказывается как строить линейные уравнения, системы уравнений
Результаты, представленные в работе, имеют практическую значимость. Работа
иллюстрирована диаграммами, ответами учащихся.
Работа
представляет интерес и в целом соответствует требованиям, предъявляемым для
участия в научно – практической конференции обучающихся городского округа город
Выкса. Рецензент выражает автору благодарность за проделанную работу и желает
дальнейших научных успехов.
Рецензент
работы: учитель
Рощина Л.В.
ПРИМЕНЕНИЕ EXCEL В ПРЕПОДАВАНИИ МАТЕМАТИКИ
В современном обществе использование информационных технологий становится необходимым практически в любой сфере деятельности человека. Овладение навыками этих технологий еще за школьной партой во многом определяет успешность будущей профессиональной подготовки нынешних учеников. Опыт показывает, что овладение этими навыками протекает гораздо эффективней, если происходит не только на уроках информатики, а находит свое продолжение и развитие на уроках учителей-предметников. Этот подход выдвигает новые требования к подготовке учителя-предметника, ставит перед ним новые проблемы, заставляет осваивать новую технику и создавать новые методики преподавания, основанные на использовании современной информационной среды обучения. Преподавание математики, в силу особенностей самого предмета, представляет собой наиболее благоприятную сферу для применения современных информационных технологий. Проводимая работа в этом направлении содержит как чисто демонстрационную составляющую, дающую ученикам расширенные представления о возможностях использования информационных технологий, так и составляющую, требующую активного применения учениками знаний, полученных на уроках информатики. В процессе преподавания математики, информационные технологии могут использоваться в различных формах. Одним из самых удачных является внедрение табличного процессора EXCEL.
Excel, пожалуй, самая популярная сегодня программа электронных таблиц. Она входит в офисный пакет MS Office. Ею пользуются деловые люди и ученые, бухгалтеры и журналисты. С ее помощью ведут разнообразные списки, каталоги и таблицы, составляют финансовые и статистические отчеты, обсчитывают данные опросов общественного мнения и состояние торгового предприятия, обрабатывают результаты научного эксперимента, ведут учет, готовят презентационные материалы.
Excel сумеет вычислить суммы по столбцам и строкам таблицы, взять проценты, подсчитать среднее арифметическое, банковский процент или дисперсию; в нем вообще можно использовать множество стандартных функций – финансовых, математических, логических, статистических.
Оформление таблиц может быть самым разнообразным, возможности форматирования данных – как в хорошем текст-процессоре: можно менять шрифты, начертания, выделять строки, столбцы или отдельные ячейки текста цветом, рамочками и линеечками, закрашивать области фоном или цветом, строить по табличным данным графики и диаграммы, вставлять в таблицу картинки и т.п.
Надо сказать, что программа достаточно мощная, возможности ее весьма обширны. Одних только математических, логических, бухгалтерских, статистических функций, которые Excel умеет выполнять над табличными данными – более 200 штук. Именно поэтому применение Excel в математике весьма эффективно и дает большие возможности учителю предметнику. В процессе преподавания математики Excel может использоваться в изучении многих тем:
- решение уравнений n-й степени;
- решение систем линейных уравнений;
- работа с матрицей;
- построение графиков функций;
- графическое решение систем уравнений;
- тест, созданный средствами Excel и т.д.
Рассмотрим некоторые примеры применения Excel на уроках математики:
- Построить график функции:
- В первой строке записываются заголовки столбцов
- В первом столбце пишем значения х от нижней до верхней границы с заданным шагом. В нашем случае от -4 до 4 и с шагом 0,5
- Во втором столбце находятся значения у, которые вычисляются по формуле: =$С$1*СТЕПЕНЬ(А2;2), где С1 это ссылка на ячейку с коэффициентом а
Рисунок 1
- Выделяем диапазон ячеек А1:В18 и выбираем пункт меню Вставка
диаграмма. Выбираем тип диаграммы – точечная, вид – сглаженные линии.
- по требованию к оформлению изменяем внешний вид полученного графика
Рисунок 2
2. Решить графически систему уравнений:
Сначала построим таблицу, содержащую значения аргумента х и значения у обоих уравнений системы:
Рисунок 3
- В первой строке записываются заголовки столбцов
- В первом столбце пишем значения х от -3 до 3 с шагом 0,2
- Во втором столбце находятся значения у первого уравнения, которые вычисляются по формуле: =СТЕПЕНЬ(А2;2)+5 (при копировании динамическая ссылка изменится)
- Во третьем столбце находятся значения у второго уравнения, которые вычисляются по формуле: =6*А2+12 (при копировании динамическая ссылка также изменится)
Рисунок 4
- Выделяем заполненную таблицу и на основе этих данных вставляем диаграмму: тип – точечная, вид – гладкие кривые
- По требованиям настроить внешний вид графика (подписи, масштаб осей, шаг осей, фон, цвет линий и т.д.)
На диаграмме видно, что оба графика имеют точки пересечения – эти координаты точек и есть решения системы.
Примечание: для более точного решения можно выбрать меньший шаг.
- Решить систему линейных уравнений:
- пусть в ячейках А1, В1, С1 будут находиться значения переменных х1, х2, х3 соответственно. Сейчас они пусты;
- в ячейки А3:С5 запишем систему уравнений в матричном виде:
- в ячейки Е3:Е5 запишем формулы, выражающие каждое уравнение системы
Рисунок 5
Рисунок 6
- далее выбираем пункт меню сервис
поиск решения. Если этого пункта нет, то выбираем пункт меню сервис
надстройки и ставим галочку напротив пункта «поиск решения»
- в появившемся диалоговом окне вводим данные: в качестве целевой ячейки выберем ячейку с формулой первого уравнения системы (на ее месте может быть любое другое уравнение системы). Выберем ячейку равной значению 15 (т.е. значение первого уравнения).
- В пункте «изменяя ячейки» выберем диапазон ячеек, в которых должны находиться переменные, т.е. диапазон А1:С1
- В области «ограничения» с помощью кнопки «добавить» введите равенства, в левой части которых находятся формулы в остальных уравнений системы, а в правой части находятся ссылки на ячейки со значениями этих уравнений.
- Жмем кнопку «выполнить»
Рисунок 7
- Если решение существует, то оно будет введено в ячейки переменных и покажется диалоговое окно об успешном решении системы.
Рисунок 8
- Создать тест по математике
Весь тест строится на формулах Ехсеl из раздела «Логические». Сначала оформляются вопросы. Под вопросами указываются варианты ответов. Перед каждым вариантом ответа оставляем пустую ячейку предназначенную для выбора ответа. Тестируемый должен поставить напротив правильного варианта ответа знак «+», а остальные ячейки оставить пустыми, иначе ответ не засчитается. Также необходимо выделить один столбец, в котором будет вестись подсчет набранных баллов. В окончательном результате этот столбец необходимо будет скрыть.
Рисунок 9
После каждого вопроса в столбце набранных баллов необходимо ввести формулу:
=ЕСЛИ(И(А12=””;A13=”+”;A14=””);”1”;””).
Формула «если» содержит условие И(А12=””;A13=”+”;A14=””). В данном случае оно сложное и говорит о том что правильный вариант ответа – второй. В ячейке А13 напротив правильного варианта ответа должен стоять плюсик, а остальные ячейки должны оставаться пустыми. При соблюдении этого условия выполняется первая часть формулы — ”1” – то есть в ячейку заносится значение 1 (цена вопроса). Количество вариантов ответов может быть любым, и количество правильных ответов – тоже. В этом случае необходимо отредактировать условие. Соответственно, при сложных вопросах может быть и больше цена вопроса. При несоблюдении условия (вопрос остается без ответа, либо выбраны неверные ответы) выполняется вторая часть формулы — “”. Ячейке не присваивается никакое значение.
После составления одного вопроса, его можно скопировать и на этой основе создавать другие вопросы, просто изменив текст и отредактировав условие правильности. При копировании динамическая ссылка изменится.
По завершении всех вопросов в столбце подсчета баллов необходимо ввести формулу суммы баллов — =СУММ(G1:G66) – от первой ячейки столбца до предыдущей той, в которую записывается сама формула.
Под всеми вопросами выделяем цветом одну ячейку.
Рисунок 10
После завершения тестирования ученик будет вводить в нее слово «готово» и в ячейке справа будет выведен результат.
Рисунок 11
В ячейку справа заносится формула =ЕСЛИ(A67=»готово»;СЦЕПИТЬ(«Ваш результат — «;G67;» баллов из 8 возможных»);»»). Условие — ученик вносит в синюю ячейку слово «готово». Действие на условие – в ячейку заносится текст, содержащий результат ученика.
Содержание
- Основные математические формулы в Excel (смотрите и учитесь)
- Основы Формул
- 1. Каждая формула в Excel начинается с “=”
- 2. Формулы показываются на панели формул Excel.
- 3. Как собрать формулу
- Базовая статистика
- Среднее
- Медиана
- Минимум
- Максимум
- Циклические вычисления
- Циклические вычисления и нахождение корней уравнения
- Функции ЧЁТН и НЕЧЁТ
- Функции ОКРВНИЗ, ОКРВВЕРХ
- Функции ЦЕЛОЕ и ОТБР
- Функция ПРОИЗВЕД
- Функция ОСТАТ
- Функция КОРЕНЬ
- Функция ЧИСЛОКОМБ
- Функция ЕЧИСЛО
- Формула ЧАСТНОЕ()
- Формула СУММЕСЛИ()
- Формулы ОКРУГЛ(), ОКРУГЛВВЕРХ(), ОКРУГЛВНИЗ()
- Использование ссылок
- ABS
- СТЕПЕНЬ
- СЛУЧМЕЖДУ
- РИМСКОЕ
- LOG
- Заключение
Если изучение по видеороликам, это ваш стиль, посмотрите видео ниже, чтобы пройти по этому уроку. В противном случае продолжайте читать подробное описание того, как работать с каждой математической формулой Excel.
Основы Формул
Прежде чем мы начнем, давайте рассмотрим, как использовать любую формулу в Microsoft Excel. Независимо от того, работаете ли вы с математическими формулами в этом учебнике или любыми другими, эти советы помогут вам овладеть Excel.
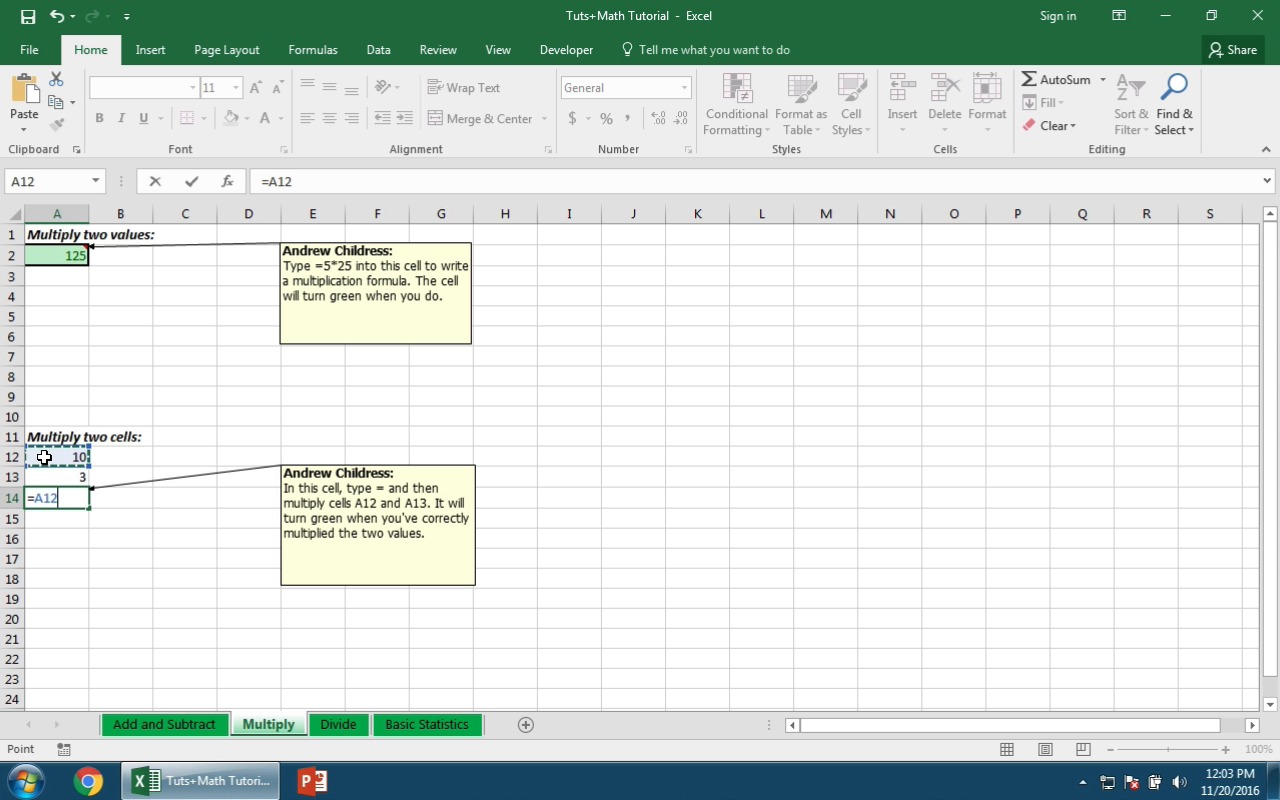
1. Каждая формула в Excel начинается с “=”
Чтобы ввести формулу, щелкните любую ячейку в Microsoft Excel и введите знак равенства на клавиатуре. Так начинается формула.
После знака равенства вы можете размещать в ячейке невероятно разнообразные вещи. Попробуйте ввести =4+4 в качестве вашей первой формулы и нажмите Enter, чтобы отобразить результат. Excel выведет 8, но формула останется за кулисами электронной таблицы.
2. Формулы показываются на панели формул Excel.
Когда вы вводите формулу в ячейку, вы можете увидеть результат в ячейке сразу после нажатия клавиши ввода. Но когда вы выбираете ячейку, вы можете увидеть формулу для этой ячейки на панели формул.
Чтобы использовать пример выше, ячейка отобразит «8», но когда мы нажмем на эту ячейку, панель формул покажет, что ячейка складывает 4 и 4.
3. Как собрать формулу
В приведенном выше примере мы набрали простую формулу для складывания двух чисел. Но вам не обязательно вводить числа, вы также можете ссылаться на другие ячейки.
Excel — это сетка ячеек, а столбцы идут слева направо, каждая назначена на букву, а строки пронумерованы. Каждая ячейка является пересечением строки и столбца. Например, ячейка, где пересекаются столбцы A и строка 3, называется A3.
Предположим, что у меня две ячейки с простыми числами, например 1 и 2, и они находятся в ячейках A2 и A3. Когда я набираю формулу, я могу начать формулу с «=», как всегда. Затем я могу ввести:
=A2+A3
…чтобы сложить эти два числа вместе. Очень распространено иметь лист со значениями и отдельный лист, где выполняются вычисления. Соблюдайте все эти советы при работе с этим руководством. Для каждой из формул вы можете ссылаться на ячейки или непосредственно вводить числовые значения в формулу.
Если вам нужно изменить формулу, которую вы уже набрали, дважды щелкните по ячейке. Вы сможете настроить значения в формуле.
Базовая статистика
Используйте вкладку “Basic Statistics” в книге для практики.
Теперь, когда вы знаете основные математические операторы, давайте перейдем к чему-то более продвинутому. Базовая статистика полезна для обзора набора данных и принятия обоснованных решений. Давайте рассмотрим несколько популярных простых статистических формул.
Среднее
Чтобы использовать формулу среднего в Excel, начните формулу с помощью =СРЗНАЧ(, а затем введите свои значения. Разделите каждое число запятой. Когда вы нажмёте клавишу ввода, Excel вычислит и выведет среднее значение.
=СРЗНАЧ(1;3;5;7;10)
Лучший способ рассчитать среднее это ввести ваши значения в отдельные ячейки в одном столбце.
=СРЗНАЧ(A2:A5)
Медиана
Медиана набора данных это значение, которое находится посередине. Если вы взяли числовые значения и выставили их в порядке от наименьшего к самому большому, медиана была бы ровно посередине этого списка.
=МЕДИАНА(1;3;5;7;10)
Я бы рекомендовал ввести ваши значения в список ячеек, а затем использовать формулу медианы над списком ячеек со значениями, введенными в них.
=МЕДИАНА(A2:A5)
Минимум
Если у вас есть набор данных и вы хотите держать на виду наименьшее значение, полезно использовать формулу МИН в Excel. Вы можете использовать формулу МИН со списком чисел, разделенных точкой с запятыми, чтобы найти самое маленькое значение в наборе. Это очень полезно при работе с большими наборами данных.
=МИН(1;3;5;7;9)
Возможно, вы захотите найти минимальное значение в списке данных, что вполне возможно с помощью такой формулы, как:
=МИН(A1:E1)
Максимум
Формула МАКС в Excel — полная противоположность МИН
=МАКС(1;3;5;7;9)
Или же, вы можете выбрать список значений в ячейках, и Excel вернет наибольшее из набора с этой формулой:
=МАКС(A1:E1)
Циклические вычисления
Если зависимые ячейки Excel образуют цикл, то говорят, что имеют место циклические ссылки (circular references). В обычном режиме Excel обнаруживает цикл и выдает сообщение о возникшей ситуации, требуя устранить циклические ссылки. Следуя обычной семантике, он не может провести вычисления, так как циклические ссылки порождают бесконечные вычисления. Есть два выхода из этой ситуации, – устранить циклические ссылки или изменить настройку в машине вычислений так, чтобы такие вычисления стали возможными. В последнем случае, естественно, требуется, чтобы число повторений цикла было конечным. Excel допускает переход к новой семантике, обеспечивающей проведение циклических вычислений. Вручную, для этого достаточно на вкладке Вычисления (меню Сервис, пункт Параметры) включить флажок Итерации и при необходимости изменить число повторений цикла в окошке “Максимум итераций”. Можно также задать точность вычислений в окошке “Максимальное изменение”, что также приводит к ограничению числа повторений цикла. По умолчанию максимальное число итераций и точность вычислений соответственно имеют значения 100 и 0,0001. Понятно, что включить циклические вычисления и задать значения параметров, определяющих окончание цикла, можно и программно.
Укажем, особенности семантики циклических вычислений:
- Формулы, связанные циклическими ссылками, вычисляются многократно.
- Запись формул на листе определяет порядок их вычисления. Формулы вычисляются сверху вниз, слева направо.
- Число повторений цикла определяется параметрами, заданными на вкладке Вычисления. Цикл заканчивается при достижении максимального числа итераций или, когда изменения значений во всех ячейках не превосходят заданной точности.
В каких же ситуациях требуется прибегать к циклическим вычислениям? Это, возможно, следует делать, когда речь идет о реализации итерационного процесса, вычислениях по рекуррентным соотношениям. У нас уже были примеры реализации итерационных процессов, например, вычисление суммы ряда, задающего экспоненту, в которых не применялись циклические ссылки. Платой за это было использование дополнительных ячеек таблицы Excel. Правда, появлялись и новые возможности, – возможность построить график, проанализировать процесс сходимости и т.д. Тем не менее, программисту, привыкшему к традиционным языкам, и привыкшему “с детства” экономить на переменных, может показаться странным предложенное решение задачи о нахождении корня уравнения, где на экран выводятся результаты всех приближений. В Excel экономия ячеек не главная задача. Тем не менее, при реализации итерационных процессов можно, конечно, и в Excel иметь одну единственную ячейку X, значение которой изменяется, начиная от начального приближения до искомого результата. Это в большей степени соответствует понятию переменной в языках программирования.
Циклические вычисления и нахождение корней уравнения
Покажем, как можно использовать циклические вычисления на примере задачи нахождения корня уравнения методом Ньютона. Для простоты я начну с квадратного уравнения, а позже рассмотрю и более “серьезные” уравнения. Итак, рассмотрим квадратное уравнение: X2 -5X+6 =0. Найти корень этого (и любого другого уравнения) можно, используя всего одну единственную ячейку Excel. Для этого достаточно включить режим циклических вычислений и ввести в произвольную ячейку с именем, скажем X, рекуррентную формулу, задающую вычисления по Ньютону:
где F и F1 задают соответственно выражения, вычисляющие функцию и производную. Для нашего квадратного уравнения после ввода формулы в ней появится значение 2, соответствующее одному из корней уравнения. А как получить второй корень? Обычно, это можно сделать путем изменения начального приближения. В нашем случае начальное приближение не задавалось, итерационный процесс вычислений начинался со значения, хранимого в ячейке X по умолчанию и равного нулю. Как же задать начальное приближение в циклических вычислениях? Возникшая проблема не связана с данной конкретной задачей. Она возникает всегда в циклических вычислениях, – до начала цикла надо задать начальные установки. В рекуррентных соотношениях всегда есть некоторый начальный отрезок. Решать задачу задания начальных установок в каждом случае можно по-разному. Я продемонстрирую один прием, основанный на использовании функции ЕСЛИ. Вот как выглядит “настоящее” решение этой задачи, использующее 4 ячейки, две из которых нужны по существу дела, а две используются для повышения наглядности процесса вычислений:
- В ячейку с именем Xinit я ввел начальное приближение.
- В ячейку Xcur, в которой и будет идти циклический счет, ввел формулу:
= ЕСЛИ(Xcur =0; Xinit; Xcur - (6- Xcur *(5- Xcur))/(2* Xcur -5))
- В две другие вспомогательные ячейки я поместил текст этой формулы и формулу, задающую вычисление функции в точке Xcur, позволяющую следить за качеством решения.
- Заметьте, что на первом шаге вычислений, функция IF (ЕСЛИ) поместит в ячейку Xcur начальное значение, а затем уже начнет счет по формуле на последующих шагах.
- Чтобы сменить начальное приближение, недостаточно изменить содержимое ячейки Xinit и запустить процесс вычислений. В этом случае вычисления будут продолжены, начиная с последнего вычисленного значения. Чтобы обнулить значение, хранящееся в ячейке Xcur, нужно заново записать туда формулу. Для этого достаточно выбрать ячейку и выделить текст формулы непосредственно в окне ее редактирования. Щелчок по Enter начнет вычисления с новым начальным приближением.
Функции ЧЁТН и НЕЧЁТ
Для выполнения операций округления можно использовать функции ЧЁТН (EVEN) и НЕЧЁТ (ODD). Функция ЧЁТН округляет число вверх до ближайшего четного целого числа. Функция НЕЧЁТ округляет число вверх до ближайшего нечетного целого числа. Отрицательные числа округляются не вверх, а вниз. Функции имеют следующий синтаксис:
=ЧЁТН(число)
=НЕЧЁТ(число)
Функции ОКРВНИЗ, ОКРВВЕРХ
Функции ОКРВНИЗ (FLOOR) и ОКРВВЕРХ (CEILING) тоже можно использовать для выполнения операций округления. Функция ОКРВНИЗ округляет число вниз до ближайшего кратного для заданного множителя, а функция ОКРВВЕРХ округляет число вверх до ближайшего кратного для заданного множителя. Эти функции имеют следующий синтаксис:
=ОКРВНИЗ(число;множитель)
=ОКРВВЕРХ(число;множитель)
Значения число и множитель должны быть числовыми и иметь один и тот же знак. Если они имеют различные знаки, то будет выдана ошибка.
Функции ЦЕЛОЕ и ОТБР
Функция ЦЕЛОЕ (INT) округляет число вниз до ближайшего целого и имеет следующий синтаксис:
=ЦЕЛОЕ(число)
Аргумент – число – это число, для которого надо найти следующее наименьшее целое число.
Рассмотрим формулу:
=ЦЕЛОЕ(10,0001)
Эта формула возвратит значение 10, как и следующая:
=ЦЕЛОЕ(10,999)
Функция ОТБР (TRUNC) отбрасывает все цифры справа от десятичной запятой независимо от знака числа. Необязательный аргумент количество_цифр задает позицию, после которой производится усечение. Функция имеет следующий синтаксис:
=ОТБР(число;количество_цифр)
Если второй аргумент опущен, он принимается равным нулю. Следующая формула возвращает значение 25:
=ОТБР(25,490)
Функции ОКРУГЛ, ЦЕЛОЕ и ОТБР удаляют ненужные десятичные знаки, но работают они различно. Функция ОКРУГЛ округляет вверх или вниз до заданного числа десятичных знаков. Функция ЦЕЛОЕ округляет вниз до ближайшего целого числа, а функция ОТБР отбрасывает десятичные разряды без округления. Основное различие между функциями ЦЕЛОЕ и ОТБР проявляется в обращении с отрицательными значениями. Если вы используете значение -10,900009 в функции ЦЕЛОЕ, результат оказывается равен -11, но при использовании этого же значения в функции ОТБР результат будет равен -10.
Функция ПРОИЗВЕД
Функция ПРОИЗВЕД (PRODUCT) перемножает все числа, задаваемые ее аргументами, и имеет следующий синтаксис:
=ПРОИЗВЕД(число1;число2…)
Эта функция может иметь до 30 аргументов. Excel игнорирует любые пустые ячейки, текстовые и логические значения.
Функция ОСТАТ
Функция ОСТАТ (MOD) возвращает остаток от деления и имеет следующий синтаксис:
=ОСТАТ(число;делитель)
Значение функции ОСТАТ – это остаток, получаемый при делении аргумента число на делитель. Например, следующая функция возвратит значение 1, то есть остаток, получаемый при делении 19 на 14:
=ОСТАТ(19;14)
Если число меньше чем делитель, то значение функции равно аргументу число. Например, следующая функция возвратит число 25:
=ОСТАТ(25;40)
Если число точно делится на делитель, функция возвращает 0. Если делитель равен 0, функция ОСТАТ возвращает ошибочное значение.
Функция КОРЕНЬ
Функция КОРЕНЬ (SQRT) возвращает положительный квадратный корень из числа и имеет следующий синтаксис:
=КОРЕНЬ(число)
Аргумент число должен быть положительным числом. Например, следующая функция возвращает значение 4:
КОРЕНЬ(16)
Если число отрицательное, КОРЕНЬ возвращает ошибочное значение.
Функция ЧИСЛОКОМБ
Функция ЧИСЛОКОМБ (COMBIN) определяет количество возможных комбинаций или групп для заданного числа элементов. Эта функция имеет следующий синтаксис:
=ЧИСЛОКОМБ(число;число_выбранных)
Аргумент число – это общее количество элементов, а число_выбранных – это количество элементов в каждой комбинации. Например, для определения количества команд с 5 игроками, которые могут быть образованы из 10 игроков, используется формула:
=ЧИСЛОКОМБ(10;5)
Результат будет равен 252. Т.е., может быть образовано 252 команды.
Функция ЕЧИСЛО
Функция ЕЧИСЛО (ISNUMBER) определяет, является ли значение числом, и имеет следующий синтаксис:
=ЕЧИСЛО(значение)
Пусть вы хотите узнать, является ли значение в ячейке А1 числом. Следующая формула возвращает значение ИСТИНА, если ячейка А1 содержит число или формулу, возвращающую число; в противном случае она возвращает ЛОЖЬ:
=ЕЧИСЛО(А1)
Формула ЧАСТНОЕ()
Тоже одна из простых операций в математике. В Экселе выполняется тоже несложно: у функции ЧАСТНОЕ() есть два аргумента: делимое и делитель.
В выделенной ячейке выводится частное:

Формула СУММЕСЛИ()
Оператор СУММЕСЛИ() находит сумму чисел. Главное отличие этой функции от СУММ() в том, что здесь в качестве аргумента можно задавать условие (только одно), которое будет показывать, какие значения будут использованы в расчетах, а какие — нет.
В качестве условий могут выступать неравенства со знаками больше, меньше или не равно («>», «<», «< >»). Число, которое не соответствует введенному условию, не будет включен в суммирование.
На рисунке изображено суммирование всех чисел, которые больше 0.
Оранжевым выделены те числа, которые будут включены в расчет функцией СУММЕСЛИ().
Остальные числа просто будут игнорироваться:

Например, нужно посчитать общую стоимость всех проданных фруктов.
Для этого воспользуемся следующей формулой:

Формулы ОКРУГЛ(), ОКРУГЛВВЕРХ(), ОКРУГЛВНИЗ()
Функция ОКРУГЛ() предназначена для округления значения до заданного количества знаков после запятой. В качестве первого аргумента выступают, как обычно, числа или диапазон ячеек, второго – разряд, до которого нужно округлить число.
Например, округление значения до второго знака после запятой:

Если в качестве второго аргумента выступает 0, то число будет округляться до ближайшего целого:

Второй аргумент может быть и отрицательным, тогда округление будет происходить до требуемого знака перед запятой:

Если необходимо округлить в сторону меньшего или большего по модулю числа используют функции ОКРУГЛВНИЗ(), ОКРУГЛВВЕРХ(), соответственно:


Замечание: многие могут решить, что функции округления бесполезны, так как можно просто убрать/добавить дополнительный знак после запятой с помощью кнопок увеличить/уменьшить разрядность.
На самом деле, это не так.
Дело в том, что увеличение или уменьшение разрядности влияет только на «внешний вид» ячейки, то есть на то, как мы число видим.
Само число, при этом, не меняется. Функции округления же полностью меняют вид числа, убирая лишние разряды.
Использование ссылок
При работе с Excel можно применять в работе различные виды ссылок. Начинающим пользователям доступны простейшие из них. Важно научиться использовать все форматы в своей работе.
Существуют:
- простые;
- ссылки на другой лист;
- абсолютные;
- относительные ссылки.
Простые адреса используются чаще всего. Простые ссылки могут быть выражены следующим образом:
- пересечение столбца и строки (А4);
- массив ячеек по столбцу А со строки 5 до 20 (А5:А20);
- диапазон клеток по строке 5 со столбца В до R (В5:R5);
- все ячейки строки (10:10);
- все клетки в диапазоне с 10 по 15 строку (10:15);
- по аналогии обозначаются и столбцы: В:В, В:К;
- все ячейки диапазона с А5 до С4 (А5:С4).
Следующий формат адресов: ссылки на другой лист. Оформляется это следующим образом: Лист2!А4:С6. Подобный адрес вставляется в любую функцию.
ABS
С помощью математической формулы ABS производится расчет числа по модулю. У этого оператора один аргумент – «Число», то есть, ссылка на ячейку, содержащую числовые данные. Диапазон в роли аргумента выступать не может. Синтаксис имеет следующий вид:
=ABS(число)
СТЕПЕНЬ
Из названия понятно, что задачей оператора СТЕПЕНЬ является возведение числа в заданную степень. У данной функции два аргумента: «Число» и «Степень». Первый из них может быть указан в виде ссылки на ячейку, содержащую числовую величину. Второй аргумент указывается степень возведения. Из всего вышесказанного следует, что синтаксис этого оператора имеет следующий вид:
=СТЕПЕНЬ(число;степень)
СЛУЧМЕЖДУ
Довольно специфическая задача у формулы СЛУЧМЕЖДУ. Она состоит в том, чтобы выводить в указанную ячейку любое случайное число, находящееся между двумя заданными числами. Из описания функционала данного оператора понятно, что его аргументами является верхняя и нижняя границы интервала. Синтаксис у него такой:
=СЛУЧМЕЖДУ(Нижн_граница;Верхн_граница)
РИМСКОЕ
Данная функция позволяет преобразовать арабские числа, которыми по умолчанию оперирует Excel, в римские. У этого оператора два аргумента: ссылка на ячейку с преобразуемым числом и форма. Второй аргумент не является обязательным. Синтаксис имеет следующий вид:
=РИМСКОЕ(Число;Форма)
LOG
С помощью этого оператора определяется логарифм числа по заданному основанию. Синтаксис функции представлен в виде:
=LOG(Число;Основание)
Необходимо заполнить два аргумента: Число и Основание логарифма (если его не указать, программа примет значение по умолчанию, равное 10).
Также для десятичного логарифма предусмотрена отдельная функция – LOG10.
Заключение
Таким образом, мы разобрали самые популярные математические функции, которые используются в Excel. Однако возможности программы гораздо шире, и в ее инструментарии можно найти функцию для успешного выполнения практически любой задачи.
Источники
- https://business.tutsplus.com/ru/tutorials/how-to-use-excel-math-formulas–cms-27554
- https://www.intuit.ru/studies/courses/114/114/lecture/3315
- http://on-line-teaching.com/excel/lsn021.html
- https://blog.sf.education/matematicheskie-funkczii-v-excel/
- https://FB.ru/article/445487/matematicheskie-funktsii-v-excel-osobennosti-i-primeryi
- https://lumpics.ru/mathematical-functions-in-excel/
- https://MicroExcel.ru/matematicheskie-funktsii/
КУРС
EXCEL ACADEMY
Научитесь использовать все прикладные инструменты из функционала MS Excel.
Microsoft Excel – одна из самых популярных и легкодоступных программ для представителей разный специальностей. Сегодня мы рассмотрим, пожалуй, одну из самых используемых групп формул – математические формулы.
Начнем с того, как найти их среди прочего функционала. Есть несколько путей того, как открыть список математических формул.
Самый простой способ – нажать на кнопку «Формулы» на панели управления. Затем выбрать из перечня тип функций: «Математические».
Перед вами появится выпадающий длинный список всех существующих операторов:

Всего в Excel около 80 математических и тригонометрических функций. Мы рассмотрим не все, только самые распространенные из них, а также обратим внимание на некоторые нюансы, о которых вы, возможно, не знали. Если в статье вы не нашли нужную вам функцию, то скачивайте наш бесплатный гайд «Математические функции в Excel».
Для разминки вспомним самые простые формулы.
1. Формулы СУММ(), ПРОИЗВЕД()
Эти операции имеют схожую структуру и одинаковый тип аргументов, поэтому мы их объединили в один блок. СУММ() служит для сложения данных в нескольких ячейках, ПРОИЗВЕД() – очевидно, для нахождения произведения.
Аргументами этих функций могут быть числа, диапазоны, ссылки на ячейку, в которой содержится числовое значение. Количество элементов не может быть больше 30.
СУММ() и ПРОИЗВЕД() пропускают пустые ячейки, ячейки текстового формата и логические значения. Операторы вносят результат вычислений в отдельную, ранее выделенную курсором ячейку:

Аналогично для формулы ПРОИЗВЕД():

2. Формула ЧАСТНОЕ()
Тоже одна из простых операций в математике. В Excel выполняется тоже несложно: у функции ЧАСТНОЕ() есть два аргумента: делимое и делитель.
В выделенной ячейке выводится частное:

3. Формула СУММЕСЛИ()
Оператор СУММЕСЛИ() находит сумму чисел. Главное отличие этой функции от СУММ() в том, что здесь в качестве аргумента можно задавать условие (только одно), которое будет показывать, какие значения будут использованы в расчетах, а какие – нет.
В качестве условий могут выступать неравенства со знаками больше, меньше или не равно («>», «<», «< >»). Число, которое не соответствует введенному условию, не будет включен в суммирование.
На рисунке 5 изображено суммирование всех чисел, которые больше 0.
Оранжевым выделены те числа, которые будут включены в расчет функцией СУММЕСЛИ().
Остальные числа просто будут игнорироваться:

Кроме постоянных аргументов, существует еще и дополнительный – «Диапазон суммирования». Он добавляется тогда, когда необходимо просуммировать один диапазон, а условия выбирать по другому диапазону.
Например, нужно посчитать общую стоимость всех проданных фруктов.
Для этого воспользуемся следующей формулой:

То есть сначала пишем диапазон, по которому проверяем условие, затем само ограничение и в конце диапазон чисел, которые надо суммировать. В примере на рисунке 6 выше, соответственно, все строки из категории «Овощи» в расчет включены не будут.
4. Формулы ОКРУГЛ(), ОКРУГЛВВЕРХ(), ОКРУГЛВНИЗ()
Функция ОКРУГЛ() предназначена для округления значения до заданного количества знаков после запятой. В качестве первого аргумента выступают, как обычно, числа или диапазон ячеек, второго – разряд, до которого нужно округлить число.
Например, округление значения до второго знака после запятой:

Если в качестве второго аргумента выступает 0, то число будет округляться до ближайшего целого:

Второй аргумент может быть и отрицательным, тогда округление будет происходить до требуемого знака перед запятой:

Если необходимо округлить в сторону меньшего или большего по модулю числа используют функции ОКРУГЛВНИЗ(), ОКРУГЛВВЕРХ(), соответственно:


Замечание: многие могут решить, что функции округления бесполезны, так как можно просто убрать/добавить дополнительный знак после запятой с помощью кнопок увеличить/уменьшить разрядность.
На самом деле, это не так.
Дело в том, что увеличение или уменьшение разрядности влияет только на «внешний вид» ячейки, то есть на то, как мы число видим.
Само число, при этом, не меняется. Функции округления же полностью меняют вид числа, убирая лишние разряды.
5. Формулы ОТБР(), ЦЕЛОЕ()
Эти функции очень похожи на предыдущие, но работают немного по-другому.
ОТБР() убирает все цифры справа от запятой и у положительных, и у отрицательных чисел. На первом месте в скобках после оператора пишется значение, а на втором – разряд, после которого удалятся все знаки.
Если второй аргумент пропущен, то по умолчанию ставится 0:

ЦЕЛОЕ() – функция, которая выдает в качестве результата наименьшее целое число, стоящее перед аргументом:

На положительные числа операторы влияют почти одинаково, а вот на отрицательные – нет.
Функция ЦЕЛОЕ(-5,6) выдаст результат (-6), а ОТБР(-5,6;0) выдаст (-5), хотя в то же время для числа 5,3 результат обеих функций будет одинаковый – число (5).
6. Формула ABS()
Математическая формула ABS() позволяет получить число по модулю. Как обычно, аргументами оператора является число или ссылка на ячейку.

Эту функцию удобно использовать, например, когда необходимо найти количество дней между датами. Из школьной программы многие знают, что нужно из большего вычитать меньшее.
Но что делать если дана огромная таблица, где трудно определить, где какое значение? Здесь нам помогает оператор ABS(), который переводит отрицательное число в положительное.

7. Формула КОРЕНЬ()
КОРЕНЬ() – довольно легкая функция с одним аргументом (числом или ссылкой на ячейку), которая находит квадратный корень числа:

Замечание. Для извлечения корня другой степени (не квадратного) можно пользоваться функцией СТЕПЕНЬ().
8. Формула СТЕПЕНЬ()
Функция СТЕПЕНЬ() позволяет возвести число в любую степень, в том числе извлечь корень (то есть возвести число в дробную степень).
Например, чтобы извлечь кубический корень из числа 8, необходимо воспользоваться формулой, как на рисунке 17.1.


Помимо математической функции СТЕПЕНЬ(), можно пользоваться оператором “^”, но он выглядит менее опрятно в формулах.
Если вам интересно узнать больше о других математических функциях, напишите об этом ниже в комментариях. Записывайтесь на открытый онлайн-курс «Аналитика в Excel», если хотите научиться выполнять рутинную работу в программе быстрее.
КУРС
EXCEL ACADEMY
Научитесь использовать все прикладные инструменты из функционала MS Excel.
Блог SF Education
Investment Banking
5 примеров экономии времени в Excel
Содержание статьи Что для работодателя главное в сотруднике? Добросовестность, ответственность, профессионализм и, конечно же, умение пользоваться отведенным временем! Предлагаем познакомиться с очень нужными, на…
Как работает сотрудник одной из компаний «большой тройки»?
Ты работаешь в компании «большой тройки (имеются в виду три крупнейших консалтинговых компании: McKinsey, Boston Consulting Group и Bain & Company), в которых мечтают работать тысячи подписчиков наших каналов и читателей vc.ru. Что это значит для тебя?
Russian (Pусский) translation by Ellen Nelson (you can also view the original English article)
Сложно радоваться изучению математики. Многие из нас предпочитают избегать этого на протяжении всей жизни. Это ещë одна причина использовать Microsoft Excel для получения идеальных вычислений.
Не думайте об этих формулах Excel, как о математике ради математики. Вместо этого представьте, как эти формулы могут помочь вам автоматизировать вашу жизнь и убрать проблему вычислений вручную. В конце этого урока вы получите навыки, необходимые для выполнения всех следующих действий, например:
- Вычислить средний балл экзаменов.
- Быстро суммировать счета, которые вы выдали клиентам.
- Использовать базовые статистические данные для обзора набора данных по тенденциям и показателям.
Однако вам не обязательно быть бухгалтером для освоения математики в Excel. Чтобы следовать по этому руководству, обязательно загрузите пример книги Excel или нажмите синюю кнопку Download Attachment в правой части этого урока — в любом случае его можно использовать бесплатно.
В книге Excel есть комментарии и инструкции по использованию этих формул. По мере того, как вы будете следовать этому руководству, я научу вас некоторым основным «математическим» навыкам. Давайте начнем.
Основные математические формулы в Excel (смотрите и учитесь)
Если изучение по видеороликам, это ваш стиль, посмотрите видео ниже, чтобы пройти по этому уроку. В противном случае продолжайте читать подробное описание того, как работать с каждой математической формулой Excel. Основы Формул
Основы Формул
Прежде чем мы начнем, давайте рассмотрим, как использовать любую формулу в Microsoft Excel. Независимо от того, работаете ли вы с математическими формулами в этом учебнике или любыми другими, эти советы помогут вам овладеть Excel.
1. Каждая формула в Excel начинается с «=»
Чтобы ввести формулу, щелкните любую ячейку в Microsoft Excel и введите знак равенства на клавиатуре. Так начинается формула.
После знака равенства вы можете размещать в ячейке невероятно разнообразные вещи. Попробуйте ввести =4+4 в качестве вашей первой формулы и нажмите Enter, чтобы отобразить результат. Excel выведет 8, но формула останется за кулисами электронной таблицы.
2. Формулы показываются на панели формул Excel.
Когда вы вводите формулу в ячейку, вы можете увидеть результат в ячейке сразу после нажатия клавиши ввода. Но когда вы выбираете ячейку, вы можете увидеть формулу для этой ячейки на панели формул.
Чтобы использовать пример выше, ячейка отобразит «8», но когда мы нажмем на эту ячейку, панель формул покажет, что ячейка складывает 4 и 4.
3. Как собрать формулу
В приведенном выше примере мы набрали простую формулу для складывания двух чисел. Но вам не обязательно вводить числа, вы также можете ссылаться на другие ячейки.
Excel — это сетка ячеек, а столбцы идут слева направо, каждая назначена на букву, а строки пронумерованы. Каждая ячейка является пересечением строки и столбца. Например, ячейка, где пересекаются столбцы A и строка 3, называется A3.
Предположим, что у меня две ячейки с простыми числами, например 1 и 2, и они находятся в ячейках A2 и A3. Когда я набираю формулу, я могу начать формулу с «=», как всегда. Затем я могу ввести:
=A2+A3
…чтобы сложить эти два числа вместе. Очень распространено иметь лист со значениями и отдельный лист, где выполняются вычисления. Соблюдайте все эти советы при работе с этим руководством. Для каждой из формул вы можете ссылаться на ячейки или непосредственно вводить числовые значения в формулу.
Если вам нужно изменить формулу, которую вы уже набрали, дважды щелкните по ячейке. Вы сможете настроить значения в формуле.
Арифметика в Excel
Теперь мы рассмотрим математические формулы Excel и рассмотрим, как их использовать. Начнем с изучения базовой арифметической формулы. Это основа математических операций.
1. Сложение и вычитание
Сложение и вычитание — две основные математические формулы в Excel. Независимо от того, складываете ли вы список бизнес-расходов за месяц или баланс вашей чековой книжки в цифровом виде, операторы сложения и вычитания невероятно полезны.
Используйте вкладку «Add and Subtract» в книге, которую вы скачали для практики.
Сложение значений
Пример:
=24+48
или, ссылаемся на значения в ячейках:
=A2+A3
Совет: попытайтесь сложить пять или шесть значений и посмотрите, что получится. Разделите каждое значение знаком плюс.
Вычитание значений
Пример:
=75-25-10
или, ссылаемся на значения в ячейках:
=A3-A2
2. Умножение
Для умножения, используйте знак *. Используйте умножение вместо сложения того же числа снова и снова.
Используйте вкладку «Multiply» в книге для практики.
Пример:
=5*4
или, ссылаемся на значения в ячейках:
=A2*A3
3. Деление
Деление полезно при разделении элементов на группы, например. Используйте оператор «/» для деления чисел или значений в ячейках ваших таблиц.
Используйте вкладку «Divide» в книге для практики.
Пример:
=20/10
или, ссылаемся на значения в ячейках:
=A5/B2
Базовая статистика
Используйте вкладку «Basic Statistics» в книге для практики.
Теперь, когда вы знаете основные математические операторы, давайте перейдем к чему-то более продвинутому. Базовая статистика полезна для обзора набора данных и принятия обоснованных решений. Давайте рассмотрим несколько популярных простых статистических формул.
1. Среднее
Чтобы использовать формулу среднего в Excel, начните формулу с помощью =СРЗНАЧ(, а затем введите свои значения. Разделите каждое число запятой. Когда вы нажмёте клавишу ввода, Excel вычислит и выведет среднее значение.
=СРЗНАЧ(1;3;5;7;10)
Лучший способ рассчитать среднее это ввести ваши значения в отдельные ячейки в одном столбце.
=СРЗНАЧ(A2:A5)
2. Медиана
Медиана набора данных это значение, которое находится посередине. Если вы взяли числовые значения и выставили их в порядке от наименьшего к самому большому, медиана была бы ровно посередине этого списка.
=МЕДИАНА(1;3;5;7;10)
Я бы рекомендовал ввести ваши значения в список ячеек, а затем использовать формулу медианы над списком ячеек со значениями, введенными в них.
=МЕДИАНА(A2:A5)
3. Минимум
Если у вас есть набор данных и вы хотите держать на виду наименьшее значение, полезно использовать формулу МИН в Excel. Вы можете использовать формулу МИН со списком чисел, разделенных точкой с запятыми, чтобы найти самое маленькое значение в наборе. Это очень полезно при работе с большими наборами данных.
=МИН(1;3;5;7;9)
Возможно, вы захотите найти минимальное значение в списке данных, что вполне возможно с помощью такой формулы, как:
=МИН(A1:E1)
4. Максимум
Формула МАКС в Excel — полная противоположность МИН; оно сообщает вам, какое значение в наборе является самым большим. Вы можете использовать его со списком чисел, разделенных точкой с запятой:
=МАКС(1;3;5;7;9)
Или же, вы можете выбрать список значений в ячейках, и Excel вернет наибольшее из набора с этой формулой:
=МАКС(A1:E1)
Повторяйте и продолжайте обучение
Надеюсь, этот учебный материал по математическим формулам Excel поможет вам больше узнать о том, что Excel может сделать для вас. С достаточной практикой, скоро вы станете владеть Excel более естественно, вместо того, чтобы схватить калькулятор или выполнять вычисления на бумаге. Таблицы собирают данные, а формулы помогают нам понять или изменять эти данные. Операции могут быть основными, но лежат в основе важных электронных таблиц в каждой компании.
Всегда полезно посмотреть один урок, чтобы начать обучение дальше. Вот некоторые предложения
- Для более продвинутого формата математики на подобие уравнений, официальная документация Microsoft имеет страницу под названием «Вставка или изменение формулы или выражения». (Прим.пер.: просто замените en-us на ru-ru в адресной строке.)
- Tuts+ инструктор Боб Флиссер имеет хороший учебник по вычислению процентов в Excel.
Каковы другие математические навыки, которые вы используете в Excel? Оставьте ответ в комментариях, если вы знаете отличную формулу, которую я не знаю.
В программе Excel разработчиками заложено огромное количество различных функций, но, пользователи чаще всего пользуются математическими. Давайте рассмотрим их и подробнее остановимся на самых популярных.
-
Использование математических функций в программе
- СУММ
- СУММЕСЛИ
- ПРОИЗВЕД
- ЧАСТНОЕ
- СТЕПЕНЬ
- КОРЕНЬ
- ОКРУГЛ
- ABS
- LOG
- ОСТАТОК
- Заключение
Использование математических функций в программе
В категорию математических функций входит более 60 различных операторов, которые позволяют выполнять различные вычисления.
Вставить функцию в свободную ячейку таблицы можно по-разному:
- Жмем кнопку “Вставить функцию” (fx) слева от строки формул. Выполнить данное действие можно, находясь в любой вкладке.
- Переключаемся во вкладку “Формулы”. Здесь также представлена кнопка “Вставить функцию” – в левом углу ленты инструментов.
- Нажимаем комбинацию клавиш Shift+F3, чтобы вызвать Мастер функций.
Результатом любого из вышеописанных способов будет открытие окна вставки функции. Здесь мы выбираем категорию “Математические”.
Теперь, когда категория выбрана, в поле ниже отмечаем требуемую функцию и щелкаем OK.
После этого откроется окно с аргументами для заполнения.
Примечание: Если мы, находясь во вкладке “Формулы”, в группе инструментов “Библиотека функций” нажмем по значку математических функций, сразу откроется список операторов, которые мы можем выбрать, минуя окно вставки функции.
Стоит учитывать, что в предлагаемом перечне присутствуют не все операторы, но самые необходимые здесь все же есть, и в большинстве случаев их достаточно.
Теперь перейдем к детальному рассмотрению самых популярных функций.
СУММ
Пожалуй, это самая популярная функция, которая используется в Эксель. С помощью нее выполняется суммирование числовых данных. Формула функции:
=СУММ(число1;число2;...)
В аргументах можно указать как конкретные числа, так и ссылки на ячейки, содержащие числовые значения. Причем указать координаты можно вручную (с помощью клавиш клавиатуры) или методом клика/выделения непосредственно в самой таблице.
Для перехода к заполнению следующего аргумента достаточно кликнуть по полю напротив него или нажать клавишу Tab.
СУММЕСЛИ
Данная функция позволяет считать сумму чисел с заданным условиями, с помощью которых будет выполняться отбор значений, учитывающихся в суммировании. Формула выглядит следующим образом:
=СУММЕСЛИ(Диапазон;Критерий;Диапазон_суммирования)
В аргументах функции указывается диапазон ячеек (вручную или путем выделения в таблице), значения которых нужно просуммировать. В качестве критерия можно задать следующие условия (в кавычках):
- больше (“>”)
- меньше (“<“)
- не равно (“<>”)
Аргумент “Диапазон_сумирования” заполнять не обязательно.
ПРОИЗВЕД
С помощью данного оператора выполняется умножение чисел. Синтаксис выглядит следующим образом:
=ПРОИЗВЕД(число;число;…)
В аргументах функции, как и в СУММ, можно указывать как конкретные числа, так и адреса ячеек (диапазоны ячеек), которые содержат числовые значения.
ЧАСТНОЕ
Чаще всего для деления используется формула со знаком “/” между делимым и делителем: =Число1/Число2.
Однако в программе также есть отдельная функция для выполнения деления, синтаксис которой представлен ниже:
=ЧАСТНОЕ(Числитель;Знаменатель)
Заполнить нужно два аргумента: Числитель (Делимое) и Знаменатель (Делитель).
СТЕПЕНЬ
Оператор позволяет возвести число в указанную степень. Формула выглядит так:
=СТЕПЕНЬ(число;степень)
В аргументах функции указывается само число, а также, степень, в которую нужно его возвести.
КОРЕНЬ
С помощью данного оператора можно извлечь квадратный корень из числа. Синтаксис выглядит следующим образом:
=КОРЕНЬ(число)
Заполнить требуется только один аргумент – “Число”.
ОКРУГЛ
Функция применяется для выполнения еще одного распространенного математического действия – округления чисел (по общематематическим правилам, т.е., к ближайшему по модулю значению). Синтаксис функции представлен ниже:
=ОКРУГЛ(число;число_разрядов)
В аргументе “Число” указывается значение, которое требуется округлить. В числе разрядов, соответственно, пишем количество цифр, которые хотим оставить после запятой.
Также, в Excel доступны операторы ОКРУГЛВВЕРХ и ОКРУГЛВНИЗ, которые, как следует из их названий, используются для округления до ближайшего верхнего и нижнего числа, соответственно (по модулю).
ABS
Позволяет получить модуль числа. Формула функции представлена ниже:
=ABS(число)
Заполнить нужно всего один аргумент – “Число”, модуль которого требуется найти.
LOG
С помощью этого оператора определяется логарифм числа по заданному основанию. Синтаксис функции представлен в виде:
=LOG(Число;Основание)
Необходимо заполнить два аргумента: Число и Основание логарифма (если его не указать, программа примет значение по умолчанию, равное 10).
Также для десятичного логарифма предусмотрена отдельная функция – LOG10.
ОСТАТОК
Применяется для получения остатка от деления чисел. Формула оператора выглядит следующим образом:
=ОСТАТ(чило;делитель)
Для того, чтобы получить результат, требуется заполнить значения двух аргументов: Число и Делитель.
Заключение
Таким образом, мы разобрали самые популярные математические функции, которые используются в Excel. Однако возможности программы гораздо шире, и в ее инструментарии можно найти функцию для успешного выполнения практически любой задачи.
Содержание
- 1 Автосуммирование
- 2 Тиражирование формул при помощи маркера заполнения
- 3 Относительные и абсолютные ссылки
- 3.1 Создание имени
- 3.2 Создание нескольких имен
- 4 Ошибки в формулах
- 5 Функции в Excel
- 6 Построение вычислительных таблиц
Формула — это математическое выражение, которое создается для вычисления результата и которое может зависеть от содержимого других ячеек. Формула в ячейке может содержать данные, ссылки на другие ячейки, а также обозначение действий, которые необходимо выполнить.
Использование ссылок на ячейки позволяет пересчитывать результат по формулам, когда происходят изменения содержимого ячеек, включенных в формулы.
В Excel формулы начинаются со знака =. Скобки ( ) могут использоваться для определения порядка математических операции.
Excel поддерживает следующие операторы:
- Арифметические операции:
- сложение (+);
- умножение (*);
- нахождение процента (%);
- вычитание (-);
- деление (/);
- экспонента (^).
- Операторы сравнения:
- = равно;
- < меньше;
- > больше;
- = больше или равно;
- не равно.
- Операторы связи:
- : диапазон;
- ; объединение;
- & оператор соединения текстов.
| Формула | Составляющие элементы |
| =27+36 =А1+А2-АЗ =45%*АЗ , |
Цифры Ссылки на ячейки Цифры и ссылки на ячейки |
| =СУММ(А1:А5), =МАКС(АЗ:А5) |
Предварительно определенные функции |
| =(А1+А2)/АЗ | Ссылки на ячейки при заданном порядке действий |
Таблица 22. Примеры формул
Упражнение
Вставка формулы -25-А1+АЗ
Предварительно введите любые числа в ячейки А1 и A3.
- Выберите необходимую ячейку, например В1.
- Начните ввод формулы со знака=.
- Введите число 25, затем оператор (знак -).
- Введите ссылку на первый операнд, например щелчком мыши на нужную ячейку А1.
- Введите следующий оператор(знак +).
- Щелкните мышью в той ячейке, которая является вторым операндом в формуле.
- Завершите ввод формулы нажатием клавиши Enter. В ячейке В1 получите результат.
Автосуммирование
Кнопка Автосумма (AutoSum) — ∑ может использоваться для автоматического создания формулы, которая суммирует область соседних ячеек, находящихся непосредственно слева в данной строке и непосредственно выше в данном столбце.
- Выберите ячейку, в которую надо поместить результат суммирования.
- Щелкните кнопку Автосумма — ∑ или нажмите комбинацию клавиш Alt+=. Excel примет решение, какую область включить в диапазон суммирования, и выделит ее пунктирной движущейся рамкой, называемой границей.
- Нажмите Enter для принятия области, которую выбрала программа Excel, или выберите с помощью мыши новую область и затем нажмите Enter.
Функция «Автосумма» автоматически трансформируется в случае добавления и удаления ячеек внутри области.
Упражнение
Создание таблицы и расчет по формулам
- Введите числовые данные в ячейки, как показано в табл. 23.
| А | В | С | D | Б | F | |
| Распределение сотрудников по образованию | ||||||
| Магнолия | Лилия | Фиалка | Всего | |||
| Высшее | 25 | 20 | 9 | |||
| Среднее спец. | 28 | 23 | 21 | |||
| ПТУ | 27 | 58 | 20 | |||
| в | Другое | 8 | 10 | 9 | ||
| Всего | ||||||
| Без высшего |
Таблица 23. Исходная таблица данных
- Выберите ячейку В7, в которой будет вычислена сумма по вертикали.
- Щелкните кнопку Автосумма — ∑ или нажмите Alt+=.
- Повторите действия пунктов 2 и 3 для ячеек С7 и D7.
Вычислите количество сотрудников без высшего образования (по формуле В7-ВЗ).
- Выберите ячейку В8 и наберите знак (=).
- Щелкните мышью в ячейке В7, которая является первым операндом в формуле.
- Введите с клавиатуры знак (-) и щелкните мышью в ячейке ВЗ, которая является вторым операндом в формуле (будет введена формула).
- Нажмите Enter (в ячейке В8 будет вычислен результат).
- Повторите пункты 5-8 для вычислений по соответствующим формулам в ячейках С8 и 08.
- Сохраните файл с именем Образование_сотрудников.х1s.
Таблица 24. Результат расчета
| А | B | С | D | Е | F | |
| Распределение сотрудников по образованию | ||||||
| Магнолия | Лилия | Фиалка | Всего | |||
| Высшее | 25 | 20 | 9 | |||
| Среднее спец. | 28 | 23 | 21 | |||
| ПТУ | 27 | 58 | 20 | |||
| Другое | 8 | 10 | 9 | |||
| Всего | 88 | 111 | 59 | |||
| Без высшего | 63 | 91 | 50 |
Тиражирование формул при помощи маркера заполнения
Область ячеек (ячейка) может быть размножена при помощи использования маркера заполнения. Как было показано в предыдущем разделе, маркер заполнения представляет собой контрольную точку в правом нижнем углу выделенной ячейки.
Часто бывает необходимо размножать не только данные, но и формулы, содержащие адресные ссылки. Процесс тиражирования формул при помощи маркера заполнения позволяет колировать формулу при одновременном изменении адресных ссылок в формуле.
- Выберите ячейку, содержащую формулу для тиражирования.
- Перетащите маркер заполнения в нужном направлении. Формула будет размножена во всех ячейках.
Обычно этот процесс используется при копировании формул внутри строк или столбцов, содержащих однотипные данные. При тиражировании формул с помощью маркера заполнения меняются так называемые относительные адреса ячеек в формуле (подробно относительные и абсолютные ссылки будут описаны далее).
Упражнение
Тиражирование формул
1.Откройте файл Образование_сотрудников.х1s.
- Введите в ячейку ЕЗ формулу для автосуммирования ячеек =СУММ(ВЗ:03).
- Скопируйте, перетащив маркер заполнения, формулу в ячейки Е4:Е8.
- Просмотрите как меняются относительные адреса ячеек в полученных формулах (табл. 25) и сохраните файл.
| А | В | С | D | Е | F | |
| Распределение сотрудников по образованию | ||||||
| Магнолия | Лилия | Фиалка | Всего | |||
| Высшее | 25 | 20 | 9 | =СУММ{ВЗ:03) | ||
| Среднее спец. | 28 | 23 | 21 | =СУММ(В4:04) | ||
| ПТУ | 27 | 58 | 20 | =СУММ(В5:05) | ||
| Другое | 8 | 10 | 9 | =СУММ(В6:06) | ||
| Всего | 88 | 111 | 58 | =СУММ(В7:07) | ||
| Без высшего | 63 | 91 | 49 | =СУММ(В8:08) |
Таблица 25. Изменение адресов ячеек при тиражировании формул
Относительные и абсолютные ссылки
Формулы, реализующие вычисления в таблицах, для адресации ячеек используют так называемые ссылки. Ссылка на ячейку может быть относительной или абсолютной.
Использование относительных ссылок аналогично указанию направления движения по улице — «идти три квартала на север, затем два квартала на запад». Следование этим инструкциям из различных начальных мест будет приводить в разные места назначения.
Обычно ссылки на ячейки описываются и используются как относительные (формат записи А1). Когда формула, содержащая эти ссылки, копируется, происходит изменение формулы для поддержания относительности ссылок.
Например, формула, которая суммирует числа в столбце или строке, затем часто копируется для других номеров строк или столбцов. В таких формулах используются относительные ссылки (см. предыдущий пример в табл. 25).
Абсолютная ссылка на ячейку .иди область ячеек будет всегда ссылаться на один и тот же адрес строки и столбца. При сравнении с направлениями улиц это будет примерно следующее: «Идите на пересечение Арбата и Бульварного кольца». Вне зависимости от места старта это будет приводить к одному и тому же месту. Если формула требует, чтобы адрес ячейки оставался неизменным при копировании, то должна использоваться абсолютная ссылка (формат записи $А$1). Например, когда формула вычисляет доли от общей суммы, ссылка на ячейку, содержащую общую сумму, не должна изменяться при копировании.
Абсолютная ссылка может быть создана только при наборе формулы, перед адресом строки и столбца вводится знак доллара — $.
Для создания абсолютной ссылки удобно использовать клавишу абсолютной ссылки F4, которая осуществляет преобразование относительной ссылки в абсолютную и наоборот.
Знак доллара ($) появится как перед ссылкой на столбец, так и перед ссылкой на строку (например, $С$2), Последовательное нажатие F4 будет добавлять или убирать знак перед номером столбца или строки в ссылке (С$2 или $С2 — так называемые смешанные ссылки).
Упражнение
Создание абсолютной ссылки
- Создайте таблицу, аналогичную представленной ниже.
| A | B | C | |
| Часовая ставка | 100р. | ||
| Ф. И. 0 . | Часов | Зарплата | |
| Иванов | 40 | ||
| Петров | 30 | ||
| Сидоров | 25 |
Таблица 26. Расчет зарплаты
- В ячейку СЗ введите формулу для расчета зарплаты Иванова =В1*ВЗ.
При тиражировании формулы данного примера с относительными ссылками в ячейке С4 появляется сообщение об ошибке (#ЗНАЧ!), так как изменится относительный адрес ячейки В1, и в ячейку С4 скопируется формула =В2*В4;
- Задайте абсолютную ссылку на ячейку В1, поставив курсор в строке формул на В1 и нажав клавишу F4, Формула в ячейке СЗ будет иметь вид =$В$1*ВЗ.
- Скопируйте формулу в ячейки С4 и С5.
- Сохраните файл (табл. 27) под именем Зарплата.xls.
| A | B | C | |
| 1 | Часовая ставка | 100р. | |
| ФИО | Часов | Зарплата | |
| 3 | Иванов | 40 | 4000р. |
| 4 | Петров | 30 | 3000р. |
| 5 | Сидоров | 25 | 2500р. |
Таблица 27. Итоги расчета зарплаты
Имена в формулах
Имена в формулах легче запомнить, чем адреса ячеек, поэтому вместо абсолютных ссылок можно использовать именованные области (одна или несколько ячеек). Необходимо соблюдать следующие правила при создании имен:
- имена могут содержать не более 255 символов;
- имена должны начинаться с буквы и могут содержать любой символ, кроме пробела;
- имена не должны быть похожи на ссылки, такие, как ВЗ, С4;
- имена не должны использовать функции Excel, такие, как СУММ, ЕСЛИ и т. п.
В меню Вставка, Имя существуют две различные команды создания именованных областей: Создать и Присвоить.
Команда Создать позволяет задать (ввести) требуемое имя (только одно)команда Присвоить использует метки, размещенные на рабочем листе, в качестве имен областей (разрешается создавать сразу несколько имен).
Создание имени
- Выделите ячейку В1 (табл. 26).
- Выберите в меню Вставка, Имя (Insert, Name) команду Присвоить (Define).
- Введите имя Часовая ставка и нажмите ОК.
- Выделите ячейку В1 и убедитесь, что в поле имени указано Часовая ставка.
Создание нескольких имен
- Выделите ячейки ВЗ:С5 (табл. 27).
- Выберите в меню Вставка, Имя (Insert, Name) команду Создать (Create), появится диалоговое окно Создать имена (рис. 88).
- Убедитесь, что переключатель в столбце слева помечен и нажмите ОК.
- Выделите ячейки ВЗ:СЗ и убедитесь, что в поле имени указано Иванов.
Рис. 88. Диалоговое окно Создать имена
Можно в формулу вставить имя вместо абсолютной ссылки.
- В строке формул установите курсор в то место, где будет добавлено имя.
- Выберите в меню Вставка, Имя (Insert, Name) команду Вставить (Paste), появится диалоговое окно Вставить имена.
- Выберите нужное имя из списка и нажмите ОК.
Ошибки в формулах
Бели при вводе формул или данных допущена ошибка, то в результирующей ячейке появляется сообщение об ошибке. Первым символом всех значений ошибок является символ #. Значения ошибок зависят от вида допущенной ошибки.
Excel может распознать далеко не все ошибки, но те, которые обнаружены, надо уметь исправить.
Ошибка # # # # появляется, когда вводимое число не умещается в ячейке. В этом случае следует увеличить ширину столбца.
Ошибка #ДЕЛ/0! появляется, когда в формуле делается попытка деления на нуль. Чаще всего это случается, когда в качестве делителя используется ссылка на ячейку, содержащую нулевое или пустое значение.
Ошибка #Н/Д! является сокращением термина «неопределенные данные». Эта ошибка указывает на использование в формуле ссылки на пустую ячейку.
Ошибка #ИМЯ? появляется, когда имя, используемое в формуле, было удалено или не было ранее определено. Для исправления определите или исправьте имя области данных, имя функции и др.
Ошибка #ПУСТО! появляется, когда задано пересечение двух областей, которые в действительности не имеют общих ячеек. Чаще всего ошибка указывает, что допущена ошибка при вводе ссылок на диапазоны ячеек.
Ошибка #ЧИСЛО! появляется, когда в функции с числовым аргументом используется неверный формат или значение аргумента.
Ошибка #ССЫЛКА! появляется, когда в формуле используется недопустимая ссылка на ячейку. Например, если ячейки были удалены или в эти ячейки было помещено содержимое других ячеек.
Ошибка #ЗНАЧ! появляется, когда в формуле используется недопустимый тип аргумента или операнда. Например, вместо числового или логического значения для оператора или функции введен текст.
Кроме перечисленных ошибок, при вводе формул может появиться циклическая ссылка.
Циклическая ссылка возникает тогда, когда формула прямо или косвенно включает ссылки на свою собственную ячейку. Циклическая ссылка может вызывать искажения в вычислениях на рабочем листе и поэтому рассматривается как ошибка в большинстве приложений. При вводе циклической ссылки появляется предупредительное сообщение (рис. 89).
Рис. 89. Циклическая ссылка
Индикатор циклической ссылки в строке состояния показывает ««ссылку на последнюю зависимую формулу.
Когда формула, содержащая циклическую ссылку, находится на рабочем листе, появится сообщение, указанное на рис. 89.
Для исправления ошибки удалите ячейку, которая вызвала циклическую ссылку, отредактируйте или введите заново формулу.
Более сложные вычисления в таблицах Excel осуществляются с помощью специальных функций (рис. 90). Список категорий функций доступен при выборе команды Функция в меню Вставка (Insert, Function).
Финансовые функции осуществляют такие расчеты, как вычисление суммы платежа по ссуде, величину выплаты прибыли на вложения и др.
Функции Дата и время позволяют работать со значениями даты и времени в формулах. Например, можно использовать в формуле текущую дату, воспользовавшись функцией СЕГОДНЯ.
Рис. 90. Мастер функций
Математические функции выполняют простые и сложные математические вычисления, например вычисление суммы диапазона ячеек, абсолютной величины числа, округление чисел и др.
Статистические функции позволяют выполнять статистический анализ данных. Например, можно определить среднее значение и дисперсию по выборке и многое другое.
Функции Ссылки и массивы позволяют осуществить поиск данных в списках или таблицах, найти ссылку на ячейку в массиве. Например, для поиска значения в строке таблицы используется функция ГПР.
Функции работы с базами данных можно использовать для выполнения расчетов и для отбора записей по условию.
Текстовые функции предоставляют пользователю возможность обработки текста. Например, можно объединить несколько строк с помощью функции СЦЕПИТЬ.
Логические функции предназначены для проверки одного или нескольких условий. Например, функция ЕСЛИ позволяет определить, выполняется ли указанное условие, и возвращает одно значение, если условие истинно, и другое, если оно ложно.
Функции Проверка свойств и значений предназначены для определения данных, хранимых в ячейке. Эти функции проверяют значения в ячейке по условию и возвращают в зависимости от результата значения ИСТИНА или ЛОЖЬ.
Для вычислений в таблице с помощью встроенных функций рекомендуется использовать мастер функций. Диалоговое окно мастера функций доступно при выборе команды Функция в меню Вставка или нажатии кнопки на стандартной панели инструментов. В процессе диалога с мастером требуется задать аргументы выбранной функции, для этого необходимо заполнить поля в диалоговом окне соответствующими значениями или адресами ячеек таблицы.
Упражнение
Вычисление величины среднего значения для каждой строки в файле Образование.хls.
- Выделите ячейку F3 и нажмите на кнопку мастера функций.
- В первом окне диалога мастера функций из категории Статистические выберите функцию СРЗНАЧ, нажмите на кнопку Далее.
- Во втором диалоговом окне мастера функций должны быть заданы аргументы. Курсор ввода находится в поле ввода первого аргумента. В это поле в качестве аргумента число! введите адрес диапазона B3:D3 (рис. 91).
- Нажмите ОК.
- Скопируйте полученную формулу в ячейки F4:F6 и сохраните файл (табл. 28).
Рис. 91. Ввод аргумента в мастере функций
Таблица 28. Таблица результатов расчета с помощью мастера функций
| А | В | С | D | Е | F | |
| Распределение сотрудников по образованию | ||||||
| Магнолия | Лилия | Фиалка | Всего | Среднее | ||
| Высшее | 25 | 20 | 9 | 54 | 18 | |
| Среднее спец. | 28 | 23 | 21 | 72 | 24 | |
| ПТУ | 27 | 58 | 20 | 105 | 35 | |
| в | Другое | 8 | 10 | 9 | 27 | 9 |
| Всего | 88 | 111 | 59 | 258 | 129 |
Для ввода диапазона ячеек в окно мастера функций можно мышью обвести на рабочем листе таблицы этот диапазон (в примере B3:D3). Если окно мастера функций закрывает нужные ячейки, можно передвинуть окно диалога. После выделения диапазона ячеек (B3:D3) вокруг него появится бегущая пунктирная рамка, а в поле аргумента автоматически появится адрес выделенного диапазона ячеек.
Примеры применения функций программы для создания таблиц с данными. Управление и форматирование диапазонов ячеек для преобразования их в таблицу.
Построение вычислительных таблиц
Копирование данных листа стандартными средствами Excel.
Способы копирования диапазонов с помощью быстрых клавиш и контекстного меню. Копирование форматов ячеек без значений.
Как добавить ячейки в таблицу Excel.
Вставка и удаление ячеек в таблицы на листе. Добавление диапазонов в таблицу. Горячие клавиши для вставки пустых ячеек.
Как вставить строку или столбец в Excel между строками и столбцами.
Вставка и удаление строк и колонок листа. Горячие клавиши для быстрого добавления и удаления строки и колонки. Редактирование таблиц прайс-листов.
Как переместить и скопировать лист Excel в другую книгу.
Управление книгами при копировании или перемещении листов между ними. Пример как переместить или скопировать лист в другой файл.
Перемещение и расстановка листов в документе Excel.
Копирование, перемещение и создание нескольких листов одновременно. Полный контроль над листами рабочей книги.
Создание, копирование и перемещение листов в книгах Excel.
Управление листами рабочих книг. Добавление, перемещение и копирование листов вместе с их содержимым.
Редактирование строк и столбцов в таблицах.
Практические примеры по редактированию и группировки данных в таблицах с добавлением, удалением, скрытием строк и столбцлов.
Создание и управление таблицами в Excel.
Работа с таблицами данных, от простого создания до сложных корректировок таблиц.
1 2
Таблицы в Excel представляют собой ряд строк и столбцов со связанными данными, которыми вы управляете независимо друг от друга.
Работая в Excel с таблицами, вы сможете создавать отчеты, делать расчеты, строить графики и диаграммы, сортировать и фильтровать информацию.
Если ваша работа связана с обработкой данных, то навыки работы с таблицами в Эксель помогут вам сильно сэкономить время и повысить эффективность.
Как работать в Excel с таблицами. Пошаговая инструкция
Прежде чем работать с таблицами в Эксель, последуйте рекомендациям по организации данных:
- Данные должны быть организованы в строках и столбцах, причем каждая строка должна содержать информацию об одной записи, например о заказе;
- Первая строка таблицы должна содержать короткие, уникальные заголовки;
- Каждый столбец должен содержать один тип данных, таких как числа, валюта или текст;
- Каждая строка должна содержать данные для одной записи, например, заказа. Если применимо, укажите уникальный идентификатор для каждой строки, например номер заказа;
- В таблице не должно быть пустых строк и абсолютно пустых столбцов.
1. Выделите область ячеек для создания таблицы
Выделите область ячеек, на месте которых вы хотите создать таблицу. Ячейки могут быть как пустыми, так и с информацией.
2. Нажмите кнопку “Таблица” на панели быстрого доступа
На вкладке “Вставка” нажмите кнопку “Таблица”.
3. Выберите диапазон ячеек
В всплывающем вы можете скорректировать расположение данных, а также настроить отображение заголовков. Когда все готово, нажмите “ОК”.
4. Таблица готова. Заполняйте данными!
Поздравляю, ваша таблица готова к заполнению! Об основных возможностях в работе с умными таблицами вы узнаете ниже.
Форматирование таблицы в Excel
Для настройки формата таблицы в Экселе доступны предварительно настроенные стили. Все они находятся на вкладке “Конструктор” в разделе “Стили таблиц”:
Если 7-ми стилей вам мало для выбора, тогда, нажав на кнопку, в правом нижнем углу стилей таблиц, раскроются все доступные стили. В дополнении к предустановленным системой стилям, вы можете настроить свой формат.
Помимо цветовой гаммы, в меню “Конструктора” таблиц можно настроить:
- Отображение строки заголовков – включает и отключает заголовки в таблице;
- Строку итогов – включает и отключает строку с суммой значений в колонках;
- Чередующиеся строки – подсвечивает цветом чередующиеся строки;
- Первый столбец – выделяет “жирным” текст в первом столбце с данными;
- Последний столбец – выделяет “жирным” текст в последнем столбце;
- Чередующиеся столбцы – подсвечивает цветом чередующиеся столбцы;
- Кнопка фильтра – добавляет и убирает кнопки фильтра в заголовках столбцов.
Как добавить строку или столбец в таблице Excel
Даже внутри уже созданной таблицы вы можете добавлять строки или столбцы. Для этого кликните на любой ячейке правой клавишей мыши для вызова всплывающего окна:
- Выберите пункт “Вставить” и кликните левой клавишей мыши по “Столбцы таблицы слева” если хотите добавить столбец, или “Строки таблицы выше”, если хотите вставить строку.
- Если вы хотите удалить строку или столбец в таблице, то спуститесь по списку в сплывающем окне до пункта “Удалить” и выберите “Столбцы таблицы”, если хотите удалить столбец или “Строки таблицы”, если хотите удалить строку.
Как отсортировать таблицу в Excel
Для сортировки информации при работе с таблицей, нажмите справа от заголовка колонки “стрелочку”, после чего появится всплывающее окно:
В окне выберите по какому принципу отсортировать данные: “по возрастанию”, “по убыванию”, “по цвету”, “числовым фильтрам”.
Как отфильтровать данные в таблице Excel
Для фильтрации информации в таблице нажмите справа от заголовка колонки “стрелочку”, после чего появится всплывающее окно:
- “Текстовый фильтр” отображается когда среди данных колонки есть текстовые значения;
- “Фильтр по цвету” также как и текстовый, доступен когда в таблице есть ячейки, окрашенные в отличающийся от стандартного оформления цвета;
- “Числовой фильтр” позволяет отобрать данные по параметрам: “Равно…”, “Не равно…”, “Больше…”, “Больше или равно…”, “Меньше…”, “Меньше или равно…”, “Между…”, “Первые 10…”, “Выше среднего”, “Ниже среднего”, а также настроить собственный фильтр.
- В всплывающем окне, под “Поиском” отображаются все данные, по которым можно произвести фильтрацию, а также одним нажатием выделить все значения или выбрать только пустые ячейки.
Если вы хотите отменить все созданные настройки фильтрации, снова откройте всплывающее окно над нужной колонкой и нажмите “Удалить фильтр из столбца”. После этого таблица вернется в исходный вид.
Как посчитать сумму в таблице Excel
Для того чтобы посчитать сумму колонки в конце таблицы, нажмите правой клавишей мыши на любой ячейке и вызовите всплывающее окно:
В списке окна выберите пункт “Таблица” => “Строка итогов”:
Внизу таблица появится промежуточный итог. Нажмите левой клавишей мыши на ячейке с суммой.
В выпадающем меню выберите принцип промежуточного итога: это может быть сумма значений колонки, “среднее”, “количество”, “количество чисел”, “максимум”, “минимум” и т.д.
Как в Excel закрепить шапку таблицы
Таблицы, с которыми приходится работать, зачастую крупные и содержат в себе десятки строк. Прокручивая таблицу “вниз” сложно ориентироваться в данных, если не видно заголовков столбцов. В Эксель есть возможность закрепить шапку в таблице таким образом, что при прокрутке данных вам будут видны заголовки колонок.
Для того чтобы закрепить заголовки сделайте следующее:
- Перейдите на вкладку “Вид” в панели инструментов и выберите пункт “Закрепить области”:
- Выберите пункт “Закрепить верхнюю строку”:
- Теперь, прокручивая таблицу, вы не потеряете заголовки и сможете легко сориентироваться где какие данные находятся:
Как перевернуть таблицу в Excel
Представим, что у нас есть готовая таблица с данными продаж по менеджерам:
На таблице сверху в строках указаны фамилии продавцов, в колонках месяцы. Для того чтобы перевернуть таблицу и разместить месяцы в строках, а фамилии продавцов нужно:
- Выделить таблицу целиком (зажав левую клавишу мыши выделить все ячейки таблицы) и скопировать данные (CTRL+C):
- Переместить курсор мыши на свободную ячейку и нажать правую клавишу мыши. В открывшемся меню выбрать “Специальная вставка” и нажать на этом пункте левой клавишей мыши:
- В открывшемся окне в разделе “Вставить” выбрать “значения” и поставить галочку в пункте “транспонировать”:
- Готово! Месяцы теперь размещены по строкам, а фамилии продавцов по колонкам. Все что остается сделать – это преобразовать полученные данные в таблицу.
В этой статье вы ознакомились с принципами работы в Excel с таблицами, а также основными подходами в их создании. Пишите свои вопросы в комментарии!