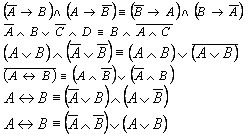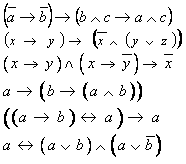Типовое задание № 2
(базовый уровень,
время – 3 мин)
Тема:
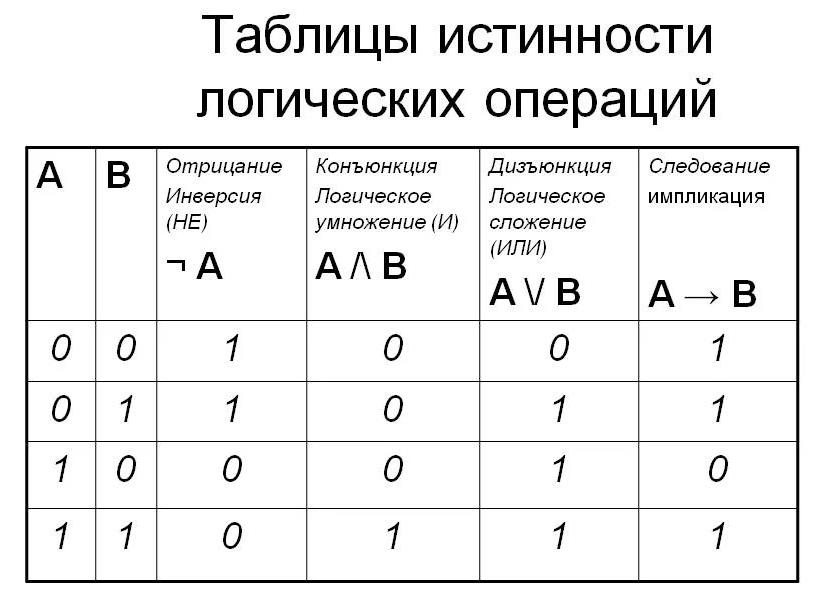
Анализ таблиц истинности логических выражений.
Что проверяется:
Умение строить таблицы
истинности и логические схемы.
1.5.1.
Высказывания, логические операции, кванторы, истинность высказывания
1.1.6.
Умение строить модели объектов, систем и процессов в виде таблицы истинности
для логического высказывания
Про обозначения
К
сожалению, обозначения логических операций И, ИЛИ и НЕ, принятые в «серьезной»
математической логике (Ù,Ú,¬), неудобны, интуитивно
непонятны и никак не проявляют аналогии с обычной алгеброй. Автор, к своему
стыду, до сих пор иногда путает Ù и Ú.
Поэтому на его уроках операция «НЕ» обозначается чертой сверху, «И» – знаком
умножения (поскольку это все же логическое умножение), а «ИЛИ» – знаком «+»
(логическое сложение). В разных учебниках используют разные обозначения. К
счастью, в начале задания ЕГЭ приводится расшифровка закорючек (Ù,Ú,¬), что еще раз подчеркивает проблему.
Что нужно знать:
условные
обозначения логических операций
¬ A, не
A (отрицание, инверсия)
A Ù B, A и B (логическое
умножение, конъюнкция)
A Ú B, A или B
(логическое сложение, дизъюнкция)
A → B импликация (следование)
A º B
эквивалентность (равносильность)
операцию «импликация» можно выразить через «ИЛИ» и «НЕ»:
A → B = ¬ A Ú B или в других обозначениях A → B =
иногда для упрощения выражений полезны формулы де Моргана:
¬ (A Ù
B) = ¬ A Ú ¬ B
¬ (A Ú
B) = ¬ A Ù ¬ B
если в выражении нет скобок, сначала выполняются все операции
«НЕ», затем – «И», затем – «ИЛИ», «импликация», и самая последняя –
«эквивалентность»
таблица
истинности выражения определяет его значения при всех возможных комбинациях
исходных данных
если
известна только часть таблицы истинности, соответствующее логическое выражение
однозначно определить нельзя, поскольку частичной таблице могут соответствовать
несколько разных логических выражений (не совпадающих для других вариантов
входных данных);
количество
разных логических функций, удовлетворяющих неполной таблице истинности, равно , где
– число отсутствующих строк; например, полная
таблица истинности выражения с тремя переменными содержит 23=8 строчек, если
заданы только 6 из них, то можно найти 28-6=22=4 разных логических функции,
удовлетворяющие этим 6 строчкам (но отличающиеся в двух оставшихся)
логическая
сумма A + B + C + … равна 0 (выражение ложно) тогда и только тогда, когда все
слагаемые одновременно равны нулю, а в остальных случаях равна 1 (выражение
истинно)
логическое
произведение A · B · C · … равно 1 (выражение истинно) тогда и только тогда,
когда все сомножители одновременно равны единице, а в остальных случаях равно 0
(выражение ложно)
логическое
следование (импликация) А→В равна 0 тогда и только тогда, когда A (посылка)
истинна, а B (следствие) ложно
эквивалентность
АºB равна 1 тогда и только тогда,
когда оба значения одновременно равны 0 или одновременно равны 1
По материалам К.Ю. Полякова с сайта ЕГЭ по информатике: подготовка к
ЕГЭ-2022 по информатике, разбор задач ЕГЭ-2022 по информатике, материалы для
подготовки к ЕГЭ (kpolyakov.spb.ru)
Решение задач
второго типа в MS Excel
Алгоритм решения
1.
Составить таблицу входных значения, перечисляя все комбинации переменных в
порядке возрастания двоичного кода. Для этого подсчитать n число переменных в
исходном выражении, выписать наборы входных переменных. Количество
наборов входных переменных 2n.
2. Для каждой строки находим логическое решение. Для этого:
·
Подсчитать
общее число логических операций в выражении;
·
Установить последовательность
выполнения логических операций с учетом скобок и приоритетов.
3. Выполнить поиск значения функции,
отсортировать данное значение по искомой части (1 или 0).
4. Сопоставить исходную таблицу и вновь
полученную.
Используемые фукции в MS Excel
|
Операция |
Функция |
|
|
Отрицание |
=НЕ |
=ЕСЛИ(A2=1;0;1) |
|
Дизъюнкция |
=ИЛИ |
=ЕСЛИ(ИЛИ(A2=1;B2=1);1;0) |
|
Конъюнкция |
=И |
=ЕСЛИ(И(A2=1;B2=1);1;0) |
|
Импликация |
=ЕСЛИ(И(A2=1;B2=0);0;1) |
|
|
Эквиваленция |
=ЕСЛИ(A2=B2;1;0) |
Примеры:
1 (Задача 158 с сайта К.Ю.
Полякова). Логическая
функция F задаётся выражением ¬x Ù y Ù (w ® z). На рисунке приведён фрагмент
таблицы истинности функции F, содержащий все наборы аргументов, при
которых функция F истинна. Определите, какому столбцу таблицы истинности
функции F соответствует каждая из переменных x, y, z,
w.
|
? |
? |
? |
? |
F |
|
1 |
0 |
0 |
0 |
1 |
|
1 |
0 |
1 |
0 |
1 |
|
1 |
0 |
1 |
1 |
1 |

z, w в том порядке, в котором идут соответствующие им столбцы.
Решение
1.
Подсчитаем количество переменных: x, y, z, w – 4 переменных, следовательно,
ищем количество наборов по формуле: 2n
= 24 = 16 наборов. Заполняем разными возможными вариантами (см.
рисунок)
2.
Определим наборы операций:
1) ¬x
2) (w ®
z)
3) ¬x Ù y Ù
(w ® z)
Ищем
результаты действий.
Результат вычислений Введенные
формулы
Следующий
шаг это отфильтровать значения 1 по столбцу H:
Сопоставим
с условием:

Анализируем:
0
– всегда X 1 – всегда Y 011 – Z 001
— W
|
y |
x |
z |
w |
F |
|
1 |
0 |
0 |
0 |
1 |
|
1 |
0 |
1 |
0 |
1 |
|
1 |
0 |
1 |
1 |
1 |
Ответ:
YXZW
2(Задача 168 с сайта К.Ю.
Полякова). Логическая
функция F задаётся выражением
x Ú (¬y
Ú z Ú ¬w) Ù (y Ú ¬z). На рисунке приведён фрагмент
таблицы истинности функции F, содержащий все наборы аргументов, при
которых функция F ложна. Определите, какому столбцу таблицы истинности
функции F соответствует каждая из переменных x, y, z,
w.
|
? |
? |
? |
? |
F |
|
0 |
0 |
1 |
0 |
0 |
|
1 |
0 |
0 |
1 |
0 |
|
1 |
0 |
1 |
0 |
0 |
В
ответе напишите буквы x, y, z, w в том порядке, в
котором идут соответствующие им столбцы.

|
W |
X |
Z |
Y |
F |
|
|
0 |
1 |
0 |
0 |
|
1 |
0 |
0 |
1 |
0 |
|
1 |
0 |
1 |
0 |
0 |
Ответ:
WXZY
3(Задача 178 с сайта К.Ю.
Полякова). Логическая
функция F задаётся выражением (Øz ÚØ
y) ® (x º z). На рисунке приведён частично
заполненный фрагмент таблицы истинности функции F, содержащий
неповторяющиеся строки. Определите, какому столбцу таблицы истинности функции F
соответствует каждая из переменных x, y, z.
В
ответе напишите буквы x, y, z в том порядке, в котором
идут соответствующие им столбцы. Буквы в ответе пишите подряд, никаких
разделителей между буквами ставить не нужно.
Ответ:
YXZ
4 (Задача 188 с сайта К.Ю.
Полякова).
Логическая функция F задаётся выражением (w Ù y) Ú ((x ® w) º (y ® z)). На рисунке приведён частично
заполненный фрагмент таблицы истинности функции F, содержащий неповторяющиеся
строки. Определите, какому столбцу таблицы истинности функции F соответствует
каждая из переменных x, y, z, w.
|
? |
? |
? |
? |
F |
|
1 |
0 |
|||
|
1 |
1 |
0 |
||
|
1 |
1 |
1 |
0 |
В
ответе напишите буквы x, y, z, w в том порядке, в котором идут соответствующие
им столбцы. Буквы в ответе пишите подряд, никаких разделителей между буквами
ставить не нужно.
Ответ:
ZWYX
5 (Задача 198 с сайта К.Ю.
Полякова).
Логическая функция F задаётся выражением
(w ® y) Ù ((x ® z) º (y ® x)). На рисунке приведён частично заполненный фрагмент таблицы
истинности функции F, содержащий неповторяющиеся строки. Определите, какому столбцу
таблицы истинности функции F соответствует каждая из переменных x, y, z, w.
|
? |
? |
? |
? |
F |
|
1 |
0 |
1 |
||
|
0 |
1 |
1 |
||
|
0 |
1 |
0 |
1 |
1 |
В
ответе напишите буквы x, y, z, w в том порядке, в котором идут соответствующие
им столбцы. Буквы в ответе пишите подряд, никаких разделителей между буквами
ставить не нужно.
Ответ:
WZXY
Практическая работа №2
«Построение таблиц истинности в MS Excel»
Цель работы:
Научиться использовать логические функции программы Excel при построении таблиц истинности.
Задание 1. Доказать законы де Моргана с помощью таблиц истинности в ЭТ Excel.
Загрузить Excel .Создать структуру электронной таблицы.
Заполнить электронную таблицу данными. Используя логические функции произвести расчеты.
Вы должны получить:
Вы проверили и убедились, что
Задание 2 Проверить с помощью ЭТ закон де Моргана
Задание 3 Проверить с помощью ЭТ сочетательный закон .
Задание 4 Установить в ЭТ истинность высказывания .
Задание 5 Установить в ЭТ является ли высказывание тавтологией?
Задание 6 Установить в ЭТ равносильны ли высказывания: ;
;
=И(А2;В2)
=И(А3;В3)
=И(А4;В4)
=И(А5;В5)
=НЕ(С2)
=НЕ(С3)
=НЕ(С4)
=НЕ(С5)
=НЕ(А2)
=НЕ(А3)
=НЕ(А4)
=НЕ(А5)
=ИЛИ(Е2;F2)
=НЕ(В3)
=НЕ(В4)
=НЕ(В5)
=ИЛИ(Е3;F3)
=ИЛИ(Е4;F4)
=ИЛИ(Е5;F5)
=НЕ(В2)
Фев 04 2021
Вроде простая вещь — нужно вычислить результат для нескольких булевых переменных
Читаем основную статью
Компьютер
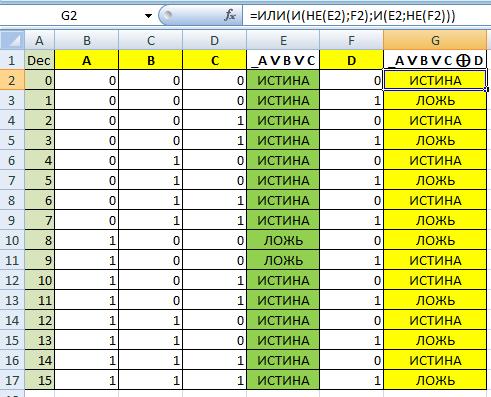
Вроде всё просто. Но вот такой пример вида _A ∨ B ∨ C ⊕ D
Переводим на русский язык (с математического языка) — нужно сделать таблицу истинности для выражения
не A или B или C иск.или D
для всех вариантов переменных A,B.C.D, которые могут принимать значения «Истина» / «Ложь»
Или на английском (для программирования) = not.A.or.B.or.C.xor.D
Задача на булеву алгебру не сложная — но у нас четыре переменных и 16 строк в таблице (да, 24 = 16). А если таких переменных будет 5, то в таблице будет 32 строки.
Но у нас есть Excel (Execute Cell), который прекрасно понимает формулы логики. Достаточно правильно написать формулу для одной строки — и потом мышкой перетащить эту формулу на остальные строки. Готово!
Итак по частям.
Логическая операция это операция над высказываниями, позволяющая составлять новые высказывания путём соединения более простых.
Логическая связка это союзы или выражения, которые употребляются в естественном языке для соединения простых высказываний в сложные.
Логические операции
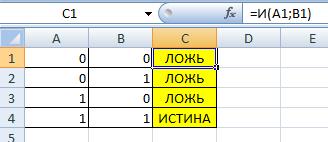
Логическая операция И (Конъюнкция)
Конъюнкция (от лат. conjunctio — «союз, связь») — логическая операция, по смыслу максимально приближенная к союзу «и». Синонимы: логическое «И», логическое умножение, иногда просто «И»
И таблица истинности (AND таблица истинности)
=И(A1;B1)
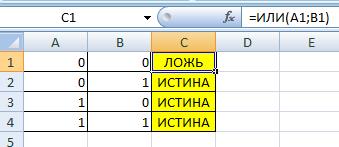
Логическая операция ИЛИ (Дизъюнкция)
Дизъюнкция (от лат. disjunctio — «разобщение») — логическое сложение, логическое ИЛИ, включа́ющее ИЛИ; иногда просто ИЛИ — логическая операция, по своему применению максимально приближённая к союзу «или» в смысле «или то, или это, или оба сразу»
ИЛИ таблица истинности (OR таблица истинности)
=ИЛИ(A1;B1)
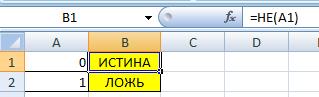
Логическая операция отрицания (Инверсия)
Инверсия (от лат. inversio «переворачивание; перестановка») — отрицание — переворачивание смысла, замена «белого» «чёрным»
НЕ таблица истинности (NOT таблица истинности)
=НЕ(A1)
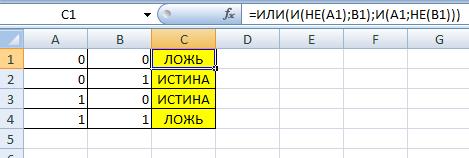
Логическая операция XOR (исключающее ИЛИ)
XOR таблица истинности
В Excel 2007 её нет.
В более современных версиях она есть. Но мы её можем собрать самостоятельно.
=ИЛИ(И(НЕ(A1);B1);И(A1;НЕ(B1)))
Логические связки
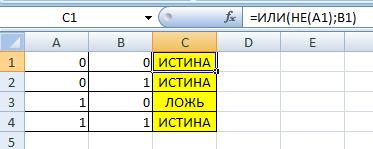
Логическая связка Импликация (прямая)
Логическая связка как A → B
используем аналог _A V B
=ИЛИ(НЕ(A1);B1)
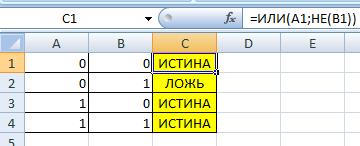
Логическая связка Импликация (обратная)
Логическая связка как A ← B
используем аналог A V _B
=ИЛИ(A1;НЕ(B1))
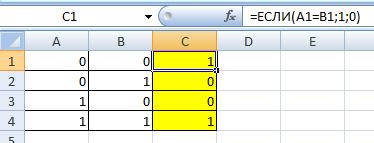
Логическая связка ТОЖДЕСТВО
Используем ЕСЛИ, чтобы логическая связка получилась
=ЕСЛИ(A1=B1;1;0)
или вывод текстом
=ЕСЛИ(A1=B1;"ИСТИНА";"ЛОЖЬ")
Собираем таблицу истинности
Не обязательно собирать всё в одной ячейке. Можно сделать столбцы для промежуточных вычислений.
Для нашего примера _A ∨ B ∨ C ⊕ D
Удобно.
Последние публикации
- Статьи от: Автор
- Рубрика: Блог
- Сортировка: дата публикации по убыванию
Классический вход Windows 7
Публикация 2 года назад
Как это было в Windows XP Для входа в систему нужно указать: пользователь (login)
пароль В Windows 7 сделали по умолчанию стандартный вход в систему Мышкой выбираем пользователя и вводим только пароль (если он установлен). Как вернуть классический вход в систему Windows 7 и зачем это нужно? Для работы на локальной машине — конечно удобнее стандартный вход. А вот если Вы подключаетесь к удаленной машине через RDP — то ввода только пароля недостаточно. Читаем статью RDP — удаленный рабочий стол Большое количество ботов со всего мира подберет Ваш пароль достаточно быстро (в логах будет по 5-10 попыток в секунду). Читаем статью Включаем шифрование…
(Читать полностью…)
Процессоры AMD FX и их «ядра»

Публикация 2 года назад
Немного маркетинга в тему — ядра процессоров AMD FX и ядра процессоров Intel AMD FX (AM3+) — хорошие были процессоры. Но есть нюанс. AMD использовала хитрую терминологию — «ядра» и «модули». Это была вершина маркетинга 
Одно…
(Читать полностью…)
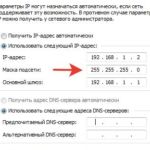
Загадочная «маска подсети» — это просто
Публикация 2 года назад
Многие видели в Windows свойства адаптера сети при ручной настройке Многие даже понимают, что IP-адрес 192.168.1.1 — это запись в десятичной форме 32-х бит адреса IP v4 с разбивкой на оксеты (по 8 бит). Что такое «маска подсети»?
Которая 255.255.255.0. И зачем она нужна? Посмотрим в таком же двоичном виде — легко видеть, что это 24 единицы подряд Это просто так айтишники шутят 
(Читать полностью…)
Вычисляем большие числа

Публикация 2 года назад
Самое известное большое число googol — отсюда собственно название Google 10100 = это 1 единица и 100 нулей Хорошо. А например, 2512 — это сколько? Калькулятор Windows говорит, что это 1,3 * 10154 Тоже неплохо, да и больше чем googol на 54 порядка 
(Читать полностью…)
Как соединить два роутера проводом?
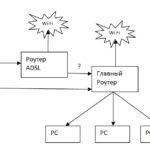
Публикация 3 года назад
Предположим, у нас есть «Главный роутер», который управляем всеми нашими устройствами PC. И еще есть: у «Главного роутера» второй WAN-порт
бесхозный ADSL роутер Простой вопрос — как сделать резервирование интернета? Что бы при отсутствии основного интернета можно было подключить и использовать «Роутер ADSL»? Основная статья про сеть здесь Варианты в лоб: использовать только «Роутер ADSL» — но это придется к нему переподключать все конечные ПК
и сетку Wi-Fi придется перестраивать для переподключения мобильных устройств Нехорошо 
(Читать полностью…)
Как не надо устанавливать SSD M.2

Публикация 3 года назад
Иногда вот такая жесть бывает при установке SSD M.2. Небольшой изгиб, так сказать. Основная статья про M.2 тут Интерфейс NVMe и разъемы M.2 и U.2 Как это получилось? Обычно так бывает при самостоятельной сборке ПК из новых комплектующих. SSD M.2 устанавливается под 45% в разъем на плате и потом прижимается винтиком, которые вкручивается в другой винтик на материнской плате. Но почему этот основной винтик «пенек» может отсутствовать на материнской плате? Вот тут хорошо видно проблему 
или кладет все…
(Читать полностью…)
Как набрать немецкие умляуты (umlaut) на обычной клавиатуре в России?

Публикация 3 года назад
Будем разбираться с немецкими умляутами Делаем свой набор горячих клавиш (hotkey) для умляутов
Самый удобный вариант 
R Alt A
Ä
ä O
Ö
ö U
Ü
ü S
ẞ
ß Здесь символы A, O, U и S — это не буквы, а кнопки на клавиатуре. Как это сделать? Используем программу QuickTextPaste — в ней можно завязать не только отдельные буквы, и целые части текста. Настройки хранятся в C:UsersNameAppDataRoamingQuickTextPasteQuickTextPaste.ini Использование простое: добавляем комбинацию клавиш
…
(Читать полностью…)
1) закрепить знания об основных логических операциях и таблицах истинности логических выражений; 2) сформировать навыки построения таблиц истинности (в том числе с использованием электронных таблиц MS Excel); 3) решение задач на построение таблиц истинности логических выражений в электронных таблицах.
Просмотр содержимого документа
«lab_rab_excel»
Просмотр содержимого документа
«Инструкция к работе»
Просмотр содержимого документа
«фрагмент раб тетради к уроку МТВправ»
Просмотр содержимого документа
«технологическая карта урока МТВ правка»
Просмотр содержимого презентации
«к уроку»
В настоящее время применение информационных
технологий становится неотъемлемой частью
образовательного процесса. Компьютер наиболее
полно удовлетворяет дидактическим требованиям и
позволяет адаптировать процесс обучения к
индивидуальным особенностям учащихся.
Компьютерные технологии активно внедряются в
процесс обучения и диагностики, позволяют
упростить процесс отработки навыков и умений и
оценки знаний учащихся.
В данной работе рассматривается применение
табличного процессора MS Excel при изучении основ
логики.
Существует множество задач, в которых исходные
и результатные данные должны быть представлены в
табличной форме. Электронные таблицы
представляют собой удобный инструмент для
автоматизации таких вычислений. Решения многих
вычислительных задач на ЭВМ, которые раньше
можно было осуществить только путем
программирования, стало возможно реализовать.
Использование математических формул в
электронных таблицах позволяет представить
взаимосвязь между различными параметрами
некоторой реальной системы. Основное свойство
электронных таблиц – мгновенный пересчет формул
при изменении значений входящих в них операндов.
Благодаря этому свойству, таблица представляет
собой удобный инструмент для организации
численного эксперимента:
- подбор параметров,
- прогноз поведения моделируемой системы,
- анализ зависимостей,
- планирование.
В электронных таблицах предусмотрен также
графический режим работы, который дает
возможность графического представления (в виде
графиков, диаграмм) числовой информации,
содержащейся в таблице.
В процессе изучения алгебры логики учащиеся
знакомятся с такими понятиями как: высказывание,
таблицы истинности, логические функции и
логические операции. Алгебра логики является
разделом математической логики, в которой
изучаются методы доказательства истинности (1)
или ложности (0) сложных логических конструкций,
составленных из простых высказываний, на основе
истинности или ложности последних. Для
закрепления полученных знаний возможно
использование табличного процессора MS Excel и его
функций.
Для реализации функций булевой алгебры
используются логические функции: ЕСЛИ, И, ИЛИ, НЕ,
ИСТИНА и ЛОЖЬ. При работе с функциями в MS Excel
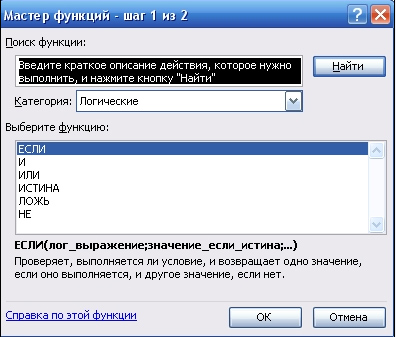
используется мастер функций (Вставка Функция…), в котором отображается
имя функции, ее описание и аргументы.
Рисунок 1. Окно мастера функций
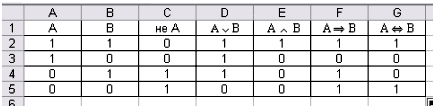
Первоначально следует создать таблицу
основных логических операций:
Рисунок 2. Таблица истинности основных
логических операций
При составлении таблицы истинности
используются следующие формулы:
- Инверсия: =ЕСЛИ(A2=1;0;1);
- Дизъюнкция: =ЕСЛИ(ИЛИ(A2=1;B2=1);1;0);
- Конъюнкция: =ЕСЛИ(И(A2=1;B2=1);1;0);
- Импликация: =ЕСЛИ(И(A2=1;B2=0);0;1);
- Эквивалентность: =ЕСЛИ(A2=B2;1;0).
В последующей работе данная таблица может
использоваться учащимися как основа для
выполнения заданий лабораторной работы.
Учащимся может быть предложена следующая
работа.
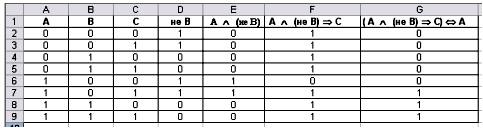
Задание: Построить таблицу истинности для
формулы (A
B
C)
A, используя MS Excel.
Алгоритм:
- Определить количество наборов входных
переменных, по формуле: Q = 2n, где n –
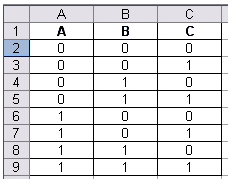
количество переменных. Q = 23 = 8. - Внести в таблицу все наборы входных переменных:
Рисунок 3. Исходные данные
- Определить количество логических операций и
порядок их выполнения:
- Заполнить столбцы результатами выполнения
логических операций в обозначенной
последовательности.
Для этого в ячейку D2 ввести формулу: =ЕСЛИ(B2=1;0;1);
в E2: =ЕСЛИ(И(A2=1;D2=1);1;0);
в F2: =ЕСЛИ(И(E2=1;C2=0);0;1);
в G2: =ЕСЛИ(F2=A2;1;0).
Заполнение остальных строк произвести путем
копирования введенной формулы.
Рисунок 4. Результат выполнения работы
Табличный процессор может быть использован для
закрепления не только материала математической
логики, но и для основ теории вероятностей и
математической статистики.
Задачи для самостоятельного решения
Определить с помощью таблиц истинности
равносильность формул.
Определить являются ли формулы тавтологиями.