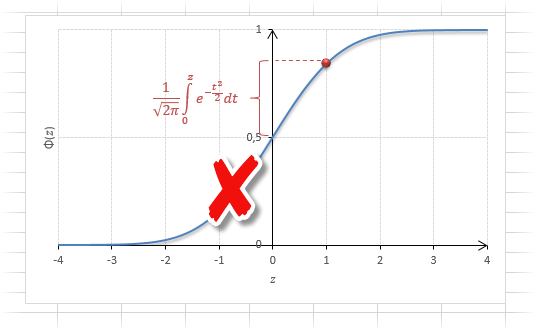
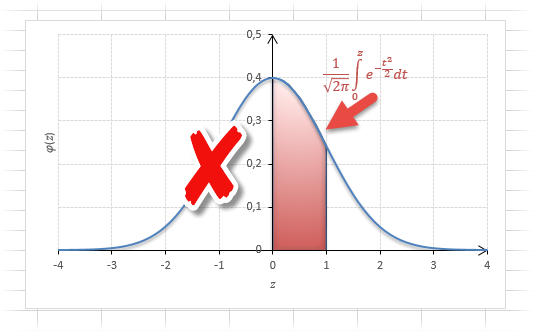
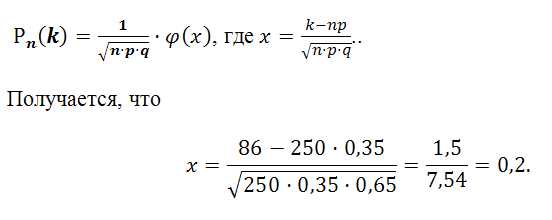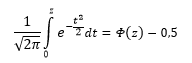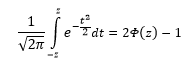Таблица значений функции лапласа excel - Word и Excel - помощь в работе с программами

Содержание

Функция Лапласа
- Оператор НОРМ.СТ.РАСП
- Решение задачи
Вопросы и ответы

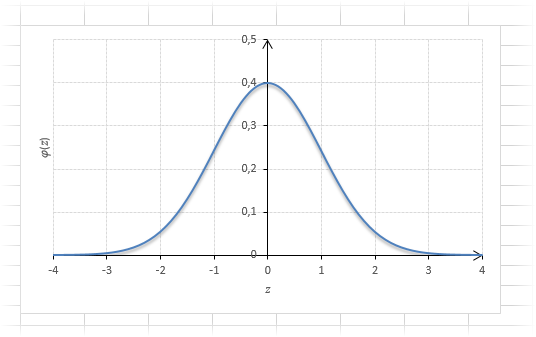
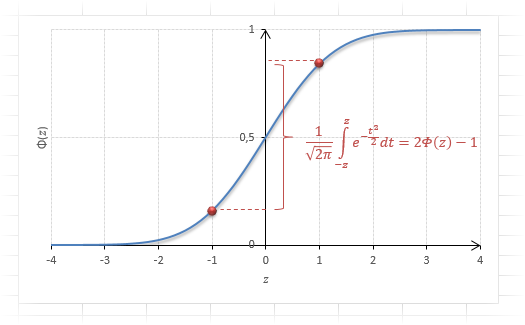
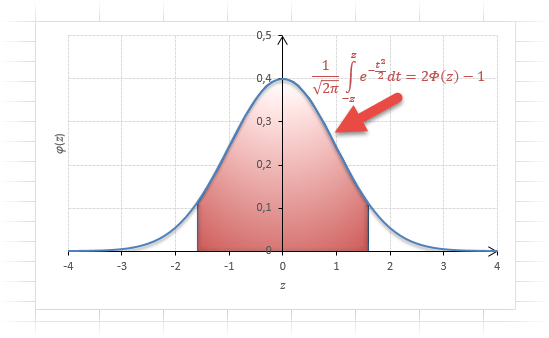
Одной из самых известных неэлементарных функций, которая применяется в математике, в теории дифференциальных уравнений, в статистике и в теории вероятностей является функция Лапласа. Решение задач с ней требует существенной подготовки. Давайте выясним, как можно с помощью инструментов Excel произвести вычисление данного показателя.

Функция Лапласа

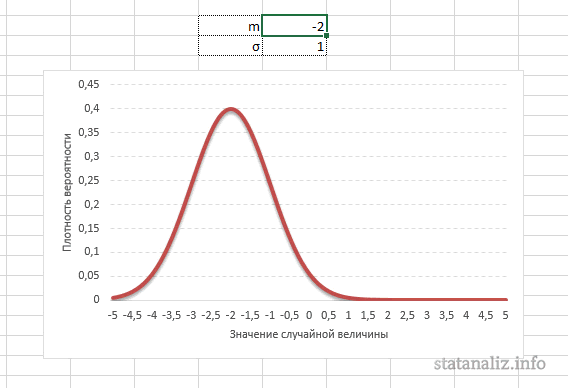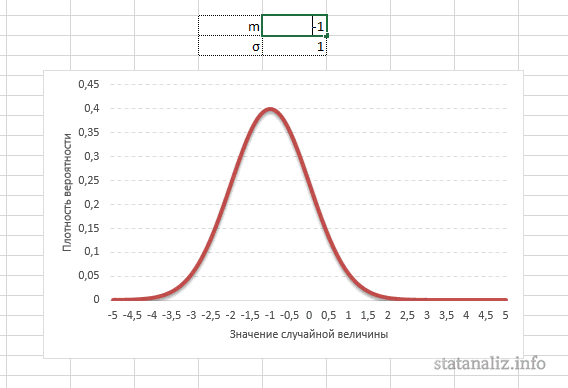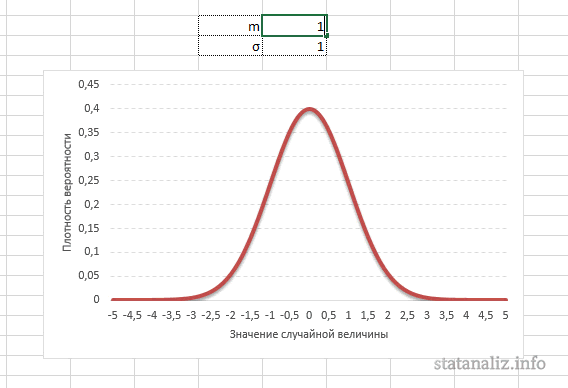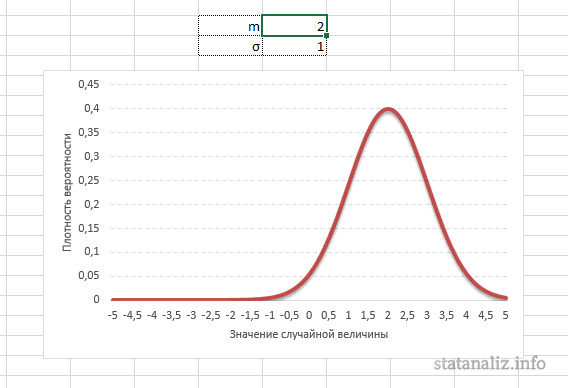
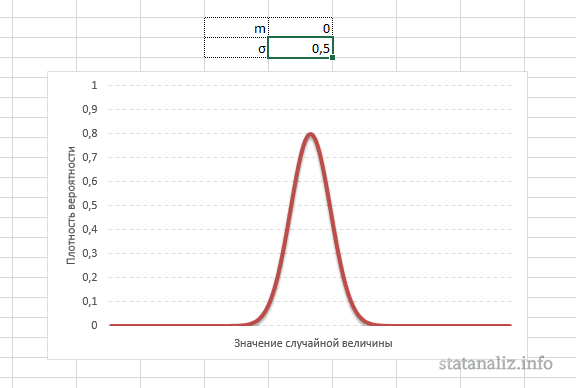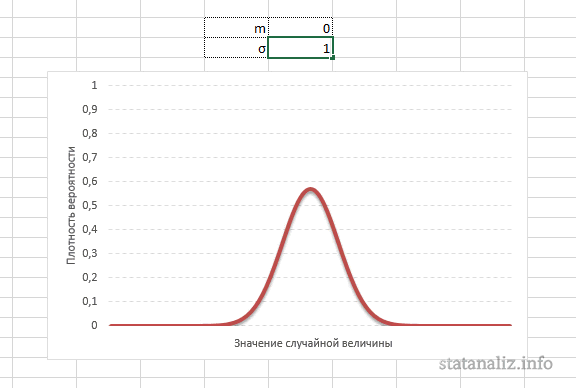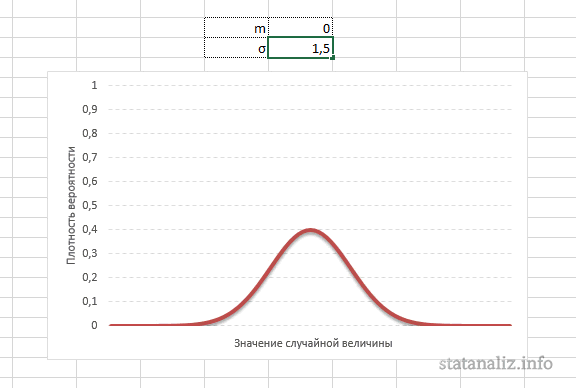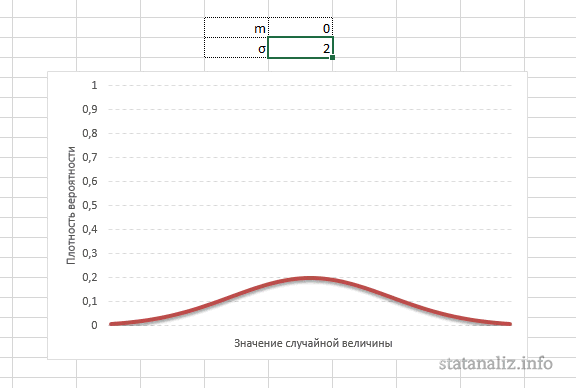
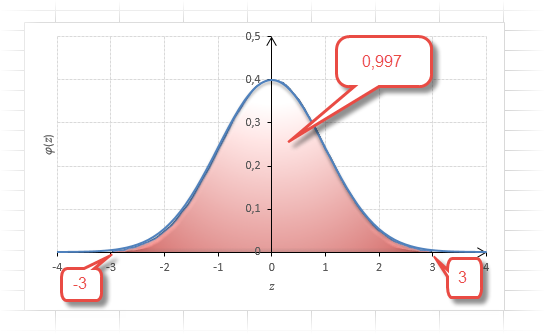
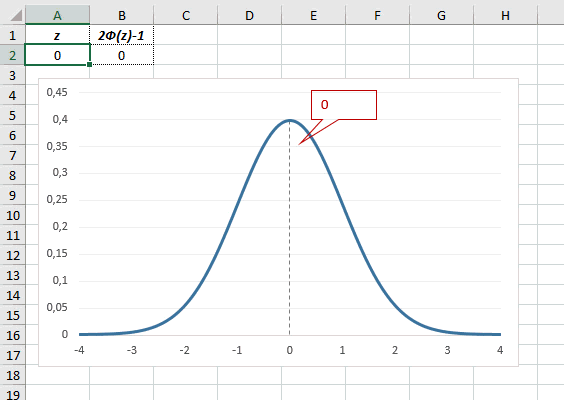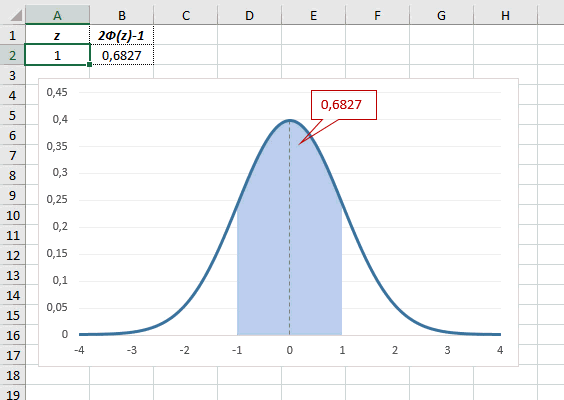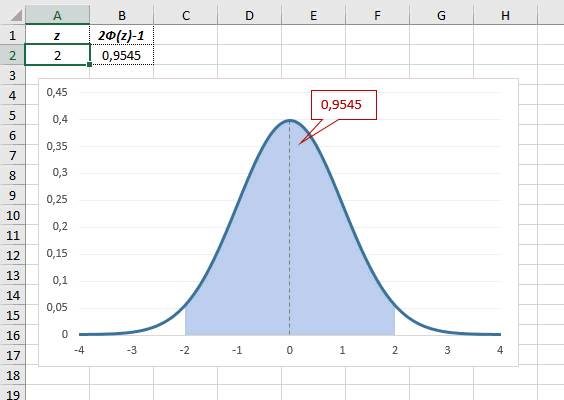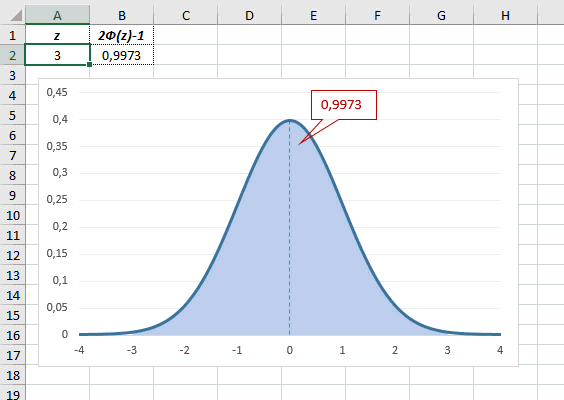
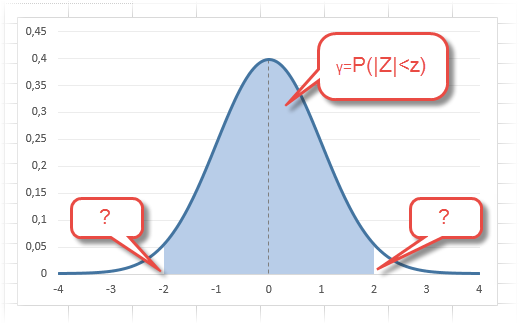
Функция Лапласа имеет широкое прикладное и теоретическое применение. Например, она довольно часто используется для решения дифференциальных уравнений. У этого термина существует ещё одно равнозначное название – интеграл вероятности. В некоторых случаях основой для решения является построение таблицы значений.

Оператор НОРМ.СТ.РАСП

В Экселе указанная задача решается с помощью оператора НОРМ.СТ.РАСП. Его название является сокращением от термина «нормальное стандартное распределение». Так как его главной задачей является возврат в выделенную ячейку стандартного нормального интегрального распределения. Данный оператор относится к статистической категории стандартных функций Excel.

В Excel 2007 и в более ранних версиях программы этот оператор назывался НОРМСТРАСП. Он в целях совместимости оставлен и в современных версиях приложений. Но все-таки в них рекомендуется использование более продвинутого аналога – НОРМ.СТ.РАСП.

Синтаксис оператора НОРМ.СТ.РАСП выглядит следующим образом:

=НОРМ.СТ.РАСП(z;интегральная)

Устаревший оператор НОРМСТРАСП записывается так:

=НОРМСТРАСП(z)

Как видим, в новом варианте к существующему аргументу «Z» добавлен аргумент «Интегральная». Нужно заметить, что каждый аргумент является обязательным.

Аргумент «Z» указывает числовое значение, для которого производится построение распределения.

Аргумент «Интегральная» представляет собой логическое значение, которое может иметь представление «ИСТИНА» («1») или «ЛОЖЬ» («0»). В первом случае в указанную ячейку возвращается интегральная функция распределения, а во втором – весовая функция распределения.

Решение задачи

Для того чтобы выполнить требуемое вычисление для переменной применяется следующая формула:

=НОРМ.СТ.РАСП(z;интегральная(1))-0,5

Теперь давайте на конкретном примере рассмотрим использование оператора НОРМ.СТ.РАСП для решения конкретной задачи.

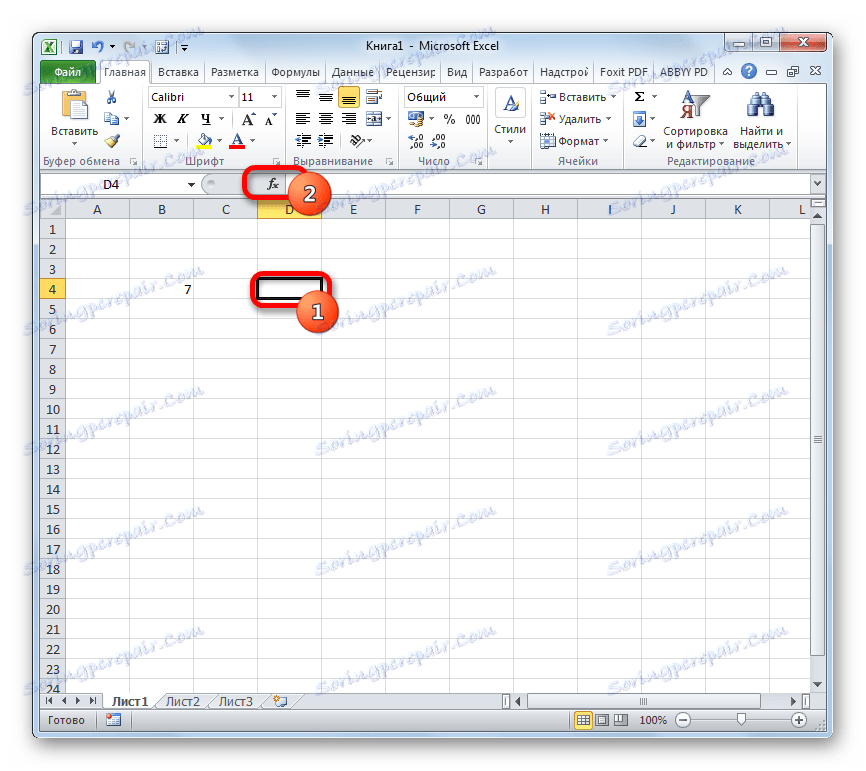
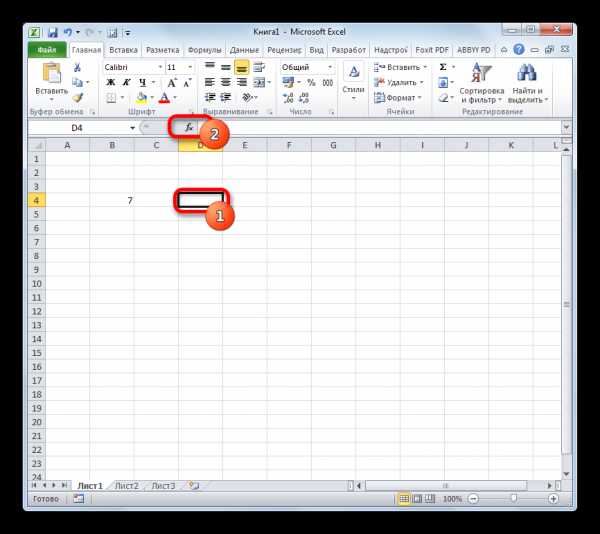
Выделяем ячейку, куда будет выводиться готовый результат и щелкаем по значку «Вставить функцию», расположенному около строки формул.

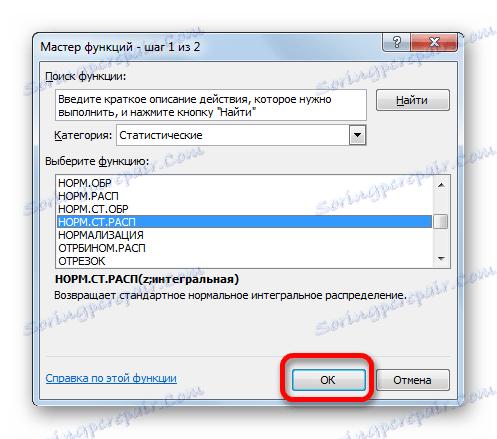
После открытия Мастера функций переходим в категорию «Статистические» или «Полный алфавитный перечень». Выделяем наименование «НОРМ.СТ.РАСП» и жмем на кнопку «OK».

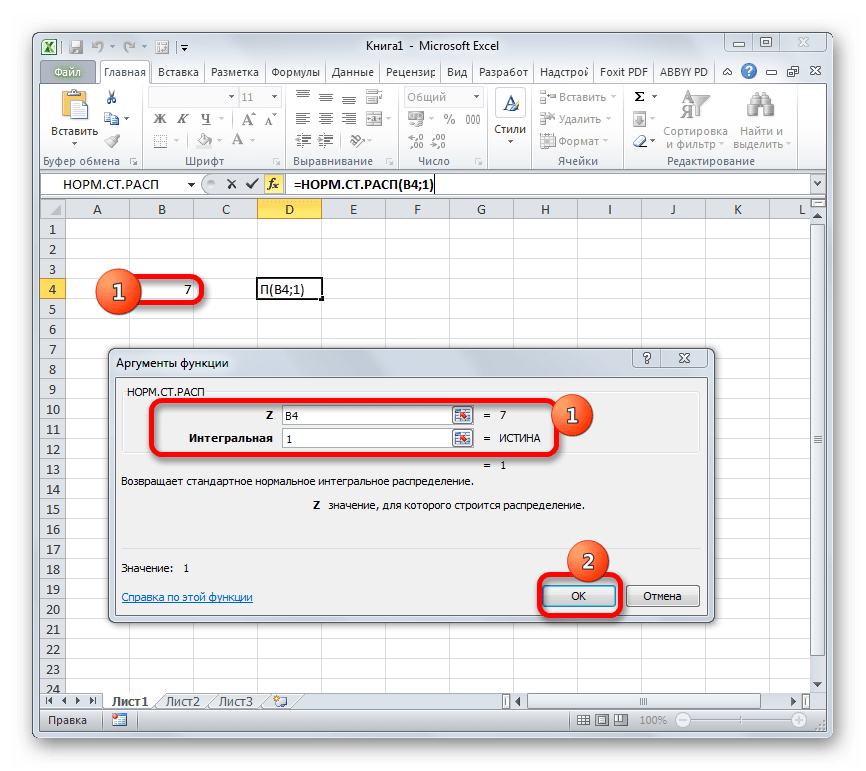
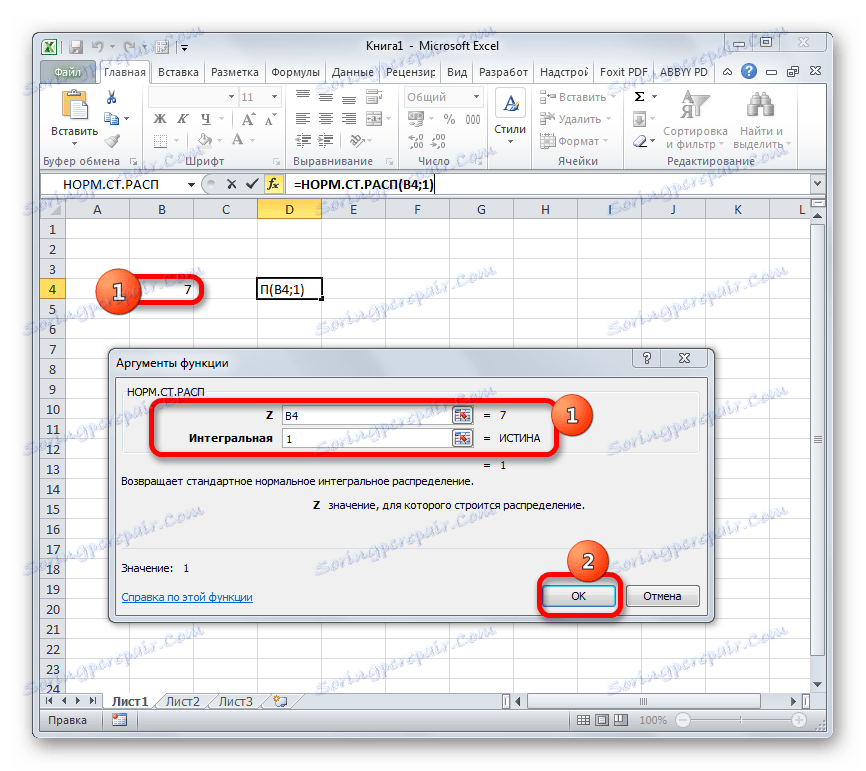
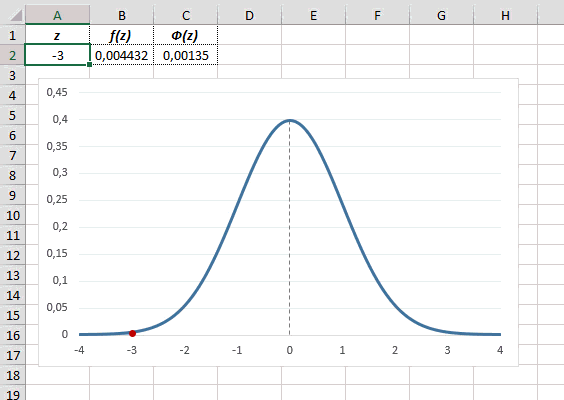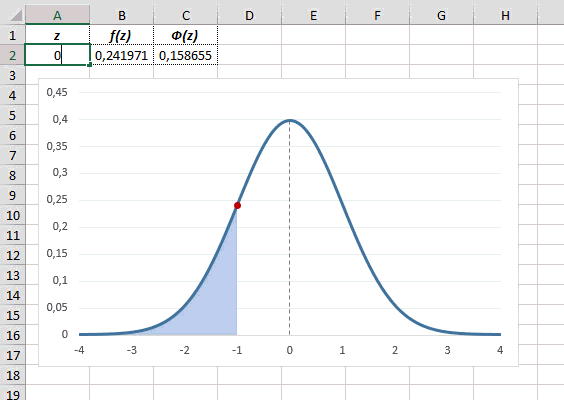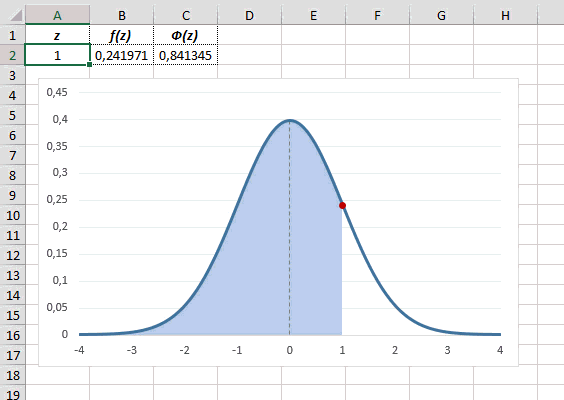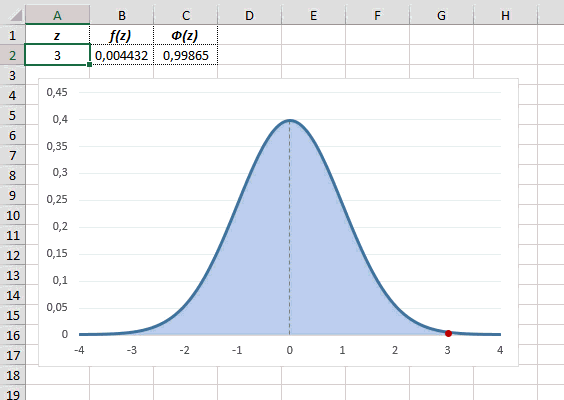
Происходит активация окна аргументов оператора НОРМ.СТ.РАСП. В поле «Z» вводим переменную, к которой нужно произвести расчет. Также этот аргумент может быть представлен в виде ссылки на ячейку, которая содержит эту переменную. В поле «Интегральная» вводим значение «1». Это означает, что оператор после вычисления вернет в качестве решения интегральную функцию распределения. После того, как выполнены вышеперечисленные действия, жмем на кнопку «OK».

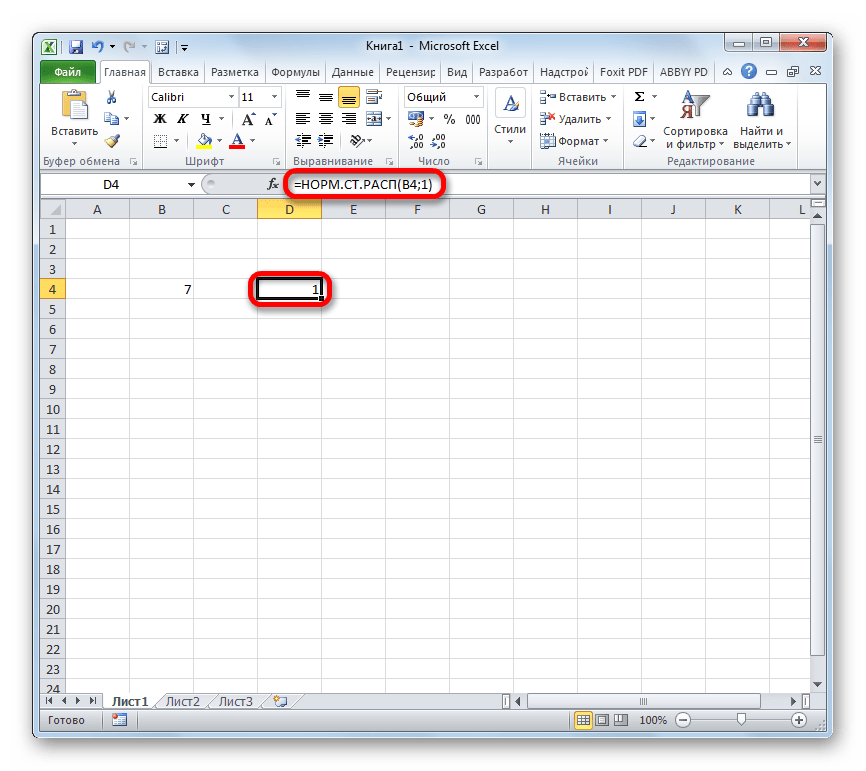
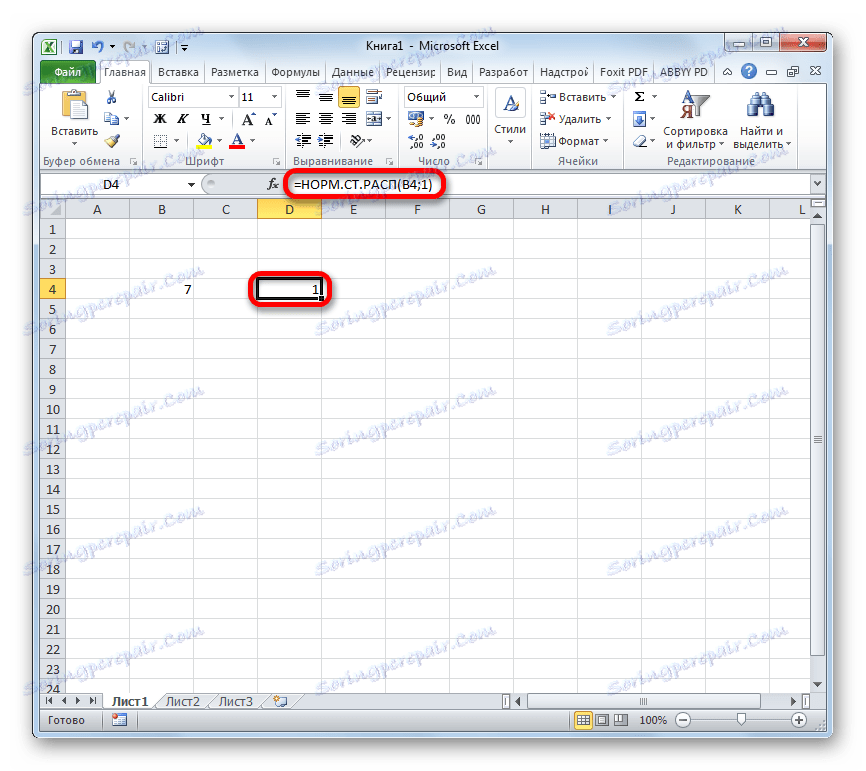
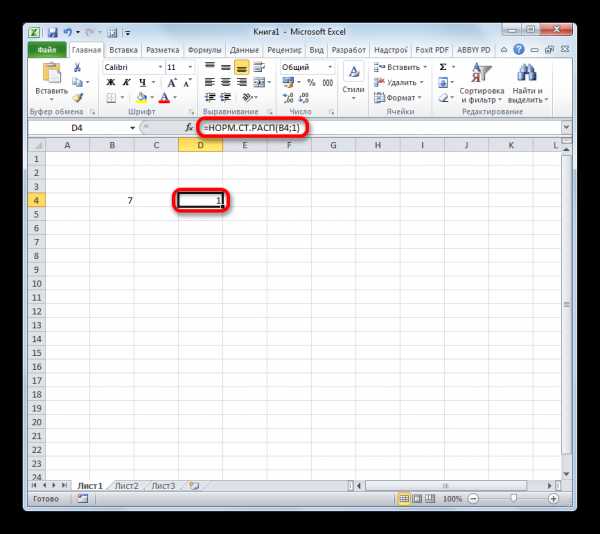
После этого результат обработки данных оператором НОРМ.СТ.РАСП будет выведен в ячейку, которая указана в первом пункте данного руководства.

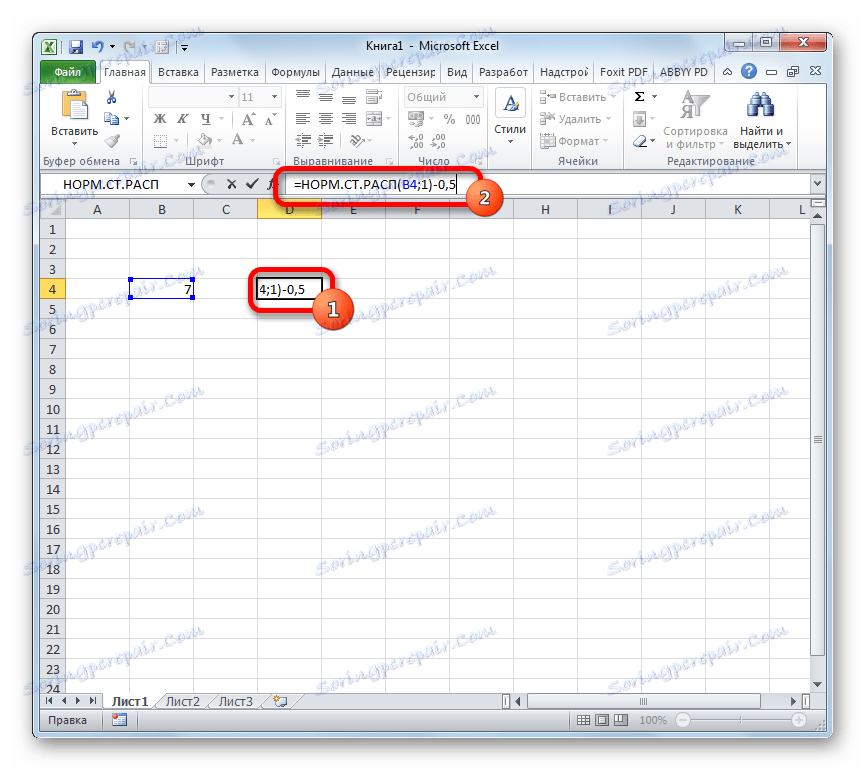
Но и это ещё не все. Мы вычислили только стандартное нормальное интегральное распределение. Для того, чтобы посчитать значение функции Лапласа, нужно от него отнять число 0,5. Выделяем ячейку, содержащую выражение. В строке формул после оператора НОРМ.СТ.РАСП дописываем значение: -0,5.

Для того, чтобы произвести вычисление, жмем на кнопку Enter. Полученный результат и будет искомым значением.

Как видим, вычислить функцию Лапласа для конкретного заданного числового значения в программе Excel не составляет особенного труда. Для этих целей применяется стандартный оператор НОРМ.СТ.РАСП.

Еще статьи по данной теме:

Помогла ли Вам статья?

Источник

Функция Лапласа и другие табличные статистические функции: считаем в Excel

При решении таких типовых задач математической статистики, как построение доверительных интервалов или проверка гипотез о параметрах случайных величин, широко используются несколько табличных функций, например,
функция Лапласа
или
квантили распределения хи-квадрат.

В наше время совершенно необязательно обращаться за недостающими в формуле величинами к толстым
справочникам со статистическими таблицами, можно всё посчитать непосредственно в Excel:

Формула =НОРМСТРАСП(x)-0,5 вычисляет значение функции Лапласа от аргумента x (подставьте вместо x соответствующую ячейку). При этом Ф(-x)=-Ф(x), а при x>3,85 значение Ф(x)=0,5.

Вычислить значение обратной функции Лапласа от аргумента x можно формулой =НОРМСТОБР(x). В Excel функция НОРМСТОБР (1-eps/2) даст требуемое критическое значение, соответствующее уровню значимости критерия, равному eps. Например, для критерия с критическим уровнем 0,05 (5%) формула НОРМСТОБР(1-0,05/2)=1,96

Критические точки t-критерия можно вычислить с помощью формулы =СТЬЮДРАСПОБР(α;n), где α – уровень значимости (вероятность γ или надёжность 1-γ), n – число степеней свободы (например, объём выборки в задачах о построении доверительных интервалов). При числе степеней свободы n≥30 распределение сводится к нормальному с параметрами α=0, σ=корень(n/(n-2)).

Критические точки распределения Пирсона χ² можно вычислить с помощью формулы =ХИ2ОБР(a;n), где a – уровень значимости, n – число степеней свободы.

Получить значение функции плотности распределения Пуассона можно с помощью формулы =ПУАССОН(n;λ;0), где n – число степеней свободы (количество событий), λ – среднее число появлений события (ожидаемое численное значение).

В ряде случаев для расчёта с заданным значением параметра γ функции Excel может понадобиться передать аргумент функции α=1-γ, смотрите внимательно встроенную справку по функциям.

Математическая статистика — лекции и примеры в Excel

12.03.2013, 17:18 [54615 просмотров]

Источник

Распределение Лапласа зависит от двух параметров n и p; характеристики распределения выражаются через эти параметры: a = np, . При расчетах вручную используют таблицы дифференциальной и интегральной функции Лапласа . Тогда , где . Эта формула обычно называется как «локальная теорема Лапласа». Интегральная функция Лапласа используется для вычисления вероятности попадания m в заданный интервал: P(m₁ £ m £ m₂) = Ф(t_m₂) – Ф(t_m₁). Эта формула обычно называется как «интегральная теорема Лапласа». При расчетах на компьютере для этих же целей используется функция Excel: НОРМРАСП(m;a;s_m;0) – возвращает значения вероятности Pn(m) и НОРМРАСП(m;a;s_m;1) – возвращает значения интегральной функции распределения Лапласа F(m) = Ф(t_m) + 0,5 (функция F(m) отличается постоянным слагаемым от функции Ф(t_m)). Считается, что предельные формулы Лапласа можно применять при n ³ 30, a = np ³ 5 и nq ³ 5. Интегральную формулу Лапласа можно уточнить, если расширить интервал [m₁ ; m₂] на полшага влево и вправо: P(m₁ £ m £ m₂) = F(m₂ + 1 /₂) – F(m₁ – 1 /₂). Предлагается прямыми расчетами проверить точность локальной, интегральной и скорректированной интегральной формул Лапласа для n = 10, 20, 30, 40, 50 и p = 0,3. Фрагмент рабочего листа Excel приведен ниже.

A	B	C	D	E	F	G	H	I	J
Распределение Лапласа
Pn(m)=НОРМРАСП(m;a;Sm;0)	a=np	Sm=КОРЕНЬ(npq)
P(m1£m£m2)=НОРМРАСП(m2;a;Sm;1)–НОРМРАСП(m1;a;Sm;1)	Интегральная теорема
P(m1£m£m2)=НОРМРАСП(m2+1/2;a;Sm;1)–НОРМРАСП(m1-1/2;a;Sm;1) (Скорректированная)
Бернулли
n =	Ф(2)-Ф(-1)=	0,81859	P([m1;m2])	n=10	n=20	n=30	n=40	n=50
p =	0,3	Bernully	0,8401	0,87577	0,90647	0,87422	0,83588
q =	0,7	M-Sm=	1,550862	Laplas	0,73571	0,80996	0,86082	0,83047	0,79069
a = M =	M+2Sm=	5,898275	Correct	0,84183	0,87469	0,90419	0,87395	0,83753
Dm =	2,1	m1 =	Error%	-12,43%	-7,51%	-5,04%	-5,00%	-5,41%
Sm =	1,449138	m2 =	ErrCorr%	0,21%	-0,12%	-0,25%	-0,03%	0,20%
Б е р н у л л и
m	n=10	F(m)	Laplas	P(a)	n=10	n=20	n=30	n=40	n=50
0,028248	0,028248	0,032298	Bernully	0,26683	0,19164	0,15729	0,13657	0,12235
0,121061	0,149308	0,106215	Laplas	0,27530	0,19466	0,15894	0,13765	0,12312
0,233474	0,382783	0,216969	Correct	0,26993	0,19275	0,15790	0,13697	0,12263
0,266828	0,649611	0,275296	Error%	3,17%	1,58%	1,05%	0,79%	0,63%
0,200121	0,849732	0,216969	ErrCorr%	1,16%	0,58%	0,39%	0,29%	0,23%
0,102919	0,952651	0,106215
0,036757	0,989408	0,032298
0,009002	0,998410	0,006100
0,001447	0,999856	0,000716
0,000138	0,999994	5,22E-05
5,909E-06	1,000000	2,36E-06

Слева в столбцах А, В расположен блок расчетов по формуле Бернулли (сейчас принято n = 10). В соседнем столбце С приведены значения кумуляты (накопленных вероятностей) F(m) = S P_n(k), вычисленных по реккурентной формуле F(m) = F(m–1) + P_n(m), где F(0) = P_n(0) = q n . С помощью кумуляты одним вычитанием определяются вероятности попадания случайной величины m в любые заданные интервалы P(m₁ £ m £ m₂) = F(m₂) – F(m₁–1). Так, вероятность P(2£ m £6) можно вычислить как разность F(6) – F(1) = 0,989408 – 0,149308 = 0,840140; это же значение можно получить непосредственно, складывая вероятности P_n(m) для m =2, 3, 4, 5, 6 (цифры на сером фоне в столбце В). В следующем столбце D вычислены вероятности по локальной формуле Лапласа. По результатам расчетов построены графики распределения Бернулли и распределения Лапласа с теми же характеристиками. Изменяя n в ячейке В6, можно наблюдать, насколько хорошо распределение Бернулли описывается предельным распределением Лапласа. Ниже приведены два сравнительных графика для n = 10 и n = 20, откуда видно, что уже при n ³ 20 распределение Бернулли для р = 0,3 практически совпадает с предельным распределением. Таким образом, мы убедились, что локальная формула Лапласа достаточно точная.

Переходим к проверке точности расчетов по интегральной формуле Лапласа. Рассмотрим вероятность попадания случайной величины m в интервал [M – Sm; M + 2Sm]. Теоретически указанная вероятность вычисляется как разность Ф(2) – Ф(-1) = 0,81859. Однако формула эта выведена для непрерывного распределения, а распределение Лапласа – дискретное. Поэтому теоретическое значение (или близкое к нему) может быть получено только для очень большого n > 200. Проверим это утверждение. Выше над блоком расчетов по формуле Бернулли в столбцах C, D вычислены границы интервала: M – Sm = 1,551 и M + 2Sm = 5,898; полученные границы округлены до ближайших целых m₁ = 2, m₂ = 6. Необходимо сравнить точное значение P(2£ m £6) = 0,8401, полученное ранее с помощью кумуляты распределения Бернулли, с соответствующим значением по интегральной формуле Лапласа P(2£ m £6) » НОРМРАСП(6;a;Sm;1)–НОРМРАСП(2;a;Sm;1) = 0,73571. По сравнению с точным значением (0,8401) ошибка составила -12,43%. Эти расчеты оформлены в виде таблицы в строках 6–11 столбцы E, F. При изменении n в ячейке B6 все цифры в столбце F автоматически корректируются. Для того, чтобы сохранить результаты предыдущих расчетов, они были cкопированы Специальной вставкой – Только значения в продолжение таблицы вправо (столбцы G, H, I, J). Рассматривая заполненную таблицу (диапазон E6:J11), убеждаемся в довольно медленном приближении предельной формулы к точному значению. Теперь мы можем оценить эффективность скорректированной интегральной формулы Лапласа P(2 £ m £ 6) = НОРМРАСП(6,5;a;Sm;1)–НОРМРАСП(1,5;a;Sm;1) , которая уже для n = 10 привела к практически точному значению 0,8418 (погрешность 0,21%). Эффективность скорректированной формулы была также проверена на вычислении вероятности моды (наивероятнейшего значения m = a = np). Эти расчеты выполнены в таблице диапазона E13:J18. Интегральная функция Лапласа здесь дает значение 0, поэтому в таблице использовалась локальная формула Лапласа. Погрешности локальной формулы небольшие и быстро убывают с увеличением n (при n = 20 погрешность составляет всего 1,6%). Скорректированная интегральная формула оказалась еще более точной; она дает практически точные значения уже при n = 10.

Вычисление функции Лапласа в Microsoft Excel

Функция Лапласа

Оператор НОРМ.СТ.РАСП

Синтаксис оператора НОРМ.СТ.РАСП выглядит следующим образом:

Устаревший оператор НОРМСТРАСП записывается так:

Аргумент «Z» указывает числовое значение, для которого производится построение распределения.

Решение задачи

Для того чтобы выполнить требуемое вычисление для переменной применяется следующая формула:

«Вставить функцию»

После открытия Мастера функций переходим в категорию «Статистические» или «Полный алфавитный перечень». Выделяем наименование «НОРМ.СТ.РАСП» и жмем на кнопку «OK».

Происходит активация окна аргументов оператора НОРМ.СТ.РАСП. В поле «Z» вводим переменную, к которой нужно произвести расчет. Также этот аргумент может быть представлен в виде ссылки на ячейку, которая содержит эту переменную. В поле «Интегральная» вводим значение «1». Это означает, что оператор после вычисления вернет в качестве решения интегральную функцию распределения. После того, как выполнены вышеперечисленные действия, жмем на кнопку «OK».

После этого результат обработки данных оператором НОРМ.СТ.РАСП будет выведен в ячейку, которая указана в первом пункте данного руководства.

Но и это ещё не все. Мы вычислили только стандартное нормальное интегральное распределение. Для того, чтобы посчитать значение функции Лапласа, нужно от него отнять число 0,5. Выделяем ячейку, содержащую выражение. В строке формул после оператора НОРМ.СТ.РАСП дописываем значение: -0,5.

Для того, чтобы произвести вычисление, жмем на кнопку Enter. Полученный результат и будет искомым значением.

Мы рады, что смогли помочь Вам в решении проблемы.

Добавьте сайт Lumpics.ru в закладки и мы еще пригодимся вам.
Отблагодарите автора, поделитесь статьей в социальных сетях.

Опишите, что у вас не получилось. Наши специалисты постараются ответить максимально быстро.

Обчислення функції Лапласа в Microsoft Excel

Однією з найвідоміших неелементарних функцій, яка застосовується в математиці, в теорії диференціальних рівнянь, в статистиці і в теорії ймовірностей є функція Лапласа. Рішення задач з нею потребує суттєвого підготовки. Давайте з’ясуємо, як можна за допомогою інструментів Excel зробити обчислення даного показника.

функція Лапласа

Функція Лапласа має широке прикладне і теоретичне застосування. Наприклад, вона досить часто використовується для вирішення диференціальних рівнянь. Цей термін існує ще одне рівнозначне назва — інтеграл ймовірності. У деяких випадках основою для вирішення є побудова таблиці значень.

оператор НОРМ.СТ.РАСП

У Ексель зазначена завдання вирішується за допомогою оператора НОРМ.СТ.РАСП. Його назва є скороченням від терміна «нормальне стандартний розподіл». Так як його головним завданням є повернення в виділену клітинку стандартного нормального інтегрального розподілу. Даний оператор відноситься до статистичної категорії стандартних функцій Excel.

В Excel 2007 і в більш ранніх версіях програми цей оператор називався НОРМСТРАСП. Він з метою сумісності залишений і в сучасних версіях додатків. Але все-таки в них рекомендується використання більш просунутого аналога — НОРМ.СТ.РАСП.

Синтаксис оператора НОРМ.СТ.РАСП виглядає наступним чином:

Застарілий оператор НОРМСТРАСП записується так:

Як бачимо, в новому варіанті до існуючого аргументу «Z» доданий аргумент «Інтегральна». Потрібно зауважити, що кожен аргумент є обов’язковим.

Аргумент «Z» вказує числове значення, для якого проводиться побудова розподілу.

Аргумент «Інтегральна» являє собою логічне значення, яке може мати уявлення «ІСТИНА» ( «1») або «БРЕХНЯ» ( «0»). У першому випадку в зазначену осередок повертається інтегральна функція розподілу, а в другому — вагова функція розподілу.

Рішення завдання

Для того щоб виконати необхідну обчислення для змінної застосовується наступна формула:

Тепер давайте на конкретному прикладі розглянемо використання оператора НОРМ.СТ.РАСП для вирішення конкретного завдання.

Виділяємо осередок, куди буде виводитися готовий результат і клацаємо по значку «Вставити функцію», розташованому біля рядка формул.

Після відкриття Майстра функцій переходимо в категорію «Статистичні» або «Повний алфавітний перелік». Виділяємо найменування «НОРМ.СТ.РАСП» і тиснемо на кнопку «OK».

Відбувається активація вікна аргументів оператора НОРМ.СТ.РАСП. В поле «Z» вводимо змінну, до якої потрібно провести розрахунок. Також цей аргумент може бути представлений у вигляді посилання на осередок, яка містить цю змінну. В поле «Інтегральна» вводимо значення «1». Це означає, що оператор після обчислення поверне в якості рішення інтегральну функцію розподілу. Після того, як виконані перераховані вище дії, тиснемо на кнопку «OK».

Після цього результат обробки даних оператором НОРМ.СТ.РАСП буде виведений в клітинку, яка вказана в першому пункті даного керівництва.

Але і це ще не все. Ми вирахували тільки стандартний нормальний інтегральний розподіл. Для того, щоб порахувати значення функції Лапласа, потрібно від нього забрати число 0,5. Виділяємо осередок, що містить вираз. У рядку формул після оператора НОРМ.СТ.РАСП дописуємо значення: -0,5.

Для того, щоб зробити обчислення, тиснемо на кнопку Enter. Отриманий результат і буде шуканим значенням.

Як бачимо, обчислити функцію Лапласа для конкретного заданого числового значення в програмі Excel не складає особливих труднощів. Для цих цілей застосовується стандартний оператор НОРМ.СТ.РАСП.

Функция Лапласа и другие табличные статистические функции: в Excel формуле

Привет, сегодня поговорим про функция лапласа, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое функция лапласа,другие табличные статистические в excel формуле , настоятельно рекомендую прочитать все из категории Теория вероятностей. Математическая статистика и Стохастический анализ

функция лапласа и другие табличные статистические функции: считаем в Excel

При решении таких типовых задач математической статистики, как построение доверительных интервалов или проверка гипотез о параметрах случайных величин, широко используются несколько табличных функций, например, функция Лапласа или квантили распределения хи- квадрат .

В наше время совершенно необязательно обращаться за недостающими в формуле величинами к толстым справочникам со статистическими таблицами, можно все посчитать непосредственно в Excel:

Формула =НОРМСТРАСП(x)-0,5 вычисляет значение функции Лапласа от аргумента x (подставьте вместо x соответствующую ячейку) . Об этом говорит сайт https://intellect.icu . При этом Ф(-x)=-Ф(x) , а при x>3,85 значение Ф(x)=0,5 .

Вычислить значение обратной функции Лапласа от аргумента x можно формулой =НОРМСТОБР(x) . В Excel функция НОРМСТОБР (1-eps/2) даст требуемое критическое значение, соответствующее уровню значимости критерия, равному eps. Например, для критерия с критическим уровнем 0,05 (5%) формула НОРМСТОБР(1-0,05/2)=1,96

Критические точки t-критерия можно вычислить с помощью формулы =СТЬЮДРАСПОБР(α,n) , где α – уровень значимости ( вероятность γ или надежность 1-γ ), n – число степеней свободы (например, объем выборки в задачах о построении доверительных интервалов). При числе степеней свободы n≥30 распределение сводится к нормальному с параметрами α=0 , σ= корень (n/(n-2)) .

Критические точки распределения Пирсона χ 2 можно вычислить с помощью формулы =ХИ2ОБР(a,n) , где a – уровень значимости, n – число степеней свободы.

Получить значение функции плотности распределения Пуассона можно с помощью формулы =ПУАССОН(n,λ,0) , где n – число степеней свободы (количество событий), λ – среднее число появлений события (ожидаемое численное значение).

В ряде случаев для расчета с заданным значением параметра γ функции Excel может понадобиться передать аргумент функции α=1-γ , смотрите внимательно встроенную справку по функциям.

Распределение Стьюдента

Понравилась статья про функция лапласа? Откомментируйте её Надеюсь, что теперь ты понял что такое функция лапласа,другие табличные статистические в excel формуле и для чего все это нужно, а если не понял, или есть замечания, то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория вероятностей. Математическая статистика и Стохастический анализ

Функция лапласа в excel

БлогNot. Функция Лапласа и другие табличные статистические функции: считаем в Excel

Функция Лапласа и другие табличные статистические функции: считаем в Excel

При решении таких типовых задач математической статистики, как построение доверительных интервалов или проверка гипотез о параметрах случайных величин, широко используются несколько табличных функций, например, функция Лапласа или квантили распределения хи-квадрат.

В наше время совершенно необязательно обращаться за недостающими в формуле величинами к толстым справочникам со статистическими таблицами, можно всё посчитать непосредственно в Excel:

Формула =НОРМСТРАСП(x)-0,5 вычисляет значение функции Лапласа от аргумента x (подставьте вместо x соответствующую ячейку). При этом Ф(-x)=-Ф(x) , а при x>3,85 значение Ф(x)=0,5 .

Критические точки t-критерия можно вычислить с помощью формулы =СТЬЮДРАСПОБР(α;n) , где α – уровень значимости (вероятность γ или надёжность 1-γ ), n – число степеней свободы (например, объём выборки в задачах о построении доверительных интервалов). При числе степеней свободы n≥30 распределение сводится к нормальному с параметрами α=0 , σ=корень(n/(n-2)) .

Критические точки распределения Пирсона χ 2 можно вычислить с помощью формулы =ХИ2ОБР(a;n) , где a – уровень значимости, n – число степеней свободы.

Получить значение функции плотности распределения Пуассона можно с помощью формулы =ПУАССОН(n;λ;0) , где n – число степеней свободы (количество событий), λ – среднее число появлений события (ожидаемое численное значение).

В ряде случаев для расчёта с заданным значением параметра γ функции Excel может понадобиться передать аргумент функции α=1-γ , смотрите внимательно встроенную справку по функциям.

Математическая статистика — лекции и примеры в Excel

12.03.2013, 17:18; рейтинг: 43632

Функция Лапласа

Оператор НОРМ.СТ.РАСП

Синтаксис оператора НОРМ.СТ.РАСП выглядит следующим образом:

Устаревший оператор НОРМСТРАСП записывается так:

Аргумент «Z» указывает числовое значение, для которого производится построение распределения.

Решение задачи

Для того чтобы выполнить требуемое вычисление для переменной применяется следующая формула:

«Вставить функцию»

Для того, чтобы произвести вычисление, жмем на кнопку Enter. Полученный результат и будет искомым значением.

функція Лапласа

оператор НОРМ.СТ.РАСП

Синтаксис оператора НОРМ.СТ.РАСП виглядає наступним чином:

Застарілий оператор НОРМСТРАСП записується так:

Аргумент «Z» вказує числове значення, для якого проводиться побудова розподілу.

Рішення завдання

Для того щоб виконати необхідну обчислення для змінної застосовується наступна формула:

Виділяємо осередок, куди буде виводитися готовий результат і клацаємо по значку «Вставити функцію», розташованому біля рядка формул.

Для того, щоб зробити обчислення, тиснемо на кнопку Enter. Отриманий результат і буде шуканим значенням.

Источник

Таблица значений локальной функции Лапласа
- Значения плотности стандартного нормального распределения
3.2. Формула Лапласа — Мои статьи — Каталог статей
Таблица значений локальной функции Лапласа
Функция Лапласа в Excel
- Функция Лапласа
  - Оператор НОРМ.СТ.РАСП
  - Решение задачи
  - Помогла ли вам эта статья?
Локальная теорема Муавра — Лапласа
таблица значений функции Лапласа
Интегральная теорема Муавра-Лапласа
- Что такое «интегральная теорема Муавра-Лапласса»?
- Задача № 1
  - Нюансы решения
- Задача № 2
  - Каверзные вопросы
- Задача № 3
  - Решение пункта б)
  - Решение пункта а)
- Ключевые моменты

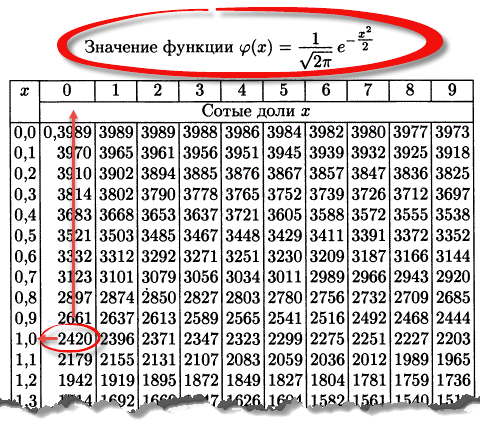
Таблица значений локальной функции Лапласа

Значения плотности стандартного нормального распределения

	0	1	2	3	4	5	6	7	8	9
0,0	0,398942	0,398922	0,398862	0,398763	0,398623	0,398444	0,398225	0,397966	0,397668	0,397330
0,1	0,396953	0,396536	0,396080	0,395585	0,395052	0,394479	0,393868	0,393219	0,392531	0,391806
0,2	0,391043	0,390242	0,389404	0,388529	0,387617	0,386668	0,385683	0,384663	0,383606	0,382515
0,3	0,381388	0,380226	0,379031	0,377801	0,376537	0,375240	0,373911	0,372548	0,371154	0,369728
0,4	0,368270	0,366782	0,365263	0,363714	0,362135	0,360527	0,358890	0,357225	0,355533	0,353812
0,5	0,352065	0,350292	0,348493	0,346668	0,344818	0,342944	0,341046	0,339124	0,337180	0,335213
0,6	0,333225	0,331215	0,329184	0,327133	0,325062	0,322972	0,320864	0,318737	0,316593	0,314432
0,7	0,312254	0,310060	0,307851	0,305627	0,303389	0,301137	0,298872	0,296595	0,294305	0,292004
0,8	0,289692	0,287369	0,285036	0,282694	0,280344	0,277985	0,275618	0,273244	0,270864	0,268477
0,9	0,266085	0,263688	0,261286	0,258881	0,256471	0,254059	0,251644	0,249228	0,246809	0,244390
1,0	0,241971	0,239551	0,237132	0,234714	0,232297	0,229882	0,227470	0,225060	0,222653	0,220251
1,1	0,217852	0,215458	0,213069	0,210686	0,208308	0,205936	0,203571	0,201214	0,198863	0,196520
1,2	0,194186	0,191860	0,189543	0,187235	0,184937	0,182649	0,180371	0,178104	0,175847	0,173602
1,3	0,171369	0,169147	0,166937	0,164740	0,162555	0,160383	0,158225	0,156080	0,153948	0,151831
1,4	0,149727	0,147639	0,145564	0,143505	0,141460	0,139431	0,137417	0,135418	0,133435	0,131468
1,5	0,129518	0,127583	0,125665	0,123763	0,121878	0,120009	0,118157	0,116323	0,114505	0,112704
1,6	0,110921	0,109155	0,107406	0,105675	0,103961	0,102265	0,100586	0,098925	0,097282	0,095657
1,7	0,094049	0,092459	0,090887	0,089333	0,087796	0,086277	0,084776	0,083293	0,081828	0,080380
1,8	0,078950	0,077538	0,076143	0,074766	0,073407	0,072065	0,070740	0,069433	0,068144	0,066871
1,9	0,065616	0,064378	0,063157	0,061952	0,060765	0,059595	0,058441	0,057304	0,056183	0,055079
2,0	0,053991	0,052919	0,051864	0,050824	0,049800	0,048792	0,047800	0,046823	0,045861	0,044915
2,1	0,043984	0,043067	0,042166	0,041280	0,040408	0,039550	0,038707	0,037878	0,037063	0,036262
2,2	0,035475	0,034701	0,033941	0,033194	0,032460	0,031740	0,031032	0,030337	0,029655	0,028985
2,3	0,028327	0,027682	0,027048	0,026426	0,025817	0,025218	0,024631	0,024056	0,023491	0,022937
2,4	0,022395	0,021862	0,021341	0,020829	0,020328	0,019837	0,019356	0,018885	0,018423	0,017971
2,5	0,017528	0,017095	0,016670	0,016254	0,015848	0,015449	0,015060	0,014678	0,014305	0,013940
2,6	0,013583	0,013234	0,012892	0,012558	0,012232	0,011912	0,011600	0,011295	0,010997	0,010706
2,7	0,010421	0,010143	0,009871	0,009606	0,009347	0,009094	0,008846	0,008605	0,00837	0,008140
2,8	0,007915	0,007697	0,007483	0,007274	0,007071	0,006873	0,006679	0,006491	0,006307	0,006127
2,9	0,005953	0,005782	0,005616	0,005454	0,005296	0,005143	0,004993	0,004847	0,004705	0,004567
3,0	0,004432	0,004301	0,004173	0,004049	0,003928	0,003810	0,003695	0,003584	0,003475	0,003370
3,1	0,003267	0,003167	0,00307	0,002975	0,002884	0,002794	0,002707	0,002623	0,002541	0,002461
3,2	0,002384	0,002309	0,002236	0,002165	0,002096	0,002029	0,001964	0,001901	0,001840	0,001780
3,3	0,001723	0,001667	0,001612	0,001560	0,001508	0,001459	0,001411	0,001364	0,001319	0,001275
3,4	0,001232	0,001191	0,001151	0,001112	0,001075	0,001038	0,001003	0,000969	0,000936	0,000904
3,5	0,000873	0,000843	0,000814	0,000785	0,000758	0,000732	0,000706	0,000681	0,000657	0,000634
3,6	0,000612	0,00059	0,000569	0,000549	0,000529	0,000510	0,000492	0,000474	0,000457	0,000441
3,7	0,000425	0,000409	0,000394	0,000380	0,000366	0,000353	0,000340	0,000327	0,000315	0,000303
3,8	0,000292	0,000281	0,000271	0,000260	0,000251	0,000241	0,000232	0,000223	0,000215	0,000207
3,9	0,000199	0,000191	0,000184	0,000177	0,000170	0,000163	0,000157	0,000151	0,000145	0,000139
4,0	0,000134	0,000129	0,000124	0,000119	0,000114	0,000109	0,000105	0,000101	0,000097	0.000093

Вернуться Статистические таблицы

helpstat.ru

3.2. Формула Лапласа — Мои статьи — Каталог статей

Локальная теорема Лапласа. Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна р (0 < р < 1), событие наступит ровно k раз (последовательность не важна), приближенно равна (при этом чем больше n, тем точнее вероятность):

Значения функции находятся в таблице для функции ф (х).

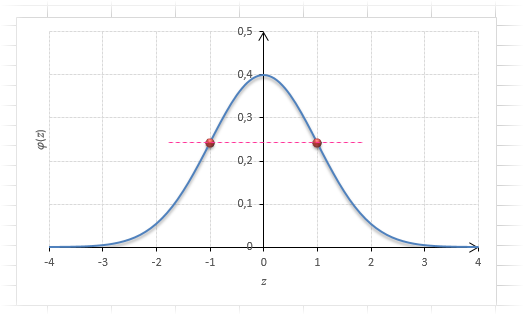
Важно помнить, что функция ф (х) — четная

=> ф (-х) = ф (х).

Интегральная теорема Лапласа. Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна р (0 < р < 1), событие наступит не менее k₁ раз и не более k₂ раз, приближенно равна:

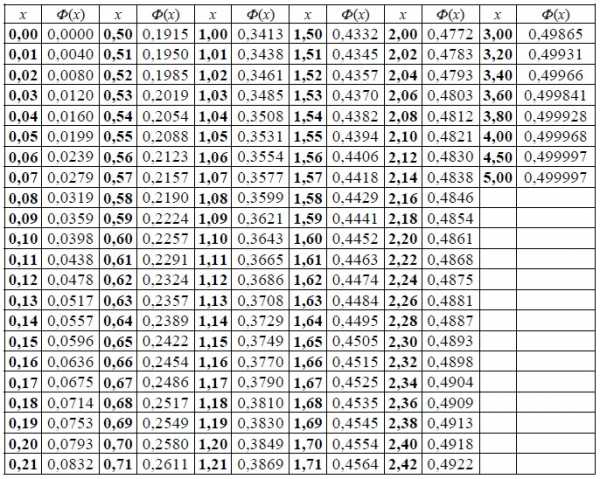
Для нахождения значений используют таблицу функции Лапласа для х:

0 , если же х>5, то автоматически Ф(х) = 0,5.

Функции Лапласа нечетная, т.е. Ф (-х) = — Ф(х).

Задача 1. Найдите вероятность того, что число зачисленных абитуриентов в институт психологии равно 86 из 250, подавших заявления. если вероятность зачисления для каждого абитуриента равна 0,35.

Решение

По условию задачи: р = 0.35; q = 0,65; n = 250;k = 86. В связи с тем, что n = 250 достаточно большое число, то целесообразней воспользоваться локальной теоремой Лапласа:

По таблице № 1 значений функции Лапласа найдем значение при х = 0,2, т.е. ф (х) = 0,391.

Тогда вероятность зачисления 86 абитуриентов в институт психологии равна

Ответ: 0,052.

Задача 2. Известно, что вероятность появления в семье мальчика равна 40 %. Сколько семей необходимо опросить, чтобы с вероятностью 0,75 утверждать, что в этих семьях родились мальчики, если всего в опросе участвовало 150 детей?

Решение

По условию задачи: n = 150; р = 0,4; q = 0,6.

Тогда, пусть было опрошено а– семей. Чтобы найти неизвестное а, при условии, что n p q > 10, воспользуемся интегральной теоремой Лапласа:

В результате, получаем неравенство:

Из таблицы № 2 для функции Лапласа получаем соответствующие значения, при Ф(х) > 0,25, то х > 0,67. Тогда неравенство принимает вид:

Следовательно, необходимо будет опросить 62 семьи, чтобы с вероятностью 0,75 утверждать, что в каждой из них ребенок – мальчик.

Ответ: 62.

Задача 3. Вероятность встретить на улице в солнечный день человека с зонтом равна 0,01. Чему равна вероятность того, что из 1 000 встречных мимо вас пройдет не более 4 человек с зонтами.

Решение

Пусть событие А – {мимо вас пройдет не более 4 человек с зонтами в солнечный день}; тогда событие А₀– {мимо вас не пройдет ни один человек с зонтом в солнечный день}; событие А₁– {мимо вас пройдет 1 человек с зонтом в солнечный день};событие А₂– {мимо вас пройдет 2 человека с зонтами в солнечный день};событие А₃– {мимо вас пройдет 3 человека с зонтами в солнечный день}; событие А₄– {мимо вас пройдет 4 человека с зонтами в солнечный день}.

Получается, что событие А есть сумма событий А₀; А₁;А₂;А₃;А₄:

А = А₀+А₁+А₂+А₃+А₄.

Так как события А₀; А₁;А₂;А₃;А₄ несовместны, то соответственно вероятность события. А есть:

Р(А) = Р(А₀) + Р(А₁) +Р(А₂) + Р(А₃) +Р(А₄).

Ответ: 0,777.

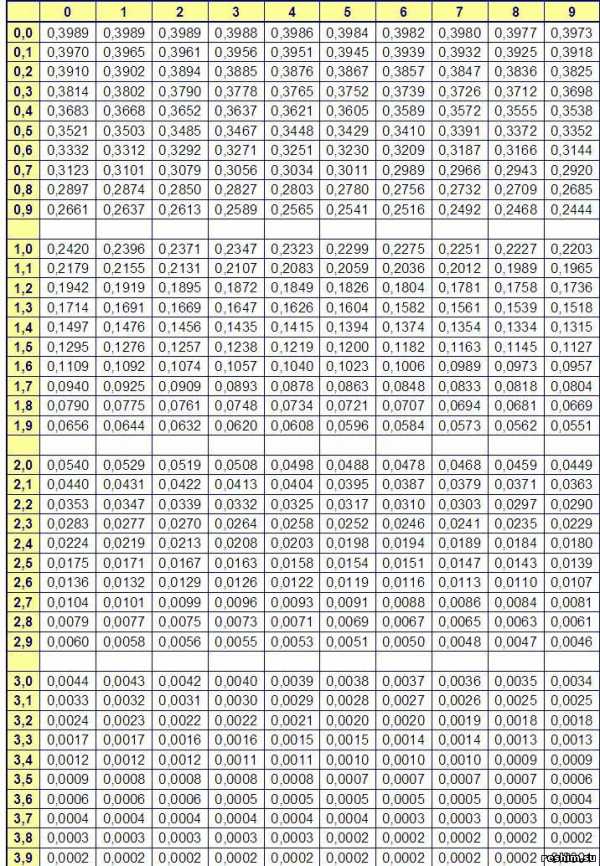
Пользоваться таблицей несложно: вначале смотрим на столбец, а потом на строку, например, Ф(0,22) = 0,3894; Ф(2,99) = 0,0046.

Таблица значений локальной функции Лапласа (таб. № 1)

Таблица значений интегральной функции Лапласа (таб. № 2)

stochastic5.ucoz.net

Таблица значений локальной функции Лапласа

Таблица значений
локальной
функции
Лапласа

01234567890,00,39890,39890,39890,39880,39860,39840,39820,39800,39770,39730,10,39700,39650,39610,39560,39510,39450,39390,39320,39250,39180,20,39100,39020,38940,38850,38760,38670,38570,38470,38360,38250,30,38140,38020,37900,37780,37650,37520,37390,37260,37120,36980,40,36830,36680,36520,36370,36210,36050,35890,35720,35550,35380,50,35210,35030,34850,34670,34480,34290,34100,33910,33720,33520,60,33320,33120,32920,32710,32510,32300,32090,31870,31660,31440,70,31230,31010,30790,30560,30340,30110,29890,29660,29430,29200,80,28970,28740,28500,28270,28030,27800,27560,27320,27090,26850,90,26610,26370,26130,25890,25650,25410,25160,24920,24680,2444 1,00,24200,23960,23710,23470,23230,22990,22750,22510,22270,22031,10,21790,21550,21310,21070,20830,20590,20360,20120,19890,19651,20,19420,19190,18950,18720,18490,18260,18040,17810,17580,17361,30,17140,16910,16690,16470,16260,16040,15820,15610,15390,15181,40,14970,14760,14560,14350,14150,13940,13740,13540,13340,13151,50,12950,12760,12570,12380,12190,12000,11820,11630,11450,11271,60,11090,10920,10740,10570,10400,10230,10060,09890,09730,09571,70,09400,09250,09090,08930,08780,08630,08480,08330,08180,08041,80,07900,07750,07610,07480,07340,07210,07070,06940,06810,06691,90,06560,06440,06320,06200,06080,05960,05840,05730,05620,0551 2,00,05400,05290,05190,05080,04980,04880,04780,04680,04590,04492,10,04400,04310,04220,04130,04040,03950,03870,03790,03710,03632,20,03530,03470,03390,03320,03250,03170,03100,03030,02970,02902,30,02830,02770,02700,02640,02580,02520,02460,02410,02350,02292,40,02240,02190,02130,02080,02030,01980,01940,01890,01840,01802,50,01750,01710,01670,01630,01580,01540,01510,01470,01430,01392,60,01360,01320,01290,01260,01220,01190,01160,01130,01100,01072,70,01040,01010,00990,00960,00930,00910,00880,00860,00840,00812,80,00790,00770,00750,00730,00710,00690,00670,00650,00630,00612,90,00600,00580,00560,00550,00530,00510,00500,00480,00470,0046 3,00,00440,00430,00420,00400,00390,00380,00370,00360,00350,00343,10,00330,00320,00310,00300,00290,00280,00270,00260,00250,00253,20,00240,00230,00220,00220,00210,00200,00200,00190,00180,00183,30,00170,00170,00160,00160,00150,00150,00140,00140,00130,00133,40,00120,00120,00120,00110,00110,00100,00100,00100,00090,00093,50,00090,00080,00080,00080,00080,00070,00070,00070,00070,00063,60,00060,00060,00060,00050,00050,00050,00050,00050,00050,00043,70,00040,00040,00040,00040,00040,00040,00030,00030,00030,00033,80,00030,00030,00030,00030,00030,00020,00020,00020,00020,00023,90,00020,00020,00020,00020,00020,00020,00020,00020,00020,0001

studfiles.net

Функция Лапласа в Excel

Функция Лапласа

Оператор НОРМ.СТ.РАСП

Синтаксис оператора НОРМ.СТ.РАСП выглядит следующим образом:

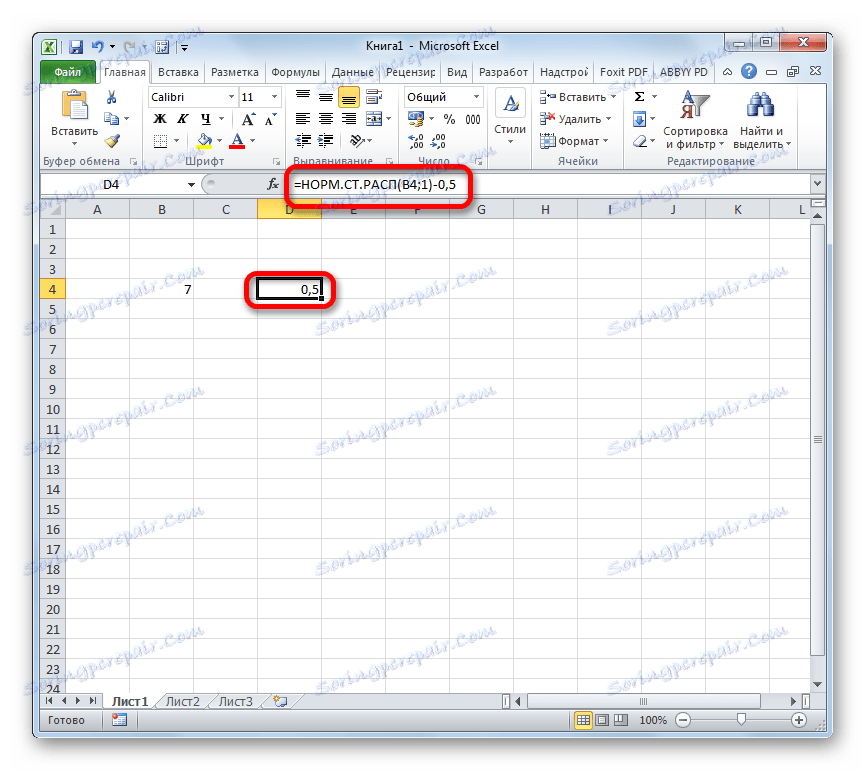
=НОРМ.СТ.РАСП(z;интегральная)

Устаревший оператор НОРМСТРАСП записывается так:

=НОРМСТРАСП(z)

Аргумент «Z» указывает числовое значение, для которого производится построение распределения.

Решение задачи

Для того чтобы выполнить требуемое вычисление для переменной применяется следующая формула:

=НОРМ.СТ.РАСП(z;интегральная(1))-0,5

Выделяем ячейку, куда будет выводиться готовый результат и щелкаем по значку «Вставить функцию», расположенному около строки формул.

После открытия Мастера функций переходим в категорию «Статистические» или «Полный алфавитный перечень». Выделяем наименование «НОРМ.СТ.РАСП» и жмем на кнопку «OK».

Происходит активация окна аргументов оператора НОРМ.СТ.РАСП. В поле «Z» вводим переменную, к которой нужно произвести расчет. Также этот аргумент может быть представлен в виде ссылки на ячейку, которая содержит эту переменную. В поле «Интегральная» вводим значение «1». Это означает, что оператор после вычисления вернет в качестве решения интегральную функцию распределения. После того, как выполнены вышеперечисленные действия, жмем на кнопку «OK».

После этого результат обработки данных оператором НОРМ.СТ.РАСП будет выведен в ячейку, которая указана в первом пункте данного руководства.

Но и это ещё не все. Мы вычислили только стандартное нормальное интегральное распределение. Для того, чтобы посчитать значение функции Лапласа, нужно от него отнять число 0,5. Выделяем ячейку, содержащую выражение. В строке формул после оператора НОРМ.СТ.РАСП дописываем значение: -0,5.

Для того, чтобы произвести вычисление, жмем на кнопку Enter. Полученный результат и будет искомым значением.

Мы рады, что смогли помочь Вам в решении проблемы.

Опишите, что у вас не получилось.
Наши специалисты постараются ответить максимально быстро.

Помогла ли вам эта статья?

ДА НЕТ

lumpics.ru

Локальная теорема Муавра — Лапласа

27 октября 2011

Рассмотрим последовательность из $n$ независимых опытов, в каждом из которых событие $A$ может произойти с вероятностью $p$, либо не произойти — с вероятностью $q=1-p$. Обозначим через P
_n(k) вероятность того, что событие $A$ произойдет ровно $k$ раз из $n$ возможных.

В таком случае величину P
_n(k) можно найти по теореме Бернулли (см. урок «Схема Бернулли. Примеры решения задач»):

Эта теорема прекрасно работает, однако у нее есть недостаток. Если $n$ будет достаточно большим, то найти значение P
_n(k) становится нереально из-за огромного объема вычислений. В этом случае работает Локальная теорема Муавра — Лапласа, которая позволяют найти приближенное значение вероятности:

Локальная теорема Муавра — Лапласа. Если в схеме Бернулли число $n$ велико, а число $p$ отлично от 0 и 1, тогда:

Функция φ(x) называется функцией Гаусса. Ее значения давно вычислены и занесены в таблицу, которой можно пользоваться даже на контрольных работах и экзаменах.

Функция Гаусса обладает двумя свойствами, которые следует учитывать при работе с таблицей значений:

φ(−x) = φ(x) — функция Гаусса — четная;
При больших значениях x имеем: φ(x) ≈ 0.

Локальная теорема Муавра — Лапласа дает отличное приближение формулы Бернулли, если число испытаний n достаточно велико. Разумеется, формулировка «число испытаний достаточно велико» весьма условна, и в разных источниках называются разные цифры. Например:

Часто встречается требование: n · p · q > 10. Пожалуй, это минимальная граница;
Другие предлагают работать по этой формуле только для $n > 100$ и n · p · q > 20.

На мой взгляд, достаточно просто взглянуть на условие задачи. Если видно, что стандартная теорема Бернулли не работает из-за большого объема вычислений (например, никто не будет считать число 58! или 45!), смело применяйте Локальную теорему Муавра — Лапласа.

К тому же, чем ближе значения вероятностей $q$ и $p$ к 0,5, тем точнее формула. И, наоборот, при пограничных значениях (когда $p$ близко к 0 или 1) Локальная теорема Муавра — Лапласа дает большую погрешность, значительно отличаясь от настоящей теоремы Бернулли.

Однако будьте внимательны! Многие репетиторы по высшей математике сами ошибаются в подобных расчетах. Дело в том, что в функцию Гаусса подставляется довольно сложное число, содержащее арифметический квадратный корень и дробь. Это число обязательно надо найти еще до подстановки в функцию. Рассмотрим все на конкретных задачах:

Задача. Вероятность рождения мальчика равна 0,512. Найдите вероятность того, что среди 100 новорожденных будет ровно 51 мальчик.

Итак, всего испытаний по схеме Бернулли n = 100. Кроме того, p = 0,512, q = 1 − p = 0,488.

Поскольку n = 100 — это достаточно большое число, будем работать по Локальной теореме Муавра — Лапласа. Заметим, что n · p · q = 100 · 0,512 · 0,488 ≈ 25 > 20. Имеем:

Поскольку мы округляли значение n · p · q до целого числа, ответ тоже можно округлить: 0,07972 ≈ 0,08. Учитывать остальные цифры просто нет смысла.

Задача. Телефонная станция обслуживает 200 абонентов. Для каждого абонента вероятность того, что в течение одного часа он позвонит на станцию, равна 0,02. Найти вероятность того, что в течение часа позвонят ровно 5 абонентов.

По схеме Бернулли, n = 200, p = 0,02, q = 1 − p = 0,98. Заметим, что n = 200 — это неслабое число, поэтому используем Локальную теорему Муавра — Лапласа. Для начала найдем n · p · q = 200 · 0,02 · 0,98 ≈ 4. Конечно, 4 — это слишком мало, поэтому результаты будут неточными. Тем не менее, имеем:

Округлим ответ до второго знака после запятой: 0,17605 ≈ 0,18. Учитывать больше знаков все равно не имеет смысла, поскольку мы округляли n · p · q = 3,92 ≈ 4 (до точного квадрата).

Задача. Магазин получил 1000 бутылок водки. Вероятность того, что при перевозке бутылка разобьется, равна 0,003. Найти вероятность того, что магазин получит ровно две разбитых бутылки.

По схеме Бернулли имеем: n = 1000, p = 0,003, q = 0,997. Отсюда n · p · q = 2,991 ≈ 1,73² (подобрали ближайший точный квадрат). Поскольку число n = 1000 достаточно велико, подставляем все числа в формулу Локальной теоремы Муавра — Лапласа:

Мы сознательно оставляем лишь один знак после запятой (на самом деле там получится 0,1949…), поскольку изначально использовали довольно грубые оценки. В частности: 2,991 ≈ 1,73². Тройка в числителе внутри функции Гаусса возникла из выражения n · p = 1000 · 0,003 = 3.

Смотрите также:

Зачем нужна интегральная теорема Муавра-Лапласа и как её правильно применять?
Схема Бернулли. Примеры решения задач
Площадь круга
Уравнение касательной к графику функции
Специфика работы с логарифмами в задаче B15
Задача B5: площадь фигуры без клеток

www.berdov.com

таблица значений функции Лапласа

Сайт www.MatBuro.ru

©МатБюро — Решение задач по высшей математике, теории вероятностей

		Функция Лапласа	y =Φ(x)=	1	∫x	e−t2 / 2dt
		2π
							0

x	Φ(x)	x	Φ(x)	x		Φ(x)	x		Φ(x)
0	0
0,01	0,004	0,13	0,0517	0,25		0,0987	0,37	0,1443
0,02	0,008	0,14	0,0557	0,26		0,1026	0,38	0,148
0,03	0,012	0,15	0,0596	0,27		0,1064	0,39	0,1517
0,04	0,016	0,16	0,0636	0,28		0,1103	0,4	0,1554
0,05	0,0199	0,17	0,0675	0,29		0,1141	0,41	0,1591
0,06	0,0239	0,18	0,0714	0,3		0,1179	0,42	0,1628
0,07	0,0279	0,19	0,0753	0,31		0,1217	0,43	0,1664
0,08	0,0319	0,2	0,0793	0,32		0,1255	0,44	0,17
0,09	0,0359	0,21	0,0832	0,33		0,1293	0,45	0,1736
0,1	0,0398	0,22	0,0871	0,34		0,1331	0,46	0,1772
0,11	0,0438	0,23	0,091	0,35		0,1368	0,47	0,1808
0,12	0,0478	0,24	0,0948	0,36		0,1406	0,48	0,1844

0,49	0,1879	1,02	0,3461	1,55		0,4394	2,16	0,4846
0,5	0,1915	1,03	0,3485	1,56		0,4406	2,18	4854
0,51	0,195	1,04	0,3508	1,57		0,4418	2,2	0,4861
0,52	0,1985	1,05	0,3531	1,58		0,4429	2,22	0,4868
0,53	0,2019	1,06	0,3554	1,59		0,4441	2,24	0,4875
0,54	0,2054	1,07	0,3577	1,6		0,4452	2,26	0,4881
0,55	0,2088	1,08	0,3599	1,61		0,4463	2,28	0,4887
0,56	0,2123	1,09	0,3621	1,62		0,4474	2,3	0,4893
0,57	0,2157	1,1	0,3643	1,63		0,4484	2,32	0,4898
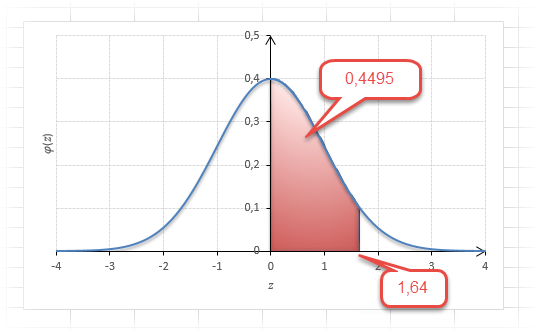
0,58	0,219	1,11	0,3665	1,64		0,4495	2,34	0,4904
0,59	0,2224	1,12	0,3686	1,65		0,4505	2,36	0,4908
0,6	0,2257	1,13	0,3708	1,66		0,4515	2,38	0,4913
0,61	0,2291	1,14	0,3729	1,67		0,4525	2,4	0,4918
0,62	0,2324	1,15	0,3749	1,68		0,4535	2,42	0,4922
0,63	0,2357	1,16	0,377	1,69		0,4545	2,44	0,4927
0,64	0,2389	1,17	0,379	1,7		0,4554	2,46	0,4931
0,65	0,2422	1,18	0,381	1,71		0,4564	2,48	0,4934
0,66	0,2454	1,19	0,383	1,72		0,4573	2,5	0,4938
0,67	0,2486	1,2	0,3849	1,73		0,4582	2,52	0,4941
0,68	0,2517	1,21	0,3869	1,74		0,4591	2,54	0,4945
0,69	0,2549	1,22	0,3888	1,75		0,4599	2,56	0,4948
0,7	0,258	1,23	0,3907	1,76		0,4608	2,58	0,4951
0,71	0,2611	1,24	0,3925	1,77		0,4616	2,6	0,4953
0,72	0,2642	1,25	0,3914	1,78		0,4625	2,62	0,4956
0,73	0,2673	1,26	0,3962	1,79		0,4633	2,64	0,4959
0,74	0.2703	1,27	0,398	1,8		0,4641	2,66	0,4961
0,75	0,2734	1,28	0,3997	1,81		0,4649	2,68	0,4963
0,76	0,2764	1,29	0,4015	1,82		0,4656	2,7	0,4965
0,77	0,2794	1,3	0,4032	1,83		0,4664	2,72	0,4967
0,78	0,2823	1,31	0,4049	1,84		0,4671	2,74	0,4969

Сайт www.MatBuro.ru

©МатБюро — Решение задач по высшей математике, теории вероятностей

x	Φ(x)	x	Φ(x)	x	Φ(x)	x	Φ(x)
0,79	0,2852	1,32	0,4066	1,85	0,4678	2,76	0,4971
0,8	0,2881	1,33	0,4082	1,86	0,4686	2,78	0,4973
0,81	0,291	1,34	0,4099	1,87	0,4693	2,8	0,4974
0,82	0,2939	1,35	0,4115	1,88	0,4699	2,82	0,4976
0,83	0,2967	1,36	0,4131	1,89	0,4706	2,84	0,4977
0.84	0,2995	1,37	0,4147	1,9	0,4713	2,86	0,4979
0,85	0,3023	1,38	0,4162	1,91	0,4719	2,88	0,498
0,86	0,3051	1,39	0,4177	1,92	0,4726	2,9	0,4981
0,87	0,3078	1,4	0,4192	1,93	0,4732	2,92	0,4982
0,88	0,3106	1,41	0,4207	1,94	0,4738	2,94	0,4984
0,89	0,3133	1,42	0,4222	1,95	0,4744	2,96	0,4985
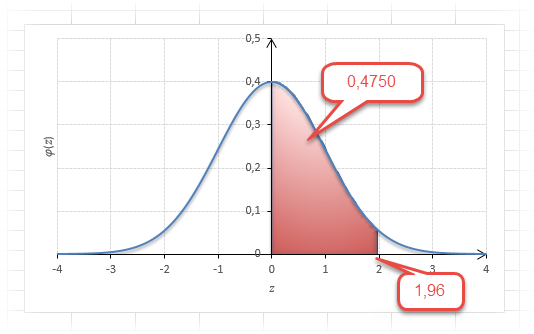
0,9	0,3159	1,43	0,4236	1,96	0,475	2,98	0,4986
0,91	0,3186	1,44	0,4251	1,97	0,4756	3	0,49865
0,92	0,3112	1,45	0,4265	1,98	0,4761	3,2	0,49931
0,93	0,3238	1,46	0,4279	1,99	0,4767	3,4	0,49966
0,94	0,3264	1,47	0,4292	2	0,4772	3,6	0,499841
0,95	0,3289	1,48	0,4306	2,02	0,4783	3,8	0,499928
0,96	0,3315	1,49	0,4319	2,04	0,4793	4	0,499968
0,97	0,334	1,5	0,4332	2,06	0,4803	4,5	0,499997
0,98	0,3365	1,51	0,4345	2,08	0,4812	5	0,5
0,99	0,3389	1,52	0,4357	2,1	0,4821
1	0,3413	1,53	0,437	2,12	0,483
1,01	0,3438	1,54	0,4382	2,14	0,4838

studfiles.net

Интегральная теорема Муавра-Лапласа

17 сентября 2015

Данная теорема является дальнейшим развитием схемы Бернулли и позволяет работать с диапазонами: какова вероятность, что число успехов будет лежать в пределах указанного отрезка.

Интегральная теорема Муавра-Лапласа. Пусть число испытаний $n$ достаточно велико, а вероятность успеха $0<,p,<1$. Пусть также$q=1-p$ — вероятность неудачного испытания. Тогда вероятность того, что число успехов будет лежать в пределах от ${{k}_{1}}$ до ${{k}_{2}}$, можно примерно посчитать по формуле:

[{{P}_{n}}left( {{k}_{1}};{{k}_{2}} right)approx Phi left( frac{{{k}_{2}}-np}{sqrt{npq}} right)-Phi left( frac{{{k}_{1}}-np}{sqrt{npq}} right)]

где

[Phi left( x right)=frac{1}{sqrt{2text{ }!!pi!!text{ }}}intlimits_{0}^{x}{{{e}^{-frac{{{t}^{2}}}{2}}}dt}]

Функция $Phi left( x right)$ называется функцией Лапласа и содержит в себе интеграл, который не считается напрямую. Как следствие, значения этой функции сведены в таблицу, которую можно загрузить прямо на этой странице.

Разумеется, в таблице приведены не все возможные значения. Для больших значений $x$ (скажем, для $x>6$ ) считают, что $Phi left( x right)approx 0,5$. Кроме того, функция Лапласа является нечётной, поэтому из неё можно выносить знак «минус»:

[Phi left( -x right)=-Phi left( x right)]

Это прямо следует из определения, в котором присутствует определённый интеграл.

Что такое «интегральная теорема Муавра-Лапласса»?

Сегодня мы разберем интегральную теорему Муавра-Лапласа. Это «старшая сестра» второй версии теоремы Муавра-Лапласа, разобранной в прошлом уроке. Во-первых, разберемся, зачем вообще нужна еще одна теорема — интегральная.

Допустим, у нас есть 1000 изделий, о которых известно, что там в среднем есть 10% брака. Однако это не означает, что в партии из 1000 изделий будет ровно 100 бракованных изделий, скорее всего, их будет 101-102 или 98, но не 100. Вероятность того, что будет ровно 100, легко считается при помощи более легкой теоремы Муавра-Лапласа, и вы можете сами убедиться, что она будет велика. В этом случае возникает вопрос: «Какова тогда вероятность, что деталей будет от 95 до 105, либо от 50 до 150?». Считать такую конструкцию при помощи первой версии теоремы Муавра-Лапласса крайне сложно, потому что нам придется отдельно посчитать, какова возможность того, что бракованных изделий будет 50, 51, 51 и так до 150, т.е. сто отдельных однотипных вычислений. Это очень трудоемко и бессмысленно. Вот именно в таких примерах нам на помощь приходит интегральная теорема Муавра-Лапласа. С назначением самой интегральной теоремы все ясно, теперь давайте разберемся с ее формулой.

Вероятность того, что при $n$-испытаниях количество успешных испытаний будет в пределах от ${{K}_{1}}$ до ${{K}_{2}}$ выражается следующей формулой:

[{{P}_{n}}left( {{K}_{1}};{{K}_{2}} right)approx Fleft( frac{{{K}_{2}}-np}{sqrt{npq}} right)-Fleft( frac{{{K}_{1}}-np}{sqrt{npq}} right)]

Сама же функция $F$ называется функцией Муавра-Лапласа, и выглядит она следующим образом:

[Fleft( x right)=frac{2}{sqrt{2text{ }!!pi!!text{ }}}{{intlimits_{0}^{x}{e}}^{-frac{{{t}^{2}}}{2}}}dt]

Сразу же скажу, что данный интеграл «красиво» не считается, поэтому вместо красивого интегрирования у вас всегда будет в распоряжении таблица значений функции Лапласа, и с помощью этой таблицы, а также некоторых способов, которые мы разберем чуть позже в этом уроке, мы и будем решать все примеры на данную интегральную теорему.

Разумеется, возникает вопрос «А что это за буквы такие — $n$, $q$, $p$?».

С $n$, я думаю, все понятно — это число испытаний.

$p$ — это вероятность успеха в каждом конкретном испытании.

$q$ — по аналогии с формулой Бернули это вероятность провала, т.е. неуспеха в каждом конкретносм испытании. Считатеся она по очень простой формуле:

[q=1-p]

Надеюсь, с буквами теперь понятно, поэтому перейдем к решению конкретных примеров.

Задача № 1

Начнем мы с довольно простой задачи, однако уже на ее примеры мы познакомимся с особенностями применения интегральной теоремы Муавра-Лапласса.

Известно, что в среднем 5% студентов носят очки. Какова вероятность того, что из 200 студентов, находящихся в аудитории, окажется не менее 10%, носящих очки?

В первую очередь, давайте запишем саму интегральную теорему Муавра-Лапласса:

[{{P}_{n}}left( {{K}_{1}};{{K}_{2}} right)approx Fleft( frac{{{K}_{2}}-np}{sqrt{npq}} right)-Fleft( frac{{{K}_{1}}-np}{sqrt{npq}} right)]

При этом полезно помнить еще одну формулу:

[Fleft( x right)=frac{2}{sqrt{2text{ }!!pi!!text{ }}}{{intlimits_{0}^{x}{e}}^{-frac{{{t}^{2}}}{2}}}dt]

Собственно, из-за этого интеграла, присутствуещего в функции Муавра-Лапласса, сама теорема и называется интегральной.

При первом взгляде на эту интегральную теорему многие ученики приходят в шок — уж больно много здесь разных конструкций, корней, вычислений и т.д. На самом деле, все очень просто, и сейчас вы сами в этом убедитесь.

Для начала давайте выпишем все значения. Итак, нам известно следующее:

Всего студентов 200 — $n=200$;
Вероятность попадания студента, который носит очки — $p=0,05$;
Вероятность того, что студенты не носят очки будет равна $1-0,05=0,95$.

Далее мы можем найти $sqrt{npq}$:

[sqrt{npq}=sqrt{200cdot 0,05cdot 0,95}=sqrt{9,5}approx 3,08]

Разумеется, такие вычисления выполняются на калькуляторе.

Кроме того, в нашей формуле, в интегральной теореме Муавра-Лапласса, мы наблюдаем выражение $np$ — произведение количества испытаний на вероятность успеха:

[np=200cdot 0,05=10]

Давайте перепишем формулу с учетом всех фактов:

[{{P}_{n}}left( {{K}_{1}};{{K}_{2}} right)approx Fleft( frac{200-10}{3,08} right)-Fleft( frac{20-10}{3,08} right)=]

[=Fleft( 61,7 right)-Fleft( 3,25 right)]

И вот здесь нас поджидает первая проблема: если мы посмотрим на таблицу значений, то значение $3,25$ здесь еще присутствует, но вот числа от $60$ и более здесь вообще не представлены. Для решения этого вопроса предлагаю взглянуть на исходную формулу Муавра-Лапласса:

[Fleft( x right)=frac{2}{sqrt{2text{ }!!pi!!text{ }}}{{intlimits_{0}^{x}{e}}^{-frac{{{t}^{2}}}{2}}}dt]

При больших «иксах» ${{e}^{-frac{{{t}^{2}}}{2}}}$ будет очень маленьким числом, т.е. возрастание $x$ дает очень маленькую, стремящуюся к «нулю» добавку к вероятности. Поэтому для всех «иксов», начиная от шести и более примерно считается, что значение функции Лапласса равно $0,5$. $$ $$

Итак, продолжим наше решение:

[{{P}_{n}}left( {{K}_{1}};{{K}_{2}} right)approx 0,5-0,49942=0,00058=5,8cdot {{10}^{-4}}]

Нюансы решения

Как видите, ничего сверхъестественного. Все применение интегральной теоремы Муавра-Лапласса сводится к следующему:

Аккуратно выписать все значения: число испытаний, вероятность и «единицу» «минус» вероятность.
Посчитать корни и величины.
Пробежаться глазами по таблице и найти значение функции в тех точках, которые мы получили.

Однако, как вы понимаете, это была самая простая задача — существуют гораздо более сложные и навороченные. И один из самых «противных» типов заданий на применение интегральной теоремы Муавра-Лапласса состоит в том, что общая вероятность, которую мы обычно рассчитываем по формуле, нам известна, а необходимо найти либо ${{K}_{1}}$, либо ${{K}_{2}}$. Вот именно сейчас такую задачу мы и решим.

Самое обидное, что именно такие чаще всего и попадаются на всяких контрольных, зачетах и экзаменах. Они будут вам встречаться на исследованиях, где необходимо определить какую-нибудь статистическую величину. Поэтому именно сейчас мы попытаемся решить такую задачу.

Задача № 2

Театр, вмещающий 1000 человек, имеет два разных входа, каждым из которых любой зритель может воспользоваться с равной вероятностью. Около каждого входа имеется свой гардероб. Сколько мест должно быть в каждом гардеробе, чтобы с вероятностью в 0,99 любой зритель смог раздеться в том гардеробе, в который он обратился сразу после входа в театр.

Я думаю, очевидно, что в данной задаче общее количество испытаний, т.е. человек, которые придут в театр, не более 1000 — $n=1000$.

Всего входов два, при этом в каждый с одинаковой вероятностью входит один и тот же человек — $p=frac{1}{2}$.

Следовательно, $q=1-frac{1}{2}=frac{1}{2}$.

Кроме того, общая возможность того, что при 1000 испытаний количество успеха попадет в искомый нами диапазон, равно 0,99 — ${{P}_{1000}}left( {{K}_{1}};{{K}_{2}} right)=0,99$. Остается разобраться с числами ${{K}_{1}}$ и ${{K}_{2}}$, т.е. границами диапазона. ${{K}_{1}}$ — наименьшее количество людей, которые могут обратиться в данный гардероб. Очевидно, будет «ноль», потому что меньше нуля прийти не может — ${{K}_{1}}=0$. Остается вопрос: «Чему равно ${{K}_{2}}$?». Именно это нам и нужно найти по условию.

Опять запишем интегральную теорему Муавра-Лапласса:

[{{P}_{1000}}left( {{K}_{1}};{{K}_{2}} right)approx Fleft( frac{{{K}_{2}}-np}{sqrt{npq}} right)-Fleft( frac{{{K}_{1}}-np}{sqrt{npq}} right)]

Посмотрим:

[np=1000cdot frac{1}{2}=500]

[sqrt{npq}=sqrt{1000cdot frac{1}{2}cdot frac{1}{2}}=sqrt{250}=5sqrt{10}=15,8]

Подставим все полученные числа в формулу, с учетом того, что ${{K}_{1}}=0$:

[{{P}_{1000}}left( {{K}_{1}};{{K}_{2}} right)approx Fleft( frac{{{K}_{2}}-500}{15,8} right)-Fleft( frac{0-500}{15,8} right)=0,99]

Теперь внимательно посмотрим на эту формулу. Отдельно посчитаем значение функции Муавра-Лапласса в следующей точке:

[Fleft( frac{-500}{15,8} right)=-Fleft( 31,6 right)=0,5]

Итого переписывая, мы получаем:

[Fleft( frac{{{K}_{2}}-500}{15,8} right)+0,5=0,99]

[Fleft( frac{{{K}_{2}}-500}{15,8} right)=+0,49]

Единственный способ, при помощи которого можно решить этот пример — это взять таблицу значений функции Муавра-Лапласса и посмотреть, когда она равна $0,49$, при каком $x$. Проблема состоит в том, что точного значения мы не найдем. Однако есть значение функции Муавра-Лапласса в точках $2,32$ и $2,34$ :

[Fleft( 2,32 right)=0,48983]

[Fleft( 2,34 right)=0,49036]

Где-то между ними лежит наша искомая величина $0,49$. А между числами $2,32$ и $2,34$ лежит величина $2,33$. Так и запишем:

[frac{{{K}_{2}}-500}{15,8}=2,33]

Теперь нам осталось решить простейшее уравнение:

[{{K}_{2}}-500=2,33cdot 15,8]

[{{K}_{2}}-500=36,8]

[{{K}_{2}}approx 536,8=537]

Ответ: 537.

Каверзные вопросы

Подождите, есть несколько вопросов. Во-первых, почему мы так легко вынесли «минус» из функции Лапласса наружу, а во-вторых, почему мы постоянно пользуемся калькулятором?

Давайте для начала посмотрим на формулу функции Муавра-Лапласса:

[Fleft( x right)=frac{2}{sqrt{2text{ }!!pi!!text{ }}}{{intlimits_{0}^{x}{e}}^{-frac{{{t}^{2}}}{2}}}dt]

Это, прежде всего, интеграл от «нуля» до $x$ в прелах четной функции, поэтому если перед $x$ внезапно появится «минус», мы можем поменять местами верхние и нижнее пределы интегрирования, при том перед самим интегралом также появится знак «минус», и больше никаких изменений не будет. Это одно из ключевых свойств определенного интеграла.

Кроме того, в таблице значений все аргументы функций приведены именно в виде десятичных дробей, поэтому считая значение функции, мы просто обязаны перевести то, что стоит у нас внутри скобок, в десятичную дробь, в том числе с помощью калькулятора.

В заключение посмотрим еще одну задачку, в которой мы не только еще раз отработаем использование стандартной формулы, но и вспомним, что такое вторая версия теоремы Муавра-Лапласса, отличная от интегральной, и в каких ситуациях она применяется.

Задача № 3

Радиотелеграфная станция передает цифровой текст. В силу наличия помех каждая цифра независимо от других может быть неправильно принята с вероятностью 0,01. Найдите вероятность того, что в принятом тексте, содержащем 1100 цифр, будет:

а) 15 ошибок;

б) менее 20 ошибок.

Решение пункта б)

Что касается б), то тут все вполне очевидно — это чистейшая теорема Муавра-Лапласса, причем интегральная. Так и запишем:

[n=1100]

[p=0,01]

[q=0,99]

[{{K}_{1}}=0]

[{{K}_{2}}=19]

Теперь запишем интегральную формулу Муавра-Лапласса:

[{{P}_{n}}left( {{K}_{1}};{{K}_{2}} right)approx Fleft( frac{{{K}_{2}}-np}{sqrt{npq}} right)-Fleft( frac{{{K}_{1}}-np}{sqrt{npq}} right)]

Посчитаем:

[np=1100cdot 0,01=11]

[sqrt{npq}=sqrt{11cdot 0,99}=sqrt{frac{11cdot 11cdot 9}{100}}=sqrt{frac{{{11}^{2}}cdot {{3}^{2}}}{{{10}^{2}}}}=frac{11cdot 3}{10}=3,3]

Осталось подставить числа в формулу:

[{{P}_{1100}}left( 0;19 right)approx Fleft( frac{19-11}{3,3} right)-Fleft( frac{0-11}{3,3} right)=]

[=Fleft( 2,42 right)+Fleft( 3,33 right)=]

[=0,49224+0,49960=0,99184approx 0,99]

Ответ: 0,99

Решение пункта а)

А теперь давайте разберемся с пунктом а). В нем от нас требуется, чтобы при тех же исходных данных, вычислить, что в итоге появится ровно 15 ошибок.

Очевидно, что это идеальная задача для применения второй версии теоремы Муавра-Лапласса — не интегральной. Давайте я ее запишу:[]

[{{P}_{n}}left( K right)approx frac{1}{sqrt{npq}}cdot varphi left( frac{K-np}{sqrt{npq}} right)]

Выпишем известные данные:

[n=1100]

[p=0,01]

[q=0,99]

Решим:

[{{P}_{1100}}left( 15 right)approx frac{1}{3,3}cdot varphi left( frac{15-11}{3,3} right)approx 0,303cdot varphi left( 1,212 right)approx ]

[approx 0,303cdot 0,1919approx 0,058]

Ответ: 0,058.

Ключевые моменты

Вот и все, что я хотел вам рассказать об интегральной теореме Муавра-Лапласса, такой, на первый взгляд сложной, но очень простой на практике. Все, что вам необходимо — это

Знать сами формулы для обеих теорем Муавра-Лапласса, в том числе, интегральной.
Грамотно считать корни и элементы $np$, которые являются матожиданием.

В ближайшее время я размещу на своем сайте целый комплект задач, посвященный теоремам Муавра-Лапласса, в том числе, интегральной. Поэтому присоединяйтесь к нам на YouTube, ставьте лайки и пишите комментарии. До новых встреч!

Смотрите также:

Локальная теорема Муавра — Лапласа
Схема Бернулли. Примеры решения задач
Тест по теории вероятностей (1 вариант)
Задача 7 — геометрический смысл производной
Периодические десятичные дроби
Задача B5: площадь фигур с вершиной в начале координат

www.berdov.com

Источник

В статье подробно показано, что такое нормальный закон распределения случайной величины и как им пользоваться при решении практически задач.

Нормальное распределение в статистике

История закона насчитывает 300 лет. Первым открывателем стал Абрахам де Муавр, который придумал аппроксимацию биномиального распределения еще 1733 году. Через много лет Карл Фридрих Гаусс (1809 г.) и Пьер-Симон Лаплас (1812 г.) вывели математические функции.

Лаплас также обнаружил замечательную закономерность и сформулировал центральную предельную теорему (ЦПТ), согласно которой сумма большого количества малых и независимых величин имеет нормальное распределение.

Нормальный закон не является фиксированным уравнением зависимости одной переменной от другой. Фиксируется только характер этой зависимости. Конкретная форма распределения задается специальными параметрами. Например, у = аx + b – это уравнение прямой. Однако где конкретно она проходит и под каким наклоном, определяется параметрами а и b. Также и с нормальным распределением. Ясно, что это функция, которая описывает тенденцию высокой концентрации значений около центра, но ее точная форма задается специальными параметрами.

Кривая нормального распределения Гаусса имеет следующий вид.

График нормального распределения напоминает колокол, поэтому можно встретить название колоколообразная кривая. У графика имеется «горб» в середине и резкое снижение плотности по краям. В этом заключается суть нормального распределения. Вероятность того, что случайная величина окажется около центра гораздо выше, чем то, что она сильно отклонится от середины.

На рисунке выше изображены два участка под кривой Гаусса: синий и зеленый. Основания, т.е. интервалы, у обоих участков равны. Но заметно отличаются высоты. Синий участок удален от центра, и имеет существенно меньшую высоту, чем зеленый, который находится в самом центре распределения. Следовательно, отличаются и площади, то бишь вероятности попадания в обозначенные интервалы.

Формула нормального распределения (плотности) следующая.

Формула состоит из двух математических констант:

π – число пи 3,142;

е – основание натурального логарифма 2,718;

двух изменяемых параметров, которые задают форму конкретной кривой:

m – математическое ожидание (в различных источниках могут использоваться другие обозначения, например, µ или a);

σ² – дисперсия;

ну и сама переменная x, для которой высчитывается плотность вероятности.

Конкретная форма нормального распределения зависит от 2-х параметров: математического ожидания (m) и дисперсии (σ²). Кратко обозначается N(m, σ²) или N(m, σ). Параметр m (матожидание) определяет центр распределения, которому соответствует максимальная высота графика. Дисперсия σ² характеризует размах вариации, то есть «размазанность» данных.

Параметр математического ожидания смещает центр распределения вправо или влево, не влияя на саму форму кривой плотности.

А вот дисперсия определяет остроконечность кривой. Когда данные имеют малый разброс, то вся их масса концентрируется у центра. Если же у данных большой разброс, то они «размазываются» по широкому диапазону.

Плотность распределения не имеет прямого практического применения. Для расчета вероятностей нужно проинтегрировать функцию плотности.

Вероятность того, что случайная величина окажется меньше некоторого значения x, определяется функцией нормального распределения:

Используя математические свойства любого непрерывного распределения, несложно рассчитать и любые другие вероятности, так как

P(a ≤ X < b) = Ф(b) – Ф(a)

Стандартное нормальное распределение

Нормальное распределение зависит от параметров средней и дисперсии, из-за чего плохо видны его свойства. Хорошо бы иметь некоторый эталон распределения, не зависящий от масштаба данных. И он существует. Называется стандартным нормальным распределением. На самом деле это обычное нормальное нормальное распределение, только с параметрами математического ожидания 0, а дисперсией – 1, кратко записывается N(0, 1).

Любое нормальное распределение легко превращается в стандартное путем нормирования:

где z – новая переменная, которая используется вместо x;
m – математическое ожидание;
σ – стандартное отклонение.

Для выборочных данных берутся оценки:

Среднее арифметическое и дисперсия новой переменной z теперь также равны 0 и 1 соответственно. В этом легко убедиться с помощью элементарных алгебраических преобразований.

В литературе встречается название z-оценка. Это оно самое – нормированные данные. Z-оценку можно напрямую сравнивать с теоретическими вероятностями, т.к. ее масштаб совпадает с эталоном.

Посмотрим теперь, как выглядит плотность стандартного нормального распределения (для z-оценок). Напомню, что функция Гаусса имеет вид:

Подставим вместо (x-m)/σ букву z, а вместо σ – единицу, получим функцию плотности стандартного нормального распределения:

График плотности:

Центр, как и ожидалось, находится в точке 0. В этой же точке функция Гаусса достигает своего максимума, что соответствует принятию случайной величиной своего среднего значения (т.е. x-m=0). Плотность в этой точке равна 0,3989, что можно посчитать даже в уме, т.к. e⁰=1 и остается рассчитать только соотношение 1 на корень из 2 пи.

Таким образом, по графику хорошо видно, что значения, имеющие маленькие отклонения от средней, выпадают чаще других, а те, которые сильно отдалены от центра, встречаются значительно реже. Шкала оси абсцисс измеряется в стандартных отклонениях, что позволяет отвязаться от единиц измерения и получить универсальную структуру нормального распределения. Кривая Гаусса для нормированных данных отлично демонстрирует и другие свойства нормального распределения. Например, что оно является симметричным относительно оси ординат. В пределах ±1σ от средней арифметической сконцентрирована большая часть всех значений (прикидываем пока на глазок). В пределах ±2σ находятся большинство данных. В пределах ±3σ находятся почти все данные. Последнее свойство широко известно под названием правило трех сигм для нормального распределения.

Функция стандартного нормального распределения позволяет рассчитывать вероятности.

Понятное дело, вручную никто не считает. Все подсчитано и размещено в специальных таблицах, которые есть в конце любого учебника по статистике.

Таблица нормального распределения

Таблицы нормального распределения встречаются двух типов:

— таблица плотности;

— таблица функции (интеграла от плотности).

Таблица плотности используется редко. Тем не менее, посмотрим, как она выглядит. Допустим, нужно получить плотность для z = 1, т.е. плотность значения, отстоящего от матожидания на 1 сигму. Ниже показан кусок таблицы.

В зависимости от организации данных ищем нужное значение по названию столбца и строки. В нашем примере берем строку 1,0 и столбец 0, т.к. сотых долей нет. Искомое значение равно 0,2420 (0 перед 2420 опущен).

Функция Гаусса симметрична относительно оси ординат. Поэтому φ(z)= φ(-z), т.е. плотность для 1 тождественна плотности для -1, что отчетливо видно на рисунке.

Чтобы не тратить зря бумагу, таблицы печатают только для положительных значений.

На практике чаще используют значения функции стандартного нормального распределения, то есть вероятности для различных z.

В таких таблицах также содержатся только положительные значения. Поэтому для понимания и нахождения любых нужных вероятностей следует знать свойства стандартного нормального распределения.

Функция Ф(z) симметрична относительно своего значения 0,5 (а не оси ординат, как плотность). Отсюда справедливо равенство:

Это факт показан на картинке:

Значения функции Ф(-z) и Ф(z) делят график на 3 части. Причем верхняя и нижняя части равны (обозначены галочками). Для того, чтобы дополнить вероятность Ф(z) до 1, достаточно добавить недостающую величину Ф(-z). Получится равенство, указанное чуть выше.

Если нужно отыскать вероятность попадания в интервал (0; z), то есть вероятность отклонения от нуля в положительную сторону до некоторого количества стандартных отклонений, достаточно от значения функции стандартного нормального распределения отнять 0,5:

Для наглядности можно взглянуть на рисунок.

На кривой Гаусса, эта же ситуация выглядит как площадь от центра вправо до z.

Довольно часто аналитика интересует вероятность отклонения в обе стороны от нуля. А так как функция симметрична относительно центра, предыдущую формулу нужно умножить на 2:

Рисунок ниже.

Под кривой Гаусса это центральная часть, ограниченная выбранным значением –z слева и z справа.

Указанные свойства следует принять во внимание, т.к. табличные значения редко соответствуют интересующему интервалу.

Для облегчения задачи в учебниках обычно публикуют таблицы для функции вида:

Если нужна вероятность отклонения в обе стороны от нуля, то, как мы только что убедились, табличное значение для данной функции просто умножается на 2.

Теперь посмотрим на конкретные примеры. Ниже показана таблица стандартного нормального распределения. Найдем табличные значения для трех z: 1,64, 1,96 и 3.

Как понять смысл этих чисел? Начнем с z=1,64, для которого табличное значение составляет 0,4495. Проще всего пояснить смысл на рисунке.

То есть вероятность того, что стандартизованная нормально распределенная случайная величина попадет в интервал от 0 до 1,64, равна 0,4495. При решении задач обычно нужно рассчитать вероятность отклонения в обе стороны, поэтому умножим величину 0,4495 на 2 и получим примерно 0,9. Занимаемая площадь под кривой Гаусса показана ниже.

Таким образом, 90% всех нормально распределенных значений попадает в интервал ±1,64σ от средней арифметической. Я не случайно выбрал значение z=1,64, т.к. окрестность вокруг средней арифметической, занимающая 90% всей площади, иногда используется для проверки статистических гипотез и расчета доверительных интервалов. Если проверяемое значение не попадает в обозначенную область, то его наступление маловероятно (всего 10%).

Для проверки гипотез, однако, чаще используется интервал, накрывающий 95% всех значений. Половина вероятности от 0,95 – это 0,4750 (см. второе выделенное в таблице значение).

Для этой вероятности z=1,96. Т.е. в пределах почти ±2σ от средней находится 95% значений. Только 5% выпадают за эти пределы.

Еще одно интересное и часто используемое табличное значение соответствует z=3, оно равно по нашей таблице 0,4986. Умножим на 2 и получим 0,997. Значит, в рамках ±3σ от средней арифметической заключены почти все значения.

Так выглядит правило 3 сигм для нормального распределения на диаграмме.

С помощью статистических таблиц можно получить любую вероятность. Однако этот метод очень медленный, неудобный и сильно устарел. Сегодня все делается на компьютере. Далее переходим к практике расчетов в Excel.

В Excel есть несколько функций для подсчета вероятностей или обратных значений нормального распределения.

Функция НОРМ.СТ.РАСП

Функция НОРМ.СТ.РАСП предназначена для расчета плотности ϕ(z) или вероятности Φ(z) по нормированным данным (z).

=НОРМ.СТ.РАСП(z;интегральная)

z – значение стандартизованной переменной

интегральная – если 0, то рассчитывается плотность ϕ(z), если 1 – значение функции Ф(z), т.е. вероятность P(Z<z).

Рассчитаем плотность и значение функции для различных z: -3, -2, -1, 0, 1, 2, 3 (их укажем в ячейке А2).

Для расчета плотности потребуется формула =НОРМ.СТ.РАСП(A2;0). На диаграмме ниже – это красная точка.

Для расчета значения функции =НОРМ.СТ.РАСП(A2;1). На диаграмме – закрашенная площадь под нормальной кривой.

В реальности чаще приходится рассчитывать вероятность того, что случайная величина не выйдет за некоторые пределы от средней (в среднеквадратичных отклонениях, соответствующих переменной z), т.е. P(|Z|<z).

Определим, чему равна вероятность попадания случайной величины в пределы ±1z, ±2z и ±3z от нуля. Потребуется формула 2Ф(z)-1, в Excel =2*НОРМ.СТ.РАСП(A2;1)-1.

На диаграмме отлично видны основные основные свойства нормального распределения, включая правило трех сигм. Функция НОРМ.СТ.РАСП – это автоматическая таблица значений функции нормального распределения в Excel.

Может стоять и обратная задача: по имеющейся вероятности P(Z<z) найти стандартизованную величину z ,то есть квантиль стандартного нормального распределения.

Функция НОРМ.СТ.ОБР

НОРМ.СТ.ОБР рассчитывает обратное значение функции стандартного нормального распределения. Синтаксис состоит из одного параметра:

=НОРМ.СТ.ОБР(вероятность)

вероятность – это вероятность.

Данная формула используется так же часто, как и предыдущая, ведь по тем же таблицам искать приходится не только вероятности, но и квантили.

Например, при расчете доверительных интервалов задается доверительная вероятность, по которой нужно рассчитать величину z.

Учитывая то, что доверительный интервал состоит из верхней и нижней границы и то, что нормальное распределение симметрично относительно нуля, достаточно получить верхнюю границу (положительное отклонение). Нижняя граница берется с отрицательным знаком. Обозначим доверительную вероятность как γ (гамма), тогда верхняя граница доверительного интервала рассчитывается по следующей формуле.

Рассчитаем в Excel значения z (что соответствует отклонению от средней в сигмах) для нескольких вероятностей, включая те, которые наизусть знает любой статистик: 90%, 95% и 99%. В ячейке B2 укажем формулу: =НОРМ.СТ.ОБР((1+A2)/2). Меняя значение переменной (вероятности в ячейке А2) получим различные границы интервалов.

Доверительный интервал для 95% равен 1,96, то есть почти 2 среднеквадратичных отклонения. Отсюда легко даже в уме оценить возможный разброс нормальной случайной величины. В общем, доверительным вероятностям 90%, 95% и 99% соответствуют доверительные интервалы ±1,64, ±1,96 и ±2,58 σ.

В целом функции НОРМ.СТ.РАСП и НОРМ.СТ.ОБР позволяют произвести любой расчет, связанный с нормальным распределением. Но, чтобы облегчить и уменьшить количество действий, в Excel есть несколько других функций. Например, для расчета доверительных интервалов средней можно использовать ДОВЕРИТ.НОРМ. Для проверки статистической гипотезы о средней арифметической есть формула Z.ТЕСТ.

Рассмотрим еще пару полезных формул с примерами.

Функция НОРМ.РАСП

Функция НОРМ.РАСП отличается от НОРМ.СТ.РАСП лишь тем, что ее используют для обработки данных любого масштаба, а не только нормированных. Параметры нормального распределения указываются в синтаксисе.

=НОРМ.РАСП(x;среднее;стандартное_откл;интегральная)

x – значение (или ссылка на ячейку), для которого рассчитывается плотность или значение функции нормального распределения

среднее – математическое ожидание, используемое в качестве первого параметра модели нормального распределения

стандартное_откл – среднеквадратичное отклонение – второй параметр модели

интегральная – если 0, то рассчитывается плотность, если 1 – то значение функции, т.е. P(X<x).

Например, плотность для значения 15, которое извлекли из нормальной выборки с матожиданием 10, стандартным отклонением 3, рассчитывается так:

Если последний параметр поставить 1, то получим вероятность того, что нормальная случайная величина окажется меньше 15 при заданных параметрах распределения. Таким образом, вероятности можно рассчитывать напрямую по исходным данным.

Функция НОРМ.ОБР

Это квантиль нормального распределения, т.е. значение обратной функции. Синтаксис следующий.

=НОРМ.ОБР(вероятность;среднее;стандартное_откл)

вероятность – вероятность

среднее – матожидание

стандартное_откл – среднеквадратичное отклонение

Назначение то же, что и у НОРМ.СТ.ОБР, только функция работает с данными любого масштаба.

Пример показан в ролике в конце статьи.

Моделирование нормального распределения

Для некоторых задач требуется генерация нормальных случайных чисел. Готовой функции для этого нет. Однако В Excel есть две функции, которые возвращают случайные числа: СЛУЧМЕЖДУ и СЛЧИС. Первая выдает случайные равномерно распределенные целые числа в указанных пределах. Вторая функция генерирует равномерно распределенные случайные числа между 0 и 1. Чтобы сделать искусственную выборку с любым заданным распределением, нужна функция СЛЧИС.

Допустим, для проведения эксперимента необходимо получить выборку из нормально распределенной генеральной совокупности с матожиданием 10 и стандартным отклонением 3. Для одного случайного значения напишем формулу в Excel.

=НОРМ.ОБР(СЛЧИС();10;3)

Протянем ее на необходимое количество ячеек и нормальная выборка готова.

Для моделирования стандартизованных данных следует воспользоваться НОРМ.СТ.ОБР.

Процесс преобразования равномерных чисел в нормальные можно показать на следующей диаграмме. От равномерных вероятностей, которые генерируются формулой СЛЧИС, проведены горизонтальные линии до графика функции нормального распределения. Затем от точек пересечения вероятностей с графиком опущены проекции на горизонтальную ось.

На выходе получаются значения с характерной концентрацией около центра. Вот так обратный прогон через функцию нормального распределения превращает равномерные числа в нормальные. Excel позволяет за несколько секунд воспроизвести любое количество выборок любого размера.

Как обычно, прилагаю ролик, где все вышеописанное показывается в действии.

Скачать файл с примером.

Поделиться в социальных сетях:

Источник