В этой статье мы сформируем на основе всех рисков, о которых речь шла в предыдущей статье (и добавив несколько новых), таблицу рисков (рис. 1). Данная таблица представляет собой шаблон, на основе которого вы можете приступить к распознаванию рисков вашего проекта. Эту таблицу можно модифицировать в соответствии с особенностями вашей отрасли и организации. Такой подход существенно повысит эффективность процесса выявления рисков в будущих проектах.
Рис. 1. Пример таблицы рисков
В приведенной на рисунке таблице указывается тип, характеристика (или влияние на проект) и категория каждого риска, а также лица, ответственные за снижение риска (или его полное устранение).
Риски разделяются на определенные категории, с которыми следует определиться еще до того, как вы приступите к процессу выявления рисков. Выполнив процесс первоначального обнаружения рисков, вы сможете при необходимости внести изменения в эти категории или добавить одну-две новые. Как правило, легче группировать риски по категориям по мере их выявления, чем возвращаться к такому группированию впоследствии. В конце проекта, анализируя свои успехи и неудачи, вы наверняка придете к выводу, что какие-то категории риска оказали большее влияние на проект, чем другие, или что вашей команде гораздо хуже удавалось выявлять внешние риски, чем связанные с управлением проектом. При анализе рисков учитывайте требования законодательства, так гражданское право регулирует взаимоотношения между юридическими лицами. Такой анализ поможет вам при выполнении дальнейших проектов, особенно, если вы сгруппируете риски по следующим категориям:
- связанные с управлением проектом;
- связанные с решением кадровых вопросов;
- финансовые;
- организационные;
- внешние;
- внутренние;
- связанные с масштабом проекта;
- связанные с календарным планом проекта;
- связанные с бюджетом проекта;
- технические;
- связанные с вопросами качества.
Следующим этапом является документирование рисков. Такое документирование лучше всего выполнять в виде двухшагового процесса. То есть сначала осуществляется процесс идентификации рисков (вместе с вашей командой), фиксируются все риски в электронной таблице и распределяются но категориям. На следующем шаге выполняется оценка рисков и анализируется их возможное влияние на проект. Эту информацию также следует зафиксировать в так называемом реестре рисков, о чем мы подробно поговорим в одной из следующих статей.
ППП
EXCEL
предлагает широкий набор средств
автоматизации статистического
моделирования данных от вычисления
параметров описательной статистики до
построения сложных прогнозных моделей.
Для этих целей в нем реализована
специальная группа статистических и
математических функций, большинство
из которых содержится в дополнении
Пакет анализа.
Список и форматы некоторых функций,
использованных в процессе анализа
рисков, приведены в табл. 1.1.
-
Таблица 1.1.
Наименование функции
Формат функции
СРЗНАЧ
СРЗНАЧ(блок
ячеек)ДИСПР
ДИСПР(блок
ячеек)СКОС
СКОС(блок
ячеек)СТАНДОТКЛОНП
СТАНДОТКЛОНП(блок
ячеек)НОЕМОБР
НОРМОБР(вероятность;
средн_энач; станд отклон)НОРМРАСП
НОРМРАСП
(х; средн знач ; станд откл; интегральная)
4.3. Анализ рисков финансовых операций
Рассмотрим
типовые задачи, которые можно решать с
использованием стандартных функций
ППП EXCEL.
Определение
основных характеристик распределения
случайной величины (СВ). Возможны
два варианта расчетов: случай, когда
вероятность осуществления случайного
события не задана и , наоборот, вероятность
осуществления случайного события задана
явно.
Определение
характеристик СВ при незаданной
вероятности осуществления событий.
В этом случае полагаем вероятность
осуществления всех событий одинаковой,
т.е. p1
= p2
=…= pn=
1/n
и можем непосредственно применить
статистические функций ППП EXCEL,
вычисляющие основные характеристики
распределения СВ (среднее значение
М(Е), дисперсию VAR(E),
стандартное отклонение (Е)).
Продемонстрируем технику их расчетов
с применением встроенных функций ППП
EXCEL.
Подготовьте исходную таблицу (рис. 1.1. ) с данными следующего примера.
Пример
1.1. Рассмотрим
возможность покупки акции недавно
образованной фирмы «Н». Предполагается,
что прогнозируется доходность по акциям
этой фирмы через год будет зависеть от
состояния спроса на ее продукцию в
течение данного периода и соответственно
равна: 12% — в случае повышенного спроса;
9% — при обычном спросе; 6% — при пониженном
спросе.
|
А |
В |
С |
|
|
1 |
Анализ |
||
|
2 |
|||
|
3 |
Прогноз |
Доходность |
|
|
4 |
Пессимистический |
6% |
|
|
5 |
Вероятный |
9% |
|
|
6 |
Оптимистический |
12% |
|
|
7 |
|||
|
8 |
Ожидаемая |
||
|
9 |
Дисперсия |
||
|
10 |
Стандартное |
||
|
11 |
Коэффициент |
Рис.
1.1. Исходная таблица для решения примера
1.1.
Осуществим
анализ риска этой операции. Прежде всего
определим среднюю доходность по акциям
фирмы «Н». Поскольку наступление
любого события в данном примере считается
равновероятным, для расчета искомой
величины можно воспользоваться функцией
СРЗНАЧ (),
указав ей в качестве аргументов блок
ячеек В4,
В6,
содержащий предполагаемые значения
доходности. Введите в ячейку В8
формулу: =СРЗНАЧ
(В4: В6) (Результат
0,09, или 9%).
Для
вычисления дисперсии и стандартного
отклонения в ячейках В9
и В10
необходимо задать следующие формулы:
=ДИСПР(В4:В6) (Результат
0,0006)
=СТАНДОТКЛОНП
(В4: В6) (Результат
0,0245, или 2,45%)
Теперь
можно легко определить значение
коэффициента вариации из соотношения
(11). Для этого
в ячейке В11
вычислим результат отношения стандартного
отклонения (В10)
к величине среднего значения (В8):
=В10/В8 (Результат
0,27)
Полученные
значения параметров позволяют сделать
вывод о невысоком риске акций фирмы
«Н».
Определение
характеристик СВ при заданной вероятности
осуществления событий.
Рассчитаем
вероятность того, что доходность по
акциям «Н» будет меньше величины
а—
(9 — 2,45 = 6,55). При этом будем исходить из
предположения, что величина доходности
r
распределена по нормальному закону
Тогда из (10)
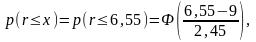
где
Ф — функция Лапласа.
Для
автоматизации расчетов, связанных с
нормальным распределением вероятностей,
в ППП EXCEL
реализован ряд специальных функций. Мы
будем использовать две функции —
НОРМРАСП()
и НОРМОБР().
Функция
НОРМРАСП (х; средн_знач; станд_откл;
интегральная)
Функция
НОРМРАСП ()
имеет следующие параметры:
х
— исследуемое значение случайной
величины,
средн_знач
— среднее значение;
станд_откл
— стандартное отклонение;
интегральная
— 0 или 1.
В
зависимости от заданного параметра
интегральная
— О (ложь) или 1 (истина) — она возвращает
плотность распределения (х)
или значение кумулятивной функции
распределения вероятностей F(x)
для нормальной случайной величины.
Определим
искомую вероятность р
(r
<. 6,55) Для
этого в ячейку В14
введем формулу:
=НОРМРАСП(6,55;
9; 2,45; 1)
(Результат 0,1586), или
=НОРМРАСП(В8-В10;
В8; В10; 1)
(Результат 0,1586)
Таким
образом, эта вероятность приблизительно
равна 16%. Соответственно вероятность
Р(r
> 6,55) будет
равна:
=1
— НОPМРАСП(В8-В10;
В8; В10; 1)
(Результат 0,8414)
На
рис. 1.2. приведен фрагмент ЭТ с расчетами
вероятностей для различных значений
ставки доходности r.
Выполнить эти расчеты самостоятельно.
Построить
графики плотности и кумулятивной функции
распределения вероятностей для примера
1.1. Для построения графиков необходимо
предварительно выполнить табуляцию
функций (х)
на интервале [а ± 3]
и F(x).
Для определения значений (х)
также используется функция НОРМРАСП
(), однако
значение параметра интегральная
при этом задается равным 0 (ложь).
|
А |
В |
С |
|
|
1 |
Анализ |
||
|
2 |
|||
|
3 |
Прогноз |
Доходность |
|
|
4 |
Пессимистический |
6% |
|
|
5 |
Вероятный |
9% |
|
|
6 |
Оптимистический |
12% |
|
|
7 |
|||
|
8 |
Ожидаемая |
9,00% |
|
|
9 |
Дисперсия |
0,0006 |
|
|
10 |
Стандартное |
2,45% |
|
|
11 |
Коэффициент |
0,27 |
|
|
12 |
|||
|
13 |
P |
0,1587 |
|
|
14 |
P |
0,8413 |
|
|
15 |
P |
0,0001 |
|
|
16 |
|||
|
17 |
рис.
1.2. Анализ риска (пример 1.1)
По
графикам убедиться, функция распределения
F(x)
возрастает на интервале от 0 до 1. Согласно
правилу сложения вероятностей при x1<x2
вероятность попадания значения случайной
величины Е
в интервал (x1;
x2)
равна
приращению функции распределения
вероятностей:
p(x1
E
< x2)=F(x2)
– F(x1)
Определим
вероятность попадания r
в интервал (а + ):
=НОРМРАСП(В8+В10;
В8; В10;1) — НОЕМРАСП(В8; В8; В10;1)
(Результат:
0,3414)
Соответственно
вероятность попадания r
в интервал (а ± )
будет равна:
=НОЕМРАСП(В8+В10;В8;В10;1)
— НОБМРАСП(В8-В10; В8; В10;1)
(Результат:
0,6828)
Вероятность
попадания г в интервал (а ± 2)
и (а ± З)
определите самостоятельно.
Полученные
результаты служат числовой иллюстрацией
правила трех сигм для нормального закона
распределения.
Функция
НОРМОБР (вероятность; средн_энач;
станд__откл)
Функция
имеет следующие параметры:
вероятность
—вероятность нормального распределения;
средн_знач
—среднее значение;
станд_откл
—стандартное отклонение.
Она
возвращает обратное нормальное
распределение для указанного среднего
и стандартного отклонения. Другими
словами, она позволяет по заданной
вероятности определить величину
исследуемой переменной (в нашем примере
доходности).
Определим
предельную величину доходности для
вероятности 84%:
=НОРМОБР
(0,84 ;В8 ;В10) (Результат:
11,45%).
Таким
образом, для заданной вероятности
величина доходности составит не более
11,45%: р(х 0,1145)
= 0,84.
Функции
ППП EXCEL,
определяющие значения параметров
распределения М(Е),
VAR(E)
и (Е),
следует применять только в тех случаях,
когда
вероятности событий равны.
Если же распределение вероятностей
задано (например, известно из предыдущего
опыта или получено методом экспертных
оценок), среднее значение, дисперсия и
стандартное отклонение рассчитываются
путем непосредственной реализации
средствами ППП EXCEL
соответствующих соотношений — (4),
(6), (7). Продемонстрируем
один из вариантов подобной реализации
на решении примера 1.2.
Пример
1.2.
Рассматривается возможность приобретения
акций двух фирм «А» и «В». Полученные
экспертные оценки предполагаемых
значений доходности по акциям и их
вероятности представлены в таблице
1.2.
Таблица
1.2.
|
Прогноз |
Вероятность |
Доходность, |
|
|
Фирма |
Фирма |
||
|
Пессимистический |
0,3 |
-70 |
10 |
|
Вероятный |
0,4 |
15 |
15 |
|
Оптимистический |
0,3 |
100 |
20 |
Подготовьте
исходную таблицу с данными примера, как
показано на рис. 1.3.
|
А |
В |
С |
D |
|
|
1 |
Анализ |
Взвешенные |
||
|
2 |
||||
|
3 |
Прогноз |
Вероятность |
Доходность |
|
|
5 |
Пессимистический |
0,30 |
-70,00% |
|
|
6 |
Вероятный |
0,40 |
15,00% |
|
|
7 |
Оптимистический |
0,30 |
100,00% |
|
|
8 |
||||
|
9 |
Ожидаемая |
|||
|
10 |
Стандартное |
|||
|
11 |
Коэффициент |
|||
|
12 |
||||
|
14 |
Интервал
(r1; |
Вероятность |
||
|
15 |
r1 |
r2 |
Рис.
1.3. Исходная таблица для решения примера
1.2.
Прежде
всего необходимо определить среднюю
величину доходности (соотношение (4)).
Наиболее простой способ — последовательно
перемножить каждую ячейку блока В5.
В7
на соответствующую ей ячейку блока С5.
С7 и суммировать
полученные значения. Нетрудно заметить,
что данная последовательность действий
представляет собой операцию нахождения
суммы произведений элементов двух
матриц. Поскольку матричные операции
достаточно часто встречаются в прикладном
анализе, для автоматизации их выполнения
в ППП EXCEL
реализована специальная группа
математических
функции..
В
частности, для выполнения необходимой
нам операции удобно использовать функцию
СУММПРОИЗВ (). Как следует из табл. 1.3.,
аргументами функции являются матрицы
одинакового размера. Введем в ячейку и
формулу:
=СУММПРОИЗВ
(В5: В7; С5: С7) (Результат:
0,15, или 15%)
Для
определения величины стандартного
отклонения необходимо сперва вычислить
дисперсию. Из (6) следует, что дисперсия
случайной величины представляет собой
сумму квадратов отклонений от среднего,
взвешенных на соответствующие вероятности.
Зададим в ячейке D5
формулу вычисления дисперсии для первого
события:
=В5*
(С5-$В$9) 2 (Результат:
0,2165).
Обратите
внимание на то, что для задания ячейки,
содержащей среднее значение (В9),
используется способ абсолютной адресации.
Это позволяет безболезненно скопировать
данную формулу в ячейки D6,D7
(в противном случае адрес ячейки,
содержащей среднее значение, был бы
настроен неправильно). Теперь можно
вычислить величину стандартного
отклонения, которая равна квадратному
корню из дисперсии (суммы ячеек D5:D7).
Для этого воспользуемся функцией КОРЕНЬ
() (см. табл. 1.3.). Введите в ячейку В10:
=КОРЕНЬ(СУММ(D5:D7)) (Результат:
0,6584, или 65,84%).
Вычисление
коэффициента вариации не представляет
особых трудностей. Для этого достаточно
просто разделить значение ячейки В10 на
значение В9. Введите в ячейку В11:
=В10/В9 (Результат:
4,39).
Вычислив
основные параметры распределения
случайной величины, можно определить
вероятность ее попадания в некоторый
интервал. В приведенной на рис. 1.4. таблице
границы первого интервала задаются в
ячейках В16
и С 16.
Определим вероятность того, что значение
доходности попадет в интервал (-70; 0).
Введите границы анализируемого интервала
в ячейки В16
и С16.
Формула вычисления вероятности в ячейке
D16
реализована с использованием уже
известной нам функцией НОРМРАСП
() и имеет
следующий вид:
=НОРМРАСП
(С16;$В$9;$В$10;1)-НОРМРАСП (В16;$В$9;$В$10;1)
(Результат:
0,31).
Снова
обращаем внимание на использование
абсолютной адресации при задании в
формулах ячеек, содержащих среднее
значение и стандартное отклонение.
|
А |
В |
С |
D |
|
|
1 |
Анализ |
|||
|
3 |
Прогноз |
Вероятность |
Доходность |
Взвешенные квадраты отклонений |
|
4 |
||||
|
5 |
Пессимистический |
0,30 |
-70,00% |
0,21675 |
|
6 |
Вероятный |
0,40 |
15,00% |
0 |
|
7 |
Оптимистический |
0,30 |
100,00% |
0,21675 |
|
9 |
Ожидаемая |
15,00% |
||
|
10 |
Стандартное |
65,84% |
||
|
11 |
Коэффициент |
4,39 |
||
|
14 |
Интервал
(r1; |
Вероятность (r1<=R<=r2) |
||
|
15 |
r1 |
r2 |
||
|
16 |
-70% |
0% |
0,31 |
|
|
17 |
15% |
65% |
0,28 |
|
|
18 |
15% |
100% |
0,4 |
|
|
19 |
-70% |
100% |
0,8 |
Рис.
1.4. Итоговая таблица анализа рисков
(фирма «А»).
Для
дальнейшего анализа достаточно указать
интересующие интервалы и скопировать
формулу в ячейке
D16
необходимое число раз. На рис 1.4. приведена
итоговая таблица, содержащая некоторые
результаты анализа риска по акциям
фирмы «А» (пример 2.) Аналогичная
таблица на рис 1.5. содержит результаты
анализа риска по акциям фирмы «В».
В
качестве упражнения попробуйте
разработать таблицу анализа рисков для
фирмы «В» самостоятельно, используя
рис 1.3. в качестве образца. Сравните
полученные результаты.
|
А |
В |
С |
D |
|
|
1 |
Анализ |
|||
|
2 |
||||
|
3 |
Прогноз |
Вероятность |
Доходность |
Взвешенные квадраты отклонений |
|
4 |
||||
|
5 |
Пессимистический |
0,3 |
10% |
0,00075 |
|
6 |
Вероятный |
0,4 |
15% |
0 |
|
7 |
Оптимистический |
0,3 |
20% |
0,00075 |
|
8 |
||||
|
9 |
Ожидаемая |
15,00% |
||
|
10 |
Стандартное |
3,87% |
||
|
11 |
Коэффициент |
0,26 |
||
|
12 |
||||
|
13 |
||||
|
14 |
Интервал (r1; r2) |
Вероятность (r1<=R<=r2) |
||
|
15 |
r1 |
r2 |
||
|
16 |
0% |
20% |
0,9 |
|
|
17 |
15% |
20% |
0,4 |
|
|
18 |
10% |
20% |
0,8 |
|
|
19 |
-10% |
0% |
0 |
Рис.
1.5. Итоговая таблица анализа рисков
(фирма «В»).
Пример
1.3.
Прогнозируемые
доходности по акциям фирм «К» и «Р»
имеют следующие распределения вероятностей
(табл.1.5)
Таблица
1.5.
|
Вероятность |
Доходность |
|
|
Акции |
Акции |
|
|
0,15 |
-15% |
—25% |
|
0,20 |
0% |
10% |
|
0,40 |
15% |
20% |
|
0,20 |
20% |
30% |
|
0,05 |
35% |
45% |
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Опубликовано 15.05.2022 Обновлено 14.08.2022
Приветствую, друзья! В этой заметке вас ждут бесплатные Excel-программы для автоматического заполнения карты профессионального риска от наших коллег, которые любезно поделились своими наработками с подписчиками Блог—Инженера. Лучи добра и вопросы вы всегда можете послать в комментариях. Также приведём полезные ссылки касательно оценки профессиональных рисков.
Обновление от 15.05.2022 – Добавлены разработки (программы) для оценки и управления профессиональными рисками от Сергея Кубинова и Линара Муллахметова + Положение об управлении профессиональными рисками.
Содержание
- Программа по ОПР от Андрея Шакаева
- Программа по ОПР от Анатолия Юдина
- Программа по ОПР и Положение об управлении профессиональными рисками от Сергея Кубинова
- Программа по ОПР от Линара Муллахметова
- Программа по ОПР от Максима Жаренкова
- Дополнительная информация и материалы по оценке профессиональных рисков
Программа по ОПР от Андрея Шакаева
Программу я делал под себя.
Формулу в карте можно конечно усовершенствовать, но мне уже неохота, так как это вопрос мы для себя закрыли.
Краткая инструкция:
Открываете лист Карта – выделяете ячейку в столбце “Выявленные потенциальные…” – нажимаете кнопку на клавиатуре “=” – переходите в лист Реестр, выбираете (выделяете ячейку с опасностью) – нажимаете Еnter.
Всё просто, осталось скачать саму программку.
Скачать > Excel-программа для автоматического заполнения карты профессионального риска (1)
Программа по ОПР от Анатолия Юдина
Оценка профессиональных рисков и создание “Карт идентификации опасностей и оценки профессиональных рисков” производится в программе “MS Excel” на основе простого организационно-технологического решения.
Программа в “MS Excel” была применена при создание “Карт идентификации опасностей и оценки профессиональных рисков” в СПб ГУП “Петербургский спортивно-концертный комплекс” в 2019 г.
Для теоретической иллюстрации и понимания процессов при создании Карт и оценки профессиональных рисков приложена презентация к Системе управления профессиональными рисками (СУПР) из ИС Специалиста по охране труда v. 10.1, созданной в “MS Access”.
В ZIP-архиве:
Excel-программ для автоматического заполнения карты профессионального риска
Инструкция по работе с Excel-программой
Презентация “Система управления профессиональными рисками”
Положение о системе управления профессиональными рисками (пример)
Скачать > Excel-программа для автоматического заполнения карты профессионального риска (2)
Программа по ОПР и Положение об управлении профессиональными рисками от Сергея Кубинова
Предлагаю для помощи в создании карт риска программу по их созданию на основе методики 5х5.
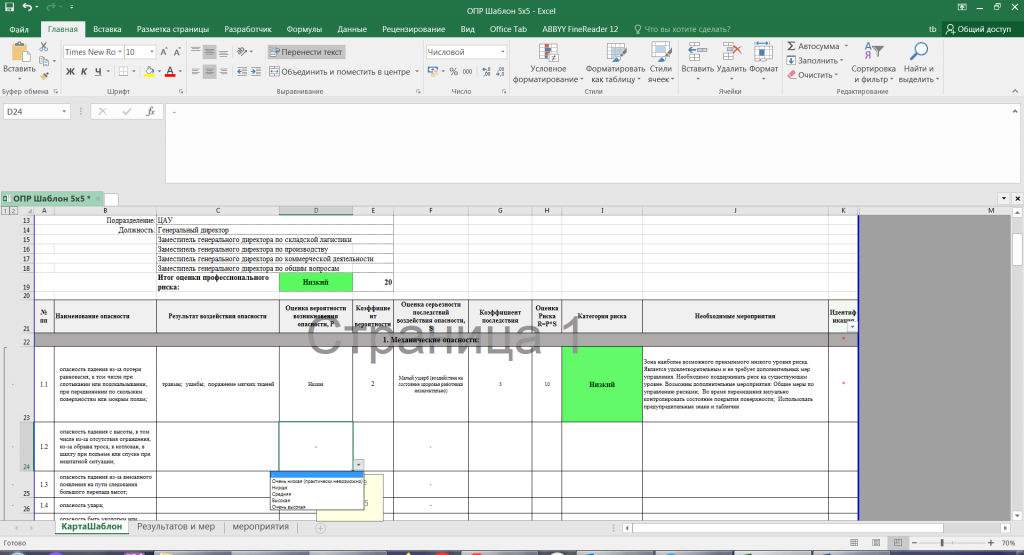
Для работы в данной программе необходимо только выбрать два значения из выпадающего списка это в столбике Оценка вероятности возникновения опасности, Р и Оценка серьезности последствий воздействия опасности, S после чего можно получить быстрый результат
Все остальные действия подтянутся автоматически.
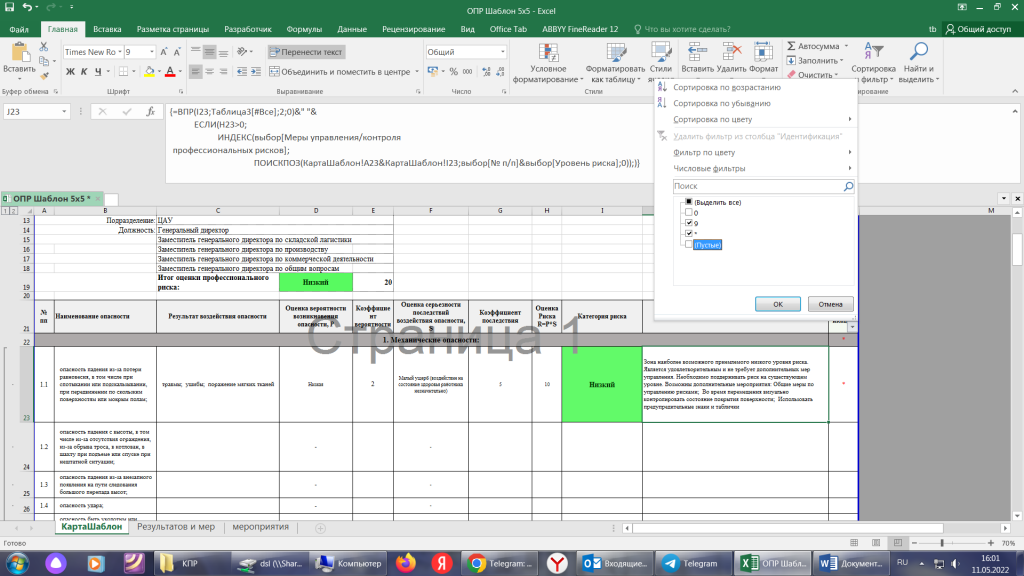
Чтобы убрать все ненужные пустые строчки, надо на столбике Идентификация убрать 2 галочки над значениями «0» и «Пустые» как показано на скриншоте 3
Остальные возможности программы как добавить мероприятия или изменить результат воздействия опасности опишу позднее.
Скачать > Excel-программа для автоматического заполнения карты профессионального риска (3)
Скачать > Положение об управлении профессиональными рисками (3)
Программа по ОПР от Линара Муллахметова
Решил поделится своей наработкой с целью упрощения составления карт идентификации, оценки и управления рисками. Форма конечно подойдёт не всем, т.к. сделана под мою организацию, но как пример или шаблон думаю можно использовать.
Как мы все знаем, руководители структурных подразделений обычно заняты и чтобы упростить задачу составления карт и хоть как-то вовлечь их в процесс оценки рисков, я разработал реестр основных операционных рисков, который и лёг в основу составления карт. Для работы с файлами у вас должны быть включены макросы, как это сделать, написано в интернете.
При запуске файла откроется вкладка “Реестр ОПР”, для очистки галочек ниже первого столбца нажмите на ячейку “Клац”, теперь выберите этап выполнения работ и щелкните один раз в первом столбце, при этом появится галочка и все значения, которые находятся правее галочки перенесутся во вкладку “Карта ОПР”. Далее можно просто скопировать значения в файл WORD или воспользоваться моим шаблоном – для этого во вкладке “Карта ОПР” нажмите на кнопку “Сформировать Карту” (при этом шаблон карты должен быть в одной папке с файлом), вуаля – карта готова, сохраните её.
Готов к любой критике или советам 🙂
Скачать > Excel-программа для автоматического заполнения карты профессионального риска (4)
Программа по ОПР от Максима Жаренкова
Так получилось, что программу опубликовали в отдельной заметке.
Скачать > Excel-программа для автоматического заполнения карты профессионального риска (5)
Дополнительная информация и материалы по оценке профессиональных рисков
- Кто не знает, вот здесь у нас народная копилка – Карты оценки рисков по профессиям и видам работ. Народные примеры и образцы
- Вот здесь можно заказать Оценку и управление профессиональными рисками:
01. Оценка профессиональных рисков “под заказ”
02. Практический курс “Оценка профессиональных рисков для работодателей”
03. Сервис РискПроф для экспертных компаний
04. Практический курс “Оценка профессиональных рисков для экспертных компаний” - Наш партнёр ФИНДИАС в рамках подписки PRO+ предлагает скидку 50% на сопровождение цифровой программы для ведения охраны труда в организациях (ФИ-ОТ), в которой есть модуль для расчёта профессиональных рисков.
На этом всё.
Продолжение следует …
Управление рисками проекта

Категория: РИСК МЕНЕДЖМЕНТ УПРАВЛЕНИЕ ПРОЕКТАМИ
Опубликовал:
10.01.2019
К списку статей
Каждый проект содержит риски. Риск — это сочетание вероятности и последствий наступления неблагоприятных событий. Если можно предположить, что в ходе проекта может (или не может) произойти что‑то негативное, то разумно управлять рисками. По мере развития проекта влияние рисков усиливается, поскольку ресурсы уже вложены, и, если прозевали какой-то риск, то его последствия могут вылиться в кругленькую сумму.
Перед началом проекта надлежит обязательно учесть все (максимально возможные) риски, чтобы потом не было мучительно больно за …
Направления, способы обнаружения рисков:
- Изучение документации по проекту (договор, техническое задание, функциональные требования и т.п.);
- Исследование бизнес- и технологических процессов;
- Анализ предположений, ограничений и допущений проекта;
- Интервьюирование / опросники ключевых участников проекта, их экспертные оценки;
- SWOT-анализ.
После того, как выявлены риски проекта, следует выделить наиболее важные, которые требуют первоочередного внимания и разрешения. Надобно подсчитать итоговые значения рисков, отсортировать их по данному параметру в порядке убывания. Образовавшийся порядковый номер — это ранг риска: 1 – самый тяжкий риск, 2 – серьезный и т. д. Риски с однаковым рангом не всегда равносильны: это могут быть риски с высокой вероятностью и низкой угрозой и наоборот.
Когда риски выявлены и оценены, необходимо решить, как реагировать на них, прежде всего на наиболее опасные.
Вашему вниманию предлагается Excel-шаблон (см. прикрепленный файл ниже) — инструмент классификации рисков посредством их идентификации, оценки влияния, вероятности, ранжирования последствий:
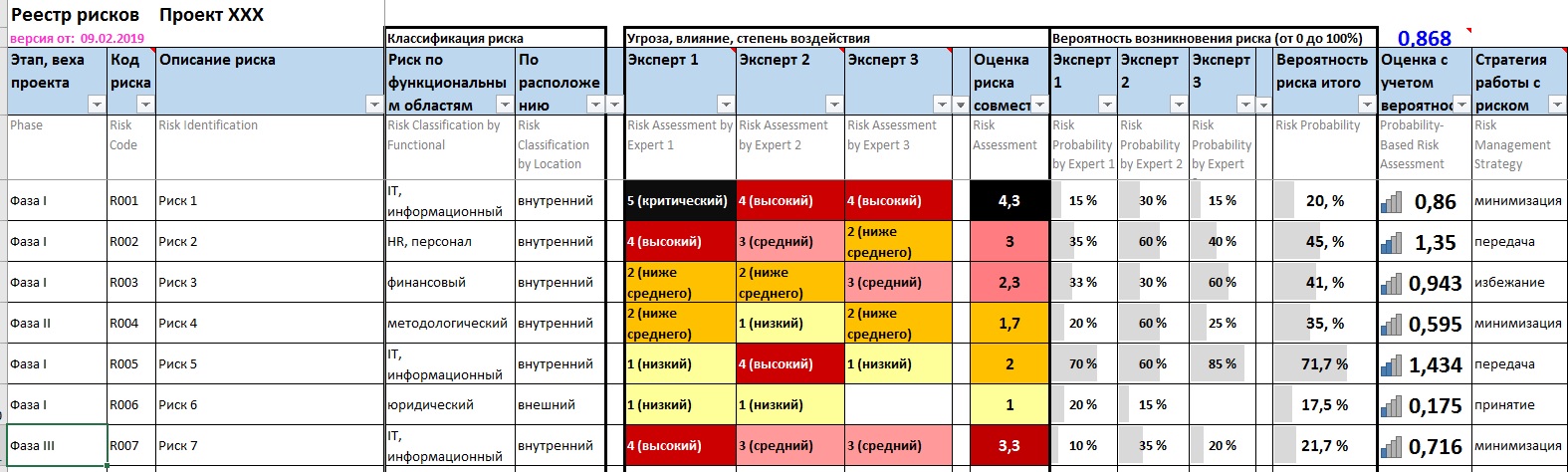
- В целях упрощения обсуждений каждому описываемому риску присваиваем уникальный код и соотносим к этапу проекта;
- Важно выявить и различать основные причины возникновения риска. У одного риска может быть несколько причин, а одна причина может являться источником нескольких рисков;
- Не менее важно заранее охарактеризовать признаки приближения риска, чтобы успеть заметить наступление риска и принять превентивные меры;
- Хорошо бы классифицировать риски как внутренние / внешние и по функциональным областям;
- Во избежание давления, взаимного влияния друг на друга ключевых участников проекта экспертные оценки по 5-ти бальной шкале степени воздействия (угрозы) рисков должны осуществляться тайным, обезличенным голосованием. Желательно учесть мнения не менее трёх специалистов, средняя совместная оценка угрозы каждого риска расчитается автоматически;
- Аналогичным способом каждый эксперт должен проставить вероятность возникновения риска (> 0 и < 100%), итоговая вероятность расчитается автоматически. Следует избегать значения 50%, которое означает, что над данным риском не думали либо старались соблюсти политес;
- Итоговая оценка по каждому риску автоматически рассчитывается как произведение совместной оценки угрозы риска и вероятности. Эти оценки ранжируем в порядке убывания и определяем самые важные риски;
- Изначально надо предотвратить такие риски, но если они все же случились, необходимо правильно реагировать на них. Нужно разработать стратегию работы с каждым риском проекта (Принятие, Избежание, Минимизация, Передача — частный случай минимизации) и выработать мероприятия по снижению риска;
- Следует зафиксировать срок реагирования по каждому риску. Некоторые риски могут требовать безотлагательной реакции, а иные терпят несколько дней;
- Необходимо определить владельца каждого риска — лицо или организационную единицу, которые имеют полномочия и несут ответственность за управление риском.
Оценивать риски нужно как перед стартом проекта, так и пересматривать их с некоторой разумной периодичностью в течение проекта, чтобы отслеживать динамику рисков и корректировать упредительные мероприятия.
dvbi.ru
2019-01-10 00:21:00Z
Последнее изменение: 2021-12-12 23:01:58Z
Возрастная аудитория: 14-70
Комментариев: 0
Теги: Примеры Управление
Связанные статьи:
Пожалуйста, проголосуйте и ниже поставьте лайк:
Следующая статья:
Обеспечение качества данных и информационных систем
Предыдущая статья:
SSAS — примеры документирования
К списку статей
Любая инвестиция нуждается в тщательных расчетах. Иначе инвестор рискует потерять вложенные средства.
На первый взгляд, бизнес прибыльный и привлекательный для инвестирования. Но это только первое впечатление. Необходим скрупулезный анализ инвестиционного проекта. И сделать это можно самостоятельно с помощью Excel, без привлечения дорогостоящих специалистов и экспертов по управлению инвестиционными портфелями.
Расчет инвестиционного проекта в Excel
Инвестор вкладывает деньги в готовое предприятие. Тогда ему необходимо оценить эффективность работы (доходность, надежность). Либо в новое дело – все расчеты проводятся на основе данных, полученных в ходе изучения рынка (инфраструктуры, доходов населения, уровня инфляции и т.д.).
Рассмотрим создание бизнеса с нуля. Рассчитаем прибыльность предприятия с помощью формул Excel. Для примера будем брать условные товары и цифры. Важно понять принцип, а подставить можно любые данные.
Итак, у нас есть идея открыть небольшой магазин. Определимся с затратами. Они бывают
- постоянными (нельзя рассчитать на единицу товара);
- переменными (можно рассчитать на единицу товара).
Первоначальные вложения – 300 000 рублей. Деньги расходуются на оформление предпринимательства, оборудование помещения, закупку первой партии товара и т.д.
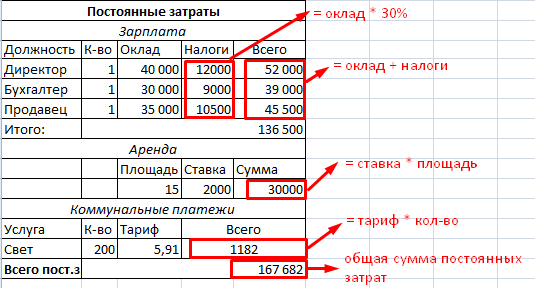
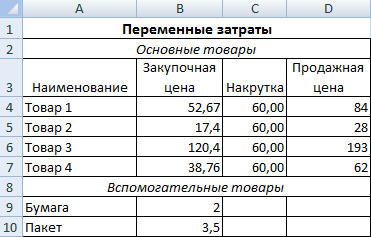
Составляем таблицу с постоянными затратами:
* Статьи расходов индивидуальны. Но принцип составления — понятен.
По такому же принципу составляем отдельно таблицу с переменными затратами:
Для нахождения цены продажи использовали формулу: =B4*(1+C4/100).
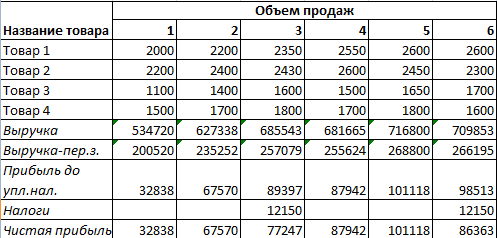
Следующий этап – прогнозируем объем продаж, выручку и прибыль. Это самый ответственный этап при составлении инвестиционного проекта.
Объем продаж условный. В реальной жизни эти цифры – результат анализа доходов населения, востребованности товаров, уровня инфляции, сезона, места нахождения торговой точки и т.д.
Для подсчета выручки использовалась формула: =СУММПРОИЗВ(B3:B6;Лист2!$D$4:$D$7). Где первый массив – объемы продаж; второй массив – цены реализации.
Выручка минус переменные затраты: =B7-СУММПРОИЗВ(B3:B6;Лист2!$B$4:$B$7).
Прибыль до уплаты налогов: =B8-Лист1!$B$14 (выручка без переменных и постоянных затрат).
Налоги ЕНВД: =Лист1!A10*1800*0,15*3 (1800 – базовая доходность по виду деятельности, 3 – количество месяцев, С12 – площадь помещения).
Чистая прибыль: прибыль – налоги.
Оценка инвестиционного проекта в Excel
Рассчитывают 4 основных показателя:
- чистый приведенный эффект (ЧПЭ, NPV);
- индекс рентабельности инвестиций (ИРИ, PI);
- внутреннюю норму доходности (ВНД, IRR);
- дисконтированный срок окупаемости (ДСО, DPP).
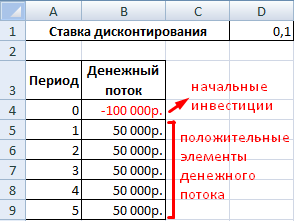
Для примера возьмем следующий вариант инвестиций:
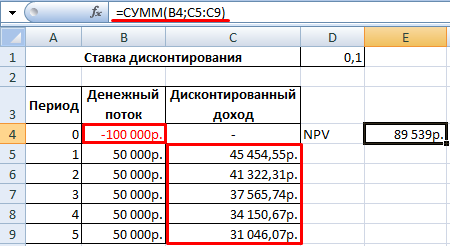
Сначала дисконтируем каждый положительный элемент денежного потока.
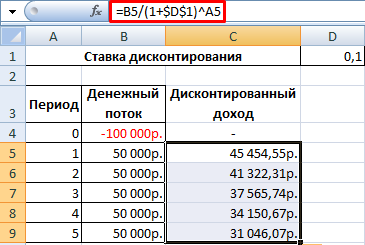
Создадим новый столбец. Введем формулу вида: = положительный элемент денежного потока / (1 + ставка дисконтирования)^ степень, равная периоду.
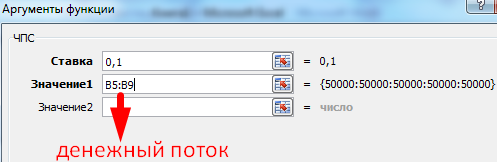
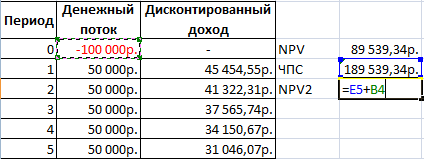
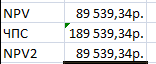
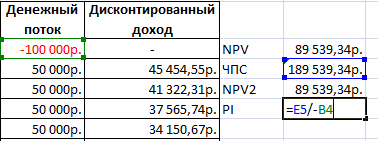
Теперь рассчитаем чистый приведенный эффект:
- С помощью функции СУММ.
- С помощью встроенной функции ЧПС.
Чтобы получить чистый приведенный эффект, складываем результат функции с суммой инвестиций.
Цифры совпали:
Найдем индекс рентабельности инвестиций. Для этого нужно разделить чистую приведенную стоимость (ЧПС) на объем инвестированных средств (со знаком «+»):
Результат – 1,90.
Посчитаем IRR инвестиционного проекта в Excel. Напомним формулу:
ВНД = ΣДПt/ (1 + ВНР)t = И.
ДПt– положительные элементы денежного потока, которые нужно продисконтировать по такой ставке, чтобы чистый приведенный эффект равнялся нулю. Внутренняя норма доходности – такая ставка дисконтирования, при которой выпадает равенство вида:
ΣДПt / (1 + ВНР)t – И = 0,
NPV = 0.
Воспользуемся инструментом «Анализ «Что-Если»»:
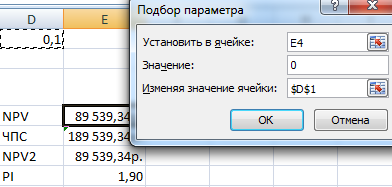
- Ставим курсор в ячейку со значением чистого приведенного эффекта. Выбираем «Данные»-«Анализ Что-Если»-«Подбор параметра».
- В открывшемся окне в строке «Значение» вводим 0 (чистый приведенный эффект должен равняться 0). В поле «Изменяя значение ячейки» ссылаемся на ставку дисконтирования. Нужно изменить ее так, чтобы соблюдалось приведенное выше равенство.
- Нажимаем ОК.
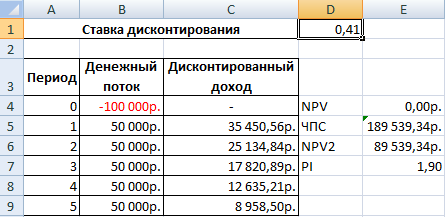
Ставка дисконтирования равняется 0,41. Следовательно, внутренняя норма доходности составила 41%.
Моделирование рисков инвестиционных проектов в Excel
Используем метод имитационного моделирования Монте-Карло. Задача – воспроизвести развитие бизнеса на основе результатов анализа известных элементов и взаимосвязей между ними.
Продемонстрируем моделирование рисков на простейшем примере. Составим условный шаблон с данными:
Ячейки, которые содержат формулы ниже подписаны своими значениями соответственно.
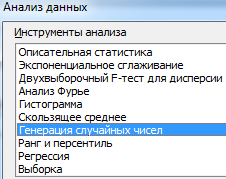
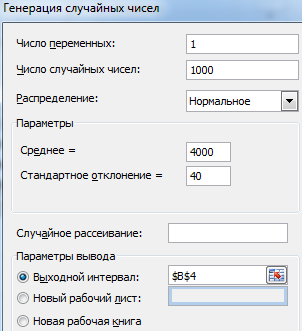
Прогнозируемые показатели – цена услуги и количество пользователей. Под этими данными делаем запись «Результаты имитации». На вкладке «Данные» нажимаем «Анализ данных» (если там нет инструмента придется подключить настройку). В открывшемся окне выбираем «Генерация случайных чисел».
Заполняем параметры следующим образом:
Нам нужно смоделировать ситуацию на основе распределений разного типа.
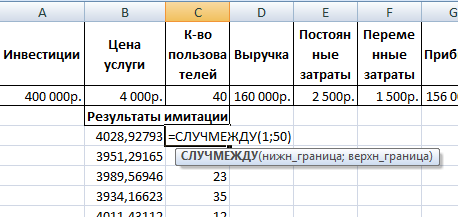
Для генерации количества пользователей воспользуемся функцией СЛУЧМЕЖДУ. Нижняя граница (при самом плохом варианте событий) – 1 пользователь. Верхняя граница (при самом хорошем варианте развития бизнеса) – 50 покупателей услуги.
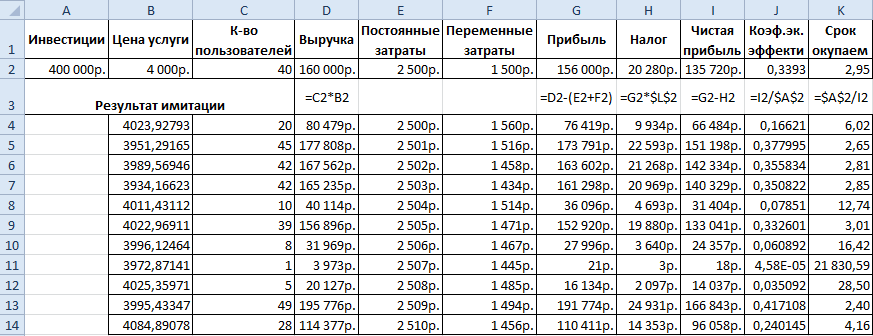
Скопируем полученные значения и формулы на весь диапазон. Для переменных затрат тоже сделаем генерацию случайных чисел. Получим эмпирическое распределение показателей эффективности проекта.
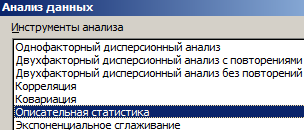
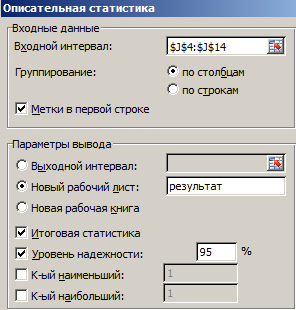
Чтобы оценить риски, нужно сделать экономико-статистический анализ. Снова воспользуемся инструментом «Анализ данных». Выбираем «Описательная статистика».
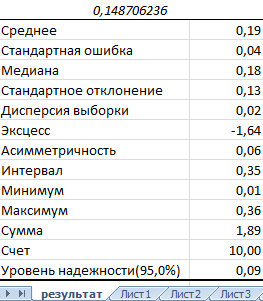
Программа выдает результат (по столбцу «Коэффициент эффективности»):
Скачать анализ инвестиционного проекта в Excel
Можно делать выводы и принимать окончательное решение.