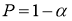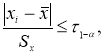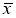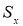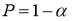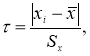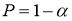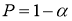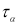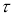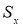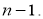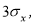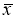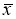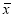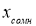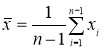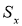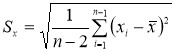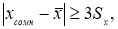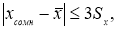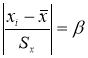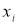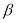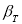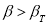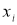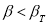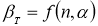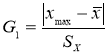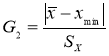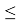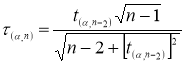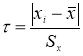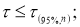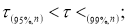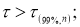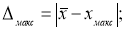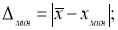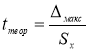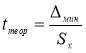Любое
из измеренных значений l
и T,
представленных в таблицах 1-3, не являются
точными величинами, так как они измерены
с определёнными погрешностями.
В
таких случаях в качестве точных значений
указанных величин принимаются их средние
арифметические, вычисляемые по формулам
(14). Тогда под погрешностью измерения
будем подразумевать модуль величины
максимального отклонения всех измеренных
величин от их среднего арифметического.
А именно, погрешность ∆1
измерения длины маятника будем определять
как:
∆1
= max
|li
— lср|,
(15)
а
погрешность ∆2
— периода колебаний маятника следует
вычислять так:
∆2
= max
|Ti
– Tср|
.
(16)
В
формулах (15) — (16) индекс i
= 1,2,3 … пробегает все номера измерений
соответствующих величин.
Обработку
результатов измерений будем производить
на компьютере в программе Microsoft
Excel
и продемонстрируем технологию необходимых
при этом расчётов на конкретных
результатах измерений.
Пусть
таблица 3 заполнена следующими фактическими
данными.
Таблица
3
|
φ0 |
||||||||||
|
n номер |
серия |
серия |
серия |
серия |
серия |
|||||
|
l, м |
T, с |
l, м |
T, с |
l, м |
T, с |
l, м |
T, с |
l, м |
T, с |
|
|
1 2 3 4 5 |
0,505 0,495 0,503 0,498 0,500 |
1,434 1,434 1,428 1,422 1,418 |
0,606 0,594 0,603 0,597 0,600 |
1,547 1,553 1,557 1,575 1,553 |
0,704 0,696 0,702 0,698 0,700 |
1,685 1,681 1,678 1,691 1,687 |
0,806 0,794 0,804 0,797 0,800 |
1,807 1,815 1,791 1,791 1,800 |
0,904 0,896 0,903 0,898 0,900 |
1,907 1,909 1,925 1,906 1,897 |
Для
каждой серии измерений необходимо по
формулам (14) вычислить lср
и Tср,
а затем построить зависимость Tср2
= f(lср).
Для удобства введём обозначения: Tср2
=
y1,
lср
= x1.
Прежде
чем перейти к указанным вычислениям,
построим в программе Excel
таблицу 3 и заготовим формат таблицы 4,
данные которой будут использованы при
построении функциональной зависимости
y1
= f(x1).
В
программе Excel
таблица 3 формируется следующим образом.
На
Листе1 рабочей книги Excel
активизируем диапазон ячеек ячейку
A1:A2,
объединим их и занесём в получившуюся
объединённую ячейку с клавиатуры
заголовок первого столбца: «n
номер измерения»,
активизируем диапазон ячеек B1:C1,
объединим их и занесём в получившуюся
объединённую ячейку с клавиатуры общий
заголовок второго и третьего столбца:
«серия
1»,
активизируем ячейку B2
и занесём в неё с клавиатуры подзаголовок
второго столбца таблицы 3: «l»,
после чего, активизируем ячейку С2 и
занесём в неё с клавиатуры подзаголовок
третьего столбца таблицы 3: «T».
Повторим указанные действия для остальных
столбцов таблицы 3. В результате выполнения
вышеуказанных действий получим формат
таблицы 3.
Теперь
заполним полученный формат данными
таблицы 3, в
результате чего получим таблицу 3 в
программе Excel.
Для
построения формата таблицы 4 в программе
Excel
на Листе1 рабочей книги Excel
активизируем ячейку A9
и вводим в неё с клавиатуры заголовок
первого столбца: «n
номер серии измерений», активизируем
ячейку B9
и вводим в неё с клавиатуры заголовок
второго столбца: «lср=x1».
Аналогично заносим с клавиатуры заголовки
третьего, четвёртого и пятого столбцов:
«Tср»,
«Tср2=y1»
и «y1
/
x1»
в ячейки C1,
D1
и E1
соответственно. Далее, активизируем
ячейку A10
и занесём в неё с клавиатуры цифру 1, в
ячейку A11
— цифру 2, активизируем диапазон ячеек
A10:A11
и выполним автозаполнение до ячейки
A14.
В
результате выполнения вышеуказанных
действий получим таблицу 4.
Таблица
4.
Технологию
заполнения первой строки таблицы 4
продемонстрируем на обработке измерений
серии 1.
Программируем
первую формулу в (14), получаем lср
и заносим в таблицу 4. Для этого активизируем
ячейку B10
и заносим с клавиатуры формулу
«=СУММ(B3:B7)*(1/5)».
Потом
программируем вторую формулу в (14). Для
этого активизируем ячейку E2
и заносим с клавиатуры формулу
«=СУММ(C3:C7)*(1/5)».
Получаем
Tср
и возводим её в квадрат, после чего
вычисляем отношение
. Для этого
активизируем ячейку D10
и заносим с клавиатуры формулу «=C10^2»,
затем активизируем ячейку E10
и заносим с клавиатуры формулу «=D10/B10».
После всех этих действий первая строка
таблицы 4 принимает вид
После
повторения указанных расчётов для
других серий Таблица 4 принимает
окончательных вид
Данные
таблицы 4 позволяют с помощью программы
Excel
построить график функциональной
зависимости y1
= f(x1).
Для
этого активизируем диапазон ячеек
D10:D14,
вызовем Мастер Функций программы Excel,
выберем тип диаграммы «Точечная», вид
первый. Подведём курсор мыши к кнопке
«Далее» и выполним однократное нажатие
левой клавиши мыши (ЛКМ). После этого
перейдём на вкладку «Ряд». Для этого
подведём курсор мыши в вкладке «Ряд»,
находящейся в верхней части окна «Мастер
Диаграмм» и выполним однократное нажатие
ЛКМ. Далее установим курсор в поле
«Значения Х», после чего подведём курсор
мыши к ячейке B10,
нажмём ЛКМ и, не отпуская её, переместим
курсор мыши до ячейки B14,
после чего отпустим ЛКМ. В результате
в поле «Значения Х» будет записана
формула «=Лист1!$B$10:$B$14».
Теперь подведём курсор мыши к кнопке
«Далее» и выполним подряд два нажатия
ЛКМ, после чего переместим курсор мыши
на кнопку «Готово» и выполним однократное
нажатие ЛКМ. На Листе1 рабочей книги
Excel
появится график функциональной
зависимости y1
= f(x1).
Активизируем строку 10 и добавим новую
строку, после чего занесём с клавиатуры
в ячейки A10:E10
цифру «0». Далее, подведём курсор мыши
к любой точке графика и выполним
однократное нажатие ЛКМ. Увеличим
диапазон данных графика, для чего
подведём курсор мыши к границе диапазона
значений y1
и передвинем маркер, расположенный в
правом верхнем углу границы, до ячейки
D10.
Аналогично
поступим с диапазоном x1.
Теперь
подведём курсор мыши к любой точке
графика и выполним однократное нажатие
правой клавиши мыши (ПКМ). В появившемся
контекстном меню подведём курсор мыши
к команде «Добавить линию тренда» и
выполним однократное нажатие ЛКМ.
Рисунок
4 иллюстрирует результат указанных
построений.
Рис
4.
Из
рисунка 4 следует, что зависимость y1
= f(x1)
имеет линейный характер и описывается
уравнением:
y1
= 4,048 x1
+ 0,0024.
(17)
Уравнение
17 показывает, что угловой коэффициент
k
из уравнения (10) оказывается равным: k
= 4,0493. Если это значение k
подставить в формулу (12), то получим
величину ускорения свободного падения.
Угловой
коэффициент k
в уравнении (10) можно вычислить и из
данных таблицы 4 по формуле:
(18)
Для
этого активизируем ячейку A17
и занесём в неё с клавиатуры формулу
«=СУММ(E11:E15)*(1/5)»
получим
k
= 4,053, т.е. число близкое к числу k,
полученному из графика, изображённого
на рисунке 4.
Очевидно,
что число
, полученное
по формуле (12) с использованием величины
k
из уравнения (17), будет обладать некоторой
погрешностью.
Чтобы
вычислить эту погрешность, вернёмся к
данным таблиц 3 и 4.
Вначале
в программе Excel
создадим формат новой таблицы 5. Для
чего на Листе1 рабочей книги Excel
активизируем ячейку A19
и занесём в неё с клавиатуры заголовок
первого столбца: «n
номер серии измерений», активизируем
ячейку B19
и занесём в неё с клавиатуры заголовок
второго столбца: «∆1
по (15)». Аналогично занесём с клавиатуры
заголовки третьего столбца: «∆2
по (16)» в ячейку C19.
Далее, активизируем ячейку A20
и занесём в неё с клавиатуры цифру 1, в
ячейку A21
— цифру 2, активизируем диапазон ячеек
A20:A21
и выполним автозаполнение до ячейки
A26.
В
результате выполнения вышеуказанных
действий получим таблицу 5.
Таблица
5.
При
программировании формул (15) и (16) необходимо
li
и Ti
каждой серии измерений брать из таблицы
3, а lср
и Tср
из данных таблицы 4.
Чтобы
вычислить ∆1
для первой серии измерений, необходимо
активизировать ячейку M3
и занести в неё с клавиатуры формулу
«=ABS(B3-B$11)»,
после чего выполним автозаполнение до
ячейки M7.
Теперь занесём с клавиатуры в ячейку
B20
формулу «=МАКС(M3:M7)».
Для
вычисления ∆2
по данным той же серии необходимо
активизировать ячейку N3
и занести в неё с клавиатуры формулу
«=ABS(C3-C$11)»,
после чего выполним автозаполнение до
ячейки N7.
Теперь занесём с клавиатуры в ячейку
C20
формулу «=МАКС(N3:N7)».
В
результате таблица 5 принимает вид
После
выполнения расчётов по (15) и (16) для данных
других серий измерений таблица 5 принимает
вид
Из
данных таблицы 5 очевидно, что для каждой
серии измерений точные значения длины
l
маятника и периода T
колебаний маятника определяются так:
l
= lср
± ∆1,
T
= Tср
± ∆2
(19)
При
этом оказывается, что ∆1
и ∆2
различны для каждой из длин маятника.
Из формул (19) следует, что прямая линия
рисунка 4 проведена с погрешностью и в
её окрестности имеет место, так называемый,
разброс экспериментальных данных.
Чтобы
учесть разброс опытных данных, вычислим
ещё две функциональные зависимости:
(Tср
+ ∆2)2
= f(lср
+ ∆1),
(20)
(Tср
— ∆2)2
= f(lср
— ∆1).
(21)
Для
вычисления зависимости (20) введём новые
обозначения:
x2
= (lср
+ ∆1),
(22)
y2
= (Tср
+ ∆2)2.
(23)
Прежде
чем приступить к вычислениям по формулам
(22) и (23), образуем формат новой таблицы
6 с помощью программы Excel
по указанному ранее алгоритму. Тогда
получим
Таблица
6.
При
вычислении x2
и y2
по (22) и (23) необходимо пользоваться
данными таблиц 4 и 5. Вначале вычисляем
x2
и полученные числа заносим таблицу 6.
Для
этого активизируем ячейку B27
и занесём в неё с клавиатуры формулу
«=B11+B20».
Затем
вычисляем y2
, для этого активизируем ячейку C27
и занесём в неё с клавиатуры формулу
«=(C11+C20)^2».
Теперь
активизируем диапазон ячеек B27:C27
и выполним автозаполнение до ячейки
C31.
После
чего таблица 6 заполнится следующими
данными
По
данным таблицы 6 строим график зависимости
y2
= y2(x2)
(см. рис. 5) по описанной ранее технологии
Из
рисунка 5 видно, что зависимость y2
= y2(x2)
определяется уравнением
y2
= 4,0886 x2
– 0,0023. (24)
Переходим
к вычислению функциональной зависимости
(21). Для этого введём две вспомогательные
формулы
x3
= lср
— ∆1
, (25)
y3
= (Tср
— ∆2)2.
(26)
Вычисление
по этим формулам производится по данным
таблиц 4 и 5, а результаты указанных
вычислений заносятся в таблицу 7. Вначале
вычисляем x3.
Для этого активизируем ячейку B34
и занесём в неё с клавиатуры формулу
«=B11-B20».
Затем
вычисляем y3
для этого активизируем ячейку C34
и занесём в неё с клавиатуры формулу
«=(C11-C20)^2».
Теперь
активизируем диапазон ячеек B34:C34
и выполним автозаполнение до ячейки
C38.
Данные
этой таблицы оказываются следующими
Функциональная
зависимость y3
= y3(x3),
построенная по данным таблицы 7, указана
на рисунке 6.
Из
рисунка 6 следует, что:
y3
= 4,0073 x3
+ 0,0071. (27)
Значения
углового коэффициента k
по данным уравнений (17), (24), (27) заносим
в таблицу 8.
Программируем
формулу (12) и вычисляем g,
соответствующее каждому значению k.
Заносим полученные значения g
в таблицу 8. Для этого активизируем
ячейку C41
и занесём в неё с клавиатуры формулу
«=(4*ПИ()^2)/B41».
После
этого выполним автозаполнения до ячейки
C43.
Теперь
вычисляем среднее значение g
по формуле:
.
Для
этого активизируем ячейку C45
и занесём в неё с клавиатуры формулу
«=(1/3)*СУММ(C41:C43)».
Оно
оказывается равным 9,75331, которое принимаем
за точное значение. Погрешность
определения данного значения g
вычисляем по формуле
Δ3
= max
|gi
– gср|
= max
|Δi|.
(28)
Для
этого активизируем ячейку D41
и занесём в неё с клавиатуры формулу
«=ABS(C41-C$45)».
После
этого выполним автозаполнения до ячейки
D43.
Вычисляем
Δi
и заносим в таблицу 8. Для этого активизируем
ячейку D45
и занесём в неё с клавиатуры формулу
«=МАКС(D41:D43)».
Из
данных таблицы 8 следует, что Δ3
= 0,098316. Таким образом, ускорение g
свободного падения, полученное на данном
приборе в результате косвенных измерений,
оказалось равным:
g
= 9,7533 ± 0,0983, (м/с2).
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
В статье рассмотрены различные критерии отбрасывания грубых погрешностей измерений, применяемые в практической деятельности, на основе рекомендаций ведущих специалистов-метрологов, а также с учетом действующих в настоящий момент нормативных документов.
Приведен пример использования Excel при оценке грубых погрешностей по критериям Стьюдента и Романовского при обработке реальных результатов измерений.
Ключевые слова:
грубые погрешности, критерии согласия, сомнительные значения, уровень значимости, нормальное распределение, критерий согласия Стьюдента, критерий Романовского, выборка, отклонения, Excel.
Одним из важнейших условий правильного применения статистических оценок является отсутствие грубых ошибок при наблюдениях. Поэтому все грубые ошибки должны быть выявлены и исключены из рассмотрения в самом начале обработки наблюдений.
Единственным достаточно надежным способом выявления грубых ошибок является тщательный анализ условий самих испытаний. При этом наблюдения, проводившиеся в нарушенных условиях, должны отбрасываться, независимо от их результата. Например, если при проведении эксперимента, связанного с электричеством, в лаборатории на некоторое время был выключен ток, то весь эксперимент обязательно нужно проводить заново, хотя результат, быть может, не сильно отличается от предыдущих измерений. Точно так же отбрасываются результаты измерений на фотопластинках с поврежденной эмульсией и вообще на любых образцах с обнаруженным позднее дефектом.
На практике, однако, не всегда удается провести подобный анализ условий испытания. Чаще всего приходится иметь дело с окончательным цифровым материалом, в котором отдельные данные вызывают сомнение лишь своим значительным отклонением от остальных. При этом сама «значительность» отклонения во многом субъективна — зачастую приходится сталкиваться со случаями, когда исследователь отбрасывает наблюдения, которые ему не понравились, как ошибочные исключительно по той причине, что они нарушают уже созданную им в воображении картину изучаемого процесса.
Строгий научный анализ готового ряда наблюдений может быть проведен лишь статистическим путем, причем должен быть достаточно хорошо известен характер распределения наблюдаемой случайной величины. В большинстве случаев исследователи исходят из нормального распределения. Каждая грубая ошибка будет соответствовать нарушению этого распределения, изменению его параметров, иными словами, нарушится однородность испытаний (или, как говорят
,
однородность наблюдений), поэтому выявление грубых ошибок можно трактовать как проверку однородности наблюдений.
Промахи, или грубые погрешности, возникают при единичном измерении и обычно устраняются путем повторных измерений. Причиной их возникновения могут быть:
- Объективная реальность (наш реальный мир отличается от идеальной модели мира, которую мы принимаем в данной измерительной задаче);
- Внезапные кратковременные изменения условий измерения (могут быть вызваны неисправностью аппаратуры или источников питания);
- Ошибка оператора (неправильное снятие показаний, неправильная запись и т. п.).
В третьем случае, если оператор в процессе измерения обнаружит промах, он вправе отбросить этот результат и провести повторные измерения.
В настоящее время определение грубой погрешности приведено в ГОСТ Р 8.736–2011: «Грубая погрешность измерения: Погрешность измерения, существенно превышающая зависящие от объективных условий измерений значения систематической и случайной погрешностей» [1, с. 6].
Общие подходы к методам отсеивания грубых погрешностей, как это уже давно принято в практике измерений, заключаются в следующем.
Задаются вероятностью
Р
или уровнем значимости
α
(
) того, что результат наблюдения содержит промах. Выявление сомнительного результата осуществляют с помощью специальных критериев. Операция отбрасывания удаленных от центра выборки сомнительных значений измеряемой величины называется «цензурированием выборки».
Проверяемая гипотеза состоит в утверждении, что результат наблюдения
x
i
не содержит грубой погрешности, т. е. является одним из значений случайной величины
x
с законом распределения Fx(x), статистические оценки параметров которого предварительно определены. Сомнительным может быть в первую очередь лишь наибольший x
max
или наименьший xmin из результатов наблюдений.
Предложим для практического использования наиболее простые методы отсева грубых погрешностей.
Если в распоряжении экспериментатора имеется выборка небольшого объема
n
≤ 25, то можно воспользоваться методом вычисления максимального относительного отклонения [2, с. 149]:
(1)
где
x
i
— крайний (наибольший или наименьший) элемент выборки, по которой подсчитывались оценки среднего значения
и среднеквадратичного отклонения
;
τ
1-
p
— табличное значение статистики
τ
, вычисленной при доверительной вероятности
.
Таким образом, для выделения аномального значения вычисляют значение статистики,
(2)
которое затем сравнивают с табличным значением
τ
1-α
:
τ
≤
τ
1-α
. Если неравенство
τ
≤
τ
1-α
соблюдается, то наблюдение не отсеивают, если не соблюдается, то наблюдение исключают. После исключения того или иного наблюдения или нескольких наблюдений характеристики эмпирического распределения должны быть пересчитаны по данным сокращенной выборки.
Квантили распределения статистики
τ
при уровнях значимости
α
= 0,10; 0,05; 0,025 и 0,01 или доверительной вероятности
=
0,90; 0,95; 0,975 и 0,99 приведены в таблице 1. На практике очень часто используют уровень значимости
α
= 0,05 (результат получается с 95 %-й доверительной вероятностью).
Функции распределения статистики
τ
определяют методами теории вероятностей. По данным таблицы, приведенной в источниках [2, с. 283; 3, с. 184] при заданной доверительной вероятности
или уровне значимости
α
можно для чисел измерения п = 3–25 найти те наибольшие значения
которые случайная величина
может еще принять по чисто случайным причинам.
Процедуру отсева можно повторить и для следующего по абсолютной величине максимального относительного отклонения, но предварительно необходимо пересчитать оценки среднего значения
и среднеквадратичного отклонения
для выборки нового объема
Таблица 1
Квантили распределения максимального относительного отклонения при отсеве грубых погрешностей [2, с. 283]
|
|
Уровень значимости |
|
Уровень значимости |
||||||
|
0,10 |
0,05 |
0,025 |
0,01 |
0,10 |
0,05 |
0,025 |
0,01 |
||
|
3 |
1,41 |
1,41 |
1,41 |
1,41 |
15 |
2,33 |
2,49 |
2,64 |
2,80 |
|
4 |
1,65 |
1,69 |
1,71 |
1,72 |
16 |
2,35 |
2,52 |
2,67 |
2,84 |
|
5 |
1,79 |
1,87 |
1,92 |
1,96 |
17 |
2,38 |
2,55 |
2,70 |
2,87 |
|
6 |
1,89 |
2,00 |
2,07 |
2,13 |
18 |
2,40 |
2,58 |
2,73 |
2,90 |
|
7 |
1,97 |
2,09 |
2,18 |
2,27 |
19 |
2,43 |
2,60 |
2,75 |
2,93 |
|
8 |
2,04 |
2,17 |
2,27 |
2,37 |
20 |
2,45 |
2,62 |
2,78 |
2,96 |
|
9 |
2,10 |
2,24 |
2,35 |
2,46 |
21 |
2,47 |
2,64 |
2,80 |
2,98 |
|
10 |
2,15 |
2,29 |
2,41 |
2,54 |
22 |
2,49 |
2,66 |
2,82 |
3,01 |
|
11 |
2,19 |
2,34 |
2,47 |
2,61 |
23 |
2,50 |
2,68 |
2,84 |
3,03 |
|
12 |
2,23 |
2,39 |
2,52 |
2,66 |
24 |
2,52 |
2,70 |
2,86 |
3,05 |
|
13 |
2,26 |
2,43 |
2,56 |
2,71 |
25 |
2,54 |
2,72 |
2,88 |
3,07 |
|
14 |
2,30 |
2,46 |
2,60 |
2,76 |
|||||
В литературе можно встретить большое количество методических рекомендаций для проведения отсева грубых погрешностей измерений, подробно рассмотренных в [4, с. 25]. Обратим внимание на некоторые из существующих критериев отсеивания грубых погрешностей.
-
Критерий «трех сигм» применяется для случая, когда измеряемая величина
x
распределена по нормальному закону. По этому критерию считается, что с вероятностью
Р
= 0,9973 и значимостью
α
= 0,0027 появление даже одной случайной погрешности, большей, чеммаловероятное событие и ее можно считать промахом, если
−
x
i
> 3
S
x
, где
S
x
—
оценка среднеквадратического отклонения (СКО) измерений. Величиныи
S
x
вычисляют без учета экстремальных значений
x
i
. Данный критерий надежен при числе измерений
n
≥ 20…50 и поэтому он широко применяется. Это правило обычно считается слишком жестким, поэтому рекомендуется назначать границу цензурирования в зависимости от объема выборки: при
6 <
n
≤100 она равна 4
S
x
; при 100 <
n
≤1000 − 4,5
S
x
; при 1000 <
n
≤10000–5
Sx
. Данное правило также используется только при нормальном распределении.
Практические вычисления проводят следующим образом [5, с. 65]:
- Выявляют сомнительное значение измеряемой величины. Сомнительным значением может быть лишь наибольшее, либо наименьшее значение наблюдения измеряемой величины.
-
Вычисляют среднее арифметическое значение выборки
без учета сомнительного значения
измеряемой величины.
(3)
-
Вычисляют оценку СКО выборки
без учета сомнительного значения
измеряемой величины.
(4)
- Вычисляют разность среднеарифметического и сомнительного значения измеряемой величины и сравнивают.
Если
то сомнительное значение отбрасывают, как промах.
Если
то сомнительное значение оставляют как равноправное в ряду наблюдений.
Данный метод «трех сигм» среди метрологов-практиков является самым популярным, достаточно надежным и удобным, так как при этом иметь под рукой какие-то таблицы нет необходимости.
-
Критерий В. И. Романовского применяется, если число измерений невелико,
n
≤ 20. При этом вычисляется соотношение
(5)
где
— результат, вызывающий сомнение,
— коэффициент, предельное значение которого
определяют по таблице 2. Если
, сомнительное значение
исключают («отбрасывают») как промах. Если
,
сомнительное значение оставляют как равноправное в ряду наблюдений [5, с. 65].
Таблица 2
Значение критерия Романовского
|
Уровень значимости, |
Число измерений, |
||||||
|
|
|
|
|
|
|
|
|
|
0,01 |
1,73 |
2,16 |
2,43 |
2,62 |
2,75 |
2,90 |
3,08 |
|
0,02 |
1,72 |
2,13 |
2,37 |
2,54 |
2,66 |
2,80 |
2,96 |
|
0,05 |
1,71 |
2,10 |
2,27 |
2,41 |
2,52 |
2,64 |
2,78 |
|
0,10 |
1,69 |
2,00 |
2,17 |
2,29 |
2,39 |
2,49 |
2,62 |
Несмотря на многообразие существующих и применяемых на практике методов отсеивания грубых погрешностей в настоящее время действует национальный стандарт ГОСТ Р 8.736–2011, который является основным нормативным документом в данной области. В новом стандарте для исключения грубых погрешностей применяется критерий Граббса.
- Статистический критерий Граббса (Смирнова) исключения грубых погрешностей основан на предположении о том, что группа результатов измерений принадлежит нормальному распределению [1, с. 8]. Для этого вычисляют критерии Граббса (Смирнова) G1 и G2, предполагая, что наибольший хmax или наименьший xmin результат измерений вызван грубыми погрешностями.
и
(6)
Сравнивают G1 и G2 с теоретическим значением GT критерия Граббса (Смирнова) при выбранном уровне значимости α. Таблица критических значений критерия Граббса (Смирнова) приведена в приложении к стандарту [1, с. 12]. Следует отметить, что критические значения критерия Граббса (Смирнова) GT отличаются от критических значений критериев
t
-статистик или значений критериев Стьюдента при одних и тех же величинах уровней значимости, что может вызывать некоторые трудности у пользователей при выборе конкретного метода отсеивания погрешностей, соответствующего нормативным документам.
Если G1>GТ, то хmax исключают как маловероятное значение. Если G2>GТ, то xmin исключают как маловероятное значение. Далее вновь вычисляют среднее арифметическое и среднее квадратическое отклонение ряда результатов измерений и процедуру проверки наличия грубых погрешностей повторяют.
Если G1
GТ, то хmax не считают промахом и его сохраняют в ряду результатов измерений. Если G2
GТ, то xmin не считают промахом и его сохраняют в ряду результатов измерений.
Отсев грубых погрешностей можно производить и для больших выборок (
n
= 50…100). Для практических целей лучше всего использовать таблицы распределения Стьюдента. Этот метод исключения аномальных значений для выборок большого объема отличается простотой, а таблицы распределения Стьюдента имеются практически в любой книге по математической статистике, кроме того, распределение Стьюдента реализовано в пакете Excel. Распределение Стьюдента относится к категории распределений, связанных с нормальным распределением. Подробно эти распределения рассмотрены в учебниках по математической статистике [3, с. 24].
Известно, что критическое значение
τ
p
(
p
— процентная точка нормирования выборочного отклонения) выражается через критическое значение распределения Стьюдента
t
α, n-2
[6, с. 26]:
(7)
Учитывая это, можно предложить следующую процедуру отсева грубых погрешностей измерения для больших выборок (
n
= 100):
1) из таблицы наблюдений выбирают наблюдение имеющее наибольшее отклонение;
2)
по формуле
вычисляют значение статистики
τ
;
3)
по таблице (или в программе Excel) находят процентные точки
t
-распределения Стьюдента
t
(
α,
n
-2
)
:
t
(95
%, 98)
= 1,6602, и
t
(
99
%, 98)
= 3,1737;
По предыдущей формуле в программе Excel вычисляют соответствующие точки
t
(95
%, 100)
= 1,66023и
t
(99
%, 100)
=3,17374.
Сравнивают значение расчетной статистики с табличными критическими значениями и принимают решение по отсеву грубых погрешностей.
Рекомендуемый метод отсева грубых погрешностей удобен еще тем, что максимальные относительные отклонения могут быть разделены на три группы: 1)
2)
3)
.
Наблюдения, попавшие в первую группу, нельзя отсеивать ни в коем случае. Наблюдения второй группы можно отсеять, если в пользу этой процедуры имеются еще и другие соображения экспериментатора (например, заключения, сделанные на основе изучения физических, химических и других свойств изучаемого явления). Наблюдения третьей группы, как правило, отсеивают всегда.
Рассмотрим далее пример с использованием средств программного пакета Excel, который позволяет снизить трудоемкость расчетов при осуществлении данной процедуры. К сожалению, в настоящее время средства Excel не позволяют автоматизировать расчеты по всем известным критериям отсеивания грубых погрешностей, поэтому проиллюстрируем рассмотренные методы с использованием доступных в Excel критериев Стьюдента.
Пример 1.
Имеется выборка из 100 шт. резисторов с номинальным сопротивлением
R
н
= (150,0 ± 5 %) кОм, которая используется для оценки качества партии резисторов (генеральная совокупность). Используя критерий Стьюдента, отсеем грубые погрешности (промахи) при измерениях.
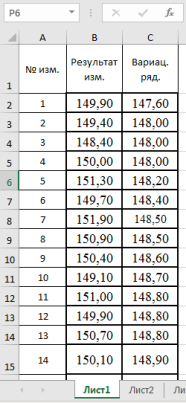
- Заносим данные измерений в таблицу Excel в ячейки В2:В101
- Составляем вариационный ряд — располагаем данные в порядке возрастания с помощью функции «Сортировка по возрастанию» в ячейках С2:С101 (рис. 1)
Рис. 1. Фрагмент диалогового окна с данными измерений и вариационного ряда
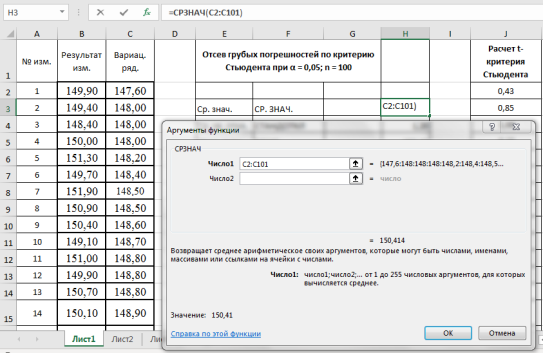
3. Находим среднее значение выборки с помощью мастера функций в категории «Статистические» и функции — СРЗНАЧ, результат в ячейке Н3 (рис. 2).
Рис. 2. Фрагмент диалогового окна при нахождении среднего значения выборки
-
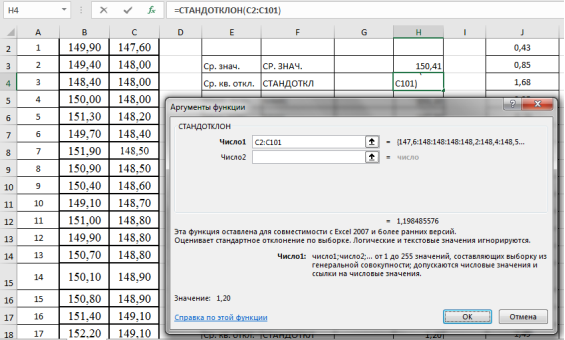
Находим среднеквадратическое отклонение —
S
x
. Выделяем ячейку Н4, вызываем «Мастер функций», категория «Статистические», функция — СТАНДОТКЛОН, результат в ячейке Н4–1,20 (рис. 3).
Рис. 3. Фрагмент диалогового окна при нахождении среднего квадратического отклонения
-
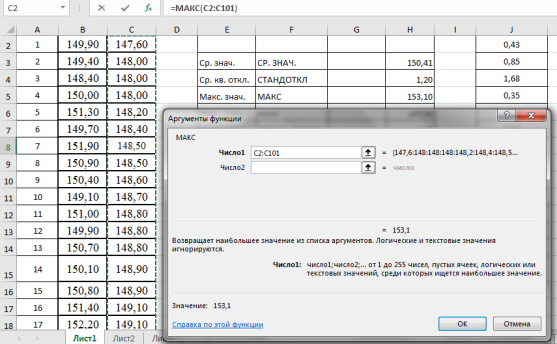
Находим максимальное значение в выборке —
x
макс
. Выделяем ячейку Н5, в категории «Статистические», функция — МАКС, выделяем мышкой вариационный ряд C2:С101, результат в ячейке Н5–153,10 (рис. 4).
Рис. 4. Фрагмент диалогового окна при нахождении максимального значения
-
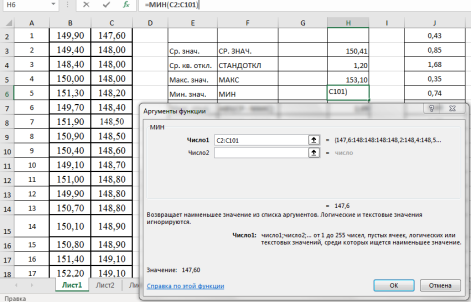
Находим минимальное значение в выборке —
x
мин
. Выделяем ячейку Н6, в категории «Статистические», функция — МИН, выделяем мышкой вариационный ряд C2:С101, результат в ячейке Н6–147,6 (рис. 5).
Рис. 5. Фрагмент диалогового окна при нахождении минимального значения
-
Находим максимальное и минимальное отклонения — Δ
макс
и Δ
мин
. Вводим в ячейки Н7 и Н8 формулы:
-
Находим теоретическое значение —
t
теор
. для максимального и минимального отклонений. Вводим в ячейки Н9 и Н12 формулу
. и
-
Находим табличное значение
t
табл.
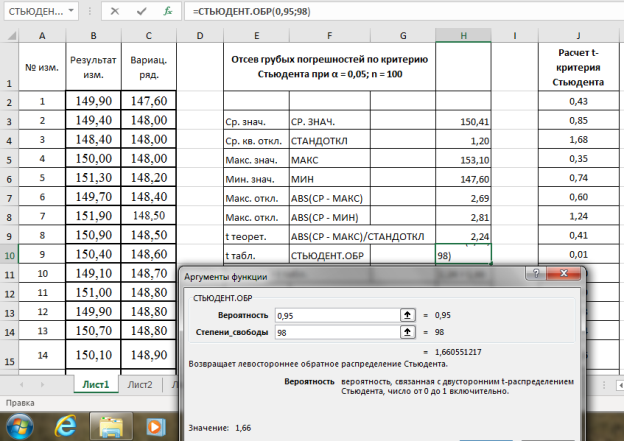
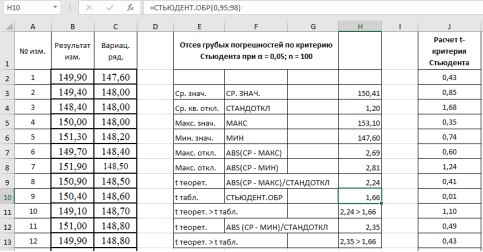
Выделяем ячейку Н10, вызываем в категории «Статистические» функцию — СТЬЮДЕНТ.ОБР, «Вероятность» — 0,95, степени свободы (
n
-2) — 98, результат в ячейке Н10–1,66 (рис. 6).
Рис. 6. Фрагмент диалогового окна при нахождении табличного значения критерия Стьюдента
-
Сравниваем теоретическое значение
t
теор
= 2,24 критерия Стьюдента для максимального значения — 153,1 кОм с табличным значением:
t
табл
.= 1,6605. - Аналогично п. 9 проверим на наличие грубой погрешности у минимального значения в выборке — 147,6 кОм. Результат в ячейке Н12–2,35 (рис. 7).
Рис. 7. Фрагмент диалогового окна при окончательном анализе данных
- Делаем вывод о наличии грубых ошибок в данных измерениях. Рассмотренная процедура подтвердила наши сомнения относительно достоверности максимального и минимального значений в данной выборке, т. е., указанные результаты могут быть отброшены из результатов измерений, и проверка может быть повторена снова без этих данных.
Пример расчета теоретического критерия Романовского по аналогичным формулам в Excel и диалоговое окно представлены на рис. 8, при условии α = 0,05, число измерений
n
= 20, β
табл
= 2,78 (из таблицы 2).
Рис. 8. Фрагмент диалогового окна при расчете критерия Романовского
Выводы
- Для использования различных критериев отбрасывания грубых погрешностей измерений необходимо учитывать требования действующих нормативных документов.
- Рассмотренный пример показал, что расчеты погрешностей по критерию Стьюдента с использованием таблиц и формул Excel значительно упрощаются, а процесс отбрасывания грубых погрешностей можно осуществить наиболее качественно и быстро.
Литература:
1. ГОСТ Р 8.736–2011 Государственная система обеспечения единства измерений. Измерения прямые многократные. Методы обработки результатов измерений. Основные положения. — М.: ФГУП Стандартинформ, 2013. — 24 с.
2. Пустыльник Е. И. Статистические методы анализа и обработки наблюдений. — М.: Наука, 1968. — 288 с.
3. Львовский Е. Н. Статистические методы построения эмпирических формул: Учеб. пособие. — М.: Высш. школа, 1982. — 224 с.
4. Фаюстов А. А. Ещё раз о критериях отсеивания грубых погрешностей. — Законодательная и прикладная метрология, 2016, № 5, с. 25–30.
5. Сергеев А. Г. Метрология: Учебник. — М.: Логос, 2005. — 272 с.
6. Большев Л. Н., Смирнов Н. В. Таблицы математической статистики. — М.: Наука, Главная редакция физико-математической литературы, 1983. — 416 с.
Основные термины (генерируются автоматически): диалоговое окно, сомнительное значение, уровень значимости, измеряемая величина, погрешность, критерий, нормальное распределение, ячейка, вариационный ряд, минимальное значение.
Содержание
- Использование описательной статистики
- Подключение «Пакета анализа»
- Размах вариации
- Вычисление коэффициента вариации
- Шаг 1: расчет стандартного отклонения
- Шаг 2: расчет среднего арифметического
- Шаг 3: нахождение коэффициента вариации
- Простая формула для расчета объема выборки
- Пример расчета объема выборки
- Задачи о генеральной доле
- По части судить о целом
- Как рассчитать объем выборки
- Как определить статистические выбросы и сделать выборку для их удаления в Excel
- Способ 1: применение расширенного автофильтра
- Способ 2: применение формулы массива
- СРЗНАЧ()
- СРЗНАЧЕСЛИ()
- МАКС()
- МИН()
Использование описательной статистики
Под описательной статистикой понимают систематизацию эмпирических данных по целому ряду основных статистических критериев. Причем на основе полученного результата из этих итоговых показателей можно сформировать общие выводы об изучаемом массиве данных.
В Экселе существует отдельный инструмент, входящий в «Пакет анализа», с помощью которого можно провести данный вид обработки данных. Он так и называется «Описательная статистика». Среди критериев, которые высчитывает данный инструмент следующие показатели:
- Медиана;
- Мода;
- Дисперсия;
- Среднее;
- Стандартное отклонение;
- Стандартная ошибка;
- Асимметричность и др.
Рассмотрим, как работает данный инструмент на примере Excel 2010, хотя данный алгоритм применим также в Excel 2007 и в более поздних версиях данной программы.
Подключение «Пакета анализа»
Как уже было сказано выше, инструмент «Описательная статистика» входит в более широкий набор функций, который принято называть Пакет анализа. Но дело в том, что по умолчанию данная надстройка в Экселе отключена. Поэтому, если вы до сих пор её не включили, то для использования возможностей описательной статистики, придется это сделать.
- Переходим во вкладку «Файл». Далее производим перемещение в пункт «Параметры».
- В активировавшемся окне параметров перемещаемся в подраздел «Надстройки». В самой нижней части окна находится поле «Управление». Нужно в нем переставить переключатель в позицию «Надстройки Excel», если он находится в другом положении. Вслед за этим жмем на кнопку «Перейти…».
- Запускается окно стандартных надстроек Excel. Около наименования «Пакет анализа» ставим флажок. Затем жмем на кнопку «OK».
После вышеуказанных действий надстройка Пакет анализа будет активирована и станет доступной во вкладке «Данные» Эксель. Теперь мы сможем использовать на практике инструменты описательной статистики.
Размах вариации
Размах вариации – разница между максимальным и минимальным значением:
Ниже приведена графическая интерпретация размаха вариации.

Видно максимальное и минимальное значение, а также расстояние между ними, которое и соответствует размаху вариации.
С одной стороны, показатель размаха может быть вполне информативным и полезным. К примеру, максимальная и минимальная стоимость квартиры в городе N, максимальная и минимальная зарплата по профессии в регионе и проч. С другой стороны, размах может быть очень широким и не иметь практического смысла, т.к. зависит лишь от двух наблюдений. Таким образом, размах вариации очень неустойчивая величина.
Вычисление коэффициента вариации
Этот показатель представляет собой отношение стандартного отклонения к среднему арифметическому. Полученный результат выражается в процентах.
В Экселе не существует отдельно функции для вычисления этого показателя, но имеются формулы для расчета стандартного отклонения и среднего арифметического ряда чисел, а именно они используются для нахождения коэффициента вариации.
Шаг 1: расчет стандартного отклонения
Стандартное отклонение, или, как его называют по-другому, среднеквадратичное отклонение, представляет собой квадратный корень из дисперсии. Для расчета стандартного отклонения используется функция СТАНДОТКЛОН. Начиная с версии Excel 2010 она разделена, в зависимости от того, по генеральной совокупности происходит вычисление или по выборке, на два отдельных варианта: СТАНДОТКЛОН.Г и СТАНДОТКЛОН.В.
Синтаксис данных функций выглядит соответствующим образом:
= СТАНДОТКЛОН(Число1;Число2;…)
= СТАНДОТКЛОН.Г(Число1;Число2;…)
= СТАНДОТКЛОН.В(Число1;Число2;…)
- Для того, чтобы рассчитать стандартное отклонение, выделяем любую свободную ячейку на листе, которая удобна вам для того, чтобы выводить в неё результаты расчетов. Щелкаем по кнопке «Вставить функцию». Она имеет внешний вид пиктограммы и расположена слева от строки формул.
Выполняется активация Мастера функций, который запускается в виде отдельного окна с перечнем аргументов. Переходим в категорию «Статистические» или «Полный алфавитный перечень». Выбираем наименование «СТАНДОТКЛОН.Г» или «СТАНДОТКЛОН.В», в зависимости от того, по генеральной совокупности или по выборке следует произвести расчет. Жмем на кнопку «OK».
Открывается окно аргументов данной функции. Оно может иметь от 1 до 255 полей, в которых могут содержаться, как конкретные числа, так и ссылки на ячейки или диапазоны. Ставим курсор в поле «Число1». Мышью выделяем на листе тот диапазон значений, который нужно обработать. Если таких областей несколько и они не смежные между собой, то координаты следующей указываем в поле «Число2» и т.д. Когда все нужные данные введены, жмем на кнопку «OK»
Шаг 2: расчет среднего арифметического
Среднее арифметическое является отношением общей суммы всех значений числового ряда к их количеству. Для расчета этого показателя тоже существует отдельная функция – СРЗНАЧ. Вычислим её значение на конкретном примере.
- Выделяем на листе ячейку для вывода результата. Жмем на уже знакомую нам кнопку «Вставить функцию».
В статистической категории Мастера функций ищем наименование «СРЗНАЧ». После его выделения жмем на кнопку «OK».
Запускается окно аргументов СРЗНАЧ. Аргументы полностью идентичны тем, что и у операторов группы СТАНДОТКЛОН. То есть, в их качестве могут выступать как отдельные числовые величины, так и ссылки. Устанавливаем курсор в поле «Число1». Так же, как и в предыдущем случае, выделяем на листе нужную нам совокупность ячеек. После того, как их координаты были занесены в поле окна аргументов, жмем на кнопку «OK».
Шаг 3: нахождение коэффициента вариации
Теперь у нас имеются все необходимые данные для того, чтобы непосредственно рассчитать сам коэффициент вариации.
- Выделяем ячейку, в которую будет выводиться результат. Прежде всего, нужно учесть, что коэффициент вариации является процентным значением. В связи с этим следует поменять формат ячейки на соответствующий. Это можно сделать после её выделения, находясь во вкладке «Главная». Кликаем по полю формата на ленте в блоке инструментов «Число». Из раскрывшегося списка вариантов выбираем «Процентный». После этих действий формат у элемента будет соответствующий.
Снова возвращаемся к ячейке для вывода результата. Активируем её двойным щелчком левой кнопки мыши. Ставим в ней знак «=». Выделяем элемент, в котором расположен итог вычисления стандартного отклонения. Кликаем по кнопке «разделить» (/) на клавиатуре. Далее выделяем ячейку, в которой располагается среднее арифметическое заданного числового ряда. Для того, чтобы произвести расчет и вывести значение, щёлкаем по кнопке Enter на клавиатуре.
Таким образом мы произвели вычисление коэффициента вариации, ссылаясь на ячейки, в которых уже были рассчитаны стандартное отклонение и среднее арифметическое. Но можно поступить и несколько по-иному, не рассчитывая отдельно данные значения.
- Выделяем предварительно отформатированную под процентный формат ячейку, в которой будет выведен результат. Прописываем в ней формулу по типу:
Вместо наименования «Диапазон значений» вставляем реальные координаты области, в которой размещен исследуемый числовой ряд. Это можно сделать простым выделением данного диапазона. Вместо оператора СТАНДОТКЛОН.В, если пользователь считает нужным, можно применять функцию СТАНДОТКЛОН.Г.
Существует условное разграничение. Считается, что если показатель коэффициента вариации менее 33%, то совокупность чисел однородная. В обратном случае её принято характеризовать, как неоднородную.
Как видим, программа Эксель позволяет значительно упростить расчет такого сложного статистического вычисления, как поиск коэффициента вариации. К сожалению, в приложении пока не существует функции, которая высчитывала бы этот показатель в одно действие, но при помощи операторов СТАНДОТКЛОН и СРЗНАЧ эта задача очень упрощается. Таким образом, в Excel её может выполнить даже человек, который не имеет высокого уровня знаний связанных со статистическими закономерностями.
Разделы: Математика
- Совершенствование умений и навыков нахождения статистических характеристик случайной величины, работа с расчетами в Excel;
- применение информационно коммутативных технологий для анализа данных; работа с различными информационными носителями.
- Сегодня мы научимся рассчитывать статистические характеристики для больших по объему выборок, используя возможности современных компьютерных технологий.
- Для начала вспомним:
– что называется случайной величиной? (Случайной величиной называют переменную величину, которая в зависимости от исхода испытания принимает одно значение из множества возможных значений.)
– Какие виды случайных величин мы знаем? (Дискретные, непрерывные.)
– Приведите примеры непрерывных случайных величин (рост дерева), дискретных случайных величин (количество учеников в классе).
– Какие статистические характеристики случайных величин мы знаем (мода, медиана, среднее выборочное значение, размах ряда).
– Какие приемы используются для наглядного представления статистических характеристик случайной величины (полигон частот, круговые и столбчатые диаграммы, гистограммы).
- Рассмотрим, применение инструментов Excel для решения статистических задач на конкретном примере.
Пример. Проведена проверка в 100 компаниях. Даны значения количества работающих в компании (чел.):
| 23 25 24 25 30 24 30 26 28 26 32 33 31 31 25 33 25 29 30 28 23 30 29 24 33 30 30 28 26 25 26 29 27 29 26 28 27 26 29 28 29 30 27 30 28 32 28 26 30 26 31 27 30 27 33 28 26 30 31 29 27 30 30 29 27 26 28 31 29 28 33 27 30 33 26 31 34 28 32 22 29 30 27 29 34 29 32 29 29 30 29 29 36 29 29 34 23 28 24 28 |
рассчитать числовые характеристики:
|
1. Занести данные в EXCEL, каждое число в отдельную ячейку.
| 23 | 25 | 24 | 25 | 30 | 24 | 30 | 26 | 28 | 26 |
| 32 | 33 | 31 | 31 | 25 | 33 | 25 | 29 | 30 | 28 |
| 23 | 30 | 29 | 24 | 33 | 30 | 30 | 28 | 26 | 25 |
| 26 | 29 | 27 | 29 | 26 | 28 | 27 | 26 | 29 | 28 |
| 29 | 30 | 27 | 30 | 28 | 32 | 28 | 26 | 30 | 26 |
| 31 | 27 | 30 | 27 | 33 | 28 | 26 | 30 | 31 | 29 |
| 27 | 30 | 30 | 29 | 27 | 26 | 28 | 31 | 29 | 28 |
| 33 | 27 | 30 | 33 | 26 | 31 | 34 | 28 | 32 | 22 |
| 29 | 30 | 27 | 29 | 34 | 29 | 32 | 29 | 29 | 30 |
| 29 | 29 | 36 | 29 | 29 | 34 | 23 | 28 | 24 | 28 |
2. Для расчета числовых характеристик используем опцию Вставка – Функция. И в появившемся окне в строке категория выберем – статистические, в списке: МОДА
В поле Число 1 ставим курсор и мышкой выделяем нашу таблицу:
Нажимаем клавишу ОК. Получили Мо = 29 (чел) – Фирм у которых в штате 29 человек больше всего.
Используя тот же путь вычисляем медиану.
Вставка – Функция – Статистические – Медиана.
В поле Число 1 ставим курсор и мышкой выделяем нашу таблицу:
Нажимаем клавишу ОК. Получили Ме = 29 (чел) – среднее значение сотрудников в фирме.
Размах ряда чисел – разница между наименьшим и наибольшим возможным значением случайной величины. Для вычисления размаха ряда нужно найти наибольшее и наименьшее значения нашей выборки и вычислить их разность.
Вставка – Функция – Статистические – МАКС.
В поле Число 1 ставим курсор и мышкой выделяем нашу таблицу:
Нажимаем клавишу ОК. Получили наибольшее значение = 36.
Вставка – Функция – Статистические – МИН.
В поле Число 1 ставим курсор и мышкой выделяем нашу таблицу:
Нажимаем клавишу ОК. Получили наименьшее значение = 22.
36 – 22 = 14 (чел) – разница между фирмой с наибольшим штатом сотрудников и фирмой с наименьшим штатом сотрудников.
Для построения диаграммы и полигона частот необходимо задать закон распределения, т.е. составить таблицу значений случайной величины и соответствующих им частот. Мы ухе знаем, что наименьшее число сотрудников в фирме = 22, а наибольшее = 36. Составим таблицу, в которой значения xi случайной величины меняются от 22 до 36 включительно шагом 1.
| xi | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 |
| ni |
Чтобы сосчитать частоту каждого значения воспользуемся
Вставка – Функция – Статистические – СЧЕТЕСЛИ.
В окне Диапазон ставим курсор и выделяем нашу выборку, а в окне Критерий ставим число 22
Нажимаем клавишу ОК, получаем значение 1, т.е. число 22 в нашей выборке встречается 1 раз и его частота =1. Аналогичным образом заполняем всю таблицу.
| xi | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 |
| ni | 1 | 3 | 4 | 5 | 11 | 9 | 13 | 18 | 16 | 6 | 4 | 6 | 3 | 0 | 1 |
Для проверки вычисляем объем выборки, сумму частот (Вставка – Функция – Математические – СУММА). Должно получиться 100 (количество всех фирм).
Чтобы построить полигон частот выделяем таблицу – Вставка – Диаграмма – Стандартные – Точечная (точечная диаграмма на которой значения соединены отрезками)
Нажимаем клавишу Далее, в Мастере диаграмм указываем название диаграммы (Полигон частот), удаляем легенду, редактируем шкалу и характеристики диаграммы для наибольшей наглядности.
Для построения столбчатой и круговой диаграмм используем тот же путь (выбирая нужный нам тип диаграммы).
Диаграмма – Стандартные – Круговая.
Диаграмма – Стандартные – Гистограмма.
4. Сегодня на уроке мы научились применять компьютерные технологии для анализа и обработки статистической информации.
Простая формула для расчета объема выборки
где: n – объем выборки;
z – нормированное отклонение, определяемое исходя из выбранного уровня доверительности. Этот показатель характеризует возможность, вероятность попадания ответов в специальный – доверительный интервал. На практике уровень доверительности часто принимают за 95% или 99%. Тогда значения z будут соответственно 1,96 и 2,58;
p – вариация для выборки, в долях. По сути, p – это вероятность того, что респонденты выберут той или иной вариант ответа. Допустим, если мы считаем, что четверть опрашиваемых выберут ответ «Да», то p будет равно 25%, то есть p = 0,25;
q = (1 – p);
e – допустимая ошибка, в долях.
Пример расчета объема выборки
Компания планирует провести социологическое исследование с целью выявить долю курящих лиц в населении города. Для этого сотрудники компании будут задавать прохожим один вопрос: «Вы курите?». Возможных вариантов ответа, таким образом, только два: «Да» и «Нет».
Объем выборки в этом случае рассчитывается следующим образом. Уровень доверительности принимается за 95%, тогда нормированное отклонение z = 1,96. Вариацию принимаем за 50%, то есть условно считаем, что половина респондентов может ответить на вопрос о том, курят ли они – «Да». Тогда p = 0,5. Отсюда находим q = 1 – p = 1 – 0,5 = 0,5. Допустимую ошибку выборки принимаем за 10%, то есть e = 0,1.
Подставляем эти данные в формулу и считаем:
Получаем объем выборки n = 96 человек.
Задачи о генеральной доле
На вопрос «Накрывает ли доверительный интервал заданное значение p0?» — можно ответить, проверив статистическую гипотезу H0:p=p0. При этом предполагается, что опыты проводятся по схеме испытаний Бернулли (независимы, вероятность p появления события А постоянна). По выборке объема n определяют относительную частоту p* появления события A: где m — количество появлений события А в серии из n испытаний. Для проверки гипотезы H0 используется статистика, имеющая при достаточно большом объеме выборки стандартное нормальное распределение (табл. 1).
Таблица 1 – Гипотезы о генеральной доле
|
Гипотеза |
H0:p=p0 | H0:p1=p2 |
| Предположения | Схема испытаний Бернулли | Схема испытаний Бернулли |
| Оценки по выборке |  |
|
| Статистика K |  |
 |
| Распределение статистики K | Стандартное нормальное N(0,1) | Стандартное нормальное N(0,1) |
Пример №1. С помощью случайного повторного отбора руководство фирмы провело выборочный опрос 900 своих служащих. Среди опрошенных оказалось 270 женщин. Постройте доверительный интервал, с вероятностью 0.95 накрывающий истинную долю женщин во всем коллективе фирмы.
Решение. По условию выборочная доля женщин составляет (относительная частота женщин среди всех опрошенных). Так как отбор является повторным, и объем выборки велик (n=900) предельная ошибка выборки определяется по формуле
(относительная частота женщин среди всех опрошенных). Так как отбор является повторным, и объем выборки велик (n=900) предельная ошибка выборки определяется по формуле
Значение uкр находим по таблице функции Лапласа из соотношения 2Ф(uкр)=γ, т.е. Функция Лапласа (приложение 1) принимает значение 0.475 при uкр=1.96. Следовательно, предельная ошибка
Функция Лапласа (приложение 1) принимает значение 0.475 при uкр=1.96. Следовательно, предельная ошибка и искомый доверительный интервал
(p – ε, p + ε) = (0.3 – 0.18; 0.3 + 0.18) = (0.12; 0.48)
Итак, с вероятностью 0.95 можно гарантировать, что доля женщин во всем коллективе фирмы находится в интервале от 0.12 до 0.48.
Пример №2. Владелец автостоянки считает день «удачным», если автостоянка заполнена более, чем на 80 %. В течение года было проведено 40 проверок автостоянки, из которых 24 оказались «удачными». С вероятностью 0.98 найдите доверительный интервал для оценки истинной доли «удачных» дней в течение года.
Решение. Выборочная доля «удачных» дней составляет
По таблице функции Лапласа найдем значение uкр при заданной
доверительной вероятности
По таблице функции Лапласа найдем значение uкр при заданной
доверительной вероятности
Ф(2.23) = 0.49, uкр = 2.33.
Считая отбор бесповторным (т.е. две проверки в один день не проводилось), найдем предельную ошибку:
где n=40, N = 365 (дней). Отсюда
где n=40, N = 365 (дней). Отсюда
и доверительный интервал для генеральной доли: (p – ε, p + ε) = (0.6 – 0.17; 0.6 + 0.17) = (0.43; 0.77)
С вероятностью 0.98 можно ожидать, что доля «удачных» дней в течение года находится в интервале от 0.43 до 0.77.
Пример №3. Проверив 2500 изделий в партии, обнаружили, что 400 изделий высшего сорта, а n–m – нет. Сколько надо проверить изделий, чтобы с уверенностью 95% определить долю высшего сорта с точностью до 0.01?
Решение ищем по формуле определения численности выборки для повторного отбора.
Ф(t) = γ/2 = 0.95/2 = 0.475 и этому значению по таблице Лапласа соответствует t=1.96
Выборочная доля w = 0.16; ошибка выборки ε = 0.01
Пример №4. Партия изделий принимается, если вероятность того, что изделие окажется соответствующим стандарту, составляет не менее 0.97. Среди случайно отобранных 200 изделий проверяемой партии оказалось 193 соответствующих стандарту. Можно ли на уровне значимости α=0,02 принять партию?
Решение. Сформулируем основную и альтернативную гипотезы.
H0:p=p0=0,97 — неизвестная генеральная доля p равна заданному значению p0=0,97. Применительно к условию — вероятность того, что деталь из проверяемой партии окажется соответствующей стандарту, равна 0.97; т.е. партию изделий можно принять.
H1:p<0,97 – вероятность того, что деталь из проверяемой партии окажется соответствующей стандарту, меньше 0.97; т.е. партию изделий нельзя принять. При такой альтернативной гипотезе критическая область будет левосторонней.
Наблюдаемое значение статистики K (таблица) вычислим при заданных значениях p0=0,97, n=200, m=193

Критическое значение находим по таблице функции Лапласа из равенства
По условию α=0,02 отсюда Ф(Ккр)=0,48 и Ккр=2,05. Критическая область левосторонняя, т.е. является интервалом (-∞;-Kkp)= (-∞;-2,05). Наблюдаемое значение Кнабл=-0,415 не принадлежит критической области, следовательно, на данном уровне значимости нет оснований отклонять основную гипотезу. Партию изделий принять можно.
Пример №5. Два завода изготавливают однотипные детали. Для оценки их качества сделаны выборки из продукции этих заводов и получены следующие результаты. Среди 200 отобранных изделий первого завода оказалось 20 бракованных, среди 300 изделий второго завода — 15 бракованных.
На уровне значимости 0.025 выяснить, имеется ли существенное различие в качестве изготавливаемых этими заводами деталей.
Решение. Это задача о сравнении генеральных долей двух совокупностей. Сформулируем основную и альтернативную гипотезы.
H0:p1=p2 — генеральные доли равны. Применительно к условию — вероятность появления бракованного изделия в продукции первого завода равна вероятности появления бракованного изделия в продукции второго завода (качество продукции одинаково).
H0:p1≠p2 — заводы изготавливают детали разного качества.
Для вычисления наблюдаемого значения статистики K (таблица) рассчитаем оценки по выборке.
Наблюдаемое значение равно

Так как альтернативная гипотеза двусторонняя, то критическое значение статистики K≈ N(0,1) находим по таблице функции Лапласа из равенства
Так как альтернативная гипотеза двусторонняя, то критическое значение статистики K≈ N(0,1) находим по таблице функции Лапласа из равенства
По условию α=0,025 отсюда Ф(Ккр)=0,4875 и Ккр=2,24. При двусторонней альтернативе область допустимых значений имеет вид (-2,24;2,24). Наблюдаемое значение Kнабл=2,15 попадает в этот интервал, т.е. на данном уровне значимости нет оснований отвергать основную гипотезу. Заводы изготавливают изделия одинакового качества.
По части судить о целом
О возможности судить о целом по части миру рассказал российский математик П.Л. Чебышев. «Закон больших чисел» простым языком можно сформулировать так: количественные закономерности массовых явлений проявляются только при
достаточном числе наблюдений
. Чем больше выборка, тем лучше случайные отклонения компенсируют друг друга и проявляется общая тенденция.
А.М. Ляпунов чуть позже сформулировал центральную предельную теорему. Она стала фундаментом для создания формул, которые позволяют рассчитать вероятность ошибки (при оценке среднего по выборке) и размер выборки, необходимый для достижения заданной точности.
Строгие формулировки:
С увеличением числа случайных величин их среднее арифметическое стремится к среднему арифметическому математических ожиданий и перестает быть случайным. Общий смысл закона больших чисел — совместное действие большого числа случайных факторов приводит к результату, почти не зависящему от случая.
Таким образом з.б.ч. гарантирует устойчивость для средних значений некоторых случайных событий при достаточно длинной серии экспериментов.
Распределение случайной величины, которая получена в результате сложения большого числа независимых случайных величин (ни одно из которых не доминирует, не вносит в сумму определяющего вклада и имеет дисперсию значительно меньшею по сравнению с дисперсией суммы) имеет распределение, близкое к нормальному.
Из ц.п.т. следует, что ошибки выборки также подчиняется нормальному распределению.
Еще раз: чтобы корректно оценивать популяцию по выборке, нам нужна не обычная выборка, а репрезентативная выборка достаточного размера. Начнем с определения этого самого размера.
Как рассчитать объем выборки
Достаточный размер выборки зависит от следующих составляющих:
- изменчивость признака (чем разнообразней показания, тем больше наблюдений нужно, чтобы это уловить);
- размер эффекта (чем меньшие эффекты мы стремимся зафиксировать, тем больше наблюдений необходимо);
- уровень доверия (уровень вероятности при который мы готовы отвергнуть нулевую гипотезу)
ЗАПОМНИТЕ
Объем выборки зависит от изменчивости признака и планируемой строгости эксперимента
Формулы для расчета объема выборки:
Формулы расчета объема выборки
Ошибка выборки значительно возрастает, когда наблюдений меньше ста. Для исследований в которых используется 30-100 объектов применяется особая статистическая методология: критерии, основанные на распределении Стьюдента или бутстрэп-анализ. И наконец, статистика совсем слаба, когда наблюдений меньше 30.
График зависимости ошибки выборки от ее объема при оценке доли признака в г.с.
Чем больше неопределенность, тем больше ошибка. Максимальная неопределенность при оценке доли — 50% (например, 50% респондентов считают концепцию хорошей, а другие 50% плохой). Если 90% опрошенных концепция понравится — это, наоборот, пример согласованности. В таких случаях оценить долю признака по выборке проще.
Для экспонирования и выделения цветом значений статистических выбросов от медианы можно использовать несколько простых формул и условное форматирование.
Первым шагом в поиске значений выбросов статистики является определение статистического центра диапазона данных. С этой целью необходимо сначала определить границы первого и третьего квартала. Определение границ квартала – значит разделение данных на 4 равные группы, которые содержат по 25% данных каждая. Группа, содержащая 25% наибольших значений, называется первым квартилем.
Границы квартилей в Excel можно легко определить с помощью простой функции КВАРТИЛЬ. Данная функция имеет 2 аргумента: диапазон данных и номер для получения желаемого квартиля.
В примере показанному на рисунке ниже значения в ячейках E1 и E2 содержат показатели первого и третьего квартиля данных в диапазоне ячеек B2:B19:

Вычитая от значения первого квартиля третьего, можно определить набор 50% статистических данных, который называется межквартильным диапазоном. В ячейке E3 определен размер межквартильного диапазона.
В этом месте возникает вопрос, как сильно данное значение может отличаться от среднего значения 50% данных и оставаться все еще в пределах нормы? Статистические аналитики соглашаются с тем, что для определения нижней и верхней границы диапазона данных можно смело использовать коэффициент расширения 1,5 умножив на значение межквартильного диапазона. То есть:
- Нижняя граница диапазона данных равна: значение первого квартиля – межкваритльный диапазон * 1,5.
- Верхняя граница диапазона данных равна: значение третьего квартиля + расширенных диапазон * 1,5.
Как показано на рисунке ячейки E5 и E6 содержат вычисленные значения верхней и нижней границы диапазона данных. Каждое значение, которое больше верхней границы нормы или меньше нижней границы нормы считается значением статистического выброса.
Чтобы выделить цветом для улучшения визуального анализа данных можно создать простое правило для условного форматирования.
Способ 1: применение расширенного автофильтра
Наиболее простым способом произвести отбор является применение расширенного автофильтра. Рассмотрим, как это сделать на конкретном примере.
- Выделяем область на листе, среди данных которой нужно произвести выборку. Во вкладке «Главная» щелкаем по кнопке «Сортировка и фильтр». Она размещается в блоке настроек «Редактирование». В открывшемся после этого списка выполняем щелчок по кнопке «Фильтр».
Есть возможность поступить и по-другому. Для этого после выделения области на листе перемещаемся во вкладку «Данные». Щелкаем по кнопке «Фильтр», которая размещена на ленте в группе «Сортировка и фильтр».
- После этого действия в шапке таблицы появляются пиктограммы для запуска фильтрования в виде перевернутых острием вниз небольших треугольников на правом краю ячеек. Кликаем по данному значку в заглавии того столбца, по которому желаем произвести выборку. В запустившемся меню переходим по пункту «Текстовые фильтры». Далее выбираем позицию «Настраиваемый фильтр…».
- Активируется окно пользовательской фильтрации. В нем можно задать ограничение, по которому будет производиться отбор. В выпадающем списке для столбца содержащего ячейки числового формата, который мы используем для примера, можно выбрать одно из пяти видов условий:
- равно;
- не равно;
- больше;
- больше или равно;
- меньше.
Давайте в качестве примера зададим условие так, чтобы отобрать только значения, по которым сумма выручки превышает 10000 рублей. Устанавливаем переключатель в позицию «Больше». В правое поле вписываем значение «10000». Чтобы произвести выполнение действия, щелкаем по кнопке «OK».
- Как видим, после фильтрации остались только строчки, в которых сумма выручки превышает 10000 рублей.
- Но в этом же столбце мы можем добавить и второе условие. Для этого опять возвращаемся в окно пользовательской фильтрации. Как видим, в его нижней части есть ещё один переключатель условия и соответствующее ему поле для ввода. Давайте установим теперь верхнюю границу отбора в 15000 рублей. Для этого выставляем переключатель в позицию «Меньше», а в поле справа вписываем значение «15000».
Кроме того, существует ещё переключатель условий. У него два положения «И» и «ИЛИ». По умолчанию он установлен в первом положении. Это означает, что в выборке останутся только строчки, которые удовлетворяют обоим ограничениям. Если он будет выставлен в положение «ИЛИ», то тогда останутся значения, которые подходят под любое из двух условий. В нашем случае нужно выставить переключатель в положение «И», то есть, оставить данную настройку по умолчанию. После того, как все значения введены, щелкаем по кнопке «OK».
- Теперь в таблице остались только строчки, в которых сумма выручки не меньше 10000 рублей, но не превышает 15000 рублей.
- Аналогично можно настраивать фильтры и в других столбцах. При этом имеется возможность сохранять также фильтрацию и по предыдущим условиям, которые были заданы в колонках. Итак, посмотрим, как производится отбор с помощью фильтра для ячеек в формате даты. Кликаем по значку фильтрации в соответствующем столбце. Последовательно кликаем по пунктам списка «Фильтр по дате» и «Настраиваемый фильтр».
- Снова запускается окно пользовательского автофильтра. Выполним отбор результатов в таблице с 4 по 6 мая 2016 года включительно. В переключателе выбора условий, как видим, ещё больше вариантов, чем для числового формата. Выбираем позицию «После или равно». В поле справа устанавливаем значение «04.05.2016». В нижнем блоке устанавливаем переключатель в позицию «До или равно». В правом поле вписываем значение «06.05.2016». Переключатель совместимости условий оставляем в положении по умолчанию – «И». Для того, чтобы применить фильтрацию в действии, жмем на кнопку «OK».
- Как видим, наш список ещё больше сократился. Теперь в нем оставлены только строчки, в которых сумма выручки варьируется от 10000 до 15000 рублей за период с 04.05 по 06.05.2016 включительно.
- Мы можем сбросить фильтрацию в одном из столбцов. Сделаем это для значений выручки. Кликаем по значку автофильтра в соответствующем столбце. В выпадающем списке щелкаем по пункту «Удалить фильтр».
- Как видим, после этих действий, выборка по сумме выручки будет отключена, а останется только отбор по датам (с 04.05.2016 по 06.05.2016).
- В данной таблице имеется ещё одна колонка – «Наименование». В ней содержатся данные в текстовом формате. Посмотрим, как сформировать выборку с помощью фильтрации по этим значениям.
Кликаем по значку фильтра в наименовании столбца. Последовательно переходим по наименованиям списка «Текстовые фильтры» и «Настраиваемый фильтр…».
- Опять открывается окно пользовательского автофильтра. Давайте сделаем выборку по наименованиям «Картофель» и «Мясо». В первом блоке переключатель условий устанавливаем в позицию «Равно». В поле справа от него вписываем слово «Картофель». Переключатель нижнего блока так же ставим в позицию «Равно». В поле напротив него делаем запись – «Мясо». И вот далее мы выполняем то, чего ранее не делали: устанавливаем переключатель совместимости условий в позицию «ИЛИ». Теперь строчка, содержащая любое из указанных условий, будет выводиться на экран. Щелкаем по кнопке «OK».
- Как видим, в новой выборке существуют ограничения по дате (с 04.05.2016 по 06.05.2016) и по наименованию (картофель и мясо). По сумме выручки ограничений нет.
- Полностью удалить фильтр можно теми же способами, которые использовались для его установки. Причем неважно, какой именно способ применялся. Для сброса фильтрации, находясь во вкладке «Данные» щелкаем по кнопке «Фильтр», которая размещена в группе «Сортировка и фильтр».
Второй вариант предполагает переход во вкладку «Главная». Там выполняем щелчок на ленте по кнопке «Сортировка и фильтр» в блоке «Редактирование». В активировавшемся списке нажимаем на кнопку «Фильтр».
При использовании любого из двух вышеуказанных методов фильтрация будет удалена, а результаты выборки – очищены. То есть, в таблице будет показан весь массив данных, которыми она располагает.
Способ 2: применение формулы массива
Сделать отбор можно также применив сложную формулу массива. В отличие от предыдущего варианта, данный метод предусматривает вывод результата в отдельную таблицу.
- На том же листе создаем пустую таблицу с такими же наименованиями столбцов в шапке, что и у исходника.
- Выделяем все пустые ячейки первой колонки новой таблицы. Устанавливаем курсор в строку формул. Как раз сюда будет заноситься формула, производящая выборку по указанным критериям. Отберем строчки, сумма выручки в которых превышает 15000 рублей. В нашем конкретном примере, вводимая формула будет выглядеть следующим образом:
=ИНДЕКС(A2:A29;НАИМЕНЬШИЙ(ЕСЛИ(15000<=C2:C29;СТРОКА(C2:C29);"");СТРОКА()-СТРОКА($C$1))-СТРОКА($C$1))Естественно, в каждом конкретном случае адрес ячеек и диапазонов будет свой. На данном примере можно сопоставить формулу с координатами на иллюстрации и приспособить её для своих нужд.
- Так как это формула массива, то для того, чтобы применить её в действии, нужно нажимать не кнопку Enter, а сочетание клавиш Ctrl+Shift+Enter. Делаем это.
- Выделив второй столбец с датами и установив курсор в строку формул, вводим следующее выражение:
=ИНДЕКС(B2:B29;НАИМЕНЬШИЙ(ЕСЛИ(15000<=C2:C29;СТРОКА(C2:C29);"");СТРОКА()-СТРОКА($C$1))-СТРОКА($C$1))Жмем сочетание клавиш Ctrl+Shift+Enter.
- Аналогичным образом в столбец с выручкой вписываем формулу следующего содержания:
=ИНДЕКС(C2:C29;НАИМЕНЬШИЙ(ЕСЛИ(15000<=C2:C29;СТРОКА(C2:C29);"");СТРОКА()-СТРОКА($C$1))-СТРОКА($C$1))Опять набираем сочетание клавиш Ctrl+Shift+Enter.
Во всех трех случаях меняется только первое значение координат, а в остальном формулы полностью идентичны.
- Как видим, таблица заполнена данными, но внешний вид её не совсем привлекателен, к тому же, значения даты заполнены в ней некорректно. Нужно исправить эти недостатки. Некорректность даты связана с тем, что формат ячеек соответствующего столбца общий, а нам нужно установить формат даты. Выделяем весь столбец, включая ячейки с ошибками, и кликаем по выделению правой кнопкой мыши. В появившемся списке переходим по пункту «Формат ячейки…».
- В открывшемся окне форматирования открываем вкладку «Число». В блоке «Числовые форматы» выделяем значение «Дата». В правой части окна можно выбрать желаемый тип отображения даты. После того, как настройки выставлены, жмем на кнопку «OK».
- Теперь дата отображается корректно. Но, как видим, вся нижняя часть таблицы заполнена ячейками, которые содержат ошибочное значение «#ЧИСЛО!». По сути, это те ячейки, данных из выборки для которых не хватило. Более привлекательно было бы, если бы они отображались вообще пустыми. Для этих целей воспользуемся условным форматированием. Выделяем все ячейки таблицы, кроме шапки. Находясь во вкладке «Главная» кликаем по кнопке «Условное форматирование», которая находится в блоке инструментов «Стили». В появившемся списке выбираем пункт «Создать правило…».
- В открывшемся окне выбираем тип правила «Форматировать только ячейки, которые содержат». В первом поле под надписью «Форматировать только ячейки, для которых выполняется следующее условие» выбираем позицию «Ошибки». Далее жмем по кнопке «Формат…».
- В запустившемся окне форматирования переходим во вкладку «Шрифт» и в соответствующем поле выбираем белый цвет. После этих действий щелкаем по кнопке «OK».
- На кнопку с точно таким же названием жмем после возвращения в окно создания условий.
Теперь у нас имеется готовая выборка по указанному ограничению в отдельной надлежащим образом оформленной таблице.
СРЗНАЧ()
Статистическая функция СРЗНАЧ возвращает среднее арифметическое своих аргументов.
Данная функция может принимать до 255 аргументов и находить среднее сразу в нескольких несмежных диапазонах и ячейках:
Если в рассчитываемом диапазоне встречаются пустые или содержащие текст ячейки, то они игнорируются. В примере ниже среднее ищется по четырем ячейкам, т.е. (4+15+11+22)/4 = 13
Если необходимо вычислить среднее, учитывая все ячейки диапазона, то можно воспользоваться статистической функцией СРЗНАЧА. В следующем примере среднее ищется уже по 6 ячейкам, т.е. (4+15+11+22)/6 = 8,6(6).
Статистическая функция СРЗНАЧ может использовать в качестве своих аргументов математические операторы и различные функции Excel:
СРЗНАЧЕСЛИ()
Если необходимо вернуть среднее арифметическое значений, которые удовлетворяют определенному условию, то можно воспользоваться статистической функцией СРЗНАЧЕСЛИ. Следующая формула вычисляет среднее чисел, которые больше нуля:
В данном примере для подсчета среднего и проверки условия используется один и тот же диапазон, что не всегда удобно. На этот случай у функции СРЗНАЧЕСЛИ существует третий необязательный аргумент, по которому можно вычислять среднее. Т.е. по первому аргументу проверяем условие, по третьему – находим среднее.
Допустим, в таблице ниже собрана статистика по стоимости лекарств в городе. В одной аптеке лекарство стоит дороже, в другой дешевле. Чтобы посчитать стоимость анальгина в среднем по городу, воспользуемся следующей формулой:
Если требуется соблюсти несколько условий, то всегда можно применить статистическую функцию СРЗНАЧЕСЛИМН, которая позволяет считать среднее арифметическое ячеек, удовлетворяющих двум и более критериям.
МАКС()
Статистическая функция МАКС возвращает наибольшее значение в диапазоне ячеек:
МИН()
Статистическая функция МИН возвращает наименьшее значение в диапазоне ячеек:
Источники
- https://lumpics.ru/descriptive-statistics-in-excel/
- https://statanaliz.info/statistica/opisanie-dannyx/variatsiya-razmakh-srednee-linejnoe-otklonenie/
- https://www.hd01.ru/info/kak-poschitat-razmah-v-excel/
- http://galyautdinov.ru/post/formula-vyborki-prostaya
- https://math.semestr.ru/group/interval-estimation-share.php
- https://tidydata.ru/sample-size
- https://exceltable.com/formuly/raschet-statisticheskih-vybrosov
- https://lumpics.ru/how-to-make-a-sample-in-excel/
- https://office-guru.ru/excel/statisticheskie-funkcii-excel-kotorye-neobhodimo-znat-96.html
Содержание
- 1 Использование описательной статистики
- 1.1 Подключение «Пакета анализа»
- 1.2 Применение инструмента «Описательная статистика»
- 1.3 Помогла ли вам эта статья?
- 1.4 Статистические процедуры Пакета анализа
- 1.5 Статистические функции библиотеки встроенных функций Excel
Пользователи Эксель знают, что данная программа имеет очень широкий набор статистических функций, по уровню которых она вполне может потягаться со специализированными приложениями. Но кроме того, у Excel имеется инструмент, с помощью которого производится обработка данных по целому ряду основных статистических показателей буквально в один клик.
Этот инструмент называется «Описательная статистика». С его помощью можно в очень короткие сроки, использовав ресурсы программы, обработать массив данных и получить о нем информацию по целому ряду статистических критериев. Давайте взглянем, как работает данный инструмент, и остановимся на некоторых нюансах работы с ним.
Использование описательной статистики
Под описательной статистикой понимают систематизацию эмпирических данных по целому ряду основных статистических критериев. Причем на основе полученного результата из этих итоговых показателей можно сформировать общие выводы об изучаемом массиве данных.
В Экселе существует отдельный инструмент, входящий в «Пакет анализа», с помощью которого можно провести данный вид обработки данных. Он так и называется «Описательная статистика». Среди критериев, которые высчитывает данный инструмент следующие показатели:
- Медиана;
- Мода;
- Дисперсия;
- Среднее;
- Стандартное отклонение;
- Стандартная ошибка;
- Асимметричность и др.
Рассмотрим, как работает данный инструмент на примере Excel 2010, хотя данный алгоритм применим также в Excel 2007 и в более поздних версиях данной программы.
Подключение «Пакета анализа»
Как уже было сказано выше, инструмент «Описательная статистика» входит в более широкий набор функций, который принято называть Пакет анализа. Но дело в том, что по умолчанию данная надстройка в Экселе отключена. Поэтому, если вы до сих пор её не включили, то для использования возможностей описательной статистики, придется это сделать.
- Переходим во вкладку «Файл». Далее производим перемещение в пункт «Параметры».
- В активировавшемся окне параметров перемещаемся в подраздел «Надстройки». В самой нижней части окна находится поле «Управление». Нужно в нем переставить переключатель в позицию «Надстройки Excel», если он находится в другом положении. Вслед за этим жмем на кнопку «Перейти…».
- Запускается окно стандартных надстроек Excel. Около наименования «Пакет анализа» ставим флажок. Затем жмем на кнопку «OK».
После вышеуказанных действий надстройка Пакет анализа будет активирована и станет доступной во вкладке «Данные» Эксель. Теперь мы сможем использовать на практике инструменты описательной статистики.
Применение инструмента «Описательная статистика»
Теперь посмотрим, как инструмент описательная статистика можно применить на практике. Для этих целей используем готовую таблицу.
- Переходим во вкладку «Данные» и выполняем щелчок по кнопке «Анализ данных», которая размещена на ленте в блоке инструментов «Анализ».
- Открывается список инструментов, представленных в Пакете анализа. Ищем наименование «Описательная статистика», выделяем его и щелкаем по кнопке «OK».
- После выполнения данных действий непосредственно запускается окно «Описательная статистика».
В поле «Входной интервал» указываем адрес диапазона, который будет подвергаться обработке этим инструментом. Причем указываем его вместе с шапкой таблицы. Для того, чтобы внести нужные нам координаты, устанавливаем курсор в указанное поле. Затем, зажав левую кнопку мыши, выделяем на листе соответствующую табличную область. Как видим, её координаты тут же отобразятся в поле. Так как мы захватили данные вместе с шапкой, то около параметра «Метки в первой строке» следует установить флажок. Тут же выбираем тип группирования, переставив переключатель в позицию «По столбцам» или «По строкам». В нашем случае подходит вариант «По столбцам», но в других случаях, возможно, придется выставить переключатель иначе.
Выше мы говорили исключительно о входных данных. Теперь переходим к разбору настроек параметров вывода, которые расположены в этом же окне формирования описательной статистики. Прежде всего, нам нужно определиться, куда именно будут выводиться обработанные данные:
- Выходной интервал;
- Новый рабочий лист;
- Новая рабочая книга.
В первом случае нужно указать конкретный диапазон на текущем листе или его верхнюю левую ячейку, куда будет выводиться обработанная информация. Во втором случае следует указать название конкретного листа данной книги, где будет отображаться результат обработки. Если листа с таким наименованием в данный момент нет, то он будет создан автоматически после того, как вы нажмете на кнопку «OK». В третьем случае никаких дополнительных параметров указывать не нужно, так как данные будут выводиться в отдельном файле Excel (книге). Мы выбираем вывод результатов на новом рабочем листе под названием «Итоги».
Далее, если вы хотите чтобы выводилась также итоговая статистика, то нужно установить флажок около соответствующего пункта. Также можно установить уровень надежности, поставив галочку около соответствующего значения. По умолчанию он будет равен 95%, но его можно изменить, внеся другие числа в поле справа.
Кроме этого, можно установить галочки в пунктах «K-ый наименьший» и «K-ый наибольший», установив значения в соответствующих полях. Но в нашем случае этот параметр так же, как и предыдущий, не является обязательным, поэтому флажки мы не ставим.
После того, как все указанные данные внесены, жмем на кнопку «OK».
- После выполнения этих действий таблица с описательной статистикой выводится на отдельном листе, который был нами назван «Итоги». Как видим, данные представлены сумбурно, поэтому их следует отредактировать, расширив соответствующие колонки для более удобного просмотра.
- После того, как данные «причесаны» можно приступать к их непосредственному анализу. Как видим, при помощи инструмента описательной статистики были рассчитаны следующие показатели:
- Асимметричность;
- Интервал;
- Минимум;
- Стандартное отклонение;
- Дисперсия выборки;
- Максимум;
- Сумма;
- Эксцесс;
- Среднее;
- Стандартная ошибка;
- Медиана;
- Мода;
- Счет.
Если какие-то из вышеуказанных данных для конкретного вида анализа не нужны, то их можно удалить, чтобы они не мешали. Далее производится анализ с учетом статистических закономерностей.
Урок: Статистические функции в Excel
Как видим, с помощью инструмента «Описательная статистика» можно сразу получить результат по целому ряду критериев, которые в ином случае рассчитывались с применением отдельно предназначенной для каждого расчета функцией, что заняло бы значительное время у пользователя. А так, все эти расчеты можно получить практически в один клик, использовав соответствующий инструмент — Пакета анализа.
Мы рады, что смогли помочь Вам в решении проблемы.
Задайте свой вопрос в комментариях, подробно расписав суть проблемы. Наши специалисты постараются ответить максимально быстро.
Помогла ли вам эта статья?
Да Нет
Сортировка данных в Excel
Таблицы Excel можно использовать для создания баз данных, т.е. совокупности определенным образом организованной информации. В таблицах хранят информацию о сотрудниках, клиентах, поставщиках различной продукции, ценах, книгах, фильмах, фотографиях и т.д. Как правило, для таких баз данных используется табличный способ организации. Они содержат большое количество данных, а с большим количеством данных не всегда просто работать. Для этого и необходима обработка данных.
- сортировку списков;
- выборку данных по определенным критериям;
- вычисление промежуточных сумм;
- вычисление средних значений;
- вычисление отклонений от определенного значения;
- построение сводных таблиц.
Как сделать фильтр в Excel
Базы данных очень удобны для хранения информации, но мы создаем их для того, чтобы получать нужную для нас справку, когда возникает подобная необходимость.
Например, нам нужно расписание железнодорожных поездов, которые отправляются в Москву в пятницу после четырех часов дня и т.п.
Поиск нужной информации осуществляется путем отбора строк, удовлетворяющих некоторому критерию. В большинстве случаев критерием отбора является равенство содержимого ячейки определенному значению.
Помимо сравнения на равенство, при отборе записей можно использовать и другие операции сравнения. Например, больше, меньше, больше или равно, меньше или равно. Использование этих операций позволяет сформулировать критерий запроса менее строго. Например, если требуется найти информацию о человеке, фамилия которого начинается с «Ку», то в качестве критерия можно использовать правило «содержимое ячейки Фамилия больше или равно Ку и содержимое ячейки Фамилия меньше Л».
Промежуточные итоги в Excel
Одним из методов обработки данных является подведение итогов. Пусть, например, есть таблица расходов. Для того чтобы узнать, сколько потрачено в каждом месяце, необходимо подвести итог за каждый месяц.
- 1. Выделить диапазон, содержащий данные и заголовки столбцов, в которых данные находятся. В рассматриваемом примере это вся таблица, на фото представлена только ее часть.
- 2. На вкладке Данные -> Структура выбрать команду Промежуточный итог.
- 3. В появившемся диалоговом окне Промежуточные итоги в поле — При каждом изменении в:, требуется задать столбец, при изменении содержимого которого будет вычислена промежуточная сумма. В данном случае это Дата. В поле Операция выбрать операцию из списка, которую нужно выполнить над обрабатываемыми данными. В нашем случае это Сумма. В поле — Добавить итоги по:, установить флажок в том столбце, в котором находятся обрабатываемые данные.
Сводные таблицы Excel 2010
Сводная таблица позволяет выполнить более тонкий анализ данных, чем простое подведение итога. Что такое сводная таблица и как ее построить, рассмотрим на примере.
Пусть есть таблица, в которой находится информация о расходах.
Основными средствами анализа статистических данных в Excel являются статистические процедуры надстройки Пакет анализа (Analysis ToolРак) и статистические функции библиотеки встроенных функций. Основные сведения обо всех этих средствах имеются в электронной справочной системе Excel.
Однако качество описаний статистических процедур и функций, приведенных в этой системе, заставляет желать лучшего. Некоторые из этих описаний не очень понятны, в них имеются неточности, а подчас и просто ошибки (это относится как к англоязычному оригиналу, так и к русскому переводу). Эти недостатки с завидным постоянством повторяются и во многих пособиях по Excel. Найти необходимые пособия в интернете можно быстро если скачать бесплатно Амиго браузер с усовершенствованным поисковым алгоритмом.
Статистические процедуры Пакета анализа
Наиболее развитыми средствами анализа данных являются статистические процедуры Пакета анализа. Они обладают большими возможностями, чем статистические функции. С их помощью можно решать более сложные задачи обработки статистических данных и выполнять более тонкий анализ этих данных.
В Пакет анализа входят следующие статистические процедуры:
- генерация случайных чисел (Random number generation);
- выборка (Sampling);
- гистограмма (Histogram);
- описательная статистика (Descriptive statistics);
- ранги персентиль (Rank and percentile);
- двухвыборочный z-тест для средних (z-Test: Two Sample for Means);
- двухвыборочный t-тест для средних с одинаковыми дисперсиями (t-Test: Two-Sample Assuming Equal Variances);
- двухвыборочный t-тест для средних с различными дисперсиями (t-Test: Two-Sample Assuming Unequal Variances);
- парный двухвыборочный t-тест для средних (t-Test: Paired Two Sample for Means);
- двухвыборочный F-тест да я дисперсий (F-Test: Two Sample for Variances);
- коварнация (Covariance);
- корреляция (Correlation);
- рецессия (Regression);
- однофакторный дисперсионный анализ (ANOVA: Single Factor);
- двухфакторный дисперсионный анализ без повторений (ANOVA: Two Factor Without Replication);
- двухфакторный дисперсионный анализ с повторениями (ANOVA: Two Factor With Replication);
- скользящее среднее (Moving Average);
- экспоненциальное сглаживание (Exponential Smoothing);
- анализ Фурье (Fourier Analysis).
Для доступа к процедурам Пакета анализа необходимо в меню Сервис (Tools) щелкнуть указателем мыши на строке Анализ данных (Data Analysis). Откроется диалоговое окно с соответствующим названием, в котором перечислены процедуры статистического анализа данных (рис. 1).
Рис.1. Диалоговое окно Анализ данных
Для того чтобы запустить в работу нужную статистическую процедуру, нужно выделить ее указателем мыши и щелкнуть на кнопке ОК. На экране появится диалоговое окно вызванной процедуры. На рис. 2 для примера показано диалоговое окно процедуры Описательная статистика (Descriptive statistics).
Рис.2. Диалоговое окно процедуры Описательная статистика
Диалоговое окно каждой процедуры содержит элементы управления: поля ввода, раскрывающиеся списки, переключатели, флажки и т. п. Эти элементы позволяют задать нужные параметры используемой процедуры. Некоторые элементы управления имеют специфический характер, присущий одной процедуре или небольшой группе процедур. Назначение таких элементов управления будет рассмотрено при описании соответствующих процедур. Другие элементы управления присутствуют в диалоговых окнах почти всех статистических процедур.
К числу общих для большинства процедур элементов управления относятся:
- поле ввода Входной интервал (Input Range). В это поле вводится ссылка на диапазон, содержащий статистические данные, подлежащие обработке. Входной диапазон может быть столбцом пли группой столбцов (строкой или группой строк);
- переключатель Группирование (Grouped By). В том случае, когда входной диапазон представляет собой столбец или группу столбцов, переключатель устанавливается в положение по столбцам (Columns). Если же входной диапазон представляет собой строку или группу строк, то переключатель устанавливается в положение по строкам (Rows). Более точным названием этого переключателя было бы название Расположение;
- флажок Метки (Labels in First Row). Флажок устанавливается в тех случаях, когда первая строка (первый столбец) входного диапазона содержит заголовки. Если такие заголовки отсутствуют, флажок Метки не устанавливают. При этом Excel автоматически создает и выводит на экран стандартные названия для данных выходного диапазона (Столбец1, Столбец2,… или Строка 1. Строка2,…);
- переключатели Выходной интервал/Новый рабочий лист/Новая книга (Output Range/New Worksheet/New Workbook). Эти переключатели определяют место вывода таблицы, содержащей результаты реализации статистической процедуры. В группе может быть выбран только одни переключатель.
При выборе переключателя Выходной интервал таблица результатов решения выводится на тот же рабочий лист, на котором находятся исходные данные. Справа от переключателя открывается поле ввода, в которое надо ввести ссылку на левую верхнюю ячейку таблицы результатов. Если возникает опасность наложения таблицы результатов на уже заполненные ячейки, на экране появляется сообщение о такой опасности. В ответ на это сообщение пользователь должен разрешить удаление старых данных и вывод на их место новых.
В положении Новый рабочий лист открывается новый лист рабочей книги. На этот лист, начиная с ячейки А1, и выводится таблица результатов решения. Справа от переключателя имеется поле ввода, в которое в случае необходимости можно ввести имя нового рабочего листа. При выборе переключателя Новая рабочая книга открывается новая рабочая книга. На первый лист этой новой книги, начиная с ячейки А1, выводится таблица результатов решения.
Следует заметить, что результаты;, получаемые с помощью статистических процедур Пакета анализа, не имеют постоянной связи с исходными данными — в случае изменения исходных данных результаты решения автоматически не изменяются. В том случае, когда необходимо получить результаты, автоматически изменяющиеся вместе с исходными данными, нужно использовать подходящие статистические функции библиотеки встроенных функций.
Эффективным и очень удобным в использовании средством парного регрессионного анализа и анализа временных рядов является процедура Добавить линию тренда (Add Trendline), входящая в комплекс графических средств Excel.
Статистические функции библиотеки встроенных функций Excel
Табличный процессор Excel имеет библиотеку встроенных функции рабочего листа (Worksheet function). Одним из разделов этой библиотеки является раздел Статистические функции. В этот раздел входят 83 функции, предназначенные для решения некоторых наиболее востребованных задач теории вероятностей и математической статистики.
Аргументы статистических функций должны быть числами или ссылками на диапазоны, которые содержат числа Если аргумент, который является массивом или ссылкой, содержит тексты, логические значения или пустые ячейки, то такие значения игнорируются, однако ячейки с нулевыми значениями учитываются.
Когда в качестве какого-либо аргумента встроенной статистической функции введен текст, функция выдает сообщение об ошибке #ЗНАЧ! (#VALUE!). Если в качестве аргумента, который по определению должен быть целым числом, введено число не целое, Excel использует в качестве аргумента целую часть этот числа. Никакие сообщения об этом «несанкционированном округлении» на экран не выводятся.
Сводные таблицы
- Подробности
- Создано 27 Апрель 2011
| Содержание |
|---|
| Термины многомерного анализа данных |
| Многомерные данные, измерения |
| OLAP |
| Виртуальный куб данных |
| Сводная таблица |
| Редактирование сводных таблиц |
| Подготовка многомерных данных |
| От автофильтра к сводному отчету |
| Свойства и форматирование |
| Сводная диаграмма |
| Доступ к внешним данным |
Первый интерфейс сводных таблиц, называемых также сводными отчеты, был включен в состав Excel еще в 1993м году (версии Excel 5.0). Несмотря на множество полезных функциональных возможностей, он практически не применяется в работе большинством пользователей Excel. Даже опытные пользователи зачастую подразумевают под термином «сводный отчет» нечто построенное с помощью сложных формул. Попробуем популяризировать использование сводных таблиц в повседневной работе экономистов. В статье обсуждаются теоретические основы создания сводных отчетов, даются практические рекомендации по их использованию, а также приводится пример доступа к данным на основе нескольких таблиц.
Термины многомерного анализа данных
Большинство экономистов слышали термины «многомерные данные», «виртуальный куб», «OLAP-технологии» и т.п. Но при детальном разговоре обычно выясняется, что почти все не очень представляют, о чем идет речь. То есть люди подразумевают нечто сложное и обычно не имеющее отношение к их повседневной деятельности. На самом деле это не так.
Многомерные данные, измерения
Можно с уверенностью утверждать, что экономисты практически постоянно сталкиваются с многомерными данными, но пытаются представить их в предопределенном виде с помощью электронных таблиц. Под многомерностью здесь подразумевается возможность ввода, просмотра или анализа одной и той же информации с изменением внешнего вида, применением различных группировок и сортировок данных. Например, план продаж можно проанализировать по следующим критериям:
- виды или группы товаров;
- бренды или категории товаров;
- периоды (месяц, квартал, год);
- покупатели или группы покупателей;
- регионы продаж
- и т.п.
Каждый из приведенных критериев в терминах многомерного анализа данных называется «измерением». Можно сказать, что измерение характеризует информацию по определенному набору значений. Специальным типом измерения многомерной информации являются «данные». В нашем примере данными плана продаж могут являться:
- объем продаж;
- цена продажи;
- индивидуальная скидка
- и т.п.
Теоретически данные могут также являться стандартным измерением многомерной информации (например, можно сгруппировать данные по цене продажи), но обычно все-таки данные являются специальным типом значений.
Таким образом, можно сказать, что в практической работе экономисты используются два типа информации: многомерные данные (фактические и плановые числа, имеющие множество признаков) и справочники (характеристики или измерения данных).
OLAP
Аббревиатура OLAP (online analytical processing) в дословном переводе звучит как «аналитическая обработка в реальном времени». Определение не очень конкретное, под него можно подвести практически любой отчет любого программного продукта. По смыслу OLAP подразумевает технологию работы со специальными отчетами, включая программное обеспечение, для получения и анализа как раз многомерных структурированных данных. Одним из популярных программных продуктов, реализующих OLAP-технологии, является SQL Server Analysis Server. Некоторые даже ошибочно считают его единственным представителем программной реализации данной концепции.
Виртуальный куб данных
«Виртуальный куб» (многомерный куб, OLAP-куб) — это специальный термин, предложенный некоторыми поставщиками специализированного программного обеспечения. OLAP-системы обычно готовят и хранят данные в собственных структурах, а специальные интерфейсы анализа (например, сводные отчеты Excel) обращаются к данным этих виртуальных кубов. При этом использование подобного выделенного хранилища совсем не обязательно для обработки многомерной информации. В общем случае, виртуальный куб – это и есть массив специально оптимизированных многомерных данных, который используется для создания сводных отчетов. Он может быть получен как через специализированные программные средства, так и через простой доступ к таблицам базы данных или любой другой источник, например к таблице Excel.
Сводная таблица
«Сводный отчет» (сводная таблица, Pivot Table) — это пользовательский интерфейс для отображения многомерных данных. С помощью данного интерфейса можно группировать, сортировать, фильтровать и менять расположение данных с целью получения различных аналитических выборок. Обновление отчета производится простыми средствами пользовательского интерфейса, данные автоматически агрегируются по заданным правилам, при этом не требуется дополнительный или повторный ввод какой-либо информации. Интерфейс сводных таблиц Excel является, пожалуй, самым популярным программным продуктом для работы с многомерными данными. Он поддерживает в качестве источника данных как внешние источники данных (OLAP-кубам и реляционным базам данных), так и внутренние диапазоны электронных таблиц. Начиная с версии 2000 (9.0), Excel поддерживает также графическую форму отображения многомерных данных – сводная диаграмма (Pivot Chart).
Реализованный в Excel интерфейс сводных таблиц позволяет расположить измерения многомерных данных в области рабочего листа. Для простоты можно представлять себе сводную таблицу, как отчет, лежащий сверху диапазона ячеек (на самом деле есть определенная привязка форматов ячеек к полям сводной таблицы). Сводная таблица Excel имеет четыре области отображения информации: фильтр, столбцы, строки и данные. Измерения данных именуются полями сводной таблицы. Эти поля имеют собственные свойства и формат отображения.
Еще раз хочется обратить внимание, что сводная таблица Excel предназначена исключительно для анализа данных без возможности редактирования информации. Ближе по смыслу было бы повсеместное употребление термина «сводный отчет» (Pivot Report), и именно так этот интерфейс и назывался до 2000го года. Но почему-то в последующих версиях разработчики от него отказались.
Редактирование сводных таблиц
По своему определению OLAP-технология, в принципе, не подразумевает возможность изменения исходных данных при работе с отчетами. Тем не менее, на рынке сформировался целый класс программных систем, реализующих возможности как анализа, так и непосредственного редактирования данных в многомерных таблицах. В основном такие системы ориентированы на решение задач бюджетирования.
Используя встроенные средства автоматизации Excel, можно решить множество нестандартных задач. Пример реализации редактирования для сводных таблиц Excel на основе данных рабочего листа можно найти на нашем сайте.
Подготовка многомерных данных
Подойдем к практическому применению сводных таблиц. Попробуем проанализировать данные о продажах в различных направлениях. Файл pivottableexample.xls состоит из нескольких листов. Лист Пример содержит основную информацию о продажах за определенный период. Для простоты примера будем анализировать единственный числовой показатель – объем продажи в кг. Имеются следующие ключевые измерения данных: продукция, покупатель и перевозчик (транспортная компания). Кроме того, имеются несколько дополнительных измерений данных, являющихся признаками продукта: тип, бренд, категория, поставщик, а также покупателя: тип. Эти данные собраны на листе Справочники. На практике подобных измерений может быть гораздо больше.
Лист Пример содержит стандартное средство анализа данных – автофильтр. Глядя на пример заполнения таблицы, очевидно, что нормальному анализу поддаются данные о продажах по датам (они расположены по столбцам). Кроме того, используя автофильтр можно попробовать просуммировать данные по сочетаниям одного или нескольких ключевых критериев. Совершенно отсутствует информация о брендах, категориях и типах. Нет возможности сгруппировать данные с автоматическим суммированием по определенному ключу (например, по покупателям). Кроме того, набор дат зафиксирован, и просмотреть итоговую информацию за определенный период, например, 3 дня, автоматическими средствами не удастся.
Вообще, наличие предопределенного расположения даты в данном примере – главный недостаток таблицы. Расположив даты по столбцам, мы как бы предопределили измерение этой таблицы, таким образом, лишив себя возможности использовать анализ с помощью сводных таблиц.
Во-первых, надо избавиться от этого недостатка – т.е. убрать предопределенное расположение одного из измерений исходных данных. Пример корректной таблицы – лист Продажи.
Таблица имеет форму журнала ввода информации. Здесь дата является равноправным измерением данных. Также следует заметить, что для последующего анализа в сводных таблицах совершенно безразлично относительное положение строк друг относительно друга (иначе говоря, сортировка). Этими свойствами обладают записи в реляционных базах данных. Именно на анализ больших объемов баз данных ориентирован в первую очередь интерфейс сводных таблиц. Поэтому необходимо придерживаться этих правил и при работе с источником данных в виде диапазонов ячеек. При этом никто не запрещает использовать в работе интерфейсные средства Excel – сводные таблицы анализируют только данные, а форматирование, фильтры, группировки и сортировки исходных ячеек могут быть произвольными.
От автофильтра к сводному отчету
Теоретически на данных листа Продажи уже можно проводить анализ в трех измерениях: товары, покупатели и перевозчики. Данные о свойствах продукции и покупателей на данном листе отсутствуют, что, соответственно, не позволит показать их и в сводной таблице. В нормальном режиме создания сводной таблицы для исходных данных Excel не позволяет связывать данные нескольких таблиц по определенным полям. Обойти это ограничение можно программными средствами – см. пример-дополнение к данной статье на нашем сайте. Чтобы не прибегать к программным методам обработки информации (тем более, что они и не универсальны), следует добавить дополнительные характеристики непосредственно в форму ввода журнала – см. лист ПродажиАнализ.
 |
Применение функций VLOOKUP позволяет легко дополнить исходные данные недостающими характеристиками. Теперь, применяя автофильтр, можно анализировать данные в различных измерениях. Но остается нерешенной проблема группировок. Например, отследить сумму только по брендам на определенные даты достаточно проблематично. Если ограничиваться формулами Excel, то нужно строить дополнительные выборки, используя функцию SUMIF.
Теперь посмотрим какие возможности дает интерфейс сводных таблиц. На листе СводАнализ построено несколько отчетов на основе диапазона ячеек с данными листа ПродажиАнализ.
Первая таблица анализа построена через интерфейс Excel 2007 Лента Вставка Сводная таблица (в Excel 2000-2003 меню Данные Сводная таблица).
Вторая и третья таблицы созданы через копирование и последующую настройку. Источник данных для всех таблиц один и тот же. Можете это проверить, изменив исходные данные, затем надо обновить данные сводных отчетов.
С нашей точки зрения, преимущества в наглядности информации очевидны. Вы можете менять местами фильтры, столбцы и строки и, скрывать определенные группы значений любых измерений, применять ручное перетаскивание и автоматическую сортировку.
Свойства и форматирование
Кроме непосредственного отображения данных, имеется большой набор возможностей по отображению внешнего вида сводных таблиц. Лишние данные можно скрывать, используя фильтры. Для единичного элемента или поля проще пользоваться пунктом контекстного меню Удалить (в версии 2000-2003 Скрыть).
 |
Для полей данных таблицы можно задать единый формат отображения. Это делается не через формат ячейки, а через специальный диалог настройки формата поля.
 |
Задавать отображение других элементов сводной таблицы также желательно не через форматирование ячейки, а через настройку поля или элемента сводной таблицы. Для этого необходимо подвести указатель мыши к нужному элементу, дождаться появления специальной формы курсора (в виде стрелки), затем через одинарный клик выделить выбранный элемент. После выделения можно изменять вид через ленту, контекстное меню или вызывать стандартный диалог формата ячейки:
 |
Кроме формата отображения в ячейках, сводная таблица включает несколько специальных свойств, управляющих внешним видом и расположением элементов. Диалоги настройки проще всего вызываются через контекстное меню: Параметры сводной таблицы или Параметры поля сводной таблицы.
Кроме того, в Excel 2007 появилось множество предопределенных стилей отображения сводной таблицы:
 |
Сводная диаграмма
Нажав кнопку на ленте «Сводная диаграмма», можно сформировать специальный тип диаграммы, отображающей данные сводной таблицы:
 |
Обратите внимание, что в диаграмме активны управляющие фильтры и области перетаскивания.
Доступ к внешним данным
Как уже отмечалось, пожалуй, наибольший эффект от применения сводных таблиц можно получить при доступе к данным внешних источников – OLAP-кубам и запросам к базам данных. Такие источники обычно хранят большие объемы информации, а также имеют предопределенную реляционную структуру, что позволяет легко определить измерения многомерных данных (поля сводной таблицы).
Excel поддерживает множество типов источников внешних данных:
 |
Наибольшего эффекта от использования внешних источников информации можно добиться, применяя средства автоматизации (программы VBA) как для получения данных, так и для их предварительной обработки в сводных таблицах.
Смотри также
» Динамический источник данных сводной таблицы
При работе со сводными таблицами несколько раз сталкивался с проблемой, когда новые данные не попадали в отчет. Сводная таблица была…
» Обработка больших объемов данных. Часть 3. Сводные таблицы
Третья статья, посвященная обработке больших объемов данных с помощью Excel, описывает преимущества использования сводных таблиц….
» Сводная таблица Excelfin.ru
Надстройка предназначена для создания сводных таблиц на основе нескольких диапазонов данных файла Excel. Пользовательский интерфейс в…
» Сводный отчет на основе нескольких таблиц Excel
В стандартном режиме Excel позволяет строить сводные отчеты на основе диапазона ячеек, расположенного на одном рабочем листе. Собрать…
» Обновление списков сводной таблицы
При работе со сводными таблицами, сохраненными в качестве отчетов и использующих обновляемые исходные данные, выпадающие списки полей…