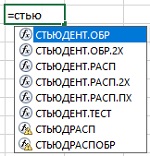
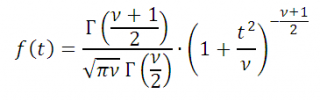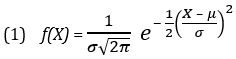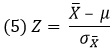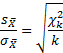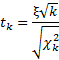Рассмотрим Распределение Стьюдента (t-распределение). С помощью функции MS EXCEL
СТЬЮДЕНТ.РАСП()
построим графики функции распределения и плотности вероятности, поясним применение этого распределения для целей математической статистики.
Распределение Стьюдента
(также называется
t
-распределением
) применяется в различных методах математической статистики:
-
при построении
доверительных интервалов для среднего
(используется функция
ДОВЕРИТ.СТЬЮДЕНТ()
); -
для
оценки различия двух выборочных средних
(используется функция
СТЬЮДЕНТ.ТЕСТ()
); -
при
проверке гипотез (выборка небольшого размера, стандартное отклонение не известно)
,
- в линейном регрессионном анализе (при проверке гипотез на значимость отдельных регрессионных коэффициентов).
Определение
: Если случайная величина Z распределена по
стандартному нормальному закону
N(0;1) и случайная величина U имеет
распределение ХИ-квадрат
с ν степенями свободы, то случайная величина T=Z/√(U/v) имеет
t-распределение
.
Плотность распределения
Стьюдента
выражается формулой:
при −∞ < t < ∞
СОВЕТ
: Подробнее о
Функции распределения
и
Плотности вероятности
см. статью
Функция распределения и плотность вероятности в MS EXCEL
.
Распределение
Стьюдента
(англ.
Student
’
s
t
—
distribution
)
зависит от одного параметра, который называется
степенью свободы
(
df
,
degrees
of
freedom
). Например, при
построении доверительного интервала для среднего
число степеней свободы
равно df=n-1, где n – размер
выборки
. При увеличении
числа степеней свободы
это распределение стремится к
стандартному нормальному распределению
.
В центральной части распределения (около 0) при df=25, относительная разница со
стандартным нормальным распределением
составляет порядка 1%, а при df=100 разница составляет 0,25%.
По аналогии со
стандартным нормальным распределением
,
t
-распределение
часто называется «стандартизированным», т.к. у него нет параметра отвечающего за положение (
среднее
всегда равно 0).
Дисперсию
t
-распределения
можно вычислить по формуле =df/(df-2)
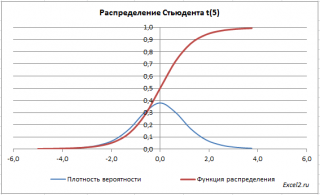
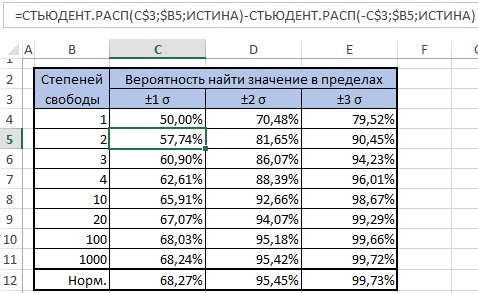
Графики функций
В
файле примера на листе График
приведены
графики плотности распределения
вероятности и
интегральной функции распределения
.
График
плотности распределения Стьюдента
, как и
стандартного
нормального распределения
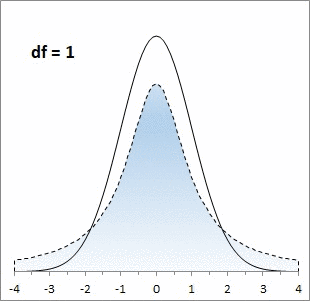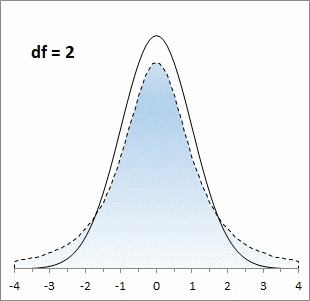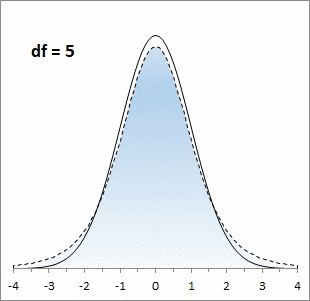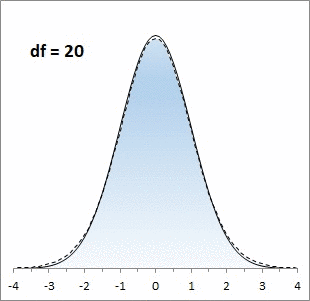
, является симметричным и колоколообразным, но с более тяжелыми хвостами.
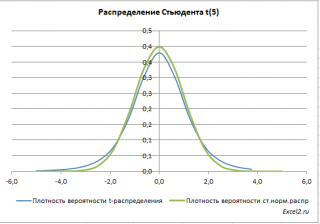
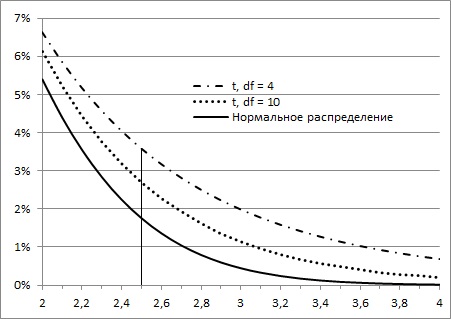
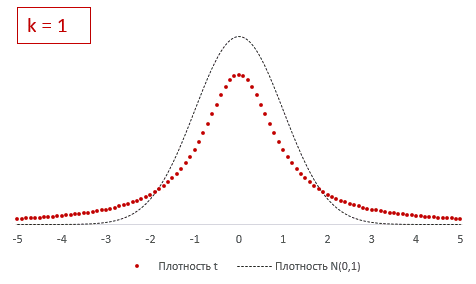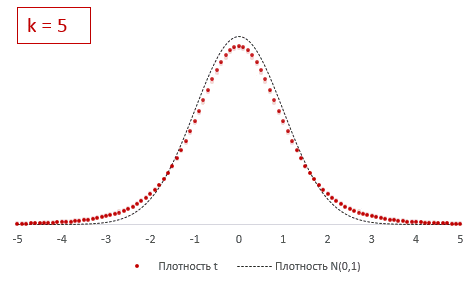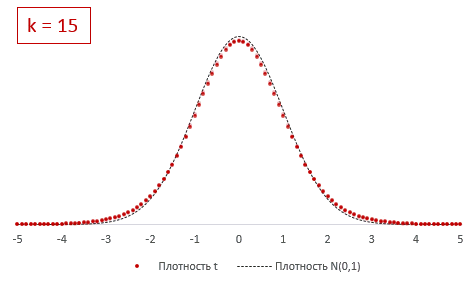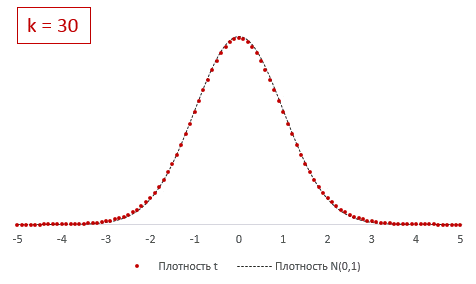
Ниже для сравнения приведены графики
плотности стандартного нормального распределения
и
распределения Стьюдента.
Примечание
: Для построения
функции распределения
и
плотности вероятности
можно использовать диаграмму типа
График
или
Точечная
(со сглаженными линиями и без точек). Подробнее о построении диаграмм читайте статью
Основные типы диаграмм
.
t-распределение в MS EXCEL
В MS EXCEL, начиная с версии 2010, для
t-распределения
имеется функция
СТЬЮДЕНТ.РАСП()
, английское название — T.DIST(), которая позволяет вычислить
плотность вероятности
(см. формулу выше) и
интегральную функцию распределения
(вероятность, что случайная величина Х, имеющая
распределение Стьюдента
, примет значение меньше или равное х, P(X <= x)).
Примечание
: В
файле примера на листе Функции
приведены основные функции MS EXCEL, связанные с этим распределением.
Кроме этой функции в MS EXCEL имеется еще довольно много других функций, относящихся к данному распределению, но по большому счету их функционал покрывается функцией
СТЬЮДЕНТ.РАСП()
.
Кроме того,
СТЬЮДЕНТ.РАСП()
является единственной функцией, которая возвращает
плотность вероятности
(третий аргумент должен быть равным ЛОЖЬ). Остальные функции возвращают
интегральную функцию распределения
, т.е. вероятность того, что случайная величина примет значение из указанного диапазона: P(X <= x), P(X > x) или даже P(|X| > x).
Очевидно, что справедливо равенство
=СТЬЮДЕНТ.РАСП.ПХ(x;n)+СТЬЮДЕНТ.РАСП(x;n;ИСТИНА)=1
т.к. первое слагаемое вычисляет вероятность P(X > x), а второе P(X <= x).
До MS EXCEL 2010 в EXCEL была только функция
СТЬЮДРАСП()
, которая позволяет вычислить
функцию распределения
(точнее — правостороннюю вероятность, т.е. P(X>x)) и объединяет возможности нескольких новых функций MS EXCEL 2010:
СТЬЮДЕНТ.РАСП(x; n; ЛОЖЬ)
,
СТЬЮДЕНТ.РАСП.ПХ()
,
СТЬЮДЕНТ.РАСП.2Х()
. Функция
СТЬЮДРАСП()
оставлена в MS EXCEL 2010 для совместимости.
-
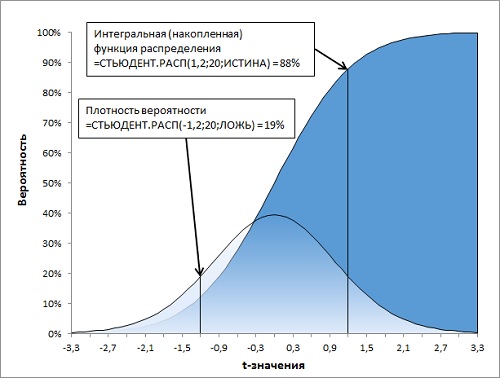
Если значение аргумента «хвосты» = 1, функция
СТЬЮДРАСП()
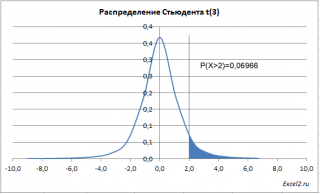
вычисляет правостороннюю вероятность P(X > x), где X — случайная переменная, соответствующая t-распределению. Под термином «хвост» подразумевается «хвост» распределения, в данном случае правый. На графике
плотности вероятности
этому «хвосту» будет соответствовать площадь фигуры под графиком (выделена синим), которая ограничена слева вертикальной линией X = x.
-
Если значение аргумента «хвосты» = 2, функция
СТЬЮДРАСП()
вычисляет вероятность P(|X| > x) или другими словами P(X > x или X < -x). Т.е. формула
=СТЬЮДРАСП(x;n;2)
эквивалентна
=СТЬЮДРАСП(x;n;1)*2
-
Функцией
СТЬЮДРАСП()
значения x < 0 не поддерживаются и нельзя записать
СТЬЮДРАСП(-x;n;1)
. Чтобы вычислить вероятность P(X <= x), в том числе и для отрицательных х, используйте формулу
=ЕСЛИ(x>0;СТЬЮДРАСП(x;n;1);1-СТЬЮДРАСП(-x;n;1))
.
Примеры
Найдем вероятность, что случайная величина Х примет значение меньше или равное заданного
x
: P(X <=
x
). Это можно сделать несколькими функциями:
=СТЬЮДЕНТ.РАСП(x; n; ИСТИНА)
или
=1-СТЬЮДЕНТ.РАСП(-x; n; ИСТИНА)
, используется свойство симметричности плотности распределения относительно оси Х.
=1-СТЬЮДЕНТ.РАСП.ПХ(x;n)
или
=СТЬЮДЕНТ.РАСП.ПХ(-x;n)
, функция
СТЬЮДЕНТ.РАСП.ПХ()
возвращает вероятность P(X > x), так называемую правостороннюю вероятность, поэтому, чтобы найти P(X <= x), необходимо вычесть ее результат от 1 или воспользоваться свойством t-распределения t(-х)=1-t(x).
=1-СТЬЮДЕНТ.РАСП.2Х(x;n)/2
или
=1-СТЬЮДРАСП(x;n;2)/2
, в этой формуле
х
может принимать только положительные значения (подробнее об этой функции см. ниже);
=1-СТЬЮДРАСП(x; n; 1)
, в этой формуле
х
может принимать только положительные значения, функция
СТЬЮДРАСП()
, как и
СТЬЮДЕНТ.РАСП.ПХ()
, возвращает «правостороннюю вероятность», т.е. P(X > x).
Аналогичные вычисления для P(X > x) и P(|X| > x) приведены в
файле примера на листе Функции
, в том числе и для x<0.
Обратная функция t-распределения
Обратная функция используется для вычисления
альфа
—
квантилей
, т.е. для вычисления значений
x
при заданной вероятности
альфа
, причем
х
должен удовлетворять выражению P{X<=x}=
альфа
.
Функция
СТЬЮДЕНТ.ОБР()
используется для вычисления как двухсторонних, так и
односторонних доверительных интервалов
. А функции
СТЬЮДЕНТ.ОБР.2Х()
и
СТЬЮДРАСПОБР()
созданы специально для вычисления
квантилей
, необходимых для расчета двусторонних
доверительных интервалов:
в качестве аргумента нужно указывать
уровень значимости
альфа
, а не
альфа/2
, как для
СТЬЮДЕНТ.ОБР()
.
Вышеуказанные функции можно взаимозаменять, т.к. нижеуказанные формулы возвращают одинаковый результат:
=СТЬЮДЕНТ.ОБР(альфа;n) =-СТЬЮДРАСПОБР(альфа*2;n) =-СТЬЮДЕНТ.ОБР.2Х(альфа*2;n)
Некоторые примеры расчетов приведены в
файле примера на листе Функции
.
Примечание
: Ниже приведено соответствие русских и английских названий функций:
СТЬЮДЕНТ.РАСП.ПХ()
— англ. название T.DIST.RT, т.е. T-DISTribution Right Tail, the right-tailed Student’s t-distribution
СТЬЮДЕНТ.РАСП.2Х()
— англ. название T.DIST.2T, т.е. T-DISTribution 2 Tails
СТЬЮДЕНТ.ОБР()
— англ. название T.INV, т.е. T-distribution INVerse
СТЬЮДРАСП()
— англ. название TDIST, т.е. T-DISTribution
СТЬЮДРАСПОБР()
— англ. название TINV, т.е. T-distribution INVerse (the right-tailed inverse of the Student’s t-distribution)
СТЬЮДЕНТ.ОБР.2Х()
— англ. название T.INV.2T
Функции MS EXCEL, использующие t-распределение
Как было сказано выше, при
построении доверительных интервалов
используется функция
ДОВЕРИТ.СТЬЮДЕНТ()
— англ. название CONFIDENCE.T.
Например, формула
=ДОВЕРИТ.СТЬЮДЕНТ(альфа;СТАНДОТКЛОН.В(B20:B79); СЧЁТ(B20:B79))
эквивалентна классической формуле для вычисления доверительного интервала
=СТЬЮДЕНТ.ОБР(1-альфа/2; СЧЁТ(B20:B79)-1)* СТАНДОТКЛОН.В(B20:B79)/КОРЕНЬ(СЧЁТ(B20:B79))
где предполагается, что
выборка
находится в диапазоне
B20:B79
.
Как видим, особых преимуществ в использовании
ДОВЕРИТ.СТЬЮДЕНТ()
нет.
Другая функция —
СТЬЮДЕНТ.ТЕСТ()
— англ. название T.TEST, используется для
оценки различия двух выборочных средних
.
Оценка параметров распределения
Т.к. обычно
t-распределение
используется для целей математической статистики (вычисление
доверительных интервалов,
проверки гипотез и др.),
и практически никогда для построения моделей реальных величин, то для этого распределения обсуждение оценки параметров распределения здесь не производится.
СОВЕТ
: О других распределениях MS EXCEL можно прочитать в статье
Распределения случайной величины в MS EXCEL
.
Рассматриваемая функция возвращает значение t, соответствующее условию P(|x|>t)=p. Здесь x является значением некоторой случайной величины с распределением Стьюдента, у которого число степеней свобод соответствует k (второй аргумент функции СТЮДРАСПОБР).
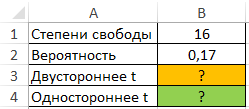
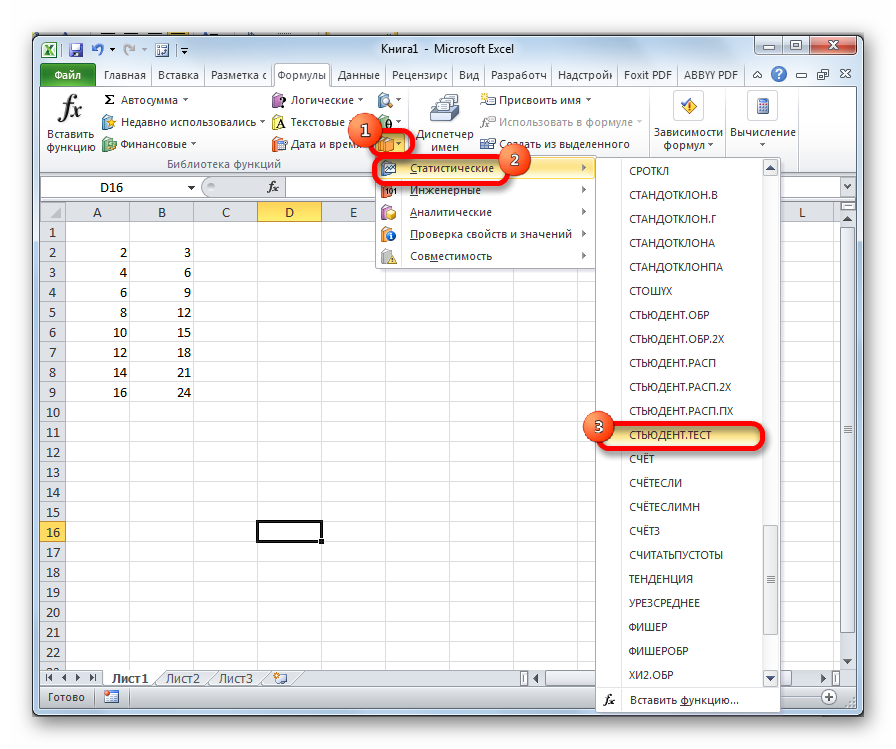
Пример 1. Определить односторонне и двустороннее t-значения для распределения Стьюдента, характеризующееся вероятностью 0,17 и числом степени свобод 16.
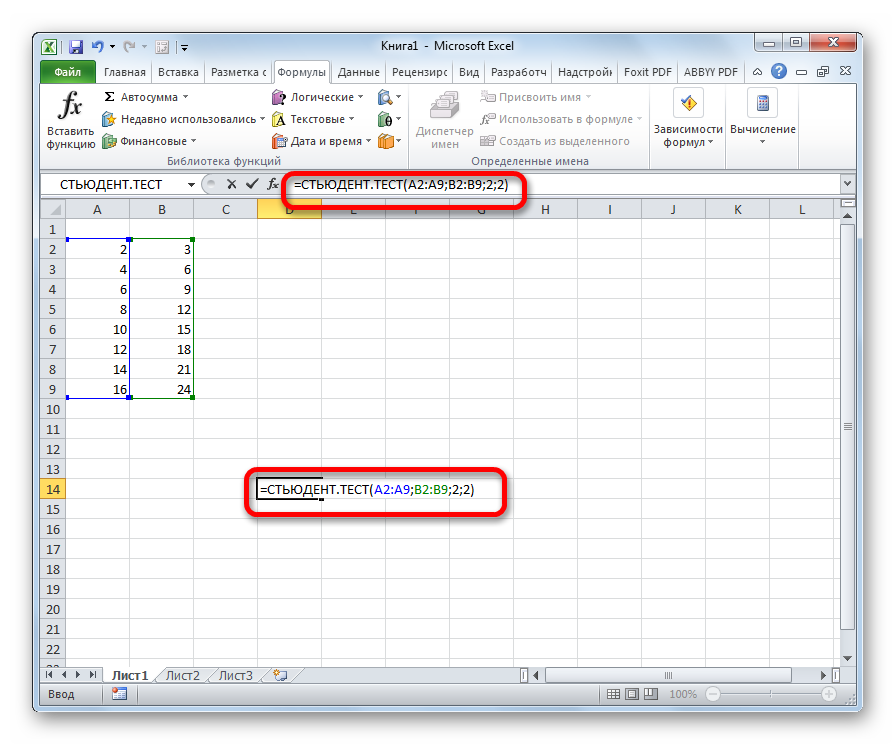
Теперь перейдем непосредственно к вопросу, как рассчитать данный показатель в Экселе. Его можно произвести через функцию СТЬЮДЕНТ.ТЕСТ. В версиях Excel 2007 года и ранее она называлась ТТЕСТ. Впрочем, она была оставлена и в позднейших версиях в целях совместимости, но в них все-таки рекомендуется использовать более современную — СТЬЮДЕНТ.ТЕСТ. Данную функцию можно использовать тремя способами, о которых подробно пойдет речь ниже.
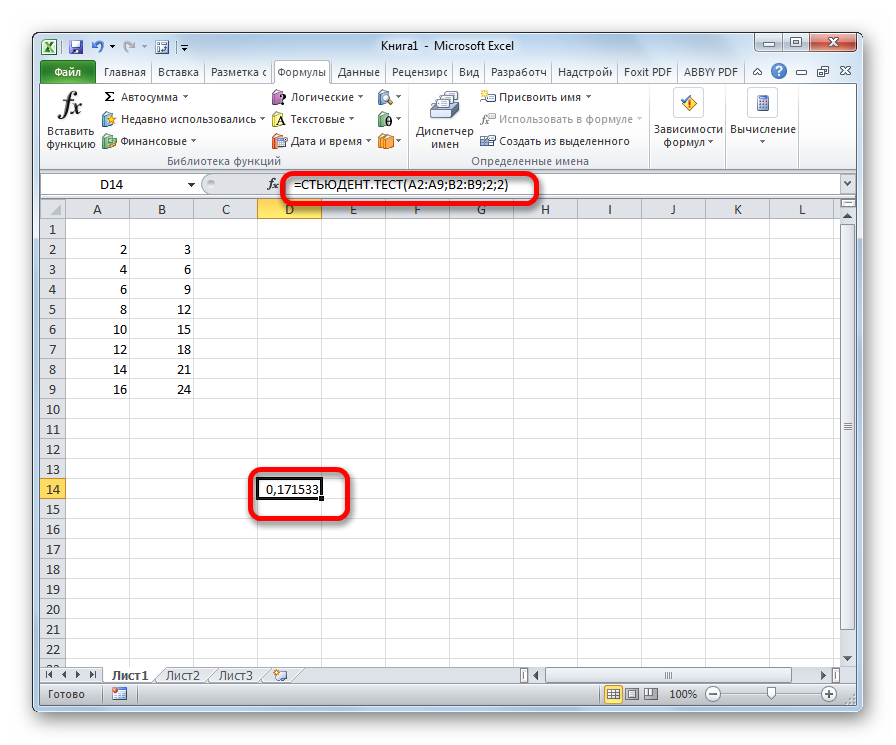
Проще всего производить вычисления данного показателя через Мастер функций.
Выполняется расчет, а результат выводится на экран в заранее выделенную ячейку.
Функцию СТЬЮДЕНТ.ТЕСТ можно вызвать также путем перехода во вкладку «Формулы» с помощью специальной кнопки на ленте.
Этапы статистического вывода (statistic inference)
- Первый из них – это вопрос, который мы хотим изучить с помощью статистических методов. То есть первый этап: что изучаем? И какие у нас есть предположения относительно результата? Этот этап называется этап статистических гипотез.
- Второй этап – нужно определиться с тем, какие у нас есть в реальности данные для того, чтобы ответить на первый вопрос. Этот этап – тип данных.
- Третий этап состоит в том, чтобы выбрать корректный для применения в данной ситуации статистический критерий.
- Четвертый этап это логичный этап применения интерпретации любой формулы, какие результаты мы получили.
- Пятый этап это создание, синтез выводов относительно первого, второго, третьего, четвертого, пятого этапа, то есть что же получили и что же это в реальности значит.
Пример использования т-критерия Стьюдента
А пример будет достаточно простой: мне интересно, стали ли люди выше за последние 100 лет. Для этого нужно подобрать некоторые данные. Я обнаружил интересную информацию в достаточно известной статье The Guardian (Tall story’s men and women have grown taller over last century, Study Shows (The Guardian, July 2016), которая сравнивает средний возраст человека в разных странах в 1914 году и в аналогичных странах в 2014 году.
Там приведены данные практически по всем государствам. Однако, я взял лишь 5 стран для простоты вычислений: это Россия, Германия, Китай, США и ЮАР, соответственно 1914 год и 2014 год.
Общее количество наблюдений – 5 в 1914 году в группе 1914 года и общее значение также 5 в 2014 году. Будем думать опять же для простоты, что эти данные сопоставимы, и с ними можно работать.
Дальше нужно выбрать критерии – критерии, по которым мы будем давать ответ. Равны ли средние по росту в 1914 году x̅1914 и в 2014 году x̅2014. Я считаю, что нет. Поэтому моя гипотеза это то, что они не равны (x̅1914≠x̅2014). Соответственно альтернативная гипотеза моему предположению, так называемая нулевая гипотеза (нулевая гипотеза консервативна, обратная вашей, часто говорит об отсутствии статистически значимых связей/зависимостей) будет говорить о том, что они между собой на самом деле равны (x̅1914=x̅2014), то есть о том, что все эти находки случайны, и я, по сути, не прав.
Для чего используется t-критерий Стьюдента?
t-критерий Стьюдента используется для определения статистической значимости различий средних величин. Может применяться как в случаях сравнения независимых выборок (например, группы больных сахарным диабетом и группы здоровых), так и при сравнении связанных совокупностей (например, средняя частота пульса у одних и тех же пациентов до и после приема антиаритмического препарата). В последнем случае рассчитывается парный t-критерий Стьюдента
В каких случаях можно использовать t-критерий Стьюдента?
Для применения t-критерия Стьюдента необходимо, чтобы исходные данные имели нормальное распределение. Также имеет значение равенство дисперсий (распределения) сравниваемых групп (гомоскедастичность). При неравных дисперсиях применяется t-критерий в модификации Уэлча (Welch’s t).
При отсутствии нормального распределения сравниваемых выборок вместо t-критерия Стьюдента используются аналогичные методы непараметрической статистики, среди которых наиболее известными является U-критерий Манна — Уитни.
Как интерпретировать значение t-критерия Стьюдента?
Полученное значение t-критерия Стьюдента необходимо правильно интерпретировать. Для этого нам необходимо знать количество исследуемых в каждой группе (n1 и n2). Находим число степеней свободы f по следующей формуле:
f = (n1 + n2) – 2
После этого определяем критическое значение t-критерия Стьюдента для требуемого уровня значимости (например, p=0,05) и при данном числе степеней свободы f по таблице (см. ниже).
Сравниваем критическое и рассчитанное значения критерия:
- Если рассчитанное значение t-критерия Стьюдента равно или больше критического, найденного по таблице, делаем вывод о статистической значимости различий между сравниваемыми величинами.
- Если значение рассчитанного t-критерия Стьюдента меньше табличного, значит различия сравниваемых величин статистически не значимы.
Внесите исходные данные группы
Вы можете внести данные для расчета критерия Т-Стьюдента поочередно вручную или скопировать их из вашего Excel файла.
Внесите исходные данные группы
Вы можете внести данные поочередно вручную или скопировать их из вашего Excel файла.
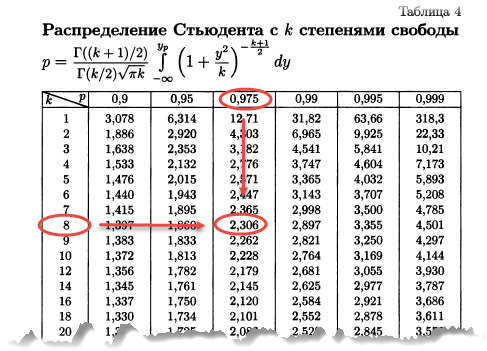
Критические точки распределения Стьюдента
| Число степеней свободы k |
Уровень значимости α (двусторонняя критическая область) | |||||
| 0.10 | 0.05 | 0.02 | 0.01 | 0.002 | 0.001 | |
| 1 | 6.31 | 12.7 | 31.82 | 63.7 | 318.3 | 637.0 |
| 2 | 2.92 | 4.30 | 6.97 | 9.92 | 22.33 | 31.6 |
| 3 | 2.35 | 3.18 | 4.54 | 5.84 | 10.22 | 12.9 |
| 4 | 2.13 | 2.78 | 3.75 | 4.60 | 7.17 | 8.61 |
| 5 | 2.01 | 2.57 | 3.37 | 4.03 | 5.89 | 6.86 |
| 6 | 1.94 | 2.45 | 3.14 | 3.71 | 5.21 | 5.96 |
| 7 | 1.89 | 2.36 | 3.00 | 3.50 | 4.79 | 5.40 |
| 8 | 1.86 | 2.31 | 2.90 | 3.36 | 4.50 | 5.04 |
| 9 | 1.83 | 2.26 | 2.82 | 3.25 | 4.30 | 4.78 |
| 10 | 1.81 | 2.23 | 2.76 | 3.17 | 4.14 | 4.59 |
| 11 | 1.80 | 2.20 | 2.72 | 3.11 | 4.03 | 4.44 |
| 12 | 1.78 | 2.18 | 2.68 | 3.05 | 3.93 | 4.32 |
| 13 | 1.77 | 2.16 | 2.65 | 3.01 | 3.85 | 4.22 |
| 14 | 1.76 | 2.14 | 2.62 | 2.98 | 3.79 | 4.14 |
| 15 | 1.75 | 2.13 | 2.60 | 2.95 | 3.73 | 4.07 |
| 16 | 1.75 | 2.12 | 2.58 | 2.92 | 3.69 | 4.01 |
| 17 | 1.74 | 2.11 | 2.57 | 2.90 | 3.65 | 3.95 |
| 18 | 1.73 | 2.10 | 2.55 | 2.88 | 3.61 | 3.92 |
| 19 | 1.73 | 2.09 | 2.54 | 2.86 | 3.58 | 3.88 |
| 20 | 1.73 | 2.09 | 2.53 | 2.85 | 3.55 | 3.85 |
| 21 | 1.72 | 2.08 | 2.52 | 2.83 | 3.53 | 3.82 |
| 22 | 1.72 | 2.07 | 2.51 | 2.82 | 3.51 | 3.79 |
| 23 | 1.71 | 2.07 | 2.50 | 2.81 | 3.59 | 3.77 |
| 24 | 1.71 | 2.06 | 2.49 | 2.80 | 3.47 | 3.74 |
| 25 | 1.71 | 2.06 | 2.49 | 2.79 | 3.45 | 3.72 |
| 26 | 1.71 | 2.06 | 2.48 | 2.78 | 3.44 | 3.71 |
| 27 | 1.71 | 2.05 | 2.47 | 2.77 | 3.42 | 3.69 |
| 28 | 1.70 | 2.05 | 2.46 | 2.76 | 3.40 | 3.66 |
| 29 | 1.70 | 2.05 | 2.46 | 2.76 | 3.40 | 3.66 |
| 30 | 1.70 | 2.04 | 2.46 | 2.75 | 3.39 | 3.65 |
| 40 | 1.68 | 2.02 | 2.42 | 2.70 | 3.31 | 3.55 |
| 60 | 1.67 | 2.00 | 2.39 | 2.66 | 3.23 | 3.46 |
| 120 | 1.66 | 1.98 | 2.36 | 2.62 | 3.17 | 3.37 |
| ∞ | 1.64 | 1.96 | 2.33 | 2.58 | 3.09 | 3.29 |
| 0.05 | 0.025 | 0.01 | 0.005 | 0.001 | 0.0005 | |
| Уровень значимости α (односторонняя критическая область) |
Условия применения t-критерия Стьюдента
Несмотря на то, что открытие Стьюдента в свое время совершило переворот в статистике, t-критерий все же довольно сильно ограничен в возможностях применения, т.к. сам по себе происходит из предположения о нормальном распределении исходных данных. Если данные не являются нормальными (что обычно и бывает), то и t-критерий уже не будет иметь распределения Стьюдента. Однако в силу действия центральной предельной теоремы средняя даже у ненормальных данных быстро приобретает колоколообразную форму распределения.
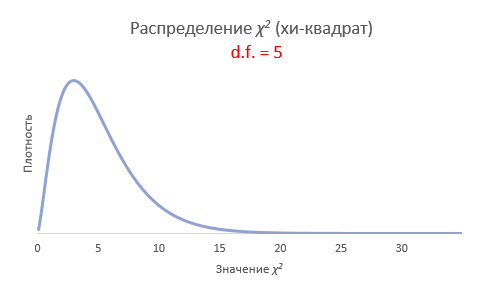
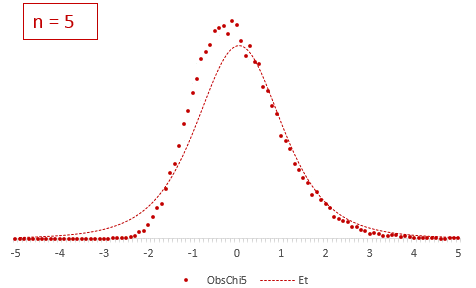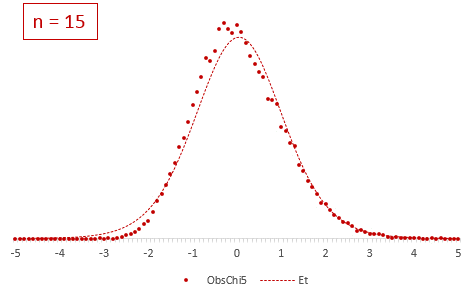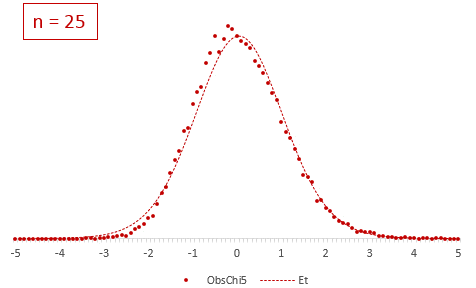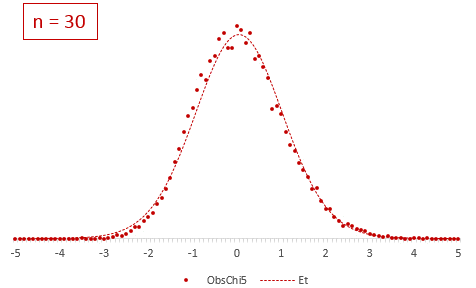
Рассмотрим, для примера, данные, имеющие выраженный скос вправо, как у распределения хи-квадрат с 5-ю степенями свободы.

Теперь создадим 20 тысяч выборок и будет наблюдать, как меняется распределение средних в зависимости от их объема.

Отличие довольно заметно в малых выборках до 15-20-ти наблюдений. Но дальше оно стремительно исчезает. Таким образом, ненормальность распределения – это, конечно, нехорошо, но некритично.
Больше всего t-критерий «боится» выбросов, т.е. аномальных отклонений. Возьмем 20 тыс. нормальных выборок по 15 наблюдений и в часть из них добавим по одному случайном выбросу.

Картина получается нерадостная. Фактические частоты средних сильно отличаются от теоретических. Использование t-распределения в такой ситуации становится весьма рискованной затеей.
Итак, в не очень малых выборках (от 15-ти наблюдений) t-критерий относительно устойчив к ненормальному распределению исходных данных. А вот выбросы в данных сильно искажают распределение t-критерия, что, в свою очередь, может привести к ошибкам статистического вывода, поэтому от аномальных наблюдений следует избавиться. Часто из выборки удаляют все значения, выходящие за пределы ±2 стандартных отклонения от средней.
Пример проверки гипотезы о математическом ожидании с помощью t- критерия Стьюдента в MS Excel
В Excel есть несколько функций, связанных с t-распределением. Рассмотрим их.
СТЬЮДЕНТ.РАСП – «классическое» левостороннее t-распределение Стьюдента. На вход подается значение t-критерия, количество степеней свободы и опция (0 или 1), определяющая, что нужно рассчитать: плотность или значение функции. На выходе получаем, соответственно, плотность или вероятность того, что случайная величина окажется меньше указанного в аргументе t-критерия, т.е. левосторонний p-value.
СТЬЮДЕНТ.РАСП.2Х – двухсторонне распределение. В качестве аргумента подается абсолютное значение (по модулю) t-критерия и количество степеней свободы. На выходе получаем вероятность получить такое или еще больше значение t-критерия (по модулю), т.е. фактический уровень значимости (p-value).
СТЬЮДЕНТ.РАСП.ПХ – правостороннее t-распределение. Так, 1-СТЬЮДЕНТ.РАСП(2;5;1) = СТЬЮДЕНТ.РАСП.ПХ(2;5) = 0,05097. Если t-критерий положительный, то полученная вероятность – это p-value.
СТЬЮДЕНТ.ОБР – используется для расчета левостороннего обратного значения t-распределения. В качестве аргумента подается вероятность и количество степеней свободы. На выходе получаем соответствующее этой вероятности значение t-критерия. Отсчет вероятности идет слева. Поэтому для левого хвоста нужен сам уровень значимости α, а для правого 1 — α.
СТЬЮДЕНТ.ОБР.2Х – обратное значение для двухстороннего распределения Стьюдента, т.е. значение t-критерия (по модулю). Также на вход подается уровень значимости α. Только на этот раз отсчет ведется с двух сторон одновременно, поэтому вероятность распределяется на два хвоста. Так, СТЬЮДЕНТ.ОБР(1-0,025;5) = СТЬЮДЕНТ.ОБР.2Х(0,05;5) = 2,57058
СТЬЮДЕНТ.ТЕСТ – функция для проверки гипотезы о равенстве математических ожиданий в двух выборках. Заменяет кучу расчетов, т.к. достаточно указать лишь два диапазона с данными и еще пару параметров. На выходе получим p-value.
ДОВЕРИТ.СТЬЮДЕНТ – расчет доверительного интервала средней с учетом t-распределения.
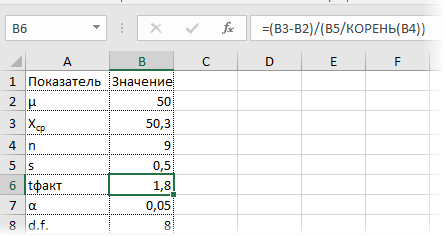
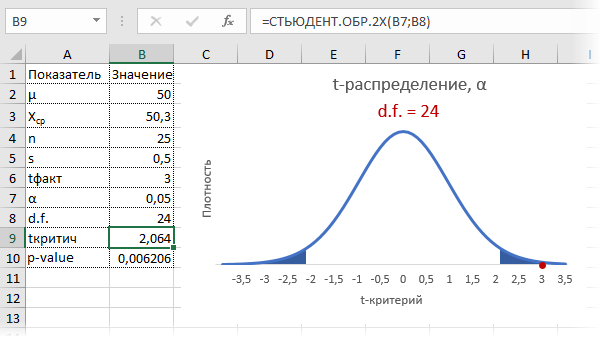
Рассмотрим такой учебный пример. На предприятии фасуют цемент в мешки по 50кг. В силу случайности в отдельно взятом мешке допускается некоторое отклонение от ожидаемой массы, но генеральная средняя должна оставаться 50кг. В отделе контроля качества случайным образом взвесили 9 мешков и получили следующие результаты: средняя масса (X̅) составила 50,3кг, среднеквадратичное отклонение (s) – 0,5кг.
Согласуется ли полученный результат с нулевой гипотезой о том, что генеральная средняя равна 50кг? Другими словами, можно ли получить такой результат по чистой случайности, если оборудование работает исправно и выдает среднее наполнение 50 кг? Если гипотеза не будет отклонена, то полученное различие вписывается в диапазон случайных колебаний, если же гипотеза будет отклонена, то, скорее всего, в настройках аппарата, заполняющего мешки, произошел сбой. Требуется его проверка и настройка.
Краткое условие в обще принятых обозначениях выглядит так.
H0: μ = 50 кг
Ha: μ ≠ 50 кг
Есть основания предположить, что распределение заполняемости мешков подчиняются нормальному распределению (или не сильно от него отличается). Значит, для проверки гипотезы о математическом ожидании можно использовать t-критерий Стьюдента. Случайные отклонения могут происходить в любую сторону, значит нужен двусторонний t-критерий.
Вначале применим допотопные средства: ручной расчет t-критерия и сравнение его с критическим табличным значением. Расчетный t-критерий:
Теперь определим, выходит ли полученное число за критический уровень при уровне значимости α = 0,05. Воспользуемся таблицей для критерия Стьюдента (есть в любом учебнике по статистике).

По столбцам идет вероятность правой части распределения, по строкам – число степеней свободы. Нас интересует двусторонний t-критерий с уровнем значимости 0,05, что равносильно t-значению для половины уровня значимости справа: 1 — 0,05/2 = 0,975. Количество степеней свободы – это объем выборки минус 1, т.е. 9 — 1 = 8. На пересечении находим табличное значение t-критерия – 2,306. Если бы мы использовали стандартное нормальное распределение, то критической точкой было бы значение 1,96, а тут она больше, т.к. t-распределение на небольших выборках имеет более приплюснутый вид.
Сравниваем фактическое (1,8) и табличное значение (2.306). Расчетный критерий оказался меньше табличного. Следовательно, имеющиеся данные не противоречат гипотезе H0 о том, что генеральная средняя равна 50 кг (но и не доказывают ее). Это все, что мы можем узнать, используя таблицы. Можно, конечно, еще p-value попробовать найти, но он будет приближенным. А, как правило, именно p-value используется для проверки гипотез. Поэтому далее переходим в Excel.
Готовой функции для расчета t-критерия в Excel нет. Но это и не страшно, ведь формула t-критерия Стьюдента довольно проста и ее можно легко соорудить прямо в ячейке Excel.

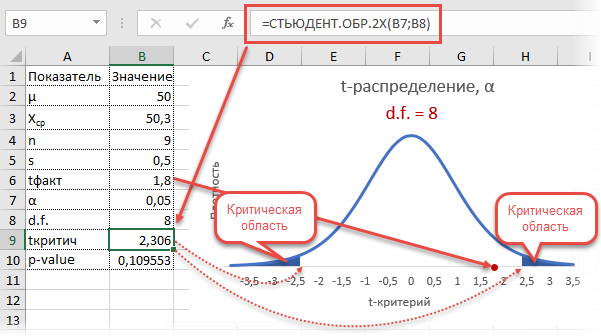
Получили те же 1,8. Найдем вначале критическое значение. Альфа берем 0,05, критерий двусторонний. Нужна функция обратного значения t-распределения для двухсторонней гипотезы СТЬЮДЕНТ.ОБР.2Х.

Полученное значение отсекает критическую область. Наблюдаемый t-критерий в нее не попадает, поэтому гипотеза не отклоняется.
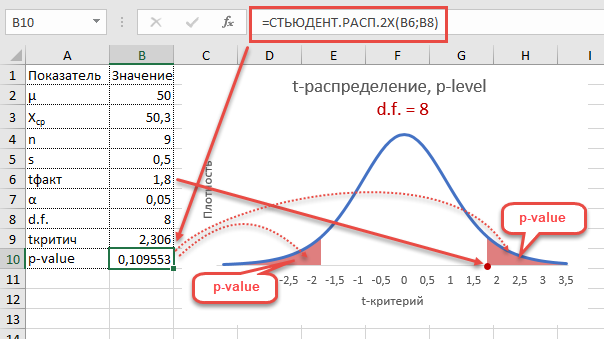
Однако это тот же способ проверки гипотезы с помощью табличного значения. Более информативно будет рассчитать p-value, т.е. вероятность получить наблюдаемое или еще большее отклонение от средней 50кг, если эта гипотеза верна. Потребуется функция распределения Стьюдента для двухсторонней гипотезы СТЬЮДЕНТ.РАСП.2Х.

P-value равен 0,1096, что больше допустимого уровня значимости 0,05 – гипотезу не отклоняем. Но теперь можно судить о степени доказательства. P-value оказался довольно близок к тому уровню, когда гипотеза отклоняется, а это наводит на разные мысли. Например, что выборка оказалась слишком мала для обнаружения значимого отклонения.
Пусть через некоторое время отдел контроля снова решил проверить, как выдерживается стандарт заполняемости мешков. На этот раз для большей надежности было отобрано не 9, а 25 мешков. Интуитивно понятно, что разброс средней уменьшится, а, значит, и шансов найти сбой в системе становится больше.
Допустим, были получены те же значения средней и стандартного отклонения по выборке, что и в первый раз (50,3 и 0,5 соответственно). Рассчитаем t-критерий.
Критическое значение для 24-х степеней свободы и α = 0,05 составляет 2,064. На картинке ниже видно, что t-критерий попадает в область отклонения гипотезы.

Можно сделать вывод о том, что с доверительной вероятностью более 95% генеральная средняя отличается от 50кг. Для большей убедительности посмотрим на p-value (последняя строка в таблице). Вероятность получить среднюю с таким или еще большим отклонением от 50, если гипотеза верна, составляет 0,0062, или 0,62%, что при однократном измерении практически невозможно. В общем, гипотезу отклоняем, как маловероятную.
Источники
- https://exceltable.com/funkcii-excel/raspredeleniya-styudenta-styudraspobr
- https://lumpics.ru/calculation-student-test-in-excel/
- https://lit-review.ru/biostatistika/t-kriterijj-styudenta-za-12-minut/
- https://medstatistic.ru/methods/methods.html
- https://statpsy.ru/t-student/onlajn-raschet-kriteriya-t-styudenta-dlya-nezavisimyh-vyborok/
- https://math.semestr.ru/corel/table-student.php
- https://statanaliz.info/statistica/proverka-gipotez/raspredelenie-t-kriteriya-styudenta-dlya-proverki-gipotezy-i-rascheta-doveritelnogo-intervala-v-ms-excel/
Функция СТЮДРАСПОБР предназначена для расчета значения квантиля уровня, соответствующего известной вероятности (указывается в качестве первого аргумента), распределения Стьюдента для известных степеней свободы и возвращает обратное t-распределение.
Распределение Стьюдента и нормальное распределение в Excel
Рассматриваемая функция возвращает значение t, соответствующее условию P(|x|>t)=p. Здесь x является значением некоторой случайной величины с распределением Стьюдента, у которого число степеней свобод соответствует k (второй аргумент функции СТЮДРАСПОБР).
Примечания:
- Распределение Стьюдента является одним из видов распределения случайной величины, близкое к нормальному распределению с характерным отличием – сниженная концентрацией отклонений в средней части распределения. Иное название – t-распределение.
- Квантилем считается некоторое значение, которое с определенной вероятностью (фиксированной) не будет превышено случайной величиной.
- Функция СТЮДРАСПОБР считается устаревшей начиная с версии MS Office 2010. Она оставлена для обеспечения совместимости с другими табличными редакторами и документами, созданными в более старых версиях табличного редактора. В новых версиях следует использовать усовершенствованные аналоги: СТЬЮДЕНТ.ОБР.2Х или СТЬЮДЕНТ.ОБР.
Подробнее о нормальном распределении читайте: НОРМСТРАСП функция стандартного нормального распределения в Excel.
Ниже рассмотрим примеры использования функции СТЮДРАСПОБР в Excel.
Определение одностороннего и двустороннего t распределение Стьюдента
Пример 1. Определить односторонне и двустороннее t-значения для распределения Стьюдента, характеризующееся вероятностью 0,17 и числом степени свобод 16.
Вид таблицы данных:
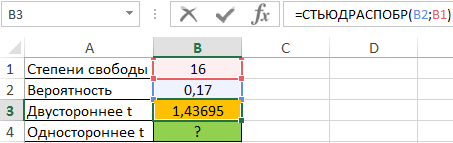
Для расчета двустороннего t-значения используем функцию:
=СТЬЮДРАСПОБР(B2;B1)
Результат вычислений:
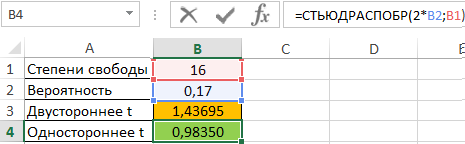
Для двустороннего t используем удвоенное значение вероятности:
=СТЬЮДРАСПОБР(2*B2;B1)
В результате получим:
Число степеней свободы в распределении Стьюдента
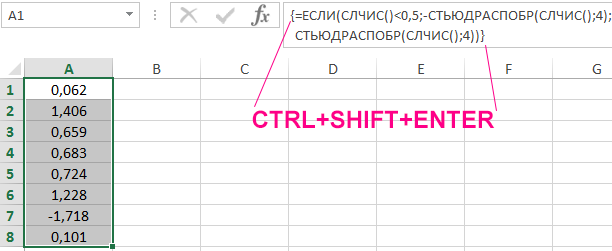
Пример 2. Сгенерировать 8 случайных чисел с использованием функции СЛЧИС, для которых распределение Стьюдента имеет 4 степени свободы.
Поскольку вероятность того, что случайна величина примет как отрицательное, так и положительное значение является одинаковой и равна 0,5 (распределение Стьюдента симметрично относительно вертикальной оси графика), используем функцию ЕСЛИ для проверки значений.
Выделим 8 ячеек и запишем следующую функцию (вводить как формулу массива CTRL+SHIFT+Enter):
То есть, если случайное значение вероятности, сгенерированное функцией СЛЧИС меньше 0,5, будет сгенерировано отрицательное t-значение, иначе – положительное.
Результат вычислений:
Как пользоваться функцией распределения Стьюдента СТЮДРАСПОБР В EXCEL
Функция имеет следующий синтаксис:
=СТЬЮДРАСПОБР(вероятность;степени_свободы)
Описание аргументов:
- вероятность – обязательный для заполнения, принимает числовое значение вероятности для двустороннего распределения Стьюдента из диапазона от 0 (не включительно) до 1.
- степени_свободы – обязательный для заполнения, принимает числовое значение степеней свободы, которые определяют исследуемое распределение.
Примечания:
- Если один из аргументов функции указан в виде значения нечислового типа данных, результатом выполнения рассматриваемой функции будет код ошибки #ЗНАЧ!. Логические значения, имена и текстовые строки, преобразуемые в числа, не приводят к возникновению ошибки. Например, функция =СТЮДРАСПОБР(“0,4”;ИСТИНА) вернет значение 1,32638.
- Если аргумент вероятность задан числом, не находящимся в промежутке от 0 (не включительно) до 1, функция СТЮДРАСПОБР вернет код ошибки #ЧИСЛО!. Аналогичная ошибка возникает, если аргумент степени_свободы задан числом, которое меньше 1.
- Для расчета односторонней t-величины следует в качестве аргумента вероятность указать значение удвоенной вероятности.
Большинству из нас хорошо знакома колоколообразная кривая нормального распределения. Она отлично работает, когда выборки большие, но занижает значения на «хвостах», когда выборки малые. Для описания статистики малых выборок была разработана t-статистика Стьюдента. Она также симметрична и подчиняется колоколообразному распределению, но дает лучшую оценку для малых выборок. В отличие от нормального распределения t-статистика не одна, а представлена целым семейством распределений. Дополнительный параметр – размер выборки или число степеней свободы.
Рис. 1. Нормальная кривая и кривые t-распределения; df – число степеней свободы (от англ. degrees of freedom); gif-файл создан с помощью бесплатного сервиса ezgif.com, на который меня навела Евгения Крюкова
Скачать заметку в формате Word или pdf, примеры в формате Excel
Подход пивовара
В начале XX века Уильяму Сили Госсету, химику и статистику ирландской пивоваренной компании Guinness, потребовалось установить, какой из двух сортов ячменя дает лучшее пиво с большим выходом.[1] Ранее была разработана статистика нормального распределения, позволяющая находить доверительный интервал на основе случайной выборки, состоящей из не менее чем 30 объектов. К сожалению, у Госсета не было возможности протестировать большое число партий пива, изготовленных из каждого сорта ячменя. Однако он не отказался от своей затеи измерить то, что как будто не поддавалось оценке, и решил вывести новый вид распределения для крайне малых выборок. К 1908 г. Госсет разработал новый эффективный метод, который назвал t-статистикой, и захотел опубликовать результаты своей работы.
Однако у Guinness уже были проблемы с разглашением коммерческой тайны, и служащим компании было запрещено публиковать любую информацию о бизнес-процессах. Госсет понимал значение своей работы. Ему сильнее хотелось рассказать о своей идее, чем добиться немедленного признания. Поэтому он опубликовал статью под псевдонимом Стьюдент. И хотя истинный автор давно известен, практически во всех работах по статистике метод называется t-статистикой Стьюдента.
От физических значений к z-статистике
Колоколообразная кривая нормального распределения описывается формулой:
где f(X) – вероятность значения Х; f(X) откладывается по оси ординат; е — основание натурального логарифма; μ — математическое ожидание генеральной совокупности, σ — стандартное отклонение генеральной совокупности, X — произвольное значение непрерывной случайной величины; X откладывается по оси абсцисс; –∞ < X < +∞ (о вычислении μ и σ подробнее см. Определение среднего значения, вариации и формы распределения. Описательные статистики).
Формула (1) довольно сложная, и в докомпьютерную эру статистики использовали заранее рассчитанные таблицы. Поскольку составление таблиц для всего разнообразия Х, μ и σ дело неподъемное, была придумана стандартизация, которая состоит в приведении физических величин к z-единицам, путем простой арифметической подстановки
В этом случае всё многообразие нормальных кривых сводится к единому стандартизованному распределению:
где математическое ожидание (среднее) стандартизованного нормального распределения μ = 0, а стандартное отклонение σ = 1. Фактически, z – это десятичное число, для которого σ = 1, μ = 0.
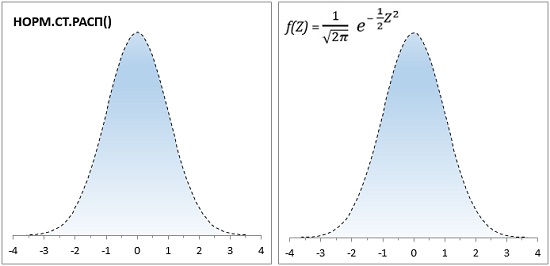
Сейчас функция в Excel НОРМ.РАСП(x;среднее;стандартное_откл;интегральная) значительно упростила работу с формулой (1). Однако, заложенная традиция сохранилась, и статистики обсуждают особенности распределения, критические границы и т.п. в терминах стандартного нормального распределения (рис. 2). Для последнего в Excel используется функция НОРМ.СТ.РАСП(z;интегральная).
Рис. 2. Формула (3) реализована в Excel с помощью функции НОРМ.СТ.РАСП(); по оси абсцисс – z-единицы, по оси ординат – вероятность.
Для перехода от стандартного распределения к физическим величинам нужно применить обратное преобразование:
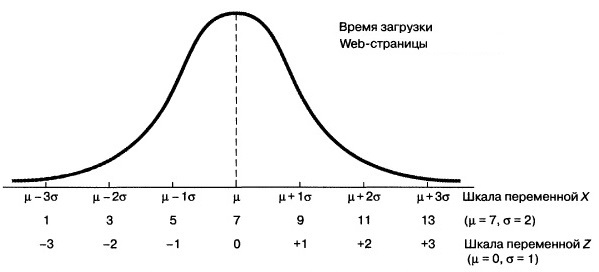
Допустим вы изучаете время загрузки некой Web-страницы, и выясняете, что оно распределено нормально, причем математическое ожидание равно μ = 7с, а стандартное отклонение σ = 2с. Как показывает рис. 3, каждому значению переменной X соответствует нормированное значение Z, полученное с помощью формулы преобразования (2). Следовательно, время загрузки, равное 9с, на одну стандартную единицу превышает математическое ожидание: Z = (9 – 7) / 2 = +1, а время загрузки равное 1с на три z-единицы (стандартных отклонения) меньше математического ожидания: Z = (1 – 7) / 2 = –3.
Рис. 3. Преобразование физических значений в z-значения для μ = 7, σ = 2
Описанные выше z-единицы используют для индивидуальных оценок, т.е. для измерений, приписываемых отдельным элементам выборки (например, рост каждого ученика школы). Если в качестве точек кривой нормального распределения берутся средние значения выборок (например, средний рост учеников различных классов), используют термин z-значение или z-статистика:[2]
где X̅ – среднее значение выборки (средний рост учеников 5А класса), μ – среднее значение генеральной совокупности (средний рост всех учеников школы), – стандартная ошибка средних (стандартное отклонение среднего роста учеников отдельных классов от среднего роста всех учеников школы). Последняя рассчитывается по формуле:
где σ – стандартная ошибка индивидуальных значений, n – размер выборки (число учеников в классе).
t-значение
Допустим, вы предполагаете, что дизельные двигатели автомобилей определенной модели выбрасывают в атмосферу больше оксида азота, чем заявлено в рекламных объявлениях. Вы знаете, что стандарт устанавливает ограничение на выбросы – не более 0,4 грамма на милю пробега. Вы хотели бы сравнить эмпирически полученные результаты не со средним по генеральной совокупности, а с этим стандартом – 0,4 г/милю. Это целевое значение, а не параметр генеральной совокупности. Вы тестируете пять автомобилей данной модели и измеряете уровень выброса оксида азота в дорожных условиях. Далее вы вычисляете среднее количество выбросов оксида азота для пяти автомобилей и находите стандартное отклонение. Наконец, вы находите величину:
где X̅ – средний уровень выбросов диоксида азота для пяти автомобилей; μ = 0,4 – установленный стандартом граничный уровень выбросов оксида азота;[3] s — стандартное отклонение уровня выбросов оксида азота по результатам для пяти автомобилей.
Это отношение очень похоже на формулу (2) для z-значения, но в действительности это t-значение. z- и t-значения отличаются тем, что для нахождения t-значения используется стандартное отклонение, полученное на основе выборочных результатов s, а не известное значение параметра генеральной совокупности σ. Использование латинской буквы s вместо греческой буквы σ для обозначения стандартного отклонения напоминает о том, что в данном случае значение стандартного отклонения является выборочной оценкой (статистикой), а не известным параметром.
Плотность распределения t-значений рассчитывается не с помощью формулы (3), а существенно сложнее. Я не привожу её здесь, поскольку сейчас в лоб ее никто не считает. Все используют готовые функции в статистических пакетах.
В Excel есть ряд функций, работающих с t-статистикой (рис. 4). Функции, имена которых включают часть РАСП, принимают t-значение в качестве аргумента и возвращают вероятность. Функции, имена которых включают часть ОБР, принимают значение вероятности в качестве аргумента и возвращают t-значение. Две последние функции на рис. 4 устарели и оставлены для обратной совместимости с более ранними версиями Excel.
Рис. 4. Семейство функций в Excel, работающих с t-статистикой Стьюдента
Степени свободы
Кривая t-распределения аналогична стандартной нормальной кривой, но ее форма немного меняется в зависимости от количества наблюдений, использованных для ее построения. В общем случае количество степеней свободы df = n – k, где n — количество наблюдений в выборке, а k — количество статистик, фиксированных для выборки. Например, если мы просто изучаем выборку, то k = 1, так как мы зафиксировали только среднее значение выборки. Если мы изучаем регрессионную зависимость от одной переменной, то k = 2; зафиксированы две статистики: среднее по выборке и наклон регрессионной кривой. Каждая дополнительная независимая переменная в регрессионной зависимости уменьшает число степеней свободы на единицу.
Во все функции Excel, предназначенные для работы с t-распределением, вторым аргументом входит количество степеней свободы df. Этот параметр необходим Excel для того, чтобы правильно вычислить форму кривой плотности t-распределения и вернуть корректное значение вероятности t-значения, заданного с помощью первого аргумента. Так для одного и того же z-значения = t-значению = 2,5 вероятность встретить его зависит от размера выборки (числа степеней свободы; рис. 5).
Рис. 5. Вероятность появления z- или t-значения зависит от того, какое распределение используется
То, насколько толстыми или тяжелыми являются хвосты t-распределения можно выразить количественно (рис. 6). Так, например, в пределах одного стандартного отклонение от среднего при нормальном распределении находится 68,27% значений. Для t-распределения с двумя степенями свободы такая вероятность существенно меньше – 57,74%.
Рис. 6. Сравнение нормального и t-распределений
Функции Excel для работы с t-распределением
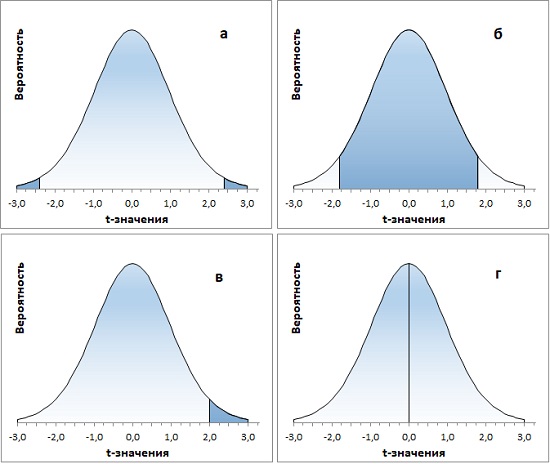
Рассмотрим работу функций Excel подробнее. Функция =СТЬЮДЕНТ.РАСП(t-значение;df;интегральная) возвращает левостороннее t-распределение Стьюдента (рис. 7). t-значение должно быть стандартизовано согласно формуле (7), т.е., выражено в долях стандартного отклонения σ при математическом ожидание генеральной совокупности µ = 0. Последний аргумент функции СТЬЮДЕНТ.РАСП() является логическим значением. Если он равен ЛОЖЬ, возвращается функция плотности распределения, т.е., вероятность для одного t-значения – Р(Х=t). Если он равен ИСТИНА, функция возвращает интегральное (накопленное) значение, т.е., вероятность попасть в интервал от минус бесконечности до t-значения – Р(Х≤t).
Рис. 7. Левостороннее t-распределение Стьюдента, функция Excel СТЬЮДЕНТ.РАСП()
Если функцию СТЬЮДЕНТ.РАСП() дополнить простыми арифметическими действиями, можно решить множество задач, связанных с t-распределением. Некоторые из них представлены ниже (рис. 8; во всех случаях df = 20):
- какова вероятность найти значение за пределами диапазона ±2,4σ от среднего значения Р(|Х|≥2,4)? =СТЬЮДЕНТ.РАСП(-2,4;20;ИСТИНА)*2
- какова вероятность найти значение внутри диапазона ±1,8σ от среднего значения Р(|Х|≤1,8)? =СТЬЮДЕНТ.РАСП(1,8;20;ИСТИНА)-СТЬЮДЕНТ.РАСП(-1,8;20;ИСТИНА) или, учитывая симметричность t-распределения, =(0,5-СТЬЮДЕНТ.РАСП(-1,8;20;ИСТИНА))*2
- какова вероятность найти значение справа от 2σ Р(Х≥2)?
=1-СТЬЮДЕНТ.РАСП(2;20;ИСТИНА) - какова вероятность среднего значения Р(Х=0)?
=СТЬЮДЕНТ.РАСП(0;20;ЛОЖЬ)
Рис. 8. Функция Excel СТЬЮДЕНТ.РАСП() позволяет решать основные задачи с t-распределением
Функция СТЬЮДЕНТ.РАСП.ПХ() возвращает правостороннее t-распределение, причем только интегральное. Т.е., она показывает накопленную вероятность, начиная с правой точки +∞ при движении влево – Р(X≥t).[4] У функции только два аргумента: t-значение и число степеней свободы. Она чуть более удобна, чем СТЬЮДЕНТ.РАСП() в задачах, где нас интересует вероятность обнаружить то или иное значение правого хвоста. Для примера (в) выше (см. также рис. 8в) формула будет такой: =СТЬЮДЕНТ.РАСП.ПХ(2;20).
Функция СТЬЮДЕНТ.РАСП.2Х() возвращает двустороннее t-распределение Стьюдента – P(|X|≥t) или P(X≥t или X≤-t). Как и функция СТЬЮДЕНТ.РАСП.ПХ(), она имеет два аргумента (t-значение и число степеней свободы), и возвращает только интегральное значение. Функция СТЬЮДЕНТ.РАСП.2Х() показывает накопленную вероятность для двух симметричных хвостов. Она чуть более удобна, чем СТЬЮДЕНТ.РАСП() в задачах, где нас интересует вероятность обнаружить два хвоста сразу. При этом задать нужно t-значение правого хвоста (отрицательные t-значения функция не принимает). Для примера (а) выше (см. также рис. 9а) формула будет такой: =СТЬЮДЕНТ.РАСП.2Х(2,4;20).
t-критерий
Одно из важных применений t-статистики связано с ответом на вопрос, насколько выборка характерна для генеральной совокупности? Например, если в генеральной совокупности среднее μ, а в выборке – х̅, какова вероятность, что выборка сделана из этой генеральной совокупности, а не из другой?
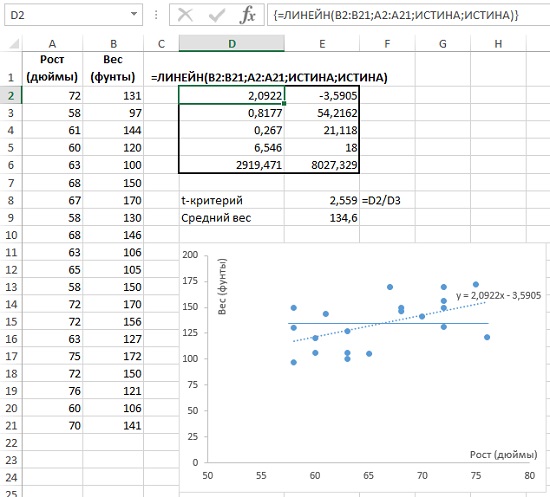
Рассмотрим пример (рис. 9). Исследуется зависимость веса от роста. Функция массива ЛИНЕЙН() (ячейки D2:E6), возвращает, в частности, наклон регрессионной кривой, он же коэффициент регрессии (ячейка D2) и стандартную ошибку коэффициента регрессии (ячейка D3). На рис. 9 данные роста и веса помещены на точечную диаграмму. На ней изображена регрессионная прямая (пунктирная линия; чтобы вывести ее, кликните в области диаграммы правой кнопкой мыши, и выберите опцию Добавить линию тренда…). Выведена также и формула регрессионной кривой y = 2,0922x – 3,5905 (естественно, коэффициент при х равен значению в ячейке D2).
t-критерий параметра = значение параметра, деленное на стандартную ошибку параметра
В нашем случае t-критерий коэффициента регрессии = коэффициент регрессии / стандартная ошибка коэффициента регрессии = 2,0922 / 0,8177 = 2,559 (ячейка Е8).
Рис. 9. Коэффициент регрессии = 2,0922 и t-критерий коэффициента регрессии = 2,559
Допустим, в генеральной совокупности вес не зависит от роста (нулевая гипотеза; на рис. 9 изображена сплошной прямой). Это значит, что коэффициент регрессии генеральной совокупности равен 0. В нашей выборке из 20 человек, мы обнаружили линейную зависимость веса от роста с коэффициентом регрессии (коэффициентом при х) = 2,0922. Если нормировать эту величину на стандартную ошибку, мы получим безразмерную величину = 2,559. Т.е., подсчитанный нами коэффициент регрессии в выборке на 2,559 сигм отстоит от нуля.
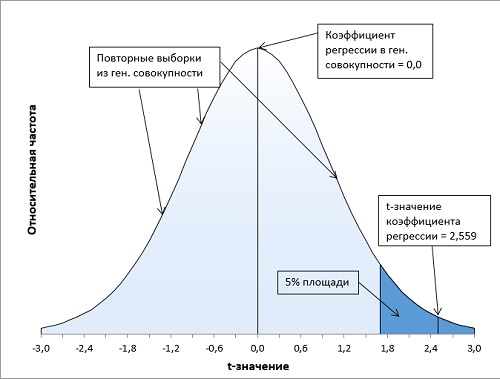
Насколько невероятно (или вероятно) получить такое отклонение в выборке, если в генеральной совокупности коэффициент регрессии = 0? Можно ли дать определение того, какое событие можно считать «невероятным». Считать ли его таковым, если оно происходит один раз в серии из 20 испытаний? Или в серии из 100 испытаний? А может быть, из 1000 испытаний? Как правило, событие считают «невероятным», если оно может произойти не чаще, чем в одном случае из двадцати.
Итак, в качестве нулевой гипотезы можно принять, что вес не зависит от роста. В качестве альтернативной гипотезы мы предположим, что вес положительно коррелирован с ростом (чем больше рост, тем больше вес). Мы отклоним нулевую гипотезу, только если t-значение коэффициента регрессии попадет в правый хвост распределения в область, соответствующую 5% всей площади под кривой (α = 0,05). Это, как раз, произойдет не чаше, чем один раз на двадцать выборок (рис. 10).
Рис. 10. Расположение t-значения коэффициента регрессии (2,559) на кривой t-распределения Стьюдента (df = 18) показывает, что его вероятность около 1% не превышает α-уровень = 5%. Нулевая гипотеза может быть отвергнута. Статистики выборки говорят о зависимости веса от роста.
Расчет t-значения, соответствующего заданному уровню значимости
Проблема выбора «уровня невероятности», т.е. уровня статистической значимости, или α-уровня, десятилетиями будоражила статистиков. Найти ответы на подобные вопросы зачастую очень трудно, и многие исследователи лишь пожимают плечами и выбирают для альфа-уровня одно из общепринятых значений: р < 0,05 или р < 0,01. Почему именно такие значения?
Главная причина — это то, что в течение многих лет исследователи должны были полагаться на справочные таблицы, позволяющие найти такое t-значение, которое можно было бы считать «статистически значимым» на уровне 0,05 или 0,01 (таблиц для других α-значений практически не было). В наше время определение критического значения t-статистики при любом заданном уровне значимости не составляет труда.
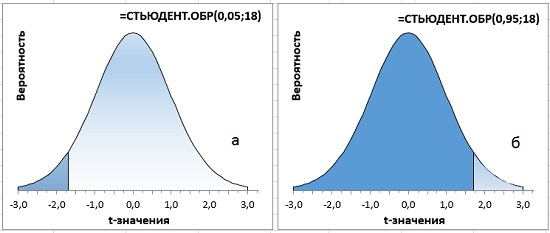
В Excel есть две функции для расчета t-критерия по уровню значимости (вероятности). СТЬЮДЕНТ.ОБР(вероятность;степени_свободы) возвращает левостороннее обратное t-распределение. В качестве первого аргумента функция принимает накопленную вероятность, начиная с –∞. Как правило, используется для односторонних тестов. В случае использования в двустороннем тесте α-значение следует разделить на 2. Например, t-значение для 5%-ного уровня значимости на рис. 10 можно найти с помощью формул =–СТЬЮДЕНТ.ОБР(0,05;18) или =СТЬЮДЕНТ.ОБР(1–0,05;18). В обоих случаях ответ 1,7341. В первом случае СТЬЮДЕНТ.ОБР(0,05;18) возвращает значение –1,7341, соответствующее 5%, накопленным от –∞ до –1,7341 (рис. 11а). Для получения окончательного ответа нужно воспользоваться свойством симметрии кривой распределения, и добавить знак минус перед функцией. Во втором случае СТЬЮДЕНТ.ОБР(1–0,05;18) возвращает значение 1,7341, соответствующее 95%, накопленным от –∞ до 1,7341 (рис. 11б).
Рис. 11. Односторонний t-критерий с уровнем значимости α = 5%
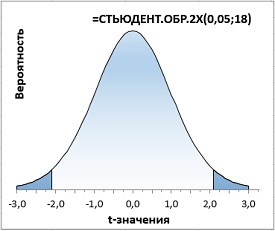
Вторая функция =СТЬЮДЕНТ.ОБР.2Х() используется в двусторонних тестах, когда мы допускаем, что исследуемое значение может отклоняться в обе стороны от среднего. В формулу следует подставить α-уровень значимости, функция сама разобьет его на две части и вернет значение, соответствующее двум симметричным хвостам (рис. 12; сравните с рис. 11а).
Рис. 12. Двусторонний t-критерий с уровнем значимости α = 5%
Ошибка первого рода
Предположим, перед вами стоит задача увеличить трафик нескольких веб-сайтов. Вы договариваетесь с владельцем популярного рекламного сайта о том, чтобы на его страницах отображались ссылки на 16 сайтов, случайным образом выбираемых из списка сайтов, контролируемых вашей компанией. Другие ваши 16 сайтов, также выбираемые случайным образом, не будут продвигаться в течение месяца.
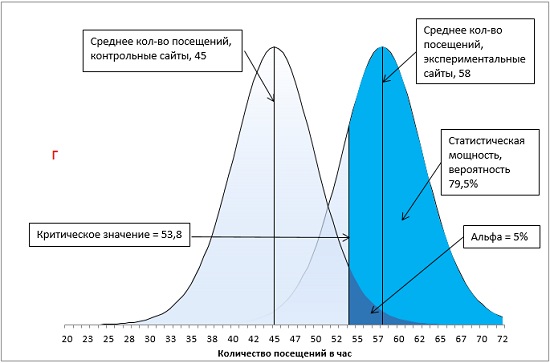
Вы намереваетесь сравнить между собой средние показатели посещений сайтов, ссылки на которые специально продвигаются поставщиком рекламных услуг, и остальных сайтов. Вы останавливаете свой выбор на направленной гипотезе с альфа-уровнем 0,05: только если специально продвигаемые сайты характеризуются большим средним количеством посещений и только если различие между двумя группами сайтов настолько велико, что при многократном повторении данного испытания оно может случайно встретиться не чаще, чем в одном случае из 20, вы будете отбрасывать гипотезу о том, что специальное продвижение сайта не влияет на среднее количество его посещений.
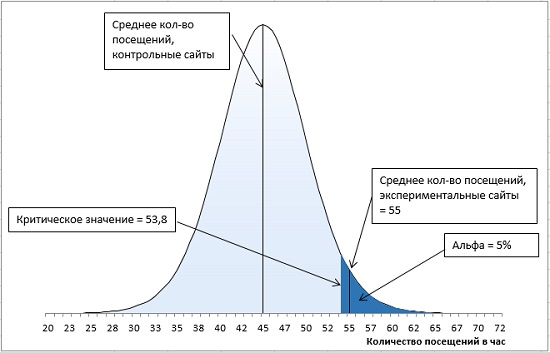
Через месяц вы получаете свои данные и обнаруживаете, что средний показатель для вашей контрольной группы – сайтов, не получающих специального продвижения, – составляет 45 посещений в час, а для продвигаемых сайтов – 55 посещений в час. Стандартная ошибка среднего равна 5.
Итак, у нас имеется контрольная группа из 16 сайтов (df = 15), правосторонний однонаправленный тест с α-уровнем = 0,05. t-значение определяется по формуле =-СТЬЮДЕНТ.ОБР(0,05;15) и равно 1,7531. Критическое значение посещаемости определяется по формуле (4) и равно: t-значение * стандартное отклонение выборки + среднее по выборке = 1,7531 * 5 + 45 = 53,8. Среднее по экспериментальной группе (55) больше критического t-значения (55 > 53,8). Мы можем отвергнуть нулевую и принять альтернативную гипотезу – продвижение сайтов влияет на посещаемость (рис. 13).
Рис. 13. Попадание среднего значения внутрь α-уровня позволяет отвергнуть нулевую гипотезу
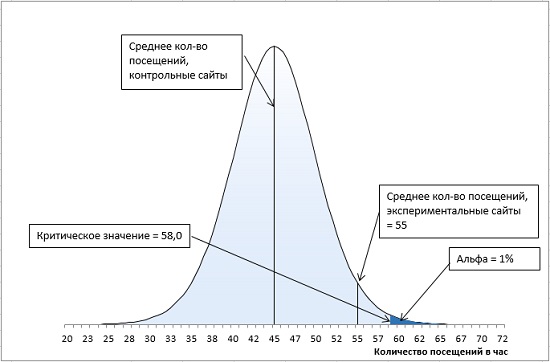
Но, значение альфа-уровня полностью контролируется нами — это наше правило принятия решений. Если бы мы установили для альфа-уровня значение 0,01, мы бы не отвергли нулевую гипотезу (рис. 14). Мы могли бы сказать, что среднее экспериментальной группы происходит из той же генеральной совокупности, что и среднее контрольной группы. Итак, статистическая ошибка I рода: мы отвергаем нулевую гипотезу, когда она верна.
Рис. 14. Для α-уровня = 0,01 среднее экспериментальной группы не позволяет отвергнуть нулевую гипотезу
Что же мешает установить α-уровень достаточно маленьким, и не отвергать нулевую гипотезу, когда она верна? …Ошибка II рода, заключающаяся в том, что мы не принимаем альтернативную гипотезу, хотя она верна.
Ошибка второго рода
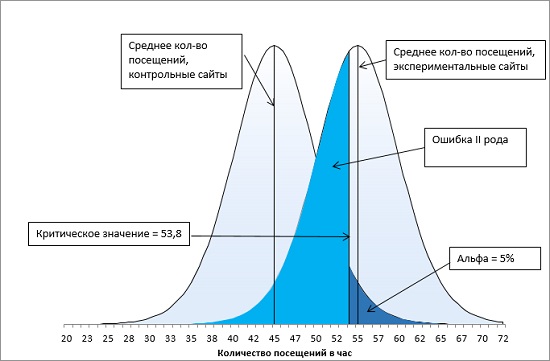
Представьте, что существуют две генеральные совокупности: одна из них состоит из сайтов, не получающих специального продвижения, вторая — из сайтов, получающих продвижение. Если вы повторите свое месячное исследование сотни или даже тысячи раз, то, возможно, получите две колоколообразные кривые (рис. 15).
Рис. 15. Ошибка второго рода при α-уровне = 0,05
Иногда среднее значение экспериментальной группы будет происходить из правого хвоста левой кривой распределения исключительно из-за выборочной ошибки. Поскольку в данном случае среднее экспериментальной группы превышает среднее контрольной группы более чем на 1,75 стандартной ошибки (попадает в область α-уровня = 0,05), вы должны отвергнуть нулевую гипотезу, даже если обе генеральные совокупности в действительности имеют одно и то же среднее. Такое неверное отбрасывание нулевой гипотезы, когда в действительности она является истинной, мы назвали ошибкой I рода. В терминах рис. 15 ошибка I рода – приписывание среднего результата экспериментальной выборки, равное 55, правой кривой, а не хвосту левой кривой.
Кривая слева представляет генеральную совокупность веб-сайтов, не получающих специального продвижения. На протяжении месяца частота посещений для некоторых из этих сайтов (очень немногих) составит всего 25 посещений в час, тогда как для других, столь же немногочисленных, – 62 посещения в час. Но 90% всех средних показателей выборок лежат в диапазоне 36,2–53,8 посещений в час.
Кривая справа представляет специально продвигаемые сайты. Как правило, показатели для них примерно на 10 посещений в час выше, чем для сайтов, представленных кривой слева. Их общее среднее составляет 55 посещений в час. Однако большая часть этой информации скрыта от вас. У вас отсутствуют данные о генеральной совокупности, и вы располагаете только результатами двух извлеченных вами выборок, но и этого вам будет вполне достаточно.
Рассмотрим правую кривую на рис. 15. Площадь под этой кривой от минимальных до критического значения (равного 53,8) выделена ярко голубым. Она определяет вероятность ошибки II рода. Средние выборок, проистекающие из этой области, мы относим к левой кривой, а не к правой. Для количественной оценки вероятности ошибки II рода найдем t-значение границы для правой кривой по формуле (7):
Вероятность того, что значение относится к правой кривой и лежит в диапазоне t-значений от –∞ до –0,247 определяется формулой =СТЬЮДЕНТ.РАСП(-0,247;15;ИСТИНА) = 0,404. Т.е., при выбранном нами α-уровне = 0,05 с вероятностью 40,4% мы отклоним альтернативную гипотезу, хотя она верна!
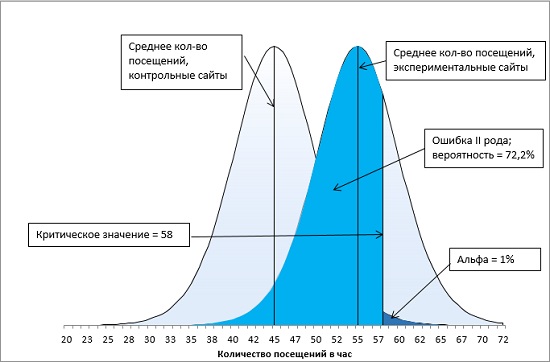
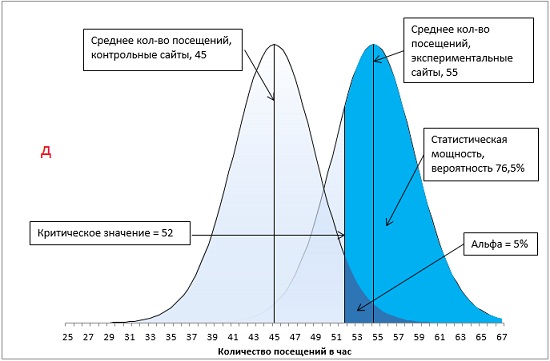
Что произойдет, если мы выберем α-уровень = 0,01, как на рис. 14? Вероятность ошибки II рода увеличится до 72,2% (рис. 16).
Рис. 16. Ошибка второго рода при α-уровне = 0,01
Статистическая мощность
Вероятность, количественно определяющую величину ошибки второго рода, называют β (на рис. 16 β = 72,2%). А вероятность р = (1 – β) – статистической мощностью (рис. 17).
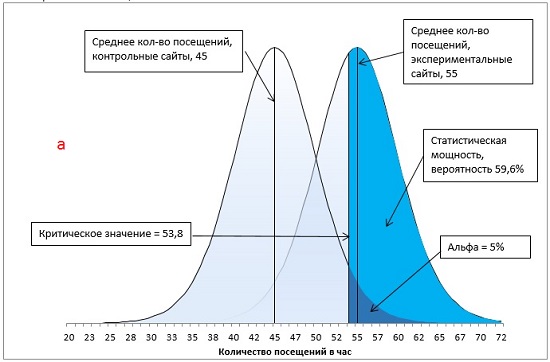
Рис. 17. Статистическая мощность исследования при α-уровне = 0,05
Чем выше статистическая мощность, тем больше вероятность того, что мы отклоним нулевую гипотезу и примем альтернативную гипотезу. На мощность влияют четыре основных фактора:
- Тип теста (переход от двунаправленного теста к однонаправленному увеличивает мощность).
- Уровень α, то есть вероятность ошибки I рода: более высокая α увеличивает мощность.
- Разница между средними значениями выборок (мощность выше при большей разнице).
- Стандартная ошибка среднего (чем ниже ошибка, тем мощность выше).
Давайте на нашем примере рассмотрим, как каждый из указанных факторов изменяет мощность, считая, что факторы меняться по одному (рис 18; расчеты и формулы можно найти в файле Excel).
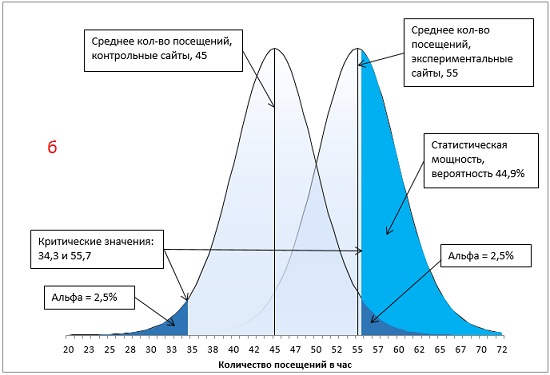
Рис. 18. Методы увеличения статистической мощности: а) базовый вариант; б) ненаправленная гипотеза; в) увеличение α с 0,05 до 0,1; г) увеличение разницы между средними экспериментальной и контрольной групп с 10 до 13 посещений в час; д) увеличение размера групп с 16 до 24 сайтов.
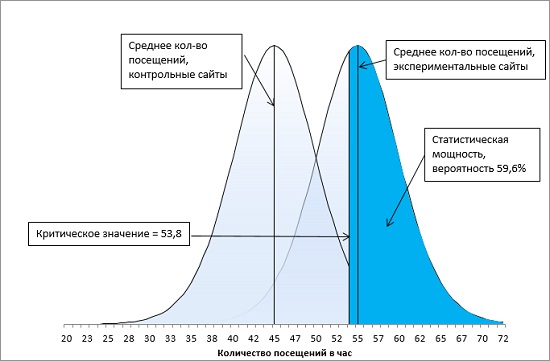
Первый метод повышения статистической мощности связан с подготовкой эксперимента. Если вместо ненаправленной гипотезы (двуххвостовой тест) использовать направленную (однохвостовой тест), вся величина α-уровня отнесется к одному хвосту распределения (сравните рис. 18а и 18б). В результате критическое значение сместится в сторону среднего значения распределения. Чем ближе критическое значение к среднему, тем более вероятно, что вы получите результат, превышающий критическое значение, что увеличивает статистическую мощность тестов. В нашем примере, мощность возрастет с 44,9% до 59,6%.
Второй метод повышения мощности теста предлагает ослабить α-уровень. Например, увеличивая α от 0,05 до 0,10, вы увеличиваете вероятность совершения ошибки I рода, но уменьшаете вероятность совершения ошибки II рода (сравните рис. 18а и 18в). В нашем примере, мощность возросла с 59,6% до 74%.
Оставшиеся два метода повышения статистической мощности основаны на формуле расчета t-статистики:
где t – t-значение для среднего выборки (а не для индивидуального значения), X̅ – среднее значение выборки, μ – среднее значение генеральной совокупности (или среднее значение контрольной выборки), – стандартная ошибка средних по выборкам (а не индивидуальных значений), равная:
где s – стандартная ошибка индивидуальных значений, n – размер выборки.
Для увеличения t-статистики (и, как следствие, статистической мощности) нужно, либо увеличить числитель, либо уменьшить знаменатель в формуле (8). Для увеличения разности X̅ – μ требуется внесение изменений в проведение эксперимента. Как это сделать, непростой вопрос, решаемый в каждом конкретном случае. В нашем примере, увеличение X̅ с 55 до 58 посещений в час при неизменном μ = 45, приведет к росту статистической мощности с 59,6% до 79,5% (рис. 18г).
И, наконец, уменьшение величины знаменателя тестовой статистики в формуле (8), есть не что иное, как уменьшение стандартной ошибки . Одним из способов уменьшения стандартной ошибки является увеличение размера выборки, n. В соответствии с формулой (9), чем больше n, тем меньше . В нашем примере, при неизменной стандартной ошибке индивидуальных значений s, увеличение контрольной и экспериментальной групп с 16 до 24 сайтов приведет к уменьшению с 5 до 4,1 и росту мощности с 59,6% до 76,5% (рис. 18д).
Один из хороших способов познакомиться с влиянием разных факторов на мощность – это поэкспериментировать с графическим калькулятором мощности, например, здесь.
Основные положения заметки
t-статистика Стьюдента используется вместо нормального распределения: а) для малых выборок; б) если стандартное отклонение генеральной совокупности σ не известно.
t-распределение представлено семейством распределений; дополнительный параметр – размер выборки или число степеней свободы.
Число степеней свободы равно размеру выборки минус число фиксированных статистик выборки (среднее, коэффициент регрессии, …)
Чем больше степеней свободы, тем ближе t-распределение к нормальному.
Функции в Excel, имена которых включают часть РАСП, принимают t-значение в качестве аргумента и возвращают вероятность. Функции, имена которых включают часть ОБР, принимают значение вероятности в качестве аргумента и возвращают t-значение.
Для подстановки в функции Excel значения предварительно должны быть стандартизованы.
Ошибка I рода: отбрасывание нулевой гипотезы, когда в действительности она является истинной. Ошибка II рода: не принятие альтернативной гипотезы, хотя она верна. Чем больше ошибка первого рода, тем меньше ошибка второго рода.
Критерий отнесения события к маловероятному является произвольным. Традиционно маловероятным считают событие, происходящее не чаще, чем 1 раз из 20 попыток.
Один из основных методов уменьшения ошибки второго рода – увеличение элементов в выборке.
[1] При написании замети использованы материалы книг: Дуглас Хаббард. Как измерить всё, что угодно, Левин и др. Статистика для менеджеров, Сара Бослаф. Статистика для всех, Конрад Карлберг. Регрессионный анализ в Microsoft Excel.
[2] На самом деле, можно встретить довольно много различных терминов в отношении нормированных значений z. Ориентируйтесь не на названия, а на суть понятий.
[3] Могут высказать справедливое замечание, что не следует обозначать граничный уровень так же, как и математическое ожидание генеральной совокупности µ. Соглашусь, но всё же использую обозначение, поскольку, в иных задачах здесь часто фигурирует именно математическое ожидание генеральной совокупности µ.
[4] Некоторые авторы указывают знак меньше или равно для левостороннего распределения Р(Х≤t), и больше для правостороннего Р(X>t). Однако, для t=0 значения СТЬЮДЕНТ.РАСП(0;df;ИСТИНА) = СТЬЮДЕНТ.РАСП.ПХ(0;df) = 0,5 для любого значения df. На мой взгляд, Excel при интегральном расчете трактует границу, как исчезающе малую. Поэтому, нет разницы, использовать знак ≥ или >.
Проверка статистической гипотезы позволяет сделать строгий вывод о характеристиках генеральной совокупности на основе выборочных данных. Гипотезы бывают разные. Одна из них – это гипотеза о средней (математическом ожидании). Суть ее в том, чтобы на основе только имеющейся выборки сделать корректное заключение о том, где может или не может находится генеральная средняя (точную правду мы никогда не узнаем, но можем сузить круг поиска).
Распределение Стьюдента
Общий подход в проверке гипотез описан здесь, поэтому сразу к делу. Предположим для начала, что выборка извлечена из нормальной совокупности случайных величин X с генеральной средней μ и дисперсией σ2. Средняя арифметическая из этой выборки, очевидно, сама является случайной величиной. Если извлечь много таких выборок и посчитать по ним средние, то они также будут иметь нормальное распределение с математическим ожиданием μ и дисперсией
Тогда случайная величина
имеет стандартное нормальное распределение со всеми вытекающими отсюда последствиями. Например, с вероятностью 95% ее значение не выйдет за пределы ±1,96.
Однако такой подход будет корректным, если известна генеральная дисперсия. В реальности, как правило, она не известна. Вместо нее берут оценку – несмещенную выборочную дисперсию:
где
Возникает вопрос: будет ли генеральная средняя c вероятностью 95% находиться в пределах ±1,96sx̅. Другими словами, являются ли распределения случайных величин
и
эквивалентными.
Впервые этот вопрос был поставлен (и решен) одним химиком, который трудился на пивной фабрике Гиннесса в г. Дублин (Ирландия). Химика звали Уильям Сили Госсет и он брал пробы пива для проведения химического анализа. В какой-то момент, видимо, Уильяма стали терзать смутные сомнения на счет распределения средних. Оно получалось немного более размазанным, чем должно быть у нормального распределения.
Собрав математическое обоснование и рассчитав значения функции обнаруженного им распределения, химик из Дублина Уильям Госсет написал заметку, которая была опубликована в мартовском выпуске 1908 года журнала «Биометрика» (главред – Карл Пирсон). Гиннесс строго-настрого запретил выдавать секреты пивоварения, и Госсет подписался псевдонимом Стьюдент.
Несмотря на то что, К. Пирсон уже изобрел распределение Хи-квадрат, все-таки всеобщее представление о нормальности еще доминировало. Никто не собирался думать, что распределение выборочных оценок может быть не нормальным. Поэтому статья У. Госсета осталась практически не замеченной и забытой. И только Рональд Фишер по достоинству оценил открытие Госсета. Фишер использовал новое распределение в своих работах и дал ему название t-распределение Стьюдента. Критерий для проверки гипотез, соответственно, стал t-критерием Стьюдента. Так произошла «революция» в статистике, которая шагнула в эру анализа выборочных данных. Это был краткий экскурс в историю.
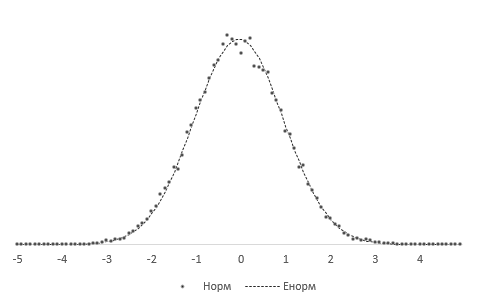
Посмотрим, что же мог увидеть У. Госсет. Сгенерируем 20 тысяч нормальных выборок из 6-ти наблюдений со средней (X̅) 50 и среднеквадратичным отклонением (σ) 10. Затем нормируем выборочные средние, используя генеральную дисперсию:
Получившиеся 20 тысяч средних сгруппируем в интервалы длинной 0,1 и подсчитаем частоты. Изобразим на диаграмме фактическое (Norm) и теоретическое (ENorm) распределение частот выборочных средних.
Точки (наблюдаемые частоты) практически совпадают с линией (теоретическими частотами). Оно и понятно, ведь данные взяты из одной и то же генеральной совокупности, а отличия – это лишь ошибки выборки.
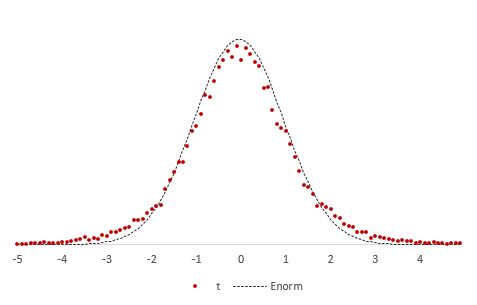
Проведем новый эксперимент. Нормируем средние, используя выборочную дисперсию.
Снова подсчитаем частоты и нанесем их на диаграмму в виде точек, оставив для сравнения линию стандартного нормального распределения. Обозначим эмпирическое частоты средних, скажем, через букву t.
Видно, что распределения на этот раз не очень-то и совпадают. Близки, да, но не одинаковы. Хвосты стали более «тяжелыми».
У Госсета-Стьюдента не было последней версии MS Excel, но именно этот эффект он и заметил. Почему так получается? Объяснение заключается в том, что случайная величина
зависит не только от ошибки выборки (числителя), но и от стандартной ошибки средней (знаменателя), которая также является случайной величиной.
Давайте немного разберемся, какое распределение должно быть у такой случайной величины. Вначале придется кое-что вспомнить (или узнать) из математической статистики. Есть такая теорема Фишера, которая гласит, что в выборке из нормального распределения:
1. средняя X̅ и выборочная дисперсия s2 являются независимыми величинами;
2. соотношение выборочной и генеральной дисперсии, умноженное на количество степеней свободы, имеет распределение χ2(хи-квадрат) с таким же количеством степеней свободы, т.е.
где k – количество степеней свободы (на английском degrees of freedom (d.f.))
Вернемся к распределению средней. Разделим числитель и знаменатель выражения
на σX̅. Получим
Числитель – это стандартная нормальная случайная величина (обозначим ξ (кси)). Знаменатель выразим из теоремы Фишера.
Тогда исходное выражение примет вид
Это и есть t-критерий Стьюдента в общем виде (стьюдентово отношение). Вывести функцию его распределения можно уже непосредственно, т.к. распределения обеих случайных величин в данном выражении известны. Оставим это удовольствие математикам.
Функция t-распределения Стьюдента имеет довольно сложную для понимания формулу, поэтому не имеет смысла ее разбирать. Вероятности и квантили t-критерия приведены в специальных таблицах распределения Стьюдента и забиты в функции разных ПО вроде Excel.
Итак, вооружившись новыми знаниями, вы сможете понять официальное определение распределения Стьюдента.
Случайной величиной, подчиняющейся распределению Стьюдента с k степенями свободы, называется отношение независимых случайных величин
где ξ распределена по стандартному нормальному закону, а χ2k подчиняется распределению χ2 c k степенями свободы.
Таким образом, формула критерия Стьюдента для средней арифметической
есть частный случай стьюдентова отношения
Из формулы и определения следует, что распределение т-критерия Стьюдента зависит лишь от количества степеней свободы.
При k > 30 t-критерий практически не отличается от стандартного нормального распределения.
В отличие от хи-квадрат, t-критерий может быть одно- и двусторонним. Обычно пользуются двусторонним, предполагая, что отклонение может происходить в обе стороны от средней. Но если условие задачи допускает отклонение только в одну сторону, то разумно применять односторонний критерий. От этого немного увеличивается мощность критерия.
Несмотря на то, что открытие Стьюдента в свое время совершило переворот в статистике, t-критерий все же довольно сильно ограничен в возможностях применения, т.к. сам по себе происходит из предположения о нормальном распределении исходных данных. Если данные не являются нормальными (что обычно и бывает), то и t-критерий уже не будет иметь распределения Стьюдента. Однако в силу действия центральной предельной теоремы средняя даже у ненормальных данных быстро приобретает колоколообразную форму распределения.
Рассмотрим, для примера, данные, имеющие выраженный скос вправо, как у распределения хи-квадрат с 5-ю степенями свободы.
Теперь создадим 20 тысяч выборок и будет наблюдать, как меняется распределение средних в зависимости от их объема.
Отличие довольно заметно в малых выборках до 15-20-ти наблюдений. Но дальше оно стремительно исчезает. Таким образом, ненормальность распределения – это, конечно, нехорошо, но некритично.
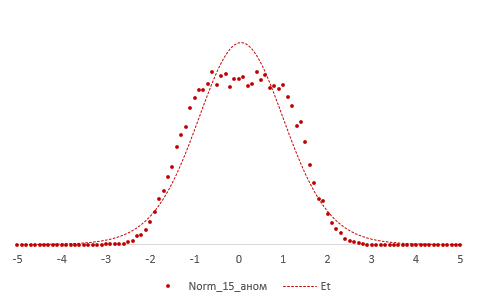
Больше всего t-критерий «боится» выбросов, т.е. аномальных отклонений. Возьмем 20 тыс. нормальных выборок по 15 наблюдений и в часть из них добавим по одному случайном выбросу.
Картина получается нерадостная. Фактические частоты средних сильно отличаются от теоретических. Использование t-распределения в такой ситуации становится весьма рискованной затеей.
Итак, в не очень малых выборках (от 15-ти наблюдений) t-критерий относительно устойчив к ненормальному распределению исходных данных. А вот выбросы в данных сильно искажают распределение t-критерия, что, в свою очередь, может привести к ошибкам статистического вывода, поэтому от аномальных наблюдений следует избавиться. Часто из выборки удаляют все значения, выходящие за пределы ±2 стандартных отклонения от средней.
Пример проверки гипотезы о математическом ожидании с помощью t- критерия Стьюдента в MS Excel
В Excel есть несколько функций, связанных с t-распределением. Рассмотрим их.
СТЬЮДЕНТ.РАСП – «классическое» левостороннее t-распределение Стьюдента. На вход подается значение t-критерия, количество степеней свободы и опция (0 или 1), определяющая, что нужно рассчитать: плотность или значение функции. На выходе получаем, соответственно, плотность или вероятность того, что случайная величина окажется меньше указанного в аргументе t-критерия, т.е. левосторонний p-value.
СТЬЮДЕНТ.РАСП.2Х – двухсторонне распределение. В качестве аргумента подается абсолютное значение (по модулю) t-критерия и количество степеней свободы. На выходе получаем вероятность получить такое или еще больше значение t-критерия (по модулю), т.е. фактический уровень значимости (p-value).
СТЬЮДЕНТ.РАСП.ПХ – правостороннее t-распределение. Так, 1-СТЬЮДЕНТ.РАСП(2;5;1) = СТЬЮДЕНТ.РАСП.ПХ(2;5) = 0,05097. Если t-критерий положительный, то полученная вероятность – это p-value.
СТЬЮДЕНТ.ОБР – используется для расчета левостороннего обратного значения t-распределения. В качестве аргумента подается вероятность и количество степеней свободы. На выходе получаем соответствующее этой вероятности значение t-критерия. Отсчет вероятности идет слева. Поэтому для левого хвоста нужен сам уровень значимости α, а для правого 1 — α.
СТЬЮДЕНТ.ОБР.2Х – обратное значение для двухстороннего распределения Стьюдента, т.е. значение t-критерия (по модулю). Также на вход подается уровень значимости α. Только на этот раз отсчет ведется с двух сторон одновременно, поэтому вероятность распределяется на два хвоста. Так, СТЬЮДЕНТ.ОБР(1-0,025;5) = СТЬЮДЕНТ.ОБР.2Х(0,05;5) = 2,57058
СТЬЮДЕНТ.ТЕСТ – функция для проверки гипотезы о равенстве математических ожиданий в двух выборках. Заменяет кучу расчетов, т.к. достаточно указать лишь два диапазона с данными и еще пару параметров. На выходе получим p-value.
ДОВЕРИТ.СТЬЮДЕНТ – расчет доверительного интервала средней с учетом t-распределения.
Рассмотрим такой учебный пример. На предприятии фасуют цемент в мешки по 50кг. В силу случайности в отдельно взятом мешке допускается некоторое отклонение от ожидаемой массы, но генеральная средняя должна оставаться 50кг. В отделе контроля качества случайным образом взвесили 9 мешков и получили следующие результаты: средняя масса (X̅) составила 50,3кг, среднеквадратичное отклонение (s) – 0,5кг.
Согласуется ли полученный результат с нулевой гипотезой о том, что генеральная средняя равна 50кг? Другими словами, можно ли получить такой результат по чистой случайности, если оборудование работает исправно и выдает среднее наполнение 50 кг? Если гипотеза не будет отклонена, то полученное различие вписывается в диапазон случайных колебаний, если же гипотеза будет отклонена, то, скорее всего, в настройках аппарата, заполняющего мешки, произошел сбой. Требуется его проверка и настройка.
Краткое условие в обще принятых обозначениях выглядит так.
H0: μ = 50 кг
Ha: μ ≠ 50 кг
Есть основания предположить, что распределение заполняемости мешков подчиняются нормальному распределению (или не сильно от него отличается). Значит, для проверки гипотезы о математическом ожидании можно использовать t-критерий Стьюдента. Случайные отклонения могут происходить в любую сторону, значит нужен двусторонний t-критерий.
Вначале применим допотопные средства: ручной расчет t-критерия и сравнение его с критическим табличным значением. Расчетный t-критерий:
Теперь определим, выходит ли полученное число за критический уровень при уровне значимости α = 0,05. Воспользуемся таблицей для критерия Стьюдента (есть в любом учебнике по статистике).
По столбцам идет вероятность правой части распределения, по строкам – число степеней свободы. Нас интересует двусторонний t-критерий с уровнем значимости 0,05, что равносильно t-значению для половины уровня значимости справа: 1 — 0,05/2 = 0,975. Количество степеней свободы – это объем выборки минус 1, т.е. 9 — 1 = 8. На пересечении находим табличное значение t-критерия – 2,306. Если бы мы использовали стандартное нормальное распределение, то критической точкой было бы значение 1,96, а тут она больше, т.к. t-распределение на небольших выборках имеет более приплюснутый вид.
Сравниваем фактическое (1,8) и табличное значение (2.306). Расчетный критерий оказался меньше табличного. Следовательно, имеющиеся данные не противоречат гипотезе H0 о том, что генеральная средняя равна 50 кг (но и не доказывают ее). Это все, что мы можем узнать, используя таблицы. Можно, конечно, еще p-value попробовать найти, но он будет приближенным. А, как правило, именно p-value используется для проверки гипотез. Поэтому далее переходим в Excel.
Готовой функции для расчета t-критерия в Excel нет. Но это и не страшно, ведь формула t-критерия Стьюдента довольно проста и ее можно легко соорудить прямо в ячейке Excel.
Получили те же 1,8. Найдем вначале критическое значение. Альфа берем 0,05, критерий двусторонний. Нужна функция обратного значения t-распределения для двухсторонней гипотезы СТЬЮДЕНТ.ОБР.2Х.
Полученное значение отсекает критическую область. Наблюдаемый t-критерий в нее не попадает, поэтому гипотеза не отклоняется.
Однако это тот же способ проверки гипотезы с помощью табличного значения. Более информативно будет рассчитать p-value, т.е. вероятность получить наблюдаемое или еще большее отклонение от средней 50кг, если эта гипотеза верна. Потребуется функция распределения Стьюдента для двухсторонней гипотезы СТЬЮДЕНТ.РАСП.2Х.
P-value равен 0,1096, что больше допустимого уровня значимости 0,05 – гипотезу не отклоняем. Но теперь можно судить о степени доказательства. P-value оказался довольно близок к тому уровню, когда гипотеза отклоняется, а это наводит на разные мысли. Например, что выборка оказалась слишком мала для обнаружения значимого отклонения.
Пусть через некоторое время отдел контроля снова решил проверить, как выдерживается стандарт заполняемости мешков. На этот раз для большей надежности было отобрано не 9, а 25 мешков. Интуитивно понятно, что разброс средней уменьшится, а, значит, и шансов найти сбой в системе становится больше.
Допустим, были получены те же значения средней и стандартного отклонения по выборке, что и в первый раз (50,3 и 0,5 соответственно). Рассчитаем t-критерий.
Критическое значение для 24-х степеней свободы и α = 0,05 составляет 2,064. На картинке ниже видно, что t-критерий попадает в область отклонения гипотезы.
Можно сделать вывод о том, что с доверительной вероятностью более 95% генеральная средняя отличается от 50кг. Для большей убедительности посмотрим на p-value (последняя строка в таблице). Вероятность получить среднюю с таким или еще большим отклонением от 50, если гипотеза верна, составляет 0,0062, или 0,62%, что при однократном измерении практически невозможно. В общем, гипотезу отклоняем, как маловероятную.
Расчет доверительного интервала для математического ожидания с помощью t-распределения Стьюдента в Excel
С проверкой гипотез тесно связан еще один статистический метод – расчет доверительных интервалов. Если в полученный интервал попадает значение, соответствующее нулевой гипотезе, то это равносильно тому, что нулевая гипотеза не отклоняется. В противном случае, гипотеза отклоняется с соответствующей доверительной вероятностью. В некоторых случаях аналитики вообще не проверяют гипотез в классическом виде, а рассчитывают только доверительные интервалы. Такой подход позволяет извлечь еще больше полезной информации.
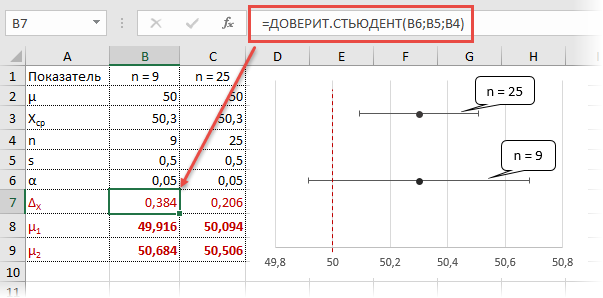
Рассчитаем доверительные интервалы для средней при 9 и 25 наблюдениях. Для этого воспользуемся функцией Excel ДОВЕРИТ.СТЬЮДЕНТ. Здесь, как ни странно, все довольно просто. В аргументах функции нужно указать только уровень значимости α, стандартное отклонение по выборке и размер выборки. На выходе получим полуширину доверительного интервала, то есть значение которое нужно отложить по обе стороны от средней. Проведя расчеты и нарисовав наглядную диаграмму, получим следующее.
Как видно, при выборке в 9 наблюдений значение 50 попадает в доверительный интервал (гипотеза не отклоняется), а при 25-ти наблюдениях не попадает (гипотеза отклоняется). При этом в эксперименте с 25-ю мешками можно утверждать, что с вероятностью 97,5% генеральная средняя превышает 50,1 кг (нижняя граница доверительного интервала равна 50,094кг). А это довольно ценная информация.
Таким образом, мы решили одну и ту же задачу тремя способами:
1. Древним подходом, сравнивая расчетное и табличное значение t-критерия
2. Более современным, рассчитав p-value, добавив степень уверенности при отклонении гипотезы.
3. Еще более информативным, рассчитав доверительный интервал и получив минимальное значение генеральной средней.
Важно помнить, что t-критерий относится к параметрическим методам, т.к. основан на нормальном распределении (у него два параметра: среднее и дисперсия). Поэтому для его успешного применения важна хотя бы приблизительная нормальность исходных данных и отсутствие выбросов.
Напоследок предлагаю видеоролик о том, как рассчитать критерий Стьюдента и проверить гипотезу о генеральной средней в Excel.
Иногда просят объяснить, как делаются такие наглядные диаграммы с распределением. Ниже можно скачать файл, где проводились расчеты для этой статьи.
Скачать файл с примером.
Всего доброго, будьте здоровы.
Поделиться в социальных сетях:
Содержание
- Определение термина
- Расчет показателя в Excel
- Способ 1: Мастер функций
- Способ 2: работа со вкладкой «Формулы»
- Способ 3: ручной ввод
- Вопросы и ответы
Одним из наиболее известных статистических инструментов является критерий Стьюдента. Он используется для измерения статистической значимости различных парных величин. Microsoft Excel обладает специальной функцией для расчета данного показателя. Давайте узнаем, как рассчитать критерий Стьюдента в Экселе.
Определение термина
Но, для начала давайте все-таки выясним, что представляет собой критерий Стьюдента в общем. Данный показатель применяется для проверки равенства средних значений двух выборок. То есть, он определяет достоверность различий между двумя группами данных. При этом, для определения этого критерия используется целый набор методов. Показатель можно рассчитывать с учетом одностороннего или двухстороннего распределения.
Теперь перейдем непосредственно к вопросу, как рассчитать данный показатель в Экселе. Его можно произвести через функцию СТЬЮДЕНТ.ТЕСТ. В версиях Excel 2007 года и ранее она называлась ТТЕСТ. Впрочем, она была оставлена и в позднейших версиях в целях совместимости, но в них все-таки рекомендуется использовать более современную — СТЬЮДЕНТ.ТЕСТ. Данную функцию можно использовать тремя способами, о которых подробно пойдет речь ниже.
Способ 1: Мастер функций
Проще всего производить вычисления данного показателя через Мастер функций.
- Строим таблицу с двумя рядами переменных.
- Кликаем по любой пустой ячейке. Жмем на кнопку «Вставить функцию» для вызова Мастера функций.
- После того, как Мастер функций открылся. Ищем в списке значение ТТЕСТ или СТЬЮДЕНТ.ТЕСТ. Выделяем его и жмем на кнопку «OK».
- Открывается окно аргументов. В полях «Массив1» и «Массив2» вводим координаты соответствующих двух рядов переменных. Это можно сделать, просто выделив курсором нужные ячейки.
В поле «Хвосты» вписываем значение «1», если будет производиться расчет методом одностороннего распределения, и «2» в случае двухстороннего распределения.
В поле «Тип» вводятся следующие значения:
- 1 – выборка состоит из зависимых величин;
- 2 – выборка состоит из независимых величин;
- 3 – выборка состоит из независимых величин с неравным отклонением.
Когда все данные заполнены, жмем на кнопку «OK».
Выполняется расчет, а результат выводится на экран в заранее выделенную ячейку.
Способ 2: работа со вкладкой «Формулы»
Функцию СТЬЮДЕНТ.ТЕСТ можно вызвать также путем перехода во вкладку «Формулы» с помощью специальной кнопки на ленте.
- Выделяем ячейку для вывода результата на лист. Выполняем переход во вкладку «Формулы».
- Делаем клик по кнопке «Другие функции», расположенной на ленте в блоке инструментов «Библиотека функций». В раскрывшемся списке переходим в раздел «Статистические». Из представленных вариантов выбираем «СТЬЮДЕНТ.ТЕСТ».
- Открывается окно аргументов, которые мы подробно изучили при описании предыдущего способа. Все дальнейшие действия точно такие же, как и в нём.
Способ 3: ручной ввод
Формулу СТЬЮДЕНТ.ТЕСТ также можно ввести вручную в любую ячейку на листе или в строку функций. Её синтаксический вид выглядит следующим образом:
= СТЬЮДЕНТ.ТЕСТ(Массив1;Массив2;Хвосты;Тип)
Что означает каждый из аргументов, было рассмотрено при разборе первого способа. Эти значения и следует подставлять в данную функцию.
После того, как данные введены, жмем кнопку Enter для вывода результата на экран.
Как видим, вычисляется критерий Стьюдента в Excel очень просто и быстро. Главное, пользователь, который проводит вычисления, должен понимать, что он собой представляет и какие вводимые данные за что отвечают. Непосредственный расчет программа выполняет сама.
Еще статьи по данной теме:
Помогла ли Вам статья?
Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel Web App Excel 2010 Excel для Mac 2011 Excel Starter 2010 Еще…Меньше
Возвращает левостороннее t-распределение Стьюдента. T-распределение используется для проверки гипотез при малом объеме выборки. Данную функцию можно использовать вместо таблицы критических значений t-распределения.
Синтаксис
СТЬЮДЕНТ.РАСП(x;степени_свободы;интегральная)
Аргументы функции СТЬЮДЕНТ.РАСП описаны ниже.
-
X Обязательный. Числовое значение, для которого требуется вычислить распределение.
-
Степени_свободы Обязательный. Целое, указывающее число степеней свободы.
-
Интегральная — обязательный аргумент. Логическое значение, определяющее форму функции. Если аргумент «интегральная» имеет значение ИСТИНА, функция СТЬЮДЕНТ.РАСП возвращает интегральную функцию распределения; если этот аргумент имеет значение ЛОЖЬ, возвращается функция плотности распределения.
Замечания
-
Если какой-либо из аргументов не является числом, то Т.#VALUE! значение ошибки #ЗНАЧ!.
-
Если значение аргумента «степени_свободы» < 1, функция СТЬЮДЕНТ.РАСП возвращает значение ошибки. Значение «степени_свободы» не может быть меньше 1.
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
|
Формула |
Описание |
Результат |
|
=СТЬЮДЕНТ.РАСП(60;1;ИСТИНА) |
Левостороннее t-распределение СТЬЮДЕНТА для 60, возвращаемое как интегральная функция распределения с 1 степенью свободы. |
0,99469533 |
|
=СТЬЮДЕНТ.РАСП(8;3;ЛОЖЬ) |
Левостороннее t-распределение СТЬЮДЕНТА для 8, возвращаемое как весовая функция распределения с 3 степенями свободы. |
0,00073691 |
К началу страницы
Нужна дополнительная помощь?
Критерий Стьюдента – обобщенное название группы статистических тестов (обычно перед словом “критерий” добавляется латинская буква “t”). Чаще всего он применяется для проверки равенства средних значений в двух выборках. Давайте посмотрим, как рассчитать данный критерий в программе Excel с помощью специальной функции.
-
Расчет t-критерия Стьюдента
- Метод 1: пользуемся Мастером функций
- Метод 2: вставляем функцию через “Формулы”
- Метод 3: ручной ввод формулы
- Заключение
Для того, чтобы выполнить соответствующие расчеты, понадобится функция “СТЬЮДЕНТ.ТЕСТ”, в ранних версиях Excel (2007 и старше) – “ТТЕСТ”, которая есть и в современных редакциях для сохранения совместимости со старыми документам.
Использовать функцию можно по-разному. Давайте разберем каждый вариант отдельно на примере таблицы с двумя рядами-столбцами числовых значений.
Метод 1: пользуемся Мастером функций
Этот способ хорош тем, что не нужно запоминать формулу функции (список ее аргументов). Итак, алгоритм действий следующий:
- Встаем в любую свободную ячейку, затем щелкаем по значку “Вставить функцию” слева от строки формул.
- В открывшемся окне Мастера функций выбираем категорию “Полный алфавитный перечень”, в списке ниже находим оператор “СТЬЮДЕНТ.ТЕСТ”, отмечаем его и щелкаем OK.
- На экране отобразится окно, в котором заполняем аргументы функции, после чего нажимаем OK:
- “Массив1” и “Массив2” – указываем диапазоны ячеек, содержащие ряды чисел (в нашем случае это “A2:A7” и “B2:B7”). Мы можем сделать это вручную, введя координаты с клавиатуры, или просто выделяем нужные элементы в самой таблице.
- “Хвосты” – пишем цифру “1”, если требуется выполнить расчет методом одностороннего распределения, или “2” – для двухстороннего.
- “Тип” – в этом поле указываем: “1” – если выборка состоит из зависимых величин; “2” – из независимых; “3” – из независимых величин с неравным отклонением.
- В результате в нашей ячейке с функцией появится рассчитанное значение критерия.
Метод 2: вставляем функцию через “Формулы”
- Переключаемся во вкладку “Формулы”, где также представлена кнопка “Вставить функцию”, которая нам и нужна.
- В результате откроется Мастер функций, дальнейшие действия в котором аналогичны описанным выше.
Через вкладку “Формулы” функцию “СТЬЮДЕНТ.ТЕСТ” можно запустить по-другому:
- В группе инструментов “Библиотека функций” жмем по значку “Другие функции”, после чего раскроется список, в котором выбираем раздел “Статистические”. Пролистав предложенный перечень мы сможем найти нужный нам оператор.
- На экране отобразится окно для заполнения аргументов, с которым мы уже познакомились ранее.
Метод 3: ручной ввод формулы
Опытные пользователи могут обходиться без Мастера функций и в требуемой ячейке сразу вводить формулу со ссылками на нужные диапазоны данных и прочими параметрами. Синтаксис функции в общем виде выглядит так:
= СТЬЮДЕНТ.ТЕСТ(Массив1;Массив2;Хвосты;Тип)
Каждый из аргументов мы разобрали в первом разделе публикации. Все, что остается сделать после набора формулы – нажать Enter для выполнения расчета.
Заключение
Таким образом, рассчитать t-критерий Стьюдента в программе Excel можно с помощью специальной функции, которую можно запустить разными способами. Также у пользователя есть возможность сразу ввести формулу функции в нужной ячейке, однако в этом случае придется запоминать ее синтаксис, что может быть хлопотно из-за того, что применяется она не так часто.