Таблица простых чисел excel

Таблица простых чисел

Простое число — это целое число больше единицы, единственными делителями которого являются только оно само и единица.

Все остальные натуральные числа называются составными. Число 1 не является ни простым, ни составным.

Tаблица простых чисел

Tаблица простых чисел

Tаблица простых чисел до 1000

Tаблица простых чисел до 997

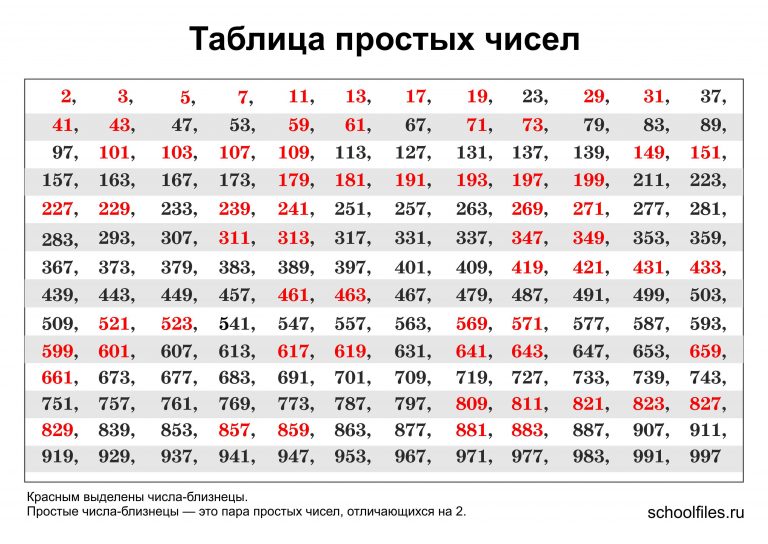
Простые числа от 1 до 997

Так-же вы можете скачать таблицу простых чисел в Excel:

Простые числа.xls

Источник

Допустим, вы решили за год скопить 100000 ₽. Тогда вам нужно начать примерно с 75 ₽ и каждую неделю откладывать на 75 ₽ больше. В этом случае к концу года вы получите в копилке 103350 ₽. Бесплатный шаблон для печати — тут.

Таблица (список) простых чисел до 3000. Генератор онлайн.

2 3 5 7 11 13 17 19 23 29
31 37 41 43 47 53 59 61 67 71
73 79 83 89 97 101 103 107 109 113
127 131 137 139 149 151 157 163 167 173
179 181 191 193 197 199 211 223 227 229
233 239 241 251 257 263 269 271 277 281
283 293 307 311 313 317 331 337 347 349
353 359 367 373 379 383 389 397 401 409
419 421 431 433 439 443 449 457 461 463
467 479 487 491 499 503 509 521 523 541
547 557 563 569 571 577 587 593 599 601
607 613 617 619 631 641 643 647 653 659
661 673 677 683 691 701 709 719 727 733
739 743 751 757 761 769 773 787 797 809
811 821 823 827 829 839 853 857 859 863
877 881 883 887 907 911 919 929 937 941
947 953 967 971 977 983 991 997

Таблица (список) простых чисел до 1000000. Генератор онлайн.

Для удобства таблица разбита на 4 страницы. Первая страница отвечает за дни 1-100, вторая — 101-200, третья — 201-300 и четвертая — 301-365. Это сделано для того, чтобы после того, как вы распечатаете таблицу, вы могли пользоваться ею без лупы 😀 Как копить деньги по таблице шаблон с произвольным шагом.

Таблица для копилки — M$M

Ниже я предлагаю вам несколько вариантов таблиц, любую из которых вы можете бесплатно скачать, распечатать и начать действовать. Честно говоря, таких ситуаций, даже если вы выберете 100-дневный марафон, будет много. Что уж там говорить о годе? В течение года количество пропусков может достичь размеров, угрожающих выполнению всего плана!

Знайка, самый умный эксперт в Цветочном городе

Мнение эксперта

Знайка, самый умный эксперт в Цветочном городе

Если у вас есть вопросы, задавайте их мне!

Задать вопрос эксперту

52-недельный марафон — базовая версия Если вы решите копить в течение года, откладывая каждый день, вам нужно будет сделать это 365 раз. На мой взгляд, проще откладывать раз в неделю. Почему же? Да все просто! Если вы решите копить в течение года, откладывая каждый день, вам нужно будет сделать это 365 раз! А если каждую неделю — всего 52 раза.

Эта схема аналогична базовой версии 52-недельного марафона, где мы копим 41340 ₽, за исключением того, что наиболее крупную сумму вы откладываете в первую неделю, а затем каждую неделю эта сумма уменьшается на выбранный шаг.

Копим по таблице 10100 ₽ за 100 дней

2 3 5 7 11 13 17 19 23 29
31 37 41 43 47 53 59 61 67 71
73 79 83 89 97 101 103 107 109 113
127 131 137 139 149 151 157 163 167 173
179 181 191 193 197 199 211 223 227 229
233 239 241 251 257 263 269 271 277 281
283 293 307 311 313 317 331 337 347 349
353 359 367 373 379 383 389 397 401 409
419 421 431 433 439 443 449 457 461 463
467 479 487 491 499 503 509 521 523 541
547 557 563 569 571 577 587 593 599 601
607 613 617 619 631 641 643 647 653 659
661 673 677 683 691 701 709 719 727 733
739 743 751 757 761 769 773 787 797 809
811 821 823 827 829 839 853 857 859 863
877 881 883 887 907 911 919 929 937 941
947 953 967 971 977 983 991 997

Вам пора перейти от трат к накоплениям

После того, как вы скачаете шаблон, распечатайте его на принтере и повесьте на видное место, чтобы не забывать о вашей цели. Каждую неделю откладывайте требуемое количество денег в копилку и делайте отметку в соответствующей строчке. Как копить деньги по таблице шаблон с произвольным шагом.

52-недельный марафон. Цель — 300000 ₽

Ниже я предлагаю вам несколько вариантов таблиц, любую из которых вы можете бесплатно скачать, распечатать и начать действовать. Честно говоря, таких ситуаций, даже если вы выберете 100-дневный марафон, будет много. Что уж там говорить о годе? В течение года количество пропусков может достичь размеров, угрожающих выполнению всего плана!

Знайка, самый умный эксперт в Цветочном городе

Мнение эксперта

Знайка, самый умный эксперт в Цветочном городе

Если у вас есть вопросы, задавайте их мне!

Задать вопрос эксперту

Как копить деньги по таблице, откладывая раз в неделю Если вы решите копить в течение года, откладывая каждый день, вам нужно будет сделать это 365 раз. На мой взгляд, проще откладывать раз в неделю. Почему же? Да все просто! Если вы решите копить в течение года, откладывая каждый день, вам нужно будет сделать это 365 раз! А если каждую неделю — всего 52 раза.

После того, как вы скачаете шаблон, распечатайте его на принтере и повесьте на видное место, чтобы не забывать о вашей цели. Каждую неделю откладывайте требуемое количество денег в копилку и делайте отметку в соответствующей строчке.

Список простых чисел от 1 до 1000:

Эта схема аналогична базовой версии 52-недельного марафона, где мы копим 41340 ₽, за исключением того, что наиболее крупную сумму вы откладываете в первую неделю, а затем каждую неделю эта сумма уменьшается на выбранный шаг. Каждый день сумма возрастает, но это и интересно.

Как накопить по таблице 5050 ₽ за 100 дней

Если откладывать в день по 10 и делать это, к примеру, 100 дней подряд, то вы скопите 10 x 100 1000 , если по 50 5000 , если по 100 1000. Честно говоря, таких ситуаций, даже если вы выберете 100-дневный марафон, будет много. Что уж там говорить о годе? В течение года количество пропусков может достичь размеров, угрожающих выполнению всего плана!

Знайка, самый умный эксперт в Цветочном городе

Мнение эксперта

Знайка, самый умный эксперт в Цветочном городе

Если у вас есть вопросы, задавайте их мне!

Задать вопрос эксперту

Копим по таблице 25250 ₽ за 100 дней Для того чтобы за 100 дней накопить 25250 , необходимо выбрать шаг 5. Более подробно я рассказываю о том, как планировать бюджет, в статье «Планирование семейного бюджета: простое руководство». Несмотря на название, эта статья прекрасно подходит как тем, у кого есть семья, так и тем, кто ею еще не успел обзавестись.

Источник

Простое число – это положительное натуральное число, которое имеет только два положительных натуральных делителя: единицу и самого себя.

Противоположностью простых чисел являются составные числа. Составное число – это положительное натуральное число, которое имеет, по крайней мере, один положительный делитель, отличный от одного или самого себя.

Взаимно простые числа – числа A и B, не имеющие никаких общих делителей, за исключением единицы.

  • Примеры простых, составных и взаимно простых чисел

  • Таблица простых чисел

  • Вопросы – ответы

Примеры простых, составных и взаимно простых чисел

  1. Число 2 является простым числом, т.к. имеет всего два делителя – 1 и 2:
    • 2/1 = 2
    • 2/2 = 1
  2. Число 15 не является простым числом, потому что имеет делители – 1, 3, 5, 15:
    • 15/1 = 15
    • 15/3 = 5
    • 15/5 = 3
    • 15/15 = 1
  3. Число 13 является простым числом, т.к. имеет только два делителя – 1 и 13:
    • 13/1 = 13
    • 13/13 = 1
  4. Числа 2 и 5 являются взаимно простыми, т.к. имеют только один общий делитель – число 1:
    1. 2/1 = 2
    2. 2/2 = 1
    3. 5/1 = 5
    4. 5/5 = 1

Таблица простых чисел

Ниже представлена таблица простых чисел от 2 до 997, которую можно распечатать, чтобы всегда иметь под рукой в случае необходимости.

2 3 5 7 11 13 17 19 23 29 31 37
41 43 47 53 59 61 67 71 73 79 83 89
97 101 103 107 109 113 127 131 137 139 149 151
157 163 167 173 179 181 191 193 197 199 211 223
227 229 233 239 241 251 257 263 269 271 277 281
283 293 307 311 313 317 331 337 347 349 353 359
367 373 379 383 389 397 401 409 419 421 431 433
439 443 449 457 461 463 467 479 487 491 499 503
509 521 523 541 547 557 563 569 571 577 587 593
599 601 607 613 617 619 631 641 643 647 653 659
661 673 677 683 691 701 709 719 727 733 739 743
751 757 761 769 773 787 797 809 811 821 823 827
829 839 853 857 859 863 877 881 883 887 907 911
919 929 937 941 947 953 967 971 977 983 991 997

microexcel.ru

Вопросы – ответы

  1. Является ли число 1 простым?
    Число 1 не является простым по определению – оно имеет только один делитель.
  2. Является ли число 0 простым?
    Число 0 не является простым – оно не является положительным числом и имеет бесконечное количество делителей.
Источник

Содержание

  1. Сколько нулей в числе
  2. Простые числа до 1000
  3. Зачем это нужно?
  4. Самое большое простое число, которое известно.
  5. Наименьшее и наибольшее простое число
  6. Метод Марена Мерсенна
  7. Таблица простых чисел
  8. Некоторые свойства простых чисел.
  9. Взаимно простые числа – определение и примеры
  10. Метод простых чисел Ферма
  11. Последовательность простых чисел
  12. Множество простых чисел
  13. Попарно простые числа – определения и примеры
  14. Как определить взаимно простые числа?
  15. Основная теорема арифметики
  16. Пример
  17. Действия с простыми числами.
  18. Что такое составные числа
  19. Интересная информация
  20. Каким числом является 1?
  21. Решето Эратосфена

Сколько нулей в числе

Узнать количество нулей, и сколько десятков, сотен, тысяч, миллионов, миллиардов, триллионов содержится в любом числе.

Сколько нулей в числе

Простые числа до 1000

101 103 107 109 113 127 131 137 139 149 151
157 163 167 173 179 181 191 193 197 199 211 223
227 229 233 239 241 251 257 263 269 271 277 281
283 293 307 311 313 317 331 337 347 349 353 359
367 373 379 383 389 397 401 409 419 421 431 433
439 443 449 457 461 463 467 479 487 491 499 503
509 521 523 541 547 557 563 569 571 577 587 593
599 601 607 613 617 619 631 641 643 647 653 659
661 673 677 683 691 701 709 719 727 733 739 743
751 757 761 769 773 787 797 809 811 821 823 827
829 839 853 857 859 863 877 881 883 887 907 911
919 929 937 941 947 953 967 971 977 983 991 997

Зачем это нужно?

Зачем нужно деление на простые и составные числа в математике? Все просто, это нужно, чтобы упростить разложение на множители. Вместо того, чтобы долго искать на какие числа, собственно, раскладывать большое значение, можно просто воспользоваться таблицей.

А разложение на простые множители в свою очередь помогает в определении наибольшего общего делителя и наименьшего общего кратного. Эти значения нужны для сложения, вычитания и сравнения дробей.

Самое большое простое число, которое известно.

Самое большое известное простое число – это 257885161 – 1. Это число состоит из 17 425 170 десятичных цифр и называется простое число Мерсенна (M57885161).

Наименьшее и наибольшее простое число

Самым меньшим значением, делящимся на себя и 1, является 2. Это единственное простое значение, являющееся четным. Остальные всегда делятся на два, то есть получают третий делитель.

Простых чисел много и их количество стремится к бесконечности, потому узнать самое большое невозможно.

Нескончаемость ряда была доказана еще до нашей эры Евклидом. Он предложил перемножить все известные исследуемые значения и прибавить к ним единицу.

При его делении в любом случае будет оставаться остаток, то есть отнести к составным невозможно. Что противоречит тому факту, что были использованы все известные простые числа, в том числе и самое большое. Значит, предположение о конечности ряда является неверным.

В настоящее время известно значение, имеющее около 25 миллионов знаков. Оно относится к наибольшему из открытых наукой, это 282 589 933

Метод Марена Мерсенна

Метод простого числа Мерсенна – это специальный метод нахождения определенного вида простого числа, известный как простые числа Мерсенна. Название для этого метода происходит от французского монаха Марин Мерсенн, который первым определил его. Простые числа Мерсенна-это те, которые сводимы к виду 2n-1, где n-простое число. Первые несколько чисел в этом методе являются 2, 3, 5, 7, 13, 17, 19, 31, 61, и 89. Долгое время метод простых чисел Мерсенна представлял собой тяжёлую работу, так как при переходе к более высоким простым числам он был очень трудоемким.

Марен Мерсенн Французский математик

Однако, с появлением компьютеров, они теперь могли выполнять эти вычислительные вычисления, которые раньше делались людьми самым кропотливым и трудоемким образом. Мы определенно достигли более высоких простых чисел Мерсенна и простых чисел на общем уровне. Поиск простых чисел так же активен, как и другие численные поиски, выполняемые компьютерами. Другой числовой поиск, аналогичный движению простых чисел, заключается в добавлении десятичных разрядов к некоторым иррациональным числам, таким как пи (отношение длины окружности к диаметру). Однако непрерывный поиск следующего по величине простого числа существенно сложнее, чем поиск следующей цифры числа Пи.

Даже самые большие компьютеры (суперкомпьютеры) тратят значительное количество времени, чтобы проверить, является ли новое число (которое обычно ошеломляюще огромным) само по себе простым числом, и требуется еще больше времени, чтобы проверить, является ли число основным числом Мерсенна. По этой причине числа Мерсенна представляют большой интерес в области кибербезопасности и криптографии, особенно в отношении шифрования.

В августе 2008 года системный администратор UCLA Эдсон Смит нашел наиболее значимое простое число, известное на тот момент. Смит установил программное обеспечение для Great Internet Mersenne Prime Search (Gimps), проекта распределенных вычислений на добровольной основе. Это число было простым числом Мерсенна длиной 12 978 189 цифр. Чтобы дать представление о том, насколько он велик, на его написание уйдет почти два с половиной месяца, а в случае печати он растянется на 50 км!

Таблица простых чисел

Простые числа, для удобства их дальнейшего использования, записывают в таблицу, которую называют таблицей простых чисел. Ниже представлена таблица простых чисел до 1 000.

Возникает логичный вопрос: «Почему мы заполнили таблицу простых чисел только до 1 000, разве нельзя составить таблицу всех существующих простых чисел»?

Ответим сначала на первую часть этого вопроса. Для большинства задач, при решении которых придется использовать простые числа, нам будет вполне достаточно простых чисел в пределах тысячи. В остальных случаях, скорее всего, придется прибегать к каким-либо специальным приемам решения. Хотя, несомненно, мы можем составить таблицу простых чисел до сколь угодно большого конечного целого положительного числа, будь то 10 000 или 1 000 000 000, в следующем пункте мы поговорим о методах составления таблиц простых чисел, в частности, разберем способ, получивший название решето Эратосфена.

Теперь разберемся с возможностью (а точнее с невозможностью) составления таблицы всех существующих простых чисел. Мы не можем составить таблицу всех простых чисел, потому что простых чисел бесконечно много. Последнее утверждение представляет собой теорему, которую мы докажем после следующей вспомогательной теоремы.

Теорема.

Наименьший положительный и отличный от 1 делитель натурального числа, большего единицы, является простым числом.

Доказательство.

Пусть a – натуральное число, большее единицы, и b – наименьший положительный и отличный от единицы делитель числа a. Докажем, что b – простое число методом от противного.

Предположим, что b – составное число. Тогда существует делитель числа b (обозначим его b1), который отличен как от 1, так и от b. Если также учесть, что абсолютная величина делителя не превосходит абсолютной величины делимого (это мы знаем из свойств делимости), то должно выполняться условие 1<b1<b.

Так как число a делится на b по условию, и мы сказали, что b делится на b1, то понятие делимости позволяет говорить о существовании таких целых чисел q и q1, что a=b·q и b=b1·q1, откуда a= b1·(q1·q). Из правил умножения целых чисел следует, что произведение двух целых чисел есть целое число, тогда равенство a=b1·(q1·q) указывает на то, что b1 является делителем числа a. Учитывая полученные выше неравенства 1<b1<b, мы получаем противоречие условию, что b – наименьший положительный и отличный от единицы делитель числа a.

Теперь мы можем доказать, что простых чисел бесконечно много.

Теорема.

Простых чисел бесконечно много.

Предположим, что это не так. То есть, предположим, что простых чисел всего n штук, и эти простые числа есть p1, p2, …, pn. Покажем, что мы всегда можем найти простое число, отличное от указанных.

Рассмотрим число, p равное p1·p2·…·pn+1. Понятно, что это число отлично от каждого из простых чисел p1, p2, …, pn. Если число p – простое, то теорема доказана. Если же это число составное, то в силу предыдущей теоремы существует простой делитель этого числа (обозначим его pn+1). Покажем, что этот делитель не совпадает ни с одним из чисел p1, p2, …, pn.

Если бы это было не так, то по свойствам делимости произведение p1·p2·…·pn делилось бы на pn+1. Но на pn+1 делится и число p, равное сумме p1·p2·…·pn+1. Отсюда следует, что на pn+1 должно делиться второе слагаемое этой суммы, которое равно единице, а это невозможно.

Так доказано, что всегда может быть найдено новое простое число, не заключающееся среди любого количества наперед заданных простых чисел. Следовательно, простых чисел бесконечно много.

Итак, в силу того, что простых чисел бесконечно много, при составлении таблиц простых чисел всегда ограничивают себя сверху каким-либо числом, обычно, 100, 1 000, 10 000 и т.д.

Некоторые свойства простых чисел.

Допустим, p — простое, и p делит ab, тогда p делит a либо b.

Кольцо вычетов Zn будет называться полем только в случае, если n — простое.

Характеристика всех полей — это нуль либо простое число.

Когда p — простое, а a — натуральное, значит, ap-a можно поделить на p (малая теорема Ферма).

Когда G — конечная группа, у которой порядок |G| делят на p, значит, у G есть элемент порядка p (теорема Коши).

Когда G — конечная группа, и pn — самая высокая степень p, делящая |G|, значит, у G есть подгруппа порядка pn, которая называется силовская подгруппа, кроме того, число силовских подгрупп соответствует pk+1 для некоего целого k (теоремы Силова).

Натуральное p > 1 будет простым лишь в случае, если (p-1)! + 1 можно подулить на p (теорема Вильсона).

Когда n > 1 — натуральное, значит, есть простое p: n < p < 2 n (постулат Бертрана).

Ряд чисел, которые обратны к простым, расходится. Кроме того, при .

Всякая арифметическая прогрессия типа a, a + q, a + 2 q, a + 3 q, … , где a, q > 1 — целые взаимно простые числа, содержит нескончаемое число простых чисел (Теорема Дирихле о простых числах в арифметической прогрессии).

Любое простое число, которое большее тройки, можно представить как 6k+1 либо 6k-1, где k — натуральное число. Исходя из этого, когда разность нескольких последовательных простых чисел (при k>1) одинаковая, значит, она точно делится на шесть — к примеру: 251-257-263-269; 199-211-223; 20183-20201-20219.

Когда p > 3 — простое число, значит, p2-1 делится на 24 (работает и на нечётных чисел, которые не делятся на три).

Теорема Грина-Тао. Есть бесконечные арифметические прогрессии, которые состоят из простых чисел.

Ни одно простое число нельзя представить как nk-1, где n>2, k>1. Другими словами, число, которое следует за простым, не может быть квадратом либо более высокой степенью с основанием, которое больше двух. Можно сделать вывод, что когда простое число представлено как 2k-1, значит k — простое.

Ни одно простое число нельзя представить как n2k+1+1, где n>1, k>0. Другими словами, число, которое предшествует простому, не может быть кубом либо более высокой нечётной степенью с основанием, которое больше единицы.

Есть многочлены, у которых множество неотрицательных значений при положительных значениях переменных совпадает с множеством простых чисел. Пример:

Этот многочлен содержит 26 переменных, имеет 25. Самая низкая степень для известных многочленов представленного вида — пять при 42 переменных; самое маленькое количество переменных — десять при степени приблизительно 1,6·1045.

Взаимно простые числа – определение и примеры

Понятие взаимно простых чисел дается как для двух целых чисел, так и для их большего числа. Сначала приведем определение двух взаимно простых чисел. Это определение дается через наибольший общий делитель чисел, так что рекомендуем сначала разобраться с материалом указанной статьи.

Определение.

Два целых числа a и b называются взаимно простыми, если их наибольший общий делитель равен единице, то есть, НОД(a, b)=1.

Из определения взаимно простых чисел следует, что два взаимно простых числа имеют лишь один положительный общий делитель, который равен единице. А всего общих делителей у двух взаимно простых чисел две штуки – это числа 1 и −1.

Приведем примеры взаимно простых чисел.

Числа 5 и 11 являются взаимно простыми. Действительно, и 5 и 11 – простые числа, следовательно, их положительным общим делителем является только число 1, что подтверждает взаимную простоту чисел 5 и 11.

Заметим, что два простых числа всегда являются взаимно простыми. Однако, два числа не обязательно должны быть простыми, чтобы быть взаимно простыми. Либо одно из них, либо они оба могут быть составными и при этом являться взаимно простыми. Приведем пример, иллюстрирующий это высказывание.

Два составных числа 8 и −9 являются взаимно простыми. Обоснуем это. Для этого найдем наибольший общий делитель этих чисел, записав все делители чисел 8 и −9 (при необходимости смотрите статью число делителей числа, все делители числа). Делителями восьмерки является любое из чисел ±1, ±2, ±4, ±8−9 есть числа ±1, ±3, ±9. Следовательно, НОД(8, −9)=1, поэтому, по определению 8 и −9 – два взаимно простых числа.

А вот числа 45 и 500 не являются взаимно простыми, так как имеют положительный общий делитель, отличный от единицы, которым является число 5 (делимость чисел 45 и 500 на 5 очевидна, если знать признак делимости на 5). Другой парой не взаимно простых чисел является пара 3 и −201, так как 3 есть их общий положительный делитель (делимость числа −201 на 3 легко устанавливается при помощи признака делимости на 3).

Часто встречаются задания, в которых требуется доказать, что данные целые числа являются взаимно простыми. Доказательство сводится к вычислению наибольшего общего делителя данных чисел и проверке НОД на его равенство единице. Полезно также перед вычислением НОД заглянуть в таблицу простых чисел: вдруг исходные целые числа являются простыми, а мы знаем, что наибольший общий делитель простых чисел равен единице. Рассмотрим решение примера.

Пример.

Докажите, что числа 84 и 275 являются взаимно простыми.

Решение.

Очевидно, что данные числа не являются простыми, поэтому мы не можем сразу говорить о взаимной простоте чисел 84 и 275, и нам придется вычислять НОД. Используем алгоритм Евклида для нахождения НОД: 275=84·3+23, 84=23·3+15, 23=15·1+8, 15=8·1+7, 8=7·1+1, 7=7·1, следовательно, НОД(84, 275)=1. Этим доказано, что числа 84 и 275 взаимно простые.

Определение взаимно простых чисел можно расширить для трех и большего количества чисел.

Определение.

Целые числа a1, a2, …, ak, k>2 называются взаимно простыми, если наибольший общий делитель этих чисел равен единице.

Из озвученного определения следует, что если некоторый набор целых чисел имеет положительный общий делитель, отличный от единицы, то данные целые числа не являются взаимно простыми.

Приведем примеры. Три целых числа −99, 17 и −27 являются взаимно простыми. Любая совокупность простых чисел составляет набор взаимно простых чисел, к примеру, 2, 3, 11, 19, 151, 293 и 677 – взаимно простые числа. А четыре числа 12, −9, 900 и −72 не являются взаимно простыми, так как они имеют положительный общий делитель 3, отличный от 1. Числа 17, 85 и 187 тоже не взаимно простые, так как каждое из них делится на 17.

Обычно далеко не очевидно, что некоторые числа являются взаимно простыми, и этот факт приходится доказывать. Для выяснения, являются ли данные числа взаимно простыми, приходится находить наибольший общий делитель этих чисел, и на основании определения взаимно простых чисел делать вывод.

Пример.

Являются ли числа 331, 463 и 733 взаимно простыми?

Решение.

Заглянув в таблицу простых чисел, мы обнаружим, что каждое из чисел 331, 463 и 733 – простое. Следовательно, они имеют единственный положительный общий делитель – единицу. Таким образом, три числа 331, 463 и 733 есть взаимно простые числа.

Ответ:

Да.

Пример.

Докажите, что числа −14, 105, −2 107 и −91 не являются взаимно простыми.

Решение.

Чтобы доказать, что данные числа не взаимно простые, можно найти их НОД и убедиться, что он не равен единице. Так и поступим.

Так как делители целых отрицательных чисел совпадают с делителями соответствующих противоположных чисел, то НОД(−14, 105, 2 107, −91)=НОД(14, 105, 2 107, 91). Обратившись к материалу статьи нахождение наибольшего общего делителя трех и большего количества чисел, выясняем, что НОД(14, 105, 2 107, 91)=7. Следовательно, наибольший общий делитель исходных чисел равен семи, поэтому эти числа не являются взаимно простыми.

Метод простых чисел Ферма

Число Ферма, как и число Мерсенна, представляет собой особый вид простого числа . Название происходит от математика 17-го века и юриста Пьера де Ферма. Число Ферма похоже на число Мерсенна… с одной маленькой поправкой. Давайте возьмем число Ферма Fm , где мы можем определить Fm как 2m +1. Здесь m снова равно 2, возведенному в степень n или 2n .

Пьер де Ферма (фр. Pierre de Fermat, 17 августа 1601 — 12 января 1665) — французский математик-самоучка, один из создателей аналитической геометрии, математического анализа, теории вероятностей и теории чисел.

Фермат был твердо убежден в том, что все числа вышеуказанной формы – это простые числа. В дальнейшем он сказал, что он будет производить простые числа для всех целочисленных значений m. Что делает эти числа уникальными и красивыми, но очень хитрыми, так это то, что простые числа становятся чрезвычайно большими очень быстро, даже в пределах первых четырех итераций. Чтобы доказать это, возьмем n в качестве следующих значений, n=0, 1, 2, 3 и 4.

Когда n = 0, m = 20 = 1; поэтому F0 = 2 1 + 1 = 2 + 1 = 3, что является простым. Когда n = 1, m = 21 = 2; поэтому F1 = 22 + 1 = 4 + 1 = 5, что является простым. Когда n = 2, m = 22 = 4; следовательно, F2 = 24 + 1 = 16 + 1 = 17, что является простым. Когда n = 3, m = 23 = 8; следовательно, F3 = 28 + 1 = 256 + 1 = 257, что является простым. Когда n = 4, m = 24 = 16; следовательно, F4 = 216 + 1 = 65536 + 1 = 65537, что является простым числом. Теперь, как вы можете заметить, к тому времени, когда мы достигнем F5, значение достигает 4 294 967 297.

На сегодняшний день мы достигли только F11, даже со всеми лучшими компьютерами и параллельными вычислениями и большой точностью. В конце концов, однако, мы можем сказать, что поиск простых чисел всегда будет идти до бесконечности и дальше!

Последовательность простых чисел

Есть целые алгоритмы, помогающие получать новое, ранее неизвестное значение.

Существуют таблицы, в которых собраны найденные числа, имеющие не больше двух делителей, например, до 200, 1000 или больше.

Последовательность можно продолжать бесконечно, начинается она так: 2, 3, 5, 7, 11, 13, 17, 19 и т. д.

Множество простых чисел

Множествами называются совокупности элементов, объединенных в одно целое общими свойствами.

Для изучаемых объектов к ним относятся:

  • принадлежность к натуральным;

  • наличие максимум двух делителей.

Простые числа можно определить, используя решето Эратосфена. Нужно выписать в ряд все значения, с которыми предстоит работать. Выбрать самое маленькое и вычеркнуть его, затем продолжать действие, убирая кратные ему.

Например, в ряду от 1 до 100 первым таким объектом будет 2. Поэтому и вычеркивать нужно значения, кратные двойке, то есть те, которые делятся на нее.

По окончании из оставшихся выбрать новое простое, искать кратные ему и также убирать. Повторять, пока это представляется возможным.

В итоге, все составные окажутся зачеркнутыми.

Эратосфен использовал свое открытие следующим образом. Он брал папирус, записывал на нем необходимые значения, при отборе прокалывал неподходящие острым предметом (отсюда название «решето Эратосфена»). Поэтому они как будто просеивались через сито, и в списке оставались видимыми только необходимые.

Попарно простые числа – определения и примеры

Через взаимно простые числа дается определение попарно простых чисел.

Определение.

Целые числа a1, a2, …, ak, каждое из которых взаимно просто со всеми остальными, называют попарно простыми числами.

Приведем пример попарно простых чисел. Числа 14, 9, 17, и −25 – попарно простые, так как пары чисел 14 и 9, 14 и 17, 14 и −25, 9 и 17, 9 и −25, 17 и −25 представляют собой взаимно простые числа. Здесь же заметим, что попарно простые числа всегда являются взаимно простыми.

С другой стороны, взаимно простые числа далеко не всегда являются попарно простыми, это подтверждает следующий пример. Числа 8, 16, 5 и 15 не являются попарно простыми, так как числа 8 и 16 не взаимно простые. Однако, числа 8, 16, 5 и 15 – взаимно простые. Таким образом, 8, 16, 5 и 15 – взаимно простые числа, но не попарно простые.

Следует особо выделить совокупность некоторого количества простых чисел. Эти числа всегда являются и взаимно простыми и попарно простыми. Например, 71, 443, 857, 991 – и попарно простые, и взаимно простые числа.

Также понятно, что когда речь идет о двух целых числах, то для них понятия «попарно простые» и «взаимно простые» совпадают.

Как определить взаимно простые числа?

Для того чтобы определить взаимно простые числа, можно воспользоваться двумя алгоритмами:

  • Разложить каждое из чисел на множители и искать общие простые множители. Если такие есть, то числа не являются взаимно простыми. Если общих множителей нет, числа можно считать взаимно простыми.
  • Делить каждое из чисел поочередно на простые множители. Этот способ проще в исполнении, так как не требует большой внимательности и сосредоточенности. Но такая проверка не подойдет для больших чисел, слишком долгой может получится проверка. Поэтому более надежным будет использовать первый вариант.

Относительно друг друга два простых числа всегда будут взаимно простыми. А если одно из чисел, делится на другое нацело, то эти числа точно не являются взаимно простыми.

Основная теорема арифметики

Натуральное число можно представить в виде произведения простых чисел.

Такое разложение будет единственным и может отличаться только порядком множителей.

Это понятие носит название основной теоремы арифметики и используется очень часто.

Посмотрим на примерах, как всё тут работает.

Разложить 6 можно двумя способами, расположив по-разному простые множители: 3 умножить на 2 или 2 умножить на 3

(mathbf{6 = 3cdot2 = 2cdot3})

Если попытаемся разложить число 48 на простые множители, то получим:

(mathbf{48 = 2cdot24 = 2cdot2cdot12 = 2cdot2cdot2cdot6= 2cdot2cdot2cdot2cdot3})

Чтобы всё сделать правильно при разложении, нужно выделить простой множитель, с оставшимся числом поступить так же и повторять действия, пока не получатся все простые множители.

Посмотрим еще один пример и возьмем 122.

Это число делится без остатка на два, так как оно чётное, получаем 61. Шестьдесят один – это простое число.

Таким образом, разложение числа 122 на простые множители выглядит так:

(mathbf{122 = 2cdot61})

Возьмем еще большее число, к примеру, 462. При разложении на простые множители получим:

(mathbf{462 = 2cdot3cdot7cdot11})

Бывают такие случаи, когда в числовом ряду простые числа стоят через одно составное. Рядом они стоять не могут, ведь каждое второе число будет чётным, значит, оно уже не будет являться простым.

Если простые числа стоят через одно составное, например, 3 и 5 или 71 и 73, или 461 и 463, то они называются «близнецами».

С развитием вычислительной техники было доказано, что простые числа с увеличением располагаются всё дальше друг от друга. Это создаёт проблему при поиске каждого нового простого числа.

Пример 1

Используя основную теорему арифметики, разложите на простые множители числа 72, 228, 896, 994, 105, 98

Решение:

$$mathbf{72 = 8cdot9=4cdot2cdot3cdot3=2cdot2cdot2cdot3cdot3}$$

$$mathbf{228= 12cdot19 = 4cdot3cdot19=2cdot2cdot3cdot19}$$

$$mathbf{896 = 64cdot14 = 4cdot16cdot2cdot7= 2cdot2cdot2cdot2cdot2cdot2cdot2cdot7}$$

$$mathbf{994 = 2cdot7cdot71}$$

$$mathbf{105= 3cdot5cdot7}$$

$$mathbf{98 = 2cdot14 =2cdot2cdot7}$$

Пример 2

Сколько делителей имеет каждое из чисел: 31, 25, 100, 189, 325, 558, 194?

Решение:

Число 31 имеет два делителя: 1, 31

Число 25 имеет три делителя: 1, 5, 25

Число 100 имеет девять делителей: 1, 2, 4, 5, 10, 20, 25, 50, 100

Число 189 имеет восемь делителей: 1, 3, 7, 9, 21, 27, 63, 189

Число 325 имеет шесть делителей: 1, 5, 13, 25, 65, 325

Число 558 имеет двенадцать делителей: 1, 2, 3, 6, 9, 18, 31, 62, 93, 186, 279, 558

Число 194 имеет четыре делителя: 1, 2, 97, 194

Пример 3

Какое из чисел 129, 565, 441, 70, 237, 816 имеет самое большое количество делителей?

Решение:

Число 129 имеет четыре делителя: 1, 3, 43, 129

Число 565 имеет четыре делителя: 1, 5, 113, 565

Число 441 имеет девять делителей: 1, 3, 7, 9, 21, 49, 63, 147, 441

Число 70 имеет восемь делителей: 1, 2, 5, 7, 10, 14, 35, 70

Число 237 имеет четыре делителя: 1, 3, 79, 237

Число 816 имеет двадцать делителей: 1, 2, 3, 4, 6, 8, 12, 16, 17, 24, 34, 48, 51, 68, 102, 136, 204, 272, 408, 816

Самое большое количество делителей имеет число 816

У меня есть дополнительная информация к этой части урока!

Перед вами кусочек таблицы простых чисел до 1000. По ней можно увидеть, что единственное простое чётное число – это двойка.

На самом деле простых чисел гораздо больше, и самое большое из найдённых на данный момент содержит 23 249 425 десятичных цифр. Вдумайтесь, больше 23 миллионов цифр в записи числа!

Пример

Определим, являются ли взаимно простыми числа 1729 и 282

Определение начинается с разложения на множители:

1729=7*13*19

282=2*3*47

Обратите внимание, что для разложения таких чисел придется использовать метод перебора. Согласно таблице простых чисел каждый множитель проверяется, после чего деление продолжается. Подбирать множители нужно от маленьких чисел к большим, то есть от 2 и выше.

Как видно, общих множителей у двух чисел нет. Это значит, что числа можно считать взаимно простыми. Не нужно пугаться, если среди множителей попадаются достаточно большие числа. Среди учеников существует миф, что простые числа редко бывают больше 20, это не так. Просто такие числа проще использовать в задачах, чтобы набить руку. На экзамене или в контрольной сложность числа для разложения может быть абсолютно любой

Действия с простыми числами.

1. Произведение простых чисел.

2. Разность простых чисел.

3. Сумма простых чисел.

4. Деление простых чисел.

Что такое составные числа

Нетрудно догадаться, что составных чисел в разы больше, чем простых. Составным числом является число, которое не является простым. Вот и все определение, в этом нет ничего сложного.

Разберемся с тем, почему эта группа чисел называется составными. Разберемся на примере, возьмем уже знакомое нам число 13 и умножим его на другое простое число: 2.

13*2=26 – в результате получилось составное число, которое можно разделить на 1,2,13,26. Это число состоит из двух множителей: 2 и 13. Значит, составными числами называют числа, которые состоят из нескольких простых множителей. Иначе говоря, в состав числа входят 2 и более простых множителя.

По аналогии с простыми числами, составные числа называют сложные. Разделение чисел на простые и сложные запомнить куда проще, чем деление на простые и составные.

Интересная информация

В глубокой древности началось изучение так называемых совершенных и дружественных чисел.

Некоторые из учёных пытались выражать на языке чисел всё, что наблюдали вокруг себя. Даже нематематические понятия дружбы, справедливости и совершенства переводились на язык чисел.

Если число равно сумме всех возможных делителей без него самого, то оно называется совершенным.

Например, самыми элементарными из них будут 6 и 28:

6 = 1 + 2 + 3,

28 = 1 + 2 + 4 + 7 + 14.

Если сумма всех возможных делителей числа (кроме него самого) равна второму числу, а сумма всех возможных делителей второго (без него самого) равна первому, то это уже дружественные числа.

Если верить историческим фактам, математик Пифагор считал, что его другом может быть «тот, кто является моим вторым Я, как числа 220 и 284»

Список делителей для 220: 1, 2, 4, 5, 10, 11, 20, 22, 44, 55 и 110, сумма делителей равна 284

Список делителей для 284: 1, 2, 4, 71 и 142, сумма делителей равна 220.

Пару дружественных чисел 1184 и 1210 обнаружил в 1866г. итальянский школьник Никколо Паганини, полный тёзка великого скрипача.

Любопытно, что эту пару «проглядели» все великие математики.

Каким числом является 1?

Интересными числами в классификации являются 0 и 1. Разберемся с 1. Согласно определению, простое число имеет два делителя: 1 и само себя. Но для единицы 1 это и есть второй делитель, а ,значит, число имеет всего один делитель и не попадает в группу простых чисел.

Само собой, к составным числам 1 так же отнести нельзя, поэтому 1 считается числом вне категорий.

Решето Эратосфена

Сейчас мы обсудим способы составления таблиц простых чисел. Предположим, что нам нужно составить таблицу простых чисел до 100.

Самым очевидным методом решения этой задачи является последовательная проверка целых положительных чисел, начиная с 2, и заканчивая 100, на наличие положительного делителя, который больше 1 и меньше проверяемого числа (из свойств делимости мы знаем, что абсолютная величина делителя не превосходит абсолютной величины делимого, отличного от нуля). Если такой делитель не найден, то проверяемое число является простым, и оно заносится в таблицу простых чисел. Если же такой делитель найден, то проверяемое число является составным, оно НЕ заносится в таблицу простых чисел. После этого происходит переход к следующему числу, которое аналогично проверяется на наличие делителя.

Опишем несколько первых шагов.

Начинаем с числа 2. Число 2 не имеет положительных делителей, кроме 1 и 2. Следовательно, оно простое, поэтому, заносим его в таблицу простых чисел. Здесь следует сказать, что 2 является наименьшим простым числом. Переходим к числу 3. Его возможным положительным делителем, отличным от 1 и 3, является число 2. Но 3 на 2 не делится, поэтому, 3 – простое число, и его также нужно занести в таблицу простых чисел. Переходим к числу 4. Его положительными делителями, отличными от 1 и 4, могут быть числа 2 и 3, проверим их. Число 4 делится на 2, поэтому, 4 – составное число, и его не нужно заносить в таблицу простых чисел. Обратим внимание на то, что 4 – наименьшее составное число. Переходим к числу 5. Проверяем, являются ли его делителем хотя бы одно из чисел 2, 3, 4. Так как 5 не делится ни на 2, ни на 3, ни на 4, то оно простое, и его надо записать в таблицу простых чисел. Дальше происходит переход к числам 6, 7, и так далее до 100.

Такой подход к составлению таблицы простых чисел является далеко не идеальным. Так или иначе, он имеет право на существование. Отметим, что при этом способе построения таблицы целых чисел можно использовать признаки делимости, которые немного ускорят процесс поиска делителей.

Существует более удобный способ для составления таблицы простых чисел, называемый решето Эратосфена. Присутствующее в названии слово «решето» не случайно, так как действия этого метода помогают как бы «просеять» сквозь решето Эратосфена целые числа, большие единицы, чтобы отделить простые от составных.

Покажем решето Эратосфена в действии при составлении таблицы простых чисел до 50.

Сначала записываем по порядку числа 2, 3, 4, …, 50.

Первое записанное число 2 является простым. Теперь от числа 2 последовательно перемещаемся вправо на два числа и зачеркиваем эти числа, пока не доберемся до конца составляемой таблицы чисел. Так будут вычеркнуты все числа, кратные двум.

Первым следующим за 2 невычеркнутым числом является 3. Это число простое. Теперь от числа 3 последовательно перемещаемся вправо на три числа (учитывая и уже зачеркнутые числа) и вычеркиваем их. Так будут вычеркнуты все числа, кратные трем.

Первым следующим за 3 невычеркнутым числом является 5. Это число простое. Теперь от числа 5 последовательно перемещаемся вправо на 5 чисел (учитываем и зачеркнутые ранее числа) и вычеркиваем их. Так будут вычеркнуты все числа, кратные пяти.

Дальше вычеркиваем числа, кратные 7, затем, кратные 11 и так далее. Процесс заканчивается, когда не останется чисел для вычеркивания. Ниже показана законченная таблица простых чисел до 50, полученная с помощью решета Эратосфена. Все незачеркнутые числа являются простыми, а все зачеркнутые числа – составными.

Давайте еще сформулируем и докажем теорему, которая позволит ускорить процесс составления таблицы простых чисел при помощи решета Эратосфена.

Теорема.

Наименьший положительный и отличный от единицы делитель составного числа a не превосходит , где – арифметический квадратный корень из a.

Доказательство.

Обозначим буквой b наименьший и отличный от единицы делитель составного числа a (число b является простым, что следует из теоремы, доказанной в самом начале предыдущего пункта). Тогда существует такое целое число q, что a=b·q (здесь q – положительное целое число, что следует из правил умножения целых чисел), причем (при b>q нарушится условие, что b – наименьший делитель числа a, так как q также является делителем числа a в силу равенства a=q·b). Умножив обе части неравенства на положительное и большее единицы целое число b (это нам позволяют сделать свойства числовых неравенств), получаем , откуда и .

Что же нам дает доказанная теорема, касательно решета Эратосфена?

Во-первых, вычеркивание составных чисел, кратных простому числу b следует начинать с числа, равного (это следует из неравенства ). Например, вычеркивание чисел, кратных двум, следует начинать с числа 4, кратных трем – с числа 9, кратных пяти – с числа 25, и так далее.

Во-вторых, составление таблицы простых чисел до числа n с помощью решета Эратосфена можно считать законченным тогда, когда будут вычеркнуты все составные числа, кратные простым числам, не превосходящим . В нашем примере n=50 (так как мы составляем таблицу простых чисел до 50) и , поэтому решето Эратосфена должно отсеять все составные числа, кратные простым числам 2, 3, 5 и 7, которые не превосходят арифметического квадратного корня из 50. То есть, нам дальше не нужно заниматься поиском и вычеркиванием чисел, кратных простым числам 11, 13, 17, 19, 23 и так далее до 47, так как они уже будут вычеркнуты, как кратные меньшим простым числам 2, 3, 5 и 7.

Источники

  • https://www.calc.ru/Tablitsa-Prostykh-Chisel-Do-10-000.html
  • https://Tablici.info/tablitsa-prostyh-chisel.html
  • https://obrazovaka.ru/matematika/sostavnye-chisla-primery.html
  • https://www.calc.ru/Chisla-Prostyye-Chisla.html
  • https://nauka.club/matematika/prostye-chisla.html
  • https://new-science.ru/kak-najti-prostye-prostye-chisla/
  • http://www.cleverstudents.ru/divisibility/prime_and_composite_numbers.html
  • http://www.cleverstudents.ru/divisibility/coprime_numbers.html
  • https://obrazovaka.ru/matematika/vzaimno-prostye-chisla-primery-6-klass.html
  • https://ladle.ru/education/matematika/6class/prostye-i-sostavnye
Источник

Вы когда-нибудь пытались в Excel перечислить все простые числа между двумя заданными числами? В этой статье я расскажу о некоторых интересных методах решения этой задачи.

Сгенерировать все простые числа между двумя заданными числами с помощью формул

Генерация всех простых чисел между двумя заданными числами с помощью функции, определяемой пользователем

стрелка синий правый пузырь Сгенерировать все простые числа между двумя заданными числами с помощью формул

Объединение Определить имя функции и формулы, вы можете перечислить или сгенерировать все простые числа между двумя конкретными числами. Пожалуйста, сделайте следующее:

1. Создайте имя первого диапазона, нажав Формулы > Менеджер именИ в Менеджер имен диалоговое окно, нажмите Новинки кнопку, см. снимок экрана:

список документов простые числа 1

2. В Новое имя диалоговое окно в Имя и фамилия текстовое поле, пожалуйста, введите дальность в качестве имени диапазона, а затем введите эту формулу: = СТРОКА (КОСВЕННАЯ (Лист1! $ B $ 1 & «:» & Лист1! $ B $ 2)) (Sheet1 ваш текущий рабочий лист, который вы использовали, B1 и B2 являются начальным и конечным числами, которые вы указали) в Относится к текстовое поле, затем щелкните OK кнопку, чтобы вернуться к прежнему диалогу. Смотрите скриншот:

список документов простые числа 2

3. Продолжайте нажимать Новинки кнопку, чтобы создать другое имя диапазона, в Новое имя диалоговое окно введите имя простое число в Имя и фамилия текстовое поле, а затем введите эту формулу: =SMALL(IF(MMULT(—(IF(rng>TRANSPOSE(rng-Sheet1!$B$1+2),MOD(rng,(rng>TRANSPOSE(rng-Sheet1!$B$1+2))*TRANSPOSE(rng-Sheet1!$B$1+2)))=0),rng-Sheet1!$B$1+2)=0,rng),ROW(INDIRECT(«1:»&Sheet1!$B$2))) (дальность это первое имя диапазона, которое вы создали на шаге 2) в Относится к текстовое поле, см. снимок экрана:

список документов простые числа 3

4. Затем нажмите OK и закройте диалоговые окна, выберите один столбец, в котором вы хотите перечислить все простые числа, и введите эту формулу: = ЕСЛИОШИБКА (штрих; «»)(простое число — это имя диапазона, которое вы создали на шаге 3) в строке формул, а затем нажмите CTRL + SHIFT + ВВОД вместе, все простые числа между заданными двумя числами перечислены, как показано на следующем снимке экрана:

список документов простые числа 4

стрелка синий правый пузырь Генерация всех простых чисел между двумя заданными числами с помощью функции, определяемой пользователем

Если первый метод несколько сложен, здесь вы можете применить Функция, определяемая пользователем решить его.

1. Удерживайте ALT + F11 , чтобы открыть Microsoft Visual Basic для приложений окно.

2. Нажмите Вставить > Модулии вставьте следующий код в Модули Окно.

Код VBA: генерировать все простые числа между двумя конкретными числами:

Function PRIME(St, En As Long)
'Updateby Extendoffice 20160613
Dim num As String
For n = St To En
    For m = 2 To n - 1
        If n Mod m = 0 Then GoTo 20:
    Next m
    num = num & n & ","
20:
Next n
PRIME = num
End Function

3. Затем сохраните и закройте этот код, вернитесь на рабочий лист, введите эту формулу: = простое число (10,100) (10 — начальный номер, а 100 — конечное число, между которым вы хотите получить простые числа, вы можете изменить их по своему усмотрению), а затем нажмите Enter key, и все простые числа отображаются в одной ячейке, см. снимок экрана:

список документов простые числа 5

Лучшие инструменты для работы в офисе

Kutools for Excel Решит большинство ваших проблем и повысит вашу производительность на 80%

  • Снова использовать: Быстро вставить сложные формулы, диаграммы и все, что вы использовали раньше; Зашифровать ячейки с паролем; Создать список рассылки и отправлять электронные письма …
  • Бар Супер Формулы (легко редактировать несколько строк текста и формул); Макет для чтения (легко читать и редактировать большое количество ячеек); Вставить в отфильтрованный диапазон…
  • Объединить ячейки / строки / столбцы без потери данных; Разделить содержимое ячеек; Объединить повторяющиеся строки / столбцы… Предотвращение дублирования ячеек; Сравнить диапазоны…
  • Выберите Дубликат или Уникальный Ряды; Выбрать пустые строки (все ячейки пустые); Супер находка и нечеткая находка во многих рабочих тетрадях; Случайный выбор …
  • Точная копия Несколько ячеек без изменения ссылки на формулу; Автоматическое создание ссылок на несколько листов; Вставить пули, Флажки и многое другое …
  • Извлечь текст, Добавить текст, Удалить по позиции, Удалить пробел; Создание и печать промежуточных итогов по страницам; Преобразование содержимого ячеек в комментарии…
  • Суперфильтр (сохранять и применять схемы фильтров к другим листам); Расширенная сортировка по месяцам / неделям / дням, периодичности и др .; Специальный фильтр жирным, курсивом …
  • Комбинируйте книги и рабочие листы; Объединить таблицы на основе ключевых столбцов; Разделить данные на несколько листов; Пакетное преобразование xls, xlsx и PDF…
  • Более 300 мощных функций. Поддерживает Office/Excel 2007-2021 и 365. Поддерживает все языки. Простое развертывание на вашем предприятии или в организации. Полнофункциональная 30-дневная бесплатная пробная версия. 60-дневная гарантия возврата денег.

вкладка kte 201905

Вкладка Office: интерфейс с вкладками в Office и упрощение работы

  • Включение редактирования и чтения с вкладками в Word, Excel, PowerPoint, Издатель, доступ, Visio и проект.
  • Открывайте и создавайте несколько документов на новых вкладках одного окна, а не в новых окнах.
  • Повышает вашу продуктивность на 50% и сокращает количество щелчков мышью на сотни каждый день!

офисный дно

Источник
 

VDM

Пользователь

Сообщений: 779
Регистрация: 22.12.2012

Здравствуйте уважаемые Форумчане!  

  Возник (не прикладной пока) вопрос:  
Существует ли в Excel возможность получить в каком либо виде последовательность простых (натуральных) чисел, то есть чисел которые делятся без остатка только на себя и единицу (1,2,3,5,7,11…)?  
Например функция аргумент — порядковый номер такого числа, возвращаемое значение — само простое число.  
(1-1) (2-2) (3-3) (4-5) (5-7)  
Или это чисто математический вопрос?  
Поиском ничего не нашел.  
Спасибо.
 

Alex_ST

Пользователь

Сообщений: 2746
Регистрация: 22.12.2012

На лицо ужасный, добрый внутри

На сколько я помню ещё школьную математику, проблема вычисления ряда простых чисел так и не решена вообще (формулы вычисления числового ряда нет).  
А Ёксель что, умнее всех математиков мира?  
Можно решить только макросом и только долгим нудным перебором.

С уважением, Алексей (ИМХО: Excel-2003 — THE BEST!!!)
<#0>

 

VDM

Пользователь

Сообщений: 779
Регистрация: 22.12.2012

{quote}{login=Alex_ST}{date=17.08.2010 11:13}{thema=}{post}На сколько я помню ещё школьную математику, проблема вычисления ряда простых чисел так и не решена    
Можно решить только макросом и только долгим нудным перебором.{/post}{/quote}  
Да, стыдно сказать а я вот не помню чтобы нам такое рассказывали в школьной программе. Толи с памятью, то ли со вниманием, то ли с учителями проблеммы  …  
Конечно, сейчас представил а что там за миллиардами миллиардов.., и кто всё это будет считать…  
Хотя переформулируя вопрос представить себе «зарезервированную» просчитанную последовательность-список (на пример до 10^6, или 10^9) наверное можно. Думал может есть в Екселе.  

  99336
 

алгоритм простой  
начиная с 5 только нечетные делить только на выявленные ранее простые числа (до корня квадратного из искомого числа округленного вверх)
 

А как это на примере будет выглядеть?
 

VDM

Пользователь

Сообщений: 779
Регистрация: 22.12.2012

{quote}{login=Vlad}{date=17.08.2010 11:51}{thema=}{post}А как это на примере будет выглядеть?{/post}{/quote}  

  Да, согласен — не очень понятен алгоритм и его практическая реализация.
 

Option Base 1  
Sub fff()  
Dim i&, j&, igr&, ii&, ir&, iy&, ik&, iii&  
Dim pri()  
jrr = 100  
ReDim pri(1 To jrr)  
pri(1) = 3  
ii = 1  
For i = 5 To jrr Step 2  
igr = Abs(Int(-i ^ 0.5))  
For iy = 1 To jrr  
If pri(iy) >= igr Then  
iii = iy  
Exit For  
End If  
Next iy  
For ik = 1 To iii  
If i Mod pri(ik) = 0 Then Exit For  
ir = ii + 1  
Next ik  
If ir — ii = 1 Then  
ii = ii + 1  
pri(ii) = i  
End If  
Next i  
MsgBox Join(pri)  
End Sub  
странно, что деление на 5 проскакивает сито  
требуется доработка
 

Alex_ST

Пользователь

Сообщений: 2746
Регистрация: 22.12.2012

На лицо ужасный, добрый внутри

Формулы ряда НЕ СУЩЕСТВУЕТ!  
Есть методы построения последовательности.  
Самый древний (3 в. до н. э.) способ получения ряда простых чисел — «Решето Эратосфена»:  
Из натурального ряда чисел  
2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14…  
— вычеркивают кратные двум (4, 6, 8, 10, 12,…)  
— кратные трем (6, 9, 12, 15,…)  
— кратные пяти (10, 15, 20, 25, 30,…)  
— кратные семи (14, 21, 28, 35, 42, 49,…)  
и т. д.  

  Таким образом все составные числа будут просеяны, и останутся только простые числа 2, 3, 5, 7, 11, 13…    
(

http://www.wikiznanie.ru/ru-wz/index.php/Решето_Эратосфена

)

С уважением, Алексей (ИМХО: Excel-2003 — THE BEST!!!)
<#0>

 

KuklP

Пользователь

Сообщений: 14868
Регистрация: 21.12.2012

E-mail и реквизиты в профиле.

Так:  
Public Sub Eratosfen_grating()  
Dim n As Integer, r As Integer, i As Integer, s As Double, k As Integer, j As Integer  
On Error Resume Next  
n = CInt(InputBox(«Number»))  
If n > 200 Then  
r = n (Log(n) — 2) + 1  
Else  
r = CInt(1.6 * n / Log(n) + 1)  
End If  
j = 3  
Dim p()  
ReDim p®  
p(1) = 1: p(2) = 2: p(3) = 3  
For k = 3 To n Step 2  
i = 2: s = Sqr(k)  
Cv:  
i = i + 1  
If p(i) > s Then p(j) = k: j = j + 1: GoTo Cv1  
If CInt(k / p(i)) * p(i) <> k Then GoTo Cv  
Cv1:  
Next  
For i = 1 To r  
If p(i) = 0 Then  
Stop  
Exit Sub  
End If  
Cells(i, 1) = p(i)  
Next  
‘Stop  
End Sub

Я сам — дурнее всякого примера! …

 

Вот мой вариант… на основе алгоритма Alex_ST  
Зы. хотел проверить до 1 000 000 — ждал около часа, надоело….
 

kim

Пользователь

Сообщений: 3139
Регистрация: 23.12.2012

Игорь

{quote}{login=Alex_ST}{date=17.08.2010 11:13}{thema=}{post}На сколько я помню ещё школьную математику, проблема вычисления ряда простых чисел так и не решена вообще (формулы вычисления числового ряда нет).  
А Ёксель что, умнее всех математиков мира?  
Можно решить только макросом и только долгим нудным перебором.{/post}{/quote}  

  Зато формулой можно пометить простые числа…
 

KuklP

Пользователь

Сообщений: 14868
Регистрация: 21.12.2012

E-mail и реквизиты в профиле.

{quote}{login=Михаил}{date=17.08.2010 08:05}{thema=}{post}Вот мой вариант… на основе алгоритма Alex_ST  
Зы. хотел проверить до 1 000 000 — ждал около часа, надоело….{/post}{/quote}  
Видимо из-за РеДимов в цикле(или зацикливается при переполнении).  
Вот это примерный посчет к-ва простых чисел®, при общем числе n:  
If n > 200 Then  
r = n (Log(n) — 2) + 1  
Else  
r = CLng(1.6 * n / Log(n) + 1)  
End If  

  у меня:  
Ввод: 360000(больше не считает гад). за 12.97с 30758 чисел  
У Вас так и не дождался, прервал.

Я сам — дурнее всякого примера! …

 

MCH

Пользователь

Сообщений: 3875
Регистрация: 22.12.2012

{quote}{login=Михаил}{date=17.08.2010 08:05}{thema=}{post}Вот мой вариант… на основе алгоритма Alex_ST  
Зы. хотел проверить до 1 000 000 — ждал около часа, надоело….{/post}{/quote}  

  По алгоритму неизвестного от 17.08.2010, 11:44 на основании файла от Михаила post_146715.xls  
800000 — 3 секунды  

  P.S.: мой первый макрос, сделал в QBASIC (учил когда-то в школе) и переложил в VBA
 

KuklP

Пользователь

Сообщений: 14868
Регистрация: 21.12.2012

E-mail и реквизиты в профиле.

Класс.

Я сам — дурнее всякого примера! …

 

Почему не хочет считать от 1 000 000? (2010, мильон строк для чисел?)
 

{quote}{login=Михаил}{date=17.08.2010 10:27}{thema=MCH}{post}Почему не хочет считать от 1 000 000? (2010, мильон строк для чисел?){/post}{/quote}  

  у меня 2003 поэтому ограничиваюсь результатом в 65536 найденых натуральных числел, на бОльших суммах не могу проверить, да и в VBA не силен
 

kim

Пользователь

Сообщений: 3139
Регистрация: 23.12.2012

Игорь

{quote}{login=Михаил}{date=17.08.2010 10:27}{thema=MCH}{post}Почему не хочет считать от 1 000 000? (2010, мильон строк для чисел?){/post}{/quote}  

  Может пересохранить файл в xlsx?
 

{quote}{login=kim}{date=17.08.2010 10:42}{thema=Re: MCH}{post}{quote}{login=Михаил}{date=17.08.2010 10:27}{thema=MCH}{post}Почему не хочет считать от 1 000 000? (2010, мильон строк для чисел?){/post}{/quote}  

  Может пересохранить файл в xlsx?{/post}{/quote}Да я просто копирую макрос в книгу 2010.. до 800 000 считает, а выше 900 000 — Type mismatch
 

MCH

Пользователь

Сообщений: 3875
Регистрация: 22.12.2012

<<Почему не хочет считать от 1 000 000? (2010, мильон строк для чисел>  
у меня 2003 поэтому ограничиваюсь результатом в 65536 найденых натуральных числел, на бОльших суммах не могу проверить, да и в VBA не силен>  

  Проблема в Range(Cells(1, 1), Cells(count, 1)) = Application.WorksheetFunction.Transpose(a) при попытке вывести более 65536 значений выдает ошибку 400. Заменив данную строчку на цыкл, через который выводятся данные, считает 1 000 000 — 8 секунд (3,9 секунды без вывода значений); 10 000 000 — менее 2х минут
 

Для интересУ проверил скорость различных версий, на 10 000 000, вот результат:  

  за 248,12с (19,42) в 2010  
за 221,39с (19,29) в 2007  
за 56,95с (19,29) в 2003  

      20204
 

MCH

Пользователь

Сообщений: 3875
Регистрация: 22.12.2012

<<Для интересУ проверил скорость различных версий, на 10 000 000, вот результат:  

  за 248,12с (19,42) в 2010  
за 221,39с (19,29) в 2007  
за 56,95с (19,29) в 2003  
>>  

  считает одинаково, а выводит по разному. и судя по скорости машинка у Вас быстрая, значительно быстрее моей :(

 

{quote}{login=MCH}{date=18.08.2010 02:06}{thema=Re: }{post} и судя по скорости машинка у Вас быстрая, значительно быстрее моей :({/post}{/quote}  
моя (1000’000, в 2003)  
за 3,8с  (0,98)   78499 чисел    
Ваша  
за 8,5с   (3,89) 78499 чисел
 

VDM

Пользователь

Сообщений: 779
Регистрация: 22.12.2012

#23

18.08.2010 12:00:18

Спасибо Всем — здорово и познавательно! И формулы и макросы!  

  По последнему предложенному коду, 2003 экс:  

  за 5,28с (0,88) 78499 чисел 1000000  
за 6,66с (2,06) 148934 чисел 2000000  
за 44,62с (17) 664580 чисел 10000000
Источник

Пробовали ли вы когда-нибудь в Excel перечислить все простые числа между двумя заданными числами? В этой статье я расскажу о некоторых интересных методах решения этой задачи.

Генерация всех простых чисел между двумя заданными числами с помощью формул

Генерация всех простых чисел между двумя заданными числами с помощью функции, определяемой пользователем

Генерация всех простых чисел между двумя заданными числами с помощью формул

Потрясающе! Использование эффективных вкладок в Excel, таких как Chrome, Firefox и Safari!
Сэкономьте 50% своего времени и сократите тысячи щелчков мышью каждый день!

Комбинируя функцию Define Name и формулы, вы можете перечислить или сгенерировать все простые числа между двумя конкретными числами. Пожалуйста, сделайте следующее:

1 . Создайте имя первого диапазона, нажав Формулы > Диспетчер имен и в диалоговом окне Диспетчер имен нажмите New , см. снимок экрана:

2 . В диалоговом окне Новое имя в текстовом поле Имя введите rng в качестве имени диапазона, а затем введите эту формулу: = ROW (INDIRECT (Sheet1! $ B $ 1 & “:” & Sheet1! $ B $ 2)) ( Sheet1 – это ваш текущий рабочий лист, который вы использовали, и являются начальным и конечным числами, которые вы указали) в текстовое поле Относится к , затем нажмите кнопку OK , чтобы вернуться к предыдущему диалоговому окну. См. Снимок экрана:

3 . Нажмите кнопку Создать , чтобы создать другое имя диапазона, в диалоговом окне Новое имя введите имя prime в текстовое поле Имя , а затем введите эту формулу: = SMALL (IF (MMULT (- (IF (rng> TRANSPOSE (rng-Sheet1! $ B $ 1 + 2) ), MOD (rng, (rng> TRANSPOSE (rng-Sheet1! $ B $ 1 + 2)) * TRANSPOSE (rng-Sheet1! $ B $ 1 + 2))) = 0), rng-Sheet1! $ B $ 1 + 2 ) = 0, rng), ROW (INDIRECT (“1:” & Sheet1! $ B $ 2))) ( rng – первое имя диапазона, которое вы создали на шаге 2), в текстовое поле Относится к , см. снимок экрана:

4 . Затем нажмите OK , закройте диалоговые окна и выберите один столбец, в котором вы хотите перечислить все простые числа, и введите следующую формулу: = ЕСЛИОШИБКА (простое число, “”) ( prime – это имя диапазона, созданное на шаге 3) в строку формул, а затем нажмите CTRL + SHIFT + Вместе с клавишами ENTER все простые числа между заданными двумя числами отображаются, как показано на следующем снимке экрана:

Создает все простые числа между двумя заданные числа с функцией, определяемой пользователем

Если первый метод несколько сложен, здесь вы можете применить функцию, определяемую пользователем , чтобы решить эту проблему.

1 . Удерживая нажатыми клавиши ALT + F11 , откройте окно Microsoft Visual Basic для приложений .

2 . Нажмите Вставить > Module и вставьте следующий код в окно Module .

Код VBA: генерировать все простые числа между двумя определенными числами:

3 . Затем сохраните и закройте этот код, вернитесь на рабочий лист, введите следующую формулу: = prime (10,100) ( 10 – это начальный номер, а – конечный номер, между которыми вы хотите получить простые числа, вы можете изменить их по своему усмотрению), а затем нажмите клавишу Enter , и все простые числа отобразятся в одной ячейке, см. снимок экрана:

Источник

Понравилась статья? Поделить с друзьями:
  • Таблица расчета калорий excel
  • Таблица простой функции в excel
  • Таблица расходных материалов в excel
  • Таблица расчета заработной платы в excel с формулами скачать
  • Таблица производства работ в excel скачать