Цель данной работы: показать, как
электронные таблицы MicrosoftExcel могут помочь
учителю математики в совершенствовании
преподавания и обучения.
В настоящее время уже нет ни одного учителя,
утверждающего, что применение компьютерных
технологий на уроке математики неэффективно.
Вопрос уже другой: как сделать чтобы применение
компьютера стало естественной потребностью, не
вызывало различных дополнительных проблем,
чтобы компьютер экономил время учителя,
разгружал его.
В большинстве же случаев учитель, применяя
информационные технологии, сталкивается с рядом
проблем:
- сложность приобретения электронных учебников;
- много времени тратится на ознакомление с их
структурой, особенностями поиска, использования,
редактирования материалов; - невозможность быстро адаптировать
мультимедийные материалы к своим конкретным
условиям; - задания трудно «вписать» в структуру урока;
- многие замечательные программы требуют
специального обучения.
Электронные таблицы MicrosoftExcelвходят в
полный пакет офисных программ Microsoft, что
позволяет учителю на любом компьютере применять
их на уроках математики, а также ученикам при
выполнении домашних заданий. В данной работе
представлены «наработки» использования
электронных таблиц MicrosoftExcel на уроках
математики.
1. Использование встроенных функций для
выполнения стандартных вычислений
Excelсодержит более 900 встроенных функций. Функции
– это уже готовые, встроенные в Excel
формулы, которым присвоены уникальные имена.
Среди этого разнообразия есть функции, созданные
специально для финансовых, инженерных,
статистических и других специфических расчётов.
Каждая функция состоит из трёх обязательных
элементов.
Знак равенства (=). Признак того, что в
данную ячейку введена функция или формула, а не
данные какого-либо другого типа.
Имя функции. Характеризует тип
выполняемых операций.
Аргументы. Значения, на основе которых
выполняются вычисления. Аргументы вводят в
круглых скобках сразу после имени функции.
Аргументами могут быть числа, адреса ячеек,
текст, выражения, содержащие другие функции.
Функции, используемые на уроках математики.
СУММ(В2:В5) – вычисление суммы числовых значений
диапазона ячеек начиная с В2 до В5.
СУММ(В2:В5;100;К4) – вычисление суммы числовых
значений диапазона ячеек В2:В5, числа 100 и значения
ячейки К4.
СУММЕСЛИ(В2:В5;”>10”) – вычисление суммы чисел,
больших 10, из диапазона ячеек В2:В5.
СРЗНАЧ(В2:В5) – вычисление среднего значения для
диапазона ячеек В2:В5.
МАКС(В2:В5) – вычисление максимального значения
из диапазона ячеек В2:В5.
МИН(В2:В5) – вычисление минимального значения из
диапазона ячеек В2:В5.
СЧЕТ(В2:В5) – подсчёт общего количества чисел из
диапазона ячеек В2:В5.
СЧЕТЕСЛИ(В2:В5;”<5”) – вычисление количества
чисел меньших 5, из диапазона ячеек В2:В5.
СТЕПЕНЬ(В1;А4) – вычисление значения степени с
основанием В1 и показателем степени А4.
КОРЕНЬ(В1) – вычисление значения квадратного
корня.
Задание 1.1:
Дана последовательность чисел: 25; –61; 0; –82;
18; –11; 0; 30; 15; –31; 0; –58; 22. С помощью встроенных
функций найдите: общее количество чисел,
количество положительных чисел, количество
отрицательных чисел, количество нулей,
максимальное значение, минимальное значение,
среднее значение, сумму всех чисел, сумму
положительных чисел, сумму отрицательных чисел,
сумму максимального и минимального значений.
Приложение 1_1.xls.
Задание 1.2:
Найти значение выражения: 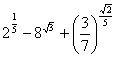
Приложение 1_2.xls.
2. Построение графиков функций
Рассмотрим примеры построения графиков
следующих функций с помощью ЭТ.
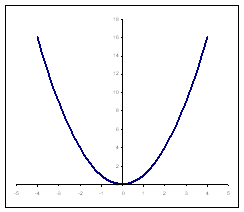
Пример 2.1:
Построить график функции y= х2,
где –4 < х < 4, с шагом 0,5.
| А | В | |
| 1 | х | У |
| 2 | –4 | =А2^2 |
| 3 | –3,5 | 12,25 |
| 4 | –3 | 9 |
| 5 | –2,5 | 6,25 |
| 6 | –2 | 4 |
| 7 | –1,5 | 2,25 |
| 8 | –1 | 1 |
| 9 | –0,5 | 0,25 |
| 10 | 0 | 0 |
| 11 | 0,5 | 0,25 |
| … | … | … |
| 18 | 4 | 16 |
1. В диапазон ячеек А2:А18 введите
значение переменной х от –4 до 4 с шагом 0,5.
2. В ячейку В2 введите формулы:
=А2*А2 или А2^2 или СТЕПЕНЬ(А2;2).
3. Выделите ячейку В2, установите
указатель мыши на маркере заполнения этого
диапазона и протащите его вниз так, чтобы
заполнить диапазон В2:В18.
4. Выделить диапазон ячеек А2:В18.
5. Панель инструментов – Мастер
диаграмм – Тип (точечная) – Вид (плавная линия).
Готово.
Приложение 2_1.xls.
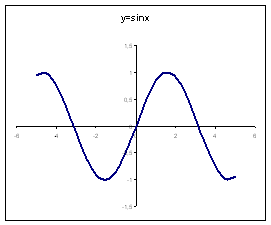
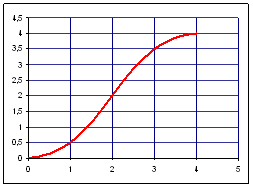
Пример 2.2:
Построить график функции у = sinx, при
х є [–5;5], с шагом 0,5.
| А | В | |
| 1 | x |
y |
| 2 | –5 | =sin(A2) |
| 3 | –4,5 | 0,97753 |
| 4 | –4 | 0,756802 |
| 5 | –3,5 | 0,350783 |
| 6 | –3 | –0,14112 |
| 7 | –2,5 | –0,59847 |
| … |
… |
… |
| 18 | 3 | 0,14112 |
1. В диапазон ячеек А2:А20 введите
значение переменной х от –5 до 5 с шагом 0,5.
2. В ячейку В2 введите формулу: =sin(A2)
3. Выделите ячейку В2, установите
указатель мыши на маркере заполнения этого
диапазона и протащите его вниз так, чтобы
заполнить диапазон В2 : В22.
4. Выделить диапазон ячеек А2 : В18.
5. Панель инструментов – Мастер
диаграмм – Тип (точечная) – Вид (плавная линия).
Готово.
Приложение 2_2.xls.
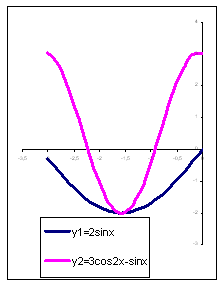
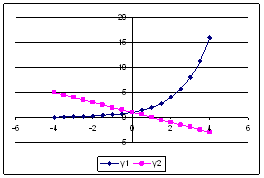
Пример 2.3.
Построить в одной системе координат графики
следующих двух функций y1 = 2sinx и у2
= 3cos2x– sinx при x є [–3;0] с шагом 0,2.
|
А |
В |
С |
|
| 1 | х |
у1 |
у2 |
| 2 | –3 | =2*sin(A2) | =3*cos(2*A2)–sin(A2) |
| 3 | –2,8 | –0,66998 | 2,661686 |
| 4 | –2,6 | –1,031 | 1,921051 |
| 5 | –2,4 | –1,35093 | 0,93796 |
| 6 | –2,2 | –1,61699 | –0,1135 |
| 7 | –2 | –1,81859 | –1,05163 |
| 8 | –1,8 | –1,9477 | –1,71643 |
| 9 | –1,6 | –1,99915 | –1,99531 |
| 10 | –1,4 | –1,9709 | –1,84122 |
| … | … | … | |
| 17 | 0 | 0 | 2 |
1. В ячейки А1, В1 и С1 введите x, y1, у2
соответственно.
2. В диапазон ячеек А2:А17 введите
значения переменной от –3 до 0 с шагом 0,2.
3. В ячейку В2 и С2 ввести формулы: =2*sin(A2) и
=3*cos(2*A2)–sin(A2).
4. Заполнить оставшиеся ячейки с помощью
Автозаполнения. Для этого выделите диапазон
В2:С2, установив указатель мыши на маркере
заполнения этого диапазона и протащите его вниз
так, чтобы заполнить диапазон В2:С17.
5. Выделите диапазон ячеек А1: С17.
6. Панель инструментов – Мастер
диаграмм – Тип (точечная) – Вид (плавная линия).
Готово.
Приложение 2_3.xls.
3. Преобразование графика:
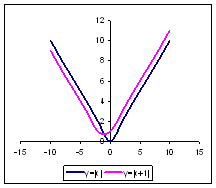
Пример 3.4.
Постройте график функции у=|x| на отрезке
[–10;10] с шагом 2. Преобразовать его: построить
график y = |x +1|
| А | В | С | |
| 1 | х | у1 | у2 |
| 2 | –10 | =ABS(А2) | =ABS(A2+1) |
| 3 | –8 | 8 | 7 |
| 4 | –6 | 6 | 5 |
| 5 | –4 | 4 | 3 |
| 6 | –2 | 2 | 1 |
| 7 | 0 | 0 | 1 |
| 8 | 2 | 2 | 3 |
| 9 | 4 | 4 | 5 |
| 10 | 6 | 6 | 7 |
| 11 | 8 | 8 | 9 |
| 12 | 10 | 10 | 11 |
1. В столбце А постройте
таблицу значений при различных значениях
аргумента;
2. В ячейку В2 введите формулу =ABS(А2);
3. Постройте график функции на данном
листе с помощью Мастера Диаграмм.
4. Добавьте столбец y = |x + 1| и найдите
значения функции при данных значениях аргумента
– в ячейку С2 введите формулу =АBS(А2+1);
5. Выделите график и выполните команду
ДИАГРАММА – ДОБАВИТЬ ДАННЫЕ.
6. Выделите диапазон значений
функции y = | x + 1 | и постройте новый график.
7. Поменяйте y = | x + 1 | на y = | x –1 |, при
этом поменяйте формулу. Что произойдёт с
графиком?
Приложение3_4. xls.
4.1. Использование логических функций
при построении графиков функций
Логические функции предназначены для проверки
выполнения условия или для проверки нескольких
условий. Эта проверка осуществляется на основе
значений ИСТИНА или ЛОЖЬ.
=ЕСЛИ(условие; выражение1; выражение2)
Функция ЕСЛИ позволяет определить,
выполняется ли указанное условие. Если условие
истинно, то значением ячейки будет выражение 1,
в противном случае – выражение2.
Например: =ЕСЛИ(В5>20;”тепло”;”холодно”)
Если значение в ячейке В5>20, то выводится
сообщение «тепло», в противном случае – «холодно».
Совместно с функцией ЕСЛИ используются
логические операции И, ИЛИ, НЕ.
Например: =ЕСЛИ(И(Е4<3;Н92>=13);”выиграет”;”проиграет”)
Если значение в ячейке Е4<3 и Н92>=13, то выводится
сообщение «выиграет», в противном случае –
«проиграет».
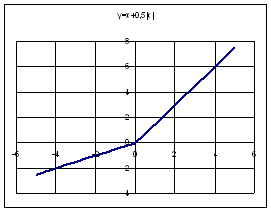
Пример 4.5. (построение графика
функции с одним условием)
Постройте график функции у=х+0,5|x| на
отрезке [–5;5] с шагом 0,5.
Данную функцию можно задать двумя формулами. Используя эти
формулы, переведем на язык Электронных Таблиц.
| А | В | |
| 1 | х | у |
| 2 | –5 | =ЕСЛИ(А2<0;0,5*A2;1,5*A2) |
Приложение4_5. xls.
Пример 4.6
(построение графика функции с двумя
условиями)
Постройте график функции
| А | В | |
| 1 | х | у |
| 2 | 0 | 0 |
| 3 | 1 | =ЕСЛИ(И(A3>=0;A2<=2);1/2*A3^2;(4–0,5*(4–A3)^2)) |
Приложение4_6. xls.
4.2.Использование логических функций при
решение геометрических задач.
С помощью логических функций в Электронных
Таблицах можно выполнять решение геометрических
задач.
Пример 4.7
Построить таблицу для определения возможности
нахождения периметра треугольника по заданным
значениям его сторон. По теореме «Неравенство
треугольника» (Каждая сторона треугольника
меньше суммы двух других сторон), Электронная
Таблица проверяет, существует треугольник с
данными сторонами или не существует. Если
треугольник существует, то вычисляется периметр
треугольника.
| 1 сторона | 2 сторона | 3 сторона | существование треугольника | периметр треугольника |
| 3 | 5 | 7 | =ЕСЛИ(И(A2<E2;B2<F2;C2<D2);»существует»;»не существует») |
15 |
| 4 | 4 | 8 | не существует | нет |
| 1 | 2 | 3 | не существует | нет |
| 5 | 2 | 4 | существует | 11 |
| 0,7 | 1,2 | 3,5 | не существует | нет |
| 1,8 | 2 | 3 | существует | 6,8 |
| 5 | 5 | 10 | не существует | нет |
| 5,7 | 2,9 | 8 | существует | 16,6 |
Приложение4_7. xls.
5. Графическое решение уравнений
Пример 5.8: Решить графически
уравнение: 2х = – х + 1
Рассмотрим две функции: у1
= 2х и у2 = – х+ 1.
Построим в одной системе координат графики этих
функций на отрезке [– 4;4] с шагом 0,5. По графику
функции определяем решение уравнения: х = 0
| А | В | С | |
| 1 | х | у1 | у2 |
| 2 | –4 | =СТЕПЕНЬ(2;А2) | =–1*А2+1 |
| 3 | –3,5 | 0,088388 | 4,5 |
| … | … | … | … |
| 9 | 0 | 1 | 1 |
| .. | … | … | … |
| 18 | 4 | 16 | –3 |
Приложение5_8. xls.
Пример 5.9: Показать графически,
что уравнение имеет решение:
Рассмотрим две функции: у1=
log2x и у2 = –2х+1.
Построим в одной системе координат графики этих
функций на отрезке [0,1;4,1] с шагом 0,5. При
построении видим, что графики пересекаются,
следовательно, уравнение имеет решение.
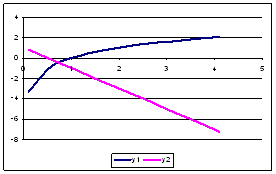
| А | В | С | |
| 1 | х | у1 | у2 |
| 2 | 0,1 | =LOG(A2;2) | =–2*A2+1 |
| 3 | 0,6 | –0,73697 | –0,2 |
Приложение5_9. xls.
6. Создание тренажёров и тестов в Excel
Создание теста и тренажёров по математике с
помощью электронных таблиц Excel,
предназначенного для заполнения на компьютере, с
автоматической проверкой правильных ответов.
Будем использовать функцию ЕСЛИ для
проверки правильности ответов.
Приведём пример создания теста: (Пример
6.10)
| А | В | С | D | E | |
| 1 | 1. Выполните действия: | 1) 1,52 | |||
| 2 | 0,256:0,8+1,2•0,01 | 2) 0,44 | =ЕСЛИ(С2=3;1;0) | ||
| 3 | 3) 0,332 | ||||
| 4 | 4) 4,52 | ||||
| … | |||||
| … | |||||
| 11 | 2. Укажите числа, кратные 9, | 1) 149; 154 | |||
| 12 | удовлетворяющие неравенству: | 2) 144; 152 | =ЕСЛИ(С12=4;1;0) | ||
| 13 | 142 < y <153 | 3) 145; 150 | |||
| 14 | 4) 144; 153 | ||||
| … | |||||
| … | |||||
| 30 | Всего баллов | =СУММ(D2;D7D12…) | |||
| 31 | оценка: | =ЕСЛИ(D30>=17;5;ЕСЛИ(D30>=11;4; ЕСЛИ(D30>=6;3;2))) |
Приложение6_10. xls.
Проверка правильностиответов:
Функция ЕСЛИ устанавливает одно
значение, если заданное условие истинно, и другое
– если оно ложно. В ячейки С2, С12…
вводятся варианты ответов 1, 2, 3 или 4. В ячейках D2,
D12… идёт проверка результатов. Таким
образом, наша функция ЕСЛИ будет
выдавать в ячейках D1, D12…будет выдавать единицу,
если ответ ученика совпал с правильным ответом, и
ноль в случае несовпадения.
Вычисление суммы:
В ячейке D30 находим сумму баллов, используя
функцию СУММ. При этом адреса ячеек отделяем “;”.
Отображение результатов теста:
С помощью функции ЕСЛИ в ячейке D31 идёт проверка
результатов.
Скрытые столбцы:
Наш тест вполне работоспособен, однако столбец
D было бы хорошо “спрятать”, чтобы учащийся не
мог сразу определить, что дал верный или неверный
ответ. Для этого выделите столбец D, щёлкнув в их
заголовки. В меню Формат выберите СтолбецСкрыть.
Столбец станет невидимым.
Если необходимо вновь сделать столбец доступным
для просмотра и редактирования, выделите два
соседних столбца, между которыми находится
скрытый столбец. В меню Формат выбрать СтолбецОтобразить.
Столбец станет видимым.
Приведём пример создания тренажёра: (Пример
6.11)
В столбце G с помощью функции ЕСЛИ
идёт проверка правильности ответов. Если в
ячейке F1 будет занесено число –3, то
таблица выдаст “Правильно”, в противном
случае “Неправильно”.
| А | И | С | D | E | F | G | |
| 1 | 1 | –9 | + | 6 | = | =ЕСЛИ(F5=0;»»;ЕСЛИ(F5=B5+D5; «Правильно»;»Неправильно»)) |
|
| 2 | 2 | –18 | + | 12 | = | ||
| 3 | 3 | –5 | + | –7 | = | ||
| 4 | 4 | 12 | + | –19 | = | ||
| 5 | 5 | 6 | + | 21 | = | ||
| 6 | 6 | 7 | + | 19 | = | ||
| 7 | 7 | 5 | + | –15 | = | ||
| 8 | 8 | 3,7 | + | 0,3 | = | ||
| 9 | 9 | –8 | + | –7,5 | = | ||
| 10 | 10 | –9 | + | 0,8 | = |
Приложение 6_11.xls.
Муниципальное бюджетное образовательное
учреждение
Досчатинская средняя школа
г.о.г. Выкса
Исследовательская работа на тему:
«Microsoft Excel –
на уроках математики»
Физико-математическое отделение
Секция математика
Работу выполнил: ученица 8Б класса
Обыденнова Дарья Сергеевна
Руководитель:
учитель математики и физики
Рощина Людмила Валерьевна,
2019
год
Оглавление
|
Введение |
3-4 |
|
Обзор |
5 |
|
Глава |
6-11 |
|
1.1 |
6-7 |
|
1.2 Таблицы в Microsoft |
7 |
|
1.3 Возможности табличного 1.4 |
8-9 9-11 |
|
Глава 2. Практическая часть…………………………………………. |
11-13 |
|
2.1 Решение уравнения графическим способом……………………. |
8-19 |
|
Заключение…………………………………………………………… |
20 |
|
Литература……………………………………………………………. |
21 |
|
Приложение…………………………………………………………… |
22-23 |
Введение
В школьной
программе по математике, в 7 классе изучаются линейные функции, их свойства и
графики, а в 8 – обратные пропорциональные, квадратичные и графики функций y=√х,
системы уравнений решающиеся графическим способом. При изучении, этой
темы возникает необходимость построения графиков элементарных функций и
уравнений выше второй степени. Для изучения свойств этих функций MicrosoftExcel
предлагает широкие возможности, которые в школьных учебниках по информатике не
оговариваются.
Программа от MicrosoftExcel или электронные таблицы была создана
для более удобной работы пользователя с таблицами данных, причём
преимущественно данная работа производится с числовыми значениями.
Основной особенностью MS Excel выступает его возможность
использовать формулы для того, чтобы описывать между значениями разных ячеек
различные связи. Следует отметить, что по заданным формулам расчёт будет
выполняться автоматически. Если человек изменяет значение какой-либо ячейки, то
сразу же автоматически произойдёт перерасчёт значений всех остальных ячеек,
которые связаны с ней формульными отношениями, благодаря чему обновится вся
таблица и данные, которые находятся в ней.
Табличный процессор Excel позволяет осуществлять вычисления. Там
не одна сотня различных функций (математических, логических, текстовых,
статистических и т.д.). В Excel можно осуществлять бухгалтерские расчеты,
строить графики и диаграммы.
При работе в MS Excelна уроках информатики, заметили, что далеко
не все функции редактора мы изучили. Особенно стало интересно знать: где и как
в расчетных таблицах применяются элементы управления? Можно
ли решить системы уравнений средствами табличного процессора?
Представленная работа состоит из двух частей. В первой
рассматриваются структура, возможности и области применения программыExcel. Во
второй части проведены исследования по изучению возможностей табличного
процессора: использование элементов управления и решение систем уравнений
графическим способом.
Гипотеза: С помощью MS
Excel можно решать математические уравнения и системы.
Цель работы: выявление возможности таблицы MS Excel на примерах построения
функции уравнения и решения графическим способом системы уравнений.
Задачи:
1.Рассмотреть программу Excel.
2. Выявить возможности
табличного процессора Excel.
3.Научится решать
уравнения графическим способом.
4.Решить систему
уравнений графическим способом.
5.Провести анализ
проделанной работы, сделать выводы.
Методы исследования:
·
Анализ литературы по проблеме исследования.
·
Практическая работа.
·
Анализ результатов.
Объектисследования – процесс
построения графиков элементарных функций при помощи ПК.
Предмет исследования — методика
использования ПК при построении графиков функций.
Обзор
литературы
1.
В своей работе я использовала несколько
книг. В книге Уокенбах Дж. «Диаграммы в Excel», перевод с английского
А.Г.Сысонюка. В книге рассматривается вопрос по построению диаграмм, подробно
рассказывается обо всех типах диаграмм их свойствах и возможностях.
2.
Из учебника алгебры 8 класса А.Г.Мерзляк,
я использовала линейные уравнения и системы уравнений, состоящие из нескольких
уравнений.
Глава 1. Теоретическая часть
1.1 Рассмотреть
программу Excel.
14
января 1985 года появилась самая популярная, на сегодняшний день, программа в
мире – Microsoft Excel. Excel был первым табличным процессором, позволявшим
пользователю менять внешний вид таблицы на экране: шрифты,
символыи
внешний вид ячеек. Он также первым представил метод умного пересчёта ячеек —
обновления только ячеек, зависящих от изменённых ячеек: раньше табличные
процессоры пересчитывали все ячейки; это делалось либо после каждого изменения
(что на больших таблицах долго), либо по команде пользователя (что могло
вводить пользователя в заблуждение не пересчитанными значениями). Excel – это
широко распространеннаякомпьютерная программа. Нужна она для
проведения расчетов, составления таблиц и диаграмм, вычисления простых и
сложных функций. Она входит в состав пакета Microsoft Office. Это такой набор
программ для работы в офисе. Самые популярные приложения в нем — Word и Excel.
Microsoft Excel представляет собой большую таблицу, в которую можно вносить
данные, то есть печатать слова и цифры. Также, используя функции этой
программы, можно производить с цифрами разные манипуляции: складывать,
вычитать, умножать, делить и многое другое.
Многие
люди думают, что Excel – это только таблицы. Они убеждены, что все таблицы на
компьютере составляются именно в этой программе. Но это не так. Эта программа
нужна, в первую очередь, для вычислений.
Если
требуется не только расчертить таблицу со словами и цифрами, но еще и
произвести с цифрами какие-либо действия (сложить, умножить, вычислить процент
и т.д), тогда Вам нужно работать в Microsoft Excel. А если же нужно составить
таблицу без вычислений, то есть ввести уже готовые данные, то быстрее и удобнее
это сделать в программе Microsoft Word.
Эксэль,
по сравнению с Вордом, конечно, сложнее. И лучше начинать работать в этой
программе уже после того, как освоите Word. Чтобы изучить Excel досконально, потребуется
немало времени. Но, как показывает практика, большинству для работы достаточно
лишь базовых навыков.
С помощьюмExcel можно анализировать большие
массивы данных. В Excel можно использовать больше 400 математических,
статистических, финансовых и других специализированных функций, связывать
разные таблицы между собой, выбирать произвольные форматы представления данных,
создавать иерархические структуры. Воистину безграничные методы графического
представления данных: кроме нескольких десятков встроенных типов диаграмм,
можно создавать свои, что настраиваются типы, помогают наглядно отобразить
тематику диаграммы.
1.2 Таблицы в Microsoft
Excel.
Построение
всякого графика начинается с таблицы. Самый быстрый способ построения диаграммы
– выделить таблицу и нажать F11,
но без таблицы даже самый простой метод не проходит. Размещать её можно на
любом для вас листе рабочей книге, а так же в любом месте страницы. Зачастую
таблица имеет самый простой и обычный вид, но иногда для получения нужного вида
графика приходится потрудиться. При наборе таблицы совершенно неважно, что у
вас будет строками, а что – столбцами. Можно набирать как вам удобно, и легко
потом менять строки и столбцы местами. Данные из одной и той же таблицы могут
использоваться в нескольких графиках и диаграммах. Дизайн таблицы ни в коем
случае не влияет на дизайн графика. После того как вы набрали таблицу, вам
нужно её выделить. Если это специально набранный квадрат данных, то здесь
проблем не возникнет. Если данные разбросаны по большей таблице, то выделяйте
куски, держа при этом нажатым CTRL.
Это позволяем выделять несмежные области.
1.3 Возможности
табличного процессора Microsoft Excel.
Табличные
процессоры имеют очень широкие функциональные и дополнительные возможности,
обеспечивающие удобную и продуктивную работу пользователя (Приложение 1).
Контекстная
подсказка. Вызывается из контекстного меню или нажатием соответствующей кнопки
в пиктографическом меню.
Контекстное
меню. Разворачивается по щелчку кнопки (правой) мыши на выбранном объекте. Речь
идет, например, о месте таблицы, где в данный момент хочет работать
пользователь. Наиболее часто используемые функции обработки, доступные в данной
ситуации, собраны в контекстном меню (Приложение 2).
Справочная
система. Организована в виде гипертекста и позволяет легко и быстро
осуществлять поиск нужной темы.
Рабочие
группы или рабочие папки. Документы можно соединять в рабочие папки, так что
они могут рассматриваться как одно единое целое, если речь идет о копировании,
загрузке, изменении или других процедурах. В нижней части электронной таблицы
расположен алфавитный указатель (регистр), который обеспечивает доступ к
рабочим листам. Пользователь может задавать название листам в папке (вместо
алфавитного указателя), что делает наглядным содержимое регистра, а значит
облегчает поиск и переход от документа к документу.
Средства
оформления и вывода на печать таблиц. Для удобства пользователя предусмотрены
все функции, обеспечивающие печать таблиц, такие как выбор размера страницы,
разбивка на страницы, установка размера полей страниц, оформление колонтитулов,
а также предварительный просмотр получившейся страницы
Для удобства вычисления в табличных процессорах имеются встроенные
функции, а именно: математические, статистические, финансовые, функции даты и
времени, логические и другие. Менеджер функций позволяет выбрать нужную функцию
и, проставив значения, получить результат (Приложение 3).
Диаграммы.Современный табличный процессор состоит из построения
различного типа двумерных, трехмерных и смешанных диаграмм. Насчитывается более
20 различных типов и подтипов диаграмм, которые можно построить в современной
системе данного класса. А возможности оформления диаграмм также многообразны и
доступны, например, вставка и оформление легенд, меток данных; оформление осей
— возможность вставки линий сеток и другие. Помимо этого, современные системы
работы с электронными таблицами снабжены такими мощными средствами построения и
анализа деловой графики, как вставка планок погрешностей, возможность
построения тренда и выбор функции линии тренда (Приложение 4).
1.4
Типы диаграмм в Microsoft Excel.
1.4.1
Гистограммы
Данные
в столбцах или строках листа можно представить в виде гистограммы. В гистограмме категории обычно отображаются по
горизонтальной оси, а значения — по вертикальной оси, как показано на этой
диаграмме (приложение 5).
1.4.2
Графики (приложение 6).
Данные,
расположенные в столбцах или строках листа, можно представить в виде графика.
Графики позволяют изображать непрерывное изменение данных с течением времени в
едином масштабе и идеально подходят для представления тенденций изменения
данных с равными интервалами. На графиках данные категорий равномерно
распределяются вдоль горизонтальной оси, а все значения равномерно
распределяются вдоль вертикальной оси. Графики можно использовать, если метки
категорий являются текстовыми и представляют значения, разделённые равными
интервалами, например, месяцы, кварталы или финансовые годы. Это особенно важно
при наличии нескольких рядов: для отображения одного ряда можно использовать
точечную диаграмму. Также графики можно использовать при наличии нескольких
разделённых равными интервалами числовых меток, в частности, лет. Если числовых
меток больше десяти, вместо графика лучше использовать точечную диаграмму.
1.4.3
Круговые диаграммы (приложение 7)
Данные
в одном столбце или строке листа можно представить в виде круговой диаграммы.
Круговая диаграмма демонстрирует размер элементов одного ряда данных
относительно суммы элементов. Точки данных на круговой диаграмме выводятся как
проценты от всего круга.
Круговую
диаграмму рекомендуется использовать, если:
-нужно
отобразить только один ряд данных;
-все
значения ваших данных неотрицательны;
-почти
все значения данных больше нуля;
—имеется
не более семи категорий, каждой из которых соответствуют части общего круга.
1.4.4 Линейчатые
диаграммы (приложение 
Данные
в столбцах или строках листа можно представить в виде линейчатой диаграммы.
Линейчатые диаграммы используют для сравнения отдельных элементов. В диаграммах
этого типа категории обычно располагаются по вертикальной оси, а
величины — по горизонтальной.
1.4.5 Точечные
диаграммы (приложение 9)
Данные
в столбцах и строках листа можно представить в виде точечной диаграммы.
Точечная диаграмма показывает отношения между численными значениями в
нескольких рядах данных или отображает две группы чисел как один ряд координат
x и y. Точечная диаграмма имеет две оси значений, при этом одни числовые
значения выводятся вдоль горизонтальной оси (оси X), а другие — вдоль
вертикальной оси (оси Y). На точечной диаграмме эти значения объединяются в
одну точку и выводятся через неравные интервалы или кластеры. Точечные
диаграммы обычно используются для иллюстрации и сравнения числовых значений,
например научных, статистических или технических данных.
1.4.6
Поверхностные
диаграммы (приложение 10)
Данные
в столбцах или строках листа можно представить в виде поверхностной диаграммы. Поверхностная
диаграмма полезна, если требуется найти оптимальные комбинации данных из двух
наборов. Как на топографической карте, области, относящиеся к одинаковым
диапазонам, при этом выделяются цветами и штриховкой. Поверхностные
диаграммы можно использовать для иллюстрации категорий и наборов данных,
представляющих собой числовые значения.
Глава
2. Практическая часть.
2.1
Решение уравнения графическим способом.
Работать
я буду в Microsoft Excel 2010.
Пример
1. Вначале я покажу, как строить простейшее
линейное уравнение у=2·х+5. Для этого зададим переменную х и
запишем уравнение в таблицу.
Зададим
переменную и составим формулу.
Создаем
значения для постоянной у.
Строим
график. Обводим ячейки А2:В9. Выбираем позицию «вставка», далее «точечная
диаграмма»
Получаем
график линейного уравнения.
Пример
2. Следующимя построю систему уравнений,
возьму её из учебника алгебры 8 класса.
Система:
Задаем
для первого уравнения переменную и находим постоянную.
Теперь
задаём для второго уравнения переменную и находим постоянную
Строим
график этих уравнений.
Получаем
точку пересечений (5,3), это и будет ответ нашей системы уравнения.
Пример
3. Возьмём более сложную функцию
Задаем
переменную и находим «у» для наших уравнений.
Выбираем
точечную диаграмму
Так как в нашей системе есть линейные уравнения и парабола, то для
каждого уравнения добавляем по отдельности линию тренда
Получаем графическое решение нашей системы, также можем поменять
название. Находим точку пересечения у=9, х=3.
Пример 4. Построим
более сложную систему, которую мы еще не проходили, и решить самостоятельно я
её не смогу. Моя система состоит из квадратного трёхчлена и кубического
уравнения.
Сначала введем переменную х и запишем формулы. Проведем
расчёты, вот что получили.
Выбираем
точечную диаграмму.
Нажимаем по очереди на точечную диаграмму, выбираем линию тренда.
Так как у нас уравнения со степенями, то нажимаем на полиномиальную линию
тренда, со степенью 2, и то же самое делаем с кубическим уравнением, только
ставим степень 3.
Построив
графики, выбираем источник данных и изменяем имя ряда.
Вывод.
Программа
MicrosoftExcel
– одна из наиболее практически значимых, востребованных. Электронные таблицы не
только позволяют автоматизировать расчеты, но и являются эффективным средством
моделирования различных вариантов и ситуаций. Меняя значения исходных данных,
можно проследить за изменением получаемых результатов и из множества вариантов
решения задачи выбрать наиболее подходящий.
Цель
моей работы достигнута, задачи выполнены. Я считаю, что моя гипотеза
подтвердилась, математические уравнения и системы можно решать графическим способом
с помощью программы MicrosoftExcel.
Использование
компьютерной программы при изучении позволяет повысить эффективность работы учеников
на уроке, избежать монотонных, однообразных действий при построении графиков
функций, поддержать интерес детей к математике. Использование ПК дает
возможность работать в одинаковом, достаточно быстром темпе. Конечно, на уроке
времени не хватает, но можно организовать
дополнительные занятия или задавать домашние задание предназначенные для
построения графиков функций при помощи компьютера, с целью повышения
эффективности работы учащихся на уроках, побуждение и поддержание интереса к
математике, показ необходимости знаний по математике и информатики в реальной
жизни
Литература
3.
Бурьков Д.В.: Практикум по информатике. — М.:
Дашков и К, 2010
4.
Гобарева Я.Л.: Технология экономических
расчетов средствами MS Exsel. — М.: КноРус, 2009
5.
Мерзляк А.Г.: Алгебра, 8 класс. – М.:
Вентана-Граф, 2018. – 256 с.
6.
Уокенбах Дж. Диаграммы в Excel
Интренет – ресурсы:
1. studbooks.net
2. lumpics.ru
3. exceltable.com
4. poisk-ru.ru
Приложение
|
Приложение 1. |
Приложение 2. Контекстное меню |
||
|
Приложение 3. Вычисления |
Приложение |
||
|
Приложение 5. Гистограмма |
Приложение |
||
|
Приложение |
Приложение |
||
|
Приложение 9. Точечные диаграммы. |
Приложение 10. Поверхностные диаграммы. |
||
Рецензия
на
исследовательскую работу: MicrosoftExcel – на
уроках математике.
Автор
работы: учащийся 8 класса, 14 лет
Работа
представлена на 17 страницах (основной текст – 15 страниц, приложение – 2
страницы). Структура работы соответствует требованиям конкурса.
Работа
носит исследовательский характер и посвящена изучению построения функций и
системы уравнений в программе Excel. Цели и
задачи соответствуют заданным исследованиям. В главе 1 рассмотрена сама
программа Excel и подробно
рассказывается об основных возможностях Всемирной паутины. В практической части
подробно рассказывается как строить линейные уравнения, системы уравнений
Результаты, представленные в работе, имеют практическую значимость. Работа
иллюстрирована диаграммами, ответами учащихся.
Работа
представляет интерес и в целом соответствует требованиям, предъявляемым для
участия в научно – практической конференции обучающихся городского округа город
Выкса. Рецензент выражает автору благодарность за проделанную работу и желает
дальнейших научных успехов.
Рецензент
работы: учитель
Рощина Л.В.
ПРИМЕНЕНИЕ EXCEL В ПРЕПОДАВАНИИ МАТЕМАТИКИ
В современном обществе использование информационных технологий становится необходимым практически в любой сфере деятельности человека. Овладение навыками этих технологий еще за школьной партой во многом определяет успешность будущей профессиональной подготовки нынешних учеников. Опыт показывает, что овладение этими навыками протекает гораздо эффективней, если происходит не только на уроках информатики, а находит свое продолжение и развитие на уроках учителей-предметников. Этот подход выдвигает новые требования к подготовке учителя-предметника, ставит перед ним новые проблемы, заставляет осваивать новую технику и создавать новые методики преподавания, основанные на использовании современной информационной среды обучения. Преподавание математики, в силу особенностей самого предмета, представляет собой наиболее благоприятную сферу для применения современных информационных технологий. Проводимая работа в этом направлении содержит как чисто демонстрационную составляющую, дающую ученикам расширенные представления о возможностях использования информационных технологий, так и составляющую, требующую активного применения учениками знаний, полученных на уроках информатики. В процессе преподавания математики, информационные технологии могут использоваться в различных формах. Одним из самых удачных является внедрение табличного процессора EXCEL.
Excel, пожалуй, самая популярная сегодня программа электронных таблиц. Она входит в офисный пакет MS Office. Ею пользуются деловые люди и ученые, бухгалтеры и журналисты. С ее помощью ведут разнообразные списки, каталоги и таблицы, составляют финансовые и статистические отчеты, обсчитывают данные опросов общественного мнения и состояние торгового предприятия, обрабатывают результаты научного эксперимента, ведут учет, готовят презентационные материалы.
Excel сумеет вычислить суммы по столбцам и строкам таблицы, взять проценты, подсчитать среднее арифметическое, банковский процент или дисперсию; в нем вообще можно использовать множество стандартных функций – финансовых, математических, логических, статистических.
Оформление таблиц может быть самым разнообразным, возможности форматирования данных – как в хорошем текст-процессоре: можно менять шрифты, начертания, выделять строки, столбцы или отдельные ячейки текста цветом, рамочками и линеечками, закрашивать области фоном или цветом, строить по табличным данным графики и диаграммы, вставлять в таблицу картинки и т.п.
Надо сказать, что программа достаточно мощная, возможности ее весьма обширны. Одних только математических, логических, бухгалтерских, статистических функций, которые Excel умеет выполнять над табличными данными – более 200 штук. Именно поэтому применение Excel в математике весьма эффективно и дает большие возможности учителю предметнику. В процессе преподавания математики Excel может использоваться в изучении многих тем:
- решение уравнений n-й степени;
- решение систем линейных уравнений;
- работа с матрицей;
- построение графиков функций;
- графическое решение систем уравнений;
- тест, созданный средствами Excel и т.д.
Рассмотрим некоторые примеры применения Excel на уроках математики:
- Построить график функции:
- В первой строке записываются заголовки столбцов
- В первом столбце пишем значения х от нижней до верхней границы с заданным шагом. В нашем случае от -4 до 4 и с шагом 0,5
- Во втором столбце находятся значения у, которые вычисляются по формуле: =$С$1*СТЕПЕНЬ(А2;2), где С1 это ссылка на ячейку с коэффициентом а
Рисунок 1
- Выделяем диапазон ячеек А1:В18 и выбираем пункт меню Вставка
диаграмма. Выбираем тип диаграммы – точечная, вид – сглаженные линии.
- по требованию к оформлению изменяем внешний вид полученного графика
Рисунок 2
2. Решить графически систему уравнений:
Сначала построим таблицу, содержащую значения аргумента х и значения у обоих уравнений системы:
Рисунок 3
- В первой строке записываются заголовки столбцов
- В первом столбце пишем значения х от -3 до 3 с шагом 0,2
- Во втором столбце находятся значения у первого уравнения, которые вычисляются по формуле: =СТЕПЕНЬ(А2;2)+5 (при копировании динамическая ссылка изменится)
- Во третьем столбце находятся значения у второго уравнения, которые вычисляются по формуле: =6*А2+12 (при копировании динамическая ссылка также изменится)
Рисунок 4
- Выделяем заполненную таблицу и на основе этих данных вставляем диаграмму: тип – точечная, вид – гладкие кривые
- По требованиям настроить внешний вид графика (подписи, масштаб осей, шаг осей, фон, цвет линий и т.д.)
На диаграмме видно, что оба графика имеют точки пересечения – эти координаты точек и есть решения системы.
Примечание: для более точного решения можно выбрать меньший шаг.
- Решить систему линейных уравнений:
- пусть в ячейках А1, В1, С1 будут находиться значения переменных х1, х2, х3 соответственно. Сейчас они пусты;
- в ячейки А3:С5 запишем систему уравнений в матричном виде:
- в ячейки Е3:Е5 запишем формулы, выражающие каждое уравнение системы
Рисунок 5
Рисунок 6
- далее выбираем пункт меню сервис
поиск решения. Если этого пункта нет, то выбираем пункт меню сервис
надстройки и ставим галочку напротив пункта «поиск решения»
- в появившемся диалоговом окне вводим данные: в качестве целевой ячейки выберем ячейку с формулой первого уравнения системы (на ее месте может быть любое другое уравнение системы). Выберем ячейку равной значению 15 (т.е. значение первого уравнения).
- В пункте «изменяя ячейки» выберем диапазон ячеек, в которых должны находиться переменные, т.е. диапазон А1:С1
- В области «ограничения» с помощью кнопки «добавить» введите равенства, в левой части которых находятся формулы в остальных уравнений системы, а в правой части находятся ссылки на ячейки со значениями этих уравнений.
- Жмем кнопку «выполнить»
Рисунок 7
- Если решение существует, то оно будет введено в ячейки переменных и покажется диалоговое окно об успешном решении системы.
Рисунок 8
- Создать тест по математике
Весь тест строится на формулах Ехсеl из раздела «Логические». Сначала оформляются вопросы. Под вопросами указываются варианты ответов. Перед каждым вариантом ответа оставляем пустую ячейку предназначенную для выбора ответа. Тестируемый должен поставить напротив правильного варианта ответа знак «+», а остальные ячейки оставить пустыми, иначе ответ не засчитается. Также необходимо выделить один столбец, в котором будет вестись подсчет набранных баллов. В окончательном результате этот столбец необходимо будет скрыть.
Рисунок 9
После каждого вопроса в столбце набранных баллов необходимо ввести формулу:
=ЕСЛИ(И(А12=””;A13=”+”;A14=””);”1”;””).
Формула «если» содержит условие И(А12=””;A13=”+”;A14=””). В данном случае оно сложное и говорит о том что правильный вариант ответа – второй. В ячейке А13 напротив правильного варианта ответа должен стоять плюсик, а остальные ячейки должны оставаться пустыми. При соблюдении этого условия выполняется первая часть формулы — ”1” – то есть в ячейку заносится значение 1 (цена вопроса). Количество вариантов ответов может быть любым, и количество правильных ответов – тоже. В этом случае необходимо отредактировать условие. Соответственно, при сложных вопросах может быть и больше цена вопроса. При несоблюдении условия (вопрос остается без ответа, либо выбраны неверные ответы) выполняется вторая часть формулы — “”. Ячейке не присваивается никакое значение.
После составления одного вопроса, его можно скопировать и на этой основе создавать другие вопросы, просто изменив текст и отредактировав условие правильности. При копировании динамическая ссылка изменится.
По завершении всех вопросов в столбце подсчета баллов необходимо ввести формулу суммы баллов — =СУММ(G1:G66) – от первой ячейки столбца до предыдущей той, в которую записывается сама формула.
Под всеми вопросами выделяем цветом одну ячейку.
Рисунок 10
После завершения тестирования ученик будет вводить в нее слово «готово» и в ячейке справа будет выведен результат.
Рисунок 11
В ячейку справа заносится формула =ЕСЛИ(A67=»готово»;СЦЕПИТЬ(«Ваш результат — «;G67;» баллов из 8 возможных»);»»). Условие — ученик вносит в синюю ячейку слово «готово». Действие на условие – в ячейку заносится текст, содержащий результат ученика.
Электронные таблицы на уроках математики
Шайдуллова Любовь Радиковна
учитель математики и информатики
Все современные технологии призваны сделать нашу жизнь удобнее. И
информационные – не исключение. С появлением компьютера выполнение
многих процессов стало не только быстрее, но еще надежнее и эффективнее.
Проникновение современных информационных технологий в сферу
образования позволяет качественно изменить методы и организационные
формы обучения, сделав его более удобным и доступным. Электронные
таблицы позволяют учителю на любом компьютере применять их на уроках
математики, а также ученикам при выполнении домашних заданий. В
конспекте представлены возможности использования электронных
таблиц Microsoft Excel на уроках математики.
Цель:
научить строить графики элементарных математических
функций с помощью табличного процессора Excel; показать возможности
программы Excel для решения задач по математике.
Задачи :
образовательные: познакомить учащихся с электронной таблицей;
сформировать умение записывать математические выражения в Excel;
сформировать навыки построения графиков элементарных функций в
электронной таблице.
развивающие: развить самостоятельность; развивать умение применять
полученные знания на практике.
воспитательные: приобщать учащихся к информационной культуре;
воспитывать чувство уверенности в себе и своих знаниях.
Вычисления значений выражений
Для выполнения различных вычислений в таблицах Excel используют
формулы и функции.
Формулы – это выражение, начинающееся со знака равенства и
состоящее из числовых величин, адресов ячеек, функций, имен, которые
соединены знаками арифметических операций. К знакам арифметических
операций, которые используются в Excel относятся: сложение; вычитание;
умножение; деление; возведение в степень.
Функция, это множество точек (x, y), удовлетворяющее выражению
y=f(x). Поэтому, нам необходимо заполнить массив таких точек, а Excel
построит нам на их основе график функции. Функции Excel — это специальные, заранее созданные формулы для
сложных вычислений, в которые пользователь должен ввести только
аргументы. Функции состоят из двух частей: имени функции и одного или
нескольких аргументов. Имя функции описывает операцию, которую эта
функция выполняет. Аргументы функции Excel задают значения или ячейки,
используемые функцией, они всегда заключены в круглые скобки.
Аргументами могут быть числа, адреса ячеек, текст, выражения, содержащие
другие функции.
Математические функции (некоторые из них)
Название функции
СУММ(A2:A6)
СУММ(А2;В10;С5:К12)
СУММЕСЛИ(А2:А6,»>5″)
ПРОИЗВЕД(число1;число2…)
СТЕПЕНЬ(В1;А4)
КОРЕНЬ(число)
СРЗНАЧ(A2:A6)
МАКС(A2:A6)
МИН(A2:A6)
Действия функции
суммирует множество чисел
получает сумму чисел в ячейках А2, В10 и в ячейках от
С5 до К12
суммирование чисел из диапазона А2:А6,
превышающие 5
перемножает все числа, задаваемые ее аргументами
вычисление значения степени с основанием В1 и
показателем степени А4
нахождение квадратного корня из числа
возвращает среднее арифметическое значение для
диапазона ячеек A2:A6
вычисление максимального значения из диапазона ячеек
A2:A6
вычисление минимального значения из диапазона ячеек
A2:A6
ОКРУГЛ(число; число разрядов) округляет значение до требуемого количества
СЧЕТ(A2:A6)
десятичных знаков. Количество десятичных знаков
указывается во втором аргументе
Подсчитывает количество чисел из диапазона ячеек
A2:A6
СЧЁТЕСЛИ(диапазон;критерий) подсчитывает количество ячеек, отвечающих
определенному условию
Покажем на примере использование каждой из выше перечисленных
функций.
Даны числа: 2; 17; 43; 13; 24; 36; 100; 65,56; 18; 0; 15; 49; 10; 8; 18. С
помощью функций найдите:
1. общее количество чисел,
2. количество положительных чисел,
3. количество отрицательных чисел,
4. максимальное значение,
5. минимальное значение,
6. среднее значение,
7. сумму всех чисел, 8. произведение всех чисел,
9. сумму отрицательных чисел,
10. корень максимального числа,
11. округлить число
Ключ к заданию:
Формулы вносятся в ячейки N4N14.
1. общее количество чисел =СЧЁТ(A2:O2)
2. количество положительных чисел =СЧЁТЕСЛИ(A2:O2;»>0″)
3. количество отрицательных чисел =СЧЁТЕСЛИ(A2:O2;»<0″)
4. максимальное значение =МАКС(A2:O2)
5. минимальное значение =МИН(A2:O2)
6. среднее значение =СРЗНАЧ(A2:O2)
7. сумму всех чисел =СУММ(A2:O2)
8. произведение всех чисел =ПРОИЗВЕД(A2:O2)
9. сумму отрицательных чисел =СУММЕСЛИ(A2:O2;»<0″)
10. корень максимального числа =КОРЕНЬ(N7)
11. округлить число =ОКРУГЛ(H2;1)
Построение графиков функций — еще одна из возможностей Excel.
Рассмотрим процесс построение графиков некоторых математических
функций: линейной, квадратичной и обратной пропорциональности.
Линейная функция: y=2x3 Графиком линейной функции является прямая, которую можно
построить по двум точкам. Строим таблицу:
В ячейку В2 вносится формула =2*А23. В ячейку В3 формулу можно
ввести аналогично (изменив А2 на А3) или использовать маркер
автозаполнения.
графиков
функций в Microsoft
Для построения
Office
Excel используется тип диаграммы Точечная. Для этого требуется два
ряда значений: Х и Y значения, которые должны быть соответственно
расположены в левом и правом столбцах. Можно совместить построение
нескольких графиков. Такая возможность используется для графического
решения систем уравнений с двумя переменными, при проведении
сравнения анализа значений y при одних и тех же значениях x.
Выполняем команды Вставка – Диаграммы – Точечная – со
значениями, соединенная сглаживающими линиями. Построим графики функций y= x2 и y= x3 на интервале [4;4] с шагом 1.
Для построения необходимо:
1. Заполнить таблицу значений: в диапазон ячеек B1:J1 введите
значение переменной х от –4 до 4 с шагом 1. В ячейку В2 введите формулы:
=B1*B1 или B1^2 или СТЕПЕНЬ(B1;2). В ячейку C2 формулу можно ввести
аналогично (изменив B1 на C1) или использовать маркер автозаполнения.
2. Выделить таблицу и указать тип диаграммы Точечная.
3. Выбрать формат точечной диаграммы с гладкими кривыми.
4. В Макете указать название диаграммы «y=x^2»
5. Должен получиться график: Аналогично строим график функции y= x3
В ячейку В2 введите формулы: =А2*А2*A2 или А2^3 или СТЕПЕНЬ(А2;3).
Любые другие графики непрерывных функций строятся аналогично.
Если функция кусочная, то необходимо каждый «кусочек» графика
объединить в одной области диаграмм.
Рассмотрим это на примере обратной пропорциональности у=1/х.
Функция определена на интервалах (∞;0) и (0; +∞). Создадим график
функции на интервалах: [4;0) и (0; 4]. Подготовим две таблички, где х
изменяется с шагом 0,5.
На диаграмму вы должны добавить два ряда — для первой и второй
таблички соответственно Получаем график функции y=1/x.
Список использованной литературы
1. Алгебра. 7 класс. Учебник. Макарычев Ю.Н., Миндюк Н.Г., Нешков
К.И., Суворова С.Б. М.: Просвещение, 2013. 256с.
2. Алгебра. 8 класс. Учебник. Макарычев Ю.Н. и др. М.: Просвещение,
2013. 287с.
3. Алгебра. 9 класс. Учебник. Макарычев Ю.Н., Миндюк Н.Г. и др. 21е
изд. М.: Просвещение,2014.— 271с.
4. Обучающие курсы, видео и учебники по Excel 2013 [электронный
ресурс] https://support.office.com/ruru/article Обучающиекурсывидео
иучебникипоExcel2013.
5. Процессоры электронных таблиц
[электронный ресурс]
http://www.lessonstva.info/edu/einf2/m2t2_1.html.
«ИСПОЛЬЗОВАНИЕ ПРОГРАММЫ MICROSOFT EXCEL НА УРОКАХ МАТЕМАТИКИ»
Переход от индустриального к информационному обществу с широким проникновением информационных технологий во все сферы практической деятельности открывает новые возможности для модернизации содержания обучения и методов преподавания.
Богатейшие возможности представления информации на компьютере позволяют изменять и неограниченно обогащать содержание образования. Выполнение заданий и упражнений с помощью компьютера создает возможность для повышения интенсивности урока.
В своей работе я использую компьютер при изучении следующих тем:
- «Показательная, логарифмическая и степенная функции, их свойства и графики»;
- «Свойства и графики тригонометрических функций»;
- «Исследование функций и построение графиков».
Когда графики функций учащиеся строят на бумаге, возникают существенные пространственные ограничения. Как правило, график изображается лишь в окрестности начала системы координат и в область бесконечности должен продолжаться учащимися мысленно. Для развития пространственного воображения и правильного формирования понятий, связанных с данными темами, компьютер становится незаменим.
При выполнении заданий на построение графиков я применяю математические возможности Microsoft Excel.
При построении на компьютере показательных и логарифмических функций учащиеся находят область определения и область значений, определяют, какая из этих функций является возрастающей, а какая убывающей, что важно в дальнейшем для решения показательных и логарифмических неравенств.
При изучении темы «Свойства и графики тригонометрических функций» учащиеся на компьютере, с помощью средств Microsoft Excel, строят графики функций и
. На этих графиках учащиеся также находят область определения и область значений, определяют четность, нечетность и периодичность функций. Здесь можно хорошо видеть сжатие и растяжение тригонометрических функций.
Учащиеся хорошо понимают процесс исследования функции, но когда дело доходит до построения графиков возникает проблема с тем, как изобразить на бумаге промежутки возрастания и убывания функции. Далеко не все учащиеся обладают необходимым пространственным воображением, в результате чего формируются поверхностные знания по данной теме.
Помимо того, что учащиеся овладевают математическими знаниями по вышеперечисленным темам, они еще и отрабатывают свои умения и навыки работы в среде Microsoft Excel, а именно ввод формул, вставку функций, построение диаграмм и т.д.
Такие уроки, на мой взгляд, очень эффективны, т.к. учащиеся получают знания в процессе самостоятельной творческой работы. Преподаватель, выступая в роли посредника, создает ситуацию активного поиска и практической деятельности.
Таким образом, использование компьютера, как на уроках, так и во внеурочное время – это не дань моде, не способ переложить на плечи компьютера многогранный творческий труд преподавателя, а лишь одно из средств, позволяющее интенсифицировать образовательный процесс и активизировать познавательную деятельность учащихся.