Таблица для логиста excel

Сегодня мы живем в эпоху перепроизводства. Теперь логистика является ключевым фактором влияния на конечную стоимость товара для потребителя. Роль логистики в бизнесе сложно переоценить. Как говорил американский генерал Джон Першинг: «Пехота выигрывает сражения, а логистика — побеждает войны». Визуализация данных о функционировании логистических цепочек поставок существенно упрощает работу для всех сотрудников. От рядовых водителей до целого департамента топ-менеджеров корпорации. Вашему вниманию презентуется наше первое решение в Excel для визуального анализа логистики и управления цепочками поставок.

Пример бизнес-идеи для анализа управления логистикой в Excel

Для приведения примера практического использования дашборда по логистическим показателям, традиционно моделируем новую ситуацию с Техническим Заданием (ТЗ) разработчика презентаций отчетов.

Описание бизнес-идеи как исходные данные к презентации

В Министерстве Сельского Хозяйства США разработали новую технологию для производства искусственных дров из травы. Согласно технологическому составу рецепта в сырьевую смесь должны добавляться щепки древесины до 40% по отношению к траве 60%. В процессе прессования предварительно подготовленного сырья: правильно высушенной измельченной травы и щепок из древесины под давлением выделяется древесный клей, который служит натуральным связующим веществом. В результате на выходе пресса экструдера получается брикет экологичных искусственных дров из травы.

Данная технология создала прибыльную и привлекательную бизнес-идею основанную на переработке растительных отходов в искусственные био-дрова:

Два базовых компонента для прибыльного производства био-дров:

1. Основной компонент – сено 60%. Повсюду много скошенной травы. Ее тысячами тон по всем штатам США ежегодно собирают с газонов приусадебных участков и школ, парков. После чего закапывают в грунт для гумуса.



2. Второй компонент – древесная щепка 40%. Его можно получать из быстрорастущего тополя Quaking Aspen. Этот осинообразный тополь является самым популярным деревом на всей территории Северной Америки. Высота Quaking Aspen достигает до 35 м, а скорость роста около 2,7 метра за год. Если потребуются большие объемы древесной щепы, то Quaking Aspen можно быстро выращивать в частных питомниках. Древесина из дерева Quaking Aspen непригодна для мебели, досок и не подходит даже на дрова. Но идеально подходит как связующий компонент для переработки сухой травы в энергетический продукт с повышенным спросом у потребителей.

Интересный факт! Quaking Aspen – признано самым старым растением, которое сохранилось до сегодняшних дней на нашей планете. Самая большая колониальная структура корня этого дерева называется лесом Пандо, он расположен в штате Юта (США). Этот лес состоит из огромной рощи деревьев Quaking Aspen и покрывает площадь 43 гектара. Но что особенно интересно, лес Пандо состоит только из одного вида дерева Quaking Aspen и обладает единым корнем. На сегодняшний день Пандо является самым большим живым организмом на нашей планете с весом 6 000 тонн.

Искусственные био-дрова при сгорании выделяют в разы меньше вредных веществ по сравнению с обычными дровами. Они практически не засоряют дымоходы каминов. В процессе производства био-дров могут быть добавлены эфирные аромамасла и другие полезные добавки для эффектных изменений в процессе их сгорания в камине:

• насыщение помещения приятными и полезными ароматами эфирных масел;
• изменение цвета огня;
• безвредные натуральные добавки для отпугивания насекомых.

Особенно популярные искусственные дрова с добавками ароматов: мяты, лаванды и эвкалипта.

По этой же технологии производятся не только брикеты, но и пеллеты для использования их в котлах с автоматической подачей твердого топлива. На такой ценный энергетический продукт уже имеется большой спрос. Тем более что дрова дорожают с каждым годом. Рентабельность бизнеса по производству дров из травы легко достигает уровня 100%, но половина расходов уходит на логистику.

Интересный факт! В период 2030-2040 года наступает цикл снижения солнечной активности в нашей галактике. Такое бывает раз на 400 лет. В этот цикл нас ждет мини ледниковый период. Средняя температура на планете снизится.

До 2030-го года важно успеть наладить логистику доставки дров во всем мире.

При этом фирменный производитель искусственных дров и пеллетов из травы должен уделять особое внимание логистике для контроля расходов.



ТЗ для разработки визуализации данных логистики в Excel

Все аспекты вышеописанной бизнес-идеи включаются в техническое задание для разработчика визуализации данных в Excel.

Топ-3 перевозимых грузов:

1. Закупка сырья – сено скошенной травы с газонов и бревна тополя Quaking Aspen.
2. Главный реализуемый продукт – искусственные дрова для каминов с аромамаслами и натуральными добавками.
3. Дополнительный товар для расширения ассортимента с целью увеличения продаж – пеллеты для заправки котлов длительного автоматного горения с функцией автоматической подачи твердого топлива.

Доставку грузов осуществляют три водителя. По 5-ти маршрутам. У первых двоих водителей по 2 маршрута и третьего только 1.

Основные производственные мощности расположены в городе Нью-Йорк. Поэтому доставка производимой продукции по США будет реализована в направлении из Нью-Йорка. А поставки сырья в обратном направлении – соответственно. Фирма на этапе развития. Ее сеть реализации товаров налажена только по 8-ми городам в разных штатах США:

1. Нью-Йорк – штат Нью-Йорк.
2. Нэшвилл – штат Теннесси.
3. Чикаго – штат Иллинойс.
4. Даллас – штат Техас.
5. Денвер – штат Колорадо.
6. Лос-Анджелес – штат Калифорния.
7. Сан-Франциско – штат Калифорния.
8. Сиэтл – Вашингтон.

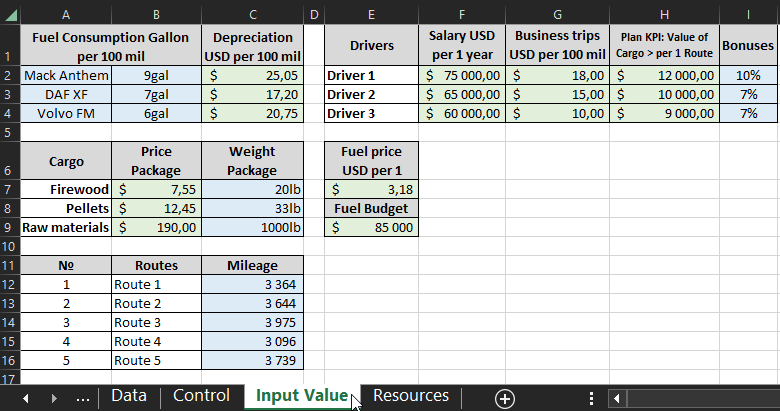
У каждого маршрута свое расстояние в милях, что влияет на различные логистические факторы. Все параметры дашборда заполняются исходными значениями на листе «Input Value»:

1. Расход топлива автомобиля в галлонах на 100 миль.
2. Амортизация за каждое пройденные 100 миль на грузовике.
3. Зарплата для каждого водителя.
4. Лимиты командировочных расходов на 100 миль.
5. План KPI – только при превышении выполнения плана будут выплачены соответственные премиальные бонусы.
6. Размер бонусных вознаграждений за перевыполнение плана KPI отдельно по каждому водителю.
7. Стоимость одной упаковки груза.
8. Вес упаковки грузов в фунтах.
9. Стоимость 1-го галлона топлива.
10. Годовой бюджет выделенный на топливо для заправки грузовиков.
11. Расстояние продолжительности каждого маршрута в милях.

Можно изменять только окрашенные ячейки в синий и зеленый цвет.

Внимание! После изменения значений параметров на листе «Input Value» не забудьте обновить сводные таблицы Excel. Для этого перейдите на лист «Control» и поместите курсор Excel в ячейку любой сводной таблицы. Затем выберите опцию: PivotTable Analyze → Data → Refresh → Refresh All.

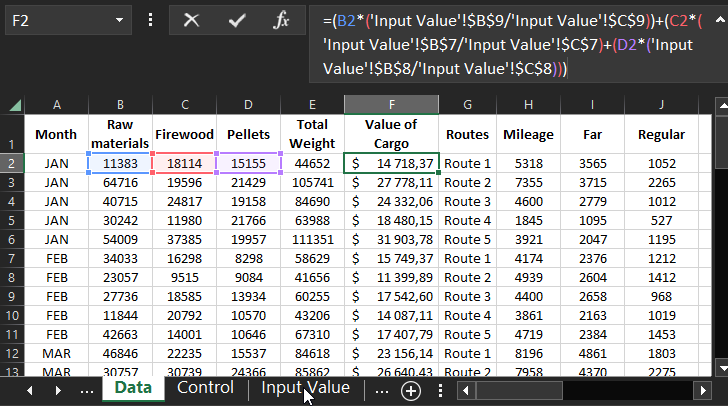
Исходные данные статистики функционирования логистики заполняются на листе «Data» в соответственных столбцах без формул:

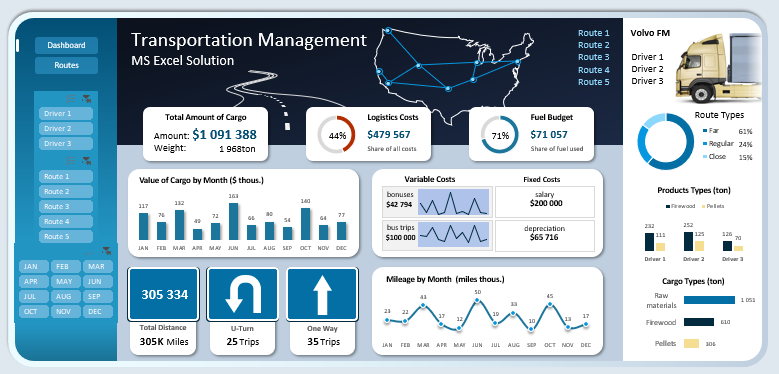
Структура дашборда для оценки эффективности логистики в Excel

Дашборд для анализа эффективности управления логистикой имеет сложную структуру и состоит из множества блоков. Рассмотрим все предназначения каждого из них.

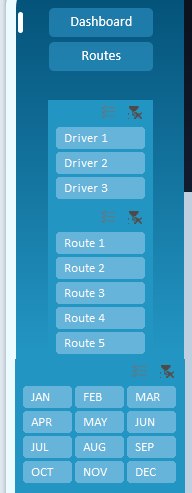
Слева находится панель управления дашбордом которая состоит из 4-х блоков кнопок:

Первые две кнопки предназначены для переключения между двумя режимами:

1. Визуальный анализ общей картины эффективности логистики на дашборде.
2. Презентация показателей маршрутов транспортировки грузов по городам США.

Ниже блок из 3-х кнопок для разделения данных с помощью фильтра отдельно по каждому водителю.

Далее идет блок из 5-ти кнопок для сегментирования показателей по маршрутам.

На четвертом блоке панели управления расположены кнопки выборки данных по месяцам. Структура кнопок в формате ¾ чтобы удобно было выбирать как по месяцам, так и по кварталам.

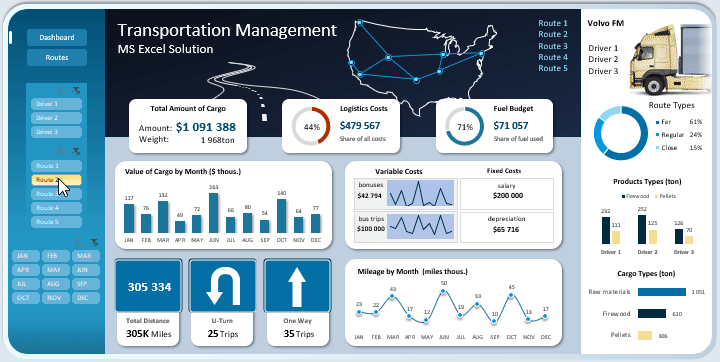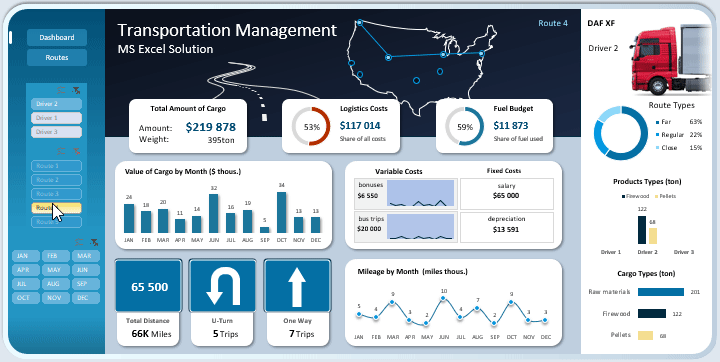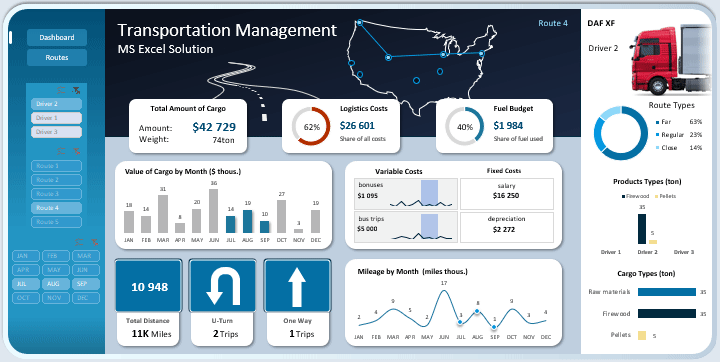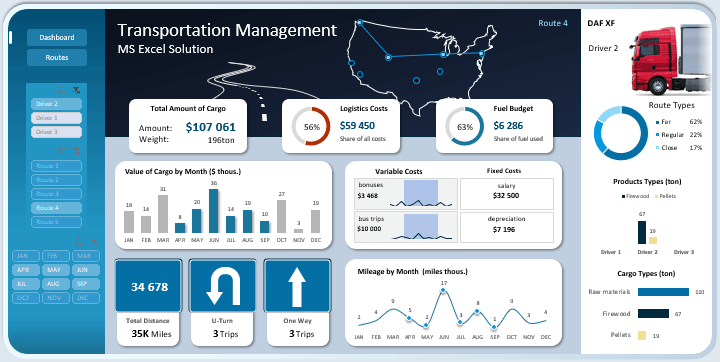
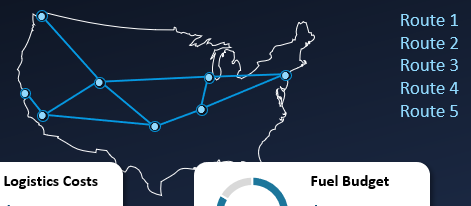
В центре в шапке дашборда расположен интерактивный Map Chart для схематического представления направления маршрутов через ключевые города доставки грузов.

При выборе одного маршрута или целой группы, схема логистической цепочки на карте США изменяется соответственно.

Ниже расположены 3 блока первого плана с итоговыми ключевыми значениями:

1. Суммарная стоимость перевезенного груза за учетный период, а также его суммарный вес. Фактически этот показатель равен показателю обороту компании или максимально приближенный ему.
2. Суммарный показатель логистических расходов. На диаграмме отображается доля расходов на логистику в общем обороте финансовых средств.
3. Суммарный расход топлива и его доля в выделенном бюджете в этом учетном периоде.

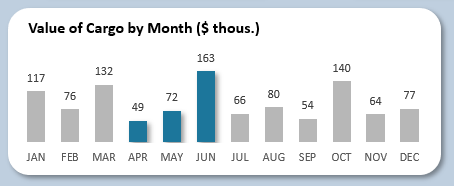
Ниже под блоками находиться Bar Chart суммарной стоимости перевозимых грузов по месяцам:

Даннвй Bar Chart умеет экспонировать выбранные учетные периоды на панели управления дашбордом. Так подсвечены показатели за второй квартал.

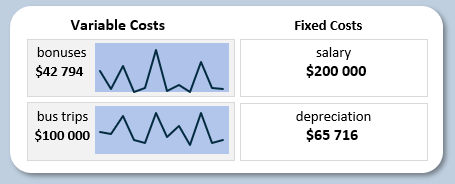
С правой стороны блок графиков и показателей расходов:

Второстепенные логистические расходы на оплату:

• заработная плата;
• бонусные вознаграждения;
• амортизация;
• командировочные.

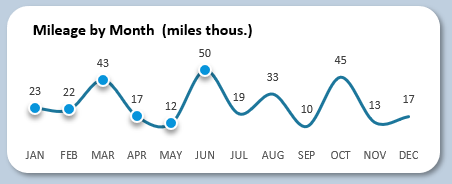
Сразу под этим блоком график изменения динамики пройденной дистанции в милях по месяцам:

График также умеет экспонировать выбранные периоды с помощью маркеров. На картинке показано как выглядит выбранный период – первое полугодие.

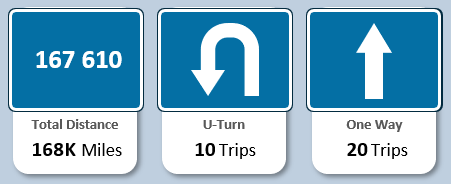
Слева находятся сразу 3 блока показателей пробега:

1. Суммарная пройденная дистанция.
2. Не до конца пройдена дистанция маршрута.
3. Количество полностью пройденных дистанций маршрутов или больше.

В верхнем правом углу дашборда расположен слайдер с фото автомобилей выбранных водителей:

При выборе водителя отображается фото его соответсвенного автомобиля. А также при переключении между маршрутами, автоматически выбирается ответственный водитель за данный маршрут и его грузовик.

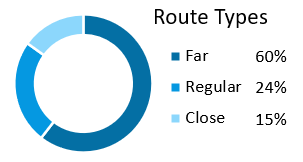
Ниже представлен Pie Chart разделен на сегменты категорий оценки пройденной дистанции:

здесь анализируем соотношение количества пройденных дистанций с разными категориями расстояний:

• долгий маршрут;
• средний;
• короткий.

На первый взгляд необычный, но очень важный логистический показатель для быстрого перепланирования схемы маршрутов. А также для тестирования стратегий масштабирования покрытия и охвата новых территорий.

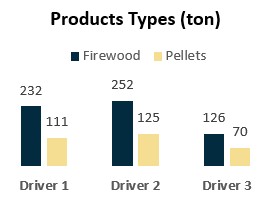
График с группировкой для сравнительного анализа перевозимых товаров по отношению к водителям:

Ассортиментная корзина состоит всего лишь из двух позиций: био-дрова и пеллеты. Каждый водитель доставил разное количество тонн готовой производимой продукции в разных товарных группах.

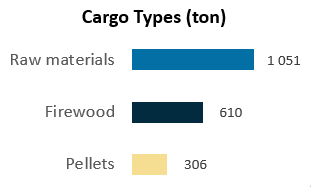
Сравнительный график распределения количества тон груза по категориям товаров:

Из материалов сырья были произведены дрова и пеллеты и все они перевозились по нашей логистической цепочке в процессах закупки и реализации на существенно покрытой территории США.

Общая картина дашборда для визуального анализа выглядит так:

Скачать анализ логистики и управления цепочками поставок в Excel

В следующей статье мы разберем второй экран дашборда для анализа управления маршрутами. Там вас ждет более интересное решение в Map Chart для презентации схем маршрутов через ключевые города США и многое другое:

Как сделать Map Chart для управления логистикой в Excel

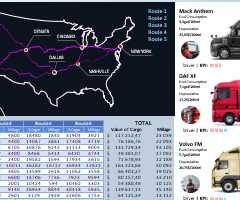
Весь функционал этого шаблона реализован без использования макросов. Файл открытый и подходит для любой политики безопасности на любом офисе.

Тема – логистика для визуализации данных слишком широка, чтобы охватить одним примером все возможности Excel в данной сфере аналитики. Поэтому в дальнейшем будут еще не раз представлены новые шаблоны для решений логистических задач в Excel c интерактивной визуализацией данных на дашборде.

Excel –  очень функциональная программа. Она может использоваться для решения огромного пласта задач, с которыми приходится сталкиваться в бизнесе. Одна из самых распространённых –  транспортная задача. Представим, что нам нужно понять, какой способ перевозки от производителя к конечному покупателю самый оптимальный по затратам времени, денег и других ресурсов. Эта проблема довольно популярная, независимо от того, в какой сфере работает бизнес. Поэтому давайте более подробно разберемся, как её реализовать с помощью Excel.

Описание транспортной задачи

Итак, у нас есть два контрагента, которые постоянно взаимодействуют друг с другом. В нашем случае это  покупатель и продавец. Нам нужно посчитать, как перевозить товары таким образом, чтобы издержки были минимальны. Для этого нужно представить все данные в схематической или матричной форме. В Эксель используем последний вариант. В целом, выделяют два типа транспортных задач:

1. Закрытые. В этом случае спрос и предложение находятся в балансе.
2. Открытые. Здесь нет равенства между спросом и предложением. Чтобы получить решение этой задачи, нужно сперва ее привести к первому типу, уравняв спрос и предложение. Для этого нужно ввести дополнительный показатель – наличие условного покупателя или продавца. Кроме этого, нужно внести определенные изменения в таблицу издержек.

Как включить функцию “Поиск решения” в Excel

Для решения транспортных задач в Excel существует специальная функция, которая называется «Поиск решения». Она не активирована по умолчанию, поэтому нужно сделать следующие шаги:

1. Открыть меню «Файл», которое находится в левом верхнем углу окна программы.
2. После этого нажимаем на кнопку с параметрами.
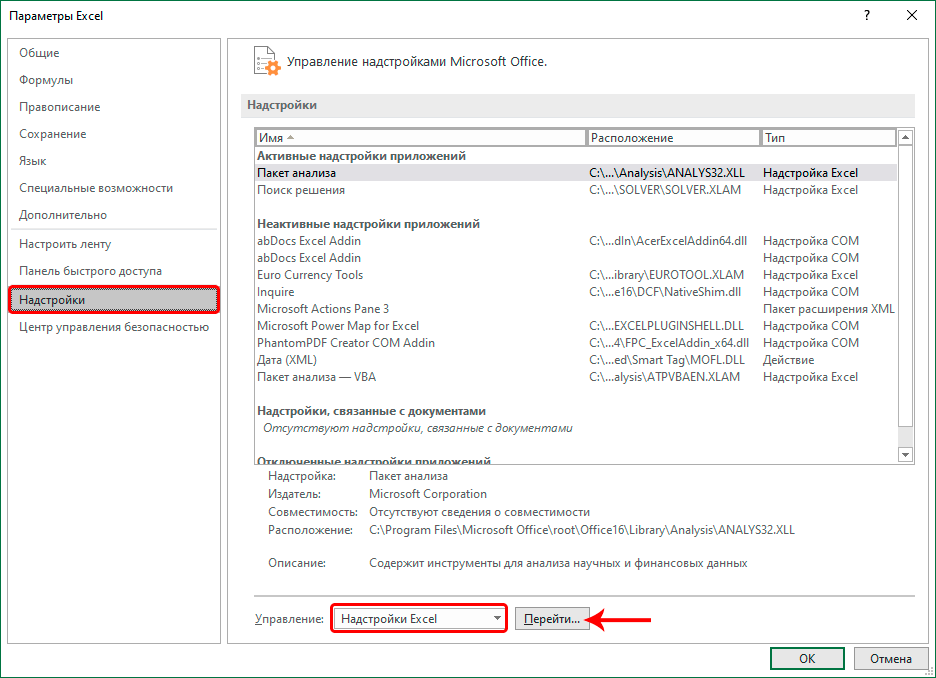
3. Далее находим подраздел «Настройки» и переходим в меню управления надстройками. Это маленькие программы, которые выполняются в рамках среды Microsoft Excel. Видим, что сначала мы нажали на меню «Надстройки», а потом в правой части внизу выставили пункт «Надстройки Excel» и нажали на кнопку «Перейти». Все нужные действия выделены красными прямоугольниками и стрелочками.
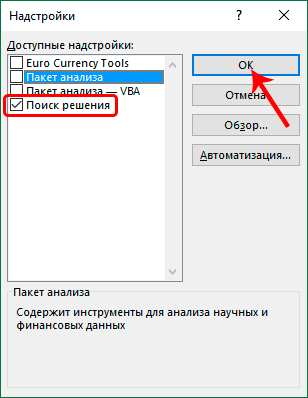
4. Далее включаем надстройку «Поиск решения», после чего подтверждаем свои действия нажатием клавиши ОК. Исходя из описания настройки, мы видим, что она предназначена для анализа сложных данных, таких как научные и финансовые.
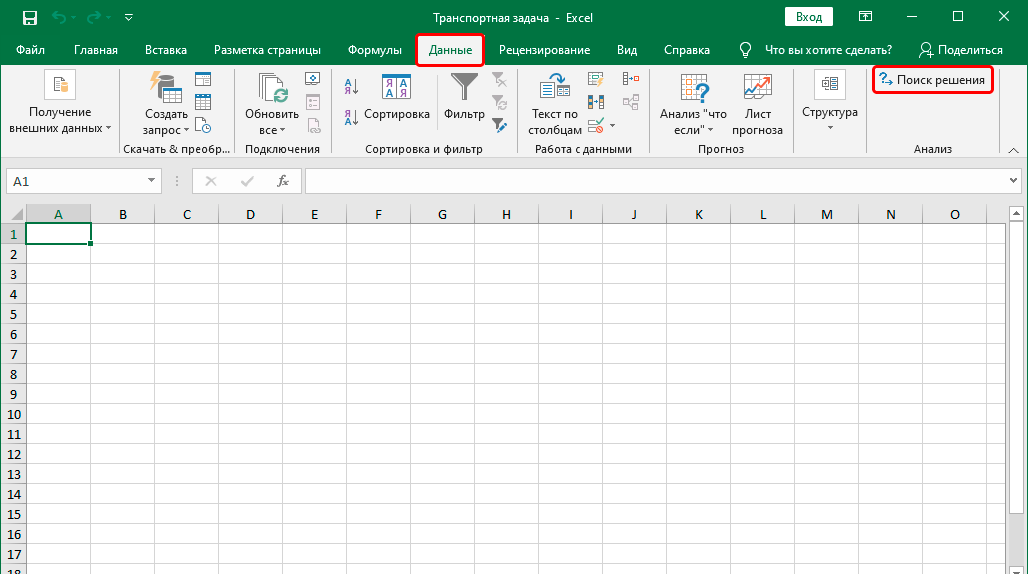
5. После этого переходим во вкладку «Данные», где видим новую кнопку, которая называется так же, как и надстройка. Ее можно найти в группе инструментов «Анализ».

Осталось только кликнуть по этой кнопке, и мы переходим к решению транспортной задачи. Но перед этим следует немного подробнее поговорить про инструмент «Поиск решения» в Excel. Это специальное дополнение Эксель, которое дает возможность находить самое быстрое решение задачи. Характерная особенность – учет ограничений, которые пользователь задает на этапе подготовки. Если говорить простым языком, это подпрограмма, дающая возможность определить самый лучший способ достижения определенной задачи. К таким задачам могут относиться следующие:

1. Инвестирование, загрузка склада или любая другая подобная деятельность. В том числе, и доставка товара.
2. Лучший способ. Сюда входят такие задачи, как достижение максимальной прибыли при минимальных издержках, способы достижения самого лучшего качества при имеющихся ресурсах и так далее.

Кроме транспортных задач, эта надстройка используется и для таких целей:

1. Разработка плана производства. То есть, сколько нужно выработать единиц товара, чтобы достичь максимального дохода.
2. Найти распределение рабочих сил по разным видам работ, чтобы суммарные затраты на производство товара или услуг были самыми маленькими.
3. Установить, сколько минимально времени понадобится на то, чтобы выполнить все работы.

Как видим, задачи бывают самыми разными. Универсальное правило применения этой надстройки – необходимо перед решением задачи создать модель, которая бы соответствовала ключевым характеристикам поставленной проблемы. Моделью является совокупность функций, которые используют переменные в качестве своих аргументов. То есть, значения, которые могут изменяться.

Важно учесть, что оптимизация набора значений осуществляется исключительно по одному показателю, который называется целевой функцией.

Надстройка «Поиск решения» осуществляет перебор разных значений переменных, которые передаются целевой функции таким образом, чтобы она была максимальной, минимальной или равной определенному значению (именно это и является ограничением). Есть еще одна функция, которая несколько похожая по своему принципу действия, и какую нередко путают с «Поиском решения». Называется она «Подбор параметра». Но если копнуть более глубоко, то разница между ними колоссальная:

1. Функция «Подбор параметра» не работает больше, чем с одной переменной.
2. Она не предусматривает возможности задавать ограничения для переменных.
3. Способна определять только равенство целевой функции определенному значению, но не дает возможности находить максимум и минимум. Поэтому для нашей задачи она не подходит.
4. Способна эффективно вычислять лишь если модельно линейного типа. Если модель нелинейная, то она находит значение, которое наиболее близкое к изначальному.

Транспортная задача по своей структуре значительно сложнее, поэтому надстройки «Подбор параметра» для этого недостаточно. Давайте разберемся более детально, как реализовать на практике функцию «Поиск решения» на примере транспортной задачи.

Пример решения транспортной задачи в Excel

Для того, чтобы наглядно продемонстрировать, как на практике решать транспортные задачи в Excel, давайте приведем пример.

Условия задачи

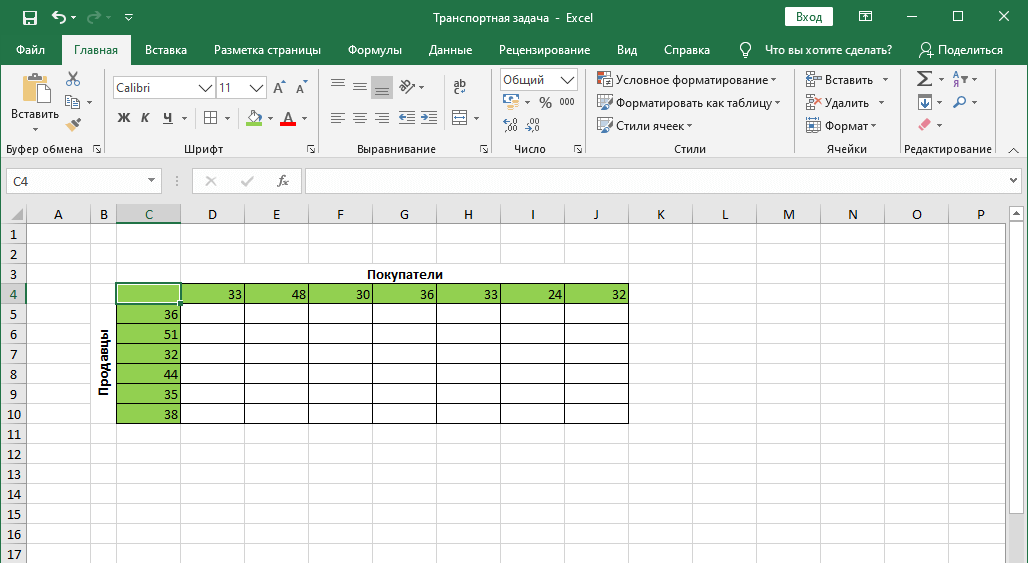
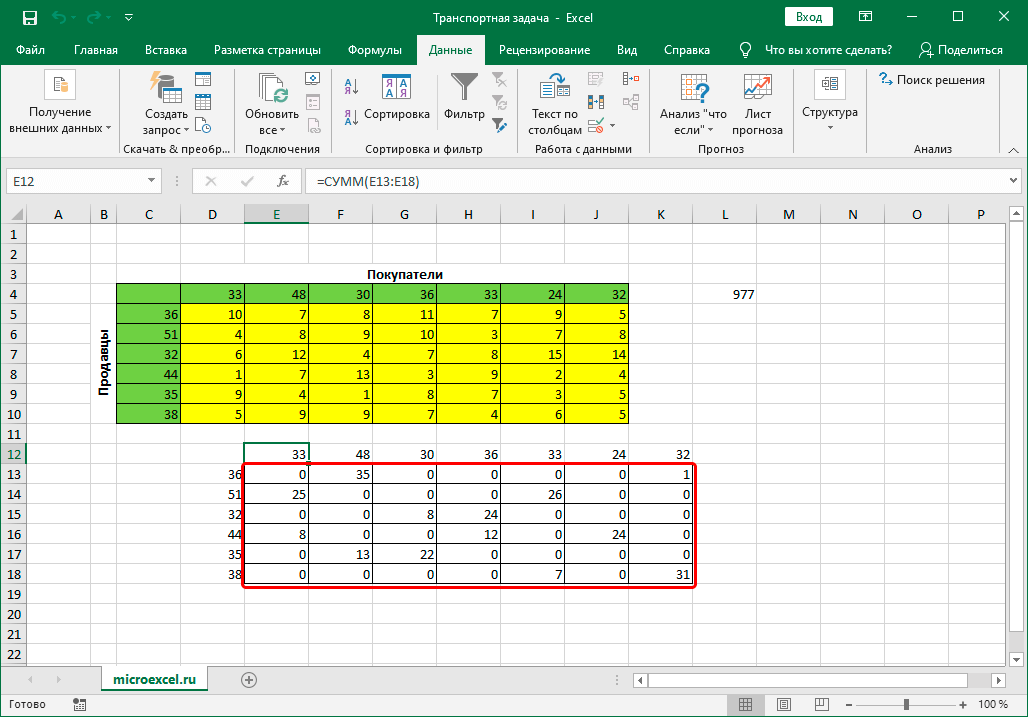
Предположим, у нас есть 6 продавцов и 7 покупателей. Спрос и предложение между ними распространяется соответственно следующим способом: 36, 51, 32, 44, 35 и 38 единиц – продавцы и 33, 48, 30, 36, 33, 24 и 32 единицы – покупатели. Если просуммировать все эти значения, то обнаружится, что спрос и предложение находятся в балансе. Следовательно, эта задача закрытого типа, которая решается очень просто.

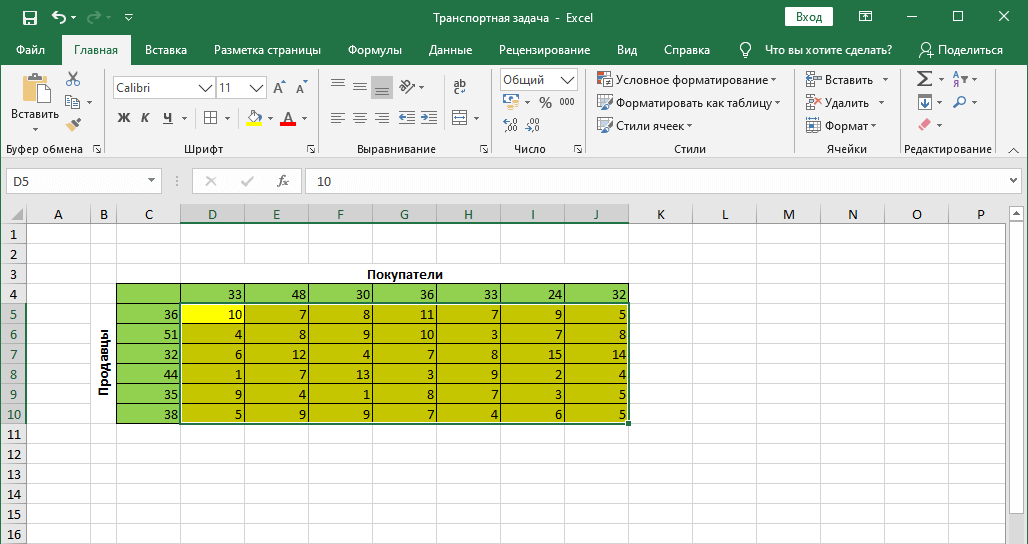
Кроме этого, у нас есть информация о том, сколько нужно потратить на перевозку из пункта А в пункт Б (они на примере выделены желтыми ячейками).

Решение – пошаговый алгоритм

Теперь, после того, как мы ознакомились с таблицами с исходными данными, можем воспользоваться следующим алгоритмом, чтобы решить эту задачу:

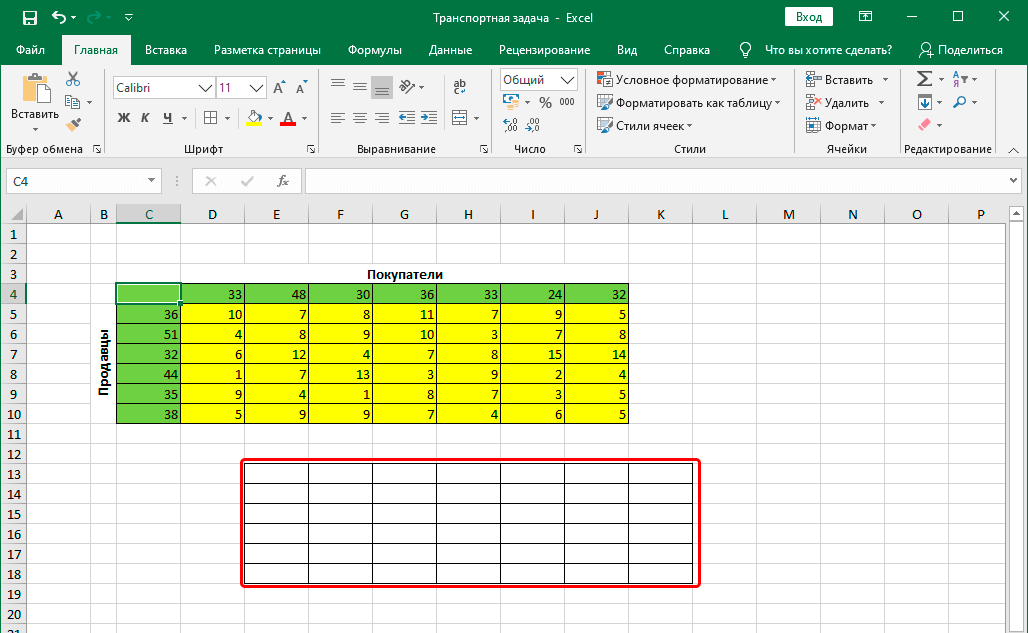
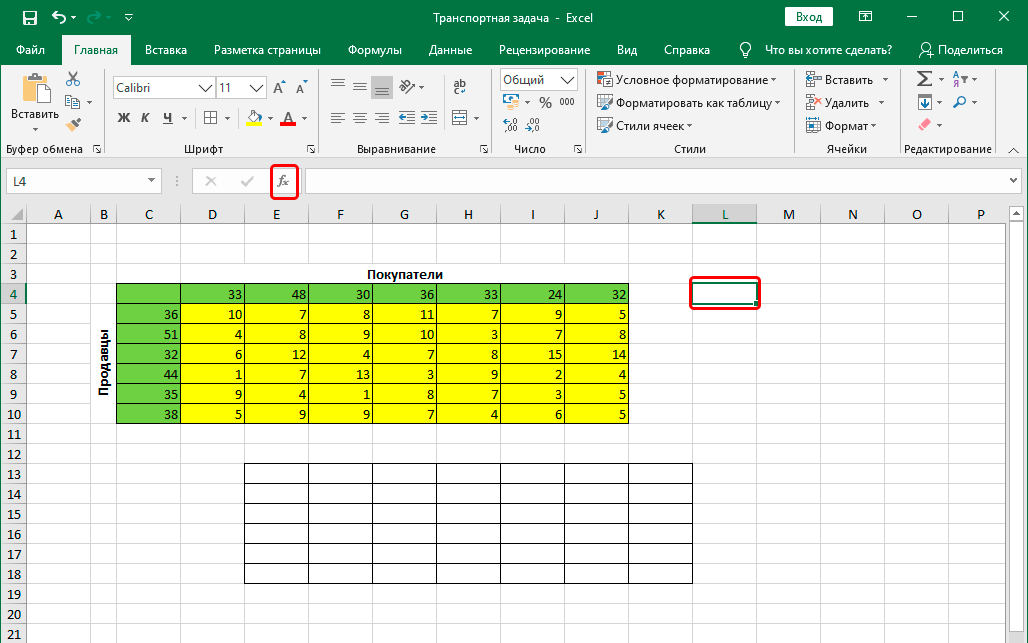
1. Сперва делаем таблицу, состоящую из 6 строк и 7 колонок.
2. После этого переходим в какую-угодно ячейку, не содержащую никаких значений и при этом лежащую за пределами новосозданной таблицы и вставляем функцию. Для этого нажимаем на кнопку fx, которая находится слева от строки ввода функции.
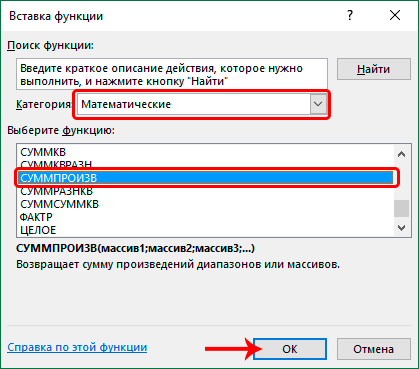
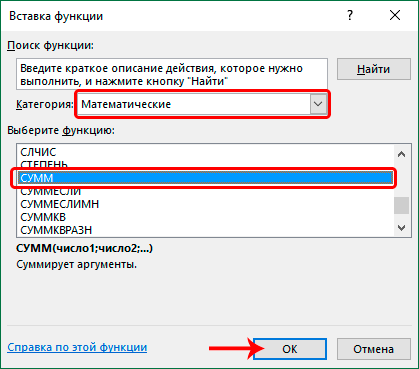
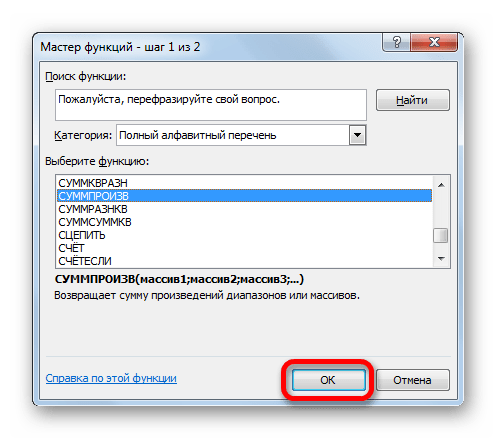
3. У нас появляется окно, в котором нам нужно выбрать категорию «Математические». А какая функция нас интересует? Та, которая выделена на этом скриншоте. Функция СУММИПРОИЗВ умножает диапазоны или массивы между собой и суммирует их. Как раз то, что нам нужно. После этого нажимаем клавишу ОК.
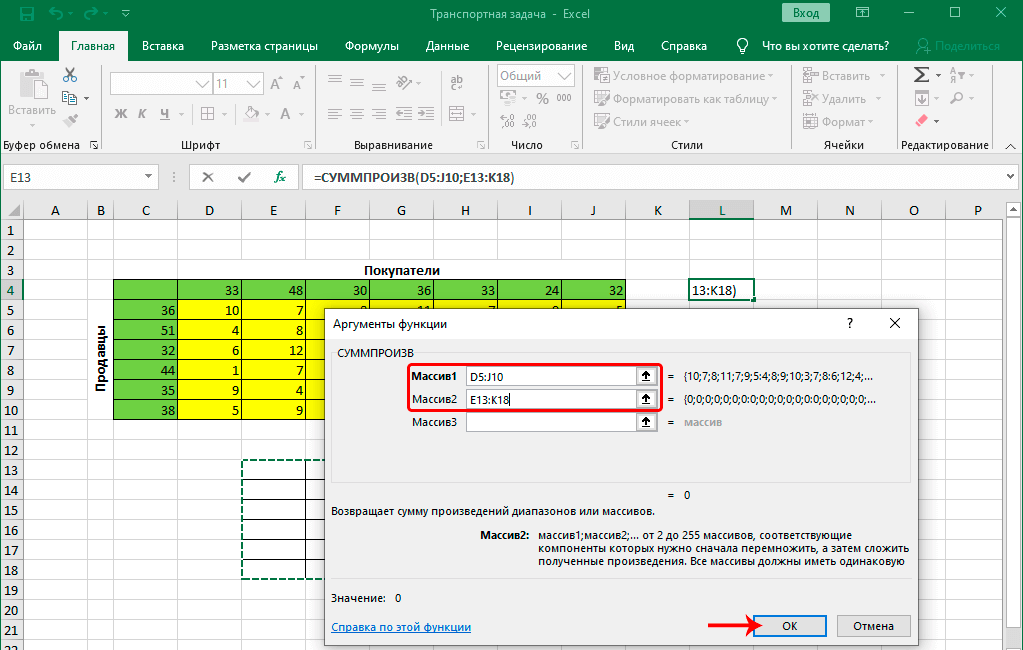
4. Далее на экране появится окно, в котором необходимо указать параметры функции. Они следующие:
   1. Массив 1. Это первый аргумент, в котором записываем тот диапазон, который выделен жёлтым  цветом. Задать параметры функции можно как используя клавиатуру, так и выделив соответствующую область с помощью левой кнопки мыши.
   2. Массив 2. Это второй аргумент, в качестве которого выступает новосозданная таблица. Действия выполняются аналогичным образом.

Подтверждаем свое действие нажатием клавиши ОК.

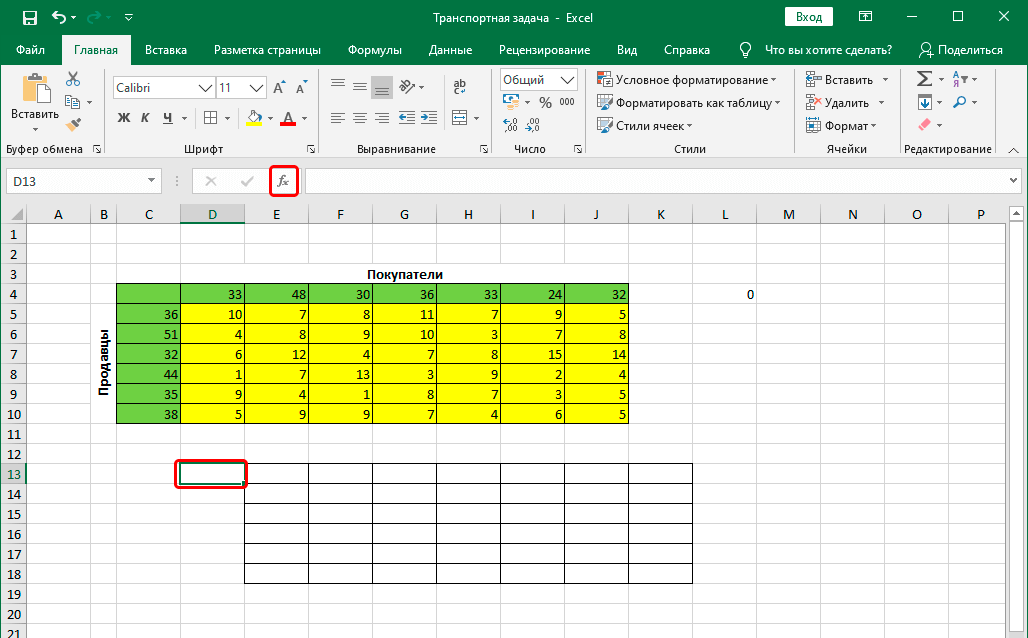
1. После этого делаем левый клик мыши по той ячейке, которая служит верхней левой в новосозданной таблице. Теперь снова нажимаем кнопку вставки функции.
2. Выбираем ту же категорию, что и в предыдущем случае. Но на этот раз нас интересует функция СУММ.
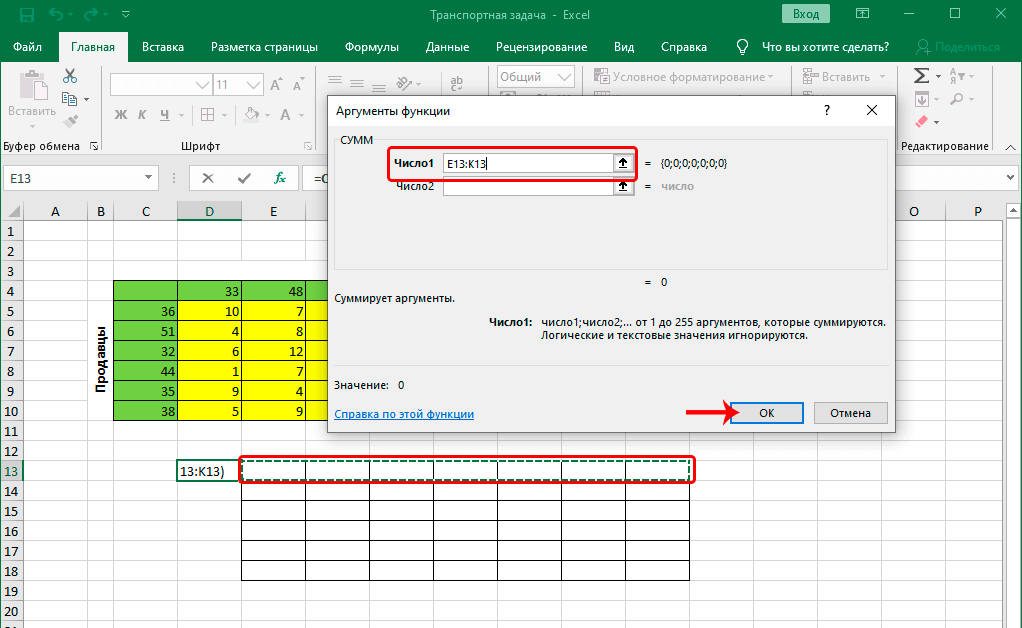
3. Теперь наступил этап заполнения аргументов. В качестве первого аргумента записываем верхнюю строку таблицы, которую мы создали в начале. Точно так же, как и раньше, это можно сделать путем выделения этих ячеек на листе, так и вручную. Подтверждаем свои действия нажатием клавиши ОК.
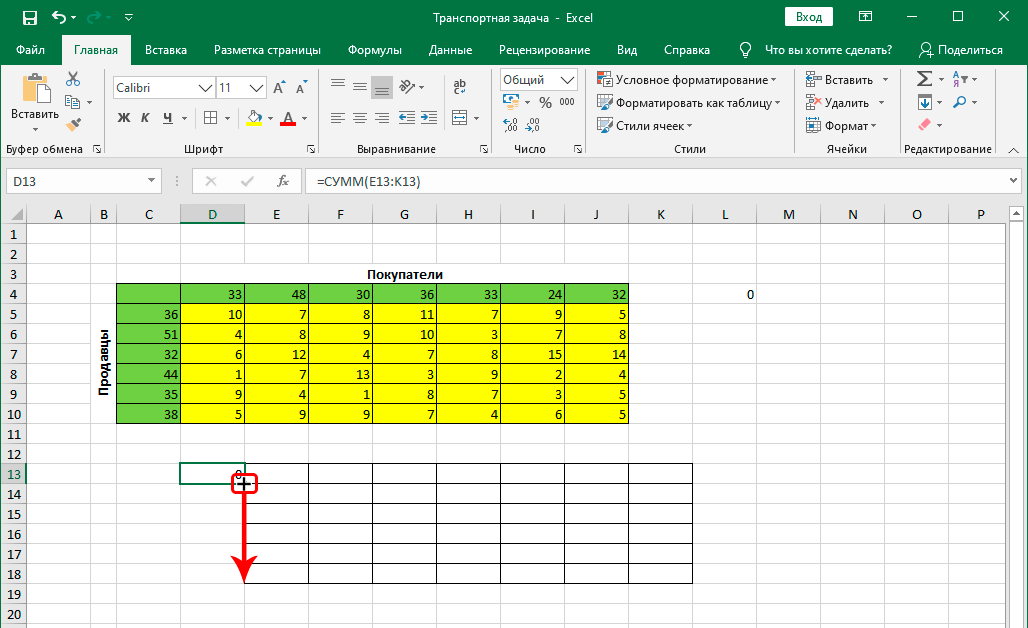
4. Увидим результаты в ячейке с функцией. В данном случае это ноль. Далее переносим курсор в правый нижний угол, после чего появится маркер автозаполнения. Выглядит он, как маленький чёрный плюсик. Если он появился, зажимаем левую кнопку мыши и перемещаем курсор до последней ячейки в нашей таблице.
5. Это дает нам возможность перенести формулу во все остальные ячейки и получить правильные результаты без необходимости выполнения дополнительных расчетов.
6. Следующий шаг – выбор левой верхней ячейки и вставка функции СУММ в нее. После этого заносим аргументы и с помощью маркера автозаполнения заполняем все оставшиеся ячейки.
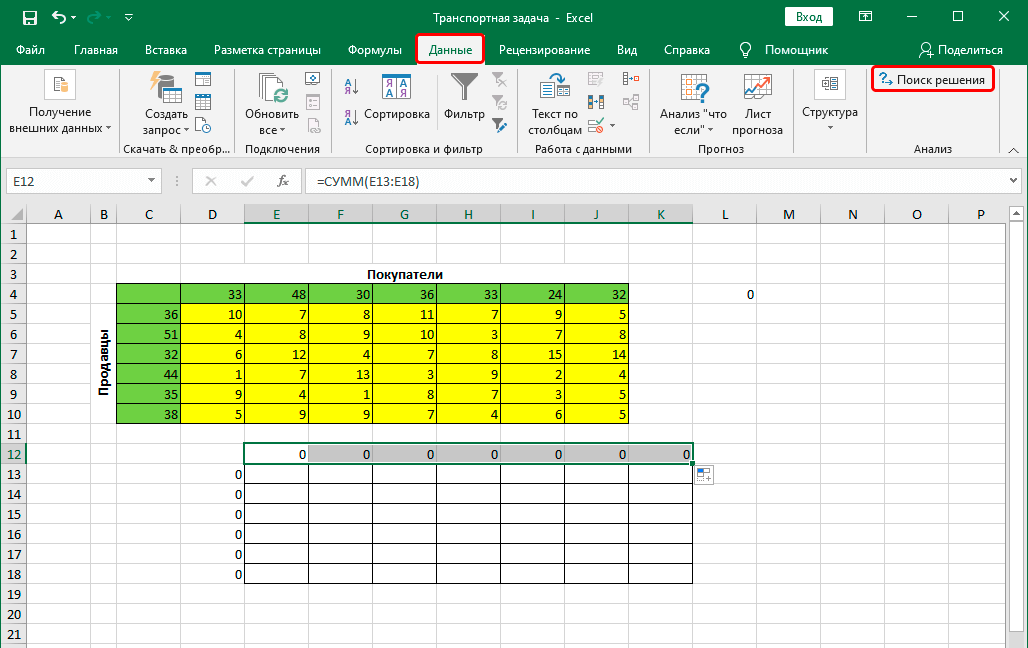
7. После этого приступаем непосредственно к решению задачи. Для этого воспользуемся дополнением, которое мы включили ранее. Переходим на вкладку «Данные», и там находим инструмент «Поиск решения». Нажимаем по этой кнопке.
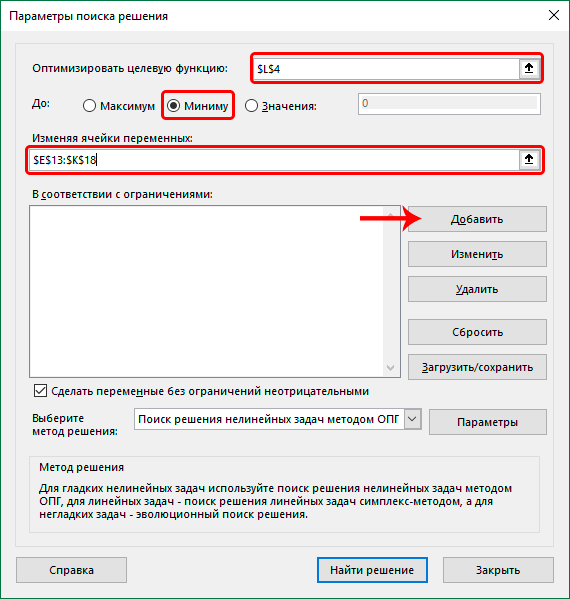
8. Теперь перед нашим взором появилось окошко, через которое можно настроить параметры нашего дополнения. Давайте каждый из этих параметров разберем:
   1. Оптимизировать целевую функцию. Здесь нам нужно выбрать ячейку, содержащую функцию СУММПРОИЗВ. Видим, что эта опция дает возможность выбрать функцию, для которой будет осуществляться поиск решения.
   2. До. Здесь выставляем опцию «Минимум».
   3. Изменяя ячейки переменных. Здесь указываем диапазон, соответствующий той таблице, которую мы создавали в самом начале (за исключением суммирующей строки и столбца).
   4. В соответствии с ограничениями. Здесь нам нужно добавить ограничения, нажав кнопку «Добавить».
   5. Мы помним, какое ограничение нам нужно создать – сумма значений спросов покупателей и предложений продавцов должны быть одинаковыми.
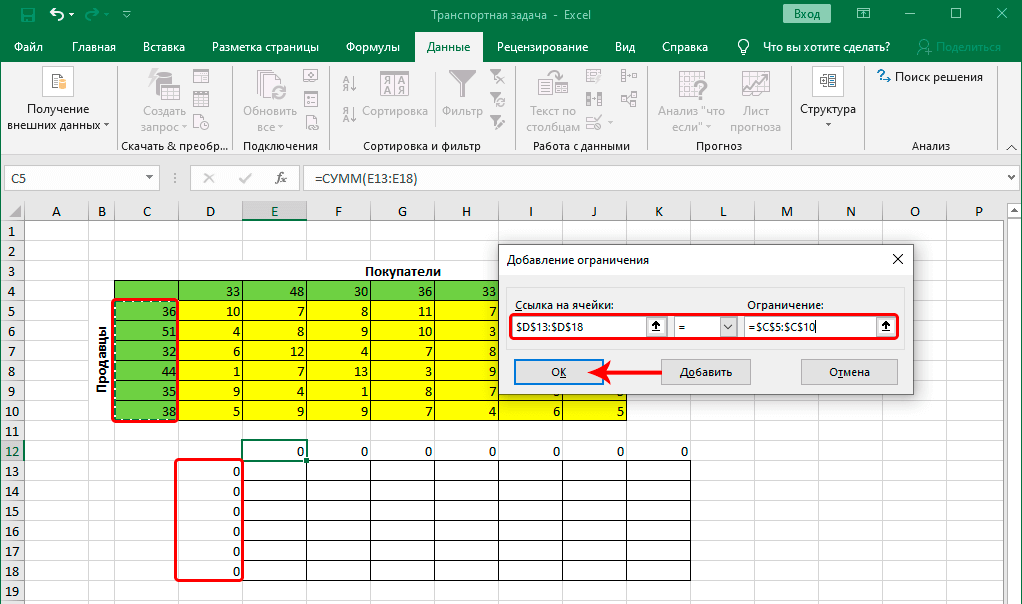
9. Задача ограничений осуществляется следующим образом:
   1. Ссылка на ячейки. Здесь заносим диапазон таблицы для расчётов.
   2. Условия. Это математическая операция на предмет соответствия которой проверяется диапазон, заданный в первом поле ввода.
   3. Значение условия или ограничение. Сюда заносим подходящую колонку в исходной таблице.
   4. После того, как все действия будут выполнены, нажимаем кнопку ОК, тем самым подтверждая наши действия.

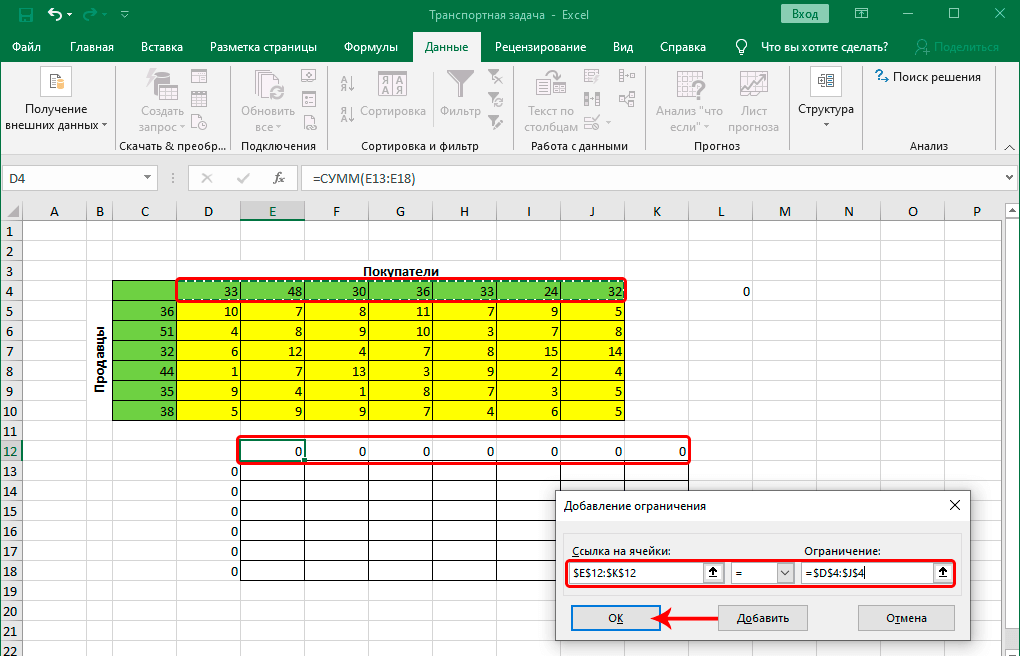
Точно такие же операции производим для верхних строк, задавая следующее условие: они должны быть равны.

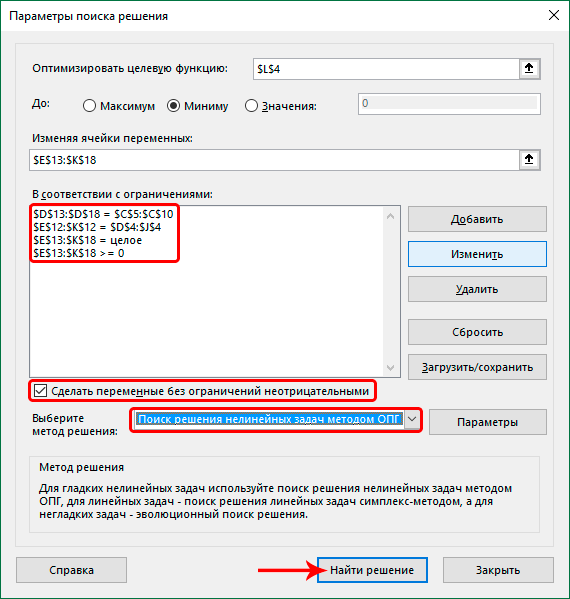
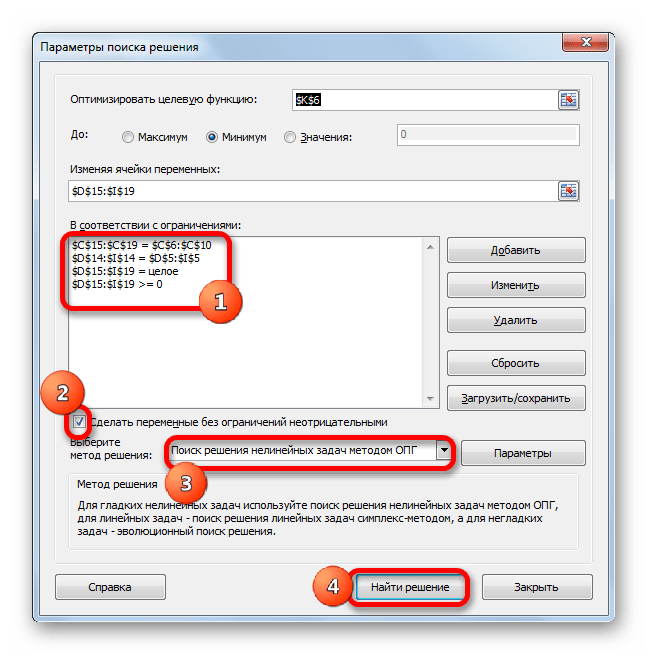
Следующий этап – задание условий. Нам необходимо установить следующие критерии для суммы ячеек в таблице – больше или равно нулю, целое число. В результате у нас появляется такой перечень условий, при которых задача решается. Здесь нужно убедиться, что поставлен флажок возле опции «Сделать переменные без ограничений неотрицательными». Также в нашей ситуации требуется, чтобы был выбран метод решения задачи – «Поиск решения нелинейных задач методов ОПГ». Теперь можно смело говорить, что настройка осуществлена. Поэтому осталось только выполнить расчеты. Для этого нажимаем на кнопку «Найти решение».

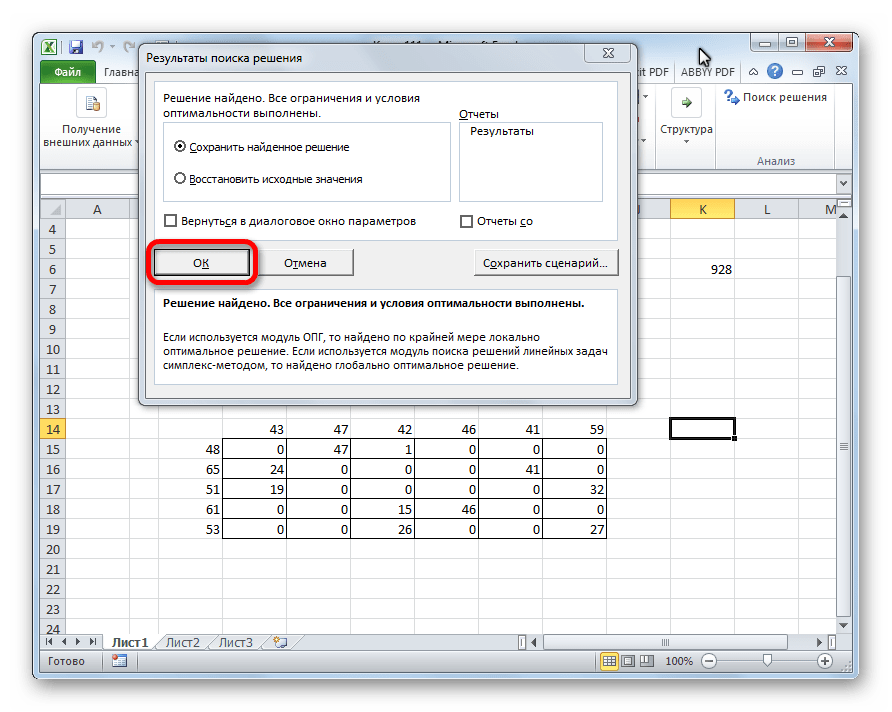
После этого все данные будут рассчитаны автоматически, а потом Эксель покажет окно с результатами. Оно необходимо для того, чтобы перепроверить работу компьютера, поскольку возможны ошибки, если условия ранее были заданы неверно. Если все правильно, то нажимаем кнопку «ОК» и видим готовую таблицу.

Если же оказывается, что у нас задача стала открытого типа, то это плохо, поскольку нужно отредактировать исходную таблицу так, чтобы задача превратилась в закрытую. Тем не менее, когда это сделать, оставшийся алгоритм будет такой же.

Заключение

Как видим, Excel может использоваться и для очень сложных вычислений, которые на первый взгляд не доступны простой компьютерной программе, которая установлена почти у каждого. Тем не менее, это так. Сегодня мы уже рассмотрели продвинутый уровень использования. Данная тема не такая простая, но как говорится, дорогу осилит идущий. Главное – следовать плану действий, и точно выполнять все действия, указанные выше. Тогда ошибок не возникнет, а программа самостоятельно выполнит все необходимые расчеты. Не нужно будет думать, какую функцию использовать и так далее.

Содержание

• Общее описание транспортной задачи
• Инструменты для решения транспортной задачи в Эксель
• Пример решения транспортной задачи в Excel
  • Условия задачи
  • Решение задачи
• Вопросы и ответы

Транспортная задача представляет собой задачу поиска наиболее оптимального варианта перевозок однотипного товара от поставщика к потребителю. Её основой является модель, широко применяемая в различных сферах математики и экономики. В Microsoft Excel имеются инструменты, которые значительно облегчают решение транспортной задачи. Выясним, как их использовать на практике.

Общее описание транспортной задачи

Главной целью транспортной задачи является поиск оптимального плана перевозок от поставщика к потребителю при минимальных затратах. Условия такой задачи записываются в виде схемы или матрицы. Для программы Excel используется матричный тип.

Если общий объем товара на складах поставщика равен величине спроса, транспортная задача именуется закрытой. Если эти показатели не равны, то такую транспортную задачу называют открытой. Для её решения условия следует привести к закрытому типу. Для этого добавляют фиктивного продавца или фиктивного покупателя с запасами или потребностями равными разнице между спросом и предложением в реальной ситуации. При этом в таблице издержек добавляется дополнительный столбец или строка с нулевыми значениями.

Инструменты для решения транспортной задачи в Эксель

Для решения транспортной задачи в Excel используется функция «Поиск решения». Проблема в том, что по умолчанию она отключена. Для того, чтобы включить данный инструмент, нужно выполнить определенные действия.

1. Делаем перемещение во вкладку «Файл».



2. Кликаем по подразделу «Параметры».



3. В новом окне переходим по надписи «Надстройки».



4. В блоке «Управление», который находится внизу открывшегося окна, в выпадающем списке останавливаем выбор на пункте «Надстройки Excel». Делаем клик по кнопке «Перейти…».



5. Запускается окно активации надстроек. Устанавливаем флажок возле пункта «Поиск решения». Кликаем по кнопке «OK».



6. Вследствие этих действий во вкладке «Данные» в блоке настроек «Анализ» на ленте появится кнопка «Поиск решения». Она нам и понадобится при поиске решения транспортной задачи.

Урок: функция «Поиск решения» в Экселе

Теперь давайте разберем конкретный пример решения транспортной задачи.

Условия задачи

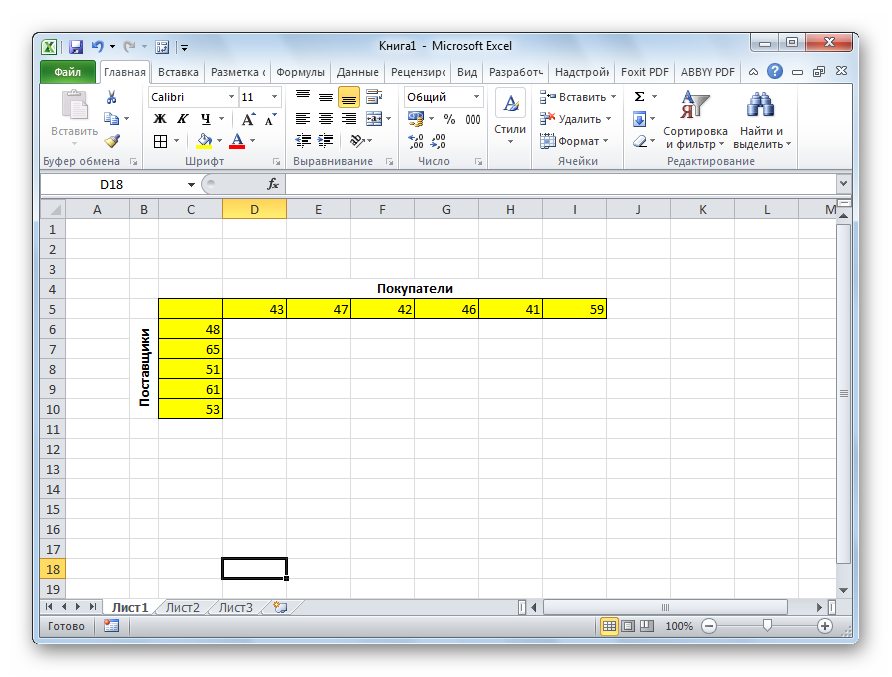
Имеем 5 поставщиков и 6 покупателей. Объёмы производства этих поставщиков составляют 48, 65, 51, 61, 53 единиц. Потребность покупателей: 43, 47, 42, 46, 41, 59 единиц. Таким образом, общий объем предложения равен величине спроса, то есть, мы имеем дело с закрытой транспортной задачей.

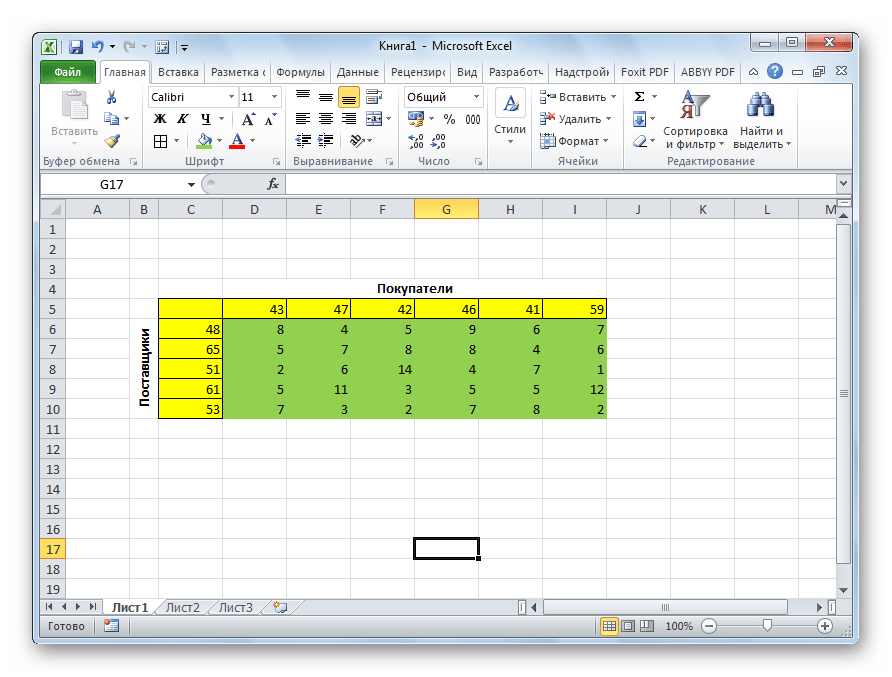
Кроме того, по условию дана матрица затрат перевозок из одного пункта в другой, которая отображена на иллюстрации ниже зеленым цветом.

Решение задачи

Перед нами стоит задача при условиях, о которых было сказано выше, свести транспортные расходы к минимуму.

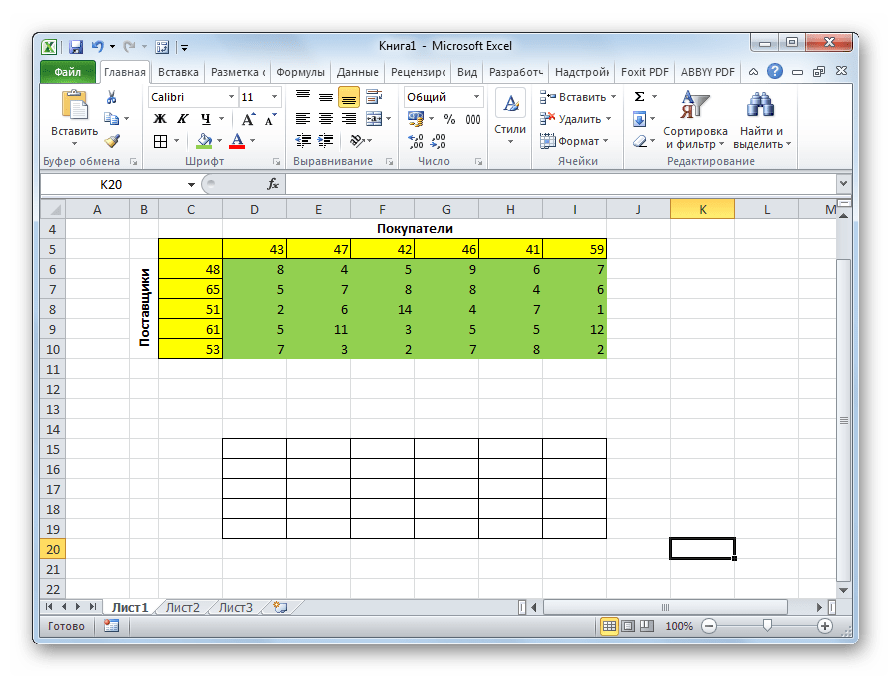
1. Для того, чтобы решить задачу, строим таблицу с точно таким же количеством ячеек, как и у вышеописанной матрицы затрат.



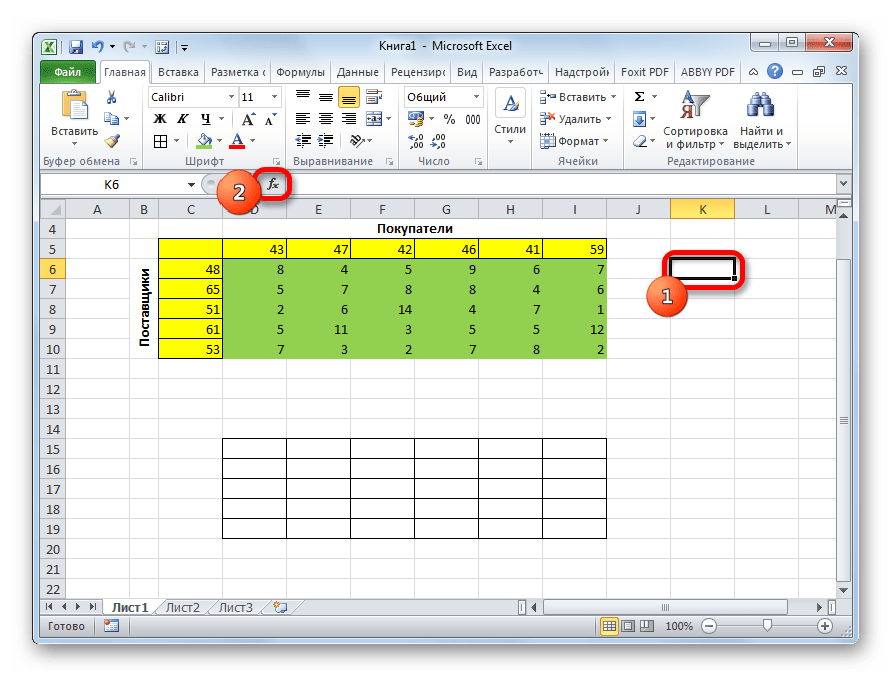
2. Выделяем любую пустую ячейку на листе. Кликаем по значку «Вставить функцию», размещенному слева от строки формул.



3. Открывается «Мастер функций». В списке, который предлагает он, нам следует отыскать функцию СУММПРОИЗВ. Выделяем её и жмем на кнопку «OK».



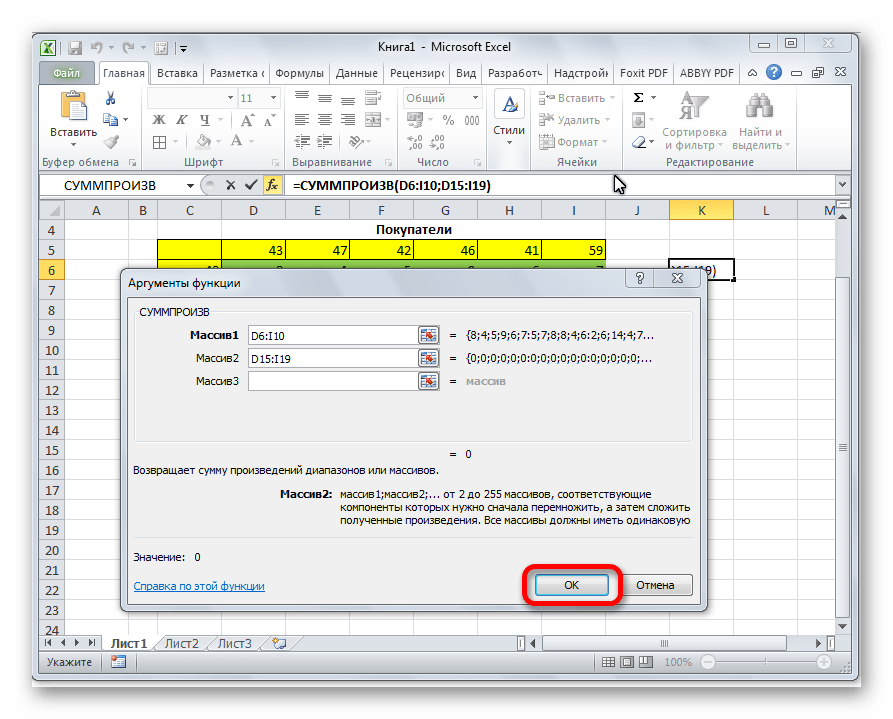
4. Открывается окно ввода аргументов функции СУММПРОИЗВ. В качестве первого аргумента внесем диапазон ячеек матрицы затрат. Для этого достаточно выделить курсором данные ячейки. Вторым аргументом выступит диапазон ячеек таблицы, которая была приготовлена для расчетов. Затем, жмем на кнопку «OK».



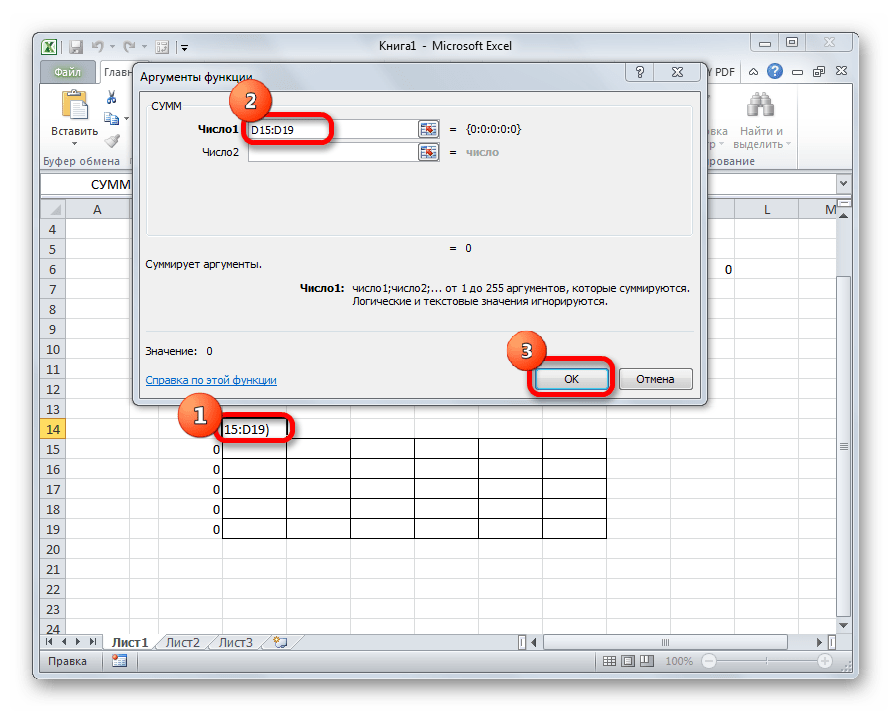
5. Кликаем по ячейке, которая расположена слева от верхней левой ячейки таблицы для расчетов. Как и в прошлый раз вызываем Мастер функций, открываем в нём аргументы функции СУММ. Кликнув по полю первого аргумента, выделяем весь верхний ряд ячеек таблицы для расчетов. После того, как их координаты занесены в соответствующее поле, кликаем по кнопке «OK».



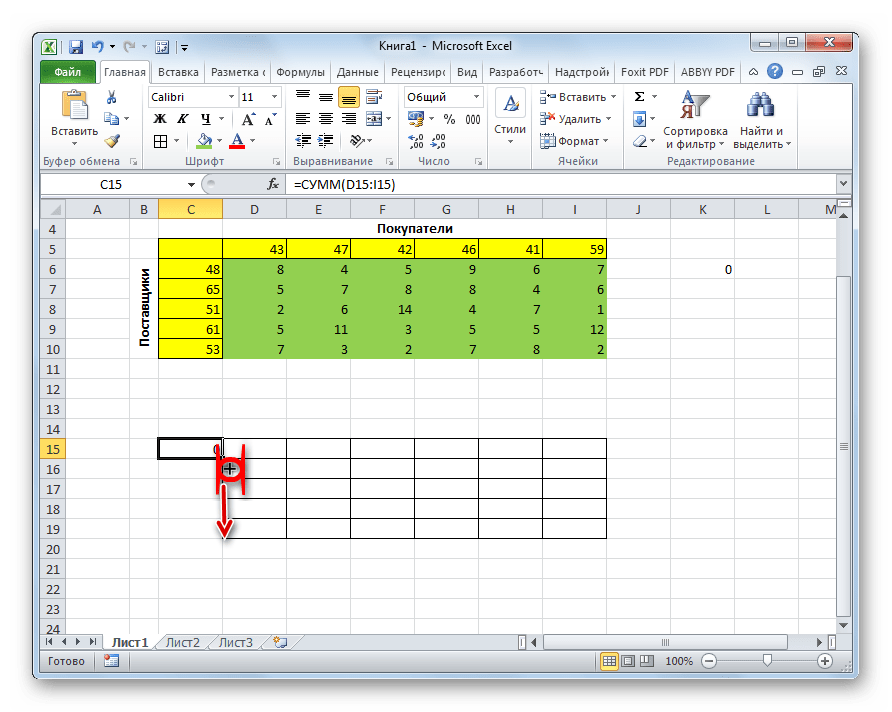
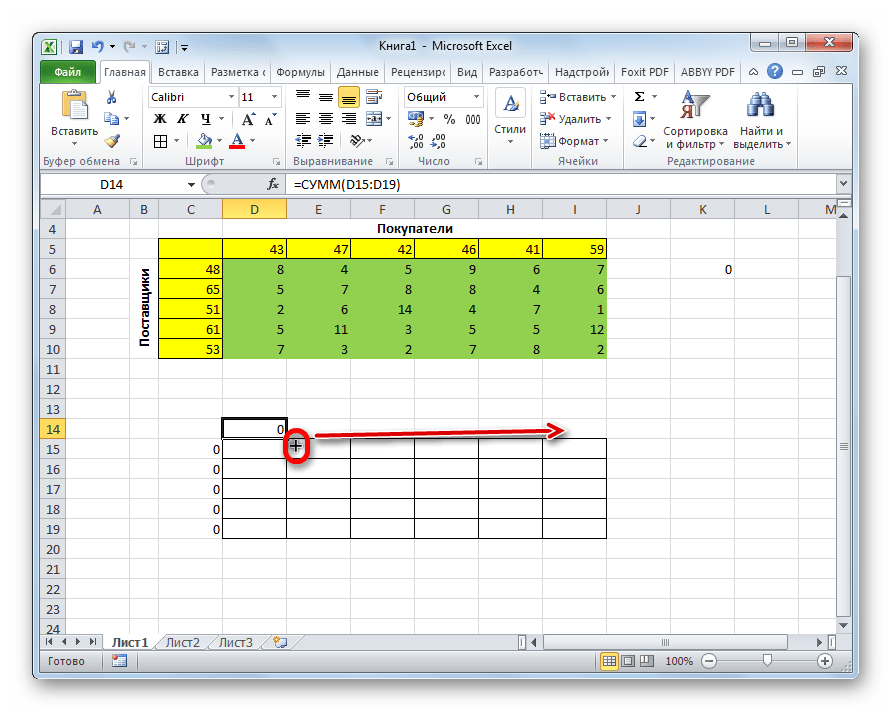
6. Становимся в нижний правый угол ячейки с функцией СУММ. Появляется маркер заполнения. Жмем на левую кнопку мыши и тянем маркер заполнения вниз до конца таблицы для расчета. Таким образом мы скопировали формулу.



7. Кликаем по ячейке размещенной сверху от верхней левой ячейки таблицы для расчетов. Как и в предыдущий раз вызываем функцию СУММ, но на этот раз в качестве аргумента используем первый столбец таблицы для расчетов. Жмем на кнопку «OK».



8. Копируем маркером заполнения формулу на всю строку.



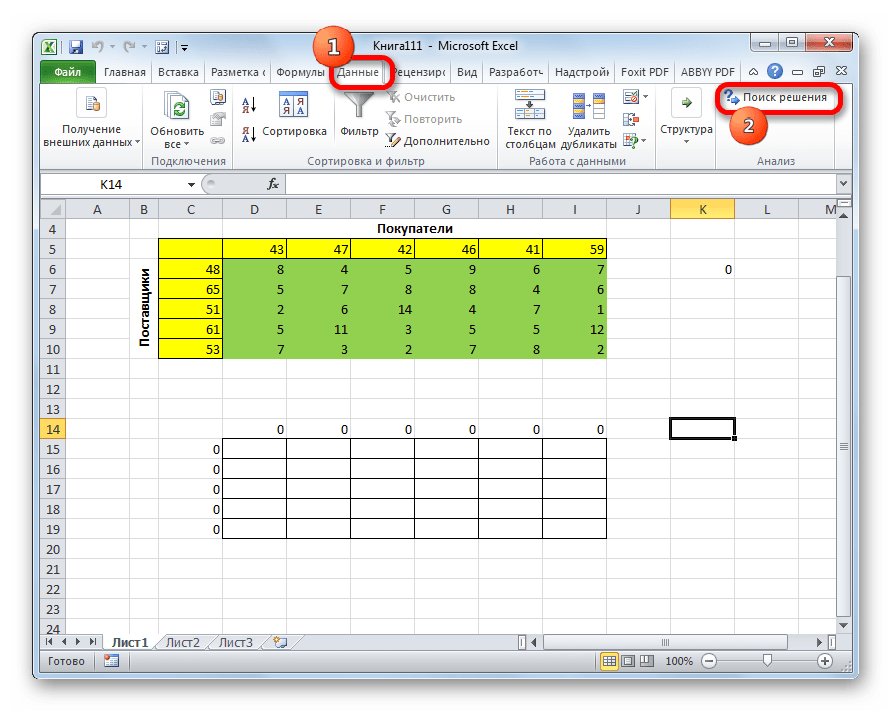
9. Переходим во вкладку «Данные». Там в блоке инструментов «Анализ» кликаем по кнопке «Поиск решения».



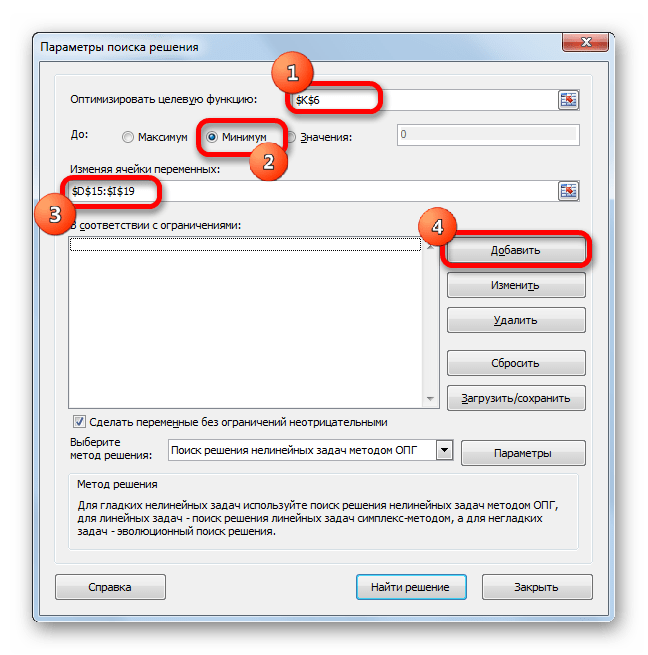
10. Открываются параметры поиска решения. В поле «Оптимизировать целевую функцию» указываем ячейку, содержащую функцию СУММПРОИЗВ. В блоке «До» устанавливаем значение «Минимум». В поле «Изменяя ячейки переменных» указываем весь диапазон таблицы для расчета. В блоке настроек «В соответствии с ограничениями» жмем на кнопку «Добавить», чтобы добавить несколько важных ограничений.



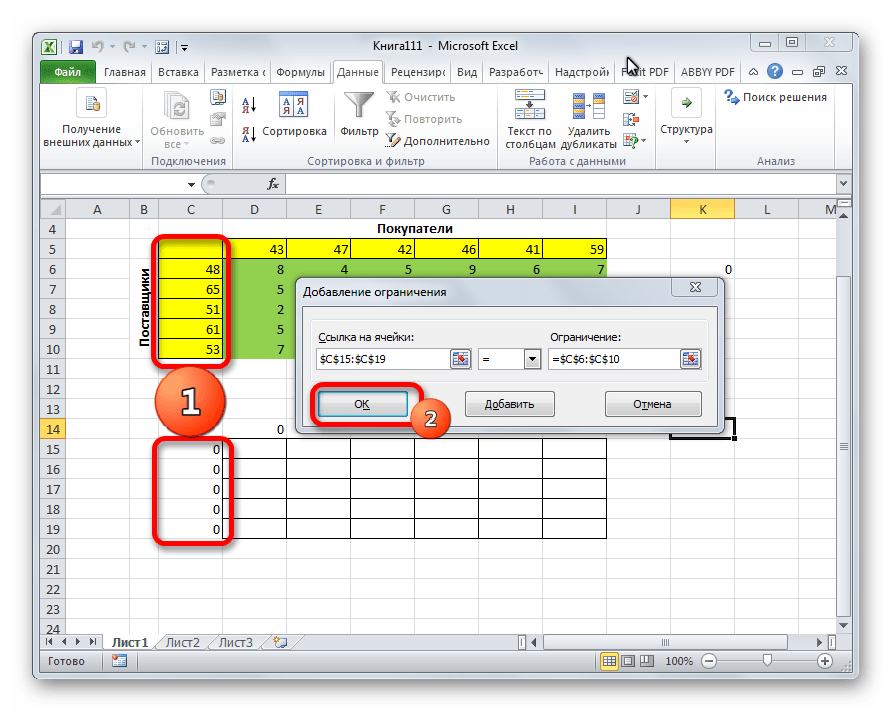
11. Запускается окно добавления ограничения. Прежде всего, нам нужно добавить условие того, что сумма данных в строках таблицы для расчетов должна быть равна сумме данных в строках таблицы с условием. В поле «Ссылка на ячейки» указываем диапазон суммы в строках таблицы расчетов. Затем выставляем знак равно (=). В поле «Ограничение» указываем диапазон сумм в строках таблицы с условием. После этого, жмем на кнопку «OK».



12. Аналогичным образом добавляем условие, что столбцы двух таблиц должны быть равны между собой. Добавляем ограничение, что сумма диапазона всех ячеек в таблице для расчета должна быть большей или равной 0, а также условие, что она должна быть целым числом. Общий вид ограничений должен быть таким, как представлен на изображении ниже. Обязательно проследите, чтобы около пункта «Сделать переменные без ограничений неотрицательными» стояла галочка, а методом решения был выбран «Поиск решения нелинейных задач методом ОПГ». После того, как все настройки указаны, жмем на кнопку «Найти решение».



13. После этого происходит расчет. Данные выводятся в ячейки таблицы для расчета. Открывается окно результатов поиска решения. Если результаты вас удовлетворяют, жмите на кнопку «OK».

Как видим, решение транспортной задачи в Excel сводится к правильному формированию вводных данных. Сами расчеты выполняет вместо пользователя программа.

Еще статьи по данной теме:

Помогла ли Вам статья?

Эксель можно использовать для решения широкого спектра задач, в том числе, для нахождения наилучшего способа осуществления перевозок от производителя (продавца) к потребителю (покупателю). Давайте посмотрим, каким образом это можно реализовать в программе.

Транспортная задача: описание

С помощью транспортной задачи можно найти наилучший вариант перевозки с минимальными издержками между двумя взаимодействующими контрагентами (в рамках данной статьи будем рассматривать покупателей и продавцов). Чтобы приступить к решению, нужно представить исходные данные в схематичном или матричном виде. Последний вариант применяется в Эксель.

Транспортные задачи бывают двух типов:

• Закрытая – совокупное предложение продавца равняется общему спросу.
• Открытая – спрос и предложение не равны. Чтобы решить такую задачу, нужно сначала привести ее к закрытому типу. В этом случае добавляется условный покупатель или продавец с недостающим количеством спроса или предложения. Также в таблицу издержек следует внести соответствующую запись (с нулевыми значениями).

Подготовительный этап: включение функции “Поиск решения”

Чтобы решить транспортную задачу в Эксель, нужно воспользоваться функцией “Поиск решения”, которую нужно предварительно активировать, т.к. изначально она не включена. Алгоритм действий следующий:

1. Открываем меню “Файл”.
2. В перечне слева выбираем пункт “Параметры”.
3. В параметрах кликаем по подразделу “Надстройки”. Затем в правой части окна в самом низу, выбрав значение “Надстройки Excel” для параметра “Управление”, щелкаем по кнопке “Перейти”.
4. В открывшемся окне ставим галочку напротив надстройки “Поиск решения” и жмем OK.
5. В результате, если мы перейдем во вкладу “Данные”, то увидим здесь кнопку “Поиск решения” в группе инструментов “Анализ”.

Пример задачи и ее решение

Чтобы лучше понять, как решать транспортные задачи в Excel, давайте рассмотрим конкретный практический пример.

Условия задачи

Допустим, у нас есть 6 продавцов и 7 покупателей. Предложение продавцов составляет 36, 51, 32, 44, 35 и 38 единиц. Спрос покупателей следующий: 33, 48, 30, 36, 33, 24 и 32 единицы. Суммарные количества по спросу и предложению равны, следовательно, это транспортная задача закрытого типа.

Также, мы имеем данные по издержкам перевозок из одного пункта в другой (ячейки с желтым фоном).

Алгоритм решения

Итак, приступи к решению нашей задачи:

1. Для начала строим таблицу, количество строк и столбцов в которой соответствует числу продавцов и покупателей, соответственно.
2. Перейдя в любую свободную ячейку щелкаем по кнопке “Вставить функцию” (fx).
3. В открывшемся окне выбираем категорию “Математические”, в списке операторов отмечаем “СУММПРОИЗВ”, после чего щелкаем OK.
4. На экране отобразится окно, в котором нужно заполнить аргументы:
   • в поле для ввода значения напротив первого аргумента “Массив1” указываем координаты диапазона ячеек матрицы затрат (с желтым фоном). Сделать это можно, используя клавиши на клавиатуре, или просто выделив нужную область в самой таблице с помощью зажатой левой кнопки мыши.
   • в качестве значения второго аргумента “Массив2” указываем диапазон ячеек новой таблицы (либо вручную, либо выделив нужные элементы на листе).
   • по готовности жмем OK.
5. Щелкаем по ячейке, расположенной слева от самого верхнего левого элемента новой таблицы, после чего снова жмем кнопку “Вставить функцию”.
6. На этот раз нам нужна функция “СУММ”, которая также, находится в категории “Математические”.
7. Теперь нужно заполнить аргументы. В качестве значения аргумента “Число1” указываем верхнюю строку созданной для расчетов таблицы (целиком) – вручную или методом выделения на листе. Жмем кнопку OK, когда все готово.
8. В ячейке с функцией появится результат, равный нулю. Наводим указатель мыши на ее правый нижний угол, и когда появится Маркер заполнения в виде черного плюсика, зажав левую кнопку мыши тянем его до конца таблицы.
9. Это позволит скопировать формулу и получить аналогичные результаты для остальных строк.
10. Выбираем ячейку, которая находится сверху от самого верхнего левого элемента созданной таблицы. Аналогично описанным выше действиям вставляем в нее функцию “СУММ”.
11. В значении аргумента “Число1” теперь указываем (вручную или с помощью выделения на листе) все ячейки первого столбца, после чего кликаем OK.
12. С помощью Маркера заполнения выполняем копирование формулы на оставшиеся ячейки строки.
13. Переключаемся во вкладку “Данные”, где жмем по кнопке функции “Поиск решения” (группа инструментов “Анализ”).
14. Перед нами появится окно с параметрами функции:
    • в качестве значения параметра “Оптимизировать целевую функцию” указываем координаты ячейки, в которую ранее была вставлена функция “СУММПРОИЗВ”.
    • для параметра “До” выбираем вариант – “Минимум”.
    • в области для ввода значений напротив параметра “Изменяя ячейки переменных” указываем диапазон ячеек новой таблицы (без суммирующей строки и столбца).
    • нажимаем кнопку “Добавить” в блоке “В соответствии с ограничениями”.
15. Откроется небольшое окошко, в котором мы можем добавить ограничение – сумма значений первых столбцов исходной и созданной таблицы должны быть равны.
    • становимся в поле “Ссылка на ячейки”, после чего указываем нужный диапазон данных в таблице для расчетов.
    • затем выбираем знак “равно”.
    • в качестве значения для параметра “Ограничение” указываем координаты  аналогичного столбца в исходной таблице.
    • щелкаем OK по готовности.
16. Таким же способом добавляем условие по равенству сумм верхних строк таблиц.
17. Также добавляем следующие условия касательно суммы ячеек в таблице для расчетов (диапазон совпадает с тем, который мы указали для параметра “Изменяя ячейки переменных”):
    • больше или равно нулю;
    • целое число.
18. В итоге получаем следующий список условий в поле “В соответствии с ограничениями”. Проверяем, чтобы обязательно была поставлена галочка напротив опции “Сделать переменные без ограничений неотрицательными”, а также, чтобы в качестве метода решения стояло значение “Поиск решения нелинейных задач методов ОПГ”. Когда все готово, нажимаем “Найти решение”.
19. В результате будет выполнен расчет и отобразится окно с результатами поиска решения. Оцениваем их, и в случае, когда они нас устраивают, нажимаем OK.
20. Все готово, мы получили таблицу с заполненными данными и транспортную задачу можно считать успешно решенной.

Заключение

Таким образом, с помощью программы Эксель достаточно просто решить транспортную задачу. Самое главное – правильно заполнить начальные данные и четко следовать плану действий, и тогда проблем быть не должно, т.к. программа все расчеты выполнит сама.