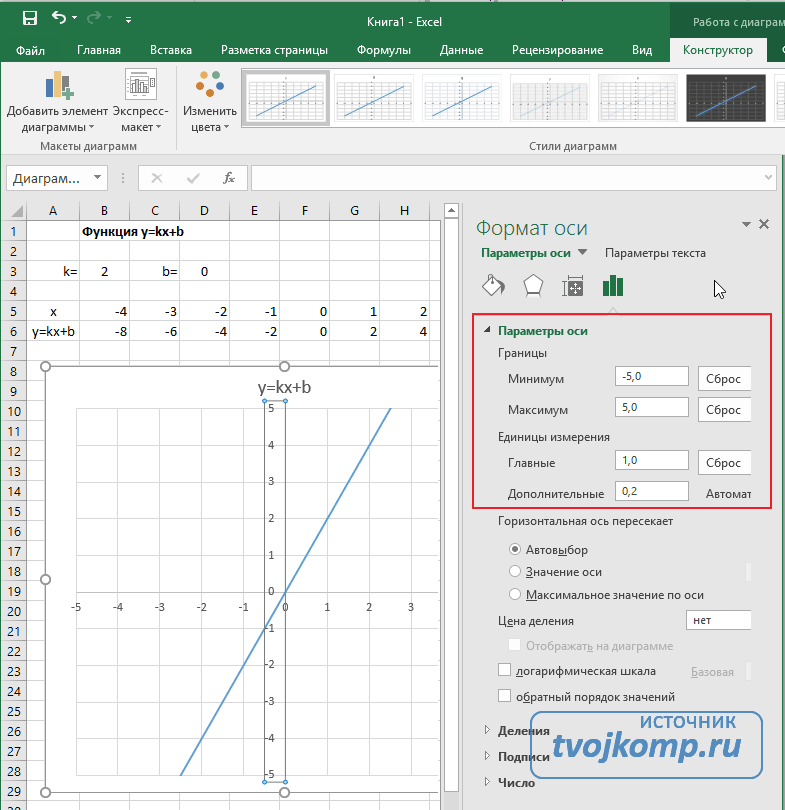
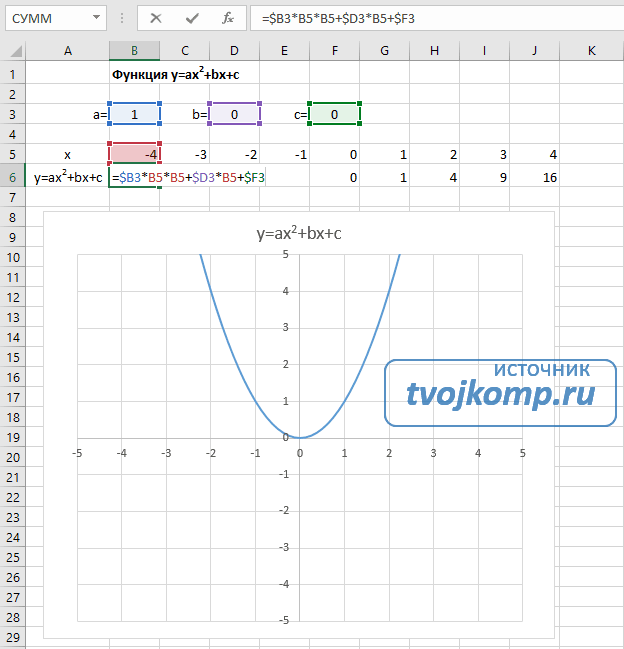
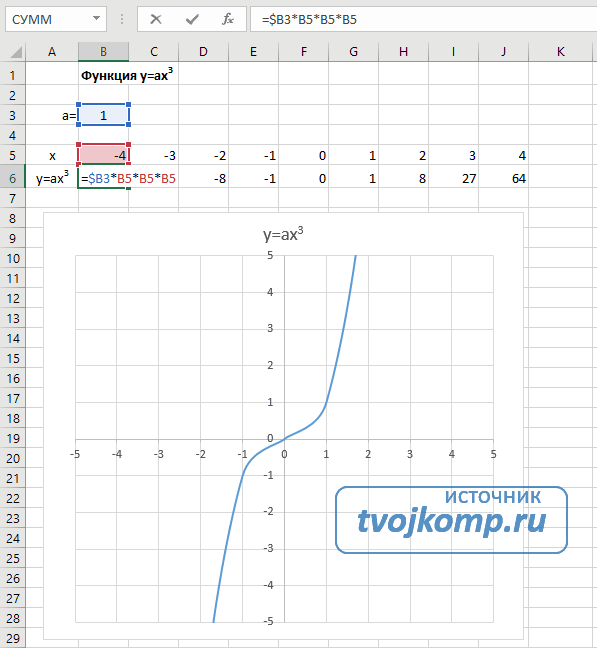
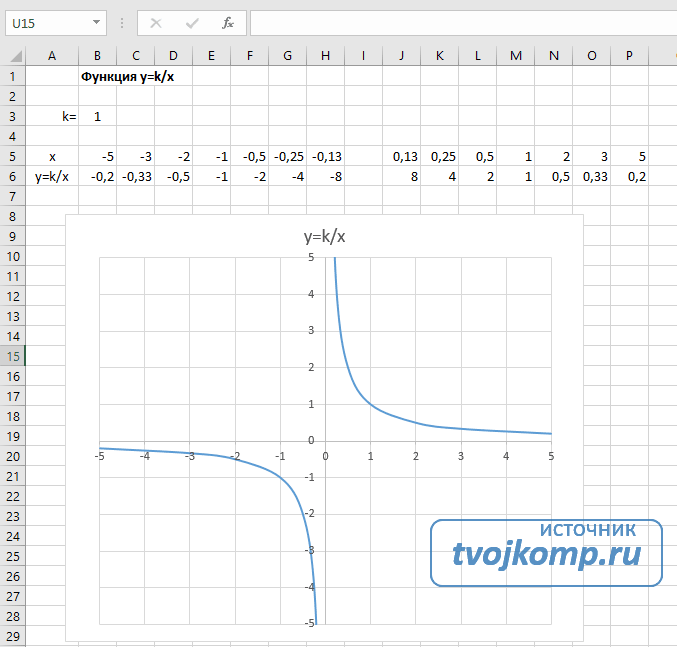
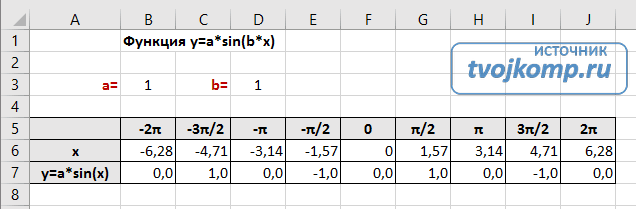
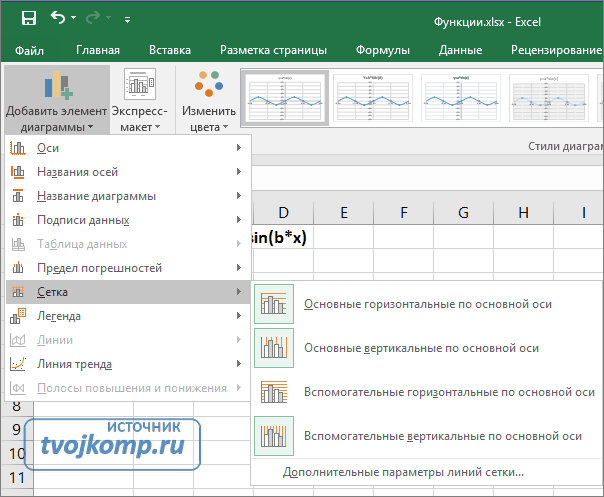
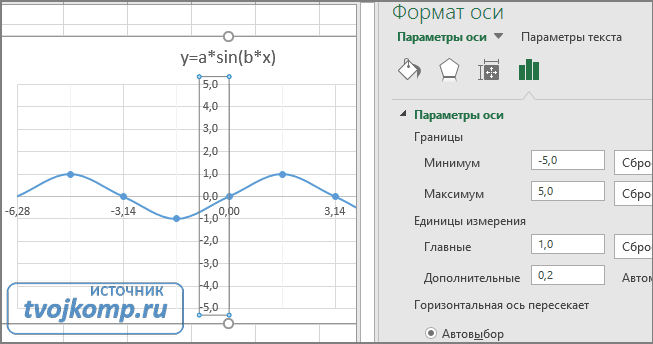
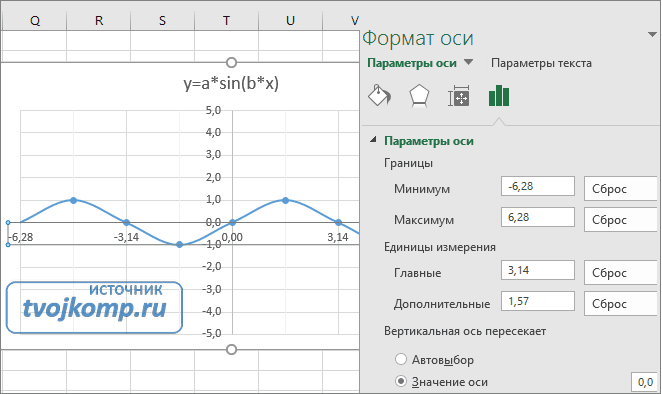
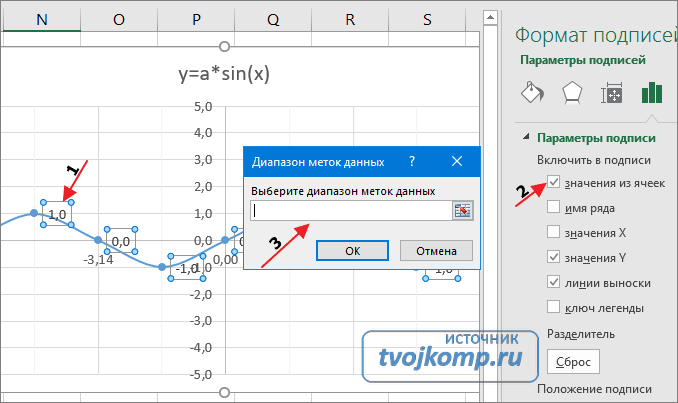
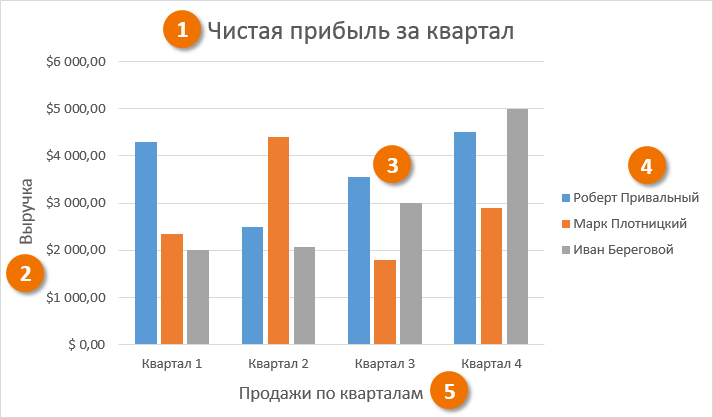
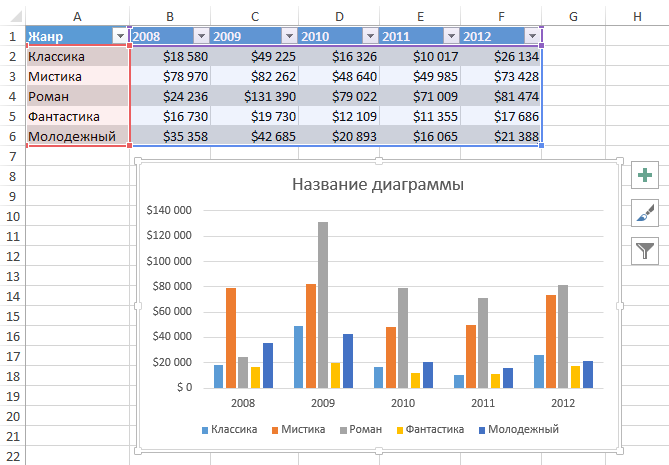
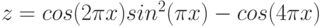Пример 1
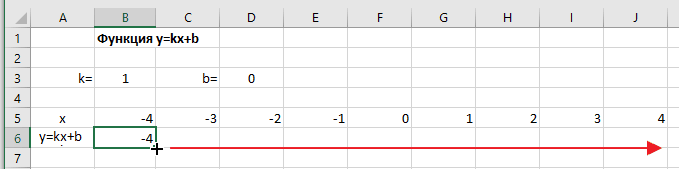
Дана функция:
Нужно построить ее график на промежутке [-5;5] с шагом равным 1.
Создание таблицы
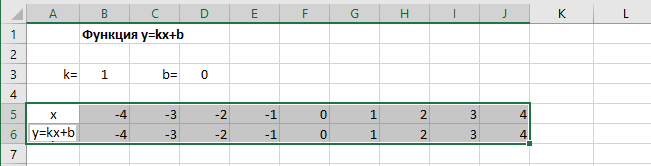
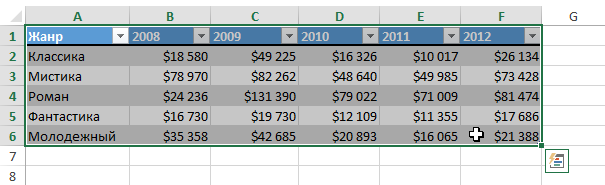
Создадим таблицу, первый столбец назовем переменная x (ячейка А1), второй — переменная y (ячейка В1). Для удобства в ячейку В1 запишем саму функцию, чтобы было понятно, какой график будем строить. Введем значения -5, -4 в ячейки А2 и А3 соответственно, выделим обе ячейки и скопируем вниз. Получим последовательность от -5 до 5 с шагом 1.
Вычисление значений функции
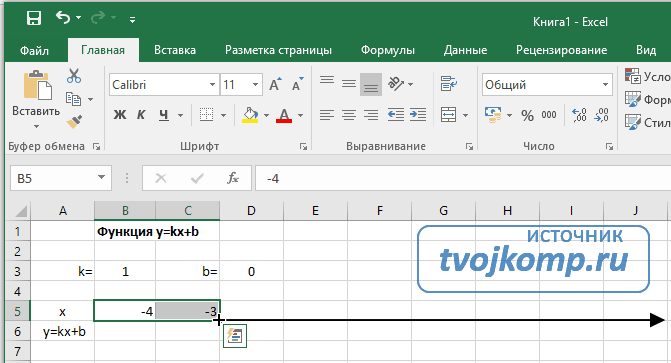
Нужно вычислить значения функции в данных точках. Для этого в ячейке В2 создадим формулу, соответствующую заданной функции, только вместо x будем вводить значение переменной х, находящееся в ячейке слева (-5).
Важно: для возведения в степень используется знак ^, который можно получить с помощью комбинации клавиш Shift+6 на английской раскладке клавиатуры. Обязательно между коэффициентами и переменной нужно ставить знак умножения * (Shift+8).
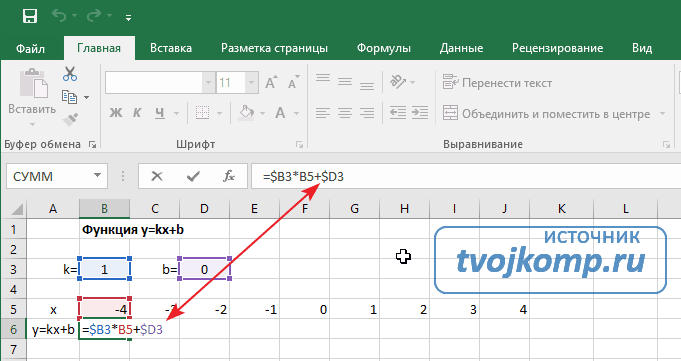
Ввод формулы завершаем нажатием клавиши Enter. Мы получим значение функции в точке x=-5. Скопируем полученную формулу вниз.
Мы получили последовательность значений функции в точках на промежутке [-5;5] с шагом 1.
Построение графика
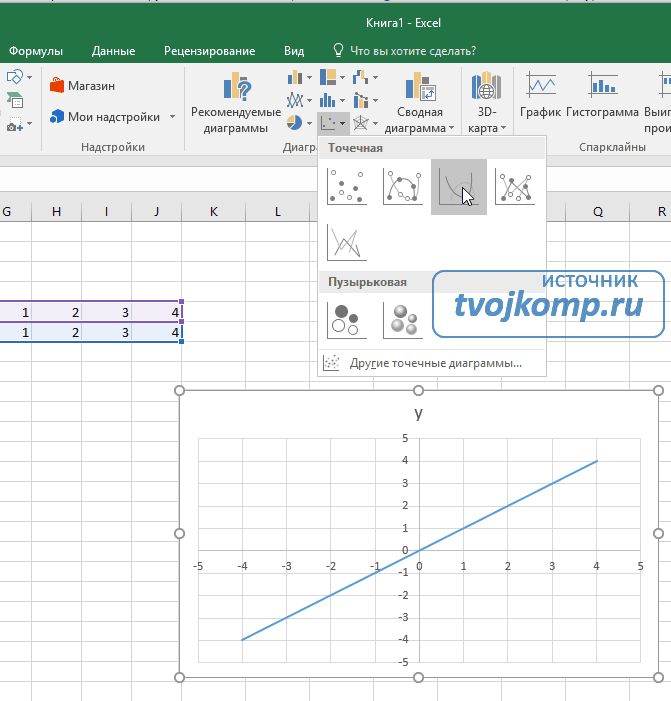
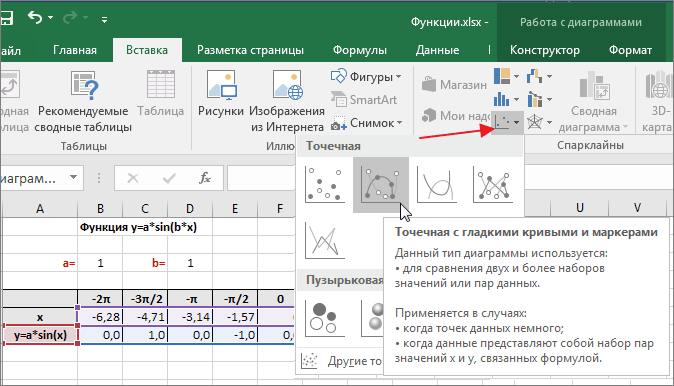
Выделим диапазон значений переменной x и функции y. Перейдем на вкладку Вставка и в группе Диаграммы выберем Точечная (можно выбрать любую из точечных диаграмм, но лучше использовать вид с гладкими кривыми).
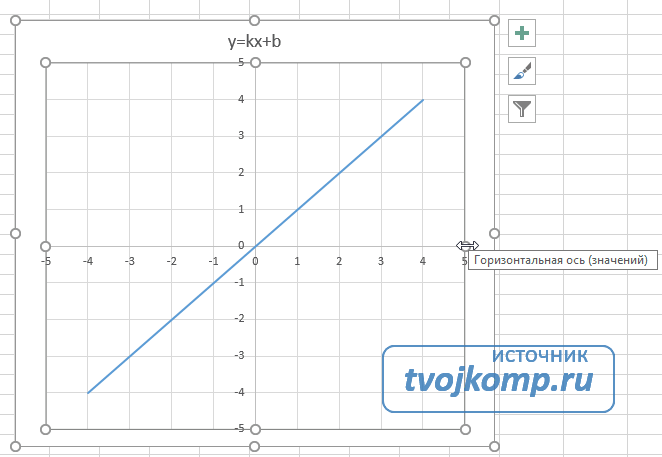
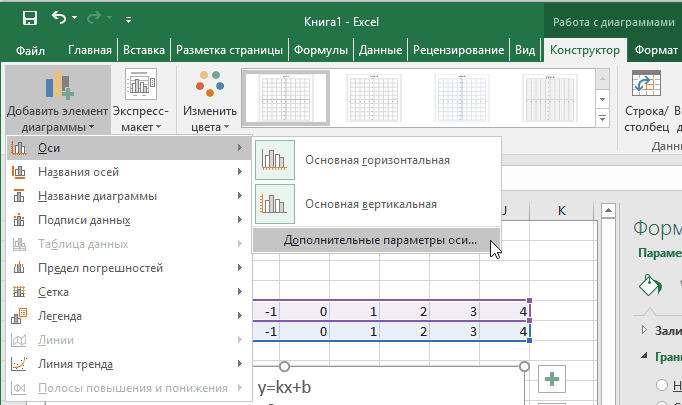
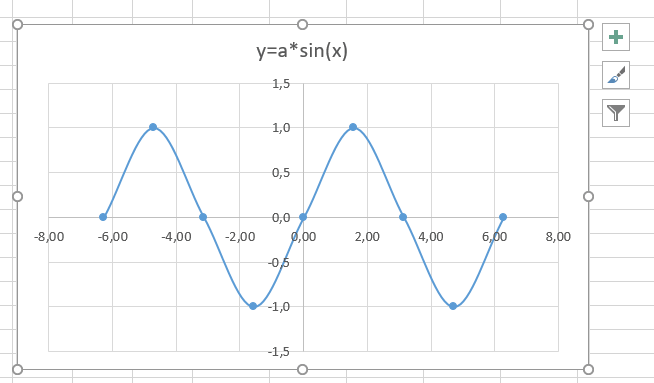
Мы получили график данной функции. Используя вкладки Конструктор, Макет, Формат, можно изменить параметры графика.
Пример 2
Даны функции:
и y=50x+2. Нужно построить графики этих функций в одной системе координат.
Создание таблицы и вычисление значений функций
Таблицу для первой функции мы уже построили, добавим третий столбец — значения функции y=50x+2 на том же промежутке [-5;5]. Заполняем значения этой функции. Для этого в ячейку C2 вводим формулу, соответствующую функции, только вместо x берем значение -5, т.е. ячейку А2. Копируем формулу вниз.
Мы получили таблицу значений переменной х и обеих функций в этих точках.
Построение графиков
Для построения графиков выделяем значения трёх столбцов, на вкладке Вставка в группе Диаграммы выбираем Точечная.
Мы получили графики функций в одной системе координат. Используя вкладки Конструктор, Макет, Формат, можно изменить параметры графиков.
Последний пример удобно использовать, если нужно найти точки пересечения функций с помощью графиков. При этом можно изменить значения переменной x, выбрать другой промежуток или взять другой шаг (меньше или больше, чем 1). При этом столбцы В и С менять не нужно, диаграмму тоже. Все изменения произойдут сразу же после ввода других значений переменной x. Такая таблица является динамической.
Кратко об авторе:

Спасибо за Вашу оценку. Если хотите, чтобы Ваше имя
стало известно автору, войдите на сайт как пользователь
и нажмите Спасибо еще раз. Ваше имя появится на этой стрнице.
Вариант 1: График функции X^2
В качестве первого примера для Excel рассмотрим самую популярную функцию F(x)=X^2. График от этой функции в большинстве случаев должен содержать точки, что мы и реализуем при его составлении в будущем, а пока разберем основные составляющие.
- Создайте строку X, где укажите необходимый диапазон чисел для графика функции.
- Ниже сделайте то же самое с Y, но можно обойтись и без ручного вычисления всех значений, к тому же это будет удобно, если они изначально не заданы и их нужно рассчитать.
- Нажмите по первой ячейке и впишите
=B1^2, что значит автоматическое возведение указанной ячейки в квадрат. - Растяните функцию, зажав правый нижний угол ячейки, и приведя таблицу в тот вид, который продемонстрирован на следующем скриншоте.
- Диапазон данных для построения графика функции указан, а это означает, что можно выделять его и переходить на вкладку «Вставка».
- На ней сразу же щелкайте по кнопке «Рекомендуемые диаграммы».
- В новом окне перейдите на вкладку «Все диаграммы» и в списке найдите «Точечная».
- Подойдет вариант «Точечная с гладкими кривыми и маркерами».
- После ее вставки в таблицу обратите внимание, что мы добавили равнозначный диапазон отрицательных и плюсовых значений, чтобы получить примерно стандартное представление параболы.
- Сейчас вы можете поменять название диаграммы и убедиться в том, что маркеры значений выставлены так, как это нужно для дальнейшего взаимодействия с этим графиком.
- Из дополнительных возможностей отметим копирование и перенос графика в любой текстовый редактор. Для этого щелкните в нем по пустому месту ПКМ и из контекстного меню выберите «Копировать».
- Откройте лист в используемом текстовом редакторе и через это же контекстное меню вставьте график или используйте горячую клавишу Ctrl + V.
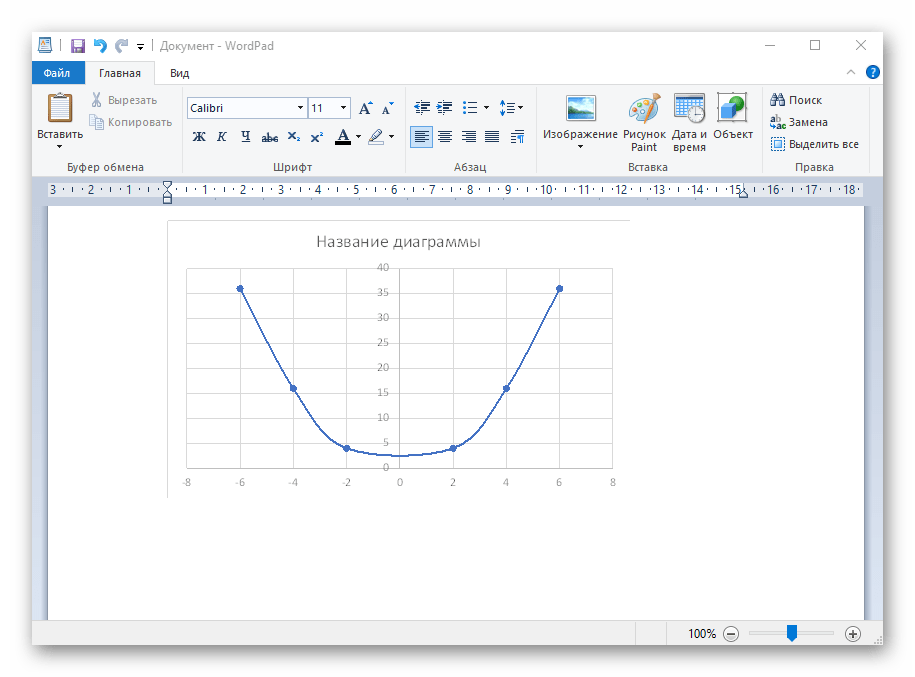
Если график должен быть точечным, но функция не соответствует указанной, составляйте его точно в таком же порядке, формируя требуемые вычисления в таблице, чтобы оптимизировать их и упростить весь процесс работы с данными.
Вариант 2: График функции y=sin(x)
Функций очень много и разобрать их в рамках этой статьи просто невозможно, поэтому в качестве альтернативы предыдущему варианту предлагаем остановиться на еще одном популярном, но сложном — y=sin(x). То есть изначально есть диапазон значений X, затем нужно посчитать синус, чему и будет равняться Y. В этом тоже поможет созданная таблица, из которой потом и построим график функции.
- Для удобства укажем всю необходимую информацию на листе в Excel. Это будет сама функция sin(x), интервал значений от -1 до 5 и их шаг весом в 0.25.
- Создайте сразу два столбца — X и Y, куда будете записывать данные.
- Запишите самостоятельно первые два или три значения с указанным шагом.
- Далее растяните столбец с X так же, как обычно растягиваете функции, чтобы автоматически не заполнять каждый шаг.
- Перейдите к столбцу Y и объявите функцию
=SIN(, а в качестве числа укажите первое значение X. - Сама функция автоматически высчитает синус заданного числа.
- Растяните столбец точно так же, как это было показано ранее.
- Если чисел после запятой слишком много, уменьшите разрядность, несколько раз нажав по соответствующей кнопке.
- Выделите столбец с Y и перейдите на вкладку «Вставка».
- Создайте стандартный график, развернув выпадающее меню.
- График функции от y=sin(x) успешно построен и отображается правильно. Редактируйте его название и отображаемые шаги для простоты понимания.


Еще статьи по данной теме:
Помогла ли Вам статья?
График функции – графическое представление математического выражения, показывающее его решение. Для построения обычно используются линейные графики с точками, с чем прекрасно справляется Microsoft Excel. Кроме того, в нем еще можно выполнить автоматические расчеты, быстро подставив нужные значения.
Существует огромное количество функций, поэтому в качестве примера я разберу только две самые наглядные, чтобы вы поняли базовые правила составления подобных элементов в таблице.
График функции F(x) = X^2
Функция X^2 – одна из самых популярных математических функций, которую разбирают еще на уроках в школе. На графике необходимо показать точки Y, что в Excel реализовывается следующим образом:
-
Создайте строку на листе в программе, вписав туда известные значения X.
-
Сделайте то же самое и с Y. Пока значения этой оси координат неизвестны. Чтобы определить их, нам нужно выполнить простые расчеты.
-
Поэтому в качестве значения для каждой ячейки укажите формулу, которая посчитает квадрат числа, указанного в строке X. Для этого впишите =A1^2, заменив номер ячейки.
-
Теперь достаточно зажать левую кнопку мыши на нижней точки готовой ячейки и растянуть таблицу, чтобы формула автоматически подставилась в остальные ячейки, и вы могли сразу ознакомиться с результатом.
-
Перейдите на вкладку вставки и выберите раздел с рекомендуемыми диаграммами.
-
В списке отыщите точечную диаграмму, которая подойдет для составления подходящего графика.
-
Вставьте ее в таблицу и ознакомьтесь с результатом. На следующем скриншоте вы видите параболу и значения X, при которых она получилась правильной (такую часто показывают в примерах на математике).
Всего 7 простых шагов потребовалось для достижения желаемого результата. Вы можете подставлять свои значения в таблицу и изменять их в любое время, следя за тем, как перестраивается график функций.
Комьюнити теперь в Телеграм
Подпишитесь и будьте в курсе последних IT-новостей
Подписаться
График функции y=sin(x)
y=sin(x) – вторая функция, которую мы возьмем за пример. Может показаться, что ее составление осуществляется сложнее, хотя на самом деле это не так. Дело в том, что Excel сам посчитает значения, а вам останется только задать известные числа и вставить простой линейный график для вывода результатов на экран.
-
Если вам будет проще, впишите в отдельную клетку функцию, укажите интервал и шаг. Так вы не запутаетесь при дальнейшем заполнении ячеек.
-
Добавьте два столбца, в которые будут вписаны значения каждой оси. Это нужно не только для обозначения чисел, но и для их вычисления при помощи функций программы.
-
Начните вписывать значения X с необходимым интервалом и шагом. Кстати, вы можете заполнить всего несколько полей, а затем растянуть клетки таким же образом, как было показано в предыдущем примере, чтобы они подставились автоматически до конца вашего интервала.
-
Теперь более сложное, но не страшное действие – определение значения Y. Понятно, что он равняется синусу X, значит, нужно вписать функцию =SIN(A1), где вместо A1 используйте нужную ячейку, а затем растяните функцию на оставшийся интервал.
-
На следующем скриншоте вы видите результат заполнения таблицы. Используйте округление для удаления лишних знаков после запятой.
-
Вставьте обычную линейчатую диаграмму и ознакомьтесь с результатом.
На примере этих двух функций уже можно понять, как работает построение графиков в Экселе. При использовании других функций просто учитывайте особенности заполнения ячеек и не забывайте о том, что вам не нужно ничего считать, поскольку Excel все сделает за вас после указания необходимой формулы.
П/р №17 Создание таблиц значений функций в электронных таблицах
Аппаратное и программное обеспечение. Компьютер с установленной операционной системой Windows или Linux.
Цель работы. Научиться создавать таблицы значений функций в заданном диапазоне значений аргумента и с заданным шагом его изменения.
Задание. В электронных таблицах Microsoft Excel и OpenOffice.org Calc создать таблицы значений квадратичной функции y=x 2 — 3 и функции квадратного корня 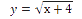
Создание таблиц значений функций в электронных таблицах Microsoft Excel и OpenOffice.org Calc
1. В операционной системе Windows запустить электронные таблиц Microsoft Excel командой [Программы — Microsoft Excel] или электронные таблицы OpenOffice.org Calc командой [Программы — OpenOffice — OpenOffice Calc].
Или:
в операционной системе Linux запустить электронные таблицы OpenOffice.org Calc командой [Офис — OpenOffice Calc].
В созданном документе присвоить листу имя Функция.
Введем значения аргумента функции в первую строку электронных таблиц.
2. В ячейку А1 ввести название строки значений аргумента (например, х), а в ячейку B1 минимальное значение аргумента (число -4).
В ячейку С1 ввести формулу =B1+1.
Выделить диапазон ячеек C1:J1 и скопировать формулу во все ячейки этого диапазона с помощью команды [Правка — Заполнить — Вправо].
Введём значения функции y=x 2 — 3 во вторую строку электронной таблицы. Ввод формулы для вычисления функции произвести с клавиатуры.
3. В ячейку A2 ввести название строки значений функции
(например, y = x^2-3)
В ячейку B2 ввести формулу =B1^2-3.
Выделить диапазон ячеек B2:J2 и скопировать формулу во все ячейки этого диапазона с помощью команды [Правка — Заполнить — Вправо].
Введём значения функции 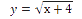
4. В ячейку А3 ввести название название строки значений функции (например, y=КОРЕНЬ(x+4)).
В электронных таблицах Microsoft Excel для ввода функций воспользуемся Мастером функций . (По форме он несколько отличается от Мастера Функций электронных таблиц OpenOffice.org Calc.)
5. Выделить ячейку B3 и ввести команду [Вставка — Функция. ]. В диалоговом окне Мастер функций — шаг 1 из 2 в списке Категория : выбрать Математические , а в списке Выберите функцию: выбрать вариант Корень . Нажать кнопку ОК .
6. На появившейся панели Аргументы функции в поле Число вести B1+4. Нажать кнопку ОК .
7. Выделить диапазон ячеек B3:J3 и скопировать формулу во все ячейки этого диапазона с помощью команды [Правка — Заполнить — Вправо]. В результате будет получена таблица значений функций.
8. Для отображения в ячейках чисел с заданной точностью выделить диапазон ячеек и ввести команду [Формат — Ячейки. ].
В появившемся диалоговом окне Формат ячеек на вкладке Число выбрать в списке Числовые форматы формат Числовой и установить с помощью счетчика Число десятичных знаков: 1.
Урок информатики по теме: «Excel: Построение графиков функций по заданным параметрам»
- Харченко Наталья Владимировна, преподаватель информатики
Разделы: Математика, Информатика
Цели урока:
Задачи урока:
Тип урока:
Учебники:
Информатика. Базовый курс 2-е издание/Под ред. С.В. Симоновича. — СПб.: Питер, 2004.-640с.:ил.
Технические и программные средства:
Раздаточный материал:
Ход урока
Организационный момент
Проверка готовности учащихся к уроку, отметка отсутствующих, объявление темы и цели урока
Проверка домашнего задания. (фронтальный опрос)
Вопросы для проверки
Объяснение нового материала.
При объяснении нового материала может быть использован файл Excel с шаблонами задач (Приложение 1), который выводится на экран с помощью проектора
Сегодня мы рассмотрим применение табличного процессора Excel для графиков функций. На предыдущих практических вы уже строили диаграммы к различным задачам, используя Мастер диаграмм. Графики функций, так же как и диаграммы строятся с помощью Мастера диаграмм программы Excel.
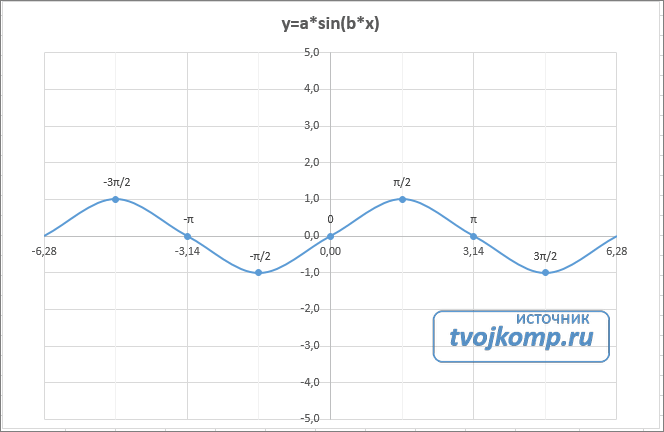
Рассмотрим построение графиков функций на примере функции у = sin x.
Вид данного графика хорошо известен вам по урокам математики, попробуем построить его средствами Excel.
Программа будет строить график по точкам: точки с известными значениями будут плавно соединяться линией. Эти точки нужно указать программе, поэтому, сначала создается таблица значений функции у = f(х).
Чтобы создать таблицу, нужно определить
Задача 1.Построить график функции у = sin x на отрезке [— 2; 2] с шагом h = 0,5.
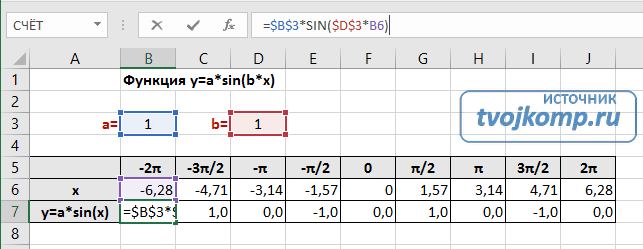
1. Заполним таблицу значений функции. В ячейку С4 введем первое значение отрезка: — 2 2. В ячейку D4 введем формулу, которая будет добавлять к лево-стоящей ячейки шаг: = В4 + $A$4 3. Маркером заполнения ячейки D4 заполним влево ячейки строки 4, до тех пор, пока получим значение другого конца отрезка: 2. 4. Выделим ячейку С5, вызовем Мастер функций, в категории математические выберем функцию SIN, в качестве аргумента функции выберем ячейку С4. 5. Маркером заполнения распространим эту формулу в ячейках строки 5 до конца таблицы.
Таким образом, мы получили таблицу аргументов (х) и значений (у) функции у = sin x на отрезке [-2;2] с шагом h = 0,5 :
6. Следующий шаг. Выделим таблицу и вызовем Мастер диаграмм. На первом шаге выберем во вкладке Нестандартные Гладкие графики. 7. На втором шаге во вкладке Ряд выполним:
В поле Ряд необходимо выделить ряд х и нажать на кнопку «Удалить» (график изменений х нам не нужен. График функции — это график изменения значений у)
В поле Подписи оси Х нажать на кнопку. Выделить в таблице ячейки со значениями х и нажмите на кнопку . Подписи по горизонтальной оси станут такими, как у нас в таблице.
8. На третьем шаге заполним вкладку Заголовки.
9. Пример полученного графика.
На самом деле пока это мало похоже на график функции в нашем привычном понимании.
Для форматирования графика:
Во вкладке Шкала установим: пересечение с осью ОУ установите номер категории 5 (чтобы ось ОУ пересекала ось ОХ в категории с подписью 0, а это пятая по счету категория).
Во вкладке шрифт установите размер шрифта 8пт. Нажмите на кнопку ОК.
Остальные изменения выполняются аналогично.
Для закрепления рассмотрим еще одну задачу на построение графика функций. Эту задачу попробуйте решить самостоятельно, сверяясь с экраном проектора.
Применение полученных знаний.
Пригласить к проектору студента и сформулировать следующую задачу.
Задача 2. Построить график функции у = х 3 на отрезке [— 3; 3] с шагом h = 0,5.
1. Создать следующую таблицу: Создать таблица значений функции у = f(х).
2. В ячейку С4 ввести первое значение отрезка: —3 3. В ячейку D4 ввести формулу, которая будет добавлять к лево-стоящей ячейки шаг: = В4 + $A$4 4. Маркером заполнения ячейки D3 заполнить влево ячейки строки 3, до тех пор, пока не будет получено значение другого конца отрезка: 3. 5. В ячейку С5 ввести формулу вычисления значения функции: = С4^3 6. Маркером заполнения скопировать формулу в ячейки строки 5 до конца таблицы.
Таким образом, должна получиться таблица аргументов (х) и значений (у) функции у = х 3 на отрезке [—3;3] с шагом h = 0,5:
7. Выделить таблицу и вызвать мастер диаграмм. На первом шаге выбрать во второй вкладке Гладкие графики. 8. На втором шаге во вкладке Ряд выполнить:
- В поле Ряд выделить ряд х и нажать на кнопку «Удалить» (график изменений х нам не нужен. График функции — это график изменения значений у)
- В поле Подписи оси Х нажать на кнопку . Выделить в таблице ячейки со значениями х и нажать на кнопку . Подписи по горизонтальной оси станут такими, как у нас в таблице.
9. На третьем шаге заполнить вкладку Заголовки.
10. Пример полученного графика: 11. Оформить график. 12. Установить параметры страницы и размеры диаграмм таким образом, что бы все поместилось на одном листе альбомной ориентации. 13. Создать колонтитулы для данного листа (Вид Колонтитулы. ): 14. Верхний колонтитул слева: график функции у = x 3
Сохранить документ своей папке под именем График.
Самостоятельная работа.
Работа по карточкам с индивидуальными заданиями. (Приложение 2)
Пример карточки, с задачей в общем виде, выводится на экран с помощью проектора.
1. Построить график функции y=f(x) на отрезке [a;b] с шагом h=c 2. Установить параметры страницы и размеры графика таким образом, что бы все поместилось на одном листе альбомной ориентации. 3. Создать колонтитулы для данного листа (Вид Колонтитулы. ):
- Верхний колонтитул слева: график функции y=f(x)
- Нижний колонтитул в центре: ваши Ф.И.О. и дата
4. Сохранить в своей папке под именем «Зачетный график» 5. Вывести документ на печать.
После выполнения задания правильность каждого варианта проверяется с помощью проектора.
Урок информатики по теме: «Excel: Построение графиков функций по заданным параметрам»
Информатика. Базовый курс 2-е издание/Под ред. С.В. Симоновича. — СПб.: Питер, 2004.-640с.:ил.
- Персональные компьютеры;
- Приложение Windows – электронные таблицы Excel.
- Проектор
- Карточки с индивидуальными заданиями на построение графиков функций.
- Организационный момент – 3 мин.
- Проверка домашнего задания –10 мин.
- Объяснение нового материала –20 мин.
- Применение полученных знаний –20 мин.
- Самостоятельная работа. – 20 мин
- Подведение итогов урока. Домашнее задание – 7 мин.
Ход урока
Организационный момент
Проверка готовности учащихся к уроку, отметка отсутствующих, объявление темы и цели урока
Проверка домашнего задания. (фронтальный опрос)
- Что представляет собой рабочая область программы Excel?
- Как определяется адрес ячейки?
- Как изменить ширину столбца, высоту строки?
- Как ввести формулу в Excel?
- Что такое маркер заполнения и для чего он нужен?
- Что такое относительная адресация ячеек?
- Что такое абсолютная адресация ячеек? Как она задается?
- Что такое колонтитулы? Как они задаются?
- Как задать поля печатного документа? Как изменить ориентацию бумаги?
- Что такое функциональная зависимость у = f(х)? Какая переменная является зависимой, а какая независимой?
- Как ввести функцию в Excel?
- Что такое график функции у = f(х)?
- Как построить диаграмму в Excel?
Объяснение нового материала.
При объяснении нового материала может быть использован файл Excel с шаблонами задач (Приложение 1), который выводится на экран с помощью проектора
Сегодня мы рассмотрим применение табличного процессора Excel для графиков функций. На предыдущих практических вы уже строили диаграммы к различным задачам, используя Мастер диаграмм. Графики функций, так же как и диаграммы строятся с помощью Мастера диаграмм программы Excel.
Рассмотрим построение графиков функций на примере функции у = sin x.
Вид данного графика хорошо известен вам по урокам математики, попробуем построить его средствами Excel.
Программа будет строить график по точкам: точки с известными значениями будут плавно соединяться линией. Эти точки нужно указать программе, поэтому, сначала создается таблица значений функции у = f(х).
- отрезок оси ОХ, на котором будет строиться график.
- шаг переменной х, т.е. через какой промежуток будут вычисляться значения функции.
Задача 1.Построить график функции у = sin x на отрезке [– 2; 2] с шагом h = 0,5.
1. Заполним таблицу значений функции. В ячейку С4 введем первое значение отрезка: – 2
2. В ячейку D4 введем формулу, которая будет добавлять к лево-стоящей ячейки шаг: = В4 + $A$4
3. Маркером заполнения ячейки D4 заполним влево ячейки строки 4, до тех пор, пока получим значение другого конца отрезка: 2.
4. Выделим ячейку С5, вызовем Мастер функций, в категории математические выберем функцию SIN, в качестве аргумента функции выберем ячейку С4.
5. Маркером заполнения распространим эту формулу в ячейках строки 5 до конца таблицы.
Таким образом, мы получили таблицу аргументов (х) и значений (у) функции у = sin x на отрезке [-2;2] с шагом h = 0,5 :
| x | -2 | -1,75 | -1,5 | -1,25 | -1 | -0,75 | -0,5 | -0,25 | 0 | 0,25 | 0,5 | 0,75 | 1 | 1,25 | 1,5 | 1,75 | 2 |
| y | -0,9092 | -0,9839 | -0,9974 | -0,9489 | -0,8414 | -0,6816 | -0,4794 | -0,2474 | 0 | 0,2474 | 0,4794 | 0,6816 | 0,8414 | 0,9489 | 0,9974 | 0,9839 | 0,9092 |
6. Следующий шаг. Выделим таблицу и вызовем Мастер диаграмм. На первом шаге выберем во вкладке Нестандартные Гладкие графики.
7. На втором шаге во вкладке Ряд выполним:
В поле Ряд необходимо выделить ряд х и нажать на кнопку “Удалить” (график изменений х нам не нужен. График функции – это график изменения значений у)
В поле Подписи оси Х нажать на кнопку. Выделить в таблице ячейки со значениями х и нажмите на кнопку . Подписи по горизонтальной оси станут такими, как у нас в таблице.
8. На третьем шаге заполним вкладку Заголовки.
На самом деле пока это мало похоже на график функции в нашем привычном понимании.
- Вызовем контекстное меню оси ОУ. Затем, выберем пункт Формат оси…. Во вкладке Шкала установим: цена основного деления: 1. Во вкладке Шрифт установим размер шрифта 8пт.
- Вызовем контекстное меню оси ОХ. Выберем пункт Формат оси….
Во вкладке Шкала установим: пересечение с осью ОУ установите номер категории 5 (чтобы ось ОУ пересекала ось ОХ в категории с подписью 0, а это пятая по счету категория).
Во вкладке шрифт установите размер шрифта 8пт. Нажмите на кнопку ОК.
Остальные изменения выполняются аналогично.
Для закрепления рассмотрим еще одну задачу на построение графика функций. Эту задачу попробуйте решить самостоятельно, сверяясь с экраном проектора.
Применение полученных знаний.
Пригласить к проектору студента и сформулировать следующую задачу.
Задача 2. Построить график функции у = х 3 на отрезке [– 3; 3] с шагом h = 0,5.
1. Создать следующую таблицу: Создать таблица значений функции у = f(х).
2. В ячейку С4 ввести первое значение отрезка: –3
3. В ячейку D4 ввести формулу, которая будет добавлять к лево-стоящей ячейки шаг: = В4 + $A$4
4. Маркером заполнения ячейки D3 заполнить влево ячейки строки 3, до тех пор, пока не будет получено значение другого конца отрезка: 3.
5. В ячейку С5 ввести формулу вычисления значения функции: = С4^3
6. Маркером заполнения скопировать формулу в ячейки строки 5 до конца таблицы.
Таким образом, должна получиться таблица аргументов (х) и значений (у) функции у = х 3 на отрезке [–3;3] с шагом h = 0,5:
| х | -3 | -2,5 | -2 | -1,5 | -1 | -0,5 | 0 | 0,5 | 1 | 1,5 | 2 | 2,5 | 3 |
| y | -27 | -15,625 | -8 | -3,375 | -1 | -0,125 | 0 | 0,125 | 1 | 3,375 | 8 | 15,625 | 27 |
7. Выделить таблицу и вызвать мастер диаграмм. На первом шаге выбрать во второй вкладке Гладкие графики.
8. На втором шаге во вкладке Ряд выполнить:
- В поле Ряд выделить ряд х и нажать на кнопку “Удалить” (график изменений х нам не нужен. График функции – это график изменения значений у)
- В поле Подписи оси Х нажать на кнопку . Выделить в таблице ячейки со значениями х и нажать на кнопку . Подписи по горизонтальной оси станут такими, как у нас в таблице.
9. На третьем шаге заполнить вкладку Заголовки.
10. Пример полученного графика:
11. Оформить график.
12. Установить параметры страницы и размеры диаграмм таким образом, что бы все поместилось на одном листе альбомной ориентации.
13. Создать колонтитулы для данного листа (Вид Колонтитулы…):
14. Верхний колонтитул слева: график функции у = x 3
Сохранить документ своей папке под именем График.
Самостоятельная работа.
Работа по карточкам с индивидуальными заданиями. (Приложение 2)
Пример карточки, с задачей в общем виде, выводится на экран с помощью проектора.
1. Построить график функции y=f(x) на отрезке [a;b] с шагом h=c
2. Установить параметры страницы и размеры графика таким образом, что бы все поместилось на одном листе альбомной ориентации.
3. Создать колонтитулы для данного листа (Вид Колонтитулы…):
- Верхний колонтитул слева: график функции y=f(x)
- Нижний колонтитул в центре: ваши Ф.И.О. и дата
4. Сохранить в своей папке под именем “Зачетный график”
5. Вывести документ на печать.
После выполнения задания правильность каждого варианта проверяется с помощью проектора.
Информация воспринимается легче, если представлена наглядно. Один из способов презентации отчетов, планов, показателей и другого вида делового материала – графики и диаграммы. В аналитике это незаменимые инструменты.
Построить график в Excel по данным таблицы можно несколькими способами. Каждый из них обладает своими преимуществами и недостатками для конкретной ситуации. Рассмотрим все по порядку.
Простейший график изменений
График нужен тогда, когда необходимо показать изменения данных. Начнем с простейшей диаграммы для демонстрации событий в разные промежутки времени.
Допустим, у нас есть данные по чистой прибыли предприятия за 5 лет:
| Год | Чистая прибыль* |
| 2010 | 13742 |
| 2011 | 11786 |
| 2012 | 6045 |
| 2013 | 7234 |
| 2014 | 15605 |
* Цифры условные, для учебных целей.
Заходим во вкладку «Вставка». Предлагается несколько типов диаграмм:
Выбираем «График». Во всплывающем окне – его вид. Когда наводишь курсор на тот или иной тип диаграммы, показывается подсказка: где лучше использовать этот график, для каких данных.
Выбрали – скопировали таблицу с данными – вставили в область диаграммы. Получается вот такой вариант:
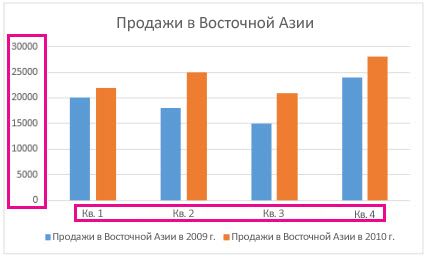
Прямая горизонтальная (синяя) не нужна. Просто выделяем ее и удаляем. Так как у нас одна кривая – легенду (справа от графика) тоже убираем. Чтобы уточнить информацию, подписываем маркеры. На вкладке «Подписи данных» определяем местоположение цифр. В примере – справа.
Улучшим изображение – подпишем оси. «Макет» – «Название осей» – «Название основной горизонтальной (вертикальной) оси»:
Заголовок можно убрать, переместить в область графика, над ним. Изменить стиль, сделать заливку и т.д. Все манипуляции – на вкладке «Название диаграммы».
Вместо порядкового номера отчетного года нам нужен именно год. Выделяем значения горизонтальной оси. Правой кнопкой мыши – «Выбрать данные» — «Изменить подписи горизонтальной оси». В открывшейся вкладке выбрать диапазон. В таблице с данными – первый столбец. Как показано ниже на рисунке:
Можем оставить график в таком виде. А можем сделать заливку, поменять шрифт, переместить диаграмму на другой лист («Конструктор» — «Переместить диаграмму»).
График с двумя и более кривыми
Допустим, нам нужно показать не только чистую прибыль, но и стоимость активов. Данных стало больше:
Но принцип построения остался прежним. Только теперь есть смысл оставить легенду. Так как у нас 2 кривые.
Добавление второй оси
Как добавить вторую (дополнительную) ось? Когда единицы измерения одинаковы, пользуемся предложенной выше инструкцией. Если же нужно показать данные разных типов, понадобится вспомогательная ось.
Сначала строим график так, будто у нас одинаковые единицы измерения.
Выделяем ось, для которой хотим добавить вспомогательную. Правая кнопка мыши – «Формат ряда данных» – «Параметры ряда» — «По вспомогательной оси».
Нажимаем «Закрыть» — на графике появилась вторая ось, которая «подстроилась» под данные кривой.
Это один из способов. Есть и другой – изменение типа диаграммы.
Щелкаем правой кнопкой мыши по линии, для которой нужна дополнительная ось. Выбираем «Изменить тип диаграммы для ряда».
Определяемся с видом для второго ряда данных. В примере – линейчатая диаграмма.
Всего несколько нажатий – дополнительная ось для другого типа измерений готова.
Строим график функций в Excel
Вся работа состоит из двух этапов:
- Создание таблицы с данными.
- Построение графика.
Пример: y=x(√x – 2). Шаг – 0,3.
Составляем таблицу. Первый столбец – значения Х. Используем формулы. Значение первой ячейки – 1. Второй: = (имя первой ячейки) + 0,3. Выделяем правый нижний угол ячейки с формулой – тянем вниз столько, сколько нужно.
В столбце У прописываем формулу для расчета функции. В нашем примере: =A2*(КОРЕНЬ(A2)-2). Нажимаем «Ввод». Excel посчитал значение. «Размножаем» формулу по всему столбцу (потянув за правый нижний угол ячейки). Таблица с данными готова.
Переходим на новый лист (можно остаться и на этом – поставить курсор в свободную ячейку). «Вставка» — «Диаграмма» — «Точечная». Выбираем понравившийся тип. Щелкаем по области диаграммы правой кнопкой мыши – «Выбрать данные».
Выделяем значения Х (первый столбец). И нажимаем «Добавить». Открывается окно «Изменение ряда». Задаем имя ряда – функция. Значения Х – первый столбец таблицы с данными. Значения У – второй.
Жмем ОК и любуемся результатом.
С осью У все в порядке. На оси Х нет значений. Проставлены только номера точек. Это нужно исправить. Необходимо подписать оси графика в excel. Правая кнопка мыши – «Выбрать данные» — «Изменить подписи горизонтальной оси». И выделяем диапазон с нужными значениями (в таблице с данными). График становится таким, каким должен быть.
Наложение и комбинирование графиков
Построить два графика в Excel не представляет никакой сложности. Совместим на одном поле два графика функций в Excel. Добавим к предыдущей Z=X(√x – 3). Таблица с данными:
Выделяем данные и вставляем в поле диаграммы. Если что-то не так (не те названия рядов, неправильно отразились цифры на оси), редактируем через вкладку «Выбрать данные».
А вот наши 2 графика функций в одном поле.
Графики зависимости
Данные одного столбца (строки) зависят от данных другого столбца (строки).
Построить график зависимости одного столбца от другого в Excel можно так:
Условия: А = f (E); В = f (E); С = f (E); D = f (E).
Выбираем тип диаграммы. Точечная. С гладкими кривыми и маркерами.
Выбор данных – «Добавить». Имя ряда – А. Значения Х – значения А. Значения У – значения Е. Снова «Добавить». Имя ряда – В. Значения Х – данные в столбце В. Значения У – данные в столбце Е. И по такому принципу всю таблицу.
Скачать все примеры графиков
Готовые примеры графиков и диаграмм в Excel скачать:
Как сделать шаблон, дашборд, диаграмму или график для создания красивого отчета удобного для визуального анализа в Excel? Выбирайте примеры диаграмм с графиками для интерактивной визуализации данных с умных таблиц Excel и используйте их для быстрого принятия правильных решений. Бесплатно скачивайте готовые шаблоны динамических диаграмм для использования их в дашбордах, отчетах или презентациях.
Точно так же можно строить кольцевые и линейчатые диаграммы, гистограммы, пузырьковые, биржевые и т.д. Возможности Excel разнообразны. Вполне достаточно, чтобы наглядно изобразить разные типы данных.
Цель работы:
- научиться строить графики в Excel;
- развить самостоятельность;
- развить навыки мыслительной деятельности, включая каждого учащегося в учебно – познавательный процесс и создавая условия для работы каждого в индивидуальном темпе;
Оборудование:
- ПЭВМ, сеть, проектор;
- опорный конспект, план практической работы, варианты для самостоятельной работы учащихся.
| Этапы | План урока + опорный конспект | Средства обучения |
| I | Подготовительный. Постановка учебных задач. Устное разъяснение порядка работы на уроке, тема урока. |
— |
| II | Повторение.
Фронтальный опрос изученного материала. Вопросы:
|
проектор |
| III | Объяснение нового материала и подготовка к практической работе:
|
Проектор, раздаточный материал |
| IV | Выполнение проектной практической работы:
|
Компьютер |
| V | Итоги:
|
Проектор, раздаточный материал, компьютер |
Опорный конспект
Построение совмещенных графиков в Microsoft Office Excel -2007.
Для построения графиков функций Y(X) в Microsoft Office Excel используется тип диаграммы Точечная:
Для этого требуется два ряда значений: Х и Y значения, которые должны быть соответственно расположены в левом и правом столбцах.
Можно совместить построение нескольких графиков. Такая возможность используется для графического решения систем уравнений с двумя переменными, при проведении сравнения анализа значений y при одних и тех же значениях x.
ПРИМЕР.
(Используется при объяснении материала через проектор.)
Построить графики функций y1= x 2 и y2= x 3 на интервале [- 3 ; 3] с шагом 0,5.
Алгоритм выполнения задания:
1. Заполнить таблицу значений:
2. Выделить таблицу и указать тип диаграммы Точечная.
3. Выбрать формат точечной диаграммы с гладкими кривыми.
4. В Макете указать название диаграммы «Графики», дать название осей: X и Y
5. Должен получиться график:
P.S. В версии 97-2003 для получения графика, представленного на рисунке надо провести редактирование.
Раздаточный материал
Варианты
ВАРИАНТ 1
Построить графики функций y1= x 2 -1, y2= x 2+1 иy=К·(y1/ y2)на интервале [- 3 ; 3] с шагом 0,3.
ВАРИАНТ 2
Построить графики функций y1= и y2= 2х на интервале [- 3 ; 3] с шагом 0,5.
ВАРИАНТ 3
Построить графики функций y1= , y2=
на интервале [- 0,5 ; 9] с шагом 0,5.
ВАРИАНТ 4
Построить графики функций y1=, y2=
на интервале [- 5 ; -0,5] с шагом 0,5.
ВАРИАНТ 5
Построить графики функций y1= , y2=
на интервале [0,5 ; 5] с шагом 0,5.
Диаграммы позволяют наглядно представить данные, чтобы произвести наибольшее впечатление на аудиторию. Узнайте, как создать диаграмму и добавить линию тренда. Вы можете начать документ с рекомендуемой диаграммы или выбрать один из наших шаблонов предварительно созданных диаграмм.
Создание диаграммы
-
Выберите данные для диаграммы.
-
На вкладке Вставка нажмите кнопку Рекомендуемые диаграммы.
-
На вкладке Рекомендуемые диаграммы выберите диаграмму для предварительного просмотра.
Примечание: Можно выделить нужные данные для диаграммы и нажать клавиши ALT+F1, чтобы сразу создать диаграмму, однако результат может оказаться не самым лучшим. Если подходящая диаграмма не отображается, перейдите на вкладку Все диаграммы, чтобы просмотреть все типы диаграмм.
-
Выберите диаграмму.
-
Нажмите кнопку ОК.
Добавление линии тренда
-
Выберите диаграмму.
-
На вкладке Конструктор нажмите кнопку Добавить элемент диаграммы.
-
Выберите пункт Линия тренда, а затем укажите тип линии тренда: Линейная, Экспоненциальная, Линейный прогноз или Скользящее среднее.
Примечание: Часть содержимого этого раздела может быть неприменима к некоторым языкам.
Диаграммы отображают данные в графическом формате, который может помочь вам и вашей аудитории визуализировать связи между данными. При создании диаграммы доступно множество типов диаграмм (например, гистограмма с накоплением или трехмерная разрезанная круговая диаграмма). После создания диаграммы ее можно настроить, применив экспресс-макеты или стили.
Диаграмма содержит несколько элементов, таких как заголовок, подписи осей, условные обозначения и линии сетки. Вы можете скрыть или показать эти элементы, а также изменить их расположение и форматирование.
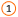

Диаграмму можно создать в Excel, Word и PowerPoint. Однако данные диаграммы вводятся и сохраняются на листе Excel. При вставке диаграммы в Word или PowerPoint открывается новый лист в Excel. При сохранении документа Word или презентации PowerPoint с диаграммой данные Excel для этой диаграммы автоматически сохраняются в документе Word или презентации PowerPoint.
Примечание: Коллекция книг Excel заменяет прежний мастер диаграмм. По умолчанию коллекция книг Excel открывается при запуске Excel. В коллекции можно просматривать шаблоны и создавать на их основе новые книги. Если коллекция книг Excel не отображается, в меню Файл выберите пункт Создать на основе шаблона.
-
В меню Вид выберите пункт Разметка страницы.
-
На вкладке Вставка щелкните стрелку рядом с кнопкой Диаграмма.
-
Выберите тип диаграммы и дважды щелкните нужную диаграмму.
При вставке диаграммы в приложение Word или PowerPoint открывается лист Excel с таблицей образцов данных.
-
В приложении Excel замените образец данных данными, которые нужно отобразить на диаграмме. Если эти данные уже содержатся в другой таблице, их можно скопировать оттуда и вставить вместо образца данных. Рекомендации по упорядочиванию данных в соответствии с типом диаграммы см. в таблице ниже.
Тип диаграммы
Расположение данных
Диаграмма с областями, линейчатая диаграмма, гистограмма, кольцевая диаграмма, график, лепестковая диаграмма или поверхностная диаграмма
Данные расположены в столбцах или строках, как в следующих примерах:
Последовательность 1
Последовательность 2
Категория А
10
12
Категория Б
11
14
Категория В
9
15
или
Категория А
Категория Б
Последовательность 1
10
11
Последовательность 2
12
14
Пузырьковая диаграмма
Данные расположены в столбцах, причем значения x — в первом столбце, а соответствующие значения y и размеры пузырьков — в смежных столбцах, как в следующих примерах:
Значения X
Значение Y 1
Размер 1
0,7
2,7
4
1,8
3,2
5
2,6
0,08
6
Круговая диаграмма
Один столбец или строка данных и один столбец или строка меток данных, как в следующих примерах:
Продажи
Кв. 1
25
Кв. 2
30
Кв. 3
45
или
Кв. 1
Кв. 2
Кв. 3
Продажи
25
30
45
Биржевая диаграмма
Данные расположены по столбцам или строкам в указанном ниже порядке с использованием названий или дат в качестве подписей, как в следующих примерах:
Открыть
Максимум
Минимум
Закрыть
1/5/02
44
55
11
25
1/6/02
25
57
12
38
или
1/5/02
1/6/02
Открыть
44
25
Максимум
55
57
Минимум
11
12
Закрыть
25
38
X Y (точечная) диаграмма
Данные расположены по столбцам, причем значения x — в первом столбце, а соответствующие значения y — в смежных столбцах, как в следующих примерах:
Значения X
Значение Y 1
0,7
2,7
1,8
3,2
2,6
0,08
или
Значения X
0,7
1,8
2,6
Значение Y 1
2,7
3,2
0,08
-
Чтобы изменить число строк и столбцов, включенных в диаграмму, наведите указатель мыши на нижний правый угол выбранных данных, а затем перетащите угол, чтобы выбрать дополнительные данные. В приведенном ниже примере таблица расширяется, чтобы включить дополнительные категории и последовательности данных.
-
Чтобы увидеть результаты изменений, вернитесь в приложение Word или PowerPoint.
Примечание: При закрытии документа Word или презентации PowerPoint с диаграммой таблица данных Excel для этой диаграммы закроется автоматически.
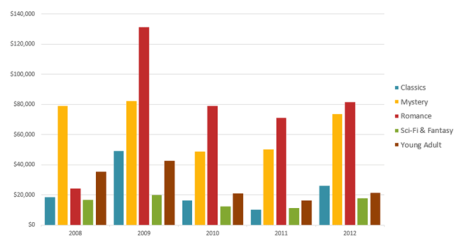
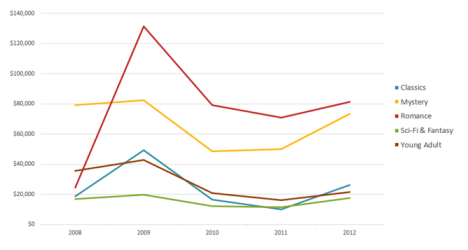
После создания диаграммы можно изменить способ отображения строк и столбцов таблицы в диаграмме. Например, в первой версии диаграммы строки данных таблицы могут отображаться по вертикальной оси (значение), а столбцы — по горизонтальной оси (категория). В следующем примере диаграмма акцентирует продажи по инструментам.
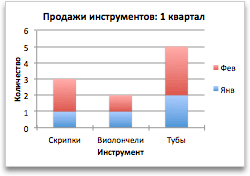
Однако если требуется сконцентрировать внимание на продажах по месяцам, можно изменить способ построения диаграммы.
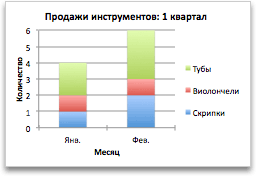
-
В меню Вид выберите пункт Разметка страницы.
-
Щелкните диаграмму.
-
Откройте вкладку Конструктор и нажмите кнопку Строка/столбец.
Если команда «Строка/столбец» недоступна
Элемент Строка/столбец доступен только при открытой таблице данных диаграммы Excel и только для определенных типов диаграмм. Вы также можете изменить данные, щелкнув диаграмму, а затем отредактировать лист в Excel.
-
В меню Вид выберите пункт Разметка страницы.
-
Щелкните диаграмму.
-
Откройте вкладку Конструктор и нажмите кнопку Экспресс-макет.
-
Выберите нужную разметку.
Чтобы сразу же отменить примененный экспресс-макет, нажмите клавиши
+ Z.
Стили диаграмм — это набор дополняющих цветов и эффектов, которые можно применить к диаграмме. При выборе стиля диаграммы изменения влияют на всю диаграмму.
-
В меню Вид выберите пункт Разметка страницы.
-
Щелкните диаграмму.
-
Откройте вкладку Конструктор и выберите нужный стиль.
Чтобы просмотреть другие стили, наведите курсор на интересующий вас элемент и щелкните
.
Чтобы сразу же отменить примененный стиль, нажмите клавиши
+Z.
-
В меню Вид выберите пункт Разметка страницы.
-
Щелкните диаграмму и откройте вкладку Конструктор.
-
Нажмите кнопку Добавить элемент диаграммы.
-
Выберите пункт Название диаграммы, чтобы задать параметры форматирования названия, а затем вернитесь к диаграмме, чтобы ввести название в поле Название диаграммы.
См. также
Обновление данных в существующей диаграмме
Типы диаграмм
Создание диаграммы
Вы можете создать диаграмму для данных в Excel в Интернете. В зависимости от данных можно создать гистограмму, линию, круговую диаграмму, линейчатую диаграмму, область, точечную или радиолокационную диаграмму.
-
Щелкните в любом месте данных, для которых требуется создать диаграмму.
Чтобы отобразить определенные данные на диаграмме, можно также выбрать данные.
-
Выберите «> диаграммы> и нужный тип диаграммы.
-
В открываемом меню выберите нужный вариант. Наведите указатель мыши на диаграмму, чтобы узнать больше о ней.
Совет: Ваш выбор не применяется, пока вы не выбираете параметр в меню команд «Диаграммы». Рассмотрите возможность просмотра нескольких типов диаграмм: при указании элементов меню рядом с ними отображаются сводки, которые помогут вам решить эту задачу.
-
Чтобы изменить диаграмму (заголовки, условные обозначения, метки данных), выберите вкладку «Диаграмма», а затем выберите » Формат».
-
В области диаграммы при необходимости измените параметр. Вы можете настроить параметры для заголовка диаграммы, условных обозначений, названий осей, заголовков рядов и т. д.
Типы диаграмм
Рекомендуется просмотреть данные и решить, какой тип диаграммы лучше всего подходит. Доступные типы перечислены ниже.
Данные в столбцах или строках листа можно представить в виде гистограммы. В гистограмме категории обычно отображаются по горизонтальной оси, а значения — по вертикальной оси, как показано на этой диаграмме:
Типы гистограмм
-
Кластеризованный столбецНа гистограмме с группировкой значения выводятся в виде плоских столбцов. Используйте этот тип диаграммы при наличии категорий, представляющих:
-
диапазоны значений (например, количество элементов);
-
специфические шкалы (например, шкала Ликерта с масками, такими как «Полностью согласен», «Согласен», «Не знаю», «Не согласен», «Полностью не согласен»);
-
неупорядоченные имена (например, названия элементов, географические названия или имена людей).
-
-
Столбец с стеками Гистограмма с накоплением представляет значения в виде плоских столбцов с накоплением. Используйте этот тип диаграммы, когда есть несколько ряд данных и нужно подчеркнуть итоговое значение.
-
Столбец с стеком на 100 %Нормированная гистограмма представляет значения в виде плоских нормированных столбцов с накоплением для представления 100 %. Используйте этот тип диаграммы, когда есть несколько рядов данных и нужно подчеркнуть их вклад в итоговое значение, особенно если итоговое значение одинаково для всех категорий.
Данные, расположенные в столбцах или строках листа, можно представить в виде графика. На графиках данные категорий равномерно распределяются вдоль горизонтальной оси, а все значения равномерно распределяются вдоль вертикальной оси. Графики позволяют отображать непрерывное изменение данных с течением времени на оси с равномерным распределением и идеально подходят для представления тенденций изменения данных с равными интервалами, такими как месяцы, кварталы или финансовые годы.
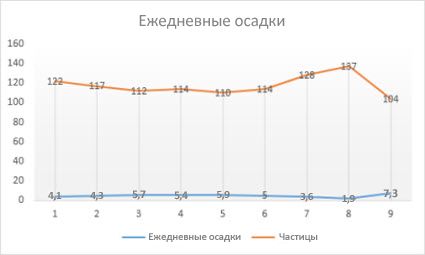
Типы графиков
-
Линии и линии с маркерамиГрафики с маркерами, отмечающими отдельные значения данных, или без маркеров можно использовать для отображения динамики изменения данных с течением времени или по категориям данных, разделенным равными интервалами, особенно когда точек данных много и порядок их представления существенен. Если категорий данных много или значения являются приблизительными, используйте график без маркеров.
-
Линия с стеками и линия с маркерамиГрафики с накоплением, отображаемые как с маркерами для конкретных значений данных, так и без них, могут отображать динамику изменения вклада каждого значения с течением времени или по категориям данных, разделенным равными интервалами.
-
100 % линий с стеками и 100 % стеками с маркерамиНормированные графики с накоплением с маркерами, отмечающими отдельные значения данных, или без маркеров могут отображать динамику вклада каждой величины в процентах с течением времени или по категориям данных, разделенным равными интервалами. Если категорий данных много или значения являются приблизительными, используйте нормированный график с накоплением без маркеров.
Примечания:
-
Графики лучше всего подходят для вывода нескольких рядов данных— если нужно отобразить только один ряд данных, вместо графика рекомендуется использовать точечную диаграмму.
-
На графиках с накоплением данные суммируются, что может быть нежелательно. Увидеть накопление на графике бывает непросто, поэтому иногда вместо него стоит воспользоваться графиком другого вида либо диаграммой с областями с накоплением.
-
Данные в одном столбце или строке листа можно представить в виде круговой диаграммы. Круговая диаграмма отображает размер элементов одного ряд данных относительно суммы элементов. точки данных на круговой диаграмме выводятся как проценты от всего круга.
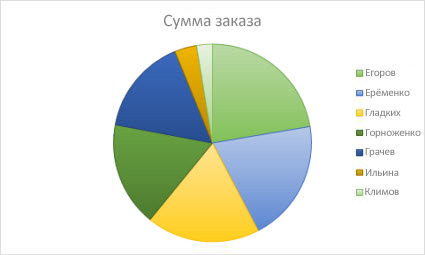
Круговую диаграмму рекомендуется использовать, если:
-
нужно отобразить только один ряд данных;
-
все значения ваших данных неотрицательны;
-
почти все значения данных больше нуля;
-
имеется не более семи категорий, каждой из которых соответствуют части общего круга.
Данные, расположенные только в столбцах или строках листа, можно представить в виде кольцевой диаграммы. Как и круговая диаграмма, кольцевая диаграмма отображает отношение частей к целому, но может содержать несколько ряд данных.
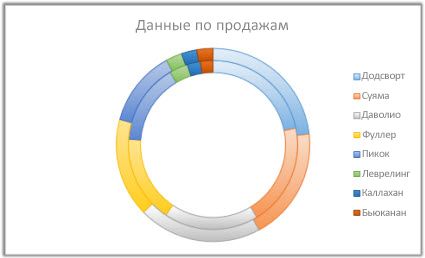
Совет: Восприятие кольцевых диаграмм затруднено. Вместо них можно использовать линейчатые диаграммы с накоплением или гистограммы с накоплением.
Данные в столбцах или строках листа можно представить в виде линейчатой диаграммы. Линейчатые диаграммы используют для сравнения отдельных элементов. В диаграммах этого типа категории обычно располагаются по вертикальной оси, а величины — по горизонтальной.
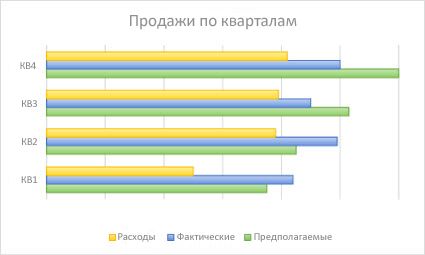
Линейчатые диаграммы рекомендуется использовать, если:
-
метки осей имеют большую длину;
-
выводимые значения представляют собой длительности.
Типы линейчатых диаграмм
-
КластерныйНа линейчатой диаграмме с группировкой значения выводятся в виде плоских столбцов.
-
Линейчатая диаграмма с стекамиЛинейчатая диаграмма с накоплением показывает вклад отдельных величин в общую сумму в виде плоских столбцов.
-
Стека на 100 %Этот тип диаграмм позволяет сравнить по категориям процентный вклад каждой величины в общую сумму.
Данные в столбцах или строках листа можно представить в виде диаграммы с областями. Диаграммы с областями могут использоваться для отображения изменений величин с течением времени и привлечения внимания к итоговому значению в соответствии с тенденцией. Отображая сумму значений рядов, такая диаграмма также наглядно показывает вклад каждого ряда.
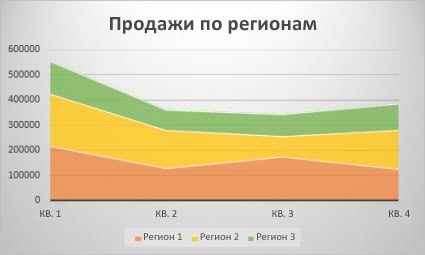
Типы диаграмм с областями
-
ОбластиДиаграммы с областями отображают изменение величин с течением времени или по категориям. Обычно вместо диаграмм с областями без накопления рекомендуется использовать графики, так как данные одного ряда могут быть скрыты за данными другого ряда.
-
Область с накоплениемДиаграммы с областями с накоплением показывают изменения вклада каждой величины с течением времени или по категориям в двухмерном виде.
-
На 100 % с накоплением диаграммы с областями с накоплением показывают тенденцию процентного участия каждого значения с течением времени или других данных категории.
Данные в столбцах и строках листа можно представить в виде точечной диаграммы. Поместите данные по оси X в одну строку или столбец, а соответствующие данные по оси Y — в соседние строки или столбцы.
Точечная диаграмма имеет две оси значений: горизонтальную (X) и вертикальную (Y). На точечной диаграмме значения «x» и «y» объединяются в одну точку данных и выводятся через неравные интервалы или кластеры. Точечные диаграммы обычно используются для отображения и сравнения числовых значений, например научных, статистических или технических данных.
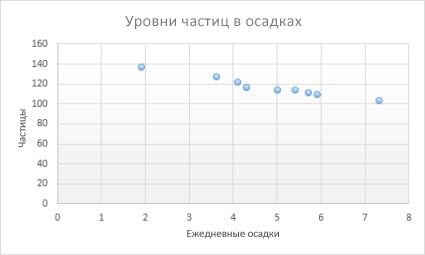
Точечные диаграммы рекомендуется использовать, если:
-
требуется изменять масштаб горизонтальной оси;
-
требуется использовать для горизонтальной оси логарифмическую шкалу;
-
значения расположены на горизонтальной оси неравномерно;
-
на горизонтальной оси имеется множество точек данных;
-
требуется настраивать независимые шкалы точечной диаграммы для отображения дополнительных сведений о данных, содержащих пары сгруппированных полей со значениями;
-
требуется отображать не различия между точками данных, а аналогии в больших наборах данных;
-
требуется сравнивать множество точек данных без учета времени; чем больше данных будет использовано для построения точечной диаграммы, тем точнее будет сравнение.
Типы точечных диаграмм
-
РазбросДиаграмма этого типа позволяет отображать точки данных без соединительных линий для сравнения пар значений.
-
Точечная с плавными линиями и маркерами и точечная с плавными линиямиНа этой диаграмме точки данных соединены сглаживающими линиями. Такие линии могут отображаться с маркерами или без них. Сглаживающую кривую без маркеров следует использовать, если точек данных достаточно много.
-
Точечная с прямыми линиями и маркерами и точечная с прямыми линиямиНа этой диаграмме показаны линии прямого соединения между точками данных. Прямые линии могут отображаться с маркерами или без них.
Данные в столбцах или строках листа можно представить в виде лепестковой диаграммы. Лепестковая диаграмма позволяет сравнить агрегированные значения нескольких ряд данных.
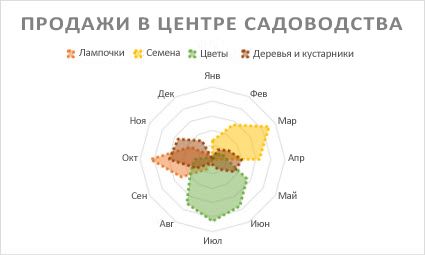
Типы лепестковых диаграмм
-
Радиолокационные и радиолокационные диаграммы с маркерами с маркерами для отдельных точек данных или без них отображают изменения значений относительно центральной точки.
-
Заполненный лепесткНа лепестковой диаграмме с областями области, заполненные рядами данных, выделены цветом.
Добавление или изменение заголовка диаграммы
Вы можете добавить или изменить заголовок диаграммы, настроить ее внешний вид и включить ее в диаграмму.
-
Щелкните в любом месте диаграммы, чтобы отобразить на ленте вкладку Диаграмма.
-
Нажмите Формат, чтобы открыть параметры форматирования диаграммы.
-
На панели » Диаграмма» разверните раздел «Заголовок диаграммы«.
-
Добавьте или измените заголовок диаграммы в соответствии со своими потребностями.
-
Используйте переключатель, чтобы скрыть заголовок, если вы не хотите, чтобы на диаграмме отображались заголовки.
Добавление названий осей для улучшения удобочитаемости диаграммы
Добавление заголовков к горизонтальным и вертикальным осям на диаграммах с осями упрощает их чтение. Названия осей нельзя добавлять к диаграммам без осей, таким как круговые и кольцевые диаграммы.
Как и заголовки диаграмм, названия осей помогают пользователям, просматривая диаграмму, понять, что такое данные.
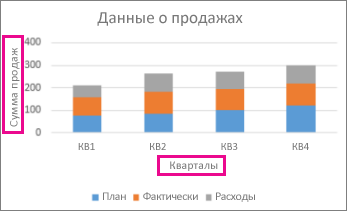
-
Щелкните в любом месте диаграммы, чтобы отобразить на ленте вкладку Диаграмма.
-
Нажмите Формат, чтобы открыть параметры форматирования диаграммы.
-
На панели диаграммы разверните раздел «Горизонтальная ось » или » Вертикальная ось».
-
Добавьте или измените параметры горизонтальной оси или вертикальной оси в соответствии со своими потребностями.
-
Разверните заголовок оси.
-
Измените заголовок оси и форматирование.
-
Используйте переключатель, чтобы отобразить или скрыть заголовок.
Изменение меток оси
Метки оси отображаются под горизонтальной осью и рядом с вертикальной осью. Диаграмма использует текст в исходных данных для этих меток оси.
Чтобы изменить текст меток категорий на горизонтальной или вертикальной оси:
-
Щелкните ячейку с текстом метки, который вы хотите изменить.
-
Введите нужный текст и нажмите клавишу ВВОД.
Метки осей на диаграмме автоматически обновляются новым текстом.
Совет: Метки осей отличаются от заголовков осей, которые можно добавить для описания того, что отображается на осях. Названия осей не отображаются на диаграмме автоматически.
Удаление меток оси
Чтобы удалить метки на горизонтальной или вертикальной оси:
-
Щелкните в любом месте диаграммы, чтобы отобразить на ленте вкладку Диаграмма.
-
Нажмите Формат, чтобы открыть параметры форматирования диаграммы.
-
На панели диаграммы разверните раздел «Горизонтальная ось » или » Вертикальная ось».
-
В раскрывающемся списке «Положение метки» выберите«Нет «, чтобы метки не отображались на диаграмме.
Дополнительные сведения
Вы всегда можете задать вопрос специалисту Excel Tech Community или попросить помощи в сообществе Answers community.
Аннотация:
Цель работы: научиться определять значения функций и строить графики, а также использовать логические функции в табличном процессоре Excel.
Содержание работы:
Построение графика функции с одной переменной.
Построение графика функции с двумя условиями.
Построение графика функции с тремя условиями.
Построение двух графиков в одной системе координат.
Построение поверхности.
Порядок выполнения работы:
Изучить методические указания.
Выполнить задания.
Оформить отчет и ответить на контрольные вопросы.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
Построение графика функции
Процесс построения графика функции состоит из двух этапов:
- создание таблицы значений функции
- непосредственного построения ее графика.
Для построения графика функции необходимо первоначально построить таблицу ее значений при различных значениях аргумента, причем аргумент изменяют обычно с фиксированным шагом. Шаг выбирают небольшим, так чтобы таблица значений функции отражала ее поведение на интервале табуляции.
Рассмотрим технологию построения графика на примере функции 
![$xin [0; 1]$](https://intuit.ru/sites/default/files/tex_cache/da5cff3c7142ff2260693225ac8b1877.png)
Создание таблицы значений функции
В нашем случае возьмем в качестве шага изменения аргумента, например, 0.1. Нам надо найти у(0), у(0.1), у(0.2), …, у(1). С этой целью в ячейки диапазона A1:А11 последовательно введем 0, 0.1, …, 1, т. е. значения переменной х. Отметим, что эта последовательность значений представляет собой арифметическую прогрессию.
Ввести в ячейки диапазона ряд последовательных значений, образующих арифметическую прогрессию, можно двумя способами.
Первый способ заключается в следующем:
- В ячейки А1 и А2 введите первый и второй члены арифметической прогрессии, т.е. 0 и 0,1
- Выделите диапазон ячеек А1:А2.
- Расположите указатель мыши на маркере заполнения выделенного диапазона (рис. 4.1
рис.
4.1) и протяните его вниз (в данном случае на диапазон A3:А11) до тех пор, пока не получится числовой ряд нужной длины (рис. 4.2
рис.
4.2).
Второй способ позволяет пользоваться диалоговым окном Прогрессия. Для этого:
- В ячейку А1 введите первый член арифметической профессии.
- Выберите команду Главная > Редактирование > Заполнить > Прогрессия.
- В появившемся диалоговом окне Прогрессия (рис. 4.3
рис.
4.3) в группе Расположение выбираем переключатель по столбцам, а в группе Тип – переключатель арифметическая. В поле Шаг введите значение 0,1, а в поле Предельное значение – 1. - Нажмите кнопку ОК.
Рис.
4.1.
Вид указателя мыши на маркере заполнения
Рис.
4.2.
Арифметическая последовательность, построенная по первым ее двум членам с помощью маркера заполнения
Рис.
4.3.
Диалоговое окно Прогрессия
Диалоговое окно Прогрессия закроется, а на рабочем листе автоматически будет построена требуемая прогрессия.
Примечание. Диалоговое окно Прогрессия, отображаемое на экране выбором команды Главная > Редактировать > Заполнить > Прогрессия, также позволяет создавать геометрические прогрессии.
В ячейку В1 введите формулу: =СОS(ПИ( )*А1)^2.
Ввод формул в ячейку можно производить либо с клавиатуры, либо с помощью диалогового окна Мастер функций, которое отображается на экране либо выбором команды Формулы > Вставить Функцию, либо нажатием кнопки Вставка функции
Продемонстрируем работу с мастером функций на примере ввода упомянутой выше формулы.
- Выберите ячейку В1.
- Нажмите кнопку Вставка функции
панели инструментов Стандартная, либо выберите команду Формулы > Вставить Функцию. На экране отобразится диалоговое окно Мастер функций – шаг 1 из 2 (рис. 4.4
рис.
4.4). Оно состоит из двух частей: - Категория – со списком двенадцати категорий функций;
- Функция – со списком имен функций, входящих в выбранную категорию.
Категория Полный алфавитный перечень содержит все встроенные функции и их имена упорядочены в алфавитном порядке, категория 10 недавно использовавшихся содержит имена десяти последних примененных функций. Эта категория ускоряет вызов функций, постоянно используемых пользователем.
- Функция cos относится к категории Математические. Выберите эту функцию и нажмите кнопку ОК. На экране отобразится панель формул (рис. 4.5
рис.
4.5).
Рис.
4.4.
Диалоговое окно Мастер функций – шаг 1 из 2
Рис.
4.5.
Панель формул
В поле Число вводится аргумент функции – в рассматриваемом примере это ПИ ()*А1. С помощью клавиатуры в это поле введите только ПИ ( )*, а ссылку на ячейку А1 в формулу добавьте, щелкнув по ячейке А1 на рабочем листе. Конечно, ее можно было также ввести с клавиатуры, но предложенный способ дает дополнительную проверку правильности ввода. После нажатия кнопки ОК в ячейку В1 будет введена формула:
Примечание. При использовании мастера функции перед вводом формулы в ячейку не надо вводить знак =, он вставляется в формулу автоматически.
- С помощью клавиатуры добавьте в формуле =COS(ПИ ())*А1 операцию возведения в квадрат функции cos. После всех описанных действий в ячейке В1 должна появиться формула =COS(ПИ()*Al)^2
Таким образом, пока найдено значение функции cos2(x) для значения х из ячейки A1. Теперь нам осталось найти значения этой функции для диапазона ячеек А2:А11.
Для этого:
- Выберите ячейку В1.
- Расположите указатель мыши на маркере заполнения выделенной ячейки и протяните его вниз на диапазон В2:В11.
Процесс создания таблицы значений функции завершен (рис. 4.6
рис.
4.6).
На рис. 4.6
рис.
4.6 на правом рабочем листе приведены формулы, введенные в ячейки рабочего листа. Для того чтобы в ячейках рабочего листа отображались не значения, а формулы, надо выбрать команду Формулы > Зависимости формул и Показать формулы.
Рис.
4.6.
Результат табуляции функции до и после форматирования данных
На среднем рабочем листе (рис. 4.6
рис.
4.6) приведен результат табуляции функции. Выглядит он не очень презентабельно: после десятичной точки отображается различное количество десятичных знаков. Кроме того, происходит перемешивание числового и экспоненциального форматов.
А именно, в ячейке В6 вместо 0 отображается 3.75Е-33, что приблизительно и равно нулю. Поэтому форматы надо привести к какому-то общему виду, например, как показано на левом рабочем листе: значения аргумента выводятся в числовом формате с точностью до одного знака после десятичной точки, а значения функции – с точностью до трех знаков после десятичной точки. Отформатируем, например, значения аргумента.
Для этого надо выбрать диапазон A1:A11. Это можно сделать, например, следующим способом. Выберите ячейку А1, а затем при нажатой клавише <Shift> выделите ячейку А11. Диапазон А1:А11 выбран.
Переходим к форматированию данных. Выберите команду Главная > Число. В появившемся диалоговом окне Формат ячеек: Число в списке Числовые форматы выберите Числовой, а в поле Число десятичных знаков введите 1. Нажмите кнопку ОК. Данные в Al:A11 будут отформатированы, как показано на левом рабочем листе (рис. 4.6
рис.
4.6). Аналогичным образом разберитесь с диапазоном В1:В11.
Построение графика
Перейдем теперь к конструированию графика cos2(xх) функции по существующей таблице значений аргументов и соответствующих значений функции. Для этого:
- Выберите команду Вставка > Диаграмма.
- В появившемся диалоговом окне Мастер диаграмм на выберите вариант График, а в списке Вид укажите стандартный график (рис. 4.7
рис.
4.7). Нажмите кнопку Далее. - Чтобы изменить (шаг 2 из 4): источник данных диаграммы (которое позднее переименовывается в окно Исходные данные) необходимо нажать на график, затем выбрать вкладку Конструктор, затем вкладку Данные, Выбрать данные. В поле Диапазон автоматически будет введена ссылка на необходимый диапазон в абсолютном формате. Проверьте его, удалите 1 ряд. В итоге у вас должно получится, что Диапазон, =Лист1!$В1$:$В$11.
Обратите внимание на полученный график функции, отображаемый на вкладке Диапазон данных. В нем по оси ординат откладываются значения функции, а вот по оси абсцисс порядковые номера точек, а не значения аргумента.
Для того чтобы по оси абсцисс откладывались значения аргумента, надо выделить диаграмму и воспользоваться командой Конструктор > Данные > Выбрать данные, далее Подписи горизонтальной оси (категории) > Изменить и указать диапазон ячеек в которых расположен аргумент х функции.
Рис.
4.7.
Вкладка Стандартные диалогового окна Мастер диаграмм (шаг 1 из 4): тип диаграммы
Рис.
4.8.
Вкладка Диапазон данных диалогового окна Исходные данные
Создав диаграмму, можно изменить любой из ее элементов. Например, можно изменить вид осей, добавить название диаграммы, переместить или скрыть легенду, а также добавить дополнительные элементы.
Чтобы изменить диаграмму, выполните одно или несколько из указанных ниже действий.
- Изменение вида осей диаграммы. Можно указать масштаб осей и изменить промежутки между значениями или категориями. Для удобства чтения диаграммы можно добавить на оси деления указать величину промежутков между ними.
- Добавление к диаграмме названий и меток данных. Для пояснения отображенных на диаграмме данных можно добавить название диаграммы, названия осей и метки данных.
- Добавление легенды и таблицы данных Можно отобразить или скрыть легенду, изменить ее расположение или элементы. Для некоторых диаграмм также можно отобразить таблицу данных, в которой содержатся ключи легенды и значения, представленные на диаграмме.
- Применение специальных параметров для диаграмм разных типов Для различных типов диаграмм можно применять различные специальные линии (например, коридор колебания и линии тренда), полосы (например, полосы повышения и понижения и планки погрешностей), маркеры данных и т.д.
Вместо того чтобы добавлять или изменять элементы диаграммы и форматировать их вручную, можно быстро применить к данным готовый макет или стиль диаграммы. В приложении Excel существует множество полезных готовых макетов и стилей, которые можно адаптировать, изменив вручную макет или формат отдельных элементов диаграммы, таких как область диаграммы, область построения, ряды данных и легенда.
При использовании готового макета диаграммы на ней в определенном порядке отображается заданный набор элементов (например, названия, легенда, таблица данных или метки данных). Можно подобрать подходящий макет из предоставленных для диаграмм конкретного типа.
При использовании готового стиля диаграммы ее форматирование основано на примененной теме документа, поэтому внешний вид диаграммы будет соответствовать цветам темы (набору цветов), шрифтам темы (набору шрифтов заголовков и основного текста) и эффектам темы (набору границ и заливок), принятым в организации или заданным пользователем.
Собственные стили или макеты диаграмм создавать нельзя, но можно создать шаблоны диаграмм, содержащие нужный макет и форматирование.
Помимо применения готового стиля диаграммы можно легко изменить форматирование ее отдельных элементов, например маркеров данных, области диаграммы, области построения, чисел и текста в названиях и подписях, что привлечет внимание и сделает диаграмму оригинальной. Можно также применять стили фигур и стили WordArt или форматировать фигуры и текст в элементах диаграммы вручную.
Чтобы изменить форматирование диаграммы, выполните одно или несколько из указанных ниже действий:
- Заливка элементов диаграммы. Для привлечения внимания к определенным элементам диаграммы можно залить их цветом, текстурой, рисунком или применить градиентную заливку.
- Изменение контуров элементов диаграммы. Для выделения элементов диаграммы можно изменить цвет, стиль или толщину линий.
- Добавление специальных эффектов к элементам диаграммы. Для придания диаграмме завершенности к ее элементам можно применить специальные эффекты, например тень, отражение, свечение, сглаживание краев, рельеф или объемное вращение.
- Форматирование текста и чисел Текст и числа в названиях, подписях и надписях на диаграмме можно форматировать так же, как текст и числа на листе. Чтобы выделить текст или число, можно даже применять стили WordArt.
Рис.
4.9.
Вкладка Конструктор: параметры диаграммы
Рис.
4.10.
Диалоговое окно Макет: параметры диаграммы
Рис.
4.11.
Результат построения графика функции
Математические функции рабочего листа
Наиболее часто употребляемые стандартные математические функции рабочего листа приведены в табл. 4.1
таблица
4.1.
| Функция (рус.) | Функция (англ.) | Описание |
|---|---|---|
| 1 | 2 | 3 |
| ABS (число) | ABS (number) | Возвращает абсолютную величину аргумента |
| ACOS (число) | ACOS (number) | Возвращает арккосинус аргумента |
| ASIN (число) | ASIN (number) | Возвращает арксинус аргумента |
| ATAN (число) | ATAN (number) | Возвращает арктангенс аргумента |
| COS (число) | COS (number) | Возвращает косинус аргумента |
| EXP (число) | EXP (number) | Возвращает экспоненту аргумента, т.е результат возведения основания натурального логарифма в степень, равную значению аргумента |
| LN (число) | LN (number) | Возвращает натуральный логарифм аргумента |
| LOG (число) | LOG (number) | Возвращает логарифм аргумента по данному основанию, если основание опущено, то оно полагается равным 10 |
| LOG10 (число; основание) | LOG10 (number; base) | Возвращает десятичный логарифм аргумента |
| SIN (число) | SIN (number) | Возвращает синус аргумента |
| TAN (число) | TAN (number) | Возвращает тангенс аргумента |
| ЗНАК (число) | SGN (number) | Возвращает знак аргумента |
| ОСТАТ (число; делитель) | MOD (number1; number1) | Возвращает остаток от деления числа на делитель |
| ПИ ( ) | PI ( ) | Возвращает значение числа ? с точностью до 15 знаков (в данном случае 3.14159265358979). обратите внимание на то, что функция ПИ ( ) не имеет аргумента |
| СЛЧИС ( ) | RND ( ) | Возвращает случайное число между 0 и 1. Чтобы получить случайное вещественное число между a и b, можно использовать следующую формулу: СЛЧИС ( )*(b-a)+a |
| ЦЕЛОЕ (число) | INT (number) | Округляет число до ближайшего меньшего целого |
График функции с двумя условиями
Рассмотрим пример построения графика функции при ![$хin[0;1]$$](https://intuit.ru/sites/default/files/tex_cache/5bbd057004769c8519124b98a54a24bf.png)
График строится по принципам, представленным в п. 4.1 «Построение графика функции»
«Построение графиков функций и использование логических формул»
, за исключением того, что в ячейку В1 вводится формула:
=ЕСЛИ(А1<0.5;(1+ABS(0.2-А1))/(1+А1+А1^2);А1^ (1/3))
Примечание. Обратите внимание на то, что для возведения в степень в коде используется соответствующая операция, т.е. А1^(1/3), а не функция рабочего листа степень, т. е. степень (А1; 1/3). В обоих случаях получается один и тот же результат, но, применение операции возведения в степень здесь более разумно, т. к. делает код более очевидным.
В коде фигурирует функция логического ветвления Если (IF), которая имеет следующий синтаксис:
ЕСЛИ (лог выражение; значение_если_истина; значение_если_ложь)
Рассмотрим ее аргументы:
- лог выражение – это любое значение или выражение, принимающее значения истина или ложь. Например, А10=100 – это логическое выражение; если значение в ячейке А10 равно 100, то выражение принимает значение ИСТИНА. В противном случае – ЛОЖЬ. Данный аргумент может быть использован в любом операторе сравнения.
- значение_если_истина – это значение, которое возвращается, если лог выражение равно ИСТИНА. Например, если этот аргумент – строка «План реализации выполнен» и лог выражение равно ИСТИНА, тогда функция ЕСЛИ отобразит текст План реализации выполнен. Если лог выражение равно, ИСТИНА, а значение_если_истина пусто, то возвращается значение 0. Чтобы отобразить слово ИСТИНА, необходимо использовать логическое значение ИСТИНА для этого аргумента. значение_если_истина может быть формулой.
- значение_если_ложь – это значение, которое возвращается, если лог выражение равно ЛОЖЬ. Например, если этот аргумент – строка «План реализации перевыполнен» и лог выражение равно ЛОЖЬ, то функция ЕСЛИ отобразит текст План реализации перевыполнен. Если лог выражение равно ЛОЖЬ, а значение_если_ложь опущено (т. е. после значение_если_истина нет точки с запятой), то возвращается логическое значение ЛОЖЬ. Если лог выражение равно ЛОЖЬ, а значение_если_ложь пусто (т. е. после значение_если_истина стоит точка с запятой с последующей закрывающей скобкой), то возвращается значение 0. значение_если_ложь может быть формулой.
Логические функции
В MS Excel имеются функции логических условий, перечисленные в табл. 4.2.
таблица
4.2
| Функция (рус.) | Функция (англ.) | Описание |
|---|---|---|
| 1 | 2 | 3 |
| И (лог знач1; лог знач2; …) | AND (arg1, arg2, …) | Логическое умножение. |
| Возвращает значение ИСТИНА, если все аргументы имеют значение ИСТИНА; возвращает значение ЛОЖЬ, если хотя бы один аргумент имеет значение ЛОЖЬ. | ||
| Например, И (2+2=4; 2+3=5) возвращает значение ИСТИНА. | ||
| Если ячейка В4содержит число из интервала от 1 до 100, то функция И (1<В4; В4<100) возвращает значение ИСТИНА, а в противном случае – ЛОЖЬ. | ||
| ИЛИ (лог знач1; лог знач2; …) | OR (arg1, arg2, …) | Логическое сложение. |
| Возвращает ИСТИНА, если хотя бы один из аргументов имеет значение ИСТИНА; возвращает ЛОЖЬ, если все аргументы имеют значение ЛОЖЬ. | ||
| Например, И (2+2=4; 2+3=6) возвращает значение ИСТИНА. | ||
| Если ячейка В4 содержит число меньше 1 или больше 100, то ИЛИ (В4<1; В4>100) возвращает значение ИСТИНА, а в противном случае – ЛОЖЬ. | ||
| НЕ (лог знач) | NOT (arg) | Логическое отрицание. Изменяет на противоположное значение логическое значение своего аргумента. Например, НЕ (2+5=5) возвращает значение ИСТИНА. |
| Если ячейка В4 содержит число меньше 1 или больше 100, то НЕ (ИЛИ(В4<1;В4>100)) возвращает ЛОЖЬ, а в противном случае – ЛОЖЬ. |
Примечание. Кроме функции ЕСЛИ в MS Excel имеются еще две функции, использующие логические условия. Это функции:
СЧЁТЕСЛИ (COUNTIF) – подсчитывает количество ячеек внутри диапазона, удовлетворяющих заданному критерию;
СУММЕСЛИ (SUMIF) – суммирует значения тех ячеек диапазона, удовлетворяющих заданному критерию.
График функции с тремя условиями
Рассмотрим пример построения графика функции у при ![$xin [0; 1]$](https://intuit.ru/sites/default/files/tex_cache/da5cff3c7142ff2260693225ac8b1877.png)
График строится так, как описано в разд. «Построение графика функции» ранее в этой работе, за исключением того, что в ячейку В1 вводится формула:
=ЕСЛИ(А1<0.2;1+ LN(1+A1); ЕСЛИ(И(А1>=0.2;А1<=0.8); (1+А1^(1/2))/(1+А1);2*ЕХР(-2*А1)))
Тот же самый результат можно получить, введя в ячейку В1 более простую формулу:
=ЕСЛИ (A1<0.2; 1+LN (1+A1); ЕСЛИ (А1<=0.8; (1+А1^(1/2))/(1+А1); 2*ЕХР(-2*А1)))
Два графика в одной системе координат
Рассмотрим пример построения в одной системе координат при ![$хin [-3; 0]$](https://intuit.ru/sites/default/files/tex_cache/3402e4268486a77799e4db4dfaf5dc40.png)
- y = 2sin(x)
- z = 3 cos(2x) – sin(x)
Итак, начнем процесс построений.
- В ячейки А1, В1 и С1 введите соответственно х, у и z.
- Выделите диапазон А1:С1. Выберите команду Главная. На вкладке
Выравнивание появившегося диалогового окна Формат ячеек в группе Выравнивание в списке по горизонтали укажите значение по правому краю. Нажмите кнопку ОК. Заголовки столбцов окажутся выровненными по правому краю.
- В диапазон ячеек А2:А17 введите значения аргумента х от -3 до 0 с шагом 0.2.
- В ячейки В2 и С2 введите формулы: =2*SIN(A2), =3*COS(2*A2)-SIN(A2)
- Выделите диапазон В2:С2, расположите указатель мыши на маркере заполнения этого диапазона и пробуксируйте его вниз так, чтобы заполнить диапазон В3:С17.
- Выделите диапазон В3:С17. Выберите команду Вставка > Диаграмма.
- В появившемся диалоговом окне Мастер диаграмм (шаг 1 из 4): тип диаграммы выберите значение График. Нажмите кнопку Далее.
- На вкладке Данные > выбрать данные диалогового окна Исходные данные в поле ввода Подписи оси X укажите ссылку на диапазон А2:А17, значения из которого откладываются по оси абсцисс (рис. 4.12
рис.
4.12). В списке Ряд приводятся ряды данных, откладываемых по оси ординат (в нашем случае имеется два ряда данных). Эти ряды автоматически определяются на основе ссылки, указанной в поле ввода Диапазон предыдущего шага алгоритма. В поле Значения автоматически выводится ссылка на диапазон, соответствующий выбранному ряду из списка Ряд. В поле ввода Имя отображается ссылка на ячейку, в которой содержится заголовок соответствующего ряда. Этот заголовок в дальнейшем используется мастером диаграмм для создания легенды.
Рис.
4.12.
Вкладка Ряд диалогового окна Исходные данные до задания имен рядов
- Выберите в списке Ряд элемент Ряд1. В поле ввода Имя укажите ссылку на ячейку В1, значение из которой будет использоваться в качестве идентификатора данного ряда. Вводить эту ссылку надо не с клавиатуры, а выбором с рабочего листа ячейки В1. Это приведет к тому, что в поле Имя автоматически будет введена ссылка на ячейку в абсолютном формате. В данном случае, =Лист1!$В$1. Теперь осталось только щелкнуть на элементе Ряд1 списка Ряд. Это приведет к тому, что элемент Ряд1 поменяется на у, т. е. на то значение, которое содержится в ячейке В1. Аналогично поступите с элементом Ряд2 списка Ряд. Сначала выберите его, затем в поле ввода Имя укажите ссылку на ячейку С1, а потом щелкните на элементе Ряд2. На рис. 4.13
рис.
4.13 показана вкладка Ряд диалогового окна Исходные данные после задания имен рядов. Теперь можно нажать кнопку Далее. - В появившемся диалоговом окне Мастер диаграмм (шаг 3 из 4): параметры диаграммы на вкладке Заголовки в поле Название диаграммы введите График двух функций, в поле Ось X(категорий) введите х, в поле Ось Y(значений) введите у и z. На вкладке Легенда установите флажок Добавить легенду. Нажмите кнопку Далее.
- Нажмите кнопку Готово.
Результат проделанных шагов представлен на рисунке 4.14
рис.
4.14.
Рис.
4.13.
Вкладка Ряд диалогового окна Исходные данные после задания имен рядов
Для большей презентабельности построенной диаграммы в ней были произведены следующие изменения по сравнению с оригиналом:
- Изменена ориентация подписи оси ординат с вертикальной на горизонтальную. Для этого выберите подпись оси ординат. Нажмите правую кнопку мыши и в появившемся контекстном меню укажите команду Формат названия оси. На вкладке Выравнивание диалогового окна Формат названия оси в группе Ориентация установите горизонтальную ориентацию. Нажмите кнопку ОК.
- Для того чтобы пользователю было легче отличить, какая линия является графиком функции у, а какая – z, изменен вид графика функции z. С этой целью выделите график функции z. Нажмите правую кнопку мыши и в появившемся контекстном меню выберите команду Формат рядов данных. На вкладке Вид диалогового окна Формат ряда данных, используя элементы управления групп Маркер и Линия, установите необходимый вид линии графика. Нажмите кнопку ОК.
- Изменен фон графика. С этой целью выделите диаграмму (но не область построения). Нажмите правую кнопку мыши и в появившемся контекстном меню выберите команду Формат области диаграммы. На вкладке Вид диалогового окна Формат области диаграммы установите флажок скругленные углы, а используя элементы управления группы Заливка, установите цвет и вид заливки фона. Нажмите кнопку ОК.
Рис.
4.14.
Графики функций у(х) и z(x), построенные в одной системе координат
Построение поверхности
Продемонстрируем технологию построения поверхностей на примере следующей функции, зависящей от двух аргументов:
$z = x^{2}-y^{2}$ при ![$$хin [-2; 2], уin [-1; 1]$](https://intuit.ru/sites/default/files/tex_cache/9ba0e461aae4f553cbb9279438619e6b.png)
Прежде чем воспользоваться мастером диаграмм, надо построить таблицу значений функции z по обоим ее аргументам, например, по аргументу х от -2 до 2 с шагом 0.2, а по у от -1 до 1 с шагом 0.2.
Для этого:
- Введите в ячейку А2 значение -2, а в ячейку А3 значение -1.8. Выберите диапазон ячеек А2:А3. Расположите указатель мыши на маркере заполнения этого диапазона и протяните его на диапазон А4:А22. Таким, образом, значения аргумента х протабулированы от -2 до 2 с шагом 0.2.
- Введите в ячейку В1 значение -1, а в ячейку С1 значение -0.8. Выберите диапазон ячеек В1:С1. Расположите указатель мыши на маркере заполнения этого диапазона и протяните его на диапазон D1:L1. Значения аргумента у протабулированы от -1 до 1 с шагом 0.2.
- В ячейку В2 введите формулу: =$А2^2 – В$1^2.
- Выберите ячейку В2, расположите указатель мыши на маркере ее заполнения и протяните его вниз на диапазон В2:L22.
На левом рабочем листе (рис. 4.15
рис.
4.15) показан результат табуляции функции, зависящей от двух аргументов, а на правом – часть формул, которые были введены в ячейке при копировании формулы, введенной в ячейку В2, перемещением маркера заполнения на диапазон В2:L22.
Рис.
4.15.
Таблица значений функции, зависящей от двух аргументов
Примечание. Использование в формуле абсолютной ссылки на строку и столбец существенно. Напомним, что знак $ в имени ячейки, стоящий перед номером строки, создает абсолютную ссылку на строку, а перед именем столбца – абсолютную ссылку на столбец. Поэтому при буксировке формулы из ячейки В2 на диапазоны B2:L22, в ячейках этого диапазона будут найдены значения функции z при соответствующих значениях аргументов х и у.
Перейдем к конструированию поверхности по результатам табуляции. Для этого:
- Выберите команду Вставка > Диаграмма.
- В появившемся диалоговом окне Мастер диаграмм (шаг 1 из 4): тип диаграммы на вкладке Стандартные в списке Тип выберите значение Поверхность, а в списке Вид укажите стандартную поверхность. Нажмите кнопку Далее.
- В следующем диалоговом окне мастера диаграмм на вкладке Диапазон данных выберите переключатель Ряды в столбцах, т. к. данные располагаются в столбцах. В поле ввода Диапазон приведите ссылку на диапазон данных A1:L22, т. е. диапазон, который содержит в себе как значения аргументов, так и значения функции. Нажмите кнопку Далее.
- В появившемся диалоговом окне Мастер диаграмм (шаг 1 из 4): в параметры диаграммы на вкладке Заголовки в поле Название диаграммы введите поверхность, в поле Ось X (категорий) укажите х, в поле Ось Y (рядов данных) задайте у, в поле Ось Z (значений) введите z. На вкладке Легенда сбросьте флажок Добавить легенду. Нажмите кнопку Готово.
- Поверхность построена, как показано на рисунке 4.16
рис.
4.16.
Рис.
4.16.
Построенная поверхность и диалоговое окно Формат трехмерной проекции
Примечание. MS Excel разрешает пользователю не только изменять размеры рабочей области диаграммы посредством маркеров изменения размеров, но и ориентацию поверхности в пространстве. Для этого достаточно выделить диаграмму, а затем выбрать команду Диаграмма > Объемный вид. На экране отобразится диалоговое окно Формат трехмерной проекции, элементы которого как раз и позволяют изменять ориентацию поверхности в пространстве.
ЗАДАНИЯ
Вариант 1.
1. Построить в разных системах координат при ![$хin [-2; 2]$](https://intuit.ru/sites/default/files/tex_cache/729acb6c58a2ee33ae416d2c9a29dd92.png)
2. Построить в одной системе координат при ![$хin [-2; 2]$](https://intuit.ru/sites/default/files/tex_cache/729acb6c58a2ee33ae416d2c9a29dd92.png)
3. Построить поверхность 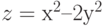
![$x,yin[-1; 1]$](https://intuit.ru/sites/default/files/tex_cache/1dccee169ef8cd4747131b25d37db985.png)
Вариант 2.
1. Построить в разных системах координат при ![$хin [-2; 2]$](https://intuit.ru/sites/default/files/tex_cache/729acb6c58a2ee33ae416d2c9a29dd92.png)
2. Построить в одной системе координат при ![$хin [-2; 2]$](https://intuit.ru/sites/default/files/tex_cache/729acb6c58a2ee33ae416d2c9a29dd92.png)
3. Построить поверхность 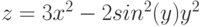
![$x, yin [-1; 1]$](https://intuit.ru/sites/default/files/tex_cache/53a8791dec1fce35a5f3ac0dd9605a3b.png)
Вариант 3.
1. Построить в разных системах координат при ![$xin[-2; 1.5]$](https://intuit.ru/sites/default/files/tex_cache/075d390c8429b09a75c1effe8b21041a.png)
2. Построить в одной системе координат при ![$хin [-2; 2]$](https://intuit.ru/sites/default/files/tex_cache/729acb6c58a2ee33ae416d2c9a29dd92.png)
3. Построить поверхность 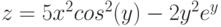
![$х,yin [-1; 1]$](https://intuit.ru/sites/default/files/tex_cache/7ee0738641bdcce8309351197a490d5c.png)
Вариант 4.
1. Построить в разных системах координат при ![$хin [-1.5; 1.5]$](https://intuit.ru/sites/default/files/tex_cache/f8ea986285591f482f6425385ca5802c.png)
2. Построить в одной системе координат при ![$хin [-2; 2]$](https://intuit.ru/sites/default/files/tex_cache/729acb6c58a2ee33ae416d2c9a29dd92.png)
3. Построить поверхность при мммх,yin [-1; 1]/ммм
Вариант 5.
1. Построить в разных системах координат при ![$хin [-1.8; 1.8]$](https://intuit.ru/sites/default/files/tex_cache/78bc9ae987003e9c6801db7908c6bfbd.png)
2. Построить в одной системе координат при ![$хin [0; 3]$](https://intuit.ru/sites/default/files/tex_cache/153306b868b619790149dea95767b4f9.png)
3. Построить поверхность 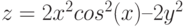
![$х,yin [-l; 1]$](https://intuit.ru/sites/default/files/tex_cache/f4f9de170788cb6bf2d9bec5dd801e0d.png)
Вариант 6.
1. Построить в разных системах координат при ![$хin [-2; 1.8]$](https://intuit.ru/sites/default/files/tex_cache/0dbcf9e9bff0f78d00043ecdd4c74666.png)
2. Построить в одной системе координат при ![$хin [-3; 0]$](https://intuit.ru/sites/default/files/tex_cache/3402e4268486a77799e4db4dfaf5dc40.png)
3. Построить поверхность 
![$х,yin [-1; 1]$](https://intuit.ru/sites/default/files/tex_cache/7ee0738641bdcce8309351197a490d5c.png)
Вариант 7.
1. Построить в разных системах координат при ![$хin [-1.7; 1.5]$](https://intuit.ru/sites/default/files/tex_cache/68c9476760c3d9265176b82bcc296063.png)
2. Построить в одной системе координат при ![$хin [-3;0]$](https://intuit.ru/sites/default/files/tex_cache/625e1ce96d5bf506d83f626e5934b564.png)
3. Построить поверхность 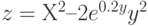
![$х,yin [-1;1]$](https://intuit.ru/sites/default/files/tex_cache/afd39bc8d16e67ea25b0fc35595fbb39.png)
Вариант 8.
1. Построить в разных системах координат при ![$хin [-1.5; 1.8]$](https://intuit.ru/sites/default/files/tex_cache/2629a936172ba4ce71bd2c2e792ee4c2.png)
2. Построить в одной системе координат при ![$хin [0; 2]$](https://intuit.ru/sites/default/files/tex_cache/e94a4675aee01c07248634bc60a09c53.png)
3. Построить поверхность при
Вариант 9.
1. Построить в разных системах координат при ![$хin [-1.4; 1.9]$](https://intuit.ru/sites/default/files/tex_cache/6c9405fb2d3d680c40a2b90ec8452bf2.png)
2. Построить в одной системе координат при ![$хin [0;2]$](https://intuit.ru/sites/default/files/tex_cache/adbba029f8747f8b59bce37c40dcc3a5.png)
3. Построить поверхность при
Вариант 10.
1. Построить в разных системах координат при ![$хin [-1.4; 1.4]$](https://intuit.ru/sites/default/files/tex_cache/077a3284889a9378e887806bcf4ea6f6.png)
2. Построить в одной системе координат при ![$хin [0; 2]$](https://intuit.ru/sites/default/files/tex_cache/e94a4675aee01c07248634bc60a09c53.png)
3. Построить поверхность z = 3x2sin2(x) – 5e2yу при ![$х,yin [-1; 1]$](https://intuit.ru/sites/default/files/tex_cache/7ee0738641bdcce8309351197a490d5c.png)
КОНТРОЛЬНЫЕ ВОПРОСЫ
- Из каких этапов состоит процесс построения графика функции?
- Какими способами можно ввести в ячейки диапазона ряд последовательных значений, образующих арифметическую прогрессию?
- Как подписать ось X значениями аргумента?
Содержание статьи (кликните для открытия/закрытия)
- Построение графика линейной функции в Excel
- Подготовка расчетной таблицы
- Построение графика функции
- Построение графиков других функций
- Квадратичная функция y=ax2+bx+c
- Кубическая парабола y=ax3
- Гипербола y=k/x
- Построение тригонометрических функций sin(x) и cos(x)
Построение графика зависимости функции является характерной математической задачей. Все, кто хотя бы на уровне школы знаком с математикой, выполняли построение таких зависимостей на бумаге. В графике отображается изменение функции в зависимости от значения аргумента. Современные электронные приложения позволяют осуществить эту процедуру за несколько кликов мышью. Microsoft Excel поможет вам в построении точного графика для любой математической функции. Давайте разберем по шагам, как построить график функции в excel по её формуле
Построение графиков в Excel 2016 значительно улучшилось и стало еще проще чем в предыдущих версиях. Разберем пример построения графика линейной функции y=kx+b на небольшом интервале [-4;4].
Подготовка расчетной таблицы
В таблицу заносим имена постоянных k и b в нашей функции. Это необходимо для быстрого изменения графика без переделки расчетных формул.
Далее строим таблицу значений линейной функции:
- В ячейки A5 и A6 вводим соответственно обозначения аргумента и саму функцию. Запись в виде формулы будет использована в качестве названия диаграммы.
- Вводим в ячейки B5 и С5 два значения аргумента функции с заданным шагом (в нашем примере шаг равен единице).
- Выделяем эти ячейки.
- Наводим указатель мыши на нижний правый угол выделения. При появлении крестика (смотри рисунок выше), зажимаем левую кнопку мыши и протягиваем вправо до столбца J.
Ячейки автоматически будут заполнены числами, значения которых различаются заданным шагом.
Далее в строку значений функции в ячейку B6 записываем формулу =$B3*B5+$D3
Внимание! Запись формулы начинается со знака равно(=). Адреса ячеек записываются на английской раскладке. Обратите внимание на абсолютные адреса со знаком доллара.
Чтобы завершить ввод формулы нажмите клавишу Enter или галочку слева от строки формул вверху над таблицей.
Копируем эту формулу для всех значений аргумента. Протягиваем вправо рамку от ячейки с формулой до столбца с конечными значениями аргумента функции.
Построение графика функции
Выделяем прямоугольный диапазон ячеек A5:J6.
Переходим на вкладку Вставка в ленте инструментов. В разделе Диаграмма выбираем Точечная с гладкими кривыми (см. рисунок ниже).Получим диаграмму.
После построения координатная сетка имеет разные по длине единичные отрезки. Изменим ее перетягивая боковые маркеры до получения квадратных клеток.
Теперь можно ввести новые значения постоянных k и b для изменения графика. И видим, что при попытке изменить коэффициент график остается неизменным, а меняются значения на оси. Исправляем. Кликните на диаграмме, чтобы ее активировать. Далее на ленте инструментов во вкладке Работа с диаграммами на вкладке Конструктор выбираем Добавить элемент диаграммы — Оси — Дополнительные параметры оси..
В правой части окна появиться боковая панель настроек Формат оси.
- Кликните на раскрывающийся список Параметры оси.
- Выберите Вертикальная ось (значений).
- Кликните зеленый значок диаграммы.
- Задайте интервал значений оси и единицы измерения (обведено красной рамкой). Ставим единицы измерения Максимум и минимум (Желательно симметричные) и одинаковые для вертикальной и горизонтальной осей. Таким образом, мы делаем мельче единичный отрезок и соответственно наблюдаем больший диапазон графика на диаграмме.И главную единицу измерения — значение 1.
- Повторите тоже для горизонтальной оси.
Теперь, если поменять значения K и b , то получим новый график с фиксированной сеткой координат.
Построение графиков других функций
Теперь, когда у нас есть основа в виде таблицы и диаграммы, можно строить графики других функций, внося небольшие корректировки в нашу таблицу.
Квадратичная функция y=ax2+bx+c
Выполните следующие действия:
- В первой строке меняем заголовок
- В третьей строке указываем коэффициенты и их значения
- В ячейку A6 записываем обозначение функции
- В ячейку B6 вписываем формулу =$B3*B5*B5+$D3*B5+$F3
- Копируем её на весь диапазон значений аргумента вправо
Получаем результат
Кубическая парабола y=ax3
Для построения выполните следующие действия:
- В первой строке меняем заголовок
- В третьей строке указываем коэффициенты и их значения
- В ячейку A6 записываем обозначение функции
- В ячейку B6 вписываем формулу =$B3*B5*B5*B5
- Копируем её на весь диапазон значений аргумента вправо
Получаем результат
Гипербола y=k/x
Для построения гиперболы заполните таблицу вручную (смотри рисунок ниже). Там где раньше было нулевое значение аргумента оставляем пустую ячейку.
Далее выполните действия:
- В первой строке меняем заголовок.
- В третьей строке указываем коэффициенты и их значения.
- В ячейку A6 записываем обозначение функции.
- В ячейку B6 вписываем формулу =$B3/B5
- Копируем её на весь диапазон значений аргумента вправо.
- Удаляем формулу из ячейки I6.
Для корректного отображения графика нужно поменять для диаграммы диапазон исходных данных, так как в этом примере он больше чем в предыдущих.
- Кликните диаграмму
- На вкладке Работа с диаграммами перейдите в Конструктор и в разделе Данные нажмите Выбрать данные.
- Откроется окно мастера ввода данных
- Выделите мышкой прямоугольный диапазон ячеек A5:P6
- Нажмите ОК в окне мастера.
Получаем результат
Построение тригонометрических функций sin(x) и cos(x)
Рассмотрим пример построения графика тригонометрической функции y=a*sin(b*x).
Сначала заполните таблицу как на рисунке ниже
В первой строке записано название тригонометрической функции.
В третьей строке прописаны коэффициенты и их значения. Обратите внимание на ячейки, в которые вписаны значения коэффициентов.
В пятой строке таблицы прописываются значения углов в радианах. Эти значения будут использоваться для подписей на графике.
В шестой строке записаны числовые значения углов в радианах. Их можно прописать вручную или используя формулы соответствующего вида =-2*ПИ(); =-3/2*ПИ(); =-ПИ(); =-ПИ()/2; …
В седьмой строке записываются расчетные формулы тригонометрической функции.
В нашем примере =$B$3*SIN($D$3*B6). Адреса B3 и D3 являются абсолютными. Их значения – коэффициенты a и b, которые по умолчанию устанавливаются равными единице.
После заполнения таблицы приступаем к построению графика.
Выделяем диапазон ячеек А6:J7. В ленте выбираем вкладку Вставка в разделе Диаграммы указываем тип Точечная и вид Точечная с гладкими кривыми и маркерами.
В итоге получим диаграмму.
Теперь настроим правильное отображение сетки, так чтобы точки графика лежали на пересечении линий сетки. Выполните последовательность действий Работа с диаграммами –Конструктор – Добавить элемент диаграммы – Сетка и включите три режима отображения линий как на рисунке.
Теперь зайдите в пункт Дополнительные параметры линий сетки. У вас появится боковая панель Формат области построения. Произведем настройки здесь.
Кликните в диаграмме на главную вертикальную ось Y (должна выделится рамкой). В боковой панели настройте формат оси как на рисунке.
Кликните главную горизонтальную ось Х (должна выделится) и также произведите настройки согласно рисунку.
Теперь сделаем подписи данных над точками. Снова выполняем Работа с диаграммами –Конструктор – Добавить элемент диаграммы – Подписи данных – Сверху. У вас подставятся значения числами 1 и 0, но мы заменим их значениями из диапазона B5:J5.
Кликните на любом значении 1 или 0 (рисунок шаг 1) и в параметрах подписи поставьте галочку Значения из ячеек (рисунок шаг 2). Вам будет сразу же предложено указать диапазон с новыми значениями (рисунок шаг 3). Указываем B5:J5.
Вот и все. Если сделали правильно, то и график будет замечательным. Вот такой.
Чтобы получить график функции cos(x), замените в расчетной формуле и в названии sin(x) на cos(x).
Аналогичным способом можно строить графики других функций. Главное правильно записать вычислительные формулы и построить таблицу значений функции. Надеюсь, что вам была полезна данная информация.
Дополнительные статьи по теме:
- Знакомство с таблицами в Excel
- Изменение строк и столбцов в Excel
- Работа с ячейками: объединение, изменение, защита…
- Ошибки в формулах: почему excel не считает
- Использования условий в формулах Excel
- Функция CЧЕТЕСЛИМН
- Работа с текстовыми функциями Excel
- Все уроки по Microsoft Excel
Дорогой читатель! Вы посмотрели статью до конца.
Получили вы ответ на свой вопрос? Напишите в комментариях пару слов. Если ответа не нашли, укажите что искали или откройте содержание блога.
ОЧЕНЬ ВАЖНО! Оцени лайком или дизлайком статью!

В большинстве случаев возникают затруднения при чтении книг Excel, содержащих большое количество информации. К счастью Excel располагает прекрасным инструментом визуализации данных – построением диаграмм. В этом уроке мы познакомимся с основными типами диаграмм, из каких элементов они состоят, а также построим нашу первую диаграмму.
Диаграммы в Excel способны графически представлять данные, что позволяет легче воспринимать большие объемы информации и оценивать ее. Excel предлагает самые различные типы диаграмм. Среди этого многообразия Вы можете подобрать именно ту диаграмму, которая наиболее точно подходит под Ваши нужды. Чтобы использовать диаграммы максимально эффективно, необходимо знать, как ими пользоваться в Excel. Итак, приступим к знакомству.
Содержание
- Типы диаграмм
- 1. Гистограмма
- 2. График
- 3. Круговые диаграммы
- 4. Линейчатая диаграмма
- 5. Диаграммы с областями
- 6. Поверхностные диаграммы
- Элементы диаграмм
- Как построить диаграмму в Excel
Типы диаграмм
Как Вы уже знаете, Excel располагает большим разнообразием типов диаграмм, каждый из которых имеет свои преимущества. Далее мы познакомимся с некоторыми из них:
1. Гистограмма
Гистограмма – это один из наиболее распространенных типов диаграмм. Гистограммы используют вертикальные столбцы для представления данных. Их можно применять в самых различных ситуациях, но чаще всего они используются для сравнения значений.
2. График
Графики, наряду с гистограммами, также очень популярны. Графики идеальны в отображении изменения непрерывных данных, а также для демонстрации трендов. Точки на графике соединяются линиями, позволяя увидеть динамику с течением времени.
3. Круговые диаграммы
Круговые диаграммы подходят для демонстрации пропорций, т.е. части чего-то относительно целого. Каждое значение представлено в виде доли (сектора) от суммы всех значений (круга). Круговая диаграмма строится для одного ряда данных и, как правило, содержит до 5-8 секторов. Такой подход очень полезен, когда нужно сравнить данные друг с другом.
Значения, используемые для построения круговой диаграммы, должны быть положительными. В противном случае Excel преобразует их в положительные, автоматически отбросив знак «минус».
4. Линейчатая диаграмма
Линейчатые диаграммы – это те же гистограммы, повернутые на 90 градусов, т.е. для представления информации используются не вертикальные столбцы, а горизонтальные.
5. Диаграммы с областями
Диаграммы с областями очень похожи на графики, за исключением того, что области под линиями заполнены цветом.
6. Поверхностные диаграммы
Поверхностные диаграммы в Excel позволяют представить информацию в виде 3D перспективы. Лучше всего эти диаграммы подходят для больших объемов данных, чтобы видеть сразу весь спектр информации.
Элементы диаграмм
Разобравшись с типами диаграмм, следующее, что необходимо сделать, это понять из чего она состоит. Диаграммы в Excel содержат 5 основных элементов, давайте рассмотрим их:
- Заголовок диаграммы должен четко описывать, что представлено на ней.
- Вертикальная ось (также известная как ось Y) является вертикальной частью диаграммы. На вертикальной оси отображаются значения столбцов, поэтому ее называют осью значений. В текущем примере величиной измерения является чистая выручка от продаж каждого продавца.
- Ряд данных состоит из связанных точек (значений) на диаграмме. В текущем примере синие столбы отражает выручку от продаж Роберта Привального. Мы понимаем, что выручка относится именно к этому продавцу, благодаря легенде в правой части диаграммы. Анализируя ряды данных, можно увидеть, что Роберт был лучшим продавцом в первом и третьем квартале и вторым во втором и четвертом.
- Легенда указывает принадлежность каждого ряда к кому-либо или чему-либо. В текущем примере легенда содержит 3 цвета с соответствующими продавцами. Видя легенду достаточно легко определить к какому продавцу относится каждый из столбцов.
- Горизонтальная ось (также известная как ось X) является горизонтальной частью диаграммы. Горизонтальная ось представляет категории. В данном примере каждый квартал содержит свою группу.
Как построить диаграмму в Excel
- Выделите ячейки, на основе которых Вы хотите построить диаграмму, включая заголовки столбцов и названия строк. Эти ячейки являются источником данных для диаграммы. В нашем примере мы выбрали диапазон ячеек A1:F6.
- На вкладке Вставка, выберите необходимую диаграмму. В нашем примере мы выберем Гистограмму.
- В раскрывающемся меню укажите подходящий тип гистограммы.
- Выбранная диаграмма появится на листе Excel.
Если Вы не уверены, какой тип диаграммы использовать, команда Рекомендуемые диаграммы предложит различные варианты на базе исходных данных.
Оцените качество статьи. Нам важно ваше мнение:












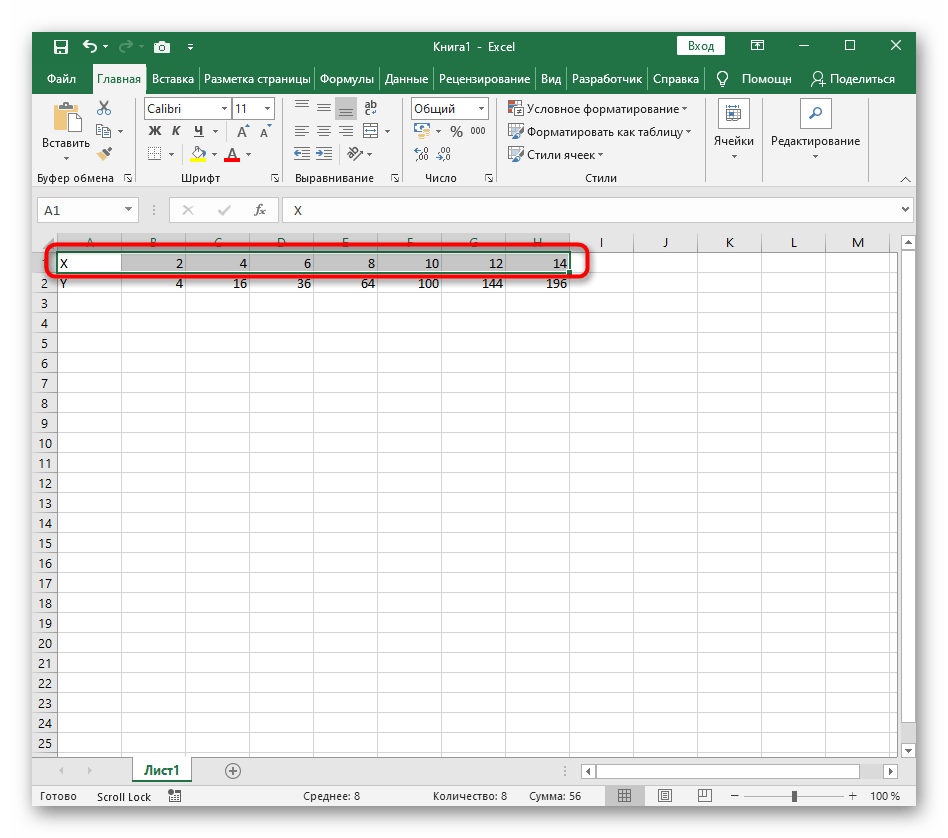
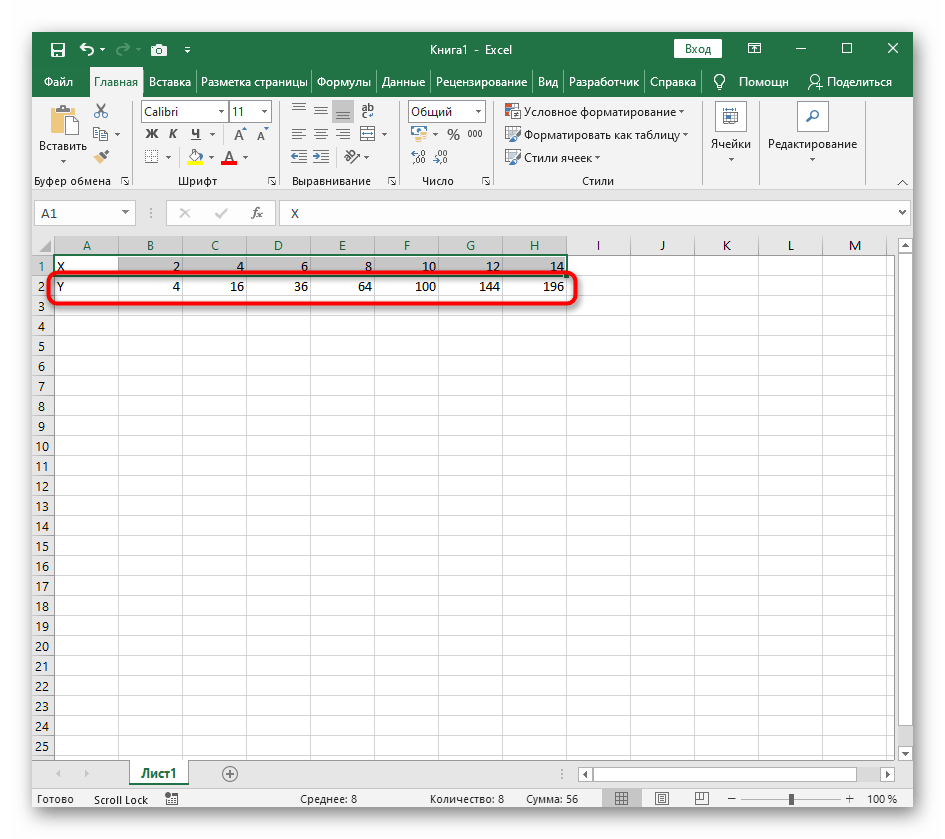
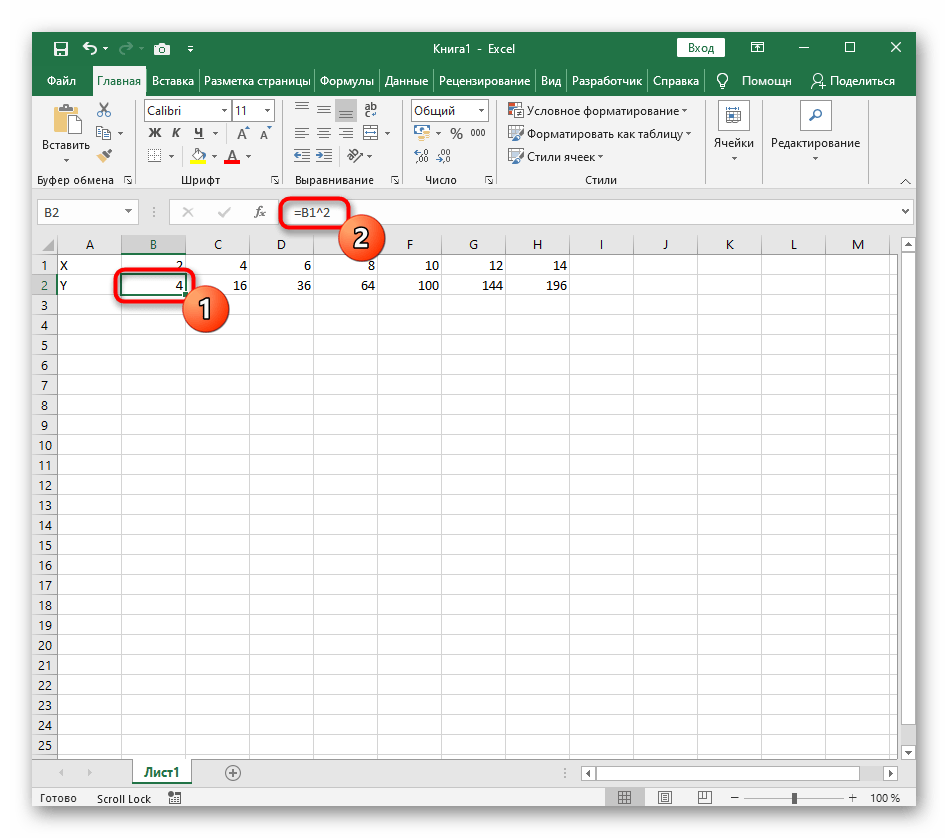
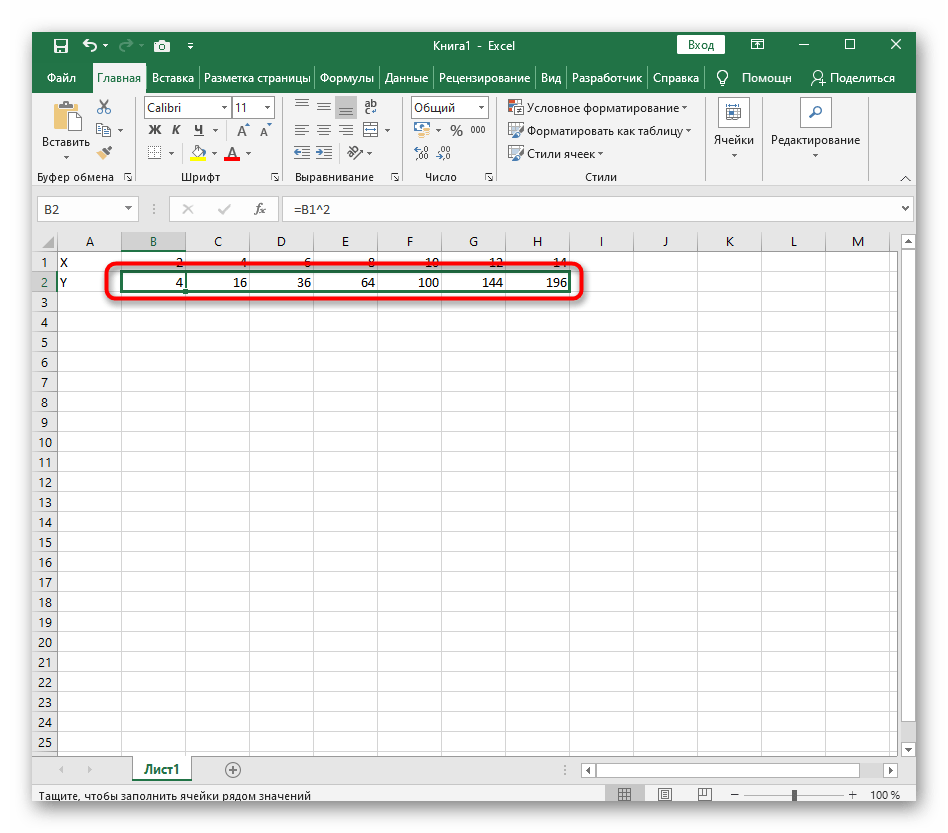
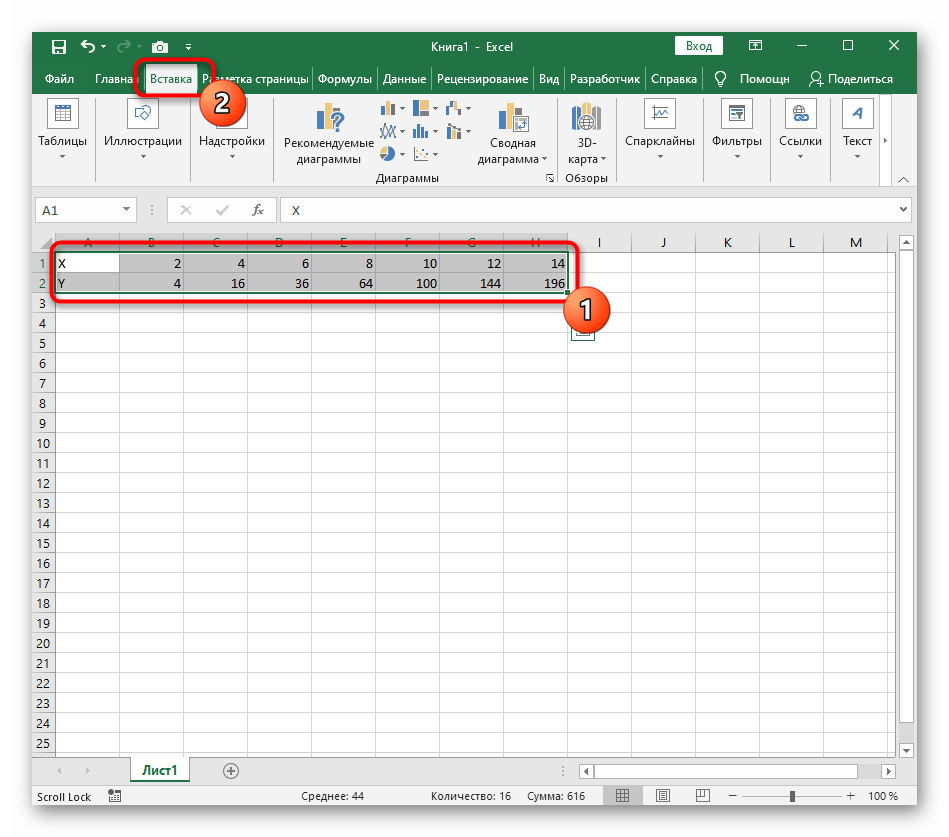
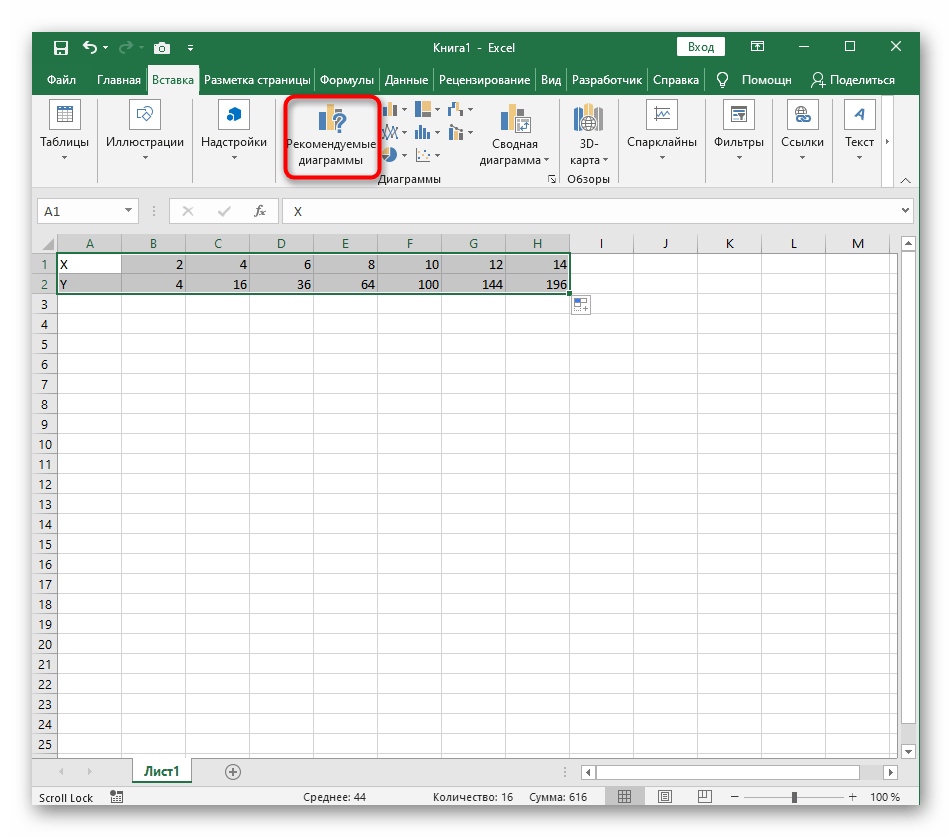
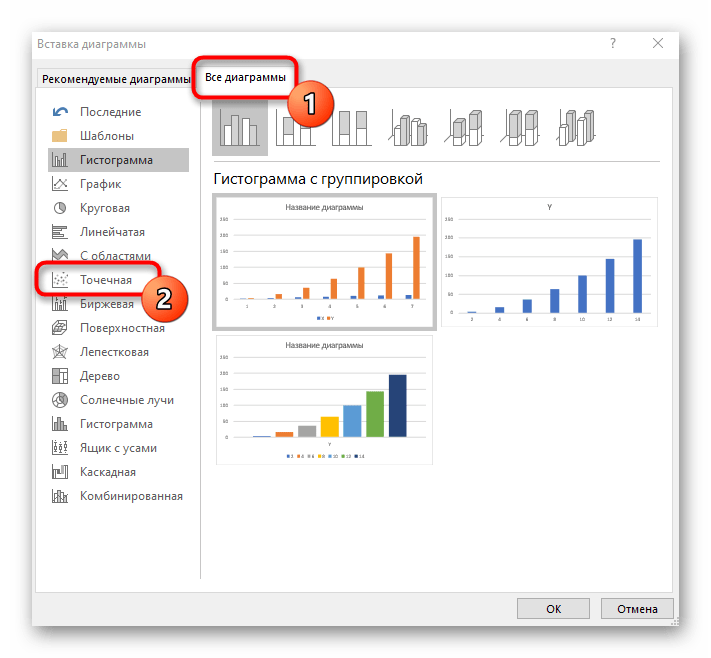
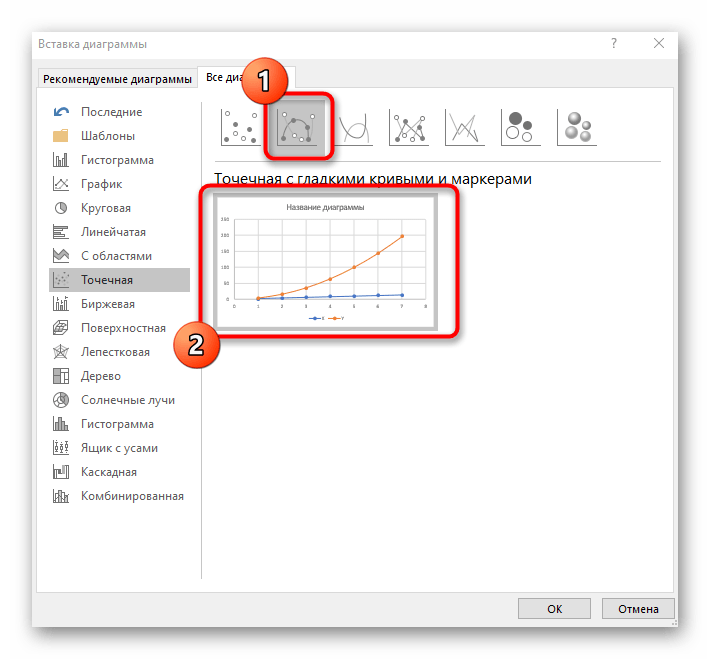
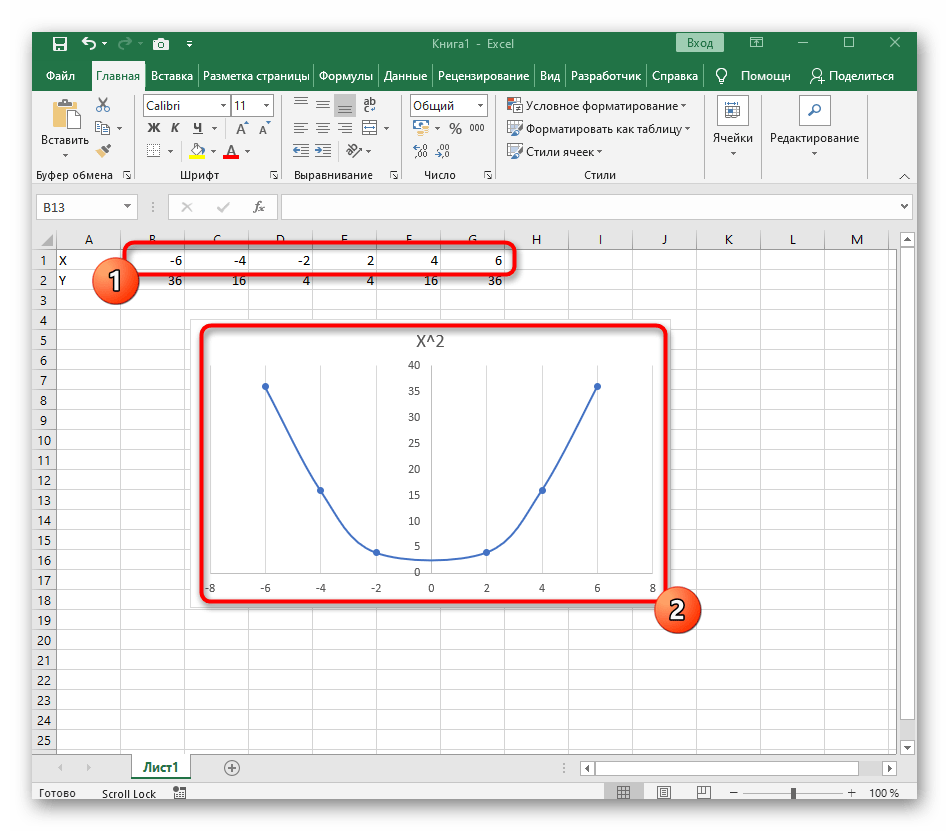
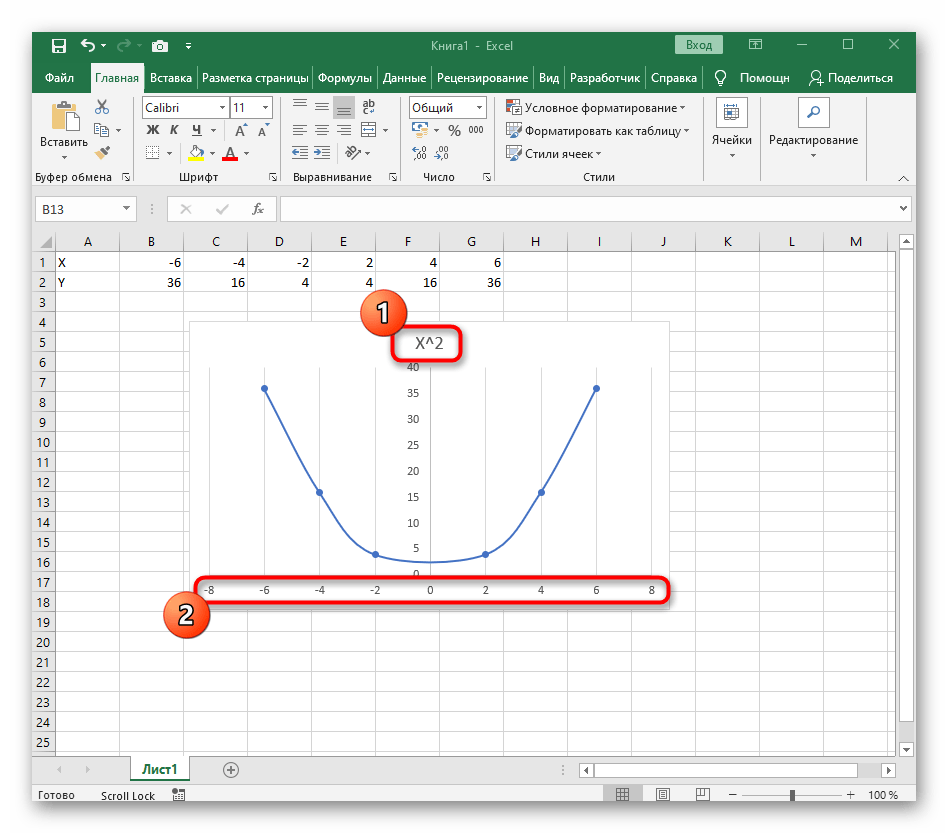









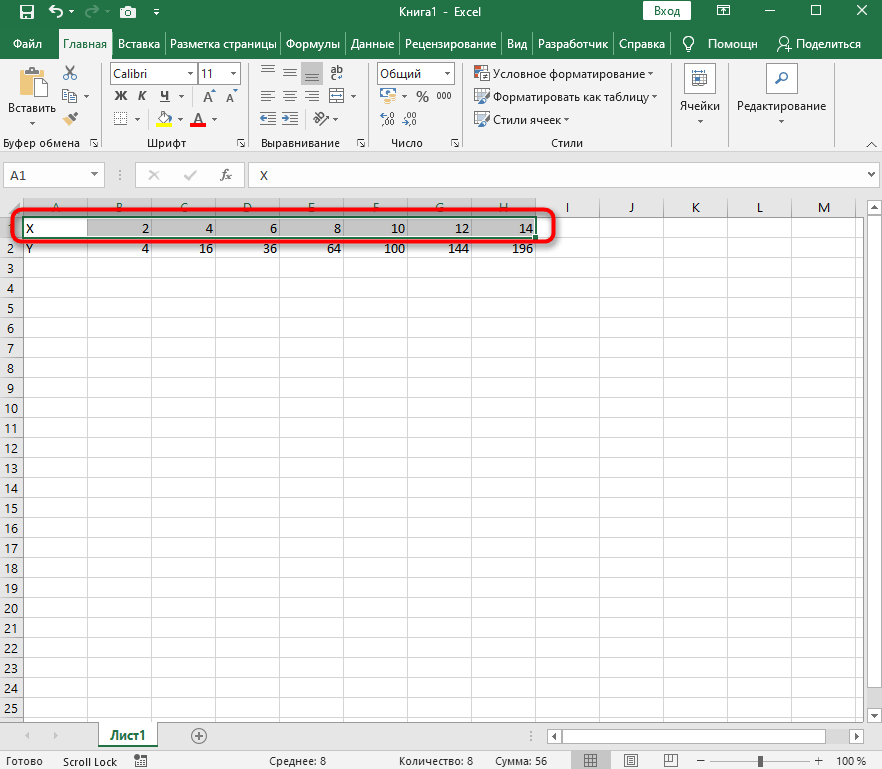
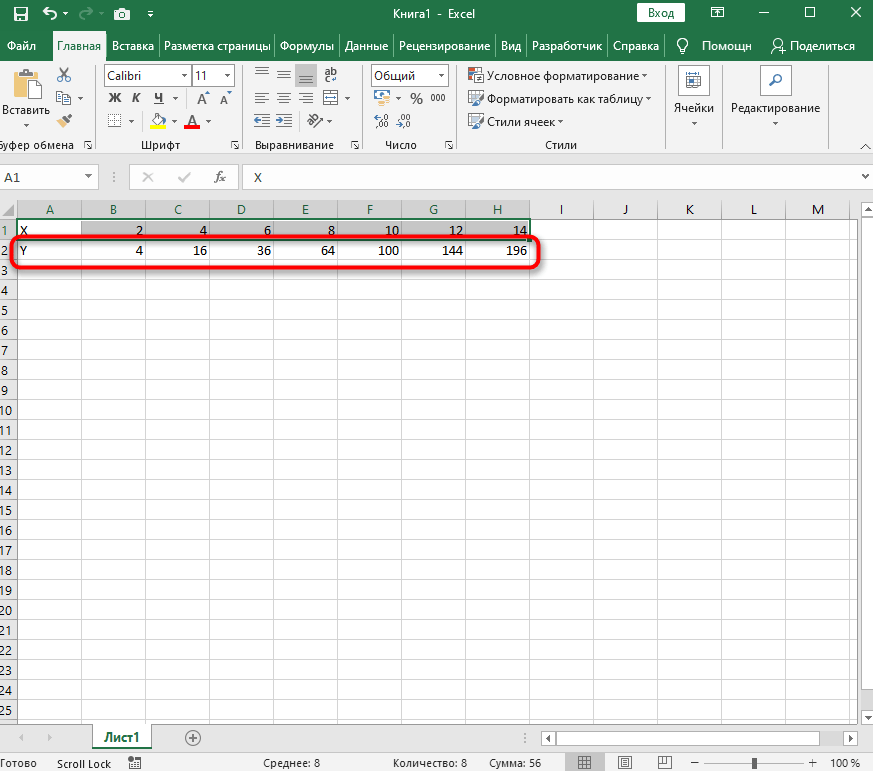
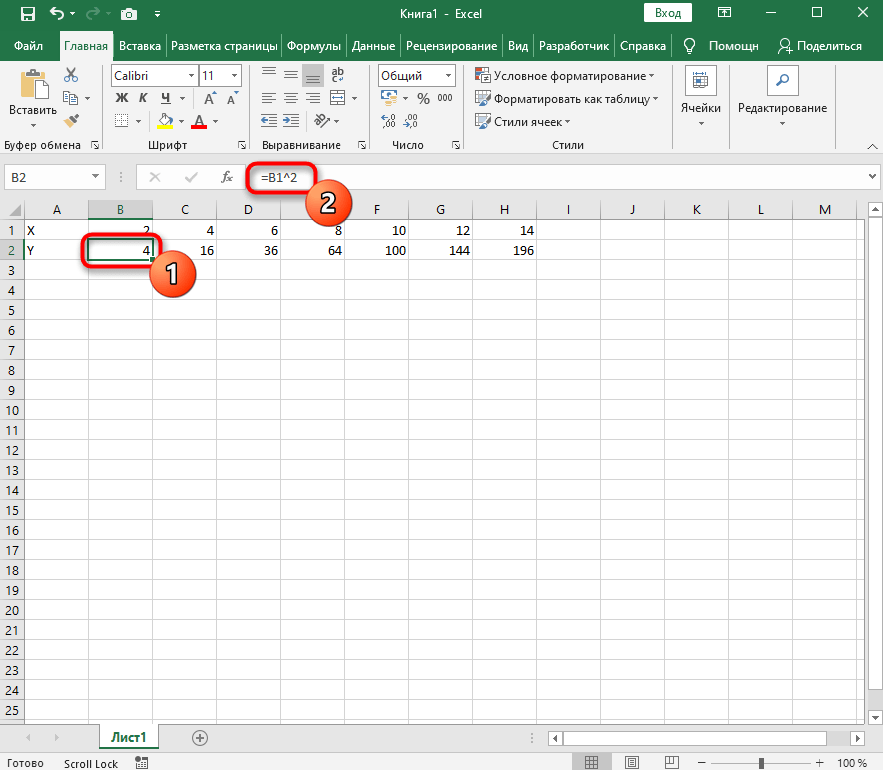
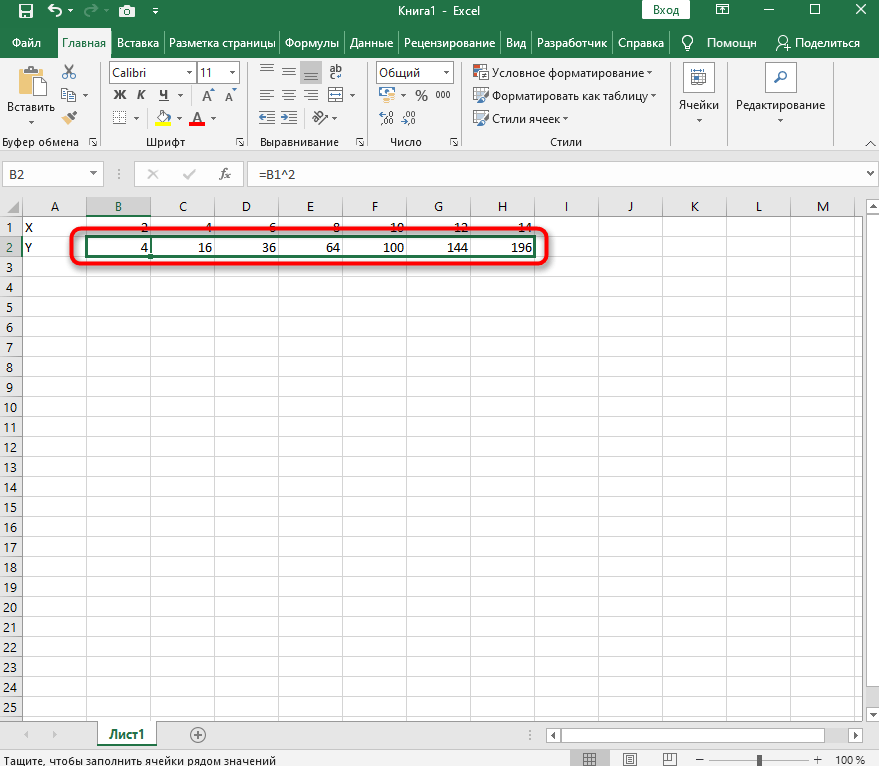
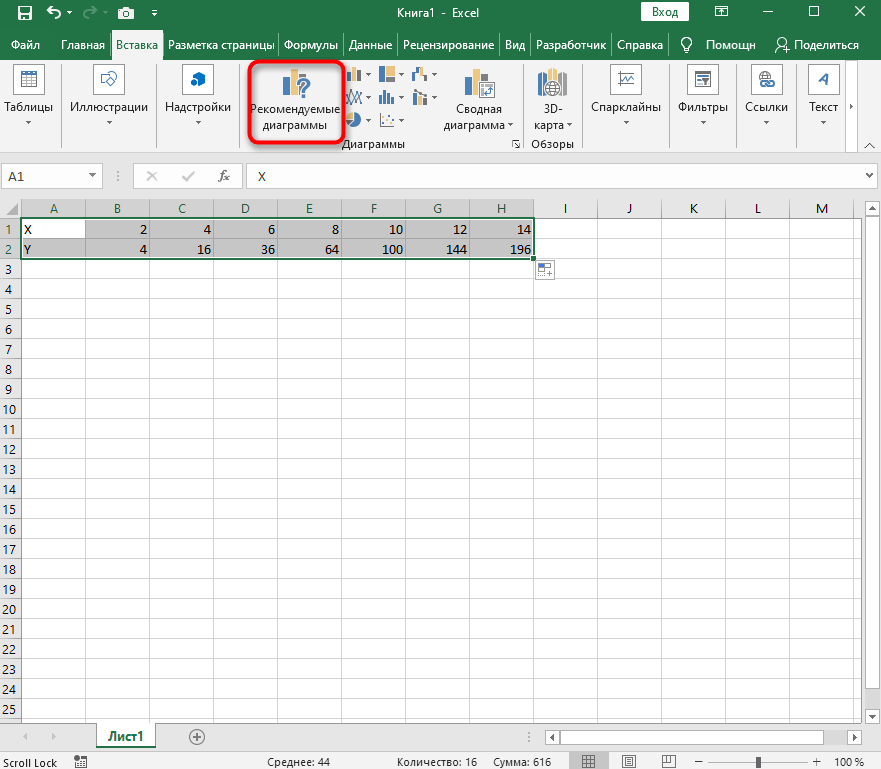
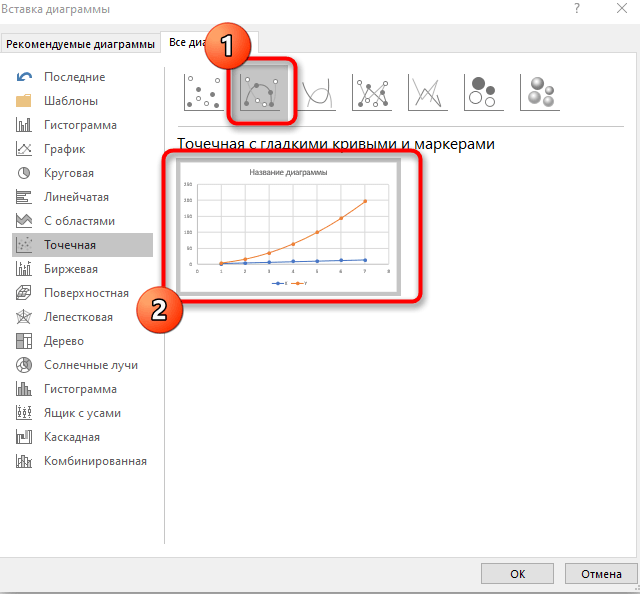
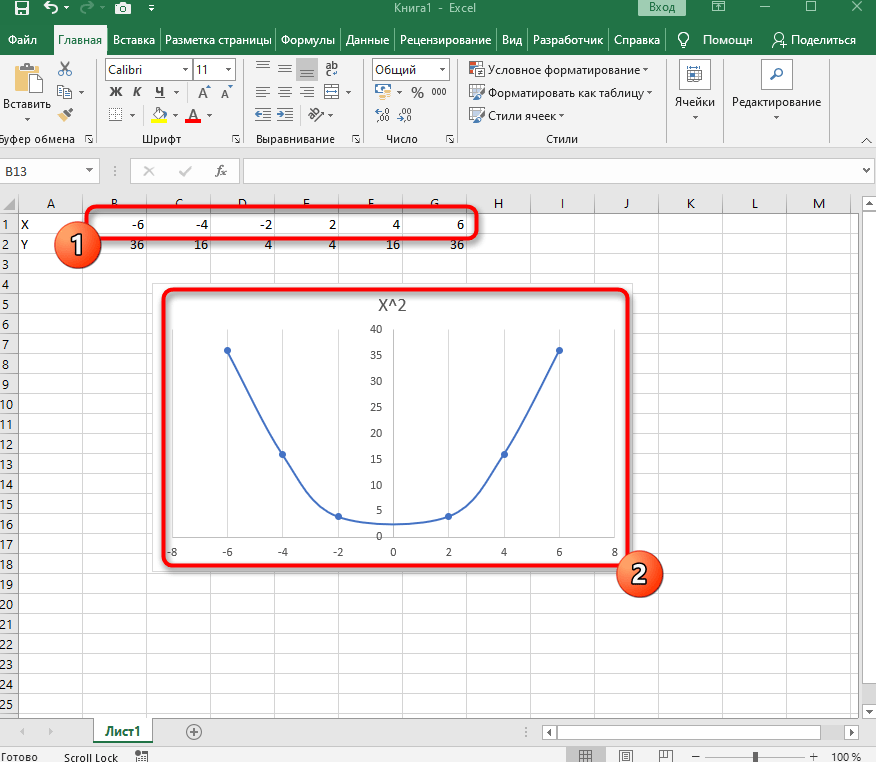
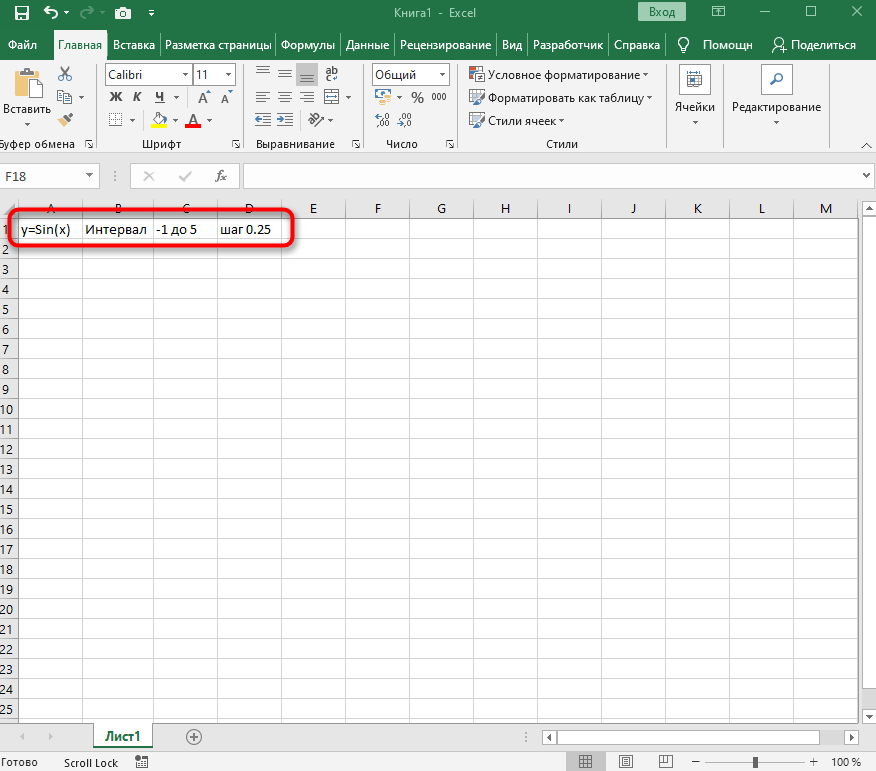
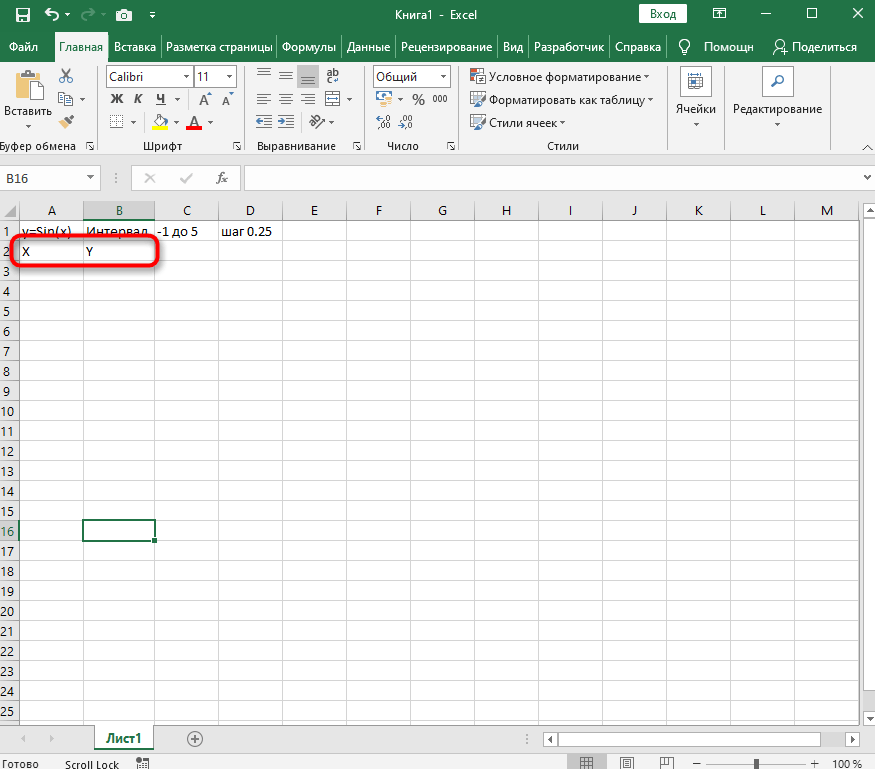
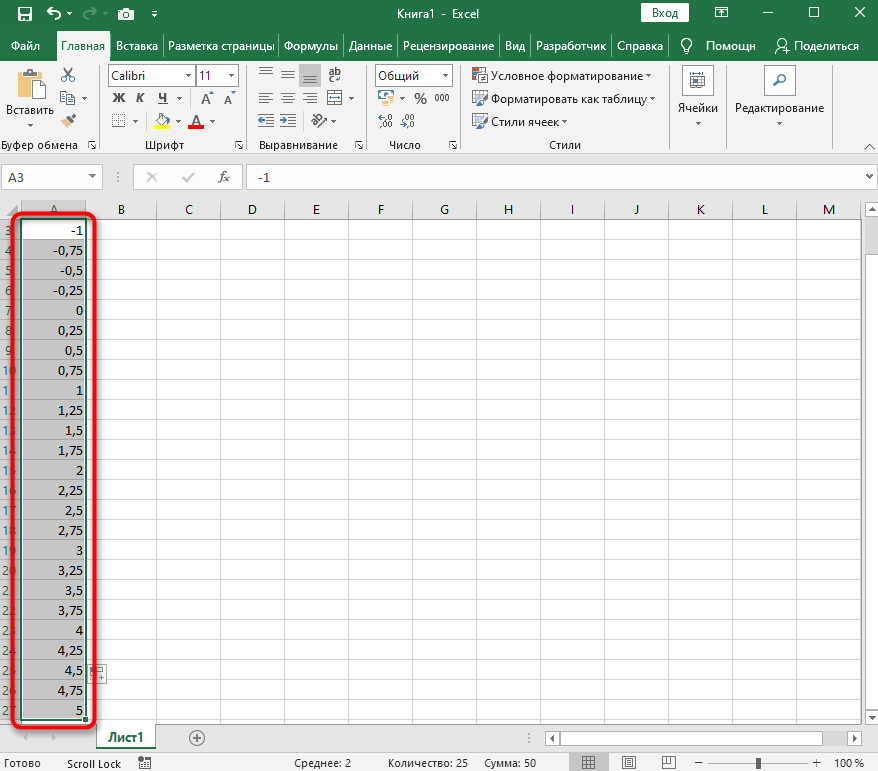
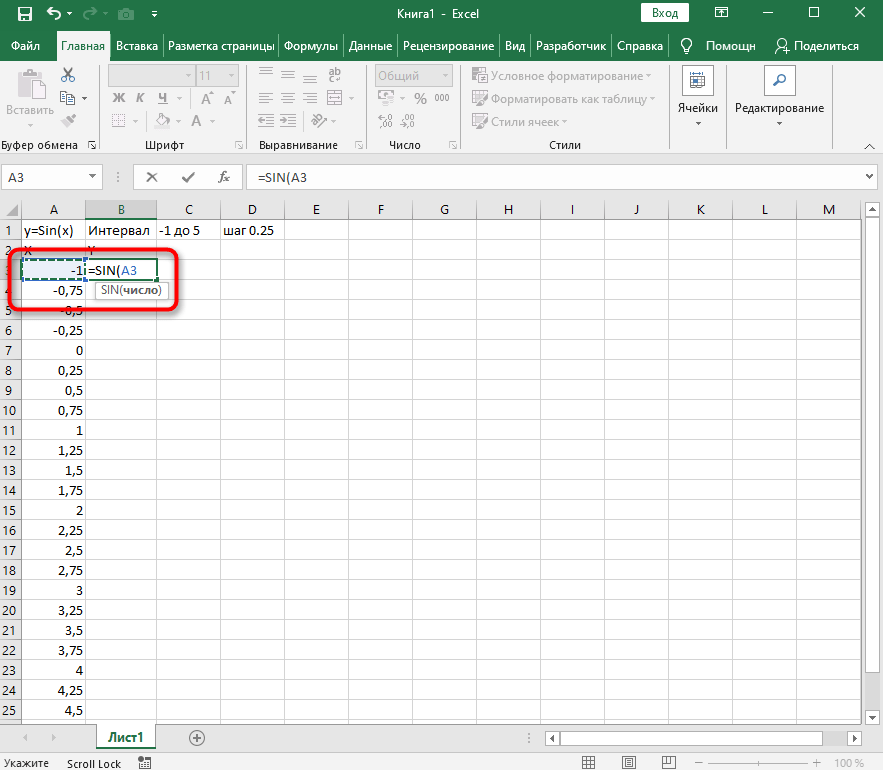
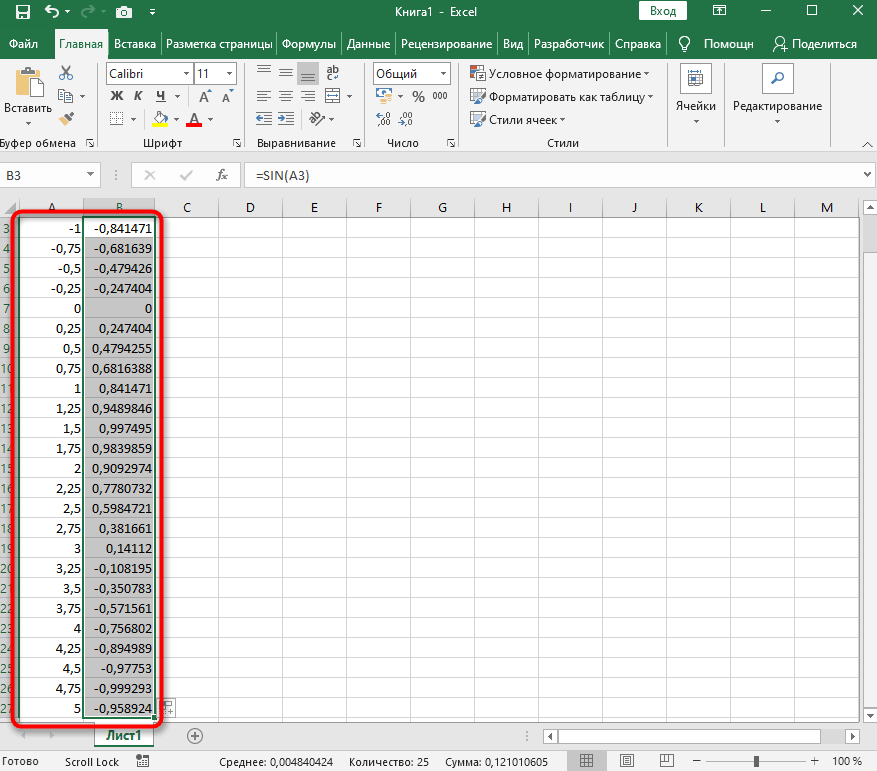
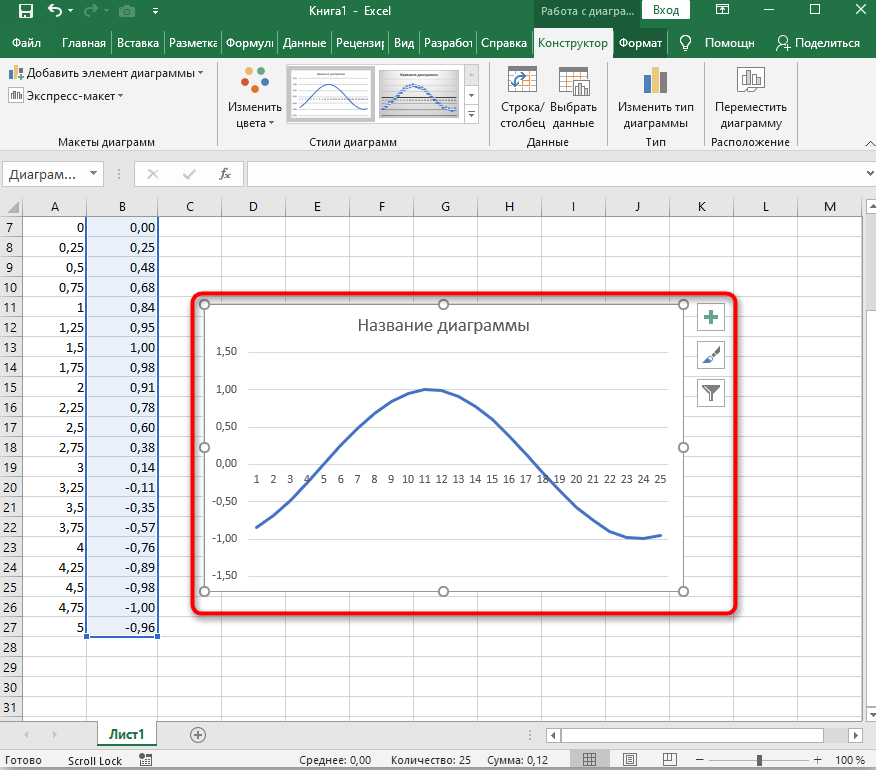
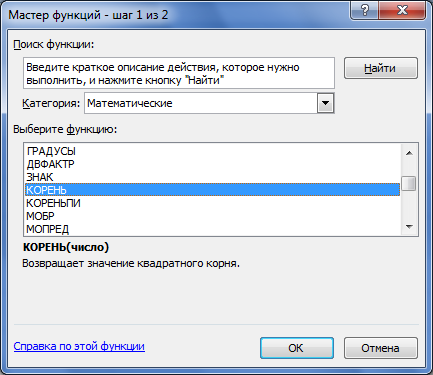
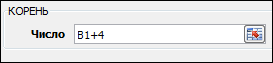





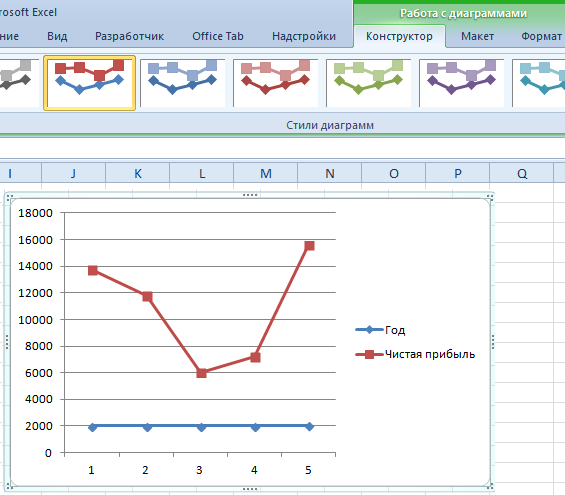
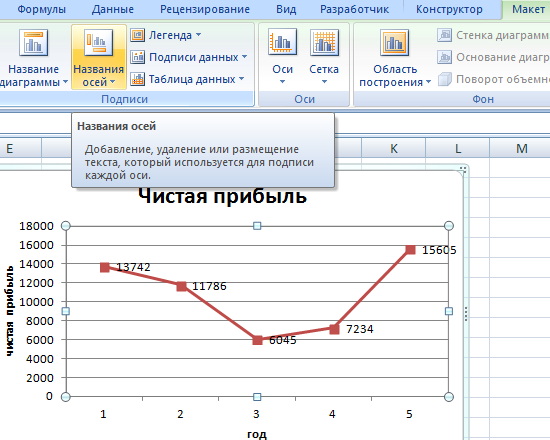
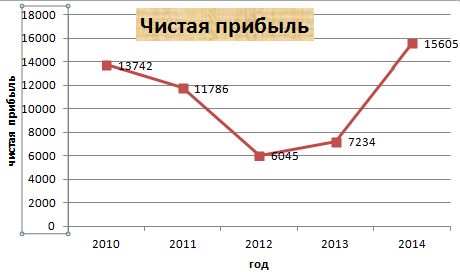
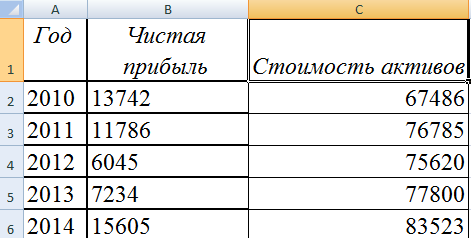
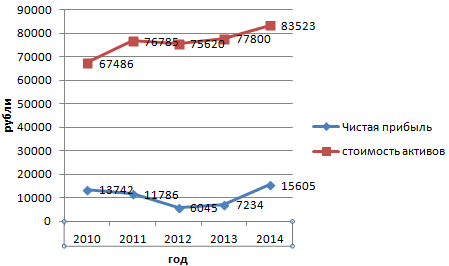
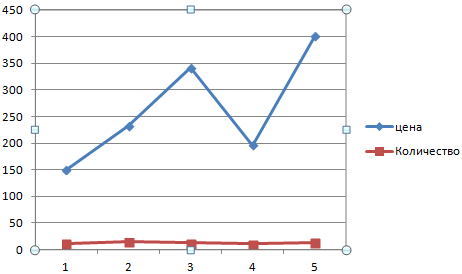
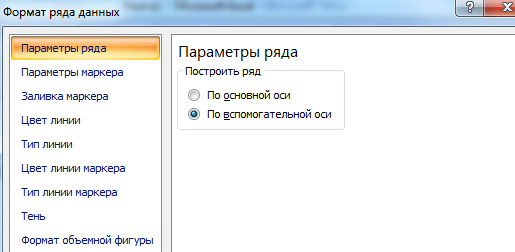
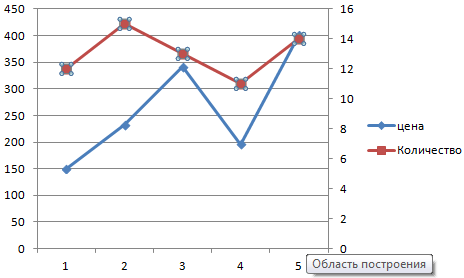
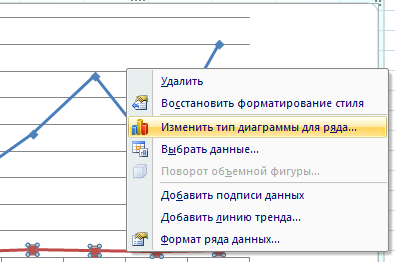
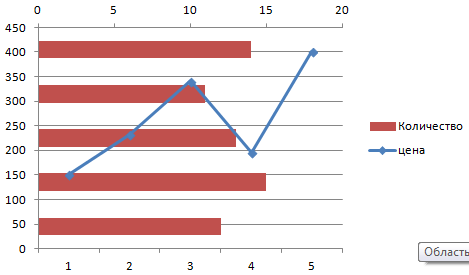
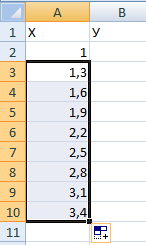
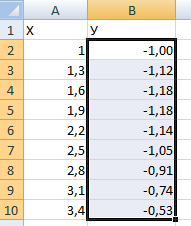
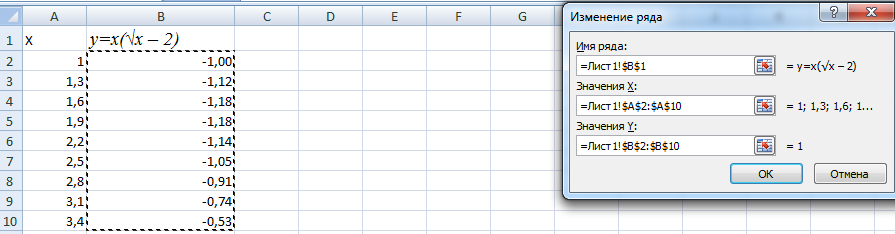
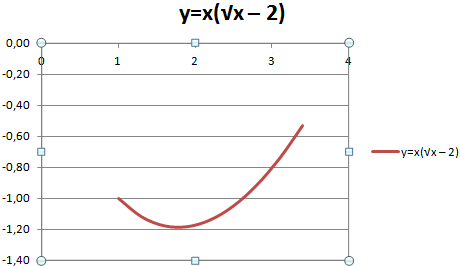
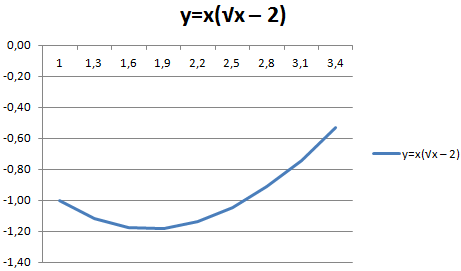
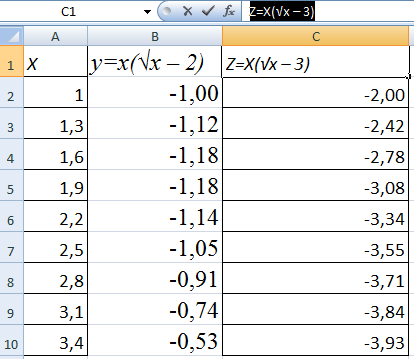
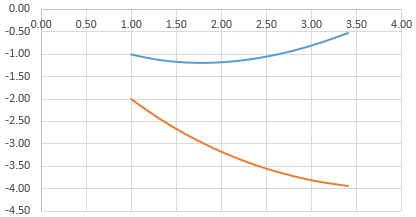
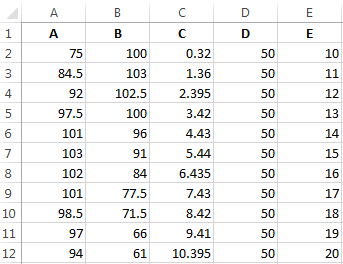
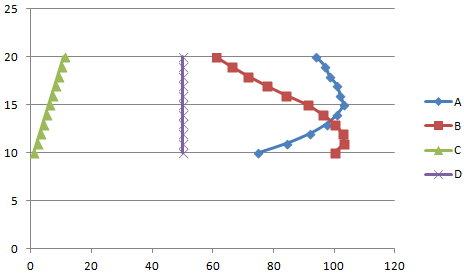
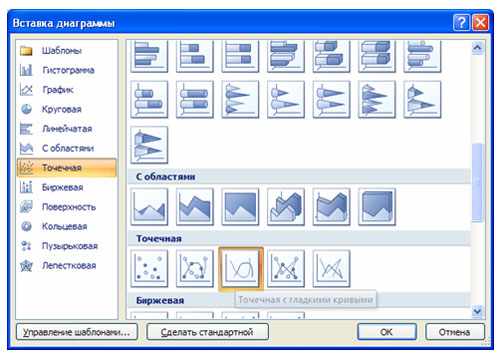
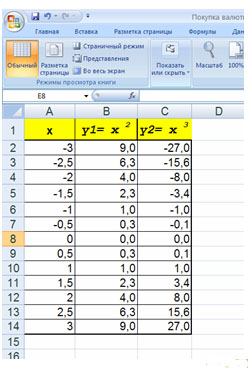
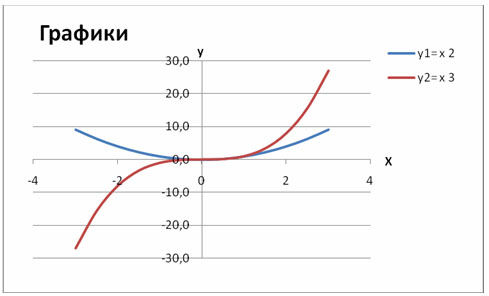
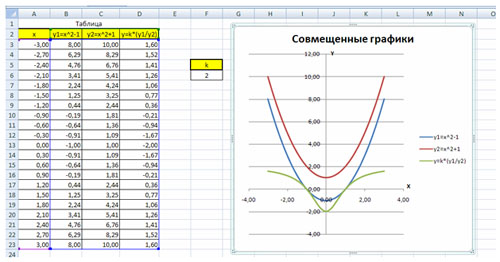
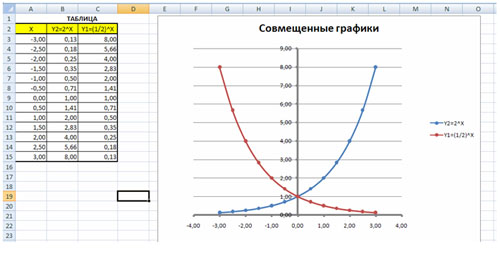
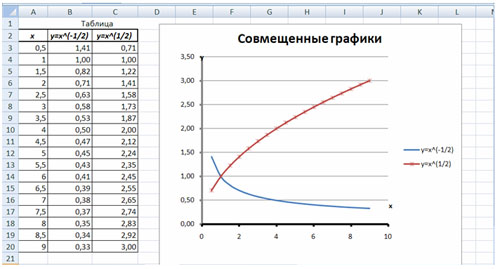
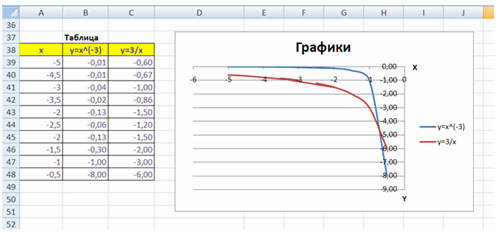
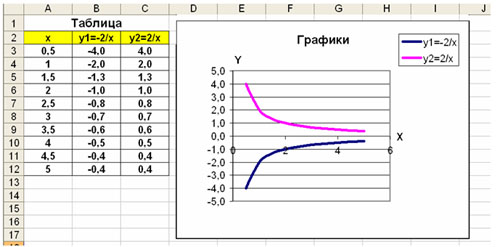

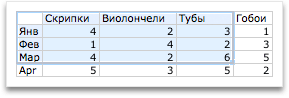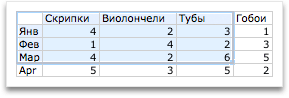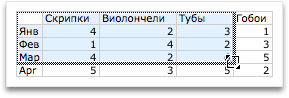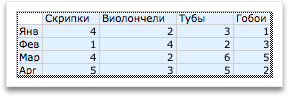

 + Z.
+ Z.
 .
.


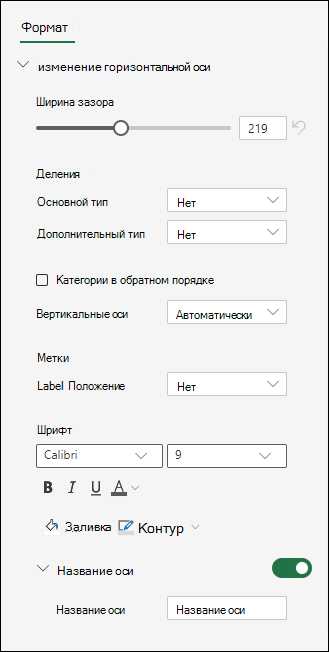
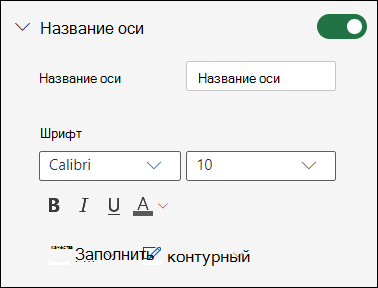
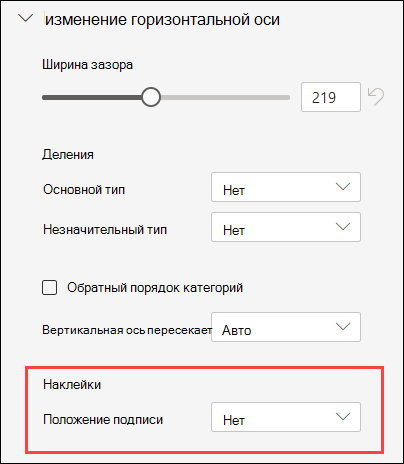











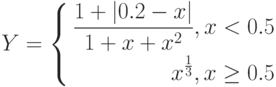
![$$
Y=left{
begin{aligned}
% nonumber to remove numbering (before each equation)
1+ln(1+x), x<0.2\
frac{1+x^{frac{1}{2}}}{1+x}, xin[0.2;0.8]\
2e^{-2x}, x>0.8
end{aligned}
right.
$$](https://intuit.ru/sites/default/files/tex_cache/4205ce0704c58087ee2090c98d69defd.png)






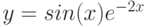
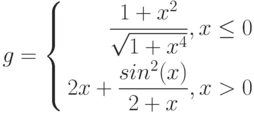
![$$
z=left{
begin{aligned}
frac{1+|x|}{sqrt[3]{1+x+x^{2}}},xleq-1\
2ln(1+x^{2}+frac{1+cos^{4}(x)}{2+x},xin [-1;0]\
(1+x)^{frac{3}{5}}, xgeq0
end{aligned}
right.
$$](https://intuit.ru/sites/default/files/tex_cache/0c4fbe6f0e5d1dfcbce7a704e471a929.png)
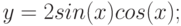
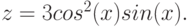
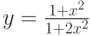
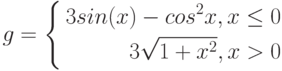
![$$
z=left{
begin{aligned}
frac{1+x}{sqrt[3]{1+x^{2}}},xleq0\
-x+2e^{-2x},xin(0,1)\
|2-x|^{frac{1}{3}},xgeq1
end{aligned}
right.
$$](https://intuit.ru/sites/default/files/tex_cache/b018b9edd908f216df636f345c6a0e0e.png)
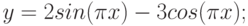
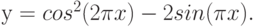
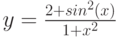
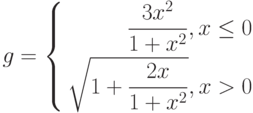
![$$
z=left{
begin{aligned}
3x+sqrt{1+x^{2}},x<0\
2cos(x)e^{-2x},xin[0,1]\
2sin(3x),x>1
end{aligned}
right.
$$](https://intuit.ru/sites/default/files/tex_cache/96eae18012c8cec7fa3195cb7cb16718.png)


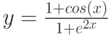
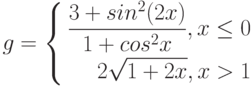
![$$
z=left{
begin{aligned}
sqrt{1+frac{x^{2}}{1+x^{2}}},x<0\
2cos^{2}(x),xin[0,1]\
sqrt{1+|2sin(3x)|^{frac{1}{3}}},x>1
end{aligned}
right.
$$](https://intuit.ru/sites/default/files/tex_cache/0e0bd3f1b2b59b98e1d0aac6b9e4e060.png)

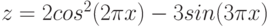
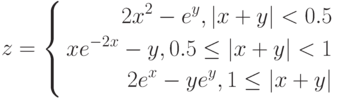
![$$y=sqrt[4]{1+e^{3x}}$$](https://intuit.ru/sites/default/files/tex_cache/38d26ef341d2e8b1539e5db30dd8d0fb.png)
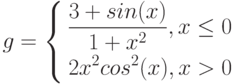
![$$
z=left{
begin{aligned}
|x|^{frac{1}{3}}, x<0\
-2x+frac{x}{1+x}, xin[0,1]\
frac{|3-x|}{1+x}, xgeq1
end{aligned}
right.
$$](https://intuit.ru/sites/default/files/tex_cache/a336bbbfe739b8a27a42bc552dbba85d.png)
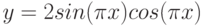

![$$
g=left{
begin{aligned}
sqrt{1+2x^{2}-sin(x)}, xleq0\
frac{2+x}{sqrt[3]{2+e^{-0.1x}}}, x>0
end{aligned}
right.
$$](https://intuit.ru/sites/default/files/tex_cache/bf750a63e0bf1e99dcdc62a82b5ae8a1.png)
![$$
z=left{
begin{aligned}
frac{1+x}{1+x^{2}}, x<0\
sqrt{1+frac{x}{1+x}}, xin[0,1]\
2|sin(3x)|, xgeq1
end{aligned}
right.
$$](https://intuit.ru/sites/default/files/tex_cache/0ba53b8c4d394ba14c7bea0640198a67.png)
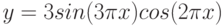
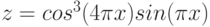
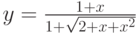
![$$
g=left{
begin{aligned}
sqrt{1+x^{2}}, x<0\
frac{1+x}{1+sqrt[3]{1+e^{-0.2x}}}, x>0
end{aligned}
right.
$$](https://intuit.ru/sites/default/files/tex_cache/0c5f92dffe784f474d4780a60de478e2.png)
![$$
z=left{
begin{aligned}
frac{1+x+x^{2}}{1+x^{2}}, x<0\
sqrt{1+frac{2x}{1+x^{2}}}, xin[0,1]\
2|0.5+sin(x)|, xgeq1
end{aligned}
right.
$$](https://intuit.ru/sites/default/files/tex_cache/ea55ab481bac3e0b5e9e38e088173fa3.png)

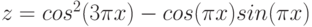
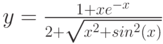
![$$
g=left{
begin{aligned}
sqrt{1+|x|}, xleq0\
frac{1+3x}{2+sqrt[3]{1+x}}, x>0
end{aligned}
right.
$$](https://intuit.ru/sites/default/files/tex_cache/5b2dfdc96ef1d57aec714b337234e6ad.png)
![$$
z=left{
begin{aligned}
1+frac{3+x}{1+x^{2}}, x<0\
sqrt{1+(1-x)^{2}},xin[0,1]\
frac{1+x}{1+cos^{2}(x)}, xgeq1
end{aligned}
right.
$$](https://intuit.ru/sites/default/files/tex_cache/d7447bf6d7e359d4eca3921d80e719a8.png)
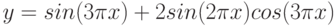

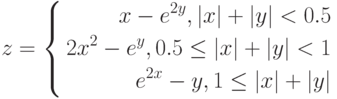
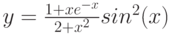
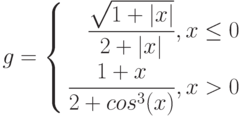
![$$
z=left{
begin{aligned}
frac{1+2x}{1+x^{2}}, x<0\
sin^{2}(x)sqrt{1+x},xin[0,1]\
sin^{2}(x)e^{0.2x}, xgeq1
end{aligned}
right.
$$](https://intuit.ru/sites/default/files/tex_cache/12bdc437bdea736bdda75cef4a7e722c.png)
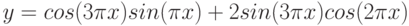
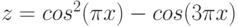
![$х,yin [-1; 1]$$](https://intuit.ru/sites/default/files/tex_cache/1398b5df6d8c02912de8ea030fafac71.png)
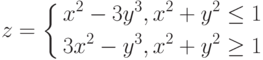
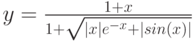
![$$
g=left{
begin{aligned}
sqrt[3]{1+x^{2}}, xleq0\
sin^{2}(x)+frac{1+x}{1+cos^{2}(x)}, x>0
end{aligned}
right.
$$](https://intuit.ru/sites/default/files/tex_cache/5144de1617b0997002fd47d479761ecb.png)
![$$
z=left{
begin{aligned}
frac{|x|}{1+x^{2}}e^{-2x}, x<0\
sqrt{1+x^{2}},xin[0,1]\
frac{1+sin(x)}{1+x}+3x, xgeq1
end{aligned}
right.
$$](https://intuit.ru/sites/default/files/tex_cache/fc2d46b4be846a82407b051315db3f0a.png)