Таблично заданная функция excel - Word и Excel - помощь в работе с программами

Электронные таблицы EXCEL можно использовать при
изучении многих разделов физики, математики и
других предметов. Одной из данных тем является
математическая тема: “Анализ элементарных
функций”. Данная работа посвящена использованию
электронных таблиц EXCEL в анализе элементарных
функций.

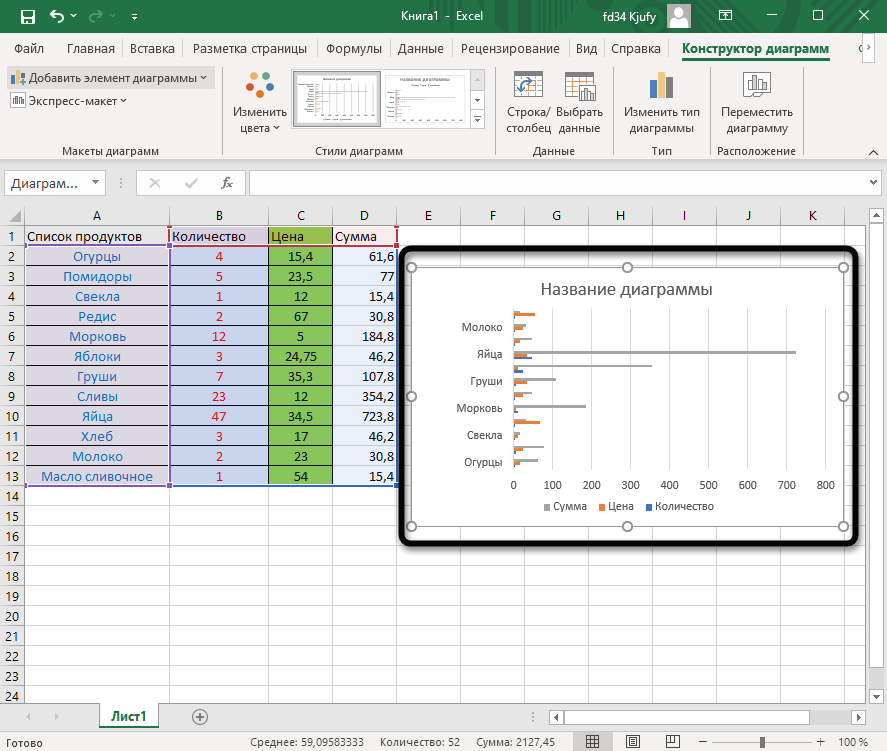
Рис. 1 (см. Приложение 2)

На рис.1 представлена некоторая функция,
заданная с помощью таблицы, построение которой
приведено в Приложении 1.

Особенность анализа функций с помощью
электронных таблиц заключается в том, что анализ
проводится на дискретной информации.
Действительно, количество значений исследуемой
функции конечно и дано (как правило) с некоторым
постоянным шагом по аргументу.

При анализе исходной функции необходимо решить
следующие задачи:

определение максимума (минимума) данной функции
на заданном интервале,
определение возрастания и/или убывания функции
на заданном интервале,
определение четности заданной функции,
определение периодичности заданной функции,
определение значения первой производной данной
функции и наличия экстремумов.

Для решения этих задач потребуется построить
таблицы ВводаИсходнойИнформации, таблицы
ВыводаРезультатов, Расчетной таблицы для
обработки информации и дополнительно построим
Вспомогательную таблицу. Таблицу
ВводаИсходнойИнформации и основу Расчетной
таблицу построены при введении значений
исследуемой функции в Приложении 1 и показанной
на рис.1. Построим решения задач анализа.

Приложение 1

Задача 1.
Для заданной функции на заданном интервале
аргумента определить ее минимальное и
максимальное значения.

Решение.
Для решения этой задачи построим таблицу
ВыводаРезультатов в виде

D E

1 комментарии Значения

2 Макс f(X) <формула>

3 Мин f(X) <формула>

В мастере функций Excel имеются функции МАКС(…) и
МИН(…), позволяющие решить нашу задачу. Для этого
необходимо в ячейки Е2 и Е3 ввести соответственно
формулы:

E2 => [=МАКС(с10:с50)]
и
E3 => [=МИН(с10:с50)]

Примечание. Если “протяжка” велась до
другой строки, то в интервале ссылок указать
соответствующий номер строки.

ЗАДАЧА РЕШЕНА.

Задача 2.
Определение возрастания и/или убывания функции
на заданном интервале.

Решение.
Для решения данной задачи в расчетной таблице
необходимо построить столбец D, в котором знак
будет указывать на возрастание или убывание
функции в данной точке. Для этого в ячейку D11
введем формулу

D11 => [=ЕСЛИ(a11<>””;ЗНАК(D11-D10);””)]
и “протянем” ее до строки №50.

И там, где знак положительный, функция
возрастает, а там, где знак отрицательный,
функция – убывает.

Далее построим вспомогательную таблицу, в
которой определим количество признаков
возрастания и убывания функции

F G

1 КОММЕНТАРИИ ЗНАЧЕНИЯ

2 Признак возрастания <формула>

3 Признак убывания <формула>

Для этого в ячейки g2 и g3 соответственно вводим
формулы:

G2 => [=СуммЕсли(d11:d50;”>0”)]
G3 => [=СуммЕсли(d11:d50;”<0”)]

Таблицу ВыводаРезультатов дополним строкой

D E

1 комментарии значения

2 Макс f(X) =МАКС(с10:с50)

3 Мин f(X) =МИН(с10:с50)

4 Возрастание/Убывание <формула>

И для определения характера изменения заданной
функции остается ввести в ячейку Е4 формулу:

E4 => [=ЕСЛИ(g2>0; ЕСЛИ(g3<0;”и то и
другое”;”возрастает”);”убывает”)

ЗАДАЧА РЕШЕНА.

Задача 3.
Определение четности данной.

Решение.
Для решения данной задачи необходимо знание
аналитического представления исходной функции,
так как признаком четности функции является
равенство f(X) = f(-X).

Для решения данной задачи в расчетной таблице
построим дополнительный столбец. В ячейку Е10
введем формулу

E10 => [=f(b10) – f(-b10)]
и “протянуть” ее до строки №50.

Таблицу ВыводаРезультатов дополним строкой

D E

1 комментарии значения

2 Макс f(X) =МАКС(с10:с50)

3 Мин f(X) =МИН(с10:с50)

4 Возрастание/Убывание [=ЕСЛИ(g2>0; ЕСЛИ(g3<0;”и то и
другое”;”возрастает”);”убывает”)

5 четность <формула>

В ячейку Е4 таблицы ВыводаРезультатов вводим
формулу.

E4 => [ЕСЛИ(ABS(СУММ(E10:E50))<0,000001; “ЧЕТНАЯ”;
“НЕЧЕТНАЯ”)

ЗАДАЧА РЕШЕНА.

Задача 4.
Определить является ли введенный период
периодом заданной функции.

Решение.
Для решения данной задачи необходимо знание
аналитического представления исходной функции,
так как признаком периодичности функции
является равенство f(Х) = f(X+<период>).

Для данной задачи добавим в таблице
ВводаИсходнойИнформации строку №6, в которой
введем численное значение предполагаемого
периода.

А В

1 КОММЕНТАРИИ ЗНАЧЕНИЯ

2 Xn <значение>

3 Xk <значение>

4 Shag <значение>

5 N <формула>

6 период <значение>

В ячейку В6 вводится число – предполагаемый
период заданной функции.

Далее для решения данной задачи построим
дополнительный столбец в расчетной таблице, для
этого в ячейку F11 введем формулу

F10 => [=ЕСЛИ(a10<>””;f(b10)-f(b10+$b$6);””)]

и “потягиваем” эту формулу до строки №50.

В таблице ВыводаРезультатов добавим строчку.

D E

1 комментарии значения

2 Макс f(X) =МАКС(с10:с50)

3 Мин f(X) =МИН(с10:с50)

4 четность =ЕСЛИ(g2>0; ЕСЛИ(g3<0;”и то и
другое”;”возрастает”);”убывает”)

5 период <формула>

В ячейке Е5 необходимо ввести формулу

Е5 => [=ЕСЛИ(СУММ(f10:f50)<0,01;”период”;”не
период”)]

Если данное значение предполагаемого периода
не подходит, то его можно изменить.

ЗАДАЧА РЕШЕНА.

Задача 5.
Для заданной функции определить:

значения первой производной данной функции,
наличия и количество экстремумов.

Решение.
Для решения первой части задачи, то есть
определения первой производной воспользуемся ее
разностным определение.

Построим столбец. Для этого в ячейку G11 вводим
формулу:

G11 => [= ЕСЛИ(a11<>””; ABS((c11-c10)/(b11-b10));””)]

и “протягиваем ее до строки с №50.

В результате получаем разностные приближенные
значения первой производной заданной функции в
заданных точках.

Для решения второй части задачи, то есть
определения наличия и количества экстремумов на
заданной функции в таблицу ВыводаРезультатов
дополнить строкой.

D E

1 комментарии значения

2 Макс f(X) =МАКС(с10:с50)

3 Мин f(X) =МИН(с10:с50)

4 четность =ЕСЛИ(g2>0; ЕСЛИ(g3<0;”и то и
другое”;”возрастает”);”убывает”)

5 период [=ЕСЛИ(СУММ(f10:f50)<0,01;”период”;
”не период”)]

6 Количество Экстремумов. <формула>

В ячейке Е6 необходимо ввести формулу

E6 => [=СчетЕсли(g11:g50;”<0,05”)]

ЗАДАЧА РЕШЕНА.

Рис 2, см. Приложение 3

На рис.2 приведена построенная таблица
решения задач.

Предложенные в данной работе задачи можно
использовать на интегрированных уроках
информатика-математика, на уроках информатики
при изучении электронных таблиц, в частности, в
теме: “Мастер функций”.

Источник

Формула, она же функция, – одна из основных составляющих электронных таблиц, создаваемых при помощи программы Microsoft Excel. Разработчики добавили огромное количество разных функций, предназначенных для выполнения как простых, так и сложных расчетов. К тому же пользователю разрешено самостоятельно производить математические операции, что тоже можно назвать своеобразной реализацией формул. Именно о работе с этими компонентами и пойдет речь далее.

Я разберу основы работы с формулами и полезные «фишки», способные упростить процесс взаимодействия с таблицами.

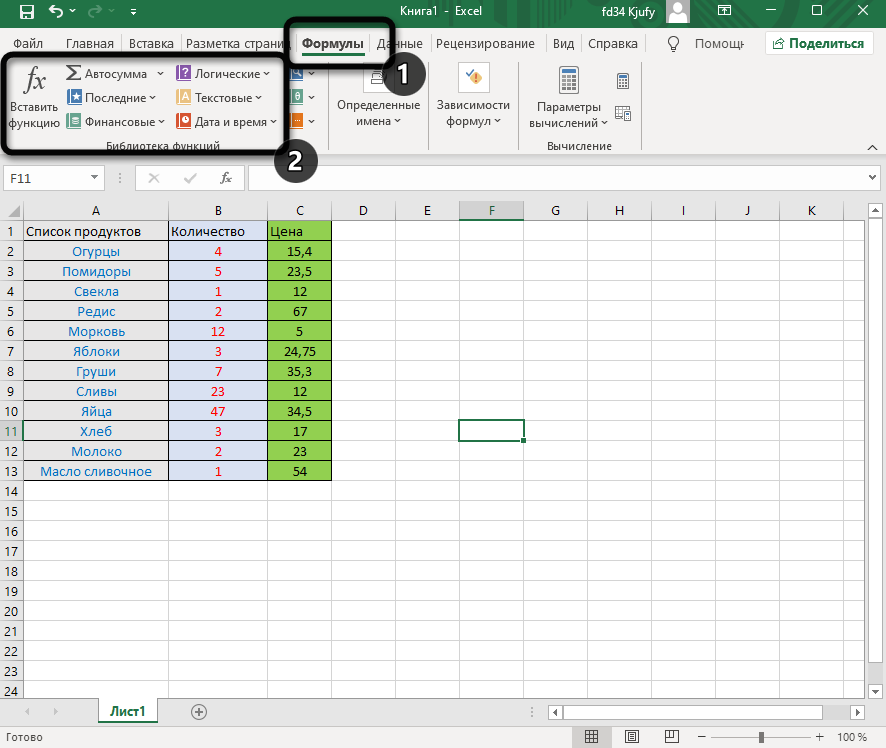
Поиск перечня доступных функций в Excel

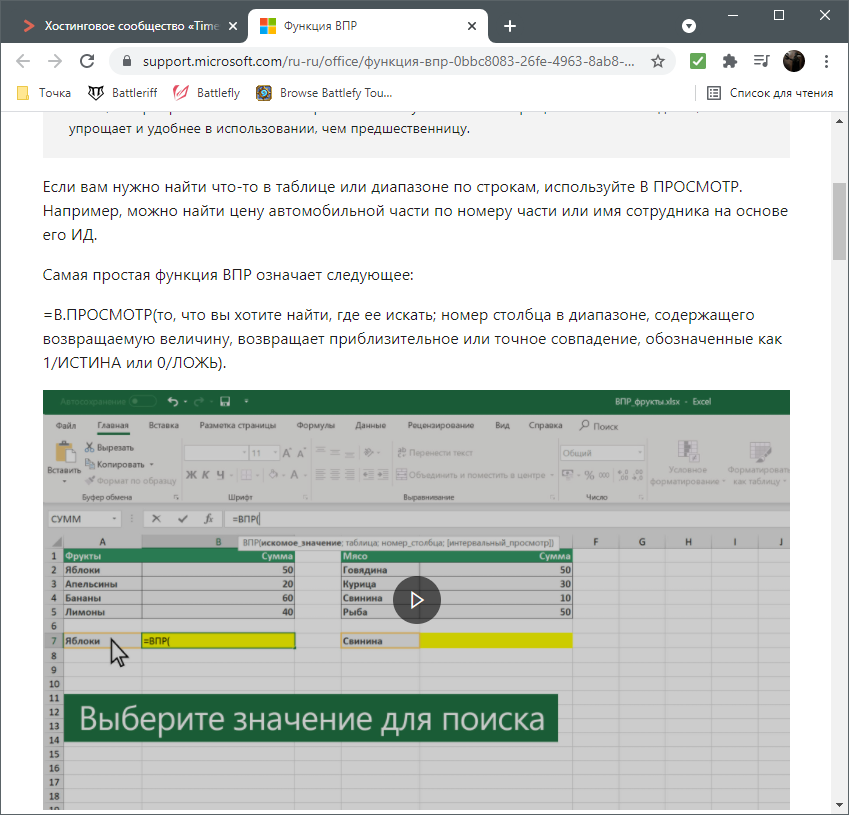
Если вы только начинаете свое знакомство с Microsoft Excel, полезно будет узнать, какие функции существуют, для чего предназначены и как происходит их создание. Для этого в программе есть графическое меню с отображением всего списка формул и кратким описанием действия расчетов.

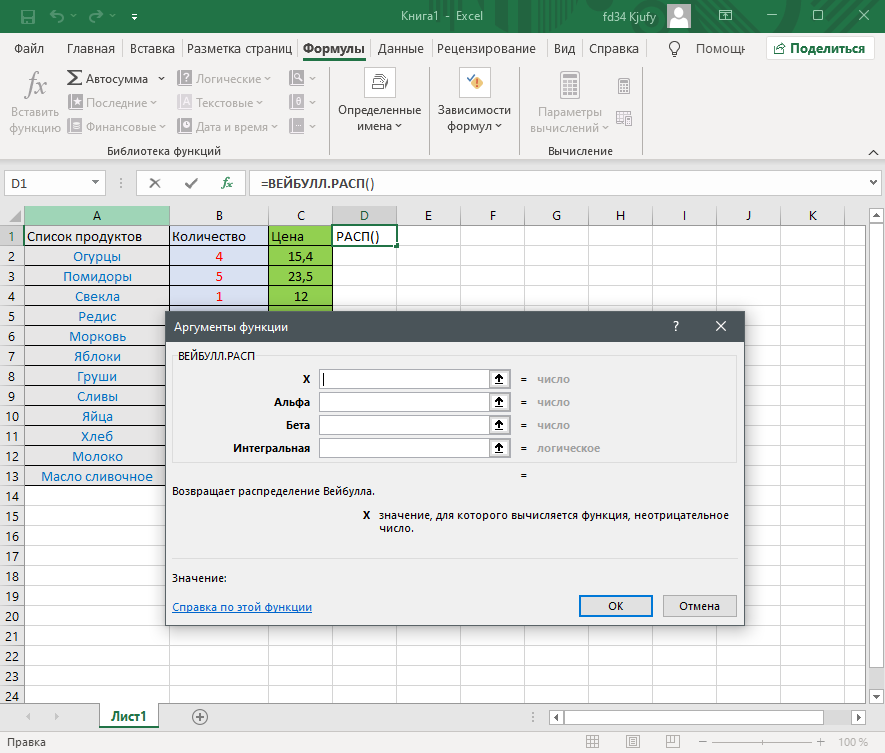
Откройте вкладку «Формулы» и нажмите на кнопку «Вставить функцию» либо разверните список с понравившейся вам категорией функций.
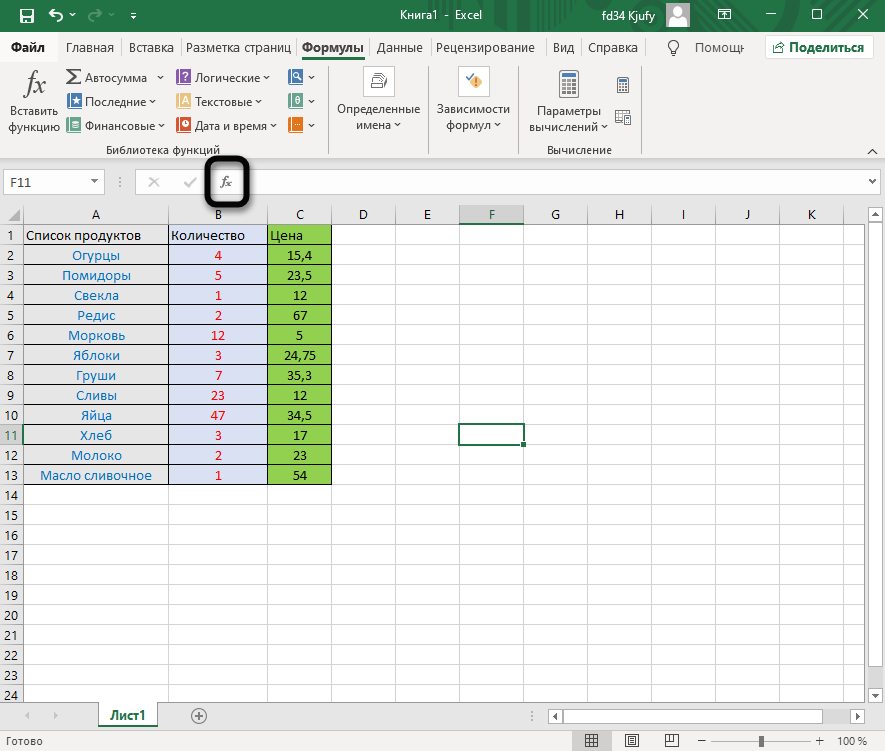
Вместо этого всегда можно кликнуть по значку с изображением «Fx» для открытия окна «Вставка функции».
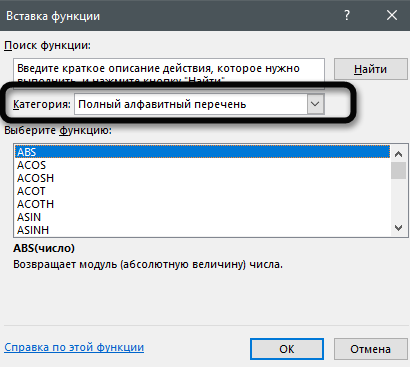
В этом окне переключите категорию на «Полный алфавитный перечень», чтобы в списке ниже отобразились все доступные формулы в Excel, расположенные в алфавитном порядке.
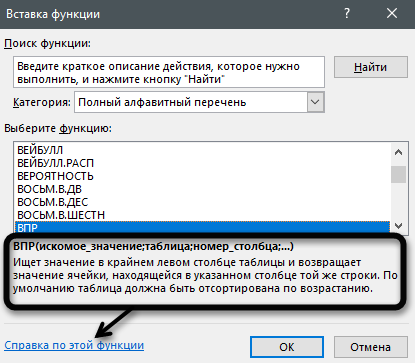
Выделите любую строку левой кнопкой мыши и прочитайте краткое описание снизу. В скобках показан синтаксис функции, который необходимо соблюдать во время ее написания, чтобы все аргументы и значения совпадали, а вычисления происходило корректно. Нажмите «Справка по этой функции», если хотите открыть страницу о ней в официальной документации Microsoft.
В браузере вы увидите большое количество информации по выбранной формуле как в текстовом, так и в формате видео, что позволит самостоятельно разобраться с принципом ее работы.

Отмечу, что наличие подобной информации на русском языке, еще и в таком развернутом виде, делает процесс знакомства с ПО еще более простым, особенно когда речь идет о переходе к более сложным функциям, действующим не совсем очевидным образом. Не стесняйтесь и переходите на упомянутые страницы, чтобы получить справку от специалистов и узнать что-то новое, что хотя бы минимально или даже значительно ускорит рабочий процесс.

Комьюнити теперь в Телеграм

Подпишитесь и будьте в курсе последних IT-новостей

Вставка функции в таблицу

Теперь давайте разберемся с тем, как в Excel задать формулу, то есть добавить ее в таблицу, обеспечив вычисление определенных значений. Вы можете писать функции как самостоятельно, объявляя их название после знака «=», так и использовать графическое меню, переход к которому осуществляется так, как это было показано выше. В Комьюнити уже есть статья «Как вставить формулу в Excel», поэтому я рекомендую нажать по выделенной ссылке и перейти к прочтению полезного материала.

Использование математических операций в Excel

Если необходимо выполнить математические действия с ячейками или конкретными числами, в Excel тоже создается формула, поскольку все записи, начинающиеся с «=» в ячейке, считаются функциями. Все знаки для математических операций являются стандартными, то есть «*»– умножить, «/» – разделить и так далее. Следует отметить, что для возведения в степень используется знак «^». Вкратце рассмотрим объявление подобных функций.

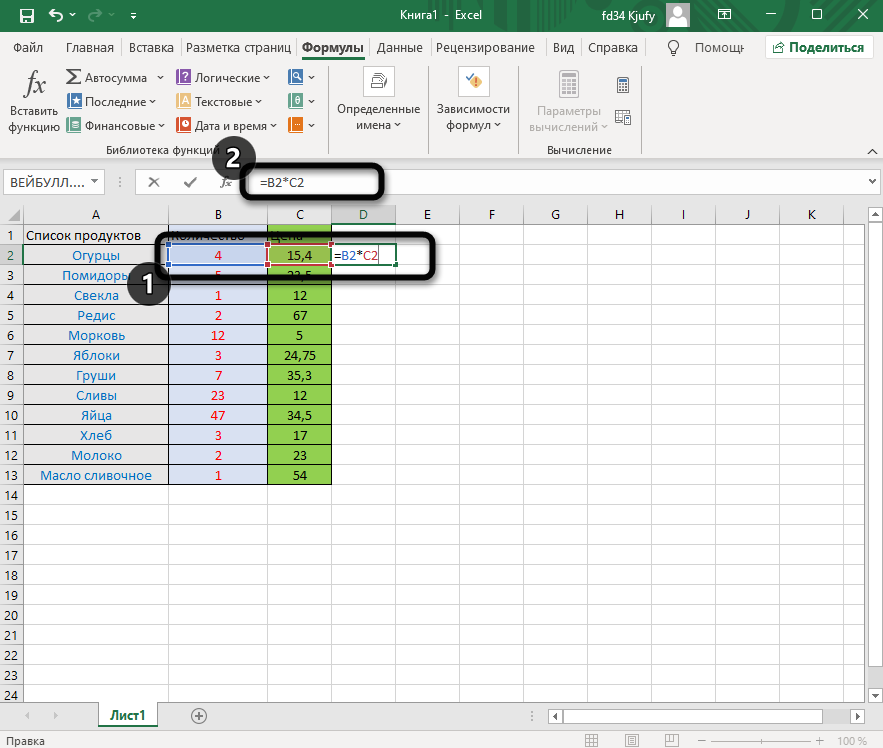
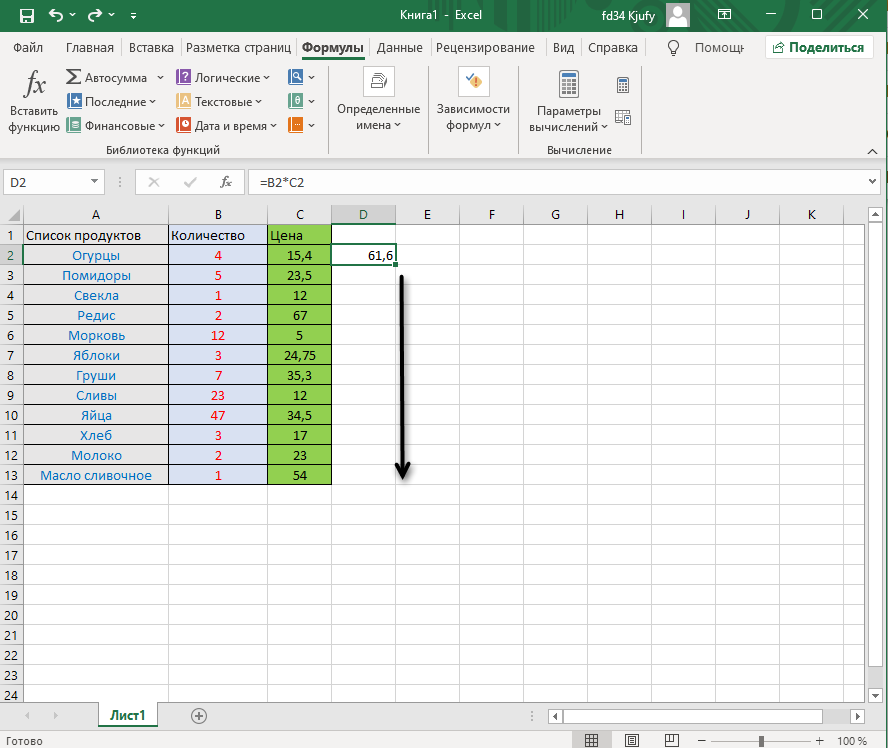
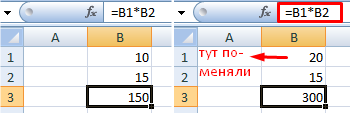
Выделите любую пустую ячейку и напишите в ней знак «=», объявив тем самым функцию. В качестве значения можете взять любое число, написать номер ячейки (используя буквенные и цифровые значения слева и сверху) либо выделить ее левой кнопкой мыши. На следующем скриншоте вы видите простой пример =B2*C2, то есть результатом функции будет перемножение указанных ячеек друг на друга.

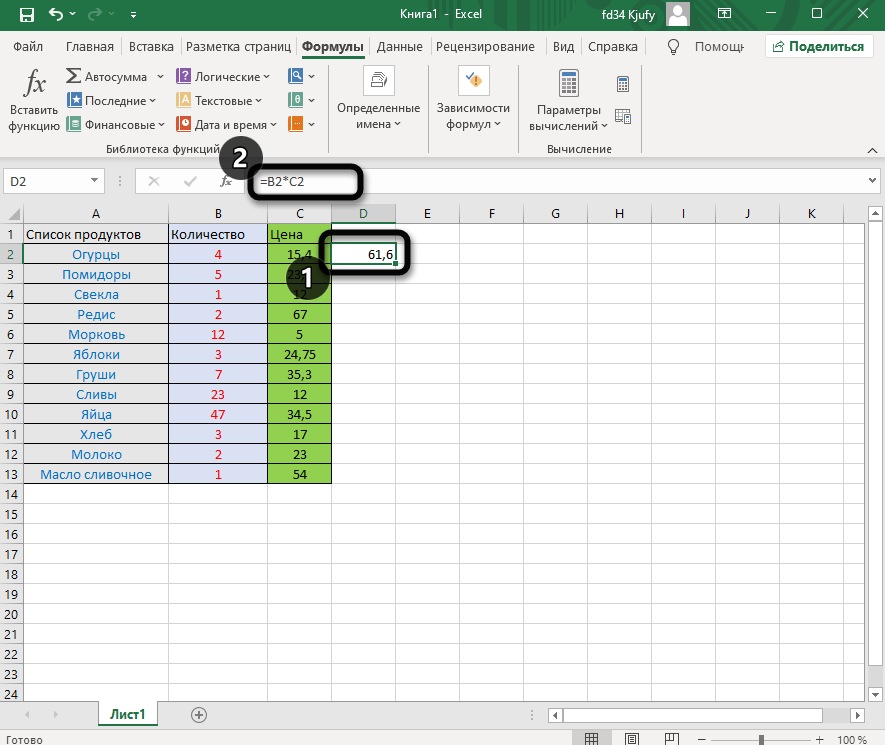
После заполнения данных нажмите Enter и ознакомьтесь с результатом. Если синтаксис функции соблюден, в выбранной ячейке появится число, а не уведомление об ошибке.

Попробуйте самостоятельно использовать разные математические операции, добавляя скобки, чередуя цифры и ячейки, чтобы быстрее разобраться со всеми возможностями математических операций и в будущем применять их, когда это понадобится.

Растягивание функций и обозначение константы

Работа с формулами в Эксель подразумевает и выполнение более сложных действий, связанных с заполнением строк всей таблицы и связыванием нескольких разных значений. В этом разделе статьи я объединю сразу две разных темы, поскольку они тесно связаны между собой и обе упрощают взаимодействие с открытым в программе проектом.

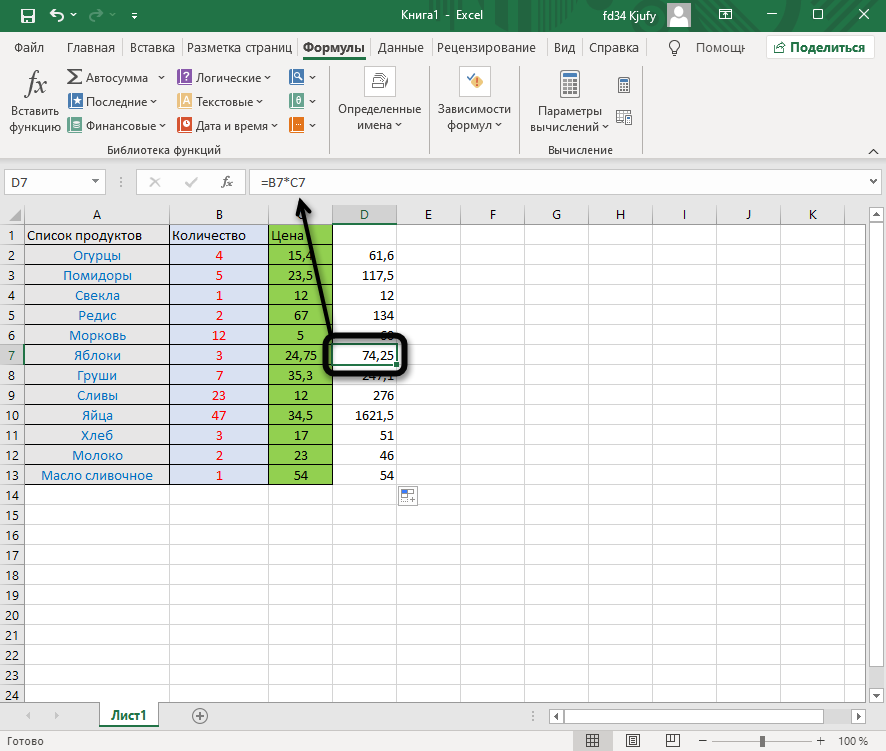
Для начала остановимся на растягивании функции. Для этого вам необходимо ввести ее в одной ячейке и убедиться в получении корректного результата. Затем зажмите точку в правом нижнем углу ячейки и проведите вниз.

В итоге вы должны увидеть, что функция растянулась на выбранный диапазон, а значения в ней подставлены автоматически. Так, изначальная функция имела вид =B2*C2, но после растягивания вниз последующие значения подставились автоматически (от B3*C3 до B13*C13, что видно на следующем изображении). Точно так же растягивание работает с СУММ и другими простыми формулами, где используется несколько аргументов.

Константа, или абсолютная ссылка, – обозначение, закрепляющее конкретную ячейку, столбец или строку, чтобы при растягивании функции выбранное значение не заменялось, а оставалось таким же.

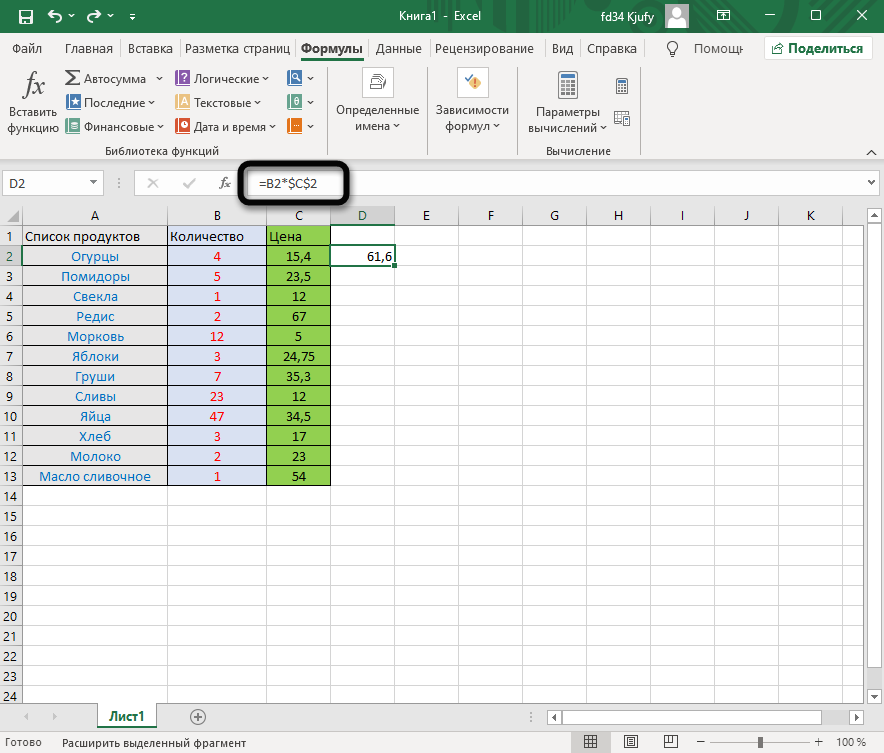
Сначала разберемся с тем, как задать константу. В качестве примера сделаем постоянной и строку, и столбец, то есть закрепим ячейку. Для этого поставьте знак «$» как возле буквы, так и цифры ячейки, чтобы в результате получилось такое написание, как показано на следующем изображении.

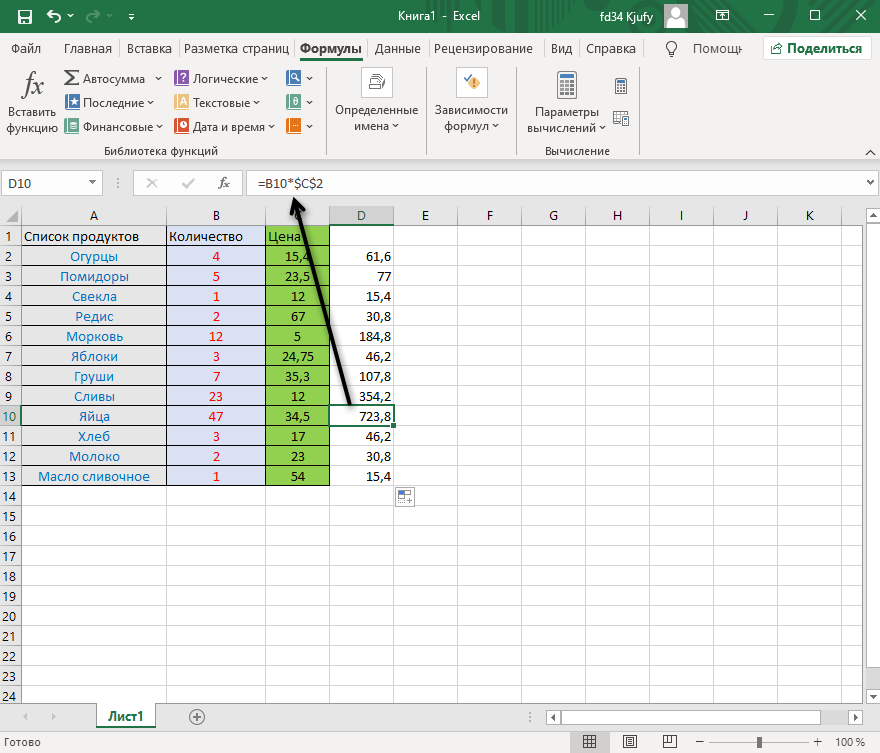
Растяните функцию и обратите внимание на то, что постоянное значение таким же и осталось, то есть произошла замена только первого аргумента. Сейчас это может показаться сложным, но стоит вам самостоятельно реализовать подобную задачу, как все станет предельно ясно, и в будущем вы вспомните, что для выполнения конкретных задач можно использовать подобную хитрость.

В закрепление темы рассмотрим три константы, которые можно обозначить при записи функции:

$В$2 – при растяжении либо копировании остаются постоянными столбец и строка.
B$2 – неизменна строка.
$B2 – константа касается только столбца.

Построение графиков функций

Графики функций – тема, косвенно связанная с использованием формул в Excel, поскольку подразумевает не добавление их в таблицу, а непосредственное составление таблицы по формуле, чтобы затем сформировать из нее диаграмму либо линейный график. Сейчас детально останавливаться на этой теме не будем, но если она вас интересует, перейдите по ссылке ниже для прочтения другой моей статьи по этой теме.

Читайте также: Как построить график функции в Excel

В этой статье вы узнали, какие есть функции в Excel, как сделать формулу и использовать полезные возможности программы, делающие процесс взаимодействия с электронными таблицами проще. Применяйте полученные знания для самостоятельной практики и поставленных задач, требующих проведения расчетов и их автоматизации.

Источник

Пример 1

Дана функция:

Нужно построить ее график на промежутке [-5;5] с шагом равным 1.

Создание таблицы

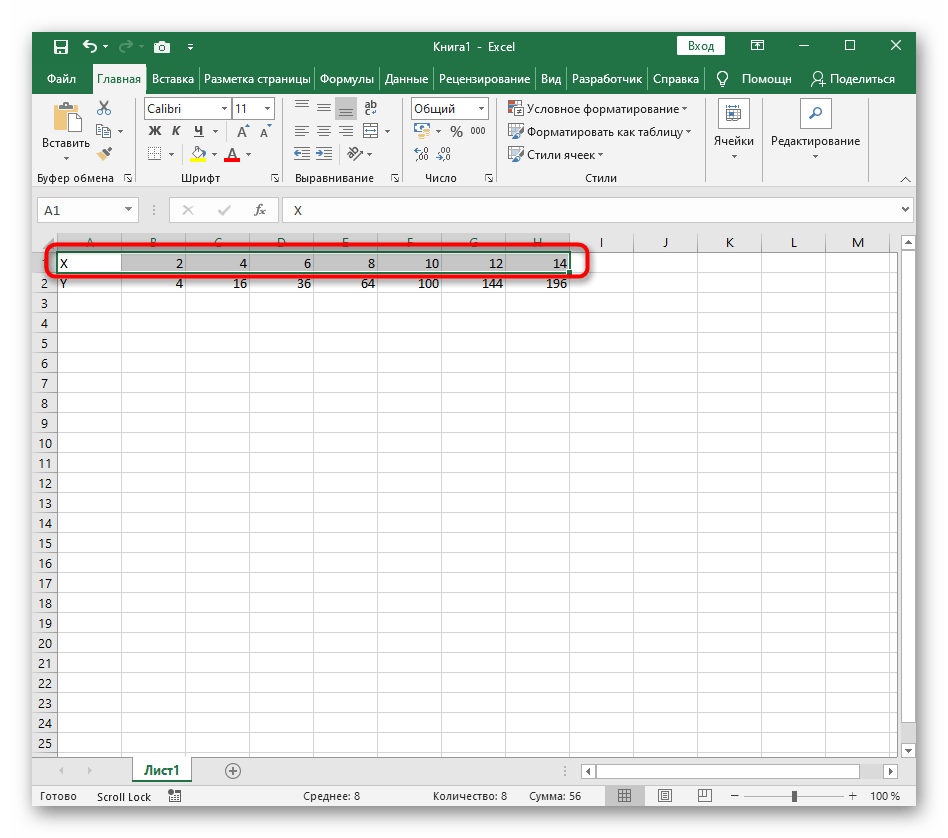
Создадим таблицу, первый столбец назовем переменная x (ячейка А1), второй — переменная y (ячейка В1). Для удобства в ячейку В1 запишем саму функцию, чтобы было понятно, какой график будем строить. Введем значения -5, -4 в ячейки А2 и А3 соответственно, выделим обе ячейки и скопируем вниз. Получим последовательность от -5 до 5 с шагом 1.

Вычисление значений функции

Нужно вычислить значения функции в данных точках. Для этого в ячейке В2 создадим формулу, соответствующую заданной функции, только вместо x будем вводить значение переменной х, находящееся в ячейке слева (-5).

Важно: для возведения в степень используется знак ^, который можно получить с помощью комбинации клавиш Shift+6 на английской раскладке клавиатуры. Обязательно между коэффициентами и переменной нужно ставить знак умножения * (Shift+8).

Ввод формулы завершаем нажатием клавиши Enter. Мы получим значение функции в точке x=-5. Скопируем полученную формулу вниз.

Мы получили последовательность значений функции в точках на промежутке [-5;5] с шагом 1.

Построение графика

Выделим диапазон значений переменной x и функции y. Перейдем на вкладку Вставка и в группе Диаграммы выберем Точечная (можно выбрать любую из точечных диаграмм, но лучше использовать вид с гладкими кривыми).

Мы получили график данной функции. Используя вкладки Конструктор, Макет, Формат, можно изменить параметры графика.

Пример 2

Даны функции:

и y=50x+2. Нужно построить графики этих функций в одной системе координат.

Создание таблицы и вычисление значений функций

Таблицу для первой функции мы уже построили, добавим третий столбец — значения функции y=50x+2 на том же промежутке [-5;5]. Заполняем значения этой функции. Для этого в ячейку C2 вводим формулу, соответствующую функции, только вместо x берем значение -5, т.е. ячейку А2. Копируем формулу вниз.

Мы получили таблицу значений переменной х и обеих функций в этих точках.

Построение графиков

Для построения графиков выделяем значения трёх столбцов, на вкладке Вставка в группе Диаграммы выбираем Точечная.

Мы получили графики функций в одной системе координат. Используя вкладки Конструктор, Макет, Формат, можно изменить параметры графиков.

Последний пример удобно использовать, если нужно найти точки пересечения функций с помощью графиков. При этом можно изменить значения переменной x, выбрать другой промежуток или взять другой шаг (меньше или больше, чем 1). При этом столбцы В и С менять не нужно, диаграмму тоже. Все изменения произойдут сразу же после ввода других значений переменной x. Такая таблица является динамической.

Кратко об авторе:

Шамарина Татьяна Николаевна — учитель физики, информатики и ИКТ, МКОУ «СОШ», с. Саволенка Юхновского района Калужской области. Автор и преподаватель дистанционных курсов по основам компьютерной грамотности, офисным программам. Автор статей, видеоуроков и разработок.

Спасибо за Вашу оценку. Если хотите, чтобы Ваше имя
стало известно автору, войдите на сайт как пользователь
и нажмите Спасибо еще раз. Ваше имя появится на этой стрнице.

Источник

Вариант 1: График функции X^2

В качестве первого примера для Excel рассмотрим самую популярную функцию F(x)=X^2. График от этой функции в большинстве случаев должен содержать точки, что мы и реализуем при его составлении в будущем, а пока разберем основные составляющие.

Создайте строку X, где укажите необходимый диапазон чисел для графика функции.

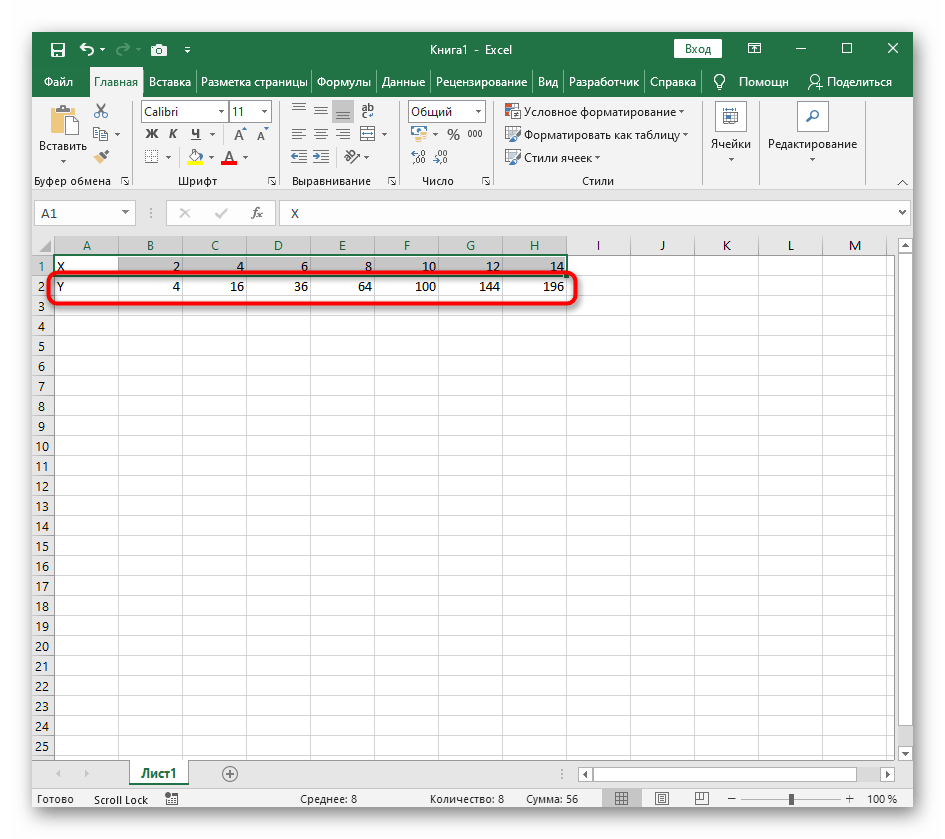
Ниже сделайте то же самое с Y, но можно обойтись и без ручного вычисления всех значений, к тому же это будет удобно, если они изначально не заданы и их нужно рассчитать.

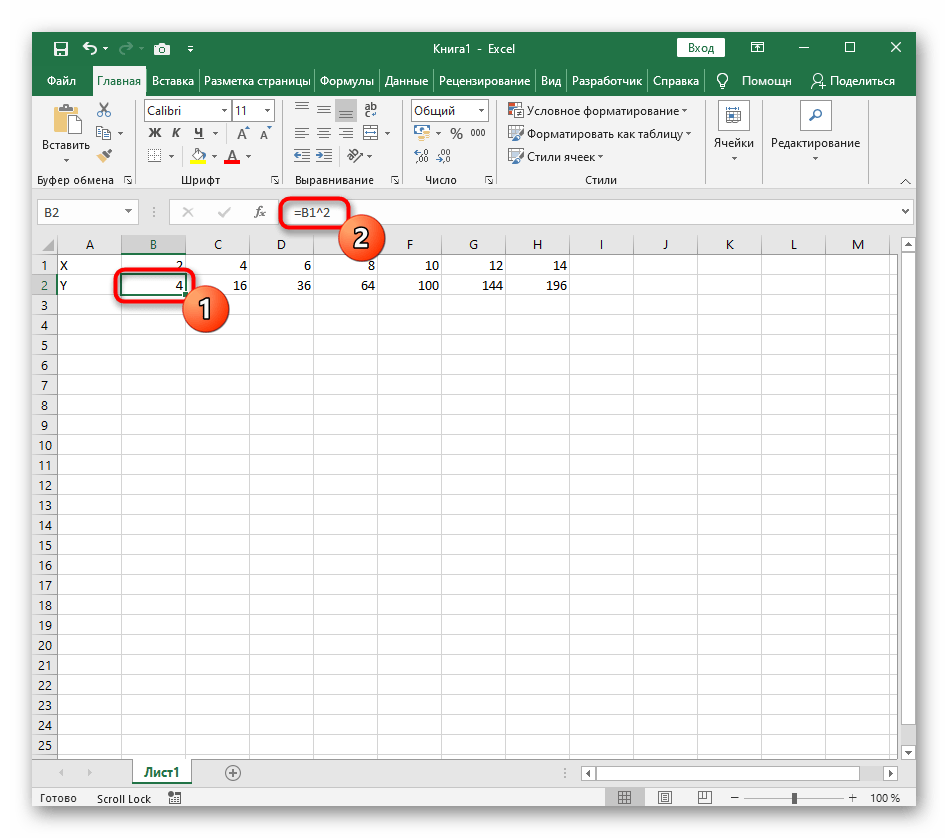
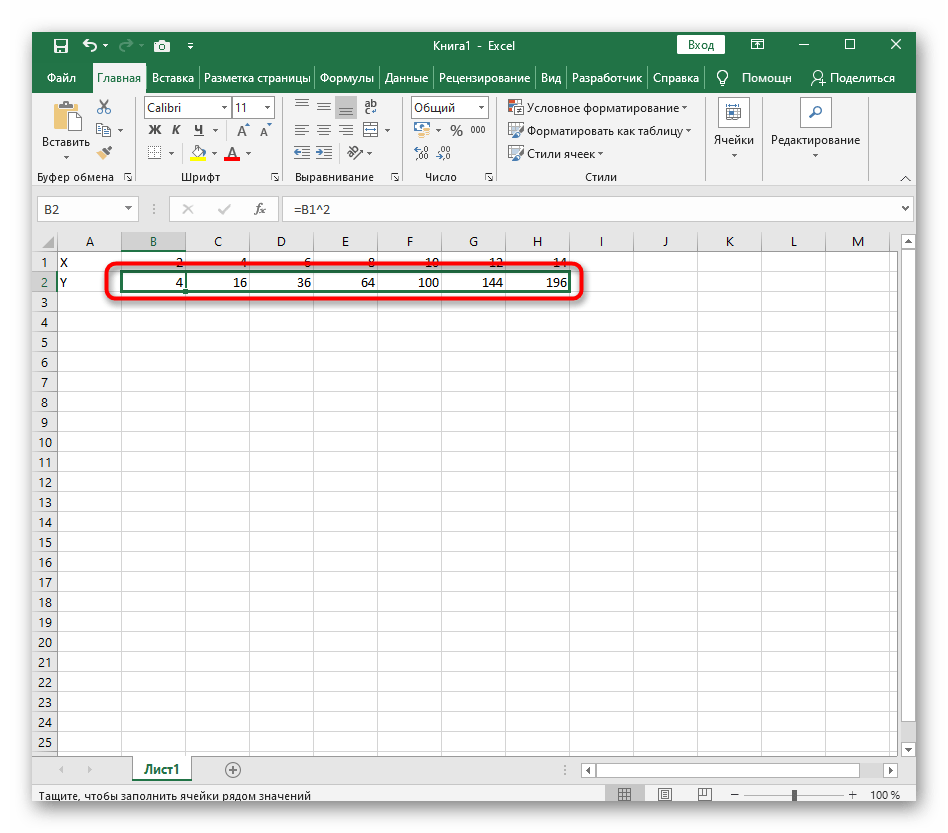
Нажмите по первой ячейке и впишите =B1^2, что значит автоматическое возведение указанной ячейки в квадрат.

Растяните функцию, зажав правый нижний угол ячейки, и приведя таблицу в тот вид, который продемонстрирован на следующем скриншоте.

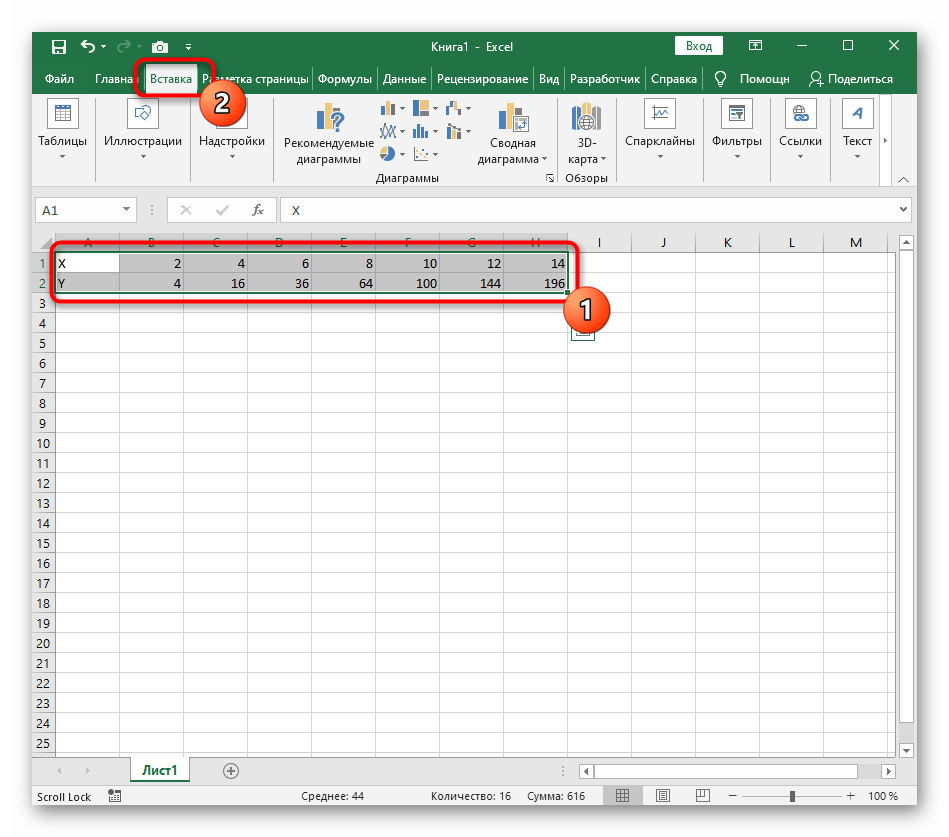
Диапазон данных для построения графика функции указан, а это означает, что можно выделять его и переходить на вкладку «Вставка».

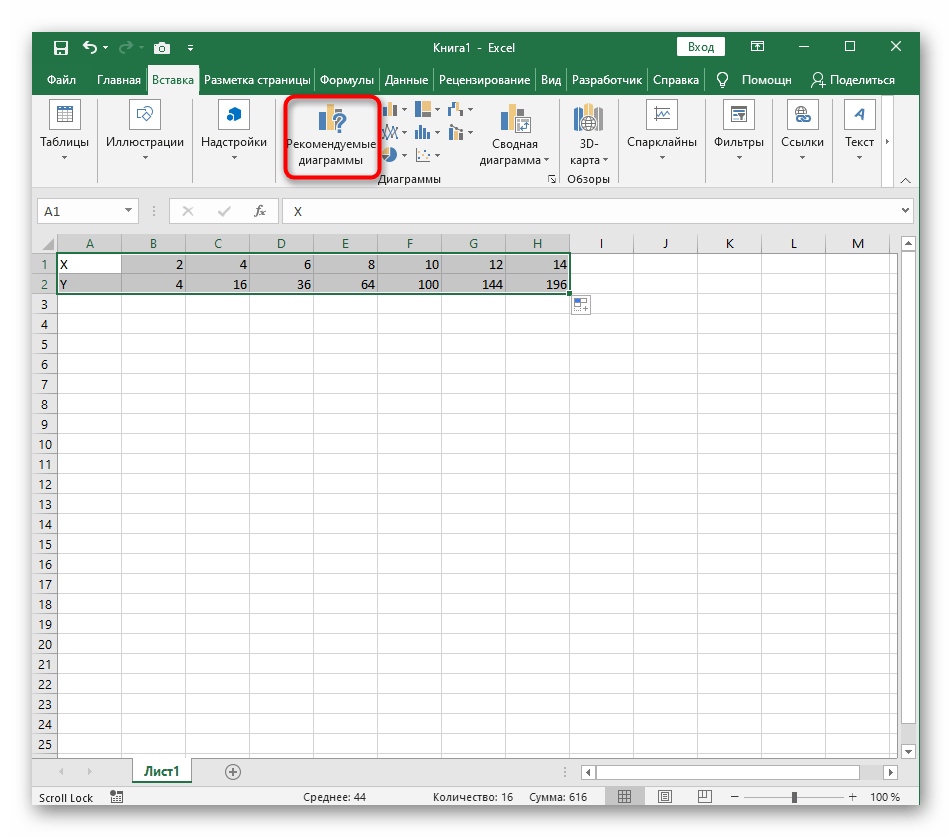
На ней сразу же щелкайте по кнопке «Рекомендуемые диаграммы».

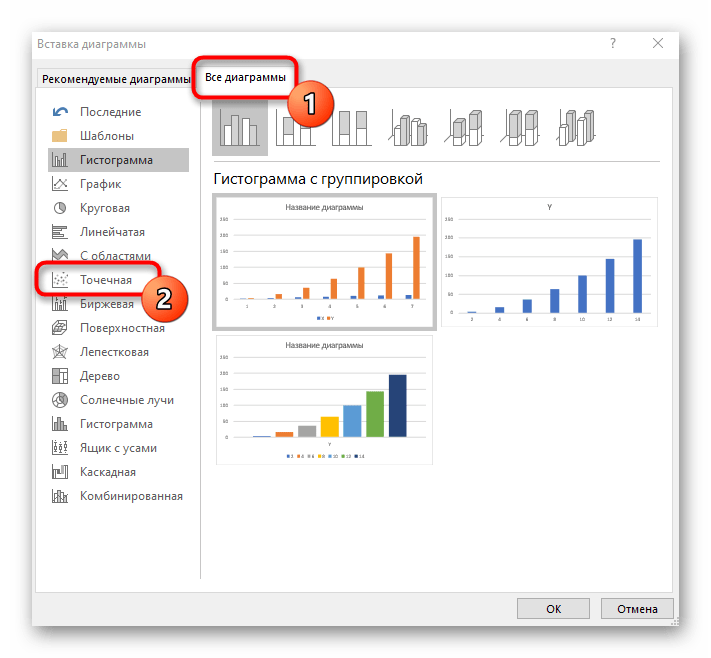
В новом окне перейдите на вкладку «Все диаграммы» и в списке найдите «Точечная».

Подойдет вариант «Точечная с гладкими кривыми и маркерами».

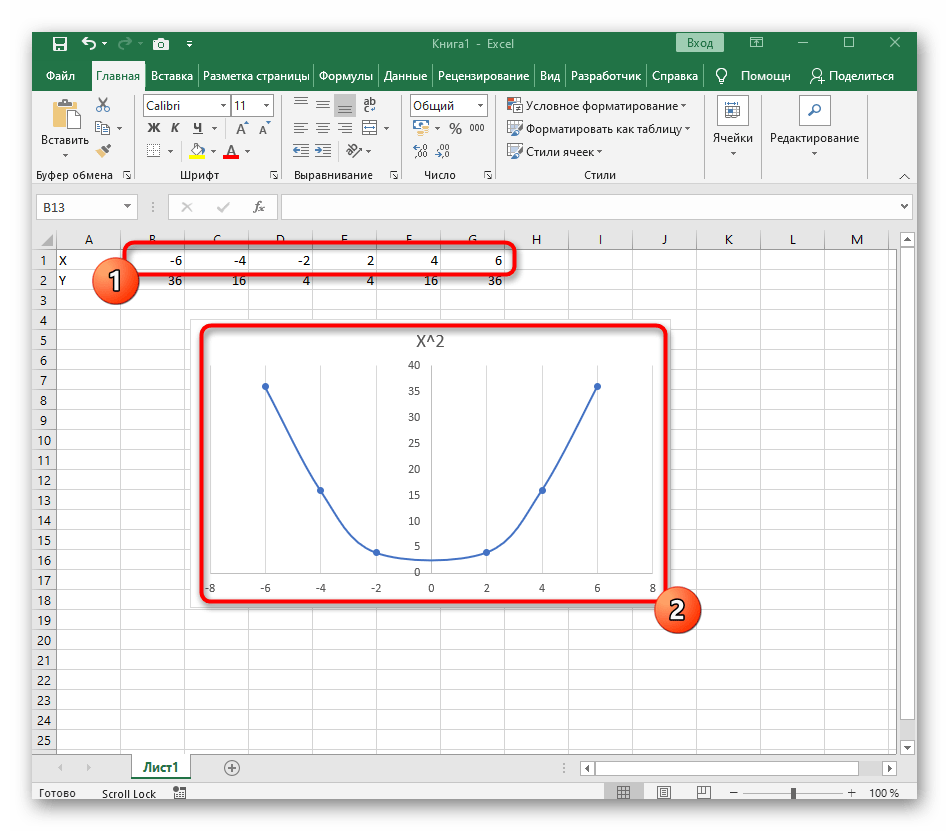
После ее вставки в таблицу обратите внимание, что мы добавили равнозначный диапазон отрицательных и плюсовых значений, чтобы получить примерно стандартное представление параболы.

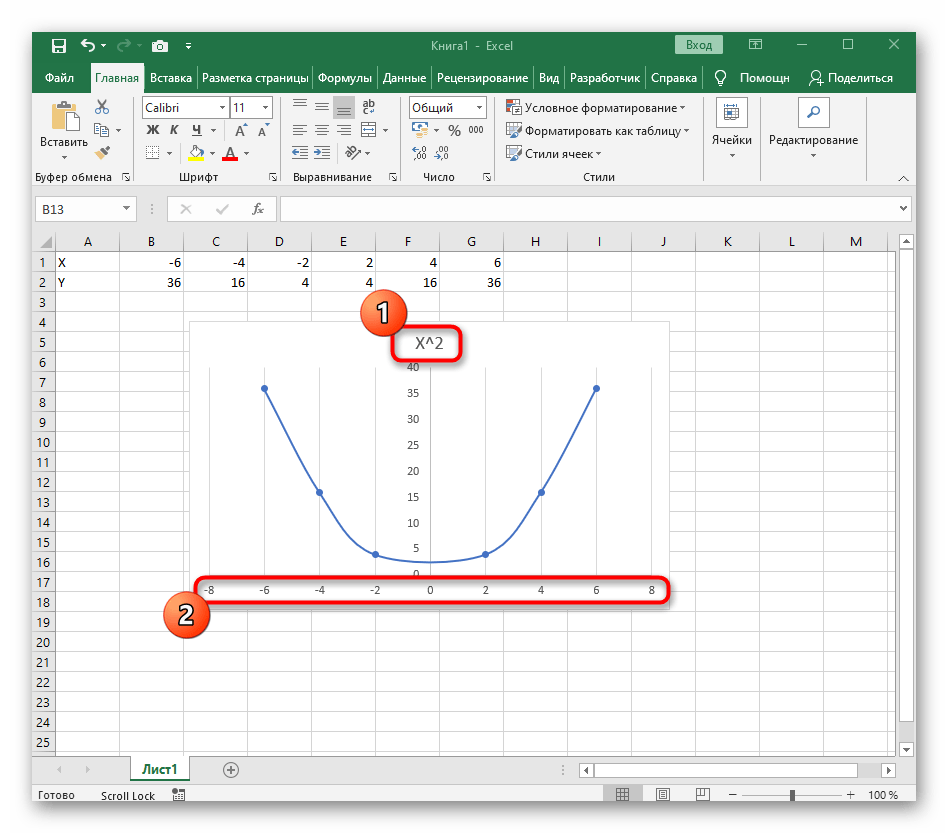
Сейчас вы можете поменять название диаграммы и убедиться в том, что маркеры значений выставлены так, как это нужно для дальнейшего взаимодействия с этим графиком.

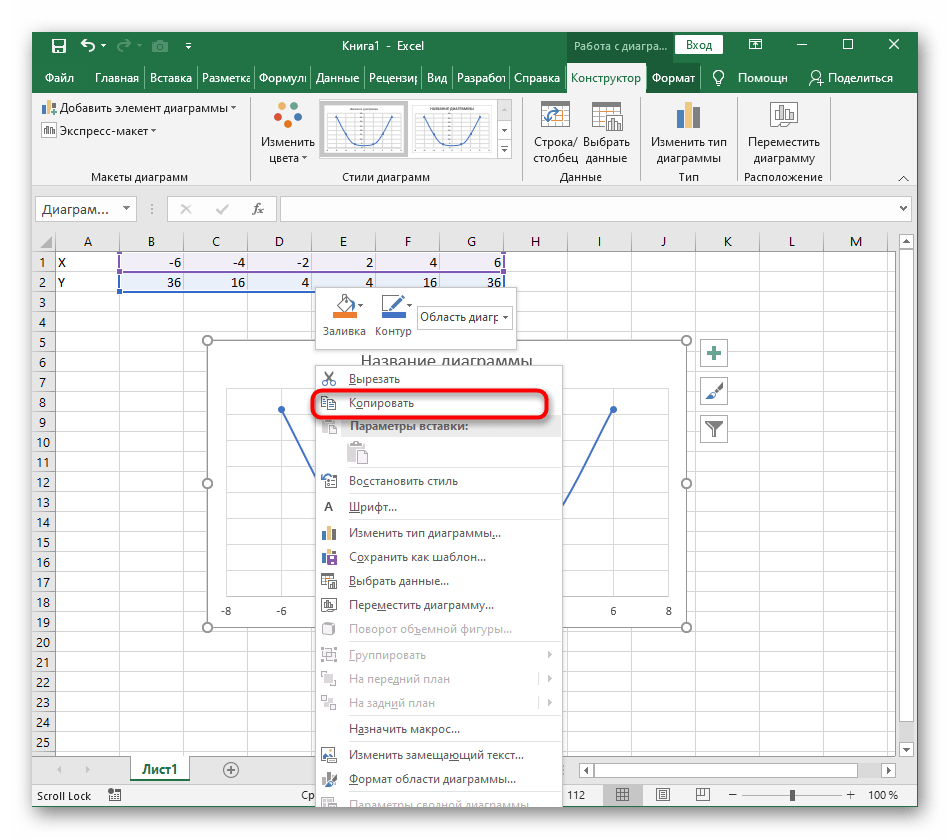
Из дополнительных возможностей отметим копирование и перенос графика в любой текстовый редактор. Для этого щелкните в нем по пустому месту ПКМ и из контекстного меню выберите «Копировать».

Откройте лист в используемом текстовом редакторе и через это же контекстное меню вставьте график или используйте горячую клавишу Ctrl + V.

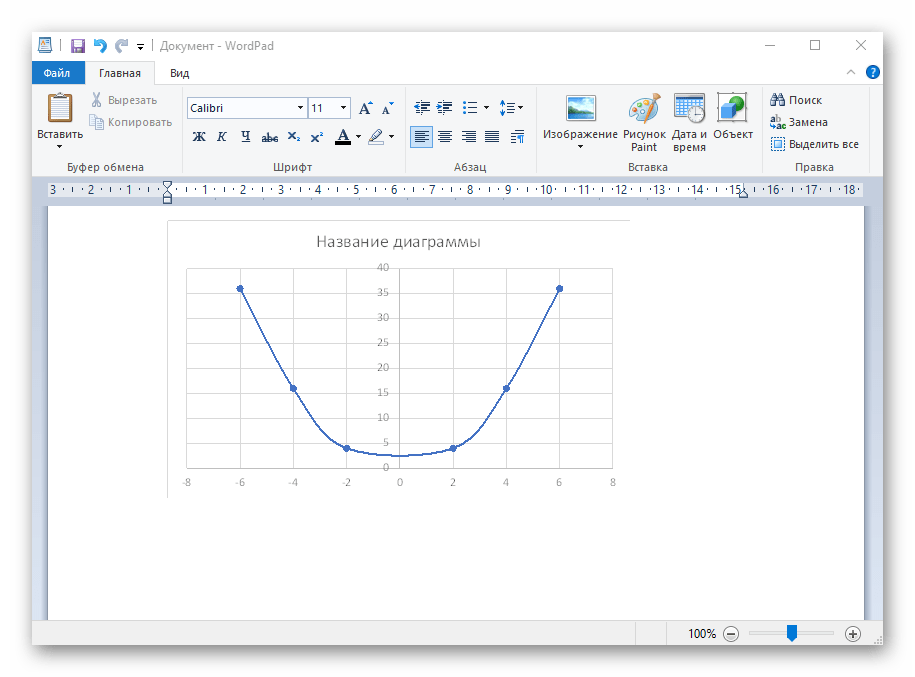
Если график должен быть точечным, но функция не соответствует указанной, составляйте его точно в таком же порядке, формируя требуемые вычисления в таблице, чтобы оптимизировать их и упростить весь процесс работы с данными.

Вариант 2: График функции y=sin(x)

Функций очень много и разобрать их в рамках этой статьи просто невозможно, поэтому в качестве альтернативы предыдущему варианту предлагаем остановиться на еще одном популярном, но сложном — y=sin(x). То есть изначально есть диапазон значений X, затем нужно посчитать синус, чему и будет равняться Y. В этом тоже поможет созданная таблица, из которой потом и построим график функции.

Для удобства укажем всю необходимую информацию на листе в Excel. Это будет сама функция sin(x), интервал значений от -1 до 5 и их шаг весом в 0.25.

Создайте сразу два столбца — X и Y, куда будете записывать данные.

Запишите самостоятельно первые два или три значения с указанным шагом.

Далее растяните столбец с X так же, как обычно растягиваете функции, чтобы автоматически не заполнять каждый шаг.

Перейдите к столбцу Y и объявите функцию =SIN(, а в качестве числа укажите первое значение X.

Сама функция автоматически высчитает синус заданного числа.

Растяните столбец точно так же, как это было показано ранее.

Если чисел после запятой слишком много, уменьшите разрядность, несколько раз нажав по соответствующей кнопке.

Выделите столбец с Y и перейдите на вкладку «Вставка».

Создайте стандартный график, развернув выпадающее меню.

График функции от y=sin(x) успешно построен и отображается правильно. Редактируйте его название и отображаемые шаги для простоты понимания.

Еще статьи по данной теме:

Помогла ли Вам статья?

Источник

Задания к лабораторной работе

по Excel

Оглавление

Задание №1

Варианты заданий

Задание №2

Варианты заданий

Задание №3

Варианты заданий

Задание №4

Задание №1

1. Вычислить значение функции

для х=1 и у=2 двумя способами:

а) в ячейку А1 запишем 1 значение х, а в В1 запишем значение у 2 и тогда в ячейку С1 запишем вышеуказанную формулу, ввод формулы всегда начинается со знака = , значок ^- операция возведение в степень, *- операция умножение

б)

Для записи формулы по варианту б) необходимо ячейкам A2 и B2 присвоить имена соответственно х и у. Для этого:

Выделить ячейку, в которую будем записывать значение х и выполнить

Вставка-Имя-Присвоить(в Office-2003)

Формула- выбрать Присвоить (в Office-2007)

,откроется диалоговое окно, в котором подтвердить новое имя ячейки х, аналогично выполнить для у и записать формулу в ячейку С2, при нажатии Enter получим результат.

Перейти на Лист2.

2.а) составить таблицу, содержащую фамилии студентов ( не менее 5 фамилий),их рост и возраст;

б) найти средний рост и возраст;

в) построить вертикальную столбчатую диаграмму на одном листе с данными, содержащую рост и возраст каждого студента.

Среднее значение роста вычислить с помощью мастера функций ,используя функцию Срзнач, а среднее значение возраста вычислить с помощью автосуммы : вычислить сумму и разделить ее на количество

Перейти на Лист3.

3. а) составить таблицу значений функции y=sin(x), для х принадлежащего отрезку [20^o,60^o] c шагом h =3^o;

б) построить по данным таблицы график функции y=sin(x)

Столбцы А и В заполнить ,используя автозаполнение: для этого поместить в ячейки В2 и В3 соответственно 20 и 23 ,выделить обе ячейки ,подвести указатель мыши к маленькому черному квадрату и нажать левую кнопку мыши и ,не отпуская ее ,провести по всем ячейкам данного столбца, таким же образом ,заполнить столбец А.Установить курсор в ячейку С2,поместить в нее знак = и вызвать мастер функций.

Вставка-Мастер функций (в Office-2003)

Формулы (в Office-2007)

Выбрать категорию функций Математическая в открывшемся диалоговом окне и в списке справа отыскать функцию радианы для перевода углов из градусов в радианы. Откроется другое диалоговое окно, в котором необходимо указать адрес ячейки для которой выполняется операция. Адрес ячейки указать с помощью мыши. За черный квадрат распространить формулу на остальные ячейки столбца С.Аналогичные действия выполнить со столбцом D.

Для построения графика выделить отдельно столбцы Х(радианы) и У, используя клавишу Ctrl.

Вызвать мастер диаграмм: Вставка-Мастер диаграмм (в Office-2003)

Вставка (в Office-2007 )

выбрать Точечная, просмотреть все открывающиеся диалоговые окна и задать имя графику и ответить на все вопросы мастера. График построить на листе с исходными данными.

4. Создание макроса.

Вернуться на Лист2.

Удалить диаграмму и записать макрос создания диаграммы.

Выполнить команду

Сервис-Макрос-Начатьзапись (вOffice-2003)

Вид-Макросы-Записьмакроса (в Office-2007)

Появится диалоговое окно, в котором будет предложено дать имя макросу, можно оставить предложенное имя.

Выделить данные для диаграммы и вызвать мастер диаграмм, построить диаграмму и выполнить команду

Сервис-Макрос-Остановитьзапись (в Office-2003)

Вид-Макросы-Остановитьзапись.(в Office-2007)

Макрос будет записан. Его можно просмотреть или выполнить.

Сервис–Макросы-Макрос (в Office-2003)

Вид-Макросы-Макросы(в Office-2007)

выбрать из предложенного списка имя макроса:

— для просмотра текста- войти

-для выполнения — выполнить.

Перейти на Лист3 удалить график и создать самостоятельно макрос создания графика. Пиктограммы работы с макросами также можно найти на ленте Разработчик

5. Настройка рабочей панели для запуска макросов

Сервис-Настройка-Панели инструментов-Создать-Настраиваемая1 (в Office—2003)

В окне документа появится пустая панель.

Выбрать из Сервис-Настройка–Команда-Макросы (в Office-2003)

Появится настраиваемая кнопка для запуска макроса. Перенести кнопку на настраиваемую панель и с помощью контекстного меню назначить имя макроса, который будет связан с этой кнопкой. С помощью контекстного меню можно изменить вид кнопки и назначить ей другой макрос.

Создать кнопки запуска макросов для построения диаграммы и графика.

В Office-2007 можно кнопки вызова макросов поместить в панель быстрого доступа.

Если панель быстрого доступа отсутствует, то на пиктограмме Макросы(Вид) через контекстное меню добавить панель быстрого доступа, а если она есть, то настроить ее:

Открывается окно Параметры Excel, в котором выбратьНастройка, затем команду

Макросы (В окне Настройка панели быстрого доступа) и добавитькнопку для запуска макросов

Варианты индивидуальных заданий

1.а) Составить таблицу значений функции y=2sin(x)cos(x), для х принадлежащего отрезку [0^o,360^o] c шагом h =45^o.

б) Построить по данным таблицы график функции y=2sin(x)cos(x).

в) Создать макрос графика.

2.а) Составить таблицу значений функции y=tg(x), для х принадлежащего отрезку [0^o,180^o] c шагом h =30^o.

б) Построить по данным таблицы график функции y=tg(x).

в) Создать макрос графика.

3.а) Составить таблицу значений функции y=e^x, для х принадлежащего отрезку [1,5] c шагом h =1.

б) Построить по данным таблицы график функции y=e^x.

в) Создать макрос графика.

4.a) Составить таблицу значений функции y=sin(x)+cos(x), для х принадлежащего отрезку

[-180^o,=180^o] c шагом h =30^o.

б) Построить по данным таблицы график функции y=sin(x)+cos(x).

в) Создать макрос графика.

5.a) Составить таблицу значений функции y=ln(x), для х принадлежащего отрезку [1,10] c шагом h =1.

б) Построить по данным таблицы график функции y=ln(x).

в) Создать макрос графика.

6.a) Составить таблицу значений функции y=xsin(x), для х принадлежащего отрезку [0^o,360^o] c шагом h =30^o.

б) Построить по данным таблицы график функции y=xsin(x).

в) Создать макрос графика.

7.a) Составить таблицу значений функции y=xcos(x), для х принадлежащего отрезку

[-180^o,360^o] c шагом h =30^o.

б) Построить по данным таблицы график функции y=xcos(x).

в) Создать макрос графика.

8.a) Составить таблицу значений функции y=sin²(x), для х принадлежащего отрезку [30^o,180^o] c шагом h =10^o.

б) Построить по данным таблицы график функции y=sin²(x).

в) Создать макрос графика.

9.a) Составить таблицу значений функции y=cos²(x)+x, для х принадлежащего отрезку [20^o,90^o] c шагом h =5^o.

б) Построить по данным таблицы график функции y=cos²(x)+x.

в) Создать макрос графика.

10.a) Составить таблицу значений функции y=ctg(x), для х принадлежащего отрезку

[-180^o,180^o] c шагом h =60^o.

б) Построить по данным таблицы график функции y=ctg(x).

в) Создать макрос графика.

11.a). Составить таблицу значений функции y=tg(x)+ctg(x), для х принадлежащего отрезку [0^o,360^o] c шагом h =45^o.

б) Построить по данным таблицы график функции y=tg(x)+ctg(x).

в) Создать макрос графика.

) Составить таблицу значений функции y=x ²sin(x), для х принадлежащего отрезку [20^o,90^o] c шагом h =5^o.

б) Построить по данным таблицы график функции y=x ²sin(x).

в) Создать макрос графика.

13.a) Составить таблицу значений функции y=xln(x), для х принадлежащего отрезку [1,6] c шагом h =1.

б) Построить по данным таблицы график функции y=xln(x).

в) Создать макрос графика.

14.a) Составить таблицу значений функции y=e^xln(x), для х принадлежащего отрезку [2,20] c шагом h =2.

б). Построить по данным таблицы график функции y=e^xln(x);.

в) Создать макрос графика.

Задание №2

Работа с матрицами

1. Умножить матрицу А₂,з на В₃,з и получить матрицу С₂,з

Задаем значения элементам матриц А и В
Выделяем место для результирующей матрицы С |
В строку формул записываем знак =
С помощью мастера функций находим функцию МУМНОЖ.
Задаем для нее исходные данные (параметры) с помощью мыши
Активизируем строку формул
Нажимаем одновременно 3 клавиши .ctrl+shift+enter.
Результат появляется в результирующей матрице

2. Найти для матрицы A транспонированную матрицу, используя функцию ТРАНСП

3. Для матрицы В найти обратную матрицу с помощью функции МОБР

4. Решение системы уравнений методом обращения матриц.

Задана система линейных уравнений

x1+2x2+3x3 = 4

4x1+3x2+2x3=1 (1)

x1+3x2+2x3 = 4

В матричной форме система (1) имеет вид

А_3,3 · Х_3,1 =В_3,1 (2), где А_3,3-матрица коэффициентов при неизвестных

B_3,1-вектор правых частей

Вектор неизвестных Х_3,1 может быть найден по формуле

Х_3,1=А_3,3^-1· В_3,1 (5)

А_3,3^-1— обратная матрица

Решение задачи выполнить в таблице

1.Ввести в таблицу значения матрицы коэффициентов А_3,3

2.Ввести в таблицу значения вектора В_3,1

3.Выделить место для обратной матрицы А_3,3^-1

4.Вызвать мастер функций, отыскать функцию Мобр, которая вычисляет обратную матрицу.

5.Открывается диалоговое окно, в которое надо ввести адрес исходной матрицы коэффициентов. Нажать клавишу ctrl и обвести мышью исходную матрицу. Проверить записанный адрес. Если все нормально, щелкнуть мышью по строке формул (в ней появится курсор) и нажать 3 клавиши одновременно ctrl+shift+enter.

В выделенных ячейках появятся значения обратной матрицы.

6.Выделить место для результата (вектор неизвестных) Х_3,1.

7.С помощью мастера функций найти функцию МУМНОЖ.

8.Откроется диалоговое окно, в которое надо ввести два адреса:

-адрес обратной матрицы (массив1)

-адрес вектора правых частей (массив2) .Выполнить выделение обязательно мышью

Активизировать строку формул , чтобы в ней появился курсор и нажать клавиши ctrl+shift+enter.

Варианты индивидуальных заданий

1. 2х1+х2-5х3+х4=8 2. 3х1-х2=5

х1-3х2-6х4=9 -2х1+х2+х3=0

2х2-х3+2х4=-5 2х1-х2+4х3=15

х1+4х2-7х3+6х4=0

3. 7,9х1+5,6х2+5,7х3-7,2х4=6,68 4. 6х1-х2-х3=11,33

8,5х1-4,8х2+0,8х3+3,5х4=9,95 -х1+6х2-х3=32

4,3х1+4,2х2-3,2х3+9,3х4=8,6 -х1-х2+6х3=42

3,2х1-1,4х2-8,9х3+3,3х4=1

5. 3х1+х2-х3+2х4=6 6. 10х1+х2+х3=12

-5х1+х2+3х3-4х4=-12 2х1+10х2+х3=13

2х1+х3-х4=1 2х1+2х2+10х3=14

х1-5х2+3х3-3х4=3

7. 2х1-х2-х3=-3 8. х1-0,2х2-0,2х3=0,6

3х1+5х2-2х3=1 -0,1х1+х2-0,2х3=0,7

х1-4х2+10х3=0 -0,1х1-0,1х2+х3=0,8

9. 3х1-х2= 5,2 10. 2х1+х2-5х3+х4=8

-2х1+х2+х3=0 х1-3х2-6х4=9

2х1-х2+4х3=15,4 2х2-х3+2х4=-5

х1+4х2-7х3+6х4=0

11. 6х1-х2-х3=11,33 12. х1+3х2-2х3-2х5=0,5

-х1+6х2-х3=32 3х1+4х2-5х3+х4-3х5=5,4

-х1-х2+6х3=42 -2х1-5х2+3х3-2х4+2х5=5,0

х2-2х3+5х4+3х5=7,5

-2х1-3х2+2х3+3х4+4х5=3,3

13. 3х1+х2-х3+2х4=6 14. 4х1+0,24х2-0,08х3=8

-5х1+х2+3х3-4х4=-12 0,09х1+3х2-0,15х3=9

2х1+х3-х4=1 0,04х1-0,08х2+4х3=20

х1-5х2+3х3-3х4=3

Задание №3

Логическая функция Если

Пример№1 -начисление премии в зависимости от должности

Ст. инспектор получает 2500 руб., инспектор-2000руб.

Установить курсор в С2 ,с помощью мастера функций выбрать категорию Логические и функцию ЕСЛИ
В диалоговом окне Аргументы функции задать необходимые параметры

В строке Логическое выражение необходимо указать адрес ячейки должности 1-ой записи(для этого щелкнуть мышкой по ячейке В2 и в строке логическое выражение появится адрес В2, дописать =”Ст.инспектор” т.е. логическое выражение будет иметь вид В2=”Ст.инспектор”

3. В строке значение, если истина записать 2500

4. В строке значение, если ложь записать 2000 и подтвердить ОК

Скопировать формулу в другие ячейки
Построить гистограмму

Пример №2

Если х>0 и x<y найти сумму чисел, иначе вычислить разность чисел

Задать столбик значений х с шагом 5 от -50 до 50
Вычислить столбик значений у по формуле у=х+5(адреса ячеек выбирать мышкой)
Установить курсор в С2, с помощью мастера функций выбрать категорию Логические и функцию И
В диалоговом окне Аргументы функции задать необходимые параметры

Логическое условие 1 для ячейки со значением -50 будет А2>0

Логическое условие 2 для ячейки со значением -50 будет А2<B2 и подтвердить ОК

Скопировать формулу в другие ячейки столбца С
Установить курсор в D2 , с помощью мастера функций выбрать категорию Логические и функцию Если
В диалоговом окне Аргументы функции задать необходимые параметры

Логическое выражение-адрес C2 , в строке значение, если истина А2+В2,

В строке значение, если ложь А2-В2

8. Полученное значение скопировать в остальные ячейки столбца D

9. Построить график зависимости результирующего значения функции от х

Построение гистограммы и графика описано в задании №1

Варианты заданий

1.Если х>5 или х≤-20 вычислить у=1+tgx иначе вычислить у=х².

Задать изменение х от -100 до 100 с шагом 10. Построить график зависимости у(х).

2.Если х принадлежит интервалу (4,20) вычислить значение функции по формуле y=х²+1 иначе вычислить значение функции по формуле y=sinх, задать изменение х от -60 до 60 с шагом 4. Построить график зависимости у(х).

3.Если х<-15 или х>10 вычислить у=x+5 иначе вычислить у=lnx.

Задать изменение х от -40 до 40 с шагом 5. Построить график зависимости у(х).

4.Если х принадлежит отрезку [5,8] вычислить значение функции по формуле y=cosx иначе вычислить значение функции по формуле y=x²+x , задать изменение х от -5 до 10 с шагом 1. Построить график зависимости у(х).

5.Если х<-1 или х<20 вычислить у=e^x иначе вычислить у=sin(x+4)

Задать изменение х от -50 до 50 с шагом 5 Построить график зависимости у(х).

6.Если х>-10 и х<40 вычислить у=x+2 иначе вычислить у=cosx+x

Задать изменение х от -50 до 50 с шагом 5 Построить график зависимости у(х).

7.Если x>0 и y<-4 вычислить произведение чисел, иначе сумму.

Задать изменение х от -20 до 20 с шагом 5, а у вычислить по формуле х-2 Построить график зависимости у(х).

8.Если х<-5 или х>10 вычислить у=x³+5 иначе вычислить у=ln(x+2).

Задать изменение х от -40 до 40 с шагом 5. Построить график зависимости у(х).

9.Если х принадлежит отрезку [3,10] вычислить значение функции по формуле y=xcosx иначе вычислить значение функции по формуле y=x+4 , задать изменение х от -4 до 20 с шагом 2 Построить график зависимости у(х).

10.Если х>10 или х≤-20 вычислить у=sinx+cosx иначе вычислить у=х².

Задать изменение х от -50 до 50 с шагом 10. Построить график зависимости у(х).

11. Если х принадлежит интервалу (8,30) вычислить значение функции по формуле y=х²+1 иначе вычислить значение функции по формуле y=2sin(х+2) , задать изменение х от -60 до 60 с шагом 10. Построить график зависимости у(х).

12.Если x>-6 и y<х вычислить произведение чисел, иначе разность.

Задать изменение х от -20 до 20 с шагом 5, а у вычислить по формуле х-2 Построить график зависимости у(х).

13. Если х принадлежит интервалу (-10,30) вычислить значение функции по формуле y=х²+1 иначе вычислить значение функции по формуле y=tgx+ctgx , задать изменение х от -60 до 60 с шагом 10. Построить график зависимости у(х).

14. Если х не принадлежит отрезку [-4,10] вычислить значение функции по формуле y=2cosx иначе вычислить значение функции по формуле y=x+2 , задать изменение х от -10 до 20 с шагом 2

Задание №4

Лабораторная работа по базам данных в ЭТ Excel.

Создать БД в виде таблицы 1.

Таблица1

Ввести 3 записи.
Создать форму для ввода данных.

а)Для этого выделить все поля без 1-ой строки

б) В меню выбрать пункт Данные-Форма(2003) ВкладкаДанные(2007)

Появится форма для ввода данных.Поля Общий размер и Общая стоимость сделать вычисляемыми.Общий размер вычислить как сумму ячеек с адресами D3+E3+F3

Общая стоимость должна быть вычислена по формуле D3*G3+E3*H3+F3*I3

В форму ввести еще 5 записей.

4.Выполнить сортировку данных по номеру садового участка и ФИО.

Для этого выделить данные.

В пункте меню Данные выбрать сортировку

5. С помощью пункта меню Данные выбрать Автофильтр и отобрать данные о садовых участках, у которых самые неплодородные земли. Выделить данные без 1-ой строки и

выполнить команду Данные-Фильтр-Автофильтр

В строке заголовка таблицы появятся стрелки раскрывающегося списка. Щелкнуть на значок неплодородные земли и задать условие выбора. Условие задать таким образом, чтобы в списке осталось3-4 владельца садового участка. Условие задается в диалоговом окне. Показать преподавателю и восстановить базу данных.

6. Расширенный фильтр. Выдать на экран владельцев , у которых самые плодородные земли и больше всего строений. Для этого скопировать БД (базу данных) на новый лист и назвать лист Расширенный .Задать диапазон условий ниже БД. Для задания условий использовать операции отношения <,=,>,=,<>. Скопировать область заголовка на свободное место за БД и задать условия выбора в полях Плодородные земли и строения. Затем установить курсор в БД и выдать команду Данные–Фильтр-Расширенный фильтр откроется диалоговое окно , в котором необходимо задать

1). Скопировать результат на новое место

2). В строке исходный диапазон указать адрес БД.

3). В строке условие задать диапазон условий.

4). Для результата отвести место на свободном поле после диапазона условий

и закрыть диалоговое окно. Если такие записи есть в вашей БД, то они будут выведены на экран. Для задания условий использовать операции отношения <,>,<>,>=,<=,=

7.Выдать в мерию список владельцев садовых участков, у которых самые неплодородные земли и меньше всего строений, т.е. нуждающихся в материальной помощи. Скопировать БД на новый лист и выбрать таких владельцев с помощью расширенного фильтра. Скопировать список на новый лист, назвать его список. Оформить с заголовком Список, выдать дату с помощью функции Сегодня. Список должен содержать следующие столбцы: Имя владельца, номер садового участка, общий размер участка, размер неплодородной земли и количество строений, остальные столбцы скрыть Формат-Столбцы -Скрыть.

Источник

Михаил Витер

Эксперт по предмету «Информационные технологии»

Задать вопрос автору статьи

Определение 1

Аппроксимация табличных функций в Excel — это определение аппроксимирующей функции, которая является близкой к заданной.

Понятие аппроксимации

Среди разных методик прогнозирования следует отдельно выделить метод аппроксимации. С его помощью имеется возможность осуществления приблизительных подсчетов и вычисления планируемых показателей, за счёт подмены исходных объектов на более простые. В Excel также присутствует возможность применения этого метода с целью выполнения прогнозов и анализа.

Название этого метода произошло от латинского слова “proxima”, то есть, «ближайшая». Как раз приближение за счет упрощения и сглаживания некоторых показателей, формирование из них тенденции и считается его основой. Но эту методику можно применять не только для прогнозирования, но и для изучения уже полученных результатов. Поскольку аппроксимация выступает, по существу, как упрощение исходных данных, а упрощенную версию легче изучать.

Аппроксимация табличных функций в Excel

Основным инструментом, при помощи которого реализуется сглаживание в Excel, является формирование линии тренда. Суть заключается в том, что на базе уже существующих показателей выполняется достраивание графика функции на будущие периоды. Основным предназначением линии тренда очевидно является формирование прогнозов или определение общей тенденции.

Эта линия может быть построена с использованием одного из следующих типов аппроксимации:
линейная,
экспоненциальная,
логарифмическая,
полиномиальная,
* степенная.

Рассмотрим некоторые из этих вариантов более подробно, и начнем с линейной аппроксимации, которая фактически является линейным сглаживанием. Прежде всего, следует рассмотреть наиболее простую версию аппроксимации, то есть, при помощи линейной функции.

Замечание 1

Сначала необходимо построить график, на базе которого будет осуществляться процедура сглаживания.

«Аппроксимация табличных функций в Excel » 👇

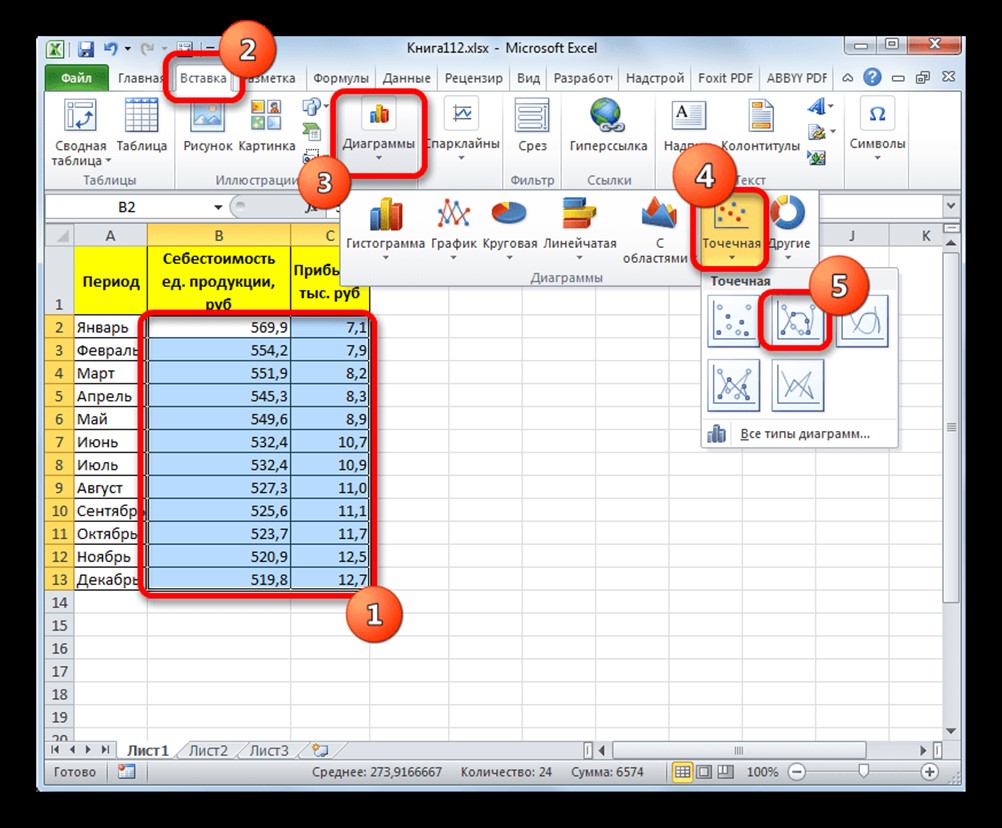
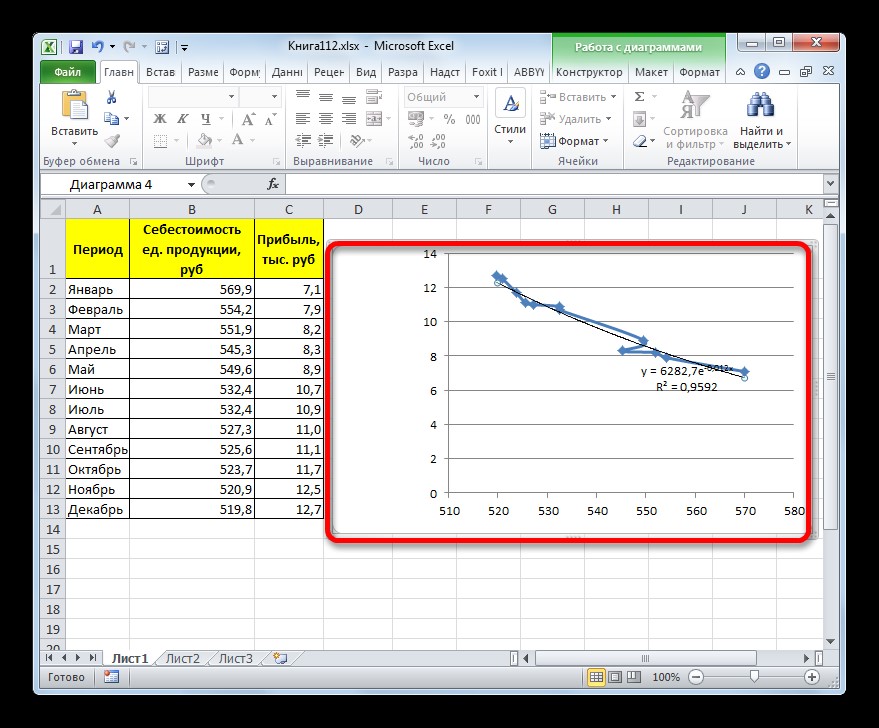
Чтобы построить график, необходимо взять таблицу, в которой, например, помесячно указывается себестоимость единицы продукции, выпускаемой организацией, и соответствующая прибыль за данный период. Графическая функция, которую необходимо построить, будет отображать зависимость роста прибыли от уменьшения себестоимости продукции. При построении графика сначала надо выделить столбцы «Себестоимость единицы продукции» и «Прибыль». После этого следует переместиться на вкладку «Вставка». Затем на ленте в блоке инструментов «Диаграммы» выполнить щелчок указателем мыши по кнопке «Точечная». В открывшемся списке нужно выбрать наименование «Точечная с гладкими кривыми и маркерами». Как раз такой вид диаграмм больше всего подходит для работы с линией тренда, а, следовательно, и для использования метода аппроксимации в Excel.

Рисунок 1. Параметры для построения графика. Автор24 — интернет-биржа студенческих работ

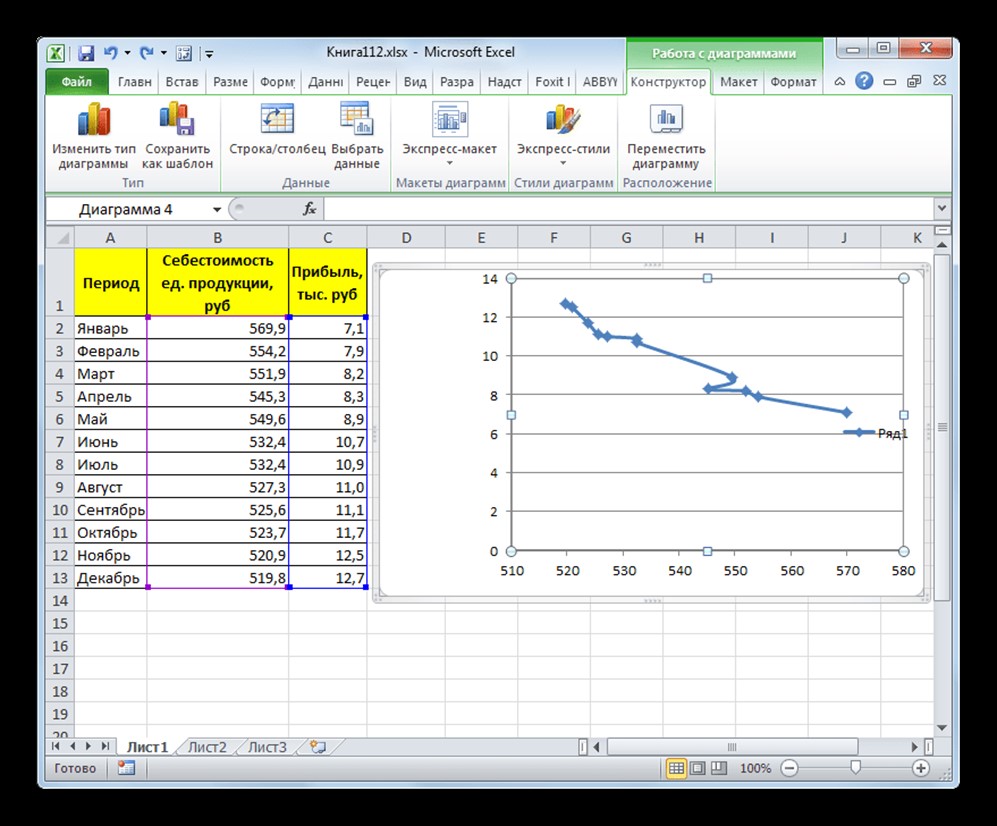
Затем будет построен следующий график:

Рисунок 2. Точечная с гладкими кривыми и маркерами. Автор24 — интернет-биржа студенческих работ

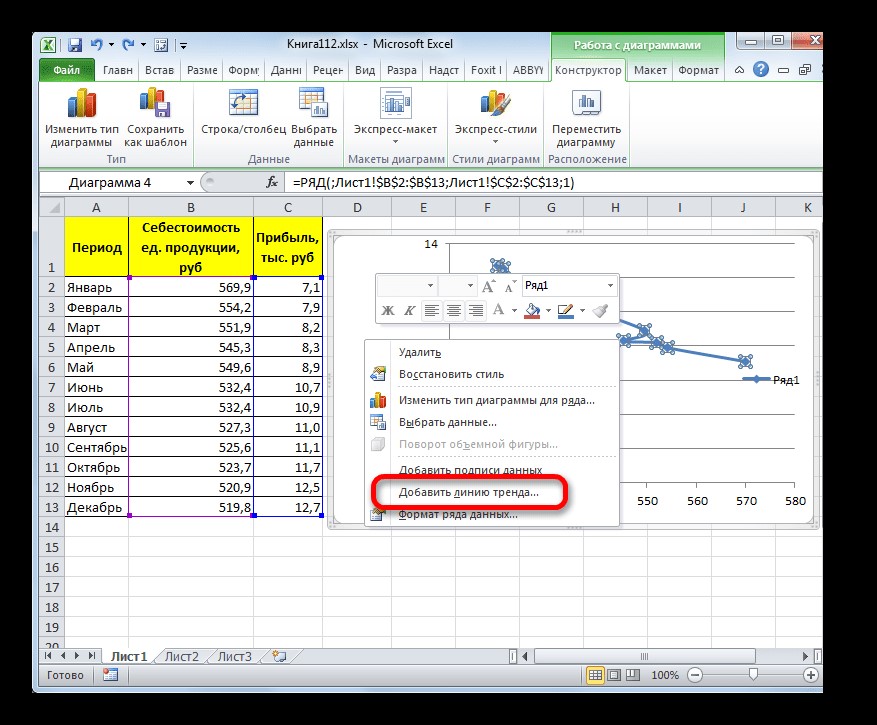
Чтобы добавить линию тренда, необходимо выделить график кликом правой кнопки мыши, после чего появится контекстное меню. Следует осуществить выбор в нем пункта «Добавить линию тренда…».

Рисунок 3. Добавить линию тренда на график. Автор24 — интернет-биржа студенческих работ

Имеется и другой вариант добавления линии тренда. В дополнительной группе вкладок на ленте «Работа с диаграммами» следует переместиться во вкладку «Макет». Затем в блоке инструментов «Анализ» необходимо сделать щелчок по кнопке «Линия тренда», после чего откроется список. Поскольку в нашем случае рассматривается применение линейной аппроксимации, то из предложенных позиций следует выбрать «Линейное приближение».

Если же был выбран первый вариант действий с добавлением через контекстное меню, то далее будет открыто окно формата. В блоке параметров «Построение линии тренда (аппроксимация и сглаживание)» необходимо установить переключатель в позицию «Линейная». Если это необходимо, то следует поставить галочку около позиции «Показывать уравнение на диаграмме». После данных действий на диаграмме будет отображено уравнение сглаживающей функции.

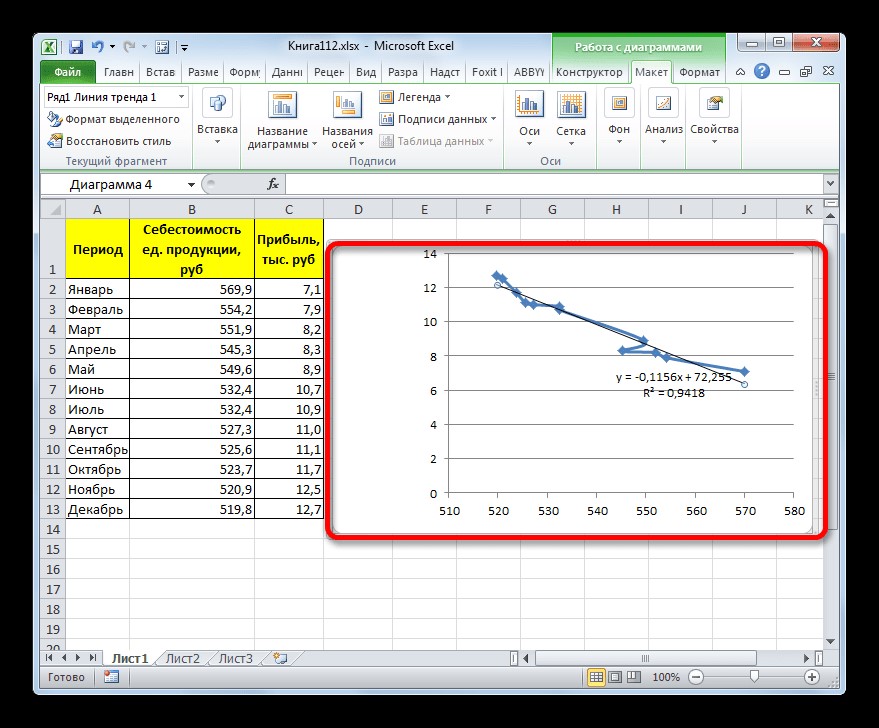
Кроме того, для сравнения разных вариантов аппроксимации можно установить галочку около пункта «Поместить на диаграмму величину достоверной аппроксимации (R^2)». Этот показатель варьируется в диапазоне от нуля до единицы. Чем его значение больше, тем точнее выполнена аппроксимация. Считается, что если величина данного показателя равна 0,85 и выше, то сглаживание может считаться достоверным, а если показатель ниже, то его достоверность ниже допустимой. После проведения всех вышеуказанных настроек, следует нажать на кнопку «Закрыть», размещенную в нижней части окна. Появится линия тренда.

Рисунок 4. Отображение линии тренда. Автор24 — интернет-биржа студенческих работ

При выполнении линейной аппроксимации линия тренда обозначается черной прямой линией. Приведенный тип сглаживания может быть использован в самых простых случаях, когда данные меняются достаточно быстро и зависимость величины функции от аргумента является очевидной. Сглаживание, которое применяется в этом варианте, может быть описано следующей формулой:

y = ax + b.

Для конкретного варианта, приведенного выше, формула будет иметь следующий вид:

y = ‒ 0,1156x + 72,255.

Значение достоверности аппроксимации в рассмотренном случае равняется 0,9418, что считается достаточно приемлемым результатом, который характеризует сглаживание как достоверное.

Далее рассмотрим экспоненциальный тип аппроксимации в Excel. Для изменения типа линии тренда, следует выделить ее кликом правой кнопки мыши и в открывшемся меню нужно выбрать пункт «Формат линии тренда…». После этого будет запущено уже применявшееся ранее окно формата. В блоке выбора типа аппроксимации необходимо установить переключатель в положение «Экспоненциальная». Остальные настройки следует оставить такими же, как и в первом варианте, и затем выполнить щелчок по кнопке «Закрыть». После этого линия тренда будет построена на графике, как показано на рисунке ниже:

Рисунок 5. Экспоненциальный тип аппроксимации. Автор24 — интернет-биржа студенческих работ

При использовании этого метода линия тренда обладает несколько изогнутой формой. Причем уровень достоверности равняется 0,9592, что выше, чем при использовании линейной аппроксимации.

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Источник

Добавил:

Upload

Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Предмет:

Файл:

Чсил.методы. УП 09.doc

Скачиваний:

Добавлен:

29.08.2019

Размер:

3.23 Mб

Скачать

В табличном
процессоре Excel
для интерполяции с помощью формулы
Лагранжа можно воспользоваться
соответствующей таблицей (таблица 5.1).

А также для
аппроксимации Excel
имеет удобные встроенные средства.
Самый наглядный способ – использование
графического представления данных:

Необходимо ввести
таблицу данных и построить по ним
точечную диаграмму;
Выделив диаграмму,
через главное меню выполнить команды
Диаграмма

Добавить линию тренда
(рис. 5.1) Тренд (тенденция) – термин для
обозначения линии графика аппраксимируемой
функции.
В открывшемся
диалоговом окне на закладке Тип
необходимо
выбрать один из видов функции, предлагаемых
для аппроксимации (рис. 5.1). Таким образом
перебирая различные виды функций можно
подобрать линию тренда наиболее
подходящую к заданным значениям
В том же диалоговом
окне, перейдя к закладке Параметры
необходимо установить галочку на флажке
показывать
уравнение на диаграмме
– после выполнения команд на диаграмме
появляется уравнение, которое
соответствует линии тренда и является
искомой функцией (рис. 5.2).

В закладке
Параметры
можно также установить галочку на флажке
поместить
на диаграмму величину достоверности
аппроксимации R^2.
В статистике данная величина называется
коэффициентом
детерминированности,она
показывает насколько точной получилась
построенная функция (рис. 5.2).

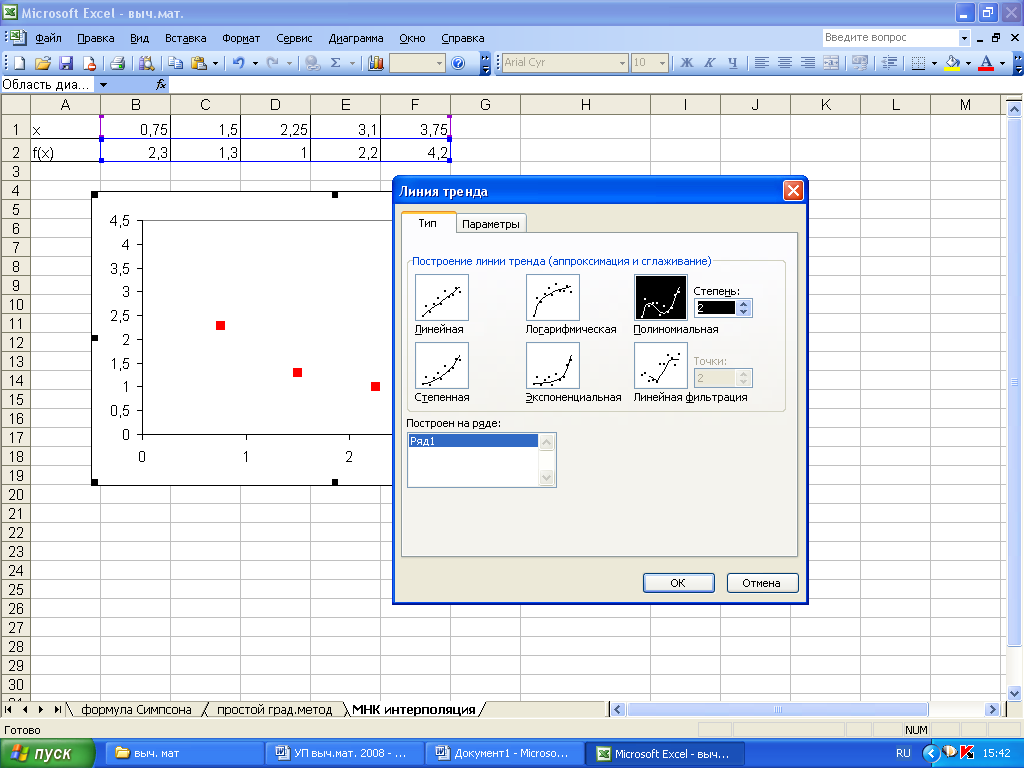
Рисунок
5.1. Получение линии тренда при аппроксимации
функции в Excel

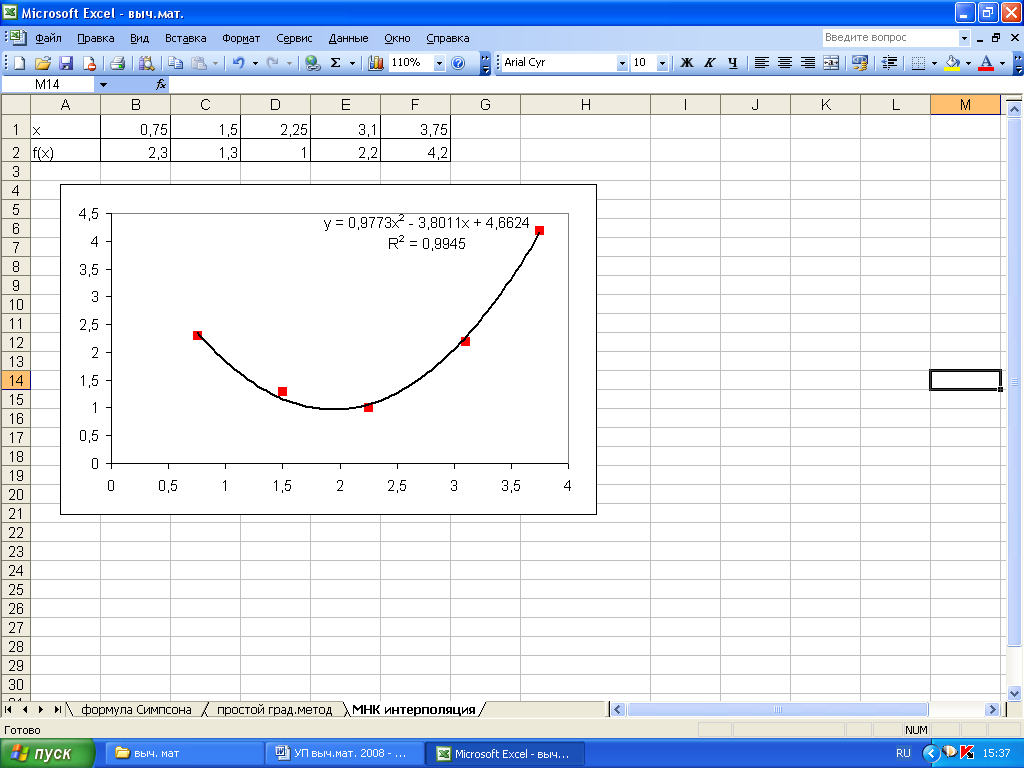
Рисунок
5.2. Результат аппроксимации функции в
Excel

Интерполяцию или
экстраполяцию можно получить, используя
функцию ПРЕДСКАЗ в мастере
функций
(рис. 5.3).

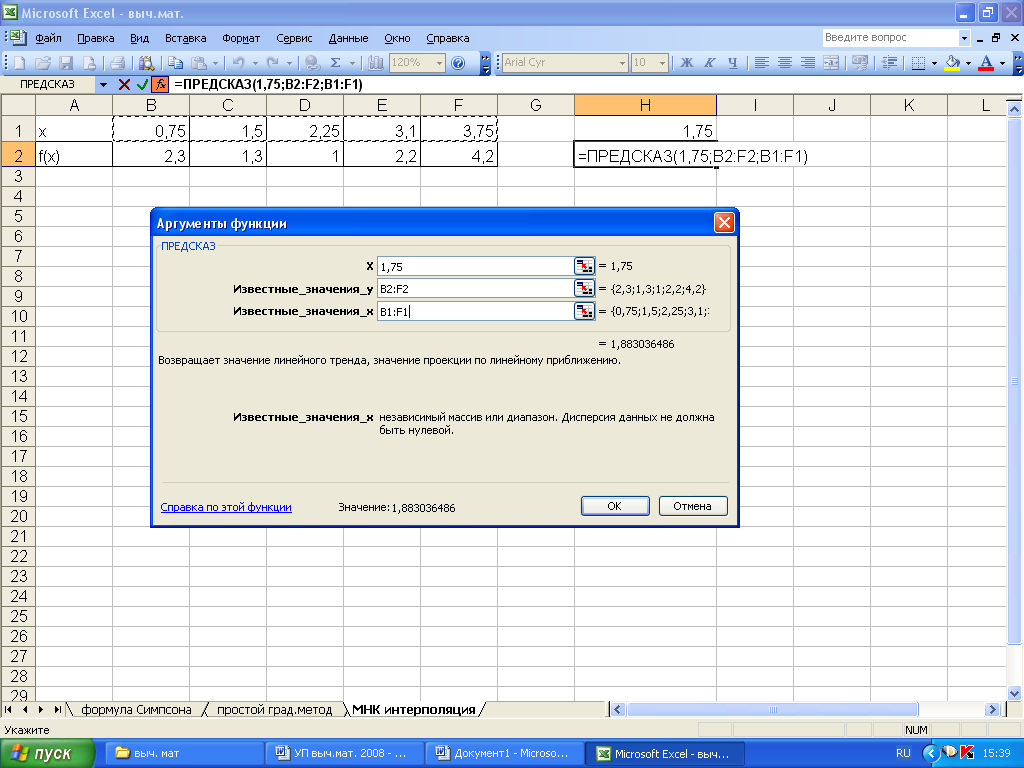
Рисунок
5.3. Нахождение интерполяционного значения
функции в табличном процессоре Excel

Задания для самостоятельного решения

x	2,0	2,2	2,4	2,6	2,8	3,0
f(x)	8,69	11,44	14,70	18,53	22,98	28,10

1. Для таблично заданной
функции получить эмпирическую формулу
с помощью математических программных
средств (табличный процессор Excel,
MATCAD,
MATLAB).

x	1,4	1,5	1,6	1,7	1,8	1,9
f(x)	-1,67	-1,80	-1,93	-2,05	-2,18	-2,30

2. Для таблично заданной
функции получить эмпирическую формулу
с помощью математических программных
средств (табличный процессор Excel,
MATCAD,
MATLAB).

Практическая работа №6

Тема: «Составление
интерполяционного многочлена Лагранжа»

Цели:
освоение применения интерполяционного
многочлена Лагранжа для вычисления
значения функции по промежуточному
значению аргумента;

Задание1.
Для функции, заданной таблицей узловых
значений, составить формулу интерполяционного
многочлена Лагранжа, вычислить с его
помощью одно значение функции для
промежуточного значения аргумента х^*.

Исходные данные
для задания 1:

Вариант 1.
х^*
= 0,7

х	-1	0	3	4
f(x)	-3	5	2	-6

Вариант 2.
х^*
= 2,4

х	2	3	5	6
f(x)	4	1	7	2

Вариант 3.
х^*
= 0,7

х	0	2	3	5
f(x)	-1	-4	2	-8

Вариант 4.
х^*
= 7,3

х	7	9	13	15
f(x)	2	-2	3	-4

Вариант 5.
х^*
= 3,6

х	-3	-1	3	5
f(x)	7	-1	4	-6

Вариант 6.
х^*
= 1,7

х	1	2	4	7
f(x)	-3	-7	2	8

Вариант 7.
х^*
= 2,7

х	2	4	5	7
f(x)	9	-3	6	-2

Вариант 8.
х^*
= 0,7

х	-4	-2	0	3
f(x)	2	8	5	10

Вариант 9.
х^*
= 2,8

х	2	4	7	8
f(x)	-1	-6	3	12

Вариант 10.
х^*
= 0,7

х	0	1	4	6
f(x)	7	-1	8	2

Вариант 11.
х^*
= 2,7

Х	-1	-1	2	4
f(x)	4	9	1	6

Вариант 12.
х^*
= 3,4

Х	-1	1,5	3	5
f(x)	4	-7	1	-8

Вариант 13.
х^*
= – 4,5

Х	-9	-7	— 4	-1
f(x)	3	-3	4	-9

Вариант 14.
х^*
= 1,3

Х	-8	-5	0	2
f(x)	9	-2	4	6

Вариант 15.
х^*
= –3,6

Х	-7	-5	— 4	-1
f(x)	4	— 4	5	10

Вариант 16.
х^*
= 2,7

Х	1	4	9	11
f(x)	-2	9	3	-7

Вариант 17.
х^*
= 8,5

Х	7	8	9	13
f(x)	6	-2	7	-10

Вариант 18.
х^*
= 0,7

Х	-4	0	2	5
f(x)	4	8	-2	-9

Вариант 19.
х^*
= 2,8

Х	-3	-1	1	3
f(x)	11	-1	6	-2

Вариант 20.
х^*
= 0,7

х	0	3	8	11
f(x)	1	5	— 4	-8

Задание 2.
Вычислить значение заданной функции
f(x)
для промежуточного значения аргумента
х^*
по интерполяционному многочлену Лагранжа
с помощью вычислительной таблицы.
Сравните результат интерполирования
со значением функции, которое вычислите,
используя ее аналитическое выражение.

Задание 3. Для
таблично заданной функции получить
эмпирическую формулу с помощью
математических программных средств
(табличный процессор Excel).
Сравнить полученную формулу с заданным
аналитическим выражением.

Исходные данные
для задания 2, 3:

Вариант 1.
х^*
= 3,8

х	1,3	2,1	3,7	4,5	6,1	7,7	8,5
f(x)	1,7777	4,5634	13,8436	20,3952	37,3387	59,4051	72,3593

Вариант 2.
х^*
= 3,5

х	1,2	1,9	3,3	4,7	5,4	6,8	7,5
f(x)	0,3486	1,0537	1,7844	2,2103	2,3712	2,6322	2,7411

Вариант 3.
х^*
= 0,5

х	-3,2	-0,8	0,4	2,8	4,0	6,4	7,6
f(x)	-1,9449	-0,6126	0,3097	1,8068	2,0913	1,4673	0,6797

Вариант 4.
х^*
= 4,8

х	1,3	2,1	3,7	4,5	6,1	7,7	8,5
f(x)	1,7777	4,5634	13,8436	20,3952	37,3387	59,4051	72,3593

Вариант 5.
х^*
= 4,1

х	1,3	2,1	3,7	4,5	6,1	7,7	8,5
f(x)	1,7777	4,5634	13,8436	20,3952	37,3387	59,4051	72,3593

Вариант 6.
х^*
= 3,9

х	1,2	1,9	3,3	4,7	5,4	6,8	7,5
f(x)	0,3486	1,0537	1,7844	2,2103	2,3712	2,6322	2,7411

Вариант 7.
х^*
= 3,3

х	-3,2	-0,8	0,4	2,8	4,0	6,4	7,6
f(x)	-1,9449	-0,6126	0,3097	1,8068	2,0913	1,4673	0,6797

Вариант 8.
х^*
= 4,0

х	1,3	2,1	3,7	4,5	6,1	7,7	8,5
f(x)	1,7777	4,5634	13,8436	20,3952	37,3387	59,4051	72,3593

Вариант 9.
х^*
= 2,9

х	1,3	2,1	3,7	4,5	6,1	7,7	8,5
f(x)	1,7777	4,5634	13,8436	20,3952	37,3387	59,4051	72,3593

Вариант 10.
х^*
= 5,3

х	1,2	1,9	3,3	4,7	5,4	6,8	7,5
f(x)	0,3486	1,0537	1,7844	2,2103	2,3712	2,6322	2,7411

Вариант 11.
х^*
= 4,1

х	-3,2	-0,8	0,4	2,8	4,0	6,4	7,6
f(x)	-1,9449	-0,6126	0,3097	1,8068	2,0913	1,4673	0,6797

Вариант 12.
х^*
= 6,6

х	1,2	1,9	3,3	4,7	5,4	6,8	7,5
f(x)	0,3486	1,0537	1,7844	2,2103	2,3712	2,6322	2,7411

Вариант 13.
х^*
= 4,4

х	1,3	2,1	3,7	4,5	6,1	7,7	8,5
f(x)	1,7777	4,5634	13,8436	20,3952	37,3387	59,4051	72,3593

Вариант 14.
х^*
= 5,2

х	-3,2	-0,8	0,4	2,8	4,0	6,4	7,6
f(x)	-1,9449	-0,6126	0,3097	1,8068	2,0913	1,4673	0,6797

Вариант 15.
х^*
= 3,7

х	1,2	1,9	3,3	4,7	5,4	6,8	7,5
f(x)	0,3486	1,0537	1,7844	2,2103	2,3712	2,6322	2,7411

Вариант 16.
х^*
= 0,4

х	1,3	2,1	3,7	4,5	6,1	7,7	8,5
f(x)	1,7777	4,5634	13,8436	20,3952	37,3387	59,4051	72,3593

Вариант 17.
х^*
= 7,5

х	-3,2	-0,8	0,4	2,8	4,0	6,4	7,6
f(x)	-1,9449	-0,6126	0,3097	1,8068	2,0913	1,4673	0,6797

Вариант 18.
х^*
= 2,5

х	1,2	1,9	3,3	4,7	5,4	6,8	7,5
f(x)	0,3486	1,0537	1,7844	2,2103	2,3712	2,6322	2,7411

Вариант 19.
х^*
= 6,8

х	1,3	2,1	3,7	4,5	6,1	7,7	8,5
f(x)	1,7777	4,5634	13,8436	20,3952	37,3387	59,4051	72,3593

Вариант 20.
х^*
= – 1,7

х	-3,2	-0,8	0,4	2,8	4,0	6,4	7,6
f(x)	-1,9449	-0,6126	0,3097	1,8068	2,0913	1,4673	0,6797

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Содержание статьи (кликните для открытия/закрытия)

Построение графика линейной функции в Excel
Подготовка расчетной таблицы
Построение графика функции
Построение графиков других функций
Квадратичная функция y=ax2+bx+c
Кубическая парабола y=ax3
Гипербола y=k/x
Построение тригонометрических функций sin(x) и cos(x)

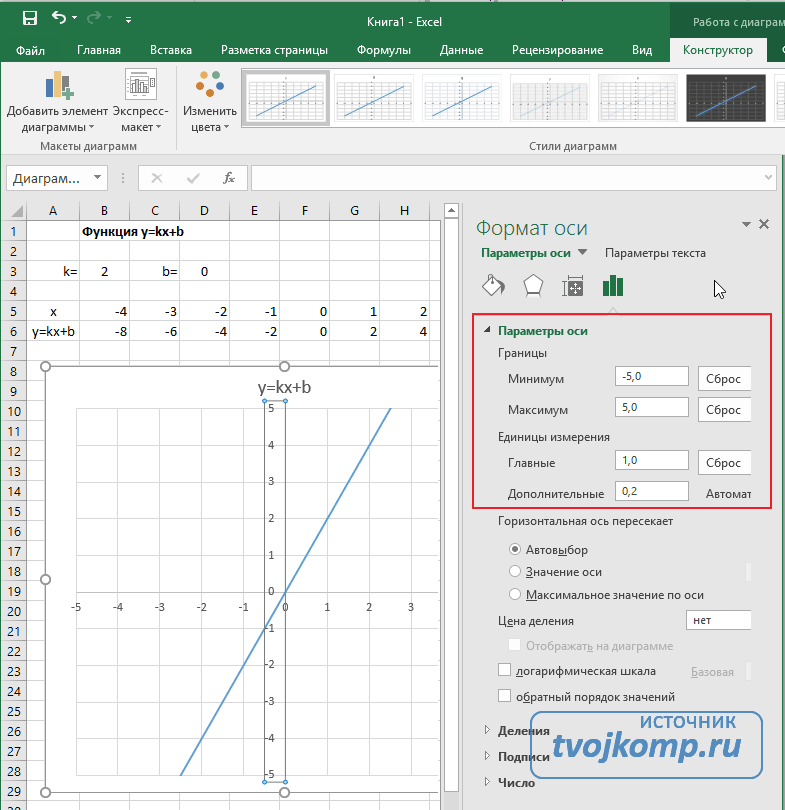
Построение графика зависимости функции является характерной математической задачей. Все, кто хотя бы на уровне школы знаком с математикой, выполняли построение таких зависимостей на бумаге. В графике отображается изменение функции в зависимости от значения аргумента. Современные электронные приложения позволяют осуществить эту процедуру за несколько кликов мышью. Microsoft Excel поможет вам в построении точного графика для любой математической функции. Давайте разберем по шагам, как построить график функции в excel по её формуле

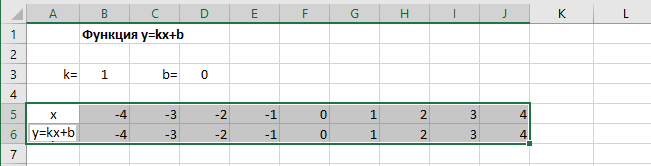
Построение графиков в Excel 2016 значительно улучшилось и стало еще проще чем в предыдущих версиях. Разберем пример построения графика линейной функции y=kx+b на небольшом интервале [-4;4].

Подготовка расчетной таблицы

В таблицу заносим имена постоянных k и b в нашей функции. Это необходимо для быстрого изменения графика без переделки расчетных формул.

Установка шага значений аргумента функции

Далее строим таблицу значений линейной функции:

В ячейки A5 и A6 вводим соответственно обозначения аргумента и саму функцию. Запись в виде формулы будет использована в качестве названия диаграммы.
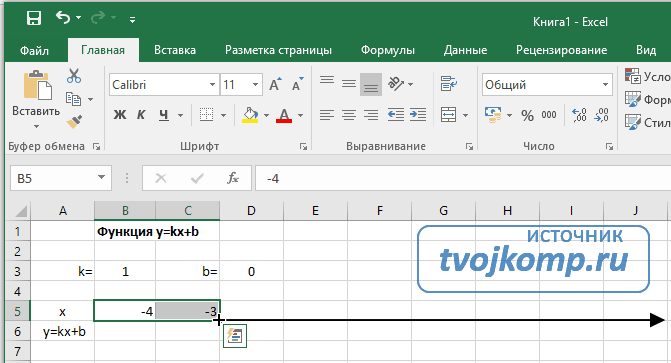
Вводим в ячейки B5 и С5 два значения аргумента функции с заданным шагом (в нашем примере шаг равен единице).
Выделяем эти ячейки.
Наводим указатель мыши на нижний правый угол выделения. При появлении крестика (смотри рисунок выше), зажимаем левую кнопку мыши и протягиваем вправо до столбца J.

Ячейки автоматически будут заполнены числами, значения которых различаются заданным шагом.

Автозаполнение значений аргумента функции

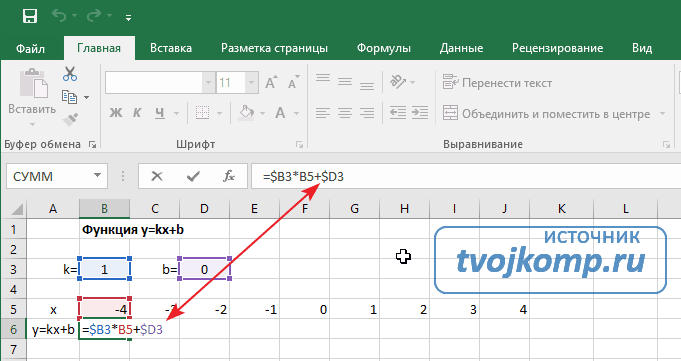
Далее в строку значений функции в ячейку B6 записываем формулу =$B3*B5+$D3

Внимание! Запись формулы начинается со знака равно(=). Адреса ячеек записываются на английской раскладке. Обратите внимание на абсолютные адреса со знаком доллара.

Запись расчётной формулы для значений функции

Чтобы завершить ввод формулы нажмите клавишу Enter или галочку слева от строки формул вверху над таблицей.

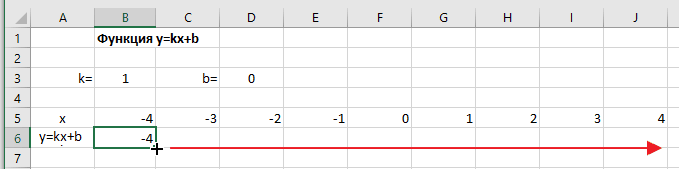
Копируем эту формулу для всех значений аргумента. Протягиваем вправо рамку от ячейки с формулой до столбца с конечными значениями аргумента функции.

Копирование формулы

Построение графика функции

Выделяем прямоугольный диапазон ячеек A5:J6.

Выделение таблицы функции

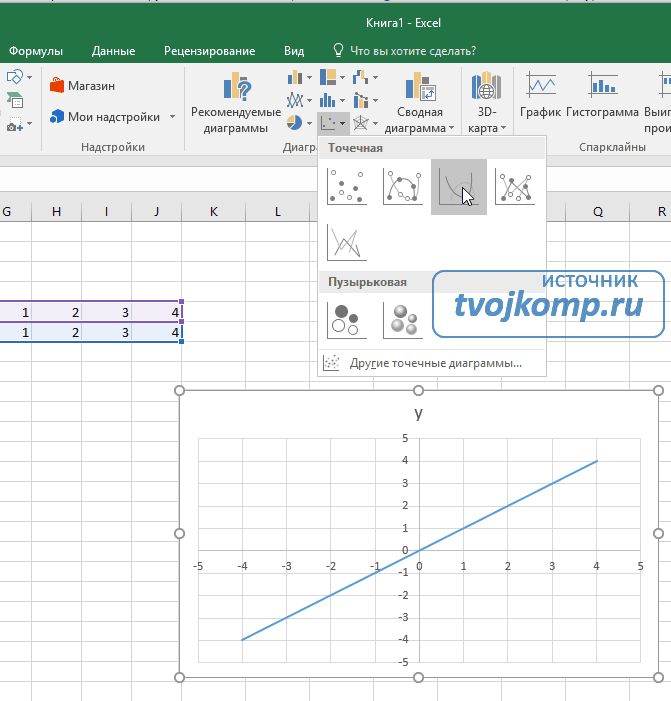
Переходим на вкладку Вставка в ленте инструментов. В разделе Диаграмма выбираем Точечная с гладкими кривыми (см. рисунок ниже).Получим диаграмму.

Построение диаграммы типа «График»

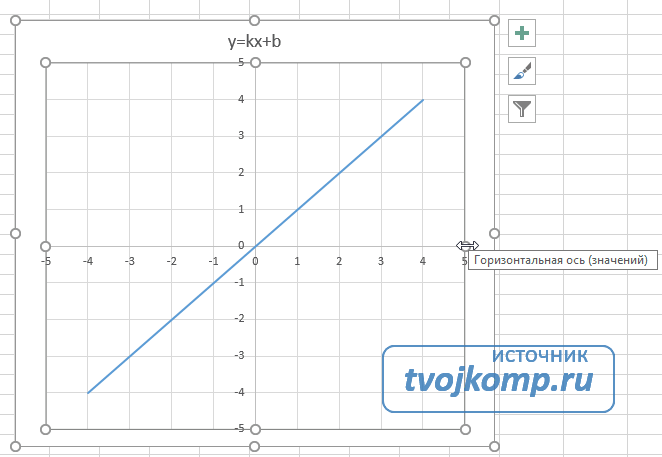
После построения координатная сетка имеет разные по длине единичные отрезки. Изменим ее перетягивая боковые маркеры до получения квадратных клеток.

График линейной функции

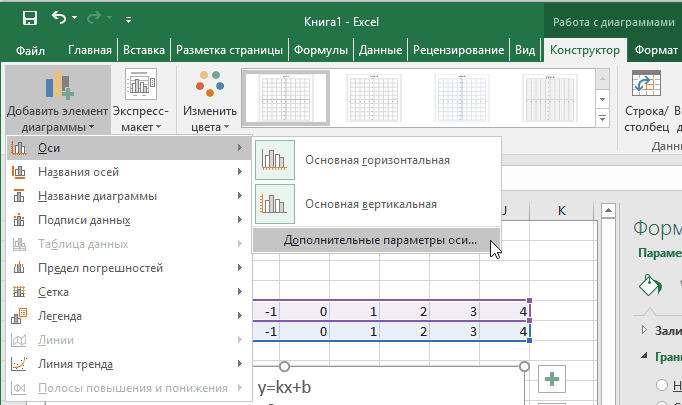
Теперь можно ввести новые значения постоянных k и b для изменения графика. И видим, что при попытке изменить коэффициент график остается неизменным, а меняются значения на оси. Исправляем. Кликните на диаграмме, чтобы ее активировать. Далее на ленте инструментов во вкладке Работа с диаграммами на вкладке Конструктор выбираем Добавить элемент диаграммы — Оси — Дополнительные параметры оси..

Вход в режим изменения параметров координатных осей

В правой части окна появиться боковая панель настроек Формат оси.

Редактирование параметров координатной оси

Кликните на раскрывающийся список Параметры оси.
Выберите Вертикальная ось (значений).
Кликните зеленый значок диаграммы.
Задайте интервал значений оси и единицы измерения (обведено красной рамкой). Ставим единицы измерения Максимум и минимум (Желательно симметричные) и одинаковые для вертикальной и горизонтальной осей. Таким образом, мы делаем мельче единичный отрезок и соответственно наблюдаем больший диапазон графика на диаграмме.И главную единицу измерения — значение 1.
Повторите тоже для горизонтальной оси.

Теперь, если поменять значения K и b , то получим новый график с фиксированной сеткой координат.

Построение графиков других функций

Теперь, когда у нас есть основа в виде таблицы и диаграммы, можно строить графики других функций, внося небольшие корректировки в нашу таблицу.

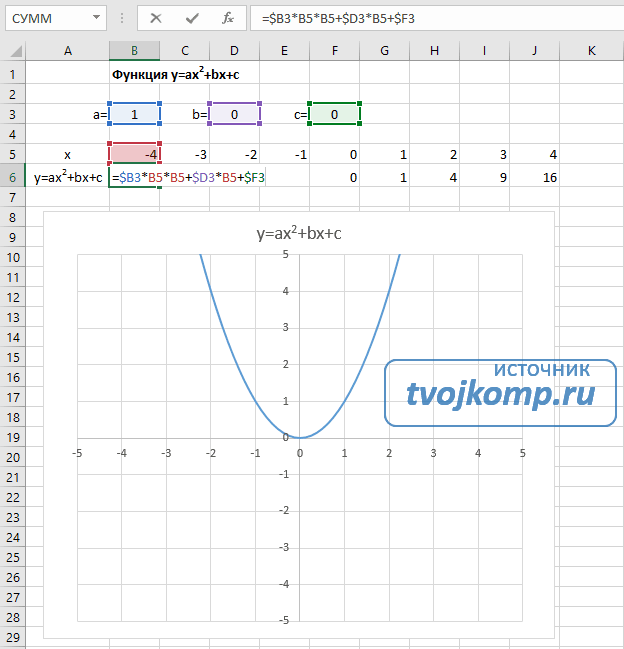
Квадратичная функция y=ax²+bx+c

Выполните следующие действия:

В первой строке меняем заголовок
В третьей строке указываем коэффициенты и их значения
В ячейку A6 записываем обозначение функции
В ячейку B6 вписываем формулу =$B3*B5*B5+$D3*B5+$F3
Копируем её на весь диапазон значений аргумента вправо

Получаем результат

График квадратичной функции

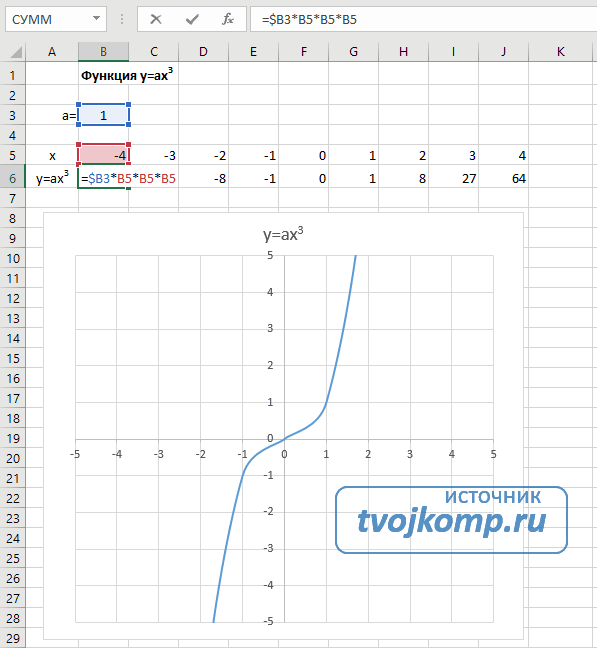
Кубическая парабола y=ax³

Для построения выполните следующие действия:

В первой строке меняем заголовок
В третьей строке указываем коэффициенты и их значения
В ячейку A6 записываем обозначение функции
В ячейку B6 вписываем формулу =$B3*B5*B5*B5
Копируем её на весь диапазон значений аргумента вправо

Получаем результат

График кубической параболы

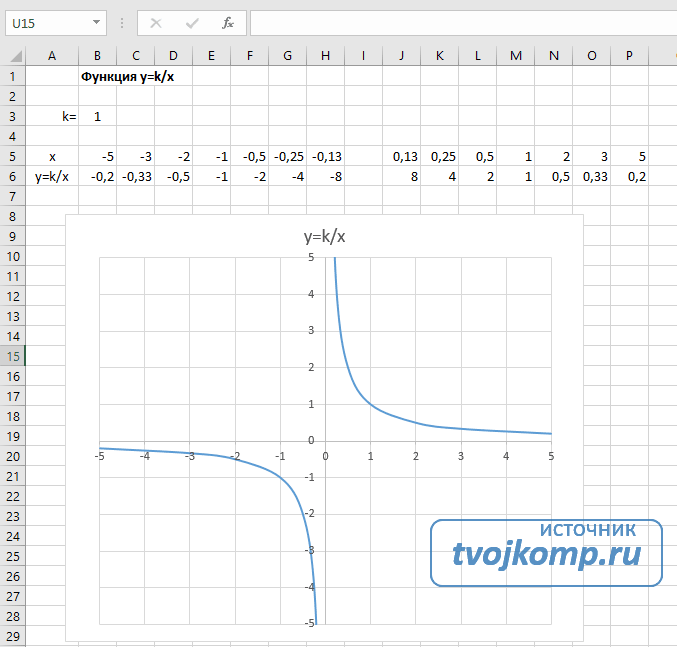
Гипербола y=k/x

Для построения гиперболы заполните таблицу вручную (смотри рисунок ниже). Там где раньше было нулевое значение аргумента оставляем пустую ячейку.

Далее выполните действия:

В первой строке меняем заголовок.
В третьей строке указываем коэффициенты и их значения.
В ячейку A6 записываем обозначение функции.
В ячейку B6 вписываем формулу =$B3/B5
Копируем её на весь диапазон значений аргумента вправо.
Удаляем формулу из ячейки I6.

Для корректного отображения графика нужно поменять для диаграммы диапазон исходных данных, так как в этом примере он больше чем в предыдущих.

Кликните диаграмму
На вкладке Работа с диаграммами перейдите в Конструктор и в разделе Данные нажмите Выбрать данные.
Откроется окно мастера ввода данных
Выделите мышкой прямоугольный диапазон ячеек A5:P6
Нажмите ОК в окне мастера.

Получаем результат

График гиперболы

Построение тригонометрических функций sin(x) и cos(x)

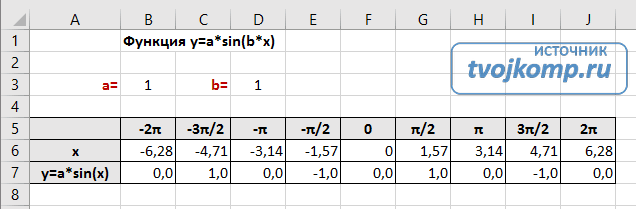
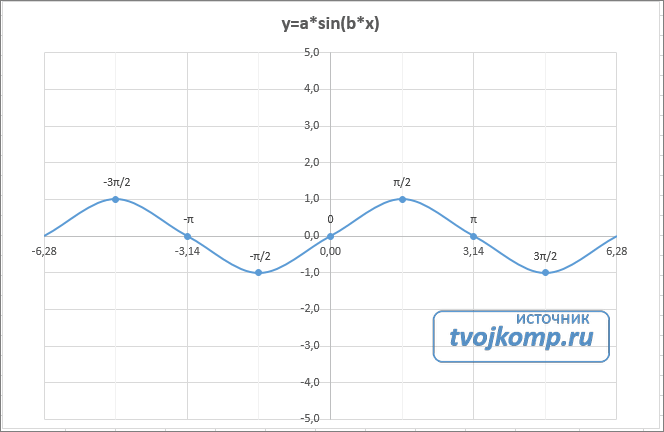
Рассмотрим пример построения графика тригонометрической функции y=a*sin(b*x).
Сначала заполните таблицу как на рисунке ниже

Таблица значений функции sin(x)

В первой строке записано название тригонометрической функции.
В третьей строке прописаны коэффициенты и их значения. Обратите внимание на ячейки, в которые вписаны значения коэффициентов.
В пятой строке таблицы прописываются значения углов в радианах. Эти значения будут использоваться для подписей на графике.
В шестой строке записаны числовые значения углов в радианах. Их можно прописать вручную или используя формулы соответствующего вида =-2*ПИ(); =-3/2*ПИ(); =-ПИ(); =-ПИ()/2; …
В седьмой строке записываются расчетные формулы тригонометрической функции.

Запись расчетной формулы функции sin(x) в Excel

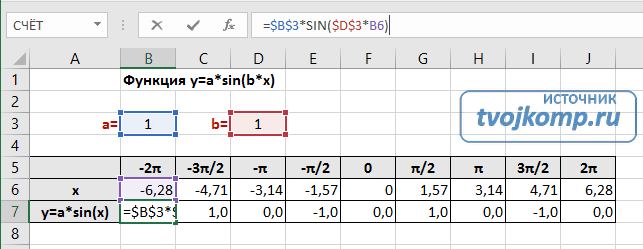
В нашем примере =$B$3*SIN($D$3*B6). Адреса B3 и D3 являются абсолютными. Их значения – коэффициенты a и b, которые по умолчанию устанавливаются равными единице.
После заполнения таблицы приступаем к построению графика.

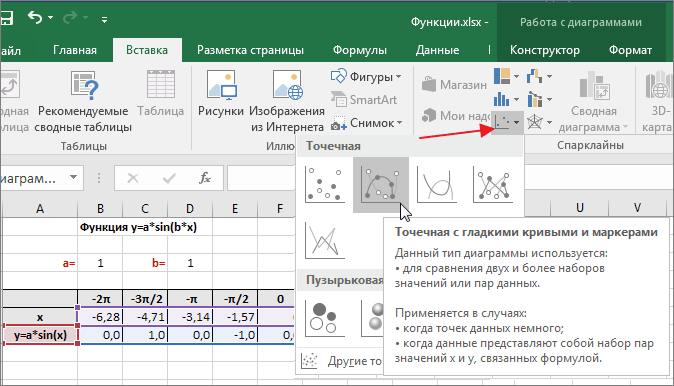
Выделяем диапазон ячеек А6:J7. В ленте выбираем вкладку Вставка в разделе Диаграммы указываем тип Точечная и вид Точечная с гладкими кривыми и маркерами.

Построение диаграммы Точечная с гладкими кривыми

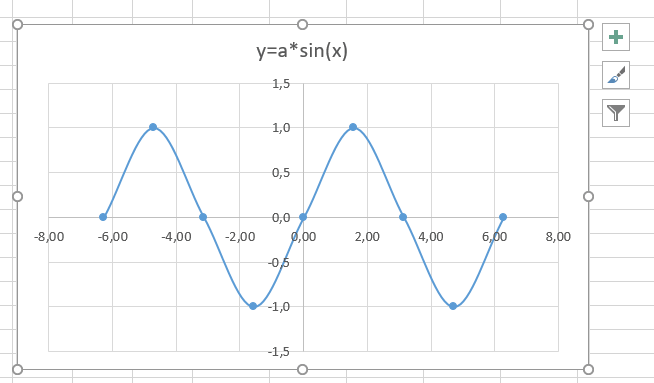
В итоге получим диаграмму.

График sin(x) после вставки диаграммы

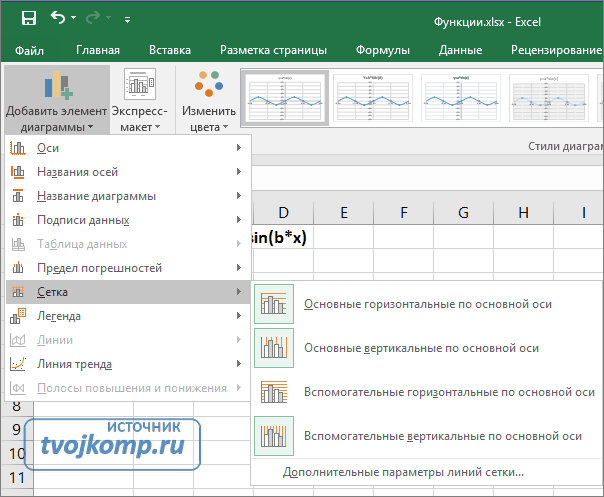
Теперь настроим правильное отображение сетки, так чтобы точки графика лежали на пересечении линий сетки. Выполните последовательность действий Работа с диаграммами –Конструктор – Добавить элемент диаграммы – Сетка и включите три режима отображения линий как на рисунке.

Настройка сетки при построении графика

Теперь зайдите в пункт Дополнительные параметры линий сетки. У вас появится боковая панель Формат области построения. Произведем настройки здесь.

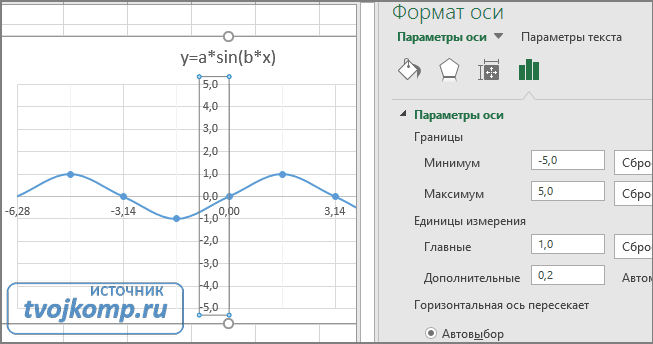
Кликните в диаграмме на главную вертикальную ось Y (должна выделится рамкой). В боковой панели настройте формат оси как на рисунке.

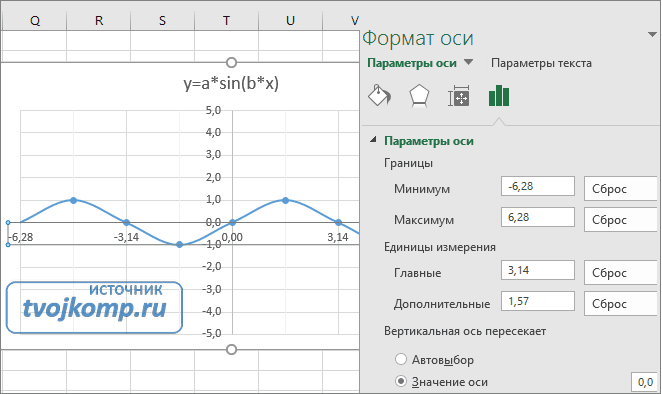
Кликните главную горизонтальную ось Х (должна выделится) и также произведите настройки согласно рисунку.

Настройка формата горизонтальной оси Х графика функции

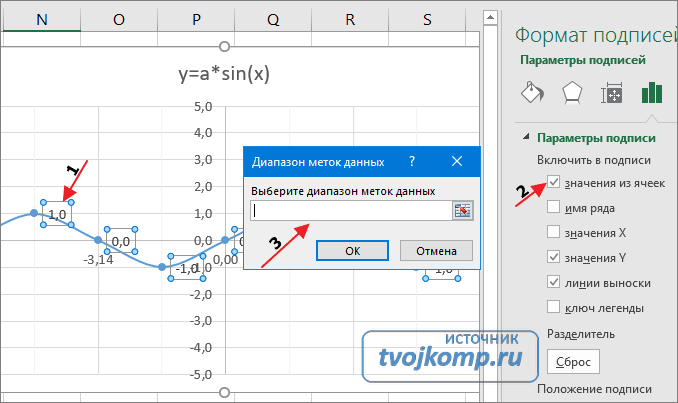
Теперь сделаем подписи данных над точками. Снова выполняем Работа с диаграммами –Конструктор – Добавить элемент диаграммы – Подписи данных – Сверху. У вас подставятся значения числами 1 и 0, но мы заменим их значениями из диапазона B5:J5.
Кликните на любом значении 1 или 0 (рисунок шаг 1) и в параметрах подписи поставьте галочку Значения из ячеек (рисунок шаг 2). Вам будет сразу же предложено указать диапазон с новыми значениями (рисунок шаг 3). Указываем B5:J5.

Вот и все. Если сделали правильно, то и график будет замечательным. Вот такой.

Чтобы получить график функции cos(x), замените в расчетной формуле и в названии sin(x) на cos(x).

Аналогичным способом можно строить графики других функций. Главное правильно записать вычислительные формулы и построить таблицу значений функции. Надеюсь, что вам была полезна данная информация.

Дополнительные статьи по теме:

Знакомство с таблицами в Excel
Изменение строк и столбцов в Excel
Работа с ячейками: объединение, изменение, защита…
Ошибки в формулах: почему excel не считает
Использования условий в формулах Excel
Функция CЧЕТЕСЛИМН
Работа с текстовыми функциями Excel
Все уроки по Microsoft Excel

Дорогой читатель! Вы посмотрели статью до конца.
Получили вы ответ на свой вопрос? Напишите в комментариях пару слов. Если ответа не нашли, укажите что искали или откройте содержание блога.

ОЧЕНЬ ВАЖНО! Оцени лайком или дизлайком статью!

Источник

Формула предписывает программе Excel порядок действий с числами, значениями в ячейке или группе ячеек. Без формул электронные таблицы не нужны в принципе.

Конструкция формулы включает в себя: константы, операторы, ссылки, функции, имена диапазонов, круглые скобки содержащие аргументы и другие формулы. На примере разберем практическое применение формул для начинающих пользователей.

Формулы в Excel для чайников

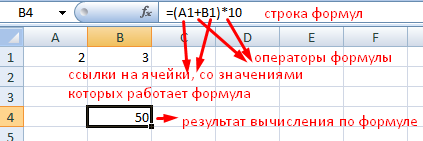
Чтобы задать формулу для ячейки, необходимо активизировать ее (поставить курсор) и ввести равно (=). Так же можно вводить знак равенства в строку формул. После введения формулы нажать Enter. В ячейке появится результат вычислений.

В Excel применяются стандартные математические операторы:

Оператор	Операция	Пример
+ (плюс)	Сложение	=В4+7
— (минус)	Вычитание	=А9-100
* (звездочка)	Умножение	=А3*2
/ (наклонная черта)	Деление	=А7/А8
^ (циркумфлекс)	Степень	=6^2
= (знак равенства)	Равно
<	Меньше
>	Больше
<=	Меньше или равно
>=	Больше или равно
<>	Не равно

Символ «*» используется обязательно при умножении. Опускать его, как принято во время письменных арифметических вычислений, недопустимо. То есть запись (2+3)5 Excel не поймет.

Программу Excel можно использовать как калькулятор. То есть вводить в формулу числа и операторы математических вычислений и сразу получать результат.

Но чаще вводятся адреса ячеек. То есть пользователь вводит ссылку на ячейку, со значением которой будет оперировать формула.

При изменении значений в ячейках формула автоматически пересчитывает результат.

Ссылки можно комбинировать в рамках одной формулы с простыми числами.

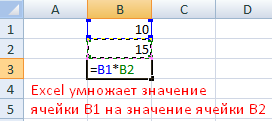
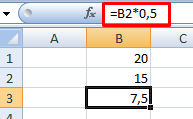
Оператор умножил значение ячейки В2 на 0,5. Чтобы ввести в формулу ссылку на ячейку, достаточно щелкнуть по этой ячейке.

В нашем примере:

Поставили курсор в ячейку В3 и ввели =.
Щелкнули по ячейке В2 – Excel «обозначил» ее (имя ячейки появилось в формуле, вокруг ячейки образовался «мелькающий» прямоугольник).
Ввели знак *, значение 0,5 с клавиатуры и нажали ВВОД.

Если в одной формуле применяется несколько операторов, то программа обработает их в следующей последовательности:

%, ^;
*, /;
+, -.

Поменять последовательность можно посредством круглых скобок: Excel в первую очередь вычисляет значение выражения в скобках.

Как в формуле Excel обозначить постоянную ячейку

Различают два вида ссылок на ячейки: относительные и абсолютные. При копировании формулы эти ссылки ведут себя по-разному: относительные изменяются, абсолютные остаются постоянными.

Все ссылки на ячейки программа считает относительными, если пользователем не задано другое условие. С помощью относительных ссылок можно размножить одну и ту же формулу на несколько строк или столбцов.

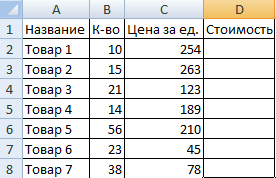
Вручную заполним первые графы учебной таблицы. У нас – такой вариант:

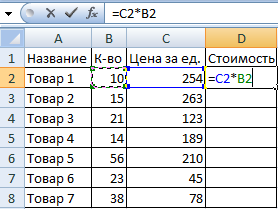
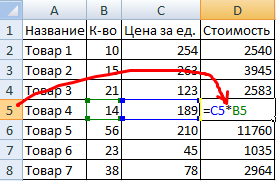
Вспомним из математики: чтобы найти стоимость нескольких единиц товара, нужно цену за 1 единицу умножить на количество. Для вычисления стоимости введем формулу в ячейку D2: = цена за единицу * количество. Константы формулы – ссылки на ячейки с соответствующими значениями.

Нажимаем ВВОД – программа отображает значение умножения. Те же манипуляции необходимо произвести для всех ячеек. Как в Excel задать формулу для столбца: копируем формулу из первой ячейки в другие строки. Относительные ссылки – в помощь.

Находим в правом нижнем углу первой ячейки столбца маркер автозаполнения. Нажимаем на эту точку левой кнопкой мыши, держим ее и «тащим» вниз по столбцу.

Отпускаем кнопку мыши – формула скопируется в выбранные ячейки с относительными ссылками. То есть в каждой ячейке будет своя формула со своими аргументами.

Ссылки в ячейке соотнесены со строкой.

Формула с абсолютной ссылкой ссылается на одну и ту же ячейку. То есть при автозаполнении или копировании константа остается неизменной (или постоянной).

Чтобы указать Excel на абсолютную ссылку, пользователю необходимо поставить знак доллара ($). Проще всего это сделать с помощью клавиши F4.

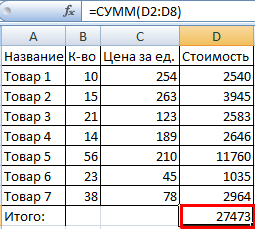
Создадим строку «Итого». Найдем общую стоимость всех товаров. Выделяем числовые значения столбца «Стоимость» плюс еще одну ячейку. Это диапазон D2:D9

Воспользуемся функцией автозаполнения. Кнопка находится на вкладке «Главная» в группе инструментов «Редактирование».

После нажатия на значок «Сумма» (или комбинации клавиш ALT+«=») слаживаются выделенные числа и отображается результат в пустой ячейке.

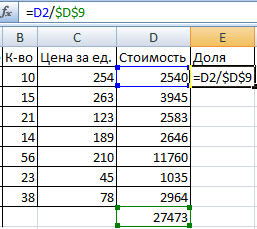
Сделаем еще один столбец, где рассчитаем долю каждого товара в общей стоимости. Для этого нужно:

Разделить стоимость одного товара на стоимость всех товаров и результат умножить на 100. Ссылка на ячейку со значением общей стоимости должна быть абсолютной, чтобы при копировании она оставалась неизменной.

Чтобы получить проценты в Excel, не обязательно умножать частное на 100. Выделяем ячейку с результатом и нажимаем «Процентный формат». Или нажимаем комбинацию горячих клавиш: CTRL+SHIFT+5

Копируем формулу на весь столбец: меняется только первое значение в формуле (относительная ссылка). Второе (абсолютная ссылка) остается прежним. Проверим правильность вычислений – найдем итог. 100%. Все правильно.

При создании формул используются следующие форматы абсолютных ссылок:

$В$2 – при копировании остаются постоянными столбец и строка;
B$2 – при копировании неизменна строка;
$B2 – столбец не изменяется.

Как составить таблицу в Excel с формулами

Чтобы сэкономить время при введении однотипных формул в ячейки таблицы, применяются маркеры автозаполнения. Если нужно закрепить ссылку, делаем ее абсолютной. Для изменения значений при копировании относительной ссылки.

Простейшие формулы заполнения таблиц в Excel:

Перед наименованиями товаров вставим еще один столбец. Выделяем любую ячейку в первой графе, щелкаем правой кнопкой мыши. Нажимаем «Вставить». Или жмем сначала комбинацию клавиш: CTRL+ПРОБЕЛ, чтобы выделить весь столбец листа. А потом комбинация: CTRL+SHIFT+»=», чтобы вставить столбец.
Назовем новую графу «№ п/п». Вводим в первую ячейку «1», во вторую – «2». Выделяем первые две ячейки – «цепляем» левой кнопкой мыши маркер автозаполнения – тянем вниз.

По такому же принципу можно заполнить, например, даты. Если промежутки между ними одинаковые – день, месяц, год. Введем в первую ячейку «окт.15», во вторую – «ноя.15». Выделим первые две ячейки и «протянем» за маркер вниз.

Найдем среднюю цену товаров. Выделяем столбец с ценами + еще одну ячейку. Открываем меню кнопки «Сумма» — выбираем формулу для автоматического расчета среднего значения.

Чтобы проверить правильность вставленной формулы, дважды щелкните по ячейке с результатом.

Источник

	D	E
1	комментарии	Значения
2	Макс f(X)	<формула>
3	Мин f(X)	<формула>

	F	G
1	КОММЕНТАРИИ	ЗНАЧЕНИЯ
2	Признак возрастания	<формула>
3	Признак убывания	<формула>

	А	В
1	КОММЕНТАРИИ	ЗНАЧЕНИЯ
2	Xn	<значение>
3	Xk	<значение>
4	Shag	<значение>
5	N	<формула>
6	период	<значение>

Поиск перечня доступных функций в Excel

Вставка функции в таблицу

Использование математических операций в Excel

Растягивание функций и обозначение константы

Построение графиков функций

Создание таблицы

Вычисление значений функции

Построение графика

Создание таблицы и вычисление значений функций

Построение графиков

Вариант 1: График функции X^2

Вариант 2: График функции y=sin(x)

Еще статьи по данной теме:

Помогла ли Вам статья?

Сервис-Настройка-Панели инструментов-Создать-Настраиваемая1 (в Office—2003)

Понятие аппроксимации

Аппроксимация табличных функций в Excel

Задания для самостоятельного решения

Практическая работа №6

Подготовка расчетной таблицы

Построение графика функции

Построение графиков других функций

Квадратичная функция y=ax2+bx+c

Кубическая парабола y=ax3

Гипербола y=k/x

Построение тригонометрических функций sin(x) и cos(x)

Формулы в Excel для чайников

Как в формуле Excel обозначить постоянную ячейку

Как составить таблицу в Excel с формулами

Квадратичная функция y=ax²+bx+c

Кубическая парабола y=ax³