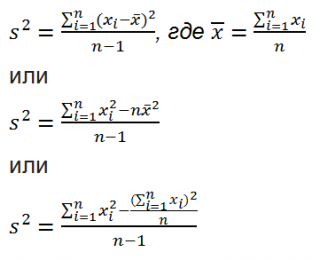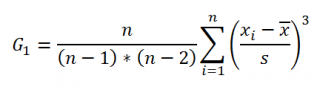Статистика расчеты microsoft excel

В учебном пособии даны методы статистической обработки данных с применением Microsoft Excel. Рассмотрены выборочный метод, дисперсионный, корреляционный и индексный анализы, приведен материал о расчетах средних величин и показателей вариации, рядах динамики, описательной статистики, раскрыто содержание статистических показателей. Подробно описаны действия в программе Microsoft Excel, приведены примеры и скриншоты с расчетными формулами.

Мы используем куки-файлы, чтобы вы могли быстрее и удобнее пользоваться сайтом. Подробнее

Статистическая обработка данных – это сбор, упорядочивание, обобщение и анализ информации с возможностью определения тенденции и прогноза по изучаемому явлению. В Excel есть огромное количество инструментов, которые помогают проводить исследования в данной области. Последние версии этой программы в плане возможностей практически ничем не уступают специализированным приложениям в области статистики. Главными инструментами для выполнения расчетов и анализа являются функции. Давайте изучим общие особенности работы с ними, а также подробнее остановимся на отдельных наиболее полезных инструментах.

Статистические функции

Как и любые другие функции в Экселе, статистические функции оперируют аргументами, которые могут иметь вид постоянных чисел, ссылок на ячейки или массивы.

Выражения можно вводить вручную в определенную ячейку или в строку формул, если хорошо знать синтаксис конкретного из них. Но намного удобнее воспользоваться специальным окном аргументов, которое содержит подсказки и уже готовые поля для ввода данных. Перейти в окно аргумента статистических выражений можно через «Мастер функций» или с помощью кнопок «Библиотеки функций» на ленте.

Запустить Мастер функций можно тремя способами:

1. Кликнуть по пиктограмме «Вставить функцию» слева от строки формул.



2. Находясь во вкладке «Формулы», кликнуть на ленте по кнопке «Вставить функцию» в блоке инструментов «Библиотека функций».



3. Набрать на клавиатуре сочетание клавиш Shift+F3.

При выполнении любого из вышеперечисленных вариантов откроется окно «Мастера функций».

Затем нужно кликнуть по полю «Категория» и выбрать значение «Статистические».

После этого откроется список статистических выражений. Всего их насчитывается более сотни. Чтобы перейти в окно аргументов любого из них, нужно просто выделить его и нажать на кнопку «OK».

Для того, чтобы перейти к нужным нам элементам через ленту, перемещаемся во вкладку «Формулы». В группе инструментов на ленте «Библиотека функций» кликаем по кнопке «Другие функции». В открывшемся списке выбираем категорию «Статистические». Откроется перечень доступных элементов нужной нам направленности. Для перехода в окно аргументов достаточно кликнуть по одному из них.

Урок: Мастер функций в Excel

МАКС

Оператор МАКС предназначен для определения максимального числа из выборки. Он имеет следующий синтаксис:

=МАКС(число1;число2;…)

В поля аргументов нужно ввести диапазоны ячеек, в которых находится числовой ряд. Наибольшее число из него эта формула выводит в ту ячейку, в которой находится сама.

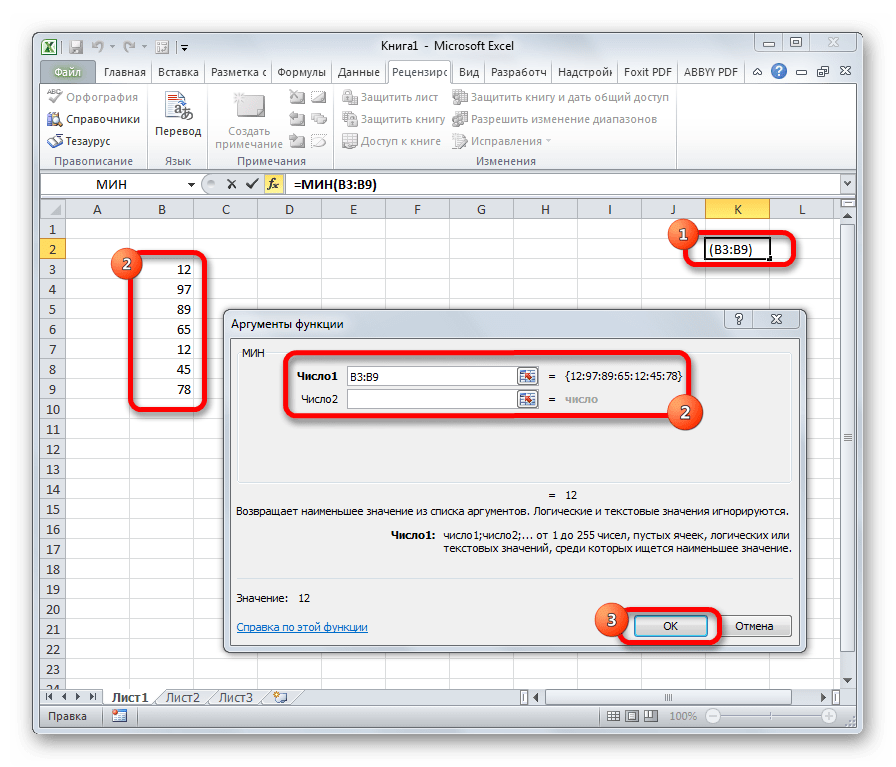
МИН

По названию функции МИН понятно, что её задачи прямо противоположны предыдущей формуле – она ищет из множества чисел наименьшее и выводит его в заданную ячейку. Имеет такой синтаксис:

=МИН(число1;число2;…)

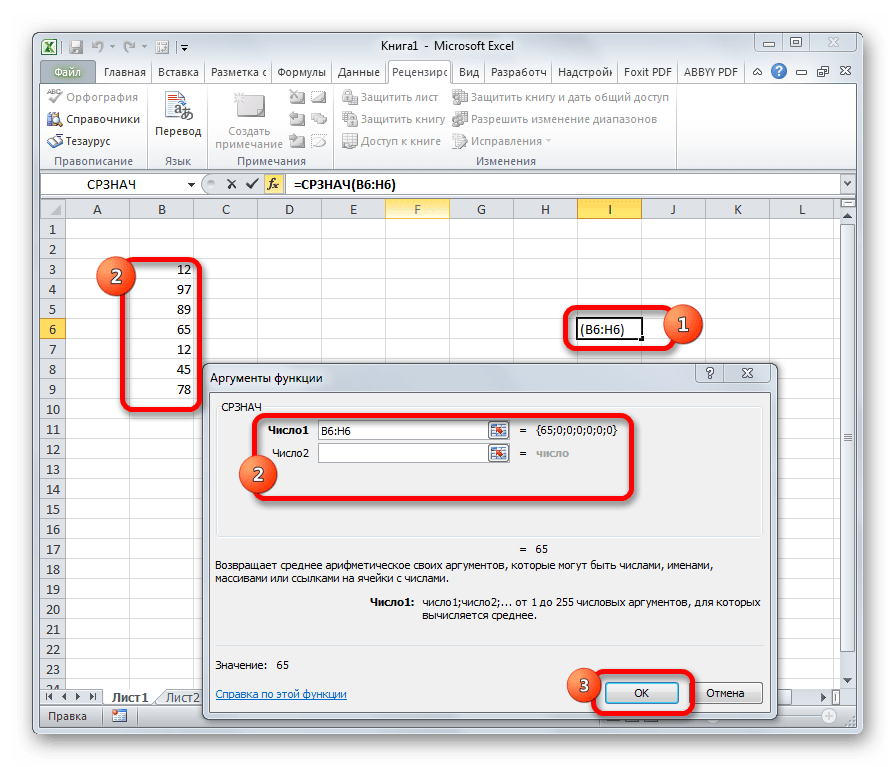
СРЗНАЧ

Функция СРЗНАЧ ищет число в указанном диапазоне, которое ближе всего находится к среднему арифметическому значению. Результат этого расчета выводится в отдельную ячейку, в которой и содержится формула. Шаблон у неё следующий:

=СРЗНАЧ(число1;число2;…)

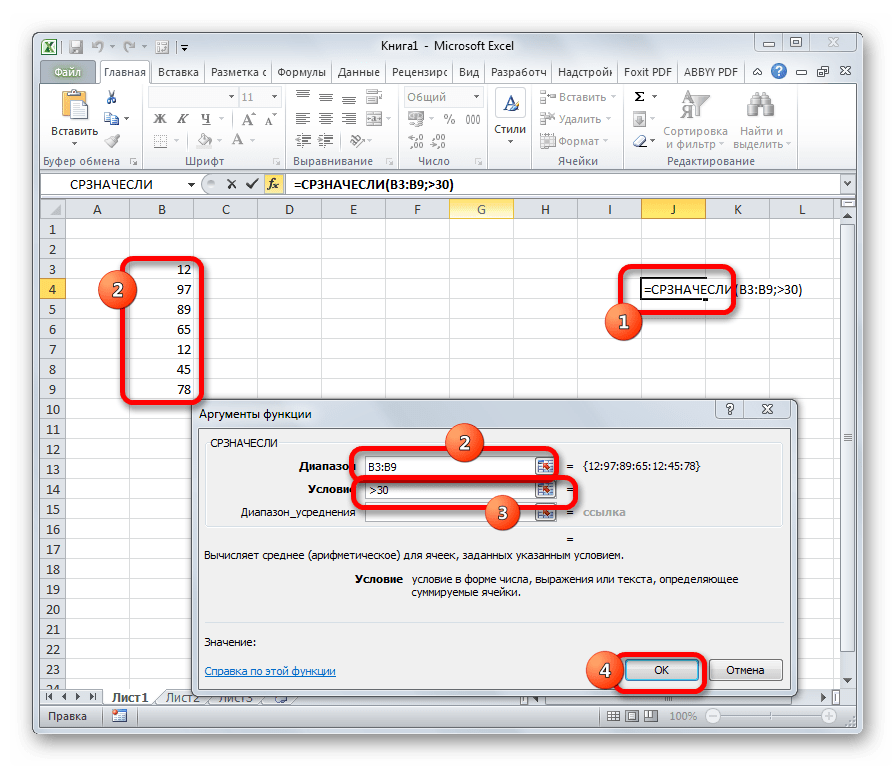
СРЗНАЧЕСЛИ

Функция СРЗНАЧЕСЛИ имеет те же задачи, что и предыдущая, но в ней существует возможность задать дополнительное условие. Например, больше, меньше, не равно определенному числу. Оно задается в отдельном поле для аргумента. Кроме того, в качестве необязательного аргумента может быть добавлен диапазон усреднения. Синтаксис следующий:

=СРЗНАЧЕСЛИ(число1;число2;…;условие;[диапазон_усреднения])

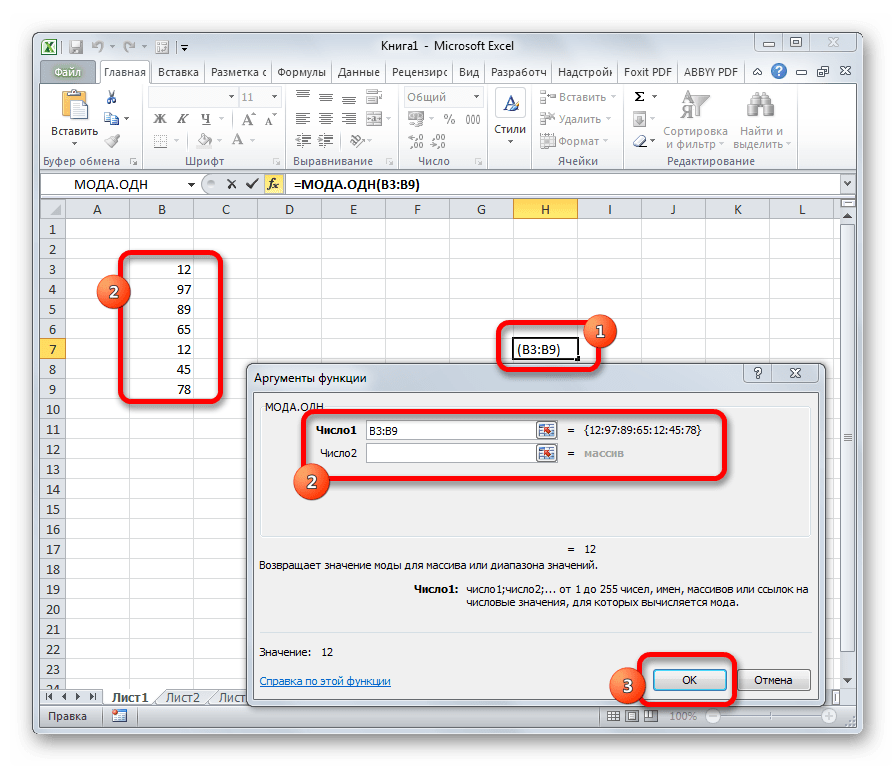
МОДА.ОДН

Формула МОДА.ОДН выводит в ячейку то число из набора, которое встречается чаще всего. В старых версиях Эксель существовала функция МОДА, но в более поздних она была разбита на две: МОДА.ОДН (для отдельных чисел) и МОДА.НСК(для массивов). Впрочем, старый вариант тоже остался в отдельной группе, в которой собраны элементы из прошлых версий программы для обеспечения совместимости документов.

=МОДА.ОДН(число1;число2;…)

=МОДА.НСК(число1;число2;…)

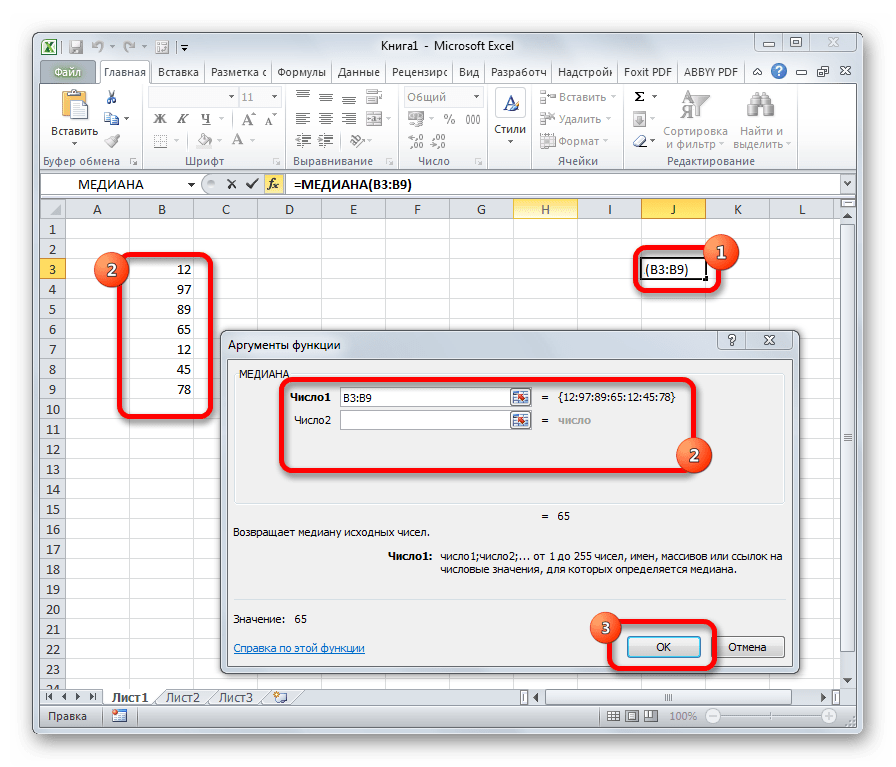
МЕДИАНА

Оператор МЕДИАНА определяет среднее значение в диапазоне чисел. То есть, устанавливает не среднее арифметическое, а просто среднюю величину между наибольшим и наименьшим числом области значений. Синтаксис выглядит так:

=МЕДИАНА(число1;число2;…)

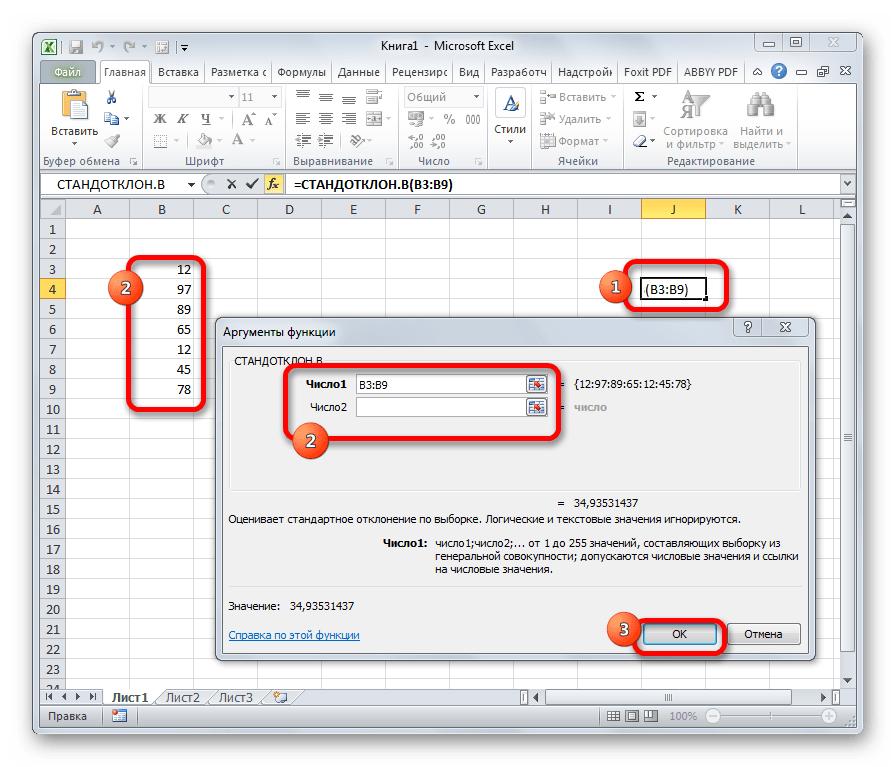
СТАНДОТКЛОН

Формула СТАНДОТКЛОН так же, как и МОДА является пережитком старых версий программы. Сейчас используются современные её подвиды – СТАНДОТКЛОН.В и СТАНДОТКЛОН.Г. Первая из них предназначена для вычисления стандартного отклонения выборки, а вторая – генеральной совокупности. Данные функции используются также для расчета среднего квадратичного отклонения. Синтаксис их следующий:

=СТАНДОТКЛОН.В(число1;число2;…)

=СТАНДОТКЛОН.Г(число1;число2;…)

Урок: Формула среднего квадратичного отклонения в Excel

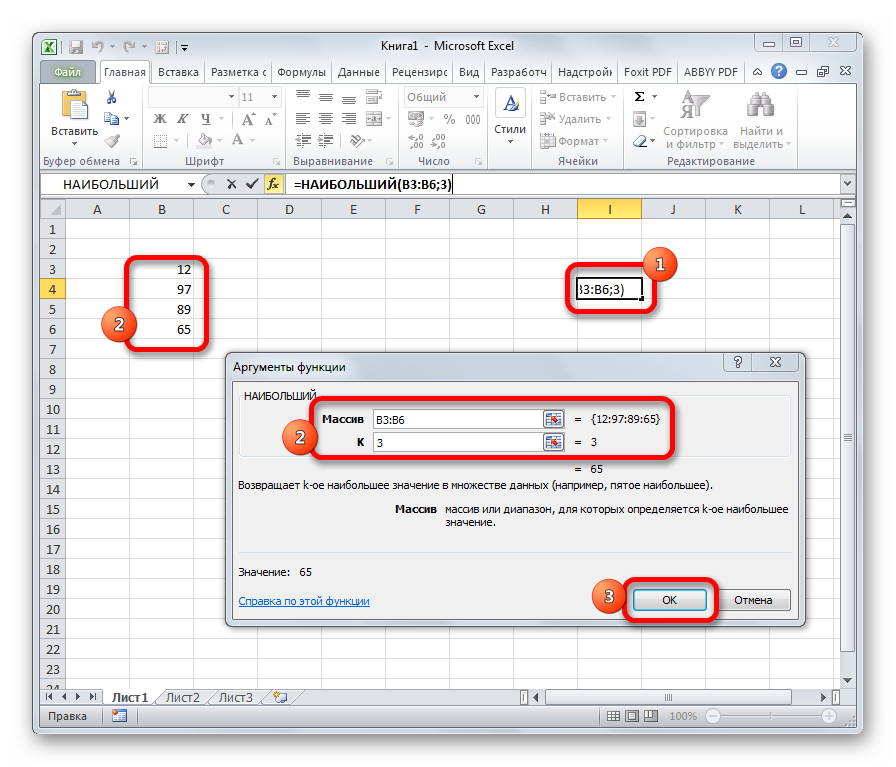
НАИБОЛЬШИЙ

Данный оператор показывает в выбранной ячейке указанное в порядке убывания число из совокупности. То есть, если мы имеем совокупность 12,97,89,65, а аргументом позиции укажем 3, то функция в ячейку вернет третье по величине число. В данном случае, это 65. Синтаксис оператора такой:

=НАИБОЛЬШИЙ(массив;k)

В данном случае, k — это порядковый номер величины.

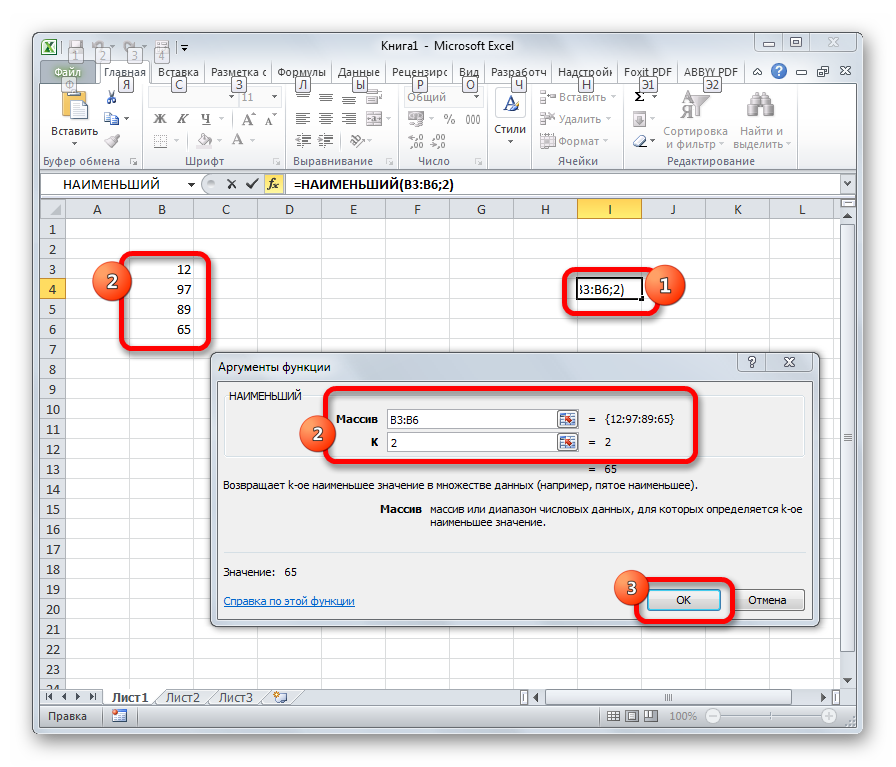
НАИМЕНЬШИЙ

Данная функция является зеркальным отражением предыдущего оператора. В ней также вторым аргументом является порядковый номер числа. Вот только в данном случае порядок считается от меньшего. Синтаксис такой:

=НАИМЕНЬШИЙ(массив;k)

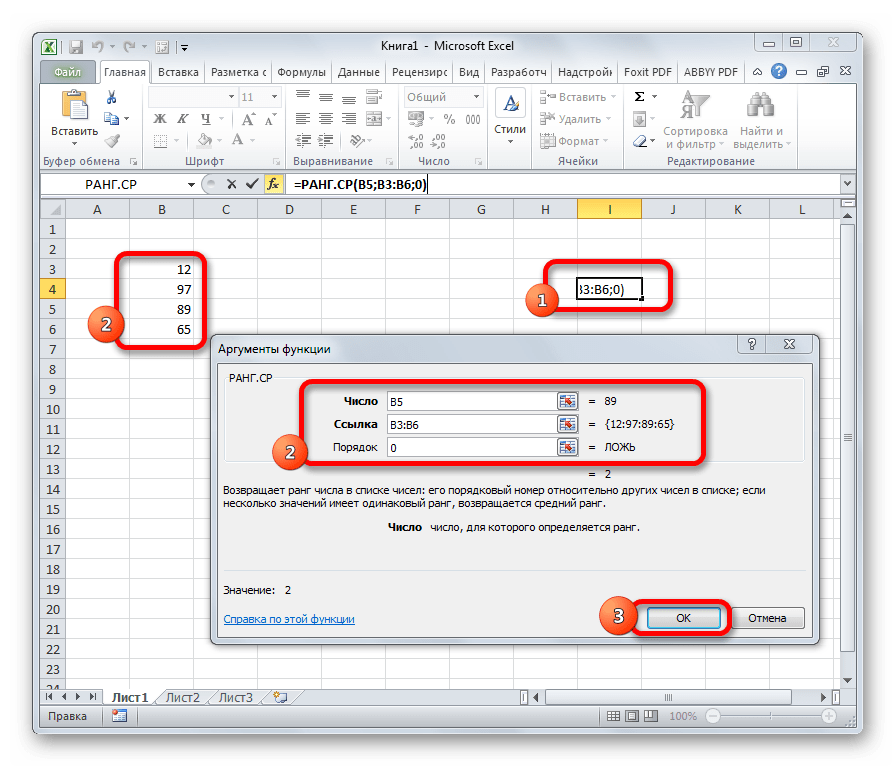
РАНГ.СР

Эта функция имеет действие, обратное предыдущим. В указанную ячейку она выдает порядковый номер конкретного числа в выборке по условию, которое указано в отдельном аргументе. Это может быть порядок по возрастанию или по убыванию. Последний установлен по умолчанию, если поле «Порядок» оставить пустым или поставить туда цифру 0. Синтаксис этого выражения выглядит следующим образом:

=РАНГ.СР(число;массив;порядок)

Выше были описаны только самые популярные и востребованные статистические функции в Экселе. На самом деле их в разы больше. Тем не менее, основной принцип действий у них похожий: обработка массива данных и возврат в указанную ячейку результата вычислительных действий.

Вычисление статистических
характеристик

В Excelимеется несколько
способов вычисления статистических
характеристик:

• по
  формулам;

• с помощью
  статистических функций;

• с помощью
  надстройки Пакет анализа.

Таблица
3

Статистическая величина	Формула	Функция
Сумма		СУММ()
Среднее арифметическое		Срзнач()
Среднее линейное отклонение		Сроткл()
Дисперсия по генеральной совокупности		Диспр()
Дисперсия по выборке		Дисп()
Среднее квадратичное отклонение		Стандотклонп()
Смещенное среднее отклонение (по выборке)		Стандотклон()

В таблице 3 приведены формулы и
соответствующие им функции для вычисления
некоторых статистических характеристик.

Кроме того, имеются функции для вычисления
следующих статистических характеристик:

• количество
  значений – СЧЕТ();

• максимум
  ‑ Макс();

• минимум
  ‑ Мин();

• мода ‑
  Мода();

• медиана
  ‑ Медиана().

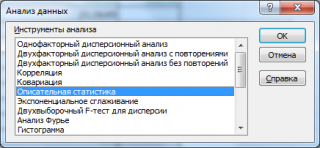
Чтобы воспользоваться надстройкой
Пакет анализа, надо:

1. На вкладке
   Данныев группеАнализвыбрать
   командуАнализ данных.

2. В
   открывшемся диалоговом окне выбрать
   строку Описательная статистика.

3. В поле
   Входной интервалуказать диапазон
   данных, для которых надо получить
   статистические оценки.

4. Если
   диапазон данных выделен вместе с
   заголовком, установить флажок Метки
   в первой строке;

5. Выбрать
   вариант размещения выходных данных:
   текущий рабочий лист, новый рабочий
   лист или новая рабочая книга.

В случае размещения выходных данных
на текущем листе включить режим Выходной
интервали указать левую верхнюю
ячейку диапазона, в который должны быть
выведены результаты.

1. Установить
   флажок Итоговая статистика.

2. Щелкнуть
   по кнопке ОК.

Экстраполяция

Экстраполяция– это прогнозирование
неизвестных значений путем продолжения
функции за границы области известных
значений.

Экстраполяцию динамического ряда в
Excelможно выполнить
различными способами.

I способ– про
помощи операции автозаполнения:

1. Выделить
   ряд данных.

2. Правой
   кнопкой мыши протащить маркер заполнения
   на нужное количество ячеек.

3. В
   открывшемся контекстном меню выбрать
   нужный пункт:

• Линейное
  приближение– для заполнения ячеек
  значениями, вычисленными на основе
  аппроксимации исходных данных линейной
  функцией;

• Экспоненциальное
  приближение‑ для заполнения
  ячеек значениями, вычисленными на
  основе аппроксимации исходных данных
  экспоненциальной функцией;

• Прогрессия– заполнение ячеек арифметической
  или геометрической прогрессией.

II способ– про
помощи встроенных функций:

• ПРЕДСКАЗ()
  – линейная экстраполяция для отдельной
  точки;

• ТЕНДЕНЦИЯ()
  – линейная экстраполяция для массива
  точек;

• РОСТ() –
  экспоненциальная экстраполяция для
  массива точек.

Построение линии тренда

Линия тренда– графическое
представление направления изменения
данных в ряде данных. Линии тренда
используются при прогнозировании.

Для построения на диаграмме линии
тренда надо:

1. Щелкнуть
   правой кнопкой мыши по любому маркеру
   диаграммы.

2. В
   открывшемся контекстном меню выбрать
   команду Добавить линию тренда;

3. В
   открывшемся диалоговом окне на вкладке
   Параметры линии трендав группеПостроение линии трендавыбрать
   нужный вариант: экспоненциальная,
   линейная, логарифмическая, полиномиальная,
   степенная и т.д.

4. В группе
   Прогнозуказать, на сколько периодов
   вперед и (или) назад надо выполнить
   прогноз.

5. При
   необходимости установить флажок
   Показывать уравнение на диаграмме.

6. При
   необходимости изменить форматы линии
   на вкладках Тип линии,Цвет линиииТень.

7. Закрыть
   диалоговое окно.

Корреляционно-регрессионный
анализ

Целью корреляционно-регрессионного
анализа является изучение зависимостей
между двумя или несколькими показателями.

Корреляцияхарактеризует тесноту
связи между случайными величинами.
Если коэффициент корреляции равен +1
или -1, то связь считается функциональной,
Если коэффициент корреляции равен 0,
считается, что связь отсутствует.

Различают парную корреляцию, когда
исследуется зависимость показателя
от одного параметра, имножественную
корреляцию, когда показатель зависит
от нескольких параметров.

Для определения коэффициента парной
корреляции в Excelпредназначена функция КОРРЕЛ(),
аргументами которой являются массивы
значений случайных величин.

Коэффициент корреляции можно определить
с помощью надстройки Пакет анализа:

1. На вкладке
   Данныев группеАнализвыбрать
   командуАнализ данных.

2. В
   открывшемся диалоговом окне выбрать
   строку Корреляция.

3. В
   открывшемся диалоговом окне:

• указать
  входной интервал;

• выбрать
  способ группирования данных: по строкам
  или по столбца;

• указать
  левую верхнюю ячейку выходного
  интервала.

1. Щелкнуть
   по кнопке ОК.

Регрессионный анализпредназначен
для выявления аналитической зависимости
между показателями, т.е. для нахождения
уравнения регрессии.

Для нахождения уравнения регрессии в
Excelпредназначена функция
ЛИНЕЙН(). С помощью этой функции
вычисляются коэффициенты уравнения
прямой, которая наилучшим образом
аппроксимирует имеющиеся данные.

В случае nпеременных
уравнение регрессии имеет вид

.

Функция ЛИНЕЙН() возвращает массив
коэффициентов
.
Аргументами функции являются массив
значенийyи массив
значений переменных.

Если yесть функция
одной переменной, то массивы значенийxиyмогут иметь любую форму (один столбец,
одна строка, несколько столбцов и строк)
при условии, что они имеют одинаковую
размерность.

Если yесть функция
нескольких переменных, то массив
значенийyдолжен
быть одномерным, т.е. занимать один
столбец (или одну строку), а массив
значенийxдолжен
занимать несколько столбцов (или строк),
при этом каждый столбец (или строка)
будут интерпретироваться как отдельная
переменная.

Кроме того, функция ЛИНЕЙН() имеет
логический аргумент Конст, который
определяет значение свободного членаb: еслиКонст=ЛОЖЬ,
то полагаетсяb=0.

Функция ЛИНЕЙН() может также возвращать
дополнительную регрессионную статистику.
Для этого надо присвоить логическому
аргументу Статистиказначение
ИСТИНА.

Поскольку функция ЛИНЕЙН() возвращает
массив значений, поэтому перед вводом
формулы надо выделить n+1
ячейку, а закончить ввод формулы –
нажатием клавишCtrl+Shift+Enter.

Коэффициенты уравнения регрессии и
регрессионную статистику можно получить
с помощью надстройки Пакет анализа:

1. На вкладке
   Данныев группеАнализвыбрать
   командуАнализ данных.

2. В
   открывшемся диалоговом окне выбрать
   строку Регрессия.

3. В
   открывшемся диалоговом окне:

• указать
  входной интервал значений y;

• указать
  входной интервал значений x;

• выбрать
  способ вычисления константы b(0: да или нет);

• указать
  левую верхнюю ячейку выходного
  интервала.

1. Щелкнуть
   по кнопке ОК.

Частотный анализ

Распределение частот в Excelможно создать несколькими способами:

• с помощью
  функции ЧАСТОТА();

• с
  использованием надстройки Пакет
  анализа;

• с помощью
  сводных таблиц.

Функция ЧАСТОТА() возвращает количество
значений из диапазона данных, попадающих
в каждый интервал группировки.

Аргументами этой функции являются
массив данных и массив интервалов
группировки.

Массив верхних границ интервалов
группировки можно определить по формуле:

=МИН(массив)+{1:2:…:n}*(МАКС(массив)-МИН(массив))/n

Здесь массив– диапазон данных;n– количество интервалов группировки.

Формула массива верхних границ и функция
ЧАСТОТА() возвращают массив ячеек,
поэтому перед их вводом надо выделить
столбец из nячеек,
а закончить ввод– нажатием клавишCtrl+Shift+Enter.

Чтобы создать распределение частот с
помощью надстройки Пакет анализа,
надо:

1. На вкладке
   Данныев группеАнализвыбрать
   командуАнализ данных.

2. В
   открывшемся диалоговом окне выбрать
   строку Гистограмма.

3. В
   открывшемся диалоговом окне:

• в поле
  Входной интервалуказать диапазон
  данных;

• в поле
  Интервал кармановуказать массив
  верхних границ интервалов;

• в поле
  Выходной интервалуказать левую
  верхнюю ячейку выходного интервала;

• для
  графического отображения распределения
  частот (гистограммы) установить флажок
  Вывод графика.

1. Щелкнуть
   по кнопке ОК.

Распределение частот можно получить,
создав сводную таблицус группировкой
по полю, содержащему числовые данные.
При этом в качестве начального значения
задается минимальное значение диапазона,
конечного значения – максимальное,
шага – интервал группировки, равный
(МАКС(массив)-МИН(массив))/n.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Рассмотрим инструмент Описательная статистика, входящий в надстройку Пакет Анализа. Рассчитаем показатели выборки: среднее, медиана, мода, дисперсия, стандартное отклонение и др.

Задача

описательной статистики

(descriptive statistics) заключается в том, чтобы с использованием математических инструментов свести сотни значений

выборки

к нескольким итоговым показателям, которые дают представление о

выборке

.В качестве таких статистических показателей используются:

среднее

,

медиана

,

мода

,

дисперсия, стандартное отклонение

и др.

Опишем набор числовых данных с помощью определенных показателей. Для чего нужны эти показатели? Эти показатели позволят сделать определенные

статистические выводы о распределении

, из которого была взята

выборка

. Например, если у нас есть

выборка

значений толщины трубы, которая изготавливается на определенном оборудовании, то на основании анализа этой

выборки

мы сможем сделать, с некой определенной вероятностью, заключение о состоянии процесса изготовления.

Содержание статьи:

• Надстройка Пакет анализа;
• Среднее выборки

  ;

• Медиана выборки

  ;

• Мода выборки

  ;

• Мода и среднее значение

  ;

• Дисперсия выборки

  ;

• Стандартное отклонение выборки

  ;

• Стандартная ошибка

  ;

• Ассиметричность

  ;

• Эксцесс выборки

  ;

• Уровень надежности

  .

Надстройка Пакет анализа

Для вычисления статистических показателей одномерных

выборок

, используем

надстройку Пакет анализа

. Затем, все показатели рассчитанные надстройкой, вычислим с помощью встроенных функций MS EXCEL.

СОВЕТ

: Подробнее о других инструментах надстройки

Пакет анализа

и ее подключении – читайте в статье

Надстройка Пакет анализа MS EXCEL

.

Выборку

разместим на

листе

Пример

в файле примера

в диапазоне

А6:А55

(50 значений).

Примечание

: Для удобства написания формул для диапазона

А6:А55

создан

Именованный диапазон

Выборка.

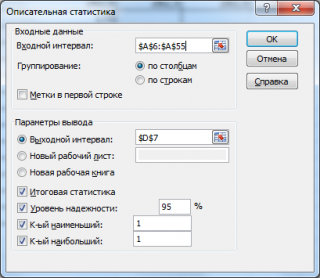
В диалоговом окне

Анализ данных

выберите инструмент

Описательная статистика

.

После нажатия кнопки

ОК

будет выведено другое диалоговое окно,

в котором нужно указать:

• 
  входной интервал
  
  (Input Range) – это диапазон ячеек, в котором содержится массив данных. Если в указанный диапазон входит текстовый заголовок набора данных, то нужно поставить галочку в поле
  
  Метки в первой строке (
  
  Labels
  
  in
  
  first
  
  row
  
  ).
  
  В этом случае заголовок будет выведен в
  
  Выходном интервале.
  
  Пустые ячейки будут проигнорированы, поэтому нулевые значения необходимо обязательно указывать в ячейках, а не оставлять их пустыми;
• 
  выходной интервал
  
  (Output Range). Здесь укажите адрес верхней левой ячейки диапазона, в который будут выведены статистические показатели;
• 
  Итоговая статистика (
  
  Summary
  
  Statistics
  
  )
  
  . Поставьте галочку напротив этого поля – будут выведены основные показатели выборки:
  
  среднее, медиана, мода, стандартное отклонение
  
  и др.;
• Также можно поставить галочки напротив полей
  
  Уровень надежности (
  
  Confidence
  
  Level
  
  for
  
  Mean
  
  )
  
  ,
  
  К-й наименьший
  
  (Kth Largest) и
  
  К-й наибольший
  
  (Kth Smallest).

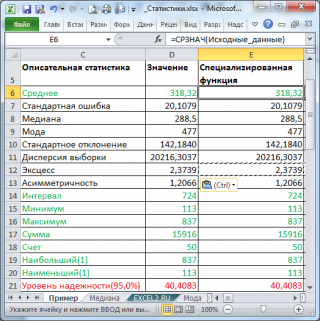
В результате будут выведены следующие статистические показатели:

Все показатели выведены в виде значений, а не формул. Если массив данных изменился, то необходимо перезапустить расчет.

Если во

входном интервале

указать ссылку на несколько столбцов данных, то будет рассчитано соответствующее количество наборов показателей. Такой подход позволяет сравнить несколько наборов данных. При сравнении нескольких наборов данных используйте заголовки (включите их во

Входной интервал

и установите галочку в поле

Метки в первой строке

). Если наборы данных разной длины, то это не проблема — пустые ячейки будут проигнорированы.

Зеленым цветом на картинке выше и в

файле примера

выделены показатели, которые не требуют особого пояснения. Для большинства из них имеется специализированная функция:

• 
  Интервал
  
  (Range) — разница между максимальным и минимальным  значениями;
• 
  Минимум
  
  (Minimum) – минимальное значение в диапазоне ячеек, указанном во
  
  Входном интервале
  
  (см.

  статью про функцию
  
  МИН()
  
  );

• 
  Максимум
  
  (Maximum)– максимальное значение (см.

  статью про функцию
  
  МАКС()
  
  );

• 
  Сумма
  
  (Sum) – сумма всех значений (см.

  статью про функцию
  
  СУММ()
  
  );

• 
  Счет
  
  (Count) – количество значений во
  
  Входном интервале
  
  (пустые ячейки игнорируются, см.

  статью про функцию
  
  СЧЁТ()
  
  );

• 
  Наибольший
  
  (Kth Largest) – выводится К-й наибольший. Например, 1-й наибольший – это максимальное значение (см.

  статью про функцию
  
  НАИБОЛЬШИЙ()
  
  );

• 
  Наименьший
  
  (Kth Smallest) – выводится К-й наименьший. Например, 1-й наименьший – это минимальное значение (см.

  статью про функцию
  
  НАИМЕНЬШИЙ()
  
  ).

Ниже даны подробные описания остальных показателей.

Среднее выборки

Среднее

(mean, average) или

выборочное среднее

или

среднее выборки

(sample average) представляет собой

арифметическое среднее

всех значений массива. В MS EXCEL для вычисления среднего выборки используется функция

СРЗНАЧ()

.

Выборочное среднее

является «хорошей» (несмещенной и эффективной) оценкой

математического ожидания

случайной величины (подробнее см. статью

Среднее и Математическое ожидание в MS EXCEL

).

Медиана выборки

Медиана

(Median) – это число, которое является серединой множества чисел (в данном случае выборки): половина чисел множества больше, чем

медиана

, а половина чисел меньше, чем

медиана

. Для определения

медианы

необходимо сначала

отсортировать множество чисел

. Например,

медианой

для чисел 2, 3, 3,

4

, 5, 7, 10 будет 4.

Если множество содержит четное количество чисел, то вычисляется

среднее

для двух чисел, находящихся в середине множества. Например,

медианой

для чисел 2, 3,

3

,

5

, 7, 10 будет 4, т.к. (3+5)/2.

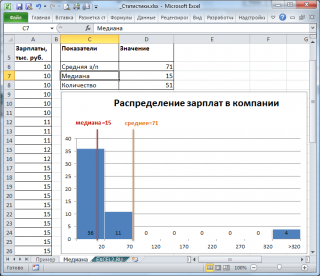
Если имеется длинный хвост распределения, то

Медиана

лучше, чем

среднее значение

, отражает «типичное» или «центральное» значение. Например, рассмотрим несправедливое распределение зарплат в компании, в которой руководство получает существенно больше, чем основная масса сотрудников.

Очевидно, что средняя зарплата (71 тыс. руб.) не отражает тот факт, что 86% сотрудников получает не более 30 тыс. руб. (т.е. 86% сотрудников получает зарплату в более, чем в 2 раза меньше средней!). В то же время медиана (15 тыс. руб.) показывает, что

как минимум

у 50% сотрудников зарплата меньше или равна 15 тыс. руб.

Для определения

медианы

в MS EXCEL существует одноименная функция

МЕДИАНА()

, английский вариант — MEDIAN().

Медиану

также можно вычислить с помощью формул

=КВАРТИЛЬ.ВКЛ(Выборка;2) =ПРОЦЕНТИЛЬ.ВКЛ(Выборка;0,5).

Подробнее о

медиане

см. специальную статью

Медиана в MS EXCEL

.

СОВЕТ

: Подробнее про

квартили

см. статью, про

перцентили (процентили)

см. статью.

Мода выборки

Мода

(Mode) – это наиболее часто встречающееся (повторяющееся) значение в

выборке

. Например, в массиве (1; 1;

2

;

2

;

2

; 3; 4; 5) число 2 встречается чаще всего – 3 раза. Значит, число 2 – это

мода

. Для вычисления

моды

используется функция

МОДА()

, английский вариант MODE().

Примечание

: Если в массиве нет повторяющихся значений, то функция вернет значение ошибки #Н/Д. Это свойство использовано в статье

Есть ли повторы в списке?

Начиная с

MS EXCEL 2010

вместо функции

МОДА()

рекомендуется использовать функцию

МОДА.ОДН()

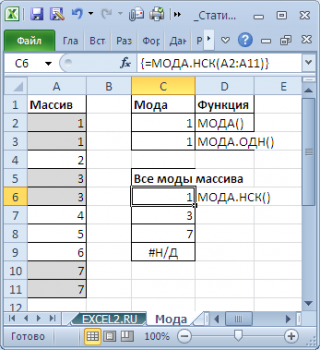
, которая является ее полным аналогом. Кроме того, в MS EXCEL 2010 появилась новая функция

МОДА.НСК()

, которая возвращает несколько наиболее часто повторяющихся значений (если количество их повторов совпадает). НСК – это сокращение от слова НеСКолько.

Например, в массиве (1; 1;

2

;

2

;

2

; 3;

4

;

4

;

4

; 5) числа 2 и 4 встречаются наиболее часто – по 3 раза. Значит, оба числа являются

модами

. Функции

МОДА.ОДН()

и

МОДА()

вернут значение 2, т.к. 2 встречается первым, среди наиболее повторяющихся значений (см.

файл примера

, лист

Мода

).

Чтобы исправить эту несправедливость и была введена функция

МОДА.НСК()

, которая выводит все

моды

. Для этого ее нужно ввести как

формулу массива

.

Как видно из картинки выше, функция

МОДА.НСК()

вернула все три

моды

из массива чисел в диапазоне

A2:A11

: 1; 3 и 7. Для этого, выделите диапазон

C6:C9

, в

Строку формул

введите формулу

=МОДА.НСК(A2:A11)

и нажмите

CTRL+SHIFT+ENTER

. Диапазон

C

6:

C

9

охватывает 4 ячейки, т.е. количество выделяемых ячеек должно быть больше или равно количеству

мод

. Если ячеек больше чем м

о

д, то избыточные ячейки будут заполнены значениями ошибки #Н/Д. Если

мода

только одна, то все выделенные ячейки будут заполнены значением этой

моды

.

Теперь вспомним, что мы определили

моду

для выборки, т.е. для конечного множества значений, взятых из

генеральной совокупности

. Для

непрерывных случайных величин

вполне может оказаться, что выборка состоит из массива на подобие этого (0,935; 1,211; 2,430; 3,668; 3,874; …), в котором может не оказаться повторов и функция

МОДА()

вернет ошибку.

Даже в нашем массиве с

модой

, которая была определена с помощью

надстройки Пакет анализа

, творится, что-то не то. Действительно,

модой

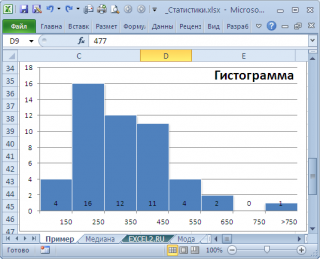
нашего массива значений является число 477, т.к. оно встречается 2 раза, остальные значения не повторяются. Но, если мы посмотрим на

гистограмму распределения

, построенную для нашего массива, то увидим, что 477 не принадлежит интервалу наиболее часто встречающихся значений (от 150 до 250).

Проблема в том, что мы определили

моду

как наиболее часто встречающееся значение, а не как наиболее вероятное. Поэтому,

моду

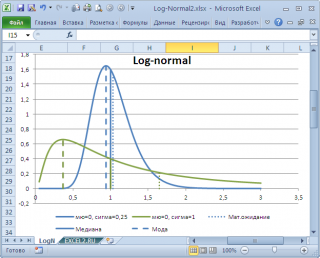
в учебниках статистики часто определяют не для выборки (массива), а для функции распределения. Например, для

логнормального распределения

мода

(наиболее вероятное значение непрерывной случайной величины х), вычисляется как

exp

(

m

—

s

²

)

, где m и s параметры этого распределения.

Понятно, что для нашего массива число 477, хотя и является наиболее часто повторяющимся значением, но все же является плохой оценкой для

моды

распределения, из которого взята

выборка

(наиболее вероятного значения или для которого плотность вероятности распределения максимальна).

Для того, чтобы получить оценку

моды

распределения, из

генеральной совокупности

которого взята

выборка

, можно, например, построить

гистограмму

. Оценкой для

моды

может служить интервал наиболее часто встречающихся значений (самого высокого столбца). Как было сказано выше, в нашем случае это интервал от 150 до 250.

Вывод

: Значение

моды

для

выборки

, рассчитанное с помощью функции

МОДА()

, может ввести в заблуждение, особенно для небольших выборок. Эта функция эффективна, когда случайная величина может принимать лишь несколько дискретных значений, а размер

выборки

существенно превышает количество этих значений.

Например, в рассмотренном примере о распределении заработных плат (см. раздел статьи выше, о Медиане),

модой

является число 15 (17 значений из 51, т.е. 33%). В этом случае функция

МОДА()

дает хорошую оценку «наиболее вероятного» значения зарплаты.

Примечание

: Строго говоря, в примере с зарплатой мы имеем дело скорее с

генеральной совокупностью

, чем с

выборкой

. Т.к. других зарплат в компании просто нет.

О вычислении

моды

для распределения

непрерывной случайной величины

читайте статью

Мода в MS EXCEL

.

Мода и среднее значение

Не смотря на то, что

мода

– это наиболее вероятное значение случайной величины (вероятность выбрать это значение из

Генеральной совокупности

максимальна), не следует ожидать, что

среднее значение

обязательно будет близко к

моде

.

Примечание

:

Мода

и

среднее

симметричных распределений совпадает (имеется ввиду симметричность

плотности распределения

).

Представим, что мы бросаем некий «неправильный» кубик, у которого на гранях имеются значения (1; 2; 3; 4; 6; 6), т.е. значения 5 нет, а есть вторая 6.

Модой

является 6, а среднее значение – 3,6666.

Другой пример. Для

Логнормального распределения

LnN(0;1)

мода

равна =EXP(m-s2)= EXP(0-1*1)=0,368, а

среднее значение

1,649.

Дисперсия выборки

Дисперсия выборки

или

выборочная дисперсия (

sample

variance

) характеризует разброс значений в массиве, отклонение от

среднего

.

Из формулы №1 видно, что

дисперсия выборки

это сумма квадратов отклонений каждого значения в массиве

от среднего

, деленная на размер выборки минус 1.

В MS EXCEL 2007 и более ранних версиях для вычисления

дисперсии выборки

используется функция

ДИСП()

. С версии MS EXCEL 2010 рекомендуется использовать ее аналог — функцию

ДИСП.В()

.

Дисперсию

можно также вычислить непосредственно по нижеуказанным формулам (см.

файл примера

):

=КВАДРОТКЛ(Выборка)/(СЧЁТ(Выборка)-1) =(СУММКВ(Выборка)-СЧЁТ(Выборка)*СРЗНАЧ(Выборка)^2)/ (СЧЁТ(Выборка)-1)

– обычная формула

=СУММ((Выборка -СРЗНАЧ(Выборка))^2)/ (СЧЁТ(Выборка)-1)

–

формула массива

Дисперсия выборки

равна 0, только в том случае, если все значения равны между собой и, соответственно, равны

среднему значению

.

Чем больше величина

дисперсии

, тем больше разброс значений в массиве относительно

среднего

.

Размерность

дисперсии

соответствует квадрату единицы измерения исходных значений. Например, если значения в выборке представляют собой измерения веса детали (в кг), то размерность

дисперсии

будет кг

²

. Это бывает сложно интерпретировать, поэтому для характеристики разброса значений чаще используют величину равную квадратному корню из

дисперсии – стандартное отклонение

.

Подробнее о

дисперсии

см. статью

Дисперсия и стандартное отклонение в MS EXCEL

.

Стандартное отклонение выборки

Стандартное отклонение выборки

(Standard Deviation), как и

дисперсия

, — это мера того, насколько широко разбросаны значения в выборке

относительно их среднего

.

По определению,

стандартное отклонение

равно квадратному корню из

дисперсии

:

Стандартное отклонение

не учитывает величину значений в

выборке

, а только степень рассеивания значений вокруг их

среднего

. Чтобы проиллюстрировать это приведем пример.

Вычислим стандартное отклонение для 2-х

выборок

: (1; 5; 9) и (1001; 1005; 1009). В обоих случаях, s=4. Очевидно, что отношение величины стандартного отклонения к значениям массива у

выборок

существенно отличается.

В MS EXCEL 2007 и более ранних версиях для вычисления

Стандартного отклонения выборки

используется функция

СТАНДОТКЛОН()

. С версии MS EXCEL 2010 рекомендуется использовать ее аналог

СТАНДОТКЛОН.В()

.

Стандартное отклонение

можно также вычислить непосредственно по нижеуказанным формулам (см.

файл примера

):

=КОРЕНЬ(КВАДРОТКЛ(Выборка)/(СЧЁТ(Выборка)-1)) =КОРЕНЬ((СУММКВ(Выборка)-СЧЁТ(Выборка)*СРЗНАЧ(Выборка)^2)/(СЧЁТ(Выборка)-1))

Подробнее о

стандартном отклонении

см. статью

Дисперсия и стандартное отклонение в MS EXCEL

.

Стандартная ошибка

В

Пакете анализа

под термином

стандартная ошибка

имеется ввиду

Стандартная ошибка среднего

(Standard Error of the Mean, SEM).

Стандартная ошибка среднего

— это оценка

стандартного отклонения

распределения

выборочного среднего

.

Примечание

: Чтобы разобраться с понятием

Стандартная ошибка среднего

необходимо прочитать о

выборочном распределении

(см. статью

Статистики, их выборочные распределения и точечные оценки параметров распределений в MS EXCEL

) и статью про

Центральную предельную теорему

.

Стандартное отклонение распределения выборочного среднего

вычисляется по формуле σ/√n, где n — объём

выборки, σ — стандартное отклонение исходного

распределения, из которого взята

выборка

. Т.к. обычно

стандартное отклонение

исходного распределения неизвестно, то в расчетах вместо

σ

используют ее оценку

s

—

стандартное отклонение выборки

. А соответствующая величина s/√n имеет специальное название —

Стандартная ошибка среднего.

Именно эта величина вычисляется в

Пакете анализа.

В MS EXCEL

стандартную ошибку среднего

можно также вычислить по формуле

=СТАНДОТКЛОН.В(Выборка)/ КОРЕНЬ(СЧЁТ(Выборка))

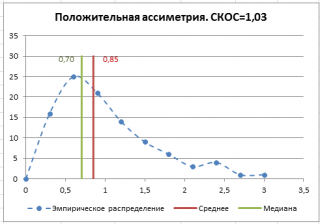
Асимметричность

Асимметричность

или

коэффициент асимметрии

(skewness) характеризует степень несимметричности распределения (

плотности распределения

) относительно его

среднего

.

Положительное значение

коэффициента асимметрии

указывает, что размер правого «хвоста» распределения больше, чем левого (относительно среднего). Отрицательная асимметрия, наоборот, указывает на то, что левый хвост распределения больше правого.

Коэффициент асимметрии

идеально симметричного распределения или выборки равно 0.

Примечание

:

Асимметрия выборки

может отличаться расчетного значения асимметрии теоретического распределения. Например,

Нормальное распределение

является симметричным распределением (

плотность его распределения

симметрична относительно

среднего

) и, поэтому имеет асимметрию равную 0. Понятно, что при этом значения в

выборке

из соответствующей

генеральной совокупности

не обязательно должны располагаться совершенно симметрично относительно

среднего

. Поэтому,

асимметрия выборки

, являющейся оценкой

асимметрии распределения

, может отличаться от 0.

Функция

СКОС()

, английский вариант SKEW(), возвращает коэффициент

асимметрии выборки

, являющейся оценкой

асимметрии

соответствующего распределения, и определяется следующим образом:

где n – размер

выборки

, s –

стандартное отклонение выборки

.

В

файле примера на листе СКОС

приведен расчет коэффициента

асимметрии

на примере случайной выборки из

распределения Вейбулла

, которое имеет значительную положительную

асимметрию

при параметрах распределения W(1,5; 1).

Эксцесс выборки

Эксцесс

показывает относительный вес «хвостов» распределения относительно его центральной части.

Для того чтобы определить, что относится к хвостам распределения, а что к его центральной части, можно использовать границы μ +/-

σ

.

Примечание

: Не смотря на старания профессиональных статистиков, в литературе еще попадается определение

Эксцесса

как меры «остроконечности» (peakedness) или сглаженности распределения. Но, на самом деле, значение

Эксцесса

ничего не говорит о форме пика распределения.

Согласно определения,

Эксцесс

равен четвертому

стандартизированному моменту:

Для

нормального распределения

четвертый момент равен 3*σ

⁴

, следовательно,

Эксцесс

равен 3. Многие компьютерные программы используют для расчетов не сам

Эксцесс

, а так называемый Kurtosis excess, который меньше на 3. Т.е. для

нормального распределения

Kurtosis excess равен 0. Необходимо быть внимательным, т.к. часто не очевидно, какая формула лежит в основе расчетов.

Примечание

: Еще большую путаницу вносит перевод этих терминов на русский язык. Термин Kurtosis происходит от греческого слова «изогнутый», «имеющий арку». Так сложилось, что на русский язык оба термина Kurtosis и Kurtosis excess переводятся как

Эксцесс

(от англ. excess — «излишек»). Например, функция MS EXCEL

ЭКСЦЕСС()

на самом деле вычисляет Kurtosis excess.

Функция

ЭКСЦЕСС()

, английский вариант KURT(), вычисляет на основе значений выборки несмещенную оценку

эксцесса распределения

случайной величины и определяется следующим образом:

Как видно из формулы MS EXCEL использует именно Kurtosis excess, т.е. для выборки из

нормального распределения

формула вернет близкое к 0 значение.

Если задано менее четырех точек данных, то функция

ЭКСЦЕСС()

возвращает значение ошибки #ДЕЛ/0!

Вернемся к

распределениям случайной величины

.

Эксцесс

(Kurtosis excess) для

нормального распределения

всегда равен 0, т.е. не зависит от параметров распределения μ и σ. Для большинства других распределений

Эксцесс

зависит от параметров распределения: см., например,

распределение Вейбулла

или

распределение Пуассона

, для котрого

Эксцесс

= 1/λ.

Уровень надежности

Уровень

надежности

— означает вероятность того, что

доверительный интервал

содержит истинное значение оцениваемого параметра распределения.

Вместо термина

Уровень

надежности

часто используется термин

Уровень доверия

. Про

Уровень надежности

(Confidence Level for Mean) читайте статью

Уровень значимости и уровень надежности в MS EXCEL

.

Задав значение

Уровня

надежности

в окне

надстройки Пакет анализа

, MS EXCEL вычислит половину ширины

доверительного интервала для оценки среднего (дисперсия неизвестна)

.

Тот же результат можно получить по формуле (см.

файл примера

):

=ДОВЕРИТ.СТЬЮДЕНТ(1-0,95;s;n)

s —

стандартное отклонение выборки

, n – объем

выборки

.

Подробнее см. статью про

построение доверительного интервала для оценки среднего (дисперсия неизвестна)

.