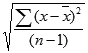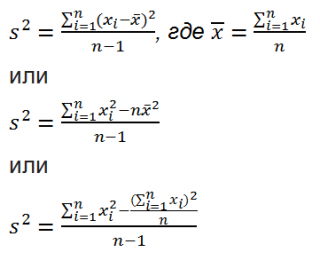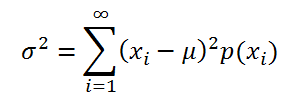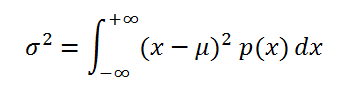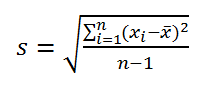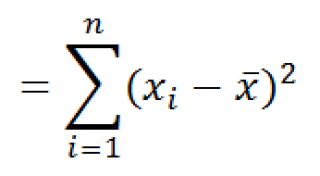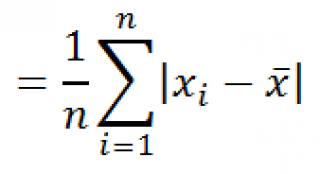Стандотклон по английски excel

Примечание: 
Мы стараемся как можно оперативнее обеспечивать вас актуальными справочными материалами на вашем языке. Эта страница переведена автоматически, поэтому ее текст может содержать неточности и грамматические ошибки. Для нас важно, чтобы эта статья была вам полезна. Просим вас уделить пару секунд и сообщить, помогла ли она вам, с помощью кнопок внизу страницы. Для удобства также приводим
ссылку на оригинал (на английском языке)
.

Оценивает стандартное отклонение по выборке. Стандартное отклонение — это мера того, насколько широко разбросаны точки данных относительно их среднего.

Синтаксис

СТАНДОТКЛОН(число1;число2;…)

Число1, число2,..     — от 1 до 30 числовых аргументов, соответствующих выборке из генеральной совокупности.

Замечания

• Логические значения, такие как ИСТИНА или ЛОЖЬ, а также текст игнорируются. Если текст и логические значения не должны игнорироваться, следует использовать функцию СТАНДОТКЛОНА.

• Функция СТАНДОТКЛОН предполагает, что аргументы являются только выборкой из генеральной совокупности. Если данные представляют всю генеральную совокупность, то стандартное отклонение следует вычислять с помощью функции СТАНДОТКЛОНП.

• Стандартное отклонение вычисляется с использованием «несмещенного» метода или метода «n-1».

• Функция СТАНДОТКЛОН вычисляется по следующей формуле:

  

Пример

Предположим, что из инструментов, отштампованных одной и той же машиной, выбраны наугад 10 штук и испытаны на прочность.

С1	С2	С3	С4	С5	С6	С7	С8	С9	С10	Формула	Описание (результат)
1345	1301	1368	1322	1310	1370	1318	1350	1303	1299	=СТАНДОТКЛОН([С1]; [С2]; [С3]; [С4]; [С5]; [С6]; [С7]; [С8]; [С9]; [С10])	Стандартное отклонение предела прочности (27,46391572)

Вычислим в

MS

EXCEL

дисперсию и стандартное отклонение выборки. Также вычислим дисперсию случайной величины, если известно ее распределение.

Сначала рассмотрим

дисперсию

, затем

стандартное отклонение

.

Дисперсия выборки

Дисперсия выборки

(

выборочная дисперсия,

sample

variance

) характеризует разброс значений в массиве относительно

среднего

.

Все 3 формулы математически эквивалентны.

Из первой формулы видно, что

дисперсия выборки

это сумма квадратов отклонений каждого значения в массиве

от среднего

, деленная на размер выборки минус 1.

В MS EXCEL 2007 и более ранних версиях для вычисления

дисперсии

выборки

используется функция

ДИСП()

, англ. название VAR, т.е. VARiance. С версии MS EXCEL 2010 рекомендуется использовать ее аналог

ДИСП.В()

, англ. название VARS, т.е. Sample VARiance. Кроме того, начиная с версии MS EXCEL 2010 присутствует функция

ДИСП.Г(),

англ. название VARP, т.е. Population VARiance, которая вычисляет

дисперсию

для

генеральной совокупности

. Все отличие сводится к знаменателю: вместо n-1 как у

ДИСП.В()

, у

ДИСП.Г()

в знаменателе просто n. До MS EXCEL 2010 для вычисления дисперсии генеральной совокупности использовалась функция

ДИСПР()

.

Дисперсию выборки

можно также вычислить непосредственно по нижеуказанным формулам (см.

файл примера

)

=КВАДРОТКЛ(Выборка)/(СЧЁТ(Выборка)-1)

=(СУММКВ(Выборка)-СЧЁТ(Выборка)*СРЗНАЧ(Выборка)^2)/ (СЧЁТ(Выборка)-1)

– обычная формула

=СУММ((Выборка -СРЗНАЧ(Выборка))^2)/ (СЧЁТ(Выборка)-1

) –

формула массива

Дисперсия выборки

равна 0, только в том случае, если все значения равны между собой и, соответственно, равны

среднему значению

. Обычно, чем больше величина

дисперсии

, тем больше разброс значений в массиве.

Дисперсия выборки

является точечной оценкой

дисперсии

распределения случайной величины, из которой была сделана

выборка

. О построении

доверительных интервалов

при оценке

дисперсии

можно прочитать в статье

Доверительный интервал для оценки дисперсии в MS EXCEL

.

Дисперсия случайной величины

Чтобы вычислить

дисперсию

случайной величины, необходимо знать ее

функцию распределения

.

Для

дисперсии

случайной величины Х часто используют обозначение Var(Х).

Дисперсия

равна

математическому ожиданию

квадрата отклонения от среднего E(X): Var(Х)=E[(X-E(X))

²

]

Если случайная величина имеет

дискретное распределение

, то

дисперсия

вычисляется по формуле:

где x

_i

– значение, которое может принимать случайная величина, а μ – среднее значение (

математическое ожидание случайной величины

), р(x) – вероятность, что случайная величина примет значение х.

Если случайная величина имеет

непрерывное распределение

, то

дисперсия

вычисляется по формуле:

где р(x) –

плотность вероятности

.

Для распределений, представленных в MS EXCEL

,

дисперсию

можно вычислить аналитически, как функцию от параметров распределения. Например, для

Биномиального распределения

дисперсия

равна произведению его параметров: n*p*q.

Примечание

:

Дисперсия,

является

вторым центральным моментом

, обозначается D[X], VAR(х), V(x). Второй центральный момент — числовая характеристика распределения случайной величины, которая является мерой разброса случайной величины относительно

математического ожидания

.

Примечание

: О распределениях в MS EXCEL можно прочитать в статье

Распределения случайной величины в MS EXCEL

.

Размерность

дисперсии

соответствует квадрату единицы измерения исходных значений. Например, если значения в выборке представляют собой измерения веса детали (в кг), то размерность дисперсии будет кг

²

. Это бывает сложно интерпретировать, поэтому для характеристики разброса значений чаще используют величину равную квадратному корню из

дисперсии

–

стандартное отклонение

.

Некоторые свойства

дисперсии

:

Var(Х+a)=Var(Х), где Х — случайная величина, а — константа.

Var(aХ)=a

²

Var(X)

Var(Х)=E[(X-E(X))

²

]=E[X

²

-2*X*E(X)+(E(X))

²

]=E(X

²

)-E(2*X*E(X))+(E(X))

²

=E(X

²

)-2*E(X)*E(X)+(E(X))

²

=E(X

²

)-(E(X))

²

Это свойство дисперсии используется в

статье про линейную регрессию

.

Var(Х+Y)=Var(Х) + Var(Y) + 2*Cov(Х;Y), где Х и Y — случайные величины, Cov(Х;Y) — ковариация этих случайных величин.

Если случайные величины независимы (independent), то их

ковариация

равна 0, и, следовательно, Var(Х+Y)=Var(Х)+Var(Y). Это свойство дисперсии используется при выводе

стандартной ошибки среднего

.

Покажем, что для независимых величин Var(Х-Y)=Var(Х+Y). Действительно, Var(Х-Y)= Var(Х-Y)= Var(Х+(-Y))= Var(Х)+Var(-Y)= Var(Х)+Var(-Y)= Var(Х)+(-1)

²

Var(Y)= Var(Х)+Var(Y)= Var(Х+Y). Это свойство дисперсии используется для построения

доверительного интервала для разницы 2х средних

.

Примечание

: квадратный корень из дисперсии случайной величины называется Среднеквадратическое отклонение (или другие названия — среднее квадратическое отклонение, среднеквадратичное отклонение, квадратичное отклонение, стандартное отклонение, стандартный разброс).

Стандартное отклонение выборки

Стандартное отклонение выборки

— это мера того, насколько широко разбросаны значения в выборке относительно их

среднего

.

По определению,

стандартное отклонение

равно квадратному корню из

дисперсии

:

Стандартное отклонение

не учитывает величину значений в

выборке

, а только степень рассеивания значений вокруг их

среднего

. Чтобы проиллюстрировать это приведем пример.

Вычислим стандартное отклонение для 2-х выборок: (1; 5; 9) и (1001; 1005; 1009). В обоих случаях, s=4. Очевидно, что отношение величины стандартного отклонения к значениям массива у выборок существенно отличается. Для таких случаев используется

Коэффициент вариации

(Coefficient of Variation, CV) — отношение

Стандартного отклонения

к среднему

арифметическому

, выраженного в процентах.

В MS EXCEL 2007 и более ранних версиях для вычисления

Стандартного отклонения выборки

используется функция

=СТАНДОТКЛОН()

, англ. название STDEV, т.е. STandard DEViation. С версии MS EXCEL 2010 рекомендуется использовать ее аналог

=СТАНДОТКЛОН.В()

, англ. название STDEV.S, т.е. Sample STandard DEViation.

Кроме того, начиная с версии MS EXCEL 2010 присутствует функция

СТАНДОТКЛОН.Г()

, англ. название STDEV.P, т.е. Population STandard DEViation, которая вычисляет

стандартное отклонение

для

генеральной совокупности

. Все отличие сводится к знаменателю: вместо n-1 как у

СТАНДОТКЛОН.В()

, у

СТАНДОТКЛОН.Г()

в знаменателе просто n.

Стандартное отклонение

можно также вычислить непосредственно по нижеуказанным формулам (см.

файл примера

)

=КОРЕНЬ(КВАДРОТКЛ(Выборка)/(СЧЁТ(Выборка)-1)) =КОРЕНЬ((СУММКВ(Выборка)-СЧЁТ(Выборка)*СРЗНАЧ(Выборка)^2)/(СЧЁТ(Выборка)-1))

Другие меры разброса

Функция

КВАДРОТКЛ()

вычисляет с умму квадратов отклонений значений от их

среднего

. Эта функция вернет тот же результат, что и формула

=ДИСП.Г(

Выборка

)*СЧЁТ(

Выборка

)

, где

Выборка

— ссылка на диапазон, содержащий массив значений выборки (

именованный диапазон

). Вычисления в функции

КВАДРОТКЛ()

производятся по формуле:

Функция

СРОТКЛ()

является также мерой разброса множества данных. Функция

СРОТКЛ()

вычисляет среднее абсолютных значений отклонений значений от

среднего

.  Эта функция вернет тот же результат, что и формула

=СУММПРОИЗВ(ABS(Выборка-СРЗНАЧ(Выборка)))/СЧЁТ(Выборка)

, где

Выборка

— ссылка на диапазон, содержащий массив значений выборки.

Вычисления в функции

СРОТКЛ

()

производятся по формуле:

Английское название функции STDEV.S() было переведено на 18 языка/языков. Для всех остальных языков применяется английское название функции. Существуют различия в переводах в разных Excel версиях

Наличие

Excel Версии	Наличие	Категория
Excel (Office 365)	Да	Статистические
Excel 2013	Да	Статистические
Excel 2010	Да	Статистические
Excel 2007	Нет	—
Excel 2003	Нет	—

Ссылка язык

язык	Обозначение
English	STDEV.S

Переводы

язык	Обозначение
Basque	DESBEST.S
Catalan	DESVEST.M
Czech	SMODCH.VÝBĚR.S
Danish	STDAFV.S
Finnish	KESKIHAJONTA.S
French	ECARTYPE.STANDARD
Galician	DESVEST.M
German	STABW.S
Hungarian	SZÓR.M
Italian	DEV.ST.C
Norwegian	STDAV.S
Polish	ODCH.STANDARD.PRÓBKI
Portuguese, Brazil	DESVPAD.A
Portuguese, Portugal	DESVPAD.S
Russian	СТАНДОТКЛОН.В
Spanish	DESVEST.M
Swedish	STDAV.S
Turkish	STDSAPMA.S

Отличающиеся переводы для Excel 2010 SP1

язык	Обозначение
Danish	STDAFVS

Отличающиеся переводы для Excel 2010

язык	Обозначение
Danish	STDAFVS

Ссылки на службу поддержки Microsoft для функции СТАНДОТКЛОН.В()

Примечание: Microsoft находится в процессе переработки ссылок и содержания службы поддержки . Поэтому в настоящее время не исключено, что некоторые из указанных ссылок не работают или ведут на ошибочную страницу. Ссылки будут актуализированы как только это будет возможно.

язык
Arabic	Finnish	Kazakh	Russian
Basque	French	Konkani	Serbian
Bulgarian	Galician	Korean	Slovak
Catalan	German	Latvian	Slovenian
Chinese — Simplified	Greek	Lithuanian	Spanish
Chinese — Traditional	Gujarati	Malaysian	Swedish
Croatian	Hebrew	Marathi	Thai
Czech	Hindi	Norwegian	Turkish
Danish	Hungarian	Polish	Ukrainian
Dutch	Indonesian	Portuguese, Brazil	Vietnamese
English	Italian	Portuguese, Portugal	—
Estonian	Japanese	Romanian	—