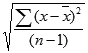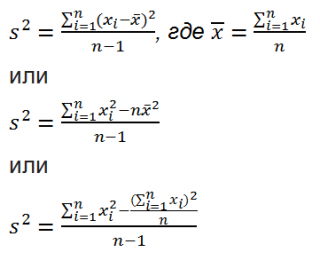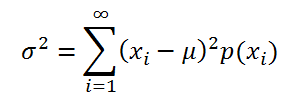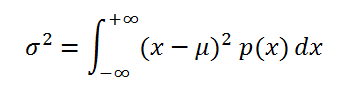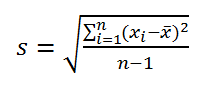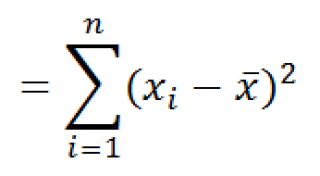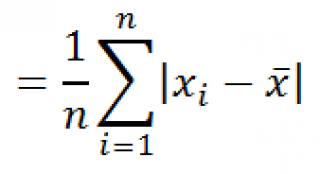Стандартное отклонение ряда excel

В этой статье описаны синтаксис формулы и использование функции СТАНДОТКЛОНА в Microsoft Excel.

Описание

Оценивает стандартное отклонение по выборке. Стандартное отклонение — это мера того, насколько широко разбросаны точки данных относительно их среднего.

Синтаксис

СТАНДОТКЛОНА(значение1;[значение2];…)

Аргументы функции СТАНДОТКЛОНА описаны ниже.

• Значение1,значение2,…    Аргумент «значение1» является обязательным, последующие значения необязательные. От 1 до 255 значений, соответствующих выборке из генеральной совокупности. Вместо аргументов, разделяемых точкой с запятой, можно использовать массив или ссылку на массив.

Замечания

• Функция СТАНДОТКЛОНА предполагает, что аргументы являются только выборкой из генеральной совокупности. Если данные представляют всю генеральную совокупность, то стандартное отклонение следует вычислять с помощью функции СТАНДОТКЛОНПА.

• Стандартное отклонение вычисляется с использованием «n-1» метода.

• Допускаются следующие аргументы: числа; имена, массивы или ссылки, содержащие числа; текстовые представления чисел; логические значения, такие как ИСТИНА и ЛОЖЬ, в ссылке.

• Аргументы, содержащие значение ИСТИНА, интерпретируются как 1; аргументы, содержащие текст или значение ЛОЖЬ, интерпретируются как 0 (ноль).

• Если аргументом является массив или ссылка, учитываются только значения массива или ссылки. Пустые ячейки и текст в массиве или ссылке игнорируются.

• Аргументы, представляющие собой значения ошибок или текст, не преобразуемый в числа, вызывают ошибку.

• Чтобы не включать логические значения и текстовые представления чисел в ссылку как часть вычисления, используйте функцию СТАНДОТКЛОН.

• Функция СТАНДОТКЛОНА вычисляется по следующей формуле:

  

  где x — выборочное среднее СРЗНАЧ(значение1,значение2,…), а n — размер выборки.

Пример

Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.

Данные
Прочность
1345
1301
1368
1322
1310
1370
1318
1350
1303
1299
Формула	Описание (результат)	Результат
=СТАНДОТКЛОНА(A3:A12)	Стандартное отклонение предела прочности для всех инструментов (27,46391572)	27,46391572

---

Среднее значение представляет собой среднее значение в наборе данных. Это дает нам хорошее представление о том, где находится центр набора данных.

Стандартное отклонение показывает, насколько разбросаны значения в наборе данных. Это дает нам представление о том, насколько близко наблюдения сгруппированы вокруг среднего значения.

Используя только эти два значения, мы можем многое понять о распределении значений в наборе данных.

Чтобы вычислить среднее значение набора данных в Excel, мы можем использовать функцию = СРЗНАЧ (диапазон) , где диапазон — это диапазон значений.

Чтобы вычислить стандартное отклонение набора данных, мы можем использовать функцию =STDEV.S(Range) , где Range — это диапазон значений.

В этом руководстве объясняется, как использовать эти функции на практике.

Техническое примечание

Обе функции СТАНДОТКЛОН() и СТАНДОТКЛОН.С() вычисляют стандартное отклонение выборки .

Вы можете использовать функцию STDEV.P() для вычисления стандартного отклонения совокупности , если ваш набор данных представляет всю совокупность значений.

Однако в большинстве случаев мы работаем с выборочными данными, а не со всей совокупностью, поэтому мы используем функцию СТАНДОТКЛОН.С().

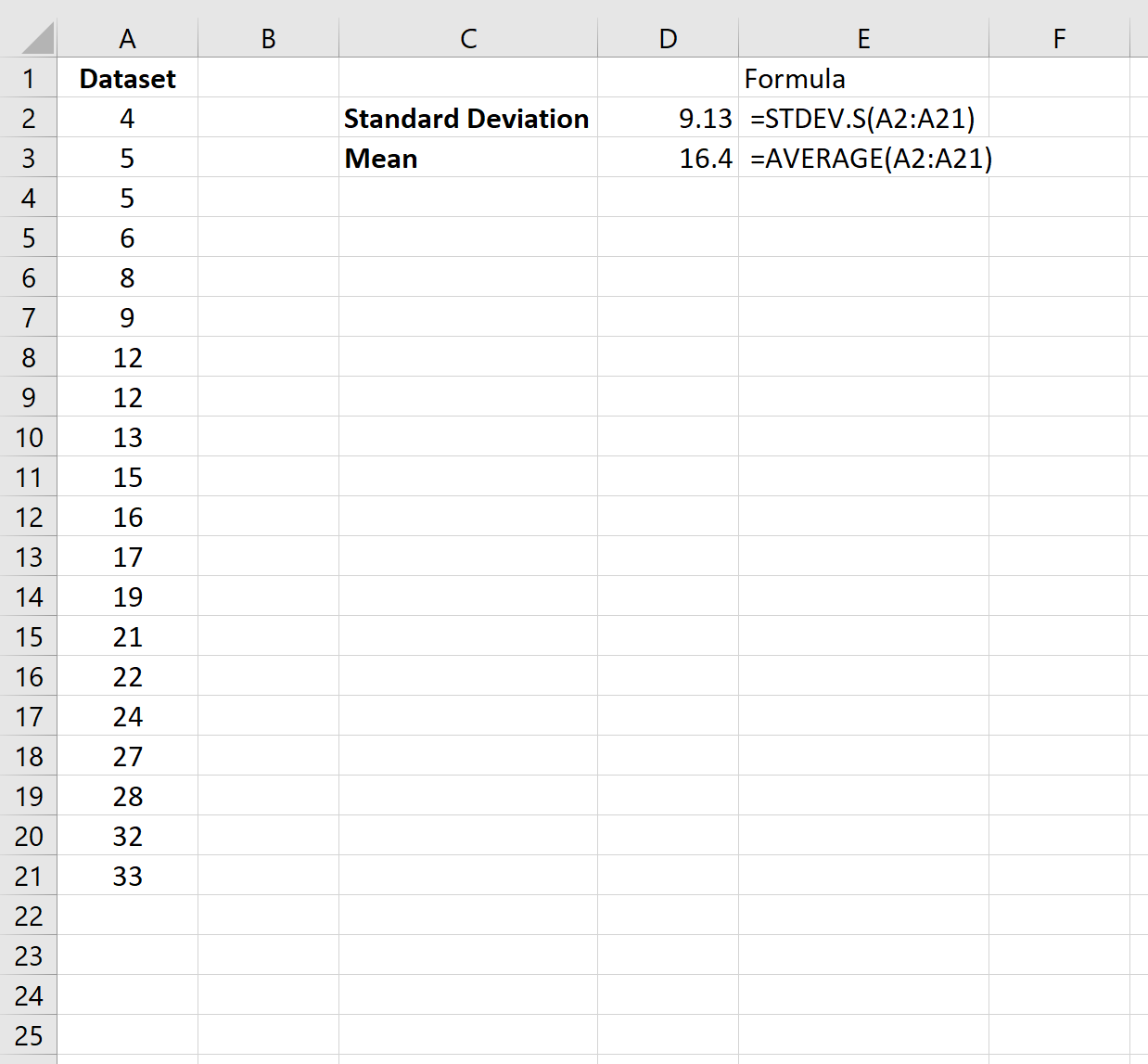
Пример 1: Среднее и стандартное отклонение одного набора данных

На следующем снимке экрана показано, как рассчитать среднее значение и стандартное отклонение одного набора данных в Excel:

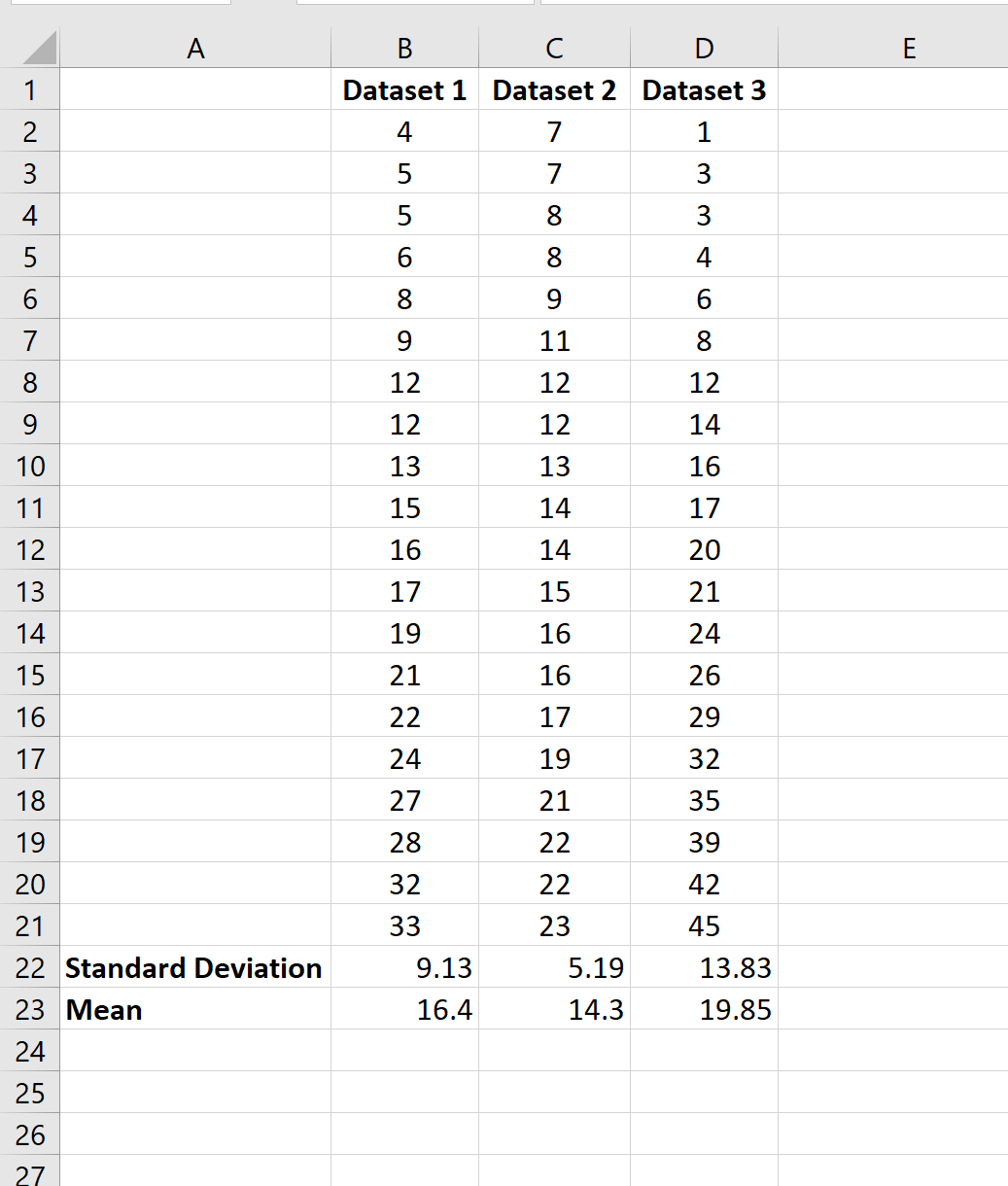
Среднее значение набора данных составляет 16,4 , а стандартное отклонение — 9,13 .

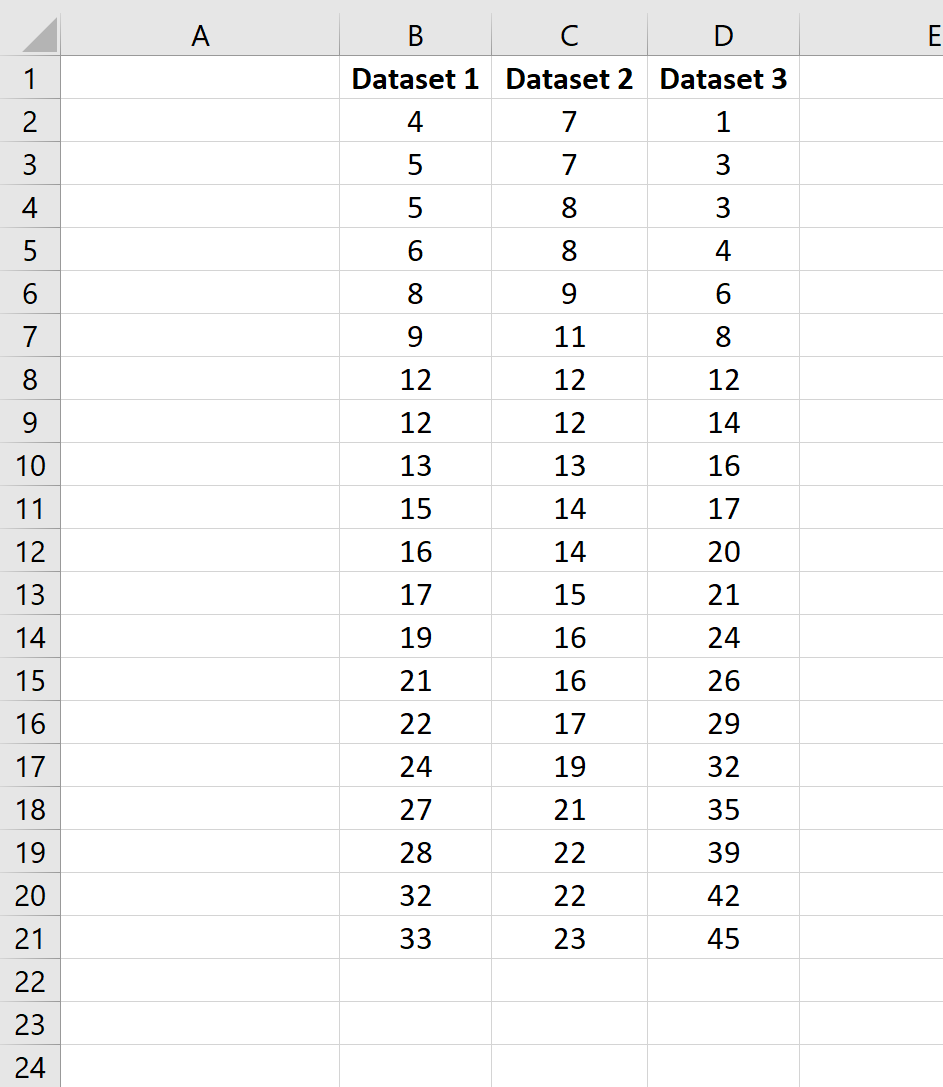
Пример 2: Среднее и стандартное отклонение нескольких наборов данных

Предположим, у нас есть несколько наборов данных в Excel:

Чтобы вычислить среднее значение и стандартное отклонение первого набора данных, мы можем использовать следующие две формулы:

• Среднее значение: =СРЗНАЧ(B2:B21)
• Стандартное отклонение: =STDEV.S(B2:B21)

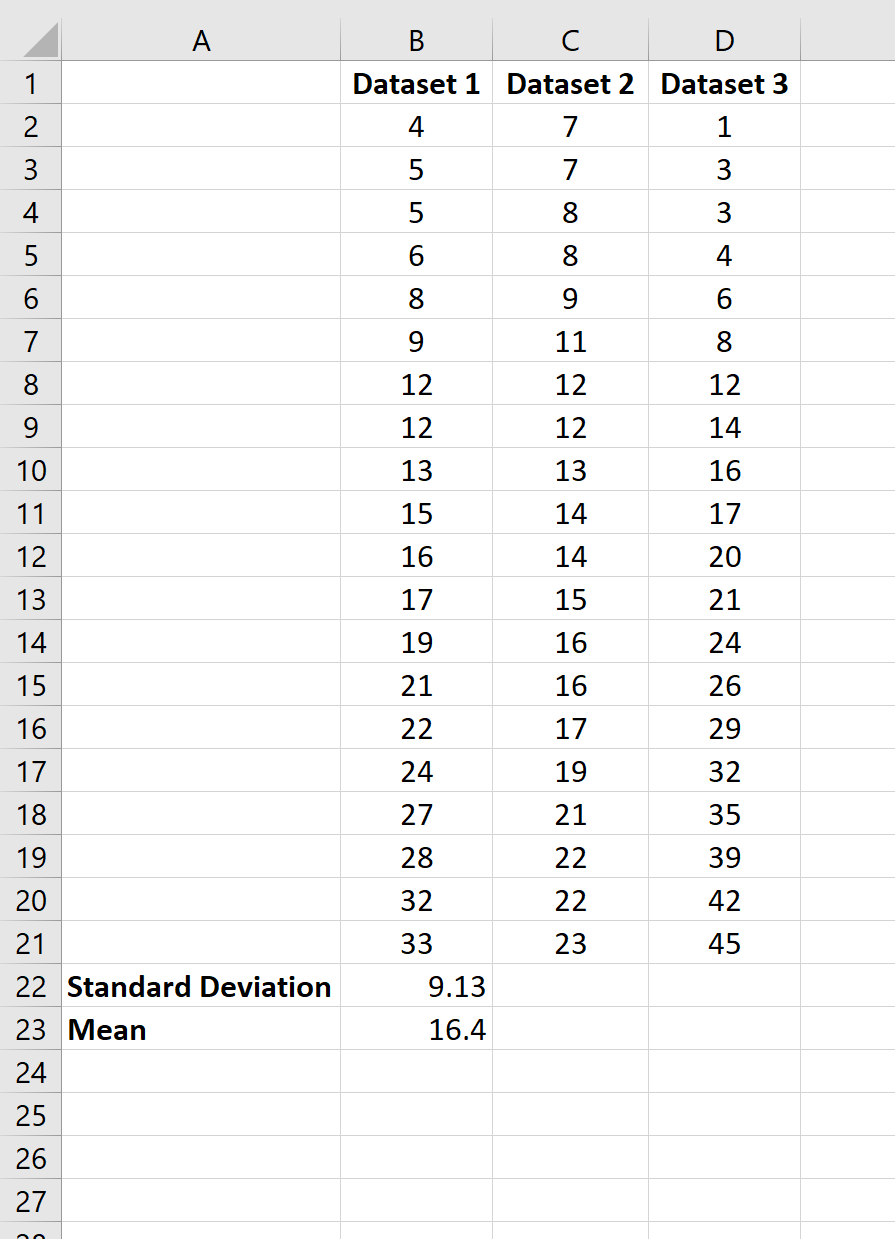
Затем мы можем выделить ячейки B22: B23 и навести указатель мыши на правый нижний угол ячейки B23, пока не появится крошечный +.Затем мы можем щелкнуть и перетащить формулы в следующие два столбца:

Дополнительные ресурсы

Как рассчитать сводку из пяти чисел в Excel
Как рассчитать межквартильный диапазон (IQR) в Excel
Как рассчитать стандартную ошибку среднего в Excel

Была ли эта статья полезной?

Вычислим в

MS

EXCEL

дисперсию и стандартное отклонение выборки. Также вычислим дисперсию случайной величины, если известно ее распределение.

Сначала рассмотрим

дисперсию

, затем

стандартное отклонение

.

Дисперсия выборки

Дисперсия выборки

(

выборочная дисперсия,

sample

variance

) характеризует разброс значений в массиве относительно

среднего

.

Все 3 формулы математически эквивалентны.

Из первой формулы видно, что

дисперсия выборки

это сумма квадратов отклонений каждого значения в массиве

от среднего

, деленная на размер выборки минус 1.

В MS EXCEL 2007 и более ранних версиях для вычисления

дисперсии

выборки

используется функция

ДИСП()

, англ. название VAR, т.е. VARiance. С версии MS EXCEL 2010 рекомендуется использовать ее аналог

ДИСП.В()

, англ. название VARS, т.е. Sample VARiance. Кроме того, начиная с версии MS EXCEL 2010 присутствует функция

ДИСП.Г(),

англ. название VARP, т.е. Population VARiance, которая вычисляет

дисперсию

для

генеральной совокупности

. Все отличие сводится к знаменателю: вместо n-1 как у

ДИСП.В()

, у

ДИСП.Г()

в знаменателе просто n. До MS EXCEL 2010 для вычисления дисперсии генеральной совокупности использовалась функция

ДИСПР()

.

Дисперсию выборки

можно также вычислить непосредственно по нижеуказанным формулам (см.

файл примера

)

=КВАДРОТКЛ(Выборка)/(СЧЁТ(Выборка)-1)

=(СУММКВ(Выборка)-СЧЁТ(Выборка)*СРЗНАЧ(Выборка)^2)/ (СЧЁТ(Выборка)-1)

– обычная формула

=СУММ((Выборка -СРЗНАЧ(Выборка))^2)/ (СЧЁТ(Выборка)-1

) –

формула массива

Дисперсия выборки

равна 0, только в том случае, если все значения равны между собой и, соответственно, равны

среднему значению

. Обычно, чем больше величина

дисперсии

, тем больше разброс значений в массиве.

Дисперсия выборки

является точечной оценкой

дисперсии

распределения случайной величины, из которой была сделана

выборка

. О построении

доверительных интервалов

при оценке

дисперсии

можно прочитать в статье

Доверительный интервал для оценки дисперсии в MS EXCEL

.

Дисперсия случайной величины

Чтобы вычислить

дисперсию

случайной величины, необходимо знать ее

функцию распределения

.

Для

дисперсии

случайной величины Х часто используют обозначение Var(Х).

Дисперсия

равна

математическому ожиданию

квадрата отклонения от среднего E(X): Var(Х)=E[(X-E(X))

²

]

Если случайная величина имеет

дискретное распределение

, то

дисперсия

вычисляется по формуле:

где x

_i

– значение, которое может принимать случайная величина, а μ – среднее значение (

математическое ожидание случайной величины

), р(x) – вероятность, что случайная величина примет значение х.

Если случайная величина имеет

непрерывное распределение

, то

дисперсия

вычисляется по формуле:

где р(x) –

плотность вероятности

.

Для распределений, представленных в MS EXCEL

,

дисперсию

можно вычислить аналитически, как функцию от параметров распределения. Например, для

Биномиального распределения

дисперсия

равна произведению его параметров: n*p*q.

Примечание

:

Дисперсия,

является

вторым центральным моментом

, обозначается D[X], VAR(х), V(x). Второй центральный момент — числовая характеристика распределения случайной величины, которая является мерой разброса случайной величины относительно

математического ожидания

.

Примечание

: О распределениях в MS EXCEL можно прочитать в статье

Распределения случайной величины в MS EXCEL

.

Размерность

дисперсии

соответствует квадрату единицы измерения исходных значений. Например, если значения в выборке представляют собой измерения веса детали (в кг), то размерность дисперсии будет кг

²

. Это бывает сложно интерпретировать, поэтому для характеристики разброса значений чаще используют величину равную квадратному корню из

дисперсии

–

стандартное отклонение

.

Некоторые свойства

дисперсии

:

Var(Х+a)=Var(Х), где Х — случайная величина, а — константа.

Var(aХ)=a

²

Var(X)

Var(Х)=E[(X-E(X))

²

]=E[X

²

-2*X*E(X)+(E(X))

²

]=E(X

²

)-E(2*X*E(X))+(E(X))

²

=E(X

²

)-2*E(X)*E(X)+(E(X))

²

=E(X

²

)-(E(X))

²

Это свойство дисперсии используется в

статье про линейную регрессию

.

Var(Х+Y)=Var(Х) + Var(Y) + 2*Cov(Х;Y), где Х и Y — случайные величины, Cov(Х;Y) — ковариация этих случайных величин.

Если случайные величины независимы (independent), то их

ковариация

равна 0, и, следовательно, Var(Х+Y)=Var(Х)+Var(Y). Это свойство дисперсии используется при выводе

стандартной ошибки среднего

.

Покажем, что для независимых величин Var(Х-Y)=Var(Х+Y). Действительно, Var(Х-Y)= Var(Х-Y)= Var(Х+(-Y))= Var(Х)+Var(-Y)= Var(Х)+Var(-Y)= Var(Х)+(-1)

²

Var(Y)= Var(Х)+Var(Y)= Var(Х+Y). Это свойство дисперсии используется для построения

доверительного интервала для разницы 2х средних

.

Примечание

: квадратный корень из дисперсии случайной величины называется Среднеквадратическое отклонение (или другие названия — среднее квадратическое отклонение, среднеквадратичное отклонение, квадратичное отклонение, стандартное отклонение, стандартный разброс).

Стандартное отклонение выборки

Стандартное отклонение выборки

— это мера того, насколько широко разбросаны значения в выборке относительно их

среднего

.

По определению,

стандартное отклонение

равно квадратному корню из

дисперсии

:

Стандартное отклонение

не учитывает величину значений в

выборке

, а только степень рассеивания значений вокруг их

среднего

. Чтобы проиллюстрировать это приведем пример.

Вычислим стандартное отклонение для 2-х выборок: (1; 5; 9) и (1001; 1005; 1009). В обоих случаях, s=4. Очевидно, что отношение величины стандартного отклонения к значениям массива у выборок существенно отличается. Для таких случаев используется

Коэффициент вариации

(Coefficient of Variation, CV) — отношение

Стандартного отклонения

к среднему

арифметическому

, выраженного в процентах.

В MS EXCEL 2007 и более ранних версиях для вычисления

Стандартного отклонения выборки

используется функция

=СТАНДОТКЛОН()

, англ. название STDEV, т.е. STandard DEViation. С версии MS EXCEL 2010 рекомендуется использовать ее аналог

=СТАНДОТКЛОН.В()

, англ. название STDEV.S, т.е. Sample STandard DEViation.

Кроме того, начиная с версии MS EXCEL 2010 присутствует функция

СТАНДОТКЛОН.Г()

, англ. название STDEV.P, т.е. Population STandard DEViation, которая вычисляет

стандартное отклонение

для

генеральной совокупности

. Все отличие сводится к знаменателю: вместо n-1 как у

СТАНДОТКЛОН.В()

, у

СТАНДОТКЛОН.Г()

в знаменателе просто n.

Стандартное отклонение

можно также вычислить непосредственно по нижеуказанным формулам (см.

файл примера

)

=КОРЕНЬ(КВАДРОТКЛ(Выборка)/(СЧЁТ(Выборка)-1)) =КОРЕНЬ((СУММКВ(Выборка)-СЧЁТ(Выборка)*СРЗНАЧ(Выборка)^2)/(СЧЁТ(Выборка)-1))

Другие меры разброса

Функция

КВАДРОТКЛ()

вычисляет с умму квадратов отклонений значений от их

среднего

. Эта функция вернет тот же результат, что и формула

=ДИСП.Г(

Выборка

)*СЧЁТ(

Выборка

)

, где

Выборка

— ссылка на диапазон, содержащий массив значений выборки (

именованный диапазон

). Вычисления в функции

КВАДРОТКЛ()

производятся по формуле:

Функция

СРОТКЛ()

является также мерой разброса множества данных. Функция

СРОТКЛ()

вычисляет среднее абсолютных значений отклонений значений от

среднего

.  Эта функция вернет тот же результат, что и формула

=СУММПРОИЗВ(ABS(Выборка-СРЗНАЧ(Выборка)))/СЧЁТ(Выборка)

, где

Выборка

— ссылка на диапазон, содержащий массив значений выборки.

Вычисления в функции

СРОТКЛ

()

производятся по формуле:

На чтение 5 мин Опубликовано 15.01.2021

Для вычисления среднеквадратического отклонения в Microsoft Office Excel используется специальная формула, которой можно пользоваться несколькими способами. О них пойдет речь в данной статье.

Содержание

1. Как вычислить среднее квадратическое отклонение в Excel
2. Способ 1. С помощью Мастера функций
3. Способ 2. Расчет стандартного отклонения в разделе «Формулы»
4. Способ 3. Ручной ввод формулы среднеквадратичного отклонения в Эксель
5. Способ 4. Ручной подсчет
6. Заключение

Как вычислить среднее квадратическое отклонение в Excel

Это один из показателей вариации. В теории вероятностей этот показатель рассчитывается по формуле:

В Эксель пользователю не нужно будет вручную рассчитывать среднеквадратичное отклонение. Существует ряд способов, позволяющих найти эту величину в кратчайшие сроки с помощью встроенных в Excel инструментов. Далее будут рассмотрены самые распространенные из них.

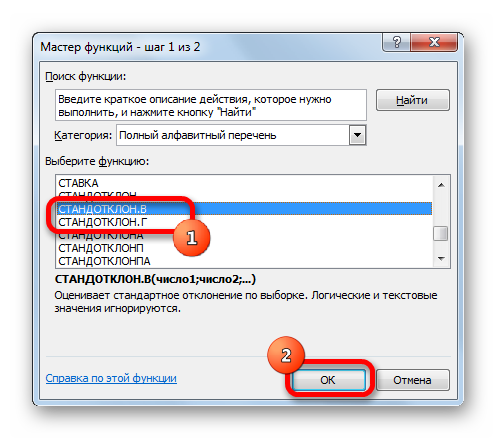
Способ 1. С помощью Мастера функций

Данный метод расчета стандартного отклонения в Excel занимает минимальное количество времени. Вычисление производится следующим образом:

1. Левой клавишей манипулятора на рабочем листе программы выделить ячейку, в которой будет отображаться результат вычисления.
2. Кликнуть по кнопке «Вставка функции», расположенной с левой стороны от строки ввода.

1. После выполнения предыдущего действия откроется окошко Мастера функций. Здесь пользователю потребуется найти строку «СТАНДОТКЛОН.В», выделить ее ЛКМ и нажать на «ОК» внизу меню. В списке функций также есть записи «СТАНДОТКЛОН.Г» и просто «СТАНДОТКЛОН». На них нажимать не нужно!

1. В следующем окне аргументов функции необходимо прописать числа совокупности в каждом поле. Если эти значения уже написаны на рабочем листе Excel, то можно указать координаты соответствующих ячеек.
2. Нажать на «ОК» внизу меню «Аргументы функции», когда все строчки будут заполнены.

1. Проверить результат. В выделенной на первом этапе ячейке будет прописано число. Это и есть среднее квадратичное отклонение.

Обратите внимание! Если после выполнения вышеуказанных манипуляций в ячейке будут отображаться знаки «###», то значит результатом является большое число, и ячейку нужно растянуть.

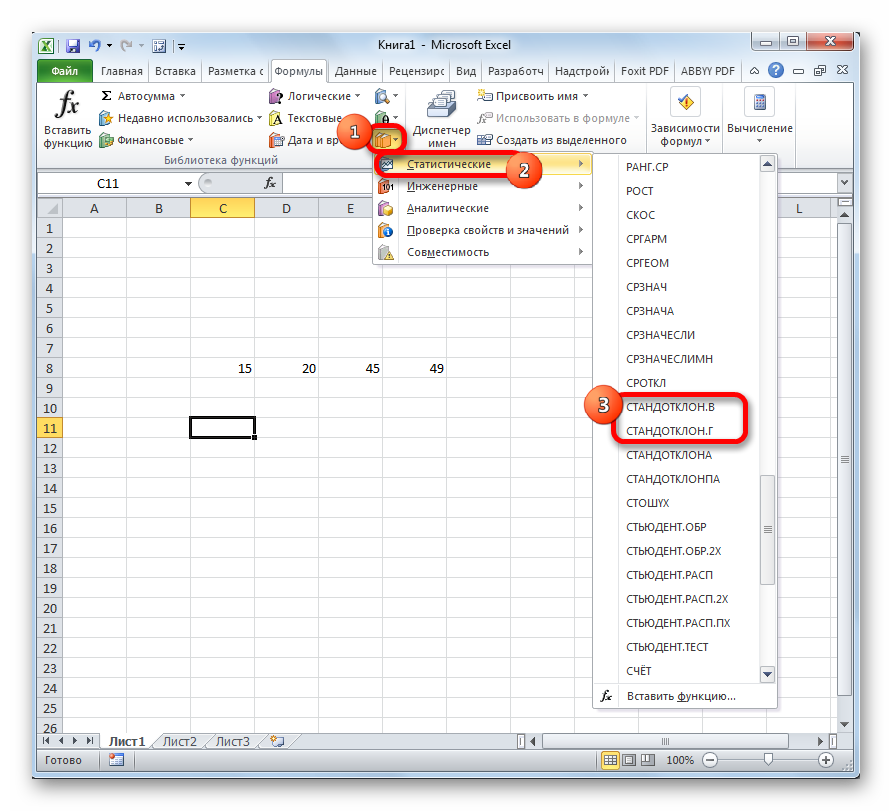
Способ 2. Расчет стандартного отклонения в разделе «Формулы»

Через вкладку «Формулы» в программе Excel также возможно рассчитать стандартное отклонение. Алгоритм вычисления состоит из следующих шагов:

1. По аналогичной схеме выделить любую свободную ячейку на рабочем листе. В этот элемент в дальнейшем будет выводиться результат.
2. В графе инструментов сверху главного меню программы найти слово «Формулы» и щелкнуть по нему ЛКМ.

1. В открывшейся области найти подраздел «Библиотека функций, а затем развернуть вкладку «Другие функции».
2. В контекстном меню выбрать тип «Статистические» и поставить курсор мышки на это слово.
3. Развернется дополнительное контекстное окно, в котором пользователю необходимо щелкнуть по строчке «СТАНДОТКЛОН.В».

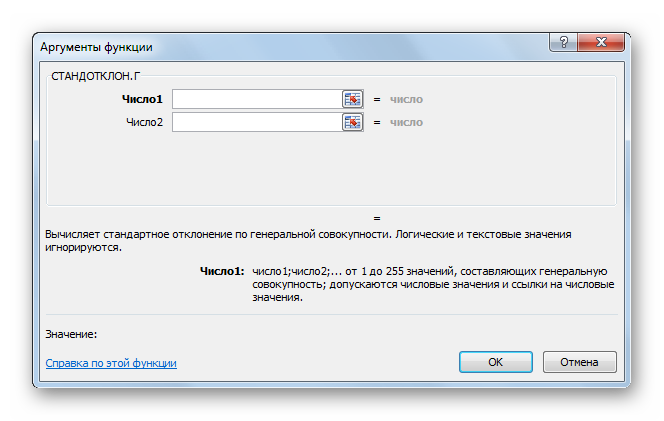
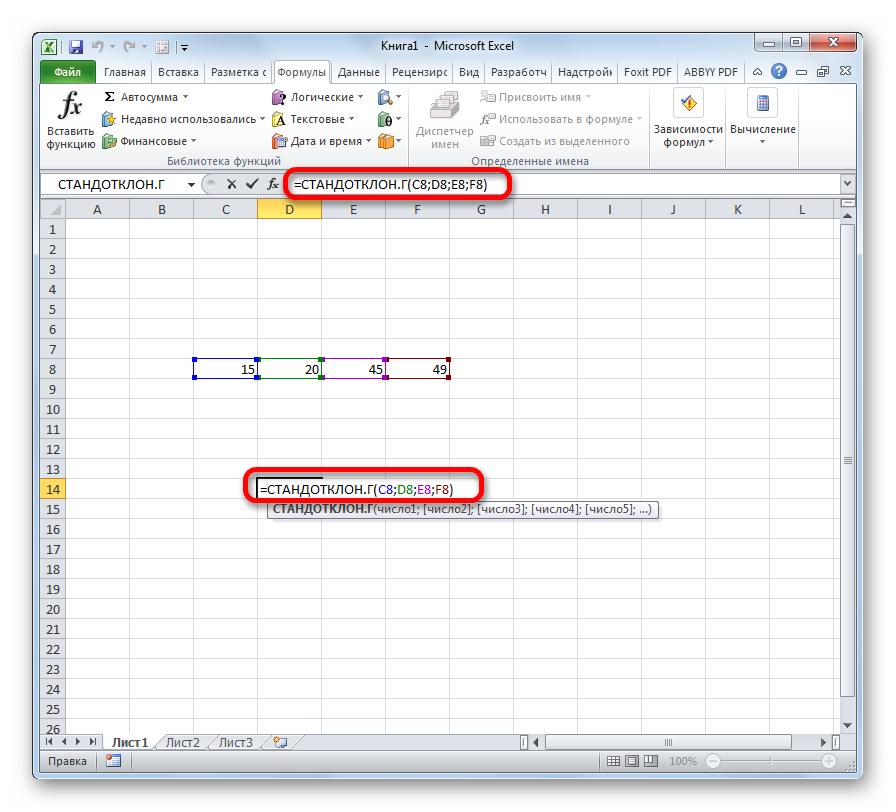
1. В запустившемся окне «Аргументы функции» надо заполнить два поля, указав координаты соответствующих ячеек на рабочем листе или в табличном массиве. Нужные значения также можно прописать вручную.
2. После выполнения этих манипуляций нажать на «ОК».

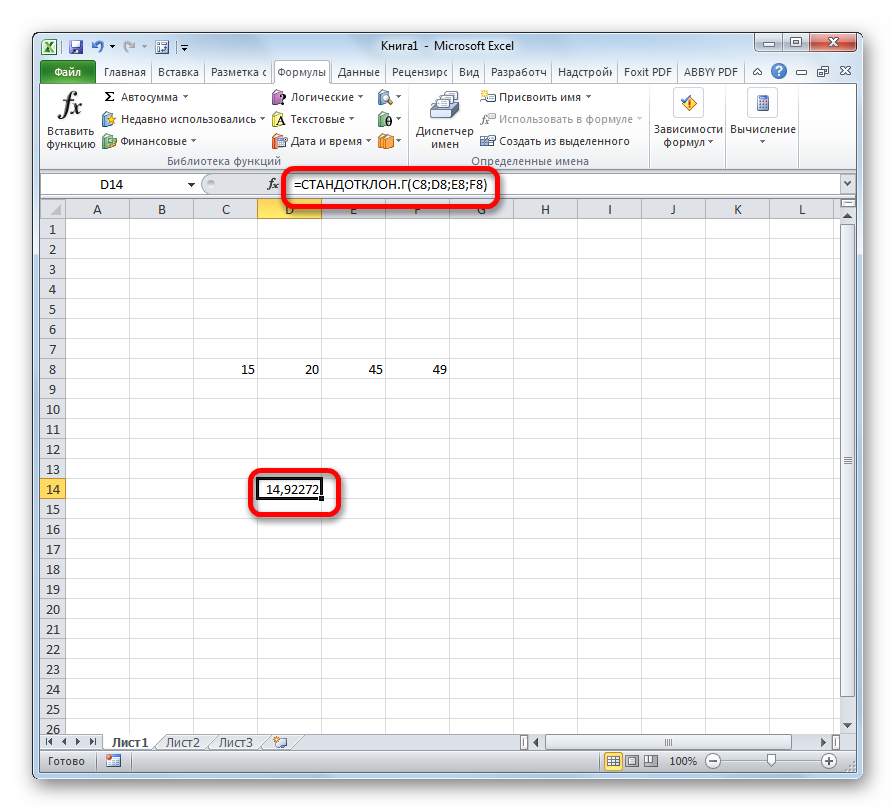
1. Удостовериться, что в указанной ранее ячейке отобразился результат работы формулы – число, характеризующее среднеквадратичное отклонение.

Важно! Если необходимо посчитать стандартное отклонение у нескольких параметров, то исходную формулу можно растянуть на оставшиеся ячейки табличного массива.

Способ 3. Ручной ввод формулы среднеквадратичного отклонения в Эксель

Чтобы рассчитать стандартное отклонение в Microsoft Office Excel, можно ввести специальную формулу с клавиатуры, результат будет одинаковым. Такой метод вычисления заключается в выполнении следующих этапов:

1. Поставить курсор мыши в ячейку, куда будет выводиться результат.
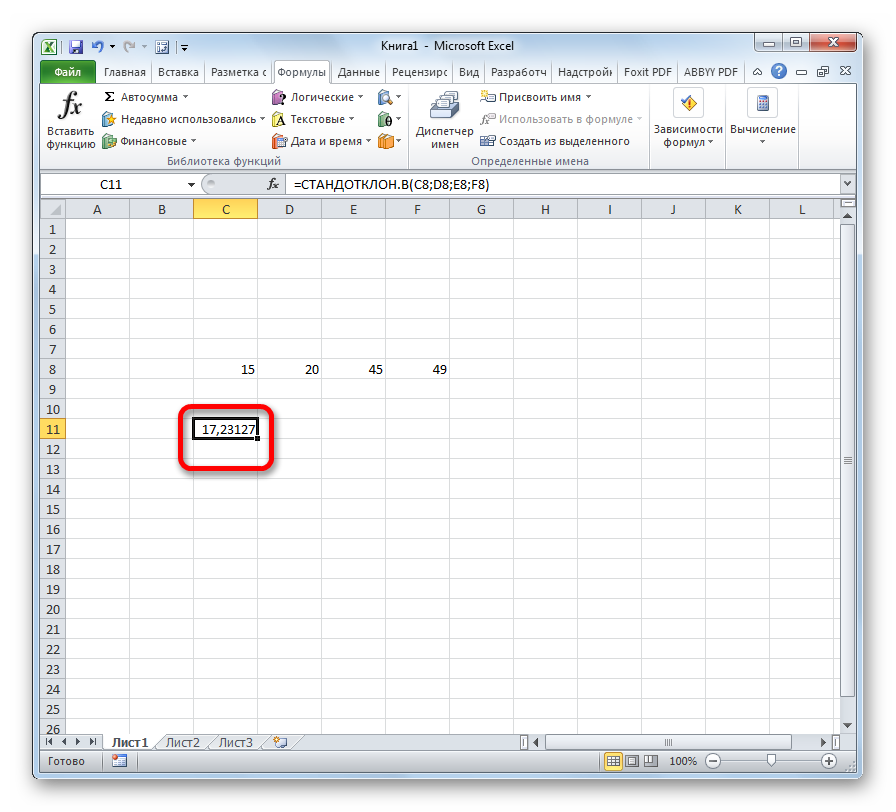
2. В выделенный элемент ввести с клавиатуры формулу «=СТАНДОТКЛОН.В(а,b,c,d)». Вместо букв в скобках нужно указать соответствующие аргументы. Это числа из табличного массива данных.

1. Нажать на «Enter» для завершения процедуры.
2. Проверить результат. В итоге в ячейке должно отобразиться конкретное значение среднеквадратичного отклонения.

Дополнительная информация! Также для расчета можно использовать формулу «СТАНОТКЛОН.Г()». Получится идентичный результат. Данный метод будет работать независимо от версии программного обеспечения.

Способ 4. Ручной подсчет

Такую операцию в Microsoft Office Excel нецелесообразно выполнять. Данный метод основан на применении обычного калькулятора, который также присутствует в Эксель. Для ручного счета необходимо проделать следующие действия по алгоритму:

1. Левой клавишей манипулятора выделить ячейку табличного массива, в которую будет выводиться результат.
2. Поставить знак «=» и с клавиатуры компьютера прописать числовые значения для расчета среднеквадратичного отклонения, указывая координаты соответствующих ячеек из таблички. Здесь надо подставлять параметры в формулу из первого рисунка.
3. После написания формулы нажать на «Enter» и убедиться, что в ячейке отобразился результат стандартного отклонения.

Обратите внимание! Формулу для вычисления среднеквадратичного отклонения, написанную вручную в Excel, также можно растянуть на оставшиеся ячейки для их автоматического заполнения.

Заключение

Таким образом, стандартное отклонение в Microsoft Office Excel рассчитывается с помощью формулы или выбора соответствующей функции. Основные методы вычисления данного параметра были рассмотрены выше.

Оцените качество статьи. Нам важно ваше мнение: