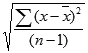Станд отклонение в excel на английском

Синтаксис

СТАНДОТКЛОН(число1,[число2],...])

Аргументы (Аргумент. Значение, предоставляющее информацию для действия, события, метода, свойства, функции или процедуры.) функции СТАНДОТКЛОН описаны ниже.

• Число1     Обязательный. Первый числовой аргумент, соответствующий выборке из генеральной совокупности.
• Число2…     Необязательный. Числовые аргументы 2—255, соответствующие выборке из генеральной совокупности. Вместо аргументов, разделенных точкой с запятой, можно использовать массив или ссылку на массив.

Дополнительная информация (источник)

Функция СТАНДОТКЛОН.В возвращает значение стандартного отклонения, рассчитанного для определенного диапазона числовых значений.

Функция СТАНДОТКЛ.Г используется для определения стандартного отклонения генеральной совокупности числовых значений и возвращает величину стандартного отклонения с учетом, что переданные значения являются всей генеральной совокупностью, а не выборкой.

Функция СТАНДОТКЛОНА возвращает значение стандартного отклонения для некоторого диапазона чисел, которые являются выборкой, а не всей генеральной совокупностью.

Функция СТАНДОТЛОНПА возвращает значение стандартного отклонения для всей генеральной совокупности, переданной в качестве ее аргументов.

Примеры использования СТАНДОТКЛОН.В, СТАНДОТКЛОН.Г, СТАНДОТКЛОНА и СТАНДОТКЛОНПА

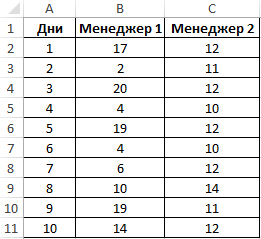
Пример 1. На предприятии работают два менеджера по привлечению клиентов. Данные о количестве обслуженных клиентов в день каждым менеджером фиксируются в таблице Excel. Определить, какой из двух сотрудников работает эффективнее.

Таблица исходных данных:

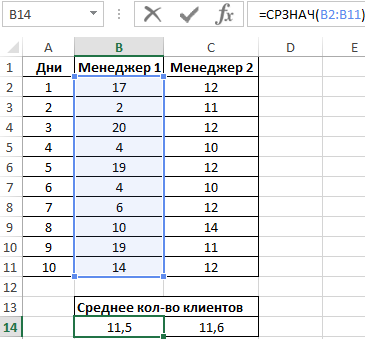
Вначале рассчитаем среднее количество клиентов, с которыми работали менеджеры ежедневно:

=СРЗНАЧ(B2:B11)

Данная функция выполняет расчет среднего арифметического значения для диапазона B2:B11, содержащего данные о количестве клиентов, принимаемых ежедневно первым менеджером. Аналогично рассчитаем среднее количество клиентов за день у второго менеджера. Получим:

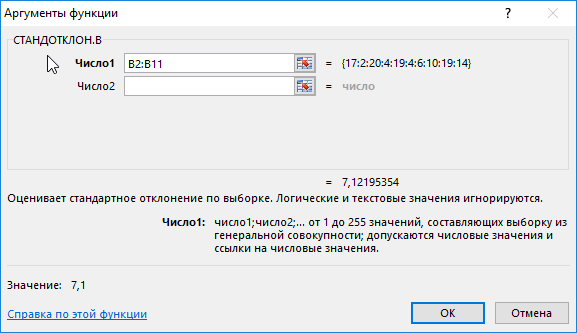
На основе полученных значений создается впечатление, что оба менеджера работают примерно одинаково эффективно. Однако визуально виден сильный разброс значений числа клиентов у первого менеджера. Произведем расчет стандартного отклонения по формуле:

=СТАНДОТКЛОН.В(B2:B11)

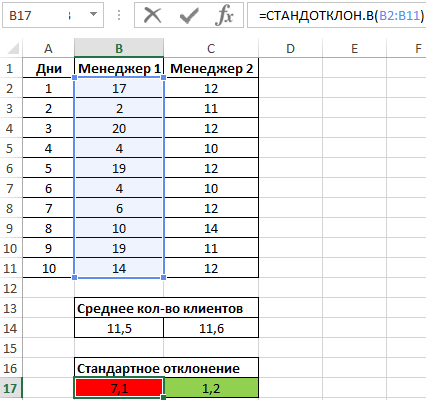
B2:B11 – диапазон исследуемых значений. Аналогично определим стандартное отклонение для второго менеджера и получим следующие результаты:

Как видно, показатели работы первого менеджера отличаются высокой вариабельностью (разбросом) значений, в связи с чем среднее арифметическое значение абсолютно не отражает реальную картину эффективности работы. Отклонение 1,2 свидетельствует о более стабильной, а, значит, и эффективной работе второго менеджера.



Пример использования функции СТАНДОТКЛОНА в Excel

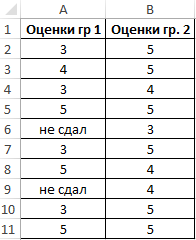
Пример 2. В двух различных группах студентов колледжа проводился экзамен по одной и той же дисциплине. Оценить успеваемость студентов.

Таблица исходных данных:

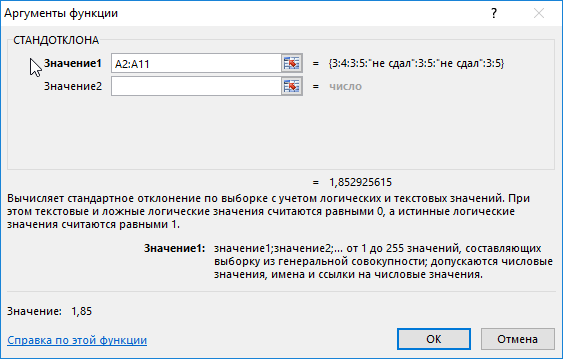
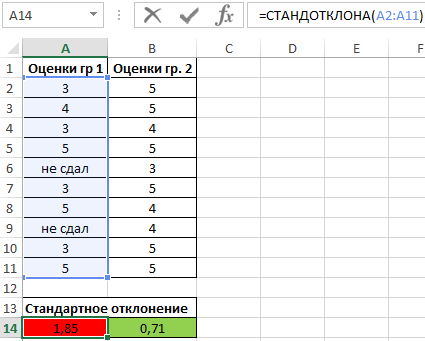
Определим стандартное отклонение значений для первой группы по формуле:

=СТАНДОТКЛОНА(A2:A11)

Аналогичный расчет произведем для второй группы. В результате получим:

Полученные значения свидетельствуют о том, что студенты второй группы намного лучше подготовились к экзамену, поскольку разброс значений оценок относительно небольшой. Обратите внимание на то, что функция СТАНДОТКЛОНА преобразует текстовое значение «не сдал» в числовое значение 0 (нуль) и учитывает его в расчетах.

Пример функции СТАНДОТКЛОН.Г в Excel

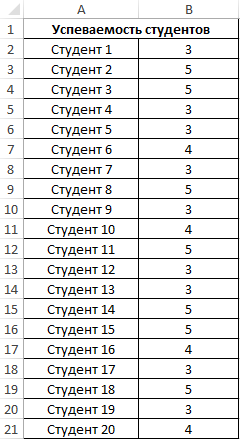
Пример 3. Определить эффективность подготовки студентов к экзамену для всех групп университета.

Примечание: в отличие от предыдущего примера, будет анализироваться не выборка (несколько групп), а все число студентов – генеральная совокупность. Студенты, не сдавшие экзамен, не учтены.

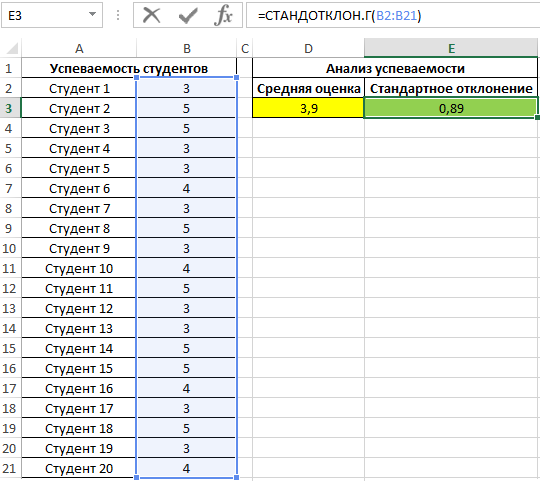
Заполним таблицу данных:

Для оценки эффективности будем оперировать двумя показателями: средняя оценка и разброс значений. Для определения среднего арифметического используем функцию:

=СРЗНАЧ(B2:B21)

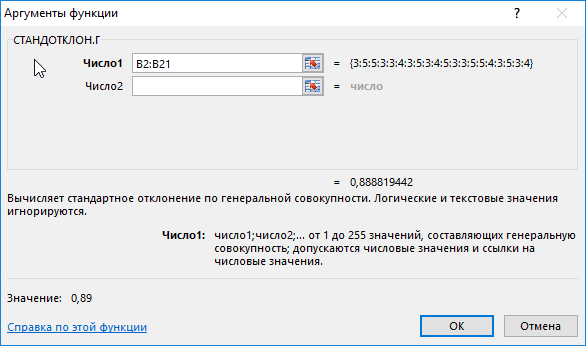
Для определения отклонения введем формулу:

=СТАНДОТКЛОН.Г(B2:B21)

В результате получим:

Полученные данные свидетельствует об успеваемости немного ниже среднего (<4), величина разброса характеризует довольно большое количество студентов, получивших 5 и 3 соответственно (учитывая, что анализировались только данные из диапазона от 3 до 5).

Пример функции СТАНДОТКЛОНПА в Excel

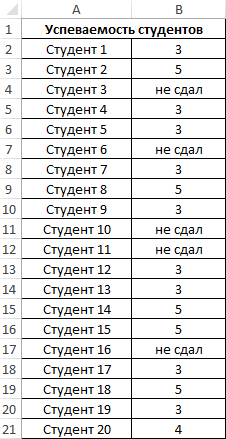
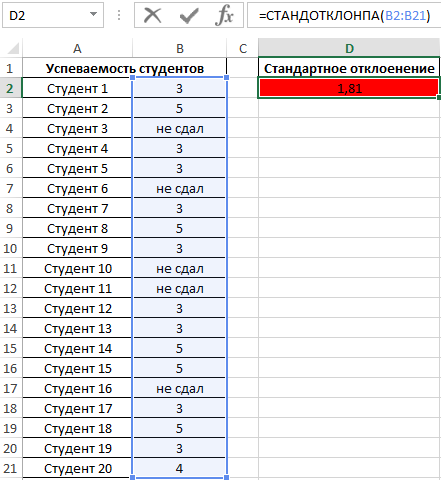
Пример 4. Проанализировать успеваемость студентов по результатам сдачи экзамена с учетом тех студентов, которым не удалось сдать этот экзамен.

Таблица данных:

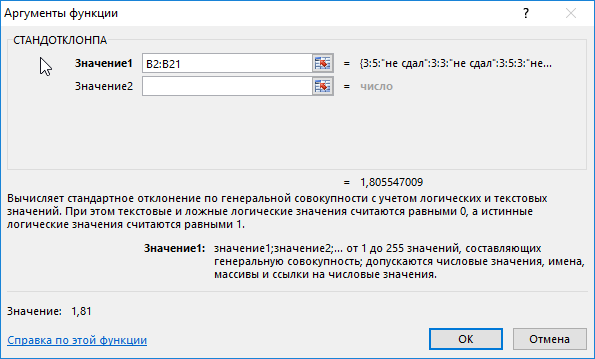
В данном примере также анализируем генеральную совокупность, однако некоторые поля данных содержат текстовые значения. Для определения стандартного отклонения используем функцию:

=СТАНДОТКЛОНПА(B2:B21)

В результате получим:

Высокий разброс значений в последовательности свидетельствует о большом числе не сдавших экзамен студентов.

Особенности использования СТАНДОТКЛОН.В, СТАНДОТКЛОН.Г, СТАНДОТКЛОНА и СТАНДОТКЛОНПА

Функции СТАНДОТКЛОНА И СТАНДОТКЛОНПА имеют идентичную синтаксическую запись типа:

=ФУНКЦИЯ (значение1; [значение2];…)

Описание:

• ФУНКЦИЯ – одна из двух рассмотренных выше функций;
• значение1 – обязательный аргумент, характеризующий одно из значений выборки (либо генеральной совокупности);
• [значени2] – необязательный аргумент, характеризующий второе значение исследуемого диапазона.

Примечания:

1. В качестве аргументов функций могут быть переданы имена, числовые значения, массивы, ссылки на диапазоны числовых данных, логические значения и ссылки на них.
2. Обе функции игнорируют пустые значения и текстовые данные, содержащиеся в диапазоне переданных данных.
3. Функции возвращают код ошибки #ЗНАЧ!, если в качестве аргументов были переданы значения ошибок или текстовые данные, которые не могут быть преобразованы в числовые значения.

Функции СТАНДОТКЛОН.В и СТАНДОТКЛОН.Г имеют следующую синтаксическую запись:

=ФУНКЦИЯ(число1;[число2];…)

Описание:

• ФУНКЦИЯ – любая из функций СТАНДОТКЛОН.В или СТАНДОТКЛОН.Г;
• число1 – обязательный аргумент, характеризующий числовое значение, взятое из выборки или всей генеральной совокупности;
• число2 – необязательный аргумент, характеризующий второе числовое значение исследуемого диапазона.

Примечание: обе функции не включают в процесс вычисления числа, представленные в виде текстовых данных, а также логические значения ИСТИНА и ЛОЖЬ.

Примечания:

1. Стандартное отклонение широко используется в статистических расчетах, когда нахождение среднего значения диапазона величин не дает верное представление о распределении данных. Оно демонстрирует принцип распределения величин относительно среднего значения в конкретной выборке или всей последовательности целиком. В Примере 1 будет наглядно рассмотрено практическое применение данного статистического параметра.
2. Функции СТАНДОТКЛОНА и СТАНДОТКЛОН.В следует использовать для анализа только части генеральной совокупности и производят расчет по первой формуле, а СТАНДОТКЛОН.Г и СТАНДОТКЛОНПА должны принимать на вход данные о всей генеральной совокупности и производят расчет по второй формуле.
3. В Excel содержатся встроенные функции СТАНДОТКЛОН и СТАНДОТКЛОНП, оставленные для совместимости с более старыми версиями Microsoft Office. Они могут быть не включены в более поздние версии программы, поэтому их использование не рекомендуется.
4. Для нахождения стандартного отклонения используются две распространенные формулы: S=√((∑_(i=1)^n▒(x_i-x_ср )^2 )/(n-1)) и S=√((∑_(i=1)^n▒(x_i-x_ср )^2 )/n), где:

• S – искомое значение стандартного отклонения;
• n – рассматриваемый диапазон значений (выборка);
• x_i – отдельно взятое значение из выборки;
• x_ср – среднее арифметическое значение для рассматриваемого диапазона.