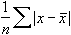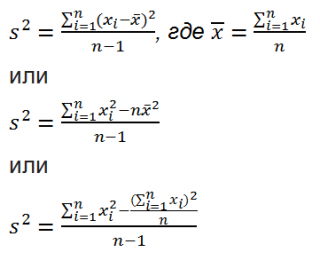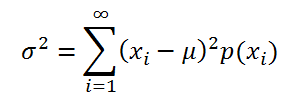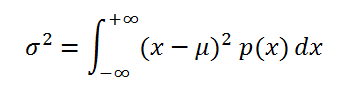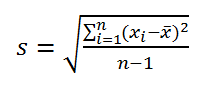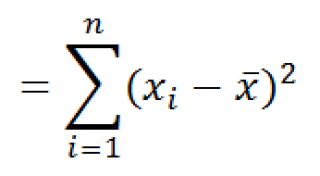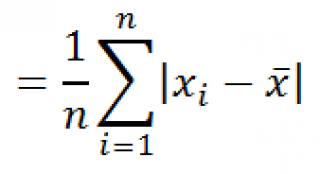Сроткл в excel что это

В этой статье описаны синтаксис формулы и использование СОВПАД
 в Microsoft Excel.

Описание

Возвращает среднее абсолютных значений отклонений точек данных от среднего. СРОТКЛ является мерой разброса множества данных.

Синтаксис

СРОТКЛ(число1;[число2];…)

Аргументы функции СРОТКЛ описаны ниже.

• Число1, число2,…    — аргумент «число1» является обязательным, следующие за ним — нет. От 1 до 255 аргументов, для которых необходимо определить среднее абсолютных отклонений. Вместо аргументов, разделенных точками с запятой, можно использовать массив или ссылку на массив.

Замечания

• На результат СРОТКЛ влияют единицы измерения входных данных.

• Аргументы должны быть либо числами, либо именами, массивами или ссылками, содержащими числа.

• Учитываются логические значения и текстовые представления чисел, которые непосредственно введены в список аргументов.

• Если аргумент, который является массивом или ссылкой, содержит текст, логические значения или пустые ячейки, то такие значения игнорируются; однако, ячейки, которые содержат нулевые значения, учитываются.

• Уравнение для среднего отклонения:

  

Пример

Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.

Данные	Описание
4	Среднее абсолютное отклонение чисел в ячейках A2:A8 от среднего (1,020408)
5
6
7
5
4
3
Формула	Результат
=СРОТКЛ(A2:A8)	1,020408

Функция СРОТКЛ в Excel используется для анализа числового ряда, передаваемого в качестве аргумента, и возвращает число, соответствующее среднему значению, рассчитанному для модулей отклонений относительно среднего арифметического для исследуемого ряда.

Примеры методов анализа числовых рядов в Excel

Смысл данной функции становится предельно ясен после рассмотрения примера. Допустим, на протяжении суток каждые 3 часа фиксировались показатели температуры воздуха. Был получен следующий ряд значений: 16, 14, 17, 21, 25, 26, 22, 18. С помощью функции СРЗНАЧ можно определить среднее значение температуры – 19,88 (округлим до 20). Для определения отклонения каждого значения от среднего необходимо вычесть из него полученное среднее значение. Например, для первого замера температуры это будет равно 16-20=-4. Получаем ряд значений: -4, -6, -3, 1, 5, 6, 2, -2. Поскольку СРОТКЛ по определению работает с модулями отклонений, итоговый ряд значений имеет вид: 4, 6, 3, 1, 5, 6, 2, 2. Теперь нужно получить среднее значение для данного ряда с помощью функции СРЗНАЧ – примерно 3,63. Именно таков алгоритм работы рассматриваемой функции.

Таким образом, значение, вычисляемое функцией СРОТКЛ, можно рассчитать с помощью формулы массива без использования этой функции. Допустим, перечисленные результаты замеров температур записаны в столбец (ячейки A1:A8). Тогда для определения среднего значения отклонений можно использовать формулу =СРЗНАЧ(ABS(A1:A8-СРЗНАЧ(A1:A8))). Однако, рассматриваемая функция значительно упрощает расчеты.

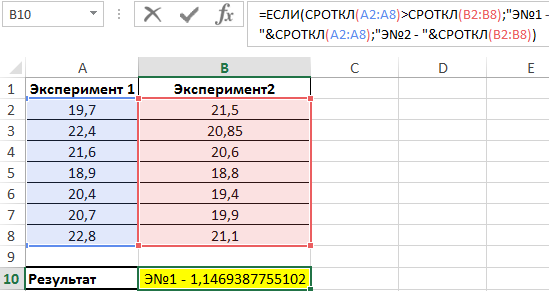
Пример 1. Имеются два ряда значений, представляющих собой результаты наблюдений одного и того же физического явления, сделанные в ходе двух различных экспериментов. Определить, среднее отклонение от среднего значения результатов для какого эксперимента является максимальным?

Вид таблицы данных:

Используем следующую формулу:

Сравниваем результаты, возвращаемые функцией СРОТКЛ для первого и второго ряда чисел с использованием функции ЕСЛИ, возвращаем соответствующий результат.

Полученное значение:

В результате мы получили среднее отклонение от среднего значения. Это весьма интересная функция для технического анализа финансовых рынков, прогнозов курсов валют и даже позволяет повысить шансы выигрышей в лотереях.



Формула расчета линейного коэффициента вариации в Excel

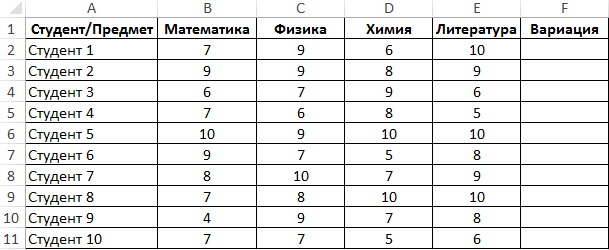
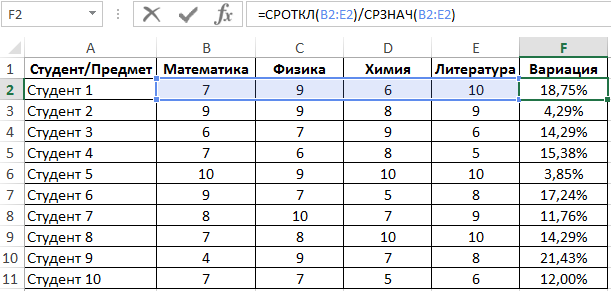
Пример 2. Студенты сдали экзамены по различным предметам. Определить число студентов, которые удовлетворяют следующему критерию успеваемости – линейный коэффициент вариации оценок не превышает 15%.

Вид таблицы данных:

Линейный коэффициент вариации определяется как отношение среднего отклонения к среднему значению. Для расчета используем следующую формулу:

Растянем ее вниз по столбцу и получим следующие значения:

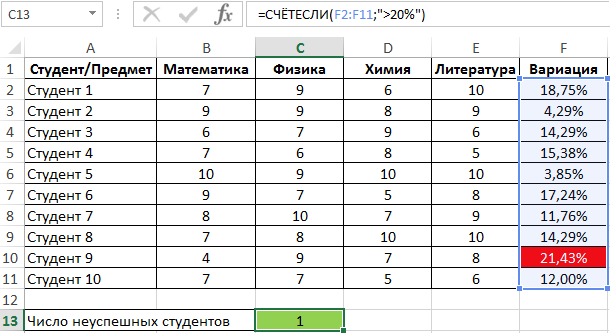
Для определения числа неуспешных студентов по указанному критерию используем функцию:

Полученный результат:

Правила использования функции СРОТКЛ в Excel

Функция имеет следующий синтаксис:

=СРОТКЛ(число1;[число2];…)

Описание аргументов:

• число1 – обязательный, принимает числовое значение, характеризующее первый член ряда значений, для которых необходимо определить среднее отклонение от среднего;
• [число2];… — необязательный, принимает второе и последующие значения из исследуемого числового ряда.

Примечания:

1. При использовании функции СРОТКЛ удобнее задавать первый аргумент в виде ссылки на диапазон ячеек, например =СРОТКЛ(A1:A8) вместо перечисления (=СРОТКЛ(A1;A2:A3…;A8)).
2. В качестве аргумента функции может быть передана константа массива, например =СРОТКЛ({2;5;4;7;10}).
3. Для получения достоверного результата необходимо привести все значения ряда к единой системе измерения величин. Например, если часть длин указана в мм, а остальные – в см, результат расчетов будет некорректен. Необходимо преобразовать все значения в мм или см соответственно.
4. Если в качестве аргументов функции переданы нечисловые данные, которые не могут быть преобразованы к числам, функция вернет код ошибки #ЧИСЛО!. Если хотя бы одно значение из ряда является числовым, функция выполнит расчет, не возвращая код ошибки.
5. Не преобразуемые к числам текстовые строки и пустые ячейки не учитываются в расчете. Если ячейка содержит значение 0 (нуль), оно будет учтено.
6. Логические данные автоматически преобразуются к числовым: ИСТИНА – 1, ЛОЖЬ – 0 соответственно.

Вычислим в

MS

EXCEL

дисперсию и стандартное отклонение выборки. Также вычислим дисперсию случайной величины, если известно ее распределение.

Сначала рассмотрим

дисперсию

, затем

стандартное отклонение

.

Дисперсия выборки

Дисперсия выборки

(

выборочная дисперсия,

sample

variance

) характеризует разброс значений в массиве относительно

среднего

.

Все 3 формулы математически эквивалентны.

Из первой формулы видно, что

дисперсия выборки

это сумма квадратов отклонений каждого значения в массиве

от среднего

, деленная на размер выборки минус 1.

В MS EXCEL 2007 и более ранних версиях для вычисления

дисперсии

выборки

используется функция

ДИСП()

, англ. название VAR, т.е. VARiance. С версии MS EXCEL 2010 рекомендуется использовать ее аналог

ДИСП.В()

, англ. название VARS, т.е. Sample VARiance. Кроме того, начиная с версии MS EXCEL 2010 присутствует функция

ДИСП.Г(),

англ. название VARP, т.е. Population VARiance, которая вычисляет

дисперсию

для

генеральной совокупности

. Все отличие сводится к знаменателю: вместо n-1 как у

ДИСП.В()

, у

ДИСП.Г()

в знаменателе просто n. До MS EXCEL 2010 для вычисления дисперсии генеральной совокупности использовалась функция

ДИСПР()

.

Дисперсию выборки

можно также вычислить непосредственно по нижеуказанным формулам (см.

файл примера

)

=КВАДРОТКЛ(Выборка)/(СЧЁТ(Выборка)-1)

=(СУММКВ(Выборка)-СЧЁТ(Выборка)*СРЗНАЧ(Выборка)^2)/ (СЧЁТ(Выборка)-1)

– обычная формула

=СУММ((Выборка -СРЗНАЧ(Выборка))^2)/ (СЧЁТ(Выборка)-1

) –

формула массива

Дисперсия выборки

равна 0, только в том случае, если все значения равны между собой и, соответственно, равны

среднему значению

. Обычно, чем больше величина

дисперсии

, тем больше разброс значений в массиве.

Дисперсия выборки

является точечной оценкой

дисперсии

распределения случайной величины, из которой была сделана

выборка

. О построении

доверительных интервалов

при оценке

дисперсии

можно прочитать в статье

Доверительный интервал для оценки дисперсии в MS EXCEL

.

Дисперсия случайной величины

Чтобы вычислить

дисперсию

случайной величины, необходимо знать ее

функцию распределения

.

Для

дисперсии

случайной величины Х часто используют обозначение Var(Х).

Дисперсия

равна

математическому ожиданию

квадрата отклонения от среднего E(X): Var(Х)=E[(X-E(X))

²

]

Если случайная величина имеет

дискретное распределение

, то

дисперсия

вычисляется по формуле:

где x

_i

– значение, которое может принимать случайная величина, а μ – среднее значение (

математическое ожидание случайной величины

), р(x) – вероятность, что случайная величина примет значение х.

Если случайная величина имеет

непрерывное распределение

, то

дисперсия

вычисляется по формуле:

где р(x) –

плотность вероятности

.

Для распределений, представленных в MS EXCEL

,

дисперсию

можно вычислить аналитически, как функцию от параметров распределения. Например, для

Биномиального распределения

дисперсия

равна произведению его параметров: n*p*q.

Примечание

:

Дисперсия,

является

вторым центральным моментом

, обозначается D[X], VAR(х), V(x). Второй центральный момент — числовая характеристика распределения случайной величины, которая является мерой разброса случайной величины относительно

математического ожидания

.

Примечание

: О распределениях в MS EXCEL можно прочитать в статье

Распределения случайной величины в MS EXCEL

.

Размерность

дисперсии

соответствует квадрату единицы измерения исходных значений. Например, если значения в выборке представляют собой измерения веса детали (в кг), то размерность дисперсии будет кг

²

. Это бывает сложно интерпретировать, поэтому для характеристики разброса значений чаще используют величину равную квадратному корню из

дисперсии

–

стандартное отклонение

.

Некоторые свойства

дисперсии

:

Var(Х+a)=Var(Х), где Х — случайная величина, а — константа.

Var(aХ)=a

²

Var(X)

Var(Х)=E[(X-E(X))

²

]=E[X

²

-2*X*E(X)+(E(X))

²

]=E(X

²

)-E(2*X*E(X))+(E(X))

²

=E(X

²

)-2*E(X)*E(X)+(E(X))

²

=E(X

²

)-(E(X))

²

Это свойство дисперсии используется в

статье про линейную регрессию

.

Var(Х+Y)=Var(Х) + Var(Y) + 2*Cov(Х;Y), где Х и Y — случайные величины, Cov(Х;Y) — ковариация этих случайных величин.

Если случайные величины независимы (independent), то их

ковариация

равна 0, и, следовательно, Var(Х+Y)=Var(Х)+Var(Y). Это свойство дисперсии используется при выводе

стандартной ошибки среднего

.

Покажем, что для независимых величин Var(Х-Y)=Var(Х+Y). Действительно, Var(Х-Y)= Var(Х-Y)= Var(Х+(-Y))= Var(Х)+Var(-Y)= Var(Х)+Var(-Y)= Var(Х)+(-1)

²

Var(Y)= Var(Х)+Var(Y)= Var(Х+Y). Это свойство дисперсии используется для построения

доверительного интервала для разницы 2х средних

.

Примечание

: квадратный корень из дисперсии случайной величины называется Среднеквадратическое отклонение (или другие названия — среднее квадратическое отклонение, среднеквадратичное отклонение, квадратичное отклонение, стандартное отклонение, стандартный разброс).

Стандартное отклонение выборки

Стандартное отклонение выборки

— это мера того, насколько широко разбросаны значения в выборке относительно их

среднего

.

По определению,

стандартное отклонение

равно квадратному корню из

дисперсии

:

Стандартное отклонение

не учитывает величину значений в

выборке

, а только степень рассеивания значений вокруг их

среднего

. Чтобы проиллюстрировать это приведем пример.

Вычислим стандартное отклонение для 2-х выборок: (1; 5; 9) и (1001; 1005; 1009). В обоих случаях, s=4. Очевидно, что отношение величины стандартного отклонения к значениям массива у выборок существенно отличается. Для таких случаев используется

Коэффициент вариации

(Coefficient of Variation, CV) — отношение

Стандартного отклонения

к среднему

арифметическому

, выраженного в процентах.

В MS EXCEL 2007 и более ранних версиях для вычисления

Стандартного отклонения выборки

используется функция

=СТАНДОТКЛОН()

, англ. название STDEV, т.е. STandard DEViation. С версии MS EXCEL 2010 рекомендуется использовать ее аналог

=СТАНДОТКЛОН.В()

, англ. название STDEV.S, т.е. Sample STandard DEViation.

Кроме того, начиная с версии MS EXCEL 2010 присутствует функция

СТАНДОТКЛОН.Г()

, англ. название STDEV.P, т.е. Population STandard DEViation, которая вычисляет

стандартное отклонение

для

генеральной совокупности

. Все отличие сводится к знаменателю: вместо n-1 как у

СТАНДОТКЛОН.В()

, у

СТАНДОТКЛОН.Г()

в знаменателе просто n.

Стандартное отклонение

можно также вычислить непосредственно по нижеуказанным формулам (см.

файл примера

)

=КОРЕНЬ(КВАДРОТКЛ(Выборка)/(СЧЁТ(Выборка)-1)) =КОРЕНЬ((СУММКВ(Выборка)-СЧЁТ(Выборка)*СРЗНАЧ(Выборка)^2)/(СЧЁТ(Выборка)-1))

Другие меры разброса

Функция

КВАДРОТКЛ()

вычисляет с умму квадратов отклонений значений от их

среднего

. Эта функция вернет тот же результат, что и формула

=ДИСП.Г(

Выборка

)*СЧЁТ(

Выборка

)

, где

Выборка

— ссылка на диапазон, содержащий массив значений выборки (

именованный диапазон

). Вычисления в функции

КВАДРОТКЛ()

производятся по формуле:

Функция

СРОТКЛ()

является также мерой разброса множества данных. Функция

СРОТКЛ()

вычисляет среднее абсолютных значений отклонений значений от

среднего

.  Эта функция вернет тот же результат, что и формула

=СУММПРОИЗВ(ABS(Выборка-СРЗНАЧ(Выборка)))/СЧЁТ(Выборка)

, где

Выборка

— ссылка на диапазон, содержащий массив значений выборки.

Вычисления в функции

СРОТКЛ

()

производятся по формуле:

Просмотров:
1 866

В статистике, да и в некоторых других расчетах используется среднее отклонение значения от всех значений диапазона. Для вычисления среднего отклонения в Excel используется функция СРОТКЛ.

Описание

Если открыть описание функции в справочнике по Excel, то можно увидеть что функция возвращает среднее абсолютных значений отклонений точек данных от среднего. Кроме того сказано что данная функция является мерой разброса множества данных. Сложно звучит, хотя на практике вычисление, производимое данной функцией не так трудно понять. Для начала рассмотрим синтаксис функции.

Синтаксис

СРОТКЛ(число1[;число2]…)

число1 – первое значение или ссылка

число2 – второе значение или ссылка

функция в качестве параметров может принимать как обычные
числа, которых может быть от 1 до 255, так и ссылки на массивы, как и сами
массивы. Необходимо отметить, что на результат функции влияют единицы измерения
входных данных.

Как и во многих других функциях при указании в качестве
аргумента диапазона значений или массива, функция производит вычисления избирательно
для значений набора.  Так строки,
логические значения и пустые ячейки пропускаются, но при этом ячейка, содержащая
0 (ноль) учитывается. Связанно это с тем, что функция производит вычисления над
числовыми значениями.

Примеры

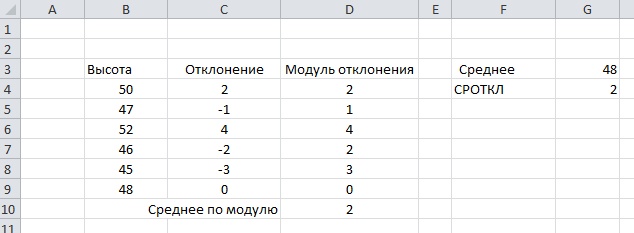
Пусть имеется рабочий лист со следующими значениями:

Анализировать мы будем диапазон от В4 до В9 содержащий
значения измеренных высот. В ячейку G4 введем функцию среднего отклонения

=СРОТКЛ(B4:B9)

Результатом выполнения функции будет значение 2. Так как же
вычисляется значение: введем в ячейку G3 функцию вычисляющую среднее значение для исходного набора
значений

=СРЗНАЧ(B4:B9)

Результатом будет значение 48. Теперь посчитаем в ячейках столбца
С для каждого исходного значения его отклонение от среднего. Так отклонение
числа 50 будет 2 (50-48), а отклонение значения 45 будет -3 (45-48). Но как мы
знаем из описания функция возвращает среднее от абсолютных значений, те
значений по модулю, поэтому в столбце D введем функцию возвращающую модуль
значений отклонения. Положительные числа и ноль останутся без изменений, а
отрицательные значения станут положительными. И теперь посчитаем среднее
значение по модулю отклонения:

=СРЗНАЧ(D4:D9)

Результат будет так же значение 2. То есть среднее значение
абсолютных значений отклонения числа от среднего значения по диапазону. То же
самое что возвращает функция СРОТКЛ.

Функция СРОТКЛ возвращает среднее абсолютных значений отклонений точек данных от среднего.

Описание функции СРОТКЛ

Возвращает среднее абсолютных значений отклонений точек данных от среднего. СРОТКЛ является мерой разброса множества данных.

Синтаксис

=СРОТКЛ(число1; [число2]; …)

Аргументы

Замечания

• На результат СРОТКЛ влияют единицы измерения входных данных.
• Аргументы должны быть либо числами, либо именами, массивами или ссылками, содержащими числа.
• Учитываются логические значения и текстовые представления чисел, которые непосредственно введены в список аргументов.
• Если аргумент, который является массивом или ссылкой, содержит текст, логические значения или пустые ячейки, то такие значения игнорируются; однако, ячейки, которые содержат нулевые значения, учитываются.
• Уравнение для среднего отклонения:
  

Пример