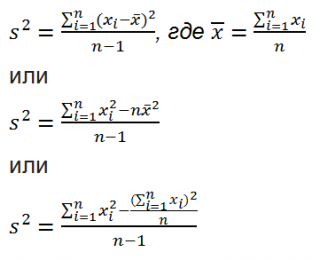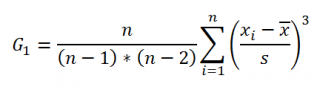Инфоурок
›
Другое
›Презентации›Статистический анализ данных в MS Excel
Скачать материал

Скачать материал


- Сейчас обучается 264 человека из 64 регионов


- Сейчас обучается 395 человек из 62 регионов




Описание презентации по отдельным слайдам:
-
1 слайд
Статистический анализ данных в MS Excel
1. Обзор и характеристика основных статистических функций, входящих в MS Excel.
2. Работа с пакетом анализа данных в MS Excel.
Литература:
1. Г.И. Просветов Анализ данных с помощью Excel. Задачи и решения. М: 2009
2. А.Ю. Козлов, В.С. Мхитарян, В.Ф. Шишов Статистический анализ данных в MS Excel М: 2012 -
2 слайд
Понятие анализа данных
Анализ данных – область математики и информатики, занимающая построением и исследованием наиболее общих математических методов и вычислительных алгоритмов извлечения знаний из экспериментальных данных.
Анализ данных – это процесс исследования, фильтрации, преобразования и моделирования данных с целью извлечения полезной информации и принятия решения. -
3 слайд
Статистические функции MS Excel
Все статистические функции, входящие в MS Excel можно разбить на восемь подразделов:
1.Предварительная обработка данных;
2.Определение характеристик положения;
3.Определение корреляции, ковариации;
4.Определение характеристик рассеивания
5.Интервальное оценивание (определение вероятности попадания дискретной случайной величины в интервал);
6.Определения параметров распределения непрерывной случайной величины;
7.Определение параметров распределения дискретной случайной величины;
8.Построение уравнения регрессии и прогнозирования. -
4 слайд
Предварительная обработка данных
Подсчет количества значений (СЧЕТ).
Определение экстремальных значений совокупности данных (МАКС, МИН)
Подсчет частот из массива данных, попадающих в заданные интервалы (ЧАСТОТА)
Оценка относительного положения точки (ПРОЦЕНТРАНГ)
Определение величины, соответствующей ее относительному положению (ПЕРСЕНТИЛЬ)
Определение числа перестановок (ПЕРЕСТ)
Определение ранга чисел в списке чисел (РАНГ) -
5 слайд
Предварительная обработка данных
Массив данных
СЧЕТ
МАКС
ЧАСТОТА
ПРОЦЕНТРАНГ
ПЕРСЕНТИЛЬ
РАНГ -
6 слайд
Определение характеристик положения
Определение среднего (СРЗНАЧ, СРГЕОМ)
Определение моды в интервале данных или массиве (МОДА)
Определение медианы (МЕДИАНА)
Определение квартилей (КВАРТИЛЬ) -
7 слайд
Определение характеристик положения
Массив данных
СРГЕОМ
СРЗНАЧ
МОДА
МЕДИАНА
КВАРТИЛЬ -
8 слайд
Определение характеристик рассеивания
Определение среднего линейного отклонения (СРОТКЛ)
Определение суммы квадратов отклонения (ДИСП)
Вычисление стандартного (среднего квадратического) отклонения (СТАНДОТКЛОН)
Определения асимметрии распределения (СКОС)
Определения эксцесса (ЭКСЦЕСС) -
9 слайд
Определение характеристик рассеивания
Массив данных
СРОТКЛ
КВАДРОТКЛ
ДИСП
СТАНДОТКЛОН
СКОС
ЭКСЦЕСС -
10 слайд
Зависимость случайных величин
Определение ковариации (КОВАР)
Определение коэффициента корреляции (КОРРЕЛ) -
11 слайд
Зависимость случайных величин
Массив данных
КОВАР
КОРРЕЛ -
12 слайд
Интервальное оценивание
Определение доверительного интервала для среднего (ДОВЕРИТ)
Определение вероятности попадания дискретной случайной величины в интервал (ВЕРОЯТНОСТЬ) -
13 слайд
Интервальное оценивание
Массив данных
ДОВЕРИТ
ВЕРОЯТНОСТЬ -
14 слайд
Определение параметров распределения непрерывных случайных величин
Определение значения функции распределения и функции плотности нормального распределения (НОРМРАСПР)
Определение аргумента по значению функции распределения (НОРМОБР)
Определение вероятности статистики z при проверке гипотизы о равенстве статистической оценки математического ожидания заданному значению (ZТЕСТ)
Определение значений функций распределения отличных от нормальных (ЛОГНОРМРАСП, СТЬЮДРАСП…)
Проверка гипотезы о равенстве дисперсий (ФТЕСТ) -
15 слайд
Определение параметров распределения непрерывных случайных величин
НОРМРАСП
НОРМОБР
Массив данных
ZТЕСТ
ФТЕСТ -
16 слайд
Построение уравнения регрессии и прогнозирование
Определение параметров линейной регрессии (ЛИНЕЙН)
Определение значений результативного признака по линейному уравнению регрессии (ТЕНДЕНЦИЯ)
Определение значения уравнения регрессии вида y=b0+b1x в заданной точке (ПРЕДСКАЗ) -
17 слайд
Построение уравнения регрессии и прогнозирование
ЛИНЕЙН
ТЕНДЕНЦИЯ
Массив данных
ПРЕДСКАЗ -
18 слайд
Работа с пакетом анализа данных в MS Excel.
-
19 слайд
Работа с пакетом анализа данных в MS Excel.
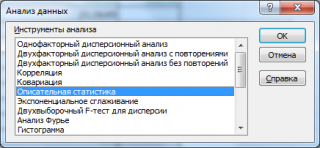
В пакет анализа данных входят следующие инструменты:
1.Генерация случайных чисел
2.Выборка
3.Гистограмма
4.Описательная статистика
5.Скользящее среднее
6.Экспоненциальное сглаживание
7.Ковариционный анализ
8.Корреляционный анализ
9.Двухвыборочный F-тест для дисперсий
10. Двухвыборочныйz-тест для средних
11.Парный двухвыборочный t-тест для средних
12. Двухвыборочный t-тест с одинаковыми дисперсиями
13. Двухвыборочный t-тест с разными дисперсиями
14. Дисперсионный анализ
15. Регрессия
16.Ранг и персентиль
17. Анализ Фурье -
20 слайд
Генерация случайных чисел
Окно инструмента Генерация случайных чисел содержит следующие основные параметры:
-Число переменных При помощи этого параметра можно получать многомерную выборку (количество столбцов)
-Число случайных чисел Определяется число точек данных (число реализаций), которое вы хотите генерировать для каждой переменной
-Случайное рассеивание Вводится произвольное значение, для которого необходимо генерировать случайные числа. Применяется для повторной генерации (повторное получение той же совокупности) -
21 слайд
Выборка
В пакете Анализ данных инструмент Выборка используется для создания выборки из генеральной совокупности, рассматривая входной диапазон как генеральную совокупность -
22 слайд
Гистограмма
Гистограмма применяется для графического изображения интервального вариационного ряда -
23 слайд
Описательная статистика
Описательная статистика использует совокупность методов, позволяющих делать научно обоснованные выводы о числовых параметрах распределения генеральной совокупности по случайной выборке из нее
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 212 255 материалов в базе
- Выберите категорию:
- Выберите учебник и тему
- Выберите класс:
-
Тип материала:
-
Все материалы
-
Статьи
-
Научные работы
-
Видеоуроки
-
Презентации
-
Конспекты
-
Тесты
-
Рабочие программы
-
Другие методич. материалы
-
Найти материалы
Другие материалы
- 27.12.2020
- 4749
- 2
- 27.12.2020
- 4952
- 11
- 27.12.2020
- 5787
- 13
- 27.12.2020
- 5023
- 9
- 27.12.2020
- 4058
- 1
- 27.12.2020
- 3884
- 0
- 27.12.2020
- 3907
- 1
- 27.12.2020
- 3300
- 4
Вам будут интересны эти курсы:
-
Курс повышения квалификации «Основы туризма и гостеприимства»
-
Курс повышения квалификации «Организация научно-исследовательской работы студентов в соответствии с требованиями ФГОС»
-
Курс повышения квалификации «Формирование компетенций межкультурной коммуникации в условиях реализации ФГОС»
-
Курс повышения квалификации «Экономика предприятия: оценка эффективности деятельности»
-
Курс профессиональной переподготовки «Клиническая психология: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Введение в сетевые технологии»
-
Курс профессиональной переподготовки «Логистика: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Применение MS Word, Excel в финансовых расчетах»
-
Курс повышения квалификации «Основы менеджмента в туризме»
-
Курс повышения квалификации «Психодинамический подход в консультировании»
-
Курс профессиональной переподготовки «Корпоративная культура как фактор эффективности современной организации»
-
Курс профессиональной переподготовки «Деятельность по хранению музейных предметов и музейных коллекций в музеях всех видов»
-
Курс профессиональной переподготовки «Организация системы менеджмента транспортных услуг в туризме»
-
Курс профессиональной переподготовки «Техническая диагностика и контроль технического состояния автотранспортных средств»
-
Настоящий материал опубликован пользователем Гущина Мадина Ивановна. Инфоурок является
информационным посредником и предоставляет пользователям возможность размещать на сайте
методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них
сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайтЕсли Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с
сайта, Вы можете оставить жалобу на материал.Удалить материал
-
- На сайте: 2 года и 3 месяца
- Подписчики: 0
- Всего просмотров: 47156
-
Всего материалов:
217
Microsoft
Excel содержит большое число встроенных
функций категории Статистические,
а также
специализированные информационные
технологии статистического анализа,
реализуемые Пакетом анализа. «Пакет
анализа» – надстройка
Microsoft Excel, устанавливаемая с помощью
команды меню СервисНадстройка.
После
установки
надстройки
Пакет
анализа в меню команды Сервис
появляется
новый пункт – Анализ
данных.
Для
анализа наиболее часто используется
описательная статистика данных,
статистические методы прогнозирования
значений.
Описательная статистика
Это самый
распространенный прием анализа данных,
с помощью которого вычисляются
статистические характеристики массива
значений экономических показателей:
-
Средние
оценки, имеют ту же размерность, что и
сама случайная величина, в том числе:
-
Средняя
арифметическая – математическое
ожидание случайной величины, соответствует
встроенной функции СРЗНАЧ. -
Средняя
геометрическая – оценка средних темпов
роста, поиск значения, равноудаленного
от других значений, соответствует
встроенной функции СРГЕОМ. -
Средняя
гармоническая – оценка средней суммы
обратных величин, соответствует
встроенной функции СРГАРМ.
Между средними
величинами существует соотношение:
-
Показатели
вариации:
-
Общее
число значений в массиве, соответствует
встроенной функции СЧЕТ. -
Сумма
всех значений переменных в массиве,
соответствует встроенной функции СУММ. -
Дисперсия
случайной величины, соответствует
встроенной функции ДИСП
(дисперсия по выборке) или ДИСПР
(дисперсия
по генеральной совокупности). Дисперсия
имеет размерность в квадрате, характеризует
рассеивание значений случайной величины
относительно средней арифметической. -
Стандартное
отклонение, соответствует встроенной
функции СТАНДОТКЛОН
(стандартное
отклонение по выборке), СТАНДОТКЛОНП
(стандартное
отклонение по генеральной совокупности).
Стандартное отклонение имеет ту же
размерность, что и случайная величина. -
Средний
модуль отклонений, который нивелирует
знак отклонения от среднего и является
показателем силы вариации, соответствует
встроенной функции СРОТКЛ. -
Уровень
надежности (доверительный интервал)
для среднего значения, соответствует
встроенной функции ДОВЕРИТ. -
Средняя
квадратическая ошибка, вычисляется
как отношение СТАНДОТКЛОН
к корню квадратному из числа элементов
выборки. -
Минимальное
значение случайной величины, соответствует
встроенной функции МИН. -
Максимальное
значение случайной величины, соответствует
встроенной функции МАКС. -
Интервал
– размах вариации, равный разности
максимального и минимального значения
переменной (МАКС–МИН). -
Порядковое
наибольшее значений, соответствует
встроенной функции НАИБОЛЬШИЙ. -
Порядковое
наименьшее значение соответствует
встроенной функции – функция НАИМЕНЬШИЙ.
-
Мера
взаимного расположения данных в массиве
значений, соответствует встроенным
функциям: МОДА, КВАРТИЛЬ, МЕДИАНА,
ПЕРСЕНТИЛЬ, ПРОЦЕНТРАНГ.
Мода
– наиболее
вероятное значение случайной величины.
При симметричном распределении
относительно среднего мода совпадает
с математическим ожиданием. Мода может
отсутствовать, либо распределение может
быть многомодальным.
Квантили распределения
— величина
значения признака, делящая совокупность
на n равных
частей. Различают номера квантилей: 0 –
соответствует минимальному значению
величины; 1 — первая четверть (квартиль)
значений или (25-я персентиль; 2 – медиана
или 50-я персентиль; 3 — третья четверть
(квартиль) или 75-я персентиль; 4 –
максимальное значение величины.
-
Форма
распределения случайной величины,
соответствует встроенным функциям
СКОС,
ЭКСЦЕСС.
Асимметрия
(скос) – безразмерная величина,
характеристика асимметричности случайной
величины
относительно ее математического
ожидания. Эксцесс
– безразмерный
коэффициент, характеристика формы
(островершинности или плосковершинности)
кривой распределения вероятности.
Эксцесс равен нулю для нормального
распределения, положителен для
островершинных и отрицателен для
плосковершинных кривых.
Пакет
анализа запускается командой меню
СервисАнализ
данных. В
диалоговом
окне Инструменты
анализа выбирается
Описательная
статистика. Исходные
данные для анализа располагаются в
ячейках строк или столбцов таблицы.
Описательная
статистика Пакета
анализа
вычисляет показатели:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Результаты
описательной статистики выводятся в
указанное место (текущий лист, другой
лист, новая книга).
Последовательность
действий (исходные данные для анализа
представлены на рабочем листе):
-
Команда
меню СервисАнализ
данных, выбрать
метод Описательная
статистика. -
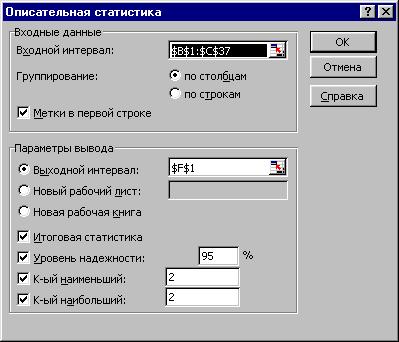
Указать
параметры описательной статистики
(рис. 16):
-
Входной
интервал – блок ячеек, содержащий
анализируемые значения. Можно одновременно
выделить смежные столбцы исходных
данных.
Рисунок
16
-
Группирование
– по столбцам/строкам. -
Флажок
Метки в первой строке выбран/не выбран. -
Выходной
интервал – Новый рабочий лист/Новая
книга/Определенная ячейка текущего
листа. -
Флажок
Итоговая статистика – выбран/не выбран
(выбор флажка обеспечивает вывод всей
описательной статистики). -
Уровень
надежности – 95% (стандартно, но можно
любой). -
K-й
наименьший – 2 (произвольно). -
K-й
наибольший – 2 (произвольно). -
Нажать
кнопку ОК.
Результаты
описательной статистики – табл. 14.
Таблица
14
|
Показатель |
Массив |
Массив |
|
Среднее |
13591,92 |
9564,75 |
|
Стандартная |
116,0136 |
127,61271 |
|
Медиана |
13821 |
9547,5 |
|
Мода |
#Н/Д |
9540 |
|
Стандартное |
696,0820303 |
765,6762604 |
|
Дисперсия |
484530,1929 |
586260,1357 |
|
Эксцесс |
-0,341929136 |
-0,809054 |
|
Асимметричность |
-0,823444644 |
0,016596 |
|
Интервал |
2441 |
2587 |
|
Минимум |
12054 |
8375 |
|
Максимум |
14495 |
10962 |
|
Сумма |
489309 |
344331 |
|
Счет |
36 |
36 |
|
Наибольший(2) |
14480 |
10932 |
|
Наименьший(2) |
12063 |
8377 |
|
Уровень |
235,52 |
259,07 |
Основными средствами анализа статистических данных в Excel являются статистические процедуры надстройки Пакет анализа (Analysis ToolРак) и статистические функции библиотеки встроенных функций. Основные сведения обо всех этих средствах имеются в электронной справочной системе Excel.
Однако качество описаний статистических процедур и функций, приведенных в этой системе, заставляет желать лучшего. Некоторые из этих описаний не очень понятны, в них имеются неточности, а подчас и просто ошибки (это относится как к англоязычному оригиналу, так и к русскому переводу). Эти недостатки с завидным постоянством повторяются и во многих пособиях по Excel. Найти необходимые пособия в интернете можно быстро если скачать бесплатно Амиго браузер с усовершенствованным поисковым алгоритмом.
Статистические процедуры Пакета анализа
Наиболее развитыми средствами анализа данных являются статистические процедуры Пакета анализа. Они обладают большими возможностями, чем статистические функции. С их помощью можно решать более сложные задачи обработки статистических данных и выполнять более тонкий анализ этих данных.
В Пакет анализа входят следующие статистические процедуры:
- генерация случайных чисел (Random number generation);
- выборка (Sampling);
- гистограмма (Histogram);
- описательная статистика (Descriptive statistics);
- ранги персентиль (Rank and percentile);
- двухвыборочный z-тест для средних (z-Test: Two Sample for Means);
- двухвыборочный t-тест для средних с одинаковыми дисперсиями (t-Test: Two-Sample Assuming Equal Variances);
- двухвыборочный t-тест для средних с различными дисперсиями (t-Test: Two-Sample Assuming Unequal Variances);
- парный двухвыборочный t-тест для средних (t-Test: Paired Two Sample for Means);
- двухвыборочный F-тест да я дисперсий (F-Test: Two Sample for Variances);
- коварнация (Covariance);
- корреляция (Correlation);
- рецессия (Regression);
- однофакторный дисперсионный анализ (ANOVA: Single Factor);
- двухфакторный дисперсионный анализ без повторений (ANOVA: Two Factor Without Replication);
- двухфакторный дисперсионный анализ с повторениями (ANOVA: Two Factor With Replication);
- скользящее среднее (Moving Average);
- экспоненциальное сглаживание (Exponential Smoothing);
- анализ Фурье (Fourier Analysis).
Для доступа к процедурам Пакета анализа необходимо в меню Сервис (Tools) щелкнуть указателем мыши на строке Анализ данных (Data Analysis). Откроется диалоговое окно с соответствующим названием, в котором перечислены процедуры статистического анализа данных (рис. 1).
Рис.1. Диалоговое окно Анализ данных
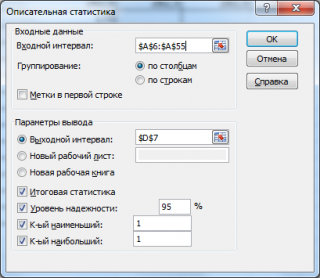
Для того чтобы запустить в работу нужную статистическую процедуру, нужно выделить ее указателем мыши и щелкнуть на кнопке ОК. На экране появится диалоговое окно вызванной процедуры. На рис. 2 для примера показано диалоговое окно процедуры Описательная статистика (Descriptive statistics).
Рис.2. Диалоговое окно процедуры Описательная статистика
Диалоговое окно каждой процедуры содержит элементы управления: поля ввода, раскрывающиеся списки, переключатели, флажки и т. п. Эти элементы позволяют задать нужные параметры используемой процедуры. Некоторые элементы управления имеют специфический характер, присущий одной процедуре или небольшой группе процедур. Назначение таких элементов управления будет рассмотрено при описании соответствующих процедур. Другие элементы управления присутствуют в диалоговых окнах почти всех статистических процедур.
К числу общих для большинства процедур элементов управления относятся:
- поле ввода Входной интервал (Input Range). В это поле вводится ссылка на диапазон, содержащий статистические данные, подлежащие обработке. Входной диапазон может быть столбцом пли группой столбцов (строкой или группой строк);
- переключатель Группирование (Grouped By). В том случае, когда входной диапазон представляет собой столбец или группу столбцов, переключатель устанавливается в положение по столбцам (Columns). Если же входной диапазон представляет собой строку или группу строк, то переключатель устанавливается в положение по строкам (Rows). Более точным названием этого переключателя было бы название Расположение;
- флажок Метки (Labels in First Row). Флажок устанавливается в тех случаях, когда первая строка (первый столбец) входного диапазона содержит заголовки. Если такие заголовки отсутствуют, флажок Метки не устанавливают. При этом Excel автоматически создает и выводит на экран стандартные названия для данных выходного диапазона (Столбец1, Столбец2,… или Строка 1. Строка2,…);
- переключатели Выходной интервал/Новый рабочий лист/Новая книга (Output Range/New Worksheet/New Workbook). Эти переключатели определяют место вывода таблицы, содержащей результаты реализации статистической процедуры. В группе может быть выбран только одни переключатель.
При выборе переключателя Выходной интервал таблица результатов решения выводится на тот же рабочий лист, на котором находятся исходные данные. Справа от переключателя открывается поле ввода, в которое надо ввести ссылку на левую верхнюю ячейку таблицы результатов. Если возникает опасность наложения таблицы результатов на уже заполненные ячейки, на экране появляется сообщение о такой опасности. В ответ на это сообщение пользователь должен разрешить удаление старых данных и вывод на их место новых.
В положении Новый рабочий лист открывается новый лист рабочей книги. На этот лист, начиная с ячейки А1, и выводится таблица результатов решения. Справа от переключателя имеется поле ввода, в которое в случае необходимости можно ввести имя нового рабочего листа. При выборе переключателя Новая рабочая книга открывается новая рабочая книга. На первый лист этой новой книги, начиная с ячейки А1, выводится таблица результатов решения.
Следует заметить, что результаты;, получаемые с помощью статистических процедур Пакета анализа, не имеют постоянной связи с исходными данными — в случае изменения исходных данных результаты решения автоматически не изменяются. В том случае, когда необходимо получить результаты, автоматически изменяющиеся вместе с исходными данными, нужно использовать подходящие статистические функции библиотеки встроенных функций.
Эффективным и очень удобным в использовании средством парного регрессионного анализа и анализа временных рядов является процедура Добавить линию тренда (Add Trendline), входящая в комплекс графических средств Excel.
Статистические функции библиотеки встроенных функций Excel
Табличный процессор Excel имеет библиотеку встроенных функции рабочего листа (Worksheet function). Одним из разделов этой библиотеки является раздел Статистические функции. В этот раздел входят 83 функции, предназначенные для решения некоторых наиболее востребованных задач теории вероятностей и математической статистики.
Аргументы статистических функций должны быть числами или ссылками на диапазоны, которые содержат числа Если аргумент, который является массивом или ссылкой, содержит тексты, логические значения или пустые ячейки, то такие значения игнорируются, однако ячейки с нулевыми значениями учитываются.
Когда в качестве какого-либо аргумента встроенной статистической функции введен текст, функция выдает сообщение об ошибке #ЗНАЧ! (#VALUE!). Если в качестве аргумента, который по определению должен быть целым числом, введено число не целое, Excel использует в качестве аргумента целую часть этот числа. Никакие сообщения об этом «несанкционированном округлении» на экран не выводятся.
Содержание
- Статистические функции
- МАКС
- МИН
- СРЗНАЧ
- СРЗНАЧЕСЛИ
- МОДА.ОДН
- МЕДИАНА
- СТАНДОТКЛОН
- НАИБОЛЬШИЙ
- НАИМЕНЬШИЙ
- РАНГ.СР
- Вопросы и ответы
Статистическая обработка данных – это сбор, упорядочивание, обобщение и анализ информации с возможностью определения тенденции и прогноза по изучаемому явлению. В Excel есть огромное количество инструментов, которые помогают проводить исследования в данной области. Последние версии этой программы в плане возможностей практически ничем не уступают специализированным приложениям в области статистики. Главными инструментами для выполнения расчетов и анализа являются функции. Давайте изучим общие особенности работы с ними, а также подробнее остановимся на отдельных наиболее полезных инструментах.
Статистические функции
Как и любые другие функции в Экселе, статистические функции оперируют аргументами, которые могут иметь вид постоянных чисел, ссылок на ячейки или массивы.
Выражения можно вводить вручную в определенную ячейку или в строку формул, если хорошо знать синтаксис конкретного из них. Но намного удобнее воспользоваться специальным окном аргументов, которое содержит подсказки и уже готовые поля для ввода данных. Перейти в окно аргумента статистических выражений можно через «Мастер функций» или с помощью кнопок «Библиотеки функций» на ленте.
Запустить Мастер функций можно тремя способами:
- Кликнуть по пиктограмме «Вставить функцию» слева от строки формул.
- Находясь во вкладке «Формулы», кликнуть на ленте по кнопке «Вставить функцию» в блоке инструментов «Библиотека функций».
- Набрать на клавиатуре сочетание клавиш Shift+F3.
При выполнении любого из вышеперечисленных вариантов откроется окно «Мастера функций».
Затем нужно кликнуть по полю «Категория» и выбрать значение «Статистические».
После этого откроется список статистических выражений. Всего их насчитывается более сотни. Чтобы перейти в окно аргументов любого из них, нужно просто выделить его и нажать на кнопку «OK».
Для того, чтобы перейти к нужным нам элементам через ленту, перемещаемся во вкладку «Формулы». В группе инструментов на ленте «Библиотека функций» кликаем по кнопке «Другие функции». В открывшемся списке выбираем категорию «Статистические». Откроется перечень доступных элементов нужной нам направленности. Для перехода в окно аргументов достаточно кликнуть по одному из них.
Урок: Мастер функций в Excel
МАКС
Оператор МАКС предназначен для определения максимального числа из выборки. Он имеет следующий синтаксис:
=МАКС(число1;число2;…)
В поля аргументов нужно ввести диапазоны ячеек, в которых находится числовой ряд. Наибольшее число из него эта формула выводит в ту ячейку, в которой находится сама.
МИН
По названию функции МИН понятно, что её задачи прямо противоположны предыдущей формуле – она ищет из множества чисел наименьшее и выводит его в заданную ячейку. Имеет такой синтаксис:
=МИН(число1;число2;…)
СРЗНАЧ
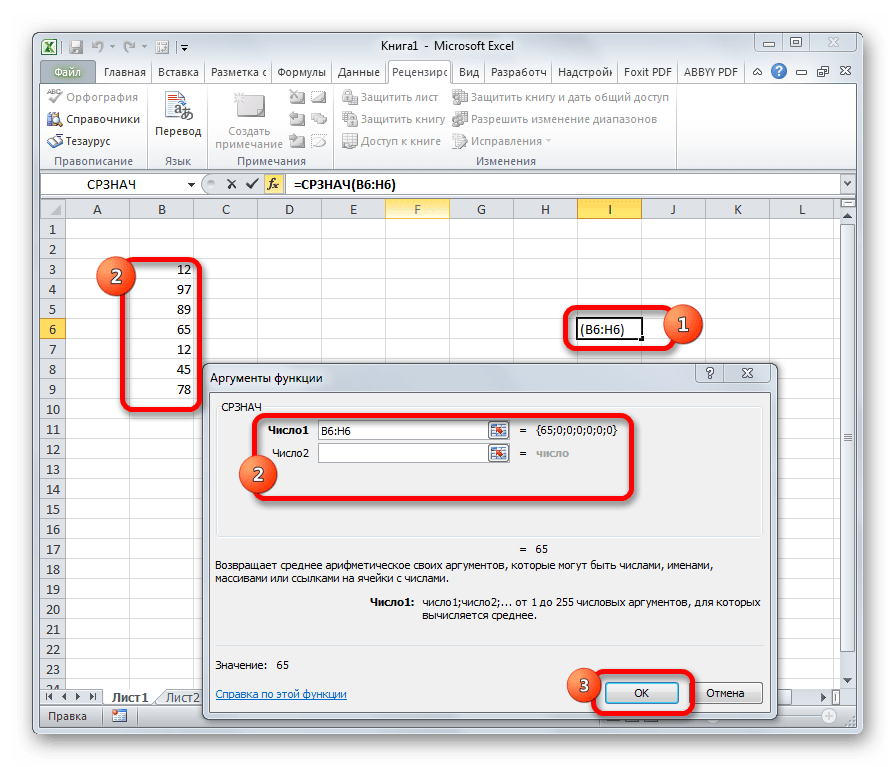
Функция СРЗНАЧ ищет число в указанном диапазоне, которое ближе всего находится к среднему арифметическому значению. Результат этого расчета выводится в отдельную ячейку, в которой и содержится формула. Шаблон у неё следующий:
=СРЗНАЧ(число1;число2;…)
СРЗНАЧЕСЛИ
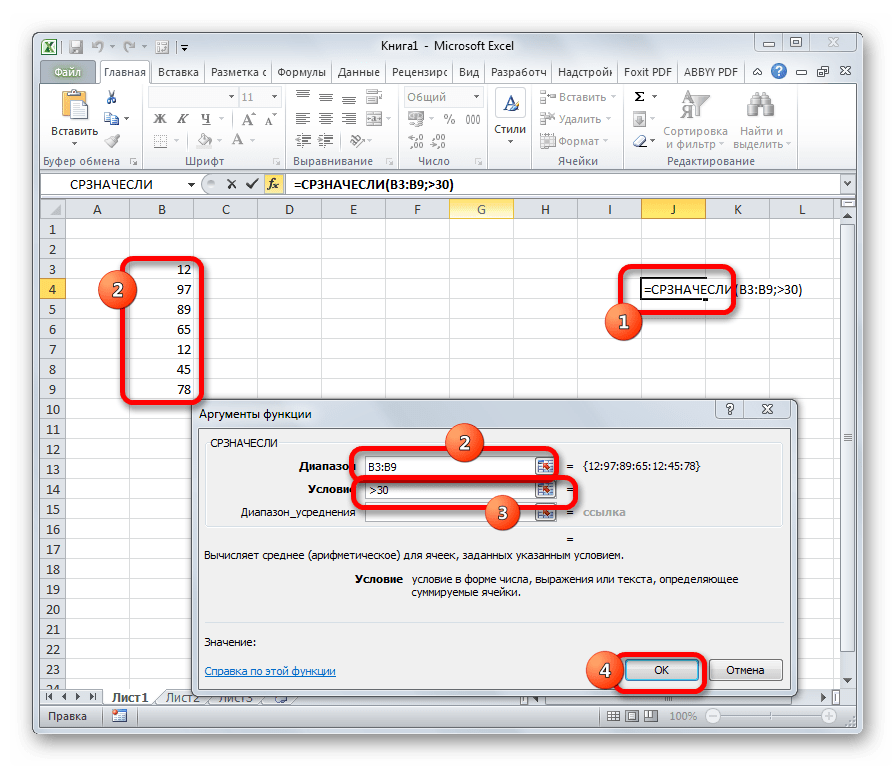
Функция СРЗНАЧЕСЛИ имеет те же задачи, что и предыдущая, но в ней существует возможность задать дополнительное условие. Например, больше, меньше, не равно определенному числу. Оно задается в отдельном поле для аргумента. Кроме того, в качестве необязательного аргумента может быть добавлен диапазон усреднения. Синтаксис следующий:
=СРЗНАЧЕСЛИ(число1;число2;…;условие;[диапазон_усреднения])
МОДА.ОДН
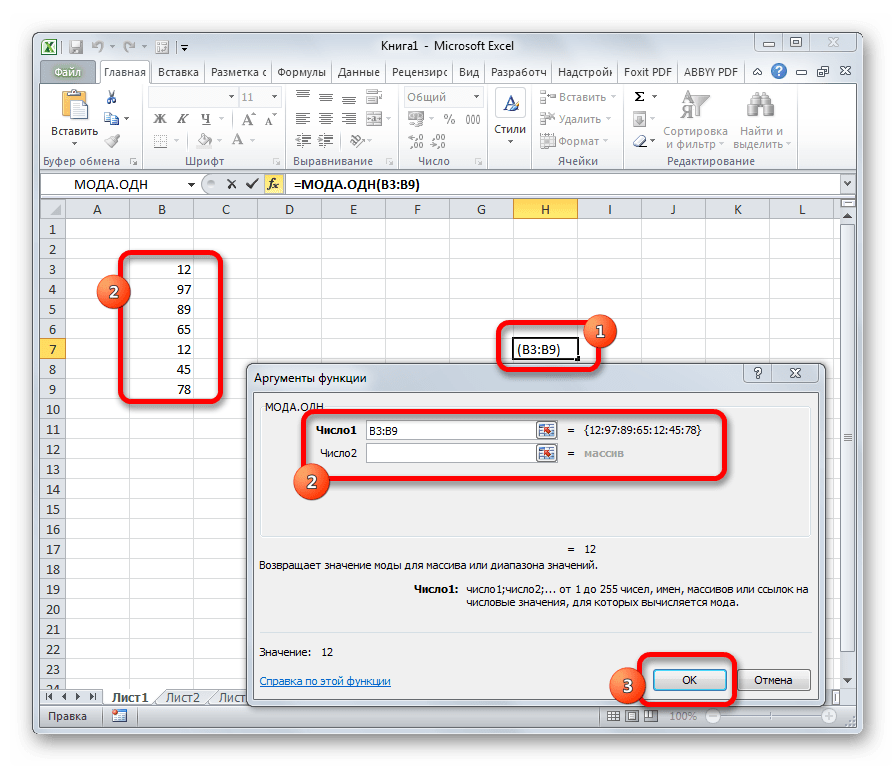
Формула МОДА.ОДН выводит в ячейку то число из набора, которое встречается чаще всего. В старых версиях Эксель существовала функция МОДА, но в более поздних она была разбита на две: МОДА.ОДН (для отдельных чисел) и МОДА.НСК(для массивов). Впрочем, старый вариант тоже остался в отдельной группе, в которой собраны элементы из прошлых версий программы для обеспечения совместимости документов.
=МОДА.ОДН(число1;число2;…)
=МОДА.НСК(число1;число2;…)
МЕДИАНА
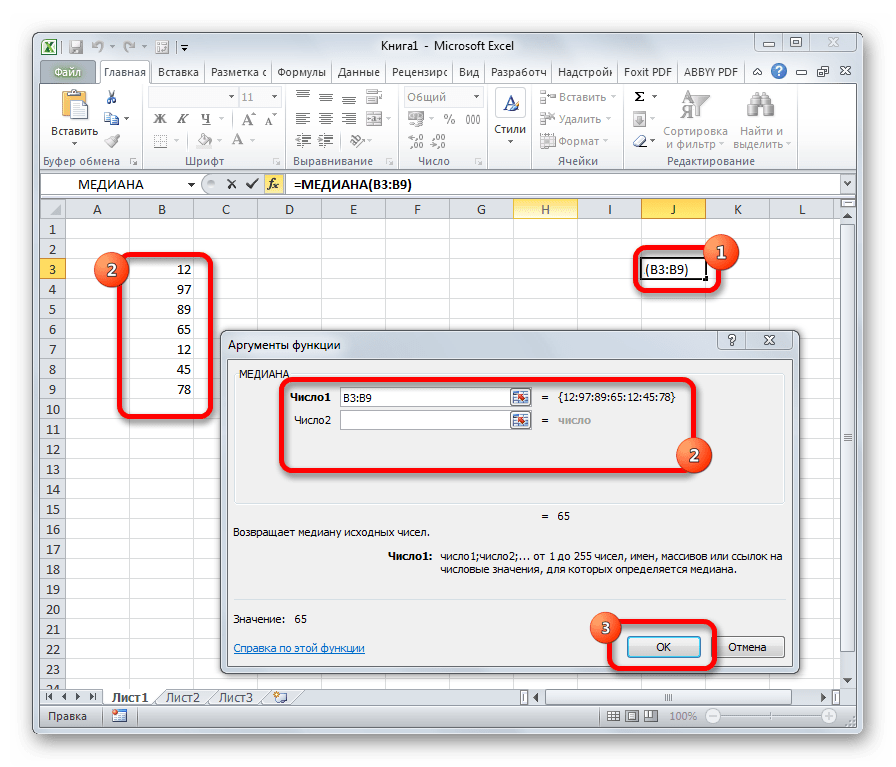
Оператор МЕДИАНА определяет среднее значение в диапазоне чисел. То есть, устанавливает не среднее арифметическое, а просто среднюю величину между наибольшим и наименьшим числом области значений. Синтаксис выглядит так:
=МЕДИАНА(число1;число2;…)
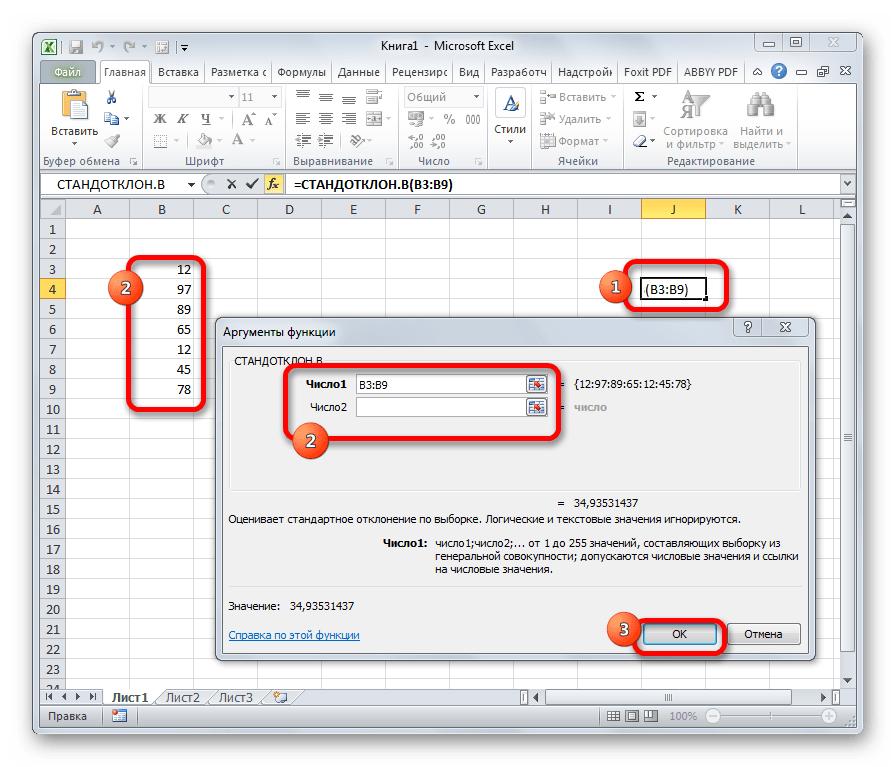
СТАНДОТКЛОН
Формула СТАНДОТКЛОН так же, как и МОДА является пережитком старых версий программы. Сейчас используются современные её подвиды – СТАНДОТКЛОН.В и СТАНДОТКЛОН.Г. Первая из них предназначена для вычисления стандартного отклонения выборки, а вторая – генеральной совокупности. Данные функции используются также для расчета среднего квадратичного отклонения. Синтаксис их следующий:
=СТАНДОТКЛОН.В(число1;число2;…)
=СТАНДОТКЛОН.Г(число1;число2;…)
Урок: Формула среднего квадратичного отклонения в Excel
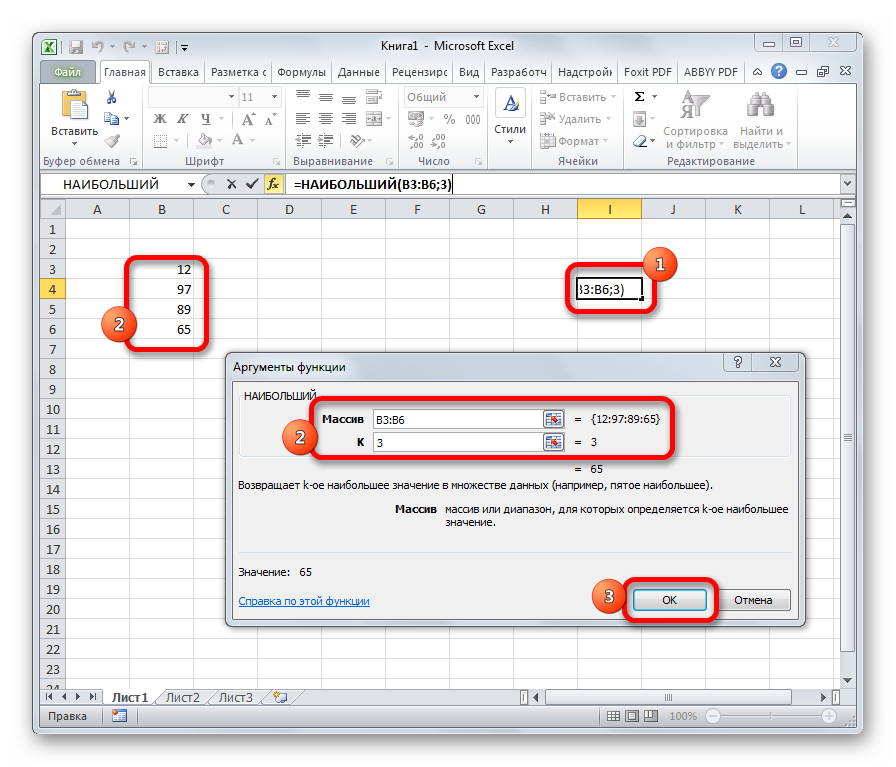
НАИБОЛЬШИЙ
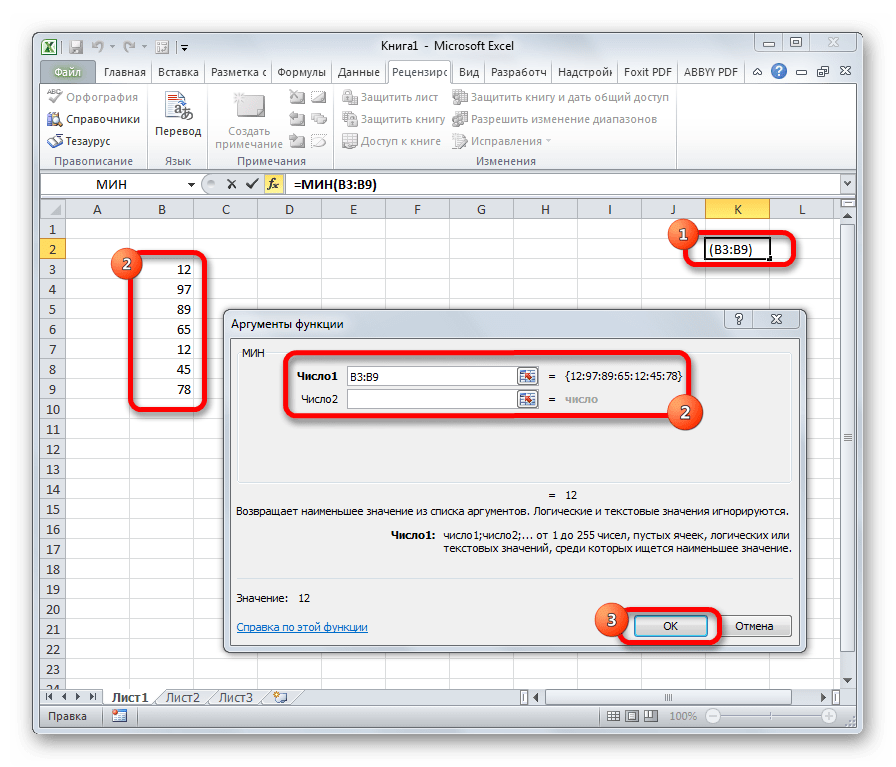
Данный оператор показывает в выбранной ячейке указанное в порядке убывания число из совокупности. То есть, если мы имеем совокупность 12,97,89,65, а аргументом позиции укажем 3, то функция в ячейку вернет третье по величине число. В данном случае, это 65. Синтаксис оператора такой:
=НАИБОЛЬШИЙ(массив;k)
В данном случае, k — это порядковый номер величины.
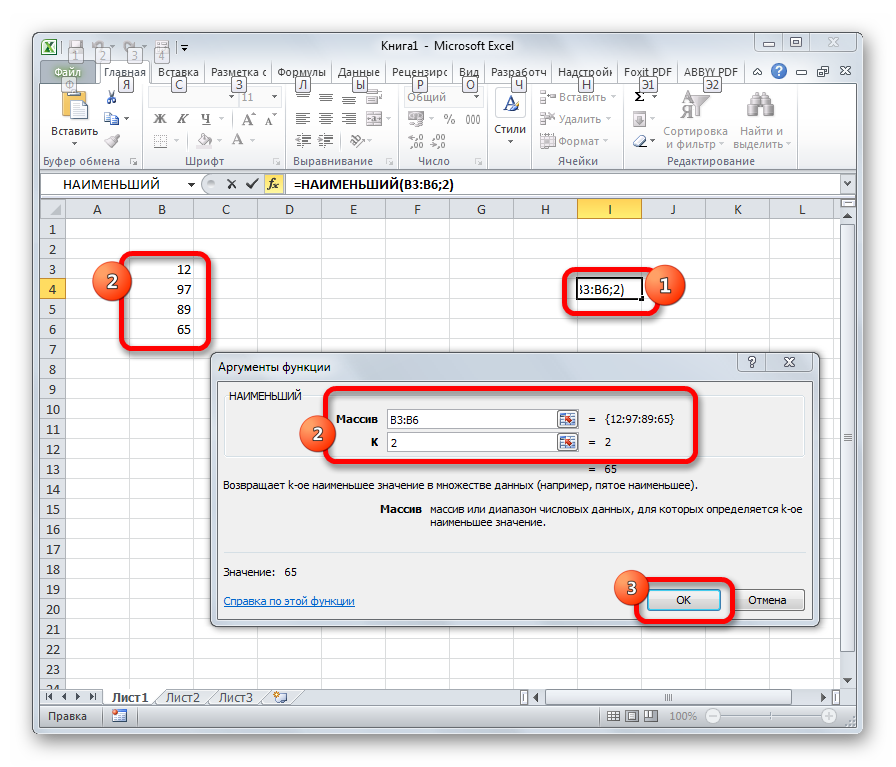
НАИМЕНЬШИЙ
Данная функция является зеркальным отражением предыдущего оператора. В ней также вторым аргументом является порядковый номер числа. Вот только в данном случае порядок считается от меньшего. Синтаксис такой:
=НАИМЕНЬШИЙ(массив;k)
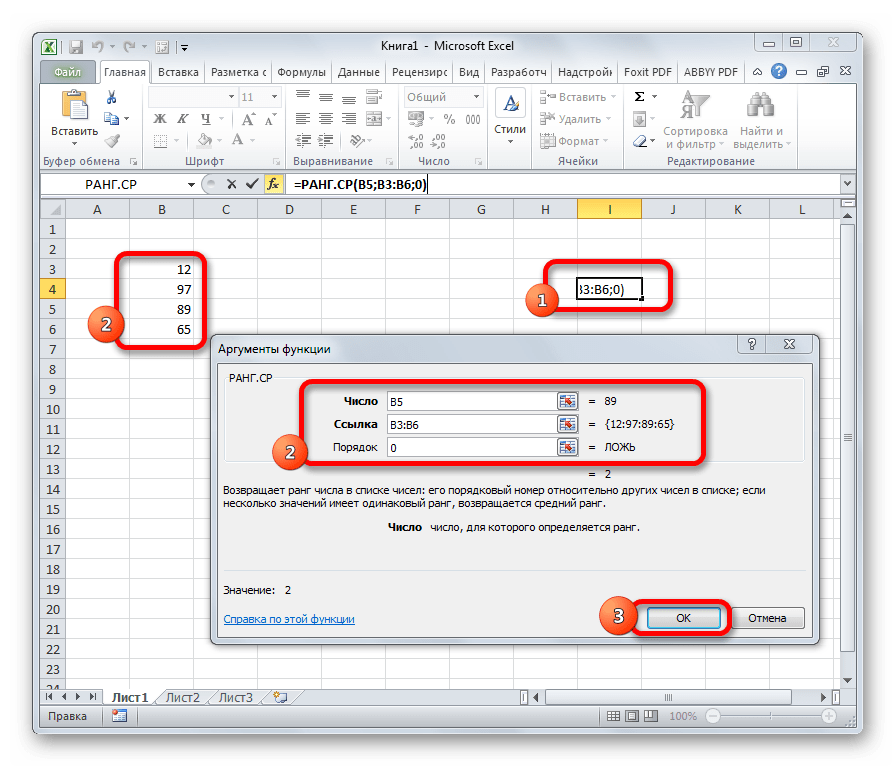
РАНГ.СР
Эта функция имеет действие, обратное предыдущим. В указанную ячейку она выдает порядковый номер конкретного числа в выборке по условию, которое указано в отдельном аргументе. Это может быть порядок по возрастанию или по убыванию. Последний установлен по умолчанию, если поле «Порядок» оставить пустым или поставить туда цифру 0. Синтаксис этого выражения выглядит следующим образом:
=РАНГ.СР(число;массив;порядок)
Выше были описаны только самые популярные и востребованные статистические функции в Экселе. На самом деле их в разы больше. Тем не менее, основной принцип действий у них похожий: обработка массива данных и возврат в указанную ячейку результата вычислительных действий.
Рассмотрим инструмент Описательная статистика, входящий в надстройку Пакет Анализа. Рассчитаем показатели выборки: среднее, медиана, мода, дисперсия, стандартное отклонение и др.
Задача
описательной статистики
(descriptive statistics) заключается в том, чтобы с использованием математических инструментов свести сотни значений
выборки
к нескольким итоговым показателям, которые дают представление о
выборке
.В качестве таких статистических показателей используются:
среднее
,
медиана
,
мода
,
дисперсия, стандартное отклонение
и др.
Опишем набор числовых данных с помощью определенных показателей. Для чего нужны эти показатели? Эти показатели позволят сделать определенные
статистические выводы о распределении
, из которого была взята
выборка
. Например, если у нас есть
выборка
значений толщины трубы, которая изготавливается на определенном оборудовании, то на основании анализа этой
выборки
мы сможем сделать, с некой определенной вероятностью, заключение о состоянии процесса изготовления.
Содержание статьи:
- Надстройка Пакет анализа;
-
Среднее выборки
;
-
Медиана выборки
;
-
Мода выборки
;
-
Мода и среднее значение
;
-
Дисперсия выборки
;
-
Стандартное отклонение выборки
;
-
Стандартная ошибка
;
-
Ассиметричность
;
-
Эксцесс выборки
;
-
Уровень надежности
.
Надстройка Пакет анализа
Для вычисления статистических показателей одномерных
выборок
, используем
надстройку Пакет анализа
. Затем, все показатели рассчитанные надстройкой, вычислим с помощью встроенных функций MS EXCEL.
СОВЕТ
: Подробнее о других инструментах надстройки
Пакет анализа
и ее подключении – читайте в статье
Надстройка Пакет анализа MS EXCEL
.
Выборку
разместим на
листе
Пример
в файле примера
в диапазоне
А6:А55
(50 значений).
Примечание
: Для удобства написания формул для диапазона
А6:А55
создан
Именованный диапазон
Выборка.
В диалоговом окне
Анализ данных
выберите инструмент
Описательная статистика
.
После нажатия кнопки
ОК
будет выведено другое диалоговое окно,
в котором нужно указать:
входной интервал
(Input Range) – это диапазон ячеек, в котором содержится массив данных. Если в указанный диапазон входит текстовый заголовок набора данных, то нужно поставить галочку в поле
Метки в первой строке (
Labels
in
first
row
).
В этом случае заголовок будет выведен в
Выходном интервале.
Пустые ячейки будут проигнорированы, поэтому нулевые значения необходимо обязательно указывать в ячейках, а не оставлять их пустыми;
выходной интервал
(Output Range). Здесь укажите адрес верхней левой ячейки диапазона, в который будут выведены статистические показатели;
Итоговая статистика (
Summary
Statistics
)
. Поставьте галочку напротив этого поля – будут выведены основные показатели выборки:
среднее, медиана, мода, стандартное отклонение
и др.;-
Также можно поставить галочки напротив полей
Уровень надежности (
Confidence
Level
for
Mean
)
,
К-й наименьший
(Kth Largest) и
К-й наибольший
(Kth Smallest).
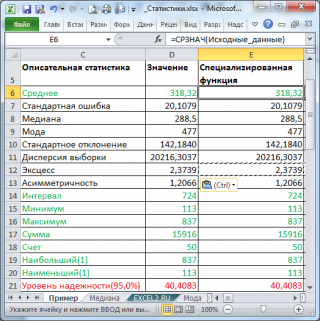
В результате будут выведены следующие статистические показатели:
Все показатели выведены в виде значений, а не формул. Если массив данных изменился, то необходимо перезапустить расчет.
Если во
входном интервале
указать ссылку на несколько столбцов данных, то будет рассчитано соответствующее количество наборов показателей. Такой подход позволяет сравнить несколько наборов данных. При сравнении нескольких наборов данных используйте заголовки (включите их во
Входной интервал
и установите галочку в поле
Метки в первой строке
). Если наборы данных разной длины, то это не проблема — пустые ячейки будут проигнорированы.
Зеленым цветом на картинке выше и в
файле примера
выделены показатели, которые не требуют особого пояснения. Для большинства из них имеется специализированная функция:
Интервал
(Range) — разница между максимальным и минимальным значениями;
Минимум
(Minimum) – минимальное значение в диапазоне ячеек, указанном во
Входном интервале
(см.статью про функцию
МИН()
);
Максимум
(Maximum)– максимальное значение (см.статью про функцию
МАКС()
);
Сумма
(Sum) – сумма всех значений (см.статью про функцию
СУММ()
);
Счет
(Count) – количество значений во
Входном интервале
(пустые ячейки игнорируются, см.статью про функцию
СЧЁТ()
);
Наибольший
(Kth Largest) – выводится К-й наибольший. Например, 1-й наибольший – это максимальное значение (см.статью про функцию
НАИБОЛЬШИЙ()
);
Наименьший
(Kth Smallest) – выводится К-й наименьший. Например, 1-й наименьший – это минимальное значение (см.статью про функцию
НАИМЕНЬШИЙ()
).
Ниже даны подробные описания остальных показателей.
Среднее выборки
Среднее
(mean, average) или
выборочное среднее
или
среднее выборки
(sample average) представляет собой
арифметическое среднее
всех значений массива. В MS EXCEL для вычисления среднего выборки используется функция
СРЗНАЧ()
.
Выборочное среднее
является «хорошей» (несмещенной и эффективной) оценкой
математического ожидания
случайной величины (подробнее см. статью
Среднее и Математическое ожидание в MS EXCEL
).
Медиана выборки
Медиана
(Median) – это число, которое является серединой множества чисел (в данном случае выборки): половина чисел множества больше, чем
медиана
, а половина чисел меньше, чем
медиана
. Для определения
медианы
необходимо сначала
отсортировать множество чисел
. Например,
медианой
для чисел 2, 3, 3,
4
, 5, 7, 10 будет 4.
Если множество содержит четное количество чисел, то вычисляется
среднее
для двух чисел, находящихся в середине множества. Например,
медианой
для чисел 2, 3,
3
,
5
, 7, 10 будет 4, т.к. (3+5)/2.
Если имеется длинный хвост распределения, то
Медиана
лучше, чем
среднее значение
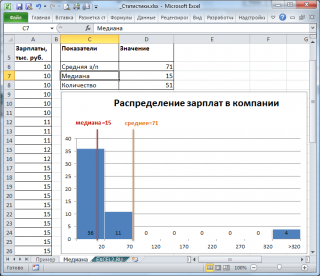
, отражает «типичное» или «центральное» значение. Например, рассмотрим несправедливое распределение зарплат в компании, в которой руководство получает существенно больше, чем основная масса сотрудников.
Очевидно, что средняя зарплата (71 тыс. руб.) не отражает тот факт, что 86% сотрудников получает не более 30 тыс. руб. (т.е. 86% сотрудников получает зарплату в более, чем в 2 раза меньше средней!). В то же время медиана (15 тыс. руб.) показывает, что
как минимум
у 50% сотрудников зарплата меньше или равна 15 тыс. руб.
Для определения
медианы
в MS EXCEL существует одноименная функция
МЕДИАНА()
, английский вариант — MEDIAN().
Медиану
также можно вычислить с помощью формул
=КВАРТИЛЬ.ВКЛ(Выборка;2) =ПРОЦЕНТИЛЬ.ВКЛ(Выборка;0,5).
Подробнее о
медиане
см. специальную статью
Медиана в MS EXCEL
.
СОВЕТ
: Подробнее про
квартили
см. статью, про
перцентили (процентили)
см. статью.
Мода выборки
Мода
(Mode) – это наиболее часто встречающееся (повторяющееся) значение в
выборке
. Например, в массиве (1; 1;
2
;
2
;
2
; 3; 4; 5) число 2 встречается чаще всего – 3 раза. Значит, число 2 – это
мода
. Для вычисления
моды
используется функция
МОДА()
, английский вариант MODE().
Примечание
: Если в массиве нет повторяющихся значений, то функция вернет значение ошибки #Н/Д. Это свойство использовано в статье
Есть ли повторы в списке?
Начиная с
MS EXCEL 2010
вместо функции
МОДА()
рекомендуется использовать функцию
МОДА.ОДН()
, которая является ее полным аналогом. Кроме того, в MS EXCEL 2010 появилась новая функция
МОДА.НСК()
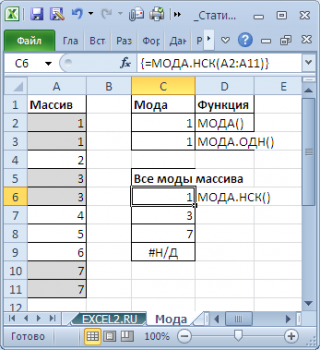
, которая возвращает несколько наиболее часто повторяющихся значений (если количество их повторов совпадает). НСК – это сокращение от слова НеСКолько.
Например, в массиве (1; 1;
2
;
2
;
2
; 3;
4
;
4
;
4
; 5) числа 2 и 4 встречаются наиболее часто – по 3 раза. Значит, оба числа являются
модами
. Функции
МОДА.ОДН()
и
МОДА()
вернут значение 2, т.к. 2 встречается первым, среди наиболее повторяющихся значений (см.
файл примера
, лист
Мода
).
Чтобы исправить эту несправедливость и была введена функция
МОДА.НСК()
, которая выводит все
моды
. Для этого ее нужно ввести как
формулу массива
.
Как видно из картинки выше, функция
МОДА.НСК()
вернула все три
моды
из массива чисел в диапазоне
A2:A11
: 1; 3 и 7. Для этого, выделите диапазон
C6:C9
, в
Строку формул
введите формулу
=МОДА.НСК(A2:A11)
и нажмите
CTRL+SHIFT+ENTER
. Диапазон
C
6:
C
9
охватывает 4 ячейки, т.е. количество выделяемых ячеек должно быть больше или равно количеству
мод
. Если ячеек больше чем м
о
д, то избыточные ячейки будут заполнены значениями ошибки #Н/Д. Если
мода
только одна, то все выделенные ячейки будут заполнены значением этой
моды
.
Теперь вспомним, что мы определили
моду
для выборки, т.е. для конечного множества значений, взятых из
генеральной совокупности
. Для
непрерывных случайных величин
вполне может оказаться, что выборка состоит из массива на подобие этого (0,935; 1,211; 2,430; 3,668; 3,874; …), в котором может не оказаться повторов и функция
МОДА()
вернет ошибку.
Даже в нашем массиве с
модой
, которая была определена с помощью
надстройки Пакет анализа
, творится, что-то не то. Действительно,
модой
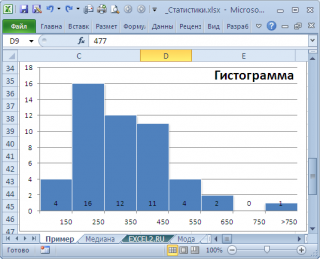
нашего массива значений является число 477, т.к. оно встречается 2 раза, остальные значения не повторяются. Но, если мы посмотрим на
гистограмму распределения
, построенную для нашего массива, то увидим, что 477 не принадлежит интервалу наиболее часто встречающихся значений (от 150 до 250).
Проблема в том, что мы определили
моду
как наиболее часто встречающееся значение, а не как наиболее вероятное. Поэтому,
моду
в учебниках статистики часто определяют не для выборки (массива), а для функции распределения. Например, для
логнормального распределения
мода
(наиболее вероятное значение непрерывной случайной величины х), вычисляется как
exp
(
m
—
s
2
)
, где m и s параметры этого распределения.
Понятно, что для нашего массива число 477, хотя и является наиболее часто повторяющимся значением, но все же является плохой оценкой для
моды
распределения, из которого взята
выборка
(наиболее вероятного значения или для которого плотность вероятности распределения максимальна).
Для того, чтобы получить оценку
моды
распределения, из
генеральной совокупности
которого взята
выборка
, можно, например, построить
гистограмму
. Оценкой для
моды
может служить интервал наиболее часто встречающихся значений (самого высокого столбца). Как было сказано выше, в нашем случае это интервал от 150 до 250.
Вывод
: Значение
моды
для
выборки
, рассчитанное с помощью функции
МОДА()
, может ввести в заблуждение, особенно для небольших выборок. Эта функция эффективна, когда случайная величина может принимать лишь несколько дискретных значений, а размер
выборки
существенно превышает количество этих значений.
Например, в рассмотренном примере о распределении заработных плат (см. раздел статьи выше, о Медиане),
модой
является число 15 (17 значений из 51, т.е. 33%). В этом случае функция
МОДА()
дает хорошую оценку «наиболее вероятного» значения зарплаты.
Примечание
: Строго говоря, в примере с зарплатой мы имеем дело скорее с
генеральной совокупностью
, чем с
выборкой
. Т.к. других зарплат в компании просто нет.
О вычислении
моды
для распределения
непрерывной случайной величины
читайте статью
Мода в MS EXCEL
.
Мода и среднее значение
Не смотря на то, что
мода
– это наиболее вероятное значение случайной величины (вероятность выбрать это значение из
Генеральной совокупности
максимальна), не следует ожидать, что
среднее значение
обязательно будет близко к
моде
.
Примечание
:
Мода
и
среднее
симметричных распределений совпадает (имеется ввиду симметричность
плотности распределения
).
Представим, что мы бросаем некий «неправильный» кубик, у которого на гранях имеются значения (1; 2; 3; 4; 6; 6), т.е. значения 5 нет, а есть вторая 6.
Модой
является 6, а среднее значение – 3,6666.
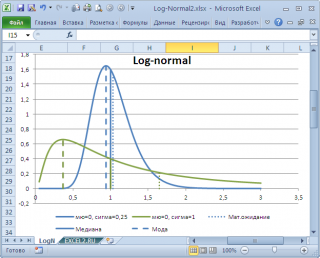
Другой пример. Для
Логнормального распределения
LnN(0;1)
мода
равна =EXP(m-s2)= EXP(0-1*1)=0,368, а
среднее значение
1,649.
Дисперсия выборки
Дисперсия выборки
или
выборочная дисперсия (
sample
variance
) характеризует разброс значений в массиве, отклонение от
среднего
.
Из формулы №1 видно, что
дисперсия выборки
это сумма квадратов отклонений каждого значения в массиве
от среднего
, деленная на размер выборки минус 1.
В MS EXCEL 2007 и более ранних версиях для вычисления
дисперсии выборки
используется функция
ДИСП()
. С версии MS EXCEL 2010 рекомендуется использовать ее аналог — функцию
ДИСП.В()
.
Дисперсию
можно также вычислить непосредственно по нижеуказанным формулам (см.
файл примера
):
=КВАДРОТКЛ(Выборка)/(СЧЁТ(Выборка)-1) =(СУММКВ(Выборка)-СЧЁТ(Выборка)*СРЗНАЧ(Выборка)^2)/ (СЧЁТ(Выборка)-1)
– обычная формула
=СУММ((Выборка -СРЗНАЧ(Выборка))^2)/ (СЧЁТ(Выборка)-1)
–
формула массива
Дисперсия выборки
равна 0, только в том случае, если все значения равны между собой и, соответственно, равны
среднему значению
.
Чем больше величина
дисперсии
, тем больше разброс значений в массиве относительно
среднего
.
Размерность
дисперсии
соответствует квадрату единицы измерения исходных значений. Например, если значения в выборке представляют собой измерения веса детали (в кг), то размерность
дисперсии
будет кг
2
. Это бывает сложно интерпретировать, поэтому для характеристики разброса значений чаще используют величину равную квадратному корню из
дисперсии – стандартное отклонение
.
Подробнее о
дисперсии
см. статью
Дисперсия и стандартное отклонение в MS EXCEL
.
Стандартное отклонение выборки
Стандартное отклонение выборки
(Standard Deviation), как и
дисперсия
, — это мера того, насколько широко разбросаны значения в выборке
относительно их среднего
.
По определению,
стандартное отклонение
равно квадратному корню из
дисперсии
:
Стандартное отклонение
не учитывает величину значений в
выборке
, а только степень рассеивания значений вокруг их
среднего
. Чтобы проиллюстрировать это приведем пример.
Вычислим стандартное отклонение для 2-х
выборок
: (1; 5; 9) и (1001; 1005; 1009). В обоих случаях, s=4. Очевидно, что отношение величины стандартного отклонения к значениям массива у
выборок
существенно отличается.
В MS EXCEL 2007 и более ранних версиях для вычисления
Стандартного отклонения выборки
используется функция
СТАНДОТКЛОН()
. С версии MS EXCEL 2010 рекомендуется использовать ее аналог
СТАНДОТКЛОН.В()
.
Стандартное отклонение
можно также вычислить непосредственно по нижеуказанным формулам (см.
файл примера
):
=КОРЕНЬ(КВАДРОТКЛ(Выборка)/(СЧЁТ(Выборка)-1)) =КОРЕНЬ((СУММКВ(Выборка)-СЧЁТ(Выборка)*СРЗНАЧ(Выборка)^2)/(СЧЁТ(Выборка)-1))
Подробнее о
стандартном отклонении
см. статью
Дисперсия и стандартное отклонение в MS EXCEL
.
Стандартная ошибка
В
Пакете анализа
под термином
стандартная ошибка
имеется ввиду
Стандартная ошибка среднего
(Standard Error of the Mean, SEM).
Стандартная ошибка среднего
— это оценка
стандартного отклонения
распределения
выборочного среднего
.
Примечание
: Чтобы разобраться с понятием
Стандартная ошибка среднего
необходимо прочитать о
выборочном распределении
(см. статью
Статистики, их выборочные распределения и точечные оценки параметров распределений в MS EXCEL
) и статью про
Центральную предельную теорему
.
Стандартное отклонение распределения выборочного среднего
вычисляется по формуле σ/√n, где n — объём
выборки, σ — стандартное отклонение исходного
распределения, из которого взята
выборка
. Т.к. обычно
стандартное отклонение
исходного распределения неизвестно, то в расчетах вместо
σ
используют ее оценку
s
—
стандартное отклонение выборки
. А соответствующая величина s/√n имеет специальное название —
Стандартная ошибка среднего.
Именно эта величина вычисляется в
Пакете анализа.
В MS EXCEL
стандартную ошибку среднего
можно также вычислить по формуле
=СТАНДОТКЛОН.В(Выборка)/ КОРЕНЬ(СЧЁТ(Выборка))
Асимметричность
Асимметричность
или
коэффициент асимметрии
(skewness) характеризует степень несимметричности распределения (
плотности распределения
) относительно его
среднего
.
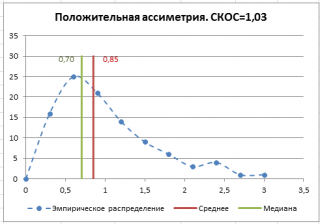
Положительное значение
коэффициента асимметрии
указывает, что размер правого «хвоста» распределения больше, чем левого (относительно среднего). Отрицательная асимметрия, наоборот, указывает на то, что левый хвост распределения больше правого.
Коэффициент асимметрии
идеально симметричного распределения или выборки равно 0.
Примечание
:
Асимметрия выборки
может отличаться расчетного значения асимметрии теоретического распределения. Например,
Нормальное распределение
является симметричным распределением (
плотность его распределения
симметрична относительно
среднего
) и, поэтому имеет асимметрию равную 0. Понятно, что при этом значения в
выборке
из соответствующей
генеральной совокупности
не обязательно должны располагаться совершенно симметрично относительно
среднего
. Поэтому,
асимметрия выборки
, являющейся оценкой
асимметрии распределения
, может отличаться от 0.
Функция
СКОС()
, английский вариант SKEW(), возвращает коэффициент
асимметрии выборки
, являющейся оценкой
асимметрии
соответствующего распределения, и определяется следующим образом:
где n – размер
выборки
, s –
стандартное отклонение выборки
.
В
файле примера на листе СКОС
приведен расчет коэффициента
асимметрии
на примере случайной выборки из
распределения Вейбулла
, которое имеет значительную положительную
асимметрию
при параметрах распределения W(1,5; 1).
Эксцесс выборки
Эксцесс
показывает относительный вес «хвостов» распределения относительно его центральной части.
Для того чтобы определить, что относится к хвостам распределения, а что к его центральной части, можно использовать границы μ +/-
σ
.
Примечание
: Не смотря на старания профессиональных статистиков, в литературе еще попадается определение
Эксцесса
как меры «остроконечности» (peakedness) или сглаженности распределения. Но, на самом деле, значение
Эксцесса
ничего не говорит о форме пика распределения.
Согласно определения,
Эксцесс
равен четвертому
стандартизированному моменту:
Для
нормального распределения
четвертый момент равен 3*σ
4
, следовательно,
Эксцесс
равен 3. Многие компьютерные программы используют для расчетов не сам
Эксцесс
, а так называемый Kurtosis excess, который меньше на 3. Т.е. для
нормального распределения
Kurtosis excess равен 0. Необходимо быть внимательным, т.к. часто не очевидно, какая формула лежит в основе расчетов.
Примечание
: Еще большую путаницу вносит перевод этих терминов на русский язык. Термин Kurtosis происходит от греческого слова «изогнутый», «имеющий арку». Так сложилось, что на русский язык оба термина Kurtosis и Kurtosis excess переводятся как
Эксцесс
(от англ. excess — «излишек»). Например, функция MS EXCEL
ЭКСЦЕСС()
на самом деле вычисляет Kurtosis excess.
Функция
ЭКСЦЕСС()
, английский вариант KURT(), вычисляет на основе значений выборки несмещенную оценку
эксцесса распределения
случайной величины и определяется следующим образом:
Как видно из формулы MS EXCEL использует именно Kurtosis excess, т.е. для выборки из
нормального распределения
формула вернет близкое к 0 значение.
Если задано менее четырех точек данных, то функция
ЭКСЦЕСС()
возвращает значение ошибки #ДЕЛ/0!
Вернемся к
распределениям случайной величины
.
Эксцесс
(Kurtosis excess) для
нормального распределения
всегда равен 0, т.е. не зависит от параметров распределения μ и σ. Для большинства других распределений
Эксцесс
зависит от параметров распределения: см., например,
распределение Вейбулла
или
распределение Пуассона
, для котрого
Эксцесс
= 1/λ.
Уровень надежности
Уровень
надежности
— означает вероятность того, что
доверительный интервал
содержит истинное значение оцениваемого параметра распределения.
Вместо термина
Уровень
надежности
часто используется термин
Уровень доверия
. Про
Уровень надежности
(Confidence Level for Mean) читайте статью
Уровень значимости и уровень надежности в MS EXCEL
.
Задав значение
Уровня
надежности
в окне
надстройки Пакет анализа
, MS EXCEL вычислит половину ширины
доверительного интервала для оценки среднего (дисперсия неизвестна)
.
Тот же результат можно получить по формуле (см.
файл примера
):
=ДОВЕРИТ.СТЬЮДЕНТ(1-0,95;s;n)
s —
стандартное отклонение выборки
, n – объем
выборки
.
Подробнее см. статью про
построение доверительного интервала для оценки среднего (дисперсия неизвестна)
.
В статье рассказывается:
- Суть и методы анализа данных
- Активация и запуск функций анализа данных в Excel
- 4 техники анализа данных в Excel
-
Пройди тест и узнай, какая сфера тебе подходит:
айти, дизайн или маркетинг.Бесплатно от Geekbrains
Анализ данных в Excel не ограничен простыми функциями деления, умножения, суммирования и сведения значений из разных ячеек. Данный программный продукт от Microsoft – это мощный комплекс, позволяющий работать со сводными таблицами, подтягивать информацию из внешних отчетов, интерпретировать ее, выстраивая наглядные диаграммы и графики.
Чтобы начать работать с данным блоком функций, их нужно активировать в Excel. Никаких сложностей на подготовительном этапе возникнуть не должно – всё делается довольно просто. С аналитикой чуть посложнее, но справиться можно. О том, как выполняется анализ данных в Excel, вы узнаете из нашего материала.
Суть и методы анализа данных
Американский учёный-статистик Джон Тьюки в 1961 году сформулировал определение анализа данных. Под ним он подразумевал как сами процедуры анализа, так и методы интерпретации результатов этих процедур, а также способы планирования сбора данных в целях упрощения и уточнения анализа и результаты математической статистики, используемые для анализа.
В связи с этим анализ данных представляет собой деятельность по извлечению крупных неструктурированных данных из самых разных источников, а также их реорганизацию в информацию, которая может быть использована в целях:
- ответа на вопросы;
- проверки гипотез;
- принятия решений;
- опровержения теорий.
Есть несколько способов анализа данных, которые распространяются на многочисленные области, от маркетинга до науки. Можно выделить несколько базовых вариантов:
Сбор данных
Data Mining – это анализ больших информационных объемов в целях получения прежде неоткрытых, полезных моделей данных, нестандартных данных, а также выявления зависимостей. Стоит упомянуть, что в качестве главной задачи выступает извлечение не самих данных, а шаблонов и знаний из больших информационных объемов.
Анализ данных производится на основе различных методов информатики, в том числе систем искусственного интеллекта, машинного обучения, статистики и баз данных.
Шаблоны, которые извлекаются посредством интеллектуального анализа данных, могут определяться как сводка входных данных. Они в свою очередь могут быть применены в последующем анализе либо для извлечения более детализированных результатов прогнозирования системой поддержки принятия решений.
Скачать файл
Бизнес-аналитика
Суть бизнес-аналитики заключается в сборе и трансформации больших объемов неструктурированных бизнес-данных, что, в свою очередь, необходимо для упрощения определения, разработки и формирования новых стратегических бизнес-возможностей.
Иными словами, главная задача бизнес-аналитики — сделать процесс интерпретации больших объемов данных более простым, чтобы выявлять новые возможности. Все это способствует разработке результативной стратегии, базирующейся на концепциях, которые могут сформировать конкурентное преимущество на рынке и стабилизировать компанию в долгосрочной перспективе.
Статистический анализ
Статистику можно определить как изучение произведенного сбора, анализа, интерпретации, представления и организации данных.
В процессе анализа данных применяют 2 базовых метода статистики:
- Описательная статистика
Данная разновидность статистики предполагает суммирование данных от всей совокупности или выборки посредством числовых дескрипторов. В качестве этих дескрипторов выступают:
- среднее значение, стандартное отклонение для непрерывных данных;
- частота, процент для категориальных данных.
Топ-30 самых востребованных и высокооплачиваемых профессий 2023
Поможет разобраться в актуальной ситуации на рынке труда
Подборка 50+ ресурсов об IT-сфере
Только лучшие телеграм-каналы, каналы Youtube, подкасты, форумы и многое другое для того, чтобы узнавать новое про IT
ТОП 50+ сервисов и приложений от Geekbrains
Безопасные и надежные программы для работы в наши дни
Уже скачали 20426
- Статистическая статистика
В этом случае применяются образцы в выборочных данных в целях формирования выводов о представленной совокупности или учета случайности. Выделяют следующие разновидности выводов:
- ответы на вопросы да / нет о данных (проверка гипотез);
- оценка числовых характеристик данных (оценка);
- описание связей в данных (корреляция);
- моделирование отношений в данных (к примеру, регрессионный анализ).
Прогнозная аналитика
Predictive Analytics применяет статистические модели в целях анализа нынешних и исторических данных. Это необходимо для создания прогнозов относительно дальнейших или иных неизвестных событий. В предпринимательстве эта разновидность анализа применяется в целях определения рисков и возможностей, способствующих принятию правильных решений.
Текстовая аналитика
Text Analytics (Text Mining, Text Data Mining) — это процесс извлечения из текста информации высокого уровня качества. Можно выделить несколько составляющих анализа текста:
- процесс структурирования исходного текста;
- извлечение шаблонов из структурированных данных с применением метода изучения статистических шаблонов и др.;
- оценка и интерпретация полученной информации.
С помощью Microsoft Excel можно использовать целый ряд средств и методов для анализа и интерпретации данных. При этом данные могут быть получены из разных источников. Имеется несколько вариантов трансформации и форматирования данных. Анализ можно осуществлять посредством различных команд, функций и инструментов программы.

Читайте также
В частности, к ним можно отнести условное форматирование, диапазоны, таблицы, текстовые функции, функции даты, функции времени, финансовые функции, промежуточные итоги, быстрый анализ, аудит формул, инструмент Inquire, анализ «что, если», решатели, модель данных, PowerPivot, PowerView, PowerMap и многое другое.
Активация и запуск функций анализа данных в Excel
Excel представляет собой не только редактор таблиц, а еще и отличный инструмент, позволяющий производить всевозможные математические и статистические расчеты. Программа отличается широким функционалом, позволяющим осуществлять вышеописанные процедуры. Однако некоторые из этих функций неактивны по умолчанию. Анализ данных в Excel является как раз такой скрытой возможностью.
Если вы хотите активировать данную функцию, то следует зайти в настройки Microsoft Excel. Причем для разных версий утилиты (2010, 2013 и 2016 года) последовательность действий будет примерно одна и та же. Несущественные расхождения в алгоритме действий имеются лишь для версии 2007 года.
Только до 20.04
Скачай подборку тестов, чтобы определить свои самые конкурентные скиллы
Список документов:



Чтобы получить файл, укажите e-mail:
Подтвердите, что вы не робот,
указав номер телефона:
Уже скачали 7503
Итак, необходимо выполнить следующие действия:
- Нажать на вкладку «Файл» (либо на логотип Microsoft Office в верхнем левом углу экрана для версии 2007 года).
- Нажать на один из пунктов в левой части открывшегося окна — «Параметры».
- Перейти в подраздел «Надстройки» (второй с конца в списке в левой части окна).
- Здесь нужно обратить внимание на нижнюю часть окна. Следует найти параметр «Управление». Обратите внимание на значение в выпадающей форме — вы должны увидеть «Надстройки Excel». Далее следует нажать на вкладку «Перейти…» справа от этого пункта. Если же в выпадающей форме вы увидите какое-то другое значение, нужно будет сначала вписать то, которое мы указали выше.
- В открывшемся окне доступных надстроек найдите пункт «Пакет анализа» и поставьте возле него галочку. Затем нажмите на кнопку «OK» (в правой верхней части).
Выполнив все перечисленные действия, вы активируете нужную функцию и получите соответствующие инструменты. Найти их можно в ленте Excel.
Чтобы открыть тот или иной инструмент анализа данных, нужно произвести следующие действия:
- Зайти в раздел «Данные».
- Найти блок инструментов «Анализ», который расположен на правом краю ленты и нажать на «Анализ данных».
- Выбрать конкретный инструмент из появившегося списка. Наиболее полезными считаются:
- корреляция;
- гистограмма;
- регрессия;
- выборка;
- экспоненциальное сглаживание;
- генератор случайных чисел;
- описательная статистика;
- анализ Фурье;
- различные виды дисперсионного анализа и т.д.
Выбрав нужный инструмент, нажмите на кнопку «OK». Каждый из доступных инструментов работает на основе своего собственного алгоритма.
Таким образом, блок функций «Пакет анализа» включается с помощью всего лишь нескольких простых шагов. При этом если не знать четкую последовательность действий, пользователю сложно найти нужную кнопку.
4 техники анализа данных в Excel
Сводные таблицы
Это важнейший инструмент для обработки больших информационных объемов. Сводные таблицы позволяют быстро делать выводы на основе неструктурированных данных без ручной сортировки и фильтрации. Создание и настройка таблиц осуществляется довольно быстро. Однако от того, какой именно вариант отображения результата вам нужен, будет зависеть алгоритм настройки.
Кроме того, у пользователя есть возможность создавать сводные диаграммы на базе сводных таблиц. При изменении таблиц диаграммы будут обновляться в автоматическом режиме. Скажем, если вы на регулярной основе формируете отчёты по одним и тем же параметрам, то такая функция вам очень пригодится.
Можно вписать какие угодно исходные параметры, например, данные по продажам, отгрузкам, доставкам и т.д.
Для использования сводной таблицы вам необходимо:
- Открыть файл с таблицей, данные которой необходимо проанализировать.
- Выделить диапазон данных для анализа.
- Перейти на вкладку «Вставка», а затем «Таблица». Далее нужно нажать на «Сводная таблица» (для macOS на вкладке «Данные» в группе «Анализ»). Если вы сделали все правильно, то появится диалоговое окно «Создание сводной таблицы».
- Настроить отображение данных, которые есть у вас в таблице.
3D-карты
Благодаря этому методу визуализации данных с географической привязкой вы сможете проанализировать данные и выявить закономерности, имеющие региональное происхождение.
Однако вам не нужно указывать координаты, ведь если правильно ввести географическое название в таблице, программа сделает все сама.
Для применения инструмента вас нужно:
- Открыть файл с таблицей, информацию из которой необходимо визуализировать. К примеру, с данными по разным городам и странам.
- Подготовить данные для отображения на карте. Для этого нужно нажать на «Главная» и перейти на вкладку «Форматировать как таблицу».
- Обозначить диапазон данных для анализа.
- На вкладке «Вставка» вы увидите кнопку «3D-карта».
На карте имеются точки, обозначающие города. Однако нам нужно увидеть информацию, которая привязана к этим городам, например, суммы, отображающиеся через высоту столбика. Если навести курсор на столбик, то вы увидите сумму.
Вместе с тем, довольно полезной считается круговая диаграмма по годам, в которой размер круга зависит от суммы.
Лист прогнозов
В бизнес-процессах имеют место сезонные закономерности. Их, конечно же, нужно учитывать во время планирования. Для этой цели лучше всего подходит «Лист прогноза», который является самым точным инструментом для осуществления прогнозов в рамках Excel. Его применяют для планирования деятельности коммерческих, финансовых, маркетинговых и прочих служб.
Чтобы сделать прогноз, необходимо иметь информацию за предыдущие периоды. Чем больше информации будет внесено, тем более точный прогноз вы получите (минимальный объём информации для хорошего прогноза — 1 год). Учтите, что нужны одинаковые интервалы между точками данных (скажем, месяц или равное количество дней).
Чтобы использовать данную функцию, вам необходимо:
- Открыть таблицу с данными за период и соответствующими ему параметрами, к примеру, от года.
- Выделить 2 ряда данных.
- На вкладке «Данные» нажать на кнопку «Лист прогноза».
- В окне «Создание листа прогноза» выбрать подходящий график или гистограмму для визуализации прогноза.
- Определить дату окончания прогноза.

Читайте также
Быстрый анализ
Данный инструмент позволяет выполнять процедуры анализа в кратчайшие сроки. Чтобы получить необходимые данные, достаточно нажать всего на несколько кнопок. Вам не нужно будет производить никаких расчетов или указывать какие-либо формулы. Единственное что от вас потребуется — выделить нужный диапазон и выбрать тип результата, который вам необходим на выходе.
Благодаря данному инструменту вы можете формировать всевозможные разновидности диаграмм или спарклайны (микрографики прямо в ячейке) буквально в два счета.
Чтобы работать с инструментом, вам нужно:
- Открыть таблицу с данными для анализа.
- Выделить необходимый для анализа диапазон.
- Во время выделения диапазона в нижней части высвечивается кнопка «Быстрый анализ».
Нажав на эту кнопку, вы сможете произвести целый ряд различных действий, которые предложит программа. К примеру, найти итоги. Кроме того, можно узнать суммы, которые проставляются внизу.
Быстрый анализ предполагает несколько способов форматирования. Чтобы узнать, какие значения больше, а какие меньше, нужно перейти в ячейки гистограммы.
Плюс ко всему, вы можете выставить в ячейках значки разных цветов: зелёные — самые большие значения, красные — самые меньшие.
Все эти инструменты позволят вам ускорить процесс анализа данных и сделать его более простым. Используя различные функции, вы сможете с легкостью освоить Microsoft Excel и извлечь из него максимальную пользу.