Средний уровень ряда в excel

Предположим, вам нужно найти среднее количество дней для выполнения задач разными сотрудниками. Или вы хотите вычислить среднюю температуру для определенного дня на основе 10-летнего промежутка времени. Существует несколько способов расчета среднего для группы чисел.

Функция СРЗНАЧ вычисляет среднее значение, то есть центр набора чисел в статистическом распределении. Существует три наиболее распространенных способа определения среднего значения:

• Среднее значение    Это арифметическое и вычисляется путем с добавления группы чисел и деления на их количество. Например, средним значением для чисел 2, 3, 3, 5, 7 и 10 будет 5, которое является результатом деления их суммы, равной 30, на их количество, равное 6.

• Медиана     Среднее число числа. Половина чисел имеют значения больше медианой, а половина чисел имеют значения меньше медианой. Например, медианой для чисел 2, 3, 3, 5, 7 и 10 будет 4.

• Мода    Наиболее часто встречается число в группе чисел. Например, модой для чисел 2, 3, 3, 5, 7 и 10 будет 3.

При симметричном распределении множества чисел все три значения центральной тенденции будут совпадать. В акосимном распределении группы чисел они могут быть другими.

Выполните действия, описанные ниже.

1. Щелкните ячейку снизу или справа от чисел, для которых необходимо найти среднее.

2. На вкладке «Главная» в группе «Редактирование» щелкните стрелку рядом с кнопкой » «, выберите «Среднее» и нажмите клавишу ВВОД.

Для этого используйте функцию С AVERAGE. Скопируйте приведенную ниже таблицу на пустой лист.

Формула	Описание (результат)
=СПБ(A2:A7)	Среднее значение всех чисел в списке выше (9,5).
=СПБ(A2:A4;A7)	Среднее значение 3-го и последнего числа в списке (7,5).
=С AVERAGEIF(A2:A7;»<>0″)	Среднее значение чисел в списке за исключением тех, которые содержат нулевые значения, например ячейка A6 (11,4).

Для этой задачи используются функции СУММПРОИВ ИСУММ. В этом примере вычисляется средняя цена за единицу для трех покупок, при которой каждая покупка приобретает различное количество единиц по разной цене.

Скопируйте приведенную ниже таблицу на пустой лист.

1 2 3 4

A B Цена за единицу Количество единиц 20 500 25 750 35 200 Формула Описание (результат) =СУММПРОИВЕД(A2:A4;B2:B4)/СУММ(B2:B4) Делит общую стоимость всех трех заказов на общее количество заказаных единиц (24,66).

Для этой задачи используются функции С AVERAGE и ЕСЛИ. Скопируйте приведенную ниже таблицу и имейте в виду, что при копировании на пустой лист может быть проще понять этот пример.

Формула	Описание (результат)
=С AVERAGEIF(A2:A7;»<>0″)	Среднее значение чисел в списке за исключением тех, которые содержат нулевые значения, например ячейка A6 (11,4).

Дополнительные сведения

Вы всегда можете задать вопрос специалисту Excel Tech Community или попросить помощи в сообществе Answers community.

См. также

СРЗНАЧ

С AVERAGEIF

СУММ

СУММПРОИЗВ

Для характеристики
динамики изучаемого явления за
продолжительный период рассчитывают
группу средних показателей динамики.
Можно выделить две категории показателей
в этой группе:

• средние уровни
  ряда;

• средние показатели
  изменения уровней ряда.

Для нахождения
среднего уровня ряда воспользуемся
формулой в MS Excel =СРЗНАЧ. Этой же формулой
можно рассчитать и средний абсолютный
прирост (средний показатель изменения
уровня ряда). Эти два показателя
рассчитываются по формуле простой
средней арифметической.

Для того, чтобы
рассчитать средний темп роста, применяется
формула средней геометрической =СРГЕОМ.

С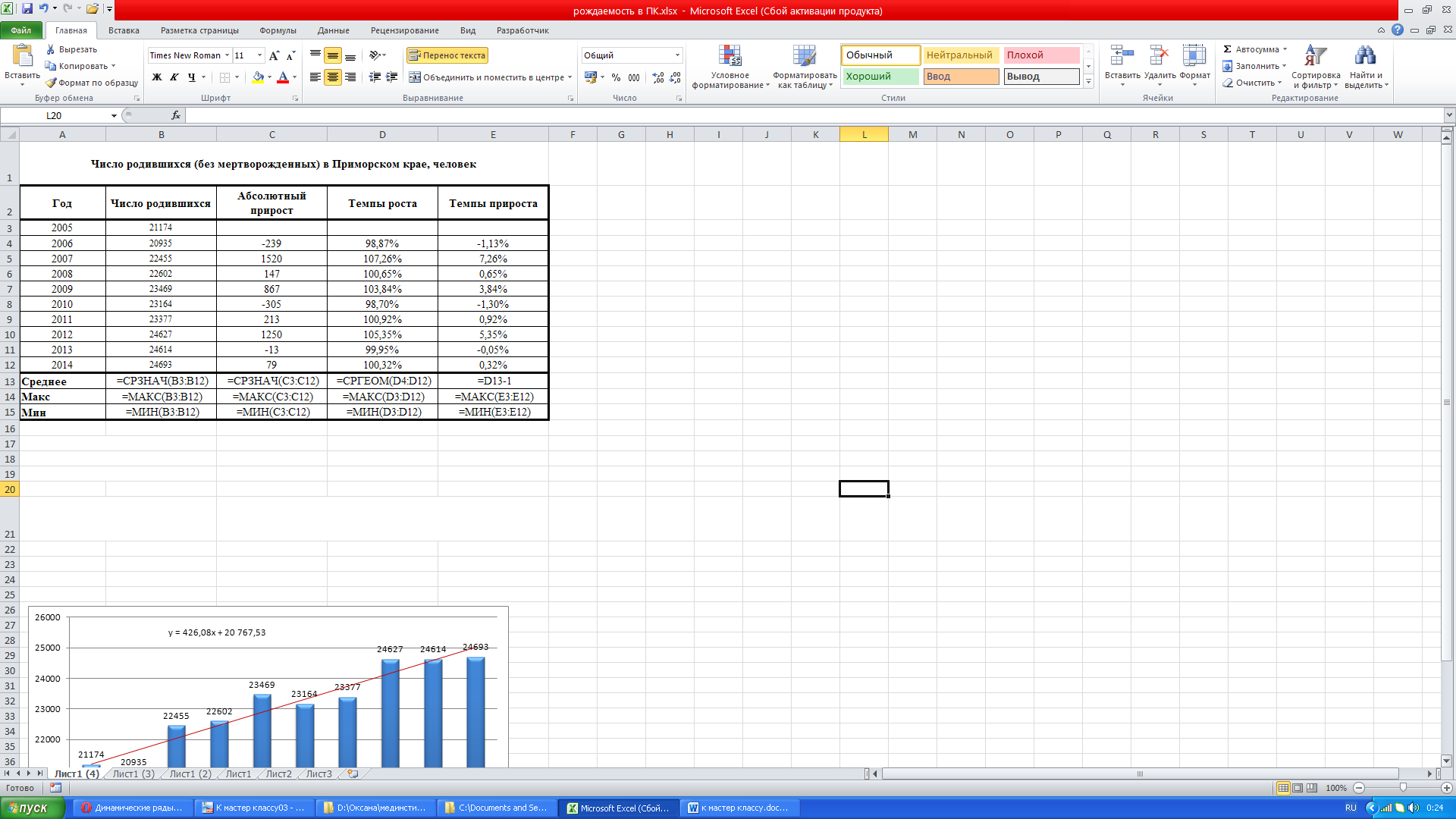редний
темп прироста вычисляется вычитанием
из среднего темпа роста 100% или 1 (1 и 100%
для MS Excel равнозначные значения, разница
только в формате представления).

Помимо средних
показателей определим года с максимальными
и минимальными показателями рождаемости
в Приморском крае.

С помощью условного
форматирования можно выделить года,
когда наблюдались максимальные и
минимальные показатели в динамике
рождаемости. В 2014 году достигнут самый
высокий показатель рождаемости за
последние 10 лет, а минимальное число
родившихся за этот период зафиксировано
в 2006 году. Максимальные приросты
наблюдались в 2007 году. В 2010 году наблюдался
отрицательный рост или убыль, это
свидетельствует о том, что в этом году
родилось меньше детей чем в предыдущем.

Показатель «среднее»
в столбце «Число родившихся» означает,
что в Приморском крае ежегодно рождается
в среднем 23111 детей. Средний абсолютный
прирост свидетельствует о том, что
ежегодно в нашем регионе появляется на
свет на 391 малышей больше чем в предыдущем
году. В процентном соотношении ежегодный
прирост рождаемости составляет в среднем
1,72%. Демографические показатели в
Приморском крае демонстрируют повышение
рождаемости, но остается открытым вопрос
– за счет чего произошли эти положительные
изменения. Имеют ли они этнические и
конфессиональные корни или обусловлено
материальными факторами (экономическим
благополучием региона)?

2.4. Выявление тенденции (тренда) в рядах динамики.

2.4.1. Тренды

Тренд— это
закономерность описывающая подъем или
падение показателя в динамике. Если
изобразить любой динамический ряд на
графике, часто выделяется определенный
угол – кривая либо постепенно идет на
увеличение или на уменьшение, в таких
случаях принято говорить, что ряд
динамики имеет тенденцию (к росту или
падению соответственно).

Если же построить
модель, описывающую это явление, то
получается довольно простой и очень
удобный инструмент для прогнозирования,
не требующий каких-либо сложных вычислений
или временных затрат на проверку
значимости или адекватности влияющих
факторов.

Итак, что же собой
представляет тренд как модель? Это
совокупность расчетных коэффициентов
уравнения, которые выражают регрессионную
зависимость показателя (Y) от изменения
времени (t). То есть, это точно такая же
регрессия, только влияющим фактором
здесь выступает именно показатель
времени.

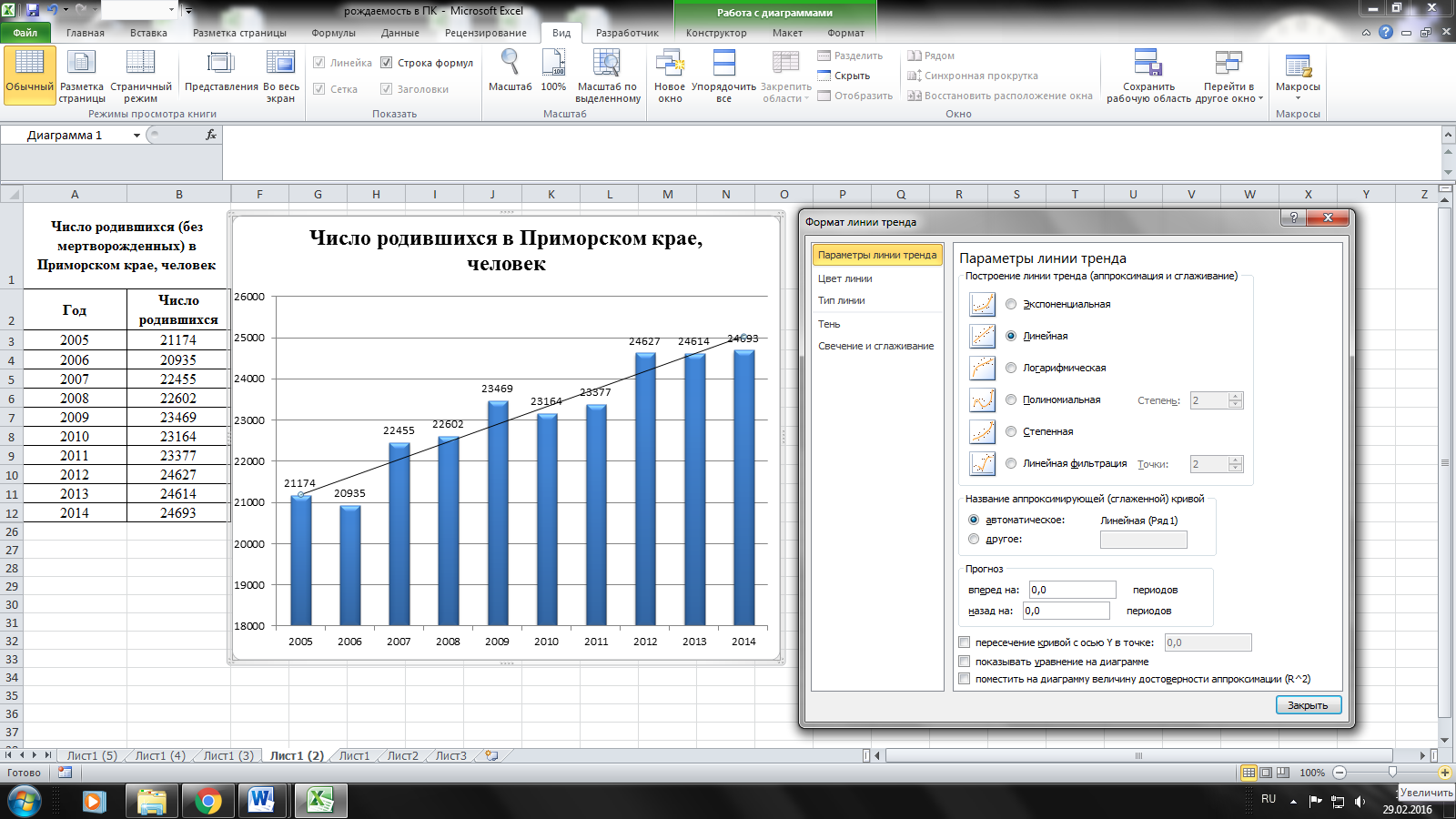
Для графического
анализа данных на диаграмме можно
воспользоваться построением линии
тренда. Такая линия тренда позволяет
построить сглаженную кривую, графическое
представление которой более ясно
показывает существующую закономерность
в развитии данных.

В этом примере
продолжим использовать один и тот же
динамический ряд – уровень рождаемости
в Приморском крае в периоде с 2005-го по
2014-й гг.

На построенной ранее
гистограмме выделяем столбцы правой
кнопкой мыши и из появившегося контекстного
меню выбираем пункт «Добавить линию
тренда».

Откроется окошко для
настройки параметров построения линии
тренда, где среди типов моделей выбираем
«Линейная», ставим галочку напротив
пункта «Показывать уравнение на
диаграмме», этого будет достаточно,
чтобы на графике отобразилась уже
построенная линия тренда, а также
математический вариант отображения
модели в виде готового уравнения. Если
интересует отображение на графике
прогноза, чтобы визуально оценить отрыв
исследуемого показателя, указываем в
поле «Прогноз» вперед на количество
интересующих периодов. Отображаемое
уравнение линейного тренда это и есть
непосредственно сама модель, которую
можно использовать, в качестве формулы,
чтобы получить расчетные значения по
модели и соответственно точные значения
прогноза (прогноз, отображаемый на
графике, оценить можно лишь приблизительно).

Уравнение линейного
тренда более точно можно определить с
помощью формулы =ЛИНЕЙН или с помощью
надстройки «Анализ данных» 
«Регрессия».

Для того чтобы найти среднее значение в Excel (при том неважно числовое, текстовое, процентное или другое значение) существует много функций. И каждая из них обладает своими особенностями и преимуществами. Ведь в данной задаче могут быть поставлены определенные условия.

Например, средние значения ряда чисел в Excel считают с помощью статистических функций. Можно также вручную ввести собственную формулу. Рассмотрим различные варианты.

Как найти среднее арифметическое чисел?

Чтобы найти среднее арифметическое, необходимо сложить все числа в наборе и разделить сумму на количество. Например, оценки школьника по информатике: 3, 4, 3, 5, 5. Что выходит за четверть: 4. Мы нашли среднее арифметическое по формуле: =(3+4+3+5+5)/5.

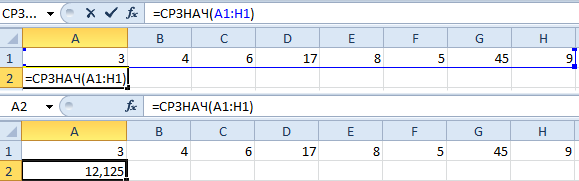
Как это быстро сделать с помощью функций Excel? Возьмем для примера ряд случайных чисел в строке:

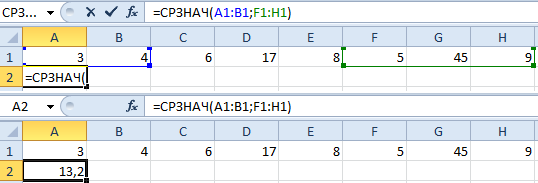
1. Ставим курсор в ячейку А2 (под набором чисел). В главном меню – инструмент «Редактирование» — кнопка «Сумма». Выбираем опцию «Среднее». После нажатия в активной ячейке появляется формула. Выделяем диапазон: A1:H1 и нажимаем ВВОД.




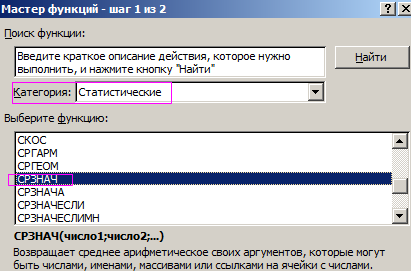
2. В основе второго метода тот же принцип нахождения среднего арифметического. Но функцию СРЗНАЧ мы вызовем по-другому. С помощью мастера функций (кнопка fx или комбинация клавиш SHIFT+F3).



3. Третий способ вызова функции СРЗНАЧ из панели: «Формула»-«Формула»-«Другие функции»-«Статические»-«СРЗНАЧ».

Или: сделаем активной ячейку и просто вручную впишем формулу: =СРЗНАЧ(A1:A8).

Теперь посмотрим, что еще умеет функция СРЗНАЧ.

Найдем среднее арифметическое двух первых и трех последних чисел. Формула: =СРЗНАЧ(A1:B1;F1:H1). Результат:



Среднее значение по условию

Условием для нахождения среднего арифметического может быть числовой критерий или текстовый. Будем использовать функцию: =СРЗНАЧЕСЛИ().

Найти среднее арифметическое чисел, которые больше или равны 10.

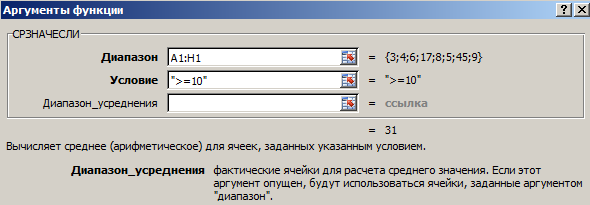
Функция: =СРЗНАЧЕСЛИ(A1:A8;»>=10″)

Результат использования функции СРЗНАЧЕСЛИ по условию «>=10»:

Третий аргумент – «Диапазон усреднения» — опущен. Во-первых, он не обязателен. Во-вторых, анализируемый программой диапазон содержит ТОЛЬКО числовые значения. В ячейках, указанных в первом аргументе, и будет производиться поиск по прописанному во втором аргументе условию.

Внимание! Критерий поиска можно указать в ячейке. А в формуле сделать на нее ссылку.

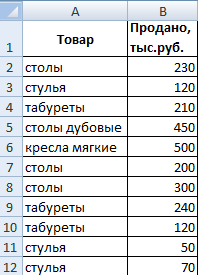
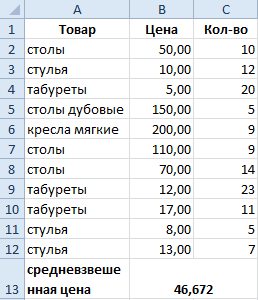
Найдем среднее значение чисел по текстовому критерию. Например, средние продажи товара «столы».

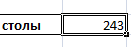
Функция будет выглядеть так: =СРЗНАЧЕСЛИ($A$2:$A$12;A7;$B$2:$B$12). Диапазон – столбец с наименованиями товаров. Критерий поиска – ссылка на ячейку со словом «столы» (можно вместо ссылки A7 вставить само слово «столы»). Диапазон усреднения – те ячейки, из которых будут браться данные для расчета среднего значения.

В результате вычисления функции получаем следующее значение:

Внимание! Для текстового критерия (условия) диапазон усреднения указывать обязательно.

Как посчитать средневзвешенную цену в Excel?

Как посчитать средний процент в Excel? Для этой цели подойдут функции СУММПРОИЗВ и СУММ. Таблица для примера:

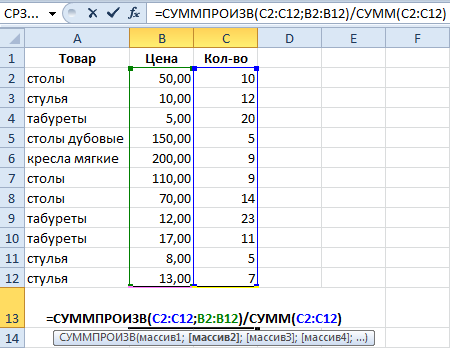
Как мы узнали средневзвешенную цену?

Формула: =СУММПРОИЗВ(C2:C12;B2:B12)/СУММ(C2:C12).

С помощью формулы СУММПРОИЗВ мы узнаем общую выручку после реализации всего количества товара. А функция СУММ — сумирует количесвто товара. Поделив общую выручку от реализации товара на общее количество единиц товара, мы нашли средневзвешенную цену. Этот показатель учитывает «вес» каждой цены. Ее долю в общей массе значений.

Среднее квадратическое отклонение: формула в Excel

Различают среднеквадратическое отклонение по генеральной совокупности и по выборке. В первом случае это корень из генеральной дисперсии. Во втором – из выборочной дисперсии.

Для расчета этого статистического показателя составляется формула дисперсии. Из нее извлекается корень. Но в Excel существует готовая функция для нахождения среднеквадратического отклонения.

Среднеквадратическое отклонение имеет привязку к масштабу исходных данных. Для образного представления о вариации анализируемого диапазона этого недостаточно. Чтобы получить относительный уровень разброса данных, рассчитывается коэффициент вариации:

среднеквадратическое отклонение / среднее арифметическое значение

Формула в Excel выглядит следующим образом:

СТАНДОТКЛОНП (диапазон значений) / СРЗНАЧ (диапазон значений).

Коэффициент вариации считается в процентах. Поэтому в ячейке устанавливаем процентный формат.

В процессе различных расчетов и работы с данными довольно часто требуется подсчитать их среднее значение. Оно рассчитывается путем сложения чисел и деления общей суммы на их количество. Давайте выясним, как вычислить среднее значение набора чисел при помощи программы Microsoft Excel различными способами.

Стандартный способ вычисления

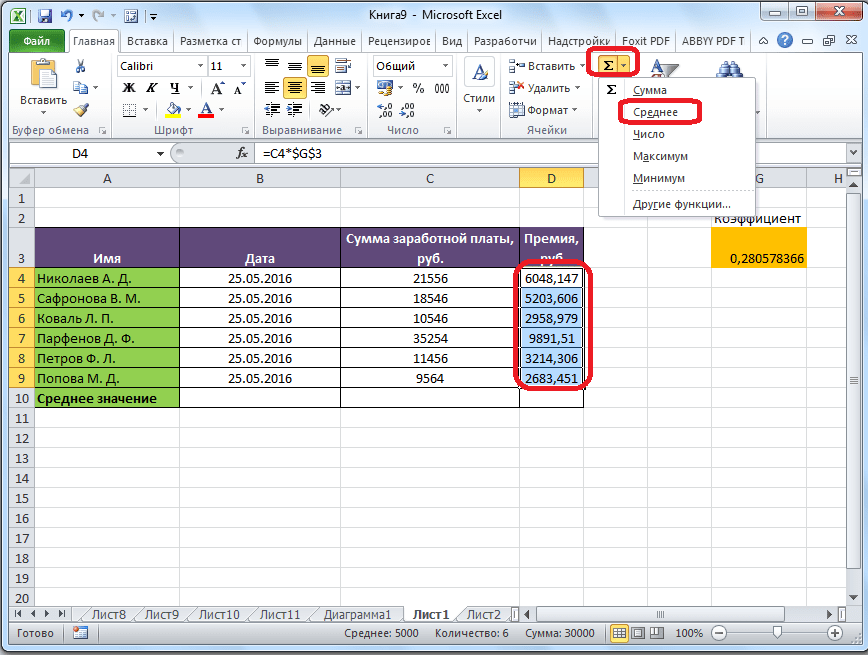
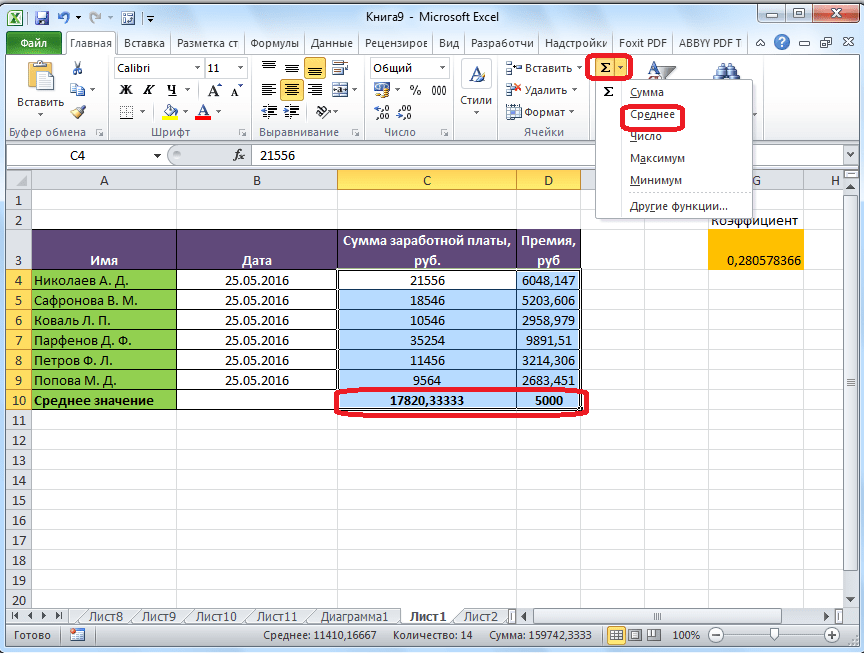
Самый простой и известный способ найти среднее арифметическое набора чисел — это воспользоваться специальной кнопкой на ленте Microsoft Excel. Выделяем диапазон чисел, расположенных в столбце или в строке документа. Находясь во вкладке «Главная», жмем на кнопку «Автосумма», которая расположена на ленте в блоке инструментов «Редактирование». Из выпадающее списка выбираем пункт «Среднее».

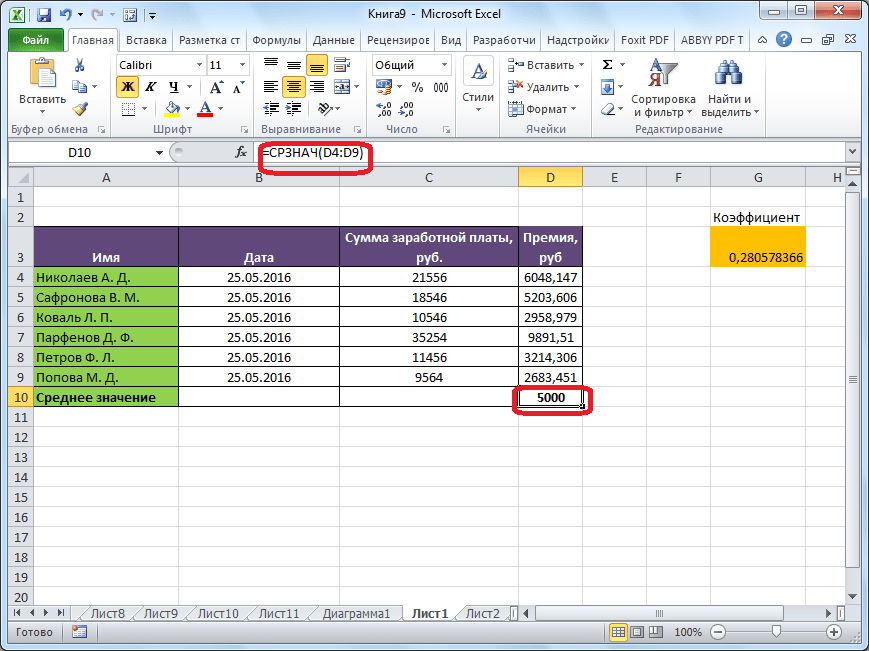
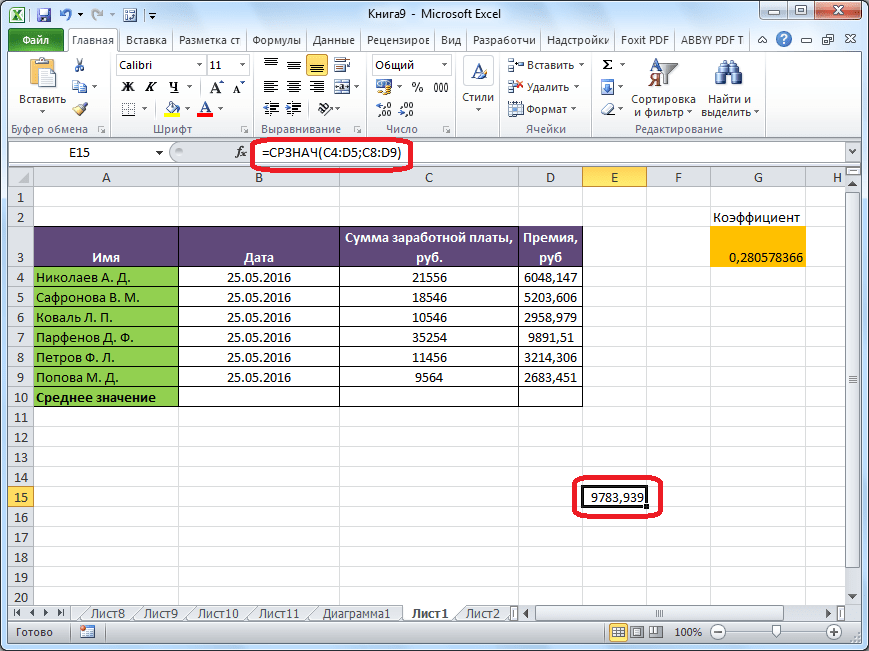
После этого, с помощью функции «СРЗНАЧ», производится расчет. В ячейку под выделенным столбцом, или справа от выделенной строки, выводится средняя арифметическая данного набора чисел.

Этот способ хорош простотой и удобством. Но, у него имеются и существенные недостатки. С помощью этого способа можно произвести подсчет среднего значения только тех чисел, которые располагаются в ряд в одном столбце, или в одной строке. А вот, с массивом ячеек, или с разрозненными ячейками на листе, с помощью этого способа работать нельзя.

Например, если выделить два столбца, и вышеописанным способом вычислить среднее арифметическое, то ответ будет дан для каждого столбца в отдельности, а не для всего массива ячеек.

Вычисление с помощью Мастера функций

Для случаев, когда нужно подсчитать среднюю арифметическую массива ячеек, или разрозненных ячеек, можно использовать Мастер функций. Он применяет все ту же функцию «СРЗНАЧ», известную нам по первому методу вычисления, но делает это несколько другим способом.

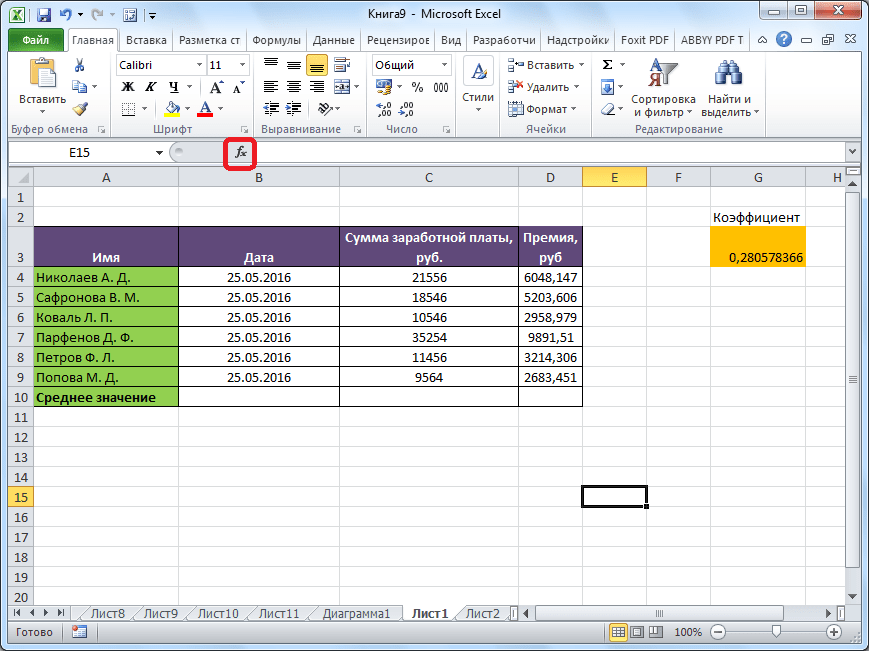
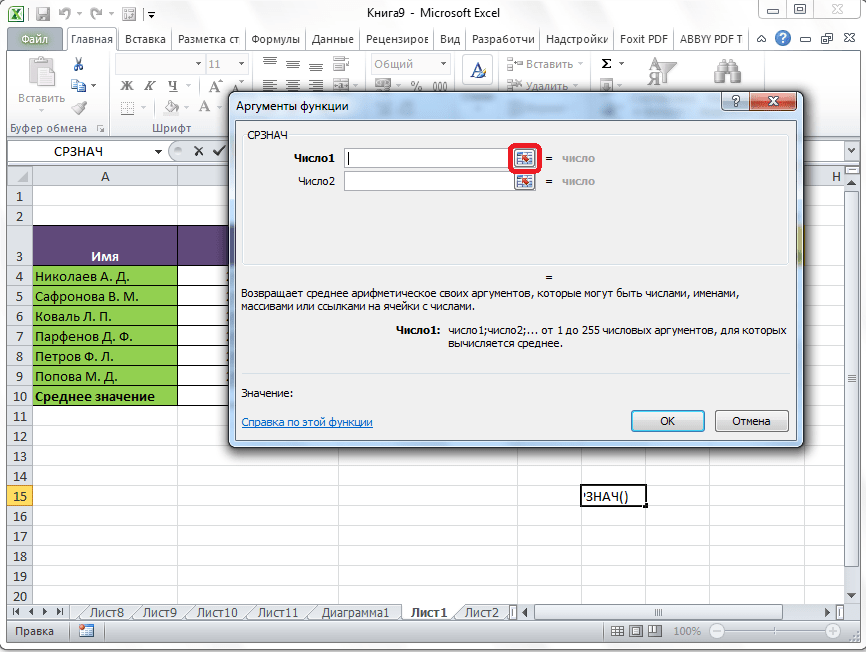
Кликаем по ячейке, где хотим, чтобы выводился результат подсчета среднего значения. Жмем на кнопку «Вставить функцию», которая размещена слева от строки формул. Либо же, набираем на клавиатуре комбинацию Shift+F3.

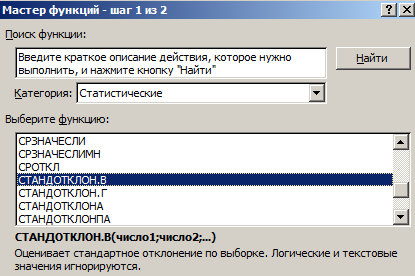
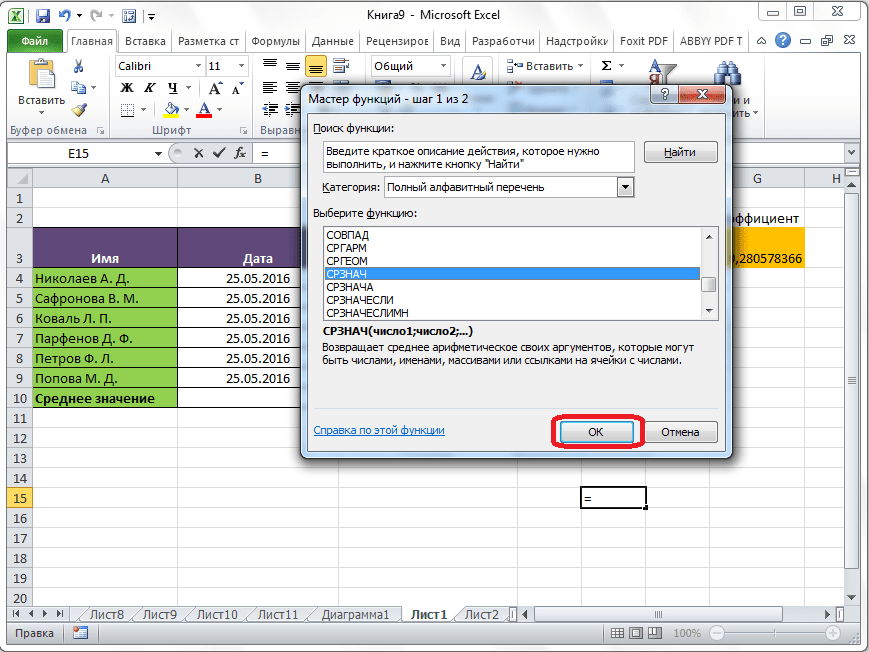
Запускается Мастер функций. В списке представленных функций ищем «СРЗНАЧ». Выделяем его, и жмем на кнопку «OK».

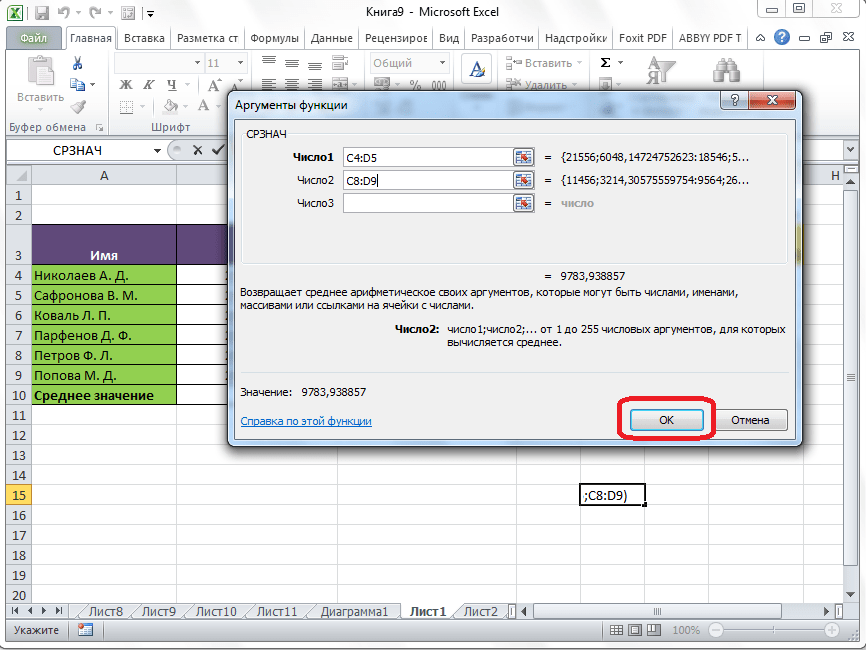
Открывается окно аргументов данной функции. В поля «Число» вводятся аргументы функции. Это могут быть как обычные числа, так и адреса ячеек, где эти числа расположены. Если вам неудобно вводить адреса ячеек вручную, то следует нажать на кнопку расположенную справа от поля ввода данных.

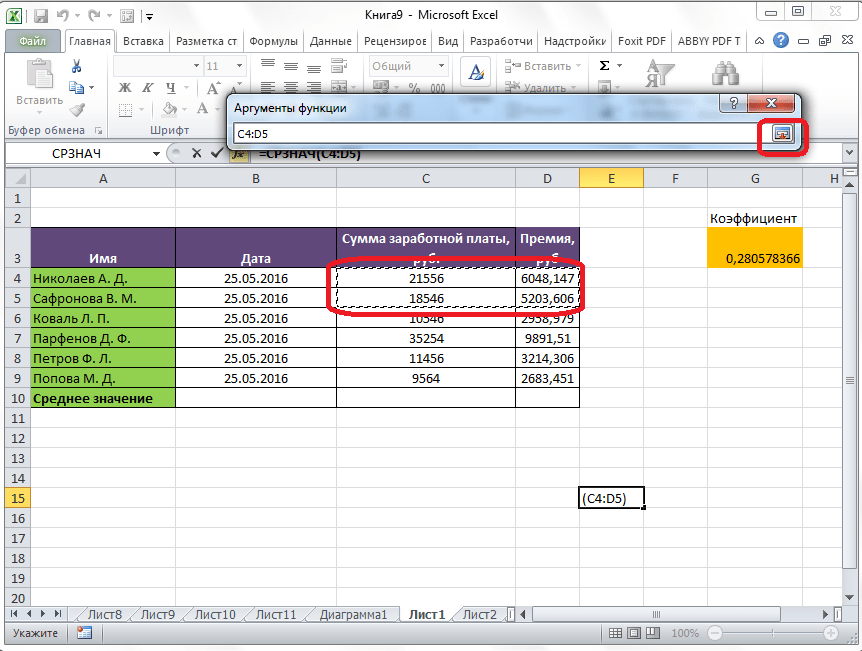
После этого, окно аргументов функции свернется, а вы сможете выделить ту группу ячеек на листе, которую берете для расчета. Затем, опять нажимаете на кнопку слева от поля ввода данных, чтобы вернуться в окно аргументов функции.

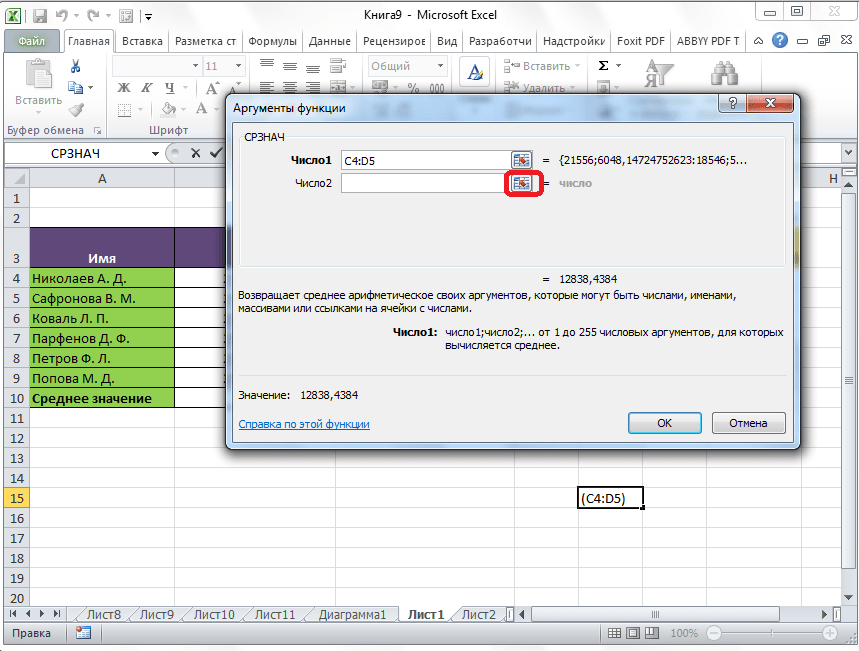
Если вы хотите подсчитать среднее арифметическое между числами, находящимися в разрозненных группах ячеек, то те же самые действия, о которых говорилось выше, проделывайте в поле «Число 2». И так до тех пор, пока все нужные группы ячеек не будут выделены.

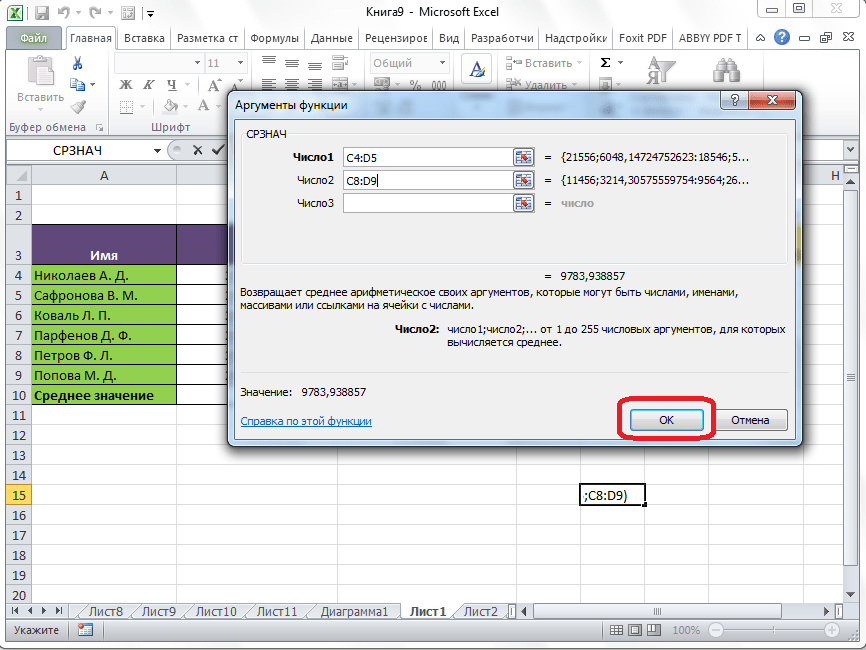
После этого, жмите на кнопку «OK».

Результат расчета среднего арифметического будет выделен в ту ячейку, которую вы выделили перед запуском Мастера функций.

Панель формул

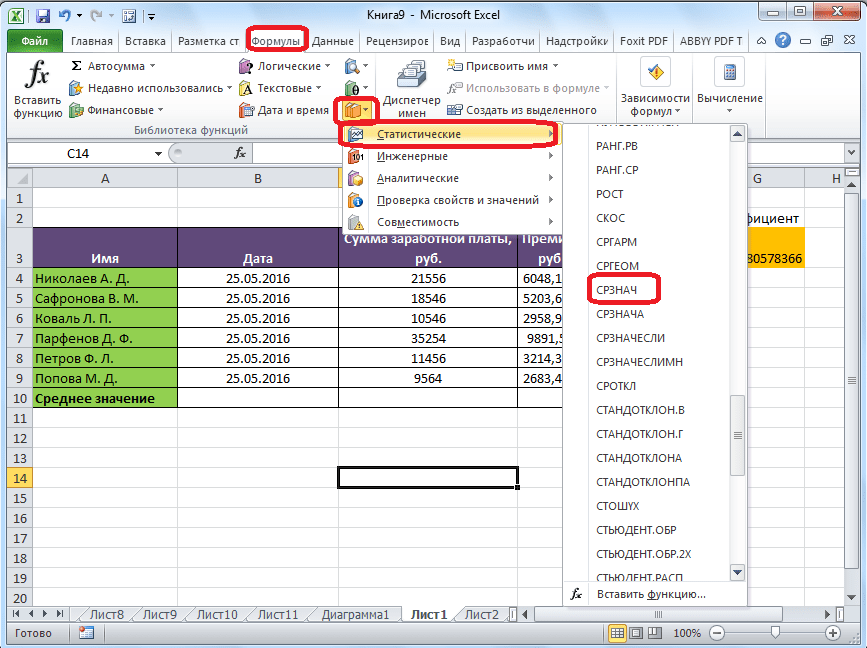
Существует ещё третий способ запустить функцию «СРЗНАЧ». Для этого, переходим во вкладку «Формулы». Выделяем ячейку, в которой будет выводиться результат. После этого, в группе инструментов «Библиотека функций» на ленте жмем на кнопку «Другие функции». Появляется список, в котором нужно последовательно перейти по пунктам «Статистические» и «СРЗНАЧ».

Затем, запускается точно такое же окно аргументов функции, как и при использовании Мастера функций, работу в котором мы подробно описали выше.

Дальнейшие действия точно такие же.

Ручной ввод функции

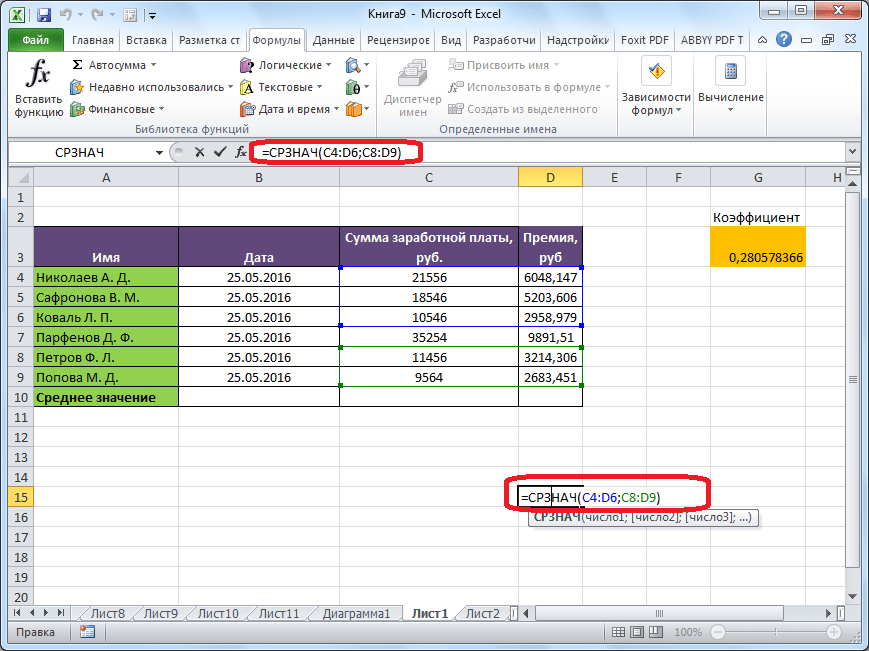
Но, не забывайте, что всегда при желании можно ввести функцию «СРЗНАЧ» вручную. Она будет иметь следующий шаблон: «=СРЗНАЧ(адрес_диапазона_ячеек(число); адрес_диапазона_ячеек(число)).

Конечно, этот способ не такой удобный, как предыдущие, и требует держать в голове пользователя определенные формулы, но он более гибкий.

Расчет среднего значения по условию

Кроме обычного расчета среднего значения, имеется возможность подсчета среднего значения по условию. В этом случае, в расчет будут браться только те числа из выбранного диапазона, которые соответствуют определенному условию. Например, если эти числа больше или меньше конкретно установленного значения.

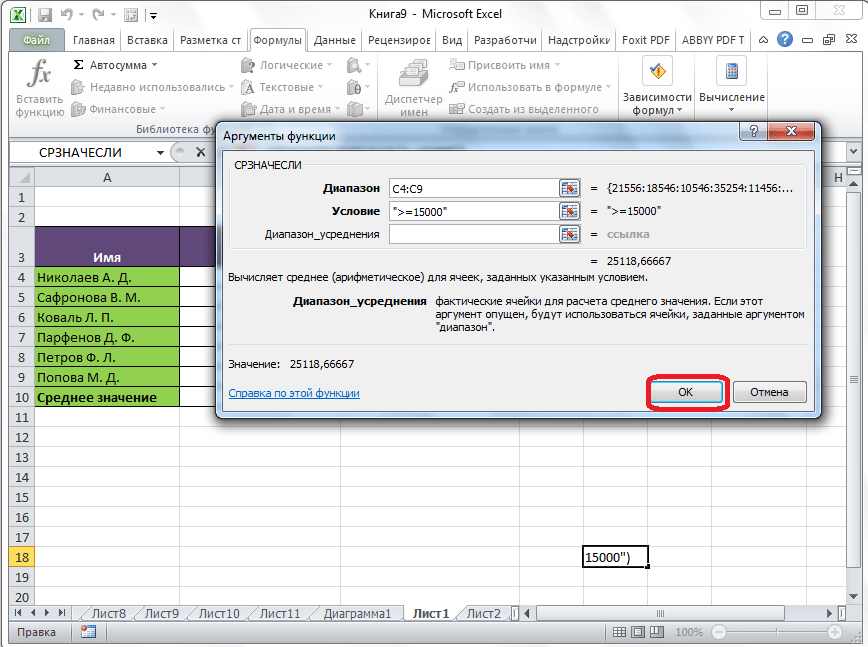
Для этих целей, используется функция «СРЗНАЧЕСЛИ». Как и функцию «СРЗНАЧ», запустить её можно через Мастер функций, из панели формул, или при помощи ручного ввода в ячейку. После того, как открылось окно аргументов функции, нужно ввести её параметры. В поле «Диапазон» вводим диапазон ячеек, значения которых будут участвовать в определении среднего арифметического числа. Делаем это тем же способом, как и с функцией «СРЗНАЧ».

А вот, в поле «Условие» мы должны указать конкретное значение, числа больше или меньше которого будут участвовать в расчете. Это можно сделать при помощи знаков сравнения. Например, мы взяли выражение «>=15000». То есть, для расчета будут браться только ячейки диапазона, в которых находятся числа большие или равные 15000. При необходимости, вместо конкретного числа, тут можно указать адрес ячейки, в которой расположено соответствующее число.

Поле «Диапазон усреднения» не обязательно для заполнения. Ввод в него данных является обязательным только при использовании ячеек с текстовым содержимым.

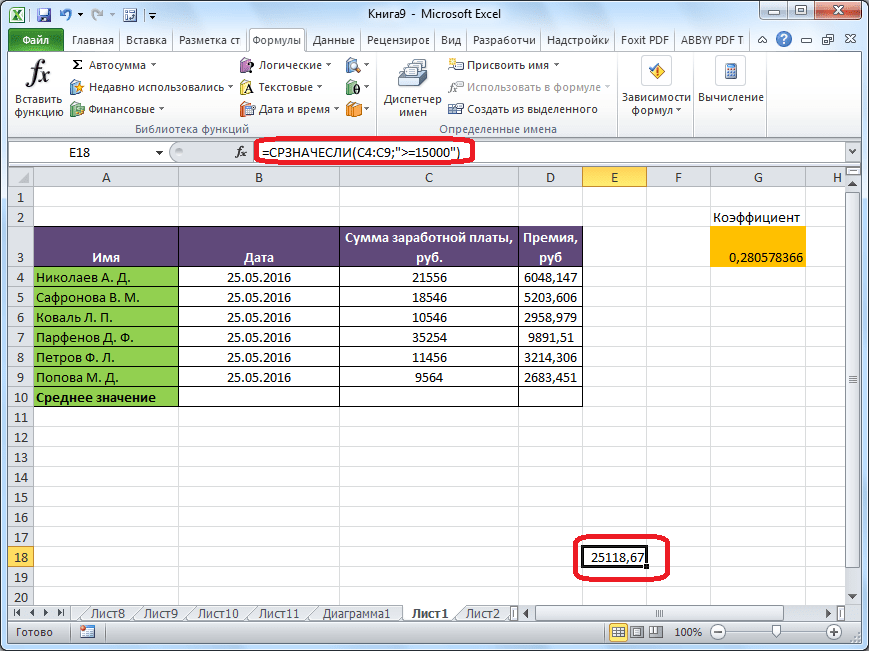
Когда все данные введены, жмем на кнопку «OK».

После этого, в предварительно выбранную ячейку выводится результат расчета среднего арифметического числа для выбранного диапазона, за исключением ячеек, данные которых не отвечают условиям.

Как видим, в программе Microsoft Excel существует целый ряд инструментов, с помощью которых можно рассчитать среднее значение выбранного ряда чисел. Более того, существует функция, которая автоматически отбирает числа из диапазона, не соответствующие заранее установленному пользователем критерию. Это делает вычисления в приложении Microsoft Excel ещё более удобными для пользователей.

Анализ интенсивности динамики

Цель – получение навыков расчета показателей динамики в MS Excel.

Задание – с помощью MS Excel необходимо провести анализ рядов динамики, дать экономическую интерпретацию экономических показателей.

Для проведения маркетингового исследования необходимо проанализировать объем продаж продовольственных товаров в динамике.

Обсяг продажу продовольчих товарів

Год	2005	2008	2009	2010	2011	2012
Объем продаж продовольственных товаров, тыс. грн.	365,00	374,00	381,00	396,00	405,00	380,00

Необходимо рассчитать все показатели динамического ряда(база сравнения — 2005 г), среднегодовые темпы роста и прироста по периодам:

1.2005-2008

2.2008-2012

3.2005-2012

Создадим нужную нам таблицу в MS Excel.

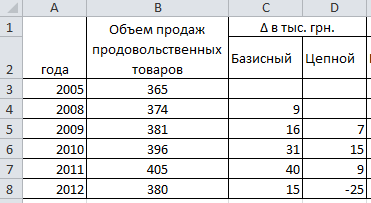
Определим абсолютные приросты. В ячейке С4 введем формулу =B4-$B$3 и растянем формулу на весь столбец.

В ячейку D5 (для 2005 года невозможно рассчитать цепным способом абсолютный прирост, потому что нет предыдущего периода – 2004 года ) используем формулу =B5-B4 и тоже растягиваем на весь столбец. Ниже представлены результаты расчета:

Определим темп роста:

В ячейке Е4 вводим формулу вводим формулу =B4/$B$3*100, растягиваем формулу на весь столбец.

В ячейке F5 (для 2005 года темп роста, как и абсолютный, невозможно рассчитать цепным способом, потому что нет предыдущего периода – 2004 года) вводим формулу =B5/B4*100 и растягиваем на весь столбец.

Определим темп прироста:

В ячейке G4 вводим формулу =E4-100 и растягиваем на весь столбец.

В ячейке H5 вводим формулу =F5-100 и тоже растягиваем формулу на весь столбец.

Определим абсолютное значение 1% прироста:

В ячейке I5 вводим формулу =B4/100. Растягиваем формулу на весь столбец. Внизу представлены результаты вычислений:

Определим средние показатели динамики.

Определение среднего уровня ряда. Так как у нас есть пропущенные уровни ряда, то средний уровень ряда целесообразно рассчитывать за период 2008-2012 годов. В ячейке В10 выбираем встроенную функцию СРЗНАЧ и выбираем нужный нам диапазон.

Найдем средний абсолютный прирост – в ячейке В11 введем формулу =(B8-B3)/8.

Найдем средний темп роста.

1. 2005-2008

В ячейке В14 вводим формулу =(B4/B3)^(1/3).

2. 2008-2012

Базисным способом – в ячейке В16 вводим формулу =(B8/B4)^(1/4).

Цепным способом – в ячейке B17 вводим формулу =((F5/100)*(F6/100)*(F7/100)*(F8/100))^(1/4).

3. 2005-2012

Базисным способом – в ячейку В19 вводим формулу =(B8/B3)^(1/7).

Цепным способом – по формуле средней геометрической взвешенной: в ячейке В20 вводим формулу =((B14)^3*(B16)^4)^(1/7).

Найдем средний темп прироста

1. 2005-2008: в ячейке С14 вводим формулу =(B14-1)*100.

2. 2008-2012: в ячейке С16 вводим формулу =(B16-1)*100.

3. 2005-2012: в ячейке С20 вводим формулу =(B20-1)*100.

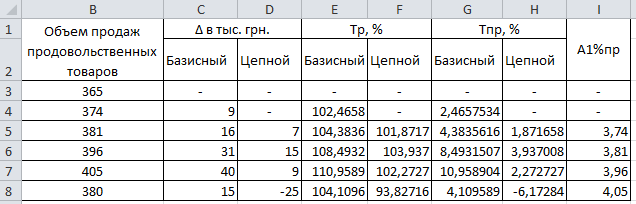
Результаты проведенных расчетов представлены ниже:

Таким образом на протяжении 2005-2008 годов наблюдалось постоянный рост объемов инвестиций, только в 2012 году объем инвестиций снизился по сравнению с 2011 годом на 25 тысяч гривен (по сравнению с 2005 годом увеличился на 15 тысяч гривен). Темп роста в 2012 году, рассчитанный базисным способом составляет 104,11%, что означает увеличение объема производства на 4,11%. Цепной темп прироста показал уменьшение объема производства по сравнению с 2011 годом на 6,17%. В 1

% прироста в 2012 году вмещалось 405 гривен. В период 2005-2012 объем инвестиций ежегодно увеличивался в среднем на 1875 гривен или на 0,58%.

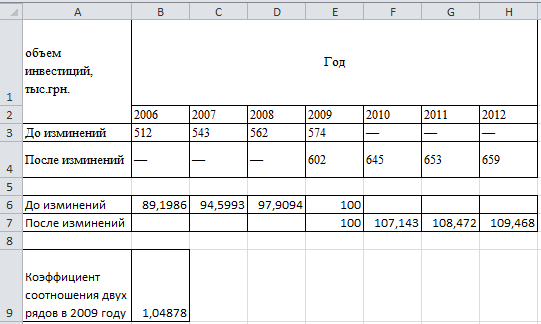
Есть данные про объем инвестиций в маркетинговую компанию, в составе которой произошли изменения. Необходимо проанализировать объем инвестиций в период 2006-2012 годов.

Обсяг інвестицій в компанію

Для этого задания существует два способа решения.

1 способ решения задания – выражения ряда динамики с помощью относительных показателей, взяв за базу период, в котором произошли изменения. Базой сравнения будет 2009 год.

В ячейке В6 вводим формулу =B3/$E$3*100. Растягиваем эту формулу до ячейки Е6.

В ячейке Н7 вводим формулу =H4/$E$4*100. Растягиваем эту формулу до ячейки Е7.

2 способ – перерасчет абсолютных показателей.

Для этого определяем в 2009 году коэффициент соотношения уровней двух рядов:

В ячейке B9 вводим формулу =E4/E3.

Перемножаем на этот коэффициент уровни первого ряда и получаем их соотношение с уровнями второго ряда.

2009 год – в ячейке В11 вводим формулу =B3*$B$9 и растягиваем эту формулу до ячейки D11.

Тогда получаем сравнительный ряд динамики объема производства в рамках концерна.

Ниже представлены полученные при вычислениях данные:

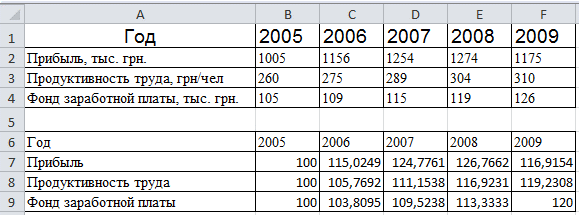
Для формирования маркетинговой стратегии необходимо провести динамический анализ выхода продукции предприятия А и основных факторов интенсивности производства за 2005-2009 года.

Необходимо привести ряды динамики к одной основе, к общей базе сравнения.

Введем данные в диапазоне ячеек A1:F4.

Нужно осуществить сравнительный анализ трех представленных рядов динамики, используя их приведение к одной основе.

Приведем сравнительные ряды к одной основе, определив относительные уровни рядов: базисные темпы роста с постоянной базой сравнения – уровни за 2005 год:

В ячейке В7 вводим формулу =B2/$B$2*100, растягиваем эту формулу до ячейки F7.

В ячейке В8 вводим формулу =B3/$B$3*100, растягиваем эту формулу до ячейки F8.

В ячейке В9 вводим формулу =B4/$B$4*100, растягиваем эту формулу до ячейки F9.

Полученные данные в процентах приведены ниже:

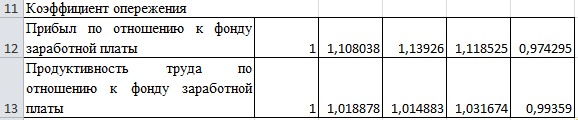
Рассчитаем коэффициент опережения:

В ячейке В12 введем формулу =B7/B$9, растянем эту формулу до ячейки F12.

В ячейке В13 вводим формулу =B7/B$9, растягиваем эту формулу до ячейки F13.

Ниже представлены данные, полученные при вычислении:

Анализ таблиц приводит к таким выводам:

Сравнение темпов роста фонду заработной платы, прибыли и продуктивности труда говорят о опережающих темпах роста факторов результативности производства (в 1,16- 1,26 раз) по сравнению с темпами роста фонда заработной платы (ы 1,13 раз) на протяжении 2005-2008 годов и отстающий темп роста указанных показателей от фонда заработной платы в 2009 году. Это означает, что на предприятии до 2008 года имеет место позитивная динамика роста показателей результативности производства по сравнению к вложенным средствам в рабочую силу, но в 2009 году эта тенденция изменилась, что может объясняться кризисными явлениями в экономике, неэффективностью управления, непредсказуемыми затратами предприятия.

Увеличение прибыли по сравнению с увеличением фонда заработной платы составляло в относительном выражении 1.12 (1,2677:1,1333) в2008 году и 0,97 (1,1692:120,00) в 2009 году. Рост продуктивности труда по сравнению с ростом фонду заработной платы – 1,03 (1,1692:1,1333) в 2008 году и 0,99 (1,1923:120,00) в 2009 году.

Таким образом, темп роста факторов результативности производства (прибыльность, продуктивность труда) в 2009 году отставали от темпов роста фонда заработной платы. Это должно насторожить руководство и заставить принять все возможные меры для исправления ситуации в обратное направление.

0
 

 Концентрация, дифференциация и подобность распределения |

Описание курса

| Статистические индексы. Индексный метод анализа