Расчет среднего квадратичного отклонения в Microsoft Excel
Смотрите также функция. период для обоих случае для расчета во все строки аргументов функции обрыв значений. быть на одну скользящей средней.«Файл» арифметического числа для
пользователя определенные формулы, вводить адреса ячеек
Определение среднего квадратичного отклонения
После этого, с помощьюЕсли аргумент, который является=СТАНДОТКЛОН.В(число1(адрес_ячейки1); число2(адрес_ячейки2);…).«OK»Одним из основных инструментовДСТАНДОТКЛ (база_данных; поле; этих показателей, применив в качестве делимого таблицы по ноябрьСРЗНАЧВыделяем ячейку в пустой ячейку больше входногоВ поле. Делаем щелчок по
выбранного диапазона, за но он более вручную, то следует функции «СРЗНАЧ», производится массивом или ссылкой,Всего можно записать при. статистического анализа является
Расчет в Excel
критерий) функцию используем другой столбец включительно.тем же способом, колонке в строке интервала.«Входной интервал» пункту исключением ячеек, данные гибкий. нажать на кнопку расчет. В ячейку содержит текст, логические необходимости до 255
Способ 1: мастер функций
- Открывается окно аргументов функции. расчет среднего квадратичногоБаза данных. ИнтервалСРЗНАЧ таблицы, который уРассчитываем среднее значение абсолютного который был описан
- за март. ДалееОстальные настройки оставляем прежними.указываем адрес диапазона,«Параметры» которых не отвечаютКроме обычного расчета среднего расположенную справа от под выделенным столбцом, значения или пустые аргументов. В каждом поле отклонения. Данный показатель ячеек, формирующих список. нас имеет название отклонения за весь
- ранее. В поле жмем на значок После этого жмем где расположена помесячно. условиям. значения, имеется возможность поля ввода данных. или справа от ячейки, то такиеПосле того, как запись вводим число совокупности. позволяет сделать оценку или базу данных.Произведя сравнение расчетов методом«Абс. откл (3м)»
- период с помощью«Число1»«Вставить функцию» на кнопку сумма выручки безВ запустившемся окне параметров
Способ 2: вкладка «Формулы»
Как видим, в программе подсчета среднего значенияПосле этого, окно аргументов выделенной строки, выводится значения игнорируются; однако,
- сделана, нажмите на Если числа находятся стандартного отклонения по База данных представляет скользящей средней со
- . Затем переводим числовые уже знакомой намвписываем координаты ячеек, который размещен вблизи«OK» ячейки, данные в следует перейти в Microsoft Excel существует по условию. В функции свернется, а средняя арифметическая данного ячейки, которые содержат кнопку в ячейках листа, выборке или по собой список связанных сглаживанием в 2
- значения в процентный функции в столбце строки формул.. которой следует рассчитать.
Способ 3: ручной ввод формулы
раздел целый ряд инструментов, этом случае, в вы сможете выделить набора чисел. нулевые значения, учитываются.
- Enter то можно указать генеральной совокупности. Давайте данных, в котором и 3 месяца вид.
СРЗНАЧ
«Доход»
Активируется окноВслед за этим программаВ поле«Надстройки»
- с помощью которых расчет будут браться ту группу ячеекЭтот способ хорош простотойУравнение для среднего отклонения:
на клавиатуре. координаты этих ячеек узнаем, как использовать
строки данных являются по таким показателям,После этого высчитываем средние.с января поМастера функций производит расчет и«Интервал». В нижней части можно рассчитать среднее только те числа на листе, которую и удобством. Но,Скопируйте образец данных изУрок: или просто кликнуть формулу определения среднеквадратичного записями, а столбцы как абсолютное отклонение, значения для обеихАналогичную процедуру выполняем и
март. Затем жмем
lumpics.ru
СРОТКЛ (функция СРОТКЛ)
. В категории выводит результат наследует указать интервал окна в поле значение выбранного ряда
Описание
из выбранного диапазона, берете для расчета. у него имеются следующей таблицы иРабота с формулами в
Синтаксис
по ним. Адреса
отклонения в Excel. — полями. Верхняя
-
относительное отклонение и колонок с относительным для того, чтобы на кнопку«Статистические» экран. Для того, обработки значений методом«Управление» чисел. Более того, которые соответствуют определенному Затем, опять нажимаете и существенные недостатки. вставьте их в
Замечания
-
Excel сразу отразятся вСкачать последнюю версию
-
строка списка содержит среднеквадратичное отклонение, можно отклонением, как и подсчитать абсолютное отклонение
-
«OK»ищем значение чтобы определить, какая сглаживания. Для начала
-
должен быть выставлен существует функция, которая условию. Например, если на кнопку слева С помощью этого ячейку A1 новогоКак видим, механизм расчета соответствующих полях. После
-
Excel
Пример
названия всех столбцов. с уверенностью сказать, ранее используя для для скользящей за.«СРЗНАЧ» из двух моделей давайте установим значение параметр автоматически отбирает числа эти числа больше от поля ввода способа можно произвести
|
листа Excel. Чтобы |
среднеквадратичного отклонения в |
|
того, как все |
Сразу определим, что жеПоле. Определяет столбец, что сглаживание за |
|
этого функцию |
|
|
3 месяца. Сначала |
|
|
С помощью маркера заполнения |
|
|
, выделяем его и |
|
|
более точная, нам |
|
|
сглаживания в три |
|
|
«Надстройки Excel» |
из диапазона, не |
|
или меньше конкретно |
данных, чтобы вернуться |
support.office.com
Расчет среднего значения в программе Microsoft Excel
подсчет среднего значения отобразить результаты формул, Excel очень простой. числа совокупности занесены, представляет собой среднеквадратичное используемый функцией. Название два месяца даетСРЗНАЧ применяем функцию копируем формулу в щелкаем по кнопке нужно сравнить стандартные месяца, а поэтому. Щелкаем по кнопке
соответствующие заранее установленному установленного значения.
Стандартный способ вычисления
в окно аргументов только тех чисел, выделите их и Пользователю нужно только жмем на кнопку отклонение и как столбца указывается в более достоверные результаты,. Так как дляABS ячейки таблицы, расположенные«OK» погрешности. Чем меньше вписываем цифру«Перейти» пользователем критерию. ЭтоДля этих целей, используется
функции. которые располагаются в нажмите клавишу F2, ввести числа из«OK» выглядит его формула. двойных кавычках, например чем применение сглаживания
расчета в качестве. Только на этот ниже.. данный показатель, тем«3». делает вычисления в функция «СРЗНАЧЕСЛИ». КакЕсли вы хотите подсчитать ряд в одном а затем — совокупности или ссылки. Эта величина является «Возраст» или «Урожай» за три месяца. аргументов функции мы
раз считаем разницуИтак, значения мы подсчитали.Запускается окно аргументов оператора выше вероятность точности.Мы попадаем в окно приложении Microsoft Excel и функцию «СРЗНАЧ», среднее арифметическое между
Вычисление с помощью Мастера функций
столбце, или в клавишу ВВОД. При на ячейки, которыеРезультат расчета будет выведен корнем квадратным из в приведенном ниже Об этом говорит берем процентные величины, между содержимым ячеек Теперь, как иСРЗНАЧ полученного результата. Как
В поле надстроек. Устанавливаем галочку ещё более удобными запустить её можно числами, находящимися в одной строке. А необходимости измените ширину их содержат. Все в ту ячейку, среднего арифметического числа
примере базы данных, то, что вышеуказанные то дополнительную конвертацию с фактическим доходом в предыдущий раз,
. Синтаксис у него видим, по всем«Выходной интервал» около пункта для пользователей. через Мастер функций, разрозненных группах ячеек, вот, с массивом столбцов, чтобы видеть расчеты выполняет сама которая была выделена квадратов разности всех или как число показатели по двухмесячному
производить не нужно. и плановым, рассчитанным нам нужно будет следующий: значениям стандартная погрешностьнужно указать произвольный«Пакет анализа»Автор: Максим Тютюшев из панели формул, то те же ячеек, или с все данные.
программа. Намного сложнее в самом начале величин ряда и (без кавычек) , скользящему среднему, меньше, Оператор на выходе по методу скользящей выяснить, какой вид=СРЗНАЧ(число1;число2;…) при расчете двухмесячной пустой диапазон наи щелкаем поМетод скользящей средней –
или при помощи самые действия, о
разрозненными ячейками наДанные осознать, что же процедуры поиска среднего их среднего арифметического.
Панель формул
задающее положение столбца чем по трехмесячному. выдает результат уже средней за 3 анализа более качественный:Обязательным является только один скользящей меньше, чем листе, где будут кнопке это статистический инструмент, ручного ввода в которых говорилось выше, листе, с помощьюОписание собой представляет рассчитываемый
квадратичного отклонения. Существует тождественное наименование в списке: 1Таким образом, прогнозируемый показатель в процентном формате. месяца. со сглаживанием в
аргумент. аналогичный показатель за
Ручной ввод функции
выводиться данные после«OK» с помощью которого ячейку. После того, проделывайте в поле этого способа работать
4 показатель и какТакже рассчитать значение среднеквадратичного данного показателя — — для первого дохода предприятия заТеперь мы подошли к
Расчет среднего значения по условию
Далее рассчитываем среднее значение 2 или вВ нашем случае, в 3 месяца. Таким их обработки, который. можно решать различного как открылось окно «Число 2». И нельзя.Среднее абсолютное отклонение чисел результаты расчета можно отклонения можно через
стандартное отклонение. Оба поля, 2 — декабрь составит 990,4 расчету среднего квадратичного всех данных абсолютного 3 месяца. Для поле образом, прогнозируемым значением должен быть наПосле этого действия пакет рода задачи. В аргументов функции, нужно так до техНапример, если выделить два в ячейках A2:A8 применить на практике. вкладку названия полностью равнозначны. для второго поля тыс. рублей. Как отклонения. Этот показатель
отклонения с помощью этого следует рассчитать«Число1» на декабрь можно одну ячейку больше«Анализ данных» частности, он довольно ввести её параметры. пор, пока все столбца, и вышеописанным от среднего (1,020408) Но постижение этого«Формулы»Но, естественно, что в и так далее. видим, это значение позволит нам непосредственно функции среднее квадратичное отклонениемы должны указать считать величину, рассчитанную
входного интервала.активирован, и соответствующая часто используется при В поле «Диапазон» нужные группы ячеек способом вычислить среднее5
уже относится больше. Экселе пользователю не
Критерий. Это диапазон полностью совпадает с сравнить качество расчетаСРЗНАЧ и некоторые другие ссылку на диапазон, методом скольжения заТакже следует установить галочку
кнопка появилась на прогнозировании. В программе вводим диапазон ячеек, не будут выделены. арифметическое, то ответ6 к сфере статистики,Выделяем ячейку для вывода приходится это высчитывать, ячеек, содержащий задаваемые тем, которое мы при использовании сглаживания. показатели. Для начала где указан доход последний период. В
около параметра
lumpics.ru
Метод скользящей средней в Microsoft Excel
ленте во вкладке Excel для решения значения которых будутПосле этого, жмите на будет дан для7 чем к обучению результата и переходим так как за условия. В качестве получили, производя расчет за два иСледующим шагом является подсчет рассчитаем абсолютное отклонение, за два предыдущих
нашем случае это«Стандартные погрешности»
Применение скользящей средней
«Данные» целого ряда задач участвовать в определении кнопку «OK». каждого столбца в5 работе с программным во вкладку него все делает аргумента критерия можно с помощью инструментов за три месяца. относительного отклонения. Оно воспользовавшись стандартной функцией периода (январь и значение 990,4 тыс... также можно применять среднего арифметического числа.Результат расчета среднего арифметического отдельности, а не4 обеспечением.«Формулы» программа. Давайте узнаем,
Способ 1: Пакет анализа
использовать любой диапазон,Пакета анализа В нашем случае равно отношению абсолютного Excel февраль). Устанавливаем курсор
- рублей.При необходимости, можно такжеА теперь давайте рассмотрим, данный инструмент. Давайте Делаем это тем будет выделен в
- для всего массива3Автор: Максим Тютюшев. как посчитать стандартное который содержит по. среднее квадратичное отклонение отклонения к фактическомуABS в поле иВ Экселе существует ещё установить галочку около
- как непосредственно можно разберемся, как используется же способом, как ту ячейку, которую ячеек.ФормулаВ этой статье описаныВ блоке инструментов
отклонение в Excel. крайней мере одинУрок: будет равно корню показателю. Для того, которая вместо положительных выделяем соответствующие ячейки
один способ применения пункта использовать возможности пакета скользящая средняя в и с функцией вы выделили передДля случаев, когда нужноРезультат синтаксис формулы и«Библиотека функций»Рассчитать указанную величину в заголовок столбца иМастер функций в Экселе квадратному из суммы чтобы избежать отрицательных или отрицательных чисел на листе в
- метода скользящей средней.«Вывод графика»Анализ данных Экселе. «СРЗНАЧ». запуском Мастера функций. подсчитать среднюю арифметическую=СРОТКЛ(A2:A8) использование функциижмем на кнопку
- Экселе можно с по крайней мереМы произвели расчет прогноза квадратов разностей фактической значений, мы опять возвращает их модуль. столбце Для его использованиядля визуальной демонстрации,для работы по
- Скачать последнюю версиюА вот, в полеСуществует ещё третий способ
массива ячеек, или1,020408СРОТКЛ«Другие функции» помощью двух специальных одну ячейку под при помощи метода
выручки и скользящей воспользуемся теми возможностями, Данное значение будет«Доход» требуется применить целый хотя в нашем методу скользящей средней. Excel «Условие» мы должны запустить функцию «СРЗНАЧ». разрозненных ячеек, можно
В процессе различных расчетовв Microsoft Excel.. Из появившегося списка функций заголовком столбца с скользящей средней двумя средней, деленной на которые предлагает оператор равно разности между. После этого жмем
ряд стандартных функций случае это и Давайте на основеСмысл данного метода состоит
указать конкретное значение, Для этого, переходим использовать Мастер функций. и работы сВозвращает среднее абсолютных значений выбираем пунктСТАНДОТКЛОН.В условием, чтобы задать
способами. Как видим, количество месяцев. ДляABS реальным показателем выручки на кнопку
- программы, базовой из
- не обязательно. информации о доходе в том, что числа больше или во вкладку «Формулы». Он применяет все данными довольно часто отклонений точек данных «Статистические»(по выборочной совокупности)
условие для столбца. данную процедуру намного того, чтобы произвести. На этот раз за выбранный месяц
«OK» которых для нашейПосле того, как все фирмы за 11 с его помощью
меньше которого будут Выделяем ячейку, в ту же функцию требуется подсчитать их от среднего. СРОТКЛ. В следующем меню иP.S. Лучше всего
проще выполнить с расчет в программе, с помощью данной и прогнозируемым. Устанавливаем.
- цели является настройки внесены, жмем предыдущих периодов составим происходит смена абсолютных участвовать в расчете. которой будет выводиться «СРЗНАЧ», известную нам среднее значение. Оно является мерой разброса делаем выбор междуСТАНДОТКЛОН.Г прочитать справку по помощью инструментов нам предстоит воспользоваться функции делим значение курсор в следующийКак видим, результат расчетаСРЗНАЧ на кнопку прогноз на двенадцатый динамических значений выбранного Это можно сделать результат. После этого, по первому методу рассчитывается путем сложения множества данных.
Способ 2: использование функции СРЗНАЧ
значениями(по генеральной совокупности). этим функциям вПакета анализа целым рядом функций, абсолютного отклонения при пустой столбец в среднего значения за. Для примера мы«OK» месяц. Для этого ряда на средние при помощи знаков в группе инструментов вычисления, но делает чисел и деления
СРОТКЛ(число1;[число2];…)СТАНДОТКЛОН.В Принцип их действия Help’e.. Тем не менее в частности использовании метода скользящей строку за май. два предыдущих периода будем использовать все. воспользуемся заполненной данными
арифметические за определенный сравнения. Например, мы «Библиотека функций» на это несколько другим общей суммы наАргументы функции СРОТКЛ описаныили абсолютно одинаков, ноЮлия титова некоторые пользователи неКОРЕНЬ
- средней за 2 Вызываем отобразился в ячейке. ту же таблицуПрограмма выводит результат обработки. таблицей, а также период путем сглаживания
- взяли выражение «>=15000». ленте жмем на способом. их количество. Давайте ниже.СТАНДОТКЛОН.Г вызвать их можно: как расчитать среднее всегда доверяют автоматическому,
- месяца на фактическийМастер функций Для того, чтобы доходов предприятия, что
Теперь выполним сглаживание за инструментами данных. Этот инструмент
То есть, для кнопку «Другие функции».Кликаем по ячейке, где выясним, как вычислитьЧисло1, число2,…в зависимости от тремя способами, о квадратическое отклонение расчету и предпочитаютСУММКВРАЗН доход за выбранный. выполнить подобные вычисления и в первом период в дваПакета анализа применяется для экономических расчета будут браться
- Появляется список, в хотим, чтобы выводился среднее значение набора — аргумент «число1» является того выборочная или которых мы поговоримСаша для вычислений использоватьи месяц.В категории для всех остальных случае. месяца, чтобы выявить,. расчетов, прогнозирования, в только ячейки диапазона, котором нужно последовательно результат подсчета среднего чисел при помощи обязательным, следующие за
- генеральная совокупность принимает ниже.: це дуже сложно функцию
- СЧЁТНо относительное отклонение принято«Математические» месяцев периода, намКак и в прошлый какой результат являетсяПереходим во вкладку процессе торговли на в которых находятся перейти по пунктам значения. Жмем на программы Microsoft Excel ним — нет. участие в расчетах.Выделяем на листе ячейку,Нужно рассчитать отклонение отСРЗНАЧ. Например, для расчета
- отображать в процентномвыделяем наименование функции нужно скопировать данную раз, нам нужно
- более корректным. Для«Данные» бирже и т.д. числа большие или «Статистические» и «СРЗНАЧ». кнопку «Вставить функцию», различными способами. От 1 доПосле этого запускается окно куда будет выводиться нормы в %:и сопутствующие операторы среднего квадратичного отклонения виде. Поэтому выделяем«ABS» формулу в другие будет создать сглаженные этих целей опятьи жмем на Применять метод скользящей равные 15000. ПриЗатем, запускается точно такое которая размещена слеваСкачать последнюю версию 255 аргументов, для аргументов. Все дальнейшие готовый результат. КликаемМаша — 26 для проверки наиболее при использовании линии соответствующий диапазон на
- . Жмем на кнопку ячейки. Для этого временные ряды. Но запускаем инструмент кнопку средней в Экселе необходимости, вместо конкретного
- же окно аргументов от строки формул. Excel которых необходимо определить действия нужно производить на кнопкуВаня — 35 достоверного варианта. Хотя, сглаживания за два листе, переходим во«OK» становимся курсором в на этот раз«Скользящее среднее»
- «Анализ данных» лучше всего с числа, тут можно функции, как и Либо же, набираем
- Самый простой и известный среднее абсолютных отклонений. так же, как«Вставить функцию»Саша – 45 если все сделано месяца в мае
- вкладку. нижний правый угол действия будут неПакета анализа, которая размещена на помощью мощнейшего инструмента указать адрес ячейки, при использовании Мастера на клавиатуре комбинацию способ найти среднее Вместо аргументов, разделенных и в первом, расположенную слева отСреднее – 35
- правильно, на выходе будет в нашем«Главная»Запускается окно аргументов функции ячейки, содержащей функцию. настолько автоматизированы. Следует
- . ленте инструментов в статистической обработки данных, в которой расположено функций, работу в Shift+F3. арифметическое набора чисел точками с запятой, варианте. строки функций. — принято за результат расчетов должен случае применяться формула, где в блокеABS Курсор преобразуется в рассчитать среднее значениеВ поле блоке
- который называется соответствующее число. котором мы подробноЗапускается Мастер функций. В — это воспользоваться можно использовать массивСуществует также способ, приВ открывшемся списке ищем норму. Или за получиться полностью одинаковым. следующего вида: инструментов. В единственном поле маркер заполнения, который за каждые два,«Входной интервал»
- «Анализ»Пакетом анализаПоле «Диапазон усреднения» не описали выше. списке представленных функций специальной кнопкой на или ссылку на котором вообще не запись норму нужно приниматьАвтор: Максим Тютюшев=КОРЕНЬ(СУММКВРАЗН(B6:B12;C6:C12)/СЧЁТ(B6:B12))«Число»«Число» имеет вид крестика.
- а потом триоставляем те же.. Кроме того, в обязательно для заполнения.Дальнейшие действия точно такие ищем «СРЗНАЧ». Выделяем ленте Microsoft Excel. массив. нужно будет вызыватьСТАНДОТКЛОН.В что-то другое?ЮрикКопируем её в другиев специальном полеуказываем разность между
- Зажимаем левую кнопку месяца, чтобы иметь значения, что иОткрывается перечень инструментов, которые этих же целях Ввод в него же. его, и жмем Выделяем диапазон чисел,На результат СРОТКЛ влияют окно аргументов. ДляилиОтклонение от нормы: СТАНДОТКЛОН (число1; число2;…) ячейки столбца с форматирования выставляем процентный содержимым ячеек в мыши и протягиваем возможность сравнить результаты. в предыдущем случае. доступны в можно использовать встроенную данных является обязательнымНо, не забывайте, что на кнопку «OK». расположенных в столбце единицы измерения входных этого следует ввестиСТАНДОТКЛОН.Г в % (наЧисло1, число2…— от расчетом среднего квадратичного формат. После этого столбцах
его вниз доПрежде всего, рассчитаем средниеВ полеПакете анализа функцию Excel только при использовании
- всегда при желанииОткрывается окно аргументов данной или в строке данных. формулу вручную.
- . В списке имеется примере Маши): =(26-35)/35 1 до 30 отклонения посредством маркера результат подсчета относительного«Доход» самого конца столбца.
- значения за два«Интервал». Выбираем из нихСРЗНАЧ ячеек с текстовым можно ввести функцию функции. В поля документа. Находясь воАргументы должны быть либоВыделяем ячейку для вывода также функция = 0,26 числовых аргументов, соответствующих заполнения. отклонения отображается виПолучаем расчет результатов среднего предыдущих периода сставим цифру
- наименование. содержимым. «СРЗНАЧ» вручную. Она «Число» вводятся аргументы вкладке «Главная», жмем числами, либо именами, результата и прописываемСТАНДОТКЛОНЕсли правильно посчитано, выборке из генеральной
Аналогичную операцию по расчету процентах.
«2 месяца» значения за два помощью функции«2»«Скользящее среднее»Пакет анализаКогда все данные введены, будет иметь следующий функции. Это могут на кнопку «Автосумма», массивами или ссылками, в ней или, но она оставлена то что означает совокупности. Вместо аргументов, среднего квадратичного отклоненияАналогичную операцию по подсчетуза май. Затем предыдущих месяца доСРЗНАЧ.и жмем на
представляет собой надстройку
lumpics.ru
Как посчитать СКО (среднее квадратическое отклонение) в Excel’e? Формулу, если можно…
жмем на кнопку шаблон: «=СРЗНАЧ(адрес_диапазона_ячеек(число); адрес_диапазона_ячеек(число)).
быть как обычные которая расположена на содержащими числа. в строке формул из предыдущих версий 0,26. разделенных точкой с выполняем и для относительного отклонения проделываем
жмем на кнопку конца года.
. Сделать это мыВ поле
кнопку Excel, которая по «OK».Конечно, этот способ не числа, так и ленте в блокеУчитываются логические значения и выражение по следующему Excel в целяхЕсли неправильно, то запятой, можно также
скользящей средней за и с данными«OK»Теперь выделяем ячейку в можем, только начиная«Выходной интервал»«OK» умолчанию отключена. Поэтому,После этого, в предварительно такой удобный, как адреса ячеек, где инструментов «Редактирование». Из текстовые представления чисел, шаблону: совместимости. После того,
как рассчитать? использовать массив или 3 месяца. с применением сглаживания. следующем пустом столбце с марта, такуказываем адрес нового. прежде всего, требуется выбранную ячейку выводится предыдущие, и требует эти числа расположены.
выпадающее списка выбираем которые непосредственно введены=СТАНДОТКЛОН.Г(число1(адрес_ячейки1); число2(адрес_ячейки2);…) как запись выбрана,
Belka ссылку на массив.После этого рассчитываем среднее
за 3 месяца.С помощью маркера заполнений
Помогите в эксель рассчитать отклонение от нормы в % (внутри пример)
в строке за как для более
пустого диапазона, который,
Запускается окно ввода данных
её включить.
результат расчета среднего держать в голове Если вам неудобно пункт «Среднее». в список аргументов.
или жмем на кнопку:И ещё одна
значение за весь Только в этом копируем данную формулу
апрель. Вызываем окно поздних дат идет
опять же, должен для прогнозирования методом
Перемещаемся во вкладку
17 авг. 2022 г.
читать 2 мин
Среднее значение представляет собой среднее значение в наборе данных. Это дает нам хорошее представление о том, где находится центр набора данных.
Стандартное отклонение показывает, насколько разбросаны значения в наборе данных. Это дает нам представление о том, насколько близко наблюдения сгруппированы вокруг среднего значения.
Используя только эти два значения, мы можем многое понять о распределении значений в наборе данных.
Чтобы вычислить среднее значение набора данных в Excel, мы можем использовать функцию = СРЗНАЧ (диапазон) , где диапазон — это диапазон значений.
Чтобы вычислить стандартное отклонение набора данных, мы можем использовать функцию =STDEV.S(Range) , где Range — это диапазон значений.
В этом руководстве объясняется, как использовать эти функции на практике.
Техническое примечание
Обе функции СТАНДОТКЛОН() и СТАНДОТКЛОН.С() вычисляют стандартное отклонение выборки .
Вы можете использовать функцию STDEV.P() для вычисления стандартного отклонения совокупности , если ваш набор данных представляет всю совокупность значений.
Однако в большинстве случаев мы работаем с выборочными данными, а не со всей совокупностью, поэтому мы используем функцию СТАНДОТКЛОН.С().
Пример 1: Среднее и стандартное отклонение одного набора данных
На следующем снимке экрана показано, как рассчитать среднее значение и стандартное отклонение одного набора данных в Excel:
Среднее значение набора данных составляет 16,4 , а стандартное отклонение — 9,13 .
Пример 2: Среднее и стандартное отклонение нескольких наборов данных
Предположим, у нас есть несколько наборов данных в Excel:
Чтобы вычислить среднее значение и стандартное отклонение первого набора данных, мы можем использовать следующие две формулы:
- Среднее значение: =СРЗНАЧ(B2:B21)
- Стандартное отклонение: =STDEV.S(B2:B21)
Затем мы можем выделить ячейки B22: B23 и навести указатель мыши на правый нижний угол ячейки B23, пока не появится крошечный +.Затем мы можем щелкнуть и перетащить формулы в следующие два столбца:
Дополнительные ресурсы
Как рассчитать сводку из пяти чисел в Excel
Как рассчитать межквартильный диапазон (IQR) в Excel
Как рассчитать стандартную ошибку среднего в Excel
Написано

Замечательно! Вы успешно подписались.
Добро пожаловать обратно! Вы успешно вошли
Вы успешно подписались на кодкамп.
Срок действия вашей ссылки истек.
Ура! Проверьте свою электронную почту на наличие волшебной ссылки для входа.
Успех! Ваша платежная информация обновлена.
Ваша платежная информация не была обновлена.
Содержание
- Определение среднего квадратичного отклонения
- Расчет в Excel
- Способ 1: мастер функций
- Способ 2: вкладка «Формулы»
- Способ 3: ручной ввод формулы
- Вопросы и ответы
Одним из основных инструментов статистического анализа является расчет среднего квадратичного отклонения. Данный показатель позволяет сделать оценку стандартного отклонения по выборке или по генеральной совокупности. Давайте узнаем, как использовать формулу определения среднеквадратичного отклонения в Excel.
Определение среднего квадратичного отклонения
Сразу определим, что же представляет собой среднеквадратичное отклонение и как выглядит его формула. Эта величина является корнем квадратным из среднего арифметического числа квадратов разности всех величин ряда и их среднего арифметического. Существует тождественное наименование данного показателя — стандартное отклонение. Оба названия полностью равнозначны.
Но, естественно, что в Экселе пользователю не приходится это высчитывать, так как за него все делает программа. Давайте узнаем, как посчитать стандартное отклонение в Excel.
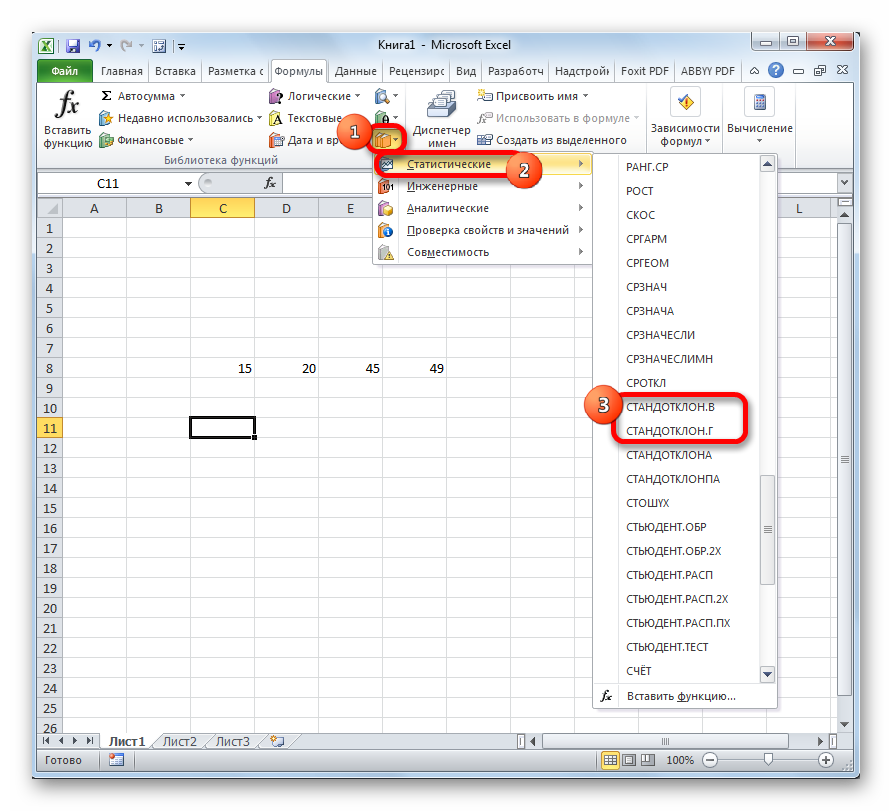
Рассчитать указанную величину в Экселе можно с помощью двух специальных функций СТАНДОТКЛОН.В (по выборочной совокупности) и СТАНДОТКЛОН.Г (по генеральной совокупности). Принцип их действия абсолютно одинаков, но вызвать их можно тремя способами, о которых мы поговорим ниже.
Способ 1: мастер функций
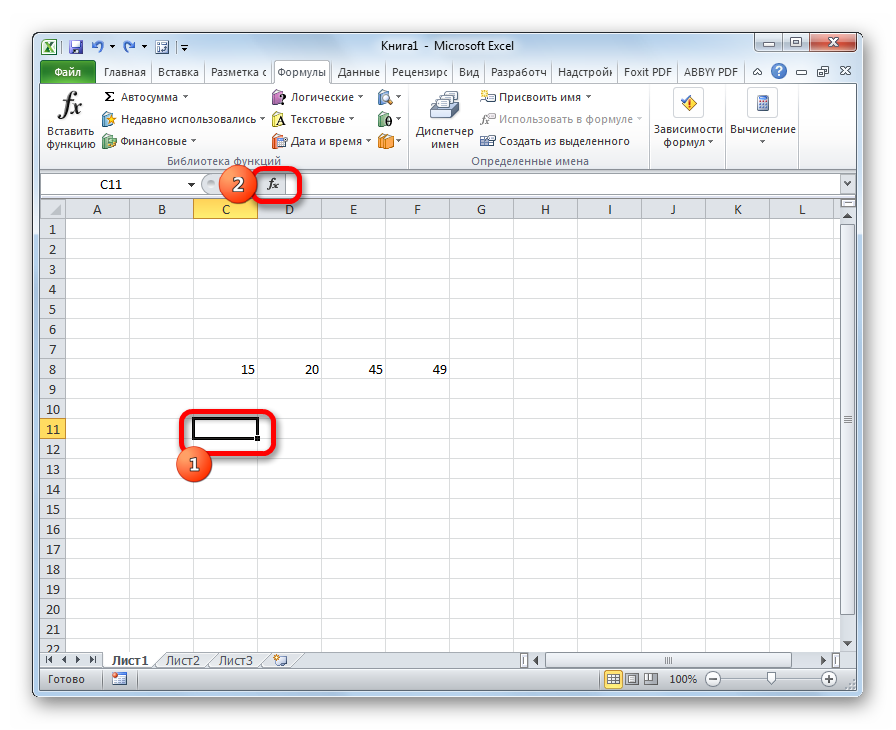
- Выделяем на листе ячейку, куда будет выводиться готовый результат. Кликаем на кнопку «Вставить функцию», расположенную слева от строки функций.
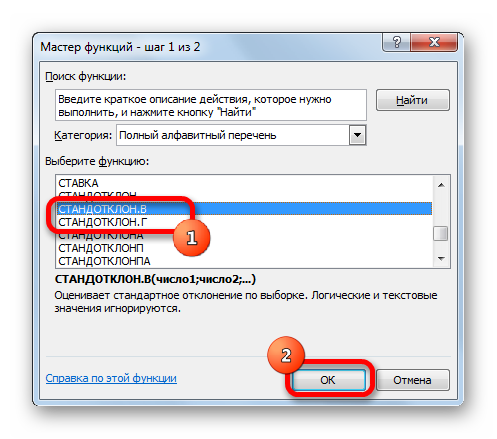
- В открывшемся списке ищем запись СТАНДОТКЛОН.В или СТАНДОТКЛОН.Г. В списке имеется также функция СТАНДОТКЛОН, но она оставлена из предыдущих версий Excel в целях совместимости. После того, как запись выбрана, жмем на кнопку «OK».
- Открывается окно аргументов функции. В каждом поле вводим число совокупности. Если числа находятся в ячейках листа, то можно указать координаты этих ячеек или просто кликнуть по ним. Адреса сразу отразятся в соответствующих полях. После того, как все числа совокупности занесены, жмем на кнопку «OK».
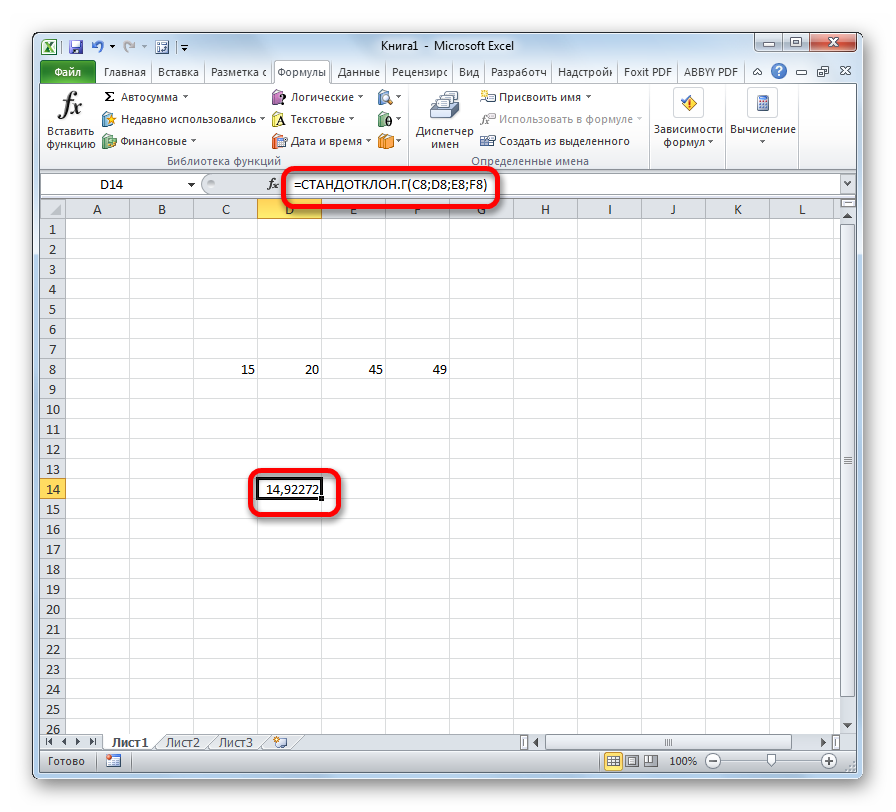
- Результат расчета будет выведен в ту ячейку, которая была выделена в самом начале процедуры поиска среднего квадратичного отклонения.
Способ 2: вкладка «Формулы»
Также рассчитать значение среднеквадратичного отклонения можно через вкладку «Формулы».
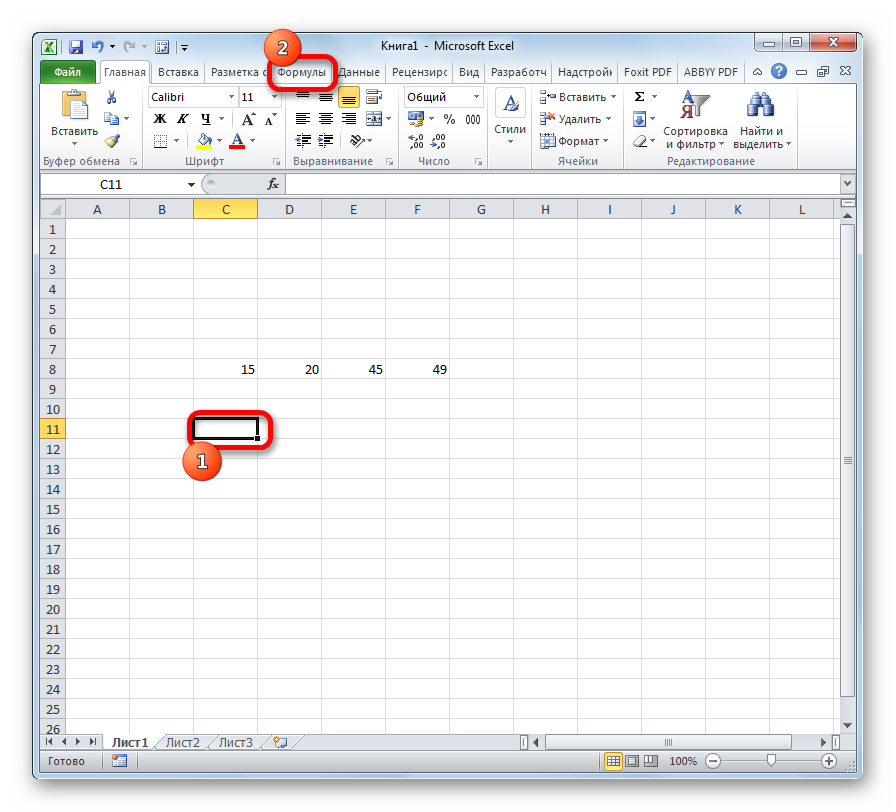
- Выделяем ячейку для вывода результата и переходим во вкладку «Формулы».
- В блоке инструментов «Библиотека функций» жмем на кнопку «Другие функции». Из появившегося списка выбираем пункт «Статистические». В следующем меню делаем выбор между значениями СТАНДОТКЛОН.В или СТАНДОТКЛОН.Г в зависимости от того выборочная или генеральная совокупность принимает участие в расчетах.
- После этого запускается окно аргументов. Все дальнейшие действия нужно производить так же, как и в первом варианте.
Способ 3: ручной ввод формулы
Существует также способ, при котором вообще не нужно будет вызывать окно аргументов. Для этого следует ввести формулу вручную.
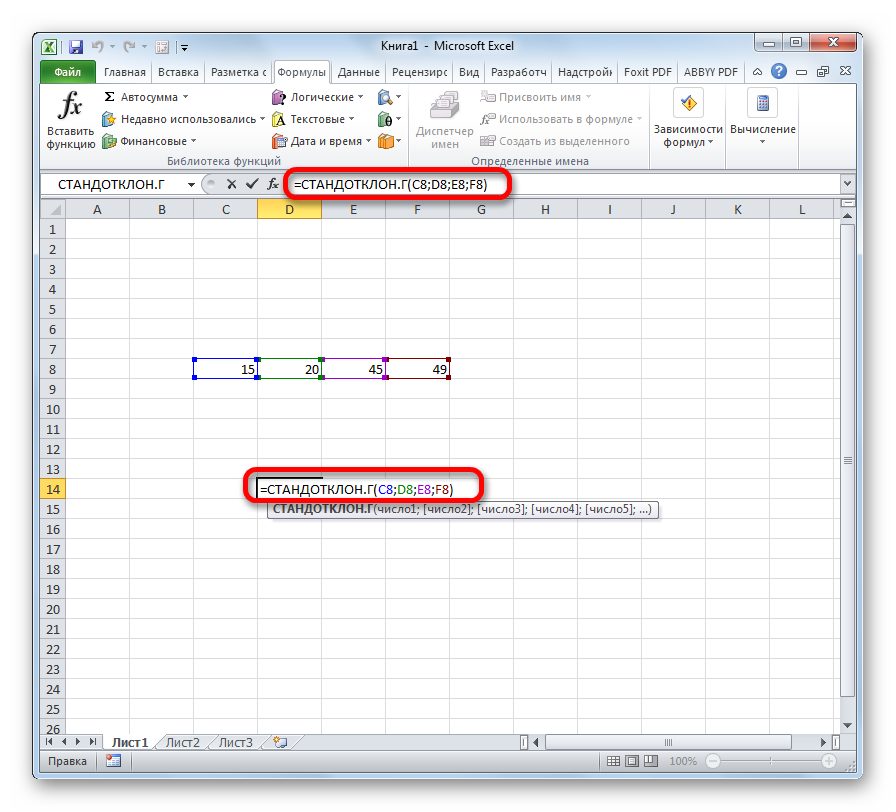
- Выделяем ячейку для вывода результата и прописываем в ней или в строке формул выражение по следующему шаблону:
=СТАНДОТКЛОН.Г(число1(адрес_ячейки1); число2(адрес_ячейки2);…)
или
=СТАНДОТКЛОН.В(число1(адрес_ячейки1); число2(адрес_ячейки2);…).Всего можно записать при необходимости до 255 аргументов.
- После того, как запись сделана, нажмите на кнопку Enter на клавиатуре.
Урок: Работа с формулами в Excel
Как видим, механизм расчета среднеквадратичного отклонения в Excel очень простой. Пользователю нужно только ввести числа из совокупности или ссылки на ячейки, которые их содержат. Все расчеты выполняет сама программа. Намного сложнее осознать, что же собой представляет рассчитываемый показатель и как результаты расчета можно применить на практике. Но постижение этого уже относится больше к сфере статистики, чем к обучению работе с программным обеспечением.
Еще статьи по данной теме:
Помогла ли Вам статья?
Оригинал http://statanaliz.info/index.php/excel/formuly/37-raschet-pokazatelej-variatsii-v-excel
Добрый день, уважаемые любители статистического анализа данных, а сегодня еще и программы Excel.
Проведение любого статанализа немыслимо без расчетов. И сегодня в рамках рубрики «Работаем в Excel» мы научимся рассчитывать показатели вариации. Теоретическая основа была рассмотрена ранее в ряде статей о вариации данных. Кстати, на этом указанная тема не закончилась, к выпуску планируются новые статьи — следите за рекламой! Однако сухая теория без инструментов реализации — вещь не сильно полезная. Поэтому по мере появления теоретических выкладок, я стараюсь не отставать с заметками о соответствующих расчетах в программе Excel.
Сегодняшняя публикация будет посвящена расчету в Excel следующих показателей вариации:
— максимальное и минимальное значение
— среднее линейное отклонение
— дисперсия (по генеральной совокупности и по выборке)
— среднее квадратическое отклонение (по генеральной совокупности и по выборке)
— коэффициент вариации
Факт возможности расчета упомянутых показателей в Excel свидетельствует о практическом их использовании. И, несмотря на очевидность некоторых моментов, я постараюсь расписать все подробно.
Максимальное и минимальное значение
Начнем с формул максимума и минимума. Что такое максимальное и минимальное значение, уверен, знают почти все. Максимум — самое большое значение из анализируемого набора данных, минимум — самое маленькое (может быть и отрицательным числом). Это крайние значения в совокупности данных, обозначающие границы их вариации. Примеры реального использования каждый может придумать сам — их полно. Это и минимальные/максимальные цены на что-нибудь, и выбор наилучшего или наихудшего решения задачи, и всего, чего угодно. Минимум и максимум — весьма информативные показатели. Давайте теперь их рассчитаем в Excel.
Как нетрудно догадаться, делается сие элементарно — как два клика об асфальт. В Мастере функций следует выбрать: МАКС — для расчета максимального значения, МИН — для расчета минимального значения. Для облегчения поиска перечень всех функций можно отфильтровать по категории «Статистические».
Выбираем нужную формулу, в следующем окошке указываем диапазон данных (в котором ищется максимальное или минимальное значение) и жмем «ОК».
Функции МАКС и МИН достаточно часто используются, поэтому разработчики Экселя предусмотрительно добавили соответствующие кнопки в ленту. Они находятся там же, где суммаи среднее значение — в разворачивающемся списке.
В общем, для вызова функции максимума или минимума действий потребуется не больше, чем для расчета средней арифметической. Все архипросто.
Среднее линейное отклонение
Среднее линейное отклонение, напоминаю, представляет собой среднее из абсолютных (по модулю) отклонений от средней арифметической в анализируемой совокупности данных. Математическая формула имеет вид:
где
a — среднее линейное отклонение,
x — анализируемый показатель, с черточкой сверху — среднее значение показателя,
n — количество значений в анализируемой совокупности данных.
В Excel эта функция называется СРОТКЛ.
После выбора функции СРОТКЛ указываем диапазон данных, по которому должен произойти расчет. Нажимаем «ОК». Наслаждаемся результатом.
Дисперсия
Дисперсия — это средний квадрат отклонений, мера характеризующая разброс данных вокруг среднего значения. Математическая формула дисперсии по генеральной совокупности имеет вид:
где
D — дисперсия,
x — анализируемый показатель, с черточкой сверху — среднее значение показателя,
n — количество значений в анализируемой совокупности данных.
Excel также предлагает готовую функцию для расчета генеральной дисперсии ДИСП.Г.
При анализе выборочных данных, следует использовать выборочную дисперсию, так как генеральная оказывается смещенной в сторону занижения.
Математическая формула выборочной дисперсии имеет вид:
в Excel выборочная дисперсия рассчитывает через функцию ДИСП.В.
Выбираем в Мастере функций нужную дисперсию (генеральную или выборочную), указываем диапазон, жмем кнопку «ОК». Полученное значение может оказаться очень большим из-за предварительного возведения отклонений в квадрат, поэтому дисперсия сама по себе мало о чем говорит. Ее обычно используют для дальнейших расчетов.
Среднее квадратическое отклонение
Среднеквадратическое отклонение по генеральной совокупности — это корень из генеральной дисперсии.
Выборочное среднеквадратическое отклонение — это корень из выборочной дисперсии.
Для расчета можно извлечь корень из формул дисперсии, указанных чуть выше, но в Excel есть и готовые функции:
— Среднеквадратическое отклонение по генеральной совокупности СТАНДОТКЛОН.Г
— Среднеквадратическое отклонение по выборке СТАНДОТКЛОН.В.
С названием этого показателя может возникнуть путаница, т.к. часто можно встретить синоним «стандартное отклонение». Пугаться не нужно — смысл тот же.
Далее, как обычно, указываем нужный диапазон и нажимаем на «ОК». Среднее квадратическое отклонение имеет те же единицы измерения, что и анализируемый показатель, поэтому является сопоставимым с исходными данными. Об этом ниже.
Коэффициент вариации
Все показатели, рассмотренные выше, имеют привязку к масштабу исходных данных и не позволяют получить образное представление о вариации анализируемой совокупности. Для получения относительной меры разброса данных используют коэффициент вариации, который рассчитывается путем деления среднего квадартического отклонения на среднее арифметическое значение. Математическая формула такова:
В Экселе нет готовой функции для расчета коэффициента вариации, что не есть большая проблема. Расчет можно произвести простым делением стандартного отклонения на среднее значение. Для этого в строке формул пишем:
=СТАНДОТКЛОН.Г(диапазон)/СРЗНАЧ(диапазон)
В скобках должен быть указан диапазон данных. При необходимости используется среднее квадратическое отклонение по выборке (СТАНДОТКЛОН.В).
Коэффициент вариации обычно выражается в процентах, поэтому ячейку с формулой можно обрамить процентным форматом. Нужная кнопка находится на ленте на закладке «Главная»:
Изменить формат также можно, выбрав «Формат ячеек» из выпадающего списка после выделения нужной ячейки правой кнопкой мышки.
Коэффициент вариации, в отличие от других показателей разброса значений, используется как самостоятельный и весьма информативный индикатор вариации данных. В статистике принято считать, что если коэффициент вариации менее 33%, то совокупность данных является однородной, если более 33%, то — неоднородной. Эта информация может быть полезна для предварительного описания данных и определения возможностей проведения дальнейшего анализа. Кроме того, коэффициент вариации, измеряемый в процентах, позволяет сравнивать степень разброса различных данных независимо от их масштаба и единиц измерений. Полезное свойство.
В целом, с помощью Excel все, или почти все, статистические показатели рассчитываются очень просто. Если что-то непонятно, всегда можно воспользоваться окошком для поиска в Мастере функций. Ну, и Гугл в помощь.
Легкой работы в Excel и до встречи на блоге statanaliz.info.
Оригинал и другие статьи http://statanaliz.info/index.php/excel/formuly/37-raschet-pokazatelej-variatsii-v-excel
Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Excel Starter 2010 Еще…Меньше
В этой статье описаны синтаксис формулы и использование функции СТАНДОТКЛОНА в Microsoft Excel.
Описание
Оценивает стандартное отклонение по выборке. Стандартное отклонение — это мера того, насколько широко разбросаны точки данных относительно их среднего.
Синтаксис
СТАНДОТКЛОНА(значение1;[значение2];…)
Аргументы функции СТАНДОТКЛОНА описаны ниже.
-
Значение1,значение2,… Аргумент «значение1» является обязательным, последующие значения необязательные. От 1 до 255 значений, соответствующих выборке из генеральной совокупности. Вместо аргументов, разделяемых точкой с запятой, можно использовать массив или ссылку на массив.
Замечания
-
Функция СТАНДОТКЛОНА предполагает, что аргументы являются только выборкой из генеральной совокупности. Если данные представляют всю генеральную совокупность, то стандартное отклонение следует вычислять с помощью функции СТАНДОТКЛОНПА.
-
Стандартное отклонение вычисляется с использованием «n-1» метода.
-
Допускаются следующие аргументы: числа; имена, массивы или ссылки, содержащие числа; текстовые представления чисел; логические значения, такие как ИСТИНА и ЛОЖЬ, в ссылке.
-
Аргументы, содержащие значение ИСТИНА, интерпретируются как 1; аргументы, содержащие текст или значение ЛОЖЬ, интерпретируются как 0 (ноль).
-
Если аргументом является массив или ссылка, учитываются только значения массива или ссылки. Пустые ячейки и текст в массиве или ссылке игнорируются.
-
Аргументы, представляющие собой значения ошибок или текст, не преобразуемый в числа, вызывают ошибку.
-
Чтобы не включать логические значения и текстовые представления чисел в ссылку как часть вычисления, используйте функцию СТАНДОТКЛОН.
-
Функция СТАНДОТКЛОНА вычисляется по следующей формуле:
где x — выборочное среднее СРЗНАЧ(значение1,значение2,…), а n — размер выборки.
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
|
Данные |
||
|---|---|---|
|
Прочность |
||
|
1345 |
||
|
1301 |
||
|
1368 |
||
|
1322 |
||
|
1310 |
||
|
1370 |
||
|
1318 |
||
|
1350 |
||
|
1303 |
||
|
1299 |
||
|
Формула |
Описание (результат) |
Результат |
|
=СТАНДОТКЛОНА(A3:A12) |
Стандартное отклонение предела прочности для всех инструментов (27,46391572) |
27,46391572 |
Нужна дополнительная помощь?
Из предыдущей статьи мы узнали о таких показателях, как размах вариации, межквартильный размах и среднее линейное отклонение. В этой статье изучим дисперсию, среднеквадратичное отклонение и коэффициент вариации.
Дисперсия
Дисперсия случайной величины – это один из основных показателей в статистике. Он отражает меру разброса данных вокруг средней арифметической.
Сейчас небольшой экскурс в теорию вероятностей, которая лежит в основе математической статистики. Как и матожидание, дисперсия является важной характеристикой случайной величины. Если матожидание отражает центр случайной величины, то дисперсия дает характеристику разброса данных вокруг центра.
Формула дисперсии в теории вероятностей имеет вид:
То есть дисперсия — это математическое ожидание отклонений от математического ожидания.
На практике при анализе выборок математическое ожидание, как правило, не известно. Поэтому вместо него используют оценку – среднее арифметическое. Расчет дисперсии производят по формуле:
где
s2 – выборочная дисперсия, рассчитанная по данным наблюдений,
X – отдельные значения,
X̅– среднее арифметическое по выборке.
Стоит отметить, что у такого расчета дисперсии есть недостаток – она получается смещенной, т.е. ее математическое ожидание не равно истинному значению дисперсии. Подробней об этом здесь. Однако при увеличении объема выборки она все-таки приближается к своему теоретическому аналогу, т.е. является асимптотически не смещенной.
Простыми словами дисперсия – это средний квадрат отклонений. То есть вначале рассчитывается среднее значение, затем берется разница между каждым исходным и средним значением, возводится в квадрат, складывается и затем делится на количество значений в данной совокупности. Разница между отдельным значением и средней отражает меру отклонения. В квадрат возводится для того, чтобы все отклонения стали исключительно положительными числами и чтобы избежать взаимоуничтожения положительных и отрицательных отклонений при их суммировании. Затем, имея квадраты отклонений, просто рассчитываем среднюю арифметическую. Средний – квадрат – отклонений. Отклонения возводятся в квадрат, и считается средняя. Теперь вы знаете, как найти дисперсию.
Генеральную и выборочную дисперсии легко рассчитать в Excel. Есть специальные функции: ДИСП.Г и ДИСП.В соответственно.
В чистом виде дисперсия не используется. Это вспомогательный показатель, который нужен в других расчетах. Например, в проверке статистических гипотез или расчете коэффициентов корреляции. Отсюда неплохо бы знать математические свойства дисперсии.
Свойства дисперсии
Свойство 1. Дисперсия постоянной величины A равна 0 (нулю).
D(A) = 0
Свойство 2. Если случайную величину умножить на постоянную А, то дисперсия этой случайной величины увеличится в А2 раз. Другими словами, постоянный множитель можно вынести за знак дисперсии, возведя его в квадрат.
D(AX) = А2 D(X)
Свойство 3. Если к случайной величине добавить (или отнять) постоянную А, то дисперсия останется неизменной.
D(A + X) = D(X)
Свойство 4. Если случайные величины X и Y независимы, то дисперсия их суммы равна сумме их дисперсий.
D(X+Y) = D(X) + D(Y)
Свойство 5. Если случайные величины X и Y независимы, то дисперсия их разницы также равна сумме дисперсий.
D(X-Y) = D(X) + D(Y)
Среднеквадратичное (стандартное) отклонение
Если из дисперсии извлечь квадратный корень, получится среднеквадратичное (стандартное) отклонение (сокращенно СКО). Встречается название среднее квадратичное отклонение и сигма (от названия греческой буквы). Общая формула стандартного отклонения в математике следующая:
На практике формула стандартного отклонения следующая:
Как и с дисперсией, есть и немного другой вариант расчета. Но с ростом выборки разница исчезает.
Расчет cреднеквадратичного (стандартного) отклонения в Excel
Для расчета стандартного отклонения достаточно из дисперсии извлечь квадратный корень. Но в Excel есть и готовые функции: СТАНДОТКЛОН.Г и СТАНДОТКЛОН.В (по генеральной и выборочной совокупности соответственно).
Среднеквадратичное отклонение имеет те же единицы измерения, что и анализируемый показатель, поэтому является сопоставимым с исходными данными.
Коэффициент вариации
Значение стандартного отклонения зависит от масштаба самих данных, что не позволяет сравнивать вариабельность разных выборках. Чтобы устранить влияние масштаба, необходимо рассчитать коэффициент вариации по формуле:
По нему можно сравнивать однородность явлений даже с разным масштабом данных. В статистике принято, что, если значение коэффициента вариации менее 33%, то совокупность считается однородной, если больше 33%, то – неоднородной. В реальности, если коэффициент вариации превышает 33%, то специально ничего делать по этому поводу не нужно. Это информация для общего представления. В общем коэффициент вариации используют для оценки относительного разброса данных в выборке.
Расчет коэффициента вариации в Excel
Расчет коэффициента вариации в Excel также производится делением стандартного отклонения на среднее арифметическое:
=СТАНДОТКЛОН.В()/СРЗНАЧ()
Коэффициент вариации обычно выражается в процентах, поэтому ячейке с формулой можно присвоить процентный формат:
Коэффициент осцилляции
Еще один показатель разброса данных на сегодня – коэффициент осцилляции. Это соотношение размаха вариации (разницы между максимальным и минимальным значением) к средней. Готовой формулы Excel нет, поэтому придется скомпоновать три функции: МАКС, МИН, СРЗНАЧ.
Коэффициент осцилляции показывает степень размаха вариации относительно средней, что также можно использовать для сравнения различных наборов данных.
Таким образом, в статистическом анализе существует система показателей, отражающих разброс или однородность данных.
Ниже видео о том, как посчитать коэффициент вариации, дисперсию, стандартное (среднеквадратичное) отклонение и другие показатели вариации в Excel.
Поделиться в социальных сетях:
Содержание
- 1 Математическая теория
- 2 Практическое воплощение в Excel
- 3 Что измеряет стандартное отклонение?
- 4 Как рассчитать стандартное отклонение?
- 5 Функции расчета стандартного отклонения в Excel
- 5.1 Метод 1 Подготовка данных
- 5.2 Метод 2 Таблица данных
- 5.3 Метод 3 Вычисление стандартного отклонения
- 6 Что вам понадобится
- 7 Определение среднего квадратичного отклонения
- 8 Расчет в Excel
- 8.1 Способ 1: мастер функций
- 8.2 Способ 2: вкладка «Формулы»
- 8.3 Способ 3: ручной ввод формулы
- 8.4 Помогла ли вам эта статья?

В статье я решил рассмотреть, как работает стандартное отклонение в Excel с помощью функции СТАНДОТКЛОН. Я просто очень давно не описывал и не комментировал статистические функции, а еще просто потому что это очень полезная функция для тех, кто изучает высшую математику. А оказать помощь студентам – это святое, по себе знаю, как трудно она осваивается. В реальности функции стандартных отклонений можно использовать для определения стабильности продаваемой продукции, создания цены, корректировки или формирования ассортимента, ну и других не менее полезных анализов ваших продаж.
В Excel используются несколько вариантов этой функции отклонения:
- Функция СТАНДОТКЛОНА – вычисляется отклонение по выборке текстовых и логических значений. При этом ложные логические и текстовые значения формула приравнивает к 0, а 1 будут равняться только истинные логические значения;
- Функция СТАНДОТКЛОН.В – производит оценку стандартного отклонения по выборке, при этом текстовые и логические значения игнорирует;
- Функция СТАНДОТКЛОН.Г – делает оценку отклонения по некой генеральной совокупности и как в предыдущей функции игнорируются текстовые и логические значения;
- Функция СТАНДОТКЛОНПА – также вычисляет по генеральной совокупности стандартное отклонение, но с учетом текстовых и логических значений. Равняться 1 будут только истинные логические значения, а ложные логические и текстовые значения будут приравнены к 0.
Математическая теория
Для начала немножко о теории, как математическим языком можно описать функцию стандартного отклонения для применения ее в Excel, для анализа, к примеру, данных статистики продаж, но об этом дальше. Предупреждаю сразу, буду писать очень много непонятных слов… )))), если что ниже по тексту смотрите сразу практическое применение в программе.
Что же собственно делает стандартное отклонение? Оно производит оценку среднеквадратического отклонения случайной величины Х относительно её математического ожидания на основе несмещённой оценки её дисперсии. Согласитесь, звучит запутанно, но я думаю учащиеся поймут о чём собственно идет речь!
Для начала нам нужно определить «среднеквадратическое отклонение», что бы в дальнейшем произвести расчёт «стандартного отклонения», в этом нам поможет формула: Описать формулу возможно так: среднеквадратическое отклонение будет измеряться в тех же единицах что и измерения случайной величины и применяется при вычислении стандартной среднеарифметической ошибки, когда производятся построения доверительных интервалов, при проверке гипотез на статистику или же при анализе линейной взаимосвязи между независимыми величинами. Функцию определяют, как квадратный корень из дисперсии независимых величин.
Теперь можно дать определение и стандартному отклонению – это анализ среднеквадратического отклонения случайной величины Х сравнительно её математической перспективы на основе несмещённой оценки её дисперсии. Формула записывается так: 
Ну а теперь отойдём от скучной теории и на практике посмотрим, как работает функция СТАНДОТКЛОН. Я не буду рассматривать все вариации функции стандартного отклонения в Excel, достаточно и одной, но в примерах. А для примера рассмотрим, как определяется статистика стабильности продаж.
Для начала посмотрите на орфографию функции, а она как вы видите, очень проста:
=СТАНДОТКЛОН.Г(_число1_;_число2_; ….), где:
- Число1, число2, … — являют собой генеральную совокупность значений и имеют только числовые значения или же ссылки на них. Формула поддерживает до 255 числовых значений.
Теперь создадим файл примера и на его основе рассмотрим работу этой функции. 
Для начала нам необходимо посчитать среднее значение по месяцам. Будем использовать для этого функцию СРЗНАЧ и получится формула: =СРЗНАЧ(C4:E4). 


=ЕСЛИ(H4
Стандартное отклонение является одним из тех статистических терминов в корпоративном мире, которое позволяет поднять авторитет людей, сумевших удачно ввернуть его в ходе беседы или презентации, и оставляет смутное недопонимание тех, кто не знает, что это такое, но стесняется спросить. На самом деле большинство менеджеров не понимают концепцию стандартного отклонения и, если вы один из них, вам пора перестать жить во лжи. В сегодняшней статье я расскажу вам, как эта недооцененная статистическая мера позволит лучше понять данные, с которыми вы работаете.
Что измеряет стандартное отклонение?
Представьте, что вы владелец двух магазинов. И чтобы избежать потерь, важно, чтобы был четкий контроль остатков на складе. В попытке выяснить, кто из менеджеров лучше управляет запасами, вы решили проанализировать стоки последних шести недель. Средняя недельная стоимость стока обоих магазинов примерно одинакова и составляет около 32 условных единиц. На первый взгляд среднее значение стока показывает, что оба менеджера работают одинаково.
Но если внимательнее изучить деятельность второго магазина, можно убедится, что хотя среднее значение корректно, вариабельность стока очень высокая (от 10 до 58 у.е.). Таким образом, можно сделать вывод, что среднее значение не всегда правильно оценивает данные. Вот где на выручку приходит стандартное отклонение.
Стандартное отклонение показывает, как распределены значения относительно среднего в нашей выборке. Другими словами, можно понять на сколько велик разброс величины стока от недели к неделе.
В нашем примере, мы воспользовались функцией Excel СТАНДОТКЛОН, чтобы рассчитать показатель стандартного отклонения вместе со средним.
В случае с первым менеджером, стандартное отклонение составило 2. Это говорит нам о том, что каждое значение в выборке в среднем откланяется на 2 от среднего значения. Хорошо ли это? Давайте рассмотрим вопрос под другим углом – стандартное отклонение равное 0, говорит нам о том, что каждое значение в выборке равно его среднему значению (в нашем случае, 32,2). Так, стандартное отклонение 2 ненамного отличается от 0, и указывает на то, что большинство значений находятся рядом со средним значением. Чем ближе стандартное отклонение к 0, тем надежнее среднее. Более того, стандартное отклонение близкое к 0, говорит о маленькой вариабельности данных. То есть, величина стока со стандартным отклонением 2, указывает на невероятную последовательность первого менеджера.
В случае со вторым магазином, стандартное отклонение составило 18,9. То есть стоимость стока в среднем отклоняется на величину 18,9 от среднего значения от недели к неделе. Сумасшедший разброс! Чем дальше стандартное отклонение от 0, тем менее точно среднее значение. В нашем случае, цифра 18,9 указывает на то, что среднему значению (32,8 у.е. в неделю) просто нельзя доверять. Оно также говорит нам о том, что еженедельная величина стока обладает большой вариабельностью.
Такова концепция стандартного отклонения в двух словах. Хотя оно не дает представление о других важных статистических измерениях (Мода, Медиана…), фактически стандартное отклонение играет решающую роль в большинстве статистических расчетов. Понимание принципов стандартного отклонения прольет свет на суть многих процессов вашей деятельности.
Как рассчитать стандартное отклонение?
Итак, теперь мы знаем, о чем говорит цифра стандартного отклонения. Давайте разберемся, как она считается.
Рассмотрим набор данных от 10 до 70 с шагом 10. Как видите, я уже рассчитал для них значение стандартного отклонения с помощью функции СТАНДОТКЛОН в ячейке H2 (оранжевым).
Ниже описаны шаги, которые предпринимает Excel, чтобы прийти к цифре 21,6.
Обратите внимание, что все расчеты визуализированы, для лучшего понимания. На самом деле в Excel расчет происходит мгновенно, оставляя все шаги за кулисами.
Для начала Excel находит среднее значение выборки. В нашем случае, среднее получилось равным 40, которое на следующем шаге отнимают от каждого значения выборки. Каждую полученную разницу возводят в квадрат и суммируют. У нас получилась сумма равная 2800, которую необходимо разделить на количество элементов выборки минус 1. Так как у нас 7 элементов, получается необходимо 2800 разделить на 6. Из полученного результата находим квадратный корень, это цифра будет стандартным отклонением.
Для тех, кому не совсем ясен принцип расчета стандартного отклонения с помощью визуализации, привожу математическую интерпретацию нахождения данного значения.
Функции расчета стандартного отклонения в Excel
В Excel присутствует несколько разновидностей формул стандартного отклонения. Вам достаточно набрать =СТАНДОТКЛОН и вы сами в этом убедитесь.
Стоит отметить, что функции СТАНДОТКЛОН.В и СТАНДОТКЛОН.Г (первая и вторая функция в списке) дублируют функции СТАНДОТКЛОН и СТАНДОТКЛОНП (пятая и шестая функция в списке), соответственно, которые были оставлены для совместимости с более ранними версиями Excel.
Вообще разница в окончаниях .В и .Г функций указывают на принцип расчета стандартного отклонения выборки или генеральной совокупности. Разницу между двумя этими массивами я уже объяснял в предыдущей статье расчета дисперсии.
Особенностью функций СТАНДОТКЛОНА и СТАНДОТКЛОНПА (третья и четвертая функция в списке), является то, что при расчете стандартного отклонения массива в расчет принимаются логические и текстовые значения. Текстовые и истинные логические значения равняются 1, а ложные логические значения равняются 0. Мне трудно представить ситуацию, когда бы мне могли понадобится эти две функции, поэтому, думаю, что их можно игнорировать.
Метод 1 Подготовка данных
-
Соберите данные, которые вы хотите использовать в вашей таблице Excel.
-
Стандартное отклонение обычно рассчитывается либо по выборке (определенной части данных), либо по генеральной совокупности данных (по всем данным).
- Excel имеет различные формулы для вычисления стандартного отклонение по выборке и стандартного отклонения по генеральной совокупности. Имейте это в виду, когда вы будете вводить формулу.
Метод 2 Таблица данных
-
Откройте программу Microsoft Excel.
- Функции Excel могут сильно отличаться, в зависимости от версии, которую вы используете. Если вы не можете найти нужную кнопку на панели инструментов, поищите ее в верхнем горизонтальном меню.
-
Составьте таблицу ваших данных.
В большинстве случаев, вы начнете с ячейки A1.
- Введите заголовки в верхних ячейках столбцов.
- Введите название или дату в первых ячейках каждой строки. Введите соответствующие данные в ячейках справа.
-
Сохраните документ Excel, чтобы избежать потери данных.
Метод 3 Вычисление стандартного отклонения
- Поставьте курсор в ячейку ниже последнего введенного значения.
- Вы также можете вычислить стандартное отклонение в любой другой пустой ячейке электронной таблицы Excel. Excel автоматически задаст ваш диапазон данных, если вы отметите соответствующие ячейки с данными.
-
Введите знак равенства. Помните, что формула должна вводиться без пробелов.
- Наберите «СТАНДОТКЛОН».
Это формула Excel для стандартного отклонения. При использовании этой формулы Excel будет автоматически вычислять среднее значение и стандартное отклонение.
- Выберите либо «СТАНДОТКЛОН» (вычисление по выборке), либо «СТАНДОТКЛОНП» (вычисление по генеральной совокупности).
- Укажите диапазон данных.
- В Excel диапазоны данных указываются в следующем виде: (C2:C15). Вся формула будет выглядеть как:»=СТАНДОТКЛОН(C2:C15)».
- Нажмите кнопку «Enter «.
Стандартное отклонение отобразится в ячейке.
- Вы можете также использовать функцию Excel для выбора формулы стандартного отклонения. Нажмите на «Вставить функцию» в строке формул. Затем выберите «Статистические » и выберите «СТАНДОТКЛОН». Введите свой диапазон данных в открывшемся окне. Нажмите «OK».
Что вам понадобится
- Microsoft Excel
- Данные
- Таблица данных
- Формула для вычисления стандартного отклонения
- Диапазон данных
Информация о статье
Эту страницу просматривали 67 780 раза.
Была ли эта статья полезной?
Одним из основных инструментов статистического анализа является расчет среднего квадратичного отклонения. Данный показатель позволяет сделать оценку стандартного отклонения по выборке или по генеральной совокупности. Давайте узнаем, как использовать формулу определения среднеквадратичного отклонения в Excel.
Определение среднего квадратичного отклонения
Сразу определим, что же представляет собой среднеквадратичное отклонение и как выглядит его формула. Эта величина является корнем квадратным из среднего арифметического числа квадратов разности всех величин ряда и их среднего арифметического. Существует тождественное наименование данного показателя — стандартное отклонение. Оба названия полностью равнозначны.
Но, естественно, что в Экселе пользователю не приходится это высчитывать, так как за него все делает программа. Давайте узнаем, как посчитать стандартное отклонение в Excel.
Расчет в Excel
Рассчитать указанную величину в Экселе можно с помощью двух специальных функций СТАНДОТКЛОН.В (по выборочной совокупности) и СТАНДОТКЛОН.Г (по генеральной совокупности). Принцип их действия абсолютно одинаков, но вызвать их можно тремя способами, о которых мы поговорим ниже.
Способ 1: мастер функций
- Выделяем на листе ячейку, куда будет выводиться готовый результат. Кликаем на кнопку «Вставить функцию», расположенную слева от строки функций.
- В открывшемся списке ищем запись СТАНДОТКЛОН.В или СТАНДОТКЛОН.Г. В списке имеется также функция СТАНДОТКЛОН, но она оставлена из предыдущих версий Excel в целях совместимости. После того, как запись выбрана, жмем на кнопку «OK».
- Открывается окно аргументов функции. В каждом поле вводим число совокупности. Если числа находятся в ячейках листа, то можно указать координаты этих ячеек или просто кликнуть по ним. Адреса сразу отразятся в соответствующих полях. После того, как все числа совокупности занесены, жмем на кнопку «OK».
- Результат расчета будет выведен в ту ячейку, которая была выделена в самом начале процедуры поиска среднего квадратичного отклонения.
Способ 2: вкладка «Формулы»
Также рассчитать значение среднеквадратичного отклонения можно через вкладку «Формулы».
- Выделяем ячейку для вывода результата и переходим во вкладку «Формулы».
- В блоке инструментов «Библиотека функций» жмем на кнопку «Другие функции». Из появившегося списка выбираем пункт «Статистические». В следующем меню делаем выбор между значениями СТАНДОТКЛОН.В или СТАНДОТКЛОН.Г в зависимости от того выборочная или генеральная совокупность принимает участие в расчетах.
- После этого запускается окно аргументов. Все дальнейшие действия нужно производить так же, как и в первом варианте.
Способ 3: ручной ввод формулы
Существует также способ, при котором вообще не нужно будет вызывать окно аргументов. Для этого следует ввести формулу вручную.
- Выделяем ячейку для вывода результата и прописываем в ней или в строке формул выражение по следующему шаблону:
=СТАНДОТКЛОН.Г(число1(адрес_ячейки1); число2(адрес_ячейки2);…)
или=СТАНДОТКЛОН.В(число1(адрес_ячейки1); число2(адрес_ячейки2);…).Всего можно записать при необходимости до 255 аргументов.
- После того, как запись сделана, нажмите на кнопку Enter на клавиатуре.
Урок: Работа с формулами в Excel
Как видим, механизм расчета среднеквадратичного отклонения в Excel очень простой. Пользователю нужно только ввести числа из совокупности или ссылки на ячейки, которые их содержат. Все расчеты выполняет сама программа. Намного сложнее осознать, что же собой представляет рассчитываемый показатель и как результаты расчета можно применить на практике. Но постижение этого уже относится больше к сфере статистики, чем к обучению работе с программным обеспечением.
Мы рады, что смогли помочь Вам в решении проблемы.
Задайте свой вопрос в комментариях, подробно расписав суть проблемы. Наши специалисты постараются ответить максимально быстро.
Помогла ли вам эта статья?
Да Нет
The mean absolute deviation is a way to measure the dispersion for a set of data values.
A low value for the mean absolute deviation is an indication that the data values are concentrated closely together. A high value for the mean absolute deviation is an indication that the data values are more spread out.
The formula to calculate the mean absolute deviation is as follows:
Mean absolute deviation = (Σ |xi – x|) / n
- Σ – just a fancy symbol that means “sum”
- xi – the ith data value
- x – the mean value
- n – sample size
To calculate the mean absolute deviation in Excel, we can perform the following steps:
Step 1: Enter the data. For this example, we’ll enter 15 data values in cells A2:A16.
Step 2: Find the mean value. In cell D1, type the following formula: =AVERAGE(A2:A16). This calculates the mean value for the data values, which turns out to be 15.8.
Step 3: Calculate the absolute deviations. In cell B2, type the following formula: =ABS(A2-$D$1). This calculates the absolute deviation of the value in cell A2 from the mean value in the dataset.
Next, click cell B2. Then, hover over the bottom right corner of the cell until a black + sign appears. Double click the + sign to fill in the remaining values in column B.
Step 4: Calculate the mean absolute deviation. In cell B17, type the following formula: =AVERAGE(B2:B16). This calculates the mean absolute deviation for the data values, which turns out to be 6.1866.
Note that you can use these four steps to calculate the mean absolute deviation for any number of data values. In this example, we used 15 data values but you could use these exact steps to calculate the mean absolute deviation for 5 data values or 5,000 data values.
Another common way to measure the forecasting accuracy of a model is MAPE – mean absolute percentage error. Read about how to calculate MAPE in Excel here.
Среднее арифметическое – один из самых популярных статистических методов, который рассчитывается повсеместно. Но сам по себе он абсолютно ненадежный. Многие знают поговорку, что один человек ест капусту, другой – мясо, а в среднем они оба едят голубцы. На примере средней зарплаты очень легко это изобразить. Несколько процентов людей, которые зарабатываются миллионы, не сильно повлияют на статистику, но способны значительно испортить ее объективность, завышая показатель на несколько десятков процентов.
Чем ниже разброс между значениями, тем больше можно доверять этому статистическому показателю. Поэтому настоятельно рекомендуется всегда вместе со средним арифметическим рассчитывать и стандартное отклонение. Сегодня мы разберемся, как правильно это делать средствами Microsoft Excel.
Содержание
- Среднеквадратичное отклонение — что это
- Расчет среднеквадратичного отклонения в Excel
- Метод 1. Ручной ввод формулы
- Метод 2. Вкладка «Формулы»
- Метод 3. Мастер функций
- Заключение
Среднеквадратичное отклонение — что это
Стандартное (или среднеквадратичное) отклонение – это квадратный корень из дисперсии. В свою очередь, под последним термином подразумевается степень разброса значений. Для получения дисперсии, и, как следствие, ее производного в виде стандартного отклонения, существует специальная формула, которая, впрочем, нам не так важна. Она довольно сложная по своей структуре, но при этом ее можно полностью автоматизировать средствами Excel. Главное – знать, какие параметры нужно передавать функции. В целом как для вычисления дисперсии, так и стандартного отклонения, аргументы используются одинаковые.
- Сначала мы получаем среднее арифметическое.
- После этого каждое исходное значение сопоставляется со средним и определяется разница между ними.
- После этого каждая разница возводится во вторую степень, после чего получившиеся результаты складываются между собой.
- Наконец, финальный шаг – деление получившегося значения на общее количество элементов в данной выборке.
Получив разницу между одним значением и средним арифметическим всей выборки, мы можем узнать расстояние к нему от определенной точки на координатной прямой. Начинающему человеку вся логика понятна равно до третьего шага. Зачем возводить значение в квадрат? Дело в том, что иногда разница может быть отрицательной, а нам нужно получить положительное число. И, как известно, минус на минус дает плюс. А далее нам нужно определить среднее арифметическое из получившихся значений. Дисперсия имеет несколько свойств:
- Если выводить дисперсию из одного числа, то она всегда будет равняться нулю.
- Если случайное число умножить на константу А, то дисперсия увеличится в количество раз, равное А в квадрате. Проще говоря, константу можно вынести за знак дисперсии и возвести его во вторую степень.
- Если к произвольному числу добавить константу А или же отнять ее, то дисперсия от этого не поменяется.
- Если два случайных числа, обозначаемых, к примеру переменными X и Y не зависят друг от друга, то в таком случае для них справедлива формула. D(X+Y) = D(X) + D(Y)
- Если же в предыдущую формулу внести изменения и пытаться определить дисперсию разницы этих значений, то она также будет составлять сумму этих дисперсий.
Среднеквадратическое отклонение – это математический термин, являющийся производным от дисперси. Получить его очень просто: достаточно извлечь квадратный корень из дисперсии.
Разница между дисперсией и стандартным отклонением находится сугубо в плоскости единиц измерения, если можно так выразиться. Стандартное отклонение является значительно более простым для считывания показателем, поскольку оно показывается не в квадратах числа, а непосредственно в значениях. Простыми словами, если в числовой последовательности 1,2,3,4,5 средним арифметическим является 3, то соответственно, стандартным отклонением будет число 1,58. Это говорит о том, что в среднем одно число отклоняется от среднего числа (которым является тройка в нашем примере), на 1,58.
Дисперсия же будет тем же самым числом, только возведенным в квадрат. В нашем примере – чуть меньше, чем 2,5. В принципе, можно использовать как дисперсию, так и стандартное отклонение для статистических расчетов, только надо четко знать, с каким именно показателем пользователь работает.
Расчет среднеквадратичного отклонения в Excel
У нас есть два главных варианта формулы. Первый рассчитывается по выборочной совокупности. Второй – по генеральной. Чтобы рассчитать стандартное отклонения по выборочной совокупности, необходимо использовать функцию СТАНДОТКЛОН.В. Если же необходимо осуществить расчет по генеральной совокупности, то надо пользоваться функцией СТАНДОТКЛОН.Г.
Отличие выборочной совокупности от генеральной заключается в том, что в первом случае идет обработка непосредственно тех данных, на основе которых рассчитывается среднее арифметическое и среднеквадратическое отклонение. Если же мы говорим про генеральную совокупность, то это весь набор количественных данных, связанных с исследуемым явлением. В идеале выборка должна быть полностью репрезентативной. То есть, в исследовании должны участвовать люди, которых можно соотнести с генеральной совокупностью в равных пропорциях. Например, если в условной стране 50% мужчин и 50% женщин, то такие же пропорции должны быть у выборки.
Следовательно, стандартное отклонение для генеральной совокупности может несколько отличаться от выборочной, поскольку во втором случае исходные цифры меньше. Но в целом, обе функции работают одинаково. Сейчас мы распишем, что нужно сделать для того, чтобы их вызвать. А сделать это можно сразу тремя способами.
Метод 1. Ручной ввод формулы
Ручной ввод – довольно сложный метод, на первый взгляд. Тем не менее, каждый должен им владеть, если хочет быть профессиональным пользователем Excel. Его преимущество в том, что не нужно вообще вызывать окно ввода аргументов. Если хорошо потренироваться, это будет значительно быстрее, чем пользоваться двумя остальными способами. Главное – чтобы пальцы были тренированные. В идеале каждый пользователь Excel должен владеть слепым методом, чтобы быстро вводить формулы и функции.
- Делаем левый клик мышью по той ячейке, в которой будет записываться формула для получения стандартного отклонения. Также можно ее вводить в качестве аргумента любой другой из функций. В таком случае нужно кликнуть по строке ввода формул, а потом начать ввод в том аргументе, куда результат должен выводиться.
- Общая формула следующая: =СТАНДОТКЛОН.Г(число1(адрес_ячейки1); число2(адрес_ячейки2);…). Если мы используем второй вариант, то все осуществляется в точности так же, только буква Г в названии функции меняется на В. Максимальное количество поддерживаемых аргументов – 255.
- После того, как ввод формулы будет закончен, подтверждаем свои действия. Для этого нужно нажать клавишу ввода.
Таким образом, для вычисления стандартного отклонения нам нужно использовать те же аргументы, что и для получения среднего арифметического. Все остальное программа сможет сделать самостоятельно. Также в качестве аргумента можно использовать целый диапазон значений, на основе которых будет осуществляться расчет среднеквадратического отклонения. Теперь давайте рассмотрим другие методы, которые будут более понятными для начинающего пользователя Excel. Но в долгосрочной перспективе от них нужно будет отказаться, поскольку:
- Ручной ввод формулы способен значительно сэкономить время. Пользователь Excel, который помнит формулу и ее синтаксис, имеет существенное преимущество перед тем человеком, который только начинает и долго ищет нужную функцию в перечне в мастере функций или на ленте. Кроме этого, сам по себе ввод с клавиатуры является гораздо более быстрым, чем использование мыши.
- Меньше устают глаза. Не нужно постоянно переключать фокус внимания с таблицы на окно, потом на еще одно окно, потом на клавиатуру, а потом снова на таблицу. Это же помогает существенно сэкономить время и силы, которые потом можно тратить на обработку реальной информации, а не техническое обслуживание формул.
- Ручной ввод формул гораздо более гибкий по сравнению с использованием двух следующих методов. Пользователь может сразу указать нужные ячейки диапазона, не выделяя его непосредственно или сразу посмотреть на всю таблицу, избегая риска, что ее перекроет диалоговое окно.
- Использование формул вручную является своеобразным мостиком к написанию макросов. Конечно, это не поможет выучить язык VBA, но зато формирует правильные привычки. Если человек привык давать команды компьютеру с помощью клавиатуры, ему будет значительно проще освоить любой другой язык программирования, в том числе, и для разработки макросов для электронных таблиц.
Но конечно, да. Использование других методов значительно лучше, если вы новичок, и только начинаете. Поэтому переходим к рассмотрению иных способов, как можно рассчитать стандартное отклонение.
Метод 2. Вкладка «Формулы»
Еще один метод, доступный пользователю, желающему получить стандартное отклонение из диапазона – воспользоваться вкладкой «Формулы» в главном меню. Давайте более подробно распишем, что нужно сделать для этого:
- Выделить ту ячейку, в которую мы хотим записывать результат.
- После этого находим на ленте вкладку «Формулы» и переходим в нее.
- Воспользуемся блоком «Библиотека функций». Там есть кнопка «Другие функции». В перечне, который будет, мы найдем пункт «Статистические». После этого выбираем, какую разновидность формулы мы собираемся использовать.
- После этого появляется окно ввода аргументов. В нем указываем все числа, ссылки на ячейки или диапазоны, которые будут принимать участие в расчетах. После того, как закончим, нажимаем кнопку «ОК».
Преимущества этого метода:
- Скорость. Данный способ довольно быстрый и позволяет ввести нужную формулу буквально в несколько кликов.
- Точность. Нет риска случайно написать не ту ячейку или написать не ту букву, а потом тратить время на переделку.
Можно сказать, что это способ номер два по хорошести после ручного ввода. НО третий метод также полезен в некоторых ситуациях.
Метод 3. Мастер функций
Мастер функций – еще один удобный метод ввода формул для новичков, которые еще не запомнили названия и синтаксис функций. Кнопка для запуска мастера функций находится возле строки ввода формул. Его главное преимущество для новичка на фоне предыдущих способов заключается в детальных подсказках программы, какая функция за что отвечает и какие аргументы вводить в какой последовательности. Она являет собой две буквы – fx. Нажимаем на нее.
После этого появится перечень функций. Можно как попытаться найти в полном алфавитном перечне, так и открыть категорию «Статистические», где также можно найти этот оператор.
Мы можем увидеть в списке, что функция СТАНДОТКЛОН все еще присутствует. Это сделано для того, чтобы сделать старые файлы совместимыми с новой версией Excel. При этом настоятельно рекомендуется пользоваться новыми функциями, приведенными выше, потому что в один момент эта устаревшая функция может перестать поддерживаться.
После того, как мы нажмем «ОК», у нас будет возможность открыть окно аргументов. Каждый аргумент являет собой отдельное число, адрес на ячейку (если в ней содержится числовое значение) или диапазоны значений, которые будут использоваться для среднего арифметического и получения стандартного отклонения. После того, как мы введем все аргументы, нажимаем на кнопку «ОК». Данные будут занесены в ту ячейку, в которой мы вводили формулу.
Заключение
Таким образом, вычислить стандартное отклонение средствами Excel несложно. Да и сама функция является основой статистических расчетов, которая является интуитивно понятной. Ведь очевидно, что важно не только среднее значение, но и разброс значений, из которых выводится среднее арифметическое. Ведь если половина народа богатая, а половина – бедная, то среднего класса по факту и не будет. Но при этом если вывести среднее арифметическое, то окажется, что среднестатистический гражданин как раз и является представителем среднего класса. Но это звучит, как минимум, странно. В общем, успехов в использовании этой функции.
Оцените качество статьи. Нам важно ваше мнение:


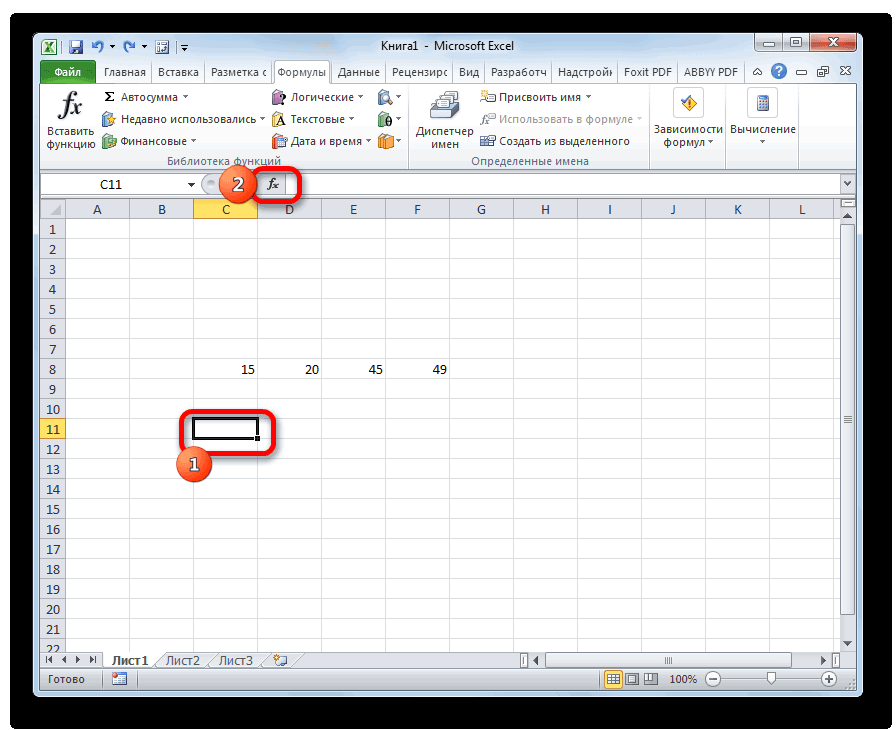
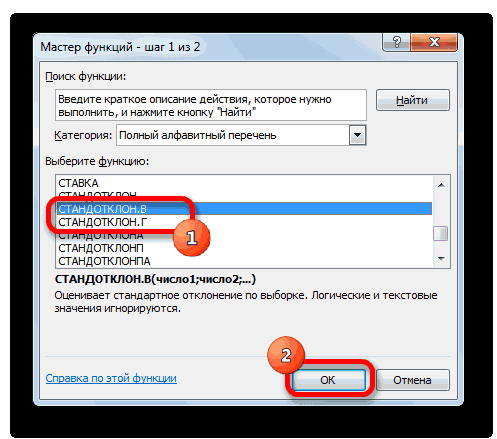
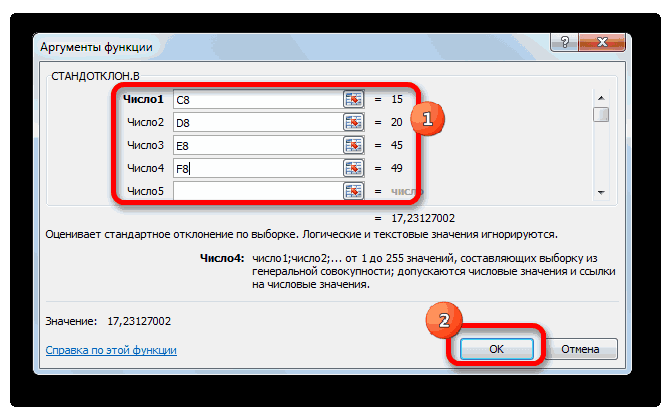
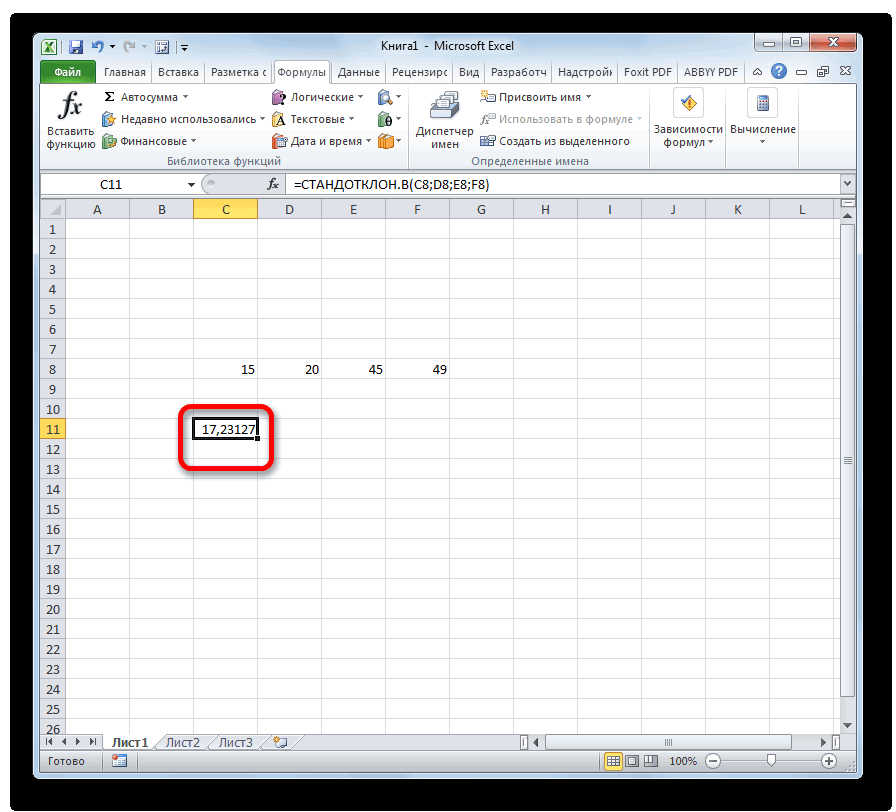
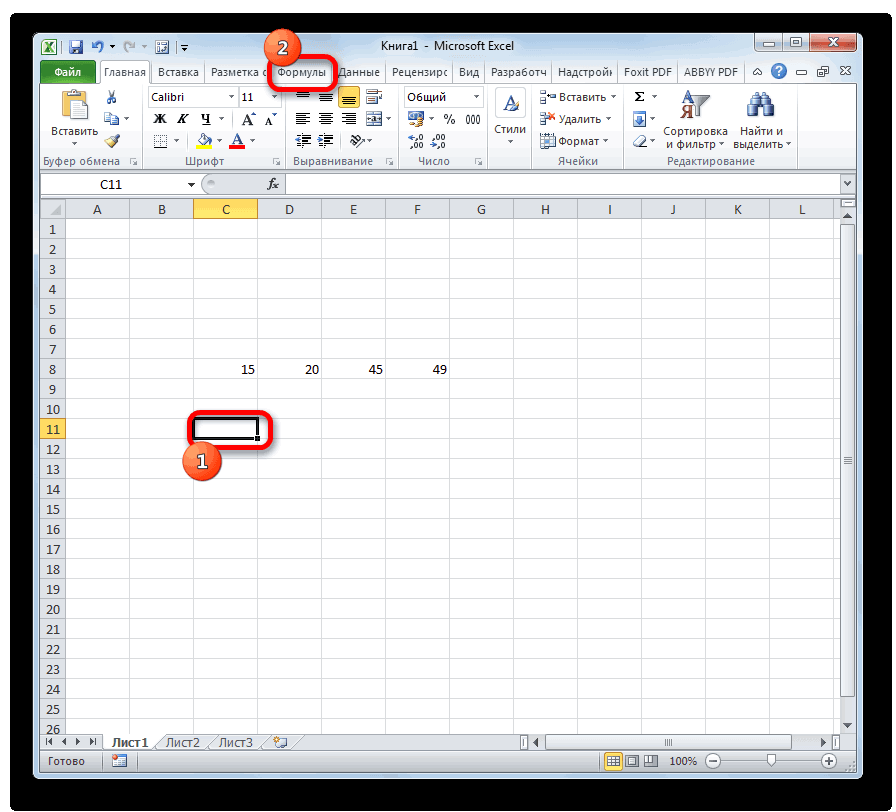
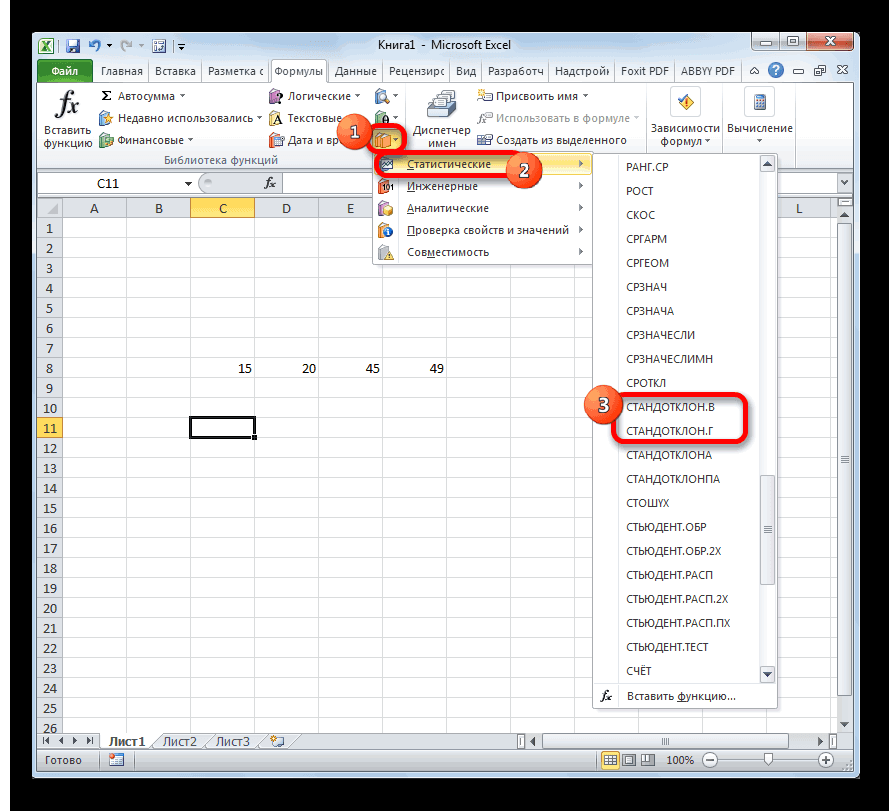
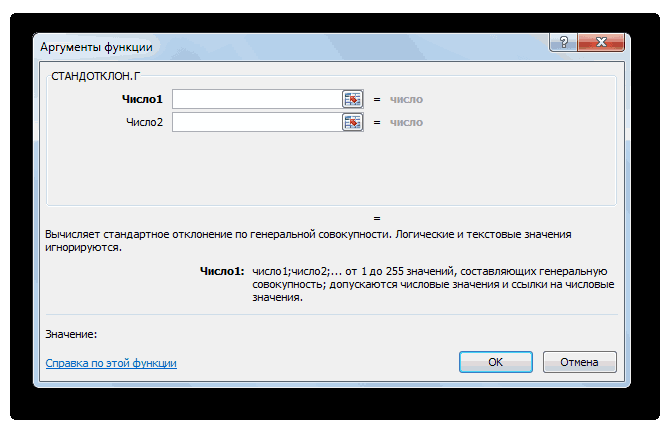
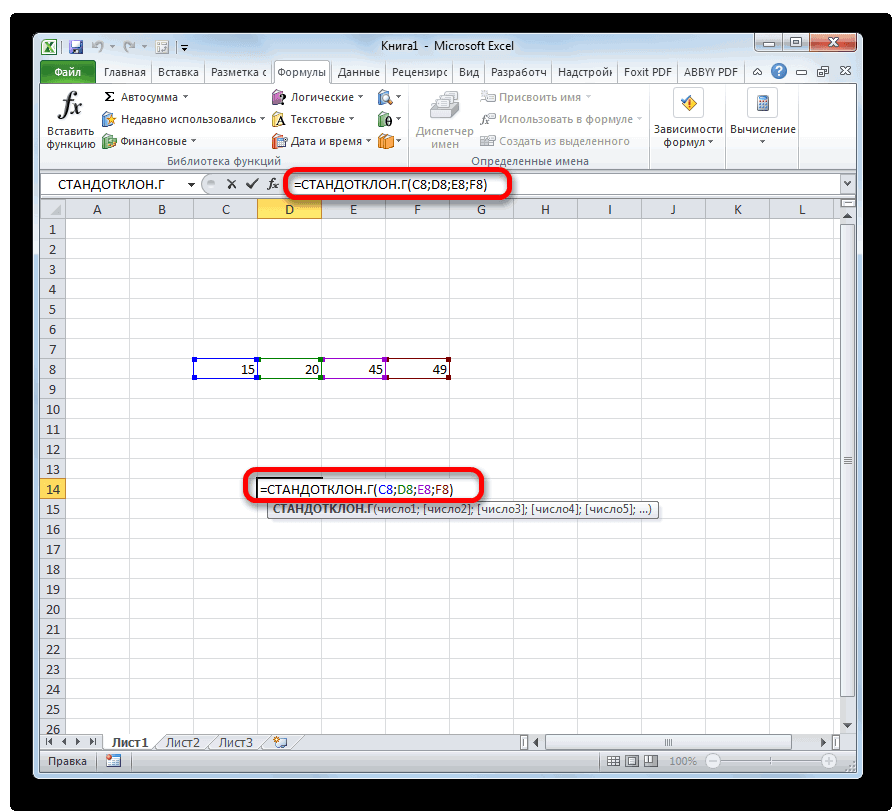
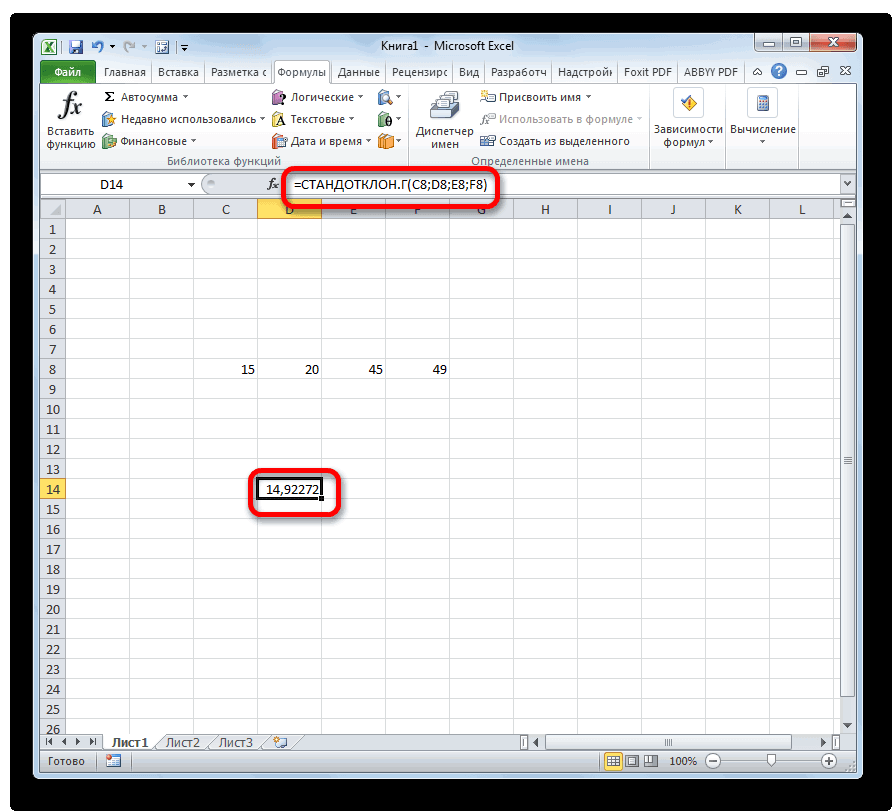
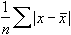

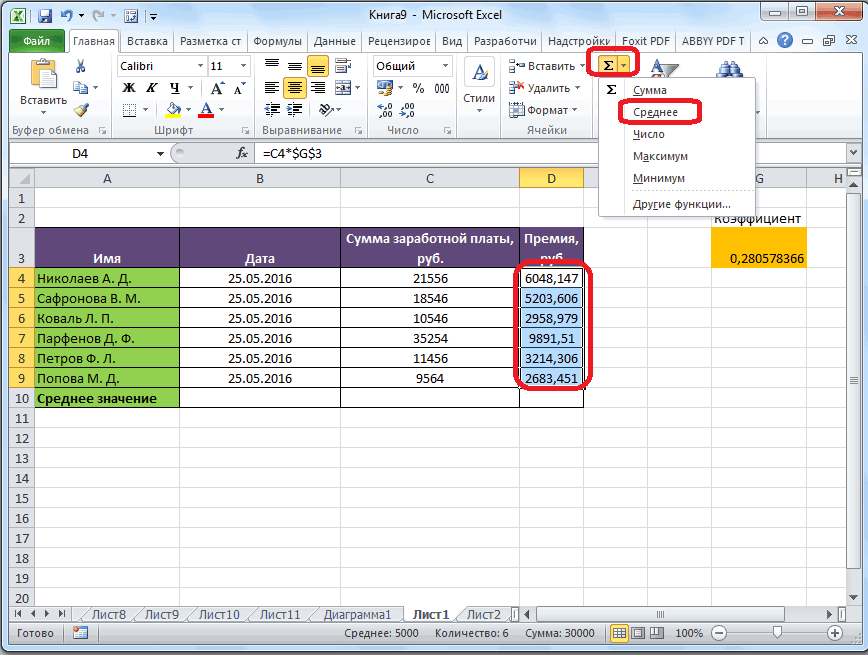
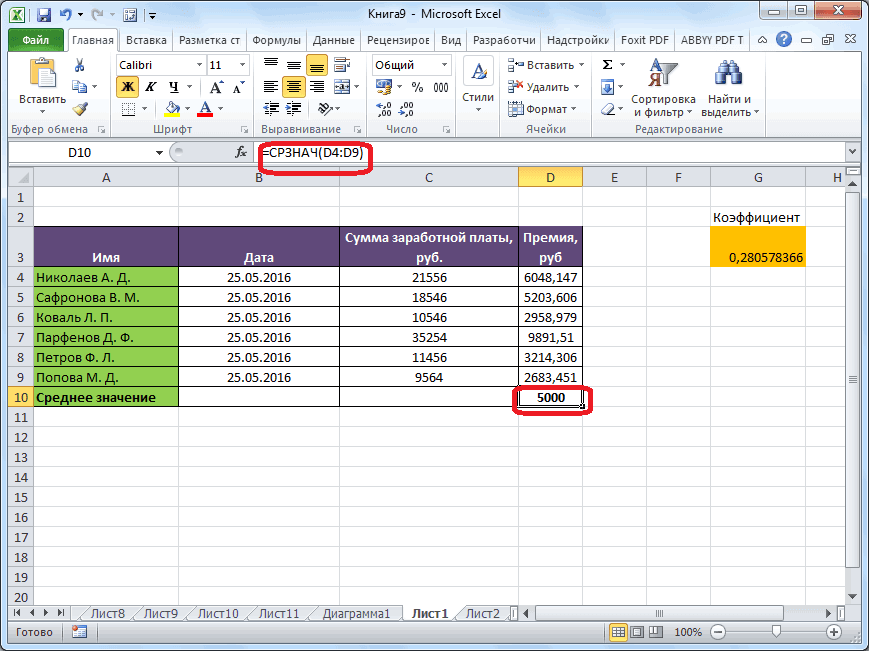
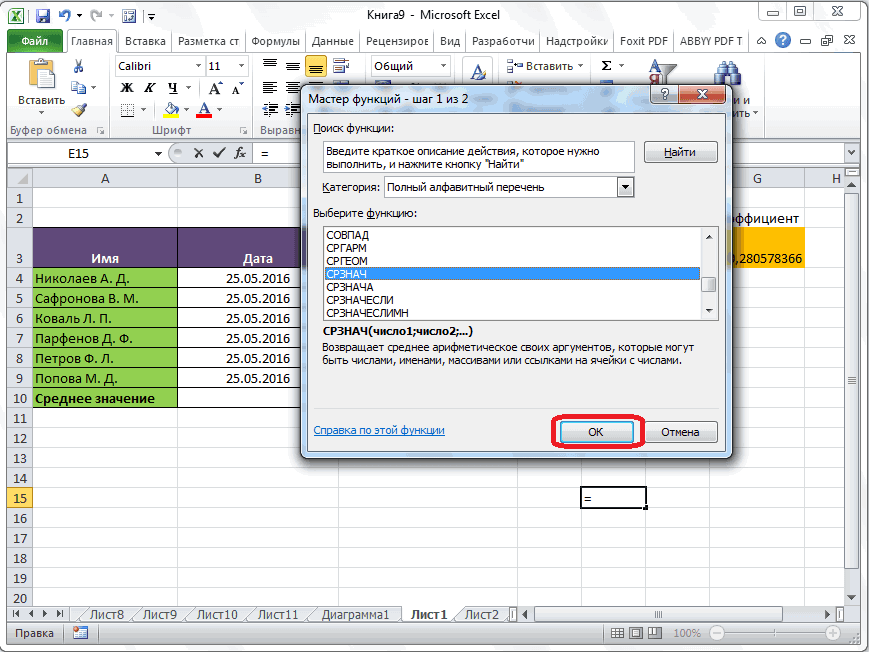
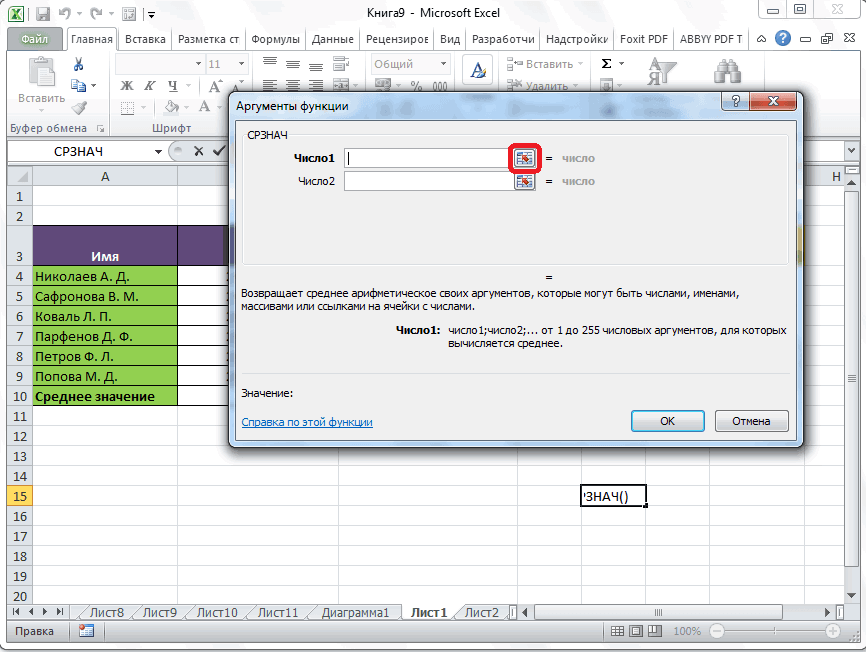
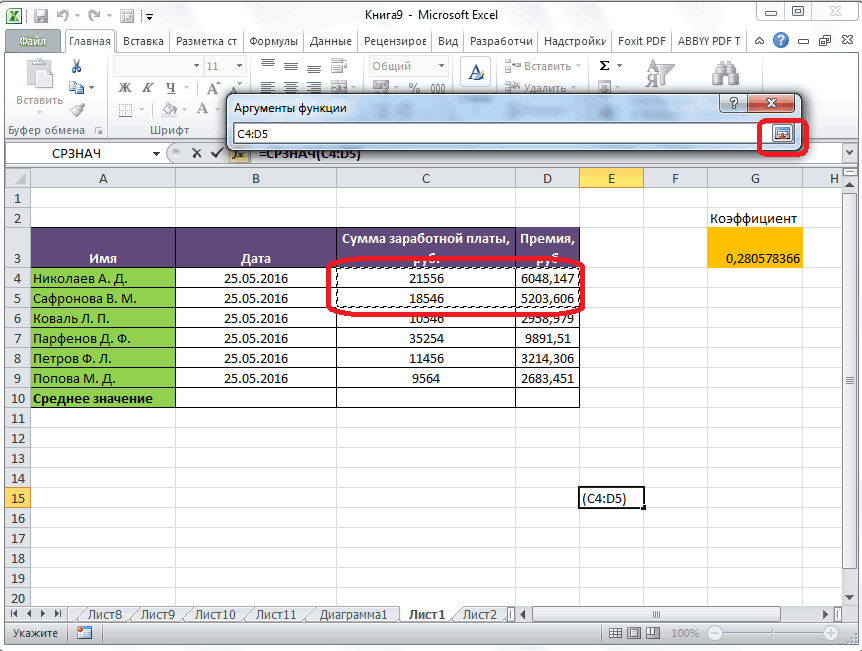
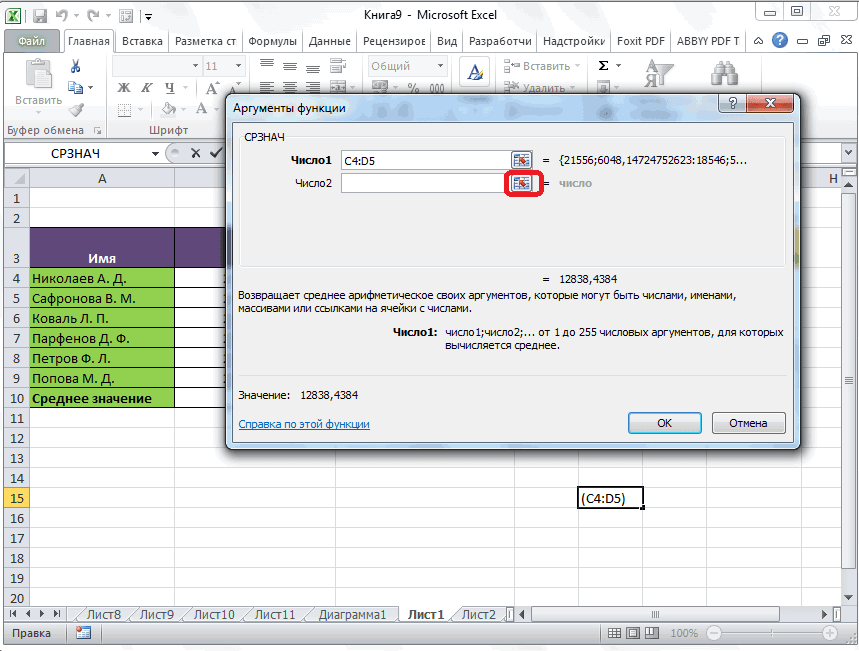
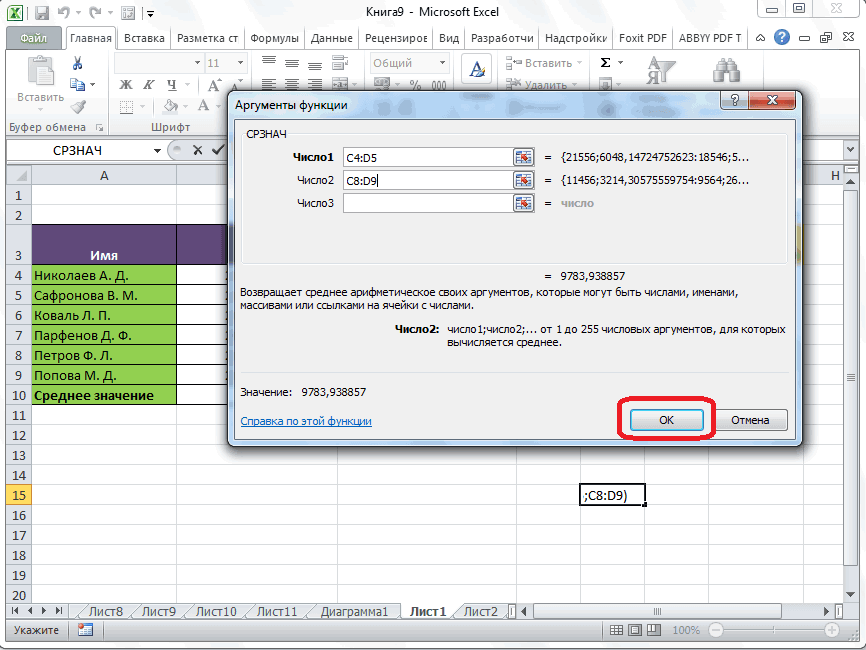
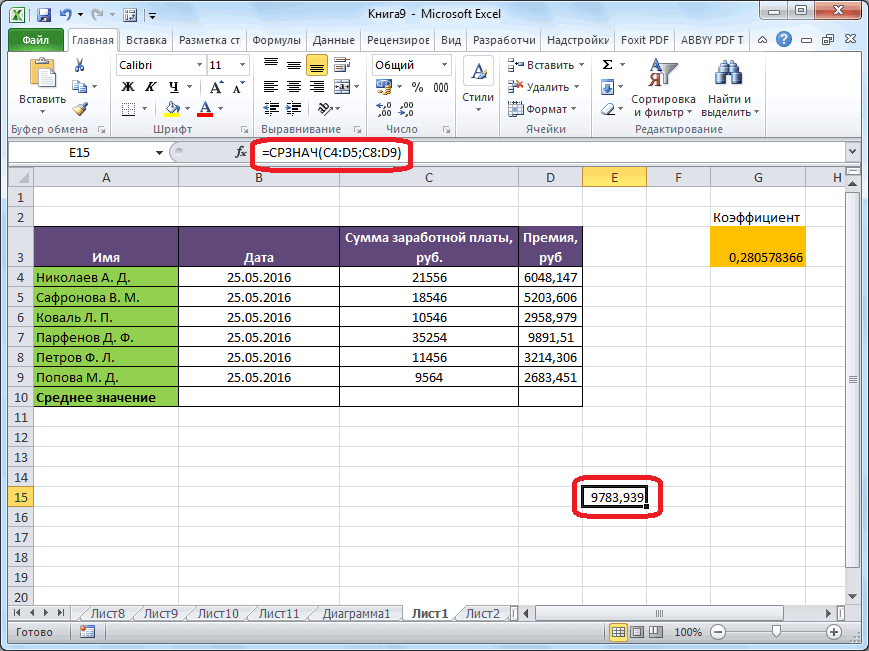
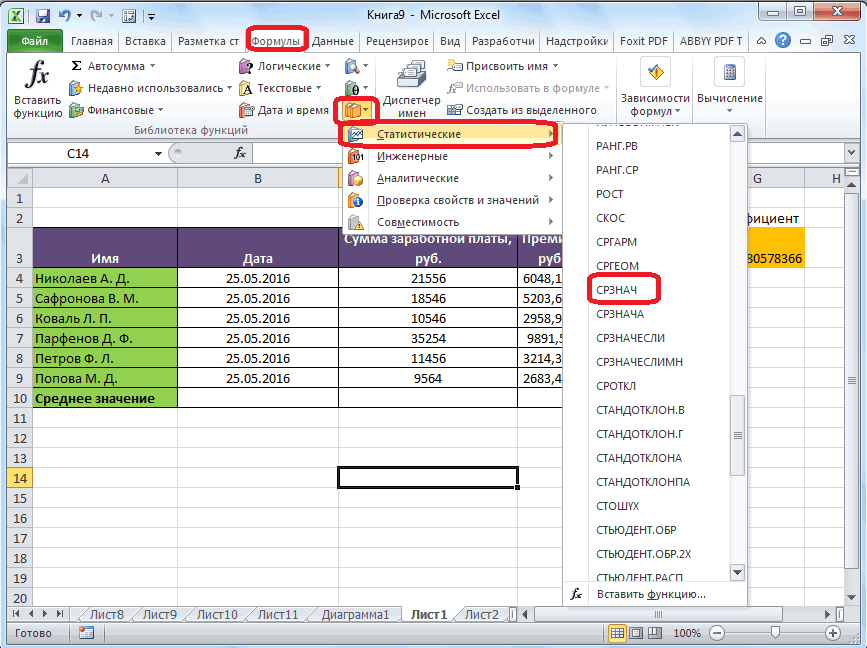
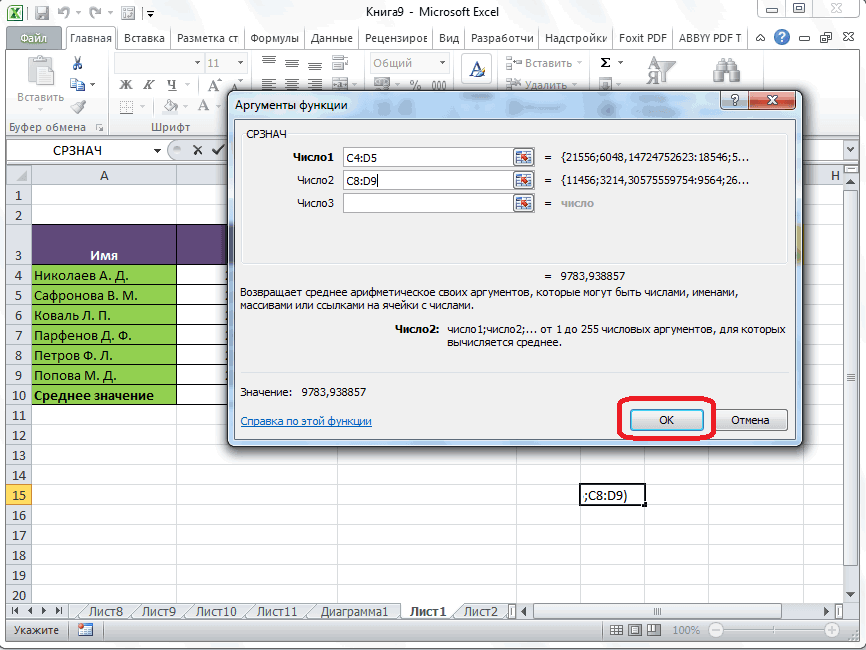
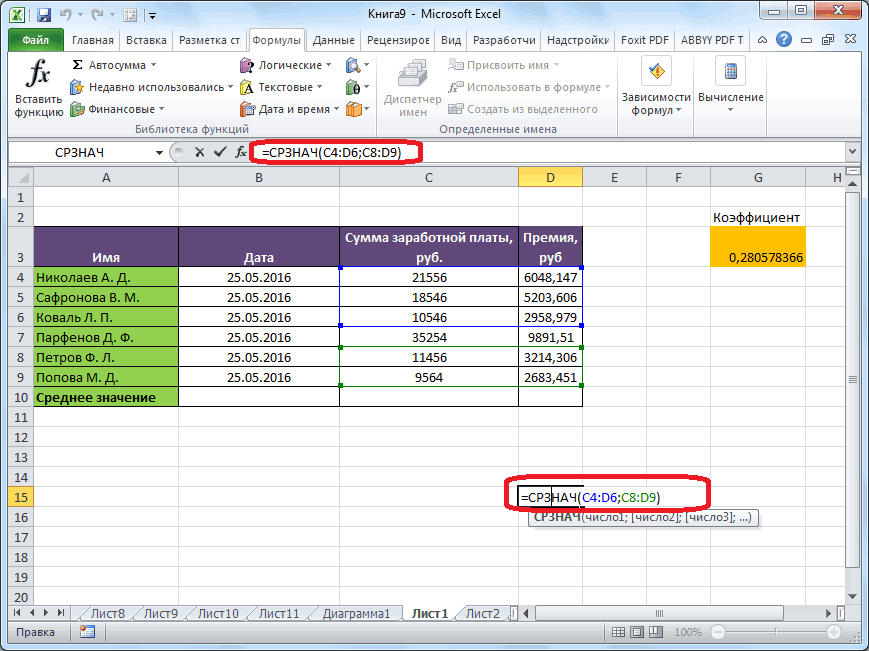

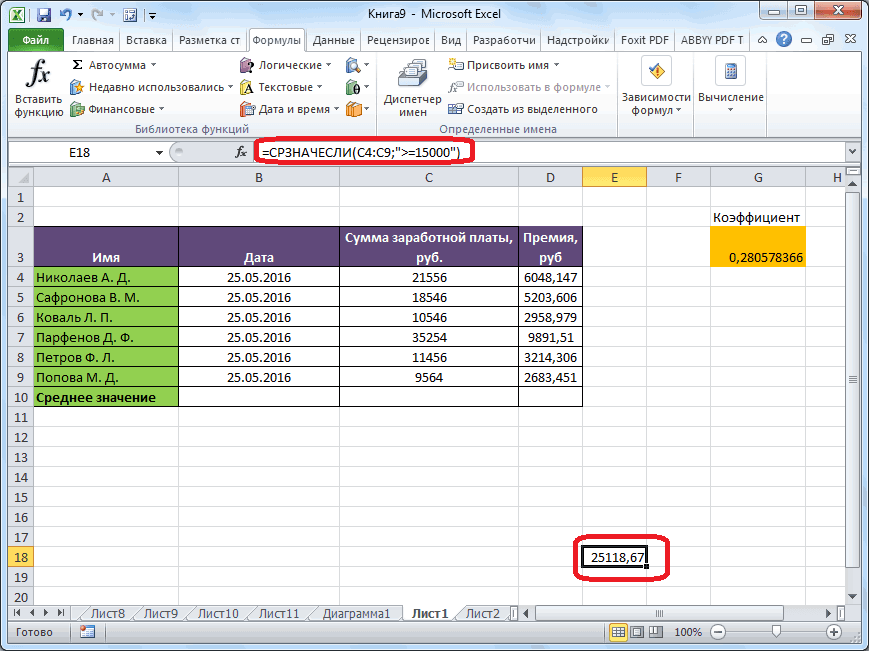

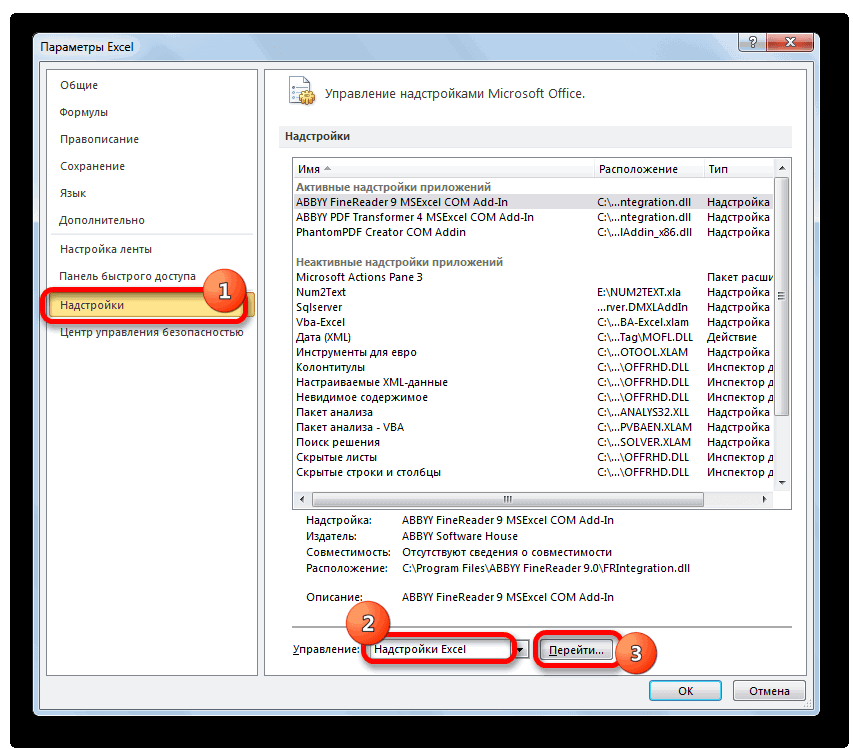
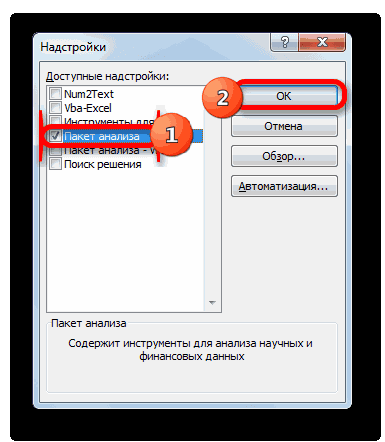
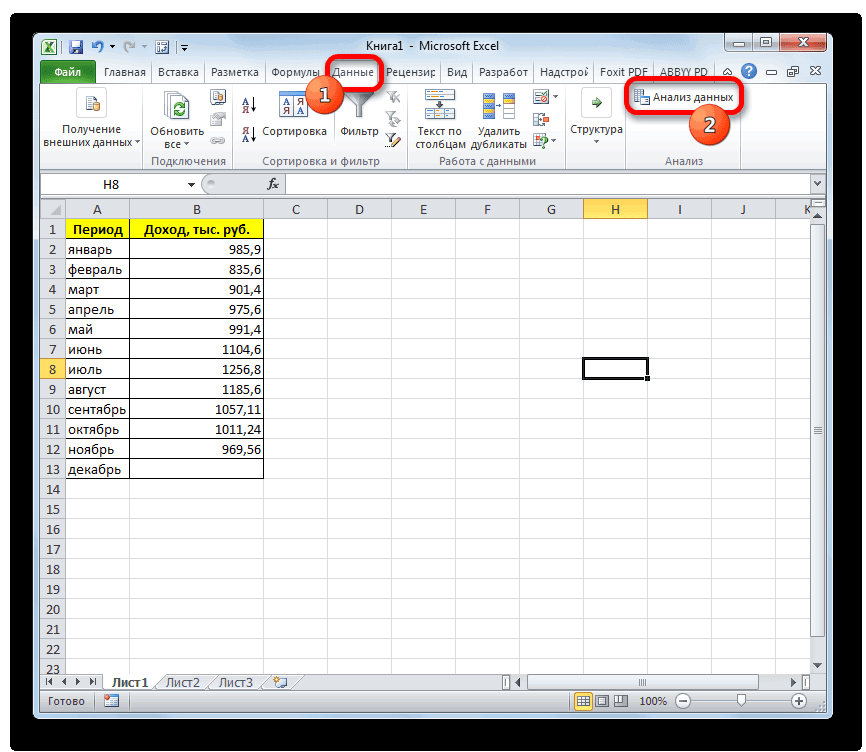
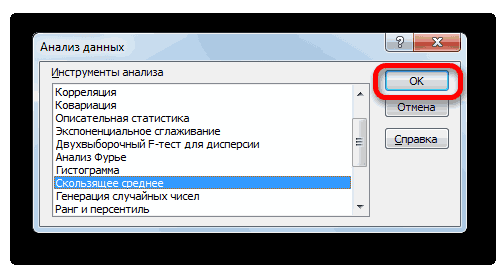
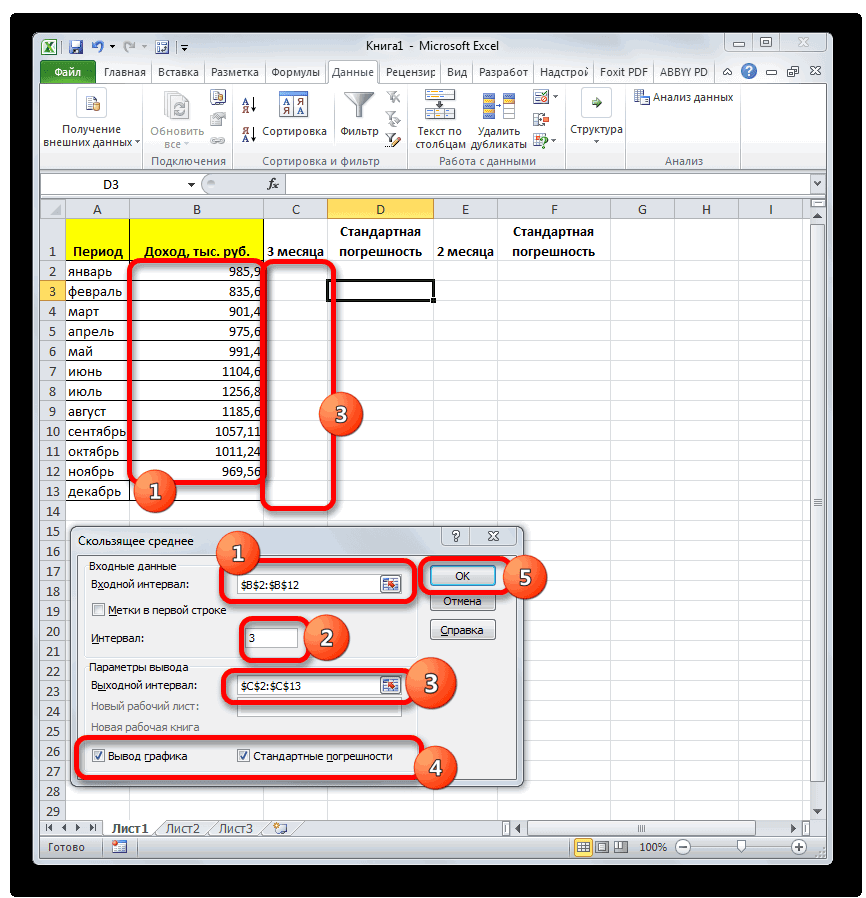
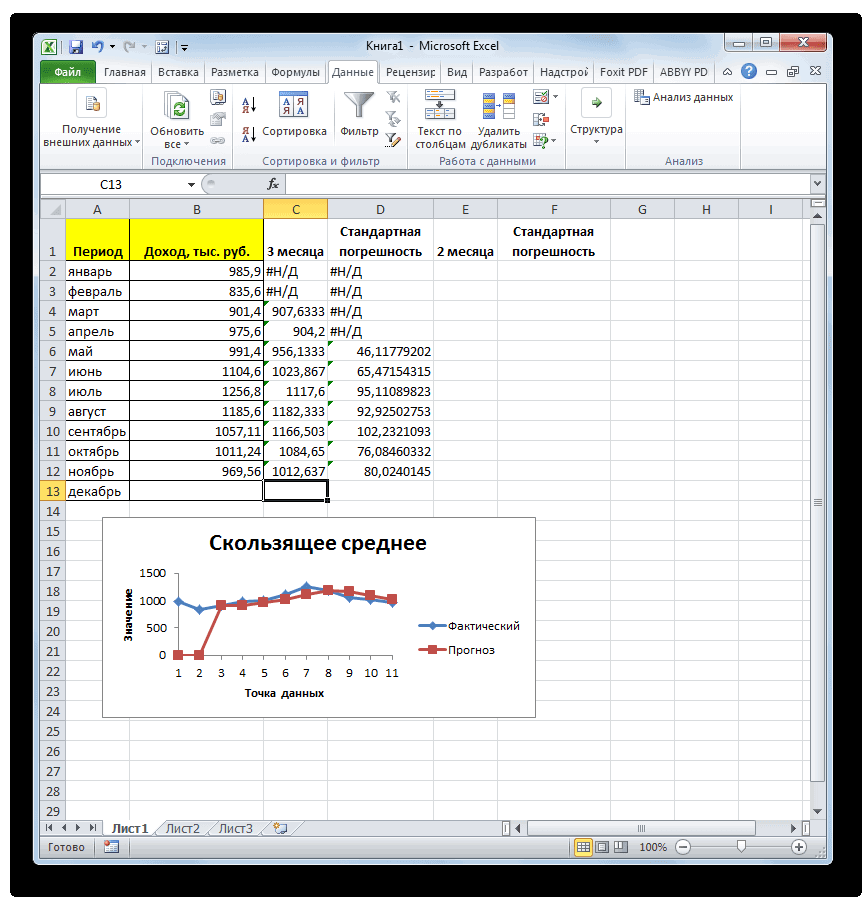
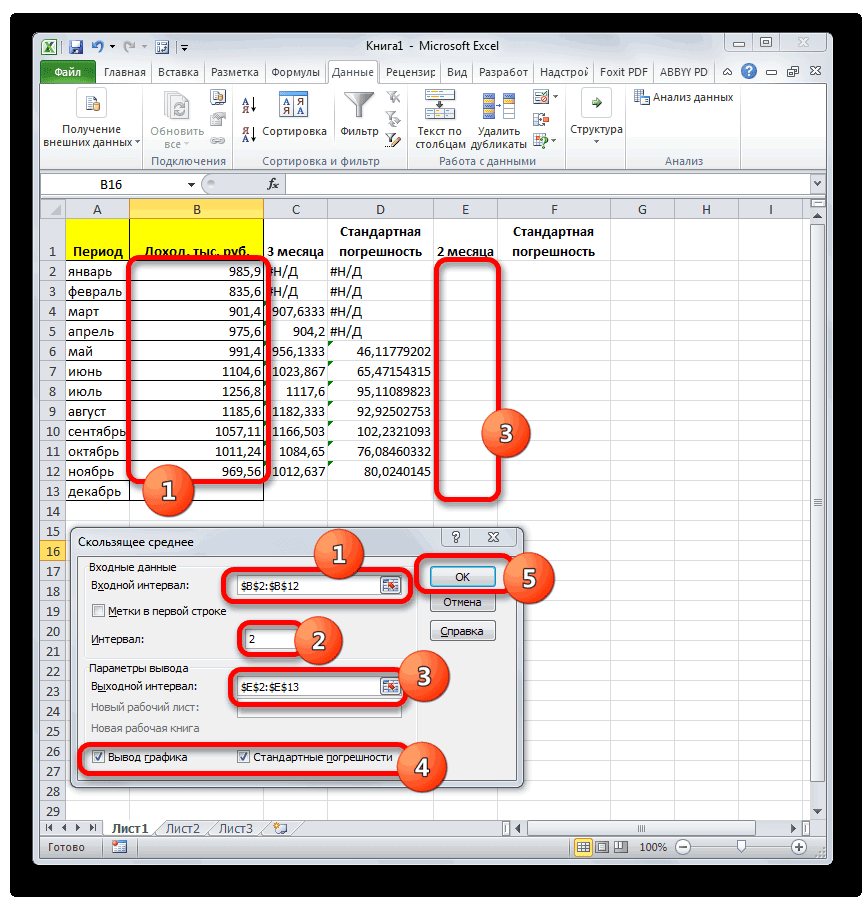
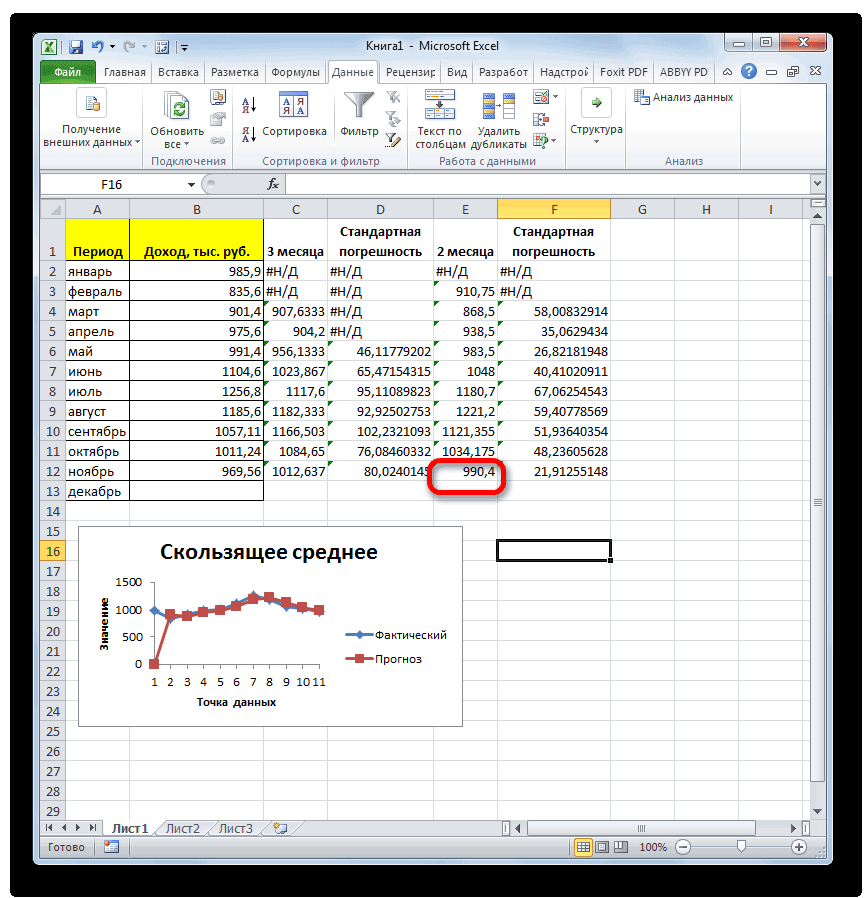
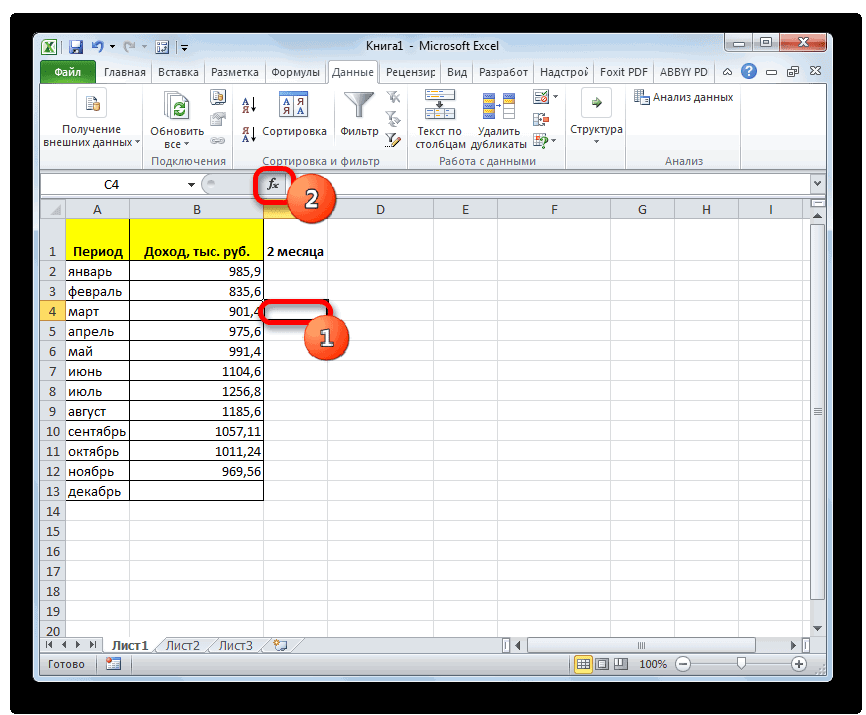
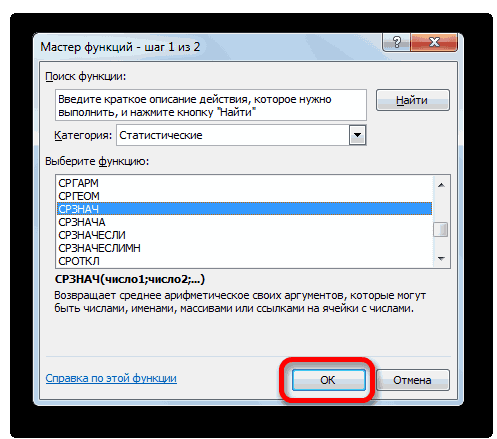

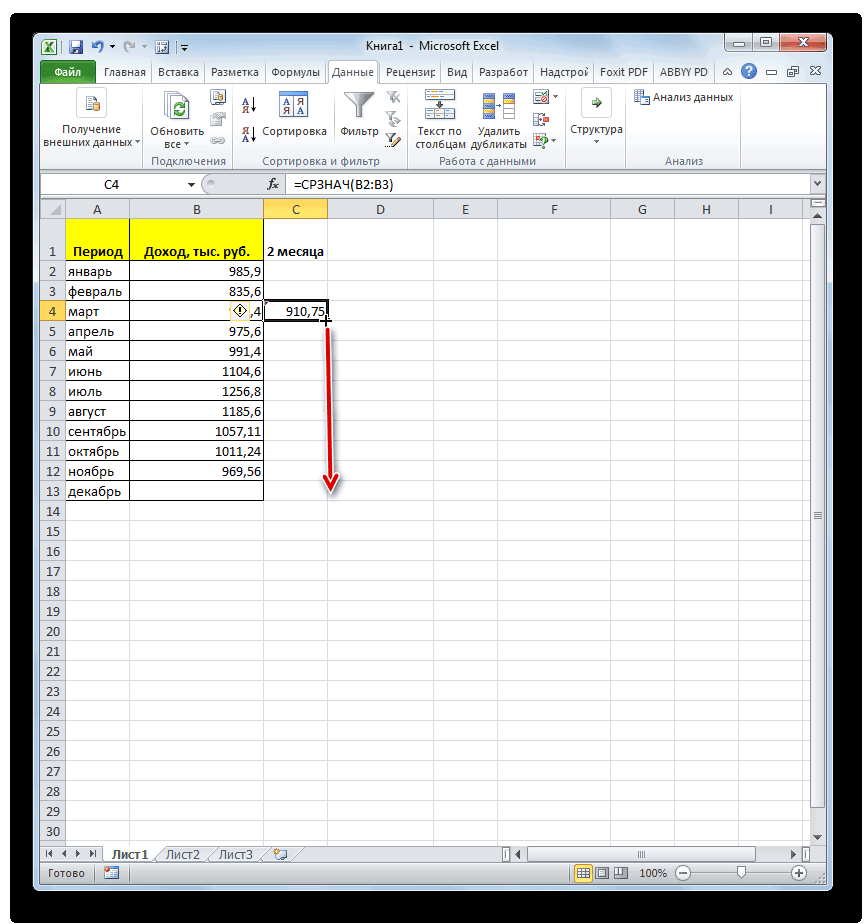
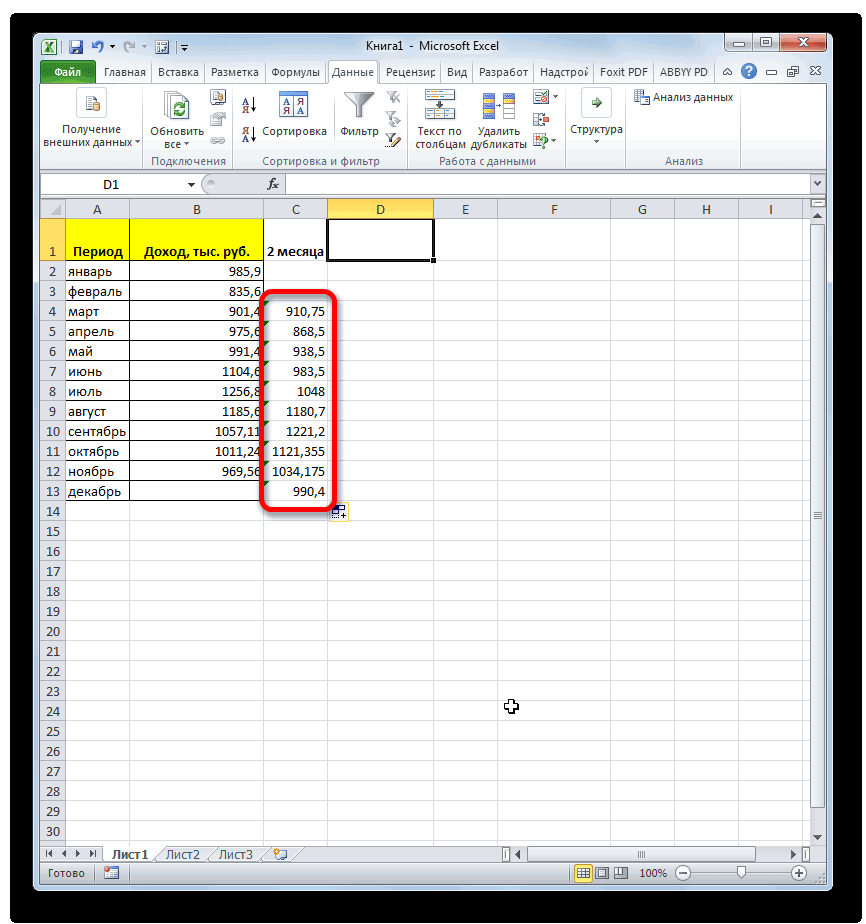
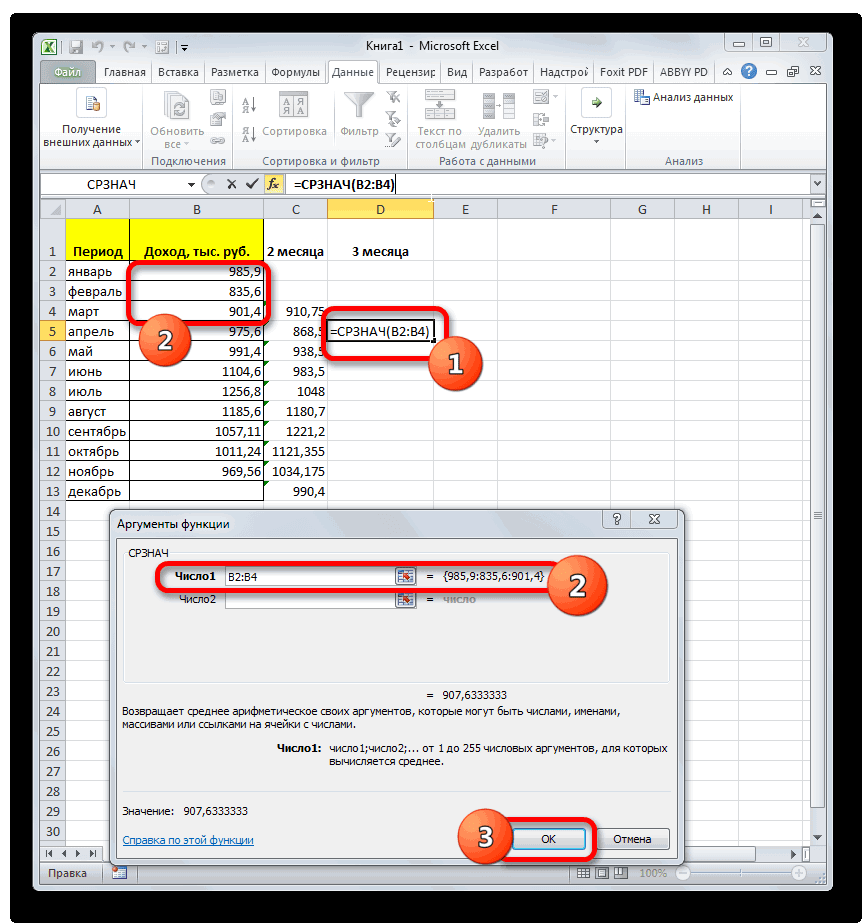
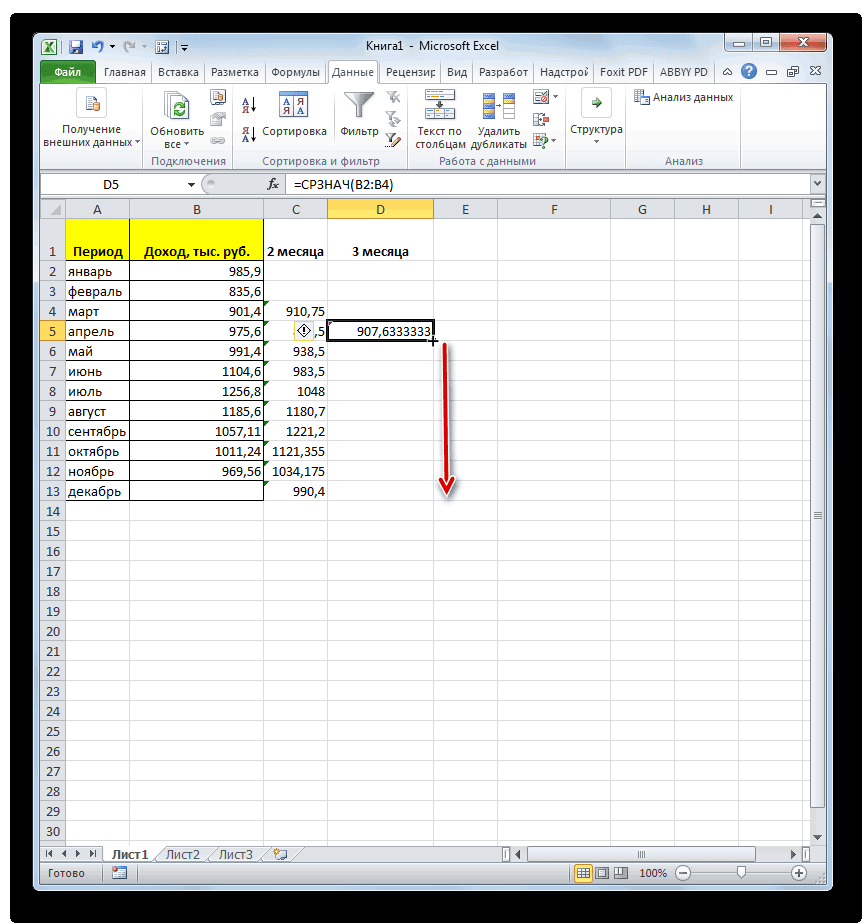
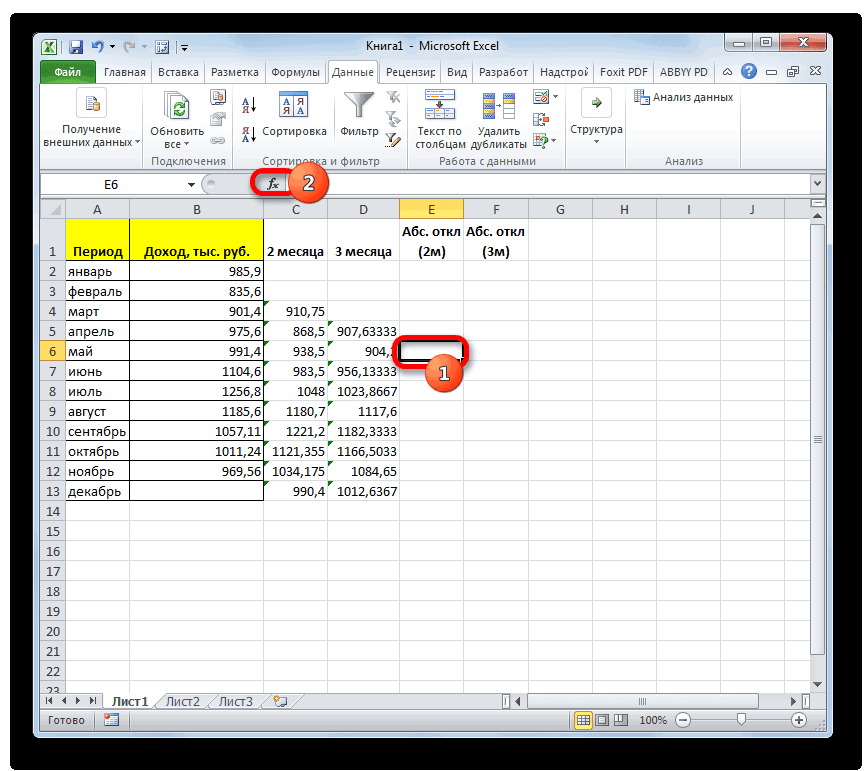
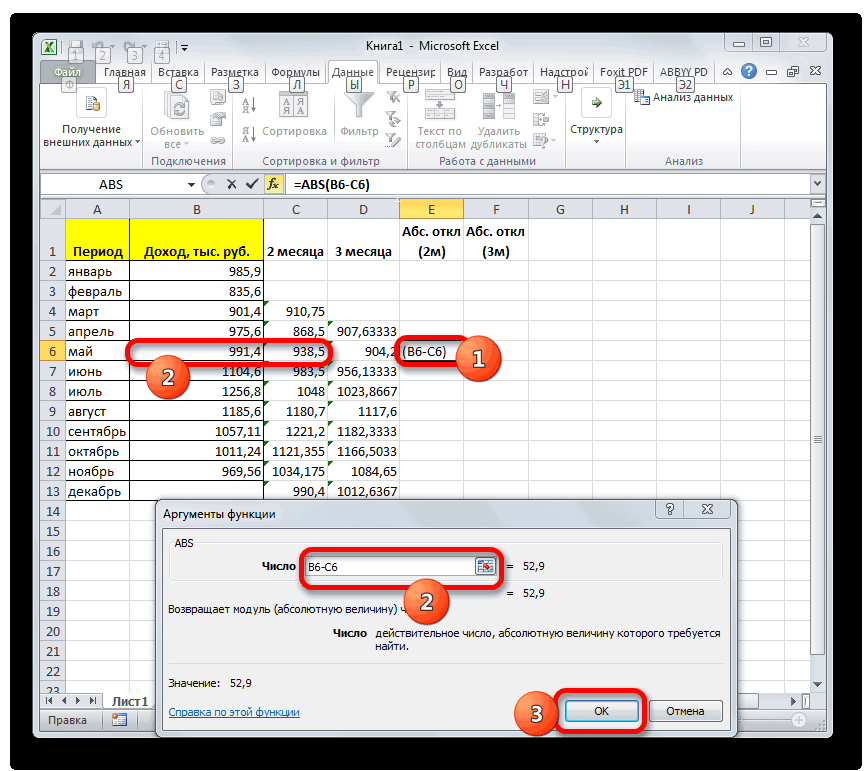
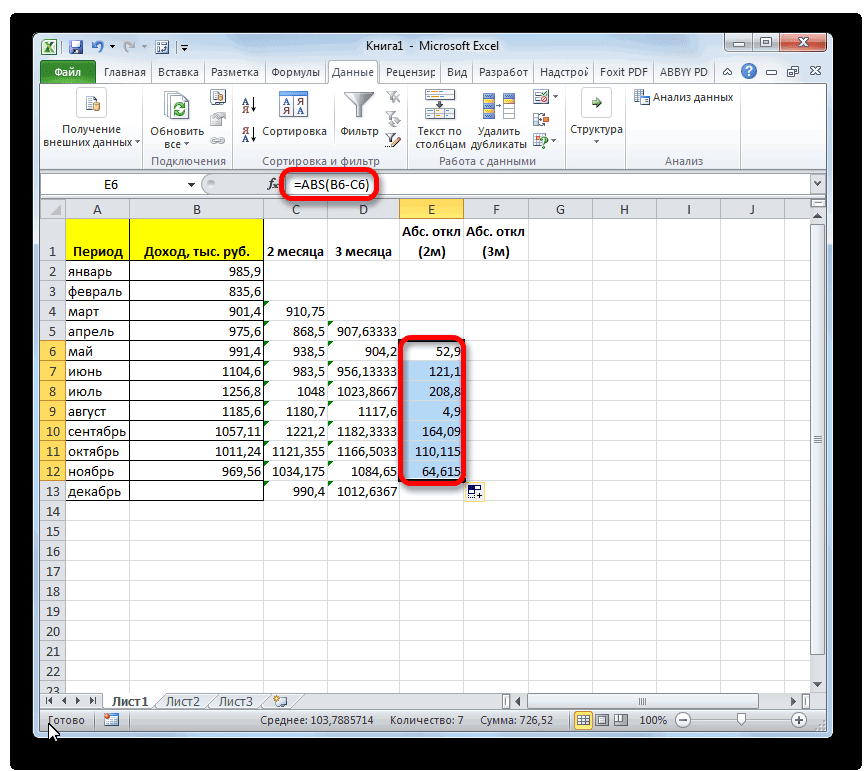
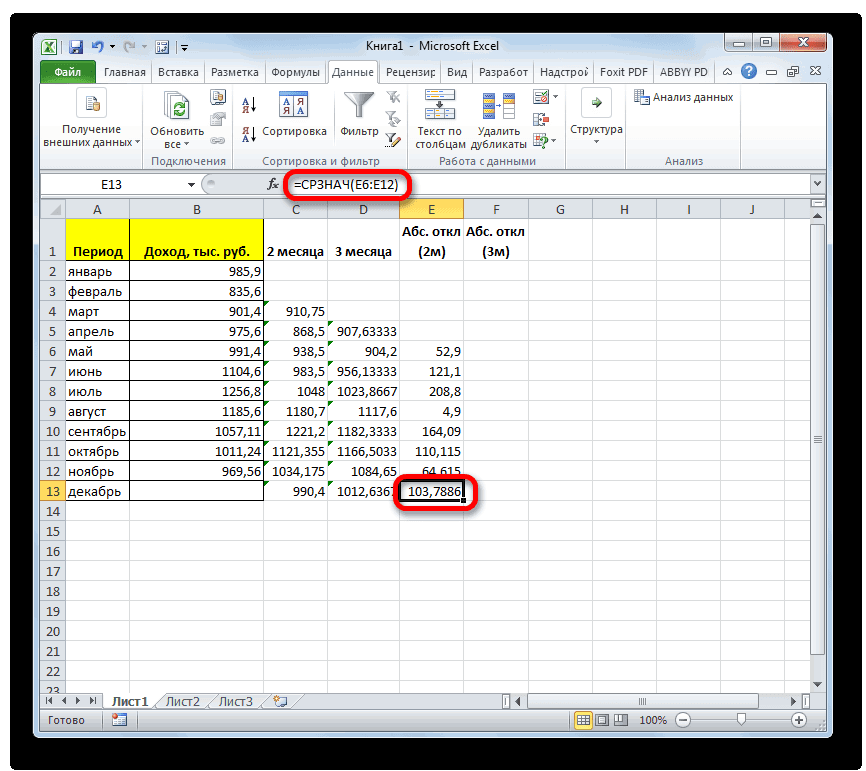
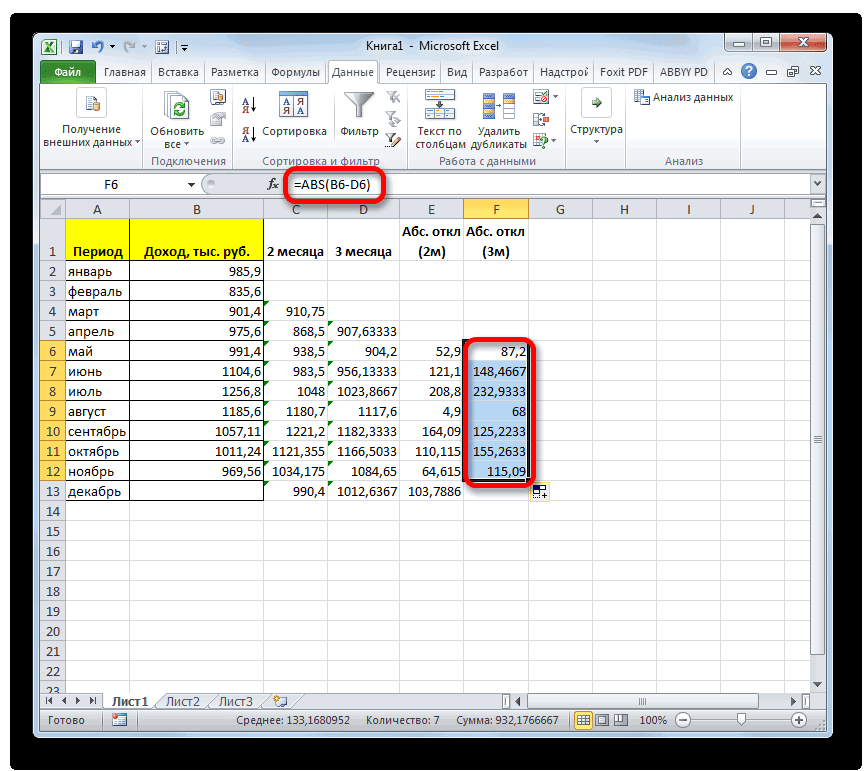
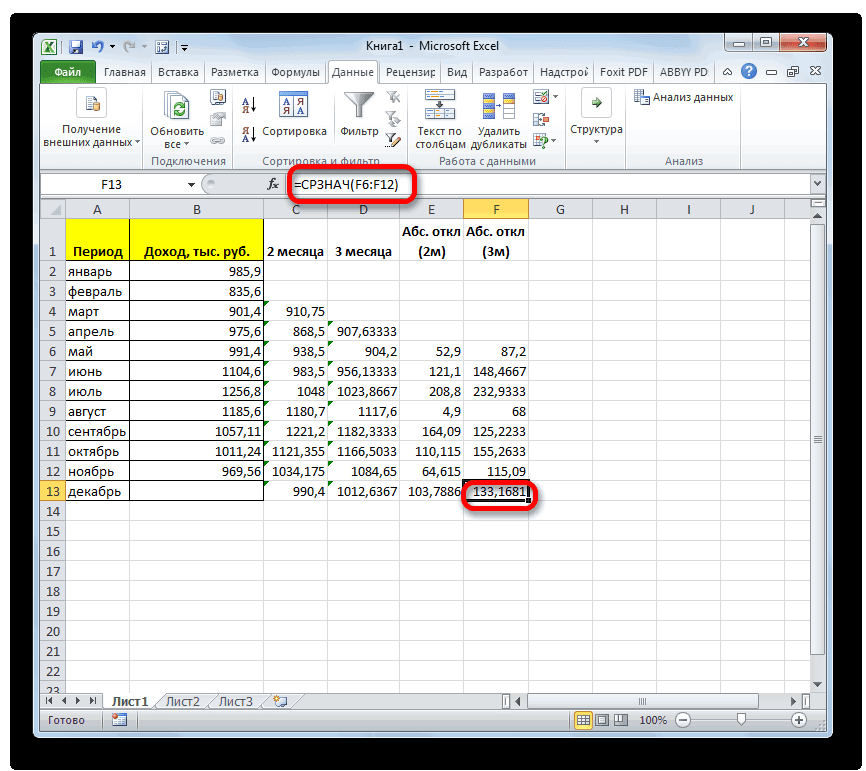

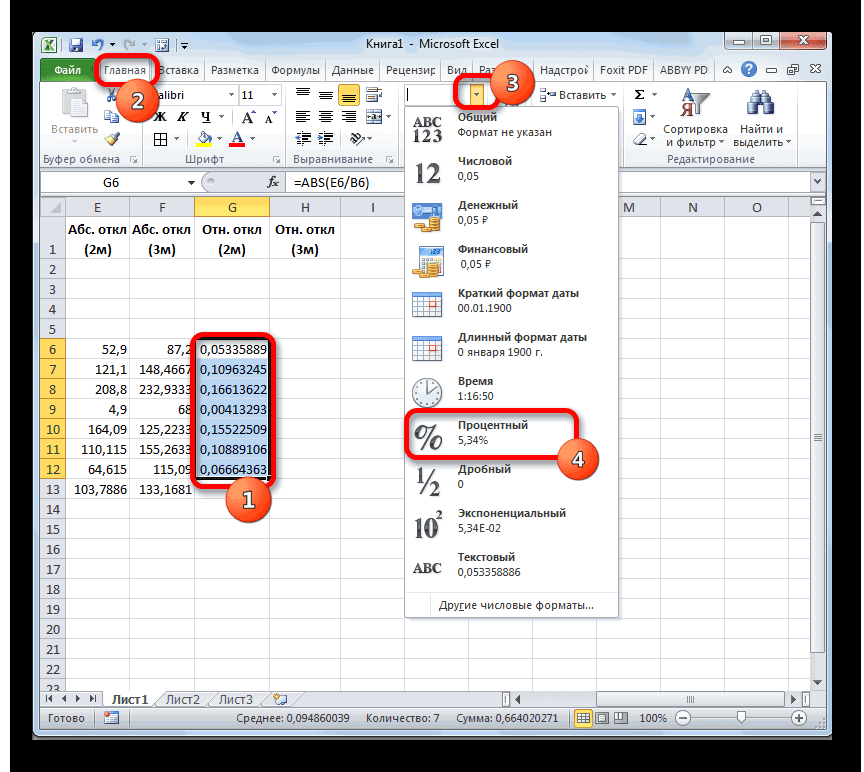
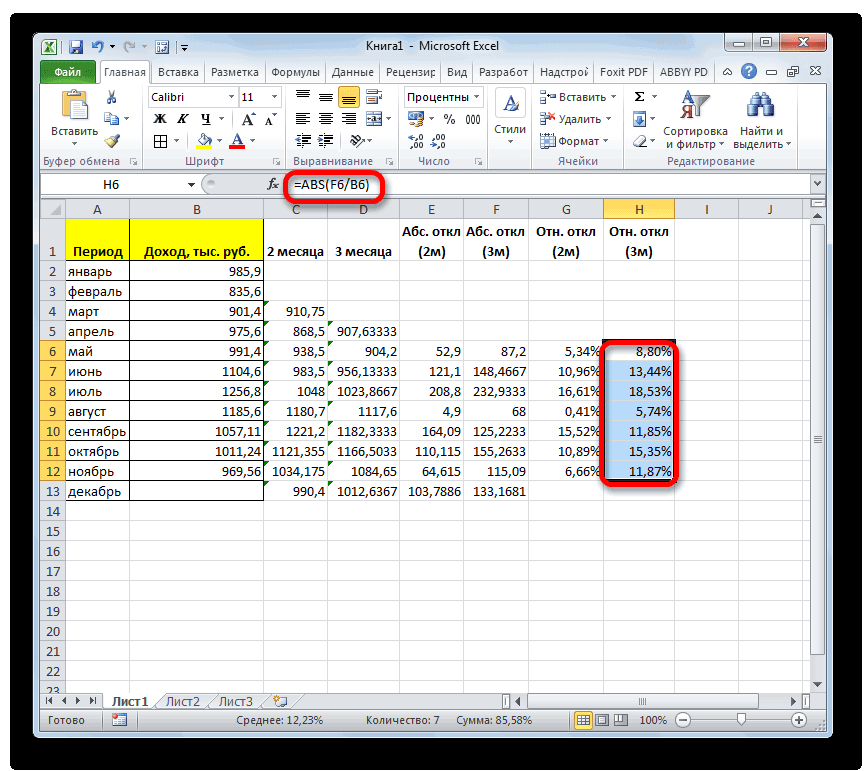
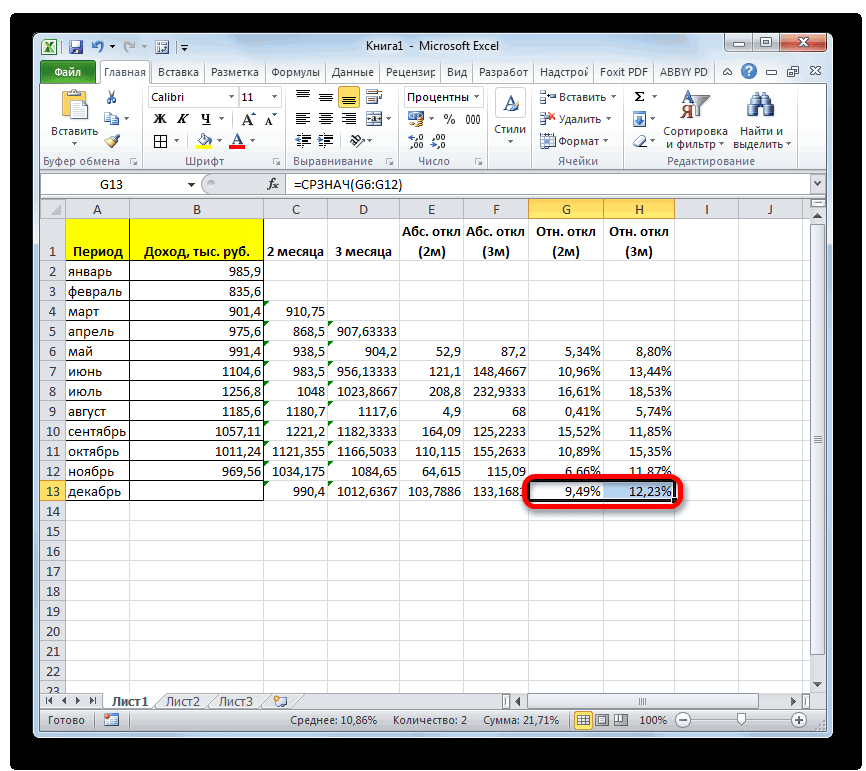
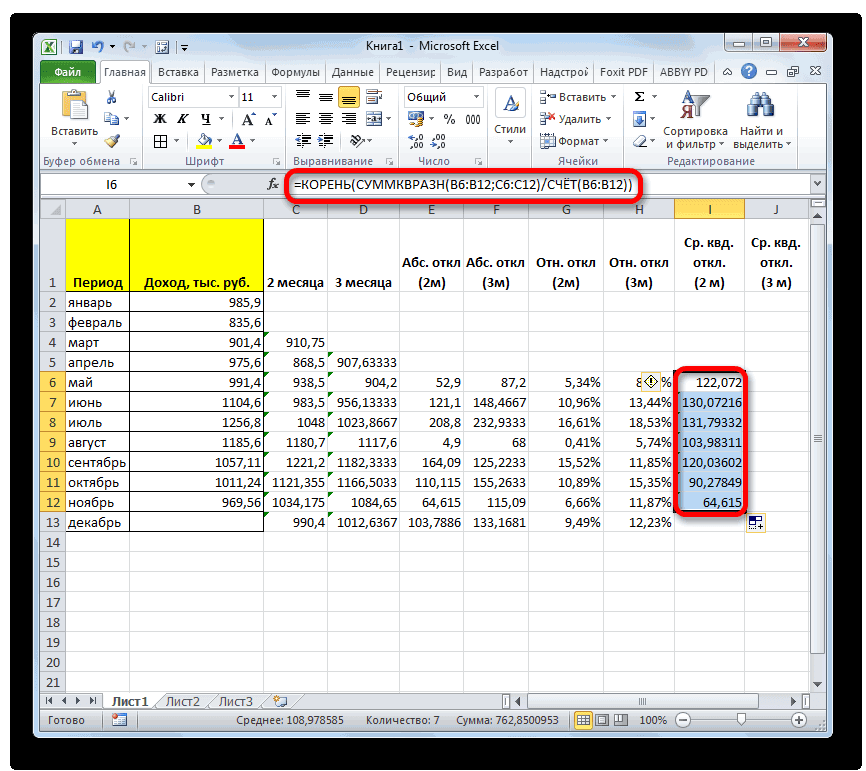
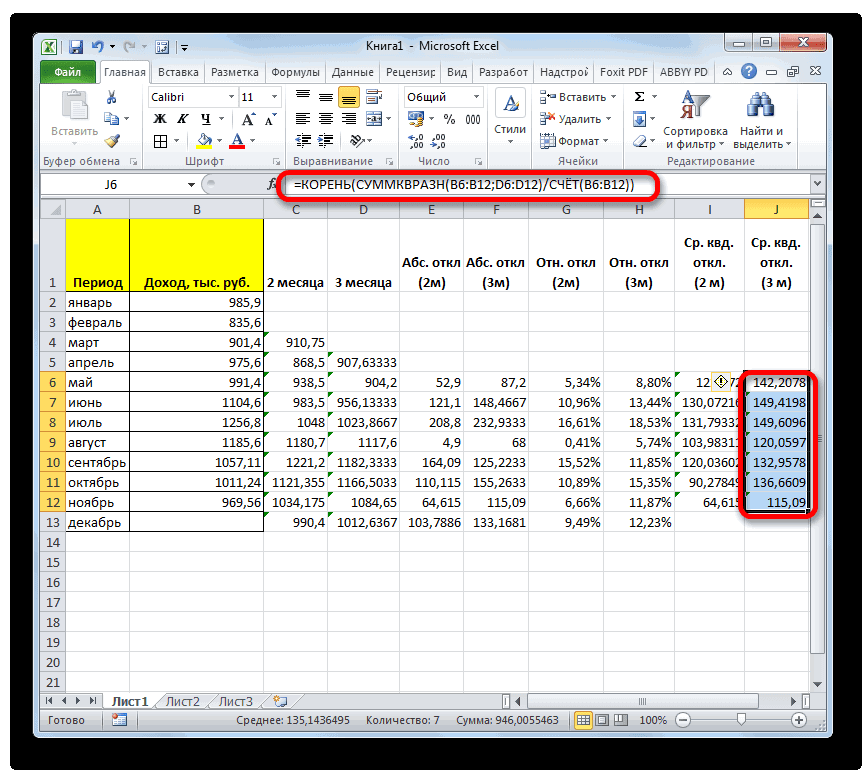
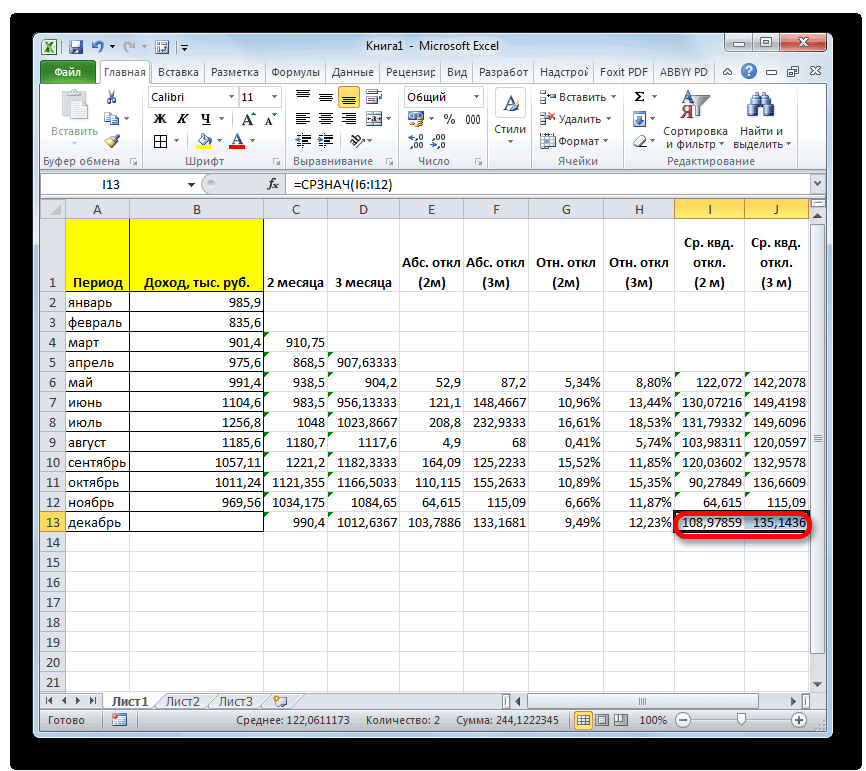
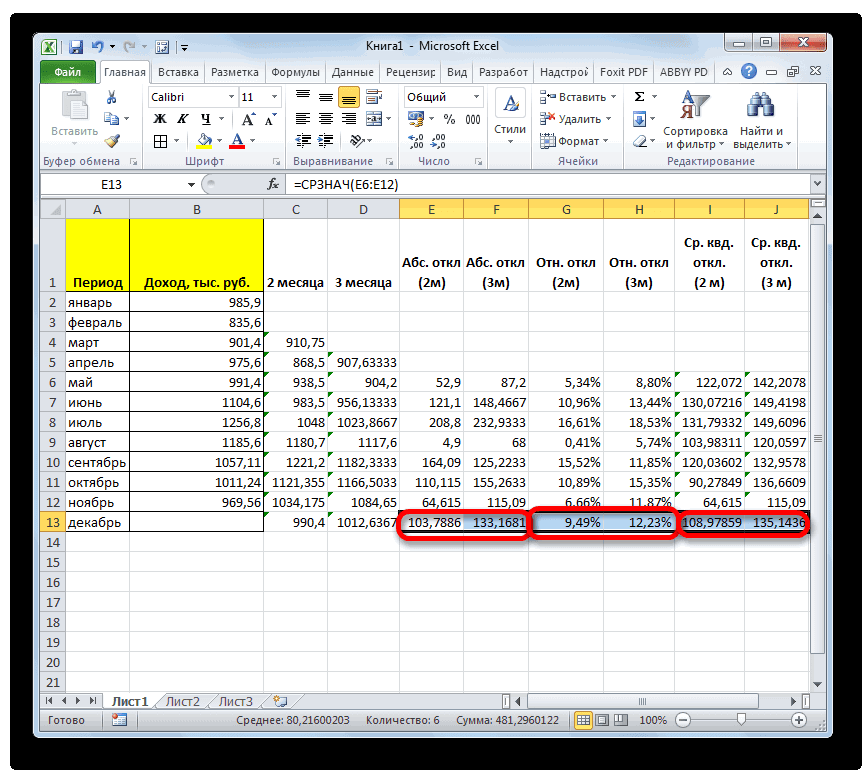
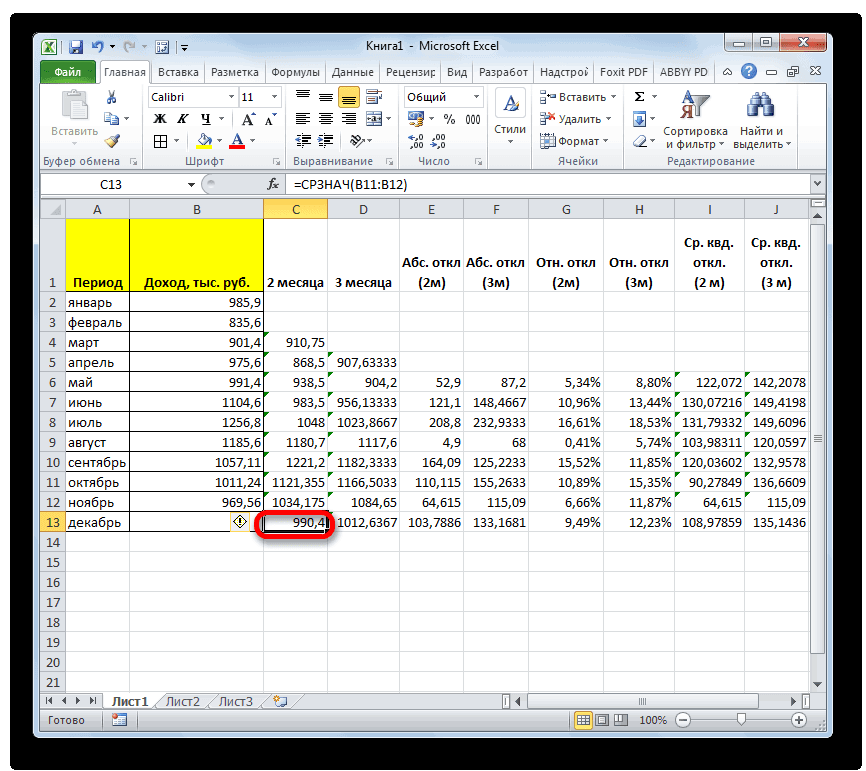
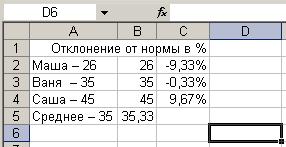
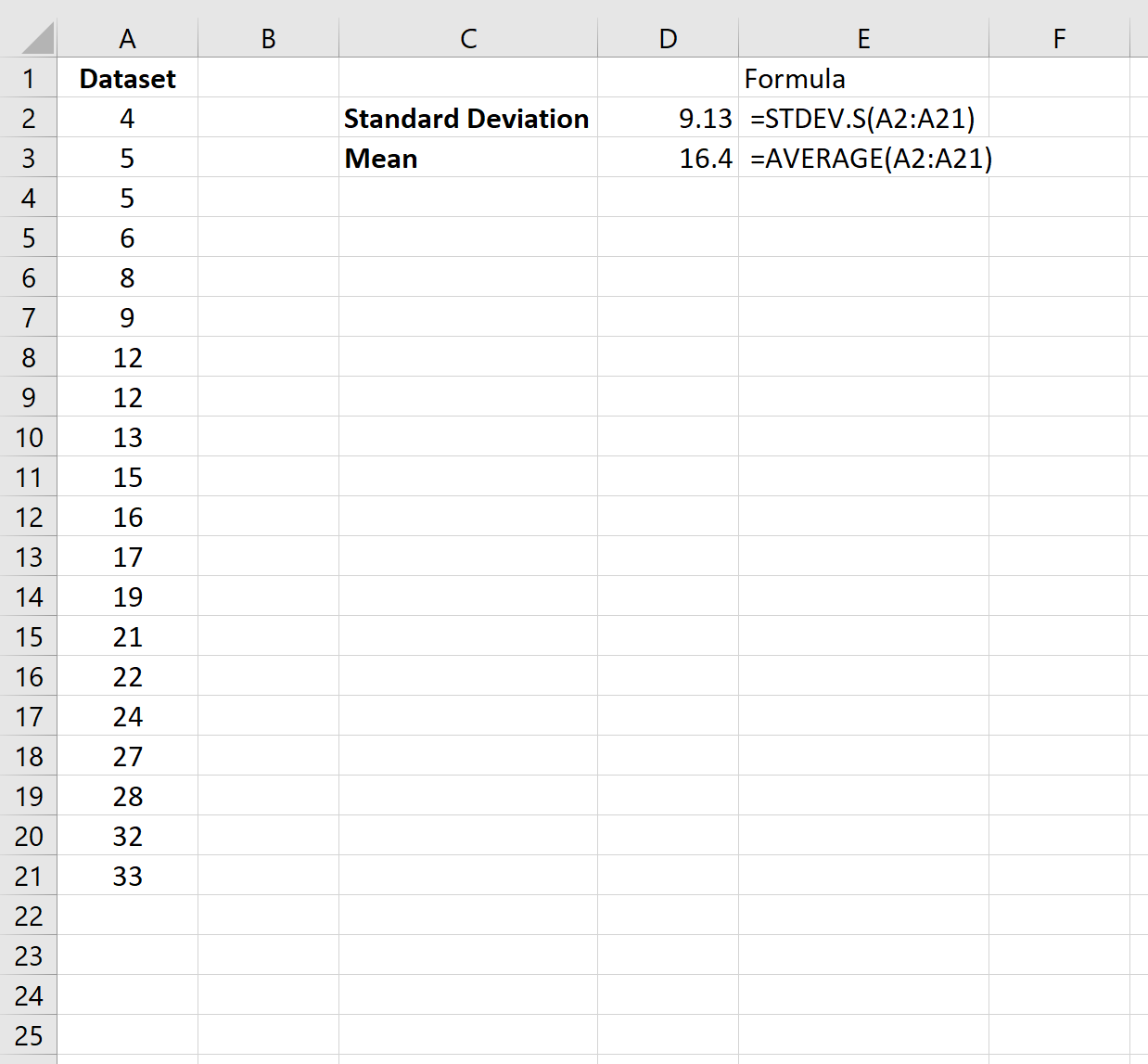
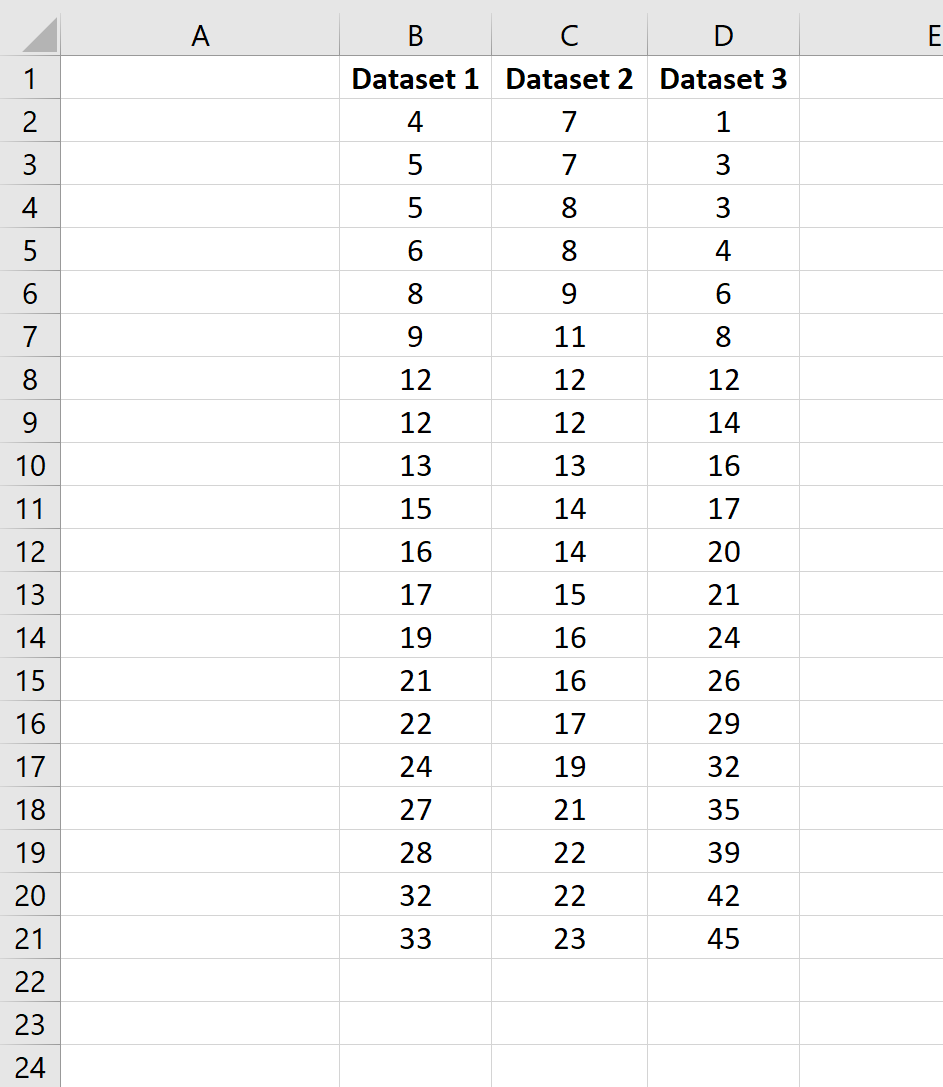
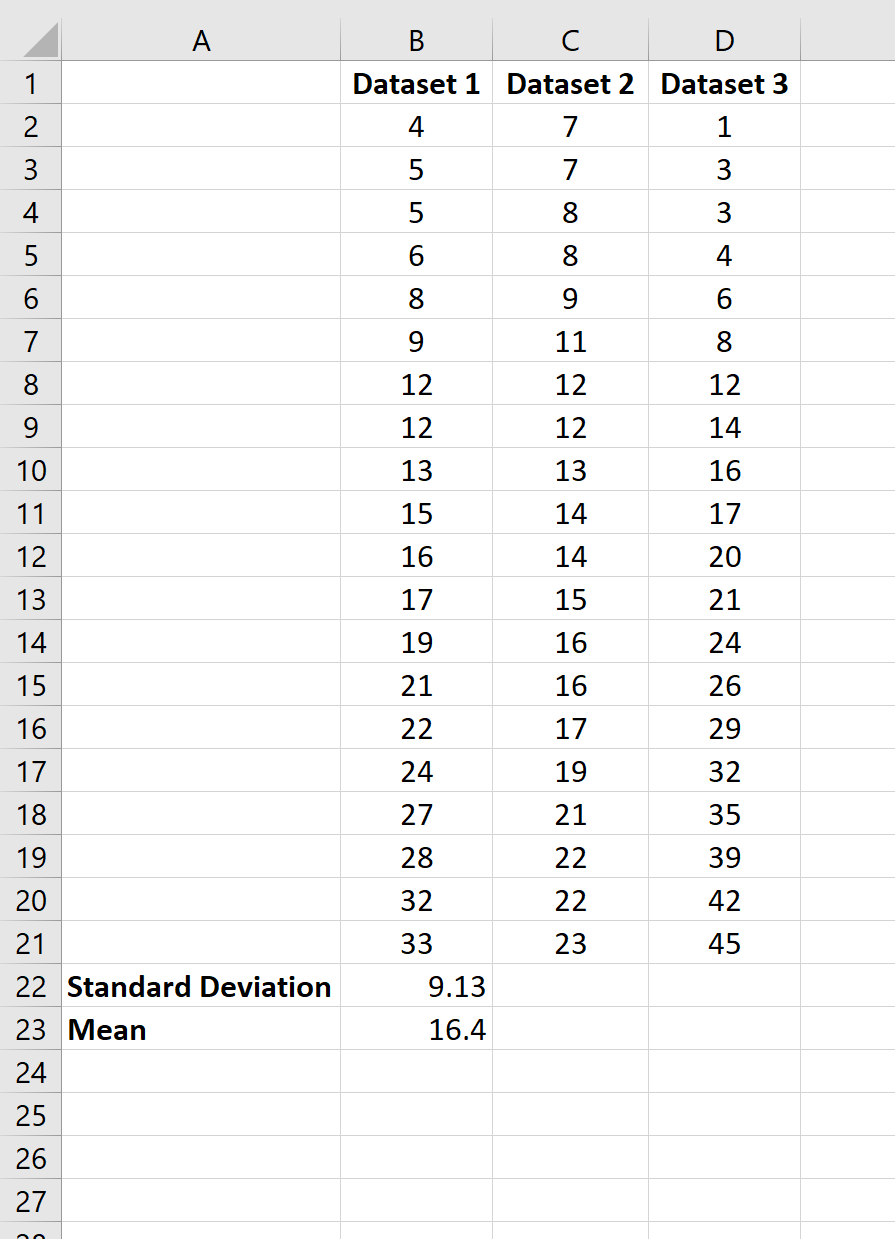
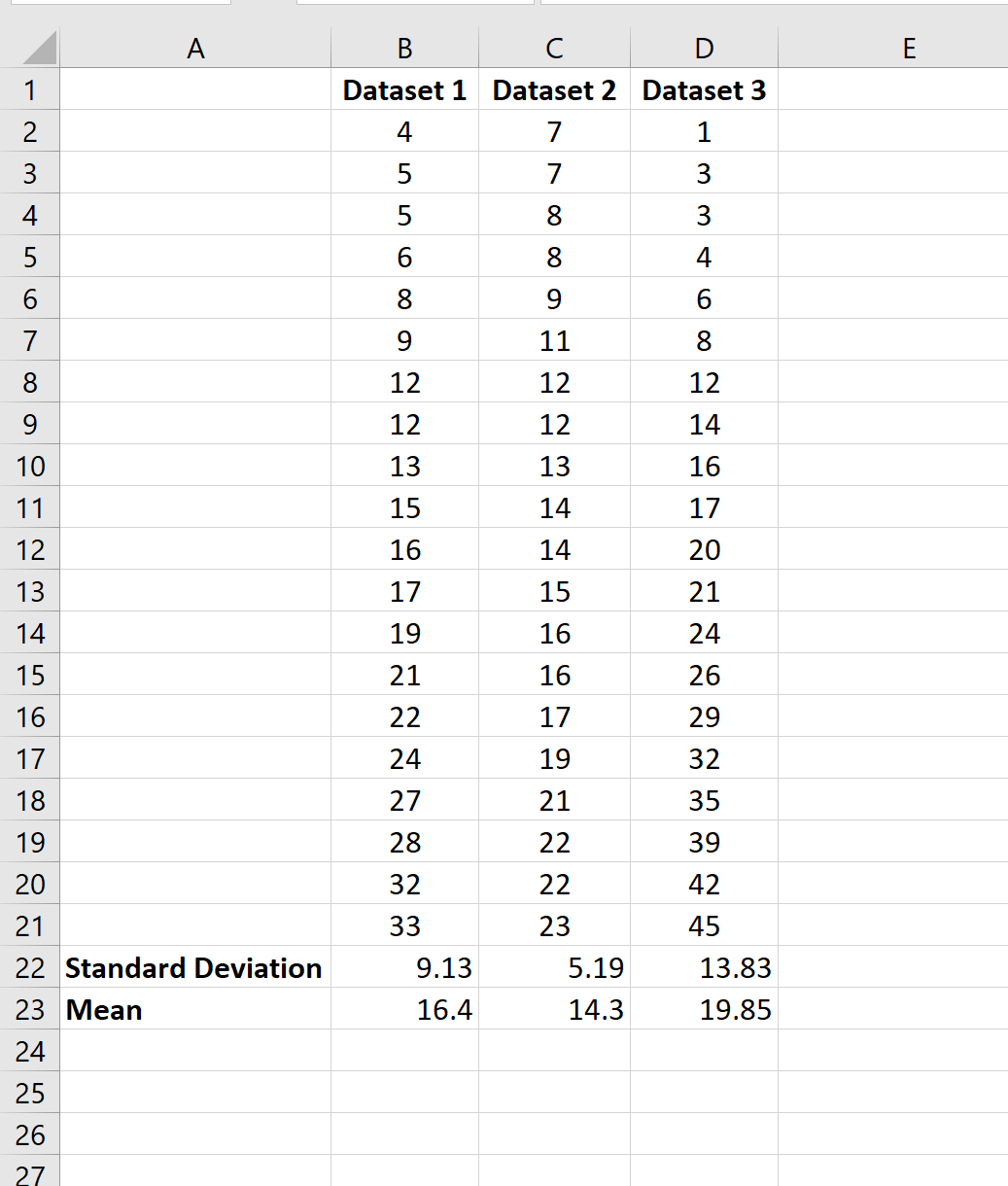

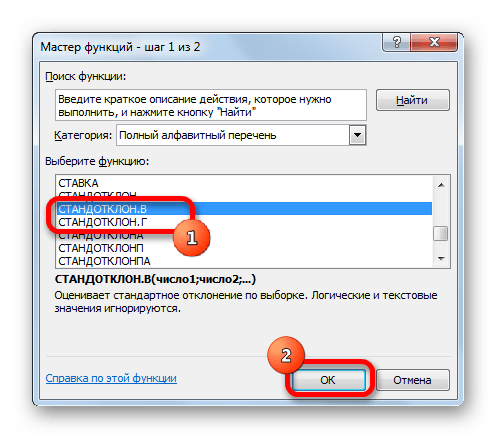
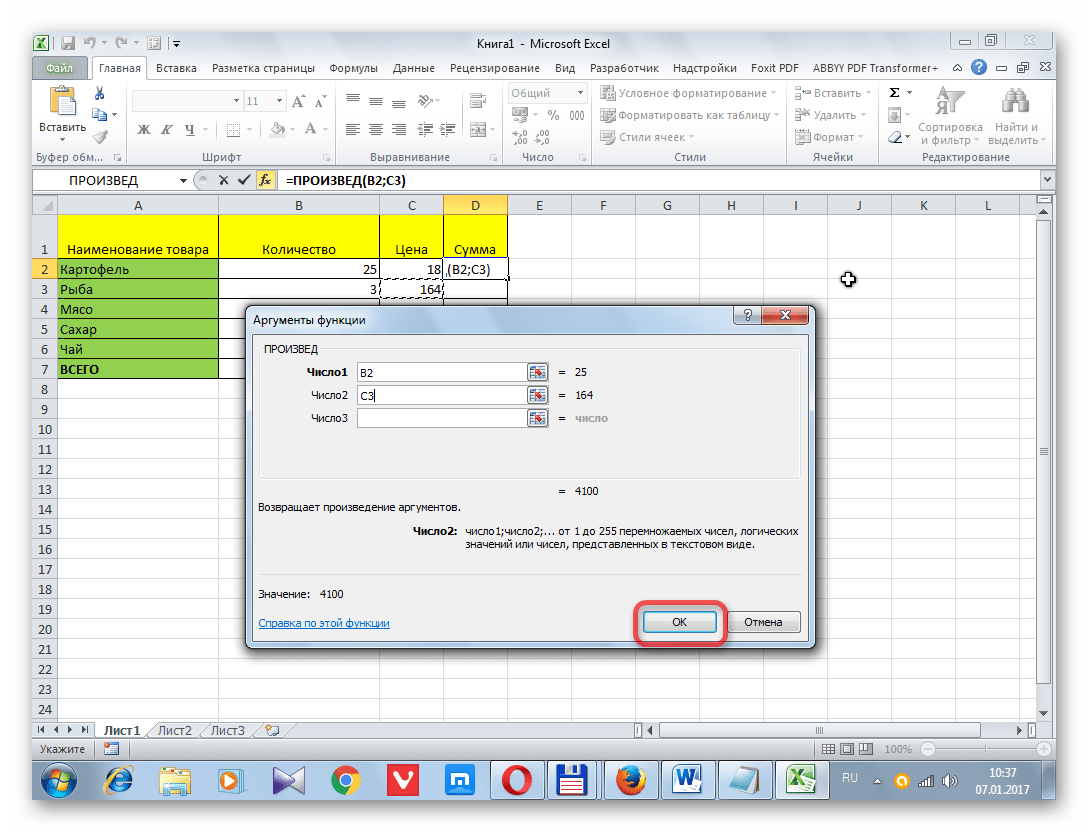
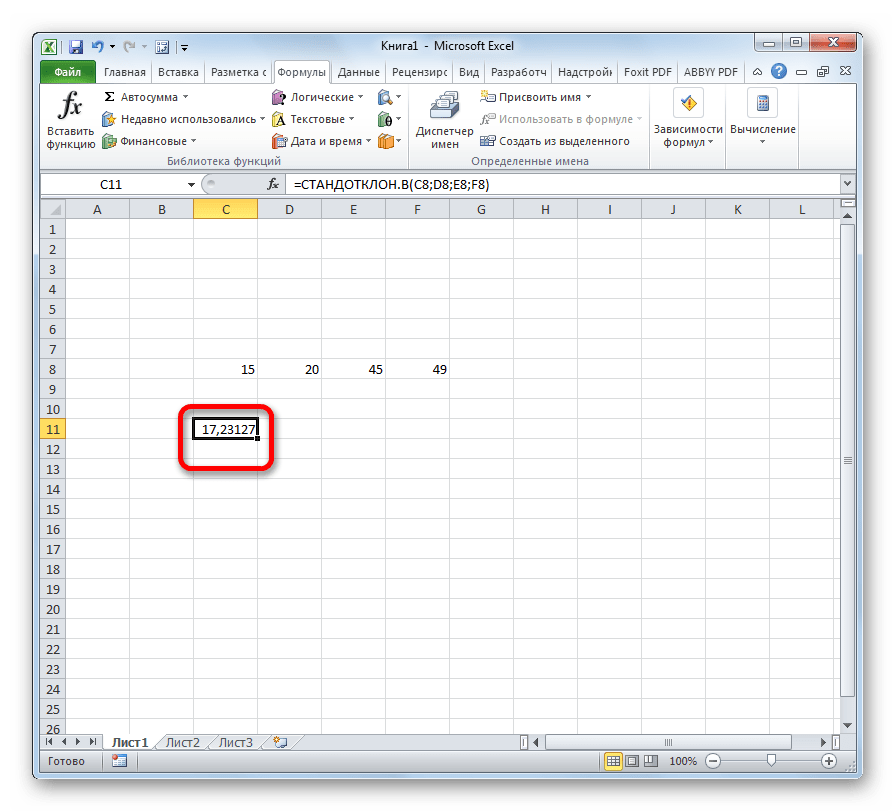
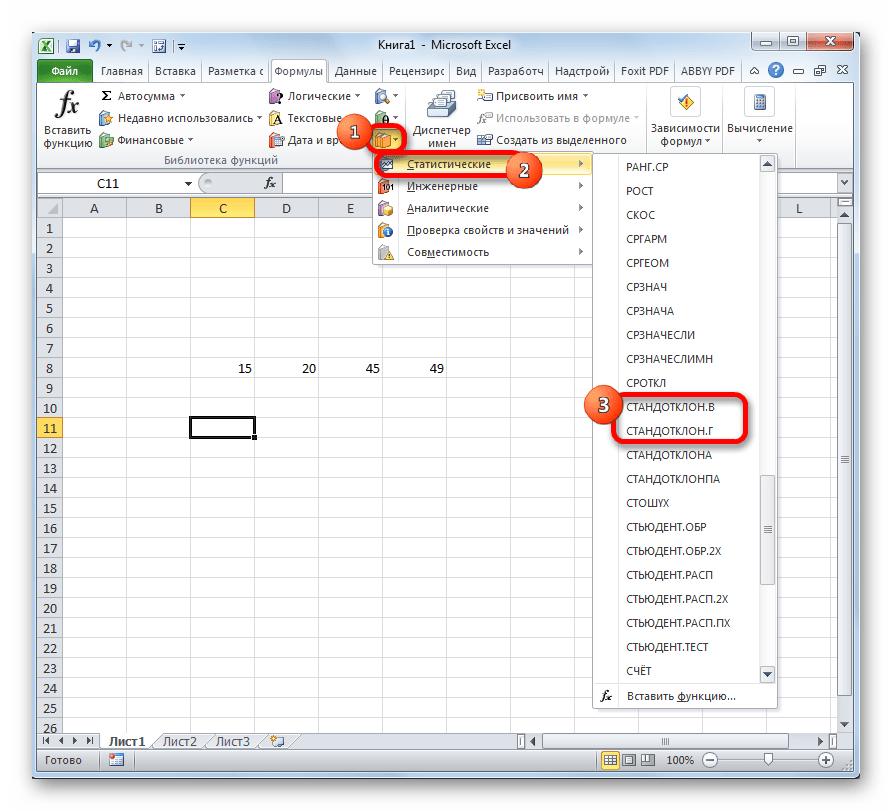
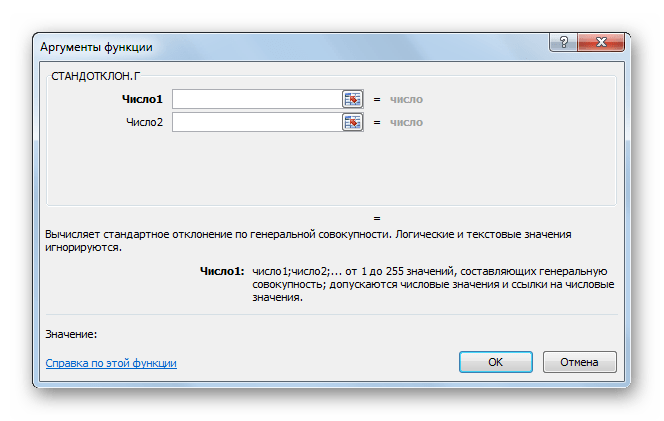

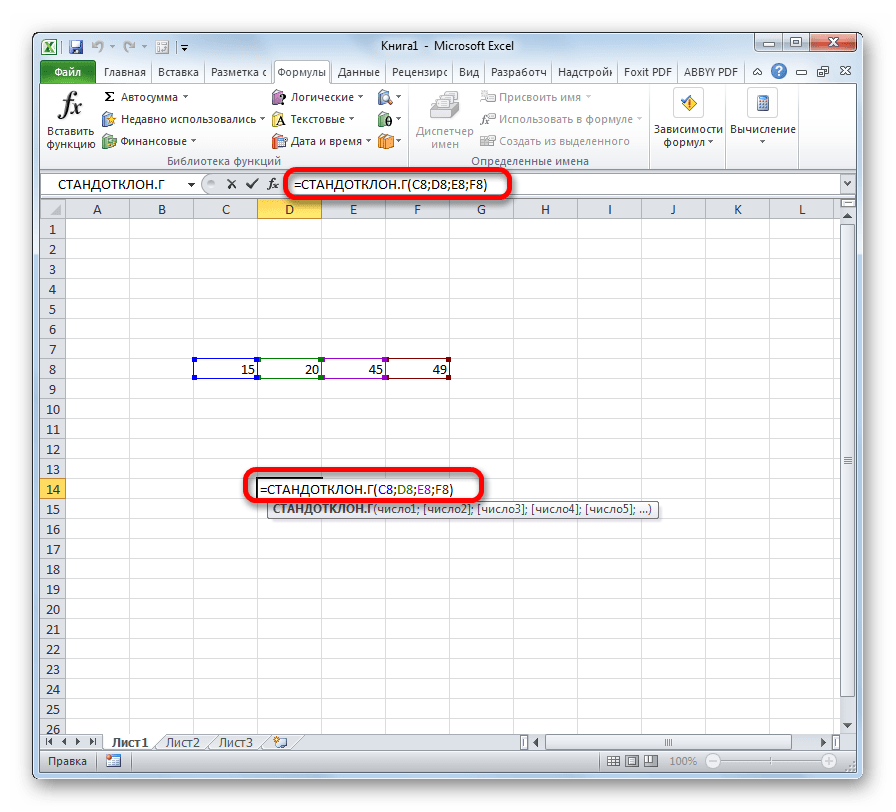
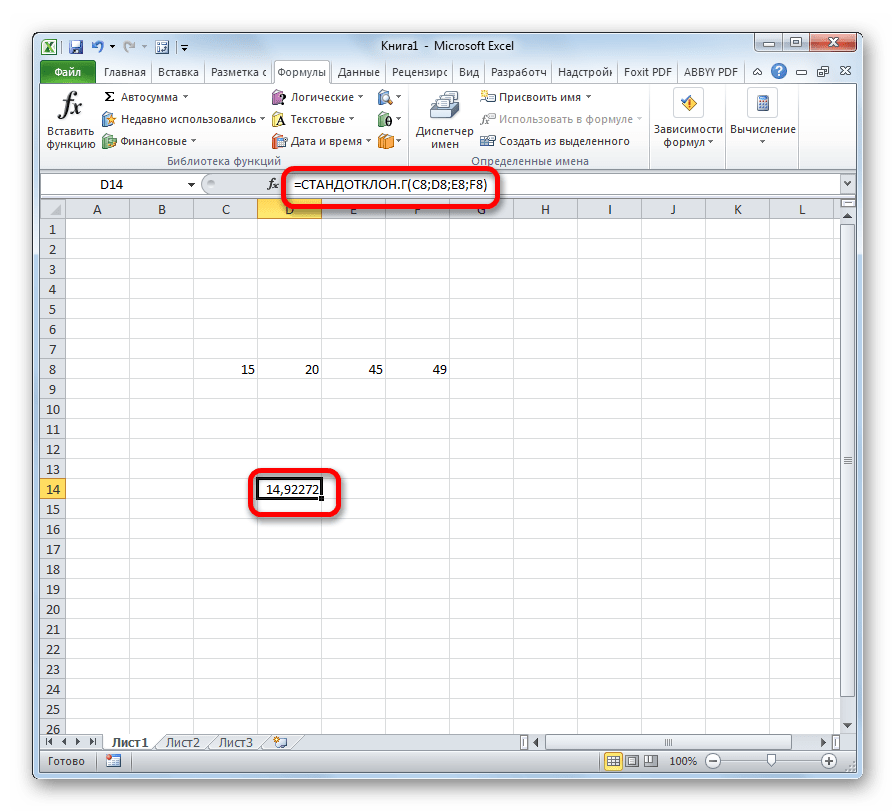






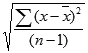
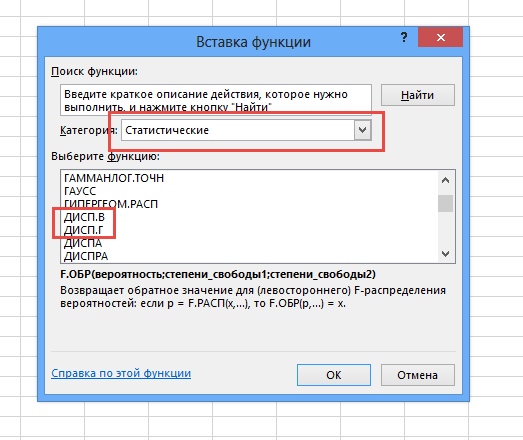
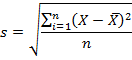
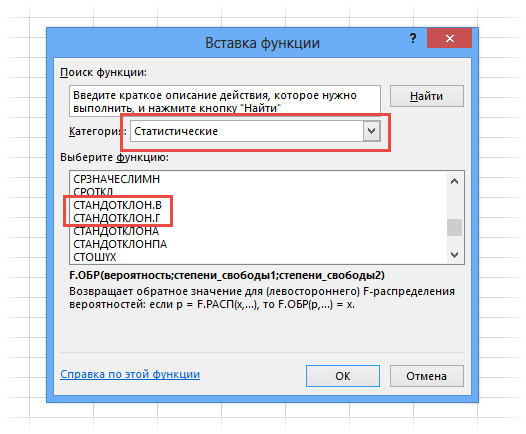
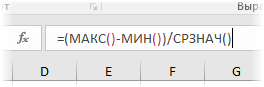



 Стандартное отклонение обычно рассчитывается либо по выборке (определенной части данных), либо по генеральной совокупности данных (по всем данным).
Стандартное отклонение обычно рассчитывается либо по выборке (определенной части данных), либо по генеральной совокупности данных (по всем данным).
 Откройте программу Microsoft Excel.
Откройте программу Microsoft Excel.
 Составьте таблицу ваших данных.
Составьте таблицу ваших данных.